code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
Run on Mac CPU - requires `num_workers=0` in a few places when get error
# Lesson 1 - What's your pet
Welcome to lesson 1! For those of you who are using a Jupyter Notebook for the first time, you can learn about this useful tool in a tutorial we prepared specially for you; click `File`->`Open` now and click `00_notebook_tutorial.ipynb`.
In this lesson we will build our first image classifier from scratch, and see if we can achieve world-class results. Let's dive in!
Every notebook starts with the following three lines; they ensure that any edits to libraries you make are reloaded here automatically, and also that any charts or images displayed are shown in this notebook.
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
We import all the necessary packages. We are going to work with the [fastai V1 library](http://www.fast.ai/2018/10/02/fastai-ai/) which sits on top of [Pytorch 1.0](https://hackernoon.com/pytorch-1-0-468332ba5163). The fastai library provides many useful functions that enable us to quickly and easily build neural networks and train our models.
```
from fastai.vision import *
from fastai.metrics import error_rate
import fastai
fastai.__version__
from fastai.utils.show_install import *
show_install()
```
If you're using a computer with an unusually small GPU, you may get an out of memory error when running this notebook. If this happens, click Kernel->Restart, uncomment the 2nd line below to use a smaller *batch size* (you'll learn all about what this means during the course), and try again.
```
#bs = 64
bs = 16 # uncomment this line if you run out of memory even after clicking Kernel->Restart
```
## Looking at the data
We are going to use the [Oxford-IIIT Pet Dataset](http://www.robots.ox.ac.uk/~vgg/data/pets/) by [O. M. Parkhi et al., 2012](http://www.robots.ox.ac.uk/~vgg/publications/2012/parkhi12a/parkhi12a.pdf) which features 12 cat breeds and 25 dogs breeds. Our model will need to learn to differentiate between these 37 distinct categories. According to their paper, the best accuracy they could get in 2012 was 59.21%, using a complex model that was specific to pet detection, with separate "Image", "Head", and "Body" models for the pet photos. Let's see how accurate we can be using deep learning!
We are going to use the `untar_data` function to which we must pass a URL as an argument and which will download and extract the data.
```
help(untar_data)
URLs.PETS
path = untar_data(URLs.PETS); path
path.ls()
path_anno = path/'annotations'
path_img = path/'images'
```
The first thing we do when we approach a problem is to take a look at the data. We _always_ need to understand very well what the problem is and what the data looks like before we can figure out how to solve it. Taking a look at the data means understanding how the data directories are structured, what the labels are and what some sample images look like.
The main difference between the handling of image classification datasets is the way labels are stored. In this particular dataset, labels are stored in the filenames themselves. We will need to extract them to be able to classify the images into the correct categories. Fortunately, the fastai library has a handy function made exactly for this, `ImageDataBunch.from_name_re` gets the labels from the filenames using a [regular expression](https://docs.python.org/3.6/library/re.html).
```
fnames = get_image_files(path_img)
fnames[:5]
np.random.seed(2)
pat = re.compile(r'/([^/]+)_\d+.jpg$')
?data.show_batch
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(), size=224, bs=bs, num_workers=0
).normalize(imagenet_stats)
data.show_batch(rows=3, figsize=(7,6))
print(data.classes)
len(data.classes),data.c
```
## Training: resnet34
Now we will start training our model. We will use a [convolutional neural network](http://cs231n.github.io/convolutional-networks/) backbone and a fully connected head with a single hidden layer as a classifier. Don't know what these things mean? Not to worry, we will dive deeper in the coming lessons. For the moment you need to know that we are building a model which will take images as input and will output the predicted probability for each of the categories (in this case, it will have 37 outputs).
We will train for 4 epochs (4 cycles through all our data).
```
learn = create_cnn(data, models.resnet34, metrics=error_rate)
learn.model
```
below cell taske 3:45 on GPU. On Mac CPU, this was going to take 2 hours
```
learn.fit_one_cycle(4)
learn.save('stage-1')
```
## Results
Let's see what results we have got.
We will first see which were the categories that the model most confused with one another. We will try to see if what the model predicted was reasonable or not. In this case the mistakes look reasonable (none of the mistakes seems obviously naive). This is an indicator that our classifier is working correctly.
Furthermore, when we plot the confusion matrix, we can see that the distribution is heavily skewed: the model makes the same mistakes over and over again but it rarely confuses other categories. This suggests that it just finds it difficult to distinguish some specific categories between each other; this is normal behaviour.
```
interp = ClassificationInterpretation.from_learner(learn)
losses,idxs = interp.top_losses()
len(data.valid_ds)==len(losses)==len(idxs)
interp.plot_top_losses(9, figsize=(15,11))
doc(interp.plot_top_losses)
interp.plot_confusion_matrix(figsize=(12,12), dpi=60)
interp.most_confused(min_val=2)
```
## Unfreezing, fine-tuning, and learning rates
Since our model is working as we expect it to, we will *unfreeze* our model and train some more.
```
learn.unfreeze()
learn.fit_one_cycle(1)
learn.load('stage-1');
learn.lr_find()
learn.recorder.plot()
learn.unfreeze()
learn.fit_one_cycle(2, max_lr=slice(1e-6,1e-4))
```
That's a pretty accurate model!
## Training: resnet50
Now we will train in the same way as before but with one caveat: instead of using resnet34 as our backbone we will use resnet50 (resnet34 is a 34 layer residual network while resnet50 has 50 layers. It will be explained later in the course and you can learn the details in the [resnet paper](https://arxiv.org/pdf/1512.03385.pdf)).
Basically, resnet50 usually performs better because it is a deeper network with more parameters. Let's see if we can achieve a higher performance here. To help it along, let's us use larger images too, since that way the network can see more detail. We reduce the batch size a bit since otherwise this larger network will require more GPU memory.
```
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(),
size=299, bs=bs//2).normalize(imagenet_stats)
learn = create_cnn(data, models.resnet50, metrics=error_rate)
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(8)
learn.save('stage-1-50')
```
It's astonishing that it's possible to recognize pet breeds so accurately! Let's see if full fine-tuning helps:
```
learn.unfreeze()
learn.fit_one_cycle(3, max_lr=slice(1e-6,1e-4))
```
If it doesn't, you can always go back to your previous model.
```
learn.load('stage-1-50');
interp = ClassificationInterpretation.from_learner(learn)
interp.most_confused(min_val=2)
```
## Other data formats
```
path = untar_data(URLs.MNIST_SAMPLE); path
tfms = get_transforms(do_flip=False)
data = ImageDataBunch.from_folder(path, ds_tfms=tfms, size=26)
data.show_batch(rows=3, figsize=(5,5))
learn = create_cnn(data, models.resnet18, metrics=accuracy)
learn.fit(2)
df = pd.read_csv(path/'labels.csv')
df.head()
data = ImageDataBunch.from_csv(path, ds_tfms=tfms, size=28)
data.show_batch(rows=3, figsize=(5,5))
data.classes
data = ImageDataBunch.from_df(path, df, ds_tfms=tfms, size=24)
data.classes
fn_paths = [path/name for name in df['name']]; fn_paths[:2]
pat = r"/(\d)/\d+\.png$"
data = ImageDataBunch.from_name_re(path, fn_paths, pat=pat, ds_tfms=tfms, size=24)
data.classes
data = ImageDataBunch.from_name_func(path, fn_paths, ds_tfms=tfms, size=24,
label_func = lambda x: '3' if '/3/' in str(x) else '7')
data.classes
labels = [('3' if '/3/' in str(x) else '7') for x in fn_paths]
labels[:5]
data = ImageDataBunch.from_lists(path, fn_paths, labels=labels, ds_tfms=tfms, size=24)
data.classes
```
|
github_jupyter
|
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai.vision import *
from fastai.metrics import error_rate
import fastai
fastai.__version__
from fastai.utils.show_install import *
show_install()
#bs = 64
bs = 16 # uncomment this line if you run out of memory even after clicking Kernel->Restart
help(untar_data)
URLs.PETS
path = untar_data(URLs.PETS); path
path.ls()
path_anno = path/'annotations'
path_img = path/'images'
fnames = get_image_files(path_img)
fnames[:5]
np.random.seed(2)
pat = re.compile(r'/([^/]+)_\d+.jpg$')
?data.show_batch
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(), size=224, bs=bs, num_workers=0
).normalize(imagenet_stats)
data.show_batch(rows=3, figsize=(7,6))
print(data.classes)
len(data.classes),data.c
learn = create_cnn(data, models.resnet34, metrics=error_rate)
learn.model
learn.fit_one_cycle(4)
learn.save('stage-1')
interp = ClassificationInterpretation.from_learner(learn)
losses,idxs = interp.top_losses()
len(data.valid_ds)==len(losses)==len(idxs)
interp.plot_top_losses(9, figsize=(15,11))
doc(interp.plot_top_losses)
interp.plot_confusion_matrix(figsize=(12,12), dpi=60)
interp.most_confused(min_val=2)
learn.unfreeze()
learn.fit_one_cycle(1)
learn.load('stage-1');
learn.lr_find()
learn.recorder.plot()
learn.unfreeze()
learn.fit_one_cycle(2, max_lr=slice(1e-6,1e-4))
data = ImageDataBunch.from_name_re(path_img, fnames, pat, ds_tfms=get_transforms(),
size=299, bs=bs//2).normalize(imagenet_stats)
learn = create_cnn(data, models.resnet50, metrics=error_rate)
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(8)
learn.save('stage-1-50')
learn.unfreeze()
learn.fit_one_cycle(3, max_lr=slice(1e-6,1e-4))
learn.load('stage-1-50');
interp = ClassificationInterpretation.from_learner(learn)
interp.most_confused(min_val=2)
path = untar_data(URLs.MNIST_SAMPLE); path
tfms = get_transforms(do_flip=False)
data = ImageDataBunch.from_folder(path, ds_tfms=tfms, size=26)
data.show_batch(rows=3, figsize=(5,5))
learn = create_cnn(data, models.resnet18, metrics=accuracy)
learn.fit(2)
df = pd.read_csv(path/'labels.csv')
df.head()
data = ImageDataBunch.from_csv(path, ds_tfms=tfms, size=28)
data.show_batch(rows=3, figsize=(5,5))
data.classes
data = ImageDataBunch.from_df(path, df, ds_tfms=tfms, size=24)
data.classes
fn_paths = [path/name for name in df['name']]; fn_paths[:2]
pat = r"/(\d)/\d+\.png$"
data = ImageDataBunch.from_name_re(path, fn_paths, pat=pat, ds_tfms=tfms, size=24)
data.classes
data = ImageDataBunch.from_name_func(path, fn_paths, ds_tfms=tfms, size=24,
label_func = lambda x: '3' if '/3/' in str(x) else '7')
data.classes
labels = [('3' if '/3/' in str(x) else '7') for x in fn_paths]
labels[:5]
data = ImageDataBunch.from_lists(path, fn_paths, labels=labels, ds_tfms=tfms, size=24)
data.classes
| 0.465873 | 0.987277 |
# Building a simple time series model
```
%matplotlib inline
```
We'll be using the international airline passenger data available from [here](https://datamarket.com/data/set/22u3/international-airline-passengers-monthly-totals-in-thousands-jan-49-dec-60#!ds=22u3&display=line). This particular dataset is included with `river` in the `datasets` module.
```
from river import datasets
for x, y in datasets.AirlinePassengers():
print(x, y)
break
```
The data is as simple as can be: it consists of a sequence of months and values representing the total number of international airline passengers per month. Our goal is going to be to predict the number of passengers for the next month at each step. Notice that because the dataset is small -- which is usually the case for time series -- we could just fit a model from scratch each month. However for the sake of example we're going to train a single model online. Although the overall performance might be potentially weaker, training a time series model online has the benefit of being scalable if, say, you have have [thousands of time series to manage](http://www.unofficialgoogledatascience.com/2017/04/our-quest-for-robust-time-series.html).
We'll start with a very simple model where the only feature will be the [ordinal date](https://www.wikiwand.com/en/Ordinal_date) of each month. This should be able to capture some of the underlying trend.
```
from river import compose
from river import linear_model
from river import preprocessing
def get_ordinal_date(x):
return {'ordinal_date': x['month'].toordinal()}
model = compose.Pipeline(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression())
)
```
We'll write down a function to evaluate the model. This will go through each observation in the dataset and update the model as it goes on. The prior predictions will be stored along with the true values and will be plotted together.
```
from river import metrics
import matplotlib.pyplot as plt
def evaluate_model(model):
metric = metrics.Rolling(metrics.MAE(), 12)
dates = []
y_trues = []
y_preds = []
for x, y in datasets.AirlinePassengers():
# Obtain the prior prediction and update the model in one go
y_pred = model.predict_one(x)
model.learn_one(x, y)
# Update the error metric
metric.update(y, y_pred)
# Store the true value and the prediction
dates.append(x['month'])
y_trues.append(y)
y_preds.append(y_pred)
# Plot the results
fig, ax = plt.subplots(figsize=(10, 6))
ax.grid(alpha=0.75)
ax.plot(dates, y_trues, lw=3, color='#2ecc71', alpha=0.8, label='Ground truth')
ax.plot(dates, y_preds, lw=3, color='#e74c3c', alpha=0.8, label='Prediction')
ax.legend()
ax.set_title(metric)
```
Let's evaluate our first model.
```
evaluate_model(model)
```
The model has captured a trend but not the right one. Indeed it thinks the trend is linear whereas we can visually see that the growth of the data increases with time. In other words the second derivative of the series is positive. This is a well know problem in time series forecasting and there are thus many ways to handle it; for example by using a [Box-Cox transform](https://www.wikiwand.com/en/Power_transform). However we are going to do something a bit different, and instead linearly detrend the series using a `Detrender`. We'll set `window_size` to 12 in order to use a rolling mean of size 12 for detrending. The `Detrender` will center the target in 0, which means that we don't need an intercept in our linear regression. We can thus set `intercept_lr` to 0.
```
from river import stats
from river import time_series
model = compose.Pipeline(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(intercept_lr=0)),
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
```
Now let's try and capture the monthly trend by one-hot encoding the month name.
```
import calendar
def get_month(x):
return {
calendar.month_name[month]: month == x['month'].month
for month in range(1, 13)
}
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month', compose.FuncTransformer(get_month)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(intercept_lr=0))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
```
This seems pretty decent. We can take a look at the weights of the linear regression to get an idea of the importance of each feature.
```
model.regressor['lin_reg'].weights
```
As could be expected the months of July and August have the highest weights because these are the months where people typically go on holiday abroad. The month of December has a low weight because this is a month of festivities in most of the Western world where people usually stay at home.
Our model seems to understand which months are important, but it fails to see that the importance of each month grows multiplicatively as the years go on. In other words our model is too shy. We can fix this by increasing the learning rate of the `LinearRegression`'s optimizer.
```
from river import optim
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month', compose.FuncTransformer(get_month)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
```
This is starting to look good! Naturally in production we would tune the learning rate, ideally in real-time.
Before finishing, we're going to introduce a cool feature extraction trick based on [radial basis function kernels](https://www.wikiwand.com/en/Radial_basis_function_kernel). The one-hot encoding we did on the month is a good idea but if you think about it is a bit rigid. Indeed the value of each feature is going to be 0 or 1, depending on the month of each observation. We're basically saying that the month of September is as distant to the month of August as it is to the month of March. Of course this isn't true, and it would be nice if our features would reflect this. To do so we can simply calculate the distance between the month of each observation and all the months in the calendar. Instead of simply computing the distance linearly, we're going to use a so-called *Gaussian radial basic function kernel*. This is a bit of a mouthful but for us it boils down to a simple formula, which is:
$$d(i, j) = exp(-\frac{(i - j)^2}{2\sigma^2})$$
Intuitively this computes a similarity between two months -- denoted by $i$ and $j$ -- which decreases the further apart they are from each other. The $sigma$ parameter can be seen as a hyperparameter than can be tuned -- in the following snippet we'll simply ignore it. The thing to take away is that this results in smoother predictions than when using a one-hot encoding scheme, which is often a desirable property. You can also see trick in action [in this nice presentation](http://www.youtube.com/watch?v=68ABAU_V8qI&t=4m45s).
```
import math
def get_month_distances(x):
return {
calendar.month_name[month]: math.exp(-(x['month'].month - month) ** 2)
for month in range(1, 13)
}
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month_distances', compose.FuncTransformer(get_month_distances)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
```
We've managed to get a good looking prediction curve with a reasonably simple model. What's more our model has the advantage of being interpretable and easy to debug. There surely are more rocks to squeeze (e.g. tune the hyperparameters, use an ensemble model, etc.) but we'll leave that as an exercice to the reader.
As a finishing touch we'll rewrite our pipeline using the `|` operator, which is called a "pipe".
```
extract_features = compose.TransformerUnion(get_ordinal_date, get_month_distances)
scale = preprocessing.StandardScaler()
learn = linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
)
model = extract_features | scale | learn
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
```
|
github_jupyter
|
%matplotlib inline
from river import datasets
for x, y in datasets.AirlinePassengers():
print(x, y)
break
from river import compose
from river import linear_model
from river import preprocessing
def get_ordinal_date(x):
return {'ordinal_date': x['month'].toordinal()}
model = compose.Pipeline(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression())
)
from river import metrics
import matplotlib.pyplot as plt
def evaluate_model(model):
metric = metrics.Rolling(metrics.MAE(), 12)
dates = []
y_trues = []
y_preds = []
for x, y in datasets.AirlinePassengers():
# Obtain the prior prediction and update the model in one go
y_pred = model.predict_one(x)
model.learn_one(x, y)
# Update the error metric
metric.update(y, y_pred)
# Store the true value and the prediction
dates.append(x['month'])
y_trues.append(y)
y_preds.append(y_pred)
# Plot the results
fig, ax = plt.subplots(figsize=(10, 6))
ax.grid(alpha=0.75)
ax.plot(dates, y_trues, lw=3, color='#2ecc71', alpha=0.8, label='Ground truth')
ax.plot(dates, y_preds, lw=3, color='#e74c3c', alpha=0.8, label='Prediction')
ax.legend()
ax.set_title(metric)
evaluate_model(model)
from river import stats
from river import time_series
model = compose.Pipeline(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(intercept_lr=0)),
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
import calendar
def get_month(x):
return {
calendar.month_name[month]: month == x['month'].month
for month in range(1, 13)
}
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month', compose.FuncTransformer(get_month)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(intercept_lr=0))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
model.regressor['lin_reg'].weights
from river import optim
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month', compose.FuncTransformer(get_month)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
import math
def get_month_distances(x):
return {
calendar.month_name[month]: math.exp(-(x['month'].month - month) ** 2)
for month in range(1, 13)
}
model = compose.Pipeline(
('features', compose.TransformerUnion(
('ordinal_date', compose.FuncTransformer(get_ordinal_date)),
('month_distances', compose.FuncTransformer(get_month_distances)),
)),
('scale', preprocessing.StandardScaler()),
('lin_reg', linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
))
)
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
extract_features = compose.TransformerUnion(get_ordinal_date, get_month_distances)
scale = preprocessing.StandardScaler()
learn = linear_model.LinearRegression(
intercept_lr=0,
optimizer=optim.SGD(0.03)
)
model = extract_features | scale | learn
model = time_series.Detrender(regressor=model, window_size=12)
evaluate_model(model)
| 0.815049 | 0.990282 |
```
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import KFold
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import cross_val_score
weather = pd.read_csv("weather3_180703.csv")
weather['date'] = pd.to_datetime(weather["date"])
station = weather[weather['station_nbr'] == 15]
station['date'].count()
# ls == ๋ชจ๋ ๊ฐ์ด 0์ธ ๊ฒ
ls = []
ls1 = []
for i in station.columns:
if station[i].count() == 0:
ls.append(i)
if station[i].isna().sum() != 0:
ls1.append(i)
ls, ls1
for i in station.columns:
count_null = station[i].isna().sum()
print(i, ":", count_null, "(",round((count_null / len(station) * 100),2),"%",")")
train = pd.read_csv("train.csv")
train.date = pd.to_datetime(train.date)
train.tail()
key = pd.read_csv("key.csv")
station = station.merge(key)
station = station.merge(train)
station.tail()
station['log1p_units'] = np.log1p(station.units)
target1 = station['units']
target2 = station['log1p_units']
station.drop(columns=['units','log1p_units'],inplace=True)
station.tail()
df1 = pd.concat([station,target1], axis=1)
df2 = pd.concat([station,target2], axis=1)
df2.to_csv('station15.csv', sep=',', index=False)
if df2.columns.tolist() and ls:
print('๊ณตํต ๋ณ์ ์์')
print(df2.columns.tolist() and ls)
else:
print('๊ณตํต ๋ณ์ ์์')
df2.columns
ls, ls1
```
### 1. ๋ณ์๋ณํ: df2 (log1p_units)
```
all_var = 'log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(depart) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(sunrise) + scale(sunset) + scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ C(resultdir) + scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + C(daytime) + 0'
model2 = sm.OLS.from_formula('log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2)
result2 = model2.fit()
print(result2.summary())
```
### 2. ๋ณ์๋ณํ : df2 (log1p_units) + ์์๋ผ์ด์ด ์ ๊ฑฐ
```
# ์์๋ผ์ด์ด ์ ๊ฑฐ
# Cook's distance > 2 ์ธ ๊ฐ ์ ๊ฑฐ
influence = result2.get_influence()
cooks_d2, pvals = influence.cooks_distance
fox_cr = 4 / (len(df2) - 2)
idx_outlier = np.where(cooks_d2 > fox_cr)[0]
len(idx_outlier)
idx = list(set(range(len(df2))).difference(idx_outlier))
df2_1 = df2.iloc[idx, :].reset_index(drop=True)
df2_1
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
ls1
```
### 3. VIF ํ์ธ
```
from statsmodels.stats.outliers_influence import variance_inflation_factor
# all_cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
# 'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
# 'windchill', 'depart', 'sunrise', 'sunset', 'snowfall' ]
cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
'windchill', 'snowfall' ]
y = df2_1.loc[:,cols]
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(y.values, i) for i in range(y.shape[1])]
vif["features"] = y.columns
vif = vif.sort_values("VIF Factor", ascending=False).reset_index(drop=True)
vif
```
### 4. VIF ๊ทผ๊ฑฐ, ๋นผ๊ณ ๋ค์ Model ๋๋ฆผ.
```
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
```
### 5. VIF ์ฌํ์ธ
```
from statsmodels.stats.outliers_influence import variance_inflation_factor
# all_cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
# 'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
# 'windchill', 'depart', 'sunrise', 'sunset', 'snowfall' ]
cols = ['cool', 'snowfall', 'preciptotal', 'resultspeed', 'avgspeed']
y = df2_1.loc[:,cols]
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(y.values, i) for i in range(y.shape[1])]
vif["features"] = y.columns
vif = vif.sort_values("VIF Factor", ascending=False).reset_index(drop=True)
vif
```
### 6. VIF ๊ทผ๊ฑฐ, stnpressure, sealevel, dewpoint, windchill, wetbulb, relative_humility, sunset์ ์ธํ๊ณ Model ๋๋ฆผ.
```
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(cool)\
+ scale(snowfall) + scale(preciptotal) + C(year) + C(month) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
```
### Anova ๋ถ์์ ํตํด p-value๊ฐ 0.05๋ณด๋ค ํฐ๊ฒ์ ์ ์ธ
```
anova_result2_1 = sm.stats.anova_lm(result2_1).sort_values(by=['PR(>F)'], ascending = False)
anova_result2_1[anova_result2_1['PR(>F)'] <= 0.05]
```
### ์ต์ข
Anova ๋ถ์๊ณผ TIF ํต๊ณผํ ๋ณ์๋ค์ ๋ฐํ์ผ๋ก ์ต์ข
๋ชจ๋ธ์์ฑ
```
# OLS - df2_1_1
model2_1 = sm.OLS.from_formula('log1p_units ~ C(year) + C(month) + \
+ C(item_nbr) + C(weekend) + 0', data = df2_1)
result = model2_1.fit()
result2_1 = model2_1.fit()
print(result2_1.summary())
from patsy import dmatrix
# ๋
๋ฆฝ๋ณ์์ ์ข
์๋ณ์๋ก ๋๋๊ธฐ
df2_1_X = df2_1.drop(columns=['log1p_units'])
df2_1_target = df2_1['log1p_units']
formula = 'C(year) + C(month) + C(weekend) + C(item_nbr) + 0'
dfX = dmatrix(formula, df2_1_X, return_type='dataframe')
dfy = pd.DataFrame(df2_1_target, columns=["log1p_units"])
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
model = LinearRegression()
cv = KFold(10)
scores = np.zeros(10)
for i, (train_index, test_index) in enumerate(cv.split(dfX)):
X_train = dfX.values[train_index]
y_train = dfy.values[train_index]
X_test = dfX.values[test_index]
y_test = dfy.values[test_index]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
scores[i] = r2_score(y_test, y_pred)
scores
```
|
github_jupyter
|
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import KFold
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.model_selection import cross_val_score
weather = pd.read_csv("weather3_180703.csv")
weather['date'] = pd.to_datetime(weather["date"])
station = weather[weather['station_nbr'] == 15]
station['date'].count()
# ls == ๋ชจ๋ ๊ฐ์ด 0์ธ ๊ฒ
ls = []
ls1 = []
for i in station.columns:
if station[i].count() == 0:
ls.append(i)
if station[i].isna().sum() != 0:
ls1.append(i)
ls, ls1
for i in station.columns:
count_null = station[i].isna().sum()
print(i, ":", count_null, "(",round((count_null / len(station) * 100),2),"%",")")
train = pd.read_csv("train.csv")
train.date = pd.to_datetime(train.date)
train.tail()
key = pd.read_csv("key.csv")
station = station.merge(key)
station = station.merge(train)
station.tail()
station['log1p_units'] = np.log1p(station.units)
target1 = station['units']
target2 = station['log1p_units']
station.drop(columns=['units','log1p_units'],inplace=True)
station.tail()
df1 = pd.concat([station,target1], axis=1)
df2 = pd.concat([station,target2], axis=1)
df2.to_csv('station15.csv', sep=',', index=False)
if df2.columns.tolist() and ls:
print('๊ณตํต ๋ณ์ ์์')
print(df2.columns.tolist() and ls)
else:
print('๊ณตํต ๋ณ์ ์์')
df2.columns
ls, ls1
all_var = 'log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(depart) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(sunrise) + scale(sunset) + scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ C(resultdir) + scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + C(daytime) + 0'
model2 = sm.OLS.from_formula('log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2)
result2 = model2.fit()
print(result2.summary())
# ์์๋ผ์ด์ด ์ ๊ฑฐ
# Cook's distance > 2 ์ธ ๊ฐ ์ ๊ฑฐ
influence = result2.get_influence()
cooks_d2, pvals = influence.cooks_distance
fox_cr = 4 / (len(df2) - 2)
idx_outlier = np.where(cooks_d2 > fox_cr)[0]
len(idx_outlier)
idx = list(set(range(len(df2))).difference(idx_outlier))
df2_1 = df2.iloc[idx, :].reset_index(drop=True)
df2_1
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(tmax) + scale(tmin) + scale(tavg) + scale(dewpoint) + scale(wetbulb) + scale(heat) + scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(stnpressure) + scale(sealevel) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + scale(relative_humility) + scale(windchill) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
ls1
from statsmodels.stats.outliers_influence import variance_inflation_factor
# all_cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
# 'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
# 'windchill', 'depart', 'sunrise', 'sunset', 'snowfall' ]
cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
'windchill', 'snowfall' ]
y = df2_1.loc[:,cols]
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(y.values, i) for i in range(y.shape[1])]
vif["features"] = y.columns
vif = vif.sort_values("VIF Factor", ascending=False).reset_index(drop=True)
vif
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(cool)\
+ scale(snowfall) + scale(preciptotal) + scale(resultspeed) \
+ scale(avgspeed) + C(year) + C(month) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
from statsmodels.stats.outliers_influence import variance_inflation_factor
# all_cols = ['tmax','tmin','tavg','dewpoint','wetbulb','heat','cool','preciptotal',\
# 'stnpressure','sealevel','resultspeed','avgspeed','relative_humility',\
# 'windchill', 'depart', 'sunrise', 'sunset', 'snowfall' ]
cols = ['cool', 'snowfall', 'preciptotal', 'resultspeed', 'avgspeed']
y = df2_1.loc[:,cols]
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(y.values, i) for i in range(y.shape[1])]
vif["features"] = y.columns
vif = vif.sort_values("VIF Factor", ascending=False).reset_index(drop=True)
vif
# OLS - df2_1
model2_1 = sm.OLS.from_formula('log1p_units ~ scale(cool)\
+ scale(snowfall) + scale(preciptotal) + C(year) + C(month) + C(weekend) \
+ C(rainY) + C(store_nbr) + C(item_nbr) + 0', data = df2_1)
result2_1 = model2_1.fit()
print(result2_1.summary())
anova_result2_1 = sm.stats.anova_lm(result2_1).sort_values(by=['PR(>F)'], ascending = False)
anova_result2_1[anova_result2_1['PR(>F)'] <= 0.05]
# OLS - df2_1_1
model2_1 = sm.OLS.from_formula('log1p_units ~ C(year) + C(month) + \
+ C(item_nbr) + C(weekend) + 0', data = df2_1)
result = model2_1.fit()
result2_1 = model2_1.fit()
print(result2_1.summary())
from patsy import dmatrix
# ๋
๋ฆฝ๋ณ์์ ์ข
์๋ณ์๋ก ๋๋๊ธฐ
df2_1_X = df2_1.drop(columns=['log1p_units'])
df2_1_target = df2_1['log1p_units']
formula = 'C(year) + C(month) + C(weekend) + C(item_nbr) + 0'
dfX = dmatrix(formula, df2_1_X, return_type='dataframe')
dfy = pd.DataFrame(df2_1_target, columns=["log1p_units"])
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
model = LinearRegression()
cv = KFold(10)
scores = np.zeros(10)
for i, (train_index, test_index) in enumerate(cv.split(dfX)):
X_train = dfX.values[train_index]
y_train = dfy.values[train_index]
X_test = dfX.values[test_index]
y_test = dfy.values[test_index]
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
scores[i] = r2_score(y_test, y_pred)
scores
| 0.545528 | 0.791821 |
### Project: Create a neural network class
---
Based on previous code examples, develop a neural network class that is able to classify any dataset provided. The class should create objects based on the desired network architecture:
1. Number of inputs
2. Number of hidden layers
3. Number of neurons per layer
4. Number of outputs
5. Learning rate
The class must have the train, and predict functions.
Test the neural network class on the datasets provided below: Use the input data to train the network, and then pass new inputs to predict on. Print the expected label and the predicted label for the input you used. Print the accuracy of the training after predicting on different inputs.
Use matplotlib to plot the error that the train method generates.
**Don't forget to install Keras and tensorflow in your environment!**
---
### Import the needed Packages
```
import numpy as np
import matplotlib.pyplot as plt
# Needed for the mnist data
from keras.datasets import mnist
from keras.utils import to_categorical
```
### Define the class
```
class NeuralNetwork:
def __init__(self, architecture, alpha):
'''
layers: List of integers which represents the architecture of the network.
alpha: Learning rate.
'''
# TODO: Initialize the list of weights matrices, then store
# the network architecture and learning rate
inputs, layers, neurons, outputs = architecture
self.alpha = alpha
self.layers = layers
self.neurons = neurons
self.w1 = np.random.randn(inputs, neurons)
self.w2 = np.zeros((layers - 1, neurons, neurons))
for i in range(layers - 1):
self.w2[i] = np.random.randn(neurons, neurons)
self.w3 = np.random.randn(neurons, outputs)
self.b1 = np.random.randn(neurons)
self.b2 = np.random.randn(layers - 1, neurons)
self.b3 = np.random.randn(outputs)
self.wT = []
pass
def __repr__(self):
# construct and return a string that represents the network
# architecture
return "NeuralNetwork: {}".format( "-".join(str(l) for l in self.layers))
@staticmethod
def softmax(X):
# applies the softmax function to a set of values
expX = np.exp(X)
return expX / expX.sum(axis=1, keepdims=True)
def sigmoid(self, x):
# the sigmoid for a given input value
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_deriv(self, x):
# the derivative of the sigmoid
return x * (1 - x)
def predict(self, inputs):
# TODO: Define the predict function
self.wT = np.zeros((self.layers, inputs.shape[0], self.neurons))
self.wT[0] = self.sigmoid(np.dot(inputs, self.w1) + self.b1)
for i in range(self.layers - 1):
self.wT[i + 1] = self.sigmoid(np.dot(self.wT[i], self.w2[i]) + self.b2[i])
return self.softmax(np.dot(self.wT[len(self.wT) - 1], self.w3) + self.b3)
def train(self, inputs, labels, epochs = 1000, displayUpdate = 100):
# TODO: Define the training step for the network. It should include the forward and back propagation
# steps, the updating of the weights, and it should print the error every 'displayUpdate' epochs
# It must return the errors so that they can be displayed with matplotlib
e = []
for i in range(epochs):
p = self.predict(inputs)
e1 = labels - p
e.append(np.average(np.abs(e1)))
d3 = e1 * self.sigmoid_deriv(p)
e2 = np.dot(d3, self.w3.T)
d2 = e2 * self.sigmoid_deriv(self.wT[-1])
b4 = np.sum(d3)
self.b3 += b4 * self.alpha
self.w3 += np.dot(self.wT[-1].T, d3) * self.alpha
self.w1 += np.dot(inputs.T, d2) * self.alpha
b4 = np.sum(d2)
self.b1 += b4 * self.alpha
for j in range(self.layers - 1):
temp = (len(self.w2) - 1) - j
temp2 = (len(self.wT) - 2) - j
e2 = np.dot(d2, self.w2[temp])
self.w2[temp] += np.dot(self.wT[temp2].T, d2) * self.alpha
b2 = np.sum(d2)
self.b2[j] += b2 * self.alpha
d2 = e2 * self.sigmoid_deriv(self.wT[temp2])
if i % displayUpdate == 0:
print("Error: ", e[-1])
return e
```
### Test datasets
#### XOR
```
# input dataset
XOR_inputs = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
# labels dataset
XOR_labels = np.array([[0,1,1,0]]).T
hot_labels = np.zeros((4, 2))
for i in range(4):
hot_labels[i, XOR_labels[i]] = 1
#TODO: Test the class with the XOR data
arch = [2, 1, 4, 2]
NN = NeuralNetwork(arch, 0.5)
test = NN.train(XOR_inputs, hot_labels, 10000, 1000)
f, p = plt.subplots(1,1)
p.set_xlabel('Epoch')
p.set_ylabel('Error')
p.plot(test)
```
#### Multiple classes
```
# Creates the data points for each class
class_1 = np.random.randn(700, 2) + np.array([0, -3])
class_2 = np.random.randn(700, 2) + np.array([3, 3])
class_3 = np.random.randn(700, 2) + np.array([-3, 3])
feature_set = np.vstack([class_1, class_2, class_3])
labels = np.array([0]*700 + [1]*700 + [2]*700)
one_hot_labels = np.zeros((2100, 3))
for i in range(2100):
one_hot_labels[i, labels[i]] = 1
plt.figure(figsize=(10,10))
plt.scatter(feature_set[:,0], feature_set[:,1], c=labels, s=30, alpha=0.5)
plt.show()
#TODO: Test the class with the multiple classes data
arch2 = [2, 2, 5, 3]
NN2 = NeuralNetwork(arch2, 0.01)
test2 = NN2.train(feature_set, one_hot_labels, 10000, 1000)
f, p2 = plt.subplots(1,1)
p2.set_xlabel('Epoch')
p2.set_ylabel('Error')
p2.plot(test2)
```
#### On the mnist data set
---
Train the network to classify hand drawn digits.
For this data set, if the training step is taking too long, you can try to adjust the architecture of the network to have fewer layers, or you could try to train it with fewer input. The data has already been loaded and preprocesed so that it can be used with the network.
---
```
# Load the train and test data from the mnist data set
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Plot a sample data point
plt.title("Label: " + str(train_labels[0]))
plt.imshow(train_images[0], cmap="gray")
# Standardize the data
# Flatten the images
train_images = train_images.reshape((60000, 28 * 28))
# turn values from 0-255 to 0-1
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
# Create one hot encoding for the labels
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
# TODO: Test the class with the mnist data. Test the training of the network with the test_images data, and
# record the accuracy of the classification.
arch3 = [train_images.shape[1], 1, 64, 10]
NN3 = NeuralNetwork(arch3, 0.0005)
test3 = NN3.train(train_images[0:5000], train_labels[0:5000], 1000, 100)
f, p3 = plt.subplots(1,1)
p3.set_xlabel('Epoch')
p3.set_ylabel('Error')
p3.plot(test3)
test4 = NN3.predict(test_images[0:1000])
# create one hot encoding on the test data
one_hot_test_labels = to_categorical(test_labels[0:1000])
np.set_printoptions(precision = 3, suppress= True, linewidth = 50)
# turn predictions to one hot encoding labels
predictions = np.copy(test4)
predictions[predictions > 0.5] = 1
predictions[predictions < 0.5] = 0
error_predictions = []
for index, (prediction, label) in enumerate(zip(predictions[0:10], one_hot_test_labels[0:10])):
if not np.array_equal(prediction,label):
error_predictions.append((index, prediction, label))
f, plots = plt.subplots((len(error_predictions)+3-1)//3, 3, figsize=(20,10))
plots = [plot for sublist in plots for plot in sublist]
for img, plot in zip(error_predictions, plots):
plot.imshow(test_images[img[0]].reshape(28,28), cmap = "gray")
plot.set_title('Prediction: ' + str(img[1]))
```
After predicting on the *test_images*, use matplotlib to display some of the images that were not correctly classified. Then, answer the following questions:
1. **Why do you think those were incorrectly classified?**
The inconsistency of the numbers in the images made the model fail in some results.
2. **What could you try doing to improve the classification accuracy?**
Adding more training data, and tweaking the parameters.
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
# Needed for the mnist data
from keras.datasets import mnist
from keras.utils import to_categorical
class NeuralNetwork:
def __init__(self, architecture, alpha):
'''
layers: List of integers which represents the architecture of the network.
alpha: Learning rate.
'''
# TODO: Initialize the list of weights matrices, then store
# the network architecture and learning rate
inputs, layers, neurons, outputs = architecture
self.alpha = alpha
self.layers = layers
self.neurons = neurons
self.w1 = np.random.randn(inputs, neurons)
self.w2 = np.zeros((layers - 1, neurons, neurons))
for i in range(layers - 1):
self.w2[i] = np.random.randn(neurons, neurons)
self.w3 = np.random.randn(neurons, outputs)
self.b1 = np.random.randn(neurons)
self.b2 = np.random.randn(layers - 1, neurons)
self.b3 = np.random.randn(outputs)
self.wT = []
pass
def __repr__(self):
# construct and return a string that represents the network
# architecture
return "NeuralNetwork: {}".format( "-".join(str(l) for l in self.layers))
@staticmethod
def softmax(X):
# applies the softmax function to a set of values
expX = np.exp(X)
return expX / expX.sum(axis=1, keepdims=True)
def sigmoid(self, x):
# the sigmoid for a given input value
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_deriv(self, x):
# the derivative of the sigmoid
return x * (1 - x)
def predict(self, inputs):
# TODO: Define the predict function
self.wT = np.zeros((self.layers, inputs.shape[0], self.neurons))
self.wT[0] = self.sigmoid(np.dot(inputs, self.w1) + self.b1)
for i in range(self.layers - 1):
self.wT[i + 1] = self.sigmoid(np.dot(self.wT[i], self.w2[i]) + self.b2[i])
return self.softmax(np.dot(self.wT[len(self.wT) - 1], self.w3) + self.b3)
def train(self, inputs, labels, epochs = 1000, displayUpdate = 100):
# TODO: Define the training step for the network. It should include the forward and back propagation
# steps, the updating of the weights, and it should print the error every 'displayUpdate' epochs
# It must return the errors so that they can be displayed with matplotlib
e = []
for i in range(epochs):
p = self.predict(inputs)
e1 = labels - p
e.append(np.average(np.abs(e1)))
d3 = e1 * self.sigmoid_deriv(p)
e2 = np.dot(d3, self.w3.T)
d2 = e2 * self.sigmoid_deriv(self.wT[-1])
b4 = np.sum(d3)
self.b3 += b4 * self.alpha
self.w3 += np.dot(self.wT[-1].T, d3) * self.alpha
self.w1 += np.dot(inputs.T, d2) * self.alpha
b4 = np.sum(d2)
self.b1 += b4 * self.alpha
for j in range(self.layers - 1):
temp = (len(self.w2) - 1) - j
temp2 = (len(self.wT) - 2) - j
e2 = np.dot(d2, self.w2[temp])
self.w2[temp] += np.dot(self.wT[temp2].T, d2) * self.alpha
b2 = np.sum(d2)
self.b2[j] += b2 * self.alpha
d2 = e2 * self.sigmoid_deriv(self.wT[temp2])
if i % displayUpdate == 0:
print("Error: ", e[-1])
return e
# input dataset
XOR_inputs = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
# labels dataset
XOR_labels = np.array([[0,1,1,0]]).T
hot_labels = np.zeros((4, 2))
for i in range(4):
hot_labels[i, XOR_labels[i]] = 1
#TODO: Test the class with the XOR data
arch = [2, 1, 4, 2]
NN = NeuralNetwork(arch, 0.5)
test = NN.train(XOR_inputs, hot_labels, 10000, 1000)
f, p = plt.subplots(1,1)
p.set_xlabel('Epoch')
p.set_ylabel('Error')
p.plot(test)
# Creates the data points for each class
class_1 = np.random.randn(700, 2) + np.array([0, -3])
class_2 = np.random.randn(700, 2) + np.array([3, 3])
class_3 = np.random.randn(700, 2) + np.array([-3, 3])
feature_set = np.vstack([class_1, class_2, class_3])
labels = np.array([0]*700 + [1]*700 + [2]*700)
one_hot_labels = np.zeros((2100, 3))
for i in range(2100):
one_hot_labels[i, labels[i]] = 1
plt.figure(figsize=(10,10))
plt.scatter(feature_set[:,0], feature_set[:,1], c=labels, s=30, alpha=0.5)
plt.show()
#TODO: Test the class with the multiple classes data
arch2 = [2, 2, 5, 3]
NN2 = NeuralNetwork(arch2, 0.01)
test2 = NN2.train(feature_set, one_hot_labels, 10000, 1000)
f, p2 = plt.subplots(1,1)
p2.set_xlabel('Epoch')
p2.set_ylabel('Error')
p2.plot(test2)
# Load the train and test data from the mnist data set
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Plot a sample data point
plt.title("Label: " + str(train_labels[0]))
plt.imshow(train_images[0], cmap="gray")
# Standardize the data
# Flatten the images
train_images = train_images.reshape((60000, 28 * 28))
# turn values from 0-255 to 0-1
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255
# Create one hot encoding for the labels
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
# TODO: Test the class with the mnist data. Test the training of the network with the test_images data, and
# record the accuracy of the classification.
arch3 = [train_images.shape[1], 1, 64, 10]
NN3 = NeuralNetwork(arch3, 0.0005)
test3 = NN3.train(train_images[0:5000], train_labels[0:5000], 1000, 100)
f, p3 = plt.subplots(1,1)
p3.set_xlabel('Epoch')
p3.set_ylabel('Error')
p3.plot(test3)
test4 = NN3.predict(test_images[0:1000])
# create one hot encoding on the test data
one_hot_test_labels = to_categorical(test_labels[0:1000])
np.set_printoptions(precision = 3, suppress= True, linewidth = 50)
# turn predictions to one hot encoding labels
predictions = np.copy(test4)
predictions[predictions > 0.5] = 1
predictions[predictions < 0.5] = 0
error_predictions = []
for index, (prediction, label) in enumerate(zip(predictions[0:10], one_hot_test_labels[0:10])):
if not np.array_equal(prediction,label):
error_predictions.append((index, prediction, label))
f, plots = plt.subplots((len(error_predictions)+3-1)//3, 3, figsize=(20,10))
plots = [plot for sublist in plots for plot in sublist]
for img, plot in zip(error_predictions, plots):
plot.imshow(test_images[img[0]].reshape(28,28), cmap = "gray")
plot.set_title('Prediction: ' + str(img[1]))
| 0.461502 | 0.987628 |
# Ungraded Lab: Build a Multi-output Model
In this lab, we'll show how you can build models with more than one output. The dataset we will be working on is available from the [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/Energy+efficiency). It is an Energy Efficiency dataset which uses the bulding features (e.g. wall area, roof area) as inputs and has two outputs: Cooling Load and Heating Load. Let's see how we can build a model to train on this data.
## Imports
```
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Dense, Input
from sklearn.model_selection import train_test_split
```
## Utilities
We define a few utilities for data conversion and visualization to make our code more neat.
```
def format_output(data):
y1 = data.pop('Y1')
y1 = np.array(y1)
y2 = data.pop('Y2')
y2 = np.array(y2)
return y1, y2
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
def plot_diff(y_true, y_pred, title=''):
plt.scatter(y_true, y_pred)
plt.title(title)
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.axis('equal')
plt.axis('square')
plt.xlim(plt.xlim())
plt.ylim(plt.ylim())
plt.plot([-100, 100], [-100, 100])
plt.show()
def plot_metrics(metric_name, title, ylim=5):
plt.title(title)
plt.ylim(0, ylim)
plt.plot(history.history[metric_name], color='blue', label=metric_name)
plt.plot(history.history['val_' + metric_name], color='green', label='val_' + metric_name)
plt.show()
```
## Prepare the Data
We download the dataset and format it for training.
```
# Get the data from UCI dataset
URL = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00242/ENB2012_data.xlsx'
# Use pandas excel reader
df = pd.read_excel(URL)
df = df.sample(frac=1).reset_index(drop=True)
# Split the data into train and test with 80 train / 20 test
train, test = train_test_split(df, test_size=0.2)
train_stats = train.describe()
# Get Y1 and Y2 as the 2 outputs and format them as np arrays
train_stats.pop('Y1')
train_stats.pop('Y2')
train_stats = train_stats.transpose()
train_Y = format_output(train)
test_Y = format_output(test)
# Normalize the training and test data
norm_train_X = norm(train)
norm_test_X = norm(test)
```
## Build the Model
Here is how we'll build the model using the functional syntax. Notice that we can specify a list of outputs (i.e. `[y1_output, y2_output]`) when we instantiate the `Model()` class.
```
# Define model layers.
input_layer = Input(shape=(len(train .columns),))
first_dense = Dense(units='128', activation='relu')(input_layer)
second_dense = Dense(units='128', activation='relu')(first_dense)
# Y1 output will be fed directly from the second dense
y1_output = Dense(units='1', name='y1_output')(second_dense)
third_dense = Dense(units='64', activation='relu')(second_dense)
# Y2 output will come via the third dense
y2_output = Dense(units='1', name='y2_output')(third_dense)
# Define the model with the input layer and a list of output layers
model = Model(inputs=input_layer, outputs=[y1_output, y2_output])
print(model.summary())
```
## Configure parameters
We specify the optimizer as well as the loss and metrics for each output.
```
# Specify the optimizer, and compile the model with loss functions for both outputs
optimizer = tf.keras.optimizers.SGD(lr=0.001)
model.compile(optimizer=optimizer,
loss={'y1_output': 'mse', 'y2_output': 'mse'},
metrics={'y1_output': tf.keras.metrics.RootMeanSquaredError(),
'y2_output': tf.keras.metrics.RootMeanSquaredError()})
```
## Train the Model
```
# Train the model for 500 epochs
history = model.fit(norm_train_X, train_Y,
epochs=500, batch_size=10, validation_data=(norm_test_X, test_Y))
```
## Evaluate the Model and Plot Metrics
```
# Test the model and print loss and mse for both outputs
loss, Y1_loss, Y2_loss, Y1_rmse, Y2_rmse = model.evaluate(x=norm_test_X, y=test_Y)
print("Loss = {}, Y1_loss = {}, Y1_mse = {}, Y2_loss = {}, Y2_mse = {}".format(loss, Y1_loss, Y1_rmse, Y2_loss, Y2_rmse))
# Plot the loss and mse
Y_pred = model.predict(norm_test_X)
plot_diff(test_Y[0], Y_pred[0], title='Y1')
plot_diff(test_Y[1], Y_pred[1], title='Y2')
plot_metrics(metric_name='y1_output_root_mean_squared_error', title='Y1 RMSE', ylim=6)
plot_metrics(metric_name='y2_output_root_mean_squared_error', title='Y2 RMSE', ylim=7)
```
|
github_jupyter
|
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Dense, Input
from sklearn.model_selection import train_test_split
def format_output(data):
y1 = data.pop('Y1')
y1 = np.array(y1)
y2 = data.pop('Y2')
y2 = np.array(y2)
return y1, y2
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
def plot_diff(y_true, y_pred, title=''):
plt.scatter(y_true, y_pred)
plt.title(title)
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.axis('equal')
plt.axis('square')
plt.xlim(plt.xlim())
plt.ylim(plt.ylim())
plt.plot([-100, 100], [-100, 100])
plt.show()
def plot_metrics(metric_name, title, ylim=5):
plt.title(title)
plt.ylim(0, ylim)
plt.plot(history.history[metric_name], color='blue', label=metric_name)
plt.plot(history.history['val_' + metric_name], color='green', label='val_' + metric_name)
plt.show()
# Get the data from UCI dataset
URL = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00242/ENB2012_data.xlsx'
# Use pandas excel reader
df = pd.read_excel(URL)
df = df.sample(frac=1).reset_index(drop=True)
# Split the data into train and test with 80 train / 20 test
train, test = train_test_split(df, test_size=0.2)
train_stats = train.describe()
# Get Y1 and Y2 as the 2 outputs and format them as np arrays
train_stats.pop('Y1')
train_stats.pop('Y2')
train_stats = train_stats.transpose()
train_Y = format_output(train)
test_Y = format_output(test)
# Normalize the training and test data
norm_train_X = norm(train)
norm_test_X = norm(test)
# Define model layers.
input_layer = Input(shape=(len(train .columns),))
first_dense = Dense(units='128', activation='relu')(input_layer)
second_dense = Dense(units='128', activation='relu')(first_dense)
# Y1 output will be fed directly from the second dense
y1_output = Dense(units='1', name='y1_output')(second_dense)
third_dense = Dense(units='64', activation='relu')(second_dense)
# Y2 output will come via the third dense
y2_output = Dense(units='1', name='y2_output')(third_dense)
# Define the model with the input layer and a list of output layers
model = Model(inputs=input_layer, outputs=[y1_output, y2_output])
print(model.summary())
# Specify the optimizer, and compile the model with loss functions for both outputs
optimizer = tf.keras.optimizers.SGD(lr=0.001)
model.compile(optimizer=optimizer,
loss={'y1_output': 'mse', 'y2_output': 'mse'},
metrics={'y1_output': tf.keras.metrics.RootMeanSquaredError(),
'y2_output': tf.keras.metrics.RootMeanSquaredError()})
# Train the model for 500 epochs
history = model.fit(norm_train_X, train_Y,
epochs=500, batch_size=10, validation_data=(norm_test_X, test_Y))
# Test the model and print loss and mse for both outputs
loss, Y1_loss, Y2_loss, Y1_rmse, Y2_rmse = model.evaluate(x=norm_test_X, y=test_Y)
print("Loss = {}, Y1_loss = {}, Y1_mse = {}, Y2_loss = {}, Y2_mse = {}".format(loss, Y1_loss, Y1_rmse, Y2_loss, Y2_rmse))
# Plot the loss and mse
Y_pred = model.predict(norm_test_X)
plot_diff(test_Y[0], Y_pred[0], title='Y1')
plot_diff(test_Y[1], Y_pred[1], title='Y2')
plot_metrics(metric_name='y1_output_root_mean_squared_error', title='Y1 RMSE', ylim=6)
plot_metrics(metric_name='y2_output_root_mean_squared_error', title='Y2 RMSE', ylim=7)
| 0.881857 | 0.987228 |
# SELF-DRIVING CAR: Finding Lane Lines.
## Project: Finding Lane Lines on the Road.
The goal of the project is to identify lane lines on the road. Given the test images and videos, end goal was to create a pipeline of code to achive the output as show in example folder [P1_example.mp4](examples/P1_example.mp4). For this project I have used Jupyter notebook to execute
the project and you can see [this online](https://classroom.udacity.com/courses/ud1111) course from Udacity to know more about the tools used for the project.
## STEPS TO FIND LANE LINES
For lane detection on a video, we have to pass some steps that you can see below
1. Getting each frame from video
2. Making grayscale each frame
3. Detecting edges by using Canny Algorithm
4. Finding Lane by using Hough Algorithm
5. Improving output and making a new video as a result
In the project I have created the pipeline of the code, which takes Image as the input and image is passed though the pipeline
(Series of algorithms).
## Canny Edge Detection
Honestly we can detect the lane lines on the image by providing few discription on RGB threshold value and the pattern of the lane
but the system will not be robust by this. To make the system robust, we have to use the computer vision algorithms.
To make the system robust we have to detect the objects by their edges. To get the edges of the object we first convert the image to gray and then we have to compute the gradiant and by doing that we can find the edge by mesuring the level of change in gradient values between the pixels.
```
edges = cv2.Canny(gray, low_threshold, high_threshold)
```
As you can see, just the important lines of the image which have strong edges have remained. The main question is, how we can extract straight lines from an image. The Hough Algorithm can answer this question.
## HOUGH TRANSFORM
The Hough transform is a feature extraction technique used in image analysis, computer vision, and digital image processing. The purpose of the technique is to find imperfect instances of objects within a certain class of shapes by a voting procedure. This voting procedure is carried out in a parameter space, from which object candidates are obtained as local maxima in a so-called accumulator space that is explicitly constructed by the algorithm for computing the Hough transform. The classical Hough transform was concerned with the identification of lines in the image, but later the Hough transform has been extended to identifying positions of arbitrary shapes, most commonly circles or ellipses. A line in image space can be represented as a single point in parameter space, or Hough Space. We use this theory for detecting lines in a picture. So for achieving this goal, we should add the result of the Canny Algorithm to Hough.
Hough Algorithm has some parameters which have role key in tuning algorithm fine. You can either put a long time for tuning parameters of algorithm or put an especial mask for eliminating other unuseful areas from the picture. Check the difference between using masked area and just tuning parameters of the Hough Algorithm. In the below images you can see the detected lines as red color.
Without Area Selection(unMasked)
```
vertices = np.array([[(0, imshape[0]), (0, 0), (imshape[1], 0), (imshape[1], imshape[0])]], dtype=np.int32)
```
Suitable Area Selection(Masked)
```
vertices = np.array([[(0,imshape[0]),(460, 318), (490, 318), (imshape[1],imshape[0])]], dtype=np.int32)
```
But you can see in the above image that the left lane is not continues and some frames will result as shown in below image
To over come above issue, we have to apply below logic on output of Hough Image.After getting x1,y1,x2,y2 from cv2.HoughLinesP call, we have to average and/or extrapolate the line segments we've detected to map out the full extent of the lane lines.
```
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
```
To extrapolate and find the mean we have to convert the line obtained in Image domain to Hough parameter domain and find the mean of M and B points obtained and derive the lane lines from the mean parameter points obtained.
```
# Get the mean of all the lines values
AvgPositiveM = mean(mPositiveValues)
AvgNegitiveM = mean(mNegitiveValues)
AvgLeftB = mean(bLeftValues)
AvgRightB = mean(bRightValues)
# use average slopes to generate line using ROI endpoints
if AvgPositiveM != 0:
x1_Left = (y_max - AvgLeftB)/AvgPositiveM
y1_Left = y_max
x2_Left = (y_min - AvgLeftB)/AvgPositiveM
y2_Left = y_min
cv2.line(img, (int(x1_Left), int(y1_Left)), (int(x2_Left), int(y2_Left)), color, thickness) #avg Left Line
if AvgNegitiveM != 0:
x1_Right = (y_max - AvgRightB)/AvgNegitiveM
y1_Right = y_max
x2_Right = (y_min - AvgRightB)/AvgNegitiveM
y2_Right = y_min
# define average left and right lines
cv2.line(img, (int(x1_Right), int(y1_Right)), (int(x2_Right), int(y2_Right)), color, thickness) #avg Right Line
```
After adding above code in our logic we will get the result as in below image
Above algorithm works fine for videos as well considering videos are series of images.
|
github_jupyter
|
edges = cv2.Canny(gray, low_threshold, high_threshold)
vertices = np.array([[(0, imshape[0]), (0, 0), (imshape[1], 0), (imshape[1], imshape[0])]], dtype=np.int32)
vertices = np.array([[(0,imshape[0]),(460, 318), (490, 318), (imshape[1],imshape[0])]], dtype=np.int32)
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
# Get the mean of all the lines values
AvgPositiveM = mean(mPositiveValues)
AvgNegitiveM = mean(mNegitiveValues)
AvgLeftB = mean(bLeftValues)
AvgRightB = mean(bRightValues)
# use average slopes to generate line using ROI endpoints
if AvgPositiveM != 0:
x1_Left = (y_max - AvgLeftB)/AvgPositiveM
y1_Left = y_max
x2_Left = (y_min - AvgLeftB)/AvgPositiveM
y2_Left = y_min
cv2.line(img, (int(x1_Left), int(y1_Left)), (int(x2_Left), int(y2_Left)), color, thickness) #avg Left Line
if AvgNegitiveM != 0:
x1_Right = (y_max - AvgRightB)/AvgNegitiveM
y1_Right = y_max
x2_Right = (y_min - AvgRightB)/AvgNegitiveM
y2_Right = y_min
# define average left and right lines
cv2.line(img, (int(x1_Right), int(y1_Right)), (int(x2_Right), int(y2_Right)), color, thickness) #avg Right Line
| 0.589244 | 0.993807 |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Gena/palettes_crameri_oleron_dem.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Gena/palettes_crameri_oleron_dem.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Gena/palettes_crameri_oleron_dem.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
```
Map = geemap.Map(center=[40,-100], zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
from ee_plugin.contrib import palettes
dem = ee.Image("AHN/AHN2_05M_RUW").convolve(ee.Kernel.gaussian(0.5, 0.3, 'meters'))
extrusion = 3
weight = 0.7
palette = palettes.crameri['oleron'][50]
rgb = dem.visualize(**{'min': 0, 'max': 3, 'palette': palette })
hsv = rgb.unitScale(0, 255).rgbToHsv()
hs = ee.Terrain.hillshade(dem.multiply(extrusion), 315, 35).unitScale(0, 255)
hs = hs.multiply(weight).add(hsv.select('value').multiply(1 - weight))
saturation = hsv.select('saturation').multiply(0.5)
hsv = hsv.addBands(hs.rename('value'), ['value'], True)
hsv = hsv.addBands(saturation, ['saturation'], True)
rgb = hsv.hsvToRgb()
# rgb = rgb.updateMask(dem.unitScale(0, 3))
Map.addLayer(rgb, {}, 'Dutch AHN DEM', True)
Map.setCenter(4.5618, 52.1664, 18)
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
Map = geemap.Map(center=[40,-100], zoom=4)
Map
# Add Earth Engine dataset
from ee_plugin.contrib import palettes
dem = ee.Image("AHN/AHN2_05M_RUW").convolve(ee.Kernel.gaussian(0.5, 0.3, 'meters'))
extrusion = 3
weight = 0.7
palette = palettes.crameri['oleron'][50]
rgb = dem.visualize(**{'min': 0, 'max': 3, 'palette': palette })
hsv = rgb.unitScale(0, 255).rgbToHsv()
hs = ee.Terrain.hillshade(dem.multiply(extrusion), 315, 35).unitScale(0, 255)
hs = hs.multiply(weight).add(hsv.select('value').multiply(1 - weight))
saturation = hsv.select('saturation').multiply(0.5)
hsv = hsv.addBands(hs.rename('value'), ['value'], True)
hsv = hsv.addBands(saturation, ['saturation'], True)
rgb = hsv.hsvToRgb()
# rgb = rgb.updateMask(dem.unitScale(0, 3))
Map.addLayer(rgb, {}, 'Dutch AHN DEM', True)
Map.setCenter(4.5618, 52.1664, 18)
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
| 0.447219 | 0.960768 |
**Jupyter Kernel**:
* If you are in SageMaker Notebook instance, please make sure you are using **conda_pytorch_latest_p36** kernel
* If you are on SageMaker Studio, please make sure you are using **SageMaker JumpStart PyTorch 1.0** kernel
**Run All**:
* If you are in SageMaker notebook instance, you can go to *Cell tab -> Run All*
* If you are in SageMaker Studio, you can go to *Run tab -> Run All Cells*
## Training our Classifier from scratch
Depending on an application, sometimes image classification is enough. In this notebook, we see how to train and deploy an accurate classifier from scratch on **NEU-CLS** dataset
```
import json
import numpy as np
import sagemaker
from sagemaker.s3 import S3Downloader
sagemaker_session = sagemaker.Session()
sagemaker_config = json.load(open("../stack_outputs.json"))
role = sagemaker_config["IamRole"]
solution_bucket = sagemaker_config["SolutionS3Bucket"]
region = sagemaker_config["AWSRegion"]
solution_name = sagemaker_config["SolutionName"]
bucket = sagemaker_config["S3Bucket"]
```
First, we download our **NEU-CLS** dataset from our public S3 bucket
```
from sagemaker.s3 import S3Downloader
original_bucket = f"s3://{solution_bucket}-{region}/{solution_name}"
original_data = f"{original_bucket}/data/NEU-CLS.zip"
original_sources = f"{original_bucket}/build/lib/source_dir.tar.gz"
print("original data: ")
S3Downloader.list(original_data)
```
For easiler data processing, depending on the dataset, we unify the class and label names using the scripts from `prepare_data`
```
%%time
RAW_DATA_PATH= !echo $PWD/raw_neu_cls
RAW_DATA_PATH = RAW_DATA_PATH.n
DATA_PATH = !echo $PWD/neu_cls
DATA_PATH = DATA_PATH.n
!mkdir -p $RAW_DATA_PATH
!aws s3 cp $original_data $RAW_DATA_PATH
!mkdir -p $DATA_PATH
!python ../src/prepare_data/neu.py $RAW_DATA_PATH/NEU-CLS.zip $DATA_PATH
```
After data preparation, we need to setup some paths that will be used throughtout the notebook
```
prefix = "neu-cls"
neu_cls_s3 = f"s3://{bucket}/{prefix}"
sources = f"{neu_cls_s3}/code/"
train_output = f"{neu_cls_s3}/output/"
neu_cls_prepared_s3 = f"{neu_cls_s3}/data/"
!aws s3 sync $DATA_PATH $neu_cls_prepared_s3 --quiet # remove the --quiet flag to view sync outputs
s3_checkpoint = f"{neu_cls_s3}/checkpoint/"
sm_local_checkpoint_dir = "/opt/ml/checkpoints/"
!aws s3 cp $original_sources $sources
```
## Visualization
Let examine some datasets that we will use later by providing an `ID`
```
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import torch
from PIL import Image
from torch.utils.data import DataLoader
try:
import sagemaker_defect_detection
except ImportError:
import sys
from pathlib import Path
ROOT = Path("../src").resolve()
sys.path.insert(0, str(ROOT))
from sagemaker_defect_detection import NEUCLS
def visualize(image, label, predicted=None):
if not isinstance(image, Image.Image):
image = Image.fromarray(image)
plt.figure(dpi=120)
if predicted is not None:
plt.title(f"label: {label}, prediction: {predicted}")
else:
plt.title(f"label: {label}")
plt.axis("off")
plt.imshow(image)
return
dataset = NEUCLS(DATA_PATH, split="train")
ID = 0
assert 0 <= ID <= 300
image, label = dataset[ID]
visualize(image, label)
```
We train our model with `resnet34` backbone for **50 epochs** and obtains about **99%** test accuracy, f1-score, precision and recall as follows
```
%%time
import logging
from os import path as osp
from sagemaker.pytorch import PyTorch
NUM_CLASSES = 6
BACKBONE = "resnet34"
assert BACKBONE in [
"resnet34",
"resnet50",
], "either resnet34 or resnet50. Make sure to be consistent with model_fn in classifier.py"
EPOCHS = 50
SEED = 123
hyperparameters = {
"backbone": BACKBONE,
"num-classes": NUM_CLASSES,
"epochs": EPOCHS,
"seed": SEED,
}
assert not isinstance(sagemaker_session, sagemaker.LocalSession), "local session as share memory cannot be altered"
model = PyTorch(
entry_point="classifier.py",
source_dir=osp.join(sources, "source_dir.tar.gz"),
role=role,
train_instance_count=1,
train_instance_type="ml.g4dn.2xlarge",
hyperparameters=hyperparameters,
py_version="py3",
framework_version="1.5",
sagemaker_session=sagemaker_session, # Note: Do not use local session as share memory cannot be altered
output_path=train_output,
checkpoint_s3_uri=s3_checkpoint,
checkpoint_local_path=sm_local_checkpoint_dir,
# container_log_level=logging.DEBUG,
)
model.fit(neu_cls_prepared_s3)
```
Then, we deploy our model which takes about **8 minutes** to complete
```
%%time
predictor = model.deploy(
initial_instance_count=1,
instance_type="ml.m5.xlarge",
endpoint_name=sagemaker_config["SolutionPrefix"] + "-classification-endpoint",
)
```
## Inference
We are ready to test our model by providing some test data and compare the actual labels with the predicted one
```
from sagemaker_defect_detection import get_transform
from sagemaker_defect_detection.utils.visualize import unnormalize_to_hwc
ID = 100
assert 0 <= ID <= 300
test_dataset = NEUCLS(DATA_PATH, split="test", transform=get_transform("test"), seed=SEED)
image, label = test_dataset[ID]
outputs = predictor.predict(image.unsqueeze(0).numpy())
_, predicted = torch.max(torch.from_numpy(np.array(outputs)), 1)
image_unnorm = unnormalize_to_hwc(image)
visualize(image_unnorm, label, predicted.item())
```
## Optional: Delete the endpoint and model
When you are done with the endpoint, you should clean it up.
All of the training jobs, models and endpoints we created can be viewed through the SageMaker console of your AWS account.
```
predictor.delete_model()
predictor.delete_endpoint()
```
|
github_jupyter
|
import json
import numpy as np
import sagemaker
from sagemaker.s3 import S3Downloader
sagemaker_session = sagemaker.Session()
sagemaker_config = json.load(open("../stack_outputs.json"))
role = sagemaker_config["IamRole"]
solution_bucket = sagemaker_config["SolutionS3Bucket"]
region = sagemaker_config["AWSRegion"]
solution_name = sagemaker_config["SolutionName"]
bucket = sagemaker_config["S3Bucket"]
from sagemaker.s3 import S3Downloader
original_bucket = f"s3://{solution_bucket}-{region}/{solution_name}"
original_data = f"{original_bucket}/data/NEU-CLS.zip"
original_sources = f"{original_bucket}/build/lib/source_dir.tar.gz"
print("original data: ")
S3Downloader.list(original_data)
%%time
RAW_DATA_PATH= !echo $PWD/raw_neu_cls
RAW_DATA_PATH = RAW_DATA_PATH.n
DATA_PATH = !echo $PWD/neu_cls
DATA_PATH = DATA_PATH.n
!mkdir -p $RAW_DATA_PATH
!aws s3 cp $original_data $RAW_DATA_PATH
!mkdir -p $DATA_PATH
!python ../src/prepare_data/neu.py $RAW_DATA_PATH/NEU-CLS.zip $DATA_PATH
prefix = "neu-cls"
neu_cls_s3 = f"s3://{bucket}/{prefix}"
sources = f"{neu_cls_s3}/code/"
train_output = f"{neu_cls_s3}/output/"
neu_cls_prepared_s3 = f"{neu_cls_s3}/data/"
!aws s3 sync $DATA_PATH $neu_cls_prepared_s3 --quiet # remove the --quiet flag to view sync outputs
s3_checkpoint = f"{neu_cls_s3}/checkpoint/"
sm_local_checkpoint_dir = "/opt/ml/checkpoints/"
!aws s3 cp $original_sources $sources
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import torch
from PIL import Image
from torch.utils.data import DataLoader
try:
import sagemaker_defect_detection
except ImportError:
import sys
from pathlib import Path
ROOT = Path("../src").resolve()
sys.path.insert(0, str(ROOT))
from sagemaker_defect_detection import NEUCLS
def visualize(image, label, predicted=None):
if not isinstance(image, Image.Image):
image = Image.fromarray(image)
plt.figure(dpi=120)
if predicted is not None:
plt.title(f"label: {label}, prediction: {predicted}")
else:
plt.title(f"label: {label}")
plt.axis("off")
plt.imshow(image)
return
dataset = NEUCLS(DATA_PATH, split="train")
ID = 0
assert 0 <= ID <= 300
image, label = dataset[ID]
visualize(image, label)
%%time
import logging
from os import path as osp
from sagemaker.pytorch import PyTorch
NUM_CLASSES = 6
BACKBONE = "resnet34"
assert BACKBONE in [
"resnet34",
"resnet50",
], "either resnet34 or resnet50. Make sure to be consistent with model_fn in classifier.py"
EPOCHS = 50
SEED = 123
hyperparameters = {
"backbone": BACKBONE,
"num-classes": NUM_CLASSES,
"epochs": EPOCHS,
"seed": SEED,
}
assert not isinstance(sagemaker_session, sagemaker.LocalSession), "local session as share memory cannot be altered"
model = PyTorch(
entry_point="classifier.py",
source_dir=osp.join(sources, "source_dir.tar.gz"),
role=role,
train_instance_count=1,
train_instance_type="ml.g4dn.2xlarge",
hyperparameters=hyperparameters,
py_version="py3",
framework_version="1.5",
sagemaker_session=sagemaker_session, # Note: Do not use local session as share memory cannot be altered
output_path=train_output,
checkpoint_s3_uri=s3_checkpoint,
checkpoint_local_path=sm_local_checkpoint_dir,
# container_log_level=logging.DEBUG,
)
model.fit(neu_cls_prepared_s3)
%%time
predictor = model.deploy(
initial_instance_count=1,
instance_type="ml.m5.xlarge",
endpoint_name=sagemaker_config["SolutionPrefix"] + "-classification-endpoint",
)
from sagemaker_defect_detection import get_transform
from sagemaker_defect_detection.utils.visualize import unnormalize_to_hwc
ID = 100
assert 0 <= ID <= 300
test_dataset = NEUCLS(DATA_PATH, split="test", transform=get_transform("test"), seed=SEED)
image, label = test_dataset[ID]
outputs = predictor.predict(image.unsqueeze(0).numpy())
_, predicted = torch.max(torch.from_numpy(np.array(outputs)), 1)
image_unnorm = unnormalize_to_hwc(image)
visualize(image_unnorm, label, predicted.item())
predictor.delete_model()
predictor.delete_endpoint()
| 0.340485 | 0.750233 |
## Unit 5 | Assignment - The Power of Plots
## Background
What good is data without a good plot to tell the story?
So, let's take what you've learned about Python Matplotlib and apply it to some real-world situations. For this assignment, you'll need to complete **1 of 2** Data Challenges. As always, it's your choice which you complete. _Perhaps_, choose the one most relevant to your future career.
## Option 1: Pyber
The ride sharing bonanza continues! Seeing the success of notable players like Uber and Lyft, you've decided to join a fledgling ride sharing company of your own. In your latest capacity, you'll be acting as Chief Data Strategist for the company. In this role, you'll be expected to offer data-backed guidance on new opportunities for market differentiation.
You've since been given access to the company's complete recordset of rides. This contains information about every active driver and historic ride, including details like city, driver count, individual fares, and city type.
Your objective is to build a [Bubble Plot](https://en.wikipedia.org/wiki/Bubble_chart) that showcases the relationship between four key variables:
* Average Fare ($) Per City
* Total Number of Rides Per City
* Total Number of Drivers Per City
* City Type (Urban, Suburban, Rural)
In addition, you will be expected to produce the following three pie charts:
* % of Total Fares by City Type
* % of Total Rides by City Type
* % of Total Drivers by City Type
As final considerations:
* You must use the Pandas Library and the Jupyter Notebook.
* You must use the Matplotlib and Seaborn libraries.
* You must include a written description of three observable trends based on the data.
* You must use proper labeling of your plots, including aspects like: Plot Titles, Axes Labels, Legend Labels, Wedge Percentages, and Wedge Labels.
* Remember when making your plots to consider aesthetics!
* You must stick to the Pyber color scheme (Gold, Light Sky Blue, and Light Coral) in producing your plot and pie charts.
* When making your Bubble Plot, experiment with effects like `alpha`, `edgecolor`, and `linewidths`.
* When making your Pie Chart, experiment with effects like `shadow`, `startangle`, and `explosion`.
* You must include an exported markdown version of your Notebook called `README.md` in your GitHub repository.
* See [Example Solution](Pyber/Pyber_Example.pdf) for a reference on expected format.
Observations:
1. There number of riders impacts the fare, the more riders around, the cheaper the fair
2. The numbers of riders changes based on city type -- Urban cities have the most riders, followed by suburban cities, and lastly, rural cities.
3. There seems to be no relationship between number of drivers and city types. There are Urban cities with not many drivers, and rural cities, with many drivers. It seems to be completely unique to each city.
```
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import colors
ride_path = "raw_data/ride_data.csv"
city_path = "raw_data/city_data.csv"
rides = pd.read_csv(ride_path)
cities = pd.read_csv(city_path)
#print(rides.head())
#cities.head()
data = pd.merge(cities, rides, how="outer")
#data.head()
#data.count()
means = data.groupby("city").mean()
means.head()
sums = data.groupby("city").sum()
sums.head()
counts = data.groupby("city").count()
#counts["driver_count"].head()
# Create unique dfs for each city type
urban = data.loc[data["type"] == "Urban"]
suburbs = data.loc[data["type"] == "Suburban"]
rural = data.loc[data["type"] == "Rural"]
a = .65
ec = "white"
# plot each unique city type separately
plt.scatter(urban.groupby("city").count()["fare"],
urban.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Urban",
color = "gold")
plt.scatter(suburbs.groupby("city").count()["fare"],
suburbs.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Surburban",
color = "cyan")
plt.scatter(rural.groupby("city").count()["fare"],
rural.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Rural",
color = "coral")
plt.style.use("dark_background")
#plt.scatter(counts["driver_count"],means["fare"],s = counts["driver_count"])
plt.title("Pyber Ride Sharing Data (2016)")
plt.xlabel("Total Number of Rides")
plt.ylabel("Mean Fare ($)")
plt.legend(title = "City Type")
plt.xlim(0,40)
plt.show()
## Circle Size Represents number of drivers in City
## xlim setting eliminates single city outside of range
fare_urban = urban["fare"].sum()
fare_sub = suburbs["fare"].sum()
fare_rural = rural["fare"].sum()
fares = [fare_urban,
fare_rural,
fare_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels1 = "Urban","Rural","Suburban"
plt.pie(fares, labels = labels1, explode = explode, colors=colors, startangle = 90, autopct="%.0f%%")
plt.title("% of Total Fares by City Type")
plt.show()
rides_urban = urban["fare"].count()
rides_sub = suburbs["fare"].count()
rides_rural = rural["fare"].count()
rides = [rides_urban,
rides_rural,
rides_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels2 = "Urban","Rural","Suburban"
plt.pie(rides, labels = labels2, explode = explode, colors = colors, startangle = 90, autopct="%.0f%%,")
plt.title("% of Total Rides by City Type")
plt.show()
drivers_urban = urban["driver_count"].sum()
drivers_sub = suburbs["driver_count"].sum()
drivers_rural = rural["driver_count"].sum()
drivers = [drivers_urban,
drivers_rural,
drivers_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels3 = "Urban","Rural","Suburban"
plt.pie(rides, labels = labels3, explode = explode , colors = colors, startangle = 90, autopct="%.0f%%")
plt.title("% of Total Drivers by City Type")
plt.show()
```
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import colors
ride_path = "raw_data/ride_data.csv"
city_path = "raw_data/city_data.csv"
rides = pd.read_csv(ride_path)
cities = pd.read_csv(city_path)
#print(rides.head())
#cities.head()
data = pd.merge(cities, rides, how="outer")
#data.head()
#data.count()
means = data.groupby("city").mean()
means.head()
sums = data.groupby("city").sum()
sums.head()
counts = data.groupby("city").count()
#counts["driver_count"].head()
# Create unique dfs for each city type
urban = data.loc[data["type"] == "Urban"]
suburbs = data.loc[data["type"] == "Suburban"]
rural = data.loc[data["type"] == "Rural"]
a = .65
ec = "white"
# plot each unique city type separately
plt.scatter(urban.groupby("city").count()["fare"],
urban.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Urban",
color = "gold")
plt.scatter(suburbs.groupby("city").count()["fare"],
suburbs.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Surburban",
color = "cyan")
plt.scatter(rural.groupby("city").count()["fare"],
rural.groupby("city").mean()["fare"],
s = counts["driver_count"]*3,
alpha = a,
edgecolor = ec,
label = "Rural",
color = "coral")
plt.style.use("dark_background")
#plt.scatter(counts["driver_count"],means["fare"],s = counts["driver_count"])
plt.title("Pyber Ride Sharing Data (2016)")
plt.xlabel("Total Number of Rides")
plt.ylabel("Mean Fare ($)")
plt.legend(title = "City Type")
plt.xlim(0,40)
plt.show()
## Circle Size Represents number of drivers in City
## xlim setting eliminates single city outside of range
fare_urban = urban["fare"].sum()
fare_sub = suburbs["fare"].sum()
fare_rural = rural["fare"].sum()
fares = [fare_urban,
fare_rural,
fare_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels1 = "Urban","Rural","Suburban"
plt.pie(fares, labels = labels1, explode = explode, colors=colors, startangle = 90, autopct="%.0f%%")
plt.title("% of Total Fares by City Type")
plt.show()
rides_urban = urban["fare"].count()
rides_sub = suburbs["fare"].count()
rides_rural = rural["fare"].count()
rides = [rides_urban,
rides_rural,
rides_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels2 = "Urban","Rural","Suburban"
plt.pie(rides, labels = labels2, explode = explode, colors = colors, startangle = 90, autopct="%.0f%%,")
plt.title("% of Total Rides by City Type")
plt.show()
drivers_urban = urban["driver_count"].sum()
drivers_sub = suburbs["driver_count"].sum()
drivers_rural = rural["driver_count"].sum()
drivers = [drivers_urban,
drivers_rural,
drivers_sub]
explode = (0, .08, .08)
colors = ["gold","coral","cyan"]
labels3 = "Urban","Rural","Suburban"
plt.pie(rides, labels = labels3, explode = explode , colors = colors, startangle = 90, autopct="%.0f%%")
plt.title("% of Total Drivers by City Type")
plt.show()
| 0.291283 | 0.906446 |
## Capstone Project 1 Proposal: Supplier Pricing Prediction
### Project Scope:
Caterpillar (construction equipment manufacturer) relies on a variety of suppliers to manufacture tube assemblies for their equipment. These assemblies are required in their equipment to lift, load and transport heavy construction loads. We are provided with detailed tube, component, and annual volume datasets. Our goal is to build and train a model that can predict how much a supplier will quote for a given tube assembly based on given supplier pricing.
```
#load libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import glob as gl
from functools import reduce # ask about this library
import warnings
warnings.filterwarnings('ignore')
# Read multiple files together and concatinating all fileds in to one file: Approach 1
csv_files = gl.glob('*.csv')
print('Number of Files:','\n',len(csv_files),'\n''Filenames:','\n', csv_files)
df_data= []
for csv_file in csv_files:
df = pd.read_csv(csv_file)
df_data.append(df)
df_full= pd.concat(df_data)
df_full.info()
#head of BOM table
df_data[8].head()
df_bom_t.iloc[0:, 3:].head()
#Melting BOM table
df_bom = df_data[8]
df_bom_melt= df_bom.melt(id_vars='tube_assembly_id',value_vars = ['component_id_1', 'component_id_2','component_id_3','component_id_4','component_id_5','component_id_6','component_id_7','component_id_8'],value_name= 'component_id')
df_bom_t = (df_bom_melt.merge(df_bom, how = 'inner', on = 'tube_assembly_id')).drop(columns= ['component_id_1', 'component_id_2','component_id_3','component_id_4','component_id_5','component_id_6','component_id_7','component_id_8'])
df_bom_t.head()
#df_bom_t.dropna(axis= 'columns', how = 'all')
#(df_bom_t[df_bom_t[3:].isnull()== True]).dropna(how = 'all' ,axis = 'columns')
df_bom_t.iloc[0:, 3:].notnull().sum().plot(kind='bar')
```
### Join datasets using Primary Key: Tube_Assembly_Id
```
#load dataset for Tube (df_t), Bill of Material(df_b), Specs (df_s) and set tube_assembly_id as index
df_t = pd.read_csv('tube.csv', index_col='tube_assembly_id')
df_b = pd.read_csv('bill_of_materials.csv', index_col='tube_assembly_id')
df_s = pd.read_csv('specs.csv', index_col='tube_assembly_id')
df_tr= pd.read_csv('train_set.csv', index_col='tube_assembly_id', parse_dates=True)
#Join loaded datasets along common index tube_assembly_id using left join.
df_tb = df_t.join(other = df_b, on ='tube_assembly_id', how='left')
df_tbs = df_tb.join(other = df_s, on ='tube_assembly_id', how= 'left')
df_primary = df_tbs.join(other = df_tr, on ='tube_assembly_id', how= 'left')
df_primary.head()
column = df_primary.columns.drop('cost')
df_primary_pivot = df_primary.pivot_table(index= 'tube_assembly_id',
columns = ['material_id'],
values= ['cost'],
aggfunc='mean')
df_primary_pivot=df_primary_pivot.transpose()
df_primary_pivot
```
## Join datasets using Secondary Key: Component_Id
```
#load component tables and join along seconday key component_id
tables = ['components.csv',
'comp_adaptor.csv',
'comp_boss.csv',
'comp_elbow.csv',
'comp_float.csv',
'comp_hfl.csv',
'comp_nut.csv',
'comp_other.csv',
'comp_sleeve.csv',
'comp_straight.csv',
'comp_tee.csv',
'comp_threaded.csv']
df_comps = [pd.read_csv(table, index_col='component_id') for table in tables]
#code idea from stackoverflow
#df_0_11= df_comps[0].join(df_comps[1:], on='component_id', how = 'left').....class type error
#df_comps= reduce(lambda left,right: pd.merge(left,right,on='component_id'), tables)
#Join various component types along common index component_id using left join.
df_0_1= df_comps[0].merge(df_comps[1], on = 'component_id', how = 'left')
df_0_2 = df_0_1.merge(df_comps[2], on = 'component_id', how = 'left')
df_0_3 = df_0_2.merge(df_comps[3], on = 'component_id', how = 'left')
df_0_4 = df_0_3.merge(df_comps[4], on = 'component_id', how = 'left')
df_0_5 = df_0_4.merge(df_comps[5], on = 'component_id', how = 'left')
df_0_6 = df_0_5.merge(df_comps[6], on = 'component_id', how = 'left')
df_0_7 = df_0_6.merge(df_comps[7], on = 'component_id', how = 'left')
df_0_8 = df_0_7.merge(df_comps[8], on = 'component_id', how = 'left')
df_0_9 = df_0_8.merge(df_comps[9], on = 'component_id', how = 'left')
df_0_10 = df_0_9.merge(df_comps[10], on = 'component_id', how = 'left')
df_0_11 = df_0_10.merge(df_comps[11], on = 'component_id', how = 'left')
df_comps[1].head()
# Load component types and map component, connection and end types of the tube assembly
df_comp_type = pd.read_csv('type_component.csv', index_col='component_type_id')
df_connection_type = pd.read_csv('type_connection.csv', index_col='connection_type_id')
df_end_type = pd.read_csv('type_end_form.csv', index_col='end_form_id')
df_test=df_0_11.merge(df_comp_type, on ='component_type_id', how = 'left')
df_0_11.reset_index().head().columns
df_0_11.head()
df_comps[1].head()
```
|
github_jupyter
|
#load libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import glob as gl
from functools import reduce # ask about this library
import warnings
warnings.filterwarnings('ignore')
# Read multiple files together and concatinating all fileds in to one file: Approach 1
csv_files = gl.glob('*.csv')
print('Number of Files:','\n',len(csv_files),'\n''Filenames:','\n', csv_files)
df_data= []
for csv_file in csv_files:
df = pd.read_csv(csv_file)
df_data.append(df)
df_full= pd.concat(df_data)
df_full.info()
#head of BOM table
df_data[8].head()
df_bom_t.iloc[0:, 3:].head()
#Melting BOM table
df_bom = df_data[8]
df_bom_melt= df_bom.melt(id_vars='tube_assembly_id',value_vars = ['component_id_1', 'component_id_2','component_id_3','component_id_4','component_id_5','component_id_6','component_id_7','component_id_8'],value_name= 'component_id')
df_bom_t = (df_bom_melt.merge(df_bom, how = 'inner', on = 'tube_assembly_id')).drop(columns= ['component_id_1', 'component_id_2','component_id_3','component_id_4','component_id_5','component_id_6','component_id_7','component_id_8'])
df_bom_t.head()
#df_bom_t.dropna(axis= 'columns', how = 'all')
#(df_bom_t[df_bom_t[3:].isnull()== True]).dropna(how = 'all' ,axis = 'columns')
df_bom_t.iloc[0:, 3:].notnull().sum().plot(kind='bar')
#load dataset for Tube (df_t), Bill of Material(df_b), Specs (df_s) and set tube_assembly_id as index
df_t = pd.read_csv('tube.csv', index_col='tube_assembly_id')
df_b = pd.read_csv('bill_of_materials.csv', index_col='tube_assembly_id')
df_s = pd.read_csv('specs.csv', index_col='tube_assembly_id')
df_tr= pd.read_csv('train_set.csv', index_col='tube_assembly_id', parse_dates=True)
#Join loaded datasets along common index tube_assembly_id using left join.
df_tb = df_t.join(other = df_b, on ='tube_assembly_id', how='left')
df_tbs = df_tb.join(other = df_s, on ='tube_assembly_id', how= 'left')
df_primary = df_tbs.join(other = df_tr, on ='tube_assembly_id', how= 'left')
df_primary.head()
column = df_primary.columns.drop('cost')
df_primary_pivot = df_primary.pivot_table(index= 'tube_assembly_id',
columns = ['material_id'],
values= ['cost'],
aggfunc='mean')
df_primary_pivot=df_primary_pivot.transpose()
df_primary_pivot
#load component tables and join along seconday key component_id
tables = ['components.csv',
'comp_adaptor.csv',
'comp_boss.csv',
'comp_elbow.csv',
'comp_float.csv',
'comp_hfl.csv',
'comp_nut.csv',
'comp_other.csv',
'comp_sleeve.csv',
'comp_straight.csv',
'comp_tee.csv',
'comp_threaded.csv']
df_comps = [pd.read_csv(table, index_col='component_id') for table in tables]
#code idea from stackoverflow
#df_0_11= df_comps[0].join(df_comps[1:], on='component_id', how = 'left').....class type error
#df_comps= reduce(lambda left,right: pd.merge(left,right,on='component_id'), tables)
#Join various component types along common index component_id using left join.
df_0_1= df_comps[0].merge(df_comps[1], on = 'component_id', how = 'left')
df_0_2 = df_0_1.merge(df_comps[2], on = 'component_id', how = 'left')
df_0_3 = df_0_2.merge(df_comps[3], on = 'component_id', how = 'left')
df_0_4 = df_0_3.merge(df_comps[4], on = 'component_id', how = 'left')
df_0_5 = df_0_4.merge(df_comps[5], on = 'component_id', how = 'left')
df_0_6 = df_0_5.merge(df_comps[6], on = 'component_id', how = 'left')
df_0_7 = df_0_6.merge(df_comps[7], on = 'component_id', how = 'left')
df_0_8 = df_0_7.merge(df_comps[8], on = 'component_id', how = 'left')
df_0_9 = df_0_8.merge(df_comps[9], on = 'component_id', how = 'left')
df_0_10 = df_0_9.merge(df_comps[10], on = 'component_id', how = 'left')
df_0_11 = df_0_10.merge(df_comps[11], on = 'component_id', how = 'left')
df_comps[1].head()
# Load component types and map component, connection and end types of the tube assembly
df_comp_type = pd.read_csv('type_component.csv', index_col='component_type_id')
df_connection_type = pd.read_csv('type_connection.csv', index_col='connection_type_id')
df_end_type = pd.read_csv('type_end_form.csv', index_col='end_form_id')
df_test=df_0_11.merge(df_comp_type, on ='component_type_id', how = 'left')
df_0_11.reset_index().head().columns
df_0_11.head()
df_comps[1].head()
| 0.340814 | 0.799794 |
## **Association Analysis - Sequential Pattern Mining (SPM)**
### 1. Introduction and algorithm description
- This notebook uses the real time itemset dataset to demonstrate the association rule mining algorithms below which are provided by the hana_ml.<br>
<br>
- **SPM(Sequential Pattern Mining)**
The sequential pattern mining algorithm searches for frequent patterns in sequence databases. A sequence database consists of ordered elements or events. For example, a customer first buys bread, then eggs and cheese, and then milk. This forms a sequence consisting of three ordered events. We consider an event or a subsequent event is frequent if its support, which is the number of sequences that contain this event or subsequence, is greater than a certain value. This algorithm finds patterns in input sequences satisfying user defined minimum support.
**Understand Sequence Pattern Mining before going into practice**<br>
- T1: Find all subsets of items that occur with a specific sequence in all other transactions:
e.g {Playing cricket -> high ECG -> Sweating}
- T2: Find all rules that correlate the order of one set of items after that another set of items in the transaction database:
e.g 72% of users who perform a web search then make a long eye gaze
over the ads follow that by a successful add-click
**Prerequisites**<br>
โ The input data does not contain null value.<br>
โ There are no duplicated items in each transaction<br>
### **Setup Connection**
```
url, port, user, pwd = Settings.load_config("../config/e2edata.ini")
# the connection
#print(url , port , user , pwd)
connection_context = dataframe.ConnectionContext(url, port, user, pwd)
print(connection_context.connection.isconnected())
```
### **Load Data for SPM**
<br>
Check if the table already exist in your schema
Select * from PAL_SPM_DATA_TBL <br>
## Dataset
we will analyze the store data for frequent pattern mining ,this is the sample data which is available on SAP's help webpage.
- **Attribute Information**<br>
CUSTID - Customer ID <br>
TRANSID - Transaction ID <BR>
ITEMS - Item of Transaction
### **Import Packages**
First, import packages needed in the data loading.
```
from hana_ml import dataframe
from data_load_utils import DataSets, Settings
```
## **Setup Connection**
In our case, the data is loaded into a table called "PAL_APRIORI_TRANS_TBL" in HANA from a csv file "apriori_item_data.csv". To do that, a connection to HANA is created and then passed to the data loader. To create a such connection, a config file, config/e2edata.ini is used to control the connection parameters. A sample section in the config file is shown below which includes HANA url, port, user and password information.<br>
<br>
###################<br>
[hana]<br>
url=host-url<br>
user=username<br>
passwd=userpassword<br>
port=3xx15<br>
<br>
###################<br>
```
url, port, user, pwd = Settings.load_config("../config/e2edata.ini")
# the connection
#print(url , port , user , pwd)
connection_context = dataframe.ConnectionContext(url, port, user, pwd)
print(connection_context.connection.isconnected())
```
**Load Data**<br>
Then, the function DataSets.load_spm_data() is used to decide load or reload the data from scratch. If it is the first time to load data, an exmaple of return message is shown below:
ERROR:hana_ml.dataframe:Failed to get row count for the current Dataframe, (259, 'invalid table name: Could not find table/view<BR>
PAL_SPM_DATA_TBL in schema DM_PAL: line 1 col 37 (at pos 36)')<br>
Table PAL_SPM_DATA_TBL doesn't exist in schema DM_PAL<br>
Creating table PAL_SPM_DATA_TBL in schema DM_PAL ....<br>
Drop unsuccessful<br>
Creating table DM_PAL.PAL_SPM_DATA_TBL<br>
Data Loaded:100%<br>
#####################<br>
```
data_tbl = DataSets.load_spm_data(connection_context)
```
**if data is already loaded into HANA**
```
data_tbl = DataSets.load_spm_data(connection_context)
print("Table Name is: " +str(data_tbl))
import pandas as pd
```
#### Create dataframes using Pandas Dataframes for data load from SAP HANA
```
##Create a dataframe df from PAL_SPM_TRANS_TBL for the following steps.
df_spm = pd.DataFrame(columns=['CUSTID' , 'TRANSID' , 'ITEMS'])
df_spm = dataframe.create_dataframe_from_pandas(connection_context=connection_context, pandas_df=df_spm, table_name=data_tbl, force=False, replace=True)
data_tbl = DataSets.load_spm_data(connection_context)
print("Table Name is: " +str(data_tbl))
df = df_spm
df.collect().head(100) ##Display Data
df.dropna() ##Drop NAN if any of the blank record is present in your dataset
print("Toal Number of Records : " + str(df.count()))
print("Columns:")
df.columns
```
## **Filter**
```
df.filter("CUSTID = 'A'").head(10).collect()
df.filter('TRANSID = 1').head(100).collect()
df.filter("ITEMS = 'Apple'").head(10).collect()
```
### **Group by column**
```
df.agg([('count' , 'ITEMS' , 'TOTAL TRANSACTIONS')] , group_by='ITEMS').head(100).collect()
df.agg([('count' , 'CUSTID', 'TOTAL TRANSACTIONS')] , group_by='CUSTID').head(100).collect()
df.agg([('count' , 'TRANSID', 'TOTAL TRANSACTIONS')] , group_by='TRANSID').head(100).collect()
```
**Display the most popular items**
```
import matplotlib.pyplot as plt
from wordcloud import WordCloud
plt.rcParams['figure.figsize'] = (10, 10)
wordcloud = WordCloud(background_color = 'white', width = 500, height = 500, max_words = 120).generate(str(df_spm.head(100).collect()))
plt.imshow(wordcloud)
plt.axis('off')
plt.title('Most Popular Items',fontsize = 10)
plt.show()
```
### Import SPM Method from HANA ML Library
```
df.filter("ITEMS = 'Blueberry'").head(100).count()
from hana_ml.algorithms.pal.association import SPM
```
### **Setup SPM instance**
```
sp = SPM(conn_context=connection_context,
min_support=0.5,
relational=False,
ubiquitous=1.0,
max_len=10,
min_len=1,
calc_lift=True)
sp.fit(data=df_spm, customer='CUSTID', transaction='TRANSID', item='ITEMS')
```
**Result Analysis**:<br>
- Itemset Apple has support 1.0 indicates the frequencey of the item in all the transactions , most frequent item - confidence & lift is 0 for all the single items which states there is no antecedent & consequent item of them
- Consider (Apple , Blueberry): Support is .88 (Frequeny of these items together is 88%) , Confidence is 88% means if someone is buying Apple then 88% chances they will also have blueberry in theri bucket , lif is .89 close to 1 indicates high Asscoiation of items
- Benefit of having such kind of result is Storekeepers can easily look into purchasing Trends for their Shops
```
sp.result_.collect()
```
**Attributes**
**result_**
(DataFrame) The overall fequent pattern mining result, structured as follows: - 1st column : mined fequent patterns, - 2nd column : support values, - 3rd column : confidence values, - 4th column : lift values. Available only when relational is False.
**pattern_**
(DataFrame) Result for mined requent patterns, structured as follows: - 1st column : pattern ID, - 2nd column : transaction ID, - 3rd column : items.
**stats_**
(DataFrame) Statistics for frequent pattern mining, structured as follows: - 1st column : pattern ID, - 2nd column : support values, - 3rd column : confidence values, - 4th column : lift values.
|
github_jupyter
|
url, port, user, pwd = Settings.load_config("../config/e2edata.ini")
# the connection
#print(url , port , user , pwd)
connection_context = dataframe.ConnectionContext(url, port, user, pwd)
print(connection_context.connection.isconnected())
from hana_ml import dataframe
from data_load_utils import DataSets, Settings
url, port, user, pwd = Settings.load_config("../config/e2edata.ini")
# the connection
#print(url , port , user , pwd)
connection_context = dataframe.ConnectionContext(url, port, user, pwd)
print(connection_context.connection.isconnected())
data_tbl = DataSets.load_spm_data(connection_context)
data_tbl = DataSets.load_spm_data(connection_context)
print("Table Name is: " +str(data_tbl))
import pandas as pd
##Create a dataframe df from PAL_SPM_TRANS_TBL for the following steps.
df_spm = pd.DataFrame(columns=['CUSTID' , 'TRANSID' , 'ITEMS'])
df_spm = dataframe.create_dataframe_from_pandas(connection_context=connection_context, pandas_df=df_spm, table_name=data_tbl, force=False, replace=True)
data_tbl = DataSets.load_spm_data(connection_context)
print("Table Name is: " +str(data_tbl))
df = df_spm
df.collect().head(100) ##Display Data
df.dropna() ##Drop NAN if any of the blank record is present in your dataset
print("Toal Number of Records : " + str(df.count()))
print("Columns:")
df.columns
df.filter("CUSTID = 'A'").head(10).collect()
df.filter('TRANSID = 1').head(100).collect()
df.filter("ITEMS = 'Apple'").head(10).collect()
df.agg([('count' , 'ITEMS' , 'TOTAL TRANSACTIONS')] , group_by='ITEMS').head(100).collect()
df.agg([('count' , 'CUSTID', 'TOTAL TRANSACTIONS')] , group_by='CUSTID').head(100).collect()
df.agg([('count' , 'TRANSID', 'TOTAL TRANSACTIONS')] , group_by='TRANSID').head(100).collect()
import matplotlib.pyplot as plt
from wordcloud import WordCloud
plt.rcParams['figure.figsize'] = (10, 10)
wordcloud = WordCloud(background_color = 'white', width = 500, height = 500, max_words = 120).generate(str(df_spm.head(100).collect()))
plt.imshow(wordcloud)
plt.axis('off')
plt.title('Most Popular Items',fontsize = 10)
plt.show()
df.filter("ITEMS = 'Blueberry'").head(100).count()
from hana_ml.algorithms.pal.association import SPM
sp = SPM(conn_context=connection_context,
min_support=0.5,
relational=False,
ubiquitous=1.0,
max_len=10,
min_len=1,
calc_lift=True)
sp.fit(data=df_spm, customer='CUSTID', transaction='TRANSID', item='ITEMS')
sp.result_.collect()
| 0.159938 | 0.924959 |
```
import os
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
%matplotlib inline /* required to execute hist() in jupyter*/
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20, 15))
plt.show()
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train + ", len(test_set), "test")
import hashlib
def test_set_check(identifiler, test_ratio, hash):
return hash(np.int64(identifiler)).digest()[-1] < 256 * test_ratio
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
test_set.head()
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace = True)
housing["income_cat"].hist()
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set["income_cat"].value_counts() / len(strat_test_set)
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)
housing = strat_train_set.copy()
housing.plot(kind="scatter", x="longitude", y="latitude")
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100, label="population", figsize=(10, 7), c="median_house_value", cmap= plt.get_cmap("jet"), colorbar=True,)
plt.legend()
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
from pandas.tools.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
```
|
github_jupyter
|
import os
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
%matplotlib inline /* required to execute hist() in jupyter*/
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20, 15))
plt.show()
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set), "train + ", len(test_set), "test")
import hashlib
def test_set_check(identifiler, test_ratio, hash):
return hash(np.int64(identifiler)).digest()[-1] < 256 * test_ratio
def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
test_set.head()
housing["income_cat"] = np.ceil(housing["median_income"] / 1.5)
housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace = True)
housing["income_cat"].hist()
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set["income_cat"].value_counts() / len(strat_test_set)
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)
housing = strat_train_set.copy()
housing.plot(kind="scatter", x="longitude", y="latitude")
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100, label="population", figsize=(10, 7), c="median_house_value", cmap= plt.get_cmap("jet"), colorbar=True,)
plt.legend()
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
from pandas.tools.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
| 0.373304 | 0.428473 |
# Read in the data
```
import pandas as pd
import numpy
import re
data_files = [
"ap_2010.csv",
"class_size.csv",
"demographics.csv",
"graduation.csv",
"hs_directory.csv",
"sat_results.csv"
]
data = {}
for f in data_files:
d = pd.read_csv("schools/{0}".format(f))
data[f.replace(".csv", "")] = d
```
# Read in the surveys
```
all_survey = pd.read_csv("schools/survey_all.txt", delimiter="\t", encoding='windows-1252')
d75_survey = pd.read_csv("schools/survey_d75.txt", delimiter="\t", encoding='windows-1252')
survey = pd.concat([all_survey, d75_survey], axis=0)
survey["DBN"] = survey["dbn"]
survey_fields = [
"DBN",
"rr_s",
"rr_t",
"rr_p",
"N_s",
"N_t",
"N_p",
"saf_p_11",
"com_p_11",
"eng_p_11",
"aca_p_11",
"saf_t_11",
"com_t_11",
"eng_t_11",
"aca_t_11",
"saf_s_11",
"com_s_11",
"eng_s_11",
"aca_s_11",
"saf_tot_11",
"com_tot_11",
"eng_tot_11",
"aca_tot_11",
]
survey = survey.loc[:,survey_fields]
data["survey"] = survey
```
# Add DBN columns
```
pd.show_versions()
data["hs_directory"]["DBN"] = data["hs_directory"]["dbn"]
def pad_csd(num):
string_representation = str(num)
if len(string_representation) > 1:
return string_representation
else:
return "0" + string_representation
data["class_size"]["padded_csd"] = data["class_size"]["CSD"].apply(pad_csd)
data["class_size"]["DBN"] = data["class_size"]["padded_csd"] + data["class_size"]["SCHOOL CODE"]
```
# Convert columns to numeric
```
cols = ['SAT Math Avg. Score', 'SAT Critical Reading Avg. Score', 'SAT Writing Avg. Score']
for c in cols:
data["sat_results"][c] = pd.to_numeric(data["sat_results"][c], errors="coerce")
data['sat_results']['sat_score'] = data['sat_results'][cols[0]] + data['sat_results'][cols[1]] + data['sat_results'][cols[2]]
def find_lat(loc):
coords = re.findall("\(.+, .+\)", loc)
lat = coords[0].split(",")[0].replace("(", "")
return lat
def find_lon(loc):
coords = re.findall("\(.+, .+\)", loc)
lon = coords[0].split(",")[1].replace(")", "").strip()
return lon
data["hs_directory"]["lat"] = data["hs_directory"]["Location 1"].apply(find_lat)
data["hs_directory"]["lon"] = data["hs_directory"]["Location 1"].apply(find_lon)
data["hs_directory"]["lat"] = pd.to_numeric(data["hs_directory"]["lat"], errors="coerce")
data["hs_directory"]["lon"] = pd.to_numeric(data["hs_directory"]["lon"], errors="coerce")
```
# Condense datasets
```
class_size = data["class_size"]
class_size = class_size[class_size["GRADE "] == "09-12"]
class_size = class_size[class_size["PROGRAM TYPE"] == "GEN ED"]
class_size = class_size.groupby("DBN").agg(numpy.mean)
class_size.reset_index(inplace=True)
data["class_size"] = class_size
data["demographics"] = data["demographics"][data["demographics"]["schoolyear"] == 20112012]
data["graduation"] = data["graduation"][data["graduation"]["Cohort"] == "2006"]
data["graduation"] = data["graduation"][data["graduation"]["Demographic"] == "Total Cohort"]
```
# Convert AP scores to numeric
```
cols = ['AP Test Takers ', 'Total Exams Taken', 'Number of Exams with scores 3 4 or 5']
for col in cols:
data["ap_2010"][col] = pd.to_numeric(data["ap_2010"][col], errors="coerce")
```
# Combine the datasets
```
combined = data["sat_results"]
combined = combined.merge(data["ap_2010"], on="DBN", how="left")
combined = combined.merge(data["graduation"], on="DBN", how="left")
to_merge = ["class_size", "demographics", "survey", "hs_directory"]
for m in to_merge:
combined = combined.merge(data[m], on="DBN", how="inner")
combined = combined.fillna(combined.mean())
combined = combined.fillna(0)
```
# Add a school district column for mapping
```
def get_first_two_chars(dbn):
return dbn[0:2]
combined["school_dist"] = combined["DBN"].apply(get_first_two_chars)
combined.corr().info()
```
# Find correlations
```
correlations = combined.corr()
correlations = correlations["sat_score"]
print(correlations)
```
# Plotting survey correlations
```
type(correlations[survey_fields])
# Remove DBN since it's a unique identifier, not a useful numerical value for correlation.
if "DBN" in survey_fields:
survey_fields.remove("DBN")
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 4))
ax.bar(range(len(survey_fields)), correlations[survey_fields])
ax.set_xticks(range(len(survey_fields)))
ax.set_xticklabels(survey_fields, rotation=90)
ax.set_title("Correlation (r-value) for survey fields")
combined.columns
```
## Investigate perceived safety's correlation to SAT scores.
```
import seaborn as sns
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["saf_s_11"], y=combined["sat_score"])
```
From the scatter plot above it appears that a perceived level of safety positively correlates positively with SAT scores, i.e. the safer a school is perceived to be the higher the SAT scores from students at that school will be. This is corroborated by the correlation score of 0.337639 for `saf_s_11` to `sat_score`.
```
import numpy as np
safety = combined.groupby("school_dist").agg(np.mean)
safety.head()
from mpl_toolkits.basemap import Basemap
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.set_title("Safety Perception")
ax2 = fig.add_subplot(122)
ax2.set_title("SAT Score")
# create a Basemap instance
m = Basemap(
projection='merc',
llcrnrlat=40.496044,
urcrnrlat=40.915256,
llcrnrlon=-74.255735,
urcrnrlon=-73.700272,
resolution='i',
ax=ax1
)
m2 = Basemap(
projection='merc',
llcrnrlat=40.496044,
urcrnrlat=40.915256,
llcrnrlon=-74.255735,
urcrnrlon=-73.700272,
resolution='i',
ax=ax2
)
# draw the maps
m.drawmapboundary(fill_color='#85A6D9')
m.drawcoastlines(color='#6D5F47', linewidth=.4)
m.drawrivers(color='#6D5F47', linewidth=.4)
m2.drawmapboundary(fill_color='#85A6D9')
m2.drawcoastlines(color='#6D5F47', linewidth=.4)
m2.drawrivers(color='#6D5F47', linewidth=.4)
# get the district lat/lons
district_lons = safety["lon"].tolist()
district_lats = safety["lat"].tolist()
# plot each district's safety score on the map
m.scatter(x=district_lons,
y=district_lats,
ax=ax1,
s=20,
zorder=2,
latlon=True,
c=safety["saf_s_11"],
cmap="RdYlGn")
m2.scatter(x=district_lons,
y=district_lats,
ax=ax2,
s=20,
zorder=2,
latlon=True,
c=safety["sat_score"],
cmap="RdYlGn")
```
Areas of the city that are perceived to be safer in general have higher SAT scores, but the correlation is not especially strong.
### Investigate racial differences for NYC SAT scores
```
racial_fields = ['white_per',
'asian_per',
'black_per',
'hispanic_per']
fig, ax = plt.subplots(figsize=(12, 4))
ax.bar(range(len(racial_fields)), correlations[racial_fields])
ax.set_xticks(range(len(racial_fields)))
ax.set_xticklabels(racial_fields, rotation=90)
ax.set_title("Correlation (r-value) for racial fields")
```
The above bar plot shows a positive correlation for White and Asian races and a negative correlation for Black and Hispanic races.
```
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["hispanic_per"], y=combined["sat_score"])
```
The above shows a negative trend in terms of correlation between the percentage of Hispanics and SAT scores, i.e. the higher percentage of Hispanics in a school the lower will be the average SAT score.
```
print("NYC Schools with 95% or greater Hispanic populations:")
combined[combined["hispanic_per"] > 95]["SCHOOL NAME"].tolist()
```
The above schools with overwhelmingly hispanic populations are international schools and/or located within sections of NYC with high percentage of Latinx immigrants.
```
print("NYC Schools with 10% or less Hispanic populations with an average SAT score above 1800:")
combined[(combined["hispanic_per"] < 10) & (combined["sat_score"] > 1800)]["SCHOOL NAME"].tolist()
```
## Gender differences in SAT scores in NYC
```
gender_percentage_cols = ['male_per', 'female_per']
fig, ax = plt.subplots()
ax.bar(range(len(gender_percentage_cols)), correlations[gender_percentage_cols])
ax.set_xticks(range(len(gender_percentage_cols)))
ax.set_xticklabels(gender_percentage_cols, rotation=90)
ax.set_title("Correlation (r-value) for gender fields")
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["female_per"], y=combined["sat_score"])
```
The above scatter plot shows a slight positive correlation between a school's percentage of female students and SAT scores.
```
combined[(combined["female_per"] > 60) & (combined["sat_score"] > 1700)]["SCHOOL NAME"]
```
The above shows that high schools in NYC where the student body is predominantly female and where the average SAT score is above 1800 are schools where the curriculum is focused on arts and humanities.
```
# compute the percentage of AP test takers, assign into a new column
combined["ap_per"] = combined["AP Test Takers "] / combined["total_enrollment"]
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["ap_per"], y=combined["sat_score"])
```
The above scatter plot shows only a slight positive correlation between AP test takers and SAT scores. somewhat counterintuitively.
Using the same sort of plotting we'll see if there's any correlation between class size adn SAT scores:
```
# print(data["class_size"].columns)
# perform a merge using an inner join on the DBN column
sizes_to_scores = data["class_size"][["DBN", "AVERAGE CLASS SIZE"]].merge(combined[["DBN", "sat_score"]],
how='inner',
on="DBN")
sizes_to_scores.reset_index("DBN")
sizes_to_scores.head()
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=sizes_to_scores["AVERAGE CLASS SIZE"], y=sizes_to_scores["sat_score"])
```
|
github_jupyter
|
import pandas as pd
import numpy
import re
data_files = [
"ap_2010.csv",
"class_size.csv",
"demographics.csv",
"graduation.csv",
"hs_directory.csv",
"sat_results.csv"
]
data = {}
for f in data_files:
d = pd.read_csv("schools/{0}".format(f))
data[f.replace(".csv", "")] = d
all_survey = pd.read_csv("schools/survey_all.txt", delimiter="\t", encoding='windows-1252')
d75_survey = pd.read_csv("schools/survey_d75.txt", delimiter="\t", encoding='windows-1252')
survey = pd.concat([all_survey, d75_survey], axis=0)
survey["DBN"] = survey["dbn"]
survey_fields = [
"DBN",
"rr_s",
"rr_t",
"rr_p",
"N_s",
"N_t",
"N_p",
"saf_p_11",
"com_p_11",
"eng_p_11",
"aca_p_11",
"saf_t_11",
"com_t_11",
"eng_t_11",
"aca_t_11",
"saf_s_11",
"com_s_11",
"eng_s_11",
"aca_s_11",
"saf_tot_11",
"com_tot_11",
"eng_tot_11",
"aca_tot_11",
]
survey = survey.loc[:,survey_fields]
data["survey"] = survey
pd.show_versions()
data["hs_directory"]["DBN"] = data["hs_directory"]["dbn"]
def pad_csd(num):
string_representation = str(num)
if len(string_representation) > 1:
return string_representation
else:
return "0" + string_representation
data["class_size"]["padded_csd"] = data["class_size"]["CSD"].apply(pad_csd)
data["class_size"]["DBN"] = data["class_size"]["padded_csd"] + data["class_size"]["SCHOOL CODE"]
cols = ['SAT Math Avg. Score', 'SAT Critical Reading Avg. Score', 'SAT Writing Avg. Score']
for c in cols:
data["sat_results"][c] = pd.to_numeric(data["sat_results"][c], errors="coerce")
data['sat_results']['sat_score'] = data['sat_results'][cols[0]] + data['sat_results'][cols[1]] + data['sat_results'][cols[2]]
def find_lat(loc):
coords = re.findall("\(.+, .+\)", loc)
lat = coords[0].split(",")[0].replace("(", "")
return lat
def find_lon(loc):
coords = re.findall("\(.+, .+\)", loc)
lon = coords[0].split(",")[1].replace(")", "").strip()
return lon
data["hs_directory"]["lat"] = data["hs_directory"]["Location 1"].apply(find_lat)
data["hs_directory"]["lon"] = data["hs_directory"]["Location 1"].apply(find_lon)
data["hs_directory"]["lat"] = pd.to_numeric(data["hs_directory"]["lat"], errors="coerce")
data["hs_directory"]["lon"] = pd.to_numeric(data["hs_directory"]["lon"], errors="coerce")
class_size = data["class_size"]
class_size = class_size[class_size["GRADE "] == "09-12"]
class_size = class_size[class_size["PROGRAM TYPE"] == "GEN ED"]
class_size = class_size.groupby("DBN").agg(numpy.mean)
class_size.reset_index(inplace=True)
data["class_size"] = class_size
data["demographics"] = data["demographics"][data["demographics"]["schoolyear"] == 20112012]
data["graduation"] = data["graduation"][data["graduation"]["Cohort"] == "2006"]
data["graduation"] = data["graduation"][data["graduation"]["Demographic"] == "Total Cohort"]
cols = ['AP Test Takers ', 'Total Exams Taken', 'Number of Exams with scores 3 4 or 5']
for col in cols:
data["ap_2010"][col] = pd.to_numeric(data["ap_2010"][col], errors="coerce")
combined = data["sat_results"]
combined = combined.merge(data["ap_2010"], on="DBN", how="left")
combined = combined.merge(data["graduation"], on="DBN", how="left")
to_merge = ["class_size", "demographics", "survey", "hs_directory"]
for m in to_merge:
combined = combined.merge(data[m], on="DBN", how="inner")
combined = combined.fillna(combined.mean())
combined = combined.fillna(0)
def get_first_two_chars(dbn):
return dbn[0:2]
combined["school_dist"] = combined["DBN"].apply(get_first_two_chars)
combined.corr().info()
correlations = combined.corr()
correlations = correlations["sat_score"]
print(correlations)
type(correlations[survey_fields])
# Remove DBN since it's a unique identifier, not a useful numerical value for correlation.
if "DBN" in survey_fields:
survey_fields.remove("DBN")
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 4))
ax.bar(range(len(survey_fields)), correlations[survey_fields])
ax.set_xticks(range(len(survey_fields)))
ax.set_xticklabels(survey_fields, rotation=90)
ax.set_title("Correlation (r-value) for survey fields")
combined.columns
import seaborn as sns
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["saf_s_11"], y=combined["sat_score"])
import numpy as np
safety = combined.groupby("school_dist").agg(np.mean)
safety.head()
from mpl_toolkits.basemap import Basemap
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.set_title("Safety Perception")
ax2 = fig.add_subplot(122)
ax2.set_title("SAT Score")
# create a Basemap instance
m = Basemap(
projection='merc',
llcrnrlat=40.496044,
urcrnrlat=40.915256,
llcrnrlon=-74.255735,
urcrnrlon=-73.700272,
resolution='i',
ax=ax1
)
m2 = Basemap(
projection='merc',
llcrnrlat=40.496044,
urcrnrlat=40.915256,
llcrnrlon=-74.255735,
urcrnrlon=-73.700272,
resolution='i',
ax=ax2
)
# draw the maps
m.drawmapboundary(fill_color='#85A6D9')
m.drawcoastlines(color='#6D5F47', linewidth=.4)
m.drawrivers(color='#6D5F47', linewidth=.4)
m2.drawmapboundary(fill_color='#85A6D9')
m2.drawcoastlines(color='#6D5F47', linewidth=.4)
m2.drawrivers(color='#6D5F47', linewidth=.4)
# get the district lat/lons
district_lons = safety["lon"].tolist()
district_lats = safety["lat"].tolist()
# plot each district's safety score on the map
m.scatter(x=district_lons,
y=district_lats,
ax=ax1,
s=20,
zorder=2,
latlon=True,
c=safety["saf_s_11"],
cmap="RdYlGn")
m2.scatter(x=district_lons,
y=district_lats,
ax=ax2,
s=20,
zorder=2,
latlon=True,
c=safety["sat_score"],
cmap="RdYlGn")
racial_fields = ['white_per',
'asian_per',
'black_per',
'hispanic_per']
fig, ax = plt.subplots(figsize=(12, 4))
ax.bar(range(len(racial_fields)), correlations[racial_fields])
ax.set_xticks(range(len(racial_fields)))
ax.set_xticklabels(racial_fields, rotation=90)
ax.set_title("Correlation (r-value) for racial fields")
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["hispanic_per"], y=combined["sat_score"])
print("NYC Schools with 95% or greater Hispanic populations:")
combined[combined["hispanic_per"] > 95]["SCHOOL NAME"].tolist()
print("NYC Schools with 10% or less Hispanic populations with an average SAT score above 1800:")
combined[(combined["hispanic_per"] < 10) & (combined["sat_score"] > 1800)]["SCHOOL NAME"].tolist()
gender_percentage_cols = ['male_per', 'female_per']
fig, ax = plt.subplots()
ax.bar(range(len(gender_percentage_cols)), correlations[gender_percentage_cols])
ax.set_xticks(range(len(gender_percentage_cols)))
ax.set_xticklabels(gender_percentage_cols, rotation=90)
ax.set_title("Correlation (r-value) for gender fields")
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["female_per"], y=combined["sat_score"])
combined[(combined["female_per"] > 60) & (combined["sat_score"] > 1700)]["SCHOOL NAME"]
# compute the percentage of AP test takers, assign into a new column
combined["ap_per"] = combined["AP Test Takers "] / combined["total_enrollment"]
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=combined["ap_per"], y=combined["sat_score"])
# print(data["class_size"].columns)
# perform a merge using an inner join on the DBN column
sizes_to_scores = data["class_size"][["DBN", "AVERAGE CLASS SIZE"]].merge(combined[["DBN", "sat_score"]],
how='inner',
on="DBN")
sizes_to_scores.reset_index("DBN")
sizes_to_scores.head()
# use the Seaborn function regplot to make a scatterplot
sns.regplot(x=sizes_to_scores["AVERAGE CLASS SIZE"], y=sizes_to_scores["sat_score"])
| 0.370225 | 0.787768 |
```
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set_theme()
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
# create datasets
def generate_in_distribution_data(n, mu, pi_in):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
X_0 = np.random.multivariate_normal(mu_0, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(mu_1, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def generate_out_distribution_data(n, mu, pi_out, theta):
n_1 = int(n*pi_out)
n_0 = int(n*(1-pi_out))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
theta = np.radians(theta)
c, s = np.cos(theta), np.sin(theta)
R = np.array(((c, s), (-s, c)))
X_0 = np.random.multivariate_normal(np.matmul(R, mu_0.T).T, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(np.matmul(R, mu_1.T).T, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
```
## Bivariate Single-Head LDA
Consider a generic binary LDA aimed at learning the target task. The projection vector is estimated according to the following expression:
$$ \omega = \argmax_{\omega} \frac{(\omega^\top \bar{X}_1 - \omega^\top \bar{X}_0 )^2}{\omega^\top S_w \omega} $$
where,
$$ S_w = \frac{n_1 S_{1} + n_0 S_{0}}{n} $$
Here, $S_{1}, S_{0}, {X}_{0}, \bar{X}_{1}$ are sample covariance matrices of target class 1 and target class 0, and sample means of target class 0 and class 1 respectively.
The above maximization problem yields the following expression for the projection vector:
$$ \omega = (S_0 + S_1)^{-1}(\bar{X}_1 - \bar{X}_0) $$
After the projection vector is estimated, the threshold $c$ is estimated by,
$$ c = \frac{\omega^\top \bar{X}_{0} + \omega^\top \bar{X}_{1}}{2} $$
Now consider an OOD task that has the same label distribution as the target task. We feed a mxiture (naively combined) of target and OOD data into our generic LDA. Hence, the class sample covariances and class sample means are estimated using this mixture, instead of just the target data.
```
def compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out):
X = np.concatenate((X_in, X_out), axis=-1)
Y = np.concatenate((Y_in, Y_out))
X_0 = X[:, Y == 0]
X_0_bar = np.mean(X_0, axis=-1, keepdims=True)
X_centered = X_0 - X_0_bar
S_0 = np.matmul(X_centered, X_centered.T)/len(Y[Y==0])
X_1 = X[:, Y == 1]
X_1_bar = np.mean(X_1, axis=-1, keepdims=True)
X_centered = X_1 - X_1_bar
S_1 = np.matmul(X_centered, X_centered.T)/len(Y[Y==1])
omega = np.matmul(np.linalg.inv(S_0 + S_1), X_1_bar - X_0_bar)
# estimate threshold
X_projected = np.matmul(omega.T, X).squeeze()
c = (np.mean(X_projected[Y == 0]) + np.mean(X_projected[Y == 1]))/2
return omega, c
def compute_empirical_risk(X, Y, omega, c):
Y_pred = (np.matmul(omega.T, X) > c).astype('int')
risk = 1 - np.mean(Y_pred == Y)
return risk
def visualize_projection_vector(n, m, theta, mu=3, pi_in=0.5, pi_out=0.5):
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out)
m = omega[1]/omega[0]
x = np.arange(-5, 5, 0.1)
y = m*x
fig, ax = plt.subplots()
ax.scatter(X_in[:, Y_in==0][0, :], X_in[:, Y_in==0][1, :], c='b')
ax.scatter(X_in[:, Y_in==1][0, :], X_in[:, Y_in==1][1, :], c='b')
ax.scatter(X_out[:, Y_out==0][0, :], X_out[:, Y_out==0][1, :], c='r')
ax.scatter(X_out[:, Y_out==1][0, :], X_out[:, Y_out==1][1, :], c='r')
ax.plot(x, y, 'k')
ax.set_xlim([-5, 5])
ax.set_ylim([-5, 5])
def run_simulation(
n = 4,
n_test = 500,
mu = 3,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 21, 1),
reps = 1000,
):
X_test, y_test = generate_in_distribution_data(n_test, mu, pi_in)
df = pd.DataFrame()
i = 0
for m in m_sizes:
for r, rep in enumerate(range(reps)):
df.at[i, "m"] = m
df.at[i, "r"] = r
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
for theta in Theta:
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out)
df.at[i, str(theta)] = compute_empirical_risk(X_test, y_test, omega, c)
i+=1
dfm = df.melt(['m', 'r'], var_name='Theta', value_name='Risk')
fig, ax = plt.subplots(figsize=(10, 10), facecolor='white')
ax = sns.lineplot(data=dfm, x="m", y="Risk", hue="Theta", ax=ax, markers=True, ci=95, lw=2)
ax.set_ylabel("Expected Risk")
ax.set_xlabel(r"$m/n, n={}$".format(n))
# ax.set_xlim([0, 100])
return df
```
### Visual the Estimated Projection Vectors
```
visualize_projection_vector(
n=10,
m=100,
theta=10
)
visualize_projection_vector(
n=10,
m=100,
theta=90
)
visualize_projection_vector(
n=100,
m=100,
theta=45
)
visualize_projection_vector(
n=100,
m=100,
theta=90
)
```
### Simulations
```
df = run_simulation(
n = 10,
n_test = 500,
mu = 1,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 100, 5),
reps = 1000,
)
```
## Bivariate Multi-Head LDA
In the multi-head LDA, first a projection vector is learnt using both the target ($n$) and OOD ($m$) data. In our case, we consider target and OOD tasks to be both binary classification tasks. Hence, there are four classes in total. Under these conditions, the projection vector is estimated according to the following expression (frequently used in the multi-class LDA):
$$ \omega = \argmax_{\omega} \frac{\omega^\top S_b \omega}{\omega^\top S_w \omega} $$
where,
$$ S_b = \frac{1}{n+m} \sum_{i=1}^{n+m} (X_i - \bar{X}) (X_i - \bar{X})^\top $$
$$ S_w = \frac{n_1 S_{t1} + n_0 S_{t0} + m_1 S_{o1} + m_0 S_{o0}}{n+m} $$
Here, $S_{t1}, S_{t0}, S_{o1}, S_{o0}$ are sample covariance matrices of target class 1, target class 0, OOD class 1, and OOD class 0, repectively.
The above maximization problem yields that the projection vector is the eigenvector corresponding to $\lambda_{max}(S_w^{-1} S_b)$.
After the projection vector is estimated, the threshold $c_{in}$ is estimated by,
$$ c_{in} = \frac{\omega^\top \bar{X}_{t0} + \omega^\top \bar{X}_{t1}}{2} $$
where $\bar{X}_{t0}, \bar{X}_{t1}$ are sample means of target class 0 and class 1 respectively.
```
# support functions
def generate_in_distribution_data(n, mu, pi_in):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
X_0 = np.random.multivariate_normal(mu_0, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(mu_1, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def generate_out_distribution_data(n, mu, pi_in, theta):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
theta = np.radians(theta)
c, s = np.cos(theta), np.sin(theta)
R = np.array(((c, s), (-s, c)))
X_0 = np.random.multivariate_normal(np.matmul(R, mu_0.T).T, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(np.matmul(R, mu_1.T).T, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out):
N = len(Y_in) + len(Y_out)
X_in_0 = X_in[:, Y_in == 0]
X_in_0_bar = np.nan_to_num(np.mean(X_in_0, axis=-1, keepdims=True))
X_centered = X_in_0 - X_in_0_bar
S_w_in_0 = np.matmul(X_centered, X_centered.T)
X_in_1 = X_in[:, Y_in == 1]
X_in_1_bar = np.nan_to_num(np.mean(X_in_1, axis=-1, keepdims=True))
X_centered = X_in_1 - X_in_1_bar
S_w_in_1 = np.matmul(X_centered, X_centered.T)
X_out_0 = X_out[:, Y_out == 0]
X_out_0_bar = np.nan_to_num(np.mean(X_out_0, axis=-1, keepdims=True))
X_centered = X_out_0 - X_out_0_bar
S_w_out_0 = np.matmul(X_centered, X_centered.T)
X_out_1 = X_out[:, Y_out == 1]
X_out_1_bar = np.nan_to_num(np.mean(X_out_1, axis=-1, keepdims=True))
X_centered = X_out_1 - X_out_1_bar
S_w_out_1 = np.matmul(X_centered, X_centered.T)
S_w = (S_w_in_0 + S_w_in_1 + S_w_out_0 + S_w_out_1)/N
# S_b according to "A generalization of LDA in MLE framework"
X = np.concatenate((X_in, X_out), axis=-1)
X_bar = np.mean(X, axis=-1, keepdims=True)
X_centered = X - X_bar
S_b = np.matmul(X_centered, X_centered.T)/N
# S_b according to Bishop's Book + other sources
m_k = np.concatenate((X_in_0_bar, X_in_1_bar, X_out_0_bar, X_out_1_bar), axis=-1)
m_k_centered = m_k - np.mean(m_k, axis=-1, keepdims=True)
S_bn = len(Y_in[Y_in==0])*np.matmul(m_k_centered[:, [0]], m_k_centered[:, [0]].T) +\
len(Y_in[Y_in==1])*np.matmul(m_k_centered[:, [1]], m_k_centered[:, [1]].T) +\
len(Y_out[Y_out==0])*np.matmul(m_k_centered[:, [2]], m_k_centered[:, [2]].T) +\
len(Y_out[Y_out==1])*np.matmul(m_k_centered[:, [3]], m_k_centered[:, [3]].T)
S_bn /= N
# estimate projection vector
e, v = np.linalg.eig(np.matmul(np.linalg.inv(S_w), S_bn))
omega = v[:, np.argmax(e)].reshape(2, 1)
# estimate threshold
X_in_projected = np.matmul(omega.T, X_in).squeeze()
c_in = (np.mean(X_in_projected[Y_in == 0]) + np.mean(X_in_projected[Y_in == 1]))/2
return omega, c_in
def compute_empirical_risk(X, Y, omega, c):
Y_pred = (np.matmul(omega.T, X) > c).astype('int')
risk = 1 - np.mean(Y_pred == Y)
return risk
def visualize_projection_vector(n, m, theta, mu=3, pi_in=0.5, pi_out=0.5):
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out)
m = omega[1]/omega[0]
x = np.arange(-5, 5, 0.1)
y = m*x
fig, ax = plt.subplots()
ax.scatter(X_in[:, Y_in==0][0, :], X_in[:, Y_in==0][1, :], c='b')
ax.scatter(X_in[:, Y_in==1][0, :], X_in[:, Y_in==1][1, :], c='b')
ax.scatter(X_out[:, Y_out==0][0, :], X_out[:, Y_out==0][1, :], c='r')
ax.scatter(X_out[:, Y_out==1][0, :], X_out[:, Y_out==1][1, :], c='r')
ax.plot(x, y, 'k')
ax.set_xlim([-5, 5])
ax.set_ylim([-5, 5])
def run_simulation(
n = 4,
n_test = 500,
mu = 3,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 21, 1),
reps = 1000,
):
X_test, y_test = generate_in_distribution_data(n_test, mu, pi_in)
df = pd.DataFrame()
i = 0
for m in m_sizes:
for r, rep in enumerate(range(reps)):
df.at[i, "m"] = m
df.at[i, "r"] = r
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
for theta in Theta:
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out)
df.at[i, str(theta)] = compute_empirical_risk(X_test, y_test, omega, c)
i+=1
dfm = df.melt(['m', 'r'], var_name='Theta', value_name='Risk')
fig, ax = plt.subplots(figsize=(10, 10), facecolor='white')
ax = sns.lineplot(data=dfm, x="m", y="Risk", hue="Theta", ax=ax, markers=True, ci=95, lw=2)
ax.set_ylabel("Expected Risk")
ax.set_xlabel(r"$m/n, n={}$".format(n))
# ax.set_xlim([0, 100])
return df
```
### Visualize the Estimated Projection Vector
```
visualize_projection_vector(
n=100,
m=100,
theta=0
)
visualize_projection_vector(
n=10,
m=100,
theta=90
)
visualize_projection_vector(
n=100,
m=100,
theta=45
)
visualize_projection_vector(
n=100,
m=100,
theta=90
)
```
### Simulations
```
df = run_simulation(
n = 10,
n_test = 500,
mu = 1,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 100, 5),
reps = 1000,
)
```
|
github_jupyter
|
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set_theme()
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
# create datasets
def generate_in_distribution_data(n, mu, pi_in):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
X_0 = np.random.multivariate_normal(mu_0, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(mu_1, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def generate_out_distribution_data(n, mu, pi_out, theta):
n_1 = int(n*pi_out)
n_0 = int(n*(1-pi_out))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
theta = np.radians(theta)
c, s = np.cos(theta), np.sin(theta)
R = np.array(((c, s), (-s, c)))
X_0 = np.random.multivariate_normal(np.matmul(R, mu_0.T).T, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(np.matmul(R, mu_1.T).T, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out):
X = np.concatenate((X_in, X_out), axis=-1)
Y = np.concatenate((Y_in, Y_out))
X_0 = X[:, Y == 0]
X_0_bar = np.mean(X_0, axis=-1, keepdims=True)
X_centered = X_0 - X_0_bar
S_0 = np.matmul(X_centered, X_centered.T)/len(Y[Y==0])
X_1 = X[:, Y == 1]
X_1_bar = np.mean(X_1, axis=-1, keepdims=True)
X_centered = X_1 - X_1_bar
S_1 = np.matmul(X_centered, X_centered.T)/len(Y[Y==1])
omega = np.matmul(np.linalg.inv(S_0 + S_1), X_1_bar - X_0_bar)
# estimate threshold
X_projected = np.matmul(omega.T, X).squeeze()
c = (np.mean(X_projected[Y == 0]) + np.mean(X_projected[Y == 1]))/2
return omega, c
def compute_empirical_risk(X, Y, omega, c):
Y_pred = (np.matmul(omega.T, X) > c).astype('int')
risk = 1 - np.mean(Y_pred == Y)
return risk
def visualize_projection_vector(n, m, theta, mu=3, pi_in=0.5, pi_out=0.5):
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out)
m = omega[1]/omega[0]
x = np.arange(-5, 5, 0.1)
y = m*x
fig, ax = plt.subplots()
ax.scatter(X_in[:, Y_in==0][0, :], X_in[:, Y_in==0][1, :], c='b')
ax.scatter(X_in[:, Y_in==1][0, :], X_in[:, Y_in==1][1, :], c='b')
ax.scatter(X_out[:, Y_out==0][0, :], X_out[:, Y_out==0][1, :], c='r')
ax.scatter(X_out[:, Y_out==1][0, :], X_out[:, Y_out==1][1, :], c='r')
ax.plot(x, y, 'k')
ax.set_xlim([-5, 5])
ax.set_ylim([-5, 5])
def run_simulation(
n = 4,
n_test = 500,
mu = 3,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 21, 1),
reps = 1000,
):
X_test, y_test = generate_in_distribution_data(n_test, mu, pi_in)
df = pd.DataFrame()
i = 0
for m in m_sizes:
for r, rep in enumerate(range(reps)):
df.at[i, "m"] = m
df.at[i, "r"] = r
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
for theta in Theta:
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_singlehead_decision_rule(X_in, Y_in, X_out, Y_out)
df.at[i, str(theta)] = compute_empirical_risk(X_test, y_test, omega, c)
i+=1
dfm = df.melt(['m', 'r'], var_name='Theta', value_name='Risk')
fig, ax = plt.subplots(figsize=(10, 10), facecolor='white')
ax = sns.lineplot(data=dfm, x="m", y="Risk", hue="Theta", ax=ax, markers=True, ci=95, lw=2)
ax.set_ylabel("Expected Risk")
ax.set_xlabel(r"$m/n, n={}$".format(n))
# ax.set_xlim([0, 100])
return df
visualize_projection_vector(
n=10,
m=100,
theta=10
)
visualize_projection_vector(
n=10,
m=100,
theta=90
)
visualize_projection_vector(
n=100,
m=100,
theta=45
)
visualize_projection_vector(
n=100,
m=100,
theta=90
)
df = run_simulation(
n = 10,
n_test = 500,
mu = 1,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 100, 5),
reps = 1000,
)
# support functions
def generate_in_distribution_data(n, mu, pi_in):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
X_0 = np.random.multivariate_normal(mu_0, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(mu_1, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def generate_out_distribution_data(n, mu, pi_in, theta):
n_1 = int(n*pi_in)
n_0 = int(n*(1-pi_in))
mu_1 = np.array([mu, 0])
mu_0 = -mu_1
theta = np.radians(theta)
c, s = np.cos(theta), np.sin(theta)
R = np.array(((c, s), (-s, c)))
X_0 = np.random.multivariate_normal(np.matmul(R, mu_0.T).T, np.identity(2), n_0).T
X_1 = np.random.multivariate_normal(np.matmul(R, mu_1.T).T, np.identity(2), n_1).T
X = np.concatenate((X_0, X_1), axis=-1)
Y = np.concatenate((np.zeros(n_0), np.ones(n_1)))
return X, Y
def compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out):
N = len(Y_in) + len(Y_out)
X_in_0 = X_in[:, Y_in == 0]
X_in_0_bar = np.nan_to_num(np.mean(X_in_0, axis=-1, keepdims=True))
X_centered = X_in_0 - X_in_0_bar
S_w_in_0 = np.matmul(X_centered, X_centered.T)
X_in_1 = X_in[:, Y_in == 1]
X_in_1_bar = np.nan_to_num(np.mean(X_in_1, axis=-1, keepdims=True))
X_centered = X_in_1 - X_in_1_bar
S_w_in_1 = np.matmul(X_centered, X_centered.T)
X_out_0 = X_out[:, Y_out == 0]
X_out_0_bar = np.nan_to_num(np.mean(X_out_0, axis=-1, keepdims=True))
X_centered = X_out_0 - X_out_0_bar
S_w_out_0 = np.matmul(X_centered, X_centered.T)
X_out_1 = X_out[:, Y_out == 1]
X_out_1_bar = np.nan_to_num(np.mean(X_out_1, axis=-1, keepdims=True))
X_centered = X_out_1 - X_out_1_bar
S_w_out_1 = np.matmul(X_centered, X_centered.T)
S_w = (S_w_in_0 + S_w_in_1 + S_w_out_0 + S_w_out_1)/N
# S_b according to "A generalization of LDA in MLE framework"
X = np.concatenate((X_in, X_out), axis=-1)
X_bar = np.mean(X, axis=-1, keepdims=True)
X_centered = X - X_bar
S_b = np.matmul(X_centered, X_centered.T)/N
# S_b according to Bishop's Book + other sources
m_k = np.concatenate((X_in_0_bar, X_in_1_bar, X_out_0_bar, X_out_1_bar), axis=-1)
m_k_centered = m_k - np.mean(m_k, axis=-1, keepdims=True)
S_bn = len(Y_in[Y_in==0])*np.matmul(m_k_centered[:, [0]], m_k_centered[:, [0]].T) +\
len(Y_in[Y_in==1])*np.matmul(m_k_centered[:, [1]], m_k_centered[:, [1]].T) +\
len(Y_out[Y_out==0])*np.matmul(m_k_centered[:, [2]], m_k_centered[:, [2]].T) +\
len(Y_out[Y_out==1])*np.matmul(m_k_centered[:, [3]], m_k_centered[:, [3]].T)
S_bn /= N
# estimate projection vector
e, v = np.linalg.eig(np.matmul(np.linalg.inv(S_w), S_bn))
omega = v[:, np.argmax(e)].reshape(2, 1)
# estimate threshold
X_in_projected = np.matmul(omega.T, X_in).squeeze()
c_in = (np.mean(X_in_projected[Y_in == 0]) + np.mean(X_in_projected[Y_in == 1]))/2
return omega, c_in
def compute_empirical_risk(X, Y, omega, c):
Y_pred = (np.matmul(omega.T, X) > c).astype('int')
risk = 1 - np.mean(Y_pred == Y)
return risk
def visualize_projection_vector(n, m, theta, mu=3, pi_in=0.5, pi_out=0.5):
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out)
m = omega[1]/omega[0]
x = np.arange(-5, 5, 0.1)
y = m*x
fig, ax = plt.subplots()
ax.scatter(X_in[:, Y_in==0][0, :], X_in[:, Y_in==0][1, :], c='b')
ax.scatter(X_in[:, Y_in==1][0, :], X_in[:, Y_in==1][1, :], c='b')
ax.scatter(X_out[:, Y_out==0][0, :], X_out[:, Y_out==0][1, :], c='r')
ax.scatter(X_out[:, Y_out==1][0, :], X_out[:, Y_out==1][1, :], c='r')
ax.plot(x, y, 'k')
ax.set_xlim([-5, 5])
ax.set_ylim([-5, 5])
def run_simulation(
n = 4,
n_test = 500,
mu = 3,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 21, 1),
reps = 1000,
):
X_test, y_test = generate_in_distribution_data(n_test, mu, pi_in)
df = pd.DataFrame()
i = 0
for m in m_sizes:
for r, rep in enumerate(range(reps)):
df.at[i, "m"] = m
df.at[i, "r"] = r
X_in, Y_in = generate_in_distribution_data(n, mu, pi_in)
for theta in Theta:
X_out, Y_out = generate_out_distribution_data(m, mu, pi_out, theta)
omega, c = compute_multihead_decision_rule(X_in, Y_in, X_out, Y_out)
df.at[i, str(theta)] = compute_empirical_risk(X_test, y_test, omega, c)
i+=1
dfm = df.melt(['m', 'r'], var_name='Theta', value_name='Risk')
fig, ax = plt.subplots(figsize=(10, 10), facecolor='white')
ax = sns.lineplot(data=dfm, x="m", y="Risk", hue="Theta", ax=ax, markers=True, ci=95, lw=2)
ax.set_ylabel("Expected Risk")
ax.set_xlabel(r"$m/n, n={}$".format(n))
# ax.set_xlim([0, 100])
return df
visualize_projection_vector(
n=100,
m=100,
theta=0
)
visualize_projection_vector(
n=10,
m=100,
theta=90
)
visualize_projection_vector(
n=100,
m=100,
theta=45
)
visualize_projection_vector(
n=100,
m=100,
theta=90
)
df = run_simulation(
n = 10,
n_test = 500,
mu = 1,
pi_in = 0.5,
pi_out = 0.5,
Theta = [0, 10, 45, 90],
m_sizes = np.arange(0, 100, 5),
reps = 1000,
)
| 0.487307 | 0.806243 |
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
path = tf.keras.utils.get_file('sunspots.csv',
' https://storage.googleapis.com/laurencemoroney-blog.appspot.com/Sunspots.csv')
print (path)
df = pd.read_csv(path, index_col='Date', parse_dates=True)
df.drop(df.columns[df.columns.str.contains('unnamed',case = False)],axis = 1, inplace = True)
df.columns = ['Sunspots'] # reaname column
df.plot(figsize=(10,6))
series = np.array(df['Sunspots'],float)
time = np.array(df.index)
plt.figure(figsize=(10, 6))
plot_series(time, series)
split_time = 3000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 30
batch_size = 32
shuffle_buffer_size = 1000
from tensorflow.keras.preprocessing.sequence import TimeseriesGenerator
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle = True)
def model_forecast(model, series, window_size):
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(32).prefetch(1)
forecast = model.predict(ds)
return forecast
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
window_size = 64
batch_size = 256
n_features = 1
# needed for lstm model.
x_train = x_train.reshape((len(x_train), n_features))
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle=True)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=32, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
model.summary()
lr_schedule = tf.keras.callbacks.LearningRateScheduler(lambda epoch: 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(generator, epochs=100, callbacks=[lr_schedule])
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-8, 1e-4, 0, 60])
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
window_size = 64
batch_size = 256
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle=True)
# needed for lstm model.
x_train = x_train.reshape((len(x_train), n_features))
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=60, kernel_size = 5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
model.summary()
# using optimal lr from the first model's graph
optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(generator,epochs=500)
# We need to make it 2 dimimention - because RNN needs 3D
series_2d = np.array(df['Sunspots'],float)
print(series_2d.shape)
series_2d = series_2d.reshape((len(series_2d), n_features))
print(series_2d.shape)
rnn_forecast=[]
for time in range(len(series_2d) - window_size):
rnn_forecast.append(model.predict(series_2d[time : time + window_size][np.newaxis]))
rnn_forecast = rnn_forecast[split_time - window_size:]
rnn_forecast = np.array(rnn_forecast)[:, 0, 0]
rnn_forecast.shape
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast)
rnn_forecast_x = model_forecast(model, series_2d[..., np.newaxis], window_size)
rnn_forecast_x = rnn_forecast_x[split_time - window_size:-1, -1, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast_x)
tf.keras.metrics.mean_absolute_error(x_valid, rnn_forecast_x)
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r')
plt.title('Training loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss"])
plt.figure()
zoomed_loss = loss[200:]
zoomed_epochs = range(200,500)
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(zoomed_epochs, zoomed_loss, 'r')
plt.title('Training loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss"])
plt.figure()
#print(rnn_forecast)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
path = tf.keras.utils.get_file('sunspots.csv',
' https://storage.googleapis.com/laurencemoroney-blog.appspot.com/Sunspots.csv')
print (path)
df = pd.read_csv(path, index_col='Date', parse_dates=True)
df.drop(df.columns[df.columns.str.contains('unnamed',case = False)],axis = 1, inplace = True)
df.columns = ['Sunspots'] # reaname column
df.plot(figsize=(10,6))
series = np.array(df['Sunspots'],float)
time = np.array(df.index)
plt.figure(figsize=(10, 6))
plot_series(time, series)
split_time = 3000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 30
batch_size = 32
shuffle_buffer_size = 1000
from tensorflow.keras.preprocessing.sequence import TimeseriesGenerator
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle = True)
def model_forecast(model, series, window_size):
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(32).prefetch(1)
forecast = model.predict(ds)
return forecast
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
window_size = 64
batch_size = 256
n_features = 1
# needed for lstm model.
x_train = x_train.reshape((len(x_train), n_features))
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle=True)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=32, kernel_size=5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
model.summary()
lr_schedule = tf.keras.callbacks.LearningRateScheduler(lambda epoch: 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(generator, epochs=100, callbacks=[lr_schedule])
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-8, 1e-4, 0, 60])
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
window_size = 64
batch_size = 256
generator = TimeseriesGenerator(x_train, x_train,
length = window_size, sampling_rate = 1,
batch_size = batch_size, shuffle=True)
# needed for lstm model.
x_train = x_train.reshape((len(x_train), n_features))
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=60, kernel_size = 5,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.LSTM(60, return_sequences=True),
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 400)
])
model.summary()
# using optimal lr from the first model's graph
optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(generator,epochs=500)
# We need to make it 2 dimimention - because RNN needs 3D
series_2d = np.array(df['Sunspots'],float)
print(series_2d.shape)
series_2d = series_2d.reshape((len(series_2d), n_features))
print(series_2d.shape)
rnn_forecast=[]
for time in range(len(series_2d) - window_size):
rnn_forecast.append(model.predict(series_2d[time : time + window_size][np.newaxis]))
rnn_forecast = rnn_forecast[split_time - window_size:]
rnn_forecast = np.array(rnn_forecast)[:, 0, 0]
rnn_forecast.shape
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast)
rnn_forecast_x = model_forecast(model, series_2d[..., np.newaxis], window_size)
rnn_forecast_x = rnn_forecast_x[split_time - window_size:-1, -1, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast_x)
tf.keras.metrics.mean_absolute_error(x_valid, rnn_forecast_x)
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r')
plt.title('Training loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss"])
plt.figure()
zoomed_loss = loss[200:]
zoomed_epochs = range(200,500)
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(zoomed_epochs, zoomed_loss, 'r')
plt.title('Training loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss"])
plt.figure()
#print(rnn_forecast)
| 0.850002 | 0.661841 |
# A Whirlwind Tour of Python
*Jake VanderPlas*
<img src="fig/cover-large.gif">
These are the Jupyter Notebooks behind my O'Reilly report,
[*A Whirlwind Tour of Python*](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp).
The full notebook listing is available [on Github](https://github.com/jakevdp/WhirlwindTourOfPython).
*A Whirlwind Tour of Python* is a fast-paced introduction to essential
components of the Python language for researchers and developers who are
already familiar with programming in another language.
The material is particularly aimed at those who wish to use Python for data
science and/or scientific programming, and in this capacity serves as an
introduction to my upcoming book, *The Python Data Science Handbook*.
These notebooks are adapted from lectures and workshops I've given on these
topics at University of Washington and at various conferences, meetings, and
workshops around the world.
## Index
1. [Introduction](00-Introduction.ipynb)
2. [How to Run Python Code](01-How-to-Run-Python-Code.ipynb)
3. [Basic Python Syntax](02-Basic-Python-Syntax.ipynb)
4. [Python Semantics: Variables](03-Semantics-Variables.ipynb)
5. [Python Semantics: Operators](04-Semantics-Operators.ipynb)
6. [Built-In Scalar Types](05-Built-in-Scalar-Types.ipynb)
7. [Built-In Data Structures](06-Built-in-Data-Structures.ipynb)
8. [Control Flow Statements](07-Control-Flow-Statements.ipynb)
9. [Defining Functions](08-Defining-Functions.ipynb)
10. [Errors and Exceptions](09-Errors-and-Exceptions.ipynb)
11. [Iterators](10-Iterators.ipynb)
12. [List Comprehensions](11-List-Comprehensions.ipynb)
13. [Generators and Generator Expressions](12-Generators.ipynb)
14. [Modules and Packages](13-Modules-and-Packages.ipynb)
15. [Strings and Regular Expressions](14-Strings-and-Regular-Expressions.ipynb)
16. [Preview of Data Science Tools](15-Preview-of-Data-Science-Tools.ipynb)
17. [Resources for Further Learning](16-Further-Resources.ipynb)
18. [Appendix: Code To Reproduce Figures](17-Figures.ipynb)
## License
This material is released under the "No Rights Reserved" [CC0](LICENSE)
license, and thus you are free to re-use, modify, build-on, and enhance
this material for any purpose.
That said, I request (but do not require) that if you use or adapt this material,
you include a proper attribution and/or citation; for example
> *A Whirlwind Tour of Python* by Jake VanderPlas (OโReilly). Copyright 2016 OโReilly Media, Inc., 978-1-491-96465-1
Read more about CC0 [here](https://creativecommons.org/share-your-work/public-domain/cc0/).
|
github_jupyter
|
# A Whirlwind Tour of Python
*Jake VanderPlas*
<img src="fig/cover-large.gif">
These are the Jupyter Notebooks behind my O'Reilly report,
[*A Whirlwind Tour of Python*](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp).
The full notebook listing is available [on Github](https://github.com/jakevdp/WhirlwindTourOfPython).
*A Whirlwind Tour of Python* is a fast-paced introduction to essential
components of the Python language for researchers and developers who are
already familiar with programming in another language.
The material is particularly aimed at those who wish to use Python for data
science and/or scientific programming, and in this capacity serves as an
introduction to my upcoming book, *The Python Data Science Handbook*.
These notebooks are adapted from lectures and workshops I've given on these
topics at University of Washington and at various conferences, meetings, and
workshops around the world.
## Index
1. [Introduction](00-Introduction.ipynb)
2. [How to Run Python Code](01-How-to-Run-Python-Code.ipynb)
3. [Basic Python Syntax](02-Basic-Python-Syntax.ipynb)
4. [Python Semantics: Variables](03-Semantics-Variables.ipynb)
5. [Python Semantics: Operators](04-Semantics-Operators.ipynb)
6. [Built-In Scalar Types](05-Built-in-Scalar-Types.ipynb)
7. [Built-In Data Structures](06-Built-in-Data-Structures.ipynb)
8. [Control Flow Statements](07-Control-Flow-Statements.ipynb)
9. [Defining Functions](08-Defining-Functions.ipynb)
10. [Errors and Exceptions](09-Errors-and-Exceptions.ipynb)
11. [Iterators](10-Iterators.ipynb)
12. [List Comprehensions](11-List-Comprehensions.ipynb)
13. [Generators and Generator Expressions](12-Generators.ipynb)
14. [Modules and Packages](13-Modules-and-Packages.ipynb)
15. [Strings and Regular Expressions](14-Strings-and-Regular-Expressions.ipynb)
16. [Preview of Data Science Tools](15-Preview-of-Data-Science-Tools.ipynb)
17. [Resources for Further Learning](16-Further-Resources.ipynb)
18. [Appendix: Code To Reproduce Figures](17-Figures.ipynb)
## License
This material is released under the "No Rights Reserved" [CC0](LICENSE)
license, and thus you are free to re-use, modify, build-on, and enhance
this material for any purpose.
That said, I request (but do not require) that if you use or adapt this material,
you include a proper attribution and/or citation; for example
> *A Whirlwind Tour of Python* by Jake VanderPlas (OโReilly). Copyright 2016 OโReilly Media, Inc., 978-1-491-96465-1
Read more about CC0 [here](https://creativecommons.org/share-your-work/public-domain/cc0/).
| 0.525612 | 0.903847 |
<a href="https://colab.research.google.com/github/RuperttAryeenWind/datascience/blob/master/machine-learning/courses/linkedin_ai/day1/LRExample.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
# drive.mount('/content/drive', force_remount=True)
drive.mount('/content/drive')
%matplotlib inline
import pandas
import numpy
import scipy
import statistics
import matplotlib
import seaborn
import math
# load data
!pwd
d = pandas.read_csv('/content/drive/My Drive/Aravind/Education/Artificial Intelligence/data/Homes76/homes76.dat.txt', sep='\t')
d.head()
d.tail()
# rename columns
cols = ['id', 'Price', 'Size', 'Lot', 'Bath', 'Bed', 'BathBed', 'Year', 'Age',
'Agesq', 'Garage', 'Status', 'Active', 'Elem', 'Edison Elementary',
'Harris Elementary', 'Adams Elementary', 'Crest Elementary', 'Parker Elementary']
cols = { d.columns.values[i]:cols[i] for i in range(len(cols))}
d.rename(index=str, columns=cols, inplace = True)
d.head()
colsForCorr = ["Size", "Lot", "Bath", "Bed", "BathBed", "Year", "Age",
"Agesq", "Garage", "Active", "Edison Elementary", "Harris Elementary",
"Adams Elementary", "Crest Elementary", "Parker Elementary"]
d_corrTest = d.loc[:, colsForCorr]
d_corrTest.corr(method='spearman') # Other methods: 'pearson', 'kendall'
d.dtypes
# perform some elemenatry data treatment
d['Lot'] = [ str(di) for di in d['Lot']]
d.dtypes
d.shape
yColumn = 'Price'
vars = ["Size", "Lot", "Bath", "Bed", "Year", "Age",
"Garage", "Elem"]
catvars = ["Lot", "Elem"]
d_forTrain = d.loc[:, [yColumn] + vars]
d_forTrain.head()
d_forTrain.shape
d_forTrain.describe(include = "all")
for ci in catvars:
print(ci)
print(d_forTrain[ci].value_counts())
pandas.get_dummies(d_forTrain["Elem"], drop_first=False)
def build_dummies(d, colname):
"""
Convert categorical variables to one-hot encodings
"""
col = d[colname]
di = pandas.get_dummies(col, drop_first = False)
cols = di.columns.values
cmap = { cols[i]:(colname + "_" + cols[i]) for i in range(len(cols))}
di.rename(index=str, columns=cmap, inplace = True)
return(di)
dframes = [ build_dummies(d_forTrain, ci) for ci in catvars]
indicator_vars = [ di.columns.values for di in dframes ]
indicator_vars = [item for sublist in indicator_vars for item in sublist]
# print(indicator_vars)
model_vars = list(set(vars) - set(catvars)) + indicator_vars
print(model_vars)
df = pandas.concat([ d_forTrain ] + dframes, axis = 1)
df.head()
df.shape
```
## Training
```
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
predictor_name, *feature_names = df.columns.values
feature_names.remove("Lot")
feature_names.remove("Elem")
```
### Creating test and train samples
[Train and test split](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html)
```
X_all = df.loc[:, feature_names]
X_all.head()
Y_all = df.loc[:, [ predictor_name ]]
X_train, X_test, Y_train, Y_test = train_test_split(X_all.values, Y_all.values)
```
### Linear regression
[Linear Regression library](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html)
```
regModel = LinearRegression(fit_intercept=True, normalize=True, copy_X=True)
regModel.fit(X_train, Y_train)
predictions = regModel.predict(X_test)
for i in range(len(predictions)):
print(predictions[i], Y_test[i])
```
Model Evaluation
```
regModel.score(X_train, Y_train)
regModel.score(X_test, Y_test)
residuals = Y_test - predictions
predDF = pandas.DataFrame(predictions, columns=["predictions"])
priceDF = pandas.DataFrame(Y_test, columns=["prices"])
plotDF = pandas.concat([ predDF, priceDF ], axis=1)
plotDF.head()
seaborn.scatterplot(x = "predictions", y = "prices", data=plotDF)
```
|
github_jupyter
|
from google.colab import drive
# drive.mount('/content/drive', force_remount=True)
drive.mount('/content/drive')
%matplotlib inline
import pandas
import numpy
import scipy
import statistics
import matplotlib
import seaborn
import math
# load data
!pwd
d = pandas.read_csv('/content/drive/My Drive/Aravind/Education/Artificial Intelligence/data/Homes76/homes76.dat.txt', sep='\t')
d.head()
d.tail()
# rename columns
cols = ['id', 'Price', 'Size', 'Lot', 'Bath', 'Bed', 'BathBed', 'Year', 'Age',
'Agesq', 'Garage', 'Status', 'Active', 'Elem', 'Edison Elementary',
'Harris Elementary', 'Adams Elementary', 'Crest Elementary', 'Parker Elementary']
cols = { d.columns.values[i]:cols[i] for i in range(len(cols))}
d.rename(index=str, columns=cols, inplace = True)
d.head()
colsForCorr = ["Size", "Lot", "Bath", "Bed", "BathBed", "Year", "Age",
"Agesq", "Garage", "Active", "Edison Elementary", "Harris Elementary",
"Adams Elementary", "Crest Elementary", "Parker Elementary"]
d_corrTest = d.loc[:, colsForCorr]
d_corrTest.corr(method='spearman') # Other methods: 'pearson', 'kendall'
d.dtypes
# perform some elemenatry data treatment
d['Lot'] = [ str(di) for di in d['Lot']]
d.dtypes
d.shape
yColumn = 'Price'
vars = ["Size", "Lot", "Bath", "Bed", "Year", "Age",
"Garage", "Elem"]
catvars = ["Lot", "Elem"]
d_forTrain = d.loc[:, [yColumn] + vars]
d_forTrain.head()
d_forTrain.shape
d_forTrain.describe(include = "all")
for ci in catvars:
print(ci)
print(d_forTrain[ci].value_counts())
pandas.get_dummies(d_forTrain["Elem"], drop_first=False)
def build_dummies(d, colname):
"""
Convert categorical variables to one-hot encodings
"""
col = d[colname]
di = pandas.get_dummies(col, drop_first = False)
cols = di.columns.values
cmap = { cols[i]:(colname + "_" + cols[i]) for i in range(len(cols))}
di.rename(index=str, columns=cmap, inplace = True)
return(di)
dframes = [ build_dummies(d_forTrain, ci) for ci in catvars]
indicator_vars = [ di.columns.values for di in dframes ]
indicator_vars = [item for sublist in indicator_vars for item in sublist]
# print(indicator_vars)
model_vars = list(set(vars) - set(catvars)) + indicator_vars
print(model_vars)
df = pandas.concat([ d_forTrain ] + dframes, axis = 1)
df.head()
df.shape
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
predictor_name, *feature_names = df.columns.values
feature_names.remove("Lot")
feature_names.remove("Elem")
X_all = df.loc[:, feature_names]
X_all.head()
Y_all = df.loc[:, [ predictor_name ]]
X_train, X_test, Y_train, Y_test = train_test_split(X_all.values, Y_all.values)
regModel = LinearRegression(fit_intercept=True, normalize=True, copy_X=True)
regModel.fit(X_train, Y_train)
predictions = regModel.predict(X_test)
for i in range(len(predictions)):
print(predictions[i], Y_test[i])
regModel.score(X_train, Y_train)
regModel.score(X_test, Y_test)
residuals = Y_test - predictions
predDF = pandas.DataFrame(predictions, columns=["predictions"])
priceDF = pandas.DataFrame(Y_test, columns=["prices"])
plotDF = pandas.concat([ predDF, priceDF ], axis=1)
plotDF.head()
seaborn.scatterplot(x = "predictions", y = "prices", data=plotDF)
| 0.229881 | 0.846451 |
# KNAP2 gene analysis
This notebook can be run locally or on a remote cloud computer by clicking the badge below:
[](https://mybinder.org/v2/gh/statisticalbiotechnology/cb2030/master?filepath=nb%2Flinear%2FKNAP2.ipynb)
This example is taken from from [statomics](https://statomics.github.io).
Data from https://doi.org/10.1093/jnci/djj052
### Background
Histologic grade in breast cancer provides clinically important prognostic information. Researchers examined whether histologic grade was associated with gene expression profiles of breast cancers and whether such profiles could be used to improve histologic grading. In this tutorial we will assess the impact of histologic grade on expression of the KPNA2 gene that is known to be associated with poor BC prognosis. The patients, however, do not only differ in the histologic grade, but also on their lymph node status. The lymph nodes were not affected (0) or surgically removed (1). We first load our data.
```
import pandas as pd
import seaborn as sns
import numpy as np
from statsmodels.compat import urlopen
try:
gene_table = pd.read_csv('brc.txt')
except: # recent pandas can read URL without urlopen
url = 'https://raw.githubusercontent.com/statOmics/statisticalGenomicsCourse/master/tutorial1/gse2990BreastcancerOneGene.txt'
fh = urlopen(url)
gene_table = pd.read_table(fh, sep=" ")
gene_table.to_csv('brc.txt')
gene_table.drop(columns=['Unnamed: 0'], inplace=True)
```
# Analysis
We first log the KNAP2 gene expression values. It is common to assume a log normal distribution of transcription values.
```
gene_table["log_gene"] = np.log(gene_table["gene"])
gene_table
```
We first plot the exression values of the KNAP2 gene for grade 1 and grade 3 cancers, and compare the ones sitting in patients where lymph nodes are or ar not surgically removed.
```
sns.boxplot(y="log_gene",x="grade",hue="node",data=gene_table)
```
Overall it seems like there is a large differnce in KNAP2 expression between grade 1 and grade 3 cancers. We test if the difference is significant.
```
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'log_gene ~ C(grade)'
lm = ols(formula, gene_table).fit()
print(anova_lm(lm))
```
The difference is indeed very significant.
We expand the model to also test for differences for removed lymph nodes, as well as an interaction term between cancer grade and node removal.
```
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'log_gene ~ C(grade) + C(node) + C(grade):C(node)'
lm = ols(formula, gene_table).fit()
#print(lm.summary())
print(anova_lm(lm))
```
All three terms are significant on a p<0.05 level. So there is a difference in expression between patients with and without surgicaly removed lymph nodes, between grade 1 and grade 3 tumors, and the two previously changes are linked. Visually, this makes sence by our previous boxplot, as the mean expression values of node 0/1 differ with differnt signs for grade 1 and grade 3 tumors.
Now we continue by investigating if we can see any significant differences of KNAP2 expressions given their size.
```
sns.lmplot(y="log_gene",x="size",hue="node",col="grade",data=gene_table)
```
We first test if there is a significant dependence on tumor size, first alone and subsequently also counting away the effects of the difference in grade and node status.
```
formula = 'log_gene ~ size'
lm2 = ols(formula, gene_table).fit()
print(anova_lm(lm2))
formula = 'log_gene ~ C(grade) + C(node) + size'
lm2 = ols(formula, gene_table).fit()
print(anova_lm(lm2))
```
In either of the tests the KNAP2 expression do not significantly depend on tumor size. We then see if there is an interaction between size and tumor grade.
```
formula = 'log_gene ~ C(grade) + size + size:C(grade)'
lm3 = ols(formula, gene_table).fit()
print(anova_lm(lm3))
```
The test suggest that KNAP2 expression depends on an interaction between tumor size and grade.
|
github_jupyter
|
import pandas as pd
import seaborn as sns
import numpy as np
from statsmodels.compat import urlopen
try:
gene_table = pd.read_csv('brc.txt')
except: # recent pandas can read URL without urlopen
url = 'https://raw.githubusercontent.com/statOmics/statisticalGenomicsCourse/master/tutorial1/gse2990BreastcancerOneGene.txt'
fh = urlopen(url)
gene_table = pd.read_table(fh, sep=" ")
gene_table.to_csv('brc.txt')
gene_table.drop(columns=['Unnamed: 0'], inplace=True)
gene_table["log_gene"] = np.log(gene_table["gene"])
gene_table
sns.boxplot(y="log_gene",x="grade",hue="node",data=gene_table)
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'log_gene ~ C(grade)'
lm = ols(formula, gene_table).fit()
print(anova_lm(lm))
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'log_gene ~ C(grade) + C(node) + C(grade):C(node)'
lm = ols(formula, gene_table).fit()
#print(lm.summary())
print(anova_lm(lm))
sns.lmplot(y="log_gene",x="size",hue="node",col="grade",data=gene_table)
formula = 'log_gene ~ size'
lm2 = ols(formula, gene_table).fit()
print(anova_lm(lm2))
formula = 'log_gene ~ C(grade) + C(node) + size'
lm2 = ols(formula, gene_table).fit()
print(anova_lm(lm2))
formula = 'log_gene ~ C(grade) + size + size:C(grade)'
lm3 = ols(formula, gene_table).fit()
print(anova_lm(lm3))
| 0.206094 | 0.994493 |
```
import pickle
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('talk')
%matplotlib inline
running_in_drive = False
images_path = '../presentation/images'
models_path = './Azin_models'
data_path = '../../data'
if running_in_drive:
images_path = '/content/drive/MyDrive/GA/images'
models_path = '/content/drive/MyDrive/GA/models'
data_path = '/content/drive/MyDrive/GA/data'
def read_data():
"""
Reads the preprocessed data
"""
path = f'{data_path}/processed_data.csv'
df = pd.read_csv(path)
df = df[['text', 'sentiment', 'Content Length', 'Content Word Count', 'emojis', 'num_comments','subreddit', 'label']]
df.columns = df.columns.str.title()
return df
df = read_data()
df.head()
df.groupby('Subreddit')['Num_Comments'].mean()
df.groupby('Subreddit')['Sentiment'].agg(['max', 'mean', 'min'])
plt.figure(figsize=(8,6))
g = sns.histplot(df, x='Sentiment', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=150);
sns.despine(top=True);
g.set_xlim(-1, 1)
plt.suptitle('Sentiment Scores', fontsize=20);
plt.savefig(f'{images_path}/sentiment_dist.png', bbox_inches='tight', dpi=300)
plt.figure(figsize=(8,6))
df_with_emojis = df[df['Emojis'].str.len()>0]
g = sns.histplot(df_with_emojis, x='Sentiment', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=45);
sns.despine(top=True);
g.set_xlim(-1, 1)
plt.suptitle('Sentiment Scores for Posts with Emojis', fontsize=20);
plt.savefig(f'{images_path}/sentiment_dist_emoji.png', bbox_inches='tight', dpi=300)
# define a function for extracting
# the punctuations
import re
def check_find_punctuations(text):
"""
# regular expression containing
# all punctuation
"https://www.geeksforgeeks.org/extract-punctuation-from-the-specified-column-of-dataframe-using-regex/"
"""
try:
result = re.findall(r'[!"\$%&\'()*+,\-.\/:;=#@?\[\\\]^_`{|}~]*',
text)
# form a string
string = "".join(result)
# list of strings return
return string
except Exception as e:
return ''
def find_punctuations_length_normalized(text):
"""
# regular expression containing
# all punctuation
"https://www.geeksforgeeks.org/extract-punctuation-from-the-specified-column-of-dataframe-using-regex/"
"""
try:
result = re.findall(r'[!"\$%&\'()*+,\-.\/:;=#@?\[\\\]^_`{|}~]*',
text)
# form a string
string = "".join(result)
# list of strings return
return len(string)/len(text)
except Exception as e:
return 0
df['Normalized Punctuation Length'] = df['Text'].apply(lambda x : find_punctuations_length_normalized(x))
plt.figure(figsize=(8,6))
data = df[df['Content Length']>0]
g = sns.histplot(data, x='Normalized Punctuation Length', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=150);
sns.despine(top=True);
#g.set_xlim(0, 1)
plt.suptitle('Use of Punctuations', fontsize=20);
plt.savefig(f'{images_path}/normalized_punctuation_dist.png', bbox_inches='tight', dpi=300)
```
|
github_jupyter
|
import pickle
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('talk')
%matplotlib inline
running_in_drive = False
images_path = '../presentation/images'
models_path = './Azin_models'
data_path = '../../data'
if running_in_drive:
images_path = '/content/drive/MyDrive/GA/images'
models_path = '/content/drive/MyDrive/GA/models'
data_path = '/content/drive/MyDrive/GA/data'
def read_data():
"""
Reads the preprocessed data
"""
path = f'{data_path}/processed_data.csv'
df = pd.read_csv(path)
df = df[['text', 'sentiment', 'Content Length', 'Content Word Count', 'emojis', 'num_comments','subreddit', 'label']]
df.columns = df.columns.str.title()
return df
df = read_data()
df.head()
df.groupby('Subreddit')['Num_Comments'].mean()
df.groupby('Subreddit')['Sentiment'].agg(['max', 'mean', 'min'])
plt.figure(figsize=(8,6))
g = sns.histplot(df, x='Sentiment', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=150);
sns.despine(top=True);
g.set_xlim(-1, 1)
plt.suptitle('Sentiment Scores', fontsize=20);
plt.savefig(f'{images_path}/sentiment_dist.png', bbox_inches='tight', dpi=300)
plt.figure(figsize=(8,6))
df_with_emojis = df[df['Emojis'].str.len()>0]
g = sns.histplot(df_with_emojis, x='Sentiment', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=45);
sns.despine(top=True);
g.set_xlim(-1, 1)
plt.suptitle('Sentiment Scores for Posts with Emojis', fontsize=20);
plt.savefig(f'{images_path}/sentiment_dist_emoji.png', bbox_inches='tight', dpi=300)
# define a function for extracting
# the punctuations
import re
def check_find_punctuations(text):
"""
# regular expression containing
# all punctuation
"https://www.geeksforgeeks.org/extract-punctuation-from-the-specified-column-of-dataframe-using-regex/"
"""
try:
result = re.findall(r'[!"\$%&\'()*+,\-.\/:;=#@?\[\\\]^_`{|}~]*',
text)
# form a string
string = "".join(result)
# list of strings return
return string
except Exception as e:
return ''
def find_punctuations_length_normalized(text):
"""
# regular expression containing
# all punctuation
"https://www.geeksforgeeks.org/extract-punctuation-from-the-specified-column-of-dataframe-using-regex/"
"""
try:
result = re.findall(r'[!"\$%&\'()*+,\-.\/:;=#@?\[\\\]^_`{|}~]*',
text)
# form a string
string = "".join(result)
# list of strings return
return len(string)/len(text)
except Exception as e:
return 0
df['Normalized Punctuation Length'] = df['Text'].apply(lambda x : find_punctuations_length_normalized(x))
plt.figure(figsize=(8,6))
data = df[df['Content Length']>0]
g = sns.histplot(data, x='Normalized Punctuation Length', hue='Subreddit', kde=True, legend=True, alpha=.45, bins=150);
sns.despine(top=True);
#g.set_xlim(0, 1)
plt.suptitle('Use of Punctuations', fontsize=20);
plt.savefig(f'{images_path}/normalized_punctuation_dist.png', bbox_inches='tight', dpi=300)
| 0.461259 | 0.261991 |
## Webscraping example 1: TESCO website
```
%matplotlib inline
# Some importing
import re
import numpy as np
import pandas as pd
import requests
from bs4 import BeautifulSoup
import matplotlib.pyplot as plt
import seaborn; seaborn.set()
```
The URL we are trying to scrape is https://www.tesco.com/groceries/en-GB/shop/fresh-food/chilled-fruit-juice-and-smoothies/all
```
URL = 'https://www.tesco.com/groceries/en-GB/shop/fresh-food/chilled-fruit-juice-and-smoothies/all'
```
### Getting the content of a webpage
Web scraping can be done in several programming languages: Python, R, Java etc.
The main thing you need it's a library which can access the internet, basically that is able to send HTTP requests.
In Python we have a library call [requests](http://docs.python-requests.org/en/master/)
We then need a parser (mostly to make our lives easier) which transforms the returned content by the requests library in a structure (a tree structure) which then we can access to retrieve elements
```
def get_content(url):
try:
response = requests.get(url)
except:
print("Ops! Something went wrong!")
return None
if response.status_code == 200:
html_doc = response.text
return BeautifulSoup(html_doc, 'html.parser')
return None
html = get_content(URL)
html
```
### Getting the products details in the page
#### Things to look at:
* chack the webpage structure
* find patterns in the naming of the containers for the item
* understand the pagination structure
```
def get_product(el):
product = dict()
title = el.find('a', attrs={'class': 'product-tile--title product-tile--browsable'})
if title:
product['product-tile'] = title.text
else:
product['product-tile'] = ''
price = el.find('div', attrs={'class': 'price-control-wrapper'})
if price:
product['price'] = float(price.text.replace("ยฃ", ""))
else:
product['price'] = np.nan
ppw = el.find('div', attrs={'class': 'price-per-quantity-weight'})
if ppw:
product['price-per-quantity-weight'] = ppw.text
else:
product['price-per-quantity-weight'] = ''
return product
def get_elements(page):
ul = page.find('ul', attrs={'class': 'product-list grid'})
if ul:
lis = ul.find_all('li', attrs={'class': re.compile('^product-list--list-item')})
items = []
for li in lis:
items.append(get_product(li))
return items
return []
get_elements(html)
```
## Putting all together: handling pagination
```
def get_data(url):
products = []
# First page
html = get_content(URL)
buttons = html.find_all('li', attrs={'class': 'pagination-btn-holder'})
last = int(buttons[-2].text[0])
products.extend(get_elements(html))
# Get everything
for i in range(1, last):
content = get_content(URL + '?page=' + str(i+1))
products.extend(get_elements(content))
return products
p = get_data(URL)
```
## Putting the data in a dataframe
```
df = pd.DataFrame(p)
df.head()
df.info()
df.price.describe()
df.price.hist(bins=15, figsize=(10,7))
```
|
github_jupyter
|
%matplotlib inline
# Some importing
import re
import numpy as np
import pandas as pd
import requests
from bs4 import BeautifulSoup
import matplotlib.pyplot as plt
import seaborn; seaborn.set()
URL = 'https://www.tesco.com/groceries/en-GB/shop/fresh-food/chilled-fruit-juice-and-smoothies/all'
def get_content(url):
try:
response = requests.get(url)
except:
print("Ops! Something went wrong!")
return None
if response.status_code == 200:
html_doc = response.text
return BeautifulSoup(html_doc, 'html.parser')
return None
html = get_content(URL)
html
def get_product(el):
product = dict()
title = el.find('a', attrs={'class': 'product-tile--title product-tile--browsable'})
if title:
product['product-tile'] = title.text
else:
product['product-tile'] = ''
price = el.find('div', attrs={'class': 'price-control-wrapper'})
if price:
product['price'] = float(price.text.replace("ยฃ", ""))
else:
product['price'] = np.nan
ppw = el.find('div', attrs={'class': 'price-per-quantity-weight'})
if ppw:
product['price-per-quantity-weight'] = ppw.text
else:
product['price-per-quantity-weight'] = ''
return product
def get_elements(page):
ul = page.find('ul', attrs={'class': 'product-list grid'})
if ul:
lis = ul.find_all('li', attrs={'class': re.compile('^product-list--list-item')})
items = []
for li in lis:
items.append(get_product(li))
return items
return []
get_elements(html)
def get_data(url):
products = []
# First page
html = get_content(URL)
buttons = html.find_all('li', attrs={'class': 'pagination-btn-holder'})
last = int(buttons[-2].text[0])
products.extend(get_elements(html))
# Get everything
for i in range(1, last):
content = get_content(URL + '?page=' + str(i+1))
products.extend(get_elements(content))
return products
p = get_data(URL)
df = pd.DataFrame(p)
df.head()
df.info()
df.price.describe()
df.price.hist(bins=15, figsize=(10,7))
| 0.285073 | 0.727637 |
# Transfer Learning
In this notebook, you'll learn how to use pre-trained networks to solved challenging problems in computer vision. Specifically, you'll use networks trained on [ImageNet](http://www.image-net.org/) [available from torchvision](http://pytorch.org/docs/0.3.0/torchvision/models.html).
ImageNet is a massive dataset with over 1 million labeled images in 1000 categories. It's used to train deep neural networks using an architecture called convolutional layers. I'm not going to get into the details of convolutional networks here, but if you want to learn more about them, please [watch this](https://www.youtube.com/watch?v=2-Ol7ZB0MmU).
Once trained, these models work astonishingly well as feature detectors for images they weren't trained on. Using a pre-trained network on images not in the training set is called transfer learning. Here we'll use transfer learning to train a network that can classify our cat and dog photos with near perfect accuracy.
With `torchvision.models` you can download these pre-trained networks and use them in your applications. We'll include `models` in our imports now.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
```
Most of the pretrained models require the input to be 224x224 images. Also, we'll need to match the normalization used when the models were trained. Each color channel was normalized separately, the means are `[0.485, 0.456, 0.406]` and the standard deviations are `[0.229, 0.224, 0.225]`.
```
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(test_data, batch_size=64)
```
We can load in a model such as [DenseNet](http://pytorch.org/docs/0.3.0/torchvision/models.html#id5). Let's print out the model architecture so we can see what's going on.
```
model = models.densenet121(pretrained=True)
model
```
This model is built out of two main parts, the features and the classifier. The features part is a stack of convolutional layers and overall works as a feature detector that can be fed into a classifier. The classifier part is a single fully-connected layer `(classifier): Linear(in_features=1024, out_features=1000)`. This layer was trained on the ImageNet dataset, so it won't work for our specific problem. That means we need to replace the classifier, but the features will work perfectly on their own. In general, I think about pre-trained networks as amazingly good feature detectors that can be used as the input for simple feed-forward classifiers.
```
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(1024, 500)),
('relu', nn.ReLU()),
('fc2', nn.Linear(500, 2)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
```
With our model built, we need to train the classifier. However, now we're using a **really deep** neural network. If you try to train this on a CPU like normal, it will take a long, long time. Instead, we're going to use the GPU to do the calculations. The linear algebra computations are done in parallel on the GPU leading to 100x increased training speeds. It's also possible to train on multiple GPUs, further decreasing training time.
PyTorch, along with pretty much every other deep learning framework, uses [CUDA](https://developer.nvidia.com/cuda-zone) to efficiently compute the forward and backwards passes on the GPU. In PyTorch, you move your model parameters and other tensors to the GPU memory using `model.to('cuda')`. You can move them back from the GPU with `model.to('cpu')` which you'll commonly do when you need to operate on the network output outside of PyTorch. As a demonstration of the increased speed, I'll compare how long it takes to perform a forward and backward pass with and without a GPU.
```
import time
for device in ['cpu', 'cuda']:
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.001)
model.to(device)
for ii, (inputs, labels) in enumerate(trainloader):
# Move input and label tensors to the GPU
inputs, labels = inputs.to(device), labels.to(device)
start = time.time()
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if ii==3:
break
print(f"Device = {device}; Time per batch: {(time.time() - start)/3:.3f} seconds")
```
You can write device agnostic code which will automatically use CUDA if it's enabled like so:
```python
# at beginning of the script
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
...
# then whenever you get a new Tensor or Module
# this won't copy if they are already on the desired device
input = data.to(device)
model = MyModule(...).to(device)
```
From here, I'll let you finish training the model. The process is the same as before except now your model is much more powerful. You should get better than 95% accuracy easily.
>**Exercise:** Train a pretrained models to classify the cat and dog images. Continue with the DenseNet model, or try ResNet, it's also a good model to try out first. Make sure you are only training the classifier and the parameters for the features part are frozen.
```
## TODO: Use a pretrained model to classify the cat and dog images
# Using the provided solution. I'll try a different one later.
# Use GPU if it's available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
model = models.densenet121(pretrained=True)
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
model.classifier = nn.Sequential(nn.Linear(1024, 256),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(256, 2),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.003)
model.to(device);
epochs = 1
steps = 0
running_loss = 0
print_every = 5
for epoch in range(epochs):
for inputs, labels in trainloader:
steps += 1
# Move input and label tensors to the default device
inputs, labels = inputs.to(device), labels.to(device)
optimizer.zero_grad()
logps = model.forward(inputs)
loss = criterion(logps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % print_every == 0:
test_loss = 0
accuracy = 0
model.eval()
with torch.no_grad():
for inputs, labels in testloader:
inputs, labels = inputs.to(device), labels.to(device)
logps = model.forward(inputs)
batch_loss = criterion(logps, labels)
test_loss += batch_loss.item()
# Calculate accuracy
ps = torch.exp(logps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor)).item()
print(f"Epoch {epoch+1}/{epochs}.. "
f"Train loss: {running_loss/print_every:.3f}.. "
f"Test loss: {test_loss/len(testloader):.3f}.. "
f"Test accuracy: {accuracy/len(testloader):.3f}")
running_loss = 0
model.train()
```
|
github_jupyter
|
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
from torchvision import datasets, transforms, models
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(test_data, batch_size=64)
model = models.densenet121(pretrained=True)
model
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
from collections import OrderedDict
classifier = nn.Sequential(OrderedDict([
('fc1', nn.Linear(1024, 500)),
('relu', nn.ReLU()),
('fc2', nn.Linear(500, 2)),
('output', nn.LogSoftmax(dim=1))
]))
model.classifier = classifier
import time
for device in ['cpu', 'cuda']:
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.001)
model.to(device)
for ii, (inputs, labels) in enumerate(trainloader):
# Move input and label tensors to the GPU
inputs, labels = inputs.to(device), labels.to(device)
start = time.time()
outputs = model.forward(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if ii==3:
break
print(f"Device = {device}; Time per batch: {(time.time() - start)/3:.3f} seconds")
# at beginning of the script
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
...
# then whenever you get a new Tensor or Module
# this won't copy if they are already on the desired device
input = data.to(device)
model = MyModule(...).to(device)
## TODO: Use a pretrained model to classify the cat and dog images
# Using the provided solution. I'll try a different one later.
# Use GPU if it's available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
model = models.densenet121(pretrained=True)
# Freeze parameters so we don't backprop through them
for param in model.parameters():
param.requires_grad = False
model.classifier = nn.Sequential(nn.Linear(1024, 256),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(256, 2),
nn.LogSoftmax(dim=1))
criterion = nn.NLLLoss()
# Only train the classifier parameters, feature parameters are frozen
optimizer = optim.Adam(model.classifier.parameters(), lr=0.003)
model.to(device);
epochs = 1
steps = 0
running_loss = 0
print_every = 5
for epoch in range(epochs):
for inputs, labels in trainloader:
steps += 1
# Move input and label tensors to the default device
inputs, labels = inputs.to(device), labels.to(device)
optimizer.zero_grad()
logps = model.forward(inputs)
loss = criterion(logps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % print_every == 0:
test_loss = 0
accuracy = 0
model.eval()
with torch.no_grad():
for inputs, labels in testloader:
inputs, labels = inputs.to(device), labels.to(device)
logps = model.forward(inputs)
batch_loss = criterion(logps, labels)
test_loss += batch_loss.item()
# Calculate accuracy
ps = torch.exp(logps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor)).item()
print(f"Epoch {epoch+1}/{epochs}.. "
f"Train loss: {running_loss/print_every:.3f}.. "
f"Test loss: {test_loss/len(testloader):.3f}.. "
f"Test accuracy: {accuracy/len(testloader):.3f}")
running_loss = 0
model.train()
| 0.720467 | 0.991255 |
```
import torch
import torchvision
import torch.nn as nn
import numpy as np
import torch.utils.data as data
import torchvision.transforms as transforms
import torchvision.datasets as dsets
from torch.autograd import Variable
from matplotlib import pyplot as plt
%matplotlib inline
from __future__ import print_function
```
## Basic autograd
```
x = Variable(torch.Tensor([1]), requires_grad=True)
w = Variable(torch.Tensor([2]), requires_grad=True)
b = Variable(torch.Tensor([3]), requires_grad=True)
# Build a computational graph
y = w * x + b
# Compute gradients.
y.backward()
# print out the gradients.
print(x.grad.data)
print(w.grad.data)
print(b.grad.data)
# Sample data for linear model y = w * x + b
x = Variable(torch.rand(30, 2))
w = Variable(torch.Tensor([2, 3]).view(2, -1))
y = torch.mm(x, w) + 1.0
y[:5]
linear = nn.Linear(2, 1)
print('w: ', linear.weight.data)
print('b: ',linear.bias.data)
# Build Loss and Optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(linear.parameters(), lr=0.01)
# forward propagation
pred = linear(x)
# compute loss
loss = criterion(pred, y)
print('loss:', loss.data[0])
# backpropagation
loss.backward()
# Gradients
print('dL/dw', linear.weight.grad)
print('dL/db', linear.bias.grad)
# optimization
optimizer.step()
# Print out the loss after optimization.
pred = linear(x)
loss = criterion(pred, y)
print('loss after 1 step optimization: ', loss.data[0])
linear.zero_grad()
loss.backward()
print('w: ', linear.weight.data)
print('b: ', linear.bias.data)
```
## Input pipeline
```
# Download and construct dataset
train_dataset = dsets.CIFAR10(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=4, shuffle=True, num_workers=4)
images, labels = next(iter(train_loader))
class_names = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
def imshow(img, title=None, mean=0, std=1):
npimg = img.numpy().transpose((1, 2, 0))
npimg = std * npimg + mean
npimg = np.clip(npimg, 0, 1)
plt.imshow(npimg)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
out = torchvision.utils.make_grid(images)
imshow(out, title=[class_names[x] for x in labels])
print(label)
# Data Loader
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=10,
shuffle=True,
num_workers=2)
data_iter = iter(train_loader)
images, labels = data_iter.next()
```
## Logistic Regression with MNIST
```
# Hyper parameters
input_size = 28 * 28
output_size = 10
num_epoches = 5
batch_size = 100
learning_rate = 0.001
# load MNIST dataset
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
train_dataset = dsets.MNIST(root='../../data/',
train=True,
download=True,
transform=transform)
test_dataset = dsets.MNIST(root='../../data/',
train=False,
transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=2)
test_loader = torch.utils.data.DataLoader(test_dataset,
batch_size=batch_size,
shuffle=False,
num_workers=2)
train_dataset.train_data.size()
images, labels = next(iter(train_loader))
print(labels.view(4,1))
batch_size = 4
nb_digits = 10
# Dummy input that HAS to be 2D for the scatter (you can use view(-1,1) if needed)
y = torch.LongTensor(batch_size,1).random_() % nb_digits
# One hot encoding buffer that you create out of the loop and just keep reusing
y_onehot = torch.FloatTensor(batch_size, nb_digits)
# In your for loop
y_onehot.zero_()
y_onehot.scatter_(1, y, 1)
print(y)
print(y_onehot)
labels_onehot = torch.FloatTensor(batch_size, 10)
labels_onehot.zero_()
labels_onehot.scatter_(1, labels.view(4, 1), 1)
labels_onehot
labels.size()
def one_hot(labels, num_classes):
out = torch.zeros(labels.size(0), num_classes)
out.scatter_(1, labels, 1)
return out
one_hot(labels.view(4, 1), 10)
# visualize the first batch
out = torchvision.utils.make_grid(images)
mean = np.array([0.1307])
std = np.array([0.3081])
imshow(out, title=[x for x in labels], mean=mean, std=std)
# train model
for epoch in range(num_epoches):
for i, (images, labels) in enumerate(train_loader):
images = Variable(images.view(-1, 28 * 28))
labels = Variable(labels)
optimizer.zero_grad()
outputs = model(images)
# convert labels to one-hot
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if (i+1) % 100 == 0:
print ('Epoch: [%d/%d], Step: [%d/%d], Loss: %.4f'
% (epoch+1, num_epoches, i+1, len(train_dataset)//batch_size, loss.data[0]))
```
|
github_jupyter
|
import torch
import torchvision
import torch.nn as nn
import numpy as np
import torch.utils.data as data
import torchvision.transforms as transforms
import torchvision.datasets as dsets
from torch.autograd import Variable
from matplotlib import pyplot as plt
%matplotlib inline
from __future__ import print_function
x = Variable(torch.Tensor([1]), requires_grad=True)
w = Variable(torch.Tensor([2]), requires_grad=True)
b = Variable(torch.Tensor([3]), requires_grad=True)
# Build a computational graph
y = w * x + b
# Compute gradients.
y.backward()
# print out the gradients.
print(x.grad.data)
print(w.grad.data)
print(b.grad.data)
# Sample data for linear model y = w * x + b
x = Variable(torch.rand(30, 2))
w = Variable(torch.Tensor([2, 3]).view(2, -1))
y = torch.mm(x, w) + 1.0
y[:5]
linear = nn.Linear(2, 1)
print('w: ', linear.weight.data)
print('b: ',linear.bias.data)
# Build Loss and Optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(linear.parameters(), lr=0.01)
# forward propagation
pred = linear(x)
# compute loss
loss = criterion(pred, y)
print('loss:', loss.data[0])
# backpropagation
loss.backward()
# Gradients
print('dL/dw', linear.weight.grad)
print('dL/db', linear.bias.grad)
# optimization
optimizer.step()
# Print out the loss after optimization.
pred = linear(x)
loss = criterion(pred, y)
print('loss after 1 step optimization: ', loss.data[0])
linear.zero_grad()
loss.backward()
print('w: ', linear.weight.data)
print('b: ', linear.bias.data)
# Download and construct dataset
train_dataset = dsets.CIFAR10(root='../../data/',
train=True,
transform=transforms.ToTensor(),
download=True)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=4, shuffle=True, num_workers=4)
images, labels = next(iter(train_loader))
class_names = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
def imshow(img, title=None, mean=0, std=1):
npimg = img.numpy().transpose((1, 2, 0))
npimg = std * npimg + mean
npimg = np.clip(npimg, 0, 1)
plt.imshow(npimg)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
out = torchvision.utils.make_grid(images)
imshow(out, title=[class_names[x] for x in labels])
print(label)
# Data Loader
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=10,
shuffle=True,
num_workers=2)
data_iter = iter(train_loader)
images, labels = data_iter.next()
# Hyper parameters
input_size = 28 * 28
output_size = 10
num_epoches = 5
batch_size = 100
learning_rate = 0.001
# load MNIST dataset
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
train_dataset = dsets.MNIST(root='../../data/',
train=True,
download=True,
transform=transform)
test_dataset = dsets.MNIST(root='../../data/',
train=False,
transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=2)
test_loader = torch.utils.data.DataLoader(test_dataset,
batch_size=batch_size,
shuffle=False,
num_workers=2)
train_dataset.train_data.size()
images, labels = next(iter(train_loader))
print(labels.view(4,1))
batch_size = 4
nb_digits = 10
# Dummy input that HAS to be 2D for the scatter (you can use view(-1,1) if needed)
y = torch.LongTensor(batch_size,1).random_() % nb_digits
# One hot encoding buffer that you create out of the loop and just keep reusing
y_onehot = torch.FloatTensor(batch_size, nb_digits)
# In your for loop
y_onehot.zero_()
y_onehot.scatter_(1, y, 1)
print(y)
print(y_onehot)
labels_onehot = torch.FloatTensor(batch_size, 10)
labels_onehot.zero_()
labels_onehot.scatter_(1, labels.view(4, 1), 1)
labels_onehot
labels.size()
def one_hot(labels, num_classes):
out = torch.zeros(labels.size(0), num_classes)
out.scatter_(1, labels, 1)
return out
one_hot(labels.view(4, 1), 10)
# visualize the first batch
out = torchvision.utils.make_grid(images)
mean = np.array([0.1307])
std = np.array([0.3081])
imshow(out, title=[x for x in labels], mean=mean, std=std)
# train model
for epoch in range(num_epoches):
for i, (images, labels) in enumerate(train_loader):
images = Variable(images.view(-1, 28 * 28))
labels = Variable(labels)
optimizer.zero_grad()
outputs = model(images)
# convert labels to one-hot
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
if (i+1) % 100 == 0:
print ('Epoch: [%d/%d], Step: [%d/%d], Loss: %.4f'
% (epoch+1, num_epoches, i+1, len(train_dataset)//batch_size, loss.data[0]))
| 0.881647 | 0.906777 |
## Model Deployment with Spark Serving
In this example, we try to predict incomes from the *Adult Census* dataset. Then we will use Spark serving to deploy it as a realtime web service.
First, we import needed packages:
```
import os
if os.environ.get("AZURE_SERVICE", None) == "Microsoft.ProjectArcadia":
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
import sys
import numpy as np
import pandas as pd
```
Now let's read the data and split it to train and test sets:
```
data = spark.read.parquet("wasbs://[email protected]/AdultCensusIncome.parquet")
data = data.select(["education", "marital-status", "hours-per-week", "income"])
train, test = data.randomSplit([0.75, 0.25], seed=123)
train.limit(10).toPandas()
```
`TrainClassifier` can be used to initialize and fit a model, it wraps SparkML classifiers.
You can use `help(synapse.ml.TrainClassifier)` to view the different parameters.
Note that it implicitly converts the data into the format expected by the algorithm. More specifically it:
tokenizes, hashes strings, one-hot encodes categorical variables, assembles the features into a vector
etc. The parameter `numFeatures` controls the number of hashed features.
```
from synapse.ml.train import TrainClassifier
from pyspark.ml.classification import LogisticRegression
model = TrainClassifier(model=LogisticRegression(), labelCol="income", numFeatures=256).fit(train)
```
After the model is trained, we score it against the test dataset and view metrics.
```
from synapse.ml.train import ComputeModelStatistics, TrainedClassifierModel
prediction = model.transform(test)
prediction.printSchema()
metrics = ComputeModelStatistics().transform(prediction)
metrics.limit(10).toPandas()
```
First, we will define the webservice input/output.
For more information, you can visit the [documentation for Spark Serving](https://github.com/Microsoft/SynapseML/blob/master/docs/mmlspark-serving.md)
```
from pyspark.sql.types import *
from synapse.ml.io import *
import uuid
serving_inputs = spark.readStream.server() \
.address("localhost", 8898, "my_api") \
.option("name", "my_api") \
.load() \
.parseRequest("my_api", test.schema)
serving_outputs = model.transform(serving_inputs) \
.makeReply("scored_labels")
server = serving_outputs.writeStream \
.server() \
.replyTo("my_api") \
.queryName("my_query") \
.option("checkpointLocation", "file:///tmp/checkpoints-{}".format(uuid.uuid1())) \
.start()
```
Test the webservice
```
import requests
data = u'{"education":" 10th","marital-status":"Divorced","hours-per-week":40.0}'
r = requests.post(data=data, url="http://localhost:8898/my_api")
print("Response {}".format(r.text))
import requests
data = u'{"education":" Masters","marital-status":"Married-civ-spouse","hours-per-week":40.0}'
r = requests.post(data=data, url="http://localhost:8898/my_api")
print("Response {}".format(r.text))
import time
time.sleep(20) # wait for server to finish setting up (just to be safe)
server.stop()
```
|
github_jupyter
|
import os
if os.environ.get("AZURE_SERVICE", None) == "Microsoft.ProjectArcadia":
from pyspark.sql import SparkSession
spark = SparkSession.builder.getOrCreate()
import sys
import numpy as np
import pandas as pd
data = spark.read.parquet("wasbs://[email protected]/AdultCensusIncome.parquet")
data = data.select(["education", "marital-status", "hours-per-week", "income"])
train, test = data.randomSplit([0.75, 0.25], seed=123)
train.limit(10).toPandas()
from synapse.ml.train import TrainClassifier
from pyspark.ml.classification import LogisticRegression
model = TrainClassifier(model=LogisticRegression(), labelCol="income", numFeatures=256).fit(train)
from synapse.ml.train import ComputeModelStatistics, TrainedClassifierModel
prediction = model.transform(test)
prediction.printSchema()
metrics = ComputeModelStatistics().transform(prediction)
metrics.limit(10).toPandas()
from pyspark.sql.types import *
from synapse.ml.io import *
import uuid
serving_inputs = spark.readStream.server() \
.address("localhost", 8898, "my_api") \
.option("name", "my_api") \
.load() \
.parseRequest("my_api", test.schema)
serving_outputs = model.transform(serving_inputs) \
.makeReply("scored_labels")
server = serving_outputs.writeStream \
.server() \
.replyTo("my_api") \
.queryName("my_query") \
.option("checkpointLocation", "file:///tmp/checkpoints-{}".format(uuid.uuid1())) \
.start()
import requests
data = u'{"education":" 10th","marital-status":"Divorced","hours-per-week":40.0}'
r = requests.post(data=data, url="http://localhost:8898/my_api")
print("Response {}".format(r.text))
import requests
data = u'{"education":" Masters","marital-status":"Married-civ-spouse","hours-per-week":40.0}'
r = requests.post(data=data, url="http://localhost:8898/my_api")
print("Response {}".format(r.text))
import time
time.sleep(20) # wait for server to finish setting up (just to be safe)
server.stop()
| 0.325092 | 0.927429 |
# Problem Statement: TASK 1
```
# importing functools for reduce()
import functools
# initializing list
lst = [1,5,3,2,9]
# using reduce function to compute sum of the above list
#print ("The sum of the list elements is : ",end="")
#print (functools.reduce(lambda a,b : a+b,lst))
# using own myreduce function
def myreduce(a,b):
return a+b
sum = functools.reduce(myreduce,lst)
print ("The sum of the list elements is : ",sum)
#Using lambda function we can perform the same task
#sum = functools.reduce(lambda a,b : a+b,lst)
#print ("The sum of the list elements is : ",sum)
```
Q1.2 Write a Python program to implement your own myfilter() function which works exactly like Python's built-in function filter().
```
# using filter function to check the numbers are prime number or not
def myfilter_isPrime(x):
for n in range(2,x):
if x%n==0:
return False
else:
return True
fltrObj=filter(myfilter_isPrime, range(20))
print ('Prime numbers between 1-20:', list(fltrObj))
```
```
#['A', 'C', 'A', 'D', 'G', 'I', โLโ, โ Dโ]
word = 'ACADGILD'
ch_list = [ch for ch in word]
print ("ACADGILD => " + str(ch_list))
#['x', 'xx', 'xxx', 'xxxx', 'y', 'yy', 'yyy', 'yyyy', 'z', 'zz', 'zzz', 'zzzz']
lst = ['x','y','z']
result = [item*num for item in lst for num in range(1,5)]
print("['x','y','z'] => " + str(result))
#['x', 'y', 'z', 'xx', 'yy', 'zz', 'xx', 'yy', 'zz', 'xxxx', 'yyyy', 'zzzz']
lst = ['x','y','z']
result = [item*num for num in range(1,5) for item in lst]
print("['x','y','z'] => " + str(result))
#[[2], [3], [4], [3], [4], [5], [4], [5], [6]]
lst = [2,3,4]
result = [ [item+num] for item in lst for num in range(0,3)]
print("[2,3,4] =>" + str(result))
#[[2, 3, 4, 5], [3, 4, 5, 6], [4, 5, 6, 7], [5, 6, 7, 8]]
lst = [2,3,4,5]
result = [[item+num for item in lst] for num in range(0,4)]
print("[2,3,4,5] =>" + str(result))
#[(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3)]
lst = [1,2,3]
result = [(y,x) for x in lst for y in lst]
print("[1,2,3] =>" + str(result))
```
Q3 Implement a function longestWord() that takes a list of words and returns the longest one.
```
#define function longestWord
def longestWord(words_lst):
word_len = []
for n in words_lst:
word_len.append((len(n), n))
word_len.sort()
return word_len[-1][1]
print(longestWord(["Machine Learning", "Deep Learning","computer vision" ,"Airtificial Intelligence"]))
```
# Task 2:
Q1.1 Write a Python Program(with class concepts) to find the area of the triangle using the below formula.
area = (s*(s-a)*(s-b)*(s-c)) ** 0.5
Function to take the length of the sides of triangle from user should be defined in the parent class and function to calculate the area should be defined in subclass.
```
import sys
import math
class Triangle():
def __init__(self):
self.a = float(input('Enter first side: '))
self.b = float(input('Enter second side: '))
self.c = float(input('Enter third side: '))
class Area_of_triangle(Triangle):
def findArea(self):
s=(self.a + self.b + self.c)/2
area=float(math.sqrt(s*(s-self.a)*(s-self.b)*(s-self.c)))
#area = (s*(s-self.a)*(s-self.b)*(s-self.c)) ** 0.5
return area
if __name__ == "__main__":
a = Area_of_triangle()
print("Area of the Triangle is :",a.findArea())
```
Q1.2 Write a function filter_long_words() that takes a list of words and an integer n and returns the list of words that are longer than n.
```
def filter_long_words(wordlist,n):
return filter(lambda word:len(word)>n, wordlist)
def main():
words = input("Enter the list of words separated by comma: ").split(',')
length = int(input("Minimum length of words to keep: "))
print("Words longer than {} are {}".format(length,', '.join(filter_long_words(words, length))))
if __name__ == "__main__":
main()
#If we want the return value to be list then we can use
#words = filter_long_words(["ML","Deep","Learning"],4)
#print("List of words longer than n:",list(words))
```
```
def map_to_lengths_lists(words):
return [len(word) for word in words]
if __name__ == "__main__":
words = ['ab','cde','erty']
print("Length of words in the list are :",map_to_lengths_lists(words))
```
```
def is_vowel(char):
#store values in tuple as the vowels are fixed
vowels = ('a', 'e', 'i', 'o', 'u')
if char not in vowels:
return False
return True
if __name__ == "__main__":
ch = str(input("Enter the character: "))
print(is_vowel(ch))
```
|
github_jupyter
|
# importing functools for reduce()
import functools
# initializing list
lst = [1,5,3,2,9]
# using reduce function to compute sum of the above list
#print ("The sum of the list elements is : ",end="")
#print (functools.reduce(lambda a,b : a+b,lst))
# using own myreduce function
def myreduce(a,b):
return a+b
sum = functools.reduce(myreduce,lst)
print ("The sum of the list elements is : ",sum)
#Using lambda function we can perform the same task
#sum = functools.reduce(lambda a,b : a+b,lst)
#print ("The sum of the list elements is : ",sum)
# using filter function to check the numbers are prime number or not
def myfilter_isPrime(x):
for n in range(2,x):
if x%n==0:
return False
else:
return True
fltrObj=filter(myfilter_isPrime, range(20))
print ('Prime numbers between 1-20:', list(fltrObj))
#['A', 'C', 'A', 'D', 'G', 'I', โLโ, โ Dโ]
word = 'ACADGILD'
ch_list = [ch for ch in word]
print ("ACADGILD => " + str(ch_list))
#['x', 'xx', 'xxx', 'xxxx', 'y', 'yy', 'yyy', 'yyyy', 'z', 'zz', 'zzz', 'zzzz']
lst = ['x','y','z']
result = [item*num for item in lst for num in range(1,5)]
print("['x','y','z'] => " + str(result))
#['x', 'y', 'z', 'xx', 'yy', 'zz', 'xx', 'yy', 'zz', 'xxxx', 'yyyy', 'zzzz']
lst = ['x','y','z']
result = [item*num for num in range(1,5) for item in lst]
print("['x','y','z'] => " + str(result))
#[[2], [3], [4], [3], [4], [5], [4], [5], [6]]
lst = [2,3,4]
result = [ [item+num] for item in lst for num in range(0,3)]
print("[2,3,4] =>" + str(result))
#[[2, 3, 4, 5], [3, 4, 5, 6], [4, 5, 6, 7], [5, 6, 7, 8]]
lst = [2,3,4,5]
result = [[item+num for item in lst] for num in range(0,4)]
print("[2,3,4,5] =>" + str(result))
#[(1, 1), (2, 1), (3, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3)]
lst = [1,2,3]
result = [(y,x) for x in lst for y in lst]
print("[1,2,3] =>" + str(result))
#define function longestWord
def longestWord(words_lst):
word_len = []
for n in words_lst:
word_len.append((len(n), n))
word_len.sort()
return word_len[-1][1]
print(longestWord(["Machine Learning", "Deep Learning","computer vision" ,"Airtificial Intelligence"]))
import sys
import math
class Triangle():
def __init__(self):
self.a = float(input('Enter first side: '))
self.b = float(input('Enter second side: '))
self.c = float(input('Enter third side: '))
class Area_of_triangle(Triangle):
def findArea(self):
s=(self.a + self.b + self.c)/2
area=float(math.sqrt(s*(s-self.a)*(s-self.b)*(s-self.c)))
#area = (s*(s-self.a)*(s-self.b)*(s-self.c)) ** 0.5
return area
if __name__ == "__main__":
a = Area_of_triangle()
print("Area of the Triangle is :",a.findArea())
def filter_long_words(wordlist,n):
return filter(lambda word:len(word)>n, wordlist)
def main():
words = input("Enter the list of words separated by comma: ").split(',')
length = int(input("Minimum length of words to keep: "))
print("Words longer than {} are {}".format(length,', '.join(filter_long_words(words, length))))
if __name__ == "__main__":
main()
#If we want the return value to be list then we can use
#words = filter_long_words(["ML","Deep","Learning"],4)
#print("List of words longer than n:",list(words))
def map_to_lengths_lists(words):
return [len(word) for word in words]
if __name__ == "__main__":
words = ['ab','cde','erty']
print("Length of words in the list are :",map_to_lengths_lists(words))
def is_vowel(char):
#store values in tuple as the vowels are fixed
vowels = ('a', 'e', 'i', 'o', 'u')
if char not in vowels:
return False
return True
if __name__ == "__main__":
ch = str(input("Enter the character: "))
print(is_vowel(ch))
| 0.148232 | 0.866189 |
# Generate Datasets
```
from sklearn.datasets.samples_generator import make_blobs
from matplotlib import pyplot as plt
import pandas as pd
data, label = make_blobs(n_samples=500, centers=3, n_features=2)
# scatter plot, dots colored by class value
df_data_normal = pd.DataFrame(dict(x=data[:,0], y=data[:,1], label=label))
colors = {0:'b', 1:'g', 2:'r', 3:'c', 4:'m', 5:'y', 6:'k'}
fig, ax = plt.subplots()
grouped = df_data_normal.groupby('label')
for key, group in grouped:
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key])
plt.show()
df_data_normal.to_csv('../data/2d_clustering_normal.csv', index=False)
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
x,y = df_data_normal['x'], df_data_normal['y']
plt.scatter(x,y,color='g')
plt.show()
import numpy as np
def gauss_2d(mu, sigma, num_samples):
x = np.random.normal(mu[0], sigma[0], num_samples)
y = np.random.normal(mu[1], sigma[1], num_samples)
return (x, y)
```
#### Data with different density
```
from matplotlib import pyplot as plt
x_para_mu = [i/2 for i in range(-50, 50)]
y_para_mu = [i*i/15 for i in x_para_mu]
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x_para_mu,y_para_mu,color='g')
plt.show()
# Generate the dataset
import numpy
sigma = 1.5
mu_x = x_para_mu
mu_y = y_para_mu
x, y = gauss_2d([mu_x[0], mu_y[0]], [sigma, sigma], 10)
for i in range(1, len(mu_x)):
mu = [mu_x[i], mu_y[i]]
x_samp, y_samp = gauss_2d(mu, [sigma, sigma], 10)
x,y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([30, 5], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([0, 40], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([-30, 10], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add random noise
x_samp, y_samp = gauss_2d([0, 20], [5, 10], 10)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x,y,color='g')
plt.show()
```
### Writing to a file
```
import pandas as pd
df_data_sin = pd.DataFrame(dict(x=x, y=y)) # convert
df_data_sin.to_csv('../data/2d_data_para.csv', header=True, index=False)
from matplotlib import pyplot as plt
import math
x_sin_mu = [i/10 for i in range(0, 100)]
y_sin_mu = [(math.sin(i)+1)*5 for i in x_sin_mu]
print(len(x_sin_mu), len(y_sin_mu))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x_sin_mu, y_sin_mu, color='g')
plt.show()
# Generate the dataset
import numpy
sigma = 0.2
mu_x = x_sin_mu
mu_y = y_sin_mu
x, y = gauss_2d([mu_x[0], mu_y[0]], [sigma, sigma], 10)
for i in range(1, len(mu_x)):
mu = [mu_x[i], mu_y[i]]
x_samp, y_samp = gauss_2d(mu, [sigma, sigma], 10)
x,y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([8, 0.5], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([1, 1], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([5, 9], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add random noise
x_samp, y_samp = gauss_2d([5, 5], [3,3], 10)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x,y,color='g')
plt.show()
```
### Writing to a file
```
import pandas as pd
df_data_sin = pd.DataFrame(dict(x=x, y=y)) # convert
df_data_sin.to_csv('../data/2d_data_sin.csv', header=True, index=False)
```
|
github_jupyter
|
from sklearn.datasets.samples_generator import make_blobs
from matplotlib import pyplot as plt
import pandas as pd
data, label = make_blobs(n_samples=500, centers=3, n_features=2)
# scatter plot, dots colored by class value
df_data_normal = pd.DataFrame(dict(x=data[:,0], y=data[:,1], label=label))
colors = {0:'b', 1:'g', 2:'r', 3:'c', 4:'m', 5:'y', 6:'k'}
fig, ax = plt.subplots()
grouped = df_data_normal.groupby('label')
for key, group in grouped:
group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key])
plt.show()
df_data_normal.to_csv('../data/2d_clustering_normal.csv', index=False)
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
x,y = df_data_normal['x'], df_data_normal['y']
plt.scatter(x,y,color='g')
plt.show()
import numpy as np
def gauss_2d(mu, sigma, num_samples):
x = np.random.normal(mu[0], sigma[0], num_samples)
y = np.random.normal(mu[1], sigma[1], num_samples)
return (x, y)
from matplotlib import pyplot as plt
x_para_mu = [i/2 for i in range(-50, 50)]
y_para_mu = [i*i/15 for i in x_para_mu]
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x_para_mu,y_para_mu,color='g')
plt.show()
# Generate the dataset
import numpy
sigma = 1.5
mu_x = x_para_mu
mu_y = y_para_mu
x, y = gauss_2d([mu_x[0], mu_y[0]], [sigma, sigma], 10)
for i in range(1, len(mu_x)):
mu = [mu_x[i], mu_y[i]]
x_samp, y_samp = gauss_2d(mu, [sigma, sigma], 10)
x,y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([30, 5], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([0, 40], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([-30, 10], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add random noise
x_samp, y_samp = gauss_2d([0, 20], [5, 10], 10)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x,y,color='g')
plt.show()
import pandas as pd
df_data_sin = pd.DataFrame(dict(x=x, y=y)) # convert
df_data_sin.to_csv('../data/2d_data_para.csv', header=True, index=False)
from matplotlib import pyplot as plt
import math
x_sin_mu = [i/10 for i in range(0, 100)]
y_sin_mu = [(math.sin(i)+1)*5 for i in x_sin_mu]
print(len(x_sin_mu), len(y_sin_mu))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x_sin_mu, y_sin_mu, color='g')
plt.show()
# Generate the dataset
import numpy
sigma = 0.2
mu_x = x_sin_mu
mu_y = y_sin_mu
x, y = gauss_2d([mu_x[0], mu_y[0]], [sigma, sigma], 10)
for i in range(1, len(mu_x)):
mu = [mu_x[i], mu_y[i]]
x_samp, y_samp = gauss_2d(mu, [sigma, sigma], 10)
x,y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([8, 0.5], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([1, 1], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add three randomly generated
x_samp, y_samp = gauss_2d([5, 9], [sigma, sigma], 20)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
# Add random noise
x_samp, y_samp = gauss_2d([5, 5], [3,3], 10)
x, y = np.hstack((x, x_samp)), np.hstack((y, y_samp))
plt.figure(figsize=(8,6))
plt.subplot(1,1,1)
plt.scatter(x,y,color='g')
plt.show()
import pandas as pd
df_data_sin = pd.DataFrame(dict(x=x, y=y)) # convert
df_data_sin.to_csv('../data/2d_data_sin.csv', header=True, index=False)
| 0.631026 | 0.931836 |
```
import json
import glob
import malaya
from unidecode import unidecode
import re
tokenizer = malaya.preprocessing._SocialTokenizer().tokenize
rules_normalizer = malaya.texts._tatabahasa.rules_normalizer
def is_number_regex(s):
if re.match("^\d+?\.\d+?$", s) is None:
return s.isdigit()
return True
def detect_money(word):
if word[:2] == 'rm' and is_number_regex(word[2:]):
return True
else:
return False
def preprocessing(string):
tokenized = tokenizer(unidecode(string))
tokenized = [w.lower() for w in tokenized if len(w) > 1]
tokenized = ['<NUM>' if is_number_regex(w) else w for w in tokenized]
tokenized = ['<MONEY>' if detect_money(w) else w for w in tokenized]
return tokenized
english, bahasa = [], []
files = glob.glob('Malaya-Dataset/english-malay/*.json')
for file in files:
with open(file) as fopen:
x = json.load(fopen)
for l, r in x:
english.append(l)
bahasa.append(r)
len(english), len(bahasa)
from tqdm import tqdm
x, y = [], []
for i in tqdm(range(len(english))):
p = preprocessing(english[i])
u = preprocessing(bahasa[i])
if len(p) <= 100 and len(p) > 3 and len(u) > 3:
x.append(p)
y.append(u)
len(x), len(y)
```
## Limit to 100k only, too big
```
english = x[:100000]
bahasa = y[:100000]
import collections
def build_dataset(words, n_words, atleast=1):
count = [['PAD', 0], ['GO', 1], ['EOS', 2], ['UNK', 3]]
counter = collections.Counter(words).most_common(n_words)
counter = [i for i in counter if i[1] >= atleast]
count.extend(counter)
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
index = dictionary.get(word, 0)
if index == 0:
unk_count += 1
data.append(index)
count[0][1] = unk_count
reversed_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reversed_dictionary
import itertools
concat = list(itertools.chain(*english))
vocabulary_size_english = len(list(set(concat)))
data, count, dictionary_english, rev_dictionary_english = build_dataset(concat, vocabulary_size_english)
print('vocab from size: %d'%(vocabulary_size_english))
print('Most common words', count[4:10])
print('Sample data', data[:10], [rev_dictionary_english[i] for i in data[:10]])
concat = list(itertools.chain(*bahasa))
vocabulary_size_bahasa = len(list(set(concat)))
data, count, dictionary_bahasa, rev_dictionary_bahasa = build_dataset(concat, vocabulary_size_bahasa)
print('vocab from size: %d'%(vocabulary_size_bahasa))
print('Most common words', count[4:10])
print('Sample data', data[:10], [rev_dictionary_bahasa[i] for i in data[:10]])
with open('dictionary.json', 'w') as fopen:
json.dump({'english':{'dictionary': dictionary_english,
'rev_dictionary': rev_dictionary_english},
'bahasa':{
'dictionary': dictionary_bahasa,
'rev_dictionary': rev_dictionary_bahasa
}}, fopen)
with open('english-malay.json', 'w') as fopen:
json.dump([english, bahasa], fopen)
```
|
github_jupyter
|
import json
import glob
import malaya
from unidecode import unidecode
import re
tokenizer = malaya.preprocessing._SocialTokenizer().tokenize
rules_normalizer = malaya.texts._tatabahasa.rules_normalizer
def is_number_regex(s):
if re.match("^\d+?\.\d+?$", s) is None:
return s.isdigit()
return True
def detect_money(word):
if word[:2] == 'rm' and is_number_regex(word[2:]):
return True
else:
return False
def preprocessing(string):
tokenized = tokenizer(unidecode(string))
tokenized = [w.lower() for w in tokenized if len(w) > 1]
tokenized = ['<NUM>' if is_number_regex(w) else w for w in tokenized]
tokenized = ['<MONEY>' if detect_money(w) else w for w in tokenized]
return tokenized
english, bahasa = [], []
files = glob.glob('Malaya-Dataset/english-malay/*.json')
for file in files:
with open(file) as fopen:
x = json.load(fopen)
for l, r in x:
english.append(l)
bahasa.append(r)
len(english), len(bahasa)
from tqdm import tqdm
x, y = [], []
for i in tqdm(range(len(english))):
p = preprocessing(english[i])
u = preprocessing(bahasa[i])
if len(p) <= 100 and len(p) > 3 and len(u) > 3:
x.append(p)
y.append(u)
len(x), len(y)
english = x[:100000]
bahasa = y[:100000]
import collections
def build_dataset(words, n_words, atleast=1):
count = [['PAD', 0], ['GO', 1], ['EOS', 2], ['UNK', 3]]
counter = collections.Counter(words).most_common(n_words)
counter = [i for i in counter if i[1] >= atleast]
count.extend(counter)
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
index = dictionary.get(word, 0)
if index == 0:
unk_count += 1
data.append(index)
count[0][1] = unk_count
reversed_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reversed_dictionary
import itertools
concat = list(itertools.chain(*english))
vocabulary_size_english = len(list(set(concat)))
data, count, dictionary_english, rev_dictionary_english = build_dataset(concat, vocabulary_size_english)
print('vocab from size: %d'%(vocabulary_size_english))
print('Most common words', count[4:10])
print('Sample data', data[:10], [rev_dictionary_english[i] for i in data[:10]])
concat = list(itertools.chain(*bahasa))
vocabulary_size_bahasa = len(list(set(concat)))
data, count, dictionary_bahasa, rev_dictionary_bahasa = build_dataset(concat, vocabulary_size_bahasa)
print('vocab from size: %d'%(vocabulary_size_bahasa))
print('Most common words', count[4:10])
print('Sample data', data[:10], [rev_dictionary_bahasa[i] for i in data[:10]])
with open('dictionary.json', 'w') as fopen:
json.dump({'english':{'dictionary': dictionary_english,
'rev_dictionary': rev_dictionary_english},
'bahasa':{
'dictionary': dictionary_bahasa,
'rev_dictionary': rev_dictionary_bahasa
}}, fopen)
with open('english-malay.json', 'w') as fopen:
json.dump([english, bahasa], fopen)
| 0.230227 | 0.583945 |
## 3.6 ๅๅปบๅ่กจ
ๅจๅ
ๅฎน่กจ่พพไธ๏ผๅ่กจๆฏไธ็ง้ๅธธๆๆ็ๆนๅผ๏ผๅฎๅฐๆไธ่ฎบ่ฟฐๅ
ๅฎนๅๆ่ฅๅนฒไธชๆก็ฎ่ฟ่ก็ฝๅ๏ผ่ฝ่พพๅฐ็ฎๆๆผ่ฆใ้็ฎ็ด่ง็่กจ่พพๆๆใๅจ่ฎบๆๅไฝไธญ๏ผๅ่กจไธๅคฑไธบไธ็ง่ฎฉๅ
ๅฎนๆธ
ๆฐๆไบ็่ฎบ่ฟฐๆนๅผใ
้ๅธธๆฅ่ฏด๏ผๅ่กจๆๅๅฑๅ่กจๅๅคๅฑๅ่กจ๏ผๅคๅฑๅ่กจๆ ๅคไนๆฏๆๅคๅฑๅ่กจไธญๅตๅฅไบไธๅฑ็่ณๆดๅคๅฑๅ่กจใๅ
ทไฝๆฅ่ฏด๏ผๅ่กจไธป่ฆๆไธ็ง็ฑปๅ๏ผๅณๆ ๅบๅ่กจใๆๅบๅ่กจๅ้่ฟฐๆงๅ่กจ๏ผๅ
ถไธญ๏ผๆ ๅบๅ่กจๅๆๅบๅ่กจๆฏ็ธๅฏนๅธธ็จ็ๅ่กจ็ฑปๅ๏ผLaTeX้ๅฏน่ฟไธ็งๅ่กจๆไพไบไธไบๅบๆฌ็ฏๅข๏ผ
- ๆ ๅบๅ่กจ็ไฝฟ็จๆนๆณไธบ๏ผ
```tex
\begin{itemize}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{itemize}
```
- ๆๅบๅ่กจ็ไฝฟ็จๆนๆณไธบ๏ผ
```tex
\begin{enumerate}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{enumerate}
```
- ้่ฟฐๆงๅ่กจ็ไฝฟ็จๆนๆณไธบ๏ผ
```tex
\begin{description}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{description}
```
ๅจ่ฟไธ็งๅ่กจไธญ๏ผๆไปฌๅๅปบ็ๆฏไธ้กนๅ่กจๅ
ๅฎน้ฝ้่ฆ็ดง้`\item`ๅฝไปคไนๅใๅฝ็ถ๏ผๆๆถๅ๏ผๆไปฌไนๅฏไปฅๆ นๆฎ้่ฆ้ๆฉๅ้็ๅ่กจ็ฑปๅใ่ฐๆดๅ่กจ็ฌฆๅท็่ณ่ก้ด่ท็ญใ
### 3.6.1 ๆ ๅบๅ่กจ
LaTeXไธญ็ๆ ๅบๅ่กจ็ฏๅขไธ่ฌ็จ็นๅฎ็ฌฆๅท๏ผๅฆๅ็นใๆๅท๏ผไฝไธบๅ่กจไธญๆฏไธชๆก็ฎ็่ตทๅงๆ ๅฟ๏ผไปฅ็คบๆๅซไบๅธธ่งๆๆฌใๅฏไปฅๅฟฝ็ฅไธปๆฌกๆ่
ๅ
ๅ้กบๅบๅ
ณ็ณป็ๆก็ฎๆๅ้ฝๅฏไปฅไฝฟ็จๆ ๅบๅ่กจ็ฏๅขๆฅ็ผๅ๏ผๆ ๅบๅ่กจๆถๅพๅคๆๆกฃๆๅธธ็จ็ๅ่กจ็ฑปๅ๏ผไน่ขซ็งฐไธบๅธธ่งๅ่กจใ
ใ**ไพ1**ใไฝฟ็จๆ ้ๅ่กจ็ฏๅขๅๅปบไธไธช็ฎๅ็ๆ ๅบๅ่กจใ
```tex
\documentclass[12pt]{article}
\begin{document}
\begin{itemize}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.1ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_1.png" width="300" />
</p>
<center><b>ๅพ3.6.1</b> ็ผ่ฏๅๅ่กจ</center>
ๅจๆ ๅบๅ่กจ็ฏๅขไธญ๏ผๆฏไธชๆก็ฎ้ฝๆฏไปฅๆก็ฎๅฝไปค`\item`ๅผๅคด็๏ผไธ่ฌ้ป่ฎค็่ตทๅง็ฌฆๅทๆฏtextbullet๏ผๅณๅคงๅ็น็ฌฆๅท๏ผๅฝ็ถ๏ผไนๅฏไปฅๆ นๆฎ้่ฆ่ฐๆด่ตทๅง็ฌฆๅทใ
ใ**ไพ2**ใๅจๆ ้ๅ่กจ็ฏๅขไธญไฝฟ็จๆๅทไฝไธบๆก็ฎ็่ตทๅง็ฌฆๅทใ
```tex
\documentclass[12pt]{article}
\begin{document}
\begin{itemize}
\item Python % ๆก็ฎ1๏ผ่ตทๅง็ฌฆๅทไธบๅคงๅ็น
\item LaTeX % ๆก็ฎ2๏ผ่ตทๅง็ฌฆๅทไธบๅคงๅ็น
\item[*] GitHub % ๆก็ฎ3๏ผ่ตทๅง็ฌฆๅทไธบๆๅท
\end{itemize}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.2ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_2.png" width="300" />
</p>
<center><b>ๅพ3.6.2</b> ็ผ่ฏๅๅ่กจ</center>
ๅฆๆๆณ่ฆๅฐๆๆๆก็ฎ็็ฌฆๅท้ฝ่ฟ่ก่ฐๆด๏ผๅนถ็ปไธไธบๆไธไธช็นๅฎ็ฌฆๅท๏ผๅๅฏไปฅไฝฟ็จ`\renewcommand`ๅฝไปค่ฟ่ก่ชๅฎไนใ
ใ**ไพ3**ใ่ชๅฎไนๆก็ฎ็่ตทๅง็ฌฆๅทไธบ้ป่ฒๆนๅ๏ผblack square๏ผใ
```tex
\documentclass[12pt]{article}
\usepackage{amssymb}
\begin{document}
\begin{itemize}
\renewcommand{\labelitemi}{\scriptsize$\blacksquare$}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.3ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_3.png" width="300" />
</p>
<center><b>ๅพ3.6.3</b> ็ผ่ฏๅๅ่กจ</center>
ๅ
ถไธญ๏ผๅฝไปค`\labelitemi`ๆฏ็ฑไธ้จๅ็ปๆ๏ผๅณ`label`๏ผๆ ็ญพ๏ผใ`item`๏ผๆก็ฎ๏ผใ`i`๏ผไธ็บง๏ผ๏ผๆๆถๅ๏ผๅฆๆ้่ฆๅๅปบๅค็บงๅ่กจ๏ผๅๅฏไปฅ็ฑปไผผ่ฟ้ไฝฟ็จๅฝไปค`\labelitemii`๏ผๅฏนๅบไบไบ็บงๅ่กจ๏ผ็่ณ`\labelitemiii`๏ผๅฏนๅบไบไธ็บงๅ่กจ๏ผใ
### 3.6.2 ๆๅบๅ่กจ
ๆๅบๅ่กจไน่ขซ็งฐไธบ็ผๅทๅ่กจใๅจๆๅบๅ่กจไธญ๏ผๆฏไธชๆก็ฎไนๅ้ฝๆไธไธชๆ ๅท๏ผๅฎๆฏ็ฑๆ ๅฟๅๅบๅทไธค้จๅ็ปๆ๏ผๅบๅท่ชไธ่ไธ๏ผไป1ๅผๅงๅๅบๆๅ๏ผๆ ๅฟๅฏไปฅๆฏๆฌๅทๆๅฐๅ็น็ญ็ฌฆๅทใ็ธไบไน้ดๆๅฏๅ็ๅ
ณ่๏ผ้ๅธธๆฏๆ่ฟ็จ้กบๅบๆๆฏ้่ฆ็จๅบฆๆๅ็ๆก็ฎ้ฝๅฏไปฅ้็จๆๅบๅ่กจ็ฏๅข็ผๅใๆๅบๅ่กจ็ฏๅข`enumerate`ไปฅๅบๅทไฝไธบๅ่กจ็่ตทๅงๆ ๅฟ๏ผๆฏไธชๆก็ฎๅฝไปคitemๅฐๅจๆฏไธชๆก็ฎไนๅ่ชๅจๅ ไธไธไธชๆ ๅทๆก็ฎๅฝไปค`item`็ๆ็้ป่ฎคๆ ๅทๆ ทๅผไธบ้ฟๆไผฏๆฐๅญๅ ๅฐๅ็นใ
ใ**ไพ4**ใๅๅปบไธไธช็ฎๅ็ๆๅบๅ่กจใ
```tex
\documentclass[12pt]{article}
\begin{document}
\begin{enumerate}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{enumerate}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.4ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_4.png" width="300" />
</p>
<center><b>ๅพ3.6.4</b> ็ผ่ฏๅๅ่กจ</center>
ๆๅบๅ่กจๅๆ ทๅฏไปฅ่ฟ่ก็ธไบๅตๅฅ๏ผๆๅคๅฏไปฅ่พพๅฐๅๅฑ๏ผไธบไบไพฟไบๅบๅ๏ผไธไป
ๆฏๅฑๅ่กจ็ๆก็ฎๆฎต่ฝ้ฝๆไธๅ็จๅบฆ็ๅทฆ็ผฉ่ฟ๏ผไบๆๆฏๅฑๅ่กจไธญๆก็ฎ็ๆ ๅทไนๅไธ็ธๅ๏ผๅ
ถไธญๅบๅท็่ฎกๆฐๅฝขๅผไธๆก็ฎๆๅจ็ๅฑๆฌกๆๅ
ณ๏ผๆ ๅฟๆ็จ็็ฌฆๅท้ค็ฌฌ2ๅฑๆฏๅๆฌๅทๅค๏ผๅ
ถไปๅๅฑ้ฝๆฏๅฐๅ็นใ
ใ**ไพ5**ใๅๅปบไธไธช็ฎๅ็ๅตๅฅ4ๅฑ็ๆๅบๅ่กจใ
```tex
\documentclass[12pt]{article}
\begin{document}
\begin{enumerate}
\item pencil
\item calculator
\item ruler
\item notebook
\begin{enumerate}
\item notes
\begin{enumerate}
\item note A
\begin{enumerate}
\item note a
\end{enumerate}
\item note B
\end{enumerate}
\item homework
\item assessments
\end{enumerate}
\end{enumerate}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.5ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_5.png" width="300" />
</p>
<center><b>ๅพ3.6.5</b> ็ผ่ฏๅๅ่กจ</center>
### 3.6.3 ้่ฟฐๆงๅ่กจ
็ธๆฏๆ ๅบๅ่กจๅๆๅบๅ่กจ๏ผ้่ฟฐๆงๅ่กจ็ไฝฟ็จ้ข็่พไฝ๏ผๅฎๅธธ็จไบๅฏนไธ็ปไธไธๆฏ่ฏญ่ฟ่ก่งฃ้่ฏดๆใ้่ฟฐๆงๅ่กจ็ฏๅขไธบ`description`ใๅจ`description`็ฏๅขๅฝไปคไธญ๏ผๆฏไธช่ฏๆก้ฝๆฏ้่ฆๅๅซ่ฟ่ก้่ฟฐ็่ฏ่ฏญ๏ผๆฏไธช้่ฟฐๅฏไปฅๆฏไธไธชๆๅคไธชๆๆฌๆฎต่ฝใ่ฟ็งๅฝขๅผๅพๅ่ฏๅ
ธ๏ผๅ ๆญค่ฏธๅฆๅ่ฏ่งฃ้่ฏดๆไน็ฑป็ๅ่กจๅฐฑๅฏไปฅ้็จ่งฃ่ฏดๅ่กจ็ฏๅขๆฅ็ผๅใๅจ้่ฟฐๆงๅ่กจ็ฏๅขไธญ๏ผ่ขซ่งฃ้็่ฏๆก็ๆ ผๅผๆฏ็จ`descriptionlabel`ๅฎไน็ใ
ใ**ไพ6**ใๅๅปบไธไธช็ฎๅ็้่ฟฐๆงๅ่กจใ
```tex
\documentclass[12pt]{article}
\begin{document}
\begin{description}
\item [CNN] Convolutional Neural Networks
\item [RNN] Recurrent Neural Network
\item [CRNN] Convolutional Recurrent Neural Network
\end{description}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.6ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_6.png" width="300" />
</p>
<center><b>ๅพ3.6.6</b> ็ผ่ฏๅๅ่กจ</center>
### 3.6.4 ่ชๅฎไนๅ่กจๆ ผๅผ
ไฝฟ็จ็ณป็ป้ป่ฎค็LaTeXๅ่กจ็ฏๅขๆ็็ๅ่กจไธไธไธๆไน้ดไปฅๅๅ่กจๆก็ฎไน้ด้ฝ้ๅ ๆไธๆฎตๅ็ด็ฉบ็ฝ๏ผๆๆพๆๅซไบๅ่กจ็ฏๅขไนๅค็ๆๆฌๆ ผๅผ๏ผ้ๅธธๅ่กจไธญ็ๆก็ฎๅ
ๅฎน้ฝๅพ็ฎ็ญ๏ผ่ฟๆ ทไผ้ ๆๅพๅค็ฉบ็ฝ๏ผไฝฟๅพๅ่กจ็่ตทๆฅๅพ็จ็๏ผไธๅๅๆๆฌไน้ด็ๅ่ฐๆง่พๅทฎใๅ ๆญค๏ผๆไปฌ้่ฆ่ชๅฎไนๅ่กจๆ ผๅผใไฝฟ็จ `enumitem`ๅฎๅ
ๅฏไปฅ่ฐๆด`enumerate`ๆ`itemize`็ไธไธๅทฆๅณ็ผฉ่ฟ้ด่ทใ
#### ๅ็ด้ด่ท
- `topsep` ๅ่กจ็ฏๅขไธไธๆไน้ด็่ท็ฆป
- `parsep` ๆก็ฎ้้ขๆฎต่ฝไน้ด็่ท็ฆป
- `itemsep` ๆก็ฎไน้ด็่ท็ฆป
- `partopsep` ๆก็ฎไธไธ้ขๆฎต่ฝ็่ท็ฆป
#### ๆฐดๅนณ้ด่ท
- `leftmargin` ๅ่กจ็ฏๅขๅทฆ่พน็็ฉบ็ฝ้ฟๅบฆ
- `rightmargin` ๅ่กจ็ฏๅขๅณ่พน็็ฉบ็ฝ้ฟๅบฆ
- `labelsep` ๆ ๅทไธๅ่กจ็ฏๅขๅทฆไพง็่ท็ฆป
- `itemindent` ๆก็ฎ็็ผฉ่ฟ่ท็ฆป
- `labelwidth` ๆ ๅท็ๅฎฝๅบฆ
- `listparindent` ๆก็ฎไธ้ขๆฎต่ฝ็็ผฉ่ฟ่ท็ฆป
ใ**ไพ7**ใไฝฟ็จ`enumitem`ๅฎๅ
ๅฏไปฅ่ฐๆดๆ ๅบๅ่กจ้ด่ทใ
```tex
\documentclass[12pt]{article}
\usepackage{enumitem}
\begin{document}
Default spacing:
\begin{itemize}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
Custom Spacing:
\begin{itemize}[itemsep= 15 pt,topsep = 20 pt]
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
```
็ผ่ฏไธ่ฟฐไปฃ็ ๏ผๅพๅฐๅ่กจๅฆๅพ3.6.7ๆ็คบใ
<p align="center">
<img align="middle" src="graphics/example3_6_7.png" width="300" />
</p>
<center><b>ๅพ3.6.7</b> ็ผ่ฏๅๅ่กจ</center>
ใๅๆพใ[**3.5 ็ผ่พๆๅญ**](https://nbviewer.jupyter.org/github/xinychen/latex-cookbook/blob/main/chapter-3/section5.ipynb)
ใ็ปง็ปญใ[**3.7 ๅๅปบ้กต็ใ้กต่ๅ่ๆณจ**](https://nbviewer.jupyter.org/github/xinychen/latex-cookbook/blob/main/chapter-3/section7.ipynb)
### License
<div class="alert alert-block alert-danger">
<b>This work is released under the MIT license.</b>
</div>
|
github_jupyter
|
\begin{itemize}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{itemize}
\begin{enumerate}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{enumerate}
\begin{description}
\item Item 1 % ๆก็ฎ1
\item Item 2 % ๆก็ฎ2
\end{description}
\documentclass[12pt]{article}
\begin{document}
\begin{itemize}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
\documentclass[12pt]{article}
\begin{document}
\begin{itemize}
\item Python % ๆก็ฎ1๏ผ่ตทๅง็ฌฆๅทไธบๅคงๅ็น
\item LaTeX % ๆก็ฎ2๏ผ่ตทๅง็ฌฆๅทไธบๅคงๅ็น
\item[*] GitHub % ๆก็ฎ3๏ผ่ตทๅง็ฌฆๅทไธบๆๅท
\end{itemize}
\end{document}
\documentclass[12pt]{article}
\usepackage{amssymb}
\begin{document}
\begin{itemize}
\renewcommand{\labelitemi}{\scriptsize$\blacksquare$}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
\documentclass[12pt]{article}
\begin{document}
\begin{enumerate}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{enumerate}
\end{document}
\documentclass[12pt]{article}
\begin{document}
\begin{enumerate}
\item pencil
\item calculator
\item ruler
\item notebook
\begin{enumerate}
\item notes
\begin{enumerate}
\item note A
\begin{enumerate}
\item note a
\end{enumerate}
\item note B
\end{enumerate}
\item homework
\item assessments
\end{enumerate}
\end{enumerate}
\end{document}
\documentclass[12pt]{article}
\begin{document}
\begin{description}
\item [CNN] Convolutional Neural Networks
\item [RNN] Recurrent Neural Network
\item [CRNN] Convolutional Recurrent Neural Network
\end{description}
\end{document}
\documentclass[12pt]{article}
\usepackage{enumitem}
\begin{document}
Default spacing:
\begin{itemize}
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
Custom Spacing:
\begin{itemize}[itemsep= 15 pt,topsep = 20 pt]
\item Python % ๆก็ฎ1
\item LaTeX % ๆก็ฎ2
\item GitHub % ๆก็ฎ3
\end{itemize}
\end{document}
| 0.382603 | 0.973544 |
# Speech Processing Labs: How to use these notebooks
This repository includes lab notebooks for the University of Edinburgh course: Speech Processing (LASC11158/LASC10061). This will contain notebooks with materials you should go through before meeting with your tutor. Some of them will have an interactive component that you can run directly in the notebook (i.e. [signals](./signals)), but most will require you to use some external tools (e.g. Praat for [phon](./phon), Festival for TTS, HTK for ASR).
## 1 Finding the notebooks
You can find the latest version of the notebooks in this [github](https://guides.github.com/activities/hello-world/) repository:
https://github.com/laic/uoe_speech_processing_course
These notebooks are [Jupyter notebooks](https://jupyter.org). These provide an interactive way to run python code and write nicely formatted text using [Markdown](https://www.markdownguide.org/cheat-sheet/). Once you've got your own copy of the notebooks you can use them to run the interactive bits and also make your own notes for your tutorials (or develop your own code if you like!)
The notebooks are available in a public repository so you don't need a github account to access it, but you might like to get one anyway.
## 2 Viewing the notebooks
You can view the notebooks directly via the github link above by just browsing through the links. However, this won't let you run the interactive bits or add your own notes, and probably won't let you directly play the audio links.
## 3 Getting your own copy
To get your own copy of the repository you will need to 'clone' it using git commands. How you do this will depend a little on how you want to run them. Here are the two main options.
### The Easy Online Way: Edina Noteable
University of Edinburgh students have access to [Edina Noteable](https://www.ed.ac.uk/information-services/learning-technology/noteable): the university's online Jupyter Notebook server.
This allows you to use Jupyter Notebooks, Python and all the extra packages we need through your browser (you don't need to install anything on your side).
You can find lots of information on how to use Edina Noteable (including some videos) [here](https://noteable.edina.ac.uk/user_guide/#hide_ge_2).
How to get these notebooks on Noteable:
* Start up Noteable by going to the following URL in your browser login in with your EASE username and password:
* https://noteable.edina.ac.uk/login
* Select Standard Notebook (if you're given an option) and click on the start button
* You'll then see the jupyter start directory, showing you links to the files in it (probably empty at this point).
* You can now import the notebook git repository by clicking the +GitRepo button and putting in the git repo address:
* https://github.com/laic/uoe_speech_processing_course
* After a bit of processing, you should now be able to see a link called `uoe_speech_processing_course`. If you click on this, you should see the notebooks.
* Click on a notebook (files ending with .ipynb) to start it!
<div class="alert alert-success" role="alert">
If your internet connection is fairly fast and stable, using Edina Noteable for this is probably your best option (just remember to save any changes you make to your notebooks often!).
</div>
#### Alternative: Using the Noteable terminal ####
Noteable also supports a unix terminal interface. If you're happy using the unix command line, you can click on the 'new' drop down menu (found to the right of the +GitRepo button) and start a new terminal instance.
You should then see a [unix shell](https://missing.csail.mit.edu/2020/course-shell/) interface in the browser. You could then, for example, use the git clone command to get the repo:
```
git clone https://github.com/laic/uoe_speech_processing_course
```
This isn't really necessary for our class work, but it may be useful thing for you to get familiar with in the future. For example, you'll need to use the terminal if you want to clone a private git repository. Once you've got the hang of it, it can also be a lot easier to use the terminal to do a lot of things, e.g. organize your files using shell commands.
<div class="alert alert-warning" role="alert">
If you're using Noteable, you might as well just use it through your normal computer browser (i.e. not through the virtual machine or guacamole!). It'll save your computer a little bit of work.
</div>
### The Normal Way: Running Jupyter Notebooks on your computer
You can also run Jupyter Notebooks locally on your own computer. Once you have everything installed, you should be able to go through all the lab materials offline. To do this, you'll need to have a few things installed:
* Python 3.x
* Jupyter notebook
* numpy
* matplotlib
If you already have Python 3 installed, you could just use `pip` to get the rest. But, I'd recommend using some version of anaconda (e.g. miniconda, the lightweight version of anaconda) because it will be useful for many other things later.
#### Install Python 3.8 and Miniconda
Download the Miniconda 3.8 installer. You'll need to choose the appropriate version for your operating system (Window, MacOs or Linux) and the number of bits your CPU uses (64 or 32).
* https://docs.conda.io/en/latest/miniconda.html
You can find installation instructions for different operating systems (e.g. Windows) here:
* https://conda.io/projects/conda/en/latest/user-guide/install/index.html
Here are the basic instructions for installing miniconda on the unix shell:
Once you've downloaded the installer, open up a terminal and go to the directory you installed it into (probably `Downloads`).
Run the following command to check the downloaded file isn't corrupted. You can check that the string it returns matches SHA256 hash listed next to the download link you used.
```
sha256sum ./Miniconda3-latest-Linux-x86_64.sh
```
Change the permissions on the Miniconda installer so you can run it ('u' for user, 'x' for execute):
```
chmod u+x ./Miniconda3-latest-Linux-x86_64.sh
```
And then run the installer script:
```
./Miniconda3-latest-Linux-x86_64.sh
```
The installer will ask you a bunch of questions (agree to the license etc) which you basically have to say yes to if you want to use Miniconda. You can also choose where it installs Miniconda, but usually the default location (in your home directory) is fine.
#### Create a conda environment
You'll then need to close and reopen your terminal. Now run the following command to create a new Python 3 environment called `slp` (actually you can call it whatever you want!).
```
conda create -n slp python=3
```
Now, activate the environment.
```
conda activate slp
```
Doing this basically means that you're telling the shell to use this version of python instead of the default version of python on your computer (For example, on Guacamole the default version of python is 2.7, which is a version of python no longer being maintained). Activating the environment also means you can download python packages in a systematic way and you (probably) won't run into permission problems on computers where you don't have administrator access.
In general, it's good practice you use python enviroments for your projects so that you can keep track of dependencies. New updates to python packages can sometimes mess up how old code works, so if you want someone else to run your code, having a specific conda environment means someone else (maybe even your future self?) can easily recreate the conditions in which your code was created on a different machine.
#### Install Jupyter Notebooks and other dependencies
Now we need can use conda to install a bunch of stuff, i.e. jupyter notebooks:
```
conda install -c conda-forge notebook numpy matplotlib ipython
```
Now we can finally startup jupyter notebooks! Note you need to be in the slp environment we just created for this to work (i.e. run `conda activate slp` before this).
```
jupyter notebook
```
This command starts a local notebook server and will give you a link to it. Open that link in your browser and you're all set!
Note: You'll need to get the notebook repository from github the 'normal way'. First, you'll need to [install git](https://git-scm.com/downloads). After that, go to the directory you want to download the notebooks into and run the following command:
```
git clone https://github.com/laic/uoe_speech_processing_course
```
You should now see a directory call `uoe_speech_processing_course` in the directory where you called the `git clone` command.
You can also potentially use a [github desktop user interface](https://desktop.github.com) to clone the repository.
<div class="alert alert-warning" role="alert">
The remote desktop service, Guacamole, uses python 2.7 by so you'll need to set up a python 3 enviroment to run these labs. <strong>But</strong>, as noted above, if you're ok working online you should probably just use the Edina Noteable servers!
</div>
#### Jupyter Notebooks official install info:
* https://jupyter.org/install
* https://jupyter.readthedocs.io/en/latest/running.html
### Downloading a zip file of the repo
You can also download the repository as zip file from the github page. However, we'd recommend you either use Edina Noteable or take a minute and figure out how to use the git clone command as this will make it easier to get an updates to the repository later.
## 4 Running the Notebooks in Interactive Mode
As mentioned above, once you've got your notebooks on Edina Noteable, clicking on an .ipynb file should start running it.
If want to run a notebook server locally on your own machine, you'll have to start it up on the command line:
```
jupyter notebook
```
Amongst the terminal output you should see a (localhost) link which you can then go to in your browser.
You can then navigate to the `uoe_speech_processing_course` directory from that browser page and start up a notebook.
### Some Very Basic Jupyter Notebook Commands
You definitely don't need to be a Jupyter expert to use these notebooks for this course. You basically just need to run every cell in turn! Here's the very bare bones of what you need to know.
#### Cells:
Jupyter notebooks have two types of cells:
* **Code cells:** i.e. code you can actually run
* **Markdown cells:** html-ish writing cells, where you can write your notes (like this one you're reading now).
* You can include various types of formatting: [Markdown reference](https://wordpress.com/support/markdown-quick-reference/)
* You can also write equations in [latex math mode](https://towardsdatascience.com/write-markdown-latex-in-the-jupyter-notebook-10985edb91fd)
After you've written something in a cell, you can run it by clicking the _Run_ button on the menu bar.
<div class="alert alert-warning" role="alert">
You don't have to run the cells in the order they appear on the page. When you run a code cell the variables set there will retain those values for the next cell you run. This means that variables are updated in the order that you run the cells, not necessarily the order they appear on the page!
</div>
#### Try it out!
If you're already in interactive mode (i.e. viewing this very jupyter notebook on a jupyter server rather than on github.com) you can try the following code cell:
* Click on the next cell
* Edit the python code to print out your own name instead of `YOUR_NAME_HERE`
* Press Shift-Enter to run the code
* You should see the output directly under the cell
```
print("Hello! My name is YOUR_NAME_HERE")
a = 793 ## This is a comment
b = 13 ## You could also change this value and see a change in the second sentence printed out
print("Did you know that %d + %d = %d?" % (a, b, a+b))
print("Did you know that {} + {} = {}?".format(a, b, a+b)) #python 3 format()
print(f"Did you know that {a} + {b} = {a+b}?") #python 3 f-string
```
Now, Run the next code cell a few times to to see that the value of the variable `a` gets updated every time you run the cell
```
a = a + b
print("Did you know that %d + %d = %d?" % (a, b, a+b))
```
* Double click on this _markdown_ cell to edit it!
* (**WRITE SOMETHING HERE**)
* Then press `Shift-Enter` to run the cell and finishing editing it!
### Basic keyboard shortcuts
As you go through a notebook, you'll probably soon find yourself wanting to use the keyboard shortcuts. Here are the most common ones:
* Click on a code cell to edit it
* Double click on a rendered Markdown cell to edit it
* `Ctrl-Enter`: Run the current cell (this is Cmd-Enter on a Mac)
* `Shift-Enter`: Run the current cell and move to the next
* Useful if you're moving through a notebook (which is what you'll likely be doing)
* `Alt-Enter`: Run the current cell and insert another after it
* Useful if you're writing a notebook!
If you click on the small keyboard icon on the menu bar (next to the cell type), you'll see many more command short cuts.
**Note**: You'll need to double click on a markdown cell to edit it (if it's already been run).
#### Try it out!
* Select one of the code cells above and type `shift-enter` on the keyboard to run that cell and move onto the next
* Select a cell above and type `alt-enter` to run the cell and add another (code) cell below it
* To delete an unwanted cell, first click outside of the code box or press the `Esc` key, and then press the `x` key (you can also press the `z` key to undo an action!)
```
#### Select this code cell and type 'Esc' then 'm' to turn it into a Markdown cell
#### Select this markdown cell and type 'Esc' then 'y' to turn it back into a code cell
```
### More on how to use Jupyter Notebooks
There are many tutorials about using Jupyter Notebooks on the internet. If you've never used them before, it's a good idea to go through at least one to get used to how they work.
* [A very quick overview from the Jupyter docs](https://nbviewer.jupyter.org/github/jupyter/notebook/blob/master/docs/source/examples/Notebook/Notebook%20Basics.ipynb)
* [An interactive tutorial from the Binder project that's made up of Jupyter notebooks](https://gke.mybinder.org/v2/gh/ipython/ipython-in-depth/master?filepath=binder/Index.ipynb)
* [Jupyter docs](https://jupyter-notebook.readthedocs.io/en/stable/notebook.html)
## 5 Updating the repository
If you've already cloned the repository somewhere, you can get the lastest version by going to the `uoe_speech_processing_course` directory in a terminal
and typing in the following command:
```
git pull
```
To update the repo in Edina Noteable you'll have to use the terminal interface.
<div class="alert alert-warning" role="alert">
This may cause merge conflicts (i.e., your version local clashes with the new version) if you've modified and saved the notebooks already (which you should be doing!). We'll try to avoid this by making sure we create notebooks with different names if we update one you might already have worked on. In practice, though, merging and resolving conflicts is a very normal thing in software engineering when you're working with other people. You can read more about updating repositories in the [github documentation](https://docs.github.com/en/github/using-git/getting-changes-from-a-remote-repository)
</div>
## 6 More info on git (and github)
Nowadays pretty much everyone uses git, often via github, for sharing and tracking code (i.e. version control). We won't really use it beyond hosting this repository in this course. However, knowing some basic git is really quite essential for working with code these days so it's worth spending some time learning a bit about this.
* [The github guide to git](https://guides.github.com/introduction/git-handbook/)
## 7 What should I do for tutorials/labs?
The goal of these labs is to get you to think through the concepts introduced in the lecture videos. The labs **aren't** about coding (that's what the CPSLP course is for). For notebooks that have python code included, you don't need to understand all the workings of the code and you definitely won't need to reproduce it. However, we do want you to get some exposure to how these abstract concepts get translated into concrete programming (and do something a bit interactive with the computer and each other!).
The main tasks for the labs are these:
* Go through the notebooks and discuss the answers to the questions with your tutorial group before meeting your tutor.
* Don't worry if you can't answer all the questions in the exercises - bring them to your tutor!
* Discuss what you've learned and share any questions that you may have with your tutor:
* Everyone in the group should take a turn leading this discussion with the tutor. Note this **doesn't** mean that person should do all the work for the week. That person should just be noting what the group did as a whole.
## 8 Help!
People taking this course come from lots of different backgrounds. If you run into trouble or this is all a bit much, ask for help! Your first port of all call should be the forum on the [speech zone website](http://speech.zone/courses/speech-processing/).
```
## A spare code cell!
```
|
github_jupyter
|
git clone https://github.com/laic/uoe_speech_processing_course
sha256sum ./Miniconda3-latest-Linux-x86_64.sh
chmod u+x ./Miniconda3-latest-Linux-x86_64.sh
./Miniconda3-latest-Linux-x86_64.sh
conda create -n slp python=3
conda activate slp
conda install -c conda-forge notebook numpy matplotlib ipython
jupyter notebook
git clone https://github.com/laic/uoe_speech_processing_course
jupyter notebook
print("Hello! My name is YOUR_NAME_HERE")
a = 793 ## This is a comment
b = 13 ## You could also change this value and see a change in the second sentence printed out
print("Did you know that %d + %d = %d?" % (a, b, a+b))
print("Did you know that {} + {} = {}?".format(a, b, a+b)) #python 3 format()
print(f"Did you know that {a} + {b} = {a+b}?") #python 3 f-string
a = a + b
print("Did you know that %d + %d = %d?" % (a, b, a+b))
#### Select this code cell and type 'Esc' then 'm' to turn it into a Markdown cell
#### Select this markdown cell and type 'Esc' then 'y' to turn it back into a code cell
git pull
## A spare code cell!
| 0.396302 | 0.953319 |
## CSCI-UA 9473 Final Assignment
Total: 55pts
### Muhammad Wajahat Mirza
### Part III. Reinforcement learning (10pts)
In this last exercise, we will tackle a simple reinforcement learning problem. Consider the map given below. There are 5 rooms + the garden. We would like to train an agent to get out of the house as quickly as possible. To set up the evironment, we will consider 6 possible state (the rooms in which the agent is located) and 6 possible actions (moving from one room to any other room).
The Q-table can thus be encoded by a $6$ by $6$ matrix. We will consider three types of rewards. Impossible moves (example 1 to 4) will be penalized by $1$. possible moves will be associated to a $0$ reward. Finally any move leading to an escape (e.g. 2 to 6) will be rewarded by 100.
```
from IPython.display import Image
Image('QLearningImage2.png',width=600,height=600)
```
## Question III.1 (5pts)
As a first approach, we will just run a couple of pure exploration iterations. Just fill out the loop below and run a couple of
## Solution
### Random Greedy Method: Brute Force
There was unclarity in the way Question was asked!
```
import numpy as np
import random
exit_moves = [(0,1),(4,3),(3,1),(2,5),(1,5)]
state, action = 6, 6
exit = 5
Curr_Room = 4
R = np.matrix(np.ones(shape=[state,action]))
R = R * -1
```
### Initiating R Matrix and Random Greedy Move Functions
```
def update_R(exit_moves,R):
for row in exit_moves:
R[row] = 0
if row[1] == exit:
R[row] = 100
row = row[::-1]
R[row] = 0
R[exit,exit] = 100
return R
R = update_R(exit_moves,R)
print("\nUpdated Reward Matrix with possible moves:\n",R)
def greedy_move(Curr_Room,R):
reward_state = R[Curr_Room,]
all_possible_act = np.where(R[Curr_Room,] >= 0)[1]
return all_possible_act
all_Moves = greedy_move(Curr_Room,R)
def rand_move(all_Moves):
curr_action = random.choice(all_Moves)
return curr_action
rand_action = rand_move(all_Moves)
```
### Iterative Brute Force Method. This part is executed 15 times to avoid runtime Error.
#### Room is chosen Randomly. It is part of random explorative technique
```
print("\nSince No exploitative Moves were made, some of the anticipated moves may not be correct!\n")
done = False
c = 0
while c < 10:
if Curr_Room != exit:
new_room = random.choice([0,1,2,3,4,5])
all_Moves = greedy_move(new_room,R)
rand_room = rand_move(all_Moves)
all_rooms_moves = [x+1 for x in all_Moves]
print("For Room {}, All possible moves are: {}\n".format(new_room+1, all_rooms_moves))
Curr_Room = rand_room
else:
new_room = random.choice([0,1,2,3,4,5])
Curr_Room = new_room
print("Exit Room has been chosen Randomly. Greedy program terminated. \n")
c+=1
print("\nBrute Force Greedy method Stopped!")
```
## Question III.2 (5pts)
Now that you can solve the greedy approach. We will start to exploit and we will do that through the use of a $Q$ table. In this case, as indicated in the statement of the exercise, the Q-table is 6x6. Train the agent by alternating between exploitation and exploration.
Since we want to update the $Q$-table, we will now add a line of the form
$$Q[s, a] \leftarrow (1-\alpha)Q[s,a] + \alpha\left(R[a] + \gamma\max_{a'}Q[s',a']\right)$$
When in the exploration framework, we will sample the action at random as in Question III.1. When in the exploitation framework however, we will simply choose the action as the one that maximizes the entry in the $Q$-table for the particular state at which we are. Hence we have $a^* = \underset{a}{\operatorname{argmax}} Q[s,a]$.
Code this epsilon-greedy approach below. You can start $\epsilon =0.8$
Take a sufficiently small learning rate (you can for example start with 0.5) and a relatively large discount factor $\gamma=0.9$ (You can later change those values to see how they affec the learning)
Once you are done with the algorithm, try a couple of different values for $\epsilon$ and describe the evolution in the learning.
## Solution
### Unlike Q III.1, this solution provides most accurate and efficient pathway for Quickest Exit
#### Import Required Libraries
```
import numpy as np
import random
```
#### All possible moves in the given house
```
exit_moves = [(0,1),(4,3),(3,1),(2,5),(1,5)]
act_num = ([(x[0]+1, x[1]+1) for x in exit_moves])
print("\nAll Possible moves that can be made for exit:\n",act_num,"\n")
state, action = 6, 6
exit = 5
```
### Initializing Reward Matrix with -1 Values
```
reward_mat = np.matrix(np.ones(shape=[state,action]))
reward_mat = reward_mat * -1
print("\nReward Matrix initialized with '-1'.\n\n",reward_mat)
```
### Updating Reward Matrix
If possible move == True:
update it to "2"
elif possible move == Exit:
update it to "100"
else:
keep it as "-1"
```
def update_reward(exit_moves,reward_mat):
for row in exit_moves:
reward_mat[row] = 0
if row[1] == exit:
reward_mat[row] = 100
row = row[::-1]
reward_mat[row] = 0
reward_mat[exit,exit] = 100
return reward_mat
reward_mat = update_reward(exit_moves,reward_mat)
print("\nUpdated Reward Matrix with possible moves:\n",reward_mat)
```
### Initializing Brain Matrix
This Matrix will be used to iterate through possible moves
```
brain_mat = np.matrix(np.zeros(shape=[state,action]))
print("\nThis is Brain Matrix:\n",brain_mat)
```
### Function Possible moves to get all possible actions
```
def possible_move(curr_state):
reward_state = reward_mat[curr_state,]
all_possible_act = np.where(reward_state >= 0)[1]
return all_possible_act
# ====================================================================================
# Put the any Room number here for training purposes
# ====================================================================================
room_train = 2
# ====================================================================================
# One is subtracted because all the rooms at the begining were '-1' for index purposes
curr_state = room_train - 1
# ====================================================================================
all_possible_act = possible_move(curr_state)
out_num = ([(x+1) for x in all_possible_act])
print("\nPossible moves from room {} are:\nRooms: {}".format(curr_state+1, out_num))
```
### From all the available moves, pick one randomly
```
def random_move(all_possible_act):
curr_action = random.choice(all_possible_act)
return curr_action
curr_action = random_move(all_possible_act)
print("\nThe random choice of move from room {} is {}\n".format(curr_state+1,curr_action +1))
```
### Updating our Q-Matrix or Brain Matrix
Use the following Equation for Update
$$Q[s, a] \leftarrow (1-\alpha)Q[s,a] + \alpha\left(R[a] + \gamma\max_{a'}Q[s',a']\right)$$
```
gamma = 0.8
alpha = 0.5
def brain_update(brain_mat,curr_state,curr_action,gamma,alpha):
max_brain = np.max(brain_mat[curr_action,])
first_term = (1-alpha)*(brain_mat[curr_state,curr_action])
second_term = alpha * (reward_mat[curr_state,curr_action] + gamma * max_brain)
brain_mat[curr_state,curr_action] = first_term + second_term
return brain_mat
brain_mat = brain_update(brain_mat,curr_state, curr_action, gamma,alpha)
```
### Train our Q-learning Model
```
def iter_brain_update(curr_state, all_possible_act, brain_mat, gamma,alpha):
rooms = [0,1,2,3,4,5]
for i in range(1,100,1):
new_curr_state = random.choice(rooms)
new_possible_moves = possible_move(new_curr_state)
new_random_move = random_move(new_possible_moves)
brain_mat = brain_update(brain_mat,new_curr_state, new_random_move, gamma,alpha)
brain_mat = brain_mat/np.max(brain_mat)*100
print("Brain Matrix after training: \n{}".format(brain_mat))
return brain_mat
brain_mat = iter_brain_update(curr_state, all_possible_act, brain_mat, gamma,alpha)
```
## Test our Model and Append Quickest Possible Routes for Exit
```
def test(curr_room,exit,brain_mat):
path = []
path.append(curr_room)
while curr_room != exit:
next_room = np.where(brain_mat[curr_room,] == np.max(brain_mat[curr_room,]))[1]
path.append(next_room[0])
if len(next_room) > 1:
next_room = random.choice(next_room)
else:
next_room = next_room
curr_room = next_room
return path
print("House Map")
Image('QLearningImage2.png',width=600,height=600)
# ====================================================================================
# Finding Quickest Paths from any Room to Room 6 which is Exit in this house
# ====================================================================================
all_room = [1,2,3,4,5,6]
for room in all_room:
path = test(room-1,exit,brain_mat)
path = [x+1 for x in path]
print("\nQuickest path from room {} to 'Room 6' is to follow rooms in this order: {}\n".format(path[0], path))
```
## End of Code For Reinforcement Learning
# End of Assignment
|
github_jupyter
|
from IPython.display import Image
Image('QLearningImage2.png',width=600,height=600)
import numpy as np
import random
exit_moves = [(0,1),(4,3),(3,1),(2,5),(1,5)]
state, action = 6, 6
exit = 5
Curr_Room = 4
R = np.matrix(np.ones(shape=[state,action]))
R = R * -1
def update_R(exit_moves,R):
for row in exit_moves:
R[row] = 0
if row[1] == exit:
R[row] = 100
row = row[::-1]
R[row] = 0
R[exit,exit] = 100
return R
R = update_R(exit_moves,R)
print("\nUpdated Reward Matrix with possible moves:\n",R)
def greedy_move(Curr_Room,R):
reward_state = R[Curr_Room,]
all_possible_act = np.where(R[Curr_Room,] >= 0)[1]
return all_possible_act
all_Moves = greedy_move(Curr_Room,R)
def rand_move(all_Moves):
curr_action = random.choice(all_Moves)
return curr_action
rand_action = rand_move(all_Moves)
print("\nSince No exploitative Moves were made, some of the anticipated moves may not be correct!\n")
done = False
c = 0
while c < 10:
if Curr_Room != exit:
new_room = random.choice([0,1,2,3,4,5])
all_Moves = greedy_move(new_room,R)
rand_room = rand_move(all_Moves)
all_rooms_moves = [x+1 for x in all_Moves]
print("For Room {}, All possible moves are: {}\n".format(new_room+1, all_rooms_moves))
Curr_Room = rand_room
else:
new_room = random.choice([0,1,2,3,4,5])
Curr_Room = new_room
print("Exit Room has been chosen Randomly. Greedy program terminated. \n")
c+=1
print("\nBrute Force Greedy method Stopped!")
import numpy as np
import random
exit_moves = [(0,1),(4,3),(3,1),(2,5),(1,5)]
act_num = ([(x[0]+1, x[1]+1) for x in exit_moves])
print("\nAll Possible moves that can be made for exit:\n",act_num,"\n")
state, action = 6, 6
exit = 5
reward_mat = np.matrix(np.ones(shape=[state,action]))
reward_mat = reward_mat * -1
print("\nReward Matrix initialized with '-1'.\n\n",reward_mat)
def update_reward(exit_moves,reward_mat):
for row in exit_moves:
reward_mat[row] = 0
if row[1] == exit:
reward_mat[row] = 100
row = row[::-1]
reward_mat[row] = 0
reward_mat[exit,exit] = 100
return reward_mat
reward_mat = update_reward(exit_moves,reward_mat)
print("\nUpdated Reward Matrix with possible moves:\n",reward_mat)
brain_mat = np.matrix(np.zeros(shape=[state,action]))
print("\nThis is Brain Matrix:\n",brain_mat)
def possible_move(curr_state):
reward_state = reward_mat[curr_state,]
all_possible_act = np.where(reward_state >= 0)[1]
return all_possible_act
# ====================================================================================
# Put the any Room number here for training purposes
# ====================================================================================
room_train = 2
# ====================================================================================
# One is subtracted because all the rooms at the begining were '-1' for index purposes
curr_state = room_train - 1
# ====================================================================================
all_possible_act = possible_move(curr_state)
out_num = ([(x+1) for x in all_possible_act])
print("\nPossible moves from room {} are:\nRooms: {}".format(curr_state+1, out_num))
def random_move(all_possible_act):
curr_action = random.choice(all_possible_act)
return curr_action
curr_action = random_move(all_possible_act)
print("\nThe random choice of move from room {} is {}\n".format(curr_state+1,curr_action +1))
gamma = 0.8
alpha = 0.5
def brain_update(brain_mat,curr_state,curr_action,gamma,alpha):
max_brain = np.max(brain_mat[curr_action,])
first_term = (1-alpha)*(brain_mat[curr_state,curr_action])
second_term = alpha * (reward_mat[curr_state,curr_action] + gamma * max_brain)
brain_mat[curr_state,curr_action] = first_term + second_term
return brain_mat
brain_mat = brain_update(brain_mat,curr_state, curr_action, gamma,alpha)
def iter_brain_update(curr_state, all_possible_act, brain_mat, gamma,alpha):
rooms = [0,1,2,3,4,5]
for i in range(1,100,1):
new_curr_state = random.choice(rooms)
new_possible_moves = possible_move(new_curr_state)
new_random_move = random_move(new_possible_moves)
brain_mat = brain_update(brain_mat,new_curr_state, new_random_move, gamma,alpha)
brain_mat = brain_mat/np.max(brain_mat)*100
print("Brain Matrix after training: \n{}".format(brain_mat))
return brain_mat
brain_mat = iter_brain_update(curr_state, all_possible_act, brain_mat, gamma,alpha)
def test(curr_room,exit,brain_mat):
path = []
path.append(curr_room)
while curr_room != exit:
next_room = np.where(brain_mat[curr_room,] == np.max(brain_mat[curr_room,]))[1]
path.append(next_room[0])
if len(next_room) > 1:
next_room = random.choice(next_room)
else:
next_room = next_room
curr_room = next_room
return path
print("House Map")
Image('QLearningImage2.png',width=600,height=600)
# ====================================================================================
# Finding Quickest Paths from any Room to Room 6 which is Exit in this house
# ====================================================================================
all_room = [1,2,3,4,5,6]
for room in all_room:
path = test(room-1,exit,brain_mat)
path = [x+1 for x in path]
print("\nQuickest path from room {} to 'Room 6' is to follow rooms in this order: {}\n".format(path[0], path))
| 0.293101 | 0.984426 |
# Implementing the `MiniBach` model
## Part 4: Generating an accompaniment for an arbitrary melody
In this step, we use the model trained on Part 3 to generate the three lower voices for a given soprano melodic line.
The model trained during Part 3 has been saved as `trained_model.h5`.
We can use this model to predict the accompaniment of an arbitrary melody.
```
import tensorflow as tf
from tensorflow import keras
import numpy as np
import pandas as pd
import music21
model = tf.keras.models.load_model('trained_model.h5')
```
This is a very rudimentary syntax for encoding our melody:
- Each token represents a sixteenth note
- The special token `--` denotes a *hold* symbol (in the generated scores, it becomes a tie)
- The pipe symbol `|` is just there for visual aid, separating blocks of four sixteenth notes (or one quarter note)
- The same can be said about the newlines, they separate the melody into four blocks (measures) with four quarter notes each
```
given_melody = '''
A4 -- -- -- |G#4 -- -- -- |A4 -- -- -- |F4 -- -- -- |
D4 -- -- -- |-- -- -- -- |D4 -- -- -- |-- -- -- -- |
E4 -- -- -- |F#4 -- -- -- |G#4 -- -- -- |A4 -- B4 -- |
C5 -- -- -- |C4 -- -- -- |E4 -- -- -- |-- -- -- -- |
'''
given_melody = given_melody.replace('\n', '').replace('|', '')
tokens = given_melody.split()
```
After organizing the tokens of the input melody, we need to encode it in a one-hot-encoded representation.
This process is fairly similar to how it was done in Part 2, so I won't describe it here.
```
SOPRANO_MIN = 57
SOPRANO_MAX = 81
ALTO_MIN = 52
ALTO_MAX = 74
TENOR_MIN = 48
TENOR_MAX = 69
BASS_MIN = 36
BASS_MAX = 64
ranges = {
'soprano': {midinumber: (midinumber - SOPRANO_MIN + 1) for midinumber in range(SOPRANO_MIN, SOPRANO_MAX + 1)},
'alto': {midinumber: (midinumber - ALTO_MIN + 1) for midinumber in range(ALTO_MIN, ALTO_MAX + 1)},
'tenor': {midinumber: (midinumber - TENOR_MIN + 1) for midinumber in range(TENOR_MIN, TENOR_MAX + 1)},
'bass': {midinumber: (midinumber - BASS_MIN + 1) for midinumber in range(BASS_MIN, BASS_MAX + 1)},
}
reverse_ranges = {
'soprano': {(midinumber - SOPRANO_MIN + 1): midinumber for midinumber in range(SOPRANO_MIN, SOPRANO_MAX + 1)},
'alto': {(midinumber - ALTO_MIN + 1): midinumber for midinumber in range(ALTO_MIN, ALTO_MAX + 1)},
'tenor': {(midinumber - TENOR_MIN + 1): midinumber for midinumber in range(TENOR_MIN, TENOR_MAX + 1)},
'bass': {(midinumber - BASS_MIN + 1): midinumber for midinumber in range(BASS_MIN, BASS_MAX + 1)},
}
def encode_note(n, rang):
if n == '--' or n == 'Rest':
ret = 0
else:
note = music21.note.Note(n)
ret = ranges[rang][note.pitch.midi]
return ret
def one_hot_encode(idx, rang):
length = len(ranges[rang].values())
ret = [0] * (length + 1)
ret[idx] = 1
return ret
s = [encode_note(n, 'soprano') for n in tokens]
x = np.array([[one_hot_encode(idx, 'soprano') for idx in s]])
x = x.reshape(1, -1)
```
The melody has been encoded, so we can pass it to the model and collect the predictions from the `MiniBach` model.
```
predictions = model.predict(x)
predictions = predictions.reshape(-1)
soprano = x.reshape(64, -1)
alto = predictions[:1536].reshape(64, -1)
tenor = predictions[1536:3008].reshape(64, -1)
bass = predictions[3008:4928].reshape(64, -1)
music = {
'soprano': soprano,
'alto': alto,
'tenor': tenor,
'bass': bass
}
def decode_note(n, rang):
if n == 0:
ret = '--'
else:
note = music21.note.Note(type='16th')
note.pitch.midi = reverse_ranges[rang][n]
ret = note
return ret
generation = {
'soprano': [],
'alto': [],
'tenor': [],
'bass': []
}
for sixteenth in range(64):
for part, notes in music.items():
this_note = decode_note(np.argmax(notes[sixteenth]), part)
if this_note == '--':
last_note = generation[part][-1]
this_note = music21.note.Note(last_note.pitch.nameWithOctave, type='16th')
if last_note.tie:
this_note.tie = music21.tie.Tie('continue')
else:
last_note.tie = music21.tie.Tie('start')
generation[part][-1] = last_note
this_note.tie = music21.tie.Tie('continue')
else:
if sixteenth > 0:
last_note = generation[part][-1]
if last_note.tie:
last_note.tie = music21.tie.Tie('stop')
generation[part].append(this_note)
```
The predictions have been generated, decoded, and turned into music notes with the `music21` library. We can give a glance to the 4-part choral (1 given soprano + 3 generated voices).
```
df = pd.DataFrame(generation)
df
```
In order to play the score, I use `music21` to generate an output `MusicXML` file.
```
s = music21.stream.Stream()
s.append(df.soprano.to_list())
a = music21.stream.Stream()
a.append(df.alto.to_list())
t = music21.stream.Stream()
t.append(df.tenor.to_list())
b = music21.stream.Stream()
b.append(df.bass.to_list())
stream = music21.stream.Stream([s,a,t,b])
stream.write('musicxml', 'generated_choral.musicxml')
```
And that's it, a generated choral using the `MiniBach` model.
The `MusicXML` file can be played using a music notation software like MuseScore, Sibelius, Finale, or Dorico.
An alternative option is to export it as `midi`, although midi-generated scores are oftentimes weird looking!
Thanks for checking, and please refer to the original book that describes the `MiniBach` architecture for more details:
> Briot, Jean-Pierre, Gaรซtan Hadjeres, and Franรงois Pachet. 2017. โDeep Learning Techniques for Music Generation - A Survey.โ CoRR abs/1709.01620. http://arxiv.org/abs/1709.01620.
|
github_jupyter
|
import tensorflow as tf
from tensorflow import keras
import numpy as np
import pandas as pd
import music21
model = tf.keras.models.load_model('trained_model.h5')
given_melody = '''
A4 -- -- -- |G#4 -- -- -- |A4 -- -- -- |F4 -- -- -- |
D4 -- -- -- |-- -- -- -- |D4 -- -- -- |-- -- -- -- |
E4 -- -- -- |F#4 -- -- -- |G#4 -- -- -- |A4 -- B4 -- |
C5 -- -- -- |C4 -- -- -- |E4 -- -- -- |-- -- -- -- |
'''
given_melody = given_melody.replace('\n', '').replace('|', '')
tokens = given_melody.split()
SOPRANO_MIN = 57
SOPRANO_MAX = 81
ALTO_MIN = 52
ALTO_MAX = 74
TENOR_MIN = 48
TENOR_MAX = 69
BASS_MIN = 36
BASS_MAX = 64
ranges = {
'soprano': {midinumber: (midinumber - SOPRANO_MIN + 1) for midinumber in range(SOPRANO_MIN, SOPRANO_MAX + 1)},
'alto': {midinumber: (midinumber - ALTO_MIN + 1) for midinumber in range(ALTO_MIN, ALTO_MAX + 1)},
'tenor': {midinumber: (midinumber - TENOR_MIN + 1) for midinumber in range(TENOR_MIN, TENOR_MAX + 1)},
'bass': {midinumber: (midinumber - BASS_MIN + 1) for midinumber in range(BASS_MIN, BASS_MAX + 1)},
}
reverse_ranges = {
'soprano': {(midinumber - SOPRANO_MIN + 1): midinumber for midinumber in range(SOPRANO_MIN, SOPRANO_MAX + 1)},
'alto': {(midinumber - ALTO_MIN + 1): midinumber for midinumber in range(ALTO_MIN, ALTO_MAX + 1)},
'tenor': {(midinumber - TENOR_MIN + 1): midinumber for midinumber in range(TENOR_MIN, TENOR_MAX + 1)},
'bass': {(midinumber - BASS_MIN + 1): midinumber for midinumber in range(BASS_MIN, BASS_MAX + 1)},
}
def encode_note(n, rang):
if n == '--' or n == 'Rest':
ret = 0
else:
note = music21.note.Note(n)
ret = ranges[rang][note.pitch.midi]
return ret
def one_hot_encode(idx, rang):
length = len(ranges[rang].values())
ret = [0] * (length + 1)
ret[idx] = 1
return ret
s = [encode_note(n, 'soprano') for n in tokens]
x = np.array([[one_hot_encode(idx, 'soprano') for idx in s]])
x = x.reshape(1, -1)
predictions = model.predict(x)
predictions = predictions.reshape(-1)
soprano = x.reshape(64, -1)
alto = predictions[:1536].reshape(64, -1)
tenor = predictions[1536:3008].reshape(64, -1)
bass = predictions[3008:4928].reshape(64, -1)
music = {
'soprano': soprano,
'alto': alto,
'tenor': tenor,
'bass': bass
}
def decode_note(n, rang):
if n == 0:
ret = '--'
else:
note = music21.note.Note(type='16th')
note.pitch.midi = reverse_ranges[rang][n]
ret = note
return ret
generation = {
'soprano': [],
'alto': [],
'tenor': [],
'bass': []
}
for sixteenth in range(64):
for part, notes in music.items():
this_note = decode_note(np.argmax(notes[sixteenth]), part)
if this_note == '--':
last_note = generation[part][-1]
this_note = music21.note.Note(last_note.pitch.nameWithOctave, type='16th')
if last_note.tie:
this_note.tie = music21.tie.Tie('continue')
else:
last_note.tie = music21.tie.Tie('start')
generation[part][-1] = last_note
this_note.tie = music21.tie.Tie('continue')
else:
if sixteenth > 0:
last_note = generation[part][-1]
if last_note.tie:
last_note.tie = music21.tie.Tie('stop')
generation[part].append(this_note)
df = pd.DataFrame(generation)
df
s = music21.stream.Stream()
s.append(df.soprano.to_list())
a = music21.stream.Stream()
a.append(df.alto.to_list())
t = music21.stream.Stream()
t.append(df.tenor.to_list())
b = music21.stream.Stream()
b.append(df.bass.to_list())
stream = music21.stream.Stream([s,a,t,b])
stream.write('musicxml', 'generated_choral.musicxml')
| 0.424651 | 0.89566 |
```
import pandas as pd
import numpy as np
WEAPON_COLUMNS = ['A1-weapon', 'A2-weapon', 'A3-weapon', 'A4-weapon', 'B1-weapon', 'B2-weapon', 'B3-weapon', 'B4-weapon']
RANK_COLUMNS = ['A1-rank', 'A2-rank', 'A3-rank', 'A4-rank', 'B1-rank', 'B2-rank', 'B3-rank', 'B4-rank']
LEVEL_COLUMNS = ['A1-level', 'A2-level', 'A3-level', 'A4-level', 'B1-level', 'B2-level', 'B3-level', 'B4-level']
train_data = pd.read_csv("data/train_data.csv", index_col="id")
test_data = pd.read_csv("data/test_data.csv", index_col="id")
train_data
```
## ๆฌ ๆๅค่ฃๅฎ
```
def complete(data):
for col_name in WEAPON_COLUMNS:
data[col_name] = data[col_name].fillna('NULL')
for col_name in LEVEL_COLUMNS:
data[col_name] = data[col_name].fillna(0)
for col_name in RANK_COLUMNS:
data[col_name] = data[col_name].fillna('n')
complete(train_data)
complete(test_data)
```
## ใจใณใณใผใใผ
```
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelBinarizer
train_data["mode"].unique().reshape(-1, 1)
```
### Mode
```
# TODO: sparseใTrueใซใใ๏ผ
mode_encoder = LabelBinarizer()
mode_encoder.fit(train_data["mode"].unique())
def make_mode(data):
return pd.DataFrame(mode_encoder.transform(data), columns=mode_encoder.classes_)
```
### Stage
```
stage_encoder = LabelBinarizer()
stage_encoder.fit(train_data["stage"].unique())
def make_stage(data):
return pd.DataFrame(stage_encoder.transform(data), columns=stage_encoder.classes_)
make_stage(train_data["stage"])
```
### Weapon
ๅ
จ้จใง140็จฎ้ก๏ผ
```
weapon_encoder = LabelBinarizer()
all_weapons = pd.concat([train_data[x] for x in WEAPON_COLUMNS]).dropna().unique()
weapon_encoder.fit(all_weapons)
def make_weapon(data):
return pd.DataFrame(weapon_encoder.transform(data), columns=weapon_encoder.classes_)
```
### Rank
ๆๅใงๆฑบใใฆใใพใ
```
# TODO: ๆ่ฆใงๆฐๅญใคใใฆใใ
rank_map = {'n': 0, 'c-': 1, 'c': 2, 'c+': 3, 'b-': 4, 'b': 5, 'b+': 6, 'a-': 7, 'a': 8, 'a+': 9, 's': 10, 's+': 11, 'x': 12}
def encode_rank(rank):
try:
return rank_map[rank]
except KeyError:
return 0
```
## ๆจๆบๅ
### Level
```
from sklearn.preprocessing import StandardScaler
level_scaler = StandardScaler()
levels = np.concatenate([train_data[x].values for x in LEVEL_COLUMNS], axis=0).reshape(-1, 1)
level_scaler.fit(levels)
level_scaler.transform([[200]])
```
### Rank
```
rank_scaler = StandardScaler()
rank_mapper = np.vectorize(encode_rank)
rank_scaler = rank_scaler.fit(rank_mapper(np.concatenate([train_data[x].values for x in RANK_COLUMNS], axis=0)).reshape(-1, 1))
rank_scaler.transform([[21]])
```
## ใใผใฟไฝๆ
```
# nawabariใจใใๆๅคใง้ใๅค
def make_weapon_bias(data, player):
weapon_col = player + '-weapon'
level_col = player + '-level'
rank_col = player + '-rank'
weapon_data = make_weapon(data[weapon_col])
# nawabariใชใ1,ใใๆๅคใฏ0
nawabari_data = np.where(data['mode'] == 'nawabari', 1, 0).reshape(-1, 1)
level_data = level_scaler.transform(data[level_col].values.reshape(-1, 1)) * nawabari_data
# nawabariใชใ0,ใใๆๅคใฏ1
nawabari_inv_data = nawabari_data * -1 + 1
rank_data = rank_scaler.transform(rank_mapper(data['A1-rank']).reshape(-1, 1)) * nawabari_inv_data
weapon_data = weapon_data.values * (level_data + rank_data)
return pd.DataFrame(weapon_data, columns=weapon_encoder.classes_)
make_weapon_bias(train_data[0:3], 'A1')
rank_scaler.transform(rank_mapper(train_data['A1-rank']).reshape(-1, 1))
def make_data(data, with_y=False):
mode_data = make_mode(data['mode'])
stage_data = make_stage(data['stage'])
a_data = make_weapon_bias(data, 'A1') + make_weapon_bias(data, 'A2') + make_weapon_bias(data, 'A3') + make_weapon_bias(data, 'A4')
b_data = make_weapon_bias(data, 'B1') + make_weapon_bias(data, 'B2') + make_weapon_bias(data, 'B3') + make_weapon_bias(data, 'B4')
X = pd.concat([mode_data, stage_data, a_data, b_data], axis=1)
if with_y:
y = data['y']
return X, y
return X
train_X, train_y = make_data(train_data, with_y=True)
test_X = make_data(test_data)
test_X.head()
train_X.shape
```
## ๅญฆ็ฟ
```
import tensorflow as tf
from tensorflow import keras
model = keras.Sequential([
keras.layers.Dense(256, activation='relu', input_shape=(train_X.shape[1],)),
keras.layers.Dropout(0.2),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dropout(0.2),
keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(train_X, train_y, batch_size=128, epochs=10, verbose=1)
train_pred_proba = model.predict(train_X)
train_pred_proba
train_pred = np.where(train_pred_proba > 0.5, 1, 0)
from sklearn.metrics import accuracy_score
accuracy_score(train_y, train_pred)
```
## ใในใ
```
test_X
from datetime import datetime
test_pred_proba = model.predict(test_X)
test_pred_proba
test_pred = np.where(test_pred_proba > 0.5, 1, 0)
np.count_nonzero(np.isnan(test_pred_proba))
test_pred
submit_df = pd.DataFrame(test_pred, columns=['y'])
submit_df.index.name = 'id'
submit_df
now = datetime.now()
submit_df.to_csv('submission_{}.csv'.format(now.strftime("%Y%m%d_%H%M%S")))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
WEAPON_COLUMNS = ['A1-weapon', 'A2-weapon', 'A3-weapon', 'A4-weapon', 'B1-weapon', 'B2-weapon', 'B3-weapon', 'B4-weapon']
RANK_COLUMNS = ['A1-rank', 'A2-rank', 'A3-rank', 'A4-rank', 'B1-rank', 'B2-rank', 'B3-rank', 'B4-rank']
LEVEL_COLUMNS = ['A1-level', 'A2-level', 'A3-level', 'A4-level', 'B1-level', 'B2-level', 'B3-level', 'B4-level']
train_data = pd.read_csv("data/train_data.csv", index_col="id")
test_data = pd.read_csv("data/test_data.csv", index_col="id")
train_data
def complete(data):
for col_name in WEAPON_COLUMNS:
data[col_name] = data[col_name].fillna('NULL')
for col_name in LEVEL_COLUMNS:
data[col_name] = data[col_name].fillna(0)
for col_name in RANK_COLUMNS:
data[col_name] = data[col_name].fillna('n')
complete(train_data)
complete(test_data)
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelBinarizer
train_data["mode"].unique().reshape(-1, 1)
# TODO: sparseใTrueใซใใ๏ผ
mode_encoder = LabelBinarizer()
mode_encoder.fit(train_data["mode"].unique())
def make_mode(data):
return pd.DataFrame(mode_encoder.transform(data), columns=mode_encoder.classes_)
stage_encoder = LabelBinarizer()
stage_encoder.fit(train_data["stage"].unique())
def make_stage(data):
return pd.DataFrame(stage_encoder.transform(data), columns=stage_encoder.classes_)
make_stage(train_data["stage"])
weapon_encoder = LabelBinarizer()
all_weapons = pd.concat([train_data[x] for x in WEAPON_COLUMNS]).dropna().unique()
weapon_encoder.fit(all_weapons)
def make_weapon(data):
return pd.DataFrame(weapon_encoder.transform(data), columns=weapon_encoder.classes_)
# TODO: ๆ่ฆใงๆฐๅญใคใใฆใใ
rank_map = {'n': 0, 'c-': 1, 'c': 2, 'c+': 3, 'b-': 4, 'b': 5, 'b+': 6, 'a-': 7, 'a': 8, 'a+': 9, 's': 10, 's+': 11, 'x': 12}
def encode_rank(rank):
try:
return rank_map[rank]
except KeyError:
return 0
from sklearn.preprocessing import StandardScaler
level_scaler = StandardScaler()
levels = np.concatenate([train_data[x].values for x in LEVEL_COLUMNS], axis=0).reshape(-1, 1)
level_scaler.fit(levels)
level_scaler.transform([[200]])
rank_scaler = StandardScaler()
rank_mapper = np.vectorize(encode_rank)
rank_scaler = rank_scaler.fit(rank_mapper(np.concatenate([train_data[x].values for x in RANK_COLUMNS], axis=0)).reshape(-1, 1))
rank_scaler.transform([[21]])
# nawabariใจใใๆๅคใง้ใๅค
def make_weapon_bias(data, player):
weapon_col = player + '-weapon'
level_col = player + '-level'
rank_col = player + '-rank'
weapon_data = make_weapon(data[weapon_col])
# nawabariใชใ1,ใใๆๅคใฏ0
nawabari_data = np.where(data['mode'] == 'nawabari', 1, 0).reshape(-1, 1)
level_data = level_scaler.transform(data[level_col].values.reshape(-1, 1)) * nawabari_data
# nawabariใชใ0,ใใๆๅคใฏ1
nawabari_inv_data = nawabari_data * -1 + 1
rank_data = rank_scaler.transform(rank_mapper(data['A1-rank']).reshape(-1, 1)) * nawabari_inv_data
weapon_data = weapon_data.values * (level_data + rank_data)
return pd.DataFrame(weapon_data, columns=weapon_encoder.classes_)
make_weapon_bias(train_data[0:3], 'A1')
rank_scaler.transform(rank_mapper(train_data['A1-rank']).reshape(-1, 1))
def make_data(data, with_y=False):
mode_data = make_mode(data['mode'])
stage_data = make_stage(data['stage'])
a_data = make_weapon_bias(data, 'A1') + make_weapon_bias(data, 'A2') + make_weapon_bias(data, 'A3') + make_weapon_bias(data, 'A4')
b_data = make_weapon_bias(data, 'B1') + make_weapon_bias(data, 'B2') + make_weapon_bias(data, 'B3') + make_weapon_bias(data, 'B4')
X = pd.concat([mode_data, stage_data, a_data, b_data], axis=1)
if with_y:
y = data['y']
return X, y
return X
train_X, train_y = make_data(train_data, with_y=True)
test_X = make_data(test_data)
test_X.head()
train_X.shape
import tensorflow as tf
from tensorflow import keras
model = keras.Sequential([
keras.layers.Dense(256, activation='relu', input_shape=(train_X.shape[1],)),
keras.layers.Dropout(0.2),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dropout(0.2),
keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(train_X, train_y, batch_size=128, epochs=10, verbose=1)
train_pred_proba = model.predict(train_X)
train_pred_proba
train_pred = np.where(train_pred_proba > 0.5, 1, 0)
from sklearn.metrics import accuracy_score
accuracy_score(train_y, train_pred)
test_X
from datetime import datetime
test_pred_proba = model.predict(test_X)
test_pred_proba
test_pred = np.where(test_pred_proba > 0.5, 1, 0)
np.count_nonzero(np.isnan(test_pred_proba))
test_pred
submit_df = pd.DataFrame(test_pred, columns=['y'])
submit_df.index.name = 'id'
submit_df
now = datetime.now()
submit_df.to_csv('submission_{}.csv'.format(now.strftime("%Y%m%d_%H%M%S")))
| 0.404037 | 0.723016 |
```
%load_ext autoreload
%autoreload 2
db_file = "../data/users.json"
output_file = "../data/contacts.csv"
max_codeplug = 200000
import json
import io
import pandas as pd
import csv
users = json.load(open(db_file))
users_buffer = io.StringIO(json.dumps(users.get("users")))
all_users = pd.read_json(users_buffer, orient="records")
all_users['country_index'] = all_users['country'].str.lower()
all_users['city_index'] = all_users['city'].str.lower()
all_users
all_users = all_users.sort_values(by=["country_index", "radio_id"], ascending=[True, False])
all_users
callsign_per_country = all_users.groupby(by=["country_index"])["radio_id"].agg(["count"]).sort_values(by="count", ascending=False)
callsign_per_country
callsign_per_country["cumsum"] = callsign_per_country["count"].cumsum()
callsign_per_country
most_callsigns_per_country = callsign_per_country.query(f"cumsum <= {max_codeplug}")
most_callsigns_per_country = most_callsigns_per_country.reset_index()
most_callsigns_per_country
least_callsigns_per_country = callsign_per_country.query(f"cumsum > {max_codeplug}")
least_callsigns_per_country
all_merged_users = all_users.merge(callsign_per_country, how="outer", on=["country_index"], indicator=True)
potential_codeplug_users = all_merged_users.query("_merge == 'both'").drop(columns=["_merge"])
extra_users = all_merged_users.query("_merge == 'left_only'").drop(columns=["_merge"])
codeplug_users = potential_codeplug_users.query(f"cumsum <= {max_codeplug}")
codeplug_users
delta_max = max_codeplug - len(codeplug_users)
delta_max
extra_cp_users = potential_codeplug_users.query(f"cumsum > {max_codeplug}").sort_values(by=["count", "radio_id"], ascending=[False, False])
extra_cp_users = extra_cp_users.head(delta_max)
codeplug_users = pd.concat([codeplug_users, extra_cp_users], ignore_index=True)
codeplug_users
codeplug_users = codeplug_users.drop(columns=["country_index", "city_index", "count", "cumsum", "id"])
def join_name(u: pd.Series) -> str:
if str(u.fname).endswith(u.surname) or u.surname is None or u.surname.strip().lower() in ["", "none"]:
return u.fname
else:
return f"{u.fname} {u.surname}"
codeplug_users['full name'] = codeplug_users.apply(join_name, axis='columns')
codeplug_users
codeplug_users["radio_id_idx"] = codeplug_users["radio_id"].astype(int)
codeplug_users = codeplug_users.sort_values(by="radio_id_idx").drop(columns=["radio_id_idx"])
fullname = False
if fullname:
codeplug_users = codeplug_users[["radio_id", "callsign", "Name", "city", "state", "country", "remarks"]]
colnames = {
'radio_id': "Radio ID",
'callsign': "Callsign",
'city': "City",
'state': "State",
'country': "Country",
'remarks': "Remarks"
}
else:
codeplug_users = codeplug_users[["radio_id", "callsign", "fname", "surname", "city", "state", "country"]]
colnames = {
'radio_id': "Radio ID",
'callsign': "Callsign",
'fname': "Name",
'surname': "City",
'city': "State",
'state': "Country",
'country': "Remarks"
}
codeplug_users = codeplug_users.rename(columns=colnames)
codeplug_users
codeplug_users['No.'] = (codeplug_users.reset_index(drop=True).index + 1).to_list()
codeplug_users
column_order = ["No.","Radio ID","Callsign","Name","City","State","Country","Remarks", "Call Type", "Call Alert"]
codeplug_users.loc[:, "Call Type"] = "Private Call"
codeplug_users.loc[:, "Call Alert"] = "None"
codeplug_users[column_order].to_csv(output_file,
index=None, quoting=csv.QUOTE_ALL, line_terminator='\r\n')
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
db_file = "../data/users.json"
output_file = "../data/contacts.csv"
max_codeplug = 200000
import json
import io
import pandas as pd
import csv
users = json.load(open(db_file))
users_buffer = io.StringIO(json.dumps(users.get("users")))
all_users = pd.read_json(users_buffer, orient="records")
all_users['country_index'] = all_users['country'].str.lower()
all_users['city_index'] = all_users['city'].str.lower()
all_users
all_users = all_users.sort_values(by=["country_index", "radio_id"], ascending=[True, False])
all_users
callsign_per_country = all_users.groupby(by=["country_index"])["radio_id"].agg(["count"]).sort_values(by="count", ascending=False)
callsign_per_country
callsign_per_country["cumsum"] = callsign_per_country["count"].cumsum()
callsign_per_country
most_callsigns_per_country = callsign_per_country.query(f"cumsum <= {max_codeplug}")
most_callsigns_per_country = most_callsigns_per_country.reset_index()
most_callsigns_per_country
least_callsigns_per_country = callsign_per_country.query(f"cumsum > {max_codeplug}")
least_callsigns_per_country
all_merged_users = all_users.merge(callsign_per_country, how="outer", on=["country_index"], indicator=True)
potential_codeplug_users = all_merged_users.query("_merge == 'both'").drop(columns=["_merge"])
extra_users = all_merged_users.query("_merge == 'left_only'").drop(columns=["_merge"])
codeplug_users = potential_codeplug_users.query(f"cumsum <= {max_codeplug}")
codeplug_users
delta_max = max_codeplug - len(codeplug_users)
delta_max
extra_cp_users = potential_codeplug_users.query(f"cumsum > {max_codeplug}").sort_values(by=["count", "radio_id"], ascending=[False, False])
extra_cp_users = extra_cp_users.head(delta_max)
codeplug_users = pd.concat([codeplug_users, extra_cp_users], ignore_index=True)
codeplug_users
codeplug_users = codeplug_users.drop(columns=["country_index", "city_index", "count", "cumsum", "id"])
def join_name(u: pd.Series) -> str:
if str(u.fname).endswith(u.surname) or u.surname is None or u.surname.strip().lower() in ["", "none"]:
return u.fname
else:
return f"{u.fname} {u.surname}"
codeplug_users['full name'] = codeplug_users.apply(join_name, axis='columns')
codeplug_users
codeplug_users["radio_id_idx"] = codeplug_users["radio_id"].astype(int)
codeplug_users = codeplug_users.sort_values(by="radio_id_idx").drop(columns=["radio_id_idx"])
fullname = False
if fullname:
codeplug_users = codeplug_users[["radio_id", "callsign", "Name", "city", "state", "country", "remarks"]]
colnames = {
'radio_id': "Radio ID",
'callsign': "Callsign",
'city': "City",
'state': "State",
'country': "Country",
'remarks': "Remarks"
}
else:
codeplug_users = codeplug_users[["radio_id", "callsign", "fname", "surname", "city", "state", "country"]]
colnames = {
'radio_id': "Radio ID",
'callsign': "Callsign",
'fname': "Name",
'surname': "City",
'city': "State",
'state': "Country",
'country': "Remarks"
}
codeplug_users = codeplug_users.rename(columns=colnames)
codeplug_users
codeplug_users['No.'] = (codeplug_users.reset_index(drop=True).index + 1).to_list()
codeplug_users
column_order = ["No.","Radio ID","Callsign","Name","City","State","Country","Remarks", "Call Type", "Call Alert"]
codeplug_users.loc[:, "Call Type"] = "Private Call"
codeplug_users.loc[:, "Call Alert"] = "None"
codeplug_users[column_order].to_csv(output_file,
index=None, quoting=csv.QUOTE_ALL, line_terminator='\r\n')
| 0.254231 | 0.167661 |
# [`vtreat`](https://github.com/WinVector/pyvtreat) Nested Model Bias Warning
For quite a while we have been teaching estimating variable re-encodings on the exact same data they
are later *naively* using to train a model on leads to an undesirable nested model bias. The `vtreat`
package (both the [`R` version](https://github.com/WinVector/vtreat) and
[`Python` version](https://github.com/WinVector/pyvtreat)) both incorporate a cross-frame method
that allows one to use all the training data both to build learn variable re-encodings and to correctly train a subsequent model (for an example please see our recent [PyData LA talk](http://www.win-vector.com/blog/2019/12/pydata-los-angeles-2019-talk-preparing-messy-real-world-data-for-supervised-machine-learning/)).
The next version of `vtreat` will warn the user if they have improperly used the same data for both `vtreat` impact code inference and downstream modeling. So in addition to us warning you not to do this, the package now also checks and warns against this situation.
## Set up the Example
This example is copied from [some of our classification documentation](https://github.com/WinVector/pyvtreat/blob/master/Examples/Classification/Classification.md).
Load modules/packages.
```
import pkg_resources
import pandas
import numpy
import numpy.random
import vtreat
import vtreat.util
numpy.random.seed(2019)
```
Generate example data.
* `y` is a noisy sinusoidal function of the variable `x`
* `yc` is the output to be predicted: : whether `y` is > 0.5.
* Input `xc` is a categorical variable that represents a discretization of `y`, along some `NaN`s
* Input `x2` is a pure noise variable with no relationship to the output
```
def make_data(nrows):
d = pandas.DataFrame({'x': 5*numpy.random.normal(size=nrows)})
d['y'] = numpy.sin(d['x']) + 0.1*numpy.random.normal(size=nrows)
d.loc[numpy.arange(3, 10), 'x'] = numpy.nan # introduce a nan level
d['xc'] = ['level_' + str(5*numpy.round(yi/5, 1)) for yi in d['y']]
d['x2'] = numpy.random.normal(size=nrows)
d.loc[d['xc']=='level_-1.0', 'xc'] = numpy.nan # introduce a nan level
d['yc'] = d['y']>0.5
return d
training_data = make_data(500)
training_data.head()
outcome_name = 'yc' # outcome variable / column
outcome_target = True # value we consider positive
```
## Demonstrate the Warning
Now that we have the data, we want to treat it prior to modeling: we want training data where all the input variables are numeric and have no missing values or `NA`s.
First create the data treatment transform design object, in this case a treatment for a binomial classification problem.
We use the training data `training_data` to fit the transform and the return a treated training set: completely numeric, with no missing values.
```
treatment = vtreat.BinomialOutcomeTreatment(
outcome_name=outcome_name, # outcome variable
outcome_target=outcome_target, # outcome of interest
cols_to_copy=['y'], # columns to "carry along" but not treat as input variables
)
train_prepared = treatment.fit_transform(training_data, training_data['yc'])
```
`train_prepared` is prepared in the correct way to use the same training data for inferring the impact-coded variables, using `.fit_transform()` instead of `.fit().transform()`.
We prepare new test or application data as follows.
```
test_data = make_data(100)
test_prepared = treatment.transform(test_data)
```
The issue is: for training data we should not call `transform()`, but instead use the value returned by `.fit_transform()`.
The point is we should not do the following:
```
train_prepared_wrong = treatment.transform(training_data)
```
Notice we now get a warning that we should not have done this, and in doing so we may have a nested model bias data leak.
And that is the new nested model bias warning feature.
The `R`-version of this document can be found [here](https://github.com/WinVector/vtreat/blob/master/Examples/Classification/ClassificationWarningExample.md).
|
github_jupyter
|
import pkg_resources
import pandas
import numpy
import numpy.random
import vtreat
import vtreat.util
numpy.random.seed(2019)
def make_data(nrows):
d = pandas.DataFrame({'x': 5*numpy.random.normal(size=nrows)})
d['y'] = numpy.sin(d['x']) + 0.1*numpy.random.normal(size=nrows)
d.loc[numpy.arange(3, 10), 'x'] = numpy.nan # introduce a nan level
d['xc'] = ['level_' + str(5*numpy.round(yi/5, 1)) for yi in d['y']]
d['x2'] = numpy.random.normal(size=nrows)
d.loc[d['xc']=='level_-1.0', 'xc'] = numpy.nan # introduce a nan level
d['yc'] = d['y']>0.5
return d
training_data = make_data(500)
training_data.head()
outcome_name = 'yc' # outcome variable / column
outcome_target = True # value we consider positive
treatment = vtreat.BinomialOutcomeTreatment(
outcome_name=outcome_name, # outcome variable
outcome_target=outcome_target, # outcome of interest
cols_to_copy=['y'], # columns to "carry along" but not treat as input variables
)
train_prepared = treatment.fit_transform(training_data, training_data['yc'])
test_data = make_data(100)
test_prepared = treatment.transform(test_data)
train_prepared_wrong = treatment.transform(training_data)
| 0.234494 | 0.973139 |
Feature Engineering
```
import pandas as pd
import numpy as np
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from xgboost import XGBRegressor
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
scaler = preprocessing.StandardScaler()
xtrain[numerical_cols] = scaler.fit_transform(xtrain[numerical_cols])
xvalid[numerical_cols] = scaler.transform(xvalid[numerical_cols])
xtest[numerical_cols] = scaler.transform(xtest[numerical_cols])
model = XGBRegressor(
random_state=fold,
tree_method='gpu_hist',
gpu_id=0,
predictor="gpu_predictor"
)
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
for col in numerical_cols:
df[col] = np.log1p(df[col])
df_test[col] = np.log1p(df_test[col])
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(
random_state=fold,
tree_method='gpu_hist',
gpu_id=0,
predictor="gpu_predictor"
)
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
poly = preprocessing.PolynomialFeatures(degree=3, interaction_only=True, include_bias=False)
train_poly = poly.fit_transform(df[numerical_cols])
test_poly = poly.fit_transform(df_test[numerical_cols])
df_poly = pd.DataFrame(train_poly, columns=[f"poly_{i}" for i in range(train_poly.shape[1])])
df_test_poly = pd.DataFrame(test_poly, columns=[f"poly_{i}" for i in range(test_poly.shape[1])])
df = pd.concat([df, df_poly], axis=1)
df_test = pd.concat([df_test, df_test_poly], axis=1)
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ohe = preprocessing.OneHotEncoder(sparse=False, handle_unknown="ignore")
xtrain_ohe = ohe.fit_transform(xtrain[object_cols])
xvalid_ohe = ohe.transform(xvalid[object_cols])
xtest_ohe = ohe.transform(xtest[object_cols])
xtrain_ohe = pd.DataFrame(xtrain_ohe, columns=[f"ohe_{i}" for i in range(xtrain_ohe.shape[1])])
xvalid_ohe = pd.DataFrame(xvalid_ohe, columns=[f"ohe_{i}" for i in range(xvalid_ohe.shape[1])])
xtest_ohe = pd.DataFrame(xtest_ohe, columns=[f"ohe_{i}" for i in range(xtest_ohe.shape[1])])
xtrain = pd.concat([xtrain, xtrain_ohe], axis=1)
xvalid = pd.concat([xvalid, xvalid_ohe], axis=1)
xtest = pd.concat([xtest, xtest_ohe], axis=1)
# this part is missing in the video:
xtrain = xtrain.drop(object_cols, axis=1)
xvalid = xvalid.drop(object_cols, axis=1)
xtest = xtest.drop(object_cols, axis=1)
# missing part ends
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from xgboost import XGBRegressor
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
scaler = preprocessing.StandardScaler()
xtrain[numerical_cols] = scaler.fit_transform(xtrain[numerical_cols])
xvalid[numerical_cols] = scaler.transform(xvalid[numerical_cols])
xtest[numerical_cols] = scaler.transform(xtest[numerical_cols])
model = XGBRegressor(
random_state=fold,
tree_method='gpu_hist',
gpu_id=0,
predictor="gpu_predictor"
)
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
for col in numerical_cols:
df[col] = np.log1p(df[col])
df_test[col] = np.log1p(df_test[col])
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(
random_state=fold,
tree_method='gpu_hist',
gpu_id=0,
predictor="gpu_predictor"
)
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if col.startswith("cont")]
df_test = df_test[useful_features]
poly = preprocessing.PolynomialFeatures(degree=3, interaction_only=True, include_bias=False)
train_poly = poly.fit_transform(df[numerical_cols])
test_poly = poly.fit_transform(df_test[numerical_cols])
df_poly = pd.DataFrame(train_poly, columns=[f"poly_{i}" for i in range(train_poly.shape[1])])
df_test_poly = pd.DataFrame(test_poly, columns=[f"poly_{i}" for i in range(test_poly.shape[1])])
df = pd.concat([df, df_poly], axis=1)
df_test = pd.concat([df_test, df_test_poly], axis=1)
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = preprocessing.OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
df = pd.read_csv("../input/30days-folds/train_folds.csv")
df_test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
useful_features = [c for c in df.columns if c not in ("id", "target", "kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
df_test = df_test[useful_features]
final_predictions = []
scores = []
for fold in range(5):
xtrain = df[df.kfold != fold].reset_index(drop=True)
xvalid = df[df.kfold == fold].reset_index(drop=True)
xtest = df_test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ohe = preprocessing.OneHotEncoder(sparse=False, handle_unknown="ignore")
xtrain_ohe = ohe.fit_transform(xtrain[object_cols])
xvalid_ohe = ohe.transform(xvalid[object_cols])
xtest_ohe = ohe.transform(xtest[object_cols])
xtrain_ohe = pd.DataFrame(xtrain_ohe, columns=[f"ohe_{i}" for i in range(xtrain_ohe.shape[1])])
xvalid_ohe = pd.DataFrame(xvalid_ohe, columns=[f"ohe_{i}" for i in range(xvalid_ohe.shape[1])])
xtest_ohe = pd.DataFrame(xtest_ohe, columns=[f"ohe_{i}" for i in range(xtest_ohe.shape[1])])
xtrain = pd.concat([xtrain, xtrain_ohe], axis=1)
xvalid = pd.concat([xvalid, xvalid_ohe], axis=1)
xtest = pd.concat([xtest, xtest_ohe], axis=1)
# this part is missing in the video:
xtrain = xtrain.drop(object_cols, axis=1)
xvalid = xvalid.drop(object_cols, axis=1)
xtest = xtest.drop(object_cols, axis=1)
# missing part ends
model = XGBRegressor(random_state=fold, tree_method='gpu_hist', gpu_id=0, predictor="gpu_predictor")
model.fit(xtrain, ytrain)
preds_valid = model.predict(xvalid)
test_preds = model.predict(xtest)
final_predictions.append(test_preds)
rmse = mean_squared_error(yvalid, preds_valid, squared=False)
print(fold, rmse)
scores.append(rmse)
print(np.mean(scores), np.std(scores))
| 0.421314 | 0.470068 |
# Day and Night Image Classifier
---
The day/night image dataset consists of 200 RGB color images in two categories: day and night. There are equal numbers of each example: 100 day images and 100 night images.
We'd like to build a classifier that can accurately label these images as day or night, and that relies on finding distinguishing features between the two types of images!
*Note: All images come from the [AMOS dataset](http://cs.uky.edu/~jacobs/datasets/amos/) (Archive of Many Outdoor Scenes).*
### Import resources
Before you get started on the project code, import the libraries and resources that you'll need.
```
import cv2 # computer vision library
import helpers
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
```
## Training and Testing Data
The 200 day/night images are separated into training and testing datasets.
* 60% of these images are training images, for you to use as you create a classifier.
* 40% are test images, which will be used to test the accuracy of your classifier.
First, we set some variables to keep track of some where our images are stored:
image_dir_training: the directory where our training image data is stored
image_dir_test: the directory where our test image data is stored
```
# Image data directories
image_dir_training = "day_night_images/training/"
image_dir_test = "day_night_images/test/"
```
## Load the datasets
These first few lines of code will load the training day/night images and store all of them in a variable, `IMAGE_LIST`. This list contains the images and their associated label ("day" or "night").
For example, the first image-label pair in `IMAGE_LIST` can be accessed by index:
``` IMAGE_LIST[0][:]```.
```
# Using the load_dataset function in helpers.py
# Load training data
IMAGE_LIST = helpers.load_dataset(image_dir_training)
```
## Construct a `STANDARDIZED_LIST` of input images and output labels.
This function takes in a list of image-label pairs and outputs a **standardized** list of resized images and numerical labels.
```
# Standardize all training images
STANDARDIZED_LIST = helpers.standardize(IMAGE_LIST)
```
## Visualize the standardized data
Display a standardized image from STANDARDIZED_LIST.
```
# Display a standardized image and its label
# Select an image by index
image_num = 0
selected_image = STANDARDIZED_LIST[image_num][0]
selected_label = STANDARDIZED_LIST[image_num][1]
# Display image and data about it
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label [1 = day, 0 = night]: " + str(selected_label))
```
# Feature Extraction
Create a feature that represents the brightness in an image. We'll be extracting the **average brightness** using HSV colorspace. Specifically, we'll use the V channel (a measure of brightness), add up the pixel values in the V channel, then divide that sum by the area of the image to get the average Value of the image.
## RGB to HSV conversion
Below, a test image is converted from RGB to HSV colorspace and each component is displayed in an image.
```
# Convert and image to HSV colorspace
# Visualize the individual color channels
image_num = 0
test_im = STANDARDIZED_LIST[image_num][0]
test_label = STANDARDIZED_LIST[image_num][1]
# Convert to HSV
hsv = cv2.cvtColor(test_im, cv2.COLOR_RGB2HSV)
# Print image label
print('Label: ' + str(test_label))
# HSV channels
h = hsv[:,:,0]
s = hsv[:,:,1]
v = hsv[:,:,2]
# Plot the original image and the three channels
f, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(20,10))
ax1.set_title('Standardized image')
ax1.imshow(test_im)
ax2.set_title('H channel')
ax2.imshow(h, cmap='gray')
ax3.set_title('S channel')
ax3.imshow(s, cmap='gray')
ax4.set_title('V channel')
ax4.imshow(v, cmap='gray')
```
---
### Find the average brightness using the V channel
This function takes in a **standardized** RGB image and returns a feature (a single value) that represent the average level of brightness in the image. We'll use this value to classify the image as day or night.
```
# Find the average Value or brightness of an image
def avg_brightness(rgb_image):
# Convert image to HSV
hsv = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2HSV)
# Add up all the pixel values in the V channel
sum_brightness = np.sum(hsv[:,:,2])
## TODO: Calculate the average brightness using the area of the image
# and the sum calculated above
avg = sum_brightness/(rgb_image.shape[0]*rgb_image.shape[1])
return avg
# Testing average brightness levels
# Look at a number of different day and night images and think about
# what average brightness value separates the two types of images
# As an example, a "night" image is loaded in and its avg brightness is displayed
image_num = 190
test_im = STANDARDIZED_LIST[image_num][0]
avg = avg_brightness(test_im)
print('Avg brightness: ' + str(avg))
plt.imshow(test_im)
for img in range(len(STANDARDIZED_LIST)):
avg = avg_brightness(STANDARDIZED_LIST[img][0])
print(str(STANDARDIZED_LIST[img][1]) + " - " + str(avg))
```
|
github_jupyter
|
import cv2 # computer vision library
import helpers
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
# Image data directories
image_dir_training = "day_night_images/training/"
image_dir_test = "day_night_images/test/"
# Using the load_dataset function in helpers.py
# Load training data
IMAGE_LIST = helpers.load_dataset(image_dir_training)
# Standardize all training images
STANDARDIZED_LIST = helpers.standardize(IMAGE_LIST)
# Display a standardized image and its label
# Select an image by index
image_num = 0
selected_image = STANDARDIZED_LIST[image_num][0]
selected_label = STANDARDIZED_LIST[image_num][1]
# Display image and data about it
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label [1 = day, 0 = night]: " + str(selected_label))
# Convert and image to HSV colorspace
# Visualize the individual color channels
image_num = 0
test_im = STANDARDIZED_LIST[image_num][0]
test_label = STANDARDIZED_LIST[image_num][1]
# Convert to HSV
hsv = cv2.cvtColor(test_im, cv2.COLOR_RGB2HSV)
# Print image label
print('Label: ' + str(test_label))
# HSV channels
h = hsv[:,:,0]
s = hsv[:,:,1]
v = hsv[:,:,2]
# Plot the original image and the three channels
f, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(20,10))
ax1.set_title('Standardized image')
ax1.imshow(test_im)
ax2.set_title('H channel')
ax2.imshow(h, cmap='gray')
ax3.set_title('S channel')
ax3.imshow(s, cmap='gray')
ax4.set_title('V channel')
ax4.imshow(v, cmap='gray')
# Find the average Value or brightness of an image
def avg_brightness(rgb_image):
# Convert image to HSV
hsv = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2HSV)
# Add up all the pixel values in the V channel
sum_brightness = np.sum(hsv[:,:,2])
## TODO: Calculate the average brightness using the area of the image
# and the sum calculated above
avg = sum_brightness/(rgb_image.shape[0]*rgb_image.shape[1])
return avg
# Testing average brightness levels
# Look at a number of different day and night images and think about
# what average brightness value separates the two types of images
# As an example, a "night" image is loaded in and its avg brightness is displayed
image_num = 190
test_im = STANDARDIZED_LIST[image_num][0]
avg = avg_brightness(test_im)
print('Avg brightness: ' + str(avg))
plt.imshow(test_im)
for img in range(len(STANDARDIZED_LIST)):
avg = avg_brightness(STANDARDIZED_LIST[img][0])
print(str(STANDARDIZED_LIST[img][1]) + " - " + str(avg))
| 0.635562 | 0.991836 |
```
%matplotlib inline
```
Compute and Reduce with Tuple Inputs
=======================================
**Author**: `Ziheng Jiang <https://github.com/ZihengJiang>`_
Often we want to compute multiple outputs with the same shape within
a single loop or perform reduction that involves multiple values like
:code:`argmax`. These problems can be addressed by tuple inputs.
In this tutorial, we will introduce the usage of tuple inputs in TVM.
```
from __future__ import absolute_import, print_function
import tvm
from tvm import te
import numpy as np
```
Describe Batchwise Computation
------------------------------
For operators which have the same shape, we can put them together as
the inputs of :any:`te.compute`, if we want them to be scheduled
together in the next schedule procedure.
```
n = te.var("n")
m = te.var("m")
A0 = te.placeholder((m, n), name="A0")
A1 = te.placeholder((m, n), name="A1")
B0, B1 = te.compute((m, n), lambda i, j: (A0[i, j] + 2, A1[i, j] * 3), name="B")
# The generated IR code would be:
s = te.create_schedule(B0.op)
print(tvm.lower(s, [A0, A1, B0, B1], simple_mode=True))
```
Describe Reduction with Collaborative Inputs
--------------------------------------------
Sometimes, we require multiple inputs to express some reduction
operators, and the inputs will collaborate together, e.g. :code:`argmax`.
In the reduction procedure, :code:`argmax` need to compare the value of
operands, also need to keep the index of operand. It can be expressed
with :py:func:`te.comm_reducer` as below:
```
# x and y are the operands of reduction, both of them is a tuple of index
# and value.
def fcombine(x, y):
lhs = tvm.tir.Select((x[1] >= y[1]), x[0], y[0])
rhs = tvm.tir.Select((x[1] >= y[1]), x[1], y[1])
return lhs, rhs
# our identity element also need to be a tuple, so `fidentity` accepts
# two types as inputs.
def fidentity(t0, t1):
return tvm.tir.const(-1, t0), tvm.te.min_value(t1)
argmax = te.comm_reducer(fcombine, fidentity, name="argmax")
# describe the reduction computation
m = te.var("m")
n = te.var("n")
idx = te.placeholder((m, n), name="idx", dtype="int32")
val = te.placeholder((m, n), name="val", dtype="int32")
k = te.reduce_axis((0, n), "k")
T0, T1 = te.compute((m,), lambda i: argmax((idx[i, k], val[i, k]), axis=k), name="T")
# the generated IR code would be:
s = te.create_schedule(T0.op)
print(tvm.lower(s, [idx, val, T0, T1], simple_mode=True))
```
<div class="alert alert-info"><h4>Note</h4><p>For ones who are not familiar with reduction, please refer to
`general-reduction`.</p></div>
Schedule Operation with Tuple Inputs
------------------------------------
It is worth mentioning that although you will get multiple outputs
with one batch operation, but they can only be scheduled together
in terms of operation.
```
n = te.var("n")
m = te.var("m")
A0 = te.placeholder((m, n), name="A0")
B0, B1 = te.compute((m, n), lambda i, j: (A0[i, j] + 2, A0[i, j] * 3), name="B")
A1 = te.placeholder((m, n), name="A1")
C = te.compute((m, n), lambda i, j: A1[i, j] + B0[i, j], name="C")
s = te.create_schedule(C.op)
s[B0].compute_at(s[C], C.op.axis[0])
# as you can see in the below generated IR code:
print(tvm.lower(s, [A0, A1, C], simple_mode=True))
```
Summary
-------
This tutorial introduces the usage of tuple inputs operation.
- Describe normal batchwise computation.
- Describe reduction operation with tuple inputs.
- Notice that you can only schedule computation in terms of operation instead of tensor.
|
github_jupyter
|
%matplotlib inline
from __future__ import absolute_import, print_function
import tvm
from tvm import te
import numpy as np
n = te.var("n")
m = te.var("m")
A0 = te.placeholder((m, n), name="A0")
A1 = te.placeholder((m, n), name="A1")
B0, B1 = te.compute((m, n), lambda i, j: (A0[i, j] + 2, A1[i, j] * 3), name="B")
# The generated IR code would be:
s = te.create_schedule(B0.op)
print(tvm.lower(s, [A0, A1, B0, B1], simple_mode=True))
# x and y are the operands of reduction, both of them is a tuple of index
# and value.
def fcombine(x, y):
lhs = tvm.tir.Select((x[1] >= y[1]), x[0], y[0])
rhs = tvm.tir.Select((x[1] >= y[1]), x[1], y[1])
return lhs, rhs
# our identity element also need to be a tuple, so `fidentity` accepts
# two types as inputs.
def fidentity(t0, t1):
return tvm.tir.const(-1, t0), tvm.te.min_value(t1)
argmax = te.comm_reducer(fcombine, fidentity, name="argmax")
# describe the reduction computation
m = te.var("m")
n = te.var("n")
idx = te.placeholder((m, n), name="idx", dtype="int32")
val = te.placeholder((m, n), name="val", dtype="int32")
k = te.reduce_axis((0, n), "k")
T0, T1 = te.compute((m,), lambda i: argmax((idx[i, k], val[i, k]), axis=k), name="T")
# the generated IR code would be:
s = te.create_schedule(T0.op)
print(tvm.lower(s, [idx, val, T0, T1], simple_mode=True))
n = te.var("n")
m = te.var("m")
A0 = te.placeholder((m, n), name="A0")
B0, B1 = te.compute((m, n), lambda i, j: (A0[i, j] + 2, A0[i, j] * 3), name="B")
A1 = te.placeholder((m, n), name="A1")
C = te.compute((m, n), lambda i, j: A1[i, j] + B0[i, j], name="C")
s = te.create_schedule(C.op)
s[B0].compute_at(s[C], C.op.axis[0])
# as you can see in the below generated IR code:
print(tvm.lower(s, [A0, A1, C], simple_mode=True))
| 0.592431 | 0.951706 |
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from scripts_step_lr_schedulers import *
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
```
# Load data
```
# Unzip files
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_1.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_2.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_3.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_4.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_5.tar.gz
database_base_path = '/kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
'MAX_LEN': 96,
'BATCH_SIZE': 32,
'EPOCHS': 4,
'LEARNING_RATE': 3e-5,
'ES_PATIENCE': 4,
'N_FOLDS': 5,
"question_size": 4,
'base_model_path': base_path + 'roberta-base-tf_model.h5',
'config_path': base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
## Learning rate schedule
```
lr_min = 1e-6
lr_max = config['LEARNING_RATE']
train_size = len(k_fold[k_fold['fold_1'] == 'train'])
step_size = train_size // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
decay = .9985
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [exponential_schedule_with_warmup(tf.cast(x, tf.float32), warmup_steps=1, lr_start=lr_max, lr_max=lr_max, lr_min=lr_min, decay=decay) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.LSTM(128, return_sequences=True)(last_hidden_state)
x = layers.Dropout(.1)(x)
x_start = layers.TimeDistributed(layers.Dense(1))(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.TimeDistributed(layers.Dense(1))(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
```
# Train
```
AUTO = tf.data.experimental.AUTOTUNE
strategy = tf.distribute.get_strategy()
k_fold_best = k_fold.copy()
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid.shape[1] // config['BATCH_SIZE']
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
optimizer = optimizers.Adam(learning_rate=lambda: exponential_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32),
warmup_steps=1, lr_start=lr_max,
lr_max=lr_max, lr_min=lr_min, decay=decay))
model.compile(optimizer, loss={'y_start': losses.CategoricalCrossentropy(),
'y_end': losses.CategoricalCrossentropy()})
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=False, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED),
validation_data=(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED)),
epochs=config['EPOCHS'],
steps_per_epoch=step_size,
validation_steps=valid_step_size,
callbacks=[checkpoint, es],
verbose=2).history
history_list.append(history)
model.save_weights('last_' + model_path)
# Make predictions (last model)
predict_eval_df(k_fold, model, x_train, x_valid, get_test_dataset, decode, n_fold, tokenizer, config, config['question_size'])
# Make predictions (best model)
model.load_weights(model_path)
predict_eval_df(k_fold_best, model, x_train, x_valid, get_test_dataset, decode, n_fold, tokenizer, config, config['question_size'])
### Delete data dir
shutil.rmtree(base_data_path)
```
# Model loss graph
```
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation (best model)
```
display(evaluate_model_kfold(k_fold_best, config['N_FOLDS']).style.applymap(color_map))
```
# Model evaluation (last model)
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
|
github_jupyter
|
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from scripts_step_lr_schedulers import *
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
# Unzip files
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_1.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_2.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_3.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_4.tar.gz
!tar -xf /kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/fold_5.tar.gz
database_base_path = '/kaggle/input/tweet-dataset-5fold-roberta-base-96-complete/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
'MAX_LEN': 96,
'BATCH_SIZE': 32,
'EPOCHS': 4,
'LEARNING_RATE': 3e-5,
'ES_PATIENCE': 4,
'N_FOLDS': 5,
"question_size": 4,
'base_model_path': base_path + 'roberta-base-tf_model.h5',
'config_path': base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
lr_min = 1e-6
lr_max = config['LEARNING_RATE']
train_size = len(k_fold[k_fold['fold_1'] == 'train'])
step_size = train_size // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
decay = .9985
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [exponential_schedule_with_warmup(tf.cast(x, tf.float32), warmup_steps=1, lr_start=lr_max, lr_max=lr_max, lr_min=lr_min, decay=decay) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.LSTM(128, return_sequences=True)(last_hidden_state)
x = layers.Dropout(.1)(x)
x_start = layers.TimeDistributed(layers.Dense(1))(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.TimeDistributed(layers.Dense(1))(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
AUTO = tf.data.experimental.AUTOTUNE
strategy = tf.distribute.get_strategy()
k_fold_best = k_fold.copy()
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid.shape[1] // config['BATCH_SIZE']
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
optimizer = optimizers.Adam(learning_rate=lambda: exponential_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32),
warmup_steps=1, lr_start=lr_max,
lr_max=lr_max, lr_min=lr_min, decay=decay))
model.compile(optimizer, loss={'y_start': losses.CategoricalCrossentropy(),
'y_end': losses.CategoricalCrossentropy()})
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=False, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED),
validation_data=(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED)),
epochs=config['EPOCHS'],
steps_per_epoch=step_size,
validation_steps=valid_step_size,
callbacks=[checkpoint, es],
verbose=2).history
history_list.append(history)
model.save_weights('last_' + model_path)
# Make predictions (last model)
predict_eval_df(k_fold, model, x_train, x_valid, get_test_dataset, decode, n_fold, tokenizer, config, config['question_size'])
# Make predictions (best model)
model.load_weights(model_path)
predict_eval_df(k_fold_best, model, x_train, x_valid, get_test_dataset, decode, n_fold, tokenizer, config, config['question_size'])
### Delete data dir
shutil.rmtree(base_data_path)
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
display(evaluate_model_kfold(k_fold_best, config['N_FOLDS']).style.applymap(color_map))
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
| 0.565539 | 0.288168 |
```
import gym, importlib, sys, warnings, IPython
import tensorflow as tf
import itertools
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%autosave 240
warnings.filterwarnings("ignore")
print(tf.__version__)
sys.path.append('../../embodied_arch/')
import embodied as emg
from embodied_misc import ActionPolicyNetwork, SensoriumNetworkTemplate
importlib.reload(emg)
```
## Cartpole Benchmark Setup
```
actor = lambda s: ActionPolicyNetwork(s, hSeq=(10,), gamma_reg=1e-1)
sensor = lambda st, out_dim: SensoriumNetworkTemplate(st, hSeq=(32,), out_dim=out_dim, gamma_reg=1e-1)
tf.reset_default_graph()
importlib.reload(emg)
env = gym.make('CartPole-v0')
# cprf = emg.EmbodiedAgentRF(name="cp-emb", env_=env,
# space_size = (4,1),latentDim=8,
# alpha=0.52, actorNN=actor, sensorium=sensor
# )
cprf = emg.EmbodiedAgentRFBaselined(name="cp-emb-b", env_=env,
space_size = (4,1),latentDim=8,
alpha_p=0.52, alpha_v=0.52, actorNN=actor, sensorium=sensor )
print(cprf, cprf.s_size, cprf.a_size)
saver = tf.train.Saver(max_to_keep=1) #n_epochs = 1000
sess = tf.InteractiveSession()
cprf.init_graph(sess)
num_episodes = 100
n_epochs = 2001
## Verify step + play set up
state = cprf.env.reset()
print(state, cprf.act(state, sess))
cprf.env.step(cprf.act(state, sess))
cprf.play(sess)
len(cprf.episode_buffer)
```
## Baseline
```
print('Baselining untrained pnet...')
uplen0 = []
for k in range(num_episodes):
cprf.play(sess)
uplen0.append(cprf.last_total_return) # uplen0.append(len(cprf.episode_buffer))
if k%20 == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
base_perf = np.mean(uplen0)
print("\nCartpole stays up for an average of {} steps".format(base_perf))
```
## Train
```
# Train pnet on cartpole episodes
print('Training...')
saver = tf.train.Saver(max_to_keep=1)
cprf.work(sess, saver, num_epochs = n_epochs)
```
## Test
```
# Test pnet!
print('Testing...')
uplen = []
for k in range(num_episodes):
cprf.play(sess)
uplen.append(cprf.last_total_return) # uplen.append(len(cprf.episode_buffer))
if k%20 == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
trained_perf = np.mean(uplen)
print("\nCartpole stays up for an average of {} steps compared to baseline {} steps".format(trained_perf, base_perf) )
```
## Evaluate
```
fig, axs = plt.subplots(2, 1, sharex=True)
sns.boxplot(uplen0, ax = axs[0])
axs[0].set_title('Baseline Episode Lengths')
sns.boxplot(uplen, ax = axs[1])
axs[1].set_title('Trained Episode Lengths')
buf = []
last_total_return, d, s = 0, False, cprf.env.reset()
while (len(buf) < 1000) and not d:
a_t = cprf.act(s, sess)
s1, r, d, *rest = cprf.env.step(a_t)
cprf.env.render()
buf.append([s, a_t, float(r), s1])
last_total_return += float(r)
s = s1
print("\r\tEpisode Length", len(buf), end="")
sess.close()
```
|
github_jupyter
|
import gym, importlib, sys, warnings, IPython
import tensorflow as tf
import itertools
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%autosave 240
warnings.filterwarnings("ignore")
print(tf.__version__)
sys.path.append('../../embodied_arch/')
import embodied as emg
from embodied_misc import ActionPolicyNetwork, SensoriumNetworkTemplate
importlib.reload(emg)
actor = lambda s: ActionPolicyNetwork(s, hSeq=(10,), gamma_reg=1e-1)
sensor = lambda st, out_dim: SensoriumNetworkTemplate(st, hSeq=(32,), out_dim=out_dim, gamma_reg=1e-1)
tf.reset_default_graph()
importlib.reload(emg)
env = gym.make('CartPole-v0')
# cprf = emg.EmbodiedAgentRF(name="cp-emb", env_=env,
# space_size = (4,1),latentDim=8,
# alpha=0.52, actorNN=actor, sensorium=sensor
# )
cprf = emg.EmbodiedAgentRFBaselined(name="cp-emb-b", env_=env,
space_size = (4,1),latentDim=8,
alpha_p=0.52, alpha_v=0.52, actorNN=actor, sensorium=sensor )
print(cprf, cprf.s_size, cprf.a_size)
saver = tf.train.Saver(max_to_keep=1) #n_epochs = 1000
sess = tf.InteractiveSession()
cprf.init_graph(sess)
num_episodes = 100
n_epochs = 2001
## Verify step + play set up
state = cprf.env.reset()
print(state, cprf.act(state, sess))
cprf.env.step(cprf.act(state, sess))
cprf.play(sess)
len(cprf.episode_buffer)
print('Baselining untrained pnet...')
uplen0 = []
for k in range(num_episodes):
cprf.play(sess)
uplen0.append(cprf.last_total_return) # uplen0.append(len(cprf.episode_buffer))
if k%20 == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
base_perf = np.mean(uplen0)
print("\nCartpole stays up for an average of {} steps".format(base_perf))
# Train pnet on cartpole episodes
print('Training...')
saver = tf.train.Saver(max_to_keep=1)
cprf.work(sess, saver, num_epochs = n_epochs)
# Test pnet!
print('Testing...')
uplen = []
for k in range(num_episodes):
cprf.play(sess)
uplen.append(cprf.last_total_return) # uplen.append(len(cprf.episode_buffer))
if k%20 == 0: print("\rEpisode {}/{}".format(k, num_episodes),end="")
trained_perf = np.mean(uplen)
print("\nCartpole stays up for an average of {} steps compared to baseline {} steps".format(trained_perf, base_perf) )
fig, axs = plt.subplots(2, 1, sharex=True)
sns.boxplot(uplen0, ax = axs[0])
axs[0].set_title('Baseline Episode Lengths')
sns.boxplot(uplen, ax = axs[1])
axs[1].set_title('Trained Episode Lengths')
buf = []
last_total_return, d, s = 0, False, cprf.env.reset()
while (len(buf) < 1000) and not d:
a_t = cprf.act(s, sess)
s1, r, d, *rest = cprf.env.step(a_t)
cprf.env.render()
buf.append([s, a_t, float(r), s1])
last_total_return += float(r)
s = s1
print("\r\tEpisode Length", len(buf), end="")
sess.close()
| 0.232833 | 0.478529 |
```
import copy
import time
import numpy as np
np.set_printoptions(precision=8, suppress=True, linewidth=400, threshold=100)
import gym
class SensorimotorAutoencoderAgents(object):
'''
a group of autoencoders, each with the ability to encode one transition
that work together to form a predictive sensorimotor inference engine.
basically they map the space, distributedly, so that they can find a path
from any observation to any other observation - they know how to manipulate
the environment.
they have overlapping input bits, but no two have the same inputs. some
have no inputs from the environment at all, and instead get inputs only
from other autoencoders. There are typically many autoencoders. they
automatically wire themselves up (inefficienty, but successfully).
'''
def __init__(self, env, encoders_n=12):
self.env = env
self.encoders = self.generate_encoders(encoders_n)
def generate_encoders(self, n):
''' https://blog.keras.io/building-autoencoders-in-keras.html '''
from keras.layers import Input, Dense
from keras.models import Model
encoders = []
for i in range(n):
# this is the size of our encoded representations
encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats
# this is our input placeholder
input_img = Input(shape=(784,))
# "encoded" is the encoded representation of the input
encoded = Dense(encoding_dim, activation='relu')(input_img)
# "decoded" is the lossy reconstruction of the input
decoded = Dense(784, activation='sigmoid')(encoded)
# this model maps an input to its reconstruction
autoencoder = Model(input_img, decoded)
# Let's also create a separate encoder model:
# this model maps an input to its encoded representation
encoder = Model(input_img, encoded)
# As well as the decoder model:
# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))
# retrieve the last layer of the autoencoder model
# Here we need to change this:
# we want the decoder_layer to be the next timestep so we can train the
# autoencoder on the transition from
# one observation+action to a new observation:
decoder_layer = autoencoder.layers[-1]
# create the decoder model
decoder = Model(encoded_input, decoder_layer(encoded_input))
# autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
encoders.append(autoencoder)
# now wire them up up so they share latents to each other's inputs (at random)
# also wire them up at random to the environment, and the action space...
return encoders
def step(self, obs):
# they are predicting what action they will take. at first the observation
# stands in as a random seed to activate the network, but soon they
# wire up in a hierarchy and take actions to acheive what they think
# they will see, instead of providing goals, you provide an image of
# what you want them to see at the top layer of the hierarchy...
sampled = env.action_space.sample()
print(f'action sampled: {sampled}')
return sampled
class SimpleCube(gym.Env):
''' a Rubiks Cube with only two colors. so that every face can be binary '''
metadata = {'render.modes': ['human']}
def __init__(self):
super(SimpleCube, self).__init__()
self.action_space = self._action_space()
self.observation_space = self._observation_space()
# should change the state to be a list of np array?
self.cube_state =[
1, 1, 1, 1,
1, 1, 1, 1,
0,
0, 0, 0,
1, 1, 1,
1, 1, 1,
0, 0, 0,
0, 0,
1, 1,
1, 1,
0, 0,
0, 0, 0,
1, 1, 1,
1, 1, 1,
0, 0,
0, 0, 0, 0,
0, 0, 0, 0]
self.solved_state = copy.deepcopy(self.cube_state)
self.do_right = {
3: 16, 16: 45, 45: 32, 32: 3,
4: 26, 26: 44, 44: 23, 23: 4,
5: 36, 36: 43, 43: 12, 12: 5,
14: 25, 25: 34, 34: 24, 24: 14,
35: 33, 33: 13, 13: 15, 15: 35, }
self.do_left = {
7: 10, 10: 41, 41: 38, 38: 7,
8: 22, 22: 48, 48: 27, 27: 8,
1: 30, 30: 47, 47: 18, 18: 1,
19: 9, 9: 29, 29: 39, 39: 19,
20: 21, 21: 40, 40: 28, 28: 20, }
self.do_top = {
9: 12, 12: 15, 15: 18, 18: 9,
10: 13, 13: 16, 16: 19, 19: 10,
11: 14, 14: 17, 17: 20, 20: 11,
1: 3, 3: 5, 5: 7, 7: 1,
2: 4, 4: 6, 6: 8, 8: 2, }
self.do_under = {
30: 33, 33: 36, 36: 39, 39: 30,
31: 34, 34: 37, 37: 40, 40: 31,
32: 35, 35: 38, 38: 29, 29: 32,
41: 43, 43: 45, 45: 47, 47: 41,
42: 44, 44: 46, 46: 48, 48: 42, }
self.do_front = {
1: 13, 13: 43, 43: 29, 29: 1,
2: 24, 24: 42, 42: 21, 21: 2,
3: 33, 33: 41, 41: 9, 9: 3,
10: 12, 12: 32, 32: 30, 30: 10,
11: 23, 23: 31, 31: 22, 22: 11, }
self.do_back = {
7: 15, 15: 45, 45: 39, 39: 7,
6: 25, 25: 46, 46: 28, 28: 6,
5: 35, 35: 47, 47: 19, 19: 5,
18: 16, 16: 36, 36: 38, 38: 18,
17: 26, 26: 37, 37: 27, 27: 17, }
def step(self, action):
return self._request(action)
def reset(self):
return self._request(None)[0]
def render(self, mode='human', close=False):
action, obs, reward, done, info = self.state
if action == None: print("{}\n".format(obs))
else: print("{}\t\t--> {:.18f}{}\n{}\n".format(action, reward, (' DONE!' if done else ''), obs))
def _action_space(self):
'''
left, right, top, under, front, back
this is a deterministic env, it doesn't change unless you change it,
therefore, no opperation isn't available.
'''
return gym.spaces.Discrete(6)
def _observation_space(self):
return gym.spaces.Box(low=np.NINF, high=np.inf, shape=(48,), dtype=np.float64)
def _request(self, action):
cube = copy.deepcopy(self.cube_state)
if isinstance(action, int):
action = {
0: 'left', 1: 'right',
2: 'top', 3: 'under',
4: 'front', 5: 'back'}.get(action, None)
if action is not None:
for k, v in eval(f'self.do_{action}').items():
self.cube_state[k] = cube[v]
obs = self.cube_state
reward = np.float64(0.0) # real AGI doesn't need spoonfed 'rewards'
done = False
info = {}
self.state = (action, obs, reward, done, info)
return obs, reward, done, info
env = SimpleCube()
env.seed(0)
print("agent: env.action_space {}".format(env.action_space))
agent = SensorimotorAutoencoderAgents(env)
for i_episode in range(1):
obs = env.reset()
env.render()
for t_timesteps in range(1000):
action = agent.step(obs)
obs, reward, done, info = env.step(action)
env.close()
```
|
github_jupyter
|
import copy
import time
import numpy as np
np.set_printoptions(precision=8, suppress=True, linewidth=400, threshold=100)
import gym
class SensorimotorAutoencoderAgents(object):
'''
a group of autoencoders, each with the ability to encode one transition
that work together to form a predictive sensorimotor inference engine.
basically they map the space, distributedly, so that they can find a path
from any observation to any other observation - they know how to manipulate
the environment.
they have overlapping input bits, but no two have the same inputs. some
have no inputs from the environment at all, and instead get inputs only
from other autoencoders. There are typically many autoencoders. they
automatically wire themselves up (inefficienty, but successfully).
'''
def __init__(self, env, encoders_n=12):
self.env = env
self.encoders = self.generate_encoders(encoders_n)
def generate_encoders(self, n):
''' https://blog.keras.io/building-autoencoders-in-keras.html '''
from keras.layers import Input, Dense
from keras.models import Model
encoders = []
for i in range(n):
# this is the size of our encoded representations
encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats
# this is our input placeholder
input_img = Input(shape=(784,))
# "encoded" is the encoded representation of the input
encoded = Dense(encoding_dim, activation='relu')(input_img)
# "decoded" is the lossy reconstruction of the input
decoded = Dense(784, activation='sigmoid')(encoded)
# this model maps an input to its reconstruction
autoencoder = Model(input_img, decoded)
# Let's also create a separate encoder model:
# this model maps an input to its encoded representation
encoder = Model(input_img, encoded)
# As well as the decoder model:
# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))
# retrieve the last layer of the autoencoder model
# Here we need to change this:
# we want the decoder_layer to be the next timestep so we can train the
# autoencoder on the transition from
# one observation+action to a new observation:
decoder_layer = autoencoder.layers[-1]
# create the decoder model
decoder = Model(encoded_input, decoder_layer(encoded_input))
# autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
encoders.append(autoencoder)
# now wire them up up so they share latents to each other's inputs (at random)
# also wire them up at random to the environment, and the action space...
return encoders
def step(self, obs):
# they are predicting what action they will take. at first the observation
# stands in as a random seed to activate the network, but soon they
# wire up in a hierarchy and take actions to acheive what they think
# they will see, instead of providing goals, you provide an image of
# what you want them to see at the top layer of the hierarchy...
sampled = env.action_space.sample()
print(f'action sampled: {sampled}')
return sampled
class SimpleCube(gym.Env):
''' a Rubiks Cube with only two colors. so that every face can be binary '''
metadata = {'render.modes': ['human']}
def __init__(self):
super(SimpleCube, self).__init__()
self.action_space = self._action_space()
self.observation_space = self._observation_space()
# should change the state to be a list of np array?
self.cube_state =[
1, 1, 1, 1,
1, 1, 1, 1,
0,
0, 0, 0,
1, 1, 1,
1, 1, 1,
0, 0, 0,
0, 0,
1, 1,
1, 1,
0, 0,
0, 0, 0,
1, 1, 1,
1, 1, 1,
0, 0,
0, 0, 0, 0,
0, 0, 0, 0]
self.solved_state = copy.deepcopy(self.cube_state)
self.do_right = {
3: 16, 16: 45, 45: 32, 32: 3,
4: 26, 26: 44, 44: 23, 23: 4,
5: 36, 36: 43, 43: 12, 12: 5,
14: 25, 25: 34, 34: 24, 24: 14,
35: 33, 33: 13, 13: 15, 15: 35, }
self.do_left = {
7: 10, 10: 41, 41: 38, 38: 7,
8: 22, 22: 48, 48: 27, 27: 8,
1: 30, 30: 47, 47: 18, 18: 1,
19: 9, 9: 29, 29: 39, 39: 19,
20: 21, 21: 40, 40: 28, 28: 20, }
self.do_top = {
9: 12, 12: 15, 15: 18, 18: 9,
10: 13, 13: 16, 16: 19, 19: 10,
11: 14, 14: 17, 17: 20, 20: 11,
1: 3, 3: 5, 5: 7, 7: 1,
2: 4, 4: 6, 6: 8, 8: 2, }
self.do_under = {
30: 33, 33: 36, 36: 39, 39: 30,
31: 34, 34: 37, 37: 40, 40: 31,
32: 35, 35: 38, 38: 29, 29: 32,
41: 43, 43: 45, 45: 47, 47: 41,
42: 44, 44: 46, 46: 48, 48: 42, }
self.do_front = {
1: 13, 13: 43, 43: 29, 29: 1,
2: 24, 24: 42, 42: 21, 21: 2,
3: 33, 33: 41, 41: 9, 9: 3,
10: 12, 12: 32, 32: 30, 30: 10,
11: 23, 23: 31, 31: 22, 22: 11, }
self.do_back = {
7: 15, 15: 45, 45: 39, 39: 7,
6: 25, 25: 46, 46: 28, 28: 6,
5: 35, 35: 47, 47: 19, 19: 5,
18: 16, 16: 36, 36: 38, 38: 18,
17: 26, 26: 37, 37: 27, 27: 17, }
def step(self, action):
return self._request(action)
def reset(self):
return self._request(None)[0]
def render(self, mode='human', close=False):
action, obs, reward, done, info = self.state
if action == None: print("{}\n".format(obs))
else: print("{}\t\t--> {:.18f}{}\n{}\n".format(action, reward, (' DONE!' if done else ''), obs))
def _action_space(self):
'''
left, right, top, under, front, back
this is a deterministic env, it doesn't change unless you change it,
therefore, no opperation isn't available.
'''
return gym.spaces.Discrete(6)
def _observation_space(self):
return gym.spaces.Box(low=np.NINF, high=np.inf, shape=(48,), dtype=np.float64)
def _request(self, action):
cube = copy.deepcopy(self.cube_state)
if isinstance(action, int):
action = {
0: 'left', 1: 'right',
2: 'top', 3: 'under',
4: 'front', 5: 'back'}.get(action, None)
if action is not None:
for k, v in eval(f'self.do_{action}').items():
self.cube_state[k] = cube[v]
obs = self.cube_state
reward = np.float64(0.0) # real AGI doesn't need spoonfed 'rewards'
done = False
info = {}
self.state = (action, obs, reward, done, info)
return obs, reward, done, info
env = SimpleCube()
env.seed(0)
print("agent: env.action_space {}".format(env.action_space))
agent = SensorimotorAutoencoderAgents(env)
for i_episode in range(1):
obs = env.reset()
env.render()
for t_timesteps in range(1000):
action = agent.step(obs)
obs, reward, done, info = env.step(action)
env.close()
| 0.782372 | 0.506164 |
# Running Tune experiments with Dragonfly
In this tutorial we introduce Dragonfly, while running a simple Ray Tune experiment. Tuneโs Search Algorithms integrate with Dragonfly and, as a result, allow you to seamlessly scale up a Dragonfly optimization process - without sacrificing performance.
Dragonfly is an open source python library for scalable Bayesian optimization. Bayesian optimization is used optimizing black-box functions whose evaluations are usually expensive. Beyond vanilla optimization techniques, Dragonfly provides an array of tools to scale up Bayesian optimisation to expensive large scale problems. These include features/functionality that are especially suited for high dimensional spaces (optimizing with a large number of variables), parallel evaluations in synchronous or asynchronous settings (conducting multiple evaluations in parallel), multi-fidelity optimization (using cheap approximations to speed up the optimization process), and multi-objective optimisation (optimizing multiple functions simultaneously).
Bayesian optimization does not rely on the gradient of the objective function, but instead, learns from samples of the search space. It is suitable for optimizing functions that are nondifferentiable, with many local minima, or even unknown but only testable. Therefore, it belongs to the domain of "derivative-free optimization" and "black-box optimization". In this example we minimize a simple objective to briefly demonstrate the usage of Dragonfly with Ray Tune via `DragonflySearch`. It's useful to keep in mind that despite the emphasis on machine learning experiments, Ray Tune optimizes any implicit or explicit objective. Here we assume `dragonfly-opt==0.1.6` library is installed. To learn more, please refer to the [Dragonfly website](https://dragonfly-opt.readthedocs.io/).
```
# !pip install ray[tune]
!pip install dragonfly-opt==0.1.6
```
Click below to see all the imports we need for this example.
You can also launch directly into a Binder instance to run this notebook yourself.
Just click on the rocket symbol at the top of the navigation.
```
import numpy as np
import time
import ray
from ray import tune
from ray.tune.suggest import ConcurrencyLimiter
from ray.tune.suggest.dragonfly import DragonflySearch
```
Let's start by defining a optimization problem. Suppose we want to figure out the proportions of water and several salts to add to an ionic solution with the goal of maximizing it's ability to conduct electricity. The objective here is explicit for demonstration, yet in practice they often come out of a black-box (e.g. a physical device measuring conductivity, or reporting the results of a long-running ML experiment). We artificially sleep for a bit (`0.02` seconds) to simulate a more typical experiment. This setup assumes that we're running multiple `step`s of an experiment and try to tune relative proportions of 4 ingredients-- these proportions should be considered as hyperparameters. Our `objective` function will take a Tune `config`, evaluates the `conductivity` of our experiment in a training loop,
and uses `tune.report` to report the `conductivity` back to Tune.
```
def objective(config):
"""
Simplistic model of electrical conductivity with added Gaussian noise to simulate experimental noise.
"""
for i in range(config["iterations"]):
vol1 = config["LiNO3_vol"] # LiNO3
vol2 = config["Li2SO4_vol"] # Li2SO4
vol3 = config["NaClO4_vol"] # NaClO4
vol4 = 10 - (vol1 + vol2 + vol3) # Water
conductivity = vol1 + 0.1 * (vol2 + vol3) ** 2 + 2.3 * vol4 * (vol1 ** 1.5)
conductivity += np.random.normal() * 0.01
tune.report(timesteps_total=i, objective=conductivity)
time.sleep(0.02)
```
Next we define a search space. The critical assumption is that the optimal hyperparameters live within this space. Yet, if the space is very large, then those hyperparameters may be difficult to find in a short amount of time.
```
search_space = {
"iterations": 100,
"LiNO3_vol": tune.uniform(0, 7),
"Li2SO4_vol": tune.uniform(0, 7),
"NaClO4_vol": tune.uniform(0, 7)
}
ray.init(configure_logging=False)
```
Now we define the search algorithm from `DragonflySearch` with `optimizer` and `domain` arguments specified in a common way. We also use `ConcurrencyLimiter` to constrain to 4 concurrent trials.
```
algo = DragonflySearch(
optimizer="bandit",
domain="euclidean",
)
algo = ConcurrencyLimiter(algo, max_concurrent=4)
```
The number of samples is the number of hyperparameter combinations that will be tried out. This Tune run is set to `1000` samples.
(you can decrease this if it takes too long on your machine).
```
num_samples = 100
# Reducing samples for smoke tests
num_samples = 10
```
Finally, we run the experiment to `"min"`imize the "mean_loss" of the `objective` by searching `search_config` via `algo`, `num_samples` times. This previous sentence is fully characterizes the search problem we aim to solve. With this in mind, notice how efficient it is to execute `tune.run()`.
```
analysis = tune.run(
objective,
metric="objective",
mode="max",
name="dragonfly_search",
search_alg=algo,
num_samples=num_samples,
config=search_space
)
```
Below are the recommended relative proportions of water and each salt found to maximize conductivity in the ionic solution (according to the simple model):
```
print("Best hyperparameters found: ", analysis.best_config)
ray.shutdown()
```
|
github_jupyter
|
# !pip install ray[tune]
!pip install dragonfly-opt==0.1.6
import numpy as np
import time
import ray
from ray import tune
from ray.tune.suggest import ConcurrencyLimiter
from ray.tune.suggest.dragonfly import DragonflySearch
def objective(config):
"""
Simplistic model of electrical conductivity with added Gaussian noise to simulate experimental noise.
"""
for i in range(config["iterations"]):
vol1 = config["LiNO3_vol"] # LiNO3
vol2 = config["Li2SO4_vol"] # Li2SO4
vol3 = config["NaClO4_vol"] # NaClO4
vol4 = 10 - (vol1 + vol2 + vol3) # Water
conductivity = vol1 + 0.1 * (vol2 + vol3) ** 2 + 2.3 * vol4 * (vol1 ** 1.5)
conductivity += np.random.normal() * 0.01
tune.report(timesteps_total=i, objective=conductivity)
time.sleep(0.02)
search_space = {
"iterations": 100,
"LiNO3_vol": tune.uniform(0, 7),
"Li2SO4_vol": tune.uniform(0, 7),
"NaClO4_vol": tune.uniform(0, 7)
}
ray.init(configure_logging=False)
algo = DragonflySearch(
optimizer="bandit",
domain="euclidean",
)
algo = ConcurrencyLimiter(algo, max_concurrent=4)
num_samples = 100
# Reducing samples for smoke tests
num_samples = 10
analysis = tune.run(
objective,
metric="objective",
mode="max",
name="dragonfly_search",
search_alg=algo,
num_samples=num_samples,
config=search_space
)
print("Best hyperparameters found: ", analysis.best_config)
ray.shutdown()
| 0.443359 | 0.991075 |
```
!pip install tfx==0.22.0
import os
import sys
import tensorflow as tf
from tfx.orchestration.experimental.interactive.interactive_context import InteractiveContext
from tfx.utils.dsl_utils import external_input
from tfx.components import CsvExampleGen
context = InteractiveContext(pipeline_root='../tfx')
base_dir = os.getcwd()
data_dir = "../data"
examples = external_input(os.path.join(base_dir, data_dir))
example_gen = CsvExampleGen(input=examples)
context.run(example_gen)
from tfx.components import StatisticsGen
statistics_gen = StatisticsGen(
examples=example_gen.outputs['examples'])
context.run(statistics_gen)
context.show(statistics_gen.outputs['statistics'])
from tfx.components import SchemaGen
schema_gen = SchemaGen(
statistics=statistics_gen.outputs['statistics'],
infer_feature_shape=True)
context.run(schema_gen)
context.show(schema_gen.outputs['schema'])
from tfx.components import ExampleValidator
example_validator = ExampleValidator(
statistics=statistics_gen.outputs['statistics'],
schema=schema_gen.outputs['schema'])
context.run(example_validator)
context.show(example_validator.outputs['anomalies'])
transform_file = os.path.join(base_dir, '../components/module.py')
from tfx.components import Transform
transform = Transform(
examples=example_gen.outputs['examples'],
schema=schema_gen.outputs['schema'],
module_file=transform_file)
context.run(transform)
trainer_file = os.path.join(base_dir, '../components/module.py')
from tfx.components import Trainer
from tfx.proto import trainer_pb2
from tfx.components.base import executor_spec
from tfx.components.trainer.executor import GenericExecutor
TRAINING_STEPS = 1000
EVALUATION_STEPS = 100
trainer = Trainer(
module_file=trainer_file,
custom_executor_spec=executor_spec.ExecutorClassSpec(GenericExecutor),
examples=transform.outputs['transformed_examples'],
schema=schema_gen.outputs['schema'],
transform_graph=transform.outputs['transform_graph'],
train_args=trainer_pb2.TrainArgs(num_steps=TRAINING_STEPS),
eval_args=trainer_pb2.EvalArgs(num_steps=EVALUATION_STEPS))
context.run(trainer)
```
### Load TensorBoard
```
model_artifact_dir = trainer.outputs['model'].get()[0].uri
log_dir = os.path.join(model_artifact_dir, 'logs/')
%load_ext tensorboard
%tensorboard --logdir {log_dir}
```
### Evaluate the model
```
from tfx.components import ResolverNode
from tfx.dsl.experimental import latest_blessed_model_resolver
from tfx.types import Channel
from tfx.types.standard_artifacts import Model
from tfx.types.standard_artifacts import ModelBlessing
model_resolver = ResolverNode(
instance_name='latest_blessed_model_resolver',
resolver_class=latest_blessed_model_resolver.LatestBlessedModelResolver,
model=Channel(type=Model),
model_blessing=Channel(type=ModelBlessing))
context.run(model_resolver)
# nb it always blesses on first run even if below threshold
import tensorflow_model_analysis as tfma
eval_config=tfma.EvalConfig(
model_specs=[tfma.ModelSpec(label_key='consumer_disputed')],
slicing_specs=[tfma.SlicingSpec(), tfma.SlicingSpec(feature_keys=['product'])],
metrics_specs=[
tfma.MetricsSpec(metrics=[
tfma.MetricConfig(class_name='BinaryAccuracy'),
tfma.MetricConfig(class_name='ExampleCount'),
tfma.MetricConfig(class_name='AUC')
],
thresholds={
'AUC':
tfma.config.MetricThreshold(
value_threshold=tfma.GenericValueThreshold(
lower_bound={'value': 0.65}),
change_threshold=tfma.GenericChangeThreshold(
direction=tfma.MetricDirection.HIGHER_IS_BETTER,
absolute={'value': 0.01}))}
)])
from tfx.components import Evaluator
evaluator = Evaluator(
examples=example_gen.outputs['examples'],
model=trainer.outputs['model'],
baseline_model=model_resolver.outputs['model'],
eval_config=eval_config)
context.run(evaluator)
#NB TFMA visualizations will not run in Jupyter Lab
import tensorflow_model_analysis as tfma
# Get the TFMA output result path and load the result.
PATH_TO_RESULT = evaluator.outputs['evaluation'].get()[0].uri
tfma_result = tfma.load_eval_result(PATH_TO_RESULT)
tfma.view.render_slicing_metrics(tfma_result)
from tfx.components.pusher.component import Pusher
from tfx.proto import pusher_pb2
_serving_model_dir = "./tfx-9Apr/serving_model_dir"
pusher = Pusher(
model=trainer.outputs['model'],
model_blessing=evaluator.outputs['blessing'],
push_destination=pusher_pb2.PushDestination(
filesystem=pusher_pb2.PushDestination.Filesystem(
base_directory=_serving_model_dir)))
context.run(pusher)
```
### Extra stuff
```
!mkdir -p ../tfx-9Apr/serving_model_dir
!jupyter nbextension enable --py widgetsnbextension --sys-prefix
!jupyter nbextension install --py --symlink tensorflow_model_analysis --sys-prefix
!jupyter nbextension enable --py tensorflow_model_analysis --sys-prefix
# THEN REFRESH BROWSER PAGE!
PATH_TO_RESULT = evaluator.outputs['evaluation'].get()[0].uri
print(tfma.load_validation_result(PATH_TO_RESULT))
# Show data sliced by product
tfma.view.render_slicing_metrics(
tfma_result, slicing_column='product')
# fairness indicators direct from pipeline
# https://colab.research.google.com/github/tensorflow/fairness-indicators/blob/master/fairness_indicators/examples/Fairness_Indicators_Lineage_Case_Study.ipynb
```
|
github_jupyter
|
!pip install tfx==0.22.0
import os
import sys
import tensorflow as tf
from tfx.orchestration.experimental.interactive.interactive_context import InteractiveContext
from tfx.utils.dsl_utils import external_input
from tfx.components import CsvExampleGen
context = InteractiveContext(pipeline_root='../tfx')
base_dir = os.getcwd()
data_dir = "../data"
examples = external_input(os.path.join(base_dir, data_dir))
example_gen = CsvExampleGen(input=examples)
context.run(example_gen)
from tfx.components import StatisticsGen
statistics_gen = StatisticsGen(
examples=example_gen.outputs['examples'])
context.run(statistics_gen)
context.show(statistics_gen.outputs['statistics'])
from tfx.components import SchemaGen
schema_gen = SchemaGen(
statistics=statistics_gen.outputs['statistics'],
infer_feature_shape=True)
context.run(schema_gen)
context.show(schema_gen.outputs['schema'])
from tfx.components import ExampleValidator
example_validator = ExampleValidator(
statistics=statistics_gen.outputs['statistics'],
schema=schema_gen.outputs['schema'])
context.run(example_validator)
context.show(example_validator.outputs['anomalies'])
transform_file = os.path.join(base_dir, '../components/module.py')
from tfx.components import Transform
transform = Transform(
examples=example_gen.outputs['examples'],
schema=schema_gen.outputs['schema'],
module_file=transform_file)
context.run(transform)
trainer_file = os.path.join(base_dir, '../components/module.py')
from tfx.components import Trainer
from tfx.proto import trainer_pb2
from tfx.components.base import executor_spec
from tfx.components.trainer.executor import GenericExecutor
TRAINING_STEPS = 1000
EVALUATION_STEPS = 100
trainer = Trainer(
module_file=trainer_file,
custom_executor_spec=executor_spec.ExecutorClassSpec(GenericExecutor),
examples=transform.outputs['transformed_examples'],
schema=schema_gen.outputs['schema'],
transform_graph=transform.outputs['transform_graph'],
train_args=trainer_pb2.TrainArgs(num_steps=TRAINING_STEPS),
eval_args=trainer_pb2.EvalArgs(num_steps=EVALUATION_STEPS))
context.run(trainer)
model_artifact_dir = trainer.outputs['model'].get()[0].uri
log_dir = os.path.join(model_artifact_dir, 'logs/')
%load_ext tensorboard
%tensorboard --logdir {log_dir}
from tfx.components import ResolverNode
from tfx.dsl.experimental import latest_blessed_model_resolver
from tfx.types import Channel
from tfx.types.standard_artifacts import Model
from tfx.types.standard_artifacts import ModelBlessing
model_resolver = ResolverNode(
instance_name='latest_blessed_model_resolver',
resolver_class=latest_blessed_model_resolver.LatestBlessedModelResolver,
model=Channel(type=Model),
model_blessing=Channel(type=ModelBlessing))
context.run(model_resolver)
# nb it always blesses on first run even if below threshold
import tensorflow_model_analysis as tfma
eval_config=tfma.EvalConfig(
model_specs=[tfma.ModelSpec(label_key='consumer_disputed')],
slicing_specs=[tfma.SlicingSpec(), tfma.SlicingSpec(feature_keys=['product'])],
metrics_specs=[
tfma.MetricsSpec(metrics=[
tfma.MetricConfig(class_name='BinaryAccuracy'),
tfma.MetricConfig(class_name='ExampleCount'),
tfma.MetricConfig(class_name='AUC')
],
thresholds={
'AUC':
tfma.config.MetricThreshold(
value_threshold=tfma.GenericValueThreshold(
lower_bound={'value': 0.65}),
change_threshold=tfma.GenericChangeThreshold(
direction=tfma.MetricDirection.HIGHER_IS_BETTER,
absolute={'value': 0.01}))}
)])
from tfx.components import Evaluator
evaluator = Evaluator(
examples=example_gen.outputs['examples'],
model=trainer.outputs['model'],
baseline_model=model_resolver.outputs['model'],
eval_config=eval_config)
context.run(evaluator)
#NB TFMA visualizations will not run in Jupyter Lab
import tensorflow_model_analysis as tfma
# Get the TFMA output result path and load the result.
PATH_TO_RESULT = evaluator.outputs['evaluation'].get()[0].uri
tfma_result = tfma.load_eval_result(PATH_TO_RESULT)
tfma.view.render_slicing_metrics(tfma_result)
from tfx.components.pusher.component import Pusher
from tfx.proto import pusher_pb2
_serving_model_dir = "./tfx-9Apr/serving_model_dir"
pusher = Pusher(
model=trainer.outputs['model'],
model_blessing=evaluator.outputs['blessing'],
push_destination=pusher_pb2.PushDestination(
filesystem=pusher_pb2.PushDestination.Filesystem(
base_directory=_serving_model_dir)))
context.run(pusher)
!mkdir -p ../tfx-9Apr/serving_model_dir
!jupyter nbextension enable --py widgetsnbextension --sys-prefix
!jupyter nbextension install --py --symlink tensorflow_model_analysis --sys-prefix
!jupyter nbextension enable --py tensorflow_model_analysis --sys-prefix
# THEN REFRESH BROWSER PAGE!
PATH_TO_RESULT = evaluator.outputs['evaluation'].get()[0].uri
print(tfma.load_validation_result(PATH_TO_RESULT))
# Show data sliced by product
tfma.view.render_slicing_metrics(
tfma_result, slicing_column='product')
# fairness indicators direct from pipeline
# https://colab.research.google.com/github/tensorflow/fairness-indicators/blob/master/fairness_indicators/examples/Fairness_Indicators_Lineage_Case_Study.ipynb
| 0.496826 | 0.314202 |
<img src = "images/Logo.png" width = 220, align = "left">
<h1 align=center><font size = 6><span style="color:blue">Case Study: Advertising</span></font></h1>
<h2 align=center><font size = 5>Lab Exercise 3.2</font></h2>
<h3 align=center><font size = 4><b>Advanced Machine Learning Made Easy<br></b><small>From Theory to Practice with NumPy and scikit-learn<br><i>Volume 1: Generalized Linear Models</i></font></h3>
## Introduction
The Advertising dataset consists of sales of that product in 200 different markets, along with advertising budgets for the product in each of those markets for three different media: TV, radio, and newspaper. Our task is to find a linear model that could help in creating an association between advertising and sales. Then we can use this model to predict sales based on the three media budgets. Thus, as a data scientist, our task is to suggest, based on this data and the obtained (linear) model, a marketing plan for next year that would result in higher product sales. That is, we can instruct our client to adjust advertising budgets, thereby indirectly increasing sales while keeping our advertising budget the same.<br>
**Note**: *The following exercise is based on the book "An Introduction to Statistical Learning - with Applications in R" by Gareth James, Daniela Witten, Trevor Hastie and Robert Tibshirani. Both the book and the dataset can be found at http://www-bcf.usc.edu/~gareth/ISL/*
### Table of contents
1. [Reading the data](#ReadingData)
2. [Analyzing the data](#AnalyzingData)
3. [Scatter plot of the data](#ScatterPlot)
4. [Fitting a multiple linear regression model](#LinearModelFit)
5. [Feature selection](#FeatureSelection)
6. [Confidence and prediction intervals, confidence regions](#ConfidenceRegions)
7. [Removing the additive assumption](#AdditiveAssumptionRemoval)
## 1. Reading the data <a name="ReadingData"></a>
As a first step, we import the required libraries.
```
import numpy as np
from numpy.linalg import matrix_rank, inv, svd
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import f_regression
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import os
%matplotlib inline
```
Then we read the dataset directly from the homepage of the book "*An Introduction to Statistical Learning - with Applications in R*" by Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani. Let's print out the dataset.
**Note**: *In case "urlopen error" is thrown due to moved webpage, comment out the first line and uncomment the line below.*
```
data = pd.read_csv('http://faculty.marshall.usc.edu/gareth-james/ISL/Advertising.csv', index_col=0) # Reading from web page
#data = pd.read_csv(os.path.join('data','Advertising.csv')) # Uncomment this line in case the above line trows an error
data
```
As we can see, the advertising budgets for *TV*, *radio*, *newspaper*,in thousands of dollars, are the independent variables, $x_1,x_2,x_3$, while *sales*sales, in thousands of units, is the dependent variable $y$. There are $N=200$ observations.
## 2. Analyzing the data <a name="AnalyzingData"></a>
Before creating the linear model, we should check that there is no invalid entry in the dataset (-inf and +inf is also considered NaN, e.i., not a number). You might also create short statistics for each variable to check if there is no unusual entry (e.g., minimum or maximum value far away from the mean).
```
pd.options.mode.use_inf_as_na = True
print(data.isnull().values.any())
data.describe()
```
You may also create the boxplot to check the distribution of the data.
```
boxprops = dict(linestyle='-', linewidth=2, color='k')
medianprops = dict(linestyle='-', linewidth=2, color='k')
data.boxplot(column=['TV','radio','newspaper','sales'],fontsize=12,grid=False,boxprops=boxprops, medianprops=medianprops)
plt.title("Boxplot of the 'Advertising' dataset",fontsize=14)
plt.show()
```
Only the newspaper variable shows two outliers.
Extract the input and output values from the pandas dataframe into matrix $\mathbf{\dot X}$ and vector $\mathbf{y}$. Also, extract the number of observations and the number of features available in the dataset.
```
X=np.array(data[["TV","radio","newspaper"]])
y_=np.array(data["sales"])[:,np.newaxis]
N,D=X.shape
print("Number of observations =",N)
print("Number of features =", D)
```
Now, let's insert a column at the beginning of $\mathbf X$ corresponding to the constant term (intercept) to obtain the design matrix $\mathbf{\dot X}$.
```
Xdot=np.insert(X,0,np.ones(N),axis=1)
```
#### Check for collinearity
First, check the rank of the design matrix.
```
print("Rank of the design matrix is:",matrix_rank(Xdot))
```
The rank of the design matrix is equal to the number of coefficients, including the intercept.<br>
Next, calculate the condition number.
```
from numpy.linalg import eigh
eigval,eigvect=eigh(Xdot.T@Xdot)
print("Eigenvalues of the product matrix:")
print(eigval[:,np.newaxis])
print("Condition number =",np.sqrt(eigval.max()/eigval.min()))
```
You can also use the *cond* method of NumPy library to calculate the condition number.
```
from numpy.linalg import cond
print(cond(Xdot))
```
The condition number is not very big which does not suggest any collinearity issue.<br>
Finally, calculate the variance inflation factor (VIF).
```
from statsmodels.stats.outliers_influence import variance_inflation_factor
print("VIF for TV =",variance_inflation_factor(Xdot,1))
print("VIF for radio =",variance_inflation_factor(Xdot,2))
print("VIF for newspaper =",variance_inflation_factor(Xdot,3))
```
As can be observed, the VIF values are close to 1, which indicates no collinearity among predictors.
## 2. Scatter plot of the data <a name="ScatterPlot"></a>
Let's first make a separate scatter plot of the *sales* as a function of *TV*, *radio*, and *newspaper*. Also, plot the estimated regression lines for each scatter plot and annotate each plot with the Pearson correlation coefficient.
```
fig, ax = plt.subplots(1, 3, figsize=(14, 4))
xvarlist=['TV','radio','newspaper']
linregr=LinearRegression()
for i in range(D):
ax[i].scatter(X[:,i],y_,s=20)
x_=X[:,i].reshape(-1,1)
linregr.fit(x_,y_)
ax[i].plot([x_.min(),x_.max()],linregr.predict(np.array([[x_.min()],[x_.max()]])),c='r')
ax[i].set_xlabel(list(data.columns.values)[i],fontsize=14)
ax[i].set_ylabel(list(data.columns.values)[D],fontsize=14)
ax[i].set_title('Sales vs. '+xvarlist[i],fontsize=16)
ax[i].annotate('r = '+'%.2f'%np.corrcoef(np.append(X,y_,axis=1), rowvar=False)[:,-1][i],\
xy=(X.mean(axis=0)[i],2),color='red',fontsize=12)
plt.show()
```
The above plot displays sales, in thousands of units, as a function of TV, radio, and newspaper advertising expenditure, in thousands of dollars, for 200 different markets. We can observe, that each red line (as the estimated regression line) represents a simple linear regression model that can be used to predict sales using TV, radio, and newspaper, respectively.
You should also observe that the Pearson correlation coefficient is quite high for TV and radio and still significant for the newspaper.
The above figures are a good starting point in analyzing multi-dimensional input data. But you may also want to check whether there is any correlation between the independent variables. So you may also want to create a separate scatter plot between the pair of independent variables.
This can be done in a condensed format using the so-called matrix of scatter plots which can be easily created with the *seeborn* library.
```
import seaborn as sns
sns.pairplot(data)
plt.show()
```
*Pandas* library also has *scatter_matrix* method for plotting the scatter plot matrix.
```
pd.plotting.scatter_matrix(data,figsize=(14,14),s=100)
plt.show()
```
The matrix of the scatter plot is symmetric, and the scatter plots of the last row (or last column) represents the scatter plot of the *sales* as a function of *TV*, *radio*, and *newspaper* shown before. We have also the scatter plot between the input variables, so it can be checked visually if there is any correlation between them. The diagonal figures show the histograms of the variables (inputs, respective output).
Checking the scatter plot between *radio* and *TV* (first plot in the second row), respective between *newspaper* and *TV* or *newspaper* and *radio* (first two plots in the third row) shows no any evidence of correlation among independent variables.
We can also create an OLS summary of the individual regressions.
```
from scipy import stats
conflevel=95
alpha=1-conflevel/100
df=N-2
tscore=abs(stats.t.ppf(alpha/2, df))
pd.options.display.float_format = '{:,.3f}'.format
def OLSresults(x_,y_):
linregr=LinearRegression()
linregr.fit(x_,y_)
r_=y_-linregr.predict(x_)
MSE=r_.T@r_/(N-2)
s_w=float(np.squeeze(np.sqrt(MSE/np.sum((x_-x_.mean())**2))))
s_b=float(np.squeeze(s_w*np.sqrt(x_.T@x_/N)))
table=pd.DataFrame(columns=["Input","Coefficient","Std. error","t-statistic","p-value","[0.025","0.975]"])
t_stat=linregr.intercept_[0]/s_b
pval = stats.t.sf(np.abs(t_stat),df)*2
LCL=linregr.intercept_[0]-tscore*s_b
UCL=linregr.intercept_[0]+tscore*s_b
table=table.append({"Input":"Intercept","Coefficient":linregr.intercept_[0],"Std. error":s_b,"t-statistic":t_stat,\
"p-value":pval,"[0.025":LCL,"0.975]":UCL},ignore_index=True)
t_stat=linregr.coef_[0][0]/s_w
pval = stats.t.sf(np.abs(t_stat),df)*2
LCL=linregr.coef_[0][0]-tscore*s_w
UCL=linregr.coef_[0][0]+tscore*s_w
table=table.append({"Input":list(data.columns.values)[i],"Coefficient":linregr.coef_[0][0],"Std. error":s_w,\
"t-statistic":t_stat,"p-value":pval,"[0.025":LCL,"0.975]":UCL},ignore_index=True)
return table,MSE,linregr.score(x_,y_),r_
R=[]
print("============================================================================")
for i in range(D):
x_=X[:,i].reshape(-1,1)
print(OLSresults(x_,y_)[0])
print('----------------------------------------------------------------------------')
print("RSE=%f, R-squared=%f\n"%(float(np.sqrt(OLSresults(x_,y_)[1])),OLSresults(x_,y_)[2]))
print("============================================================================")
R.append(OLSresults(x_,y_)[3])
R=np.array(R).squeeze().T # Store the residual vectors
```
The above OLS results show the simple linear regression models of each media when the other two media are not considered. As we can observe, all 3 media has a significantly nonzero coefficient.
Let's check the residual plot for each regression.
```
fig, ax = plt.subplots(1, 3, figsize=(14, 4))
ax[0].scatter(X[:,0],R[:,0],s=15)
ax[0].plot([X[:,0].min(),X[:,0].max()],[0,0],'--r',lw=2)
ax[1].scatter(X[:,1],R[:,1],s=15)
ax[1].plot([X[:,1].min(),X[:,1].max()],[0,0],'--r',lw=2)
ax[2].scatter(X[:,2],R[:,2],s=15)
ax[2].plot([X[:,2].min(),X[:,2].max()],[0,0],'--r',lw=2)
ax[0].set_xlabel('TV',fontsize=12)
ax[1].set_xlabel('radio',fontsize=12)
ax[2].set_xlabel('newspaper',fontsize=12)
ax[0].set_ylabel('Residuals',fontsize=12)
fig.suptitle("Scatter plot of the residuals for each SLR", fontsize=14)
plt.show()
```
From the residual plot, you might suspect the presence of heteroskedasticity for *TV* and *radio*.
Let's create the OLS using the *statsmodels* library and check for homoskedasticity using the Goldfeld-Quandt test.
```
from statsmodels.formula.api import ols
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
results = ols(formula = 'sales ~ TV', data=data).fit()
print(results.summary(title='OLS Results for TV vs. sales'))
name = ['F statistic', 'p-value']
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
results = ols(formula = 'sales ~ radio', data=data).fit()
print(results.summary(title='OLS Results for radio vs. sales'))
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
results = ols(formula = 'sales ~ newspaper', data=data).fit()
print(results.summary(title='OLS Results for newspaper vs. sales'))
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
```
Based on the Goldfeld-Quandt test, we can conclude that the residuals have constant variance.<br>
Next, create the normal probability plots for the residuals for each regression to check the normality of the residuals.
```
fig, ax = plt.subplots(1, 3, figsize=(16, 5))
stats.probplot(np.ravel(R[:,0]), plot=ax[0])
stats.probplot(np.ravel(R[:,1]), plot=ax[1])
stats.probplot(np.ravel(R[:,2]), plot=ax[2])
ax[0].set_title('QQ-plot of residuals for sales vs. TV')
ax[1].set_title('QQ-plot of residuals for sales vs. radio')
ax[2].set_title('QQ-plot of residuals for sales vs. newspaper')
fig.suptitle("Normal probability plot for the residuals of each SLR", fontsize=14)
plt.show()
```
From the normal probability plots, we can conclude that the residuals of each simple linear regression have an approximately normal distribution. Thus, we can rely on standard errors and confidence intervals created with OLS. So far so good.
However, the approach of fitting a separate simple linear regression model for each predictor is not entirely satisfactory because each of the media budgets is associated with a separate regression equation and ignores the other two media in forming estimates for the regression coefficients. If the media budgets are correlated with each other, then this can lead to very misleading estimates of the individual media effects on sales. You may also observe that the R-squared value is quite low for *radio vs. sales*, and especially very low for *newspaper vs. sales*.
## 4. Fitting a multiple linear regression model <a name="LinearModelFit"></a>
For the above reasons, we should rather fit a multiple linear regression model to see if it has any extra value. Using the same instance of the *scikit-learn* class, we fit a linear model considering all 3 media types.
**Note:** *You should pass the input matrix without the intercept, and not the design matrix to the fit method.*
```
linregr.fit(X,y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(3),["TV coef. =","Radio coef. =","Newspaper coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X,y_))
print("R-squared adjusted =",1-(1-linregr.score(X,y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X)).T@(y_-linregr.predict(X))/(N-2))
print("RMSE =",np.sqrt(MSE))
```
We can see that the R-squared value is increased significantly, being almost 0.9. Thus, 90% of the sales variability is explained by our model. Moreover, now the root mean square error (RMSE) dropped significantly.
As we can observe, the coefficients of *TV* and *radio* have been slightly decreased compared to what we obtained from the individual single linear regression models. More interestingly, the coefficient for the newspaper became almost zero.
Using the *statsmodel* library, we can create further statistics for this multiple linear regression model.
```
results = ols(formula = 'sales ~ TV + radio + newspaper', data=data).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
```
The F-test shows that our multiple linear regression model is significantly better than the average model (with all slope coefficients set to zero). That is, at least one of the regression coefficient is significantly different from zero.
Although the exact value for the coefficient of the newspaper is not zero, the null hypothesis for t-statistic cannot be rejected (i.e., $w_3=0$), and the confidence interval not only includes the zero value, but the center of the confidence interval is near zero. This illustrates that the simple and multiple regression coefficients can be quite different.
Let's also print out the residual plot. Because there are three input variables, not all of them can be used on the horizontal axis when creating a 2D residual plot. In the case of multiple linear regression, the only way to have a 2D residual plot is to have the linear combination of the input variables on the horizontal axis. This is exactly the predicted value, $\hat y$.
```
plt.scatter(results.resid, results.predict())
plt.title('Scatter plot of the residuals',fontsize=14)
plt.xlabel('$\hat y$',fontsize=12)
plt.ylabel('Residuals',fontsize=12)
plt.show()
```
From the residual plot, you might suspect the presence of heteroskedasticity, but the Goldfeld-Quandt test shows otherwise. So we can rely on the standard errors and confidence intervals.
Finally, check the normality of the residuals graphically.
```
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].hist(results.resid)
ax[0].set_title('Histogram of the residuals',fontsize=12)
stats.probplot(results.resid,plot=ax[1])
plt.show()
```
There seem to be one outlier (see the value close to -8 on the histogram), but otherwise the residual plot slightly resembles to a normal distribution. So we can rely on the standard errors and confidence intervals.
## 5. Feature selection <a name="FeatureSelection"></a>
According to the t-test in the previous section, we ended up that we cannot reject the null hypothesis that the regression coefficient of the newspaper is zero. So let's select only the *TV* and *radio* as features in our next model. <br>
But before doing so, let's check the correlation matrix of the three predictor variables and response variables to see the degree of correlation between them.
```
pd.DataFrame(data=np.corrcoef(np.append(X,y_,axis=1), rowvar=False)\
,index=['TV','radio','newspaper','sales'],columns=['TV','radio','newspaper','sales'])
```
Notice that the correlation between radio and newspaper is greater than 0.35. This reveals a tendency to spend more on newspaper advertising in markets where more is spent on radio advertising or vice verso. However, the multiple linear regression model suggests that the budget spent on the newspaper advartising does not increase our sales.
Notice that the correlation between radio and newspaper is greater than 0.35. This reveals a tendency to spend more on newspaper advertising in markets where more is spent on radio advertising, or vice verso. However, the multiple linear regression model suggests that the budget spent on newspaper advertising does not increase our sales.
Even though there is some positive correlation between the radio and newspaper budget, the variance inflation factors do not show any sign of multicollinearity between the independent variables, as we already found out during data analysis.
Let's try to fit a linear regression model using only the *TV* and *radio* as predictors.
```
linregr.fit(X[:,0:2],y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(2),["TV coef. =","Radio coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X[:,0:2],y_))
print("R-squared adjusted =",1-(1-linregr.score(X[:,0:2],y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X[:,0:2])).T@(y_-linregr.predict(X[:,0:2]))/(N-2))
print("RMSE =",np.sqrt(MSE))
```
More statistics can be obtained with *statmodels* library.
```
results = ols(formula = 'sales ~ TV + radio', data=data).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
sigma=np.sqrt(results.mse_resid)
print("RMSE =",np.sqrt(results.mse_resid))
```
As can be observed, with only two predictors (*TV* and *radio*), we obtain the same R-squared value as with three, and the F-statistic becomes even slightly greater than before.
In conclusion, we can state that the sales are predicted very well with only two predictors (advertising expenditure on TV and radio). We can state that a unit change in the advertising expenditure of TV will provide an increase of 0.0458 unit increase in sales while keeping expenditure on radio advertising fix, and a unit change in the advertising expenditure of radio will provide an increase of 0.1880 unit increase in sales while keeping expenditure on TV advertising fix. That also means that advertising on radio is more efficient, because one thousand dollar additional budget spent only on radio advertising will end up in 188 additional unit sales in contrast to only 46 additional unit sales if that additional budget is spent on TV advertising.
Thus, we can use our multiple linear regression model for predicting the sales based on advertising expenditure on different media, but we should keep in mind the uncertainty of our prediction.
Although the Goldfeld-Quandt test does not reject the homoskedasticity, the p-value is quite close to the 0.05 threshold. Let's check the normality of the residuals using histogram and QQ-plot.
```
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].hist(results.resid)
stats.probplot(results.resid,plot=ax[1])
plt.show()
```
Again, we can see one outlier around -8 (see on the left of the histogram above). Let's check what happens if we remove this observation and create a regression with the remaining dataset.
```
data1=data.drop(index=131)
results = ols(formula = 'sales ~ TV + radio', data=data1).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
sigma=np.sqrt(results.mse_resid)
print("RMSE =",np.sqrt(results.mse_resid))
```
Both the R-squared value and the F-statistic slightly increased while the regression coefficients for TV and radio slightly altered (coefficient for TV slightly decreased and for radio slightly increased). However, the regression coefficients are not modified significantly, thus, the outlier should not be considered an influential point.
What is more important that the Goldfeld-Quandt test now provides more evidence against heteroskedasticity, and the Skew gets closer to 0 while the Kurtosis gets closer to 3. The latter two can be considered as signs for the correctness of the normality assumption. As a conclusion, we can rely on the standard error and confidence interval shown by the OLS results. This is even true for the OLS based on the whole dataset as the outlier is not an influential point.
## 5. Confidence and prediction intervals, confidence regions <a name="ConfidenceRegions"></a>
#### Confidence and prediction intervals
Confidence and prediction intervals can be created in a similar way as we did for the simple linear regression. The only difference is, that because there are more than one independent variable, the confidence and prediction intervals cannot be shown graphically, except when we have only two variables (like in this case with 'TV" and 'Radio'). Because both the confidence and prediction interval of the estimated conditional mean depends on the Mahalanobis distance of the input from the center of the input data, let's calculate first the center of the input and the inverse of the sample covariance matrix.
```
mu_=X[:,0:2].mean(axis=0)[:,np.newaxis]
Sigma=1/(N-1)*(X[:,0:-1]-mu_.T).T@(X[:,0:-1]-mu_.T)
Sigma_1=inv(Sigma)
```
Then draw a scatter plot of the observations together with the estimated regression plane in 3D, respective the boundary of the prediction interval, which represents hyperparabolic planes. The confidence interval for the conditional mean is not drawn to keep the graph readable.
**Note:** *The 3D plot will open in a new window where you can rotate the plot to see from a different angle. The execution of code will not continue until you close the window.*
```
%matplotlib qt
w0=linregr.intercept_
w_=linregr.coef_.T
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:,0], X[:,1], y_, c='b', alpha=1)
# Creating the meshgrid for x (TV), y (radio) and calculating the value of z (sales)
xx, yy = np.meshgrid(np.arange(0,300,5), np.arange(0,50,5))
y_mean = w0+w_[0,0]*xx+w_[1,0]*yy
# Plotting the estimated conditional mean surface
zz = y_mean
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Blues, linewidth=0, antialiased=False, alpha=0.7)
# Calculating the Mahalanobis distance for the meshgrid
imax,jmax=xx.shape
d_M2=np.array([[float(np.array([xx[i,j]-mu_[0,0],yy[i,j]-mu_[1,0]])[:,np.newaxis].T@Sigma_1@\
np.array([xx[i,j]-mu_[0,0],yy[i,j]-mu_[1,0]])[:,np.newaxis]) for j in range(jmax)] for i in range(imax)])
# Plotting the boundary surface for the prediction interval
zz = y_mean+tscore*np.sqrt(MSE)*np.sqrt(1+1/N+1/(N-1)*d_M2)
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Reds, linewidth=0, antialiased=False, alpha=0.7)
zz = y_mean-tscore*np.sqrt(MSE)*np.sqrt(1+1/N+1/(N-1)*d_M2)
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Reds, linewidth=0, antialiased=False, alpha=0.7)
ax.set_xlabel('TV',fontsize=12)
ax.set_ylabel('radio',fontsize=12)
ax.set_zlabel('Sales',fontsize=12)
plt.title('Estimated regression plane with prediction interval',fontsize=14)
plt.show(block=True)
```
To understand the confidence and prediction intervals let's take an example.
For example, given that 10000 USD is spent on TV advertising and 90000 USD is spent on radio advertising in each market, the estimated mean of the average sale is:
```
linregr.fit(X[:,0:2],y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
xnew_=np.array([[1],[10],[90]])
yhatnew=float(xnew_.T@w_)
print("Estimated average sale:",yhatnew*1000)
```
The 95% confidence interval is:
```
alpha=0.05
tscore=abs(stats.t.ppf(alpha/2, df))
[1000*float(yhatnew-tscore*sigma*np.sqrt(xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_)),\
1000*float(yhatnew+tscore*sigma*np.sqrt(xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_))]
```
and the 95% prediction interval is:
```
[1000*float(yhatnew-tscore*sigma*np.sqrt(1+xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_)),\
1000*float(yhatnew+tscore*sigma*np.sqrt(1+xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_))]
```
#### Confidence regions
We already created the individual confidence intervals for the regression coefficients. Now, let's create a joint confidence region as a rectangle from the individual confidence intervals, respective also create the confidence rectangle using the Bonferroni correction method. We should also create the ellipse of the confidence region.
```
from matplotlib.patches import Ellipse
import matplotlib.patches as mpatches
%matplotlib inline
xlim=0.02
ylim=0.02
ax= plt.subplot(111)
w_=linregr.coef_.T
#Plot the center
ax.scatter(w_[0],w_[1])
# Plot the 95% confidence ellipse
U,Diag,V=svd(X[:,0:2].T@X[:,0:2]/(3*MSE*stats.f.ppf(1-0.05,2,198)))
width,height=np.sqrt(1/Diag)
theta=np.degrees(np.arctan2(V[0,1],V[0,0]))
ellipsoid=Ellipse(w_.ravel(), width, height, theta, edgecolor='r', fc='None',lw=3)
ax.add_patch(ellipsoid)
# Plot the confidence rectangle
tscore=abs(stats.t.ppf(alpha/2, df))
w1min,w2min=w_-tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
w1max,w2max=w_+tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
ax.plot([w1min,w1min],[w_[1]-ylim,w2max],'k--')
ax.plot([w1max,w1max],[w_[1]-ylim,w2max],'k--')
ax.plot([w_[0]-xlim,w1max],[w2min,w2min],'k--')
ax.plot([w_[0]-xlim,w1max],[w2max,w2max],'k--')
# Plot the Bonferroni confidence rectangle
tscore=abs(stats.t.ppf(alpha/4, df))
w1min,w2min=w_-tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
w1max,w2max=w_+tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
ax.plot([w1min,w1min],[w_[1]-ylim,w2max],'b--')
ax.plot([w1max,w1max],[w_[1]-ylim,w2max],'b--')
ax.plot([w_[0]-xlim,w1max],[w2min,w2min],'b--')
ax.plot([w_[0]-xlim,w1max],[w2max,w2max],'b--')
red_patch = mpatches.Patch(color='red', label='Confidence ellipse')
black_patch = mpatches.Patch(color='black', label='Confidence rectangle')
blue_patch = mpatches.Patch(color='blue', label='Bonferroni rectangle')
plt.legend(handles=[red_patch,black_patch,blue_patch])
plt.xlim(w_[0]-xlim, w_[0]+xlim)
plt.ylim(w_[1]-ylim, w_[1]+ylim)
plt.xlabel('TV',fontsize=12)
plt.ylabel('radio',fontsize=12)
plt.title("Confidence regions for 'TV' and 'radio' regr. coeff.",fontsize=14)
plt.show()
```
As we can observe, the Bonferroni correction makes the individual confidence intervals wider, while the confidence ellipse is much narrower than what the naive confidence rectangle provides.
## 6. Removing the additive assumption <a name="AdditiveAssumptionRemoval"></a>
**Note:** *This part is related to $\textbf{Removing Beyond the OLS Assumptions}$ of the book. You may check this part of the lab exercise only after reading the relavand section of the book (3.6.2 Removing the Additive Assumption).*
So far so good! You created a model that explains around 90% percent of the variability of the sales. So you can go to your boss to present your work. Your linear model has the form of
$\hat y=w_0 + w_1 x_1 + w_2 x_2$<br>
where $x_1$ represents the *TV* and $x_2$ the *radio* independent variable.
However, your boss has some doubts about the validity of your model. Especially that your model suggests, it is better to spend the budget on radio advertising than on TV, which seems to be unrealistic. If you want to maximize your sales with a given fix advertising budget, you should advertise on the radio only. Now that you got the feedback from your boss, you have to make your homework again and create a model, which provides a more realistic result.
Previously, we concluded that both TV and radio seem to be associated with sales. The linear models that formed the basis for this conclusion assumed that the effect on sales of increasing one advertising medium is independent of the amount spent on the other media. For example, the average effect on sales of a one-unit increase in TV is always $w_1$, regardless of the amount spent on radio. But this simple model may be incorrect. Suppose that spending money on radio advertising increases the effectiveness of TV advertising. In marketing, this is known as a synergy effect, and in statistics, it is referred to as an interaction effect. Let's consider the linear model:
$\hat y^\star=w_0^\star + w_1^\star x_1 + w_2^\star x_2 + w_3^\star x_1 x_2 $
and denote with $x_3=x_1 x_2$. Let's create this interaction effect as a third predictor.
```
data['TVxRadio'] = data['TV']*data['radio']
data
```
Then create the OLS summary with *statsmodels* library.
```
model = ols(formula = 'sales ~ TV + radio + TVxRadio', data=data).fit()
print(model.summary())
```
The results strongly suggest that the model that includes the interaction term is superior to the model that contains only the main effects. The p-value for the interaction term, *TVxRadio*, is extremely low, indicating that there is strong evidence for the alternative hypothesis of $w_3\neq 0$. Even if this interaction effect has a very low coefficient, the standard error is extremely low. In other words, a true relationship is not additive. The R-squared value is also increased from 89.7% to 96.8%.
You may use the *scikit-learn* library to obtain the same result. You may also find that the RMSE also dropped to 0.94.
```
X1=data[['TV','radio','TVxRadio']].to_numpy()
N,D=X1.shape
linregr.fit(X1,y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(3),["TV coef. =","Radio coef. =","TV x Radio coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X,y_))
print("R-squared adjusted =",1-(1-linregr.score(X1,y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X1)).T@(y_-linregr.predict(X1))/(N-2))
print("RSE =",np.sqrt(MSE))
```
What is more important than the R-squared value is that the conclusion drawn from your model is different. With only additive assumption, you may suggest that the optimal solution to maximize the sales with a given advertising budget of 100 thousand dollars would be to use only the radio medium. In such a case, your model would predict almost 22 thousand units in sales with that advertising budget. However, with the non-additive assumption, you will get a more realistic result, which suggests that the advertising budget should be split equally between TV and radio. In this case, however, the predicted sales are below 12 thousand units, which is only slightly more than half of what the additive assumption predicted.
```
budget=100
linregr.fit(X[:,0:2],y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
ratio_=np.linspace(0.01,100,100)
yhat_=w_[0]+w_[1]*budget/(1+ratio_)+w_[2]*budget*ratio_/(1+ratio_)
plt.plot(ratio_,yhat_,label='Additive model')
linregr.fit(X1,y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
ratio_=np.linspace(0.01,100,100)
yhat_=w_[0]+w_[1]*budget/(1+ratio_)+w_[2]*budget*ratio_/(1+ratio_)+w_[3]*budget**2*ratio_/(1+ratio_)**2
plt.plot(ratio_,yhat_,label='Non-additive model')
plt.title('Sales vs. radio to TV budget ratio', fontsize=14)
plt.xlabel(r'ratio [$\frac{\mathrm{radio}}{\mathrm{TV}}$] for fixed budget of \$100,000',fontsize=12)
plt.ylabel('sales [thousands of units]',fontsize=12)
plt.legend()
plt.show()
```
You can print out the maximum sales value for the non-additive model.
```
print('Maximum sales in thousand of units with advertising budget of 100,000$ =',yhat_.max())
```
We can find out the radio to TV advertising expenditure ratio for the non-additive model with maximum sales.
```
print('Radio to TV advertising expenditure ratio for maximized sales =',np.argmax(yhat_))
```
Wow! Not only your model explains now 97% of the variability of the sales, but more importantly provides more realistic scenario regarding how you should spend the advertising budget to maximize the sales, namely the budget shall be split equally between the two media: radio and TV. There is also a surprise in the outcome, the predicited maximum sales value is much lower, only slightly more than half of what the first model suggested. That is a good example why the R-squared value should not be taken as granted and common sense should be also used.
<img src = "images/AML1-Cover.png" width = 110, align = "left" style="margin:0px 20px">
<span style="color:blue">**Note:**</span> This Jupyter Notebook is accompanying the book: <br> $\qquad$ <b>Advanced Machine Learning Made Easy</b> <br> $\qquad$ From Theory to Practice with NumPy and scikit-learn <br> $\qquad$ <i> Volume 1: Generalized Linear Models</i><br>
by Ferenc Farkas, Ph.D.
If you find this Notebook useful, please support me by buying the book at [Leanpub](http://leanpub.com/AML1). <br>
Copyright notice: This Jupyter Notebook is made available under the [MIT License](https://opensource.org/licenses/MIT).
|
github_jupyter
|
import numpy as np
from numpy.linalg import matrix_rank, inv, svd
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import f_regression
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import os
%matplotlib inline
data = pd.read_csv('http://faculty.marshall.usc.edu/gareth-james/ISL/Advertising.csv', index_col=0) # Reading from web page
#data = pd.read_csv(os.path.join('data','Advertising.csv')) # Uncomment this line in case the above line trows an error
data
pd.options.mode.use_inf_as_na = True
print(data.isnull().values.any())
data.describe()
boxprops = dict(linestyle='-', linewidth=2, color='k')
medianprops = dict(linestyle='-', linewidth=2, color='k')
data.boxplot(column=['TV','radio','newspaper','sales'],fontsize=12,grid=False,boxprops=boxprops, medianprops=medianprops)
plt.title("Boxplot of the 'Advertising' dataset",fontsize=14)
plt.show()
X=np.array(data[["TV","radio","newspaper"]])
y_=np.array(data["sales"])[:,np.newaxis]
N,D=X.shape
print("Number of observations =",N)
print("Number of features =", D)
Xdot=np.insert(X,0,np.ones(N),axis=1)
print("Rank of the design matrix is:",matrix_rank(Xdot))
from numpy.linalg import eigh
eigval,eigvect=eigh(Xdot.T@Xdot)
print("Eigenvalues of the product matrix:")
print(eigval[:,np.newaxis])
print("Condition number =",np.sqrt(eigval.max()/eigval.min()))
from numpy.linalg import cond
print(cond(Xdot))
from statsmodels.stats.outliers_influence import variance_inflation_factor
print("VIF for TV =",variance_inflation_factor(Xdot,1))
print("VIF for radio =",variance_inflation_factor(Xdot,2))
print("VIF for newspaper =",variance_inflation_factor(Xdot,3))
fig, ax = plt.subplots(1, 3, figsize=(14, 4))
xvarlist=['TV','radio','newspaper']
linregr=LinearRegression()
for i in range(D):
ax[i].scatter(X[:,i],y_,s=20)
x_=X[:,i].reshape(-1,1)
linregr.fit(x_,y_)
ax[i].plot([x_.min(),x_.max()],linregr.predict(np.array([[x_.min()],[x_.max()]])),c='r')
ax[i].set_xlabel(list(data.columns.values)[i],fontsize=14)
ax[i].set_ylabel(list(data.columns.values)[D],fontsize=14)
ax[i].set_title('Sales vs. '+xvarlist[i],fontsize=16)
ax[i].annotate('r = '+'%.2f'%np.corrcoef(np.append(X,y_,axis=1), rowvar=False)[:,-1][i],\
xy=(X.mean(axis=0)[i],2),color='red',fontsize=12)
plt.show()
import seaborn as sns
sns.pairplot(data)
plt.show()
pd.plotting.scatter_matrix(data,figsize=(14,14),s=100)
plt.show()
from scipy import stats
conflevel=95
alpha=1-conflevel/100
df=N-2
tscore=abs(stats.t.ppf(alpha/2, df))
pd.options.display.float_format = '{:,.3f}'.format
def OLSresults(x_,y_):
linregr=LinearRegression()
linregr.fit(x_,y_)
r_=y_-linregr.predict(x_)
MSE=r_.T@r_/(N-2)
s_w=float(np.squeeze(np.sqrt(MSE/np.sum((x_-x_.mean())**2))))
s_b=float(np.squeeze(s_w*np.sqrt(x_.T@x_/N)))
table=pd.DataFrame(columns=["Input","Coefficient","Std. error","t-statistic","p-value","[0.025","0.975]"])
t_stat=linregr.intercept_[0]/s_b
pval = stats.t.sf(np.abs(t_stat),df)*2
LCL=linregr.intercept_[0]-tscore*s_b
UCL=linregr.intercept_[0]+tscore*s_b
table=table.append({"Input":"Intercept","Coefficient":linregr.intercept_[0],"Std. error":s_b,"t-statistic":t_stat,\
"p-value":pval,"[0.025":LCL,"0.975]":UCL},ignore_index=True)
t_stat=linregr.coef_[0][0]/s_w
pval = stats.t.sf(np.abs(t_stat),df)*2
LCL=linregr.coef_[0][0]-tscore*s_w
UCL=linregr.coef_[0][0]+tscore*s_w
table=table.append({"Input":list(data.columns.values)[i],"Coefficient":linregr.coef_[0][0],"Std. error":s_w,\
"t-statistic":t_stat,"p-value":pval,"[0.025":LCL,"0.975]":UCL},ignore_index=True)
return table,MSE,linregr.score(x_,y_),r_
R=[]
print("============================================================================")
for i in range(D):
x_=X[:,i].reshape(-1,1)
print(OLSresults(x_,y_)[0])
print('----------------------------------------------------------------------------')
print("RSE=%f, R-squared=%f\n"%(float(np.sqrt(OLSresults(x_,y_)[1])),OLSresults(x_,y_)[2]))
print("============================================================================")
R.append(OLSresults(x_,y_)[3])
R=np.array(R).squeeze().T # Store the residual vectors
fig, ax = plt.subplots(1, 3, figsize=(14, 4))
ax[0].scatter(X[:,0],R[:,0],s=15)
ax[0].plot([X[:,0].min(),X[:,0].max()],[0,0],'--r',lw=2)
ax[1].scatter(X[:,1],R[:,1],s=15)
ax[1].plot([X[:,1].min(),X[:,1].max()],[0,0],'--r',lw=2)
ax[2].scatter(X[:,2],R[:,2],s=15)
ax[2].plot([X[:,2].min(),X[:,2].max()],[0,0],'--r',lw=2)
ax[0].set_xlabel('TV',fontsize=12)
ax[1].set_xlabel('radio',fontsize=12)
ax[2].set_xlabel('newspaper',fontsize=12)
ax[0].set_ylabel('Residuals',fontsize=12)
fig.suptitle("Scatter plot of the residuals for each SLR", fontsize=14)
plt.show()
from statsmodels.formula.api import ols
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
results = ols(formula = 'sales ~ TV', data=data).fit()
print(results.summary(title='OLS Results for TV vs. sales'))
name = ['F statistic', 'p-value']
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
results = ols(formula = 'sales ~ radio', data=data).fit()
print(results.summary(title='OLS Results for radio vs. sales'))
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
results = ols(formula = 'sales ~ newspaper', data=data).fit()
print(results.summary(title='OLS Results for newspaper vs. sales'))
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
fig, ax = plt.subplots(1, 3, figsize=(16, 5))
stats.probplot(np.ravel(R[:,0]), plot=ax[0])
stats.probplot(np.ravel(R[:,1]), plot=ax[1])
stats.probplot(np.ravel(R[:,2]), plot=ax[2])
ax[0].set_title('QQ-plot of residuals for sales vs. TV')
ax[1].set_title('QQ-plot of residuals for sales vs. radio')
ax[2].set_title('QQ-plot of residuals for sales vs. newspaper')
fig.suptitle("Normal probability plot for the residuals of each SLR", fontsize=14)
plt.show()
linregr.fit(X,y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(3),["TV coef. =","Radio coef. =","Newspaper coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X,y_))
print("R-squared adjusted =",1-(1-linregr.score(X,y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X)).T@(y_-linregr.predict(X))/(N-2))
print("RMSE =",np.sqrt(MSE))
results = ols(formula = 'sales ~ TV + radio + newspaper', data=data).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
print("RMSE =",np.sqrt(results.mse_resid))
plt.scatter(results.resid, results.predict())
plt.title('Scatter plot of the residuals',fontsize=14)
plt.xlabel('$\hat y$',fontsize=12)
plt.ylabel('Residuals',fontsize=12)
plt.show()
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].hist(results.resid)
ax[0].set_title('Histogram of the residuals',fontsize=12)
stats.probplot(results.resid,plot=ax[1])
plt.show()
pd.DataFrame(data=np.corrcoef(np.append(X,y_,axis=1), rowvar=False)\
,index=['TV','radio','newspaper','sales'],columns=['TV','radio','newspaper','sales'])
linregr.fit(X[:,0:2],y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(2),["TV coef. =","Radio coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X[:,0:2],y_))
print("R-squared adjusted =",1-(1-linregr.score(X[:,0:2],y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X[:,0:2])).T@(y_-linregr.predict(X[:,0:2]))/(N-2))
print("RMSE =",np.sqrt(MSE))
results = ols(formula = 'sales ~ TV + radio', data=data).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
sigma=np.sqrt(results.mse_resid)
print("RMSE =",np.sqrt(results.mse_resid))
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
ax[0].hist(results.resid)
stats.probplot(results.resid,plot=ax[1])
plt.show()
data1=data.drop(index=131)
results = ols(formula = 'sales ~ TV + radio', data=data1).fit()
print(results.summary())
test = sms.het_goldfeldquandt(results.resid, results.model.exog)
print("\nGoldfeld-Quandt test:\n",lzip(name, test))
sigma=np.sqrt(results.mse_resid)
print("RMSE =",np.sqrt(results.mse_resid))
mu_=X[:,0:2].mean(axis=0)[:,np.newaxis]
Sigma=1/(N-1)*(X[:,0:-1]-mu_.T).T@(X[:,0:-1]-mu_.T)
Sigma_1=inv(Sigma)
%matplotlib qt
w0=linregr.intercept_
w_=linregr.coef_.T
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:,0], X[:,1], y_, c='b', alpha=1)
# Creating the meshgrid for x (TV), y (radio) and calculating the value of z (sales)
xx, yy = np.meshgrid(np.arange(0,300,5), np.arange(0,50,5))
y_mean = w0+w_[0,0]*xx+w_[1,0]*yy
# Plotting the estimated conditional mean surface
zz = y_mean
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Blues, linewidth=0, antialiased=False, alpha=0.7)
# Calculating the Mahalanobis distance for the meshgrid
imax,jmax=xx.shape
d_M2=np.array([[float(np.array([xx[i,j]-mu_[0,0],yy[i,j]-mu_[1,0]])[:,np.newaxis].T@Sigma_1@\
np.array([xx[i,j]-mu_[0,0],yy[i,j]-mu_[1,0]])[:,np.newaxis]) for j in range(jmax)] for i in range(imax)])
# Plotting the boundary surface for the prediction interval
zz = y_mean+tscore*np.sqrt(MSE)*np.sqrt(1+1/N+1/(N-1)*d_M2)
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Reds, linewidth=0, antialiased=False, alpha=0.7)
zz = y_mean-tscore*np.sqrt(MSE)*np.sqrt(1+1/N+1/(N-1)*d_M2)
surf = ax.plot_surface(xx, yy, zz, cmap=cm.Reds, linewidth=0, antialiased=False, alpha=0.7)
ax.set_xlabel('TV',fontsize=12)
ax.set_ylabel('radio',fontsize=12)
ax.set_zlabel('Sales',fontsize=12)
plt.title('Estimated regression plane with prediction interval',fontsize=14)
plt.show(block=True)
linregr.fit(X[:,0:2],y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
xnew_=np.array([[1],[10],[90]])
yhatnew=float(xnew_.T@w_)
print("Estimated average sale:",yhatnew*1000)
alpha=0.05
tscore=abs(stats.t.ppf(alpha/2, df))
[1000*float(yhatnew-tscore*sigma*np.sqrt(xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_)),\
1000*float(yhatnew+tscore*sigma*np.sqrt(xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_))]
[1000*float(yhatnew-tscore*sigma*np.sqrt(1+xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_)),\
1000*float(yhatnew+tscore*sigma*np.sqrt(1+xnew_.T@inv(Xdot[:,:-1].T@Xdot[:,:-1])@xnew_))]
from matplotlib.patches import Ellipse
import matplotlib.patches as mpatches
%matplotlib inline
xlim=0.02
ylim=0.02
ax= plt.subplot(111)
w_=linregr.coef_.T
#Plot the center
ax.scatter(w_[0],w_[1])
# Plot the 95% confidence ellipse
U,Diag,V=svd(X[:,0:2].T@X[:,0:2]/(3*MSE*stats.f.ppf(1-0.05,2,198)))
width,height=np.sqrt(1/Diag)
theta=np.degrees(np.arctan2(V[0,1],V[0,0]))
ellipsoid=Ellipse(w_.ravel(), width, height, theta, edgecolor='r', fc='None',lw=3)
ax.add_patch(ellipsoid)
# Plot the confidence rectangle
tscore=abs(stats.t.ppf(alpha/2, df))
w1min,w2min=w_-tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
w1max,w2max=w_+tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
ax.plot([w1min,w1min],[w_[1]-ylim,w2max],'k--')
ax.plot([w1max,w1max],[w_[1]-ylim,w2max],'k--')
ax.plot([w_[0]-xlim,w1max],[w2min,w2min],'k--')
ax.plot([w_[0]-xlim,w1max],[w2max,w2max],'k--')
# Plot the Bonferroni confidence rectangle
tscore=abs(stats.t.ppf(alpha/4, df))
w1min,w2min=w_-tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
w1max,w2max=w_+tscore*np.sqrt(np.diag(MSE*inv(X[:,0:2].T@X[:,0:2])))[:,np.newaxis]
ax.plot([w1min,w1min],[w_[1]-ylim,w2max],'b--')
ax.plot([w1max,w1max],[w_[1]-ylim,w2max],'b--')
ax.plot([w_[0]-xlim,w1max],[w2min,w2min],'b--')
ax.plot([w_[0]-xlim,w1max],[w2max,w2max],'b--')
red_patch = mpatches.Patch(color='red', label='Confidence ellipse')
black_patch = mpatches.Patch(color='black', label='Confidence rectangle')
blue_patch = mpatches.Patch(color='blue', label='Bonferroni rectangle')
plt.legend(handles=[red_patch,black_patch,blue_patch])
plt.xlim(w_[0]-xlim, w_[0]+xlim)
plt.ylim(w_[1]-ylim, w_[1]+ylim)
plt.xlabel('TV',fontsize=12)
plt.ylabel('radio',fontsize=12)
plt.title("Confidence regions for 'TV' and 'radio' regr. coeff.",fontsize=14)
plt.show()
data['TVxRadio'] = data['TV']*data['radio']
data
model = ols(formula = 'sales ~ TV + radio + TVxRadio', data=data).fit()
print(model.summary())
X1=data[['TV','radio','TVxRadio']].to_numpy()
N,D=X1.shape
linregr.fit(X1,y_)
print("Intercept =",linregr.intercept_[0])
for i,media in zip(range(3),["TV coef. =","Radio coef. =","TV x Radio coef. ="]):
print(media,linregr.coef_[0][i])
print("R-squared =",linregr.score(X,y_))
print("R-squared adjusted =",1-(1-linregr.score(X1,y_))*(N-1)/(N-D-1))
MSE=float((y_-linregr.predict(X1)).T@(y_-linregr.predict(X1))/(N-2))
print("RSE =",np.sqrt(MSE))
budget=100
linregr.fit(X[:,0:2],y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
ratio_=np.linspace(0.01,100,100)
yhat_=w_[0]+w_[1]*budget/(1+ratio_)+w_[2]*budget*ratio_/(1+ratio_)
plt.plot(ratio_,yhat_,label='Additive model')
linregr.fit(X1,y_)
w_=list(linregr.intercept_)
w_.extend(list(linregr.coef_[0]))
w_=np.array(w_)[:,np.newaxis]
ratio_=np.linspace(0.01,100,100)
yhat_=w_[0]+w_[1]*budget/(1+ratio_)+w_[2]*budget*ratio_/(1+ratio_)+w_[3]*budget**2*ratio_/(1+ratio_)**2
plt.plot(ratio_,yhat_,label='Non-additive model')
plt.title('Sales vs. radio to TV budget ratio', fontsize=14)
plt.xlabel(r'ratio [$\frac{\mathrm{radio}}{\mathrm{TV}}$] for fixed budget of \$100,000',fontsize=12)
plt.ylabel('sales [thousands of units]',fontsize=12)
plt.legend()
plt.show()
print('Maximum sales in thousand of units with advertising budget of 100,000$ =',yhat_.max())
print('Radio to TV advertising expenditure ratio for maximized sales =',np.argmax(yhat_))
| 0.585101 | 0.990777 |
# UE ROLL Blue speaker detection
A model trained to detect Blue UE roll blutooth speaker.
Only 16 images has been used for current training. Performace could be increased using more images.
#Environment Setup
```
# !pip install protobuf-compiler python-pil python-lxml python-tk
# !pip install Cython
# !pip install jupyter
# !pip install matplotlib
!pip install --upgrade tensorflow==1.13.1
# !git clone https://github.com/tensorflow/models.git
# %cd /Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research
# !protoc object_detection/protos/*.proto --python_out=.
# %set_env PYTHONPATH=/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research:/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research/slim
# !python object_detection/builders/model_builder_test.py
```
# Imports
```
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
# This is needed since the notebook is stored in the object_detection folder.
sys.path.append("..")
from object_detection.utils import ops as utils_ops
from object_detection.utils import label_map_util
from object_detection.utils import visualization_utils as vis_util
# This is needed to display the images.
%matplotlib inline
print(tf.__version__)
```
# Model preparation
## Variables
Any model exported using the `export_inference_graph.py` tool can be loaded here simply by changing `PATH_TO_FROZEN_GRAPH` to point to a new .pb file.
By default we use an "SSD with Mobilenet" model here. See the [detection model zoo](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md) for a list of other models that can be run out-of-the-box with varying speeds and accuracies.
```
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_FROZEN_GRAPH = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/IG/frozen_inference_graph.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/data/label.pbtxt'
#Number of classes
NUM_CLASSES = 1
```
## Load a (frozen) Tensorflow model into memory.
```
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_FROZEN_GRAPH, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
```
## Loading label map
Label maps map indices to category names, so that when our convolution network predicts `5`, we know that this corresponds to `airplane`. Here we use internal utility functions, but anything that returns a dictionary mapping integers to appropriate string labels would be fine
```
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
```
## Helper code
```
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
```
# Detection
```
# If you want to test the code with your images, just add path to the images to the TEST_IMAGE_PATHS.
PATH_TO_TEST_IMAGES_DIR = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/data/testImages'
TEST_IMAGE_PATHS = [ os.path.join(PATH_TO_TEST_IMAGES_DIR, 'image{}.jpg'.format(i)) for i in range(1, 3) ]
# Size, in inches, of the output images.
IMAGE_SIZE = (12, 8)
def run_inference_for_single_image(image, graph):
with graph.as_default():
with tf.Session() as sess:
# Get handles to input and output tensors
ops = tf.get_default_graph().get_operations()
all_tensor_names = {output.name for op in ops for output in op.outputs}
tensor_dict = {}
for key in [
'num_detections', 'detection_boxes', 'detection_scores',
'detection_classes', 'detection_masks'
]:
tensor_name = key + ':0'
if tensor_name in all_tensor_names:
tensor_dict[key] = tf.get_default_graph().get_tensor_by_name(
tensor_name)
if 'detection_masks' in tensor_dict:
# The following processing is only for single image
detection_boxes = tf.squeeze(tensor_dict['detection_boxes'], [0])
detection_masks = tf.squeeze(tensor_dict['detection_masks'], [0])
# Reframe is required to translate mask from box coordinates to image coordinates and fit the image size.
real_num_detection = tf.cast(tensor_dict['num_detections'][0], tf.int32)
detection_boxes = tf.slice(detection_boxes, [0, 0], [real_num_detection, -1])
detection_masks = tf.slice(detection_masks, [0, 0, 0], [real_num_detection, -1, -1])
detection_masks_reframed = utils_ops.reframe_box_masks_to_image_masks(
detection_masks, detection_boxes, image.shape[0], image.shape[1])
detection_masks_reframed = tf.cast(
tf.greater(detection_masks_reframed, 0.5), tf.uint8)
# Follow the convention by adding back the batch dimension
tensor_dict['detection_masks'] = tf.expand_dims(
detection_masks_reframed, 0)
image_tensor = tf.get_default_graph().get_tensor_by_name('image_tensor:0')
# Run inference
output_dict = sess.run(tensor_dict,
feed_dict={image_tensor: np.expand_dims(image, 0)})
# all outputs are float32 numpy arrays, so convert types as appropriate
output_dict['num_detections'] = int(output_dict['num_detections'][0])
output_dict['detection_classes'] = output_dict[
'detection_classes'][0].astype(np.uint8)
output_dict['detection_boxes'] = output_dict['detection_boxes'][0]
output_dict['detection_scores'] = output_dict['detection_scores'][0]
if 'detection_masks' in output_dict:
output_dict['detection_masks'] = output_dict['detection_masks'][0]
return output_dict
for image_path in TEST_IMAGE_PATHS:
image = Image.open(image_path)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
image_np = load_image_into_numpy_array(image)
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
output_dict = run_inference_for_single_image(image_np, detection_graph)
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
output_dict['detection_boxes'],
output_dict['detection_classes'],
output_dict['detection_scores'],
category_index,
instance_masks=output_dict.get('detection_masks'),
use_normalized_coordinates=True,
line_thickness=8)
fig = plt.figure(figsize=IMAGE_SIZE)
ax = fig.gca()
ax.grid(False)
plt.imshow(image_np)
```
|
github_jupyter
|
# !pip install protobuf-compiler python-pil python-lxml python-tk
# !pip install Cython
# !pip install jupyter
# !pip install matplotlib
!pip install --upgrade tensorflow==1.13.1
# !git clone https://github.com/tensorflow/models.git
# %cd /Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research
# !protoc object_detection/protos/*.proto --python_out=.
# %set_env PYTHONPATH=/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research:/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/models/research/slim
# !python object_detection/builders/model_builder_test.py
import numpy as np
import os
import six.moves.urllib as urllib
import sys
import tarfile
import tensorflow as tf
import zipfile
from collections import defaultdict
from io import StringIO
from matplotlib import pyplot as plt
from PIL import Image
# This is needed since the notebook is stored in the object_detection folder.
sys.path.append("..")
from object_detection.utils import ops as utils_ops
from object_detection.utils import label_map_util
from object_detection.utils import visualization_utils as vis_util
# This is needed to display the images.
%matplotlib inline
print(tf.__version__)
# Path to frozen detection graph. This is the actual model that is used for the object detection.
PATH_TO_FROZEN_GRAPH = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/IG/frozen_inference_graph.pb'
# List of the strings that is used to add correct label for each box.
PATH_TO_LABELS = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/data/label.pbtxt'
#Number of classes
NUM_CLASSES = 1
detection_graph = tf.Graph()
with detection_graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(PATH_TO_FROZEN_GRAPH, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
label_map = label_map_util.load_labelmap(PATH_TO_LABELS)
categories = label_map_util.convert_label_map_to_categories(label_map, max_num_classes=NUM_CLASSES, use_display_name=True)
category_index = label_map_util.create_category_index(categories)
def load_image_into_numpy_array(image):
(im_width, im_height) = image.size
return np.array(image.getdata()).reshape(
(im_height, im_width, 3)).astype(np.uint8)
# If you want to test the code with your images, just add path to the images to the TEST_IMAGE_PATHS.
PATH_TO_TEST_IMAGES_DIR = '/Users/wangmeijie/PycharmProjects/Flame+MaskRCNN/data/testImages'
TEST_IMAGE_PATHS = [ os.path.join(PATH_TO_TEST_IMAGES_DIR, 'image{}.jpg'.format(i)) for i in range(1, 3) ]
# Size, in inches, of the output images.
IMAGE_SIZE = (12, 8)
def run_inference_for_single_image(image, graph):
with graph.as_default():
with tf.Session() as sess:
# Get handles to input and output tensors
ops = tf.get_default_graph().get_operations()
all_tensor_names = {output.name for op in ops for output in op.outputs}
tensor_dict = {}
for key in [
'num_detections', 'detection_boxes', 'detection_scores',
'detection_classes', 'detection_masks'
]:
tensor_name = key + ':0'
if tensor_name in all_tensor_names:
tensor_dict[key] = tf.get_default_graph().get_tensor_by_name(
tensor_name)
if 'detection_masks' in tensor_dict:
# The following processing is only for single image
detection_boxes = tf.squeeze(tensor_dict['detection_boxes'], [0])
detection_masks = tf.squeeze(tensor_dict['detection_masks'], [0])
# Reframe is required to translate mask from box coordinates to image coordinates and fit the image size.
real_num_detection = tf.cast(tensor_dict['num_detections'][0], tf.int32)
detection_boxes = tf.slice(detection_boxes, [0, 0], [real_num_detection, -1])
detection_masks = tf.slice(detection_masks, [0, 0, 0], [real_num_detection, -1, -1])
detection_masks_reframed = utils_ops.reframe_box_masks_to_image_masks(
detection_masks, detection_boxes, image.shape[0], image.shape[1])
detection_masks_reframed = tf.cast(
tf.greater(detection_masks_reframed, 0.5), tf.uint8)
# Follow the convention by adding back the batch dimension
tensor_dict['detection_masks'] = tf.expand_dims(
detection_masks_reframed, 0)
image_tensor = tf.get_default_graph().get_tensor_by_name('image_tensor:0')
# Run inference
output_dict = sess.run(tensor_dict,
feed_dict={image_tensor: np.expand_dims(image, 0)})
# all outputs are float32 numpy arrays, so convert types as appropriate
output_dict['num_detections'] = int(output_dict['num_detections'][0])
output_dict['detection_classes'] = output_dict[
'detection_classes'][0].astype(np.uint8)
output_dict['detection_boxes'] = output_dict['detection_boxes'][0]
output_dict['detection_scores'] = output_dict['detection_scores'][0]
if 'detection_masks' in output_dict:
output_dict['detection_masks'] = output_dict['detection_masks'][0]
return output_dict
for image_path in TEST_IMAGE_PATHS:
image = Image.open(image_path)
# the array based representation of the image will be used later in order to prepare the
# result image with boxes and labels on it.
image_np = load_image_into_numpy_array(image)
# Expand dimensions since the model expects images to have shape: [1, None, None, 3]
image_np_expanded = np.expand_dims(image_np, axis=0)
# Actual detection.
output_dict = run_inference_for_single_image(image_np, detection_graph)
# Visualization of the results of a detection.
vis_util.visualize_boxes_and_labels_on_image_array(
image_np,
output_dict['detection_boxes'],
output_dict['detection_classes'],
output_dict['detection_scores'],
category_index,
instance_masks=output_dict.get('detection_masks'),
use_normalized_coordinates=True,
line_thickness=8)
fig = plt.figure(figsize=IMAGE_SIZE)
ax = fig.gca()
ax.grid(False)
plt.imshow(image_np)
| 0.471223 | 0.717433 |
# `photoeccentric` eccentricity fit
In this tutorial, I will use a Kepler light curve to demonstrate how to use `photoeccentric` to recover the planet's eccentricity using the photoeccentric e
ffect [(Dawson & Johnson 2012)](https://arxiv.org/pdf/1203.5537.pdf).
The code I'm using to implement the photoeccentric effect is compiled into a package called `photoeccentric`, and can be viewed/downloaded here: https://github.com/ssagear/photoeccentric
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from astropy.table import Table
import astropy.units as u
import os
import pickle
import scipy
import random
# Using `batman` to create & fit fake transit
import batman
# Using astropy BLS and scipy curve_fit to fit transit
from astropy.timeseries import BoxLeastSquares
# Using juliet & corner to find and plot (e, w) distribution
import juliet
import corner
# Using dynesty to do the same with nested sampling
import dynesty
# And importing `photoeccentric`
import photoeccentric as ph
%load_ext autoreload
%autoreload 2
# pandas display option
pd.set_option('display.float_format', lambda x: '%.5f' % x)
spectplanets = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/spectplanets.csv')
muirhead_comb = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/muirhead_comb.csv')
muirheadKOIs = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/MuirheadKOIs.csv')
lcpath = '/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/sample_lcs'
plt.rcParams['figure.figsize'] = [20, 10]
%load_ext autoreload
%autoreload 2
```
I'll define the conversions between solar mass -> kg and solar radius -> meters for convenience.
```
# smass_kg = 1.9885e30 # Solar mass (kg)
# srad_m = 696.34e6 # Solar radius (m)
```
## The Sample
I'm using the sample of "cool KOIs" from [Muirhead et al. 2013](https://iopscience.iop.org/article/10.1088/0067-0049/213/1/5), and their properites from spectroscopy published here.
I'm reading in several .csv files containing data for this sample. The data includes spectroscopy data from Muirhead et al. (2013), stellar and planet parameters from the Kepler archive, and distances/luminosities from Gaia.
```
muirhead_data = pd.read_csv("datafiles/Muirhead2013_isochrones/muirhead_data_incmissing.txt", sep=" ")
# ALL Kepler planets from exo archive
planets = pd.read_csv('datafiles/exoplanetarchive/cumulative_kois.csv')
# Take the Kepler planet archive entries for the planets in Muirhead et al. 2013 sample
spectplanets = pd.read_csv('datafiles/database/spectplanets.csv')
# Kepler-Gaia Data
kpgaia = Table.read('datafiles/Kepler-Gaia/kepler_dr2_4arcsec.fits', format='fits').to_pandas();
# Kepler-Gaia data for only the objects in our sample
muirhead_gaia = pd.read_csv("datafiles/database/muirhead_gaia.csv")
# Combined spectroscopy data + Gaia/Kepler data for our sample
muirhead_comb = pd.read_csv('datafiles/database/muirhead_comb.csv')
# Only targets from table above with published luminosities from Gaia
muirhead_comb_lums = pd.read_csv('datafiles/database/muirhead_comb_lums.csv')
# star = ph.KeplerStar(int(np.floor(float(nkoi))))
# star.get_stellar_params(isodf)
# koi = ph.KOI(nkoi, int(np.floor(float(nkoi))), isodf)
# koi.get_KIC(muirhead_comb)
# koi.planet_params_from_archive(spectplanets)
# koi.calc_a(koi.mstar, koi.rstar)
# nbuffer, nlinfit = 7, 6
# KICs = np.sort(np.unique(np.array(muirhead_comb['KIC'])))
# KOIs = np.sort(np.unique(np.array(muirhead_comb['KOI'])))
# files = ph.get_lc_files(koi.KIC, KICs, lcpath)
# koi.get_stitched_lcs(files)
# koi.get_midpoints()
# koi.remove_oot_data(nbuffer, nlinfit)
# time, flux, fluxerr = koi.time_intransit, koi.flux_intransit, koi.fluxerr_intransit
```
# Defining a "test planet"
### I'm going to pick a planet from our sample to test how well `photoeccentric` works. Here, I'm picking KOI 254.01
First, I'll use the spectroscopy data from Muirhead et al. 2013 and Gaia luminosities to constrain the mass and radius of the host star beyond the constraint published in the Exoplanet Archive. I'll do this by matching these data with stellar isochrones [MESA](https://iopscience.iop.org/article/10.3847/0004-637X/823/2/102) and using the masses/radii from the matching isochrones to constrian the stellar density.
```
nkoi = 254.01
```
I'll read in a file with the MESA stellar isochrones for low-mass stars. I'll use `ph.fit_isochrone_lum()` to find the subset of stellar isochrones that are consistent with a certain stellar parameters form Kepler-691 (Teff, Mstar, Rstar, and Gaia luminosity).
```
# # Read in MESA isochrones
isochrones = pd.read_csv('datafiles/Muirhead2013_isochrones/isochrones_sdss_spitzer_lowmass.dat', sep='\s\s+', engine='python')
```
Using `ph.fit_isochrone_lum()` to match isochrones to stellar data:
```
koi254 = muirhead_comb.loc[muirhead_comb['KOI'] == '251']
iso_lums = ph.fit_isochrone_lum(koi251, isochrones)
# Write to csv, then read back in (prevents notebook from lagging)
iso_lums.to_csv("tutorial02/iso_lums_" + str(nkoi) + ".csv")
isodf = pd.read_csv("tutorial02/iso_lums_" + str(nkoi) + ".csv")
```
Define a KeplerStar object, and use ph.get_stellar_params and the fit isochrones to get the stellar parameters.
```
SKOI = int(np.floor(float(nkoi)))
print('System KOI', SKOI)
star = ph.KeplerStar(SKOI)
star.get_stellar_params(isodf)
print('Stellar Mass (Msol): ', star.mstar)
print('Stellar Radius (Rsol): ', star.rstar)
print('Average Stellar Density (kg m^-3): ', star.rho_star)
```
Define a KOI object.
```
koi = ph.KOI(nkoi, SKOI, isodf)
koi.get_KIC(muirhead_comb)
print('KIC', koi.KIC)
```
# Fitting the light curve
```
koi.planet_params_from_archive(spectplanets)
koi.calc_a(koi.mstar, koi.rstar)
print('Stellar mass (Msun): ', koi.mstar, 'Stellar radius (Rsun): ', koi.rstar)
print('Period (Days): ', koi.period, 'Rp/Rs: ', koi.rprs)
print('a/Rs: ', koi.a_rs)
koi.i = 90.
print('i (deg): ', koi.i)
# Define the working directory
direct = 'tutorial02/' + str(nkoi) + '/'
```
First, reading in the light curves that I have saved for this planet.
```
KICs = np.sort(np.unique(np.array(muirhead_comb['KIC'])))
KOIs = np.sort(np.unique(np.array(muirhead_comb['KOI'])))
files = ph.get_lc_files(koi.KIC, KICs, lcpath)
# Stitching the light curves together, preserving the time stamps
koi.get_stitched_lcs(files)
# Getting the midpoint times
koi.get_midpoints()
plt.errorbar(koi.time-2454900, koi.flux, yerr=koi.flux_err, fmt='.')
plt.xlabel('Time')
plt.ylabel('Flux')
```
##### Removing Out of Transit Data
```
koi.remove_oot_data(7, 6)
plt.errorbar(koi.time_intransit, koi.flux_intransit, yerr=koi.fluxerr_intransit, fmt='.')
plt.xlabel('Time')
plt.ylabel('Flux')
plt.title('Transit LC Model with Noise')
nlive=1000
nsupersample=29
exptimesupersample=0.0201389
dataset, results = koi.do_tfit_juliet(direct, nsupersample=nsupersample, exptimesupersample=exptimesupersample, nlive=nlive)
res = pd.read_table(direct + 'posteriors.dat')
# Print transit fit results from Juliet
res
# Save fit planet parameters to variables for convenience
per_f = res.iloc[0][2]
t0_f = res.iloc[1][2]
rprs_f = res.iloc[2][2]
b_f = res.iloc[3][2]
a_f = res.iloc[6][2]
i_f = np.arccos(b_f*(1./a_f))*(180./np.pi)
```
Below, I print the original parameters and fit parameters, and overlay the fit light curve on the input light curve.
Because I input $e = 0.0$, the transit fitter should return the exact same parameters I input (because the transit fitter always requires $e = 0.0$).
```
# Plot the transit fit corner plot
p = results.posteriors['posterior_samples']['P_p1']
t0 = results.posteriors['posterior_samples']['t0_p1']
rprs = results.posteriors['posterior_samples']['p_p1']
b = results.posteriors['posterior_samples']['b_p1']
a = results.posteriors['posterior_samples']['a_p1']
inc = np.arccos(b*(1./a))*(180./np.pi)
params = ['Period', 't0', 'rprs', 'inc', 'a']
fs = np.vstack((p, t0, rprs, inc, a))
fs = fs.T
figure = corner.corner(fs, labels=params)
# Plot the data:
plt.errorbar(dataset.times_lc['KEPLER']-2454900, dataset.data_lc['KEPLER'], \
yerr = dataset.errors_lc['KEPLER'], fmt = '.', alpha = 0.1)
# Plot the model:
plt.plot(dataset.times_lc['KEPLER']-2454900, results.lc.evaluate('KEPLER'), c='r')
# Plot portion of the lightcurve, axes, etc.:
plt.xlabel('Time (BJD)-2454900')
plt.xlim(np.min(dataset.times_lc['KEPLER'])-2454900, np.max(dataset.times_lc['KEPLER'])-2454900)
plt.ylim(0.998, 1.002)
plt.ylabel('Relative flux')
plt.title('KOI 818.01 Kepler LC with Transit Fit')
plt.show()
```
### Determining T14 and T23
A crucial step to determining the $(e, w)$ distribution from the transit is calculating the total and full transit durations. T14 is the total transit duration (the time between first and fourth contact). T23 is the full transit duration (i.e. the time during which the entire planet disk is in front of the star, the time between second and third contact.)
Here, I'm using equations 14 and 15 from [this textbook](https://sites.astro.caltech.edu/~lah/review/transits_occultations.winn.pdf). We calculate T14 and T23 assuming the orbit must be circular, and using the fit parameters assuming the orbit is circular. (If the orbit is not circular, T14 and T23 will not be correct -- but this is what we want, because they will differ from the true T14 and T23 in a way that reveals the eccentricity of the orbit.)
```
koi.calc_durations()
print('Total Transit Duration: ', np.mean(koi.T14_dist), koi.T14_errs)
print('Full Transit Duration: ', np.mean(koi.T23_dist), koi.T23_errs)
```
# Get $g$
Print $g$ and $\sigma_{g}$:
```
koi.get_gs()
g_mean = koi.g_mean
g_sigma = koi.g_sigma
g_mean
g_sigma
koi.do_eccfit(direct)
with open(direct + '/kepewdres.pickle', 'rb') as f:
ewdres = pickle.load(f)
labels = ["w", "e"]
fig = corner.corner(ewdres.samples, labels=labels, title_kwargs={"fontsize": 12}, plot_contours=True)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from astropy.table import Table
import astropy.units as u
import os
import pickle
import scipy
import random
# Using `batman` to create & fit fake transit
import batman
# Using astropy BLS and scipy curve_fit to fit transit
from astropy.timeseries import BoxLeastSquares
# Using juliet & corner to find and plot (e, w) distribution
import juliet
import corner
# Using dynesty to do the same with nested sampling
import dynesty
# And importing `photoeccentric`
import photoeccentric as ph
%load_ext autoreload
%autoreload 2
# pandas display option
pd.set_option('display.float_format', lambda x: '%.5f' % x)
spectplanets = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/spectplanets.csv')
muirhead_comb = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/muirhead_comb.csv')
muirheadKOIs = pd.read_csv('/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/datafiles/MuirheadKOIs.csv')
lcpath = '/Users/ssagear/Dropbox (UFL)/Research/MetallicityProject/HiPerGator/HPG_Replica/sample_lcs'
plt.rcParams['figure.figsize'] = [20, 10]
%load_ext autoreload
%autoreload 2
# smass_kg = 1.9885e30 # Solar mass (kg)
# srad_m = 696.34e6 # Solar radius (m)
muirhead_data = pd.read_csv("datafiles/Muirhead2013_isochrones/muirhead_data_incmissing.txt", sep=" ")
# ALL Kepler planets from exo archive
planets = pd.read_csv('datafiles/exoplanetarchive/cumulative_kois.csv')
# Take the Kepler planet archive entries for the planets in Muirhead et al. 2013 sample
spectplanets = pd.read_csv('datafiles/database/spectplanets.csv')
# Kepler-Gaia Data
kpgaia = Table.read('datafiles/Kepler-Gaia/kepler_dr2_4arcsec.fits', format='fits').to_pandas();
# Kepler-Gaia data for only the objects in our sample
muirhead_gaia = pd.read_csv("datafiles/database/muirhead_gaia.csv")
# Combined spectroscopy data + Gaia/Kepler data for our sample
muirhead_comb = pd.read_csv('datafiles/database/muirhead_comb.csv')
# Only targets from table above with published luminosities from Gaia
muirhead_comb_lums = pd.read_csv('datafiles/database/muirhead_comb_lums.csv')
# star = ph.KeplerStar(int(np.floor(float(nkoi))))
# star.get_stellar_params(isodf)
# koi = ph.KOI(nkoi, int(np.floor(float(nkoi))), isodf)
# koi.get_KIC(muirhead_comb)
# koi.planet_params_from_archive(spectplanets)
# koi.calc_a(koi.mstar, koi.rstar)
# nbuffer, nlinfit = 7, 6
# KICs = np.sort(np.unique(np.array(muirhead_comb['KIC'])))
# KOIs = np.sort(np.unique(np.array(muirhead_comb['KOI'])))
# files = ph.get_lc_files(koi.KIC, KICs, lcpath)
# koi.get_stitched_lcs(files)
# koi.get_midpoints()
# koi.remove_oot_data(nbuffer, nlinfit)
# time, flux, fluxerr = koi.time_intransit, koi.flux_intransit, koi.fluxerr_intransit
nkoi = 254.01
# # Read in MESA isochrones
isochrones = pd.read_csv('datafiles/Muirhead2013_isochrones/isochrones_sdss_spitzer_lowmass.dat', sep='\s\s+', engine='python')
koi254 = muirhead_comb.loc[muirhead_comb['KOI'] == '251']
iso_lums = ph.fit_isochrone_lum(koi251, isochrones)
# Write to csv, then read back in (prevents notebook from lagging)
iso_lums.to_csv("tutorial02/iso_lums_" + str(nkoi) + ".csv")
isodf = pd.read_csv("tutorial02/iso_lums_" + str(nkoi) + ".csv")
SKOI = int(np.floor(float(nkoi)))
print('System KOI', SKOI)
star = ph.KeplerStar(SKOI)
star.get_stellar_params(isodf)
print('Stellar Mass (Msol): ', star.mstar)
print('Stellar Radius (Rsol): ', star.rstar)
print('Average Stellar Density (kg m^-3): ', star.rho_star)
koi = ph.KOI(nkoi, SKOI, isodf)
koi.get_KIC(muirhead_comb)
print('KIC', koi.KIC)
koi.planet_params_from_archive(spectplanets)
koi.calc_a(koi.mstar, koi.rstar)
print('Stellar mass (Msun): ', koi.mstar, 'Stellar radius (Rsun): ', koi.rstar)
print('Period (Days): ', koi.period, 'Rp/Rs: ', koi.rprs)
print('a/Rs: ', koi.a_rs)
koi.i = 90.
print('i (deg): ', koi.i)
# Define the working directory
direct = 'tutorial02/' + str(nkoi) + '/'
KICs = np.sort(np.unique(np.array(muirhead_comb['KIC'])))
KOIs = np.sort(np.unique(np.array(muirhead_comb['KOI'])))
files = ph.get_lc_files(koi.KIC, KICs, lcpath)
# Stitching the light curves together, preserving the time stamps
koi.get_stitched_lcs(files)
# Getting the midpoint times
koi.get_midpoints()
plt.errorbar(koi.time-2454900, koi.flux, yerr=koi.flux_err, fmt='.')
plt.xlabel('Time')
plt.ylabel('Flux')
koi.remove_oot_data(7, 6)
plt.errorbar(koi.time_intransit, koi.flux_intransit, yerr=koi.fluxerr_intransit, fmt='.')
plt.xlabel('Time')
plt.ylabel('Flux')
plt.title('Transit LC Model with Noise')
nlive=1000
nsupersample=29
exptimesupersample=0.0201389
dataset, results = koi.do_tfit_juliet(direct, nsupersample=nsupersample, exptimesupersample=exptimesupersample, nlive=nlive)
res = pd.read_table(direct + 'posteriors.dat')
# Print transit fit results from Juliet
res
# Save fit planet parameters to variables for convenience
per_f = res.iloc[0][2]
t0_f = res.iloc[1][2]
rprs_f = res.iloc[2][2]
b_f = res.iloc[3][2]
a_f = res.iloc[6][2]
i_f = np.arccos(b_f*(1./a_f))*(180./np.pi)
# Plot the transit fit corner plot
p = results.posteriors['posterior_samples']['P_p1']
t0 = results.posteriors['posterior_samples']['t0_p1']
rprs = results.posteriors['posterior_samples']['p_p1']
b = results.posteriors['posterior_samples']['b_p1']
a = results.posteriors['posterior_samples']['a_p1']
inc = np.arccos(b*(1./a))*(180./np.pi)
params = ['Period', 't0', 'rprs', 'inc', 'a']
fs = np.vstack((p, t0, rprs, inc, a))
fs = fs.T
figure = corner.corner(fs, labels=params)
# Plot the data:
plt.errorbar(dataset.times_lc['KEPLER']-2454900, dataset.data_lc['KEPLER'], \
yerr = dataset.errors_lc['KEPLER'], fmt = '.', alpha = 0.1)
# Plot the model:
plt.plot(dataset.times_lc['KEPLER']-2454900, results.lc.evaluate('KEPLER'), c='r')
# Plot portion of the lightcurve, axes, etc.:
plt.xlabel('Time (BJD)-2454900')
plt.xlim(np.min(dataset.times_lc['KEPLER'])-2454900, np.max(dataset.times_lc['KEPLER'])-2454900)
plt.ylim(0.998, 1.002)
plt.ylabel('Relative flux')
plt.title('KOI 818.01 Kepler LC with Transit Fit')
plt.show()
koi.calc_durations()
print('Total Transit Duration: ', np.mean(koi.T14_dist), koi.T14_errs)
print('Full Transit Duration: ', np.mean(koi.T23_dist), koi.T23_errs)
koi.get_gs()
g_mean = koi.g_mean
g_sigma = koi.g_sigma
g_mean
g_sigma
koi.do_eccfit(direct)
with open(direct + '/kepewdres.pickle', 'rb') as f:
ewdres = pickle.load(f)
labels = ["w", "e"]
fig = corner.corner(ewdres.samples, labels=labels, title_kwargs={"fontsize": 12}, plot_contours=True)
| 0.637369 | 0.877214 |
<h1> Pricing a European Call Option with the Black-Scholes Equation </h1>
The <a href="https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_equation">Black-Scholes equation</a> predicts the prices of an option from the underlying stock price, volatility, strike price, risk-free interest rate, and time to maturity.
This notebook defines the Black-Scholes equation and provides some examples that can be played with to get a better feel for the equation.
```
import numpy as np
from scipy.stats import norm
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('seaborn')
mpl.rcParams['axes.labelsize'] = 18
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['ytick.labelsize'] = 14
mpl.rcParams['font.family'] = 'serif'
```
The function below uses the Black-Scholes equation to determine the price of a <a href="https://en.wikipedia.org/wiki/Option_style#American_and_European_optionsEuropean">European</a> <a href="https://en.wikipedia.org/wiki/Call_option">call</a> option. The variable d1 determines the normal distribution describing the variation in the underlying stock price, while d2 determines the normal distribution determining the strike price.
```
def european_call_option_price(S, sigma, T, X, r, q=0):
"""returns the price of a european call option determined using the Black-Scholes equation
S: :float
Stock price of option
sigma: Volatility of option expressed on an annual basis
T: :float
Time to maturity of option, represented as fraction of a year (e.g. T=0.5 represents 6 months)
X: :float
Strike price of option
r: :float
Risk-free interest rate
q: :float
Dividend rate. Optional, default 0 (i.e. defaults to non-dividend paying)
returns
: :float
Price of european call option
"""
d1 = (np.log(S/X) + (r - q + 0.5*sigma**2)*T) / (sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
return S*np.exp(-q*T)*norm.cdf(d1) - X*np.exp(-r*T)*norm.cdf(d2)
```
As an example, consider a European call option with price ยฃ200, strike price of ยฃ220, 6 months to maturity, a risk-free interest rate of 1% and volatility of 0.2. The Black-Scholes equation values this option at ยฃ4.68. This is cheap as the stock price is less than the strike price, so it is out of the money.
```
S = 200
X = 220
T = 0.5
r = 0.01
sigma = 0.2
print(f"European call option valuation: ยฃ{np.round(european_call_option_price(S, sigma, T, X, r), 2)}")
```
Plotting the stock price from ยฃ100 to ยฃ300 we can see that for values far below the strike price, the option is worthless. This is because with only 6 months to maturity, and given the stocks volatility, it is very unlikely to end up in the money before maturity.
```
S = np.arange(100, 300)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, prices, label="Option Value")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
Increasing the volatility to 0.5 increases the liklihood of the option ending up in the money, and so the option is more valuable even at lower stock prices.
```
prices = european_call_option_price(S=S, sigma=0.5, T=T, X=X, r=r)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with higher volatility")
plt.vlines(X, ymin=prices.min(), ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(prices.min(), prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
Similarly, increasing the time to maturity to 10 years gives more time for the stock price to rise above the strike price, increasing the options value (especially given the risk free interest rate).
```
prices = european_call_option_price(S=S, sigma=sigma, T=10, X=X, r=r)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with 10 years to maturity")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
In fact, the price of the option increases with the time to maturity, though at an ever decreasing rate.
```
T = np.arange(0.5, 100)
prices = european_call_option_price(S=200, sigma=sigma, T=T, X=X, r=r)
plt.plot(T, prices, label="Option Value")
plt.ylim(0, prices.max())
plt.xlabel("Time to maturity")
plt.ylabel("Option price")
plt.legend()
```
Increasing the risk-free interest rate to 2% slightly increases the value of the option at lower stock prices, but not by much as there is only 6 months to maturity, which is not long enough for the interest rates to be important.
```
T = 0.5
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=0.02)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with higher risk-free interest")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
Here we change to a dividend paying stock, paying a continuous rate of 0.02. Similar to interest rates, with only six months to maturity this has little affect on the price.
```
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r, q=0.02)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with dividend")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
Below we see what happens when the strike price is lowered to ยฃ180. As expected, the price of the option increases as it is now in the money.
```
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=180, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with lower strike price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
```
Fixing the stock price at ยฃ200 and allowing the strike price to vary from ยฃ120 to ยฃ220 we can see that a lower strike price favourable, as it means the option is more likely to be in the money at maturity.
```
S = 200
X = np.arange(120, 320)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(X, prices, label="Option Value")
plt.vlines(S, ymin=0, ymax=prices.max(), colors='r', label="Stock Price")
plt.ylim(0, prices.max())
plt.xlabel("Strike price")
plt.ylabel("Option price")
plt.legend()
```
|
github_jupyter
|
import numpy as np
from scipy.stats import norm
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('seaborn')
mpl.rcParams['axes.labelsize'] = 18
mpl.rcParams['xtick.labelsize'] = 14
mpl.rcParams['ytick.labelsize'] = 14
mpl.rcParams['font.family'] = 'serif'
def european_call_option_price(S, sigma, T, X, r, q=0):
"""returns the price of a european call option determined using the Black-Scholes equation
S: :float
Stock price of option
sigma: Volatility of option expressed on an annual basis
T: :float
Time to maturity of option, represented as fraction of a year (e.g. T=0.5 represents 6 months)
X: :float
Strike price of option
r: :float
Risk-free interest rate
q: :float
Dividend rate. Optional, default 0 (i.e. defaults to non-dividend paying)
returns
: :float
Price of european call option
"""
d1 = (np.log(S/X) + (r - q + 0.5*sigma**2)*T) / (sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
return S*np.exp(-q*T)*norm.cdf(d1) - X*np.exp(-r*T)*norm.cdf(d2)
S = 200
X = 220
T = 0.5
r = 0.01
sigma = 0.2
print(f"European call option valuation: ยฃ{np.round(european_call_option_price(S, sigma, T, X, r), 2)}")
S = np.arange(100, 300)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, prices, label="Option Value")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
prices = european_call_option_price(S=S, sigma=0.5, T=T, X=X, r=r)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with higher volatility")
plt.vlines(X, ymin=prices.min(), ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(prices.min(), prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
prices = european_call_option_price(S=S, sigma=sigma, T=10, X=X, r=r)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with 10 years to maturity")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
T = np.arange(0.5, 100)
prices = european_call_option_price(S=200, sigma=sigma, T=T, X=X, r=r)
plt.plot(T, prices, label="Option Value")
plt.ylim(0, prices.max())
plt.xlabel("Time to maturity")
plt.ylabel("Option price")
plt.legend()
T = 0.5
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=0.02)
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with higher risk-free interest")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r, q=0.02)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with dividend")
plt.vlines(X, ymin=0, ymax=prices.max(), colors='r', label="Strike Price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
original_prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=180, r=r)
plt.plot(S, original_prices, label="Original Option Value")
plt.plot(S, prices, label="Option Value with lower strike price")
plt.ylim(0, prices.max())
plt.xlabel("Stock price")
plt.ylabel("Option price")
plt.legend()
S = 200
X = np.arange(120, 320)
prices = european_call_option_price(S=S, sigma=sigma, T=T, X=X, r=r)
plt.plot(X, prices, label="Option Value")
plt.vlines(S, ymin=0, ymax=prices.max(), colors='r', label="Stock Price")
plt.ylim(0, prices.max())
plt.xlabel("Strike price")
plt.ylabel("Option price")
plt.legend()
| 0.797557 | 0.988536 |
```
from datascience import *
from datascience.predicates import are
path_data = '../../../../data/'
import numpy as np
import matplotlib
matplotlib.use('Agg')
%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)
from urllib.request import urlopen
import re
def read_url(url):
return re.sub('\\s+', ' ', urlopen(url).read().decode())
```
# Plotting the classics
In this example, we will explore statistics for two classic novels: *The Adventures of Huckleberry Finn* by Mark Twain, and *Little Women* by Louisa May Alcott. The text of any book can be read by a computer at great speed. Books published before 1923 are currently in the *public domain*, meaning that everyone has the right to copy or use the text in any way. [Project Gutenberg](http://www.gutenberg.org/) is a website that publishes public domain books online. Using Python, we can load the text of these books directly from the web.
This example is meant to illustrate some of the broad themes of this text. Don't worry if the details of the program don't yet make sense. Instead, focus on interpreting the images generated below. Later sections of the text will describe most of the features of the Python programming language used below.
First, we read the text of both books into lists of chapters, called `huck_finn_chapters` and `little_women_chapters`. In Python, a name cannot contain any spaces, and so we will often use an underscore `_` to stand in for a space. The `=` in the lines below give a name on the left to the result of some computation described on the right. A *uniform resource locator* or *URL* is an address on the Internet for some content; in this case, the text of a book. The `#` symbol starts a comment, which is ignored by the computer but helpful for people reading the code.
```
# Read two books, fast!
huck_finn_url = 'https://www.inferentialthinking.com/data/huck_finn.txt'
huck_finn_text = read_url(huck_finn_url)
huck_finn_chapters = huck_finn_text.split('CHAPTER ')[44:]
little_women_url = 'https://www.inferentialthinking.com/data/little_women.txt'
little_women_text = read_url(little_women_url)
little_women_chapters = little_women_text.split('CHAPTER ')[1:]
```
While a computer cannot understand the text of a book, it can provide us with some insight into the structure of the text. The name `huck_finn_chapters` is currently bound to a list of all the chapters in the book. We can place them into a table to see how each chapter begins.
```
# Display the chapters of Huckleberry Finn in a table.
Table().with_column('Chapters', huck_finn_chapters)
```
Each chapter begins with a chapter number in Roman numerals, followed by the first sentence of the chapter. Project Gutenberg has printed the first word of each chapter in upper case.
|
github_jupyter
|
from datascience import *
from datascience.predicates import are
path_data = '../../../../data/'
import numpy as np
import matplotlib
matplotlib.use('Agg')
%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)
from urllib.request import urlopen
import re
def read_url(url):
return re.sub('\\s+', ' ', urlopen(url).read().decode())
# Read two books, fast!
huck_finn_url = 'https://www.inferentialthinking.com/data/huck_finn.txt'
huck_finn_text = read_url(huck_finn_url)
huck_finn_chapters = huck_finn_text.split('CHAPTER ')[44:]
little_women_url = 'https://www.inferentialthinking.com/data/little_women.txt'
little_women_text = read_url(little_women_url)
little_women_chapters = little_women_text.split('CHAPTER ')[1:]
# Display the chapters of Huckleberry Finn in a table.
Table().with_column('Chapters', huck_finn_chapters)
| 0.378229 | 0.798383 |
# BIDS v1.1.1 Notebook
## 1. Describe your dataset in a json file
```
import json
import os
import pandas as pd
import numpy as np
import ipywidgets as widgets # load library for interactive widgets (drop-down lists, button, etc.)
from ipywidgets import HBox, Label, Layout
from IPython.core.display import display, HTML
from IPython.display import clear_output
### Define some useful functions
# Button
def mybutton(mydescription):
mybuttonis = widgets.Button(
description = mydescription,
disabled = False,
button_style = '', # 'success', 'info', 'warning', 'danger' or ''
)
return mybuttonis
# Textbox
def mytextbox(placeholder):
mytextboxis = widgets.Text(
#value='Type dataset name',
placeholder=placeholder,
disabled=False,
layout=Layout(width='60%')
)
return mytextboxis
### Excel template
templates_folder = 'https://github.com/bvhpatel/DOPE/raw/master/templates' #location of the form templates
file_name = 'dataset_description.xlsx'
file_path = os.path.join(templates_folder, file_name)
file_dwld = ' Dowload file <a href= {0}>dataset_description.xlsx</a>, fill it out, and save it in your dataset'.format(file_path)
display(HTML(file_dwld))
print()
print()
### File location
xlfilepath_textbox = mytextbox(r'e.g. C:\User\Desktop\DOPEv1.1\examples\BIDS')
datafilename_box = HBox([Label('Indicate path of dataset_description.xlsx folder:'), xlfilepath_textbox])
display(datafilename_box)
### Button create json file
createjson_button = mybutton('Create json')
json_box = HBox([Label('Click here to generate json file:'), createjson_button])
display(json_box)
output = widgets.Output()
@output.capture()
def createjson_button_clicked(b):
clear_output()
print("Creating json file")
mypath = xlfilepath_textbox.value
jsonfilename = 'dataset_description'
excelpath = mypath + '\\' + jsonfilename + '.xlsx'
df = pd.read_excel(excelpath)
df.fillna('', inplace=True)
mydata = {}
count = -1
filePathNameWExt2 = mypath + '\\' + jsonfilename + '.json'
for item in df['Field']:
count += 1
mydata[item] = df['Entry'].iloc[count]
def writeToJSONFile(path, fileName, data):
filePathNameWExt = path + '\\' + fileName + '.json'
with open(filePathNameWExt, 'w') as fp:
json.dump(data, fp)
writeToJSONFile(mypath,jsonfilename,mydata)
print("json file is created at", filePathNameWExt2 )
createjson_button.on_click(createjson_button_clicked)
display(output)
```
## 2. Add details about participants
Download [participants.tsv](https://github.com/bvhpatel/DOPE/raw/master/templates/participants.tsv) and required add details (open with Excel and click Save when dope)
## 3. Organize your file according to BIDS instructions
Find guidelines in section Section 7 and 8 of [the specs manuals](https://bids.neuroimaging.io/bids_spec.pdf). Automated file organizer will be included here in the future.
## 4. Convert you DICOMs to (compressed) NIFTI
Go to [https://www.nitrc.org/projects/dcm2nii/](https://www.nitrc.org/projects/dcm2nii/)
## 5. Add specific .json files to subdirectories
Excel templates will be added in the future for automated conversion to json format.
## 6. Add a README file (Optional)
## 7. Additional instructions (Optional)
If you would like to include additional files not compatible with BIDs at this point, create a .bidsignore file in your dataset root folder with the paths that need to be excluded.
## 8. Validate your file organization using the BIDS validator
BIDS validator will be incorporated here in the future.
|
github_jupyter
|
import json
import os
import pandas as pd
import numpy as np
import ipywidgets as widgets # load library for interactive widgets (drop-down lists, button, etc.)
from ipywidgets import HBox, Label, Layout
from IPython.core.display import display, HTML
from IPython.display import clear_output
### Define some useful functions
# Button
def mybutton(mydescription):
mybuttonis = widgets.Button(
description = mydescription,
disabled = False,
button_style = '', # 'success', 'info', 'warning', 'danger' or ''
)
return mybuttonis
# Textbox
def mytextbox(placeholder):
mytextboxis = widgets.Text(
#value='Type dataset name',
placeholder=placeholder,
disabled=False,
layout=Layout(width='60%')
)
return mytextboxis
### Excel template
templates_folder = 'https://github.com/bvhpatel/DOPE/raw/master/templates' #location of the form templates
file_name = 'dataset_description.xlsx'
file_path = os.path.join(templates_folder, file_name)
file_dwld = ' Dowload file <a href= {0}>dataset_description.xlsx</a>, fill it out, and save it in your dataset'.format(file_path)
display(HTML(file_dwld))
print()
print()
### File location
xlfilepath_textbox = mytextbox(r'e.g. C:\User\Desktop\DOPEv1.1\examples\BIDS')
datafilename_box = HBox([Label('Indicate path of dataset_description.xlsx folder:'), xlfilepath_textbox])
display(datafilename_box)
### Button create json file
createjson_button = mybutton('Create json')
json_box = HBox([Label('Click here to generate json file:'), createjson_button])
display(json_box)
output = widgets.Output()
@output.capture()
def createjson_button_clicked(b):
clear_output()
print("Creating json file")
mypath = xlfilepath_textbox.value
jsonfilename = 'dataset_description'
excelpath = mypath + '\\' + jsonfilename + '.xlsx'
df = pd.read_excel(excelpath)
df.fillna('', inplace=True)
mydata = {}
count = -1
filePathNameWExt2 = mypath + '\\' + jsonfilename + '.json'
for item in df['Field']:
count += 1
mydata[item] = df['Entry'].iloc[count]
def writeToJSONFile(path, fileName, data):
filePathNameWExt = path + '\\' + fileName + '.json'
with open(filePathNameWExt, 'w') as fp:
json.dump(data, fp)
writeToJSONFile(mypath,jsonfilename,mydata)
print("json file is created at", filePathNameWExt2 )
createjson_button.on_click(createjson_button_clicked)
display(output)
| 0.196286 | 0.51251 |
# ํ๋ จ ๋ฐ์ดํฐ์
์์ฑ๊ธฐ
๋ชจ๋ธ์ ํ๋ จ์ํค๊ธฐ ์ํ ๋ฐ์ดํฐ์
์ ์์ฑํ๋ค. ๋ฐ์ดํฐ์
์ ์์ฑํ๊ธฐ ์ํด, ์๋ณธ ๋ฐ์ดํฐ ์ ์ฒ๋ฆฌ๋ฅผ ๋ ๋ฒจ๋ณ๋ก ์ํํ๋ค.
Raw : ์๋ณธ ๋ฐ์ดํฐ
Level 0 : ํจ์น ์ด๋ฏธ์ง๋ฅผ ์ถ์ถํ๊ธฐ ์ํด ์๋ณธ ๋ฐ์ดํฐ๋ฅผ ๊ฐ๊ณตํจ
Level 1 : ํจ์น ์ด๋ฏธ์ง๋ฅผ ์ถ์ถํ์ฌ ํด๋๋ณ๋ก ์ ๋ฆฌํจ
Level 2 : Upsampling ๋๋ downsampling ์ํ
Dataset : ๋ชจ๋ธ ์
๋ ฅ ๋ฐ์ดํฐ (IMAGE์ LABEL๋ก ๊ตฌ์ฑ)
```
import cv2
import numpy as np
import sys
import os
import random
```
Level ๊ฒฝ๋ก๋ฅผ ์ค์ ํฉ๋๋ค.
```
LEVEL1_TRUE_DATA_DIR = './warehouse/level1/train/true/'
LEVEL1_FALSE_DATA_DIR = './warehouse/level1/train/false/'
LEVEL2_TRUE_DATA_DIR = './warehouse/level2/train/true/'
LEVEL2_FALSE_DATA_DIR = './warehouse/level2/train/false/'
DATASET_IMAGE_PATH = './dataset/train_image_64x64_gray_447648.bin'
DATASET_LABEL_PATH = './dataset/train_label_64x64_gray_447648.bin'
```
ํ๊ฒฝ์ค์ ๋ ๊ฒฝ๋ก๊ฐ ์๋ค๋ฉด ํด๋๋ฅผ ์์ฑํ๋ค.
```
class PatchGenerator():
def __init__(self, num_patch_channel, num_patch_row, num_patch_col, num_sample_per_batch, num_batch_per_cache):
self.num_patch_channel = num_patch_channel # channel ์
self.num_patch_row = num_patch_row # row ์
self.num_patch_col = num_patch_col # col ์
self.num_sample_per_batch = num_sample_per_batch # ํ ๋ฐฐ์น ๋น ์ํ ์
self.num_batch_per_cache = num_batch_per_cache # ํ ์บ์ฌ ๋น ๋ฐฐ์น ์
def upsampling_rotate(self, angle):
def sample_size(self):
return self.num_patch_channel * self.num_patch_row * self.num_patch_col
def batch_size(self):
return self.num_sample_per_batch * self.sample_size()
def cache_size(self):
return self.num_batch_per_cache * self.batch_size()
def PrintProgress(prev_percent, curr_percent):
if prev_percent % 5 == curr_percent % 5:
return None
if curr_percent % 10 == 0:
sys.stdout.write(str(curr_percent) + '%')
sys.stdout.flush()
else:
if curr_percent % 5 == 0:
sys.stdout.write('.')
sys.stdout.flush()
```
GetLevelDataList() : Level ๊ฒฝ๋ก์์ ํ์ผ ๋ชฉ๋ก์ ๊ฐ์ง๊ณ ์ต๋๋ค.
```
def GetLevelDataList(dir_path):
level_data_list = []
for (path, dir, files) in os.walk(dir_path):
for filename in files:
ext = os.path.splitext(filename)[-1]
if ext == '.bmp' or ext == '.png' or ext == '.jpg' or ext == '.jpeg':
level_data_list.append(dir_path + filename)
return level_data_list
```
RotatePatchImage() : ์
์ํ๋ง์ ์ํด ํจ์น์ด๋ฏธ์ง๋ฅผ ํ์ ์ํต๋๋ค.
```
def RotatePatchImage(src_file_list, dst_dir):
total_count = len(src_file_list)
curr_count = 0
prev_percent = -1
for file_path in src_file_list:
cv_img = cv2.imread(file_path)
(h, w) = cv_img.shape[:2]
check = 'f'
filename = os.path.basename(file_path)
if filename.rfind('t.png') != -1:
check = 't'
for angle in range(0,360,15):
M = cv2.getRotationMatrix2D((w/2, h/2), angle, scale=1.0)
rotated = cv2.warpAffine(cv_img, M, (w, h))
dst_file_path = dst_dir + filename[:filename.rfind('.')] + '_' + str(angle) + check + '.png'
cv2.imwrite(dst_file_path, rotated)
curr_percent = int(curr_count*100/total_count)
PrintProgress(prev_percent, curr_percent)
curr_count = curr_count + 1
prev_percent = curr_percent
print('')
```
ShufflePatchImage() : ํจ์น ์ด๋ฏธ์ง๋ฅผ ํฉ์น๊ณ ์์ต๋๋ค.
```
def ShufflePatchImage(true_data_list, false_data_list):
random.shuffle(true_data_list)
random.shuffle(false_data_list)
shuffled_data_list = true_data_list + false_data_list
random.shuffle(shuffled_data_list)
return shuffled_data_list
```
GenerateDataset() : ๋ฐ์ดํฐ์
์ ์์ฑํฉ๋๋ค.
```
def GenerateDataset(data_list, out_image_file_path, out_label_file_path):
total_count = len(data_list)
curr_count = 0
prev_percent = -1
fp_label = open(out_label_file_path, 'wb')
fp_image = open(out_image_file_path, 'wb')
for data_item in data_list:
cv_img = cv2.imread(data_item)
cv_gray = cv2.cvtColor(cv_img, cv2.COLOR_BGR2GRAY)
label = '0'
if data_item.find("t.") != -1:
label = '1'
fp_label.write(label)
fp_image.write(cv_gray.tobytes())
"""
for row in cv_gray:
for val in row:
fp_image.write(val)
"""
curr_count = curr_count + 1
curr_percent = int(curr_count*100/total_count)
PrintProgress(prev_percent, curr_percent)
prev_percent = curr_percent
fp_label.close()
fp_image.close()
print('')
if __name__ == '__main__':
"""
PatchGenerator pg
pg.init(positive_dir_path, negative_dir_path)
pg.upsampling_rotate(val)
pg.upsampling_noise(...)
pg.upsampling_shift(...)
pg.upsampling_zoom(...)
pg.upsampling_horizontal_flip(...)
pg.upsampling_vertical_flip(...)
pg.generate_dataset(patch_file_path, label_file_path)
"""
# Level1 ๋ฐ์ดํฐ ๋ชฉ๋ก ๊ฐ์ ธ์ค๊ธฐ
level1_true_data_list = GetLevelDataList(LEVEL1_TRUE_DATA_DIR)
level1_false_data_list = GetLevelDataList(LEVEL1_FALSE_DATA_DIR)
print('level1 true data count :\t' + str(len(level1_true_data_list)))
print('level1 false data count :\t' + str(len(level1_false_data_list)))
# Level1 ๋ฐ์ดํฐ๋ก๋ถํฐ Level2 ๋ฐ์ดํฐ ์์ฑ
print('generate level2 true data...')
RotatePatchImage(level1_true_data_list, # Level 1 ํ์ผ ๋ชฉ๋ก (in)
LEVEL2_TRUE_DATA_DIR) # Level 2 ๊ฒฝ๋ก (out)
print('generate level2 false data...')
RotatePatchImage(level1_false_data_list, # Level 1 ํ์ผ ๋ชฉ๋ก (in)
LEVEL2_FALSE_DATA_DIR) # Level 2 ๊ฒฝ๋ก (out)
# Level2 ๋ฐ์ดํฐ ๋ชฉ๋ก ๊ฐ์ ธ์ค๊ธฐ
level2_true_data_list = GetLevelDataList(LEVEL2_TRUE_DATA_DIR)
level2_false_data_list = GetLevelDataList(LEVEL2_FALSE_DATA_DIR)
print('level2 true data count :\t' + str(len(level2_true_data_list)))
print('level2 false data count :\t' + str(len(level2_false_data_list)))
# Level2 ๋ฐ์ดํฐ๋ก๋ถํฐ Dataset ์์ฑ
print('merge and shuffle level 2 patch image...')
merge_shuffle_level2_data_list = ShufflePatchImage(level2_true_data_list, level2_false_data_list)
print('generate dataset...')
GenerateDataset(merge_shuffle_level2_data_list, DATASET_IMAGE_PATH, DATASET_LABEL_PATH)
print('dataset pacth image : \t' + DATASET_IMAGE_PATH)
print('dataset label : \t' + DATASET_LABEL_PATH)
```
|
github_jupyter
|
import cv2
import numpy as np
import sys
import os
import random
LEVEL1_TRUE_DATA_DIR = './warehouse/level1/train/true/'
LEVEL1_FALSE_DATA_DIR = './warehouse/level1/train/false/'
LEVEL2_TRUE_DATA_DIR = './warehouse/level2/train/true/'
LEVEL2_FALSE_DATA_DIR = './warehouse/level2/train/false/'
DATASET_IMAGE_PATH = './dataset/train_image_64x64_gray_447648.bin'
DATASET_LABEL_PATH = './dataset/train_label_64x64_gray_447648.bin'
class PatchGenerator():
def __init__(self, num_patch_channel, num_patch_row, num_patch_col, num_sample_per_batch, num_batch_per_cache):
self.num_patch_channel = num_patch_channel # channel ์
self.num_patch_row = num_patch_row # row ์
self.num_patch_col = num_patch_col # col ์
self.num_sample_per_batch = num_sample_per_batch # ํ ๋ฐฐ์น ๋น ์ํ ์
self.num_batch_per_cache = num_batch_per_cache # ํ ์บ์ฌ ๋น ๋ฐฐ์น ์
def upsampling_rotate(self, angle):
def sample_size(self):
return self.num_patch_channel * self.num_patch_row * self.num_patch_col
def batch_size(self):
return self.num_sample_per_batch * self.sample_size()
def cache_size(self):
return self.num_batch_per_cache * self.batch_size()
def PrintProgress(prev_percent, curr_percent):
if prev_percent % 5 == curr_percent % 5:
return None
if curr_percent % 10 == 0:
sys.stdout.write(str(curr_percent) + '%')
sys.stdout.flush()
else:
if curr_percent % 5 == 0:
sys.stdout.write('.')
sys.stdout.flush()
def GetLevelDataList(dir_path):
level_data_list = []
for (path, dir, files) in os.walk(dir_path):
for filename in files:
ext = os.path.splitext(filename)[-1]
if ext == '.bmp' or ext == '.png' or ext == '.jpg' or ext == '.jpeg':
level_data_list.append(dir_path + filename)
return level_data_list
def RotatePatchImage(src_file_list, dst_dir):
total_count = len(src_file_list)
curr_count = 0
prev_percent = -1
for file_path in src_file_list:
cv_img = cv2.imread(file_path)
(h, w) = cv_img.shape[:2]
check = 'f'
filename = os.path.basename(file_path)
if filename.rfind('t.png') != -1:
check = 't'
for angle in range(0,360,15):
M = cv2.getRotationMatrix2D((w/2, h/2), angle, scale=1.0)
rotated = cv2.warpAffine(cv_img, M, (w, h))
dst_file_path = dst_dir + filename[:filename.rfind('.')] + '_' + str(angle) + check + '.png'
cv2.imwrite(dst_file_path, rotated)
curr_percent = int(curr_count*100/total_count)
PrintProgress(prev_percent, curr_percent)
curr_count = curr_count + 1
prev_percent = curr_percent
print('')
def ShufflePatchImage(true_data_list, false_data_list):
random.shuffle(true_data_list)
random.shuffle(false_data_list)
shuffled_data_list = true_data_list + false_data_list
random.shuffle(shuffled_data_list)
return shuffled_data_list
def GenerateDataset(data_list, out_image_file_path, out_label_file_path):
total_count = len(data_list)
curr_count = 0
prev_percent = -1
fp_label = open(out_label_file_path, 'wb')
fp_image = open(out_image_file_path, 'wb')
for data_item in data_list:
cv_img = cv2.imread(data_item)
cv_gray = cv2.cvtColor(cv_img, cv2.COLOR_BGR2GRAY)
label = '0'
if data_item.find("t.") != -1:
label = '1'
fp_label.write(label)
fp_image.write(cv_gray.tobytes())
"""
for row in cv_gray:
for val in row:
fp_image.write(val)
"""
curr_count = curr_count + 1
curr_percent = int(curr_count*100/total_count)
PrintProgress(prev_percent, curr_percent)
prev_percent = curr_percent
fp_label.close()
fp_image.close()
print('')
if __name__ == '__main__':
"""
PatchGenerator pg
pg.init(positive_dir_path, negative_dir_path)
pg.upsampling_rotate(val)
pg.upsampling_noise(...)
pg.upsampling_shift(...)
pg.upsampling_zoom(...)
pg.upsampling_horizontal_flip(...)
pg.upsampling_vertical_flip(...)
pg.generate_dataset(patch_file_path, label_file_path)
"""
# Level1 ๋ฐ์ดํฐ ๋ชฉ๋ก ๊ฐ์ ธ์ค๊ธฐ
level1_true_data_list = GetLevelDataList(LEVEL1_TRUE_DATA_DIR)
level1_false_data_list = GetLevelDataList(LEVEL1_FALSE_DATA_DIR)
print('level1 true data count :\t' + str(len(level1_true_data_list)))
print('level1 false data count :\t' + str(len(level1_false_data_list)))
# Level1 ๋ฐ์ดํฐ๋ก๋ถํฐ Level2 ๋ฐ์ดํฐ ์์ฑ
print('generate level2 true data...')
RotatePatchImage(level1_true_data_list, # Level 1 ํ์ผ ๋ชฉ๋ก (in)
LEVEL2_TRUE_DATA_DIR) # Level 2 ๊ฒฝ๋ก (out)
print('generate level2 false data...')
RotatePatchImage(level1_false_data_list, # Level 1 ํ์ผ ๋ชฉ๋ก (in)
LEVEL2_FALSE_DATA_DIR) # Level 2 ๊ฒฝ๋ก (out)
# Level2 ๋ฐ์ดํฐ ๋ชฉ๋ก ๊ฐ์ ธ์ค๊ธฐ
level2_true_data_list = GetLevelDataList(LEVEL2_TRUE_DATA_DIR)
level2_false_data_list = GetLevelDataList(LEVEL2_FALSE_DATA_DIR)
print('level2 true data count :\t' + str(len(level2_true_data_list)))
print('level2 false data count :\t' + str(len(level2_false_data_list)))
# Level2 ๋ฐ์ดํฐ๋ก๋ถํฐ Dataset ์์ฑ
print('merge and shuffle level 2 patch image...')
merge_shuffle_level2_data_list = ShufflePatchImage(level2_true_data_list, level2_false_data_list)
print('generate dataset...')
GenerateDataset(merge_shuffle_level2_data_list, DATASET_IMAGE_PATH, DATASET_LABEL_PATH)
print('dataset pacth image : \t' + DATASET_IMAGE_PATH)
print('dataset label : \t' + DATASET_LABEL_PATH)
| 0.302082 | 0.900223 |
# Read Directly from IIASA Data Resources
IIASA's new [scenario explorer](https://data.ene.iiasa.ac.at/iamc-1.5c-explorer/#/workspaces) is not only a great resource on its own, but it also allows the underlying datasets to be directly queried. `pyam` takes advantage of this ability to allow you to easily pull data and work with it.
```
import pyam
```
Accessing an explorer is done via a `Connection` object. By default, all public explorers can be connected to.
```
conn = pyam.iiasa.Connection()
conn.valid_connections
```
If you have additional credentials, you can supply them as well via the `creds` key-word argument:
```
pyam.iiasa.Connection(creds=(<username>, <password>))
```
In this example, we will be pulling data from the Special Report on 1.5C explorer. This can be done either via the constructor:
```
pyam.iiasa.Connection('IXSE_SR15')
```
or, if you want to query multiple databases, via the explicit `connect()` method:
```
conn = pyam.iiasa.Connection()
conn.connect('IXSE_SR15')
```
We also provide some convenience functions to shorten the amount of code you have to write. Under the hood, `read_iiasa()` is just opening an connection to a database and making a query on that data.
In this tutorial, we will query specific subsets of data in a manner similar to `pyam.IamDataFrame.filter()`.
```
df = pyam.read_iiasa(
'IXSE_SR15',
model='MESSAGEix*',
variable=['Emissions|CO2', 'Primary Energy|Coal'],
region='World',
meta=['category']
)
```
Here we pulled out all times series data for model(s) that start with 'MESSAGEix' that are in the 'World' region and associated with the two named variables. We also added the "category" metadata, which tells us the climate impact categorisation of each scenario as assessed in the IPCC SR15.
Let's plot CO2 emissions.
```
ax = df.filter(variable='Emissions|CO2').line_plot(
color='category',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
```
And now continue doing all of your analysis!
```
ax = df.scatter(
x='Primary Energy|Coal',
y='Emissions|CO2',
color='category',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
```
## Exploring the Data Source
If you're interested in what data is actually in the data source, you can use `pyam.iiasa.Connection` to do so.
```
conn = pyam.iiasa.Connection('IXSE_SR15')
```
The `conn` object has a number of useful functions for listing what's in the dataset. A few of them are shown below.
```
conn.models().head()
conn.scenarios().head()
conn.variables().head()
conn.regions().head()
```
A number of different kinds of indicators are available for model/scenario combinations. We queried the `category` metadata in the above example, but there are many more. You can see them with
```
conn.available_metadata().head()
```
You can directly query the `Connection`, which will give you a `pd.DataFrame`
```
df = conn.query(
model='MESSAGEix*',
variable=['Emissions|CO2', 'Primary Energy|Coal'],
region='World'
)
df.head()
```
And you can easily turn this into a `pyam.IamDataFrame` to continue your analysis.
```
df = pyam.IamDataFrame(df)
ax = df.filter(variable='Primary Energy|Coal').line_plot(
color='scenario',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
```
|
github_jupyter
|
import pyam
conn = pyam.iiasa.Connection()
conn.valid_connections
pyam.iiasa.Connection(creds=(<username>, <password>))
pyam.iiasa.Connection('IXSE_SR15')
conn = pyam.iiasa.Connection()
conn.connect('IXSE_SR15')
df = pyam.read_iiasa(
'IXSE_SR15',
model='MESSAGEix*',
variable=['Emissions|CO2', 'Primary Energy|Coal'],
region='World',
meta=['category']
)
ax = df.filter(variable='Emissions|CO2').line_plot(
color='category',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
ax = df.scatter(
x='Primary Energy|Coal',
y='Emissions|CO2',
color='category',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
conn = pyam.iiasa.Connection('IXSE_SR15')
conn.models().head()
conn.scenarios().head()
conn.variables().head()
conn.regions().head()
conn.available_metadata().head()
df = conn.query(
model='MESSAGEix*',
variable=['Emissions|CO2', 'Primary Energy|Coal'],
region='World'
)
df.head()
df = pyam.IamDataFrame(df)
ax = df.filter(variable='Primary Energy|Coal').line_plot(
color='scenario',
legend=dict(loc='center left', bbox_to_anchor=(1.0, 0.5))
)
| 0.399109 | 0.971375 |
# Imports and Settings
```
# basics
import os
import time
import numpy as np
import pandas as pd
# sklearn
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, StandardScaler
# keras
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten
from keras.callbacks import TensorBoard, ModelCheckpoint
# tensorflow
import tensorflow as tf
# plotting
import matplotlib.pyplot as plt
# local
from data_loaders import load_mnist_data, load_iris_data, retrieve_predictions
from models import *
from utils import train_model_iteratively, get_model_weights, convert_weight_dict_to_dataframe
plt.style.use('ggplot')
%matplotlib inline
%load_ext autoreload
%autoreload 2
# suppress warnings
import warnings
warnings.filterwarnings('ignore')
```
# Working examples that use module functions
## MNIST working example
```
x_train_mnist, y_train_mnist, x_test_mnist, y_test_mnist = load_mnist_data()
pd.DataFrame(y_test_mnist).to_csv("y_test_mnist.csv", index=False)
baseline_mnist_model(name='mnist_test', num_classes=2).summary()
example_mnist_outdir = './data/example_mnist'
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=example_mnist_outdir, epochs=4, epochs_to_save=None,
batch_size=128, num_models=10)
mnist_preds = retrieve_mnist_preds(y_test=y_test_mnist, outdir=example_mnist_outdir)
mnist_weights = convert_weight_dict_to_dataframe(get_model_weights(example_mnist_outdir))
```
## IRIS working example
```
x_train_iris, x_test_iris, y_train_iris, y_test_iris = load_iris_data()
pd.DataFrame(y_test_iris).to_csv("y_test_iris.csv", index=False)
baseline_iris_model(name='iris_test').summary()
example_iris_outdir = './data/example_iris'
# need this to suppress tf.function retracing warning that kept coming up
tf.compat.v1.logging.set_verbosity("ERROR")
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=example_iris_outdir, epochs=15, epochs_to_save=None,
batch_size=5, num_models=2)
```
# Model Runs
## MNIST model runs
### Baseline MNIST
```
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir="./data/mnist_baseline", epochs=4, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep epochs
```
for num_epochs in [8, 12, 16]:
outdir = "./data/mnist_epoch_{}".format(num_epochs)
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=num_epochs, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep batch size
```
for batch_size in [32, 64, 256]:
outdir = "./data/mnist_batch_{}".format(batch_size)
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=4, epochs_to_save=None,
batch_size=batch_size, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep layers
```
for idx, model in enumerate([mnist_2_layers, mnist_3_layers, mnist_4_layers]):
outdir = "./data/mnist_layers_{}".format(idx+2)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=4, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
## IRIS model runs
### Baseline IRIS
```
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir="./data/iris_baseline", epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep epochs
```
for num_epochs in [100, 300, 450]:
outdir = "./data/iris_epoch_{}".format(num_epochs)
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=num_epochs, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep batch size:
```
for batch_size in [10, 20, 40]:
outdir = "./data/iris_batch_{}".format(batch_size)
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=batch_size, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep layers:
```
for idx, model in enumerate([iris_2_layers, iris_3_layers, iris_4_layers]):
outdir = "./data/iris_layers_{}".format(idx+2)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
### Sweep nodes:
```
for idx, model in enumerate([iris_3_nodes, iris_4_nodes, iris_5_nodes, iris_6_nodes]):
outdir = "./data/iris_nodes_{}".format(idx+3)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
```
|
github_jupyter
|
# basics
import os
import time
import numpy as np
import pandas as pd
# sklearn
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, StandardScaler
# keras
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Flatten
from keras.callbacks import TensorBoard, ModelCheckpoint
# tensorflow
import tensorflow as tf
# plotting
import matplotlib.pyplot as plt
# local
from data_loaders import load_mnist_data, load_iris_data, retrieve_predictions
from models import *
from utils import train_model_iteratively, get_model_weights, convert_weight_dict_to_dataframe
plt.style.use('ggplot')
%matplotlib inline
%load_ext autoreload
%autoreload 2
# suppress warnings
import warnings
warnings.filterwarnings('ignore')
x_train_mnist, y_train_mnist, x_test_mnist, y_test_mnist = load_mnist_data()
pd.DataFrame(y_test_mnist).to_csv("y_test_mnist.csv", index=False)
baseline_mnist_model(name='mnist_test', num_classes=2).summary()
example_mnist_outdir = './data/example_mnist'
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=example_mnist_outdir, epochs=4, epochs_to_save=None,
batch_size=128, num_models=10)
mnist_preds = retrieve_mnist_preds(y_test=y_test_mnist, outdir=example_mnist_outdir)
mnist_weights = convert_weight_dict_to_dataframe(get_model_weights(example_mnist_outdir))
x_train_iris, x_test_iris, y_train_iris, y_test_iris = load_iris_data()
pd.DataFrame(y_test_iris).to_csv("y_test_iris.csv", index=False)
baseline_iris_model(name='iris_test').summary()
example_iris_outdir = './data/example_iris'
# need this to suppress tf.function retracing warning that kept coming up
tf.compat.v1.logging.set_verbosity("ERROR")
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=example_iris_outdir, epochs=15, epochs_to_save=None,
batch_size=5, num_models=2)
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir="./data/mnist_baseline", epochs=4, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for num_epochs in [8, 12, 16]:
outdir = "./data/mnist_epoch_{}".format(num_epochs)
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=num_epochs, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for batch_size in [32, 64, 256]:
outdir = "./data/mnist_batch_{}".format(batch_size)
start = time.time()
train_model_iteratively(baseline_model=baseline_mnist_model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=4, epochs_to_save=None,
batch_size=batch_size, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for idx, model in enumerate([mnist_2_layers, mnist_3_layers, mnist_4_layers]):
outdir = "./data/mnist_layers_{}".format(idx+2)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_mnist, Y_train=y_train_mnist,
X_test=x_test_mnist, Y_test=y_test_mnist,
outdir=outdir, epochs=4, epochs_to_save=None,
batch_size=128, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir="./data/iris_baseline", epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for num_epochs in [100, 300, 450]:
outdir = "./data/iris_epoch_{}".format(num_epochs)
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=num_epochs, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for batch_size in [10, 20, 40]:
outdir = "./data/iris_batch_{}".format(batch_size)
start = time.time()
train_model_iteratively(baseline_model=baseline_iris_model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=batch_size, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for idx, model in enumerate([iris_2_layers, iris_3_layers, iris_4_layers]):
outdir = "./data/iris_layers_{}".format(idx+2)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
for idx, model in enumerate([iris_3_nodes, iris_4_nodes, iris_5_nodes, iris_6_nodes]):
outdir = "./data/iris_nodes_{}".format(idx+3)
start = time.time()
train_model_iteratively(baseline_model=model,
X_train=x_train_iris, Y_train=y_train_iris,
X_test=x_test_iris, Y_test=y_test_iris,
outdir=outdir, epochs=150, epochs_to_save=None,
batch_size=5, num_models=100)
print("train_model_iteratively took {} seconds\n".format(time.time() - start))
| 0.625667 | 0.798265 |
```
from google.colab import drive
drive.mount('/content/drive')
```
<a id="1"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>LIBRARIES</center></h1>
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(color_codes = True)
%matplotlib inline
```
<a id="2"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>IMPORT DATA</center></h1>
```
df = pd.read_csv('/content/drive/MyDrive/Colab Notebooks/Bank loan/bank_loan 1.csv.txt',sep = ';')
df.head()
# Check NAN Values
for i in df.columns:
print (i+": "+str(df[i].isna().sum()))
df.describe()
```
<a id="3"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>DATA VISUALIZATION</center></h1>
```
sns.countplot('y',data = df,palette= 'rocket')
plt.figure(figsize = (20,8))
sns.violinplot(x = 'job',y = 'age',data = df)
plt.figure(figsize = (20,8))
sns.violinplot(x = 'job',y = 'balance',data = df)
sns.catplot('marital','age',data = df,kind = 'bar',hue = 'job',col = 'job',col_wrap = 2)
correlation = df.corr()
plt.figure(figsize = (20,8))
sns.heatmap(correlation,annot = True, cmap = 'rocket')
plt.figure(figsize = (20,8))
sns.boxplot('age',data = df)
plt.figure(figsize = (20,8))
sns.boxplot('balance',data = df)
plt.figure(figsize = (20,8))
sns.boxplot('pdays',data = df)
```
<a id="4"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>DATA PREPROCESSING</center></h1>
```
Q1 = df['age'].quantile(0.25)
Q3 = df['age'].quantile(0.75)
IQR = Q3 - Q1
filter = (df['age'] >= Q1 - 1.5 * IQR) & (df['age']<= Q3 + 1.5 *IQR)
train1 = df.loc[filter]
print("data loss percentage {}%".format(((len(df) - len(train1))/len(df))*100))
Q1 = train1['balance'].quantile(0.25)
Q3 = train1['balance'].quantile(0.75)
IQR = Q3 - Q1
filter = (train1['balance'] >= Q1 - 1.5 * IQR) & (train1['balance']<= Q3 + 1.5 *IQR)
train2 = train1.loc[filter]
print("data loss percentage {}%".format(((len(train1) - len(train2))/len(train1))*100))
Q1 = train2['pdays'].quantile(0.25)
Q3 = train2['pdays'].quantile(0.75)
IQR = Q3 - Q1
filter = (train2['pdays'] >= Q1 - 1.25 * IQR) & (train2['pdays']<= Q3 + 1.25 *IQR)
train3 = train2.loc[filter]
print("data loss percentage {}%".format(((len(train2) - len(train3))/len(train2))*100))
from sklearn.preprocessing import LabelEncoder
#Using label encoder convert categorical variable into numerical one.
label = LabelEncoder()
train3['job'] = label.fit_transform(train3['job'])
train3['marital'] = label.fit_transform(train3['marital'])
train3['education'] = label.fit_transform(train3['education'])
train3['default'] = label.fit_transform(train3['default'])
train3['housing'] = label.fit_transform(train3['housing'])
train3['loan'] = label.fit_transform(train3['loan'])
train3['contact'] = label.fit_transform(train3['contact'])
train3['month'] = label.fit_transform(train3['month'])
train3['poutcome'] = label.fit_transform(train3['poutcome'])
x = train3.drop(['day','campaign','y'],axis = 1)
train3['y'] = pd.get_dummies(train3['y'],drop_first = True)
y = train3.iloc[:,-1]
y
## Get the Fraud and the normal dataset
Interested = train3[train3['y']==1]
Not_Interested = train3[train3['y']==0]
!pip install imblearn
from imblearn.combine import SMOTETomek
from imblearn.under_sampling import NearMiss
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor
from sklearn.svm import OneClassSVM
from pylab import rcParams
# Implementing Oversampling for Handling Imbalanced
smk = SMOTETomek(random_state=35)
X_res,y_res=smk.fit_resample(x,y)
X_res.shape,y_res.shape
y_res.value_counts()
from sklearn.preprocessing import StandardScaler
standard = StandardScaler()
std_x = standard.fit_transform(X_res)
```
<a id="5"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>DATA VALIDATION</center></h1>
```
from sklearn.model_selection import train_test_split
#Split data into Train and test format
x_train,x_test,y_train,y_test = train_test_split(std_x,y_res,test_size = 0.20,random_state =35)
print('Shape of Training Xs:{}'.format(x_train.shape))
print('shape of Test:{}'.format(x_test.shape))
```
<a id="6"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>MODEL BUILDING</center></h1>
```
# Use algoritm to train model.
from sklearn.linear_model import SGDClassifier
SGD=SGDClassifier()
SGD.fit(x_train,y_train)
y_predicted = SGD.predict(x_test)
score = SGD.score(x_test,y_test)
print(score)
print(y_predicted)
```
<a id="7"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>PERFORMANCE MATRIX</center></h1>
```
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(y_test, y_predicted)
np.set_printoptions(precision=2)
cnf_matrix
from sklearn.metrics import roc_auc_score, classification_report
print(classification_report(y_test, SGD.predict(x_test)))
```
<a id="8"></a>
<h1 style='background:#a9a799; border:0; color:black'><center>HYPERPARAMETER</center></h1>
```
from sklearn.model_selection import RandomizedSearchCV
#Randomized Search CV
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 100, stop = 1200, num = 12)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(5, 30, num = 6)]
# max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10, 15, 100]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 5, 10]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf}
print(random_grid)
# Use the random grid to search for best hyperparameters
# First create the base model to tune
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
rf = RandomForestClassifier()
# Random search of parameters, using 5 fold cross validation,
# search across 50 different combinations
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid,scoring='accuracy', n_iter = 50, cv = 5, verbose=2, random_state=42, n_jobs = 1)
rf_random.fit(x_train,y_train)
rf_random.best_params_
rf = RandomForestClassifier(n_estimators= 200,min_samples_split = 5, min_samples_leaf = 1, max_features = 'auto',max_depth = 20)
rf.fit(x_train,y_train)
score = rf.score(x_test,y_test)
print(score)
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(y_test, y_predicted)
np.set_printoptions(precision=2)
cnf_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
classes = train3["y"].value_counts()
classes.index = [str(x) for x in classes.index]
#With Normalization
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=classes.index,
title='Confusion matrix, without normalization')
# With normalization
plt.figure()
plot_confusion_matrix(cnf_matrix, classes= classes.index, normalize=True,
title='Normalized confusion matrix')
plt.show()
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(color_codes = True)
%matplotlib inline
df = pd.read_csv('/content/drive/MyDrive/Colab Notebooks/Bank loan/bank_loan 1.csv.txt',sep = ';')
df.head()
# Check NAN Values
for i in df.columns:
print (i+": "+str(df[i].isna().sum()))
df.describe()
sns.countplot('y',data = df,palette= 'rocket')
plt.figure(figsize = (20,8))
sns.violinplot(x = 'job',y = 'age',data = df)
plt.figure(figsize = (20,8))
sns.violinplot(x = 'job',y = 'balance',data = df)
sns.catplot('marital','age',data = df,kind = 'bar',hue = 'job',col = 'job',col_wrap = 2)
correlation = df.corr()
plt.figure(figsize = (20,8))
sns.heatmap(correlation,annot = True, cmap = 'rocket')
plt.figure(figsize = (20,8))
sns.boxplot('age',data = df)
plt.figure(figsize = (20,8))
sns.boxplot('balance',data = df)
plt.figure(figsize = (20,8))
sns.boxplot('pdays',data = df)
Q1 = df['age'].quantile(0.25)
Q3 = df['age'].quantile(0.75)
IQR = Q3 - Q1
filter = (df['age'] >= Q1 - 1.5 * IQR) & (df['age']<= Q3 + 1.5 *IQR)
train1 = df.loc[filter]
print("data loss percentage {}%".format(((len(df) - len(train1))/len(df))*100))
Q1 = train1['balance'].quantile(0.25)
Q3 = train1['balance'].quantile(0.75)
IQR = Q3 - Q1
filter = (train1['balance'] >= Q1 - 1.5 * IQR) & (train1['balance']<= Q3 + 1.5 *IQR)
train2 = train1.loc[filter]
print("data loss percentage {}%".format(((len(train1) - len(train2))/len(train1))*100))
Q1 = train2['pdays'].quantile(0.25)
Q3 = train2['pdays'].quantile(0.75)
IQR = Q3 - Q1
filter = (train2['pdays'] >= Q1 - 1.25 * IQR) & (train2['pdays']<= Q3 + 1.25 *IQR)
train3 = train2.loc[filter]
print("data loss percentage {}%".format(((len(train2) - len(train3))/len(train2))*100))
from sklearn.preprocessing import LabelEncoder
#Using label encoder convert categorical variable into numerical one.
label = LabelEncoder()
train3['job'] = label.fit_transform(train3['job'])
train3['marital'] = label.fit_transform(train3['marital'])
train3['education'] = label.fit_transform(train3['education'])
train3['default'] = label.fit_transform(train3['default'])
train3['housing'] = label.fit_transform(train3['housing'])
train3['loan'] = label.fit_transform(train3['loan'])
train3['contact'] = label.fit_transform(train3['contact'])
train3['month'] = label.fit_transform(train3['month'])
train3['poutcome'] = label.fit_transform(train3['poutcome'])
x = train3.drop(['day','campaign','y'],axis = 1)
train3['y'] = pd.get_dummies(train3['y'],drop_first = True)
y = train3.iloc[:,-1]
y
## Get the Fraud and the normal dataset
Interested = train3[train3['y']==1]
Not_Interested = train3[train3['y']==0]
!pip install imblearn
from imblearn.combine import SMOTETomek
from imblearn.under_sampling import NearMiss
from sklearn.ensemble import IsolationForest
from sklearn.neighbors import LocalOutlierFactor
from sklearn.svm import OneClassSVM
from pylab import rcParams
# Implementing Oversampling for Handling Imbalanced
smk = SMOTETomek(random_state=35)
X_res,y_res=smk.fit_resample(x,y)
X_res.shape,y_res.shape
y_res.value_counts()
from sklearn.preprocessing import StandardScaler
standard = StandardScaler()
std_x = standard.fit_transform(X_res)
from sklearn.model_selection import train_test_split
#Split data into Train and test format
x_train,x_test,y_train,y_test = train_test_split(std_x,y_res,test_size = 0.20,random_state =35)
print('Shape of Training Xs:{}'.format(x_train.shape))
print('shape of Test:{}'.format(x_test.shape))
# Use algoritm to train model.
from sklearn.linear_model import SGDClassifier
SGD=SGDClassifier()
SGD.fit(x_train,y_train)
y_predicted = SGD.predict(x_test)
score = SGD.score(x_test,y_test)
print(score)
print(y_predicted)
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(y_test, y_predicted)
np.set_printoptions(precision=2)
cnf_matrix
from sklearn.metrics import roc_auc_score, classification_report
print(classification_report(y_test, SGD.predict(x_test)))
from sklearn.model_selection import RandomizedSearchCV
#Randomized Search CV
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 100, stop = 1200, num = 12)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(5, 30, num = 6)]
# max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10, 15, 100]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 5, 10]
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf}
print(random_grid)
# Use the random grid to search for best hyperparameters
# First create the base model to tune
from sklearn.ensemble import RandomForestRegressor,RandomForestClassifier
rf = RandomForestClassifier()
# Random search of parameters, using 5 fold cross validation,
# search across 50 different combinations
rf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid,scoring='accuracy', n_iter = 50, cv = 5, verbose=2, random_state=42, n_jobs = 1)
rf_random.fit(x_train,y_train)
rf_random.best_params_
rf = RandomForestClassifier(n_estimators= 200,min_samples_split = 5, min_samples_leaf = 1, max_features = 'auto',max_depth = 20)
rf.fit(x_train,y_train)
score = rf.score(x_test,y_test)
print(score)
from sklearn.metrics import confusion_matrix
cnf_matrix = confusion_matrix(y_test, y_predicted)
np.set_printoptions(precision=2)
cnf_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
classes = train3["y"].value_counts()
classes.index = [str(x) for x in classes.index]
#With Normalization
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=classes.index,
title='Confusion matrix, without normalization')
# With normalization
plt.figure()
plot_confusion_matrix(cnf_matrix, classes= classes.index, normalize=True,
title='Normalized confusion matrix')
plt.show()
| 0.4206 | 0.708969 |
## Kernel SVM
## Importing the libraries
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Importing the dataset
```
dataset = pd.read_csv('Social_Network_Ads.csv')
dataset.head(10)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
```
## Splitting the dataset into the Training set and Test set
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
print(X_train)
print(y_train)
print(X_test)
print(y_test)
```
## Feature Scaling
```
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
print(X_train)
print(X_test)
```
## Training the Kernel SVM model on the Training set
```
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
```
## Predicting a new result
```
print(classifier.predict(sc.transform([[30,87000]])))
y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
```
## Predicting the Test set results
```
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
```
## Visualising the Training set results
```
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_train), y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
## Visualising the Test set results
```
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_test), y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('Social_Network_Ads.csv')
dataset.head(10)
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
print(X_train)
print(y_train)
print(X_test)
print(y_test)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
print(X_train)
print(X_test)
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
print(classifier.predict(sc.transform([[30,87000]])))
y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_train), y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_test), y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, stop = X_set[:, 0].max() + 10, step = 0.25),
np.arange(start = X_set[:, 1].min() - 1000, stop = X_set[:, 1].max() + 1000, step = 0.25))
plt.contourf(X1, X2, classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1], c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Kernel SVM (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
| 0.556641 | 0.952838 |
Import the required packages:
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
```
Installing plotly
```
!pip install plotly
```
Import plotly.express from the installed package:
```
import plotly.express as px
```
Store each of the CSV files in two different DataFrames:
```
r09 = pd.read_csv('https://raw.githubusercontent.com/PacktWorkshops/The-Data-Analysis-Workshop/master/Chapter08/Datasets/online_retail_II.csv')
r09.head()
```
Similarly, create the second DataFrame:
```
r10 = pd.read_csv('https://raw.githubusercontent.com/PacktWorkshops/The-Data-Analysis-Workshop/master/Chapter08/Datasets/online_retail_II2.csv')
r10.head()
```
Concatenate the two DataFrames into one called retail using the .concat() function and add the keys 09-10 and 10-11:
```
dfs = [r09, r10]
retail = pd.concat(dfs, keys = ['09-10', '10-11'])
retail
```
Rename the columns as we did in Exercise 8.01, Loading and Cleaning Our Data:
```
retail.rename(index = str, columns = {
'Invoice' : 'invoice',
'StockCode' : 'stock_code',
'Quantity' : 'quantity',
'InvoiceDate' : 'date',
'Price' : 'unit_price',
'Country' : 'country',
'Description' : 'desc',
'Customer ID' : 'cust_id'
}, inplace = True)
retail.head()
```
Check the statistical information for retail:
```
retail.isnull().sum().sort_values(ascending = False)
```
Fetch the details of the DataFrame by using the .describe() function.
```
retail.describe()
```
Use the .loc() function to determine how many instances in retail have 38970.0 as their unit_price value:
```
retail.loc[retail['unit_price'] == 38970.0]
```
Use the .loc() function again to determine how many instances in retail have -53594.360000 as their unit_price value:
```
retail.loc[retail['unit_price'] == -53594.360000]
```
Calculate how many negative values of unit_price and quantity are present in retail. If they are only a small percentage of the total number of instances, then remove them from retail:
```
(retail['unit_price'] <= 0).sum()
```
Similarly, find out the number of negative values of quantity:
```
(retail['quantity'] <= 0).sum()
```
Display the total number of negative instances for the unit_price and quantity columns:
```
retail[(retail['unit_price'] <= 0) & (retail['quantity'] <= 0) & (retail['cust_id'].isnull())]
```
Store the instances with missing values in another DataFrame:
```
null_retail = retail[retail.isnull().any(axis=1)]
null_retail
```
Delete the instances with missing values from retail:
```
new_retail = retail[(retail['unit_price'] > 0) & (retail['quantity'] > 0)]
new_retail.describe()
```
Plot a boxplot for unit_price to see if there are any outliers. If there are, remove those instances:
```
plt.subplots(figsize = (12, 6))
up = sns.boxplot(new_retail.unit_price)
```
Similarly, plot the unit_price boxplot for the modified values:
```
new_retail = new_retail[new_retail.unit_price < 15000]
new_retail.describe()
```
Plot a boxplot for the unit_price of the new_retail DataFrame.
```
up_new = sns.boxplot(new_retail.unit_price)
```
Plot a boxplot for quantity to see if there are any outliers. If there are, remove those instances:
```
plt.subplots(figsize = (12, 6))
q = sns.boxplot(new_retail.quantity)
```
Plot the boxplot for quantity without outliers:
```
new_retail = new_retail[new_retail.quantity < 25000]
new_retail.describe()
```
Plot a boxplot for the quantity column of the new_retail DataFrame.
```
q_new = sns.boxplot(new_retail.quantity)
```
Use the following code to get some details about the new_retail DataFrame:
```
new_retail[(new_retail.desc.isnull()) & (new_retail.cust_id.isnull())]
```
Fetch the details of the DataFrame using the .info() function:
```
new_retail.info()
```
Drop all the null values in the new DataFrame:
```
new_retail = new_retail.dropna()
new_retail.info()
```
Move the values to a new DataFrame to avoid confusion:
```
retail = new_retail
retail.head()
```
Convert the text in the desc column to lowercase:
```
retail.desc = retail.desc.str.lower()
retail.head()
```
Convert the date column into datetime format:
```
retail['date'] = pd.to_datetime(retail.date, format = '%d/%m/%Y %H:%M')
retail.head()
```
Add six new columns with the following names: year_month, year, month, day, day_of_week, and hour:
```
retail.insert(loc = 4, column = 'year_month', value = retail.date.map(lambda x: 100 * x.year + x.month))
retail.insert(loc = 5, column = 'year', value = retail.date.dt.year)
retail.insert(loc = 6, column = 'month', value = retail.date.dt.month)
retail.insert(loc = 7, column = 'day', value = retail.date.dt.day)
retail.insert(loc = 8, column ='hour', value = retail.date.dt.hour)
retail.insert(loc = 9, column='day_of_week', value=(retail.date.dt.dayofweek)+1)
retail.head()
```
Add a column called spent, which is the quantity multiplied by the unit_price:
```
retail.insert(loc = 11, column = 'spent', value = (retail['quantity'] * retail['unit_price']))
retail.head()
```
Rearrange the columns
```
retail = retail[['invoice', 'country', 'cust_id', 'stock_code', 'desc','quantity', 'unit_price', 'date', 'spent',
'year_month', 'year', 'month', 'day', 'day_of_week', 'hour']]
retail.head()
```
Determine which customers placed the most and fewest orders:
```
#orders made by each customer
ord_cust = retail.groupby(by = ['cust_id', 'country'], as_index = False)['invoice'].count()
ord_cust.head(10)
```
Plot the graph for visualizing the preceding information:
```
plt.subplots(figsize = (15, 6))
oc = plt.plot(ord_cust.cust_id, ord_cust.invoice)
plt.xlabel('Customer ID')
plt.ylabel('Number of Orders')
plt.title('Number of Orders made by Customers')
plt.show()
```
Find details about the orders per customer:
```
ord_cust.describe()
```
Determine which country has the customers that have spent the most money on orders:
```
# 5 customers who ordered the most number of times
ord_cust.sort_values(by = 'invoice', ascending = False).head()
```
Find the amount spent by customers:
```
# money spent
spent_cust = retail.groupby(by = ['cust_id', 'country'], as_index = False)['spent'].sum()
spent_cust.head()
```
Plot a graph for the amount of money spent by the customers:
```
plt.subplots(figsize = (15, 6))
sc = plt.plot(spent_cust.cust_id, spent_cust.spent)
plt.xlabel('Customer ID')
plt.ylabel('Total Amount Spent')
plt.title('Amount Spent by Customers')
plt.show()
```
Arrange the values in ascending order to get a clear picture:
```
spent_cust.sort_values(by = 'spent', ascending = False).head()
```
Get more details about the new DataFrame:
```
retail.tail()
retail.head()
```
Determine which month had the most orders:
```
#orders per month
ord_month = retail.groupby(['invoice'])['year_month'].unique().value_counts().sort_index()
ord_month
```
Plot a graph to find which month had the most orders:
```
om = ord_month.plot(kind='bar', figsize = (15, 6))
om.set_xlabel('Month')
om.set_ylabel('Number of Orders')
om.set_title('Orders per Month')
om.set_xticklabels(('Dec 09', 'Jan 10', 'Feb 10', 'Mar 10', 'Apr 10', 'May 10',
'Jun 10', 'Jul 10', 'Aug 10', 'Sep 10', 'Oct 10', 'Nov 10', 'Dec 10',
'Jan 11', 'Feb 11', 'Mar 11', 'Apr 11', 'May 11',
'Jun 11', 'Jul 11', 'Aug 11', 'Sep 11', 'Oct 11', 'Nov 11', 'Dec 11'), rotation = 'horizontal')
plt.show()
```
Determine which day of the month had the most orders:
```
# most popular time of the month to order
ord_day = retail.groupby('invoice')['day'].unique().value_counts().sort_index()
ord_day
```
Plot the graph to find the day of the month with the most orders:
```
od = ord_day.plot(kind='bar', figsize = (15, 6))
od.set_xlabel('Day of the Month')
od.set_ylabel('Number of Orders')
od.set_title('Orders per Day of the Month')
od.set_xticklabels(labels = [i for i in range (1, 32)], rotation = 'horizontal')
plt.show()
```
Determine which day of the week had the most orders:
```
# orders per day of the week
ord_dayofweek = retail.groupby('invoice')['day_of_week'].unique().value_counts().sort_index()
ord_dayofweek
```
Plot the graph to find the day of the week with the most orders:
```
odw = ord_dayofweek.plot(kind='bar', figsize = (15, 6))
odw.set_xlabel('Day of the Week')
odw.set_ylabel('Number of Orders')
odw.set_title('Orders per Day of the Week')
odw.set_xticklabels(labels = ['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun'], rotation = 'horizontal')
plt.show()
```
Determine which customers spent the most money on one item:
```
q_item = retail.groupby(by = ['desc'], as_index = False)['quantity'].sum()
q_item.head()
```
Sort the values in the quantity column in ascending order:
```
q_item.sort_values(by = 'quantity', ascending = False).head()
```
Sort the quantity of items sold per month in descending order from the retail DataFrame:
```
item_month = retail.groupby(by = ['desc', 'year_month'], as_index = False)['quantity'].sum()
item_month.sort_values(by = 'quantity', ascending = False).head()
```
Similarly, sort the most sold items of the week in descending order from the retail DataFrame:
```
item_dayofweek = retail.groupby(by = ['desc', 'day_of_week'], as_index = False)['quantity'].sum()
item_dayofweek.sort_values(by = 'quantity', ascending = False).head()
```
Finding out which item is the most sold item across all countries
```
item_coun = retail.groupby(by = ['desc', 'country'], as_index = False)['quantity'].sum()
item_coun.sort_values(by = 'quantity', ascending = False).head()
```
Now, sort the items based on customer ID, stock code, and date:
```
retail_sort = retail.sort_values(['cust_id', 'stock_code', 'date'])
retail_sort_shift1 = retail_sort.shift(1)
retail_sort_reorder = retail_sort.copy()
retail_sort_reorder['reorder'] = np.where(retail_sort['stock_code'] == retail_sort_shift1['stock_code'], 1, 0)
retail_sort_reorder.head()
```
Create a new DataFrame for the reordered items:
```
rsr = pd.DataFrame((retail_sort_reorder.groupby('desc')['reorder'].sum())).sort_values('reorder', ascending = False)
rsr.head()
```
Sort the reordered items in descending order of quantity:
```
q_up = retail.groupby(by = ['unit_price'], as_index = False)['quantity'].sum()
q_up.sort_values('quantity', ascending = False).head(10)
```
Form an array to display the correlation coefficients for unit_price and quantity columns:
```
up_arr = np.array(retail.unit_price)
q_arr = np.array(retail.quantity)
np.corrcoef(up_arr, q_arr)
```
Determine which countries the customers who placed the minimum number of orders are from:
```
ord_coun = retail.groupby(['country'])['invoice'].count().sort_values()
ord_coun.head()
```
Plot the graph to visualize the preceding output:
```
ocoun = ord_coun.plot(kind='barh', figsize = (15, 6))
ocoun.set_xlabel('Number of Orders')
ocoun.set_ylabel('Country')
ocoun.set_title('Orders per Country')
plt.show()
```
Delete the count of orders from United Kingdom as follows:
```
del ord_coun['United Kingdom']
```
Now plot the graph again:
```
ocoun2 = ord_coun.plot(kind='barh', figsize = (15, 6))
ocoun2.set_xlabel('Number of Orders')
ocoun2.set_ylabel('Country')
ocoun2.set_title('Orders per Country')
plt.show()
```
Find out the country with the most money spent on orders:
```
coun_spent = retail.groupby('country')['spent'].sum().sort_values()
cs = coun_spent.plot(kind='barh', figsize = (15, 6))
cs.set_xlabel('Amount Spent')
cs.set_ylabel('Country')
cs.set_title('Amount Spent per Country')
plt.show()
```
Delete the values for United Kingdom in the DataFrame and visualize the output in a graph:
```
del coun_spent['United Kingdom']
cs2 = coun_spent.plot(kind='barh', figsize = (15, 6))
cs2.set_xlabel('Amount Spent')
cs2.set_ylabel('Country')
cs2.set_title('Amount Spent per Country')
plt.show()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
!pip install plotly
import plotly.express as px
r09 = pd.read_csv('https://raw.githubusercontent.com/PacktWorkshops/The-Data-Analysis-Workshop/master/Chapter08/Datasets/online_retail_II.csv')
r09.head()
r10 = pd.read_csv('https://raw.githubusercontent.com/PacktWorkshops/The-Data-Analysis-Workshop/master/Chapter08/Datasets/online_retail_II2.csv')
r10.head()
dfs = [r09, r10]
retail = pd.concat(dfs, keys = ['09-10', '10-11'])
retail
retail.rename(index = str, columns = {
'Invoice' : 'invoice',
'StockCode' : 'stock_code',
'Quantity' : 'quantity',
'InvoiceDate' : 'date',
'Price' : 'unit_price',
'Country' : 'country',
'Description' : 'desc',
'Customer ID' : 'cust_id'
}, inplace = True)
retail.head()
retail.isnull().sum().sort_values(ascending = False)
retail.describe()
retail.loc[retail['unit_price'] == 38970.0]
retail.loc[retail['unit_price'] == -53594.360000]
(retail['unit_price'] <= 0).sum()
(retail['quantity'] <= 0).sum()
retail[(retail['unit_price'] <= 0) & (retail['quantity'] <= 0) & (retail['cust_id'].isnull())]
null_retail = retail[retail.isnull().any(axis=1)]
null_retail
new_retail = retail[(retail['unit_price'] > 0) & (retail['quantity'] > 0)]
new_retail.describe()
plt.subplots(figsize = (12, 6))
up = sns.boxplot(new_retail.unit_price)
new_retail = new_retail[new_retail.unit_price < 15000]
new_retail.describe()
up_new = sns.boxplot(new_retail.unit_price)
plt.subplots(figsize = (12, 6))
q = sns.boxplot(new_retail.quantity)
new_retail = new_retail[new_retail.quantity < 25000]
new_retail.describe()
q_new = sns.boxplot(new_retail.quantity)
new_retail[(new_retail.desc.isnull()) & (new_retail.cust_id.isnull())]
new_retail.info()
new_retail = new_retail.dropna()
new_retail.info()
retail = new_retail
retail.head()
retail.desc = retail.desc.str.lower()
retail.head()
retail['date'] = pd.to_datetime(retail.date, format = '%d/%m/%Y %H:%M')
retail.head()
retail.insert(loc = 4, column = 'year_month', value = retail.date.map(lambda x: 100 * x.year + x.month))
retail.insert(loc = 5, column = 'year', value = retail.date.dt.year)
retail.insert(loc = 6, column = 'month', value = retail.date.dt.month)
retail.insert(loc = 7, column = 'day', value = retail.date.dt.day)
retail.insert(loc = 8, column ='hour', value = retail.date.dt.hour)
retail.insert(loc = 9, column='day_of_week', value=(retail.date.dt.dayofweek)+1)
retail.head()
retail.insert(loc = 11, column = 'spent', value = (retail['quantity'] * retail['unit_price']))
retail.head()
retail = retail[['invoice', 'country', 'cust_id', 'stock_code', 'desc','quantity', 'unit_price', 'date', 'spent',
'year_month', 'year', 'month', 'day', 'day_of_week', 'hour']]
retail.head()
#orders made by each customer
ord_cust = retail.groupby(by = ['cust_id', 'country'], as_index = False)['invoice'].count()
ord_cust.head(10)
plt.subplots(figsize = (15, 6))
oc = plt.plot(ord_cust.cust_id, ord_cust.invoice)
plt.xlabel('Customer ID')
plt.ylabel('Number of Orders')
plt.title('Number of Orders made by Customers')
plt.show()
ord_cust.describe()
# 5 customers who ordered the most number of times
ord_cust.sort_values(by = 'invoice', ascending = False).head()
# money spent
spent_cust = retail.groupby(by = ['cust_id', 'country'], as_index = False)['spent'].sum()
spent_cust.head()
plt.subplots(figsize = (15, 6))
sc = plt.plot(spent_cust.cust_id, spent_cust.spent)
plt.xlabel('Customer ID')
plt.ylabel('Total Amount Spent')
plt.title('Amount Spent by Customers')
plt.show()
spent_cust.sort_values(by = 'spent', ascending = False).head()
retail.tail()
retail.head()
#orders per month
ord_month = retail.groupby(['invoice'])['year_month'].unique().value_counts().sort_index()
ord_month
om = ord_month.plot(kind='bar', figsize = (15, 6))
om.set_xlabel('Month')
om.set_ylabel('Number of Orders')
om.set_title('Orders per Month')
om.set_xticklabels(('Dec 09', 'Jan 10', 'Feb 10', 'Mar 10', 'Apr 10', 'May 10',
'Jun 10', 'Jul 10', 'Aug 10', 'Sep 10', 'Oct 10', 'Nov 10', 'Dec 10',
'Jan 11', 'Feb 11', 'Mar 11', 'Apr 11', 'May 11',
'Jun 11', 'Jul 11', 'Aug 11', 'Sep 11', 'Oct 11', 'Nov 11', 'Dec 11'), rotation = 'horizontal')
plt.show()
# most popular time of the month to order
ord_day = retail.groupby('invoice')['day'].unique().value_counts().sort_index()
ord_day
od = ord_day.plot(kind='bar', figsize = (15, 6))
od.set_xlabel('Day of the Month')
od.set_ylabel('Number of Orders')
od.set_title('Orders per Day of the Month')
od.set_xticklabels(labels = [i for i in range (1, 32)], rotation = 'horizontal')
plt.show()
# orders per day of the week
ord_dayofweek = retail.groupby('invoice')['day_of_week'].unique().value_counts().sort_index()
ord_dayofweek
odw = ord_dayofweek.plot(kind='bar', figsize = (15, 6))
odw.set_xlabel('Day of the Week')
odw.set_ylabel('Number of Orders')
odw.set_title('Orders per Day of the Week')
odw.set_xticklabels(labels = ['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun'], rotation = 'horizontal')
plt.show()
q_item = retail.groupby(by = ['desc'], as_index = False)['quantity'].sum()
q_item.head()
q_item.sort_values(by = 'quantity', ascending = False).head()
item_month = retail.groupby(by = ['desc', 'year_month'], as_index = False)['quantity'].sum()
item_month.sort_values(by = 'quantity', ascending = False).head()
item_dayofweek = retail.groupby(by = ['desc', 'day_of_week'], as_index = False)['quantity'].sum()
item_dayofweek.sort_values(by = 'quantity', ascending = False).head()
item_coun = retail.groupby(by = ['desc', 'country'], as_index = False)['quantity'].sum()
item_coun.sort_values(by = 'quantity', ascending = False).head()
retail_sort = retail.sort_values(['cust_id', 'stock_code', 'date'])
retail_sort_shift1 = retail_sort.shift(1)
retail_sort_reorder = retail_sort.copy()
retail_sort_reorder['reorder'] = np.where(retail_sort['stock_code'] == retail_sort_shift1['stock_code'], 1, 0)
retail_sort_reorder.head()
rsr = pd.DataFrame((retail_sort_reorder.groupby('desc')['reorder'].sum())).sort_values('reorder', ascending = False)
rsr.head()
q_up = retail.groupby(by = ['unit_price'], as_index = False)['quantity'].sum()
q_up.sort_values('quantity', ascending = False).head(10)
up_arr = np.array(retail.unit_price)
q_arr = np.array(retail.quantity)
np.corrcoef(up_arr, q_arr)
ord_coun = retail.groupby(['country'])['invoice'].count().sort_values()
ord_coun.head()
ocoun = ord_coun.plot(kind='barh', figsize = (15, 6))
ocoun.set_xlabel('Number of Orders')
ocoun.set_ylabel('Country')
ocoun.set_title('Orders per Country')
plt.show()
del ord_coun['United Kingdom']
ocoun2 = ord_coun.plot(kind='barh', figsize = (15, 6))
ocoun2.set_xlabel('Number of Orders')
ocoun2.set_ylabel('Country')
ocoun2.set_title('Orders per Country')
plt.show()
coun_spent = retail.groupby('country')['spent'].sum().sort_values()
cs = coun_spent.plot(kind='barh', figsize = (15, 6))
cs.set_xlabel('Amount Spent')
cs.set_ylabel('Country')
cs.set_title('Amount Spent per Country')
plt.show()
del coun_spent['United Kingdom']
cs2 = coun_spent.plot(kind='barh', figsize = (15, 6))
cs2.set_xlabel('Amount Spent')
cs2.set_ylabel('Country')
cs2.set_title('Amount Spent per Country')
plt.show()
| 0.441673 | 0.93276 |
When we talk about quantum computing, we actually talk about several different paradigms. The most common one is gate-model quantum computing, in the vein we discussed in the previous notebook. In this case, gates are applied on qubit registers to perform arbitrary transformations of quantum states made up of qubits.
The second most common paradigm is quantum annealing. This paradigm is often also referred to as adiabatic quantum computing, although there are subtle differences. Quantum annealing solves a more specific problem -- universality is not a requirement -- which makes it an easier, albeit still difficult engineering challenge to scale it up. The technology is up to 2000 superconducting qubits in 2018, compared to the less than 100 qubits on gate-model quantum computers. D-Wave Systems has been building superconducting quantum annealers for over a decade and this company holds the record for the number of qubits -- 2048. More recently, an IARPA project was launched to build novel superconducting quantum annealers. A quantum optics implementation was also made available by QNNcloud that implements a coherent Ising model. Its restrictions are different from superconducting architectures.
Gate-model quantum computing is conceptually easier to understand: it is the generalization of digital computing. Instead of deterministic logical operations of bit strings, we have deterministic transformations of (quantum) probability distributions over bit strings. Quantum annealing requires some understanding of physics, which is why we introduced classical and quantum many-body physics in a previous notebook. Over the last few years, quantum annealing inspired gate-model algorithms that work on current and near-term quantum computers (see the notebook on variational circuits). So in this sense, it is worth developing an understanding of the underlying physics model and how quantum annealing works, even if you are only interested in gate-model quantum computing.
While there is a plethora of quantum computing languages, frameworks, and libraries for the gate-model, quantum annealing is less well-established. D-Wave Systems offers an open source suite called Ocean. A vendor-independent solution is XACC, an extensible compilation framework for hybrid quantum-classical computing architectures, but the only quantum annealer it maps to is that of D-Wave Systems. Since XACC is a much larger initiative that extends beyond annealing, we choose a few much simpler packages from Ocean to illustrate the core concepts of this paradigm. However, before diving into the details of quantum annealing, it is worth taking a slight detour to connect the unitary evolution we discussed in a closed system and in the gate-model paradigm and the Hamiltonian describing a quantum many-body system. We also briefly discuss the adiabatic theorem, which provides the foundation why quantum annealing would work at all.
# Unitary evolution and the Hamiltonian
We introduced the Hamiltonian as an object describing the energy of a classical or quantum system. Something more is true: it gives a description of a system evolving with time. This formalism is expressed by the Schrรถdinger equation:
$$
\imath\hbar {\frac {d}{dt}}|\psi(t)\rangle = H|\psi(t)\rangle,
$$
where $\hbar$ is the reduced Planck constant. Previously we said that it is a unitary operator that evolves state. That is exactly what we get if we solve the Schrรถdinger equation for some time $t$: $U = \exp(-\imath Ht/\hbar)$. Note that we used that the Hamiltonian does not depend on time. In other words, every unitary we talked about so far has some underlying Hamiltonian.
The Schrรถdinger equation in the above form is the time-dependent variant: the state depends on time. The time-independent Schrรถndinger equation reflects what we said about the Hamiltonian describing the energy of the system:
$$
H|\psi \rangle =E|\psi \rangle,
$$
where $E$ is the total energy of the system.
# The adiabatic theorem and adiabatic quantum computing
An adiabatic process means that conditions change slowly enough for the system to adapt to the new configuration. For instance, in a quantum mechanical system, we can start from some Hamiltonian $H_0$ and slowly change it to some other Hamiltonian $H_1$. The simplest change could be a linear schedule:
$$
H(t) = (1-t) H_0 + t H_1,
$$
for $t\in[0,1]$ on some time scale. This Hamiltonian depends on time, so solving the Schrรถdinger equation is considerably more complicated. The adiabatic theorem says that if the change in the time-dependent Hamiltonian occurs slowly, the resulting dynamics remain simple: starting close to an eigenstate, the system remains close to
an eigenstate. This implies that if the system started in the ground state, if certain conditions are met, the system stays in the ground state.
We call the energy difference between the ground state and the first excited state the gap. If $H(t)$ has a nonnegative gap for each $t$ during the transition and the change happens slowly, then the system stays in the ground state. If we denote the time-dependent gap by $\Delta(t)$, a course approximation of the speed limit scales as $1/\min(\Delta(t))^2$.
This theorem allows something highly unusual. We can reach the ground state of an easy-to-solve quantum many body system, and change the Hamiltonian to a system we are interested in. For instance, we could start with the Hamiltonian $\sum_i \sigma^X_i$ -- its ground state is just the equal superposition. Let's see this on two sites:
```
import numpy as np
np.set_printoptions(precision=3, suppress=True)
X = np.array([[0, 1], [1, 0]])
IX = np.kron(np.eye(2), X)
XI = np.kron(X, np.eye(2))
H_0 = - (IX + XI)
ฮป, v = np.linalg.eigh(H_0)
print("Eigenvalues:", ฮป)
print("Eigenstate for lowest eigenvalue", v[:, 0])
```
Then we could turn this Hamiltonian slowly into a classical Ising model and read out the global solution.
<img src="../figures/annealing_process.svg" alt="Annealing process" style="width: 400px;"/>
Adiabatic quantum computation exploits this phenomenon and it is able to perform universal calculations with the final Hamiltonian being $H=-\sum_{<i,j>} J_{ij} \sigma^Z_i \sigma^Z_{j} - \sum_i h_i \sigma^Z_i - \sum_{<i,j>} g_{ij} \sigma^X_i\sigma^X_j$. Note that is not the transverse-field Ising model: the last term is an X-X interaction. If a quantum computer respects the speed limit, guarantees the finite gap, and implements this Hamiltonian, then it is equivalent to the gate model with some overhead.
The quadratic scaling on the gap does not appear too bad. So can we solve NP-hard problems faster with this paradigm? It is unlikely. The gap is highly dependent on the problem, and actually difficult problems tend to have an exponentially small gap. So our speed limit would be quadratic over the exponentially small gap, so the overall time required would be exponentially large.
# Quantum annealing
A theoretical obstacle to adiabatic quantum computing is that calculating the speed limit is clearly not trivial; in fact, it is harder than solving the original problem of finding the ground state of some Hamiltonian of interest. Engineering constraints also apply: the qubits decohere, the environment has finite temperature, and so on. *Quantum annealing* drops the strict requirements and instead of respecting speed limits, it repeats the transition (the annealing) over and over again. Having collected a number of samples, we pick the spin configuration with the lowest energy as our solution. There is no guarantee that this is the ground state.
Quantum annealing has a slightly different software stack than gate-model quantum computers. Instead of a quantum circuit, the level of abstraction is the classical Ising model -- the problem we are interested in solving must be in this form. Then, just like superconducting gate-model quantum computers, superconducting quantum annealers also suffer from limited connectivity. In this case, it means that if our problem's connectivity does not match that of the hardware, we have to find a graph minor embedding. This will combine several physical qubits into a logical qubit. The workflow is summarized in the following diagram [[1](#1)]:
<img src="../figures/quantum_annealing_workflow.png" alt="Software stack on a quantum annealer" style="width: 400px;"/>
A possible classical solver for the Ising model is the simulated annealer that we have seen before:
```
import dimod
J = {(0, 1): 1.0, (1, 2): -1.0}
h = {0:0, 1:0, 2:0}
model = dimod.BinaryQuadraticModel(h, J, 0.0, dimod.SPIN)
sampler = dimod.SimulatedAnnealingSampler()
response = sampler.sample(model, num_reads=10)
print("Energy of samples:")
print([solution.energy for solution in response.data()])
```
Let's take a look at the minor embedding problem. This part is NP-hard in itself, so we normally use probabilistic heuristics to find an embedding. For instance, for many generations of the quantum annealer that D-Wave Systems produces has unit cells containing a $K_{4,4}$ bipartite fully-connected graph, with two remote connections from each qubit going to qubits in neighbouring unit cells. A unit cell with its local and remote connections indicated is depicted following figure:
<img src="../figures/unit_cell.png" alt="Unit cell in Chimera graph" style="width: 80px;"/>
This is called the Chimera graph. The current largest hardware has 2048 qubits, consisting of $16\times 16$ unit cells of 8 qubits each. The Chimera graph is available as a `networkx` graph in the package `dwave_networkx`. We draw a smaller version, consisting of $2\times 2$ unit cells.
```
import matplotlib.pyplot as plt
import dwave_networkx as dnx
%matplotlib inline
connectivity_structure = dnx.chimera_graph(2, 2)
dnx.draw_chimera(connectivity_structure)
plt.show()
```
Let's create a graph that certainly does not fit this connectivity structure. For instance, the complete graph $K_n$ on nine nodes:
```
import networkx as nx
G = nx.complete_graph(9)
plt.axis('off')
nx.draw_networkx(G, with_labels=False)
import minorminer
embedded_graph = minorminer.find_embedding(G.edges(), connectivity_structure.edges())
```
Let's plot this embedding:
```
dnx.draw_chimera_embedding(connectivity_structure, embedded_graph)
plt.show()
```
Qubits that have the same colour corresponding to a logical node in the original problem defined by the $K_9$ graph. Qubits combined in such way form a chain. Even though our problem only has 9 variables (nodes), we used almost all 32 available on the toy Chimera graph. Let's find the maximum chain length:
```
max_chain_length = 0
for _, chain in embedded_graph.items():
if len(chain) > max_chain_length:
max_chain_length = len(chain)
print(max_chain_length)
```
The chain on the hardware is implemented by having strong couplings between the elements in a chain -- in fact, twice as strong as what the user can set. Nevertheless, long chains can break, which means we receive inconsistent results. In general, we prefer shorter chains, so we do not waste physical qubits and we obtain more reliable results.
# References
[1] M. Fingerhuth, T. Babej, P. Wittek. (2018). [Open source software in quantum computing](https://doi.org/10.1371/journal.pone.0208561). *PLOS ONE* 13(12):e0208561. <a id='1'></a>
|
github_jupyter
|
import numpy as np
np.set_printoptions(precision=3, suppress=True)
X = np.array([[0, 1], [1, 0]])
IX = np.kron(np.eye(2), X)
XI = np.kron(X, np.eye(2))
H_0 = - (IX + XI)
ฮป, v = np.linalg.eigh(H_0)
print("Eigenvalues:", ฮป)
print("Eigenstate for lowest eigenvalue", v[:, 0])
import dimod
J = {(0, 1): 1.0, (1, 2): -1.0}
h = {0:0, 1:0, 2:0}
model = dimod.BinaryQuadraticModel(h, J, 0.0, dimod.SPIN)
sampler = dimod.SimulatedAnnealingSampler()
response = sampler.sample(model, num_reads=10)
print("Energy of samples:")
print([solution.energy for solution in response.data()])
import matplotlib.pyplot as plt
import dwave_networkx as dnx
%matplotlib inline
connectivity_structure = dnx.chimera_graph(2, 2)
dnx.draw_chimera(connectivity_structure)
plt.show()
import networkx as nx
G = nx.complete_graph(9)
plt.axis('off')
nx.draw_networkx(G, with_labels=False)
import minorminer
embedded_graph = minorminer.find_embedding(G.edges(), connectivity_structure.edges())
dnx.draw_chimera_embedding(connectivity_structure, embedded_graph)
plt.show()
max_chain_length = 0
for _, chain in embedded_graph.items():
if len(chain) > max_chain_length:
max_chain_length = len(chain)
print(max_chain_length)
| 0.307982 | 0.994708 |
```
# Dependencies and Setup
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sn
from math import trunc
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
# File to Load and read
mouse_drug_data = pd.read_csv("data/mouse_drug_data.csv")
clinical_trial_data = pd.read_csv("data/clinicaltrial_data.csv")
mouse_drug_data.head()
# mouse_drug_type = mouse_drug_data[["Capomulin","Infubinol","Ketapril","Placebo"]]
# mouse_drug_type
clinical_trial_data.head()
# Combine the data into a single dataset
merge_data=pd.merge(mouse_drug_data, clinical_trial_data, on = "Mouse ID", how = "left")
# Display the data table for preview
merge_data.head()
```
## Tumor Response to Treatment
```
# Store the Mean Tumor Volume Data Grouped by Drug and Timepoint
Mean_tumor_volume = merge_data.groupby(['Drug','Timepoint']).mean()['Tumor Volume (mm3)']
Mean_tumor_volume.head()
# Convert to DataFrame
Tumor_response_df = pd.DataFrame(Mean_tumor_volume)
Tumor_response_df = Tumor_response_df.reset_index()
# Preview DataFrame
Tumor_response_df.head()
# Store the Standard Error of Tumor Volumes Grouped by Drug and Timepoint
SEM_Tumor_response = Tumor_response_df.sem
SEM_Tumor_response
# Minor Data Munging to Re-Format the Data Frames
Tumor_response = pd.pivot_table(merge_data, index='Timepoint',
columns='Drug',
values='Tumor Volume (mm3)',
aggfunc = np.mean)
# Preview that Reformatting worked
Tumor_response.head()
Tumor_response_type = Tumor_response[["Capomulin","Infubinol","Ketapril","Placebo"]]
Tumor_response_type.head()
Tumor_volume = Tumor_response_type.mean()
Tumor_volume
# Generate the Plot (with Error Bars)
Timepoint = Tumor_response_type.index
plt.figure(figsize=(12,8))
plt.errorbar(Timepoint, Tumor_response['Capomulin'],yerr=Tumor_response['Capomulin'].sem(), marker ='o', linestyle='--', label="Capomulin")
plt.errorbar(Timepoint, Tumor_response['Infubinol'],yerr=Tumor_response['Infubinol'].sem(), marker ='s', linestyle='--', label="Infubinol")
plt.errorbar(Timepoint, Tumor_response['Ketapril'],yerr=Tumor_response['Ketapril'].sem(), marker ='p', linestyle='--', label="Ketapril")
plt.errorbar(Timepoint, Tumor_response['Placebo'],yerr=Tumor_response['Placebo'].sem(), marker ='d', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Time(Days)', ylabel = 'Tumor Volume (mm3)',title = 'Tumor Response to Treatment',xlim = (0,max(Timepoint)))
plt.legend(loc = 'best', frameon=True)
plt.grid()
plt.show()
# Save the Figure
plt.savefig("errorbar.png")
```
## Metastatic Response to Treatment
```
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
Met_response_mean = merge_data.groupby(['Drug','Timepoint']).mean()[['Metastatic Sites']]
Met_response_mean.head()
# Convert to DataFrame
Met_response_mean = pd.DataFrame(Met_response_mean)
# Preview DataFrame
Met_response_mean.head()
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
Met_response_sem = merge_data.groupby(['Drug','Timepoint']).sem()[['Metastatic Sites']]
# Convert to DataFrame
Met_response_sem = pd.DataFrame(Met_response_sem)
# Preview DataFrame
Met_response_sem.head()
# Minor Data Munging to Re-Format the Data Frames
Met_response_mean = Met_response_mean.reset_index()
Met_response_pivot_mean = Met_response_mean.pivot(index="Timepoint", columns="Drug")["Metastatic Sites"]
Met_response_sem = Met_response_sem.reset_index()
Met_response_pivot_sem = Met_response_sem.pivot(index="Timepoint", columns="Drug")["Metastatic Sites"]
# Preview that Reformatting worked
Met_response_pivot_mean.head()
# Generate the Plot (with Error Bars)
Metastatic = Met_response_pivot_mean.index
plt.figure(figsize=(10,10))
plt.errorbar(Metastatic, Met_response_pivot_mean["Capomulin"],yerr=Tumor_response["Capomulin"].sem(), marker ='o', linestyle='--', label="Capomulin")
plt.errorbar(Metastatic, Met_response_pivot_mean["Infubinol"],yerr=Tumor_response["Infubinol"].sem(), marker ='s', linestyle='--', label="Infubinol")
plt.errorbar(Metastatic, Met_response_pivot_mean["Ketapril"],yerr=Tumor_response["Ketapril"].sem(), marker ='p', linestyle='--', label="Ketapril")
plt.errorbar(Metastatic, Met_response_pivot_mean["Placebo"],yerr=Tumor_response["Placebo"].sem(), marker ='d', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Treatment Duration (Days)', ylabel = 'Met. Sites',title = 'Metastatic Spread During Treatment' ,xlim = (0,max(Metastatic)))
plt.legend(loc ="best", fontsize = "medium", frameon=True)
plt.grid()
plt.show()
# Save the Figure
plt.savefig("errorbar.png")
# Save the Figure
plt.savefig("metastatic.png")
```
## Survival Rates
```
# Store the Count of Mice Grouped by Drug and Timepoint (W can pass any metric)
mouse_count = merge_data.groupby(['Drug','Timepoint']).count()[['Mouse ID']]
mouse_count.head()
# Convert to DataFrame
mouse_count_df = pd.DataFrame(mouse_count)
# Preview DataFrame
mouse_count_df.head()
# Minor Data Munging to Re-Format the Data Frames
Mouse_Data = pd.pivot_table(mouse_count, index='Timepoint', columns='Drug', values='Mouse ID', aggfunc = np.mean)
# Preview the Data Frame
Mouse_Data.head()
Mouse_Data_type = Mouse_Data[["Capomulin","Infubinol","Ketapril","Placebo"]]
Mouse_Data_type
Survival_percent = Mouse_Data_type.copy()
Survival_percent = round(Survival_percent.apply(lambda c: c / c.max() * 100, axis=0),2)
# Generate the Plot (Accounting for percentages)
Survival_rate = Survival_percent.index
plt.figure(figsize=(12,8))
plt.plot(Survival_rate, Survival_percent['Capomulin'], marker ='^', linestyle='--', label="Capomulin")
plt.plot(Survival_rate, Survival_percent['Infubinol'], marker ='p', linestyle='--', label="Infubinol")
plt.plot(Survival_rate, Survival_percent['Ketapril'], marker ='d', linestyle='--', label="Ketapril")
plt.plot(Survival_rate, Survival_percent['Placebo'], marker ='s', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Time (Days)', ylabel = 'Survival Rate(%)',title = 'Survival During Treatment',xlim = (0,max(Survival_rate)))
plt.legend(loc = 'best', frameon=True)
plt.grid()
plt.show()
#Capomulin, Infubinol, Ketapril, and Placebo
# Save the Figure
plt.savefig("survival_rate.png")
```
## Summary Bar Graph
```
# Calculate the percent changes for each drug
Drug_Change_Percent = (((Tumor_response.iloc[-1]-Tumor_response.iloc[0])/Tumor_response.iloc[0])*100)
Drug_Change_Percent
PCT_changes = (Drug_Change_Percent["Capomulin"],
Drug_Change_Percent["Infubinol"],
Drug_Change_Percent["Ketapril"],
Drug_Change_Percent["Placebo"])
# Splice the data between passing and failing drugs
fig, ax = plt.subplots()
ind = np.arange(len(PCT_changes))
width = 1
rectsPass = ax.bar(ind[0], PCT_changes[0], width, color='green')
rectsFail = ax.bar(ind[1:], PCT_changes[1:], width, color='red')
# Orient widths. Add labels, tick marks, etc.
ax.set_ylabel('% Tumor Volume Change')
ax.set_title('Tumor Change Over 45 Day Treatment')
ax.set_xticks(ind + 0.5)
ax.set_xticklabels(('Capomulin', 'Infubinol', 'Ketapril', 'Placebo'))
ax.set_autoscaley_on(False)
ax.set_ylim([-30,70])
ax.grid(True)
# Use functions to label the percentages of changes
def autolabelFail(rects):
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()/2., 3,
'%d%%' % int(height),
ha='center', va='bottom', color="white")
def autolabelPass(rects):
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()/2., -8,
'-%d%% ' % int(height),
ha='center', va='bottom', color="white")
# Call functions to implement the function calls
autolabelPass(rectsPass)
autolabelFail(rectsFail)
# Save the Figure
#fig.savefig("analysis/Fig4.png")
# Show the Figure
fig.show()
OBSERVATIONS
1. Mice that were administered Capomulin had the highest survival rate durng treatment.
2. Metastatic sites spread on the mice was lowest with the Capomulin durung treatment period.
3. The tumor response volume was lowest with the adminstation of Capomulin.
```
|
github_jupyter
|
# Dependencies and Setup
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sn
from math import trunc
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
# File to Load and read
mouse_drug_data = pd.read_csv("data/mouse_drug_data.csv")
clinical_trial_data = pd.read_csv("data/clinicaltrial_data.csv")
mouse_drug_data.head()
# mouse_drug_type = mouse_drug_data[["Capomulin","Infubinol","Ketapril","Placebo"]]
# mouse_drug_type
clinical_trial_data.head()
# Combine the data into a single dataset
merge_data=pd.merge(mouse_drug_data, clinical_trial_data, on = "Mouse ID", how = "left")
# Display the data table for preview
merge_data.head()
# Store the Mean Tumor Volume Data Grouped by Drug and Timepoint
Mean_tumor_volume = merge_data.groupby(['Drug','Timepoint']).mean()['Tumor Volume (mm3)']
Mean_tumor_volume.head()
# Convert to DataFrame
Tumor_response_df = pd.DataFrame(Mean_tumor_volume)
Tumor_response_df = Tumor_response_df.reset_index()
# Preview DataFrame
Tumor_response_df.head()
# Store the Standard Error of Tumor Volumes Grouped by Drug and Timepoint
SEM_Tumor_response = Tumor_response_df.sem
SEM_Tumor_response
# Minor Data Munging to Re-Format the Data Frames
Tumor_response = pd.pivot_table(merge_data, index='Timepoint',
columns='Drug',
values='Tumor Volume (mm3)',
aggfunc = np.mean)
# Preview that Reformatting worked
Tumor_response.head()
Tumor_response_type = Tumor_response[["Capomulin","Infubinol","Ketapril","Placebo"]]
Tumor_response_type.head()
Tumor_volume = Tumor_response_type.mean()
Tumor_volume
# Generate the Plot (with Error Bars)
Timepoint = Tumor_response_type.index
plt.figure(figsize=(12,8))
plt.errorbar(Timepoint, Tumor_response['Capomulin'],yerr=Tumor_response['Capomulin'].sem(), marker ='o', linestyle='--', label="Capomulin")
plt.errorbar(Timepoint, Tumor_response['Infubinol'],yerr=Tumor_response['Infubinol'].sem(), marker ='s', linestyle='--', label="Infubinol")
plt.errorbar(Timepoint, Tumor_response['Ketapril'],yerr=Tumor_response['Ketapril'].sem(), marker ='p', linestyle='--', label="Ketapril")
plt.errorbar(Timepoint, Tumor_response['Placebo'],yerr=Tumor_response['Placebo'].sem(), marker ='d', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Time(Days)', ylabel = 'Tumor Volume (mm3)',title = 'Tumor Response to Treatment',xlim = (0,max(Timepoint)))
plt.legend(loc = 'best', frameon=True)
plt.grid()
plt.show()
# Save the Figure
plt.savefig("errorbar.png")
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
Met_response_mean = merge_data.groupby(['Drug','Timepoint']).mean()[['Metastatic Sites']]
Met_response_mean.head()
# Convert to DataFrame
Met_response_mean = pd.DataFrame(Met_response_mean)
# Preview DataFrame
Met_response_mean.head()
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
Met_response_sem = merge_data.groupby(['Drug','Timepoint']).sem()[['Metastatic Sites']]
# Convert to DataFrame
Met_response_sem = pd.DataFrame(Met_response_sem)
# Preview DataFrame
Met_response_sem.head()
# Minor Data Munging to Re-Format the Data Frames
Met_response_mean = Met_response_mean.reset_index()
Met_response_pivot_mean = Met_response_mean.pivot(index="Timepoint", columns="Drug")["Metastatic Sites"]
Met_response_sem = Met_response_sem.reset_index()
Met_response_pivot_sem = Met_response_sem.pivot(index="Timepoint", columns="Drug")["Metastatic Sites"]
# Preview that Reformatting worked
Met_response_pivot_mean.head()
# Generate the Plot (with Error Bars)
Metastatic = Met_response_pivot_mean.index
plt.figure(figsize=(10,10))
plt.errorbar(Metastatic, Met_response_pivot_mean["Capomulin"],yerr=Tumor_response["Capomulin"].sem(), marker ='o', linestyle='--', label="Capomulin")
plt.errorbar(Metastatic, Met_response_pivot_mean["Infubinol"],yerr=Tumor_response["Infubinol"].sem(), marker ='s', linestyle='--', label="Infubinol")
plt.errorbar(Metastatic, Met_response_pivot_mean["Ketapril"],yerr=Tumor_response["Ketapril"].sem(), marker ='p', linestyle='--', label="Ketapril")
plt.errorbar(Metastatic, Met_response_pivot_mean["Placebo"],yerr=Tumor_response["Placebo"].sem(), marker ='d', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Treatment Duration (Days)', ylabel = 'Met. Sites',title = 'Metastatic Spread During Treatment' ,xlim = (0,max(Metastatic)))
plt.legend(loc ="best", fontsize = "medium", frameon=True)
plt.grid()
plt.show()
# Save the Figure
plt.savefig("errorbar.png")
# Save the Figure
plt.savefig("metastatic.png")
# Store the Count of Mice Grouped by Drug and Timepoint (W can pass any metric)
mouse_count = merge_data.groupby(['Drug','Timepoint']).count()[['Mouse ID']]
mouse_count.head()
# Convert to DataFrame
mouse_count_df = pd.DataFrame(mouse_count)
# Preview DataFrame
mouse_count_df.head()
# Minor Data Munging to Re-Format the Data Frames
Mouse_Data = pd.pivot_table(mouse_count, index='Timepoint', columns='Drug', values='Mouse ID', aggfunc = np.mean)
# Preview the Data Frame
Mouse_Data.head()
Mouse_Data_type = Mouse_Data[["Capomulin","Infubinol","Ketapril","Placebo"]]
Mouse_Data_type
Survival_percent = Mouse_Data_type.copy()
Survival_percent = round(Survival_percent.apply(lambda c: c / c.max() * 100, axis=0),2)
# Generate the Plot (Accounting for percentages)
Survival_rate = Survival_percent.index
plt.figure(figsize=(12,8))
plt.plot(Survival_rate, Survival_percent['Capomulin'], marker ='^', linestyle='--', label="Capomulin")
plt.plot(Survival_rate, Survival_percent['Infubinol'], marker ='p', linestyle='--', label="Infubinol")
plt.plot(Survival_rate, Survival_percent['Ketapril'], marker ='d', linestyle='--', label="Ketapril")
plt.plot(Survival_rate, Survival_percent['Placebo'], marker ='s', linestyle='--', label="Placebo")
plt.gca().set(xlabel = 'Time (Days)', ylabel = 'Survival Rate(%)',title = 'Survival During Treatment',xlim = (0,max(Survival_rate)))
plt.legend(loc = 'best', frameon=True)
plt.grid()
plt.show()
#Capomulin, Infubinol, Ketapril, and Placebo
# Save the Figure
plt.savefig("survival_rate.png")
# Calculate the percent changes for each drug
Drug_Change_Percent = (((Tumor_response.iloc[-1]-Tumor_response.iloc[0])/Tumor_response.iloc[0])*100)
Drug_Change_Percent
PCT_changes = (Drug_Change_Percent["Capomulin"],
Drug_Change_Percent["Infubinol"],
Drug_Change_Percent["Ketapril"],
Drug_Change_Percent["Placebo"])
# Splice the data between passing and failing drugs
fig, ax = plt.subplots()
ind = np.arange(len(PCT_changes))
width = 1
rectsPass = ax.bar(ind[0], PCT_changes[0], width, color='green')
rectsFail = ax.bar(ind[1:], PCT_changes[1:], width, color='red')
# Orient widths. Add labels, tick marks, etc.
ax.set_ylabel('% Tumor Volume Change')
ax.set_title('Tumor Change Over 45 Day Treatment')
ax.set_xticks(ind + 0.5)
ax.set_xticklabels(('Capomulin', 'Infubinol', 'Ketapril', 'Placebo'))
ax.set_autoscaley_on(False)
ax.set_ylim([-30,70])
ax.grid(True)
# Use functions to label the percentages of changes
def autolabelFail(rects):
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()/2., 3,
'%d%%' % int(height),
ha='center', va='bottom', color="white")
def autolabelPass(rects):
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()/2., -8,
'-%d%% ' % int(height),
ha='center', va='bottom', color="white")
# Call functions to implement the function calls
autolabelPass(rectsPass)
autolabelFail(rectsFail)
# Save the Figure
#fig.savefig("analysis/Fig4.png")
# Show the Figure
fig.show()
OBSERVATIONS
1. Mice that were administered Capomulin had the highest survival rate durng treatment.
2. Metastatic sites spread on the mice was lowest with the Capomulin durung treatment period.
3. The tumor response volume was lowest with the adminstation of Capomulin.
| 0.681091 | 0.792986 |
```
import pandas as pd
import numpy as np
```
### Merge Harvest data to the bridge project Data
```
db_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/final_csv/Final_with_gov_ID.csv")
harvest_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/share_of_harvest_sold.csv")
print(db_df.shape)
print(harvest_df.shape)
db_df.drop(['Unnamed: 0','Cell','Form: Form Name','Cell_ID'],axis=1,inplace=True)
harvest_df.drop('Unnamed: 0', axis=1,inplace=True)
# Merge database file on share of harvest in each RW district
df = pd.merge(db_df,harvest_df,on='District',how='inner')
# db_df['District'].nunique()
# df['District'].nunique()
# harvest_df['Mean share of harvest sold'].nunique()
# df['Mean share of harvest sold'].nunique()
```
### Cleaning and merging of Schools and Gov ID data
```
schools_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda_Schools%20(1).csv")
govt_df = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/unique_gov_id_PDS.csv')
govt_df['Sector'] = govt_df['Sector'].str.title()
schools_df['Sector'] = schools_df['Sector'].str.title()
schools_df['District'] = schools_df['District'].str.title()
# Correct spellings in schools data to match govt_data
govt_to_sch = {
'Kabagali' : 'Kabagari',
'Muringa' : 'Mulinga' ,
'Rugarika' : 'Rugalika',
'Gishali' : 'Gishari' ,
'Rugengabari' : 'Rugengabali',
'Nyagihanga':'Nyagahanga',
'Niboye': 'Niboyi',
'Save':'Gatoki',
'Tumba':'Ntuba'
}
for key,value in govt_to_sch.items():
schools_df.loc[schools_df['Sector'] == value,'Sector'] = key
b = [x for x in set(schools_df['Sector']) if x not in set(govt_df['Sector'])]
b
# Change Nyanza-Kibirizi to Nyanza-Kibilizi to match database_df
indy = schools_df[(schools_df['District'] == "Nyanza") & (schools_df['Sector'] == 'Kibirizi')].index
for i in indy:
schools_df.loc[i,['Sector']] = "Kibilizi"
schools_df.drop('Unnamed: 0',axis=1,inplace=True)
# Correct Sector names in schools data
il = [294]
for i in il:
schools_df.loc[i,['Sector']] = 'Bigogwe'
jl = [185]
for j in jl:
schools_df.loc[j,['Sector']] = 'Ngarama'
# Merge schools data on govt data
mg = pd.merge(schools_df,govt_df,on=['District','Sector'])
y = [x for x in set(mg['School Name']) if x not in set(schools_df['School Name'])]
y
q = [x for x in set(schools_df['School Name']) if x not in set(mg['School Name'])]
q
schools_df[schools_df['School Name'] == 'College Baptiste De Ngarama']
mg[mg['School Name'] == 'EAV BIGOGWE']
mg[mg['School Name'] == 'College Baptiste De Ngarama']
# schools_df.groupby(['District','Sector'],as_index=False).count()
# Get the count of schools in each sector
count_sch = mg.groupby(['Sect_ID']).count()['School Name']
count_sch.head(3)
# merge database df on school count
test_df = pd.merge(df,count_sch,on='Sect_ID')
test_df['School_count'] = test_df['School Name']
test_df.drop('School Name',axis=1,inplace=True)
current_df = test_df
# Current final df with farm harvest by District
# and number of schools in each Sector
current_df.shape
```
### Clean and Merge Sector population with the bridge project data
```
population = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda%20Administrative%20Levels%20and%20Codes%20Sector%20Population.csv')
population
current_df.head()
[i for i in set(population['Sect_ID']) if i not in set(govt_df['Sect_ID']) ]
# there are some duplicate values that we can drop.
# but Sect code 2411 is showing for two different Sectors. We cant drop that one.
# we need to change the sector code for the sector Rwaniro to 2412.
population['Sect_ID'].value_counts()
# Sector ID for Rwaniro shouldnt be 2411...it should be 2412
population[population['Sect_ID'] == 2411]
govt_df[govt_df['Sect_ID'] == 2412]
# Change Sector ID for Rwaniro to 2412
population.loc[85, 'Sect_ID'] = 2412
# make sure that the change is made in the population dataset now.
population[population['Sect_ID'] == 2412]
# drop the duplicate values from the population dataset based on Sect_ID
population = population.drop_duplicates('Sect_ID')
# make sure there are no duplicates
population['Sect_ID'].value_counts()
# merge the population data set with the bridge project to get the population by
# sector, included in the project data set
# drop the province, district, sector name and district, province ID from
# population dataset
population = population.drop(columns=['Prov_ID', 'Province', 'Dist_ID', 'District', 'Sector', 'Unnamed: 7', 'Unnamed: 8'])
# merge the two together, save new dataframe
current_df = pd.merge(current_df, population, on='Sect_ID')
current_df.head()
```
### Merge Electricity Access with bridge projects
```
electricity = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda_electricity_access_districts.csv')
electricity.head()
# update the ACcess rate to be in percent form by multiplying by 10
electricity['Access rate'] = electricity['Access rate'] * 100
electricity.head()
# check to make sure we have the same districts in the electricity
# as we do in the bridges projects dataset
sorted(electricity['District']) == sorted(set(current_df['District']))
# Because the districts are unique districts we can merge on the district name
current_df = pd.merge(current_df, electricity, on='District')
current_df.head()
```
### Merge Average Travel time to various Financial institutions
```
travel_time = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/avg_travel_time_financial_access.csv')
travel_time.head()
current_df.shape
# merge the current_df with the travel times
current_df = pd.merge(current_df, travel_time, on='District')
current_df.head()
```
### Merge banking access dataset
```
banking = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/datasets_22991_29451_rwa_exclusion.csv')
banking.rename(columns={'district': 'District'}, inplace=True)
banking.head()
current_df = pd.merge(current_df, banking, on='District')
current_df.head()
```
### Get the number of communities that a specific bridge Serves
```
# get a dataframe that has the total number of communities served
communities_served = pd.DataFrame(current_df.groupby('Project Code', as_index=False).count()[['Project Code', 'Community_Served']])
communities_served.head()
communities_served = communities_served.rename(columns={'Community_Served': 'num_communities_served'})
current_df = pd.merge(current_df, communities_served, on='Project Code')
current_df.head()
```
### Drop the duplicates for project code:
this will give us the unique bridge
```
final_df = current_df.drop_duplicates(subset='Project Code')
final_df.head()
final_df.to_csv('final_model_df.csv', index=False)
testing = pd.read_csv('/content/final_model_df.csv')
testing.dtypes
```
|
github_jupyter
|
import pandas as pd
import numpy as np
db_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/final_csv/Final_with_gov_ID.csv")
harvest_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/share_of_harvest_sold.csv")
print(db_df.shape)
print(harvest_df.shape)
db_df.drop(['Unnamed: 0','Cell','Form: Form Name','Cell_ID'],axis=1,inplace=True)
harvest_df.drop('Unnamed: 0', axis=1,inplace=True)
# Merge database file on share of harvest in each RW district
df = pd.merge(db_df,harvest_df,on='District',how='inner')
# db_df['District'].nunique()
# df['District'].nunique()
# harvest_df['Mean share of harvest sold'].nunique()
# df['Mean share of harvest sold'].nunique()
schools_df = pd.read_csv("https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda_Schools%20(1).csv")
govt_df = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/unique_gov_id_PDS.csv')
govt_df['Sector'] = govt_df['Sector'].str.title()
schools_df['Sector'] = schools_df['Sector'].str.title()
schools_df['District'] = schools_df['District'].str.title()
# Correct spellings in schools data to match govt_data
govt_to_sch = {
'Kabagali' : 'Kabagari',
'Muringa' : 'Mulinga' ,
'Rugarika' : 'Rugalika',
'Gishali' : 'Gishari' ,
'Rugengabari' : 'Rugengabali',
'Nyagihanga':'Nyagahanga',
'Niboye': 'Niboyi',
'Save':'Gatoki',
'Tumba':'Ntuba'
}
for key,value in govt_to_sch.items():
schools_df.loc[schools_df['Sector'] == value,'Sector'] = key
b = [x for x in set(schools_df['Sector']) if x not in set(govt_df['Sector'])]
b
# Change Nyanza-Kibirizi to Nyanza-Kibilizi to match database_df
indy = schools_df[(schools_df['District'] == "Nyanza") & (schools_df['Sector'] == 'Kibirizi')].index
for i in indy:
schools_df.loc[i,['Sector']] = "Kibilizi"
schools_df.drop('Unnamed: 0',axis=1,inplace=True)
# Correct Sector names in schools data
il = [294]
for i in il:
schools_df.loc[i,['Sector']] = 'Bigogwe'
jl = [185]
for j in jl:
schools_df.loc[j,['Sector']] = 'Ngarama'
# Merge schools data on govt data
mg = pd.merge(schools_df,govt_df,on=['District','Sector'])
y = [x for x in set(mg['School Name']) if x not in set(schools_df['School Name'])]
y
q = [x for x in set(schools_df['School Name']) if x not in set(mg['School Name'])]
q
schools_df[schools_df['School Name'] == 'College Baptiste De Ngarama']
mg[mg['School Name'] == 'EAV BIGOGWE']
mg[mg['School Name'] == 'College Baptiste De Ngarama']
# schools_df.groupby(['District','Sector'],as_index=False).count()
# Get the count of schools in each sector
count_sch = mg.groupby(['Sect_ID']).count()['School Name']
count_sch.head(3)
# merge database df on school count
test_df = pd.merge(df,count_sch,on='Sect_ID')
test_df['School_count'] = test_df['School Name']
test_df.drop('School Name',axis=1,inplace=True)
current_df = test_df
# Current final df with farm harvest by District
# and number of schools in each Sector
current_df.shape
population = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda%20Administrative%20Levels%20and%20Codes%20Sector%20Population.csv')
population
current_df.head()
[i for i in set(population['Sect_ID']) if i not in set(govt_df['Sect_ID']) ]
# there are some duplicate values that we can drop.
# but Sect code 2411 is showing for two different Sectors. We cant drop that one.
# we need to change the sector code for the sector Rwaniro to 2412.
population['Sect_ID'].value_counts()
# Sector ID for Rwaniro shouldnt be 2411...it should be 2412
population[population['Sect_ID'] == 2411]
govt_df[govt_df['Sect_ID'] == 2412]
# Change Sector ID for Rwaniro to 2412
population.loc[85, 'Sect_ID'] = 2412
# make sure that the change is made in the population dataset now.
population[population['Sect_ID'] == 2412]
# drop the duplicate values from the population dataset based on Sect_ID
population = population.drop_duplicates('Sect_ID')
# make sure there are no duplicates
population['Sect_ID'].value_counts()
# merge the population data set with the bridge project to get the population by
# sector, included in the project data set
# drop the province, district, sector name and district, province ID from
# population dataset
population = population.drop(columns=['Prov_ID', 'Province', 'Dist_ID', 'District', 'Sector', 'Unnamed: 7', 'Unnamed: 8'])
# merge the two together, save new dataframe
current_df = pd.merge(current_df, population, on='Sect_ID')
current_df.head()
electricity = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/Rwanda_electricity_access_districts.csv')
electricity.head()
# update the ACcess rate to be in percent form by multiplying by 10
electricity['Access rate'] = electricity['Access rate'] * 100
electricity.head()
# check to make sure we have the same districts in the electricity
# as we do in the bridges projects dataset
sorted(electricity['District']) == sorted(set(current_df['District']))
# Because the districts are unique districts we can merge on the district name
current_df = pd.merge(current_df, electricity, on='District')
current_df.head()
travel_time = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/avg_travel_time_financial_access.csv')
travel_time.head()
current_df.shape
# merge the current_df with the travel times
current_df = pd.merge(current_df, travel_time, on='District')
current_df.head()
banking = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Bridges_to_Prosperity-TeamC-ds/main/rwanda_data_files/datasets_22991_29451_rwa_exclusion.csv')
banking.rename(columns={'district': 'District'}, inplace=True)
banking.head()
current_df = pd.merge(current_df, banking, on='District')
current_df.head()
# get a dataframe that has the total number of communities served
communities_served = pd.DataFrame(current_df.groupby('Project Code', as_index=False).count()[['Project Code', 'Community_Served']])
communities_served.head()
communities_served = communities_served.rename(columns={'Community_Served': 'num_communities_served'})
current_df = pd.merge(current_df, communities_served, on='Project Code')
current_df.head()
final_df = current_df.drop_duplicates(subset='Project Code')
final_df.head()
final_df.to_csv('final_model_df.csv', index=False)
testing = pd.read_csv('/content/final_model_df.csv')
testing.dtypes
| 0.334155 | 0.799658 |
# Starfish re-creation of an in-situ sequencing pipeline
Here, we reproduce the results of a pipeline run on data collected using the gap filling and padlock probe litigation method described in [Ke, Mignardi, et. al, 2013](http://www.nature.com/nmeth/journal/v10/n9/full/nmeth.2563.html). These data represent 5 co-cultured mouse and human cells -- the main idea is to detect a single nucleotide polymorphism (SNP) in the Beta-Actin (ACTB) gene across species. The Python code below correctly re-produces the same results from the original cell profiler - matlab - imagej [pipeline](http://cellprofiler.org/examples/#InSitu) that is publicly accessible.
```
import pandas as pd
import numpy as np
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
%matplotlib inline
from showit import image, tile
```
## Raw Data
The raw data can be downloaded and formatted for analysis by running: ```python examples/get_iss_data.py ><raw data directory> <output directory> --d 1``` from the Starfish directory
```
from starfish.io import Stack
# replace <output directory> with where you saved the formatted data to with the above script
in_json = '<output directory>/org.json'
s = Stack()
s.read(in_json)
tile(s.image.squeeze(), size=10);
image(s.auxiliary_images['dots'], size=10)
```
## Register
```
from starfish.pipeline.registration import Registration
registration = Registration.fourier_shift(upsampling=1000)
registration.register(s)
tile(s.image.squeeze(), size=10);
```
## Filter
```
from starfish.filters import white_top_hat
disk_dize = 10
# filter raw images, for all hybs and channels
stack_filt = [white_top_hat(im, disk_dize) for im in s.image.squeeze()]
stack_filt = s.un_squeeze(stack_filt)
# filter dots
dots_filt = white_top_hat(s.auxiliary_images['dots'], disk_dize)
# create a 'stain' for segmentation
stain = np.mean(s.image.max_proj('ch'), axis=0)
stain = stain/stain.max()
# update stack
s.set_stack(stack_filt)
s.set_aux('dots', dots_filt)
s.set_aux('stain', stain)
# visualize
tile(s.image.squeeze(), bar=False, size=10);
image(s.auxiliary_images['dots'])
image(s.auxiliary_images['stain'])
```
## Detect
```
from starfish.spots.gaussian import GaussianSpotDetector
gsp = GaussianSpotDetector(s)
min_sigma = 4
max_sigma = 6
num_sigma=20
thresh=.01
blobs='dots'
measurement_type="max"
bit_map_flag=False
spots_df_tidy = gsp.detect(min_sigma, max_sigma, num_sigma, thresh, blobs, measurement_type, bit_map_flag)
gsp.show(figsize=(10,10))
spots_viz = gsp.spots_df_viz
spots_df_tidy.head()
spots_viz.head()
```
## Segmentation
```
from starfish.watershedsegmenter import WatershedSegmenter
dapi_thresh = .16
stain_thresh = .22
size_lim = (10, 10000)
disk_size_markers = None
disk_size_mask = None
min_dist = 57
seg = WatershedSegmenter(s.auxiliary_images['dapi'], s.auxiliary_images['stain'])
cells_labels = seg.segment(dapi_thresh, stain_thresh, size_lim, disk_size_markers, disk_size_mask, min_dist)
seg.show()
```
## Assignment
```
from starfish.assign import assign
from starfish.stats import label_to_regions
points = spots_viz.loc[:, ['x', 'y']].values
regions = label_to_regions(cells_labels)
ass = assign(regions, points, use_hull=True)
ass.groupby('cell_id',as_index=False).count().rename(columns={'spot_id':'num spots'})
ass.head()
```
## Decode
```
from starfish.decoders.iss import IssDecoder
decoder = IssDecoder(pd.DataFrame({'barcode': ['AAGC', 'AGGC'], 'gene': ['ACTB_human', 'ACTB_mouse']}),
letters=['T', 'G', 'C', 'A'])
dec = decoder.decode_euclidean(spots_df_tidy)
dec.qual.hist(bins=20)
top_barcode = dec.barcode.value_counts()[0:10]
top_barcode
```
## Visualization
```
from starfish.stats import label_to_regions
dec_filt = pd.merge(dec, spots_viz, on='spot_id',how='left')
dec_filt = dec_filt[dec_filt.qual>.25]
assert s.auxiliary_images['dapi'].shape == s.auxiliary_images['dots'].shape
rgb = np.zeros(s.auxiliary_images['dapi'].shape + (3,))
rgb[:,:,0] = s.auxiliary_images['dapi']
rgb[:,:,1] = s.auxiliary_images['dots']
do = rgb2gray(rgb)
do = do/(do.max())
image(do,size=10)
plt.plot(dec_filt[dec_filt.barcode==top_barcode.index[0]].y,
dec_filt[dec_filt.barcode==top_barcode.index[0]].x,
'ob',
markerfacecolor='None')
plt.plot(dec_filt[dec_filt.barcode==top_barcode.index[1]].y, dec_filt[dec_filt.barcode==top_barcode.index[1]].x, 'or', markerfacecolor='None')
v = pd.merge(spots_viz, ass, on='spot_id')
r = label_to_regions(cells_labels)
im = r.mask(background=[0.9, 0.9, 0.9], dims=s.auxiliary_images['dots'].shape, stroke=None, cmap='rainbow')
image(im,size=10)
v_ass = v[~v.cell_id.isnull()]
plt.plot(v_ass.y, v_ass.x, '.w')
v_uass = v[v.cell_id.isnull()]
plt.plot(v_uass.y, v_uass.x, 'xw')
```
## Cell by gene expression table
```
res = pd.merge(dec, ass, on='spot_id', how='left')
grp = res.groupby(['barcode', 'cell_id'],as_index=False).count()
exp_tab = grp.pivot(index='cell_id', columns='barcode', values = 'spot_id').fillna(0)
exp_tab
```
|
github_jupyter
|
import pandas as pd
import numpy as np
from skimage.color import rgb2gray
import matplotlib.pyplot as plt
%matplotlib inline
from showit import image, tile
from starfish.io import Stack
# replace <output directory> with where you saved the formatted data to with the above script
in_json = '<output directory>/org.json'
s = Stack()
s.read(in_json)
tile(s.image.squeeze(), size=10);
image(s.auxiliary_images['dots'], size=10)
from starfish.pipeline.registration import Registration
registration = Registration.fourier_shift(upsampling=1000)
registration.register(s)
tile(s.image.squeeze(), size=10);
from starfish.filters import white_top_hat
disk_dize = 10
# filter raw images, for all hybs and channels
stack_filt = [white_top_hat(im, disk_dize) for im in s.image.squeeze()]
stack_filt = s.un_squeeze(stack_filt)
# filter dots
dots_filt = white_top_hat(s.auxiliary_images['dots'], disk_dize)
# create a 'stain' for segmentation
stain = np.mean(s.image.max_proj('ch'), axis=0)
stain = stain/stain.max()
# update stack
s.set_stack(stack_filt)
s.set_aux('dots', dots_filt)
s.set_aux('stain', stain)
# visualize
tile(s.image.squeeze(), bar=False, size=10);
image(s.auxiliary_images['dots'])
image(s.auxiliary_images['stain'])
from starfish.spots.gaussian import GaussianSpotDetector
gsp = GaussianSpotDetector(s)
min_sigma = 4
max_sigma = 6
num_sigma=20
thresh=.01
blobs='dots'
measurement_type="max"
bit_map_flag=False
spots_df_tidy = gsp.detect(min_sigma, max_sigma, num_sigma, thresh, blobs, measurement_type, bit_map_flag)
gsp.show(figsize=(10,10))
spots_viz = gsp.spots_df_viz
spots_df_tidy.head()
spots_viz.head()
from starfish.watershedsegmenter import WatershedSegmenter
dapi_thresh = .16
stain_thresh = .22
size_lim = (10, 10000)
disk_size_markers = None
disk_size_mask = None
min_dist = 57
seg = WatershedSegmenter(s.auxiliary_images['dapi'], s.auxiliary_images['stain'])
cells_labels = seg.segment(dapi_thresh, stain_thresh, size_lim, disk_size_markers, disk_size_mask, min_dist)
seg.show()
from starfish.assign import assign
from starfish.stats import label_to_regions
points = spots_viz.loc[:, ['x', 'y']].values
regions = label_to_regions(cells_labels)
ass = assign(regions, points, use_hull=True)
ass.groupby('cell_id',as_index=False).count().rename(columns={'spot_id':'num spots'})
ass.head()
from starfish.decoders.iss import IssDecoder
decoder = IssDecoder(pd.DataFrame({'barcode': ['AAGC', 'AGGC'], 'gene': ['ACTB_human', 'ACTB_mouse']}),
letters=['T', 'G', 'C', 'A'])
dec = decoder.decode_euclidean(spots_df_tidy)
dec.qual.hist(bins=20)
top_barcode = dec.barcode.value_counts()[0:10]
top_barcode
from starfish.stats import label_to_regions
dec_filt = pd.merge(dec, spots_viz, on='spot_id',how='left')
dec_filt = dec_filt[dec_filt.qual>.25]
assert s.auxiliary_images['dapi'].shape == s.auxiliary_images['dots'].shape
rgb = np.zeros(s.auxiliary_images['dapi'].shape + (3,))
rgb[:,:,0] = s.auxiliary_images['dapi']
rgb[:,:,1] = s.auxiliary_images['dots']
do = rgb2gray(rgb)
do = do/(do.max())
image(do,size=10)
plt.plot(dec_filt[dec_filt.barcode==top_barcode.index[0]].y,
dec_filt[dec_filt.barcode==top_barcode.index[0]].x,
'ob',
markerfacecolor='None')
plt.plot(dec_filt[dec_filt.barcode==top_barcode.index[1]].y, dec_filt[dec_filt.barcode==top_barcode.index[1]].x, 'or', markerfacecolor='None')
v = pd.merge(spots_viz, ass, on='spot_id')
r = label_to_regions(cells_labels)
im = r.mask(background=[0.9, 0.9, 0.9], dims=s.auxiliary_images['dots'].shape, stroke=None, cmap='rainbow')
image(im,size=10)
v_ass = v[~v.cell_id.isnull()]
plt.plot(v_ass.y, v_ass.x, '.w')
v_uass = v[v.cell_id.isnull()]
plt.plot(v_uass.y, v_uass.x, 'xw')
res = pd.merge(dec, ass, on='spot_id', how='left')
grp = res.groupby(['barcode', 'cell_id'],as_index=False).count()
exp_tab = grp.pivot(index='cell_id', columns='barcode', values = 'spot_id').fillna(0)
exp_tab
| 0.486088 | 0.889673 |
# Hardening Plasticity
## Overview
After the elastic limit of a material is exceeded and the material yields, further increases in load are usually required for plastic flow to continue. This phenomenon is known as hardening and is broadly classified as either work or strain-hardening. Hardening theories of plasticity describe the evolution of the strength through time. This notebook
- presents an introduction to hardening plasticity,
- implements a hardening "$J_2$" plasticity model in Matmodlab for the case of linear isotropic strain hardening,
- verifies the $J_2$ model against analytic solutions.
## See Also
- [User Defined Materials](UserMaterial.ipynb)
- [Linear Elastic Material](LinearElastic.ipynb)
- [Nonhardening Plasticity](NonhardeningJ2Plasticity.ipynb)
<a name='contents'></a>
## Contents
1. <a href='#plast'>Hardening Plasticity</a>
2. <a href='#j2'>$J_2$ Plasticity</a>
2. <a href='#umat.std'>Standard Model Implementation</a>
<a name='plastic'></a>
## Hardening Plasticity
### Overview
Similar to nonhardening theories of plasticity, the hardening theory of plasticity presumes the existence of an elastic limit defined by a yield surface
$$
f\left(\pmb{\sigma}, Y\right) = 0
$$
where $f$ is the yield function. Unlike the nonhardening theory, the yield function depends not only on the mechanical stress $\pmb{\sigma}$ but also the (nonconstant) yield strength $Y$.
The rate of mechanical stress is given by
$$
\dot{\pmb{\sigma}} = \mathbb{C}{:}\dot{\pmb{\epsilon}}^{\rm e}
$$
where $\mathbb{C}$ is the elastic stiffness and $\dot{\pmb{\epsilon}}^{\rm e}$ the rate of elastic strain. Presuming that the rate of strain is the sum of elastic and plastic parts, the mechanical response is defined by
$$
\dot{\pmb{\sigma}} = \mathbb{C}{:}\left(\dot{\pmb{\epsilon}} - \dot{\pmb{\epsilon}}^{\rm p}\right)
$$
where $\dot{\pmb{\epsilon}}^{\rm p}$ is the rate of plastic strain. Replacing $\dot{\pmb{\epsilon}}^{\rm p}$ with $\dot{\lambda}\pmb{m}$, $\dot{\lambda}$ being the magnitude of $\dot{\pmb{\epsilon}}^{\rm p}$ and $\pmb{m}$ its direction, the mechanical response of the material is
$$
\dot{\pmb{\sigma}} = \mathbb{C}{:}\left(\dot{\pmb{\epsilon}} - \dot{\lambda}\pmb{m}\right)
$$
The solution to the plasticity problem is reduced to determining $\dot{\lambda}$ such that $f\left(\pmb{\sigma}(t), Y(t)\right)\leq 0 \ \forall t>0$
### Solution Process
Given the current state of stress $\pmb{\sigma}_n$, the solution to the plasticity problem begins with the hypothesis that the entire strain increment is elastic:
$$
\pmb{\sigma}_{\rm new} \stackrel{?}{=} \pmb{\sigma}_{\rm old} + \mathbb{C}{:}\dot{\pmb{\epsilon}}dt = \pmb{\sigma}^{\rm test}
$$
where the descriptor "test" is used to signal the fact that at this point $\pmb{\sigma}^{\rm test}$ is merely a hypothesized solution. The hypothesis is validated if $\pmb{\sigma}^{\rm test}$ satisfies the yield condition
$$f\left(\pmb{\sigma}^{\rm test}, Y^{\rm test}\right)\leq 0$$
so that $\pmb{\sigma}_{\rm new}=\pmb{\sigma}^{\rm test}$.
If instead the hypothesis is *falsefied*, i.e., the predicted test stress falls outside of the yield surface defined by $f=0$, the plasticity problem,
$$\begin{align}
\pmb{\sigma}_{\rm new} = \pmb{\sigma}_{\rm old} + \mathbb{C}{:}\left(\dot{\pmb{\epsilon}} - \dot{\lambda}\pmb{m}\right)dt &= \pmb{\sigma}^{\rm trial} - \dot{\lambda}\pmb{A}dt\\
f\left(\pmb{\sigma}^{\rm trial} - \dot{\lambda}\pmb{A}dt, Y\right) &= 0
\end{align}$$
where $\pmb{A}=\mathbb{C}{:}\pmb{m}$, is solved. $\dot{\pmb{\sigma}}^{\rm trial}=\mathbb{C}{:}\dot{\pmb{\epsilon}}$ is distinguished from $\dot{\pmb{\sigma}}^{\rm test}$ in that for stress driven problems $\dot{\pmb{\sigma}}^{\rm trial}$ is not necessarily known because the strain rates $\dot{\epsilon}$ are not known.
The unknown scalar $\dot{\lambda}$ is determined by noting the following observation: if $f\left(\pmb{\sigma}_{\rm old}, Y_{\rm old}\right)=0$ and, after continued loading, $f\left(\pmb{\sigma}_{\rm new}, Y_{\rm new}\right)=0$, the rate of change of $f$ itself must be zero. Thus, by the chain rule,
$$
\dot{f}{\left(\pmb{\sigma}, Y\right)}
=\frac{df}{d\pmb{\sigma}}{:}\dot{\pmb{\sigma}}
+\frac{df}{dY}\dot{Y} = 0
$$
During elastic loading, the yield strength does not change. Therefore, we presume that the rate of $Y$ is of the form
$$
\dot{Y} = \dot{\lambda}h_{Y}
$$
where $\dot{\lambda}$ is the rate of plastic strain and $h_{Y}$ the modulus of $Y$. Since $Y$ is tied to the internal state of the material, it is regarded as a "solution-dependent variable" (SDV) and $h_Y$ a SDV modulus. SDV moduli must be determined from experiment or microphysical considerations.
Substituting the expression for $\dot{Y}$ in to the consistency condition gives
$$
\frac{df}{d\pmb{\sigma}}{:}\left(\mathbb{C}{:}\dot{\epsilon}-\dot{\lambda}\pmb{A}\right) + \frac{df}{dY}\dot{\lambda}h_Y = 0
$$
Letting
$$
\pmb{n} = \frac{df}{d\pmb{\sigma}}\Big/\Big\lVert\frac{df}{d\pmb{\sigma}}\Big\rVert
$$
the preceding equation can be solved $\dot{\lambda}$, giving
$$
\dot{\lambda}
= \frac{\pmb{n}{:}\mathbb{C}{:}\dot{\epsilon}}{\pmb{n}{:}\pmb{A}+H}
$$
where
$$
H = -\frac{df}{dY}\Big/\Big\lVert\frac{df}{d\pmb{\sigma}}\Big\rVert h_Y
$$
Substituting $\dot{\lambda}$ in to the expression for stress rate gives
$$\begin{align}
\dot{\pmb{\sigma}}
&= \mathbb{C}{:}\dot{\pmb{\epsilon}} - \frac{\pmb{n}{:}\mathbb{C}{:}\dot{\epsilon}}{\pmb{n}{:}\pmb{A}+H}\pmb{A}\\
&= \mathbb{C}{:}\dot{\pmb{\epsilon}} - \frac{1}{\pmb{n}{:}\pmb{A}+H}\pmb{Q}\pmb{A}{:}\dot{\pmb{\epsilon}}\\
&= \mathbb{D}{:}\dot{\pmb{\epsilon}}
\end{align}$$
where
$$
\pmb{Q} = \mathbb{C}{:}\pmb{n}
$$
and
$$
\mathbb{D} = \mathbb{C} - \frac{1}{\pmb{n}{:}\pmb{A}+H}\pmb{Q}\pmb{A}
$$
The stress rate is then integrated through time to determine $\pmb{\sigma}$
### Integration Procedure
Unlike the nonhardening case, the expression for the stress rate
$$
\dot{\pmb{\sigma}}
= \dot{\pmb{\sigma}}^{\rm trial}
- \frac{\pmb{n}{:}\dot{\pmb{\sigma}}^{\rm trial}}{\pmb{n}{:}\pmb{A}+H}\pmb{A}
$$
*is not* a projection of the trial stress rate, but it is still true that
$$\pmb{\sigma}_{\rm new} = \pmb{\sigma}^{\rm trial} - \Gamma\pmb{A}$$
$\Gamma$ is determined by satisfying the now *evolving* yield condition. In other words, $\Gamma$ is the solution to
$$f\left(\pmb{\sigma}^{\rm trial} - \Gamma\pmb{A}, Y(\Gamma)\right)=0$$
The unknown $\Gamma$ is found such that $f\left(\pmb{\sigma}(\Gamma), Y(\Gamma)\right)=0$. The solution can be found by solving the preceding equation iteratively by applying Newton's method so that
$$
\Gamma^{i+1} = \Gamma^i
- \frac{f\left(\pmb{\sigma}(\Gamma^{n}), Y(\Gamma)\right)}
{\frac{df}{d\pmb{\sigma}}{:}\frac{d\pmb{\sigma}}{d\Gamma} + \frac{df}{dY}\frac{dY}{d\Gamma}}
= \Gamma^i
+ \frac{g\left(\pmb{\sigma}(\Gamma^{n}), Y(\Gamma)\right)}
{\pmb{n}{:}\pmb{A}-\frac{df}{dY}\frac{dY}{d\Gamma}}
$$
where $g = f\Big/\lVert df/d\pmb{\sigma}\rVert$.
When $\Gamma^{i+1}-\Gamma^i<\epsilon$, where $\epsilon$ is a small number, the iterations are complete and the updated stress can be determined.
Note that the scalar $\Gamma$ is also equal to $\Gamma=\dot{\lambda}dt$, but since $\dot{\lambda}=0$ for elastic loading, $\Gamma=\dot{\lambda}dt^p$, where $dt^p$ is the plastic part of the time step. This gives $\Gamma$ the following physical interpretation: it is the magnigute of the total plastic strain increment.
## $J_2$ Plasticity
The equations developed thus far are general in the sense that they apply to any material that can be modeled by hardening plasticity. The equations are now specialized to the case of isotropic hypoelasticity and $J_2$ plasticity by defining
$$\begin{align}
\dot{\pmb{\sigma}} &= 3K\,\mathrm{iso}\dot{\pmb{\epsilon}}^{\rm e} + 2G\,\mathrm{dev}\dot{\pmb{\epsilon}}^{\rm e} \\
f\left(\pmb{\sigma}\right) &= \sqrt{J_2} - \frac{1}{\sqrt{3}}Y\left(\epsilon^p_{eq}\right)
\end{align}
$$
where $J_2$ is the second invariant of the stress deviator, defined as
$$J_2 = \frac{1}{2}\pmb{s}{:}\pmb{s}, \quad \pmb{s} = \pmb{\sigma} - \frac{1}{3}\mathrm{tr}\left(\pmb{\sigma}\right)\pmb{I}$$
and $Y\left(\epsilon^p_{eq}\right)$ is the plastic strain dependent yield strength in tension.
Additionally, we adopt the assumption of an **associative flow rule** wherein $\pmb{m}=\pmb{n}$. Accordingly,
$$\begin{align}
\frac{df}{d\pmb{\sigma}}&=\frac{1}{2\sqrt{J_2}}\pmb{s}, &\pmb{n}=\frac{1}{\sqrt{2J_2}}\pmb{s} \\
\pmb{A}&=\frac{2G}{\sqrt{2J_2}}\pmb{s}, &\pmb{Q}=\frac{2G}{\sqrt{2J_2}}\pmb{s}
\end{align}$$
### Linear Hardening
Returning now to the definition of $Y$. Let
$$Y = Y_0 + Y_1 \epsilon^p_{eq}$$
where $Y_0$ is the initial strength and $Y_1$ is a fitting parameter. Taking the rate of $Y$ allows determining the SDV modulus $h_Y$:
$$\dot{Y} = Y_1\dot{\epsilon}^p_{eq} = h_Y\dot{\lambda}, \quad h_Y = \sqrt{\frac{2}{3}}Y_1$$
#### Required Parameters
The model as described above requires at minimum 4 parameters: 2 independent elastic moduli and the yield strength parameters $Y_0$ and $Y_1$.
#### Solution Dependent Variables
Evaluation of $Y$ requires storing and tracking the equivalent plastic strain $\epsilon_{eq}^p$
### Power-Law Hardening
A phenomenological power-law model presumes that
$$Y = Y_0 + Y_1 \left(\epsilon^p_{eq}\right)^m$$
where $Y_0$ is the initial strength and $K_1$ is a fitting parameter. Taking the rate of $Y$ allows determining the SDV modulus $h_Y$:
$$\dot{Y} = h_Y\dot{\lambda}, \quad h_Y = \sqrt{\frac{2}{3}}mY_1\left[\frac{Y-Y_0}{Y_1}\right]^{\frac{m-1}{m}}$$
#### Required Parameters
The model as described above requires at minimum 4 parameters: 2 independent elastic moduli and the yield strength parameters $Y_0$, $Y_1$, and $m$.
#### Solution Dependent Variables
Evaluation of $Y$ requires storing and tracking the equivalent plastic strain $\epsilon_{eq}^p$
### Work Hardening
A phenomenological linear work hardening model presumes that
$$Y = Y_0 + Y_1 W_P, \quad W_P = \int_0^t \pmb{\sigma}{:}\dot{\pmb{\epsilon}}^p dt$$
where $Y_0$ is the initial strength and $K_1$ is a fitting parameter. Taking the rate of $Y$ allows determining the SDV modulus $h_Y$:
$$\dot{Y} = h_Y\dot{\lambda}, \quad h_Y = mY_1\left[\frac{Y-Y_0}{Y_1}\right]^{\frac{m-1}{m}}\sqrt{\pmb{m}{:}\pmb{m}}$$
#### Required Parameters
The model as described above requires at minimum 4 parameters: 2 independent elastic moduli and the yield strength parameters $Y_0$, $Y_1$, and $m$.
#### Solution Dependent Variables
Evaluation of $Y$ requires storing and tracking the equivalent plastic strain $\epsilon_{eq}^p$
<a name='umat.std'></a>
## Model Implementation
The plastic material described above is implemented as `HardeningPlasticMaterial` in `matmodlab2/materials/plastic3.py`. `HardeningPlasticMaterial` is implemented as a subclass of the `matmodlab2.core.material.Material` class. `HardeningPlasticMaterial` defines
- `name`: *class attribute*
Used for referencing the material model in the `MaterialPointSimulator`.
- `eval`: *instance method*
Updates the material stress, stiffness (optional), and state dependent variables to the end of the time increment.
In the model, in addition to some standard functions imported from `Numpy`, several helper functions are imported from various locations in Matmodlab:
- `matmodlab.core.tensor`
- `isotropic_part`, `deviatoric_part`: computes the isotropic and deviatoric parts of a second-order symmetric tensor stored as an array of length 6
- `magnitude`: computes the magnitude $\left(\lVert x_{ij} \rVert=\sqrt{x_{ij}x_{ij}}\right)$ of a second-order symmetric tensor stored as an array of length 6
- `double_dot`: computes the double dot product of second-order symmetric tensors stored as an array of length 6
- `VOIGT`: mulitplier for converting tensor strain components to engineering strain components
### Model Source
The source of the file can be viewed by executing the following cell.
```
%pycat ../matmodlab2/materials/plastic3.py
%pylab inline
from bokeh.io import output_notebook
from bokeh.plotting import *
from matmodlab2 import *
from numpy import *
from plotting_helpers import create_figure
output_notebook()
import pandas as pd
pd.set_option('precision', 20)
```
### Verification
Exercising the elastic model through a path of uniaxial stress should result in the slope of axial stress vs. axial strain being equal to the input parameter `E` for the elastic portion. The maximum stress should be equal to the input parameter `Y`.
**Note:** the input parameters to a standard material are given as a dictionary of `name:value` pairs for each paramter. Parameters not specified are initialized to a value of zero.
```
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.004, 0, 0), frames=50)
i = where((mps1.df['E.XX'] > 0.) & (mps1.df['E.XX'] < .005))
E = mps1.df['S.XX'].iloc[i] / mps1.df['E.XX'].iloc[i]
assert allclose(E.iloc[0], 10e6, atol=1e-3, rtol=1e-3)
assert amax(mps1.df['S.XX']) - 40e3 < 1e-6
#plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
mps1.plot('E.XX', 'S.XX')
print(mps1.df[['F.XX','F.YY','F.ZZ','S.XX']])
mps1 = MaterialPointSimulator('uplastic-std')
p = {'K': 15, 'G': 10, 'Y0': 1}
mps1.material = VonMisesMaterial(**p)
mps1.run_step('EEE', (.075, 0, 0), frames=50)
mps1.plot('E.XX', 'S.XX')
print(mps1.df[['F.XX','S.XX','S.YY']])
1.020201 0.990711 0.990711
```
#### Linear Hardening
```
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3, 'Y1': 2e6}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.02, 0, 0), frames=50)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps1.df['E.XX'], mps1.df['S.XX'])
show(plot);
```
#### Nonlinear Hardening
```
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3, 'Y1': 2e4, 'm': .4}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.02, 0, 0), frames=50)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps1.df['E.XX'], mps1.df['S.XX'])
show(plot);
```
### Validation
Let us now fit experimental data
```
from pandas import read_excel
from scipy.optimize import fmin
from scipy.stats import linregress
L0 = 2.25
D0 = 0.525
A0 = pi * (D0 / 2.) ** 2
df = read_excel('aldat.xls', skiprows=9)
# subtract initial displacement and compute stress/strain
df['Crosshead displacement'] -= df['Crosshead displacement'].iloc[0]
df['Stress'] = df['Load'] / A0
df['Strain'] = log((L0 + df['Crosshead displacement']) / L0)
df['dStress'] = ediff1d(df['Stress'], to_begin=0)
df['dStrain'] = ediff1d(df['Strain'], to_begin=0)
```
#### Determine elastic response
```
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(df['Strain'], df['Stress'])
show(plot);
df = df[df['Strain'] >= 1.5e-3]
df_e = df[(df['Strain'] < .017) & (df['Strain'] > .004)].copy()
df_e['Strain'] -= df_e['Strain'].iloc[0]
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(df_e['Strain'], df_e['Stress'])
show(plot)
E = polyfit(df_e['Strain'], df_e['Stress'], 1)[0]
p = {'E': E}
plot = figure()
plot.circle(df['Strain'], df['Stress'])
ee = linspace(0, .015)
plot.line(ee, E * ee, color='red')
show(plot)
df['dEE'] = df['dStress'] / E
df['dEP'] = df['dStrain'] - df['dEE']
df['EE'] = cumsum(df['dEE'])
df['EP'] = cumsum(df['dEP'])
df['EPEQ'] = sqrt(2./3.) * df['EP']
dwp = df['dStress'] * df['dEP']
df['WP'] = cumsum(dwp)
i = df['Stress'].argmax()
df_p = df[(df['Strain'] >= .02) & (df['Strain'] < df['Strain'][i])]
#print df.loc(i)
#df_p = df[(df['Strain'] >= .03) & (df['Strain'] < .15)]
M, N = 350, 350
p1 = figure(x_axis_label='EPEQ', y_axis_label='Y',
width=M, plot_height=N,
title='Linear Hardening')
p1.circle(df_p['EPEQ'], df_p['Stress'])
p2 = figure(x_axis_label='Log[EPEQ]', y_axis_label='Log[Y]',
width=M, plot_height=N,
title='Power Law Hardening')
p2.circle(log(df_p['EPEQ']), log(df_p['Stress']))
p3 = figure(x_axis_label='EP', y_axis_label='Y',
width=M, plot_height=N,
title='Work Hardening')
p3.circle(df_p['WP'], df_p['Stress'])
p4 = figure(x_axis_label='E', y_axis_label='EE, EP',
width=M, plot_height=N)
p4.circle(df_p['EE'], df_p['Strain'], legend='EE')
p4.circle(df_p['EP'], df_p['Strain'], color='red', legend='EP')
gp = gridplot([[p1, p2], [p3, p4]])
show(gp)
```
### Power law model fit
```
p['Y0'] = 38e3
x = polyfit(log(df_p['EPEQ']), log(df_p['Stress']-p['Y0']) , 1)
p['m'] = x[0]
p['Y1'] = exp(x[1])
p, x
mps = MaterialPointSimulator('uplastic-std')
p['Nu'] = .333
mps.material = HardeningPlasticMaterial(**p)
mps.run_step('ESS', (.08, 0, 0), frames=100)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps.df['E.XX'], mps.df['S.XX'], color='red', legend='Model')
plot.circle(df['Strain'], df['Stress'], legend='Experiment')
show(plot)
```
|
github_jupyter
|
%pycat ../matmodlab2/materials/plastic3.py
%pylab inline
from bokeh.io import output_notebook
from bokeh.plotting import *
from matmodlab2 import *
from numpy import *
from plotting_helpers import create_figure
output_notebook()
import pandas as pd
pd.set_option('precision', 20)
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.004, 0, 0), frames=50)
i = where((mps1.df['E.XX'] > 0.) & (mps1.df['E.XX'] < .005))
E = mps1.df['S.XX'].iloc[i] / mps1.df['E.XX'].iloc[i]
assert allclose(E.iloc[0], 10e6, atol=1e-3, rtol=1e-3)
assert amax(mps1.df['S.XX']) - 40e3 < 1e-6
#plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
mps1.plot('E.XX', 'S.XX')
print(mps1.df[['F.XX','F.YY','F.ZZ','S.XX']])
mps1 = MaterialPointSimulator('uplastic-std')
p = {'K': 15, 'G': 10, 'Y0': 1}
mps1.material = VonMisesMaterial(**p)
mps1.run_step('EEE', (.075, 0, 0), frames=50)
mps1.plot('E.XX', 'S.XX')
print(mps1.df[['F.XX','S.XX','S.YY']])
1.020201 0.990711 0.990711
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3, 'Y1': 2e6}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.02, 0, 0), frames=50)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps1.df['E.XX'], mps1.df['S.XX'])
show(plot);
mps1 = MaterialPointSimulator('uplastic-std')
p = {'E': 10e6, 'Nu': .333, 'Y0': 40e3, 'Y1': 2e4, 'm': .4}
mps1.material = HardeningPlasticMaterial(**p)
mps1.run_step('ESS', (.02, 0, 0), frames=50)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps1.df['E.XX'], mps1.df['S.XX'])
show(plot);
from pandas import read_excel
from scipy.optimize import fmin
from scipy.stats import linregress
L0 = 2.25
D0 = 0.525
A0 = pi * (D0 / 2.) ** 2
df = read_excel('aldat.xls', skiprows=9)
# subtract initial displacement and compute stress/strain
df['Crosshead displacement'] -= df['Crosshead displacement'].iloc[0]
df['Stress'] = df['Load'] / A0
df['Strain'] = log((L0 + df['Crosshead displacement']) / L0)
df['dStress'] = ediff1d(df['Stress'], to_begin=0)
df['dStrain'] = ediff1d(df['Strain'], to_begin=0)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(df['Strain'], df['Stress'])
show(plot);
df = df[df['Strain'] >= 1.5e-3]
df_e = df[(df['Strain'] < .017) & (df['Strain'] > .004)].copy()
df_e['Strain'] -= df_e['Strain'].iloc[0]
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(df_e['Strain'], df_e['Stress'])
show(plot)
E = polyfit(df_e['Strain'], df_e['Stress'], 1)[0]
p = {'E': E}
plot = figure()
plot.circle(df['Strain'], df['Stress'])
ee = linspace(0, .015)
plot.line(ee, E * ee, color='red')
show(plot)
df['dEE'] = df['dStress'] / E
df['dEP'] = df['dStrain'] - df['dEE']
df['EE'] = cumsum(df['dEE'])
df['EP'] = cumsum(df['dEP'])
df['EPEQ'] = sqrt(2./3.) * df['EP']
dwp = df['dStress'] * df['dEP']
df['WP'] = cumsum(dwp)
i = df['Stress'].argmax()
df_p = df[(df['Strain'] >= .02) & (df['Strain'] < df['Strain'][i])]
#print df.loc(i)
#df_p = df[(df['Strain'] >= .03) & (df['Strain'] < .15)]
M, N = 350, 350
p1 = figure(x_axis_label='EPEQ', y_axis_label='Y',
width=M, plot_height=N,
title='Linear Hardening')
p1.circle(df_p['EPEQ'], df_p['Stress'])
p2 = figure(x_axis_label='Log[EPEQ]', y_axis_label='Log[Y]',
width=M, plot_height=N,
title='Power Law Hardening')
p2.circle(log(df_p['EPEQ']), log(df_p['Stress']))
p3 = figure(x_axis_label='EP', y_axis_label='Y',
width=M, plot_height=N,
title='Work Hardening')
p3.circle(df_p['WP'], df_p['Stress'])
p4 = figure(x_axis_label='E', y_axis_label='EE, EP',
width=M, plot_height=N)
p4.circle(df_p['EE'], df_p['Strain'], legend='EE')
p4.circle(df_p['EP'], df_p['Strain'], color='red', legend='EP')
gp = gridplot([[p1, p2], [p3, p4]])
show(gp)
p['Y0'] = 38e3
x = polyfit(log(df_p['EPEQ']), log(df_p['Stress']-p['Y0']) , 1)
p['m'] = x[0]
p['Y1'] = exp(x[1])
p, x
mps = MaterialPointSimulator('uplastic-std')
p['Nu'] = .333
mps.material = HardeningPlasticMaterial(**p)
mps.run_step('ESS', (.08, 0, 0), frames=100)
plot = create_figure(bokeh=True, x_axis_label='Strain', y_axis_label='Stress')
plot.line(mps.df['E.XX'], mps.df['S.XX'], color='red', legend='Model')
plot.circle(df['Strain'], df['Stress'], legend='Experiment')
show(plot)
| 0.385606 | 0.991084 |
<a href="https://colab.research.google.com/github/rezwanh001/Machine-Learning-Tutorial/blob/master/Linear_Regression_with_One_Variable.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Check the GPU
```
import tensorflow as tf
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
raise SystemError('GPU device not found')
print('Found GPU at: {}'.format(device_name))
```
### Mount the gdrive
```
from google.colab import drive
drive.mount('/content/drive')
```
## Model and Cost Function:
----------------------------------------------
* `m` = Number of training examples.
* `X's` = Input variable/Features.
* ` y's `= Outout variable/Target variable.
* `(X,y)` = one training example.
* ($X^{(i)}, y^{(i)}$) = $i$-th training example.
So here's how this supervised learning algorithm works. To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function `h : X โ y` so that `h(x)` is a โgoodโ predictor for the corresponding value of `y`. For historical reasons, this function `h` is called a hypothesis. Seen pictorially, the process is therefore like this:
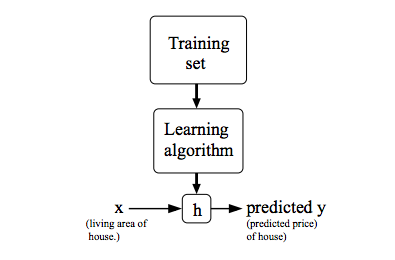
Fig-1: The Process the supervised learning algorithms.
When the target variable that weโre trying to predict is continuous, such as in our housing example, we call the learning problem a regression problem. When `y` can take on only a small number of discrete values (such as if, given the living area, we wanted to predict if a dwelling is a house or an apartment, say), we call it a classification problem.
* ***How do we represent `h`?***
$h_\theta(X)$ = $\theta_0 + \theta_1(X)$ --------------------------------------------------------------------------(i)
* ***How to fit the best possible straight line in our data?***
* Hypothesis: $h_\theta(x)$ = $\theta_0 + \theta_1x$ -----------------------------------------------------------(ii)
* $\theta_{i}$'s = Parameters.
* Idea: Choose $\theta_0$, $\theta_1$ so that $h_\theta(x)$ is close to $y$ for our training examples$(X, y)$
* Let's formalize this. So linear regression, what we're going to do is, I'm going to want to solve a minimization problem. So I'll write minimize over $\theta_0$, $\theta_1$ with following formula:
$\underset{\theta_0, \theta_1}{minimize}$ =$\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(X^{(i)}) - y^{(i)})^2$ -------------------------------(iii)
* ***Cost function:***
* $J(\theta_0, \theta_1)$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(X^{(i)}) - y^{(i)})^2$ -------------------------------------------(iv)
This cost function is also known as Squared Error Function.
It turns out that why do we take the squares of the errors. It turns out that these squared error cost function is a reasonable choice and works well for problems for most regression programs. There are other cost functions that will work pretty well. But the square cost function is probably the most commonly used one for regression problems.
We can measure the accuracy of our hypothesis function by using a **cost function**. This takes an average difference (actually a fancier version of an average) of all the results of the hypothesis with inputs from $x$'s and the actual output $y$'s.
* $J(\theta_0, \theta_1)$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(\hat{y_i} - y_i)^2$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(X^{(i)}) - y^{(i)})^2$ ----------(v)
To break it apart, it is $\frac{1}{2}\bar{x}$ where $\bar{x}$ is the mean of the squares of $h_\theta (x_{i}) - y_{i}$ or the difference between the predicted value and the actual value.
This function is otherwise called the "Squared error function", or "Mean squared error". The mean is halved $\left(\frac{1}{2}\right)$ as a convenience for the computation of the gradient descent, as the derivative term of the square function will cancel out the $\frac{1}{2}$ term.
* ***What the cost function is doing, and why we want to use it?***
* Hypothesis:
$h_\theta(x)$ = $\theta_0 + \theta_1x$
* Parameters:
$\theta_0$, $\theta_1$
* Cost Function:
$J(\theta_0, \theta_1)$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(X^{(i)}) - y^{(i)})^2$
* Goal:
$\underset{\theta_0, \theta_1}{minimize}$ $J(\theta_0, \theta_1)$
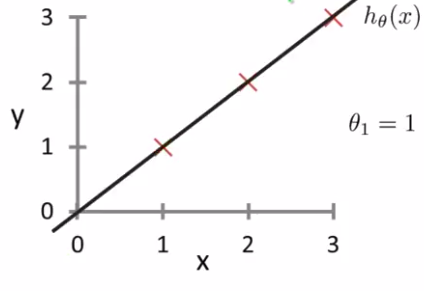
Fig-2: Plot the Hypothesis Function where $\theta_0$=$0$, $x$ is the size of house.
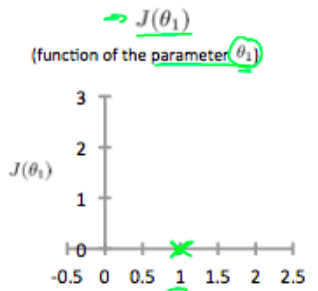
Fig-3: Plot the Cost Function where $\theta_0$=$0$, $\theta_1$=$1$.
* **Simplified**
* Hypothesis:
$h_\theta(x)$ = $\theta_1x$
* Parameters:
$\theta_1$
* Cost Function:
$J(\theta_1)$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(X^{(i)}) - y^{(i)})^2$
* Goal:
$\underset{\theta_1}{minimize}$ $J(\theta_1)$
*Two key functions we want to understand:*
1. $h_\theta(x)$ : For fixed $\theta_1$, this is a function of $x$. So the hypothsis is a finction of, what is the size of the house $x$.
2. $J(\theta_1)$: Function of the parameter $\theta_1$. In contrast, $J$, that's a function of parameter, $\theta_1$, which controls the slope of the straight line.
If we try to think of it in visual terms, our training data set is scattered on the x-y plane. We are trying to make a straight line (defined by $h_\theta(x)$) which passes through these scattered data points.
Our objective is to get the best possible line. The best possible line will be such so that the average squared vertical distances of the scattered points from the line will be the least. Ideally, the line should pass through all the points of our training data set.
Thus as a goal, we should try to minimize the cost function. In this case, $\theta_1$ = $1$ is our global minimum.
## Parameter Learning
-------------------------------------
### Gradient Descent:
* Gradient descent is an algorithm for minimizing the cost function $J$. It turns out gradient descent is a more general algorithm, and is used not only in linear regression. It's actually used all over the place in machine learning.
* Have some function, $J(\theta_0, \theta_1)$
* Want, $\underset{\theta_0, \theta_1}{min}$ $J(\theta_0, \theta_1)$
* Outline:
* Start with some $\theta_0$, $\theta_1$
* Keep changing $\theta_0$, $\theta_1$ to reduce $J(\theta_0, \theta_1)$ until we hopefully end up at a minimum.
* **Gradient descent algorithm**
* repeat until convergence {
$\theta_j := \theta_j - \alpha\frac{\delta}{\delta\theta_j} J(\theta_0, \theta_1)$
$(for j =0 and j = 1)$
}
Where, $\alpha$ = $learning$ $rate$.
And what $\alpha$ does is it basically controls how big a step we take downhill with creating descent. So if $\alpha$ is very large, then that corresponds to a very aggressive gradient descent procedure where we're trying take huge steps downhill and if $\alpha$ is very small, then we're taking little, little baby steps downhill.
* If $\alpha$ is too small, gradient descent can be slow.
* If $\alpha$ is too large, gradient descent can overshoot the minimum. It may fail to converge, or even diverge.
* What if your parameter $\theta_1$ is already at a local minimum, what do you think one step of gradient descent will do?
* **Ans:** Slope will be equal to $0$. So, Leave $\theta_1$ unchanged. So if your parameters are already at a local minimum one step with gradient descent does not absolutely nothing it doesn't your parameter, which is what you want beacause it keeps your solution at the local optimum.
* Why gradient descent can converse the local minimum even with the learning rate alpha fixed?
* **Ans:** Gradient descent can converge to a local minimum, even with the learning rate $\alpha$ fixed.
$\theta_1 := \theta_1 - \alpha \frac{\delta}{\delta\theta_1} J(\theta_1)$
As we approach a local minimum, gradient descent will automatically take smaller steps. So, on need to decrese $\alpha$ over time.
So that's the gradient descent algorithm and you can use it to try to minimize any cost function $J$, not the cost function $J$ that we defiend for linear regression.
## Gradient descent for linear regression
-------------------------------------------------------------------
### Linear Regression Model:
* **Hypothesis Function:** $h_\theta(x) = \theta_0 + \theta_1x$
* ** Squared Error Cost Function: ** $J(\theta_0, \theta_1)$ = $\frac{1}{2m}$ $\sum_{i=1}^{m}$ $(h_\theta(x^{(i)}) - y^{(i)})^2$
Apply gradient descent to minimize our squared error cost function.
The key term we need is cost function $J$ derivative term over here. So, we need to figure out what is this partial deivative term.
$\frac{\delta}{\delta\theta_j} J(\theta_0, \theta_1) = \frac{\delta}{\delta\theta_j} \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$
$\frac{\delta}{\delta\theta_j} J(\theta_0, \theta_1) = \frac{\delta}{\delta\theta_j} \frac{1}{2m} \sum_{i=1}^{m} ((\theta_0 + \theta_1x^{(i)}) - y^{(i)})^2$
Partial derivative with respect to $\theta_0$ and $\theta_1$.
* $\theta_0, J=0: \frac{\delta}{\delta\theta_0} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})$
* $\theta_1, J=1: \frac{\delta}{\delta\theta_1} J(\theta_0, \theta_1) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}).x^{(i)}$
* ***Gradient descent algorithm for linear regression:***
* repeat until convergence {
$\theta_0 := \theta_0 - \alpha \frac{\delta}{\delta\theta_j} \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})$
$\theta_1 := \theta_1 - \alpha \frac{\delta}{\delta\theta_j} \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}).x^{(i)}$
}
* ** "Batch" Gradient Descent:**
"Batch" : Each step of gradient descent uses all the training examples.
## Linear Algebra Review
------------------------------------------
* **Matrices and Vectors**
* **Matrix:** Rectangular array of Numbers.
* **Dimension of Matrix:** Number of rows $x$ numbers of columns.
* **Vector:** An $nx1$ matrix. Also called $n$-D vector. Also denoted by $\mathbb{R^n}$.
* **Notation and terms:**
* $A_{ij}$refers to the element in the $i$-th row and $j$-th column of matrix $A$.
* $A$ vector with $'n'$ rows is referred to as an $'n'$-dimensional vector.
* $v_i$ refers to the element in the $i$-th row of the vector.
* In general, all our vectors and matrices will be $1$-indexed. Note that for some programming languages, the arrays are $0$-indexed.
* Matrices are usually denoted by uppercase names while vectors are lowercase.
* "Scalar" means that an object is a single value, not a vector or matrix.
* $\mathbb{R}$ refers to the set of scalar real numbers.
* $\mathbb{R}^n$ refers to the set of $n$-dimensional vectors of real numbers.
* **Addition and scalar multiplication**
* Addition and subtraction are element-wise, so you simply add or subtract each corresponding element:
$\begin{bmatrix} a & b \newline c & d \newline \end{bmatrix} + \begin{bmatrix} w & x \newline y & z \newline \end{bmatrix} =\begin{bmatrix} a+w & b+x \newline c+y & d+z \newline \end{bmatrix}$
* In scalar division, we simply divide every element by the scalar value:
$\begin{bmatrix} a & b \newline c & d \newline \end{bmatrix} / x =\begin{bmatrix} a /x & b/x \newline c /x & d /x \newline \end{bmatrix}$
* ** Matrix-Vector multiplication **
* $Prediction = DataMetrix * Parameters$
* We map the column of the vector onto each row of the matrix, multiplying each element and summing the result.
$\begin{bmatrix} a & b \newline c & d \newline e & f \end{bmatrix} *\begin{bmatrix} x \newline y \newline \end{bmatrix} =\begin{bmatrix} a*x + b*y \newline c*x + d*y \newline e*x + f*y\end{bmatrix}$
The result is a vector. The number of columns of the matrix must equal the number of rows of the vector.
An m x n matrix multiplied by an n x 1 vector results in an m x 1 vector.
* **Matrix-Matrix Multiplication**
* We multiply two matrices by breaking it into several vector multiplications and concatenating the result
$\begin{bmatrix} a & b \newline c & d \newline e & f \end{bmatrix} *\begin{bmatrix} w & x \newline y & z \newline \end{bmatrix} =\begin{bmatrix} a*w + b*y & a*x + b*z \newline c*w + d*y & c*x + d*z \newline e*w + f*y & e*x + f*z\end{bmatrix}$
An m x n matrix multiplied by an n x o matrix results in an m x o matrix. In the above example, a 3 x 2 matrix times a 2 x 2 matrix resulted in a 3 x 2 matrix.
To multiply two matrices, the number of columns of the first matrix must equal the number of rows of the second matrix.
* ** Matrix Multiplication Properties**
* Matrices are not commutative:
$(AโB)\neq(BโA)$
* Matrices are associative:
$(AโB)โC=Aโ(BโC)$
* The identity matrix, when multiplied by any matrix of the same dimensions, results in the original matrix. It's just like multiplying numbers by 1. The identity matrix simply has 1's on the diagonal (upper left to lower right diagonal) and 0's elsewhere.
$\begin{bmatrix} 1 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & 0 & 1 \newline \end{bmatrix}$
* When multiplying the identity matrix after some matrix (AโI), the square identity matrix's dimension should match the other matrix's columns. When multiplying the identity matrix before some other matrix (IโA), the square identity matrix's dimension should match the other matrix's rows.
* **Inverse and Transpose**
* Matrices that don't have inverse are "singular" or "degenerate".
* Let $A$ be an $(mxn)$ matrix, and let $B = A^T$. Then $B$ is an $(nxm)$ matrix, and $B_{ij} = A_{ji}$
* The inverse of a matrix $A$ is denoted $A^{-1}$. Multiplying by the inverse results in the identity matrix.
* A non square matrix does not have an inverse matrix. We can compute inverses of matrices in octave with the $pinv(A)$ function and in Matlab with the $inv(A)$ function. Matrices that don't have an inverse are *singular* or *degenerate*.
* The transposition of a matrix is like rotating the matrix $90ยฐ$ in clockwise direction and then reversing it. We can compute transposition of matrices in matlab with the $transpose(A)$ function or $A'$:
$A = \begin{bmatrix} a & b \newline c & d \newline e & f \end{bmatrix}$
$A^T = \begin{bmatrix} a & c & e \newline b & d & f \newline \end{bmatrix}$
* In other words: $A_{ij} = A^{T}_{ji}$
## Linear Algebra Review: Python Code
```
## Matrix and Vector
##-------------------
### Initialize matrix A with 4 rows and 3 cols
# Load library
import numpy as np
A = np.matrix([[1,2,3], [4,5,6], [7,8, 9],[10,11,12]])
print("Matrix: \n", A)
### Initialize a vector
v = np.matrix([1,2,3])
print("Vector: ", v)
### Get the dimension of the matrix A where m = rows and n = cols
[m, n] = A.shape
print("Dim A: ", [m, n])
###You could also store it this way
dim_A = A.shape
print("dim_A: ", dim_A)
### Get the dimension of the vector v
dim_v = v.shape
print("dim_v: ", dim_v)
### Now let's index into the 2nd row and 3rth cols of matrix A.
A_23 = A.item(2-1, 3-1)
print("A_23: ", A_23)
## %%%%%%%%% Addition and Scalar Multiplication %%%%%%%%%%%%
## %--------------------------------------------------
## % Initialize matrix A and B
A = np.matrix([[1,2,4], [5,3,2]])
B = np.matrix([[1,3,4], [1,1,1]])
print("Matrix A: \n", A)
print("Matrix B: \n", B)
## % Initialize constant s
s = 2
## % See how the element-wise addition works.
add_AB = A + B
print("add_AB: \n", add_AB)
## % See how the element-wise subtraction works.
sub_AB = A - B
print("sub_AB: \n", sub_AB)
## % Divide A by s
div_As = A / s
print("div_As: \n", div_As)
## % What happens if we have a Matrix + scalar?
add_As = A + s
print("add_As: \n", add_As)
### %%%%% Matrix Vector Multiplication
## %%%-------------------------------
### % Initialize a 3 by 2 matrix
A = np.matrix([[1, 2], [3, 4],[5, 6]])
print("Matrix A: \n", A)
### % Initialize a 2 by 1 matrix
B = np.matrix([1, 2])
print("Matrix: \n", B)
### % Multiply A * B
mult_AB = A.dot(B.T)
print("mult_AB: \n", mult_AB)
### %%%% Matrix Multiplication Properties
## %%------------------------------------
## % Initialize random matrices A and B
A = np.matrix([[1,2],[4,5]])
B = np.matrix([[1,1],[0,2]])
print("Matrix A: \n", A)
print("Matrix B: \n", B)
## % Initialize a 2 by 2 identity matrix
I = np.identity(2)
print("Identity Matrix: \n", I)
### % The above notation is the same as I = [1,0;0,1]
## % What happens when we multiply I*A ?
IA = I.dot(A)
print("I*A: \n", IA)
## % How about A*I ?
AI = A.dot(I)
print("A*I: \n", AI)
## % Compute A*B
AB = np.dot(A, B)
print("A*B: \n", AB)
## % Is it equal to B*A?
BA = np.dot(B, A)
print("B*A: \n", BA)
### % Note that IA = AI but AB != BA
### %%%%% Inverse and Transpose
### %%-------------------------
## % Initialize matrix A
A = np.matrix([[1,2,0], [0,5,6], [7,0,9]])
print("Matrix A: \n", A)
## % Transpose A
A_trans = A.T
print("Matrix A_trans: \n", A_trans)
## % Take the inverse of A
A_inv = A.I
print("A_inv: \n", A_inv)
## % What is A^(-1)*A?
A_invA = np.dot(A_inv, A)
print("A_invA: \n", A_invA)
```
***References***
[1]. [Machine Learning by Andrew NG.](https://www.coursera.org/learn/machine-learning/home/welcome)
|
github_jupyter
|
import tensorflow as tf
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
raise SystemError('GPU device not found')
print('Found GPU at: {}'.format(device_name))
from google.colab import drive
drive.mount('/content/drive')
## Matrix and Vector
##-------------------
### Initialize matrix A with 4 rows and 3 cols
# Load library
import numpy as np
A = np.matrix([[1,2,3], [4,5,6], [7,8, 9],[10,11,12]])
print("Matrix: \n", A)
### Initialize a vector
v = np.matrix([1,2,3])
print("Vector: ", v)
### Get the dimension of the matrix A where m = rows and n = cols
[m, n] = A.shape
print("Dim A: ", [m, n])
###You could also store it this way
dim_A = A.shape
print("dim_A: ", dim_A)
### Get the dimension of the vector v
dim_v = v.shape
print("dim_v: ", dim_v)
### Now let's index into the 2nd row and 3rth cols of matrix A.
A_23 = A.item(2-1, 3-1)
print("A_23: ", A_23)
## %%%%%%%%% Addition and Scalar Multiplication %%%%%%%%%%%%
## %--------------------------------------------------
## % Initialize matrix A and B
A = np.matrix([[1,2,4], [5,3,2]])
B = np.matrix([[1,3,4], [1,1,1]])
print("Matrix A: \n", A)
print("Matrix B: \n", B)
## % Initialize constant s
s = 2
## % See how the element-wise addition works.
add_AB = A + B
print("add_AB: \n", add_AB)
## % See how the element-wise subtraction works.
sub_AB = A - B
print("sub_AB: \n", sub_AB)
## % Divide A by s
div_As = A / s
print("div_As: \n", div_As)
## % What happens if we have a Matrix + scalar?
add_As = A + s
print("add_As: \n", add_As)
### %%%%% Matrix Vector Multiplication
## %%%-------------------------------
### % Initialize a 3 by 2 matrix
A = np.matrix([[1, 2], [3, 4],[5, 6]])
print("Matrix A: \n", A)
### % Initialize a 2 by 1 matrix
B = np.matrix([1, 2])
print("Matrix: \n", B)
### % Multiply A * B
mult_AB = A.dot(B.T)
print("mult_AB: \n", mult_AB)
### %%%% Matrix Multiplication Properties
## %%------------------------------------
## % Initialize random matrices A and B
A = np.matrix([[1,2],[4,5]])
B = np.matrix([[1,1],[0,2]])
print("Matrix A: \n", A)
print("Matrix B: \n", B)
## % Initialize a 2 by 2 identity matrix
I = np.identity(2)
print("Identity Matrix: \n", I)
### % The above notation is the same as I = [1,0;0,1]
## % What happens when we multiply I*A ?
IA = I.dot(A)
print("I*A: \n", IA)
## % How about A*I ?
AI = A.dot(I)
print("A*I: \n", AI)
## % Compute A*B
AB = np.dot(A, B)
print("A*B: \n", AB)
## % Is it equal to B*A?
BA = np.dot(B, A)
print("B*A: \n", BA)
### % Note that IA = AI but AB != BA
### %%%%% Inverse and Transpose
### %%-------------------------
## % Initialize matrix A
A = np.matrix([[1,2,0], [0,5,6], [7,0,9]])
print("Matrix A: \n", A)
## % Transpose A
A_trans = A.T
print("Matrix A_trans: \n", A_trans)
## % Take the inverse of A
A_inv = A.I
print("A_inv: \n", A_inv)
## % What is A^(-1)*A?
A_invA = np.dot(A_inv, A)
print("A_invA: \n", A_invA)
| 0.708313 | 0.987228 |
```
# ๆฅ็ๅฝๅๆ่ฝฝ็ๆฐๆฎ้็ฎๅฝ, ่ฏฅ็ฎๅฝไธ็ๅๆด้ๅฏ็ฏๅขๅไผ่ชๅจ่ฟๅ
# View dataset directory.
# This directory will be recovered automatically after resetting environment.
!ls /home/aistudio/data
# ๆฅ็ๅทฅไฝๅบๆไปถ, ่ฏฅ็ฎๅฝไธ็ๅๆดๅฐไผๆไน
ไฟๅญ. ่ฏทๅๆถๆธ
็ไธๅฟ
่ฆ็ๆไปถ, ้ฟๅ
ๅ ่ฝฝ่ฟๆ
ข.
# View personal work directory.
# All changes under this directory will be kept even after reset.
# Please clean unnecessary files in time to speed up environment loading.
!ls /home/aistudio/work
# ๅฆๆ้่ฆ่ฟ่กๆไน
ๅๅฎ่ฃ
, ้่ฆไฝฟ็จๆไน
ๅ่ทฏๅพ, ๅฆไธๆนไปฃ็ ็คบไพ:
# If a persistence installation is required,
# you need to use the persistence path as the following:
!mkdir /home/aistudio/external-libraries
!pip install beautifulsoup4 -t /home/aistudio/external-libraries
# ๅๆถๆทปๅ ๅฆไธไปฃ็ , ่ฟๆ ทๆฏๆฌก็ฏๅข(kernel)ๅฏๅจ็ๆถๅๅช่ฆ่ฟ่กไธๆนไปฃ็ ๅณๅฏ:
# Also add the following code,
# so that every time the environment (kernel) starts,
# just run the following code:
import sys
sys.path.append('/home/aistudio/external-libraries')
```
# ไธป่ฆไปฃ็ ๅๅ
ถ่ฏดๆ
## ้่ฟpaddlesegๅฎ็ฐ
ๆญฅ้ชค๏ผ
1.ๅฏนไบๆฐๆฎ่ฟ่ก้ขๅค็๏ผๅฝขๆๅฏ่ขซpaddleseg่ฏปๅ็labelๅพ็
2.ๅๅๆฐๆฎ้๏ผๆ นๆฎๅพ็็ฎๅฝ็ๆtxtๆไปถ
3.้
็ฝฎ็ธๅ
ณๆไปถ ไฝฟ็จsetrไธdnlnetๆจกๅ ๅๅซๅฏนๆฐๆฎ่ฟ่ก่ฎญ็ป
4.่ๅๆจกๅ่ฟ่กๆจ็
5.ๅ็ผฉ้ขๆตๅพ็
### ๆฐๆฎๅๅคๅ้ขๅค็้จๅ
```
#่งฃๅๆฐๆฎ้
!unzip -qo data/data102901/train_50k_mask.zip -d data/
!unzip -oq data/data102901/Bๆฆๆต่ฏๆฐๆฎ้.zip -d data/
!unzip -oq data/data102901/train_image.zip -d data/
!unzip -oq /home/aistudio/data/data102949/model.zip
!unzip -oq /home/aistudio/PaddleSeg.zip
import sys
import paddle
import numpy as np
import os
import matplotlib.pyplot as plt
from PIL import Image
from tqdm import tqdm
import random
#ๅฏนlabelๅพ็่ฟ่กๅๅพๅไบๅผๅๅค็
#PaddleSeg้็จๅ้้็ๆ ๆณจๅพ็๏ผๆฏไธ็งๅ็ด ๅผไปฃ่กจไธ็ง็ฑปๅซ๏ผๅ็ด ๆ ๆณจ็ฑปๅซ้่ฆไป0ๅผๅง้ๅข
import cv2
import matplotlib.pyplot as plt
for filename in os.listdir("data/train_50k_mask"):
print(filename)
k=os.path.join("data/train_50k_mask",filename)
for filenamel in os.listdir(k):
kt=os.path.join(k,filenamel)
img = cv2.imread(kt)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
difference = (img_gray.max() - img_gray.min()) // 2
_, img_binary = cv2.threshold(img_gray, difference, 1, cv2.THRESH_BINARY)
cv2.imwrite(kt, img_binary)
plt.imshow(img_binary)
plt.show()
import sys
import paddle
import numpy as np
import os
import matplotlib.pyplot as plt
from PIL import Image
import random
#่ฏปๅ
ฅๆฐๆฎ็ฎๅฝ๏ผๆผๆฅimagesไธlabels
datas_list=[]
for filename in os.listdir("data/train_image"):
k=os.path.join("data/train_image",filename)
kt=os.path.join("data/train_50k_mask",filename)
for filenamel in os.listdir(k):
datas_list.append([os.path.join(k,filenamel),os.path.join(kt,filenamel)])
#ๆไนฑๆฐๆฎ
random.shuffle(datas_list)
#ๅๅๆฐๆฎ้
train_list= datas_list[ : int(len(datas_list)*0.9)]
test_list = datas_list[int(len(datas_list)*0.9):]
print(len(train_list))
print(len(test_list))
#็ๆtxtๆไปถ
with open('train.txt',"a+") as train_file:
for k in range(len(train_list)):
train_file.write("%s %s\n"%(train_list[k][0],train_list[k][1]))
with open('val.txt',"a+") as train_file:
for k in range(len(test_list)):
train_file.write("%s %s\n"%(test_list[k][0],test_list[k][1]))
import glob
path = glob.glob('data/test_image/*')
f = open('test.txt', 'w')
for i in path:
f.write(i+'\n')
f.close()
%cd ~/
```
### ่ฎญ็ป้จๅ
#### ๆฐๆฎๅขๅผบ
ไฝฟ็จไบpaddlesegๅ
็ฝฎ็RandomHorizontalFlipใRandomVerticalFlipใRandomDistortใResize็ญๆนๅผๅฏนๆฐๆฎ่ฟ่กๅค็
#### ไฝฟ็จsetrๆจกๅ ไปฅไธไธบsetrๆจกๅ็้
็ฝฎๆไปถ
```
batch_size: 32
iters: 40000
train_dataset:
type: Dataset
dataset_root: /home/aistudio
train_path: /home/aistudio/train.txt
num_classes: 2
transforms:
- type: RandomHorizontalFlip
- type: RandomVerticalFlip
- type: RandomDistort
brightness_range: 0.4
contrast_range: 0.4
saturation_range: 0.4
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: train
val_dataset:
type: Dataset
dataset_root: /home/aistudio
val_path: /home/aistudio/val.txt
num_classes: 2
transforms:
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: val
model:
type: SegmentationTransformer
backbone:
type: ViT_large_patch16_384
pretrained: https://bj.bcebos.com/paddleseg/dygraph/vit_large_patch16_384.tar.gz
num_classes: 2
backbone_indices: [9, 14, 19, 23]
head: pup
align_corners: True
optimizer:
type: sgd
momentum: 0.9
weight_decay: 4.0e-5
lr_scheduler:
type: PolynomialDecay
learning_rate: 0.01
end_lr: 1.0e-4
power: 0.9
loss:
types:
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
coef: [1, 0.4, 0.4, 0.4, 0.4]
```
```
#ๅผๅง่ฎญ็ป
!python PaddleSeg/train.py --config setr.yaml --do_eval --use_vdl --save_dir /home/aistudio/output_setr --save_interval 2000
```
#### ไฝฟ็จDNLNetๆจกๅ ไปฅไธไธบDNLNetๆจกๅ็้
็ฝฎๆไปถ
```
batch_size: 32
iters: 40000
train_dataset:
type: Dataset
dataset_root: /home/aistudio
train_path: /home/aistudio/train.txt
num_classes: 2
transforms:
- type: RandomHorizontalFlip
- type: RandomVerticalFlip
- type: RandomDistort
brightness_range: 0.4
contrast_range: 0.4
saturation_range: 0.4
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: train
val_dataset:
type: Dataset
dataset_root: /home/aistudio
val_path: /home/aistudio/val.txt
num_classes: 2
transforms:
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: val
model:
type: DNLNet
backbone:
type: ResNet50_vd
output_stride: 8
pretrained: https://bj.bcebos.com/paddleseg/dygraph/resnet50_vd_ssld_v2.tar.gz
optimizer:
type: sgd
momentum: 0.9
weight_decay: 4.0e-5
lr_scheduler:
type: PolynomialDecay
learning_rate: 0.01
end_lr: 0
power: 0.9
loss:
types:
- type: CrossEntropyLoss
- type: CrossEntropyLoss
coef: [1, 0.4]
```
```
#ๅผๅง่ฎญ็ป
!python PaddleSeg/train.py --config DNLNet.yaml --do_eval --use_vdl --save_dir /home/aistudio/output_DNLNet_1 --save_interval 2000
```
#### ไธคไธชๆจกๅ็ๅๆฐไฟๅญไธ็ธๅบ็save_dir ็ฎๅฝไธ๏ผๆญคๅค็ฑไบ้กน็ฎๅคงๅฐ้ๅถๅ็ผฉไบmodelๆฐๆฎ้ๅ
### ๆจกๅ่ๅ
#### ๆญคๅคๅ่ๅผๆบ้กน็ฎ [ๆจกๅ่ๅ-่ฟไธๆญฅๆๅ็ฒพๅบฆ](https://aistudio.baidu.com/aistudio/projectdetail/1698818?channel=0&channelType=0&shared=1)
```
#ๅผๅง้ช่ฏ
!python PaddleSeg/val.py --config_1 DNLNet.yaml --model_path_1 dnl.pdparams --config_2 setr.yaml --model_path_2 ster.pdparams
#ๅผๅง้ขๆต
!python PaddleSeg/predict.py --config_1 DNLNet.yaml --model_path_1 dnl.pdparams --config_2 setr.yaml --model_path_2 ster.pdparams --image_path data/test_image --save_dir output/result --aug_pred --flip_horizontal --flip_vertical
%cd PaddleSeg
!zip -r -oq /home/aistudio/PaddleSeg.zip ./
#ๅ็ผฉ้ขๆตๆไปถไพฟไบๆไบค
%cd output/result/results
!zip -r -oq /home/aistudio/preddouble.zip ./
%cd /home/aistudio
```
่ฏท็นๅป[ๆญคๅค](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576)ๆฅ็ๆฌ็ฏๅขๅบๆฌ็จๆณ. <br>
Please click [here ](https://ai.baidu.com/docs#/AIStudio_Project_Notebook/a38e5576) for more detailed instructions.
|
github_jupyter
|
# ๆฅ็ๅฝๅๆ่ฝฝ็ๆฐๆฎ้็ฎๅฝ, ่ฏฅ็ฎๅฝไธ็ๅๆด้ๅฏ็ฏๅขๅไผ่ชๅจ่ฟๅ
# View dataset directory.
# This directory will be recovered automatically after resetting environment.
!ls /home/aistudio/data
# ๆฅ็ๅทฅไฝๅบๆไปถ, ่ฏฅ็ฎๅฝไธ็ๅๆดๅฐไผๆไน
ไฟๅญ. ่ฏทๅๆถๆธ
็ไธๅฟ
่ฆ็ๆไปถ, ้ฟๅ
ๅ ่ฝฝ่ฟๆ
ข.
# View personal work directory.
# All changes under this directory will be kept even after reset.
# Please clean unnecessary files in time to speed up environment loading.
!ls /home/aistudio/work
# ๅฆๆ้่ฆ่ฟ่กๆไน
ๅๅฎ่ฃ
, ้่ฆไฝฟ็จๆไน
ๅ่ทฏๅพ, ๅฆไธๆนไปฃ็ ็คบไพ:
# If a persistence installation is required,
# you need to use the persistence path as the following:
!mkdir /home/aistudio/external-libraries
!pip install beautifulsoup4 -t /home/aistudio/external-libraries
# ๅๆถๆทปๅ ๅฆไธไปฃ็ , ่ฟๆ ทๆฏๆฌก็ฏๅข(kernel)ๅฏๅจ็ๆถๅๅช่ฆ่ฟ่กไธๆนไปฃ็ ๅณๅฏ:
# Also add the following code,
# so that every time the environment (kernel) starts,
# just run the following code:
import sys
sys.path.append('/home/aistudio/external-libraries')
#่งฃๅๆฐๆฎ้
!unzip -qo data/data102901/train_50k_mask.zip -d data/
!unzip -oq data/data102901/Bๆฆๆต่ฏๆฐๆฎ้.zip -d data/
!unzip -oq data/data102901/train_image.zip -d data/
!unzip -oq /home/aistudio/data/data102949/model.zip
!unzip -oq /home/aistudio/PaddleSeg.zip
import sys
import paddle
import numpy as np
import os
import matplotlib.pyplot as plt
from PIL import Image
from tqdm import tqdm
import random
#ๅฏนlabelๅพ็่ฟ่กๅๅพๅไบๅผๅๅค็
#PaddleSeg้็จๅ้้็ๆ ๆณจๅพ็๏ผๆฏไธ็งๅ็ด ๅผไปฃ่กจไธ็ง็ฑปๅซ๏ผๅ็ด ๆ ๆณจ็ฑปๅซ้่ฆไป0ๅผๅง้ๅข
import cv2
import matplotlib.pyplot as plt
for filename in os.listdir("data/train_50k_mask"):
print(filename)
k=os.path.join("data/train_50k_mask",filename)
for filenamel in os.listdir(k):
kt=os.path.join(k,filenamel)
img = cv2.imread(kt)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
difference = (img_gray.max() - img_gray.min()) // 2
_, img_binary = cv2.threshold(img_gray, difference, 1, cv2.THRESH_BINARY)
cv2.imwrite(kt, img_binary)
plt.imshow(img_binary)
plt.show()
import sys
import paddle
import numpy as np
import os
import matplotlib.pyplot as plt
from PIL import Image
import random
#่ฏปๅ
ฅๆฐๆฎ็ฎๅฝ๏ผๆผๆฅimagesไธlabels
datas_list=[]
for filename in os.listdir("data/train_image"):
k=os.path.join("data/train_image",filename)
kt=os.path.join("data/train_50k_mask",filename)
for filenamel in os.listdir(k):
datas_list.append([os.path.join(k,filenamel),os.path.join(kt,filenamel)])
#ๆไนฑๆฐๆฎ
random.shuffle(datas_list)
#ๅๅๆฐๆฎ้
train_list= datas_list[ : int(len(datas_list)*0.9)]
test_list = datas_list[int(len(datas_list)*0.9):]
print(len(train_list))
print(len(test_list))
#็ๆtxtๆไปถ
with open('train.txt',"a+") as train_file:
for k in range(len(train_list)):
train_file.write("%s %s\n"%(train_list[k][0],train_list[k][1]))
with open('val.txt',"a+") as train_file:
for k in range(len(test_list)):
train_file.write("%s %s\n"%(test_list[k][0],test_list[k][1]))
import glob
path = glob.glob('data/test_image/*')
f = open('test.txt', 'w')
for i in path:
f.write(i+'\n')
f.close()
%cd ~/
batch_size: 32
iters: 40000
train_dataset:
type: Dataset
dataset_root: /home/aistudio
train_path: /home/aistudio/train.txt
num_classes: 2
transforms:
- type: RandomHorizontalFlip
- type: RandomVerticalFlip
- type: RandomDistort
brightness_range: 0.4
contrast_range: 0.4
saturation_range: 0.4
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: train
val_dataset:
type: Dataset
dataset_root: /home/aistudio
val_path: /home/aistudio/val.txt
num_classes: 2
transforms:
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: val
model:
type: SegmentationTransformer
backbone:
type: ViT_large_patch16_384
pretrained: https://bj.bcebos.com/paddleseg/dygraph/vit_large_patch16_384.tar.gz
num_classes: 2
backbone_indices: [9, 14, 19, 23]
head: pup
align_corners: True
optimizer:
type: sgd
momentum: 0.9
weight_decay: 4.0e-5
lr_scheduler:
type: PolynomialDecay
learning_rate: 0.01
end_lr: 1.0e-4
power: 0.9
loss:
types:
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
- type: CrossEntropyLoss
coef: [1, 0.4, 0.4, 0.4, 0.4]
#ๅผๅง่ฎญ็ป
!python PaddleSeg/train.py --config setr.yaml --do_eval --use_vdl --save_dir /home/aistudio/output_setr --save_interval 2000
batch_size: 32
iters: 40000
train_dataset:
type: Dataset
dataset_root: /home/aistudio
train_path: /home/aistudio/train.txt
num_classes: 2
transforms:
- type: RandomHorizontalFlip
- type: RandomVerticalFlip
- type: RandomDistort
brightness_range: 0.4
contrast_range: 0.4
saturation_range: 0.4
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: train
val_dataset:
type: Dataset
dataset_root: /home/aistudio
val_path: /home/aistudio/val.txt
num_classes: 2
transforms:
- type: Resize
target_size: [256, 256]
- type: Normalize
mode: val
model:
type: DNLNet
backbone:
type: ResNet50_vd
output_stride: 8
pretrained: https://bj.bcebos.com/paddleseg/dygraph/resnet50_vd_ssld_v2.tar.gz
optimizer:
type: sgd
momentum: 0.9
weight_decay: 4.0e-5
lr_scheduler:
type: PolynomialDecay
learning_rate: 0.01
end_lr: 0
power: 0.9
loss:
types:
- type: CrossEntropyLoss
- type: CrossEntropyLoss
coef: [1, 0.4]
#ๅผๅง่ฎญ็ป
!python PaddleSeg/train.py --config DNLNet.yaml --do_eval --use_vdl --save_dir /home/aistudio/output_DNLNet_1 --save_interval 2000
#ๅผๅง้ช่ฏ
!python PaddleSeg/val.py --config_1 DNLNet.yaml --model_path_1 dnl.pdparams --config_2 setr.yaml --model_path_2 ster.pdparams
#ๅผๅง้ขๆต
!python PaddleSeg/predict.py --config_1 DNLNet.yaml --model_path_1 dnl.pdparams --config_2 setr.yaml --model_path_2 ster.pdparams --image_path data/test_image --save_dir output/result --aug_pred --flip_horizontal --flip_vertical
%cd PaddleSeg
!zip -r -oq /home/aistudio/PaddleSeg.zip ./
#ๅ็ผฉ้ขๆตๆไปถไพฟไบๆไบค
%cd output/result/results
!zip -r -oq /home/aistudio/preddouble.zip ./
%cd /home/aistudio
| 0.249813 | 0.645399 |
# Which Plot Type Should I Use?
**This a _brief_ listing of common graphs and their functions**
The functions below are but a little tasting of common plots, and I'm not specifying parameters beyond the utterly necessary. `pd` and `sns` functions get their flexibility from the wide assortment of parameters you can alter. Changing the parameters a bit can produce large (and interesting!) alterations. For example, `col` and `hue` typically _**multiply**_ the amount of info in a graph.
You can either read the function's documentation (and I frequently do!) via `SHIFT+TAB` or look through the
graph example galleries [here](https://www.data-to-viz.com) and [here](https://python-graph-gallery.com) until you see graphs with features you want, and then you can look at how they are made.
```{tip}
I would absolutely bookmark these links:
- [data to viz](https://www.data-to-viz.com)
- [py graph gallary](https://python-graph-gallery.com)
- [seaborn gallery](https://seaborn.pydata.org/examples/index.html)
```
## Common plot functions
````{dropdown} Examining one variable
```{note}
Below, if I call something like `df['variable'].<someplottype>` that means we are using `pandas` built in plotting methods. Else, we call `sns` to use `seaborn`.
```
If the variable is called $x$ in the dataset,
| Graph | Code example |
|:---|:---|
| frequency count | `df['x'].value_counts().plot.bar() # built in pandas fnc` <br> `df['x'].value_counts()[:10].plot.bar() # only the top 10 values` <br> `sns.countplot(data=df, x='x') ` |
| histogram | `sns.displot(data=df, x='x')` <br> `sns.displot(data=df, x='x',bins=15) # lots of opts, one is num of bins` |
| KDE (Kernel density est.) | `sns.displot(data=df, x='x',kind='kde')` <br> `sns.displot(data=df, x='x',kde=True) # includes both kde and hist by default` |
| boxplot | `sns.boxplot(x="x", data=df)` |
The `countplot`/bar graph counts frequency of values (# of times that value exists) within a variable, and is best when there are fewer possible values or when the variable is categorical instead of numerical (e.g. the color of a car).
The others examine the distribution of values for numerical variables (not categorical) and also work on continuous variables or those with many values.
````
````{dropdown} Examining one variable by group
If you want to examine $y$ for each group in $group$
| Graph | Code example |
|:---|:---|
| boxplot | `sns.boxplot(x="group",y="y", data=df)` |
| distplot | `sns.FacetGrid(temp_df, hue="group").map(sns.kdeplot, "y")` <br><br> `kdeplot` is the KDE plot portion of `distplot`. <br> FacetGrid is something we should defer talking about.... |
| violinplot | `sns.catplot(x="group",y="y", data=df, kind='violin')` <br> **`catplot`** can quickly plot many different types of categorical plots! |
```{tip}
Most functions accept some subset of `hue`, `row`, `col`, `style`, `size`. Each of these add [new facets](#faceting) to your graphs. Facets are ways of either repeating graphs for different subgroups or overlaying figures for different subgroups on each other.
```
````
````{dropdown} Examining two variables
| Graph | Code example |
|:---|:---|
| line | `sns.lineplot(x="x", y="y", data=df)` |
| scatterplot | `sns.scatterplot(x="x", y="y", data=df)` |
| scatter + density | `sns.jointplot(x="x", y="y", data=df)` |
| with fit line | `sns.jointplot(x="x", y="y", data=df,kind=reg) # regress to get fit` |
| hexbin | `sns.jointplot(x=x, y=y, kind="hex") # possibly better than scatter with larger data` |
| topograph | `sns.jointplot(x=x, y=y, kind="kde") topo map with kde on sides` |
| pairwise scatter | `sns.pairplot(df[['x','y','z']])` <br> `sns.pairplot(df[['x','y','z']],kind='reg) # add fit lines` |
````
````{dropdown} Examining two variables by group
| Graph | Code example |
|:---|:---|
| line | `sns.lineplot(x="x", y="y", data=df,hue='group')` |
| scatterplot | `sns.scatterplot(x="x", y="y", data=df,hue='group')` |
| pairplot | `sns.pairplot(df,hue='group')`
You will come across times where you think the relationship between $x$ and $y$ might on a third variable, $z$, or maybe even a fourth variable $w$. For example, age and income are related, but the relationship is different for college educated women than it is for high-school only men.
If you want to examine the relationship of $x$ and $y$ for each group in $group$, you can do so using any two-way plot type (scatter and its cousins).
```{admonition} Hue vs Col
Some functions achieve the group analysis with a `hue` argument (give different groups different colors) and some do it with `col` (give different groups different subfigures).
```
````
## Faceting
**Facets** allow you to present more info on a graph by designing a plot for a subset of the data, and quickly repeating it for other parts.
You can think of facets as either
1. creating subfigures
- the `pairplot` below creates subfigures for each combination of variables in the dataset
- the [Anscombe example](04b-whyplot.html#summary-statistics-don-t-show-relationships) makes subfigures for subsets of the data
2. or overlaying figures on top of each other in a single figure
- the categorical `boxplot` below does this for each sub group
- the ["omitted group effects"](04b-whyplot.html#finding-group-effects)
Let's look at some examples quickly:
```
import seaborn as sns
import matplotlib.pyplot as plt
iris = sns.load_dataset("iris")
sns.pairplot(iris)
plt.suptitle('Faceting by repeating scatter plots for each pair of variables',fontsize=18)
plt.subplots_adjust(top=0.95) # Reduce plot to make room for the title
plt.show()
# note: .set(title) doesn't work here - it tries to title the individual subfigures (axes)
# to title the whole thing, I had to use suptitle.
sns.pairplot(iris, hue="species")
plt.suptitle('Faceting by overlaying figures by group',fontsize=18)
plt.subplots_adjust(top=0.95) # Reduce plot to make room for the title
plt.show()
```
Boxplot by group: Just use the `x` and `y` arguments together.
```
sns.boxplot(x="species",y="petal_width", data=iris,)
plt.show()
```
An example of faceting via the `col` argument. Using `row` instead does what you'd think. Protip: You can use `row` and `col` together to make a grid of groups.
```
sns.lmplot(data=iris,x='petal_width',y="petal_length",col="species")
plt.show()
sns.lmplot(data=iris,x='petal_width',y="petal_length",col="species")
plt.show()
sns.lmplot(data=iris,x='petal_width',y="petal_length",hue="species")
plt.show()
```
### I want to `Facet` my figure, but...
**Problem:** The variable you want to facet/group by is
- (A) continuous variable
- or (B) a variable with too many values.
**Solutions:**
- (A) - partition/slice/factor your variable into bins using `panda`'s [`cut` function](https://pandas.pydata.org/pandas-docs/version/0.23.4/generated/pandas.cut.html).
- (B) - re-factor the variables into a smaller number of groups, or only graph some of them.
**For example:** Say you want to plot how age and death are related, and you want to plot this for healthy people and less-healthy people. So you collect the BMI of individuals in your sample. Let's say that BMI can take 25 values from 15 to 40. The problem is plotting 20 sub-figures is probably excessive. The solution is to use the `cut` function to create a new variable which is four bins of BMI [according to the UK's NHS](https://www.nhs.uk/common-health-questions/lifestyle/what-is-the-body-mass-index-bmi/): underweight (BMI<18.5), healthy (BMI 18.5-24.5), overweight (BMI 24.5-30), obese (BMI>30).
## Practice: Thinking and planning
**Questions:** Which type of graph (bar, line, or histogram) would you use?
1. The volume of apples picked at an orchard based on the type of apple (Granny Smith, Fuji, etcetera).
2. The number of points for each game in a basketball season for a team.
3. The count of apartment buildings in Chicago by the number of individual units.
**Answers**
```{dropdown} Q1
This is a nominal categorical example, and hence, a pretty straightforward bar graph target.
```
```{dropdown} Q2
This is a (nearly) continuous variable, with 82 observations (games). 82 bars is too much for a bar chart. But a line chart, histogram (or density plot), or boxplot would all work.
```
```{dropdown} Q3
Density chart would work, but you could also use a histogram as long as you "bin" apartment buildings (<10 units, 10-50 units, etc...) Note that this variable will be skewed because only a few buildings have 500+ units.
```
|
github_jupyter
|
## Common plot functions
If the variable is called $x$ in the dataset,
| Graph | Code example |
|:---|:---|
| frequency count | `df['x'].value_counts().plot.bar() # built in pandas fnc` <br> `df['x'].value_counts()[:10].plot.bar() # only the top 10 values` <br> `sns.countplot(data=df, x='x') ` |
| histogram | `sns.displot(data=df, x='x')` <br> `sns.displot(data=df, x='x',bins=15) # lots of opts, one is num of bins` |
| KDE (Kernel density est.) | `sns.displot(data=df, x='x',kind='kde')` <br> `sns.displot(data=df, x='x',kde=True) # includes both kde and hist by default` |
| boxplot | `sns.boxplot(x="x", data=df)` |
The `countplot`/bar graph counts frequency of values (# of times that value exists) within a variable, and is best when there are fewer possible values or when the variable is categorical instead of numerical (e.g. the color of a car).
The others examine the distribution of values for numerical variables (not categorical) and also work on continuous variables or those with many values.
import seaborn as sns
import matplotlib.pyplot as plt
iris = sns.load_dataset("iris")
sns.pairplot(iris)
plt.suptitle('Faceting by repeating scatter plots for each pair of variables',fontsize=18)
plt.subplots_adjust(top=0.95) # Reduce plot to make room for the title
plt.show()
# note: .set(title) doesn't work here - it tries to title the individual subfigures (axes)
# to title the whole thing, I had to use suptitle.
sns.pairplot(iris, hue="species")
plt.suptitle('Faceting by overlaying figures by group',fontsize=18)
plt.subplots_adjust(top=0.95) # Reduce plot to make room for the title
plt.show()
sns.boxplot(x="species",y="petal_width", data=iris,)
plt.show()
sns.lmplot(data=iris,x='petal_width',y="petal_length",col="species")
plt.show()
sns.lmplot(data=iris,x='petal_width',y="petal_length",col="species")
plt.show()
sns.lmplot(data=iris,x='petal_width',y="petal_length",hue="species")
plt.show()
```{dropdown} Q2
This is a (nearly) continuous variable, with 82 observations (games). 82 bars is too much for a bar chart. But a line chart, histogram (or density plot), or boxplot would all work.
| 0.822617 | 0.985552 |
# Mixed lubrication modelling by the semi system approach
Slippy contains the powerful unified Reynoldโs solver which can solve a wide variety of lubrication problems from Hertzian contact/ boundary lubrication to mixed lubrication and full EHL contacts. This can be done for non-Newtonian fluids including user defined or built-in models and rough surfaces. Using sub models for wear, friction, flash temperature, tribofilm growth, etc. full simulations can be carried out with any user defined behaviour.
Clearly this is a powerful and flexible tool. In this notebook, we will use this solver to solve the oil lubricated contact between a ball and a plane. This process has the steps defined below:
- Import slippy
- Solve the Hertzian contact problem as an initial guess for the solution and to set sensible bounds for the solution domain
- Make the surfaces
- Assign materials to the surfaces
- Make the lubricant and assign non-Newtonian sub models to it
- Make a contact model with the surfaces and the lubricant
- Make a Reynoldโs solver object
- Make a lubrication model step with the Reynoldโs solver
- Add this step to the contact model
- Data check the contact model
- Solve the contact model
- Analyse the result
```
%matplotlib inline
# Importing slippy
import slippy
slippy.CUDA = False
import slippy.surface as S
import slippy.contact as C
```
# Defining constants
The next cell contains all the constants which we will use in the model, these can be edited for different situations:
```
radius = 0.01905 # The radius of the ball
load = 800 # The load on the ball in N
rolling_speed = 4 # The rolling speed in m/s (The mean speed of the surfaces)
youngs_modulus = 200e9 # The youngs modulus of the surfaces
p_ratio = 0.3 # The poission's ratio of the surfaces
grid_size = 65 # The number of points in the descretisation grid
eta_0 = 0.096 # Coefficient in the roelands pressure-viscosity equation
roelands_p_0 = 1/5.1e-9# Coefficient in the roelands pressure-viscosity equation
roelands_z = 0.68 # Coefficient in the roelands pressure-viscosity equation
```
# Solving the Hertzian problem
Slippy contains a comprehensive hertz solver that will provide all the parameters we need to initialise the solution. This can be found in the contact sub package:
```
# Solving the hertzian contact
hertz_result = C.hertz_full([radius, radius], [float('inf'), float('inf')],
[youngs_modulus, youngs_modulus],
[p_ratio, p_ratio], load)
hertz_pressure = hertz_result['max_pressure']
hertz_a = hertz_result['contact_radii'][0]
hertz_deflection = hertz_result['total_deflection']
hertz_pressure_function = hertz_result['pressure_f']
```
# Making the surface objects
Next, we will make define the geometry of the contacting surfaces. We can use analytically defined surfaces for this. In any contact model the 'master' surface must be discretised to the resolution of the solution grid. We can discretise the round surface to the correct grid size by setting its shape and extent and setting generate to True when the surface is made.
We can view the surface profile by calling the show() method on the surface.
```
ball = S.RoundSurface((radius,)*3, shape = (grid_size, grid_size),
extent=(hertz_a*4,hertz_a*4), generate = True)
flat = S.FlatSurface()
ball.show()
```
# Assigning materials to the surfaces
Now we must define how the surfaces deflect under load. This is done by setting the material property of the surfaces. If we wanted to model pure HDL, we could set theses to rigid materials, but here we will model full EHL by using an elastic material.
Any material object that supplies a displacement_from_surface_loads method can be used here.
```
steel = C.Elastic('steel', {'E' : youngs_modulus, 'v' : p_ratio})
ball.material = steel
flat.material = steel
```
# Making the lubricant
Now we must define how the lubricant flows under pressure and any non-Newtonian behaviour that we want to model. Our lubricant must have sub models for each of the fluid parameters in our chosen Reynoldโs solver's requires property. In this case that is the non-dimensional viscosity and the non-dimensional pressure. If any of the needed models are missed it will be caught in the data check stage.
Here we will add a Roelandโs model for the viscosity and a Dowson Higginson model for the density. These are defined as shown below:
Roeland's:
$$\frac{\eta(P)}{\eta_0} = exp\left(\left(ln(\eta_0)+9.67\right)\left(-1+\left(1+\frac{P p_h}{p_0}\right)^z\right)\right)$$
In which $P$ is the non dimensional pressure, $\frac{\eta(P)}{\eta_0}$ is the non dimensional viscosity, $p_h$ is the Hertzian pressure and $p_o$, $\eta_0$ are parameters specific to each oil.
Dowson-Higginson:
$$\frac{\rho(P)}{\rho_0} = \frac{5.9e8+1.34p_hP}{5.9e8+p_hP}$$
In which $P$ is the non dimensional pressure, $\frac{\rho(P)}{\rho_0}$ is the non dimensional density, and $p_h$ is the Hertzian pressure and $\rho_0$ is the density at ambient pressure.
**Sub models added to the lubricant will be run on every iteration of the solver. Models for wear or friction etc should be added to the step or the contact model, these are run on each step after the normal contact has been solved.**
```
print(C.UnifiedReynoldsSolver.requires) # looking at the requires property of our chosen solver
oil = C.Lubricant('oil') # Making a lubricant object to contain our sub models
oil.add_sub_model('nd_viscosity', C.lubricant_models.nd_roelands(eta_0, roelands_p_0, hertz_pressure, roelands_z))
oil.add_sub_model('nd_density', C.lubricant_models.nd_dowson_higginson(hertz_pressure)) # adding dowson higginson
```
# Making a contact model
Now we will make a contact model to coordinate solving our steps, contact models can contain any number of solution steps to be solved. They also handle file output for long simulations. For our single step simulation, we do not need file outputs.
The first argument of the contact model is the name, this will be used for the log file and the output files. The second argument is the master surface, this must be discretised.
```
my_model = C.ContactModel('lubrication_test', ball, flat, oil)
```
# Making a Reynoldโs solver
There are many ways to solve a Reynoldโs equation, as such Reynoldโs solvers are separate object in slippy. The Reynoldโs solver you choose will depend on the situation you are trying to model but these can be used interchangeably in the lubrication steps.
Our Reynoldโs solver is non dimensional and as such must take all the parameters which are used to non-denationalise the problem, the exact parameters needed will change from solver to solver, the documentation for your particular solver should be consulted.
```
reynolds = C.UnifiedReynoldsSolver(time_step = 0,
grid_spacing = ball.grid_spacing,
hertzian_pressure = hertz_pressure,
radius_in_rolling_direction=radius,
hertzian_half_width=hertz_a,
dimentional_viscosity=eta_0,
dimentional_density=872)
```
# Making a lubrication step and adding it to the model
The unified Reynoldโs solver only solves the fluid pressure problem. To solve the full EHL problem we need to use this with a model step. This step coordinates solving each of the semi systems (fluid pressure, material deflection, pressure-viscosity, pressure-density) as well as checking for convergence in the solution.
To make the solution converge faster we can provide an initial guess of the pressure distribution from the Hertzian solution we found earlier. We can also add any options which we want to pass to the material objects, and iteration controls like the required accuracy, the maximum number of iterations and the relaxation factor used for the pressure result.
Lastly, we need to add this step to our contact model.
```
# Find the hertzian pressure distribution as an initial guess
X, Y = ball.get_points_from_extent()
X, Y = X + ball._total_shift[0], Y + ball._total_shift[1]
hertzian_pressure_dist = hertz_pressure_function(X, Y)
# Making the step object
step = C.IterSemiSystem('main', reynolds, rolling_speed, 1, no_time=True, normal_load=load,
initial_guess=[hertz_deflection, hertzian_pressure_dist],
relaxation_factor=0.05, max_it_interference=3000)
# Adding the step to the contact model
my_model.add_step(step)
```
# Data checking the model
There are many potential problems that can arise during solution of a contact model. data checking the model will ensure that during the solution each requirement of all the sub models, Reynoldโs solvers, steps, and outputs will be fulfilled when they are called. A model failing to write your required outputs can waste a lot of time, so it is always best not to skip this step.
*It will not ensure that your result will converge or that the result will resemble reality in any way. For this you must validate against experimental measurements, tinker with iteration controls or do some maths (hopefully not).*
```
my_model.data_check()
```
# Solving the model
Now we are ready to solve the model!
This is easy, by default the solve method will return the final state of the model as a dict, it will also write all requested outputs to a file.
```
state = my_model.solve()
print(f"Result converged: {state['converged']}")
```
# Plotting our results
To plot our results we need to import some plotting packages
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
```
# Full pressure distribution
```
fig = plt.figure(figsize=(8,5))
ax = fig.gca(projection='3d')
ax.plot_trisurf(X.flatten()/hertz_a, Y.flatten()/hertz_a, state['nd_pressure'].flatten(),
cmap=plt.cm.viridis, linewidth=0.2)
ax.set_xlabel('ND length')
ax.set_ylabel('ND length')
ax.set_zlabel('ND pressure')
ax.set_title('Pressure distribution')
plt.show()
```
# Gap
```
state['gap'][state['gap']<0.5e-9] = 0.5e-9
plt.imshow(np.log(state['gap']))
```
# Central pressure distribution
```
plt.plot(X[:,0]/hertz_a,state['nd_pressure'][:,32], label='Lubricated')
plt.plot(X[:,0]/hertz_a,hertzian_pressure_dist[:,32]/hertz_pressure, label='Hertz')
ax = plt.gca()
ax.set_xlabel('Nondimensional length')
ax.set_ylabel('Nondimensional pressure')
ax.set_title('Central pressure distribution')
```
# Central film thickness
```
plt.plot(X[:,0]/hertz_a, state['gap'][:,32]/hertz_a)
ax = plt.gca()
ax.set_xlabel('Nondimensional length')
ax.set_ylabel('Nondimensional film thickness')
ax.set_title('Central film thickness')
```
|
github_jupyter
|
%matplotlib inline
# Importing slippy
import slippy
slippy.CUDA = False
import slippy.surface as S
import slippy.contact as C
radius = 0.01905 # The radius of the ball
load = 800 # The load on the ball in N
rolling_speed = 4 # The rolling speed in m/s (The mean speed of the surfaces)
youngs_modulus = 200e9 # The youngs modulus of the surfaces
p_ratio = 0.3 # The poission's ratio of the surfaces
grid_size = 65 # The number of points in the descretisation grid
eta_0 = 0.096 # Coefficient in the roelands pressure-viscosity equation
roelands_p_0 = 1/5.1e-9# Coefficient in the roelands pressure-viscosity equation
roelands_z = 0.68 # Coefficient in the roelands pressure-viscosity equation
# Solving the hertzian contact
hertz_result = C.hertz_full([radius, radius], [float('inf'), float('inf')],
[youngs_modulus, youngs_modulus],
[p_ratio, p_ratio], load)
hertz_pressure = hertz_result['max_pressure']
hertz_a = hertz_result['contact_radii'][0]
hertz_deflection = hertz_result['total_deflection']
hertz_pressure_function = hertz_result['pressure_f']
ball = S.RoundSurface((radius,)*3, shape = (grid_size, grid_size),
extent=(hertz_a*4,hertz_a*4), generate = True)
flat = S.FlatSurface()
ball.show()
steel = C.Elastic('steel', {'E' : youngs_modulus, 'v' : p_ratio})
ball.material = steel
flat.material = steel
print(C.UnifiedReynoldsSolver.requires) # looking at the requires property of our chosen solver
oil = C.Lubricant('oil') # Making a lubricant object to contain our sub models
oil.add_sub_model('nd_viscosity', C.lubricant_models.nd_roelands(eta_0, roelands_p_0, hertz_pressure, roelands_z))
oil.add_sub_model('nd_density', C.lubricant_models.nd_dowson_higginson(hertz_pressure)) # adding dowson higginson
my_model = C.ContactModel('lubrication_test', ball, flat, oil)
reynolds = C.UnifiedReynoldsSolver(time_step = 0,
grid_spacing = ball.grid_spacing,
hertzian_pressure = hertz_pressure,
radius_in_rolling_direction=radius,
hertzian_half_width=hertz_a,
dimentional_viscosity=eta_0,
dimentional_density=872)
# Find the hertzian pressure distribution as an initial guess
X, Y = ball.get_points_from_extent()
X, Y = X + ball._total_shift[0], Y + ball._total_shift[1]
hertzian_pressure_dist = hertz_pressure_function(X, Y)
# Making the step object
step = C.IterSemiSystem('main', reynolds, rolling_speed, 1, no_time=True, normal_load=load,
initial_guess=[hertz_deflection, hertzian_pressure_dist],
relaxation_factor=0.05, max_it_interference=3000)
# Adding the step to the contact model
my_model.add_step(step)
my_model.data_check()
state = my_model.solve()
print(f"Result converged: {state['converged']}")
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
fig = plt.figure(figsize=(8,5))
ax = fig.gca(projection='3d')
ax.plot_trisurf(X.flatten()/hertz_a, Y.flatten()/hertz_a, state['nd_pressure'].flatten(),
cmap=plt.cm.viridis, linewidth=0.2)
ax.set_xlabel('ND length')
ax.set_ylabel('ND length')
ax.set_zlabel('ND pressure')
ax.set_title('Pressure distribution')
plt.show()
state['gap'][state['gap']<0.5e-9] = 0.5e-9
plt.imshow(np.log(state['gap']))
plt.plot(X[:,0]/hertz_a,state['nd_pressure'][:,32], label='Lubricated')
plt.plot(X[:,0]/hertz_a,hertzian_pressure_dist[:,32]/hertz_pressure, label='Hertz')
ax = plt.gca()
ax.set_xlabel('Nondimensional length')
ax.set_ylabel('Nondimensional pressure')
ax.set_title('Central pressure distribution')
plt.plot(X[:,0]/hertz_a, state['gap'][:,32]/hertz_a)
ax = plt.gca()
ax.set_xlabel('Nondimensional length')
ax.set_ylabel('Nondimensional film thickness')
ax.set_title('Central film thickness')
| 0.575588 | 0.986764 |
# ะะฐะดะฐัะฐ 1
ะัะพะตะบัะธัะพะฒะฐะฝะธะต ััะฝะบัะธะน ะดะปั ะฟะพัััะพะตะฝะธั ะพะฑััะฐััะธั
ะผะพะดะตะปะตะน ะฟะพ ะดะฐะฝะฝัะผ. ะ ะดะฐะฝะฝะพะน ะทะฐะดะฐัะฐ ะฒะฐะผ ะฝัะถะฝะพ ัะฐะทัะฐะฑะพัะฐัั ะฟัะพัะพัะธะฟั ััะฝะบัะธะน(ะพะฑััะฒะปะตะฝะธะต ััะฝะบัะธะน ะฑะตะท ัะตะฐะปะธะทะฐัะธะน) ะดะปั ะทะฐะดะฐัะธ ะฐะฝะฐะปะธะทะฐ ะดะฐะฝะฝัั
ะธะท ะผะฐัะธะฝะฝะพะณะพ ะพะฑััะตะฝะธั, ะดะพะปะถะฝั ะฑััั ัััะตะฝั ัะปะตะดัััะธะต ัะฐะณะธ:
* ะะฐะณััะทะบะฐ ะดะฐะฝะฝัั
ะธะท ะฒะฝะตัะฝะธั
ะธััะพัะฝะธะบะพะฒ
* ะะฑัะฐะฑะพัะบะฐ ะฝะต ะทะฐะดะฐะฝะฝัั
ะทะฝะฐัะตะฝะธะน - ะฟัะพะฟััะบะพะฒ
* ะฃะดะฐะปะตะฝะธะต ะฝะต ะธะฝัะพัะผะฐัะธะฒะฝัั
ะฟัะธะทะฝะฐะบะพะฒ ะธ ะพะฑัะตะบัะพะฒ
* ะะพะปััะตะฝะธะต ะผะพะดะตะปะธ ะดะปั ะพะฑััะตะฝะธั
* ะัะตะฝะบะฐ ะบะฐัะตััะฒะฐ ะผะพะดะตะปะธ
* ะกะพั
ัะฐะฝะตะฝะธะต ะผะพะดะตะปะธ ะฒ ัะฐะนะป
```
def prototype(params1, lambda1):
pass
prototype((1,2), lambda x: x/2)
def load_external(source, mode='raw'):
'''
Load dataset from source with choosen mode
Parameters:
source - filepath or url
mode - preprocess mode
Returns:
loaded dataset
'''
pass
def process_gaps(dataset, mode='remove'):
'''
Remove/fill data gaps
Parameters:
dataset - processing data
mode - action over gaps: 'remove'/'fill'
'''
pass
def remove_unessential(dataset):
'''
Remove unnecessary dataset columns and rows
Parameters:
dataset - processing data
'''
pass
def create_model(dataset, structure, **args):
'''
Create model with defined structure
Parameters:
dataset
structure - model structure
args - additional structure parameters
Returns:
created model
'''
pass
def evaluate_model(model, test_dataset):
'''
Evaluates model fitness to given dataset
Parameters:
model - model to evaluate
test_dataset - data input and output
Returns:
float number from 0.0(unfit model) to 1.0(perfect model)
'''
pass
def save_model(filepath, model):
'''
Save given model to file.
Parameters:
filepath - saving path
model - model to be saved
Returns:
False if could not save model
True if model has been saved successfully
'''
pass
dataset = load_external('dataset.csv')
process_gaps(dataset, 'fill')
remove_unessential(dataset)
... (get model structure)
model = create_model(train_dataset, structure)
... (training)
eval = evaluate_model(model, test_dataset)
if eval >= MIN_FITNESS:
save_model('trained_model.model', model)
```
# ะะฐะดะฐัะฐ 2
ะะฐะดะฐัะฐ ะฟะพะฒััะตะฝะฝะพะน ัะปะพะถะฝะพััะธ. ะ ะตะฐะปะธะทะพะฒะฐัั ะฒัะฒะพะด ััะตัะณะพะปัะฝะธะบะฐ ะฟะฐัะบะฐะปั, ัะตัะตะท ััะฝะบัะธั. ะัะธะผะตั ััะตัะณะพะปัะฝะธะบะฐ:
ะะปัะฑะธะฝะฐ 10 ะฟะพ ัะผะพะปัะฐะฝะธั
```
def pascal_triangle(depth=10, use_min_width=False):
if depth < 0:
print('error: negative depth')
return
layers = [[1]]
for cur_depth in range(1, depth+1):
prev_layer = layers[cur_depth - 1]
layers.append([1])
for i in range(cur_depth - 1):
layers[cur_depth].append(prev_layer[i] + prev_layer[i + 1])
layers[cur_depth].append(1)
lengths = []
if use_min_width:
for i in range(depth):
lengths.append(len(str(layers[depth][i])))
lengths.append(len(str(layers[depth - 1][i])))
lengths.append(len(str(layers[depth][depth]))) # always equals 1
else:
max_len = len(str(layers[depth][depth//2]))
lengths = [max_len]*(2*depth + 1)
for cur_depth in range(depth + 1):
offset = depth - cur_depth
len_offset = 0
for i in range(offset):
len_offset += lengths[i]
layer = layers[cur_depth]
print(' '*len_offset, end='')
for i in range(cur_depth):
len_gap = lengths[offset + 2*i] - len(str(layer[i]))
len_right = len_gap // 2
len_left = len_gap - len_right
print(' '*len_left, end='')
print(layer[i], end='')
print(' '*len_right, end='')
len_next_gap = lengths[offset + 2*i + 1]
print(' '*len_next_gap, end='')
len_gap = lengths[offset + 2*cur_depth] - len(str(layer[cur_depth]))
len_right = len_gap // 2
len_left = len_gap - len_right
print(' '*len_left, end='')
print(layer[cur_depth], end='')
print(' '*len_right, end='')
print(' '*len_offset, end='\n')
pascal_triangle(10, True)
pascal_triangle(10)
print('\n\n')
pascal_triangle(17, True)
pascal_triangle(15)
```
|
github_jupyter
|
def prototype(params1, lambda1):
pass
prototype((1,2), lambda x: x/2)
def load_external(source, mode='raw'):
'''
Load dataset from source with choosen mode
Parameters:
source - filepath or url
mode - preprocess mode
Returns:
loaded dataset
'''
pass
def process_gaps(dataset, mode='remove'):
'''
Remove/fill data gaps
Parameters:
dataset - processing data
mode - action over gaps: 'remove'/'fill'
'''
pass
def remove_unessential(dataset):
'''
Remove unnecessary dataset columns and rows
Parameters:
dataset - processing data
'''
pass
def create_model(dataset, structure, **args):
'''
Create model with defined structure
Parameters:
dataset
structure - model structure
args - additional structure parameters
Returns:
created model
'''
pass
def evaluate_model(model, test_dataset):
'''
Evaluates model fitness to given dataset
Parameters:
model - model to evaluate
test_dataset - data input and output
Returns:
float number from 0.0(unfit model) to 1.0(perfect model)
'''
pass
def save_model(filepath, model):
'''
Save given model to file.
Parameters:
filepath - saving path
model - model to be saved
Returns:
False if could not save model
True if model has been saved successfully
'''
pass
dataset = load_external('dataset.csv')
process_gaps(dataset, 'fill')
remove_unessential(dataset)
... (get model structure)
model = create_model(train_dataset, structure)
... (training)
eval = evaluate_model(model, test_dataset)
if eval >= MIN_FITNESS:
save_model('trained_model.model', model)
def pascal_triangle(depth=10, use_min_width=False):
if depth < 0:
print('error: negative depth')
return
layers = [[1]]
for cur_depth in range(1, depth+1):
prev_layer = layers[cur_depth - 1]
layers.append([1])
for i in range(cur_depth - 1):
layers[cur_depth].append(prev_layer[i] + prev_layer[i + 1])
layers[cur_depth].append(1)
lengths = []
if use_min_width:
for i in range(depth):
lengths.append(len(str(layers[depth][i])))
lengths.append(len(str(layers[depth - 1][i])))
lengths.append(len(str(layers[depth][depth]))) # always equals 1
else:
max_len = len(str(layers[depth][depth//2]))
lengths = [max_len]*(2*depth + 1)
for cur_depth in range(depth + 1):
offset = depth - cur_depth
len_offset = 0
for i in range(offset):
len_offset += lengths[i]
layer = layers[cur_depth]
print(' '*len_offset, end='')
for i in range(cur_depth):
len_gap = lengths[offset + 2*i] - len(str(layer[i]))
len_right = len_gap // 2
len_left = len_gap - len_right
print(' '*len_left, end='')
print(layer[i], end='')
print(' '*len_right, end='')
len_next_gap = lengths[offset + 2*i + 1]
print(' '*len_next_gap, end='')
len_gap = lengths[offset + 2*cur_depth] - len(str(layer[cur_depth]))
len_right = len_gap // 2
len_left = len_gap - len_right
print(' '*len_left, end='')
print(layer[cur_depth], end='')
print(' '*len_right, end='')
print(' '*len_offset, end='\n')
pascal_triangle(10, True)
pascal_triangle(10)
print('\n\n')
pascal_triangle(17, True)
pascal_triangle(15)
| 0.564579 | 0.9434 |
# 1. Get variables
```
keyvaultlsname = 'Ls_KeyVault_01'
adls2lsname = 'Ls_AdlsGen2_01'
```
# 2. Linked Services Setup: KV and ADLS Gen2
```
from pyspark.sql import SparkSession
sc = SparkSession.builder.getOrCreate()
token_library = sc._jvm.com.microsoft.azure.synapse.tokenlibrary.TokenLibrary
storage_account = token_library.getSecretWithLS(keyvaultlsname, "datalakeaccountname")
spark.conf.set("spark.storage.synapse.linkedServiceName", adls2lsname)
spark.conf.set("fs.azure.account.oauth.provider.type", "com.microsoft.azure.synapse.tokenlibrary.LinkedServiceBasedTokenProvider")
```
# 3. Create Schemas
```
spark.sql(f"CREATE SCHEMA IF NOT EXISTS dw LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS lnd LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS interim LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS malformed LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
```
# 4. Create Fact Tables
```
spark.sql(f"DROP TABLE IF EXISTS dw.fact_parking")
spark.sql(f"CREATE TABLE dw.fact_parking(dim_date_id STRING,dim_time_id STRING, dim_parking_bay_id STRING, dim_location_id STRING, dim_st_marker_id STRING, status STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/fact_parking/'")
spark.sql(f"REFRESH TABLE dw.fact_parking")
```
# 5. Create Dimension Tables
```
spark.sql(f"DROP TABLE IF EXISTS dw.dim_st_marker")
spark.sql(f"CREATE TABLE dw.dim_st_marker(dim_st_marker_id STRING, st_marker_id STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_st_marker/'")
spark.sql(f"REFRESH TABLE dw.dim_st_marker")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_location")
spark.sql(f"CREATE TABLE dw.dim_location(dim_location_id STRING,lat FLOAT, lon FLOAT, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_location/'")
spark.sql(f"REFRESH TABLE dw.dim_location")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_parking_bay")
spark.sql(f"CREATE TABLE dw.dim_parking_bay(dim_parking_bay_id STRING, bay_id INT,`marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_parking_bay/'")
spark.sql(f"REFRESH TABLE dw.dim_parking_bay")
```
# 6. Create dim date and time
```
from pyspark.sql.functions import col
spark.sql(f"DROP TABLE IF EXISTS dw.dim_date")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_time")
# DimDate
dimdate = spark.read.csv(f"abfss://datalake@{storage_account}.dfs.core.windows.net/data/seed/dim_date/dim_date.csv", header=True)
dimdate.write.saveAsTable("dw.dim_date")
# DimTime
dimtime = spark.read.csv(f"abfss://datalake@{storage_account}.dfs.core.windows.net/data/seed/dim_time/dim_time.csv", header=True)
dimtime.write.saveAsTable("dw.dim_time")
```
# 7. Create interim and error tables
```
spark.sql(f"DROP TABLE IF EXISTS interim.parking_bay")
spark.sql(f"CREATE TABLE interim.parking_bay(bay_id INT, `last_edit` TIMESTAMP, `marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, `the_geom` STRUCT<`coordinates`: ARRAY<ARRAY<ARRAY<ARRAY<DOUBLE>>>>, `type`: STRING>, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/interim/interim.parking_bay/'")
spark.sql(f"REFRESH TABLE interim.parking_bay")
spark.sql(f"DROP TABLE IF EXISTS interim.sensor")
spark.sql(f"CREATE TABLE interim.sensor(bay_id INT, `st_marker_id` STRING, `lat` FLOAT, `lon` FLOAT, `location` STRUCT<`coordinates`: ARRAY<DOUBLE>, `type`: STRING>, `status` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/interim/interim.sensor/'")
spark.sql(f"REFRESH TABLE interim.sensor")
spark.sql(f"DROP TABLE IF EXISTS malformed.parking_bay")
spark.sql(f"CREATE TABLE malformed.parking_bay(bay_id INT, `last_edit` TIMESTAMP,`marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, `the_geom` STRUCT<`coordinates`: ARRAY<ARRAY<ARRAY<ARRAY<DOUBLE>>>>, `type`: STRING>, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/malformed/malformed.parking_bay/'")
spark.sql(f"REFRESH TABLE malformed.parking_bay")
spark.sql(f"DROP TABLE IF EXISTS malformed.sensor")
spark.sql(f"CREATE TABLE malformed.sensor(bay_id INT,`st_marker_id` STRING,`lat` FLOAT,`lon` FLOAT,`location` STRUCT<`coordinates`: ARRAY<DOUBLE>, `type`: STRING>,`status` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/malformed/malformed.parking_bay/'")
spark.sql(f"REFRESH TABLE malformed.sensor")
```
|
github_jupyter
|
keyvaultlsname = 'Ls_KeyVault_01'
adls2lsname = 'Ls_AdlsGen2_01'
from pyspark.sql import SparkSession
sc = SparkSession.builder.getOrCreate()
token_library = sc._jvm.com.microsoft.azure.synapse.tokenlibrary.TokenLibrary
storage_account = token_library.getSecretWithLS(keyvaultlsname, "datalakeaccountname")
spark.conf.set("spark.storage.synapse.linkedServiceName", adls2lsname)
spark.conf.set("fs.azure.account.oauth.provider.type", "com.microsoft.azure.synapse.tokenlibrary.LinkedServiceBasedTokenProvider")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS dw LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS lnd LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS interim LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"CREATE SCHEMA IF NOT EXISTS malformed LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data'")
spark.sql(f"DROP TABLE IF EXISTS dw.fact_parking")
spark.sql(f"CREATE TABLE dw.fact_parking(dim_date_id STRING,dim_time_id STRING, dim_parking_bay_id STRING, dim_location_id STRING, dim_st_marker_id STRING, status STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/fact_parking/'")
spark.sql(f"REFRESH TABLE dw.fact_parking")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_st_marker")
spark.sql(f"CREATE TABLE dw.dim_st_marker(dim_st_marker_id STRING, st_marker_id STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_st_marker/'")
spark.sql(f"REFRESH TABLE dw.dim_st_marker")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_location")
spark.sql(f"CREATE TABLE dw.dim_location(dim_location_id STRING,lat FLOAT, lon FLOAT, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_location/'")
spark.sql(f"REFRESH TABLE dw.dim_location")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_parking_bay")
spark.sql(f"CREATE TABLE dw.dim_parking_bay(dim_parking_bay_id STRING, bay_id INT,`marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/dw/dim_parking_bay/'")
spark.sql(f"REFRESH TABLE dw.dim_parking_bay")
from pyspark.sql.functions import col
spark.sql(f"DROP TABLE IF EXISTS dw.dim_date")
spark.sql(f"DROP TABLE IF EXISTS dw.dim_time")
# DimDate
dimdate = spark.read.csv(f"abfss://datalake@{storage_account}.dfs.core.windows.net/data/seed/dim_date/dim_date.csv", header=True)
dimdate.write.saveAsTable("dw.dim_date")
# DimTime
dimtime = spark.read.csv(f"abfss://datalake@{storage_account}.dfs.core.windows.net/data/seed/dim_time/dim_time.csv", header=True)
dimtime.write.saveAsTable("dw.dim_time")
spark.sql(f"DROP TABLE IF EXISTS interim.parking_bay")
spark.sql(f"CREATE TABLE interim.parking_bay(bay_id INT, `last_edit` TIMESTAMP, `marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, `the_geom` STRUCT<`coordinates`: ARRAY<ARRAY<ARRAY<ARRAY<DOUBLE>>>>, `type`: STRING>, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/interim/interim.parking_bay/'")
spark.sql(f"REFRESH TABLE interim.parking_bay")
spark.sql(f"DROP TABLE IF EXISTS interim.sensor")
spark.sql(f"CREATE TABLE interim.sensor(bay_id INT, `st_marker_id` STRING, `lat` FLOAT, `lon` FLOAT, `location` STRUCT<`coordinates`: ARRAY<DOUBLE>, `type`: STRING>, `status` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/interim/interim.sensor/'")
spark.sql(f"REFRESH TABLE interim.sensor")
spark.sql(f"DROP TABLE IF EXISTS malformed.parking_bay")
spark.sql(f"CREATE TABLE malformed.parking_bay(bay_id INT, `last_edit` TIMESTAMP,`marker_id` STRING, `meter_id` STRING, `rd_seg_dsc` STRING, `rd_seg_id` STRING, `the_geom` STRUCT<`coordinates`: ARRAY<ARRAY<ARRAY<ARRAY<DOUBLE>>>>, `type`: STRING>, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/malformed/malformed.parking_bay/'")
spark.sql(f"REFRESH TABLE malformed.parking_bay")
spark.sql(f"DROP TABLE IF EXISTS malformed.sensor")
spark.sql(f"CREATE TABLE malformed.sensor(bay_id INT,`st_marker_id` STRING,`lat` FLOAT,`lon` FLOAT,`location` STRUCT<`coordinates`: ARRAY<DOUBLE>, `type`: STRING>,`status` STRING, load_id STRING, loaded_on TIMESTAMP) USING parquet LOCATION 'abfss://datalake@{storage_account}.dfs.core.windows.net/data/malformed/malformed.parking_bay/'")
spark.sql(f"REFRESH TABLE malformed.sensor")
| 0.512205 | 0.54056 |
ไธบไบๆดๅฅฝๅฐ็ๆPyTorchๅๅฏนๆฏๅ
ถไธๅ
ถไปๆกๆถ็ๅบๅซ๏ผๅฐๅฎ็ฝไธ็ไพ็จ่ชๅทฑ้ฝๅไธ้ๅนถๅๆด่ฏฆ็ป็ๆณจ้ใไพ็จไธญ๏ผๅชๅฟซ้ๅฎ็ฐไธคๅฑ็ฅ็ป็ฝ็ป็ๆ ธๅฟ้จๅ๏ผๅ ๆญค่ฎญ็ปๆฐๆฎๆฏ้ๆบ็ๆ็๏ผ่ไธๅชๅฎ็ฐไบๅฏนๅๆฐ็ๆดๆฐ่ฐๆด๏ผๆชๆถๅๅฏนไปฃไปทๅฝๆฐ็ไผๅ่ฟ็จใๅฎๆๅ
จๅฅไพ็จ๏ผไผๅฏน็ฅ็ป็ฝ็ป็ๅๅ้้ๅๅๅไผ ๆญๆๆดๅฅฝ็็่งฃใๅ
ทไฝๅฎ็ฐ็ๆนๆณๆ๏ผ
1. ๅฉ็จNumpyๅฎ็ฐ (CPU)
2. ๅฉ็จPyTorch็tensorๅฎ็ฐ (CPUๅGPU)
3. ๅฉ็จPyTorch็autogradๆจกๅๅฎ็ฐ
4. ๅฉ็จTensorflowๅฎ็ฐ๏ผๅฏนๆฏ้ๆๅพไธๅจๆๅพ็ๅบๅซ
#### 1. Numpyๅฎ็ฐ
```
import numpy as np
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ
w1 = np.random.randn(D_in, D_hidden)
w2 = np.random.randn(D_hidden, D_out)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
h_linear = x.dot(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = np.maximum(h_linear, 0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.dot(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * np.sum(np.square(y_pred - y)) #sum squared error as loss
# ๅๅๆฑๅฏผ
grad_y_pred = y_pred - y #10x5
grad_w2 = h_relu.T.dot(grad_y_pred) #30x10 and 10x5 produce the dimension of w2: 30x5
grad_h_relu = grad_y_pred.dot(w2.T) #30x5 and 10x5 produce the dimension of h_relu: 10x30
grad_h = grad_h_relu.copy()
grad_h[h_linear < 0] = 0 #ๆฟไปฃ้ๅฏน้ๅซๅฑๅฏผๆฐไธญ็่ดๆฐไธบ้ถ
grad_w1 = x.T.dot(grad_h) #20x10 and 10x30 produce 20x30
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
```
#### 2. PyTorch็tensorๅฎ็ฐ
ๅช้ๅฐnumpy็็จๅบ็จไฝ่ฐๆดๅฐฑ่ฝๅฎ็ฐtensor็ๅฎ็ฐ๏ผไป่ๆฏ็จๅบ่ฝๅค้จ็ฝฒๅฐGPUไธ่ฟ็ฎใ
```
import torch as T
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ
x = T.randn(N, D_in)
y = T.randn(N, D_out)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ
w1 = T.randn(D_in, D_hidden)
w2 = T.randn(D_hidden, D_out)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
#mm should also work as x is a matrix. The matrix multiplication will be summarized in another post
h_linear = x.matmul(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = h_linear.clamp(min=0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.matmul(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * (y_pred - y).pow(2).sum() #sum squared error as loss
# ๅๅๆฑๅฏผ
grad_y_pred = y_pred - y #10x5
grad_w2 = h_relu.t().mm(grad_y_pred) #30x10 and 10x5 produce the dimension of w2: 30x5
grad_h_relu = grad_y_pred.dot(w2.t()) #30x5 and 10x5 produce the dimension of h_relu: 10x30
grad_h = grad_h_relu.clone()
grad_h[h_linear < 0] = 0 #ๆฟไปฃ้ๅฏน้ๅซๅฑๅฏผๆฐไธญ็่ดๆฐไธบ้ถ
grad_w1 = x.t().mm(grad_h) #20x10 and 10x30 produce 20x30
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
```
#### 3. ๅฉ็จPyTorch็Tensorๅautogradๅฎ็ฐ
ไธคๅฑ็ฝ็ป็ๅๅๆฑๅฏผๆฏ่พๅฎนๆ๏ผไฝๅฆๆๅฑๆฐๅ ๅค๏ผๅจๆๅจๆฑๅฏผๅฐฑไผๅๅพๅพๅคๆใๅ ๆญคๆทฑๅบฆๅญฆไน ๅนณๅฐ้ฝๆไพไบ่ชๅจๆฑๅฏผๅ่ฝ๏ผPyTorch็Autogradไธญ็่ชๅจๆฑๅฏผๅ่ฝๅฏไปฅไฝฟๅๅๆฑๅฏผ็ฎๆทไธ็ตๆดปใ่ฆๆณจๆ็ๆฏ่ฎก็ฎๅพ็ๆๅปบ้่ฆ็จautogradไธญ็Variableๅฐ้่ฆๅนถๅ
ฅ่ฎก็ฎๅพไธญ็ๅ้่ฟ่กๅฐ่ฃ
๏ผๅนถ่ฎพ็ฝฎ็ธๅ
ณๅฑๆงใ
```
import torch as T
from torch.autograd import Variable
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ, ๅนถ็จVariableๅฏน่พๅ
ฅ่พๅบ่ฟ่กๅฐ่ฃ
๏ผๅๆถๅจ่ฎก็ฎๅพๅฝขไธญไธ่ฆๆฑๆฑๅฏผ
x = Variable(T.randn(N, D_in), requires_grad=False)
y = Variable(T.randn(N, D_out), requires_grad=False)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ๏ผๅนถ็จVariableๅฐ่ฃ
๏ผๅๆถ่ฆๆฑๆฑๅฏผ
w1 = Variable(T.randn(D_in, D_hidden), requires_grad=True)
w2 = Variable(T.randn(D_hidden, D_out), requires_grad=True)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
#mm should also work as x is a matrix. The matrix multiplication will be summarized in another post
h_linear = x.matmul(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = h_linear.clamp(min=0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.matmul(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * (y_pred - y).pow(2).sum() #sum squared error as loss
loss.backward()
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1.data -= learning_rate * w1.grad.data #note that we are updating the 'data' of Variable w1
w2.data -= learning_rate * w2.grad.data
#PyTorchไธญ๏ผๅฐgradไธญ็ๅผๅจๅพช็ฏไธญ่ฟ่ก็ดฏ็งฏ๏ผๅฝไธ้กปๆญคๆไฝๆถ๏ผๅบๆธ
้ถ
w1.grad.data.zero_()
w2.grad.data.zero_()
```
|
github_jupyter
|
import numpy as np
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ
w1 = np.random.randn(D_in, D_hidden)
w2 = np.random.randn(D_hidden, D_out)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
h_linear = x.dot(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = np.maximum(h_linear, 0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.dot(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * np.sum(np.square(y_pred - y)) #sum squared error as loss
# ๅๅๆฑๅฏผ
grad_y_pred = y_pred - y #10x5
grad_w2 = h_relu.T.dot(grad_y_pred) #30x10 and 10x5 produce the dimension of w2: 30x5
grad_h_relu = grad_y_pred.dot(w2.T) #30x5 and 10x5 produce the dimension of h_relu: 10x30
grad_h = grad_h_relu.copy()
grad_h[h_linear < 0] = 0 #ๆฟไปฃ้ๅฏน้ๅซๅฑๅฏผๆฐไธญ็่ดๆฐไธบ้ถ
grad_w1 = x.T.dot(grad_h) #20x10 and 10x30 produce 20x30
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
import torch as T
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ
x = T.randn(N, D_in)
y = T.randn(N, D_out)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ
w1 = T.randn(D_in, D_hidden)
w2 = T.randn(D_hidden, D_out)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
#mm should also work as x is a matrix. The matrix multiplication will be summarized in another post
h_linear = x.matmul(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = h_linear.clamp(min=0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.matmul(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * (y_pred - y).pow(2).sum() #sum squared error as loss
# ๅๅๆฑๅฏผ
grad_y_pred = y_pred - y #10x5
grad_w2 = h_relu.t().mm(grad_y_pred) #30x10 and 10x5 produce the dimension of w2: 30x5
grad_h_relu = grad_y_pred.dot(w2.t()) #30x5 and 10x5 produce the dimension of h_relu: 10x30
grad_h = grad_h_relu.clone()
grad_h[h_linear < 0] = 0 #ๆฟไปฃ้ๅฏน้ๅซๅฑๅฏผๆฐไธญ็่ดๆฐไธบ้ถ
grad_w1 = x.t().mm(grad_h) #20x10 and 10x30 produce 20x30
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
import torch as T
from torch.autograd import Variable
#ๅ
ๅฎไน็ฝ็ป็ปๆ: batch_size, Input Dimension, Hidden Dimension, Output Dimension
N, D_in, D_hidden, D_out = 10, 20, 30, 5
#้ๆบ็ๆ่พๅ
ฅๅ่พๅบๆฐๆฎ, ๅนถ็จVariableๅฏน่พๅ
ฅ่พๅบ่ฟ่กๅฐ่ฃ
๏ผๅๆถๅจ่ฎก็ฎๅพๅฝขไธญไธ่ฆๆฑๆฑๅฏผ
x = Variable(T.randn(N, D_in), requires_grad=False)
y = Variable(T.randn(N, D_out), requires_grad=False)
#ๅฏน่พๅ
ฅๅฑๅ่พๅบๅฑ็ๅๆฐ่ฟ่กๅๅงๅ๏ผๅนถ็จVariableๅฐ่ฃ
๏ผๅๆถ่ฆๆฑๆฑๅฏผ
w1 = Variable(T.randn(D_in, D_hidden), requires_grad=True)
w2 = Variable(T.randn(D_hidden, D_out), requires_grad=True)
learning_rate = 0.001
#ๅพช็ฏๆดๆฐๅๆฐ๏ผๆฏไธชๅพช็ฏๅๅๅๅๅๅ่ฎก็ฎไธๆฌก
for i in xrange(50):
# ่ฎก็ฎๅๅ้้
#mm should also work as x is a matrix. The matrix multiplication will be summarized in another post
h_linear = x.matmul(w1) #10x20 and 20x30 produce 10x30, which is the shape of h_linear
h_relu = h_linear.clamp(min=0) #note one have to use np.maximum but not np.max, 10x30
y_pred = h_relu.matmul(w2) #10x30 and 30x5 produce 10x5
#ๅฎไนไปฃไปทๅฝๆฐ
loss = 0.5 * (y_pred - y).pow(2).sum() #sum squared error as loss
loss.backward()
#ๆขฏๅบฆไธ้ๆณๆดๆฐๅๆฐ
w1.data -= learning_rate * w1.grad.data #note that we are updating the 'data' of Variable w1
w2.data -= learning_rate * w2.grad.data
#PyTorchไธญ๏ผๅฐgradไธญ็ๅผๅจๅพช็ฏไธญ่ฟ่ก็ดฏ็งฏ๏ผๅฝไธ้กปๆญคๆไฝๆถ๏ผๅบๆธ
้ถ
w1.grad.data.zero_()
w2.grad.data.zero_()
| 0.466359 | 0.909103 |
# Control Flow Statements
## If
if some_condition:
algorithm
```
x = 12
if x >10:
print "Hello"
```
## If-else
if some_condition:
algorithm
else:
algorithm
```
x = 12
if x > 10:
print "hello"
else:
print "world"
```
## if-elif
if some_condition:
algorithm
elif some_condition:
algorithm
else:
algorithm
```
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
else:
print "x=y"
```
if statement inside a if statement or if-elif or if-else are called as nested if statements.
```
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
if x==10:
print "x=10"
else:
print "invalid"
else:
print "x=y"
```
## Loops
### For
for variable in something:
algorithm
```
for i in range(5):
print i
```
In the above example, i iterates over the 0,1,2,3,4. Every time it takes each value and executes the algorithm inside the loop. It is also possible to iterate over a nested list illustrated below.
```
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
print list1
```
A use case of a nested for loop in this case would be,
```
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
for x in list1:
print x
```
### While
while some_condition:
algorithm
```
i = 1
while i < 3:
print(i ** 2)
i = i+1
print('Bye')
```
## Break
As the name says. It is used to break out of a loop when a condition becomes true when executing the loop.
```
for i in range(100):
print i
if i>=7:
break
```
## Continue
This continues the rest of the loop. Sometimes when a condition is satisfied there are chances of the loop getting terminated. This can be avoided using continue statement.
```
for i in range(10):
if i>4:
print "The end."
continue
elif i<7:
print i
```
## List Comprehensions
Python makes it simple to generate a required list with a single line of code using list comprehensions. For example If i need to generate multiples of say 27 I write the code using for loop as,
```
res = []
for i in range(1,11):
x = 27*i
res.append(x)
print res
```
Since you are generating another list altogether and that is what is required, List comprehensions is a more efficient way to solve this problem.
```
[27*x for x in range(1,11)]
```
That's it!. Only remember to enclose it in square brackets
Understanding the code, The first bit of the code is always the algorithm and then leave a space and then write the necessary loop. But you might be wondering can nested loops be extended to list comprehensions? Yes you can.
```
[27*x for x in range(1,20) if x<=10]
```
Let me add one more loop to make you understand better,
```
[27*z for i in range(50) if i==27 for z in range(1,11)]
```
|
github_jupyter
|
x = 12
if x >10:
print "Hello"
x = 12
if x > 10:
print "hello"
else:
print "world"
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
else:
print "x=y"
x = 10
y = 12
if x > y:
print "x>y"
elif x < y:
print "x<y"
if x==10:
print "x=10"
else:
print "invalid"
else:
print "x=y"
for i in range(5):
print i
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
print list1
list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for list1 in list_of_lists:
for x in list1:
print x
i = 1
while i < 3:
print(i ** 2)
i = i+1
print('Bye')
for i in range(100):
print i
if i>=7:
break
for i in range(10):
if i>4:
print "The end."
continue
elif i<7:
print i
res = []
for i in range(1,11):
x = 27*i
res.append(x)
print res
[27*x for x in range(1,11)]
[27*x for x in range(1,20) if x<=10]
[27*z for i in range(50) if i==27 for z in range(1,11)]
| 0.038062 | 0.810329 |
<a href="https://colab.research.google.com/github/donw385/DS-Unit-1-Sprint-2-Data-Wrangling/blob/master/module2-join-datasets/LS_DS_122_Join_datasets.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science_
# Join datasets
Objectives
- concatenate data with pandas
- merge data with pandas
Links
- [Pandas Cheat Sheet](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf)
- Combine Data Sets: Standard Joins
- Python Data Science Handbook
- [Chapter 3.6](https://jakevdp.github.io/PythonDataScienceHandbook/03.06-concat-and-append.html), Combining Datasets: Concat and Append
- [Chapter 3.7](https://jakevdp.github.io/PythonDataScienceHandbook/03.07-merge-and-join.html), Combining Datasets: Merge and Join
## Download data
Weโll work with a dataset of [3 Million Instacart Orders, Open Sourced](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2)!
```
import pandas as pd
!wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
!tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
%cd instacart_2017_05_01
```
## Goal: Reproduce this example
The first two orders for user id 1:
```
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*vYGFQCafJtGBBX5mbl0xyw.png'
example = Image(url=url, width=600)
display(example)
```
## Load data
Here's a list of all six CSV filenames
```
!ls -lh
```
For each CSV
- Load it with pandas
- Look at the dataframe's shape
- Look at its head (first rows)
- `display(example)`
- Which columns does it have in common with the example we want to reproduce?
### aisles
### departments
### order_products__prior
```
order_products_prior = pd.read_csv('order_products__prior.csv')
```
### order_products__train
```
order_products_train = pd.read_csv('order_products__train.csv')
```
### orders
```
orders = pd.read_csv('orders.csv')
```
### products
```
products = pd.read_csv('products.csv')
```
## Concatenate order_products__prior and order_products__train
```
#append columns, add, axis=1, but better to add axis = column
order_products = pd.concat([order_products_prior,order_products_train])
order_products.head()
#validate working properly
assert len(order_products) == len(order_products_prior) + len(order_products_train)
#validate columns
assert len(order_products.columns) == len(order_products_prior.columns) == len(order_products_train.columns)
```
## Get a subset of orders โ the first two orders for user id 1
```
condition = (orders.user_id==1) & (orders.order_number <= 2)
columns = ['user_id', 'order_id','order_number','order_dow','order_hour_of_day']
subset = orders.loc[condition,columns]
subset.head()
```
## Merge dataframes
```
columns =['order_id','add_to_cart_order','product_id']
merged = pd.merge(subset, order_products[columns], how='inner', on='order_id')
subset.shape, merged.shape
merged['product_name'] = products['product_name']
merged.head()
final = pd.merge(merged,products[['product_id','product_name']])
final = final.sort_values(by=['order_number', 'add_to_cart_order'])
final.columns = [column.replace('_', ' ')
for column in final]
```
```
final.head()
```
# Assignment
These are the top 10 most frequently ordered products. How many times was each ordered?
1. Banana
2. Bag of Organic Bananas
3. Organic Strawberries
4. Organic Baby Spinach
5. Organic Hass Avocado
6. Organic Avocado
7. Large Lemon
8. Strawberries
9. Limes
10. Organic Whole Milk
First, write down which columns you need and which dataframes have them.
Next, merge these into a single dataframe.
Then, use pandas functions from the previous lesson to get the counts of the top 10 most frequently ordered products.
## Stretch challenge
The [Instacart blog post](https://tech.instacart.com/3-million-instacart-orders-open-sourced-d40d29ead6f2) has a visualization of "**Popular products** purchased earliest in the day (green) and latest in the day (red)."
The post says,
> "We can also see the time of day that users purchase specific products.
> Healthier snacks and staples tend to be purchased earlier in the day, whereas ice cream (especially Half Baked and The Tonight Dough) are far more popular when customers are ordering in the evening.
> **In fact, of the top 25 latest ordered products, the first 24 are ice cream! The last one, of course, is a frozen pizza.**"
Your challenge is to reproduce the list of the top 25 latest ordered popular products.
We'll define "popular products" as products with more than 2,900 orders.
```
total = pd.merge(order_products, products)
total.head()
total.shape, order_products.shape, products.shape
product_counts = total['product_name'].value_counts().sort_index()
#answer to assignment
product_counts.sort_values(ascending=False).head(10)
df = pd.merge(order_products[['order_id','product_id']],products[['product_id','product_name']])
df=pd.merge(df,orders[['order_id','order_hour_of_day']])
df.head()
times_and_sales= (df.groupby('product_name').order_hour_of_day.agg(['mean','count']).rename(columns={'mean':'average time','count':'total sales'}))
times_and_sales.head()
popular=times_and_sales[times_and_sales['total sales']>2900]
popular.sort_values(by='average time',ascending=False).head(25)
```
|
github_jupyter
|
import pandas as pd
!wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
!tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
%cd instacart_2017_05_01
from IPython.display import display, Image
url = 'https://cdn-images-1.medium.com/max/1600/1*vYGFQCafJtGBBX5mbl0xyw.png'
example = Image(url=url, width=600)
display(example)
!ls -lh
order_products_prior = pd.read_csv('order_products__prior.csv')
order_products_train = pd.read_csv('order_products__train.csv')
orders = pd.read_csv('orders.csv')
products = pd.read_csv('products.csv')
#append columns, add, axis=1, but better to add axis = column
order_products = pd.concat([order_products_prior,order_products_train])
order_products.head()
#validate working properly
assert len(order_products) == len(order_products_prior) + len(order_products_train)
#validate columns
assert len(order_products.columns) == len(order_products_prior.columns) == len(order_products_train.columns)
condition = (orders.user_id==1) & (orders.order_number <= 2)
columns = ['user_id', 'order_id','order_number','order_dow','order_hour_of_day']
subset = orders.loc[condition,columns]
subset.head()
columns =['order_id','add_to_cart_order','product_id']
merged = pd.merge(subset, order_products[columns], how='inner', on='order_id')
subset.shape, merged.shape
merged['product_name'] = products['product_name']
merged.head()
final = pd.merge(merged,products[['product_id','product_name']])
final = final.sort_values(by=['order_number', 'add_to_cart_order'])
final.columns = [column.replace('_', ' ')
for column in final]
final.head()
total = pd.merge(order_products, products)
total.head()
total.shape, order_products.shape, products.shape
product_counts = total['product_name'].value_counts().sort_index()
#answer to assignment
product_counts.sort_values(ascending=False).head(10)
df = pd.merge(order_products[['order_id','product_id']],products[['product_id','product_name']])
df=pd.merge(df,orders[['order_id','order_hour_of_day']])
df.head()
times_and_sales= (df.groupby('product_name').order_hour_of_day.agg(['mean','count']).rename(columns={'mean':'average time','count':'total sales'}))
times_and_sales.head()
popular=times_and_sales[times_and_sales['total sales']>2900]
popular.sort_values(by='average time',ascending=False).head(25)
| 0.267217 | 0.978343 |
# Decision Tree & Optuna Example
Example showing how to use the Optuna library (https://optuna.readthedocs.io/en/stable/) for Bayesian hyperparameter optimization (via tree of parzen estimator)
```
%load_ext watermark
%watermark -p scikit-learn,optuna
```
## Dataset
```
from sklearn import model_selection
from sklearn.model_selection import train_test_split
from sklearn import datasets
data = datasets.load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
X_train_sub, X_valid, y_train_sub, y_valid = \
train_test_split(X_train, y_train, test_size=0.2, random_state=1, stratify=y_train)
print('Train/Valid/Test sizes:', y_train.shape[0], y_valid.shape[0], y_test.shape[0])
```
## Hyperopt
```
from hyperopt import Trials, STATUS_OK, tpe, hp, fmin
import hyperopt.pyll.stochastic
```
Some random sampling examples:
```
hyperopt.pyll.stochastic.sample(hp.loguniform('test', 1e-5, 1)) # range e^{low} to e^{high}
hyperopt.pyll.stochastic.sample(hp.qloguniform('test', 1e-5, 1, 0.1)) # rounded to 0.1
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import StratifiedKFold
import numpy as np
import optuna
def optimization_objective(trial, X_train, y_train, cv=5):
params = {
'min_samples_split': trial.suggest_int('min_samples_split', 2, 10),
'min_impurity_decrease': trial.suggest_uniform('min_impurity_decrease', 0.0, 0.5),
'max_depth': trial.suggest_categorical('max_depth', [6, 16, None])
}
cv_iterator = StratifiedKFold(n_splits=cv, shuffle=True, random_state=123)
cv_scores = np.zeros(cv)
for idx, (train_sub_idx, valid_idx) in enumerate(cv_iterator.split(X_train, y_train)):
X_train_sub, X_valid = X_train[train_sub_idx], X_train[valid_idx]
y_train_sub, y_valid = y_train[train_sub_idx], y_train[valid_idx]
model = DecisionTreeClassifier(**params, random_state=123)
model.fit(X_train_sub, y_train_sub)
preds = model.score(X_valid, y_valid)
cv_scores[idx] = preds
return np.mean(cv_scores)
study = optuna.create_study(direction="maximize", study_name="DT Classifier")
def func(trial):
return optimization_objective(trial, X_train, y_train)
study.optimize(func, n_trials=50);
print(f"Best CV accuracy: {study.best_value:.5f}")
print("Best params:")
for key, value in study.best_params.items():
print(f"\t{key}: {value}")
model = DecisionTreeClassifier(random_state=123, **study.best_params)
model.fit(X_train, y_train)
print(f"Training Accuracy: {model.score(X_train, y_train):0.2f}")
print(f"Test Accuracy: {model.score(X_test, y_test):0.2f}")
```
|
github_jupyter
|
%load_ext watermark
%watermark -p scikit-learn,optuna
from sklearn import model_selection
from sklearn.model_selection import train_test_split
from sklearn import datasets
data = datasets.load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
X_train_sub, X_valid, y_train_sub, y_valid = \
train_test_split(X_train, y_train, test_size=0.2, random_state=1, stratify=y_train)
print('Train/Valid/Test sizes:', y_train.shape[0], y_valid.shape[0], y_test.shape[0])
from hyperopt import Trials, STATUS_OK, tpe, hp, fmin
import hyperopt.pyll.stochastic
hyperopt.pyll.stochastic.sample(hp.loguniform('test', 1e-5, 1)) # range e^{low} to e^{high}
hyperopt.pyll.stochastic.sample(hp.qloguniform('test', 1e-5, 1, 0.1)) # rounded to 0.1
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import StratifiedKFold
import numpy as np
import optuna
def optimization_objective(trial, X_train, y_train, cv=5):
params = {
'min_samples_split': trial.suggest_int('min_samples_split', 2, 10),
'min_impurity_decrease': trial.suggest_uniform('min_impurity_decrease', 0.0, 0.5),
'max_depth': trial.suggest_categorical('max_depth', [6, 16, None])
}
cv_iterator = StratifiedKFold(n_splits=cv, shuffle=True, random_state=123)
cv_scores = np.zeros(cv)
for idx, (train_sub_idx, valid_idx) in enumerate(cv_iterator.split(X_train, y_train)):
X_train_sub, X_valid = X_train[train_sub_idx], X_train[valid_idx]
y_train_sub, y_valid = y_train[train_sub_idx], y_train[valid_idx]
model = DecisionTreeClassifier(**params, random_state=123)
model.fit(X_train_sub, y_train_sub)
preds = model.score(X_valid, y_valid)
cv_scores[idx] = preds
return np.mean(cv_scores)
study = optuna.create_study(direction="maximize", study_name="DT Classifier")
def func(trial):
return optimization_objective(trial, X_train, y_train)
study.optimize(func, n_trials=50);
print(f"Best CV accuracy: {study.best_value:.5f}")
print("Best params:")
for key, value in study.best_params.items():
print(f"\t{key}: {value}")
model = DecisionTreeClassifier(random_state=123, **study.best_params)
model.fit(X_train, y_train)
print(f"Training Accuracy: {model.score(X_train, y_train):0.2f}")
print(f"Test Accuracy: {model.score(X_test, y_test):0.2f}")
| 0.752649 | 0.964589 |
# Jupyter Notebook
A [Jupyter Notebook](http://jupyter.org/index.html) is an HTML-based notebook which allows you to create and share documents that contain live code, equations, visualizations and explanatory text. It allows a clean presentation of computational results as HTML or PDF reports and is well suited for interactive tasks such as data cleaning, transformation and exploration, numerical simulation, statistical modeling, machine learning and more. It runs everywhere (Window, Mac, Linux, Cloud) and supports multiple languages through various kernels, e.g. Python, R, Julia, Matlab.
## Modes
When inside a notebook, there are two modes:
1. **Edit mode**: as its name tells, you are editing a cell (writing something). The selected cell has a <span style="color: green;">green</span> border.
2. **Command mode**: this mode allows you to interact with the notebook structure. The selected cell has a <span style="color: blue;">blue</span> border.
When in command mode, press `<Enter>` or click to *enter* edit mode. When in edit mode, press `<Esc>` to *leave* edit mode and enter command mode.
## Keyboard shortcuts
Something that you should know is that you can perform a lot of actions using specific keyboard shortcuts. That way you never have to remove your hands from the keys to reach the mouse. You can keep your brain connected directly to the screen, allowing your ideas to flow smoothly to the editor :) Productivity improvement guaranteed!
## Cells
A notebook is composed of **cells**. Each cell has a *type*, the most relevant being the *Code* and the *[Markdown](https://en.wikipedia.org/wiki/Markdown)* types. You can interact with the cells in different ways. We will go through the basic actions that you can perform.
### Insert a cell
The first thing is of course to **create** a cell. You always create cells *relatively to the selected one* (the one that has a colored border). There are several ways to do that:
1. **Using the menu.** Click on `Insert -> Insert Cell Above/Bellow`.
2. **Using a shortcut.** When in command mode, press `<A>` (**a**bove) or `<B>` (**b**ellow).
Insert cells bellow this one using the two methods.
### Delete a cell
You can of course **delete** a cell. Again, there are two ways to do so. After selecting a cell to delete, you can:
1. In the menu, select `Edit -> Delete Cells`.
2. When in command mode, press `<DD>` (**d**elete, twice because it is a risky operation...).
You can still *undo* it using the `Edit -> Undo [move]` menu.
Delete the following two cells.
```
# This cell does not contain anything useful. Delete it using the menu.
# This cell is also useless. Delete it using the keyboard shortcut.
```
### Execute a cell
We have not done anything meaningful so far. To really make use of the notebook, we need to be able to **execute** the cells. Executing a Markdown cell will only *render* its content. Executing a Code cell will actually evaluate it. Potential outputs (print, plot, ...) will be displayed right bellow the cell. Again, there are several ways to do that:
1. Using the menu, select one of `Cell -> Run [something]`.
2. Using the toolbar, click on the "play" button (the triangle with a bar on its right, next to the big square).
3. Using the keyboard, you have several options:
- `<Ctrl>-<Enter>` will execute the cell and keep it selected.
- `<Shift>-<Enter>` will execute the cell and select the one bellow.
- `<Alt>-<Enter>` will execute the cell and insert a new one bellow.
Execute the following cell with the different methods.
```
a = 2
b = 3
print("Hi there! Did you know a + b = %d ?" % (a + b))
```
### Select the cell type
You can change the cell type in the toolbar at the top of the screen. Select the desired type in the dropdown menu. You can also use the keyboad. When in command mode:
- Press `<M>` to change the type to **M**arkdown.
- Press `<Y>` to change the type to Code.
The following cell contains some Markdown text, but its type is set on code. Fix it!
```
### This is a 3rd-level heading
This is some *normal* text.
```
### More advanced
There exists more actions to interact with your notebook, such as:
- Spliting cells
- Merging cells
- Moving cells up and down
- Restarting the kernel
- Clearing the outputs
But we leave it to the curious reader or the eager user to find them out by herself.
## Relevant features
Here comes a non-exhaustive of relevant features that are widely used when developing in notebooks.
### Magic cells and lines
Jupyter provides a bunch of magic commands. Line magics start with `%` and involve only one line (meaning that you can mix them with other things, like code). Cell magics start with `%%` and involve the whole cell.
Examples of useful magic commands are:
- `%%time`: display a report of the execution time of the cell
- `%matplotlib inline`: display the plots in the cell output and not in a new window (see notebook `2-data-science`)
- Automatically reload Python modules to avoid restarting the kernel (see notebook `1-python`):
```
%reload_ext autoreload
%autoreload 2
```
You can list all the magic commands with `%lsmagic`.
```
%lsmagic
```
### Latex
In your Markdown cells, you can also include $\LaTeX$ equations using the usual delimiters `$` (inline equation) and `$$` (block equation).
Here is an example of the [most beautiful equation](https://www.quora.com/What-is-the-most-beautiful-equation/answer/Tracy-Chou?srid=dVcP):
$$
e^{\pi i} + 1 = 0
$$
You can also define a whole cell as Latex by using the cell magics `%%latex` at the beginning of a *Code* cell.
### Shell commands
You can also run shell commands directly in the cells by starting the line with `!`:
```
!ls -alh
```
### Sharing
A notebook is just a [JSON](https://en.wikipedia.org/wiki/JSON) file. You can therefore easily share it with other people or display it on [notebook viewer](https://nbviewer.jupyter.org) platforms. Export it using `File -> Download as -> Notebook`. Several output formats are moreover available. Keep in mind the **HTML** format.
## References
You should definitely take the **User Interface Tour** and read through the **Keyboard Shortcuts**, both located in the help menu. If you are interested, here is a link to the complete [documentation](http://jupyter-notebook.readthedocs.io/en/latest/).
|
github_jupyter
|
# This cell does not contain anything useful. Delete it using the menu.
# This cell is also useless. Delete it using the keyboard shortcut.
a = 2
b = 3
print("Hi there! Did you know a + b = %d ?" % (a + b))
### This is a 3rd-level heading
This is some *normal* text.
%reload_ext autoreload
%autoreload 2
%lsmagic
!ls -alh
| 0.275227 | 0.977023 |
<a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fcurriculum-notebooks&branch=master&subPath=Mathematics/HorizontalAndVerticalTranslations/effects-of-horizontal-and-vertical-translations.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
```
%%html
<p>The raw code for this IPython notebook is hidden for easier reading. If you want to see it,
<button onclick="javascript:code_toggle()">CLICK HERE TO SHOW/HIDE CODE</button>
</p>
<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
import numpy as np
import ipywidgets as widgets
from plotly import graph_objs as go
```
# Introduction
This notebook introduces the topic of translating a function both vertically and horizontally. Although this may sound hard, all it really means is that we can move the graph of a function up and down (vertically) and from side to side (horizontally). By the end of this lesson, you will better understand what it means to translate a function, how a translation affects the function's graph, and how a translation affects the equation that defines the function.
## Background and simple example
Translations are used in many mathematical applications. When a function is translated, either horizontally or vertically, we get a new function. Let's start with a simple example.
Take the equation $y=x^2$, which is the formula for a parabola. We can graph it by plotting a series of x values horizontally, paired with the square of those values vertically. You will get the following graph:
```
x = np.linspace(-4,4,200)
fig = go.Figure(data = go.Scatter(x = x, y = x**2))
fig.update_layout(title='$\mbox{A parabola, }y=x^2$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
```
Notice, for instance, the point $x=4$ has square $y = 4^2 = 16$ and the parabola does indeed pass through the point $(x,y) = (4,16).$
#### Vertical shift
To shift this graph upwards (vertically), say by five, we just add 5 to the function $x^2$:
```
x = np.linspace(-4,4,200)
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=x**2,
mode='lines',
name='original'))
fig.add_trace(go.Scatter(x=x, y=x**2 + 5,
mode='lines',
name='vertical shift'))
fig.update_layout(title='$\mbox{A parabola, }y=x^2, \mbox{ and shifted up, } y=x^2 + 5$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
```
#### Horizontal shift
To shift this graph to the right (horizontally), say by two, we just **subtract** 2 from the x in function $x^2$, to get $y = (x-2)^2$:
```
x = np.linspace(-4,6,200)
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=x**2,
mode='lines',
name='original'))
fig.add_trace(go.Scatter(x=x, y=(x-2)**2,
mode='lines',
name='horizontal shift'))
fig.add_trace(go.Scatter(x=[0], y=[0],
mode='markers',
name='original vertex'))
fig.add_trace(go.Scatter(x=[2], y=[0],
mode='markers',
name='shifted vertex'))
fig.update_layout(title='$\mbox{A parabola, }y=x^2, \mbox{ and shifted right, } y=(x-2)^2$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
```
## Ask yourself
Notice to raise the function up, we added 5 to $x^2$. To move the function to the right, we **subtracted** 2 from the x variable, $x^2$ become $(x-2)^2$. Does this make sense to you?
If not, think about moving the vertex of the parabola to the right. To move it from (0,0) to (2,0), we need the squaring function to have a minimum at $x=2$. The function $(x-2)^2$ does have its minimum at 2, as desired.
## Application example
Think about throwing a ball up in the air. Imagine you are being timed by your friend, and that you throw the ball in the air as soon as your friend says 'Go'. If we drew a graph of how high the ball goes over time, the graph might look something like this:
```
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5,
mode='lines',name='path')
fig = go.Figure()
fig.add_trace(t1)
fig.update_layout(title='Parabolic path of a thrown ball',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
```
There's something wrong with this graph, though. At time 0, when you throw the ball, the ball has a height of 0 meters. So this graph is saying that you threw the ball from the ground, i.e. your hand was on the ground when you threw the ball. This is completely impossible, so we'll adjust the graph. Let's say that, with your arm extended above your head, you're about 2.2 m tall. To make things easier, let's imagine that you throw the ball with your arm fully extended and you catch the ball with your arm fully extended. The graph of the height of the ball over time should now look like this:
```
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5 + 2.2,
mode='lines',
name='path'
)
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic path of a thrown ball, shifted up a bit',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
```
Alright, now this makes a bit more sense. The ball starts at height 2.2 m, is in the air for 2 seconds, and then you catch it when it is 2.2 m high.
What we've just seen is a *vertical* translation, since the graph of the ball's height got moved *up*.
Now let's imagine that you throw and catch the ball at the same height, but when your friend says 'Go' you wait for 1 second to throw the ball. The graph of the height of the ball now looks like this:
```
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x + 1,
y = -5*(x-1)**2 + 5 + 2.2)
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic path of a thrown ball, shifted up and to the right',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
```
This is the same graph as before, but it's been moved to the *right*. This is a *horizontal* translation. Just for comparison, let's see all three graphs together.
```
# Hide this.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5,
name = 'Original path')
t2 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5 + 2.2,
name = 'Path translated up')
t3 = go.Scatter(
x = x + 1,
y = -5*(x-1)**2 + 5 + 2.2,
name = 'Path translated up and to the right')
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(t2)
fig.add_trace(t3)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic paths of three thrown balls',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
```
## Checking In
After seeing the example of throwing the ball into the air, see if you can answer these questions.
- How does a **vertical** translation affect the graph of a function?
- How does a **horizontal** translation affect the graph of a function?
- What other real-world application could use translations?
You've seen an example of how translations affect the *graph* of a function, now let's talk about how translations affect the *equation* of a function. This can get tricky, so it's important to imagine the graph of the function moving around as we apply translations.
### More examples
Let's look at the function $f(x) = x$. The graph of this function is a diagonal line. Let's take a look.
```
# Create the x and y variables for plotting the function.
x = np.linspace(-10,10,200)
# Assign the variables for plotting.
f_graph = go.Scatter(
x = x,
y = x,
name = 'f(x)')
# Assign the plot to a figure.
fig = go.Figure(f_graph)
# Plot the function.
fig.update_layout(title='Plot of a diagonal line',
xaxis_title='x values',
yaxis_title='y = f(x)')
fig.show()
```
You can move your mouse cursor over the graph to get some values of the function. Let's write some values down in a table.
\begin{array}{c|c}
x & y=f(x) \\ \hline
-2 & -2 \\
-1 & -1 \\
0 & 0 \\
1 & 1 \\
2 & 2
\end{array}
Now what would happen if we added 2 to every $y$ value? For one thing, the table would now look like this:
\begin{array}{c|c}
x & y=f(x) + 2 \\ \hline
-2 & -2 + 2 = 0 \\
-1 & -1 + 2 = 1 \\
0 & 0 + 2 = 2 \\
1 & 1 + 2 = 3 \\
2 & 2 + 2 = 4
\end{array}
Now how does that affect the graph? Let's plot it to find out.
```
x = np.linspace(-10,10,200)
# Two traces for plotting.
f_graph = go.Scatter(
x = x,
y = x,
name = 'f(x)')
f_translated = go.Scatter(
x = x,
y = x+2,
name = 'f(x) + 2')
data = [f_graph, f_translated]
fig = go.Figure([f_graph,f_translated])
fig.update_layout(title='Plot of two diagonal lines: y = x and y = x + 2',
xaxis_title='x values',
yaxis_title='y = f(x), y = f(x) + 2')
fig.show()
```
From this graph, we can see that adding 2 to every $y$-value moved the graph of $f(x)$ up 2 units.
Remember, we expressed this idea of 'adding 2 to every function output' very clearly using algebra. We let $y=f(x)$ be the function values, and then used the expression $f(x) + 2$ to translate every function value up by 2 units.
In general, we can write the vertical translation of a function $f(x)$ by $v$ units by the expression
$$ f(x) + v. $$
WAIT A MINUTE!! This notation makes it seem like we can only translate functions **up**! We need to keep in mind that if we wanted to translate a function **down**, then we would select a **negative** value for $v$. The translations resulting from values of $v$ are shown in the this table:
Value of $v$ | Effect on graph of function
:-- | :--
Positive | Translates **up**
Negative | Translates **down**
You can play with different values of $v$ in the widget that comes after the next section.
## Horizontal Translations
Now you're getting used to vertical translations, so let's move to the next concept: moving a function from side to side. We'll use the same function from the last section, $f(x) = x$.
Suppose we add 2 to every function input value. In other words, before we put an $x$ value into our function, we add 2 to it. The table of function inputs and outputs now looks like this:
\begin{array}{c|c}
x + 2 & y=f(x) \\ \hline
-2+2 = 0 & -2 \\
-1+2 = 1 & -1 \\
0+2 = 2 & 0 \\
1+2 = 3 & 1 \\
2+2 = 4 & 2
\end{array}
Now let's plot the result of shifting the function inputs. It's ok to be uneasy about the $y$-values in the above table. We'll explain that right after we look at the graph of the translated function.
```
x = np.linspace(-10,10,200)
y1 = x
y2 = x+2
g1 = go.Scatter(
x = x,
y = y1,
name = 'Original function')
g2 = go.Scatter(
x = x,
y = y2,
name = 'Translated function')
fig = go.Figure([g1,g2])
fig.update_layout(title='Plot of two diagonal lines: y = x and y = (x+2)',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
```
This plot shows something unexpected. When we added 2 to the $x$ values, the whole graph of the function moved to the *left*. Maybe you expected the graph of the function to move to the right.
Let's keep in mind what actually happened when we added 2 to the $x$ values. By adding 2 units to $x=1$, for example, we essentially told the function to take on the output value it would normally take on at $x=3$, but instead when $x=1$.
In general, we can express any horizontal translation by $h$ units using the algebraic expression:
$$ f(x-h). $$
The effects of different values of $h$ are given in this table:
Value of $h$ | Effect on graph of function
:-- | :--
Positive | Translates **left**
Negative | Translates **right**
### Combining Vertical and Horizontal Translations
Now it's time for you to play with different vertical and horizontal translations. The widget below lets you set values for $v$ and $h$, and you will see how the displayed equation of the function changes. We'll use the function $y = \arctan(x-h) + v$.
```
# Hide this.
x = np.linspace(-10,10,200)
fig = go.Figure(go.Scatter(x=x,y=x**2))
fig.update_layout(title='y=arctan(x-(0.0)) + (0.0)',
xaxis_title='x values', xaxis_range=[-5,5],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-5,5],yaxis_zeroline=True)
def View1(h, v):
fig.update_layout(title='y = arctan(x -(' + str(h) + ')) + (' + str(v) + ')',
xaxis_title='x values', xaxis_range=[-5,5],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-5,5],yaxis_zeroline=True)
x = np.linspace(-10,10,200)
fig.update_traces(x=x,y = np.arctan(x - h) + v)
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View1,
v = (-5,5,0.5),
h = (-5,5,0.5),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
```
### *Exercise*
The graph is an arc with its highest point at the coordinate pair $(x,y)=(2,0)$. Move the graph so that the top of the arc is at $(2,-3)$, $(-4,6)$, $(10,0)$, and $(0,10)$. What are the values of $v$ and $h$ at each of these places?
```
# Hide this.
def func(x, v, h):
return np.abs(np.sqrt(4-(x-2+h)**2)) - 2 + v
x1 = np.linspace(-10,10,200)
fig = go.Figure(go.Scatter(x=x1,y=func(x1,0.0,0.0)))
fig.update_layout(title='y = y = f(x-h) + v, an arc',
xaxis_title='x values', xaxis_range=[-10,10],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-10,10],yaxis_zeroline=True)
fig.update_xaxes(tick0=2.0, dtick=2.0)
fig.update_yaxes(tick0=2.0, dtick=2.0)
def View(v, h):
x1 = np.linspace(-10,10,200)
fig.update_traces(x=x1,y = func(x1, v, h))
fig.update_layout(title='y = f(x-h) + v, an arc')
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View,
v = (-10,10,1),
h = (-10,10,1),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
```
### *Exercises*
<ol>
<li> Write the expression for translating the function $f(x) = \sqrt{x}$ **down** by 4 units and **right** by 3 units. </li>
<li> The graph of the function $f(x) = x^2 - 2x - 3 = (x+1)(x-3)$ touches the $x$-axis at the two points $x=-1$ and $x=3$. What vertical translation can be applied to this function so that it only touches the $x$-axis when $x=1$? </li>
<li> What happens to the graph of a constant function $f(x)=c$ when the function is translated horizontally? Vertically? </li>
<li> Write a Python function that allows the user to specify input values 'x', an output function to be translated 'f', and the vertical and horizontal translation parameters $k$ and $h$. Your function should have four inputs: x, f, $h$, and $k$. A template is provided in the next cell. Show that your function works on the function 'testf'. </li>
</ol>
```
%%html
<button onclick="javascript:code_toggle()">CLICK HERE TO SHOW THE CODE CELL FOR THIS EXERCISE.</button>
# Write your translation function from Exercise 4 here.
def translate(x, f, v, h):
return f(x) # put your formula here
pass
# A test function
def testf(x):
return np.exp(-x**2)*0.4
# Test your translation function here.
h = 1 # Replace with a value of h
v = 0 # Replace with a value of v
x = np.linspace(-10,10,200)
y = translate(x, testf, v, h)
# Uncomment these lines to plot the translated function (select the lines and press 'CTRL /').
#fig = go.Figure([go.Scatter(x=x,y=y,name='Translated'),go.Scatter(x=x,y=testf(x),name='Original')])
#fig.show()
```
### *Exercise*
In the maze below, use horizontal and vertical translations to move the dot from its current position to the red circle. There are lots of ways to get there, but try to find the fastest possible route. Don't travel through any buildings!
```
# Hide this.
# These are the coordinates for each 'building' rectangle. They are in the form
# x0, x1, y0, y1.
b_coords = [[-9.8,-6.2,-7.8,-6.2], [-9.8,-1.2,-9.8,-9.2], [-4.8,-0.2,-7.8,-0.2],
[-8.8,-1.2,0.2,3.8], [-8.8,-6.2,-4.8,-1.2], [0.2,8.8,-8.8,-8.2],
[1.2,9.8,-6.8,-1.2], [0.2,7.8,0.2,4.8], [9.2,9.8,0.2,9.8],
[9.2,9.8,0.2,9.8], [0.2,7.8,6.2,8.8], [-3.8,-1.2,5.2,7.8],
[-9.8,-5.2,5.2,9.8], [-3.8,-1.2,9.2,9.8]]
def View(v, h):
trace = go.Scatter(x=[0],y=[0],mode='markers')
layout = {
'xaxis': {
'range': [-10, 10],
'zeroline': True
},
'yaxis': {
'range': [-10, 10],
'zeroline': True
},
'shapes': [
# filled circle
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'fillcolor': 'rgba(50, 171, 96, 0.7)',
'x0': -9+h,
'y0': -9+v,
'x1': -8+h,
'y1': -8+v,
'line': {'color': 'rgba(50, 171, 96, 1)'}
},
# end point
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'fillcolor': 'rgba(255, 0, 0, 0.7)',
'x0': -1,
'y0': 8,
'x1': 0,
'y1': 9,
'line': {'color': 'rgba(255, 0, 0, 1)'}
}
]
}
# Add the 'building' obstacles.
for i in range(len(b_coords)):
building = {'type':'rect','xref':'x','yref':'y',
'fillcolor':'rgba(102, 51, 0, 0.7)','line':{'color':'rgba(102, 51, 0, 1)'},
'x0':b_coords[i][0],'x1':b_coords[i][1],'y0':b_coords[i][2],'y1':b_coords[i][3]}
layout['shapes'].append(building)
fig = go.Figure(data=[trace],layout=layout)
fig.update_layout(title='Using the sliders, move the green circle to the red one.')
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View,
v = (-20,20,1),
h = (-20,20,1),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
```
# What have we learned?
Translating a function just takes adding or subtracting number to the function definition.
The function $y=f(x)$ is moved up by two units when we change it to $y=f(x)+2$.
The function $y=f(x)$ is moved to the right by two units when we change it to $y=f(x-2)$.
Notice for vertical moves, the number 2 is added **outside** the function. For horizontal moves, the number 2 is subtracted **inside** the function, next to the variable $x$.
[](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
github_jupyter
|
%%html
<p>The raw code for this IPython notebook is hidden for easier reading. If you want to see it,
<button onclick="javascript:code_toggle()">CLICK HERE TO SHOW/HIDE CODE</button>
</p>
<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
import numpy as np
import ipywidgets as widgets
from plotly import graph_objs as go
x = np.linspace(-4,4,200)
fig = go.Figure(data = go.Scatter(x = x, y = x**2))
fig.update_layout(title='$\mbox{A parabola, }y=x^2$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
x = np.linspace(-4,4,200)
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=x**2,
mode='lines',
name='original'))
fig.add_trace(go.Scatter(x=x, y=x**2 + 5,
mode='lines',
name='vertical shift'))
fig.update_layout(title='$\mbox{A parabola, }y=x^2, \mbox{ and shifted up, } y=x^2 + 5$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
x = np.linspace(-4,6,200)
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=x**2,
mode='lines',
name='original'))
fig.add_trace(go.Scatter(x=x, y=(x-2)**2,
mode='lines',
name='horizontal shift'))
fig.add_trace(go.Scatter(x=[0], y=[0],
mode='markers',
name='original vertex'))
fig.add_trace(go.Scatter(x=[2], y=[0],
mode='markers',
name='shifted vertex'))
fig.update_layout(title='$\mbox{A parabola, }y=x^2, \mbox{ and shifted right, } y=(x-2)^2$',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5,
mode='lines',name='path')
fig = go.Figure()
fig.add_trace(t1)
fig.update_layout(title='Parabolic path of a thrown ball',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5 + 2.2,
mode='lines',
name='path'
)
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic path of a thrown ball, shifted up a bit',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
# This code to be hidden.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x + 1,
y = -5*(x-1)**2 + 5 + 2.2)
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic path of a thrown ball, shifted up and to the right',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
# Hide this.
x = np.linspace(0,2,200)
t1 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5,
name = 'Original path')
t2 = go.Scatter(
x = x,
y = -5*(x-1)**2 + 5 + 2.2,
name = 'Path translated up')
t3 = go.Scatter(
x = x + 1,
y = -5*(x-1)**2 + 5 + 2.2,
name = 'Path translated up and to the right')
fig = go.Figure()
fig.add_trace(t1)
fig.add_trace(t2)
fig.add_trace(t3)
fig.add_trace(go.Scatter(x=[0], y=[0], mode='markers',name='origin'))
fig.update_layout(title='Parabolic paths of three thrown balls',
xaxis_title='Time (seconds)',
yaxis_title='Height (meters)')
fig.show()
# Create the x and y variables for plotting the function.
x = np.linspace(-10,10,200)
# Assign the variables for plotting.
f_graph = go.Scatter(
x = x,
y = x,
name = 'f(x)')
# Assign the plot to a figure.
fig = go.Figure(f_graph)
# Plot the function.
fig.update_layout(title='Plot of a diagonal line',
xaxis_title='x values',
yaxis_title='y = f(x)')
fig.show()
x = np.linspace(-10,10,200)
# Two traces for plotting.
f_graph = go.Scatter(
x = x,
y = x,
name = 'f(x)')
f_translated = go.Scatter(
x = x,
y = x+2,
name = 'f(x) + 2')
data = [f_graph, f_translated]
fig = go.Figure([f_graph,f_translated])
fig.update_layout(title='Plot of two diagonal lines: y = x and y = x + 2',
xaxis_title='x values',
yaxis_title='y = f(x), y = f(x) + 2')
fig.show()
x = np.linspace(-10,10,200)
y1 = x
y2 = x+2
g1 = go.Scatter(
x = x,
y = y1,
name = 'Original function')
g2 = go.Scatter(
x = x,
y = y2,
name = 'Translated function')
fig = go.Figure([g1,g2])
fig.update_layout(title='Plot of two diagonal lines: y = x and y = (x+2)',
xaxis_title='x values',
yaxis_title='y values')
fig.show()
# Hide this.
x = np.linspace(-10,10,200)
fig = go.Figure(go.Scatter(x=x,y=x**2))
fig.update_layout(title='y=arctan(x-(0.0)) + (0.0)',
xaxis_title='x values', xaxis_range=[-5,5],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-5,5],yaxis_zeroline=True)
def View1(h, v):
fig.update_layout(title='y = arctan(x -(' + str(h) + ')) + (' + str(v) + ')',
xaxis_title='x values', xaxis_range=[-5,5],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-5,5],yaxis_zeroline=True)
x = np.linspace(-10,10,200)
fig.update_traces(x=x,y = np.arctan(x - h) + v)
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View1,
v = (-5,5,0.5),
h = (-5,5,0.5),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
# Hide this.
def func(x, v, h):
return np.abs(np.sqrt(4-(x-2+h)**2)) - 2 + v
x1 = np.linspace(-10,10,200)
fig = go.Figure(go.Scatter(x=x1,y=func(x1,0.0,0.0)))
fig.update_layout(title='y = y = f(x-h) + v, an arc',
xaxis_title='x values', xaxis_range=[-10,10],xaxis_zeroline=True,
yaxis_title='y values', yaxis_range=[-10,10],yaxis_zeroline=True)
fig.update_xaxes(tick0=2.0, dtick=2.0)
fig.update_yaxes(tick0=2.0, dtick=2.0)
def View(v, h):
x1 = np.linspace(-10,10,200)
fig.update_traces(x=x1,y = func(x1, v, h))
fig.update_layout(title='y = f(x-h) + v, an arc')
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View,
v = (-10,10,1),
h = (-10,10,1),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
%%html
<button onclick="javascript:code_toggle()">CLICK HERE TO SHOW THE CODE CELL FOR THIS EXERCISE.</button>
# Write your translation function from Exercise 4 here.
def translate(x, f, v, h):
return f(x) # put your formula here
pass
# A test function
def testf(x):
return np.exp(-x**2)*0.4
# Test your translation function here.
h = 1 # Replace with a value of h
v = 0 # Replace with a value of v
x = np.linspace(-10,10,200)
y = translate(x, testf, v, h)
# Uncomment these lines to plot the translated function (select the lines and press 'CTRL /').
#fig = go.Figure([go.Scatter(x=x,y=y,name='Translated'),go.Scatter(x=x,y=testf(x),name='Original')])
#fig.show()
# Hide this.
# These are the coordinates for each 'building' rectangle. They are in the form
# x0, x1, y0, y1.
b_coords = [[-9.8,-6.2,-7.8,-6.2], [-9.8,-1.2,-9.8,-9.2], [-4.8,-0.2,-7.8,-0.2],
[-8.8,-1.2,0.2,3.8], [-8.8,-6.2,-4.8,-1.2], [0.2,8.8,-8.8,-8.2],
[1.2,9.8,-6.8,-1.2], [0.2,7.8,0.2,4.8], [9.2,9.8,0.2,9.8],
[9.2,9.8,0.2,9.8], [0.2,7.8,6.2,8.8], [-3.8,-1.2,5.2,7.8],
[-9.8,-5.2,5.2,9.8], [-3.8,-1.2,9.2,9.8]]
def View(v, h):
trace = go.Scatter(x=[0],y=[0],mode='markers')
layout = {
'xaxis': {
'range': [-10, 10],
'zeroline': True
},
'yaxis': {
'range': [-10, 10],
'zeroline': True
},
'shapes': [
# filled circle
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'fillcolor': 'rgba(50, 171, 96, 0.7)',
'x0': -9+h,
'y0': -9+v,
'x1': -8+h,
'y1': -8+v,
'line': {'color': 'rgba(50, 171, 96, 1)'}
},
# end point
{
'type': 'circle',
'xref': 'x',
'yref': 'y',
'fillcolor': 'rgba(255, 0, 0, 0.7)',
'x0': -1,
'y0': 8,
'x1': 0,
'y1': 9,
'line': {'color': 'rgba(255, 0, 0, 1)'}
}
]
}
# Add the 'building' obstacles.
for i in range(len(b_coords)):
building = {'type':'rect','xref':'x','yref':'y',
'fillcolor':'rgba(102, 51, 0, 0.7)','line':{'color':'rgba(102, 51, 0, 1)'},
'x0':b_coords[i][0],'x1':b_coords[i][1],'y0':b_coords[i][2],'y1':b_coords[i][3]}
layout['shapes'].append(building)
fig = go.Figure(data=[trace],layout=layout)
fig.update_layout(title='Using the sliders, move the green circle to the red one.')
fig.show()
import warnings
import sys
if not sys.warnoptions:
warnings.simplefilter("ignore")
interactive_plot = widgets.interactive(View,
v = (-20,20,1),
h = (-20,20,1),
continuous_update=True,
wait=True)
output = interactive_plot.children[-1]
output.layout.height = '600px'
output.layout.width = '600px'
output.clear_output(wait=True)
interactive_plot
| 0.642993 | 0.962743 |
# My Own Learner
> Notebook for exercises making my own learner class.
- toc: true
- badges: true
- comments: true
- categories: [jupyter]
```
import fastbook
fastbook.setup_book()
from fastbook import *
from fastai.vision.widgets import *
## MyLearner class
class MyLearner():
def __init__(self, dls : DataLoaders, model, loss_func, opt_func, metrics, lr=1e-3):
self.dls = dls
self.model = model
self.loss_func = loss_func
self.opt_func = opt_func
self.metrics = metrics
self.lr = lr
self.opt = self.opt_func([p for p in self.model.parameters() if p.requires_grad], lr=self.lr)
def fit(self, n_epoch):
for i in range(n_epoch):
self.train_epoch()
print(f"t_loss: {round(float(self.loss), 4)} acc: {self.validate_epoch()}", end='\n')
def train_epoch(self):
for xb,yb in self.dls.train:
self.calc_grad(xb, yb)
self.opt.step()
self.opt.zero_grad()
def calc_grad(self, xb, yb):
self.preds = self.model(xb)
self.loss_grad = self.loss_func(self.preds, yb)
self.loss = self.loss_grad.clone()
self.loss_grad.backward()
def validate_epoch(self):
accs = [self.metrics(self.model(xb), yb) for xb,yb in self.dls.valid]
return round(torch.stack(accs).mean().item(), 4)
class BasicOptim:
def __init__(self, params, lr):
self.params = params
self.lr = lr
def step(self, *args, **kwargs):
for p in self.params:
p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
## Models
# Linear model
def linear1(xb): return xb@weights + bias
# Simple neural network
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
## Test MyLearner class
# Load in training data
path = untar_data(URLs.MNIST_SAMPLE)
Path.BASE_PATH = path
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
#Package training data into data loader
dataSet = list(zip(train_x,train_y))
dataLoad = DataLoader(dataSet, batch_size=256)
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
validDataLoad = DataLoader(valid_dset, batch_size=256)
batch = train_x[:4]
batch.shape
preds = linear1(batch)
loss = learner.mnist_loss(preds, train_y[:4])
loss
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
learner = MyLearner()
learner.calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
weights.grad.zero_()
bias.grad.zero_()
learner.batch_accuracy(linear1(train_x[:4]), train_y[:4])
learner.validate_epoch(linear1, validDataLoad)
lr = 1.
params = weights,bias
learner.train_epoch(linear1, lr, params, dataLoad)
learner.validate_epoch(linear1, validDataLoad)
for i in range(20):
learner.train_epoch(linear1, lr, params, dataLoad)
print(learner.validate_epoch(linear1, validDataLoad), end=' ')
images, targes = dataLoad.dataset[1]
len(images)
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
my_net = nn.Sequential(
nn.Linear(28*28,128),
nn.ReLU(),
nn.Linear(128,64),
nn.ReLU(),
nn.Linear(64,1),
)
dls = DataLoaders(dataLoad, validDataLoad)
my_learner = MyLearner(dls, my_net, loss_func=mnist_loss, opt_func=SGD, metrics=batch_accuracy)
my_learner.fit(40)
```
|
github_jupyter
|
import fastbook
fastbook.setup_book()
from fastbook import *
from fastai.vision.widgets import *
## MyLearner class
class MyLearner():
def __init__(self, dls : DataLoaders, model, loss_func, opt_func, metrics, lr=1e-3):
self.dls = dls
self.model = model
self.loss_func = loss_func
self.opt_func = opt_func
self.metrics = metrics
self.lr = lr
self.opt = self.opt_func([p for p in self.model.parameters() if p.requires_grad], lr=self.lr)
def fit(self, n_epoch):
for i in range(n_epoch):
self.train_epoch()
print(f"t_loss: {round(float(self.loss), 4)} acc: {self.validate_epoch()}", end='\n')
def train_epoch(self):
for xb,yb in self.dls.train:
self.calc_grad(xb, yb)
self.opt.step()
self.opt.zero_grad()
def calc_grad(self, xb, yb):
self.preds = self.model(xb)
self.loss_grad = self.loss_func(self.preds, yb)
self.loss = self.loss_grad.clone()
self.loss_grad.backward()
def validate_epoch(self):
accs = [self.metrics(self.model(xb), yb) for xb,yb in self.dls.valid]
return round(torch.stack(accs).mean().item(), 4)
class BasicOptim:
def __init__(self, params, lr):
self.params = params
self.lr = lr
def step(self, *args, **kwargs):
for p in self.params:
p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
## Models
# Linear model
def linear1(xb): return xb@weights + bias
# Simple neural network
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
## Test MyLearner class
# Load in training data
path = untar_data(URLs.MNIST_SAMPLE)
Path.BASE_PATH = path
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
#Package training data into data loader
dataSet = list(zip(train_x,train_y))
dataLoad = DataLoader(dataSet, batch_size=256)
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
validDataLoad = DataLoader(valid_dset, batch_size=256)
batch = train_x[:4]
batch.shape
preds = linear1(batch)
loss = learner.mnist_loss(preds, train_y[:4])
loss
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
learner = MyLearner()
learner.calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
weights.grad.zero_()
bias.grad.zero_()
learner.batch_accuracy(linear1(train_x[:4]), train_y[:4])
learner.validate_epoch(linear1, validDataLoad)
lr = 1.
params = weights,bias
learner.train_epoch(linear1, lr, params, dataLoad)
learner.validate_epoch(linear1, validDataLoad)
for i in range(20):
learner.train_epoch(linear1, lr, params, dataLoad)
print(learner.validate_epoch(linear1, validDataLoad), end=' ')
images, targes = dataLoad.dataset[1]
len(images)
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
my_net = nn.Sequential(
nn.Linear(28*28,128),
nn.ReLU(),
nn.Linear(128,64),
nn.ReLU(),
nn.Linear(64,1),
)
dls = DataLoaders(dataLoad, validDataLoad)
my_learner = MyLearner(dls, my_net, loss_func=mnist_loss, opt_func=SGD, metrics=batch_accuracy)
my_learner.fit(40)
| 0.783409 | 0.739069 |
# ๅญฆ็ฟๆธใฎVGGใขใใซใไฝฟ็จใใ่ปข็งปๅญฆ็ฟ
## ็ฎ็
- PyTorch ใง ImageNet ใใผใฟใปใใใงใฎๅญฆ็ฟๆธใขใใซใใญใผใใงใใใใใซใชใ
- ็ปๅๅ้ก็จใขใใซใงใใVGGใขใใซใซใคใใฆ็่งฃใใ
- ๅ
ฅๅ็ปๅใฎใตใคใบใ่ฒใๅคๆใงใใใใใซใชใ
## ImageNet ใใผใฟใปใใ
- ในใฟใณใใฉใผใๅคงๅญฆใใคใณใฟใผใใใไธใใ็ปๅใ้ใใฆๅ้กใใใใผใฟใปใใ
- ILSVRC (ImageNet Large Scale Visual Recognition Challenge) ใณใณใในใใงไฝฟ็จใใใ
### ILSVRC2012 ใใผใฟใปใใ
- ImageNet ใใผใฟใปใใใฎใใกใILSVRC 2012ๅนดใฎใณใณใในใใงไฝฟ็จใใใใใผใฟใปใใ
- ็ปๅๅ้กใฎๅญฆ็ฟๆธใขใใซใฎๆฎใฉใฏใใฎใใผใฟใปใใใๅ
ใซใใใฆใใ
- ็ปๅๆฐ:
- ใฏใฉในๆฐ: 1,000็จฎ้ก
- ๅญฆ็ฟ็จใใผใฟ: 120ไธๆ
- ๆค่จผ็จใใผใฟ: 5ไธๆ
- ใในใ็จใใผใฟ: 10ไธๆ
## VGG-16 ใขใใซ
- 2014ๅนดใฎ ILSVRC ใณใณใในใใง2ไฝใซใชใฃใ็ณใฟ่พผใฟใใฅใผใฉใซใใใใฏใผใฏใขใใซ
- ใชใใฏในใใฉใผใๅคงๅญฆใฎ VGG (Visual Geometry Group) ใใผใ ใไฝๆใใ16ๅฑคใใๆงๆใใใใขใใซ
```
import os.path
if not os.path.exists('./pytorch_advanced/'):
!git clone https://github.com/YutaroOgawa/pytorch_advanced.git
```
## ็ปๅๅ้กใฎๆบๅใใกใคใซ
```
import os
import urllib.request
import zipfile
# ใใฉใซใใdataใใๅญๅจใใชใๅ ดๅใฏไฝๆใใ
data_dir = './data/'
if not os.path.exists(data_dir):
os.mkdir(data_dir)
# ImageNetใฎclass_indexใใใฆใณใญใผใใใ
## Kerasใง็จๆใใใฆใใใใฎใๅฉ็จ
## https://github.com/fchollet/deep-learning-models/blob/master/imagenet_utils.py
url = "https://s3.amazonaws.com/deep-learning-models/image-models/imagenet_class_index.json"
save_path = os.path.join(data_dir, "imagenet_class_index.json")
if not os.path.exists(save_path):
urllib.request.urlretrieve(url, save_path)
# ใขใชใจใใใฎ็ปๅใใผใฟใใใฆใณใญใผใใ่งฃๅ
## PyTorchใฎใใฅใผใใชใขใซใง็จๆใใใฆใใใใฎใๅฉ็จ
## https://pytorch.org/tutorials/beginner/transfer_learning_tutorial.html
url = "https://download.pytorch.org/tutorial/hymenoptera_data.zip"
save_path = os.path.join(data_dir, "hymenoptera_data.zip")
if not os.path.exists(save_path):
urllib.request.urlretrieve(url, save_path)
# ZIPใใกใคใซใ่ชญใฟ่พผใฟ
zip = zipfile.ZipFile(save_path)
zip.extractall(data_dir) # ZIPใ่งฃๅ
zip.close() # ZIPใใกใคใซใใฏใญใผใบ
# ZIPใใกใคใซใๆถๅป
os.remove(save_path)
```
## ใใใฑใผใธใฎimportใจPyTorchใฎใใผใธใงใณใ็ขบ่ช
```
# ๅฟ
่ฆใใใฑใผใธใฎimport
import numpy as np
import json
from PIL import Image
import matplotlib.pyplot as plt
# matplotlibใฎใฐใฉใใNotebookใซinline่กจ็คบ
%matplotlib inline
# PyTorch้ข้ฃใใใฑใผใธใฎimport
import torch
import torchvision
from torchvision import models, transforms
# PyTorchใฎใใผใธใงใณ็ขบ่ช
print('PyTorch Version: ', torch.__version__)
print('Torchvision Version: ', torchvision.__version__)
```
## VGG-16ใฎๅญฆ็ฟๆธใฟใขใใซใใญใผใ
```
# ๅญฆ็ฟๆธใฟใฎVGG-16ใขใใซใใญใผใ
# ๅใใฆๅฎ่กใใ้ใฏใๅญฆ็ฟๆธใฟใใฉใกใผใฟใใใฆใณใญใผใใใใใใๅฎ่กใซๆ้ใใใใ
# VGG-16ใขใใซใฎใคใณในใฟใณในใ็ๆ
use_pretrained = True # ๅญฆ็ฟๆธใฟใฎใใฉใกใผใฟใไฝฟ็จ
net = models.vgg16(pretrained=use_pretrained)
net.eval() # ๆจ่ซใขใผใใซ่จญๅฎ
# ใขใใซใฎใใใใฏใผใฏๆงๆใๅบๅ
print(net)
```
## ๅ
ฅๅ็ปๅใฎๅๅฆ็ใฏใฉในใไฝๆ
```
# ๅ
ฅๅ็ปๅใฎๅๅฆ็ใฏใฉใน
class BaseTransform()
"""
็ปๅๅๅฆ็ใฏใฉใน็ๆใ
Attributes
----------
resize : int
ใชใตใคใบๅ
ใฎ็ปๅใฎๅคงใใใ
mean : (R, G, B)
ๅ่ฒใใฃใใซใฎๅนณๅๅคใ
std : (R, G, B)
ๅ่ฒใใฃใใซใฎๆจๆบๅๅทฎใ
"""
def __init__(self, resize, mean, std):
self.base_transform = transforms.Compose([
transforms.Resize(resize), # ็ญใ่พบใฎ้ทใใresizeใฎๅคงใใใซใชใ
transforms.CenterCrop(resize), # ็ปๅไธญๅคฎใresize ร resizeใงๅใๅใ
transforms.ToTensor(), # Torchใใณใฝใซใซๅคๆ
transforms.Normalize(mean, std) # ่ฒๆ
ๅ ฑใฎๆจๆบๅ
])
def __call__(self, img):
"""
็ปๅใฎใตใคใบใใชใตใคใบใใ่ฒใๆจๆบๅใใใ
Parameters
----------
img : PIL.Image
ใชใตใคใบๅฏพ่ฑกใฎ็ปๅใชใใธใงใฏใใ
Returns
-------
resized_image : PIL.Image
ใชใตใคใบๅพใฎ็ปๅใชใใธใงใฏใใ
"""
return self.base_transform(img)
# ็ปๅๅๅฆ็ใฎๅไฝใ็ขบ่ช
# 1. ็ปๅ่ชญใฟ่พผใฟ
image_file_path = './pytorch_advanced/1_image_classification/data/goldenretriever-3724972_640.jpg'
img = Image.open(image_file_path) # [้ซใ][ๅน
][่ฒRGB]
# 2. ๅ
ใฎ็ปๅใฎ่กจ็คบ
plt.imshow(img)
plt.show()
# 3. ็ปๅใฎๅๅฆ็ใจๅฆ็ๆธใฟ็ปๅใฎ่กจ็คบ
resize = 224
mean = (0.485, 0.456, 0.406)
std = (0.229, 0.224, 0.225)
transform = BaseTransform(resize, mean, std)
img_transformed = transform(img) # torch.Size([3, 224, 224])
# (่ฒใ้ซใใๅน
)ใ (้ซใใๅน
ใ่ฒ)ใซๅคๆใใ0-1ใซๅคใๅถ้ใใฆ่กจ็คบ
img_transformed = img_transformed.numpy().transpose((1, 2, 0))
img_transformed = np.clip(img_transformed, 0, 1)
plt.imshow(img_transformed)
plt.show()
```
## ๅบๅ็ตๆใใใฉใใซใไบๆธฌใใๅพๅฆ็ใฏใฉในใไฝๆ
```
# ILSVRCใฎใฉใใซๆ
ๅ ฑใใญใผใใ่พๆๆธๅๅคๆฐใ็ๆ
ILSVRC_class_index = json.load(open('./data/imagenet_class_index.json', 'r'))
ILSVRC_class_index
# ๅบๅ็ตๆใใใฉใใซใไบๆธฌใใๅพๅฆ็ใฏใฉใน
class ILSVRCPredictor():
"""
ILSVRCใใผใฟใซๅฏพใใใขใใซใฎๅบๅใใใฉใใซใๆฑใใใ
Attributes
----------
class_index : dictionary
ใฏใฉในindexใจใฉใใซๅใๅฏพๅฟใใใ่พๆธๅๅคๆฐใ
"""
def __init__(self, class_index):
self.class_index = class_index
def predict_max(self, out):
"""
็ขบ็ๆๅคงใฎILSVRCใฎใฉใใซๅใๅๅพใใใ
Parameters
----------
out : torch.Size([1, 1000])
Netใใใฎๅบๅใ
Returns
-------
predicted_label_name : str
ๆใไบๆธฌ็ขบ็ใ้ซใใฉใใซใฎๅๅใ
"""
maxid = np.argmax(out.detach().numpy())
predicted_label_name = self.class_index[str(maxid)][1]
return predicted_label_name
```
## ๅญฆ็ฟๆธใฟVGGใขใใซใงๆๅ
ใฎ็ปๅใไบๆธฌ
```
# ILSVRCใฎใฉใใซๆ
ๅ ฑใใญใผใใ่พๆๆธๅๅคๆฐใ็ๆ
ILSVRC_class_index = json.load(open('./data/imagenet_class_index.json', 'r'))
# ILSVRCPredictorใฎใคใณในใฟใณในใ็ๆ
predictor = ILSVRCPredictor(ILSVRC_class_index)
# ๅ
ฅๅ็ปๅใ่ชญใฟ่พผใ
image_file_path = './pytorch_advanced/1_image_classification/data/goldenretriever-3724972_640.jpg'
img = Image.open(image_file_path) # [้ซใ][ๅน
][่ฒRGB]
# ๅๅฆ็ใฎๅพใใใใใตใคใบใฎๆฌกๅ
ใ่ฟฝๅ
transform = BaseTransform(resize, mean, std) # ๅๅฆ็ใฏใฉในไฝๆ
img_transformed = transform(img) # torch.Size([3, 224, 224])
inputs = img_transformed.unsqueeze_(0) # torch.Size([1, 3, 224, 224])
# ใขใใซใซๅ
ฅๅใใใขใใซๅบๅใใฉใใซใซๅคๆ
out = net(inputs) # torch.Size([1, 1000])
result = predictor.predict_max(out)
# ไบๆธฌ็ตๆใๅบๅ
print("ๅ
ฅๅ็ปๅใฎไบๆธฌ็ตๆ๏ผ", result)
```
โ ็ปๅใ่ฆใฆใใใใgolden_retrieverใใซๅ้กใใใใจไธๆใๆจๆธฌใงใใฆใใ
|
github_jupyter
|
import os.path
if not os.path.exists('./pytorch_advanced/'):
!git clone https://github.com/YutaroOgawa/pytorch_advanced.git
import os
import urllib.request
import zipfile
# ใใฉใซใใdataใใๅญๅจใใชใๅ ดๅใฏไฝๆใใ
data_dir = './data/'
if not os.path.exists(data_dir):
os.mkdir(data_dir)
# ImageNetใฎclass_indexใใใฆใณใญใผใใใ
## Kerasใง็จๆใใใฆใใใใฎใๅฉ็จ
## https://github.com/fchollet/deep-learning-models/blob/master/imagenet_utils.py
url = "https://s3.amazonaws.com/deep-learning-models/image-models/imagenet_class_index.json"
save_path = os.path.join(data_dir, "imagenet_class_index.json")
if not os.path.exists(save_path):
urllib.request.urlretrieve(url, save_path)
# ใขใชใจใใใฎ็ปๅใใผใฟใใใฆใณใญใผใใ่งฃๅ
## PyTorchใฎใใฅใผใใชใขใซใง็จๆใใใฆใใใใฎใๅฉ็จ
## https://pytorch.org/tutorials/beginner/transfer_learning_tutorial.html
url = "https://download.pytorch.org/tutorial/hymenoptera_data.zip"
save_path = os.path.join(data_dir, "hymenoptera_data.zip")
if not os.path.exists(save_path):
urllib.request.urlretrieve(url, save_path)
# ZIPใใกใคใซใ่ชญใฟ่พผใฟ
zip = zipfile.ZipFile(save_path)
zip.extractall(data_dir) # ZIPใ่งฃๅ
zip.close() # ZIPใใกใคใซใใฏใญใผใบ
# ZIPใใกใคใซใๆถๅป
os.remove(save_path)
# ๅฟ
่ฆใใใฑใผใธใฎimport
import numpy as np
import json
from PIL import Image
import matplotlib.pyplot as plt
# matplotlibใฎใฐใฉใใNotebookใซinline่กจ็คบ
%matplotlib inline
# PyTorch้ข้ฃใใใฑใผใธใฎimport
import torch
import torchvision
from torchvision import models, transforms
# PyTorchใฎใใผใธใงใณ็ขบ่ช
print('PyTorch Version: ', torch.__version__)
print('Torchvision Version: ', torchvision.__version__)
# ๅญฆ็ฟๆธใฟใฎVGG-16ใขใใซใใญใผใ
# ๅใใฆๅฎ่กใใ้ใฏใๅญฆ็ฟๆธใฟใใฉใกใผใฟใใใฆใณใญใผใใใใใใๅฎ่กใซๆ้ใใใใ
# VGG-16ใขใใซใฎใคใณในใฟใณในใ็ๆ
use_pretrained = True # ๅญฆ็ฟๆธใฟใฎใใฉใกใผใฟใไฝฟ็จ
net = models.vgg16(pretrained=use_pretrained)
net.eval() # ๆจ่ซใขใผใใซ่จญๅฎ
# ใขใใซใฎใใใใฏใผใฏๆงๆใๅบๅ
print(net)
# ๅ
ฅๅ็ปๅใฎๅๅฆ็ใฏใฉใน
class BaseTransform()
"""
็ปๅๅๅฆ็ใฏใฉใน็ๆใ
Attributes
----------
resize : int
ใชใตใคใบๅ
ใฎ็ปๅใฎๅคงใใใ
mean : (R, G, B)
ๅ่ฒใใฃใใซใฎๅนณๅๅคใ
std : (R, G, B)
ๅ่ฒใใฃใใซใฎๆจๆบๅๅทฎใ
"""
def __init__(self, resize, mean, std):
self.base_transform = transforms.Compose([
transforms.Resize(resize), # ็ญใ่พบใฎ้ทใใresizeใฎๅคงใใใซใชใ
transforms.CenterCrop(resize), # ็ปๅไธญๅคฎใresize ร resizeใงๅใๅใ
transforms.ToTensor(), # Torchใใณใฝใซใซๅคๆ
transforms.Normalize(mean, std) # ่ฒๆ
ๅ ฑใฎๆจๆบๅ
])
def __call__(self, img):
"""
็ปๅใฎใตใคใบใใชใตใคใบใใ่ฒใๆจๆบๅใใใ
Parameters
----------
img : PIL.Image
ใชใตใคใบๅฏพ่ฑกใฎ็ปๅใชใใธใงใฏใใ
Returns
-------
resized_image : PIL.Image
ใชใตใคใบๅพใฎ็ปๅใชใใธใงใฏใใ
"""
return self.base_transform(img)
# ็ปๅๅๅฆ็ใฎๅไฝใ็ขบ่ช
# 1. ็ปๅ่ชญใฟ่พผใฟ
image_file_path = './pytorch_advanced/1_image_classification/data/goldenretriever-3724972_640.jpg'
img = Image.open(image_file_path) # [้ซใ][ๅน
][่ฒRGB]
# 2. ๅ
ใฎ็ปๅใฎ่กจ็คบ
plt.imshow(img)
plt.show()
# 3. ็ปๅใฎๅๅฆ็ใจๅฆ็ๆธใฟ็ปๅใฎ่กจ็คบ
resize = 224
mean = (0.485, 0.456, 0.406)
std = (0.229, 0.224, 0.225)
transform = BaseTransform(resize, mean, std)
img_transformed = transform(img) # torch.Size([3, 224, 224])
# (่ฒใ้ซใใๅน
)ใ (้ซใใๅน
ใ่ฒ)ใซๅคๆใใ0-1ใซๅคใๅถ้ใใฆ่กจ็คบ
img_transformed = img_transformed.numpy().transpose((1, 2, 0))
img_transformed = np.clip(img_transformed, 0, 1)
plt.imshow(img_transformed)
plt.show()
# ILSVRCใฎใฉใใซๆ
ๅ ฑใใญใผใใ่พๆๆธๅๅคๆฐใ็ๆ
ILSVRC_class_index = json.load(open('./data/imagenet_class_index.json', 'r'))
ILSVRC_class_index
# ๅบๅ็ตๆใใใฉใใซใไบๆธฌใใๅพๅฆ็ใฏใฉใน
class ILSVRCPredictor():
"""
ILSVRCใใผใฟใซๅฏพใใใขใใซใฎๅบๅใใใฉใใซใๆฑใใใ
Attributes
----------
class_index : dictionary
ใฏใฉในindexใจใฉใใซๅใๅฏพๅฟใใใ่พๆธๅๅคๆฐใ
"""
def __init__(self, class_index):
self.class_index = class_index
def predict_max(self, out):
"""
็ขบ็ๆๅคงใฎILSVRCใฎใฉใใซๅใๅๅพใใใ
Parameters
----------
out : torch.Size([1, 1000])
Netใใใฎๅบๅใ
Returns
-------
predicted_label_name : str
ๆใไบๆธฌ็ขบ็ใ้ซใใฉใใซใฎๅๅใ
"""
maxid = np.argmax(out.detach().numpy())
predicted_label_name = self.class_index[str(maxid)][1]
return predicted_label_name
# ILSVRCใฎใฉใใซๆ
ๅ ฑใใญใผใใ่พๆๆธๅๅคๆฐใ็ๆ
ILSVRC_class_index = json.load(open('./data/imagenet_class_index.json', 'r'))
# ILSVRCPredictorใฎใคใณในใฟใณในใ็ๆ
predictor = ILSVRCPredictor(ILSVRC_class_index)
# ๅ
ฅๅ็ปๅใ่ชญใฟ่พผใ
image_file_path = './pytorch_advanced/1_image_classification/data/goldenretriever-3724972_640.jpg'
img = Image.open(image_file_path) # [้ซใ][ๅน
][่ฒRGB]
# ๅๅฆ็ใฎๅพใใใใใตใคใบใฎๆฌกๅ
ใ่ฟฝๅ
transform = BaseTransform(resize, mean, std) # ๅๅฆ็ใฏใฉในไฝๆ
img_transformed = transform(img) # torch.Size([3, 224, 224])
inputs = img_transformed.unsqueeze_(0) # torch.Size([1, 3, 224, 224])
# ใขใใซใซๅ
ฅๅใใใขใใซๅบๅใใฉใใซใซๅคๆ
out = net(inputs) # torch.Size([1, 1000])
result = predictor.predict_max(out)
# ไบๆธฌ็ตๆใๅบๅ
print("ๅ
ฅๅ็ปๅใฎไบๆธฌ็ตๆ๏ผ", result)
| 0.503662 | 0.942823 |
## Dependencies
```
import json, glob
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras import layers
from tensorflow.keras.models import Model
```
# Load data
```
test = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/test.csv')
print('Test samples: %s' % len(test))
display(test.head())
```
# Model parameters
```
input_base_path = '/kaggle/input/160roberta-base/'
with open(input_base_path + 'config.json') as json_file:
config = json.load(json_file)
config
# vocab_path = input_base_path + 'vocab.json'
# merges_path = input_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
vocab_path = base_path + 'roberta-base-vocab.json'
merges_path = base_path + 'roberta-base-merges.txt'
config['base_model_path'] = base_path + 'roberta-base-tf_model.h5'
config['config_path'] = base_path + 'roberta-base-config.json'
model_path_list = glob.glob(input_base_path + '*.h5')
model_path_list.sort()
print('Models to predict:')
print(*model_path_list, sep = "\n")
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
```
# Pre process
```
test['text'].fillna('', inplace=True)
test["text"] = test["text"].apply(lambda x: x.lower())
test["text"] = test["text"].apply(lambda x: x.strip())
x_test, x_test_aux, x_test_aux_2 = get_data_test(test, tokenizer, config['MAX_LEN'], preprocess_fn=preprocess_roberta_test)
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.Dropout(.1)(last_hidden_state)
x_start = layers.Dense(1)(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dense(1)(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
```
# Make predictions
```
NUM_TEST_IMAGES = len(test)
test_start_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
test_end_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
for model_path in model_path_list:
print(model_path)
model = model_fn(config['MAX_LEN'])
model.load_weights(model_path)
test_preds = model.predict(get_test_dataset(x_test, config['BATCH_SIZE']))
test_start_preds += test_preds[0]
test_end_preds += test_preds[1]
```
# Post process
```
test['start'] = test_start_preds.argmax(axis=-1)
test['end'] = test_end_preds.argmax(axis=-1)
test['text_len'] = test['text'].apply(lambda x : len(x))
test['text_wordCnt'] = test['text'].apply(lambda x : len(x.split(' ')))
test["end"].clip(0, test["text_len"], inplace=True)
test["start"].clip(0, test["end"], inplace=True)
test['selected_text'] = test.apply(lambda x: decode(x['start'], x['end'], x['text'], config['question_size'], tokenizer), axis=1)
test["selected_text"].fillna(test["text"], inplace=True)
```
# Visualize predictions
```
display(test.head(10))
```
# Test set predictions
```
submission = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/sample_submission.csv')
submission['selected_text'] = test["selected_text"]
submission.to_csv('submission.csv', index=False)
submission.head(10)
```
|
github_jupyter
|
import json, glob
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras import layers
from tensorflow.keras.models import Model
test = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/test.csv')
print('Test samples: %s' % len(test))
display(test.head())
input_base_path = '/kaggle/input/160roberta-base/'
with open(input_base_path + 'config.json') as json_file:
config = json.load(json_file)
config
# vocab_path = input_base_path + 'vocab.json'
# merges_path = input_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
vocab_path = base_path + 'roberta-base-vocab.json'
merges_path = base_path + 'roberta-base-merges.txt'
config['base_model_path'] = base_path + 'roberta-base-tf_model.h5'
config['config_path'] = base_path + 'roberta-base-config.json'
model_path_list = glob.glob(input_base_path + '*.h5')
model_path_list.sort()
print('Models to predict:')
print(*model_path_list, sep = "\n")
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
test['text'].fillna('', inplace=True)
test["text"] = test["text"].apply(lambda x: x.lower())
test["text"] = test["text"].apply(lambda x: x.strip())
x_test, x_test_aux, x_test_aux_2 = get_data_test(test, tokenizer, config['MAX_LEN'], preprocess_fn=preprocess_roberta_test)
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.Dropout(.1)(last_hidden_state)
x_start = layers.Dense(1)(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dense(1)(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
NUM_TEST_IMAGES = len(test)
test_start_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
test_end_preds = np.zeros((NUM_TEST_IMAGES, config['MAX_LEN']))
for model_path in model_path_list:
print(model_path)
model = model_fn(config['MAX_LEN'])
model.load_weights(model_path)
test_preds = model.predict(get_test_dataset(x_test, config['BATCH_SIZE']))
test_start_preds += test_preds[0]
test_end_preds += test_preds[1]
test['start'] = test_start_preds.argmax(axis=-1)
test['end'] = test_end_preds.argmax(axis=-1)
test['text_len'] = test['text'].apply(lambda x : len(x))
test['text_wordCnt'] = test['text'].apply(lambda x : len(x.split(' ')))
test["end"].clip(0, test["text_len"], inplace=True)
test["start"].clip(0, test["end"], inplace=True)
test['selected_text'] = test.apply(lambda x: decode(x['start'], x['end'], x['text'], config['question_size'], tokenizer), axis=1)
test["selected_text"].fillna(test["text"], inplace=True)
display(test.head(10))
submission = pd.read_csv('/kaggle/input/tweet-sentiment-extraction/sample_submission.csv')
submission['selected_text'] = test["selected_text"]
submission.to_csv('submission.csv', index=False)
submission.head(10)
| 0.461017 | 0.310015 |
```
from featuretools.primitives import TransformPrimitive
from featuretools.tests.testing_utils import make_ecommerce_entityset
from featuretools.variable_types import DatetimeTimeIndex, NaturalLanguage, Numeric
import featuretools as ft
import numpy as np
import re
```
```
class StringCount(TransformPrimitive):
'''Count the number of times the string value occurs.'''
name = 'string_count'
input_types = [NaturalLanguage]
return_type = Numeric
def __init__(self, string=None):
self.string = string
def get_function(self):
def string_count(column):
assert self.string is not None, "string to count needs to be defined"
# this is a naive implementation used for clarity
counts = [text.lower().count(self.string) for text in column]
return counts
return string_count
```
```
es = make_ecommerce_entityset()
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="sessions",
agg_primitives=["sum", "mean", "std"],
trans_primitives=[StringCount(string="the")],
)
feature_matrix[[
'STD(log.STRING_COUNT(comments, string=the))',
'SUM(log.STRING_COUNT(comments, string=the))',
'MEAN(log.STRING_COUNT(comments, string=the))',
]]
```
```
class CaseCount(TransformPrimitive):
'''Return the count of upper case and lower case letters of a text.'''
name = 'case_count'
input_types = [NaturalLanguage]
return_type = Numeric
number_output_features = 2
def get_function(self):
def case_count(array):
# this is a naive implementation used for clarity
upper = np.array([len(re.findall('[A-Z]', i)) for i in array])
lower = np.array([len(re.findall('[a-z]', i)) for i in array])
return upper, lower
return case_count
```
```
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="sessions",
agg_primitives=[],
trans_primitives=[CaseCount],
)
feature_matrix[[
'customers.CASE_COUNT(favorite_quote)[0]',
'customers.CASE_COUNT(favorite_quote)[1]',
]]
```
```
class HourlySineAndCosine(TransformPrimitive):
'''Returns the sine and cosine of the hour.'''
name = 'hourly_sine_and_cosine'
input_types = [DatetimeTimeIndex]
return_type = Numeric
number_output_features = 2
def get_function(self):
def hourly_sine_and_cosine(column):
sine = np.sin(column.dt.hour)
cosine = np.cos(column.dt.hour)
return sine, cosine
return hourly_sine_and_cosine
def generate_names(self, base_feature_names):
name = self.generate_name(base_feature_names)
return f'{name}[sine]', f'{name}[cosine]'
```
```
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="log",
agg_primitives=[],
trans_primitives=[HourlySineAndCosine],
)
feature_matrix.head()[[
'HOURLY_SINE_AND_COSINE(datetime)[sine]',
'HOURLY_SINE_AND_COSINE(datetime)[cosine]',
]]
```
|
github_jupyter
|
from featuretools.primitives import TransformPrimitive
from featuretools.tests.testing_utils import make_ecommerce_entityset
from featuretools.variable_types import DatetimeTimeIndex, NaturalLanguage, Numeric
import featuretools as ft
import numpy as np
import re
class StringCount(TransformPrimitive):
'''Count the number of times the string value occurs.'''
name = 'string_count'
input_types = [NaturalLanguage]
return_type = Numeric
def __init__(self, string=None):
self.string = string
def get_function(self):
def string_count(column):
assert self.string is not None, "string to count needs to be defined"
# this is a naive implementation used for clarity
counts = [text.lower().count(self.string) for text in column]
return counts
return string_count
es = make_ecommerce_entityset()
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="sessions",
agg_primitives=["sum", "mean", "std"],
trans_primitives=[StringCount(string="the")],
)
feature_matrix[[
'STD(log.STRING_COUNT(comments, string=the))',
'SUM(log.STRING_COUNT(comments, string=the))',
'MEAN(log.STRING_COUNT(comments, string=the))',
]]
class CaseCount(TransformPrimitive):
'''Return the count of upper case and lower case letters of a text.'''
name = 'case_count'
input_types = [NaturalLanguage]
return_type = Numeric
number_output_features = 2
def get_function(self):
def case_count(array):
# this is a naive implementation used for clarity
upper = np.array([len(re.findall('[A-Z]', i)) for i in array])
lower = np.array([len(re.findall('[a-z]', i)) for i in array])
return upper, lower
return case_count
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="sessions",
agg_primitives=[],
trans_primitives=[CaseCount],
)
feature_matrix[[
'customers.CASE_COUNT(favorite_quote)[0]',
'customers.CASE_COUNT(favorite_quote)[1]',
]]
class HourlySineAndCosine(TransformPrimitive):
'''Returns the sine and cosine of the hour.'''
name = 'hourly_sine_and_cosine'
input_types = [DatetimeTimeIndex]
return_type = Numeric
number_output_features = 2
def get_function(self):
def hourly_sine_and_cosine(column):
sine = np.sin(column.dt.hour)
cosine = np.cos(column.dt.hour)
return sine, cosine
return hourly_sine_and_cosine
def generate_names(self, base_feature_names):
name = self.generate_name(base_feature_names)
return f'{name}[sine]', f'{name}[cosine]'
feature_matrix, features = ft.dfs(
entityset=es,
target_entity="log",
agg_primitives=[],
trans_primitives=[HourlySineAndCosine],
)
feature_matrix.head()[[
'HOURLY_SINE_AND_COSINE(datetime)[sine]',
'HOURLY_SINE_AND_COSINE(datetime)[cosine]',
]]
| 0.747616 | 0.83025 |
```
import os
os.environ["CUDA_VISIBLE_DEVICES"]="0"
import pandas as pd
import numpy as np
import gc
from PIL import Image
from tqdm.auto import tqdm
# pytorch lighting
import pytorch_lightning as pl
from src.config import *
from src.dataset import *
from src.models import *
import warnings
warnings.filterwarnings('ignore')
data_dir = '/data/siim-covid19-detection/'
test_csv_path = data_dir + 'sample_submission.csv'
df_test = pd.read_csv(test_csv_path)
df_test
id_laststr_list = []
for i in range(df_test.shape[0]):
id_laststr_list.append(df_test.loc[i,'id'][-1])
df_test['id_last_str'] = id_laststr_list
df_test
study_len = df_test[df_test['id_last_str'] == 'y'].shape[0]
study_len
test_df = pd.read_csv(test_csv_path)
test_df
test_df['negative'] = 0
test_df['typical'] = 0
test_df['indeterminate'] = 0
test_df['atypical'] = 0
test_df
label_cols = test_df.columns[2:]
label_cols
CFG = Config
def to_tensor(x, **kwargs):
if x.ndim==2 :
x = np.expand_dims(x,2)
x = np.transpose(x,(2,0,1)).astype('float32') / 255.
x = torch.from_numpy(x)
return x
def get_preprocessing():
"""Construct preprocessing transform
Args:
preprocessing_fn (callbale): data normalization function
(can be specific for each pretrained neural network)
Return:
transform: albumentations.Compose
"""
_transform = [
# A.Lambda(image=preprocessing_fn),
A.Lambda(image=to_tensor, mask=to_tensor),
]
return A.Compose(_transform)
def get_val_transforms(CFG):
return A.Compose([
A.Resize(CFG.image_size, CFG.image_size),
# A.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], max_pixel_value=255.0, p=1.0),
# ToTensorV2(),
],p=1.0)
class SIIMTestDataset(Dataset):
def __init__(self, df, transforms=None, preprocessing=None):
super().__init__()
self.df = df
self.transforms = transforms
self.preprocessing = preprocessing
self.length = len(df)
def __len__(self):
return self.length
def __getitem__(self, index):
d = self.df.iloc[index]
split = d.id.split('_')[-1]
if split == 'study':
image_path = '/home/chen/ai-competition/siim-covid19-detection/test/study/%s.png' % (d.id)
else:
image_path = '/home/chen/ai-competition/siim-covid19-detection/test/image/%s.png' % (d.id)
image = cv2.imread(image_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
if image is None:
raise FileNotFoundError(image_path)
# apply augmentations
if self.transforms:
image = self.transforms(image=image)['image']
else:
image = torch.from_numpy(image)
# apply preprocessing
if self.preprocessing:
sample = self.preprocessing(image=image)
image = sample['image']
return image
test_dataset = SIIMTestDataset(test_df, transforms=get_val_transforms(CFG), preprocessing=get_preprocessing())
test_loader = DataLoader(test_dataset, 32, num_workers=4, shuffle=False)
class SIIMPLModel(pl.LightningModule):
def __init__(self):
super(SIIMPLModel,self).__init__()
self.model = SIIMMaskNet(CFG.model_name, CFG.num_classes, pretrained=False)
def forward(self, x):
return self.model(x)
def do_predict(model, test_loader, tta=['']):
print(f'tta is {tta}')
test_probability = []
test_num = 0
tk0 = tqdm(enumerate(test_loader), total=len(test_loader))
for t, (image) in tk0:
batch_size = image.size(0)
image = image.to(device)
#<todo> TTA
model.eval()
with torch.no_grad():
probability = []
logit, mask = model(image)
probability.append(F.softmax(logit,-1))
if 'flip' in tta:
logit, mask = model(torch.flip(image,dims=(3,)))
probability.append(F.softmax(logit,-1))
if 'scale' in tta:
# size=None, scale_factor=None, mode='nearest', align_corners=None, recompute_scale_factor=None):
logit, mask = model(F.interpolate(image, scale_factor=1.25, mode='bilinear', align_corners=False))
probability.append(F.softmax(logit,-1))
#--------------
probability = torch.stack(probability,0).mean(0)
test_num += batch_size
test_probability.append(probability.data.cpu().numpy())
assert(test_num == len(test_loader.dataset))
probability = np.concatenate(test_probability)
return probability
# ====================================================
# Helper functions
# ====================================================
def inference(model, states, test_loader, device, ttas):
probs = 0
for (state,tta) in zip(states,ttas):
model = model.load_from_checkpoint(state)
model.to(device)
probability = do_predict(model, test_loader, tta)
probs += probability**0.5
probs = probs/len(states)
return probs
# ====================================================
# inference
# ====================================================
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
### init pl model
pl_model = SIIMPLModel()
#### drop duplicate images and save one 6227
models_path = f'/data/output/pl-siim-covid19-study-classification/\
{CFG.model_name}_folds_cutout_{CFG.image_size}_30e_Adam_GradualWarmupSchedulerV2_\
LabelSmoothingBinaryCrossEntropy_ls0.0_lovasz0.0_v2_dropdup'
### effnet-b5 best cv=0.3877336, lb=0.535
states = [
f'{models_path}/{CFG.model_name}/fold_0/epoch=17_mAP=0.387950.ckpt',
f'{models_path}/{CFG.model_name}/fold_1/epoch=17_mAP=0.401342.ckpt',
f'{models_path}/{CFG.model_name}/fold_2/epoch=17_mAP=0.382397.ckpt',
f'{models_path}/{CFG.model_name}/fold_3/epoch=20_mAP=0.370457.ckpt',
f'{models_path}/{CFG.model_name}/fold_4/epoch=18_mAP=0.396522.ckpt',
]
fold_ttas = [
['flip'],
['flip'],
['flip'],
['flip'],
['flip'],
]
predictions = inference(pl_model, states, test_loader, device, fold_ttas)
predictions
test_df[label_cols] = predictions
test_df
# test_df.to_csv(f'./predicts/{CFG.model_name}_folds_{CFG.image_size}_study_siim_test_ricord_pseudo_v3_flip.csv',index=False)
```
|
github_jupyter
|
import os
os.environ["CUDA_VISIBLE_DEVICES"]="0"
import pandas as pd
import numpy as np
import gc
from PIL import Image
from tqdm.auto import tqdm
# pytorch lighting
import pytorch_lightning as pl
from src.config import *
from src.dataset import *
from src.models import *
import warnings
warnings.filterwarnings('ignore')
data_dir = '/data/siim-covid19-detection/'
test_csv_path = data_dir + 'sample_submission.csv'
df_test = pd.read_csv(test_csv_path)
df_test
id_laststr_list = []
for i in range(df_test.shape[0]):
id_laststr_list.append(df_test.loc[i,'id'][-1])
df_test['id_last_str'] = id_laststr_list
df_test
study_len = df_test[df_test['id_last_str'] == 'y'].shape[0]
study_len
test_df = pd.read_csv(test_csv_path)
test_df
test_df['negative'] = 0
test_df['typical'] = 0
test_df['indeterminate'] = 0
test_df['atypical'] = 0
test_df
label_cols = test_df.columns[2:]
label_cols
CFG = Config
def to_tensor(x, **kwargs):
if x.ndim==2 :
x = np.expand_dims(x,2)
x = np.transpose(x,(2,0,1)).astype('float32') / 255.
x = torch.from_numpy(x)
return x
def get_preprocessing():
"""Construct preprocessing transform
Args:
preprocessing_fn (callbale): data normalization function
(can be specific for each pretrained neural network)
Return:
transform: albumentations.Compose
"""
_transform = [
# A.Lambda(image=preprocessing_fn),
A.Lambda(image=to_tensor, mask=to_tensor),
]
return A.Compose(_transform)
def get_val_transforms(CFG):
return A.Compose([
A.Resize(CFG.image_size, CFG.image_size),
# A.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], max_pixel_value=255.0, p=1.0),
# ToTensorV2(),
],p=1.0)
class SIIMTestDataset(Dataset):
def __init__(self, df, transforms=None, preprocessing=None):
super().__init__()
self.df = df
self.transforms = transforms
self.preprocessing = preprocessing
self.length = len(df)
def __len__(self):
return self.length
def __getitem__(self, index):
d = self.df.iloc[index]
split = d.id.split('_')[-1]
if split == 'study':
image_path = '/home/chen/ai-competition/siim-covid19-detection/test/study/%s.png' % (d.id)
else:
image_path = '/home/chen/ai-competition/siim-covid19-detection/test/image/%s.png' % (d.id)
image = cv2.imread(image_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
if image is None:
raise FileNotFoundError(image_path)
# apply augmentations
if self.transforms:
image = self.transforms(image=image)['image']
else:
image = torch.from_numpy(image)
# apply preprocessing
if self.preprocessing:
sample = self.preprocessing(image=image)
image = sample['image']
return image
test_dataset = SIIMTestDataset(test_df, transforms=get_val_transforms(CFG), preprocessing=get_preprocessing())
test_loader = DataLoader(test_dataset, 32, num_workers=4, shuffle=False)
class SIIMPLModel(pl.LightningModule):
def __init__(self):
super(SIIMPLModel,self).__init__()
self.model = SIIMMaskNet(CFG.model_name, CFG.num_classes, pretrained=False)
def forward(self, x):
return self.model(x)
def do_predict(model, test_loader, tta=['']):
print(f'tta is {tta}')
test_probability = []
test_num = 0
tk0 = tqdm(enumerate(test_loader), total=len(test_loader))
for t, (image) in tk0:
batch_size = image.size(0)
image = image.to(device)
#<todo> TTA
model.eval()
with torch.no_grad():
probability = []
logit, mask = model(image)
probability.append(F.softmax(logit,-1))
if 'flip' in tta:
logit, mask = model(torch.flip(image,dims=(3,)))
probability.append(F.softmax(logit,-1))
if 'scale' in tta:
# size=None, scale_factor=None, mode='nearest', align_corners=None, recompute_scale_factor=None):
logit, mask = model(F.interpolate(image, scale_factor=1.25, mode='bilinear', align_corners=False))
probability.append(F.softmax(logit,-1))
#--------------
probability = torch.stack(probability,0).mean(0)
test_num += batch_size
test_probability.append(probability.data.cpu().numpy())
assert(test_num == len(test_loader.dataset))
probability = np.concatenate(test_probability)
return probability
# ====================================================
# Helper functions
# ====================================================
def inference(model, states, test_loader, device, ttas):
probs = 0
for (state,tta) in zip(states,ttas):
model = model.load_from_checkpoint(state)
model.to(device)
probability = do_predict(model, test_loader, tta)
probs += probability**0.5
probs = probs/len(states)
return probs
# ====================================================
# inference
# ====================================================
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
### init pl model
pl_model = SIIMPLModel()
#### drop duplicate images and save one 6227
models_path = f'/data/output/pl-siim-covid19-study-classification/\
{CFG.model_name}_folds_cutout_{CFG.image_size}_30e_Adam_GradualWarmupSchedulerV2_\
LabelSmoothingBinaryCrossEntropy_ls0.0_lovasz0.0_v2_dropdup'
### effnet-b5 best cv=0.3877336, lb=0.535
states = [
f'{models_path}/{CFG.model_name}/fold_0/epoch=17_mAP=0.387950.ckpt',
f'{models_path}/{CFG.model_name}/fold_1/epoch=17_mAP=0.401342.ckpt',
f'{models_path}/{CFG.model_name}/fold_2/epoch=17_mAP=0.382397.ckpt',
f'{models_path}/{CFG.model_name}/fold_3/epoch=20_mAP=0.370457.ckpt',
f'{models_path}/{CFG.model_name}/fold_4/epoch=18_mAP=0.396522.ckpt',
]
fold_ttas = [
['flip'],
['flip'],
['flip'],
['flip'],
['flip'],
]
predictions = inference(pl_model, states, test_loader, device, fold_ttas)
predictions
test_df[label_cols] = predictions
test_df
# test_df.to_csv(f'./predicts/{CFG.model_name}_folds_{CFG.image_size}_study_siim_test_ricord_pseudo_v3_flip.csv',index=False)
| 0.537527 | 0.370937 |
# Understanding CNN's with a CAM - A Class Activation Map
> In this article we will look at how Class Acivation Maps (CAM's) can be used to understand and interpret the decisions that Convolutional Neural Networks (CNN's) make.
- toc: true
- comments: true
- image: images/cam.png
- categories: [deep-learning-theory]
```
#hide
!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
from fastbook import *
```
## Introduction
In this article we will look at how Class Acivation Maps (CAM's) can be used to understand and interpret the decisions that Convolutional Neural Networks (CNN's) make.
## CAM and Pytorch hooks
A Class Activation Map (CAM) and help us understand why Convolutional Neural Networks (CNN's) make the descisions they do. CAM's do this by looking at the outputs of the last convolutional layer just before the average pooling layer - combined with the predictions, to give a heatmap visualisation of why the model made that descision.
At each point in our final convolutional layer, we have as many channels as in the last linear layer. We can compute a dot product of those activations with the final weights to get for each location in our feature map, the score of the feature that was used to make that decision. In other words, we can identify the relationships between the parts of the network that are most active in generating the correct choice.
We can access activations inside the network using Pytorch hooks. **Wheras fastai callbacks allow you to inject code into the training loop, Pytorch hooks allow you to inject code into the forward and backward calculations themselves.**.
Lets see an example looking at a dataset of cats and dogs.
```
path = untar_data(URLs.PETS)/'images'
def is_cat(x): return x[0].isupper()
dls = ImageDataLoaders.from_name_func(
path, get_image_files(path), valid_pct=0.2, seed=21,
label_func=is_cat, item_tfms=Resize(224))
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1)
```
We can get a cat image. For CAM we want to store the activations of the last convolutional layer, lets create a hook function in a class with a state.
```
img = PILImage.create(image_cat())
x, = first(dls.test_dl([img]))
class Hook():
def hook_func(self, m, i, o): self.stored = o.detach().clone()
```
We can then instantiate a hook and attach it to any layer, in this case the last layer of the CNN body.
```
hook_output = Hook()
hook = learn.model[0].register_forward_hook(hook_output.hook_func)
```
Then we can grab a batch of images and feed it through our model.
```
with torch.no_grad(): output = learn.model.eval()(x)
```
Then we can extract our stored activations
```
act = hook_output.stored[0]
```
And check our predictions.
```
F.softmax(output, dim=-1)
```
So 0 means dog, but just to check.
```
dls.vocab
```
So the model seems quite confident the image is a cat.
To perform our dot product of the weight matrix with the activations we can use *einsum*.
```
x.shape
cam_map = torch.einsum('ck,kij->cij', learn.model[1][-1].weight, act)
cam_map.shape
```
So for each image in the batch, we get a 7x7 channel map that tells us which activations were higher or lower, which will allow us to see what parts of the image most influenced the models choice.
```
x_dec = TensorImage(dls.train.decode((x,))[0][0])
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map[1].detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
```
The parts in bright yellow correspond to higher activations and purple lower activations. So we can see the paws are the main area that made the model decide it was a cat. Its good to remove a hook once used as it can leak memory.
```
hook.remove()
```
We can manage hooks better by using a class, to handle all these things automatically.
```
class Hook():
def __init__(self, m):
self.hook = m.register_forward_hook(self.hook_func)
def hook_func(self, m, i, o): self.stored = o.detach().clone()
def __enter__(self, *args): return self
def __exit__(self, *args): self.hook.remove()
with Hook(learn.model[0]) as hook:
with torch.no_grad(): output = learn.model.eval()(x.cuda())
act = hook.stored
```
This Hook class is provided by fastai. This approach only works for the last layer.
## Gradient CAM
The previous approach only works for the last layer, but what if we want to look at activations for earlier layers? Gradient CAM lets us do this. Normally the gradients for weights are not stored after the backward pass, but we can store them, and then pick them up with a hook.
```
class HookBwd():
def __init__(self, m):
self.hook = m.register_backward_hook(self.hook_func)
def hook_func(self, m, gi, go): self.stored = go[0].detach().clone()
def __enter__(self, *args): return self
def __exit__(self, *args): self.hook.remove()
```
Let's try this approach on the last layer, as we did before. However we can use this approach to calculate the gradients for any layer, with respect to the output.
```
cls = 1
with HookBwd(learn.model[0]) as hookg:
with Hook(learn.model[0]) as hook:
output = learn.model.eval()(x.cuda())
act = hook.stored
output[0,cls].backward()
grad = hookg.stored
```
The weights for the Grad-CAM approach are given by the average of our gradients accross the feature/channel map.
```
w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
```
Let's now try this on a different layer, the second to last ResNet group layer.
```
with HookBwd(learn.model[0][-2]) as hookg:
with Hook(learn.model[0][-2]) as hook:
output = learn.model.eval()(x.cuda())
act = hook.stored
output[0,cls].backward()
grad = hookg.stored
w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
```
## Conclusion
In this article we saw how we can use Class Activation Map's to understand and interpret the choices a CNN makes.
|
github_jupyter
|
#hide
!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
from fastbook import *
path = untar_data(URLs.PETS)/'images'
def is_cat(x): return x[0].isupper()
dls = ImageDataLoaders.from_name_func(
path, get_image_files(path), valid_pct=0.2, seed=21,
label_func=is_cat, item_tfms=Resize(224))
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1)
img = PILImage.create(image_cat())
x, = first(dls.test_dl([img]))
class Hook():
def hook_func(self, m, i, o): self.stored = o.detach().clone()
hook_output = Hook()
hook = learn.model[0].register_forward_hook(hook_output.hook_func)
with torch.no_grad(): output = learn.model.eval()(x)
act = hook_output.stored[0]
F.softmax(output, dim=-1)
dls.vocab
x.shape
cam_map = torch.einsum('ck,kij->cij', learn.model[1][-1].weight, act)
cam_map.shape
x_dec = TensorImage(dls.train.decode((x,))[0][0])
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map[1].detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
hook.remove()
class Hook():
def __init__(self, m):
self.hook = m.register_forward_hook(self.hook_func)
def hook_func(self, m, i, o): self.stored = o.detach().clone()
def __enter__(self, *args): return self
def __exit__(self, *args): self.hook.remove()
with Hook(learn.model[0]) as hook:
with torch.no_grad(): output = learn.model.eval()(x.cuda())
act = hook.stored
class HookBwd():
def __init__(self, m):
self.hook = m.register_backward_hook(self.hook_func)
def hook_func(self, m, gi, go): self.stored = go[0].detach().clone()
def __enter__(self, *args): return self
def __exit__(self, *args): self.hook.remove()
cls = 1
with HookBwd(learn.model[0]) as hookg:
with Hook(learn.model[0]) as hook:
output = learn.model.eval()(x.cuda())
act = hook.stored
output[0,cls].backward()
grad = hookg.stored
w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
with HookBwd(learn.model[0][-2]) as hookg:
with Hook(learn.model[0][-2]) as hook:
output = learn.model.eval()(x.cuda())
act = hook.stored
output[0,cls].backward()
grad = hookg.stored
w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
interpolation='bilinear', cmap='magma');
| 0.600423 | 0.987129 |
```
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
%matplotlib inline
import matplotlib.pyplot as plt
X, y = load_diabetes().data, load_diabetes().target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
slr = LinearRegression()
slr.fit(X_train, y_train)
print(slr.coef_)
print(slr.intercept_)
plt.plot(X, y, 'o')
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
```
# Ridge
```
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=10.0).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=0.1).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
```
# Lasso
```
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.001).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
```
|
github_jupyter
|
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
%matplotlib inline
import matplotlib.pyplot as plt
X, y = load_diabetes().data, load_diabetes().target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
slr = LinearRegression()
slr.fit(X_train, y_train)
print(slr.coef_)
print(slr.intercept_)
plt.plot(X, y, 'o')
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=10.0).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=0.1).fit(X_train, y_train)
print(ridge.coef_)
print(ridge.intercept_)
y_train_pred = ridge.predict(X_train)
y_test_pred = ridge.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.001).fit(X_train, y_train)
print(lasso.coef_)
y_train_pred = lasso.predict(X_train)
y_test_pred = lasso.predict(X_test)
print('MSE train: %.3f, test: %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 train: %.3f, test: %.3f' % (r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
| 0.846546 | 0.883387 |
```
%autosave 0
```
*This notebook is part of course materials for CS 345: Machine Learning Foundations and Practice at Colorado State University.
Original versions were created by Asa Ben-Hur.
The content is availabe [on GitHub](https://github.com/asabenhur/CS345).*
*The text is released under the [CC BY-SA license](https://creativecommons.org/licenses/by-sa/4.0/), and code is released under the [MIT license](https://opensource.org/licenses/MIT).*
<img style="padding: 10px; float:right;" alt="CC-BY-SA icon.svg in public domain" src="https://upload.wikimedia.org/wikipedia/commons/d/d0/CC-BY-SA_icon.svg" width="125">
<a href="https://colab.research.google.com/github//asabenhur/CS345/blob/master/notebooks/module01_01_intro.ipynb">
<img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
# CS345 Course introduction
### What is machine learning
**Machine learning:** the construction and study of systems that learn from data.
Machine learning is an interdisciplinary field that requires background in multiple areas:
* Linear algebra for working with vectors and matrices
* Statistics and probability for reasoning about uncertainty
* Calculus for optimization
* Programming for efficient implementation of the algorithms
### Supervised learning
Example problem: handwritten digit recognition.
Some examples from the [MNIST dataset](https://en.wikipedia.org/wiki/MNIST_database):
<img style="padding: 10px; float:center;" alt="MNIST dataset by Josef Steppan CC BY-SA 4.0" src="https://upload.wikimedia.org/wikipedia/commons/2/27/MnistExamples.png" width="350">
### Course objectives
The machine learning toolbox:
* Formulating a problem as an ML problem
* Understanding a variety of ML algorithms
* Running and interpreting ML experiments
* Understanding what makes ML work โ theory and practice
### Python
Why Pytnon?
<img style="float: right;" src="https://www.python.org/static/community_logos/python-logo.png" width="200">
* A concise and intuitive language
* Simple, easy to learn syntax
* Highly readable, compact code
* Supports object oriented and functional programming
* Strong support for integration with other languages (C,C++,Java)
* Cross-platform compatibility
* Free
* Makes programming fun!
**We assume you already know the basics of Python**. The website has some resources you can use to come up to speed. The author of the textbook we are using has a set of notebooks for learning Python:
[A Whirlwind Tour of the Python Language](https://github.com/jakevdp/WhirlwindTourOfPython).
### Why Python for machine learning
Over the past decade or so Python has emerged as one of the primary data science / machine learning languages. In addition to the points mentioned above, here are a few additional aspects of Python that make it great for data science:
* An interpreted language โ allows for interactive data analysis
* Libraries for plotting and vector/matrix computation
* Many machine learning packages available: scikit-learn, TensorFlow, PyTorch
* Language of choice for many ML practitioners (other options: R)
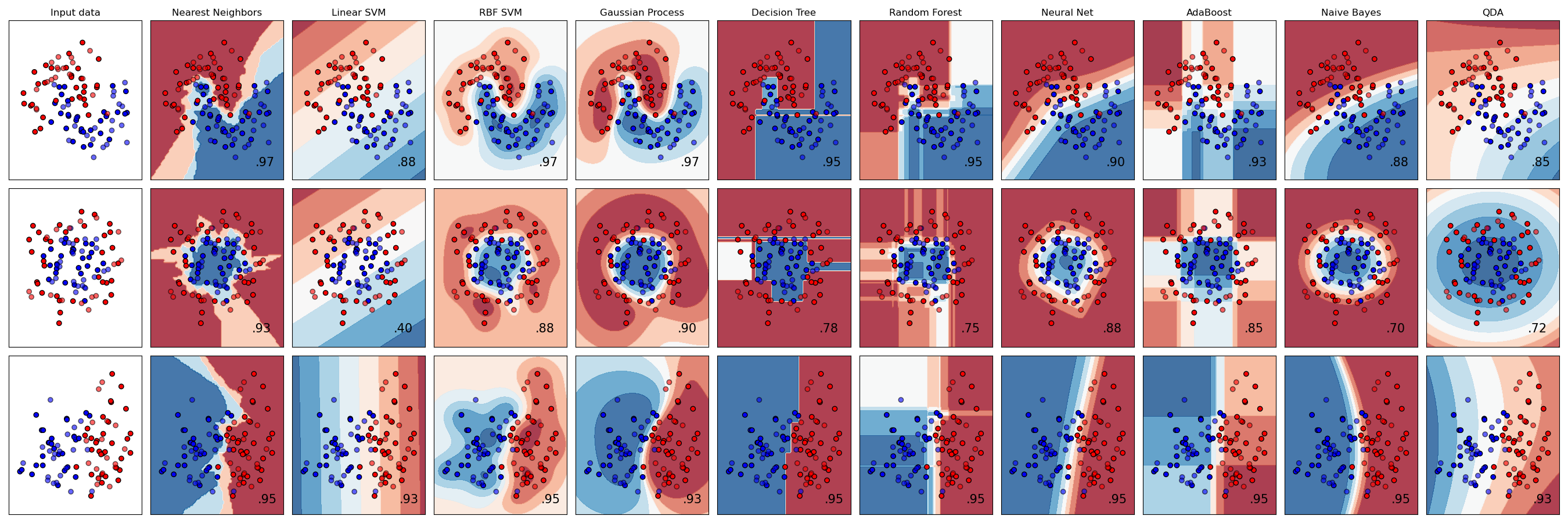
### The tools we will cover in this course:
* ``Numpy``: highly efficient manipulation of vectors and matrices
* ``Matplotlib``: data visualization
### Python version and environment
<img style="float: right;" src="https://upload.wikimedia.org/wikipedia/en/c/cd/Anaconda_Logo.png" alt="drawing" width="150"/>
Use version 3.X of Python.
If setting up Python on your personal machine, we recommend the [anaconda](https://www.anaconda.com/distribution/) Python distribution which is a data-science oriented distribution that includes all the tools we will use in this course.
### IPython and the Jupyter Notebook
The Jupyter notebook is a browser-based interface to the ``IPython`` Python shell.
In addition to executing Python/IPython statements, the notebook allows the user to include formatted text, static and dynamic visualizations, mathematical equations, and much more.
**It is the standard way of sharing data science analyses.**
<img style="float: right;" src="https://jupyter.org/assets/main-logo.svg" width="100">
To invoke the jupyter notebook use the command:
```bash
jupyter notebook
```
which brings up the Jupyter notebook browser. To open a specific notebook:
```bash
jupyter notebook notebook_name.ipynb
```
There are two primary types of cells in Jupyter:
```
# this is a code cell
```
This is a **markdown** cell. You can type *text* and good looking equations
$$f(x) = \frac{1}{2\pi} e^{-2 x^2 / \sigma^2}$$
```
print("Hello world!")
2 + 2
```
You can run shell commands:
```
!ls
```
The `%` sign is used for *magic commands*, which are iPython shell commands. For example, to find what other magic commands there are
```
%lsmagic
```
The `%timeit` magic is one that we will use quite regularly. Let's learn what it's for:
```
%timeit?
```
Now try this:
```
import antigravity
```
### Mastering the Jupyter notebook
To be more productive in using notebooks, I highly recommend exploring the notebook keyboard shortcuts.
Here is a useful [blog post](https://www.dataquest.io/blog/jupyter-notebook-tips-tricks-shortcuts/) that provides a detailed overview.
You will also need to know the basics of Markdown syntax.
One of the nice features of the Jupyter notebook is that it supports writing mathematical equation using LaTex. Here are a couple of examples of what you can do with LaTex:
$$
\sum_{i=1}^N x_i^2 + \alpha
$$
And here is the markup that generated this formula
```latex
$$
\sum_{i=1}^N x_i^2 + \alpha
$$
```
All LaTex commands are preceded by a `\`, and as you can see, it is quite intuitive!
|
github_jupyter
|
%autosave 0
jupyter notebook
There are two primary types of cells in Jupyter:
This is a **markdown** cell. You can type *text* and good looking equations
$$f(x) = \frac{1}{2\pi} e^{-2 x^2 / \sigma^2}$$
You can run shell commands:
The `%` sign is used for *magic commands*, which are iPython shell commands. For example, to find what other magic commands there are
The `%timeit` magic is one that we will use quite regularly. Let's learn what it's for:
Now try this:
### Mastering the Jupyter notebook
To be more productive in using notebooks, I highly recommend exploring the notebook keyboard shortcuts.
Here is a useful [blog post](https://www.dataquest.io/blog/jupyter-notebook-tips-tricks-shortcuts/) that provides a detailed overview.
You will also need to know the basics of Markdown syntax.
One of the nice features of the Jupyter notebook is that it supports writing mathematical equation using LaTex. Here are a couple of examples of what you can do with LaTex:
$$
\sum_{i=1}^N x_i^2 + \alpha
$$
And here is the markup that generated this formula
| 0.563378 | 0.986891 |
# Custom SVI Objectives
Pyro provides support for various optimization-based approaches to Bayesian inference, with `Trace_ELBO` serving as the basic implementation of SVI (stochastic variational inference).
See the [docs](http://docs.pyro.ai/en/dev/inference_algos.html#module-pyro.infer.svi) for more information on the various SVI implementations and SVI
tutorials [I](http://pyro.ai/examples/svi_part_i.html),
[II](http://pyro.ai/examples/svi_part_ii.html),
and [III](http://pyro.ai/examples/svi_part_iii.html) for background on SVI.
In this tutorial we show how advanced users can modify and/or augment the variational
objectives (alternatively: loss functions) provided by Pyro to support special use cases.
1. [Basic SVI Usage](#Basic-SVI-Usage)
1. [A Lower Level Pattern](#A-Lower-Level-Pattern)
2. [Example: Custom Regularizer](#Example:-Custom-Regularizer)
3. [Example: Scaling the Loss](#Example:-Scaling-the-Loss)
4. [Example: Mixing Optimizers](#Example:-Mixing-Optimizers)
5. [Example: Custom ELBO](#Example:-Custom-ELBO)
6. [Example: KL Annealing](#Example:-KL-Annealing)
## Basic SVI Usage
We first review the basic usage pattern of `SVI` objects in Pyro. We assume that the user
has defined a `model` and a `guide`. The user then creates an optimizer and an `SVI` object:
```python
optimizer = pyro.optim.Adam({"lr": 0.001, "betas": (0.90, 0.999)})
svi = pyro.infer.SVI(model, guide, optimizer, loss=pyro.infer.Trace_ELBO())
```
Gradient steps can then be taken with a call to `svi.step(...)`. The arguments to `step()` are then
passed to `model` and `guide`.
### A Lower-Level Pattern
The nice thing about the above pattern is that it allows Pyro to take care of various
details for us, for example:
- `pyro.optim.Adam` dynamically creates a new `torch.optim.Adam` optimizer whenever a new parameter is encountered
- `SVI.step()` zeros gradients between gradient steps
If we want more control, we can directly manipulate the differentiable loss method of
the various `ELBO` classes. For example, (assuming we know all the parameters in advance)
this is equivalent to the previous code snippet:
```python
# define optimizer and loss function
optimizer = torch.optim.Adam(my_parameters, {"lr": 0.001, "betas": (0.90, 0.999)})
loss_fn = pyro.infer.Trace_ELBO.differentiable_loss
# compute loss
loss = loss_fn(model, guide)
loss.backward()
# take a step and zero the parameter gradients
optimizer.step()
optimizer.zero_grad()
```
## Example: Custom Regularizer
Suppose we want to add a custom regularization term to the SVI loss. Using the above
usage pattern, this is easy to do. First we define our regularizer:
```python
def my_custom_L2_regularizer(my_parameters):
reg_loss = 0.0
for param in my_parameters:
reg_loss = reg_loss + param.pow(2.0).sum()
return reg_loss
```
Then the only change we need to make is:
```diff
- loss = loss_fn(model, guide)
+ loss = loss_fn(model, guide) + my_custom_L2_regularizer(my_parameters)
```
## Example: Scaling the Loss
Depending on the optimization algorithm, the scale of the loss may or not matter. Suppose
we want to scale our loss function by the number of datapoints before we differentiate it.
This is easily done:
```diff
- loss = loss_fn(model, guide)
+ loss = loss_fn(model, guide) / N_data
```
Note that in the case of SVI, where each term in the loss function is a log probability
from the model or guide, this same effect can be achieved using [`poutine.scale`](http://docs.pyro.ai/en/dev/poutine.html#pyro.poutine.scale). For
example we can use the `poutine.scale` decorator to scale both the model and guide:
```python
@poutine.scale(scale=1.0/N_data)
def model(...):
pass
@poutine.scale(scale=1.0/N_data)
def guide(...):
pass
```
## Example: Mixing Optimizers
The various optimizers in `pyro.optim` allow the user to specify optimization settings (e.g. learning rates) on
a per-parameter basis. But what if we want to use different optimization algorithms for different parameters?
We can do this using Pyro's `MultiOptimizer` (see below), but we can also achieve the same thing if we directly manipulate `differentiable_loss`:
```python
adam = torch.optim.Adam(adam_parameters, {"lr": 0.001, "betas": (0.90, 0.999)})
sgd = torch.optim.SGD(sgd_parameters, {"lr": 0.0001})
loss_fn = pyro.infer.Trace_ELBO.differentiable_loss
# compute loss
loss = loss_fn(model, guide)
loss.backward()
# take a step and zero the parameter gradients
adam.step()
sgd.step()
adam.zero_grad()
sgd.zero_grad()
```
For completeness, we also show how we can do the same thing using [MultiOptimizer](http://docs.pyro.ai/en/dev/optimization.html?highlight=multi%20optimizer#module-pyro.optim.multi), which allows
us to combine multiple Pyro optimizers. Note that since `MultiOptimizer` uses `torch.autograd.grad` under the hood (instead of `torch.Tensor.backward()`), it has a slightly different interface; in particular the `step()` method also takes parameters as inputs.
```python
def model():
pyro.param('a', ...)
pyro.param('b', ...)
...
adam = pyro.optim.Adam({'lr': 0.1})
sgd = pyro.optim.SGD({'lr': 0.01})
optim = MixedMultiOptimizer([(['a'], adam), (['b'], sgd)])
with pyro.poutine.trace(param_only=True) as param_capture:
loss = elbo.differentiable_loss(model, guide)
params = {'a': pyro.param('a'), 'b': pyro.param('b')}
optim.step(loss, params)
```
## Example: Custom ELBO
In the previous three examples we bypassed creating a `SVI` object and directly manipulated
the differentiable loss function provided by an `ELBO` implementation. Another thing we
can do is create custom `ELBO` implementations and pass those into the `SVI` machinery.
For example, a simplified version of a `Trace_ELBO` loss function might look as follows:
```python
# note that simple_elbo takes a model, a guide, and their respective arguments as inputs
def simple_elbo(model, guide, *args, **kwargs):
# run the guide and trace its execution
guide_trace = poutine.trace(guide).get_trace(*args, **kwargs)
# run the model and replay it against the samples from the guide
model_trace = poutine.trace(
poutine.replay(model, trace=guide_trace)).get_trace(*args, **kwargs)
# construct the elbo loss function
return -1*(model_trace.log_prob_sum() - guide_trace.log_prob_sum())
svi = SVI(model, guide, optim, loss=simple_elbo)
```
Note that this is basically what the `elbo` implementation in ["mini-pyro"](https://github.com/uber/pyro/blob/dev/pyro/contrib/minipyro.py) looks like.
### Example: KL Annealing
In the [Deep Markov Model Tutorial](http://pyro.ai/examples/dmm.html) the ELBO variational objective
is modified during training. In particular the various KL-divergence terms between latent random
variables are scaled downward (i.e. annealed) relative to the log probabilities of the observed data.
In the tutorial this is accomplished using `poutine.scale`. We can accomplish the same thing by defining
a custom loss function. This latter option is not a very elegant pattern but we include it anyway to
show the flexibility we have at our disposal.
```python
def simple_elbo_kl_annealing(model, guide, *args, **kwargs):
# get the annealing factor and latents to anneal from the keyword
# arguments passed to the model and guide
annealing_factor = kwargs.pop('annealing_factor', 1.0)
latents_to_anneal = kwargs.pop('latents_to_anneal', [])
# run the guide and replay the model against the guide
guide_trace = poutine.trace(guide).get_trace(*args, **kwargs)
model_trace = poutine.trace(
poutine.replay(model, trace=guide_trace)).get_trace(*args, **kwargs)
elbo = 0.0
# loop through all the sample sites in the model and guide trace and
# construct the loss; note that we scale all the log probabilities of
# samples sites in `latents_to_anneal` by the factor `annealing_factor`
for site in model_trace.values():
if site["type"] == "sample":
factor = annealing_factor if site["name"] in latents_to_anneal else 1.0
elbo = elbo + factor * site["fn"].log_prob(site["value"]).sum()
for site in guide_trace.values():
if site["type"] == "sample":
factor = annealing_factor if site["name"] in latents_to_anneal else 1.0
elbo = elbo - factor * site["fn"].log_prob(site["value"]).sum()
return -elbo
svi = SVI(model, guide, optim, loss=simple_elbo_kl_annealing)
svi.step(other_args, annealing_factor=0.2, latents_to_anneal=["my_latent"])
```
|
github_jupyter
|
optimizer = pyro.optim.Adam({"lr": 0.001, "betas": (0.90, 0.999)})
svi = pyro.infer.SVI(model, guide, optimizer, loss=pyro.infer.Trace_ELBO())
# define optimizer and loss function
optimizer = torch.optim.Adam(my_parameters, {"lr": 0.001, "betas": (0.90, 0.999)})
loss_fn = pyro.infer.Trace_ELBO.differentiable_loss
# compute loss
loss = loss_fn(model, guide)
loss.backward()
# take a step and zero the parameter gradients
optimizer.step()
optimizer.zero_grad()
def my_custom_L2_regularizer(my_parameters):
reg_loss = 0.0
for param in my_parameters:
reg_loss = reg_loss + param.pow(2.0).sum()
return reg_loss
- loss = loss_fn(model, guide)
+ loss = loss_fn(model, guide) + my_custom_L2_regularizer(my_parameters)
- loss = loss_fn(model, guide)
+ loss = loss_fn(model, guide) / N_data
@poutine.scale(scale=1.0/N_data)
def model(...):
pass
@poutine.scale(scale=1.0/N_data)
def guide(...):
pass
adam = torch.optim.Adam(adam_parameters, {"lr": 0.001, "betas": (0.90, 0.999)})
sgd = torch.optim.SGD(sgd_parameters, {"lr": 0.0001})
loss_fn = pyro.infer.Trace_ELBO.differentiable_loss
# compute loss
loss = loss_fn(model, guide)
loss.backward()
# take a step and zero the parameter gradients
adam.step()
sgd.step()
adam.zero_grad()
sgd.zero_grad()
def model():
pyro.param('a', ...)
pyro.param('b', ...)
...
adam = pyro.optim.Adam({'lr': 0.1})
sgd = pyro.optim.SGD({'lr': 0.01})
optim = MixedMultiOptimizer([(['a'], adam), (['b'], sgd)])
with pyro.poutine.trace(param_only=True) as param_capture:
loss = elbo.differentiable_loss(model, guide)
params = {'a': pyro.param('a'), 'b': pyro.param('b')}
optim.step(loss, params)
# note that simple_elbo takes a model, a guide, and their respective arguments as inputs
def simple_elbo(model, guide, *args, **kwargs):
# run the guide and trace its execution
guide_trace = poutine.trace(guide).get_trace(*args, **kwargs)
# run the model and replay it against the samples from the guide
model_trace = poutine.trace(
poutine.replay(model, trace=guide_trace)).get_trace(*args, **kwargs)
# construct the elbo loss function
return -1*(model_trace.log_prob_sum() - guide_trace.log_prob_sum())
svi = SVI(model, guide, optim, loss=simple_elbo)
def simple_elbo_kl_annealing(model, guide, *args, **kwargs):
# get the annealing factor and latents to anneal from the keyword
# arguments passed to the model and guide
annealing_factor = kwargs.pop('annealing_factor', 1.0)
latents_to_anneal = kwargs.pop('latents_to_anneal', [])
# run the guide and replay the model against the guide
guide_trace = poutine.trace(guide).get_trace(*args, **kwargs)
model_trace = poutine.trace(
poutine.replay(model, trace=guide_trace)).get_trace(*args, **kwargs)
elbo = 0.0
# loop through all the sample sites in the model and guide trace and
# construct the loss; note that we scale all the log probabilities of
# samples sites in `latents_to_anneal` by the factor `annealing_factor`
for site in model_trace.values():
if site["type"] == "sample":
factor = annealing_factor if site["name"] in latents_to_anneal else 1.0
elbo = elbo + factor * site["fn"].log_prob(site["value"]).sum()
for site in guide_trace.values():
if site["type"] == "sample":
factor = annealing_factor if site["name"] in latents_to_anneal else 1.0
elbo = elbo - factor * site["fn"].log_prob(site["value"]).sum()
return -elbo
svi = SVI(model, guide, optim, loss=simple_elbo_kl_annealing)
svi.step(other_args, annealing_factor=0.2, latents_to_anneal=["my_latent"])
| 0.930272 | 0.988391 |
## 1. Single Layer Perceptron
### 1) import modules
```
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
from modules import single_layer_perceptron
```
### 2) define placeholder for INPUT & LABELS
```
INPUT = tf.placeholder(tf.float32, [None, 28*28]) # ํ๋ จ์ฉ ๋ฐ์ดํฐ ์ฃผ์
๊ณต๊ฐ ํ๋ณด 1 x 784, 784๋๋ฉ์ ผ
LABELS = tf.placeholder(tf.int32, [None]) # ๋ ์ด๋ธ ์ฐจ์ ์์, shape ๋์ ์ผ๋ก ์ ์, ๋ฐฐ์น์ฌ์ด์ฆ None์ผ๋ก ์ ์ 100x1 ๋ฐฐ์น์ฌ์ด์ฆ 100์ธ ๊ฒฝ์ฐ
```
### 3) define slp model with single_layer_percentorn function
<img src="./images/slp_r.png" alt="slp model" width=1000 align="left"/>
```
prediction = single_layer_perceptron(INPUT, output_dim=10) # ์ฌ๊ธฐ ๋ชจ๋ธ๋ง ๋ฐ๋
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits( # ์ํํธ๋งฅ์ค ์ฒ๋ฆฌ ํด์ค
labels=LABELS, logits=prediction
)
cost = tf.reduce_mean(cross_entropy) # ์ฐจ์ด ๊ณ์ฐํด์ ํ๊ท ๋
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # ํ
์ํ๋ก์ฐ ์ ๊ณต ๊ธฐ๋ณธ ํจ์
```
### 4) load data
```
mnist = input_data.read_data_sets("./data/", one_hot=True) # ๋ฐ์ดํฐ ๋ฐ์ ์ด
```
### 5) start training
#### - set training parameters : batch size, learning rate, total loop
```
BATCH_SIZE = 100
LEARNING_RATE = 0.01
TOTAL_LOOP = 10000 # ๋ง ๋ฒ ํ๋ จ
```
- arrA = [[0,0,0,0,1],
[0,1,0,0,0]]
- np.where(arrA) => ([0,1], [4,1]) # true ๊ฐ ์ธ๋ฑ์ค ๋ฐํ
- ref) https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.where.html?highlight=numpy%20where#numpy.where
```
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for loop in range(1, TOTAL_LOOP + 1):
train_images, train_labels = mnist.train \
.next_batch(BATCH_SIZE)
train_labels = np.where(train_labels)[1]
#100x10
_, loss = sess.run(
[optimizer, cost], # ์ตํฐ๋ง์ด์ ธ ๋ฐ ์ํค๋ฉด ๋จ cost ์ฐ๊ฒฐ๋์ด ์์
feed_dict={
INPUT: train_images,
LABELS: train_labels
}
)
if loop % 500 == 0 or loop == 0:
print("loop: %05d,"%(loop), "loss:", loss) # ๋๋ฒ๊น
์ฉ, ์ตํฐ๋ง์ด์ ๊ฐ ๊ฐ์ ธ์ฌ ํ์๋ ์๋ค, loss ์ค์ด๋๋์ง ํ์ธ 500๊ฐ ๋ง๋ค ํ์ธ
print("Training Finished! (loss : " + str(loss) + ")")
```
### 6) test performance
- test image shape: (100, 784)
- test label shape: (100, 10)
- arrB = [[0, 1, 2],[3, 4, 5]]
- np.argmax(arrB) => 5
- np.argmax(arrB, axis=0) => [1, 1, 1] axis=0 ํ์ถ ๋น๊ต
- np.argmax(arrB, axis=1) => [2, 2] axis=1 ์ปฌ๋ผ์ถ๋น๊ต
- ref) https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.argmax.html
```
TEST_SAMPLE_SIZE = 100 # 100๊ฐ ์ด๋ฏธ์ง์ ๋ํด ํ์ธ
TEST_NUMBER = 5
accuracy_save = dict()
for number in range(1, 1+TEST_NUMBER):
test_images, test_labels = mnist.test \
.next_batch(TEST_SAMPLE_SIZE)
pred_result = sess.run(
prediction,
feed_dict={INPUT: test_images}
)
pred_number = np.argmax(pred_result, axis=1) # 100x1
label_number = np.where(test_labels)[1] #100x1
accuracy_save[number] = np.sum(pred_number == label_number)
print("Accuracy:", accuracy_save)
print("Total mean Accuracy:",
np.mean(list(accuracy_save.values())) # ํ๊ท ๋
)
```
|
github_jupyter
|
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
from modules import single_layer_perceptron
INPUT = tf.placeholder(tf.float32, [None, 28*28]) # ํ๋ จ์ฉ ๋ฐ์ดํฐ ์ฃผ์
๊ณต๊ฐ ํ๋ณด 1 x 784, 784๋๋ฉ์ ผ
LABELS = tf.placeholder(tf.int32, [None]) # ๋ ์ด๋ธ ์ฐจ์ ์์, shape ๋์ ์ผ๋ก ์ ์, ๋ฐฐ์น์ฌ์ด์ฆ None์ผ๋ก ์ ์ 100x1 ๋ฐฐ์น์ฌ์ด์ฆ 100์ธ ๊ฒฝ์ฐ
prediction = single_layer_perceptron(INPUT, output_dim=10) # ์ฌ๊ธฐ ๋ชจ๋ธ๋ง ๋ฐ๋
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits( # ์ํํธ๋งฅ์ค ์ฒ๋ฆฌ ํด์ค
labels=LABELS, logits=prediction
)
cost = tf.reduce_mean(cross_entropy) # ์ฐจ์ด ๊ณ์ฐํด์ ํ๊ท ๋
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # ํ
์ํ๋ก์ฐ ์ ๊ณต ๊ธฐ๋ณธ ํจ์
mnist = input_data.read_data_sets("./data/", one_hot=True) # ๋ฐ์ดํฐ ๋ฐ์ ์ด
BATCH_SIZE = 100
LEARNING_RATE = 0.01
TOTAL_LOOP = 10000 # ๋ง ๋ฒ ํ๋ จ
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for loop in range(1, TOTAL_LOOP + 1):
train_images, train_labels = mnist.train \
.next_batch(BATCH_SIZE)
train_labels = np.where(train_labels)[1]
#100x10
_, loss = sess.run(
[optimizer, cost], # ์ตํฐ๋ง์ด์ ธ ๋ฐ ์ํค๋ฉด ๋จ cost ์ฐ๊ฒฐ๋์ด ์์
feed_dict={
INPUT: train_images,
LABELS: train_labels
}
)
if loop % 500 == 0 or loop == 0:
print("loop: %05d,"%(loop), "loss:", loss) # ๋๋ฒ๊น
์ฉ, ์ตํฐ๋ง์ด์ ๊ฐ ๊ฐ์ ธ์ฌ ํ์๋ ์๋ค, loss ์ค์ด๋๋์ง ํ์ธ 500๊ฐ ๋ง๋ค ํ์ธ
print("Training Finished! (loss : " + str(loss) + ")")
TEST_SAMPLE_SIZE = 100 # 100๊ฐ ์ด๋ฏธ์ง์ ๋ํด ํ์ธ
TEST_NUMBER = 5
accuracy_save = dict()
for number in range(1, 1+TEST_NUMBER):
test_images, test_labels = mnist.test \
.next_batch(TEST_SAMPLE_SIZE)
pred_result = sess.run(
prediction,
feed_dict={INPUT: test_images}
)
pred_number = np.argmax(pred_result, axis=1) # 100x1
label_number = np.where(test_labels)[1] #100x1
accuracy_save[number] = np.sum(pred_number == label_number)
print("Accuracy:", accuracy_save)
print("Total mean Accuracy:",
np.mean(list(accuracy_save.values())) # ํ๊ท ๋
)
| 0.523664 | 0.958577 |
# ะฃัะพะบ 4
# ะะฐััะธัั ะธ ะผะฐััะธัะฝัะต ะพะฟะตัะฐัะธะธ. ะงะฐััั 2
## ะะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั
ะ ะฐััะผะพััะธะผ ะฟัะพะธะทะฒะพะปัะฝัั ะบะฒะฐะดัะฐัะฝัั ะผะฐััะธัั ะฟะพััะดะบะฐ $n$:
$$A=\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\cdots & \cdots & \ddots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}\\
\end{pmatrix}.$$
ะก ะบะฐะถะดะพะน ัะฐะบะพะน ะผะฐััะธัะตะน ัะฒัะถะตะผ ัะธัะปะตะฝะฝัั ั
ะฐัะฐะบัะตัะธััะธะบั, ะฝะฐะทัะฒะฐะตะผัั _ะพะฟัะตะดะตะปะธัะตะปะตะผ_, ัะพะพัะฒะตัััะฒัััะธะผ ััะพะน ะผะฐััะธัะต.
ะกัะฐะทั ะทะฐะผะตัะธะผ, ััะพ ะฟะพะฝััะธะต ะพะฟัะตะดะตะปะธัะตะปั ะธะผะตะตั ัะผััะป __ัะพะปัะบะพ ะดะปั ะบะฒะฐะดัะฐัะฝัั
ะผะฐััะธั__.
ะัะปะธ ะฟะพััะดะพะบ $n$ ะผะฐััะธัั ัะฐะฒะตะฝ ะตะดะธะฝะธัะต, ัะพ ะตััั ััะฐ ะผะฐััะธัะฐ ัะพััะพะธั ะธะท ะพะดะฝะพะณะพ ัะปะตะผะตะฝัะฐ $a_{11}$, ะพะฟัะตะดะตะปะธัะตะปะตะผ, ัะพะพัะฒะตัััะฒัััะธะผ ัะฐะบะพะน ะผะฐััะธัะต, ะฝะฐะทะพะฒะตะผ ัะฐะผ ััะพั ัะปะตะผะตะฝั.
ะัะปะธ ะฟะพััะดะพะบ ะผะฐััะธัั ัะฐะฒะตะฝ $2$, ัะพ ะตััั ะผะฐััะธัะฐ ะธะผะตะตั ะฒะธะด
$$A=\begin{pmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{pmatrix},$$
ัะพ ะพะฟัะตะดะตะปะธัะตะปะตะผ ะฒัะพัะพะณะพ ะฟะพััะดะบะฐ, ัะพะพัะฒะตัััะฒัััะธะผ ัะฐะบะพะน ะผะฐััะธัะต, ะฝะฐะทะพะฒะตะผ ัะธัะปะพ, ัะฐะฒะฝะพะต
$$a_{11}a_{22} - a_{12}a_{21}.$$
ะกะปะพะฒะตัะฝะพ ััะพ ะฟัะฐะฒะธะปะพ ะผะพะถะฝะพ ััะพัะผัะปะธัะพะฒะฐัั ัะฐะบ: _ะพะฟัะตะดะตะปะธัะตะปั ะฒัะพัะพะณะพ ะฟะพััะดะบะฐ, ัะพะพัะฒะตัััะฒัััะธะน ะผะฐััะธัะต $A$, ัะฐะฒะตะฝ ัะฐะทะฝะพััะธ ะฟัะพะธะทะฒะตะดะตะฝะธั ัะปะตะผะตะฝัะพะฒ, ััะพััะธั
ะฝะฐ ะณะปะฐะฒะฝะพะน ะดะธะฐะณะพะฝะฐะปะธ ััะพะน ะผะฐััะธัั, ะธ ัะปะตะผะตะฝัะพะฒ, ััะพััะธั
ะฝะฐ ะตะต ะฟะพะฑะพัะฝะพะน ะดะธะฐะณะพะฝะฐะปะธ._
ะะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั $A$ ะพะฑะพะทะฝะฐัะฐะตััั ะบะฐะบ $detA$, ะธะปะธ $|A|$, ัะพ ะตััั ะพะฟัะตะดะตะปะธัะตะปั ะฒัะพัะพะณะพ ะฟะพััะดะบะฐ ะผะพะถะฝะพ ะทะฐะฟะธัะฐัั ะบะฐะบ
$$detA=|A|=\begin{vmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{vmatrix}=a_{11}a_{22} - a_{12}a_{21}.$$
ะัะดะตะผ ะดะฒะธะณะฐัััั ะดะฐะปััะต ะธ ะฒัััะฝะธะผ ะฟะพะฝััะธะต ะพะฟัะตะดะตะปะธัะตะปั ะดะปั ะผะฐััะธั ะฟะพััะดะบะฐ $n\geq2.$
ะะปั ััะพะณะพ ะฒะฒะตะดะตะผ ะฟะพะฝััะธะต ะผะธะฝะพัะฐ. _ะะธะฝะพัะพะผ_ ะปัะฑะพะณะพ ัะปะตะผะตะฝัะฐ $a_{ij}$ ะผะฐััะธัั $n$-ะณะพ ะฟะพััะดะบะฐ ะฝะฐะทะพะฒะตะผ ะพะฟัะตะดะตะปะธัะตะปั ะฟะพััะดะบะฐ $n-1$, ัะพะพัะฒะตัััะฒัััะธะน ะผะฐััะธัะต, ะบะพัะพัะฐั ะฟะพะปััะฐะตััั ะธะท ะธัั
ะพะดะฝะพะน ะผะฐััะธัั ะฟััะตะผ ะฒััะตัะบะธะฒะฐะฝะธั $i$-ะน ัััะพะบะธ ะธ $j$-ะณะพ ััะพะปะฑัะฐ (ัััะพะบะธ ะธ ััะพะปะฑัะฐ, ะฝะฐ ะฟะตัะตัะตัะตะฝะธะธ ะบะพัะพััั
ััะพะธั ัะปะตะผะตะฝั $a_{ij}$). ะะฑะพะทะฝะฐัะฐัั ะผะธะฝะพั ะฑัะดะตะผ ัะธะผะฒะพะปะพะผ $M_{ij}$.
ะะฟัะตะดะตะปะธัะตะปะตะผ ะผะฐััะธัั ะฟะพััะดะบะฐ $n$ ะฝะฐะทะพะฒะตะผ ัะธัะปะพ, ัะฐะฒะฝะพะต
$$detA=\begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\cdots & \cdots & \ddots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}\\
\end{vmatrix} =
\sum_{j=1}^{n}(-1)^{j+1}a_{1j}M_{1j}.$$
ะญัะฐ ัะพัะผัะปะฐ ะฟัะตะดััะฐะฒะปัะตั ัะพะฑะพะน ะฟัะฐะฒะธะปะพ ัะพััะฐะฒะปะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปั ะฟะพััะดะบะฐ $n$ ะฟะพ ัะปะตะผะตะฝัะฐะผ ะฟะตัะฒะพะน ัััะพะบะธ ะธ ะผะธะฝะพัะฐะผ $M_{1j}$, ัะฒะปัััะธะผะธัั ะพะฟัะตะดะตะปะธัะตะปัะผะธ ะฟะพััะดะบะฐ $n-1$.
ะะฐะผะตัะธะผ, ััะพ ะฟัะธ $n=2$ ะฟัะฐะฒะธะปะพ ัะพะฒะฟะฐะดะฐะตั ั ะฒะฒะตะดะตะฝะฝัะผ ัะฐะฝะตะต ะฟัะฐะฒะธะปะพะผ ะฟะพะปััะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปั ะดะปั ะผะฐััะธั ะฒัะพัะพะณะพ ะฟะพััะดะบะฐ: ะฒ ััะพะผ ัะปััะฐะต ะผะธะฝะพัั ัะปะตะผะตะฝัะพะฒ ะฟะตัะฒะพะน ัััะพะบะธ ะธะผะตัั ะฒะธะด $M_{11}=a_{22}$, $M_{12}=a_{21}$.
__ะขะตะพัะตะผะฐ__
ะัะธ ะปัะฑะพะผ ะฟัะพะธะทะฒะพะปัะฝะพะผ ะฝะพะผะตัะต ัััะพะบะธ $i~(i=1,2,...,n)$ ะดะปั ะพะฟัะตะดะตะปะธัะตะปั ะฟะพััะดะบะฐ $n$ ัะฟัะฐะฒะตะดะปะธะฒะฐ ัะพัะผัะปะฐ
$$detA = \sum_{j=1}^{n}(-1)^{i+j}a_{ij}M_{ij},$$
ะฝะฐะทัะฒะฐะตะผะฐั _ัะฐะทะปะพะถะตะฝะธะตะผ ััะพะณะพ ะพะฟัะตะดะตะปะธัะตะปั ะฟะพ $i$-ะน ัััะพะบะต._
__ะขะตะพัะตะผะฐ__
ะัะธ ะปัะฑะพะผ ะฟัะพะธะทะฒะพะปัะฝะพะผ ะฝะพะผะตัะต ััะพะปะฑัะฐ $j~(j=1,2,...,n)$ ะดะปั ะพะฟัะตะดะตะปะธัะตะปั ะฟะพััะดะบะฐ $n$ ัะฟัะฐะฒะตะดะปะธะฒะฐ ัะพัะผัะปะฐ
$$detA = \sum_{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij},$$
ะฝะฐะทัะฒะฐะตะผะฐั _ัะฐะทะปะพะถะตะฝะธะตะผ ััะพะณะพ ะพะฟัะตะดะตะปะธัะตะปั ะฟะพ $j$-ะผั ััะพะปะฑัั._
ะขะฐะบะธะผ ะพะฑัะฐะทะพะผ, ะพะฟัะตะดะตะปะธัะตะปั ะผะพะถะตั ะฑััั ััะพัะผะธัะพะฒะฐะฝ ัะฐะทะปะพะถะตะฝะธะตะผ ะบะฐะบ ะฟะพ ะฟัะพะธะทะฒะพะปัะฝะพะน ัััะพะบะต ะธัั
ะพะดะฝะพะน ะผะฐััะธัั, ัะฐะบ ะธ ะฟะพ ะฟัะพะธะทะฒะพะปัะฝะพะผั ะตะต ััะพะปะฑัั.
__ะัะธะผะตั__
ะััะธัะปะธะผ ะพะฟัะตะดะตะปะธัะตะปั
$$\begin{vmatrix}
1 & 1 & 1\\
1 & 1 & 4\\
2 & 3 & 6
\end{vmatrix}.$$
__ะ ะตัะตะฝะธะต__
$$\begin{vmatrix}
1 & 2 & 1\\
1 & 1 & 4\\
2 & 3 & 6
\end{vmatrix}=
1\cdot\begin{vmatrix}
1 & 4\\
3 & 6
\end{vmatrix}-
2\cdot\begin{vmatrix}
1 & 4\\
2 & 6
\end{vmatrix}+
1\cdot\begin{vmatrix}
1 & 1\\
2 & 3
\end{vmatrix}=1\cdot(1\cdot6-3\cdot4)-2\cdot(1\cdot6-2\cdot4)+1\cdot(1\cdot3-2\cdot1)=-6+4+1=-1.
$$
__ะัะธะผะตั__
ะะฐะนะดะตะผ ะพะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั
$$A=\begin{pmatrix}
-1 & -4 & 0 & -2 \\
0 & 1 & 5 & 4 \\
3 & 1 & 1 & 0 \\
-1 & 0 & 2 & 2\\
\end{pmatrix},$$
ัะฐะทะปะพะถะธะฒ ะตะณะพ<br>
1) ะฟะพ ัะปะตะผะตะฝัะฐะผ 2-ะณะพ ััะพะปะฑัะฐ;<br>
2) ะฟะพ ัะปะตะผะตะฝัะฐะผ 3-ะน ัััะพะบะธ.
__ะ ะตัะตะฝะธะต__
1. ะ ะฐะทะปะพะถะตะฝะธะต ะพะฟัะตะดะตะปะธัะตะปัั 4-ะณะพ ะฟะพััะดะบะฐ ะฟะพ ัะปะตะผะตะฝัะฐะผ 2-ะณะพ ััะพะปะฑัะฐ ะฑัะดะตั ะธะผะตัั ะฒะธะด
$$\begin{vmatrix}
a_{11} & a_{12} & a_{13} & a_{14}\\
a_{21} & a_{22} & a_{23} & a_{24}\\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}\\
\end{vmatrix} =
(-1)^{1+2}a_{12}\begin{vmatrix}
a_{21} & a_{23} & a_{24}\\
a_{31} & a_{33} & a_{34} \\
a_{41} & a_{43} & a_{44}\\
\end{vmatrix} + (-1)^{2+2}a_{22}\begin{vmatrix}
a_{11} & a_{13} & a_{14}\\
a_{31} & a_{33} & a_{34} \\
a_{41} & a_{43} & a_{44}\\
\end{vmatrix} + (-1)^{3+2}a_{32}\begin{vmatrix}
a_{11} & a_{13} & a_{14}\\
a_{21} & a_{23} & a_{24}\\
a_{41} & a_{43} & a_{44}\\
\end{vmatrix} + (-1)^{4+2}a_{42}\begin{vmatrix}
a_{11} & a_{13} & a_{14}\\
a_{21} & a_{23} & a_{24}\\
a_{31} & a_{33} & a_{34} \\
\end{vmatrix}.$$
ะขะฐะบะธะผ ะพะฑัะฐะทะพะผ, ะดะปั ะผะฐััะธัั $A$
$$\begin{vmatrix}
-1 & -4 & 0 & -2 \\
0 & 1 & 5 & 4 \\
3 & 1 & 1 & 0 \\
-1 & 0 & 2 & 2\\
\end{vmatrix} = 4\begin{vmatrix}
0 & 5 & 4 \\
3 & 1 & 0\\
-1 & 2 & 2 \\
\end{vmatrix} + \begin{vmatrix}
-1 & 0 & -2\\
3 & 1 & 0\\
-1 & 2 & 2 \\
\end{vmatrix} - \begin{vmatrix}
-1 & 0 & -2\\
0 & 5 & 4\\
-1 & 2 & 2 \\
\end{vmatrix} + 0.$$
ะขะฐะบ ะทะฐะดะฐัะฐ ะฝะฐั
ะพะถะดะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปั 4-ะณะพ ะฟะพััะดะบะฐ ัะฒะพะดะธััั ะบ ะฝะฐั
ะพะถะดะตะฝะธั ััะตั
ะพะฟัะตะดะตะปะธัะตะปะตะน 3-ะณะพ ะฟะพััะดะบะฐ. ะััะธัะปะธะผ ะฟะตัะฒัะน, ัะฐะทะปะพะถะธะฒ ะฟะพ ะฟะตัะฒะพะน ัััะพะบะต:
$$\begin{vmatrix}
0 & 5 & 4 \\
3 & 1 & 0\\
-1 & 2 & 2 \\
\end{vmatrix} =
0\begin{vmatrix}
1 & 0\\
2 & 2 \\
\end{vmatrix}
-5\begin{vmatrix}
3 & 0\\
-1 & 2 \\
\end{vmatrix} +
4\begin{vmatrix}
3 & 1\\
-1 & 2\\
\end{vmatrix} = 0\cdot(1\cdot2-2\cdot0)
-5\cdot(3\cdot2 - (-1)\cdot 0) + 4\cdot(3\cdot2 - (-1)\cdot1) = -2.$$
ะะฝะฐะปะพะณะธัะฝะพ ะฒััะธัะปัะตะผ
$$\begin{vmatrix}
-1 & 0 & -2\\
3 & 1 & 0\\
-1 & 2 & 2 \\
\end{vmatrix} =
(-1)\begin{vmatrix}
1 & 0\\
2 & 2 \\
\end{vmatrix} -
0\begin{vmatrix}
3 & 0\\
-1 & 2 \\
\end{vmatrix} +
(-2)\begin{vmatrix}
3 & 1\\
-1 & 2 \\
\end{vmatrix} =
(-1)\cdot(1\cdot2-2\cdot0) - 0\cdot(3\cdot2-(-1)\cdot0) + (-2)\cdot(3\cdot2-(-1)\cdot1) = -16,$$
$$\begin{vmatrix}
-1 & 0 & -2\\
0 & 5 & 4\\
-1 & 2 & 2 \\
\end{vmatrix} =
(-1)\begin{vmatrix}
5 & 4\\
2 & 2 \\
\end{vmatrix} -
0\begin{vmatrix}
0 & 4\\
-1 & 2 \\
\end{vmatrix} +
(-2)\begin{vmatrix}
0 & 5\\
-1 & 2\\
\end{vmatrix} =
(-1)\cdot(5\cdot2 - 2\cdot4) - 0\cdot(0\cdot2-(-1)\cdot4) + (-2)\cdot(0\cdot2-(-1)\cdot5) = -12.$$
ะะพะดััะฐะฒะปัั ะฟะพะปััะตะฝะฝัะต ะทะฝะฐัะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปะตะน ะฒ ะธัั
ะพะดะฝะพะต ัะฐะทะปะพะถะตะฝะธะต, ะฟะพะปััะธะผ
$$|A| = 4\cdot(-2) + (-16) - (-12) = -12.$$
2. ะ ะฐะทะปะพะถะตะฝะธะต ะพะฟัะตะดะตะปะธัะตะปัั 4-ะณะพ ะฟะพััะดะบะฐ ะฟะพ ัะปะตะผะตะฝัะฐะผ 3-ะน ัััะพะบะธ ะฑัะดะตั ะธะผะตัั ะฒะธะด
$$\begin{vmatrix}
a_{11} & a_{12} & a_{13} & a_{14}\\
a_{21} & a_{22} & a_{23} & a_{24}\\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}\\
\end{vmatrix} =
(-1)^{3+1}a_{31}\begin{vmatrix}
a_{12} & a_{13} & a_{14}\\
a_{22} & a_{23} & a_{24}\\
a_{42} & a_{43} & a_{44}\\
\end{vmatrix} +
(-1)^{3+2}a_{32}\begin{vmatrix}
a_{11} & a_{13} & a_{14}\\
a_{21} & a_{23} & a_{24}\\
a_{41} & a_{43} & a_{44}\\
\end{vmatrix} +
(-1)^{3+3}a_{33}\begin{vmatrix}
a_{11} & a_{12} & a_{14}\\
a_{21} & a_{22} & a_{24}\\
a_{41} & a_{42} & a_{44}\\
\end{vmatrix} +
(-1)^{3+4}a_{34}\begin{vmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{41} & a_{42} & a_{43}
\end{vmatrix}.$$
ะะปั ะผะฐััะธัั $A$:
$$\begin{vmatrix}
-1 & -4 & 0 & -2 \\
0 & 1 & 5 & 4 \\
3 & 1 & 1 & 0 \\
-1 & 0 & 2 & 2\\
\end{vmatrix} = 3\begin{vmatrix}
-4 & 0 & -2 \\
1 & 5 & 4 \\
0 & 2 & 2\\
\end{vmatrix} -\begin{vmatrix}
-1 & 0 & -2 \\
0 & 5 & 4 \\
-1 & 2 & 2\\
\end{vmatrix} + \begin{vmatrix}
-1 & -4 & -2 \\
0 & 1 & 4 \\
-1 & 0 & 2\\
\end{vmatrix} - 0.$$
ะะฐะนะดะตะผ ะพะฟัะตะดะตะปะธัะตะปะธ ััะตััะตะณะพ ะฟะพััะดะบะฐ:
$$\begin{vmatrix}
-4 & 0 & -2 \\
1 & 5 & 4 \\
0 & 2 & 2\\
\end{vmatrix} = (-4)\cdot(5\cdot2-2\cdot4) - 0\cdot(1\cdot2 - 0\cdot4) + (-2)\cdot(1\cdot2-0\cdot5)= -12,$$
$$\begin{vmatrix}
-1 & 0 & -2 \\
0 & 5 & 4 \\
-1 & 2 & 2\\
\end{vmatrix} = (-1)\cdot(5\cdot2-2\cdot4) - 0\cdot(0\cdot2-(-1)\cdot4) + (-2)\cdot(0\cdot2-(-1)\cdot5)= -12,$$
$$\begin{vmatrix}
-1 & -4 & -2 \\
0 & 1 & 4 \\
-1 & 0 & 2\\
\end{vmatrix} = (-1)\cdot(1\cdot2-0\cdot4) - (-4)\cdot(0\cdot2-(-1)\cdot4) + (-2)\cdot(0\cdot0-(-1)\cdot1) = 12.$$
ะะพะดััะฐะฒะปัั ะฟะพะปััะตะฝะฝัะต ะทะฝะฐัะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปะตะน ะฒ ะธัั
ะพะดะฝะพะต ัะฐะทะปะพะถะตะฝะธะต, ะฟะพะปััะธะผ
$$|A| = 3\cdot(-12) - (-12) + 12 = -12.$$
### ะััะฐะถะตะฝะธะต ะพะฟัะตะดะตะปะธัะตะปั ะฝะตะฟะพััะตะดััะฒะตะฝะฝะพ ัะตัะตะท ะตะณะพ ัะปะตะผะตะฝัั
ะฃััะฐะฝะพะฒะธะผ ัะพัะผัะปั ะฝะฐั
ะพะถะดะตะฝะธั ะดะตัะตัะผะธะฝะฐะฝัะฐ $n$-ะณะพ ะฟะพััะดะบะฐ ะฝะตะฟะพััะตะดััะฒะตะฝะฝะพ ัะตัะตะท ะตะณะพ ัะปะตะผะตะฝัั (ะผะธะฝัั ะผะธะฝะพัั).
ะะปั ััะพะณะพ ะฒะฒะตะดะตะผ ะฟะพะฝััะธั ะฟะตัะตััะฐะฝะพะฒะพะบ ะธ ััะฐะฝัะฟะพะทะธัะธะน ะฝะฐ ะผะฝะพะถะตััะฒะต.
_ะะตัะตััะฐะฝะพะฒะบะพะน_ ะฝะฐ ะผะฝะพะถะตััะฒะต $S=\{1,2,3,...,n\}$ ะฝะฐะทัะฒะฐะตััั ะผะฝะพะถะตััะฒะพ ัะตั
ะถะต ัะธัะตะป, ัะฟะพััะดะพัะตะฝะฝะพะต ะฝะตะบะพัะพััะผ ะพะฑัะฐะทะพะผ:
$$\{1,2,3,4\}\Rightarrow\{3,4,1,2\}.$$
_ะขัะฐะฝัะฟะพะทะธัะธะตะน_ ะฝะฐะทัะฒะฐะตััั ัะฐะบะฐั ะฟะตัะตััะฐะฝะพะฒะบะฐ, ะฒ ะบะพัะพัะพะน ะฟะตัะตััะฐะฒะปะตะฝั ะผะตััะฐะผะธ ัะพะปัะบะพ ะดะฒะฐ ัะปะตะผะตะฝัะฐ ะผะฝะพะถะตััะฒะฐ, ะฒ ัะพ ะฒัะตะผั ะบะฐะบ ะพััะฐะปัะฝัะต ัะปะตะผะตะฝัั ะพััะฐัััั ะฝะฐ ัะฒะพะธั
ะผะตััะฐั
:
$$\{1,2,3,4\}\Rightarrow\{\underline{4},2,3,\underline{1}\}.$$
ะัะฑัั ะฟะตัะตััะฐะฝะพะฒะบั ะผะพะถะฝะพ ัะตะฐะปะธะทะพะฒะฐัั ะฟััะตะผ ะฝะตัะบะพะปัะบะธั
ะฟะพัะปะตะดะพะฒะฐัะตะปัะฝัั
ััะฐะฝัะฟะพะทะธัะธะน. ะะฐะฟัะธะผะตั, ะฟะตัะตััะฐะฝะพะฒะบะฐ $\{3,4,1,2\}$ ะฟัะตะดััะฐะฒะปัะตั ัะพะฑะพะน ะฟะพัะปะตะดะพะฒะฐัะตะปัะฝะพััั ััะตั
ััะฐะฝัะฟะพะทะธัะธะน:
$$\{\underline{1},2,\underline{3},4\}\Rightarrow\{3,\underline{2},1,\underline{4}\}\Rightarrow\{3,4,1,2\}.$$
ะัะธะฝััะพ,ััะพ ะฟะตัะตััะฐะฝะพะฒะบะฐ ัะพะดะตัะถะธั __ะธะฝะฒะตััะธั__ ัะปะตะผะตะฝัะพะฒ $i_{j}$ ะธ $i_{k}$, ะตัะปะธ $i_{j}>i_{k}$ ะฟัะธ $j<k.$
ะะฐะฟัะธะผะตั, ะฝะฐัะฐ ะฟะตัะตััะฐะฝะพะฒะบะฐ $\{3,4,1,2\}$ ัะพะดะตัะถะธั ัะตัััะต ะธะฝะฒะตััะธะธ:
- $3$ ะธ $1$, ัะฐะบ ะบะฐะบ ัะธัะปะพ $3$ ััะพะธั ัะปะตะฒะฐ ะพั ะผะตะฝััะตะณะพ ัะธัะปะฐ $1$, ะธ ะฟะพ ะฐะฝะฐะปะพะณะธะธ ัะปะตะดัััะธะต:
- $3$ ะธ $2$;
- $4$ ะธ $1$;
- $4$ ะธ $2$.
ะงะธัะปะพ ะธะฝะฒะตััะธะน ะพะฟัะตะดะตะปัะตั __ัะตัะฝะพััั__ ะฟะตัะตััะฐะฝะพะฒะบะธ. ะขะพ ะตััั ะฟะตัะตััะฐะฝะพะฒะบะฐ ััะธัะฐะตััั ัะตัะฝะพะน, ะตัะปะธ ะพะฝะฐ ัะพะดะตัะถะธั ัะตัะฝะพะต ัะธัะปะพ ะธะฝะฒะตััะธะน ะธ ะฝะตัะตัะฝะพะน, ะตัะปะธ ะฝะตัะตัะฝะพะต ัะธัะปะพ.
_ะะปั ะผะฝะพะถะตััะฒะฐ $S=\{1,2,3,...,n\}$ ัััะตััะฒัะตั $n!$ ัะฐะทะปะธัะฝัั
ะฟะตัะตััะฐะฝะพะฒะพะบ._
__ะัะธะผะตั__
ะะพะทัะผะตะผ ะผะฝะพะถะตััะฒะพ $\{1,2,3\}$. ะะฝะพ ะฑัะดะตั ัะพะดะตัะถะฐัั $3!=6$ ะฟะตัะตััะฐะฝะพะฒะพะบ:
$$\{1,2,3\}, \{2,1,3\}, \{2,3,1\}, \{3,2,1\}, \{3,1,2\}, \{1,3,2\}.$$
ะัะธ ััะพะผ:
- ะฟะตัะตััะฐะฝะพะฒะบะธ $\{1,2,3\}$, $\{2,3,1\}$ ะธ $\{3,1,2\}$ ะฑัะดัั ัะฒะปััััั ัะตัะฝัะผะธ;
- ะฟะตัะตััะฐะฝะพะฒะบะธ $\{2,1,3\}$, $\{3,2,1\}$ ะธ $\{1,3,2\}$ ะฑัะดัั ัะฒะปััััั ะฝะตัะตัะฝัะผะธ.
__ะะตัะฝะตะผัั ะบ ะฟะพะฝััะธั ะพะฟัะตะดะตะปะธัะตะปั__
ะะพะทัะผะตะผ ะบะฒะฐะดัะฐัะฝัั ะผะฐััะธัั $A$ $n$-ะณะพ ะฟะพััะดะบะฐ (ัะฐะทะผะตัะฐ $n\times n$) ะธ ะผะฝะพะถะตััะฒะพ $\{k_{1}, k_{2}, ...,k_{n}\}$, ัะฒะปัััะตะตัั ะฝะตะบะพัะพัะพะน ะฟะตัะตััะฐะฝะพะฒะบะพะน ัะฟะพััะดะพัะตะฝะฝะพะณะพ ะผะฝะพะถะตััะฒะฐ ะฝะฐัััะฐะปัะฝัั
ัะธัะตะป $\{1,2,...,n\}$.
ะ ะฐััะผะพััะธะผ ะฟัะพะธะทะฒะตะดะตะฝะธะต, ัะพะดะตัะถะฐัะตะต $n$ ะผะฐััะธัะฝัั
ัะปะตะผะตะฝัะพะฒ, ะฒะทัััั
ะฟะพ ะพะดะฝะพะผั ะธะท ะบะฐะถะดะพะน ัััะพะบะธ, ัะพััะฐะฒะปะตะฝะฝะพะต ัะปะตะดัััะธะผ ะพะฑัะฐะทะพะผ:
$$a_{1k_{1}}a_{2k_{2}}...a_{nk_{n}}.$$
ะะตัะฒัะน ะผะฝะพะถะธัะตะปั ัะฒะปะตััั ัะปะตะผะตะฝัะพะผ ะธะท ะฟะตัะฒะพะน ัััะพะบะธ ะธ $k_{1}$ ััะพะปะฑัะฐ, ะฒัะพัะพะน โ ะธะท ะฒัะพัะพะน ัััะพะบะธ ะธ $k_{2}$ ััะพะปะฑัะฐ ะธย ั.ย ะด.
ะัะฟะพะผะฝะธะผ, ััะพ ัััะตััะฒัะตั $n!$ ัะฐะทะปะธัะฝัั
ะฟะตัะตััะฐะฝะพะฒะพะบ $\{k_{1}, k_{2}, ...,k_{n}\}$ ะธะท ะธะฝะดะตะบัะพะฒ ััะพะปะฑัะพะฒ. ะะฐะถะดะฐั ะธะท ะฝะธั
ะฑัะดะตั ัะพัะผะธัะพะฒะฐัั ะฟัะพะธะทะฒะตะดะตะฝะธะต ัะบะฐะทะฐะฝะฝะพะณะพ ะฒะธะดะฐ. ะัะธะฟะธัะตะผ ะบะฐะถะดะพะผั ัะฐะบะพะผั ะฟัะพะธะทะฒะตะดะตะฝะธั ะทะฝะฐะบ $ยซ+ยป$, ะตัะปะธ ะฟะตัะตััะฐะฝะพะฒะบะฐ $\{k_{1}, k_{2}, ...,k_{n}\}$ ัะตัะฝะฐั, ะธ $ยซ-ยป$, ะตัะปะธ ะฝะตัะตัะฝะฐั.
ะงัะพะฑั ะพะฟะธัะฐัั ััะพ ะผะฐัะตะผะฐัะธัะตัะบะธ, ะฒะฒะตะดะตะผ ะฒััะฐะถะตะฝะธะต $P\{k_{1}, k_{2}, ...,k_{n}\}$, ะบะพัะพัะพะต ะฑัะดะตั ะพะฑะพะทะฝะฐัะฐัั ัะธัะปะพ ะธะฝะฒะตััะธะน ะฒ ัะพะพัะฒะตัััะฒัััะตะน ะฟะตัะตััะฐะฝะพะฒะบะต. ะ ััะพะผ ัะปััะฐะต ัะดะพะฑะฝะพ ะพะฟัะตะดะตะปััั ะทะฝะฐะบ ะฟัะพะธะทะฒะตะดะตะฝะธั ัะฐะบะธะผ ะพะฑัะฐะทะพะผ:
$$(-1)^{P\{k_{1}, k_{2}, ...,k_{n}\}}=\begin{cases}
+1 & \text{ ะฒ ัะปััะฐะต ัะตัะฝะพะน ะฟะตัะตััะฐะฝะพะฒะบะธ, } \\
-1 & \text{ ะฒ ัะปััะฐะต ะฝะตัะตัะฝะพะน ะฟะตัะตััะฐะฝะพะฒะบะธ. }
\end{cases}$$
ะกัะผะผะฐ ะฒัะตั
ะฒะพะทะผะพะถะฝัั
ะฟัะพะธะทะฒะตะดะตะฝะธะน ัะปะตะผะตะฝัะพะฒ ะผะฐััะธัั $A$, ะพะฟะธัะฐะฝะฝัั
ะฒััะตัะบะฐะทะฐะฝะฝัะผ ะพะฑัะฐะทะพะผ, ะธ ะฑัะดะตั ัะฒะปััััั ะพะฟัะตะดะตะปะธัะตะปะตะผ ะผะฐััะธัั $A$:
$$detA=\sum_{\{k_{1}, k_{2}, ...,k_{n}\}}a_{1k_{1}}a_{2k_{2}}...a_{nk_{n}}(-1)^{P\{k_{1}, k_{2}, ...,k_{n}\}}.$$
ะะฐะฝะฝะพะต ะฟัะฐะฒะธะปะพ ัะฐะบะถะต ะผะพะถะฝะพ ะฒัะฒะตััะธ ะธะท ัะพัะผัะปั ะพะฟัะตะดะตะปะตะฝะธั ัะตัะตะท ะผะธะฝะพัั. ะก ะฒัะฒะพะดะพะผ ะผะพะถะฝะพ ะพะทะฝะฐะบะพะผะธัััั ะฒ ะบะฝะธะณะต ะ.ย ะ.ย ะะปัะธะฝะฐ ะธ ะญ.ย ะ.ย ะะพะทะฝัะบะฐ ยซะะธะฝะตะนะฝะฐั ะฐะปะณะตะฑัะฐยป ะธะท ัะฟะธัะบะฐ ะปะธัะตัะฐัััั.
ะ ัะปััะฐะต $n=2$ ัะพัะผัะปะฐ ัะปะตะผะตะฝัะฐัะฝะพ ะฟัะพะฒะตััะตััั, ะตัะปะธ ะฟัะธะฝััั ะฒะพ ะฒะฝะธะผะฐะฝะธะต, ััะพ ัััะตััะฒัะตั ะฒัะตะณะพ ะดะฒะต ะฟะตัะตััะฐะฝะพะฒะบะธ ะผะฝะพะถะตััะฒะฐ $\{1,2\}$: $\{1,2\}$ ะธ $\{2,1\}$, ะฟะตัะฒะฐั ะธะท ะบะพัะพััั
ัะฒะปัะตััั ัะตัะฝะพะน, ะฒัะพัะฐั โ ะฝะตัะตัะฝะพะน. ะขะฐะบะธะผ ะพะฑัะฐะทะพะผ, ะฟะพะปััะธะผ
$$\begin{vmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{vmatrix}=a_{11}a_{22} - a_{12}a_{21}.$$
ะ NumPy ะพะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั ะฒััะธัะปัะตััั ั ะฟะพะผะพััั ััะฝะบัะธะธ `numpy.linalg.det(a)`, ะณะดะต `a` โ ะผะฐััะธัะฐ.
__ะัะธะผะตั__
ะะฐะนะดะตะผ ะพะฟัะตะดะตะปะธัะตะปะธ ะธะท ะฟัะธะผะตัะพะฒ ะฒััะต ั ะฟะพะผะพััั Python:
```
import numpy as np
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]])
print(f'ะะฐััะธัะฐ:\n{a}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(a):.0f}')
b = np.array([[-1, -4, 0, -2], [0, 1, 5, 4], [3, 1, 1, 0], [-1, 0, 2, 2]])
print(f'ะะฐััะธัะฐ:\n{b}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(b):.0f}')
```
### ะกะฒะพะนััะฒะฐ ะพะฟัะตะดะตะปะธัะตะปะตะน
__1.__ ะะฟัะตะดะตะปะธัะตะปั ััะฐะฝัะฟะพะฝะธัะพะฒะฐะฝะฝะพะน ะผะฐััะธัั ัะฐะฒะตะฝ ะพะฟัะตะดะตะปะธัะตะปั ะธัั
ะพะดะฝะพะน:
$$detA^{T}=detA.$$
__2.__ ะฃะผะฝะพะถะตะฝะธะต ัััะพะบะธ ะธะปะธ ััะพะปะฑัะฐ ะผะฐััะธัั ะฝะฐ ัะธัะปะพ $\lambda$ ะฟัะธะฒะตะดะตั ะบ ัะผะฝะพะถะตะฝะธั ะพะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั ะฝะฐ ัะพ ะถะต ัะธัะปะพ.
- ะะพะบะฐะทะฐัะตะปัััะฒะพ ััะพะณะพ ัะฒะพะนััะฒะฐ ัะปะตะผะตะฝัะฐัะฝะพ, ัะฐะบ ะบะฐะบ, ะธัั
ะพะดั ะธะท ัะพัะผัะปั ะพะฟัะตะดะตะปะธัะตะปั, ะผะฝะพะถะธัะตะปั ะธะท ััะพะน ัััะพะบะธ ะฑัะดะตั ะฒ ะบะฐะถะดะพะผ ะธะท ัะปะฐะณะฐะตะผัั
ะฟัะธ ะฝะฐั
ะพะถะดะตะฝะธะธ ะพะฟัะตะดะตะปะธัะตะปั ัะฐะทะปะพะถะตะฝะธะตะผ ะฟะพ ััะพะน ัััะพะบะต/ััะพะปะฑัั, ััะพ ัะฐะฒะฝะพะทะฝะฐัะฝะพ ะตะณะพ ัะผะฝะพะถะตะฝะธั ะฝะฐ ััะพ ัะธัะปะพ.
__3.__ ะะตัะตััะฐะฝะพะฒะบะฐ ะปัะฑัั
ะดะฒัั
ัััะพะบ ะธะปะธ ััะพะปะฑัะพะฒ ะผะฐััะธัั ะฟัะธะฒะพะดะธั ะบ ะธะทะผะตะฝะตะฝะธั ะทะฝะฐะบะฐ ะพะฟัะตะดะตะปะธัะตะปั.
- ะญัะพ ะฟัะพะธัั
ะพะดะธั ะธะท-ะทะฐ ัะพะณะพ, ััะพ ะดะพะฟะพะปะฝะธัะตะปัะฝะฐั ััะฐะฝัะฟะพะทะธัะธั ะผะตะฝัะตั ัะตัะฝะพััั ะฟะตัะตััะฐะฝะพะฒะบะธ.
__4.__ ะัะปะธ ะผะฐััะธัะฐ ะธะผะตะตั ะฝัะปะตะฒัั ัััะพะบั ะธะปะธ ััะพะปะฑะตั, ัะพ ะพะฟัะตะดะตะปะธัะตะปั ัะฐะฒะตะฝ ะฝัะปั.
- ะะพ ะฐะฝะฐะปะพะณะธะธ ั ะฟัะฝะบัะพะผ 2: ะฒ ะบะฐะถะดะพะผ ะธะท ัะปะฐะณะฐะตะผัั
ะฑัะดะตั ะผะฝะพะถะธัะตะปั โ ัะปะตะผะตะฝั ะธะท ััะพะน ัััะพะบะธ (ััะพะปะฑัะฐ), ะฐ ะทะฝะฐัะธั, ะฒัะต ะพะฝะธ ะพะฑะฝัะปัััั.
__5.__ ะัะปะธ ะดะฒะต ัััะพะบะธ (ััะพะปะฑัะฐ) ะผะฐััะธัั ัะฐะฒะฝั ะผะตะถะดั ัะพะฑะพะน, ัะพ ะพะฟัะตะดะตะปะธัะตะปั ััะพะน ะผะฐััะธัั ัะฐะฒะตะฝ ะฝัะปั.
- ะกะพะณะปะฐัะฝะพ ัะฒะพะนััะฒั 3, ะฟะตัะตััะฐะฝะพะฒะบะฐ ะดะฒัั
ัััะพะบ (ััะพะปะฑัะพะฒ) ะฟัะธะฒะพะดะธั ะบ ัะผะตะฝะต ะทะฝะฐะบะฐ ะพะฟัะตะดะตะปะธัะตะปั. ะก ะดััะณะพะน ััะพัะพะฝั, ะตัะปะธ ัััะพะบะธ ัะฐะฒะฝั, ัะพ ะพะฟัะตะดะตะปะธัะตะปั ะธะทะผะตะฝะธัััั ะฝะต ะดะพะปะถะตะฝ. ะะฑะฐ ััะธ ััะปะพะฒะธั ะพะดะฝะพะฒัะตะผะตะฝะฝะพ ะฒัะฟะพะปะฝััััั, ัะพะปัะบะพ ะบะพะณะดะฐ ะพะฟัะตะดะตะปะธัะตะปั ัะฐะฒะตะฝ ะฝัะปั:
$$detA=-detA \Rightarrow detA=0.$$
__6.__ ะัะปะธ ะดะฒะต ัััะพะบะธ (ััะพะปะฑัะฐ) ะผะฐััะธัั ะปะธะฝะตะนะฝะพ ะทะฐะฒะธัะธะผั, ัะพ ะพะฟัะตะดะตะปะธัะตะปั ััะพะน ะผะฐััะธัั ัะฐะฒะตะฝ ะฝัะปั.
- ะกะพะณะปะฐัะฝะพ ัะฒะพะนััะฒั 2, ะผะฝะพะถะธัะตะปั ัััะพะบะธ (ััะพะปะฑัะฐ) ะผะพะถะฝะพ ะฒัะฝะตััะธ ะทะฐ ะทะฝะฐะบ ะพะฟัะตะดะตะปะธัะตะปั. ะัะฝะตัั ัะฐะบะธะผ ะพะฑัะฐะทะพะผ ะผะฝะพะถะธัะตะปั ะฟัะพะฟะพััะธะพะฝะฐะปัะฝะพััะธ, ะผั ะฟะพะปััะธะผ ะผะฐััะธัั, ะธะผะตัััั ะดะฒะต ะพะดะธะฝะฐะบะพะฒัั
ัััะพะบะธ (ััะพะปะฑัะฐ). ะกะพะณะปะฐัะฝะพ ัะฒะพะนััะฒั 5, ะพะฟัะตะดะตะปะธัะตะปั ัะฐะบะพะน ะผะฐััะธัั ัะฐะฒะตะฝ ะฝัะปั.
__7.__ ะะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั ััะตัะณะพะปัะฝะพะณะพ ะฒะธะดะฐ ัะฐะฒะตะฝ ะฟัะพะธะทะฒะตะดะตะฝะธั ัะปะตะผะตะฝัะพะฒ, ััะพััะธั
ะฝะฐ ะตะต ะณะปะฐะฒะฝะพะน ะดะธะฐะณะพะฝะฐะปะธ:
$$\begin{vmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
0 & a_{22} & a_{23} & \cdots & a_{2n}\\
0 & 0 & a_{33} & \cdots & a_{3n}\\
\cdots & \cdots & \cdots & \ddots & \cdots\\
0 & 0 & 0 & \cdots & a_{nn}
\end{vmatrix}=a_{11}\cdot a_{22}\cdot ... \cdot a_{nn}.$$
__8.__ ะัะปะธ ะผะฐััะธัะฐ $A$ ะพััะพะณะพะฝะฐะปัะฝะฐ, ัะพ ะพะฟัะตะดะตะปะธัะตะปั ัะฐะบะพะน ะผะฐััะธัั
$$detA = \pm1.$$
__9.__ ะะปั ะดะฒัั
ะบะฒะฐะดัะฐัะฝัั
ะผะฐััะธั ะพะดะธะฝะฐะบะพะฒะพะณะพ ัะฐะทะผะตัะฐ
$$det(AB)=detA\cdot detB.$$
__10.__ ะัะปะธ ัะปะตะผะตะฝัั ัััะพะบะธ (ััะพะปะฑัะฐ) ะผะฐััะธัั ัะฒะปััััั ัะตะทัะปััะฐัะพะผ ััะผะผั, ัะพ
$$\begin{vmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{k1}+b_{k1} & a_{k2}+b_{k2} & a_{k3}+b_{k3} & \cdots & a_{kn}+b_{kn}\\
\cdots & \cdots & \cdots & \ddots & \cdots\\
a_{1n} & a_{2n} & a_{3n} & \cdots & a_{nn}
\end{vmatrix}=
\begin{vmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{k1} & a_{k2} & a_{k3} & \cdots & a_{kn}\\
\cdots & \cdots & \cdots & \ddots & \cdots\\
a_{1n} & a_{2n} & a_{3n} & \cdots & a_{nn}
\end{vmatrix}+
\begin{vmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
b_{k1} & b_{k2} & b_{k3} & \cdots & b_{kn}\\
\cdots & \cdots & \cdots & \ddots & \cdots\\
a_{1n} & a_{2n} & a_{3n} & \cdots & a_{nn}
\end{vmatrix}.$$
__11.__ ะัะปะธ ะบ ะพะดะฝะพะน ะธะท ัััะพะบ ะผะฐััะธัั ะฟัะธะฑะฐะฒะธัั ะดััะณัั, ัะผะฝะพะถะตะฝะฝัั ะฝะฐ ัะธัะปะพ, ะตะต ะพะฟัะตะดะตะปะธัะตะปั ะฝะต ะธะทะผะตะฝะธััั:
$$\begin{vmatrix}
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{i1} & a_{i2} & a_{i3} & \cdots & a_{in}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{k1}& a_{k2}& a_{k3} & \cdots & a_{kn}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
\end{vmatrix}=
\begin{vmatrix}
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{i1} & a_{i2} & a_{i3} & \cdots & a_{in}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
a_{k1}+\lambda a_{i1} & a_{k2}+\lambda a_{i2}& a_{k3}+\lambda a_{i3} & \cdots & a_{kn}+\lambda a_{in}\\
\cdots & \cdots & \cdots & \cdots & \cdots\\
\end{vmatrix}.$$
- ะขะฐะบะพะน ะพะฟัะตะดะตะปะธัะตะปั ะผะพะถะฝะพ ะฑัะดะตั ะฟัะตะดััะฐะฒะธัั ะฒ ะฒะธะดะต ััะผะผั ะดะฒัั
, ะฟะตัะฒัะน ะธะท ะบะพัะพััั
ะฑัะดะตั ัะฐะฒะตะฝ ะธัั
ะพะดะฝะพะผั, ะฐ ะฒัะพัะพะน ะฑัะดะตั ัะพะดะตัะถะฐัั ะปะธะฝะตะนะฝะพ ะทะฐะฒะธัะธะผัะต ัััะพะบะธ, ะฒ ัะฒัะทะธ ั ัะตะผ ะพะฑัะฐัะธััั ะฒ ะฝะพะปั.
__ะัะธะผะตั__
ะััะธัะปะธะผ ะพะฟัะตะดะตะปะธัะตะปั
$$\begin{vmatrix}
2 & -4 & 1\\
-3 & 2 & 5\\
1 & 2 & 3
\end{vmatrix}.$$
__ะ ะตัะตะฝะธะต__
ะขะฐะบ ะบะฐะบ ะฟัะธ ะฟัะธะฑะฐะฒะปะตะฝะธะธ ะบ ัััะพะบะต ะดััะณะพะน ัััะพะบะธ, ัะผะฝะพะถะตะฝะฝะพะน ะฝะฐ ัะธัะปะพ, ะพะฟัะตะดะตะปะธัะตะปั ะฝะต ะผะตะฝัะตััั, ะผั ะผะพะถะตะผ ะพัััะตััะฒะธัั ะฝะตะบะพัะพััะต ะฟัะตะพะฑัะฐะทะพะฒะฐะฝะธั ะดะปั ะพะฑะฝัะปะตะฝะธั ะผะฐะบัะธะผะฐะปัะฝะพะณะพ ะบะพะปะธัะตััะฒะฐ ัะปะตะผะตะฝัะพะฒ:
- ะฟัะตะพะฑัะฐะทัะตะผ ะฟะตัะฒัั ัััะพะบั, ะฒัััั ััะตััั, ัะผะฝะพะถะตะฝะฝัั ะฝะฐ 2;
- ะฟัะตะพะฑัะฐะทัะตะผ ะฒัะพััั ัััะพะบั, ะฟัะธะฑะฐะฒะธะฒ ะบ ะฝะตะน ััะตััั, ัะผะฝะพะถะตะฝะฝัั ะฝะฐ 3.
ะะพะปััะธะผ:
$$\begin{vmatrix}
2 & -4 & 1\\
-3 & 2 & 5\\
1 & 2 & 3
\end{vmatrix}=
\begin{vmatrix}
0 & -8 & -5\\
0 & 8 & 14\\
1 & 2 & 3
\end{vmatrix}.$$
ะะฐะปะตะต ะฟะพะผะตะฝัะตะผ ะผะตััะฐะผะธ ะฟะตัะฒัั ะธ ััะตััั ัััะพะบะธ (ะฟัะธ ััะพะผ ะทะฝะฐะบ ะพะฟัะตะดะตะปะธัะตะปั ะธะทะผะตะฝะธััั, ะฟะพ ัะฒะพะนััะฒั 3):
$$-\begin{vmatrix}
1 & 2 & 3\\
0 & 8 & 14\\
0 & -8 & -5
\end{vmatrix}.$$
ะ ะฟัะธะฑะฐะฒะธะผ ะบ ััะตััะตะน ัััะพะบะต ะฒัะพััั:
$$-\begin{vmatrix}
1 & 2 & 3\\
0 & 8 & 14\\
0 & 0 & 9
\end{vmatrix}.$$
ะั ะฟะพะปััะธะปะธ ะผะฐััะธัั ััะตัะณะพะปัะฝะพะณะพ ะฒะธะดะฐ, ะพะฟัะตะดะตะปะธัะตะปั ะบะพัะพัะพะน ัะฐะฒะตะฝ ะฟัะพะธะทะฒะตะดะตะฝะธั ะดะธะฐะณะพะฝะฐะปัะฝัั
ัะปะตะผะตะฝัะพะฒ:
$$-\begin{vmatrix}
1 & 2 & 3\\
0 & 8 & 14\\
0 & 0 & 9
\end{vmatrix}=-1\cdot8\cdot9=-72.$$
ะัะพะฒะตัะธะผ ั ะฟะพะผะพััั Python:
```
a = np.array([[2, -4, 1], [-3, 2, 5], [1, 2, 3]])
print(f'ะะฐััะธัะฐ:\n{a}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(a):.0f}')
```
__ะะฟัะตะดะตะปะตะฝะธะต__
ะะฐััะธัะฐ ะฝะฐะทัะฒะฐะตััั _ัะธะฝะณัะปััะฝะพะน_, ะธะปะธ _ะฒััะพะถะดะตะฝะฝะพะน_, ะตัะปะธ ะตะต ะพะฟัะตะดะตะปะธัะตะปั ัะฐะฒะตะฝ ะฝัะปั.
## ะ ะฐะฝะณ ะผะฐััะธัั
ะะฒะตะดะตะผ ะฟะพะฝััะธะต ะผะธะฝะพัะฐ $k$-ะณะพ ะฟะพััะดะบะฐ.
_ะะธะฝะพัะพะผ $k$-ะณะพ ะฟะพััะดะบะฐ_ ะผะฐััะธัั $A$ ัะฐะทะผะตัะฐ $m\times n$ ะฑัะดะตะผ ะฝะฐะทัะฒะฐัั ะพะฟัะตะดะตะปะธัะตะปั $k$-ะณะพ ะฟะพััะดะบะฐ ($k$ ะฝะต ะฟัะตะฒะพัั
ะพะดะธั ะผะตะฝััะตะต ะธะท $m$ ะธ $n$) ั ัะปะตะผะตะฝัะฐะผะธ, ะปะตะถะฐัะธะผะธ ะฝะฐ ะฟะตัะตัะตััะตะฝะธะธ ะปัะฑัั
$k$ ัััะพะบ ะธ ะปัะฑัั
$k$ ััะพะปะฑัะพะฒ ะผะฐััะธัั $A$.
__ะะฟัะตะดะตะปะตะฝะธะต__
ะัะตะดะฟะพะปะพะถะธะผ, ััะพ ั
ะพัั ะฑั ะพะดะธะฝ ะธะท ัะปะตะผะตะฝัะพะฒ ะผะฐััะธัั $A$ ะพัะปะธัะตะฝ ะพั ะฝัะปั. ะขะพะณะดะฐ ะฝะฐะนะดะตััั ัะตะปะพะต ะฟะพะปะพะถะธัะตะปัะฝะพะต ัะธัะปะพ $r$, ัะฐะบะพะต, ััะพ:<br>
1) ั ะผะฐััะธัั $A$ ะธะผะตะตััั ะผะธะฝะพั $r$-ะณะพ ะฟะพััะดะบะฐ, ะพัะปะธัะฝัะน ะพั ะฝัะปั;<br>
2) ะปัะฑะพะน ะผะธะฝะพั ะฟะพััะดะบะฐ $r+1$ ะธ ะฒััะต ัะฐะฒะตะฝ ะฝัะปั.
ะงะธัะปะพ $r$, ัะดะพะฒะปะตัะฒะพััััะตะต ััะธะผ ััะตะฑะพะฒะฐะฝะธัะผ, ะฝะฐะทะพะฒะตะผ _ัะฐะฝะณะพะผ ะผะฐััะธัั $A$_ ะธ ะพะฑะพะทะฝะฐัะธะผ $rankA$, ะฐ ะผะธะฝะพั $r$-ะณะพ ะฟะพััะดะบะฐ โ _ะฑะฐะทะธัะฝัะผ ะผะธะฝะพัะพะผ_.
ะะฝัะผะธ ัะปะพะฒะฐะผะธ, ัะฐะฝะณ ะผะฐััะธัั โ ััะพ ะฟะพััะดะพะบ ะตะต ะผะฐะบัะธะผะฐะปัะฝะพะณะพ ะฝะตะฒััะพะถะดะตะฝะฝะพะณะพ (ะธะปะธ ะฑะฐะทะธัะฝะพะณะพ) ะผะธะฝะพัะฐ.
__ะะฟัะตะดะตะปะตะฝะธะต__
_ะกััะพัะฝัะผ ัะฐะฝะณะพะผ ะผะฐััะธัั_ ะฝะฐะทัะฒะฐะตััั ะผะฐะบัะธะผะฐะปัะฝะพะต ัะธัะปะพ ะปะธะฝะตะนะฝะพ ะฝะตะทะฐะฒะธัะธะผัั
ัััะพะบ ััะพะน ะผะฐััะธัั.
_ะกัะพะปะฑัะพะฒัะผ ัะฐะฝะณะพะผ ะผะฐััะธัั_ ะฝะฐะทัะฒะฐะตััั ะผะฐะบัะธะผะฐะปัะฝะพะต ัะธัะปะพ ะปะธะฝะตะนะฝะพ ะฝะตะทะฐะฒะธัะธะผัั
ััะพะปะฑัะพะฒ ััะพะน ะผะฐััะธัั.
__ะขะตะพัะตะผะฐ__
_ะกััะพัะฝัะน ัะฐะฝะณ ะผะฐััะธัั ะฒัะตะณะดะฐ ัะพะฒะฟะฐะดะฐะตั ั ััะพะปะฑัะพะฒัะผ ะธ ัะฐะฒะตะฝ ะผะฐะบัะธะผะฐะปัะฝะพะผั ัะฐะทะผะตัั ะตะต ะฝะตะฒััะพะถะดะตะฝะฝะพะณะพ ะผะธะฝะพัะฐ._
ะัะธ ัะฐะฑะพัะต ั ัะฐะฝะณะพะผ ะผะฐััะธัั ะฒะฐะถะฝะพ ะทะฝะฐัั, ะบะฐะบะธะต ะฟัะตะพะฑัะฐะทะพะฒะฐะฝะธั ะผะฐััะธั ะฝะต ะฟัะธะฒะพะดัั ะบ ะธะทะผะตะฝะตะฝะธั ะธั
ัะฐะฝะณะฐ:
- ััะฐะฝัะฟะพะฝะธัะพะฒะฐะฝะธะต;
- ะฟะตัะตััะฐะฝะพะฒะบะฐ ะผะตััะฐะผะธ ะดะฒัั
ัััะพะบ (ััะพะปะฑัะพะฒ);
- ัะผะฝะพะถะตะฝะธะต ะฒัะตั
ัะปะตะผะตะฝัะพะฒ ัััะพะบะธ (ััะพะปะฑัะฐ) ะฝะฐ ัะธัะปะพ, ะฝะต ัะฐะฒะฝะพะต ะฝัะปั;
- ะฟัะธะฑะฐะฒะปะตะฝะธะต ะบะพ ะฒัะตะผ ัะปะตะผะตะฝัะฐะผ ัััะพะบะธ (ััะพะปะฑัะฐ) ัะพะพัะฒะตัััะฒัััะธั
ัะปะตะผะตะฝัะพะฒ ะดััะณะพะน ัััะพะบะธ (ััะพะปะฑัะฐ);
- ะฒัะฑัะฐััะฒะฐะฝะธะต ะฝัะปะตะฒะพะน ัััะพะบะธ (ััะพะปะฑัะฐ);
- ะฒัะฑัะฐััะฒะฐะฝะธะต ัััะพะบะธ (ััะพะปะฑัะฐ), ัะฒะปัััะตะนัั ะปะธะฝะตะนะฝะพะน ะบะพะผะฑะธะฝะฐัะธะตะน ะดััะณะธั
ัััะพะบ (ััะพะปะฑัะพะฒ).
__ะัะธะผะตั__
ะะฐะนะดะตะผ ัะฐะฝะณ ะผะฐััะธัั
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
2 & 5 & 8 & 11 & 14\\
3 & 9 & 14 & 20 & 26\\
5 & 14 & 22 & 31 & 40
\end{pmatrix}.$$
ะงะตัะฒะตััะฐั ัััะพะบะฐ ัะฒะปัะตััั ััะผะผะพะน ะฒัะพัะพะน ะธ ััะตััะตะน ัััะพะบ, ะฐ ะทะฝะฐัะธั, ะตะต ะผะพะถะฝะพ ะพัะฑัะพัะธัั:
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
2 & 5 & 8 & 11 & 14\\
3 & 9 & 14 & 20 & 26
\end{pmatrix}.$$
ะะท ะฒัะพัะพะน ะธ ััะตััะตะน ัััะพะบ ะฒัััะตะผ ะฟะตัะฒัั, ัะผะฝะพะถะตะฝะฝัั ะฝะฐ $2$ ะธ $3$ ัะพะพัะฒะตัััะฒะตะฝะฝะพ:
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
0 & 1 & 2 & 3 & 4\\
0 & 2 & 5 & 8 & 11
\end{pmatrix}.$$
ะ ะฒัััะตะผ ะธะท ััะตััะตะน ัััะพะบะธ ะฒัะพััั, ัะผะฝะพะถะตะฝะฝัั ะฝะฐ $2$:
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
0 & 1 & 2 & 3 & 4\\
0 & 0 & 1 & 2 & 3
\end{pmatrix}.$$
ะขะฐะบะธะผ ะพะฑัะฐะทะพะผ, ัะฐะฝะณ ะผะฐััะธัั ัะฐะฒะตะฝ $3$.
ะ ะบะพะฝัะตะบััะต ะผะฐัะธะฝะฝะพะณะพ ะพะฑััะตะฝะธั ััะฐ ั
ะฐัะฐะบัะตัะธััะธะบะฐ ะพัะพะฑะตะฝะฝะพ ะฒะฐะถะฝะฐ, ัะฐะบ ะบะฐะบ ะฝะฐะปะธัะธะต ะปะธะฝะตะนะฝะพ ะทะฐะฒะธัะธะผัั
ัััะพะบ ะฒ ะพะฑััะฐััะตะน ะฒัะฑะพัะบะต ะฟัะธะฒะพะดะธั ะบ ะธะทะฑััะพัะฝะพััะธ ะธะฝัะพัะผะฐัะธะธ ะธ ััะปะพะถะฝะตะฝะธั ะผะพะดะตะปะธ. ะขะฐะบะธะต ัััะพะบะธ ะธะท ะพะฑััะฐััะธั
ะฒัะฑะพัะพะบ ะผะพะถะฝะพ ัะดะฐะปััั ะฑะตะท ััะตัะฑะฐ ะดะปั ัะพัะฝะพััะธ ะฟะพะปััะฐะตะผะพะน ะผะพะดะตะปะธ, ะพัััะตััะฒะปัั ัะถะฐัะธะต ะดะฐะฝะฝัั
ะฑะตะท ะฟะพัะตัั.
ะ NumPy ัะฐะฝะณ ะผะฐััะธัั ะฒััะธัะปัะตััั ั ะฟะพะผะพััั ััะฝะบัะธะธ `numpy.linalg.matrix_rank(a)`, ะณะดะต `a` โ ะผะฐััะธัะฐ.
ะัะพะผะต ะฟัะพัะตะณะพ, ั ะฟะพะผะพััั ัะฐะฝะณะฐ ะผะฐััะธัั ะผะพะถะฝะพ ะฟัะพะฒะตัััั ะฒะตะบัะพัั ะฝะฐ ะปะธะฝะตะนะฝัั ะทะฐะฒะธัะธะผะพััั.
ะะผะตั ะฝะตัะบะพะปัะบะพ ะฒะตะบัะพัะพะฒ, ะผั ะผะพะถะตะผ ัะพััะฐะฒะธัั ะธะท ะฝะธั
ะผะฐััะธัั, ะณะดะต ััะธ ะฒะตะบัะพัั ะฑัะดัั ัะฒะปััััั ัััะพะบะฐะผะธ ะธะปะธ ััะพะปะฑัะฐะผะธ. ะะตะบัะพัั ะฑัะดัั ะปะธะฝะตะนะฝะพ ะฝะตะทะฐะฒะธัะธะผั ัะพะณะดะฐ ะธ ัะพะปัะบะพ ัะพะณะดะฐ, ะบะพะณะดะฐ ัะฐะฝะณ ะฟะพะปััะตะฝะฝะพะน ะผะฐััะธัั ัะพะฒะฟะฐะดะตั ั ัะธัะปะพะผ ะฒะตะบัะพัะพะฒ.
```
x = [1, 2, 3]
y = [2, 2, 2]
z = [3, 3, 3]
a = np.array([x, y, z])
r = np.linalg.matrix_rank(a)
print(f'ะ ะฐะฝะณ ะผะฐััะธัั: {r}')
```
## ะะพะฝััะธะต ะพะฑัะฐัะฝะพะน ะผะฐััะธัั
ะะฐััะธัะฐ $B$ ะฝะฐะทัะฒะฐะตััั _ะฟัะฐะฒะพะน ะพะฑัะฐัะฝะพะน ะผะฐััะธัะตะน_ ะบ $A$, ะตัะปะธ
$$AB=E,$$
ะณะดะต $E$ โ ะตะดะธะฝะธัะฝะฐั ะผะฐััะธัะฐ.
ะะฐััะธัะฐ $C$ ะฝะฐะทัะฒะฐะตััั _ะปะตะฒะพะน ะพะฑัะฐัะฝะพะน ะผะฐััะธัะตะน_ ะบ $A$, ะตัะปะธ
$$CA=E.$$
__ะฃัะฒะตัะถะดะตะฝะธะต__
ะัะปะธ ะดะปั ะผะฐััะธัั $A$ ัััะตััะฒััั ะปะตะฒะฐั ะธ ะฟัะฐะฒะฐั ะพะฑัะฐัะฝัะต ะผะฐััะธัั, ัะพ ะพะฝะธ ัะพะฒะฟะฐะดะฐัั ะผะตะถะดั ัะพะฑะพะน.
__ะขะตะพัะตะผะฐ__
ะะปั ัะพะณะพ, ััะพะฑั ะดะปั ะผะฐััะธัั $A$ ัััะตััะฒะพะฒะฐะปะธ ะปะตะฒะฐั ะธ ะฟัะฐะฒะฐั ะพะฑัะฐัะฝัะต ะผะฐััะธัั, ะฝะตะพะฑั
ะพะดะธะผะพ ะธ ะดะพััะฐัะพัะฝะพ, ััะพะฑั ะพะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั $A$ ะฑัะป ะพัะปะธัะตะฝ ะพั ะฝัะปั.
ะขะฐะบะธะผ ะพะฑัะฐะทะพะผ, ะฒ ัะปััะฐะต ะฝะตะฒััะพะถะดะตะฝะฝัั
ะผะฐััะธั ะผะพะถะฝะพ ะพะฟััะบะฐัั ัะตัะผะธะฝั ยซะปะตะฒะฐัยป ะธ ยซะฟัะฐะฒะฐัยป, ะธ ะณะพะฒะพัะธัั ะฟัะพััะพ ะพ ะผะฐััะธัะต, _ะพะฑัะฐัะฝะพะน ะฟะพ ะพัะฝะพัะตะฝะธั ะบ ะผะฐััะธัะต_ $A$, ะธ ะพะฑะพะทะฝะฐัะฐัั ะตะต ัะธะผะฒะพะปะพะผ $A^{-1}$:
$$A^{-1}A=AA^{-1}=E,$$
ะณะดะต $E$ โ ะตะดะธะฝะธัะฝะฐั ะผะฐััะธัะฐ.
ะัะปะธ ะดะปั ะผะฐััะธัั $A$ ัััะตััะฒัะตั ะพะฑัะฐัะฝะฐั ะผะฐััะธัะฐ, ัะพ ะพะฝะฐ ะตะดะธะฝััะฒะตะฝะฝะฐ.
_ะัะปะธ ะผะฐััะธัะฐ ะฒััะพะถะดะตะฝะฐ, ัะพ ั ะฝะตะต ะฝะตั ะพะฑัะฐัะฝะพะน ะผะฐััะธัั._
- __ะะพะบะฐะทะฐัะตะปัััะฒะพ__
ะะพะฟัััะธะผ, ะผะฐััะธัะฐ $A$ ะฒััะพะถะดะตะฝะฐ, ัะพ ะตััั $detA=0$, ะธ ะดะปั ะฝะตะต ัััะตััะฒัะตั ะพะฑัะฐัะฝะฐั ะผะฐััะธัะฐ $A^{-1}$. ะขะพะณะดะฐ ะธะท ัะพะพัะฝะพัะตะฝะธั $A\cdot A^{-1}=E$ ะฟะพะปััะธะผ, ััะพ $detA\cdot detA^{-1}=detE=1$, ะพัะบัะดะฐ ัะปะตะดัะตั, ััะพ $detA\neq0$, ััะพ ะฟัะพัะธะฒะพัะตัะธั ััะปะพะฒะธั. ะขะพ ะตััั, ะตัะปะธ ั ะผะฐััะธัั ะตััั ะพะฑัะฐัะฝะฐั, ะทะฝะฐัะธั, ะผะฐััะธัะฐ ะฝะตะฒััะพะถะดะตะฝะฐ. ะงัะพ ะธ ััะตะฑะพะฒะฐะปะพัั ะดะพะบะฐะทะฐัั.
__ะะฐั
ะพะถะดะตะฝะธะต ะพะฑัะฐัะฝะพะน ะผะฐััะธัั (ะผะตัะพะด ะฟัะธัะพะตะดะธะฝะตะฝะฝะพะน ะผะฐััะธัั)__
ะะปั ะฒะฒะพะดะฐ ะฐะปะณะพัะธัะผะฐ ะฝะฐั
ะพะถะดะตะฝะธั ะพะฑัะฐัะฝะพะน ะผะฐััะธัั ะบ ะผะฐััะธัะต $A$ ะฒะฒะตะดะตะผ ะฟะพะฝััะธะต ะฐะปะณะตะฑัะฐะธัะตัะบะพะณะพ ะดะพะฟะพะปะฝะตะฝะธั.
_ะะปะณะตะฑัะฐะธัะตัะบะธะผ ะดะพะฟะพะปะฝะตะฝะธะตะผ_ ัะปะตะผะตะฝัะฐ $a_{ij}$ ะบะฒะฐะดัะฐัะฝะพะน ะผะฐััะธัั $A$ ะฟะพััะดะบะฐ $n$ ะฝะฐะทัะฒะฐัั ะผะธะฝะพั $M_{ij}$, ัะผะฝะพะถะตะฝะฝัะน ะฝะฐ $(-1)^{i+j}$, ะธ ะพะฑะพะทะฝะฐัะฐัั $A_{ij}$:
$$A_{ij}=(-1)^{i+j}M_{ij}.$$
ะะปะณะพัะธัะผ ะฝะฐั
ะพะถะดะตะฝะธั ะพะฑัะฐัะฝะพะน ะผะฐััะธัั ัะปะตะดัััะธะน:
1. ะะฐะนัะธ ะพะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั $A$ ะธ ัะฑะตะดะธัััั, ััะพ $detA\neq0$;
2. ะกะพััะฐะฒะธัั ะฐะปะณะตะฑัะฐะธัะตัะบะธะต ะดะพะฟะพะปะฝะตะฝะธั $A_{ij}$ ะดะปั ะบะฐะถะดะพะณะพ ัะปะตะผะตะฝัะฐ ะผะฐััะธัั $A$ ะธ ะทะฐะฟะธัะฐัั ะผะฐััะธัั $A^{*}=(A_{ij})$ ะธะท ะฝะฐะนะดะตะฝะฝัั
ะฐะปะณะตะฑัะฐะธัะตัะบะธั
ะดะพะฟะพะปะฝะตะฝะธะน.
3. ะะฐะฟะธัะฐัั ะพะฑัะฐัะฝัั ะผะฐััะธัั, ะพะฟัะตะดะตะปะตะฝะฝัั ะฟะพ ัะพัะผัะปะต
$$A^{-1}=\frac{1}{detA}\cdot A^{*T}.$$
ะะฐััะธัั $A^{*T}$ ัะฐััะพ ะฝะฐะทัะฒะฐัั _ะฟัะธัะพะตะดะธะฝะตะฝะฝะพะน (ัะพัะทะฝะพะน)_ ะบ ะผะฐััะธัะต $A$.
__ะัะธะผะตั__
ะะฐะนะดะตะผ ะพะฑัะฐัะฝัั ะผะฐััะธัั ะดะปั ะผะฐััะธัั
$$A = \begin{pmatrix}
1 & 2 & 1\\
1 & 1 & 4\\
2 & 3 & 6
\end{pmatrix}.$$
__ะ ะตัะตะฝะธะต__
1. ะะฐะนะดะตะผ ะพะฟัะตะดะตะปะธัะตะปั:
$$\begin{vmatrix}
1 & 2 & 1\\
1 & 1 & 4\\
2 & 3 & 6
\end{vmatrix} = -6 + 4 + 1 = -1. $$
2. ะะฐะนะดะตะผ ะฐะปะณะตะฑัะฐะธัะตัะบะธะต ะดะพะฟะพะปะฝะตะฝะธั ะดะปั ะบะฐะถะดะพะณะพ ัะปะตะผะตะฝัะฐ:
$$A_{11}=(-1)^{2}\begin{vmatrix}
1 & 4\\
3 & 6
\end{vmatrix} = -6,~
A_{12}=(-1)^{3}\begin{vmatrix}
1 & 4\\
2 & 6
\end{vmatrix} = 2,~
A_{13}=(-1)^{4}\begin{vmatrix}
1 & 1\\
2 & 3
\end{vmatrix} = 1,$$
$$A_{21}=(-1)^{3}\begin{vmatrix}
2 & 1\\
3 & 6
\end{vmatrix} = -9,~
A_{22}=(-1)^{4}\begin{vmatrix}
1 & 1\\
2 & 6
\end{vmatrix} = 4,~
A_{23}=(-1)^{5}\begin{vmatrix}
1 & 2\\
2 & 3
\end{vmatrix} = 1,$$
$$A_{31}=(-1)^{4}\begin{vmatrix}
2 & 1\\
1 & 4\\
\end{vmatrix} = 7,~
A_{32}=(-1)^{5}\begin{vmatrix}
1 & 1\\
1 & 4
\end{vmatrix} = -3,~
A_{33}=(-1)^{6}\begin{vmatrix}
1 & 2\\
1 & 1\\
\end{vmatrix} = -1.$$
ะะพะปััะตะฝะฝะฐั ะผะฐััะธัะฐ ะธะท ะฐะปะณะตะฑัะฐะธัะตัะบะธั
ะดะพะฟะพะปะฝะตะฝะธะน:
$$A^{*} = \begin{pmatrix}
-6 & 2 & 1\\
-9 & 4 & 1\\
7 & -3 & -1
\end{pmatrix},~
A^{*T} = \begin{pmatrix}
-6 & -9 & 7\\
2 & 4 & -3\\
1 & 1 & -1
\end{pmatrix}.$$
3. ะัะฟะพะปัะทัั ัะพัะผัะปั ะธะท ะฐะปะณะพัะธัะผะฐ, ะฟะพะปััะธะผ
$$A^{-1} = \frac{1}{(-1)}\cdot \begin{pmatrix}
-6 & -9 & 7\\
2 & 4 & -3\\
1 & 1 & -1
\end{pmatrix} = \begin{pmatrix}
6 & 9 & -7\\
-2 & -4 & 3\\
-1 & -1 & 1
\end{pmatrix}.$$
ะ NumPy ะพะฑัะฐัะฝัะต ะผะฐััะธัั ะฒััะธัะปััััั ั ะฟะพะผะพััั ััะฝะบัะธะธ `numpy.linalg.inv(a)`, ะณะดะต `a` โ ะผะฐััะธัะฐ.
```
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=float)
b = np.linalg.inv(a)
print(f'ะะฐััะธัะฐ A:\n{a}\n')
print(f'ะะฐััะธัะฐ B, ะพะฑัะฐัะฝะฐั ะบ A:\n{b}\n')
print(f'ะะฐััะธัะฐ AB (ะดะพะปะถะฝะฐ ะฑััั ะตะดะธะฝะธัะฝะพะน):\n{a.dot(b)}')
```
## ะัะฐะบัะธัะตัะบะพะต ะทะฐะดะฐะฝะธะต
ะัะต ะทะฐะดะฐะฝะธั ัะตะบะพะผะตะฝะดัะตััั ะฒัะฟะพะปะฝััั ะฒัััะฝัั, ะทะฐัะตะผ ะฟัะพะฒะตััั ะฟะพะปััะตะฝะฝัะต ัะตะทัะปััะฐัั ั ะธัะฟะพะปัะทะพะฒะฐะฝะธะตะผ Numpy.
__1.__ ะััะธัะปะธัั ะพะฟัะตะดะตะปะธัะตะปั:
a)
$$\begin{vmatrix}
sinx & -cosx\\
cosx & sinx
\end{vmatrix};$$
ะฑ)
$$\begin{vmatrix}
4 & 2 & 3\\
0 & 5 & 1\\
0 & 0 & 9
\end{vmatrix};$$
ะฒ)
$$\begin{vmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{vmatrix}.$$
__2.__ ะะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั $A$ ัะฐะฒะตะฝ $4$. ะะฐะนัะธ:
ะฐ) $det(A^{2})$;
ะฑ) $det(A^{T})$;
ะฒ) $det(2A)$.
__3.__ ะะพะบะฐะทะฐัั, ััะพ ะผะฐััะธัะฐ
$$\begin{pmatrix}
-2 & 7 & -3\\
4 & -14 & 6\\
-3 & 7 & 13
\end{pmatrix}$$
ะฒััะพะถะดะตะฝะฝะฐั.
__4.__ ะะฐะนัะธ ัะฐะฝะณ ะผะฐััะธัั:
ะฐ) $\begin{pmatrix}
1 & 2 & 3\\
1 & 1 & 1\\
2 & 3 & 4
\end{pmatrix};$
ะฑ) $\begin{pmatrix}
0 & 0 & 2 & 1\\
0 & 0 & 2 & 2\\
0 & 0 & 4 & 3\\
2 & 3 & 5 & 6
\end{pmatrix}.$
## ะะธัะตัะฐัััะฐ
1. ะะปัะธะฝ ะ.ย ะ., ะะพะทะฝัะบ ะญ.ย ะ. ะะธะฝะตะนะฝะฐั ะฐะปะณะตะฑัะฐ: ะฃัะตะฑ. ะดะปั ะฒัะทะพะฒ. โ 6-ะต ะธะทะด. โ ะ.: ะคะธะทะผะฐัะปะธั, 2005.
2. ะคะพััะฐะนั ะะถ., ะะพะปะตั ะ. ะงะธัะปะตะฝะฝะพะต ัะตัะตะฝะธะต ัะธััะตะผ ะปะธะฝะตะนะฝัั
ะฐะปะณะตะฑัะฐะธัะตัะบะธั
ััะฐะฒะฝะตะฝะธะน. โ ะ.: ะะธั, 1969.
3. ะะพัััะธะบะธะฝ ะ.ย ะ., ะะฐะฝะธะฝ ะฎ.ย ะ. ะะธะฝะตะนะฝะฐั ะฐะปะณะตะฑัะฐ ะธ ะณะตะพะผะตััะธั. ะฃัะตะฑ. ะฟะพัะพะฑะธะต ะดะปั ะฒัะทะพะฒ. โ 2-ะต ะธะทะด. โ ะ.: ะะฐัะบะฐ, ะะปะฐะฒะฝะฐั ัะตะดะฐะบัะธั ัะธะทะธะบะพ-ะผะฐัะตะผะฐัะธัะตัะบะพะน ะปะธัะตัะฐัััั, 1986.
## ะะพะฟะพะปะฝะธัะตะปัะฝัะต ะผะฐัะตัะธะฐะปั:
1. [ะะฟัะตะดะตะปะธัะตะปั ะผะฐััะธัั ะฒ NumPy](https://docs.scipy.org/doc/numpy-1.14.2/reference/generated/numpy.linalg.det.html)
2. [ะ ะฐะฝะณ ะผะฐััะธัั ะฒ NumPy](https://docs.scipy.org/doc/numpy-1.14.2/reference/generated/numpy.linalg.matrix_rank.html)
3. [ะะฑัะฐัะตะฝะธะต ะผะฐััะธั ะฒ NumPy](https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.inv.html)
|
github_jupyter
|
import numpy as np
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]])
print(f'ะะฐััะธัะฐ:\n{a}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(a):.0f}')
b = np.array([[-1, -4, 0, -2], [0, 1, 5, 4], [3, 1, 1, 0], [-1, 0, 2, 2]])
print(f'ะะฐััะธัะฐ:\n{b}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(b):.0f}')
a = np.array([[2, -4, 1], [-3, 2, 5], [1, 2, 3]])
print(f'ะะฐััะธัะฐ:\n{a}')
print(f'ะะฟัะตะดะตะปะธัะตะปั:\n{np.linalg.det(a):.0f}')
x = [1, 2, 3]
y = [2, 2, 2]
z = [3, 3, 3]
a = np.array([x, y, z])
r = np.linalg.matrix_rank(a)
print(f'ะ ะฐะฝะณ ะผะฐััะธัั: {r}')
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=float)
b = np.linalg.inv(a)
print(f'ะะฐััะธัะฐ A:\n{a}\n')
print(f'ะะฐััะธัะฐ B, ะพะฑัะฐัะฝะฐั ะบ A:\n{b}\n')
print(f'ะะฐััะธัะฐ AB (ะดะพะปะถะฝะฐ ะฑััั ะตะดะธะฝะธัะฝะพะน):\n{a.dot(b)}')
| 0.116349 | 0.94868 |
## Introduction to the Interstellar Medium
### Jonathan Williams
### Figure 11.8: show the appearance of the M82 SED at different redshifts
#### first fit a smooth curve (7th order polynomial) to a digitized M82 SED and then reshift that representation
#### redshift formulae in Hogg 1999 (https://arxiv.org/abs/astro-ph/9905116v4)
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage.filters import gaussian_filter1d as smooth
from scipy import interpolate
%matplotlib inline
def fit_profile():
# fits a 7th order polynomial to the SED
fig = plt.figure(figsize=(8,5))
ax1 = fig.add_subplot(111)
# read in a more finely sampled version of the M82 SED the same source as M82_SED.ipynb
nu_GHz, Fnu_Jy = np.genfromtxt('M82_radio_SED2.txt', unpack=True, delimiter=',')
wl = 3e2/nu_GHz # millimeters
wl_interp = np.logspace(-1.5,2.3,100)
isort = np.argsort(wl)
p = np.polyfit(np.log10(wl[isort]), np.log10(Fnu_Jy[isort]), 7)
Fnu_interp = 10**np.polyval(p, np.log10(wl_interp))
ax1.plot(wl, Fnu_Jy, 'b-', lw=1)
ax1.plot(wl_interp, Fnu_interp, 'k-', lw=5, alpha=0.3)
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_ylabel(r"$F_\nu$ (Jy)", fontsize=16)
plt.show()
return p
def shift_profile(p):
# redshift the polynomial fit for the SED
# as this shows the broad features and is best for illustration (no distracting wiggles...)
fig = plt.figure(figsize=(8,5))
ax1 = fig.add_subplot(111)
wl0 = np.logspace(-1.5,1.7,100)
Fnu0 = 10**np.polyval(p, np.log10(wl0))
Fnu0 *= 1000 # mJy
# Einstein de Sitter universe, Omega_M=1, Omega_Lambda=0
H0 = 67 # km/s/Mpc
h = H0/100
DH = 3000/h # Mpc
# Lambda CDM, Omega_M=0.3, Omega_Lambda=0.7 (Omega_k=0)
Omega_M = 0.3
Omega_Lambda = 0.7
dz = 0.05
zC = np.arange(0,10,dz)
DC = np.zeros(len(zC))
for i in range(1,len(zC)):
E = np.sqrt(Omega_M*(1+zC[i])**3 + Omega_Lambda)
DC[i] = DC[i-1] + dz/E
DC *= DH
fC = interpolate.interp1d(zC, DC)
# M82 distance
d_M82 = 3.5 # Mpc
zrange = [0.5,1,2,3,4,5, 6]
label = ['z=0.5', '1', '2', '3', '4', '5', '6']
for i in range(len(zrange)):
z = zrange[i]
# Einstein-de Sitter
#DM = DH * 2 * (z+1-np.sqrt(1+z)) / (1+z)
# Lambda CDM
DM = fC(z)
DL = (1+z) * DM
Fz = (1+z) * (d_M82/DL)**2 * Fnu0
wlz = (1+z) * wl0
ax1.plot(wlz, Fz, color='black', lw=2, alpha=np.sqrt(0.5/z))
ax1.text(1.05*wlz[-1], Fz[-1], label[i], ha='left')
ax1.set_xlim(0.03, 500)
ax1.set_ylim(1e-5, 10.0)
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_xlabel(r"$\lambda$ (mm)", fontsize=16)
ax1.set_ylabel(r"$F_\nu$ (mJy)", fontsize=16)
ax1.text(0.2, 1e-3, 'Dust', ha='center', fontsize=12)
ax1.text(60, 0.03, 'Synchrotron', ha='center', fontsize=12)
x_labels = ['0.1','1','10','100']
x_loc = np.array([float(x) for x in x_labels])
ax1.set_xticks(x_loc)
ax1.set_xticklabels(x_labels)
fig.tight_layout(rect=[0.0,0.0,1.0,1.0])
plt.savefig('M82_SED_redshifted.pdf')
pfit = fit_profile()
print(pfit)
shift_profile(pfit)
```
|
github_jupyter
|
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage.filters import gaussian_filter1d as smooth
from scipy import interpolate
%matplotlib inline
def fit_profile():
# fits a 7th order polynomial to the SED
fig = plt.figure(figsize=(8,5))
ax1 = fig.add_subplot(111)
# read in a more finely sampled version of the M82 SED the same source as M82_SED.ipynb
nu_GHz, Fnu_Jy = np.genfromtxt('M82_radio_SED2.txt', unpack=True, delimiter=',')
wl = 3e2/nu_GHz # millimeters
wl_interp = np.logspace(-1.5,2.3,100)
isort = np.argsort(wl)
p = np.polyfit(np.log10(wl[isort]), np.log10(Fnu_Jy[isort]), 7)
Fnu_interp = 10**np.polyval(p, np.log10(wl_interp))
ax1.plot(wl, Fnu_Jy, 'b-', lw=1)
ax1.plot(wl_interp, Fnu_interp, 'k-', lw=5, alpha=0.3)
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_ylabel(r"$F_\nu$ (Jy)", fontsize=16)
plt.show()
return p
def shift_profile(p):
# redshift the polynomial fit for the SED
# as this shows the broad features and is best for illustration (no distracting wiggles...)
fig = plt.figure(figsize=(8,5))
ax1 = fig.add_subplot(111)
wl0 = np.logspace(-1.5,1.7,100)
Fnu0 = 10**np.polyval(p, np.log10(wl0))
Fnu0 *= 1000 # mJy
# Einstein de Sitter universe, Omega_M=1, Omega_Lambda=0
H0 = 67 # km/s/Mpc
h = H0/100
DH = 3000/h # Mpc
# Lambda CDM, Omega_M=0.3, Omega_Lambda=0.7 (Omega_k=0)
Omega_M = 0.3
Omega_Lambda = 0.7
dz = 0.05
zC = np.arange(0,10,dz)
DC = np.zeros(len(zC))
for i in range(1,len(zC)):
E = np.sqrt(Omega_M*(1+zC[i])**3 + Omega_Lambda)
DC[i] = DC[i-1] + dz/E
DC *= DH
fC = interpolate.interp1d(zC, DC)
# M82 distance
d_M82 = 3.5 # Mpc
zrange = [0.5,1,2,3,4,5, 6]
label = ['z=0.5', '1', '2', '3', '4', '5', '6']
for i in range(len(zrange)):
z = zrange[i]
# Einstein-de Sitter
#DM = DH * 2 * (z+1-np.sqrt(1+z)) / (1+z)
# Lambda CDM
DM = fC(z)
DL = (1+z) * DM
Fz = (1+z) * (d_M82/DL)**2 * Fnu0
wlz = (1+z) * wl0
ax1.plot(wlz, Fz, color='black', lw=2, alpha=np.sqrt(0.5/z))
ax1.text(1.05*wlz[-1], Fz[-1], label[i], ha='left')
ax1.set_xlim(0.03, 500)
ax1.set_ylim(1e-5, 10.0)
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_xlabel(r"$\lambda$ (mm)", fontsize=16)
ax1.set_ylabel(r"$F_\nu$ (mJy)", fontsize=16)
ax1.text(0.2, 1e-3, 'Dust', ha='center', fontsize=12)
ax1.text(60, 0.03, 'Synchrotron', ha='center', fontsize=12)
x_labels = ['0.1','1','10','100']
x_loc = np.array([float(x) for x in x_labels])
ax1.set_xticks(x_loc)
ax1.set_xticklabels(x_labels)
fig.tight_layout(rect=[0.0,0.0,1.0,1.0])
plt.savefig('M82_SED_redshifted.pdf')
pfit = fit_profile()
print(pfit)
shift_profile(pfit)
| 0.638272 | 0.923454 |
<a href="https://colab.research.google.com/github/We-Want-it-That-Way/Analysis-of-Plot/blob/main/Analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import pandas as pd
import numpy as np
import math
H=pd.DataFrame({'Name of pulsar':['J0205+6449','J0218+4232','J0437-4715','J0534+2200','J1105-6107','J1124-5916','J1617-5055','J1930+1852','J2124-3358','J2229+6114'],'po':[0.06571592849324,0.00232309053151224,0.005757451936712637,0.0333924123,0.0632021309179,0.13547685441,0.069356847,0.136855046957,0.00493111494309662,0.05162357393],'pdot':[1.93754256e-13,7.73955e-20,5.729215e-20,4.20972e-13,1.584462e-14,7.52566e-13,1.351e-13,7.5057e-13,2.05705e-20,7.827e-14],'D in Kpc':[3.200,3.150,0.157,2.000,2.360, 5.000, 4.743, 7.000, 0.410, 3.000],'Age':[5.37e+03,4.76e+08,1.59e+09,1.26e+03,6.32e+04,2.85e+03, 8.13e+03, 2.89e+03, 3.8e+09, 1.05e+04],'R_L':['NaN',466.36,13.52,2200.00,'NaN','NaN','NaN','NaN', 2.86, 13.50],'B_s':[3.61e+12,4.29e+08,4.29e+08,3.79e+12,1.01e+12,1.02e+13,3.1e+12,1.03e+13,3.22e+08,2.03e+12],
'Edot':[2.7e+37,2.4e+35,1.2e+34,4.5e+38,2.5e+36,1.2e+37,1.6e+37,1.2e+37,6.8e+33,2.2e+37],
'Edot2':[2.6e+36,2.5e+34,4.8e+35,1.1e+38,4.4e+35,4.8e+35,7.1e+35,2.4e+35,2.4e+35,2.5e+36],
'B_sI':[3.61e+12,4.27e+08,2.85e+08,3.79e+12,np.nan,np.nan,np.nan,np.nan, 1.92e+08,np.nan],
'B_Lc':[1.19e+05,3.21e+05,2.85e+04,9.55e+05,3.76e+04,3.85e+04, 8.70e+04, 3.75e+04, 2.52e+04, 1.39e+05]})
H
import pandas as pd
import numpy as np
import math
A=pd.DataFrame({'Name of pulsar':['J0537-6910',np.nan,'J0543+2329','J1811-1925','J1846-0258','J0628+0909','J0633+1746','J0636-4549','J1811-4930','J1812-1718'],'po':[0.0161222220245,np.nan,0.245983683333,0.06466700,0.32657128834,3.763733080,0.2370994416923,1.98459736713,1.4327041968,1.20537444137],'pdot':[5.1784338e-14,np.nan,1.541956e-14,4.40e-14,7.107450e-12,0.5479e-15,1.097087e-14,3.1722e-15,2.254e-15,1.9077e-14],'D in Kpc':[49.700,np.nan,1.565,5.000,5.800,1.771,0.190,0.383,1.447,3.678],'R_L':[np.nan,np.nan,71.03,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan],'Age':[4.93e+03,np.nan,2.53e+05,2.33e+04,728,3.59e+07,3.42e+05,9.91e+06,1.01e+07,1e+06],'B_s':[9.25e+11,np.nan,1.97e+12,1.71e+12,4.88e+13,8.35e+11,1.63e+12,2.54e+12,1.82e+12,4.85e+12],'Edot':[4.9e+38,np.nan,4.1e+34,6.4e+36,8.1e+36,1.1e+31,3.2e+34,1.6e+31,3.0e+31,4.3e+32],'Edot2':[2.0e+35,np.nan,1.7e+34,2.6e+35,2.4e+35,3.6e+30,9.0e+35,1.1e+32,1.4e+31,3.2e+31],'B_sI':[np.nan,np.nan,1.97e+12,np.nan,np.nan,np.nan,1.63e+12,np.nan,np.nan,np.nan],'B_Lc':[2.07e+06,np.nan,1.24e+03,5.92e+04,1.31e+04,4.09e+00,1.15e+03,3.05e+00,5.80e+00,2.60e+01]})
A
import pandas as pd
import numpy as np
import math
R=pd.DataFrame({'Name of pulsar':['J0100-7211','J0525-6607','J1708-4008','J1808-2024','J1809-1943','J1841-0456','J1907+0919','J2301+5852','J1745-2900','J0525-6607'],'po':[8.020392, 0.35443759451370,11.0062624,7.55592,5.540742829,11.7889784, 5.198346,6.9790709703,3.763733080,8.0470],'pdot':[1.88e-11, 7.36052e-17,1.960e-11,5.49e-10,2.8281e-12,4.092e-11,9.2e-11,4.7123e-13,1.756e-11,6.5e-11],'D in Kpc':[59.700, 1.841,3.800,13.000,3.600,9.600,np.nan,3.300,8.300,np.nan],'R_L':[np.nan, 66.09,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan],'Age':[6.76e+03,7.63e+07,8.9e+03,218,3.1e+04,4.57e+03,895,2.35e+05,3.4e+03,1.96e+03],'B_s':[3.93e+14,1.63e+11,4.7e+14,2.06e+15,1.27e+14,7.03e+14,7e+14,5.8e+13,2.6e+14,7.32e+14],'Edot':[1.4e+33,6.5e+31,5.8e+32,5.0e+34,6.6e+32,9.9e+32,2.6e+34,5.5e+31,1.3e+34,4.9e+33],'Edot2':[4.0e+29,1.9e+31,4.0e+31,3.0e+32,5.1e+31,1.1e+31,np.nan,5.0e+30,1.9e+32,np.nan],'B_sI':[np.nan, 1.62e+11,np.nan,2.06e+15, 1.27e+14,np.nan,np.nan, 5.80e+13,2.60e+14,np.nan],'B_Lc':[7.14e+00,3.44e+01,3.30e+00,4.48e+01,6.98e+00,4.02e+00,4.67e+01,1.60e+00,4.57e+01,1.32e+01]})
R
o=pd.concat([H,A,R],ignore_index=True)
o['category']=['HE','He_hwd','He_hwd','HE','X_ray','HE','HE','HE','HE','HE','NRAD','HE','X_ray','NRAD','NRAD','RRAT','HE','-','-','-','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_HE','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_HE','AXP_NRAD']
o
```
# ## Tryng for R, using the empirical equation
# ### $R_{NS} = \frac{\dot{E}^{1/6}}{B_{s}^{1/3}P^{2/3}}$
```
R = (((o['Edot'])**(1/6))/((o['B_s'])**(1/3))*((o['po'])**(2/3)))
o['Radius']=R
```
Inertia
```
k = o['Edot']
l = o['po']
m = o['pdot']
MI = (k*l**3)/(4*((3.14)**2)*m)
o['I']=MI
```
# ### From I , B, P and Pdot
# ### From relation : $R_{ns} = (\frac{IP\dot{P}}{B_{s}^{2}})^{1/6}$
```
R2 = ((o['I']*o['pdot']*o['po'])/(o['B_s']**2))**(1/6)
o['R_2']=R2
```
Magnetic Momentum
```
k = MI
l = o['po']
m = o['pdot']
moment = ((3*l*m*k*((3*10**8)**3))**(1/2))/(8**(1/2)*np.pi)
o['M_moment']=moment
```
Pdouble dot, Magnetic index values
```
o['pdoubledot'] = [4.362022e-74,1.435485e-77,1.645689e-78,3.594040e-73,3.765140e-75,3.983752e-74,2.725094e-74,3.599818e-74,8.226702e-79,2.852902e-74,2.014969e-73,1.900034e-76,2.471356e-76,1.021682e-74,6.672220e-74,3.756395e-80,1.915326e-76,7.661261e-79,1.449304e-81,1.315667e-77,2.843571e-76,5.792669e-79,1.571104e-76,9.862808e-75,9.023199e-77,2.863310e-76,3.339180e-75,9.204737e-78,1.206434e-75,9.555010e-76]
o['m_index'] = [2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0]
```
Breaking index, Energy Density
```
b=o['po']*o['pdoubledot']
i=o['pdot']**2
bi=b/i
o['b_i']=2-bi
o['E_Density']= [5.197004e+23,7.329435e+15,1.344718e+16,5.730662e+23,4.070692e+22,4.158539e+24,3.816843e+23,4.189682e+24,4.140784e+15,1.647759e+23,3.404310e+22,1.063169e+23,1.544215e+23,1.159887e+23,9.465151e+25,8.407745e+22,1.063169e+23,2.564554e+23,1.314073e+23,9.385028e+23,6.146583e+27,1.063405e+21,8.793794e+27,1.690987e+29,6.391975e+26,1.965530e+28,1.949545e+28,1.339982e+26,2.700298e+27,2.132199e+28]
```
# ### also $L_{ang} = \frac{4\pi}{5} \frac{MR^{2}}{P}$
# ### $M = \frac{5PL_{ang}}{4\pi R^{2}}$
```
ang_mom = o['I']*((2*np.pi)/o['po'])
o['A_M']= ang_mom
M_ = (5*o['po']*ang_mom)/(4*(np.pi)*(R**2))
Mc=M_/(2*10**30)
o['M_cal']=Mc
lum = (o['I']*o['pdot'])/(o['po'])**3
o['lum']=lum
np.random.seed(0)
o
o.iloc[0:11,[0,1,10]].sort_values(by='po',ascending=True)
```
```
o.iloc[0:11,[0,10]].min()
from scipy import stats
from mlxtend.preprocessing import minmax_scaling
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
```
Higher Energy pulsar without HE + Binary, all the values
```
Hp=o.iloc[[0,3,5,6,7,9,11,16,8],:]
Hp
```
High Energy with the Exception He+ White helium dwarf companion
```
Hpe=o.iloc[[0,1,2,3,5,6,7,8,9,11,16],:]
Hpe
sns.scatterplot(x=np.log10(Hp['B_Lc']), y=np.log10(Hp['po']),hue=Hp['Name of pulsar'])
plt.title('High Energy pulsars With out binary $B_{Lc}$ vs p')
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(Hpe['B_Lc']), y=np.log10(Hpe['po']), hue=Hpe['Name of pulsar'])
plt.title('High Energy pulsars With binary $B_{Lc}$ vs p')
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(A['B_Lc']), y=np.log10(A['po']))
plt.title("Non Radio $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP")
```
AXP_ NRAD with out High Energy
```
Axp=o.iloc[[20,21,22,23,25,26,27,29],:]
Axp
sns.scatterplot(x=np.log10(Axp['B_Lc']), y=np.log10(Axp['po']))
plt.title("Axp With out High Energy $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
```
Axp with High Energy Emission
```
Axp_e=o.iloc[20: ,:]
Axp_e
sns.scatterplot(x=np.log10(Axp_e['B_Lc']), y=np.log10(Axp_e['po']), hue=Axp_e['category'])
plt.title("Axp With High Energy $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(o['lum']), y=np.log10(o['R_2']),hue=o['category'])
plt.title("Lum vs R")
plt.xlabel("logLuminosity")
plt.ylabel("logRadius(km)")
```
rough
```
sns.scatterplot(x=np.log10(o['lum']), y=np.log10(o['pdot']),hue=o['category'])
plt.title("Lum vs p")
plt.xlabel("logLuminosity")
plt.ylabel("logpdot(s)")
sns.scatterplot(x=np.log10(o['Edot']), y=np.log10(o['I']),hue=o['category'])
plt.title("$\dot{E}$ vs I")
plt.xlabel("log$\dot{E}$")
plt.ylabel("log I")
sns.scatterplot(x=(o['po']), y=(o['B_s']),hue=o['category'])
plt.title("p vs $B_{s}$")
plt.xlabel("peroid(s)")
plt.ylabel("$B_{Lc}$")
Mm=o['M_moment']
Mm.to_csv("Mm.csv")
sns.scatterplot(x=np.log10(o['pdot']), y=(o['M_moment']),hue=o['category'])
plt.title("$\dot{P}$ vs m")
plt.xlabel("$\dot{P}$")
plt.ylabel(" m")
sns.scatterplot(x=(Hp['pdot']), y=(Hp['M_moment']),hue=Hp['category'])
plt.title("$\dot{P}$ vs m")
plt.xlabel("$\dot{P}$")
plt.ylabel(" m")
```
Missing Values
```
missing_values_count = o.isnull().sum()
missing_values_count
```
Data Cleaning
```
m1=o.dropna()
m2 = o.dropna(axis=1)
m2.to_csv("final.csv")
```
Scaling and Normalising the data just for checking
* scaled data
* Normalised data
```
from scipy import stats
from mlxtend.preprocessing import minmax_scaling
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
original_po=m2['po']
scaled_data = minmax_scaling(original_po, columns=[0])
fig, ax = plt.subplots(1,2)
sns.distplot(original_po, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(scaled_data, ax=ax[1])
ax[1].set_title("Scaled data")
normalized_data = stats.boxcox(original_po)
fig, ax=plt.subplots(1,2)
sns.distplot(original_po, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(normalized_data[0], ax=ax[1])
ax[1].set_title("Normalized data")
normalized_data
import pandas as pd
pd.plotting.register_matplotlib_converters()
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
print("Setup Complete")
def square(number):
return number ** 2
num= [1, 2, 3, 4, 5]
squared = map(square, num)
z=list(squared)
data= pd.DataFrame({'x':num,'y':z})
sns.scatterplot(x=data['x'], y=data['y'])
def square(number):
return number ** 2
num= [1, 2, 3, 4, 5,100,100.5]
squared = map(square, num)
z=list(squared)
data= pd.DataFrame({'x':num,'y':z})
sns.scatterplot(x=data['x'], y=data['y'])
data['y']
ly =stats.boxcox(data['y'])
lx=stats.boxcox(data['x'])
x=[1, 2, 3, 4, 5,100,100.5]
lx
y=[0. , 1.24702552, 1.86112761, 2.25218084, 2.53230088,
4.89466943, 4.89704865]
x =[0. , 0.62351275, 0.93056379, 1.1260904 , 1.26615041,2.4473346 , 2.44852421]
sns.scatterplot(x=x, y=y)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import math
H=pd.DataFrame({'Name of pulsar':['J0205+6449','J0218+4232','J0437-4715','J0534+2200','J1105-6107','J1124-5916','J1617-5055','J1930+1852','J2124-3358','J2229+6114'],'po':[0.06571592849324,0.00232309053151224,0.005757451936712637,0.0333924123,0.0632021309179,0.13547685441,0.069356847,0.136855046957,0.00493111494309662,0.05162357393],'pdot':[1.93754256e-13,7.73955e-20,5.729215e-20,4.20972e-13,1.584462e-14,7.52566e-13,1.351e-13,7.5057e-13,2.05705e-20,7.827e-14],'D in Kpc':[3.200,3.150,0.157,2.000,2.360, 5.000, 4.743, 7.000, 0.410, 3.000],'Age':[5.37e+03,4.76e+08,1.59e+09,1.26e+03,6.32e+04,2.85e+03, 8.13e+03, 2.89e+03, 3.8e+09, 1.05e+04],'R_L':['NaN',466.36,13.52,2200.00,'NaN','NaN','NaN','NaN', 2.86, 13.50],'B_s':[3.61e+12,4.29e+08,4.29e+08,3.79e+12,1.01e+12,1.02e+13,3.1e+12,1.03e+13,3.22e+08,2.03e+12],
'Edot':[2.7e+37,2.4e+35,1.2e+34,4.5e+38,2.5e+36,1.2e+37,1.6e+37,1.2e+37,6.8e+33,2.2e+37],
'Edot2':[2.6e+36,2.5e+34,4.8e+35,1.1e+38,4.4e+35,4.8e+35,7.1e+35,2.4e+35,2.4e+35,2.5e+36],
'B_sI':[3.61e+12,4.27e+08,2.85e+08,3.79e+12,np.nan,np.nan,np.nan,np.nan, 1.92e+08,np.nan],
'B_Lc':[1.19e+05,3.21e+05,2.85e+04,9.55e+05,3.76e+04,3.85e+04, 8.70e+04, 3.75e+04, 2.52e+04, 1.39e+05]})
H
import pandas as pd
import numpy as np
import math
A=pd.DataFrame({'Name of pulsar':['J0537-6910',np.nan,'J0543+2329','J1811-1925','J1846-0258','J0628+0909','J0633+1746','J0636-4549','J1811-4930','J1812-1718'],'po':[0.0161222220245,np.nan,0.245983683333,0.06466700,0.32657128834,3.763733080,0.2370994416923,1.98459736713,1.4327041968,1.20537444137],'pdot':[5.1784338e-14,np.nan,1.541956e-14,4.40e-14,7.107450e-12,0.5479e-15,1.097087e-14,3.1722e-15,2.254e-15,1.9077e-14],'D in Kpc':[49.700,np.nan,1.565,5.000,5.800,1.771,0.190,0.383,1.447,3.678],'R_L':[np.nan,np.nan,71.03,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan],'Age':[4.93e+03,np.nan,2.53e+05,2.33e+04,728,3.59e+07,3.42e+05,9.91e+06,1.01e+07,1e+06],'B_s':[9.25e+11,np.nan,1.97e+12,1.71e+12,4.88e+13,8.35e+11,1.63e+12,2.54e+12,1.82e+12,4.85e+12],'Edot':[4.9e+38,np.nan,4.1e+34,6.4e+36,8.1e+36,1.1e+31,3.2e+34,1.6e+31,3.0e+31,4.3e+32],'Edot2':[2.0e+35,np.nan,1.7e+34,2.6e+35,2.4e+35,3.6e+30,9.0e+35,1.1e+32,1.4e+31,3.2e+31],'B_sI':[np.nan,np.nan,1.97e+12,np.nan,np.nan,np.nan,1.63e+12,np.nan,np.nan,np.nan],'B_Lc':[2.07e+06,np.nan,1.24e+03,5.92e+04,1.31e+04,4.09e+00,1.15e+03,3.05e+00,5.80e+00,2.60e+01]})
A
import pandas as pd
import numpy as np
import math
R=pd.DataFrame({'Name of pulsar':['J0100-7211','J0525-6607','J1708-4008','J1808-2024','J1809-1943','J1841-0456','J1907+0919','J2301+5852','J1745-2900','J0525-6607'],'po':[8.020392, 0.35443759451370,11.0062624,7.55592,5.540742829,11.7889784, 5.198346,6.9790709703,3.763733080,8.0470],'pdot':[1.88e-11, 7.36052e-17,1.960e-11,5.49e-10,2.8281e-12,4.092e-11,9.2e-11,4.7123e-13,1.756e-11,6.5e-11],'D in Kpc':[59.700, 1.841,3.800,13.000,3.600,9.600,np.nan,3.300,8.300,np.nan],'R_L':[np.nan, 66.09,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan,np.nan],'Age':[6.76e+03,7.63e+07,8.9e+03,218,3.1e+04,4.57e+03,895,2.35e+05,3.4e+03,1.96e+03],'B_s':[3.93e+14,1.63e+11,4.7e+14,2.06e+15,1.27e+14,7.03e+14,7e+14,5.8e+13,2.6e+14,7.32e+14],'Edot':[1.4e+33,6.5e+31,5.8e+32,5.0e+34,6.6e+32,9.9e+32,2.6e+34,5.5e+31,1.3e+34,4.9e+33],'Edot2':[4.0e+29,1.9e+31,4.0e+31,3.0e+32,5.1e+31,1.1e+31,np.nan,5.0e+30,1.9e+32,np.nan],'B_sI':[np.nan, 1.62e+11,np.nan,2.06e+15, 1.27e+14,np.nan,np.nan, 5.80e+13,2.60e+14,np.nan],'B_Lc':[7.14e+00,3.44e+01,3.30e+00,4.48e+01,6.98e+00,4.02e+00,4.67e+01,1.60e+00,4.57e+01,1.32e+01]})
R
o=pd.concat([H,A,R],ignore_index=True)
o['category']=['HE','He_hwd','He_hwd','HE','X_ray','HE','HE','HE','HE','HE','NRAD','HE','X_ray','NRAD','NRAD','RRAT','HE','-','-','-','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_HE','AXP_NRAD','AXP_NRAD','AXP_NRAD','AXP_HE','AXP_NRAD']
o
R = (((o['Edot'])**(1/6))/((o['B_s'])**(1/3))*((o['po'])**(2/3)))
o['Radius']=R
k = o['Edot']
l = o['po']
m = o['pdot']
MI = (k*l**3)/(4*((3.14)**2)*m)
o['I']=MI
R2 = ((o['I']*o['pdot']*o['po'])/(o['B_s']**2))**(1/6)
o['R_2']=R2
k = MI
l = o['po']
m = o['pdot']
moment = ((3*l*m*k*((3*10**8)**3))**(1/2))/(8**(1/2)*np.pi)
o['M_moment']=moment
o['pdoubledot'] = [4.362022e-74,1.435485e-77,1.645689e-78,3.594040e-73,3.765140e-75,3.983752e-74,2.725094e-74,3.599818e-74,8.226702e-79,2.852902e-74,2.014969e-73,1.900034e-76,2.471356e-76,1.021682e-74,6.672220e-74,3.756395e-80,1.915326e-76,7.661261e-79,1.449304e-81,1.315667e-77,2.843571e-76,5.792669e-79,1.571104e-76,9.862808e-75,9.023199e-77,2.863310e-76,3.339180e-75,9.204737e-78,1.206434e-75,9.555010e-76]
o['m_index'] = [2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0]
b=o['po']*o['pdoubledot']
i=o['pdot']**2
bi=b/i
o['b_i']=2-bi
o['E_Density']= [5.197004e+23,7.329435e+15,1.344718e+16,5.730662e+23,4.070692e+22,4.158539e+24,3.816843e+23,4.189682e+24,4.140784e+15,1.647759e+23,3.404310e+22,1.063169e+23,1.544215e+23,1.159887e+23,9.465151e+25,8.407745e+22,1.063169e+23,2.564554e+23,1.314073e+23,9.385028e+23,6.146583e+27,1.063405e+21,8.793794e+27,1.690987e+29,6.391975e+26,1.965530e+28,1.949545e+28,1.339982e+26,2.700298e+27,2.132199e+28]
ang_mom = o['I']*((2*np.pi)/o['po'])
o['A_M']= ang_mom
M_ = (5*o['po']*ang_mom)/(4*(np.pi)*(R**2))
Mc=M_/(2*10**30)
o['M_cal']=Mc
lum = (o['I']*o['pdot'])/(o['po'])**3
o['lum']=lum
np.random.seed(0)
o
o.iloc[0:11,[0,1,10]].sort_values(by='po',ascending=True)
o.iloc[0:11,[0,10]].min()
from scipy import stats
from mlxtend.preprocessing import minmax_scaling
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
Hp=o.iloc[[0,3,5,6,7,9,11,16,8],:]
Hp
Hpe=o.iloc[[0,1,2,3,5,6,7,8,9,11,16],:]
Hpe
sns.scatterplot(x=np.log10(Hp['B_Lc']), y=np.log10(Hp['po']),hue=Hp['Name of pulsar'])
plt.title('High Energy pulsars With out binary $B_{Lc}$ vs p')
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(Hpe['B_Lc']), y=np.log10(Hpe['po']), hue=Hpe['Name of pulsar'])
plt.title('High Energy pulsars With binary $B_{Lc}$ vs p')
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(A['B_Lc']), y=np.log10(A['po']))
plt.title("Non Radio $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP")
Axp=o.iloc[[20,21,22,23,25,26,27,29],:]
Axp
sns.scatterplot(x=np.log10(Axp['B_Lc']), y=np.log10(Axp['po']))
plt.title("Axp With out High Energy $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
Axp_e=o.iloc[20: ,:]
Axp_e
sns.scatterplot(x=np.log10(Axp_e['B_Lc']), y=np.log10(Axp_e['po']), hue=Axp_e['category'])
plt.title("Axp With High Energy $B_{Lc}$ vs p")
plt.xlabel("$logB_{Lc}$")
plt.ylabel("logP(s)")
sns.scatterplot(x=np.log10(o['lum']), y=np.log10(o['R_2']),hue=o['category'])
plt.title("Lum vs R")
plt.xlabel("logLuminosity")
plt.ylabel("logRadius(km)")
sns.scatterplot(x=np.log10(o['lum']), y=np.log10(o['pdot']),hue=o['category'])
plt.title("Lum vs p")
plt.xlabel("logLuminosity")
plt.ylabel("logpdot(s)")
sns.scatterplot(x=np.log10(o['Edot']), y=np.log10(o['I']),hue=o['category'])
plt.title("$\dot{E}$ vs I")
plt.xlabel("log$\dot{E}$")
plt.ylabel("log I")
sns.scatterplot(x=(o['po']), y=(o['B_s']),hue=o['category'])
plt.title("p vs $B_{s}$")
plt.xlabel("peroid(s)")
plt.ylabel("$B_{Lc}$")
Mm=o['M_moment']
Mm.to_csv("Mm.csv")
sns.scatterplot(x=np.log10(o['pdot']), y=(o['M_moment']),hue=o['category'])
plt.title("$\dot{P}$ vs m")
plt.xlabel("$\dot{P}$")
plt.ylabel(" m")
sns.scatterplot(x=(Hp['pdot']), y=(Hp['M_moment']),hue=Hp['category'])
plt.title("$\dot{P}$ vs m")
plt.xlabel("$\dot{P}$")
plt.ylabel(" m")
missing_values_count = o.isnull().sum()
missing_values_count
m1=o.dropna()
m2 = o.dropna(axis=1)
m2.to_csv("final.csv")
from scipy import stats
from mlxtend.preprocessing import minmax_scaling
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
original_po=m2['po']
scaled_data = minmax_scaling(original_po, columns=[0])
fig, ax = plt.subplots(1,2)
sns.distplot(original_po, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(scaled_data, ax=ax[1])
ax[1].set_title("Scaled data")
normalized_data = stats.boxcox(original_po)
fig, ax=plt.subplots(1,2)
sns.distplot(original_po, ax=ax[0])
ax[0].set_title("Original Data")
sns.distplot(normalized_data[0], ax=ax[1])
ax[1].set_title("Normalized data")
normalized_data
import pandas as pd
pd.plotting.register_matplotlib_converters()
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
print("Setup Complete")
def square(number):
return number ** 2
num= [1, 2, 3, 4, 5]
squared = map(square, num)
z=list(squared)
data= pd.DataFrame({'x':num,'y':z})
sns.scatterplot(x=data['x'], y=data['y'])
def square(number):
return number ** 2
num= [1, 2, 3, 4, 5,100,100.5]
squared = map(square, num)
z=list(squared)
data= pd.DataFrame({'x':num,'y':z})
sns.scatterplot(x=data['x'], y=data['y'])
data['y']
ly =stats.boxcox(data['y'])
lx=stats.boxcox(data['x'])
x=[1, 2, 3, 4, 5,100,100.5]
lx
y=[0. , 1.24702552, 1.86112761, 2.25218084, 2.53230088,
4.89466943, 4.89704865]
x =[0. , 0.62351275, 0.93056379, 1.1260904 , 1.26615041,2.4473346 , 2.44852421]
sns.scatterplot(x=x, y=y)
| 0.097133 | 0.873593 |
<a href="https://colab.research.google.com/github/priyanshgupta1998/WebScraping/blob/master/Getting_started_with_BigQuery.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Before you begin
1. Use the [Cloud Resource Manager](https://console.cloud.google.com/cloud-resource-manager) to Create a Cloud Platform project if you do not already have one.
2. [Enable billing](https://support.google.com/cloud/answer/6293499#enable-billing) for the project.
3. [Enable BigQuery](https://console.cloud.google.com/flows/enableapi?apiid=bigquery) APIs for the project.
### Provide your credentials to the runtime
```
from google.colab import auth
auth.authenticate_user()
print('Authenticated')
```
## Optional: Enable data table display
Colab includes the ``google.colab.data_table`` package that can be used to display large pandas dataframes as an interactive data table.
It can be enabled with:
```
%load_ext google.colab.data_table
```
If you would prefer to return to the classic Pandas dataframe display, you can disable this by running:
```python
%unload_ext google.colab.data_table
```
# Use BigQuery via magics
The `google.cloud.bigquery` library also includes a magic command which runs a query and either displays the result or saves it to a variable as a `DataFrame`.
```
# Display query output immediately
%%bigquery --project yourprojectid
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
# Save output in a variable `df`
%%bigquery --project yourprojectid df
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
df
```
# Use BigQuery through google-cloud-bigquery
See [BigQuery documentation](https://cloud.google.com/bigquery/docs) and [library reference documentation](https://googlecloudplatform.github.io/google-cloud-python/latest/bigquery/usage.html).
The [GSOD sample table](https://bigquery.cloud.google.com/table/bigquery-public-data:samples.gsod) contains weather information collected by NOAA, such as precipitation amounts and wind speeds from late 1929 to early 2010.
### Declare the Cloud project ID which will be used throughout this notebook
```
project_id = '[your project ID]'
```
### Sample approximately 2000 random rows
```
from google.cloud import bigquery
client = bigquery.Client(project=project_id)
sample_count = 2000
row_count = client.query('''
SELECT
COUNT(*) as total
FROM `bigquery-public-data.samples.gsod`''').to_dataframe().total[0]
df = client.query('''
SELECT
*
FROM
`bigquery-public-data.samples.gsod`
WHERE RAND() < %d/%d
''' % (sample_count, row_count)).to_dataframe()
print('Full dataset has %d rows' % row_count)
```
### Describe the sampled data
```
df.describe()
```
### View the first 10 rows
```
df.head(10)
# 10 highest total_precipitation samples
df.sort_values('total_precipitation', ascending=False).head(10)[['station_number', 'year', 'month', 'day', 'total_precipitation']]
```
# Use BigQuery through pandas-gbq
The `pandas-gbq` library is a community led project by the pandas community. It covers basic functionality, such as writing a DataFrame to BigQuery and running a query, but as a third-party library it may not handle all BigQuery features or use cases.
[Pandas GBQ Documentation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_gbq.html)
```
import pandas as pd
sample_count = 2000
df = pd.io.gbq.read_gbq('''
SELECT name, SUM(number) as count
FROM `bigquery-public-data.usa_names.usa_1910_2013`
WHERE state = 'TX'
GROUP BY name
ORDER BY count DESC
LIMIT 100
''', project_id=project_id, dialect='standard')
df.head()
```
|
github_jupyter
|
from google.colab import auth
auth.authenticate_user()
print('Authenticated')
%load_ext google.colab.data_table
%unload_ext google.colab.data_table
# Display query output immediately
%%bigquery --project yourprojectid
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
# Save output in a variable `df`
%%bigquery --project yourprojectid df
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
df
project_id = '[your project ID]'
from google.cloud import bigquery
client = bigquery.Client(project=project_id)
sample_count = 2000
row_count = client.query('''
SELECT
COUNT(*) as total
FROM `bigquery-public-data.samples.gsod`''').to_dataframe().total[0]
df = client.query('''
SELECT
*
FROM
`bigquery-public-data.samples.gsod`
WHERE RAND() < %d/%d
''' % (sample_count, row_count)).to_dataframe()
print('Full dataset has %d rows' % row_count)
df.describe()
df.head(10)
# 10 highest total_precipitation samples
df.sort_values('total_precipitation', ascending=False).head(10)[['station_number', 'year', 'month', 'day', 'total_precipitation']]
import pandas as pd
sample_count = 2000
df = pd.io.gbq.read_gbq('''
SELECT name, SUM(number) as count
FROM `bigquery-public-data.usa_names.usa_1910_2013`
WHERE state = 'TX'
GROUP BY name
ORDER BY count DESC
LIMIT 100
''', project_id=project_id, dialect='standard')
df.head()
| 0.378229 | 0.968974 |
### Contents
0. [Foreword](#Foreword)
1. [Introduction](#Introduction)
1. [Intro to VSM's](#Intro-to-Vector-Space-Models)
1. [Linguistic Motivation](#Linguistic-Motivation)
1. [Counts & Context Windows](#Counts-&-Context-Windows)
1. [Initial Exploration](#Initial-Exploration)
1. [Corpus](#Corpus)
1. [Semantics](#Words-as-Concepts)
1. [Noise obscures meaningful comparisons](#Noise-obscures-meaningful-comparisons)
1. [Visualizing word embeddings](#Visualizing-word-embeddings)
1. [Age](#Age)
1.[Trio](#Trio)
1. [Quantitative Evaluation](#Quantitative-Evaluation)
```
import pandas as pd #imports
import numpy as np
import os
import utils# general utility functions
import vsm # utils for vector space model needs
import random
from scipy.stats import spearmanr
DATA_HOME = os.path.join('data/data', 'vsmdata') # vsm related data
giga5 = pd.read_csv(
os.path.join(DATA_HOME, 'giga_window5-scaled.csv.gz'), index_col=0) #other coprpuses include yelp_20 and giga_20
giga = giga5.iloc[11:,11:] # filters emoticons in output
W = giga5.iloc[12:,12:] # same
DATA_HOME2 = os.path.join('data/data', 'wordrelatedness') #data read-in
utils.fix_random_seeds()
eval_df = pd.read_csv(
os.path.join(DATA_HOME2, "wordrelatedness-dev.csv")) # relatedness dataset for evaluation
def distance2pred(pred_df): # converts cosine distance to similarity
lis = [-1*i for i in pred_df['prediction']]
random_pred_df['prediction'] = pd.Series(lis)
return pred_df
def random_scorer(x1, x2): # random guesses as a baseline
return random.random()
```
### Foreword
Although I didnโt know it at the time, my Machine Learning journey began about a year and a half ago. Searching for a major (and life purpose), I took a survey course in Neuroscience. Inspired by Francis Crickโs own search for the soul in his book *The Astonishing Hypothesis*, I walked in with starry eyes and untempered ambition. It seems I was not alone. Before introducing the course or even himself, our professor methodically relieved us from the lofty goals we had for the field. Instead of solving conciousness, he directed our gaze to the basics. The simple act of remembering proved astonishing enough for me. Although Iโve since settled on a different field, learning and memory have become the throughline from which I view artificial intelligence. However, you wonโt find any learning algorithms in these notebooks. After blindly throwing models of increasing complexity at some problems, I realized I still didnโt know the first thing about the datasets themselves. This, then, is an exercise on a few upstream elements of ML pipelines---exploratory analysis, dimensionality reductions, and visualizations. I hope you find some utility in it, and if not, that it at least serves as an interesting read.
# Introduction
##### Vector Space Models
In many ways, the rise of Natural Language Processing (NLP) is a microcosm of MLโs own emergence. Big data and powerful processors allow previously known statistical techniques to reach their full potential. Vector Space Models (VSMs) are good example of how powerful these ideas can be at scale. A fun introduction to VSMs is the word guessing game Semantle (https://semantle.novalis.org/). Youโll notice the more related your guess is to the hidden word, the better your score is. If you guess right, or in my case give up, you can click for the nearest words to the answer. There are always some oddities but for the most part the nearest neighbors are surprisingly meaningful. That is to say, they are semantically related. In Semantle, and all Vector Space Models, each word is represented by a high dimensional vector whose components are also words. Since all vectors have the same dimensionality, we tend to call them embeddings. Imagine a VSM comprised of only four words : โcatโ, โdogโ, โappleโ, and โblueโ. A general embedding is shown, as well as mock embeddings for 'cat' and 'dog'^^. Since different words will have unique values for each component, they take on unique identities. All word embeddings, by definition though, share the same set of words they're defined through. Scrolling through the nearest neighbors on Semantle shows the components by which any word is judged. In short, the embeddings form a matrix of data, whose columns span a space we use to map words. This matrix (dataset) *is* the VSM.
##### Linguistic Motivation
Consider the sentence โ...many cattle farmers are going further into debt as grain prices increase.โ Intuitively, we know โcattleโ, โfarmerโ, and โgrainโ probably group together more than โgoingโ, โpricesโ, and โintoโ. Given just this sentence, an alien would be at a loss. However, if they could listen to every time the word โfarmerโ was uttered across the globe for a week, theyโd probably come to a similar conclusion. This is the essence of the distributional hypothesis. Summed up by linguist John Firthโs famous line, โYou shall know a word by the company it keepsโ, the idea that frequency distributions can give insight about usage is as fascinating as it is useful. Defining a notion of context and investigating the members present in that context tells us a little bit. Repeating this process over a huge corpus, say millions of news articles, tells us a lot. This is the ultimate source for the embedding values in Vector Space Models.
#### Counts & Context Windows
Letโs keep the news articles example. What we define as context is up to us. It could be a sentence or even a paragraph. Perhaps there's value to keeping the scope local though. It makes basic linguistic sense that the immediate neighbors of a word are probably more relevant. For now, letโs just define context as the immediate two words left and right of a target (center) word. This is our window. Imagine the farmer sentence is the start of the corpus. Beginning with that sentence, weโd scan through the entire corpus so each word gets to be a target. In each window of the scan, we'll look left and right of the center, observe the present words and update.
โ**Many** *cattle* *farmers* are going further into debt as grain prices increase.โ $$Window_1$$
Current neighbor words for: **Many**: cattle 1, farmers 1
โ*Many* **cattle** *farmers* *are* going further into debt as grain prices increase.โ $$Window_2$$
Current neighbor words for: **Cattle**: many 1, farmers 1, are 1
โ*Many* *cattle* **farmers** *are* *going* further into debt as grain prices increase.โ $$Window_3$$
Current neighbor words for: **Farmers**: many 1, cattle 1, are 1, going 1
The edges of a corpus wonโt have the full window but thatโs ok. To wrap it up, letโs imagine weโre at the end of the corpus.
โโฆ banned predatory credit card offers because it *encouraged* *unhealthy* **debt**.โ $$Window_n$$
Final neighbor words for: **Debt** arrive 2, *poor* 45, my 5, underlying 6, โฆ encouraged 3+1, unhealthy 7+1, โฆ zealot 1
Iโve added +1 to relay the sense of those two words updating from previous counts. Notice that at this stage the center word, debt, has many unique neighbors with a range of values. In fact, each target word has values for the whole vocabulary. If a word was never a neighbor for a target it simply has a count of zero. This ensures all embeddings are equal length. Notice if we take an array of all the center words we obtain a dataset with words as our rows and columns. In other words, it's a square matrix. It's standard to view the space as a set of word vectors/embeddings that are w-dimensional (from word_1 to word_w). Each element in a word embedding represents the *co-occurance* between that word and the wth component. If they share context often, they strongly co-occur and thus have a larger co-occurance value. See how large the 'poor' dimension is in the 'Debt' word embedding? The space created from the set of these word embeddings constitutes our VSM. Let's take a closer look at it in the *Initial Explorations* section.
#### Technical notes about the data
In practice, performance and other cost reasons add extra complexity to implementing the context window method. Since many such generated datasets already exist, often at the scale of millions or even billions of tokens, I've opted to use them. If you are curious on how to generate a co-occurance matrix from scratch, there should soon be a the notebook titled "VSM Applications in Finance". In it, I detail the steps taken to go from a corpus (stock data) to a dateset of co-occurances.
# Initial Exploration
##### Corpus
Let's use Gigaword as a corpus, a collection of 4 million articles from the Associated Press, Los Angeles Times, Washington Post, Bloomberg, and several other news agencies. We'll use a window which scans five words deep on either side of a center word. Instead of keeping the context window flat, we'll weigh it so words closer to the target count for more. For each word in the corpus we update the total list of possible neighbors (the vocabulary). After scanning through the entire corpus we obtain a wxw co-occurance matrix (datafrmae) W.
For more info on Gigaword (https://catalog.ldc.upenn.edu/LDC2011T07)
A look at W:
```
W.head(20)
```
The output shows a shortened view of all the columns in our VSM, W, from "abc" to "zoo". It also shows the full view of a few dozen rows (components), which happened to be arranged alphabetically. Notice W's diagonal elements, they represent a words' self co-occurance. It's a useful landmark since the values catch the eye, and will by definition be large. However, the meaningful view is in the components of each column. Let's look at a truncated word embedding for 'age'.
```
pd.DataFrame(W['age'])
```
The components of W with the highest co-occurance values. These word pairs (Age & 'the', Age & 'of', Age & 'at', etc) were spotted together in context windows the most number of times.
```
pd.DataFrame(W['age'].sort_values(ascending=False).head(40))
```
### Words as Concepts
This is encouraging. We see some words that seem meaningful when paired with Age. There's 'old', 'retirement', 'children', and 'died'. There are also words that have a sort of phrase partnership with Age. Golden age, under age, and average age for example. Then there are a bunch of stop words. These words occur highly with everything because they are linguistic building blocks or common usage. We can be sure the components in any of these word embeddings are large across the board.
##### Noise obscures meaningful comparisons
This quirk is intrinsic to natural language. Looking at the usage chart of English words below, we can see it follows a striking Zipfian distribution. A handful of words dominate the lexicon. An Oxford deep dive found only 10 words constituted ~ 25% of observed words(https://www.businessinsider.com/zipfs-law-and-the-most-common-words-in-english-2013-10). This noise serves as our primary challenge .
(Thanks to Adam at https://www.etymologynerd.com/)
## Visualizing word embeddings
So far we've only seen a shortened printout of word embeddings.
It might be useful to get a better idea of what we're transforming. So before we apply changes, let's take a closer look at some embeddings. We know each word vector/embedding is a column in W, characterized by w components running along its rows. Each component is a unique word in the vocabulary of the corpus (Gigaword) populating this VSM.
### Age
In the 'Age' visualization below, we see an embedding for age represented as an abstract column. The co-occurance between each component and the word embedding is a band. The large elements in W['age'], for example have the widest bands in the column. I've colored tagged the components to make the connection more evident.
For reference, here are the top five co-occurances in Age: '**the**', 'of', 'at', 'and', 'in'
### Trio
##### Gallery link: https://public.tableau.com/app/profile/jelan.samatar/viz/VisualizingWordEmbeddings/Trio
Since our VSM is comprised from a set of word vectors, the column space of W as a matrix is the equivalent to the embedding space of W as a VSM. So comparing word embeddings means making we want to make meaningful comparisons between columns. For example how does Age compare against Old and Clear. In the gallery, we see a visualization called 'Trio' of these three words. At first glance, it seems Age and Old have a more similar structure than Clear. All three, though, tend to share the largest bands. Click the marker icon in the top right of the legend title 'components' to activate the highlight function. It lets you compare by component. Although this is a tiny glimpse of the space in W, exploring it gives a nice feel for how word embeddings relate to each other. Moreover it serves as a helpful, if incomplete, visual reference for where our VSM is. It paints a picture of latent knowledge obscured by noise.
## Quantitative Evaluation
Another way to judge our VSM is by seeing how it performs on relevant tasks. How well it does it mimic human judgement on how related a given pair of words is? A dataset formed by having humans sit down and score the relatedness between word pairs is called a relatedness dataset. I've used the dataset from Stanford's Linguistic/NLP department as our evaluative dataset (https://web.stanford.edu/class/cs224u/data/).
```
DATA_HOME = os.path.join('data/data', 'wordrelatedness')
eval_df = pd.read_csv(
os.path.join(DATA_HOME, "wordrelatedness-dev.csv"))
eval_df.rename(columns={'score': 'relatedness score'})
eval_df
```
The basic idea is to use the word embeddings to predict a relatedness score. Then we'll compare the human rankings with our VSM's rankings through Spearman's $\rho$ value. For now, as a sanity check, let's see how a random guesser does.
```
random_pred_df, random_score = vsm.word_relatedness_evaluation(eval_df, giga5, distfunc=random_scorer)
random_score = (random_score*-100)
random_pred_df = distance2pred(random_pred_df)
random_pred_df.rename(columns={'score': 'relatedness score'},inplace=True)
print(f'SCORE: {round(random_score,3)} % similar to human answers')
random_pred_df
```
This serves as our initial baseline. As we make transformations on our VSM, we'll see how it performs on evaluative tasks and explore what's in it with more visualizations. This work is continued in Page 2 of this project, called *Statistical Methods*.
|
github_jupyter
|
import pandas as pd #imports
import numpy as np
import os
import utils# general utility functions
import vsm # utils for vector space model needs
import random
from scipy.stats import spearmanr
DATA_HOME = os.path.join('data/data', 'vsmdata') # vsm related data
giga5 = pd.read_csv(
os.path.join(DATA_HOME, 'giga_window5-scaled.csv.gz'), index_col=0) #other coprpuses include yelp_20 and giga_20
giga = giga5.iloc[11:,11:] # filters emoticons in output
W = giga5.iloc[12:,12:] # same
DATA_HOME2 = os.path.join('data/data', 'wordrelatedness') #data read-in
utils.fix_random_seeds()
eval_df = pd.read_csv(
os.path.join(DATA_HOME2, "wordrelatedness-dev.csv")) # relatedness dataset for evaluation
def distance2pred(pred_df): # converts cosine distance to similarity
lis = [-1*i for i in pred_df['prediction']]
random_pred_df['prediction'] = pd.Series(lis)
return pred_df
def random_scorer(x1, x2): # random guesses as a baseline
return random.random()
W.head(20)
pd.DataFrame(W['age'])
pd.DataFrame(W['age'].sort_values(ascending=False).head(40))
DATA_HOME = os.path.join('data/data', 'wordrelatedness')
eval_df = pd.read_csv(
os.path.join(DATA_HOME, "wordrelatedness-dev.csv"))
eval_df.rename(columns={'score': 'relatedness score'})
eval_df
random_pred_df, random_score = vsm.word_relatedness_evaluation(eval_df, giga5, distfunc=random_scorer)
random_score = (random_score*-100)
random_pred_df = distance2pred(random_pred_df)
random_pred_df.rename(columns={'score': 'relatedness score'},inplace=True)
print(f'SCORE: {round(random_score,3)} % similar to human answers')
random_pred_df
| 0.264074 | 0.941815 |
### *IPCC SR15 scenario assessment*
<img style="float: right; height: 80px; padding-left: 20px;" src="../_static/IIASA_logo.png">
<img style="float: right; height: 80px;" src="../_static/IAMC_logo.jpg">
# Analysis of carbon dioxide removal (CDR)
This notebook generates the assessment of carbon dioxide removal for **Figure 2.9** in the IPCC's _"Special Report on Global Warming of 1.5ยฐC"_.
The scenario data used in this analysis can be accessed and downloaded at [https://data.ene.iiasa.ac.at/iamc-1.5c-explorer](https://data.ene.iiasa.ac.at/iamc-1.5c-explorer).
## Load `pyam` package and other dependencies
```
import pandas as pd
import numpy as np
import warnings
import io
import itertools
import yaml
import math
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
plt.style.use('style_sr15.mplstyle')
%matplotlib inline
import pyam
```
## Import scenario data, categorization and specifications files
The metadata file must be generated from the notebook `sr15_2.0_categories_indicators` included in this repository.
If the snapshot file has been updated, make sure that you rerun the categorization notebook.
The last cell of this section loads and assigns a number of auxiliary lists as defined in the categorization notebook.
```
sr1p5 = pyam.IamDataFrame(data='../data/iamc15_scenario_data_world_r1.1.xlsx')
sr1p5.load_metadata('../data/sr15_metadata_indicators.xlsx')
with open("sr15_specs.yaml", 'r') as stream:
specs = yaml.load(stream, Loader=yaml.FullLoader)
rc = pyam.run_control()
for item in specs.pop('run_control').items():
rc.update({item[0]: item[1]})
cats = specs.pop('cats')
all_cats = specs.pop('all_cats')
subcats = specs.pop('subcats')
all_subcats = specs.pop('all_subcats')
plotting_args = specs.pop('plotting_args')
marker = specs.pop('marker')
```
## Downselect scenario ensemble to categories of interest for this assessment
```
df = sr1p5.filter(category=all_cats)
#df.data.iloc[:3]
df2 = sr1p5
type(df2.data)
```
## Set specifications for filter and plotting
```
filter_args = dict(df=sr1p5, category=cats, marker=None, join_meta=True)
```
## Retrieve carbon dioxide emissions and generate two auxiliary variables with net-negative CO2 emissions
For easier aggregation of the timeseries later on towards different metrics of carbon dioxide removal, we introduce both a positive net-negative timeseries (A, where the removal of 1Gt CO2 is counted as a positive value) and a timeseries where the sequestered amount is defined as a negative value (B).
```
co2 = df.filter(variable='Emissions|CO2').timeseries()
type(co2)
co2.columns
```
### A) Net-negative CO2 emissions
```
co2_nn = co2.applymap(lambda x: - min(x, 0)).reset_index()
co2_nn.variable = 'Emissions|CO2|Net-negative'
co2_nn_df = pyam.IamDataFrame(co2_nn)
df.data = df.data.append(co2_nn_df.data, ignore_index=True)
```
### B) Net-negative-negative CO2 emissions
```
co2_nn_neg = co2.applymap(lambda x: min(x, 0)).reset_index()
co2_nn_neg.variable = 'Emissions|CO2|Net-negative-negative'
co2_nn_neg_df = pyam.IamDataFrame(co2_nn_neg)
df.data = df.data.append(co2_nn_neg_df.data, ignore_index=True)
df.data.iloc[:3]
```
## Retrieve carbon dioxide emissions from agriculture, forestry and land-use
```
co2_afolu = df.filter(variable='Emissions|CO2|AFOLU').timeseries()
co_afolu_nn = co2_afolu.applymap(lambda x: - min(x, 0)).reset_index()
co_afolu_nn.variable = 'Emissions|CO2|AFOLU|Net-negative'
co_afolu_nn_df = pyam.IamDataFrame(co_afolu_nn)
df.data = df.data.append(co_afolu_nn_df.data, ignore_index=True)
```
## Determine emissions reductions from land use
### Where possible, determine AFOLU CO2 emissions reduction relative to baseline
```
base_mapping = df.meta.reset_index()[['model', 'scenario', 'baseline']].groupby(['model'])
afolu_cdr_lst = []
for mapping in base_mapping:
m = mapping[0]
_df = co_afolu_nn_df.filter(model=m, year=range(2020, 2101))
base_mapping_by_model = mapping[1].groupby(['baseline'])
for _mapping in base_mapping_by_model:
b = _mapping[0]
base = _df.filter(scenario=b).timeseries()
base.index = base.index.droplevel([1, 2, 3, 4])
for s in _mapping[1].scenario:
cdr = _df.filter(scenario=s).timeseries()
cdr.index = cdr.index.droplevel([1, 2, 3, 4])
cdr = cdr - base
cdr['scenario'] = s
afolu_cdr_lst.append(cdr)
afolu_cdr = pd.concat(afolu_cdr_lst, sort=False).reset_index()
afolu_cdr['region'] = 'World'
afolu_cdr['variable'] = 'Emissions|CO2|AFOLU|Net-negative reduction'
afolu_cdr['unit'] = 'MtCO2'
afolu_cdr_df = pyam.IamDataFrame(afolu_cdr)
```
### For scenarios that do not provide a baseline, use the self-reported land-iuse carbon sequestration timeseries
```
alofu_cdr_direct_df = df.filter(variable='Carbon Sequestration|Land Use',
scenario=['PEP*', 'IMA15*', 'LowEnergyDemand'],
year=range(2020, 2101)
)
```
### Check that methods 1 and 2 do not overlap, then merge
```
if not afolu_cdr_df.meta.index.intersection(alofu_cdr_direct_df.meta.index).empty:
print('There is an overlap of index sets!')
afolu_cdr_df.data = afolu_cdr_df.data.append(alofu_cdr_direct_df.data, ignore_index=True)
```
## Remove 'Carbon Sequestration|Land Use' from `IamDataFrame` and merge in alternative metrics
```
df.filter(variable='Carbon Sequestration|Land Use', keep=False, inplace=True)
df.data = df.data.append(afolu_cdr_df.data, ignore_index=True)
df.rename({'variable': {'Carbon Sequestration|Land Use': 'AFOLU CDR',
'Emissions|CO2|AFOLU|Net-negative reduction': 'AFOLU CDR'}}, inplace=True)
exclude_no_afolue_cdr = df.require_variable('AFOLU CDR', exclude_on_fail=True)
df.filter(exclude=False, inplace=True)
```
## Rename variables for plots
```
variable_mapping = [
('Total CDR', [
'Carbon Sequestration|CCS|Biomass',
'AFOLU CDR',
'Carbon Sequestration|Direct Air Capture',
'Carbon Sequestration|Enhanced Weathering']),
('AFOLU CDR', 'AFOLU CDR'),
('BECCS', 'Carbon Sequestration|CCS|Biomass'),
('Net negative CO2', 'Emissions|CO2|Net-negative'),
('Compensate CDR', [
'Carbon Sequestration|CCS|Biomass',
'AFOLU CDR',
'Carbon Sequestration|Direct Air Capture',
'Carbon Sequestration|Enhanced Weathering',
'Emissions|CO2|Net-negative-negative'])
]
valid_variables = []
for (name, variable) in variable_mapping:
if pyam.isstr(variable):
valid_variables.append(variable)
else:
for v in variable:
valid_variables.append(v)
df.filter(variable=valid_variables, inplace=True)
df.data.iloc[:25]
# save to an excel file
df.data.to_csv('output/CCSBySource.csv')
```
## Plot by warming category with multiple last years
```
cats.remove('Above 2C')
def marker_args(m):
return dict(zorder=4,
edgecolors=rc['edgecolors']['marker'][m],
c=rc['c']['marker'][m],
marker=rc['marker']['marker'][m],
linewidths=1)
def boxplot_cumulative_ccs(ymax, last_year, panel_label, legend=True): # should be able to include categories like this
fig = plt.figure(figsize=(8, 3))
_cats = len(cats) - 1
label_list = []
for i, (name, v) in enumerate(variable_mapping):
_df = df.filter(variable=v, year=range(2020, 2101, 10)).timeseries() / 1000 # gigatons
_df = _df.groupby(['model', 'scenario']).sum()
_df = pd.DataFrame(_df.apply(pyam.cumulative, raw=False, axis=1, first_year=2020, last_year=last_year))
_df = pyam.filter_by_meta(_df, df, category=cats, marker=None, join_meta=True)
for j, c in enumerate(cats):
__df = _df[_df.category == c]
lst = __df[0][~np.isnan(__df[0])]
pos = 0.5 / _cats * (j - _cats / 2) + i
outliers = len(lst[lst > ymax])
if outliers > 0:
plt.text(pos - 0.01 * len(cats), ymax * 1.01, outliers)
p = plt.boxplot(lst, positions=[pos], widths=(0.3 / _cats),
whis='range',
patch_artist=True)
plt.setp(p['boxes'], color=rc['color']['category'][c])
plt.setp(p['medians'], color='black')
for m in marker:
val = __df.loc[_df.marker == m, 0]
if not val.empty:
plt.scatter(x=pos, y=val, **marker_args(m),
s=40, label=None)
label_list.append(name)
for m in marker:
meta = df.filter(marker=m).timeseries()
if not meta.empty:
meta = meta.iloc[0].name[0:2]
plt.scatter(x=[], y=[], **marker_args(m), s=60, label=m)
for j, c in enumerate(cats):
plt.plot([], c=rc['color']['category'][c], label='{}'.format(c))
if legend:
plt.legend()
plt.grid(False)
plt.xlim(-0.6, (i + 0.6))
plt.xticks(range(0, i + 1), label_list)
plt.vlines(x=[_i + 0.5 for _i in range(i)], ymin=0, ymax=ymax, colors='white')
plt.ylim(0, ymax)
plt.ylabel('Cumulative CO2 until {} (GtCO2)'.format(last_year))
fig.savefig('output/fig2.9{}_cdr_{}.png'.format(panel_label, last_year))
boxplot_cumulative_ccs(340, 2050, 'a')
boxplot_cumulative_ccs(1250, 2100, 'b', legend=False)
```
## Export timeseries data to `xlsx`
```
variable_mapping
cats
df.to_excel('output/fig2.9_data_table.xlsx')
def exportDataExcel(last_year): # should be able to include categories like this
_cats = len(cats) - 1
label_list = []
for i, (name, v) in enumerate(variable_mapping):
_df = df.filter(variable=v, year=range(2020, 2101, 5)).timeseries() / 1000
_df = _df.groupby(['model', 'scenario']).sum()
_df = pyam.filter_by_meta(_df, df, category=cats, marker=None, join_meta=True)
for j, c in enumerate(cats):
__df = _df[_df.category == c]
__df.to_csv(('output/fig2.9_data_table' + name + c + '.csv'))
exportDataExcel(2100)
x = pd.read_csv(('output/fig2.9_data_tableTotal CDR1.5C low overshoot.csv'))
x['Variable'] = name
cols = x.columns
print(cols)
def combineData():
a = pd.DataFrame(columns=cols)
for i, (name, v) in enumerate(variable_mapping):
for j, c in enumerate(cats):
x = pd.read_csv(('output/fig2.9_data_table' + name + c + '.csv'))
x['Variable'] = name
a = pd.concat([a, x])
print(a.shape)
a = a.sort_values(['model', 'scenario'], ascending = (True, False))
a.to_csv('output/CombinedCsvsWithOutcome.csv')
combineData()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import warnings
import io
import itertools
import yaml
import math
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
plt.style.use('style_sr15.mplstyle')
%matplotlib inline
import pyam
sr1p5 = pyam.IamDataFrame(data='../data/iamc15_scenario_data_world_r1.1.xlsx')
sr1p5.load_metadata('../data/sr15_metadata_indicators.xlsx')
with open("sr15_specs.yaml", 'r') as stream:
specs = yaml.load(stream, Loader=yaml.FullLoader)
rc = pyam.run_control()
for item in specs.pop('run_control').items():
rc.update({item[0]: item[1]})
cats = specs.pop('cats')
all_cats = specs.pop('all_cats')
subcats = specs.pop('subcats')
all_subcats = specs.pop('all_subcats')
plotting_args = specs.pop('plotting_args')
marker = specs.pop('marker')
df = sr1p5.filter(category=all_cats)
#df.data.iloc[:3]
df2 = sr1p5
type(df2.data)
filter_args = dict(df=sr1p5, category=cats, marker=None, join_meta=True)
co2 = df.filter(variable='Emissions|CO2').timeseries()
type(co2)
co2.columns
co2_nn = co2.applymap(lambda x: - min(x, 0)).reset_index()
co2_nn.variable = 'Emissions|CO2|Net-negative'
co2_nn_df = pyam.IamDataFrame(co2_nn)
df.data = df.data.append(co2_nn_df.data, ignore_index=True)
co2_nn_neg = co2.applymap(lambda x: min(x, 0)).reset_index()
co2_nn_neg.variable = 'Emissions|CO2|Net-negative-negative'
co2_nn_neg_df = pyam.IamDataFrame(co2_nn_neg)
df.data = df.data.append(co2_nn_neg_df.data, ignore_index=True)
df.data.iloc[:3]
co2_afolu = df.filter(variable='Emissions|CO2|AFOLU').timeseries()
co_afolu_nn = co2_afolu.applymap(lambda x: - min(x, 0)).reset_index()
co_afolu_nn.variable = 'Emissions|CO2|AFOLU|Net-negative'
co_afolu_nn_df = pyam.IamDataFrame(co_afolu_nn)
df.data = df.data.append(co_afolu_nn_df.data, ignore_index=True)
base_mapping = df.meta.reset_index()[['model', 'scenario', 'baseline']].groupby(['model'])
afolu_cdr_lst = []
for mapping in base_mapping:
m = mapping[0]
_df = co_afolu_nn_df.filter(model=m, year=range(2020, 2101))
base_mapping_by_model = mapping[1].groupby(['baseline'])
for _mapping in base_mapping_by_model:
b = _mapping[0]
base = _df.filter(scenario=b).timeseries()
base.index = base.index.droplevel([1, 2, 3, 4])
for s in _mapping[1].scenario:
cdr = _df.filter(scenario=s).timeseries()
cdr.index = cdr.index.droplevel([1, 2, 3, 4])
cdr = cdr - base
cdr['scenario'] = s
afolu_cdr_lst.append(cdr)
afolu_cdr = pd.concat(afolu_cdr_lst, sort=False).reset_index()
afolu_cdr['region'] = 'World'
afolu_cdr['variable'] = 'Emissions|CO2|AFOLU|Net-negative reduction'
afolu_cdr['unit'] = 'MtCO2'
afolu_cdr_df = pyam.IamDataFrame(afolu_cdr)
alofu_cdr_direct_df = df.filter(variable='Carbon Sequestration|Land Use',
scenario=['PEP*', 'IMA15*', 'LowEnergyDemand'],
year=range(2020, 2101)
)
if not afolu_cdr_df.meta.index.intersection(alofu_cdr_direct_df.meta.index).empty:
print('There is an overlap of index sets!')
afolu_cdr_df.data = afolu_cdr_df.data.append(alofu_cdr_direct_df.data, ignore_index=True)
df.filter(variable='Carbon Sequestration|Land Use', keep=False, inplace=True)
df.data = df.data.append(afolu_cdr_df.data, ignore_index=True)
df.rename({'variable': {'Carbon Sequestration|Land Use': 'AFOLU CDR',
'Emissions|CO2|AFOLU|Net-negative reduction': 'AFOLU CDR'}}, inplace=True)
exclude_no_afolue_cdr = df.require_variable('AFOLU CDR', exclude_on_fail=True)
df.filter(exclude=False, inplace=True)
variable_mapping = [
('Total CDR', [
'Carbon Sequestration|CCS|Biomass',
'AFOLU CDR',
'Carbon Sequestration|Direct Air Capture',
'Carbon Sequestration|Enhanced Weathering']),
('AFOLU CDR', 'AFOLU CDR'),
('BECCS', 'Carbon Sequestration|CCS|Biomass'),
('Net negative CO2', 'Emissions|CO2|Net-negative'),
('Compensate CDR', [
'Carbon Sequestration|CCS|Biomass',
'AFOLU CDR',
'Carbon Sequestration|Direct Air Capture',
'Carbon Sequestration|Enhanced Weathering',
'Emissions|CO2|Net-negative-negative'])
]
valid_variables = []
for (name, variable) in variable_mapping:
if pyam.isstr(variable):
valid_variables.append(variable)
else:
for v in variable:
valid_variables.append(v)
df.filter(variable=valid_variables, inplace=True)
df.data.iloc[:25]
# save to an excel file
df.data.to_csv('output/CCSBySource.csv')
cats.remove('Above 2C')
def marker_args(m):
return dict(zorder=4,
edgecolors=rc['edgecolors']['marker'][m],
c=rc['c']['marker'][m],
marker=rc['marker']['marker'][m],
linewidths=1)
def boxplot_cumulative_ccs(ymax, last_year, panel_label, legend=True): # should be able to include categories like this
fig = plt.figure(figsize=(8, 3))
_cats = len(cats) - 1
label_list = []
for i, (name, v) in enumerate(variable_mapping):
_df = df.filter(variable=v, year=range(2020, 2101, 10)).timeseries() / 1000 # gigatons
_df = _df.groupby(['model', 'scenario']).sum()
_df = pd.DataFrame(_df.apply(pyam.cumulative, raw=False, axis=1, first_year=2020, last_year=last_year))
_df = pyam.filter_by_meta(_df, df, category=cats, marker=None, join_meta=True)
for j, c in enumerate(cats):
__df = _df[_df.category == c]
lst = __df[0][~np.isnan(__df[0])]
pos = 0.5 / _cats * (j - _cats / 2) + i
outliers = len(lst[lst > ymax])
if outliers > 0:
plt.text(pos - 0.01 * len(cats), ymax * 1.01, outliers)
p = plt.boxplot(lst, positions=[pos], widths=(0.3 / _cats),
whis='range',
patch_artist=True)
plt.setp(p['boxes'], color=rc['color']['category'][c])
plt.setp(p['medians'], color='black')
for m in marker:
val = __df.loc[_df.marker == m, 0]
if not val.empty:
plt.scatter(x=pos, y=val, **marker_args(m),
s=40, label=None)
label_list.append(name)
for m in marker:
meta = df.filter(marker=m).timeseries()
if not meta.empty:
meta = meta.iloc[0].name[0:2]
plt.scatter(x=[], y=[], **marker_args(m), s=60, label=m)
for j, c in enumerate(cats):
plt.plot([], c=rc['color']['category'][c], label='{}'.format(c))
if legend:
plt.legend()
plt.grid(False)
plt.xlim(-0.6, (i + 0.6))
plt.xticks(range(0, i + 1), label_list)
plt.vlines(x=[_i + 0.5 for _i in range(i)], ymin=0, ymax=ymax, colors='white')
plt.ylim(0, ymax)
plt.ylabel('Cumulative CO2 until {} (GtCO2)'.format(last_year))
fig.savefig('output/fig2.9{}_cdr_{}.png'.format(panel_label, last_year))
boxplot_cumulative_ccs(340, 2050, 'a')
boxplot_cumulative_ccs(1250, 2100, 'b', legend=False)
variable_mapping
cats
df.to_excel('output/fig2.9_data_table.xlsx')
def exportDataExcel(last_year): # should be able to include categories like this
_cats = len(cats) - 1
label_list = []
for i, (name, v) in enumerate(variable_mapping):
_df = df.filter(variable=v, year=range(2020, 2101, 5)).timeseries() / 1000
_df = _df.groupby(['model', 'scenario']).sum()
_df = pyam.filter_by_meta(_df, df, category=cats, marker=None, join_meta=True)
for j, c in enumerate(cats):
__df = _df[_df.category == c]
__df.to_csv(('output/fig2.9_data_table' + name + c + '.csv'))
exportDataExcel(2100)
x = pd.read_csv(('output/fig2.9_data_tableTotal CDR1.5C low overshoot.csv'))
x['Variable'] = name
cols = x.columns
print(cols)
def combineData():
a = pd.DataFrame(columns=cols)
for i, (name, v) in enumerate(variable_mapping):
for j, c in enumerate(cats):
x = pd.read_csv(('output/fig2.9_data_table' + name + c + '.csv'))
x['Variable'] = name
a = pd.concat([a, x])
print(a.shape)
a = a.sort_values(['model', 'scenario'], ascending = (True, False))
a.to_csv('output/CombinedCsvsWithOutcome.csv')
combineData()
| 0.282097 | 0.872075 |
```
import os
from pathlib import Path
import json
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score
from ue4nlp.ue_scores import *
def calc_roc_aucs(probabilities, labels, sampled_probabilities, methods):
predictions = np.argmax(probabilities, axis=-1)
errors = (labels != predictions).astype('uint8')
results = {}
for name, method_function in methods.items():
ue_scores = method_function(sampled_probabilities)
results[name] = roc_auc_score(errors, ue_scores)
max_prob = 1. - np.max(probabilities, axis=-1)
results['max_prob'] = roc_auc_score(errors, max_prob)
return results
def extract_result(time_dir, methods):
with open(Path(time_dir) / 'dev_inference.json') as f:
model_outputs = json.load(f)
return calc_roc_aucs(np.asarray(model_outputs['probabilities']),
np.asarray(model_outputs['true_labels']),
np.asarray(model_outputs['sampled_probabilities']).transpose(1, 0, 2),
methods=methods)
def extract_all_results(data_path, mc_types, frac, methods):
results = {}
for mc_type in mc_types:
mc_type_dir = data_path / mc_type / str(frac)
mc_type_results = []
for suffix in os.listdir(mc_type_dir):
suffix_dir = mc_type_dir / suffix
for date_fname in os.listdir(suffix_dir):
date_dir = suffix_dir / date_fname
for time_fname in os.listdir(date_dir):
time_dir = date_dir / time_fname
mc_type_results.append(extract_result(time_dir, methods=methods))
results[mc_type] = pd.DataFrame.from_dict(mc_type_results, orient='columns')
return results
def aggregate_results(data_path, frac, mc_types=None):
data_path = Path(data_path)
if mc_types is None:
mc_types = ['DPP_last', 'MC_last', 'MC_all']
default_methods = {
'bald': bald,
'sampled_max_prob': sampled_max_prob,
'variance': probability_variance
}
all_results = extract_all_results(data_path, mc_types=mc_types, frac=frac, methods=default_methods)
return all_results
def format_results(all_results, baseline_coords=('DPP_last', 'max_prob')):
baseline_row = baseline_coords[0]
baseline_column = baseline_coords[1]
baseline = all_results[baseline_row][baseline_column]
all_formatted_result = {}
for mc_type, results in all_results.items():
diff_res = results.drop(columns=baseline_column).subtract(baseline, axis='rows')
mean_res = diff_res.mean(axis=0)
std_res = diff_res.std(axis=0)
diff_final_res = pd.DataFrame.from_records([mean_res, std_res], index=['mean', 'std']).T
diff_final_res *= 100.
def mean_std_str(row):
return '{:.1f}ยฑ{:.1f}'.format(row[0], row[1])
formatted_results = diff_final_res.apply(mean_std_str, raw=True, axis=1)
baseline_percent = baseline*100
formatted_results.loc['baseline (max_prob)'] = mean_std_str([baseline_percent.mean(), baseline_percent.std()])
all_formatted_result[mc_type] = formatted_results
return all_formatted_result
def covert_into_series(formatted_results):
ser = pd.Series()
ser['baseline (max_prob)'] = formatted_results['DPP_last']['baseline (max_prob)']
all_series = [ser]
for mc_type, res in formatted_results.items():
ser = pd.Series()
for i in res.index:
if i == 'baseline (max_prob)':
continue
ser[f'{mc_type}_{i}'] = res[i]
all_series.append(ser)
return pd.concat(all_series)
def build_eval_table(dataset_paths, mc_types=None):
series = []
for path, frac, name in dataset_paths:
agg_res = aggregate_results(path, frac=frac, mc_types=mc_types)
formatted_res = format_results(agg_res)
ser = covert_into_series(formatted_res)
series.append((ser,name))
return pd.DataFrame.from_records([e[0] for e in series],
index=[e[1] for e in series]).T
dataset_paths = [
('../workdir/runs_results/SST-2/', 0.2, 'SST-2'),
('../workdir/runs_results/CoLA/', 0., 'CoLA'),
('../workdir/runs_results/MRPC/', 0., 'MRPC')
]
mc_types = ['DPP_last', 'MC_last', 'MC_all']
eval_table = build_eval_table(dataset_paths, mc_types=mc_types)
eval_table
index_map = {'DPP_last_bald' : ''}
print(str(eval_table.to_latex()).replace('ยฑ', '$\pm$'))
```
|
github_jupyter
|
import os
from pathlib import Path
import json
import numpy as np
import pandas as pd
from sklearn.metrics import roc_auc_score
from ue4nlp.ue_scores import *
def calc_roc_aucs(probabilities, labels, sampled_probabilities, methods):
predictions = np.argmax(probabilities, axis=-1)
errors = (labels != predictions).astype('uint8')
results = {}
for name, method_function in methods.items():
ue_scores = method_function(sampled_probabilities)
results[name] = roc_auc_score(errors, ue_scores)
max_prob = 1. - np.max(probabilities, axis=-1)
results['max_prob'] = roc_auc_score(errors, max_prob)
return results
def extract_result(time_dir, methods):
with open(Path(time_dir) / 'dev_inference.json') as f:
model_outputs = json.load(f)
return calc_roc_aucs(np.asarray(model_outputs['probabilities']),
np.asarray(model_outputs['true_labels']),
np.asarray(model_outputs['sampled_probabilities']).transpose(1, 0, 2),
methods=methods)
def extract_all_results(data_path, mc_types, frac, methods):
results = {}
for mc_type in mc_types:
mc_type_dir = data_path / mc_type / str(frac)
mc_type_results = []
for suffix in os.listdir(mc_type_dir):
suffix_dir = mc_type_dir / suffix
for date_fname in os.listdir(suffix_dir):
date_dir = suffix_dir / date_fname
for time_fname in os.listdir(date_dir):
time_dir = date_dir / time_fname
mc_type_results.append(extract_result(time_dir, methods=methods))
results[mc_type] = pd.DataFrame.from_dict(mc_type_results, orient='columns')
return results
def aggregate_results(data_path, frac, mc_types=None):
data_path = Path(data_path)
if mc_types is None:
mc_types = ['DPP_last', 'MC_last', 'MC_all']
default_methods = {
'bald': bald,
'sampled_max_prob': sampled_max_prob,
'variance': probability_variance
}
all_results = extract_all_results(data_path, mc_types=mc_types, frac=frac, methods=default_methods)
return all_results
def format_results(all_results, baseline_coords=('DPP_last', 'max_prob')):
baseline_row = baseline_coords[0]
baseline_column = baseline_coords[1]
baseline = all_results[baseline_row][baseline_column]
all_formatted_result = {}
for mc_type, results in all_results.items():
diff_res = results.drop(columns=baseline_column).subtract(baseline, axis='rows')
mean_res = diff_res.mean(axis=0)
std_res = diff_res.std(axis=0)
diff_final_res = pd.DataFrame.from_records([mean_res, std_res], index=['mean', 'std']).T
diff_final_res *= 100.
def mean_std_str(row):
return '{:.1f}ยฑ{:.1f}'.format(row[0], row[1])
formatted_results = diff_final_res.apply(mean_std_str, raw=True, axis=1)
baseline_percent = baseline*100
formatted_results.loc['baseline (max_prob)'] = mean_std_str([baseline_percent.mean(), baseline_percent.std()])
all_formatted_result[mc_type] = formatted_results
return all_formatted_result
def covert_into_series(formatted_results):
ser = pd.Series()
ser['baseline (max_prob)'] = formatted_results['DPP_last']['baseline (max_prob)']
all_series = [ser]
for mc_type, res in formatted_results.items():
ser = pd.Series()
for i in res.index:
if i == 'baseline (max_prob)':
continue
ser[f'{mc_type}_{i}'] = res[i]
all_series.append(ser)
return pd.concat(all_series)
def build_eval_table(dataset_paths, mc_types=None):
series = []
for path, frac, name in dataset_paths:
agg_res = aggregate_results(path, frac=frac, mc_types=mc_types)
formatted_res = format_results(agg_res)
ser = covert_into_series(formatted_res)
series.append((ser,name))
return pd.DataFrame.from_records([e[0] for e in series],
index=[e[1] for e in series]).T
dataset_paths = [
('../workdir/runs_results/SST-2/', 0.2, 'SST-2'),
('../workdir/runs_results/CoLA/', 0., 'CoLA'),
('../workdir/runs_results/MRPC/', 0., 'MRPC')
]
mc_types = ['DPP_last', 'MC_last', 'MC_all']
eval_table = build_eval_table(dataset_paths, mc_types=mc_types)
eval_table
index_map = {'DPP_last_bald' : ''}
print(str(eval_table.to_latex()).replace('ยฑ', '$\pm$'))
| 0.440229 | 0.192426 |
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
pageName = 'AllTests'
saveGraphs = True
savePath = 'images/graphs/'+pageName
df = pd.read_excel (r'data/latency/latency_nuvolaPunti.xlsx', sheet_name=pageName)
delayTicks = [300, 500, 750, 1000, 1500, 2000]
delayPoints = df['delay'].to_numpy()
latencyPoints = df['latency'].to_numpy()
marginErrPoints = df['marginErr'].to_numpy()
maxPoints = df['max'].to_numpy()
minPoints = df['min'].to_numpy()
plt.style.use('seaborn-whitegrid')
paper_rc = {'lines.linewidth': 1, 'lines.markersize': 10}
sns.set_context("paper", rc = paper_rc)
sns.set(style="ticks", palette="muted")
#fig, ax = plt.subplots()
if pageName in ["AllTests", "AllTest3"]:
plt.figure(figsize=(20,10))
#df.plot.scatter('delay', 'latency', color='red', s=0.5)
sns.scatterplot(x="delay", y="latency", hue="Test", palette="muted",data=df)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' scatterPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
plt.figure(figsize=(20,10))
#df.plot.scatter('delay', 'latency', color='red', s=0.5)
sns.scatterplot(x="delay", y="latency",data=df)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' scatterPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName not in ["AllTests", "AllTest3"]:
#Scatter plot with error bar
plt.figure(figsize=(20,10))
plt.errorbar(delayPoints, latencyPoints, yerr=marginErrPoints, markersize=3, fmt='o', color ='red', ecolor='black', capsize=2, barsabove = False, alpha =0.1)
plt.title("Scatter plot with error bars - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' dispersion.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Error interval mean plot
plt.figure(figsize=(20,10))
sns.pointplot('delay', 'latency', hue='Test', markers=["2", "x", "+", "^","1"], data=df, capsize=.05, yerr= marginErrPoints, height=5, aspect = 2, err_style="bars", ci=95)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Error plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' linePlotWithErrorBar.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
#Error plot
plt.figure(figsize=(20,10))
sns.pointplot('delay', 'latency', data=df, capsize=.05, yerr= marginErrPoints, err_style="bars", ci=95)
plt.title("Error plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' linePlotWithErrorBar.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Smote plot
plt.figure(figsize=(20,10))
sns.lmplot('delay', 'latency', hue ='Test',data=df, ci=None, order=5,height=10, aspect = 2, truncate=True, scatter_kws={"s": 0.5})
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' smoteInterpolation.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
plt.figure(figsize=(20,10))
sns.lmplot('delay', 'latency', hue ='Test',data=df, ci=95, order=5,height=10, aspect = 2, truncate=True, scatter_kws={"s": 0.5})
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' smoteInterpolationWithCI.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
#Smote plot
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency',data=df, ci=95, order=5, height=10, aspect = 2, truncate=True, legend_out=True, scatter_kws={"s": 5})
plt.title("Smoted line plot with CI - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if pageName == "Test1":
g.set(ylim=(0.25, 0.41))
if pageName == "Test2":
g.set(ylim=(0.7, 1.1))
if pageName == "Test3 500ms":
g.set(ylim=(17, 20.5))
if pageName == "Test3 5sec":
g.set(ylim=(22, 25))
if pageName == "Test3 10sec":
g.set(ylim=(21, 31))
if saveGraphs == True:
plt.savefig(savePath+' smoteinterpolationWithCI.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2, transparent=False)
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency',data=df, ci=None, order=5, height=10, aspect = 2, truncate=True, legend_out=True, scatter_kws={"s": 5})
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if pageName == "Test1":
g.set(ylim=(0.25, 0.41))
if pageName == "Test2":
g.set(ylim=(0.7, 1.1))
if pageName == "Test3 500ms":
g.set(ylim=(17, 20.5))
if pageName == "Test3 5sec":
g.set(ylim=(22, 25))
if pageName == "Test3 10sec":
g.set(ylim=(21, 31))
if saveGraphs == True:
plt.savefig(savePath+' smoteinterpolation.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Smote plot - confronto
plt.figure(figsize=(20,10))
g = sns.lmplot(x="delay", y="latency", col="Test", hue="Test", data=df,
col_wrap=2, ci=95, palette="muted", height=5, aspect = 2, order=5, truncate = True,
scatter_kws={"s": 4, "alpha": 1})
g = (g.set_axis_labels("Time between pkt sent (ms)", "Latency (s)"))
plt.xticks(delayTicks)
if saveGraphs == True:
plt.savefig(savePath+' confrontoSmootedLine.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency', col="Test", hue="Test", data=df, scatter_kws={"s": 1, "alpha": 1},
palette="muted", y_jitter=.02, logistic=False, truncate=True)
g = (g.set_axis_labels("Time between pkt sent (ms)", "Latency (s)"))
g.set(ylim=(0, 32))
plt.xticks(delayTicks)
if saveGraphs == True:
plt.savefig(savePath+' confrontoRegressionLine.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
plt.figure(figsize=(20,10))
sns.boxplot('delay', 'latency', palette="muted", data=df, hue="Test",width=0.3, dodge = False) #notch = True
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Box plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
sns.despine(offset=10, trim=True)
if saveGraphs == True:
plt.savefig(savePath+' boxPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
plt.figure(figsize=(20,10))
sns.boxplot('delay', 'latency', palette="muted", data=df,width=0.3, dodge = False)
#sns.swarmplot('delay', 'latency', data=df, color=".25")
plt.title("Box plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
sns.despine(offset=10, trim=True)
if saveGraphs == True:
plt.savefig(savePath+' boxPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
#sns.residplot('delay', 'latency',data=df, lowess=True, color="g")
#sns.jointplot('delay', 'latency',data=df, kind="hex", color="#4CB391")
#sns.regplot('delay', 'latency',ci=95, data=df)
```
|
github_jupyter
|
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
pageName = 'AllTests'
saveGraphs = True
savePath = 'images/graphs/'+pageName
df = pd.read_excel (r'data/latency/latency_nuvolaPunti.xlsx', sheet_name=pageName)
delayTicks = [300, 500, 750, 1000, 1500, 2000]
delayPoints = df['delay'].to_numpy()
latencyPoints = df['latency'].to_numpy()
marginErrPoints = df['marginErr'].to_numpy()
maxPoints = df['max'].to_numpy()
minPoints = df['min'].to_numpy()
plt.style.use('seaborn-whitegrid')
paper_rc = {'lines.linewidth': 1, 'lines.markersize': 10}
sns.set_context("paper", rc = paper_rc)
sns.set(style="ticks", palette="muted")
#fig, ax = plt.subplots()
if pageName in ["AllTests", "AllTest3"]:
plt.figure(figsize=(20,10))
#df.plot.scatter('delay', 'latency', color='red', s=0.5)
sns.scatterplot(x="delay", y="latency", hue="Test", palette="muted",data=df)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' scatterPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
plt.figure(figsize=(20,10))
#df.plot.scatter('delay', 'latency', color='red', s=0.5)
sns.scatterplot(x="delay", y="latency",data=df)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' scatterPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName not in ["AllTests", "AllTest3"]:
#Scatter plot with error bar
plt.figure(figsize=(20,10))
plt.errorbar(delayPoints, latencyPoints, yerr=marginErrPoints, markersize=3, fmt='o', color ='red', ecolor='black', capsize=2, barsabove = False, alpha =0.1)
plt.title("Scatter plot with error bars - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' dispersion.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Error interval mean plot
plt.figure(figsize=(20,10))
sns.pointplot('delay', 'latency', hue='Test', markers=["2", "x", "+", "^","1"], data=df, capsize=.05, yerr= marginErrPoints, height=5, aspect = 2, err_style="bars", ci=95)
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Error plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' linePlotWithErrorBar.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
#Error plot
plt.figure(figsize=(20,10))
sns.pointplot('delay', 'latency', data=df, capsize=.05, yerr= marginErrPoints, err_style="bars", ci=95)
plt.title("Error plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' linePlotWithErrorBar.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Smote plot
plt.figure(figsize=(20,10))
sns.lmplot('delay', 'latency', hue ='Test',data=df, ci=None, order=5,height=10, aspect = 2, truncate=True, scatter_kws={"s": 0.5})
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' smoteInterpolation.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
plt.figure(figsize=(20,10))
sns.lmplot('delay', 'latency', hue ='Test',data=df, ci=95, order=5,height=10, aspect = 2, truncate=True, scatter_kws={"s": 0.5})
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if saveGraphs == True:
plt.savefig(savePath+' smoteInterpolationWithCI.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
#Smote plot
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency',data=df, ci=95, order=5, height=10, aspect = 2, truncate=True, legend_out=True, scatter_kws={"s": 5})
plt.title("Smoted line plot with CI - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if pageName == "Test1":
g.set(ylim=(0.25, 0.41))
if pageName == "Test2":
g.set(ylim=(0.7, 1.1))
if pageName == "Test3 500ms":
g.set(ylim=(17, 20.5))
if pageName == "Test3 5sec":
g.set(ylim=(22, 25))
if pageName == "Test3 10sec":
g.set(ylim=(21, 31))
if saveGraphs == True:
plt.savefig(savePath+' smoteinterpolationWithCI.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2, transparent=False)
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency',data=df, ci=None, order=5, height=10, aspect = 2, truncate=True, legend_out=True, scatter_kws={"s": 5})
plt.title("Smoted line plot - "+pageName)
plt.xticks(delayTicks)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
if pageName == "Test1":
g.set(ylim=(0.25, 0.41))
if pageName == "Test2":
g.set(ylim=(0.7, 1.1))
if pageName == "Test3 500ms":
g.set(ylim=(17, 20.5))
if pageName == "Test3 5sec":
g.set(ylim=(22, 25))
if pageName == "Test3 10sec":
g.set(ylim=(21, 31))
if saveGraphs == True:
plt.savefig(savePath+' smoteinterpolation.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
#Smote plot - confronto
plt.figure(figsize=(20,10))
g = sns.lmplot(x="delay", y="latency", col="Test", hue="Test", data=df,
col_wrap=2, ci=95, palette="muted", height=5, aspect = 2, order=5, truncate = True,
scatter_kws={"s": 4, "alpha": 1})
g = (g.set_axis_labels("Time between pkt sent (ms)", "Latency (s)"))
plt.xticks(delayTicks)
if saveGraphs == True:
plt.savefig(savePath+' confrontoSmootedLine.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
plt.figure(figsize=(20,10))
g = sns.lmplot('delay', 'latency', col="Test", hue="Test", data=df, scatter_kws={"s": 1, "alpha": 1},
palette="muted", y_jitter=.02, logistic=False, truncate=True)
g = (g.set_axis_labels("Time between pkt sent (ms)", "Latency (s)"))
g.set(ylim=(0, 32))
plt.xticks(delayTicks)
if saveGraphs == True:
plt.savefig(savePath+' confrontoRegressionLine.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
if pageName in ["AllTests", "AllTest3"]:
plt.figure(figsize=(20,10))
sns.boxplot('delay', 'latency', palette="muted", data=df, hue="Test",width=0.3, dodge = False) #notch = True
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title("Box plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
sns.despine(offset=10, trim=True)
if saveGraphs == True:
plt.savefig(savePath+' boxPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
else:
plt.figure(figsize=(20,10))
sns.boxplot('delay', 'latency', palette="muted", data=df,width=0.3, dodge = False)
#sns.swarmplot('delay', 'latency', data=df, color=".25")
plt.title("Box plot - "+pageName)
plt.xlabel("Time between pkt sent (ms)")
plt.ylabel("Latency (s)")
sns.despine(offset=10, trim=True)
if saveGraphs == True:
plt.savefig(savePath+' boxPlot.png', format='png', dpi=300, bbox_inches='tight', pad_inches=0.2)
#sns.residplot('delay', 'latency',data=df, lowess=True, color="g")
#sns.jointplot('delay', 'latency',data=df, kind="hex", color="#4CB391")
#sns.regplot('delay', 'latency',ci=95, data=df)
| 0.36727 | 0.428473 |
# An Example of using sklearn Pipeline with matminer
This goes over the steps to build a model using sklearn Pipeline and matminer. Look at the intro_predicting_bulk_modulus notebook for more details about matminer and the featurizers used here.
This notebook was last updated 11/15/18 for version 0.4.5 of matminer.
**Note that in order to get the in-line plotting to work, you might need to start Jupyter notebook with a higher data rate, e.g., ``jupyter notebook --NotebookApp.iopub_data_rate_limit=1.0e10``. We recommend you do this before starting.**
## Why use Pipeline?
Pre-processing and featurizing materials data can be viewed as a series of transformations on the data, going from the initially loaded state to training ready. Pipelines are a tool for encapsulating this process in a way that enables easy replication/repeatability, presents a simple model of data transformation, and helps to avoid errant changes to the data. Pipelines chain together transformations into a single transformation. They can also be used to build end end-to-end methods for preprocessing/training/validating a model, by optionally putting an estimator at the end of the pipeline. See the [scikit-learn Pipeline documentation](http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html) for details.
```
# Load sklearn modules
from sklearn.pipeline import FeatureUnion, Pipeline
from sklearn.base import TransformerMixin, BaseEstimator
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR, LinearSVR
from sklearn.decomposition import PCA, NMF
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import RepeatedKFold, cross_val_score, cross_val_predict, train_test_split, GridSearchCV, RandomizedSearchCV
import numpy as np
from pandas import DataFrame
from scipy.stats import randint as sp_randint
# Load featurizers and conversion functions
from matminer.featurizers.composition import ElementProperty, OxidationStates
from matminer.featurizers.structure import DensityFeatures
from matminer.featurizers.conversions import CompositionToOxidComposition, StrToComposition
```
## Loading the Dataset
Matminer comes pre-loaded with several example data sets you can use. Below, we'll load a data set of computed elastic properties of materials which is sourced from the paper: "Charting the complete elastic properties of inorganic crystalline compounds", M. de Jong *et al.*, Sci. Data. 2 (2015) 150009.
```
from matminer.datasets.convenience_loaders import load_elastic_tensor
df = load_elastic_tensor() # loads dataset in a pandas DataFrame
unwanted_columns = ["volume", "nsites", "compliance_tensor", "elastic_tensor",
"elastic_tensor_original", "K_Voigt", "G_Voigt", "K_Reuss", "G_Reuss"]
df = df.drop(unwanted_columns, axis=1)
# seperate out values to be estimated
y = df['K_VRH'].values
```
## Data Preprocessing
The conversion functions in matminer need to be run before the pipeline as a data preprocessing step.
```
df = StrToComposition().featurize_dataframe(df, "formula")
df = CompositionToOxidComposition().featurize_dataframe(df, "composition")
```
## Helper Functions
The matminer library uses pandas DataFrames, where sklearn.pipeline mainly looks at things as numpy arrays, so helper methods are needed to seperate out columns from the DataFrame for pipeline. To be used in pipeline they need to be transformers, meaning they implement a transform method. (A fit method that does nothing is also needed)
```
from matminer.utils.pipeline import DropExcluded, ItemSelector
```
## Making Feature Union Pipeline for Featurizers
This creates a pipeline that transforms preprocessed data to featurized data usable in sklearn. It can be used to transform data on its own or as part of another pipeline. It is possible to cache values in the pipeline so that this is only done once.
This Feature Union pipeline has three parts, ``drop`` which drops unwanted columns, ``density`` which adds density features, and ``oxidation`` which adds oxidation state features. These are combined by ``FeatureUnion`` to create the final dataset. The ``drop`` transform acts as an identity+filter, passing through the original data minus the unwanted columns.
```
# columns to remove before regression
excluded = ["G_VRH", "K_VRH", "elastic_anisotropy", "formula", "material_id",
"poisson_ratio", "structure", "composition", "composition_oxid"]
# featurization transformations
featurizer = FeatureUnion(
transformer_list=[
('drop', DropExcluded(excluded)),
('density', Pipeline([
('select', ItemSelector("structure")),
('density_feat', DensityFeatures())
])),
('element', Pipeline([
('select', ItemSelector("composition")),
('oxidation_feat', ElementProperty.from_preset(preset_name="magpie"))
])),
('oxidation', Pipeline([
('select', ItemSelector("composition_oxid")),
('oxidation_feat', OxidationStates())
])),
]
)
```
## Making a Regression Pipeline
This is a simple pipeline combining the featurizer transformer pipeline with a linear regression estimator.
```
# make the pipeline
pipeline = Pipeline([
('featurize', featurizer),
('regress', LinearRegression()),
])
pipeline.fit(df, y)
# get fit statistics
print('training R2 = ' + str(round(pipeline.score(df, y), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y, y_pred=pipeline.predict(df))))
```
## Making a Random Forest Pipeline
This is the same, but with a random forest regression instead. The only line changed is the one defining ``regress`` in the pipeline.
```
# make the pipeline
pipeline = Pipeline([
('featurize', featurizer),
('regress', RandomForestRegressor(n_estimators=50, random_state=1)),
])
pipeline.fit(df, y)
# get fit statistics
print('training R2 = ' + str(round(pipeline.score(df, y), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y, y_pred=pipeline.predict(df))))
```
## Cross Validation
To run cross validation, the featurizer transformation can't be in a pipeline with the regressor, as the initial form of the data cannot be used with KFold. This is because the transformer adds and removes columns, it's more than just a simple function of the data. Instead the final featurized data can be computed beforehand, here as ``X``.
```
X = featurizer.transform(df)
```
Define a KFold for cross validation. Using RepeatedKFold can reduce variance in the cross val score without increasing the number of folds, this is similar to bootstrapping, as the data is randomly subsampled multiple times by the KFold and then averaged. Using repeated folds is a good way to reduce variance if there is sufficient compute time to do so. For very computationally expensive models, such as DNNs, it is common to use a single train/validation split (not counting the excluded test data).
```
crossvalidation = RepeatedKFold(n_splits=5, n_repeats=3, random_state=1)
```
This is the same linear regression as before, now with RepeatedKFold cross validation. This gives a better estimate of how well the model will generalize than looking at training error. Cross validation usually gives a pessimistic estimate, and in practice the best performing model will be retrained on the full set of train/val data before testing.
```
lr = LinearRegression()
scores = cross_val_score(lr, X, y, scoring='neg_mean_squared_error', cv=crossvalidation, n_jobs=1)
rmse_scores = [np.sqrt(abs(s)) for s in scores]
r2_scores = cross_val_score(lr, X, y, scoring='r2', cv=crossvalidation, n_jobs=1)
print('Cross-validation results:')
print('Folds: %i, mean R2: %.3f' % (len(scores), np.mean(np.abs(r2_scores))))
print('Folds: %i, mean RMSE: %.3f' % (len(scores), np.mean(np.abs(rmse_scores))))
```
This is the same with the random forest regressor.
```
# compute cross validation scores for random forest model
rf = RandomForestRegressor(n_estimators=50, random_state=1)
r2_scores = cross_val_score(rf, X, y, scoring='r2', cv=crossvalidation, n_jobs=1)
scores = cross_val_score(rf, X, y, scoring='neg_mean_squared_error', cv=crossvalidation, n_jobs=1)
rmse_scores = [np.sqrt(abs(s)) for s in scores]
print('Cross-validation results:')
print('Folds: %i, mean R2: %.3f' % (len(scores), np.mean(np.abs(r2_scores))))
print('Folds: %i, mean RMSE: %.3f' % (len(scores), np.mean(np.abs(rmse_scores))))
```
## Model Selection with Grid Search
A pipeline can be used with Grid Search or Random Search for model selection and hyper-parameter optimization. This can include normalization, scaling, whitening, PCA / dimensionality reduction, basis expansion, or any other preprocessing or data transformation steps.
Setting up a pipeline is design pattern that gives a straight forward abd repeatable method of processing the data and training a model. This can make it easy to try many different models and perform model selection with a hyper-parameter optimization scheme like grid search.
Before doing model selection, the data should be split into a training set and a holdout test set. This tries to measure the generality of the model, predicting how it may perform on real data. Without a test set there is no way to measure if the model has likely overfit the training data.
Note: The best model is chosen by cross validation score, and only the final model (after being retrained on all train/val data) is evaluated on the test set. Evaluating multiple models on the test set and choosing the best of them is an almost sure way of leading to overfitting or overestimating the true performance/generality of the model, exactly what we are trying to avoid by creating a hold out test set.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
rf = RandomForestRegressor(n_estimators=50, random_state=1)
param_grid = [
{'n_estimators': [10,15,20,25,30,50,100]},
]
gs = GridSearchCV(rf, param_grid, n_jobs=4, cv=5)
gs.fit(X_train, y_train)
print(gs.best_score_)
print(gs.best_params_)
print(gs.score(X_test, y_test))
```
## Random Search
Random search is another possible option for hyper-parameter selection, and usually outperforms grid search both in theory and in practice (see Random Search for Hyper-Parameter Optimization by Bergstra & Bengio). This is true especially in higher dimentional hyper-parameter spaces. This shows an example of a scaling step in the pipeline, which can improve performance for some types of models.
```
pipe = Pipeline([
('scale', StandardScaler()),
('regress', RandomForestRegressor(random_state=1)),
])
param_dist = {'regress__n_estimators': sp_randint(10,150)}
gs = RandomizedSearchCV(pipe, param_dist, cv=crossvalidation, n_jobs=-1)
gs.fit(X_train, y_train)
print('best crossval score ' + str(round(gs.best_score_, 3)))
print('best params ' + str(gs.best_params_))
# get fit statistics
print('training R2 = ' + str(round(gs.score(X_train, y_train), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y_train, y_pred=gs.predict(X_train))))
print('test R2 = ' + str(round(gs.score(X_test, y_test), 3)))
print('test RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y_test, y_pred=gs.predict(X_test))))
```
|
github_jupyter
|
# Load sklearn modules
from sklearn.pipeline import FeatureUnion, Pipeline
from sklearn.base import TransformerMixin, BaseEstimator
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR, LinearSVR
from sklearn.decomposition import PCA, NMF
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import RepeatedKFold, cross_val_score, cross_val_predict, train_test_split, GridSearchCV, RandomizedSearchCV
import numpy as np
from pandas import DataFrame
from scipy.stats import randint as sp_randint
# Load featurizers and conversion functions
from matminer.featurizers.composition import ElementProperty, OxidationStates
from matminer.featurizers.structure import DensityFeatures
from matminer.featurizers.conversions import CompositionToOxidComposition, StrToComposition
from matminer.datasets.convenience_loaders import load_elastic_tensor
df = load_elastic_tensor() # loads dataset in a pandas DataFrame
unwanted_columns = ["volume", "nsites", "compliance_tensor", "elastic_tensor",
"elastic_tensor_original", "K_Voigt", "G_Voigt", "K_Reuss", "G_Reuss"]
df = df.drop(unwanted_columns, axis=1)
# seperate out values to be estimated
y = df['K_VRH'].values
df = StrToComposition().featurize_dataframe(df, "formula")
df = CompositionToOxidComposition().featurize_dataframe(df, "composition")
from matminer.utils.pipeline import DropExcluded, ItemSelector
# columns to remove before regression
excluded = ["G_VRH", "K_VRH", "elastic_anisotropy", "formula", "material_id",
"poisson_ratio", "structure", "composition", "composition_oxid"]
# featurization transformations
featurizer = FeatureUnion(
transformer_list=[
('drop', DropExcluded(excluded)),
('density', Pipeline([
('select', ItemSelector("structure")),
('density_feat', DensityFeatures())
])),
('element', Pipeline([
('select', ItemSelector("composition")),
('oxidation_feat', ElementProperty.from_preset(preset_name="magpie"))
])),
('oxidation', Pipeline([
('select', ItemSelector("composition_oxid")),
('oxidation_feat', OxidationStates())
])),
]
)
# make the pipeline
pipeline = Pipeline([
('featurize', featurizer),
('regress', LinearRegression()),
])
pipeline.fit(df, y)
# get fit statistics
print('training R2 = ' + str(round(pipeline.score(df, y), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y, y_pred=pipeline.predict(df))))
# make the pipeline
pipeline = Pipeline([
('featurize', featurizer),
('regress', RandomForestRegressor(n_estimators=50, random_state=1)),
])
pipeline.fit(df, y)
# get fit statistics
print('training R2 = ' + str(round(pipeline.score(df, y), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y, y_pred=pipeline.predict(df))))
X = featurizer.transform(df)
crossvalidation = RepeatedKFold(n_splits=5, n_repeats=3, random_state=1)
lr = LinearRegression()
scores = cross_val_score(lr, X, y, scoring='neg_mean_squared_error', cv=crossvalidation, n_jobs=1)
rmse_scores = [np.sqrt(abs(s)) for s in scores]
r2_scores = cross_val_score(lr, X, y, scoring='r2', cv=crossvalidation, n_jobs=1)
print('Cross-validation results:')
print('Folds: %i, mean R2: %.3f' % (len(scores), np.mean(np.abs(r2_scores))))
print('Folds: %i, mean RMSE: %.3f' % (len(scores), np.mean(np.abs(rmse_scores))))
# compute cross validation scores for random forest model
rf = RandomForestRegressor(n_estimators=50, random_state=1)
r2_scores = cross_val_score(rf, X, y, scoring='r2', cv=crossvalidation, n_jobs=1)
scores = cross_val_score(rf, X, y, scoring='neg_mean_squared_error', cv=crossvalidation, n_jobs=1)
rmse_scores = [np.sqrt(abs(s)) for s in scores]
print('Cross-validation results:')
print('Folds: %i, mean R2: %.3f' % (len(scores), np.mean(np.abs(r2_scores))))
print('Folds: %i, mean RMSE: %.3f' % (len(scores), np.mean(np.abs(rmse_scores))))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
rf = RandomForestRegressor(n_estimators=50, random_state=1)
param_grid = [
{'n_estimators': [10,15,20,25,30,50,100]},
]
gs = GridSearchCV(rf, param_grid, n_jobs=4, cv=5)
gs.fit(X_train, y_train)
print(gs.best_score_)
print(gs.best_params_)
print(gs.score(X_test, y_test))
pipe = Pipeline([
('scale', StandardScaler()),
('regress', RandomForestRegressor(random_state=1)),
])
param_dist = {'regress__n_estimators': sp_randint(10,150)}
gs = RandomizedSearchCV(pipe, param_dist, cv=crossvalidation, n_jobs=-1)
gs.fit(X_train, y_train)
print('best crossval score ' + str(round(gs.best_score_, 3)))
print('best params ' + str(gs.best_params_))
# get fit statistics
print('training R2 = ' + str(round(gs.score(X_train, y_train), 3)))
print('training RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y_train, y_pred=gs.predict(X_train))))
print('test R2 = ' + str(round(gs.score(X_test, y_test), 3)))
print('test RMSE = %.3f' % np.sqrt(mean_squared_error(y_true=y_test, y_pred=gs.predict(X_test))))
| 0.824073 | 0.987794 |
<img src="https://nlp.johnsnowlabs.com/assets/images/logo.png" width="180" height="50" style="float: left;">
## Rule-based Sentiment Analysis
In the following example, we walk-through a simple use case for our straight forward SentimentDetector annotator.
This annotator will work on top of a list of labeled sentences which can have any of the following features
positive
negative
revert
increment
decrement
Each of these sentences will be used for giving a score to text
#### 1. Call necessary imports and set the resource path to read local data files
```
#Imports
import sys
sys.path.append('../../')
import sparknlp
from pyspark.sql import SparkSession
from pyspark.ml import Pipeline
from pyspark.sql.functions import array_contains
from sparknlp.annotator import *
from sparknlp.common import RegexRule
from sparknlp.base import DocumentAssembler, Finisher
```
#### 2. Load SparkSession if not already there
```
import sparknlp
spark = sparknlp.start()
print("Spark NLP version: ", sparknlp.version())
print("Apache Spark version: ", spark.version)
! rm /tmp/sentiment.parquet.zip
! rm -rf /tmp/sentiment.parquet
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/sentiment.parquet.zip -P /tmp
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/lemma-corpus-small/lemmas_small.txt -P /tmp
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/sentiment-corpus/default-sentiment-dict.txt -P /tmp
! unzip /tmp/sentiment.parquet.zip -d /tmp/
data = spark. \
read. \
parquet("/tmp/sentiment.parquet"). \
limit(10000).cache()
data.show()
```
#### 3. Create appropriate annotators. We are using Sentence Detection, Tokenizing the sentences, and find the lemmas of those tokens. The Finisher will only output the Sentiment.
```
document_assembler = DocumentAssembler() \
.setInputCol("text")
sentence_detector = SentenceDetector() \
.setInputCols(["document"]) \
.setOutputCol("sentence")
tokenizer = Tokenizer() \
.setInputCols(["sentence"]) \
.setOutputCol("token")
lemmatizer = Lemmatizer() \
.setInputCols(["token"]) \
.setOutputCol("lemma") \
.setDictionary("/tmp/lemmas_small.txt", key_delimiter="->", value_delimiter="\t")
sentiment_detector = SentimentDetector() \
.setInputCols(["lemma", "sentence"]) \
.setOutputCol("sentiment_score") \
.setDictionary("/tmp/default-sentiment-dict.txt", ",")
finisher = Finisher() \
.setInputCols(["sentiment_score"]) \
.setOutputCols(["sentiment"])
```
#### 4. Train the pipeline, which is only being trained from external resources, not from the dataset we pass on. The prediction runs on the target dataset
```
pipeline = Pipeline(stages=[document_assembler, sentence_detector, tokenizer, lemmatizer, sentiment_detector, finisher])
model = pipeline.fit(data)
result = model.transform(data)
```
#### 5. filter the finisher output, to find the positive sentiment lines
```
result.where(array_contains(result.sentiment, "positive")).show(10,False)
```
|
github_jupyter
|
#Imports
import sys
sys.path.append('../../')
import sparknlp
from pyspark.sql import SparkSession
from pyspark.ml import Pipeline
from pyspark.sql.functions import array_contains
from sparknlp.annotator import *
from sparknlp.common import RegexRule
from sparknlp.base import DocumentAssembler, Finisher
import sparknlp
spark = sparknlp.start()
print("Spark NLP version: ", sparknlp.version())
print("Apache Spark version: ", spark.version)
! rm /tmp/sentiment.parquet.zip
! rm -rf /tmp/sentiment.parquet
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/sentiment.parquet.zip -P /tmp
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/lemma-corpus-small/lemmas_small.txt -P /tmp
! wget -N https://s3.amazonaws.com/auxdata.johnsnowlabs.com/public/resources/en/sentiment-corpus/default-sentiment-dict.txt -P /tmp
! unzip /tmp/sentiment.parquet.zip -d /tmp/
data = spark. \
read. \
parquet("/tmp/sentiment.parquet"). \
limit(10000).cache()
data.show()
document_assembler = DocumentAssembler() \
.setInputCol("text")
sentence_detector = SentenceDetector() \
.setInputCols(["document"]) \
.setOutputCol("sentence")
tokenizer = Tokenizer() \
.setInputCols(["sentence"]) \
.setOutputCol("token")
lemmatizer = Lemmatizer() \
.setInputCols(["token"]) \
.setOutputCol("lemma") \
.setDictionary("/tmp/lemmas_small.txt", key_delimiter="->", value_delimiter="\t")
sentiment_detector = SentimentDetector() \
.setInputCols(["lemma", "sentence"]) \
.setOutputCol("sentiment_score") \
.setDictionary("/tmp/default-sentiment-dict.txt", ",")
finisher = Finisher() \
.setInputCols(["sentiment_score"]) \
.setOutputCols(["sentiment"])
pipeline = Pipeline(stages=[document_assembler, sentence_detector, tokenizer, lemmatizer, sentiment_detector, finisher])
model = pipeline.fit(data)
result = model.transform(data)
result.where(array_contains(result.sentiment, "positive")).show(10,False)
| 0.264263 | 0.947186 |
# <img style="float: left; padding-right: 10px; width: 45px" src="https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png"> CS-109B Advanced Data Science
## Lab 6: Recurrent Neural Networks
**Harvard University**<br>
**Spring 2019**<br>
**Lab instructor:** Srivatsan Srinivasan<br>
**Instructors:** Pavlos Protopapas and Mark Glickman<br>
**Authors:** Srivatsan Srinivasan, Pavlos Protopapas
```
# RUN THIS CELL TO PROPERLY HIGHLIGHT THE EXERCISES
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2019-CS109B/master/content/styles/cs109.css").text
HTML(styles)
```
## Learning Goals
In this lab we will look at Recurrent Neural Networks (RNNs), LSTMs and their building blocks.
By the end of this lab, you should:
- know how to put together the building blocks used in RNNs and its variants (GRU, LSTM) in `keras` with an example.
- have a good undertanding on how sequences - any dataset that has some temporal semantics (time series, natural language, images etc.) fit into and benefit from a recurrent architecture
- be familiar with preprocessing text, dynamic embeddings
- be familiar with gradient issues on RNNs processing longer sentence lengths
- understand different kinds of LSTM architectures - classifier, sequence to sequence models and their far-reaching applications
## 1. IMDB Review Classification Battlefield - Contestants : Feedforward, CNN, RNN, LSTM
In this task, we are going to do sentiment classification on a movie review dataset. We are going to build a feedforward net, a convolutional neural net, a recurrent net and combine one or more of them to understand performance of each of them. A sentence can be thought of as a sequence of words which have semantic connections across time. By semantic connection, we mean that the words that occur earlier in the sentence influence the sentence's structure and meaning in the latter part of the sentence. There are also semantic connections backwards in a sentence, in an ideal case (in which we use RNNs from both directions and combine their outputs). But for the purpose of this tutorial, we are going to restrict ourselves to only uni-directional RNNs.
```
import numpy
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM, SimpleRNN
from keras.layers.embeddings import Embedding
from keras.layers import Flatten
from keras.preprocessing import sequence
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
from keras.layers.embeddings import Embedding
import numpy as np
# fix random seed for reproducibility
numpy.random.seed(1)
# We want to have a finite vocabulary to make sure that our word matrices are not arbitrarily small
vocabulary_size = 10000
#We also want to have a finite length of reviews and not have to process really long sentences.
max_review_length = 500
```
#### TOKENIZATION
For practical data science applications, we need to convert text into tokens since the machine understands only numbers and not really English words like humans can. As a simple example of tokenization, we can see a small example.
Assume we have 5 sentences. This is how we tokenize them into numbers once we create a dictionary.
1. i have books - [1, 4, 7]
2. interesting books are useful [10,2,9,8]
3. i have computers [1,4,6]
4. computers are interesting and useful [6,9,11,10,8]
5. books and computers are both valuable. [2,10,2,9,13,12]
6. Bye Bye [7,7]
Create tokens for vocabulary based on frequency of occurrence. Hence, we assign the following tokens
I-1, books-2, computers-3, have-4, are-5, computers-6,bye-7, useful-8, are-9, and-10,interesting-11, valuable-12, both-13
Thankfully, in our dataset it is internally handled and each sentence is represented in such tokenized form.
#### Load data
```
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=vocabulary_size)
print('Number of reviews', len(X_train))
print('Length of first and fifth review before padding', len(X_train[0]) ,len(X_train[4]))
print('First review', X_train[0])
print('First label', y_train[0])
```
#### Preprocess data
Pad sequences in order to ensure that all inputs have same sentence length and dimensions.
```
X_train = sequence.pad_sequences(X_train, maxlen=max_review_length)
X_test = sequence.pad_sequences(X_test, maxlen=max_review_length)
print('Length of first and fifth review after padding', len(X_train[0]) ,len(X_train[4]))
```
### MODEL 1(a) : FEEDFORWARD NETWORKS WITHOUT EMBEDDINGS
Let us build a single layer feedforward net with 250 nodes. Each input would be a 500-dim vector of tokens since we padded all our sequences to size 500.
<b> EXERCISE </b> : Calculate the number of parameters involved in this network and implement a feedforward net to do classification without looking at cells below.
```
model = Sequential()
model.add(Dense(250, activation='relu',input_dim=max_review_length))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
```
#### Discussion : Why was the performance bad ? What was wrong with tokenization ?
### MODEL 1(b) : FEEDFORWARD NETWORKS WITH EMBEDDINGS
#### What is an embedding layer ?
An embedding is a linear projection from one vector space to another. We usually use embeddings to project the one-hot encodings of words on to a lower-dimensional continuous space so that the input surface is dense and possibly smooth. According to the model, an embedding layer is just a transformation from $\mathbb{R}^{inp}$ to $\mathbb{R}^{emb}$
```
embedding_dim = 100
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
#inputs will be converted from batch_size * sentence_length to batch_size*sentence_length*embedding _dim
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
# Fit the model
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
```
### MODEL 2 : CONVOLUTIONAL NEURAL NETWORKS
Text can be thought of as 1-dimensional sequence and we can apply 1-D Convolutions over a set of words. Let us walk through convolutions on text data with this blog.
http://debajyotidatta.github.io/nlp/deep/learning/word-embeddings/2016/11/27/Understanding-Convolutions-In-Text/
Fit a 1D convolution with 200 filters, kernel size 3 followed by a feedforward layer of 250 nodes and ReLU, sigmoid activations as appropriate.
```
# create the model
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=200, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
```
### MODEL 3 : SIMPLE RNN
Two of the best blogs that help understand the workings of a RNN and LSTM are
1. http://karpathy.github.io/2015/05/21/rnn-effectiveness/
2. http://colah.github.io/posts/2015-08-Understanding-LSTMs/
Mathematically speaking, a simple RNN does the following. It constructs a set of hidden states using the state variable from the previous timestep and the input at current time. Mathematically, a simpleRNN can be defined by the following relation.
<center>$h_t = \sigma(W([h_{t-1},x_{t}])+b)$
If we extend this recurrence relation to the length of sequences we have in hand, we have our RNN network constructed.
<img src="files/fig/LSTM_classification.jpg" width="400">
```
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(SimpleRNN(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
```
#### RNNs and vanishing/exploding gradients
Let us use sigmoid activations as example. Derivative of a sigmoid can be written as
<center> $\sigma'(x) = \sigma(x) \cdot \sigma(1-x)$. </center>
<img src = "files/fig/vanishing_gradients.png">
Remember RNN is a "really deep" feedforward network (when unrolled in time). Hence, backpropagation happens from $h_t$ all the way to $h_1$. Also realize that sigmoid gradients are multiplicatively dependent on the value of sigmoid. Hence, if the non-activated output of any layer $h_l$ is < 0, then $\sigma$ tends to 0, effectively "vanishing" gradient. Any layer that the current layer backprops to $H_{1:L-1}$ do not learn anything useful out of the gradients.
#### LSTMs and GRU
LSTM and GRU are two sophisticated implementations of RNN which essentially are built on what we call as gates. A gate is a probability number between 0 and 1. For instance, LSTM is built on these state updates
Note : L is just a linear transformation L(x) = W*x + b.
$f_t = \sigma(L([h_{t-1},x_t))$
$i_t = \sigma(L([h_{t-1},x_t))$
$o_t = \sigma(L([h_{t-1},x_t))$
$\hat{C}_t = \tanh(L([h_{t-1},x_t))$
$C_t = f_t * C_{t-1}+i_t*\hat{C}_t$ (Using the forget gate, the neural network can learn to control how much information it has to retain or forget)
$h_t = o_t * \tanh(c_t)$
### MODEL 4 : LSTM
In the next step, we will implement a LSTM model to do classification. Use the same architecture as before. Try experimenting with increasing the number of nodes, stacking multiple layers, applyong dropouts etc. Check the number of parameters that this model entails.
```
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
```
### MODEL 5 : CNN + LSTM
CNNs are good at learning spatial features and sentences can be thought of as 1-D spatial vectors (dimension being connotated by the sequence ordering among the words in the sentence.). We apply a LSTM over the features learned by the CNN (after a maxpooling layer). This leverages the power of CNNs and LSTMs combined. We expect the CNN to be able to pick out invariant features across the 1-D spatial structure(i.e. sentence) that characterize good and bad sentiment. This learned spatial features may then be learned as sequences by an LSTM layer followed by a feedforward for classification.
```
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=32, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
```
### CONCLUSION
We saw the power of sequence models and how they are useful in text classification. They give a solid performance, low memory footprint (thanks to shared parameters) and are able to understand and leverage the temporally connected information contained in the inputs. There is still an open debate about the performance vs memory benefits of CNNs vs RNNs in the research community.
## 2. 231+432 = 665.... It's not ? Let's ask our LSTM
In this exercise, we are going to teach addition to our model. Given two numbers (<999), the model outputs their sum (<9999). The input is provided as a string '231+432' and the model will provide its output as ' 663' (Here the empty space is the padding character). We are not going to use any external dataset and are going to construct our own dataset for this exercise.
The exercise we attempt to do effectively "translates" a sequence of characters '231+432' to another sequence of characters ' 663' and hence, this class of models are called sequence-to-sequence models. Such architectures have profound applications in several real-life tasks such as machine translation, summarization, image captioning etc.
```
from __future__ import print_function
from keras.models import Sequential
from keras import layers
from keras.layers import Dense, RepeatVector, TimeDistributed
import numpy as np
from six.moves import range
```
#### The less interesting data generation and preprocessing
```
class CharacterTable(object):
def __init__(self, chars):
self.chars = sorted(set(chars))
self.char_indices = dict((c, i) for i, c in enumerate(self.chars))
self.indices_char = dict((i, c) for i, c in enumerate(self.chars))
#One-hot encodes
def encode(self, C, num_rows):
x = np.zeros((num_rows, len(self.chars)))
for i, c in enumerate(C):
x[i, self.char_indices[c]] = 1
return x
#Decodes a one-hot encoding
def decode(self, x, calc_argmax=True):
if calc_argmax:
x = x.argmax(axis=-1)
return ''.join(self.indices_char[x] for x in x)
TRAINING_SIZE = 50000
DIGITS = 3
MAXOUTPUTLEN = DIGITS + 1
MAXLEN = DIGITS + 1 + DIGITS
chars = '0123456789+ '
ctable = CharacterTable(chars)
def return_random_digit():
return np.random.choice(list('0123456789'))
def generate_number():
num_digits = np.random.randint(1, DIGITS + 1)
return int(''.join( return_random_digit()
for i in range(num_digits)))
def data_generate(num_examples):
questions = []
expected = []
seen = set()
print('Generating data...')
while len(questions) < TRAINING_SIZE:
a, b = generate_number(), generate_number()
#Remove already seen elements
key = tuple(sorted((a, b)))
if key in seen:
continue
seen.add(key)
# Pad the data with spaces such that it is always MAXLEN.
q = '{}+{}'.format(a, b)
query = q + ' ' * (MAXLEN - len(q))
ans = str(a + b)
# Answers can be of maximum size DIGITS + 1.
ans += ' ' * (MAXOUTPUTLEN - len(ans))
questions.append(query)
expected.append(ans)
print('Total addition questions:', len(questions))
return questions, expected
def encode_examples(questions,answers):
x = np.zeros((len(questions), MAXLEN, len(chars)), dtype=np.bool)
y = np.zeros((len(questions), DIGITS + 1, len(chars)), dtype=np.bool)
for i, sentence in enumerate(questions):
x[i] = ctable.encode(sentence, MAXLEN)
for i, sentence in enumerate(answers):
y[i] = ctable.encode(sentence, DIGITS + 1)
indices = np.arange(len(y))
np.random.shuffle(indices)
return x[indices],y[indices]
q,a = data_generate(TRAINING_SIZE)
x,y = encode_examples(q,a)
split_at = len(x) - len(x) // 10
x_train, x_val, y_train, y_val = x[:split_at], x[split_at:],y[:split_at],y[split_at:]
print('Training Data shape:')
print('X : ', x_train.shape)
print('Y : ', y_train.shape)
print('Sample Question(in encoded form) : ', x_train[0], y_train[0])
print('Sample Question(in decoded form) : ', ctable.decode(x_train[0]),'Sample Output : ', ctable.decode(y_train[0]))
```
#### Let's learn two wrapper functions in Keras - TimeDistributed and RepeatVector with some dummy examples.
**TimeDistributed** is a wrapper function call that applies an input operation on all the timesteps of an input data. For instance I have a feedforward network which converts a 10-dim vector to a 5-dim vector, then wrapping this timedistributed layer on that feedforward operation would convert a batch_size \* sentence_len \* vector_len(=10) to batch_size \* sentence_len \* output_len(=5)
```
model = Sequential()
#Inputs to it will be batch_size*time_steps*input_vector_dim(to Dense) . Output will be batch_size*time_steps* output_vector_dim
#Here dense converts a 5-dim input vector to a 8-dim vector.
model.add(TimeDistributed(Dense(8), input_shape=(3, 5)))
input_array = np.random.randint(10, size=(1,3,5))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)
```
**RepeatVector** repeats the vector a specified number of times. Dimension changes from batch_size * number of elements to batch_size* number of repetitions * number of elements.
```
model = Sequential()
#converts from 1*10 to 1 * 6
model.add(Dense(6, input_dim=10))
print(model.output_shape)
#converts from 1*6 to 1*3*6
model.add(RepeatVector(3))
print(model.output_shape)
input_array = np.random.randint(1000, size=(1, 10))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)
# note: `None` is the batch dimension
print('Input : ', input_array[0])
print('Output : ', output_array[0])
```
### MODEL ARCHITECTURE
<img src="files/fig/LSTM_addition.jpg" width="400">
Note : Whenever you are initializing a LSTM in Keras, by the default the option return_sequences = False. This means that at the end of the step the next component will only get to see the final hidden layer's values. On the other hand, if you set return_sequences = True, the LSTM component will return the hidden layer at each time step. It means that the next component should be able to consume inputs in that form.
Think how this statement is relevant in terms of this model architecture and the TimeDistributed module we just learned.
Build an encoder and decoder both single layer 128 nodes and an appropriate dense layer as needed by the model.
```
#Hyperaparams
RNN = layers.LSTM
HIDDEN_SIZE = 128
BATCH_SIZE = 128
LAYERS = 1
print('Build model...')
model = Sequential()
#ENCODING
model.add(RNN(HIDDEN_SIZE, input_shape=(MAXLEN, len(chars))))
model.add(RepeatVector(MAXOUTPUTLEN))
#DECODING
for _ in range(LAYERS):
model.add(RNN(HIDDEN_SIZE, return_sequences=True))
model.add(TimeDistributed(layers.Dense(len(chars), activation='softmax')))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model.summary()
```
Let's check how well our model trained.
```
for iteration in range(1, 2):
print()
model.fit(x_train, y_train,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(x_val, y_val))
# Select 10 samples from the validation set at random so we can visualize
# errors.
print('Finished iteration ', iteration)
numcorrect = 0
numtotal = 20
for i in range(numtotal):
ind = np.random.randint(0, len(x_val))
rowx, rowy = x_val[np.array([ind])], y_val[np.array([ind])]
preds = model.predict_classes(rowx, verbose=0)
q = ctable.decode(rowx[0])
correct = ctable.decode(rowy[0])
guess = ctable.decode(preds[0], calc_argmax=False)
print('Question', q, end=' ')
print('True', correct, end=' ')
print('Guess', guess, end=' ')
if guess == correct :
print('Good job')
numcorrect += 1
else:
print('Fail')
print('The model scored ', numcorrect*100/numtotal,' % in its test.')
```
#### EXERCISE
* Try changing the hyperparams, use other RNNs, more layers, check if increasing the number of epochs is useful.
* Try reversing the data from validation set and check if commutative property of addition is learned by the model. Try printing the hidden layer with two inputs that are commutative and check if the hidden representations it learned are same or similar. Do we expect it to be true ? If so, why ? If not why ? You can access the layer using an index with model.layers and layer.output will give the output of that layer.
* Try doing addition in the RNN model the same way we do by hand. Reverse the order of digits and at each time step, input two digits get an output use the hidden layer and input next two digits and so on.(units in the first time step, tens in the second time step etc.)
|
github_jupyter
|
# RUN THIS CELL TO PROPERLY HIGHLIGHT THE EXERCISES
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2019-CS109B/master/content/styles/cs109.css").text
HTML(styles)
import numpy
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM, SimpleRNN
from keras.layers.embeddings import Embedding
from keras.layers import Flatten
from keras.preprocessing import sequence
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
from keras.layers.embeddings import Embedding
import numpy as np
# fix random seed for reproducibility
numpy.random.seed(1)
# We want to have a finite vocabulary to make sure that our word matrices are not arbitrarily small
vocabulary_size = 10000
#We also want to have a finite length of reviews and not have to process really long sentences.
max_review_length = 500
(X_train, y_train), (X_test, y_test) = imdb.load_data(num_words=vocabulary_size)
print('Number of reviews', len(X_train))
print('Length of first and fifth review before padding', len(X_train[0]) ,len(X_train[4]))
print('First review', X_train[0])
print('First label', y_train[0])
X_train = sequence.pad_sequences(X_train, maxlen=max_review_length)
X_test = sequence.pad_sequences(X_test, maxlen=max_review_length)
print('Length of first and fifth review after padding', len(X_train[0]) ,len(X_train[4]))
model = Sequential()
model.add(Dense(250, activation='relu',input_dim=max_review_length))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
embedding_dim = 100
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
#inputs will be converted from batch_size * sentence_length to batch_size*sentence_length*embedding _dim
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
# Fit the model
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=2, batch_size=128, verbose=2)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
# create the model
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=200, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(250, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(SimpleRNN(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
model = Sequential()
model.add(Embedding(vocabulary_size, embedding_dim, input_length=max_review_length))
model.add(Conv1D(filters=32, kernel_size=3, padding='same', activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, epochs=3, batch_size=64)
# Final evaluation of the model
scores = model.evaluate(X_test, y_test, verbose=0)
print("Accuracy: %.2f%%" % (scores[1]*100))
from __future__ import print_function
from keras.models import Sequential
from keras import layers
from keras.layers import Dense, RepeatVector, TimeDistributed
import numpy as np
from six.moves import range
class CharacterTable(object):
def __init__(self, chars):
self.chars = sorted(set(chars))
self.char_indices = dict((c, i) for i, c in enumerate(self.chars))
self.indices_char = dict((i, c) for i, c in enumerate(self.chars))
#One-hot encodes
def encode(self, C, num_rows):
x = np.zeros((num_rows, len(self.chars)))
for i, c in enumerate(C):
x[i, self.char_indices[c]] = 1
return x
#Decodes a one-hot encoding
def decode(self, x, calc_argmax=True):
if calc_argmax:
x = x.argmax(axis=-1)
return ''.join(self.indices_char[x] for x in x)
TRAINING_SIZE = 50000
DIGITS = 3
MAXOUTPUTLEN = DIGITS + 1
MAXLEN = DIGITS + 1 + DIGITS
chars = '0123456789+ '
ctable = CharacterTable(chars)
def return_random_digit():
return np.random.choice(list('0123456789'))
def generate_number():
num_digits = np.random.randint(1, DIGITS + 1)
return int(''.join( return_random_digit()
for i in range(num_digits)))
def data_generate(num_examples):
questions = []
expected = []
seen = set()
print('Generating data...')
while len(questions) < TRAINING_SIZE:
a, b = generate_number(), generate_number()
#Remove already seen elements
key = tuple(sorted((a, b)))
if key in seen:
continue
seen.add(key)
# Pad the data with spaces such that it is always MAXLEN.
q = '{}+{}'.format(a, b)
query = q + ' ' * (MAXLEN - len(q))
ans = str(a + b)
# Answers can be of maximum size DIGITS + 1.
ans += ' ' * (MAXOUTPUTLEN - len(ans))
questions.append(query)
expected.append(ans)
print('Total addition questions:', len(questions))
return questions, expected
def encode_examples(questions,answers):
x = np.zeros((len(questions), MAXLEN, len(chars)), dtype=np.bool)
y = np.zeros((len(questions), DIGITS + 1, len(chars)), dtype=np.bool)
for i, sentence in enumerate(questions):
x[i] = ctable.encode(sentence, MAXLEN)
for i, sentence in enumerate(answers):
y[i] = ctable.encode(sentence, DIGITS + 1)
indices = np.arange(len(y))
np.random.shuffle(indices)
return x[indices],y[indices]
q,a = data_generate(TRAINING_SIZE)
x,y = encode_examples(q,a)
split_at = len(x) - len(x) // 10
x_train, x_val, y_train, y_val = x[:split_at], x[split_at:],y[:split_at],y[split_at:]
print('Training Data shape:')
print('X : ', x_train.shape)
print('Y : ', y_train.shape)
print('Sample Question(in encoded form) : ', x_train[0], y_train[0])
print('Sample Question(in decoded form) : ', ctable.decode(x_train[0]),'Sample Output : ', ctable.decode(y_train[0]))
model = Sequential()
#Inputs to it will be batch_size*time_steps*input_vector_dim(to Dense) . Output will be batch_size*time_steps* output_vector_dim
#Here dense converts a 5-dim input vector to a 8-dim vector.
model.add(TimeDistributed(Dense(8), input_shape=(3, 5)))
input_array = np.random.randint(10, size=(1,3,5))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)
model = Sequential()
#converts from 1*10 to 1 * 6
model.add(Dense(6, input_dim=10))
print(model.output_shape)
#converts from 1*6 to 1*3*6
model.add(RepeatVector(3))
print(model.output_shape)
input_array = np.random.randint(1000, size=(1, 10))
print("Shape of input : ", input_array.shape)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print("Shape of output : ", output_array.shape)
# note: `None` is the batch dimension
print('Input : ', input_array[0])
print('Output : ', output_array[0])
#Hyperaparams
RNN = layers.LSTM
HIDDEN_SIZE = 128
BATCH_SIZE = 128
LAYERS = 1
print('Build model...')
model = Sequential()
#ENCODING
model.add(RNN(HIDDEN_SIZE, input_shape=(MAXLEN, len(chars))))
model.add(RepeatVector(MAXOUTPUTLEN))
#DECODING
for _ in range(LAYERS):
model.add(RNN(HIDDEN_SIZE, return_sequences=True))
model.add(TimeDistributed(layers.Dense(len(chars), activation='softmax')))
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
model.summary()
for iteration in range(1, 2):
print()
model.fit(x_train, y_train,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(x_val, y_val))
# Select 10 samples from the validation set at random so we can visualize
# errors.
print('Finished iteration ', iteration)
numcorrect = 0
numtotal = 20
for i in range(numtotal):
ind = np.random.randint(0, len(x_val))
rowx, rowy = x_val[np.array([ind])], y_val[np.array([ind])]
preds = model.predict_classes(rowx, verbose=0)
q = ctable.decode(rowx[0])
correct = ctable.decode(rowy[0])
guess = ctable.decode(preds[0], calc_argmax=False)
print('Question', q, end=' ')
print('True', correct, end=' ')
print('Guess', guess, end=' ')
if guess == correct :
print('Good job')
numcorrect += 1
else:
print('Fail')
print('The model scored ', numcorrect*100/numtotal,' % in its test.')
| 0.756088 | 0.972805 |
```
!pip install qiskit
```
# General Tech Versions/Info
- **Python:** 3.7.10
- **Qiskit**: {'qiskit': '0.24.0',
'qiskit-aer': '0.7.6',
'qiskit-aqua': '0.8.2',
'qiskit-ibmq-provider': '0.12.1',
'qiskit-ignis': '0.5.2',
'qiskit-terra': '0.16.4'}
- Run on Google Colab
- Requires 20 qubits + 6 bits
```
from qiskit import (
IBMQ,
QuantumCircuit,
execute,
Aer,
QuantumRegister,
ClassicalRegister,
transpile,
)
from qiskit.ignis.mitigation.measurement import complete_meas_cal, tensored_meas_cal, CompleteMeasFitter,TensoredMeasFitter
from qiskit.test.mock import FakeSydney, FakeMontreal
import numpy as np
import math
import random
import time
import pandas as pd
# CNOT gates for applying the Steane Code
CNOT_GATES = [[1,0], [1,4], [1,5], [2,0], [2,4], [2,6], [3,4], [3,5],[3,6],[7, 12],[7, 13],[8,7] ,[8, 11],[8, 12], [9,7],[9, 11],[9, 13],[10, 11],[10, 12],[10, 13]]
REV_CNOT_GATES = [[10, 13],[10, 12],[10, 11],[9, 13],[9, 11],[9,7],[8, 12],[8, 11],[8,7],[7, 13],[7, 12],[3,6],[3,5],[3,4],[2,6],[2,4],[2,0],[1,5],[1,4],[1,0]]
```
#User Defined Values
Please edit these values before running on quantum computer:
```
# COMPUTATION CONFIGURATIONS
NUM_SHOTS = 1
NUM_DIFF_PROGRAMS = 1
NUM_ITERATIONS = 1
NUM_RANDOM_ITERATIONS = 1
# SPECIFY NUMBER OF RANDOM SEEDS FOR TRANSPILING QUANTUM CIRCUITS
NUM_SEEDS = 150
# SET PHYSICAL TO VIRTUAL QUBIT MAPPING OF QUANTUM MACHINE
unpermuted_layout = [8,11,13,19,14,20,16,1,2,7,12,6,4,10]
syndrome_layout = [5,9,18,0,3,15]
# SET LOCATION FOR SAVING DATA
from google.colab import drive
drive.mount('/content/drive')
# SET FILENAMES FOR DATA SAVING
filename_0 = "/content/drive/My Drive/Results/general_info_20Q.txt"
filename_error = "/content/drive/My Drive/Results/error_results_20Q.csv"
filename_mit = "/content/drive/My Drive/Results/mit_results_20Q.csv"
filename_decoded = "/content/drive/My Drive/Results/decoded_results_20Q.csv"
# SET QUANTUM COMPUTER BACKEND OF YOUR CHOICE
fake_mtrl = FakeMontreal()
# BACKEND = AerSimulator.from_backend(fake_mtrl)
BACKEND = Aer.get_backend('qasm_simulator')
```
# Server Class (Main Code)
```
class Server():
def __init__(self):
print('Server initialized')
def generate_point(self, size=14):
"""
Generate a random point as password
Parameters:
size (int): number of qubits in circuit to be encrypted
Returns:
point (str): the combination of key1 and key2 in binary form
key1 ([int]): permutation key in integer form
key2 ([[int], [int]]): one-time pad component of the password, comprised of the x key and z key respectively
"""
# get permutation key
bin_key1, key1 = self.generate_permutation_key()
# get OTP key
x_key = np.random.randint(2, size=size)
z_key = np.random.randint(2, size=size)
key2 = [x_key.tolist(), z_key.tolist()]
# combine keys to get point
a = ''.join(bin_key1)
b = ''.join(map(str, x_key.tolist()))
c = ''.join(map(str,z_key.tolist()))
point = a+b+c
return point, key1, key2
def generate_permutation_key(self, size=14):
"""
Generate a random permutation of list(range(size))
Parameters:
size (int): size of list
Returns:
key ([str]): the permuted list in binary form
dec_key ([int]): the permuted list in decimal form
"""
key_dec = list(range(size))
rng = np.random.default_rng()
rng.shuffle(key_dec)
f = '0' + str(math.ceil(math.log2(size))) + 'b'
# get the permutation in binary form
key = [format(x, f) for x in key_dec]
return key, key_dec
def sample_challenge_point(self, point, size=14):
"""
Sample a random point q from the distribution in which with approx.
probability 0.5, point (the parameter) is sampled,
and with approx. probability 0.5, a random point excluding point (the parameter) is uniformly chosen
Parameters:
point (str): the point that will be sampled with probability 0.5 in the distribution
size (int): number of qubits that point encrypts for
Returns:
sample (str): challenge point taken from distribution
"""
# generate a random valid point that has a permutation and one-time pad keys
key1, key_dec = self.generate_permutation_key()
key1 = "".join(key1)
key2_dec = random.randint(0, (2**(size*2))-1)
key2_bin = format(key2_dec,'0'+str(size*2)+'b')
random_point = str(key1) + str(key2_bin)
# keep sampling for a random point uniformly until the random_point is not equivalent to point
while random_point == point:
key2_dec = random.randint(0, (2**(size*2))-1)
key2_bin = format(key2_dec,'0'+str(size*2)+'b')
random_point = str(key1) + str(key2_bin)
# sample from challenge distribution in which with approx. 50%, random_point is selected, and 50%, point is selected
sample = np.random.choice([random_point, point])
return sample
def protect(self, permuted_cnots, hadamards, x_key, z_key, init_data = [0,0,0,0,0,0,0,'+',0,0,0,0,0,0], size=14):
"""
Encodes a program
Parameters:
permuted_cnots ([[int,int]]): all permuted CNOT gates to be applied
hadamards ([int]): all hadamard gates to be applied
x_key ([int]): all pauli-X gates to be applied
z_key ([int]): all pauli-Z gates to be applied
init_data (list): initialized qubit states
size (int): size of the quantum circuit
Returns:
circuit (qiskit's QuantumCircuit): encoded program
"""
# initialize quantum circuit
qr = QuantumRegister(size)
circuit = QuantumCircuit(qr)
# initialize the states of the quantum circuit
for i in range(size):
if init_data[i] == '+':
circuit.h(i)
elif init_data[i] == 1:
circuit.x(i)
elif init_data[i] == '-':
circuit.x(i)
circuit.h(i)
circuit.barrier()
# apply delegated one-time pad
for i in range(size):
if x_key[i] == 1 and init_data[i] == 0:
circuit.x(i)
elif z_key[i] == 1 and init_data[i] == '+':
circuit.z(i)
circuit.barrier()
# apply hadamard gates
for i in hadamards:
circuit.h(i)
circuit.barrier()
# apply cnot gates
for cnots in permuted_cnots:
circuit.cx(cnots[0], cnots[1])
circuit.barrier()
return circuit
def get_syndrome_circuit(self, challenge_input, program, size=14, syndrome_cnots =[[0, 14], [2, 14], [4, 14], [6, 14], [1, 15], [2, 15], [5, 15], [6, 15], [3, 16], [4, 16], [5, 16], [6, 16], [7, 17], [9, 17], [11, 17], [13, 17], [8, 18], [9, 18], [12, 18], [13, 18], [10, 19], [11, 19], [12, 19], [13, 19]]):
"""
Creates a circuit that detects for single bit and phase flip errors
Parameters:
challenge_input (str): point used to decrypt program
program (qiskit's QuantumCircuit): program for finding error syndromes
size (int): the number of qubits in the program
syndrome_cnots ([int,int]): CNOT gates for obtaining error syndromes
Returns:
syndrome_circuit (qiskit's QuantumCircuit): program for calculating error syndromes
"""
key1, key2 = self.point_to_keys(challenge_input)
# initialize quantum circuit
qr = QuantumRegister(size+int(size/7*3))
cr = ClassicalRegister(size+int(size/7*3))
syndrome_circuit = QuantumCircuit(qr, cr)
# add program to new quantum circuit
syndrome_circuit.append(program, range(size))
# apply gates to decrypt the circuit
for i in range(size,size+int(size/7*3)):
syndrome_circuit.h(i)
for gate in syndrome_cnots:
syndrome_circuit.cx(gate[1], key1.index(gate[0]))
for i in range(size,size+int(size/7*3)):
syndrome_circuit.h(i)
syndrome_circuit.barrier()
syndrome_circuit.measure(qr,cr)
return syndrome_circuit
def get_syndrome_circuit_mit_measures(self, mit_values, challenge_input, program, size=14, syndrome_cnots =[[0, 14], [2, 14], [4, 14], [6, 14], [1, 15], [2, 15], [5, 15], [6, 15], [3, 16], [4, 16], [5, 16], [6, 16], [7, 17], [9, 17], [11, 17], [13, 17], [8, 18], [9, 18], [12, 18], [13, 18], [10, 19], [11, 19], [12, 19], [13, 19]]):
"""
Creates a circuit that detects bit and phase flip errors but measures only a subset of qubits;
Used for tensored error mitigation
Parameters:
mit_values ([int]): subset of qubits to be measured
challenge_input (str): point used to decrypt program
program (qiskit's QuantumCircuit): program for finding error syndromes
size (int): the number of qubits in the program
syndrome_cnots ([int,int]): CNOT gates for obtaining error syndromes
Returns:
syndrome_program (qiskit's QuantumCircuit): program for calculating error syndromes with partial qubit measurement
"""
key1, key2 = self.point_to_keys(challenge_input)
qr = QuantumRegister(size+int(size/7*3))
cr = ClassicalRegister(len(mit_values))
syndrome_program = QuantumCircuit(qr, cr)
syndrome_program.append(program, range(size))
for i in range(size,size+int(size/7*3)):
syndrome_program.h(i)
for gate in syndrome_cnots:
syndrome_program.cx(gate[1], key1.index(gate[0]))
for i in range(size,size+int(size/7*3)):
syndrome_program.h(i)
syndrome_program.barrier()
for i in range(len(mit_values)):
syndrome_program.measure(qr[mit_values[i]], cr[i])
return syndrome_program
def point_to_keys(self, point, size=14):
"""
Derives the permutation and one-time pad keys from a point
Parameters:
point(str): point for deriving keys from
size (int): number of qubits in program
Returns:
circuit (circuit): protected program
"""
inc = math.ceil(math.log2(size))
key1 = [int(point[i:i+inc],2) for i in range(0, len(point[:-size*2]), inc)]
key2_x = [int(value) for value in point[-size*2:-size]]
key2_z = [int(value) for value in point[-size:]]
return key1, [key2_x, key2_z]
def permute_classical(self, key1, orig_cnots, hadamards = [1,2,3,8,9,10], size=14):
"""
Provides the locations of CNOT and Hadamard gates based on a permutated list
Parameters:
key1 ([int]): permutated list
orig_cnots ([[int,int]]): the location of unpermuted CNOT gates
hadamards ([int]): the location of unpermuted Hadamard gates
size (int): number of qubits in program
Returns:
new_cnot_gates ([[int,int]]): permuted CNOT gates
new_hadamard_gates ([int]): permuted Hadamard gates
"""
new_hadamard_gates = [0]*len(hadamards)
new_cnot_gates = [0]*len(orig_cnots)
for i in range(len(orig_cnots)):
new_cnot_gates[i] = [key1.index(orig_cnots[i][0]), key1.index(orig_cnots[i][1])]
for i in range(len(hadamards)):
new_hadamard_gates[i] = key1.index(hadamards[i])
return new_cnot_gates, new_hadamard_gates
def get_OTP_classical_key(self, key, permutation_key, cnots, hadamards):
"""
Gets the delegated one-time pad key, where the one-time pad key is delegated to the beginning of the program
Parameters:
key ([[int],[int]]): the one-time pad key to be delegated
permutation_key ([int]): permutation
cnots ([[int,int]]): all CNOT gates
hadamards ([int]): all Hadamard gates
Returns:
new_x_key ([int]): delegated Pauli-X gates of one-time pad
new_z_key ([int]): delegated Pauli-Z gates of one-time pad
"""
x_key = key[0]
z_key = key[1]
for cnot in cnots:
a = x_key[cnot[0]]
b = z_key[cnot[0]]
c = x_key[cnot[1]]
d = z_key[cnot[1]]
x_key[cnot[0]] = a
z_key[cnot[0]] = b+d
x_key[cnot[1]] = a+c
z_key[cnot[1]] = d
for i in hadamards:
x_key[i], z_key[i] = z_key[i], x_key[i]
new_x_key = [i%2 for i in x_key]
new_z_key = [i%2 for i in z_key]
return new_x_key, new_z_key
def undo_circuit(self, point, program, rev_cnots=[[3,6],[3,5],[3,4],[2,6],[2,4],[2,0],[1,5],[1,4],[1,0],[0,6],[0,5],[10, 13],[10, 12],[10, 11],[9, 13],[9, 11],[9, 7],[8, 12],[8, 11],[8, 7],[7, 13],[7, 12]], size=14):
"""
Applies all the operations in reverse order as to undo the original program
Parameters:
point (str): the point for encoding the program
program (qiskit's QuantumCircuit): circuit to be undoed
rev_cnots ([[int,int]]): the reverse sequence of CNOT gates that were applied in the program
size (int): number of qubits in program
Returns:
undo_circuit (qiskit's QuantumCircuit): the program that has been undoed
"""
key1, key2 = self.point_to_keys(point)
permuted_cnots, hg = self.permute_classical(key1, rev_cnots)
qr = QuantumRegister(size)
cr_trap = ClassicalRegister(size)
undo_circuit = QuantumCircuit(qr, cr_trap)
undo_circuit.append(program, range(size))
for cnot in permuted_cnots:
undo_circuit.cx(cnot[0], cnot[1])
undo_circuit.barrier()
for gate in hg:
undo_circuit.h(gate)
undo_circuit.barrier()
undo_circuit.measure(qr, cr_trap)
return undo_circuit
def reverse_cnots(self, cnots):
"""
Reverse the order of CNOTs
Parameters:
cnots ([[int,int]]): original order of cnots
Returns:
rev_cnots ([[int,int]]): reversed order of cnots
"""
rev_cnots = []
for i in range(len(cnots)):
rev_cnots.append(cnots[len(cnots)-i-1])
return rev_cnots
def get_random_mit_pattern_single(self, size=20, num_qubits = 10):
"""
Selected single qubit pattern for tensored error mitigation
Parameters:
size(int): total number of qubits in the program
num_qubits(int): number of qubits to be selected
Returns:
mit_pattern (list): pattern for tensored error mitigation, comprised of single qubits
mit_values ([int]): a random subset of all qubits in mit_pattern
"""
mit_vals = random.sample(list(range(size)),num_qubits)
mit_pattern = [[x] for x in mit_vals]
return mit_pattern, mit_vals
def get_permuted_cnots(self, permutation_key, cnots):
"""
Gets the permuted set of CNOTs to be applied for the syndrome programs
Parameters:
permutation_key([int]): permutation
cnots([[int,int]]): CNOT gates to be applied
Returns:
new_permuted_cnots ([[int,int]]): permutation of CNOT gates
"""
num_aux_qubits = int((len(permutation_key)/7)*3)
# get the list of auxiliary qubits for obtaining error syndromes
aux_qubits = list(range(len(permutation_key),len(permutation_key)+num_aux_qubits))
key = permutation_key + aux_qubits
new_permuted_cnots = [0]*len(cnots)
for i in range(len(cnots)):
new_permuted_cnots[i] = [key.index(cnots[i][0]), key.index(cnots[i][1])]
return new_permuted_cnots
def get_random_mit_pattern_all(self, permutation_key, steane_cnots = [[1,0], [1,4], [1,5], [2,0], [2,4], [2,6], [3,4], [3,5],[3,6],[7, 12],[7, 13],[8,7] ,[8, 11],[8, 12], [9,7],[9, 11],[9, 13],[10, 11],[10, 12],[10, 13]], syndrome_cnots = [[14, 0], [14, 2], [14, 4], [14, 6], [15, 1], [15, 2], [15, 5], [15, 6], [16, 3], [16, 4], [16, 5], [16, 6], [17, 7], [17, 9], [17, 11], [17, 13], [18, 8], [18, 9], [18, 12], [18, 13], [19, 10], [19, 11], [19, 12], [19, 13]], size=20, num_qubits = 10):
"""
Selected single and double qubit patterns for tensored error mitigation
Parameters:
permutation_key([int]): permutation
steane_cnots ([[int,int]]): all cnot gates for the Steane encoding
syndrome_cnots ([[int,int]]): all cnot gates for calculating the error syndromes
size(int): total number of qubits in the program
num_qubits(int): number of qubits to be selected
Returns:
mit_pattern (list): pattern for tensored error mitigation, comprised of single and qubit pairs
mit_values ([int]): a random subset of all qubits in mit_pattern
"""
permuted_steane_cnots = self.get_permuted_cnots(permutation_key, steane_cnots)
permuted_syndrome_cnots = self.get_permuted_cnots(permutation_key, syndrome_cnots)
cnots = permuted_steane_cnots + permuted_syndrome_cnots
# number of qubit pairs to include in pattern
num_cnots = random.choice(range(10//2))
count = 0
cnot_pairs = []
cnot_values = []
while count != num_cnots:
val = random.choice(range(len(cnots)))
if cnots[val] not in cnot_pairs:
if cnots[val][0] not in cnot_values and cnots[val][1] not in cnot_values:
cnot_pairs.append(cnots[val])
cnot_values.append(cnots[val][0])
cnot_values.append(cnots[val][1])
count = count +1
singles = random.sample(set(list(range(20)))-set(cnot_values),num_qubits-(num_cnots*2))
s = [[x] for x in singles[:]]
mit_values = cnot_values + singles
mit_patterns = cnot_pairs + s
return mit_patterns,mit_values
def prepare_meas_filter(self, mit_pattern, backend, num_shots, size=20):
"""
Prepare a tensored error mitigation measurement filter based on specified mit_pattern
Parameters:
mit_pattern([int]): pattern used for tensored error mitigation
backend(qiskit's IBMQBackend): specified backend for preparing measurement filter
num_shots(int): number of shots for backend
size(int): number of qubits in program
Returns:
meas_filter (qiskit's TensoredMeasFitter.filter): prepared measurement filter
"""
qr = QuantumRegister(size)
qulayout = range(size)
meas_calibs, state_labels = tensored_meas_cal(mit_pattern=mit_pattern, qr=qr, circlabel='mcal')
for circ in meas_calibs:
print(circ.name)
job = execute(meas_calibs, backend=backend, shots=num_shots)
cal_results = job.result()
meas_fitter = TensoredMeasFitter(cal_results, mit_pattern=mit_pattern)
meas_filter = meas_fitter.filter
return meas_filter
```
#Tests
```
# initiate the server
server = Server()
start = time.time()
fields = ['is_point', 'point_value', 'challenge_point_value', 'key_1', 'key_2', 'challenge_key_1', 'challenge_key_2', 'mit_pattern_single','mit_pattern_all']
results_info = pd.DataFrame(columns=fields)
results_info_decoded = pd.DataFrame(columns=fields)
sp_list= []
sp_mit_single_list =[]
sp_mit_all_list = []
dp_list = []
meas_filter_singles = []
meas_filter_alls = []
def get_programs_for_test(server, challenge_input, program, permutation_key,sp_list, sp_mit_single_list, sp_mit_all_list,dp_list, meas_filter_singles, meas_filter_alls, rev_cnots=REV_CNOT_GATES, backend=BACKEND, num_shots=NUM_SHOTS):
"""
Prepares circuits for execution
Parameters:
server (Server): Server instance
challenge_input (str): challenge point for testing programs
program (qiskit's QuantumCicuit): the encoded program for applying tests
permutation_key ([int]): permutation ordering
sp_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits
sp_mit_single_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits with partial measurement and single qubit patterns
sp_mit_all_list ([qiskit's QuantumCircuits]): list of prepared quantum circuits with syndromes with partial measurement and single and qubit pair patterns
dp_list ([qiskit's QuantumCircuits]): list of prepared undoed quantum circuits
meas_filter_singles ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_single_list circuits
meas_filter_alls ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_all_list circuits
rev_cnots ([[int,int]]): cnot gates to be applied for undoing the circuit
backend (qiskit's IBMQBackend): specified backend for preparing measurement filter
num_shots (int): number of shots for backend
Returns:
sp_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits
sp_mit_single_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits with partial measurement and single qubit patterns
sp_mit_all_list ([qiskit's QuantumCircuits]): list of prepared quantum circuits with syndromes with partial measurement and single and double qubit patterns
dp_list ([qiskit's QuantumCircuits]): list of prepared undoed quantum circuits
meas_filter_singles ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_single_list circuits
meas_filter_alls ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_all_list circuits
mit_pattern_s ([[int]]): subset of single qubits used in tensored error mitigation, based on the circuits sp_mit_single_list
mit_pattern_all (list): subset of single and double qubits used in tensored error mitigation, based on the circuits sp_mit_all_list
"""
syndrome_program = server.get_syndrome_circuit(challenge_input,program)
mit_pattern_s, mit_val_s = server.get_random_mit_pattern_single()
mit_pattern_all, mit_val_all = server.get_random_mit_pattern_all(permutation_key)
syndrome_program_mit_single = server.get_syndrome_circuit_mit_measures(mit_val_s, challenge_input, program)
syndrome_program_mit_all = server.get_syndrome_circuit_mit_measures(mit_val_all,challenge_input,program)
decoded_program = server.undo_circuit(challenge_input, program, rev_cnots=rev_cnots)
meas_filter_s = server.prepare_meas_filter(mit_pattern_s, backend, num_shots)
meas_filter_all = server.prepare_meas_filter(mit_pattern_all, backend, num_shots)
sp_list = sp_list + [syndrome_program]
sp_mit_single_list =sp_mit_single_list + [syndrome_program_mit_single]
sp_mit_all_list = sp_mit_all_list + [syndrome_program_mit_all]
dp_list = dp_list + [decoded_program]
meas_filter_singles = meas_filter_singles + [meas_filter_s]
meas_filter_alls = meas_filter_alls + [meas_filter_all]
return sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all
def prepare_for_test(server, cnots = CNOT_GATES):
"""
Prepare inputs for test
Parameters:
server (Server): instance of Server for preparing inputs
cnots ([[int,int]]): cnot gates to be applied
Returns:
p (str): point
k1 ([int]): permutation key
key2 ([[int],[int]]): one-time pad key
permuted_cnots([[int,int]]): cnot gates post permutation
permuted_hadamards ([int]): hadamard gates post permutation
x_key ([int]): all delegated pauli-X gates to be applied for one-time pad (key2)
z_key ([int]): all delegated pauli-Z gates to be applied for one-time pad (key2)
data (list): qubits' intial states
"""
p, k1, k2 = server.generate_point()
key2 = [k2[0][:], k2[1][:]]
permuted_cnots, permuted_hadamards = server.permute_classical(k1, cnots)
rev = server.reverse_cnots(permuted_cnots)
x_key, z_key = server.get_OTP_classical_key(k2,k1, rev,permuted_hadamards)
data = [0]*14
data[k1.index(7)] = '+'
return p, k1, key2, permuted_cnots, permuted_hadamards, x_key, z_key, data
```
> ### Test 1.1: Point = Challenge Input Correctness Check
```
print("_____________PART A: Challenge Input == Point_____________")
for i in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# set challenge_input
challenge_input = p
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = i*NUM_ITERATIONS+k
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
```
> ### Test 1.2: Point != Challenge Input, w/ 1 permutation error Correctness Check
```
print("\n_____________PART B: Challenge Input != Point - one Permutation Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,2,False)
edited_k1 = k1[:]
edited_k1[i[0]], edited_k1[i[1]] = k1[i[1]], k1[i[0]]
f = '0' + str(math.ceil(math.log2(14))) + 'b'
new_key1 = [format(x, f) for x in edited_k1]
challenge_input = str("".join(new_key1)) + str(p[-28:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS)
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-","-"]
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
```
> ### Test 1.3: Point != Challenge Input, w/ 1 X error Correctness Check
```
print("\n_____________PART C: Challenge Input != Point - one X Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,1,False)
index = (i[0]-28)
challenge_input = str(p[:index]) + str((int(p[index])+1)%2) + str(p[index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*2)
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2,"-","-"]
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
print(len(results_info))
```
> ### Test 1.4: Point != Challenge Input, w/ 1 Z error Correctness Check
```
print("\n_____________PART D: Challenge Input != Point - one Z-Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,1,False)
index = (i[0]-14)
print(index)
if i == 13:
challenge_input = str(p[:index]) + str((int(p[index])+1)%2)
else:
challenge_input = str(p[:index]) + str((int(p[index])+1)%2) + str(p[index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*3)
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
```
> ### Test 1.5: Point != Challenge Input, w/ 1 X, Z error EACH
```
print("\n_____________PART E: Challenge Input != Point - one X and Z Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.sort(np.random.choice(14,2,True))
x_error_index = i[0] - 28
z_error_index = i[1] - 14
if i[1] == 13:
challenge_input = str(p[:x_error_index]) + str((int(p[x_error_index])+1)%2) + str(p[x_error_index+1: z_error_index])
else:
challenge_input = str(p[:x_error_index]) + str((int(p[x_error_index])+1)%2) + str(p[x_error_index+1: z_error_index])+ str((int(p[z_error_index])+1)%2)+ str(p[z_error_index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*4)
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
```
> ### Test 1.6: Point != Challenge Input, w/ random error Correctness Check
```
print("\n_____________PART F: Random Challenge Input_____________")
for i in range(NUM_RANDOM_ITERATIONS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
challenge_input = server.sample_challenge_point(p)
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = (NUM_ITERATIONS*NUM_DIFF_PROGRAMS*5)+i
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
```
# Execute Circuits prepared in Tests
### Transpiling Circuits
---
```
def get_transpiled_circuit_and_depth(circuit_list, backend, init_qubits, opt_level = 2, num_seeds = 1):
"""
Gets the list of transpiled circuits with the least gate depths based on the random seeds of the specified quantum backend
Parameters:
circuit_list ([qiskit's QuantumCircuit]): list of circuits to be transpiled
backend (qiskit's IBMQBackend): specified quantum computer for transpiling the circuits
init_qubits ([int]): mapping of virtual to physical qubits
opt_level (int): the optimization level of the transpiled circuits
num_seeds (int): the number of random seeds to iterate through
Returns:
transpiled_list ([qiskit's QuantumCircuit]): transpiled circuits with the least gate depths
transpiled_depths ([int]): corresponding gate depths of transpiled_list
"""
transpiled_list = []
transpiled_depths = []
for i in range(len(circuit_list)):
min_circ = transpile(circuit_list[i], backend, initial_layout=init_qubits[i])
min_depth = min_circ.depth()
for j in range(num_seeds):
transpiled_circ = transpile(circuit_list[i], backend, initial_layout=init_qubits[i],optimization_level=opt_level)
depth = transpiled_circ.depth()
if depth < min_depth:
min_depth = depth
min_circ = transpiled_circ
transpiled_list.append(min_circ)
transpiled_depths.append(min_circ.depth())
return transpiled_list, transpiled_depths
# getting the virtual to physical qubit mapping for all circuits
# mapping is based on the permutation of the circuits and the ideal physical ordering of the quantum computer
init_qubits= []
init_qubits_msg = []
for key1 in results_info.challenge_key_1:
k1 = key1[:]
for i in range(len(k1)):
k1[i]= unpermuted_layout[k1[i]]
init_qubits_msg.append(k1[:])
for j in syndrome_layout:
k1.append(j)
init_qubits.append(k1)
# getting all the transpiled circuits
transpiled_sp_list, transpiled_sp_depths = get_transpiled_circuit_and_depth(sp_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_singles_list, transpiled_sp_singles_depths = get_transpiled_circuit_and_depth(sp_mit_single_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_all_list, transpiled_sp_all_depths = get_transpiled_circuit_and_depth(sp_mit_all_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_msg_list, transpiled_sp_msg_depths = get_transpiled_circuit_and_depth(dp_list, BACKEND, init_qubits_msg, num_seeds = NUM_SEEDS)
```
> ### Run Transpiled Circuits on Quantum Computers & Saving to Files
```
# execute jobs of transpiled error syndrome programs
job = execute(transpiled_sp_list, BACKEND, shots=NUM_SHOTS)
results_sim = job.result()
counts = results_sim.get_counts()
counts = [str(x) for x in counts]
# saving data
results_info.insert(9, "device_counts",counts)
results_info.insert(10, "circuit_depth", transpiled_sp_depths)
results_info.to_csv(filename_error)
mit_counts_singles = []
mit_counts_all = []
# execute jobs of transpiled error syndrome programs (with partial qubit measurement) for error mitigation
job_s = execute(transpiled_sp_singles_list, BACKEND, shots=NUM_SHOTS)
job_all = execute(transpiled_sp_all_list, BACKEND, shots=NUM_SHOTS)
results_sim_s = job_s.result()
counts_s = results_sim_s.get_counts()
results_sim_all = job_all.result()
counts_all = results_sim_all.get_counts()
# get the mitigated counts of the transpiled error syndrome (with partial qubit measurement)
for j in range(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*5+ NUM_RANDOM_ITERATIONS):
mitigated_counts = meas_filter_singles[j].apply(counts_s[j])
mit_counts_singles.append(str(mitigated_counts))
mitigated_counts = meas_filter_alls[j].apply(counts_all[j])
mit_counts_all.append(str(mitigated_counts))
# saving data
results_info.insert(11, "raw_singles", counts_s)
results_info.insert(12,"raw_all", counts_all)
results_info.insert(13, "mitigated_counts_singles",mit_counts_singles)
results_info.insert(14, "singles_circuit_depth", transpiled_sp_singles_depths)
results_info.insert(15, "mitigated_counts_all",mit_counts_all)
results_info.insert(16, "all_circuit_depth", transpiled_sp_all_depths)
results_info.to_csv(filename_mit)
# execute jobs of undoed programs
job = execute(transpiled_sp_msg_list, BACKEND, shots=NUM_SHOTS)
results_sim = job.result()
de_counts = results_sim.get_counts()
# saving data
results_info_decoded.insert(8, "device_counts",de_counts)
results_info_decoded.insert(9, "circuit_depth", transpiled_sp_msg_depths)
results_info_decoded.to_csv(filename_decoded)
# saving some generic data
with open(filename_0, 'w') as writefile:
x = time.time() - start
writefile.write("--------------------ELAPSED TIME: \n")
writefile.write(str(x))
writefile.write("\n________________________________COUNTS_____________________________________\n")
writefile.write(str(counts))
writefile.write("\n________________________________DECODED_COUNTS_____________________________________\n")
writefile.write(str(de_counts))
```
|
github_jupyter
|
!pip install qiskit
from qiskit import (
IBMQ,
QuantumCircuit,
execute,
Aer,
QuantumRegister,
ClassicalRegister,
transpile,
)
from qiskit.ignis.mitigation.measurement import complete_meas_cal, tensored_meas_cal, CompleteMeasFitter,TensoredMeasFitter
from qiskit.test.mock import FakeSydney, FakeMontreal
import numpy as np
import math
import random
import time
import pandas as pd
# CNOT gates for applying the Steane Code
CNOT_GATES = [[1,0], [1,4], [1,5], [2,0], [2,4], [2,6], [3,4], [3,5],[3,6],[7, 12],[7, 13],[8,7] ,[8, 11],[8, 12], [9,7],[9, 11],[9, 13],[10, 11],[10, 12],[10, 13]]
REV_CNOT_GATES = [[10, 13],[10, 12],[10, 11],[9, 13],[9, 11],[9,7],[8, 12],[8, 11],[8,7],[7, 13],[7, 12],[3,6],[3,5],[3,4],[2,6],[2,4],[2,0],[1,5],[1,4],[1,0]]
# COMPUTATION CONFIGURATIONS
NUM_SHOTS = 1
NUM_DIFF_PROGRAMS = 1
NUM_ITERATIONS = 1
NUM_RANDOM_ITERATIONS = 1
# SPECIFY NUMBER OF RANDOM SEEDS FOR TRANSPILING QUANTUM CIRCUITS
NUM_SEEDS = 150
# SET PHYSICAL TO VIRTUAL QUBIT MAPPING OF QUANTUM MACHINE
unpermuted_layout = [8,11,13,19,14,20,16,1,2,7,12,6,4,10]
syndrome_layout = [5,9,18,0,3,15]
# SET LOCATION FOR SAVING DATA
from google.colab import drive
drive.mount('/content/drive')
# SET FILENAMES FOR DATA SAVING
filename_0 = "/content/drive/My Drive/Results/general_info_20Q.txt"
filename_error = "/content/drive/My Drive/Results/error_results_20Q.csv"
filename_mit = "/content/drive/My Drive/Results/mit_results_20Q.csv"
filename_decoded = "/content/drive/My Drive/Results/decoded_results_20Q.csv"
# SET QUANTUM COMPUTER BACKEND OF YOUR CHOICE
fake_mtrl = FakeMontreal()
# BACKEND = AerSimulator.from_backend(fake_mtrl)
BACKEND = Aer.get_backend('qasm_simulator')
class Server():
def __init__(self):
print('Server initialized')
def generate_point(self, size=14):
"""
Generate a random point as password
Parameters:
size (int): number of qubits in circuit to be encrypted
Returns:
point (str): the combination of key1 and key2 in binary form
key1 ([int]): permutation key in integer form
key2 ([[int], [int]]): one-time pad component of the password, comprised of the x key and z key respectively
"""
# get permutation key
bin_key1, key1 = self.generate_permutation_key()
# get OTP key
x_key = np.random.randint(2, size=size)
z_key = np.random.randint(2, size=size)
key2 = [x_key.tolist(), z_key.tolist()]
# combine keys to get point
a = ''.join(bin_key1)
b = ''.join(map(str, x_key.tolist()))
c = ''.join(map(str,z_key.tolist()))
point = a+b+c
return point, key1, key2
def generate_permutation_key(self, size=14):
"""
Generate a random permutation of list(range(size))
Parameters:
size (int): size of list
Returns:
key ([str]): the permuted list in binary form
dec_key ([int]): the permuted list in decimal form
"""
key_dec = list(range(size))
rng = np.random.default_rng()
rng.shuffle(key_dec)
f = '0' + str(math.ceil(math.log2(size))) + 'b'
# get the permutation in binary form
key = [format(x, f) for x in key_dec]
return key, key_dec
def sample_challenge_point(self, point, size=14):
"""
Sample a random point q from the distribution in which with approx.
probability 0.5, point (the parameter) is sampled,
and with approx. probability 0.5, a random point excluding point (the parameter) is uniformly chosen
Parameters:
point (str): the point that will be sampled with probability 0.5 in the distribution
size (int): number of qubits that point encrypts for
Returns:
sample (str): challenge point taken from distribution
"""
# generate a random valid point that has a permutation and one-time pad keys
key1, key_dec = self.generate_permutation_key()
key1 = "".join(key1)
key2_dec = random.randint(0, (2**(size*2))-1)
key2_bin = format(key2_dec,'0'+str(size*2)+'b')
random_point = str(key1) + str(key2_bin)
# keep sampling for a random point uniformly until the random_point is not equivalent to point
while random_point == point:
key2_dec = random.randint(0, (2**(size*2))-1)
key2_bin = format(key2_dec,'0'+str(size*2)+'b')
random_point = str(key1) + str(key2_bin)
# sample from challenge distribution in which with approx. 50%, random_point is selected, and 50%, point is selected
sample = np.random.choice([random_point, point])
return sample
def protect(self, permuted_cnots, hadamards, x_key, z_key, init_data = [0,0,0,0,0,0,0,'+',0,0,0,0,0,0], size=14):
"""
Encodes a program
Parameters:
permuted_cnots ([[int,int]]): all permuted CNOT gates to be applied
hadamards ([int]): all hadamard gates to be applied
x_key ([int]): all pauli-X gates to be applied
z_key ([int]): all pauli-Z gates to be applied
init_data (list): initialized qubit states
size (int): size of the quantum circuit
Returns:
circuit (qiskit's QuantumCircuit): encoded program
"""
# initialize quantum circuit
qr = QuantumRegister(size)
circuit = QuantumCircuit(qr)
# initialize the states of the quantum circuit
for i in range(size):
if init_data[i] == '+':
circuit.h(i)
elif init_data[i] == 1:
circuit.x(i)
elif init_data[i] == '-':
circuit.x(i)
circuit.h(i)
circuit.barrier()
# apply delegated one-time pad
for i in range(size):
if x_key[i] == 1 and init_data[i] == 0:
circuit.x(i)
elif z_key[i] == 1 and init_data[i] == '+':
circuit.z(i)
circuit.barrier()
# apply hadamard gates
for i in hadamards:
circuit.h(i)
circuit.barrier()
# apply cnot gates
for cnots in permuted_cnots:
circuit.cx(cnots[0], cnots[1])
circuit.barrier()
return circuit
def get_syndrome_circuit(self, challenge_input, program, size=14, syndrome_cnots =[[0, 14], [2, 14], [4, 14], [6, 14], [1, 15], [2, 15], [5, 15], [6, 15], [3, 16], [4, 16], [5, 16], [6, 16], [7, 17], [9, 17], [11, 17], [13, 17], [8, 18], [9, 18], [12, 18], [13, 18], [10, 19], [11, 19], [12, 19], [13, 19]]):
"""
Creates a circuit that detects for single bit and phase flip errors
Parameters:
challenge_input (str): point used to decrypt program
program (qiskit's QuantumCircuit): program for finding error syndromes
size (int): the number of qubits in the program
syndrome_cnots ([int,int]): CNOT gates for obtaining error syndromes
Returns:
syndrome_circuit (qiskit's QuantumCircuit): program for calculating error syndromes
"""
key1, key2 = self.point_to_keys(challenge_input)
# initialize quantum circuit
qr = QuantumRegister(size+int(size/7*3))
cr = ClassicalRegister(size+int(size/7*3))
syndrome_circuit = QuantumCircuit(qr, cr)
# add program to new quantum circuit
syndrome_circuit.append(program, range(size))
# apply gates to decrypt the circuit
for i in range(size,size+int(size/7*3)):
syndrome_circuit.h(i)
for gate in syndrome_cnots:
syndrome_circuit.cx(gate[1], key1.index(gate[0]))
for i in range(size,size+int(size/7*3)):
syndrome_circuit.h(i)
syndrome_circuit.barrier()
syndrome_circuit.measure(qr,cr)
return syndrome_circuit
def get_syndrome_circuit_mit_measures(self, mit_values, challenge_input, program, size=14, syndrome_cnots =[[0, 14], [2, 14], [4, 14], [6, 14], [1, 15], [2, 15], [5, 15], [6, 15], [3, 16], [4, 16], [5, 16], [6, 16], [7, 17], [9, 17], [11, 17], [13, 17], [8, 18], [9, 18], [12, 18], [13, 18], [10, 19], [11, 19], [12, 19], [13, 19]]):
"""
Creates a circuit that detects bit and phase flip errors but measures only a subset of qubits;
Used for tensored error mitigation
Parameters:
mit_values ([int]): subset of qubits to be measured
challenge_input (str): point used to decrypt program
program (qiskit's QuantumCircuit): program for finding error syndromes
size (int): the number of qubits in the program
syndrome_cnots ([int,int]): CNOT gates for obtaining error syndromes
Returns:
syndrome_program (qiskit's QuantumCircuit): program for calculating error syndromes with partial qubit measurement
"""
key1, key2 = self.point_to_keys(challenge_input)
qr = QuantumRegister(size+int(size/7*3))
cr = ClassicalRegister(len(mit_values))
syndrome_program = QuantumCircuit(qr, cr)
syndrome_program.append(program, range(size))
for i in range(size,size+int(size/7*3)):
syndrome_program.h(i)
for gate in syndrome_cnots:
syndrome_program.cx(gate[1], key1.index(gate[0]))
for i in range(size,size+int(size/7*3)):
syndrome_program.h(i)
syndrome_program.barrier()
for i in range(len(mit_values)):
syndrome_program.measure(qr[mit_values[i]], cr[i])
return syndrome_program
def point_to_keys(self, point, size=14):
"""
Derives the permutation and one-time pad keys from a point
Parameters:
point(str): point for deriving keys from
size (int): number of qubits in program
Returns:
circuit (circuit): protected program
"""
inc = math.ceil(math.log2(size))
key1 = [int(point[i:i+inc],2) for i in range(0, len(point[:-size*2]), inc)]
key2_x = [int(value) for value in point[-size*2:-size]]
key2_z = [int(value) for value in point[-size:]]
return key1, [key2_x, key2_z]
def permute_classical(self, key1, orig_cnots, hadamards = [1,2,3,8,9,10], size=14):
"""
Provides the locations of CNOT and Hadamard gates based on a permutated list
Parameters:
key1 ([int]): permutated list
orig_cnots ([[int,int]]): the location of unpermuted CNOT gates
hadamards ([int]): the location of unpermuted Hadamard gates
size (int): number of qubits in program
Returns:
new_cnot_gates ([[int,int]]): permuted CNOT gates
new_hadamard_gates ([int]): permuted Hadamard gates
"""
new_hadamard_gates = [0]*len(hadamards)
new_cnot_gates = [0]*len(orig_cnots)
for i in range(len(orig_cnots)):
new_cnot_gates[i] = [key1.index(orig_cnots[i][0]), key1.index(orig_cnots[i][1])]
for i in range(len(hadamards)):
new_hadamard_gates[i] = key1.index(hadamards[i])
return new_cnot_gates, new_hadamard_gates
def get_OTP_classical_key(self, key, permutation_key, cnots, hadamards):
"""
Gets the delegated one-time pad key, where the one-time pad key is delegated to the beginning of the program
Parameters:
key ([[int],[int]]): the one-time pad key to be delegated
permutation_key ([int]): permutation
cnots ([[int,int]]): all CNOT gates
hadamards ([int]): all Hadamard gates
Returns:
new_x_key ([int]): delegated Pauli-X gates of one-time pad
new_z_key ([int]): delegated Pauli-Z gates of one-time pad
"""
x_key = key[0]
z_key = key[1]
for cnot in cnots:
a = x_key[cnot[0]]
b = z_key[cnot[0]]
c = x_key[cnot[1]]
d = z_key[cnot[1]]
x_key[cnot[0]] = a
z_key[cnot[0]] = b+d
x_key[cnot[1]] = a+c
z_key[cnot[1]] = d
for i in hadamards:
x_key[i], z_key[i] = z_key[i], x_key[i]
new_x_key = [i%2 for i in x_key]
new_z_key = [i%2 for i in z_key]
return new_x_key, new_z_key
def undo_circuit(self, point, program, rev_cnots=[[3,6],[3,5],[3,4],[2,6],[2,4],[2,0],[1,5],[1,4],[1,0],[0,6],[0,5],[10, 13],[10, 12],[10, 11],[9, 13],[9, 11],[9, 7],[8, 12],[8, 11],[8, 7],[7, 13],[7, 12]], size=14):
"""
Applies all the operations in reverse order as to undo the original program
Parameters:
point (str): the point for encoding the program
program (qiskit's QuantumCircuit): circuit to be undoed
rev_cnots ([[int,int]]): the reverse sequence of CNOT gates that were applied in the program
size (int): number of qubits in program
Returns:
undo_circuit (qiskit's QuantumCircuit): the program that has been undoed
"""
key1, key2 = self.point_to_keys(point)
permuted_cnots, hg = self.permute_classical(key1, rev_cnots)
qr = QuantumRegister(size)
cr_trap = ClassicalRegister(size)
undo_circuit = QuantumCircuit(qr, cr_trap)
undo_circuit.append(program, range(size))
for cnot in permuted_cnots:
undo_circuit.cx(cnot[0], cnot[1])
undo_circuit.barrier()
for gate in hg:
undo_circuit.h(gate)
undo_circuit.barrier()
undo_circuit.measure(qr, cr_trap)
return undo_circuit
def reverse_cnots(self, cnots):
"""
Reverse the order of CNOTs
Parameters:
cnots ([[int,int]]): original order of cnots
Returns:
rev_cnots ([[int,int]]): reversed order of cnots
"""
rev_cnots = []
for i in range(len(cnots)):
rev_cnots.append(cnots[len(cnots)-i-1])
return rev_cnots
def get_random_mit_pattern_single(self, size=20, num_qubits = 10):
"""
Selected single qubit pattern for tensored error mitigation
Parameters:
size(int): total number of qubits in the program
num_qubits(int): number of qubits to be selected
Returns:
mit_pattern (list): pattern for tensored error mitigation, comprised of single qubits
mit_values ([int]): a random subset of all qubits in mit_pattern
"""
mit_vals = random.sample(list(range(size)),num_qubits)
mit_pattern = [[x] for x in mit_vals]
return mit_pattern, mit_vals
def get_permuted_cnots(self, permutation_key, cnots):
"""
Gets the permuted set of CNOTs to be applied for the syndrome programs
Parameters:
permutation_key([int]): permutation
cnots([[int,int]]): CNOT gates to be applied
Returns:
new_permuted_cnots ([[int,int]]): permutation of CNOT gates
"""
num_aux_qubits = int((len(permutation_key)/7)*3)
# get the list of auxiliary qubits for obtaining error syndromes
aux_qubits = list(range(len(permutation_key),len(permutation_key)+num_aux_qubits))
key = permutation_key + aux_qubits
new_permuted_cnots = [0]*len(cnots)
for i in range(len(cnots)):
new_permuted_cnots[i] = [key.index(cnots[i][0]), key.index(cnots[i][1])]
return new_permuted_cnots
def get_random_mit_pattern_all(self, permutation_key, steane_cnots = [[1,0], [1,4], [1,5], [2,0], [2,4], [2,6], [3,4], [3,5],[3,6],[7, 12],[7, 13],[8,7] ,[8, 11],[8, 12], [9,7],[9, 11],[9, 13],[10, 11],[10, 12],[10, 13]], syndrome_cnots = [[14, 0], [14, 2], [14, 4], [14, 6], [15, 1], [15, 2], [15, 5], [15, 6], [16, 3], [16, 4], [16, 5], [16, 6], [17, 7], [17, 9], [17, 11], [17, 13], [18, 8], [18, 9], [18, 12], [18, 13], [19, 10], [19, 11], [19, 12], [19, 13]], size=20, num_qubits = 10):
"""
Selected single and double qubit patterns for tensored error mitigation
Parameters:
permutation_key([int]): permutation
steane_cnots ([[int,int]]): all cnot gates for the Steane encoding
syndrome_cnots ([[int,int]]): all cnot gates for calculating the error syndromes
size(int): total number of qubits in the program
num_qubits(int): number of qubits to be selected
Returns:
mit_pattern (list): pattern for tensored error mitigation, comprised of single and qubit pairs
mit_values ([int]): a random subset of all qubits in mit_pattern
"""
permuted_steane_cnots = self.get_permuted_cnots(permutation_key, steane_cnots)
permuted_syndrome_cnots = self.get_permuted_cnots(permutation_key, syndrome_cnots)
cnots = permuted_steane_cnots + permuted_syndrome_cnots
# number of qubit pairs to include in pattern
num_cnots = random.choice(range(10//2))
count = 0
cnot_pairs = []
cnot_values = []
while count != num_cnots:
val = random.choice(range(len(cnots)))
if cnots[val] not in cnot_pairs:
if cnots[val][0] not in cnot_values and cnots[val][1] not in cnot_values:
cnot_pairs.append(cnots[val])
cnot_values.append(cnots[val][0])
cnot_values.append(cnots[val][1])
count = count +1
singles = random.sample(set(list(range(20)))-set(cnot_values),num_qubits-(num_cnots*2))
s = [[x] for x in singles[:]]
mit_values = cnot_values + singles
mit_patterns = cnot_pairs + s
return mit_patterns,mit_values
def prepare_meas_filter(self, mit_pattern, backend, num_shots, size=20):
"""
Prepare a tensored error mitigation measurement filter based on specified mit_pattern
Parameters:
mit_pattern([int]): pattern used for tensored error mitigation
backend(qiskit's IBMQBackend): specified backend for preparing measurement filter
num_shots(int): number of shots for backend
size(int): number of qubits in program
Returns:
meas_filter (qiskit's TensoredMeasFitter.filter): prepared measurement filter
"""
qr = QuantumRegister(size)
qulayout = range(size)
meas_calibs, state_labels = tensored_meas_cal(mit_pattern=mit_pattern, qr=qr, circlabel='mcal')
for circ in meas_calibs:
print(circ.name)
job = execute(meas_calibs, backend=backend, shots=num_shots)
cal_results = job.result()
meas_fitter = TensoredMeasFitter(cal_results, mit_pattern=mit_pattern)
meas_filter = meas_fitter.filter
return meas_filter
# initiate the server
server = Server()
start = time.time()
fields = ['is_point', 'point_value', 'challenge_point_value', 'key_1', 'key_2', 'challenge_key_1', 'challenge_key_2', 'mit_pattern_single','mit_pattern_all']
results_info = pd.DataFrame(columns=fields)
results_info_decoded = pd.DataFrame(columns=fields)
sp_list= []
sp_mit_single_list =[]
sp_mit_all_list = []
dp_list = []
meas_filter_singles = []
meas_filter_alls = []
def get_programs_for_test(server, challenge_input, program, permutation_key,sp_list, sp_mit_single_list, sp_mit_all_list,dp_list, meas_filter_singles, meas_filter_alls, rev_cnots=REV_CNOT_GATES, backend=BACKEND, num_shots=NUM_SHOTS):
"""
Prepares circuits for execution
Parameters:
server (Server): Server instance
challenge_input (str): challenge point for testing programs
program (qiskit's QuantumCicuit): the encoded program for applying tests
permutation_key ([int]): permutation ordering
sp_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits
sp_mit_single_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits with partial measurement and single qubit patterns
sp_mit_all_list ([qiskit's QuantumCircuits]): list of prepared quantum circuits with syndromes with partial measurement and single and qubit pair patterns
dp_list ([qiskit's QuantumCircuits]): list of prepared undoed quantum circuits
meas_filter_singles ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_single_list circuits
meas_filter_alls ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_all_list circuits
rev_cnots ([[int,int]]): cnot gates to be applied for undoing the circuit
backend (qiskit's IBMQBackend): specified backend for preparing measurement filter
num_shots (int): number of shots for backend
Returns:
sp_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits
sp_mit_single_list ([qiskit's QuantumCircuits]): list of prepared syndrome quantum circuits with partial measurement and single qubit patterns
sp_mit_all_list ([qiskit's QuantumCircuits]): list of prepared quantum circuits with syndromes with partial measurement and single and double qubit patterns
dp_list ([qiskit's QuantumCircuits]): list of prepared undoed quantum circuits
meas_filter_singles ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_single_list circuits
meas_filter_alls ([qiskit's TensoredMeasFitter.filter]): list of tensored measurement filters for sp_mit_all_list circuits
mit_pattern_s ([[int]]): subset of single qubits used in tensored error mitigation, based on the circuits sp_mit_single_list
mit_pattern_all (list): subset of single and double qubits used in tensored error mitigation, based on the circuits sp_mit_all_list
"""
syndrome_program = server.get_syndrome_circuit(challenge_input,program)
mit_pattern_s, mit_val_s = server.get_random_mit_pattern_single()
mit_pattern_all, mit_val_all = server.get_random_mit_pattern_all(permutation_key)
syndrome_program_mit_single = server.get_syndrome_circuit_mit_measures(mit_val_s, challenge_input, program)
syndrome_program_mit_all = server.get_syndrome_circuit_mit_measures(mit_val_all,challenge_input,program)
decoded_program = server.undo_circuit(challenge_input, program, rev_cnots=rev_cnots)
meas_filter_s = server.prepare_meas_filter(mit_pattern_s, backend, num_shots)
meas_filter_all = server.prepare_meas_filter(mit_pattern_all, backend, num_shots)
sp_list = sp_list + [syndrome_program]
sp_mit_single_list =sp_mit_single_list + [syndrome_program_mit_single]
sp_mit_all_list = sp_mit_all_list + [syndrome_program_mit_all]
dp_list = dp_list + [decoded_program]
meas_filter_singles = meas_filter_singles + [meas_filter_s]
meas_filter_alls = meas_filter_alls + [meas_filter_all]
return sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all
def prepare_for_test(server, cnots = CNOT_GATES):
"""
Prepare inputs for test
Parameters:
server (Server): instance of Server for preparing inputs
cnots ([[int,int]]): cnot gates to be applied
Returns:
p (str): point
k1 ([int]): permutation key
key2 ([[int],[int]]): one-time pad key
permuted_cnots([[int,int]]): cnot gates post permutation
permuted_hadamards ([int]): hadamard gates post permutation
x_key ([int]): all delegated pauli-X gates to be applied for one-time pad (key2)
z_key ([int]): all delegated pauli-Z gates to be applied for one-time pad (key2)
data (list): qubits' intial states
"""
p, k1, k2 = server.generate_point()
key2 = [k2[0][:], k2[1][:]]
permuted_cnots, permuted_hadamards = server.permute_classical(k1, cnots)
rev = server.reverse_cnots(permuted_cnots)
x_key, z_key = server.get_OTP_classical_key(k2,k1, rev,permuted_hadamards)
data = [0]*14
data[k1.index(7)] = '+'
return p, k1, key2, permuted_cnots, permuted_hadamards, x_key, z_key, data
print("_____________PART A: Challenge Input == Point_____________")
for i in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# set challenge_input
challenge_input = p
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = i*NUM_ITERATIONS+k
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
print("\n_____________PART B: Challenge Input != Point - one Permutation Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,2,False)
edited_k1 = k1[:]
edited_k1[i[0]], edited_k1[i[1]] = k1[i[1]], k1[i[0]]
f = '0' + str(math.ceil(math.log2(14))) + 'b'
new_key1 = [format(x, f) for x in edited_k1]
challenge_input = str("".join(new_key1)) + str(p[-28:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS)
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-","-"]
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
print("\n_____________PART C: Challenge Input != Point - one X Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,1,False)
index = (i[0]-28)
challenge_input = str(p[:index]) + str((int(p[index])+1)%2) + str(p[index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*2)
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2,"-","-"]
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
print(len(results_info))
print("\n_____________PART D: Challenge Input != Point - one Z-Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.random.choice(14,1,False)
index = (i[0]-14)
print(index)
if i == 13:
challenge_input = str(p[:index]) + str((int(p[index])+1)%2)
else:
challenge_input = str(p[:index]) + str((int(p[index])+1)%2) + str(p[index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*3)
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
print("\n_____________PART E: Challenge Input != Point - one X and Z Error_____________")
for j in range(NUM_DIFF_PROGRAMS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
i = np.sort(np.random.choice(14,2,True))
x_error_index = i[0] - 28
z_error_index = i[1] - 14
if i[1] == 13:
challenge_input = str(p[:x_error_index]) + str((int(p[x_error_index])+1)%2) + str(p[x_error_index+1: z_error_index])
else:
challenge_input = str(p[:x_error_index]) + str((int(p[x_error_index])+1)%2) + str(p[x_error_index+1: z_error_index])+ str((int(p[z_error_index])+1)%2)+ str(p[z_error_index+1:])
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
for k in range(NUM_ITERATIONS):
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = j*NUM_ITERATIONS+k +(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*4)
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
print("\n_____________PART F: Random Challenge Input_____________")
for i in range(NUM_RANDOM_ITERATIONS):
p, k1, key2, cnots, hadamards, x_key, z_key, data = prepare_for_test(server)
program = server.protect(cnots, hadamards, x_key, z_key, init_data=data)
# prepare challenge input
challenge_input = server.sample_challenge_point(p)
challenge_key1, challenge_key2 = server.point_to_keys(challenge_input)
sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls, mit_pattern_s, mit_pattern_all = get_programs_for_test(server, challenge_input, program, k1, sp_list, sp_mit_single_list, sp_mit_all_list, dp_list, meas_filter_singles, meas_filter_alls)
index = (NUM_ITERATIONS*NUM_DIFF_PROGRAMS*5)+i
results_info.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, mit_pattern_s, mit_pattern_all]
results_info_decoded.loc[index] = [str(p) == str(challenge_input), p, challenge_input, k1, key2, challenge_key1, challenge_key2, "-", "-"]
def get_transpiled_circuit_and_depth(circuit_list, backend, init_qubits, opt_level = 2, num_seeds = 1):
"""
Gets the list of transpiled circuits with the least gate depths based on the random seeds of the specified quantum backend
Parameters:
circuit_list ([qiskit's QuantumCircuit]): list of circuits to be transpiled
backend (qiskit's IBMQBackend): specified quantum computer for transpiling the circuits
init_qubits ([int]): mapping of virtual to physical qubits
opt_level (int): the optimization level of the transpiled circuits
num_seeds (int): the number of random seeds to iterate through
Returns:
transpiled_list ([qiskit's QuantumCircuit]): transpiled circuits with the least gate depths
transpiled_depths ([int]): corresponding gate depths of transpiled_list
"""
transpiled_list = []
transpiled_depths = []
for i in range(len(circuit_list)):
min_circ = transpile(circuit_list[i], backend, initial_layout=init_qubits[i])
min_depth = min_circ.depth()
for j in range(num_seeds):
transpiled_circ = transpile(circuit_list[i], backend, initial_layout=init_qubits[i],optimization_level=opt_level)
depth = transpiled_circ.depth()
if depth < min_depth:
min_depth = depth
min_circ = transpiled_circ
transpiled_list.append(min_circ)
transpiled_depths.append(min_circ.depth())
return transpiled_list, transpiled_depths
# getting the virtual to physical qubit mapping for all circuits
# mapping is based on the permutation of the circuits and the ideal physical ordering of the quantum computer
init_qubits= []
init_qubits_msg = []
for key1 in results_info.challenge_key_1:
k1 = key1[:]
for i in range(len(k1)):
k1[i]= unpermuted_layout[k1[i]]
init_qubits_msg.append(k1[:])
for j in syndrome_layout:
k1.append(j)
init_qubits.append(k1)
# getting all the transpiled circuits
transpiled_sp_list, transpiled_sp_depths = get_transpiled_circuit_and_depth(sp_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_singles_list, transpiled_sp_singles_depths = get_transpiled_circuit_and_depth(sp_mit_single_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_all_list, transpiled_sp_all_depths = get_transpiled_circuit_and_depth(sp_mit_all_list, BACKEND, init_qubits, num_seeds = NUM_SEEDS)
transpiled_sp_msg_list, transpiled_sp_msg_depths = get_transpiled_circuit_and_depth(dp_list, BACKEND, init_qubits_msg, num_seeds = NUM_SEEDS)
# execute jobs of transpiled error syndrome programs
job = execute(transpiled_sp_list, BACKEND, shots=NUM_SHOTS)
results_sim = job.result()
counts = results_sim.get_counts()
counts = [str(x) for x in counts]
# saving data
results_info.insert(9, "device_counts",counts)
results_info.insert(10, "circuit_depth", transpiled_sp_depths)
results_info.to_csv(filename_error)
mit_counts_singles = []
mit_counts_all = []
# execute jobs of transpiled error syndrome programs (with partial qubit measurement) for error mitigation
job_s = execute(transpiled_sp_singles_list, BACKEND, shots=NUM_SHOTS)
job_all = execute(transpiled_sp_all_list, BACKEND, shots=NUM_SHOTS)
results_sim_s = job_s.result()
counts_s = results_sim_s.get_counts()
results_sim_all = job_all.result()
counts_all = results_sim_all.get_counts()
# get the mitigated counts of the transpiled error syndrome (with partial qubit measurement)
for j in range(NUM_ITERATIONS*NUM_DIFF_PROGRAMS*5+ NUM_RANDOM_ITERATIONS):
mitigated_counts = meas_filter_singles[j].apply(counts_s[j])
mit_counts_singles.append(str(mitigated_counts))
mitigated_counts = meas_filter_alls[j].apply(counts_all[j])
mit_counts_all.append(str(mitigated_counts))
# saving data
results_info.insert(11, "raw_singles", counts_s)
results_info.insert(12,"raw_all", counts_all)
results_info.insert(13, "mitigated_counts_singles",mit_counts_singles)
results_info.insert(14, "singles_circuit_depth", transpiled_sp_singles_depths)
results_info.insert(15, "mitigated_counts_all",mit_counts_all)
results_info.insert(16, "all_circuit_depth", transpiled_sp_all_depths)
results_info.to_csv(filename_mit)
# execute jobs of undoed programs
job = execute(transpiled_sp_msg_list, BACKEND, shots=NUM_SHOTS)
results_sim = job.result()
de_counts = results_sim.get_counts()
# saving data
results_info_decoded.insert(8, "device_counts",de_counts)
results_info_decoded.insert(9, "circuit_depth", transpiled_sp_msg_depths)
results_info_decoded.to_csv(filename_decoded)
# saving some generic data
with open(filename_0, 'w') as writefile:
x = time.time() - start
writefile.write("--------------------ELAPSED TIME: \n")
writefile.write(str(x))
writefile.write("\n________________________________COUNTS_____________________________________\n")
writefile.write(str(counts))
writefile.write("\n________________________________DECODED_COUNTS_____________________________________\n")
writefile.write(str(de_counts))
| 0.665628 | 0.785946 |
# Jupyter Notebooks
## ฮคฮน ฮตฮฏฮฝฮฑฮน ฯฮฟ Project Jupyter;
ฮคฮฟ Project Jupyter ฮตฮฏฮฝฮฑฮน ฮญฮฝฮฑฯ ฮผฮท ฮบฮตฯฮดฮฟฯฮบฮฟฯฮนฮบฯฯ ฮฟฯฮณฮฑฮฝฮนฯฮผฯฯ ฯฮฟฯ
ฮดฮทฮผฮนฮฟฯ
ฯฮณฮฎฮธฮทฮบฮต ฮผฮต ฯฮบฮฟฯฯ ฯฮทฮฝ ฮฑฮฝฮฌฯฯฯ
ฮพฮท ฮปฮฟฮณฮนฯฮผฮนฮบฮฟฯ ฮฑฮฝฮฟฮนฯฯฮฟฯ ฮบฯฮดฮนฮบฮฑ, ฮฑฮฝฮฟฮนฯฯฯฮฝ ฯฯฮฟฯฯฯฯฮฝ ฮบฮฑฮน ฯ
ฯฮทฯฮตฯฮนฯฮฝ ฮณฮนฮฑ ฮดฮนฮฑฮดฯฮฑฯฯฮนฮบฮฟฯฯ ฯ
ฯฮฟฮปฮฟฮณฮนฯฯฮญฯ ฯฮต ฮดฮตฮบฮฌฮดฮตฯ ฮณฮปฯฯฯฮตฯ ฯฯฮฟฮณฯฮฑฮผฮผฮฑฯฮนฯฮผฮฟฯ. ฮฮฝฮฑ ฮฑฯฯ ฯฮฑ ฯฯฮฟฮณฯฮฌฮผฮผฮฑฯฮฑ ฯฮฟฯ
ฮฑฮฝฮญฯฯฯ
ฮพฮฑฮฝ ฮบฮฑฮน ฯ
ฯฮฟฯฯฮทฯฮฏฮถฮฟฯ
ฮฝ ฮตฮฏฮฝฮฑฮน ฯฮฟ Jupyeter Notebooks.
---
## ฮ ฯฯ ฮฝฮฑ ฮตฮณฮบฮฑฯฮฑฯฯฮฎฯฯ ฯฮฟ Jupyter ฯฯฮฟ ฮผฮทฯฮฌฮฝฮทฮผฮฑ ฮผฮฟฯ
;
### Linux
#### Arch linux
ฮฃฯฮฑ arch linux ฮฑฯฮปฯฯ ฮตฮบฯฮตฮปฮญฯฯฮต ฯฮฟ ฮตฮพฮฎฯ:
```
!yes | sudo pacman -S jupyter-notebook python-ipykernel
```
*ฮ ฯฮฟฯฮฟฯฮฎ*, ฮผฮทฮฝ ฮบฮฌฮฝฮตฯฮต ฮฑฮฝฯฮนฮณฯฮฑฯฮฎ ฯฮฟฮฝ ฯฮฑฯฮฑฮบฯฮฎฯฮฑ !
#### Ubuntu linux
ฮฃฯฮฑ ubuntu linux ฮตฮบฯฮตฮปฮญฯฯฮต ฯฮฑ ฮตฮพฮฎฯ:
```
%%bash
sudo apt install python3-pip python3-dev
pip install jupyter
```
#### ฮ ฯฯ ฮฝฮฑ ฮบฮฌฮฝฯ ฯฮนฮฟ ฯฯฮฟฯฮฒฮฌฯฮนฮผฮฟ ฯฮฟ Jupyter;
ฮฮนฮฑ ฮฝฮฑ ฮตฮบฯฮตฮปฮญฯฮฟฯ
ฮผฮต ฯฮฟ Jupyter ฮธฮฑ ฯฯฮญฯฮตฮน ฮฝฮฑ ฯฮฟ ฮตฮบฯฮตฮปฮญฯฮฟฯ
ฮผฮต ฮฑฯฯ ฯฮท ฮณฯฮฑฮผฮผฮฎ ฮตฮฝฯฮฟฮปฯฮฝ.
```
!jupyter lab
```
ฮฎ
```
!jupyter lab & disown %jupyter
```
ฮบฮฑฮน ฮณฮนฮฑ ฮฝฮฑ ฯฮฟ ฮบฮปฮตฮฏฯฮฟฯ
ฮผฮต
```
!pkill jupyter
```
### Windows
ฮฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฮฑฮบฮฟฮปฮฟฯ
ฮธฮฎฯฮตฯฮต ฮฑฯ
ฯฯฮฝ ฯฮฟฮฝ [ฮฟฮดฮทฮณฯ](https://medium.com/@kswalawage/install-python-and-jupyter-notebook-to-windows-10-64-bit-66db782e1d02).
ฮฯฮฟฯฮตฮฏฯฮต ฮฝฮฑ ฯฮฟ ฮบฮฑฯฮตฮฒฮฌฯฮตฯฮต ฮผฮต ฯฮฟ anacoda, conda ฮฎ pip.
```
!pip install jupyter
```
---
## Kernels
ฮฮน ฯฯ
ฯฮฎฮฝฮตฯ ฮตฮฏฮฝฮฑฮน ฯฮฑ ฯฯฮฟฮณฯฮฌฮผฮผฮฑฯฮฑ ฯฮฟฯ
ฮตฮบฯฮตฮปฮฟฯฮฝ ฯฮฟฮฝ ฮบฯฮดฮนฮบฮฑ.
---
## Shortcuts
- Ctrl + Enter: Run Cell
- Shift + Enter: Run Cell and Select Below
- Alt + Enter: Run Cell and Insert Below
---
## Magics
- lsmagic
- matplotlib inline
- html
- bash
```
%lsmagic
%%bash
bash --version
```
---
## Ipython magic commands
```
import time
def method_a():
time.sleep(1)
def method_b():
time.sleep(2)
%timeit method_a()
%timeit method_b()
```
---
## Plots
```
import matplotlib.pyplot as plt
points = [
[1, 1, "Red"], [1, 4, "Red"], [1, 9, "Black"], [5, 3,"Black"],
[5, 6, "Red"], [6, 1, "Black"], [6, 2, "Black"], [6, 5, "Black"],
[6, 8, "Red"], [8, 1, "Red"], [9, 3, "Black"], [2, 9, "Black"]
]
plt.title("Points")
plt.xlabel("x")
plt.ylabel("y")
char = 'A'
for point in points:
plt.plot(point[1],point[0], "o", label=char, color=point[2])
char = chr(ord(char) + 1)
plt.legend()
plt.show()
from matplotlib.widgets import Button
import matplotlib.pyplot as plt
import numpy as np
print("Gradient Descent f(x) = X^3-3*x^2")
x_root = float(input("x0 (3-4): "))
b = float(input("b (0.01-0.05): "))
y0 = []
x_root_arr = []
x_axis = np.r_[-1:4:0.01]
x_axis0 = np.zeros(x_axis.size)
y_axis = np.r_[-5:25:0.01]
y_axis0 = np.zeros(y_axis.size)
# 3(x_root^2)-6x_root > 10^-3
while abs(3 * pow(x_root, 2) - 6 * x_root) > pow(10, -3):
# x_root-b(3x_root^2-6x_root)
x_root = x_root - b * (3 * pow(x_root, 2) - 6 * x_root)
x_root_arr.append(x_root)
# x_axis^3-3x_axis^2
y = pow(x_axis, 3) - 3 * pow(x_axis, 2)
# 3x_axis^2-6x_axis
y1 = 3 * pow(x_axis, 2) - 6 * x_axis
# x_root^3-3x_root^2
y0.append(pow(x_root, 3) - 3 * pow(x_root, 2))
plt.title("Gradient Descent f(x) = x^3-3x^2")
plt.xlabel("x")
plt.ylabel("f(x)\\f'(x)")
plt.plot(x_axis, x_axis0, "--", label="X-axis")
plt.plot(y_axis0, y_axis, "--", label="Y-axis")
plt.plot(x_axis, y, "k-", label="f(x)")
plt.plot(x_axis, y1, "g-", label="f'(x)")
plt.plot(x_root_arr, y0, "r-",label="x_root")
plt.legend()
plt.show()
```
---
## Pandas
```
import pandas as pd
import numpy as np
df = pd.DataFrame(np.random.randn(10,5))
df
print(df.columns)
df[1]
df[1][2:5]
df.describe()
```
## Widgets
```
import ipywidgets as widgets
widgets.IntSlider()
import ipywidgets as widgets
widgets.Button(description='Press Me')
```
---
<a href="ipynb/jupyter.ipynb" download>Download the ipynb file</a>
---
# ฮฮตฯ ฮตฯฮฏฯฮทฯ
- [ฮ ฮฑฯฮฑฮดฮตฮฏฮณฮผฮฑฯฮฑ](https://nbviewer.jupyter.org/)
- [ฮฆฮตฯฮนฮฝฮฌ ฮธฮญฮผฮฑฯฮฑ ฮตฮพฮตฯฮฌฯฮตฯฮฝ](https://www.youtube.com/watch?v=dQw4w9WgXcQ)
|
github_jupyter
|
!yes | sudo pacman -S jupyter-notebook python-ipykernel
%%bash
sudo apt install python3-pip python3-dev
pip install jupyter
!jupyter lab
!jupyter lab & disown %jupyter
!pkill jupyter
!pip install jupyter
%lsmagic
%%bash
bash --version
import time
def method_a():
time.sleep(1)
def method_b():
time.sleep(2)
%timeit method_a()
%timeit method_b()
import matplotlib.pyplot as plt
points = [
[1, 1, "Red"], [1, 4, "Red"], [1, 9, "Black"], [5, 3,"Black"],
[5, 6, "Red"], [6, 1, "Black"], [6, 2, "Black"], [6, 5, "Black"],
[6, 8, "Red"], [8, 1, "Red"], [9, 3, "Black"], [2, 9, "Black"]
]
plt.title("Points")
plt.xlabel("x")
plt.ylabel("y")
char = 'A'
for point in points:
plt.plot(point[1],point[0], "o", label=char, color=point[2])
char = chr(ord(char) + 1)
plt.legend()
plt.show()
from matplotlib.widgets import Button
import matplotlib.pyplot as plt
import numpy as np
print("Gradient Descent f(x) = X^3-3*x^2")
x_root = float(input("x0 (3-4): "))
b = float(input("b (0.01-0.05): "))
y0 = []
x_root_arr = []
x_axis = np.r_[-1:4:0.01]
x_axis0 = np.zeros(x_axis.size)
y_axis = np.r_[-5:25:0.01]
y_axis0 = np.zeros(y_axis.size)
# 3(x_root^2)-6x_root > 10^-3
while abs(3 * pow(x_root, 2) - 6 * x_root) > pow(10, -3):
# x_root-b(3x_root^2-6x_root)
x_root = x_root - b * (3 * pow(x_root, 2) - 6 * x_root)
x_root_arr.append(x_root)
# x_axis^3-3x_axis^2
y = pow(x_axis, 3) - 3 * pow(x_axis, 2)
# 3x_axis^2-6x_axis
y1 = 3 * pow(x_axis, 2) - 6 * x_axis
# x_root^3-3x_root^2
y0.append(pow(x_root, 3) - 3 * pow(x_root, 2))
plt.title("Gradient Descent f(x) = x^3-3x^2")
plt.xlabel("x")
plt.ylabel("f(x)\\f'(x)")
plt.plot(x_axis, x_axis0, "--", label="X-axis")
plt.plot(y_axis0, y_axis, "--", label="Y-axis")
plt.plot(x_axis, y, "k-", label="f(x)")
plt.plot(x_axis, y1, "g-", label="f'(x)")
plt.plot(x_root_arr, y0, "r-",label="x_root")
plt.legend()
plt.show()
import pandas as pd
import numpy as np
df = pd.DataFrame(np.random.randn(10,5))
df
print(df.columns)
df[1]
df[1][2:5]
df.describe()
import ipywidgets as widgets
widgets.IntSlider()
import ipywidgets as widgets
widgets.Button(description='Press Me')
| 0.308086 | 0.724432 |
# Starbucks Capstone Challenge
### Introduction
This data set contains simulated data that mimics customer behavior on the Starbucks rewards mobile app. Once every few days, Starbucks sends out an offer to users of the mobile app. An offer can be merely an advertisement for a drink or an actual offer such as a discount or BOGO (buy one get one free). Some users might not receive any offer during certain weeks.
Not all users receive the same offer, and that is the challenge to solve with this data set.
Your task is to combine transaction, demographic and offer data to determine which demographic groups respond best to which offer type. This data set is a simplified version of the real Starbucks app because the underlying simulator only has one product whereas Starbucks actually sells dozens of products.
Every offer has a validity period before the offer expires. As an example, a BOGO offer might be valid for only 5 days. You'll see in the data set that informational offers have a validity period even though these ads are merely providing information about a product; for example, if an informational offer has 7 days of validity, you can assume the customer is feeling the influence of the offer for 7 days after receiving the advertisement.
You'll be given transactional data showing user purchases made on the app including the timestamp of purchase and the amount of money spent on a purchase. This transactional data also has a record for each offer that a user receives as well as a record for when a user actually views the offer. There are also records for when a user completes an offer.
Keep in mind as well that someone using the app might make a purchase through the app without having received an offer or seen an offer.
### Example
To give an example, a user could receive a discount offer buy 10 dollars get 2 off on Monday. The offer is valid for 10 days from receipt. If the customer accumulates at least 10 dollars in purchases during the validity period, the customer completes the offer.
However, there are a few things to watch out for in this data set. Customers do not opt into the offers that they receive; in other words, a user can receive an offer, never actually view the offer, and still complete the offer. For example, a user might receive the "buy 10 dollars get 2 dollars off offer", but the user never opens the offer during the 10 day validity period. The customer spends 15 dollars during those ten days. There will be an offer completion record in the data set; however, the customer was not influenced by the offer because the customer never viewed the offer.
# Data Sets
The data is contained in three files:
* portfolio.json - containing offer ids and meta data about each offer (duration, type, etc.)
* profile.json - demographic data for each customer
* transcript.json - records for transactions, offers received, offers viewed, and offers completed
Here is the schema and explanation of each variable in the files:
**portfolio.json**
* id (string) - offer id
* offer_type (string) - type of offer ie BOGO, discount, informational
* difficulty (int) - minimum required spend to complete an offer
* reward (int) - reward given for completing an offer
* duration (int) - time for offer to be open, in days
* channels (list of strings)
**profile.json**
* age (int) - age of the customer
* became_member_on (int) - date when customer created an app account
* gender (str) - gender of the customer (note some entries contain 'O' for other rather than M or F)
* id (str) - customer id
* income (float) - customer's income
**transcript.json**
* event (str) - record description (ie transaction, offer received, offer viewed, etc.)
* person (str) - customer id
* time (int) - time in hours since start of test. The data begins at time t=0
* value - (dict of strings) - either an offer id or transaction amount depending on the record
```
import pandas as pd
import numpy as np
import math
import json
import pickle
import matplotlib.pyplot as plt
% matplotlib inline
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import make_scorer, fbeta_score, accuracy_score
# read in the json files
portfolio = pd.read_json('data/portfolio.json', orient='records', lines=True)
profile = pd.read_json('data/profile.json', orient='records', lines=True)
transcript = pd.read_json('data/transcript.json', orient='records', lines=True)
portfolio
portfolio.shape
profile.head()
profile.info()
def profile_clean(df=profile):
df['year']=df['became_member_on'].apply(lambda x:str(x)[0:4])
df['month']=df['became_member_on'].apply(lambda x:float(str(x)[4:6].strip('0')))
df['day']=df['became_member_on'].apply(lambda x:str(x)[6:8])
df.drop('became_member_on', axis=1, inplace=True)
df['age']=df['age'].apply(lambda x:x if x != 118 else np.nan)
df['more_nan']= df.isnull().sum(axis=1)
df['more_nan'] = df['more_nan'].apply(lambda x: 1 if x==3 else 0)
profile_clean()
profile.shape
profile.head()
profile.year.unique()
profile.info()
profile.id.nunique()
transcript.head()
transcript.shape
transcript.query('event=="offer viewed"').time.nunique()
transcript.time.max()
transcript['value']=transcript['value'].apply(lambda x: x.values())
transactions = transcript.query('event == "transaction"')
transactions['value'] = transactions.value.apply(lambda x:float(str(x).strip("dict_values(['([])")))
transactions.head()
mean_t = transactions.groupby('person').mean()['value']
number_t = transactions.groupby('person').count()['event']
mean_t.shape
profile_t = profile.set_index('id').join(mean_t).join(number_t)
profile_t.head()
profile_t.rename(columns={'value':'value_mean', 'event': 'count'}, inplace=True)
profile_t.head()
offer_received = transcript.query('event == "offer received"')
offer_received.shape
offer_received.head()
offer_received['offer_id']=offer_received.value.apply(lambda x:str(x).strip("dict_values(['([])"))
offer_received.drop('value', axis=1, inplace=True)
offer_received.head()
offer_received.drop('time', axis=1).duplicated().sum()
offer_received.duplicated().sum()
offer_viewed = transcript.query('event == "offer viewed"')
offer_viewed['offer_id']=offer_viewed.value.apply(lambda x:str(x).strip("dict_values(['([])"))
offer_viewed.drop('value', axis=1, inplace=True)
offer_viewed.head()
offer_viewed.shape
offer_viewed.duplicated().sum()
offer_viewed.drop('time', axis=1).duplicated().sum()
offer_completed = transcript.query('event == "offer completed"')
offer_completed['value'] = offer_completed['value'].apply(lambda x:str(x).strip("dict_values(['([])"))
offer_completed.head()
offer_completed['offer_id']=offer_completed['value'].apply(lambda x: x.split("',")[0])
offer_completed['reward']=offer_completed['value'].apply(lambda x:x.split("',")[1])
offer_completed.drop('value', axis=1, inplace=True)
offer_completed.head()
offer_completed.info()
offer_completed.duplicated().sum()
offer_completed.drop_duplicates(inplace=True)
offer_completed.drop('time', axis=1).duplicated().sum()
def event_merge(early, later, l_sufx, r_sufx):
df = pd.merge(early.drop('event', axis=1), later.drop('event', axis=1),
on =['person', 'offer_id'],
suffixes=(l_sufx, r_sufx))
df['delay'] = df['time'+r_sufx]-df['time'+l_sufx]
df=df.query('delay>0')
df=df.loc[df.groupby(['person','time'+l_sufx])['delay'].idxmin()]
return df
completed = event_merge(offer_viewed, offer_completed, l_sufx='_viewed', r_sufx='_completed')
completed.head()
completed.shape
completed.duplicated().any()
viewed = event_merge(offer_received, offer_viewed, l_sufx='_received', r_sufx='_viewed')
viewed.head()
viewed.duplicated().any()
viewed.shape
portfolio.rename(columns={'id':'offer_id'}, inplace=True)
portfolio.head()
viewed=viewed.merge(portfolio, on='offer_id')
viewed.head()
viewed.info()
viewed = viewed[viewed['time_viewed']-viewed['time_received'] < viewed['duration']*24]
viewed_in = viewed.query('time_received+duration*24<=714')
viewed_in.head()
viewed_in.shape
progress = pd.merge(viewed_in, completed, how='left', on=['person','time_viewed'], suffixes=('_viewed', '_completed'))
progress.head()
progress.drop(['offer_id_completed','reward_completed'], axis=1, inplace=True)
progress.head()
progress.rename(columns={'offer_id_viewed':'offer_id', 'reward_viewed':'reward'},inplace=True)
progress.head()
progress.info()
def offer_id_setting(o_id):
new_o_id = portfolio[portfolio['offer_id']==o_id].index.values.astype(str)
return new_o_id
progress['offer_id']=progress['offer_id'].apply(offer_id_setting)
progress.head()
progress = progress.merge(profile_t, left_on='person', right_on=profile_t.index)
progress.head()
progress.shape
progress['result']=progress['time_completed'].apply(lambda x: 0 if pd.isnull(x) else 1)
progress.head()
progress.shape
with open('PROGRESS.pkl', 'wb') as f:
pickle.dump(progress,f)
progress = pd.read_pickle('PROGRESS.pkl')
progress.head()
progress.info()
progress[~(progress['time_completed']-progress['time_received'] > progress['duration']*24)].shape
progress = progress[~(progress['time_completed']-progress['time_received'] > progress['duration']*24)]
progress['value_mean'].fillna(value=0, inplace=True)
progress['count'].fillna(value=0, inplace=True)
progress.describe()
progress.boxplot(column=['value_mean']);
plt.xticks([1],['Average transaction value']);
IQR = progress['value_mean'].quantile(0.75)-progress['value_mean'].quantile(0.25)
upper_bound=progress['value_mean'].quantile(0.75)+IQR*1.5
upper_bound
progress['value_mean'].quantile(0.98)
progress[~(progress['value_mean']>upper_bound)].shape
progress=progress[progress['value_mean']<upper_bound]
progress.query('offer_type=="informational"')['result'].mean()
progress.query('offer_type=="bogo"')['result'].mean()
progress.query('offer_type=="discount"')['result'].mean()
progress[progress['more_nan']==1].query('offer_type=="bogo"')['result'].mean()
progress[progress['more_nan']==1].query('offer_type=="discount"')['result'].mean()
progress[progress['more_nan']==0].query('offer_type=="bogo"')['result'].mean()
progress[progress['more_nan']==0].query('offer_type=="discount"')['result'].mean()
```
| Users | BOGO | discount |
| --- | --- | --- |
| Without personal imformation | 0.06 | 0.22 |
| With personal imformation | 0.42 | 0.61 |
| Total | 0.36 | 0.55 |
```
progress.info()
progress_l_nan = progress[progress['more_nan']==0]
progress_m_nan = progress[progress['more_nan']==1]
def hist_offer(cate, feature, df=progress_l_nan):
cate_df = df[df['offer_type']==cate]
number=cate_df.shape[0]
cate_1 = cate_df[cate_df['result']==1][feature]
cate_0 = cate_df[cate_df['result']==0][feature]
kwargs = dict(alpha=0.3, bins=15)
plt.hist(cate_0, **kwargs, color='g', align='mid', label='Uncompleted')
plt.hist(cate_1, **kwargs, color='r', align='mid', label='Completed')
plt.gca().set(title= (feature+' distribution of '+cate+ ' offer').capitalize(), ylabel='Frequency', xlabel=feature.capitalize())
plt.legend();
kwargs = dict(alpha=0.3, bins=15)
plt.hist(progress_l_nan[progress_l_nan['result']==0]['gender'], **kwargs, color='g', label='Unompleted');
plt.hist(progress_l_nan[progress_l_nan['result']==1]['gender'], **kwargs, color='r', label='Completed');
plt.gca().set(title='Gender Distribution', ylabel='Frequency', xlabel='Gender')
plt.legend();
hist_offer( 'bogo', 'gender')
hist_offer('discount', 'gender')
hist_offer( 'bogo', 'age')
hist_offer( 'discount', 'age')
hist_offer('bogo', 'income')
hist_offer('discount', 'income')
hist_offer('bogo', 'year')
hist_offer( 'discount', 'year')
hist_offer('bogo', 'count')
hist_offer('discount', 'count')
hist_offer('discount', 'value_mean')
hist_offer('bogo', 'value_mean')
progress_l_nan.info()
model = progress_l_nan.query('offer_type != "informational"')[['delay_viewed', 'difficulty', 'duration', 'offer_type',
'reward', 'age', 'gender', 'income', 'year', 'month',
'value_mean', 'count', 'result']]
model.head()
model[['2013','2014','2015','2016','2017','2018']] = pd.get_dummies(model['year'])
model[['gender_F', 'gender_M', 'gender_O']] = pd.get_dummies(model['gender'])
model['bogo'] = model['offer_type'].apply(lambda x: 1 if x =="bogo" else 0)
model.drop(['year','gender', 'offer_type'], axis=1, inplace=True)
model.head()
X = model.drop('result', axis=1)
y = model['result']
X.describe()
X.loc[:,:'count'].hist(figsize=(15,10));
#log-transformation
X['delay_viewed'] = X['delay_viewed'].apply(lambda x: np.log(x + 1))
X['count'] = X['count'].apply(lambda x: np.log(x + 1))
X['value_mean'] = X['value_mean'].apply(lambda x: np.log(x + 1))
X_transformed=pd.DataFrame(data=X)
scaler = MinMaxScaler()
X_transformed[X.columns] = scaler.fit_transform(X)
X_transformed.head()
X_transformed.describe()
X_train, X_test, y_train, y_test = train_test_split(X_transformed, y, test_size=0.2, random_state=42)
RF_clf = RandomForestClassifier(n_estimators=200,
random_state=42,
n_jobs=-1)
RF_clf.fit(X_train, y_train)
y_train_pred = RF_clf.predict(X_train).reshape(-1,1)
y_test_pred = RF_clf.predict(X_test).reshape(-1,1)
print('accuracy train: %.3f, test: %.3f' % (
accuracy_score(y_train, y_train_pred),
accuracy_score(y_test, y_test_pred)))
print('f0.5_score train: %.3f, test: %.3f' % (
fbeta_score(y_train, y_train_pred, beta=0.5),
fbeta_score(y_test, y_test_pred, beta=0.5)))
clf
param_grid={'n_estimators':[100, 200, 300],
'max_depth':[15, 20, 30],
'min_samples_split': [20,30,40],
'random_state':[42],
'n_jobs':[-1]}
scorer = make_scorer(fbeta_score, beta=0.5)
grid_obj = GridSearchCV(RandomForestClassifier(),param_grid, scoring = scorer)
grid_obj.fit(X_train, y_train)
best_r = grid_obj.best_estimator_
best_predictions = best_r.predict(X_test).reshape(-1,1)
y_train_grid = best_r.predict(X_train).reshape(-1,1)
print('accuracy train: %.3f, test: %.3f' % (
accuracy_score(y_train, y_train_grid ),
accuracy_score(y_test, best_predictions)))
print('f0.5_score train: %.3f, test: %.3f' % (
fbeta_score(y_train, y_train_grid, beta=0.5),
fbeta_score(y_test, best_predictions, beta=0.5)))
```
| Data | Accuracy | F-score |
| --- | --- | --- |
| Training data | 0.821 | 0.810 |
| Test data | 0.755 | 0.754 |
```
print (grid_obj.best_estimator_)
```
|
github_jupyter
|
import pandas as pd
import numpy as np
import math
import json
import pickle
import matplotlib.pyplot as plt
% matplotlib inline
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import make_scorer, fbeta_score, accuracy_score
# read in the json files
portfolio = pd.read_json('data/portfolio.json', orient='records', lines=True)
profile = pd.read_json('data/profile.json', orient='records', lines=True)
transcript = pd.read_json('data/transcript.json', orient='records', lines=True)
portfolio
portfolio.shape
profile.head()
profile.info()
def profile_clean(df=profile):
df['year']=df['became_member_on'].apply(lambda x:str(x)[0:4])
df['month']=df['became_member_on'].apply(lambda x:float(str(x)[4:6].strip('0')))
df['day']=df['became_member_on'].apply(lambda x:str(x)[6:8])
df.drop('became_member_on', axis=1, inplace=True)
df['age']=df['age'].apply(lambda x:x if x != 118 else np.nan)
df['more_nan']= df.isnull().sum(axis=1)
df['more_nan'] = df['more_nan'].apply(lambda x: 1 if x==3 else 0)
profile_clean()
profile.shape
profile.head()
profile.year.unique()
profile.info()
profile.id.nunique()
transcript.head()
transcript.shape
transcript.query('event=="offer viewed"').time.nunique()
transcript.time.max()
transcript['value']=transcript['value'].apply(lambda x: x.values())
transactions = transcript.query('event == "transaction"')
transactions['value'] = transactions.value.apply(lambda x:float(str(x).strip("dict_values(['([])")))
transactions.head()
mean_t = transactions.groupby('person').mean()['value']
number_t = transactions.groupby('person').count()['event']
mean_t.shape
profile_t = profile.set_index('id').join(mean_t).join(number_t)
profile_t.head()
profile_t.rename(columns={'value':'value_mean', 'event': 'count'}, inplace=True)
profile_t.head()
offer_received = transcript.query('event == "offer received"')
offer_received.shape
offer_received.head()
offer_received['offer_id']=offer_received.value.apply(lambda x:str(x).strip("dict_values(['([])"))
offer_received.drop('value', axis=1, inplace=True)
offer_received.head()
offer_received.drop('time', axis=1).duplicated().sum()
offer_received.duplicated().sum()
offer_viewed = transcript.query('event == "offer viewed"')
offer_viewed['offer_id']=offer_viewed.value.apply(lambda x:str(x).strip("dict_values(['([])"))
offer_viewed.drop('value', axis=1, inplace=True)
offer_viewed.head()
offer_viewed.shape
offer_viewed.duplicated().sum()
offer_viewed.drop('time', axis=1).duplicated().sum()
offer_completed = transcript.query('event == "offer completed"')
offer_completed['value'] = offer_completed['value'].apply(lambda x:str(x).strip("dict_values(['([])"))
offer_completed.head()
offer_completed['offer_id']=offer_completed['value'].apply(lambda x: x.split("',")[0])
offer_completed['reward']=offer_completed['value'].apply(lambda x:x.split("',")[1])
offer_completed.drop('value', axis=1, inplace=True)
offer_completed.head()
offer_completed.info()
offer_completed.duplicated().sum()
offer_completed.drop_duplicates(inplace=True)
offer_completed.drop('time', axis=1).duplicated().sum()
def event_merge(early, later, l_sufx, r_sufx):
df = pd.merge(early.drop('event', axis=1), later.drop('event', axis=1),
on =['person', 'offer_id'],
suffixes=(l_sufx, r_sufx))
df['delay'] = df['time'+r_sufx]-df['time'+l_sufx]
df=df.query('delay>0')
df=df.loc[df.groupby(['person','time'+l_sufx])['delay'].idxmin()]
return df
completed = event_merge(offer_viewed, offer_completed, l_sufx='_viewed', r_sufx='_completed')
completed.head()
completed.shape
completed.duplicated().any()
viewed = event_merge(offer_received, offer_viewed, l_sufx='_received', r_sufx='_viewed')
viewed.head()
viewed.duplicated().any()
viewed.shape
portfolio.rename(columns={'id':'offer_id'}, inplace=True)
portfolio.head()
viewed=viewed.merge(portfolio, on='offer_id')
viewed.head()
viewed.info()
viewed = viewed[viewed['time_viewed']-viewed['time_received'] < viewed['duration']*24]
viewed_in = viewed.query('time_received+duration*24<=714')
viewed_in.head()
viewed_in.shape
progress = pd.merge(viewed_in, completed, how='left', on=['person','time_viewed'], suffixes=('_viewed', '_completed'))
progress.head()
progress.drop(['offer_id_completed','reward_completed'], axis=1, inplace=True)
progress.head()
progress.rename(columns={'offer_id_viewed':'offer_id', 'reward_viewed':'reward'},inplace=True)
progress.head()
progress.info()
def offer_id_setting(o_id):
new_o_id = portfolio[portfolio['offer_id']==o_id].index.values.astype(str)
return new_o_id
progress['offer_id']=progress['offer_id'].apply(offer_id_setting)
progress.head()
progress = progress.merge(profile_t, left_on='person', right_on=profile_t.index)
progress.head()
progress.shape
progress['result']=progress['time_completed'].apply(lambda x: 0 if pd.isnull(x) else 1)
progress.head()
progress.shape
with open('PROGRESS.pkl', 'wb') as f:
pickle.dump(progress,f)
progress = pd.read_pickle('PROGRESS.pkl')
progress.head()
progress.info()
progress[~(progress['time_completed']-progress['time_received'] > progress['duration']*24)].shape
progress = progress[~(progress['time_completed']-progress['time_received'] > progress['duration']*24)]
progress['value_mean'].fillna(value=0, inplace=True)
progress['count'].fillna(value=0, inplace=True)
progress.describe()
progress.boxplot(column=['value_mean']);
plt.xticks([1],['Average transaction value']);
IQR = progress['value_mean'].quantile(0.75)-progress['value_mean'].quantile(0.25)
upper_bound=progress['value_mean'].quantile(0.75)+IQR*1.5
upper_bound
progress['value_mean'].quantile(0.98)
progress[~(progress['value_mean']>upper_bound)].shape
progress=progress[progress['value_mean']<upper_bound]
progress.query('offer_type=="informational"')['result'].mean()
progress.query('offer_type=="bogo"')['result'].mean()
progress.query('offer_type=="discount"')['result'].mean()
progress[progress['more_nan']==1].query('offer_type=="bogo"')['result'].mean()
progress[progress['more_nan']==1].query('offer_type=="discount"')['result'].mean()
progress[progress['more_nan']==0].query('offer_type=="bogo"')['result'].mean()
progress[progress['more_nan']==0].query('offer_type=="discount"')['result'].mean()
progress.info()
progress_l_nan = progress[progress['more_nan']==0]
progress_m_nan = progress[progress['more_nan']==1]
def hist_offer(cate, feature, df=progress_l_nan):
cate_df = df[df['offer_type']==cate]
number=cate_df.shape[0]
cate_1 = cate_df[cate_df['result']==1][feature]
cate_0 = cate_df[cate_df['result']==0][feature]
kwargs = dict(alpha=0.3, bins=15)
plt.hist(cate_0, **kwargs, color='g', align='mid', label='Uncompleted')
plt.hist(cate_1, **kwargs, color='r', align='mid', label='Completed')
plt.gca().set(title= (feature+' distribution of '+cate+ ' offer').capitalize(), ylabel='Frequency', xlabel=feature.capitalize())
plt.legend();
kwargs = dict(alpha=0.3, bins=15)
plt.hist(progress_l_nan[progress_l_nan['result']==0]['gender'], **kwargs, color='g', label='Unompleted');
plt.hist(progress_l_nan[progress_l_nan['result']==1]['gender'], **kwargs, color='r', label='Completed');
plt.gca().set(title='Gender Distribution', ylabel='Frequency', xlabel='Gender')
plt.legend();
hist_offer( 'bogo', 'gender')
hist_offer('discount', 'gender')
hist_offer( 'bogo', 'age')
hist_offer( 'discount', 'age')
hist_offer('bogo', 'income')
hist_offer('discount', 'income')
hist_offer('bogo', 'year')
hist_offer( 'discount', 'year')
hist_offer('bogo', 'count')
hist_offer('discount', 'count')
hist_offer('discount', 'value_mean')
hist_offer('bogo', 'value_mean')
progress_l_nan.info()
model = progress_l_nan.query('offer_type != "informational"')[['delay_viewed', 'difficulty', 'duration', 'offer_type',
'reward', 'age', 'gender', 'income', 'year', 'month',
'value_mean', 'count', 'result']]
model.head()
model[['2013','2014','2015','2016','2017','2018']] = pd.get_dummies(model['year'])
model[['gender_F', 'gender_M', 'gender_O']] = pd.get_dummies(model['gender'])
model['bogo'] = model['offer_type'].apply(lambda x: 1 if x =="bogo" else 0)
model.drop(['year','gender', 'offer_type'], axis=1, inplace=True)
model.head()
X = model.drop('result', axis=1)
y = model['result']
X.describe()
X.loc[:,:'count'].hist(figsize=(15,10));
#log-transformation
X['delay_viewed'] = X['delay_viewed'].apply(lambda x: np.log(x + 1))
X['count'] = X['count'].apply(lambda x: np.log(x + 1))
X['value_mean'] = X['value_mean'].apply(lambda x: np.log(x + 1))
X_transformed=pd.DataFrame(data=X)
scaler = MinMaxScaler()
X_transformed[X.columns] = scaler.fit_transform(X)
X_transformed.head()
X_transformed.describe()
X_train, X_test, y_train, y_test = train_test_split(X_transformed, y, test_size=0.2, random_state=42)
RF_clf = RandomForestClassifier(n_estimators=200,
random_state=42,
n_jobs=-1)
RF_clf.fit(X_train, y_train)
y_train_pred = RF_clf.predict(X_train).reshape(-1,1)
y_test_pred = RF_clf.predict(X_test).reshape(-1,1)
print('accuracy train: %.3f, test: %.3f' % (
accuracy_score(y_train, y_train_pred),
accuracy_score(y_test, y_test_pred)))
print('f0.5_score train: %.3f, test: %.3f' % (
fbeta_score(y_train, y_train_pred, beta=0.5),
fbeta_score(y_test, y_test_pred, beta=0.5)))
clf
param_grid={'n_estimators':[100, 200, 300],
'max_depth':[15, 20, 30],
'min_samples_split': [20,30,40],
'random_state':[42],
'n_jobs':[-1]}
scorer = make_scorer(fbeta_score, beta=0.5)
grid_obj = GridSearchCV(RandomForestClassifier(),param_grid, scoring = scorer)
grid_obj.fit(X_train, y_train)
best_r = grid_obj.best_estimator_
best_predictions = best_r.predict(X_test).reshape(-1,1)
y_train_grid = best_r.predict(X_train).reshape(-1,1)
print('accuracy train: %.3f, test: %.3f' % (
accuracy_score(y_train, y_train_grid ),
accuracy_score(y_test, best_predictions)))
print('f0.5_score train: %.3f, test: %.3f' % (
fbeta_score(y_train, y_train_grid, beta=0.5),
fbeta_score(y_test, best_predictions, beta=0.5)))
print (grid_obj.best_estimator_)
| 0.323487 | 0.975225 |
```
# default_exp learner
#export
from local.torch_basics import *
from local.test import *
from local.layers import *
from local.data.all import *
from local.notebook.showdoc import *
from local.optimizer import *
#export
_all_ = ['CancelFitException', 'CancelEpochException', 'CancelTrainException', 'CancelValidException', 'CancelBatchException']
```
# Learner
> Basic class for handling the training loop
We'll use the following for testing purposes (a basic linear regression problem):
```
from torch.utils.data import TensorDataset
def synth_dbunch(a=2, b=3, bs=16, n_train=10, n_valid=2, cuda=False):
def get_data(n):
x = torch.randn(int(bs*n))
return TensorDataset(x, a*x + b + 0.1*torch.randn(int(bs*n)))
train_ds = get_data(n_train)
valid_ds = get_data(n_valid)
tfms = Cuda() if cuda else None
train_dl = TfmdDL(train_ds, bs=bs, shuffle=True, after_batch=tfms, num_workers=0)
valid_dl = TfmdDL(valid_ds, bs=bs, after_batch=tfms, num_workers=0)
return DataBunch(train_dl, valid_dl)
class RegModel(Module):
def __init__(self): self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
def forward(self, x): return x*self.a + self.b
```
## Callback -
```
#export core
_camel_re1 = re.compile('(.)([A-Z][a-z]+)')
_camel_re2 = re.compile('([a-z0-9])([A-Z])')
def camel2snake(name):
s1 = re.sub(_camel_re1, r'\1_\2', name)
return re.sub(_camel_re2, r'\1_\2', s1).lower()
test_eq(camel2snake('ClassAreCamel'), 'class_are_camel')
#export
def class2attr(self, cls_name):
return camel2snake(re.sub(rf'{cls_name}$', '', self.__class__.__name__) or cls_name.lower())
#export
class Callback(GetAttr):
"Basic class handling tweaks of the training loop by changing a `Learner` in various events"
_default='learn'
def __repr__(self): return type(self).__name__
def __call__(self, event_name):
"Call `self.{event_name}` if it's defined"
getattr(self, event_name, noop)()
@property
def name(self):
"Name of the `Callback`, camel-cased and with '*Callback*' removed"
return class2attr(self, 'Callback')
```
The training loop is defined in `Learner` a bit below and consists in a minimal set of instructions: looping through the data we:
- compute the output of the model from the input
- calculate a loss between this output and the desired target
- compute the gradients of this loss with respect to all the model parameters
- update the parameters accordingly
- zero all the gradients
Any tweak of this training loop is defined in a `Callback` to avoid over-complicating the code of the training loop, and to make it easy to mix and match different techniques (since they'll be defined in different callbacks). A callback can implement actions on the following events:
- `begin_fit`: called before doing anything, ideal for initial setup.
- `begin_epoch`: called at the beginning of each epoch, useful for any behavior you need to reset at each epoch.
- `begin_train`: called at the beginning of the training part of an epoch.
- `begin_batch`: called at the beginning of each batch, just after drawing said batch. It can be used to do any setup necessary for the batch (like hyper-parameter scheduling) or to change the input/target before it goes in the model (change of the input with techniques like mixup for instance).
- `after_pred`: called after computing the output of the model on the batch. It can be used to change that output before it's fed to the loss.
- `after_loss`: called after the loss has been computed, but before the backward pass. It can be used to add any penalty to the loss (AR or TAR in RNN training for instance).
- `after_backward`: called after the backward pass, but before the update of the parameters. It can be used to do any change to the gradients before said update (gradient clipping for instance).
- `after_step`: called after the step and before the gradients are zeroed.
- `after_batch`: called at the end of a batch, for any clean-up before the next one.
- `after_train`: called at the end of the training phase of an epoch.
- `begin_validate`: called at the beginning of the validation phase of an epoch, useful for any setup needed specifically for validation.
- `after_validate`: called at the end of the validation part of an epoch.
- `after_epoch`: called at the end of an epoch, for any clean-up before the next one.
- `after_fit`: called at the end of training, for final clean-up.
```
show_doc(Callback.__call__)
tst_cb = Callback()
tst_cb.call_me = lambda: print("maybe")
test_stdout(lambda: tst_cb("call_me"), "maybe")
show_doc(Callback.__getattr__)
```
This is a shortcut to avoid having to write `self.learn.bla` for any `bla` attribute we seek, and just write `self.bla`.
```
mk_class('TstLearner', 'a')
class TstCallback(Callback):
def batch_begin(self): print(self.a)
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
test_stdout(lambda: cb('batch_begin'), "1")
```
Note that it only works to get the value of the attribute, if you want to change it, you have to manually access it with `self.learn.bla`. In the example below, `self.a += 1` creates an `a` attribute of 2 in the callback instead of setting the `a` of the learner to 2:
```
class TstCallback(Callback):
def batch_begin(self): self.a += 1
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
cb('batch_begin')
test_eq(cb.a, 2)
test_eq(cb.learn.a, 1)
```
A proper version needs to write `self.learn.a = self.a + 1`:
```
class TstCallback(Callback):
def batch_begin(self): self.learn.a = self.a + 1
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
cb('batch_begin')
test_eq(cb.learn.a, 2)
show_doc(Callback.name, name='Callback.name')
test_eq(TstCallback().name, 'tst')
class ComplicatedNameCallback(Callback): pass
test_eq(ComplicatedNameCallback().name, 'complicated_name')
```
### TrainEvalCallback -
```
#export
class TrainEvalCallback(Callback):
"`Callback` that tracks the number of iterations done and properly sets training/eval mode"
def begin_fit(self):
"Set the iter and epoch counters to 0, put the model and the right device"
self.learn.train_iter,self.learn.pct_train = 0,0.
self.model.to(self.dbunch.device)
def after_batch(self):
"Update the iter counter (in training mode)"
if not self.training: return
self.learn.pct_train += 1./(self.n_iter*self.n_epoch)
self.learn.train_iter += 1
def begin_train(self):
"Set the model in training mode"
self.learn.pct_train=self.epoch/self.n_epoch
self.model.train()
self.learn.training=True
def begin_validate(self):
"Set the model in validation mode"
self.model.eval()
self.learn.training=False
show_doc(TrainEvalCallback, title_level=3)
```
This `Callback` is automatically added in every `Learner` at initialization.
```
#hide
#test of the TrainEvalCallback below in Learner.fit
show_doc(TrainEvalCallback.begin_fit)
show_doc(TrainEvalCallback.after_batch)
show_doc(TrainEvalCallback.begin_train)
show_doc(TrainEvalCallback.begin_validate)
```
### GatherPredsCallback -
```
#export
class GatherPredsCallback(Callback):
"`Callback` that saves the predictions and targets, optionally `with_loss`"
def __init__(self, with_input=False, with_loss=False): store_attr(self, "with_input,with_loss")
def begin_batch(self):
if self.with_input: self.inputs.append((to_detach(self.xb)))
def begin_validate(self):
"Initialize containers"
self.preds,self.targets = [],[]
if self.with_input: self.inputs=[]
if self.with_loss: self.losses = []
def after_batch(self):
"Save predictions, targets and potentially losses"
self.preds.append(to_detach(self.pred))
self.targets.append(to_detach(self.yb))
if self.with_loss: self.losses.append(to_detach(self.loss))
show_doc(GatherPredsCallback, title_level=3)
show_doc(GatherPredsCallback.begin_validate)
show_doc(GatherPredsCallback.after_batch)
```
## Callbacks control flow
It happens that we may want to skip some of the steps of the training loop: in gradient accumulation, we don't aways want to do the step/zeroing of the grads for instance. During an LR finder test, we don't want to do the validation phase of an epoch. Or if we're training with a strategy of early stopping, we want to be able to completely interrupt the training loop.
This is made possible by raising specific exceptions the training loop will look for (and properly catch).
```
#export
_ex_docs = dict(
CancelFitException="Skip the rest of this batch and go to `after_batch`",
CancelEpochException="Skip the rest of the training part of the epoch and go to `after_train`",
CancelTrainException="Skip the rest of the validation part of the epoch and go to `after_validate`",
CancelValidException="Skip the rest of this epoch and go to `after_epoch`",
CancelBatchException="Interrupts training and go to `after_fit`")
for c,d in _ex_docs.items(): mk_class(c,sup=Exception,doc=d)
show_doc(CancelBatchException, title_level=3)
show_doc(CancelTrainException, title_level=3)
show_doc(CancelValidException, title_level=3)
show_doc(CancelEpochException, title_level=3)
show_doc(CancelFitException, title_level=3)
```
You can detect one of those exceptions occurred and add code that executes right after with the following events:
- `after_cancel_batch`: reached imediately after a `CancelBatchException` before proceeding to `after_batch`
- `after_cancel_train`: reached imediately after a `CancelTrainException` before proceeding to `after_epoch`
- `after_cancel_valid`: reached imediately after a `CancelValidException` before proceeding to `after_epoch`
- `after_cancel_epoch`: reached imediately after a `CancelEpochException` before proceeding to `after_epoch`
- `after_cancel_fit`: reached imediately after a `CancelFitException` before proceeding to `after_fit`
```
# export
_events = L.split('begin_fit begin_epoch begin_train begin_batch after_pred after_loss \
after_backward after_step after_cancel_batch after_batch after_cancel_train \
after_train begin_validate after_cancel_validate after_validate after_cancel_epoch \
after_epoch after_cancel_fit after_fit')
mk_class('event', **_events.map_dict(),
doc="All possible events as attributes to get tab-completion and typo-proofing")
_before_inference = [event.begin_fit, event.begin_epoch, event.begin_validate]
_after_inference = [event.after_validate, event.after_epoch, event.after_fit]
# export
_all_ = ['event']
show_doc(event, name='event', title_level=3)
test_eq(event.after_backward, 'after_backward')
```
Here's the full list: *begin_fit begin_epoch begin_train begin_batch after_pred after_loss after_backward after_step after_cancel_batch after_batch after_cancel_train after_train begin_validate after_cancel_validate after_validate after_cancel_epoch after_epoch after_cancel_fit after_fit*.
```
#hide
#Full test of the control flow below, after the Learner class
```
## Learner -
```
# export
defaults.lr = slice(3e-3)
defaults.wd = 1e-2
defaults.callbacks = [TrainEvalCallback]
# export
def replacing_yield(o, attr, val):
"Context manager to temporarily replace an attribute"
old = getattr(o,attr)
try: yield setattr(o,attr,val)
finally: setattr(o,attr,old)
#export
def mk_metric(m):
"Convert `m` to an `AvgMetric`, unless it's already a `Metric`"
return m if isinstance(m, Metric) else AvgMetric(m)
#export
def save_model(file, model, opt, with_opt=True):
"Save `model` to `file` along with `opt` (if available, and if `with_opt`)"
if opt is None: with_opt=False
state = get_model(model).state_dict()
if with_opt: state = {'model': state, 'opt':opt.state_dict()}
torch.save(state, file)
# export
def load_model(file, model, opt, with_opt=None, device=None, strict=True):
"Load `model` from `file` along with `opt` (if available, and if `with_opt`)"
if isinstance(device, int): device = torch.device('cuda', device)
state = torch.load(file)
hasopt = set(state)=={'model', 'opt'}
model_state = state['model'] if hasopt else state
get_model(model).load_state_dict(model_state, strict=strict)
if hasopt and ifnone(with_opt,True):
try: opt.load_state_dict(state['opt'])
except:
if with_opt: warn("Could not load the optimizer state.")
elif with_opt: warn("Saved filed doesn't contain an optimizer state.")
x = [(tensor([1]),),(tensor([2]),),(tensor([3]),)]
y = [(tensor([1]),tensor([1])),(tensor([2]),tensor([2])),(tensor([3]),tensor([3]))]
#export
def detuplify(x):
"If `x` is a tuple with one thing, extract it"
return x[0] if len(x)==1 else x
# export
class Learner():
def __init__(self, dbunch, model, loss_func=None, opt_func=SGD, lr=defaults.lr, splitter=trainable_params, cbs=None,
cb_funcs=None, metrics=None, path=None, model_dir='models', wd_bn_bias=False, train_bn=True):
store_attr(self, "dbunch,model,opt_func,lr,splitter,model_dir,wd_bn_bias,train_bn")
self.training,self.logger,self.opt,self.cbs = False,print,None,L()
#TODO: infer loss_func from data
if loss_func is None:
loss_func = getattr(dbunch.train_ds, 'loss_func', None)
assert loss_func is not None, "Could not infer loss function from the data, please pass a loss function."
self.loss_func = loss_func
self.path = path if path is not None else getattr(dbunch, 'path', Path('.'))
self.metrics = L(metrics).map(mk_metric)
self.add_cbs(cbf() for cbf in L(defaults.callbacks)+L(cb_funcs))
self.add_cbs(cbs)
self.model.to(self.dbunch.device)
def add_cbs(self, cbs): L(cbs).map(self.add_cb)
def remove_cbs(self, cbs): L(cbs).map(self.remove_cb)
def add_cb(self, cb):
old = getattr(self, cb.name, None)
assert not old or isinstance(old, type(cb)), f"self.{cb.name} already registered"
cb.learn = self
setattr(self, cb.name, cb)
self.cbs.append(cb)
def remove_cb(self, cb):
cb.learn = None
if hasattr(self, cb.name): delattr(self, cb.name)
if cb in self.cbs: self.cbs.remove(cb)
@contextmanager
def added_cbs(self, cbs):
self.add_cbs(cbs)
yield
self.remove_cbs(cbs)
def __call__(self, event_name): L(event_name).map(self._call_one)
def _call_one(self, event_name):
assert hasattr(event, event_name)
[cb(event_name) for cb in sort_by_run(self.cbs)]
def _bn_bias_state(self, with_bias): return bn_bias_params(self.model, with_bias).map(self.opt.state)
def create_opt(self):
self.opt = self.opt_func(self.splitter(self.model), lr=self.lr)
if not self.wd_bn_bias:
for p in self._bn_bias_state(True ): p['do_wd'] = False
if self.train_bn:
for p in self._bn_bias_state(False): p['force_train'] = True
def _split(self, b):
i = getattr(self.dbunch, 'n_inp', 1 if len(b)==1 else len(b)-1)
self.xb,self.yb = b[:i],b[i:]
def all_batches(self):
self.n_iter = len(self.dl)
for o in enumerate(self.dl): self.one_batch(*o)
def one_batch(self, i, b):
self.iter = i
try:
self._split(b); self('begin_batch')
self.pred = self.model(*self.xb); self('after_pred')
if len(self.yb) == 0: return
self.loss = self.loss_func(self.pred, *self.yb); self('after_loss')
if not self.training: return
self.loss.backward(); self('after_backward')
self.opt.step(); self('after_step')
self.opt.zero_grad()
except CancelBatchException: self('after_cancel_batch')
finally: self('after_batch')
def _do_begin_fit(self, n_epoch):
self.n_epoch,self.loss = n_epoch,tensor(0.); self('begin_fit')
def _do_epoch_train(self):
try:
self.dl = self.dbunch.train_dl; self('begin_train')
self.all_batches()
except CancelTrainException: self('after_cancel_train')
finally: self('after_train')
def _do_epoch_validate(self):
try:
self.dl = self.dbunch.valid_dl; self('begin_validate')
with torch.no_grad(): self.all_batches()
except CancelValidException: self('after_cancel_validate')
finally: self('after_validate')
def fit(self, n_epoch, lr=None, wd=defaults.wd, cbs=None, reset_opt=False):
with self.added_cbs(cbs):
if reset_opt or not self.opt: self.create_opt()
self.opt.set_hypers(wd=wd, lr=self.lr if lr is None else lr)
try:
self._do_begin_fit(n_epoch)
for epoch in range(n_epoch):
try:
self.epoch=epoch; self('begin_epoch')
self._do_epoch_train()
self._do_epoch_validate()
except CancelEpochException: self('after_cancel_epoch')
finally: self('after_epoch')
except CancelFitException: self('after_cancel_fit')
finally: self('after_fit')
def validate(self, ds_idx=1, dl=None, cbs=None):
self.epoch,self.n_epoch,self.loss = 0,1,tensor(0.)
self.dl = self.dbunch.dls[ds_idx] if dl is None else dl
with self.added_cbs(cbs), self.no_logging():
self(_before_inference)
self.all_batches()
self(_after_inference)
return self.recorder.values[-1]
def get_preds(self, ds_idx=1, dl=None, with_input=False, with_loss=False, decoded=False, act=None):
self.epoch,self.n_epoch,self.loss = 0,1,tensor(0.)
self.dl = self.dbunch.dls[ds_idx] if dl is None else dl
cb = GatherPredsCallback(with_input=with_input, with_loss=with_loss)
with self.no_logging(), self.added_cbs(cb), self.loss_not_reduced():
self(_before_inference)
self.all_batches()
self(_after_inference)
if act is None: act = getattr(self.loss_func, 'activation', noop)
preds = act(torch.cat(cb.preds))
if decoded: preds = getattr(sellf.loss_func, 'decodes', noop)(preds)
res = (preds, detuplify(tuple(torch.cat(o) for o in zip(*cb.targets))))
if with_input: res = (tuple(torch.cat(o) for o in zip(*cb.inputs)),) + res
if with_loss: res = res + (torch.cat(cb.losses),)
return res
def predict(self, item):
dl = test_dl(self.dbunch, [item])
inp,preds,_ = self.get_preds(dl=dl, with_input=True)
dec_preds = getattr(self.loss_func, 'decodes', noop)(preds)
i = getattr(self.dbunch, 'n_inp', -1)
full_dec = self.dbunch.decode_batch((*inp,dec_preds))[0][i:]
return detuplify(full_dec),dec_preds[0],preds[0]
@contextmanager
def no_logging(self): return replacing_yield(self, 'logger', noop)
@contextmanager
def loss_not_reduced(self):
if hasattr(self.loss_func, 'reduction'): return replacing_yield(self.loss_func, 'reduction', 'none')
else: return replacing_yield(self, 'loss_func', partial(self.loss_func, reduction='none'))
def save(self, file, with_opt=True):
#TODO: if rank_distrib(): return # don't save if slave proc
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
save_model(file, self.model, getattr(self,'opt',None), with_opt)
def load(self, file, with_opt=None, device=None, strict=True):
if device is None: device = self.dbunch.device
if self.opt is None: self.create_opt()
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
load_model(file, self.model, self.opt, with_opt=with_opt, device=device, strict=strict)
return self
Learner.x,Learner.y = add_props(lambda i,x: detuplify((x.xb,x.yb)[i]))
#export
add_docs(Learner, "Group together a `model`, some `dbunch` and a `loss_func` to handle training",
add_cbs="Add `cbs` to the list of `Callback` and register `self` as their learner",
add_cb="Add `cb` to the list of `Callback` and register `self` as their learner",
remove_cbs="Remove `cbs` from the list of `Callback` and deregister `self` as their learner",
remove_cb="Add `cb` from the list of `Callback` and deregister `self` as their learner",
added_cbs="Context manage that temporarily adds `cbs`",
create_opt="Create an optimizer with `lr`",
one_batch="Train or evaluate `self.model` on batch `(xb,yb)`",
all_batches="Train or evaluate `self.model` on all batches of `self.dl`",
fit="Fit `self.model` for `n_epoch` using `cbs`. Optionally `reset_opt`.",
validate="Validate on `dl` with potential new `cbs`.",
get_preds="Get the predictions and targets on the `ds_idx`-th dbunchset, optionally `with_input` and `with_loss`",
predict="Return the prediction on `item`, fully decoded, loss function decoded and probabilities",
no_logging="Context manager to temporarily remove `logger`",
loss_not_reduced="A context manager to evaluate `loss_func` with reduction set to none.",
save="Save model and optimizer state (if `with_opt`) to `self.path/self.model_dir/file`",
load="Load model and optimizer state (if `with_opt`) from `self.path/self.model_dir/file` using `device`"
)
```
`opt_func` will be used to create an optimizer when `Learner.fit` is called, with `lr` as a learning rate. `splitter` is a function taht takes `self.model` and returns a list of parameter groups (or just one parameter group if there are no different parameter groups). The default is `trainable_params`, which returns all trainable parameters of the model.
`cbs` is one or a list of `Callback`s to pass to the `Learner`, and `cb_funcs` is one or a list of functions returning a `Callback` that will be called at init. Each `Callback` is registered as an attribute of `Learner` (with camel case). At creation, all the callbacks in `defaults.callbacks` (`TrainEvalCallback` and `Recorder`) are associated to the `Learner`.
`metrics` is an optional list of metrics, that can be either functions or `Metric`s (see below).
### Training loop
```
#Test init with callbacks
def synth_learner(n_train=10, n_valid=2, cuda=False, lr=defaults.lr, **kwargs):
data = synth_dbunch(n_train=n_train,n_valid=n_valid, cuda=cuda)
return Learner(data, RegModel(), loss_func=MSELossFlat(), lr=lr, **kwargs)
tst_learn = synth_learner()
test_eq(len(tst_learn.cbs), 1)
assert isinstance(tst_learn.cbs[0], TrainEvalCallback)
assert hasattr(tst_learn, ('train_eval'))
tst_learn = synth_learner(cbs=TstCallback())
test_eq(len(tst_learn.cbs), 2)
assert isinstance(tst_learn.cbs[1], TstCallback)
assert hasattr(tst_learn, ('tst'))
tst_learn = synth_learner(cb_funcs=TstCallback)
test_eq(len(tst_learn.cbs), 2)
assert isinstance(tst_learn.cbs[1], TstCallback)
assert hasattr(tst_learn, ('tst'))
#A name that becomes an existing attribute of the Learner will throw an exception (here add_cb)
class AddCbCallback(Callback): pass
test_fail(lambda: synth_learner(cbs=AddCbCallback()))
show_doc(Learner.fit)
#Training a few epochs should make the model better
learn = synth_learner(cb_funcs=TstCallback, lr=1e-2)
xb,yb = learn.dbunch.one_batch()
init_loss = learn.loss_func(learn.model(xb), yb)
learn.fit(2)
assert learn.loss < init_loss
#hide
#Test of TrainEvalCallback
class TestTrainEvalCallback(Callback):
run_after=TrainEvalCallback
def begin_fit(self):
test_eq([self.pct_train,self.train_iter], [0., 0])
self.old_pct_train,self.old_train_iter = self.pct_train,self.train_iter
def begin_batch(self): test_eq(next(self.model.parameters()).device, find_device(self.xb))
def after_batch(self):
if self.training:
test_eq(self.pct_train , self.old_pct_train+1/(self.n_iter*self.n_epoch))
test_eq(self.train_iter, self.old_train_iter+1)
self.old_pct_train,self.old_train_iter = self.pct_train,self.train_iter
def begin_train(self):
assert self.training and self.model.training
test_eq(self.pct_train, self.epoch/self.n_epoch)
self.old_pct_train = self.pct_train
def begin_validate(self):
assert not self.training and not self.model.training
learn = synth_learner(cb_funcs=TestTrainEvalCallback)
learn.fit(1)
#Check order is properly taken into account
learn.cbs = L(reversed(learn.cbs))
#hide
#cuda
#Check model is put on the GPU if needed
learn = synth_learner(cb_funcs=TestTrainEvalCallback, cuda=True)
learn.fit(1)
#hide
#Check wd is not applied on bn/bias when option wd_bn_bias=False
class _TstModel(nn.Module):
def __init__(self):
super().__init__()
self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
self.tst = nn.Sequential(nn.Linear(4,5), nn.BatchNorm1d(3))
self.tst[0].bias.data,self.tst[1].bias.data = torch.randn(5),torch.randn(3)
def forward(self, x): return x * self.a + self.b
class _PutGrad(Callback):
def after_backward(self):
for p in self.learn.model.tst.parameters():
p.grad = torch.ones_like(p.data)
learn = synth_learner(n_train=5, opt_func = partial(SGD, wd=1, true_wd=True), cb_funcs=_PutGrad)
learn.model = _TstModel()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1, lr=1e-2)
end = list(learn.model.tst.parameters())
assert not torch.allclose(end[0]-init[0], -0.05 * torch.ones_like(end[0]))
for i in [1,2,3]: test_close(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
show_doc(Learner.one_batch)
```
This is an internal method called by `Learner.fit`. If passed, `i` is the index of this iteration in the epoch. In training method, this does a full training step on the batch (compute predictions, loss, gradients, update the model parameters and zero the gradients). In validation mode, it stops at the loss computation.
```
# export
class VerboseCallback(Callback):
"Callback that prints the name of each event called"
def __call__(self, event_name):
print(event_name)
super().__call__(event_name)
#hide
class TestOneBatch(VerboseCallback):
def __init__(self, xb, yb, i):
self.save_xb,self.save_yb,self.i = xb,yb,i
self.old_pred,self.old_loss = None,tensor(0.)
def begin_batch(self):
self.old_a,self.old_b = self.model.a.data.clone(),self.model.b.data.clone()
test_eq(self.iter, self.i)
test_eq(self.save_xb, *self.xb)
test_eq(self.save_yb, *self.yb)
if hasattr(self.learn, 'pred'): test_eq(self.pred, self.old_pred)
def after_pred(self):
self.old_pred = self.pred
test_eq(self.pred, self.model.a.data * self.x + self.model.b.data)
test_eq(self.loss, self.old_loss)
def after_loss(self):
self.old_loss = self.loss
test_eq(self.loss, self.loss_func(self.old_pred, self.save_yb))
for p in self.model.parameters():
if not hasattr(p, 'grad') or p.grad is not None: test_eq(p.grad, tensor([0.]))
def after_backward(self):
self.grad_a = (2 * self.x * (self.pred.data - self.y)).mean()
self.grad_b = 2 * (self.pred.data - self.y).mean()
test_close(self.model.a.grad.data, self.grad_a)
test_close(self.model.b.grad.data, self.grad_b)
test_eq(self.model.a.data, self.old_a)
test_eq(self.model.b.data, self.old_b)
def after_step(self):
test_close(self.model.a.data, self.old_a - self.lr * self.grad_a)
test_close(self.model.b.data, self.old_b - self.lr * self.grad_b)
self.old_a,self.old_b = self.model.a.data.clone(),self.model.b.data.clone()
test_close(self.model.a.grad.data, self.grad_a)
test_close(self.model.b.grad.data, self.grad_b)
def after_batch(self):
for p in self.model.parameters(): test_eq(p.grad, tensor([0.]))
#hide
learn = synth_learner()
b = learn.dbunch.one_batch()
learn = synth_learner(cbs=TestOneBatch(*b, 42), lr=1e-2)
#Remove train/eval
learn.cbs = learn.cbs[1:]
#Setup
learn.loss,learn.training = tensor(0.),True
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
learn.model.train()
batch_events = ['begin_batch', 'after_pred', 'after_loss', 'after_backward', 'after_step', 'after_batch']
test_stdout(lambda: learn.one_batch(42, b), '\n'.join(batch_events))
test_stdout(lambda: learn.one_batch(42, b), '\n'.join(batch_events)) #Check it works for a second batch
show_doc(Learner.all_batches)
#hide
learn = synth_learner(n_train=5, cbs=VerboseCallback())
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
with redirect_stdout(io.StringIO()):
learn._do_begin_fit(1)
learn.epoch,learn.dl = 0,learn.dbunch.train_dl
learn('begin_epoch')
learn('begin_train')
test_stdout(learn.all_batches, '\n'.join(batch_events * 5))
test_eq(learn.train_iter, 5)
valid_events = ['begin_batch', 'after_pred', 'after_loss', 'after_batch']
with redirect_stdout(io.StringIO()):
learn.dl = learn.dbunch.valid_dl
learn('begin_validate')
test_stdout(learn.all_batches, '\n'.join(valid_events * 2))
test_eq(learn.train_iter, 5)
#hide
learn = synth_learner(n_train=5, cbs=VerboseCallback())
test_stdout(lambda: learn._do_begin_fit(42), 'begin_fit')
test_eq(learn.n_epoch, 42)
test_eq(learn.loss, tensor(0.))
#hide
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
learn.epoch = 0
test_stdout(lambda: learn._do_epoch_train(), '\n'.join(['begin_train'] + batch_events * 5 + ['after_train']))
#hide
test_stdout(learn._do_epoch_validate, '\n'.join(['begin_validate'] + valid_events * 2+ ['after_validate']))
```
### Serializing
```
show_doc(Learner.save)
```
`file` can be a `Path`, a `string` or a buffer.
```
show_doc(Learner.load)
```
`file` can be a `Path`, a `string` or a buffer. Use `device` to load the model/optimizer state on a device different from the one it was saved.
```
learn = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
xb,yb = learn.dbunch.one_batch()
init_loss = learn.loss_func(learn.model(xb), yb)
learn.fit(1)
learn.save('tmp')
assert (Path.cwd()/'models/tmp.pth').exists()
learn1 = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
learn1 = learn1.load('tmp')
test_eq(learn.model.a, learn1.model.a)
test_eq(learn.model.b, learn1.model.b)
test_eq(learn.opt.state_dict(), learn1.opt.state_dict())
learn.save('tmp1', with_opt=False)
learn1 = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
learn1 = learn1.load('tmp1')
test_eq(learn.model.a, learn1.model.a)
test_eq(learn.model.b, learn1.model.b)
test_ne(learn.opt.state_dict(), learn1.opt.state_dict())
shutil.rmtree('models')
```
### Callback handling
```
show_doc(Learner.__call__)
show_doc(Learner.add_cb)
learn = synth_learner()
learn.add_cb(TestTrainEvalCallback())
test_eq(len(learn.cbs), 2)
assert isinstance(learn.cbs[1], TestTrainEvalCallback)
test_eq(learn.train_eval.learn, learn)
show_doc(Learner.add_cbs)
learn.add_cbs([TestTrainEvalCallback(), TestTrainEvalCallback()])
test_eq(len(learn.cbs), 4)
show_doc(Learner.remove_cb)
cb = learn.cbs[1]
learn.remove_cb(learn.cbs[1])
test_eq(len(learn.cbs), 3)
assert cb.learn is None
assert not getattr(learn,'test_train_eval',None)
show_doc(Learner.remove_cbs)
cb = learn.cbs[1]
learn.remove_cbs(learn.cbs[1:])
test_eq(len(learn.cbs), 1)
```
When writing a callback, the following attributes of `Learner` are available:
- `model`: the model used for training/validation
- `data`: the underlying `DataBunch`
- `loss_func`: the loss function used
- `opt`: the optimizer used to udpate the model parameters
- `opt_func`: the function used to create the optimizer
- `cbs`: the list containing all `Callback`s
- `dl`: current `DataLoader` used for iteration
- `x`/`xb`: last input drawn from `self.dl` (potentially modified by callbacks). `xb` is always a tuple (potentially with one element) and `x` is detuplified. You can only assign to `xb`.
- `y`/`yb`: last target drawn from `self.dl` (potentially modified by callbacks). `yb` is always a tuple (potentially with one element) and `y` is detuplified. You can only assign to `yb`.
- `pred`: last predictions from `self.model` (potentially modified by callbacks)
- `loss`: last computed loss (potentially modified by callbacks)
- `n_epoch`: the number of epochs in this training
- `n_iter`: the number of iterations in the current `self.dl`
- `epoch`: the current epoch index (from 0 to `n_epoch-1`)
- `iter`: the current iteration index in `self.dl` (from 0 to `n_iter-1`)
The following attributes are added by `TrainEvalCallback` and should be available unless you went out of your way to remove that callback:
- `train_iter`: the number of training iterations done since the beginning of this training
- `pct_train`: from 0. to 1., the percentage of training iterations completed
- `training`: flag to indicate if we're in training mode or not
The following attribute is added by `Recorder` and should be available unless you went out of your way to remove that callback:
- `smooth_loss`: an exponentially-averaged version of the training loss
### Control flow testing
```
#hide
batch_events = ['begin_batch', 'after_pred', 'after_loss', 'after_backward', 'after_step', 'after_batch']
batchv_events = ['begin_batch', 'after_pred', 'after_loss', 'after_batch']
train_events = ['begin_train'] + batch_events + ['after_train']
valid_events = ['begin_validate'] + batchv_events + ['after_validate']
epoch_events = ['begin_epoch'] + train_events + valid_events + ['after_epoch']
cycle_events = ['begin_fit'] + epoch_events + ['after_fit']
#hide
learn = synth_learner(n_train=1, n_valid=1)
test_stdout(lambda: learn.fit(1, cbs=VerboseCallback()), '\n'.join(cycle_events))
#hide
class TestCancelCallback(VerboseCallback):
def __init__(self, cancel_at=event.begin_batch, exception=CancelBatchException, train=None):
def _interrupt():
if train is None or train == self.training: raise exception()
setattr(self, cancel_at, _interrupt)
#hide
#test cancel batch
for i,e in enumerate(batch_events[:-1]):
be = batch_events[:i+1] + ['after_cancel_batch', 'after_batch']
bev = be if i <3 else batchv_events
cycle = cycle_events[:3] + be + ['after_train', 'begin_validate'] + bev + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(cancel_at=e)), '\n'.join(cycle))
#CancelBatchException not caught if thrown in any other event
for e in cycle_events:
if e not in batch_events[:-1]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(cancel_at=e)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i < len(batch_events) else [])
be += ['after_cancel_train', 'after_train']
cycle = cycle_events[:3] + be + ['begin_validate'] + batchv_events + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelTrainException, True)), '\n'.join(cycle))
#CancelTrainException not caught if thrown in any other event
for e in cycle_events:
if e not in ['begin_train'] + batch_events[:-1]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelTrainException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i < len(batchv_events) else []) + ['after_cancel_validate']
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelValidException, False)), '\n'.join(cycle))
#CancelValidException not caught if thrown in any other event
for e in cycle_events:
if e not in ['begin_validate'] + batch_events[:3]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelValidException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel epoch
#In train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i<len(batch_events) else [])
cycle = cycle_events[:3] + be + ['after_train', 'after_cancel_epoch'] + cycle_events[-2:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelEpochException, True)), '\n'.join(cycle))
#In valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i<len(batchv_events) else [])
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev
cycle += ['after_validate', 'after_cancel_epoch'] + cycle_events[-2:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelEpochException, False)), '\n'.join(cycle))
#In begin epoch
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_epoch', CancelEpochException, False)),
'\n'.join(cycle_events[:2] + ['after_cancel_epoch'] + cycle_events[-2:]))
#CancelEpochException not caught if thrown in any other event
for e in ['begin_fit', 'after_epoch', 'after_fit']:
if e not in ['begin_validate'] + batch_events[:3]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelEpochException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel fit
#In begin fit
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_fit', CancelFitException)),
'\n'.join(['begin_fit', 'after_cancel_fit', 'after_fit']))
#In begin epoch
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_epoch', CancelFitException, False)),
'\n'.join(cycle_events[:2] + ['after_epoch', 'after_cancel_fit', 'after_fit']))
#In train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i<len(batch_events) else [])
cycle = cycle_events[:3] + be + ['after_train', 'after_epoch', 'after_cancel_fit', 'after_fit']
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelFitException, True)), '\n'.join(cycle))
#In valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i<len(batchv_events) else [])
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev
cycle += ['after_validate', 'after_epoch', 'after_cancel_fit', 'after_fit']
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelFitException, False)), '\n'.join(cycle))
#CancelEpochException not caught if thrown in any other event
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback('after_fit', CancelEpochException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
```
## Metrics -
```
#export
@docs
class Metric():
"Blueprint for defining a metric"
def reset(self): pass
def accumulate(self, learn): pass
@property
def value(self): raise NotImplementedError
@property
def name(self): return class2attr(self, 'Metric')
_docs = dict(
reset="Reset inner state to prepare for new computation",
name="Name of the `Metric`, camel-cased and with Metric removed",
accumulate="Use `learn` to update the state with new results",
value="The value of the metric")
show_doc(Metric, title_level=3)
```
Metrics can be simple averages (like accuracy) but sometimes their computation is a little bit more complex and can't be averaged over batches (like precision or recall), which is why we need a special class for them. For simple functions that can be computed as averages over batches, we can use the class `AvgMetric`, otherwise you'll need to implement the following methods.
> Note: If your `Metric` has state depending on tensors, don't forget to store it on the CPU to avoid any potential memory leaks.
```
show_doc(Metric.reset)
show_doc(Metric.accumulate)
show_doc(Metric.value, name='Metric.value')
show_doc(Metric.name, name='Metric.name')
#export
class AvgMetric(Metric):
"Average the values of `func` taking into account potential different batch sizes"
def __init__(self, func): self.func = func
def reset(self): self.total,self.count = 0.,0
def accumulate(self, learn):
bs = find_bs(learn.yb)
self.total += to_detach(self.func(learn.pred, *learn.yb))*bs
self.count += bs
@property
def value(self): return self.total/self.count if self.count != 0 else None
@property
def name(self): return self.func.__name__
show_doc(AvgMetric, title_level=3)
learn = synth_learner()
tst = AvgMetric(lambda x,y: (x-y).abs().mean())
t,u = torch.randn(100),torch.randn(100)
tst.reset()
for i in range(0,100,25):
learn.pred,learn.yb = t[i:i+25],(u[i:i+25],)
tst.accumulate(learn)
test_close(tst.value, (t-u).abs().mean())
#hide
#With varying batch size
tst.reset()
splits = [0, 30, 50, 60, 100]
for i in range(len(splits )-1):
learn.pred,learn.yb = t[splits[i]:splits[i+1]],(u[splits[i]:splits[i+1]],)
tst.accumulate(learn)
test_close(tst.value, (t-u).abs().mean())
#export
class AvgLoss(Metric):
"Average the losses taking into account potential different batch sizes"
def reset(self): self.total,self.count = 0.,0
def accumulate(self, learn):
bs = find_bs(learn.yb)
self.total += to_detach(learn.loss.mean())*bs
self.count += bs
@property
def value(self): return self.total/self.count if self.count != 0 else None
@property
def name(self): return "loss"
show_doc(AvgLoss, title_level=3)
tst = AvgLoss()
t = torch.randn(100)
tst.reset()
for i in range(0,100,25):
learn.yb,learn.loss = t[i:i+25],t[i:i+25].mean()
tst.accumulate(learn)
test_close(tst.value, t.mean())
#hide
#With varying batch size
tst.reset()
splits = [0, 30, 50, 60, 100]
for i in range(len(splits )-1):
learn.yb,learn.loss = t[splits[i]:splits[i+1]],t[splits[i]:splits[i+1]].mean()
tst.accumulate(learn)
test_close(tst.value, t.mean())
#export
class AvgSmoothLoss(Metric):
"Smooth average of the losses (exponentially weighted with `beta`)"
def __init__(self, beta=0.98): self.beta = beta
def reset(self): self.count,self.val = 0,tensor(0.)
def accumulate(self, learn):
self.count += 1
self.val = torch.lerp(to_detach(learn.loss.mean()), self.val, self.beta)
@property
def value(self): return self.val/(1-self.beta**self.count)
show_doc(AvgSmoothLoss, title_level=3)
tst = AvgSmoothLoss()
t = torch.randn(100)
tst.reset()
val = tensor(0.)
for i in range(4):
learn.loss = t[i*25:(i+1)*25].mean()
tst.accumulate(learn)
val = val*0.98 + t[i*25:(i+1)*25].mean()*(1-0.98)
test_close(val/(1-0.98**(i+1)), tst.value)
```
## Recorder --
```
#export
from fastprogress.fastprogress import format_time
def _maybe_item(t):
t = t.value
return t.item() if isinstance(t, Tensor) and t.numel()==1 else t
#export
class Recorder(Callback):
"Callback that registers statistics (lr, loss and metrics) during training"
run_after = TrainEvalCallback
def __init__(self, add_time=True, train_metrics=False, beta=0.98):
self.add_time,self.train_metrics = add_time,train_metrics
self.loss,self.smooth_loss = AvgLoss(),AvgSmoothLoss(beta=beta)
def begin_fit(self):
"Prepare state for training"
self.lrs,self.losses,self.values = [],[],[]
names = self._valid_mets.attrgot('name')
if self.train_metrics: names = names.map('train_{}') + names.map('valid_{}')
else: names = L('train_loss', 'valid_loss') + names[1:]
if self.add_time: names.append('time')
self.metric_names = 'epoch'+names
self.smooth_loss.reset()
def after_batch(self):
"Update all metrics and records lr and smooth loss in training"
if len(self.yb) == 0: return
mets = L(self.smooth_loss) + (self._train_mets if self.training else self._valid_mets)
for met in mets: met.accumulate(self.learn)
if not self.training: return
self.lrs.append(self.opt.hypers[-1]['lr'])
self.losses.append(self.smooth_loss.value)
self.learn.smooth_loss = self.smooth_loss.value
def begin_epoch(self):
"Set timer if `self.add_time=True`"
self.cancel_train,self.cancel_valid = False,False
if self.add_time: self.start_epoch = time.time()
self.log = L(getattr(self, 'epoch', 0))
def begin_train (self): self._train_mets.map(Self.reset())
def begin_validate(self): self._valid_mets.map(Self.reset())
def after_train (self): self.log += self._train_mets.map(_maybe_item)
def after_validate(self): self.log += self._valid_mets.map(_maybe_item)
def after_cancel_train(self): self.cancel_train = True
def after_cancel_validate(self): self.cancel_valid = True
def after_epoch(self):
"Store and log the loss/metric values"
self.values.append(self.log[1:].copy())
if self.add_time: self.log.append(format_time(time.time() - self.start_epoch))
self.logger(self.log)
@property
def _train_mets(self):
if getattr(self, 'cancel_train', False): return L()
return L(self.loss) + (self.metrics if self.train_metrics else L())
@property
def _valid_mets(self):
if getattr(self, 'cancel_valid', False): return L()
return L(self.loss) + self.metrics
def plot_loss(self, skip_start=5): plt.plot(self.losses[skip_start:])
#export
add_docs(Recorder,
begin_train = "Reset loss and metrics state",
after_train = "Log loss and metric values on the training set (if `self.training_metrics=True`)",
begin_validate = "Reset loss and metrics state",
after_validate = "Log loss and metric values on the validation set",
after_cancel_train = "Ignore training metrics for this epoch",
after_cancel_validate = "Ignore validation metrics for this epoch",
plot_loss = "Plot the losses from `skip_start` and onward")
defaults.callbacks = [TrainEvalCallback, Recorder]
```
By default, metrics are computed on the validation set only, although that can be changed with `training_metrics=True`. `beta` is the weight used to compute the exponentially weighted average of the losses (which gives the `smooth_loss` attribute to `Learner`).
```
#Test printed output
def tst_metric(out, targ): return F.mse_loss(out, targ)
learn = synth_learner(n_train=5, metrics=tst_metric)
pat = r"[tensor\(\d.\d*\), tensor\(\d.\d*\), tensor\(\d.\d*\), 'dd:dd']"
test_stdout(lambda: learn.fit(1), pat, regex=True)
#hide
class TestRecorderCallback(Callback):
run_after=Recorder
def begin_fit(self):
self.train_metrics,self.add_time = self.recorder.train_metrics,self.recorder.add_time
self.beta = self.recorder.smooth_loss.beta
for m in self.metrics: assert isinstance(m, Metric)
test_eq(self.recorder.smooth_loss.val, 0.)
#To test what the recorder logs, we use a custom logger function.
self.learn.logger = self.test_log
self.old_smooth,self.count = tensor(0.),0
def after_batch(self):
if self.training:
self.count += 1
test_eq(len(self.recorder.lrs), self.count)
test_eq(self.recorder.lrs[-1], self.opt.hypers[-1]['lr'])
test_eq(len(self.recorder.losses), self.count)
smooth = (1 - self.beta**(self.count-1)) * self.old_smooth * self.beta + self.loss * (1-self.beta)
smooth /= 1 - self.beta**self.count
test_close(self.recorder.losses[-1], smooth, eps=1e-4)
test_close(self.smooth_loss, smooth, eps=1e-4)
self.old_smooth = self.smooth_loss
self.bs += find_bs(self.yb)
test_eq(self.recorder.loss.count, self.bs)
if self.train_metrics or not self.training:
for m in self.metrics: test_eq(m.count, self.bs)
self.losses.append(self.loss.detach().cpu())
def begin_epoch(self):
if self.add_time: self.start_epoch = time.time()
self.log = [self.epoch]
def begin_train(self):
self.bs = 0
self.losses = []
for m in self.recorder._train_mets: test_eq(m.count, self.bs)
def after_train(self):
res = tensor(self.losses).mean()
self.log += [res, res] if self.train_metrics else [res]
test_eq(self.log, self.recorder.log)
self.losses = []
def begin_validate(self):
self.bs = 0
self.losses = []
for m in [self.recorder.loss] + self.metrics: test_eq(m.count, self.bs)
def test_log(self, log):
res = tensor(self.losses).mean()
self.log += [res, res]
if self.add_time: self.log.append(format_time(time.time() - self.start_epoch))
test_eq(log, self.log)
#hide
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.fit(1)
test_eq(learn.recorder.metric_names, ['epoch', 'train_loss', 'valid_loss', 'tst_metric', 'time'])
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.recorder.train_metrics=True
learn.fit(1)
test_eq(learn.recorder.metric_names,
['epoch', 'train_loss', 'train_tst_metric', 'valid_loss', 'valid_tst_metric', 'time'])
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.recorder.add_time=False
learn.fit(1)
test_eq(learn.recorder.metric_names, ['epoch', 'train_loss', 'valid_loss', 'tst_metric'])
#hide
#Test numpy metric
def tst_metric_np(out, targ): return F.mse_loss(out, targ).numpy()
learn = synth_learner(n_train=5, metrics=tst_metric_np)
learn.fit(1)
```
### Callback internals
```
show_doc(Recorder.begin_fit)
show_doc(Recorder.begin_epoch)
show_doc(Recorder.begin_validate)
show_doc(Recorder.after_batch)
show_doc(Recorder.after_epoch)
```
### Plotting tools
```
show_doc(Recorder.plot_loss)
#hide
learn.recorder.plot_loss(skip_start=1)
```
## Inference functions
```
show_doc(Learner.no_logging)
learn = synth_learner(n_train=5, metrics=tst_metric)
with learn.no_logging():
test_stdout(lambda: learn.fit(1), '')
test_eq(learn.logger, print)
show_doc(Learner.validate)
#Test result
learn = synth_learner(n_train=5, metrics=tst_metric)
res = learn.validate()
test_eq(res[0], res[1])
x,y = learn.dbunch.valid_ds.tensors
test_close(res[0], F.mse_loss(learn.model(x), y))
#hide
#Test other dl
res = learn.validate(dl=learn.dbunch.train_dl)
test_eq(res[0], res[1])
x,y = learn.dbunch.train_ds.tensors
test_close(res[0], F.mse_loss(learn.model(x), y))
#Test additional callback is executed.
cycle = cycle_events[:2] + ['begin_validate'] + batchv_events * 2 + cycle_events[-3:]
test_stdout(lambda: learn.validate(cbs=VerboseCallback()), '\n'.join(cycle))
show_doc(Learner.loss_not_reduced)
#hide
test_eq(learn.loss_func.reduction, 'mean')
with learn.loss_not_reduced():
test_eq(learn.loss_func.reduction, 'none')
x,y = learn.dbunch.one_batch()
p = learn.model(x)
losses = learn.loss_func(p, y)
test_eq(losses.shape, y.shape)
test_eq(losses, F.mse_loss(p,y, reduction='none'))
test_eq(learn.loss_func.reduction, 'mean')
show_doc(Learner.get_preds)
```
Depending on the `loss_func` attribute of `Learner`, an activation function will be picked automatically so that the predictions make sense. For instance if the loss is a case of cross-entropy, a softmax will be applied, or if the loss is binary cross entropy with logits, a sigmoid will be applied. If you want to make sure a certain activation function is applied, you can pass it with `act`.
> Note: If you want to use the option `with_loss=True` on a custom loss function, make sure you have implemented a `reduction` attribute that supports 'none'
```
#Test result
learn = synth_learner(n_train=5, metrics=tst_metric)
preds,targs = learn.get_preds()
x,y = learn.dbunch.valid_ds.tensors
test_eq(targs, y)
test_close(preds, learn.model(x))
preds,targs = learn.get_preds(act = torch.sigmoid)
test_eq(targs, y)
test_close(preds, torch.sigmoid(learn.model(x)))
#Test get_preds work with ds not evenly dividble by bs
learn = synth_learner(n_train=2.5, metrics=tst_metric)
preds,targs = learn.get_preds(ds_idx=0)
#hide
#Test other dataset
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
dl = TfmdDL(TensorDataset(x, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, y)
test_close(preds, learn.model(x))
#Test with loss
preds,targs,losses = learn.get_preds(dl=dl, with_loss=True)
test_eq(targs, y)
test_close(preds, learn.model(x))
test_close(losses, F.mse_loss(preds, targs, reduction='none'))
#Test with inputs
inps,preds,targs = learn.get_preds(dl=dl, with_input=True)
test_eq(*inps,x)
test_eq(targs, y)
test_close(preds, learn.model(x))
#hide
#Test with no target
learn = synth_learner(n_train=5)
x = torch.randn(16*5)
dl = TfmdDL(TensorDataset(x), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, ())
#hide
#Test with targets that are tuples
def _fake_loss(x,y,z,reduction=None): return F.mse_loss(x,y)
learn = synth_learner(n_train=5)
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
learn.dbunch.n_inp=1
learn.loss_func = _fake_loss
dl = TfmdDL(TensorDataset(x, y, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, [y,y])
#hide
#Test with inputs that are tuples
class _TupleModel(Module):
def __init__(self, model): self.model=model
def forward(self, x1, x2): return self.model(x1)
learn = synth_learner(n_train=5)
#learn.dbunch.n_inp=2
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
learn.model = _TupleModel(learn.model)
learn.dbunch = DataBunch(TfmdDL(TensorDataset(x, x, y), bs=16),TfmdDL(TensorDataset(x, x, y), bs=16))
inps,preds,targs = learn.get_preds(ds_idx=0, with_input=True)
test_eq(inps, [x,x])
#hide
#Test auto activation function is picked
learn = synth_learner(n_train=5)
learn.loss_func = BCEWithLogitsLossFlat()
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
dl = TfmdDL(TensorDataset(x, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_close(preds, torch.sigmoid(learn.model(x)))
show_doc(Learner.predict)
```
It returns a tuple of three elements with, in reverse order,
- the prediction from the model, potentially passed through the activation of the loss function (if it has one)
- the decoded prediction, using the poential `decodes` method from it
- the fully decoded prediction, using the transforms used to buil the `DataSource`/`DataBunch`
```
class _FakeLossFunc(Module):
reduction = 'none'
def forward(self, x, y): return F.mse_loss(x,y)
def activation(self, x): return x+1
def decodes(self, x): return 2*x
class _Add1(Transform):
def encodes(self, x): return x+1
def decodes(self, x): return x-1
learn = synth_learner(n_train=5)
dl = TfmdDL(DataSource(torch.arange(50), tfms = [L(), [_Add1()]]))
learn.dbunch = DataBunch(dl, dl)
learn.loss_func = _FakeLossFunc()
inp = tensor([2.])
out = learn.model(inp).detach()+1 #applying model + activation
dec = 2*out #decodes from loss function
full_dec = dec-1 #decodes from _Add1
test_eq(learn.predict(tensor([2.])), [full_dec, dec, out])
```
## Transfer learning
```
#export
@patch
def freeze_to(self:Learner, n):
if self.opt is None: self.create_opt()
self.opt.freeze_to(n)
@patch
def freeze(self:Learner): self.freeze_to(-1)
@patch
def unfreeze(self:Learner): self.freeze_to(0)
add_docs(Learner,
freeze_to="Freeze parameter groups up to `n`",
freeze="Freeze up to last parameter group",
unfreeze="Unfreeze the entire model")
#hide
class _TstModel(nn.Module):
def __init__(self):
super().__init__()
self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
self.tst = nn.Sequential(nn.Linear(4,5), nn.BatchNorm1d(3))
self.tst[0].bias.data,self.tst[1].bias.data = torch.randn(5),torch.randn(3)
def forward(self, x): return x * self.a + self.b
class _PutGrad(Callback):
def after_backward(self):
for p in self.learn.model.tst.parameters():
if p.requires_grad: p.grad = torch.ones_like(p.data)
def _splitter(m): return [list(m.tst[0].parameters()), list(m.tst[1].parameters()), [m.a,m.b]]
learn = synth_learner(n_train=5, opt_func = partial(SGD), cb_funcs=_PutGrad, splitter=_splitter, lr=1e-2)
learn.model = _TstModel()
learn.freeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear was not trained
for i in [0,1]: assert torch.allclose(end[i],init[i])
#bn was trained even frozen since `train_bn=True` by default
for i in [2,3]: assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
#hide
learn = synth_learner(n_train=5, opt_func = partial(SGD), cb_funcs=_PutGrad, splitter=_splitter, train_bn=False, lr=1e-2)
learn.model = _TstModel()
learn.freeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear and bn were not trained
for i in range(4): assert torch.allclose(end[i],init[i])
learn.freeze_to(-2)
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear was not trained
for i in [0,1]: assert torch.allclose(end[i],init[i])
#bn was trained
for i in [2,3]: assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
learn.unfreeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear and bn were trained
for i in range(4): assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
```
## Export -
```
#hide
from local.notebook.export import notebook2script
notebook2script(all_fs=True)
```
|
github_jupyter
|
# default_exp learner
#export
from local.torch_basics import *
from local.test import *
from local.layers import *
from local.data.all import *
from local.notebook.showdoc import *
from local.optimizer import *
#export
_all_ = ['CancelFitException', 'CancelEpochException', 'CancelTrainException', 'CancelValidException', 'CancelBatchException']
from torch.utils.data import TensorDataset
def synth_dbunch(a=2, b=3, bs=16, n_train=10, n_valid=2, cuda=False):
def get_data(n):
x = torch.randn(int(bs*n))
return TensorDataset(x, a*x + b + 0.1*torch.randn(int(bs*n)))
train_ds = get_data(n_train)
valid_ds = get_data(n_valid)
tfms = Cuda() if cuda else None
train_dl = TfmdDL(train_ds, bs=bs, shuffle=True, after_batch=tfms, num_workers=0)
valid_dl = TfmdDL(valid_ds, bs=bs, after_batch=tfms, num_workers=0)
return DataBunch(train_dl, valid_dl)
class RegModel(Module):
def __init__(self): self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
def forward(self, x): return x*self.a + self.b
#export core
_camel_re1 = re.compile('(.)([A-Z][a-z]+)')
_camel_re2 = re.compile('([a-z0-9])([A-Z])')
def camel2snake(name):
s1 = re.sub(_camel_re1, r'\1_\2', name)
return re.sub(_camel_re2, r'\1_\2', s1).lower()
test_eq(camel2snake('ClassAreCamel'), 'class_are_camel')
#export
def class2attr(self, cls_name):
return camel2snake(re.sub(rf'{cls_name}$', '', self.__class__.__name__) or cls_name.lower())
#export
class Callback(GetAttr):
"Basic class handling tweaks of the training loop by changing a `Learner` in various events"
_default='learn'
def __repr__(self): return type(self).__name__
def __call__(self, event_name):
"Call `self.{event_name}` if it's defined"
getattr(self, event_name, noop)()
@property
def name(self):
"Name of the `Callback`, camel-cased and with '*Callback*' removed"
return class2attr(self, 'Callback')
show_doc(Callback.__call__)
tst_cb = Callback()
tst_cb.call_me = lambda: print("maybe")
test_stdout(lambda: tst_cb("call_me"), "maybe")
show_doc(Callback.__getattr__)
mk_class('TstLearner', 'a')
class TstCallback(Callback):
def batch_begin(self): print(self.a)
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
test_stdout(lambda: cb('batch_begin'), "1")
class TstCallback(Callback):
def batch_begin(self): self.a += 1
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
cb('batch_begin')
test_eq(cb.a, 2)
test_eq(cb.learn.a, 1)
class TstCallback(Callback):
def batch_begin(self): self.learn.a = self.a + 1
learn,cb = TstLearner(1),TstCallback()
cb.learn = learn
cb('batch_begin')
test_eq(cb.learn.a, 2)
show_doc(Callback.name, name='Callback.name')
test_eq(TstCallback().name, 'tst')
class ComplicatedNameCallback(Callback): pass
test_eq(ComplicatedNameCallback().name, 'complicated_name')
#export
class TrainEvalCallback(Callback):
"`Callback` that tracks the number of iterations done and properly sets training/eval mode"
def begin_fit(self):
"Set the iter and epoch counters to 0, put the model and the right device"
self.learn.train_iter,self.learn.pct_train = 0,0.
self.model.to(self.dbunch.device)
def after_batch(self):
"Update the iter counter (in training mode)"
if not self.training: return
self.learn.pct_train += 1./(self.n_iter*self.n_epoch)
self.learn.train_iter += 1
def begin_train(self):
"Set the model in training mode"
self.learn.pct_train=self.epoch/self.n_epoch
self.model.train()
self.learn.training=True
def begin_validate(self):
"Set the model in validation mode"
self.model.eval()
self.learn.training=False
show_doc(TrainEvalCallback, title_level=3)
#hide
#test of the TrainEvalCallback below in Learner.fit
show_doc(TrainEvalCallback.begin_fit)
show_doc(TrainEvalCallback.after_batch)
show_doc(TrainEvalCallback.begin_train)
show_doc(TrainEvalCallback.begin_validate)
#export
class GatherPredsCallback(Callback):
"`Callback` that saves the predictions and targets, optionally `with_loss`"
def __init__(self, with_input=False, with_loss=False): store_attr(self, "with_input,with_loss")
def begin_batch(self):
if self.with_input: self.inputs.append((to_detach(self.xb)))
def begin_validate(self):
"Initialize containers"
self.preds,self.targets = [],[]
if self.with_input: self.inputs=[]
if self.with_loss: self.losses = []
def after_batch(self):
"Save predictions, targets and potentially losses"
self.preds.append(to_detach(self.pred))
self.targets.append(to_detach(self.yb))
if self.with_loss: self.losses.append(to_detach(self.loss))
show_doc(GatherPredsCallback, title_level=3)
show_doc(GatherPredsCallback.begin_validate)
show_doc(GatherPredsCallback.after_batch)
#export
_ex_docs = dict(
CancelFitException="Skip the rest of this batch and go to `after_batch`",
CancelEpochException="Skip the rest of the training part of the epoch and go to `after_train`",
CancelTrainException="Skip the rest of the validation part of the epoch and go to `after_validate`",
CancelValidException="Skip the rest of this epoch and go to `after_epoch`",
CancelBatchException="Interrupts training and go to `after_fit`")
for c,d in _ex_docs.items(): mk_class(c,sup=Exception,doc=d)
show_doc(CancelBatchException, title_level=3)
show_doc(CancelTrainException, title_level=3)
show_doc(CancelValidException, title_level=3)
show_doc(CancelEpochException, title_level=3)
show_doc(CancelFitException, title_level=3)
# export
_events = L.split('begin_fit begin_epoch begin_train begin_batch after_pred after_loss \
after_backward after_step after_cancel_batch after_batch after_cancel_train \
after_train begin_validate after_cancel_validate after_validate after_cancel_epoch \
after_epoch after_cancel_fit after_fit')
mk_class('event', **_events.map_dict(),
doc="All possible events as attributes to get tab-completion and typo-proofing")
_before_inference = [event.begin_fit, event.begin_epoch, event.begin_validate]
_after_inference = [event.after_validate, event.after_epoch, event.after_fit]
# export
_all_ = ['event']
show_doc(event, name='event', title_level=3)
test_eq(event.after_backward, 'after_backward')
#hide
#Full test of the control flow below, after the Learner class
# export
defaults.lr = slice(3e-3)
defaults.wd = 1e-2
defaults.callbacks = [TrainEvalCallback]
# export
def replacing_yield(o, attr, val):
"Context manager to temporarily replace an attribute"
old = getattr(o,attr)
try: yield setattr(o,attr,val)
finally: setattr(o,attr,old)
#export
def mk_metric(m):
"Convert `m` to an `AvgMetric`, unless it's already a `Metric`"
return m if isinstance(m, Metric) else AvgMetric(m)
#export
def save_model(file, model, opt, with_opt=True):
"Save `model` to `file` along with `opt` (if available, and if `with_opt`)"
if opt is None: with_opt=False
state = get_model(model).state_dict()
if with_opt: state = {'model': state, 'opt':opt.state_dict()}
torch.save(state, file)
# export
def load_model(file, model, opt, with_opt=None, device=None, strict=True):
"Load `model` from `file` along with `opt` (if available, and if `with_opt`)"
if isinstance(device, int): device = torch.device('cuda', device)
state = torch.load(file)
hasopt = set(state)=={'model', 'opt'}
model_state = state['model'] if hasopt else state
get_model(model).load_state_dict(model_state, strict=strict)
if hasopt and ifnone(with_opt,True):
try: opt.load_state_dict(state['opt'])
except:
if with_opt: warn("Could not load the optimizer state.")
elif with_opt: warn("Saved filed doesn't contain an optimizer state.")
x = [(tensor([1]),),(tensor([2]),),(tensor([3]),)]
y = [(tensor([1]),tensor([1])),(tensor([2]),tensor([2])),(tensor([3]),tensor([3]))]
#export
def detuplify(x):
"If `x` is a tuple with one thing, extract it"
return x[0] if len(x)==1 else x
# export
class Learner():
def __init__(self, dbunch, model, loss_func=None, opt_func=SGD, lr=defaults.lr, splitter=trainable_params, cbs=None,
cb_funcs=None, metrics=None, path=None, model_dir='models', wd_bn_bias=False, train_bn=True):
store_attr(self, "dbunch,model,opt_func,lr,splitter,model_dir,wd_bn_bias,train_bn")
self.training,self.logger,self.opt,self.cbs = False,print,None,L()
#TODO: infer loss_func from data
if loss_func is None:
loss_func = getattr(dbunch.train_ds, 'loss_func', None)
assert loss_func is not None, "Could not infer loss function from the data, please pass a loss function."
self.loss_func = loss_func
self.path = path if path is not None else getattr(dbunch, 'path', Path('.'))
self.metrics = L(metrics).map(mk_metric)
self.add_cbs(cbf() for cbf in L(defaults.callbacks)+L(cb_funcs))
self.add_cbs(cbs)
self.model.to(self.dbunch.device)
def add_cbs(self, cbs): L(cbs).map(self.add_cb)
def remove_cbs(self, cbs): L(cbs).map(self.remove_cb)
def add_cb(self, cb):
old = getattr(self, cb.name, None)
assert not old or isinstance(old, type(cb)), f"self.{cb.name} already registered"
cb.learn = self
setattr(self, cb.name, cb)
self.cbs.append(cb)
def remove_cb(self, cb):
cb.learn = None
if hasattr(self, cb.name): delattr(self, cb.name)
if cb in self.cbs: self.cbs.remove(cb)
@contextmanager
def added_cbs(self, cbs):
self.add_cbs(cbs)
yield
self.remove_cbs(cbs)
def __call__(self, event_name): L(event_name).map(self._call_one)
def _call_one(self, event_name):
assert hasattr(event, event_name)
[cb(event_name) for cb in sort_by_run(self.cbs)]
def _bn_bias_state(self, with_bias): return bn_bias_params(self.model, with_bias).map(self.opt.state)
def create_opt(self):
self.opt = self.opt_func(self.splitter(self.model), lr=self.lr)
if not self.wd_bn_bias:
for p in self._bn_bias_state(True ): p['do_wd'] = False
if self.train_bn:
for p in self._bn_bias_state(False): p['force_train'] = True
def _split(self, b):
i = getattr(self.dbunch, 'n_inp', 1 if len(b)==1 else len(b)-1)
self.xb,self.yb = b[:i],b[i:]
def all_batches(self):
self.n_iter = len(self.dl)
for o in enumerate(self.dl): self.one_batch(*o)
def one_batch(self, i, b):
self.iter = i
try:
self._split(b); self('begin_batch')
self.pred = self.model(*self.xb); self('after_pred')
if len(self.yb) == 0: return
self.loss = self.loss_func(self.pred, *self.yb); self('after_loss')
if not self.training: return
self.loss.backward(); self('after_backward')
self.opt.step(); self('after_step')
self.opt.zero_grad()
except CancelBatchException: self('after_cancel_batch')
finally: self('after_batch')
def _do_begin_fit(self, n_epoch):
self.n_epoch,self.loss = n_epoch,tensor(0.); self('begin_fit')
def _do_epoch_train(self):
try:
self.dl = self.dbunch.train_dl; self('begin_train')
self.all_batches()
except CancelTrainException: self('after_cancel_train')
finally: self('after_train')
def _do_epoch_validate(self):
try:
self.dl = self.dbunch.valid_dl; self('begin_validate')
with torch.no_grad(): self.all_batches()
except CancelValidException: self('after_cancel_validate')
finally: self('after_validate')
def fit(self, n_epoch, lr=None, wd=defaults.wd, cbs=None, reset_opt=False):
with self.added_cbs(cbs):
if reset_opt or not self.opt: self.create_opt()
self.opt.set_hypers(wd=wd, lr=self.lr if lr is None else lr)
try:
self._do_begin_fit(n_epoch)
for epoch in range(n_epoch):
try:
self.epoch=epoch; self('begin_epoch')
self._do_epoch_train()
self._do_epoch_validate()
except CancelEpochException: self('after_cancel_epoch')
finally: self('after_epoch')
except CancelFitException: self('after_cancel_fit')
finally: self('after_fit')
def validate(self, ds_idx=1, dl=None, cbs=None):
self.epoch,self.n_epoch,self.loss = 0,1,tensor(0.)
self.dl = self.dbunch.dls[ds_idx] if dl is None else dl
with self.added_cbs(cbs), self.no_logging():
self(_before_inference)
self.all_batches()
self(_after_inference)
return self.recorder.values[-1]
def get_preds(self, ds_idx=1, dl=None, with_input=False, with_loss=False, decoded=False, act=None):
self.epoch,self.n_epoch,self.loss = 0,1,tensor(0.)
self.dl = self.dbunch.dls[ds_idx] if dl is None else dl
cb = GatherPredsCallback(with_input=with_input, with_loss=with_loss)
with self.no_logging(), self.added_cbs(cb), self.loss_not_reduced():
self(_before_inference)
self.all_batches()
self(_after_inference)
if act is None: act = getattr(self.loss_func, 'activation', noop)
preds = act(torch.cat(cb.preds))
if decoded: preds = getattr(sellf.loss_func, 'decodes', noop)(preds)
res = (preds, detuplify(tuple(torch.cat(o) for o in zip(*cb.targets))))
if with_input: res = (tuple(torch.cat(o) for o in zip(*cb.inputs)),) + res
if with_loss: res = res + (torch.cat(cb.losses),)
return res
def predict(self, item):
dl = test_dl(self.dbunch, [item])
inp,preds,_ = self.get_preds(dl=dl, with_input=True)
dec_preds = getattr(self.loss_func, 'decodes', noop)(preds)
i = getattr(self.dbunch, 'n_inp', -1)
full_dec = self.dbunch.decode_batch((*inp,dec_preds))[0][i:]
return detuplify(full_dec),dec_preds[0],preds[0]
@contextmanager
def no_logging(self): return replacing_yield(self, 'logger', noop)
@contextmanager
def loss_not_reduced(self):
if hasattr(self.loss_func, 'reduction'): return replacing_yield(self.loss_func, 'reduction', 'none')
else: return replacing_yield(self, 'loss_func', partial(self.loss_func, reduction='none'))
def save(self, file, with_opt=True):
#TODO: if rank_distrib(): return # don't save if slave proc
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
save_model(file, self.model, getattr(self,'opt',None), with_opt)
def load(self, file, with_opt=None, device=None, strict=True):
if device is None: device = self.dbunch.device
if self.opt is None: self.create_opt()
file = join_path_file(file, self.path/self.model_dir, ext='.pth')
load_model(file, self.model, self.opt, with_opt=with_opt, device=device, strict=strict)
return self
Learner.x,Learner.y = add_props(lambda i,x: detuplify((x.xb,x.yb)[i]))
#export
add_docs(Learner, "Group together a `model`, some `dbunch` and a `loss_func` to handle training",
add_cbs="Add `cbs` to the list of `Callback` and register `self` as their learner",
add_cb="Add `cb` to the list of `Callback` and register `self` as their learner",
remove_cbs="Remove `cbs` from the list of `Callback` and deregister `self` as their learner",
remove_cb="Add `cb` from the list of `Callback` and deregister `self` as their learner",
added_cbs="Context manage that temporarily adds `cbs`",
create_opt="Create an optimizer with `lr`",
one_batch="Train or evaluate `self.model` on batch `(xb,yb)`",
all_batches="Train or evaluate `self.model` on all batches of `self.dl`",
fit="Fit `self.model` for `n_epoch` using `cbs`. Optionally `reset_opt`.",
validate="Validate on `dl` with potential new `cbs`.",
get_preds="Get the predictions and targets on the `ds_idx`-th dbunchset, optionally `with_input` and `with_loss`",
predict="Return the prediction on `item`, fully decoded, loss function decoded and probabilities",
no_logging="Context manager to temporarily remove `logger`",
loss_not_reduced="A context manager to evaluate `loss_func` with reduction set to none.",
save="Save model and optimizer state (if `with_opt`) to `self.path/self.model_dir/file`",
load="Load model and optimizer state (if `with_opt`) from `self.path/self.model_dir/file` using `device`"
)
#Test init with callbacks
def synth_learner(n_train=10, n_valid=2, cuda=False, lr=defaults.lr, **kwargs):
data = synth_dbunch(n_train=n_train,n_valid=n_valid, cuda=cuda)
return Learner(data, RegModel(), loss_func=MSELossFlat(), lr=lr, **kwargs)
tst_learn = synth_learner()
test_eq(len(tst_learn.cbs), 1)
assert isinstance(tst_learn.cbs[0], TrainEvalCallback)
assert hasattr(tst_learn, ('train_eval'))
tst_learn = synth_learner(cbs=TstCallback())
test_eq(len(tst_learn.cbs), 2)
assert isinstance(tst_learn.cbs[1], TstCallback)
assert hasattr(tst_learn, ('tst'))
tst_learn = synth_learner(cb_funcs=TstCallback)
test_eq(len(tst_learn.cbs), 2)
assert isinstance(tst_learn.cbs[1], TstCallback)
assert hasattr(tst_learn, ('tst'))
#A name that becomes an existing attribute of the Learner will throw an exception (here add_cb)
class AddCbCallback(Callback): pass
test_fail(lambda: synth_learner(cbs=AddCbCallback()))
show_doc(Learner.fit)
#Training a few epochs should make the model better
learn = synth_learner(cb_funcs=TstCallback, lr=1e-2)
xb,yb = learn.dbunch.one_batch()
init_loss = learn.loss_func(learn.model(xb), yb)
learn.fit(2)
assert learn.loss < init_loss
#hide
#Test of TrainEvalCallback
class TestTrainEvalCallback(Callback):
run_after=TrainEvalCallback
def begin_fit(self):
test_eq([self.pct_train,self.train_iter], [0., 0])
self.old_pct_train,self.old_train_iter = self.pct_train,self.train_iter
def begin_batch(self): test_eq(next(self.model.parameters()).device, find_device(self.xb))
def after_batch(self):
if self.training:
test_eq(self.pct_train , self.old_pct_train+1/(self.n_iter*self.n_epoch))
test_eq(self.train_iter, self.old_train_iter+1)
self.old_pct_train,self.old_train_iter = self.pct_train,self.train_iter
def begin_train(self):
assert self.training and self.model.training
test_eq(self.pct_train, self.epoch/self.n_epoch)
self.old_pct_train = self.pct_train
def begin_validate(self):
assert not self.training and not self.model.training
learn = synth_learner(cb_funcs=TestTrainEvalCallback)
learn.fit(1)
#Check order is properly taken into account
learn.cbs = L(reversed(learn.cbs))
#hide
#cuda
#Check model is put on the GPU if needed
learn = synth_learner(cb_funcs=TestTrainEvalCallback, cuda=True)
learn.fit(1)
#hide
#Check wd is not applied on bn/bias when option wd_bn_bias=False
class _TstModel(nn.Module):
def __init__(self):
super().__init__()
self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
self.tst = nn.Sequential(nn.Linear(4,5), nn.BatchNorm1d(3))
self.tst[0].bias.data,self.tst[1].bias.data = torch.randn(5),torch.randn(3)
def forward(self, x): return x * self.a + self.b
class _PutGrad(Callback):
def after_backward(self):
for p in self.learn.model.tst.parameters():
p.grad = torch.ones_like(p.data)
learn = synth_learner(n_train=5, opt_func = partial(SGD, wd=1, true_wd=True), cb_funcs=_PutGrad)
learn.model = _TstModel()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1, lr=1e-2)
end = list(learn.model.tst.parameters())
assert not torch.allclose(end[0]-init[0], -0.05 * torch.ones_like(end[0]))
for i in [1,2,3]: test_close(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
show_doc(Learner.one_batch)
# export
class VerboseCallback(Callback):
"Callback that prints the name of each event called"
def __call__(self, event_name):
print(event_name)
super().__call__(event_name)
#hide
class TestOneBatch(VerboseCallback):
def __init__(self, xb, yb, i):
self.save_xb,self.save_yb,self.i = xb,yb,i
self.old_pred,self.old_loss = None,tensor(0.)
def begin_batch(self):
self.old_a,self.old_b = self.model.a.data.clone(),self.model.b.data.clone()
test_eq(self.iter, self.i)
test_eq(self.save_xb, *self.xb)
test_eq(self.save_yb, *self.yb)
if hasattr(self.learn, 'pred'): test_eq(self.pred, self.old_pred)
def after_pred(self):
self.old_pred = self.pred
test_eq(self.pred, self.model.a.data * self.x + self.model.b.data)
test_eq(self.loss, self.old_loss)
def after_loss(self):
self.old_loss = self.loss
test_eq(self.loss, self.loss_func(self.old_pred, self.save_yb))
for p in self.model.parameters():
if not hasattr(p, 'grad') or p.grad is not None: test_eq(p.grad, tensor([0.]))
def after_backward(self):
self.grad_a = (2 * self.x * (self.pred.data - self.y)).mean()
self.grad_b = 2 * (self.pred.data - self.y).mean()
test_close(self.model.a.grad.data, self.grad_a)
test_close(self.model.b.grad.data, self.grad_b)
test_eq(self.model.a.data, self.old_a)
test_eq(self.model.b.data, self.old_b)
def after_step(self):
test_close(self.model.a.data, self.old_a - self.lr * self.grad_a)
test_close(self.model.b.data, self.old_b - self.lr * self.grad_b)
self.old_a,self.old_b = self.model.a.data.clone(),self.model.b.data.clone()
test_close(self.model.a.grad.data, self.grad_a)
test_close(self.model.b.grad.data, self.grad_b)
def after_batch(self):
for p in self.model.parameters(): test_eq(p.grad, tensor([0.]))
#hide
learn = synth_learner()
b = learn.dbunch.one_batch()
learn = synth_learner(cbs=TestOneBatch(*b, 42), lr=1e-2)
#Remove train/eval
learn.cbs = learn.cbs[1:]
#Setup
learn.loss,learn.training = tensor(0.),True
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
learn.model.train()
batch_events = ['begin_batch', 'after_pred', 'after_loss', 'after_backward', 'after_step', 'after_batch']
test_stdout(lambda: learn.one_batch(42, b), '\n'.join(batch_events))
test_stdout(lambda: learn.one_batch(42, b), '\n'.join(batch_events)) #Check it works for a second batch
show_doc(Learner.all_batches)
#hide
learn = synth_learner(n_train=5, cbs=VerboseCallback())
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
with redirect_stdout(io.StringIO()):
learn._do_begin_fit(1)
learn.epoch,learn.dl = 0,learn.dbunch.train_dl
learn('begin_epoch')
learn('begin_train')
test_stdout(learn.all_batches, '\n'.join(batch_events * 5))
test_eq(learn.train_iter, 5)
valid_events = ['begin_batch', 'after_pred', 'after_loss', 'after_batch']
with redirect_stdout(io.StringIO()):
learn.dl = learn.dbunch.valid_dl
learn('begin_validate')
test_stdout(learn.all_batches, '\n'.join(valid_events * 2))
test_eq(learn.train_iter, 5)
#hide
learn = synth_learner(n_train=5, cbs=VerboseCallback())
test_stdout(lambda: learn._do_begin_fit(42), 'begin_fit')
test_eq(learn.n_epoch, 42)
test_eq(learn.loss, tensor(0.))
#hide
learn.opt = SGD(learn.model.parameters(), lr=learn.lr)
learn.epoch = 0
test_stdout(lambda: learn._do_epoch_train(), '\n'.join(['begin_train'] + batch_events * 5 + ['after_train']))
#hide
test_stdout(learn._do_epoch_validate, '\n'.join(['begin_validate'] + valid_events * 2+ ['after_validate']))
show_doc(Learner.save)
show_doc(Learner.load)
learn = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
xb,yb = learn.dbunch.one_batch()
init_loss = learn.loss_func(learn.model(xb), yb)
learn.fit(1)
learn.save('tmp')
assert (Path.cwd()/'models/tmp.pth').exists()
learn1 = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
learn1 = learn1.load('tmp')
test_eq(learn.model.a, learn1.model.a)
test_eq(learn.model.b, learn1.model.b)
test_eq(learn.opt.state_dict(), learn1.opt.state_dict())
learn.save('tmp1', with_opt=False)
learn1 = synth_learner(cb_funcs=TstCallback, opt_func=partial(SGD, mom=0.9))
learn1 = learn1.load('tmp1')
test_eq(learn.model.a, learn1.model.a)
test_eq(learn.model.b, learn1.model.b)
test_ne(learn.opt.state_dict(), learn1.opt.state_dict())
shutil.rmtree('models')
show_doc(Learner.__call__)
show_doc(Learner.add_cb)
learn = synth_learner()
learn.add_cb(TestTrainEvalCallback())
test_eq(len(learn.cbs), 2)
assert isinstance(learn.cbs[1], TestTrainEvalCallback)
test_eq(learn.train_eval.learn, learn)
show_doc(Learner.add_cbs)
learn.add_cbs([TestTrainEvalCallback(), TestTrainEvalCallback()])
test_eq(len(learn.cbs), 4)
show_doc(Learner.remove_cb)
cb = learn.cbs[1]
learn.remove_cb(learn.cbs[1])
test_eq(len(learn.cbs), 3)
assert cb.learn is None
assert not getattr(learn,'test_train_eval',None)
show_doc(Learner.remove_cbs)
cb = learn.cbs[1]
learn.remove_cbs(learn.cbs[1:])
test_eq(len(learn.cbs), 1)
#hide
batch_events = ['begin_batch', 'after_pred', 'after_loss', 'after_backward', 'after_step', 'after_batch']
batchv_events = ['begin_batch', 'after_pred', 'after_loss', 'after_batch']
train_events = ['begin_train'] + batch_events + ['after_train']
valid_events = ['begin_validate'] + batchv_events + ['after_validate']
epoch_events = ['begin_epoch'] + train_events + valid_events + ['after_epoch']
cycle_events = ['begin_fit'] + epoch_events + ['after_fit']
#hide
learn = synth_learner(n_train=1, n_valid=1)
test_stdout(lambda: learn.fit(1, cbs=VerboseCallback()), '\n'.join(cycle_events))
#hide
class TestCancelCallback(VerboseCallback):
def __init__(self, cancel_at=event.begin_batch, exception=CancelBatchException, train=None):
def _interrupt():
if train is None or train == self.training: raise exception()
setattr(self, cancel_at, _interrupt)
#hide
#test cancel batch
for i,e in enumerate(batch_events[:-1]):
be = batch_events[:i+1] + ['after_cancel_batch', 'after_batch']
bev = be if i <3 else batchv_events
cycle = cycle_events[:3] + be + ['after_train', 'begin_validate'] + bev + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(cancel_at=e)), '\n'.join(cycle))
#CancelBatchException not caught if thrown in any other event
for e in cycle_events:
if e not in batch_events[:-1]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(cancel_at=e)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i < len(batch_events) else [])
be += ['after_cancel_train', 'after_train']
cycle = cycle_events[:3] + be + ['begin_validate'] + batchv_events + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelTrainException, True)), '\n'.join(cycle))
#CancelTrainException not caught if thrown in any other event
for e in cycle_events:
if e not in ['begin_train'] + batch_events[:-1]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelTrainException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i < len(batchv_events) else []) + ['after_cancel_validate']
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev + cycle_events[-3:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelValidException, False)), '\n'.join(cycle))
#CancelValidException not caught if thrown in any other event
for e in cycle_events:
if e not in ['begin_validate'] + batch_events[:3]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelValidException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel epoch
#In train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i<len(batch_events) else [])
cycle = cycle_events[:3] + be + ['after_train', 'after_cancel_epoch'] + cycle_events[-2:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelEpochException, True)), '\n'.join(cycle))
#In valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i<len(batchv_events) else [])
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev
cycle += ['after_validate', 'after_cancel_epoch'] + cycle_events[-2:]
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelEpochException, False)), '\n'.join(cycle))
#In begin epoch
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_epoch', CancelEpochException, False)),
'\n'.join(cycle_events[:2] + ['after_cancel_epoch'] + cycle_events[-2:]))
#CancelEpochException not caught if thrown in any other event
for e in ['begin_fit', 'after_epoch', 'after_fit']:
if e not in ['begin_validate'] + batch_events[:3]:
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback(e, CancelEpochException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#hide
#test cancel fit
#In begin fit
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_fit', CancelFitException)),
'\n'.join(['begin_fit', 'after_cancel_fit', 'after_fit']))
#In begin epoch
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback('begin_epoch', CancelFitException, False)),
'\n'.join(cycle_events[:2] + ['after_epoch', 'after_cancel_fit', 'after_fit']))
#In train
for i,e in enumerate(['begin_train'] + batch_events):
be = batch_events[:i] + (['after_batch'] if i >=1 and i<len(batch_events) else [])
cycle = cycle_events[:3] + be + ['after_train', 'after_epoch', 'after_cancel_fit', 'after_fit']
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelFitException, True)), '\n'.join(cycle))
#In valid
for i,e in enumerate(['begin_validate'] + batchv_events):
bev = batchv_events[:i] + (['after_batch'] if i >=1 and i<len(batchv_events) else [])
cycle = cycle_events[:3] + batch_events + ['after_train', 'begin_validate'] + bev
cycle += ['after_validate', 'after_epoch', 'after_cancel_fit', 'after_fit']
test_stdout(lambda: learn.fit(1, cbs=TestCancelCallback(e, CancelFitException, False)), '\n'.join(cycle))
#CancelEpochException not caught if thrown in any other event
with redirect_stdout(io.StringIO()):
cb = TestCancelCallback('after_fit', CancelEpochException)
test_fail(lambda: learn.fit(1, cbs=cb))
learn.remove_cb(cb) #Have to remove it manually
#export
@docs
class Metric():
"Blueprint for defining a metric"
def reset(self): pass
def accumulate(self, learn): pass
@property
def value(self): raise NotImplementedError
@property
def name(self): return class2attr(self, 'Metric')
_docs = dict(
reset="Reset inner state to prepare for new computation",
name="Name of the `Metric`, camel-cased and with Metric removed",
accumulate="Use `learn` to update the state with new results",
value="The value of the metric")
show_doc(Metric, title_level=3)
show_doc(Metric.reset)
show_doc(Metric.accumulate)
show_doc(Metric.value, name='Metric.value')
show_doc(Metric.name, name='Metric.name')
#export
class AvgMetric(Metric):
"Average the values of `func` taking into account potential different batch sizes"
def __init__(self, func): self.func = func
def reset(self): self.total,self.count = 0.,0
def accumulate(self, learn):
bs = find_bs(learn.yb)
self.total += to_detach(self.func(learn.pred, *learn.yb))*bs
self.count += bs
@property
def value(self): return self.total/self.count if self.count != 0 else None
@property
def name(self): return self.func.__name__
show_doc(AvgMetric, title_level=3)
learn = synth_learner()
tst = AvgMetric(lambda x,y: (x-y).abs().mean())
t,u = torch.randn(100),torch.randn(100)
tst.reset()
for i in range(0,100,25):
learn.pred,learn.yb = t[i:i+25],(u[i:i+25],)
tst.accumulate(learn)
test_close(tst.value, (t-u).abs().mean())
#hide
#With varying batch size
tst.reset()
splits = [0, 30, 50, 60, 100]
for i in range(len(splits )-1):
learn.pred,learn.yb = t[splits[i]:splits[i+1]],(u[splits[i]:splits[i+1]],)
tst.accumulate(learn)
test_close(tst.value, (t-u).abs().mean())
#export
class AvgLoss(Metric):
"Average the losses taking into account potential different batch sizes"
def reset(self): self.total,self.count = 0.,0
def accumulate(self, learn):
bs = find_bs(learn.yb)
self.total += to_detach(learn.loss.mean())*bs
self.count += bs
@property
def value(self): return self.total/self.count if self.count != 0 else None
@property
def name(self): return "loss"
show_doc(AvgLoss, title_level=3)
tst = AvgLoss()
t = torch.randn(100)
tst.reset()
for i in range(0,100,25):
learn.yb,learn.loss = t[i:i+25],t[i:i+25].mean()
tst.accumulate(learn)
test_close(tst.value, t.mean())
#hide
#With varying batch size
tst.reset()
splits = [0, 30, 50, 60, 100]
for i in range(len(splits )-1):
learn.yb,learn.loss = t[splits[i]:splits[i+1]],t[splits[i]:splits[i+1]].mean()
tst.accumulate(learn)
test_close(tst.value, t.mean())
#export
class AvgSmoothLoss(Metric):
"Smooth average of the losses (exponentially weighted with `beta`)"
def __init__(self, beta=0.98): self.beta = beta
def reset(self): self.count,self.val = 0,tensor(0.)
def accumulate(self, learn):
self.count += 1
self.val = torch.lerp(to_detach(learn.loss.mean()), self.val, self.beta)
@property
def value(self): return self.val/(1-self.beta**self.count)
show_doc(AvgSmoothLoss, title_level=3)
tst = AvgSmoothLoss()
t = torch.randn(100)
tst.reset()
val = tensor(0.)
for i in range(4):
learn.loss = t[i*25:(i+1)*25].mean()
tst.accumulate(learn)
val = val*0.98 + t[i*25:(i+1)*25].mean()*(1-0.98)
test_close(val/(1-0.98**(i+1)), tst.value)
#export
from fastprogress.fastprogress import format_time
def _maybe_item(t):
t = t.value
return t.item() if isinstance(t, Tensor) and t.numel()==1 else t
#export
class Recorder(Callback):
"Callback that registers statistics (lr, loss and metrics) during training"
run_after = TrainEvalCallback
def __init__(self, add_time=True, train_metrics=False, beta=0.98):
self.add_time,self.train_metrics = add_time,train_metrics
self.loss,self.smooth_loss = AvgLoss(),AvgSmoothLoss(beta=beta)
def begin_fit(self):
"Prepare state for training"
self.lrs,self.losses,self.values = [],[],[]
names = self._valid_mets.attrgot('name')
if self.train_metrics: names = names.map('train_{}') + names.map('valid_{}')
else: names = L('train_loss', 'valid_loss') + names[1:]
if self.add_time: names.append('time')
self.metric_names = 'epoch'+names
self.smooth_loss.reset()
def after_batch(self):
"Update all metrics and records lr and smooth loss in training"
if len(self.yb) == 0: return
mets = L(self.smooth_loss) + (self._train_mets if self.training else self._valid_mets)
for met in mets: met.accumulate(self.learn)
if not self.training: return
self.lrs.append(self.opt.hypers[-1]['lr'])
self.losses.append(self.smooth_loss.value)
self.learn.smooth_loss = self.smooth_loss.value
def begin_epoch(self):
"Set timer if `self.add_time=True`"
self.cancel_train,self.cancel_valid = False,False
if self.add_time: self.start_epoch = time.time()
self.log = L(getattr(self, 'epoch', 0))
def begin_train (self): self._train_mets.map(Self.reset())
def begin_validate(self): self._valid_mets.map(Self.reset())
def after_train (self): self.log += self._train_mets.map(_maybe_item)
def after_validate(self): self.log += self._valid_mets.map(_maybe_item)
def after_cancel_train(self): self.cancel_train = True
def after_cancel_validate(self): self.cancel_valid = True
def after_epoch(self):
"Store and log the loss/metric values"
self.values.append(self.log[1:].copy())
if self.add_time: self.log.append(format_time(time.time() - self.start_epoch))
self.logger(self.log)
@property
def _train_mets(self):
if getattr(self, 'cancel_train', False): return L()
return L(self.loss) + (self.metrics if self.train_metrics else L())
@property
def _valid_mets(self):
if getattr(self, 'cancel_valid', False): return L()
return L(self.loss) + self.metrics
def plot_loss(self, skip_start=5): plt.plot(self.losses[skip_start:])
#export
add_docs(Recorder,
begin_train = "Reset loss and metrics state",
after_train = "Log loss and metric values on the training set (if `self.training_metrics=True`)",
begin_validate = "Reset loss and metrics state",
after_validate = "Log loss and metric values on the validation set",
after_cancel_train = "Ignore training metrics for this epoch",
after_cancel_validate = "Ignore validation metrics for this epoch",
plot_loss = "Plot the losses from `skip_start` and onward")
defaults.callbacks = [TrainEvalCallback, Recorder]
#Test printed output
def tst_metric(out, targ): return F.mse_loss(out, targ)
learn = synth_learner(n_train=5, metrics=tst_metric)
pat = r"[tensor\(\d.\d*\), tensor\(\d.\d*\), tensor\(\d.\d*\), 'dd:dd']"
test_stdout(lambda: learn.fit(1), pat, regex=True)
#hide
class TestRecorderCallback(Callback):
run_after=Recorder
def begin_fit(self):
self.train_metrics,self.add_time = self.recorder.train_metrics,self.recorder.add_time
self.beta = self.recorder.smooth_loss.beta
for m in self.metrics: assert isinstance(m, Metric)
test_eq(self.recorder.smooth_loss.val, 0.)
#To test what the recorder logs, we use a custom logger function.
self.learn.logger = self.test_log
self.old_smooth,self.count = tensor(0.),0
def after_batch(self):
if self.training:
self.count += 1
test_eq(len(self.recorder.lrs), self.count)
test_eq(self.recorder.lrs[-1], self.opt.hypers[-1]['lr'])
test_eq(len(self.recorder.losses), self.count)
smooth = (1 - self.beta**(self.count-1)) * self.old_smooth * self.beta + self.loss * (1-self.beta)
smooth /= 1 - self.beta**self.count
test_close(self.recorder.losses[-1], smooth, eps=1e-4)
test_close(self.smooth_loss, smooth, eps=1e-4)
self.old_smooth = self.smooth_loss
self.bs += find_bs(self.yb)
test_eq(self.recorder.loss.count, self.bs)
if self.train_metrics or not self.training:
for m in self.metrics: test_eq(m.count, self.bs)
self.losses.append(self.loss.detach().cpu())
def begin_epoch(self):
if self.add_time: self.start_epoch = time.time()
self.log = [self.epoch]
def begin_train(self):
self.bs = 0
self.losses = []
for m in self.recorder._train_mets: test_eq(m.count, self.bs)
def after_train(self):
res = tensor(self.losses).mean()
self.log += [res, res] if self.train_metrics else [res]
test_eq(self.log, self.recorder.log)
self.losses = []
def begin_validate(self):
self.bs = 0
self.losses = []
for m in [self.recorder.loss] + self.metrics: test_eq(m.count, self.bs)
def test_log(self, log):
res = tensor(self.losses).mean()
self.log += [res, res]
if self.add_time: self.log.append(format_time(time.time() - self.start_epoch))
test_eq(log, self.log)
#hide
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.fit(1)
test_eq(learn.recorder.metric_names, ['epoch', 'train_loss', 'valid_loss', 'tst_metric', 'time'])
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.recorder.train_metrics=True
learn.fit(1)
test_eq(learn.recorder.metric_names,
['epoch', 'train_loss', 'train_tst_metric', 'valid_loss', 'valid_tst_metric', 'time'])
learn = synth_learner(n_train=5, metrics = tst_metric, cb_funcs = TestRecorderCallback)
learn.recorder.add_time=False
learn.fit(1)
test_eq(learn.recorder.metric_names, ['epoch', 'train_loss', 'valid_loss', 'tst_metric'])
#hide
#Test numpy metric
def tst_metric_np(out, targ): return F.mse_loss(out, targ).numpy()
learn = synth_learner(n_train=5, metrics=tst_metric_np)
learn.fit(1)
show_doc(Recorder.begin_fit)
show_doc(Recorder.begin_epoch)
show_doc(Recorder.begin_validate)
show_doc(Recorder.after_batch)
show_doc(Recorder.after_epoch)
show_doc(Recorder.plot_loss)
#hide
learn.recorder.plot_loss(skip_start=1)
show_doc(Learner.no_logging)
learn = synth_learner(n_train=5, metrics=tst_metric)
with learn.no_logging():
test_stdout(lambda: learn.fit(1), '')
test_eq(learn.logger, print)
show_doc(Learner.validate)
#Test result
learn = synth_learner(n_train=5, metrics=tst_metric)
res = learn.validate()
test_eq(res[0], res[1])
x,y = learn.dbunch.valid_ds.tensors
test_close(res[0], F.mse_loss(learn.model(x), y))
#hide
#Test other dl
res = learn.validate(dl=learn.dbunch.train_dl)
test_eq(res[0], res[1])
x,y = learn.dbunch.train_ds.tensors
test_close(res[0], F.mse_loss(learn.model(x), y))
#Test additional callback is executed.
cycle = cycle_events[:2] + ['begin_validate'] + batchv_events * 2 + cycle_events[-3:]
test_stdout(lambda: learn.validate(cbs=VerboseCallback()), '\n'.join(cycle))
show_doc(Learner.loss_not_reduced)
#hide
test_eq(learn.loss_func.reduction, 'mean')
with learn.loss_not_reduced():
test_eq(learn.loss_func.reduction, 'none')
x,y = learn.dbunch.one_batch()
p = learn.model(x)
losses = learn.loss_func(p, y)
test_eq(losses.shape, y.shape)
test_eq(losses, F.mse_loss(p,y, reduction='none'))
test_eq(learn.loss_func.reduction, 'mean')
show_doc(Learner.get_preds)
#Test result
learn = synth_learner(n_train=5, metrics=tst_metric)
preds,targs = learn.get_preds()
x,y = learn.dbunch.valid_ds.tensors
test_eq(targs, y)
test_close(preds, learn.model(x))
preds,targs = learn.get_preds(act = torch.sigmoid)
test_eq(targs, y)
test_close(preds, torch.sigmoid(learn.model(x)))
#Test get_preds work with ds not evenly dividble by bs
learn = synth_learner(n_train=2.5, metrics=tst_metric)
preds,targs = learn.get_preds(ds_idx=0)
#hide
#Test other dataset
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
dl = TfmdDL(TensorDataset(x, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, y)
test_close(preds, learn.model(x))
#Test with loss
preds,targs,losses = learn.get_preds(dl=dl, with_loss=True)
test_eq(targs, y)
test_close(preds, learn.model(x))
test_close(losses, F.mse_loss(preds, targs, reduction='none'))
#Test with inputs
inps,preds,targs = learn.get_preds(dl=dl, with_input=True)
test_eq(*inps,x)
test_eq(targs, y)
test_close(preds, learn.model(x))
#hide
#Test with no target
learn = synth_learner(n_train=5)
x = torch.randn(16*5)
dl = TfmdDL(TensorDataset(x), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, ())
#hide
#Test with targets that are tuples
def _fake_loss(x,y,z,reduction=None): return F.mse_loss(x,y)
learn = synth_learner(n_train=5)
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
learn.dbunch.n_inp=1
learn.loss_func = _fake_loss
dl = TfmdDL(TensorDataset(x, y, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_eq(targs, [y,y])
#hide
#Test with inputs that are tuples
class _TupleModel(Module):
def __init__(self, model): self.model=model
def forward(self, x1, x2): return self.model(x1)
learn = synth_learner(n_train=5)
#learn.dbunch.n_inp=2
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
learn.model = _TupleModel(learn.model)
learn.dbunch = DataBunch(TfmdDL(TensorDataset(x, x, y), bs=16),TfmdDL(TensorDataset(x, x, y), bs=16))
inps,preds,targs = learn.get_preds(ds_idx=0, with_input=True)
test_eq(inps, [x,x])
#hide
#Test auto activation function is picked
learn = synth_learner(n_train=5)
learn.loss_func = BCEWithLogitsLossFlat()
x = torch.randn(16*5)
y = 2*x + 3 + 0.1*torch.randn(16*5)
dl = TfmdDL(TensorDataset(x, y), bs=16)
preds,targs = learn.get_preds(dl=dl)
test_close(preds, torch.sigmoid(learn.model(x)))
show_doc(Learner.predict)
class _FakeLossFunc(Module):
reduction = 'none'
def forward(self, x, y): return F.mse_loss(x,y)
def activation(self, x): return x+1
def decodes(self, x): return 2*x
class _Add1(Transform):
def encodes(self, x): return x+1
def decodes(self, x): return x-1
learn = synth_learner(n_train=5)
dl = TfmdDL(DataSource(torch.arange(50), tfms = [L(), [_Add1()]]))
learn.dbunch = DataBunch(dl, dl)
learn.loss_func = _FakeLossFunc()
inp = tensor([2.])
out = learn.model(inp).detach()+1 #applying model + activation
dec = 2*out #decodes from loss function
full_dec = dec-1 #decodes from _Add1
test_eq(learn.predict(tensor([2.])), [full_dec, dec, out])
#export
@patch
def freeze_to(self:Learner, n):
if self.opt is None: self.create_opt()
self.opt.freeze_to(n)
@patch
def freeze(self:Learner): self.freeze_to(-1)
@patch
def unfreeze(self:Learner): self.freeze_to(0)
add_docs(Learner,
freeze_to="Freeze parameter groups up to `n`",
freeze="Freeze up to last parameter group",
unfreeze="Unfreeze the entire model")
#hide
class _TstModel(nn.Module):
def __init__(self):
super().__init__()
self.a,self.b = nn.Parameter(torch.randn(1)),nn.Parameter(torch.randn(1))
self.tst = nn.Sequential(nn.Linear(4,5), nn.BatchNorm1d(3))
self.tst[0].bias.data,self.tst[1].bias.data = torch.randn(5),torch.randn(3)
def forward(self, x): return x * self.a + self.b
class _PutGrad(Callback):
def after_backward(self):
for p in self.learn.model.tst.parameters():
if p.requires_grad: p.grad = torch.ones_like(p.data)
def _splitter(m): return [list(m.tst[0].parameters()), list(m.tst[1].parameters()), [m.a,m.b]]
learn = synth_learner(n_train=5, opt_func = partial(SGD), cb_funcs=_PutGrad, splitter=_splitter, lr=1e-2)
learn.model = _TstModel()
learn.freeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear was not trained
for i in [0,1]: assert torch.allclose(end[i],init[i])
#bn was trained even frozen since `train_bn=True` by default
for i in [2,3]: assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
#hide
learn = synth_learner(n_train=5, opt_func = partial(SGD), cb_funcs=_PutGrad, splitter=_splitter, train_bn=False, lr=1e-2)
learn.model = _TstModel()
learn.freeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear and bn were not trained
for i in range(4): assert torch.allclose(end[i],init[i])
learn.freeze_to(-2)
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear was not trained
for i in [0,1]: assert torch.allclose(end[i],init[i])
#bn was trained
for i in [2,3]: assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
learn.unfreeze()
init = [p.clone() for p in learn.model.tst.parameters()]
learn.fit(1)
end = list(learn.model.tst.parameters())
#linear and bn were trained
for i in range(4): assert torch.allclose(end[i]-init[i], -0.05 * torch.ones_like(end[i]))
#hide
from local.notebook.export import notebook2script
notebook2script(all_fs=True)
| 0.811116 | 0.831588 |
```
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 4) # Change plot sizes (in cm) - this bit of code is only relevant if you are using a juyter notebook - ignore otherwise
```
# Generalised Linear Models
## Introduction
Aims of this chapter[$^{[1]}$](#fn1):
* Develop an intuitive understanding of generalized linear models
* Learn to fit generalized linear models to count data
This chapter will step through the analysis carefully. These are not simple analyses so you should concentrate on understanding the process and the biology and think about how to present your results.
## What is a GLM?
Till now, we have adhered faithfully to the assumption of a normal (Gaussian) distribution for the response variable, at times transforming the response variable (e.g., by taking a log) to make it (approximately) normal. However, there are many scenarios where assuming a normal distribution for the response variable is just not appropriate, whether you transform it or not. The generalized linear model (GLM) analysis is (as the name suggests) a generalization of the ordinary linear regression model analysis to accommodate response variables that have non-normal error distributions. These types of (non-normal) response variables can arise quite commonly in the form of count (as in the practical example below) and binary response (present/absent, 0/1, etc.) data, but beyond that, many measures of interest in biology are just not normally distributed.
The GLM generalization of the ordinary Linear Models is made possible by using an (arbitrary) function of the dependent variable (the link function) that makes it vary *linearly* with the predicted values, thus making the problem relatively tractable statistically. We will not try to understand the mathematical underpinnings of this approach here, but instead learn through an example.
## Some (statistical) distributions
First, it's time to revisit the idea of *statistical distributions*, which you were introduced to [previously](12-ExpDesign:Data-types-and-distributions). This is because while analyzing data using GLMs, one needs to decide what particular statistical distribution best represents (or captures, or "model's") that particular dataset. For example, continuous numeric data are *often* normally distributed (e.g., weights of lecturers!). On the other hand, count data are likely to be distributed according to the Poisson distribution (e.g., numbers of plant species found in a sampling plot). And all statistical distribution are actually a *family* of distributions of different shapes (e.g., can range from right-skewed to bell-shaped) and/or scales (spread) depending upon the value of their *parameters*. For example, the Gaussian distribution can have different scales depending on the variance parameter. More on distribution parameters below.
There are actually a large number of statistical distributions [out there](https://en.wikipedia.org/wiki/List_of_probability_distributions) to choose from. But we will look at a few that GLMs support. Specifically, the `glm` procedure in R supports the following distribution "families": Binomial, Gaussian, Gamma, Inverse Gaussian, Poisson, Quasi, Quasi-Binomial, and Quasi-Poisson. You may want to look these up online (google it). You have already seen, [sampled from](12-ExpDesign:Sampling-from-distributions-in-R), and used the Gaussian distribution, so we won't go into it here. But let's look at three other distributions that are particularly useful in R.
### The Poisson distribution
The Poisson distribution family is appropriate for discrete, integer valued data. You can generate "data" that are poisson-distributed by using the function `rpois(n, lambda)` in R:
```
par(mfrow=c(1,2))
hist(rpois(1000, lambda = 1),xlab = "Value", main="")
hist(rpois(1000, lambda = 100),xlab = "Value", main="")
```
The main things to note about these plots (and poisson-distributed data):
* This distribution is appropriate for response data that can only take integer values, such as counts (technically, only for values of $\lambda \ge 1$, but this does not really concern you as far fitting glms in R is concerned).
* A single parameter $\lambda$ ("lambda") controls the shape, the scale (the range of the variable) and the location (mean value, or central tendency) of the distribution.
* Thus, this distribution can represent a variety of shapes that count data can take, from right skewed (left plot) to bell-shaped (right plot) – these variants of shapes and scales make up the Poisson distribution "family".
$\star$ Play with the above code and generate different shapes (and inevitably, scales) of poisson-distributed data.
### The Binomial distribution
The binomial distribution is appropriate for continuous-valued data that arise from repeated trials of binary (yes/no, 0/1, head/tail, suceptible/resistant) outcomes. This distribution is also the basis for the [binomial statistical test](https://en.wikipedia.org/wiki/Binomial_test). You can generate binomial-distributed "data" by using the function `rbinom(n, size, prob)` in R:
```
par(mfrow=c(1,2))
hist(rbinom(1000, 1, 0.5),xlab = "Value", main="")
hist(rbinom(1000, 100, 0.5),xlab = "Value", main="")
```
The main things to note about these plots (and Binomial-distributed data):
* The two main parameters of interest are `size` (number of trials), and `prob` (the probability of an outcome in each trial). So,
* The left plot is the distribution of outcomes of a single try of a 50:50 (0.5 probability, like a coin-flip) outcome, re-generated 1000 times (e.g., a thousand coin flips) – as expected, there are about 500 each of 0's and 1's (e.g., 0 = head, 1 = tail). Each of the 1000 such success/failure experiments is called a Bernoulli trial/experiment. For repeated experiments of a single trial, i.e., `size` = 1 in the R code above, the binomial distribution is a Bernoulli distribution (so the left plot is a bernoulli distribution).
* The right plot is the binomial distribution that you will encounter more often, which is appropriate for modeling the number of successes in a sample of a given size. In the above code, `size` = 100, with 1000 repetitions of this "experiment"). Thus in the right plot, the distribution will on average have a mean value of 50 ($0.5\times100$ trials) (recall the [Central Limit Theorem](12-ExpDesign:Data-types-and-distributions)).
* Thus, the binomial distribution family is appropriate for binomial [logistic regression](https://en.wikipedia.org/wiki/Logistic_regression), which is a GLM analysis where your sample of binary (yes/no, 0/1, etc) outcomes is fitted as a function of one or more continuous or categorical predictors.
$\star$ Play with the above code and generate variants of binomial-distributed data distributions. They will all be bell-shaped, but can take different mean and spread values.
### The Gamma distribution
The Gamma family is suitable for data that are continuous and can only take values greater than zero (positive values). Another key feature of this distribution family is that the ratio of its variance and mean is constant, so it is appropriate to model data where increasing a mean value also increases the variance as a fixed (constant) factor. Because of this property, the Gamma family is often used to fit a GLM to response variables that are times, such as waiting time, time between failure, or inverse of the rate of any event, such as an accident.
You can generate Gamma-distributed "data" by using the function `rgamma(n, shape, rate)` in R:
```
par(mfrow=c(1,2))
hist(rgamma(1000,1,1),xlab = "Value", main = "")
hist(rgamma(1000,100,1),xlab = "Value", main = "")
```
The main things to note about these plots (and Gamma-distributed data):
* The main parameters of interest are the `shape` and `rate`. The latter controls the distribution's scale (over what values the distributions spreads).
* This distribution can be right-skewed or bell-shaped, depending on choice of the `shape` parameter.
$\star$ Play with the above code and generate variants in the gamma-distributed data family.
### Other distributions
There are also the Quasi-binomial and Quasi-poisson families within R's `glm` procedure, which differ from the Binomial and Poisson families in that the dispersion parameter (variance to mean ratio) is not fixed at one, so that over-dispersion in your data (greater variability than would be expected based on the given statistical model) can be modeled. You will see an example of this below.
Thus, the first and key step while using GLMs is to determine what type of distribution best describes your response variable. We will now try put this and subsequent steps of fitting GLMs.
## A GLM example
We will use mutation data collected in the Genetics Practical by a previous year's batch.
The students were basically counting colonies looking for mutations. There were a number of bacterial strains which were different mutants of *Salmonella*. Each group applied a mutagen Nitroguanisine (NG) as well as histidine and streptomycine. A control plate was also tested.
The data file is called `PracData.csv` (so it's a comma-separated values file), and is available from TheMulQuaBio's `data` directory.
$\star$ Save the `PracData.csv` dataset into your `data` directory.
$\star$ Create a new script called MyGLM.R in your `code` directory. Use the code below to load and check your data.
$\star$ Start R and change the working directory to `code`, and read in the data:
```
colonies <- read.csv("../data/PracData.csv", stringsAsFactors = T)
str(colonies)
head(colonies)
```
Now let's explore the data first.
### Data exploration
We have a continuous response variable (`ColonyCount`) and two categorical explanatory variables (`Strain` and `Treatment`). We also have observations of halos and bacterial lawns around the treated areas (`HaloLawn`), which we will come back to at the end of this chapter.
So, with two factors as the explanatory variables, we will use box and whisker plots and boxplots to explore the data. First, we'll look at the effects of the four treatments.
```
boxplot(ColonyCount ~ Treatment, data=colonies)
```
There are two immediate things to note.
(1) The distributions of colony counts are very *skewed* โ many small counts and a few large counts. We've already seen that taking a log of data sometimes works in these cases. However, as the tables above show, we have zero counts for all treatments and $\log(0)$ is undefined. A common trick is therefore to use $\log(n+1)$ (add 1 and take a log) when dealing with count data like this:
```
colonies$logCC <- log(colonies$ColonyCount + 1)
boxplot(logCC ~ Treatment, data=colonies)
```
I hope you'll agree that this still doesn't look very convincingly like normal data, but we'll come back to this point.
(2) The colony counts are vastly different between the different treatments. It is hard to say for sure from the two plots, but it looks like colonies never grow under the histidine and streptomycine treatments. We can check that:
```
tapply(colonies$ColonyCount, colonies$Treatment, min, na.rm = TRUE)
tapply(colonies$ColonyCount, colonies$Treatment, max, na.rm = TRUE)
```
There is indeed no variation at all in colony count for histidine and streptomycine โ colonies never grow in these treatments. We don't really need statistics for this observation and, in fact, variation is needed for statistics to work. So, for the rest of this analysis, we will reduce the dataset to the control and nitroguanisine treatments.
$\star$ Update your script by including the code for these plots.
We'll use a new piece of code here to get the right subset. `var %in% c('a','b','c')` finds all the entries in `var` whose values are equal to `'a'`, `'b'` OR `'c'`.
This is new syntax, so let's make sure we understand it. For example, try the following:
```
MyData1 <- rep(c("Control", "NG", "NG"), 4)
MyData1
MyData1 %in% c("Control", "NG")
```
This is the same as doing:
```
MyData1 == "Control" | MyData1 == "NG"
```
Note that this is NOT the same as doing:
```
MyData1 == c("Control", "NG")
```
This is because concatenating the variable names `"Control"` and `"NG"` using `c()` forces R to match only pairs in that sequence, and not just that, but also only search in successive blocks of two entries. That is why above, the sub-sequence `'Control' 'NG' 'NG' 'Control' 'NG'` still returns `TRUE TRUE FALSE FALSE FALSE`, as the second occurrence of the pair `'Control' 'NG'` comes in an odd location, following a single `'NG'`.
Now, let's do the subsetting using `%in%`:
```
coloniesCN <- subset(colonies, Treatment %in% c("Control", "NG"))
str(colonies)
```
Note that this is the same as doing:
```
coloniesCN <- subset(colonies, Treatment == "Control" | Treatment == "NG")
str(coloniesCN)
```
You'll see that, although we have removed two treatments, their names still appear in the list of levels in the `str` output. R retains a list of all the levels that were originally in a factor, even when those levels aren't used any more. This will be annoying later, so
we'll use the `droplevels` function to strip them out.
```
coloniesCN <- droplevels(coloniesCN)
str(coloniesCN)
```
$\star$ Add these commands for sub-setting your data to your script file.
### Looking at strains too
Now we'll look to see how counts differ between the strains. A quick and elegant way to visualise this is to use the `ggplot2` package to get plots grouped by treatment.
```
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 4) # Change plot size
library(ggplot2)
ggplot(coloniesCN, aes(x = Strain, y= logCC)) +
geom_boxplot() + facet_grid(. ~ Treatment)
```
First impressions from this figure:
1. The strains are doing *very* different things under the two treatments. Hopefully this now leaps out at you as suggesting that the two variables (Strain and Treatment) are *interacting*.
2. The distributions are still pretty ugly โ the variances differ hugely between combinations and four combinations have a median of zero.
We can also use a barplot of means here. We'll use the original data to get the means, but can use a log scale on the $y$ axis (`log = 'y'`).
Let's do it:
```
tab <- tapply(coloniesCN$ColonyCount, list(coloniesCN$Treatment, coloniesCN$Strain), mean, na.rm=TRUE)
print(tab)
```
And then,
```
barplot(tab, beside=TRUE, log= 'y' )
```
Let's have a go at fitting an ordinary Linear model.
### A linear model
We'll fit a model of colony count as the interaction between strain and treatment and then look at the diagnostic plots. We'd do this anyway, but we're already suspicious about the variance.
```
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 6) # Change plot size
modLM <- lm(logCC ~ Strain * Treatment, data=coloniesCN)
par(mfrow=c(2,2), mar=c(3,3,3,1), mgp=c(2,0.8,0))
plot(modLM)
```
$\star$ Include Run this code and have a close look at the plots.
That normal Q-Q plot is not good. Our suspicions were justified and it doesn't look like we can use a simple log transformation. We're not even going to look at the `anova` and `summary` tables โ if the diagnostic plots are bad enough, then the model outputs are not
to be trusted.
## Fitting a GLM
In the linear models lecture, we looked at the expectation of *constant normal variance* in linear models. Whatever the combination of explanatory variables for a particular prediction, the residuals around that prediction have similar variance and are roughly normally distributed. The panel on the left in the figure below illustrates this basic idea.
---
<img src="./graphics/GLMexample.svg" width="700px">
<small> <br><center> Illustration of continuous data that follow a normal distribution (left) versus discrete, count data (right). </center></small>
---
As we have seen, count data do not have this distribution, even when logged. The panel on the right in the above figure shows the expected distribution of count data as the mean count increases with an explanatory variable.
There are three key differences between the two panels of the figure:
1. Counts can *never* be negative but can be zero.
2. Counts are always *integers* โ whole numbers โ rather than being continuous.
3. The variance of count data is *not constant*. As the average predicted count gets larger, so does the variance. Unlike the normal distribution, where variance can take any value, for count data the variance is expected to be equal to the mean.
So, we have data that are unsuitable for a linear model because they do not show constant normal variance. This is where generalised linear models come in โ we can change the model for the expected residuals to use a different distribution. For count data, this is the *Poisson* distribution.
We need to change the function we use to fit models to `glm`, but otherwise the process is very similar. The whole point of the GLM is to model the original count data more appropriately, so we will abandon the logged data too. GLMs can cope with a range of different distributions, so we have to specify the `family` of the distribution we want to use.
So let's fit a GLM to the data:
```
modPois <- glm(ColonyCount ~ Strain * Treatment, data=coloniesCN, family= 'poisson')
```
First, we'll look at the summary table for this model. We have 5 levels of strain and 2 levels of factor in the subset so we get an intercept ($i$), 4 differences for strains($s_{2-5}$), one difference for treatment ($t_2$) and then four differences for the interaction ($s_{2-5}t_2$). These combine like this:
| |Control|Nitroguanisine|
|:-|:- |:- |
|421|$i$|$i+t_2$|
|712| $i + s_2$ | $i + s_2 + t_2 + s_2 t_2$ |
|881| $i + s_3$ | $i+s_3 + t_2 + s_3 t_2$ |
|889| $ + s_4$ | $i + s_4 + t_2 + s_4 t_2$ |
|TA102| $i + s_5$ | $ + s_5 + t_2 + s_5 t_2$ |
The summary table looks like this:
```
summary(modPois)
```
This looks similar to the `summary` table for a linear model, but with some differences.
Let's Interpret this table:
* Under the control treatment, strain 421 (the intercept) has the highest number of colonies and all the other strains have lower numbers to some degree โ the differences are
negative.
* The overall effect of nitrogaunasine is to decrease the number of colonies โ again a negative coefficient โ but then the positive interactions show big increases in colony counts for nitroguanisine for specific strains. Everything is hugely significant.
* Two types of deviance are in the model output. Deviance is a measure of goodness of fit of a GLM. The null deviance shows how well the response variable is predicted by a model that includes only the intercept (overall mean). In our example, we have a value of 134445 on 293 degrees of freedom. Including the independent variables (strain and treatment) decreased the deviance to 61579 points on 284 degrees of freedom (remember, lust like linear models, the df are decreased by the number of parameters minus 1). This is a significant reduction in deviance, so the model fit is significant.
$\star$ Copy the code in this section into your script and explore the model a bit more.
### Overdispersion
There's a problem. You may have already spotted it:
```
par(mfrow = c(2, 2), mar = c(3, 3, 3, 1), mgp = c(2, 0.8, 0))
plot(modPois)
```
Actually, there are two problems. First, that Q-Q plot is still a bit dubious. More of the points are close to the line than in the linear model but there are some extreme positive residuals. Second, the magnitude of the residuals is enormous, and this is really clear in the plot in the bottom right hand corner. This plot identifies outliers and any points outside of the red dotted line are possible problems.
The problem here is *overdispersion*. The Poisson distribution predicts that the variance at a point in the model is equal to the prediction โ the mean count at that point. Our count data shows much more variance than this โ particularly that there are some huge counts given the means.
There is a simple way to check the dispersion of count data using the `summary` table: the ratio of the residual deviance to the residual degrees of freedom should be approximately 1. This expectation is actually given in the table:
`(Dispersion parameter for poisson family taken to be 1)`
In this case, the ratio is $61579/284=216.8$. That's very strongly overdispersed. Fortunately, we can allow for this by using a different model.
### Fitting a GLM using a quasi-poisson distribution
The quasi-poisson distribution family uses the data to estimate the dispersion of the model, but is otherwise very similar to using the Poisson family. Let's re-fit the GLM using this distribution.
```
modQPois <- glm(ColonyCount ~ Strain * Treatment, data = coloniesCN, family = 'quasipoisson')
```
The summary table now looks like this:
```
summary(modQPois)
```
This is pretty similar to the previous table but there are two differences. First, the dispersion parameter line has changed. Second, all the $p$ values have got less significant โ this is the effect of controlling for the overdispersion.
Let's look at the model diagnostic plots next:
```
par(mfrow = c(2, 2), mar = c(3, 3, 3, 1), mgp = c(2, 0.8, 0))
plot(modQPois)
```
The residuals and leverage plot is now ok. The Q-Q plot is not better, but is still an improvement over the original linear model. We can't improve the model fit any more โ it isn't perfect but we'll accept those imperfections. It is worth thinking about the imperfections though โ what might give rise to occasional larger than expected counts of
colonies?
We'll look at the `anova` table next. Technically, this is now analysis of deviance not analysis of variance but the concept is the same. Different tests are appropriate for different families of distribution, but we can use $F$ here:
```
anova(modQPois, test = "F")
```
Can we simplify the model? The interaction is the only term we can drop and looks highly significant, but we can check by deleting it.
```
drop.scope(modQPois)
modQPois2 <- update(modQPois, . ~ . - Strain:Treatment)
anova(modQPois, modQPois2, test = "F")
```
No, that makes the model much worse, so we now have our final model.
$\star$ Include this new model fitting in your script and check you've got the same results.
### Model predictions
We can get model predictions and standard errors using the `predict` function. There is a difference though. GLMs use an internal transformation to model the data using a *link function* and the coefficients in the summary above are on the scale of the link transformation. The link function defines the relationship between the linear predictor and the mean of the distribution function, so that an otherwise non-linear (non-normal) response can be accommodated. For quasipoisson, the default is a *log link*, which you can see in the output of `anova`. You can use `predict` to get predictions on the scale of the original *response*. You can use different link functions than the "canonical" one encoded for each distribution `family`, but covering this is outside the scope of this chapter.
```
# use expand.grid to get all combinations of factors
df <- expand.grid(Strain = levels(coloniesCN$Strain), Treatment = levels(coloniesCN$Treatment))
predict(modQPois, newdata = df, type = "response")
```
Those are the same values as the means we calculated for the barplot. Adding standard errors to barplots is more difficult for GLMs and we won't go into it here.
### Reporting the model
Reporting complicated statistics is a difficult business. There is a lot of detail involved and you want the reader to understand what you have done well enough to repeat the analysis if needed. You also have to summarise and explain the results without pages of R output.
Here are some pointers:
- What does the data show? Present a graph or a table to show the data you are about to model. *Always* include a figure or table legend and *always* refer to that figure or legend from the text.
- Have you transformed the data or used a subset? If so, why?
- What kind of model or statistical test have you used?
- With linear models, what is the response variable and what are the explanatory variables.
- Have you simplified the model and, if so, what was the most complex model you tried?
- How did you check the suitability of the model? Are there any problems with the model and, if so, what might cause them?
- If you summarise stats in text, you must include all the information about the test.
- For $F$ tests, this is $F$, the two degrees of freedom and the p value. For example: 'There is a significant interaction between treatment and strain ($F_{4,284}=32.7, p < 0.0001$)'.
- For $t$ tests, this is the coefficient, the standard error, $t$, the degrees of freedom and $p$. For example, 'Across strains, the main effect of nitroguanisine is to reduce colony counts relative to the control (estimate=-2.17, s.e= 0.51, $t=-4.26$, df=284, $p < 0.0001$)'.
- With more complex models, it is common to present either the anova table or the coefficients table as a summary of the model output. Just include the tables from R output, not the information around it. See Table 1 for an example.
- *Never* just include chunks of raw output from R.
- Most importantly, you need to convey what the interpretation of the model is. What is it telling you about the data?
*Table 1*: Coefficients from a GLM of treatment and strain as predictors of colony count.
|Estimate| Std. Error| t value |p |
|-:|:-|:-|:-|
|(Intercept)| 6.29| 0.16| 39.78 |<0.0001|
|Strain712|-1.35 | 0.35|-3.88|0.0001|
|Strain881| -3.74| 1.11| -3.36| 0.0009|
| Strain899| -7.27| 5.80| -1.25| 0.2111|
| StrainTA102| -1.45| 0.35| -4.10 |<0.0001|
| TreatmentNG| -2.17| 0.51| -4.26| <0.0001|
| Strain712:TreatmentNG| -1.05| 1.70| -0.62| 0.5353|
| Strain881:TreatmentNG| 5.31| 1.24| 4.30| <0.0001|
|Strain899:TreatmentNG| 9.54| 5.82| 1.64| 0.1025|
| StrainTA102:TreatmentNG| 3.59| 0.62| 5.79| <0.0001|
Halos and lawns
---------------
We'll keep this one simple since it is harder to analyse. The response variable (`HaloLawn`) is binary โ the plates either have a lawn or not. We'll just look at a contingency table of how many plates have halos or lawns under each combination of treatment and strain.
```
table(Halo = colonies$HaloLawn, Strain = colonies$Strain, Treatment = colonies$Treatment)
```
So, lawns and halos are never recorded from nitroguanisine or the control. They're nearly always found with histidine and different strains have different response to streptomysin. Again, treatment and strain interact. Although you can use a $\chi^2$ test with two-dimensional contingency tables to look for independence between factors, you can't with a three-way table without using more specialized tests.
We will not go any further into this, but be aware that such gnarly statistical challenges may arise at times!
-----
<a id="fn1"></a>
[1]: Here you will work with the script file `glm.R`
|
github_jupyter
|
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 4) # Change plot sizes (in cm) - this bit of code is only relevant if you are using a juyter notebook - ignore otherwise
par(mfrow=c(1,2))
hist(rpois(1000, lambda = 1),xlab = "Value", main="")
hist(rpois(1000, lambda = 100),xlab = "Value", main="")
par(mfrow=c(1,2))
hist(rbinom(1000, 1, 0.5),xlab = "Value", main="")
hist(rbinom(1000, 100, 0.5),xlab = "Value", main="")
par(mfrow=c(1,2))
hist(rgamma(1000,1,1),xlab = "Value", main = "")
hist(rgamma(1000,100,1),xlab = "Value", main = "")
colonies <- read.csv("../data/PracData.csv", stringsAsFactors = T)
str(colonies)
head(colonies)
boxplot(ColonyCount ~ Treatment, data=colonies)
colonies$logCC <- log(colonies$ColonyCount + 1)
boxplot(logCC ~ Treatment, data=colonies)
tapply(colonies$ColonyCount, colonies$Treatment, min, na.rm = TRUE)
tapply(colonies$ColonyCount, colonies$Treatment, max, na.rm = TRUE)
MyData1 <- rep(c("Control", "NG", "NG"), 4)
MyData1
MyData1 %in% c("Control", "NG")
MyData1 == "Control" | MyData1 == "NG"
MyData1 == c("Control", "NG")
coloniesCN <- subset(colonies, Treatment %in% c("Control", "NG"))
str(colonies)
coloniesCN <- subset(colonies, Treatment == "Control" | Treatment == "NG")
str(coloniesCN)
coloniesCN <- droplevels(coloniesCN)
str(coloniesCN)
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 4) # Change plot size
library(ggplot2)
ggplot(coloniesCN, aes(x = Strain, y= logCC)) +
geom_boxplot() + facet_grid(. ~ Treatment)
tab <- tapply(coloniesCN$ColonyCount, list(coloniesCN$Treatment, coloniesCN$Strain), mean, na.rm=TRUE)
print(tab)
barplot(tab, beside=TRUE, log= 'y' )
library(repr); options(repr.plot.res = 100, repr.plot.width = 6, repr.plot.height = 6) # Change plot size
modLM <- lm(logCC ~ Strain * Treatment, data=coloniesCN)
par(mfrow=c(2,2), mar=c(3,3,3,1), mgp=c(2,0.8,0))
plot(modLM)
modPois <- glm(ColonyCount ~ Strain * Treatment, data=coloniesCN, family= 'poisson')
summary(modPois)
par(mfrow = c(2, 2), mar = c(3, 3, 3, 1), mgp = c(2, 0.8, 0))
plot(modPois)
modQPois <- glm(ColonyCount ~ Strain * Treatment, data = coloniesCN, family = 'quasipoisson')
summary(modQPois)
par(mfrow = c(2, 2), mar = c(3, 3, 3, 1), mgp = c(2, 0.8, 0))
plot(modQPois)
anova(modQPois, test = "F")
drop.scope(modQPois)
modQPois2 <- update(modQPois, . ~ . - Strain:Treatment)
anova(modQPois, modQPois2, test = "F")
# use expand.grid to get all combinations of factors
df <- expand.grid(Strain = levels(coloniesCN$Strain), Treatment = levels(coloniesCN$Treatment))
predict(modQPois, newdata = df, type = "response")
table(Halo = colonies$HaloLawn, Strain = colonies$Strain, Treatment = colonies$Treatment)
| 0.501953 | 0.98366 |
# Introducing txtai
[txtai](https://github.com/neuml/txtai) executes machine-learning workflows to transform data and build AI-powered semantic search applications.
Traditional search systems use keywords to find data. Semantic search applications have an understanding of natural language and identify results that have the same meaning, not necessarily the same keywords.
Backed by state-of-the-art machine learning models, data is transformed into vector representations for search (also known as embeddings). Innovation is happening at a rapid pace, models can understand concepts in documents, audio, images and more.
The following is a summary of key features:
- ๐ Large-scale similarity search with multiple index backends ([Faiss](https://github.com/facebookresearch/faiss), [Annoy](https://github.com/spotify/annoy), [Hnswlib](https://github.com/nmslib/hnswlib))
- ๐ Create embeddings for text snippets, documents, audio, images and video. Supports transformers and word vectors.
- ๐ก Machine-learning pipelines to run extractive question-answering, zero-shot labeling, transcription, translation, summarization and text extraction
- โช๏ธ๏ธ Workflows that join pipelines together to aggregate business logic. txtai processes can be microservices or full-fledged indexing workflows.
- ๐ API bindings for [JavaScript](https://github.com/neuml/txtai.js), [Java](https://github.com/neuml/txtai.java), [Rust](https://github.com/neuml/txtai.rs) and [Go](https://github.com/neuml/txtai.go)
- โ๏ธ Cloud-native architecture that scales out with container orchestration systems (e.g. Kubernetes)
Applications range from similarity search to complex NLP-driven data extractions to generate structured databases. The following applications are powered by txtai.
- [paperai](https://github.com/neuml/paperai) - AI-powered literature discovery and review engine for medical/scientific papers
- [tldrstory](https://github.com/neuml/tldrstory) - AI-powered understanding of headlines and story text
- [neuspo](https://neuspo.com) - Fact-driven, real-time sports event and news site
- [codequestion](https://github.com/neuml/codequestion) - Ask coding questions directly from the terminal
txtai is built with Python 3.6+, [Hugging Face Transformers](https://github.com/huggingface/transformers), [Sentence Transformers](https://github.com/UKPLab/sentence-transformers) and [FastAPI](https://github.com/tiangolo/fastapi)
This notebook gives an overview of txtai and how to run similarity searches.
# Install dependencies
Install `txtai` and all dependencies.
```
%%capture
!pip install git+https://github.com/neuml/txtai
```
# Create an Embeddings instance
The Embeddings instance is the main entrypoint for txtai. An Embeddings instance defines the method used to tokenize and convert a text section into an embeddings vector.
```
%%capture
from txtai.embeddings import Embeddings
# Create embeddings model, backed by sentence-transformers & transformers
embeddings = Embeddings({"path": "sentence-transformers/nli-mpnet-base-v2"})
```
# Running similarity queries
An embedding instance relies on the underlying transformer model to build text embeddings. The following example shows how to use an transformers Embedding instance to run similarity searches for a list of different concepts.
```
data = ["US tops 5 million confirmed virus cases",
"Canada's last fully intact ice shelf has suddenly collapsed, forming a Manhattan-sized iceberg",
"Beijing mobilises invasion craft along coast as Taiwan tensions escalate",
"The National Park Service warns against sacrificing slower friends in a bear attack",
"Maine man wins $1M from $25 lottery ticket",
"Make huge profits without work, earn up to $100,000 a day"]
print("%-20s %s" % ("Query", "Best Match"))
print("-" * 50)
for query in ("feel good story", "climate change", "public health story", "war", "wildlife", "asia", "lucky", "dishonest junk"):
# Get index of best section that best matches query
uid = embeddings.similarity(query, data)[0][0]
print("%-20s %s" % (query, data[uid]))
```
The example above shows for almost all of the queries, the actual text isn't stored in the list of text sections. This is the true power of transformer models over token based search. What you get out of the box is ๐ฅ๐ฅ๐ฅ!
# Building an Embeddings index
For small lists of texts, the method above works. But for larger repositories of documents, it doesn't make sense to tokenize and convert to embeddings on each query. txtai supports building pre-computed indices which signficantly improve performance.
Building on the previous example, the following example runs an index method to build and store the text embeddings. In this case, only the query is converted to an embeddings vector each search.
```
# Create an index for the list of text
embeddings.index([(uid, text, None) for uid, text in enumerate(data)])
print("%-20s %s" % ("Query", "Best Match"))
print("-" * 50)
# Run an embeddings search for each query
for query in ("feel good story", "climate change", "public health story", "war", "wildlife", "asia", "lucky", "dishonest junk"):
# Extract uid of first result
# search result format: (uid, score)
uid = embeddings.search(query, 1)[0][0]
# Print text
print("%-20s %s" % (query, data[uid]))
```
# Embeddings load/save
Embeddings indices can be saved to disk and reloaded.
```
embeddings.save("index")
embeddings = Embeddings()
embeddings.load("index")
uid = embeddings.search("climate change", 1)[0][0]
print(data[uid])
!ls index
```
# Embeddings update/delete
Updates and deletes are supported for Embedding indices. The upsert operation will insert new data and update existing data
The following section runs a query, then updates a value changing the top result and finally deletes the updated value to revert back to the original query results.
```
# Run initial query
uid = embeddings.search("feel good story", 1)[0][0]
print("Initial: ", data[uid])
# Update data
data[0] = "See it: baby panda born"
embeddings.upsert([(0, data[0], None)])
uid = embeddings.search("feel good story", 1)[0][0]
print("After update: ", data[uid])
# Remove record just added from index
embeddings.delete([0])
# Ensure value matches previous value
uid = embeddings.search("feel good story", 1)[0][0]
print("After delete: ", data[uid])
```
# Embedding methods
Embeddings supports two methods for creating text vectors, the sentence-transformers library and word embeddings vectors. Both methods have their merits as shown below:
- [sentence-transformers](https://github.com/UKPLab/sentence-transformers)
- Creates a single embeddings vector via mean pooling of vectors generated by the transformers library.
- Supports models stored on Hugging Face's model hub or stored locally.
- See sentence-transformers for details on how to create custom models, which can be kept local or uploaded to Hugging Face's model hub.
- Base models require significant compute capability (GPU preferred). Possible to build smaller/lighter weight models that tradeoff accuracy for speed.
- word embeddings
- Creates a single embeddings vector via BM25 scoring of each word component. See this [Medium article](https://towardsdatascience.com/building-a-sentence-embedding-index-with-fasttext-and-bm25-f07e7148d240) for the logic behind this method.
- Backed by the [pymagnitude](https://github.com/plasticityai/magnitude) library. Pre-trained word vectors can be installed from the referenced link.
- See [words.py](https://github.com/neuml/txtai/blob/master/src/python/txtai/vectors/words.py) for code that can build word vectors for custom datasets.
- Significantly better performance with default models. For larger datasets, it offers a good tradeoff of speed and accuracy.
|
github_jupyter
|
%%capture
!pip install git+https://github.com/neuml/txtai
%%capture
from txtai.embeddings import Embeddings
# Create embeddings model, backed by sentence-transformers & transformers
embeddings = Embeddings({"path": "sentence-transformers/nli-mpnet-base-v2"})
data = ["US tops 5 million confirmed virus cases",
"Canada's last fully intact ice shelf has suddenly collapsed, forming a Manhattan-sized iceberg",
"Beijing mobilises invasion craft along coast as Taiwan tensions escalate",
"The National Park Service warns against sacrificing slower friends in a bear attack",
"Maine man wins $1M from $25 lottery ticket",
"Make huge profits without work, earn up to $100,000 a day"]
print("%-20s %s" % ("Query", "Best Match"))
print("-" * 50)
for query in ("feel good story", "climate change", "public health story", "war", "wildlife", "asia", "lucky", "dishonest junk"):
# Get index of best section that best matches query
uid = embeddings.similarity(query, data)[0][0]
print("%-20s %s" % (query, data[uid]))
# Create an index for the list of text
embeddings.index([(uid, text, None) for uid, text in enumerate(data)])
print("%-20s %s" % ("Query", "Best Match"))
print("-" * 50)
# Run an embeddings search for each query
for query in ("feel good story", "climate change", "public health story", "war", "wildlife", "asia", "lucky", "dishonest junk"):
# Extract uid of first result
# search result format: (uid, score)
uid = embeddings.search(query, 1)[0][0]
# Print text
print("%-20s %s" % (query, data[uid]))
embeddings.save("index")
embeddings = Embeddings()
embeddings.load("index")
uid = embeddings.search("climate change", 1)[0][0]
print(data[uid])
!ls index
# Run initial query
uid = embeddings.search("feel good story", 1)[0][0]
print("Initial: ", data[uid])
# Update data
data[0] = "See it: baby panda born"
embeddings.upsert([(0, data[0], None)])
uid = embeddings.search("feel good story", 1)[0][0]
print("After update: ", data[uid])
# Remove record just added from index
embeddings.delete([0])
# Ensure value matches previous value
uid = embeddings.search("feel good story", 1)[0][0]
print("After delete: ", data[uid])
| 0.504639 | 0.985158 |
Any learning algorithm will always have strengths and weaknesses: a single model is unlikely to fit every possible scenario. Ensembles combine multiple models to achieve higher generalization performance than any of the constituent models is capable of. How do we assemble the weak learners? We can use some sequential heuristics. For instance, given the current collection of models, we can add one more based on where that particular model performs well. Alternatively, we can look at all the correlations of the predictions between all models, and optimize for the most uncorrelated predictors. Since this latter is a global approach, it naturally maps to a quantum computer. But first, let's take a look a closer look at loss functions and regularization, two key concepts in machine learning.
# Loss Functions and Regularization
If you can solve a problem by a classical computer -- let that be a laptop or a massive GPU cluster -- there is little value in solving it by a quantum computer that costs ten million dollars. The interesting question in quantum machine learning is whether there are problems in machine learning and AI that fit quantum computers naturally, but are challenging on classical hardware. This, however, requires a good understanding of both machine learning and contemporary quantum computers.
In this course, we primarily focus on the second aspect, since there is no shortage of educational material on classical machine learning. However, it is worth spending a few minutes on going through some basics.
Let us take a look at the easiest possible problem: the data points split into two, easily distinguishable sets. We randomly generate this data set:
```
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
c1 = np.random.rand(50, 2)/5
c2 = (-0.6, 0.5) + np.random.rand(50, 2)/5
data = np.concatenate((c1, c2))
labels = np.array([0] * 50 + [1] *50)
plt.figure(figsize=(6, 6))
plt.subplot(111, xticks=[], yticks=[])
plt.scatter(data[:50, 0], data[:50, 1], color='navy')
plt.scatter(data[50:, 0], data[50:, 1], color='c');
```
Let's shuffle the data set into a training set that we are going to optimize over (2/3 of the data), and a test set where we estimate our generalization performance.
```
idx = np.arange(len(labels))
np.random.shuffle(idx)
# train on a random 2/3 and test on the remaining 1/3
idx_train = idx[:2*len(idx)//3]
idx_test = idx[2*len(idx)//3:]
X_train = data[idx_train]
X_test = data[idx_test]
y_train = labels[idx_train]
y_test = labels[idx_test]
```
We will use the package `scikit-learn` to train various machine learning models.
```
import sklearn
import sklearn.metrics
metric = sklearn.metrics.accuracy_score
```
Let's train a perceptron, which has a linear loss function $\frac{1}{N}\sum_{i=1}^N |h(x_i)-y_i)|$:
```
from sklearn.linear_model import Perceptron
model_1 = Perceptron()
model_1.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_1.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_1.predict(X_test))))
```
It does a great job. It is a linear model, meaning its decision surface is a plane. Our dataset is separable by a plane, so let's try another linear model, but this time a support vector machine. If you eyeball our dataset, you will see that to define the separation between the two classes, actually only a few points close to the margin are relevant. These are called support vectors and support vector machines aim to find them. Its objective function measures The $C$ hyperparameter controls a regularization term that penalizes the objective for the number of support vectors:
```
from sklearn.svm import SVC
model_2 = SVC(kernel='linear', C=1)
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
print('Number of support vectors:', sum(model_2.n_support_))
```
It picks only a few datapoints out of the hundred. Let's change the hyperparameter to reduce the penalty:
```
model_2 = SVC(kernel='linear', C=0.01)
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
print('Number of support vectors:', sum(model_2.n_support_))
```
You can see that the model gets confused by using two many datapoints in the final classifier. This is one example where regularization helps.
# Ensemble methods
Ensembles yield better results when there is considerable diversity among the base classifiers. If diversity is sufficient, base classifiers make different errors, and a strategic combination may reduce the total error, ideally improving generalization performance. A constituent model in an ensemble is also called a base classifier or weak learner, and the composite model a strong learner.
The generic procedure of ensemble methods has two steps. First, develop a set of base classifiers from the training data. Second, combine them to form the ensemble. In the simplest combination, the base learners vote, and the label prediction is based on majority. More involved methods weigh the votes of the base learners.
Let us import some packages and define our figure of merit as accuracy in a balanced dataset.
```
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.metrics
%matplotlib inline
metric = sklearn.metrics.accuracy_score
```
We generate a random dataset of two classes that form concentric circles:
```
np.random.seed(0)
data, labels = sklearn.datasets.make_circles()
idx = np.arange(len(labels))
np.random.shuffle(idx)
# train on a random 2/3 and test on the remaining 1/3
idx_train = idx[:2*len(idx)//3]
idx_test = idx[2*len(idx)//3:]
X_train = data[idx_train]
X_test = data[idx_test]
y_train = 2 * labels[idx_train] - 1 # binary -> spin
y_test = 2 * labels[idx_test] - 1
scaler = sklearn.preprocessing.StandardScaler()
normalizer = sklearn.preprocessing.Normalizer()
X_train = scaler.fit_transform(X_train)
X_train = normalizer.fit_transform(X_train)
X_test = scaler.fit_transform(X_test)
X_test = normalizer.fit_transform(X_test)
plt.figure(figsize=(6, 6))
plt.subplot(111, xticks=[], yticks=[])
plt.scatter(data[labels == 0, 0], data[labels == 0, 1], color='navy')
plt.scatter(data[labels == 1, 0], data[labels == 1, 1], color='c');
```
Let's train a perceptron:
```
from sklearn.linear_model import Perceptron
model_1 = Perceptron()
model_1.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_1.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_1.predict(X_test))))
```
Since its decision surface is linear, we get a poor accuracy. Would a support vector machine with a nonlinear kernel fare better?
```
from sklearn.svm import SVC
model_2 = SVC(kernel='rbf')
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
```
It performs better on the training set, but at the cost of extremely poor generalization.
Boosting is an ensemble method that explicitly seeks models that complement one another. The variation between boosting algorithms is how they combine weak learners. Adaptive boosting (AdaBoost) is a popular method that combines the weak learners in a sequential manner based on their individual accuracies. It has a convex objective function that does not penalize for complexity: it is likely to include all available weak learners in the final ensemble. Let's train AdaBoost with a few weak learners:
```
from sklearn.ensemble import AdaBoostClassifier
model_3 = AdaBoostClassifier(n_estimators=3)
model_3.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_3.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_3.predict(X_test))))
```
Its performance is marginally better than that of the SVM.
# QBoost
The idea of Qboost is that optimization on a quantum computer is not constrained to convex objective functions, therefore we can add arbitrary penalty terms and rephrase our objective [[1](#1)]. Qboost solves the following problem:
$$
\mathrm{argmin}_{w} \left(\frac{1}{N}\sum_{i=1}^{N}\left(\sum_{k=1}^{K}w_kh_k(x_i)-
y_i\right)^2+\lambda\|w\|_0\right),
$$
where $h_k(x_i)$ is the prediction of the weak learner $k$ for a training instance $k$. The weights in this formulation are binary, so this objective function is already maps to an Ising model. The regularization in the $l_0$ norm ensures sparsity, and it is not the kind of regularization we would consider classically: it is hard to optimize with this term on a digital computer.
Let us expand the quadratic part of the objective:
$$
\mathrm{argmin}_{w} \left(\frac{1}{N}\sum_{i=1}^{N}
\left( \left(\sum_{k=1}^{K} w_k h_k(x_i)\right)^{2} -
2\sum_{k=1}^{K} w_k h_k(\mathbf{x}_i)y_i + y_i^{2}\right) + \lambda \|w\|_{0}
\right).
$$
Since $y_i^{2}$ is just a constant offset, the optimization reduces to
$$
\mathrm{argmin}_{w} \left(
\frac{1}{N}\sum_{k=1}^{K}\sum_{l=1}^{K} w_k w_l
\left(\sum_{i=1}^{N}h_k(x_i)h_l(x_i)\right) -
\frac{2}{N}\sum_{k=1}^{K}w_k\sum_{i=1}^{N} h_k(x_i)y_i +
\lambda \|w\|_{0} \right).
$$
This form shows that we consider all correlations between the predictions of the weak learners: there is a summation of $h_k(x_i)h_l(x_i)$. Since this term has a positive sign, we penalize for correlations. On the other hand, the correlation with the true label, $h_k(x_i)y_i$, has a negative sign. The regularization term remains unchanged.
Let us consider all three models from the previous section as weak learners.
```
models = [model_1, model_2, model_3]
```
We calculate their predictions and set $\lambda$ to 1. The predictions are scaled to reflecting the averaging in the objective.
```
n_models = len(models)
predictions = np.array([h.predict(X_train) for h in models], dtype=np.float64)
# scale hij to [-1/N, 1/N]
predictions *= 1/n_models
ฮป = 1
```
We create the quadratic binary optimization of the objective function as we expanded above:
```
w = np.dot(predictions, predictions.T)
wii = len(X_train) / (n_models ** 2) + ฮป - 2 * np.dot(predictions, y_train)
w[np.diag_indices_from(w)] = wii
W = {}
for i in range(n_models):
for j in range(i, n_models):
W[(i, j)] = w[i, j]
```
We solve the quadratic binary optimization with simulated annealing and read out the optimal weights:
```
import dimod
sampler = dimod.SimulatedAnnealingSampler()
response = sampler.sample_qubo(W, num_reads=10)
weights = list(response.first.sample.values())
```
We define a prediction function to help with measuring accuracy:
```
def predict(models, weights, X):
n_data = len(X)
T = 0
y = np.zeros(n_data)
for i, h in enumerate(models):
y0 = weights[i] * h.predict(X) # prediction of weak classifier
y += y0
T += np.sum(y0)
y = np.sign(y - T / (n_data*len(models)))
return y
print('accuracy (train): %5.2f'%(metric(y_train, predict(models, weights, X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, predict(models, weights, X_test))))
```
The accuracy co-incides with our strongest weak learner's, the AdaBoost model. Looking at the optimal weights, this is apparent:
```
weights
```
Only AdaBoost made it to the final ensemble. The first two models perform poorly and their predictions are correlated. Yet, if you remove regularization by setting $\lambda=0$ above, the second model also enters the ensemble, decreasing overall performance. This shows that the regularization is in fact important.
# Solving by QAOA
Since eventually our problem is just an Ising model, we can also solve it on a gate-model quantum computer by QAOA. Let us explicitly map the binary optimization to the Ising model:
```
h, J, offset = dimod.qubo_to_ising(W)
```
We have to translate the Ising couplings to be suitable for solving by the QAOA routine:
```
from pyquil import Program, api
from pyquil.paulis import PauliSum, PauliTerm
from scipy.optimize import fmin_bfgs
from grove.pyqaoa.qaoa import QAOA
from forest_tools import *
qvm_server, quilc_server, fc = init_qvm_and_quilc()
qvm = api.QVMConnection(endpoint=fc.sync_endpoint, compiler_endpoint=fc.compiler_endpoint)
num_nodes = w.shape[0]
ising_model = []
for i in range(num_nodes):
ising_model.append(PauliSum([PauliTerm("Z", i, h[i])]))
for j in range(i+1, num_nodes):
ising_model.append(PauliSum([PauliTerm("Z", i, J[i, j]) * PauliTerm("Z", j, 1.0)]))
```
Next we run the optimization:
```
p = 1
Hm = [PauliSum([PauliTerm("X", i, 1.0)]) for i in range(num_nodes)]
qaoa = QAOA(qvm,
qubits=range(num_nodes),
steps=p,
ref_ham=Hm,
cost_ham=ising_model,
store_basis=True,
minimizer=fmin_bfgs,
minimizer_kwargs={'maxiter': 50})
ฮฝ, ฮณ = qaoa.get_angles()
program = qaoa.get_parameterized_program()(np.hstack((ฮฝ, ฮณ)))
measures = qvm.run_and_measure(program, range(num_nodes), trials=100)
measures = np.array(measures)
```
Let's look at the solutions found:
```
hist = plt.hist([str(m) for m in measures])
```
Finally, we extract the most likely solution:
```
count = np.unique(measures, return_counts=True, axis=0)
weights = count[0][np.argmax(count[1])]
```
Let's see the weights found by QAOA:
```
weights
```
And the final accuracy:
```
print('accuracy (train): %5.2f'%(metric(y_train, predict(models, weights, X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, predict(models, weights, X_test))))
```
# References
[1] Neven, H., Denchev, V.S., Rose, G., Macready, W.G. (2008). [Training a binary classifier with the quantum adiabatic algorithm](https://arxiv.org/abs/0811.0416). *arXiv:0811.0416*. <a id='1'></a>
|
github_jupyter
|
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
c1 = np.random.rand(50, 2)/5
c2 = (-0.6, 0.5) + np.random.rand(50, 2)/5
data = np.concatenate((c1, c2))
labels = np.array([0] * 50 + [1] *50)
plt.figure(figsize=(6, 6))
plt.subplot(111, xticks=[], yticks=[])
plt.scatter(data[:50, 0], data[:50, 1], color='navy')
plt.scatter(data[50:, 0], data[50:, 1], color='c');
idx = np.arange(len(labels))
np.random.shuffle(idx)
# train on a random 2/3 and test on the remaining 1/3
idx_train = idx[:2*len(idx)//3]
idx_test = idx[2*len(idx)//3:]
X_train = data[idx_train]
X_test = data[idx_test]
y_train = labels[idx_train]
y_test = labels[idx_test]
import sklearn
import sklearn.metrics
metric = sklearn.metrics.accuracy_score
from sklearn.linear_model import Perceptron
model_1 = Perceptron()
model_1.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_1.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_1.predict(X_test))))
from sklearn.svm import SVC
model_2 = SVC(kernel='linear', C=1)
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
print('Number of support vectors:', sum(model_2.n_support_))
model_2 = SVC(kernel='linear', C=0.01)
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
print('Number of support vectors:', sum(model_2.n_support_))
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.metrics
%matplotlib inline
metric = sklearn.metrics.accuracy_score
np.random.seed(0)
data, labels = sklearn.datasets.make_circles()
idx = np.arange(len(labels))
np.random.shuffle(idx)
# train on a random 2/3 and test on the remaining 1/3
idx_train = idx[:2*len(idx)//3]
idx_test = idx[2*len(idx)//3:]
X_train = data[idx_train]
X_test = data[idx_test]
y_train = 2 * labels[idx_train] - 1 # binary -> spin
y_test = 2 * labels[idx_test] - 1
scaler = sklearn.preprocessing.StandardScaler()
normalizer = sklearn.preprocessing.Normalizer()
X_train = scaler.fit_transform(X_train)
X_train = normalizer.fit_transform(X_train)
X_test = scaler.fit_transform(X_test)
X_test = normalizer.fit_transform(X_test)
plt.figure(figsize=(6, 6))
plt.subplot(111, xticks=[], yticks=[])
plt.scatter(data[labels == 0, 0], data[labels == 0, 1], color='navy')
plt.scatter(data[labels == 1, 0], data[labels == 1, 1], color='c');
from sklearn.linear_model import Perceptron
model_1 = Perceptron()
model_1.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_1.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_1.predict(X_test))))
from sklearn.svm import SVC
model_2 = SVC(kernel='rbf')
model_2.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_2.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_2.predict(X_test))))
from sklearn.ensemble import AdaBoostClassifier
model_3 = AdaBoostClassifier(n_estimators=3)
model_3.fit(X_train, y_train)
print('accuracy (train): %5.2f'%(metric(y_train, model_3.predict(X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, model_3.predict(X_test))))
models = [model_1, model_2, model_3]
n_models = len(models)
predictions = np.array([h.predict(X_train) for h in models], dtype=np.float64)
# scale hij to [-1/N, 1/N]
predictions *= 1/n_models
ฮป = 1
w = np.dot(predictions, predictions.T)
wii = len(X_train) / (n_models ** 2) + ฮป - 2 * np.dot(predictions, y_train)
w[np.diag_indices_from(w)] = wii
W = {}
for i in range(n_models):
for j in range(i, n_models):
W[(i, j)] = w[i, j]
import dimod
sampler = dimod.SimulatedAnnealingSampler()
response = sampler.sample_qubo(W, num_reads=10)
weights = list(response.first.sample.values())
def predict(models, weights, X):
n_data = len(X)
T = 0
y = np.zeros(n_data)
for i, h in enumerate(models):
y0 = weights[i] * h.predict(X) # prediction of weak classifier
y += y0
T += np.sum(y0)
y = np.sign(y - T / (n_data*len(models)))
return y
print('accuracy (train): %5.2f'%(metric(y_train, predict(models, weights, X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, predict(models, weights, X_test))))
weights
h, J, offset = dimod.qubo_to_ising(W)
from pyquil import Program, api
from pyquil.paulis import PauliSum, PauliTerm
from scipy.optimize import fmin_bfgs
from grove.pyqaoa.qaoa import QAOA
from forest_tools import *
qvm_server, quilc_server, fc = init_qvm_and_quilc()
qvm = api.QVMConnection(endpoint=fc.sync_endpoint, compiler_endpoint=fc.compiler_endpoint)
num_nodes = w.shape[0]
ising_model = []
for i in range(num_nodes):
ising_model.append(PauliSum([PauliTerm("Z", i, h[i])]))
for j in range(i+1, num_nodes):
ising_model.append(PauliSum([PauliTerm("Z", i, J[i, j]) * PauliTerm("Z", j, 1.0)]))
p = 1
Hm = [PauliSum([PauliTerm("X", i, 1.0)]) for i in range(num_nodes)]
qaoa = QAOA(qvm,
qubits=range(num_nodes),
steps=p,
ref_ham=Hm,
cost_ham=ising_model,
store_basis=True,
minimizer=fmin_bfgs,
minimizer_kwargs={'maxiter': 50})
ฮฝ, ฮณ = qaoa.get_angles()
program = qaoa.get_parameterized_program()(np.hstack((ฮฝ, ฮณ)))
measures = qvm.run_and_measure(program, range(num_nodes), trials=100)
measures = np.array(measures)
hist = plt.hist([str(m) for m in measures])
count = np.unique(measures, return_counts=True, axis=0)
weights = count[0][np.argmax(count[1])]
weights
print('accuracy (train): %5.2f'%(metric(y_train, predict(models, weights, X_train))))
print('accuracy (test): %5.2f'%(metric(y_test, predict(models, weights, X_test))))
| 0.458106 | 0.991347 |
# Python Basics
These assignments aim to get you acquainted with Python, which is an important requirement for all the research done at Solarillion Foundation. Apart from teaching you Python, these assignments also aim to make you a better programmer and cultivate better coding practices.
Visit these links for more details: <br>
PEP8 Practices: https://www.python.org/dev/peps/pep-0008/ <br>
Check PEP8: http://pep8online.com <br>
Python Reference: https://www.py4e.com/lessons <br>
Do use Google efficiently, and refer to StackOverflow for clarifying any programming doubts. If you're still stuck, feel free to ask a TA to help you.
Each task in the assignment comprises of at least two cells. There are function definitions wherein you will name the function(s), and write code to solve the problem at hand. You will call the function(s) in the last cell of each task, and check your output.
We encourage you to play around and learn as much as possible, and be as creative as you can get. More than anything, have fun doing these assignments. Enjoy!
# Important
* **Only the imports and functions must be present when you upload this notebook to GitHub for verification.**
* **Do not upload it until you want to get it verified. Do not change function names or add extra cells or code, or remove anything.**
* **For your rough work and four showing your code to TAs, use a different notebook with the name Module2Playground.ipynb and copy only the final functions to this notebook for verification.**
# Module 3
Scope: Algorithmic Thinking, Programming
## Imports - Always Execute First!
Import any modules and turn on any magic here:
```
from IPython import get_ipython
ipy = get_ipython()
if ipy is not None:
ipy.run_line_magic("load_ext", "pycodestyle_magic")
ipy.run_line_magic("pycodestyle_on", "")
```
## Burger Mania
```
"""
Imagine that you are a restaurant's cashier and are trying to keep records for analysing profits.
Your restaurant sells 7 different items:
1. Burgers - $4.25
2. Nuggets - $2.50
3. French Fries - $2.00
4. Small Drink - $1.25
5. Medium Drink - $1.50
6. Large Drink - $1.75
7. Salad - $3.75
Create a program to randomly generate the orders of each customer as a string of numbers
(corresponding to the item) and calculate the cost of the order. For example, if the generated
string is 5712335, the program should understand that the customer has ordered 1 burger, 1
portion of nuggets, 2 portions of fries, 2 medium drinks and 1 salad. It should then compute the
cost ($17.50). The final cost is calculated after considering discounts for combo offers and
adding 18% GST.
The combo offers are:
A) 1 Burger + 1 Portion of Fries + 1 Drink -> 20% discount
B) 1 Burger + 1 Portion of Nuggets + 1 Salad + 1 Drink -> 35% discount
The final cost of the 5712335 order is $13.4225. The profit gained each day has to be recorded for
30 days and plotted for analysis.
Note:
- There will be at least 20 customers and not more than 50 customers per day. Each customer
orders at least 3 items and not more than 7 items.
- If there is a possibility of availing multiple combo offers in an order, the program
should select the offer with maximum discount.
"""
def generate_order():
import random
"""
Function 1: generate_order()
Return: A randomly generated order string
"""
s = ""
for i in range(random.randint(3,8)):
s = s + str(random.randint(1,7))
return s
def compute_cost(s):
"""
Function 2: compute_cost(order)
Parameters: order (String)
Return: Final cost of order
"""
order = {"1":4.25,"2":2.50,"3":2.00,"4":1.25,"5":1.50,"6":1.75,"7":3.75}
amt = 0
for i in s:
amt = amt+order[i]
if(("1" in s) and ("3" in s) and (("4" in s) or ("5" in s) or ("6" in s))):
if("2" in s):
amt = amt - (0.35*amt)
else:
amy = amt - (0.2*amt)
return amt + (0.18*amt)
def simulate_restaurant():
import random
import matplotlib.pyplot as plt
"""
Function 3: simulate_restaurant()
Purpose: Simulate the restaurant's operation using the previously declared functions,
based on the constraints mentioned in the question
Output: Plot of profit over 30 days
"""
days = []
profit = []
for i in range(30):
days.append(i)
customers = random.randint(20,50)
amt = 0
for j in range(customers):
cost = compute_cost((generate_order()))
amt += cost
profit.append(amt)
plt.xlabel('Days')
plt.ylabel('Profit')
plt.plot(days,profit)
plt.show()
simulate_restaurant()
```
You're done with the Basics of Python! Give yourself a pat on the back.
Now, choose an area you want to work on - Machine Learning, Internet of Things or Microgrids - and get started with the assignments. You could also choose to do assignments from multiple areas, it's entirely up to you. Hope you have fun!
|
github_jupyter
|
from IPython import get_ipython
ipy = get_ipython()
if ipy is not None:
ipy.run_line_magic("load_ext", "pycodestyle_magic")
ipy.run_line_magic("pycodestyle_on", "")
"""
Imagine that you are a restaurant's cashier and are trying to keep records for analysing profits.
Your restaurant sells 7 different items:
1. Burgers - $4.25
2. Nuggets - $2.50
3. French Fries - $2.00
4. Small Drink - $1.25
5. Medium Drink - $1.50
6. Large Drink - $1.75
7. Salad - $3.75
Create a program to randomly generate the orders of each customer as a string of numbers
(corresponding to the item) and calculate the cost of the order. For example, if the generated
string is 5712335, the program should understand that the customer has ordered 1 burger, 1
portion of nuggets, 2 portions of fries, 2 medium drinks and 1 salad. It should then compute the
cost ($17.50). The final cost is calculated after considering discounts for combo offers and
adding 18% GST.
The combo offers are:
A) 1 Burger + 1 Portion of Fries + 1 Drink -> 20% discount
B) 1 Burger + 1 Portion of Nuggets + 1 Salad + 1 Drink -> 35% discount
The final cost of the 5712335 order is $13.4225. The profit gained each day has to be recorded for
30 days and plotted for analysis.
Note:
- There will be at least 20 customers and not more than 50 customers per day. Each customer
orders at least 3 items and not more than 7 items.
- If there is a possibility of availing multiple combo offers in an order, the program
should select the offer with maximum discount.
"""
def generate_order():
import random
"""
Function 1: generate_order()
Return: A randomly generated order string
"""
s = ""
for i in range(random.randint(3,8)):
s = s + str(random.randint(1,7))
return s
def compute_cost(s):
"""
Function 2: compute_cost(order)
Parameters: order (String)
Return: Final cost of order
"""
order = {"1":4.25,"2":2.50,"3":2.00,"4":1.25,"5":1.50,"6":1.75,"7":3.75}
amt = 0
for i in s:
amt = amt+order[i]
if(("1" in s) and ("3" in s) and (("4" in s) or ("5" in s) or ("6" in s))):
if("2" in s):
amt = amt - (0.35*amt)
else:
amy = amt - (0.2*amt)
return amt + (0.18*amt)
def simulate_restaurant():
import random
import matplotlib.pyplot as plt
"""
Function 3: simulate_restaurant()
Purpose: Simulate the restaurant's operation using the previously declared functions,
based on the constraints mentioned in the question
Output: Plot of profit over 30 days
"""
days = []
profit = []
for i in range(30):
days.append(i)
customers = random.randint(20,50)
amt = 0
for j in range(customers):
cost = compute_cost((generate_order()))
amt += cost
profit.append(amt)
plt.xlabel('Days')
plt.ylabel('Profit')
plt.plot(days,profit)
plt.show()
simulate_restaurant()
| 0.590661 | 0.960952 |
```
import pandas as pd
import numpy as np
df = pd.DataFrame({
'sales': [100, 50, 14, 94, 20, 45, 56, 18, 125],
'CTA Variant': ['A', 'B', 'C', 'A', 'C', 'B', 'B', 'C', 'A']
}, index = pd.date_range("12:30", "21:00", freq="60min")
)
df.head()
sales = pd.read_csv("sales.csv")
sales.head()
sales.loc[sales['Retailer country']=='United States', ['Revenue', 'Quantity', 'Gross profit']].head()
sales.rename({'Revenue':'Earnings'}, axis = 'columns').head()
sales['Unit cost'].quantile([0.0, 0.25,0.5,0.75,1])
def cat_gen(x):
if pd.isnull(x):
return np.nan
elif x<=2.76:
return "cheap"
elif 2.76<x<=9.0:
return "medium"
elif 9.0<x<=34.97:
return "moderate"
else:
return "expensive"
sales['Cost category'] = sales['Unit cost'].map(cat_gen)
sales['Cost category'].value_counts(dropna = True)
sales['Unit cost'] = sales['Unit cost'].astype('category')
sales.dtypes
cta = pd.read_csv('CTA_comparison.csv')
cta
cta.set_index('CTA Variant')
cta.set_index(['CTA Variant', 'views'])
cta_views = cta.groupby(['CTA Variant', 'views']).count()
cta_views
h1 = cta_views.unstack(level = 'CTA Variant')
h1
h1.stack(0)
data = pd.read_csv("conversion_rates.csv")
data.head()
data.pivot(columns = 'group', values='converted').head()
data.pivot_table(index = 'group', columns = 'converted', aggfunc= len)
import seaborn as sns
sns.set()
sns.distplot(sales['Gross profit'].dropna(), kde = False)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(42)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
ax.xaxis.set_major_locator(MultipleLocator(1.000))
ax.xaxis.set_minor_locator(AutoMinorLocator(4))
ax.yaxis.set_major_locator(MultipleLocator(1.000))
ax.yaxis.set_minor_locator(AutoMinorLocator(4))
ax.xaxis.set_minor_formatter(FuncFormatter(minor_tick))
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.tick_params(which='major', width=1.0)
ax.tick_params(which='major', length=10)
ax.tick_params(which='minor', width=1.0, labelsize=10)
ax.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
ax.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
ax.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
ax.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
ax.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
ax.set_title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
ax.set_xlabel("X axis label")
ax.set_ylabel("Y axis label")
ax.legend()
def circle(x, y, radius=0.15):
from matplotlib.patches import Circle
from matplotlib.patheffects import withStroke
circle = Circle((x, y), radius, clip_on=False, zorder=10, linewidth=1,
edgecolor='black', facecolor=(0, 0, 0, .0125),
path_effects=[withStroke(linewidth=5, foreground='w')])
ax.add_artist(circle)
def text(x, y, text):
ax.text(x, y, text, backgroundcolor="white",
ha='center', va='top', weight='bold', color='blue')
# Minor tick
circle(0.50, -0.10)
text(0.50, -0.32, "Minor tick label")
# Major tick
circle(-0.03, 4.00)
text(0.03, 3.80, "Major tick")
# Minor tick
circle(0.00, 3.50)
text(0.00, 3.30, "Minor tick")
# Major tick label
circle(-0.15, 3.00)
text(-0.15, 2.80, "Major tick label")
# X Label
circle(1.80, -0.27)
text(1.80, -0.45, "X axis label")
# Y Label
circle(-0.27, 1.80)
text(-0.27, 1.6, "Y axis label")
# Title
circle(1.60, 4.13)
text(1.60, 3.93, "Title")
# Blue plot
circle(1.75, 2.80)
text(1.75, 2.60, "Line\n(line plot)")
# Red plot
circle(1.20, 0.60)
text(1.20, 0.40, "Line\n(line plot)")
# Scatter plot
circle(3.20, 1.75)
text(3.20, 1.55, "Markers\n(scatter plot)")
# Grid
circle(3.00, 3.00)
text(3.00, 2.80, "Grid")
# Legend
circle(3.70, 3.80)
text(3.70, 3.60, "Legend")
# Axes
circle(0.5, 0.5)
text(0.5, 0.3, "Axes")
# Figure
circle(-0.3, 0.65)
text(-0.3, 0.45, "Figure")
color = 'blue'
ax.annotate('Spines', xy=(4.0, 0.35), xycoords='data',
xytext=(3.3, 0.5), textcoords='data',
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.annotate('', xy=(3.15, 0.0), xycoords='data',
xytext=(3.45, 0.45), textcoords='data',
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(42)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
plt.figure(figsize=(8, 8))
plt.subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
plt.axes().xaxis.set_major_locator(MultipleLocator(1.000))
plt.axes().xaxis.set_minor_locator(AutoMinorLocator(4))
plt.axes().yaxis.set_major_locator(MultipleLocator(1.000))
plt.axes().yaxis.set_minor_locator(AutoMinorLocator(4))
plt.axes().xaxis.set_minor_formatter(FuncFormatter(minor_tick))
plt.xticks([1.000, 2.000,3.000,4.000])
plt.yticks([1.000, 2.000,3.000,4.000])
plt.xlim(0, 4)
plt.ylim(0, 4)
plt.tick_params(which='major', width=1.0)
plt.tick_params(which='major', length=10)
plt.tick_params(which='minor', width=1.0, labelsize=10)
plt.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
plt.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
plt.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
plt.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
plt.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
plt.title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
plt.xlabel("X axis label")
plt.ylabel("Y axis label")
plt.legend()
plt.show()
```
|
github_jupyter
|
import pandas as pd
import numpy as np
df = pd.DataFrame({
'sales': [100, 50, 14, 94, 20, 45, 56, 18, 125],
'CTA Variant': ['A', 'B', 'C', 'A', 'C', 'B', 'B', 'C', 'A']
}, index = pd.date_range("12:30", "21:00", freq="60min")
)
df.head()
sales = pd.read_csv("sales.csv")
sales.head()
sales.loc[sales['Retailer country']=='United States', ['Revenue', 'Quantity', 'Gross profit']].head()
sales.rename({'Revenue':'Earnings'}, axis = 'columns').head()
sales['Unit cost'].quantile([0.0, 0.25,0.5,0.75,1])
def cat_gen(x):
if pd.isnull(x):
return np.nan
elif x<=2.76:
return "cheap"
elif 2.76<x<=9.0:
return "medium"
elif 9.0<x<=34.97:
return "moderate"
else:
return "expensive"
sales['Cost category'] = sales['Unit cost'].map(cat_gen)
sales['Cost category'].value_counts(dropna = True)
sales['Unit cost'] = sales['Unit cost'].astype('category')
sales.dtypes
cta = pd.read_csv('CTA_comparison.csv')
cta
cta.set_index('CTA Variant')
cta.set_index(['CTA Variant', 'views'])
cta_views = cta.groupby(['CTA Variant', 'views']).count()
cta_views
h1 = cta_views.unstack(level = 'CTA Variant')
h1
h1.stack(0)
data = pd.read_csv("conversion_rates.csv")
data.head()
data.pivot(columns = 'group', values='converted').head()
data.pivot_table(index = 'group', columns = 'converted', aggfunc= len)
import seaborn as sns
sns.set()
sns.distplot(sales['Gross profit'].dropna(), kde = False)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(42)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
ax.xaxis.set_major_locator(MultipleLocator(1.000))
ax.xaxis.set_minor_locator(AutoMinorLocator(4))
ax.yaxis.set_major_locator(MultipleLocator(1.000))
ax.yaxis.set_minor_locator(AutoMinorLocator(4))
ax.xaxis.set_minor_formatter(FuncFormatter(minor_tick))
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.tick_params(which='major', width=1.0)
ax.tick_params(which='major', length=10)
ax.tick_params(which='minor', width=1.0, labelsize=10)
ax.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
ax.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
ax.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
ax.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
ax.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
ax.set_title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
ax.set_xlabel("X axis label")
ax.set_ylabel("Y axis label")
ax.legend()
def circle(x, y, radius=0.15):
from matplotlib.patches import Circle
from matplotlib.patheffects import withStroke
circle = Circle((x, y), radius, clip_on=False, zorder=10, linewidth=1,
edgecolor='black', facecolor=(0, 0, 0, .0125),
path_effects=[withStroke(linewidth=5, foreground='w')])
ax.add_artist(circle)
def text(x, y, text):
ax.text(x, y, text, backgroundcolor="white",
ha='center', va='top', weight='bold', color='blue')
# Minor tick
circle(0.50, -0.10)
text(0.50, -0.32, "Minor tick label")
# Major tick
circle(-0.03, 4.00)
text(0.03, 3.80, "Major tick")
# Minor tick
circle(0.00, 3.50)
text(0.00, 3.30, "Minor tick")
# Major tick label
circle(-0.15, 3.00)
text(-0.15, 2.80, "Major tick label")
# X Label
circle(1.80, -0.27)
text(1.80, -0.45, "X axis label")
# Y Label
circle(-0.27, 1.80)
text(-0.27, 1.6, "Y axis label")
# Title
circle(1.60, 4.13)
text(1.60, 3.93, "Title")
# Blue plot
circle(1.75, 2.80)
text(1.75, 2.60, "Line\n(line plot)")
# Red plot
circle(1.20, 0.60)
text(1.20, 0.40, "Line\n(line plot)")
# Scatter plot
circle(3.20, 1.75)
text(3.20, 1.55, "Markers\n(scatter plot)")
# Grid
circle(3.00, 3.00)
text(3.00, 2.80, "Grid")
# Legend
circle(3.70, 3.80)
text(3.70, 3.60, "Legend")
# Axes
circle(0.5, 0.5)
text(0.5, 0.3, "Axes")
# Figure
circle(-0.3, 0.65)
text(-0.3, 0.45, "Figure")
color = 'blue'
ax.annotate('Spines', xy=(4.0, 0.35), xycoords='data',
xytext=(3.3, 0.5), textcoords='data',
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.annotate('', xy=(3.15, 0.0), xycoords='data',
xytext=(3.45, 0.45), textcoords='data',
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(42)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
plt.figure(figsize=(8, 8))
plt.subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
plt.axes().xaxis.set_major_locator(MultipleLocator(1.000))
plt.axes().xaxis.set_minor_locator(AutoMinorLocator(4))
plt.axes().yaxis.set_major_locator(MultipleLocator(1.000))
plt.axes().yaxis.set_minor_locator(AutoMinorLocator(4))
plt.axes().xaxis.set_minor_formatter(FuncFormatter(minor_tick))
plt.xticks([1.000, 2.000,3.000,4.000])
plt.yticks([1.000, 2.000,3.000,4.000])
plt.xlim(0, 4)
plt.ylim(0, 4)
plt.tick_params(which='major', width=1.0)
plt.tick_params(which='major', length=10)
plt.tick_params(which='minor', width=1.0, labelsize=10)
plt.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
plt.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
plt.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
plt.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
plt.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
plt.title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
plt.xlabel("X axis label")
plt.ylabel("Y axis label")
plt.legend()
plt.show()
| 0.485112 | 0.397938 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.