text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Text classification with TensorFlow Lite Model Maker
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/lite/tutorials/model_maker_text_classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/tutorials/model_maker_text_classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/tutorials/model_maker_text_classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/tensorflow/tensorflow/lite/g3doc/tutorials/model_maker_text_classification.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
The TensorFlow Lite Model Maker library simplifies the process of adapting and converting a TensorFlow model to particular input data when deploying this model for on-device ML applications.
This notebook shows an end-to-end example that utilizes the Model Maker library to illustrate the adaptation and conversion of a commonly-used text classification model to classify movie reviews on a mobile device. The text classification model classifies text into predefined categories.The inputs should be preprocessed text and the outputs are the probabilities of the categories. The dataset used in this tutorial are positive and negative movie reviews.
## Prerequisites
### Install the required packages
To run this example, install the required packages, including the Model Maker package from the [GitHub repo](https://github.com/tensorflow/examples/tree/master/tensorflow_examples/lite/model_maker).
**If you run this notebook on Colab, you may see an error message about `tensorflowjs` and `tensorflow-hub` version imcompatibility. It is safe to ignore this error as we do not use `tensorflowjs` in this workflow.**
```
!pip install -q tflite-model-maker
```
Import the required packages.
```
import numpy as np
import os
from tflite_model_maker import configs
from tflite_model_maker import ExportFormat
from tflite_model_maker import model_spec
from tflite_model_maker import text_classifier
from tflite_model_maker import TextClassifierDataLoader
import tensorflow as tf
assert tf.__version__.startswith('2')
tf.get_logger().setLevel('ERROR')
```
### Download the sample training data.
In this tutorial, we will use the [SST-2](https://nlp.stanford.edu/sentiment/index.html) (Stanford Sentiment Treebank) which is one of the tasks in the [GLUE](https://gluebenchmark.com/) benchmark. It contains 67,349 movie reviews for training and 872 movie reviews for testing. The dataset has two classes: positive and negative movie reviews.
```
data_dir = tf.keras.utils.get_file(
fname='SST-2.zip',
origin='https://dl.fbaipublicfiles.com/glue/data/SST-2.zip',
extract=True)
data_dir = os.path.join(os.path.dirname(data_dir), 'SST-2')
```
The SST-2 dataset is stored in TSV format. The only difference between TSV and CSV is that TSV uses a tab `\t` character as its delimiter instead of a comma `,` in the CSV format.
Here are the first 5 lines of the training dataset. label=0 means negative, label=1 means positive.
| sentence | label | | | |
|-------------------------------------------------------------------------------------------|-------|---|---|---|
| hide new secretions from the parental units | 0 | | | |
| contains no wit , only labored gags | 0 | | | |
| that loves its characters and communicates something rather beautiful about human nature | 1 | | | |
| remains utterly satisfied to remain the same throughout | 0 | | | |
| on the worst revenge-of-the-nerds clichés the filmmakers could dredge up | 0 | | | |
Next, we will load the dataset into a Pandas dataframe and change the current label names (`0` and `1`) to a more human-readable ones (`negative` and `positive`) and use them for model training.
```
import pandas as pd
def replace_label(original_file, new_file):
# Load the original file to pandas. We need to specify the separator as
# '\t' as the training data is stored in TSV format
df = pd.read_csv(original_file, sep='\t')
# Define how we want to change the label name
label_map = {0: 'negative', 1: 'positive'}
# Excute the label change
df.replace({'label': label_map}, inplace=True)
# Write the updated dataset to a new file
df.to_csv(new_file)
# Replace the label name for both the training and test dataset. Then write the
# updated CSV dataset to the current folder.
replace_label(os.path.join(os.path.join(data_dir, 'train.tsv')), 'train.csv')
replace_label(os.path.join(os.path.join(data_dir, 'dev.tsv')), 'dev.csv')
```
## Quickstart
There are five steps to train a text classification model:
**Step 1. Choose a text classification model archiecture.**
Here we use the average word embedding model architecture, which will produce a small and fast model with decent accuracy.
```
spec = model_spec.get('average_word_vec')
```
Model Maker also supports other model architectures such as [BERT](https://arxiv.org/abs/1810.04805). If you are interested to learn about other architecture, see the [Choose a model architecture for Text Classifier](#scrollTo=kJ_B8fMDOhMR) section below.
**Step 2. Load the training and test data, then preprocess them according to a specific `model_spec`.**
Model Maker can take input data in the CSV format. We will load the training and test dataset with the human-readable label name that were created earlier.
Each model architecture requires input data to be processed in a particular way. `TextClassifierDataLoader` reads the requirement from `model_spec` and automatically execute the necessary preprocessing.
```
train_data = TextClassifierDataLoader.from_csv(
filename='train.csv',
text_column='sentence',
label_column='label',
model_spec=spec,
is_training=True)
test_data = TextClassifierDataLoader.from_csv(
filename='dev.csv',
text_column='sentence',
label_column='label',
model_spec=spec,
is_training=False)
```
**Step 3. Train the TensorFlow model with the training data.**
The average word embedding model use `batch_size = 32` by default. Therefore you will see that it takes 2104 steps to go through the 67,349 sentences in the training dataset. We will train the model for 10 epochs, which means going through the training dataset 10 times.
```
model = text_classifier.create(train_data, model_spec=spec, epochs=10)
```
**Step 4. Evaluate the model with the test data.**
After training the text classification model using the sentences in the training dataset, we will use the remaining 872 sentences in the test dataset to evaluate how the model perform against new data it has never seen before.
As the default batch size is 32, it will take 28 steps to go through the 872 sentences in the test dataset.
```
loss, acc = model.evaluate(test_data)
```
**Step 5. Export as a TensorFlow Lite model.**
Let's export the text classification that we have trained in the TensorFlow Lite format. We will specify which folder to export the model.
You may see an warning about `vocab.txt` file does not exist in the metadata but they can be safely ignore.
```
model.export(export_dir='average_word_vec')
```
You can download the TensorFlow Lite model file using the left sidebar of Colab. Go into the `average_word_vec` folder as we specified in `export_dir` parameter above, right-click on the `model.tflite` file and choose `Download` to download it to your local computer.
This model can be integrated into an Android or an iOS app using the [NLClassifier API](https://www.tensorflow.org/lite/inference_with_metadata/task_library/nl_classifier) of the [TensorFlow Lite Task Library](https://www.tensorflow.org/lite/inference_with_metadata/task_library/overview).
See the [TFLite Text Classification sample app](https://github.com/tensorflow/examples/blob/master/lite/examples/text_classification/android/lib_task_api/src/main/java/org/tensorflow/lite/examples/textclassification/client/TextClassificationClient.java#L54) for more details on how the model is used in an working app.
*Note 1: Android Studio Model Binding does not support text classification yet so please use the TensorFlow Lite Task Library.*
*Note 2: There is a `model.json` file in the same folder with the TFLite model. It contains the JSON representation of the [metadata](https://www.tensorflow.org/lite/convert/metadata) bundled inside the TensorFlow Lite model. Model metadata helps the TFLite Task Library know what the model does and how to pre-process/post-process data for the model. You don't need to download the `model.json` file as it is only for informational purpose and its content is already inside the TFLite file.*
*Note 3: If you train a text classification model using MobileBERT or BERT-Base architecture, you will need to use [BertNLClassifier API](https://www.tensorflow.org/lite/inference_with_metadata/task_library/bert_nl_classifier) instead to integrate the trained model into a mobile app.*
The following sections walk through the example step by step to show more details.
## Choose a model architecture for Text Classifier
Each `model_spec` object represents a specific model for the text classifier. TensorFlow Lite Model Maker currently supports [MobileBERT](https://arxiv.org/pdf/2004.02984.pdf), averaging word embeddings and [BERT-Base](https://arxiv.org/pdf/1810.04805.pdf) models.
| Supported Model | Name of model_spec | Model Description | Model size |
|--------------------------|-------------------------|-----------------------------------------------------------------------------------------------------------------------|---------------------------------------------|
| Averaging Word Embedding | 'average_word_vec' | Averaging text word embeddings with RELU activation. | <1MB |
| MobileBERT | 'mobilebert_classifier' | 4.3x smaller and 5.5x faster than BERT-Base while achieving competitive results, suitable for on-device applications. | 25MB w/ quantization <br/> 100MB w/o quantization |
| BERT-Base | 'bert_classifier' | Standard BERT model that is widely used in NLP tasks. | 300MB |
In the quick start, we have used the average word embedding model. Let's switch to [MobileBERT](https://arxiv.org/pdf/2004.02984.pdf) to train a model with higher accuracy.
```
mb_spec = model_spec.get('mobilebert_classifier')
```
## Load training data
You can upload your own dataset to work through this tutorial. Upload your dataset by using the left sidebar in Colab.
<img src="https://storage.googleapis.com/download.tensorflow.org/models/tflite/screenshots/model_maker_text_classification.png" alt="Upload File" width="800" hspace="100">
If you prefer not to upload your dataset to the cloud, you can also locally run the library by following the [guide](https://github.com/tensorflow/examples/tree/master/tensorflow_examples/lite/model_maker).
To keep it simple, we will reuse the SST-2 dataset downloaded earlier. Let's use the `TestClassifierDataLoader.from_csv` method to load the data.
Please be noted that as we have changed the model architecture, we will need to reload the training and test dataset to apply the new preprocessing logic.
```
train_data = TextClassifierDataLoader.from_csv(
filename='train.csv',
text_column='sentence',
label_column='label',
model_spec=mb_spec,
is_training=True)
test_data = TextClassifierDataLoader.from_csv(
filename='dev.csv',
text_column='sentence',
label_column='label',
model_spec=mb_spec,
is_training=False)
```
The Model Maker library also supports the `from_folder()` method to load data. It assumes that the text data of the same class are in the same subdirectory and that the subfolder name is the class name. Each text file contains one movie review sample. The `class_labels` parameter is used to specify which the subfolders.
## Train a TensorFlow Model
Train a text classification model using the training data.
*Note: As MobileBERT is a complex model, each training epoch will takes about 10 minutes on a Colab GPU. Please make sure that you are using a GPU runtime.*
```
model = text_classifier.create(train_data, model_spec=mb_spec, epochs=3)
```
Examine the detailed model structure.
```
model.summary()
```
## Evaluate the model
Evaluate the model that we have just trained using the test data and measure the loss and accuracy value.
```
loss, acc = model.evaluate(test_data)
```
## Quantize the model
In many on-device ML application, the model size is an important factor. Therefore, it is recommended that you apply quantize the model to make it smaller and potentially run faster. Model Maker automatically applies the recommended quantization scheme for each model architecture but you can customize the quantization config as below.
```
config = configs.QuantizationConfig.create_dynamic_range_quantization(optimizations=[tf.lite.Optimize.OPTIMIZE_FOR_LATENCY])
config.experimental_new_quantizer = True
```
## Export as a TensorFlow Lite model
Convert the trained model to TensorFlow Lite model format with [metadata](https://www.tensorflow.org/lite/convert/metadata) so that you can later use in an on-device ML application. The label file and the vocab file are embedded in metadata. The default TFLite filename is `model.tflite`.
```
model.export(export_dir='mobilebert/', quantization_config=config)
```
The TensorFlow Lite model file can be integrated in a mobile app using the [BertNLClassifier API](https://www.tensorflow.org/lite/inference_with_metadata/task_library/bert_nl_classifier) in [TensorFlow Lite Task Library](https://www.tensorflow.org/lite/inference_with_metadata/task_library/overview). Please note that this is **different** from the `NLClassifier` API used to integrate the text classification trained with the average word vector model architecture.
The export formats can be one or a list of the following:
* `ExportFormat.TFLITE`
* `ExportFormat.LABEL`
* `ExportFormat.VOCAB`
* `ExportFormat.SAVED_MODEL`
By default, it exports only the TensorFlow Lite model file containing the model metadata. You can also choose to export other files related to the model for better examination. For instance, exporting only the label file and vocab file as follows:
```
model.export(export_dir='mobilebert/', export_format=[ExportFormat.LABEL, ExportFormat.VOCAB])
```
You can evaluate the TFLite model with `evaluate_tflite` method to measure its accuracy. Converting the trained TensorFlow model to TFLite format and apply quantization can affect its accuracy so it is recommended to evaluate the TFLite model accuracy before deployment.
```
accuracy = model.evaluate_tflite('mobilebert/model.tflite', test_data)
print('TFLite model accuracy: ', accuracy)
```
## Advanced Usage
The `create` function is the driver function that the Model Maker library uses to create models. The `model_spec` parameter defines the model specification. The `AverageWordVecModelSpec` and `BertClassifierModelSpec` classes are currently supported. The `create` function comprises of the following steps:
1. Creates the model for the text classifier according to `model_spec`.
2. Trains the classifier model. The default epochs and the default batch size are set by the `default_training_epochs` and `default_batch_size` variables in the `model_spec` object.
This section covers advanced usage topics like adjusting the model and the training hyperparameters.
### Customize the MobileBERT model hyperparameters
The model parameters you can adjust are:
* `seq_len`: Length of the sequence to feed into the model.
* `initializer_range`: The standard deviation of the `truncated_normal_initializer` for initializing all weight matrices.
* `trainable`: Boolean that specifies whether the pre-trained layer is trainable.
The training pipeline parameters you can adjust are:
* `model_dir`: The location of the model checkpoint files. If not set, a temporary directory will be used.
* `dropout_rate`: The dropout rate.
* `learning_rate`: The initial learning rate for the Adam optimizer.
* `tpu`: TPU address to connect to.
For instance, you can set the `seq_len=256` (default is 128). This allows the model to classify longer text.
```
new_model_spec = model_spec.get('mobilebert_classifier')
new_model_spec.seq_len = 256
```
### Customize the average word embedding model hyperparameters
You can adjust the model infrastructure like the `wordvec_dim` and the `seq_len` variables in the `AverageWordVecModelSpec` class.
For example, you can train the model with a larger value of `wordvec_dim`. Note that you must construct a new `model_spec` if you modify the model.
```
new_model_spec = model_spec.AverageWordVecModelSpec(wordvec_dim=32)
```
Get the preprocessed data.
```
new_train_data = TextClassifierDataLoader.from_csv(
filename='train.csv',
text_column='sentence',
label_column='label',
model_spec=new_model_spec,
is_training=True)
```
Train the new model.
```
model = text_classifier.create(new_train_data, model_spec=new_model_spec)
```
### Tune the training hyperparameters
You can also tune the training hyperparameters like `epochs` and `batch_size` that affect the model accuracy. For instance,
* `epochs`: more epochs could achieve better accuracy, but may lead to overfitting.
* `batch_size`: the number of samples to use in one training step.
For example, you can train with more epochs.
```
model = text_classifier.create(new_train_data, model_spec=new_model_spec, epochs=20)
```
Evaluate the newly retrained model with 20 training epochs.
```
new_test_data = TextClassifierDataLoader.from_csv(
filename='dev.csv',
text_column='sentence',
label_column='label',
model_spec=new_model_spec,
is_training=False)
loss, accuracy = model.evaluate(new_test_data)
```
### Change the Model Architecture
You can change the model by changing the `model_spec`. The following shows how to change to BERT-Base model.
Change the `model_spec` to BERT-Base model for the text classifier.
```
spec = model_spec.get('bert_classifier')
```
The remaining steps are the same.
|
github_jupyter
|
```
# Import libraries
import sklearn
from sklearn import model_selection
import numpy as np
np.random.seed(42)
import os
import pandas as pd
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# To plot figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "assets")
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Load the data
script_directory = os.getcwd() # Script directory
full_data_path = os.path.join(script_directory, 'data/')
DATA_PATH = full_data_path
def load_data(data_path=DATA_PATH):
csv_path = os.path.join(data_path, "train.csv")
return pd.read_csv(csv_path)
data = load_data()
```
# A brief look at the data
```
data.shape
data.head()
data["Embarked"].value_counts()
data["Sex"].value_counts()
data["Ticket"].value_counts()
data.describe()
data.describe(include=['O'])
data.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()
```
# Split the data into train and validation sets
```
# Split the data into train and validation sets before diving into analysis
train_data, validation_data = model_selection.train_test_split(data, test_size=0.2, random_state=42)
print("Train data shape:")
print(train_data.shape)
print("Train data columns:")
print(train_data.columns)
# Save the data sets
train_data.to_csv("data/train_data.csv", index=False)
validation_data.to_csv("data/validation_data.csv", index=False)
```
# Reshaping data
```
correlation_matrix = train_data.corr()
correlation_matrix["Survived"].sort_values(ascending=False)
train_set = [train_data]
#train_set.type()
for dataset in train_set:
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
pd.crosstab(train_data['Title'], train_data['Sex'])
for dataset in train_set:
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
train_data[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
for dataset in train_set:
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
train_data.head()
from sklearn.base import BaseEstimator, TransformerMixin
class TitleAdder(BaseEstimator, TransformerMixin):
def fit(self, X, y=None):
return self
def transform(self, X):
X_list = [X]
for row in X_list:
row['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
row['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
row['Title'] = dataset['Title'].replace('Mlle', 'Miss')
row['Title'] = dataset['Title'].replace('Ms', 'Miss')
row['Title'] = dataset['Title'].replace('Mme', 'Mrs')
row['Title'] = dataset['Title'].fillna(0)
X = X.drop(["Name"], axis=1)
return X
import seaborn as sns
g = sns.FacetGrid(train_data, col='Survived')
g.map(plt.hist, 'Age', bins=20)
train_data['AgeBand'] = pd.cut(train_data['Age'], bins=[0, 5, 18, 30, 38, 50, 65, 74.3, 90])
train_data[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False).mean().sort_values(by='AgeBand', ascending=True)
train_data.head(3)
train_data["AgeBucket"] = train_data["Age"] // 15 * 15
train_data[["AgeBucket", "Survived"]].groupby(['AgeBucket']).mean()
train_data['IsAlone'] = train_data['SibSp'] + train_data['Parch'] > 0
train_data[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean()
train_data[['SibSp', 'Survived']].groupby(['SibSp'], as_index=False).mean()
#train_data[['Parch', 'Survived']].groupby(['Parch'], as_index=False).mean()
import seaborn as sns
g = sns.FacetGrid(train_data, col='Survived')
g.map(plt.hist, 'Fare', bins=20)
train_data['FareBand'] = pd.qcut(train_data['Fare'], 4)
train_data[['FareBand', 'Survived']].groupby(['FareBand'], as_index=False).mean().sort_values(by='FareBand', ascending=True)
y_train = train_data["Survived"]
y_train
```
|
github_jupyter
|
```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns; sns.set()
trips = pd.read_csv('2015_trip_data.csv',
parse_dates=['starttime', 'stoptime'],
infer_datetime_format=True)
ind = pd.DatetimeIndex(trips.starttime)
trips['date'] = ind.date.astype('datetime64')
trips['hour'] = ind.hour
hourly = trips.pivot_table('trip_id', aggfunc='count',
index=['usertype', 'date'], columns='hour').fillna(0)
hourly.head()
```
## Principal Component Analysis
```
from sklearn.decomposition import PCA
data = hourly[np.arange(24)].values
data_pca = PCA(2).fit_transform(data)
hourly['projection1'], hourly['projection2'] = data_pca.T
hourly['total rides'] = hourly.sum(axis=1)
hourly.plot('projection1', 'projection2', kind='scatter', c='total rides', cmap='Blues_r');
plt.savefig('figs/pca_raw.png', bbox_inches='tight')
```
## Automated Clustering
```
from sklearn.mixture import GMM
gmm = GMM(3, covariance_type='full', random_state=2)
data = hourly[['projection1', 'projection2']]
gmm.fit(data)
# require high-probability cluster membership
hourly['cluster'] = (gmm.predict_proba(data)[:, 0] > 0.6).astype(int)
from datetime import time
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(wspace=0.1)
times = pd.date_range('0:00', '23:59', freq='H').time
times = np.hstack([times, time(23, 59, 59)])
hourly.plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='rainbow', colorbar=False, ax=ax[0]);
for i in range(2):
vals = hourly.query("cluster == " + str(i))[np.arange(24)]
vals[24] = vals[0]
ax[1].plot(times, vals.T, color=plt.cm.rainbow(255 * i), alpha=0.05, lw=0.5)
ax[1].plot(times, vals.mean(0), color=plt.cm.rainbow(255 * i), lw=3)
ax[1].set_xticks(4 * 60 * 60 * np.arange(6))
ax[1].set_ylim(0, 60);
ax[1].set_ylabel('Rides per hour');
fig.savefig('figs/pca_clustering.png', bbox_inches='tight')
fig, ax = plt.subplots(1, 2, figsize=(16, 6), sharex=True, sharey=True)
fig.subplots_adjust(wspace=0.05)
for i, col in enumerate(['Annual Member', 'Short-Term Pass Holder']):
hourly.loc[col].plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='rainbow', colorbar=False, ax=ax[i]);
ax[i].set_title(col + 's')
fig.savefig('figs/pca_annual_vs_shortterm.png', bbox_inches='tight')
usertype = hourly.index.get_level_values('usertype')
weekday = hourly.index.get_level_values('date').dayofweek < 5
hourly['commute'] = (weekday & (usertype == "Annual Member"))
fig, ax = plt.subplots()
hourly.plot('projection1', 'projection2', c='commute', kind='scatter',
cmap='binary', colorbar=False, ax=ax);
ax.set_title("Annual Member Weekdays vs Other")
fig.savefig('figs/pca_true_weekends.png', bbox_inches='tight')
```
## Identifying Mismatches
```
mismatch = hourly.query('cluster == 0 & commute')
mismatch = mismatch.reset_index('usertype')[['usertype', 'projection1', 'projection2']]
mismatch
from pandas.tseries.holiday import USFederalHolidayCalendar
cal = USFederalHolidayCalendar()
holidays = cal.holidays('2014-08', '2015-10', return_name=True)
holidays_all = pd.concat([holidays,
"2 Days Before " + holidays.shift(-2, 'D'),
"Day Before " + holidays.shift(-1, 'D'),
"Day After " + holidays.shift(1, 'D')])
holidays_all = holidays_all.sort_index()
holidays_all.head()
holidays_all.name = 'holiday name' # required for join
joined = mismatch.join(holidays_all)
joined['holiday name']
set(holidays) - set(joined['holiday name'])
fig, ax = plt.subplots()
hourly.plot('projection1', 'projection2', c='cluster', kind='scatter',
cmap='binary', colorbar=False, ax=ax);
ax.set_title("Holidays in Projected Results")
for i, ind in enumerate(joined.sort_values('projection1').index):
x, y = hourly.loc['Annual Member', ind][['projection1', 'projection2']]
if i % 2:
ytext = 20 + 3 * i
else:
ytext = -8 - 4 * i
ax.annotate(joined.loc[ind, 'holiday name'], [x, y], [x , ytext], color='black',
ha='center', arrowprops=dict(arrowstyle='-', color='black'))
ax.scatter([x], [y], c='red')
for holiday in (set(holidays) - set(joined['holiday name'])):
ind = holidays[holidays == holiday].index[0]
#ind = ind.strftime('%Y-%m-%d')
x, y = hourly.loc['Annual Member', ind][['projection1', 'projection2']]
ax.annotate(holidays.loc[ind], [x, y], [x + 20, y + 30], color='black',
ha='center', arrowprops=dict(arrowstyle='-', color='black'))
ax.scatter([x], [y], c='#00FF00')
ax.set_xlim([-60, 60])
ax.set_ylim([-60, 60])
fig.savefig('figs/pca_holiday_labels.png', bbox_inches='tight')
```
|
github_jupyter
|
# T81-558: Applications of Deep Neural Networks
**Module 13: Advanced/Other Topics**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 13 Video Material
* Part 13.1: Flask and Deep Learning Web Services [[Video]](https://www.youtube.com/watch?v=H73m9XvKHug&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_01_flask.ipynb)
* Part 13.2: Deploying a Model to AWS [[Video]](https://www.youtube.com/watch?v=8ygCyvRZ074&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_02_cloud.ipynb)
* **Part 13.3: Using a Keras Deep Neural Network with a Web Application** [[Video]](https://www.youtube.com/watch?v=OBbw0e-UroI&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_03_web.ipynb)
* Part 13.4: When to Retrain Your Neural Network [[Video]](https://www.youtube.com/watch?v=K2Tjdx_1v9g&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_13_04_retrain.ipynb)
* Part 13.5: AI at the Edge: Using Keras on a Mobile Device [[Video]]() [[Notebook]](t81_558_class_13_05_edge.ipynb)
# Part 13.3: Using a Keras Deep Neural Network with a Web Application
In this module we will extend the image API developed in Part 13.1 to work with a web application. This allows you to use a simple website to upload/predict images, such as Figure 13.WEB.
**Figure 13.WEB: AI Web Application**

To do this, we will use the same API developed in Module 13.1. However, we will now add a [ReactJS](https://reactjs.org/) website around it. This is a single page web application that allows you to upload images for classification by the neural network. If you would like to read more about ReactJS and image uploading, you can refer to the [blog post](http://www.hartzis.me/react-image-upload/) that I borrowed some of the code from. I added neural network functionality to a simple ReactJS image upload and preview example.
This example is built from the following components:
* [GitHub Location for Web App](./py/)
* [image_web_server_1.py](./py/image_web_server_1.py) - The code both to start Flask, as well as serve the HTML/JavaScript/CSS needed to provide the web interface.
* Directory WWW - Contains web assets.
* [index.html](./py/www/index.html) - The main page for the web application.
* [style.css](./py/www/style.css) - The stylesheet for the web application.
* [script.js](./py/www/script.js) - The JavaScript code for the web application.
|
github_jupyter
|
```
%%html
<style>
body {
font-family: "Cambria", cursive, sans-serif;
}
</style>
import random, time
import numpy as np
from collections import defaultdict
import operator
import matplotlib.pyplot as plt
```
## Misc functions and utilities
```
orientations = EAST, NORTH, WEST, SOUTH = [(1, 0), (0, 1), (-1, 0), (0, -1)]
turns = LEFT, RIGHT = (+1, -1)
def vector_add(a, b):
"""Component-wise addition of two vectors."""
return tuple(map(operator.add, a, b))
def turn_heading(heading, inc, headings=orientations):
return headings[(headings.index(heading) + inc) % len(headings)]
def turn_right(heading):
return turn_heading(heading, RIGHT)
def turn_left(heading):
return turn_heading(heading, LEFT)
def distance(a, b):
"""The distance between two (x, y) points."""
xA, yA = a
xB, yB = b
return math.hypot((xA - xB), (yA - yB))
def isnumber(x):
"""Is x a number?"""
return hasattr(x, '__int__')
```
## Class definitions
### Base `MDP` class
```
class MDP:
"""A Markov Decision Process, defined by an initial state, transition model,
and reward function. We also keep track of a gamma value, for use by
algorithms. The transition model is represented somewhat differently from
the text. Instead of P(s' | s, a) being a probability number for each
state/state/action triplet, we instead have T(s, a) return a
list of (p, s') pairs. We also keep track of the possible states,
terminal states, and actions for each state."""
def __init__(self, init, actlist, terminals, transitions = {}, reward = None, states=None, gamma=.9):
if not (0 < gamma <= 1):
raise ValueError("An MDP must have 0 < gamma <= 1")
if states:
self.states = states
else:
## collect states from transitions table
self.states = self.get_states_from_transitions(transitions)
self.init = init
if isinstance(actlist, list):
## if actlist is a list, all states have the same actions
self.actlist = actlist
elif isinstance(actlist, dict):
## if actlist is a dict, different actions for each state
self.actlist = actlist
self.terminals = terminals
self.transitions = transitions
#if self.transitions == {}:
#print("Warning: Transition table is empty.")
self.gamma = gamma
if reward:
self.reward = reward
else:
self.reward = {s : 0 for s in self.states}
#self.check_consistency()
def R(self, state):
"""Return a numeric reward for this state."""
return self.reward[state]
def T(self, state, action):
"""Transition model. From a state and an action, return a list
of (probability, result-state) pairs."""
if(self.transitions == {}):
raise ValueError("Transition model is missing")
else:
return self.transitions[state][action]
def actions(self, state):
"""Set of actions that can be performed in this state. By default, a
fixed list of actions, except for terminal states. Override this
method if you need to specialize by state."""
if state in self.terminals:
return [None]
else:
return self.actlist
def get_states_from_transitions(self, transitions):
if isinstance(transitions, dict):
s1 = set(transitions.keys())
s2 = set([tr[1] for actions in transitions.values()
for effects in actions.values() for tr in effects])
return s1.union(s2)
else:
print('Could not retrieve states from transitions')
return None
def check_consistency(self):
# check that all states in transitions are valid
assert set(self.states) == self.get_states_from_transitions(self.transitions)
# check that init is a valid state
assert self.init in self.states
# check reward for each state
#assert set(self.reward.keys()) == set(self.states)
assert set(self.reward.keys()) == set(self.states)
# check that all terminals are valid states
assert all([t in self.states for t in self.terminals])
# check that probability distributions for all actions sum to 1
for s1, actions in self.transitions.items():
for a in actions.keys():
s = 0
for o in actions[a]:
s += o[0]
assert abs(s - 1) < 0.001
```
### A custom MDP class to extend functionality
We will write a CustomMDP class to extend the MDP class for the problem at hand. <br>This class will implement the `T` method to implement the transition model.
```
class CustomMDP(MDP):
def __init__(self, transition_matrix, rewards, terminals, init, gamma=.9):
# All possible actions.
actlist = []
for state in transition_matrix.keys():
actlist.extend(transition_matrix[state])
actlist = list(set(actlist))
#print(actlist)
MDP.__init__(self, init, actlist, terminals=terminals, gamma=gamma)
self.t = transition_matrix
self.reward = rewards
for state in self.t:
self.states.add(state)
def T(self, state, action):
if action is None:
return [(0.0, state)]
else:
return [(prob, new_state) for new_state, prob in self.t[state][action].items()]
```
## Problem 1: Simple MDP
---
### State dependent reward function
Markov Decision Processes are formally described as processes that follow the Markov property which states that "The future is independent of the past given the present". MDPs formally describe environments for reinforcement learning and we assume that the environment is fully observable.
Let us take a toy example MDP and solve it using value iteration and policy iteration. This is a simple example adapted from a similar problem by Dr. David Silver, tweaked to fit the limitations of the current functions.
Let's say you're a student attending lectures in a university. There are three lectures you need to attend on a given day. Attending the first lecture gives you 4 points of reward. After the first lecture, you have a 0.6 probability to continue into the second one, yielding 6 more points of reward. But, with a probability of 0.4, you get distracted and start using Facebook instead and get a reward of -1. From then onwards, you really can't let go of Facebook and there's just a 0.1 probability that you will concentrate back on the lecture.
After the second lecture, you have an equal chance of attending the next lecture or just falling asleep. Falling asleep is the terminal state and yields you no reward, but continuing on to the final lecture gives you a big reward of 10 points. From there on, you have a 40% chance of going to study and reach the terminal state, but a 60% chance of going to the pub with your friends instead. You end up drunk and don't know which lecture to attend, so you go to one of the lectures according to the probabilities given above.

### Definition of transition matrix
We first have to define our Transition Matrix as a nested dictionary to fit the requirements of the MDP class.
```
t = {
'leisure': {
'facebook': {'leisure':0.9, 'class1':0.1},
'quit': {'leisure':0.1, 'class1':0.9},
'study': {},
'sleep': {},
'pub': {}
},
'class1': {
'study': {'class2':0.6, 'leisure':0.4},
'facebook': {'class2':0.4, 'leisure':0.6},
'quit': {},
'sleep': {},
'pub': {}
},
'class2': {
'study': {'class3':0.5, 'end':0.5},
'sleep': {'end':0.5, 'class3':0.5},
'facebook': {},
'quit': {},
'pub': {},
},
'class3': {
'study': {'end':0.6, 'class1':0.08, 'class2':0.16, 'class3':0.16},
'pub': {'end':0.4, 'class1':0.12, 'class2':0.24, 'class3':0.24},
'facebook': {},
'quit': {},
'sleep': {}
},
'end': {}
}
```
### Defining rewards
We now need to define the reward for each state.
```
rewards = {
'class1': 4,
'class2': 6,
'class3': 10,
'leisure': -1,
'end': 0
}
```
### Terminal state
This MDP has only one terminal state
```
terminals = ['end']
```
### Setting initial state to `Class 1`
```
init = 'class1'
```
### Read in an instance of the custom class
```
school_mdp = CustomMDP(t, rewards, terminals, init, gamma=.95)
```
### Let's see the actions and rewards of the MDP
```
school_mdp.states
school_mdp.actions('class1')
school_mdp.actions('leisure')
school_mdp.T('class1','sleep')
school_mdp.actions('end')
school_mdp.reward
```
## Value iteration
```
def value_iteration(mdp, epsilon=0.001):
"""Solving an MDP by value iteration.
mdp: The MDP object
epsilon: Stopping criteria
"""
U1 = {s: 0 for s in mdp.states}
R, T, gamma = mdp.R, mdp.T, mdp.gamma
while True:
U = U1.copy()
delta = 0
for s in mdp.states:
U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
for a in mdp.actions(s)])
delta = max(delta, abs(U1[s] - U[s]))
if delta < epsilon * (1 - gamma) / gamma:
return U
def value_iteration_over_time(mdp, iterations=20):
U_over_time = []
U1 = {s: 0 for s in mdp.states}
R, T, gamma = mdp.R, mdp.T, mdp.gamma
for _ in range(iterations):
U = U1.copy()
for s in mdp.states:
U1[s] = R(s) + gamma * max([sum([p * U[s1] for (p, s1) in T(s, a)])
for a in mdp.actions(s)])
U_over_time.append(U)
return U_over_time
def best_policy(mdp, U):
"""Given an MDP and a utility function U, determine the best policy,
as a mapping from state to action."""
pi = {}
for s in mdp.states:
pi[s] = max(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
return pi
```
## Value iteration on the school MDP
```
value_iteration(school_mdp)
value_iteration_over_time(school_mdp,iterations=10)
```
### Plotting value updates over time/iterations
```
def plot_value_update(mdp,iterations=10,plot_kw=None):
"""
Plot value updates over iterations for a given MDP.
"""
x = value_iteration_over_time(mdp,iterations=iterations)
value_states = {k:[] for k in mdp.states}
for i in x:
for k,v in i.items():
value_states[k].append(v)
plt.figure(figsize=(8,5))
plt.title("Evolution of state utilities over iteration", fontsize=18)
for v in value_states:
plt.plot(value_states[v])
plt.legend(list(value_states.keys()),fontsize=14)
plt.grid(True)
plt.xlabel("Iterations",fontsize=16)
plt.ylabel("Utilities of states",fontsize=16)
plt.show()
plot_value_update(school_mdp,15)
```
### Value iterations for various discount factors ($\gamma$)
```
for i in range(4):
mdp = CustomMDP(t, rewards, terminals, init, gamma=1-0.2*i)
plot_value_update(mdp,10)
```
### Value iteration for two different reward structures
```
rewards1 = {
'class1': 4,
'class2': 6,
'class3': 10,
'leisure': -1,
'end': 0
}
mdp1 = CustomMDP(t, rewards1, terminals, init, gamma=.95)
plot_value_update(mdp1,20)
rewards2 = {
'class1': 1,
'class2': 1.5,
'class3': 2.5,
'leisure': -4,
'end': 0
}
mdp2 = CustomMDP(t, rewards2, terminals, init, gamma=.95)
plot_value_update(mdp2,20)
value_iteration(mdp2)
```
## Policy iteration
```
def expected_utility(a, s, U, mdp):
"""The expected utility of doing a in state s, according to the MDP and U."""
return sum([p * U[s1] for (p, s1) in mdp.T(s, a)])
def policy_evaluation(pi, U, mdp, k=20):
"""Returns an updated utility mapping U from each state in the MDP to its
utility, using an approximation (modified policy iteration)."""
R, T, gamma = mdp.R, mdp.T, mdp.gamma
for i in range(k):
for s in mdp.states:
U[s] = R(s) + gamma * sum([p * U[s1] for (p, s1) in T(s, pi[s])])
return U
def policy_iteration(mdp,verbose=0):
"""Solves an MDP by policy iteration"""
U = {s: 0 for s in mdp.states}
pi = {s: random.choice(mdp.actions(s)) for s in mdp.states}
if verbose:
print("Initial random choice:",pi)
iter_count=0
while True:
iter_count+=1
U = policy_evaluation(pi, U, mdp)
unchanged = True
for s in mdp.states:
a = max(mdp.actions(s), key=lambda a: expected_utility(a, s, U, mdp))
if a != pi[s]:
pi[s] = a
unchanged = False
if unchanged:
return (pi,iter_count)
if verbose:
print("Policy after iteration {}: {}".format(iter_count,pi))
```
## Policy iteration over the school MDP
```
policy_iteration(school_mdp)
policy_iteration(school_mdp,verbose=1)
```
### Does the result match using value iteration? We use the `best_policy` function to find out
```
best_policy(school_mdp,value_iteration(school_mdp,0.01))
```
## Comparing computation efficiency (time) of value and policy iterations
Clearly values iteration method takes more iterations to reach the same steady-state compared to policy iteration technique. But how does their computation time compare? Let's find out.
### Running value and policy iteration on the school MDP many times and averaging
```
def compute_time(mdp,iteration_technique='value',n_run=1000,epsilon=0.01):
"""
Computes the average time for value or policy iteration for a given MDP
n_run: Number of runs to average over, default 1000
epsilon: Error margin for the value iteration
"""
if iteration_technique=='value':
t1 = time.time()
for _ in range(n_run):
value_iteration(mdp,epsilon=epsilon)
t2 = time.time()
print("Average value iteration took {} milliseconds".format((t2-t1)*1000/n_run))
else:
t1 = time.time()
for _ in range(n_run):
policy_iteration(mdp)
t2 = time.time()
print("Average policy iteration took {} milliseconds".format((t2-t1)*1000/n_run))
compute_time(school_mdp,'value')
compute_time(school_mdp,'policy')
```
## Q-learning
### Q-learning class
```
class QLearningAgent:
""" An exploratory Q-learning agent. It avoids having to learn the transition
model because the Q-value of a state can be related directly to those of
its neighbors.
"""
def __init__(self, mdp, Ne, Rplus, alpha=None):
self.gamma = mdp.gamma
self.terminals = mdp.terminals
self.all_act = mdp.actlist
self.Ne = Ne # iteration limit in exploration function
self.Rplus = Rplus # large value to assign before iteration limit
self.Q = defaultdict(float)
self.Nsa = defaultdict(float)
self.s = None
self.a = None
self.r = None
self.states = mdp.states
self.T = mdp.T
if alpha:
self.alpha = alpha
else:
self.alpha = lambda n: 1./(1+n)
def f(self, u, n):
""" Exploration function. Returns fixed Rplus until
agent has visited state, action a Ne number of times."""
if n < self.Ne:
return self.Rplus
else:
return u
def actions_in_state(self, state):
""" Return actions possible in given state.
Useful for max and argmax. """
if state in self.terminals:
return [None]
else:
act_list=[]
for a in self.all_act:
if len(self.T(state,a))>0:
act_list.append(a)
return act_list
def __call__(self, percept):
s1, r1 = self.update_state(percept)
Q, Nsa, s, a, r = self.Q, self.Nsa, self.s, self.a, self.r
alpha, gamma, terminals = self.alpha, self.gamma, self.terminals,
actions_in_state = self.actions_in_state
if s in terminals:
Q[s, None] = r1
if s is not None:
Nsa[s, a] += 1
Q[s, a] += alpha(Nsa[s, a]) * (r + gamma * max(Q[s1, a1]
for a1 in actions_in_state(s1)) - Q[s, a])
if s in terminals:
self.s = self.a = self.r = None
else:
self.s, self.r = s1, r1
self.a = max(actions_in_state(s1), key=lambda a1: self.f(Q[s1, a1], Nsa[s1, a1]))
return self.a
def update_state(self, percept):
"""To be overridden in most cases. The default case
assumes the percept to be of type (state, reward)."""
return percept
```
### Trial run
```
def run_single_trial(agent_program, mdp):
"""Execute trial for given agent_program
and mdp."""
def take_single_action(mdp, s, a):
"""
Select outcome of taking action a
in state s. Weighted Sampling.
"""
x = random.uniform(0, 1)
cumulative_probability = 0.0
for probability_state in mdp.T(s, a):
probability, state = probability_state
cumulative_probability += probability
if x < cumulative_probability:
break
return state
current_state = mdp.init
while True:
current_reward = mdp.R(current_state)
percept = (current_state, current_reward)
next_action = agent_program(percept)
if next_action is None:
break
current_state = take_single_action(mdp, current_state, next_action)
```
### Testing Q-learning
```
# Define an agent
q_agent = QLearningAgent(school_mdp, Ne=1000, Rplus=2,alpha=lambda n: 60./(59+n))
q_agent.actions_in_state('leisure')
run_single_trial(q_agent,school_mdp)
q_agent.Q
for i in range(200):
run_single_trial(q_agent,school_mdp)
q_agent.Q
def get_U_from_Q(q_agent):
U = defaultdict(lambda: -100.) # Large negative value for comparison
for state_action, value in q_agent.Q.items():
state, action = state_action
if U[state] < value:
U[state] = value
return U
get_U_from_Q(q_agent)
q_agent = QLearningAgent(school_mdp, Ne=100, Rplus=25,alpha=lambda n: 10/(9+n))
qhistory=[]
for i in range(100000):
run_single_trial(q_agent,school_mdp)
U=get_U_from_Q(q_agent)
qhistory.append(U)
print(get_U_from_Q(q_agent))
print(value_iteration(school_mdp,epsilon=0.001))
```
### Function for utility estimate by Q-learning by many iterations
```
def qlearning_iter(agent_program,mdp,iterations=1000,print_final_utility=True):
"""
Function for utility estimate by Q-learning by many iterations
Returns a history object i.e. a list of dictionaries, where utility estimate for each iteration is stored
q_agent = QLearningAgent(grid_1, Ne=25, Rplus=1.5,
alpha=lambda n: 10000./(9999+n))
hist=qlearning_iter(q_agent,grid_1,iterations=10000)
"""
qhistory=[]
for i in range(iterations):
run_single_trial(agent_program,mdp)
U=get_U_from_Q(agent_program)
if len(U)==len(mdp.states):
qhistory.append(U)
if print_final_utility:
print(U)
return qhistory
```
### How do the long-term utility estimates with Q-learning compare with value iteration?
```
def plot_qlearning_vi(hist, vi,plot_n_states=None):
"""
Compares and plots a Q-learning and value iteration results for the utility estimate of an MDP's states
hist: A history object from a Q-learning run
vi: A value iteration estimate for the same MDP
plot_n_states: Restrict the plotting for n states (randomly chosen)
"""
utilities={k:[] for k in list(vi.keys())}
for h in hist:
for state in h.keys():
utilities[state].append(h[state])
if plot_n_states==None:
for state in list(vi.keys()):
plt.figure(figsize=(7,4))
plt.title("Plot of State: {} over Q-learning iterations".format(str(state)),fontsize=16)
plt.plot(utilities[state])
plt.hlines(y=vi[state],xmin=0,xmax=1.1*len(hist))
plt.legend(['Q-learning estimates','Value iteration estimate'],fontsize=14)
plt.xlabel("Iterations",fontsize=14)
plt.ylabel("Utility of the state",fontsize=14)
plt.grid(True)
plt.show()
else:
for state in list(vi.keys())[:plot_n_states]:
plt.figure(figsize=(7,4))
plt.title("Plot of State: {} over Q-learning iterations".format(str(state)),fontsize=16)
plt.plot(utilities[state])
plt.hlines(y=vi[state],xmin=0,xmax=1.1*len(hist))
plt.legend(['Q-learning estimates','Value iteration estimate'],fontsize=14)
plt.xlabel("Iterations",fontsize=14)
plt.ylabel("Utility of the state",fontsize=14)
plt.grid(True)
plt.show()
```
### Testing the long-term utility learning for the small (default) grid world
```
# Define the Q-learning agent
q_agent = QLearningAgent(school_mdp, Ne=100, Rplus=2,alpha=lambda n: 100/(99+n))
# Obtain the history by running the Q-learning for many iterations
hist=qlearning_iter(q_agent,school_mdp,iterations=20000,print_final_utility=False)
# Get a value iteration estimate using the same MDP
vi = value_iteration(school_mdp,epsilon=0.001)
# Compare the utility estimates from two methods
plot_qlearning_vi(hist,vi)
for alpha in range(100,5100,1000):
q_agent = QLearningAgent(school_mdp, Ne=10, Rplus=2,alpha=lambda n: alpha/(alpha-1+n))
# Obtain the history by running the Q-learning for many iterations
hist=qlearning_iter(q_agent,school_mdp,iterations=10000,print_final_utility=False)
# Get a value iteration estimate using the same MDP
vi = value_iteration(school_mdp,epsilon=0.001)
# Compare the utility estimates from two methods
plot_qlearning_vi(hist,vi,plot_n_states=1)
```
|
github_jupyter
|
```
library('magrittr')
library('dplyr')
library('tidyr')
library('readr')
library('ggplot2')
flow_data <-
read_tsv(
'data.tsv',
col_types=cols(
`Donor`=col_factor(levels=c('Donor 25', 'Donor 34', 'Donor 35', 'Donor 40', 'Donor 41')),
`Condition`=col_factor(levels=c('No electroporation', 'Mock electroporation', 'Plasmid electroporation')),
`Cell state`=col_factor(levels=c('Unstimulated', 'Activated')),
.default=col_number()
)
)
flow_data
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_wrap(~`Cell state`+`Donor`, ncol=4) +
ylab('Percent population (%)')
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_grid(`Cell state`~`Donor`) +
ylab('Percent population (%)')
no_electro_val <- function(x) {
x[1]
}
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
select(
`Donor`:`Condition`,
`Naive: CCR7+ CD45RO-`=`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
arrange(`Condition`) %>%
group_by(`Donor`, `Cell state`, `Population`) %>%
mutate(
`Normalized_Freq_of_parent`=`Freq_of_parent`-no_electro_val(`Freq_of_parent`)
) %>%
filter(
`Condition` == 'Plasmid electroporation'
) %>%
ggplot(aes(x=`Population`, y=`Normalized_Freq_of_parent`, color=`Cell state`)) +
geom_boxplot(alpha=.3, outlier.size=0) +
geom_point(position=position_jitterdodge()) +
geom_hline(yintercept=0, color="gray") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
ylab('Percent change for plasmid electroporation\ncompared to no electroporation (%)') +
ylim(-25, 25)
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Donor`:`Condition`,
`CD3 Count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0),
`Naive: CCR7+ CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
ggplot(aes(x=`Population`, y=`Freq_of_parent`, fill=`Condition`)) +
geom_col(position="dodge") +
theme_bw() +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_grid(`Cell state`~`Donor`) +
ylab('Live cell count')
no_electro_val <- function(x) {
x[1]
}
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Donor`:`Condition`,
`CD3 Count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0),
`Naive: CCR7+ CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO- | Freq. of Parent`,
`CM: CCR7+ CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7+ CD45RO+ | Freq. of Parent`,
`EM: CCR7- CD45RO+`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO+ | Freq. of Parent`,
`EMRA: CCR7- CD45RO-`=`CD3 Count`*`Live/CD3+/CCR7- CD45RO- | Freq. of Parent`
) %>%
gather(
key=`Population`,
value=`Freq_of_parent`,
`Naive: CCR7+ CD45RO-`:`EMRA: CCR7- CD45RO-`
) %>%
arrange(`Condition`) %>%
group_by(`Donor`, `Cell state`, `Population`) %>%
mutate(
`Normalized_Freq_of_parent`=(1-(`Freq_of_parent`/no_electro_val(`Freq_of_parent`)))*100
) %>%
filter(
`Condition` == 'Plasmid electroporation',
`Normalized_Freq_of_parent` > 0
) %>%
ggplot(aes(x=`Population`, y=`Normalized_Freq_of_parent`, color=`Cell state`)) +
geom_boxplot(alpha=.3, outlier.size=0) +
geom_point(position=position_jitterdodge()) +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
ylab('Percent death for plasmid electroporation\ncompared to no electroporation (%)') +
ylim(0, 100)
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`T cell count`=`Count`*(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`/100.0)
) %>%
ggplot(aes(x=`Donor`, y=`T cell count`, fill=`Condition`)) +
geom_col(position="dodge") +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
facet_wrap(~`Cell state`, ncol=1) +
ylab('Live T cell count')
colors <- c("#FC877F", "#0EADEE", "#04B412")
flow_data %>%
filter(`Donor` != 'Donor 35') %>%
mutate(
`Live Percent (%)`=(`Live | Freq. of Parent`/100.0)*(`Live/CD3+ | Freq. of Parent`)
) %>%
ggplot(aes(x=`Donor`, y=`Live Percent (%)`, fill=`Condition`)) +
geom_col(position="dodge") +
facet_wrap(~`Cell state`, ncol=2) +
theme_bw() +
theme(axis.text.x=element_text(angle=75, hjust=1)) +
scale_fill_manual(values=colors) +
ylab('Live Percent (%)') +
ylim(0, 100)
```
|
github_jupyter
|
# Proyecto
## Instrucciones
1.- Completa los datos personales (nombre y rol USM) de cada integrante en siguiente celda.
* __Nombre-Rol__:
* Cristobal Salazar 201669515-k
* Andres Riveros 201710505-4
* Matias Sasso 201704523-k
* Javier Valladares 201710508-9
2.- Debes _pushear_ este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.
3.- Se evaluará:
- Soluciones
- Código
- Que Binder esté bien configurado.
- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error.
## I.- Sistemas de recomendación
### Introducción
El rápido crecimiento de la recopilación de datos ha dado lugar a una nueva era de información. Los datos se están utilizando para crear sistemas más eficientes y aquí es donde entran en juego los sistemas de recomendación. Los sistemas de recomendación son un tipo de sistemas de filtrado de información, ya que mejoran la calidad de los resultados de búsqueda y proporcionan elementos que son más relevantes para el elemento de búsqueda o están relacionados con el historial de búsqueda del usuario.
Se utilizan para predecir la calificación o preferencia que un usuario le daría a un artículo. Casi todas las grandes empresas de tecnología los han aplicado de una forma u otra: Amazon lo usa para sugerir productos a los clientes, YouTube lo usa para decidir qué video reproducir a continuación en reproducción automática y Facebook lo usa para recomendar páginas que me gusten y personas a seguir. Además, empresas como Netflix y Spotify dependen en gran medida de la efectividad de sus motores de recomendación para sus negocios y éxitos.
### Objetivos
Poder realizar un proyecto de principio a fin ocupando todos los conocimientos aprendidos en clase. Para ello deben cumplir con los siguientes objetivos:
* **Desarrollo del problema**: Se les pide a partir de los datos, proponer al menos un tipo de sistemas de recomendación. Como todo buen proyecto de Machine Learning deben seguir el siguiente procedimiento:
* **Lectura de los datos**: Describir el o los conjunto de datos en estudio.
* **Procesamiento de los datos**: Procesar adecuadamente los datos en estudio. Para este caso ocuparan técnicas de [NLP](https://en.wikipedia.org/wiki/Natural_language_processing).
* **Metodología**: Describir adecuadamente el procedimiento ocupado en cada uno de los modelos ocupados.
* **Resultados**: Evaluar adecuadamente cada una de las métricas propuesta en este tipo de problemas.
* **Presentación**: La presentación será levemente distinta a las anteriores, puesto que deberán ocupar la herramienta de Jupyter llamada [RISE](https://en.wikipedia.org/wiki/Natural_language_processing). Esta presentación debe durar aproximadamente entre 15-30 minutos, y deberán mandar sus videos (por youtube, google drive, etc.)
### Evaluación
* **Códigos**: Los códigos deben estar correctamente documentados (ocupando las *buenas prácticas* de python aprendidas en este curso).
* **Explicación**: La explicación de la metodología empleada debe ser clara, precisa y concisa.
* **Apoyo Visual**: Se espera que tengan la mayor cantidad de gráficos y/o tablas que puedan resumir adecuadamente todo el proceso realizado.
### Esquema del proyecto
El proyecto tendrá la siguiente estructura de trabajo:
```
- project
|
|- data
|- tmdb_5000_credits.csv
|- tmdb_5000_movies.csv
|- graficos.py
|- lectura.py
|- modelos.py
|- preprocesamiento.py
|- presentacion.ipynb
|- project.ipynb
```
donde:
* `data`: carpeta con los datos del proyecto
* `graficos.py`: módulo de gráficos
* `lectura.py`: módulo de lectura de datos
* `modelos.py`: módulo de modelos de Machine Learning utilizados
* `preprocesamiento.py`: módulo de preprocesamiento de datos
* `presentacion.ipynb`: presentación del proyecto (formato *RISE*)
* `project.ipynb`: descripción del proyecto
### Apoyo
Para que la carga del proyecto sea lo más amena posible, se les deja las siguientes referencias:
* **Sistema de recomendación**: Pueden tomar como referencia el proyecto de Kaggle [Getting Started with a Movie Recommendation System](https://www.kaggle.com/ibtesama/getting-started-with-a-movie-recommendation-system/data?select=tmdb_5000_credits.csv).
* **RISE**: Les dejo un video del Profesor Sebastían Flores denomindo *Presentaciones y encuestas interactivas en jupyter notebooks y RISE* ([link](https://www.youtube.com/watch?v=ekyN9DDswBE&ab_channel=PyConColombia)). Este material les puede ayudar para comprender mejor este nuevo concepto.
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# 過学習と学習不足について知る
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/overfit_and_underfit"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [[email protected] メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
いつものように、この例のプログラムは`tf.keras` APIを使用します。詳しくはTensorFlowの[Keras guide](https://www.tensorflow.org/guide/keras)を参照してください。
これまでの例、つまり、映画レビューの分類と燃費の推定では、検証用データでのモデルの正解率が、数エポックでピークを迎え、その後低下するという現象が見られました。
言い換えると、モデルが訓練用データを**過学習**したと考えられます。過学習への対処の仕方を学ぶことは重要です。**訓練用データセット**で高い正解率を達成することは難しくありませんが、我々は、(これまで見たこともない)**テスト用データ**に汎化したモデルを開発したいのです。
過学習の反対語は**学習不足**(underfitting)です。学習不足は、モデルがテストデータに対してまだ改善の余地がある場合に発生します。学習不足の原因は様々です。モデルが十分強力でないとか、正則化のしすぎだとか、単に訓練時間が短すぎるといった理由があります。学習不足は、訓練用データの中の関連したパターンを学習しきっていないということを意味します。
モデルの訓練をやりすぎると、モデルは過学習を始め、訓練用データの中のパターンで、テストデータには一般的ではないパターンを学習します。我々は、過学習と学習不足の中間を目指す必要があります。これから見ていくように、ちょうどよいエポック数だけ訓練を行うというのは必要なスキルなのです。
過学習を防止するための、最良の解決策は、より多くの訓練用データを使うことです。多くのデータで訓練を行えば行うほど、モデルは自然により汎化していく様になります。これが不可能な場合、次善の策は正則化のようなテクニックを使うことです。正則化は、モデルに保存される情報の量とタイプに制約を課すものです。ネットワークが少数のパターンしか記憶できなければ、最適化プロセスにより、最も主要なパターンのみを学習することになり、より汎化される可能性が高くなります。
このノートブックでは、重みの正則化とドロップアウトという、よく使われる2つの正則化テクニックをご紹介します。これらを使って、IMDBの映画レビューを分類するノートブックの改善を図ります。
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## IMDBデータセットのダウンロード
以前のノートブックで使用したエンベディングの代わりに、ここでは文をマルチホットエンコードします。このモデルは、訓練用データセットをすぐに過学習します。このモデルを使って、過学習がいつ起きるかということと、どうやって過学習と戦うかをデモします。
リストをマルチホットエンコードすると言うのは、0と1のベクトルにするということです。具体的にいうと、例えば`[3, 5]`というシーケンスを、インデックス3と5の値が1で、それ以外がすべて0の、10,000次元のベクトルに変換するということを意味します。
```
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
# 形状が (len(sequences), dimension)ですべて0の行列を作る
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0 # 特定のインデックスに対してresults[i] を1に設定する
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)
```
結果として得られるマルチホットベクトルの1つを見てみましょう。単語のインデックスは頻度順にソートされています。このため、インデックスが0に近いほど1が多く出現するはずです。分布を見てみましょう。
```
plt.plot(train_data[0])
```
## 過学習のデモ
過学習を防止するための最も単純な方法は、モデルのサイズ、すなわち、モデル内の学習可能なパラメータの数を小さくすることです(学習パラメータの数は、層の数と層ごとのユニット数で決まります)。ディープラーニングでは、モデルの学習可能なパラメータ数を、しばしばモデルの「キャパシティ」と呼びます。直感的に考えれば、パラメータ数の多いモデルほど「記憶容量」が大きくなり、訓練用のサンプルとその目的変数の間の辞書のようなマッピングをたやすく学習することができます。このマッピングには汎化能力がまったくなく、これまで見たことが無いデータを使って予測をする際には役に立ちません。
ディープラーニングのモデルは訓練用データに適応しやすいけれど、本当のチャレレンジは汎化であって適応ではないということを、肝に銘じておく必要があります。
一方、ネットワークの記憶容量が限られている場合、前述のようなマッピングを簡単に学習することはできません。損失を減らすためには、より予測能力が高い圧縮された表現を学習しなければなりません。同時に、モデルを小さくしすぎると、訓練用データに適応するのが難しくなります。「多すぎる容量」と「容量不足」の間にちょうどよい容量があるのです。
残念ながら、(層の数や、層ごとの大きさといった)モデルの適切なサイズやアーキテクチャを決める魔法の方程式はありません。一連の異なるアーキテクチャを使って実験を行う必要があります。
適切なモデルのサイズを見つけるには、比較的少ない層の数とパラメータから始めるのがベストです。それから、検証用データでの損失値の改善が見られなくなるまで、徐々に層の大きさを増やしたり、新たな層を加えたりします。映画レビューの分類ネットワークでこれを試してみましょう。
比較基準として、```Dense```層だけを使ったシンプルなモデルを構築し、その後、それより小さいバージョンと大きいバージョンを作って比較します。
### 比較基準を作る
```
baseline_model = keras.Sequential([
# `.summary` を見るために`input_shape`が必要
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
baseline_model.summary()
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### より小さいモデルの構築
今作成したばかりの比較基準となるモデルに比べて隠れユニット数が少ないモデルを作りましょう。
```
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.summary()
```
同じデータを使って訓練します。
```
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### より大きなモデルの構築
練習として、より大きなモデルを作成し、どれほど急速に過学習が起きるかを見ることもできます。次はこのベンチマークに、この問題が必要とするよりはるかに容量の大きなネットワークを追加しましょう。
```
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
bigger_model.summary()
```
このモデルもまた同じデータを使って訓練します。
```
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### 訓練時と検証時の損失をグラフにする
<!--TODO(markdaoust): This should be a one-liner with tensorboard -->
実線は訓練用データセットの損失、破線は検証用データセットでの損失です(検証用データでの損失が小さい方が良いモデルです)。これをみると、小さいネットワークのほうが比較基準のモデルよりも過学習が始まるのが遅いことがわかります(4エポックではなく6エポック後)。また、過学習が始まっても性能の低下がよりゆっくりしています。
```
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])
```
より大きなネットワークでは、すぐに、1エポックで過学習が始まり、その度合も強いことに注目してください。ネットワークの容量が大きいほど訓練用データをモデル化するスピードが早くなり(結果として訓練時の損失値が小さくなり)ますが、より過学習しやすく(結果として訓練時の損失値と検証時の損失値が大きく乖離しやすく)なります。
## 過学習防止の戦略
### 重みの正則化を加える
「オッカムの剃刀」の原則をご存知でしょうか。何かの説明が2つあるとすると、最も正しいと考えられる説明は、仮定の数が最も少ない「一番単純な」説明だというものです。この原則は、ニューラルネットワークを使って学習されたモデルにも当てはまります。ある訓練用データとネットワーク構造があって、そのデータを説明できる重みの集合が複数ある時(つまり、複数のモデルがある時)、単純なモデルのほうが複雑なものよりも過学習しにくいのです。
ここで言う「単純なモデル」とは、パラメータ値の分布のエントロピーが小さいもの(あるいは、上記で見たように、そもそもパラメータの数が少ないもの)です。したがって、過学習を緩和するための一般的な手法は、重みが小さい値のみをとることで、重み値の分布がより整然となる(正則)様に制約を与えるものです。これを「重みの正則化」と呼ばれ、ネットワークの損失関数に、重みの大きさに関連するコストを加えることで行われます。このコストには2つの種類があります。
* [L1正則化](https://developers.google.com/machine-learning/glossary/#L1_regularization) 重み係数の絶対値に比例するコストを加える(重みの「L1ノルム」と呼ばれる)。
* [L2正則化](https://developers.google.com/machine-learning/glossary/#L2_regularization) 重み係数の二乗に比例するコストを加える(重み係数の二乗「L2ノルム」と呼ばれる)。L2正則化はニューラルネットワーク用語では重み減衰(Weight Decay)と呼ばれる。呼び方が違うので混乱しないように。重み減衰は数学的にはL2正則化と同義である。
L1正則化は重みパラメータの一部を0にすることでモデルを疎にする効果があります。L2正則化は重みパラメータにペナルティを加えますがモデルを疎にすることはありません。これは、L2正則化のほうが一般的である理由の一つです。
`tf.keras`では、重みの正則化をするために、重み正則化のインスタンスをキーワード引数として層に加えます。ここでは、L2正則化を追加してみましょう。
```
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
```l2(0.001)```というのは、層の重み行列の係数全てに対して```0.001 * 重み係数の値 **2```をネットワークの損失値合計に加えることを意味します。このペナルティは訓練時のみに加えられるため、このネットワークの損失値は、訓練時にはテスト時に比べて大きくなることに注意してください。
L2正則化の影響を見てみましょう。
```
plot_history([('baseline', baseline_history),
('l2', l2_model_history)])
```
ご覧のように、L2正則化ありのモデルは比較基準のモデルに比べて過学習しにくくなっています。両方のモデルのパラメータ数は同じであるにもかかわらずです。
### ドロップアウトを追加する
ドロップアウトは、ニューラルネットワークの正則化テクニックとして最もよく使われる手法の一つです。この手法は、トロント大学のヒントンと彼の学生が開発したものです。ドロップアウトは層に適用するもので、訓練時に層から出力された特徴量に対してランダムに「ドロップアウト(つまりゼロ化)」を行うものです。例えば、ある層が訓練時にある入力サンプルに対して、普通は`[0.2, 0.5, 1.3, 0.8, 1.1]` というベクトルを出力するとします。ドロップアウトを適用すると、このベクトルは例えば`[0, 0.5, 1.3, 0, 1.1]`のようにランダムに散らばったいくつかのゼロを含むようになります。「ドロップアウト率」はゼロ化される特徴の割合で、通常は0.2から0.5の間に設定します。テスト時は、どのユニットもドロップアウトされず、代わりに出力値がドロップアウト率と同じ比率でスケールダウンされます。これは、訓練時に比べてたくさんのユニットがアクティブであることに対してバランスをとるためです。
`tf.keras`では、Dropout層を使ってドロップアウトをネットワークに導入できます。ドロップアウト層は、その直前の層の出力に対してドロップアウトを適用します。
それでは、IMDBネットワークに2つのドロップアウト層を追加しましょう。
```
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation='relu', input_shape=(NUM_WORDS,)),
keras.layers.Dropout(0.5),
keras.layers.Dense(16, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid')
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('baseline', baseline_history),
('dropout', dpt_model_history)])
```
ドロップアウトを追加することで、比較対象モデルより明らかに改善が見られます。
まとめ:ニューラルネットワークにおいて過学習を防ぐ最も一般的な方法は次のとおりです。
* 訓練データを増やす
* ネットワークの容量をへらす
* 重みの正則化を行う
* ドロップアウトを追加する
このガイドで触れていない2つの重要なアプローチがあります。データ拡張とバッチ正規化です。
|
github_jupyter
|
### An Auto correct system is an application that changes mispelled words into the correct ones.
```
# In this notebook I'll show how to implement an Auto Correct System that its very usefull.
# This auto correct system only search for spelling erros, not contextual errors.
```
*The implementation can be divided into 4 steps:*
[1]. **Identity a mispelled word.**
[2]. **Find strings n Edit Distance away**
[3]. **Filter Candidates** (*as Real Words that are spelled correct*)
[4]. **Calculate Word Probabilities.** (*Choose the most likely cadidate to be the replacement*)
### 1. Identity a mispelled Word
*To identify if a word was mispelled, you can check if the word is in the dictionary / vocabulary.*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
word_test = 'Congratulations my deah'
word_test = word_test.lower()
word_test = word_test.split()
for word in word_test:
if word in vocab:
print(f'The word: {word} is in the vocab')
else:
print(f"The word: {word} isn't in the vocabulary")
```
### 2. Find strings n Edit Distance Away
*Edit is a operation performed on a string to change into another string. Edit distance count the number of these operations*
*So **n Edit Distance** tells you how many operations away one string is from another.*
*For this application we'll use the Levenshtein Distance value's cost, where this edit value are:*
* **Insert** - Operation where you insert a letter, the cost is equal to 1.
* **Delete** - Operation where you delete a letter, the cost is equal to 1.
* **Replace** - Operation where you replace one letter to another, the cost is equal to 2.
* **Switch** - Operation where you swap 2 **adjacent** letters
*Also we'll use the Minimum Edit Distance which is the minimum number of edits needed to transform 1 string into the other, for that we are using n = 2 and the Dynamic Programming algorithm. ( will be explained when it is implemented ) for evaluate our model*
```
# To implement this operations we need to split the word into 2 parts in all possible ways
word = 'dear'
split_word = [[word[:i], word[i:]] for i in range(len(word) + 1)]
for i in split_word:
print(i)
# The delete operation need to delete each possible letter from the original word.
delete_operation = [[L + R[1:]] for L, R in split_word if R ]
for i in delete_operation:
print(i)
# The same way the insert operation need to add each possible letter from the vocab to the original word
letters = 'abcdefghijklmnopqrstuvwxyz'
insert_operation = [L + s + R for L, R in split_word for s in letters]
c = 0
print('the first insert operations: ')
print()
for i in insert_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last insert operations:')
print()
for i in insert_operation:
c += 1
if c > 126:
print(i)
# Switch Operation
switch_operation = [[L[:-1] + R[0] + L[-1] + R[1:]] for L, R in split_word if R and L]
for i in switch_operation:
print(i)
# Replace Operation
letters = 'abcdefghijklmnopqrstuvwxyz'
replace_operation = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
c = 0
print('the first replace operations: ')
print()
for i in replace_operation:
print(i)
c += 1
if c == 4:
break
c = 0
print('the last replace operations:')
print()
for i in replace_operation:
c += 1
if c > 100:
print(i)
# Remember that at the end we need to remove the word it self
replace_operation = set(replace_operation)
replace_operation.discard('dear')
```
### 3. Filter Candidates
*We only want to consider real and correctly spelled words form the candidate lists, so we need to compare to a know dictionary.*
*If the string does not appears in the dict, remove from the candidates, this way resulting in a list of actual words only*
```
vocab = ['dean','deer','dear','fries','and','coke', 'congratulations', 'my']
# for example we can use the replace operations words to filter in our vocab
filtered_words = [word for word in replace_operation if word in vocab]
print(filtered_words)
```
### 4. Calculate the words probabilities
*We need to find the most likely word from the cadidate list, to calculate the probability of a word in the
sentence we need to first calculate the word frequencies, also we want to count the total number of word in the body of texts
or corpus.*
*So we compute the probability that each word will appear if randomly selected from the corpus of words.*
$$P(w_i) = \frac{C(w_i)}{M} \tag{Eq 01}$$
*where*
$C(w_i)$ *is the total number of times $w_i$ appears in the corpus.*
$M$ *is the total number of words in the corpus.*
*For example, the probability of the word 'am' in the sentence **'I am happy because I am learning'** is:*
$$P(am) = \frac{C(w_i)}{M} = \frac {2}{7} \tag{Eq 02}.$$
### Now the we know the four steps of the Auto Correct System, we can start to implement it
```
# import libraries
import re
from collections import Counter
import numpy as np
import pandas as pd
```
*The first thing to do is the data pre processing, for this example we'll use the file called **'shakespeare.txt'** this file can be found in the directory.*
```
def process_data(filename):
"""
Input:
A file_name which is found in the current directory. We just have to read it in.
Output:
words: a list containing all the words in the corpus (text file you read) in lower case.
"""
words = []
with open(filename, 'r') as f:
text = f.read()
words = re.findall(r'\w+', text)
words = [word.lower() for word in words]
return words
words = process_data('shakespeare.txt')
vocab = set(words) # eliminate duplicates
print(f'The vocabulary has {len(vocab)} unique words.')
```
*The second step, we need to count the frequency of every word in the dictionary to later calculate the probabilities*
```
def get_count(word):
'''
Input:
word_l: a set of words representing the corpus.
Output:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
'''
word_count_dict = {}
word_count_dict = Counter(word)
return word_count_dict
word_count_dict = get_count(words)
print(f'There are {len(word_count_dict)} key par values')
print(f"The count for the word 'thee' is {word_count_dict.get('thee',0)}")
```
*Now we must calculate the probability that each word appears using the (eq 01):*
```
def get_probs(word_count_dict):
'''
Input:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
Output:
probs: A dictionary where keys are the words and the values are the probability that a word will occur.
'''
probs = {}
total_words = 0
for word, value in word_count_dict.items():
total_words += value # we add the quantity of each word appears
for word, value in word_count_dict.items():
probs[word] = value / total_words
return probs
probs = get_probs(word_count_dict)
print(f"Length of probs is {len(probs)}")
print(f"P('thee') is {probs['thee']:.4f}")
```
*Now, that we have computed $P(w_i)$ for all the words in the corpus, we'll write the functions such as delete, insert, switch and replace to manipulate strings so that we can edit the erroneous strings and return the right spellings of the words.*
```
def delete_letter(word, verbose = False):
'''
Input:
word: the string/word for which you will generate all possible words
in the vocabulary which have 1 missing character
Output:
delete_l: a list of all possible strings obtained by deleting 1 character from word
'''
delete = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
delete = [L + R[1:] for L, R in split_word if R]
if verbose: print(f"input word {word}, \nsplit_word = {split_word}, \ndelete_word = {delete}")
return delete
delete_word = delete_letter(word="cans",
verbose=True)
def switch_letter(word, verbose = False):
'''
Input:
word: input string
Output:
switches: a list of all possible strings with one adjacent charater switched
'''
switch = []
split_word = []
split_word = [[word[:i], word[i:]] for i in range(len(word))]
switch = [L[:-1] + R[0] + L[-1] + R[1:] for L, R in split_word if L and R]
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nswitch = {switch}")
return switch
switch_word_l = switch_letter(word="eta",
verbose=True)
def replace_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
replaces: a list of all possible strings where we replaced one letter from the original word.
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
replace = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word))]
replace = [L + s + (R[1:] if len(R) > 1 else '') for L, R in split_word if R for s in letters ]
# we need to remove the actual word from the list
replace = set(replace)
replace.discard(word)
replace = sorted(list(replace)) # turn the set back into a list and sort it, for easier viewing
if verbose: print(f"Input word = {word} \nsplit = {split_word} \nreplace {replace}")
return replace
replace_l = replace_letter(word='can',
verbose=True)
def insert_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
inserts: a set of all possible strings with one new letter inserted at every offset
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
insert = []
split_word = []
split_word = [(word[:i], word[i:]) for i in range(len(word) + 1 )]
insert = [L + s + R for L, R in split_word for s in letters]
if verbose: print(f"Input word {word} \nsplit = {split_word} \ninsert = {insert}")
return insert
insert = insert_letter('at', True)
print(f"Number of strings output by insert_letter('at') is {len(insert)}")
```
*Now that we have implemented the string manipulations, we'll create two functions that, given a string, will return all the possible single and double edits on that string. These will be `edit_one_letter()` and `edit_two_letters()`.*
```
def edit_one_letter(word, allow_switches = True): # The 'switch' function is a less common edit function,
# so will be selected by an "allow_switches" input argument.
"""
Input:
word: the string/word for which we will generate all possible wordsthat are one edit away.
Output:
edit_one_set: a set of words with one possible edit. Please return a set. and not a list.
"""
edit_one_set = set()
all_word, words = [] , []
words.append(insert_letter(word))
words.append(delete_letter(word))
words.append(replace_letter(word))
if allow_switches == True:
words.append(switch_letter(word))
for i in words:
for each_word in i:
if each_word == word: # we exclude the word it self
continue
all_word.append(each_word)
edit_one_set = set(all_word)
return edit_one_set
tmp_word = "at"
tmp_edit_one_set = edit_one_letter(tmp_word)
# turn this into a list to sort it, in order to view it
tmp_edit_one = sorted(list(tmp_edit_one_set))
print(f"input word: {tmp_word} \nedit_one \n{tmp_edit_one}\n")
print(f"The type of the returned object should be a set {type(tmp_edit_one_set)}")
print(f"Number of outputs from edit_one_letter('at') is {len(edit_one_letter('at'))}")
def edit_two_letters(word, allow_switches = True):
'''
Input:
word: the input string/word
Output:
edit_two_set: a set of strings with all possible two edits
'''
edit_two_set = set()
if allow_switches == True:
first_edit = edit_one_letter(word)
else:
first_edit = edit_one_letter(word, allow_switches = False)
first_edit = set(first_edit)
second_edit = []
final_edit = []
if allow_switches == True:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
else:
for each_word in first_edit:
second_edit.append(edit_one_letter(each_word, allow_switches = False))
for i in second_edit:
for each_word in i:
final_edit.append(each_word)
edit_two_set = set(final_edit)
return edit_two_set
tmp_edit_two_set = edit_two_letters("a")
tmp_edit_two_l = sorted(list(tmp_edit_two_set))
print(f"Number of strings with edit distance of two: {len(tmp_edit_two_l)}")
print(f"First 10 strings {tmp_edit_two_l[:10]}")
print(f"Last 10 strings {tmp_edit_two_l[-10:]}")
print(f"The data type of the returned object should be a set {type(tmp_edit_two_set)}")
print(f"Number of strings that are 2 edit distances from 'at' is {len(edit_two_letters('at'))}")
```
*Now we will use the `edit_two_letters` function to get a set of all the possible 2 edits on our word. We will then use those strings to get the most probable word we meant to substitute our word typing suggestion.*
```
def get_corrections(word, probs, vocab, n=2, verbose = False):
'''
Input:
word: a user entered string to check for suggestions
probs: a dictionary that maps each word to its probability in the corpus
vocab: a set containing all the vocabulary
n: number of possible word corrections you want returned in the dictionary
Output:
n_best: a list of tuples with the most probable n corrected words and their probabilities.
'''
suggestions = []
n_best = []
# look if the word exist in the vocab, if doesn't, the edit_one_letter fuction its used, if any of the letter created
# exists in the vocab, take the two letter edit function, if any of this situations are in the vocab, take the input word
suggestions = list((word in vocab) or (edit_one_letter(word).intersection(vocab)) or (edit_two_letter(word).intersection(vocab)) or word)
n_best= [[word, probs[word]] for word in (suggestions)] # make a list with the possible word and probability.
if verbose: print("entered word = ", word, "\nsuggestions = ", set(suggestions))
return n_best
my_word = 'dys'
tmp_corrections = get_corrections(my_word, probs, vocab, 2, verbose=True) # keep verbose=True
for i, word_prob in enumerate(tmp_corrections):
print(f"word {i}: {word_prob[0]}, probability {word_prob[1]:.6f}")
print(f'The highest score for all the candidates is the word {tmp_corrections[np.argmax(word_prob)][0]}')
```
*Now that we have implemented the auto-correct system, how do you evaluate the similarity between two strings? For example: 'waht' and 'what'.*
*Also how do you efficiently find the shortest path to go from the word, 'waht' to the word 'what'?*
*We will implement a dynamic programming system that will tell you the minimum number of edits required to convert a string into another string.*
### Dynamic Programming
*Dynamic Programming breaks a problem down into subproblems which can be combined to form the final solution. Here, given a string source[0..i] and a string target[0..j], we will compute all the combinations of substrings[i, j] and calculate their edit distance. To do this efficiently, we will use a table to maintain the previously computed substrings and use those to calculate larger substrings.*
*You have to create a matrix and update each element in the matrix as follows:*
$$\text{Initialization}$$
\begin{align}
D[0,0] &= 0 \\
D[i,0] &= D[i-1,0] + del\_cost(source[i]) \tag{eq 03}\\
D[0,j] &= D[0,j-1] + ins\_cost(target[j]) \\
\end{align}
*So converting the source word **play** to the target word **stay**, using an insert cost of one, a delete cost of 1, and replace cost of 2 would give you the following table:*
<table style="width:20%">
<tr>
<td> <b> </b> </td>
<td> <b># </b> </td>
<td> <b>s </b> </td>
<td> <b>t </b> </td>
<td> <b>a </b> </td>
<td> <b>y </b> </td>
</tr>
<tr>
<td> <b> # </b></td>
<td> 0</td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
</tr>
<tr>
<td> <b> p </b></td>
<td> 1</td>
<td> 2</td>
<td> 3</td>
<td> 4</td>
<td> 5</td>
</tr>
<tr>
<td> <b> l </b></td>
<td>2</td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>6</td>
</tr>
<tr>
<td> <b> a </b></td>
<td>3</td>
<td>4</td>
<td>5</td>
<td>4</td>
<td>5</td>
</tr>
<tr>
<td> <b> y </b></td>
<td>4</td>
<td>5</td>
<td>6</td>
<td>5</td>
<td>4</td>
</tr>
</table>
*The operations used in this algorithm are 'insert', 'delete', and 'replace'. These correspond to the functions that we defined earlier: insert_letter(), delete_letter() and replace_letter(). switch_letter() is not used here.*
*The diagram below describes how to initialize the table. Each entry in D[i,j] represents the minimum cost of converting string source[0:i] to string target[0:j]. The first column is initialized to represent the cumulative cost of deleting the source characters to convert string "EER" to "". The first row is initialized to represent the cumulative cost of inserting the target characters to convert from "" to "NEAR".*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistInit4.PNG' alt="alternate text" width="width" height="height" style="width:1000px;height:400px;"/> Figure 1 Initializing Distance Matrix</div>
*Note that the formula for $D[i,j]$ shown in the image is equivalent to:*
\begin{align}
\\
D[i,j] =min
\begin{cases}
D[i-1,j] + del\_cost\\
D[i,j-1] + ins\_cost\\
D[i-1,j-1] + \left\{\begin{matrix}
rep\_cost; & if src[i]\neq tar[j]\\
0 ; & if src[i]=tar[j]
\end{matrix}\right.
\end{cases}
\tag{5}
\end{align}
*The variable `sub_cost` (for substitution cost) is the same as `rep_cost`; replacement cost. We will stick with the term "replace" whenever possible.*
<div style="width:image width px; font-size:100%; text-align:center;"><img src='EditDistExample1.PNG' alt="alternate text" width="width" height="height" style="width:1200px;height:400px;"/> Figure 2 Examples Distance Matrix</div>
```
def min_edit_distance(source, target, ins_cost = 1, del_cost = 1, rep_cost = 2):
'''
Input:
source: a string corresponding to the string you are starting with
target: a string corresponding to the string you want to end with
ins_cost: an integer setting the insert cost
del_cost: an integer setting the delete cost
rep_cost: an integer setting the replace cost
Output:
D: a matrix of len(source)+1 by len(target)+1 containing minimum edit distances
med: the minimum edit distance (med) required to convert the source string to the target
'''
m = len(source)
n = len(target)
# initialize cost matrix with zeros and dimensions (m+1, n+1)
D = np.zeros((m+1, n+1), dtype = int)
# Fill in column 0, from row 1 to row m, both inclusive
for row in range(1, m+1): # Replace None with the proper range
D[row, 0] = D[row -1, 0] + del_cost
# Fill in row 0, for all columns from 1 to n, both inclusive
for column in range(1, n+1):
D[0, column] = D[0, column - 1] + ins_cost
# Loop through row 1 to row m, both inclusive
for row in range(1, m+1):
# Loop through column 1 to column n, both inclusive
for column in range(1, n+1):
# initialize r_cost to the 'replace' cost that is passed into this function
r_cost = rep_cost
# check to see if source character at the previous row
# matches the target haracter at the previous column
if source[row - 1] == target[column - 1]:
# Update the replacement cost to 0 if source and
# target are equal
r_cost = 0
# Update the cost atow, col based on previous entries in the cost matrix
# Refer to the equation calculate for D[i,j] (the mininum of the three calculated)
D[row, column] = min([D[row-1, column] + del_cost, D[row, column-1] + ins_cost, D[row-1, column-1] + r_cost])
# Set the minimum edit distance with the cost found at row m, column n
med = D[m, n]
return D, med
# testing your implementation
source = 'play'
target = 'stay'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list('#' + source)
cols = list('#' + target)
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
# testing your implementation
source = 'eer'
target = 'near'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list(source)
idx.insert(0, '#')
cols = list(target)
cols.insert(0, '#')
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
```
|
github_jupyter
|
## Birthday Paradox
In a group of 5 people, how likely is it that everyone has a unique birthday (assuming that nobody was born on February 29th of a leap year)? You may feel it is highly likely because there are $365$ days in a year and loosely speaking, $365$ is "much greater" than $5$. Indeed, as you shall see, this probability is greater than $0.9$. However, in a group of $25$ or more, what is the probability that no two persons have the same birthday? You might be surprised to know that the answer is less than a half. This is known as the "birthday paradox".
In general, for a group of $n$ people, the probability that no two persons share the same birthday can be calculated as:
\begin{align*}
P &= \frac{\text{Number of } n \text{-permutations of birthdays}}{\text{Total number of birthday assignments allowing repeated birthdays}}\\
&= \frac{365!/(365-n)!}{365^n}\\
&= \prod_{k=1}^n \frac{365-k+1}{365}
\end{align*}
Observe that this value decreases with $n$. At $n=23$, this value goes below half. The following cell simulates this event and compares the associated empirical and theoretical probabilities. You can use the slider called "iterations" to vary the number of iterations performed by the code.
```
import itertools
import random
import matplotlib.pyplot as plt
import numpy as np
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
# Range of number of people
PEOPLE = np.arange(1, 26)
# Days in year
DAYS = 365
def prob_unique_birthdays(num_people):
'''
Returns the probability that all birthdays are unique, among a given
number of people with uniformly-distributed birthdays.
'''
return (np.arange(DAYS, DAYS - num_people, -1) / DAYS).prod()
def sample_unique_birthdays(num_people):
'''
Selects a sample of people with uniformly-distributed birthdays, and
returns True if all birthdays are unique (or False otherwise).
'''
bdays = np.random.randint(0, DAYS, size=num_people)
unique_bdays = np.unique(bdays)
return len(bdays) == len(unique_bdays)
def plot_probs(iterations):
'''
Plots a comparison of the probability of a group of people all having
unique birthdays, between the theoretical and empirical probabilities.
'''
sample_prob = [] # Empirical prob. of unique-birthday sample
prob = [] # Theoretical prob. of unique-birthday sample
# Compute data points to plot
np.random.seed(1)
for num_people in PEOPLE:
unique_count = sum(sample_unique_birthdays(num_people)
for i in range(iterations))
sample_prob.append(unique_count / iterations)
prob.append(prob_unique_birthdays(num_people))
# Plot results
plt.plot(PEOPLE, prob, 'k-', linewidth = 3.0, label='Theoretical probability')
plt.plot(PEOPLE, sample_prob, 'bo-', linewidth = 3.0, label='Empirical probability')
plt.gcf().set_size_inches(20, 10)
plt.axhline(0.5, color='red', linewidth = 4.0, label='0.5 threshold')
plt.xlabel('Number of people', fontsize = 18)
plt.ylabel('Probability of unique birthdays', fontsize = 18)
plt.grid()
plt.xticks(fontsize = 18)
plt.yticks(fontsize = 18)
plt.legend(fontsize = 18)
plt.show()
interact(plot_probs,
iterations=widgets.IntSlider(min=50, value = 500, max=5050, step=200),
continuous_update=False, layout='bottom');
```
## Conditional Probability
Oftentimes it is advantageous to infer the probability of certain events conditioned on other events. Say you want to estimate the probability that it will rain on a particular day. There are copious number of factors that affect rain on a particular day, but [certain clouds are good indicators of rains](https://www.nationalgeographic.com/science/earth/earths-atmosphere/clouds/). Then the question is how likely are clouds a precursor to rains? These types of problems are called [statistical classification](https://en.wikipedia.org/wiki/Statistical_classification), and concepts such as conditional probability and Bayes rule play an important role in its solution.
Dice, coins and cards are useful examples which we can use to understand the fundamental concepts of probability. There are even more interesting real world examples where we can apply these principles to. Let us analyze the [student alcohol consumption](https://www.kaggle.com/uciml/student-alcohol-consumption) dataset and see if we can infer any information regarding a student's performance relative to the time they spend studying.
<span style="color:red">NOTE:</span> Before continuing, please download the dataset and add it to the folder where this notebook resides. If necessary, you can also review our Pandas notebook.
```
import pandas as pd
import matplotlib.pyplot as plt
```
The dataset consists of two parts, `student-por.csv` and `student-mat.csv`, represents the students' performance in Portuguese and Math courses, respectively. We will consider the scores in the Portuguese courses, and leave the math courses optionally to you.
```
data_por = pd.read_csv("student-por.csv")
```
Of the dataset's [various attributes](https://www.kaggle.com/uciml/student-alcohol-consumption/home), we will use the following two
- `G3` - final grade related with the course subject, Math or Portuguese (numeric: from 0 to 20, output target)
- `studytime` - weekly study time (numeric: 1 : < 2 hours, 2 : 2 to 5 hours, 3 : 5 to 10 hours, or 4 : > 10 hours)
```
attributes = ["G3","studytime"]
data_por = data_por[attributes]
```
We are interested in the relationship between study-time and grade performance, but to start, let us view each attribute individually.
The probability that a student's study-time falls in an interval can be approximated by
$${P(\text{study interval}) = \frac{\text{Number of students with this study interval}}{Total\ number\ of\ students}}$$
This is an emperical estimate, and in later lectures we will reason why this is a valid assumption.
```
data_temp = data_por["studytime"].value_counts()
P_studytime = pd.DataFrame((data_temp/data_temp.sum()).sort_index())
P_studytime.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime.columns = ["Probability"]
P_studytime.columns.name = "Study Interval"
P_studytime.plot.bar(figsize=(12,9),fontsize=18)
plt.ylabel("Probability",fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
```
Note that the largest number of students studied between two and five hours, and the smallest studied over 10 hours.
Let us call scores of at least 15 "high". The probability of a student getting a high score can be approximated by
$$P(\text{high score}) = \frac{\text{Number of students with high scores}}{\text{Total number of students}}$$
```
data_temp = (data_por["G3"]>=15).value_counts()
P_score15_p = pd.DataFrame(data_temp/data_temp.sum())
P_score15_p.index = ["Low","High"]
P_score15_p.columns = ["Probability"]
P_score15_p.columns.name = "Score"
print(P_score15_p)
P_score15_p.plot.bar(figsize=(10,6),fontsize=16)
plt.xlabel("Score",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Proceeding to more interesting observations, suppose we want to find the probability of the various study-intervals when the student scored high. By conditional probability, this can be calculated by:
$$P(\text{study interval}\ |\ \text{highscore})=\frac{\text{Number of students with study interval AND highscore}}{\text{Total number of students with highscore}}$$
```
score = 15
data_temp = data_por.loc[data_por["G3"]>=score,"studytime"]
P_T_given_score15= pd.DataFrame((data_temp.value_counts()/data_temp.shape[0]).sort_index())
P_T_given_score15.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_T_given_score15.columns = ["Probability"]
print("Probability of study interval given that the student gets a highscore:")
P_T_given_score15.columns.name="Study Interval"
P_T_given_score15.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Studt interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
The above metric is something we can only calculate after the students have obtained their results. But how about the other way? What if we want to **predict** the probability that a student gets a score greater than 15 given that they studied for a particular period of time . Using the estimated values we can use the **Bayes rule** to calculate this probability.
$$P(\text{student getting a highscore}\ |\ \text{study interval})=\frac{P(\text{study interval}\ |\ \text{the student scored high})P(\text{highscore})}{P(\text{study interval})}$$
```
P_score15_given_T_p = P_T_given_score15 * P_score15_p.loc["High"] / P_studytime
print("Probability of high score given study interval :")
pd.DataFrame(P_score15_given_T_p).plot.bar(figsize=(12,9),fontsize=18).legend(loc="best")
plt.xlabel("Study interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
Do you find the results surprising? Roughly speaking, the longer students study, the more likely they are to score high. However, once they study over 10 hours, their chances of scoring high decline. You may want to check whether the same phenomenon occurs for the math scores too.
## Try it yourself
If interested, you can try the same analysis for the students math scores. For example, you can get the probabilities of the different study intervals.
```
data_math = pd.read_csv("student-mat.csv")
data_temp = data_math["studytime"].value_counts()
P_studytime_m = pd.DataFrame(data_temp/data_temp.sum())
P_studytime_m.index = ["< 2 hours","2 to 5 hours","5 to 10 hours","> 10 hours"]
P_studytime_m.columns = ["Probability"]
P_studytime_m.columns.name = "Study Interval"
P_studytime_m.plot.bar(figsize=(12,9),fontsize=16)
plt.xlabel("Study Interval",fontsize=18)
plt.ylabel("Probability",fontsize=18)
```
|
github_jupyter
|
# Train a basic TensorFlow Lite for Microcontrollers model
This notebook demonstrates the process of training a 2.5 kB model using TensorFlow and converting it for use with TensorFlow Lite for Microcontrollers.
Deep learning networks learn to model patterns in underlying data. Here, we're going to train a network to model data generated by a [sine](https://en.wikipedia.org/wiki/Sine) function. This will result in a model that can take a value, `x`, and predict its sine, `y`.
The model created in this notebook is used in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) example for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview).
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/train_hello_world_model.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
**Training is much faster using GPU acceleration.** Before you proceed, ensure you are using a GPU runtime by going to **Runtime -> Change runtime type** and set **Hardware accelerator: GPU**.
## Configure Defaults
```
# Define paths to model files
import os
MODELS_DIR = 'models/'
if not os.path.exists(MODELS_DIR):
os.mkdir(MODELS_DIR)
MODEL_TF = MODELS_DIR + 'model.pb'
MODEL_NO_QUANT_TFLITE = MODELS_DIR + 'model_no_quant.tflite'
MODEL_TFLITE = MODELS_DIR + 'model.tflite'
MODEL_TFLITE_MICRO = MODELS_DIR + 'model.cc'
```
## Setup Environment
Install Dependencies
```
! pip install -q tensorflow==2
```
Set Seed for Repeatable Results
```
# Set a "seed" value, so we get the same random numbers each time we run this
# notebook for reproducible results.
# Numpy is a math library
import numpy as np
np.random.seed(1) # numpy seed
# TensorFlow is an open source machine learning library
import tensorflow as tf
tf.random.set_seed(1) # tensorflow global random seed
```
Import Dependencies
```
# Keras is TensorFlow's high-level API for deep learning
from tensorflow import keras
# Matplotlib is a graphing library
import matplotlib.pyplot as plt
# Math is Python's math library
import math
```
## Dataset
### 1. Generate Data
The code in the following cell will generate a set of random `x` values, calculate their sine values, and display them on a graph.
```
# Number of sample datapoints
SAMPLES = 1000
# Generate a uniformly distributed set of random numbers in the range from
# 0 to 2π, which covers a complete sine wave oscillation
x_values = np.random.uniform(
low=0, high=2*math.pi, size=SAMPLES).astype(np.float32)
# Shuffle the values to guarantee they're not in order
np.random.shuffle(x_values)
# Calculate the corresponding sine values
y_values = np.sin(x_values).astype(np.float32)
# Plot our data. The 'b.' argument tells the library to print blue dots.
plt.plot(x_values, y_values, 'b.')
plt.show()
```
### 2. Add Noise
Since it was generated directly by the sine function, our data fits a nice, smooth curve.
However, machine learning models are good at extracting underlying meaning from messy, real world data. To demonstrate this, we can add some noise to our data to approximate something more life-like.
In the following cell, we'll add some random noise to each value, then draw a new graph:
```
# Add a small random number to each y value
y_values += 0.1 * np.random.randn(*y_values.shape)
# Plot our data
plt.plot(x_values, y_values, 'b.')
plt.show()
```
### 3. Split the Data
We now have a noisy dataset that approximates real world data. We'll be using this to train our model.
To evaluate the accuracy of the model we train, we'll need to compare its predictions to real data and check how well they match up. This evaluation happens during training (where it is referred to as validation) and after training (referred to as testing) It's important in both cases that we use fresh data that was not already used to train the model.
The data is split as follows:
1. Training: 60%
2. Validation: 20%
3. Testing: 20%
The following code will split our data and then plots each set as a different color:
```
# We'll use 60% of our data for training and 20% for testing. The remaining 20%
# will be used for validation. Calculate the indices of each section.
TRAIN_SPLIT = int(0.6 * SAMPLES)
TEST_SPLIT = int(0.2 * SAMPLES + TRAIN_SPLIT)
# Use np.split to chop our data into three parts.
# The second argument to np.split is an array of indices where the data will be
# split. We provide two indices, so the data will be divided into three chunks.
x_train, x_test, x_validate = np.split(x_values, [TRAIN_SPLIT, TEST_SPLIT])
y_train, y_test, y_validate = np.split(y_values, [TRAIN_SPLIT, TEST_SPLIT])
# Double check that our splits add up correctly
assert (x_train.size + x_validate.size + x_test.size) == SAMPLES
# Plot the data in each partition in different colors:
plt.plot(x_train, y_train, 'b.', label="Train")
plt.plot(x_test, y_test, 'r.', label="Test")
plt.plot(x_validate, y_validate, 'y.', label="Validate")
plt.legend()
plt.show()
```
## Training
### 1. Design the Model
We're going to build a simple neural network model that will take an input value (in this case, `x`) and use it to predict a numeric output value (the sine of `x`). This type of problem is called a _regression_. It will use _layers_ of _neurons_ to attempt to learn any patterns underlying the training data, so it can make predictions.
To begin with, we'll define two layers. The first layer takes a single input (our `x` value) and runs it through 8 neurons. Based on this input, each neuron will become _activated_ to a certain degree based on its internal state (its _weight_ and _bias_ values). A neuron's degree of activation is expressed as a number.
The activation numbers from our first layer will be fed as inputs to our second layer, which is a single neuron. It will apply its own weights and bias to these inputs and calculate its own activation, which will be output as our `y` value.
**Note:** To learn more about how neural networks function, you can explore the [Learn TensorFlow](https://codelabs.developers.google.com/codelabs/tensorflow-lab1-helloworld) codelabs.
The code in the following cell defines our model using [Keras](https://www.tensorflow.org/guide/keras), TensorFlow's high-level API for creating deep learning networks. Once the network is defined, we _compile_ it, specifying parameters that determine how it will be trained:
```
# We'll use Keras to create a simple model architecture
model_1 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 8 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_1.add(keras.layers.Dense(8, activation='relu', input_shape=(1,)))
# Final layer is a single neuron, since we want to output a single value
model_1.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_1.compile(optimizer='adam', loss='mse', metrics=['mae'])
```
### 2. Train the Model
Once we've defined the model, we can use our data to _train_ it. Training involves passing an `x` value into the neural network, checking how far the network's output deviates from the expected `y` value, and adjusting the neurons' weights and biases so that the output is more likely to be correct the next time.
Training runs this process on the full dataset multiple times, and each full run-through is known as an _epoch_. The number of epochs to run during training is a parameter we can set.
During each epoch, data is run through the network in multiple _batches_. Each batch, several pieces of data are passed into the network, producing output values. These outputs' correctness is measured in aggregate and the network's weights and biases are adjusted accordingly, once per batch. The _batch size_ is also a parameter we can set.
The code in the following cell uses the `x` and `y` values from our training data to train the model. It runs for 500 _epochs_, with 64 pieces of data in each _batch_. We also pass in some data for _validation_. As you will see when you run the cell, training can take a while to complete:
```
# Train the model on our training data while validating on our validation set
history_1 = model_1.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
```
### 3. Plot Metrics
**1. Mean Squared Error**
During training, the model's performance is constantly being measured against both our training data and the validation data that we set aside earlier. Training produces a log of data that tells us how the model's performance changed over the course of the training process.
The following cells will display some of that data in a graphical form:
```
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_1.history['loss']
val_loss = history_1.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.plot(epochs, loss, 'g.', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
```
The graph shows the _loss_ (or the difference between the model's predictions and the actual data) for each epoch. There are several ways to calculate loss, and the method we have used is _mean squared error_. There is a distinct loss value given for the training and the validation data.
As we can see, the amount of loss rapidly decreases over the first 25 epochs, before flattening out. This means that the model is improving and producing more accurate predictions!
Our goal is to stop training when either the model is no longer improving, or when the _training loss_ is less than the _validation loss_, which would mean that the model has learned to predict the training data so well that it can no longer generalize to new data.
To make the flatter part of the graph more readable, let's skip the first 50 epochs:
```
# Exclude the first few epochs so the graph is easier to read
SKIP = 50
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
```
From the plot, we can see that loss continues to reduce until around 200 epochs, at which point it is mostly stable. This means that there's no need to train our network beyond 200 epochs.
However, we can also see that the lowest loss value is still around 0.155. This means that our network's predictions are off by an average of ~15%. In addition, the validation loss values jump around a lot, and is sometimes even higher.
**2. Mean Absolute Error**
To gain more insight into our model's performance we can plot some more data. This time, we'll plot the _mean absolute error_, which is another way of measuring how far the network's predictions are from the actual numbers:
```
plt.clf()
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_1.history['mae']
val_mae = history_1.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.show()
```
This graph of _mean absolute error_ tells another story. We can see that training data shows consistently lower error than validation data, which means that the network may have _overfit_, or learned the training data so rigidly that it can't make effective predictions about new data.
In addition, the mean absolute error values are quite high, ~0.305 at best, which means some of the model's predictions are at least 30% off. A 30% error means we are very far from accurately modelling the sine wave function.
**3. Actual vs Predicted Outputs**
To get more insight into what is happening, let's check its predictions against the test dataset we set aside earlier:
```
# Calculate and print the loss on our test dataset
loss = model_1.evaluate(x_test, y_test)
# Make predictions based on our test dataset
predictions = model_1.predict(x_test)
# Graph the predictions against the actual values
plt.clf()
plt.title('Comparison of predictions and actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_test, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
```
Oh dear! The graph makes it clear that our network has learned to approximate the sine function in a very limited way.
The rigidity of this fit suggests that the model does not have enough capacity to learn the full complexity of the sine wave function, so it's only able to approximate it in an overly simplistic way. By making our model bigger, we should be able to improve its performance.
## Training a Larger Model
### 1. Design the Model
To make our model bigger, let's add an additional layer of neurons. The following cell redefines our model in the same way as earlier, but with 16 neurons in the first layer and an additional layer of 16 neurons in the middle:
```
model_2 = tf.keras.Sequential()
# First layer takes a scalar input and feeds it through 16 "neurons". The
# neurons decide whether to activate based on the 'relu' activation function.
model_2.add(keras.layers.Dense(16, activation='relu', input_shape=(1,)))
# The new second layer may help the network learn more complex representations
model_2.add(keras.layers.Dense(16, activation='relu'))
# Final layer is a single neuron, since we want to output a single value
model_2.add(keras.layers.Dense(1))
# Compile the model using a standard optimizer and loss function for regression
model_2.compile(optimizer='adam', loss='mse', metrics=['mae'])
```
### 2. Train the Model ###
We'll now train the new model.
```
history_2 = model_2.fit(x_train, y_train, epochs=500, batch_size=64,
validation_data=(x_validate, y_validate))
```
### 3. Plot Metrics
Each training epoch, the model prints out its loss and mean absolute error for training and validation. You can read this in the output above (note that your exact numbers may differ):
```
Epoch 500/500
600/600 [==============================] - 0s 51us/sample - loss: 0.0118 - mae: 0.0873 - val_loss: 0.0105 - val_mae: 0.0832
```
You can see that we've already got a huge improvement - validation loss has dropped from 0.15 to 0.01, and validation MAE has dropped from 0.33 to 0.08.
The following cell will print the same graphs we used to evaluate our original model, but showing our new training history:
```
# Draw a graph of the loss, which is the distance between
# the predicted and actual values during training and validation.
loss = history_2.history['loss']
val_loss = history_2.history['val_loss']
epochs = range(1, len(loss) + 1)
# Exclude the first few epochs so the graph is easier to read
SKIP = 100
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(epochs[SKIP:], loss[SKIP:], 'g.', label='Training loss')
plt.plot(epochs[SKIP:], val_loss[SKIP:], 'b.', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
# Draw a graph of mean absolute error, which is another way of
# measuring the amount of error in the prediction.
mae = history_2.history['mae']
val_mae = history_2.history['val_mae']
plt.plot(epochs[SKIP:], mae[SKIP:], 'g.', label='Training MAE')
plt.plot(epochs[SKIP:], val_mae[SKIP:], 'b.', label='Validation MAE')
plt.title('Training and validation mean absolute error')
plt.xlabel('Epochs')
plt.ylabel('MAE')
plt.legend()
plt.tight_layout()
```
Great results! From these graphs, we can see several exciting things:
* The overall loss and MAE are much better than our previous network
* Metrics are better for validation than training, which means the network is not overfitting
The reason the metrics for validation are better than those for training is that validation metrics are calculated at the end of each epoch, while training metrics are calculated throughout the epoch, so validation happens on a model that has been trained slightly longer.
This all means our network seems to be performing well! To confirm, let's check its predictions against the test dataset we set aside earlier:
```
# Calculate and print the loss on our test dataset
loss = model_2.evaluate(x_test, y_test)
# Make predictions based on our test dataset
predictions = model_2.predict(x_test)
# Graph the predictions against the actual values
plt.clf()
plt.title('Comparison of predictions and actual values')
plt.plot(x_test, y_test, 'b.', label='Actual')
plt.plot(x_test, predictions, 'r.', label='Predicted')
plt.legend()
plt.show()
```
Much better! The evaluation metrics we printed show that the model has a low loss and MAE on the test data, and the predictions line up visually with our data fairly well.
The model isn't perfect; its predictions don't form a smooth sine curve. For instance, the line is almost straight when `x` is between 4.2 and 5.2. If we wanted to go further, we could try further increasing the capacity of the model, perhaps using some techniques to defend from overfitting.
However, an important part of machine learning is knowing when to quit, and this model is good enough for our use case - which is to make some LEDs blink in a pleasing pattern.
## Generate a TensorFlow Lite Model
### 1. Generate Models with or without Quantization
We now have an acceptably accurate model. We'll use the [TensorFlow Lite Converter](https://www.tensorflow.org/lite/convert) to convert the model into a special, space-efficient format for use on memory-constrained devices.
Since this model is going to be deployed on a microcontroller, we want it to be as tiny as possible! One technique for reducing the size of models is called [quantization](https://www.tensorflow.org/lite/performance/post_training_quantization) while converting the model. It reduces the precision of the model's weights, and possibly the activations (output of each layer) as well, which saves memory, often without much impact on accuracy. Quantized models also run faster, since the calculations required are simpler.
*Note: Currently, TFLite Converter produces TFlite models with float interfaces (input and output ops are always float). This is a blocker for users who require TFlite models with pure int8 or uint8 inputs/outputs. Refer to https://github.com/tensorflow/tensorflow/issues/38285*
In the following cell, we'll convert the model twice: once with quantization, once without.
```
# Convert the model to the TensorFlow Lite format without quantization
converter = tf.lite.TFLiteConverter.from_keras_model(model_2)
model_no_quant_tflite = converter.convert()
# # Save the model to disk
open(MODEL_NO_QUANT_TFLITE, "wb").write(model_no_quant_tflite)
# Convert the model to the TensorFlow Lite format with quantization
def representative_dataset():
for i in range(500):
yield([x_train[i].reshape(1, 1)])
# Set the optimization flag.
converter.optimizations = [tf.lite.Optimize.DEFAULT]
# Enforce full-int8 quantization (except inputs/outputs which are always float)
converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS_INT8]
# Provide a representative dataset to ensure we quantize correctly.
converter.representative_dataset = representative_dataset
model_tflite = converter.convert()
# Save the model to disk
open(MODEL_TFLITE, "wb").write(model_tflite)
```
### 2. Compare Model Sizes
```
import os
model_no_quant_size = os.path.getsize(MODEL_NO_QUANT_TFLITE)
print("Model is %d bytes" % model_no_quant_size)
model_size = os.path.getsize(MODEL_TFLITE)
print("Quantized model is %d bytes" % model_size)
difference = model_no_quant_size - model_size
print("Difference is %d bytes" % difference)
```
Our quantized model is only 224 bytes smaller than the original version, which only a tiny reduction in size! At around 2.5 kilobytes, this model is already so small that the weights make up only a small fraction of the overall size, meaning quantization has little effect.
More complex models have many more weights, meaning the space saving from quantization will be much higher, approaching 4x for most sophisticated models.
Regardless, our quantized model will take less time to execute than the original version, which is important on a tiny microcontroller!
### 3. Test the Models
To prove these models are still accurate after conversion and quantization, we'll use both of them to make predictions and compare these against our test results:
```
# Instantiate an interpreter for each model
model_no_quant = tf.lite.Interpreter(MODEL_NO_QUANT_TFLITE)
model = tf.lite.Interpreter(MODEL_TFLITE)
# Allocate memory for each model
model_no_quant.allocate_tensors()
model.allocate_tensors()
# Get the input and output tensors so we can feed in values and get the results
model_no_quant_input = model_no_quant.tensor(model_no_quant.get_input_details()[0]["index"])
model_no_quant_output = model_no_quant.tensor(model_no_quant.get_output_details()[0]["index"])
model_input = model.tensor(model.get_input_details()[0]["index"])
model_output = model.tensor(model.get_output_details()[0]["index"])
# Create arrays to store the results
model_no_quant_predictions = np.empty(x_test.size)
model_predictions = np.empty(x_test.size)
# Run each model's interpreter for each value and store the results in arrays
for i in range(x_test.size):
model_no_quant_input().fill(x_test[i])
model_no_quant.invoke()
model_no_quant_predictions[i] = model_no_quant_output()[0]
model_input().fill(x_test[i])
model.invoke()
model_predictions[i] = model_output()[0]
# See how they line up with the data
plt.clf()
plt.title('Comparison of various models against actual values')
plt.plot(x_test, y_test, 'bo', label='Actual values')
plt.plot(x_test, predictions, 'ro', label='Original predictions')
plt.plot(x_test, model_no_quant_predictions, 'bx', label='Lite predictions')
plt.plot(x_test, model_predictions, 'gx', label='Lite quantized predictions')
plt.legend()
plt.show()
```
We can see from the graph that the predictions for the original model, the converted model, and the quantized model are all close enough to be indistinguishable. This means that our quantized model is ready to use!
## Generate a TensorFlow Lite for Microcontrollers Model
Convert the TensorFlow Lite quantized model into a C source file that can be loaded by TensorFlow Lite for Microcontrollers.
```
# Install xxd if it is not available
!apt-get update && apt-get -qq install xxd
# Convert to a C source file
!xxd -i {MODEL_TFLITE} > {MODEL_TFLITE_MICRO}
# Update variable names
REPLACE_TEXT = MODEL_TFLITE.replace('/', '_').replace('.', '_')
!sed -i 's/'{REPLACE_TEXT}'/g_model/g' {MODEL_TFLITE_MICRO}
```
## Deploy to a Microcontroller
Follow the instructions in the [hello_world](https://github.com/tensorflow/tensorflow/tree/master/tensorflow/lite/micro/examples/hello_world) README.md for [TensorFlow Lite for MicroControllers](https://www.tensorflow.org/lite/microcontrollers/overview) to deploy this model on a specific microcontroller.
**Reference Model:** If you have not modified this notebook, you can follow the instructions as is, to deploy the model. Refer to the [`hello_world/train/models`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/train/models) directory to access the models generated in this notebook.
**New Model:** If you have generated a new model, then update the values assigned to the variables defined in [`hello_world/model.cc`](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/micro/examples/hello_world/model.cc) with values displayed after running the following cell.
```
# Print the C source file
!cat {MODEL_TFLITE_MICRO}
```
|
github_jupyter
|
## Conceptual description
As people interact, they tend to become more alike in their beliefs, attitudes and behaviour. In "The Dissemination of Culture: A Model with Local Convergence and Global Polarization" (1997), Robert Axelrod presents an agent-based model to explain cultural diffusion. Analogous to Schelling's segregation model, the key to this conceptualization is the emergence of polarization from the interaction of individual agents. The basic premise is that the more similar an actor is to a neighbor, the more likely that that actor will adopt one of the neighbor's traits.
In the model below, this is implemented by initializing the model by filling an excel-like grid with agents with random values [0,1] for each of four traits (music, sports, favorite color and drink).
Each step, each agent (in random order) chooses a random neighbor from the 8 neighbors proportionaly to how similar it is to each of its neighbors, and adopts one randomly selected differing trait from this neighbor. Similarity between any two agents is calculated by 1 - euclidian distance over the four traits.
To visualize the model, the four traits are transformed into 'RGBA' (Red-Green-Blue-Alpha) values; i.e. a color and an opacity. The visualizations below show the clusters of homogeneity being formed.
```
import random
import numpy as np
from mesa import Model, Agent
import mesa.time as time
from mesa.time import RandomActivation
from mesa.space import SingleGrid
from mesa.datacollection import DataCollector
class CulturalDiff(Model):
"""
Model class for the Schelling segregation model.
Parameters
----------
height : int
height of grid
width : int
height of grid
seed : int
random seed
Attributes
----------
height : int
width : int
density : float
schedule : RandomActivation instance
grid : SingleGrid instance
"""
def __init__(self, height=20, width=20, seed=None):
__init__(seed=seed)
self.height = height
self.width = width
self.schedule = time.BaseScheduler(self)
self.grid = SingleGrid(width, height, torus=True)
self.datacollector = DataCollector(model_reporters={'diversity':count_nr_cultures})
# Fill grid with agents with random traits
# Note that this implementation does not guarantee some set distribution of traits.
# Therefore, examining the effect of minorities etc is not facilitated.
for cell in self.grid.coord_iter():
agent = CulturalDiffAgent(cell, self)
self.grid.position_agent(agent, cell)
self.schedule.add(agent)
def step(self):
"""
Run one step of the model.
"""
self.datacollector.collect(self)
self.schedule.step
class CulturalDiffAgent(Agent):
"""
Schelling segregation agent
Parameters
----------
pos : tuple of 2 ints
the x,y coordinates in the grid
model : Model instance
"""
def __init__(self, pos, model):
super().__init__(pos, model)
self.pos = pos
self.profile = np.asarray([random.random() for _ in range(4)])
def step(self):
#For each neighbor, calculate the euclidian distance
# similarity is 1 - distance
neighbor_similarity_dict = []
for neighbor in self.model.grid.neighbor_iter(self.pos, moore=True):
neighbor_similarity = 1-np.linalg.norm(self.profile-neighbor.profile)
neighbor_similarity_dict[neighbor] = neighbor_similarity
# Proportional to this similarity, pick a 'random' neighbor to interact with
neighbor_to_interact = self.random.choices(list(neighbor_similarity_dict.keys()),
weights=neighbor_similarity_dict.values())[0]
# Select a trait that differs between the selected neighbor and self and change that trait in self
# we are using some numpy boolean indexing to make this short and easy
not_same_features = self.profile != neighbor_to_interact.profile
if np.any(not_same_features):
index_for_trait = self.random.choice(np.nonzero(not_same_features)[0])
self.profile[index_for_trait] = neighbor_to_interact.profile[index_for_trait]
def count_nr_cultures(model):
cultures = set()
for (cell, x,y) in model.grid.coord_iter():
if cell:
cultures.add(tuple(cell.profile))
return len(cultures)
```
# Visualization
## Static images
Visualization of this model are static images. A visualization after initialization, after 20 steps, after 50 steps, and after 200 steps is presented.
### After initialization
```
model = CulturalDiff(seed=123456789)
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import seaborn as sns
import pandas as pd
def plot_model(model, ax):
grid = np.zeros((model.height, model.width, 4))
for (cell, i, j) in model.grid.coord_iter():
color = [0,0,0,0] #in case not every cell is filled, the default colour is white
if cell is not None:
color = cell.profile
grid[i,j] = color
plt.imshow(grid)
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 20 steps
```
for i in range(20):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 50 steps
```
for i in range(30):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
### After 200 steps
```
for i in range(150):
model.step()
fig, ax = plt.subplots()
plot_model(model, ax)
plt.show()
```
|
github_jupyter
|
## Imports
```
import numpy as np
import matplotlib.pyplot as plt
%tensorflow_version 2.x
import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential, Model
from keras.layers import Flatten, Dense, LSTM, GRU, SimpleRNN, RepeatVector, Input
from keras import backend as K
from keras.utils.vis_utils import plot_model
import keras.regularizers
import keras.optimizers
```
## Load data
```
!git clone https://github.com/luisferuam/DLFBT-LAB
f = open('DLFBT-LAB/data/el_quijote.txt', 'r')
quijote = f.read()
f.close()
print(len(quijote))
```
## Input/output sequences
```
quijote_x = quijote[:-1]
quijote_y = quijote[1:]
```
## Some utility functions
```
def one_hot_encoding(data):
symbols = np.unique(data)
char_to_ix = {s: i for i, s in enumerate(symbols)}
ix_to_char = {i: s for i, s in enumerate(symbols)}
data_numeric = np.zeros(data.shape)
for s in symbols:
data_numeric[data == s] = char_to_ix[s]
one_hot_values = np.array(list(ix_to_char.keys()))
data_one_hot = 1 * (data_numeric[:, :, None] == one_hot_values[None, None, :])
return data_one_hot, symbols
def prepare_sequences(x, y, wlen):
(n, dim) = x.shape
nchunks = dim//wlen
xseq = np.array(np.split(x, nchunks, axis=1))
xseq = xseq.reshape((n*nchunks, wlen))
yseq = np.array(np.split(y, nchunks, axis=1))
yseq = yseq.reshape((n*nchunks, wlen))
return xseq, yseq
def get_data_from_strings(data_str_x, data_str_y, wlen):
"""
Inputs:
data_str_x: list of input strings
data_str_y: list of output strings
wlen: window length
Returns:
input/output data organized in batches
"""
# The batch size is the number of input/output strings:
batch_size = len(data_str_x)
# Clip all strings at length equal to the largest multiple of wlen that is
# lower than all string lengths:
minlen = len(data_str_x[0])
for c in data_str_x:
if len(c) < minlen:
minlen = len(c)
while minlen % wlen != 0:
minlen -=1
data_str_x = [c[:minlen] for c in data_str_x]
data_str_y = [c[:minlen] for c in data_str_y]
# Transform strings to numpy array:
x = np.array([[c for c in m] for m in data_str_x])
y = np.array([[c for c in m] for m in data_str_y])
# Divide into batches:
xs, ys = prepare_sequences(x, y, wlen)
# Get one-hot encoding:
xs_one_hot, xs_symbols = one_hot_encoding(xs)
ys_one_hot, ys_symbols = one_hot_encoding(ys)
# Get sparse encoding:
xs_sparse = np.argmax(xs_one_hot, axis=2)
ys_sparse = np.argmax(ys_one_hot, axis=2)
# Return:
return xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols
```
## Batches for training and test
```
batch_size = 32
seq_len = 50
longitud = len(quijote_x) // batch_size
print(longitud)
print(longitud*batch_size)
qx = [quijote_x[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
qy = [quijote_y[i*(batch_size+longitud):(i+1)*(batch_size+longitud)] for i in range(batch_size)]
xs_one_hot, ys_one_hot, xs_sparse, ys_sparse, xs_symbols, ys_symbols = get_data_from_strings(qx, qy, seq_len)
char_to_ix = {s: i for i, s in enumerate(xs_symbols)}
ix_to_char = {i: s for i, s in enumerate(ys_symbols)}
print(xs_symbols)
print(xs_symbols.shape)
print(ys_symbols)
print(ys_symbols.shape)
xs_symbols == ys_symbols
vocab_len = xs_symbols.shape[0]
print(vocab_len)
num_batches = xs_one_hot.shape[0] / batch_size
print(xs_one_hot.shape[0])
print(batch_size)
print(num_batches)
```
## Training/test partition
```
print(xs_one_hot.shape)
print(ys_one_hot.shape)
print(xs_sparse.shape)
print(ys_sparse.shape)
ntrain = int(num_batches*0.75)*batch_size
xs_one_hot_train = xs_one_hot[:ntrain]
ys_one_hot_train = ys_one_hot[:ntrain]
xs_sparse_train = xs_sparse[:ntrain]
ys_sparse_train = ys_sparse[:ntrain]
xs_one_hot_test = xs_one_hot[ntrain:]
ys_one_hot_test = ys_one_hot[ntrain:]
xs_sparse_test = xs_sparse[ntrain:]
ys_sparse_test = ys_sparse[ntrain:]
print(xs_one_hot_train.shape)
print(xs_one_hot_test.shape)
```
## Function to evaluate the model on test data
```
def evaluate_network(model, x, y, batch_size):
mean_loss = []
mean_acc = []
for i in range(0, x.shape[0], batch_size):
batch_data_x = x[i:i+batch_size, :, :]
batch_data_y = y[i:i+batch_size, :, :]
loss, acc = model.test_on_batch(batch_data_x, batch_data_y)
mean_loss.append(loss)
mean_acc.append(acc)
return np.array(mean_loss).mean(), np.array(mean_acc).mean()
```
## Function that copies the weigths from ``source_model`` to ``dest_model``
```
def copia_pesos(source_model, dest_model):
for source_layer, dest_layer in zip(source_model.layers, dest_model.layers):
dest_layer.set_weights(source_layer.get_weights())
```
## Function that samples probabilities from model
```
def categorical(p):
return (p.cumsum(-1) >= np.random.uniform(size=p.shape[:-1])[..., None]).argmax(-1)
```
## Function that generates text
```
def genera_texto(first_char, num_chars):
texto = "" + first_char
next_char = first_char
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
for i in range(num_chars):
probs = model2.predict_on_batch(next_one_hot)
next_ix = categorical(probs.ravel())
next_char = ix_to_char[next_ix]
next_one_hot = np.zeros(vocab_len)
next_one_hot[char_to_ix[next_char]] = 1.
next_one_hot = next_one_hot[None, None, :]
texto += next_char
return texto
```
## Network definition
```
K.clear_session()
nunits = 200
model1 = Sequential()
#model1.add(SimpleRNN(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model1.add(LSTM(nunits, batch_input_shape=(batch_size, seq_len, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model1.add(Dense(vocab_len, activation='softmax'))
model1.summary()
```
## Network that generates text
```
model2 = Sequential()
#model2.add(SimpleRNN(nunits, batch_input_shape=(1, 1, vocab_len),
# return_sequences=True, stateful=True, unroll=True))
model2.add(LSTM(nunits, batch_input_shape=(1, 1, vocab_len),
return_sequences=True, stateful=True, unroll=True))
model2.add(Dense(vocab_len, activation='softmax'))
model2.summary()
```
## Training
```
#learning_rate = 0.5 # Probar entre 0.05 y 5
#clip = 0.005 # Probar entre 0.0005 y 0.05
learning_rate = 0.5
clip = 0.002
#model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.SGD(lr=learning_rate, clipvalue=clip), metrics=['accuracy'])
model1.compile(loss='categorical_crossentropy', optimizer=keras.optimizers.Adam(), metrics=['accuracy'])
num_epochs = 500 # Dejar en 100, la red tarda unos 10 minutos
model1_loss = np.zeros(num_epochs)
model1_acc = np.zeros(num_epochs)
model1_loss_test = np.zeros(num_epochs)
model1_acc_test = np.zeros(num_epochs)
for epoch in range(num_epochs):
model1.reset_states()
mean_tr_loss = []
mean_tr_acc = []
for i in range(0, xs_one_hot_train.shape[0], batch_size):
batch_data_x = xs_one_hot_train[i:i+batch_size, :, :]
batch_data_y = ys_one_hot_train[i:i+batch_size, :, :]
tr_loss, tr_acc = model1.train_on_batch(batch_data_x, batch_data_y)
mean_tr_loss.append(tr_loss)
mean_tr_acc.append(tr_acc)
model1_loss[epoch] = np.array(mean_tr_loss).mean()
model1_acc[epoch] = np.array(mean_tr_acc).mean()
model1.reset_states()
model1_loss_test[epoch], model1_acc_test[epoch] = evaluate_network(model1, xs_one_hot_test, ys_one_hot_test, batch_size)
print("\rTraining epoch: %d / %d" % (epoch+1, num_epochs), end="")
print(", loss = %f, acc = %f" % (model1_loss[epoch], model1_acc[epoch]), end="")
print(", test loss = %f, test acc = %f" % (model1_loss_test[epoch], model1_acc_test[epoch]), end="")
# Genero texto:
copia_pesos(model1, model2)
model2.reset_states()
print(" >>> %s" % genera_texto('e', 200)) #, end="")
```
## Plots
```
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(model1_loss, label="train")
plt.plot(model1_loss_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(model1_acc, label="train")
plt.plot(model1_acc_test, label="test")
plt.grid(True)
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('accuracy')
plt.legend()
plt.show()
model2.reset_states()
print(genera_texto('A', 1000))
```
|
github_jupyter
|
# HRF downsampling
This short notebook is why (often) we have to downsample our predictors after convolution with an HRF.
```
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from nistats.hemodynamic_models import glover_hrf
%matplotlib inline
```
First, let's define our data. Suppose we did an experiment where we show subjects images for 4 seconds. The onset of the stimuli we're drawn semi-randomly: every 15 seconds but +/- 3 to 5 seconds. In total, the experiment lasted 5 minutes. The fMRI data we acquired during the experiment had a TR of 2 seconds.
```
TR = 2 # seconds
time_exp = 5*60 # seconds
number_of_events = 10
duration_of_events = 4
onsets_sec = np.arange(0, time_exp, 15) + np.random.uniform(3, 5, 20)
onsets_sec = np.round(onsets_sec, 3)
print("Onset events: %s" % (onsets_sec,))
```
As you can see, the onsets are not neatly synchronized to the time that we acquired the different volumes of our fMRI data, which are (with a TR of 2): `[0, 2, 4, 6, ..., 298]` seconds. In other words, the data (onsets) of our experimental paradigm are on a different scale (i.e., with a precision of milliseconds) than our fMRI data (i.e., with a precision/temporal resolution of 2 seconds)!
So, what should we do? One thing we *could* do, is to round each onset to the nearest TR. So, we'll pretend that for example an onset at 2.9 seconds happened at 2 seconds. This, however, is of course not very precise and, fortunately, not necessary. Another, and better, option is to create your design and convolve your regressors with an HRF at the time scale and temporal resolution of your onsets and *then*, as a last step, downsample your regressors to the temporal resolution of your fMRI data (which is defined by your TR).
So, given that our onsets have been measured on a millisecond scale, let's create our design with this temporal resolution. First, we'll create an empty stimulus-vector with a length of the time of the experiment in seconds times 1000 (because we want it in milliseconds):
```
stim_vector = np.zeros(time_exp * 1000)
print("Length of stim vector: %i" % stim_vector.size)
```
Now, let's convert our onsets to milliseconds:
```
onsets_msec = onsets_sec * 1000
```
Now we can define within our `stim_vector` when each onset happened. Importantly, let's assume that each stimulus lasted 4 seconds.
```
for onset in onsets_msec:
onset = int(onset)
stim_vector[onset:(onset+duration_of_events*1000)] = 1
```
Alright, let's plot it:
```
plt.plot(stim_vector)
plt.xlim(0, time_exp*1000)
plt.xlabel('Time (milliseconds)')
plt.ylabel('Activity (A.U.)')
sns.despine()
plt.show()
```
Sweet, now let's define an HRF:
```
hrf = glover_hrf(tr=TR, time_length=32, oversampling=TR*1000)
hrf = hrf / hrf.max()
plt.plot(hrf)
plt.xlabel('Time (milliseconds)')
plt.ylabel('Activity (A.U.)')
sns.despine()
plt.show()
```
Let's convolve!
```
conv = np.convolve(stim_vector, hrf)[:stim_vector.size]
conv = conv / conv.max()
conv_ds = conv[::TR*1000]
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
plt.plot(conv)
plt.subplot(1, 2, 2)
plt.plot(conv_ds)
plt.tight_layout()
sns.despine()
plt.show()
```
|
github_jupyter
|
# Table of Contents
<p><div class="lev1 toc-item"><a href="#Linear-Regression-problem" data-toc-modified-id="Linear-Regression-problem-1"><span class="toc-item-num">1 </span>Linear Regression problem</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent" data-toc-modified-id="Gradient-Descent-2"><span class="toc-item-num">2 </span>Gradient Descent</a></div><div class="lev1 toc-item"><a href="#Gradient-Descent---Classification" data-toc-modified-id="Gradient-Descent---Classification-3"><span class="toc-item-num">3 </span>Gradient Descent - Classification</a></div><div class="lev1 toc-item"><a href="#Gradient-descent-with-numpy" data-toc-modified-id="Gradient-descent-with-numpy-4"><span class="toc-item-num">4 </span>Gradient descent with numpy</a></div>
```
%matplotlib inline
from fastai.learner import *
```
In this part of the lecture we explain Stochastic Gradient Descent (SGD) which is an **optimization** method commonly used in neural networks. We will illustrate the concepts with concrete examples.
# Linear Regression problem
The goal of linear regression is to fit a line to a set of points.
```
# Here we generate some fake data
def lin(a,b,x): return a*x+b
def gen_fake_data(n, a, b):
x = s = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, y
x, y = gen_fake_data(50, 3., 8.)
plt.scatter(x,y, s=8); plt.xlabel("x"); plt.ylabel("y");
```
You want to find **parameters** (weights) $a$ and $b$ such that you minimize the *error* between the points and the line $a\cdot x + b$. Note that here $a$ and $b$ are unknown. For a regression problem the most common *error function* or *loss function* is the **mean squared error**.
```
def mse(y_hat, y): return ((y_hat - y) ** 2).mean()
```
Suppose we believe $a = 10$ and $b = 5$ then we can compute `y_hat` which is our *prediction* and then compute our error.
```
y_hat = lin(10,5,x)
mse(y_hat, y)
def mse_loss(a, b, x, y): return mse(lin(a,b,x), y)
mse_loss(10, 5, x, y)
```
So far we have specified the *model* (linear regression) and the *evaluation criteria* (or *loss function*). Now we need to handle *optimization*; that is, how do we find the best values for $a$ and $b$? How do we find the best *fitting* linear regression.
# Gradient Descent
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
# generate some more data
x, y = gen_fake_data(10000, 3., 8.)
x.shape, y.shape
x,y = V(x),V(y)
# Create random weights a and b, and wrap them in Variables.
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
a,b
learning_rate = 1e-3
for t in range(10000):
# Forward pass: compute predicted y using operations on Variables
loss = mse_loss(a,b,x,y)
if t % 1000 == 0: print(loss.data[0])
# Computes the gradient of loss with respect to all Variables with requires_grad=True.
# After this call a.grad and b.grad will be Variables holding the gradient
# of the loss with respect to a and b respectively
loss.backward()
# Update a and b using gradient descent; a.data and b.data are Tensors,
# a.grad and b.grad are Variables and a.grad.data and b.grad.data are Tensors
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
# Zero the gradients
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient Descent - Classification
For a fixed dataset $x$ and $y$ `mse_loss(a,b)` is a function of $a$ and $b$. We would like to find the values of $a$ and $b$ that minimize that function.
**Gradient descent** is an algorithm that minimizes functions. Given a function defined by a set of parameters, gradient descent starts with an initial set of parameter values and iteratively moves toward a set of parameter values that minimize the function. This iterative minimization is achieved by taking steps in the negative direction of the function gradient.
Here is gradient descent implemented in [PyTorch](http://pytorch.org/).
```
def gen_fake_data2(n, a, b):
x = np.random.uniform(0,1,n)
y = lin(a,b,x) + 0.1 * np.random.normal(0,3,n)
return x, np.where(y>10, 1., 0.)
x,y = gen_fake_data2(10000, 3., 8.)
x,y = V(x),V(y)
def nll(y_hat, y):
y_hat = torch.clamp(y_hat, 1e-5, 1-1e-5)
return (y*y_hat.log() + (1.-y)*(1.-y_hat).log()).mean()
a = V(np.random.randn(1), requires_grad=True)
b = V(np.random.randn(1), requires_grad=True)
learning_rate = 1e-2
for t in range(3000):
p = (-lin(a,b,x)).exp()
y_hat = 1./(1.+p)
loss = nll(y_hat, y)
if t % 1000 == 0:
print(np.exp(loss.data[0]), np.mean(to_np(y)==(to_np(y_hat)>0.5)))
# print(y_hat)
loss.backward()
a.data -= learning_rate * a.grad.data
b.data -= learning_rate * b.grad.data
a.grad.data.zero_()
b.grad.data.zero_()
```
Nearly all of deep learning is powered by one very important algorithm: **stochastic gradient descent (SGD)**. SGD can be seeing as an approximation of **gradient descent** (GD). In GD you have to run through *all* the samples in your training set to do a single itaration. In SGD you use *only one* or *a subset* of training samples to do the update for a parameter in a particular iteration. The subset use in every iteration is called a **batch** or **minibatch**.
# Gradient descent with numpy
```
from matplotlib import rcParams, animation, rc
from ipywidgets import interact, interactive, fixed
from ipywidgets.widgets import *
rc('animation', html='html5')
rcParams['figure.figsize'] = 3, 3
x, y = gen_fake_data(50, 3., 8.)
a_guess,b_guess = -1., 1.
mse_loss(y, a_guess, b_guess, x)
lr=0.01
def upd():
global a_guess, b_guess
y_pred = lin(a_guess, b_guess, x)
dydb = 2 * (y_pred - y)
dyda = x*dydb
a_guess -= lr*dyda.mean()
b_guess -= lr*dydb.mean()
fig = plt.figure(dpi=100, figsize=(5, 4))
plt.scatter(x,y)
line, = plt.plot(x,lin(a_guess,b_guess,x))
plt.close()
def animate(i):
line.set_ydata(lin(a_guess,b_guess,x))
for i in range(30): upd()
return line,
ani = animation.FuncAnimation(fig, animate, np.arange(0, 20), interval=100)
ani
```
|
github_jupyter
|
```
import cv2
import numpy as np
import pandas as pd
import numba
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import matplotlib
model = 'neural'
symmetric = False
nPosts = 3
if symmetric == True:
data = 'SPP/symmetric_n' if model == 'collective' else 'NN/symmetric_n'
prefix = 'coll_symmetric_' if model == 'collective' else 'symmetric_'
else:
data = 'SPP/collective_n' if model == 'collective' else 'NN/flydata_n'
prefix = 'coll_' if model == 'collective' else ''
tmin = 0
if symmetric == True:
if nPosts < 4:
tmax = 2000 if model == 'neural' else 5100
else:
tmax = 3000 if model == 'neural' else 5100
else:
if nPosts < 4:
tmax = 1200 if model == 'neural' else 5100
else:
tmax = 1900 if model == 'neural' else 6200
window_size = 600
df = pd.read_csv("/Users/vivekhsridhar/Documents/Work/Results/decision_geometry/Data/Theory/" + data + str(nPosts) + "_direct.csv")
df.head()
if symmetric:
xs = np.array((df[' x'] - 500) / 100)
df[' x'] = xs
else:
xs = np.array(df[' x'] / 100)
df[' x'] = xs
ys = np.array((df[' y'] - 500) / 100)
df[' y'] = ys
if model == 'neural':
ts = df['time']
else:
ts = df[' time']
xs = xs[ts < tmax]
ys = ys[ts < tmax]
ts = ts[ts < tmax]
if nPosts == 2:
if symmetric:
post0_x = 5.0*np.cos(np.pi)
post0_y = 5.0*np.sin(np.pi)
post1_x = 5.0*np.cos(0)
post1_y = 5.0*np.sin(0)
else:
post0_x = 5.0*np.cos(np.pi/6)
post0_y = -5.0*np.sin(np.pi/6)
post1_x = 5.0*np.cos(np.pi/6)
post1_y = 5.0*np.sin(np.pi/6)
elif nPosts == 3:
if symmetric:
post0_x = 5.0*np.cos(-2*np.pi/3)
post0_y = 5.0*np.sin(-2*np.pi/3)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/3)
post2_y = 5.0*np.sin(2*np.pi/3)
else:
post0_x = 5.0*np.cos(2*np.pi/9)
post0_y = -5.0*np.sin(2*np.pi/9)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/9)
post2_y = 5.0*np.sin(2*np.pi/9)
else:
if symmetric:
post0_x = -5.0
post0_y = 0.0
post1_x = 0.0
post1_y = 5.0
post2_x = 5.0
post2_y = 0.0
post3_x = 0.0
post3_y = -5.0
else:
post0_x = 5.0*np.cos(2*np.pi/9)
post0_y = -5.0*np.sin(2*np.pi/9)
post1_x = 5.0
post1_y = 0.0
post2_x = 5.0*np.cos(2*np.pi/9)
post2_y = 5.0*np.sin(2*np.pi/9)
if nPosts == 2:
if symmetric:
fig, ax = plt.subplots(1,1,figsize=(2,2))
else:
fig, ax = plt.subplots(1,1,figsize=(post0_x/2.5,post1_y/1.25))
else:
if symmetric:
fig, ax = plt.subplots(1,1,figsize=(2,2))
else:
fig, ax = plt.subplots(1,1,figsize=(1.25,post2_x/2))
plt.scatter(xs, ys, c='black', s=1, alpha=0.01)
ax.set_aspect('equal')
if symmetric:
if nPosts == 2:
ax.set_xticks([-4,-2,0,2,4])
ax.set_yticks([-4,-2,0,2,4])
else:
ax.set_xticks([-4,-2,0,2,4])
ax.set_yticks([-4,-2,0,2,4])
else:
if nPosts == 2:
ax.set_xticks([0,1,2,3,4])
ax.set_yticks([-2,-1,0,1,2])
plt.xlim(0,post0_x)
plt.ylim(post0_y,post1_y)
else:
ax.set_xticks([0,1,2,3,4,5])
#ax.set_yticks([-3,-2,-1,0,1,2,3])
plt.xlim(0,5)
plt.ylim(post0_y,post2_y)
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'trajectories_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
nbins = 500
peak_threshold = 0.9
def density_map(x, y, stats=True):
blur = (11, 11) if stats == True else (51, 51)
if nPosts == 2:
r = (
[[-5, 5], [-5, 5]]
if symmetric == True
else [[0, post0_x], [post0_y, post1_y]]
)
elif nPosts == 3:
r = (
[[post0_x, post1_x], [post0_y, post2_y]]
if symmetric == True
else [[0, post1_x], [post0_y, post2_y]]
)
else:
r = (
[[-5, 5], [-5, 5]]
if symmetric == True
else [[0, post1_x], [post0_y, post2_y]]
)
h, xedge, yedge, image = plt.hist2d(x, y, bins=nbins, density=True, range=r)
if nPosts == 2:
tmp_img = np.flipud(np.rot90(cv2.GaussianBlur(h, blur, 0)))
else:
tmp_img = np.flipud(np.rot90(cv2.GaussianBlur(h, blur, 0)))
tmp_img /= np.max(tmp_img)
return tmp_img
for idx,t in enumerate(range(tmin,tmax-window_size,10)):
window_min = t
window_max = t + window_size
x = xs[(ts > window_min) & (ts < window_max)]
y = ys[(ts > window_min) & (ts < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
img = tmp_img
else:
img = np.fmax(tmp_img, img)
if nPosts == 2:
x_peaks = np.where(img > peak_threshold)[1] * post0_x / nbins
y_peaks = np.where(img > peak_threshold)[0] * (post0_y - post1_y) / nbins + post1_y
elif nPosts == 3:
x_peaks = np.where(img > peak_threshold)[1] * post1_x / nbins
y_peaks = np.where(img > peak_threshold)[0] * (post0_y - post2_y) / nbins + post2_y
if nPosts == 2:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(2,2))
plt.imshow(img, extent=[-5, 5, -5.0, 5.0])
plt.xticks([-4,-2,0,2,4])
plt.yticks([-4,-2,0,2,4])
else:
fig, ax = plt.subplots(1, 1, figsize=(post0_x/2.5,post1_y/1.25))
plt.imshow(img, extent=[0, post0_x, post0_y, post1_y])
plt.xticks([0,1,2,3,4])
elif nPosts == 3:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(3.75/2,post2_y/2))
plt.imshow(img, extent=[post0_x, post1_x, post0_y, post2_y])
else:
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
plt.xticks([0,1,2,3,4,5])
else:
if symmetric == True:
fig, ax = plt.subplots(1,1, figsize=(post2_x/2,post1_y/2))
plt.imshow(img, extent=[-post2_x, post2_x, -post1_y, post1_y])
plt.xticks([-4,-2,0,2,4])
else:
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
plt.xticks([0,1,2,3,4,5])
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
```
### Identify bifurcation point using a piecewise phase-transition function
#### Get first bifurcation point
Once you have this, you can draw a line segment bisecting the angle between the point and two targets. This will be the line about which you symmetrise to get the second bifurcation point
```
def fitfunc(x, p, q, r):
return r * (np.abs((x - p)) ** q)
def fitfunc_vec_self(x, p, q, r):
y = np.zeros(x.shape)
for i in range(len(y)):
y[i] = fitfunc(x[i], p, q, r)
return y
x_fit = []
y_fit = []
if nPosts == 2:
if model == 'neural':
bif_pt = 2.5
params1 = [3, 1, 1]
else:
bif_pt = 1.2
params1 = [1.5, 1, 1]
x_sub = np.concatenate((xs, xs))
y_sub = np.concatenate((ys, -ys))
t_sub = np.concatenate((ts, ts))
tmin = np.min(t_sub)
tmax = np.max(t_sub)-100 if model == 'neural' else np.max(t_sub)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img2 = density_map(x, y, stats=False)
if idx == 0:
tmp_img = tmp_img2
else:
tmp_img = np.fmax(tmp_img2, tmp_img)
x_fit = np.where(tmp_img > peak_threshold)[1] * post0_x / nbins
y_fit = (
np.where(tmp_img > peak_threshold)[0] * (post0_y - post1_y) / nbins
+ post1_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params1, maxfev=10000
)
params1 = fit_params
else:
if model == 'neural':
bif_pt = 1
params1 = [1.2, 1, 0.5]
xs1 = xs[xs < 2.7]
ys1 = ys[xs < 2.7]
ts1 = ts[xs < 2.7]
else:
bif_pt = 0.8
params1 = [1, 1, 0.5]
xs1 = xs[xs < 2.5]
ys1 = ys[xs < 2.5]
ts1 = ts[xs < 2.5]
x_sub = np.concatenate((xs1, xs1))
y_sub = np.concatenate((ys1, -ys1))
t_sub = np.concatenate((ts1, ts1))
tmin = np.min(t_sub)
tmax = np.max(t_sub)-100 if model == 'neural' else np.max(t_sub)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img2 = density_map(x, y, stats=False)
if idx == 0:
tmp_img = tmp_img2
else:
tmp_img = np.fmax(tmp_img2, tmp_img)
x_fit = np.where(tmp_img > peak_threshold)[1] * post1_x / nbins
y_fit = (
np.where(tmp_img > peak_threshold)[0] * (post0_y - post2_y) / nbins
+ post2_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params1, maxfev=10000
)
params1 = fit_params
if nPosts == 2:
fig, ax = plt.subplots(1, 1, figsize=(post0_x/2.5,post1_y/1.25))
plt.imshow(img, extent=[0, post0_x, post0_y, post1_y])
else:
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
parameters = params1
step_len = 0.01
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
offset=0.2 if model == 'neural' else 0.5
x = (
np.arange(parameters[0], post0_x-offset, step_len)
if nPosts == 2
else np.arange(parameters[0], 3., step_len)
)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
((parameters[2] * (x - parameters[0])) ** parameters[1], -(parameters[2] * (x - parameters[0])) ** parameters[1])
)
if nPosts != 2:
bisector_xs = [params1[0], post2_x]
bisector_ys = [
0,
np.tan(np.arctan2(post2_y, post2_x - params1[0]) / 2)
* (post2_x - params1[0]),
]
plt.xticks([0,1,2,3,4])
plt.scatter(x1, y1, c="black", s=0.1)
plt.scatter(x2, y2, c="black", s=0.1)
if nPosts == 2:
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '_direct.pdf', dpi=600, bbox_inches='tight')
if nPosts == 2:
print(
"The bifurcation occurs at an angle",
2 * np.arctan2(post1_y, post1_x - params1[0]) * 180 / np.pi,
)
else:
print(
"The first bifurcation occurs at an angle",
2 * np.arctan2(post2_y, post2_x - params1[0]) * 180 / np.pi,
)
```
#### Get the second bifurcation point
For this, you must center the trajectories about the bifurcation point, get a new heatmap and rotate this by the angle of the bisector line
```
# center points about the first bifurcation
cxs = xs - params1[0]
cys = ys
cts = ts
cpost0_x = post0_x - params1[0]
cpost1_x = post1_x - params1[0]
cpost2_x = post2_x - params1[0]
@numba.njit(fastmath=True, parallel=True)
def parallel_rotate(xy, rmat):
out = np.zeros(xy.shape)
for idx in numba.prange(xy.shape[0]):
out[idx] = np.dot(rmat[idx], xy[idx])
return out
# clip all points to the left of and below 0 and points beyond post centers
ccxs = cxs[cxs > 0]
ccys = cys[cxs > 0]
ccts = cts[cxs > 0]
ccxs = ccxs[ccys > 0]
ccts = ccts[ccys > 0]
ccys = ccys[ccys > 0]
xy = np.concatenate((ccxs.reshape(-1, 1), ccys.reshape(-1, 1)), axis=1)
angle = np.full(
ccxs.shape, np.arctan2(post2_y, post2_x - params1[0]) / 2
)
rmat = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]]).T
rx, ry = parallel_rotate(xy, rmat).T
blur = (51,51)
r1 = [[0, post1_x], [post0_y, post2_y]]
tmin = np.min(ccts)
tmax = np.max(ccts)-100 if model == 'neural' else np.max(ccts)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = rx[(ccts > window_min) & (ccts < window_max)]
y = ry[(ccts > window_min) & (ccts < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
tmp_img1 = tmp_img
else:
tmp_img1 = np.fmax(tmp_img1, tmp_img)
plt.imshow(tmp_img1, extent=[r1[0][0], r1[0][1], r1[1][0], r1[1][1]])
if model == 'neural':
bif_pt = 2.2
params2 = [2.5, 1, 0.5]
else:
bif_pt = 1.8
params2 = [2, 1, 0.5]
x_sub = np.concatenate((rx, rx))
y_sub = np.concatenate((ry, -ry))
t_sub = np.concatenate((ccts, ccts))
tmin = np.min(ccts)
tmax = np.max(ccts)-100 if model == 'neural' else np.max(ccts)-500
for idx,t in enumerate(range(tmin,tmax,10)):
window_min = t
window_max = t + window_size
x = x_sub[(t_sub > window_min) & (t_sub < window_max)]
y = y_sub[(t_sub > window_min) & (t_sub < window_max)]
tmp_img = density_map(x, y, stats=False)
if idx == 0:
tmp_img1 = tmp_img
else:
tmp_img1 = np.fmax(tmp_img1, tmp_img)
x_fit = np.where(tmp_img1 > peak_threshold)[1] * post1_x / nbins
y_fit = (
np.where(tmp_img1 > peak_threshold)[0] * (post0_y - post2_y) / nbins
+ post2_y
)
x_fit = x_fit
y_fit = np.abs(y_fit)
y_fit = y_fit[x_fit > bif_pt]
x_fit = x_fit[x_fit > bif_pt]
for i in range(0,10):
fit_params, pcov = curve_fit(
fitfunc_vec_self, x_fit, y_fit, p0=params2, maxfev=10000
)
params2 = fit_params
plt.imshow(tmp_img1, extent=[r1[0][0], r1[0][1], r1[1][0], r1[1][1]])
parameters = params2
step_len = 0.01
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
x = np.arange(parameters[0], 3, step_len)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
((parameters[2] * (x - parameters[0])) ** parameters[1], -(parameters[2] * (x - parameters[0])) ** parameters[1])
)
plt.scatter(x1, y1, c="black", s=1)
plt.scatter(x2, y2, c="black", s=1)
bif2 = np.array([params2[0], 0]).reshape(1, -1)
ang = angle[0]
rmat1 = np.array([[np.cos(ang), -np.sin(ang)], [np.sin(ang), np.cos(ang)]]).T
bif2 = parallel_rotate(bif2, rmat).T
bif2[0] += params1[0]
print(
"The second bifurcation occurs at angle",
(
(
np.arctan2(post2_y - bif2[1], post2_x - bif2[0])
- np.arctan2(bif2[1] - post1_y, post1_x - bif2[0])
)
* 180
/ np.pi
)[0],
)
x1 = np.arange(step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
bcxy1 = np.concatenate((x1.reshape(-1, 1), y1.reshape(-1, 1)), axis=1)
ang1 = np.full(
x1.shape, -np.arctan2(post2_y, post2_x - params1[0]) / 2
)
rmat1 = np.array([[np.cos(ang1), -np.sin(ang1)], [np.sin(ang1), np.cos(ang1)]]).T
bcx1, bcy1 = parallel_rotate(bcxy1, rmat1).T
bx1 = bcx1 + params1[0]
fig, ax = plt.subplots(1, 1, figsize=(1.25,post2_x/2))
plt.imshow(img, extent=[0, post1_x, post0_y, post2_y])
step_len = 0.01
parameters = params2
bcxy1 = np.concatenate((x1.reshape(-1, 1), y1.reshape(-1, 1)), axis=1)
ang1 = np.full(x1.shape, -ang)
rmat1 = np.array([[np.cos(ang1), -np.sin(ang1)], [np.sin(ang1), np.cos(ang1)]]).T
bcx1, bcy1 = parallel_rotate(bcxy1, rmat1).T
bx1 = bcx1 + params1[0]
x = np.arange(parameters[0], 3.5, step_len) if model == 'neural' else np.arange(parameters[0], 3, step_len)
x2 = np.concatenate((x, x))
y2 = np.concatenate(
(
(parameters[2] * (x - parameters[0])) ** parameters[1],
-(parameters[2] * (x - parameters[0])) ** parameters[1])
)
bcxy2 = np.concatenate((x2.reshape(-1, 1), y2.reshape(-1, 1)), axis=1)
ang2 = np.full(x2.shape, -ang)
rmat2 = np.array([[np.cos(ang2), -np.sin(ang2)], [np.sin(ang2), np.cos(ang2)]]).T
bcx2, bcy2 = parallel_rotate(bcxy2, rmat2).T
bx2 = bcx2 + params1[0]
bx2 = np.concatenate((bx2, bx2))
bcy2 = np.concatenate((bcy2, -bcy2))
bcy2 = bcy2[bx2 < post1_x - 0.1]
bx2 = bx2[bx2 < post1_x - 0.1]
bx2 = bx2[np.abs(bcy2) < post2_y - 0.1]
bcy2 = bcy2[np.abs(bcy2) < post2_y - 0.1]
plt.plot(bx1, bcy1, linestyle="dashed", c="black")
plt.plot(bx1, -bcy1, linestyle="dashed", c="black")
plt.scatter(bx2, bcy2, c="black", s=0.1)
parameters = params1
step_len = 0.01
x1 = np.arange(5 * step_len, parameters[0], step_len)
y1 = np.zeros(len(x1))
# x = np.arange(parameters[0], 2.9, step_len)
# x2 = np.concatenate((x, x))
# y2 = np.concatenate(
# (
# (parameters[2] * (x - parameters[0])) ** parameters[1],
# -(parameters[2] * (x - parameters[0])) ** parameters[1],
# )
# )
plt.scatter(x1, y1, c="black", s=0.1)
# plt.scatter(x2, y2, c="black", s=0.1)
plt.xticks([0, 1, 2, 3, 4, 5])
fig.savefig('/Users/vivekhsridhar/Documents/Code/Python/fly-matrix/figures/' + prefix + 'density_n' + str(nPosts) + '.pdf', dpi=600, bbox_inches='tight')
```
|
github_jupyter
|
<h1 align="center"> TUGAS BESAR TF3101 - DINAMIKA SISTEM DAN SIMULASI </h1>
<h2 align="center"> Sistem Elektrik, Elektromekanik, dan Mekanik</h2>
<h3>Nama Anggota:</h3>
<body>
<ul>
<li>Erlant Muhammad Khalfani (13317025)</li>
<li>Bernardus Rendy (13317041)</li>
</ul>
</body>
## 1. Pemodelan Sistem Elektrik##
Untuk pemodelan sistem elektrik, dipilih rangkaian RLC seri dengan sebuah sumber tegangan seperti yang tertera pada gambar di bawah ini.
<img src="./ELEKTRIK_TUBES_3.png" style="width:50%" align="middle">
### Deskripsi Sistem
1. Input <br>
Sistem ini memiliki input sumber tegangan $v_i$, yang merupakan fungsi waktu $v_i(t)$. <br>
2. Output <br>
Sistem ini memiliki *output* arus $i_2$, yaitu arus yang mengalir pada *mesh* II. Tegangan $v_{L1}$ dan $v_{R2}$ juga dapat berfungsi sebagai *output*. Pada program ini, *output* yang akan di-*plot* hanya $v_{R2}$ dan $v_{L1}$. Nilai $i_2$ berbanding lurus terhadap nilai $v_{R2}$, sehingga bentuk grafik $i_2$ akan menyerupai bentuk grafik $v_{R2}$
3. Parameter <br>
Sistem ini memiliki parameter-parameter $R_1$, $R_2$, $L_1$, dan $C_1$. Hambatan-hambatan $R_1$ dan $R_2$ adalah parameter *resistance*. Induktor $L_1$ adalah parameter *inertance*. Kapasitor $C_1$ adalah parameter *capacitance*.
### Asumsi
1. Arus setiap *mesh* pada keadaan awal adalah nol ($i_1(0) = i_2(0) = 0$).
2. Turunan arus terhadap waktu pada setiap *mesh* adalah nol ($\frac{di_1(0)}{dt}=\frac{di_2(0)}{dt}=0$)
### Pemodelan dengan *Bond Graph*
Dari sistem rangkaian listrik di atas, akan didapatkan *bond graph* sebagai berikut.
<img src="./BG_ELEKTRIK.png" style="width:50%" align="middle">
<br>
Pada gambar di atas, terlihat bahwa setiap *junction* memenuhi aturan kausalitas. Ini menandakan bahwa rangkaian di atas bersifat *causal*. Dari *bond graph* di atas, dapat diturunkan *Ordinary Differential Equation* (ODE) seperti hasil penerapan *Kirchhoff's Voltage Law* (KVL) pada setiap *mesh*. Dalam pemodelan *bond graph* variabel-variabel dibedakan menjadi variabel *effort* dan *flow*. Sistem di atas merupakan sistem elektrik, sehingga memiliki variabel *effort* berupa tegangan ($v$) dan *flow* berupa arus ($i$).
### Persamaan Matematis - ODE
Dilakukan analisis besaran *effort* pada *1-junction* sebelah kiri. Ini akan menghasilkan:
$$
v_i = v_{R1} + v_{C1}
$$
<br>
Hasil ini sama seperti hasil dari KVL pada *mesh* I. Nilai $v_{R1}$ dan $v_{C1}$ diberikan oleh rumus-rumus:
$$
v_{R1} = R_1i_1
$$
<br>
$$
v_{C1} = \frac{1}{C_1}\int (i_1 - i_2)dt
$$
sehingga hasil KVL pada *mesh* I menjadi:
$$
v_i = R_1i_1 + \frac{1}{C_1}\int (i_1 - i_2)dt
$$
Kemudian, analisis juga dilakukan pada *1-junction* sebelah kanan, yang akan menghasilkan:
$$
v_{C1} = v_{R2} + v_{L1}
$$
<br>
Ini juga sama seperti hasil KVL pada *mesh* II. Nilai $v_{R2}$ dan $v_{L1}$ diberikan oleh rumus-rumus:
$$
v_{R2} = R_2i_2
$$
<br>
$$
v_{L1} = L_1\frac{di_2}{dt}
$$
sehingga hasil KVL pada *mesh* II menjadi:
$$
\frac{1}{C_1}\int(i_1-i_2)dt = R_2i_2 + L_1\frac{di_2}{dt}
$$
atau
$$
0 = L_1\frac{di_2}{dt} + R_2i_2 + \frac{1}{C_1}\int(i_2-i_1)dt
$$
### Persamaan Matematis - *Transfer Function*
Setelah didapatkan ODE hasil dari *bond graph*, dapat dilakukan *Laplace Transform* untuk mendapatkan fungsi transfer sistem. *Laplace Transform* pada persamaan hasil KVL *mesh* I menghasilkan:
$$
(R_1 + \frac{1}{C_1s})I_1 + (-\frac{1}{C_1s})I_2 = V_i
$$
<br>
dan pada persamaan hasil *mesh* II, akan didapatkan:
$$
(-\frac{1}{C_1s})I_1 + (L_1s + R_2 + \frac{1}{C_1s})I_2 = 0
$$
<br>
Kedua persamaan itu dieliminasi, sehingga didapatkan fungsi transfer antara $I_2$ dengan $V_i$
$$
\frac{I_2(s)}{V_i(s)} = \frac{1}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
<br>
Dari hasil *Laplace Transform* persamaan pada *mesh* II, didapatkan nilai $V_{L1}$ dari rumus
$$
V_{L1} = L_1sI_2
$$
<br>
sehingga didapatkan fungsi transfer antara $V_{L1}$ dengan $V_i$
$$
\frac{V_{L1}(s)}{V_i(s)} = \frac{L_1s}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
Sementara fungsi transfer antara $V_{R2}$ dan $V_i$ adalah
$$
\frac{V_{R2}(s)}{V_i(s)} = \frac{R_2}{R_1C_1L_1s^2 + (R_1R_2C_1 + L_1)s + R_1 + R_2}
$$
```
#IMPORTS
from ipywidgets import interact, interactive, fixed, interact_manual , HBox, VBox, Label, Layout
import ipywidgets as widgets
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
#DEFINISI SLIDER-SLIDER PARAMETER
#Slider R1
R1_slider = widgets.FloatSlider(
value=1.,
min=1.,
max=1000.,
step=1.,
description='$R_1 (\Omega)$',
readout_format='.1f',
)
#Slider R2
R2_slider = widgets.FloatSlider(
value=1.,
min=1.,
max=1000.,
step=1.,
description='$R_2 (\Omega)$',
readout_format='.1f',
)
#Slider C1
C1_slider = widgets.IntSlider(
value=1,
min=10,
max=1000,
step=1,
description='$C_1 (\mu F)$',
)
#Slider L1
L1_slider = widgets.FloatSlider(
value=0.1,
min=1.,
max=1000.,
step=0.1,
description='$L_1 (mH)$',
readout_format='.1f',
)
#DEKLARASI SELECTOR INPUT
#Slider selector input
vi_select = signal_select = widgets.Dropdown(
options=[('Step', 0), ('Impulse', 1)],
description='Tipe Sinyal:',
)
#DEKLARASI SELECTOR OUTPUT
#Output Selector
vo_select = widgets.ToggleButtons(
options=['v_R2', 'v_L1'],
description='Output:',
)
#DEKLARASI TAMBAHAN UNTUK INTERFACE
#Color button
color_select1 = widgets.ToggleButtons(
options=['blue', 'red', 'green', 'black'],
description='Color:',
)
#PENENTUAN NILAI-NILAI PARAMETER
R1 = R1_slider.value
R2 = R2_slider.value
C1 = C1_slider.value
L1 = L1_slider.value
#PENENTUAN NILAI DAN BENTUK INPUT
vform = vi_select.value
#PENENTUAN OUTPUT
vo = vo_select
#PENENTUAN PADA INTERFACE
color = color_select1.value
#Plot v_L1 menggunakan transfer function
def plot_electric (vo, R1, R2, C1, L1, vform, color):
#Menyesuaikan nilai parameter dengan satuan
R1 = R1
R2 = R2
C1 = C1*(10**-6)
L1 = L1*(10**-3)
f, ax = plt.subplots(1, 1, figsize=(8, 6))
num1 = [R2]
num2 = [L1, 0]
den = [R1*C1*L1, R1*R2*C1+L1, R1+R2]
if vo=='v_R2':
sys_vr =signal.TransferFunction(num1, den)
step_vr = signal.step(sys_vr)
impl_vr = signal.impulse(sys_vr)
if vform == 0:
ax.plot(step_vr[0], step_vr[1], color=color, label='Respon Step')
elif vform == 1:
ax.plot(impl_vr[0], impl_vr[1], color=color, label='Respon Impuls')
ax.grid()
ax.legend()
elif vo=='v_L1':
sys_vl = signal.TransferFunction(num2, den)
step_vl = signal.step(sys_vl)
impl_vl = signal.impulse(sys_vl)
#Plot respon
if vform == 0:
ax.plot(step_vl[0], step_vl[1], color=color, label='Respon Step')
elif vform == 1:
ax.plot(impl_vl[0], impl_vl[1], color=color, label='Respon Impuls')
ax.grid()
ax.legend()
ui_el = widgets.VBox([vo_select, R1_slider, R2_slider, C1_slider, L1_slider, vi_select, color_select1])
out_el = widgets.interactive_output(plot_electric, {'vo':vo_select,'R1':R1_slider,'R2':R2_slider,'C1':C1_slider,'L1':L1_slider,'vform':vi_select,'color':color_select1})
int_el = widgets.HBox([ui_el, out_el])
display(int_el)
```
### Analisis###
<h4>a. Respon Step </h4>
Dari hasil simulasi, didapatkan pengaruh perubahan-perubahan nilai parameter pada *output* sistem setelah diberikan *input* berupa sinyal *step*, di antaranya:
1. Kenaikan nilai $R_1$ akan menurunkan *steady-state gain* ($K$) sistem. Ini terlihat dari turunnya nilai *output* $v_{R2}$ pada keadaan *steady-state* dan turunnya nilai *maximum overshoot* ($M_p$) pada *output* $v_{L1}$. Perubahan nilai $R_1$ juga berbanding terbalik dengan perubahan koefisien redaman $\xi$, terlihat dari semakin jelas terlihatnya osilasi seiring dengan kenaikan nilai $R_1$. Perubahan nilai $R_1$ juga sebanding dengan perubahan nilai *settling time* ($t_s$). Ini terlihat dengan bertambahnya waktu sistem untuk mencapai nilai dalam rentang 2-5% dari nilai keadaan *steady-state*.
2. Kenaikan nilai $R_2$ akan meningkatkan *steady-state gain* ($K$) sistem dengan *output* $v_{R2}$ tetapi menurunkan *steady-state gain* ($K$) *output* $v_{L1}$. Selain itu, dapat terlihat juga bahwa perubahan nilai $R_2$ berbanding terbalik dengan nilai *settling time* ($t_s$); Saat nilai $R_2$ naik, sistem mencapai kondisi *steady-state* dalam waktu yang lebih singkat. Kenaikan nilai $R_2$ juga menyebabkan penurunan nilai *maximum overshoot* ($M_p$).
3. Perubahan nilai $C_1$ sebanding dengan perubahan nilai *settling time*, seperti yang dapat terlihat dengan bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state* seiring dengan kenaikan nilai $C_1$. Selain itu nilai $C_1$ juga berbanding terbalik dengan nilai *maximum overshoot*, ini dapat dilihat dari turunnya nilai *maximum overshoot* ketika nilai $C_1$ dinaikan. Pada saat nilai $C_1$, naik, juga terlihat kenaikan nilai *delay time* ($t_d$), *rise time* ($t_r$), dan *peak time* ($t_p$).
4. Kenaikan nilai $L_1$ mengakibatkan berkurangnya nilai frekuensi osilasi, serta meningkatkan *settling time* sistem. Perubahan nilai $L_1$ ini juga sebanding dengan *steady-state gain* sistem untuk *output* $v_{L1}$.
<h4>b. Respon Impuls </h4>
Dari hasil simulasi, didapatkan pengaruh perubahan-perubahan nilai parameter pada *output* sistem setelah diberikan *input* berupa sinyal *impulse*, di antaranya:
1. Perubahan nilai $R_1$ berbanding terbalik dengan nilai *peak response*. Kenaikan nilai $R_1$ juga menaikkan nilai *settling time* ($t_s$).
2. Kenaikan nilai $R_2$ memengaruhi nilai *peak response* $v_{R2}$, tetapi tidak berpengaruh pada *peak response* $v_{L1}$. Naiknya nilai $R_2$ juga menurunkan nilai *settling time* ($t_s$), yang terlihat dari semakin cepatnya sistem mencapai kondisi *steady-state*.
3. Kenaikan nilai $C_1$ menyebabkan turunnya nilai *peak response*. Kenaikan nilai $C_1$ juga menyebabkan kenaikan nilai *settling time* ($t_s$), yang dapat dilihat dengan bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state*.
4. Kenaikan nilai $L_1$ menyebabkan turunnya nilai *peak response*. Kenaikan nilai $L_1$ juga menurunkan nilai *settling time* ($t_s$), yang dapat dilihat dari bertambahnya waktu yang diperlukan sistem untuk mendekati keadaan *steady-state*.
## 2. Pemodelan Sistem Elektromekanik
### DC Brushed Motor Torsi Besar dengan Motor Driver
Sistem yang akan dimodelkan berupa motor driver high current BTS7960 seperti gambar pertama, dihubungkan dengan motor torsi besar dengan brush pada gambar kedua.
<div>
<img src="./1.jpg" style="width:20%" align="middle">
</div>
<div>
<img src="./2.jpg" style="width:20%" align="middle">
</div>
<p style="text-align:center"><b>Sumber gambar: KRTMI URO ITB</b></p>
### Deskripsi Sistem
1. Input <br>
Sistem ini memiliki input sinyal $V_{in}$, yang merupakan fungsi waktu $V_{in}(t)$. Tegangan $v_i(t)$ ini dapat berbentuk fungsi step, impuls, atau pulse width modulation dengan duty cycle tertentu (luaran mikrokontroller umum). <br>
2. Output <br>
Sistem ini memiliki *output* posisi sudut $\theta$, kecepatan sudut motor $\omega$, percepatan sudut motor $\alpha$, dan torsi $T$. Output ditentukan sesuai kebutuhan untuk manuver robot. Terlihat variable output bergantung pada $\theta$, $\frac {d\theta}{dt}$, dan $\frac{d^2\theta}{dt}$, sehingga dicari beberapa persamaan diferensial sesuai tiap output.
3. Parameter <br>
Sistem memiliki parameter $J,K_f,K_a,L,R,K_{emf},K_{md}$ yang diturunkan dari karakteristik subsistem mekanik dan elektrik sebagai berikut.
#### Subsistem Motor Driver
Pertama ditinjau struktur sistem dari motor driver. Motor driver yang digunakan adalah tipe MOSFET BTS7960 sehingga memiliki karakteristik dinamik yang meningkat hampir dengan instant. MOSFET dirangkai sedemikian rupa sehingga dapat digunakan untuk kontrol maju/mundur motor. Diasumsikan rise-time MOSFET cukup cepat relatif terhadap sinyal dan motor driver cukup linear, maka motor driver dapat dimodelkan sebagai sistem orde 0 dengan gain sebesar $ K_{md} $.
<img src="./4.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Sumber gambar: Datasheet BTS7960</b></p>
<img src="./5.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Model Orde 0 Motor Driver</b></p>
Maka persamaan dinamik output terhadap input dalam motor driver adalah <br>
$ V_m=K_{md}V_{in} $<br>
Sama seperti hubungan input output pada karakteristik statik.
#### Subsistem Motor
Lalu ditinjau struktur sistem dari motor torsi besar dengan inertia beban yang tidak dapat diabaikan.
<img src="./3.png" style="width:30%" align="middle">
<p style="text-align:center"><b>Sumber gambar: https://www.researchgate.net/figure/The-structure-of-a-DC-motor_fig2_260272509</b></p>
<br>
Maka dapat diturunkan persamaan diferensial untuk sistem mekanik.
<br>
<img src="./6.png" style="width:30%">
<img src="./7.png" style="width:30%">
<p style="text-align:center"><b>Sumber gambar: Chapman - Electric Machinery Fundamentals 4th Edition</b></p>
$$
T=K_a i_a
$$
dengan $T$ adalah torsi dan $K_a$ adalah konstanta proporsionalitas torsi (hasil perkalian K dengan flux) untuk arus armature $i_a$.
$$
V_{emf}=K_{emf} \omega
$$
dengan $V_{emf}$ adalah tegangan penyebab electromotive force dan $K_{emf}$ konstanta proporsionalitas tegangan emf (hasil perkalian K dengan flux pada kondisi ideal tanpa voltage drop) untuk kecepatan putar sudut dari motor.
<br>
Namun, akibat terbentuknya torsi adalah berputarnya beban dengan kecepatan sudut sebesar $\omega$ dan percepatan sudut sebesar $\alpha$. Faktor proporsionalitas terhadap percepatan sudut adalah $J$ (Inersia Putar) dan terhadap kecepatan sudut sebesar $ K_f $ (Konstanta Redam Putar) Sehingga dapat diturunkan persamaan diferensial sebagai berikut (Persamaan 1):
<br>
$$
J\alpha + K_f\omega = T
$$
$$
J\frac {d^2\theta}{dt} + K_f\frac {d\theta}{dt} = K_a i_a
$$
$$
J\frac {d\omega}{dt} + K_f \omega = K_a i_a
$$
Kemudian diturunkan persamaan diferensial untuk sistem elektrik yang terdapat pada motor sehingga $i_a$ dapat disubstitusi dengan input $V_{in}$ (Persamaan 2):
$$
L \frac{d{i_a}}{dt} + R i_a + K_{emf} \omega = V_m
$$
$$
V_m = K_{md} V_{in}
$$
$$
L \frac{d{i_a}}{dt} + R i_a + K_{emf} \omega = K_{md} V_{in}
$$
### Pemodelan dengan Fungsi Transfer
Dengan persamaan subsistem tersebut, dapat dilakukan pemodelan fungsi transfer sistem dengan transformasi ke domain laplace (s). Dilakukan penyelesaian menggunakan fungsi transfer dalam domain laplace, pertama dilakukan transfer ke domain laplace dengan asumsi
<br>
$ i_a (0) = 0 $
<br>
$ \frac {di_a}{dt} = 0 $
<br>
$ \theta (0) = 0 $
<br>
$ \omega (0) = 0 $
<br>
$ \alpha (0) = 0 $
<br>
Tidak diasumsikan terdapat voltage drop karena telah di akumulasi di $K_{emf}$, namun diasumsikan voltage drop berbanding lurus terhadap $\omega$.
<br>
Persamaan 1 menjadi:
$$
J s \omega + K_f \omega = K_a i_a
$$
Persamaan 2 menjadi:
$$
L s i_a + R i_a + K_{emf} \omega = K_{md} V_{in}
$$
$$
i_a=\frac {K_{md} V_{in}-K_{emf} \omega}{L s + R}
$$
Sehingga terbentuk fungsi transfer sistem keseluruhan dalam $\omega$ adalah:
$$
J s \omega + K_f \omega = \frac {K_a(K_{md} V_{in} - K_{emf} \omega)}{L s + R}
$$
Fungsi transfer untuk $\omega$ adalah:
$$
\omega = \frac {K_a(K_{md} V_{in}-K_{emf} \omega)}{(L s + R)(J s + K_f)}
$$
$$
\omega = \frac {K_a K_{md} V_{in}}{(L s + R)(J s + K_f)(1 + \frac {K_a K_{emf}}{(L s + R)(J s + K_f)})}
$$
$$
\frac {\omega (s)}{V_{in}(s)} = \frac {K_a K_{md}}{(L s + R)(J s + K_f)+ K_a K_{emf}}
$$
Dapat diturunkan fungsi transfer untuk theta dengan mengubah variable pada persamaan 1:
$$
J s^2 \theta + K_f s \theta = K_a i_a
$$
Persamaan 2:
$$
L s i_a + R i_a + K_{emf} s \theta = K_{md} V_{in}
$$
$$
i_a=\frac {K_{md} V_{in}-K_{emf} s \theta}{L s + R}
$$
Sehingga terbentuk fungsi transfer sistem keseluruhan dalam $\theta$ adalah:
$$
J s^2 \theta + K_f s \theta = \frac {K_a(K_{md} V_{in}-K_{emf} s \theta)}{L s + R}
$$
Fungsi transfer untuk $\theta$ adalah:
$$
\theta = \frac {K_a(K_{md} V_{in}-K_{emf} s \theta)}{(L s + R)(J s^2 + K_f s )}
$$
$$
\theta + \frac {K_a K_{emf} s \theta}{(L s + R)(J s^2 + K_f s )}= \frac {K_a K_{md} V_{in}}{(L s + R)(J s^2 + K_f s )}
$$
$$
\theta= \frac {K_a K_{md} V_{in}}{(L s + R)(J s^2 + K_f s )(1 + \frac {K_a K_{emf} s}{(L s + R)(J s^2 + K_f s )})}
$$
$$
\frac {\theta (s)}{V_{in}(s)}= \frac {K_a K_{md}}{(L s + R)(J s^2 + K_f s )+ K_a K_{emf} s}
$$
Terlihat bahwa fungsi transfer untuk $\omega$ dan $\theta$ hanya berbeda sebesar $ \frac {1}{s} $ sesuai dengan hubungan
$$
\omega = s \theta
$$
Sehingga fungsi transfer untuk $\alpha$ akan memenuhi
$$
\alpha = s\omega = s^2 \theta
$$
Sehingga fungsi transfer untuk $\alpha$ adalah:
$$
\frac {\alpha (s)}{V_{in}(s)} = \frac {K_a K_{md} s}{(L s + R)(J s + K_f)+ K_a K_{emf}}
$$
### Output
Dari fungsi transfer, diformulasikan persamaan output posisi sudut $\theta$, kecepatan sudut motor $\omega$, percepatan sudut $\alpha$, dan torsi $T$ dalam fungsi waktu (t).
$$
\theta (t) = \mathscr {L^{-1}} \{\frac {K_a K_{md} V_{in}(s)}{(L s + R)(J s^2 + K_f s )+ K_a K_{emf} s}\}
$$
<br>
$$
\omega (t) = \mathscr {L^{-1}} \{\frac {K_a K_{md} V_{in}(s)}{(L s + R)(J s + K_f)+ K_a K_{emf}}\}
$$
<br>
$$
\alpha (t)= \mathscr {L^{-1}} \{\frac {K_a K_{md} Vin_{in}(s) s}{(L s + R)(J s + K_f)+ K_a K_{emf}}\}
$$
<br>
$$
T = \frac {K_a(K_{md} V_{in}-K_{emf} \omega)}{L s + R}
$$
```
# Digunakan penyelesaian numerik untuk output
import numpy as np
from scipy.integrate import odeint
import scipy.signal as sig
import matplotlib.pyplot as plt
from sympy.physics.mechanics import dynamicsymbols, SymbolicSystem
from sympy import *
import control as control
vin = symbols ('V_{in}') #import symbol input
omega, theta, alpha = dynamicsymbols('omega theta alpha') #import symbol output
ka,kmd,l,r,j,kf,kemf,s,t = symbols ('K_a K_{md} L R J K_f K_{emf} s t')#import symbol parameter dan s
thetaOverVin = (ka*kmd)/((l*s+r)*(j*s**2+kf*s)+ka*kemf*s) #persamaan fungsi transfer theta
polyThetaOverVin = thetaOverVin.as_poly() #Penyederhanaan persamaan
polyThetaOverVin
omegaOverVin = (ka*kmd)/((l*s+r)*(j*s+kf)+ka*kemf) #persamaan fungsi transfer omega
polyOmegaOverVin = omegaOverVin.as_poly() #Penyederhanaan persamaan
polyOmegaOverVin
alphaOverVin = (ka*kmd*s)/((l*s+r)*(j*s+kf)+ka*kemf)
polyAlphaOverVin = alphaOverVin.as_poly() #Penyederhanaan persamaan
polyAlphaOverVin
torqueOverVin= ka*(kmd-kemf*((ka*kmd)/((l*s+r)*(j*s+kf)+ka*kemf)))/(l*s+r) #Penyederhanaan persamaan torsi
polyTorqueOverVin = torqueOverVin.as_poly()
polyTorqueOverVin
def plot_elektromekanik(Ka,Kmd,L,R,J,Kf,Kemf,VinType,tMax,dutyCycle,grid):
# Parameter diberi value dan model system dibentuk dalam transfer function yang dapat diolah python
Ka = Ka
Kmd = Kmd
L = L
R = R
J = J
Kf = Kf
Kemf = Kemf
# Pembuatan model transfer function
tf = control.tf
tf_Theta_Vin = tf([Ka*Kmd],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R),0])
tf_Omega_Vin = tf([Ka*Kmd],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R)])
tf_Alpha_Vin = tf([Ka*Kmd,0],[J*L,(J*R+Kf*L),(Ka*Kemf+Kf*R)])
tf_Torque_Vin = tf([Ka*Kmd],[L,R]) - tf([Kmd*Kemf*Ka**2],[J*L**2,(2*J*L*R+Kf*L**2),(J*R**2+Ka*Kemf*L+2*Kf*L*R),(Ka*Kemf*R+Kf*R**2)])
f, axs = plt.subplots(4, sharex=True, figsize=(10, 10))
# Fungsi mengatur rentang waktu analisis (harus memiliki kelipatan 1 ms)
def analysisTime(maxTime):
ts=np.linspace(0, maxTime, maxTime*100)
return ts
t=analysisTime(tMax)
if VinType== 2:
# Input pwm dalam 1 millisecond
def Pwm(dutyCycle,totalTime):
trepeat=np.linspace(0, 1, 100)
squareWave=(5*sig.square(2 * np.pi * trepeat, duty=dutyCycle))
finalInput=np.zeros(len(totalTime))
for i in range(len(squareWave)):
if squareWave[i]<0:
squareWave[i]=0
for i in range(len(totalTime)):
finalInput[i]=squareWave[i%100]
return finalInput
pwm=Pwm(dutyCycle,t)
tPwmTheta, yPwmTheta, xPwmTheta = control.forced_response(tf_Theta_Vin, T=t, U=pwm, X0=0)
tPwmOmega, yPwmOmega, xPwmOmega = control.forced_response(tf_Omega_Vin, t, pwm, X0=0)
tPwmAlpha, yPwmAlpha, xPwmAlpha = control.forced_response(tf_Alpha_Vin, t, pwm, X0=0)
tPwmTorque, yPwmTorque, xPwmTorque = control.forced_response(tf_Torque_Vin, t, pwm, X0=0)
axs[0].plot(tPwmTheta, yPwmTheta, color = 'blue', label ='Theta')
axs[1].plot(tPwmOmega, yPwmOmega, color = 'red', label ='Omega')
axs[2].plot(tPwmAlpha, yPwmAlpha, color = 'black', label ='Alpha')
axs[3].plot(tPwmTorque, yPwmTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input PWM)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input PWM)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$ (Input PWM)')
axs[3].title.set_text('Torque $(Nm)$ (Input PWM)')
elif VinType== 0:
tStepTheta, yStepTheta = control.step_response(tf_Theta_Vin,T=t, X0=0)
tStepOmega, yStepOmega = control.step_response(tf_Omega_Vin,T=t, X0=0)
tStepAlpha, yStepAlpha = control.step_response(tf_Alpha_Vin,T=t, X0=0)
tStepTorque, yStepTorque = control.step_response(tf_Torque_Vin, T=t, X0=0)
axs[0].plot(tStepTheta, yStepTheta, color = 'blue', label ='Theta')
axs[1].plot(tStepOmega, yStepOmega, color = 'red', label ='Omega')
axs[2].plot(tStepAlpha, yStepAlpha, color = 'black', label ='Alpha')
axs[3].plot(tStepTorque, yStepTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input Step)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input Step)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$(Input Step)')
axs[3].title.set_text('Torque $(Nm)$ (Input Step)')
elif VinType== 1 :
tImpulseTheta, yImpulseTheta = control.impulse_response(tf_Theta_Vin,T=t, X0=0)
tImpulseOmega, yImpulseOmega = control.impulse_response(tf_Omega_Vin,T=t, X0=0)
tImpulseAlpha, yImpulseAlpha = control.impulse_response(tf_Alpha_Vin,T=t, X0=0)
tImpulseTorque, yImpulseTorque = control.impulse_response(tf_Torque_Vin, T=t, X0=0)
axs[0].plot(tImpulseTheta, yImpulseTheta, color = 'blue', label ='Theta')
axs[1].plot(tImpulseOmega, yImpulseOmega, color = 'red', label ='Omega')
axs[2].plot(tImpulseAlpha, yImpulseAlpha, color = 'black', label ='Alpha')
axs[3].plot(tImpulseTorque, yImpulseTorque, color = 'green', label ='Torque')
axs[0].title.set_text('Theta $(rad)$ (Input Impulse)')
axs[1].title.set_text('Omega $(\\frac {rad}{ms})$ (Input Impulse)')
axs[2].title.set_text('Alpha $(\\frac {rad}{ms^2})$ (Input Impulse)')
axs[3].title.set_text('Torque $(Nm)$ (Input Impulse)')
axs[0].legend()
axs[1].legend()
axs[2].legend()
axs[3].legend()
axs[0].grid(grid)
axs[1].grid(grid)
axs[2].grid(grid)
axs[3].grid(grid)
#DEFINISI WIDGETS PARAMETER
Ka_slider = widgets.FloatSlider(
value=19.90,
min=0.1,
max=20.0,
step=0.1,
description='$K_a (\\frac {Nm}{A})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kmd_slider = widgets.FloatSlider(
value=20.0,
min=0.1,
max=20.0,
step=0.1,
description='$K_{md} (\\frac {V}{V})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
L_slider = widgets.FloatSlider(
value=20,
min=0.1,
max=100.0,
step=0.1,
description='$L (mH)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
R_slider = widgets.IntSlider(
value=5,
min=1,
max=20,
step=1,
description='$R (\Omega)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
J_slider = widgets.FloatSlider(
value=25,
min=0.1,
max=100.0,
step=0.1,
description='$J (\\frac {Nm(ms)^2}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kf_slider = widgets.FloatSlider(
value=8,
min=0.1,
max=100.0,
step=0.1,
description='$K_{f} (\\frac {Nm(ms)}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
Kemf_slider = widgets.FloatSlider(
value=19.8,
min=0.1,
max=20,
step=0.1,
description='$K_{emf} (\\frac {V(ms)}{rad})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
VinType_select = widgets.Dropdown(
options=[('Step', 0), ('Impulse', 1),('PWM',2)],
description='Tipe Sinyal Input:',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
tMax_slider = widgets.IntSlider(
value=50,
min=1,
max=500,
step=1,
description='$t_{max} (ms)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
dutyCycle_slider = widgets.FloatSlider(
value=0.5,
min=0,
max=1.0,
step=0.05,
description='$Duty Cycle (\%)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
grid_button = widgets.ToggleButton(
value=True,
description='Grid',
icon='check',
layout=Layout(width='20%', height='50px',margin='10px 10px 10px 350px'),
style={'description_width': '200px'},
)
def update_Kemf_max(*args):
Kemf_slider.max = Ka_slider.value
Ka_slider.observe(update_Kemf_max, 'value')
ui_em = widgets.VBox([Ka_slider,Kmd_slider,L_slider,R_slider,J_slider,Kf_slider,Kemf_slider,VinType_select,tMax_slider,dutyCycle_slider,grid_button])
out_em = widgets.interactive_output(plot_elektromekanik, {'Ka':Ka_slider,'Kmd':Kmd_slider,'L':L_slider,'R':R_slider,'J':J_slider,'Kf':Kf_slider,'Kemf':Kemf_slider,'VinType':VinType_select,'tMax':tMax_slider,'dutyCycle':dutyCycle_slider, 'grid':grid_button})
display(ui_em,out_em)
```
### Analisis
Karena model memiliki persamaan yang cukup kompleks sehingga tidak dapat diambil secara intuitive kesimpulan parameter terhadap output sistem, akan dilakukan percobaan menggunakan slider untuk mengubah parameter dan mengamati interaksi perubahan antara parameter. Akan dilakukan juga perubahan bentuk input dan analisa efek penggunaan PWM sebagai modulasi sinyal step dengan besar maksimum 5V terhadap output.
#### 1. Peningkatan $K_a$
Peningkatan $K_a$ menyebabkan peningkatan osilasi ($\omega_d$) dan meningkatkan gain pada output $\omega$ dan $\alpha$ serta meningkatkan gradien dari output $\theta$. Namun, gain Torque tidak terpengaruh.
#### 2. Peningkatan $K_{md}$
Peningkatan $K_{md}$ membuat amplitudo $V_{in}$ meningkat sehingga amplitudo output bertambah.
#### 3. Peningkatan $L$
Peningkatan $L$ menyebabkan peningkatan kecepatan sudut $\omega$ dan $T$ menjadi lebih lambat serta penurunan $\alpha$ yang semakin lambat sehingga menyebabkan peningkatan $\theta$ semakin lambat (peningkatan rise time).
#### 4. Peningkatan $R$
Peningkatan $R$ menyebabkan osilasi output ($\omega_d$) $\omega$, $\alpha$, dan Torque semakin kecil dan gain yang semakin kecil sehingga mengurangi gradien dari output $\theta$.
#### 5. Peningkatan $J$
Peningkatan $J$ meningkatkan gain Torque dan menurunkan gain $\theta$, $\omega$, dan $\alpha$.
#### 6. Peningkatan $K_f$
Peningkatan $K_f$ meningkatkan gain Torque dan menurunkan gain $\theta$, $\omega$, dan $\alpha$.
#### 7. Peningkatan $K_{emf}$
Peningkatan $K_{emf}$ menurunkan gain Torque, $\theta$, $\omega$, dan $\alpha$.
#### 8. Interaksi antar parameter
Perbandingan pengurangan $R$ dibanding peningkatan $K_a$ kira kira 3 kali lipat. Peningkatan pada $J$ dan $K_f$ terbatas pada peningkatan $K_a$. Secara fisis, peningkatan $K_a$ dan $K_{emf}$ terjadi secara bersamaan dan hampir sebanding (hanya dibedakan pada voltage drop pada berbagai komponen), diikuti oleh $L$ sehingga untuk $K_a$ dan $K_{emf}$ besar, waktu mencapai steady state juga semakin lama. Hal yang menarik adalah $K_a$ dan $K_{emf}$ membuat sistem memiliki gain (transfer energi) yang kecil jika hanya ditinjau dari peningkatan nilai $K_a$ dan $K_{emf}$, namun ketika diikuti peningkatan $V_{in}$ sistem memiliki transfer energi yang lebih besar daripada sebelumnya pada keadaan steady state. Jadi dapat disimpulkan bahwa $K_a$ dan $K_{emf}$ harus memiliki nilai yang cukup besar agar konfigurasi sesuai dengan input $V_{in}$ dan menghasilkan transfer energi yang efisien. Input $V_{in}$ juga harus sesuai dengan sistem $K_a$ dan $K_{emf}$ yang ada sehingga dapat memutar motor (ini mengapa terdapat voltage minimum dan voltage yang disarankan untuk menjalankan sebuah motor).
#### 9. Pengaruh Input Step
Penggunaan input step memiliki osilasi ($\omega_d$) semakin sedikit.
#### 10. Pengaruh Input Impuls
Penggunaan input impulse membuat $\theta$ mencapai steady state karena motor berhenti berputar sehingga $\omega$,$\alpha$, dan Torque memiliki nilai steady state 0.
#### 11. Pengaruh Input PWM
Penggunaan input PWM dengan duty cycle tertentu membuat osilasi yang semakin banyak, namun dengan peningkatan duty cycle, osilasi semakin sedikit (semakin mendekati sinyal step). Hal yang menarik disini adalah sinyal PWM dapat digunakan untuk mengontrol, tetapi ketika tidak digunakan pengontrol, sinyal PWM malah memberikan osilasi pada sistem.
## 3. Pemodelan Sistem Mekanik
Dimodelkan sistem mekanik sebagai berikut
<img src="./10.png" style="width:20%">
<p style="text-align: center"><b>Sistem Mekanik Sederhana dengan Bond Graph</b></p>
### Deskripsi Sistem
1. Input
$F$ sebagai gaya yang dikerjakan pada massa
2. Output
$x$ sebagai perpindahan, $v$ sebagai kecepatan, dan $a$ sebagai percepatan pada massa
3. Parameter
Dari penurunan bond graph, didapatkan parameter $k$, $b$, dan $m$
### Pemodean Transfer Function
Fungsi transfer dapat dengan mudah di turunkan dari hubungan bond graph, diasumsikan
$$
x(0)=0
$$
$$
v(0)=0
$$
$$
a(0)=0
$$
$$
m \frac {d^2 x}{dt^2} = F-kx-b\frac{dx}{dt}
$$
<br>
Transformasi laplace menghasilkan
<br>
$$
s^2 x = \frac {F}{m}-x\frac {k}{m}-sx\frac{b}{m}
$$
$$
(s^2+s\frac{b}{m}+\frac {k}{m})x=\frac {F}{m}
$$
<br>
Untuk x:
<br>
$$
\frac {x}{F}=\frac {1}{(ms^2+bs+k)}
$$
<br>
Untuk v:
<br>
$$
\frac {v}{F}=\frac {s}{(ms^2+bs+k)}
$$
<br>
Untuk a:
<br>
$$
\frac {a}{F}=\frac {s^2}{(ms^2+bs+k)}
$$
```
# Digunakan penyelesaian numerik untuk output
import numpy as np
from scipy.integrate import odeint
import scipy.signal as sig
import matplotlib.pyplot as plt
from sympy.physics.mechanics import dynamicsymbols, SymbolicSystem
from sympy import *
import control as control
def plot_mekanik(M,B,K,VinType,grid):
# Parameter diberi value dan model system dibentuk dalam transfer function yang dapat diolah python
m=M
b=B
k=K
tf = sig.TransferFunction
tf_X_F=tf([1],[m,b,k])
tf_V_F=tf([1,0],[m,b,k])
tf_A_F=tf([1,0,0],[m,b,k])
f, axs = plt.subplots(3, sharex=True, figsize=(10, 10))
if VinType==0:
tImpX,xOutImp=sig.impulse(tf_X_F)
tImpV,vOutImp=sig.impulse(tf_V_F)
tImpA,aOutImp=sig.impulse(tf_A_F)
axs[0].plot(tImpX,xOutImp, color = 'blue', label ='x')
axs[1].plot(tImpV,vOutImp, color = 'red', label ='v')
axs[2].plot(tImpA,aOutImp, color = 'green', label ='a')
axs[0].title.set_text('Perpindahan Linear $(m)$ (Input Impuls)')
axs[1].title.set_text('Kecepatan Linear $(\\frac {m}{s})$ (Input Impuls)')
axs[2].title.set_text('Percepatan Linear $(\\frac {m}{s^2})$ (Input Impuls)')
elif VinType==1:
tStepX,xOutStep=sig.step(tf_X_F)
tStepV,vOutStep=sig.step(tf_V_F)
tStepA,aOutStep=sig.step(tf_A_F)
axs[0].plot(tStepX,xOutStep, color = 'blue', label ='x')
axs[1].plot(tStepV,vOutStep, color = 'red', label ='v')
axs[2].plot(tStepA,aOutStep, color = 'green', label ='a')
axs[0].title.set_text('Perpindahan Linear $(m)$ (Input Step)')
axs[1].title.set_text('Kecepatan Linear $(\\frac {m}{s})$ (Input Step)')
axs[2].title.set_text('Percepatan Linear $(\\frac {m}{s^2})$ (Input Step)')
axs[0].legend()
axs[1].legend()
axs[2].legend()
axs[0].grid(grid)
axs[1].grid(grid)
axs[2].grid(grid)
M_slider = widgets.FloatSlider(
value=0.1,
min=0.1,
max=30.0,
step=0.1,
description='Massa $(kg)$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
B_slider = widgets.FloatSlider(
value=0.1,
min=2,
max=20.0,
step=0.1,
description='Konstanta Redaman $(\\frac {Ns}{m})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
K_slider = widgets.FloatSlider(
value=0.1,
min=0.1,
max=100.0,
step=0.1,
description='Konstanta pegas $(\\frac {N}{m})$',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
VinType_select = widgets.Dropdown(
options=[('Impulse', 0), ('Step', 1)],
description='Tipe Sinyal Input:',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
)
grid_button = widgets.ToggleButton(
value=True,
description='Grid',
icon='check',
layout=Layout(width='20%', height='50px',margin='10px 10px 10px 350px'),
style={'description_width': '200px'},
)
ui_mk = widgets.VBox([M_slider,B_slider,K_slider,VinType_select,grid_button])
out_mk = widgets.interactive_output(plot_mekanik, {'M':M_slider,'B':B_slider,'K':K_slider,'VinType':VinType_select,'grid':grid_button})
display(ui_mk,out_mk)
```
### Analisis
Berdasarkan persamaan yang cukup sederhana, sistem mekanik orde dua memiliki karakteristik berikut:
#### 1. Pengaruh peningkatan massa
Massa pada sistem berperilaku seperti komponen inersial yang meningkatkan rise time dan settling time ketika diperbesar.
#### 2. Pengaruh peningkatan konstanta redaman
Konstanta redaman berperilaku seperti komponen hambatan yang meredam sistem sehingga maximum overshoot menjadi kecil (akibat peningkatan damping ratio) ketika peningkatan konstanta redaman terjadi. Konstanta redaman juga berpengaruh pada settling time, dimana peningkatan konstanta redaman meningkatkan settling time.
#### 3. Pengaruh peningkatan konstanta pegas
Konstanta pegas berperilaku seperti komponen kapasitansi yang mengurangi besar gain dari perpindahan, mengurangi damping ratio, meningkatkan frekuensi osilasi sistem, mengurangi amplitudo kecepatan sistem, mempercepat settling time, dan mempercepat peak time, meningkatkan maximum overshoot.
#### 4. Respon terhadap impulse
Terhadap sinyal impulse, sistem mencapai posisi awal kembali dan mencapai steady state 0 untuk perpindahan, kecepatan, dan percepatan
#### 5. Respon terhadap step
Terhadap sinyal step, sistem mencapai posisi akhir sesuai
$$\frac {F}{k}$$
dan kecepatan serta percepatan 0
|
github_jupyter
|
# Game Music dataset: data cleaning and exploration
The goal with this notebook is cleaning the dataset to make it usable as well as providing a descriptive analysis of the dataset features.
## Data loading and cleaning
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from ast import literal_eval
import os
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.read_csv('midi_dataframe.csv', parse_dates=[11])
num_midis_before = len(df)
print('There is %d midi files, from %d games, with %d midis matched with tgdb'
%(num_midis_before,
len(df.groupby(['tgdb_platform', 'tgdb_gametitle'])),
(df.tgdb_gametitle.notnull().sum())))
df.head()
```
We keep only files matched with tgdb and check that every midi file is only present once, if not we drop the rows.
```
num_dup = df.duplicated(subset='file_name').sum()
df.drop_duplicates(subset='file_name', inplace=True)
print('There was %d duplicated midi files, %d midis left'%(num_dup, len(df)))
```
Since we are interested in the genre, we only keep midis that have one.
```
num_genres_na = df.tgdb_genres.isnull().sum()
df.dropna(subset=['tgdb_genres'], inplace=True)
print("We removed %d midis, %d midis left"%(num_genres_na, len(df)))
```
Then, there are some categories, such as Medleys or Piano only that are not interesting.
There is also a big "remix" scene on vgmusic, so we also remove those.
```
categories_filter = df.console.isin(['Medleys', 'Piano Only'])
remix_filter = df.title.str.contains('[Rr]emix')
df = df[~categories_filter & ~remix_filter]
print('We removed %d midis from Medleys and Piano categories'%categories_filter.sum())
print('We removed %d midis containing "remix" in their title'%remix_filter.sum())
print('%d midis left'%len(df))
```
There often exists several versions of the same midi file, most of the time denoted by 'title (1)', 'title (2)', etc.
We also consider removing those, but keeping only the one with the highest value, or if there are several with the same title, we randomly keep one.
```
num_midis_before = len(df)
df_stripped = df.copy()
df_stripped.title = df.title.str.replace('\(\d+\)', '').str.rstrip()
df_stripped['rank'] = df.title.str.extract('\((\d+)\)', expand=False)
df = df_stripped.sort_values(by='rank', ascending=False).groupby(['brand', 'console', 'game', 'title']).first().reset_index()
print("We removed %d midis, %d midis left"%(num_midis_before-len(df), len(df)))
```
We also check if the midis files are valid by using mido and trying to load them.
```
from mido import MidiFile
bad_midis = []
for file in df['file_name']:
try:
midi = MidiFile("full/" + file)
except:
bad_midis.append(file)
df = df.loc[df.file_name.apply(lambda x: x not in bad_midis)]
print("We removed %d midis, %d midis left"%(len(bad_midis), len(df)))
```
The final numbers after preliminary data cleaning are:
```
num_games = len(df.groupby(['tgdb_platform', 'tgdb_gametitle']))
print('There is %d midi files, from %d games, with %d midis matched with tgdb'
%(len(df),
num_games,
(df.tgdb_gametitle.notnull().sum())))
```
## Data Exploration
## General statistics
We first begin by some general statistics about the dataset.
The number of gaming platforms is computed.
```
print('There is %d platforms'%df.tgdb_platform.nunique())
```
Then, statistics concerning the number of games per platform are computed and plotted.
```
df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle']).groupby('tgdb_platform').size().to_frame().describe()
size= (10, 5)
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle']).groupby('tgdb_platform').size().to_frame(), ax = ax)
ax.set_xlabel("number of games per platform")
ax.set_ylabel("density")
ax.set_title("Density of the number of games per platform")
ax.set_xticks(np.arange(0, 300, 10))
ax.set_xlim(0,200)
plt.show()
```
It can be noted that the majority of platforms seem to have around 10 games, which is a sufficient sample size.
Following this, statistics concerning the number of midis per platform are computed and plotted.
```
df.groupby('tgdb_platform').size().to_frame().describe()
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.groupby('tgdb_platform').size().to_frame())
ax.set_xlabel("number of midi per platform")
ax.set_ylabel("density")
ax.set_title("Density of the number of midis per platform")
ax.set_xticks(np.arange(0, 1000, 50))
ax.set_xlim(0,1500)
plt.show()
```
It can be noted that the majority of platform have around 50 midis, which is again judged to be a sufficient sample for analysis.
Finally, statistics concerning the number of midi per game are computed and plotted.
```
df.groupby(['tgdb_platform', 'tgdb_gametitle']).size().to_frame().describe()
fig, ax = plt.subplots(figsize=size)
ax = sns.distplot(df.groupby(['tgdb_platform', 'tgdb_gametitle']).size().to_frame())
ax.set_xlabel("number of midi per game")
ax.set_ylabel("density")
ax.set_title("Density of the number of midi per game")
ax.set_xticks(np.arange(0, 40, 2))
ax.set_xlim(0,40)
plt.show()
```
It can be noted that the peak of density is at 2 midi per game. This does not matter much as we are not trying to classify music per game, but by genres.
As a general remark, it can be noticed that most of the data we have follow power laws.
### Genres analysis
We currently had list of genres, for more convenience, we rework the dataframe to make several row of a midi if it had several genres.
```
genres = df.tgdb_genres.map(literal_eval, 'ignore').apply(pd.Series).stack().reset_index(level=1, drop=True)
genres.name = 'tgdb_genres'
genres_df = df.drop('tgdb_genres', axis=1).join(genres)
print("There is %d different genres"%genres_df.tgdb_genres.nunique())
genres_df.to_csv("midi_dataframe_cleaned.csv")
```
Here follows the percentage of games belonging to each genre and of midis for each genres.
```
genres_df.drop_duplicates(subset=['tgdb_platform', 'tgdb_gametitle'])\
.groupby(['tgdb_genres']).size().to_frame()\
.sort_values(0, ascending = False)/num_games*100
```
The number of genres is 19, and could be reduced to 10 if we consider only the genres for which we have at least 3% dataset coverage or 5 if we consider only the genres for which we have at least 9% dataset coverage.
|
github_jupyter
|
# Convolutional Neural Network in Keras
Bulding a Convolutional Neural Network to classify Fashion-MNIST.
#### Set seed for reproducibility
```
import numpy as np
np.random.seed(42)
```
#### Load dependencies
```
import os
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Layer, Activation, Dense, Dropout, Conv2D, MaxPooling2D, Flatten, LeakyReLU, BatchNormalization
from tensorflow.keras.callbacks import TensorBoard, ModelCheckpoint, EarlyStopping
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.models import load_model
from keras_contrib.layers.advanced_activations.sinerelu import SineReLU
from matplotlib import pyplot as plt
%matplotlib inline
```
#### Load data
```
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
```
#### Preprocess data
Flatten and normalise input data.
```
X_train = X_train.reshape(-1, 28, 28, 1)
X_test = X_test.reshape(-1, 28, 28, 1)
X_train = X_train.astype("float32")/255.
X_test = X_test.astype("float32")/255.
# One-hot encoded categories
n_classes = 10
y_train = to_categorical(y_train, n_classes)
y_test = to_categorical(y_test, n_classes)
```
#### Design Neural Network architecture
```
model = Sequential()
model.add(Conv2D(32, 7, padding = 'same', input_shape = (28, 28, 1)))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(32, 7, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.20))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(64, 3, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.30))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Conv2D(128, 2, padding = 'same'))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Dropout(0.40))
model.add(Flatten())
model.add(Dense(512))
# model.add(LeakyReLU(alpha=0.01))
model.add(Activation('relu'))
model.add(Dropout(0.50))
model.add(Dense(10, activation = "softmax"))
model.summary()
```
#### Callbacks
```
modelCheckpoint = ModelCheckpoint(monitor='val_accuracy', filepath='model_output/weights-cnn-fashion-mnist.hdf5',
save_best_only=True, mode='max')
earlyStopping = EarlyStopping(monitor='val_accuracy', mode='max', patience=5)
if not os.path.exists('model_output'):
os.makedirs('model_output')
tensorboard = TensorBoard("logs/convnet-fashion-mnist")
```
#### Configure model
```
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
```
#### Train!
```
history = model.fit(X_train, y_train, batch_size = 128, epochs = 20, verbose = 1,
validation_split = 0.1, callbacks=[modelCheckpoint, earlyStopping, tensorboard])
```
#### Test Predictions
```
saved_model = load_model('model_output/weights-cnn-fashion-mnist.hdf5')
predictions = saved_model.predict_classes(X_test, verbose = 2)
print(predictions)
# np.std(history.history['loss'])
```
#### Test Final Accuracy
```
final_loss, final_acc = saved_model.evaluate(X_test, y_test, verbose = 2)
print("Final loss: {0:.4f}, final accuracy: {1:.4f}".format(final_loss, final_acc))
image = X_test[0].reshape(1, 28, 28, 1)
predictions = model.predict_classes(image, verbose = 2)
print(predictions)
plt.imshow(X_test[0].reshape((28, 28)), cmap='gray')
# 0 T-shirt/top
# 1 Trouser
# 2 Pullover
# 3 Dress
# 4 Coat
# 5 Sandal
# 6 Shirt
# 7 Sneaker
# 8 Bag
# 9 Ankle boot
```
|
github_jupyter
|
# Parallel GST using MPI
The purpose of this tutorial is to demonstrate how to compute GST estimates in parallel (using multiple CPUs or "processors"). The core PyGSTi computational routines are written to take advantage of multiple processors via the MPI communication framework, and so one must have a version of MPI and the `mpi4py` python package installed in order use run pyGSTi calculations in parallel.
Since `mpi4py` doesn't play nicely with Jupyter notebooks, this tutorial is a bit more clunky than the others. In it, we will create a standalone Python script that imports `mpi4py` and execute it.
We will use as an example the same "standard" single-qubit model of the first tutorial. We'll first create a dataset, and then a script to be run in parallel which loads the data. The creation of a simulated data is performed in the same way as the first tutorial. Since *random* numbers are generated and used as simulated counts within the call to `generate_fake_data`, it is important that this is *not* done in a parallel environment, or different CPUs may get different data sets. (This isn't an issue in the typical situation when the data is obtained experimentally.)
```
#Import pyGSTi and the "stardard 1-qubit quantities for a model with X(pi/2), Y(pi/2), and idle gates"
import pygsti
from pygsti.modelpacks import smq1Q_XYI
#Create experiment design
exp_design = smq1Q_XYI.get_gst_experiment_design(max_max_length=32)
pygsti.io.write_empty_protocol_data(exp_design, "example_files/mpi_gst_example", clobber_ok=True)
#Simulate taking data
mdl_datagen = smq1Q_XYI.target_model().depolarize(op_noise=0.1, spam_noise=0.001)
pygsti.io.fill_in_empty_dataset_with_fake_data(mdl_datagen, "example_files/mpi_gst_example/data/dataset.txt",
nSamples=1000, seed=2020)
```
Next, we'll write a Python script that will load in the just-created `DataSet`, run GST on it, and write the output to a file. The only major difference between the contents of this script and previous examples is that the script imports `mpi4py` and passes a MPI comm object (`comm`) to the `do_long_sequence_gst` function. Since parallel computing is best used for computationaly intensive GST calculations, we also demonstrate how to set a per-processor memory limit to tell pyGSTi to partition its computations so as to not exceed this memory usage. Lastly, note the use of the `gaugeOptParams` argument of `do_long_sequence_gst`, which can be used to weight different model members differently during gauge optimization.
```
mpiScript = """
import time
import pygsti
#get MPI comm
from mpi4py import MPI
comm = MPI.COMM_WORLD
print("Rank %d started" % comm.Get_rank())
#load in data
data = pygsti.io.load_data_from_dir("example_files/mpi_gst_example")
#Specify a per-core memory limit (useful for larger GST calculations)
memLim = 2.1*(1024)**3 # 2.1 GB
#Perform TP-constrained GST
protocol = pygsti.protocols.StandardGST("TP")
start = time.time()
results = protocol.run(data, memlimit=memLim, comm=comm)
end = time.time()
print("Rank %d finished in %.1fs" % (comm.Get_rank(), end-start))
if comm.Get_rank() == 0:
results.write() #write results (within same diretory as data was loaded from)
"""
with open("example_files/mpi_example_script.py","w") as f:
f.write(mpiScript)
```
Next, we run the script with 3 processors using `mpiexec`. The `mpiexec` executable should have been installed with your MPI distribution -- if it doesn't exist, try replacing `mpiexec` with `mpirun`.
```
! mpiexec -n 3 python3 "example_files/mpi_example_script.py"
```
Notice in the above that output within `StandardGST.run` is not duplicated (only the first processor outputs to stdout) so that the output looks identical to running on a single processor. Finally, we just need to read the saved `ModelEstimateResults` object from file and proceed with any post-processing analysis. In this case, we'll just create a report.
```
results = pygsti.io.load_results_from_dir("example_files/mpi_gst_example", name="StandardGST")
pygsti.report.construct_standard_report(
results, title="MPI Example Report", verbosity=2
).write_html('example_files/mpi_example_brief', auto_open=True)
```
Open the [report](example_files/mpi_example_brief/main.html).
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
**BikeShare Demand Forecasting**
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Compute](#Compute)
1. [Data](#Data)
1. [Train](#Train)
1. [Featurization](#Featurization)
1. [Evaluate](#Evaluate)
## Introduction
This notebook demonstrates demand forecasting for a bike-sharing service using AutoML.
AutoML highlights here include built-in holiday featurization, accessing engineered feature names, and working with the `forecast` function. Please also look at the additional forecasting notebooks, which document lagging, rolling windows, forecast quantiles, other ways to use the forecast function, and forecaster deployment.
Make sure you have executed the [configuration notebook](../../../configuration.ipynb) before running this notebook.
Notebook synopsis:
1. Creating an Experiment in an existing Workspace
2. Configuration and local run of AutoML for a time-series model with lag and holiday features
3. Viewing the engineered names for featurized data and featurization summary for all raw features
4. Evaluating the fitted model using a rolling test
## Setup
```
import azureml.core
import pandas as pd
import numpy as np
import logging
from azureml.core import Workspace, Experiment, Dataset
from azureml.train.automl import AutoMLConfig
from datetime import datetime
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.17.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
As part of the setup you have already created a <b>Workspace</b>. To run AutoML, you also need to create an <b>Experiment</b>. An Experiment corresponds to a prediction problem you are trying to solve, while a Run corresponds to a specific approach to the problem.
```
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-bikeshareforecasting'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Compute
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read this article on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your cluster.
amlcompute_cluster_name = "bike-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=4)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## Data
The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace) is paired with the storage account, which contains the default data store. We will use it to upload the bike share data and create [tabular dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
```
datastore = ws.get_default_datastore()
datastore.upload_files(files = ['./bike-no.csv'], target_path = 'dataset/', overwrite = True,show_progress = True)
```
Let's set up what we know about the dataset.
**Target column** is what we want to forecast.
**Time column** is the time axis along which to predict.
```
target_column_name = 'cnt'
time_column_name = 'date'
dataset = Dataset.Tabular.from_delimited_files(path = [(datastore, 'dataset/bike-no.csv')]).with_timestamp_columns(fine_grain_timestamp=time_column_name)
dataset.take(5).to_pandas_dataframe().reset_index(drop=True)
```
### Split the data
The first split we make is into train and test sets. Note we are splitting on time. Data before 9/1 will be used for training, and data after and including 9/1 will be used for testing.
```
# select data that occurs before a specified date
train = dataset.time_before(datetime(2012, 8, 31), include_boundary=True)
train.to_pandas_dataframe().tail(5).reset_index(drop=True)
test = dataset.time_after(datetime(2012, 9, 1), include_boundary=True)
test.to_pandas_dataframe().head(5).reset_index(drop=True)
```
## Forecasting Parameters
To define forecasting parameters for your experiment training, you can leverage the ForecastingParameters class. The table below details the forecasting parameter we will be passing into our experiment.
|Property|Description|
|-|-|
|**time_column_name**|The name of your time column.|
|**forecast_horizon**|The forecast horizon is how many periods forward you would like to forecast. This integer horizon is in units of the timeseries frequency (e.g. daily, weekly).|
|**country_or_region_for_holidays**|The country/region used to generate holiday features. These should be ISO 3166 two-letter country/region codes (i.e. 'US', 'GB').|
|**target_lags**|The target_lags specifies how far back we will construct the lags of the target variable.|
|**drop_column_names**|Name(s) of columns to drop prior to modeling|
## Train
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|forecasting|
|**primary_metric**|This is the metric that you want to optimize.<br> Forecasting supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i>
|**blocked_models**|Models in blocked_models won't be used by AutoML. All supported models can be found at [here](https://docs.microsoft.com/en-us/python/api/azureml-train-automl-client/azureml.train.automl.constants.supportedmodels.forecasting?view=azure-ml-py).|
|**experiment_timeout_hours**|Experimentation timeout in hours.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
|**compute_target**|The remote compute for training.|
|**n_cross_validations**|Number of cross validation splits.|
|**enable_early_stopping**|If early stopping is on, training will stop when the primary metric is no longer improving.|
|**forecasting_parameters**|A class that holds all the forecasting related parameters.|
This notebook uses the blocked_models parameter to exclude some models that take a longer time to train on this dataset. You can choose to remove models from the blocked_models list but you may need to increase the experiment_timeout_hours parameter value to get results.
### Setting forecaster maximum horizon
The forecast horizon is the number of periods into the future that the model should predict. Here, we set the horizon to 14 periods (i.e. 14 days). Notice that this is much shorter than the number of days in the test set; we will need to use a rolling test to evaluate the performance on the whole test set. For more discussion of forecast horizons and guiding principles for setting them, please see the [energy demand notebook](https://github.com/Azure/MachineLearningNotebooks/tree/master/how-to-use-azureml/automated-machine-learning/forecasting-energy-demand).
```
forecast_horizon = 14
```
### Config AutoML
```
from azureml.automl.core.forecasting_parameters import ForecastingParameters
forecasting_parameters = ForecastingParameters(
time_column_name=time_column_name,
forecast_horizon=forecast_horizon,
country_or_region_for_holidays='US', # set country_or_region will trigger holiday featurizer
target_lags='auto', # use heuristic based lag setting
drop_column_names=['casual', 'registered'] # these columns are a breakdown of the total and therefore a leak
)
automl_config = AutoMLConfig(task='forecasting',
primary_metric='normalized_root_mean_squared_error',
blocked_models = ['ExtremeRandomTrees'],
experiment_timeout_hours=0.3,
training_data=train,
label_column_name=target_column_name,
compute_target=compute_target,
enable_early_stopping=True,
n_cross_validations=3,
max_concurrent_iterations=4,
max_cores_per_iteration=-1,
verbosity=logging.INFO,
forecasting_parameters=forecasting_parameters)
```
We will now run the experiment, you can go to Azure ML portal to view the run details.
```
remote_run = experiment.submit(automl_config, show_output=False)
remote_run
remote_run.wait_for_completion()
```
### Retrieve the Best Model
Below we select the best model from all the training iterations using get_output method.
```
best_run, fitted_model = remote_run.get_output()
fitted_model.steps
```
## Featurization
You can access the engineered feature names generated in time-series featurization. Note that a number of named holiday periods are represented. We recommend that you have at least one year of data when using this feature to ensure that all yearly holidays are captured in the training featurization.
```
fitted_model.named_steps['timeseriestransformer'].get_engineered_feature_names()
```
### View the featurization summary
You can also see what featurization steps were performed on different raw features in the user data. For each raw feature in the user data, the following information is displayed:
- Raw feature name
- Number of engineered features formed out of this raw feature
- Type detected
- If feature was dropped
- List of feature transformations for the raw feature
```
# Get the featurization summary as a list of JSON
featurization_summary = fitted_model.named_steps['timeseriestransformer'].get_featurization_summary()
# View the featurization summary as a pandas dataframe
pd.DataFrame.from_records(featurization_summary)
```
## Evaluate
We now use the best fitted model from the AutoML Run to make forecasts for the test set. We will do batch scoring on the test dataset which should have the same schema as training dataset.
The scoring will run on a remote compute. In this example, it will reuse the training compute.
```
test_experiment = Experiment(ws, experiment_name + "_test")
```
### Retrieving forecasts from the model
To run the forecast on the remote compute we will use a helper script: forecasting_script. This script contains the utility methods which will be used by the remote estimator. We copy the script to the project folder to upload it to remote compute.
```
import os
import shutil
script_folder = os.path.join(os.getcwd(), 'forecast')
os.makedirs(script_folder, exist_ok=True)
shutil.copy('forecasting_script.py', script_folder)
```
For brevity, we have created a function called run_forecast that submits the test data to the best model determined during the training run and retrieves forecasts. The test set is longer than the forecast horizon specified at train time, so the forecasting script uses a so-called rolling evaluation to generate predictions over the whole test set. A rolling evaluation iterates the forecaster over the test set, using the actuals in the test set to make lag features as needed.
```
from run_forecast import run_rolling_forecast
remote_run = run_rolling_forecast(test_experiment, compute_target, best_run, test, target_column_name)
remote_run
remote_run.wait_for_completion(show_output=False)
```
### Download the prediction result for metrics calcuation
The test data with predictions are saved in artifact outputs/predictions.csv. You can download it and calculation some error metrics for the forecasts and vizualize the predictions vs. the actuals.
```
remote_run.download_file('outputs/predictions.csv', 'predictions.csv')
df_all = pd.read_csv('predictions.csv')
from azureml.automl.core.shared import constants
from azureml.automl.runtime.shared.score import scoring
from sklearn.metrics import mean_absolute_error, mean_squared_error
from matplotlib import pyplot as plt
# use automl metrics module
scores = scoring.score_regression(
y_test=df_all[target_column_name],
y_pred=df_all['predicted'],
metrics=list(constants.Metric.SCALAR_REGRESSION_SET))
print("[Test data scores]\n")
for key, value in scores.items():
print('{}: {:.3f}'.format(key, value))
# Plot outputs
%matplotlib inline
test_pred = plt.scatter(df_all[target_column_name], df_all['predicted'], color='b')
test_test = plt.scatter(df_all[target_column_name], df_all[target_column_name], color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
```
Since we did a rolling evaluation on the test set, we can analyze the predictions by their forecast horizon relative to the rolling origin. The model was initially trained at a forecast horizon of 14, so each prediction from the model is associated with a horizon value from 1 to 14. The horizon values are in a column named, "horizon_origin," in the prediction set. For example, we can calculate some of the error metrics grouped by the horizon:
```
from metrics_helper import MAPE, APE
df_all.groupby('horizon_origin').apply(
lambda df: pd.Series({'MAPE': MAPE(df[target_column_name], df['predicted']),
'RMSE': np.sqrt(mean_squared_error(df[target_column_name], df['predicted'])),
'MAE': mean_absolute_error(df[target_column_name], df['predicted'])}))
```
To drill down more, we can look at the distributions of APE (absolute percentage error) by horizon. From the chart, it is clear that the overall MAPE is being skewed by one particular point where the actual value is of small absolute value.
```
df_all_APE = df_all.assign(APE=APE(df_all[target_column_name], df_all['predicted']))
APEs = [df_all_APE[df_all['horizon_origin'] == h].APE.values for h in range(1, forecast_horizon + 1)]
%matplotlib inline
plt.boxplot(APEs)
plt.yscale('log')
plt.xlabel('horizon')
plt.ylabel('APE (%)')
plt.title('Absolute Percentage Errors by Forecast Horizon')
plt.show()
```
|
github_jupyter
|
```
import numpy as np # type: ignore
import onnx
import onnx.helper as h
import onnx.checker as checker
from onnx import TensorProto as tp
from onnx import save
import onnxruntime
# Builds a pipeline that resizes and crops an input.
def build_preprocessing_model(filename):
nodes = []
nodes.append(
h.make_node('Shape', inputs=['x'], outputs=['x_shape'], name='x_shape')
)
nodes.append(
h.make_node('Split', inputs=['x_shape'], outputs=['h', 'w', 'c'], axis=0, name='split_shape')
)
nodes.append(
h.make_node('Min', inputs=['h', 'w'], outputs=['min_extent'], name='min_extent')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_256'],
value=h.make_tensor(name='k256', data_type=tp.FLOAT, dims=[1], vals=[256.0]),
name='constant_256')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_1'],
value=h.make_tensor(name='k1', data_type=tp.FLOAT, dims=[1], vals=[1.0]),
name='constant_1')
)
nodes.append(
h.make_node('Cast', inputs=['min_extent'], outputs=['min_extent_f'], to=tp.FLOAT, name='min_extent_f')
)
nodes.append(
h.make_node('Div', inputs=['constant_256', 'min_extent_f'], outputs=['ratio-resize'], name='ratio-resize')
)
nodes.append(
h.make_node('Concat', inputs=['ratio-resize', 'ratio-resize', 'constant_1'], outputs=['scales-resize'],
axis=0, name='scales-resize')
)
nodes.append(
h.make_node('Resize', inputs=['x', '', 'scales-resize'], outputs=['x_resized'], mode='linear', name='x_resize')
)
# Centered crop 224x224
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_224'],
value=h.make_tensor(name='k224', data_type=tp.INT64, dims=[1], vals=[224]), name='constant_224')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['constant_2'],
value=h.make_tensor(name='k2', data_type=tp.INT64, dims=[1], vals=[2]), name='constant_2')
)
nodes.append(
h.make_node('Shape', inputs=['x_resized'], outputs=['x_shape_2'], name='x_shape_2')
)
nodes.append(
h.make_node('Split', inputs=['x_shape_2'], outputs=['h2', 'w2', 'c2'], name='split_shape_2')
)
nodes.append(
h.make_node('Concat', inputs=['h2', 'w2'], outputs=['hw'], axis=0, name='concat_2')
)
nodes.append(
h.make_node('Sub', inputs=['hw', 'constant_224'], outputs=['hw_diff'], name='sub_224')
)
nodes.append(
h.make_node('Div', inputs=['hw_diff', 'constant_2'], outputs=['start_xy'], name='div_2')
)
nodes.append(
h.make_node('Add', inputs=['start_xy', 'constant_224'], outputs=['end_xy'], name='add_224')
)
nodes.append(
h.make_node('Constant', inputs=[], outputs=['axes'],
value=h.make_tensor(name='axes_k', data_type=tp.INT64, dims=[2], vals=[0, 1]), name='axes_k')
)
nodes.append(
h.make_node('Slice', inputs=['x_resized', 'start_xy', 'end_xy', 'axes'], outputs=['x_processed'], name='x_crop')
)
# Create the graph
g = h.make_graph(nodes, 'rn50-data-pipe-resize',
[h.make_tensor_value_info('x', tp.UINT8, ['H', 'W', 3])],
[h.make_tensor_value_info('x_processed', tp.UINT8, ['H', 'W', 3])]
)
# Make the preprocessing model
op = onnx.OperatorSetIdProto()
op.version = 14
m = h.make_model(g, producer_name='onnx-preprocessing-resize-demo', opset_imports=[op])
checker.check_model(m)
# Save the model to a file
save(m, filename)
build_preprocessing_model('preprocessing.onnx')
# display images in notebook
import matplotlib.pyplot as plt
from PIL import Image, ImageDraw, ImageFont
%matplotlib inline
def show_images(images):
nsamples = len(images)
print("Output sizes: ")
for i in range(nsamples):
print(images[i].size)
fig, axs = plt.subplots(1, nsamples)
for i in range(nsamples):
axs[i].axis('off')
axs[i].imshow(images[i])
plt.show()
images = [
Image.open('../images/snail-4345504_1280.jpg'),
Image.open('../images/grasshopper-4357903_1280.jpg')
]
show_images(images)
session = onnxruntime.InferenceSession('preprocessing.onnx', None)
# Note: x_shape could be calculated from 'x' inside the graph, but we add it explicitly
# to workaround an issue with SequenceAt (https://github.com/microsoft/onnxruntime/issues/9868)
# To be removed when the issue is solved
out_images1 = []
for i in range(len(images)):
img = np.array(images[i])
result = session.run(
[],
{
'x': img,
#'x_shape': np.array(img.shape)
}
)
out_images1.append(Image.fromarray(result[0]))
show_images(out_images1)
import copy
preprocessing_model = onnx.load('preprocessing.onnx')
graph = preprocessing_model.graph
ninputs = len(graph.input)
noutputs = len(graph.output)
def tensor_shape(t):
return [d.dim_value or d.dim_param for d in t.type.tensor_type.shape.dim]
def tensor_dtype(t):
return t.type.tensor_type.elem_type
def make_tensor_seq(t, prefix='seq_'):
return h.make_tensor_sequence_value_info(prefix + t.name, tensor_dtype(t), tensor_shape(t))
def make_batch_tensor(t, prefix='batch_'):
return h.make_tensor_value_info(prefix + t.name, tensor_dtype(t), ['N', ] + tensor_shape(t))
cond_in = h.make_tensor_value_info('cond_in', onnx.TensorProto.BOOL, [])
cond_out = h.make_tensor_value_info('cond_out', onnx.TensorProto.BOOL, [])
iter_count = h.make_tensor_value_info('iter_count', onnx.TensorProto.INT64, [])
nodes = []
loop_body_inputs = [iter_count, cond_in]
loop_body_outputs = [cond_out]
for i in range(ninputs):
in_name = graph.input[i].name
nodes.append(
onnx.helper.make_node(
'SequenceAt',
inputs=['seq_' + in_name, 'iter_count'],
outputs=[in_name]
)
)
for n in graph.node:
nodes.append(n)
for i in range(noutputs):
out_i = graph.output[i]
loop_body_inputs.append(
make_tensor_seq(out_i, prefix='loop_seqin_')
)
loop_body_outputs.append(
make_tensor_seq(out_i, prefix='loop_seqout_')
)
nodes.append(
onnx.helper.make_node(
'SequenceInsert',
inputs=['loop_seqin_' + out_i.name, out_i.name],
outputs=['loop_seqout_' + out_i.name]
)
)
nodes.append(
onnx.helper.make_node(
'Identity',
inputs=['cond_in'],
outputs=['cond_out']
)
)
loop_body = onnx.helper.make_graph(
nodes=nodes,
name='loop_body',
inputs=loop_body_inputs,
outputs=loop_body_outputs,
)
# Loop
loop_graph_nodes = []
# Note: Sequence length is taken from the first input
loop_graph_nodes.append(
onnx.helper.make_node(
'SequenceLength',
inputs=['seq_' + graph.input[i].name],
outputs=['seq_len']
)
)
loop_graph_nodes.append(
onnx.helper.make_node(
'Constant',
inputs=[],
outputs=['cond'],
value=onnx.helper.make_tensor(
name='const_bool_true',
data_type=onnx.TensorProto.BOOL,
dims=(),
vals=[True]
)
)
)
loop_node_inputs = ['seq_len', 'cond']
loop_node_outputs = []
for i in range(noutputs):
out_i = graph.output[i]
loop_graph_nodes.append(
onnx.helper.make_node(
'SequenceEmpty',
dtype=tensor_dtype(out_i),
inputs=[],
outputs=['emptyseq_' + out_i.name]
)
)
loop_node_inputs.append('emptyseq_' + out_i.name)
loop_node_outputs.append('seq_out_' + out_i.name)
loop_graph_nodes.append(
onnx.helper.make_node(
'Loop',
inputs=loop_node_inputs,
outputs=loop_node_outputs,
body=loop_body
)
)
for i in range(noutputs):
out_i = graph.output[i]
loop_graph_nodes.append(
onnx.helper.make_node(
'ConcatFromSequence',
inputs=['seq_out_' + out_i.name],
outputs=['batch_' + out_i.name],
new_axis=1,
axis=0,
)
)
# graph
graph = onnx.helper.make_graph(
nodes=loop_graph_nodes,
name='loop_graph',
inputs=[make_tensor_seq(t) for t in graph.input],
outputs=[make_batch_tensor(t) for t in graph.output],
)
op = onnx.OperatorSetIdProto()
op.version = 14
model = onnx.helper.make_model(graph, producer_name='loop-test', opset_imports=[op])
onnx.checker.check_model(model)
onnx.save(model, "loop-test.onnx")
session = onnxruntime.InferenceSession("loop-test.onnx", None)
imgs = [np.array(image) for image in images]
img_shapes = [np.array(img.shape) for img in imgs]
result = session.run(
[],
{
'seq_x' : imgs,
}
)
print("Output shape: ", result[0].shape)
out_images2 = [Image.fromarray(result[0][i]) for i in range(2)]
show_images(out_images2)
```
|
github_jupyter
|
# Getting Started with BentoML
[BentoML](http://bentoml.ai) is an open-source framework for machine learning **model serving**, aiming to **bridge the gap between Data Science and DevOps**.
Data Scientists can easily package their models trained with any ML framework using BentoMl and reproduce the model for serving in production. BentoML helps with managing packaged models in the BentoML format, and allows DevOps to deploy them as online API serving endpoints or offline batch inference jobs, on any cloud platform.
This getting started guide demonstrates how to use BentoML to serve a sklearn modeld via a REST API server, and then containerize the model server for production deployment.

BentoML requires python 3.6 or above, install dependencies via `pip`:
```
# Install PyPI packages required in this guide, including BentoML
!pip install -q bentoml
!pip install -q 'scikit-learn>=0.23.2' 'pandas>=1.1.1'
```
Before started, let's discuss how BentoML's project structure would look like. For most use-cases, users can follow this minimal scaffold
for deploying with BentoML to avoid any potential errors (example project structure can be found under [guides/quick-start](https://github.com/bentoml/BentoML/tree/master/guides/quick-start)):
bento_deploy/
├── bento_packer.py # responsible for packing BentoService
├── bento_service.py # BentoService definition
├── model.py # DL Model definitions
├── train.py # training scripts
└── requirements.txt
Let's prepare a trained model for serving with BentoML. Train a classifier model on the [Iris data set](https://en.wikipedia.org/wiki/Iris_flower_data_set):
```
from sklearn import svm
from sklearn import datasets
# Load training data
iris = datasets.load_iris()
X, y = iris.data, iris.target
# Model Training
clf = svm.SVC(gamma='scale')
clf.fit(X, y)
```
## Create a Prediction Service with BentoML
Model serving with BentoML comes after a model is trained. The first step is creating a
prediction service class, which defines the models required and the inference APIs which
contains the serving logic. Here is a minimal prediction service created for serving
the iris classifier model trained above:
```
%%writefile bento_service.py
import pandas as pd
from bentoml import env, artifacts, api, BentoService
from bentoml.adapters import DataframeInput
from bentoml.frameworks.sklearn import SklearnModelArtifact
@env(infer_pip_packages=True)
@artifacts([SklearnModelArtifact('model')])
class IrisClassifier(BentoService):
"""
A minimum prediction service exposing a Scikit-learn model
"""
@api(input=DataframeInput(), batch=True)
def predict(self, df: pd.DataFrame):
"""
An inference API named `predict` with Dataframe input adapter, which codifies
how HTTP requests or CSV files are converted to a pandas Dataframe object as the
inference API function input
"""
return self.artifacts.model.predict(df)
```
This code defines a prediction service that packages a scikit-learn model and provides
an inference API that expects a `pandas.Dataframe` object as its input. BentoML also supports other API input
data types including `JsonInput`, `ImageInput`, `FileInput` and
[more](https://docs.bentoml.org/en/latest/api/adapters.html).
In BentoML, **all inference APIs are suppose to accept a list of inputs and return a
list of results**. In the case of `DataframeInput`, each row of the dataframe is mapping
to one prediction request received from the client. BentoML will convert HTTP JSON
requests into :code:`pandas.DataFrame` object before passing it to the user-defined
inference API function.
This design allows BentoML to group API requests into small batches while serving online
traffic. Comparing to a regular flask or FastAPI based model server, this can increases
the overall throughput of the API server by 10-100x depending on the workload.
The following code packages the trained model with the prediction service class
`IrisClassifier` defined above, and then saves the IrisClassifier instance to disk
in the BentoML format for distribution and deployment:
```
# import the IrisClassifier class defined above
from bento_service import IrisClassifier
# Create a iris classifier service instance
iris_classifier_service = IrisClassifier()
# Pack the newly trained model artifact
iris_classifier_service.pack('model', clf)
# Prepare input data for testing the prediction service
import pandas as pd
test_input_df = pd.DataFrame(X).sample(n=5)
test_input_df.to_csv("./test_input.csv", index=False)
test_input_df
# Test the service's inference API python interface
iris_classifier_service.predict(test_input_df)
# Start a dev model server to test out everything
iris_classifier_service.start_dev_server()
import requests
response = requests.post(
"http://127.0.0.1:5000/predict",
json=test_input_df.values.tolist()
)
print(response.text)
# Stop the dev model server
iris_classifier_service.stop_dev_server()
# Save the prediction service to disk for deployment
saved_path = iris_classifier_service.save()
```
BentoML stores all packaged model files under the
`~/bentoml/{service_name}/{service_version}` directory by default.
The BentoML file format contains all the code, files, and configs required to
deploy the model for serving.
## REST API Model Serving
To start a REST API model server with the `IrisClassifier` saved above, use
the `bentoml serve` command:
```
!bentoml serve IrisClassifier:latest
```
If you are running this notebook from Google Colab, you can start the dev server with `--run-with-ngrok` option, to gain acccess to the API endpoint via a public endpoint managed by [ngrok](https://ngrok.com/):
```
!bentoml serve IrisClassifier:latest --run-with-ngrok
```
The `IrisClassifier` model is now served at `localhost:5000`. Use `curl` command to send
a prediction request:
```bash
curl -i \
--header "Content-Type: application/json" \
--request POST \
--data '[[5.1, 3.5, 1.4, 0.2]]' \
localhost:5000/predict
```
Or with `python` and [request library](https://requests.readthedocs.io/):
```python
import requests
response = requests.post("http://127.0.0.1:5000/predict", json=[[5.1, 3.5, 1.4, 0.2]])
print(response.text)
```
Note that BentoML API server automatically converts the Dataframe JSON format into a
`pandas.DataFrame` object before sending it to the user-defined inference API function.
The BentoML API server also provides a simple web UI dashboard.
Go to http://localhost:5000 in the browser and use the Web UI to send
prediction request:

## Containerize model server with Docker
One common way of distributing this model API server for production deployment, is via
Docker containers. And BentoML provides a convenient way to do that.
Note that `docker` is __not available in Google Colab__. You will need to download and run this notebook locally to try out this containerization with docker feature.
If you already have docker configured, simply run the follow command to product a
docker container serving the `IrisClassifier` prediction service created above:
```
!bentoml containerize IrisClassifier:latest -t iris-classifier:v1
```
Start a container with the docker image built in the previous step:
```
!docker run -p 5000:5000 iris-classifier:v1 --workers=2
```
This made it possible to deploy BentoML bundled ML models with platforms such as
[Kubeflow](https://www.kubeflow.org/docs/components/serving/bentoml/),
[Knative](https://knative.dev/community/samples/serving/machinelearning-python-bentoml/),
[Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html), which
provides advanced model deployment features such as auto-scaling, A/B testing,
scale-to-zero, canary rollout and multi-armed bandit.
## Load saved BentoService
`bentoml.load` is the API for loading a BentoML packaged model in python:
```
import bentoml
import pandas as pd
bento_svc = bentoml.load(saved_path)
# Test loaded bentoml service:
bento_svc.predict(test_input_df)
```
The BentoML format is pip-installable and can be directly distributed as a
PyPI package for using in python applications:
```
!pip install -q {saved_path}
# The BentoService class name will become packaged name
import IrisClassifier
installed_svc = IrisClassifier.load()
installed_svc.predict(test_input_df)
```
This also allow users to upload their BentoService to pypi.org as public python package
or to their organization's private PyPi index to share with other developers.
`cd {saved_path} & python setup.py sdist upload`
*You will have to configure ".pypirc" file before uploading to pypi index.
You can find more information about distributing python package at:
https://docs.python.org/3.7/distributing/index.html#distributing-index*
# Launch inference job from CLI
BentoML cli supports loading and running a packaged model from CLI. With the `DataframeInput` adapter, the CLI command supports reading input Dataframe data from CLI argument or local `csv` or `json` files:
```
!bentoml run IrisClassifier:latest predict --input '{test_input_df.to_json()}' --quiet
!bentoml run IrisClassifier:latest predict \
--input-file "./test_input.csv" --format "csv" --quiet
# run inference with the docker image built above
!docker run -v $(PWD):/tmp iris-classifier:v1 \
bentoml run /bento predict --input-file "/tmp/test_input.csv" --format "csv" --quiet
```
# Deployment Options
Check out the [BentoML deployment guide](https://docs.bentoml.org/en/latest/deployment/index.html)
to better understand which deployment option is best suited for your use case.
* One-click deployment with BentoML:
- [AWS Lambda](https://docs.bentoml.org/en/latest/deployment/aws_lambda.html)
- [AWS SageMaker](https://docs.bentoml.org/en/latest/deployment/aws_sagemaker.html)
- [AWS EC2](https://docs.bentoml.org/en/latest/deployment/aws_ec2.html)
- [Azure Functions](https://docs.bentoml.org/en/latest/deployment/azure_functions.html)
* Deploy with open-source platforms:
- [Docker](https://docs.bentoml.org/en/latest/deployment/docker.html)
- [Kubernetes](https://docs.bentoml.org/en/latest/deployment/kubernetes.html)
- [Knative](https://docs.bentoml.org/en/latest/deployment/knative.html)
- [Kubeflow](https://docs.bentoml.org/en/latest/deployment/kubeflow.html)
- [KFServing](https://docs.bentoml.org/en/latest/deployment/kfserving.html)
- [Clipper](https://docs.bentoml.org/en/latest/deployment/clipper.html)
* Manual cloud deployment guides:
- [AWS ECS](https://docs.bentoml.org/en/latest/deployment/aws_ecs.html)
- [Google Cloud Run](https://docs.bentoml.org/en/latest/deployment/google_cloud_run.html)
- [Azure container instance](https://docs.bentoml.org/en/latest/deployment/azure_container_instance.html)
- [Heroku](https://docs.bentoml.org/en/latest/deployment/heroku.html)
# Summary
This is what it looks like when using BentoML to serve and deploy a model in the cloud. BentoML also supports [many other Machine Learning frameworks](https://docs.bentoml.org/en/latest/examples.html) besides Scikit-learn. The [BentoML core concepts](https://docs.bentoml.org/en/latest/concepts.html) doc is recommended for anyone looking to get a deeper understanding of BentoML.
Join the [BentoML Slack](https://join.slack.com/t/bentoml/shared_invite/enQtNjcyMTY3MjE4NTgzLTU3ZDc1MWM5MzQxMWQxMzJiNTc1MTJmMzYzMTYwMjQ0OGEwNDFmZDkzYWQxNzgxYWNhNjAxZjk4MzI4OGY1Yjg) to follow the latest development updates and roadmap discussions.
|
github_jupyter
|
# Time Complexity Examples
```
def logarithmic_problem(N):
i = N
while i > 1:
# do something
i = i // 2 # move on
%time logarithmic_problem(10000)
def linear_problem(N):
i = N
while i > 1:
# do something
i = i - 1 # move on
%time linear_problem(10000)
def quadratic_problem(N):
i = N
while i > 1:
j = N
while j > 1:
# do something
j = j - 1 # move on
i = i - 1
%time quadratic_problem(10000)
```
# Problem
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of a target(k) if found in A, and -1 otherwise.
### Brute-force solution: Linear Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def linear_search(A, k):
for idx, element in enumerate(A):
if element == k:
return idx
return -1
linear_search(A, 15)
linear_search(A, 100)
```
### Efficient solution: Binary Search
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search(A, k):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search(A, 15)
binary_search(A, 17)
```
### Binary Search common bugs:
#### BUG-1: one-off bug
not handling arrays of size=1
```
A = [5, 8, 8, 15, 16, 19, 30, 35, 40, 51]
def binary_search_bug1(A, k):
left, right = 0, len(A)-1
#HERE: < instead of <=
while left<right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
return mid
return -1
binary_search_bug1(A, 35)
binary_search_bug1(A, 30)
binary_search_bug1(A, 15)
binary_search_bug1([15], 15)
```
#### BUG-2: integer overflow
not handling the case where summing two integers can return an integer bigger than what the memory can take
```
# because python3 only imposes limits
# on float, we are going to illustrate
# this issue using floats instead of ints
import sys
right = sys.float_info.max
left = sys.float_info.max - 1000
mid = (right + left) // 2
mid
mid = (right - left)//2 + left
mid
```
## Problem variant1:
#### Search a sorted array for first occurrence of target(k)
Given an array(A) of numbers sorted in increasing order, implement a function that returns the index of the first occurence of a target(k) if found in A, and -1 otherwise.
```
A = [5, 8, 8, 8, 8, 19, 30, 35, 40, 51]
def first_occurence_search(A, k):
left, right, res = 0, len(A)-1, -1
while left<=right:
mid = (right - left)//2 + left
if A[mid] < k:
#look on the right
left = mid+1
elif A[mid] > k:
#look on the left
right = mid-1
else:
# update res
res = mid
# keep looking on the left
right = mid-1
return res
binary_search(A, 8)
first_occurence_search(A, 8)
```
## Problem variant2:
#### Search a sorted array for entry equal to its index
Given a sorted array(A) of distinct integers, implement a function that returns the index i if A[i] = i, and -1 otherwise.
```
A = [-3, 0, 2, 5, 7, 9, 18, 35, 40, 51]
def search_entry_equal_to_its_index(A):
left, right = 0, len(A)-1
while left<=right:
mid = (right - left)//2 + left
difference = A[mid] - mid
if difference < 0:
#look on the right
left = mid+1
elif difference > 0:
#look on the left
right = mid-1
else:
return mid
return -1
search_entry_equal_to_its_index(A)
```
|
github_jupyter
|
# Differentially Private Covariance
SmartNoise offers three different functionalities within its `covariance` function:
1. Covariance between two vectors
2. Covariance matrix of a matrix
3. Cross-covariance matrix of a pair of matrices, where element $(i,j)$ of the returned matrix is the covariance of column $i$ of the left matrix and column $j$ of the right matrix.
```
# load libraries
import os
import opendp.smartnoise.core as sn
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# establish data information
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
var_names = ["age", "sex", "educ", "race", "income", "married"]
data = np.genfromtxt(data_path, delimiter=',', names=True)
```
### Functionality
Below we show the relationship between the three methods by calculating the same covariance in each. We use a much larger $\epsilon$ than would ever be used in practice to show that the methods are consistent with one another.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get scalar covariance
age_income_cov_scalar = sn.dp_covariance(left = sn.to_float(wn_data['age']),
right = sn.to_float(wn_data['income']),
privacy_usage = {'epsilon': 5000},
left_lower = 0.,
left_upper = 100.,
left_rows = 1000,
right_lower = 0.,
right_upper = 500_000.,
right_rows = 1000)
# get full covariance matrix
age_income_cov_matrix = sn.dp_covariance(data = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
data_lower = [0., 0.],
data_upper = [100., 500_000],
data_rows = 1000)
# get cross-covariance matrix
cross_covar = sn.dp_covariance(left = sn.to_float(wn_data['age', 'income']),
right = sn.to_float(wn_data['age', 'income']),
privacy_usage = {'epsilon': 5000},
left_lower = [0., 0.],
left_upper = [100., 500_000.],
left_rows = 1_000,
right_lower = [0., 0.],
right_upper = [100., 500_000.],
right_rows = 1000)
# analysis.release()
print('scalar covariance:\n{0}\n'.format(age_income_cov_scalar.value))
print('covariance matrix:\n{0}\n'.format(age_income_cov_matrix.value))
print('cross-covariance matrix:\n{0}'.format(cross_covar.value))
```
### DP Covariance in Practice
We now move to an example with a much smaller $\epsilon$.
```
with sn.Analysis() as analysis:
wn_data = sn.Dataset(path = data_path, column_names = var_names)
# get full covariance matrix
cov = sn.dp_covariance(data = sn.to_float(wn_data['age', 'sex', 'educ', 'income', 'married']),
privacy_usage = {'epsilon': 1.},
data_lower = [0., 0., 1., 0., 0.],
data_upper = [100., 1., 16., 500_000., 1.],
data_rows = 1000)
analysis.release()
# store DP covariance and correlation matrix
dp_cov = cov.value
dp_corr = dp_cov / np.outer(np.sqrt(np.diag(dp_cov)), np.sqrt(np.diag(dp_cov)))
# get non-DP covariance/correlation matrices
age = list(data[:]['age'])
sex = list(data[:]['sex'])
educ = list(data[:]['educ'])
income = list(data[:]['income'])
married = list(data[:]['married'])
non_dp_cov = np.cov([age, sex, educ, income, married])
non_dp_corr = non_dp_cov / np.outer(np.sqrt(np.diag(non_dp_cov)), np.sqrt(np.diag(non_dp_cov)))
print('Non-DP Correlation Matrix:\n{0}\n\n'.format(pd.DataFrame(non_dp_corr)))
print('DP Correlation Matrix:\n{0}'.format(pd.DataFrame(dp_corr)))
fig, (ax_1, ax_2) = plt.subplots(1, 2, figsize = (9, 11))
# generate a mask for the upper triangular matrix
mask = np.triu(np.ones_like(non_dp_corr, dtype = np.bool))
# generate color palette
cmap = sns.diverging_palette(220, 10, as_cmap = True)
# get correlation plots
ax_1.title.set_text('Non-DP Correlation Matrix')
sns.heatmap(non_dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_1)
ax_1.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_1.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.title.set_text('DP Correlation Matrix')
sns.heatmap(dp_corr, mask=mask, cmap=cmap, vmax=.3, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5}, ax = ax_2)
ax_2.set_xticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
ax_2.set_yticklabels(labels = ['age', 'sex', 'educ', 'income', 'married'], rotation = 45)
```
Notice that the differentially private correlation matrix contains values outside of the feasible range for correlations, $[-1, 1]$. This is not uncommon, especially for analyses with small $\epsilon$, and is not necessarily indicative of a problem. In this scenario, we will not use these correlations for anything other than visualization, so we will leave our result as is.
Sometimes, you may get a result that does cause problems for downstream analysis. For example, say your differentially private covariance matrix is not positive semi-definite. There are a number of ways to deal with problems of this type.
1. Relax your original plans: For example, if you want to invert your DP covariance matrix and are unable to do so, you could instead take the pseudoinverse.
2. Manual Post-Processing: Choose some way to change the output such that it is consistent with what you need for later analyses. This changed output is still differentially private (we will use this idea again in the next section). For example, map all negative variances to small positive value.
3. More releases: You could perform the same release again (perhaps with a larger $\epsilon$) and combine your results in some way until you have a release that works for your purposes. Note that additional $\epsilon$ from will be consumed everytime this happens.
### Post-Processing of DP Covariance Matrix: Regression Coefficient
Differentially private outputs are "immune" to post-processing, meaning functions of differentially private releases are also differentially private (provided that the functions are independent of the underlying data in the dataset). This idea provides us with a relatively easy way to generate complex differentially private releases from simpler ones.
Say we wanted to run a linear regression of the form $income = \alpha + \beta \cdot educ$ and want to find an differentially private estimate of the slope, $\hat{\beta}_{DP}$. We know that
$$ \beta = \frac{cov(income, educ)}{var(educ)}, $$
and so
$$ \hat{\beta}_{DP} = \frac{\hat{cov}(income, educ)_{DP}}{ \hat{var}(educ)_{DP} }. $$
We already have differentially private estimates of the necessary covariance and variance, so we can plug them in to find $\hat{\beta}_{DP}$.
```
'''income = alpha + beta * educ'''
# find DP estimate of beta
beta_hat_dp = dp_cov[2,3] / dp_cov[2,2]
beta_hat = non_dp_cov[2,3] / non_dp_cov[2,2]
print('income = alpha + beta * educ')
print('DP coefficient: {0}'.format(beta_hat_dp))
print('Non-DP Coefficient: {0}'.format(beta_hat))
```
This result is implausible, as it would suggest that an extra year of education is associated with, on average, a decrease in annual income of nearly $11,000. It's not uncommon for this to be the case for DP releases constructed as post-processing from other releases, especially when they involve taking ratios.
If you find yourself in such as situation, it is often worth it to spend some extra privacy budget to estimate your quantity of interest using an algorithm optimized for that specific use case.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mashyko/object_detection/blob/master/Model_Quickload.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Tutorials Installation:
https://caffe2.ai/docs/tutorials.html
First download the tutorials source.
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/
!git clone --recursive https://github.com/caffe2/tutorials caffe2_tutorials
# Model Quickload
This notebook will show you how to quickly load a pretrained SqueezeNet model and test it on images of your choice in four main steps.
1. Load the model
2. Format the input
3. Run the test
4. Process the results
The model used in this tutorial has been pretrained on the full 1000 class ImageNet dataset, and is downloaded from Caffe2's [Model Zoo](https://github.com/caffe2/caffe2/wiki/Model-Zoo). For an all around more in-depth tutorial on using pretrained models check out the [Loading Pretrained Models](https://github.com/caffe2/caffe2/blob/master/caffe2/python/tutorials/Loading_Pretrained_Models.ipynb) tutorial.
Before this script will work, you need to download the model and install it. You can do this by running:
```
sudo python -m caffe2.python.models.download -i squeezenet
```
Or make a folder named `squeezenet`, download each file listed below to it, and place it in the `/caffe2/python/models/` directory:
* [predict_net.pb](https://download.caffe2.ai/models/squeezenet/predict_net.pb)
* [init_net.pb](https://download.caffe2.ai/models/squeezenet/init_net.pb)
Notice, the helper function *parseResults* will translate the integer class label of the top result to an English label by searching through the [inference codes file](inference_codes.txt). If you want to really test the model's capabilities, pick a code from the file, find an image representing that code, and test the model with it!
```
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/My Drive/caffe2_tutorials
!pip3 install torch torchvision
!python -m caffe2.python.models.download -i squeezenet
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import numpy as np
import operator
# load up the caffe2 workspace
from caffe2.python import workspace
# choose your model here (use the downloader first)
from caffe2.python.models import squeezenet as mynet
# helper image processing functions
import helpers
##### Load the Model
# Load the pre-trained model
init_net = mynet.init_net
predict_net = mynet.predict_net
# Initialize the predictor with SqueezeNet's init_net and predict_net
p = workspace.Predictor(init_net, predict_net)
##### Select and format the input image
# use whatever image you want (urls work too)
# img = "https://upload.wikimedia.org/wikipedia/commons/a/ac/Pretzel.jpg"
# img = "images/cat.jpg"
# img = "images/cowboy-hat.jpg"
# img = "images/cell-tower.jpg"
# img = "images/Ducreux.jpg"
# img = "images/pretzel.jpg"
# img = "images/orangutan.jpg"
# img = "images/aircraft-carrier.jpg"
img = "images/flower.jpg"
# average mean to subtract from the image
mean = 128
# the size of images that the model was trained with
input_size = 227
# use the image helper to load the image and convert it to NCHW
img = helpers.loadToNCHW(img, mean, input_size)
##### Run the test
# submit the image to net and get a tensor of results
results = p.run({'data': img})
##### Process the results
# Quick way to get the top-1 prediction result
# Squeeze out the unnecessary axis. This returns a 1-D array of length 1000
preds = np.squeeze(results)
# Get the prediction and the confidence by finding the maximum value and index of maximum value in preds array
curr_pred, curr_conf = max(enumerate(preds), key=operator.itemgetter(1))
print("Top-1 Prediction: {}".format(curr_pred))
print("Top-1 Confidence: {}\n".format(curr_conf))
# Lookup our result from the inference list
response = helpers.parseResults(results)
print(response)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img=mpimg.imread('images/flower.jpg') #image to array
# show the original image
plt.figure()
plt.imshow(img)
plt.axis('on')
plt.title('Original image = RGB')
plt.show()
```
|
github_jupyter
|
<table border="0">
<tr>
<td>
<img src="https://ictd2016.files.wordpress.com/2016/04/microsoft-research-logo-copy.jpg" style="width 30px;" />
</td>
<td>
<img src="https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/MSR-ALICE-HeaderGraphic-1920x720_1-800x550.jpg" style="width 100px;"/></td>
</tr>
</table>
# Dynamic Double Machine Learning: Use Cases and Examples
Dynamic DoubleML is an extension of the Double ML approach for treatments assigned sequentially over time periods. This estimator will account for treatments that can have causal effects on future outcomes. For more details, see [this paper](https://arxiv.org/abs/2002.07285) or the [EconML docummentation](https://econml.azurewebsites.net/).
For example, the Dynamic DoubleML could be useful in estimating the following causal effects:
* the effect of investments on revenue at companies that receive investments at regular intervals ([see more](https://arxiv.org/abs/2103.08390))
* the effect of prices on demand in stores where prices of goods change over time
* the effect of income on health outcomes in people who receive yearly income
The preferred data format is balanced panel data. Each panel corresponds to one entity (e.g. company, store or person) and the different rows in a panel correspond to different time points. Example:
||Company|Year|Features|Investment|Revenue|
|---|---|---|---|---|---|
|1|A|2018|...|\$1,000|\$10,000|
|2|A|2019|...|\$2,000|\$12,000|
|3|A|2020|...|\$3,000|\$15,000|
|4|B|2018|...|\$0|\$5,000|
|5|B|2019|...|\$100|\$10,000|
|6|B|2020|...|\$1,200|\$7,000|
|7|C|2018|...|\$1,000|\$20,000|
|8|C|2019|...|\$1,500|\$25,000|
|9|C|2020|...|\$500|\$15,000|
(Note: when passing the data to the DynamicDML estimator, the "Company" column above corresponds to the `groups` argument at fit time. The "Year" column above should not be passed in as it will be inferred from the "Company" column)
If group memebers do not appear together, it is assumed that the first instance of a group in the dataset corresponds to the first period of that group, the second instance of the group corresponds to the second period, etc. Example:
||Company|Features|Investment|Revenue|
|---|---|---|---|---|
|1|A|...|\$1,000|\$10,000|
|2|B|...|\$0|\$5,000
|3|C|...|\$1,000|\$20,000|
|4|A|...|\$2,000|\$12,000|
|5|B|...|\$100|\$10,000|
|6|C|...|\$1,500|\$25,000|
|7|A|...|\$3,000|\$15,000|
|8|B|...|\$1,200|\$7,000|
|9|C|...|\$500|\$15,000|
In this dataset, 1<sup>st</sup> row corresponds to the first period of group `A`, 4<sup>th</sup> row corresponds to the second period of group `A`, etc.
In this notebook, we show the performance of the DynamicDML on synthetic and observational data.
## Notebook Contents
1. [Example Usage with Average Treatment Effects](#1.-Example-Usage-with-Average-Treatment-Effects)
2. [Example Usage with Heterogeneous Treatment Effects](#2.-Example-Usage-with-Heterogeneous-Treatment-Effects)
```
%load_ext autoreload
%autoreload 2
import econml
# Main imports
from econml.dynamic.dml import DynamicDML
from econml.tests.dgp import DynamicPanelDGP, add_vlines
# Helper imports
import numpy as np
from sklearn.linear_model import Lasso, LassoCV, LogisticRegression, LogisticRegressionCV, MultiTaskLassoCV
import matplotlib.pyplot as plt
%matplotlib inline
```
# 1. Example Usage with Average Treatment Effects
## 1.1 DGP
We consider a data generating process from a markovian treatment model.
In the example bellow, $T_t\rightarrow$ treatment(s) at time $t$, $Y_t\rightarrow$outcome at time $t$, $X_t\rightarrow$ features and controls at time $t$ (the coefficients $e, f$ will pick the features and the controls).
\begin{align}
X_t =& (\pi'X_{t-1} + 1) \cdot A\, T_{t-1} + B X_{t-1} + \epsilon_t\\
T_t =& \gamma\, T_{t-1} + (1-\gamma) \cdot D X_t + \zeta_t\\
Y_t =& (\sigma' X_{t} + 1) \cdot e\, T_{t} + f X_t + \eta_t
\end{align}
with $X_0, T_0 = 0$ and $\epsilon_t, \zeta_t, \eta_t \sim N(0, \sigma^2)$. Moreover, $X_t \in R^{n_x}$, $B[:, 0:s_x] \neq 0$ and $B[:, s_x:-1] = 0$, $\gamma\in [0, 1]$, $D[:, 0:s_x] \neq 0$, $D[:, s_x:-1]=0$, $f[0:s_x]\neq 0$, $f[s_x:-1]=0$. We draw a single time series of samples of length $n\_panels \cdot n\_periods$.
```
# Define DGP parameters
np.random.seed(123)
n_panels = 5000 # number of panels
n_periods = 3 # number of time periods in each panel
n_treatments = 2 # number of treatments in each period
n_x = 100 # number of features + controls
s_x = 10 # number of controls (endogeneous variables)
s_t = 10 # treatment support size
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, random_seed=12345)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=12345)
true_effect = dgp.true_effect
```
## 1.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3, max_iter=1000),
model_t=MultiTaskLassoCV(cv=3, max_iter=1000),
cv=3)
est.fit(Y, T, X=None, W=W, groups=groups)
# Average treatment effect of all periods on last period for unit treatments
print(f"Average effect of default policy: {est.ate():0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(T0=baseline_policy, T1=target_policy)
print(f"Effect of target policy over baseline policy: {eff[0]:0.2f}")
# Period treatment effects + interpretation
for i, theta in enumerate(est.intercept_.reshape(-1, n_treatments)):
print(f"Marginal effect of a treatments in period {i+1} on period {n_periods} outcome: {theta}")
# Period treatment effects with confidence intervals
est.summary()
conf_ints = est.intercept__interval(alpha=0.05)
```
## 1.3 Performance Visualization
```
# Some plotting boilerplate code
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods*n_treatments)-.04, est.intercept_, yerr=(conf_ints[1] - est.intercept_,
est.intercept_ - conf_ints[0]), fmt='o', label='DynamicDML')
plt.errorbar(np.arange(n_periods*n_treatments), true_effect.flatten(), fmt='o', alpha=.6, label='Ground truth')
for t in np.arange(1, n_periods):
plt.axvline(x=t * n_treatments - .5, linestyle='--', alpha=.4)
plt.xticks([t * n_treatments - .5 + n_treatments/2 for t in range(n_periods)],
["$\\theta_{}$".format(t) for t in range(n_periods)])
plt.gca().set_xlim([-.5, n_periods*n_treatments - .5])
plt.ylabel("Effect")
plt.legend()
plt.show()
```
# 2. Example Usage with Heterogeneous Treatment Effects on Time-Invariant Unit Characteristics
We can also estimate treatment effect heterogeneity with respect to the value of some subset of features $X$ in the initial period. Heterogeneity is currently only supported with respect to such initial state features. This for instance can support heterogeneity with respect to time-invariant unit characteristics. In that case you can simply pass as $X$ a repetition of some unit features that stay constant in all periods. You can also pass time-varying features, and their time varying component will be used as a time-varying control. However, heterogeneity will only be estimated with respect to the initial state.
## 2.1 DGP
```
# Define additional DGP parameters
het_strength = .5
het_inds = np.arange(n_x - n_treatments, n_x)
# Generate data
dgp = DynamicPanelDGP(n_periods, n_treatments, n_x).create_instance(
s_x, hetero_strength=het_strength, hetero_inds=het_inds, random_seed=12)
Y, T, X, W, groups = dgp.observational_data(n_panels, s_t=s_t, random_seed=1)
ate_effect = dgp.true_effect
het_effect = dgp.true_hetero_effect[:, het_inds + 1]
```
## 2.2 Train Estimator
```
est = DynamicDML(
model_y=LassoCV(cv=3),
model_t=MultiTaskLassoCV(cv=3),
cv=3)
est.fit(Y, T, X=X, W=W, groups=groups, inference="auto")
est.summary()
# Average treatment effect for test points
X_test = X[np.arange(0, 25, 3)]
print(f"Average effect of default policy:{est.ate(X=X_test):0.2f}")
# Effect of target policy over baseline policy
# Must specify a treatment for each period
baseline_policy = np.zeros((1, n_periods * n_treatments))
target_policy = np.ones((1, n_periods * n_treatments))
eff = est.effect(X=X_test, T0=baseline_policy, T1=target_policy)
print("Effect of target policy over baseline policy for test set:\n", eff)
# Coefficients: intercept is of shape n_treatments*n_periods
# coef_ is of shape (n_treatments*n_periods, n_hetero_inds).
# first n_treatment rows are from first period, next n_treatment
# from second period, etc.
est.intercept_, est.coef_
# Confidence intervals
conf_ints_intercept = est.intercept__interval(alpha=0.05)
conf_ints_coef = est.coef__interval(alpha=0.05)
```
## 2.3 Performance Visualization
```
# parse true parameters in array of shape (n_treatments*n_periods, 1 + n_hetero_inds)
# first column is the intercept
true_effect_inds = []
for t in range(n_treatments):
true_effect_inds += [t * (1 + n_x)] + (list(t * (1 + n_x) + 1 + het_inds) if len(het_inds)>0 else [])
true_effect_params = dgp.true_hetero_effect[:, true_effect_inds]
true_effect_params = true_effect_params.reshape((n_treatments*n_periods, 1 + het_inds.shape[0]))
# concatenating intercept and coef_
param_hat = np.hstack([est.intercept_.reshape(-1, 1), est.coef_])
lower = np.hstack([conf_ints_intercept[0].reshape(-1, 1), conf_ints_coef[0]])
upper = np.hstack([conf_ints_intercept[1].reshape(-1, 1), conf_ints_coef[1]])
plt.figure(figsize=(15, 5))
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
true_effect_params.flatten(), fmt='*', label='Ground Truth')
plt.errorbar(np.arange(n_periods * (len(het_inds) + 1) * n_treatments),
param_hat.flatten(), yerr=((upper - param_hat).flatten(),
(param_hat - lower).flatten()), fmt='o', label='DynamicDML')
add_vlines(n_periods, n_treatments, het_inds)
plt.legend()
plt.show()
```
|
github_jupyter
|
```
# default_exp models.cox
```
# Cox Proportional Hazard
> SA with features apart from time
We model the the instantaneous hazard as the product of two functions, one with the time component, and the other with the feature component.
$$
\begin{aligned}
\lambda(t,x) = \lambda(t)h(x)
\end{aligned}
$$
It is important to have the seperation of these functions to arrive at an analytical solution. This is so that the time component can be integrated out to give the survival function.
$$
\begin{aligned}
\int_0^T \lambda(t,x) dt &= \int_0^T \lambda(t)h(x) dt\\
&= h(x)\int_0^T \lambda(t) dt\\
S(t) &= \exp\left(-h(x)\int_{-\infty}^t \lambda(\tau) d\tau\right)
\end{aligned}
$$
```
# export
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from sklearn.preprocessing import MaxAbsScaler, StandardScaler
from torchlife.losses import hazard_loss
from torchlife.models.ph import PieceWiseHazard
# torch.Tensor.ndim = property(lambda x: x.dim())
# hide
%load_ext autoreload
%autoreload 2
%matplotlib inline
# export
class ProportionalHazard(nn.Module):
"""
Hazard proportional to time and feature component as shown above.
parameters:
- breakpoints: time points where hazard would change
- max_t: maximum point of time to plot to.
- dim: number of input dimensions of x
- h: (optional) number of hidden units (for x only).
"""
def __init__(self, breakpoints:np.array, t_scaler:MaxAbsScaler, x_scaler:StandardScaler,
dim:int, h:tuple=(), **kwargs):
super().__init__()
self.baseλ = PieceWiseHazard(breakpoints, t_scaler)
self.x_scaler = x_scaler
nodes = (dim,) + h + (1,)
self.layers = nn.ModuleList([nn.Linear(a,b, bias=False)
for a,b in zip(nodes[:-1], nodes[1:])])
def forward(self, t, t_section, x):
logλ, Λ = self.baseλ(t, t_section)
for layer in self.layers[:-1]:
x = F.relu(layer(x))
log_hx = self.layers[-1](x)
logλ += log_hx
Λ = torch.exp(log_hx + torch.log(Λ))
return logλ, Λ
def survival_function(self, t:np.array, x:np.array) -> torch.Tensor:
if len(t.shape) == 1:
t = t[:,None]
t = self.baseλ.t_scaler.transform(t)
if len(x.shape) == 1:
x = x[None, :]
if len(x) == 1:
x = np.repeat(x, len(t), axis=0)
x = self.x_scaler.transform(x)
with torch.no_grad():
x = torch.Tensor(x)
# get the times and time sections for survival function
breakpoints = self.baseλ.breakpoints[1:].cpu().numpy()
t_sec_query = np.searchsorted(breakpoints.squeeze(), t.squeeze())
# convert to pytorch tensors
t_query = torch.Tensor(t)
t_sec_query = torch.LongTensor(t_sec_query)
# calculate cumulative hazard according to above
_, Λ = self.forward(t_query, t_sec_query, x)
return torch.exp(-Λ)
def plot_survival_function(self, t:np.array, x:np.array) -> None:
s = self.survival_function(t, x)
# plot
plt.figure(figsize=(12,5))
plt.plot(t, s)
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.show()
```
## Fitting Cox Proportional Hazard Model
```
# hide
from torchlife.data import create_db, get_breakpoints
import pandas as pd
# hide
url = "https://raw.githubusercontent.com/CamDavidsonPilon/lifelines/master/lifelines/datasets/rossi.csv"
df = pd.read_csv(url)
df.head()
# hide
df.rename(columns={'week':'t', 'arrest':'e'}, inplace=True)
breakpoints = get_breakpoints(df)
db, t_scaler, x_scaler = create_db(df, breakpoints)
# hide
from fastai.basics import Learner
x_dim = df.shape[1] - 2
model = ProportionalHazard(breakpoints, t_scaler, x_scaler, x_dim, h=(3,3))
learner = Learner(db, model, loss_func=hazard_loss)
# wd = 1e-4
# learner.lr_find()
# learner.recorder.plot()
# hide
epochs = 10
learner.fit(epochs, lr=1)
```
## Plotting hazard functions
```
model.baseλ.plot_hazard()
x = df.drop(['t', 'e'], axis=1).iloc[4]
t = np.arange(df['t'].max())
model.plot_survival_function(t, x)
# hide
from nbdev.export import *
notebook2script()
```
|
github_jupyter
|
(*** hide ***)
```
#nowarn "211"
open System
let airQuality = __SOURCE_DIRECTORY__ + "/data/airquality.csv"
```
(**
Interoperating between R and Deedle
===================================
The [R type provider](http://fslab.org/RProvider/) enables
smooth interoperation between R and F#. The type provider automatically discovers
installed packages and makes them accessible via the `RProvider` namespace.
R type provider for F# automatically converts standard data structures betwene R
and F# (such as numerical values, arrays, etc.). However, the conversion mechanism
is extensible and so it is possible to support conversion between other F# types.
The Deedle library comes with extension that automatically converts between Deedle
`Frame<R, C>` and R `data.frame` and also between Deedle `Series<K, V>` and the
[zoo package](http://cran.r-project.org/web/packages/zoo/index.html) (Z's ordered
observations).
This page is a quick overview showing how to pass data between R and Deedle.
You can also get this page as an [F# script file](https://github.com/fslaborg/Deedle/blob/master/docs/content/rinterop.fsx)
from GitHub and run the samples interactively.
<a name="setup"></a>
Getting started
---------------
To use Deedle and R provider together, all you need to do is to install the
[**Deedle.RPlugin** package](https://nuget.org/packages/Deedle.RPlugin), which
installes both as dependencies. Alternatively, you can use the [**FsLab**
package](http://www.nuget.org/packages/FsLab), which also includes additional
data access, data science and visualization libraries.
In a typical project ("F# Tutorial"), the NuGet packages are installed in the `../packages`
directory. To use R provider and Deedle, you need to write something like this:
*)
```
#load "../../packages/RProvider/RProvider.fsx"
#load "../../bin/net45/Deedle.fsx"
open RProvider
open RDotNet
open Deedle
```
(**
If you're not using NuGet from Visual Studio, then you'll need to manually copy the
file `Deedle.RProvider.Plugin.dll` from the package `Deedle.RPlugin` to the
directory where `RProvider.dll` is located (in `RProvider/lib`). Once that's
done, the R provider will automatically find the plugin.
<a name="frames"></a>
Passing data frames to and from R
---------------------------------
### From R to Deedle
Let's start by looking at passing data frames from R to Deedle. To test this, we
can use some of the sample data sets available in the `datasets` package. The R
makes all packages available under the `RProvider` namespace, so we can just
open `datasets` and access the `mtcars` data set using `R.mtcars` (when typing
the code, you'll get automatic completion when you type `R` followed by dot):
*)
(*** define-output:mtcars ***)
```
open RProvider.datasets
// Get mtcars as an untyped object
R.mtcars.Value
// Get mtcars as a typed Deedle frame
let mtcars : Frame<string, string> = R.mtcars.GetValue()
```
(*** include-value:mtcars ***)
(**
The first sample uses the `Value` property to convert the data set to a boxed Deedle
frame of type `obj`. This is a great way to explore the data, but when you want to do
some further processing, you need to specify the type of the data frame that you want
to get. This is done on line 7 where we get `mtcars` as a Deedle frame with both rows
and columns indexed by `string`.
To see that this is a standard Deedle data frame, let's group the cars by the number of
gears and calculate the average "miles per galon" value based on the gear. To visualize
the data, we use the [F# Charting library](https://github.com/fsharp/FSharp.Charting):
*)
(*** define-output:mpgch ***)
```
#load "../../packages/FSharp.Charting/lib/net45/FSharp.Charting.fsx"
open FSharp.Charting
mtcars
|> Frame.groupRowsByInt "gear"
|> Frame.getCol "mpg"
|> Stats.levelMean fst
|> Series.observations |> Chart.Column
```
(*** include-it:mpgch ***)
(**
### From Deedle to R
So far, we looked how to turn R data frame into Deedle `Frame<R, C>`, so let's look
at the opposite direction. The following snippet first reads Deedle data frame
from a CSV file (file name is in the `airQuality` variable). We can then use the
data frame as argument to standard R functions that expect data frame.
*)
```
let air = Frame.ReadCsv(airQuality, separators=";")
```
(*** include-value:air ***)
(**
Let's first try passing the `air` frame to the R `as.data.frame` function (which
will not do anything, aside from importing the data into R). To do something
slightly more interesting, we then use the `colMeans` R function to calculate averages
for each column (to do this, we need to open the `base` package):
*)
```
open RProvider.``base``
// Pass air data to R and print the R output
R.as_data_frame(air)
// Pass air data to R and get column means
R.colMeans(air)
// [fsi:val it : SymbolicExpression =]
// [fsi: Ozone Solar.R Wind Temp Month Day ]
// [fsi: NaN NaN 9.96 77.88 6.99 15.8]
```
(**
As a final example, let's look at the handling of missing values. Unlike R, Deedle does not
distinguish between missing data (`NA`) and not a number (`NaN`). For example, in the
following simple frame, the `Floats` column has missing value for keys 2 and 3 while
`Names` has missing value for the row 2:
*)
```
// Create sample data frame with missing values
let df =
[ "Floats" =?> series [ 1 => 10.0; 2 => nan; 4 => 15.0]
"Names" =?> series [ 1 => "one"; 3 => "three"; 4 => "four" ] ]
|> frame
```
(**
When we pass the data frame to R, missing values in numeric columns are turned into `NaN`
and missing data for other columns are turned into `NA`. Here, we use `R.assign` which
stores the data frame in a varaible available in the current R environment:
*)
```
R.assign("x", df)
// [fsi:val it : SymbolicExpression = ]
// [fsi: Floats Names ]
// [fsi: 1 10 one ]
// [fsi: 2 NaN <NA> ]
// [fsi: 4 15 four ]
// [fsi: 3 NaN three ]
```
(**
<a name="series"></a>
Passing time series to and from R
---------------------------------
For working with time series data, the Deedle plugin uses [the zoo package](http://cran.r-project.org/web/packages/zoo/index.html)
(Z's ordered observations). If you do not have the package installed, you can do that
by using the `install.packages("zoo")` command from R or using `R.install_packages("zoo")` from
F# after opening `RProvider.utils`. When running the code from F#, you'll need to restart your
editor and F# interactive after it is installed.
### From R to Deedle
Let's start by looking at getting time series data from R. We can again use the `datasets`
package with samples. For example, the `austres` data set gives us access to
quarterly time series of the number of australian residents:
*)
```
R.austres.Value
// [fsi:val it : obj =]
// [fsi: 1971.25 -> 13067.3 ]
// [fsi: 1971.5 -> 13130.5 ]
// [fsi: 1971.75 -> 13198.4 ]
// [fsi: ... -> ... ]
// [fsi: 1992.75 -> 17568.7 ]
// [fsi: 1993 -> 17627.1 ]
// [fsi: 1993.25 -> 17661.5 ]
```
(**
As with data frames, when we want to do any further processing with the time series, we need
to use the generic `GetValue` method and specify a type annotation to that tells the F#
compiler that we expect a series where both keys and values are of type `float`:
*)
```
// Get series with numbers of australian residents
let austres : Series<float, float> = R.austres.GetValue()
// Get TimeSpan representing (roughly..) two years
let twoYears = TimeSpan.FromDays(2.0 * 365.0)
// Calculate means of sliding windows of 2 year size
austres
|> Series.mapKeys (fun y ->
DateTime(int y, 1 + int (12.0 * (y - floor y)), 1))
|> Series.windowDistInto twoYears Stats.mean
```
(**
The current version of the Deedle plugin supports only time series with single column.
To access, for example, the EU stock market data, we need to write a short R inline
code to extract the column we are interested in. The following gets the FTSE time
series from `EuStockMarkets`:
*)
```
let ftseStr = R.parse(text="""EuStockMarkets[,"FTSE"]""")
let ftse : Series<float, float> = R.eval(ftseStr).GetValue()
```
(**
### From Deedle to R
The opposite direction is equally easy. To demonstrate this, we'll generate a simple
time series with 3 days of randomly generated values starting today:
*)
```
let rnd = Random()
let ts =
[ for i in 0.0 .. 100.0 ->
DateTime.Today.AddHours(i), rnd.NextDouble() ]
|> series
```
(**
Now that we have a time series, we can pass it to R using the `R.as_zoo` function or
using `R.assign` to store it in an R variable. As previously, the R provider automatically
shows the output that R prints for the value:
*)
```
open RProvider.zoo
// Just convert time series to R
R.as_zoo(ts)
// Convert and assing to a variable 'ts'
R.assign("ts", ts)
// [fsi:val it : string =
// [fsi: 2013-11-07 05:00:00 2013-11-07 06:00:00 2013-11-07 07:00:00 ...]
// [fsi: 0.749946652 0.580584353 0.523962789 ...]
```
(**
Typically, you will not need to assign time series to an R variable, because you can
use it directly as an argument to functions that expect time series. For example, the
following snippet applies the rolling mean function with a window size 20 to the
time series.
*)
```
// Rolling mean with window size 20
R.rollmean(ts, 20)
```
(**
This is a simple example - in practice, you can achieve the same thing with `Series.window`
function from Deedle - but it demonstrates how easy it is to use R packages with
time series (and data frames) from Deedle. As a final example, we create a data frame that
contains the original time series together with the rolling mean (in a separate column)
and then draws a chart showing the results:
*)
(*** define-output:means ***)
```
// Use 'rollmean' to calculate mean and 'GetValue' to
// turn the result into a Deedle time series
let tf =
[ "Input" => ts
"Means5" => R.rollmean(ts, 5).GetValue<Series<_, float>>()
"Means20" => R.rollmean(ts, 20).GetValue<Series<_, float>>() ]
|> frame
// Chart original input and the two rolling means
Chart.Combine
[ Chart.Line(Series.observations tf?Input)
Chart.Line(Series.observations tf?Means5)
Chart.Line(Series.observations tf?Means20) ]
```
(**
Depending on your random number generator, the resulting chart looks something like this:
*)
(*** include-it:means ***)
```
```
|
github_jupyter
|
```
from gs_quant.session import GsSession, Environment
from gs_quant.instrument import IRSwap
from gs_quant.risk import IRFwdRate, CarryScenario
from gs_quant.markets.portfolio import Portfolio
from gs_quant.markets import PricingContext
from datetime import datetime
import matplotlib.pylab as plt
import pandas as pd
import numpy as np
# external users should substitute their client id and secret; please skip this step if using internal jupyterhub
GsSession.use(Environment.PROD, client_id=None, client_secret=None, scopes=('run_analytics',))
ccy = 'EUR'
# construct a series of 6m FRAs going out 20y or so
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m')
for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
# get the fwd rates for these fras under the base sceneraio (no shift in time)
base = {}
for i, res in enumerate(results):
base[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
base_series = pd.Series(base, name='base', dtype=np.dtype(float))
# calculate the fwd rates with a shift forward of 132 business days - about 6m. This shift keeps spot rates constant.
# So 5y rate today will be 5y rate under the scenario of pricing 6m in the future.
with CarryScenario(time_shift=132, roll_to_fwds=False):
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m') for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
roll_spot = {}
for i, res in enumerate(results):
roll_spot[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
roll_spot_series = pd.Series(roll_spot, name='roll to spot', dtype=np.dtype(float))
# calculate the fwd rates with a shift forward of 132 business days - about 6m. This shift keeps fwd rates constant.
# So 5.5y rate today will be 5y rate under the scenario of pricing 6m in the future.
with CarryScenario(time_shift=132, roll_to_fwds=True):
fras = Portfolio([IRSwap('Pay', '{}m'.format(i), ccy, effective_date='{}m'.format(i-6),
fixed_rate_frequency='6m', floating_rate_frequency='6m') for i in range(6, 123, 6)])
fras.resolve()
results = fras.calc(IRFwdRate)
roll_fwd = {}
for i, res in enumerate(results):
roll_fwd[datetime.strptime(fras[i].termination_date, '%Y-%m-%d')] = res
roll_fwd_series = pd.Series(roll_fwd, name='roll to fwd', dtype=np.dtype(float))
# show the curves, the base in blue, the roll to fwd in green and the roll to spot in orange.
# note blue and green curves are not exactly on top of each other as we aren't using the curve instruments themselves
# but instead using FRAs to show a smooth curve.
base_series.plot(figsize=(20, 10))
roll_spot_series.plot()
roll_fwd_series.plot()
plt.legend()
```
|
github_jupyter
|
>This notebook is part of our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) course at [Code Heroku](http://www.codeheroku.com/).
Hey folks, today we are going to discuss about the application of gradient descent algorithm for solving machine learning problems. Let’s take a brief overview about the the things that we are going to discuss in this article:
- What is gradient descent?
- How gradient descent algorithm can help us solving machine learning problems
- The math behind gradient descent algorithm
- Implementation of gradient descent algorithm in Python
So, without wasting any time, let’s begin :)
# What is gradient descent?
Here’s what Wikipedia says: “Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function.”
Now, you might be thinking “Wait, what does that mean? What do you want to say?”
Don’t worry, we will elaborate everything about gradient descent in this article and all of it will start making sense to you in a moment :)
To understand gradient descent algorithm, let us first understand a real life machine learning problem:
Suppose you have a dataset where you are provided with the number of hours a student studies per day and the percentage of marks scored by the corresponding student. If you plot a 2D graph of this dataset, it will look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_1.png">
Now, if someone approaches you and says that a new student has taken admission and you need to predict the score of that student based on the number of hours he studies. How would you do that?
To predict the score of the new student, at first you need to find out a relationship between “Hours studied” and “Score” from the existing dataset. By taking a look over the visual graph plotting, we can see that a linear relationship can be established between these two things. So, by drawing a straight line over the data points in the graph, we can establish the relationship. Let’s see how would it look if we try to draw a straight line over the data points. It would look something like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_2.png">
Great! Now we have the relationship between “Hours Studied” and “Score”. So, now if someone asks us to predict the score of a student who studies 10 hours per day, we can just simply put Hours Studied = 10 data point over the relationship line and predict the value of his score like this:
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_3.png">
From the above picture, we can easily say that the new student who studies 10 hours per day would probably score around 60. Pretty easy, right? By the way, the relationship line that we have drawn is called the “regression” line. And because the relationship we have established is a linear relationship, the line is actually called “linear regression” line. Hence, this machine learning model that we have created is known as linear regression model.
At this point, you might have noticed that all the data points do not lie perfectly over the regression line. So, there might be some difference between the predicted value and the actual value. We call this difference as error(or cost).
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_err.png">
In machine learning world, we always try to build a model with as minimum error as possible. To achieve this, we have to calculate the error of our model in order to best fit the regression line over it. We have different kinds of error like- total error, mean error, mean squared error etc.
Total error: Summation of the absolute difference between predicted and actual value for all the data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_4.png">
Mean error: Total error / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_5.png">
Mean squared error: Summation of the square of absolute difference / number of data points. Mathematically, this is
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_6.png">
Below is an example of calculating these errors:
<img src="http://www.codeheroku.com/static/blog/images/error_calc.png">
We will use the Mean Squared Error(M.S.E) to calculate the error and determine the best linear regression line(the line with the minimum error value) for our model.
Now the question is, how would you represent a regression line in a computer?
The answer is simple. Remember the equation of a straight line? We can use the same equation in order to represent the regression line in computer. If you can’t recall it, let me quickly remind you, it’s **y = M * x + B**
<img src="http://www.codeheroku.com/static/blog/images/line_repr.png">
Here, M is the slope of the line and B is the Y intercept. Let’s quickly recall about slope and Y intercept.
Slope is the amount by which the line is rising on the Y axis for every block that you go towards right in the X axis. This tells us the direction of the line and the rate by which our line is increasing. Mathematically speaking, this means  for a specified amount of distance on the line.
From the dotted lines in the above picture, we can see that for every 2 blocks in the X axis, the line rises by 1 block in the Y axis.<br>
Hence, slope, M = ½ = 0.5<br>
And it’s a positive value, which indicates that the line is increasing in the upward direction.
Now, let’s come to Y intercept. It is the distance which tells us exactly where the line cuts the Y axis. From the above picture, we can see that the line is cutting Y axis on point (0,1). So, the Y intercept(B) in this case is the distance between (0,0) and (0,1) = 1.
Hence, the straight line on the above picture can be represented through the following equation:
y = 0.5 * x + 1
Now we know how to represent the regression line in a computer. Everything seems good so far. But, the biggest question still remains unanswered- “How would the computer know the right value of M and B for drawing the regression line with the minimum error?”
Exactly that’s why we need the gradient descent algorithm. Gradient descent is a trial and error method, which will iteratively give us different values of M and B to try. In each iteration, we will draw a regression line using these values of M and B and will calculate the error for this model. We will continue until we get the values of M and B such that the error is minimum.
Let’s have a more elaborative view of gradient descent algorithm:
Step 1: Start with random values of M and B
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s1.png">
Step 2: Adjust M and B such that error reduces
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s2.png">
Step 3: Repeat until we get the best values of M and B (until convergence)
<img src="http://www.codeheroku.com/static/blog/images/grad_desc_s3.png">
By the way, the application of gradient descent is not limited to regression problems only. It is an optimization algorithm which can be applied to any problem in general.
# The math behind gradient descent
Till now we have understood that we will use gradient descent to minimize the error for our model. But, now let us see exactly how gradient descent finds the best values of M and B for us.
Gradient descent tries to minimize the error. Right?
So, we can say that it tries to minimize the following function(cost function):
<img src="http://www.codeheroku.com/static/blog/images/gd_err_fnc.png">
At first we will take random values of M and B. So, we will get a random error corresponding to these values. Thus, a random point will be plotted on the above graph. At this point, there will be some error. So, our objective will be to reduce this error.
In general, how would you approach towards the minimum value of a function? By finding its derivative. Right? The same thing applies here.
We will obtain the partial derivative of J with respect to M and B. This will give us the direction of the slope of tangent at the given point. We would like to move in the opposite direction of the slope in order to approach towards the minimum value.
<img src="http://www.codeheroku.com/static/blog/images/gd_db_dm_calc.png">
So far, we have only got the direction of the slope and we know we need to move in its opposite direction. But, in each iteration, by how much amount we should move in the opposite direction? This amount is called the learning rate(alpha). Learning rate determines the step size of our movement towards the minimal point.
So, choosing the right learning rate is very important. If the learning rate is too small, it will take more time to converge. On the other hand, if the learning rate is very high, it may overshoot the minimum point and diverge.
<img src="http://www.codeheroku.com/static/blog/images/gd_ch_alpha.png">
To sum up, what we have till now is-
1. A random point is chosen initially by choosing random values of M and B.
2. Direction of the slope of that point is found by finding delta_m and delta_b
3. Since we want to move in the opposite direction of the slope, we will multiply -1 with both delta_m and delta_b.
4. Since delta_m and delta_b gives us only the direction, we need to multiply both of them with the learning rate(alpha) to specify the step size of each iteration.
5. Next, we need to modify the current values of M and B such that the error is reduced.
<img src="http://www.codeheroku.com/static/blog/images/gd_9.png">
6. We need to repeat steps 2 to 5 until we converge at the minimum point.
# Implementation of gradient descent using Python
This was everything about gradient descent algorithm. Now we will implement this algorithm using Python.
Let us first import all required libraries and read the dataset using Pandas library(the csv file can be downloaded from this [link](https://github.com/codeheroku/Introduction-to-Machine-Learning/tree/master/gradient%20descent/starter%20code)):
```
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("student_scores.csv") #Read csv file using Pandas library
```
Next, we need to read the values of X and Y from the dataframe and create a scatter plot of that data.
```
X = df["Hours"] #Read values of X from dataframe
Y = df["Scores"] #Read values of Y from dataframe
plt.plot(X,Y,'o') # 'o' for creating scatter plot
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
```
After that, we will initially choose m = 0 and b = 0
```
m = 0
b = 0
```
Now, we need to create a function(gradient descent function) which will take the current value of m and b and then give us better values of m and b.
```
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0] #value of x of a point
y_actual = point[1] #Actual value of y for that point
y_prediction = m*x + b #Predicted value of y for given x
error = y_prediction - y_actual #Error in the estimation
#Using alpha = 0.0005
delta_m = -1 * (error*x) * 0.0005 #Calculating delta m
delta_b = -1 * (error) * 0.0005 #Calculating delta b
m = m + delta_m #Modifying value of m for reducing error
b = b + delta_b #Modifying value of b for reducing error
return m,b #Returning better values of m and b
```
Notice, in the above code, we are using learning rate(alpha) = 0.0005 . You can try to modify this value and try this example with different learning rates.
Now we will make a function which will help us to plot the regression line on the graph.
```
def plot_regression_line(X,m,b):
regression_x = X.values #list of values of x
regression_y = [] #list of values of y
for x in regression_x:
y = m*x + b #calculating the y_prediction
regression_y.append(y) #adding the predicted value in list of y
plt.plot(regression_x,regression_y) #plot the regression line
plt.pause(1) #pause for 1 second before plotting next line
```
Now, when we will run the grad_desc() function, each time we will get a better result for regression line. Let us create a loop and run the grad_desc() function for 10 times and visualize the results.
```
for i in range(0,10):
m,b = grad_desc(X,Y,m,b) #call grad_desc() to get better m & b
plot_regression_line(X,m,b) #plot regression line with m & b
```
Finally, we need to show the plot by adding the following statement:
```
plt.show()
```
So, the full code for our program is:
```
import pandas as pd
import matplotlib.pyplot as plt
# function for plotting regression line
def plot_regression_line(X,m,b):
regression_x = X.values
regression_y = []
for x in regression_x:
y = m*x + b
regression_y.append(y)
plt.plot(regression_x,regression_y)
plt.pause(1)
df = pd.read_csv("student_scores.csv")
X = df["Hours"]
Y = df["Scores"]
plt.plot(X,Y,'o')
plt.title("Implementing Gradient Descent")
plt.xlabel("Hours Studied")
plt.ylabel("Student Score")
m = 0
b = 0
# gradient descent function
def grad_desc(X,Y,m,b):
for point in zip(X,Y):
x = point[0]
y_actual = point[1]
y_prediction = m*x + b
error = y_prediction - y_actual
delta_m = -1 * (error*x) * 0.0005
delta_b = -1 * (error) * 0.0005
m = m + delta_m
b = b + delta_b
return m,b
for i in range(0,10):
m,b = grad_desc(X,Y,m,b)
plot_regression_line(X,m,b)
plt.show()
```
Now let’s run the above program for different values of learning rate(alpha).
For alpha = 0.0005 , the output will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_1.gif">
For alpha = 0.05 , it will look like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_2.gif">
For alpha = 1, it will overshoot the minimum point and diverge like this:
<img src="http://www.codeheroku.com/static/blog/images/gd_alpha_3.gif">
The gradient descent algorithm about which we discussed in this article is called stochastic gradient descent. There are also other types of gradient descent algorithms like- batch gradient descent, mini batch gradient descent etc.
>If this article was helpful to you, check out our [Introduction to Machine Learning](http://www.codeheroku.com/course?course_id=1) Course at [Code Heroku](http://www.codeheroku.com/) for a complete guide to Machine Learning.
|
github_jupyter
|
```
import csv
import itertools
import operator
import numpy as np
import nltk
import sys
from datetime import datetime
from utils import *
import matplotlib.pyplot as plt
%matplotlib inline
vocabulary_size = 200
sentence_start_token = "START"
sentence_end_token = "END"
f = open('data/ratings_train.txt', 'r')
lines = f.readlines()
for i in range(len(lines)):
lines[i] = lines[i].replace("/n","").replace("\n","")
reader = []
for line in lines:
line_document = line.split("\t")[1]
reader.append(line_document)
f.close()
sentences = ["%s %s %s" % (sentence_start_token, x, sentence_end_token) for x in reader[:1000]]
from konlpy.tag import Twitter
pos_tagger = Twitter()
def tokenize(doc):
return ['/'.join(t) for t in pos_tagger.pos(doc, norm=True, stem=True)]
tokenized_sentences = [tokenize(row) for row in sentences]
vocab = [t for d in tokenized_sentences for t in d]
Verb_Noun_Adjective_Alpha_in_text = []
index = 0
for text in tokenized_sentences:
Verb_Noun_Adjective_Alpha_in_text.append([])
for word in text:
parts_of_speech = word.split("/")
if parts_of_speech[1] in ["Noun","Verb","Adjective"] :
Verb_Noun_Adjective_Alpha_in_text[index].append(word.split("/")[0])
elif parts_of_speech[1] in ["Alpha"] and len(parts_of_speech[0]) ==3 or len(parts_of_speech[0]) ==5:
Verb_Noun_Adjective_Alpha_in_text[index].append(word.split("/")[0])
index += 1
Verb_Noun_Adjective_Alpha_in_text_tokens = [t for d in Verb_Noun_Adjective_Alpha_in_text for t in d]
import nltk
real_tokens = nltk.Text(Verb_Noun_Adjective_Alpha_in_text_tokens, name='RNN')
real_tokens_freq = real_tokens.vocab().most_common(vocabulary_size-1)
index_to_word = [x[0] for x in real_tokens_freq]
index_to_word.append("unknown")
word_to_index = dict([(w,i) for i,w in enumerate(index_to_word)])
for i, sent in enumerate(Verb_Noun_Adjective_Alpha_in_text):
tokenized_sentences[i] = [w if w in word_to_index else "unknown" for w in sent]
```
# Make model
```
X_train = np.asarray([[word_to_index[w] for w in sent[:-1]] for sent in tokenized_sentences])
y_train = np.asarray([[word_to_index[w] for w in sent[1:]] for sent in tokenized_sentences])
X_train[0]
class RNNNumpy:
def __init__(self, word_dim, hidden_dim=100, bptt_truncate=4):
self.word_dim = word_dim
self.hidden_dim = hidden_dim
self.bptt_truncate = bptt_truncate
self.U = np.random.uniform(-np.sqrt(1./word_dim), np.sqrt(1./word_dim), (hidden_dim, word_dim))
self.V = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (word_dim, hidden_dim))
self.W = np.random.uniform(-np.sqrt(1./hidden_dim), np.sqrt(1./hidden_dim), (hidden_dim, hidden_dim))
def forward_propagation(self, x):
T = len(x)
s = np.zeros((T + 1, self.hidden_dim))
s[-1] = np.zeros(self.hidden_dim)
o = np.zeros((T, self.word_dim))
for t in np.arange(T):
s[t] = np.tanh(self.U[:,x[t]] + self.W.dot(s[t-1]))
o[t] = softmax(self.V.dot(s[t]))
return [o, s]
RNNNumpy.forward_propagation = forward_propagation
def predict(self, x):
o, s = self.forward_propagation(x)
return np.argmax(o, axis=1)
RNNNumpy.predict = predict
tokenized_sentences[0]
np.random.seed(100)
model = RNNNumpy(vocabulary_size)
#for i in range(100):
o, s = model.forward_propagation(X_train[0])
print (o.shape)
print (s.shape)
X_train[0]
y_train[0]
predictions = model.predict(X_train[0])
print (predictions.shape)
print (predictions)
def calculate_total_loss(self, x, y):
L = 0
for i in np.arange(len(y)):
o, s = self.forward_propagation(x[i])
correct_word_predictions = o[np.arange(len(y[i])), y[i]]
L += -1 * np.sum(np.log(correct_word_predictions))
return L
def calculate_loss(self, x, y):
N = np.sum((len(y_i) for y_i in y))
return self.calculate_total_loss(x,y)/N
RNNNumpy.calculate_total_loss = calculate_total_loss
RNNNumpy.calculate_loss = calculate_loss
# Limit to 1000 examples to save time
print ("Expected Loss for random predictions: %f" % np.log(vocabulary_size))
print ("Actual loss: %f" % model.calculate_loss(X_train[:1000], y_train[:1000]))
def bptt(self, x, y):
T = len(y)
# Perform forward propagation
o, s = self.forward_propagation(x)
# We accumulate the gradients in these variables
dLdU = np.zeros(self.U.shape)
dLdV = np.zeros(self.V.shape)
dLdW = np.zeros(self.W.shape)
delta_o = o
delta_o[np.arange(len(y)), y] -= 1.
# For each output backwards...
for t in np.arange(T)[::-1]:
dLdV += np.outer(delta_o[t], s[t].T)
# Initial delta calculation
delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
# Backpropagation through time (for at most self.bptt_truncate steps)
for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
# print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
dLdW += np.outer(delta_t, s[bptt_step-1])
dLdU[:,x[bptt_step]] += delta_t
# Update delta for next step
delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
return [dLdU, dLdV, dLdW]
RNNNumpy.bptt = bptt
def numpy_sdg_step(self, x, y, learning_rate):
dLdU, dLdV, dLdW = self.bptt(x, y)
self.U -= learning_rate * dLdU
self.V -= learning_rate * dLdV
self.W -= learning_rate * dLdW
RNNNumpy.sgd_step = numpy_sdg_step
def train_with_sgd(model, X_train, y_train, learning_rate=0.005, nepoch=100, evaluate_loss_after=5):
losses = []
num_examples_seen = 0
for epoch in range(nepoch):
if (epoch % evaluate_loss_after == 0):
loss = model.calculate_loss(X_train, y_train)
losses.append((num_examples_seen, loss))
time = datetime.now().strftime('%Y-%m-%d %H:%M:%S')
print ("%s: Loss after num_examples_seen=%d epoch=%d: %f" % (time, num_examples_seen, epoch, loss))
for i in range(len(y_train)):
model.sgd_step(X_train[i], y_train[i], learning_rate)
num_examples_seen += 1
print(model)
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
%timeit model.sgd_step(X_train[10], y_train[10], 0.005)
np.random.seed(10)
model = RNNNumpy(vocabulary_size)
losses = train_with_sgd(model, X_train[:100], y_train[:100], nepoch=10, evaluate_loss_after=1)
from rnn_theano import RNNTheano, gradient_check_theano
from utils import load_model_parameters_theano, save_model_parameters_theano
model = RNNTheano(vocabulary_size, hidden_dim=100)
train_with_sgd(model, X_train, y_train, nepoch=50)
save_model_parameters_theano('./data/trained-model-sion_consider.npz', model)
load_model_parameters_theano('./data/trained-model-sion_consider.npz', model)
print(len(model.V.get_value()))
def generate_sentence(model):
new_sentence = [word_to_index[sentence_start_token]]
while not new_sentence[-1] == word_to_index[sentence_end_token]:
next_word_probs = model.forward_propagation(new_sentence)
sampled_word = word_to_index["unknown"]
while sampled_word == word_to_index["unknown"]:
samples = np.random.multinomial(1, next_word_probs[-1])
sampled_word = np.argmax(samples)
new_sentence.append(sampled_word)
sentence_str = [index_to_word[x] for x in new_sentence[1:-1]]
return sentence_str
num_sentences = 2
senten_min_length = 5
for i in range(num_sentences):
sent = []
while len(sent) < senten_min_length:
sent = generate_sentence(model)
print (" ".join(sent))
```
|
github_jupyter
|
**Chapter 10 – Introduction to Artificial Neural Networks with Keras**
_This notebook contains all the sample code and solutions to the exercises in chapter 10._
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0-preview.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# TensorFlow ≥2.0-preview is required
import tensorflow as tf
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
# Perceptrons
**Note**: we set `max_iter` and `tol` explicitly to avoid warnings about the fact that their default value will change in future versions of Scikit-Learn.
```
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int)
per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42)
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])
y_pred
a = -per_clf.coef_[0][0] / per_clf.coef_[0][1]
b = -per_clf.intercept_ / per_clf.coef_[0][1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs", label="Not Iris-Setosa")
plt.plot(X[y==1, 0], X[y==1, 1], "yo", label="Iris-Setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-", linewidth=3)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="lower right", fontsize=14)
plt.axis(axes)
save_fig("perceptron_iris_plot")
plt.show()
```
# Activation functions
```
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
z = np.linspace(-5, 5, 200)
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=1, label="Step")
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=1, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
def heaviside(z):
return (z >= 0).astype(z.dtype)
def mlp_xor(x1, x2, activation=heaviside):
return activation(-activation(x1 + x2 - 1.5) + activation(x1 + x2 - 0.5) - 0.5)
x1s = np.linspace(-0.2, 1.2, 100)
x2s = np.linspace(-0.2, 1.2, 100)
x1, x2 = np.meshgrid(x1s, x2s)
z1 = mlp_xor(x1, x2, activation=heaviside)
z2 = mlp_xor(x1, x2, activation=sigmoid)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.contourf(x1, x2, z1)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: heaviside", fontsize=14)
plt.grid(True)
plt.subplot(122)
plt.contourf(x1, x2, z2)
plt.plot([0, 1], [0, 1], "gs", markersize=20)
plt.plot([0, 1], [1, 0], "y^", markersize=20)
plt.title("Activation function: sigmoid", fontsize=14)
plt.grid(True)
```
# Building an Image Classifier
First let's import TensorFlow and Keras.
```
import tensorflow as tf
from tensorflow import keras
tf.__version__
keras.__version__
```
Let's start by loading the fashion MNIST dataset. Keras has a number of functions to load popular datasets in `keras.datasets`. The dataset is already split for you between a training set and a test set, but it can be useful to split the training set further to have a validation set:
```
fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()
```
The training set contains 60,000 grayscale images, each 28x28 pixels:
```
X_train_full.shape
```
Each pixel intensity is represented as a byte (0 to 255):
```
X_train_full.dtype
```
Let's split the full training set into a validation set and a (smaller) training set. We also scale the pixel intensities down to the 0-1 range and convert them to floats, by dividing by 255.
```
X_valid, X_train = X_train_full[:5000] / 255., X_train_full[5000:] / 255.
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.
```
You can plot an image using Matplotlib's `imshow()` function, with a `'binary'`
color map:
```
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()
```
The labels are the class IDs (represented as uint8), from 0 to 9:
```
y_train
```
Here are the corresponding class names:
```
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
```
So the first image in the training set is a coat:
```
class_names[y_train[0]]
```
The validation set contains 5,000 images, and the test set contains 10,000 images:
```
X_valid.shape
X_test.shape
```
Let's take a look at a sample of the images in the dataset:
```
n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_train[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_plot', tight_layout=False)
plt.show()
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])
model.layers
model.summary()
keras.utils.plot_model(model, "my_mnist_model.png", show_shapes=True)
hidden1 = model.layers[1]
hidden1.name
model.get_layer(hidden1.name) is hidden1
weights, biases = hidden1.get_weights()
weights
weights.shape
biases
biases.shape
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
```
This is equivalent to:
```python
model.compile(loss=keras.losses.sparse_categorical_crossentropy,
optimizer=keras.optimizers.SGD(),
metrics=[keras.metrics.sparse_categorical_accuracy])
```
```
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid))
history.params
print(history.epoch)
history.history.keys()
import pandas as pd
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("keras_learning_curves_plot")
plt.show()
model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)
y_pred = model.predict_classes(X_new)
y_pred
np.array(class_names)[y_pred]
y_new = y_test[:3]
y_new
```
# Regression MLP
Let's load, split and scale the California housing dataset (the original one, not the modified one as in chapter 2):
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)
plt.plot(pd.DataFrame(history.history))
plt.grid(True)
plt.gca().set_ylim(0, 1)
plt.show()
y_pred
```
# Functional API
Not all neural network models are simply sequential. Some may have complex topologies. Some may have multiple inputs and/or multiple outputs. For example, a Wide & Deep neural network (see [paper](https://ai.google/research/pubs/pub45413)) connects all or part of the inputs directly to the output layer.
```
np.random.seed(42)
tf.random.set_seed(42)
input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_], outputs=[output])
model.summary()
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
y_pred = model.predict(X_new)
```
What if you want to send different subsets of input features through the wide or deep paths? We will send 5 features (features 0 to 4), and 6 through the deep path (features 2 to 7). Note that 3 features will go through both (features 2, 3 and 4).
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.models.Model(inputs=[input_A, input_B], outputs=[output])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:]
X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:]
X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:]
X_new_A, X_new_B = X_test_A[:3], X_test_B[:3]
history = model.fit((X_train_A, X_train_B), y_train, epochs=20,
validation_data=((X_valid_A, X_valid_B), y_valid))
mse_test = model.evaluate((X_test_A, X_test_B), y_test)
y_pred = model.predict((X_new_A, X_new_B))
```
Adding an auxiliary output for regularization:
```
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="main_output")(concat)
aux_output = keras.layers.Dense(1, name="aux_output")(hidden2)
model = keras.models.Model(inputs=[input_A, input_B],
outputs=[output, aux_output])
model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit([X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))
total_loss, main_loss, aux_loss = model.evaluate(
[X_test_A, X_test_B], [y_test, y_test])
y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])
```
# The subclassing API
```
class WideAndDeepModel(keras.models.Model):
def __init__(self, units=30, activation="relu", **kwargs):
super().__init__(**kwargs)
self.hidden1 = keras.layers.Dense(units, activation=activation)
self.hidden2 = keras.layers.Dense(units, activation=activation)
self.main_output = keras.layers.Dense(1)
self.aux_output = keras.layers.Dense(1)
def call(self, inputs):
input_A, input_B = inputs
hidden1 = self.hidden1(input_B)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
main_output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return main_output, aux_output
model = WideAndDeepModel(30, activation="relu")
model.compile(loss="mse", loss_weights=[0.9, 0.1], optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit((X_train_A, X_train_B), (y_train, y_train), epochs=10,
validation_data=((X_valid_A, X_valid_B), (y_valid, y_valid)))
total_loss, main_loss, aux_loss = model.evaluate((X_test_A, X_test_B), (y_test, y_test))
y_pred_main, y_pred_aux = model.predict((X_new_A, X_new_B))
model = WideAndDeepModel(30, activation="relu")
```
# Saving and Restoring
```
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
model.save("my_keras_model.h5")
model = keras.models.load_model("my_keras_model.h5")
model.predict(X_new)
model.save_weights("my_keras_weights.ckpt")
model.load_weights("my_keras_weights.ckpt")
```
# Using Callbacks during Training
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5", save_best_only=True)
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb])
model = keras.models.load_model("my_keras_model.h5") # rollback to best model
mse_test = model.evaluate(X_test, y_test)
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
early_stopping_cb = keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])
mse_test = model.evaluate(X_test, y_test)
class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"]))
val_train_ratio_cb = PrintValTrainRatioCallback()
history = model.fit(X_train, y_train, epochs=1,
validation_data=(X_valid, y_valid),
callbacks=[val_train_ratio_cb])
```
# TensorBoard
```
root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir()
run_logdir
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
To start the TensorBoard server, one option is to open a terminal, if needed activate the virtualenv where you installed TensorBoard, go to this notebook's directory, then type:
```bash
$ tensorboard --logdir=./my_logs --port=6006
```
You can then open your web browser to [localhost:6006](http://localhost:6006) and use TensorBoard. Once you are done, press Ctrl-C in the terminal window, this will shutdown the TensorBoard server.
Alternatively, you can load TensorBoard's Jupyter extension and run it like this:
```
%load_ext tensorboard
%tensorboard --logdir=./my_logs --port=6006
run_logdir2 = get_run_logdir()
run_logdir2
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=[8]),
keras.layers.Dense(30, activation="relu"),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=0.05))
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir2)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, tensorboard_cb])
```
Notice how TensorBoard now sees two runs, and you can compare the learning curves.
Check out the other available logging options:
```
help(keras.callbacks.TensorBoard.__init__)
```
# Hyperparameter Tuning
```
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
model = keras.models.Sequential()
model.add(keras.layers.InputLayer(input_shape=input_shape))
for layer in range(n_hidden):
model.add(keras.layers.Dense(n_neurons, activation="relu"))
model.add(keras.layers.Dense(1))
optimizer = keras.optimizers.SGD(lr=learning_rate)
model.compile(loss="mse", optimizer=optimizer)
return model
keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)
keras_reg.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)
np.random.seed(42)
tf.random.set_seed(42)
from scipy.stats import reciprocal
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
"n_hidden": [0, 1, 2, 3],
"n_neurons": np.arange(1, 100),
"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3, verbose=2)
rnd_search_cv.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[keras.callbacks.EarlyStopping(patience=10)])
rnd_search_cv.best_params_
rnd_search_cv.best_score_
rnd_search_cv.best_estimator_
rnd_search_cv.score(X_test, y_test)
model = rnd_search_cv.best_estimator_.model
model
model.evaluate(X_test, y_test)
```
# Exercise solutions
## 1. to 9.
See appendix A.
## 10.
TODO
|
github_jupyter
|
Copyright 2021 DeepMind Technologies Limited
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
#Generative Art Using Neural Visual Grammars and Dual Encoders
**Chrisantha Fernando, Piotr Mirowski, Dylan Banarse, S. M. Ali Eslami, Jean-Baptiste Alayrac, Simon Osindero**
DeepMind, 2021
##Arnheim 1
###Generate paintings from text prompts.
Whilst there are perhaps only a few scientific methods, there seem to be almost as many artistic methods as there are artists. Artistic processes appear to inhabit the highest order of open-endedness. To begin to understand some of the processes of art making it is helpful to try to automate them even partially.
In this paper, a novel algorithm for producing generative art is described which allows a user to input a text string, and which in a creative response to this string, outputs an image which interprets that string. It does so by evolving images using a hierarchical neural [Lindenmeyer system](https://en.wikipedia.org/wiki/L-system), and evaluating these images along the way using an image text dual encoder trained on billions of images and their associated text from the internet.
In doing so we have access to and control over an instance of an artistic process, allowing analysis of which aspects of the artistic process become the task of the algorithm, and which elements remain the responsibility of the artist.
This colab accompanies the paper [Generative Art Using Neural Visual Grammars and Dual Encoders](https://arxiv.org/abs/2105.00162)
##Instructions
1. Click "Connect" button in the top right corner of this Colab
1. Select Runtime -> Change runtime type -> Hardware accelerator -> GPU
1. Select High-RAM for "Runtime shape" option
1. Navigate to "Get text input"
1. Enter text for IMAGE_NAME
1. Select "Run All" from Runtime menu
# Imports
```
#@title Set CUDA version for PyTorch
import subprocess
CUDA_version = [s for s in subprocess.check_output(["nvcc", "--version"]
).decode("UTF-8").split(", ")
if s.startswith("release")][0].split(" ")[-1]
print("CUDA version:", CUDA_version)
if CUDA_version == "10.0":
torch_version_suffix = "+cu100"
elif CUDA_version == "10.1":
torch_version_suffix = "+cu101"
elif CUDA_version == "10.2":
torch_version_suffix = ""
else:
torch_version_suffix = "+cu110"
! nvidia-smi
#@title Install and import PyTorch and Clip
! pip install torch==1.7.1{torch_version_suffix} torchvision==0.8.2{torch_version_suffix} -f https://download.pytorch.org/whl/torch_stable.html
! pip install git+https://github.com/openai/CLIP.git --no-deps
! pip install ftfy regex
import torch
import torch.nn as nn
import clip
print("Torch version:", torch.__version__)
#@title Install and import ray multiprocessing
! pip install -q -U ray[default]
import ray
#@title Import all other needed libraries
import collections
import copy
import cloudpickle
import time
import numpy as np
import matplotlib.pyplot as plt
import math
from PIL import Image
from PIL import ImageDraw
from skimage import transform
#@title Load CLIP {vertical-output: true}
CLIP_MODEL = "ViT-B/32"
device = torch.device("cuda")
print(f"Downloading CLIP model {CLIP_MODEL}...")
model, _ = clip.load(CLIP_MODEL, device, jit=False)
```
# Neural Visual Grammar
### Drawing primitives
```
def to_homogeneous(p):
r, c = p
return np.stack((r, c, np.ones_like(p[0])), axis=0)
def from_homogeneous(p):
p = p / p.T[:, 2]
return p[0].astype("int32"), p[1].astype("int32")
def apply_scale(scale, lineh):
return np.stack([lineh[0, :] * scale,
lineh[1, :] * scale,
lineh[2, :]])
def apply_translation(translation, lineh, offset_r=0, offset_c=0):
r, c = translation
return np.stack([lineh[0, :] + c + offset_c,
lineh[1, :] + r + offset_r,
lineh[2, :]])
def apply_rotation(translation, rad, lineh):
r, c = translation
cos_rad = np.cos(rad)
sin_rad = np.sin(rad)
return np.stack(
[(lineh[0, :] - c) * cos_rad - (lineh[1, :] - r) * sin_rad + c,
(lineh[0, :] - c) * sin_rad + (lineh[1, :] - r) * cos_rad + r,
lineh[2, :]])
def transform_lines(line_from, line_to, translation, angle, scale,
translation2, angle2, scale2, img_siz2):
"""Transform lines by translation, angle and scale, twice.
Args:
line_from: Line start point.
line_to: Line end point.
translation: 1st translation to line.
angle: 1st angle of rotation for line.
scale: 1st scale for line.
translation2: 2nd translation to line.
angle2: 2nd angle of rotation for line.
scale2: 2nd scale for line.
img_siz2: Offset for 2nd translation.
Returns:
Transformed lines.
"""
if len(line_from.shape) == 1:
line_from = np.expand_dims(line_from, 0)
if len(line_to.shape) == 1:
line_to = np.expand_dims(line_to, 0)
# First transform.
line_from_h = to_homogeneous(line_from.T)
line_to_h = to_homogeneous(line_to.T)
line_from_h = apply_scale(scale, line_from_h)
line_to_h = apply_scale(scale, line_to_h)
translated_line_from = apply_translation(translation, line_from_h)
translated_line_to = apply_translation(translation, line_to_h)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle,
translated_line_to)
line_from_transformed = np.array(from_homogeneous(line_from_transformed))
line_to_transformed = np.array(from_homogeneous(line_to_transformed))
# Second transform.
line_from_h = to_homogeneous(line_from_transformed)
line_to_h = to_homogeneous(line_to_transformed)
line_from_h = apply_scale(scale2, line_from_h)
line_to_h = apply_scale(scale2, line_to_h)
translated_line_from = apply_translation(
translation2, line_from_h, offset_r=img_siz2, offset_c=img_siz2)
translated_line_to = apply_translation(
translation2, line_to_h, offset_r=img_siz2, offset_c=img_siz2)
translated_mid_point = (translated_line_from + translated_line_to) / 2.0
translated_mid_point = translated_mid_point[[1, 0]]
line_from_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_from)
line_to_transformed = apply_rotation(translated_mid_point,
np.pi * angle2,
translated_line_to)
return np.concatenate([from_homogeneous(line_from_transformed),
from_homogeneous(line_to_transformed)],
axis=1)
```
### Hierarchical stroke painting functions
```
# PaintingCommand
# origin_top: Origin of line defined by top level LSTM
# angle_top: Angle of line defined by top level LSTM
# scale_top: Scale for line defined by top level LSTM
# origin_bottom: Origin of line defined by bottom level LSTM
# angle_bottom: Angle of line defined by bottom level LSTM
# scale_bottom: Scale for line defined by bottom level LSTM
# position_choice: Selects between use of:
# Origin, angle and scale from both LSTM levels
# Origin, angle and scale just from top level LSTM
# Origin, angle and scale just from bottom level LSTM
# transparency: Line transparency determined by bottom level LSTM
PaintingCommand = collections.namedtuple("PaintingCommand",
["origin_top",
"angle_top",
"scale_top",
"origin_bottom",
"angle_bottom",
"scale_bottom",
"position_choice",
"transparency"])
def paint_over_image(img, strokes, painting_commands,
allow_strokes_beyond_image_edges, coeff_size=1):
"""Make marks over an existing image.
Args:
img: Image to draw on.
strokes: Stroke descriptions.
painting_commands: Top-level painting commands with transforms for the i
sets of strokes.
allow_strokes_beyond_image_edges: Allow strokes beyond image boundary.
coeff_size: Determines low res (1) or high res (10) image will be drawn.
Returns:
num_strokes: The number of strokes made.
"""
img_center = 112. * coeff_size
# a, b and c: determines the stroke width distribution (see 'weights' below)
a = 10. * coeff_size
b = 2. * coeff_size
c = 300. * coeff_size
# d: extent that the strokes are allowed to go beyond the edge of the canvas
d = 223 * coeff_size
def _clip_colour(col):
return np.clip((np.round(col * 255. + 128.)).astype(np.int32), 0, 255)
# Loop over all the top level...
t0_over = time.time()
num_strokes = sum(len(s) for s in strokes)
translations = np.zeros((2, num_strokes,), np.float32)
translations2 = np.zeros((2, num_strokes,), np.float32)
angles = np.zeros((num_strokes,), np.float32)
angles2 = np.zeros((num_strokes,), np.float32)
scales = np.zeros((num_strokes,), np.float32)
scales2 = np.zeros((num_strokes,), np.float32)
weights = np.zeros((num_strokes,), np.float32)
lines_from = np.zeros((num_strokes, 2), np.float32)
lines_to = np.zeros((num_strokes, 2), np.float32)
rgbas = np.zeros((num_strokes, 4), np.float32)
k = 0
for i in range(len(strokes)):
# Get the top-level transforms for the i-th bunch of strokes
painting_comand = painting_commands[i]
translation_a = painting_comand.origin_top
angle_a = (painting_comand.angle_top + 1) / 5.0
scale_a = 0.5 + (painting_comand.scale_top + 1) / 3.0
translation_b = painting_comand.origin_bottom
angle_b = (painting_comand.angle_bottom + 1) / 5.0
scale_b = 0.5 + (painting_comand.scale_bottom + 1) / 3.0
position_choice = painting_comand.position_choice
solid_colour = painting_comand.transparency
# Do we use origin, angle and scale from both, top or bottom LSTM levels?
if position_choice > 0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = translation_b
angle2 = angle_b
scale2 = scale_b
elif position_choice > -0.33:
translation = translation_a
angle = angle_a
scale = scale_a
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
else:
translation = translation_b
angle = angle_b
scale = scale_b
translation2 = [-img_center, -img_center]
angle2 = 0.
scale2 = 1.
# Store top-level transforms
strokes_i = strokes[i]
n_i = len(strokes_i)
angles[k:(k+n_i)] = angle
angles2[k:(k+n_i)] = angle2
scales[k:(k+n_i)] = scale
scales2[k:(k+n_i)] = scale2
translations[0, k:(k+n_i)] = translation[0]
translations[1, k:(k+n_i)] = translation[1]
translations2[0, k:(k+n_i)] = translation2[0]
translations2[1, k:(k+n_i)] = translation2[1]
# ... and the bottom level stroke definitions.
for j in range(n_i):
z_ij = strokes_i[j]
# Store line weight (we will process micro-strokes later)
weights[k] = z_ij[4]
# Store line endpoints
lines_from[k, :] = (z_ij[0], z_ij[1])
lines_to[k, :] = (z_ij[2], z_ij[3])
# Store colour and alpha
rgbas[k, 0] = z_ij[7]
rgbas[k, 1] = z_ij[8]
rgbas[k, 2] = z_ij[9]
if solid_colour > -0.5:
rgbas[k, 3] = 25.5
else:
rgbas[k, 3] = z_ij[11]
k += 1
# Draw all the strokes in a batch as sequence of length 2 * num_strokes
t1_over = time.time()
lines_from *= img_center/2.0
lines_to *= img_center/2.0
rr, cc = transform_lines(lines_from, lines_to, translations, angles, scales,
translations2, angles2, scales2, img_center)
if not allow_strokes_beyond_image_edges:
rrm = np.round(np.clip(rr, 1, d-1)).astype(int)
ccm = np.round(np.clip(cc, 1, d-1)).astype(int)
else:
rrm = np.round(rr).astype(int)
ccm = np.round(cc).astype(int)
# Plot all the strokes
t2_over = time.time()
img_pil = Image.fromarray(img)
canvas = ImageDraw.Draw(img_pil, "RGBA")
rgbas[:, :3] = _clip_colour(rgbas[:, :3])
rgbas[:, 3] = (np.clip(5.0 * np.abs(rgbas[:, 3]), 0, 255)).astype(np.int32)
weights = (np.clip(np.round(weights * b + a), 2, c)).astype(np.int32)
for k in range(num_strokes):
canvas.line((rrm[k], ccm[k], rrm[k+num_strokes], ccm[k+num_strokes]),
fill=tuple(rgbas[k]), width=weights[k])
img[:] = np.asarray(img_pil)[:]
t3_over = time.time()
if VERBOSE_CODE:
print("{:.2f}s to store {} stroke defs, {:.4f}s to "
"compute them, {:.4f}s to plot them".format(
t1_over - t0_over, num_strokes, t2_over - t1_over,
t3_over - t2_over))
return num_strokes
```
### Recurrent Neural Network Layer Generator
```
# DrawingLSTMSpec - parameters defining the LSTM architecture
# input_spec_size: Size if sequence elements
# num_lstms: Number of LSTMs at each layer
# net_lstm_hiddens: Number of hidden LSTM units
# net_mlp_hiddens: Number of hidden units in MLP layer
DrawingLSTMSpec = collections.namedtuple("DrawingLSTMSpec",
["input_spec_size",
"num_lstms",
"net_lstm_hiddens",
"net_mlp_hiddens"])
class MakeGeneratorLstm(nn.Module):
"""Block of parallel LSTMs with MLP output heads."""
def __init__(self, drawing_lstm_spec, output_size):
"""Build drawing LSTM architecture using spec.
Args:
drawing_lstm_spec: DrawingLSTMSpec with architecture parameters
output_size: Number of outputs for the MLP head layer
"""
super(MakeGeneratorLstm, self).__init__()
self._num_lstms = drawing_lstm_spec.num_lstms
self._input_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.input_spec_size,
drawing_lstm_spec.net_lstm_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True))
lstms = []
heads = []
for _ in range(self._num_lstms):
lstm_layer = nn.LSTM(
input_size=drawing_lstm_spec.net_lstm_hiddens,
hidden_size=drawing_lstm_spec.net_lstm_hiddens,
num_layers=2, batch_first=True, bias=True)
head_layer = nn.Sequential(
nn.Linear(drawing_lstm_spec.net_lstm_hiddens,
drawing_lstm_spec.net_mlp_hiddens),
torch.nn.LeakyReLU(0.2, inplace=True),
nn.Linear(drawing_lstm_spec.net_mlp_hiddens, output_size))
lstms.append(lstm_layer)
heads.append(head_layer)
self._lstms = nn.ModuleList(lstms)
self._heads = nn.ModuleList(heads)
def forward(self, x):
pred = []
x = self._input_layer(x)*10.0
for i in range(self._num_lstms):
y, _ = self._lstms[i](x)
y = self._heads[i](y)
pred.append(y)
return pred
```
### DrawingLSTM - A Drawing Recurrent Neural Network
```
Genotype = collections.namedtuple("Genotype",
["top_lstm",
"bottom_lstm",
"input_sequence",
"initial_img"])
class DrawingLSTM:
"""LSTM for processing input sequences and generating resultant drawings.
Comprised of two LSTM layers.
"""
def __init__(self, drawing_lstm_spec, allow_strokes_beyond_image_edges):
"""Create DrawingLSTM to interpret input sequences and paint an image.
Args:
drawing_lstm_spec: DrawingLSTMSpec with LSTM architecture parameters
allow_strokes_beyond_image_edges: Draw lines outside image boundary
"""
self._input_spec_size = drawing_lstm_spec.input_spec_size
self._num_lstms = drawing_lstm_spec.num_lstms
self._allow_strokes_beyond_image_edges = allow_strokes_beyond_image_edges
with torch.no_grad():
self.top_lstm = MakeGeneratorLstm(drawing_lstm_spec,
self._input_spec_size)
self.bottom_lstm = MakeGeneratorLstm(drawing_lstm_spec, 12)
self._init_all(self.top_lstm, torch.nn.init.normal_, mean=0., std=0.2)
self._init_all(self.bottom_lstm, torch.nn.init.normal_, mean=0., std=0.2)
def _init_all(self, a_model, init_func, *params, **kwargs):
"""Method for initialising model with given init_func, params and kwargs."""
for p in a_model.parameters():
init_func(p, *params, **kwargs)
def _feed_top_lstm(self, input_seq):
"""Feed all input sequences input_seq into the LSTM models."""
x_in = input_seq.reshape((len(input_seq), 1, self._input_spec_size))
x_in = np.tile(x_in, (SEQ_LENGTH, 1))
x_torch = torch.from_numpy(x_in).type(torch.FloatTensor)
y_torch = self.top_lstm(x_torch)
y_torch = [y_torch_k.detach().numpy() for y_torch_k in y_torch]
del x_in
del x_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts_top = np.clip(
np.round(self._num_lstms/2.0 * (1 + input_seq[:, 1])).astype(np.int32),
0, self._num_lstms-1)
lengths_top = np.clip(
np.round(10.0 * (1 + input_seq[:, 0])).astype(np.int32),
0, SEQ_LENGTH) + 1
intermediate_strings = []
for i in range(len(readouts_top)):
y_torch_i = y_torch[readouts_top[i]][i]
intermediate_strings.append(y_torch_i[0:lengths_top[i], :])
return intermediate_strings
def _feed_bottom_lstm(self, intermediate_strings, input_seq, coeff_size=1):
"""Feed all input sequences into the LSTM models.
Args:
intermediate_strings: top level strings
input_seq: input sequences fed to the top LSTM
coeff_size: sets centre origin
Returns:
strokes: Painting strokes.
painting_commands: Top-level painting commands with origin, angle and scale
information, as well as transparency.
"""
img_center = 112. * coeff_size
coeff_origin = 100. * coeff_size
top_lengths = []
for i in range(len(intermediate_strings)):
top_lengths.append(len(intermediate_strings[i]))
y_flat = np.concatenate(intermediate_strings, axis=0)
tiled_y_flat = y_flat.reshape((len(y_flat), 1, self._input_spec_size))
tiled_y_flat = np.tile(tiled_y_flat, (SEQ_LENGTH, 1))
y_torch = torch.from_numpy(tiled_y_flat).type(torch.FloatTensor)
z_torch = self.bottom_lstm(y_torch)
z_torch = [z_torch_k.detach().numpy() for z_torch_k in z_torch]
del tiled_y_flat
del y_torch
# There are multiple LSTM heads. For each sequence, read out the head and
# length of intermediary output to keep and return intermediary outputs.
readouts = np.clip(np.round(
NUM_LSTMS/2.0 * (1 + y_flat[:, 0])).astype(np.int32), 0, NUM_LSTMS-1)
lengths_bottom = np.clip(
np.round(10.0 * (1 + y_flat[:, 1])).astype(np.int32), 0, SEQ_LENGTH) + 1
strokes = []
painting_commands = []
offset = 0
for i in range(len(intermediate_strings)):
origin_top = [(1+input_seq[i, 2]) * img_center,
(1+input_seq[i, 3]) * img_center]
angle_top = input_seq[i, 4]
scale_top = input_seq[i, 5]
for j in range(len(intermediate_strings[i])):
k = j + offset
z_torch_ij = z_torch[readouts[k]][k]
strokes.append(z_torch_ij[0:lengths_bottom[k], :])
y_ij = y_flat[k]
origin_bottom = [y_ij[2] * coeff_origin, y_ij[3] * coeff_origin]
angle_bottom = y_ij[4]
scale_bottom = y_ij[5]
position_choice = y_ij[6]
transparency = y_ij[7]
painting_command = PaintingCommand(
origin_top, angle_top, scale_top, origin_bottom, angle_bottom,
scale_bottom, position_choice, transparency)
painting_commands.append(painting_command)
offset += top_lengths[i]
del y_flat
return strokes, painting_commands
def make_initial_genotype(self, initial_img, sequence_length,
input_spec_size):
"""Make and return initial DNA weights for LSTMs, input sequence, and image.
Args:
initial_img: Image (to be appended to the genotype)
sequence_length: Length of the input sequence (i.e. number of strokes)
input_spec_size: Number of inputs for each element in the input sequences
Returns:
Genotype NamedTuple with fields: [parameters of network 0,
parameters of network 1,
input sequence,
initial_img]
"""
dna_top = []
with torch.no_grad():
for _, params in self.top_lstm.named_parameters():
dna_top.append(params.clone())
param_size = params.numpy().shape
dna_top[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
dna_bottom = []
with torch.no_grad():
for _, params in self.bottom_lstm.named_parameters():
dna_bottom.append(params.clone())
param_size = params.numpy().shape
dna_bottom[-1] = np.random.uniform(
0.1 * DNA_SCALE, 0.3
* DNA_SCALE) * np.random.normal(size=param_size)
input_sequence = np.random.uniform(
-1, 1, size=(sequence_length, input_spec_size))
return Genotype(dna_top, dna_bottom, input_sequence, initial_img)
def draw(self, img, genotype):
"""Add to the image using the latest genotype and get latest input sequence.
Args:
img: image to add to.
genotype: as created by make_initial_genotype.
Returns:
image with new strokes added.
"""
t0_draw = time.time()
img = img + genotype.initial_img
input_sequence = genotype.input_sequence
# Generate the strokes for drawing in batch mode.
# input_sequence is between 10 and 20 but is evolved, can go to 200.
intermediate_strings = self._feed_top_lstm(input_sequence)
strokes, painting_commands = self._feed_bottom_lstm(
intermediate_strings, input_sequence)
del intermediate_strings
# Now we can go through the output strings producing the strokes.
t1_draw = time.time()
num_strokes = paint_over_image(
img, strokes, painting_commands, self._allow_strokes_beyond_image_edges,
coeff_size=1)
t2_draw = time.time()
if VERBOSE_CODE:
print(
"Draw {:.2f}s (net {:.2f}s plot {:.2f}s {:.1f}ms/strk {}".format(
t2_draw - t0_draw, t1_draw - t0_draw, t2_draw - t1_draw,
(t2_draw - t1_draw) / num_strokes * 1000, num_strokes))
return img
```
## DrawingGenerator
```
class DrawingGenerator:
"""Creates a drawing using a DrawingLSTM."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.primitives = ["c", "r", "l", "b", "p", "j"]
self.pop = []
self.size = image_size
self.fitnesses = np.zeros(1)
self.noise = 2
self.mutation_std = 0.0004
# input_spec_size, num_lstms, net_lstm_hiddens,
# net_mlp_hiddens, output_size, allow_strokes_beyond_image_edges
self.drawing_lstm = DrawingLSTM(drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def make_initial_genotype(self, initial_img, sequence_length, input_spec_size):
"""Use drawing_lstm to create initial genotypye."""
self.genotype = self.drawing_lstm.make_initial_genotype(
initial_img, sequence_length, input_spec_size)
return self.genotype
def _copy_genotype_to_generator(self, genotype):
"""Copy genotype's data into generator's parameters.
Copies the parameters in genotype (genotype.top_lstm[:] and
genotype.bottom_lstm[:]) into the parmaters for the drawing network so it
can be used to evaluate the genotype.
Args:
genotype: as created by make_initial_genotype.
Returns:
None
"""
self.genotype = copy.deepcopy(genotype)
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.top_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.top_lstm[i]))
i = i + 1
i = 0
with torch.no_grad():
for _, param in self.drawing_lstm.bottom_lstm.named_parameters():
param.copy_(torch.tensor(self.genotype.bottom_lstm[i]))
i = i + 1
def _interpret_genotype(self, genotype):
img = np.zeros((self.size, self.size, 3), dtype=np.uint8)
img = self.drawing_lstm.draw(img, genotype)
return img
def draw_from_genotype(self, genotype):
"""Copy input sequence and LSTM weights from `genotype`, run and draw."""
self._copy_genotype_to_generator(genotype)
return self._interpret_genotype(self.genotype)
def visualize_genotype(self, genotype):
"""Plot histograms of genotype"s data."""
plt.show()
inp_seq = np.array(genotype.input_sequence).flatten()
plt.title("input seq")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.top_lstm).flatten()
plt.title("LSTM top")
plt.hist(inp_seq)
plt.show()
inp_seq = np.array(genotype.bottom_lstm).flatten()
plt.title("LSTM bottom")
plt.hist(inp_seq)
plt.show()
def mutate(self, genotype):
"""Mutates `genotype`. This function is static.
Args:
genotype: genotype structure to mutate parameters of.
Returns:
new_genotype: Mutated copy of supplied genotype.
"""
new_genotype = copy.deepcopy(genotype)
new_input_seq = new_genotype.input_sequence
n = len(new_input_seq)
if np.random.uniform() < 1.0:
# Standard gaussian small mutation of input sequence.
if np.random.uniform() > 0.5:
new_input_seq += (
np.random.uniform(0.001, 0.2) * np.random.normal(
size=new_input_seq.shape))
# Low frequency large mutation of individual parts of the input sequence.
for i in range(n):
if np.random.uniform() < 2.0/n:
for j in range(len(new_input_seq[i])):
if np.random.uniform() < 2.0/len(new_input_seq[i]):
new_input_seq[i][j] = new_input_seq[i][j] + 0.5*np.random.normal()
# Adding and deleting elements from the input sequence.
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: adding")
a = np.random.uniform(-1, 1, size=(1, INPUT_SPEC_SIZE))
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.insert(new_input_seq, pos, a, axis=0)
if np.random.uniform() < 0.02:
if VERBOSE_MUTATION:
print("Mutation: deleting")
pos = np.random.randint(1, len(new_input_seq))
new_input_seq = np.delete(new_input_seq, pos, axis=0)
n = len(new_input_seq)
# Swapping two elements in the input sequence.
if np.random.uniform() < 0.01:
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
temp = copy.deepcopy(new_input_seq[element1])
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
new_input_seq[element2] = temp
# Duplicate an element in the input sequence (with some mutation).
if np.random.uniform() < 0.01:
if VERBOSE_MUTATION:
print("Mutation: duplicating")
element1 = np.random.randint(0, n)
element2 = np.random.randint(0, n)
while element1 == element2:
element2 = np.random.randint(0, n)
new_input_seq[element1] = copy.deepcopy(new_input_seq[element2])
noise = 0.05 * np.random.normal(size=new_input_seq[element1].shape)
new_input_seq[element1] += noise
# Ensure that the input sequence is always between -1 and 1
# so that positions make sense.
new_genotype = new_genotype._replace(
input_sequence=np.clip(new_input_seq, -1.0, 1.0))
# Mutates dna of networks.
if np.random.uniform() < 1.0:
for net in range(2):
for layer in range(len(new_genotype[net])):
weights = new_genotype[net][layer]
if np.random.uniform() < 0.5:
noise = 0.00001 * np.random.standard_cauchy(size=weights.shape)
weights += noise
else:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.0001, 0.006)
weights += noise
if np.random.uniform() < 0.01:
noise = np.random.normal(size=weights.shape)
noise *= np.random.uniform(0.1, 0.3)
weights = noise
# Ensure weights are between -10 and 10.
weights = np.clip(weights, -1.0, 1.0)
new_genotype[net][layer] = weights
return new_genotype
```
## Evaluator
```
class Evaluator:
"""Evaluator for a drawing."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.drawing_generator = DrawingGenerator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
self.calls = 0
def make_initial_genotype(self, img, sequence_length, input_spec_size):
return self.drawing_generator.make_initial_genotype(img, sequence_length,
input_spec_size)
def evaluate_genotype(self, pickled_genotype, id_num):
"""Evaluate genotype and return genotype's image.
Args:
pickled_genotype: pickled genotype to be evaluated.
id_num: ID number of genotype.
Returns:
dict: drawing and id_num.
"""
genotype = cloudpickle.loads(pickled_genotype)
drawing = self.drawing_generator.draw_from_genotype(genotype)
self.calls += 1
return {"drawing": drawing, "id": id_num}
def mutate(self, genotype):
"""Create a mutated version of genotype."""
return self.drawing_generator.mutate(genotype)
```
# Evolution
## Fitness calculation, tournament, and crossover
```
IMAGE_MEAN = torch.tensor([0.48145466, 0.4578275, 0.40821073]).cuda()
IMAGE_STD = torch.tensor([0.26862954, 0.26130258, 0.27577711]).cuda()
def get_fitness(pictures, use_projective_transform,
projective_transform_coefficient):
"""Run CLIP on a batch of `pictures` and return `fitnesses`.
Args:
pictures: batch if images to evaluate
use_projective_transform: Add transformed versions of the image
projective_transform_coefficient: Degree of transform
Returns:
Similarities between images and the text
"""
# Do we use projective transforms of images before CLIP eval?
t0 = time.time()
pictures_trans = np.swapaxes(np.array(pictures), 1, 3) / 244.0
if use_projective_transform:
for i in range(len(pictures_trans)):
matrix = np.eye(3) + (
projective_transform_coefficient * np.random.normal(size=(3, 3)))
tform = transform.ProjectiveTransform(matrix=matrix)
pictures_trans[i] = transform.warp(pictures_trans[i], tform.inverse)
# Run the CLIP evaluator.
t1 = time.time()
image_input = torch.tensor(np.stack(pictures_trans)).cuda()
image_input -= IMAGE_MEAN[:, None, None]
image_input /= IMAGE_STD[:, None, None]
with torch.no_grad():
image_features = model.encode_image(image_input).float()
t2 = time.time()
similarity = torch.cosine_similarity(
text_features, image_features, dim=1).cpu().numpy()
t3 = time.time()
if VERBOSE_CODE:
print(f"get_fitness init {t1-t0:.4f}s, CLIP {t2-t1:.4f}s, sim {t3-t2:.4f}s")
return similarity
def crossover(dna_winner, dna_loser, crossover_prob):
"""Create new genotype by combining two genotypes.
Randomly replaces parts of the genotype 'dna_winner' with parts of dna_loser
to create a new genotype based mostly on on both 'parents'.
Args:
dna_winner: The high-fitness parent genotype - gets replaced with child.
dna_loser: The lower-fitness parent genotype.
crossover_prob: Probability of crossover between winner and loser.
Returns:
dna_winner: The result of crossover from parents.
"""
# Copy single input signals
for i in range(len(dna_winner[2])):
if i < len(dna_loser[2]):
if np.random.uniform() < crossover_prob:
dna_winner[2][i] = copy.deepcopy(dna_loser[2][i])
# Copy whole modules
for i in range(len(dna_winner[0])):
if i < len(dna_loser[0]):
if np.random.uniform() < crossover_prob:
dna_winner[0][i] = copy.deepcopy(dna_loser[0][i])
# Copy whole modules
for i in range(len(dna_winner[1])):
if i < len(dna_loser[1]):
if np.random.uniform() < crossover_prob:
dna_winner[1][i] = copy.deepcopy(dna_loser[1][i])
return dna_winner
def truncation_selection(population, fitnesses, evaluator, use_crossover,
crossover_prob):
"""Create new population using truncation selection.
Creates a new population by copying across the best 50% genotypes and
filling the rest with (for use_crossover==False) a mutated copy of each
genotype or (for use_crossover==True) with children created through crossover
between each winner and a genotype in the bottom 50%.
Args:
population: list of current population genotypes.
fitnesses: list of evaluated fitnesses.
evaluator: class that evaluates a draw generator.
use_crossover: Whether to use crossover between winner and loser.
crossover_prob: Probability of crossover between winner and loser.
Returns:
new_pop: the new population.
best: genotype.
"""
fitnesses = np.array(-fitnesses)
ordered_fitness_ids = fitnesses.argsort()
best = copy.deepcopy(population[ordered_fitness_ids[0]])
pop_size = len(population)
if not use_crossover:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(
copy.deepcopy(population[ordered_fitness_ids[i]])))
else:
new_pop = []
for i in range(int(pop_size/2)):
new_pop.append(copy.deepcopy(population[ordered_fitness_ids[i]]))
for i in range(int(pop_size/2)):
new_pop.append(evaluator.mutate(crossover(
copy.deepcopy(population[ordered_fitness_ids[i]]),
population[ordered_fitness_ids[int(pop_size/2) + i]], crossover_prob
)))
return new_pop, best
```
##Remote workers
```
VERBOSE_DURATION = False
@ray.remote
class Worker(object):
"""Takes a pickled dna and evaluates it, returning result."""
def __init__(self, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
self.evaluator = Evaluator(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges)
def compute(self, dna_pickle, genotype_id):
if VERBOSE_DURATION:
t0 = time.time()
res = self.evaluator.evaluate_genotype(dna_pickle, genotype_id)
if VERBOSE_DURATION:
duration = time.time() - t0
print(f"Worker {genotype_id} evaluated params in {duration:.1f}sec")
return res
def create_workers(num_workers, image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges):
"""Create the workers.
Args:
num_workers: Number of parallel workers for evaluation.
image_size: Length of side of (square) image
drawing_lstm_spec: DrawingLSTMSpec for LSTM network
allow_strokes_beyond_image_edges: Whether to draw outside the edges
Returns:
List of workers.
"""
worker_pool = []
for w_i in range(num_workers):
print("Creating worker", w_i, flush=True)
worker_pool.append(Worker.remote(image_size, drawing_lstm_spec,
allow_strokes_beyond_image_edges))
return worker_pool
```
##Plotting
```
def plot_training_res(batch_drawings, fitness_history, idx=None):
"""Plot fitnesses and timings.
Args:
batch_drawings: Drawings
fitness_history: History of fitnesses
idx: Index of drawing to show, default is highest fitness
"""
_, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
if idx is None:
idx = np.argmax(fitness_history[-1])
ax1.plot(fitness_history, ".")
ax1.set_title("Fitnesses")
ax2.imshow(batch_drawings[idx])
ax2.set_title(f"{PROMPT} (fit: {fitness_history[-1][idx]:.3f})")
plt.show()
def plot_samples(batch_drawings, num_samples=16):
"""Plot sample of drawings.
Args:
batch_drawings: Batch of drawings to sample from
num_samples: Number to displa
"""
num_samples = min(len(batch_drawings), num_samples)
num_rows = int(math.floor(np.sqrt(num_samples)))
num_cols = int(math.ceil(num_samples / num_rows))
row_images = []
for c in range(0, num_samples, num_cols):
if c + num_cols <= num_samples:
row_images.append(np.concatenate(batch_drawings[c:(c+num_cols)], axis=1))
composite_image = np.concatenate(row_images, axis=0)
_, ax = plt.subplots(1, 1, figsize=(20, 20))
ax.imshow(composite_image)
ax.set_title(PROMPT)
```
## Population and evolution main loop
```
def make_population(pop_size, evaluator, image_size, input_spec_size,
sequence_length):
"""Make initial population.
Args:
pop_size: number of genotypes in population.
evaluator: An Evaluator class instance for generating initial genotype.
image_size: Size of initial image for genotype to draw on.
input_spec_size: Sequence element size
sequence_length: Initial length of sequences
Returns:
Initialised population.
"""
print(f"Creating initial population of size {pop_size}")
pop = []
for _ in range(pop_size):
a_genotype = evaluator.make_initial_genotype(
img=np.zeros((image_size, image_size, 3), dtype=np.uint8),
sequence_length=sequence_length,
input_spec_size=input_spec_size)
pop.append(a_genotype)
return pop
def evolution_loop(population, worker_pool, evaluator, num_generations,
use_crossover, crossover_prob,
use_projective_transform, projective_transform_coefficient,
plot_every, plot_batch):
"""Create population and run evolution.
Args:
population: Initial population of genotypes
worker_pool: List of workers of parallel evaluations
evaluator: image evaluator to calculate fitnesses
num_generations: number of generations to run
use_crossover: Whether crossover is used for offspring
crossover_prob: Probability that crossover takes place
use_projective_transform: Use projective transforms in evaluation
projective_transform_coefficient: Degree of projective transform
plot_every: number of generations between new plots
plot_batch: whether to show all samples in the batch then plotting
"""
population_size = len(population)
num_workers = len(worker_pool)
print("Population of {} genotypes being evaluated by {} workers".format(
population_size, num_workers))
drawings = {}
fitness_history = []
init_gen = len(fitness_history)
print(f"(Re)starting evolution at generation {init_gen}")
for gen in range(init_gen, num_generations):
# Drawing
t0_loop = time.time()
futures = []
for j in range(0, population_size, num_workers):
for i in range(num_workers):
futures.append(worker_pool[i].compute.remote(
cloudpickle.dumps(population[i+j]), i+j))
data = ray.get(futures)
for i in range(num_workers):
drawings[data[i+j]["id"]] = data[j+i]["drawing"]
batch_drawings = []
for i in range(population_size):
batch_drawings.append(drawings[i])
# Fitness evaluation using CLIP
t1_loop = time.time()
fitnesses = get_fitness(batch_drawings, use_projective_transform,
projective_transform_coefficient)
fitness_history.append(copy.deepcopy(fitnesses))
# Tournament
t2_loop = time.time()
population, best_genotype = truncation_selection(
population, fitnesses, evaluator, use_crossover, crossover_prob)
t3_loop = time.time()
duration_draw = t1_loop - t0_loop
duration_fit = t2_loop - t1_loop
duration_tournament = t3_loop - t2_loop
duration_total = t3_loop - t0_loop
if gen % plot_every == 0:
if VISUALIZE_GENOTYPE:
evaluator.drawing_generator.visualize_genotype(best_genotype)
print("Draw: {:.2f}s fit: {:.2f}s evol: {:.2f}s total: {:.2f}s".format(
duration_draw, duration_fit, duration_tournament, duration_total))
plot_training_res(batch_drawings, fitness_history)
if plot_batch:
num_samples_to_plot = int(math.pow(
math.floor(np.sqrt(population_size)), 2))
plot_samples(batch_drawings, num_samples=num_samples_to_plot)
```
# Configure and Generate
```
#@title Hyperparameters
#@markdown Evolution parameters: population size and number of generations.
POPULATION_SIZE = 10 #@param {type:"slider", min:4, max:100, step:2}
NUM_GENERATIONS = 5000 #@param {type:"integer", min:100}
#@markdown Number of workers working in parallel (should be equal to or smaller than the population size).
NUM_WORKERS = 10 #@param {type:"slider", min:4, max:100, step:2}
#@markdown Crossover in evolution.
USE_CROSSOVER = True #@param {type:"boolean"}
CROSSOVER_PROB = 0.01 #@param {type:"number"}
#@markdown Number of LSTMs, each one encoding a group of strokes.
NUM_LSTMS = 5 #@param {type:"integer", min:1, max:5}
#@markdown Number of inputs for each element in the input sequences.
INPUT_SPEC_SIZE = 10 #@param {type:"integer"}
#@markdown Length of the input sequence fed to the LSTMs (determines number of strokes).
SEQ_LENGTH = 20 #@param {type:"integer", min:20, max:200}
#@markdown Rendering parameter.
ALLOW_STROKES_BEYOND_IMAGE_EDGES = True #@param {type:"boolean"}
#@markdown CLIP evaluation: do we use projective transforms of images?
USE_PROJECTIVE_TRANSFORM = True #@param {type:"boolean"}
PROJECTIVE_TRANSFORM_COEFFICIENT = 0.000001 #@param {type:"number"}
#@markdown These parameters should be edited mostly only for debugging reasons.
NET_LSTM_HIDDENS = 40 #@param {type:"integer"}
NET_MLP_HIDDENS = 20 #@param {type:"integer"}
# Scales the values used in genotype's initialisation.
DNA_SCALE = 1.0 #@param {type:"number"}
IMAGE_SIZE = 224 #@param {type:"integer"}
VERBOSE_CODE = False #@param {type:"boolean"}
VISUALIZE_GENOTYPE = False #@param {type:"boolean"}
VERBOSE_MUTATION = False #@param {type:"boolean"}
#@markdown Number of generations between new plots.
PLOT_EVERY_NUM_GENS = 5 #@param {type:"integer"}
#@markdown Whether to show all samples in the batch when plotting.
PLOT_BATCH = True # @param {type:"boolean"}
assert POPULATION_SIZE % NUM_WORKERS == 0, "POPULATION_SIZE not multiple of NUM_WORKERS"
```
#Running the original evolutionary algorithm
This is the original inefficient version of Arnheim which uses a genetic algorithm to optimize the picture. It takes at least 12 hours to produce an image using 50 workers. In our paper we used 500-1000 GPUs which speeded things up considerably. Refer to Arnheim 2 for a far more efficient way to generate images with a similar architecture.
Try prompts like “A photorealistic chicken”. Feel free to modify this colab to include your own way of generating and evolving images like we did in figure 2 here https://arxiv.org/pdf/2105.00162.pdf.
```
# @title Get text input and run evolution
PROMPT = "an apple" #@param {type:"string"}
# Tokenize prompts and coompute CLIP features.
text_input = clip.tokenize(PROMPT).to(device)
with torch.no_grad():
text_features = model.encode_text(text_input)
ray.shutdown()
ray.init()
drawing_lstm_arch = DrawingLSTMSpec(INPUT_SPEC_SIZE,
NUM_LSTMS,
NET_LSTM_HIDDENS,
NET_MLP_HIDDENS)
workers = create_workers(NUM_WORKERS, IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_evaluator = Evaluator(IMAGE_SIZE, drawing_lstm_arch,
ALLOW_STROKES_BEYOND_IMAGE_EDGES)
drawing_population = make_population(POPULATION_SIZE, drawing_evaluator,
IMAGE_SIZE, INPUT_SPEC_SIZE, SEQ_LENGTH)
evolution_loop(drawing_population, workers, drawing_evaluator, NUM_GENERATIONS,
USE_CROSSOVER, CROSSOVER_PROB,
USE_PROJECTIVE_TRANSFORM, PROJECTIVE_TRANSFORM_COEFFICIENT,
PLOT_EVERY_NUM_GENS, PLOT_BATCH)
```
|
github_jupyter
|
# CRRT Mortality Prediction
## Model Construction
### Christopher V. Cosgriff, David Sasson, Colby Wilkinson, Kanhua Yin
The purpose of this notebook is to build a deep learning model that predicts ICU mortality in the CRRT population. The data is extracted in the `extract_cohort_and_features` notebook and stored in the `data` folder. This model will be mult-input and use GRUs to model sequence data. See the extraction file for a full description of the data extraction.
## Step 0: Envrionment Setup
```
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from IPython.display import SVG
import os
from keras.optimizers import Adam, SGD, rmsprop
from keras.models import Sequential,Model
from keras.layers import Dense, Activation, Dropout, Input, Dropout, concatenate
from keras.layers.recurrent import GRU
from keras.utils import plot_model
from keras.utils.vis_utils import model_to_dot
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, roc_curve
# for saving images
fig_fp = os.path.join('./', 'figures')
if not os.path.isdir(fig_fp):
os.mkdir(fig_fp)
%matplotlib inline
```
## Step 1: Load and Prepare Data
Here will we load in the data, and create train, validation, and testing splits.
```
# set tensors to float 32 as this is what GPUs expect
features_sequence = np.load('./features_sequence.npy').astype(np.float32)
features_static = np.load('./features_static.npy').astype(np.float32)
labels = np.load('./labels.npy').astype(np.float32)
x_seq_full_train, x_seq_test, x_static_full_train, x_static_test, y_full_train, y_test = train_test_split(
features_sequence, features_static, labels, test_size = 0.20, random_state = 42)
x_seq_train, x_seq_val, x_static_train, x_static_val, y_train, y_val = train_test_split(
x_seq_full_train, x_static_full_train, y_full_train, test_size = 0.10, random_state = 42)
```
Next we need to remove NANs from the data; we'll impute the trianing population mean, the simplest method suggested by David Sontag.
```
def impute_mean(source_data, input_data):
'''
Takes the source data, and uses it to determine means for all
features; it then applies them to the input data.
inputs:
source_data: a tensor to provide means
input_data: the data to fill in NA for
output:
output_data: data with nans imputed for each feature
'''
output_data = input_data.copy()
for feature in range(source_data.shape[1]):
feature_mean = np.nanmean(source_data[:, feature, :][np.where(source_data[:, feature, :] != 0)])
ind_output_data = np.where(np.isnan(output_data[:, feature, :]))
output_data[:, feature, :][ind_output_data] = feature_mean
return output_data
x_seq_train_original = x_seq_train.copy()
x_seq_train = impute_mean(x_seq_train_original, x_seq_train)
x_seq_val = impute_mean(x_seq_train_original, x_seq_val)
x_seq_test = impute_mean(x_seq_train_original, x_seq_test)
```
## Step 2: Build Model
### Model 1
Base model, no regularization.
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
plot_model(model, to_file='experiment_GRU-base.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-base.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'loss_svg.svg'
fig.savefig('./loss_svg.svg', bbox_inches='tight')
```
### 10% Dropout
```
# Define inputs
sequence_input = Input(shape = (x_seq_train.shape[1], x_seq_train.shape[2], ), dtype = 'float32', name = 'sequence_input')
static_input = Input(shape = (x_static_train.shape[1], ), name = 'static_input')
# Network architecture
seq_x = GRU(units = 128)(sequence_input)
# Seperate output for the GRU later
seq_aux_output = Dense(1, activation='sigmoid', name='aux_output')(seq_x)
# Merge dual inputs
x = concatenate([seq_x, static_input])
# We stack a deep fully-connected network on the merged inputs
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
x = Dropout(0.10)(x)
x = Dense(128, activation = 'relu')(x)
x = Dense(128, activation = 'relu')(x)
# Sigmoid output layer
main_output = Dense(1, activation='sigmoid', name='main_output')(x)
# optimizer
opt = rmsprop(lr = 0.00001)
# build model
model = Model(inputs = [sequence_input, static_input], outputs = [main_output, seq_aux_output])
model.compile(optimizer = opt, loss = 'binary_crossentropy', metrics = ['accuracy'], loss_weights = [1, 0.1])
# save a plot of the model
#plot_model(model, to_file='experiment_GRU-DO.svg')
# fit the model
history = model.fit([x_seq_train, x_static_train], [y_train, y_train], epochs = 500, batch_size = 128,\
validation_data=([x_seq_val, x_static_val], [y_val, y_val]),)
# plot the fit
pred_main, pred_aux = model.predict([x_seq_test, x_static_test])
roc = roc_curve(y_test, pred_main)
auc = roc_auc_score(y_test, pred_main)
fig = plt.figure(figsize=(4, 3)) # in inches
plt.plot(roc[0], roc[1], color = 'darkorange', label = 'ROC curve\n(area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color= 'navy', linestyle = '--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('%s: ROC' % 'GRU-base')
plt.legend(loc = "lower right")
fig_name = 'gru-do.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
plt.show()
# plot training and validation loss and accuracy
acc = history.history['main_output_acc']
val_acc = history.history['val_main_output_acc']
loss = history.history['main_output_loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
fig_name = 'do_loss_acc.pdf'
fig.savefig(os.path.join(fig_fp, fig_name), bbox_inches='tight')
```
|
github_jupyter
|
```
# Mount Google Drive
from google.colab import drive # import drive from google colab
ROOT = "/content/drive" # default location for the drive
print(ROOT) # print content of ROOT (Optional)
drive.mount(ROOT) # we mount the google drive at /content/drive
!pip install pennylane
from IPython.display import clear_output
clear_output()
import os
def restart_runtime():
os.kill(os.getpid(), 9)
restart_runtime()
# %matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import numpy as np
```
# Loading Raw Data
```
import tensorflow as tf
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train_flatten = x_train.reshape(x_train.shape[0], x_train.shape[1]*x_train.shape[2])/255.0
x_test_flatten = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[2])/255.0
print(x_train_flatten.shape, y_train.shape)
print(x_test_flatten.shape, y_test.shape)
x_train_0 = x_train_flatten[y_train == 0]
x_train_1 = x_train_flatten[y_train == 1]
x_train_2 = x_train_flatten[y_train == 2]
x_train_3 = x_train_flatten[y_train == 3]
x_train_4 = x_train_flatten[y_train == 4]
x_train_5 = x_train_flatten[y_train == 5]
x_train_6 = x_train_flatten[y_train == 6]
x_train_7 = x_train_flatten[y_train == 7]
x_train_8 = x_train_flatten[y_train == 8]
x_train_9 = x_train_flatten[y_train == 9]
x_train_list = [x_train_0, x_train_1, x_train_2, x_train_3, x_train_4, x_train_5, x_train_6, x_train_7, x_train_8, x_train_9]
print(x_train_0.shape)
print(x_train_1.shape)
print(x_train_2.shape)
print(x_train_3.shape)
print(x_train_4.shape)
print(x_train_5.shape)
print(x_train_6.shape)
print(x_train_7.shape)
print(x_train_8.shape)
print(x_train_9.shape)
x_test_0 = x_test_flatten[y_test == 0]
x_test_1 = x_test_flatten[y_test == 1]
x_test_2 = x_test_flatten[y_test == 2]
x_test_3 = x_test_flatten[y_test == 3]
x_test_4 = x_test_flatten[y_test == 4]
x_test_5 = x_test_flatten[y_test == 5]
x_test_6 = x_test_flatten[y_test == 6]
x_test_7 = x_test_flatten[y_test == 7]
x_test_8 = x_test_flatten[y_test == 8]
x_test_9 = x_test_flatten[y_test == 9]
x_test_list = [x_test_0, x_test_1, x_test_2, x_test_3, x_test_4, x_test_5, x_test_6, x_test_7, x_test_8, x_test_9]
print(x_test_0.shape)
print(x_test_1.shape)
print(x_test_2.shape)
print(x_test_3.shape)
print(x_test_4.shape)
print(x_test_5.shape)
print(x_test_6.shape)
print(x_test_7.shape)
print(x_test_8.shape)
print(x_test_9.shape)
```
# Selecting the dataset
Output: X_train, Y_train, X_test, Y_test
```
num_sample = 300
n_class = 4
mult_test = 0.25
X_train = x_train_list[0][:num_sample, :]
X_test = x_test_list[0][:int(mult_test*num_sample), :]
Y_train = np.zeros((n_class*X_train.shape[0],), dtype=int)
Y_test = np.zeros((n_class*X_test.shape[0],), dtype=int)
for i in range(n_class-1):
X_train = np.concatenate((X_train, x_train_list[i+1][:num_sample, :]), axis=0)
Y_train[num_sample*(i+1):num_sample*(i+2)] = int(i+1)
X_test = np.concatenate((X_test, x_test_list[i+1][:int(mult_test*num_sample), :]), axis=0)
Y_test[int(mult_test*num_sample*(i+1)):int(mult_test*num_sample*(i+2))] = int(i+1)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
```
# Dataset Preprocessing (Standardization + PCA)
## Standardization
```
def normalize(X, use_params=False, params=None):
"""Normalize the given dataset X
Args:
X: ndarray, dataset
Returns:
(Xbar, mean, std): tuple of ndarray, Xbar is the normalized dataset
with mean 0 and standard deviation 1; mean and std are the
mean and standard deviation respectively.
Note:
You will encounter dimensions where the standard deviation is
zero, for those when you do normalization the normalized data
will be NaN. Handle this by setting using `std = 1` for those
dimensions when doing normalization.
"""
if use_params:
mu = params[0]
std_filled = [1]
else:
mu = np.mean(X, axis=0)
std = np.std(X, axis=0)
#std_filled = std.copy()
#std_filled[std==0] = 1.
Xbar = (X - mu)/(std + 1e-8)
return Xbar, mu, std
X_train, mu_train, std_train = normalize(X_train)
X_train.shape, Y_train.shape
X_test = (X_test - mu_train)/(std_train + 1e-8)
X_test.shape, Y_test.shape
```
## PCA
```
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
num_component = 9
pca = PCA(n_components=num_component, svd_solver='full')
pca.fit(X_train)
np.cumsum(pca.explained_variance_ratio_)
X_train = pca.transform(X_train)
X_test = pca.transform(X_test)
print(X_train.shape, Y_train.shape)
print(X_test.shape, Y_test.shape)
```
## Norm
```
X_train = (X_train.T / np.sqrt(np.sum(X_train ** 2, -1))).T
X_test = (X_test.T / np.sqrt(np.sum(X_test ** 2, -1))).T
plt.scatter(X_train[:100, 0], X_train[:100, 1])
plt.scatter(X_train[100:200, 0], X_train[100:200, 1])
plt.scatter(X_train[200:300, 0], X_train[200:300, 1])
```
# Quantum
```
import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer, GradientDescentOptimizer
qml.enable_tape()
# Set a random seed
np.random.seed(42)
def plot_data(x, y, fig=None, ax=None):
"""
Plot data with red/blue values for a binary classification.
Args:
x (array[tuple]): array of data points as tuples
y (array[int]): array of data points as tuples
"""
if fig == None:
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
reds = y == 0
blues = y == 1
ax.scatter(x[reds, 0], x[reds, 1], c="red", s=20, edgecolor="k")
ax.scatter(x[blues, 0], x[blues, 1], c="blue", s=20, edgecolor="k")
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
# Define output labels as quantum state vectors
# def density_matrix(state):
# """Calculates the density matrix representation of a state.
# Args:
# state (array[complex]): array representing a quantum state vector
# Returns:
# dm: (array[complex]): array representing the density matrix
# """
# return state * np.conj(state).T
label_0 = [[1], [0]]
label_1 = [[0], [1]]
def density_matrix(state):
"""Calculates the density matrix representation of a state.
Args:
state (array[complex]): array representing a quantum state vector
Returns:
dm: (array[complex]): array representing the density matrix
"""
return np.outer(state, np.conj(state))
#state_labels = [label_0, label_1]
state_labels = np.loadtxt('./tetra_states.txt', dtype=np.complex_)
dev = qml.device("default.qubit", wires=1)
# Install any pennylane-plugin to run on some particular backend
@qml.qnode(dev)
def qcircuit(params, x=None, y=None):
"""A variational quantum circuit representing the Universal classifier.
Args:
params (array[float]): array of parameters
x (array[float]): single input vector
y (array[float]): single output state density matrix
Returns:
float: fidelity between output state and input
"""
for i in range(len(params[0])):
for j in range(int(len(x)/3)):
qml.Rot(*(params[0][i][3*j:3*(j+1)]*x[3*j:3*(j+1)] + params[1][i][3*j:3*(j+1)]), wires=0)
#qml.Rot(*params[1][i][3*j:3*(j+1)], wires=0)
return qml.expval(qml.Hermitian(y, wires=[0]))
X_train[0].shape
a = np.random.uniform(size=(2, 1, 9))
qcircuit(a, X_train[0], density_matrix(state_labels[3]))
tetra_class = np.loadtxt('./tetra_class_label.txt')
tetra_class
binary_class = np.array([[1, 0], [0, 1]])
binary_class
class_labels = tetra_class
class_labels[0][0]
dm_labels = [density_matrix(s) for s in state_labels]
def cost(params, x, y, state_labels=None):
"""Cost function to be minimized.
Args:
params (array[float]): array of parameters
x (array[float]): 2-d array of input vectors
y (array[float]): 1-d array of targets
state_labels (array[float]): array of state representations for labels
Returns:
float: loss value to be minimized
"""
# Compute prediction for each input in data batch
loss = 0.0
for i in range(len(x)):
f = qcircuit(params, x=x[i], y=dm_labels[y[i]])
loss = loss + (1 - f) ** 2
return loss / len(x)
# loss = 0.0
# for i in range(len(x)):
# f = 0.0
# for j in range(len(dm_labels)):
# f += (qcircuit(params, x=x[i], y=dm_labels[j]) - class_labels[y[i]][j])**2
# loss = loss + f
# return loss / len(x)
def test(params, x, y, state_labels=None):
"""
Tests on a given set of data.
Args:
params (array[float]): array of parameters
x (array[float]): 2-d array of input vectors
y (array[float]): 1-d array of targets
state_labels (array[float]): 1-d array of state representations for labels
Returns:
predicted (array([int]): predicted labels for test data
output_states (array[float]): output quantum states from the circuit
"""
fidelity_values = []
dm_labels = [density_matrix(s) for s in state_labels]
predicted = []
for i in range(len(x)):
fidel_function = lambda y: qcircuit(params, x=x[i], y=y)
fidelities = [fidel_function(dm) for dm in dm_labels]
best_fidel = np.argmax(fidelities)
predicted.append(best_fidel)
fidelity_values.append(fidelities)
return np.array(predicted), np.array(fidelity_values)
def accuracy_score(y_true, y_pred):
"""Accuracy score.
Args:
y_true (array[float]): 1-d array of targets
y_predicted (array[float]): 1-d array of predictions
state_labels (array[float]): 1-d array of state representations for labels
Returns:
score (float): the fraction of correctly classified samples
"""
score = y_true == y_pred
return score.sum() / len(y_true)
def iterate_minibatches(inputs, targets, batch_size):
"""
A generator for batches of the input data
Args:
inputs (array[float]): input data
targets (array[float]): targets
Returns:
inputs (array[float]): one batch of input data of length `batch_size`
targets (array[float]): one batch of targets of length `batch_size`
"""
for start_idx in range(0, inputs.shape[0] - batch_size + 1, batch_size):
idxs = slice(start_idx, start_idx + batch_size)
yield inputs[idxs], targets[idxs]
# Train using Adam optimizer and evaluate the classifier
num_layers = 2
learning_rate = 0.1
epochs = 100
batch_size = 32
opt = AdamOptimizer(learning_rate)
# initialize random weights
theta = np.random.uniform(size=(num_layers, 18))
w = np.random.uniform(size=(num_layers, 18))
params = [w, theta]
predicted_train, fidel_train = test(params, X_train, Y_train, state_labels)
accuracy_train = accuracy_score(Y_train, predicted_train)
predicted_test, fidel_test = test(params, X_test, Y_test, state_labels)
accuracy_test = accuracy_score(Y_test, predicted_test)
# save predictions with random weights for comparison
initial_predictions = predicted_test
loss = cost(params, X_test, Y_test, state_labels)
print(
"Epoch: {:2d} | Loss: {:3f} | Train accuracy: {:3f} | Test Accuracy: {:3f}".format(
0, loss, accuracy_train, accuracy_test
)
)
for it in range(epochs):
for Xbatch, ybatch in iterate_minibatches(X_train, Y_train, batch_size=batch_size):
params = opt.step(lambda v: cost(v, Xbatch, ybatch, state_labels), params)
predicted_train, fidel_train = test(params, X_train, Y_train, state_labels)
accuracy_train = accuracy_score(Y_train, predicted_train)
loss = cost(params, X_train, Y_train, state_labels)
predicted_test, fidel_test = test(params, X_test, Y_test, state_labels)
accuracy_test = accuracy_score(Y_test, predicted_test)
res = [it + 1, loss, accuracy_train, accuracy_test]
print(
"Epoch: {:2d} | Loss: {:3f} | Train accuracy: {:3f} | Test accuracy: {:3f}".format(
*res
)
)
qml.Rot(*(params[0][0][0:3]*X_train[0, 0:3] + params[1][0][0:3]), wires=[0])
params[1][0][0:3]
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import stellargraph as sg
from stellargraph.mapper import PaddedGraphGenerator
from stellargraph.layer import DeepGraphCNN
from stellargraph import StellarGraph
from stellargraph import datasets
from sklearn import model_selection
from IPython.display import display, HTML
from tensorflow.keras import Model
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.layers import Dense, Conv1D, MaxPool1D, Dropout, Flatten
from tensorflow.keras.losses import binary_crossentropy
import tensorflow as tf
conspiracy_5G_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/5g_corona_conspiracy/'
conspiracy_other_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/non_conspiracy/'
non_conspiracy_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/other_conspiracy/'
test_graphs_path = '/Users/maria/Desktop/twitterAnalysis/FakeNews/dataset/graphs/test_graphs/'
conspiracy_5G_N = 270
conspiracy_other_N = 1660
non_conspiracy_N = 397
test_graphs_N = 1165
conspiracy_5G = list()
for i in range(conspiracy_5G_N):
g_id = i+1
nodes_path = conspiracy_5G_path + str(g_id) + '/nodes.csv'
edges_path = conspiracy_5G_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
conspiracy_5G.append(g)
conspiracy_other = list()
for i in range(conspiracy_other_N):
g_id = i+1
nodes_path = conspiracy_other_path + str(g_id) + '/nodes.csv'
edges_path = conspiracy_other_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
conspiracy_other.append(g)
non_conspiracy = list()
for i in range(non_conspiracy_N):
g_id = i+1
nodes_path = non_conspiracy_path + str(g_id) + '/nodes.csv'
edges_path = non_conspiracy_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
non_conspiracy.append(g)
test_graphs_off = list()
for i in range(test_graphs_N):
g_id = i+1
nodes_path = test_graphs_path + str(g_id) + '/nodes.csv'
edges_path = test_graphs_path + str(g_id) + '/edges.txt'
g_nodes = pd.read_csv(nodes_path)
g_nodes = g_nodes.set_index('id')
g_edges = pd.read_csv(edges_path, header = None, sep=' ')
g_edges = g_edges.rename(columns={0: 'source', 1: 'target'})
g = StellarGraph(g_nodes, edges=g_edges)
test_graphs_off.append(g)
graphs = conspiracy_5G + conspiracy_other + non_conspiracy
graph_labels = pd.Series(np.repeat([1, -1], [conspiracy_5G_N, conspiracy_other_N+non_conspiracy_N], axis=0))
graph_labels = pd.get_dummies(graph_labels, drop_first=True)
generator = PaddedGraphGenerator(graphs=graphs)
k = 35 # the number of rows for the output tensor
layer_sizes = [32, 32, 32, 1]
dgcnn_model = DeepGraphCNN(
layer_sizes=layer_sizes,
activations=["tanh", "tanh", "tanh", "tanh"],
k=k,
bias=False,
generator=generator,
)
x_inp, x_out = dgcnn_model.in_out_tensors()
x_out = Conv1D(filters=16, kernel_size=sum(layer_sizes), strides=sum(layer_sizes))(x_out)
x_out = MaxPool1D(pool_size=2)(x_out)
x_out = Conv1D(filters=32, kernel_size=5, strides=1)(x_out)
x_out = Flatten()(x_out)
x_out = Dense(units=128, activation="relu")(x_out)
x_out = Dropout(rate=0.5)(x_out)
predictions = Dense(units=1, activation="sigmoid")(x_out)
model = Model(inputs=x_inp, outputs=predictions)
model.compile(
optimizer=Adam(lr=0.0001), loss=binary_crossentropy, metrics=["acc"],
)
train_graphs, test_graphs = model_selection.train_test_split(
graph_labels, train_size=0.9, test_size=None, stratify=graph_labels,
)
gen = PaddedGraphGenerator(graphs=graphs)
train_gen = gen.flow(
list(train_graphs.index - 1),
targets=train_graphs.values,
batch_size=50,
symmetric_normalization=False,
)
test_gen = gen.flow(
list(test_graphs.index - 1),
targets=test_graphs.values,
batch_size=1,
symmetric_normalization=False,
)
epochs = 100
history = model.fit(
train_gen, epochs=epochs, verbose=1, validation_data=test_gen, shuffle=True,
)
sg.utils.plot_history(history)
test_gen_off = PaddedGraphGenerator(graphs=test_graphs_off)
test_gen_off_f = test_gen_off.flow(graphs=test_graphs_off)
preds = model.predict(test_gen_off_f)
import matplotlib.pyplot as plt
plt.hist(preds)
print(preds)
# Sources
# https://stellargraph.readthedocs.io/en/stable/demos/graph-classification/dgcnn-graph-classification.html
```
|
github_jupyter
|
# $H(curl, \Omega)$ Elliptic Problems
$\newcommand{\dd}{\,{\rm d}}$
$\newcommand{\uu}{\mathbf{u}}$
$\newcommand{\vv}{\mathbf{v}}$
$\newcommand{\nn}{\mathbf{n}}$
$\newcommand{\ff}{\mathbf{f}}$
$\newcommand{\Hcurlzero}{\mathbf{H}_0(\mbox{curl}, \Omega)}$
$\newcommand{\Curl}{\nabla \times}$
Let $\Omega \subset \mathbb{R}^d$ be an open Liptschitz bounded set, and we look for the solution of the following problem
\begin{align}
\left\{
\begin{array}{rl}
\Curl \Curl \uu + \mu \uu &= \ff, \quad \Omega
\\
\uu \times \nn &= 0, \quad \partial\Omega
\end{array} \right.
\label{eq:elliptic_hcurl}
\end{align}
where $\ff \in \mathbf{L}^2(\Omega)$, $\mu \in L^\infty(\Omega)$ and there exists $\mu_0 > 0$ such that $\mu \geq \mu_0$ almost everywhere.
We take the Hilbert space $V := \Hcurlzero$, in which case the variational formulation corresponding to \eqref{eq:elliptic_hcurl} writes
---
Find $\uu \in V$ such that
\begin{align}
a(\uu,\vv) = l(\vv) \quad \forall \vv \in V
\label{eq:abs_var_elliptic_hcurl}
\end{align}
where
\begin{align}
\left\{
\begin{array}{rll}
a(\uu, \vv) &:= \int_{\Omega} \Curl \uu \cdot \Curl \vv + \int_{\Omega} \mu \uu \cdot \vv, & \forall \uu, \vv \in V \\
l(\vv) &:= \int_{\Omega} \vv \cdot \ff, & \forall \vv \in V
\end{array} \right.
\label{tcb:elliptic_hcurl}
\end{align}
---
We recall that in $\Hcurlzero$, the bilinear form $a$ is equivalent to the inner product and is therefor continuous and coercive. Hence, our abstract theory applies and there exists a unique solution to the problem \eqref{eq:abs_var_elliptic_hcurl}.
```
import numpy as np
from sympy import pi, cos, sin, sqrt, Matrix, Tuple, lambdify
from scipy.sparse.linalg import spsolve
from scipy.sparse.linalg import gmres as sp_gmres
from scipy.sparse.linalg import minres as sp_minres
from scipy.sparse.linalg import cg as sp_cg
from scipy.sparse.linalg import bicg as sp_bicg
from scipy.sparse.linalg import bicgstab as sp_bicgstab
from sympde.calculus import grad, dot, inner, div, curl, cross
from sympde.topology import NormalVector
from sympde.topology import ScalarFunctionSpace, VectorFunctionSpace
from sympde.topology import ProductSpace
from sympde.topology import element_of, elements_of
from sympde.topology import Square
from sympde.expr import BilinearForm, LinearForm, integral
from sympde.expr import Norm
from sympde.expr import find, EssentialBC
from psydac.fem.basic import FemField
from psydac.fem.vector import ProductFemSpace
from psydac.api.discretization import discretize
from psydac.linalg.utilities import array_to_stencil
from psydac.linalg.iterative_solvers import pcg, bicg
# ... abstract model
domain = Square('A')
B_dirichlet_0 = domain.boundary
x, y = domain.coordinates
alpha = 1.
uex = Tuple(sin(pi*y), sin(pi*x)*cos(pi*y))
f = Tuple(alpha*sin(pi*y) - pi**2*sin(pi*y)*cos(pi*x) + pi**2*sin(pi*y),
alpha*sin(pi*x)*cos(pi*y) + pi**2*sin(pi*x)*cos(pi*y))
V = VectorFunctionSpace('V', domain, kind='hcurl')
u = element_of(V, name='u')
v = element_of(V, name='v')
F = element_of(V, name='F')
# Bilinear form a: V x V --> R
a = BilinearForm((u, v), integral(domain, curl(u)*curl(v) + alpha*dot(u,v)))
nn = NormalVector('nn')
a_bc = BilinearForm((u, v), integral(domain.boundary, 1e30 * cross(u, nn) * cross(v, nn)))
# Linear form l: V --> R
l = LinearForm(v, integral(domain, dot(f,v)))
# l2 error
error = Matrix([F[0]-uex[0],F[1]-uex[1]])
l2norm = Norm(error, domain, kind='l2')
ncells = [2**3, 2**3]
degree = [2, 2]
# Create computational domain from topological domain
domain_h = discretize(domain, ncells=ncells)
# Discrete spaces
Vh = discretize(V, domain_h, degree=degree)
# Discretize bi-linear and linear form
a_h = discretize(a, domain_h, [Vh, Vh])
a_bc_h = discretize(a_bc, domain_h, [Vh, Vh])
l_h = discretize(l, domain_h, Vh)
l2_norm_h = discretize(l2norm, domain_h, Vh)
M = a_h.assemble() + a_bc_h.assemble()
b = l_h.assemble()
# Solve linear system
sol, info = pcg(M ,b, pc='jacobi', tol=1e-8)
uh = FemField( Vh, sol )
l2_error = l2_norm_h.assemble(F=uh)
print(l2_error)
```
|
github_jupyter
|
# Emotion recognition using Emo-DB dataset and scikit-learn
### Database: Emo-DB database (free) 7 emotions
The data can be downloaded from http://emodb.bilderbar.info/index-1024.html
Code of emotions
W->Anger->Wut
L->Boredom->Langeweile
E->Disgust->Ekel
A->Anxiety/Fear->Angst
F->Happiness->Freude
T->Sadness->Trauer
N->Neutral

```
import requests
import zipfile
import os
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
import itertools
import sys
sys.path.append("../")
from plots_examples import plot_confusion_matrix, plot_ROC, plot_histogram
# disvoice imports
from phonation.phonation import Phonation
from articulation.articulation import Articulation
from prosody.prosody import Prosody
from phonological.phonological import Phonological
from replearning.replearning import RepLearning
# sklearn methods
from sklearn.model_selection import RandomizedSearchCV, train_test_split
from sklearn import preprocessing
from sklearn import metrics
from sklearn import svm
```
## Download and unzip data
```
def download_url(url, save_path, chunk_size=128):
r = requests.get(url, stream=True)
with open(save_path, 'wb') as fd:
for chunk in r.iter_content(chunk_size=chunk_size):
fd.write(chunk)
PATH_data="http://emodb.bilderbar.info/download/download.zip"
download_url(PATH_data, "./download.zip")
with zipfile.ZipFile("./download.zip", 'r') as zip_ref:
zip_ref.extractall("./emo-db/")
```
## prepare labels from the dataset
we will get labels for two classification problems:
1. high vs. low arousal emotions
2. positive vs. negative emotions
```
PATH_AUDIO=os.path.abspath("./emo-db/wav")+"/"
labelsd='WLEAFTN'
labelshl= [0, 1, 0, 0, 0, 1, 1] # 0 high arousal emotion, 1 low arousal emotions
labelspn= [0, 0, 0, 0, 1, 0, 1] # 0 negative valence emotion, 1 positive valence emotion
hf=os.listdir(PATH_AUDIO)
hf.sort()
yArousal=np.zeros(len(hf))
yValence=np.zeros(len(hf))
for j in range(len(hf)):
name_file=hf[j]
label=hf[j][5]
poslabel=labelsd.find(label)
yArousal[j]=labelshl[poslabel]
yValence[j]=labelspn[poslabel]
```
## compute features using disvoice: phonation, articulation, prosody, phonological
```
phonationf=Phonation()
articulationf=Articulation()
prosodyf=Prosody()
phonologicalf=Phonological()
replearningf=RepLearning('CAE')
```
### phonation features
```
Xphonation=phonationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonation.shape)
```
### articulation features
```
Xarticulation=articulationf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xarticulation.shape)
```
### prosody features
```
Xprosody=prosodyf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xprosody.shape)
```
### phonological features
```
Xphonological=phonologicalf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xphonological.shape)
```
### representation learning features
```
Xrep=replearningf.extract_features_path(PATH_AUDIO, static=True, plots=False, fmt="npy")
print(Xrep.shape)
```
### Emotion classification using an SVM classifier
```
def classify(X, y):
# train test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.30, random_state=42)
# z-score standarization
scaler = preprocessing.StandardScaler().fit(Xtrain)
Xtrain=scaler.transform(Xtrain)
Xtest=scaler.transform(Xtest)
Results=[]
# randomized search cross-validation to optimize hyper-parameters of SVM
parameters = {'kernel':['rbf'], 'class_weight': ['balanced'],
'C':st.expon(scale=10),
'gamma':st.expon(scale=0.01)}
svc = svm.SVC()
clf=RandomizedSearchCV(svc, parameters, n_jobs=4, cv=10, verbose=1, n_iter=200, scoring='balanced_accuracy')
clf.fit(Xtrain, ytrain) # train the SVM
accDev= clf.best_score_ # validation accuracy
Copt=clf.best_params_.get('C') # best C
gammaopt=clf.best_params_.get('gamma') # best gamma
# train the SVM with the optimal hyper-parameters
cls=svm.SVC(kernel='rbf', C=Copt, gamma=gammaopt, class_weight='balanced')
cls.fit(Xtrain, ytrain)
ypred=cls.predict(Xtest) # test predictions
# check the results
acc=metrics.accuracy_score(ytest, ypred)
score_test=cls.decision_function(Xtest)
dfclass=metrics.classification_report(ytest, ypred,digits=4)
# display the results
plot_confusion_matrix(ytest, ypred, classes=["class 0", "class 1"], normalize=True)
plot_ROC(ytest, score_test)
plot_histogram(ytest, score_test, name_clases=["class 0", "class 1"])
print("Accuracy: ", acc)
print(dfclass)
```
## classify high vs. low arousal with the different feature sets
```
classify(Xphonation, yArousal)
classify(Xarticulation, yArousal)
classify(Xprosody, yArousal)
classify(Xphonological, yArousal)
classify(Xrep, yArousal)
```
## classify positive vs. negative valence with the different feature sets
```
classify(Xphonation, yValence)
classify(Xarticulation, yValence)
classify(Xprosody, yValence)
classify(Xphonological, yValence)
classify(Xrep, yValence)
```
|
github_jupyter
|
# 07 - Ensemble Methods
by [Alejandro Correa Bahnsen](http://www.albahnsen.com/) & [Iván Torroledo](http://www.ivantorroledo.com/)
version 1.3, June 2018
## Part of the class [Applied Deep Learning](https://github.com/albahnsen/AppliedDeepLearningClass)
This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US). Special thanks goes to [Kevin Markham](https://github.com/justmarkham)
Why are we learning about ensembling?
- Very popular method for improving the predictive performance of machine learning models
- Provides a foundation for understanding more sophisticated models
## Lesson objectives
Students will be able to:
- Define ensembling and its requirements
- Identify the two basic methods of ensembling
- Decide whether manual ensembling is a useful approach for a given problem
- Explain bagging and how it can be applied to decision trees
- Explain how out-of-bag error and feature importances are calculated from bagged trees
- Explain the difference between bagged trees and Random Forests
- Build and tune a Random Forest model in scikit-learn
- Decide whether a decision tree or a Random Forest is a better model for a given problem
# Part 1: Introduction
Ensemble learning is a widely studied topic in the machine learning community. The main idea behind
the ensemble methodology is to combine several individual base classifiers in order to have a
classifier that outperforms each of them.
Nowadays, ensemble methods are one
of the most popular and well studied machine learning techniques, and it can be
noted that since 2009 all the first-place and second-place winners of the KDD-Cup https://www.sigkdd.org/kddcup/ used ensemble methods. The core
principle in ensemble learning, is to induce random perturbations into the learning procedure in
order to produce several different base classifiers from a single training set, then combining the
base classifiers in order to make the final prediction. In order to induce the random permutations
and therefore create the different base classifiers, several methods have been proposed, in
particular:
* bagging
* pasting
* random forests
* random patches
Finally, after the base classifiers
are trained, they are typically combined using either:
* majority voting
* weighted voting
* stacking
There are three main reasons regarding why ensemble
methods perform better than single models: statistical, computational and representational . First, from a statistical point of view, when the learning set is too
small, an algorithm can find several good models within the search space, that arise to the same
performance on the training set $\mathcal{S}$. Nevertheless, without a validation set, there is
a risk of choosing the wrong model. The second reason is computational; in general, algorithms
rely on some local search optimization and may get stuck in a local optima. Then, an ensemble may
solve this by focusing different algorithms to different spaces across the training set. The last
reason is representational. In most cases, for a learning set of finite size, the true function
$f$ cannot be represented by any of the candidate models. By combining several models in an
ensemble, it may be possible to obtain a model with a larger coverage across the space of
representable functions.

## Example
Let's pretend that instead of building a single model to solve a binary classification problem, you created **five independent models**, and each model was correct about 70% of the time. If you combined these models into an "ensemble" and used their majority vote as a prediction, how often would the ensemble be correct?
```
import numpy as np
# set a seed for reproducibility
np.random.seed(1234)
# generate 1000 random numbers (between 0 and 1) for each model, representing 1000 observations
mod1 = np.random.rand(1000)
mod2 = np.random.rand(1000)
mod3 = np.random.rand(1000)
mod4 = np.random.rand(1000)
mod5 = np.random.rand(1000)
# each model independently predicts 1 (the "correct response") if random number was at least 0.3
preds1 = np.where(mod1 > 0.3, 1, 0)
preds2 = np.where(mod2 > 0.3, 1, 0)
preds3 = np.where(mod3 > 0.3, 1, 0)
preds4 = np.where(mod4 > 0.3, 1, 0)
preds5 = np.where(mod5 > 0.3, 1, 0)
# print the first 20 predictions from each model
print(preds1[:20])
print(preds2[:20])
print(preds3[:20])
print(preds4[:20])
print(preds5[:20])
# average the predictions and then round to 0 or 1
ensemble_preds = np.round((preds1 + preds2 + preds3 + preds4 + preds5)/5.0).astype(int)
# print the ensemble's first 20 predictions
print(ensemble_preds[:20])
# how accurate was each individual model?
print(preds1.mean())
print(preds2.mean())
print(preds3.mean())
print(preds4.mean())
print(preds5.mean())
# how accurate was the ensemble?
print(ensemble_preds.mean())
```
**Note:** As you add more models to the voting process, the probability of error decreases, which is known as [Condorcet's Jury Theorem](http://en.wikipedia.org/wiki/Condorcet%27s_jury_theorem).
## What is ensembling?
**Ensemble learning (or "ensembling")** is the process of combining several predictive models in order to produce a combined model that is more accurate than any individual model.
- **Regression:** take the average of the predictions
- **Classification:** take a vote and use the most common prediction, or take the average of the predicted probabilities
For ensembling to work well, the models must have the following characteristics:
- **Accurate:** they outperform the null model
- **Independent:** their predictions are generated using different processes
**The big idea:** If you have a collection of individually imperfect (and independent) models, the "one-off" mistakes made by each model are probably not going to be made by the rest of the models, and thus the mistakes will be discarded when averaging the models.
There are two basic **methods for ensembling:**
- Manually ensemble your individual models
- Use a model that ensembles for you
### Theoretical performance of an ensemble
If we assume that each one of the $T$ base classifiers has a probability $\rho$ of
being correct, the probability of an ensemble making the correct decision, assuming independence,
denoted by $P_c$, can be calculated using the binomial distribution
$$P_c = \sum_{j>T/2}^{T} {{T}\choose{j}} \rho^j(1-\rho)^{T-j}.$$
Furthermore, as shown, if $T\ge3$ then:
$$
\lim_{T \to \infty} P_c= \begin{cases}
1 &\mbox{if } \rho>0.5 \\
0 &\mbox{if } \rho<0.5 \\
0.5 &\mbox{if } \rho=0.5 ,
\end{cases}
$$
leading to the conclusion that
$$
\rho \ge 0.5 \quad \text{and} \quad T\ge3 \quad \Rightarrow \quad P_c\ge \rho.
$$
# Part 2: Manual ensembling
What makes a good manual ensemble?
- Different types of **models**
- Different combinations of **features**
- Different **tuning parameters**
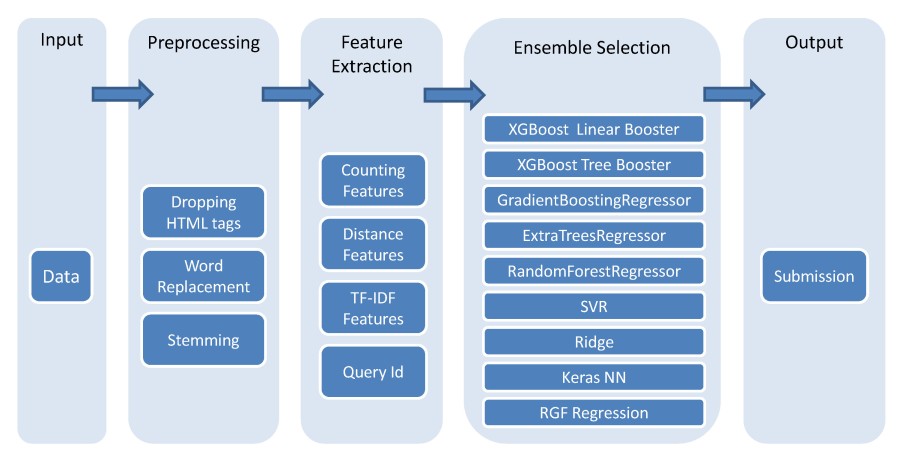
*Machine learning flowchart created by the [winner](https://github.com/ChenglongChen/Kaggle_CrowdFlower) of Kaggle's [CrowdFlower competition](https://www.kaggle.com/c/crowdflower-search-relevance)*
```
# read in and prepare the vehicle training data
import zipfile
import pandas as pd
with zipfile.ZipFile('../datasets/vehicles_train.csv.zip', 'r') as z:
f = z.open('vehicles_train.csv')
train = pd.io.parsers.read_table(f, index_col=False, sep=',')
with zipfile.ZipFile('../datasets/vehicles_test.csv.zip', 'r') as z:
f = z.open('vehicles_test.csv')
test = pd.io.parsers.read_table(f, index_col=False, sep=',')
train['vtype'] = train.vtype.map({'car':0, 'truck':1})
# read in and prepare the vehicle testing data
test['vtype'] = test.vtype.map({'car':0, 'truck':1})
train.head()
```
### Train different models
```
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsRegressor
models = {'lr': LinearRegression(),
'dt': DecisionTreeRegressor(),
'nb': GaussianNB(),
'nn': KNeighborsRegressor()}
# Train all the models
X_train = train.iloc[:, 1:]
X_test = test.iloc[:, 1:]
y_train = train.price
y_test = test.price
for model in models.keys():
models[model].fit(X_train, y_train)
# predict test for each model
y_pred = pd.DataFrame(index=test.index, columns=models.keys())
for model in models.keys():
y_pred[model] = models[model].predict(X_test)
# Evaluate each model
from sklearn.metrics import mean_squared_error
for model in models.keys():
print(model,np.sqrt(mean_squared_error(y_pred[model], y_test)))
```
### Evaluate the error of the mean of the predictions
```
np.sqrt(mean_squared_error(y_pred.mean(axis=1), y_test))
```
## Comparing manual ensembling with a single model approach
**Advantages of manual ensembling:**
- Increases predictive accuracy
- Easy to get started
**Disadvantages of manual ensembling:**
- Decreases interpretability
- Takes longer to train
- Takes longer to predict
- More complex to automate and maintain
- Small gains in accuracy may not be worth the added complexity
# Part 3: Bagging
The primary weakness of **decision trees** is that they don't tend to have the best predictive accuracy. This is partially due to **high variance**, meaning that different splits in the training data can lead to very different trees.
**Bagging** is a general purpose procedure for reducing the variance of a machine learning method, but is particularly useful for decision trees. Bagging is short for **bootstrap aggregation**, meaning the aggregation of bootstrap samples.
What is a **bootstrap sample**? A random sample with replacement:
```
# set a seed for reproducibility
np.random.seed(1)
# create an array of 1 through 20
nums = np.arange(1, 21)
print(nums)
# sample that array 20 times with replacement
print(np.random.choice(a=nums, size=20, replace=True))
```
**How does bagging work (for decision trees)?**
1. Grow B trees using B bootstrap samples from the training data.
2. Train each tree on its bootstrap sample and make predictions.
3. Combine the predictions:
- Average the predictions for **regression trees**
- Take a vote for **classification trees**
Notes:
- **Each bootstrap sample** should be the same size as the original training set.
- **B** should be a large enough value that the error seems to have "stabilized".
- The trees are **grown deep** so that they have low bias/high variance.
Bagging increases predictive accuracy by **reducing the variance**, similar to how cross-validation reduces the variance associated with train/test split (for estimating out-of-sample error) by splitting many times an averaging the results.
```
# set a seed for reproducibility
np.random.seed(123)
n_samples = train.shape[0]
n_B = 10
# create ten bootstrap samples (will be used to select rows from the DataFrame)
samples = [np.random.choice(a=n_samples, size=n_samples, replace=True) for _ in range(1, n_B +1 )]
samples
# show the rows for the first decision tree
train.iloc[samples[0], :]
```
Build one tree for each sample
```
from sklearn.tree import DecisionTreeRegressor
# grow each tree deep
treereg = DecisionTreeRegressor(max_depth=None, random_state=123)
# DataFrame for storing predicted price from each tree
y_pred = pd.DataFrame(index=test.index, columns=[list(range(n_B))])
# grow one tree for each bootstrap sample and make predictions on testing data
for i, sample in enumerate(samples):
X_train = train.iloc[sample, 1:]
y_train = train.iloc[sample, 0]
treereg.fit(X_train, y_train)
y_pred[i] = treereg.predict(X_test)
y_pred
```
Results of each tree
```
for i in range(n_B):
print(i, np.sqrt(mean_squared_error(y_pred[i], y_test)))
```
Results of the ensemble
```
y_pred.mean(axis=1)
np.sqrt(mean_squared_error(y_test, y_pred.mean(axis=1)))
```
## Bagged decision trees in scikit-learn (with B=500)
```
# define the training and testing sets
X_train = train.iloc[:, 1:]
y_train = train.iloc[:, 0]
X_test = test.iloc[:, 1:]
y_test = test.iloc[:, 0]
# instruct BaggingRegressor to use DecisionTreeRegressor as the "base estimator"
from sklearn.ensemble import BaggingRegressor
bagreg = BaggingRegressor(DecisionTreeRegressor(), n_estimators=500,
bootstrap=True, oob_score=True, random_state=1)
# fit and predict
bagreg.fit(X_train, y_train)
y_pred = bagreg.predict(X_test)
y_pred
# calculate RMSE
np.sqrt(mean_squared_error(y_test, y_pred))
```
## Estimating out-of-sample error
For bagged models, out-of-sample error can be estimated without using **train/test split** or **cross-validation**!
On average, each bagged tree uses about **two-thirds** of the observations. For each tree, the **remaining observations** are called "out-of-bag" observations.
```
# show the first bootstrap sample
samples[0]
# show the "in-bag" observations for each sample
for sample in samples:
print(set(sample))
# show the "out-of-bag" observations for each sample
for sample in samples:
print(sorted(set(range(n_samples)) - set(sample)))
```
How to calculate **"out-of-bag error":**
1. For every observation in the training data, predict its response value using **only** the trees in which that observation was out-of-bag. Average those predictions (for regression) or take a vote (for classification).
2. Compare all predictions to the actual response values in order to compute the out-of-bag error.
When B is sufficiently large, the **out-of-bag error** is an accurate estimate of **out-of-sample error**.
```
# compute the out-of-bag R-squared score (not MSE, unfortunately!) for B=500
bagreg.oob_score_
```
## Estimating feature importance
Bagging increases **predictive accuracy**, but decreases **model interpretability** because it's no longer possible to visualize the tree to understand the importance of each feature.
However, we can still obtain an overall summary of **feature importance** from bagged models:
- **Bagged regression trees:** calculate the total amount that **MSE** is decreased due to splits over a given feature, averaged over all trees
- **Bagged classification trees:** calculate the total amount that **Gini index** is decreased due to splits over a given feature, averaged over all trees
# Part 4: Random Forests
Random Forests is a **slight variation of bagged trees** that has even better performance:
- Exactly like bagging, we create an ensemble of decision trees using bootstrapped samples of the training set.
- However, when building each tree, each time a split is considered, a **random sample of m features** is chosen as split candidates from the **full set of p features**. The split is only allowed to use **one of those m features**.
- A new random sample of features is chosen for **every single tree at every single split**.
- For **classification**, m is typically chosen to be the square root of p.
- For **regression**, m is typically chosen to be somewhere between p/3 and p.
What's the point?
- Suppose there is **one very strong feature** in the data set. When using bagged trees, most of the trees will use that feature as the top split, resulting in an ensemble of similar trees that are **highly correlated**.
- Averaging highly correlated quantities does not significantly reduce variance (which is the entire goal of bagging).
- By randomly leaving out candidate features from each split, **Random Forests "decorrelates" the trees**, such that the averaging process can reduce the variance of the resulting model.
# Part 5: Building and tuning decision trees and Random Forests
- Major League Baseball player data from 1986-87: [data](https://github.com/justmarkham/DAT8/blob/master/data/hitters.csv), [data dictionary](https://cran.r-project.org/web/packages/ISLR/ISLR.pdf) (page 7)
- Each observation represents a player
- **Goal:** Predict player salary
```
# read in the data
with zipfile.ZipFile('../datasets/hitters.csv.zip', 'r') as z:
f = z.open('hitters.csv')
hitters = pd.read_csv(f, sep=',', index_col=False)
# remove rows with missing values
hitters.dropna(inplace=True)
hitters.head()
# encode categorical variables as integers
hitters['League'] = pd.factorize(hitters.League)[0]
hitters['Division'] = pd.factorize(hitters.Division)[0]
hitters['NewLeague'] = pd.factorize(hitters.NewLeague)[0]
hitters.head()
# allow plots to appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# scatter plot of Years versus Hits colored by Salary
hitters.plot(kind='scatter', x='Years', y='Hits', c='Salary', colormap='jet', xlim=(0, 25), ylim=(0, 250))
# define features: exclude career statistics (which start with "C") and the response (Salary)
feature_cols = hitters.columns[hitters.columns.str.startswith('C') == False].drop('Salary')
feature_cols
# define X and y
X = hitters[feature_cols]
y = hitters.Salary
```
## Predicting salary with a decision tree
Find the best **max_depth** for a decision tree using cross-validation:
```
# list of values to try for max_depth
max_depth_range = range(1, 21)
# list to store the average RMSE for each value of max_depth
RMSE_scores = []
# use 10-fold cross-validation with each value of max_depth
from sklearn.model_selection import cross_val_score
for depth in max_depth_range:
treereg = DecisionTreeRegressor(max_depth=depth, random_state=1)
MSE_scores = cross_val_score(treereg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_depth (x-axis) versus RMSE (y-axis)
plt.plot(max_depth_range, RMSE_scores)
plt.xlabel('max_depth')
plt.ylabel('RMSE (lower is better)')
# show the best RMSE and the corresponding max_depth
sorted(zip(RMSE_scores, max_depth_range))[0]
# max_depth=2 was best, so fit a tree using that parameter
treereg = DecisionTreeRegressor(max_depth=2, random_state=1)
treereg.fit(X, y)
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':treereg.feature_importances_}).sort_values('importance')
```
## Predicting salary with a Random Forest
```
from sklearn.ensemble import RandomForestRegressor
rfreg = RandomForestRegressor()
rfreg
```
### Tuning n_estimators
One important tuning parameter is **n_estimators**, which is the number of trees that should be grown. It should be a large enough value that the error seems to have "stabilized".
```
# list of values to try for n_estimators
estimator_range = range(10, 310, 10)
# list to store the average RMSE for each value of n_estimators
RMSE_scores = []
# use 5-fold cross-validation with each value of n_estimators (WARNING: SLOW!)
for estimator in estimator_range:
rfreg = RandomForestRegressor(n_estimators=estimator, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=5, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot n_estimators (x-axis) versus RMSE (y-axis)
plt.plot(estimator_range, RMSE_scores)
plt.xlabel('n_estimators')
plt.ylabel('RMSE (lower is better)')
```
### Tuning max_features
The other important tuning parameter is **max_features**, which is the number of features that should be considered at each split.
```
# list of values to try for max_features
feature_range = range(1, len(feature_cols)+1)
# list to store the average RMSE for each value of max_features
RMSE_scores = []
# use 10-fold cross-validation with each value of max_features (WARNING: SLOW!)
for feature in feature_range:
rfreg = RandomForestRegressor(n_estimators=150, max_features=feature, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_features (x-axis) versus RMSE (y-axis)
plt.plot(feature_range, RMSE_scores)
plt.xlabel('max_features')
plt.ylabel('RMSE (lower is better)')
# show the best RMSE and the corresponding max_features
sorted(zip(RMSE_scores, feature_range))[0]
```
### Fitting a Random Forest with the best parameters
```
# max_features=8 is best and n_estimators=150 is sufficiently large
rfreg = RandomForestRegressor(n_estimators=150, max_features=8, max_depth=3, oob_score=True, random_state=1)
rfreg.fit(X, y)
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':rfreg.feature_importances_}).sort_values('importance')
# compute the out-of-bag R-squared score
rfreg.oob_score_
```
### Reducing X to its most important features
```
# check the shape of X
X.shape
rfreg
# set a threshold for which features to include
from sklearn.feature_selection import SelectFromModel
print(SelectFromModel(rfreg, threshold=0.1, prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='median', prefit=True).transform(X).shape)
# create a new feature matrix that only includes important features
X_important = SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X)
# check the RMSE for a Random Forest that only includes important features
rfreg = RandomForestRegressor(n_estimators=150, max_features=3, random_state=1)
scores = cross_val_score(rfreg, X_important, y, cv=10, scoring='neg_mean_squared_error')
np.mean(np.sqrt(-scores))
```
## Comparing Random Forests with decision trees
**Advantages of Random Forests:**
- Performance is competitive with the best supervised learning methods
- Provides a more reliable estimate of feature importance
- Allows you to estimate out-of-sample error without using train/test split or cross-validation
**Disadvantages of Random Forests:**
- Less interpretable
- Slower to train
- Slower to predict
|
github_jupyter
|
```
import os
for dirname, _, filenames in os.walk('../input/covid19-image-dataset'):
for filename in filenames:
print(os.path.join(dirname, filename))
import tensorflow as tf
import numpy as np
import os
from matplotlib import pyplot as plt
import cv2
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Conv2D #images are two dimensional. Videos are three dimension.
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense
from keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
```
# Plotting Various Scan Reports
**Covid Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Covid/022.jpeg"))
```
**Pneumomnia Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Viral Pneumonia/020.jpeg"))
```
**Normal Patient**
```
plt.imshow(cv2.imread("../input/covid19-image-dataset/Covid19-dataset/train/Normal/018.jpeg"))
```
# Preprocessing the images
```
train_datagen=ImageDataGenerator(rescale=1/255,
shear_range=0.2,
zoom_range=2,
horizontal_flip=True)
training_set=train_datagen.flow_from_directory('../input/covid19-image-dataset/Covid19-dataset/train',
target_size=(224,224),
batch_size=32)
training_set.class_indices
test_datagen=ImageDataGenerator(rescale=1/255,
shear_range=0.2,
zoom_range=2,
horizontal_flip=True)
test_set=test_datagen.flow_from_directory('../input/covid19-image-dataset/Covid19-dataset/test',
target_size=(224,224),
batch_size=32)
test_set.class_indices
```
# Building VGG-16 architecture & Neural Network
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),strides=(1, 1),activation='relu',padding='same', input_shape=(224, 224, 3)),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(64,(3,3),strides=(1, 1) ,padding='same',activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(128,(3,3),strides=(1, 1),padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Conv2D(256,(3,3),strides=(1, 1),padding='same', activation='relu'),
tf.keras.layers.MaxPooling2D(pool_size=(2,2)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(3, activation='softmax'),
])
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model_fit = model.fit(training_set,
epochs = 71,
validation_data = test_set)
```
# Prediction
```
import numpy as np
from keras.preprocessing import image
test_image = image.load_img('../input/covid19-image-dataset/Covid19-dataset/test/Viral Pneumonia/0112.jpeg', target_size = (224, 224))
test_image = image.img_to_array(test_image)
test_image = np.expand_dims(test_image, axis = 0)
result = model.predict(test_image)
training_set.class_indices
print(result)
```
[0,0,1] which means Pneumonia. Hence our model is accurate
|
github_jupyter
|
# Collaborative filtering on Google Analytics data
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
```
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.13"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, we don't need to know anything about either the users or the content. Essentially, all we need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, we are working with newspaper articles. The company doesn't ask their users to rate the articles. However, we can use the time-spent on the page as a proxy for rating.
<p>
Normally, we would also add a time filter to this ("latest 7 days"), but our dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, we combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so we need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> We will need to save the above mapping to a file because at prediction time, we'll need to know how to map the contentId in the table above to the itemId.
<li> We'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, we created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/master/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, we write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, we use tf.contrib.learn.Experiment to handle the training loop.<p>
Make sure to replace <strong># TODO</strong> in below code.
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
def decode_example(protos, vocab_size):
# TODO
return
def remap_keys(sparse_tensor):
# Current indices of our SparseTensor that we need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of our SparseTensor that we need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
def input_cols():
return parse_tfrecords("users_for_item", args["nusers"])
return _input_fn#_subset
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, we have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This took <b>10 minutes</b> for me.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. We'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2018 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
|
github_jupyter
|
# How to make the perfect time-lapse of the Earth
This tutorial shows a detail coverage of making time-lapse animations from satellite imagery like a pro.
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#0.-Prerequisites" data-toc-modified-id="0.-Prerequisites-1">0. Prerequisites</a></span></li><li><span><a href="#1.-Removing-clouds" data-toc-modified-id="1.-Removing-clouds-2">1. Removing clouds</a></span></li><li><span><a href="#2.-Applying-co-registration" data-toc-modified-id="2.-Applying-co-registration-3">2. Applying co-registration</a></span></li><li><span><a href="#3.-Large-Area-Example" data-toc-modified-id="3.-Large-Area-Example-4">3. Large Area Example</a></span></li><li><span><a href="#4.-Split-Image" data-toc-modified-id="4.-Split-Image-5">4. Split Image</a></span></li></ul></div>
Note: This notebook requires an installation of additional packages `ffmpeg-python` and `ipyleaflet`.
```
%load_ext autoreload
%autoreload 2
import datetime as dt
import json
import os
import subprocess
from concurrent.futures import ProcessPoolExecutor
from datetime import date, datetime, time, timedelta
from functools import partial
from glob import glob
import ffmpeg
import geopandas as gpd
import imageio
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import shapely
from ipyleaflet import GeoJSON, Map, basemaps
from shapely.geometry import Polygon
from tqdm.auto import tqdm
from eolearn.core import (EOExecutor, EOPatch, EOTask, FeatureType,
LinearWorkflow, LoadTask, OverwritePermission,
SaveTask, ZipFeatureTask)
from eolearn.coregistration import ECCRegistration
from eolearn.features import LinearInterpolation, SimpleFilterTask
from eolearn.io import ExportToTiff, ImportFromTiff, SentinelHubInputTask
from eolearn.mask import CloudMaskTask
from sentinelhub import (CRS, BatchSplitter, BBox, BBoxSplitter,
DataCollection, Geometry, MimeType, SentinelHubBatch,
SentinelHubRequest, SHConfig, bbox_to_dimensions)
```
## 0. Prerequisites
In order to set everything up and make the credentials work, please check [this notebook](https://github.com/sentinel-hub/eo-learn/blob/master/examples/io/SentinelHubIO.ipynb).
```
class AnimateTask(EOTask):
def __init__(self, image_dir, out_dir, out_name, feature=(FeatureType.DATA, 'RGB'), scale_factor=2.5, duration=3, dpi=150, pad_inches=None, shape=None):
self.image_dir = image_dir
self.out_name = out_name
self.out_dir = out_dir
self.feature = feature
self.scale_factor = scale_factor
self.duration = duration
self.dpi = dpi
self.pad_inches = pad_inches
self.shape = shape
def execute(self, eopatch):
images = np.clip(eopatch[self.feature]*self.scale_factor, 0, 1)
fps = len(images)/self.duration
subprocess.run(f'rm -rf {self.image_dir} && mkdir {self.image_dir}', shell=True)
for idx, image in enumerate(images):
if self.shape:
fig = plt.figure(figsize=(self.shape[0], self.shape[1]))
plt.imshow(image)
plt.axis(False)
plt.savefig(f'{self.image_dir}/image_{idx:03d}.png', bbox_inches='tight', dpi=self.dpi, pad_inches = self.pad_inches)
plt.close()
# video related
stream = ffmpeg.input(f'{self.image_dir}/image_*.png', pattern_type='glob', framerate=fps)
stream = stream.filter('pad', w='ceil(iw/2)*2', h='ceil(ih/2)*2', color='white')
split = stream.split()
video = split[0]
# gif related
palette = split[1].filter('palettegen', reserve_transparent=True, stats_mode='diff')
gif = ffmpeg.filter([split[2], palette], 'paletteuse', dither='bayer', bayer_scale=5, diff_mode='rectangle')
# save output
os.makedirs(self.out_dir, exist_ok=True)
video.output(f'{self.out_dir}/{self.out_name}.mp4', crf=15, pix_fmt='yuv420p', vcodec='libx264', an=None).run(overwrite_output=True)
gif.output(f'{self.out_dir}/{self.out_name}.gif').run(overwrite_output=True)
return eopatch
```
## 1. Removing clouds
```
# https://twitter.com/Valtzen/status/1270269337061019648
bbox = BBox(bbox=[-73.558102,45.447728,-73.488750,45.491908], crs=CRS.WGS84)
resolution = 10
time_interval = ('2018-01-01', '2020-01-01')
print(f'Image size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=13
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
mosaicking_order='leastCC',
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.MASK, 'dataMask')
]
)
def valid_coverage_thresholder_f(valid_mask, more_than=0.95):
coverage = np.count_nonzero(valid_mask)/np.prod(valid_mask.shape)
return coverage > more_than
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'clm_service'
anim_task = AnimateTask(image_dir = './images', out_dir = './animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'clm_service_coreg'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task,
valid_mask_task,
filter_task,
anim_task,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 2. Applying co-registration
```
bbox = BBox(bbox=[34.716, 30.950, 34.743, 30.975], crs=CRS.WGS84)
resolution = 10
time_interval = ('2020-01-01', '2021-01-01')
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=14
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
]
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
]
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature=(FeatureType.DATA, 'BANDS'),
is_data_feature='dataMask',
all_bands=True,
processing_resolution=120,
mono_features=None,
mask_feature='CLM',
average_over=16,
dilation_size=12,
mono_threshold=0.2
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
filter_task = SimpleFilterTask((FeatureType.MASK, 'VALID_DATA'), valid_coverage_thresholder_f)
name = 'wo_coreg_anim'
anim_task_before = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
params = {'MaxIters': 500}
coreg_task = ECCRegistration((FeatureType.DATA, 'RGB'), channel=2, params=params)
name = 'coreg_anim'
anim_task_after = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
filter_task,
anim_task_before,
coreg_task,
anim_task_after
)
result = workflow.execute({
download_task_l2a: {'bbox': bbox, 'time_interval': time_interval}
})
```
## 3. Large Area Example
```
bbox = BBox(bbox=[21.4,-20.0,23.9,-18.0], crs=CRS.WGS84)
time_interval = ('2017-09-01', '2019-04-01')
# time_interval = ('2017-09-01', '2017-10-01')
resolution = 640
print(f'BBox size: {bbox_to_dimensions(bbox, resolution)}')
geom, crs = bbox.geometry, bbox.crs
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
area_geojson = GeoJSON(data=wgs84_geometry.geojson)
map1.add_layer(area_geojson)
map1
download_task_l2a = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l2a')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
download_task_l1c = SentinelHubInputTask(
bands_feature = (FeatureType.DATA, 'BANDS'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L1C,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'dataMask', 'dataMask_l1c')
],
aux_request_args={'dataFilter': {'previewMode': 'PREVIEW'}}
)
data_mask_merge = ZipFeatureTask({FeatureType.MASK: ['dataMask_l1c', 'dataMask_l2a']}, (FeatureType.MASK, 'dataMask'),
lambda dm1, dm2: np.all([dm1, dm2], axis=0))
cloud_masking_task = CloudMaskTask(
data_feature='BANDS',
is_data_feature='dataMask',
all_bands=True,
processing_resolution=resolution,
mono_features=('CLP', 'CLM'),
mask_feature=None,
mono_threshold=0.3,
average_over=1,
dilation_size=4
)
valid_mask_task = ZipFeatureTask({FeatureType.MASK: ['CLM', 'dataMask']}, (FeatureType.MASK, 'VALID_DATA'),
lambda clm, dm: np.all([clm == 0, dm], axis=0))
resampled_range = ('2018-01-01', '2019-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
name = 'botswana_single_raw'
anim_task_raw = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=5, dpi=200)
name = 'botswana_single'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3, dpi=200)
workflow = LinearWorkflow(
download_task_l2a,
# anim_task_raw
download_task_l1c,
data_mask_merge,
cloud_masking_task,
valid_mask_task,
interp_task,
anim_task
)
result = workflow.execute({
download_task_l2a:{'bbox': bbox, 'time_interval': time_interval},
})
```
## 4. Split Image
```
bbox = BBox(bbox=[21.3,-20.0,24.0,-18.0], crs=CRS.WGS84)
time_interval = ('2018-09-01', '2020-04-01')
resolution = 120
bbox_splitter = BBoxSplitter([bbox.geometry], bbox.crs, (6,5))
bbox_list = np.array(bbox_splitter.get_bbox_list())
info_list = np.array(bbox_splitter.get_info_list())
print(f'{len(bbox_list)} patches of size: {bbox_to_dimensions(bbox_list[0], resolution)}')
gdf = gpd.GeoDataFrame(None, crs=int(bbox.crs.epsg), geometry=[bbox.geometry for bbox in bbox_list])
geom, crs = gdf.unary_union, CRS.WGS84
wgs84_geometry = Geometry(geom, crs).transform(CRS.WGS84)
geometry_center = wgs84_geometry.geometry.centroid
map1 = Map(
basemap=basemaps.Esri.WorldImagery,
center=(geometry_center.y, geometry_center.x),
zoom=8
)
for geo in gdf.geometry:
area_geojson = GeoJSON(data=Geometry(geo, crs).geojson)
map1.add_layer(area_geojson)
map1
download_task = SentinelHubInputTask(
bands = ['B04', 'B03', 'B02'],
bands_feature = (FeatureType.DATA, 'RGB'),
resolution=resolution,
maxcc=0.9,
time_difference=timedelta(minutes=120),
data_collection=DataCollection.SENTINEL2_L2A,
max_threads=10,
additional_data=[
(FeatureType.MASK, 'CLM'),
(FeatureType.DATA, 'CLP'),
(FeatureType.MASK, 'dataMask')
]
)
valid_mask_task = ZipFeatureTask([(FeatureType.MASK, 'dataMask'), (FeatureType.MASK, 'CLM'), (FeatureType.DATA, 'CLP')], (FeatureType.MASK, 'VALID_DATA'),
lambda dm, clm, clp: np.all([dm, clm == 0, clp/255 < 0.3], axis=0))
resampled_range = ('2019-01-01', '2020-01-01', 10)
interp_task = LinearInterpolation(
feature=(FeatureType.DATA, 'RGB'),
mask_feature=(FeatureType.MASK, 'VALID_DATA'),
resample_range=resampled_range,
bounds_error=False
)
export_r = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[0])
export_g = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[1])
export_b = ExportToTiff(feature=(FeatureType.DATA, 'RGB'), folder='./tiffs/', band_indices=[2])
convert_to_uint16 = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'),
lambda x: (x*1e4).astype(np.uint16))
os.system('rm -rf ./tiffs && mkdir ./tiffs')
workflow = LinearWorkflow(
download_task,
valid_mask_task,
interp_task,
convert_to_uint16,
export_r,
export_g,
export_b
)
# Execute the workflow
execution_args = []
for idx, bbox in enumerate(bbox_list):
execution_args.append({
download_task: {'bbox': bbox, 'time_interval': time_interval},
export_r: {'filename': f'r_patch_{idx}.tiff'},
export_g: {'filename': f'g_patch_{idx}.tiff'},
export_b: {'filename': f'b_patch_{idx}.tiff'}
})
executor = EOExecutor(workflow, execution_args, save_logs=True)
executor.run(workers=10, multiprocess=False)
executor.make_report()
# spatial merge
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/r.tiff -co compress=LZW tiffs/r_patch_*.tiff && rm -rf tiffs/r_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/g.tiff -co compress=LZW tiffs/g_patch_*.tiff && rm -rf tiffs/g_patch_*.tiff', shell=True);
subprocess.run(f'gdal_merge.py -n 0 -a_nodata 0 -o tiffs/b.tiff -co compress=LZW tiffs/b_patch_*.tiff && rm -rf tiffs/b_patch_*.tiff', shell=True);
dates = pd.date_range('2019-01-01', '2020-01-01', freq='10D').to_pydatetime()
import_r = ImportFromTiff((FeatureType.DATA, 'R'), f'tiffs/r.tiff', timestamp_size=len(dates))
import_g = ImportFromTiff((FeatureType.DATA, 'G'), f'tiffs/g.tiff', timestamp_size=len(dates))
import_b = ImportFromTiff((FeatureType.DATA, 'B'), f'tiffs/b.tiff', timestamp_size=len(dates))
merge_bands_task = ZipFeatureTask({FeatureType.DATA: ['R', 'G', 'B']}, (FeatureType.DATA, 'RGB'),
lambda r, g, b: np.moveaxis(np.array([r[...,0], g[...,0], b[...,0]]), 0, -1))
def temporal_ma_f(f):
k = np.array([0.05, 0.6, 1, 0.6, 0.05])
k = k/np.sum(k)
w = len(k)//2
return np.array([np.sum([f[(i-w+j)%len(f)]*k[j] for j in range(len(k))], axis=0) for i in range(len(f))])
temporal_smoothing = ZipFeatureTask([(FeatureType.DATA, 'RGB')], (FeatureType.DATA, 'RGB'), temporal_ma_f)
name = 'botswana_multi_ma'
anim_task = AnimateTask(image_dir='./images', out_dir='./animations', out_name=name, duration=3,
dpi=400, scale_factor=3.0/1e4)
workflow = LinearWorkflow(
import_r,
import_g,
import_b,
merge_bands_task,
temporal_smoothing,
anim_task
)
result = workflow.execute()
```
## 5. Batch request
Use the evalscript from the [custom scripts repository](https://github.com/sentinel-hub/custom-scripts/tree/master/sentinel-2/interpolated_time_series) and see how to use it in the batch example in our [sentinelhub-py](https://github.com/sentinel-hub/sentinelhub-py/blob/master/examples/batch_processing.ipynb) library.
|
github_jupyter
|
##### 训练PNet
```
#导入公共文件
import os
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
from torch.autograd import Variable
import sys
sys.path.append('../')
# add other package
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from tool.plotcm import plot_confusion_matrix
import pdb
from collections import OrderedDict
from collections import namedtuple
from itertools import product
#torch.set_printoptions(linewidth=120)
from mtcnn.PNet import PNet
from mtcnn.mtcnn import RunBuilder
from mtcnn.LossFn import LossFn
from tool.imagedb import ImageDB
from tool.imagedb import TrainImageReader
from tool import image_tools
import datetime
torch.set_grad_enabled(True)
def compute_accuracy(prob_cls, gt_cls):
prob_cls = torch.squeeze(prob_cls)
gt_cls = torch.squeeze(gt_cls)
#we only need the detection which >= 0
mask = torch.ge(gt_cls,0)
#get valid element
valid_gt_cls = torch.masked_select(gt_cls,mask)
valid_prob_cls = torch.masked_select(prob_cls,mask)
size = min(valid_gt_cls.size()[0], valid_prob_cls.size()[0])
prob_ones = torch.ge(valid_prob_cls,0.6).float()
right_ones = torch.eq(prob_ones,valid_gt_cls).float()
#cms = confusion_matrix(prob_ones,right_ones,[0,1])
#print(cms)
#names = ('0','1')
#plot_confusion_matrix(cms, names)
#print(prob_cls.shape,gt_cls.shape,valid_prob_cls.shape,right_ones.shape)
## if size == 0 meaning that your gt_labels are all negative, landmark or part
return torch.div(torch.mul(torch.sum(right_ones),float(1.0)),float(size))
## divided by zero meaning that your gt_labels are all negative, landmark or part
#annotation_file = './image/imglist_anno_12.txt'
annotation_file = '../image/12/imglist_anno_12.txt' #'./image/wider_face/wider_face_train_bbx_gt.txt' #'./image/anno_train.txt'
model_store_path = '../model/Pnet'
params = OrderedDict(
lr = [.01]
,batch_size = [2000]
#,device = ["cuda", "cpu"]
,shuffle = [True]
)
end_epoch = 10
frequent = 10
#runs = RunBuilder.get_runs(params)
def train_net(imdb=None):
if imdb == None:
imagedb = ImageDB(annotation_file)
imdb = imagedb.load_imdb()
#print(imdb.num_images)
imdb = imagedb.append_flipped_images(imdb)
for run in RunBuilder.get_runs(params):
#create model path
if not os.path.exists(model_store_path):
os.makedirs(model_store_path)
#create data_loader
train_data=TrainImageReader(imdb,12,batch_size=run.batch_size,shuffle=run.shuffle)
#print(train_data.data[0].shape,len(train_data.data))
#Sprint(train_data.label[0][0])
acc=0.0
comment = f'-{run}'
lossfn = LossFn()
network = PNet()
optimizer = torch.optim.Adam(network.parameters(), lr=run.lr)
for epoch in range(end_epoch):
train_data.reset() # shuffle
epoch_acc = 0.0
#for batch_idx,(image,(gt_label,gt_bbox,gt_landmark))in enumerate(train_dat)
for batch_idx,(image,(gt_label,gt_bbox,gt_landmark))in enumerate(train_data):
im_tensor = [ image_tools.convert_image_to_tensor(image[i,:,:,:]) for i in range(image.shape[0]) ]
im_tensor = torch.stack(im_tensor)
im_tensor = Variable(im_tensor)
gt_label = Variable(torch.from_numpy(gt_label).float())
gt_bbox = Variable(torch.from_numpy(gt_bbox).float())
#gt_landmark = Variable(torch.from_numpy(gt_landmark).float())
cls_pred, box_offset_pred = network(im_tensor)
cls_loss = lossfn.cls_loss(gt_label,cls_pred)
box_offset_loss = lossfn.box_loss(gt_label,gt_bbox,box_offset_pred)
all_loss = cls_loss*1.0+box_offset_loss*0.5
if batch_idx%frequent==0:
accuracy=compute_accuracy(cls_pred,gt_label)
accuracy=compute_accuracy(cls_pred,gt_label)
show1 = accuracy.data.cpu().numpy()
show2 = cls_loss.data.cpu().numpy()
show3 = box_offset_loss.data.cpu().numpy()
# show4 = landmark_loss.data.cpu().numpy()
show5 = all_loss.data.cpu().numpy()
print("%s : Epoch: %d, Step: %d, accuracy: %s, det loss: %s, bbox loss: %s, all_loss: %s, lr:%s "%
(datetime.datetime.now(),epoch,batch_idx, show1,show2,show3,show5,run.lr))
epoch_acc = show1
#计算偏差矩阵
optimizer.zero_grad()
all_loss.backward()
optimizer.step()
pass
pass
print('save modle acc:', epoch_acc)
torch.save(network.state_dict(), os.path.join(model_store_path,"pnet_epoch_%d.pt" % epoch))
torch.save(network, os.path.join(model_store_path,"pnet_epoch_model_%d.pkl" % epoch))
pass
pass
pass
if __name__ == '__main__':
print('train Pnet Process:...')
#加载图片文件
#imagedb = ImageDB(annotation_file,'./image/train')
#gt_imdb = imagedb.load_imdb()
#gt_imdb = imagedb.append_flipped_images(gt_imdb)
train_net()
print('finish....')
#print(gt_imdb[2])
```
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 20GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
```
# Installing important modules for proper functioning. #
```
!pip install tld
```
# Importing all required modules #
```
import re
import seaborn as sns
import matplotlib.pyplot as plt
from colorama import Fore
from urllib.parse import urlparse
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, ExtraTreesClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.naive_bayes import GaussianNB
from tld import get_tld, is_tld
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import plot_roc_curve
```
# Reading the contents from the imported (csv) file provided by the Kaggle #
```
data = pd.read_csv('/kaggle/input/malicious-urls-dataset/malicious_phish.csv')
data.head()
data.isnull().sum()
count = data.type.value_counts()
count
```
# Checking data types #
## Counting the numbers of phising, malware, etc types of links from the given csv files ##
```
sns.barplot(x=count.index, y=count)
plt.xlabel('Types of links')
plt.ylabel('Counts');
```
# Representing the types of links based on their categories and types #
## removing 'www" from the given dataset ##
```
data['url'] = data['url'].replace('www.', '', regex=True)
data
```
### Removing (WWW) from the given list and allowing only http:// ###
```
rem = {"Category": {"benign": 0, "defacement": 1, "phishing":2, "malware":3}}
data['Category'] = data['type']
data = data.replace(rem)
data['url_len'] = data['url'].apply(lambda x: len(str(x)))
def process_tld(url):
try:
res = get_tld(url, as_object = True, fail_silently=False,fix_protocol=True)
pri_domain= res.parsed_url.netloc
except :
pri_domain= None
return pri_domain
data['domain'] = data['url'].apply(lambda i: process_tld(i))
data.head()
```
# 👇 extracting number of feature = ['@','?','-','=','.','#','%','+','$','!','*',',','//'] from given data set. #
```
feature = ['@','?','-','=','.','#','%','+','$','!','*',',','//']
for a in feature:
data[a] = data['url'].apply(lambda i: i.count(a))
def abnormal_url(url):
hostname = urlparse(url).hostname
hostname = str(hostname)
match = re.search(hostname, url)
if match:
return 1
else:
return 0
data['abnormal_url'] = data['url'].apply(lambda i: abnormal_url(i))
sns.countplot(x='abnormal_url', data=data);
def httpSecure(url):
htp = urlparse(url).scheme
match = str(htp)
if match=='https':
return 1
else:
return 0
data['https'] = data['url'].apply(lambda i: httpSecure(i))
sns.countplot(x='https', data=data);
```
# Training the model for realtime use #
```
def digit_count(url):
digits = 0
for i in url:
if i.isnumeric():
digits = digits + 1
return digits
data['digits']= data['url'].apply(lambda i: digit_count(i))
def letter_count(url):
letters = 0
for i in url:
if i.isalpha():
letters = letters + 1
return letters
data['letters']= data['url'].apply(lambda i: letter_count(i))
data.head()
def Shortining_Service(url):
match = re.search('bit\.ly|goo\.gl|shorte\.st|go2l\.ink|x\.co|ow\.ly|t\.co|tinyurl|tr\.im|is\.gd|cli\.gs|'
'yfrog\.com|migre\.me|ff\.im|tiny\.cc|url4\.eu|twit\.ac|su\.pr|twurl\.nl|snipurl\.com|'
'short\.to|BudURL\.com|ping\.fm|post\.ly|Just\.as|bkite\.com|snipr\.com|fic\.kr|loopt\.us|'
'doiop\.com|short\.ie|kl\.am|wp\.me|rubyurl\.com|om\.ly|to\.ly|bit\.do|t\.co|lnkd\.in|'
'db\.tt|qr\.ae|adf\.ly|goo\.gl|bitly\.com|cur\.lv|tinyurl\.com|ow\.ly|bit\.ly|ity\.im|'
'q\.gs|is\.gd|po\.st|bc\.vc|twitthis\.com|u\.to|j\.mp|buzurl\.com|cutt\.us|u\.bb|yourls\.org|'
'x\.co|prettylinkpro\.com|scrnch\.me|filoops\.info|vzturl\.com|qr\.net|1url\.com|tweez\.me|v\.gd|'
'tr\.im|link\.zip\.net',
url)
if match:
return 1
else:
return 0
data['Shortining_Service'] = data['url'].apply(lambda x: Shortining_Service(x))
sns.countplot(x='Shortining_Service', data=data);
def having_ip_address(url):
match = re.search(
'(([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.'
'([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\/)|' # IPv4
'(([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\.'
'([01]?\\d\\d?|2[0-4]\\d|25[0-5])\\/)|' # IPv4 with port
'((0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\/)' # IPv4 in hexadecimal
'(?:[a-fA-F0-9]{1,4}:){7}[a-fA-F0-9]{1,4}|'
'([0-9]+(?:\.[0-9]+){3}:[0-9]+)|'
'((?:(?:\d|[01]?\d\d|2[0-4]\d|25[0-5])\.){3}(?:25[0-5]|2[0-4]\d|[01]?\d\d|\d)(?:\/\d{1,2})?)', url) # Ipv6
if match:
return 1
else:
return 0
data['having_ip_address'] = data['url'].apply(lambda i: having_ip_address(i))
data["having_ip_address"].value_counts()
plt.figure(figsize=(15, 15))
sns.heatmap(data.corr(), linewidths=.5)
X = data.drop(['url','type','Category','domain'],axis=1)
y = data['Category']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2)
models = [DecisionTreeClassifier,RandomForestClassifier,AdaBoostClassifier,KNeighborsClassifier,SGDClassifier,
ExtraTreesClassifier,GaussianNB]
accuracy_test=[]
for m in models:
print('Model =>\033[07m {} \033[0m'.format(m))
model_ = m()
model_.fit(X_train, y_train)
pred = model_.predict(X_test)
acc = accuracy_score(pred, y_test)
accuracy_test.append(acc)
print('Test Accuracy :\033[32m \033[01m {:.2f}% \033[30m \033[0m'.format(acc*100))
print('\033[01m Classification_report \033[0m')
print(classification_report(y_test, pred))
print('\033[01m Confusion_matrix \033[0m')
cf_matrix = confusion_matrix(y_test, pred)
plot_ = sns.heatmap(cf_matrix/np.sum(cf_matrix), annot=True,fmt= '0.2%')
plt.show()
print('\033[31m End \033[0m')
output = pd.DataFrame({"Model":['Decision Tree Classifier','Random Forest Classifier',
'AdaBoost Classifier','KNeighbors Classifier','SGD Classifier',
'Extra Trees Classifier','Gaussian NB'],
"Accuracy":accuracy_test})
plt.figure(figsize=(10, 5))
plots = sns.barplot(x='Model', y='Accuracy', data=output)
for bar in plots.patches:
plots.annotate(format(bar.get_height(), '.2f'),
(bar.get_x() + bar.get_width() / 2,
bar.get_height()), ha='center', va='center',
size=15, xytext=(0, 8),
textcoords='offset points')
plt.xlabel("Models", size=14)
plt.xticks(rotation=20);
plt.ylabel("Accuracy", size=14)
plt.show()
```
|
github_jupyter
|
```
import math
import json
import pandas as pd
import numpy as np
from Bio import SeqIO
from Bio.Seq import Seq
from Bio.SeqRecord import SeqRecord
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
#make test data set to sanity check
outgroup_test = ['ATGGAGATT']
test_seqs = ['ATGGAGATT', 'ATGGAGAAT', 'ATGGAGATT',
'ATGGAGAAT', 'ATGGAGATC', 'ATCGAGATT',
'ATGGAGACT', 'ATGGAGATT', 'ATGGAGATT',
'ATGGGGATT', 'ATGCAGATT', 'ATGCAGATT', 'ATGGAGATT']
test_dates = [2010, 2010, 2011,
2012, 2012,
2013, 2013, 2013,
2014, 2014, 2014, 2014]
#given a polymorphism frequency, return bin
def frequency_binning(x):
#nan frequencies are when there is no sequence coverage at the given position
if math.isnan(x):
f_bin = float('nan')
else:
if x == 1.0:
f_bin = 'f'
elif x>=0.75:
f_bin = 'h'
elif x<0.75 and x>=0.15:
f_bin = 'm'
elif x<0.15:
f_bin='l'
return f_bin
def walk_through_sites(outgroup_seq, outgroup_aa_seq, input_file_alignment, viruses):
#at each site, count number of viruses with polymorphism
count_polymorphic = np.zeros(len(outgroup_seq))
#at each site, count totaly number of viruses
count_total_unambiguous = np.zeros(len(outgroup_seq))
count_replacement_mutations = np.zeros(len(outgroup_seq))
count_silent_mutations = np.zeros(len(outgroup_seq))
#at each site, list of nucleotide from each virus
ingroup_bases = [[] for x in range(len(outgroup_seq))]
with open(input_file_alignment, "r") as aligned_handle:
for virus in SeqIO.parse(aligned_handle, "fasta"):
#Only viruses in time window
if virus.id in viruses:
#check
if len(virus.seq) != len(outgroup_seq):
print(virus)
elif len(virus.seq) == len(outgroup_seq):
for pos in range(len(outgroup_seq)):
outgroup_nt = str(outgroup_seq[pos])
virus_nt = str(virus.seq[pos])
#skip ambiguous sites
if virus_nt != 'N':
ingroup_bases[pos].append(virus_nt)
count_total_unambiguous[pos]+=1
if virus_nt != outgroup_nt:
count_polymorphic[pos]+=1
#determine silent or replacement
codon = math.floor(pos/3)
codon_pos = pos-(codon*3)
if codon_pos == 0:
codon_nt = virus.seq[pos:(pos+3)]
elif codon_pos == 1:
codon_nt = virus.seq[(pos-1):(pos+2)]
elif codon_pos == 2:
codon_nt = virus.seq[(pos-2):(pos+1)]
codon_aa = codon_nt.translate()
outgroup_aa = outgroup_aa_seq[codon]
if codon_aa != outgroup_aa:
count_replacement_mutations[pos]+=1
elif codon_aa == outgroup_aa:
count_silent_mutations[pos]+=1
polymorphic_frequencies = count_polymorphic/count_total_unambiguous
replacement_score = count_replacement_mutations/count_total_unambiguous
freq_bins = [frequency_binning(x) for x in polymorphic_frequencies]
return freq_bins, replacement_score, ingroup_bases
def determine_site_type(outgroup, ingroup):
ingroup_bases_nan = set(ingroup)
#remove 'nan's
ingroup_bases = {x for x in ingroup_bases_nan if pd.notna(x)}
if len(ingroup_bases) == 0:
site_type = None
elif len(ingroup_bases) != 0:
#all ingroup bases are identical
if len(ingroup_bases) == 1:
if outgroup in ingroup_bases:
site_type = 1
elif outgroup not in ingroup_bases:
site_type = 2
#2 different bases in ingroup
elif len(ingroup_bases) == 2:
if outgroup in ingroup_bases:
site_type = 3
elif outgroup not in ingroup_bases:
site_type = 4
#3 different bases in ingroup
elif len(ingroup_bases) == 3:
if outgroup in ingroup_bases:
site_type = 5
elif outgroup not in ingroup_bases:
site_type = 6
#4 different bases in ingroup
elif len(ingroup_bases) == 4:
site_type = 7
return site_type
def fixation_polymorphism_score(outgroup, ingroup):
site_type = determine_site_type(outgroup, ingroup)
if site_type == None:
Fi = float('nan')
Pi = float('nan')
if site_type == 1:
Fi = 0
Pi = 0
elif site_type == 2:
Fi = 1
Pi = 0
elif site_type in [3,5,7]:
Fi = 0
Pi = 1
elif site_type == 4:
Fi = 0.5
Pi = 0.5
elif site_type == 6:
Fi = (1/3)
Pi = (2/3)
return Fi, Pi
def assign_fi_pi(outgroup_seq, ingroup_bases):
#at each site, record Fi
Fi_all = np.zeros(len(outgroup_seq))
#at each site, record Pi
Pi_all = np.zeros(len(outgroup_seq))
for pos in range(len(outgroup_seq)):
outgroup_nt = outgroup_seq[pos]
ingroup_nts = ingroup_bases[pos]
Fi, Pi = fixation_polymorphism_score(outgroup_nt, ingroup_nts)
Fi_all[pos] = Fi
Pi_all[pos] = Pi
return Fi_all, Pi_all
def calc_site_stats(cov, gene, window):
#Find percent polymorphism at each site
#Also determine whether polymorphism is silent or replacement
input_file_outgroup = '../'+str(cov)+'/auspice/seasonal_corona_'+str(cov)+'_'+str(gene)+'_root-sequence.json'
input_file_alignment = '../'+str(cov)+'/results/aligned_'+str(cov)+'_'+str(gene)+'.fasta'
metafile = '../'+str(cov)+'/results/metadata_'+str(cov)+'_'+str(gene)+'.tsv'
#Subset data based on time windows
meta = pd.read_csv(metafile, sep = '\t')
meta.drop(meta[meta['date']=='?'].index, inplace=True)
meta.dropna(subset=['date'], inplace=True)
meta['year'] = meta['date'].str[:4].astype('int')
date_range = meta['year'].max() - meta['year'].min()
#Group viruses by time windows
virus_time_subset = {}
if window == 'all':
years = str(meta['year'].min()) + '-' + str(meta['year'].max())
virus_time_subset[years] = meta['strain'].tolist()
else:
date_window_start = meta['year'].min()
date_window_end = meta['year'].min() + window
while date_window_end <= meta['year'].max():
years = str(date_window_start) + '-' + str(date_window_end)
strains = meta[(meta['year']>=date_window_start) & (meta['year']<date_window_end)]['strain'].tolist()
virus_time_subset[years] = strains
#sliding window
date_window_end += 1
date_window_start += 1
#Find outgroup sequence
outgroup_seq = ''
outgroup_aa_seq = ''
with open(input_file_outgroup, "r") as outgroup_handle:
outgroup = json.load(outgroup_handle)
outgroup_seq = SeqRecord(Seq(outgroup['nuc']))
outgroup_aa_seq = outgroup_seq.translate()
#initiate lists to record all time windows
year_windows = []
seqs_in_window = []
frequency_bins = []
fixation_scores = []
polymorphism_scores = []
replacement_scores = []
silent_scores = []
#each time window separately
for years, subset_viruses in virus_time_subset.items():
if len(subset_viruses) != 0:
year_windows.append(years)
seqs_in_window.append(len(subset_viruses))
freq_bins, replacement_score, ingroup_bases = walk_through_sites(outgroup_seq, outgroup_aa_seq,
input_file_alignment, subset_viruses)
Fi_all, Pi_all = assign_fi_pi(outgroup_seq, ingroup_bases)
silent_score = 1-replacement_score
frequency_bins.append(freq_bins)
fixation_scores.append(Fi_all)
polymorphism_scores.append(Pi_all)
replacement_scores.append(replacement_score)
silent_scores.append(silent_score)
return year_windows, seqs_in_window, frequency_bins, fixation_scores, polymorphism_scores, replacement_scores, silent_scores
#M=rm/sm
#not expected to vary through time provided that long-term effective population sizes remain sufficiently large
#For each gene, calculate M by combining site count among time points
def calc_m_ratio(cov, gene):
if gene=='spike' or gene=='s1':
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores, replacement_scores, silent_scores) = calc_site_stats(cov, 's2', 'all')
else:
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores, replacement_scores, silent_scores) = calc_site_stats(cov, gene, 'all')
sm = 0
rm = 0
for site in range(len(frequency_bins[0])):
freq_bin = frequency_bins[0][site]
if freq_bin == 'm':
sm+= (polymorphism_scores[0][site]*silent_scores[0][site])
rm+= (polymorphism_scores[0][site]*replacement_scores[0][site])
m_ratio = rm/sm
return m_ratio
def bhatt_estimators(cov, gene, window):
(year_windows, seqs_in_window, frequency_bins,
fixation_scores, polymorphism_scores,
replacement_scores, silent_scores) = calc_site_stats(cov, gene, window)
m_ratio = calc_m_ratio(cov, gene)
#Initiate lists to store a values
window_midpoint = []
adaptive_substitutions = []
#for each window, calculate bhatt estimators
for years_window in range(len(frequency_bins)):
#don't use windows with fewer than 5 sequences
if seqs_in_window[years_window] >= 5:
window_start = int(year_windows[years_window][0:4])
window_end = int(year_windows[years_window][-4:])
window_midpoint.append((window_start + window_end)/2)
sf = 0
rf = 0
sh = 0
rh = 0
sm = 0
rm = 0
sl = 0
rl = 0
#calculate number of sites in different catagories (defined by polymorphic freq at that site)
window_freq_bins = frequency_bins[years_window]
for site in range(len(window_freq_bins)):
freq_bin = window_freq_bins[site]
#ignore sites with no polymorphisms?
if freq_bin!='nan':
if freq_bin == 'f':
sf+= (fixation_scores[years_window][site]*silent_scores[years_window][site])
rf+= (fixation_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'h':
sh+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rh+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'm':
sm+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rm+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
elif freq_bin == 'l':
sl+= (polymorphism_scores[years_window][site]*silent_scores[years_window][site])
rl+= (polymorphism_scores[years_window][site]*replacement_scores[years_window][site])
# print(year_windows[years_window])
# print(sf, rf, sh, rh, sm, rm, sl, rl)
#Calculate equation 1: number of nonneutral sites
al = rl - sl*m_ratio
ah = rh - sh*m_ratio
af = rf - sf*m_ratio
#set negative a values to zero
if al < 0:
al = 0
if ah < 0:
ah = 0
if af < 0:
af = 0
# print(al, ah, af)
#Calculate the number and proportion of all fixed or high-freq sites that have undergone adaptive change
number_adaptive_substitutions = af + ah
adaptive_substitutions.append(number_adaptive_substitutions)
proportion_adaptive_sites = (af + ah)/(rf +rh)
# get coeffs of linear fit
slope, intercept, r_value, p_value, std_err = stats.linregress(window_midpoint, adaptive_substitutions)
ax = sns.regplot(x= window_midpoint, y=adaptive_substitutions,
line_kws={'label':"y={0:.1f}x+{1:.1f}".format(slope,intercept)})
plt.ylabel('number of adaptive substitutions')
plt.xlabel('year')
ax.legend()
plt.show()
```
|
github_jupyter
|
```
%matplotlib inline
```
# Wasserstein 1D with PyTorch
In this small example, we consider the following minization problem:
\begin{align}\mu^* = \min_\mu W(\mu,\nu)\end{align}
where $\nu$ is a reference 1D measure. The problem is handled
by a projected gradient descent method, where the gradient is computed
by pyTorch automatic differentiation. The projection on the simplex
ensures that the iterate will remain on the probability simplex.
This example illustrates both `wasserstein_1d` function and backend use within
the POT framework.
```
# Author: Nicolas Courty <[email protected]>
# Rémi Flamary <[email protected]>
#
# License: MIT License
import numpy as np
import matplotlib.pylab as pl
import matplotlib as mpl
import torch
from ot.lp import wasserstein_1d
from ot.datasets import make_1D_gauss as gauss
from ot.utils import proj_simplex
red = np.array(mpl.colors.to_rgb('red'))
blue = np.array(mpl.colors.to_rgb('blue'))
n = 100 # nb bins
# bin positions
x = np.arange(n, dtype=np.float64)
# Gaussian distributions
a = gauss(n, m=20, s=5) # m= mean, s= std
b = gauss(n, m=60, s=10)
# enforce sum to one on the support
a = a / a.sum()
b = b / b.sum()
device = "cuda" if torch.cuda.is_available() else "cpu"
# use pyTorch for our data
x_torch = torch.tensor(x).to(device=device)
a_torch = torch.tensor(a).to(device=device).requires_grad_(True)
b_torch = torch.tensor(b).to(device=device)
lr = 1e-6
nb_iter_max = 800
loss_iter = []
pl.figure(1, figsize=(8, 4))
pl.plot(x, a, 'b', label='Source distribution')
pl.plot(x, b, 'r', label='Target distribution')
for i in range(nb_iter_max):
# Compute the Wasserstein 1D with torch backend
loss = wasserstein_1d(x_torch, x_torch, a_torch, b_torch, p=2)
# record the corresponding loss value
loss_iter.append(loss.clone().detach().cpu().numpy())
loss.backward()
# performs a step of projected gradient descent
with torch.no_grad():
grad = a_torch.grad
a_torch -= a_torch.grad * lr # step
a_torch.grad.zero_()
a_torch.data = proj_simplex(a_torch) # projection onto the simplex
# plot one curve every 10 iterations
if i % 10 == 0:
mix = float(i) / nb_iter_max
pl.plot(x, a_torch.clone().detach().cpu().numpy(), c=(1 - mix) * blue + mix * red)
pl.legend()
pl.title('Distribution along the iterations of the projected gradient descent')
pl.show()
pl.figure(2)
pl.plot(range(nb_iter_max), loss_iter, lw=3)
pl.title('Evolution of the loss along iterations', fontsize=16)
pl.show()
```
## Wasserstein barycenter
In this example, we consider the following Wasserstein barycenter problem
$$ \\eta^* = \\min_\\eta\;\;\; (1-t)W(\\mu,\\eta) + tW(\\eta,\\nu)$$
where $\\mu$ and $\\nu$ are reference 1D measures, and $t$
is a parameter $\in [0,1]$. The problem is handled by a project gradient
descent method, where the gradient is computed by pyTorch automatic differentiation.
The projection on the simplex ensures that the iterate will remain on the
probability simplex.
This example illustrates both `wasserstein_1d` function and backend use within the
POT framework.
```
device = "cuda" if torch.cuda.is_available() else "cpu"
# use pyTorch for our data
x_torch = torch.tensor(x).to(device=device)
a_torch = torch.tensor(a).to(device=device)
b_torch = torch.tensor(b).to(device=device)
bary_torch = torch.tensor((a + b).copy() / 2).to(device=device).requires_grad_(True)
lr = 1e-6
nb_iter_max = 2000
loss_iter = []
# instant of the interpolation
t = 0.5
for i in range(nb_iter_max):
# Compute the Wasserstein 1D with torch backend
loss = (1 - t) * wasserstein_1d(x_torch, x_torch, a_torch.detach(), bary_torch, p=2) + t * wasserstein_1d(x_torch, x_torch, b_torch, bary_torch, p=2)
# record the corresponding loss value
loss_iter.append(loss.clone().detach().cpu().numpy())
loss.backward()
# performs a step of projected gradient descent
with torch.no_grad():
grad = bary_torch.grad
bary_torch -= bary_torch.grad * lr # step
bary_torch.grad.zero_()
bary_torch.data = proj_simplex(bary_torch) # projection onto the simplex
pl.figure(3, figsize=(8, 4))
pl.plot(x, a, 'b', label='Source distribution')
pl.plot(x, b, 'r', label='Target distribution')
pl.plot(x, bary_torch.clone().detach().cpu().numpy(), c='green', label='W barycenter')
pl.legend()
pl.title('Wasserstein barycenter computed by gradient descent')
pl.show()
pl.figure(4)
pl.plot(range(nb_iter_max), loss_iter, lw=3)
pl.title('Evolution of the loss along iterations', fontsize=16)
pl.show()
```
|
github_jupyter
|
```
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import numpy as np; np.random.seed(0)
import seaborn as sns
data = pd.read_csv("avocado.csv")
pd.set_option('display.max_rows', 100)
print(data)
data.head()
data.tail()
#BoxPlot_Avocado
columna_1 = data["Small Bags"]
columna_2 = data["Large Bags"]
columna_3 = data["XLarge Bags"]
columna_4 = data["Total Bags"]
myData = [columna_1,columna_2,columna_3,columna_4]
fig = plt.figure(figsize =(10, 7))
ax = fig.add_axes([0, 0, 1, 1])
bp = ax.boxplot(myData)
plt.title("Bags Boxplot")
ax.set_xticklabels(['Small Bags', 'Large Bags',
'XLarge Bags','Total Bags'])
plt.show()
#Histograma Precios Promedio
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["AveragePrice"], num_bins,
density = 1,
color ='purple',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='black')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Precio Promedio',
fontweight ="bold")
plt.show()
#Histograma de Volumen total
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Total Volume"], num_bins,
density = 1,
color ='red',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='orange')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Volumen Total',
fontweight ="bold")
#Histograma de Large Bags
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Large Bags"], num_bins,
density = 3,
color ='red',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='red')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Grandes',
fontweight ="bold")
#Histograma de Small Bags
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Small Bags"], num_bins,
density = 3,
color ='blue',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='orange')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Pequeñas',
fontweight ="bold")
#Histograma Bolsas Extra Grandes
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["XLarge Bags"], num_bins,
density = 3,
color ='brown',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='brown')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Extra Grandes',
fontweight ="bold")
np.random.seed(10**7)
mu = 121
sigma = 21
x = mu + sigma * np.random.randn(1000)
num_bins = 100
n, bins, patches = plt.hist(data["Total Bags"], num_bins,
density = 3,
color ='yellow',
alpha = 0.7)
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
plt.plot(bins, y, '--', color ='red')
plt.xlabel('X-Axis')
plt.ylabel('Y-Axis')
plt.title('Bolsas Grandes',
fontweight ="bold")
newdf = data.copy()
newdf = newdf.drop(['Date','type','year','region', 'XLarge Bags'], axis=1)
print(data.head())
data.describe(include=np.object).transpose()
ax = sns.heatmap(data)
```
|
github_jupyter
|
Центр непрерывного образования
# Программа «Python для автоматизации и анализа данных»
Неделя 3 - 1
*Ян Пиле, НИУ ВШЭ*
# Цикл for. Применение циклов к строкам, спискам, кортежам и словарям.
Циклы мы используем в тех случаях, когда нужно повторить что-нибудь n-ное количество раз. Например, у нас уже был цикл **While**
```
ss = {1,2,3}
ss.pop()
ss.pop()
i = 1
while i<=10:
print(i)
i+=1
```
Здесь мы проверяем условие *i <= 10* (оно выполнено, *i = 1*), заходим в цикл с *i = 1*, печатаем значение *i*, добавляем к нему 1 иииии... \
Снова проверяем условие *i <= 10* (оно выполнено, *i = 2*), заходим в цикл с *i = 2*, печатаем значение *i*, добавляем к нему 1 иииии... \
Делаем такие же действия, пока *i* не становится равным 11, тогда условие входа в цикл не выполняется, и цикл завершается
Как мы уже обсуждали, цикл *While* гипотетически может "уходить в бесконечность", если условие, которое проверяется на входе в цикл будет выполнено всегда, например **While True**. Такие зацикливания можно прерывать оператором **break**, НО, это надо использовать очень аккуратно
```
i = 1
while True:
print(i)
i+=1
if i==11:
break
```
### FOR
В Python цикл начинается с ключевого слова **for**, за которым следует произвольное имя переменной, которое будет хранить значения следующего объекта последовательности. Общий синтаксис **for...in** в python выглядит следующим образом:
**for** <переменная> **in** <последовательность>:
<действие>
**else:**
<действие>
Элементы “последовательности” перебираются один за другим “переменной” цикла; если быть точным, переменная указывает на элементы. Для каждого элемента выполняется “действие”.
<img src ="https://d33wubrfki0l68.cloudfront.net/09c51b2f33c74a58ae5ae12689b2c5441e6f6bb4/83a52/wp-content/uploads/2017/06/forloop.png" alt ="Test picture" style="width: 300px;"/>
Вот пример простейшего цикла **for**
```
languages = ["C", "C++", "Perl", "Python"]
for x in languages:
print(x)
```
Элементы “последовательности” перебираются один за другим “переменной” цикла; \
если быть точным, переменная указывает на элементы. Для каждого элемента выполняется “действие”.\
Здесь в роли "последовательности" у нас список
### Итерируемый объект
**Итерация** - это общий термин, который описывает процедуру взятия элементов чего-то по очереди.
В более общем смысле, это последовательность инструкций, которая повторяется определенное количество раз или до выполнения указанного условия.
**Итерируемый объект** (iterable) - это объект, который способен возвращать элементы по одному(не обязательно по порядку). Кроме того, это объект, из которого можно получить итератор.
Примеры итерируемых объектов:
* все последовательности: список, строка, кортеж
* словари и множества
* файлы
**Итератор** (iterator) - это объект, который возвращает свои элементы по одному за раз.
С точки зрения Python - это любой объект, у которого есть метод __next__. Этот метод возвращает следующий элемент, если он есть, или возвращает исключение **StopIteration**, когда элементы закончились.
Кроме того, итератор запоминает, на каком объекте он остановился в последнюю итерацию.
Сейчас сложновато: Наш цикл for проходит именно по итератору! Когда мы говорим:
for object in iterable:
do something
Мы, на самом деле, вызываем метод итерируемого объекта , который возвращает итератор.
Таким образом, создаем объект-итератор , по которому и бежит цикл for.
Для того чтобы все это увидеть, есть функция iter() В качестве аргумента ей передается итерируемый объект (словарь, список, лист и т.д.) , а она возвращает соответствующий итератор.
```
s = {1,2,3,4,5}
print(type(s))
print(type(iter(s)))
for i in iter(s):
print(i)
```
Посмотрим на встроенную функцию next(). Она должна отдавать следующий элемент итератора.
```
s = {1,2,3,4,5}
s_iter = iter(s)
print(next(s_iter))
print(next(s_iter))
print(next(s_iter))
```
Отлично! мы по одному научились перебирать элементы из итерируемого объекта. Стоит отдельно остановиться на том, что цикл **for**, в Python, устроен несколько иначе, чем в большинстве других языков. Он больше похож на **for...each**, или же **for...of**.
Например, для Javascript проход по списку с выводом на печать всех его элементов выглядит так:
```
%%js
let numbers = [10, 12, 15, 18, 20];
for (let i = 0; i < numbers.length; i += 1) {
console.log(numbers[i])
}
l = [1,2,3,4,5]
list(map(str,l))
```
Если же, мы перепишем цикл **for** с помощью цикла **while**, используя индексы, то работать такой подход будет только с последовательностями:
```
list_of_numbers = [1,2,3]
index = 0
while index < len(list_of_numbers):
print(list_of_numbers[index])
index += 1
```
А с итерируемыми объектами, последовательностями не являющимися, не будет (потому что в множестве к элементу по индексу не обращаются!):
```
set_of_numbers = {1,2,3}
index = 0
while index < len(set_of_numbers):
print(set_of_numbers[index])
index += 1
```
Ну если уж прям совсем никак без индексации, то к любому итерируемому объекту можно применить функцию enumerate(), \
которая, как следует из названия, коллекцию занумерует. Здесь мы наделали кортежей вида (индекс, элемент)
```
set_of_numbers = {1,2,3,4,5,6}
for i in enumerate(set_of_numbers):
print(i)
```
Чтобы выдавать это в человеческом виде, можно прямо после for сказать, что мы "итерируемся" по индексам и объектам. \
Выглядит это следующим образом:
```
set_of_numbers = [1,2,3]
for index, element in enumerate(set_of_numbers):
print(index, element)
```
### Немного умных слов об итераторах
**Протокол итератора**
Теперь формализуем протокол итератора целиком:
* Чтобы получить итератор мы должны передать функции iter итерируемый объект.
* Далее мы передаём итератор функции next.
* Когда элементы в итераторе закончились, порождается исключение StopIteration. (Пока представим себе исключения, как объект специального типа, который генерируется в момент ошибки или какого-то терминального события. Например, они появляются, когда мы пытаемся делить на ноль или когда что-то напутали с типами
**Особенности**:
* Любой объект, передаваемый функции iter без исключения TypeError — итерируемый объект.
* Любой объект, передаваемый функции next без исключения TypeError — итератор.
* Любой объект, передаваемый функции iter и возвращающий сам себя — итератор.
**Плюсы итераторов:**
Итераторы работают "лениво" (en. lazy). А это значит, что они не выполняют какой-либо работы, до тех пор, пока мы их об этом не попросим. А это классный функционал, потому что очень многие виды данных в память компьютера не помещаются, а "ленивый" итератор позволяет эти данные читать по кускам! Так, например, можно посчитать количество строк в текстовом файле на несколько гигабайт.
Таким образом, мы можем оптимизировать потребление ресурсов ОЗУ и CPU, а так же создавать бесконечные последовательности.
<img src ="https://files.realpython.com/media/t.ba63222d63f5.png" alt ="Test picture" style="width: 300px;"/>
На самом деле мы уже попробовали использовать цикл **for** на множествах и на списках. \
Теперь давайте систематически разберемся, как for используется с разными коллекциями
### Списки, строки, множества и кортежи
В общем, по индексированным последовательностям мы уже ходить умеем. В списках и кортежах это проход по элементам(подряд)\
а в строках это проход по буквам(в порядке следования).
```
x = 'Take a look around'
for i in x:
print(i)
# Здесь мы прошлись по элементам списка и посчитали их сумму
# В цикл вошли с total = 0 и на каждом элементе добавляли к total значение элемента
x = [1,2,3,4]
total = 0
for i in x:
total+=i
print(total)
# Здесь мы прошлись по элементам кортежа и посчитали сумму тех, которые делятся на 7 нацело
# В цикл вошли с total = 0 и на каждом элементе добавляли к total значение элементов, удовлетворяющих условию
x = (1,2,3,4,7,49,4,23,63,28,28)
total = 0
for i in x:
if i % 7 == 0:
total+=i
print(total)
# Здесь мы преобразовали кортеж из предыдущей ячейки в множество и посчитали сумму четных элементов
# В цикл вошли с total = 0 и на каждом элементе добавляли к total значение элементов, удовлетворяющих условию
x_set = set(x)
total = 0
for i in x_set:
if i % 2 == 0:
total+=i
print(total)
print(x_set)
```
### Словари
В случае словарей итерация (по умолчанию) происходит по ключам
```
d = {'foo': 1, 'bar': 2, 'baz': 3}
for k in d:
print(k)
```
Но по ключам можно вынимать и соответствующие значения
```
for k in d:
print(d[k])
```
Также можно напрямую указать, по чему мы итерируемся: по ключам, по значениям или по кортежам ключ-значение\
Помните методы **.values()** , **.keys()** и **.items()** ?
```
print(d)
for v in d.values():
print(v)
print(d)
for v in d.keys():
print(v)
print(d)
for v in d.items():
print(v)
```
А еще можно "распаковать" эти кортежи-ключ значения (примерно так же, как мы сделали для **enumerate**)
```
d = {'foo': 1, 'bar': 2, 'baz': 3}
for k, v in d.items():
print('k =', k, ', v =', v)
```
Перед тем, как начать решать какие-то задачи, остается упомянуть крайне полезную функцию **range()**. \
Простыми словами, **range()** позволяет вам генерировать ряд чисел в рамках заданного диапазона. В зависимости от того, как много аргументов вы передаете функции, вы можете решить, где этот ряд чисел начнется и закончится, а также насколько велика разница будет между двумя числами.
Есть три способа вызова **range()**:
* **range(стоп)** берет один аргумент
* **range(старт, стоп)** берет два аргумента
* **range(старт, стоп, шаг)** берет три аргумента
На деле **range()** возвращает "ленивый" итерируемый объект (Да, сейчас что-то сложно). Понимать надо следующее:\
* По range() можно итерироваться (значит это итерируемый объект)
* range() не держит все свои объекты в памяти, а достает их "по требованию" (прям как итератор!)
* Но есть и ряд отличий, который делает range() похожим на последовательности (списки, кортежи и строки)
```
# Это как раз первый случай (мы вывели все целые числа ДО трех)
for i in range(3):
print(i)
# Это второй случай (мы вывели все целые числа от 0 до 10 не включая правый конец)
for i in range(0, 10):
print(i)
# Ну а это третий случай (мы вывели все целые числа от 0 до 10 не включая правый конец с шагом 2)
# То есть нулевое, второе, четвертое и т.д.
for i in range(0, 10, 2):
print(i)
```
Шаг здесь может быть положительным или отрицательным числом, но не может быть нулем! Отрицательное число будет означать уменьшение аргумента, то есть:
```
for i in range(10, 0, -1):
print(i)
```
А теперь отличие от итераторов! У range можно обратиться к элементу или даже срезу (как в списках)
```
print(range(3)[1])
print(range(10)[2:5])
```
Немного истории: в Python 2 были функции **range** и **xrange**. Первая создавала список (прям настоящий список), а вторая - \
именно то, что теперь в Python 3 называется **range**
### Задача 1
Считайте с клавиатуры несколько чисел через пробел и выведите сумму их кубов
**Вход:** 1 2 3 \
**Выход:** 36
```
# Решение
numbers = map(int,input().split())
x = 0
for i in numbers:
x += i**2
print(x)
```
### Задача 2
Считайте с клавиатуры две последовательности чисел через пробел и выведите список уникальных общих элементов этих двух последовательностей. Сделать это можно с помощью вложенного цикла for и, например, множеств.
**Вход:**
Последовательность 1: 1 2 3
Последовательность 2: 2,2,4,7,4,3
**Выход:**
Общие элементы: [2,3]
Взяли и посчитали вложенными циклами
```
common = set()
list1 = list(map(int,input().split()))
list2 = list(map(int,input().split()))
for elem1 in list1:
for elem2 in list2:
if elem1 == elem2:
common.add(elem1)
break
print(common)
```
Но можно было и без этого. Решать можно было в несколько строк с использованием функционала множеств
```
set1 = set(map(int,input().split()))
set2 = set(map(int,input().split()))
set1.intersection(set2)
```
### Задача 3
Дан список, содержащий строки, целые числа и числа с плавающей точкой. Разбить его на три списка так, чтобы в одном остались только строки, в другом - только целые числа, а в третьем - только числа с плавающей точкой. Заметьте, что при проверке типов название типа пишется без кавычек, например **int**.
**Вход:**
Список 1: [1, 2, 5.6, 7.5, 'Boo', 1, 'RocknRoll']
**Выход:**
Список 1: [1, 2, 1]
Список 2: [5.6, 7.5]
Список 3: ['Boo', 'RocknRoll']
```
#Решение
list1 = [1, 2, 5.6, 7.5, 'Boo', 1, 'RocknRoll']
ints, floats, strings = [], [], []
for i in list1:
if type(i)==int:
ints.append(i)
elif type(i)==float:
floats.append(i)
else:
strings.append(i)
print(ints)
print(floats)
print(strings)
```
### Генераторы списков и списковые включения. aka List Comprehensions
Этот элемент языка считается его "визитной карточкой". Это своего рода метод быстро создать новый список, не применяя цикл for. Пусть мы, к примеру, хотим создать список с числами от 0 до 20
```
a = []
for i in range(20):
a.append(i)
a
```
Это же выражение можно записать с помощью спискового включения
```
a = [i for i in range(20)]
print(type(a))
print(a)
```
Что мы видим? Во-первых, на выходе такой конструкцими мы получили лист (конечно, это же СПИСКОВОЕ включение). А во-вторых, все написано в одну строчку и , кажется следует вот такой конструкции:
**new_list** = [**expression** for **member** in **iterable**]
1. **expression** какое либо вычисление, вызов метода или любое другое допустимое выражение, которое возвращает значение. В приведенном выше примере выражение i * i является квадратом значения члена.
2. **member** является объектом или значением в списке или итерируемым объекте (iterable). В приведенном выше примере значением элемента является i.
3. **iterable** список, множество, последовательность, генератор или любой другой объект, который может возвращать свои элементы по одному. В приведенном выше примере iterable является range(20).
Одним из основных преимуществ использования является то, что это единственный инструмент, который вы можете использовать в самых разных ситуациях. В дополнение к созданию стандартного списка, списки могут также использоваться для отображения и фильтрации. Вам не нужно использовать разные подходы для каждого сценария. Например, можно в раздел **expression** поставить функцию str(), которая превратит каждый элемент исходного списка в строку.
```
lst = [1,2,3,4,5,45,67,8,765,854,76]
x = [str(i) for i in lst]
x
```
Но и это еще не все. В списковое включение можно добавить какое нибудь условие (как мы это делали с **if**). Выглядеть это будет так:
new_list = [expression for member in iterable (if conditional)]
Разберем на примере:
```
lst = [1,2,3,4,5,45,67,8,765,854,76]
x = [i for i in lst if i%2 == 0] #Здесь я взял и включил в новый список только четные элементы
x
```
Более того - не зря в условии написано iterable, а не list. Значит можно попробовать проделать что-то подобное с любыми другими итерируемыми объектами. с кортежами все точно должно получиться:
```
# Предложение
sentence = '''The rocket, who was named Ted, came back
from Mars because he missed his friends.'''
# Гласные английского языка и пробел
vowels = 'aeiou '
# достанем в список все символы строки, которые не являются гласными и пробелом.
consonants = [i for i in sentence if i not in vowels]
consonants
```
А еще вот так можно было... Не зря же регулярные выражения проходили.
```
import re
re.findall(r'[^aeiou ]',sentence)
```
Мы уже поняли, что можно поместить условие в конец оператора для простой фильтрации, но что, если хочется изменить значение элемента вместо его фильтрации? В этом случае полезно поместить условное выражение в начале выражения. Выглядит это вот так:
new_list = [expression (if conditional) for member in iterable]
С помощью этого шаблона можно, например, использовать условную логику для выбора из нескольких возможных вариантов вывода. Допустим, у вас есть список цен, можно заменить отрицательные цены (это могут быть какие-то ошибки логирования) на 0 и оставить положительные значения без изменений:
```
original_prices = [1.25, -9.45, 10.22, 3.78, -5.92, 1.16]
prices = [i if i > 0 else 0 for i in original_prices]
prices
```
Здесь, наше выражение **i** содержит условный оператор, **if i> 0** else **0**. Это говорит Python выводить значение **i**, если число положительное, но менять **i** на **0**, если число отрицательное.
### Включения для множеств и словарей
Хотя **list comprehension** в Python является распространенным инструментом, вы также можете создавать множественные и словарные представления (**set and dictionary comprehensions**). **set comprehension** почти точно такое же, как представление списка. Разница лишь в том, что заданные значения обеспечивают, чтобы выходные данные не содержали дубликатов. Вы можете создать **set comprehension**, используя фигурные скобки вместо скобок:
```
quote = "life, uh, finds a way"
unique_vowels = {i for i in quote if i in 'aeiou'}
unique_vowels
```
Здесь мы вывели все уникальные гласные, которые встретились в строке
**Dictionary comprehensions** , по сути, работает так же, но с дополнительным требованием определения ключа. Ключ отделяется двоеточием.
```
squares = {i: i * i for i in range(10)}
squares
```
### Генераторы списков
По сути, это то же самое, что списковое включение, но только возвращает оно не сам список, а генератор.
```
type((i * i for i in range(10)))
```
Проверим:
```
x = (i * i for i in range(10))
next(x)
next(x)
```
Так-так, функция next работает.
```
x[4]
```
К элементам обращаться нельзя
```
x = (i * i for i in range(10))
while True:
print(next(x))
```
**StopIteration!** Опять что-то знакомое) Получается, что генератор, это , на самом деле, какой-то вид итератора. Так оно и есть. Генератор это итератор, который можно получить с помощью генераторного выражения, например, (i * i for i in range(10)) или с помощью функции-генератора (но об этом в следующей серии.
Так а зачем все это нужно-то? А вот возьмите, например, и посчитайте сумму квадратов первого миллиона чисел
```
%time
sum([i * i for i in range(1000000)])
%time
sum(i * i for i in range(1000000))
```
При использовании генератора время существенно меньше
Ура, теоретическая часть закончилась. Теперь можно порешать задачи!
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import linearsolve as ls
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
```
# Class 14: Prescott's Real Business Cycle Model I
In this notebook, we'll consider a centralized version of the model from pages 11-17 in Edward Prescott's article "Theory Ahead of Business Cycle Measurement in the Fall 1986 of the Federal Reserve Bank of Minneapolis' *Quarterly Review* (link to article: https://www.minneapolisfed.org/research/qr/qr1042.pdf). The model is just like the RBC model that we studying in the previous lecture, except that now we include an endogenous labor supply.
## Prescott's RBC Model with Labor
The equilibrium conditions for Prescott's RBC model with labor are:
\begin{align}
\frac{1}{C_t} & = \beta E_t \left[\frac{\alpha A_{t+1}K_{t+1}^{\alpha-1}L_{t+1}^{1-\alpha} +1-\delta }{C_{t+1}}\right]\\
\frac{\varphi}{1-L_t} & = \frac{(1-\alpha)A_tK_t^{\alpha}L_t^{-\alpha}}{C_t} \\
Y_t & = A_t K_t^{\alpha}L_t^{1-\alpha}\\
K_{t+1} & = I_t + (1-\delta) K_t\\
Y_t & = C_t + I_t\\
\log A_{t+1} & = \rho \log A_t + \epsilon_{t+1}
\end{align}
where $\epsilon_{t+1} \sim \mathcal{N}(0,\sigma^2)$.
The objective is use `linearsolve` to simulate impulse responses to a TFP shock using the following parameter values for the simulation:
| $$\rho$$ | $$\sigma$$ | $$\beta$$ | $$\varphi$$ | $$\alpha$$ | $$\delta $$ |
|----------|------------|-------------|-----------|------------|-------------|
| 0.75 | 0.006 | 0.99 | 1.7317 | 0.35 | 0.025 |
The value for $\beta$ implies a steady state (annualized) real interest rate of about 4 percent:
\begin{align}
4 \cdot \left(\beta^{-1} - 1\right) & \approx 0.04040
\end{align}
$\rho = 0.75$ and $\sigma = 0.006$ are consistent with the statistical properties of the cyclical component of TFP in the US. $\alpha$ is set so that, consistent with the long-run average of the US, the labor share of income is about 65 percent of GDP. The deprecation rate of capital is calibrated to be about 10 percent annually. Finally, $\varphi$ was chosen last to ensure that in the steady state households allocate about 33 percent of their available time to labor.
## Model Preparation
Before proceding, let's recast the model in the form required for `linearsolve`. Write the model with all variables moved to the left-hand side of the equations and dropping the expecations operator $E_t$ and the exogenous shock $\epsilon_{t+1}$:
\begin{align}
0 & = \beta\left[\frac{\alpha A_{t+1}K_{t+1}^{\alpha-1}L_{t+1}^{1-\alpha} +1-\delta }{C_{t+1}}\right] - \frac{1}{C_t}\\
0 & = \frac{(1-\alpha)A_tK_t^{\alpha}L_t^{-\alpha}}{C_t} - \frac{\varphi}{1-L_t}\\
0 & = A_t K_t^{\alpha}L_t^{1-\alpha} - Y_t\\
0 & = I_t + (1-\delta) K_t - K_{t+1}\\
0 & = C_t + I_t - Y_t\\
0 & = \rho \log A_t - \log A_{t+1}
\end{align}
Remember, capital and TFP are called *state variables* because they're $t+1$ values are predetermined. Output, consumption, and investment are called a *costate* or *control* variables. Note that the model as 5 equations in 5 endogenous variables.
## Initialization, Approximation, and Solution
The next several cells initialize the model in `linearsolve` and then approximate and solve it.
```
# Create a variable called 'parameters' that stores the model parameter values in a Pandas Series
parameters = pd.Series(dtype=float)
parameters['rho'] = .75
parameters['beta'] = 0.99
parameters['phi'] = 1.7317
parameters['alpha'] = 0.35
parameters['delta'] = 0.025
# Print the model's parameters
print(parameters)
# Create a variable called 'sigma' that stores the value of sigma
sigma = 0.006
# Create variable called 'var_names' that stores the variable names in a list with state variables ordered first
var_names = ['a','k','y','c','i','l']
# Create variable called 'shock_names' that stores an exogenous shock name for each state variable.
shock_names = ['e_a','e_k']
# Define a function that evaluates the equilibrium conditions of the model solved for zero. PROVIDED
def equilibrium_equations(variables_forward,variables_current,parameters):
# Parameters. PROVIDED
p = parameters
# Current variables. PROVIDED
cur = variables_current
# Forward variables. PROVIDED
fwd = variables_forward
# Define variable to store MPK. Will make things easier later.
mpk = p.alpha*fwd.a*fwd.k**(p.alpha-1)*fwd.l**(1-p.alpha)
# Define variable to store MPL. Will make things easier later.
mpl = (1-p.alpha)*fwd.a*fwd.k**p.alpha*fwd.l**-p.alpha
# Euler equation
euler_equation = p.beta*(mpk+1-p.delta)/fwd.c - 1/cur.c
# Labor-labor choice
labor_leisure = mpl/cur.c - p.phi/(1-cur.l)
# Production function
production_function = cur.a*cur.k**p.alpha*cur.l**(1-p.alpha) - cur.y
# Capital evolution. PROVIDED
capital_evolution = cur.i + (1 - p.delta)*cur.k - fwd.k
# Market clearing. PROVIDED
market_clearing = cur.c+cur.i - cur.y
# Exogenous tfp. PROVIDED
tfp_process = p.rho*np.log(cur.a) - np.log(fwd.a)
# Stack equilibrium conditions into a numpy array
return np.array([
euler_equation,
labor_leisure,
production_function,
capital_evolution,
market_clearing,
tfp_process
])
```
Next, initialize the model using `ls.model` which takes the following required arguments:
* `equations`
* `n_states`
* `var_names`
* `shock_names`
* `parameters`
```
# Initialize the model into a variable named 'rbc_model'
rbc_model = ls.model(equations = equilibrium_equations,
n_states=2,
var_names=var_names,
shock_names=shock_names,
parameters=parameters)
# Compute the steady state numerically using .compute_ss() method of rbc_model
guess = [1,4,1,1,1,0.5]
rbc_model.compute_ss(guess)
# Print the computed steady state
print(rbc_model.ss)
# Find the log-linear approximation around the non-stochastic steady state and solve using .approximate_and_solve() method of rbc_model
rbc_model.approximate_and_solve()
```
## Impulse Responses
Compute a 26 period impulse responses of the model's variables to a 0.01 unit shock to TFP in period 5.
```
# Compute impulse responses
rbc_model.impulse(T=26,t0=5,shocks=[0.01,0])
# Print the first 10 rows of the computed impulse responses to the TFP shock
print(rbc_model.irs['e_a'].head(10))
```
Construct a $2\times3$ grid of plots of simulated TFP, output, labor, consumption, investment, and capital. Be sure to multiply simulated values by 100 so that vertical axis units are in "percent deviation from steady state."
```
# Create figure. PROVIDED
fig = plt.figure(figsize=(18,8))
# Create upper-left axis. PROVIDED
ax = fig.add_subplot(2,3,1)
ax.plot(rbc_model.irs['e_a']['a']*100,'b',lw=5,alpha=0.75)
ax.set_title('TFP')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create upper-center axis. PROVIDED
ax = fig.add_subplot(2,3,2)
ax.plot(rbc_model.irs['e_a']['y']*100,'b',lw=5,alpha=0.75)
ax.set_title('Output')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create upper-right axis. PROVIDED
ax = fig.add_subplot(2,3,3)
ax.plot(rbc_model.irs['e_a']['l']*100,'b',lw=5,alpha=0.75)
ax.set_title('Labor')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.5,2])
ax.grid()
# Create lower-left axis. PROVIDED
ax = fig.add_subplot(2,3,4)
ax.plot(rbc_model.irs['e_a']['c']*100,'b',lw=5,alpha=0.75)
ax.set_title('Consumption')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.1,0.4])
ax.grid()
# Create lower-center axis. PROVIDED
ax = fig.add_subplot(2,3,5)
ax.plot(rbc_model.irs['e_a']['i']*100,'b',lw=5,alpha=0.75)
ax.set_title('Investment')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-2,8])
ax.grid()
# Create lower-right axis. PROVIDED
ax = fig.add_subplot(2,3,6)
ax.plot(rbc_model.irs['e_a']['k']*100,'b',lw=5,alpha=0.75)
ax.set_title('Capital')
ax.set_ylabel('% dev from steady state')
ax.set_ylim([-0.2,0.8])
ax.grid()
fig.tight_layout()
```
|
github_jupyter
|
# The thermodynamics of ideal solutions
*Authors: Enze Chen (University of California, Berkeley)*
This animation will show how the Gibbs free energy curves correspond to a lens phase diagram.
## Python imports
```
# General libraries
import io
import os
# Scientific computing libraries
import numpy as np
from scipy.misc import derivative
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import matplotlib.animation as animation
from PIL import Image
import cv2
from moviepy.editor import *
```
### Helper functions
```
# analytical function for the solid free energy curve
def curve_s(x, T, beta=0):
"""This function plots the Gibbs free energy curve for the solid solution.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter in J/mol.
Returns:
G_s (numpy.ndarray): An array of Gibbs free energy values in kJ/mol.
"""
S_mix = -8.314 * (np.multiply(x, np.log(x)) + np.multiply(1 - x, np.log(1 - x)))
H_mix = beta * np.multiply(x, 1 - x)
G_s = -T * S_mix + H_mix
return G_s / 1000
# analytical function for the liquid free energy curve
def curve_l(x, T, beta=0):
"""This function plots the Gibbs free energy curve for the liquid solution.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter in J/mol.
Returns:
G_l (numpy.ndarray): An array of Gibbs free energy values in kJ/mol.
"""
S_A, S_B = (52.7, 59.9)
T_A, T_B = (1890 + 273, 1205 + 273)
G_A = S_A * (T_A - T)
G_B = S_B * (T_B - T)
S_mix = -8.314 * (np.multiply(x, np.log(x)) + np.multiply(1 - x, np.log(1 - x)))
H_mix = beta * np.multiply(x, 1 - x)
G_l = x * G_B + (1 - x) * G_A - T * S_mix + H_mix
return G_l / 1000
# find the common tangent using intersections and line search
def common_tangent(x, y1, y2, T, beta=0):
"""This function calculates the common tangent of two convex curves.
Args:
x (numpy.ndarray): An array of atomic fractions of B.
y1 (numpy.ndarray): y values for curve 1.
y2 (numpy.ndarray): y values for curve 2.
T (float): The temperature in Kelvin.
beta (float): The interaction parameter for the solid solution.
Returns:
line (numpy.ndarray): y values for the common tangent.
idmin (int): Index of the x-coordinate of the first tangent point.
idmax (int): Index of the x-coordinate of the second tangent point.
"""
# Compute a derivative
dx = 1e-3
dy1 = derivative(func=curve_s, x0=x, dx=dx, args=(T, beta,))
# Make an initial guess at the minimum of curve 1
n = len(x)
idmin, idmax = (0, n)
idx = np.argmin(y1)
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
# Construct the tangent line and count intersections with curve 2
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
# They're the same curve. Used for finding miscibility gap.
# I'm assuming that the curve is symmetric
if np.linalg.norm(y1 - y2) < 1e-4:
idmin = np.argmin(y1[:int(n/2)])
idmax = np.argmin(y1[int(n/2):]) + int(n/2)
# If the tangent line intersects curve 2, shift tangent point to the left
elif nnz >= 1:
while nnz >= 1:
idx -= 1
# try-except to avoid an out-of-bounds error
try:
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
except:
break
if diff.any():
# Assign left and right indices of the tangent points
# Here we do it each time because once we miss, we can't go back
idmax = np.nonzero(diff)[0][0]
idmin = idx
# If the tangent line misses curve 2, shift tangent point to the right
elif nnz < 1:
while nnz < 1:
idx += 1
# try-except to avoid an out-of-bounds error
try:
yp = y1[idx]
xp = x[idx]
dyp = dy1[idx]
line = dyp * x + yp - dyp * xp
diff = np.diff(np.sign(y2 - line))
nnz = np.count_nonzero(diff)
except:
break
# Assign left and right indices of the tangent points
idmin = idx
idmax = np.nonzero(diff)[0][0]
# Return a tuple
return (line, idmin, idmax)
# plot the Gibbs free energy curves
def plot_Gx(T=1800, beta_s=0, beta_l=0):
"""This function is called by the widget to perform the plotting based on inputs.
Args:
T (float): The temperature in Kelvin.
beta_s (float): The interaction parameter for solids in J/mol.
beta_l (float): The interaction parameter for liquids in J/mol.
Returns:
None, but a pyplot is displayed.
"""
# For the given temperature, calculate the curves and common tangent
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
y_s = curve_s(x, T, beta_s)
y_l = curve_l(x, T, beta_l)
line, idmin, idmax = common_tangent(x, y_s, y_l, T, beta_s)
# Mostly plot settings for visual appeal
plt.rcParams.update({'figure.figsize':(8,6), 'font.size':20, \
'lines.linewidth':4, 'axes.linewidth':2})
fig, ax = plt.subplots()
ymin, ymax = (-39, 19)
ax.plot(x, y_s, c='C0', label='solid')
ax.plot(x, y_l, c='C1', label='liquid')
if abs(idmin) < n and abs(idmax) < n:
ax.plot(x[idmin:idmax], line[idmin:idmax], c='k', lw=5, ls='-.')
ax.vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=3)
ax.tick_params(top=True, right=True, direction='in', length=10, width=2)
ax.set_xlim(0, 1)
ax.set_ylim(ymin, ymax)
ax.set_xlabel(r'$x_{B}$')
ax.set_ylabel(r'$\Delta G$ (kJ/mol)')
ax.set_title('Gibbs free energy at T = {} K'.format(T), fontsize=18)
plt.legend()
plt.show()
```
## Animations using `FuncAnimation`
Finally!! VLC/Windows has buggy glitches, but the embedded HTML version looks fine.
Also, **extremely high quality and low memory footprint**!! 🎉
```
# Initialize quantities
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
liquidus = []
solidus = []
Ts = np.arange(1300, 2301, 5)
# Plot settings
plt.rcParams.update({'figure.figsize':(7,9.5), 'font.size':16})
fig, ax = plt.subplots(nrows=2, ncols=1, sharex=True)
# Initialize plot settings
ymin, ymax = -39, 19
ax[0].set_xlim(0, 1)
ax[0].set_ylim(ymin, ymax)
ax[0].set_ylabel(r'$\Delta G$ (kJ/mol)', fontsize=22)
ax[0].set_title('Binary ideal solution\nFree energy vs. composition', fontsize=20)
ax[0].tick_params(axis='both', labelsize=20)
Tmin, Tmax = 1100, 2500
ax[1].set_xlabel(r'$x_{B}$', fontsize=22)
ax[1].set_ylabel(r'$T$ (K)', fontsize=22)
ax[1].set_ylim(Tmin, Tmax)
ax[1].set_title('Phase diagram', fontsize=20)
ax[1].tick_params(axis='both', labelsize=20)
# Initialize the lines
l1, = ax[0].plot([], [], c='C1', label='liquid')
l2, = ax[0].plot([], [], c='C0', label='solid')
l3, = ax[1].plot([], [], c='C1', label='liquidus')
l4, = ax[1].plot([], [], c='C0', label='solidus')
l5, = ax[1].plot([], [], c='gray', ls='dashed', lw=4, alpha=0.5, zorder=-5)
v3, = ax[0].plot([], [], c='k', ls='-.')
v1 = ax[0].vlines(x=[0], ymin=[0], ymax=[0], linestyles='dotted', linewidth=4, color='k')
v2 = ax[1].vlines(x=[0], ymin=[0], ymax=[0], linestyles='dotted', linewidth=4, color='k')
ax[0].legend(loc='upper right')
ax[1].legend(loc='upper right')
plt.tight_layout()
# This is needed to avoid an extra loop
def init():
l1.set_data([], [])
return l1,
# This does the enumeration
def animate(i):
global ymin, ymax, Tmax, liquidus, solidus, x, n, Ts, v1, v2
T = Ts[i]
if T % 100 == 0:
print(T)
y_s = curve_s(x, T)
y_l = curve_l(x, T)
line, idmin, idmax = common_tangent(x, y_s, y_l, T) # compute common tangent
if idmin == 0 or idmin == n-1 or idmax == 0 or idmax == n-1:
liquidus.append(None)
solidus.append(None)
else:
liquidus.append(x[idmax])
solidus.append(x[idmin])
# set the data to be updated each iteration
l1.set_data(x, y_l)
l2.set_data(x, y_s)
l3.set_data(liquidus, Ts[:np.where(Ts==T)[0][0]+1])
l4.set_data(solidus, Ts[:np.where(Ts==T)[0][0]+1])
l5.set_data([0, 1], [T, T])
ax[0].annotate(text=f'$T={T}$ K', xy=(0.70, -33), fontsize=20,
bbox=dict(fc='1.0', boxstyle='round'))
# handle the tangent points
if T == 2170:
v1.remove()
v2.remove()
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
v1.remove()
v2.remove()
v3.set_data(x[idmin:idmax], line[idmin:idmax])
v1 = ax[0].vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=4, colors=['C0', 'C1'])
v2 = ax[1].vlines(x=[x[idmin], x[idmax]], ymin=T, ymax=Tmax, linestyles='dotted', linewidth=4, colors=['C0', 'C1'])
# return the artists that get updated (for blitting)
return l1, l2, l3, l4, l5, v3, v2, v1
# Create animation object
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=len(Ts), interval=1000, blit=True, repeat=False)
# Save animation as MP4 (preferred)
# anim.save('C:/Users/Enze/Desktop/test_funcanim.mp4', fps=9, dpi=300, writer='ffmpeg')
# Save animation as GIF (file size MUCH larger!)
# anim.save('C:/Users/Enze/Desktop/test_funcanim.gif', fps=9, dpi=300, writer='pillow')
plt.show()
```
## Other (sub-par) methods that I've tried...
```
# Accumulate images in a list for post-processing
n = int(1e4)
xmin, xmax = (0.001, 0.999)
x = np.linspace(xmin, xmax, n)
liquidus = []
solidus = []
Ts = np.arange(1300, 1450, 10)
plt.rcParams.update({'figure.figsize':(7,9)})
fig, ax = plt.subplots(nrows=2, ncols=1, sharex=True)
fig.tight_layout()
ymin, ymax = -39, 19
ax[0].set_xlim(0, 1)
ax[0].set_ylim(ymin, ymax)
ax[0].set_ylabel(r'$\Delta G$ (kJ/mol)')
Tmin, Tmax = 1100, 2500
ax[1].set_xlabel(r'$x_{B}$')
ax[1].set_ylabel(r'$T$ (K)')
ax[1].set_ylim(Tmin, Tmax)
images = []
for i,T in enumerate(Ts):
if T % 100 == 0:
print(T)
y_s = curve_s(x, T)
y_l = curve_l(x, T)
line, idmin, idmax = common_tangent(x, y_s, y_l, T)
if idmin == 0 or idmin == n-1 or idmax == 0 or idmax == n-1:
liquidus.append(None)
solidus.append(None)
else:
liquidus.append(x[idmax])
solidus.append(x[idmin])
ax[0].plot(x, y_s, c='C0', label='solid')
ax[0].plot(x, y_l, c='C1', label='liquid')
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
ax[0].plot(x[idmin:idmax], line[idmin:idmax], c='k', ls='-.')
v1 = ax[0].vlines(x=[x[idmin], x[idmax]], ymin=ymin, \
ymax=[line[idmin], line[idmax]], linestyles='dotted', linewidth=4, color='k')
v2 = ax[1].vlines(x=[x[idmin], x[idmax]], ymin=T, ymax=Tmax, linestyles='dotted', linewidth=4, color='k')
ax[0].legend(loc='upper right')
ax[1].plot(liquidus, Ts[:i+1], c='C1', label='liquidus')
ax[1].plot(solidus, Ts[:i+1], c='C0', label='solidus')
ax[1].plot([0, 1], [T, T], c='gray', ls='dashed', lw=4, alpha=0.5, zorder=-5)
ax[1].annotate(text=f'$T={T}$ K', xy=(0.7, 2320), fontsize=24,
bbox=dict(fc='1.0', boxstyle='round'))
# fig.savefig(f'C:/Users/Enze/Desktop/plots/fig_{T:4d}')
# Convert to PIL image for GIF
buf = io.BytesIO()
fig.savefig(buf)
buf.seek(0)
images.append(Image.open(buf))
while len(ax[0].lines) > 0:
ax[0].lines.remove(ax[0].lines[0])
while len(ax[1].lines) > 0:
ax[1].lines.remove(ax[1].lines[0])
if abs(idmin) < n and abs(idmax) < n and idmax != 0:
v1.remove()
v2.remove()
# Make a GIF by converting from PIL Image
make_gif = True
if make_gif: # Quality is pretty good!!
images[0].save('C:/Users/Enze/Desktop/test_PIL3.gif', save_all=True, append_images=images[1:], optimize=False, duration=200, loop=0)
print('Finished making GIF')
```
### Convert PIL images to mp4 using [OpenCV](https://docs.opencv.org/master/d6/d00/tutorial_py_root.html)
OK, this works!
Quality could be improved... this is where FuncAnimation native support would probably be better.
```
# This movie is very large in size!!
opencv_images = [cv2.cvtColor(np.array(i), cv2.COLOR_RGB2BGR) for i in images]
height, width, channels = opencv_images[0].shape
fourcc = cv2.VideoWriter_fourcc(*'MP4V') # can also be 'MJPG' or 'MP4V'
video = cv2.VideoWriter(filename='C:/Users/Enze/Desktop/test_opencv.mp4',
fourcc=fourcc, fps=6, frameSize=(width, height))
for i in opencv_images:
video.write(i)
cv2.destroyAllWindows()
video.release()
```
### Convert figure files using [`moviepy`](https://moviepy.readthedocs.io/en/latest/index.html)
Quality seems a little worse than OpenCV.
Also takes a longggg time lol, but the file size is very small!
```
datadir = 'C:/Users/Enze/Desktop/plots/'
clips = [ImageClip(os.path.join(datadir, m)).set_duration(0.2) for m in os.listdir(datadir)]
concat = concatenate_videoclips(clips, method='compose')
concat.write_videofile('C:/Users/Enze/Desktop/test_moviepy.mp4', fps=10)
```
|
github_jupyter
|
#### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Classification on imbalanced data
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/structured_data/imbalanced_data"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/structured_data/imbalanced_data.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This tutorial demonstrates how to classify a highly imbalanced dataset in which the number of examples in one class greatly outnumbers the examples in another. You will work with the [Credit Card Fraud Detection](https://www.kaggle.com/mlg-ulb/creditcardfraud) dataset hosted on Kaggle. The aim is to detect a mere 492 fraudulent transactions from 284,807 transactions in total. You will use [Keras](https://www.tensorflow.org/guide/keras/overview) to define the model and [class weights](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model) to help the model learn from the imbalanced data. .
This tutorial contains complete code to:
* Load a CSV file using Pandas.
* Create train, validation, and test sets.
* Define and train a model using Keras (including setting class weights).
* Evaluate the model using various metrics (including precision and recall).
* Try common techniques for dealing with imbalanced data like:
* Class weighting
* Oversampling
## Setup
```
import tensorflow as tf
from tensorflow import keras
import os
import tempfile
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sklearn
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
mpl.rcParams['figure.figsize'] = (12, 10)
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
```
## Data processing and exploration
### Download the Kaggle Credit Card Fraud data set
Pandas is a Python library with many helpful utilities for loading and working with structured data. It can be used to download CSVs into a Pandas [DataFrame](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html#pandas.DataFrame).
Note: This dataset has been collected and analysed during a research collaboration of Worldline and the [Machine Learning Group](http://mlg.ulb.ac.be) of ULB (Université Libre de Bruxelles) on big data mining and fraud detection. More details on current and past projects on related topics are available [here](https://www.researchgate.net/project/Fraud-detection-5) and the page of the [DefeatFraud](https://mlg.ulb.ac.be/wordpress/portfolio_page/defeatfraud-assessment-and-validation-of-deep-feature-engineering-and-learning-solutions-for-fraud-detection/) project
```
file = tf.keras.utils
raw_df = pd.read_csv('https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv')
raw_df.head()
raw_df[['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V26', 'V27', 'V28', 'Amount', 'Class']].describe()
```
### Examine the class label imbalance
Let's look at the dataset imbalance:
```
neg, pos = np.bincount(raw_df['Class'])
total = neg + pos
print('Examples:\n Total: {}\n Positive: {} ({:.2f}% of total)\n'.format(
total, pos, 100 * pos / total))
```
This shows the small fraction of positive samples.
### Clean, split and normalize the data
The raw data has a few issues. First the `Time` and `Amount` columns are too variable to use directly. Drop the `Time` column (since it's not clear what it means) and take the log of the `Amount` column to reduce its range.
```
cleaned_df = raw_df.copy()
# You don't want the `Time` column.
cleaned_df.pop('Time')
# The `Amount` column covers a huge range. Convert to log-space.
eps = 0.001 # 0 => 0.1¢
cleaned_df['Log Ammount'] = np.log(cleaned_df.pop('Amount')+eps)
```
Split the dataset into train, validation, and test sets. The validation set is used during the model fitting to evaluate the loss and any metrics, however the model is not fit with this data. The test set is completely unused during the training phase and is only used at the end to evaluate how well the model generalizes to new data. This is especially important with imbalanced datasets where [overfitting](https://developers.google.com/machine-learning/crash-course/generalization/peril-of-overfitting) is a significant concern from the lack of training data.
```
# Use a utility from sklearn to split and shuffle your dataset.
train_df, test_df = train_test_split(cleaned_df, test_size=0.2)
train_df, val_df = train_test_split(train_df, test_size=0.2)
# Form np arrays of labels and features.
train_labels = np.array(train_df.pop('Class'))
bool_train_labels = train_labels != 0
val_labels = np.array(val_df.pop('Class'))
test_labels = np.array(test_df.pop('Class'))
train_features = np.array(train_df)
val_features = np.array(val_df)
test_features = np.array(test_df)
```
Normalize the input features using the sklearn StandardScaler.
This will set the mean to 0 and standard deviation to 1.
Note: The `StandardScaler` is only fit using the `train_features` to be sure the model is not peeking at the validation or test sets.
```
scaler = StandardScaler()
train_features = scaler.fit_transform(train_features)
val_features = scaler.transform(val_features)
test_features = scaler.transform(test_features)
train_features = np.clip(train_features, -5, 5)
val_features = np.clip(val_features, -5, 5)
test_features = np.clip(test_features, -5, 5)
print('Training labels shape:', train_labels.shape)
print('Validation labels shape:', val_labels.shape)
print('Test labels shape:', test_labels.shape)
print('Training features shape:', train_features.shape)
print('Validation features shape:', val_features.shape)
print('Test features shape:', test_features.shape)
```
Caution: If you want to deploy a model, it's critical that you preserve the preprocessing calculations. The easiest way to implement them as layers, and attach them to your model before export.
### Look at the data distribution
Next compare the distributions of the positive and negative examples over a few features. Good questions to ask yourself at this point are:
* Do these distributions make sense?
* Yes. You've normalized the input and these are mostly concentrated in the `+/- 2` range.
* Can you see the difference between the distributions?
* Yes the positive examples contain a much higher rate of extreme values.
```
pos_df = pd.DataFrame(train_features[ bool_train_labels], columns=train_df.columns)
neg_df = pd.DataFrame(train_features[~bool_train_labels], columns=train_df.columns)
sns.jointplot(pos_df['V5'], pos_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
plt.suptitle("Positive distribution")
sns.jointplot(neg_df['V5'], neg_df['V6'],
kind='hex', xlim=(-5,5), ylim=(-5,5))
_ = plt.suptitle("Negative distribution")
```
## Define the model and metrics
Define a function that creates a simple neural network with a densly connected hidden layer, a [dropout](https://developers.google.com/machine-learning/glossary/#dropout_regularization) layer to reduce overfitting, and an output sigmoid layer that returns the probability of a transaction being fraudulent:
```
METRICS = [
keras.metrics.TruePositives(name='tp'),
keras.metrics.FalsePositives(name='fp'),
keras.metrics.TrueNegatives(name='tn'),
keras.metrics.FalseNegatives(name='fn'),
keras.metrics.BinaryAccuracy(name='accuracy'),
keras.metrics.Precision(name='precision'),
keras.metrics.Recall(name='recall'),
keras.metrics.AUC(name='auc'),
keras.metrics.AUC(name='prc', curve='PR'), # precision-recall curve
]
def make_model(metrics=METRICS, output_bias=None):
if output_bias is not None:
output_bias = tf.keras.initializers.Constant(output_bias)
model = keras.Sequential([
keras.layers.Dense(
16, activation='relu',
input_shape=(train_features.shape[-1],)),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation='sigmoid',
bias_initializer=output_bias),
])
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.BinaryCrossentropy(),
metrics=metrics)
return model
```
### Understanding useful metrics
Notice that there are a few metrics defined above that can be computed by the model that will be helpful when evaluating the performance.
* **False** negatives and **false** positives are samples that were **incorrectly** classified
* **True** negatives and **true** positives are samples that were **correctly** classified
* **Accuracy** is the percentage of examples correctly classified
> $\frac{\text{true samples}}{\text{total samples}}$
* **Precision** is the percentage of **predicted** positives that were correctly classified
> $\frac{\text{true positives}}{\text{true positives + false positives}}$
* **Recall** is the percentage of **actual** positives that were correctly classified
> $\frac{\text{true positives}}{\text{true positives + false negatives}}$
* **AUC** refers to the Area Under the Curve of a Receiver Operating Characteristic curve (ROC-AUC). This metric is equal to the probability that a classifier will rank a random positive sample higher than a random negative sample.
* **AUPRC** refers to Area Under the Curve of the Precision-Recall Curve. This metric computes precision-recall pairs for different probability thresholds.
Note: Accuracy is not a helpful metric for this task. You can 99.8%+ accuracy on this task by predicting False all the time.
Read more:
* [True vs. False and Positive vs. Negative](https://developers.google.com/machine-learning/crash-course/classification/true-false-positive-negative)
* [Accuracy](https://developers.google.com/machine-learning/crash-course/classification/accuracy)
* [Precision and Recall](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall)
* [ROC-AUC](https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc)
* [Relationship between Precision-Recall and ROC Curves](https://www.biostat.wisc.edu/~page/rocpr.pdf)
## Baseline model
### Build the model
Now create and train your model using the function that was defined earlier. Notice that the model is fit using a larger than default batch size of 2048, this is important to ensure that each batch has a decent chance of containing a few positive samples. If the batch size was too small, they would likely have no fraudulent transactions to learn from.
Note: this model will not handle the class imbalance well. You will improve it later in this tutorial.
```
EPOCHS = 100
BATCH_SIZE = 2048
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor='val_prc',
verbose=1,
patience=10,
mode='max',
restore_best_weights=True)
model = make_model()
model.summary()
```
Test run the model:
```
model.predict(train_features[:10])
```
### Optional: Set the correct initial bias.
These initial guesses are not great. You know the dataset is imbalanced. Set the output layer's bias to reflect that (See: [A Recipe for Training Neural Networks: "init well"](http://karpathy.github.io/2019/04/25/recipe/#2-set-up-the-end-to-end-trainingevaluation-skeleton--get-dumb-baselines)). This can help with initial convergence.
With the default bias initialization the loss should be about `math.log(2) = 0.69314`
```
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
```
The correct bias to set can be derived from:
$$ p_0 = pos/(pos + neg) = 1/(1+e^{-b_0}) $$
$$ b_0 = -log_e(1/p_0 - 1) $$
$$ b_0 = log_e(pos/neg)$$
```
initial_bias = np.log([pos/neg])
initial_bias
```
Set that as the initial bias, and the model will give much more reasonable initial guesses.
It should be near: `pos/total = 0.0018`
```
model = make_model(output_bias=initial_bias)
model.predict(train_features[:10])
```
With this initialization the initial loss should be approximately:
$$-p_0log(p_0)-(1-p_0)log(1-p_0) = 0.01317$$
```
results = model.evaluate(train_features, train_labels, batch_size=BATCH_SIZE, verbose=0)
print("Loss: {:0.4f}".format(results[0]))
```
This initial loss is about 50 times less than if would have been with naive initialization.
This way the model doesn't need to spend the first few epochs just learning that positive examples are unlikely. This also makes it easier to read plots of the loss during training.
### Checkpoint the initial weights
To make the various training runs more comparable, keep this initial model's weights in a checkpoint file, and load them into each model before training:
```
initial_weights = os.path.join(tempfile.mkdtemp(), 'initial_weights')
model.save_weights(initial_weights)
```
### Confirm that the bias fix helps
Before moving on, confirm quick that the careful bias initialization actually helped.
Train the model for 20 epochs, with and without this careful initialization, and compare the losses:
```
model = make_model()
model.load_weights(initial_weights)
model.layers[-1].bias.assign([0.0])
zero_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
model = make_model()
model.load_weights(initial_weights)
careful_bias_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=20,
validation_data=(val_features, val_labels),
verbose=0)
def plot_loss(history, label, n):
# Use a log scale on y-axis to show the wide range of values.
plt.semilogy(history.epoch, history.history['loss'],
color=colors[n], label='Train ' + label)
plt.semilogy(history.epoch, history.history['val_loss'],
color=colors[n], label='Val ' + label,
linestyle="--")
plt.xlabel('Epoch')
plt.ylabel('Loss')
plot_loss(zero_bias_history, "Zero Bias", 0)
plot_loss(careful_bias_history, "Careful Bias", 1)
```
The above figure makes it clear: In terms of validation loss, on this problem, this careful initialization gives a clear advantage.
### Train the model
```
model = make_model()
model.load_weights(initial_weights)
baseline_history = model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels))
```
### Check training history
In this section, you will produce plots of your model's accuracy and loss on the training and validation set. These are useful to check for overfitting, which you can learn more about in the [Overfit and underfit](https://www.tensorflow.org/tutorials/keras/overfit_and_underfit) tutorial.
Additionally, you can produce these plots for any of the metrics you created above. False negatives are included as an example.
```
def plot_metrics(history):
metrics = ['loss', 'prc', 'precision', 'recall']
for n, metric in enumerate(metrics):
name = metric.replace("_"," ").capitalize()
plt.subplot(2,2,n+1)
plt.plot(history.epoch, history.history[metric], color=colors[0], label='Train')
plt.plot(history.epoch, history.history['val_'+metric],
color=colors[0], linestyle="--", label='Val')
plt.xlabel('Epoch')
plt.ylabel(name)
if metric == 'loss':
plt.ylim([0, plt.ylim()[1]])
elif metric == 'auc':
plt.ylim([0.8,1])
else:
plt.ylim([0,1])
plt.legend()
plot_metrics(baseline_history)
```
Note: That the validation curve generally performs better than the training curve. This is mainly caused by the fact that the dropout layer is not active when evaluating the model.
### Evaluate metrics
You can use a [confusion matrix](https://developers.google.com/machine-learning/glossary/#confusion_matrix) to summarize the actual vs. predicted labels, where the X axis is the predicted label and the Y axis is the actual label:
```
train_predictions_baseline = model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_baseline = model.predict(test_features, batch_size=BATCH_SIZE)
def plot_cm(labels, predictions, p=0.5):
cm = confusion_matrix(labels, predictions > p)
plt.figure(figsize=(5,5))
sns.heatmap(cm, annot=True, fmt="d")
plt.title('Confusion matrix @{:.2f}'.format(p))
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
print('Legitimate Transactions Detected (True Negatives): ', cm[0][0])
print('Legitimate Transactions Incorrectly Detected (False Positives): ', cm[0][1])
print('Fraudulent Transactions Missed (False Negatives): ', cm[1][0])
print('Fraudulent Transactions Detected (True Positives): ', cm[1][1])
print('Total Fraudulent Transactions: ', np.sum(cm[1]))
```
Evaluate your model on the test dataset and display the results for the metrics you created above:
```
baseline_results = model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(model.metrics_names, baseline_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_baseline)
```
If the model had predicted everything perfectly, this would be a [diagonal matrix](https://en.wikipedia.org/wiki/Diagonal_matrix) where values off the main diagonal, indicating incorrect predictions, would be zero. In this case the matrix shows that you have relatively few false positives, meaning that there were relatively few legitimate transactions that were incorrectly flagged. However, you would likely want to have even fewer false negatives despite the cost of increasing the number of false positives. This trade off may be preferable because false negatives would allow fraudulent transactions to go through, whereas false positives may cause an email to be sent to a customer to ask them to verify their card activity.
### Plot the ROC
Now plot the [ROC](https://developers.google.com/machine-learning/glossary#ROC). This plot is useful because it shows, at a glance, the range of performance the model can reach just by tuning the output threshold.
```
def plot_roc(name, labels, predictions, **kwargs):
fp, tp, _ = sklearn.metrics.roc_curve(labels, predictions)
plt.plot(100*fp, 100*tp, label=name, linewidth=2, **kwargs)
plt.xlabel('False positives [%]')
plt.ylabel('True positives [%]')
plt.xlim([-0.5,20])
plt.ylim([80,100.5])
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right')
```
### Plot the AUPRC
Now plot the [AUPRC](https://developers.google.com/machine-learning/glossary?hl=en#PR_AUC). Area under the interpolated precision-recall curve, obtained by plotting (recall, precision) points for different values of the classification threshold. Depending on how it's calculated, PR AUC may be equivalent to the average precision of the model.
```
def plot_prc(name, labels, predictions, **kwargs):
precision, recall, _ = sklearn.metrics.precision_recall_curve(labels, predictions)
plt.plot(precision, recall, label=name, linewidth=2, **kwargs)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
ax = plt.gca()
ax.set_aspect('equal')
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plt.legend(loc='lower right')
```
It looks like the precision is relatively high, but the recall and the area under the ROC curve (AUC) aren't as high as you might like. Classifiers often face challenges when trying to maximize both precision and recall, which is especially true when working with imbalanced datasets. It is important to consider the costs of different types of errors in the context of the problem you care about. In this example, a false negative (a fraudulent transaction is missed) may have a financial cost, while a false positive (a transaction is incorrectly flagged as fraudulent) may decrease user happiness.
## Class weights
### Calculate class weights
The goal is to identify fraudulent transactions, but you don't have very many of those positive samples to work with, so you would want to have the classifier heavily weight the few examples that are available. You can do this by passing Keras weights for each class through a parameter. These will cause the model to "pay more attention" to examples from an under-represented class.
```
# Scaling by total/2 helps keep the loss to a similar magnitude.
# The sum of the weights of all examples stays the same.
weight_for_0 = (1 / neg) * (total / 2.0)
weight_for_1 = (1 / pos) * (total / 2.0)
class_weight = {0: weight_for_0, 1: weight_for_1}
print('Weight for class 0: {:.2f}'.format(weight_for_0))
print('Weight for class 1: {:.2f}'.format(weight_for_1))
```
### Train a model with class weights
Now try re-training and evaluating the model with class weights to see how that affects the predictions.
Note: Using `class_weights` changes the range of the loss. This may affect the stability of the training depending on the optimizer. Optimizers whose step size is dependent on the magnitude of the gradient, like `tf.keras.optimizers.SGD`, may fail. The optimizer used here, `tf.keras.optimizers.Adam`, is unaffected by the scaling change. Also note that because of the weighting, the total losses are not comparable between the two models.
```
weighted_model = make_model()
weighted_model.load_weights(initial_weights)
weighted_history = weighted_model.fit(
train_features,
train_labels,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[early_stopping],
validation_data=(val_features, val_labels),
# The class weights go here
class_weight=class_weight)
```
### Check training history
```
plot_metrics(weighted_history)
```
### Evaluate metrics
```
train_predictions_weighted = weighted_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_weighted = weighted_model.predict(test_features, batch_size=BATCH_SIZE)
weighted_results = weighted_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(weighted_model.metrics_names, weighted_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_weighted)
```
Here you can see that with class weights the accuracy and precision are lower because there are more false positives, but conversely the recall and AUC are higher because the model also found more true positives. Despite having lower accuracy, this model has higher recall (and identifies more fraudulent transactions). Of course, there is a cost to both types of error (you wouldn't want to bug users by flagging too many legitimate transactions as fraudulent, either). Carefully consider the trade-offs between these different types of errors for your application.
### Plot the ROC
```
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right')
```
### Plot the AUPRC
```
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plt.legend(loc='lower right')
```
## Oversampling
### Oversample the minority class
A related approach would be to resample the dataset by oversampling the minority class.
```
pos_features = train_features[bool_train_labels]
neg_features = train_features[~bool_train_labels]
pos_labels = train_labels[bool_train_labels]
neg_labels = train_labels[~bool_train_labels]
```
#### Using NumPy
You can balance the dataset manually by choosing the right number of random
indices from the positive examples:
```
ids = np.arange(len(pos_features))
choices = np.random.choice(ids, len(neg_features))
res_pos_features = pos_features[choices]
res_pos_labels = pos_labels[choices]
res_pos_features.shape
resampled_features = np.concatenate([res_pos_features, neg_features], axis=0)
resampled_labels = np.concatenate([res_pos_labels, neg_labels], axis=0)
order = np.arange(len(resampled_labels))
np.random.shuffle(order)
resampled_features = resampled_features[order]
resampled_labels = resampled_labels[order]
resampled_features.shape
```
#### Using `tf.data`
If you're using `tf.data` the easiest way to produce balanced examples is to start with a `positive` and a `negative` dataset, and merge them. See [the tf.data guide](../../guide/data.ipynb) for more examples.
```
BUFFER_SIZE = 100000
def make_ds(features, labels):
ds = tf.data.Dataset.from_tensor_slices((features, labels))#.cache()
ds = ds.shuffle(BUFFER_SIZE).repeat()
return ds
pos_ds = make_ds(pos_features, pos_labels)
neg_ds = make_ds(neg_features, neg_labels)
```
Each dataset provides `(feature, label)` pairs:
```
for features, label in pos_ds.take(1):
print("Features:\n", features.numpy())
print()
print("Label: ", label.numpy())
```
Merge the two together using `experimental.sample_from_datasets`:
```
resampled_ds = tf.data.experimental.sample_from_datasets([pos_ds, neg_ds], weights=[0.5, 0.5])
resampled_ds = resampled_ds.batch(BATCH_SIZE).prefetch(2)
for features, label in resampled_ds.take(1):
print(label.numpy().mean())
```
To use this dataset, you'll need the number of steps per epoch.
The definition of "epoch" in this case is less clear. Say it's the number of batches required to see each negative example once:
```
resampled_steps_per_epoch = np.ceil(2.0*neg/BATCH_SIZE)
resampled_steps_per_epoch
```
### Train on the oversampled data
Now try training the model with the resampled data set instead of using class weights to see how these methods compare.
Note: Because the data was balanced by replicating the positive examples, the total dataset size is larger, and each epoch runs for more training steps.
```
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
val_ds = tf.data.Dataset.from_tensor_slices((val_features, val_labels)).cache()
val_ds = val_ds.batch(BATCH_SIZE).prefetch(2)
resampled_history = resampled_model.fit(
resampled_ds,
epochs=EPOCHS,
steps_per_epoch=resampled_steps_per_epoch,
callbacks=[early_stopping],
validation_data=val_ds)
```
If the training process were considering the whole dataset on each gradient update, this oversampling would be basically identical to the class weighting.
But when training the model batch-wise, as you did here, the oversampled data provides a smoother gradient signal: Instead of each positive example being shown in one batch with a large weight, they're shown in many different batches each time with a small weight.
This smoother gradient signal makes it easier to train the model.
### Check training history
Note that the distributions of metrics will be different here, because the training data has a totally different distribution from the validation and test data.
```
plot_metrics(resampled_history)
```
### Re-train
Because training is easier on the balanced data, the above training procedure may overfit quickly.
So break up the epochs to give the `tf.keras.callbacks.EarlyStopping` finer control over when to stop training.
```
resampled_model = make_model()
resampled_model.load_weights(initial_weights)
# Reset the bias to zero, since this dataset is balanced.
output_layer = resampled_model.layers[-1]
output_layer.bias.assign([0])
resampled_history = resampled_model.fit(
resampled_ds,
# These are not real epochs
steps_per_epoch=20,
epochs=10*EPOCHS,
callbacks=[early_stopping],
validation_data=(val_ds))
```
### Re-check training history
```
plot_metrics(resampled_history)
```
### Evaluate metrics
```
train_predictions_resampled = resampled_model.predict(train_features, batch_size=BATCH_SIZE)
test_predictions_resampled = resampled_model.predict(test_features, batch_size=BATCH_SIZE)
resampled_results = resampled_model.evaluate(test_features, test_labels,
batch_size=BATCH_SIZE, verbose=0)
for name, value in zip(resampled_model.metrics_names, resampled_results):
print(name, ': ', value)
print()
plot_cm(test_labels, test_predictions_resampled)
```
### Plot the ROC
```
plot_roc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_roc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_roc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_roc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_roc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_roc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right')
```
### Plot the AUPRC
```
plot_prc("Train Baseline", train_labels, train_predictions_baseline, color=colors[0])
plot_prc("Test Baseline", test_labels, test_predictions_baseline, color=colors[0], linestyle='--')
plot_prc("Train Weighted", train_labels, train_predictions_weighted, color=colors[1])
plot_prc("Test Weighted", test_labels, test_predictions_weighted, color=colors[1], linestyle='--')
plot_prc("Train Resampled", train_labels, train_predictions_resampled, color=colors[2])
plot_prc("Test Resampled", test_labels, test_predictions_resampled, color=colors[2], linestyle='--')
plt.legend(loc='lower right')
```
## Applying this tutorial to your problem
Imbalanced data classification is an inherently difficult task since there are so few samples to learn from. You should always start with the data first and do your best to collect as many samples as possible and give substantial thought to what features may be relevant so the model can get the most out of your minority class. At some point your model may struggle to improve and yield the results you want, so it is important to keep in mind the context of your problem and the trade offs between different types of errors.
|
github_jupyter
|
# Caching
Interacting with files on a cloud provider can mean a lot of waiting on files downloading and uploading. `cloudpathlib` provides seamless on-demand caching of cloud content that can be persistent across processes and sessions to make sure you only download or upload when you need to.
## Are we synced?
Before `cloudpathlib`, we spent a lot of time syncing our remote and local files. There was no great solution. For example, I just need one file, but I only have a script that downloads the entire 800GB bucket (or worse, you can't remember exactly _which_ files you need 🤮). Or _even worse_, you have all the files synced to your local machine, but you suspect that some are are up-to-date and some are stale. More often that I'd like to admit, the simplest answer was to blast the whole data directory and download all over again. Bandwidth doesn't grow on trees!
## Cache me if you can
Part of what makes `cloudpathlib` so useful is that it takes care of all of that, leaving your precious mental resources free to do other things! It maintains a local cache and only downloads a file if the local version and remote versions are out of sync. Every time you read or write a file, `cloudpathlib` goes through these steps:
- Does the file exist in the cache already?
- If no, download it to the cache.
- If yes, does the cached version have the same modtime as the cloud version?
- If it is older, re-download the file and replace the old cached version with the updated version from the cloud.
- If the local one is newer, something is up! We don't want to overwrite your local changes with the version from the cloud. If we see this scenario, we'll raise an error and offer some options to resolve the versions.
## Supporting reading and writing
The cache logic also support writing to cloud files seamlessly in addition to reading. We do this by tracking when a `CloudPath` is opened and on the close of that file, we will upload the new version to the cloud if it has changed.
**Warning** we don't upload files that weren't opened for write by `cloudpathlib`. For example, if you edit a file in the cache manually in a text edior, `cloudpathlib` won't know to update that file on the cloud. If you want to write to a file in the cloud, you should use the `open` or `write` methods, for example:
```python
with my_cloud_path.open("w") as f:
f.write("My new text!")
```
This will download the file, write to the text to the local version in the cache, and when that file is closed we know to upload the changed version to the cloud.
As an example, let's look at using the [Low Altitude Disaster Imagery](https://registry.opendata.aws/ladi/) open dataset on S3. We'll view one images available of a flooding incident available on S3.
```
from cloudpathlib import CloudPath
from itertools import islice
ladi = CloudPath("s3://ladi/Images/FEMA_CAP/2020/70349")
# list first 5 images for this incident
for p in islice(ladi.iterdir(), 5):
print(p)
```
Just because we saw these images are available, it doesn't mean we have downloaded any of this data yet.
```
# Nothing in the cache yet
!tree {ladi.fspath}
```
Now let's look at just the first image from this dataset.
```
flood_image = ladi / "DSC_0001_5a63d42e-27c6-448a-84f1-bfc632125b8e.jpg"
flood_image.exists()
# Still nothing in the cache
!tree {ladi.fspath}
```
Even though we refer to a specific file and make sure it exists in the cloud, we can still do all of that work without actually downloading the file.
In order to read the file, we do have to download the data. Let's actually display the image:
```
%%time
%matplotlib inline
import matplotlib.pyplot as plt
from PIL import Image
with flood_image.open("rb") as f:
i = Image.open(f)
plt.imshow(i)
# Downloaded image file in the cache
!tree {ladi.fspath}
```
Just be using `open`, we've downloaded the file in the background to the cache. Now that it is local, we won't redownload that file unless it changes on the server. We can confirm that by checking if the file is faster to read a second time.
```
%%time
with flood_image.open("rb") as f:
i = Image.open(f)
plt.imshow(i)
```
Notice that the second display is much faster since we use the cached version!
## Keeping the cache around
By default, the cache uses [`tempfile`](https://docs.python.org/3/library/tempfile.html) this means at some point either Python or your operating system will remove whatever files you have cached. This is helpful in that it means the downloaded files get cleaned up regularly and don't necessarily clutter up your local hard drive.
However, sometimes I don't want to have to re-download files I know won't change. For example, in the LADI dataset, I may want to use the images in a Jupyter notebook and every time I restart the notebook I want to always have the downloaded files. I don't want to re-download since I know the LADI images won't be changing on S3.
We can do this just by using a `Client` that does all the downloading/uploading to a specfic folder on our local machine.
```
from cloudpathlib import S3Client
# explicitly instantiate a client that always uses the local cache
client = S3Client(local_cache_dir="data")
ladi = client.CloudPath("s3://ladi/Images/FEMA_CAP/2020/70349")
# Again, nothing in the cache yet, but we see it is all in the "data" folder
!tree {ladi.fspath}
```
Now let's look at just the first image from this dataset. Note that paths created by using the `ladi` root (e.g., by using the `/` operator below or calls like `iterdir` and `glob`) will inherit the same `Client` instance, and therefore the same `local_cache_dir` without our having to do extra work.
```
flood_image = ladi / "DSC_0002_a89f1b79-786f-4dac-9dcc-609fb1a977b1.jpg"
with flood_image.open("rb") as f:
i = Image.open(f)
plt.imshow(i)
# Now
!tree {ladi.fspath}
# let's explicitly cleanup this directory, since it is not handled for us
!rm -rf data
```
## Accessing the cached version directly (read-only)
Many Python libraries don't properly handle `PathLike` objects. These libraries often only expect a `str` to be passed when working with files or, even worse, they will call `str(p)` on a Path that is passed before using it.
To use `cloudpathlib` with these libraries, you can pass `.fspath` which will provide the path to the cached version of the file as a string.
**Warning:** Using the `.fspath` property will download the file from the cloud if it does not exist yet in the cache.
**Warning:** Since we are no longer in control of opening/closing the file, we cannot upload any changes when the file is closed. Therefore, you should treat any code where you use `fspath` as _read only_. Writes directly to `fspath` will not be uplaoded to the cloud.
## Handling conflicts
We try to be conservative in terms of not losing data—especially data stored on the cloud, which is likely to be the canonical version. Given this, we will raise exceptions in two scenarios:
`OverwriteNewerLocalError`
This exception is raised if we are asked to download a file, but our local version in the cache is newer. This likely means that the cached version has been updated, but not pushed to the cloud. To work around this you could remove the cache version explicitly if you _know_ you don't need that data. If you did write changes you need, make sure your code uses the `cloudpathlib` versions of the `open`, `write_text`, or `write_bytes` methods, which will upload your changes to the cloud automatically.
The `CloudPath.open` method supports a `force_overwrite_from_cloud` kwarg to force overwriting your local version.
`OverwriteNewerCloudError`
This exception is raised if we are asked to upload a file, but the one on the cloud is newer than our local version. This likely means that a separate process has updated the cloud version, and we don't want to overwrite and lose that new data in the cloud.
The `CloudPath.open` method supports a `force_overwrite_to_cloud` kwarg to force overwriting the cloud version.
|
github_jupyter
|
```
#Modified version of the following script from nilearn:
#https://nilearn.github.io/auto_examples/03_connectivity/plot_group_level_connectivity.html
from nilearn import datasets
from tqdm.notebook import tqdm
abide_dataset = datasets.fetch_abide_pcp(n_subjects=200)
abide_dataset.keys()
from nilearn import input_data
msdl_data = datasets.fetch_atlas_msdl()
masker = input_data.NiftiMapsMasker(
msdl_data.maps, resampling_target="data", t_r=2, detrend=True,
low_pass=.1, high_pass=.01, memory='nilearn_cache', memory_level=1).fit()
pooled_subjects = []
groups = []
for func_file, dx in tqdm(zip(abide_dataset['func_preproc'], abide_dataset['phenotypic']['DX_GROUP'])):
time_series = masker.transform(func_file)
pooled_subjects.append(time_series)
groups.append(dx)
print(f'Dataset has {len(pooled_subjects)} subjects')
n_regions = pooled_subjects[0].shape[1]
def sym_matrix_to_vec(symmetric):
tril_mask = np.tril(np.ones(symmetric.shape[-2:]), k=-1).astype(np.bool)
return symmetric[..., tril_mask]
def compute_dtw(subjects, n_regions):
dtw_output = []
for subj in subjects:
dtw_output.append(
rust_dtw.dtw_connectome(
connectome=subj,
window=100,
distance_mode="euclidean")
)
connectomes = []
#Post processing them as per paper recommendations
for vec in dtw_output:
sym = np.zeros((n_regions, n_regions))
sym[i_lower] = vec
sym += sym.T
sym *= -1
StandardScaler().fit_transform(sym)
connectomes.append(sym_matrix_to_vec(sym))
return connectomes
from sklearn.svm import LinearSVC
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from nilearn.connectome import ConnectivityMeasure
import matplotlib.pyplot as plt
import rust_dtw
import numpy as np
import copy
kinds = ['dtw', 'correlation', 'partial correlation', 'tangent']
# kinds = ['correlation']
_, classes = np.unique(groups, return_inverse=True)
cv = StratifiedShuffleSplit(n_splits=15, random_state=0, test_size=5)
pooled_subjects = np.asarray(pooled_subjects)
scores = {}
for kind in kinds:
print('PROCESSING: ', kind)
scores[kind] = []
for train, test in cv.split(pooled_subjects, classes):
if kind == 'dtw':
connectomes = compute_dtw(pooled_subjects[train], n_regions)
test_connectomes = compute_dtw(pooled_subjects[test], n_regions)
else:
connectivity = ConnectivityMeasure(kind=kind, vectorize=True)
connectomes = connectivity.fit_transform(pooled_subjects[train])
test_connectomes = connectivity.transform(pooled_subjects[test])
classifier = LinearSVC(max_iter=10000).fit(connectomes, classes[train])
# make predictions for the left-out test subjects
predictions = classifier.predict(test_connectomes)
# store the accuracy for this cross-validation fold
scores[kind].append(accuracy_score(classes[test], predictions))
import matplotlib.pyplot as plt
import seaborn
plt.style.use('seaborn-white')
seaborn.set_context('poster')
mean_scores = [np.mean(scores[kind]) for kind in kinds]
print(list(zip(mean_scores, kinds) ))
scores_std = [np.std(scores[kind]) for kind in kinds]
plt.figure(figsize=(15, 10))
positions = np.arange(len(kinds)) * .1 + .1
plt.barh(positions, mean_scores, align='center', height=.05, xerr=scores_std)
yticks = [k.replace(' ', '\n') for k in kinds]
plt.yticks(positions, yticks)
plt.gca().grid(True)
plt.gca().set_axisbelow(True)
plt.xlabel('Classification accuracy')
plt.tight_layout()
plt.savefig('accuracy.png', bbox_inches="tight", dpi=300)
```
|
github_jupyter
|
<center>
<h1>Fetal Health Classification</h1>
<img src="https://blog.pregistry.com/wp-content/uploads/2018/08/AdobeStock_90496738.jpeg">
<small>Source: Google</small>
</center>
<p>
Fetal mortality refers to stillbirths or fetal death. It encompasses any death of a fetus after 20 weeks of gestation.
Cardiotocograms (CTGs) are a simple and cost accessible option to assess fetal health, allowing healthcare professionals to take action in order to prevent child and maternal mortality.
Cardiotocography is a technical means of recording the fetal heartbeat and the uterine contractions during pregnancy. It is most commonly used in the third trimester and its purpose is to monitor fetal well-being and allow early detection of fetal distress. An abnormal CTG may indicate the need for further investigations and potential intervention.
</p>
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('../Datasets/fetal_health.csv')
```
| Variable symbol | Variable description|
| ----------------|---------------------|
|LB | Fetal heart rate baseline (beats per minute)|
|AC | Number of accelerations per second|
|FM | Number of fetal movements per second|
|UC | Number of uterine contractions per second|
|DL | Number of light decelerations per second|
|DS | Number of severe decelerations per second|
|DP | Number of prolonged decelerations per second|
|ASTV | Percentage of time with abnormal short-term variability|
|MSTV | Mean value of short-term variability|
|ALTV | Percentage of time with abnormal long-term variability|
|MLTV | Mean value of long-term variability|
|Width | Width of FHR histogram|
|Min | Minimum of FHR histogram|
|Max | Maximum of FHR histogram|
|Nmax | Number of histogram peaks|
|Nzeros | Number of histogram zeroes|
|Mode | Histogram mode|
|Median | Histogram median|
|Variance | Histogram variance|
|Tendency | Histogram tendency|
|NSP | Fetal state class code (N=Normal, S=Suspected,P=Pathological)|
Reference: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6822315/
```
df.head()
df.info()
df.describe()
df.isna().sum()
```
Thankfully, there are no NaN values in the dataset.
```
sns.countplot(x='fetal_health', data=df)
print(df['fetal_health'].value_counts())
```
We can see that there is the problem of class imbalance in this dataset. This means we cannot use **accuracy** as a metric to evaluate the performance of our model. The most appropiate metric for model evaluation can be:
1. F1 Score
2. Recall
3. Precision
Before diving deep into understanding the data and features, let us first look at what does the three different categories of fetal_health represent. Please refer to the table below for the same.
Reference: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4812878/

```
corr = df.corr()
plt.figure(figsize=(24, 20))
sns.heatmap(corr, annot=True)
plt.title("Correlation Matrix")
plt.show()
```
From the above correlation matrix, we can observe that the following features show some correlation with target variable fetal health:
1. accelerations (negative corr)
2. uterine contractions (negative corr)
3. prolonged_decelerations (positive corr)
4. abnormal short term variability (positive corr)
5. percentage of time with abnormal long term variability (positive corr)
## Model Selection
```
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.svm import LinearSVC
from sklearn.linear_model import SGDClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, f1_score, recall_score, precision_score
print("There are total "+str(len(df))+" rows in the dataset")
X = df.drop(["fetal_health"],axis=1)
Y = df["fetal_health"]
std_scale = StandardScaler()
X_sc = std_scale.fit_transform(X)
X_train, X_test, y_train,y_test = train_test_split(X_sc, Y, test_size=0.25, random_state=42)
print("There are total "+str(len(X_train))+" rows in training dataset")
print("There are total "+str(len(X_test))+" rows in test dataset")
```
If you remember, in the initial investigation of the data, we found out that we have imbalanced classes.
To handle the problem of imbalanced classes, we can use oversampling techniques. In oversampling, we populate the minority classes with some synthetic data.
Let us try some oversampling techniques and judge their performance on the above dataset.
1. SMOTE Technique
```
from imblearn.over_sampling import SMOTE
smt = SMOTE()
X_train_sm, y_train_sm = smt.fit_resample(X_train, y_train)
```
2. ADASYN
```
from imblearn.over_sampling import ADASYN
ada = ADASYN(random_state=130)
X_train_ada, y_train_ada = ada.fit_resample(X_train, y_train)
```
3. SMOTE + Tomek Links
```
from imblearn.combine import SMOTETomek
smtom = SMOTETomek(random_state=139)
X_train_smtom, y_train_smtom = smtom.fit_resample(X_train, y_train)
```
4. SMOTE + ENN
```
from imblearn.combine import SMOTEENN
smenn = SMOTEENN()
X_train_smenn, y_train_smenn = smenn.fit_resample(X_train, y_train)
def evaluate_model(clf, X_test, y_test, model_name, oversample_type):
print('--------------------------------------------')
print('Model ', model_name)
print('Data Type ', oversample_type)
y_pred = clf.predict(X_test)
f1 = f1_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
precision = precision_score(y_test, y_pred, average='weighted')
print(classification_report(y_test, y_pred))
print("F1 Score ", f1)
print("Recall ", recall)
print("Precision ", precision)
return [model_name, oversample_type, f1, recall, precision]
models = {
'DecisionTrees': DecisionTreeClassifier(random_state=42),
'RandomForest':RandomForestClassifier(random_state=42),
'LinearSVC':LinearSVC(random_state=0),
'AdaBoostClassifier':AdaBoostClassifier(random_state=42),
'SGD':SGDClassifier()
}
oversampled_data = {
'ACTUAL':[X_train, y_train],
'SMOTE':[X_train_sm, y_train_sm],
'ADASYN':[X_train_ada, y_train_ada],
'SMOTE_TOMEK':[X_train_smtom, y_train_smtom],
'SMOTE_ENN':[X_train_smenn, y_train_smenn]
}
final_output = []
for model_k, model_clf in models.items():
for data_type, data in oversampled_data.items():
model_clf.fit(data[0], data[1])
final_output.append(evaluate_model(model_clf, X_test, y_test, model_k, data_type))
final_df = pd.DataFrame(final_output, columns=['Model', 'DataType', 'F1', 'Recall', 'Precision'])
final_df.sort_values(by="F1", ascending=False)
```
### Hyperparameter Tuning
```
param_grid = {
'criterion':['gini', 'entropy'],
'max_depth': [10, 20, 40, 80, 100],
'max_features': ['auto', 'sqrt'],
'n_estimators': [200, 400, 600, 800, 1000, 2000]
}
rfc = RandomForestClassifier(random_state=42)
rfc_cv = GridSearchCV(estimator=rfc, param_grid=param_grid, cv=5, verbose=2)
rfc_cv.fit(X_train_smtom, y_train_smtom)
rfc_cv.best_params_
rf = RandomForestClassifier(n_estimators=2000, criterion='entropy', max_depth=20, max_features='auto')
rf.fit(X_train_smtom, y_train_smtom)
evaluate_model(rf, X_test, y_test, 'RandomForest', 'SMOTE+TOMEK')
import pickle
filename = 'fetal-health-model.pkl'
pickle.dump(rf, open(filename, 'wb'))
```
|
github_jupyter
|
# HHVM
## 背景介绍
HHVM 是 Facebook (现 Meta) 开发的高性能 PHP 虚拟机,宣称达到了官方解释器的 9x 性能
### 为什么会有 HHVM
#### 脚本语言
##### Pros
一般我们使用脚本语言 (Perl,Python,PHP,JavaScript)是为了以下几个目的
1. 大部分的脚本语言都拥有较为完备的外部库,能够帮助开发者快速的开发/测试
- 使用 Python 作为 ebt 的技术栈也是因为 `numpy`, `pandas` 等数据科学库的支持比别的编程语言更加的完备
2. 动态语言的特性使得开发过程变得异常轻松,可以最大程度的实现可复用性和多态性,打个比方
- Python
```python
def evaluate(model_impl, params):
return model_impl.calculate(params)
class Model(object):
def calculate(params):
sum_val = 0
for param in params:
sum_val += param
return sum_val
```
- C++
```cpp
class IModel {
public:
virtual double calculate(const vector<double> ¶ms) = 0;
virtual int calculate(const vector<int> ¶ms) = 0;
}
class Model : public IModel {
public:
double calculate(const vector<double> ¶ms) {
double sum_val = 0;
for (vector<double>::iterator it = params.begin(); it != params.end(); ++it) {
sum_val += *it;
}
return sum_val;
}
int calculate(const vector<int> ¶ms) {
int sum_val = 0;
for (vector<int>::iterator it = params.begin(); it != params.end(); ++it) {
sum_val += *it;
}
return sum_val;
}
}
double evaluate(IModel* model_impl, const vector<double> ¶ms) {
return model_impl->calculate(params);
}
int evaluate(IModel* model_impl, const vector<int> ¶ms) {
return model_impl->calculate(params);
}
```
- 模版
```cpp
// This is ok but template is not a general feature for all static typed language
template <typename T>
T evaluate(IModel* model_impl, const vector<T> ¶ms) {
return model_impl->calculate<T>(params);
}
template <typename T>
T::value_type evaluate(IModel* model_impl, const T& params) {
return model_impl->calculate<T>(params);
}
```
3. 动态语言完全是解释执行,调试成本较低。每当改动源码有所改动后,程序重新运行更加直接,只需要解释器重新读取源码即可。编译性语言需要更多的步骤与时间,例如 C++,为了从源码生成可执行程序需要 链接静态库 -> .obj -> 链接动态库 -> 可执行程序。如果是大型项目开发的话这一步骤甚至会花费几个小时。而解释执行的程序可以不需要这些步骤直接重新运行
##### Cons
但是对于有较高性能需求的 situation,编译执行反而会成为拖累。
> Although easy to implement, interpreters are generally slow, which makes scripting language prohibitive for implementing large, CPU-intensive applications. (Zhao, 2021)
Debian 有一个 [benchmark game](https://benchmarksgame-team.pages.debian.net/benchmarksgame/index.html),比较了目前比较常见的几种编程语言的运行速度/内存占用/源码大小
```
import pandas as pd
import matplotlib.pyplot as plt
benchmarks = pd.read_csv('./data/programming_language_benchmarks_game_all_measurements.csv')
benchmarks.head(10)
compile_lang_lst = ['clang', 'csharpcore', 'csharppgo', 'gcc', 'gfortran', 'go', 'gpp', 'java', 'rust', 'swift']
interpreter_lang_lst = ['node', 'perl', 'php', 'python3']
def boxplot_by_lang(data: pd.DataFrame, colname: str) -> None:
fig, ax = plt.subplots()
index = 1
for lang in compile_lang_lst:
ax.boxplot(data[data['lang'] == lang][colname],
positions=[index],
labels=[lang],
boxprops=dict(color='blue'))
index += 1
for lang in interpreter_lang_lst:
ax.boxplot(data[data['lang'] == lang][colname],
positions=[index],
labels=[lang],
boxprops=dict(color='green'))
index += 1
ax.set_title(colname, fontsize=15)
ax.tick_params(axis='x', labelrotation=45)
fig.set_size_inches(10, 6)
filtered = benchmarks[(benchmarks['status'] == 0) & (benchmarks['name'] == 'binarytrees') & (benchmarks['n'] == 21)].reset_index()
boxplot_by_lang(data=filtered, colname='elapsed(s)')
boxplot_by_lang(data=filtered, colname='mem(KB)')
boxplot_by_lang(data=filtered, colname='size(B)')
```
通过以上数据可以显然看出与编译执行语言相比,解释执行的语言在 CPU 的处理性能有明显的优势,部分编译执行的语言在内存处理(申请与回收)上也有着异常优秀的表现。
像 Meta 这样的巨型公司需要 host 的服务器是也是巨型的
<img src='./images/faceboook_datacenter_oregon.png' alt='facebook_datacenter' width='1000' />
上图是 Meta 在 Oregon 的数据中心,据说这两个 building 的造价就高达了 *$750M* (约合 *¥47.78 亿*),并且在 2020 年中 Meta 又在边上造了两个
如此巨型的数据中心的一大作用就是用来做 Facebook 的服务器主机,所以为了优化服务器的物理成本,从代码上优化服务器性能是必然的。
我们都知道 Facebook 是用 PHP 实现的,据 HHVM 的项目主持者之一的 Keith Adams 所说,Facebook 有约莫 $2 \times 10^7$ 行 PHP 代码 (2012年)。Facebook 的开发者在检查之后发现自己服务器的性能问题很大一部分就是资源的消耗就在 PHP 的解释器本身上,所以需要考虑的就是如何优化 PHP 的性能
### 如何优化 PHP 的性能
1. 使用性能更好的语言重写服务端,如 C++,GO,Java
- 重构2千万行代码?算了算了
2. 使用 RPC 将部分业务功能独立,减少 PHP 的处理,比如 Twitter 就将自己的很多业务逻辑从 Ruby on Rails 转为了 Java 和 Scala (前端由 node + react 独立实现)
<img src='./images/twitter_tech_stack.webp' alt='twitter_tech_stack' width="1000" />
- RPC 框架
<img src='./images/Thrift_homepage.png' alt='Thrift' width="1000" />
但是不解决问题
3. 以动态扩展的形式优化 PHP 的性能瓶颈,用 PHP 加载 C++ 实现的方式绕开性能瓶颈
- ebt 目前的解决方案,但是对 Facebook 这样历史包袱过重的源码仓库来说,性能瓶颈并不是 1-2 处小地方,而是不断累积的后果,并且 PHP 的扩展并不像 pybind 一样有比较成熟的加载方式
4. 优化 PHP 的解释器本身
### 如何优化 PHP 的解释器
1. 改进自己的源码
- 用 PHP 写的 PHP 性能分析工具 [XHProf](https://github.com/phacility/xhprof)
- 定位性能瓶颈处,优化代码逻辑,就像 leetcode 去做到 >99%
- 优化的不够
2. 优化 PHP 的解释器实现
- [Zend Engine](https://github.com/php/php-src/tree/master/Zend)
- 将 PHP 编译为 `opcode` 然后执行 `opcode`
- 优化 Zend 的性能代价太大,并且还要做到版本的向下兼容
3. 将 PHP 转为 C/C++,然后编译生成
- Hiphop Compiler for PHP (Zhao, 2012)
<img src='./images/hhvm_autogen.png' alt='hhvm_autogen' width="1000" />
被认为是一种 Ahead of Time 的方式,能够完成非常多的代码优化(就像 LLVM 一样),但是一个问题就是无法正确支持 PHP 中的部分特性,如 `eval()`, `create_function()` 等
> Support for eval is theoretically possible in HipHop by invoking an interpreter. However, we opted not to implement that because the use of eval exposes serious security problems and is therefore discouraged. (Zhao, 2012)
就像是在 C++ 里面 `Py_Initialize()` 启动了 Python 环境,对内存消耗和代码优化都不是很友好
4. 实现一个虚拟机,将 PHP 源码转为当前平台的机器码执行 (JVM)
- 如今的 HHVM
## HipHop Compiler for PHP (HPHPc)
### C++ 与 PHP 的特性区别
<img src='./images/php_cpp_table.png' alt='PHP_cpp_table' width='600' />
### HPHPc 的编译设计
<img src='./images/hphpc_phases.png' alt='hphpc_phases' width='600' />
```php
<?php
define("confName", "OOPSLA");
define("firstYear", 1986);
function year($edition) {
return firstYear - 1 + $edition;
}
echo "Hello " . confName . "'" . year(27);
```
#### 1. 生成 AST
读取 PHP 的源码并生成对应的 AST
<img src='./images/ast.png' alt='ast' width="1000" />
#### 2. 预分析
遍历 AST 并且记录所有符号的信息(类,函数,变量,全局 const),判断哪些符号是存在同名覆盖的情况需要考虑代码上下文。并且建立符号之间的依赖图,为后续的并行优化提供前置准备
#### 3. 预优化
处理不需要类型就能完成的油画,比如将函数转为内联函数,优化不必要的逻辑判断,移除不可能到达的代码片段等
#### 4. 判断类型
核心部分,基于 Damas-Milner constraint-based 算法判断不同符号的类型
<img src='./images/hphpc_types.png' alt='hphpc_types' width="600" />
`variant` 是 `any` 类型,所有符号在类型推断出类型前都是 `variant` 类型,在推断过程中如果成功判断为任何类型则覆盖 `variant`
#### 5. 后优化
在拥有类型之后,HipHop 编译器会根据类型信息优化包括简单的数值计算和逻辑判断在内的部分代码片段,然后再重新执行一次预优化阶段的优化逻辑
#### 6. 生成
最后编译器会遍历带有类型的,被优化后的 AST,并且生成对应的 C++ 代码,并且运行 gcc 编译 C++ 源码,生成的 C++ 部分包括
1. 类的头文件:每个 PHP 的类实现会生成对应的 C++ 头文件与对应的类声明
2. PHP 的头文件:每个 PHP 的文件(函数)会生成对应的 C++ 头文件与对应的声明
3. 具体实现文件:包含了一个或者多个声明类/函数的具体实现
4. 系统文件:不包含 PHP 的源码内容,但是会记录 Symbol Table
### 如何从 AST 生成 C++ 代码
#### 鸭子类型
除了正常标注类型的符号以外,仍然存在无法判断的 `variant` 类型,需要实现一个 `variant` 类型支持运行时处理的逻辑
#### 动态符号
指符号的具体指向需要运行时判断,如
```python
if SOME_CONDITION:
x = 10
else:
x = 'a'
```
对于这种情况,HipHop 用一张 *global symbol table* 记录了:
- 全局变量
- 动态申明的 constant
- 函数体/类实现中的静态变量
- 重复定义的函数体/类
所谓重复定义是指在不同文件中定义了同样的函数名/类名(在动态语言中这样做是合法的),GST 会在符号名后添加唯一后缀,然后根据具体 `#include` 语句引用的文件名导向不同后缀的同名函数/类实现。对于静态编译过程中出现的无法处理的**动态符号**,HipHop 会通过类似的逻辑生成临时的 *local symbol table*。
在具体处理实际的 variable 时,编译器会通过当前所处的上下文获取 LST 和 GST,从 table 中获取实际的指向。
同时,HipHop 还支持了动态添加实例属性,如
```
class SomeClass:
def __init__(self):
pass
some_instance = SomeClass()
some_instance.a = 10
print(some_instance.a)
```
为了实现这样的 feature,HipHop 还实现了一个 *property symbol table*,用于记录符号中的属性,当源码尝试访问实例/类属性时,会通过 PST 找到对应的符号。
但是 HPHPc 的痛点就是
- 无法支持 PHP 的动态方法 `eval()`, `create_function()` 等
- 并且编译后部署上线的源码重量会比 PHP 要大很多,对于2千万行的源码,这种硬性的成本是毁灭性的
## HHVM (HipHop Virtual Machine)
会什么虚拟机能够解决传统解释器的问题呢?
### JIT (Just In Time)
JVM,Numba 和 HHVM 都是对解释性语言的 jit 优化,但是尝试过 Numba 的我们也知道,jit 有可能并没有想象中的那么美好,对于一些简单的方法,jit 甚至还会拖累性能
```
def make_it_double(a: int) -> int:
return a * 2
%%timeit
make_it_double(10)
import numba
make_it_double_numba = numba.jit(make_it_double)
%%timeit
make_it_double_numba(10)
```
从上面的表现可以发现 jit 并不是那么的美好,因为 jit 这个过程也是存在性能损耗的,所以这种简单的方法反而会比普通的解释器慢
<img src='./images/hphpc_vs_hhvm.png' alt='hphpc_vs_hhvm' width="600" />
安卓的目前的运行时方案 ART (Andriod Run Time)作为 Android 上的应用和部分系统服务使用的托管式运行时,采用的就是 HPHPc 的 AOT 方案,其前身 Dalvik 使用的 JIT 方案,但是 ART 虚拟机比 Dalvik 快了一倍多。
为了保证虚拟机 jit 的性能优化,Facebook 招聘了各路神仙
- Andrei Alexandrescu,『Modern C++ Design』和『C++ Coding Standards』的作者,C++ 领域无可争议的大神
- Keith Adams,负责过 VMware 核心架构,当年 VMware 就派他一人去和 Intel 进行技术合作,足以证明在 VMM 领域他有多了解了
- Drew Paroski,在微软参与过 .NET 虚拟机开发,改进了其中的 JIT
- Jason Evans,开发了 jemalloc,减少了 Firefox 一半的内存消耗
- Sara Golemon,『Extending and Embedding PHP』的作者,PHP 内核专家
### Interpreter
HHVM 在 parse 完 PHP 源码会生成一种 Bytecode (opcode),储存在 .hhvm.hhbc 文件中索引,在执行 Bytecode 时和 Zend 类似,将不同的字节码放到不同的函数中去实现 (Subroutine threading)。具体的生成逻辑在 `hphp/runtime/vm/hhbc.cpp`
因为重新实现了解释器,HHVM 比起 HPHPc 能够提供更加优异的兼容性,理论上可以做到对 PHP 所有特性的完美兼容,但是这样的性能还是走了 Zend 的老路子,并且对于动态类型,需要实现类似于如下的判断
```cpp
VMType::Variant VMExecutionContext::add(const VMType::Variant &left, const VMType::Variant &right) {
if (this->GST[left.uid] == VMType::Int64 && this->GST[right.uid] == VMType::Int64) {
return this->IntAddImpl->exec(left, right);
}
// TODO: some other impl
}
```
而我们知道这样的 if else 条件判断对 CPU 的执行优化是严重的拖累,另一个问题是需要从数据都是储存在对象中,作为 boxed structure 每次的间接获取地址也是有成本的,所以需要 jit 的实现来完成这些工作
### JIT Impl
其实本质上 jit 和 `eval()` 是类似的,只不过 jit eval 的不是源码字符串,而是不同平台下的机器码。HHVM 实现了一个 x64 的机器码生成器(HHBBC)。
常见的 jit 触发条件有两种
- trace:记录循环执行次数,如果超过一定数量就对这段代码进行 jit
- method:记录函数执行次数,如果超过一定数量就对这个函数内的代码片段进行 jit,如果过于 hot 就直接改为 inline
关于这两种方法哪种更好在 [Lambada](http://lambda-the-ultimate.org/node/3851) 上有个帖子引来了各路大神的讨论,尤其是 Mike Pall(LuaJIT 作者) 、Andreas Gal(Mozilla VP) 和 Brendan Eich(Mozilla CTO)都发表了很多自己的观点,两者的区别不仅仅是编译的范围,还有包括局部变量处理在内的很多细节方面都不太一样。
然而 HHVM 自创了一种叫做 tracelet 的方式,根据类型划分
<img src='./images/hhvm_tracelet.png' alt='hhvm_tracelet' width="1000" />
tracelet 将一个函数划分了 3 个部分,A,C用于处理入参 `$k` 是 integer 或者 string 两种类型的情况,B 用于处理返回值,因此 HHVM 的 jit 触发更像是与类型相关,具体如何分析和拆解 tracelet 的细节在 `hphp/runtime/vm/jit` 中,太深了就不需要了解了。
当然 HHVM 的 jit 优化还体现在很多地方,比如 如果 C 比 A 更加 hot(命中次数更多),HHVM 就会在 jit 的过程中倾向于把 C 放在 A 的前面,据说这样的操作提升了 14% 的性能,因为这样更容易提前命中需要相应的类型。
### Hack
hhvm/jit 的关键是类型,而猜测类型就像上面的例子一样是一个对 CPU 非常不友好的操作,所以 HHVM 的开发者就开始考虑为 PHP 添加类型支持,推出了一个新的语言 - Hack,通过静态类型指定让 HHVM 能够更好的提供性能优化。同时也能够让代码可读性大大提升,方便 IDE 提供更多帮助,在编码阶段减少很多没有必要的 bug。
## Conclusion
HPHPc / HHVM 作为两种为动态的脚本语言提供性能优化的方案都是有可取之处的,HPHPc 能够在静态编译的过程中完成各种可能的性能优化,比起 HHVM 的优化, HPHPc 的优化能够更加稳定,AOT 是一种非常成熟的优化方案
HHVM 则能够更加完美的兼容动态语言的特性,jit 是一种近年来发展迅速的技术,迭代更新快,能够一直保持对性能的优化。
|
github_jupyter
|
# Módulo 2: Scraping con Selenium
## LATAM Airlines
<a href="https://www.latam.com/es_ar/"><img src="https://i.pinimg.com/originals/dd/52/74/dd5274702d1382d696caeb6e0f6980c5.png" width="420"></img></a>
<br>
Vamos a scrapear el sitio de Latam para averiguar datos de vuelos en funcion el origen y destino, fecha y cabina. La información que esperamos obtener de cada vuelo es:
- Precio(s) disponibles
- Horas de salida y llegada (duración)
- Información de las escalas
**¡Empecemos!**
Utilicemos lo aprendido hasta ahora para lograr el objetivo propuesto
```
import requests
from bs4 import BeautifulSoup
url = 'https://www.latam.com/es_ar/apps/personas/booking?fecha1_dia=18&fecha1_anomes=2019-12&auAvailability=1&ida_vuelta=ida&vuelos_origen=Buenos%20Aires&from_city1=BUE&vuelos_destino=Madrid&to_city1=MAD&flex=1&vuelos_fecha_salida_ddmmaaaa=18/12/2019&cabina=Y&nadults=1&nchildren=0&ninfants=0&cod_promo=#/'
r = requests.get(url)
r.status_code
s = BeautifulSoup(r.text, 'lxml')
print(s.prettify())
```
Vemos que la respuesta de la página no contiene la información que buscamos, ya que la misma aparece recién después de ejecutar el código JavaSCript que está en la respuesta.
## Selenium
Selenium es una herramienta que nos permitirá controlar un navegador y podremos utilizar las funcionalidades del motor de JavaScript para cargar el contenido que no viene en el HTML de la página. Para esto necesitamos el módulo `webdriver`.
```
from selenium import webdriver
```
Paso 1: instanciar un **driver** del navegador
```
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../chromedriver', options=options)
```
Paso 2: hacer que el navegador cargue la página web.
```
driver.get(url)
```
Paso 3: extraer la información de la página
```
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
vuelos
vuelo = vuelos[0]
vuelo
# Hora de salida
vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
boton_escalas = vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button')
boton_escalas.click()
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
segmentos
escalas = len(segmentos) - 1
escalas
segmento = segmentos[0]
# Origen
segmento.find_element_by_xpath('.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
segmento.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
segmento.find_element_by_xpath('.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
segmento.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
segmento.find_element_by_xpath('.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
segmento.find_element_by_xpath('.//span[@class="equipment-airline-number"]').text
# Modelo de avion
segmento.find_element_by_xpath('.//span[@class="equipment-airline-material"]').text
# Duracion de la escala
segmento.find_element_by_xpath('.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
driver.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
vuelo.click()
tarifas = vuelo.find_elements_by_xpath('.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
tarifas
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
print(dict_tarifa)
def obtener_precios(vuelo):
'''
Función que retorna una lista de diccionarios con las distintas tarifas
'''
tarifas = vuelo.find_elements_by_xpath('.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
return precios
def obtener_datos_escalas(vuelo):
'''
Función que retorna una lista de diccionarios con la información de
las escalas de cada vuelo
'''
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
info_escalas = []
for segmento in segmentos:
# Origen
origen = segmento.find_element_by_xpath('.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
dep_time = segmento.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
destino = segmento.find_element_by_xpath('.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
arr_time = segmento.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
duracion_vuelo = segmento.find_element_by_xpath('.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
numero_vuelo = segmento.find_element_by_xpath('.//span[@class="equipment-airline-number"]').text
# Modelo de avion
modelo_avion =segmento.find_element_by_xpath('.//span[@class="equipment-airline-material"]').text
if segmento != segmentos[-1]:
# Duracion de la escala
duracion_escala = segmento.find_element_by_xpath('.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
else:
duracion_escala = ''
data_dict={
'origen':origen,
'dep_time':dep_time,
'destino':destino,
'arr_time':arr_time,
'duracion_vuelo':duracion_vuelo,
'numero_vuelo':numero_vuelo,
'modelo_avion':modelo_avion,
'duracion_escala':duracion_escala,
}
info_escalas.append(data_dict)
return info_escalas
def obtener_tiempos(vuelo):
'''
Función que retorna un diccionario con los horarios de salida y llegada de cada
vuelo, incluyendo la duración.
Nota: la duración del vuelo no es la hora de llegada - la hora de salida porque
puede haber diferencia de horarios entre el origen y el destino.
'''
# Hora de salida
salida = vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
llegada = vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duracion
duracion = vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
tiempos = {'hora_salida': salida, 'hora_llegada': llegada, 'duracion': duracion}
return tiempos
def obtener_info(driver):
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
print(f'Se encontraron {len(vuelos)} vuelos.')
print('Iniciando scraping...')
info = []
for vuelo in vuelos:
#obtenemos los tiempos generales de cada vuelo
tiempos = obtener_tiempos(vuelo)
# Clickeamos sobre el boton de las escalas
vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button').click()
escalas = obtener_datos_escalas(vuelo)
# Cerramos el modal
driver.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
# Clickeamos el vuelo para ver los precios
vuelo.click()
precios = obtener_precios(vuelo)
vuelo.click()
info.append({'precios':precios, 'tiempos': tiempos, 'escalas':escalas})
return info
import time
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.by import By
from selenium.common.exceptions import TimeoutException
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../chromedriver', options=options)
driver.get(url)
# Introducir una demora
delay = 10
try:
# introducir demora inteligente
vuelo = WebDriverWait(driver, delay).until(EC.presence_of_element_located((By.XPATH, '//li[@class="flight"]')))
print('La página terminó de cargar')
info_vuelos = obtener_info(driver)
except TimeoutException:
print('La página tardó demasiado en cargar')
info_vuelos = []
driver.close()
info_vuelos
```
Paso 4: cerrar el navegador
```
driver.close()
```
|
github_jupyter
|
# Accessing higher energy states with Qiskit Pulse
In most quantum algorithms/applications, computations are carried out over a 2-dimensional space spanned by $|0\rangle$ and $|1\rangle$. In IBM's hardware, however, there also exist higher energy states which are not typically used. The focus of this section is to explore these states using Qiskit Pulse. In particular, we demonstrate how to excite the $|2\rangle$ state and build a discriminator to classify the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states.
We recommend reviewing the prior [chapter](https://learn.qiskit.org/course/quantum-hardware-pulses/calibrating-qubits-using-qiskit-pulse) before going through this notebook. We also suggest reading the Qiskit Pulse specifications (Ref [1](#refs)).
### Physics Background
We now give some additional background on the physics of transmon qubits, the basis for much of IBM's quantum hardware. These systems contain superconducting circuits composed of a Josephson junction and capacitor. For those unfamiliar with superconducting circuits, see the review [here](https://arxiv.org/pdf/1904.06560.pdf) (Ref. [2](#refs)). The Hamiltonian of this system is given by
$$
H = 4 E_C n^2 - E_J \cos(\phi),
$$
where $E_C, E_J$ denote the capacitor and Josephson energies, $n$ is the reduced charge number operator and $\phi$ is the reduced flux across the junction. We work in units with $\hbar=1$.
Transmon qubits are defined in the regime where $\phi$ is small, so we may expand $E_J \cos(\phi)$ in a Taylor series (ignoring constant terms)
$$
E_J \cos(\phi) \approx \frac{1}{2} E_J \phi^2 - \frac{1}{24} E_J \phi^4 + \mathcal{O}(\phi^6).
$$
The quadratic term $\phi^2$ defines the standard harmonic oscillator. Each additional term contributes an anharmonicity.
Using the relations $n \sim (a-a^\dagger), \phi \sim (a+a^\dagger)$ (for raising, lowering operators $a^\dagger, a$), it can be shown that the system resembles a Duffing oscillator with Hamiltonian
$$
H = \omega a^\dagger a + \frac{\alpha}{2} a^\dagger a^\dagger a a,
$$
where $\omega$ gives the $0\rightarrow1$ excitation frequency ($\omega \equiv \omega^{0\rightarrow1}$) and $\alpha$ is the anharmonicity between the $0\rightarrow1$ and $1\rightarrow2$ frequencies ($\alpha \equiv \omega^{1\rightarrow2} - \omega^{0\rightarrow1}$). Drive terms can be added as needed.
If we choose to specialize to the standard 2-dimensional subspace, we can make $|\alpha|$ sufficiently large or use special control techniques to suppress the higher energy states.
# Contents
[Getting started](#importing)
[Discriminating the 0, 1 and 2 states](#discrim012)
  [Computing the 1->2 Frequency](#freq12)
  [1->2 Rabi Experiment](#rabi12)
  [Build the 0, 1, 2 discriminator](#builddiscrim012)
[References](#refs)
## Getting Started <a id="importing"></a>
We begin by importing dependencies and defining some default variable values. We choose qubit 0 to run our experiments. We perform our experiments on the publicly available single qubit device `ibmq_armonk`.
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from qiskit import pulse # This is where we access all of our Pulse features!
from qiskit.circuit import Parameter # This is Parameter Class for variable parameters.
from qiskit.circuit import QuantumCircuit, Gate
from qiskit import schedule
from qiskit.tools.monitor import job_monitor
from qiskit.tools.jupyter import *
%matplotlib inline
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
backend = provider.get_backend('ibmq_manila')
backend_defaults = backend.defaults()
backend_properties = backend.properties()
# unit conversion factors -> all backend properties returned in SI (Hz, sec, etc.)
GHz = 1.0e9 # Gigahertz
MHz = 1.0e6 # Megahertz
us = 1.0e-6 # Microseconds
ns = 1.0e-9 # Nanoseconds
qubit = 0 # qubit we will analyze
default_qubit_freq = backend_defaults.qubit_freq_est[qubit] # Default qubit frequency in Hz.
print(f"Qubit {qubit} has an estimated frequency of {default_qubit_freq/ GHz} GHz.")
default_anharmonicity = backend_properties.qubits[qubit][3].value # Default anharmonicity in GHz
print(f"Default anharmonicity is {default_anharmonicity} GHz.")
# scale data (specific to each device)
scale_factor = 1e-7
# number of shots for our experiments
NUM_SHOTS = 1024
```
We define some additional helper functions.
```
def get_job_data(job, average):
"""Retrieve data from a job that has already run.
Args:
job (Job): The job whose data you want.
average (bool): If True, gets the data assuming data is an average.
If False, gets the data assuming it is for single shots.
Return:
list: List containing job result data.
"""
job_results = job.result(timeout = 120) # timeout parameter set to 120 s
result_data = []
for i in range(len(job_results.results)):
if average: # get avg data
result_data.append(np.real(job_results.get_memory(i)[qubit] * scale_factor))
else: # get single data
result_data.append(job_results.get_memory(i)[:, qubit] * scale_factor)
return result_data
def get_closest_multiple_of_16(num):
"""Compute the nearest multiple of 16. Needed because pulse enabled devices require
durations which are multiples of 16 samples.
"""
return int(num + 8 ) - (int(num + 8 ) % 16)
```
Next we include some default parameters for drive pulses.
```
# there are pulse parameters of the single qubit drive in IBM devices
x12_duration = 160
x12_sigma = 40
```
## Discriminating the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states <a id="discrim012"></a>
given we have already calibrated X gate in the qubit subspace, which is available as XGate instruction in the quantum circuit. Here we calibrate transition in the higher energy subspace with pulse gate.
We focus on exciting the $|2\rangle$ state and building a discriminator to classify $|0\rangle$, $|1\rangle$ and $2\rangle$ states from their respective IQ data points. The procedure for even higher states ($|3\rangle$, $|4\rangle$, etc.) should be similar, but we have not tested them explicitly.
The process for building the higher state discriminator is as follows:
1. Compute the $1\rightarrow2$ frequency.
2. Conduct a Rabi experiment to obtain the $\pi$ pulse amplitude for $1\rightarrow2$. To do this, we first apply a $0\rightarrow1$ $\pi$ pulse to get from the $|0\rangle$ to the $|1\rangle$ state. Then, we do a sweep of drive amplitudes at the $1\rightarrow2$ frequency obtained above.
3. Construct 3 schedules:\
a. Zero schedule: just measure the ground state.\
b. One schedule: apply a $0\rightarrow1$ $\pi$ pulse and measure.\
c. Two schedule: apply a $0\rightarrow1$ $\pi$ pulse, then a $1\rightarrow2$ $\pi$ pulse and measure.
4. Separate the data from each schedule into training and testing sets and construct an LDA model for discrimination.
### Computing the 1->2 frequency <a id="freq12"></a>
The first step in our calibration is to compute the frequency needed to go from the $1\rightarrow2$ state. There are two methods to do this:
1. Do a frequency sweep from the ground state and apply very high power. If the applied power is large enough, two peaks should be observed. One at the $0\rightarrow1$ frequency found in section [1](#discrim01) and one at the $0\rightarrow2$ frequency. The $1\rightarrow2$ frequency can be obtained by taking the difference of the two. Unfortunately, for `ibmq_armonk`, the maximum drive power of $1.0$ is not sufficient to see this transition. Instead, we turn to the second method.
2. Excite the $|1\rangle$ state by applying a $0\rightarrow1$ $\pi$ pulse. Then perform the frequency sweep over excitations of the $|1\rangle$ state. A single peak should be observed at a frequency lower than the $0\rightarrow1$ frequency which corresponds to the $1\rightarrow2$ frequency.
We follow the second method described above.
```
# smaller range sweep
num_freqs = 75
drive_power = 0.15
sweep_freqs = default_anharmonicity*GHz + np.linspace(-30*MHz, 30*MHz, num_freqs)
freq = Parameter('freq')
with pulse.build(backend=backend, default_alignment='sequential', name='Frequency sweep') as freq12_sweep_sched:
drive_chan = pulse.drive_channel(qubit)
with pulse.frequency_offset(freq, drive_chan):
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=drive_power,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
spect_gate = Gate("spect", 1, [freq])
qc_spect = QuantumCircuit(1, 1)
qc_spect.x(0)
qc_spect.append(spect_gate, [0])
qc_spect.measure(0, 0)
qc_spect.add_calibration(spect_gate, (0,), freq12_sweep_sched, [freq])
exp_spect_circs = [qc_spect.assign_parameters({freq: f}) for f in sweep_freqs]
excited_freq_sweep_job = backend.run(exp_spect_circs,
meas_level=1,
meas_return='avg',
shots=NUM_SHOTS)
job_monitor(excited_freq_sweep_job)
# Get the refined data (average)
excited_freq_sweep_data = get_job_data(excited_freq_sweep_job, average=True)
excited_sweep_freqs = default_qubit_freq + default_anharmonicity*GHz + np.linspace(-30*MHz, 30*MHz, num_freqs)
```
Let's plot and fit the refined signal, using the standard Lorentzian curve.
```
def fit_function(x_values, y_values, function, init_params):
"""Fit a function using scipy curve_fit."""
fitparams, conv = curve_fit(function, x_values, y_values, init_params, maxfev = 50000)
y_fit = function(x_values, *fitparams)
return fitparams, y_fit
# do fit in Hz
(excited_sweep_fit_params,
excited_sweep_y_fit) = fit_function(excited_sweep_freqs,
excited_freq_sweep_data,
lambda x, A, q_freq, B, C: (A / np.pi) * (B / ((x - q_freq)**2 + B**2)) + C,
[-20, 4.625*GHz, 0.06*GHz, 3*GHz] # initial parameters for curve_fit
)
# Note: we are only plotting the real part of the signal
plt.scatter(excited_sweep_freqs/GHz, excited_freq_sweep_data, color='black')
plt.plot(excited_sweep_freqs/GHz, excited_sweep_y_fit, color='red')
plt.xlim([min(excited_sweep_freqs/GHz), max(excited_sweep_freqs/GHz)])
plt.xlabel("Frequency [GHz]", fontsize=15)
plt.ylabel("Measured Signal [a.u.]", fontsize=15)
plt.title("1->2 Frequency Sweep (refined pass)", fontsize=15)
plt.show()
_, qubit_12_freq, _, _ = excited_sweep_fit_params
print(f"Our updated estimate for the 1->2 transition frequency is "
f"{round(qubit_12_freq/GHz, 7)} GHz.")
```
### 1->2 Rabi Experiment <a id="rabi12"></a>
Now that we have a good estimate for the $1\rightarrow2$ frequency, we perform a Rabi experiment to obtain the $\pi$ pulse amplitude for the $1\rightarrow2$ transition. To do so, we apply a $0\rightarrow1$ $\pi$ pulse and then sweep over drive amplitudes at the $1\rightarrow2$ frequency.
```
# experimental configuration
num_rabi_points = 75 # number of experiments (ie amplitudes to sweep out)
# Drive amplitude values to iterate over: 75 amplitudes evenly spaced from 0 to 1.0
drive_amp_min = 0
drive_amp_max = 1.0
drive_amps = np.linspace(drive_amp_min, drive_amp_max, num_rabi_points)
amp = Parameter('amp')
with pulse.build(backend=backend, default_alignment='sequential', name='Amp sweep') as rabi_sched:
drive_chan = pulse.drive_channel(qubit)
pulse.set_frequency(qubit_12_freq, drive_chan)
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=amp,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
rabi_gate = Gate("rabi", 1, [amp])
qc_rabi = QuantumCircuit(1, 1)
qc_rabi.x(0)
qc_rabi.append(rabi_gate, [0])
qc_rabi.measure(0, 0)
qc_rabi.add_calibration(rabi_gate, (0,), rabi_sched, [amp])
exp_rabi_circs = [qc_rabi.assign_parameters({amp: a}) for a in drive_amps]
rabi_12_job = backend.run(exp_rabi_circs,
meas_level=1,
meas_return='avg',
shots=NUM_SHOTS)
job_monitor(rabi_12_job)
# Get the job data (average)
rabi_12_data = get_job_data(rabi_12_job, average=True)
def baseline_remove(values):
"""Center data around 0."""
return np.array(values) - np.mean(values)
# Note: Only real part of data is plotted
rabi_12_data = np.real(baseline_remove(rabi_12_data))
(rabi_12_fit_params,
rabi_12_y_fit) = fit_function(drive_amps,
rabi_12_data,
lambda x, A, B, drive_12_period, phi: (A*np.cos(2*np.pi*x/drive_12_period - phi) + B),
[0.2, 0, 0.3, 0])
plt.scatter(drive_amps, rabi_12_data, color='black')
plt.plot(drive_amps, rabi_12_y_fit, color='red')
drive_12_period = rabi_12_fit_params[2]
pi_amp_12 = drive_12_period/2
plt.axvline(pi_amp_12, color='red', linestyle='--')
plt.axvline(pi_amp_12+drive_12_period/2, color='red', linestyle='--')
plt.annotate("", xy=(pi_amp_12+drive_12_period/2, 0), xytext=(pi_amp_12,0), arrowprops=dict(arrowstyle="<->", color='red'))
plt.annotate("$\pi$", xy=(pi_amp_12-0.03, 0.1), color='red')
plt.xlabel("Drive amp [a.u.]", fontsize=15)
plt.ylabel("Measured signal [a.u.]", fontsize=15)
plt.title('Rabi Experiment (1->2)', fontsize=20)
plt.show()
```
We plot and fit our data as before.
```
print(f"Our updated estimate for the 1->2 transition frequency is "
f"{round(qubit_12_freq/GHz, 7)} GHz.")
print(f"Pi Amplitude (1->2) = {pi_amp_12}")
```
### Build the 0, 1, 2 discriminator <a id="builddiscrim012"></a>
Finally, we build our discriminator for the $|0\rangle$, $|1\rangle$ and $|2\rangle$ states.
As a review, our three circuits are (again, recalling that our system starts in the $|0\rangle$ state):
1. Measure the $|0\rangle$ state directly (obtain $|0\rangle$ centroid).
2. Apply $0\rightarrow1$ $\pi$ pulse and then measure (obtain $|1\rangle$ centroid).
3. Apply $0\rightarrow1$ $\pi$ pulse, then $1\rightarrow2$ $\pi$ pulse, then measure (obtain $|2\rangle$ centroid).
```
with pulse.build(backend=backend, default_alignment='sequential', name='x12 schedule') as x12_sched:
drive_chan = pulse.drive_channel(qubit)
pulse.set_frequency(qubit_12_freq, drive_chan)
pulse.play(pulse.Gaussian(duration=x12_duration,
amp=pi_amp_12,
sigma=x12_sigma,
name='x12_pulse'), drive_chan)
# Create the three circuits
# 0 state
qc_ground = QuantumCircuit(1, 1)
qc_ground.measure(0, 0)
# 1 state
qc_one = QuantumCircuit(1, 1)
qc_one.x(0)
qc_one.measure(0, 0)
# 2 state
x12_gate = Gate("one_two_pulse", 1, [])
qc_x12 = QuantumCircuit(1, 1)
qc_x12.x(0)
qc_x12.append(x12_gate, [0])
qc_x12.measure(0, 0)
qc_x12.add_calibration(x12_gate, (0,), x12_sched, [])
```
We construct the program and plot the centroids in the IQ plane.
```
# Assemble the schedules into a program
IQ_012_job = backend.run([qc_ground, qc_one, qc_x12],
meas_level=1,
meas_return='single',
shots=NUM_SHOTS)
job_monitor(IQ_012_job)
# Get job data (single); split for zero, one and two
IQ_012_data = get_job_data(IQ_012_job, average=False)
zero_data = IQ_012_data[0]
one_data = IQ_012_data[1]
two_data = IQ_012_data[2]
def IQ_012_plot(x_min, x_max, y_min, y_max):
"""Helper function for plotting IQ plane for 0, 1, 2. Limits of plot given
as arguments."""
# zero data plotted in blue
plt.scatter(np.real(zero_data), np.imag(zero_data),
s=5, cmap='viridis', c='blue', alpha=0.5, label=r'$|0\rangle$')
# one data plotted in red
plt.scatter(np.real(one_data), np.imag(one_data),
s=5, cmap='viridis', c='red', alpha=0.5, label=r'$|1\rangle$')
# two data plotted in green
plt.scatter(np.real(two_data), np.imag(two_data),
s=5, cmap='viridis', c='green', alpha=0.5, label=r'$|2\rangle$')
# Plot a large dot for the average result of the 0, 1 and 2 states.
mean_zero = np.mean(zero_data) # takes mean of both real and imaginary parts
mean_one = np.mean(one_data)
mean_two = np.mean(two_data)
plt.scatter(np.real(mean_zero), np.imag(mean_zero),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.scatter(np.real(mean_one), np.imag(mean_one),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.scatter(np.real(mean_two), np.imag(mean_two),
s=200, cmap='viridis', c='black',alpha=1.0)
plt.xlim(x_min, x_max)
plt.ylim(y_min,y_max)
plt.legend()
plt.ylabel('I [a.u.]', fontsize=15)
plt.xlabel('Q [a.u.]', fontsize=15)
plt.title("0-1-2 discrimination", fontsize=15)
x_min = -5
x_max = 5
y_min = -10
y_max = 10
IQ_012_plot(x_min, x_max, y_min, y_max)
```
Now it is time to actually build the discriminator. We will use a machine learning technique called Linear Discriminant Analysis (LDA). LDA classifies an arbitrary data set into a set of categories (here $|0\rangle$, $|1\rangle$ and $|2\rangle$) by maximizing the distance between the means of each category and minimizing the variance within each category. For further detail, see [here](https://scikit-learn.org/stable/modules/lda_qda.html#id4) (Ref. [3](#refs)).
LDA generates a line called a separatrix. Depending on which side of the separatrix a given data point is on, we can determine which category it belongs to.
We use `scikit.learn` for an implementation of LDA; in a future release, this functionality will be added released directly into Qiskit-Ignis (see [here](https://github.com/Qiskit/qiskit-ignis/tree/master/qiskit/ignis/measurement/discriminator)).
We observe a third centroid corresponding to the $|2\rangle$ state. (Note: If the plot looks off, rerun the notebook.)
We begin by reshaping our result data into a format suitable for discrimination.
```
def reshape_complex_vec(vec):
"""Take in complex vector vec and return 2d array w/ real, imag entries. This is needed for the learning.
Args:
vec (list): complex vector of data
Returns:
list: vector w/ entries given by (real(vec], imag(vec))
"""
length = len(vec)
vec_reshaped = np.zeros((length, 2))
for i in range(len(vec)):
vec_reshaped[i]=[np.real(vec[i]), np.imag(vec[i])]
return vec_reshaped
```
We begin by shaping the data for LDA.
```
# Create IQ vector (split real, imag parts)
zero_data_reshaped = reshape_complex_vec(zero_data)
one_data_reshaped = reshape_complex_vec(one_data)
two_data_reshaped = reshape_complex_vec(two_data)
IQ_012_data = np.concatenate((zero_data_reshaped, one_data_reshaped, two_data_reshaped))
print(IQ_012_data.shape) # verify IQ data shape
```
Next, we split our training and testing data. The testing data is a vector containing an array of `0`'s (for the zero schedule, `1`'s (for the one schedule) and `2`'s (for the two schedule).
```
# construct vector w/ 0's, 1's and 2's (for testing)
state_012 = np.zeros(NUM_SHOTS) # shots gives number of experiments
state_012 = np.concatenate((state_012, np.ones(NUM_SHOTS)))
state_012 = np.concatenate((state_012, 2*np.ones(NUM_SHOTS)))
print(len(state_012))
# Shuffle and split data into training and test sets
IQ_012_train, IQ_012_test, state_012_train, state_012_test = train_test_split(IQ_012_data, state_012, test_size=0.5)
```
Finally, we set up our model and train it. The accuracy of our fit is printed.
```
# Set up the LDA
LDA_012 = LinearDiscriminantAnalysis()
LDA_012.fit(IQ_012_train, state_012_train)
# test on some simple data
print(LDA_012.predict([[0, 0], [-10, 0], [-15, -5]]))
# Compute accuracy
score_012 = LDA_012.score(IQ_012_test, state_012_test)
print(score_012)
```
The last step is to plot the separatrix.
```
# Plot separatrix on top of scatter
def separatrixPlot(lda, x_min, x_max, y_min, y_max, shots):
nx, ny = shots, shots
xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
np.linspace(y_min, y_max, ny))
Z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
Z = Z[:, 1].reshape(xx.shape)
plt.contour(xx, yy, Z, [0.5], linewidths=2., colors='black')
IQ_012_plot(x_min, x_max, y_min, y_max)
separatrixPlot(LDA_012, x_min, x_max, y_min, y_max, NUM_SHOTS)
```
Now that we have 3 centroids, the separatrix is no longer a line, but rather a curve containing a combination of two lines. In order to discriminate between $|0\rangle$, $|1\rangle$ and $|2\rangle$ states, our model checks where the IQ point lies relative to the separatrix and classifies the point accordingly.
## References <a id="refs"></a>
1. D. C. McKay, T. Alexander, L. Bello, M. J. Biercuk, L. Bishop, J. Chen, J. M. Chow, A. D. C ́orcoles, D. Egger, S. Filipp, J. Gomez, M. Hush, A. Javadi-Abhari, D. Moreda, P. Nation, B. Paulovicks, E. Winston, C. J. Wood, J. Wootton, and J. M. Gambetta, “Qiskit backend specifications for OpenQASM and OpenPulse experiments,” 2018, https://arxiv.org/abs/1809.03452.
2. Krantz, P. et al. “A Quantum Engineer’s Guide to Superconducting Qubits.” Applied Physics Reviews 6.2 (2019): 021318, https://arxiv.org/abs/1904.06560.
3. Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011, https://scikit-learn.org/stable/modules/lda_qda.html#id4.
```
import qiskit.tools.jupyter
%qiskit_version_table
```
|
github_jupyter
|
# Exploratory Data Analysis Using Python and BigQuery
## Learning Objectives
1. Analyze a Pandas Dataframe
2. Create Seaborn plots for Exploratory Data Analysis in Python
3. Write a SQL query to pick up specific fields from a BigQuery dataset
4. Exploratory Analysis in BigQuery
## Introduction
This lab is an introduction to linear regression using Python and Scikit-Learn. This lab serves as a foundation for more complex algorithms and machine learning models that you will encounter in the course. We will train a linear regression model to predict housing price.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](../labs/python.BQ_explore_data.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
### Import Libraries
```
# Run the chown command to change the ownership
!sudo chown -R jupyter:jupyter /home/jupyter/training-data-analyst
# Install the Google Cloud BigQuery library
!pip install --user google-cloud-bigquery==1.25.0
```
Please ignore any incompatibility warnings and errors.
**Restart** the kernel before proceeding further (On the Notebook menu - Kernel - Restart Kernel).
```
# You can use any Python source file as a module by executing an import statement in some other Python source file.
# The import statement combines two operations; it searches for the named module, then it binds the results of that search
# to a name in the local scope.
import os
import pandas as pd
import numpy as np
# Import matplotlib to visualize the model
import matplotlib.pyplot as plt
# Seaborn is a Python data visualization library based on matplotlib
import seaborn as sns
%matplotlib inline
```
### Load the Dataset
Here, we create a directory called usahousing. This directory will hold the dataset that we copy from Google Cloud Storage.
```
# Create a directory to hold the dataset
if not os.path.isdir("../data/explore"):
os.makedirs("../data/explore")
```
Next, we copy the Usahousing dataset from Google Cloud Storage.
```
# Copy the file using `gsutil cp` from Google Cloud Storage in the required directory
!gsutil cp gs://cloud-training/mlongcp/v3.0_MLonGC/toy_data/housing_pre-proc_toy.csv ../data/explore
```
Then we use the "ls" command to list files in the directory. This ensures that the dataset was copied.
```
# `ls` shows the working directory's contents.
# The `l` flag list the all files with permissions and details
!ls -l ../data/explore
```
Next, we read the dataset into a Pandas dataframe.
```
# TODO 1
# Read a comma-separated values (csv) file into a DataFrame using the read_csv() function
df_USAhousing = pd.read_csv('../data/explore/housing_pre-proc_toy.csv')
```
### Inspect the Data
```
# Get the first five rows using the head() method
df_USAhousing.head()
```
Let's check for any null values.
```
# `isnull()` finds a null value in a column and `sum()` counts it
df_USAhousing.isnull().sum()
# Get some basic statistical details using describe() method
df_stats = df_USAhousing.describe()
# Transpose index and columns of the dataframe
df_stats = df_stats.transpose()
df_stats
# Get a concise summary of a DataFrame
df_USAhousing.info()
```
Let's take a peek at the first and last five rows of the data for all columns.
```
print ("Rows : " ,df_USAhousing.shape[0])
print ("Columns : " ,df_USAhousing.shape[1])
print ("\nFeatures : \n" ,df_USAhousing.columns.tolist())
print ("\nMissing values : ", df_USAhousing.isnull().sum().values.sum())
print ("\nUnique values : \n",df_USAhousing
.nunique())
```
## Explore the Data
Let's create some simple plots to check out the data!
```
# `heatmap` plots a rectangular data in a color-encoded matrix and
# `corr` finds the pairwise correlation of all columns in the dataframe
sns.heatmap(df_USAhousing.corr())
```
Create a displot showing "median_house_value".
```
# TODO 2a
# Plot a univariate distribution of observations using seaborn `distplot()` function
sns.displot(df_USAhousing['median_house_value'])
# Set the aesthetic style of the plots
sns.set_style('whitegrid')
# Plot a histogram using `hist()` function
df_USAhousing['median_house_value'].hist(bins=30)
plt.xlabel('median_house_value')
x = df_USAhousing['median_income']
y = df_USAhousing['median_house_value']
# Scatter plot of y vs x using scatter() and `show()` display all open figures
plt.scatter(x, y)
plt.show()
```
Create a jointplot showing "median_income" versus "median_house_value".
```
# TODO 2b
# `joinplot()` draws a plot of two variables with bivariate and univariate graphs.
sns.jointplot(x='median_income',y='median_house_value',data=df_USAhousing)
# `countplot()` shows the counts of observations in each categorical bin using bars
sns.countplot(x = 'ocean_proximity', data=df_USAhousing)
# takes numeric only?
# plt.figure(figsize=(20,20))
# Draw a multi-plot on every facet using `FacetGrid()`
g = sns.FacetGrid(df_USAhousing, col="ocean_proximity")
# Pass a function and the name of one or more columns in the dataframe
g.map(plt.hist, "households");
# takes numeric only?
# plt.figure(figsize=(20,20))
# Draw a multi-plot on every facet using `FacetGrid()`
g = sns.FacetGrid(df_USAhousing, col="ocean_proximity")
# Pass a function and the name of one or more columns in the dataframe
g.map(plt.hist, "median_income");
```
You can see below that this is the state of California!
```
x = df_USAhousing['latitude']
y = df_USAhousing['longitude']
# Scatter plot of y vs x and display all open figures
plt.scatter(x, y)
plt.show()
```
# Explore and create ML datasets
In this notebook, we will explore data corresponding to taxi rides in New York City to build a Machine Learning model in support of a fare-estimation tool. The idea is to suggest a likely fare to taxi riders so that they are not surprised, and so that they can protest if the charge is much higher than expected.
## Learning objectives
* Access and explore a public BigQuery dataset on NYC Taxi Cab rides
* Visualize your dataset using the Seaborn library
First, **restart the Kernel**. Now, let's start with the Python imports that we need.
```
# Import the python libraries
from google.cloud import bigquery
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
```
<h3> Extract sample data from BigQuery </h3>
The dataset that we will use is <a href="https://console.cloud.google.com/bigquery?project=nyc-tlc&p=nyc-tlc&d=yellow&t=trips&page=table">a BigQuery public dataset</a>. Click on the link, and look at the column names. Switch to the Details tab to verify that the number of records is one billion, and then switch to the Preview tab to look at a few rows.
Let's write a SQL query to pick up interesting fields from the dataset. It's a good idea to get the timestamp in a predictable format.
```
%%bigquery
# SQL query to get a fields from dataset which prints the 10 records
SELECT
FORMAT_TIMESTAMP(
"%Y-%m-%d %H:%M:%S %Z", pickup_datetime) AS pickup_datetime,
pickup_longitude, pickup_latitude, dropoff_longitude,
dropoff_latitude, passenger_count, trip_distance, tolls_amount,
fare_amount, total_amount
# TODO 3
FROM
`nyc-tlc.yellow.trips`
LIMIT 10
```
Let's increase the number of records so that we can do some neat graphs. There is no guarantee about the order in which records are returned, and so no guarantee about which records get returned if we simply increase the LIMIT. To properly sample the dataset, let's use the HASH of the pickup time and return 1 in 100,000 records -- because there are 1 billion records in the data, we should get back approximately 10,000 records if we do this.
We will also store the BigQuery result in a Pandas dataframe named "trips"
```
%%bigquery trips
SELECT
FORMAT_TIMESTAMP(
"%Y-%m-%d %H:%M:%S %Z", pickup_datetime) AS pickup_datetime,
pickup_longitude, pickup_latitude,
dropoff_longitude, dropoff_latitude,
passenger_count,
trip_distance,
tolls_amount,
fare_amount,
total_amount
FROM
`nyc-tlc.yellow.trips`
WHERE
ABS(MOD(FARM_FINGERPRINT(CAST(pickup_datetime AS STRING)), 100000)) = 1
print(len(trips))
# We can slice Pandas dataframes as if they were arrays
trips[:10]
```
<h3> Exploring data </h3>
Let's explore this dataset and clean it up as necessary. We'll use the Python Seaborn package to visualize graphs and Pandas to do the slicing and filtering.
```
# TODO 4
# Use Seaborn `regplot()` function to plot the data and a linear regression model fit.
ax = sns.regplot(
x="trip_distance", y="fare_amount",
fit_reg=False, ci=None, truncate=True, data=trips)
ax.figure.set_size_inches(10, 8)
```
Hmm ... do you see something wrong with the data that needs addressing?
It appears that we have a lot of invalid data that is being coded as zero distance and some fare amounts that are definitely illegitimate. Let's remove them from our analysis. We can do this by modifying the BigQuery query to keep only trips longer than zero miles and fare amounts that are at least the minimum cab fare ($2.50).
Note the extra WHERE clauses.
```
%%bigquery trips
# SQL query with where clause to save the results in the trips dataframe
SELECT
FORMAT_TIMESTAMP(
"%Y-%m-%d %H:%M:%S %Z", pickup_datetime) AS pickup_datetime,
pickup_longitude, pickup_latitude,
dropoff_longitude, dropoff_latitude,
passenger_count,
trip_distance,
tolls_amount,
fare_amount,
total_amount
FROM
`nyc-tlc.yellow.trips`
WHERE
ABS(MOD(FARM_FINGERPRINT(CAST(pickup_datetime AS STRING)), 100000)) = 1
# TODO 4a
AND trip_distance > 0
AND fare_amount >= 2.5
print(len(trips))
# Use Seaborn `regplot()` function to plot the data and a linear regression model fit.
ax = sns.regplot(
x="trip_distance", y="fare_amount",
fit_reg=False, ci=None, truncate=True, data=trips)
ax.figure.set_size_inches(10, 8)
```
What's up with the streaks around 45 dollars and 50 dollars? Those are fixed-amount rides from JFK and La Guardia airports into anywhere in Manhattan, i.e. to be expected. Let's list the data to make sure the values look reasonable.
Let's also examine whether the toll amount is captured in the total amount.
```
tollrides = trips[trips["tolls_amount"] > 0]
tollrides[tollrides["pickup_datetime"] == "2012-02-27 09:19:10 UTC"]
notollrides = trips[trips["tolls_amount"] == 0]
notollrides[notollrides["pickup_datetime"] == "2012-02-27 09:19:10 UTC"]
```
Looking at a few samples above, it should be clear that the total amount reflects fare amount, toll and tip somewhat arbitrarily -- this is because when customers pay cash, the tip is not known. So, we'll use the sum of fare_amount + tolls_amount as what needs to be predicted. Tips are discretionary and do not have to be included in our fare estimation tool.
Let's also look at the distribution of values within the columns.
```
# Print the distribution of values within the columns using `describe()`
trips.describe()
```
Copyright 2021 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
github_jupyter
|
In this notebook, we'll learn how to use GANs to do semi-supervised learning.
In supervised learning, we have a training set of inputs $x$ and class labels $y$. We train a model that takes $x$ as input and gives $y$ as output.
In semi-supervised learning, our goal is still to train a model that takes $x$ as input and generates $y$ as output. However, not all of our training examples have a label $y$. We need to develop an algorithm that is able to get better at classification by studying both labeled $(x, y)$ pairs and unlabeled $x$ examples.
To do this for the SVHN dataset, we'll turn the GAN discriminator into an 11 class discriminator. It will recognize the 10 different classes of real SVHN digits, as well as an 11th class of fake images that come from the generator. The discriminator will get to train on real labeled images, real unlabeled images, and fake images. By drawing on three sources of data instead of just one, it will generalize to the test set much better than a traditional classifier trained on only one source of data.
```
%matplotlib inline
import pickle as pkl
import time
import matplotlib.pyplot as plt
import numpy as np
from scipy.io import loadmat
import tensorflow as tf
!mkdir data
from urllib.request import urlretrieve
from os.path import isfile, isdir
from tqdm import tqdm
data_dir = 'data/'
if not isdir(data_dir):
raise Exception("Data directory doesn't exist!")
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile(data_dir + "train_32x32.mat"):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='SVHN Training Set') as pbar:
urlretrieve(
'http://ufldl.stanford.edu/housenumbers/train_32x32.mat',
data_dir + 'train_32x32.mat',
pbar.hook)
if not isfile(data_dir + "test_32x32.mat"):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='SVHN Training Set') as pbar:
urlretrieve(
'http://ufldl.stanford.edu/housenumbers/test_32x32.mat',
data_dir + 'test_32x32.mat',
pbar.hook)
trainset = loadmat(data_dir + 'train_32x32.mat')
testset = loadmat(data_dir + 'test_32x32.mat')
idx = np.random.randint(0, trainset['X'].shape[3], size=36)
fig, axes = plt.subplots(6, 6, sharex=True, sharey=True, figsize=(5,5),)
for ii, ax in zip(idx, axes.flatten()):
ax.imshow(trainset['X'][:,:,:,ii], aspect='equal')
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
plt.subplots_adjust(wspace=0, hspace=0)
def scale(x, feature_range=(-1, 1)):
# scale to (0, 1)
x = ((x - x.min())/(255 - x.min()))
# scale to feature_range
min, max = feature_range
x = x * (max - min) + min
return x
class Dataset:
def __init__(self, train, test, val_frac=0.5, shuffle=True, scale_func=None):
split_idx = int(len(test['y'])*(1 - val_frac))
self.test_x, self.valid_x = test['X'][:,:,:,:split_idx], test['X'][:,:,:,split_idx:]
self.test_y, self.valid_y = test['y'][:split_idx], test['y'][split_idx:]
self.train_x, self.train_y = train['X'], train['y']
# The SVHN dataset comes with lots of labels, but for the purpose of this exercise,
# we will pretend that there are only 1000.
# We use this mask to say which labels we will allow ourselves to use.
self.label_mask = np.zeros_like(self.train_y)
self.label_mask[0:1000] = 1
self.train_x = np.rollaxis(self.train_x, 3)
self.valid_x = np.rollaxis(self.valid_x, 3)
self.test_x = np.rollaxis(self.test_x, 3)
if scale_func is None:
self.scaler = scale
else:
self.scaler = scale_func
self.train_x = self.scaler(self.train_x)
self.valid_x = self.scaler(self.valid_x)
self.test_x = self.scaler(self.test_x)
self.shuffle = shuffle
def batches(self, batch_size, which_set="train"):
x_name = which_set + "_x"
y_name = which_set + "_y"
num_examples = len(getattr(dataset, y_name))
if self.shuffle:
idx = np.arange(num_examples)
np.random.shuffle(idx)
setattr(dataset, x_name, getattr(dataset, x_name)[idx])
setattr(dataset, y_name, getattr(dataset, y_name)[idx])
if which_set == "train":
dataset.label_mask = dataset.label_mask[idx]
dataset_x = getattr(dataset, x_name)
dataset_y = getattr(dataset, y_name)
for ii in range(0, num_examples, batch_size):
x = dataset_x[ii:ii+batch_size]
y = dataset_y[ii:ii+batch_size]
if which_set == "train":
# When we use the data for training, we need to include
# the label mask, so we can pretend we don't have access
# to some of the labels, as an exercise of our semi-supervised
# learning ability
yield x, y, self.label_mask[ii:ii+batch_size]
else:
yield x, y
def model_inputs(real_dim, z_dim):
inputs_real = tf.placeholder(tf.float32, (None, *real_dim), name='input_real')
inputs_z = tf.placeholder(tf.float32, (None, z_dim), name='input_z')
y = tf.placeholder(tf.int32, (None), name='y')
label_mask = tf.placeholder(tf.int32, (None), name='label_mask')
return inputs_real, inputs_z, y, label_mask
def generator(z, output_dim, reuse=False, alpha=0.2, training=True, size_mult=128):
with tf.variable_scope('generator', reuse=reuse):
# First fully connected layer
x1 = tf.layers.dense(z, 4 * 4 * size_mult * 4)
# Reshape it to start the convolutional stack
x1 = tf.reshape(x1, (-1, 4, 4, size_mult * 4))
x1 = tf.layers.batch_normalization(x1, training=training)
x1 = tf.maximum(alpha * x1, x1)
x2 = tf.layers.conv2d_transpose(x1, size_mult * 2, 5, strides=2, padding='same')
x2 = tf.layers.batch_normalization(x2, training=training)
x2 = tf.maximum(alpha * x2, x2)
x3 = tf.layers.conv2d_transpose(x2, size_mult, 5, strides=2, padding='same')
x3 = tf.layers.batch_normalization(x3, training=training)
x3 = tf.maximum(alpha * x3, x3)
# Output layer
logits = tf.layers.conv2d_transpose(x3, output_dim, 5, strides=2, padding='same')
out = tf.tanh(logits)
return out
def discriminator(x, reuse=False, alpha=0.2, drop_rate=0., num_classes=10, size_mult=64):
with tf.variable_scope('discriminator', reuse=reuse):
x = tf.layers.dropout(x, rate=drop_rate/2.5)
# Input layer is 32x32x3
x1 = tf.layers.conv2d(x, size_mult, 3, strides=2, padding='same')
relu1 = tf.maximum(alpha * x1, x1)
relu1 = tf.layers.dropout(relu1, rate=drop_rate)
x2 = tf.layers.conv2d(relu1, size_mult, 3, strides=2, padding='same')
bn2 = tf.layers.batch_normalization(x2, training=True)
relu2 = tf.maximum(alpha * x2, x2)
x3 = tf.layers.conv2d(relu2, size_mult, 3, strides=2, padding='same')
bn3 = tf.layers.batch_normalization(x3, training=True)
relu3 = tf.maximum(alpha * bn3, bn3)
relu3 = tf.layers.dropout(relu3, rate=drop_rate)
x4 = tf.layers.conv2d(relu3, 2 * size_mult, 3, strides=1, padding='same')
bn4 = tf.layers.batch_normalization(x4, training=True)
relu4 = tf.maximum(alpha * bn4, bn4)
x5 = tf.layers.conv2d(relu4, 2 * size_mult, 3, strides=1, padding='same')
bn5 = tf.layers.batch_normalization(x5, training=True)
relu5 = tf.maximum(alpha * bn5, bn5)
x6 = tf.layers.conv2d(relu5, 2 * size_mult, 3, strides=2, padding='same')
bn6 = tf.layers.batch_normalization(x6, training=True)
relu6 = tf.maximum(alpha * bn6, bn6)
relu6 = tf.layers.dropout(relu6, rate=drop_rate)
x7 = tf.layers.conv2d(relu5, 2 * size_mult, 3, strides=1, padding='valid')
# Don't use bn on this layer, because bn would set the mean of each feature
# to the bn mu parameter.
# This layer is used for the feature matching loss, which only works if
# the means can be different when the discriminator is run on the data than
# when the discriminator is run on the generator samples.
relu7 = tf.maximum(alpha * x7, x7)
# Flatten it by global average pooling
features = raise NotImplementedError()
# Set class_logits to be the inputs to a softmax distribution over the different classes
raise NotImplementedError()
# Set gan_logits such that P(input is real | input) = sigmoid(gan_logits).
# Keep in mind that class_logits gives you the probability distribution over all the real
# classes and the fake class. You need to work out how to transform this multiclass softmax
# distribution into a binary real-vs-fake decision that can be described with a sigmoid.
# Numerical stability is very important.
# You'll probably need to use this numerical stability trick:
# log sum_i exp a_i = m + log sum_i exp(a_i - m).
# This is numerically stable when m = max_i a_i.
# (It helps to think about what goes wrong when...
# 1. One value of a_i is very large
# 2. All the values of a_i are very negative
# This trick and this value of m fix both those cases, but the naive implementation and
# other values of m encounter various problems)
raise NotImplementedError()
return out, class_logits, gan_logits, features
def model_loss(input_real, input_z, output_dim, y, num_classes, label_mask, alpha=0.2, drop_rate=0.):
"""
Get the loss for the discriminator and generator
:param input_real: Images from the real dataset
:param input_z: Z input
:param output_dim: The number of channels in the output image
:param y: Integer class labels
:param num_classes: The number of classes
:param alpha: The slope of the left half of leaky ReLU activation
:param drop_rate: The probability of dropping a hidden unit
:return: A tuple of (discriminator loss, generator loss)
"""
# These numbers multiply the size of each layer of the generator and the discriminator,
# respectively. You can reduce them to run your code faster for debugging purposes.
g_size_mult = 32
d_size_mult = 64
# Here we run the generator and the discriminator
g_model = generator(input_z, output_dim, alpha=alpha, size_mult=g_size_mult)
d_on_data = discriminator(input_real, alpha=alpha, drop_rate=drop_rate, size_mult=d_size_mult)
d_model_real, class_logits_on_data, gan_logits_on_data, data_features = d_on_data
d_on_samples = discriminator(g_model, reuse=True, alpha=alpha, drop_rate=drop_rate, size_mult=d_size_mult)
d_model_fake, class_logits_on_samples, gan_logits_on_samples, sample_features = d_on_samples
# Here we compute `d_loss`, the loss for the discriminator.
# This should combine two different losses:
# 1. The loss for the GAN problem, where we minimize the cross-entropy for the binary
# real-vs-fake classification problem.
# 2. The loss for the SVHN digit classification problem, where we minimize the cross-entropy
# for the multi-class softmax. For this one we use the labels. Don't forget to ignore
# use `label_mask` to ignore the examples that we are pretending are unlabeled for the
# semi-supervised learning problem.
raise NotImplementedError()
# Here we set `g_loss` to the "feature matching" loss invented by Tim Salimans at OpenAI.
# This loss consists of minimizing the absolute difference between the expected features
# on the data and the expected features on the generated samples.
# This loss works better for semi-supervised learning than the tradition GAN losses.
raise NotImplementedError()
pred_class = tf.cast(tf.argmax(class_logits_on_data, 1), tf.int32)
eq = tf.equal(tf.squeeze(y), pred_class)
correct = tf.reduce_sum(tf.to_float(eq))
masked_correct = tf.reduce_sum(label_mask * tf.to_float(eq))
return d_loss, g_loss, correct, masked_correct, g_model
def model_opt(d_loss, g_loss, learning_rate, beta1):
"""
Get optimization operations
:param d_loss: Discriminator loss Tensor
:param g_loss: Generator loss Tensor
:param learning_rate: Learning Rate Placeholder
:param beta1: The exponential decay rate for the 1st moment in the optimizer
:return: A tuple of (discriminator training operation, generator training operation)
"""
# Get weights and biases to update. Get them separately for the discriminator and the generator
raise NotImplementedError()
# Minimize both players' costs simultaneously
raise NotImplementedError()
shrink_lr = tf.assign(learning_rate, learning_rate * 0.9)
return d_train_opt, g_train_opt, shrink_lr
class GAN:
"""
A GAN model.
:param real_size: The shape of the real data.
:param z_size: The number of entries in the z code vector.
:param learnin_rate: The learning rate to use for Adam.
:param num_classes: The number of classes to recognize.
:param alpha: The slope of the left half of the leaky ReLU activation
:param beta1: The beta1 parameter for Adam.
"""
def __init__(self, real_size, z_size, learning_rate, num_classes=10, alpha=0.2, beta1=0.5):
tf.reset_default_graph()
self.learning_rate = tf.Variable(learning_rate, trainable=False)
inputs = model_inputs(real_size, z_size)
self.input_real, self.input_z, self.y, self.label_mask = inputs
self.drop_rate = tf.placeholder_with_default(.5, (), "drop_rate")
loss_results = model_loss(self.input_real, self.input_z,
real_size[2], self.y, num_classes,
label_mask=self.label_mask,
alpha=0.2,
drop_rate=self.drop_rate)
self.d_loss, self.g_loss, self.correct, self.masked_correct, self.samples = loss_results
self.d_opt, self.g_opt, self.shrink_lr = model_opt(self.d_loss, self.g_loss, self.learning_rate, beta1)
def view_samples(epoch, samples, nrows, ncols, figsize=(5,5)):
fig, axes = plt.subplots(figsize=figsize, nrows=nrows, ncols=ncols,
sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
ax.axis('off')
img = ((img - img.min())*255 / (img.max() - img.min())).astype(np.uint8)
ax.set_adjustable('box-forced')
im = ax.imshow(img)
plt.subplots_adjust(wspace=0, hspace=0)
return fig, axes
def train(net, dataset, epochs, batch_size, figsize=(5,5)):
saver = tf.train.Saver()
sample_z = np.random.normal(0, 1, size=(50, z_size))
samples, train_accuracies, test_accuracies = [], [], []
steps = 0
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epochs):
print("Epoch",e)
t1e = time.time()
num_examples = 0
num_correct = 0
for x, y, label_mask in dataset.batches(batch_size):
assert 'int' in str(y.dtype)
steps += 1
num_examples += label_mask.sum()
# Sample random noise for G
batch_z = np.random.normal(0, 1, size=(batch_size, z_size))
# Run optimizers
t1 = time.time()
_, _, correct = sess.run([net.d_opt, net.g_opt, net.masked_correct],
feed_dict={net.input_real: x, net.input_z: batch_z,
net.y : y, net.label_mask : label_mask})
t2 = time.time()
num_correct += correct
sess.run([net.shrink_lr])
train_accuracy = num_correct / float(num_examples)
print("\t\tClassifier train accuracy: ", train_accuracy)
num_examples = 0
num_correct = 0
for x, y in dataset.batches(batch_size, which_set="test"):
assert 'int' in str(y.dtype)
num_examples += x.shape[0]
correct, = sess.run([net.correct], feed_dict={net.input_real: x,
net.y : y,
net.drop_rate: 0.})
num_correct += correct
test_accuracy = num_correct / float(num_examples)
print("\t\tClassifier test accuracy", test_accuracy)
print("\t\tStep time: ", t2 - t1)
t2e = time.time()
print("\t\tEpoch time: ", t2e - t1e)
gen_samples = sess.run(
net.samples,
feed_dict={net.input_z: sample_z})
samples.append(gen_samples)
_ = view_samples(-1, samples, 5, 10, figsize=figsize)
plt.show()
# Save history of accuracies to view after training
train_accuracies.append(train_accuracy)
test_accuracies.append(test_accuracy)
saver.save(sess, './checkpoints/generator.ckpt')
with open('samples.pkl', 'wb') as f:
pkl.dump(samples, f)
return train_accuracies, test_accuracies, samples
!mkdir checkpoints
real_size = (32,32,3)
z_size = 100
learning_rate = 0.0003
net = GAN(real_size, z_size, learning_rate)
dataset = Dataset(trainset, testset)
batch_size = 128
epochs = 25
train_accuracies, test_accuracies, samples = train(net,
dataset,
epochs,
batch_size,
figsize=(10,5))
fig, ax = plt.subplots()
plt.plot(train_accuracies, label='Train', alpha=0.5)
plt.plot(test_accuracies, label='Test', alpha=0.5)
plt.title("Accuracy")
plt.legend()
```
When you run the fully implemented semi-supervised GAN, you should usually find that the test accuracy peaks at 69-71%. It should definitely stay above 68% fairly consistently throughout the last several epochs of training.
This is a little bit better than a [NIPS 2014 paper](https://arxiv.org/pdf/1406.5298.pdf) that got 64% accuracy on 1000-label SVHN with variational methods. However, we still have lost something by not using all the labels. If you re-run with all the labels included, you should obtain over 80% accuracy using this architecture (and other architectures that take longer to run can do much better).
```
_ = view_samples(-1, samples, 5, 10, figsize=(10,5))
!mkdir images
for ii in range(len(samples)):
fig, ax = view_samples(ii, samples, 5, 10, figsize=(10,5))
fig.savefig('images/samples_{:03d}.png'.format(ii))
plt.close()
```
Congratulations! You now know how to train a semi-supervised GAN. This exercise is stripped down to make it run faster and to make it simpler to implement. In the original work by Tim Salimans at OpenAI, a GAN using [more tricks and more runtime](https://arxiv.org/pdf/1606.03498.pdf) reaches over 94% accuracy using only 1,000 labeled examples.
|
github_jupyter
|
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from mlxtend.frequent_patterns import apriori, association_rules
from collections import Counter
# dataset = pd.read_csv("data.csv",encoding= 'unicode_escape')
dataset = pd.read_excel("Online Retail.xlsx")
dataset.head()
dataset.shape
## Verify missing value
dataset.isnull().sum().sort_values(ascending=False)
## Remove missing values
dataset1 = dataset.dropna()
dataset1.describe()
#selecting data where quantity > 0
dataset1= dataset1[dataset1.Quantity > 0]
dataset1.describe()
# Creating a new feature 'Amount' which is the product of Quantity and its Unit Price
dataset1['Amount'] = dataset1['Quantity'] * dataset1['UnitPrice']
# to highlight the Customers with most no. of orders (invoices) with groupby function
orders = dataset1.groupby(by=['CustomerID','Country'], as_index=False)['InvoiceNo'].count()
print('The TOP 5 loyal customers with most number of orders...')
orders.sort_values(by='InvoiceNo', ascending=False).head()
# Creating a subplot of size 15x6
plt.subplots(figsize=(15,6))
# Using the style bmh for better visualization
plt.style.use('bmh')
# X axis will denote the customer ID, Y axis will denote the number of orders
plt.plot(orders.CustomerID, orders.InvoiceNo)
# Labelling the X axis
plt.xlabel('Customers ID')
# Labelling the Y axis
plt.ylabel('Number of Orders')
# Title to the plot
plt.title('Number of Orders by different Customers')
plt.show()
#Using groupby function to highlight the Customers with highest spent amount (invoices)
money = dataset1.groupby(by=['CustomerID','Country'], as_index=False)['Amount'].sum()
print('The TOP 5 profitable customers with highest money spent...')
money.sort_values(by='Amount', ascending=False).head()
# Creating a subplot of size 15*6
plt.subplots(figsize=(15,6))
# X axis will denote the customer ID, Y axis will denote the amount spent
plt.plot(money.CustomerID, money.Amount)
# Using bmh style for better visualization
plt.style.use('bmh')
# Labelling the X-axis
plt.xlabel('Customers ID')
# Labelling the Y-axis
plt.ylabel('Money spent')
# Giving a suitable title to the plot
plt.title('Money Spent by different Customers')
plt.show()
# Convert InvoiceDate from object to datetime
dataset1['InvoiceDate'] = pd.to_datetime(dataset.InvoiceDate, format='%m/%d/%Y %H:%M')
# Creating a new feature called year_month, such that December 2010 will be denoted as 201012
dataset1.insert(loc=2, column='year_month', value=dataset1['InvoiceDate'].map(lambda x: 100*x.year + x.month))
# Creating a new feature for Month
dataset1.insert(loc=3, column='month', value=dataset1.InvoiceDate.dt.month)
# Creating a new feature for Day
# +1 to make Monday=1.....until Sunday=7
dataset1.insert(loc=4, column='day', value=(dataset1.InvoiceDate.dt.dayofweek)+1)
# Creating a new feature for Hour
dataset1.insert(loc=5, column='hour', value=dataset1.InvoiceDate.dt.hour)
# Using bmh style for better visualization
plt.style.use('bmh')
# Using groupby to extract No. of Invoices year-monthwise
ax = dataset1.groupby('InvoiceNo')['year_month'].unique().value_counts().sort_index().plot(kind='bar',figsize=(15,6))
# Labelling the X axis
ax.set_xlabel('Month',fontsize=15)
# Labelling the Y-axis
ax.set_ylabel('Number of Orders',fontsize=15)
# Giving suitable title to the plot
ax.set_title('Number of orders for different Months (Dec 2010 - Dec 2011)',fontsize=15)
# Providing with X tick labels
ax.set_xticklabels(('Dec_10','Jan_11','Feb_11','Mar_11','Apr_11','May_11','Jun_11','July_11','Aug_11','Sep_11','Oct_11','Nov_11','Dec_11'), rotation='horizontal', fontsize=13)
plt.show()
# Day = 6 is Saturday.no orders placed
dataset1[dataset1['day']==6]
# Using groupby to count no. of Invoices daywise
ax = dataset1.groupby('InvoiceNo')['day'].unique().value_counts().sort_index().plot(kind='bar',figsize=(15,6))
# Labelling X axis
ax.set_xlabel('Day',fontsize=15)
# Labelling Y axis
ax.set_ylabel('Number of Orders',fontsize=15)
# Giving suitable title to the plot
ax.set_title('Number of orders for different Days',fontsize=15)
# Providing with X tick labels
# Since there are no orders placed on Saturdays, we are excluding Sat from xticklabels
ax.set_xticklabels(('Mon','Tue','Wed','Thur','Fri','Sun'), rotation='horizontal', fontsize=15)
plt.show()
# Using groupby to count the no. of Invoices hourwise
ax = dataset1.groupby('InvoiceNo')['hour'].unique().value_counts().iloc[:-2].sort_index().plot(kind='bar',figsize=(15,6))
# Labelling X axis
ax.set_xlabel('Hour',fontsize=15)
# Labelling Y axis
ax.set_ylabel('Number of Orders',fontsize=15)
# Giving suitable title to the plot
ax.set_title('Number of orders for different Hours', fontsize=15)
# Providing with X tick lables ( all orders are placed between 6 and 20 hour )
ax.set_xticklabels(range(6,21), rotation='horizontal', fontsize=15)
plt.show()
dataset1.UnitPrice.describe()
# checking the distribution of unit price
plt.subplots(figsize=(12,6))
# Using darkgrid style for better visualization
sns.set_style('darkgrid')
# Applying boxplot visualization on Unit Price
sns.boxplot(dataset1.UnitPrice)
plt.show()
# Creating a new df of free items
freeproducts = dataset1[dataset1['UnitPrice'] == 0]
freeproducts.head()
# Counting how many free items were given out year-month wise
freeproducts.year_month.value_counts().sort_index()
# Counting how many free items were given out year-month wise
ax = freeproducts.year_month.value_counts().sort_index().plot(kind='bar',figsize=(12,6))
# Labelling X-axis
ax.set_xlabel('Month',fontsize=15)
# Labelling Y-axis
ax.set_ylabel('Frequency',fontsize=15)
# Giving suitable title to the plot
ax.set_title('Frequency for different Months (Dec 2010 - Dec 2011)',fontsize=15)
# Providing X tick labels
# Since there are 0 free items in June 2011, we are excluding it
ax.set_xticklabels(('Dec_10','Jan_11','Feb_11','Mar_11','Apr_11','May_11','July_11','Aug_11','Sep_11','Oct_11','Nov_11'), rotation='horizontal', fontsize=13)
plt.show()
plt.style.use('bmh')
# Using groupby to sum the amount spent year-month wise
ax = dataset1.groupby('year_month')['Amount'].sum().sort_index().plot(kind='bar',figsize=(15,6))
# Labelling X axis
ax.set_xlabel('Month',fontsize=15)
# Labelling Y axis
ax.set_ylabel('Amount',fontsize=15)
# Giving suitable title to the plot
ax.set_title('Revenue Generated for different Months (Dec 2010 - Dec 2011)',fontsize=15)
# Providing with X tick labels
ax.set_xticklabels(('Dec_10','Jan_11','Feb_11','Mar_11','Apr_11','May_11','Jun_11','July_11','Aug_11','Sep_11','Oct_11','Nov_11','Dec_11'), rotation='horizontal', fontsize=13)
plt.show()
# Creating a new pivot table which sums the Quantity ordered for each item
most_sold= dataset1.pivot_table(index=['StockCode','Description'], values='Quantity', aggfunc='sum').sort_values(by='Quantity', ascending=False)
most_sold.reset_index(inplace=True)
sns.set_style('white')
# Creating a bar plot of Description ( or the item ) on the Y axis and the sum of Quantity on the X axis
# We are plotting only the 10 most ordered items
sns.barplot(y='Description', x='Quantity', data=most_sold.head(10))
# Giving suitable title to the plot
plt.title('Top 10 Items based on No. of Sales', fontsize=14)
plt.ylabel('Item')
# choosing WHITE HANGING HEART T-LIGHT HOLDER as a sample
d_white = dataset1[dataset1['Description']=='WHITE HANGING HEART T-LIGHT HOLDER']
# WHITE HANGING HEART T-LIGHT HOLDER has been ordered 2028 times
d_white.shape
# WHITE HANGING HEART T-LIGHT HOLDER has been ordered by 856 customers
len(d_white.CustomerID.unique())
# Creating a pivot table that displays the sum of unique Customers who bought particular item
most_customers = dataset1.pivot_table(index=['StockCode','Description'], values='CustomerID', aggfunc=lambda x: len(x.unique())).sort_values(by='CustomerID', ascending=False)
most_customers
# Since the count for WHITE HANGING HEART T-LIGHT HOLDER matches above length 856, the pivot table looks correct for all items
most_customers.reset_index(inplace=True)
sns.set_style('white')
# Creating a bar plot of Description ( or the item ) on the Y axis and the sum of unique Customers on the X axis
# We are plotting only the 10 most bought items
sns.barplot(y='Description', x='CustomerID', data=most_customers.head(10))
# Giving suitable title to the plot
plt.title('Top 10 Items bought by Most no. of Customers', fontsize=14)
plt.ylabel('Item')
# Storing all the invoice numbers into a list y
y = dataset1['InvoiceNo']
y = y.to_list()
# Using set function to find unique invoice numbers only and storing them in invoices list
invoices = list(set(y))
# Creating empty list first_choices
firstchoices = []
# looping into list of unique invoice numbers
for i in invoices:
# the first item (index = 0) of every invoice is the first purchase
# extracting the item name for the first purchase
firstpurchase = dataset1[dataset1['InvoiceNo']==i]['items'].reset_index(drop=True)[0]
# Appending the first purchase name into first choices list
firstchoices.append(firstpurchase)
firstchoices[:5]
# Using counter to count repeating first choices
count = Counter(firstchoices)
# Storing the counter into a datafrane
data_first_choices = pd.DataFrame.from_dict(count, orient='index').reset_index()
# Rename columns as item and count
data_first_choices.rename(columns={'index':'item', 0:'count'},inplace=True)
# Sorting the data based on count
data_first_choices.sort_values(by='count',ascending=False)
plt.subplots(figsize=(20,10))
sns.set_style('white')
# Creating a bar plot that displays Item name on the Y axis and Count on the X axis
sns.barplot(y='item', x='count', data=data_first_choices.sort_values(by='count',ascending=False).head(10))
# Giving suitable title to the plot
plt.title('Top 10 First Choices', fontsize=14)
plt.ylabel('Item')
basket = (dataset1.groupby(['InvoiceNo', 'Description'])['Quantity'].sum().unstack().reset_index().fillna(0).set_index('InvoiceNo'))
basket.head(10)
def encode_u(x):
if x < 1:
return 0
if x >= 1:
return 1
basket = basket.applymap(encode_u)
# everything is encoded into 0 and 1
basket.head(10)
# trying out on a sample item
wooden_star = basket.loc[basket['WOODEN STAR CHRISTMAS SCANDINAVIAN']==1]
# Using apriori algorithm, creating association rules for the sample item
# Applying apriori algorithm for wooden_star
frequentitemsets = apriori(wooden_star, min_support=0.15, use_colnames=True)
# Storing the association rules into rules
wooden_star_rules = association_rules(frequentitemsets, metric="lift", min_threshold=1)
# Sorting the rules on lift and support
wooden_star_rules.sort_values(['lift','support'],ascending=False).reset_index(drop=True)
# In other words, it returns the items which are likely to be bought by user because he bought the item passed into function
def frequently_bought_t(item):
# df of item passed
item_d = basket.loc[basket[item]==1]
# Applying apriori algorithm on item df
frequentitemsets = apriori(item_d, min_support=0.15, use_colnames=True)
# Storing association rules
rules = association_rules(frequentitemsets, metric="lift", min_threshold=1)
# Sorting on lift and support
rules.sort_values(['lift','support'],ascending=False).reset_index(drop=True)
print('Items frequently bought together with {0}'.format(item))
# Returning top 6 items with highest lift and support
return rules['consequents'].unique()[:6]
frequently_bought_t('WOODEN STAR CHRISTMAS SCANDINAVIAN')
frequently_bought_t('JAM MAKING SET WITH JARS')
```
|
github_jupyter
|
```
import sys
import pickle
import numpy as np
import tensorflow as tf
import PIL.Image
%matplotlib inline
import matplotlib.pyplot as plt
```
##### Set the path to directory containing code of this case
```
new_path = r'/home/users/suihong/3-Cond_wellfacies-upload/'
sys.path.append(new_path)
```
#### Set the path to data directory; this directory includes two datasets: "trainingdata" and "testdata"
```
data_dir_test = '/scratch/users/suihong/DataSets(MultiChannels_Version4_Consistency)/'
```
#### Set path to trained network
```
# 19200 means totally 19200 thousand training images (facies models) used for the training
network_dir = '/scratch/users/suihong/ProGAN_MultiChannel_Reusults_ConditionedtoMultiConditions_TF/099-pgan-cond-Well-sinuosity-2gpu/'
network_name = 'network-snapshot-025920.pkl'
```
### 1. Fetch dataset
```
# Initialize TensorFlow session.
tf.InteractiveSession()
import dataset
# tfrecord_dir='TestData' to fetch test dataset, if tfrecord_dir='TrainingData' to fetch training dataset
# labeltypes: 0 for 'channelorientation', 1 for 'mudproportion', 2 for 'channelwidth', 3 for 'channelsinuosity'
# well_enlarge: if True, well points occupy 4x4 area, otherwise occupy 1x1 area
test_set = dataset.load_dataset(data_dir=data_dir_test, verbose=True, tfrecord_dir='TestData', labeltypes = [1,2,3], well_enlarge = True, shuffle_mb = 0, prefetch_mb = 0)
# labels are from -1 to 1
image_test, label_test = test_set.get_minibatch_imageandlabel_np(3000)
probimg_test, wellfacies_test = test_set.get_minibatch_probandwell_np(3000*8)
print(image_test.shape)
print(label_test.shape)
print(probimg_test.shape)
print(wellfacies_test.shape)
plt.imshow(wellfacies_test[55,0])
plt.imshow(image_test[60,0])
plt.colorbar()
```
#### Global features are kept and inputted into Networks with the scale of -1 to 1. To recover the global features into its original scales, use the below transformation functions.
```
# index in label_test[:,0], e.g., "0" here, needs to be adjusted according to the setting of "labeltypes = [3]" in previous "dataset.load_dataset(..)" function
#orit_test = (label_test[:,0]/2+0.5)*168-84
back_ratio_test = (label_test[:,0]/2+0.5)*0.8037109375+0.167724609375
width_test = (label_test[:,1]/2+0.5)*0.8+2.7
amwv_ratio_test = (label_test[:,2]/2+0.5)*0.4866197183098592+0.06338028169014084
```
### 2. Import pre-trained Network
```
# Initialize TensorFlow session.
tf.InteractiveSession()
# Import networks.
with open(network_dir+network_name, 'rb') as file:
G, D, Gs = pickle.load(file)
```
### 3. Evaluation of the imported pretrained Generator
### 3.1 Fetch 300 inputs from Test dataset
```
# Sample 300 global features, probability maps, and well facies data
faciesmodels_real = image_test[:3000]
labels_inspect = label_test[:3000]
proborder = np.arange(3000) * 8 + np.random.RandomState(32).randint(0, 8, size=3000)
wellfacies_inspect_init = wellfacies_test[proborder]
wellfacies_points_inspect = np.where(wellfacies_inspect_init>0, 1, 0)
wellfacies_facies_inspect = np.where(wellfacies_inspect_init<1.5, 0, 1)
wellfacies_inspect = np.concatenate([wellfacies_points_inspect, wellfacies_facies_inspect], 1)
print(labels_inspect.shape)
print(wellfacies_inspect.shape)
```
##### Create masks to only output visualize well facies against white background
```
### Enlarge areas of well points for displaying ###
wellfacies_onechannel = wellfacies_inspect[:,0:1]+wellfacies_inspect[:,1:2]
wellfacies_onechannel_mask = np.ma.masked_where(wellfacies_onechannel == 0, wellfacies_onechannel)
cmap_well = plt.cm.viridis # Can be any colormap that you want after the cm '.
cmap_well.set_bad(color='white')
```
### 3.2 General visual assessment
#### Visual assessment on realism, diversity, conditioning to global features, conditioning to well facies data
* (1) Input corresponding global features with well data into trained Generator
Second column corresponds to ground truth for well facies data and global features.
```
print(Gs.input_shapes)
fig, ax = plt.subplots(8, 16, sharex='col', sharey='row')
fig.set_size_inches(25, 12.5, forward=True)
images_plt_average = np.zeros((8,1,64,64))
for i in range (8):
ax[i, 0].imshow(wellfacies_onechannel_mask[i,0], cmap=cmap_well, vmax = 2.15)
ax[i, 1].imshow(faciesmodels_real[i,0,:,:]) # *15+50 is to create inconsistency between labels and probimg
latents_plt = np.random.randn(500, Gs.input_shapes[0][1])
labels_plt = np.repeat(np.expand_dims(labels_inspect[i,2:3], axis=0), 500, axis=0) ##
wellfacies_plt = np.repeat(np.expand_dims(wellfacies_inspect[i], axis=0), 500, axis=0)
images_plt = Gs.run(latents_plt, labels_plt, wellfacies_plt)
images_plt = np.where(images_plt< -0.3, -1, images_plt)
images_plt = np.where(images_plt> 0.3, 1, images_plt)
images_plt = np.where((images_plt> -0.4) & (images_plt< 0.4), 0, images_plt)
images_plt_a = (np.where(images_plt> -0.2, 1, images_plt) + 1)/2
images_plt_average[i] = np.average(images_plt_a, axis = 0)
for j in range(2,15):
ax[i, j].imshow(images_plt[j-2,0,:,:])
ax[i, 15].imshow(images_plt_average[i, 0])
#plt.savefig(network_dir + "Random Latents.png", dpi=200)
```
### 3.3 Evaluation of Generator's conditioning ability to global features
#### 3.3.1 Visual assessment by comparing to corresponding ground truth facies models.
* Generate facies models with increasing input sinuosity index
** Choose appropriate increasing global features from test data. **
These chosen global features will be used to simulate facies models; these facies models will be compared to ground truth facies models with the same global features in test dataset
** Choose appropriate increasing global features from test data. **
```
amwv_ratio_no = 4
amwv_ratio_test_max = np.max(amwv_ratio_test)
amwv_ratio_test_min = np.min(amwv_ratio_test)
plot_img_no = np.empty((amwv_ratio_no), dtype = np.int)
for j in range(amwv_ratio_no):
for r in range(amwv_ratio_test.shape[0]):
if amwv_ratio_test[r] >= (amwv_ratio_test_max - amwv_ratio_test_min) * j/amwv_ratio_no+amwv_ratio_test_min and \
amwv_ratio_test[r] < (amwv_ratio_test_max - amwv_ratio_test_min) * (j+1)/amwv_ratio_no+amwv_ratio_test_min and \
back_ratio_test[r] >= 0.5 and back_ratio_test[r] <0.6:
plot_img_no[j] = r
break
print(plot_img_no)
```
##### Simulate with the above chosen appropriate global features
```
# This cell is only used for evaluation of conditioning to sinuosity when the GAN is only conditioning to sinuosity and well facies data
fig, ax = plt.subplots(4, 16, sharex='col', sharey='row')
fig.set_size_inches(24, 6, forward=True)
images_plt_average = np.zeros((4,1,64,64))
images_plt_variance = np.zeros((4,1,64,64))
for i in range (4):
gt_no = plot_img_no[i]
ax[i, 0].imshow(faciesmodels_real[gt_no,0,:,:])
ax[i, 1].imshow(wellfacies_onechannel_mask[gt_no,0], cmap=cmap_well, vmax = 2.15)
latents_plt = np.random.randn(500, Gs.input_shapes[0][1])
labels_plt = np.repeat(np.expand_dims(labels_inspect[gt_no,3:4], axis=0), 500, axis=0) ##
wellfacies_plt = np.repeat(np.expand_dims(wellfacies_inspect[gt_no], axis=0), 1 * 500, axis=0)
images_plt = Gs.run(latents_plt, labels_plt, wellfacies_plt)
images_plt = np.where(images_plt< -0.3, -1, images_plt)
images_plt = np.where(images_plt> 0.3, 1, images_plt)
images_plt = np.where((images_plt> -0.4) & (images_plt< 0.4), 0, images_plt)
images_plt_a = np.where(images_plt> -0.3, 1, 0)
images_plt_average[i] = np.average(images_plt_a, axis = 0)
images_plt_variance[i] = np.var(images_plt_a, axis = 0)
for j in range(2,14):
ax[i, j].imshow(images_plt[j-2,0,:,:])
ax[i, 14].imshow(images_plt_average[i, 0], vmin = 0, vmax = 1)
ax[i, 15].imshow(images_plt_variance[i, 0], vmin = 0, vmax = 0.25)
plt.savefig(network_dir + "Condition to sinuosity1.png", dpi=200)
print(plot_img_no)
print(amwv_ratio_test[plot_img_no])
```
#### 3.3.2 Quantitative assessment by comparing to corresponding ground truth facies models.
#### * Assess channel sinuosity
#### Second quantitative evaluation method in paper.
##### 1) With input global features from test dataset, generate a number of facies model realizations;
##### 2) Use image process toolbox in Matlab to measure the channel sand sinuosity for each generated facies model and the real facies model in test dataset;
##### 3) Use blox plot to compare the distribution of calculated global features from the generated facies models and the real facies models from test dataset.
```
latents_plt = np.random.RandomState(99).randn(300, Gs.input_shapes[0][1])
labels_plt = label_test[:300, 3:4]
wellfacies_plt = wellfacies_inspect[:300]
# Run the generator to produce a set of images.
images_plt = Gs.run(latents_plt, labels_plt,wellfacies_plt)
images_plt = np.where(images_plt< -0.3, -1, images_plt)
images_plt = np.where(images_plt> 0.3, 1, images_plt)
images_plt = np.where((images_plt> -0.4) & (images_plt< 0.4), 0, images_plt)
# Save the generated facies models to measure their global features in Matlab
np.savetxt(network_dir + 'images_generated.out', np.reshape(images_plt,[-1,64]), delimiter='\n', fmt='%1.1e') # X is an array
np.savetxt(network_dir + 'input_sinuosity.out', amwv_ratio_test[:300], delimiter=',', fmt='%1.4e')
# Calculate corresponding mud facies proportion, used for falsification
props = np.average(np.where(images_plt < -0.5, 1, 0), axis = (1, 2, 3))
np.savetxt(network_dir + 'images_generated_variouswelldata.out', props, delimiter='\n', fmt='%1.4e')
```
###### Box plot
```
# statistics of generated facies models with differnt input sinuosity
atodlen1=[1.11889313640155,1.09077787644318,1.12165645035333,1.09007474127227,1.13424798563159,1.13978293428402,1.11589740130591,1.08779763348608,1.10422031446294,1.17915902056786,1.02510382912376,1.17754080734206,1.10875489964738,1.18006034468054,1.27723890880682,1.14638300311517,1.08693130776357,1.1252197699912,1.109755804729,1.16673251350461,1.06846449139615,1.17203190188304,1.16330998283785,1.0672391301468,1.08866531192593,1.12416211546016,1.08876828138484,1.13792798971085,1.08172883034534,1.21580531837135,1.16354479912917,1.08044443747823,1.10654455347437,1.10174692816356,1.15188569360076,1.1405607079217,1.18031308206105,1.18542732746059,1.1232360416386,1.08106615903648,1.03094429058473,1.09190293169268,1.11142403382545,1.16616135904274,1.10355341434478,1.16389655030855,1.16659102541762,1.13192857588692,1.07118203692042,1.1266728660161,1.07459689798195,1.09970672681694,1.10635609001926,1.13221228463309,1.11750625345516,1.14314916661737,1.20083274841309,1.20504213919236,1.18240699508685,1.08712839696534,1.2260388931612,1.12483686658524,1.13391254500886,1.11078855865792,1.1359207331302,1.22642969615047]
atodlen2=[1.23346416627969,1.18790795871182,1.13206343645113,1.15338398825942,1.35522185771154,1.25681517599675,1.25224679547042,1.29612092872378,1.24560397238837,1.1491338876045,1.25456488401029,1.23013928805078,1.19372906892008,1.22265130803079,1.21318294337388,1.28551517544856,1.25217338162324,1.10815673856744,1.14175645721712,1.20245720113621,1.26116454098179,1.23981030791812,1.10862054524809,1.19454408468376,1.26833117593655,1.17526158283443,1.3340651202328,1.20681028667095,1.28884541800114,1.29659761124924,1.17471201367372,1.2623522326848,1.27644874404882,1.27708851822535,1.20310242653192,1.20839972375883,1.2577319236707,1.19332561298605,1.19804239122632,1.27270631353138,1.15814653319549,1.17790658980959,1.28400380876366,1.274688236357,1.40724325130618,1.18431519006312,1.38478713245515,1.33262839242974,1.22182427675395,1.28858043330918,1.2480230728123,1.26572099474012]
atodlen3=[1.42192410908225,1.30050392626452,1.39992573412069,1.37263802405987,1.47959767824524,1.33871582748462,1.55702586171734,1.29703136026025,1.42648817860534,1.54277708166896,1.3413078386406,1.37451623939317,1.33874745766729,1.28142160021022,1.3640579438568,1.3312281783283,1.26124791761409,1.42836951848415,1.42330129463223,1.3824873212986,1.32318867234402,1.34780962028487,1.46170292845754,1.40062567956459,1.34601323608999,1.2991542394207,1.39879432768685,1.35982398566578,1.38103394691446,1.46038873239369,1.3695438754174,1.32504218975231,1.38660499687224,1.52656655308705,1.46086932069164,1.39252518413149,1.32385365329999,1.49312453883924,1.48530704668984,1.38268800710165,1.50227513995371,1.40363340757143,1.43564719222004,1.30066577684531,1.38946521505559,1.35515484785891,1.35373208958743,1.48410146998181,1.55720364978457]
atodlen4=[1.47854052910486,1.44875296985827,1.56205549619363,1.49967116076352,1.5110593576732,1.54660190884447,1.61775808590815,1.63299484355889,1.44380133543288,1.8768958182758,1.51801322831438,1.66702979671336,1.58709698671153,1.51647210762613,1.43256584267425,1.63567708346971,1.67397299546274,1.7805802368729,1.49779277041385,1.7116209119977,1.69743132669584,1.54304168767851,1.50029133424245,1.43418602408524,1.64933702557829,1.68593331031236,1.46346597383482,1.59628920777078,1.4938495366634,1.5193055744107,1.77318391930879,1.51501375015756,1.66865709073917,1.57122626158941,1.38764347641693,1.52438039615829,1.69678134962763,1.47333633645482,1.60123019487691,1.46272626757244,1.63630072740957,2.09612413473267,1.82043738987135,1.76016424252416,1.70838436718918,1.61712018873247,1.52252092436247,1.60551035800042,1.70797328069314,1.61350523799317,1.51520291640211,1.51784056099423,1.50671388504789,1.58125653505074,1.46183724432156,1.75201099012403,1.50460566587645,1.32495784759522,1.63960059500893,1.83595874370741,1.62801633133348,1.31987552398628,1.91973429586026,1.53907450403085,1.33521982648562,1.52347521729374,10.3066484298083,1.4467062138431,1.38666242910265,1.60423843720179,1.53993290339551,1.74443934718012,1.45756769539599,1.55009632415411,1.3521773223474,1.43932014186439,1.46019141523122,1.58652908035827,1.66918275044889,1.6224014047749,1.39148723365835,1.52729178631895,1.89642724630959,1.56554835652658,1.82062181678182,1.4529929845647,1.77689702994759,1.59889335828939,1.61332230786664,2.05694321876533,1.44468123769683,1.49215293366155,1.44791406892582,1.64402865035875,1.54780224110627,1.63894827288451,5.22306304558851,1.53235259488324,1.37752366585505,1.51948863864103,1.70012307970306,1.62365146804077,1.5619331999111,1.64510583463559,1.5848142375346,1.49508528589155,1.42645082603477,1.460990268011,2.01645794711342,1.40852830991425,1.57794744143376,1.25163213782414,1.55399420643523,1.44450010301215,1.47066214824339,1.7198627187404,1.48373251955428,1.57968195253227,1.59452089774149,1.68339687365707,1.51820707428025,1.46864477882538,1.62361567367562]
fig1, ax1 = plt.subplots()
ax1.set_title('Sinuosity assessment of generated facies models')
ax1.boxplot([atodlen1,atodlen2,atodlen3,atodlen4],showfliers=False)
plt.savefig(network_dir + "Sinuosity assessment of generated facies models.png", dpi=200)
```
### 3.4 Evaluation of Generator's conditioning ability to input well data
**Well points accuracy evaluation**
```
def get_random_well_facies_data(images_num):
well_points = np.zeros([images_num, 1, 64, 64], dtype = int)
for i in range(images_num):
well_points_num = np.random.RandomState(3*i).choice(np.arange(8, 16), 1) # Random choose the expected total number of well points
xs = np.random.choice(64, well_points_num)
ys = np.random.choice(64, well_points_num)
well_points[i, 0, xs, ys] = 1
# Using test facies models to sample faices types at well points
well_facies = np.where(well_points * image_test[:images_num]>0, 1, 0)
well_facies = np.concatenate([well_points, well_facies], 1)
return well_facies
def generate_images(realization_num, well_facies):
# Generate latent vectors.
latents_plt = np.random.randn(realization_num, Gs.input_shapes[0][1])
labels_plt = np.random.uniform(-1, 1, (realization_num, Gs.input_shapes[1][1]))
well_facies_plt = well_facies
# Run the generator to produce a set of images.
images_plt = Gs.run(latents_plt, labels_plt, well_facies_plt)
images_plt = np.where(images_plt< -0.3, -1, images_plt)
images_plt = np.where(images_plt> 0.15, 1, images_plt)
images_plt = np.where((images_plt>= -0.3) & (images_plt<= 0.15), 0, images_plt)
return images_plt
def well_points_accuracy(well_facies, fake_imgs_a):
gg = well_facies_smp_train_facies[:,0:1] + well_facies_smp_train_facies[:,1:2]
recognized_f1 = np.where((gg==2) & (well_facies_smp_train_facies[:,0:1] * (fake_imgs_a+1) > 0.8), 1, 0)
f1_prob = np.sum(recognized_f1)/np.sum(np.where(gg==2,1,0))
recognized_f0 = np.where((gg==1) & (well_facies_smp_train_facies[:,0:1] * (fake_imgs_a+2) ==1), 1, 0)
f0_prob = np.sum(recognized_f0)/np.sum(np.where(gg==1,1,0))
return f1_prob, f0_prob
def enlarge(well_facies):
### Enlarge areas of well points into 4 x 4 as inputs
with tf.device('/gpu:1'):
well_facies = tf.cast(well_facies, tf.float32)
well_facies_enlarge = tf.nn.max_pool(well_facies, ksize = [1,1,4,4], strides=[1,1,1,1], padding='SAME', data_format='NCHW')
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
well_points_el = sess.run(well_facies_enlarge)
return well_points_el
images_num = 1000
well_facies_smp_train_facies = get_random_well_facies_data(images_num)
well_facies_smp_train_facies_el = enlarge(well_facies_smp_train_facies)
fake_imgs = generate_images(images_num, well_facies_smp_train_facies_el)
f_c_prob, f_m_prob = well_points_accuracy(well_facies_smp_train_facies, fake_imgs)
print(f_c_prob) # well facies reproduction accuracy for input channel complex facies
print(f_m_prob) # well facies reproduction accuracy for input mud facies
```
### 4. Evaluation of the imported pretrained Discriminator as a global feature recognizer
#### Assess D with Test data
```
plt_data_no = 500
a = np.arange(plt_data_no)
np.random.shuffle(a)
test_img_no = a[:plt_data_no]
_, features = D.run(image_test[test_img_no]/127.5-1)
# orit_test = (label_test[:,0]/2+0.5)*168-84
# back_ratio_test = (label_test[:,1]/2+0.5)*0.8037109375+0.167724609375
# width_test = (label_test[:,2]/2+0.5)*0.8+2.7
# amwv_ratio_test = (label_test[:,3]/2+0.5)*0.4866197183098592+0.06338028169014084
features[:, 0] = (features[:, 0] /2+0.5)*0.4866197183098592+0.06338028169014084
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(6, 5, forward=True)
# labels_cor includes: orientation, background_ratio, width, amplitude/wavelength ratio, after shifting to (-1, 1)
ax.scatter(amwv_ratio_test[test_img_no], features[:, 0])
# calc the trendline
z3 = np.polyfit(amwv_ratio_test[test_img_no], features[:, 0], 1)
p3 = np.poly1d(z3)
ax.plot(amwv_ratio_test[test_img_no],p3(amwv_ratio_test[test_img_no]),"r-")
# the line equation:
print ("y=%.6fx+(%.6f)"%(z3[0],z3[1]))
ax.set_xlabel("Amplitude/wavelength ratio inputted to D")
ax.set_ylabel("Predicted amplitude/wavelength ratio by D")
#plt.savefig(network_dir +"Mud facies ratio scatter of fake vs real.png", dpi=200)
```
#### Assess D with Simulated data
*(1) Randomly Select global features data
```
print(plt_data_no)
# Generate latent vectors.
latents_plt = np.random.randn(plt_data_no, Gs.input_shapes[0][1]) # 1000 random latents *Gs.input_shapes[0][1:]=[None, 128] [None, 4]
labels_plt = labels_inspect[:plt_data_no, 2:3]
wellfacies_plt = wellfacies_inspect[:plt_data_no]
# Run the generator to produce a set of images.
images_plt = Gs.run(latents_plt, labels_plt, wellfacies_plt)
images_plt = np.where(images_plt< -0.7, -1, images_plt)
images_plt = np.where(images_plt> 0.3, 1, images_plt)
_, features = D.run(images_plt)
plt.imshow(images_plt[0,0])
features[:, 0] = (features[:, 0] / 2 + 0.5) *0.4866197183098592+0.06338028169014084
labels_plt[:, 0] = (labels_plt[:, 0] / 2 + 0.5) *0.4866197183098592+0.06338028169014084
fig, ax = plt.subplots(1, 1)
fig.set_size_inches(6, 5, forward=True)
# labels_cor includes: orientation, background_ratio, width, amplitude/wavelength ratio, after shifting to (-1, 1)
ax.scatter(labels_plt[:, 0], features[:, 0])
# calc the trendline
z3 = np.polyfit(labels_plt[:, 0], features[:, 0], 1)
p3 = np.poly1d(z3)
ax.plot(labels_plt[:, 0],p3(labels_plt[:, 0]),"r-")
# the line equation:
print ("y=%.6fx+(%.6f)"%(z3[0],z3[1]))
ax.set_xlabel("Amplitude/wavelength ratio inputted to D")
ax.set_ylabel("Predicted amplitude/wavelength ratio by D")
#plt.savefig(network_dir +"Mud facies ratio scatter of fake vs real.png", dpi=200)
```
|
github_jupyter
|
# Gaussian feedforward -- analysis
Ro Jefferson<br>
Last updated 2021-05-26
This is the companion notebook to "Gaussian_Feedforward.ipynb", and is designed to read and perform analysis on data generated by that notebook and stored in HDF5 format.
**The user must specify** the `PATH_TO_DATA` (where the HDF5 files to be read are located) and the `PATH_TO_OUTPUT` (where any plots will be written) below.
```
# Numpy, scipy, and plotting:
import numpy as np
from scipy.stats import norm # Gaussian fitting
import scipy.integrate as integrate # integration
import matplotlib.pyplot as plt # plotting
import seaborn as sns; sns.set() # nicer plotting
import pandas as pd # dataframe for use with seaborn
# File i/o:
import pickle # for unpickling MNIST data
import gzip # for opening pickled MNIST data file
import h5py # HDF5
# Miscellaneous:
import math
import random # random number generators
import re # regular expressions
import gc # garbage collection
# symbolic algebra package:
import sympy as sym
from sympy import tanh
```
## Import HDF5 data
Specify the path to the .hdf5 files containing the accuracies and hooks, and define functions to load the data as dictionaries:
```
PATH_TO_DATA = '/full/path/to/HDF5/data/'
PATH_TO_OUTPUT = '/full/path/where/plots/are/to/be/saved/'
# read file of accuracies, return dataset as dictionary:
def read_accuracies(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
acc_dict = {key : np.array(file[key]) for key in file.keys()}
return acc_dict
# read file of inputs/outputs, return dataset as dictionary:
def read_hooks(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
hook_dict = {key : np.array(file[key]) for key in file.keys()}
return hook_dict
# read file of weights, biases; return dataset as dictionary:
def read_parameters(file_name):
with h5py.File(PATH_TO_DATA + file_name, 'r') as file:
# cast elements as np.array, else returns closed file datasets:
for key in file.keys():
para_dict = {key : np.array(file[key]) for key in file.keys()}
return para_dict
# load data, ensuring consistent files:
def load_data(acc_file, hook_file, para_file, verbose=True):
accuracies = read_accuracies(acc_file)
hooks = read_hooks(hook_file)
parameters = read_parameters(para_file)
var_w = accuracies['var_weight'].item()
var_b = accuracies['var_bias'].item()
if var_w != hooks['var_weight'].item() or var_w != parameters['var_weight'].item():
raise Exception('Weight variances do not match!')
elif var_b != hooks['var_bias'].item() or var_b != parameters['var_bias'].item():
raise Exception('Bias variances do not match!')
# extract accuracies corresponding to depth in hook file:
index = np.where(accuracies['depth'] == hooks['depth'])[0] # array of matches
if index.size == 0: # empty array = no match
raise Exception('No matching depth!')
else:
acc = accuracies['accuracies'][index[0]]
print('Successfully loaded network with the following parameters:'
'\nDepth = {}\nvar_w = {}\nvar_b = {}\n'.format(hooks['depth'].item(), var_w, var_b))
# optionally print key lists:
if verbose:
print('Hook keys:\n{}\n'.format(hooks.keys()))
print('Parameter keys:\n{}\n'.format(parameters.keys()))
return acc, hooks, parameters
```
So, for example, we can read in files and extract the hyperparameters as follows:
```
accs, hooks, paras = load_data('acc-150-30.hdf5', 'e14-hooks-150-30.hdf5', 'e14-para-150-30.hdf5')
depth = hooks['depth'].item()
var_w = hooks['var_weight'].item()
var_b = hooks['var_bias'].item()
```
## Analysis functions
Here we'll define some useful functions for analyzing the results. To begin, let's write a simple function that returns the distribution of pre-/post-activations (i.e., inputs/outputs) for each layer, to see whether they remain Gaussian.
```
# return mean and variance for the layer, and optionally plot:
def view_layer(key, plot=False, truncate=1000):
layer = hooks[key][-truncate:] # use last `truncate` samples, else excessive size
sns.distplot(layer, fit=norm)
if not plot: plt.close() # optionally suppress figure
mean, std = norm.fit(layer)
return mean, std**2
# same, but accept layer as array:
def view_array(layer, plot=False):
sns.distplot(layer, fit=norm)
if not plot: plt.close() # optionally suppress figure
mean, std = norm.fit(layer)
return mean, std**2
```
Let's look at a few layers:
```
# current dataset corresponds to `wide` network option, so should remain Gaussian until the last couple layers:
view_layer('in-0', True)
view_layer('in-15', True)
view_layer('in-27', True)
view_layer('in-29', True) # only 10 neurons, don't expect Gaussian
```
Of chief importance is the fixed-point $q^*$. We can find the approximate value with the following process: first, we numerically evaluate the integral expression for $q^{\ell+1}$ as a function of $q^{\ell}$ for a grid of points. We can optionally use this to plot $q^{\ell+1}$ and the unit slope, but all we really need is the nearest datapoint (in the aforementioned grid) to the intersection, which we find by identifying the index at which the difference between these two curves changes sign. Then, we apply linear interpolation to the corresponding line segments to approximate the precise value of the intersection.
Denote the endpoints of the line segment with unit slope $(x_1, y_1=x_1)$ and $(x_2, y_2=x_2)$, and the endpoints of the segment of the $q$-curve $(x_3=x_1, y_3)$ and $(x_4=x_2, y_4)$. Then Cramer's rule reduces to the following expression for the intersection point $x=y$:
\begin{equation}
x=\frac{(x_1y_4-x_2y_3)}{(x_1-x_2)-(y_3-y_4)}
\end{equation}
```
# recursive expression for the variances, eq. (14) in my blog:
def next_q(q, var_w=1, var_b=0):
integral = integrate.quad(lambda z: np.exp(-z**2/2)*np.tanh(np.sqrt(q)*z)**2, -np.inf, np.inf)[0]/np.sqrt(2*np.pi)
return var_w*integral + var_b
# compute q* given variances, and optionally plot q^{l+1} vs. q^l:
def find_qstar(var_weight, var_bias, plot = False, domain = 2): # check between 0 and domain
# grid of points for numerical sampling:
points = np.arange(0,domain,0.05)
qnew = [next_q(q, var_weight, var_bias) for q in points]
# find index (i.e., datapoint) at which difference between curves changes sign:
flip = np.argwhere(np.diff(np.sign(qnew-points)))[0][0]
# extract line segments which contain the intersection:
seg1 = points[flip:flip+2]
seg2 = qnew[flip:flip+2]
# intersection point x=4 via Cramer's rule:
qstar = (seg1[0]*seg2[1] - seg1[1]*seg2[0])/(seg1[0] - seg1[1] - seg2[0] + seg2[1])
if plot:
line_df = pd.DataFrame({'q_l': points, 'q_{l+1}': points})
theory_df = pd.DataFrame({'q_l': points, 'q_{l+1}': qnew})
sns.lineplot('q_l', 'q_{l+1}', data=theory_df, marker='o');
sns.lineplot('q_l', 'q_{l+1}', data=line_df, marker='o');
return qstar
```
For example, for the case above, we have:
```
qstar = find_qstar(var_w, var_b, plot=True)
print(qstar)
```
Similarly, we would like to find the fixed point $\rho^*$, which is found by numerically solving a similar recursion relation, and then applying the flip-interpolation strategy above:
```
# recursive expression for the Pearson correlation coefficient, eq. (23) in my blog:
def next_rho(rho, qstar, var_w=1, var_b=0):
sq = np.sqrt(qstar)
bound = np.inf # integration bound (should be np.inf)
integral = integrate.dblquad(lambda x, y: np.exp(-x**2/2)*np.exp(-y**2/2)*np.tanh(sq*x)*np.tanh(sq*(rho*x+np.sqrt(1-rho**2)*y)),
-bound, bound, lambda x: -bound, lambda x: bound)[0]/(2*np.pi)
return (var_w*integral + var_b)/qstar
# compute rho* given q*, variances; optionally plot rho^{l+1} vs. rho^l:
def find_rhostar(qstar, var_weight, var_bias, plot = False):
# grid of points for numerical sampling:
points = np.arange(0,1.01,0.05)
rhonew = [next_rho(rho, qstar, var_weight, var_bias) for rho in points]
# find index (i.e., datapoint) at which difference between curves changes sign:
where = np.argwhere(np.diff(np.sign(rhonew-points)))
if where.size == 0:
rhostar = 1
else:
flip = np.argwhere(np.diff(np.sign(rhonew-points)))[0][0]
# extract line segments which contain the intersection:
seg1 = points[flip:flip+2]
seg2 = rhonew[flip:flip+2]
# intersection point x=4 via Cramer's rule:
rhostar = (seg1[0]*seg2[1] - seg1[1]*seg2[0])/(seg1[0] - seg1[1] - seg2[0] + seg2[1])
if plot:
line_df = pd.DataFrame({'rho_l': points, 'rho_{l+1}': points})
theory_df = pd.DataFrame({'rho_l': points, 'rho_{l+1}': rhonew})
sns.lineplot('rho_l', 'rho_{l+1}', data=theory_df, marker='o');
sns.lineplot('rho_l', 'rho_{l+1}', data=line_df, marker='o');
return rhostar
```
For example, for the $q^*$ value and associated variances above, we have:
```
rhostar = find_rhostar(qstar, var_w, var_b, True)
print(rhostar)
```
With these values in hand, we can compute the theoretical correlation length, given by eq. (27) in my blog (which is eq. (9) in Schoenholz et al.):
```
# correlation length (for the Pearson correlation coefficient):
def correlation_length(rhostar, qstar, var_w=1):
sq = np.sqrt(qstar)
bound = 100 # integration bound (should be np.inf, but that causes overflow errors)
integral = integrate.dblquad(lambda x, y: np.exp(-x**2/2)*np.exp(-y**2/2)*(1/np.cosh(sq*x))**2*(1/np.cosh(sq*(rhostar*x+np.sqrt(1-rhostar**2)*y))**2),
-bound, bound, lambda x: -bound, lambda x: bound)[0]/(2*np.pi)
return -1/np.log(var_w*integral)
correlation_length(rhostar, qstar, var_w)
```
# Probing fall-off
Theoretically, we should be able to train deeper networks at criticality, and they should all fall-off based on the correlation length. To see how our networks behave, we'll write a function that reads-in a grid-worth of accuracy data (optionally plotting the individual accuracies), and another that uses this function to make the desired scatterplot:
```
# automatically read and plot accuracies from a series of files **with the same variances**:
def read_and_plot_accs(base, start, stop, step, plot=True, write=False):
# file names in format acc-{base}-{dd}.hdf5
filenames = ['acc-{}-{}.hdf5'.format(base, dd) for dd in range(start, stop, step)]
#print('Reading {} files: {}\n'.format(len(filenames), filenames))
# get list of accuracies and corresponding depths:
acc, depth = [], []
for i in range(len(filenames)):
# load data:
acc_dict = read_accuracies(filenames[i])
acc.append(acc_dict['accuracies'])
depth.append(acc_dict['depth'].item())
# get variances from last file:
var_w = acc_dict['var_weight'].item()
var_b = acc_dict['var_bias'].item()
if plot:
#plt.rcParams['figure.figsize'] = [9, 6] # globally (!) adjust figure size
# plot each series, labelled by depth:
list_dict = {'L = {}'.format(dd) : pd.Series(acc[i])
for i,dd in enumerate(depth)}
df = pd.DataFrame(list_dict)
acc_plot = df.plot()
# format legend, title:
acc_legend = acc_plot.legend(loc='upper left', bbox_to_anchor=(1,1))
acc_plot.set_title('var_w = {}'.format(var_w)) # all var_w equal
# optionally save plot as pdf:
if write:
plt.savefig(PATH_TO_OUTPUT+'plot-{}.pdf'.format(base),
bbox_extra_artists=(acc_legend,), bbox_inches='tight')
return acc, depth, var_w, var_b
# read-in accuracies using pre-defined function above, and use this to
# make scatterplot like fig. 5 in Schoenholz et al.:
def probe_falloff(base_list, start, stop, step, plot=True, write=False):
# read accuracies, with plot suppressed:
acc_list, dep_list, w_list, b_list = [], [], [], []
for base in base_list:
acc, dep, w, b = read_and_plot_accs(base, start, stop, step, False, False)
# store final accuracy from run:
acc_list.append([a[-1] for a in acc])
# store list of depths, variances:
dep_list.append(dep)
w_list.append(w)
b_list.append(b)
# var_w gives x-values:
x_vals = []
for i in range(len(w_list)):
# make len(acc_list[i]) copies of w_list[i]:
x_vals.append([w_list[i]]*len(acc_list[i]))
x_vals = np.array(x_vals).flatten()
# depths give y-values:
y_vals = np.array(dep_list).flatten()
# accuracies give z-values (color):
z_vals = np.array(acc_list).flatten()
# optionally make scatterplot:
if plot:
scat_plot = plt.scatter(x_vals, y_vals, c=z_vals, cmap='rainbow', s=50)
plt.colorbar(scat_plot) # add colorbar as legend
# add title, axes labels:
plt.title('var_b = {}'.format(b_list[0])) # all var_b equal
plt.xlabel('var_w')
plt.ylabel('depth')
# optionally save plot as pdf:
if write:
# should all have same bias, so label with that:
plt.savefig(PATH_TO_OUTPUT+'scatterplot-{}.pdf'.format(b_list[0]),)
return x_vals, y_vals, z_vals, b_list
# read and plot:
var_list, dep_list, acc_list, b_list = probe_falloff([x for x in range(100,286,5)], 10, 70, 3, True, False)
```
How does this compare with the theoretical value of the correlation length? We can easily compute this using the $q^*$, $\rho^*$, and `correlation_length` functions above:
```
# same range of var_w values as above, for given var_b:
test_w = np.arange(1.0, 2.86, 0.05)
test_b = 0.05
qstar_test = [find_qstar(ww, test_b, False) for ww in test_w]
#print('q* = ', qstar_test)
rhostar_test = [find_rhostar(qq, ww, test_b, False) for qq, ww in zip(qstar_test, test_w)]
#print('\nrho* = {}\n'.format(rhostar_test))
xi_vals = np.array([correlation_length(rr, qq, ww) for rr,qq,ww in zip(rhostar_test,qstar_test,test_w)])
```
In principle this should never be negative, but the numerics are such that the integral can be greater than 1 near the critical point, which makes $\xi<0$. Since we can't plot infinity, let's just replace this with double the largest positive value for visualization purposes:
```
neg_index = np.where(np.array(xi_vals) < 0)[0].item() # get index of negative value
xis = np.copy(xi_vals)
xis[neg_index] = 2*max(xi_vals)
xi_df = pd.DataFrame({'var_w': test_w, 'xi': xis})
xi_plot = sns.lineplot('var_w', 'xi', data=xi_df, marker='o');
xi_plot.set_ylim(0,100);
```
This is fine, but it would be nice to overlay the theoretical curve on the grid:
```
# re-create and overlay above two plots:
def overlay_falloff(base_list, start, stop, step, write=False):
# ************ load and process data for scatterplot: ************
# read accuracies, with plot suppressed:
acc_list, dep_list, w_list, b_list = [], [], [], []
for base in base_list:
acc, dep, w, b = read_and_plot_accs(base, start, stop, step, False, False)
# store final accuracy from run:
acc_list.append([a[-1] for a in acc])
# store list of depths, variances:
dep_list.append(dep)
w_list.append(w)
b_list.append(b)
# var_w gives x-values:
x_vals = []
for i in range(len(w_list)):
# make len(acc_list[i]) copies of w_list[i]:
x_vals.append([w_list[i]]*len(acc_list[i]))
x_vals = np.array(x_vals).flatten()
# depths give y-values:
y_vals = np.array(dep_list).flatten()
# accuracies give z-values (color):
z_vals = np.array(acc_list).flatten()
# ************ process data for correlation length plot: ************
qstar = [find_qstar(ww, b_list[0], False) for ww in w_list] # all biases equal, so just use first
rhostar = [find_rhostar(qq, ww, b_list[0], False) for qq, ww in zip(qstar, w_list)]
xi_vals = np.array([correlation_length(rr, qq, ww) for rr,qq,ww in zip(rhostar, qstar, w_list)])
# ensure no negative elements (see comment about numerics near critical point above):
artificial_xi = 2*max(xi_vals) # overwrite negative values with this
for i in range(xi_vals.size):
if xi_vals[i] < 0:
xi_vals[i] = artificial_xi
# consider a few different multiples of the correlation length, for comparison with Schoenholz et al.:
three_vals = [np.pi*xx for xx in xi_vals]
six_vals = [2*np.pi*xx for xx in xi_vals]
# ************ overlay correlation length plot on scatterplot: ************
# create combination figure:
fig, ax1 = plt.subplots(figsize=(9,6))
ax2 = ax1.twinx() # share x axis
# make scatterplot:
ax1.set_xlabel(r'$\sigma_w^2$')
ax1.set_ylabel('depth')
scat_plot = ax1.scatter(x=x_vals, y=y_vals, c=z_vals, cmap='rainbow', s=120) # does not return Axes object!
ax1.tick_params(axis='y')
# truncate for cleaner visuals:
ax1.set_ylim(min(y_vals)-1, max(y_vals)+1)
ax1.set_xlim(min(w_list)-0.05, max(w_list)+0.05)
# ax1.set_title('Optional title here')
cbar = plt.colorbar(scat_plot, label='accuracy') # add colorbar as legend
# control labels/ticks position colorbar:
cbar.ax.yaxis.set_ticks_position('right')
cbar.ax.yaxis.set_label_position('left')
# overlay correlation length plot:
xi_df = pd.DataFrame({'var_w': w_list, 'xi': xi_vals})
ax2 = sns.lineplot('var_w', 'xi', data=xi_df, marker=None, color='black')
# n.b., use None instead of False, else pdf still has white horizontal ticks
xi3_df = pd.DataFrame({'var_w': w_list, 'xi': three_vals})
sns.lineplot('var_w', 'xi', data=xi3_df, marker=None, color='grey')
xi6_df = pd.DataFrame({'var_w': w_list, 'xi': six_vals})
sns.lineplot('var_w', 'xi', data=xi6_df, marker=None, color='darkgrey')
# n.b., darkgrey is *lighter* than grey, because what the fuck programmers
# truncate to same range/domain:
ax2.set_ylim(min(y_vals)-1, max(y_vals)+1)
ax2.set_xlim(min(w_list)-0.05, max(w_list)+0.05)
# turn off second labels, ticks, and grid:
ax2.set_ylabel(None)
ax2.grid(False)
ax2.axis('off')
# optionally save plot as pdf:
if write:
# should all have same bias, so label with that:
plt.savefig(PATH_TO_OUTPUT+'scatterplot-{}.pdf'.format(b_list[0]),)
return x_vals, y_vals, z_vals, b_list
overlay_falloff([x for x in range(100,286,5)], 10, 70, 3, xis, False);
```
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Azure Machine Learning Pipeline with AutoMLStep
This notebook demonstrates the use of AutoMLStep in Azure Machine Learning Pipeline.
## Introduction
In this example we showcase how you can use AzureML Dataset to load data for AutoML via AML Pipeline.
If you are using an Azure Machine Learning Notebook VM, you are all set. Otherwise, make sure you have executed the [configuration](https://aka.ms/pl-config) before running this notebook.
In this notebook you will learn how to:
1. Create an `Experiment` in an existing `Workspace`.
2. Create or Attach existing AmlCompute to a workspace.
3. Define data loading in a `TabularDataset`.
4. Configure AutoML using `AutoMLConfig`.
5. Use AutoMLStep
6. Train the model using AmlCompute
7. Explore the results.
8. Test the best fitted model.
## Azure Machine Learning and Pipeline SDK-specific imports
```
import logging
import os
import csv
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets
import pkg_resources
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.train.automl import AutoMLConfig
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.core.dataset import Dataset
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
from azureml.train.automl.runtime import AutoMLStep
# Check core SDK version number
print("SDK version:", azureml.core.VERSION)
```
## Initialize Workspace
Initialize a workspace object from persisted configuration. Make sure the config file is present at .\config.json
```
ws = Workspace.from_config()
print(ws.name, ws.resource_group, ws.location, ws.subscription_id, sep = '\n')
```
## Create an Azure ML experiment
Let's create an experiment named "automl-classification" and a folder to hold the training scripts. The script runs will be recorded under the experiment in Azure.
The best practice is to use separate folders for scripts and its dependent files for each step and specify that folder as the `source_directory` for the step. This helps reduce the size of the snapshot created for the step (only the specific folder is snapshotted). Since changes in any files in the `source_directory` would trigger a re-upload of the snapshot, this helps keep the reuse of the step when there are no changes in the `source_directory` of the step.
```
# Choose a name for the run history container in the workspace.
experiment_name = 'automlstep-classification'
project_folder = './project'
experiment = Experiment(ws, experiment_name)
experiment
```
### Create or Attach an AmlCompute cluster
You will need to create a [compute target](https://docs.microsoft.com/azure/machine-learning/service/concept-azure-machine-learning-architecture#compute-target) for your AutoML run. In this tutorial, you get the default `AmlCompute` as your training compute resource.
```
# Choose a name for your cluster.
amlcompute_cluster_name = "cpu-cluster"
found = False
# Check if this compute target already exists in the workspace.
cts = ws.compute_targets
if amlcompute_cluster_name in cts and cts[amlcompute_cluster_name].type == 'AmlCompute':
found = True
print('Found existing compute target.')
compute_target = cts[amlcompute_cluster_name]
if not found:
print('Creating a new compute target...')
provisioning_config = AmlCompute.provisioning_configuration(vm_size = "STANDARD_D2_V2", # for GPU, use "STANDARD_NC6"
#vm_priority = 'lowpriority', # optional
max_nodes = 4)
# Create the cluster.
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, provisioning_config)
# Can poll for a minimum number of nodes and for a specific timeout.
# If no min_node_count is provided, it will use the scale settings for the cluster.
compute_target.wait_for_completion(show_output = True, min_node_count = 1, timeout_in_minutes = 10)
# For a more detailed view of current AmlCompute status, use get_status().
# create a new RunConfig object
conda_run_config = RunConfiguration(framework="python")
conda_run_config.environment.docker.enabled = True
conda_run_config.environment.docker.base_image = azureml.core.runconfig.DEFAULT_CPU_IMAGE
cd = CondaDependencies.create(pip_packages=['azureml-sdk[automl]'],
conda_packages=['numpy', 'py-xgboost<=0.80'])
conda_run_config.environment.python.conda_dependencies = cd
print('run config is ready')
```
## Data
```
# The data referenced here was a 1MB simple random sample of the Chicago Crime data into a local temporary directory.
example_data = 'https://dprepdata.blob.core.windows.net/demo/crime0-random.csv'
dataset = Dataset.Tabular.from_delimited_files(example_data)
dataset.to_pandas_dataframe().describe()
dataset.take(5).to_pandas_dataframe()
```
### Review the Dataset Result
You can peek the result of a TabularDataset at any range using `skip(i)` and `take(j).to_pandas_dataframe()`. Doing so evaluates only `j` records for all the steps in the TabularDataset, which makes it fast even against large datasets.
`TabularDataset` objects are composed of a list of transformation steps (optional).
```
X = dataset.drop_columns(columns=['Primary Type', 'FBI Code'])
y = dataset.keep_columns(columns=['Primary Type'], validate=True)
print('X and y are ready!')
```
## Train
This creates a general AutoML settings object.
```
automl_settings = {
"iteration_timeout_minutes" : 5,
"iterations" : 2,
"primary_metric" : 'AUC_weighted',
"preprocess" : True,
"verbosity" : logging.INFO
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
path = project_folder,
compute_target=compute_target,
run_configuration=conda_run_config,
X = X,
y = y,
**automl_settings
)
```
You can define outputs for the AutoMLStep using TrainingOutput.
```
from azureml.pipeline.core import PipelineData, TrainingOutput
ds = ws.get_default_datastore()
metrics_output_name = 'metrics_output'
best_model_output_name = 'best_model_output'
metrics_data = PipelineData(name='metrics_data',
datastore=ds,
pipeline_output_name=metrics_output_name,
training_output=TrainingOutput(type='Metrics'))
model_data = PipelineData(name='model_data',
datastore=ds,
pipeline_output_name=best_model_output_name,
training_output=TrainingOutput(type='Model'))
```
Create an AutoMLStep.
```
automl_step = AutoMLStep(
name='automl_module',
automl_config=automl_config,
outputs=[metrics_data, model_data],
allow_reuse=True)
from azureml.pipeline.core import Pipeline
pipeline = Pipeline(
description="pipeline_with_automlstep",
workspace=ws,
steps=[automl_step])
pipeline_run = experiment.submit(pipeline)
from azureml.widgets import RunDetails
RunDetails(pipeline_run).show()
pipeline_run.wait_for_completion()
```
## Examine Results
### Retrieve the metrics of all child runs
Outputs of above run can be used as inputs of other steps in pipeline. In this tutorial, we will examine the outputs by retrieve output data and running some tests.
```
metrics_output = pipeline_run.get_pipeline_output(metrics_output_name)
num_file_downloaded = metrics_output.download('.', show_progress=True)
import json
with open(metrics_output._path_on_datastore) as f:
metrics_output_result = f.read()
deserialized_metrics_output = json.loads(metrics_output_result)
df = pd.DataFrame(deserialized_metrics_output)
df
```
### Retrieve the Best Model
```
best_model_output = pipeline_run.get_pipeline_output(best_model_output_name)
num_file_downloaded = best_model_output.download('.', show_progress=True)
import pickle
with open(best_model_output._path_on_datastore, "rb" ) as f:
best_model = pickle.load(f)
best_model
```
### Test the Model
#### Load Test Data
For the test data, it should have the same preparation step as the train data. Otherwise it might get failed at the preprocessing step.
```
dataset = Dataset.Tabular.from_delimited_files(path='https://dprepdata.blob.core.windows.net/demo/crime0-test.csv')
df_test = dataset_test.to_pandas_dataframe()
df_test = df_test[pd.notnull(df['Primary Type'])]
y_test = df_test[['Primary Type']]
X_test = df_test.drop(['Primary Type', 'FBI Code'], axis=1)
```
#### Testing Our Best Fitted Model
We will use confusion matrix to see how our model works.
```
from pandas_ml import ConfusionMatrix
ypred = best_model.predict(X_test)
cm = ConfusionMatrix(y_test['Primary Type'], ypred)
print(cm)
cm.plot()
```
|
github_jupyter
|
# Breast-Cancer Classification
```
#WOHOO already Version 2 I learned How to explore Data
```
# Library
```
# Import Dependencies
%matplotlib inline
# Start Python Imports
import math, time, random, datetime
# Data Manipulation
import numpy as np
import pandas as pd
# Visualization
import matplotlib.pyplot as plt
import missingno
import seaborn as sns
plt.style.use('seaborn-whitegrid')
# Preprocessing
from sklearn.preprocessing import OneHotEncoder, LabelEncoder, label_binarize
# Machine learning
import catboost
from sklearn.model_selection import train_test_split
from sklearn import model_selection, tree, preprocessing, metrics, linear_model
from sklearn.svm import LinearSVC
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LinearRegression, LogisticRegression, SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from catboost import CatBoostClassifier, Pool, cv
# Let's be rebels and ignore warnings for now
import warnings
warnings.filterwarnings('ignore')
```
# Exploring the dataset
```
dataset = pd.read_csv('data.csv')
dataset.drop('Unnamed: 32', inplace=True, axis=1)
dataset.head()
# Plot graphic of missing values
missingno.matrix(dataset, figsize = (30,10))
dataset.columns
print(dataset.shape)
dataset.describe()
dataset.isnull().sum()
X = dataset.iloc[:, 2:].values
y = dataset.iloc[:, 1:2].values
```
# spliting the dataset
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2)
#categorical values
from sklearn.preprocessing import LabelEncoder
label_y = LabelEncoder()
y_train = label_y.fit_transform(y_train)
y_test = label_y.transform(y_test)
```
# Method 1
## Fitting the model and analysing
```
#fitting
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(n_jobs= -1)
classifier.fit(X_train, y_train)
#predicting
y_pred = classifier.predict(X_test)
#confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred)
# classification analysis
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
# k-fold cross vallidation
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator=classifier, X=X_train, y=y_train,cv= 10, n_jobs=-1)
print(accuracies.mean(), accuracies.std())
```
# Method 2
# Function that runs the requested algorithm and returns the accuracy metrics
```
def fit_ml_algo(algo, X_train, y_train, cv):
# One Pass
model = algo.fit(X_train, y_train)
acc = round(model.score(X_train, y_train) * 100, 2)
# Cross Validation
train_pred = model_selection.cross_val_predict(algo,
X_train,
y_train,
cv=cv,
n_jobs = -1)
# Cross-validation accuracy metric
acc_cv = round(metrics.accuracy_score(y_train, train_pred) * 100, 2)
return train_pred, acc, acc_cv
start_time = time.time()
train_pred_log, acc_log, acc_cv_log = fit_ml_algo(LogisticRegression(),
X_train,
y_train,
10)
log_time = (time.time() - start_time)
print("Accuracy: %s" % acc_log)
print("Accuracy CV 10-Fold: %s" % acc_cv_log)
print("Running Time: %s" % datetime.timedelta(seconds=log_time))
```
|
github_jupyter
|
# Exploring Random Forests
```
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.datasets import load_boston, load_iris, load_wine, load_digits, \
load_breast_cancer, load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, precision_score, recall_score
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
from rfpimp import *
from distutils.version import LooseVersion
if LooseVersion(sklearn.__version__) >= LooseVersion("0.24"):
# In sklearn version 0.24, forest module changed to be private.
from sklearn.ensemble._forest import _generate_unsampled_indices
from sklearn.ensemble import _forest as forest
else:
# Before sklearn version 0.24, forest was public, supporting this.
from sklearn.ensemble.forest import _generate_unsampled_indices
from sklearn.ensemble import forest
from sklearn import tree
from dtreeviz.trees import *
def rent(n=None, bootstrap=False):
df_rent = pd.read_csv("data/rent-ideal.csv")
if n is None:
n = len(df_rent)
df_rent = df_rent.sample(n, replace=bootstrap)
X = df_rent[['bedrooms','bathrooms','latitude','longitude']]
y = df_rent['price']
return X, y
def boston():
boston = load_boston()
X = boston.data
y = boston.target
features = boston.feature_names
df = pd.DataFrame(data=X,columns=features)
df['y'] = y
return df
```
## Set up
Get the `rent-ideal.csv` data file from canvas "files area" and store in the data directory underneath your notebook directory.
```
X, y = rent()
X.head(3)
X.shape
```
## Train random forests of different sizes
As we increase the number of trees in the forest, we initially see model bias going down. It will asymptotically approach some minimum error on the testing set.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
```
Here's how to train a random forest that has a single tree:
```
rf = RandomForestRegressor(n_estimators=1)
rf.fit(X_train, y_train)
```
**Task**: Compute the MAE for the training and the testing set, printing them out.
```
mae_train = mean_absolute_error(...)
mae = mean_absolute_error(...)
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
</pre>
</details>
**Task**: Run the training and testing cycle several times to see the variance: the test scores bounce around a lot.
**Task**: Increase the number of trees (`n_estimators`) to 2, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=2)
rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
You should notice the both test MAE scores going down and bouncing around less from run to run.
**Q.** Why does the MAE score go down?
<details>
<summary>Solution</summary>
With 2 trees, the chances are that the random forest will have seen (trained on) more of the original training set, despite bootstrapping.
</details>
**Task**: Increase the number of trees (`n_estimators`) to 10, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=10)
rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores?
<details>
<summary>Solution</summary>
They are getting smaller.
</details>
**Q.** After running several times, what else do you notice?
<details>
<summary>Solution</summary>
With 10 trees, the prediction from run to run varies a lot less. We have reduced variance, improving generality.
</details>
**Task**: Increase the number of trees (`n_estimators`) to 200, retrain, and print out the results.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200)
%time rf.fit(X_train, y_train) # how long does this take?
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores from a single run?
<details>
<summary>Solution</summary>
They are a bit smaller, but not by much.
</details>
**Task**: Notice that it took a long time to train, about 10 seconds. Do the exact same thing again but this time use `n_jobs=-1` as an argument to the `RandomForestRegressor` constructor.
This tells the library to use all processing cores available on the computer processor. As long as the data is not too huge (because it must pass it around), it often goes much faster using this argument. It should take less than two seconds.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200, n_jobs=-1)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
**Q.** What you notice about the MAE scores from SEVERAL runs?
<details>
<summary>Solution</summary>
The error variance across runs is even lower (tighter).
</details>
## Examining model size and complexity
The structure of a tree is affected by a number of hyper parameters, not just the data. Goal in the section is to see the effect of altering the number of samples per leaf and the maximum number of candidate features per split. Let's start out with a handy function that uses some support code from rfpimp to examine tree size and depth:
```
def showsize(ntrees, max_features=1.0, min_samples_leaf=1):
rf = RandomForestRegressor(n_estimators=ntrees,
max_features=max_features,
min_samples_leaf=min_samples_leaf,
n_jobs=-1)
rf.fit(X_train, y_train)
n = rfnnodes(rf) # from rfpimp
h = np.median(rfmaxdepths(rf)) # rfmaxdepths from rfpimp
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:6.1f}$, test {mae:6.1f}$ using {n:9,d} tree nodes with {h:2.0f} median tree height")
```
### Effect of number of trees
For a single tree, we see about 21,000 nodes and a tree height of around 35:
```
showsize(ntrees=1)
```
**Task**: Look at the metrics for 2 trees and then 100 trees.
<details>
<summary>Solution</summary>
<pre>
showsize(ntrees=2)
showsize(ntrees=100)
</pre>
</details>
**Q.** Why does the median height of a tree stay the same when we increase the number of trees?
<details>
<summary>Solution</summary>
While the number of nodes increases with the number of trees, the height of any individual tree will stay the same because we have not fundamentally changed how it is constructing a single tree.
</details>
### Effect of increasing min samples / leaf
**Task**: Loop around a call to `showsize()` with 10 trees and min_samples_leaf=1..10
```
for i in range(...):
print(f"{i:2d} ",end='')
showsize(...)
```
<details>
<summary>Solution</summary>
<pre>
for i in range(1,10+1):
showsize(ntrees=10, min_samples_leaf=i)
</pre>
</details>
**Q.** Why do the median height of a tree and number of total nodes decrease as we increase the number of samples per leaf?
<details>
<summary>Solution</summary>
Because when the sample size gets down to `min_samples_leaf`, splitting stops, which prevents the tree from getting taller. It also restricts how many nodes total get created for the tree.
</details>
**Q.** Why does the MAE error increase?
<details>
<summary>Solution</summary>
If we include more observations in a single leaf, then the average is taken over more samples. That average is a more general prediction but less accurate.
</details>
It's pretty clear from that print out that `min_samples_leaf=1` is the best choice because it gives the minimum validation error.
### Effect of reducing max_features (rent data)
**Task:** Do another loop from `max_features` = 4 down to 1, with 1 sample per leaf. (There are 4 total features.)
```
p = X_train.shape[1]
for i in range(...):
print(f"{i:2d} ",end='')
showsize(ntrees=10, ...)
```
<details>
<summary>Solution</summary>
<pre>
p = X_train.shape[1]
for i in range(p,0,-1):
print(f"{i:2d} ",end='')
showsize(ntrees=10, max_features=i)
</pre>
</details>
For this data set, changing the available candidate features that each split does not seem to be important as the validation error does not change, nor does the height of the trees.
### Examine effects of hyper parameters on Boston data set
```
df_boston = boston()
df_boston.head(3)
X, y = df_boston.drop('y', axis=1), df_boston['y']
y *= 1000 # y is "Median value of owner-occupied homes in $1000's" so multiply by 1000
# reproducible 20% test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)
```
Let's run the metric `showsize()` function to see how many trees we should use:
```
for i in [1,5,30,50,100,150,300]:
print(f"{i:3d} trees: ", end='')
showsize(ntrees=i)
```
Seems like the sweet spot on the validation error is probably 150 trees as it gets a low validation error and has a fairly small set of trees.
Check the effect of increasing the minimum samples per leaf from 1 to 10 as we did before.
```
for i in range(1,10+1):
print(f"{i:2d} ",end='')
showsize(ntrees=150, min_samples_leaf=i)
```
The training error goes up dramatically but the validation error doesn't get too much worse.
**Q.** Which min samples per leaf would you choose?
<details>
<summary>Solution</summary>
After running a few times, it seems that using <tt>min_samples_leaf</tt>=1 or 2 is best for the validation error. But, keep in mind that this data set is pretty small and so our error values will change quite a bit depending on the sample we get for the test set.
</details>
Run a loop from the maximum number of features down to 1 for `max_features` to see the effects.
```
p = X_train.shape[1]
for i in range(p,0,-1):
print(f"{i:2d} ",end='')
showsize(ntrees=150, max_features=i, min_samples_leaf=3)
```
**Q.** Which max features would you choose?
<details>
<summary>Solution</summary>
After running a few times, it seems that using <tt>max_features</tt>=7 or 13 gets best validation error, but again it depends on the randomness of the tree construction and results will vary across runs.
</details>
Here's what the final model would look like:
```
showsize(ntrees=150, max_features=13, min_samples_leaf=1)
```
## RF prediction confidence
A random forest is a collection of decision trees, each of which contributes a prediction. The forest averages those predictions to provide the overall prediction (or takes most common vote for classification). Let's dig inside the random forest to get the individual trees out and ask them what their predictions are.
**Task**: Train a random forest with 10 trees on `X_train`, `y_train`. Use `for t in rf.estimators_` to iterate through the trees making predictions with `t` not `rf`. Print out the usual MAE scores for each tree predictor.
```
rf = RandomForestRegressor(n_estimators=10, n_jobs=-1)
rf.fit(X_train, y_train)
for t in ...:
mae_train = ...
mae = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=10, n_jobs=-1)
rf.fit(X_train, y_train)
for t in rf.estimators_:
mae_train = mean_absolute_error(y_train, t.predict(X_train))
mae = mean_absolute_error(y_test, t.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
Notice that it bounces around quite a bit.
**Task**: Select one of the `X_test` rows and print out the addicted rent price.
```
x = ... # pick single test case
x = x.values.reshape(1,-1) # Needs to be a one-row matrix
print(f"{x} => {rf.predict(x)}$")
```
<details>
<summary>Solution</summary>
<pre>
x = X_test.iloc[3,:] # pick single test case
x = x.values.reshape(1,-1)
print(f"{x} => {rf.predict(x)}$")
</pre>
</details>
**Task**: Now let's see how the forest came to that conclusion. Compute the average of the predictions obtained from every tree.
Compare that to the prediction obtained directly from the random forest (`rf.predict(X_test)`). They should be the same.
```
y_pred = ...
print(f"{x} => {y_pred}$")
```
<details>
<summary>Solution</summary>
<pre>
y_pred = np.mean([t.predict(x) for t in rf.estimators_])
print(f"{x} => {y_pred}$")
</pre>
</details>
**Task**: Compute the standard deviation of the tree estimates and print that out.
<details>
<summary>Solution</summary>
<pre>
np.std([t.predict(x) for t in rf.estimators_])
</pre>
</details>
The lower the standard deviation, the more tightly grouped the predictions were, which means we should have more confidence in our answer.
Different records will often have different standard deviations, which means we could have different levels of confidence in the various answers. This might be helpful to a bank for example that wanted to not only predict whether to give loans, but how confident the model was.
## Altering bootstrap size
**This no longer works with latest versions of scikit-learn... and the feature is not yet implemented by them* See [related github issue](https://github.com/scikit-learn/scikit-learn/issues/11993). Ah [this new features](https://github.com/scikit-learn/scikit-learn/pull/14682) covers it for trees. "Adds a max_samples kwarg to forest ensembles that limits the size of the bootstrap samples used to train each estimator."
```
X, y = rent()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)
```
**Task**: There are about 38,000 training records, change that to 19,000 and check the accuracy again.
```
rf = RandomForestRegressor(n_estimators=200) # don't compute in parallel so we can see timing
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
rf = RandomForestRegressor(n_estimators=200, max_samples=1/2)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
It's a bit less accurate, but it's faster.
**Q.** Why is it less accurate?
<details>
<summary>Solution</summary>
Each tree is seeing less of the data set during training.
</details>
**Task**: Turn off bootstrapping by adding `bootstrap=False` to the constructor of the model. This means that it will subsample rather than bootstrap. Remember that bootstrapping gets about two thirds of the data because of replacement.
```
rf = ...
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
<details>
<summary>Solution</summary>
<pre>
rf = RandomForestRegressor(n_estimators=200, n_jobs=-1, bootstrap=False)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
</pre>
</details>
That brings the accuracy back up a little bit for the test set but very much so for the training MAE score.
**Task**: Drop that size to one third of the training records then retrain and test.
```
rf = RandomForestRegressor(n_estimators=200, max_samples=1/3, n_jobs=-1)
%time rf.fit(X_train, y_train)
mae_train = mean_absolute_error(y_train, rf.predict(X_train))
mae = mean_absolute_error(y_test, rf.predict(X_test))
print(f"MAE train {mae_train:.1f}$, test {mae:.1f}$")
```
Mine is twice as fast as the full bootstrap but continues to have very tight variance because of the number of trees. The accuracy is lower, however, about what we get for the usual random forest with two trees.
|
github_jupyter
|
```
# Mount Google Drive
from google.colab import drive # import drive from google colab
ROOT = "/content/drive" # default location for the drive
print(ROOT) # print content of ROOT (Optional)
drive.mount(ROOT) # we mount the google drive at /content/drive
!pip install pennylane
from IPython.display import clear_output
clear_output()
import os
def restart_runtime():
os.kill(os.getpid(), 9)
restart_runtime()
# %matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import numpy as np
```
# Loading Raw Data
```
import tensorflow as tf
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train = x_train[:, 0:27, 0:27]
x_test = x_test[:, 0:27, 0:27]
x_train_flatten = x_train.reshape(x_train.shape[0], x_train.shape[1]*x_train.shape[2])/255.0
x_test_flatten = x_test.reshape(x_test.shape[0], x_test.shape[1]*x_test.shape[2])/255.0
print(x_train_flatten.shape, y_train.shape)
print(x_test_flatten.shape, y_test.shape)
x_train_0 = x_train_flatten[y_train == 0]
x_train_1 = x_train_flatten[y_train == 1]
x_train_2 = x_train_flatten[y_train == 2]
x_train_3 = x_train_flatten[y_train == 3]
x_train_4 = x_train_flatten[y_train == 4]
x_train_5 = x_train_flatten[y_train == 5]
x_train_6 = x_train_flatten[y_train == 6]
x_train_7 = x_train_flatten[y_train == 7]
x_train_8 = x_train_flatten[y_train == 8]
x_train_9 = x_train_flatten[y_train == 9]
x_train_list = [x_train_0, x_train_1, x_train_2, x_train_3, x_train_4, x_train_5, x_train_6, x_train_7, x_train_8, x_train_9]
print(x_train_0.shape)
print(x_train_1.shape)
print(x_train_2.shape)
print(x_train_3.shape)
print(x_train_4.shape)
print(x_train_5.shape)
print(x_train_6.shape)
print(x_train_7.shape)
print(x_train_8.shape)
print(x_train_9.shape)
x_test_0 = x_test_flatten[y_test == 0]
x_test_1 = x_test_flatten[y_test == 1]
x_test_2 = x_test_flatten[y_test == 2]
x_test_3 = x_test_flatten[y_test == 3]
x_test_4 = x_test_flatten[y_test == 4]
x_test_5 = x_test_flatten[y_test == 5]
x_test_6 = x_test_flatten[y_test == 6]
x_test_7 = x_test_flatten[y_test == 7]
x_test_8 = x_test_flatten[y_test == 8]
x_test_9 = x_test_flatten[y_test == 9]
x_test_list = [x_test_0, x_test_1, x_test_2, x_test_3, x_test_4, x_test_5, x_test_6, x_test_7, x_test_8, x_test_9]
print(x_test_0.shape)
print(x_test_1.shape)
print(x_test_2.shape)
print(x_test_3.shape)
print(x_test_4.shape)
print(x_test_5.shape)
print(x_test_6.shape)
print(x_test_7.shape)
print(x_test_8.shape)
print(x_test_9.shape)
```
# Selecting the dataset
Output: X_train, Y_train, X_test, Y_test
```
X_train = np.concatenate((x_train_list[0][:200, :], x_train_list[1][:200, :]), axis=0)
Y_train = np.zeros((X_train.shape[0],), dtype=int)
Y_train[200:] += 1
X_train.shape, Y_train.shape
X_test = np.concatenate((x_test_list[0][:500, :], x_test_list[1][:500, :]), axis=0)
Y_test = np.zeros((X_test.shape[0],), dtype=int)
Y_test[500:] += 1
X_test.shape, Y_test.shape
```
# Dataset Preprocessing
```
X_train = X_train.reshape(X_train.shape[0], 27, 27, 1)
X_test = X_test.reshape(X_test.shape[0], 27, 27, 1)
X_train.shape, X_test.shape
```
# Quantum
```
import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer, GradientDescentOptimizer
qml.enable_tape()
from tensorflow.keras.utils import to_categorical
# Set a random seed
np.random.seed(2020)
# Define output labels as quantum state vectors
def density_matrix(state):
"""Calculates the density matrix representation of a state.
Args:
state (array[complex]): array representing a quantum state vector
Returns:
dm: (array[complex]): array representing the density matrix
"""
return state * np.conj(state).T
label_0 = [[1], [0]]
label_1 = [[0], [1]]
state_labels = [label_0, label_1]
n_qubits = 2
dev = qml.device("default.qubit", wires=n_qubits)
@qml.qnode(dev)
def qcircuit(params, inputs):
"""A variational quantum circuit representing the DRC.
Args:
params (array[float]): array of parameters
inputs = [x, y]
x (array[float]): 1-d input vector
y (array[float]): single output state density matrix
Returns:
float: fidelity between output state and input
"""
# layer iteration
for l in range(len(params[0])):
# qubit iteration
for q in range(n_qubits):
# gate iteration
for g in range(int(len(inputs)/3)):
qml.Rot(*(params[0][l][3*g:3*(g+1)] * inputs[3*g:3*(g+1)] + params[1][l][3*g:3*(g+1)]), wires=q)
return [qml.expval(qml.Hermitian(density_matrix(state_labels[i]), wires=[i])) for i in range(n_qubits)]
class class_weights(tf.keras.layers.Layer):
def __init__(self):
super(class_weights, self).__init__()
w_init = tf.random_normal_initializer()
self.w = tf.Variable(
initial_value=w_init(shape=(1, 2), dtype="float32"),
trainable=True,
)
def call(self, inputs):
return (inputs * self.w)
X = tf.keras.Input(shape=(27,27,1))
conv_layer_1 = tf.keras.layers.Conv2D(filters=1, kernel_size=[3,3], strides=[2,2], name='Conv_Layer_1')(X)
conv_layer_2 = tf.keras.layers.Conv2D(filters=1, kernel_size=[3,3], strides=[2,2], name='Conv_Layer_2')(conv_layer_1)
max__pool_layer = tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, name='Max_Pool_Layer')(conv_layer_2)
reshapor_layer = tf.keras.layers.Reshape((9,), name='Reshapor_Layer')(max__pool_layer)
qlayer = qml.qnn.KerasLayer(qcircuit, {"params": (2, 1, 9)}, output_dim=2, name='Quantum_Layer')(reshapor_layer)
class_weights_layer = class_weights()(qlayer)
model = tf.keras.Model(inputs=X, outputs=class_weights_layer, name='Conv DRC')
model(X_train[0:32])
model.summary()
opt = tf.keras.optimizers.Adam(learning_rate=0.1)
model.compile(opt, loss="mse", metrics=["accuracy"])
model.fit(X_train, to_categorical(Y_train), epochs=6, batch_size=32, validation_data=(X_test, to_categorical(Y_test)), verbose=1)
predict_test = model.predict(X_test)
```
|
github_jupyter
|
## Dependencies
```
# !pip install --quiet efficientnet
!pip install --quiet image-classifiers
import warnings, json, re, glob, math
from scripts_step_lr_schedulers import *
from melanoma_utility_scripts import *
from kaggle_datasets import KaggleDatasets
from sklearn.model_selection import KFold
import tensorflow.keras.layers as L
import tensorflow.keras.backend as K
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from tensorflow.keras import optimizers, layers, metrics, losses, Model
# import efficientnet.tfkeras as efn
from classification_models.tfkeras import Classifiers
import tensorflow_addons as tfa
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
```
## TPU configuration
```
strategy, tpu = set_up_strategy()
print("REPLICAS: ", strategy.num_replicas_in_sync)
AUTO = tf.data.experimental.AUTOTUNE
```
# Model parameters
```
dataset_path = 'melanoma-256x256'
config = {
"HEIGHT": 256,
"WIDTH": 256,
"CHANNELS": 3,
"BATCH_SIZE": 64,
"EPOCHS": 20,
"LEARNING_RATE": 3e-4,
"ES_PATIENCE": 5,
"N_FOLDS": 5,
"BASE_MODEL_PATH": 'imagenet',
"DATASET_PATH": dataset_path
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
config
```
# Load data
```
database_base_path = '/kaggle/input/siim-isic-melanoma-classification/'
k_fold = pd.read_csv(database_base_path + 'train.csv')
test = pd.read_csv(database_base_path + 'test.csv')
print('Train samples: %d' % len(k_fold))
display(k_fold.head())
print(f'Test samples: {len(test)}')
display(test.head())
GCS_PATH = KaggleDatasets().get_gcs_path(dataset_path)
TRAINING_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/train*.tfrec')
TEST_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/test*.tfrec')
```
# Augmentations
```
def data_augment(image, label):
p_spatial = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_spatial2 = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_rotate = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_crop = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
### Spatial-level transforms
if p_spatial >= .2: # flips
image['input_image'] = tf.image.random_flip_left_right(image['input_image'])
image['input_image'] = tf.image.random_flip_up_down(image['input_image'])
if p_spatial >= .7:
image['input_image'] = tf.image.transpose(image['input_image'])
if p_rotate >= .8: # rotate 270º
image['input_image'] = tf.image.rot90(image['input_image'], k=3)
elif p_rotate >= .6: # rotate 180º
image['input_image'] = tf.image.rot90(image['input_image'], k=2)
elif p_rotate >= .4: # rotate 90º
image['input_image'] = tf.image.rot90(image['input_image'], k=1)
if p_spatial2 >= .7: # random rotation range 0º to 45º
image['input_image'] = transform_rotation(image['input_image'], config['HEIGHT'])
if p_crop >= .6: # crops
if p_crop >= .95:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.7), int(config['WIDTH']*.7), config['CHANNELS']])
elif p_crop >= .85:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.8), int(config['WIDTH']*.8), config['CHANNELS']])
elif p_crop >= .7:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.9), int(config['WIDTH']*.9), config['CHANNELS']])
else:
image['input_image'] = tf.image.central_crop(image['input_image'], central_fraction=.6)
image['input_image'] = tf.image.resize(image['input_image'], size=[config['HEIGHT'], config['WIDTH']])
return image, label
```
## Auxiliary functions
```
# Datasets utility functions
def read_labeled_tfrecord(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, LABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
label = tf.cast(example['target'], tf.float32)
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
data['diagnosis'] = tf.cast(tf.one_hot(example['diagnosis'], 10), tf.int32)
return {'input_image': image, 'input_meta': data}, label # returns a dataset of (image, data, label)
def read_labeled_tfrecord_eval(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, LABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
label = tf.cast(example['target'], tf.float32)
image_name = example['image_name']
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
data['diagnosis'] = tf.cast(tf.one_hot(example['diagnosis'], 10), tf.int32)
return {'input_image': image, 'input_meta': data}, label, image_name # returns a dataset of (image, data, label, image_name)
def load_dataset(filenames, ordered=False, buffer_size=-1):
ignore_order = tf.data.Options()
if not ordered:
ignore_order.experimental_deterministic = False # disable order, increase speed
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.with_options(ignore_order) # uses data as soon as it streams in, rather than in its original order
dataset = dataset.map(read_labeled_tfrecord, num_parallel_calls=buffer_size)
return dataset # returns a dataset of (image, data, label)
def load_dataset_eval(filenames, buffer_size=-1):
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.map(read_labeled_tfrecord_eval, num_parallel_calls=buffer_size)
return dataset # returns a dataset of (image, data, label, image_name)
def get_training_dataset(filenames, batch_size, buffer_size=-1):
dataset = load_dataset(filenames, ordered=False, buffer_size=buffer_size)
dataset = dataset.map(data_augment, num_parallel_calls=AUTO)
dataset = dataset.repeat() # the training dataset must repeat for several epochs
dataset = dataset.shuffle(2048)
dataset = dataset.batch(batch_size, drop_remainder=True) # slighly faster with fixed tensor sizes
dataset = dataset.prefetch(buffer_size) # prefetch next batch while training (autotune prefetch buffer size)
return dataset
def get_validation_dataset(filenames, ordered=True, repeated=False, batch_size=32, buffer_size=-1):
dataset = load_dataset(filenames, ordered=ordered, buffer_size=buffer_size)
if repeated:
dataset = dataset.repeat()
dataset = dataset.shuffle(2048)
dataset = dataset.batch(batch_size, drop_remainder=repeated)
dataset = dataset.prefetch(buffer_size)
return dataset
def get_eval_dataset(filenames, batch_size=32, buffer_size=-1):
dataset = load_dataset_eval(filenames, buffer_size=buffer_size)
dataset = dataset.batch(batch_size, drop_remainder=False)
dataset = dataset.prefetch(buffer_size)
return dataset
# Test function
def read_unlabeled_tfrecord(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, UNLABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
image_name = example['image_name']
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
return {'input_image': image, 'input_tabular': data}, image_name # returns a dataset of (image, data, image_name)
def load_dataset_test(filenames, buffer_size=-1):
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.map(read_unlabeled_tfrecord, num_parallel_calls=buffer_size)
# returns a dataset of (image, data, label, image_name) pairs if labeled=True or (image, data, image_name) pairs if labeled=False
return dataset
def get_test_dataset(filenames, batch_size=32, buffer_size=-1):
dataset = load_dataset_test(filenames, buffer_size=buffer_size)
dataset = dataset.batch(batch_size, drop_remainder=False)
dataset = dataset.prefetch(buffer_size)
return dataset
# Advanced augmentations
def transform_rotation(image, height):
# input image - is one image of size [dim,dim,3] not a batch of [b,dim,dim,3]
# output - image randomly rotated
DIM = height
XDIM = DIM%2 #fix for size 331
rotation = 45. * tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
# CONVERT DEGREES TO RADIANS
rotation = math.pi * rotation / 180.
# ROTATION MATRIX
c1 = tf.math.cos(rotation)
s1 = tf.math.sin(rotation)
one = tf.constant([1] ,dtype='float32')
zero = tf.constant([0], dtype='float32')
rotation_matrix = tf.reshape( tf.concat([c1,s1,zero, -s1,c1,zero, zero,zero,one],axis=0), [3, 3] )
# LIST DESTINATION PIXEL INDICES
x = tf.repeat( tf.range(DIM//2,-DIM//2,-1), DIM )
y = tf.tile( tf.range(-DIM//2,DIM//2),[DIM] )
z = tf.ones([DIM*DIM],dtype='int32')
idx = tf.stack( [x,y,z] )
# ROTATE DESTINATION PIXELS ONTO ORIGIN PIXELS
idx2 = K.dot(rotation_matrix,tf.cast(idx,dtype='float32'))
idx2 = K.cast(idx2,dtype='int32')
idx2 = K.clip(idx2,-DIM//2+XDIM+1,DIM//2)
# FIND ORIGIN PIXEL VALUES
idx3 = tf.stack( [DIM//2-idx2[0,], DIM//2-1+idx2[1,]] )
d = tf.gather_nd(image, tf.transpose(idx3))
return tf.reshape(d,[DIM, DIM, 3])
```
## Learning rate scheduler
```
lr_min = 1e-6
lr_start = 0
lr_max = config['LEARNING_RATE']
step_size = 26880 // config['BATCH_SIZE'] #(len(k_fold[k_fold[f'fold_{fold_n}'] == 'train']) * 2) // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
hold_max_steps = 0
warmup_steps = step_size * 5
num_cycles = 5
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [cosine_with_hard_restarts_schedule_with_warmup(tf.cast(x, tf.float32), total_steps=total_steps,
warmup_steps=warmup_steps, lr_start=lr_start,
lr_max=lr_max, lr_min=lr_min, num_cycles=num_cycles) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
```
# Model
```
def model_fn(input_shape):
input_image = L.Input(shape=input_shape, name='input_image')
BaseModel, preprocess_input = Classifiers.get('resnet18')
base_model = BaseModel(input_shape=input_shape,
weights=config['BASE_MODEL_PATH'],
include_top=False)
x = base_model(input_image)
x = L.GlobalAveragePooling2D()(x)
output = L.Dense(1, activation='sigmoid')(x)
model = Model(inputs=input_image, outputs=output)
return model
```
# Training
```
eval_dataset = get_eval_dataset(TRAINING_FILENAMES, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
image_names = next(iter(eval_dataset.unbatch().map(lambda data, label, image_name: image_name).batch(len(k_fold)))).numpy().astype('U')
image_data = eval_dataset.map(lambda data, label, image_name: data)
history_list = []
kfold = KFold(config['N_FOLDS'], shuffle=True, random_state=SEED)
for n_fold, (trn_idx, val_idx) in enumerate(kfold.split(TRAINING_FILENAMES)):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# tf.tpu.experimental.initialize_tpu_system(tpu)
K.clear_session()
### Data
train_filenames = np.array(TRAINING_FILENAMES)[trn_idx]
valid_filenames = np.array(TRAINING_FILENAMES)[val_idx]
train_size = count_data_items(train_filenames)
step_size = train_size // config['BATCH_SIZE']
# Train model
model_path = f'model_fold_{n_fold}.h5'
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
with strategy.scope():
model = model_fn((config['HEIGHT'], config['WIDTH'], config['CHANNELS']))
lr = lambda: cosine_with_hard_restarts_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32),
total_steps=total_steps, warmup_steps=warmup_steps,
lr_start=lr_start, lr_max=lr_max, lr_min=lr_min,
num_cycles=num_cycles)
optimizer = optimizers.Adam(learning_rate=lr)
model.compile(optimizer, loss=losses.BinaryCrossentropy(label_smoothing=0.05),
metrics=[metrics.AUC()])
history = model.fit(get_training_dataset(train_filenames, batch_size=config['BATCH_SIZE'], buffer_size=AUTO),
validation_data=get_validation_dataset(valid_filenames, ordered=True, repeated=False,
batch_size=config['BATCH_SIZE'], buffer_size=AUTO),
epochs=config['EPOCHS'],
steps_per_epoch=step_size,
callbacks=[checkpoint, es],
verbose=2).history
history_list.append(history)
# Make predictions
preds = model.predict(image_data)
name_preds = dict(zip(image_names, preds.reshape(len(preds))))
k_fold[f'pred_fold_{n_fold}'] = k_fold.apply(lambda x: name_preds[x['image_name']], axis=1)
valid_filenames = np.array(TRAINING_FILENAMES)[val_idx]
valid_dataset = get_eval_dataset(valid_filenames, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
valid_image_names = next(iter(valid_dataset.unbatch().map(lambda data, label, image_name: image_name).batch(count_data_items(valid_filenames)))).numpy().astype('U')
k_fold[f'fold_{n_fold}'] = k_fold.apply(lambda x: 'validation' if x['image_name'] in valid_image_names else 'train', axis=1)
```
## Model loss graph
```
for n_fold in range(config['N_FOLDS']):
print(f'Fold: {n_fold + 1}')
plot_metrics(history_list[n_fold])
```
## Model loss graph aggregated
```
plot_metrics_agg(history_list, config['N_FOLDS'])
```
# Model evaluation
```
display(evaluate_model(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Model evaluation by Subset
```
display(evaluate_model_Subset(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Confusion matrix
```
for n_fold in range(config['N_FOLDS']):
n_fold += 1
pred_col = f'pred_fold_{n_fold}'
train_set = k_fold[k_fold[f'fold_{n_fold}'] == 'train']
valid_set = k_fold[k_fold[f'fold_{n_fold}'] == 'validation']
print(f'Fold: {n_fold}')
plot_confusion_matrix(train_set['target'], np.round(train_set[pred_col]),
valid_set['target'], np.round(valid_set[pred_col]))
```
# Visualize predictions
```
k_fold['pred'] = 0
for n_fold in range(config['N_FOLDS']):
k_fold['pred'] += k_fold[f'pred_fold_{n_fold+1}'] / config['N_FOLDS']
print('Top 10 samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].head(10))
print('Top 10 positive samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].query('target == 1').head(10))
print('Top 10 predicted positive samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].query('pred > .5').head(10))
print('Label/prediction distribution')
print(f"Train positive labels: {len(k_fold[k_fold['target'] > .5])}")
print(f"Train positive predictions: {len(k_fold[k_fold['pred'] > .5])}")
print(f"Train positive correct predictions: {len(k_fold[(k_fold['target'] > .5) & (k_fold['pred'] > .5)])}")
```
# Make predictions
```
model_path_list = glob.glob('/kaggle/working/' + '*.h5')
n_models = len(model_path_list)
model_path_list.sort()
print(f'{n_models} Models to predict:')
print(*model_path_list, sep='\n')
test_dataset = get_test_dataset(TEST_FILENAMES, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
NUM_TEST_IMAGES = len(test)
test_preds = np.zeros((NUM_TEST_IMAGES, 1))
for model_path in model_path_list:
# tf.tpu.experimental.initialize_tpu_system(tpu)
K.clear_session()
print(model_path)
model = model_fn((config['HEIGHT'], config['WIDTH'], config['CHANNELS']))
model.load_weights(model_path)
test_preds += model.predict(test_dataset) / n_models
image_names = next(iter(test_dataset.unbatch().map(lambda data, image_name: image_name).batch(NUM_TEST_IMAGES))).numpy().astype('U')
name_preds = dict(zip(image_names, test_preds.reshape(len(test_preds))))
test['target'] = test.apply(lambda x: name_preds[x['image_name']], axis=1)
```
# Visualize test predictions
```
print(f"Test predictions {len(test[test['target'] > .5])}|{len(test[test['target'] <= .5])}")
print('Top 10 samples')
display(test[['image_name', 'sex', 'age_approx','anatom_site_general_challenge','target'] +
[c for c in test.columns if (c.startswith('pred_fold'))]].head(10))
print('Top 10 positive samples')
display(test[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'target'] +
[c for c in test.columns if (c.startswith('pred_fold'))]].query('target > .5').head(10))
```
# Test set predictions
```
submission = pd.read_csv(database_base_path + 'sample_submission.csv')
submission['target'] = test['target']
submission.to_csv('submission.csv', index=False)
display(submission.head(10))
display(submission.describe())
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_1_gan_intro.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 7: Generative Adversarial Networks**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 7 Material
* **Part 7.1: Introduction to GANS for Image and Data Generation** [[Video]](https://www.youtube.com/watch?v=0QnCH6tlZgc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_1_gan_intro.ipynb)
* Part 7.2: Implementing a GAN in Keras [[Video]](https://www.youtube.com/watch?v=T-MCludVNn4&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_2_Keras_gan.ipynb)
* Part 7.3: Face Generation with StyleGAN and Python [[Video]](https://www.youtube.com/watch?v=s1UQPK2KoBY&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_3_style_gan.ipynb)
* Part 7.4: GANS for Semi-Supervised Learning in Keras [[Video]](https://www.youtube.com/watch?v=ZPewmEu7644&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_4_gan_semi_supervised.ipynb)
* Part 7.5: An Overview of GAN Research [[Video]](https://www.youtube.com/watch?v=cvCvZKvlvq4&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_07_5_gan_research.ipynb)
# Part 7.1: Introduction to GANS for Image and Data Generation
A generative adversarial network (GAN) is a class of machine learning systems invented by Ian Goodfellow in 2014. [[Cite:goodfellow2014generative]](https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf) Two neural networks contest with each other in a game. Given a training set, this technique learns to generate new data with the same statistics as the training set. For example, a GAN trained on photographs can generate new photographs that look at least superficially authentic to human observers, having many realistic characteristics. Though originally proposed as a form of generative model for unsupervised learning, GANs have also proven useful for semi-supervised learning, fully supervised learning, and reinforcement learning.
This paper used neural networks to automatically generate images for several datasets that we've seen previously: MINST and CIFAR. However, it also included the Toronto Face Dataset (a private dataset used by some researchers). These generated images are given in Figure 7.GANS.
**Figure 7.GANS: GAN Generated Images**

Only sub-figure D made use of convolutional neural networks. Figures A-C make use of fully connected neural networks. As we will see in this module, the role of convolutional neural networks with GANs was greatly increased.
A GAN is called a generative model because it generates new data. The overall process of a GAN is given by the following diagram in Figure 7.GAN-FLOW.
**Figure 7.GAN-FLOW: GAN Structure**

|
github_jupyter
|
# **Solving the Definition Extraction Problem**
### **Approach 3: Using Doc2Vec model and Classifiers.**
**Doc2Vec** is a Model that represents each Document as a Vector. The goal of Doc2Vec is to create a numeric representation of a document, regardless of its length. So, the input of texts per document can be various while the output is fixed-length vectors.
Design of Doc2Vec is based on Word2Vec. But unlike words, documents do not come in logical structures such as words, so the another method has to be found. There are two implementations:
1. Paragraph Vector - Distributed Memory (PV-DM)
2. Paragraph Vector - Distributed Bag of Words (PV-DBOW)
**PV-DM** is analogous to Word2Vec continous bag of word CBOW. But instead of using just words to predict the next word, add another feature vector, which is document-unique. So, when training the word vectors W, the document vector D is trained as well, and in the end of training, it holds a numeric representation of the document.

**PV-DBOW** is analogous to Word2Vec skip gram. Instead of predicting next word, it use a document vector to classify entire words in the document.

Not: it's recommend to use a combination of both algorithms to infer the vector representation of a document.
```
from google.colab import drive
drive.mount('/content/drive')
!unzip 'drive/My Drive/wikipedia-movie-plots.zip'
import os
import nltk
import pandas as pd
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
from data_loader import DeftCorpusLoader
from sklearn.naive_bayes import GaussianNB
from sklearn import tree
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
nltk.download('punkt')
nltk.download('stopwords')
nltk.download('wordnet')
```
### **Load Doc2Vec Model Trainning Data**
```
# Load amazon review reports of movies.
with open('wiki_movie_plots_deduped.csv') as data:
corpus_list = pd.read_csv(data, sep=",", header = None)
corpus_list = corpus_list[7].tolist()[1:]
print("Corpus legnth: ", len(corpus_list))
stop_words = set(stopwords.words('english'))
porter = PorterStemmer()
qoutes_list = ["``", "\"\"", "''"]
train_corpus = []
for i, sentence in enumerate(corpus_list):
# Lower all the letters in the sentence
tokens = word_tokenize(sentence.lower())
processed_tokens = []
for j, token in enumerate(tokens):
if not token.isdigit():
if token not in stop_words and len(token) > 1 and token not in qoutes_list:
# Convert each sentence from amazon reviews to list of words that doesn't include
# stop words or any special letters or digits
processed_tokens.append(porter.stem(token))
train_corpus.append(TaggedDocument(words=processed_tokens, tags=[str(i)]))
train_corpus[:5]
```
### **Train Doc2Vec Model Based on Amazon Reviews.**
First we will define the attributes of Doc2Vec model:
* **Vector Size:** Dimensionality of the documents feature vector.
* **Min Count:** Ignores all words with total frequency lower than this.
* **Epochs:** Number of iterations (epochs) over the corpus.
* **Workers:** Use these many worker threads to train the model (faster training with multicore machines).
Second build the **Vocabulary** based on the training corpus (processed amazon reviews). Finally train the model on the training corpus.
Note: the default used algorithm is PV-DM.
```
model = Doc2Vec(vector_size=300, min_count=2, epochs=40, workers=8)
model.build_vocab(train_corpus)
model.train(train_corpus, total_examples=model.corpus_count, epochs=model.epochs)
```
### **Load DeftEval Trainning & Dev Data**
Note: as the code is executed on google colab, the path of the data is rooted from the drive. So, the path of the data need to be change if the code will be executed on the local machine.
```
deft_loader = DeftCorpusLoader("drive/My Drive/DeftEval/deft_corpus/data")
trainframe, devframe = deft_loader.load_classification_data()
deft_loader.preprocess_data(devframe)
deft_loader.clean_data(devframe)
dev_vectors = []
# Create test data vectors from Doc2Vec model
for parsed_list in devframe["Parsed"]:
dev_vectors.append(model.infer_vector(parsed_list))
deft_loader.preprocess_data(trainframe)
deft_loader.clean_data(trainframe)
train_vectors=[]
# Create training data vectors from Doc2Vec model
for parsed_list in trainframe["Parsed"]:
train_vectors.append(model.infer_vector(parsed_list))
```
### **Apply Classifiers Algorithms**
For each classifier test, **F1-score** and **Accuracy** are calculated.
**1. Naive Bayes Algorithm**
```
gnb = GaussianNB()
test_predict = gnb.fit(train_vectors, trainframe['HasDef']).predict(dev_vectors)
print(metrics.classification_report(list(devframe["HasDef"]), test_predict))
```
**2. Decision Tree Algorithm**
```
decision_tree = tree.DecisionTreeClassifier(class_weight="balanced")
test_predict = decision_tree.fit(train_vectors, trainframe['HasDef']).predict(dev_vectors)
print(metrics.classification_report(list(devframe["HasDef"]), test_predict))
```
**3. Logistic Regression Algorithm**
```
test_predict = LogisticRegression(class_weight="balanced", random_state=0).fit(train_vectors, trainframe['HasDef']).predict(dev_vectors)
print(metrics.classification_report(list(devframe["HasDef"]), test_predict))
```
|
github_jupyter
|
```
from MPyDATA import ScalarField, VectorField, PeriodicBoundaryCondition, Options, Stepper, Solver
import numpy as np
dt, dx, dy = .1, .2, .3
nt, nx, ny = 100, 15, 10
# https://en.wikipedia.org/wiki/Arakawa_grids#Arakawa_C-grid
x, y = np.mgrid[
dx/2 : nx*dx : dx,
dy/2 : ny*dy : dy
]
# vector field (u,v) components
# u - x component of the velocity field
ux, uy = np.mgrid[
0 : (nx+1)*dx : dx,
dy/2 : ny*dy : dy
]
# v - y component of the velocity field
vx, vy = np.mgrid[
dx/2 : nx*dx : dx,
0: (ny+1)*dy : dy
]
from matplotlib import pyplot, rcParams
rcParams['figure.figsize'] = [12, 8]
pyplot.quiver(ux, uy, 1, 0, pivot='mid')
pyplot.quiver(vx, vy, 0, 1, pivot='mid')
pyplot.xticks(ux[:,0])
pyplot.yticks(vy[0,:])
pyplot.scatter(x, y)
pyplot.title('Arakawa-C grid')
pyplot.grid()
pyplot.show()
from MPyDATA import ScalarField, VectorField, PeriodicBoundaryCondition, Options, Stepper, Solver
bc = [PeriodicBoundaryCondition(), PeriodicBoundaryCondition()]
options = Options()
data = np.zeros((nx, ny))
data[1,1] = 10
advectee = ScalarField(data, options.n_halo, boundary_conditions=bc)
# https://en.wikipedia.org/wiki/Stream_function
```
stream function:
$u=-\partial_y \psi$
$v=\partial_x \psi$
example flow field:
$\psi(x,y) = - w_{\text{max}} \frac{X}{\pi}
\sin\left(\pi \frac{y}{Y}\right)
\cos\left(2\pi\frac{x}{X}\right)
$
```
class Psi:
def __init__(self, *, X, Y, w_max):
self.X = X
self.Y = Y
self.w_max = w_max
def __call__(self, x, y):
return - self.w_max * self.X / np.pi * np.sin(np.pi * y/self.Y) * np.cos(2 * np.pi * x/self.X)
psi = Psi(X=nx*dx, Y=ny*dy, w_max=.6)
print(psi(0,0))
print(psi(1,1))
# https://en.wikipedia.org/wiki/Courant%E2%80%93Friedrichs%E2%80%93Lewy_condition
# C_x = u * dt / dx
# C_y = v * dt / dy
u = -(psi(ux, uy+dy/2) - psi(ux, uy-dy/2)) / dy
v = +(psi(vx+dx/2, vy) - psi(vx-dx/2, vy)) / dx
advector = VectorField([u*dt/dx, v*dt/dy], halo=options.n_halo, boundary_conditions=bc)
def plot(advectee, advector):
pyplot.scatter(x, y, s=100, c=advectee.get(), marker='s')
pyplot.quiver(ux, uy, advector.get_component(0), 0, pivot='mid', scale=10)
pyplot.quiver(vx, vy, 0, advector.get_component(1), pivot='mid', scale=10)
pyplot.xticks(ux[:,0])
pyplot.yticks(vy[0,:])
pyplot.colorbar()
pyplot.grid()
pyplot.show()
plot(advectee, advector)
stepper = Stepper(options=options, grid=(nx, ny))
solver = Solver(stepper=stepper, advectee=advectee, advector=advector)
solver.advance(20)
plot(advectee, advector)
# https://en.wikipedia.org/wiki/NetCDF
from scipy.io.netcdf import netcdf_file
with netcdf_file('test.nc', mode='w') as ncdf:
# global attributes (metadata)
ncdf.MPyDATA_options = str(options)
# dimensions
ncdf.createDimension("T", nt)
ncdf.createDimension("X", nx)
ncdf.createDimension("Y", ny)
# variables (defined over defined dimensions)
variables = {}
variables["T"] = ncdf.createVariable("T", "f", ["T"])
variables["T"].units = "seconds"
variables["T"][:] = 0
variables["X"] = ncdf.createVariable("X", "f", ["X"])
variables["X"][:] = x[:, 0]
variables["X"].units = "metres"
variables["Y"] = ncdf.createVariable("Y", "f", ["Y"])
variables["Y"][:] = y[0, :]
variables["Y"].units = "metres"
variables["advectee"] = ncdf.createVariable("advectee", "f", ["T", "X", "Y"])
# attributes (per variable)
# e.g. units above
# note: initial condition not saved
for i in range(nt):
solver.advance(nt=1)
variables["T"][i] = (i+1) * dt
variables["advectee"][i, :, :] = solver.advectee.get()
! ls -lah test.nc
! file test.nc
! ncdump -c test.nc
# https://en.wikipedia.org/wiki/Climate_and_Forecast_Metadata_Conventions
# try opening in Paraview (https://en.wikipedia.org/wiki/ParaView)...
```
|
github_jupyter
|
# NLTK
## Sentence and Word Tokenization
```
from nltk.tokenize import sent_tokenize, word_tokenize
EXAMPLE_TEXT = "Hello Mr. Smith, how are you doing today? The weather is great, and Python is awesome. The sky is pinkish-blue. You shouldn't eat cardboard."
# Sentence Tokenization
print(sent_tokenize(EXAMPLE_TEXT))
# Word Tokenization
print(word_tokenize(EXAMPLE_TEXT))
```
## Stopwords
```
from nltk.corpus import stopwords
# Printing all stopwords (english)
set(stopwords.words('english'))
example_sent = "This is a sample sentence, showing off the stop words filtration."
stop_words = set(stopwords.words('english'))
word_tokens = word_tokenize(example_sent)
filtered_sentence = [w for w in word_tokens if not w in stop_words]
print(word_tokens)
print(filtered_sentence)
```
## Stemming words
```
# Porter Stemmer is a stemming algorithm
from nltk.stem import PorterStemmer
from nltk.tokenize import sent_tokenize, word_tokenize
ps = PorterStemmer()
example_words = ["python","pythoner","pythoning","pythoned","pythonly"]
for w in example_words:
print(ps.stem(w))
new_text = "It is important to by very pythonly while you are pythoning with python. All pythoners have pythoned poorly at least once."
words = word_tokenize(new_text)
for w in words:
print(ps.stem(w))
```
## Part of Speech Tagging
# POS tag list:
CC coordinating conjunction
CD cardinal digit
DT determiner
EX existential there (like: "there is" ... think of it like "there exists")
FW foreign word
IN preposition/subordinating conjunction
JJ adjective 'big'
JJR adjective, comparative 'bigger'
JJS adjective, superlative 'biggest'
LS list marker 1)
MD modal could, will
NN noun, singular 'desk'
NNS noun plural 'desks'
NNP proper noun, singular 'Harrison'
NNPS proper noun, plural 'Americans'
PDT predeterminer 'all the kids'
POS possessive ending parent's
PRP personal pronoun I, he, she
PRP\$ possessive pronoun my, his, hers
RB adverb very, silently,
RBR adverb, comparative better
RBS adverb, superlative best
RP particle give up
TO to go 'to' the store.
UH interjection errrrrrrrm
VB verb, base form take
VBD verb, past tense took
VBG verb, gerund/present participle taking
VBN verb, past participle taken
VBP verb, sing. present, non-3d take
VBZ verb, 3rd person sing. present takes
WDT wh-determiner which
WP wh-pronoun who, what
WP$ possessive wh-pronoun whose
WRB wh-abverb where, when
#### PunktSentenceTokenizer
> This tokenizer is capable of unsupervised machine learning, so you can actually train it on any body of text that you use.
```
import nltk
from nltk.corpus import state_union
from nltk.tokenize import PunktSentenceTokenizer
# Create training and testing data
train_text = state_union.raw('2005-GWBush.txt')
sample_text = state_union.raw('2006-GWBush.txt')
# Train Punkt tokenizer
custom_sent_tokenizer = PunktSentenceTokenizer(train_text)
# Actually tokenize
tokenized = custom_sent_tokenizer.tokenize(sample_text)
print(tokenized)
# Create a function that will run through and tag all of the parts of speech per sentence
def process_content():
try:
for i in tokenized[ :5]:
words = nltk.word_tokenize(i)
tagged = nltk.pos_tag(words)
print(tagged)
except Exception as e:
print(str(e))
# Output should be a list of tuples, where the first element in the tuple is the word, and the second is the part of speech tag
process_content()
```
## Lemmatizing
> A very similar operation to stemming is called lemmatizing. The major difference between these is, as you saw earlier, stemming can often create non-existent words, whereas lemmas are actual words.
> So, your root stem, meaning the word you end up with, is not something you can just look up in a dictionary, but you can look up a lemma.
> Some times you will wind up with a very similar word, but sometimes, you will wind up with a completely different word.
```
from nltk.stem import WordNetLemmatizer
lemmatizer = WordNetLemmatizer()
print(lemmatizer.lemmatize("cats"))
print(lemmatizer.lemmatize("cacti"))
print(lemmatizer.lemmatize("geese"))
print(lemmatizer.lemmatize("rocks"))
print(lemmatizer.lemmatize("python"))
print(lemmatizer.lemmatize("better", pos="a"))
print(lemmatizer.lemmatize("best", pos="a"))
print(lemmatizer.lemmatize("run"))
print(lemmatizer.lemmatize("run",'v'))
# Here, we've got a bunch of examples of the lemma for the words that we use.
# The only major thing to note is that lemmatize takes a part of speech parameter, "pos."
# If not supplied, the default is "noun." This means that an attempt will be made to find the closest noun, which can create trouble for you.
# Keep this in mind if you use lemmatizing!
```
## Corpora
> The NLTK corpus is a massive dump of all kinds of natural language data sets
```
# Opening the Gutenberg Bible, and reading the first few lines
from nltk.tokenize import sent_tokenize, PunktSentenceTokenizer
from nltk.corpus import gutenberg
#sample text
sample = gutenberg.raw('bible-kjv.txt')
tok = sent_tokenize(sample)
for x in range(5):
print(tok[x])
```
## Wordnet
> Wordnet is a collection of words, definitions, examples of their use, synonyms, antonyms, and more.
```
# Import wordnet
from nltk.corpus import wordnet
# use the term "program" to find synsets
syns = wordnet.synsets('program')
print(syns)
#Print first synset
print(syns[0].name())
# Print only the word
print(syns[0].lemmas()[0].name())
# Definition for that first synset
print(syns[0].definition())
# Examples of the word in use
print(syns[0].examples())
# Synonyms and Antonyms
# The lemmas will be synonyms,
# and then you can use .antonyms to find the antonyms to the lemmas
synonyms = []
antonyms = []
for syn in wordnet.synsets('good'):
for l in syn.lemmas():
synonyms.append(l.name())
if l.antonyms():
antonyms.append(l.antonyms()[0].name())
print(set(synonyms))
print(set(antonyms))
# compare the similarity of two words and their tenses
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('boat.n.01')
print(w1.wup_similarity(w2))
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('car.n.01')
print(w1.wup_similarity(w2))
w1 = wordnet.synset('ship.n.01')
w2 = wordnet.synset('cat.n.01')
print(w1.wup_similarity(w2))
```
|
github_jupyter
|
```
#@title blank template
#@markdown This notebook from [github.com/matteoferla/pyrosetta_help](https://github.com/matteoferla/pyrosetta_help).
#@markdown It can be opened in Colabs via [https://colab.research.google.com/github/matteoferla/pyrosetta_help/blob/main/colabs/colabs-pyrosetta.ipynb](https://colab.research.google.com/github/matteoferla/pyrosetta_help/blob/main/colabs/colabs-pyrosetta.ipynb)
#@markdown It just for loading up PyRosetta
#@title Installation
#@markdown Installing PyRosetta with optional backup to your drive (way quicker next time!).
#@markdown Note that PyRosetta occupies some 10 GB, so you'll need to be on the 100 GB plan of Google Drive (it's one pound a month).
#@markdown The following is not the real password. However, the format is similar.
username = 'boltzmann' #@param {type:"string"}
password = 'constant' #@param {type:"string"}
#@markdown Release to install:
_release = 'release-295' #@param {type:"string"}
#@markdown Use Google Drive for PyRosetta (way faster next time, but takes up space)
#@markdown (NB. You may be prompted to follow a link and possibly authenticate and then copy a code into a box
use_drive = True #@param {type:"boolean"}
#@markdown Installing `rdkit` and `rdkit_to_params` allows the creation of custom topologies (params) for new ligands
install_rdkit = True #@param {type:"boolean"}
import sys
import platform
import os
assert platform.dist()[0] == 'Ubuntu'
py_version = str(sys.version_info.major) + str(sys.version_info.minor)
if use_drive:
from google.colab import drive
drive.mount('/content/drive')
_path = '/content/drive/MyDrive'
os.chdir(_path)
else:
_path = '/content'
if not any(['PyRosetta4.Release' in filename for filename in os.listdir()]):
assert not os.system(f'curl -u {username}:{password} https://graylab.jhu.edu/download/PyRosetta4/archive/release/PyRosetta4.Release.python{py_version}.ubuntu/PyRosetta4.Release.python{py_version}.ubuntu.{_release}.tar.bz2 -o /content/a.tar.bz2')
assert not os.system('tar -xf /content/a.tar.bz2')
assert not os.system(f'pip3 install -e {_path}/PyRosetta4.Release.python{py_version}.ubuntu.{_release}/setup/')
assert not os.system(f'pip3 install pyrosetta-help biopython')
if install_rdkit:
assert not os.system(f'pip3 install rdkit-pypi rdkit-to-params')
import site
site.main()
#@title Start PyRosetta
import pyrosetta
import pyrosetta_help as ph
no_optH = False #@param {type:"boolean"}
ignore_unrecognized_res=False #@param {type:"boolean"}
load_PDB_components=False #@param {type:"boolean"}
ignore_waters=False #@param {type:"boolean"}
extra_options= ph.make_option_string(no_optH=no_optH,
ex1=None,
ex2=None,
mute='all',
ignore_unrecognized_res=ignore_unrecognized_res,
load_PDB_components=load_PDB_components,
ignore_waters=ignore_waters)
# capture to log
logger = ph.configure_logger()
pyrosetta.init(extra_options=extra_options)
## Usual stuff
pose = ph.pose_from_alphafold2('P02144')
scorefxn = pyrosetta.get_fa_scorefxn()
relax = pyrosetta.rosetta.protocols.relax.FastRelax(scorefxn, 3)
movemap = pyrosetta.MoveMap()
movemap.set_bb(False)
movemap.set_chi(True)
relax.apply(pose)
# Note that nglview does not work with Colabs but py3Dmol does.
# install py3Dmol
os.system(f'pip3 install py3Dmol')
import site
site.main()
# run
import py3Dmol
view = py3Dmol.view(js='https://3dmol.org/build/3Dmol.js',)
view.addModel(ph.get_pdbstr(pose),'pdb')
view.zoomTo()
view
# Also note that RDKit Chem.Mol instances are not displays as representations by default.
#@title Upload to Michelanglo (optional)
#@markdown [Michelanglo](https://michelanglo.sgc.ox.ac.uk/) is a website that
#@markdown allows the creation, annotation and sharing of a webpage with an interactive protein viewport.
#@markdown ([examples](https://michelanglo.sgc.ox.ac.uk/gallery)).
#@markdown The created pages are private —they have a 1 in a quintillion change to be guessed within 5 tries.
#@markdown Registered users (optional) can add interactive annotations to pages.
#@markdown A page created by a guest is editable by registered users with the URL to it
#@markdown (this can be altered in the page settings).
#@markdown Leave blank for guest (it will not add an interactive description):
username = '' #@param {type:"string"}
password = '' #@param {type:"string"}
import os
assert not os.system(f'pip3 install michelanglo-api')
import site
site.main()
from michelanglo_api import MikeAPI, Prolink
if not username:
mike = MikeAPI.guest_login()
else:
mike = MikeAPI(username, password)
page = mike.convert_pdb(pdbblock=ph.get_pdbstr(pose),
data_selection='ligand',
data_focus='residue',
)
if username:
page.retrieve()
page.description = '## Description\n\n'
page.description += 'autogen bla bla'
page.commit()
page.show_link()
```
|
github_jupyter
|
```
import sqlite3
import pandas as pd
import numpy as np
import scipy as sp
import scipy.stats as stats
#import pylab as plt
import matplotlib.pyplot as plt
from collections import Counter
from numpy.random import choice
%matplotlib notebook
dbname = '../../data/sepsis.db'
conn = sqlite3.connect(dbname)
sql = 'SELECT * FROM "diagnoses"'
df = pd.read_sql(sql,conn)
df.head()
from importlib import reload
from fakelite3 import KungFauxPandas
kfpd = KungFauxPandas()
fdf=kfpd.read_sql(sql,conn)
fdf.head()
col = 'Code'
out_dict = dict()
colfact = df[col].factorize()
cc=Counter(colfact[0])
# convert from counts to proportions
for key in cc:
cc[key] = cc[key] / len(df)
fakes = choice(elements,p=weights, replace=True, size=len(df))
out_dict[col] = [colfact[1][xx] for xx in fakes]
len(cc.values()), len(df), len(cc)/len(df)
col = 'Code'
out_dict = dict()
colfact = df[col].factorize()
cc=Counter(colfact[0])
# convert from counts to proportions
for key in cc:
cc[key] = cc[key] / len(df)
fakes = choice(elements,p=weights, replace=True, size=len(df))
out_dict[col] = [colfact[1][xx] for xx in fakes]
#out_dict
col = 'SubjectId'
kd = stats.gaussian_kde(df[col], bw_method='silverman')
out_dict[col]=np.int64(kd.resample()[0])
df.head()
pd.crosstab(df.Codeode, df.squishcode)
np.corrcoef(df.Code, df.squishcode)
sdf = df.sample(5000)
for thiscol in sdf.columns:
if sdf[thiscol].dtype=='object':
print('Converting column ', thiscol)
sdf[thiscol] = sdf[thiscol].factorize()[0]
#np.cov(sdf)
cc = np.corrcoef(sdf.transpose())
#cc = np.cov(sdf.transpose())
#cc[5,1]
plt.imshow(cc,cmap='inferno')
plt.colorbar()
#sdf.head()
#help(np.correlate)
df.iloc[3]
from statsmodels.nonparametric import kernel_density as kd
woo = kd.KDEMultivariate(np.array(sdf.iloc[:,[2,4,9]]), var_type=3*'u')
#help(kd.KDEMultivariate)
np.array(data=sdf.sample(2000).iloc[:,[2,4,9]])
xx = range(40)
bb = list(itertools.product(xx,xx,xx))
np.array(sdf.iloc[2]).shape
from scipy.optimize import fsolve
import statsmodels.api as sm
import numpy as np
# fit
kde = woo#sm.nonparametric.KDEMultivariate() # ... you already did this
# sample
u = np.random.random()
# 1-d root-finding
def func(x):
return kde.cdf([x]) - u
#sample_x = brentq(func, -99999999, 99999999) # read brentq-docs about these constants
# constants need to be sign-changing for the function
#u = np.random.random()
#u
#sample_x = brentq(func, -99999999, 99999999)
def func(x):
return kde.cdf([x]) - u
x0=[92,4,5,3,6,7,8,9,10,11]
from scipy.optimize import minimize
darf = minimize(func,np.array(x0))
print(darf)
x0, func(x0)
func([0,0,0,0,0,3,0,0,0,0])
bork = np.mgrid[0:10,0:10, 0:10]
xx = range(4)
import itertools
ins = list(itertools.product(xx,xx,xx,xx,xx,xx,xx,xx,xx,xx))
vals = [func(i) for i in ins[1004:2004]]
func(ins[1004:2004])
func(bork[32532])
u
#kde.cdf(bork[9000:10000])
func(x0)
list(bork[0])
x0
import statsmodels.api as sm
nobs = 300
np.random.seed(1234) # Seed random generator
c1 = np.random.normal(size=(nobs,1))
c2 = np.random.normal(2, 1, size=(nobs,1))
#Estimate a bivariate distribution and display the bandwidth found:
#dens_u = sm.nonparametric.KDEMultivariate(data=[c1,c2], var_type='cc', bw='normal_reference')
#dens_u.bw
woo = sm.nonparametric.KDEMultivariate(data=sdf.iloc[:,[2,4,9]], var_type=3*'u')
woo.cdf()
len(sdf)
len(set(sdf.iloc[:,9]))
np.corrcoef(sdf.iloc[:,[2,9]])
```
|
github_jupyter
|
# 以下為 Export 成 freeze_graph 的範例程式嗎
```
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD
from keras import backend as K
import tensorflow as tf
from tensorflow.python.tools import freeze_graph, optimize_for_inference_lib
import numpy as np
```
## Exprot to frezen model 的標準作法
* 由於在 Tensorflow Lite
* 但在使用之前需要 Session 載入 Graph & Weight
* tf.train.write_graph :如果是使用 Keras 的話就是用 K.get_session().graph_def 取得 grpah ,然後輸到 phtxt
* tf.train.Saver() : 透過 K.get_session() 取得 Session ,而後透過 tf.train.Saver().save()
```
def export_model_for_mobile(model_name, input_node_name, output_node_name):
# 先暫存成另一個檔檔
tf.train.write_graph(K.get_session().graph_def, 'out', \
model_name + '_graph.pbtxt')
tf.train.Saver().save(K.get_session(), 'out/' + model_name + '.chkp')
freeze_graph.freeze_graph('out/' + model_name + '_graph.pbtxt', None, \
False, 'out/' + model_name + '.chkp', output_node_name, \
"save/restore_all", "save/Const:0", \
'out/frozen_' + model_name + '.pb', True, "")
input_graph_def = tf.GraphDef()
with tf.gfile.Open('out/frozen_' + model_name + '.pb', "rb") as f:
input_graph_def.ParseFromString(f.read())
output_graph_def = optimize_for_inference_lib.optimize_for_inference(
input_graph_def, [input_node_name], [output_node_name],
tf.float32.as_datatype_enum)
with tf.gfile.FastGFile('out/tensorflow_lite_' + model_name + '.pb', "wb") as f:
f.write(output_graph_def.SerializeToString())
```
## 創建 Graph
```
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Activation, Dropout, Flatten, Dense
from keras import backend as K
model = Sequential([
Conv2D(8, (3, 3), activation='relu', input_shape=[128,128,3]),
MaxPooling2D(pool_size=(2, 2)),
Conv2D(8, (3, 3), activation='relu'),
MaxPooling2D(pool_size=(2, 2)),
Flatten(),
Dense(128),
Activation('relu'),
Dense(7),
Activation('softmax')
])
model.summary()
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
model.load_weights("/home/kent/git/DeepLearning_ClassmatesImageClassification_jdwang2018_5_25/CNN_Classfier_32X32_jdwang_Weight_1.h5")
```
## 呼叫預設的函式
```
export_model_for_mobile('classmate_new', model.input.name.split(":")[0], model.output.name.split(":")[0])
```
|
github_jupyter
|
# 1 - Installs and imports
```
!pip install --upgrade pip
!pip install sentencepiece
!pip install transformers
from transformers import AutoTokenizer, AutoModel, TFAutoModel, AutoConfig
from transformers import AutoModelForSequenceClassification
from transformers import TFAutoModelForSequenceClassification
from transformers import pipeline
import numpy as np
from scipy.spatial.distance import cosine
from collections import defaultdict
import urllib
import numpy as np
from scipy.special import softmax
from sklearn.metrics import classification_report
```
# 2 - Fetch XLM-T model
```
MODEL = "cardiffnlp/twitter-xlm-roberta-base"
tokenizer = AutoTokenizer.from_pretrained(MODEL)
model = AutoModel.from_pretrained(MODEL)
```
# Use Cases
## 1 - Compute Tweet Similarity
```
def preprocess(text):
new_text = []
for t in text.split(" "):
t = '@user' if t.startswith('@') and len(t) > 1 else t
t = 'http' if t.startswith('http') else t
new_text.append(t)
return " ".join(new_text)
def get_embedding(text):
text = preprocess(text)
encoded_input = tokenizer(text, return_tensors='pt')
features = model(**encoded_input)
features = features[0].detach().numpy()
features_mean = np.mean(features[0], axis=0)
return features_mean
query = "Acabo de pedir pollo frito 🐣" #spanish
tweets = ["We had a great time! ⚽️", # english
"We hebben een geweldige tijd gehad! ⛩", # dutch
"Nous avons passé un bon moment! 🎥", # french
"Ci siamo divertiti! 🍝"] # italian
d = defaultdict(int)
for tweet in tweets:
sim = 1-cosine(get_embedding(query),get_embedding(tweet))
d[tweet] = sim
print('Most similar to: ',query)
print('----------------------------------------')
for idx,x in enumerate(sorted(d.items(), key=lambda x:x[1], reverse=True)):
print(idx+1,x[0])
```
## 2 - Simple inference example (with `pipelines`)
```
model_path = "cardiffnlp/twitter-xlm-roberta-base-sentiment"
sentiment_task = pipeline("sentiment-analysis", model=model_path, tokenizer=model_path)
sentiment_task("Huggingface es lo mejor! Awesome library 🤗😎")
```
# 3 - Experiment on UMSAB
## Fetch dataset (Spanish)
```
language = 'spanish'
files = """test_labels.txt
test_text.txt
train_labels.txt
train_text.txt
val_labels.txt
val_text.txt""".split('\n')
def fetch_data(language, files):
dataset = defaultdict(list)
for infile in files:
thisdata = infile.split('/')[-1].replace('.txt','')
dataset_url = f"https://raw.githubusercontent.com/cardiffnlp/xlm-t/main/data/sentiment/{language}/{infile}"
print(f'Fetching from {dataset_url}')
with urllib.request.urlopen(dataset_url) as f:
for line in f:
if thisdata.endswith('labels'):
dataset[thisdata].append(int(line.strip().decode('utf-8')))
else:
dataset[thisdata].append(line.strip().decode('utf-8'))
return dataset
dataset = fetch_data(language, files)
dataset['train_text'][:3],dataset['train_labels'][:3]
```
## Run full experiment
```
# load multilingual sentiment classifier
CUDA = True # set to true if using GPU (Runtime -> Change runtime Type -> GPU)
BATCH_SIZE = 32
MODEL = "cardiffnlp/twitter-xlm-roberta-base-sentiment"
tokenizer = AutoTokenizer.from_pretrained(MODEL)
config = AutoConfig.from_pretrained(MODEL)
model = AutoModelForSequenceClassification.from_pretrained(MODEL)
if CUDA:
model = model.to('cuda')
# helper functions
def preprocess(corpus):
outcorpus = []
for text in corpus:
new_text = []
for t in text.split(" "):
t = '@user' if t.startswith('@') and len(t) > 1 else t
t = 'http' if t.startswith('http') else t
new_text.append(t)
new_text = " ".join(new_text)
outcorpus.append(new_text)
return outcorpus
def predict(text, cuda):
text = preprocess(text)
encoded_input = tokenizer(text, return_tensors='pt', padding = True, truncation = True)
if cuda:
encoded_input.to('cuda')
output = model(**encoded_input)
scores = output[0].detach().cpu().numpy()
else:
output = model(**encoded_input)
scores = output[0].detach().numpy()
scores = softmax(scores, axis=-1)
return scores
from torch.utils.data import DataLoader
dl = DataLoader(dataset['test_text'], batch_size=BATCH_SIZE)
all_preds = []
for idx,batch in enumerate(dl):
if idx % 10 == 0:
print('Batch ',idx+1,' of ',len(dl))
text = preprocess(batch)
scores = predict(text, CUDA)
preds = np.argmax(scores, axis=-1)
all_preds.extend(preds)
print(classification_report(dataset['test_labels'], all_preds))
```
|
github_jupyter
|
This notebook presents some code to compute some basic baselines.
In particular, it shows how to:
1. Use the provided validation set
2. Compute the top-30 metric
3. Save the predictions on the test in the right format for submission
```
%pylab inline --no-import-all
import os
from pathlib import Path
import pandas as pd
# Change this path to adapt to where you downloaded the data
DATA_PATH = Path("data")
# Create the path to save submission files
SUBMISSION_PATH = Path("submissions")
os.makedirs(SUBMISSION_PATH, exist_ok=True)
```
We also load the official metric, top-30 error rate, for which we provide efficient implementations:
```
from GLC.metrics import top_30_error_rate
help(top_30_error_rate)
from GLC.metrics import top_k_error_rate_from_sets
help(top_k_error_rate_from_sets)
```
For submissions, we will also need to predict the top-30 sets for which we also provide an efficient implementation:
```
from GLC.metrics import predict_top_30_set
help(predict_top_30_set)
```
We also provide an utility function to generate submission files in the right format:
```
from GLC.submission import generate_submission_file
help(generate_submission_file)
```
# Observation data loading
We first need to load the observation data:
```
df_obs_fr = pd.read_csv(DATA_PATH / "observations" / "observations_fr_train.csv", sep=";", index_col="observation_id")
df_obs_us = pd.read_csv(DATA_PATH / "observations" / "observations_us_train.csv", sep=";", index_col="observation_id")
df_obs = pd.concat((df_obs_fr, df_obs_us))
```
Then, we retrieve the train/val split provided:
```
obs_id_train = df_obs.index[df_obs["subset"] == "train"].values
obs_id_val = df_obs.index[df_obs["subset"] == "val"].values
y_train = df_obs.loc[obs_id_train]["species_id"].values
y_val = df_obs.loc[obs_id_val]["species_id"].values
n_val = len(obs_id_val)
print("Validation set size: {} ({:.1%} of train observations)".format(n_val, n_val / len(df_obs)))
```
We also load the observation data for the test set:
```
df_obs_fr_test = pd.read_csv(DATA_PATH / "observations" / "observations_fr_test.csv", sep=";", index_col="observation_id")
df_obs_us_test = pd.read_csv(DATA_PATH / "observations" / "observations_us_test.csv", sep=";", index_col="observation_id")
df_obs_test = pd.concat((df_obs_fr_test, df_obs_us_test))
obs_id_test = df_obs_test.index.values
print("Number of observations for testing: {}".format(len(df_obs_test)))
df_obs_test.head()
```
# Sample submission file
In this section, we will demonstrate how to generate the sample submission file provided.
To do so, we will use the function `generate_submission_file` from `GLC.submission`.
The sample submission consists in always predicting the first 30 species for all the test observations:
```
first_30_species = np.arange(30)
s_pred = np.tile(first_30_species[None], (len(df_obs_test), 1))
```
We can then generate the associated submission file using:
```
generate_submission_file(SUBMISSION_PATH / "sample_submission.csv", df_obs_test.index, s_pred)
```
# Constant baseline: 30 most observed species
The first baseline consists in predicting the 30 most observed species on the train set which corresponds exactly to the "Top-30 most present species":
```
species_distribution = df_obs.loc[obs_id_train]["species_id"].value_counts(normalize=True)
top_30_most_observed = species_distribution.index.values[:30]
```
As expected, it does not perform very well on the validation set:
```
s_pred = np.tile(top_30_most_observed[None], (n_val, 1))
score = top_k_error_rate_from_sets(y_val, s_pred)
print("Top-30 error rate: {:.1%}".format(score))
```
We will however generate the associated submission file on the test using:
```
# Compute baseline on the test set
n_test = len(df_obs_test)
s_pred = np.tile(top_30_most_observed[None], (n_test, 1))
# Generate the submission file
generate_submission_file(SUBMISSION_PATH / "constant_top_30_most_present_species_baseline.csv", df_obs_test.index, s_pred)
```
# Random forest on environmental vectors
A classical approach in ecology is to train Random Forests on environmental vectors.
We show here how to do so using [scikit-learn](https://scikit-learn.org/).
We start by loading the environmental vectors:
```
df_env = pd.read_csv(DATA_PATH / "pre-extracted" / "environmental_vectors.csv", sep=";", index_col="observation_id")
X_train = df_env.loc[obs_id_train].values
X_val = df_env.loc[obs_id_val].values
X_test = df_env.loc[obs_id_test].values
```
Then, we need to handle properly the missing values.
For instance, using `SimpleImputer`:
```
from sklearn.impute import SimpleImputer
imp = SimpleImputer(
missing_values=np.nan,
strategy="constant",
fill_value=np.finfo(np.float32).min,
)
imp.fit(X_train)
X_train = imp.transform(X_train)
X_val = imp.transform(X_val)
X_test = imp.transform(X_test)
```
We can now start training our Random Forest (as there are a lot of observations, over 1.8M, this can take a while):
```
from sklearn.ensemble import RandomForestClassifier
est = RandomForestClassifier(n_estimators=16, max_depth=10, n_jobs=-1)
est.fit(X_train, y_train)
```
As there are a lot of classes (over 17K), we need to be cautious when predicting the scores of the model.
This can easily take more than 5Go on the validation set.
For this reason, we will be predict the top-30 sets by batches using the following generic function:
```
def batch_predict(predict_func, X, batch_size=1024):
res = predict_func(X[:1])
n_samples, n_outputs, dtype = X.shape[0], res.shape[1], res.dtype
preds = np.empty((n_samples, n_outputs), dtype=dtype)
for i in range(0, len(X), batch_size):
X_batch = X[i:i+batch_size]
preds[i:i+batch_size] = predict_func(X_batch)
return preds
```
We can know compute the top-30 error rate on the validation set:
```
def predict_func(X):
y_score = est.predict_proba(X)
s_pred = predict_top_30_set(y_score)
return s_pred
s_val = batch_predict(predict_func, X_val, batch_size=1024)
score_val = top_k_error_rate_from_sets(y_val, s_val)
print("Top-30 error rate: {:.1%}".format(score_val))
```
We now predict the top-30 sets on the test data and save them in a submission file:
```
# Compute baseline on the test set
s_pred = batch_predict(predict_func, X_test, batch_size=1024)
# Generate the submission file
generate_submission_file(SUBMISSION_PATH / "random_forest_on_environmental_vectors.csv", df_obs_test.index, s_pred)
```
|
github_jupyter
|
# Preprocessing for deep learning
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
plt.rcParams['axes.facecolor'] ='w'
plt.rcParams['axes.edgecolor'] = '#D6D6D6'
plt.rcParams['axes.linewidth'] = 2
```
# 1. Background
## A. Variance and covariance
### Example 1.
```
A = np.array([[1, 3, 5], [5, 4, 1], [3, 8, 6]])
print(A)
print(np.cov(A, rowvar=False, bias=True))
```
### Finding the covariance matrix with the dot product
```
def calculateCovariance(X):
meanX = np.mean(X, axis = 0)
lenX = X.shape[0]
X = X - meanX
covariance = X.T.dot(X)/lenX
return covariance
print(calculateCovariance(A))
```
## B. Visualize data and covariance matrices
```
def plotDataAndCov(data):
ACov = np.cov(data, rowvar=False, bias=True)
print('Covariance matrix:\n', ACov)
fig, ax = plt.subplots(nrows=1, ncols=2)
fig.set_size_inches(10, 10)
ax0 = plt.subplot(2, 2, 1)
# Choosing the colors
cmap = sns.color_palette("GnBu", 10)
sns.heatmap(ACov, cmap=cmap, vmin=0)
ax1 = plt.subplot(2, 2, 2)
# data can include the colors
if data.shape[1]==3:
c=data[:,2]
else:
c="#0A98BE"
ax1.scatter(data[:,0], data[:,1], c=c, s=40)
# Remove the top and right axes from the data plot
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
```
## C. Simulating data
### Uncorrelated data
```
np.random.seed(1234)
a1 = np.random.normal(2, 1, 300)
a2 = np.random.normal(1, 1, 300)
A = np.array([a1, a2]).T
A.shape
print(A[:10,:])
sns.distplot(A[:,0], color="#53BB04")
sns.distplot(A[:,1], color="#0A98BE")
plt.show()
plt.close()
plotDataAndCov(A)
plt.show()
plt.close()
```
### Correlated data
```
np.random.seed(1234)
b1 = np.random.normal(3, 1, 300)
b2 = b1 + np.random.normal(7, 1, 300)/2.
B = np.array([b1, b2]).T
plotDataAndCov(B)
plt.show()
plt.close()
```
# 2. Preprocessing
## A. Mean normalization
```
def center(X):
newX = X - np.mean(X, axis = 0)
return newX
BCentered = center(B)
print('Before:\n\n')
plotDataAndCov(B)
plt.show()
plt.close()
print('After:\n\n')
plotDataAndCov(BCentered)
plt.show()
plt.close()
```
## B. Standardization
```
def standardize(X):
newX = center(X)/np.std(X, axis = 0)
return newX
np.random.seed(1234)
c1 = np.random.normal(3, 1, 300)
c2 = c1 + np.random.normal(7, 5, 300)/2.
C = np.array([c1, c2]).T
plotDataAndCov(C)
plt.xlim(0, 15)
plt.ylim(0, 15)
plt.show()
plt.close()
CStandardized = standardize(C)
plotDataAndCov(CStandardized)
plt.show()
plt.close()
```
## C. Whitening
### 1. Zero-centering
```
CCentered = center(C)
plotDataAndCov(CCentered)
plt.show()
plt.close()
```
### 2. Decorrelate
```
def decorrelate(X):
cov = X.T.dot(X)/float(X.shape[0])
# Calculate the eigenvalues and eigenvectors of the covariance matrix
eigVals, eigVecs = np.linalg.eig(cov)
# Apply the eigenvectors to X
decorrelated = X.dot(eigVecs)
return decorrelated
plotDataAndCov(C)
plt.show()
plt.close()
CDecorrelated = decorrelate(CCentered)
plotDataAndCov(CDecorrelated)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()
```
### 3. Rescale the data
```
def whiten(X):
cov = X.T.dot(X)/float(X.shape[0])
# Calculate the eigenvalues and eigenvectors of the covariance matrix
eigVals, eigVecs = np.linalg.eig(cov)
# Apply the eigenvectors to X
decorrelated = X.dot(eigVecs)
# Rescale the decorrelated data
whitened = decorrelated / np.sqrt(eigVals + 1e-5)
return whitened
CWhitened = whiten(CCentered)
plotDataAndCov(CWhitened)
plt.xlim(-5,5)
plt.ylim(-5,5)
plt.show()
plt.close()
```
# 3. Image whitening
```
from keras.datasets import cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train.shape
X = X_train[:1000]
print(X.shape)
X = X.reshape(X.shape[0], X.shape[1]*X.shape[2]*X.shape[3])
print(X.shape)
def plotImage(X):
plt.rcParams["axes.grid"] = False
plt.figure(figsize=(1.5, 1.5))
plt.imshow(X.reshape(32,32,3))
plt.show()
plt.close()
plotImage(X[12, :])
X_norm = X / 255.
print('X.min()', X_norm.min())
print('X.max()', X_norm.max())
X_norm.mean(axis=0).shape
print(X_norm.mean(axis=0))
X_norm = X_norm - X_norm.mean(axis=0)
print(X_norm.mean(axis=0))
cov = np.cov(X_norm, rowvar=True)
cov.shape
U,S,V = np.linalg.svd(cov)
print(U.shape, S.shape)
print(np.diag(S))
print('\nshape:', np.diag(S).shape)
epsilon = 0.1
X_ZCA = U.dot(np.diag(1.0/np.sqrt(S + epsilon))).dot(U.T).dot(X_norm)
plotImage(X[12, :])
plotImage(X_ZCA[12, :])
X_ZCA_rescaled = (X_ZCA - X_ZCA.min()) / (X_ZCA.max() - X_ZCA.min())
print('min:', X_ZCA_rescaled.min())
print('max:', X_ZCA_rescaled.max())
plotImage(X[12, :])
plotImage(X_ZCA_rescaled[12, :])
```
|
github_jupyter
|
## Organização do dataset
```
def dicom2png(input_file, output_file):
try:
ds = pydicom.dcmread(input_file)
shape = ds.pixel_array.shape
# Convert to float to avoid overflow or underflow losses.
image_2d = ds.pixel_array.astype(float)
# Rescaling grey scale between 0-255
image_2d_scaled = (np.maximum(image_2d,0) / image_2d.max()) * 255.0
# Convert to uint
image_2d_scaled = np.uint8(image_2d_scaled)
# Write the PNG file
with open(output_file, 'wb') as png_file:
w = png.Writer(shape[1], shape[0], greyscale=True)
w.write(png_file, image_2d_scaled)
except:
print('Could not convert: ', input_file)
from google.colab import drive
drive.mount("/content/gdrive", force_remount=True)
import pandas as pd
import shutil
import glob
from sklearn.model_selection import train_test_split
import os
study_level = pd.read_csv("gdrive/MyDrive/covid-dataset/train_study_level.csv")
image_level = pd.read_csv("gdrive/MyDrive/covid-dataset/train_image_level.csv")
study_level['study_name'] = study_level['id'].apply(lambda x: x.replace('_study', ''))
df = pd.DataFrame()
df['image_name'] = image_level['id'].apply(lambda x: x.replace('_image', ''))
df['study_name'] = image_level['StudyInstanceUID']
merge = pd.merge(df, study_level, on='study_name')
r0 = merge['Typical Appearance'].apply(lambda x: 'typical' if x == 1 else False)
r1 = merge['Atypical Appearance'].apply(lambda x: 'atypical' if x == 1 else False)
r2 = merge['Indeterminate Appearance'].apply(lambda x: 'indeterminate' if x == 1 else False)
labels = []
for a,b,c in zip(r0, r1, r2):
if a != False:
labels.append(a)
continue
if b != False:
labels.append(b)
continue
if c != False:
labels.append(c)
continue
labels.append('not recognized')
merge['label'] = labels
shutil.copy('gdrive/MyDrive/covid-dataset/nn_train_600.zip', './')
!unzip -qq nn_train_600.zip
img_df = pd.DataFrame()
paths = glob.glob('./nn_train_600/**/*.png', recursive=True)
img_df['path'] = paths
img_df['image_name'] = img_df['path'].apply(lambda x: x.split('/')[-1].replace('.png', ''))
fndf = pd.merge(merge, img_df, on='image_name')
X, y = fndf['path'], fndf['label']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
os.makedirs('train/typical', exist_ok=True)
os.makedirs('train/indeterminate', exist_ok=True)
os.makedirs('train/atypical', exist_ok=True)
os.makedirs('test/typical', exist_ok=True)
os.makedirs('test/indeterminate', exist_ok=True)
os.makedirs('test/atypical', exist_ok=True)
def distribute_images(_paths, _labels, _folder):
for path, label in zip(_paths, _labels):
shutil.copy(path, _folder + '/' + label)
distribute_images(X_train, y_train, 'train')
distribute_images(X_test, y_test, 'test')
```
## Fine-tuning EfficientNet
```
import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.applications import EfficientNetB0, EfficientNetB1, EfficientNetB2, EfficientNetB3, EfficientNetB4, EfficientNetB5, EfficientNetB6, EfficientNetB7
from tensorflow.keras import models
from tensorflow.keras import layers
from tensorflow.keras import optimizers
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
print("Running on TPU ", tpu.cluster_spec().as_dict()["worker"])
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.TPUStrategy(tpu)
except ValueError:
print("Not connected to a TPU runtime. Using CPU/GPU strategy")
strategy = tf.distribute.MirroredStrategy()
batch_size = 64
height = 456
width = 456
input_shape = (height, width, 3)
with strategy.scope():
train_datagen = ImageDataGenerator(
rescale=1,
rotation_range=10,
width_shift_range=0.1,
height_shift_range=0.1,
shear_range=0.1,
zoom_range=0.1,
horizontal_flip=True,)
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
"train",
# All images will be resized to target height and width.
target_size=(height, width),
batch_size=batch_size,
# Since we use categorical_crossentropy loss, we need categorical labels
class_mode='categorical')
validation_generator = test_datagen.flow_from_directory(
"test",
target_size=(height, width),
batch_size=batch_size,
class_mode='categorical', shuffle=False)
with strategy.scope():
model = models.Sequential()
model.add(layers.Input(shape=(height, width, 3)))
model.add(EfficientNetB7(include_top=True, weights=None, classes=3))
model.compile(
optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"]
)
model.summary()
hist = model.fit_generator(
train_generator,
steps_per_epoch= 3382 // batch_size,
epochs=20,
validation_data=validation_generator,
validation_steps= 846 // batch_size,
verbose=1,)
def build_model(num_classes):
inputs = layers.Input(shape=(height, width, 3))
x = inputs
model = EfficientNetB5(include_top=False, input_tensor=x, weights="imagenet")
# Freeze the pretrained weights
model.trainable = False
# Rebuild top
x = layers.GlobalAveragePooling2D(name="avg_pool")(model.output)
x = layers.BatchNormalization()(x)
top_dropout_rate = 0.2
x = layers.Dropout(top_dropout_rate, name="top_dropout")(x)
outputs = layers.Dense(num_classes, activation="softmax", name="pred")(x)
# Compile
model = tf.keras.Model(inputs, outputs, name="EfficientNet")
for layer in model.layers[-20:]:
if not isinstance(layer, layers.BatchNormalization):
layer.trainable = True
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
model.compile(
optimizer=optimizer, loss="categorical_crossentropy", metrics=["accuracy"]
)
return model
with strategy.scope():
model2 = build_model(3)
model2.summary()
checkpoint_filepath = 'gdrive/MyDrive/covid-dataset'
model_checkpoint_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_filepath,
save_weights_only=True,
monitor='val_accuracy',
mode='max',
save_best_only=True)
hist = model2.fit_generator(
train_generator,
steps_per_epoch= 3382 // batch_size,
epochs=50,
validation_data=validation_generator,
validation_steps= 846 // batch_size,
verbose=1, callbacks=[model_checkpoint_callback])
def build_model(num_classes):
inputs = layers.Input(shape=(height, width, 3))
x = inputs
model = EfficientNetB5(include_top=False, input_tensor=x, weights="imagenet")
# Freeze the pretrained weights
model.trainable = False
# Rebuild top
x = layers.GlobalAveragePooling2D(name="avg_pool")(model.output)
x = layers.BatchNormalization()(x)
top_dropout_rate = 0.2
x = layers.Dropout(top_dropout_rate, name="top_dropout")(x)
outputs = layers.Dense(num_classes, activation="softmax", name="pred")(x)
# Compile
model = tf.keras.Model(inputs, outputs, name="EfficientNet")
for layer in model.layers[-20:]:
if not isinstance(layer, layers.BatchNormalization):
layer.trainable = True
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
model.compile(
optimizer=optimizer, loss="categorical_crossentropy", metrics=["accuracy"]
)
return model
model2 = build_model(3)
model2.load_weights('gdrive/MyDrive/covid-dataset')
model2.predict(validation_generator)
import numpy as np
np.unique(validation_generator.labels,
return_counts=True)
model2.evaluate(validation_generator)
y_pred = model2.predict(validation_generator)
y_true, y_pred = validation_generator.classes, np.argmax(y_pred, axis=1)
from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred)
from sklearn.metrics import classification_report, confusion_matrix
indices_class = {v:k for k,v in validation_generator.class_indices.items()}
indices_class
target_names = ['atypical', 'indeterminate', 'typical']
target_names
print('Confusion Matrix')
print(confusion_matrix(y_true, y_pred))
print('Precision: What proportion of positive identifications was actually correct?')
print('When it predicts a <Class> is true, it is correct <Precision> of the time.', '\n')
print('Recall: What proportion of actual positives was identified correctly?')
print('Correctly identifies <Recall> of all true <Class>.', '\n')
print('F1-SCORE: Combines the precision and recall of a classifier into a\nsingle metric by taking their harmonic meany.')
print('Classification Report')
print(classification_report(y_true, y_pred, target_names=target_names))
```
|
github_jupyter
|
[](https://pythonista.io)
# Entrada y salida estándar.
En la actualidad existen muchas fuentes desde las que se puede obtener y desplegar la información que un sistema de cómputo consume, gestiona y genera. Sin embargo, para el intérprete de Python la salida por defecto (salida estándar) de datos es la terminal de texto y la entrada estándar es el teclado.
En el caso de las notebooks de *Jupyter*, cada celda de código representa a la entrada estándar mediante:
```In[ ]:```
Y la salida estándar mediante:
```Out[ ]:```
**Ejemplo:**
```
3 * "Hola"
```
## Salida estándar con la funcion ```print()```.
En Python 3, la función ```print()``` se utiliza para desplegar información en la salida estándar.
La sintaxis es la siguiente:
```
print(<expresión 1>, <expresión 2>, ...<expresión 3>)
```
* La función ```print()``` evalúa y despliega una o varias expresiones.
* Si el resultado de la expresión es un objeto ```str```, este es desplegado sin los apóstrofes o las comillas que lo delimitan.
**Ejemplos:**
* La siguiente celda define el nombre ```a``` con valor igual a ```2```.
```
a = 2
```
* La siguiente celda evalúa la expresión ```a```, por lo que desplegará ```2```.
```
print(a)
```
* La siguiente celda desplegará el mensaje dentro del objeto ```"Hola"```.
```
print("Hola")
```
* En la siguiente celda la función ```print()``` desplegará dos expresiones que corresponde cada una a un objeto de tipo ```str```. Cada objeto será desplegado separado por un espacio.
* La salida será ```Hola Mundo```.
```
print("Hola", "Mundo")
```
* En la siguiente celda la función ```print()``` desplegará el resultado de una expresión de concatenación entre dos objetos de tipo ```str```. El resultado es un objeto ```str```.
* La salida será ```HolaMundo```.
```
print("Hola" + "Mundo")
```
* En la siguiente celda la función ```print()``` desplegará tres expresiones que corresponden a:
* El objeto ```'Tienes'``` de tipo ```str```.
* El objeto ```2``` de tipo ```int``` ligado al nombre ```a```.
* El objeto ```'buenos amigos'``` de tipo ```str```.
Cada expresión será desplegada separada por un espacio.
* La salida será ```Tienes 2 buenos amigos.```.
```
print("Tienes", a, "buenos amigos.")
```
* En la siguiente celda la función ```print()``` intentará desplegar el resultado de la expresión ```"Tienes" + a + "buenos amigos."```, la cual no es correcta y generará un error de tipo ```TypeError```.
```
print("Tienes" + a + "buenos amigos.")
```
### Despliegue con formato.
Para intercalar valores dentro de un formato específico de texto se utiliza el caracter sobre-escritura definodo como el signo de porcentaje ```%``` seguido de algún caracter que definirá el modo de desplegar la expresión correspondiente.
```
print("...%<caracter>..." % expresión 1)
```
```
print("...%<caracter 1>...%<caracter n>..." %(<expresión 1>,...<expresión n>))
```
|Caracter de escape|Modo de despliegue|
|:----------------:|:----------------:|
|```%s```| cadena de texto|
|```%d```| entero|
|```%o```| octal|
|```%x```| hexadecimal|
|```%f```| punto flotante|
|```%e```| punto flotante en formato exponencial|
El uso de ```%s```, equivale a aplicar la función ```str()``` al valor a desplegar.
**Ejemplos:**
```
pi = 3.141592
radio = 2
print("El perímetro de un círculo de radio %d es %f." % (radio, 2 * radio * pi))
print("El perímetro de un círculo de radio %d es %d." % (radio, 2 * radio * pi))
print("El perímetro de un circulo de radio %s es %s." % (radio, 2 * radio * pi))
print("El valor de pi es %f." % (pi))
print("El valor de pi es %e." % pi)
```
Para desplegar el signo de porcentaje ```%``` se utiliza ```%%```.
**Ejemplo:**
```
valor = 13
porciento = 15
porcentaje = (valor * porciento) / 100
print("El %d%% de %f es %f." % (porciento, valor, porcentaje))
```
#### Despliegue de cifras significativas.
Para desplegar un número específico de cifras significativas de un valor de punto flotante, se añade un punto ```.``` y el número de cifras a desplegarse después del signo de porcentaje ```%``` y antes del carácter ```f``` o ```e```.
```
%.<n>f
```
**Ejemplos:**
```
pi = 3.14169265
radio = 2
print("El perímetro de un círculo de radio igual a %d es %f." % (radio, 2 * pi * radio))
print("El perímetro de un círculo de radio igual a %d es %.2f." % (radio, 2 * pi * radio))
```
### Caracteres de escape.
Existen algunos caracteres que por su función o por la sintaxis de Python -tales como los apóstrofes, las comillas, los retornos de línea, etc.- que deben utilizar un "caracter de escape", para que puedan ser desplegados. Los caracteres de escape pueden ser introducidos después de una diagonal invertida ```\```.
|Secuencia|Despliegue|
|:-------:|:--------:|
|```\n``` |Retorno de línea|
|```\t``` |Tabulador |
|```\"``` |Comillas |
|```\'``` |Apóstrofe |
|```\\``` |Diagonal invertida|
|```\xNN``` |Caracter que corresponde al número hexadecimal *NN* en ASCII|
|```\uNN``` |Caracter que corresponde al número hexadecimal *NN* en Unicode|
**Ejemplo:**
```
print("Primera línea.\nSegunda línea\t con tabulador.")
print("Este es el signo de \"gato\" \x23.")
print("Beta: \u00DF")
print('I \u2764 YOU!')
```
## Entrada estándar con la función ```input()```.
La función por defecto de entrada estándar para Python 3 es ```input()```.
La función ```input()``` captura los caracteres provenientes de entrada estándar (el teclado) hasta que se introduce un retorno de carro <kbd>Intro</kbd> y el contenido capturado es devuelto al intérprete como una cadena de texto.
La cadena de caracteres resultante puede ser almacenada como un objeto de tipo ```str``` mediante la asignación de un nombre.
La función permite desplegar un mensaje de tipo ```str``` como parámetro.
```
input(<objeto tipo str>)
```
**Ejemplos:**
```
input()
texto = input()
type(texto)
texto
print(texto)
nombre = input("Escribe un nombre: ")
print(nombre)
```
## Entrada y salida estándar en Python 2.
### La función ```raw_input()```.
La sintaxis es la siguiente para Python 2:
```
raw_input(<objeto tipo str>)
```
**Ejemplo:**
``` python
>>> raw_input()
Hola
'Hola'
>>> texto = raw_input()
Hola
>>> type(texto)
<type 'str'>
>>> print texto
Hola
>>> nombre = raw_input("Escribe un nombre: ")
Escribe un nombre: Juan
>>> print nombre
Juan
>>>
```
### La función ```input()``` en Python 2.
Además de ```raw_input()```, existe la función ```input()```, la cual es semejante a ejecutar ```eval(raw_input())```.
Si la expresión ingresada es correcta, La función ```input()``` puede regresar valores de diversos tipos, en vez de sólo cadenas de texto.
**Ejemplo:**
``` python
>>> mensaje = "Ingresa el texto: "
>>> valor = raw_input(mensaje)
Ingresa el texto: 35 + 21
>>> type(valor)
<type 'str'>
>>> print valor
35 + 21
>>> valor = input(mensaje)
Ingresa el texto: 35 + 21
>>> type(valor)
<type 'int'>
>>> print valor
56
>>> valor = input(mensaje)
Ingresa el texto: "Hola"
>>> type(valor)
<type 'str'>
>>> print valor
Hola
>>> valor = input(mensaje)
Ingresa el texto: Hola
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<string>", line 1, in <module>
NameError: name 'Hola' is not defined
>>>
```
**NOTA:** La función ```input()```, tal como se usa en Python 2 tiene el potencial de generar diversos errores y es susceptible de vulnerabilidades de seguridad debido a que podría usarse para inyectar código malicioso. Es por eso por lo que en Python 3, ```input()``` se comporta como ```raw_input()``` y la función ```raw_input()``` fue desechada.
```
eval(input('Ingresa: '))
```
<p style="text-align: center"><a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Licencia Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/80x15.png" /></a><br />Esta obra está bajo una <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Licencia Creative Commons Atribución 4.0 Internacional</a>.</p>
<p style="text-align: center">© José Luis Chiquete Valdivieso. 2019.</p>
|
github_jupyter
|
```
# Take all JSON from Blob Container and upload to Azure Search
import globals
import os
import pickle
import json
import requests
from pprint import pprint
from azure.storage.blob import BlockBlobService
from joblib import Parallel, delayed
def processLocalFile(file_name):
json_content = {}
try:
with open(file_name, 'r') as json_file:
json_content = json.loads(json_file.read())
docID = json_content["paper_id"]
title = json_content["metadata"]["title"]
body = {"documents": []}
abstractContent = ''
id_counter = 1
if "abstract" in json_content:
for c in json_content["abstract"]:
abstractContent += c["text"] + ' '
body["documents"].append({
"language": "en",
"id": str(id_counter),
"text": c["text"]
})
id_counter += 1
abstractContent = abstractContent.strip()
body = ''
if "body_text" in json_content:
for c in json_content["body_text"]:
body += c["text"] + ' '
body = body.strip()
contributors = []
for c in json_content["metadata"]["authors"]:
midInitial = ''
for mi in c["middle"]:
midInitial += mi + ' '
if len(((c["first"] + ' ' + midInitial + c["last"]).strip())) > 2:
contributors.append((c["first"] + ' ' + midInitial + c["last"]).strip())
return {"@search.action": "mergeOrUpload", "docID": docID, "title":title, "abstractContent": abstractContent, "body": body, "contributors": contributors}
except Exception as ex:
print (blob_name, " - Error:", str(ex))
return "Error"
with open(os.path.join(globals.files_dir, 'new_files.pkl'), 'rb') as input:
new_files = pickle.load(input)
print (str(len(new_files)), 'to upload...')
documents = {"value": []}
for json_file in new_files:
# print (json_file[json_file.rindex('/')+1:].replace('.json', '').replace('.xml', ''))
documents["value"].append(processLocalFile(json_file))
if len(documents["value"]) == 100:
print ("Applying", str(len(documents["value"])), "docs...")
url = globals.endpoint + "indexes/" + globals.indexName + "/docs/index" + globals.api_version
response = requests.post(url, headers=globals.headers, json=documents)
documents = {"value": []}
if len(documents["value"]) > 0:
print ("Applying", str(len(documents["value"])), "docs...")
url = globals.endpoint + "indexes/" + globals.indexName + "/docs/index" + globals.api_version
response = requests.post(url, headers=globals.headers, json=documents)
```
|
github_jupyter
|
# Schooling in Xenopus tadpoles: Power analysis
This is a supplementary notebook that generates some simulated data, and estimates the power analysis for a schooling protocol. The analysis subroutines are the same, or very close to ones from the actual notebook (**schooling_analysis**). The results of power analysis are given, and explained, in the text below, but can also be re-created by the reader, by re-running this notebook.
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.spatial
import scipy.stats as stats
from typing import List,Tuple
```
## 1. Generate simulated data
Data is generated in the following format:
Layout of Tadpole dataframe:
x y tx ty
0 7.391 14.783 -0.159 -0.14
1 8.850 14.623 -0.180 -0.18
2 7.751 12.426 -0.260 -0.24
where each line correponds to a "tadpole"; `x` and `y` columns give the position of the "tadpole's head" (virtual, in this case), and `tx` and `ty` are the positions of the "tail", relative to the "head".
```
def simulate_data(ntads=10, schooling=0.5, alignment=0.6):
"""Simulates tadpole distribution in the dish.
n = how many tadpoles to have
schooling = the probability of being in a school (simplistic, binary approach)
r = aligment radius
alignment = alignment coefficient (1-noise_level)
"""
R_DISH = 7
TAD_LENGTH = 0.4
N_ATTEMPTS = 20 # How many attempts to place each tadpole we would make
JUMP = 1 # Jump, in cm, from one tadpole to another
do_alignment = False # Whether we should align tadpoles to their neighbors. Too fancy?
xy = np.zeros((ntads,2))
tails = np.zeros((ntads,2))
itad = 0
while itad < ntads: # Simplified Bridson’s algorithm for Poisson-disc sampling
if itad==0 or np.random.uniform()>schooling: # First point and non-schooled points placed at random
drop = np.random.uniform(0, 2*R_DISH, 2)
else:
iparent = np.random.randint(itad)
angle = np.random.uniform(0, 2*np.pi)
d = np.random.uniform(JUMP, 2*JUMP)
drop = xy[iparent,:] + np.array([np.cos(angle), np.sin(angle)])*d
if np.sqrt((drop[0]-R_DISH)**2 + (drop[1]-R_DISH)**2) > R_DISH: # Outside of a dish, won't do
continue
good_point = True
for iother in range(itad):
if np.sqrt(np.sum(np.square(drop-xy[iother,:]))) < JUMP: # Too close to another dot; won't do
good_point = False
break
if not good_point:
continue
xy[itad,:] = drop
# Make the tadpole perpendicular to the radius
tails[itad,:] = [xy[itad,1]-R_DISH, -xy[itad,0]+R_DISH]
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
if do_alignment: # Fancy mutual alignment; maybe don't use it, as it is too fancy?
if itad>0:
for iother in range(itad):
d = np.linalg.norm(xy[itad,:]-xy[iother,:])
tails[itad,:] += tails[iother,:]/(d**2)
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
angle = np.random.uniform(0, 2*np.pi)
randotail = np.array([np.cos(angle), np.sin(angle)])*TAD_LENGTH
tails[itad,:] = tails[itad,:]*alignment + randotail*(1-alignment)
tails[itad,:] = tails[itad,:]/np.linalg.norm(tails[itad,:])*TAD_LENGTH
# This code above with 3 normalizations in a row could have been prettier of course
itad += 1
return pd.DataFrame({'x':xy[:,0] , 'y':xy[:,1] , 'tx':tails[:,0] , 'ty':tails[:,1]})
def arena_plot(t):
for i in range(len(t)):
plt.plot(t.x[i]+np.array([0, t.tx[i]]), t.y[i]+np.array([0, t.ty[i]]), 'r-')
plt.plot(t.x, t.y, '.')
plt.gca().add_artist(plt.Circle((7,7), 6.9, color='blue', fill=False, linestyle='-'))
plt.xlim([0, 14])
plt.ylim([0, 14])
plt.axis('off')
return
schoolings = [1, 0.5, 0]
alignments = [1, 0.5, 0]
names = ['Lawful', 'Neutral', 'Chaotic', 'good', 'neutral', 'evil']
plt.figure(figsize=(9,9))
for i in range(3):
for j in range(3):
t = simulate_data(ntads=20, schooling=schoolings[i], alignment=alignments[j])
plt.subplot(3,3,i*3+j+1)
arena_plot(t)
plt.title(f"Schooling={schoolings[i]}, \n alignment={alignments[j]}")
#plt.title(names[j] + ' ' + names[3+i])
```
## 2. Processing Tools
An exact copy of tools from the "main notebook" (as of 2020.08.01), except that instead of extracing tadpoles from real data, here we simulate this data. (So `exctractTads` function is not actually used).
```
def getNFrames(data):
"""Returns the total number of frames."""
return max(data.Frame)+1
def extractTads(data,frame):
"""Splits the data into XY position of each head, and _relative_ XY position of each tail."""
xy = data.loc[data.Frame==frame,['X','Y']].to_numpy()
heads = xy[0::2,:]
tails = xy[1::2,:]-heads
return pd.DataFrame({'x':heads[:,0] , 'y':heads[:,1] , 'tx':tails[:,0] , 'ty':tails[:,1]})
def findNeighbors(tads): # Returns a new data frame, for edges
"""Triangulates the field, finds "neighbors". No thresholding of distance."""
xy = tads[['x','y']]
tri = scipy.spatial.Delaunay(xy,qhull_options="QJ").simplices # "QJ" is needed to retain
# all tadpoles, including isolated ones
listOfPairs = [] # Array of tuples to describe all pairs of points
flip = lambda x: (x[1],x[0]) # A local function to flip tuples
for i in range(tri.shape[0]): # Go through all edges of Delaunay triangles, include each one only once
triangle = [tuple(tri[i,[0,1]]) , tuple(tri[i,[1,2]]) , tuple(tri[i,[2,0]])]
for p in triangle:
if p not in listOfPairs and flip(p) not in listOfPairs:
listOfPairs += [p]
out = pd.DataFrame({'i':[a for (a,b) in listOfPairs] , 'j':[b for (a,b) in listOfPairs]})
return out
def findDistances(tads,pairs):
"""Calculates distances between pairs of neighboring tadpoles."""
xy = tads[['x','y']].values
dist = [np.linalg.norm(xy[p[0],]-xy[p[1],]) for p in pairs[['i','j']].values.tolist()]
pairs['dist'] = dist
return pairs
# --- Test, for the first frame
tads = simulate_data(ntads=20)
pairs = findNeighbors(tads)
pairs = findDistances(tads,pairs)
print('Layout of Tadpole dataframe:')
print(tads[:3])
print('\nLayout of Pairs dataframe:')
print(pairs[:3])
# Test figure with edge colors proportional to their distance
fig = plt.figure()
ax = fig.add_subplot(111)
xy = tads[['x','y']].values
for i in range(len(pairs)):
p = pairs[['i','j']].values.tolist()[i]
ax.plot([xy[p[0],0] , xy[p[1],0]],[xy[p[0],1] , xy[p[1],1]]) # Point
ax.plot(*([xy[p[i],_] for i in range(2)] for _ in range(2)),
color=np.array([1,0.5,0])*pairs['dist'].iloc[i]/pairs[['dist']].max().values*0.9)
# The awkward construction above draws lines between neighboring tadpoles
ax.set_aspect('equal')
```
## 3. Tools to Process Angles
Exactly same as in the main notebook (as of 2020.08.01)
```
def findAngles(tads,pairs):
'''Angles between pairs of tadpoles'''
tails = tads[['tx','ty']].values # Go from pandas to lists, to utilize list comprehension
norms = [np.linalg.norm(tails[i,]) for i in range(tails.shape[0])]
angle = [np.arccos(np.dot(tails[p[0],],tails[p[1],])/(norms[p[0]]*norms[p[1]]))
for p in pairs[['i','j']].values.tolist()]
pairs['angle'] = np.array(angle)/np.pi*180
return pairs
def niceTadFigure(ax,tads,pairs):
"""Nice picture for troubleshooting."""
xy = tads[['x','y']].values
tails = tads[['tx','ty']].values
ang = pairs[['angle']].values
for i in range(len(pairs)):
p = pairs[['i','j']].values.tolist()[i]
ax.plot(*([xy[p[i],_] for i in range(2)] for _ in range(2)),
color=np.array([0.5,0.8,1])*(1-ang[i]/max(ang))) # Tadpole-tapole Edges
for i in range(xy.shape[0]):
nm = np.linalg.norm(tails[i,])
ax.plot(xy[i,0]+[0,tails[i,0]/nm], xy[i,1]+[0,tails[i,1]/nm] , '-',color='red')
ax.set_aspect('equal')
ax.axis('off')
# --- Test, for the first frame
pairs = findAngles(tads,pairs)
fig = plt.figure()
ax = fig.add_subplot(111)
niceTadFigure(ax,tads,pairs)
#plt.savefig('crystal_pic.svg', format='svg')
```
## 4. Define full processor and dataset visualization
This function is adjusted to look like the procesisng function from the main notebook, but actually we call the simulation several times, to generate the "frames".
```
def processEverything(nsets=12, show_image=False, schooling=0.3, alignment=0.5):
"""Process one full dataset."""
if show_image:
fig = plt.figure(figsize=(10,10));
fullDf = pd.DataFrame()
for iframe in range(nsets):
tads = simulate_data(ntads=20, schooling=schooling, alignment=alignment)
pairs = findNeighbors(tads)
pairs = findDistances(tads,pairs)
angl = findAngles(tads,pairs)
fullDf = fullDf.append(pd.DataFrame({'frame': [iframe]*len(pairs)}).join(pairs))
if show_image:
ax = fig.add_subplot(4,4,iframe+1)
niceTadFigure(ax,tads,pairs)
return fullDf
out = processEverything(show_image=True)
```
## 5. Compare two different simulated datasets
Below, one dataset has high schooling coefficient (0.9), and perfect alignment (1.0), while the other has almost no schooling (0.1), and perfectly random orientation for all tadpoles (alignment=0.0).
```
# Prepare the data
out = processEverything(show_image=False, schooling=0.9, alignment=1.0)
out_treatment = processEverything(show_image=False, schooling=0.1, alignment=0.0)
def two_groups_plot(y1, y2, labels):
"""A basic two-groups plot"""
plt.plot(1+(np.random.uniform(size=y1.shape[0])-0.5)*0.3, y1, '.', alpha=0.2, zorder=-1)
plt.plot(2+(np.random.uniform(size=y2.shape[0])-0.5)*0.3, y2, '.', alpha=0.2, zorder=-1)
# Zorder is set to negative to hack around a bug in matplotlib that places errorbars below plots
plt.errorbar(1, np.mean(y1), np.std(y1), color='k', marker='s', capsize=5)
plt.errorbar(2, np.mean(y2), np.std(y2), color='k', marker='s', capsize=5)
plt.xlim(0,3)
plt.xticks(ticks=[1,2], labels=labels)
def compare_distances(out1,out2,labels):
"""Visualizes distances, reports a stat test"""
N_BINS = 10
d = out1['dist'].values
d2 = out2['dist'].values
plt.figure(figsize=(9,4))
ax = plt.subplot(121)
two_groups_plot(d, d2, labels)
plt.ylabel('Distance, cm')
ax = plt.subplot(122)
#plt.hist(d , bins=30, density=True, alpha=0.5);
#plt.hist(d2, bins=30, density=True, alpha=0.5);
y1,x1 = np.histogram(d, bins=N_BINS, density=True)
y2,x2 = np.histogram(d2, bins=N_BINS, density=True)
centers = lambda x: np.mean(np.vstack((x[:-1],x[1:])), axis=0) # Centers of each bin
plt.plot(centers(x1),y1,'.-')
plt.plot(centers(x2),y2,'.-')
plt.xlabel('Distance, cm')
plt.ylabel('Probability Density')
plt.legend(labels, loc='upper right')
print('Was the average inter-tadpole disctance different between two sets of data?')
print('(were their clumping?)')
test_results = stats.ttest_ind(d,d2)
print('T-test: t = ', test_results.statistic, '; p-value = ',test_results.pvalue)
print('\nWas the distribution shape different between two sets??')
test_results = scipy.stats.ks_2samp(d,d2)
print('Kolmogorov-Smirnov test p-value = ',test_results.pvalue)
compare_distances(out, out_treatment, ['High Schooling','Low schooling'])
#plt.savefig('distances.svg', format='svg')
```
As we can see, non-schooling tadpoles tend to be more uniformly distributed, so we observe more mid-distances and fewer low and high distances. ("More uniformly" doesn't mean that the distribution is actually uniform; it is expected to be closer to $χ^2$). Conversely, schooling tadpoles tend to be closer to each other.
As not all inter-tadpole distances were considered, but rather we rely on the Delaunay triangulation, the shape of the histogram may be rather peculiar, but it is OK. What matters is not the shape itself, but the fact that this shape is sensitive to the configuration of the swarm, as this means that it can be used to statistically compare swarms that were formed differently.
```
def compare_angles(out, out2, labels):
"""Visualizes angles, reports a stat test."""
HIST_BIN = 30 # Histogram step, in degrees
a = out['angle'].values
a2 = out2['angle'].values
#plt.hist(a , bins=np.arange(0,180+10,10), density=True, alpha=0.5);
#plt.hist(a2, bins=np.arange(0,180+10,10), density=True, alpha=0.5);
preset_bins = np.arange(0,180+HIST_BIN, HIST_BIN)
y1,x1 = np.histogram(a, bins=preset_bins, density=True)
y2,x2 = np.histogram(a2, bins=preset_bins, density=True)
centers = lambda x: np.mean(np.vstack((x[:-1],x[1:])), axis=0) # Centers of each bin
plt.plot(centers(x1),y1,'.-')
plt.plot(centers(x2),y2,'.-')
plt.xticks(np.arange(0,180+30,30))
plt.xlabel('Angle, degrees')
plt.ylabel('Probability Density')
plt.legend(labels, loc='upper right')
print('\nWas the distribution of angles different between two sets?')
test_results = scipy.stats.ks_2samp(a,a2)
print('Kolmogorov-Smirnov test p-value = ',test_results.pvalue)
compare_angles(out, out_treatment, ['Alignment','No alignment'])
#plt.savefig('angles.svg', format='svg')
```
As we can see, if tadpoles are oriented at random, the histogram of inter-tadpole angles is flat. If tadpoles school, the distribution of angles drops, as most tadpoles are co-oriented.
## 6. Power analysis
```
ntries = 50
x = np.linspace(0, 1, 21)
y = np.zeros((x.shape[0], 3))
for ival in range(len(x)):
val = x[ival]
print(f'{val:4.1f}', end=' ')
count = np.array([0,0,0])
for iattempt in range(ntries):
print('.', end='')
out1 = processEverything(show_image=False, schooling=0.5, alignment=0.5)
out2 = processEverything(show_image=False, schooling=val, alignment=val)
d = out1['dist'].values
d2 = out2['dist'].values
pttest = stats.ttest_ind(d,d2).pvalue
pks = scipy.stats.ks_2samp(d,d2).pvalue
pangles = scipy.stats.ks_2samp(out['angle'].values, out2['angle'].values).pvalue
count[0] += 1*(pttest<0.05)
count[1] += 1*(pks<0.05)
count[2] += 1*(pangles<0.05)
y[ival,:] = count/ntries
print()
plt.figure(figsize=(8,6));
plt.plot(x,y);
plt.legend(labels=["Distances, t-test","Distances, KS-test","Angles, KS-test"], bbox_to_anchor=(1.3, 1));
plt.xlabel('Coefficients for the 2nd set (1st is fixed at 0.5)');
plt.ylabel('Test power');
```
For every point of the chart above, we compare two simulated datasets. One has the **schooling** coefficient (the probability of joining an existing school) set at 0.5, and the admixture of noise to tadpole orientation (**alignment** coefficient) also set at 0.5. For the other dataset, both parameters assume all values from 0 to 1 with a 0.05 step. The sizes of both datasets are the same as in our real experiments: 20 tadpoles, 12 photos. each simulation is repeated 50 times, to estimate the power 1-β of each of the tests (with α=0.05).
We can see that the angle analysis is much more sensitive, as even a change from 0.50 to 0.55 noise admixture is detected with >95% probability. Yet, the distribution of angles is also arguably more biologically involved, as it can depend on the function of the lateral line, and the distribution of currents in the bowl, while these currents may themselves be affected by the quality of schooling (non-schooling tadpoles won't create a current). To re-iterate, the test for co-alignment is very sensitive mathematically, but may be a bit messy biologically.
The tests of spatial clumping are almost exactly the other way around: they are easy to interpret (if the tadpoles stay together, then phenomenologially the DO schoo, regardless of the mechanism), but they are not that sensitive mathematically. For this sample size, we had to change the probability of "not joining a school" by about 30% to detect a difference with 80% power. We can also see that the t-test is more sensitive to this change than the Kolmogorov-Smirnov test, although this comparison may be sensitive to this particular implementation of a spatial model.
|
github_jupyter
|
# OCR (Optical Character Recognition) from Images with Transformers
---
[Github](https://github.com/eugenesiow/practical-ml/) | More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml)
---
Notebook to recognise text automaticaly from an input image with either handwritten or printed text.
[Optical Character Recognition](https://paperswithcode.com/task/optical-character-recognition) is the task of converting images of typed, handwritten or printed text into machine-encoded text, whether from a scanned document, a photo of a document, a scene-photo (for example the text on signs and billboards in a landscape photo, license plates in cars...) or from subtitle text superimposed on an image (for example: from a television broadcast).
The [transformer models used](https://malaya-speech.readthedocs.io/en/latest/tts-singlish.html) are from Microsoft's TrOCR. The TrOCR models are encoder-decoder models, consisting of an image Transformer as encoder, and a text Transformer as decoder. We utilise the versions hosted on [huggingface.co](https://huggingface.co/models?search=microsoft/trocr) and use the awesome transformers library, for longevity and simplicity.
The notebook is structured as follows:
* Setting up the Environment
* Using the Model (Running Inference)
# Setting up the Environment
#### Dependencies and Runtime
If you're running this notebook in Google Colab, most of the dependencies are already installed and we don't need the GPU for this particular example.
If you decide to run this on many (>thousands) images and want the inference to go faster though, you can select `Runtime` > `Change Runtime Type` from the menubar. Ensure that `GPU` is selected as the `Hardware accelerator`.
We need to install huggingface `transformers` for this example to run, so execute the command below to setup the dependencies. We use the version compiled directly from the latest source (at the time of writing this is the only way to access the transforemrs TrOCR model code).
```
!pip install -q git+https://github.com/huggingface/transformers.git
```
# Using the Model (Running Inference)
Let's define a function for us to get images from the web. We execute this function to download an image with a line of handwritten text and display it.
```
import requests
from IPython.display import display
from PIL import Image
def show_image(url):
img = Image.open(requests.get(url, stream=True).raw).convert("RGB")
display(img)
return img
handwriting1 = show_image('https://fki.tic.heia-fr.ch/static/img/a01-122-02.jpg')
```
Now we want to load the model to recognise handwritten text.
Specifically we are running the following steps:
* Load the processor, `TrOCRProcessor`, which processes our input image and converts it into a sequence of fixed-size patches (resolution 16x16), which are linearly embedded. The processor also adds absolute position embeddings and this sequence is fed to the layers of the Transformer encoder.
* Load the model, `VisionEncoderDecoderModel`, which consists of the image encoder and the text decoder.
* Define `ocr_image` function - We define the function for inferencing which takes our `src_img`, the input image we have downloaded. It will then run both the processor and the model inference and produce the output OCR text that has been recognised from the image.
```
import transformers
from transformers import TrOCRProcessor, VisionEncoderDecoderModel
processor = TrOCRProcessor.from_pretrained('microsoft/trocr-base-handwritten')
model = VisionEncoderDecoderModel.from_pretrained('microsoft/trocr-base-handwritten')
def ocr_image(src_img):
pixel_values = processor(images=src_img, return_tensors="pt").pixel_values
generated_ids = model.generate(pixel_values)
return processor.batch_decode(generated_ids, skip_special_tokens=True)[0]
```
We now run our `ocr_image` function on the line of handwritten text in the image we have downloaded previously (and stored in `handwriting1`).
```
ocr_image(handwriting1)
```
Lets try on another image with handwritten text.
```
ocr_image(show_image('https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSoolxi9yWGAT5SLZShv8vVd0bz47UWRzQC19fDTeE8GmGv_Rn-PCF1pP1rrUx8kOjA4gg&usqp=CAU'))
import transformers
from transformers import TrOCRProcessor, VisionEncoderDecoderModel
print_processor = TrOCRProcessor.from_pretrained('microsoft/trocr-base-printed')
print_model = VisionEncoderDecoderModel.from_pretrained('microsoft/trocr-base-printed')
def ocr_print_image(src_img):
pixel_values = print_processor(images=src_img, return_tensors="pt").pixel_values
generated_ids = print_model.generate(pixel_values)
return print_processor.batch_decode(generated_ids, skip_special_tokens=True)[0]
```
We download an image with noisy printed text, a scanned receipt.
```
receipt = show_image('https://github.com/zzzDavid/ICDAR-2019-SROIE/raw/master/data/img/000.jpg')
```
As the model processes a line of text, we crop the image to include on of the lines of text in the receipt and send it to our model.
```
receipt_crop = receipt.crop((0, 80, receipt.size[0], 110))
display(receipt_crop)
ocr_print_image(receipt_crop)
```
More Notebooks @ [eugenesiow/practical-ml](https://github.com/eugenesiow/practical-ml) and do star or drop us some feedback on how to improve the notebooks on the [Github repo](https://github.com/eugenesiow/practical-ml/).
|
github_jupyter
|
# 初始化
```
#@markdown - **挂载**
from google.colab import drive
drive.mount('GoogleDrive')
# #@markdown - **卸载**
# !fusermount -u GoogleDrive
```
# 代码区
```
#@title K-近邻算法 { display-mode: "both" }
# 该程序实现 k-NN 对三维随机数据的分类
#@markdown [参考程序](https://github.com/wzyonggege/statistical-learning-method/blob/master/KNearestNeighbors/KNN.ipynb)
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#@markdown - **绑定数据**
class Bunch(dict):
def __init__(self,*args,**kwds):
super(Bunch,self).__init__(*args,**kwds)
self.__dict__ = self
#@markdown - **生成带标签随机数据函数**
def generate_random(sigma, N, mu1=[25., 25., 20], mu2=[30., 40., 30]):
c = sigma.shape[-1] # 生成N行c维的随机测试数据
X = np.zeros((N, c)) # 初始化X,N个样本
target = np.zeros((N,1))
for i in range(N):
if np.random.random(1) < 0.5: # 生成0-1之间随机数
X[i, :] = np.random.multivariate_normal(mu1, sigma[0, :, :], 1) # 用第一个高斯模型生成3维数据
target[i] = 1
else:
X[i, :] = np.random.multivariate_normal(mu2, sigma[1, :, :], 1) # 用第二个高斯模型生成3维数据
target[i] = -1
return X, target
#@markdown - **KNN 类**
class KNN:
def __init__(self, X_train, y_train, n_neighbors=3, p=2):
"""
parameter: n_neighbors 临近点个数, 最好选奇数
parameter: p 距离度量
"""
if n_neighbors % 2 == 0:
print('n_neighbors 最好为奇数!')
self.n = n_neighbors
self.p = p
self.X_train = X_train
self.y_train = y_train.flatten()
def predict(self, X):
# 取出n个点
knn_list = []
for i in range(self.n):
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
knn_list.append((dist, self.y_train[i]))
# 遍历得到距离最近的 n 个点
for i in range(self.n, len(self.X_train)):
max_index = knn_list.index(max(knn_list, key=lambda x: x[0]))
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
if knn_list[max_index][0] > dist:
knn_list[max_index] = (dist, self.y_train[i])
# 预测类别
knn = np.array([k[-1] for k in knn_list])
return np.sign(knn.sum()) if knn.sum() != 0 else 1
def score(self, X_test, y_test):
y_test = y_test.flatten()
right_count = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right_count += 1
return right_count / X_test.shape[0]
#@markdown - **生成带标签的随机数据**
k, N = 2, 400
# 初始化方差,生成样本与标签
sigma = np.zeros((k, 3, 3))
for i in range(k):
sigma[i, :, :] = np.diag(np.random.randint(10, 25, size=(3, )))
sample, target = generate_random(sigma, N)
feature_names = ['x_label', 'y_label', 'z_label'] # 特征数
target_names = ['gaussian1', 'gaussian2', 'gaussian3', 'gaussian4'] # 类别
data = Bunch(sample=sample, feature_names=feature_names, target=target, target_names=target_names)
sample_t, target_t = generate_random(sigma, N)
data_t = Bunch(sample=sample_t, target=target_t)
#@markdown - **模型训练**
model = KNN(data.sample, target, n_neighbors=4, p=2)
model.predict(data.sample[100])
target.flatten()[100]
#@markdown - **测试集精度**
acc = model.score(data_t.sample, data_t.target) * 100
print('Accuracy on testing set: {:.2f}%.'.format(acc))
tar_test = np.array([model.predict(x) for x in data_t.sample], dtype=np.int8) + 1
#@markdown - **显示 KNN 对测试数据的分类情况**
titles = ['Random training data', 'Classified testing data by KNN']
TAR = [target, tar_test]
DATA = [data.sample, data_t.sample]
fig = plt.figure(1, figsize=(16, 8))
fig.subplots_adjust(wspace=.01, hspace=.02)
for i, title, data_n, tar in zip([1, 2], titles, DATA, TAR):
ax = fig.add_subplot(1, 2, i, projection='3d')
if title == 'Random training data':
ax.scatter(data_n[:,0], data_n[:,1], data_n[:,2], c='b', s=35, alpha=0.4, marker='o')
else:
color=['b','g', 'r']
for j in range(N):
ax.scatter(data_n[j, 0], data_n[j, 1], data_n[j, 2], c=color[tar[j]], s=35, alpha=0.4, marker='P')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.view_init(elev=20., azim=-25)
ax.set_title(title, fontsize=14, y=0.01)
plt.show()
```
|
github_jupyter
|
# Implementing an LSTM RNN Model
------------------------
Here we implement an LSTM model on all a data set of Shakespeare works.
We start by loading the necessary libraries and resetting the default computational graph.
```
import os
import re
import string
import requests
import numpy as np
import collections
import random
import pickle
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
```
We start a computational graph session.
```
sess = tf.Session()
```
Next, it is important to set the algorithm and data processing parameters.
---------
Parameter : Descriptions
- min_word_freq: Only attempt to model words that appear at least 5 times.
- rnn_size: size of our RNN (equal to the embedding size)
- epochs: Number of epochs to cycle through the data
- batch_size: How many examples to train on at once
- learning_rate: The learning rate or the convergence paramter
- training_seq_len: The length of the surrounding word group (e.g. 10 = 5 on each side)
- embedding_size: Must be equal to the rnn_size
- save_every: How often to save the model
- eval_every: How often to evaluate the model
- prime_texts: List of test sentences
```
# Set RNN Parameters
min_word_freq = 5 # Trim the less frequent words off
rnn_size = 128 # RNN Model size
embedding_size = 100 # Word embedding size
epochs = 10 # Number of epochs to cycle through data
batch_size = 100 # Train on this many examples at once
learning_rate = 0.001 # Learning rate
training_seq_len = 50 # how long of a word group to consider
embedding_size = rnn_size
save_every = 500 # How often to save model checkpoints
eval_every = 50 # How often to evaluate the test sentences
prime_texts = ['thou art more', 'to be or not to', 'wherefore art thou']
# Download/store Shakespeare data
data_dir = 'temp'
data_file = 'shakespeare.txt'
model_path = 'shakespeare_model'
full_model_dir = os.path.join(data_dir, model_path)
# Declare punctuation to remove, everything except hyphens and apostrophes
punctuation = string.punctuation
punctuation = ''.join([x for x in punctuation if x not in ['-', "'"]])
# Make Model Directory
if not os.path.exists(full_model_dir):
os.makedirs(full_model_dir)
# Make data directory
if not os.path.exists(data_dir):
os.makedirs(data_dir)
```
Download the data if we don't have it saved already. The data comes from the [Gutenberg Project](http://www.gutenberg.org])
```
print('Loading Shakespeare Data')
# Check if file is downloaded.
if not os.path.isfile(os.path.join(data_dir, data_file)):
print('Not found, downloading Shakespeare texts from www.gutenberg.org')
shakespeare_url = 'http://www.gutenberg.org/cache/epub/100/pg100.txt'
# Get Shakespeare text
response = requests.get(shakespeare_url)
shakespeare_file = response.content
# Decode binary into string
s_text = shakespeare_file.decode('utf-8')
# Drop first few descriptive paragraphs.
s_text = s_text[7675:]
# Remove newlines
s_text = s_text.replace('\r\n', '')
s_text = s_text.replace('\n', '')
# Write to file
with open(os.path.join(data_dir, data_file), 'w') as out_conn:
out_conn.write(s_text)
else:
# If file has been saved, load from that file
with open(os.path.join(data_dir, data_file), 'r') as file_conn:
s_text = file_conn.read().replace('\n', '')
# Clean text
print('Cleaning Text')
s_text = re.sub(r'[{}]'.format(punctuation), ' ', s_text)
s_text = re.sub('\s+', ' ', s_text ).strip().lower()
print('Done loading/cleaning.')
```
Define a function to build a word processing dictionary (word -> ix)
```
# Build word vocabulary function
def build_vocab(text, min_word_freq):
word_counts = collections.Counter(text.split(' '))
# limit word counts to those more frequent than cutoff
word_counts = {key:val for key, val in word_counts.items() if val>min_word_freq}
# Create vocab --> index mapping
words = word_counts.keys()
vocab_to_ix_dict = {key:(ix+1) for ix, key in enumerate(words)}
# Add unknown key --> 0 index
vocab_to_ix_dict['unknown']=0
# Create index --> vocab mapping
ix_to_vocab_dict = {val:key for key,val in vocab_to_ix_dict.items()}
return(ix_to_vocab_dict, vocab_to_ix_dict)
```
Now we can build the index-vocabulary from the Shakespeare data.
```
# Build Shakespeare vocabulary
print('Building Shakespeare Vocab')
ix2vocab, vocab2ix = build_vocab(s_text, min_word_freq)
vocab_size = len(ix2vocab) + 1
print('Vocabulary Length = {}'.format(vocab_size))
# Sanity Check
assert(len(ix2vocab) == len(vocab2ix))
# Convert text to word vectors
s_text_words = s_text.split(' ')
s_text_ix = []
for ix, x in enumerate(s_text_words):
try:
s_text_ix.append(vocab2ix[x])
except:
s_text_ix.append(0)
s_text_ix = np.array(s_text_ix)
```
We define the LSTM model. The methods of interest are the `__init__()` method, which defines all the model variables and operations, and the `sample()` method which takes in a sample word and loops through to generate text.
```
# Define LSTM RNN Model
class LSTM_Model():
def __init__(self, embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=False):
self.embedding_size = embedding_size
self.rnn_size = rnn_size
self.vocab_size = vocab_size
self.infer_sample = infer_sample
self.learning_rate = learning_rate
if infer_sample:
self.batch_size = 1
self.training_seq_len = 1
else:
self.batch_size = batch_size
self.training_seq_len = training_seq_len
self.lstm_cell = tf.contrib.rnn.BasicLSTMCell(self.rnn_size)
self.initial_state = self.lstm_cell.zero_state(self.batch_size, tf.float32)
self.x_data = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
self.y_output = tf.placeholder(tf.int32, [self.batch_size, self.training_seq_len])
with tf.variable_scope('lstm_vars'):
# Softmax Output Weights
W = tf.get_variable('W', [self.rnn_size, self.vocab_size], tf.float32, tf.random_normal_initializer())
b = tf.get_variable('b', [self.vocab_size], tf.float32, tf.constant_initializer(0.0))
# Define Embedding
embedding_mat = tf.get_variable('embedding_mat', [self.vocab_size, self.embedding_size],
tf.float32, tf.random_normal_initializer())
embedding_output = tf.nn.embedding_lookup(embedding_mat, self.x_data)
rnn_inputs = tf.split(axis=1, num_or_size_splits=self.training_seq_len, value=embedding_output)
rnn_inputs_trimmed = [tf.squeeze(x, [1]) for x in rnn_inputs]
# If we are inferring (generating text), we add a 'loop' function
# Define how to get the i+1 th input from the i th output
def inferred_loop(prev, count):
# Apply hidden layer
prev_transformed = tf.matmul(prev, W) + b
# Get the index of the output (also don't run the gradient)
prev_symbol = tf.stop_gradient(tf.argmax(prev_transformed, 1))
# Get embedded vector
output = tf.nn.embedding_lookup(embedding_mat, prev_symbol)
return(output)
decoder = tf.contrib.legacy_seq2seq.rnn_decoder
outputs, last_state = decoder(rnn_inputs_trimmed,
self.initial_state,
self.lstm_cell,
loop_function=inferred_loop if infer_sample else None)
# Non inferred outputs
output = tf.reshape(tf.concat(axis=1, values=outputs), [-1, self.rnn_size])
# Logits and output
self.logit_output = tf.matmul(output, W) + b
self.model_output = tf.nn.softmax(self.logit_output)
loss_fun = tf.contrib.legacy_seq2seq.sequence_loss_by_example
loss = loss_fun([self.logit_output],[tf.reshape(self.y_output, [-1])],
[tf.ones([self.batch_size * self.training_seq_len])],
self.vocab_size)
self.cost = tf.reduce_sum(loss) / (self.batch_size * self.training_seq_len)
self.final_state = last_state
gradients, _ = tf.clip_by_global_norm(tf.gradients(self.cost, tf.trainable_variables()), 4.5)
optimizer = tf.train.AdamOptimizer(self.learning_rate)
self.train_op = optimizer.apply_gradients(zip(gradients, tf.trainable_variables()))
def sample(self, sess, words=ix2vocab, vocab=vocab2ix, num=10, prime_text='thou art'):
state = sess.run(self.lstm_cell.zero_state(1, tf.float32))
word_list = prime_text.split()
for word in word_list[:-1]:
x = np.zeros((1, 1))
x[0, 0] = vocab[word]
feed_dict = {self.x_data: x, self.initial_state:state}
[state] = sess.run([self.final_state], feed_dict=feed_dict)
out_sentence = prime_text
word = word_list[-1]
for n in range(num):
x = np.zeros((1, 1))
x[0, 0] = vocab[word]
feed_dict = {self.x_data: x, self.initial_state:state}
[model_output, state] = sess.run([self.model_output, self.final_state], feed_dict=feed_dict)
sample = np.argmax(model_output[0])
if sample == 0:
break
word = words[sample]
out_sentence = out_sentence + ' ' + word
return(out_sentence)
```
In order to use the same model (with the same trained variables), we need to share the variable scope between the trained model and the test model.
```
# Define LSTM Model
lstm_model = LSTM_Model(embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size)
# Tell TensorFlow we are reusing the scope for the testing
with tf.variable_scope(tf.get_variable_scope(), reuse=True):
test_lstm_model = LSTM_Model(embedding_size, rnn_size, batch_size, learning_rate,
training_seq_len, vocab_size, infer_sample=True)
```
We need to save the model, so we create a model saving operation.
```
# Create model saver
saver = tf.train.Saver(tf.global_variables())
```
Let's calculate how many batches are needed for each epoch and split up the data accordingly.
```
# Create batches for each epoch
num_batches = int(len(s_text_ix)/(batch_size * training_seq_len)) + 1
# Split up text indices into subarrays, of equal size
batches = np.array_split(s_text_ix, num_batches)
# Reshape each split into [batch_size, training_seq_len]
batches = [np.resize(x, [batch_size, training_seq_len]) for x in batches]
```
Initialize all the variables
```
# Initialize all variables
init = tf.global_variables_initializer()
sess.run(init)
```
Training the model!
```
# Train model
train_loss = []
iteration_count = 1
for epoch in range(epochs):
# Shuffle word indices
random.shuffle(batches)
# Create targets from shuffled batches
targets = [np.roll(x, -1, axis=1) for x in batches]
# Run a through one epoch
print('Starting Epoch #{} of {}.'.format(epoch+1, epochs))
# Reset initial LSTM state every epoch
state = sess.run(lstm_model.initial_state)
for ix, batch in enumerate(batches):
training_dict = {lstm_model.x_data: batch, lstm_model.y_output: targets[ix]}
c, h = lstm_model.initial_state
training_dict[c] = state.c
training_dict[h] = state.h
temp_loss, state, _ = sess.run([lstm_model.cost, lstm_model.final_state, lstm_model.train_op],
feed_dict=training_dict)
train_loss.append(temp_loss)
# Print status every 10 gens
if iteration_count % 10 == 0:
summary_nums = (iteration_count, epoch+1, ix+1, num_batches+1, temp_loss)
print('Iteration: {}, Epoch: {}, Batch: {} out of {}, Loss: {:.2f}'.format(*summary_nums))
# Save the model and the vocab
if iteration_count % save_every == 0:
# Save model
model_file_name = os.path.join(full_model_dir, 'model')
saver.save(sess, model_file_name, global_step = iteration_count)
print('Model Saved To: {}'.format(model_file_name))
# Save vocabulary
dictionary_file = os.path.join(full_model_dir, 'vocab.pkl')
with open(dictionary_file, 'wb') as dict_file_conn:
pickle.dump([vocab2ix, ix2vocab], dict_file_conn)
if iteration_count % eval_every == 0:
for sample in prime_texts:
print(test_lstm_model.sample(sess, ix2vocab, vocab2ix, num=10, prime_text=sample))
iteration_count += 1
```
Here is a plot of the training loss across the iterations.
```
# Plot loss over time
plt.plot(train_loss, 'k-')
plt.title('Sequence to Sequence Loss')
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.show()
```
|
github_jupyter
|
# Random Forest Classification
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 123)#performing datasplitting
```
### Model
A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is controlled with the <code>max_samples</code> parameter if <code>bootstrap=True</code> (default), otherwise the whole dataset is used to build each tree.
#### Model Tuning Parameters
1. n_estimators : int, default=100
> The number of trees in the forest.
2. criterion : {“gini”, “entropy”}, default=”gini”
> The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “entropy” for the information gain.
3. max_depth : int, default=None
> The maximum depth of the tree.
4. max_features : {“auto”, “sqrt”, “log2”}, int or float, default=”auto”
> The number of features to consider when looking for the best split:
5. bootstrap : bool, default=True
> Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
6. oob_score : bool, default=False
> Whether to use out-of-bag samples to estimate the generalization accuracy.
7. n_jobs : int, default=None
> The number of jobs to run in parallel. fit, predict, decision_path and apply are all parallelized over the trees. <code>None</code> means 1 unless in a joblib.parallel_backend context. <code>-1</code> means using all processors. See Glossary for more details.
8. random_state : int, RandomState instance or None, default=None
> Controls both the randomness of the bootstrapping of the samples used when building trees (if <code>bootstrap=True</code>) and the sampling of the features to consider when looking for the best split at each node (if <code>max_features < n_features</code>).
9. verbose : int, default=0
> Controls the verbosity when fitting and predicting.
```
# Build Model here
model = RandomForestClassifier(n_jobs = -1,random_state = 123)
model.fit(X_train, y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,X_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(X_test)))
```
#### Feature Importances.
The Feature importance refers to techniques that assign a score to features based on how useful they are for making the prediction.
```
plt.figure(figsize=(8,6))
n_features = len(X.columns)
plt.barh(range(n_features), model.feature_importances_, align='center')
plt.yticks(np.arange(n_features), X.columns)
plt.xlabel("Feature importance")
plt.ylabel("Feature")
plt.ylim(-1, n_features)
```
#### Creator: Thilakraj Devadiga , Github: [Profile](https://github.com/Thilakraj1998)
|
github_jupyter
|
```
from __future__ import division
import numpy as np
from numpy import *
import os
import tensorflow as tf
import PIL
from PIL import Image
import matplotlib.pyplot as plt
from skimage import data, io, filters
from matplotlib.path import Path
import matplotlib.patches as patches
import pandas as pd
path_to_strokes = "tiny/airplane.npy"
X = np.load(path_to_strokes)[()]
print('Example sketch has ', str(shape(X['airplane'][0][0])[0]), ' strokes')
print('Corresponds to photo: ', X['airplane'][1][0])
path_to_source_photos = "../tiny/photo/airplane/"
photo = os.path.join(path_to_source_photos,'n02691156_10151.jpg')
class TinyDataset():
"""tiny airplane dataset of photos and sketches for pix2svg."""
def __init__(self, npy_file, root_dir, transform=None):
"""
Args:
npy_file (string): Path to the numpy file with stroke-5 representation and corresponding photos.
# to get stroke-5 representation of svg
x['airplane'][0][5]
# to get corresponding photos
x['airplane'][1][5]
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.root_dir = root_dir
self.stroke_dir = npy_file
self.photo_dir = os.path.join(root_dir,'photo')
self.strokes = np.load(npy_file)[()]
self.transform = transform
def __len__(self):
return len(self.strokes['airplane'][0])
def __getitem__(self, idx):
img_name = os.path.join(self.photo_dir,'airplane',X['airplane'][1][idx]+ '.jpg')
photo = io.imread(img_name)
photo = photo.astype(float)
strokes = self.strokes['airplane'][0][idx]
sample = {'photo': photo, 'strokes': strokes,'name': X['airplane'][1][idx]+ '.jpg'}
if self.transform:
sample = self.transform(sample)
return sample
class ToTensor(object):
"""Convert ndarrays in sample to Tensors."""
def __call__(self, sample):
image, strokes, name = sample['photo'], sample['strokes'], sample['name']
# swap color axis because
# numpy image: H x W x C
# torch image: C X H X W
image = image.transpose((2, 0, 1))
return {'tensor': tf.divide(tf.stack(sample['photo']),255),
'strokes': strokes,
'name': name,
'photo': image}
def to_normal_strokes(big_stroke):
"""Convert from stroke-5 format (from sketch-rnn paper) back to stroke-3."""
l = 0
for i in range(len(big_stroke)):
if big_stroke[i, 4] > 0:
l = i
break
if l == 0:
l = len(big_stroke)
result = np.zeros((l, 3))
result[:, 0:2] = big_stroke[0:l, 0:2]
result[:, 2] = big_stroke[0:l, 3]
return result
def strokes_to_lines(strokes):
"""
Convert stroke-3 format to polyline format.
List contains sublist of continuous line segments (strokes).
"""
x = 0
y = 0
lines = []
line = []
for i in range(len(strokes)):
if strokes[i, 2] == 1:
x += float(strokes[i, 0])
y += float(strokes[i, 1])
line.append([x, y])
lines.append(line)
line = []
else:
x += float(strokes[i, 0])
y += float(strokes[i, 1])
line.append([x, y])
return lines
def polyline_pathmaker(lines):
x = []
y = []
codes = [Path.MOVETO] # start with moveto command always
for i,l in enumerate(lines):
for _i,_l in enumerate(l):
x.append(_l[0])
y.append(_l[1])
if _i<len(l)-1:
codes.append(Path.LINETO) # keep pen on page
else:
if i != len(lines)-1: # final vertex
codes.append(Path.MOVETO)
verts = zip(x,y)
return verts, codes
def path_renderer(verts, codes):
path = Path(verts, codes)
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax.add_patch(patch)
ax.set_xlim(0,max(max(verts)))
ax.set_ylim(0,max(max(verts)))
ax.axis('off')
plt.gca().invert_yaxis() # y values increase as you go down in image
plt.show()
%ls
## load in airplanes dataset
airplanes = TinyDataset(npy_file='/home/jefan/ptsketchy/tiny/airplane.npy',root_dir='/home/jefan/ptsketchy/tiny',transform=None)
## display given photo and corresponding sketch from stroke-5 representation
i = 100
sample = airplanes[i]
print(i, sample['photo'].shape, sample['strokes'].shape)
plt.figure()
ax = plt.subplot(121)
ax.set_title(sample['name'])
ax.axis('off')
img = np.reshape(sample['photo'],(256,256,3))
plt.imshow(img,interpolation='nearest')
ax = plt.subplot(122)
lines = strokes_to_lines(to_normal_strokes(sample['strokes']))
verts,codes = polyline_pathmaker(lines)
path_renderer(verts,codes)
plt.show()
# load in airplanes dataset
airplanes = TinyDataset(npy_file='/home/jefan/ptsketchy/tiny/airplane.npy',
root_dir='/home/jefan/ptsketchy/tiny',
transform=ToTensor())
# load in features for photos
path_to_features = 'sketchy/triplet_features'
photo_features = np.load(os.path.join(path_to_features,'photo_features.npy'))
F = photo_features
# read in filenames and generate pandas dataframe with object labels
_filenames = pd.read_csv(os.path.join(path_to_features,'photo_filenames.txt'),header=None,names=['filename'])
filenames = []
for i in range(len(_filenames)):
filenames.append(_filenames[_filenames.index==i].values[0][0])
filenames = ['sketchy' + f[1:] for f in filenames]
path = filenames
obj = [f.split('/')[3] for f in filenames]
img = [f.split('/')[4] for f in filenames]
data = {'path': path,
'object': obj,
'filename': img}
X = pd.DataFrame.from_dict(data)
# subset airplane features only
matches = X['object']=='airplane'
inds = np.where(matches==True)
X0 = X[matches]
F0 = F[inds]
# construct (11094,1024) version of photo feature matrix, called PF, that matches indexing of the sketch feature matrix
sketch_features = np.load('sketchy/airplane_features/airplane_sketch_features.npy')
_sketch_filenames = pd.read_csv('sketchy/airplane_features/airplane_sketch_filenames.txt',header=None,names=['filename'])
sketch_filenames = []
for i in range(len(_sketch_filenames)):
sketch_filenames.append(_sketch_filenames[_sketch_filenames.index==i].values[0][0])
PF = []
inds = []
for sf in sketch_filenames:
q = sf.split('/')[2]+'.jpg'
PF.append(F0[X0['filename']==q])
inds.append(np.where(X0['filename']==q)[0][0])
PF = np.squeeze(np.array(PF))
SF = sketch_features
inds = np.array(inds)
## zip together/concatenate the photo and sketch features
_F = np.hstack((PF,SF))
### now get a (11094,5) representation of the 'next stroke'
### no wait, instead, just bump up the dimensionality of these feature matrices to fit that of
### the (delta_x,delta_y) stroke representation
### Strokes dataframe ("S") is of dimensionality (55855,5).
### So, resize and re-index the feature matrix to match S.
S = pd.read_csv('tiny/stroke_dataframe.csv')
S1 = S
photo_dir = np.array([sf.split('/')[2] for sf in sketch_filenames]) # photo dir
sketch_dir = np.array(map(int,[sf.split('/')[3] for sf in sketch_filenames])) # sketch dir
stroke_png = np.array(map(int,[sf.split('/')[4].split('.')[0] for sf in sketch_filenames])) # stroke png
F = []
for index, row in S.iterrows():
# get ind of the original small (11094,5) matrix that corresponds to this row of S (55855,5)
ind = np.intersect1d(np.intersect1d(np.where(photo_dir==row['photoID']),
np.where(sketch_dir==row['sketchID'])),
np.where(stroke_png==row['strokeID']))[0]
F.append(_F[ind])
F = np.array(F)
F1 = F # protected F1 matrix
```
### convert strokes matrix from absolute to relative coordinates
```
from copy import deepcopy
unique_photos = np.unique(S1.photoID)
r = pd.DataFrame(columns=list(S1.keys()))
run_this = False
if run_this:
for i, p in enumerate(unique_photos):
print 'Processing ' + p + ': ' + str(i+1) + ' of ' + str(len(unique_photos)) + ' photos.'
s1 = S1[S1.photoID==p]
unique_sketches_of_photo = np.unique(s1.sketchID)
for sketch in unique_sketches_of_photo:
this_sketch = s1[s1.sketchID==sketch]
for index, row in this_sketch.iterrows():
_row = deepcopy(row)
if index==min(this_sketch.index): # first stroke
r = r.append(row)
this_x = row.x
this_y = row.y
else:
x_offset = _row.x-this_x
y_offset = _row.y-this_y
row.x = x_offset
row.y = y_offset
r = r.append(row)
this_x = _row.x # hold onto current row so you can compute difference with next one
this_y = _row.y
# save out relative strokes matrix as S2
S2 = r
print 'Saving out stroke_dataframe_relative.csv'
S2.to_csv('tiny/stroke_dataframe_relative.csv')
# check if S2 exists, if not, load it in
try:
S2
except:
S2 = pd.read_csv('tiny/stroke_dataframe_relative.csv')
# define S to either be ABSOLUTE strokes matrix (S1) or RELATIVE strokes matrix (S2)
S = S2
# generate 55855-long vector of photo indices
print 'generating list of photo indices based on X0'
inds = []
for index, row in S.iterrows():
q = row['photoID']+'.jpg'
inds.append(np.where(X0['filename']==q)[0][0])
inds = np.array(inds)
# generate random index to do train/val/test split
print 'generating random index to do train/val/test split'
_idx = np.arange(len(X0))
np.random.seed(seed=0)
np.random.shuffle(_idx)
train_len = int(len(_idx)*0.85)
val_len = int(len(_idx)*0.05)
test_len = int(len(_idx*0.10))
# indices of 100 photos that will go into train/val/test split
train_inds = _idx[:train_len]
val_inds = _idx[train_len:train_len+val_len]
test_inds = _idx[train_len+val_len:len(_idx)]
print 'constructing 55855 vectors that correspond to membership in train/val/test splits'
# construct 55855 vectors that correspond to membership in train/val/test splits
train_vec = np.zeros(len(F)).astype(bool)
val_vec = np.zeros(len(F)).astype(bool)
test_vec = np.zeros(len(F)).astype(bool)
for i in train_inds:
train_vec[inds==i] = True
for i in val_inds:
val_vec[inds==i] = True
for i in test_inds:
test_vec[inds==i] = True
assert sum(train_vec)+ sum(val_vec) + sum(test_vec) == len(train_vec)
print ' '
print str(sum(train_vec)/len(train_vec) * len(F)) + ' sketch intermediates to train on.'
print str(sum(val_vec)/len(val_vec) * len(F)) + ' sketch intermediates to validate on.'
print str(sum(test_vec)/len(test_vec) * len(F)) + ' sketch intermediates to test on.'
print ' '
print 'Now actually splitting data.'
# now actually split data
F_train = F[train_vec]
F_val = F[val_vec]
F_test = F[test_vec]
S_train = S[train_vec]
S_val = S[val_vec]
S_test = S[test_vec]
S_train = S_train[['x', 'y', 'pen']].copy()
S_val = S_val[['x', 'y', 'pen']].copy()
S_test = S_test[['x', 'y', 'pen']].copy()
## training helpers
def minibatch(data, minibatch_idx):
return data[minibatch_idx] if type(data) is np.ndarray else [data[i] for i in minibatch_idx]
def minibatches(data, batch_size, shuffle=True):
batches = [np.array(col) for col in zip(*data)]
return get_minibatches(batches, batch_size, shuffle)
def get_minibatches(data, minibatch_size, shuffle=True):
"""
Iterates through the provided data one minibatch at at time. You can use this function to
iterate through data in minibatches as follows:
for inputs_minibatch in get_minibatches(inputs, minibatch_size):
...
Or with multiple data sources:
for inputs_minibatch, labels_minibatch in get_minibatches([inputs, labels], minibatch_size):
...
Args:
data: there are two possible values:
- a list or numpy array
- a list where each element is either a list or numpy array
minibatch_size: the maximum number of items in a minibatch
shuffle: whether to randomize the order of returned data
Returns:
minibatches: the return value depends on data:
- If data is a list/array it yields the next minibatch of data.
- If data a list of lists/arrays it returns the next minibatch of each element in the
list. This can be used to iterate through multiple data sources
(e.g., features and labels) at the same time.
"""
list_data = type(data) is list and (type(data[0]) is list or type(data[0]) is np.ndarray)
data_size = len(data[0]) if list_data else len(data)
indices = np.arange(data_size)
if shuffle:
np.random.shuffle(indices)
for minibatch_start in np.arange(0, data_size, minibatch_size):
minibatch_indices = indices[minibatch_start:minibatch_start + minibatch_size]
yield [minibatch(d, minibatch_indices) for d in data] if list_data \
else minibatch(data, minibatch_indices), minibatch_indices
# usage notes:
# for m in get_minibatches([F_train,S_train.as_matrix()],batch_size,shuffle=True):
# print len(m),m[0].shape,m[1].shape
```
### quality assurance make sure that image classification is working as advertised based on triplet features
```
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn import svm
from sklearn import linear_model
# reminders:
# S1 is stroke matrix
# F1 is feature matrix
# PF is photo-feature matrix
# SF is sketch-feature matrix/
# get np.array of source photo labels
photos = np.array([sf.split('/')[2] for sf in sketch_filenames])
## get image classification within airplane class
run_this = 1
FEAT = SF_complete
LABELS = photos_complete
if run_this:
# split sketch feature data for linear classification
X_train, X_test, y_train, y_test = train_test_split(
FEAT, LABELS, test_size=0.2, random_state=0)
# check dimensionality of split data
print 'dimensionality of train/test split'
print X_train.shape, y_train.shape
print X_test.shape, y_test.shape
print ' '
cval = True
if cval==False:
# compute linear classification accuracy (takes a minute or so to run)
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
clf.score(X_test, y_test)
else:
# compute linear classification accuracy (takes several minutes to run)
# clf = svm.SVC(kernel='linear', C=1)
clf = linear_model.LogisticRegression(penalty='l2')
scores = cross_val_score(clf, FEAT, LABELS, cv=2)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
## SVM Accuracy: 0.41 (+/- 0.08) with cv=5 achieved on 6/26/17 on intermediate sketches
## softmax Accuracy: 0.43 (+/- 0.01) with cv=2 achieved on 9/11/17
```
#### compute pairwise euclidean distances between sketches of same class vs. different class
```
### this was done on 9/11/17 in order to debug the vgg embedding
print 'Why are there fewer sketch intermediate files than total sketch files?'
print str(len(os.listdir('./tiny/sketch/airplane'))) + ' total sketch files.'
all_sketches = os.listdir('./tiny/sketch/airplane')
all_sketches_with_intermediates = [s.split('/')[-2]+'-'+s.split('/')[-1]+'.png' for s in sketch_folders]
print str(len(all_sketches_with_intermediates)) + ' sketch files after extracting intermediates.'
missing_ones = [i for i in all_sketches if i not in all_sketches_with_intermediates]
## get just complete sketches from each sketch folder
sketch_folders = np.unique([os.path.dirname(s) for s in sketch_filenames])
complete_paths = []
SF_complete = []
photos_complete = []
for (j,s) in enumerate(sketch_folders):
complete_sketch = str(max([int(i.split('.')[0]) for i \
in os.listdir(s)])) + '.png'
complete_paths.append(os.path.join(os.path.dirname(s),complete_sketch))
SF_complete.append(SF[j])
photos_complete.append(os.path.dirname(s).split('/')[-1])
SF_complete = np.array(SF_complete)
photos_complete = np.array(photos_complete)
from sklearn.metrics.pairwise import pairwise_distances
def rmse(x):
return np.sqrt(np.sum(x**2))
euc = pairwise_distances(SF_complete,metric='euclidean')
print euc.shape
p_ind = 4
fp = 20
fig = plt.figure(figsize=(9,9))
for (_i,p_ind) in enumerate(np.arange(fp,fp+9)):
unique_photos = np.unique(photos_complete)
inds = np.where(photos_complete==unique_photos[p_ind])[0]
start = inds[0]
stop = inds[-1]
# get within-photo sketch distances
within_block = euc[start:stop+1,start:stop+1]
assert len(within_block[np.triu_indices(len(within_block),k=1)])==(len(within_block)**2-len(within_block))/2
within_distances = within_block[np.triu_indices(len(within_block),k=1)]
# get between-photo sketch distances
all_inds = np.arange(len(photos_complete))
non_matches = [i for i in all_inds if i not in inds]
_non_matches_shuff = np.random.RandomState(seed=0).permutation(non_matches)
non_matches_shuff = _non_matches_shuff[:len(inds)]
btw_distances = euc[start:stop+1,non_matches_shuff].flatten()
# plot
plt.subplot(3,3,_i+1)
h = plt.hist(within_distances,bins=20,alpha=0.3)
h = plt.hist(btw_distances,bins=20,alpha=0.3)
plt.title(str(p_ind))
plt.show()
## get image classification within airplane class
run_this = 1
FEAT = SF_complete
LABELS = photos_complete
if run_this:
# split sketch feature data for linear classification
X_train, X_test, y_train, y_test = train_test_split(
FEAT, LABELS, test_size=0.2, random_state=0)
# check dimensionality of split data
print 'dimensionality of train/test split'
print X_train.shape, y_train.shape
print X_test.shape, y_test.shape
print ' '
cval = True
if cval==False:
# compute linear classification accuracy (takes a minute or so to run)
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
clf.score(X_test, y_test)
else:
# compute linear classification accuracy (takes several minutes to run)
clf = svm.SVC(kernel='linear', C=1)
scores = cross_val_score(clf, SF, photos, cv=5)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
## Accuracy: 0.41 (+/- 0.08) achieved on 6/26/17
from glob import glob
def list_files(path, ext='jpg'):
result = [y for x in os.walk(path)
for y in glob(os.path.join(x[0], '*.%s' % ext))]
return result
airplane_dir = '/home/jefan/full_sketchy_dataset/sketches/airplane'
airplane_paths = list_files(airplane_dir,ext='png')
```
### draft of model for single minibatch
```
RANDOM_SEED = 42
tf.set_random_seed(RANDOM_SEED)
# reset entire graph
tf.reset_default_graph()
sess = tf.InteractiveSession()
# weight on offset loss
offset_weight = 100.
# learning rate
learning_rate = 0.01
# get minibatch
batch_size = 10
F_batch = F_train[:batch_size,:]
S_batch = S_train.head(n=batch_size)
# reserve numpy version
F_batch_array = F_batch
S_batch_array = S_batch.as_matrix().astype('float32')
# convert to tensorflow tensor
F_batch = tf.cast(tf.stack(F_batch,name='F_batch'),tf.float32)
S_batch = tf.cast(tf.stack(S_batch.as_matrix().astype('float32'),name='S_batch'),tf.float32)
# Layer's sizes
x_size = F_batch.shape[1] # Number of input nodes: 2048 features and 1 bias
h_size = 256 # Number of hidden nodes
y_size = S_batch.shape[1] # Number of outcomes (x,y,pen)
# Symbols
X = tf.placeholder("float", shape=[None, x_size])
y = tf.placeholder("float", shape=[None, y_size])
output = tf.placeholder("float", shape=[None,y_size])
# Weight initializations
W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W2 = tf.get_variable('W2', [h_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b2 = tf.get_variable('b2', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W3 = tf.get_variable('W3', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b3 = tf.get_variable('b3', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# forward propagation
fc1 = tf.nn.relu(tf.nn.xw_plus_b(F_batch, W1, b1,name='fc1'))
fc2 = tf.nn.relu(tf.nn.xw_plus_b(fc1, W2, b2,name='fc2'))
output = tf.nn.xw_plus_b(fc1, W3, b3,name='output')
actual_offset = tf.slice(S_batch,[0,0],[batch_size,2])
actual_pen = tf.slice(S_batch,[0,2],[batch_size,-1])
pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_weight)
pred_pen = tf.nn.softmax(tf.slice(output,[0,2],[batch_size,-1]))
# currently doesn't properly handle the pen state loss
offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
labels = actual_pen,
logits = pred_pen))
loss = tf.add(offset_loss,pen_loss)
# run backprop
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(loss)
# # get predicted stroke vector
strokes = tf.concat([pred_offset, pred_pen],axis=1)
tf.global_variables_initializer().run()
# sess.close()
updates = sess.run([fc1,output,pred_offset,
pred_pen,actual_offset, actual_pen,
offset_loss,pen_loss,loss,
train_op,strokes], feed_dict={X:F_batch_array,y:S_batch_array})
fc1 = updates[0]
output = updates[1]
pred_offset = updates[2]
pred_pen = updates[3]
actual_offset = updates[4]
actual_pen = updates[5]
offset_loss = updates[6]
pen_loss = updates[7]
loss = updates[8]
train_op = updates[9]
strokes = updates[10]
```
### run multiple batches of MLP version
```
RANDOM_SEED = 42
tf.set_random_seed(RANDOM_SEED)
# reset entire graph
tf.reset_default_graph()
# weight on offset loss
offset_weight = 0.1
# amount to multiply predicted offset values by
offset_multiplier = 100.
# learning rate
learning_rate = 0.001
# set batch size
batch_size = 10
# epoch counter
epoch_num = 0
# feed in only current features, or also features on the next time step as well?
now_plus_next = True
# initialize variables
if now_plus_next:
F = tf.placeholder("float", shape=[None, 4096]) # features (input)
else:
F = tf.placeholder("float", shape=[None, 2048]) # features (input)
S = tf.placeholder("float", shape=[None, 3]) # strokes (output)
# Layer's sizes
x_size = F.shape[1] # Number of input nodes: 2048 features and 1 bias
h_size = 256 # Number of hidden nodes
y_size = S.shape[1] # Number of outcomes (x,y,pen)
output = tf.placeholder("float", shape=[None,y_size])
# convert to tensorflow tensor
F = tf.cast(tf.stack(F,name='F'),tf.float32)
S = tf.cast(tf.stack(S,name='S'),tf.float32)
# Weight initializations
W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W2 = tf.get_variable('W2', [h_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b2 = tf.get_variable('b2', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W3 = tf.get_variable('W3', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b3 = tf.get_variable('b3', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# forward propagation
fc1 = tf.nn.relu(tf.nn.xw_plus_b(F, W1, b1,name='fc1'))
fc2 = tf.nn.relu(tf.nn.xw_plus_b(fc1, W2, b2,name='fc2'))
output = tf.nn.xw_plus_b(fc1, W3, b3,name='output')
actual_offset = tf.slice(So,[0,0],[batch_size,2])
actual_pen = tf.squeeze(tf.slice(So,[0,2],[batch_size,-1]))
pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_multiplier)
pred_pen = tf.squeeze(tf.slice(output,[0,2],[batch_size,-1]))
offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
labels = actual_pen,
logits = pred_pen))
loss = tf.add(tf.multiply(offset_weight,offset_loss),pen_loss)
# run backprop
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(loss)
# saver
save = False
saver = tf.train.Saver()
# get predicted stroke vector
strokes = tf.concat([pred_offset, tf.expand_dims(pred_pen,1)],axis=1)
# run batches
with tf.Session() as sess:
tf.global_variables_initializer().run()
for m,idx in get_minibatches([F_train,S_train.as_matrix().astype('float32')],batch_size,shuffle=True):
if m[0].shape[0]==batch_size:
F_batch = m[0]
S_batch = m[1]
# use idx to retrieve the features of the subsequent row in the feature matrix, so you
# effectively feed in sketch_so_far and sketch_so_far_plus_next_xy, as well as pen (absolute?) location and state
if (max(idx)<45040):
F_batch_next = F_train[idx+1].shape
F_now_plus_next = np.hstack((F_train[idx],F_train[idx+1]))
if (now_plus_next) & (max(idx)<45040):
updates = sess.run([offset_loss, pen_loss, loss, pred_offset], feed_dict={F:F_now_plus_next,S:S_batch})
else:
try:
updates = sess.run([offset_loss, pen_loss, loss, pred_offset], feed_dict={F:F_batch,S:S_batch})
except:
pass
offset_loss_ = updates[0]
pen_loss_ = updates[1]
loss_ = updates[2]
pred_offset_ = updates[3]
if epoch_num%200==0:
print "Epoch: " + str(epoch_num) + " | Loss: " + str(loss_) + \
" | Offset loss: " + str(offset_loss_) + " | Pen loss: " + str(pen_loss_)
# save
if save:
saver.save(sess, 'checkpoints/pix2svg_train_0')
# increment epoch number
epoch_num += 1
## meeting notes
# june 26: validate triplet network to make sure it does the task -- QA
# does it take in pen location? put in pen location, pen state
# put in sketch so far + (sketch so far +1)
# delta x, delta y -- make sure the thing it spits out, after getting squashed by tanh, or whatever, is well centered
```
### simpler version that goes from last pen offset to next pen offset
```
## now try simpler version that just tries to predict the next offset based on previous offset
RANDOM_SEED = 42
tf.set_random_seed(RANDOM_SEED)
# reset entire graph
tf.reset_default_graph()
# weight on offset loss
offset_weight = 0.8
# amount to multiply predicted offset values by
offset_multiplier = 100.
# learning rate
learning_rate = 0.001
# set batch size
batch_size = 10
# epoch counter
epoch_num = 0
# initialize variables
Si = tf.placeholder("float", shape=[None, 3]) # strokes (input)
So = tf.placeholder("float", shape=[None, 3]) # strokes (output)
# Layer's sizes
x_size = Si.shape[1] # Number of input nodes: x, y, state
h_size = 256 # Number of hidden nodes
y_size = So.shape[1] # Number of outcomes (x,y,pen)
output = tf.placeholder("float", shape=[None,y_size])
# convert to tensorflow tensor
Si = tf.cast(tf.stack(Si,name='Si'),tf.float32)
So = tf.cast(tf.stack(So,name='So'),tf.float32)
# Weight initializations
W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W2 = tf.get_variable('W2', [h_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b2 = tf.get_variable('b2', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W3 = tf.get_variable('W3', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b3 = tf.get_variable('b3', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# forward propagation
fc1 = tf.nn.relu(tf.nn.xw_plus_b(Si, W1, b1,name='fc1'))
fc2 = tf.nn.relu(tf.nn.xw_plus_b(fc1, W2, b2,name='fc2'))
output = tf.nn.xw_plus_b(fc1, W3, b3,name='output')
actual_offset = tf.slice(So,[0,0],[batch_size,2])
actual_pen = tf.squeeze(tf.slice(So,[0,2],[batch_size,-1]))
pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_multiplier)
pred_pen = tf.squeeze(tf.slice(output,[0,2],[batch_size,-1]))
offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
labels = actual_pen,
logits = pred_pen))
loss = tf.add(tf.multiply(offset_weight,offset_loss),tf.multiply(1-offset_weight,pen_loss))
# run backprop
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(loss)
# saver
save = False
saver = tf.train.Saver()
# get predicted stroke vector
strokes = tf.concat([pred_offset, tf.expand_dims(tf.round(tf.sigmoid(pred_pen)+1),1)],axis=1)
Strokes = []
# run batches
with tf.Session() as sess:
tf.global_variables_initializer().run()
for m,idx in get_minibatches(S_train.as_matrix().astype('float32')[:len(S_train)-1],batch_size,shuffle=True):
Si_batch = m # batch of current strokes
if (max(idx)<45040):
So_batch = S_train.iloc[idx+1].as_matrix().astype('float32')
updates = sess.run([offset_loss, pen_loss, loss, pred_offset, actual_pen, pred_pen, strokes], feed_dict={Si:Si_batch,So:So_batch})
offset_loss_ = updates[0]
pen_loss_ = updates[1]
loss_ = updates[2]
pred_offset_ = updates[3]
actual_pen_ = updates[4]
pred_pen_ = updates[5]
strokes_ = updates[6]
if epoch_num%200==0:
print "Epoch: " + str(epoch_num) + " | Loss: " + str(loss_) + \
" | Offset loss: " + str(offset_loss_) + " | Pen loss: " + str(pen_loss_)
# save
if save:
saver.save(sess, 'checkpoints/pix2svg_train_svg2svg_0')
# increment epoch number
epoch_num += 1
plt.scatter(strokes_[:,0],strokes_[:,1])
plt.show()
### demo of the difference between the absolute pen position and the relative pen position
plt.figure()
inds = list(S[(S.photoID=='n02691156_10151') & (S.sketchID==0)].index)
verts = zip(S1.loc[inds].x.values,S1.loc[inds].y.values)
codes = S1.loc[inds].pen.values
path = Path(verts, codes)
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax = plt.subplot(121)
ax.add_patch(patch)
ax.set_xlim(0,600)
ax.set_ylim(0,600)
ax.axis('off')
plt.gca().invert_yaxis() # y values increase as you go down in image
plt.show()
inds = list(S[(S.photoID=='n02691156_10151') & (S.sketchID==0)].index)
verts = zip(S2.loc[inds].x.values,S2.loc[inds].y.values)
codes = S2.loc[inds].pen.values
path = Path(verts, codes)
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax = plt.subplot(122)
ax.add_patch(patch)
ax.set_xlim(-200,200)
ax.set_ylim(-200,200)
ax.axis('off')
plt.gca().invert_yaxis() # y values increase as you go down in image
plt.show()
```
### predict next offset on basis of previous 4 offsets
```
RANDOM_SEED = 42
tf.set_random_seed(RANDOM_SEED)
# reset entire graph
tf.reset_default_graph()
# weight on offset loss
offset_weight = 1.
# amount to multiply predicted offset values by
offset_multiplier = 100.
# learning rate
learning_rate = 0.001
# set batch size
batch_size = 10
# epoch counter
epoch_num = 0
# initialize variables
Si4 = tf.placeholder("float", shape=[None, 3]) # strokes (input) -- 4th to last
Si3 = tf.placeholder("float", shape=[None, 3]) # strokes (input) -- 3rd to last
Si2 = tf.placeholder("float", shape=[None, 3]) # strokes (input) -- 2nd to last
Si1 = tf.placeholder("float", shape=[None, 3]) # strokes (input) -- previous one
So = tf.placeholder("float", shape=[None, 3]) # strokes (output)
# Layer's sizes
x_size = Si1.shape[1]*4 # Number of input nodes: x, y, state
h_size = 512 # Number of hidden nodes
y_size = So.shape[1] # Number of outcomes (x,y,pen)
output = tf.placeholder("float", shape=[None,y_size])
# convert to tensorflow tensor
Si4 = tf.cast(tf.stack(Si4,name='Si4'),tf.float32)
Si3 = tf.cast(tf.stack(Si3,name='Si3'),tf.float32)
Si2 = tf.cast(tf.stack(Si2,name='Si2'),tf.float32)
Si1 = tf.cast(tf.stack(Si1,name='Si1'),tf.float32)
Si = tf.concat([Si4,Si3,Si2,Si1],axis=1)
So = tf.cast(tf.stack(So,name='So'),tf.float32)
# Weight initializations
W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W2 = tf.get_variable('W2', [h_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b2 = tf.get_variable('b2', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W3 = tf.get_variable('W3', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b3 = tf.get_variable('b3', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# forward propagation
fc1 = tf.nn.relu(tf.nn.xw_plus_b(Si, W1, b1,name='fc1'))
fc2 = tf.nn.relu(tf.nn.xw_plus_b(fc1, W2, b2,name='fc2'))
output = tf.nn.xw_plus_b(fc1, W3, b3,name='output')
actual_offset = tf.slice(So,[0,0],[batch_size,2])
actual_pen = tf.squeeze(tf.slice(So,[0,2],[batch_size,-1]))
pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_multiplier)
pred_pen = tf.squeeze(tf.slice(output,[0,2],[batch_size,-1]))
offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
labels = actual_pen,
logits = pred_pen))
loss = tf.add(tf.multiply(offset_weight,offset_loss),tf.multiply(1-offset_weight,pen_loss))
# run backprop
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(loss)
# saver
save = False
saver = tf.train.Saver()
# get predicted stroke vector
strokes = tf.concat([pred_offset, tf.expand_dims(tf.round(tf.sigmoid(pred_pen)+1),1)],axis=1)
Strokes = []
# run batches
with tf.Session() as sess:
tf.global_variables_initializer().run()
for m,idx in get_minibatches(S_train.as_matrix().astype('float32')[:len(S_train)-1],batch_size,shuffle=True):
Si1_batch = m # batch of current strokes
Si2_batch = S_train.iloc[idx-1].as_matrix().astype('float32')
Si3_batch = S_train.iloc[idx-2].as_matrix().astype('float32')
Si4_batch = S_train.iloc[idx-3].as_matrix().astype('float32')
if (max(idx)<45040):
So_batch = S_train.iloc[idx+1].as_matrix().astype('float32')
updates = sess.run([offset_loss, pen_loss, loss,
pred_offset, actual_pen, pred_pen, strokes],
feed_dict={Si1:Si1_batch,Si2:Si2_batch,Si3:Si3_batch,Si4:Si4_batch,
So:So_batch})
offset_loss_ = updates[0]
pen_loss_ = updates[1]
loss_ = updates[2]
pred_offset_ = updates[3]
actual_pen_ = updates[4]
pred_pen_ = updates[5]
strokes_ = updates[6]
if epoch_num%200==0:
print "Epoch: " + str(epoch_num) + " | Loss: " + str(loss_) + \
" | Offset loss: " + str(offset_loss_) + " | Pen loss: " + str(pen_loss_)
# save
if save:
saver.save(sess, 'checkpoints/pix2svg_train_svg2svg_0')
# increment epoch number
epoch_num += 1
```
### now trying to predict mixture of gaussians rather than naive nonlinear function... because pen offsets can't be modeled by any function
reverting to trying to predict next pen offset based on single most recent pen offset
```
## now trying to predict mixture of gaussians rather than naive nonlinear function... because pen offsets can't be modeled by any function
import mdn as mdn ## import mixture density network helpers
reload(mdn)
RANDOM_SEED = 42
tf.set_random_seed(RANDOM_SEED)
# reset entire graph
tf.reset_default_graph()
# weight on offset loss
offset_weight = 0.8
# amount to multiply predicted offset values by
offset_multiplier = 100.
# learning rate
learning_rate = 0.001
# set batch size
batch_size = 10
# epoch counter
epoch_num = 0
# initialize variables
Si = tf.placeholder("float", shape=[None, 3]) # strokes (input)
So = tf.placeholder("float", shape=[None, 3]) # strokes (output)
r_cost = tf.placeholder("float", shape=[None])
x1_data = tf.placeholder("float",shape=[None])
x2_data = tf.placeholder("float",shape=[None])
pen_data = tf.placeholder("float",shape=[None])
offset_loss = tf.placeholder("float",shape=[None])
state_loss = tf.placeholder("float",shape=[None])
recon_loss = tf.placeholder("float",shape=[None])
# Layer's sizes
x_size = Si.shape[1] # Number of input nodes: x, y, state
h_size = 384 # Number of hidden nodes 6*64
# y_size = So.shape[1] # Number of outcomes (x,y,pen)
y_size = 8 ## split this into MDN parameters: first two elements are pen state logits (1 or 2), next 384/6 are for estimating the other parameters
output = tf.placeholder("float", shape=[None,y_size])
# # convert to tensorflow tensor
Si = tf.cast(tf.stack(Si,name='Si'),tf.float32)
So = tf.cast(tf.stack(So,name='So'),tf.float32)
# Weight initializations
W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W2 = tf.get_variable('W2', [h_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b2 = tf.get_variable('b2', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
W3 = tf.get_variable('W3', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
b3 = tf.get_variable('b3', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# forward propagation
fc1 = tf.nn.relu(tf.nn.xw_plus_b(Si, W1, b1,name='fc1'))
fc2 = tf.nn.relu(tf.nn.xw_plus_b(fc1, W2, b2,name='fc2'))
output = tf.nn.xw_plus_b(fc2, W3, b3,name='output')
# get mixture distribution parameters
out = mdn.get_mixture_coef(output)
[o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr, o_pen, o_pen_logits] = out ## each of these are the size of the batch
# get target for prediction
target = So # shape: (batch_size, 3)
[x1_data, x2_data, pen_data] = tf.split(target, 3, 1)
x1_data = tf.squeeze(x1_data) # shape (batch_size,)
x2_data = tf.squeeze(x2_data) # shape (batch_size,)
pen_data = tf.squeeze(pen_data) # shape (batch_size,)
pen_data = tf.subtract(pen_data,1) # classes need to be in the range [0, num_classes-1]
# compute reconstruction loss
offset_loss, state_loss = mdn.get_lossfunc(o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr,
o_pen_logits, x1_data, x2_data, pen_data)
offset_loss = tf.squeeze(offset_loss)
recon_loss = tf.add(offset_loss,state_loss)
loss = tf.reduce_sum(recon_loss,axis=0)
# # run backprop
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for m,idx in get_minibatches(S_train.as_matrix().astype('float32')[:len(S_train)-1],batch_size,shuffle=True):
Si_batch = m # batch of current strokes
if (max(idx)<45040):
So_batch = S_train.iloc[idx+1].as_matrix().astype('float32')
results = sess.run([o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr, o_pen, o_pen_logits, offset_loss, state_loss, recon_loss, loss], feed_dict={Si:Si_batch,So:So_batch})
_o_pi = results[0]
_o_mu1 = results[1]
_o_mu2 = results[2]
_o_sigma1 = results[3]
_o_sigma2 = results[4]
_o_corr = results[5]
_o_pen = results[6]
_o_pen_logits = results[7]
_offset_loss = results[8]
_state_loss = results[9]
_recon_loss = results[10]
_loss = results[11]
if epoch_num%100==0:
print('Epoch Num: ', epoch_num, 'Reconstruction Loss:', _loss)
epoch_num += 1
a = tf.constant([2.,2.,1.,2.,2.,1.,1.,2.,1.,2.])
b = tf.constant([1.,1.,1.,1.,1.,1.,1.,1.,1.,1.])
c = tf.reshape(a,[-1,10])
### reshape with a -1 nests a tensor, so one that is originally of shape (10,) becomes (1,10)
d = tf.split(c,10,1)
e = tf.constant([-0.4])
result = tf.nn.softmax_cross_entropy_with_logits(labels=a,logits=b)
sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())
print result.eval()
print a.eval(), a.get_shape()
print c.eval(), c.get_shape()
print tf.nn.softmax(c).eval()
print tf.nn.softmax(e).eval()
sess.close()
# NSAMPLE = 1000
x_data = np.float32(np.random.uniform(-10.5, 10.5, (1, NSAMPLE))).T
r_data = np.float32(np.random.normal(size=(NSAMPLE,1)))
y_data = np.float32(np.sin(0.75*x_data)*7.0+x_data*0.5+r_data*1.0)
# plt.figure(figsize=(8, 8))
# plot_out = plt.plot(x_data,y_data,'ro',alpha=0.3)
# plt.show()
# temp_data = x_data
# x_data = y_data
# y_data = temp_data
# plt.figure(figsize=(8, 8))
# plot_out = plt.plot(x_data,y_data,'ro',alpha=0.3)
# plt.show()
import mdn as mdn
mdn
x1 = tf.random_normal([1], mean=0, stddev=0.1)
x2 = tf.random_normal([1], mean=1, stddev=0.1)
mu1 = tf.constant(0., dtype=tf.float32)
mu2 = tf.constant(1., dtype=tf.float32)
s1 = tf.constant(1., dtype=tf.float32)
s2 = tf.constant(1., dtype=tf.float32)
rho = tf.constant(0., dtype=tf.float32)
result = mdn.tf_2d_normal(x1, x2, mu1, mu2, s1, s2, rho)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
print x1.eval()
print x2.eval()
print result.eval()
sess.close()
## self contained example of sinusoidal function fitting
NSAMPLE = 1000
x_data = np.float32(np.random.uniform(-10.5, 10.5, (1, NSAMPLE))).T
r_data = np.float32(np.random.normal(size=(NSAMPLE,1)))
y_data = np.float32(np.sin(0.75*x_data)*7.0+x_data*0.5+r_data*1.0)
x = tf.placeholder(dtype=tf.float32, shape=[None,1])
y = tf.placeholder(dtype=tf.float32, shape=[None,1])
NHIDDEN = 20
W = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=1.0, dtype=tf.float32))
b = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=1.0, dtype=tf.float32))
W_out = tf.Variable(tf.random_normal([NHIDDEN,1], stddev=1.0, dtype=tf.float32))
b_out = tf.Variable(tf.random_normal([1,1], stddev=1.0, dtype=tf.float32))
hidden_layer = tf.nn.tanh(tf.matmul(x, W) + b)
y_out = tf.matmul(hidden_layer,W_out) + b_out
lossfunc = tf.nn.l2_loss(y_out-y)
train_op = tf.train.RMSPropOptimizer(learning_rate=0.1, decay=0.8).minimize(lossfunc)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
NEPOCH = 1000
for i in range(NEPOCH):
sess.run(train_op,feed_dict={x: x_data, y: y_data})
x_test = np.float32(np.arange(-10.5,10.5,0.1))
x_test = x_test.reshape(x_test.size,1)
y_test = sess.run(y_out,feed_dict={x: x_test})
plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', x_test,y_test,'bo',alpha=0.3)
plt.show()
sess.close()
NHIDDEN = 24
STDEV = 0.5
KMIX = 24 # number of mixtures
NOUT = KMIX * 3 # pi, mu, stdev
x = tf.placeholder(dtype=tf.float32, shape=[None,1], name="x")
y = tf.placeholder(dtype=tf.float32, shape=[None,1], name="y")
Wh = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=STDEV, dtype=tf.float32))
bh = tf.Variable(tf.random_normal([1,NHIDDEN], stddev=STDEV, dtype=tf.float32))
Wo = tf.Variable(tf.random_normal([NHIDDEN,NOUT], stddev=STDEV, dtype=tf.float32))
bo = tf.Variable(tf.random_normal([1,NOUT], stddev=STDEV, dtype=tf.float32))
hidden_layer = tf.nn.tanh(tf.matmul(x, Wh) + bh)
output = tf.matmul(hidden_layer,Wo) + bo
def get_mixture_coef(output):
out_pi = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")
out_sigma = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")
out_mu = tf.placeholder(dtype=tf.float32, shape=[None,KMIX], name="mixparam")
out_pi, out_sigma, out_mu = tf.split(output,3,1)
max_pi = tf.reduce_max(out_pi, 1, keep_dims=True)
out_pi = tf.subtract(out_pi, max_pi)
out_pi = tf.exp(out_pi)
normalize_pi = tf.reciprocal(tf.reduce_sum(out_pi, 1, keep_dims=True))
out_pi = tf.multiply(normalize_pi, out_pi)
out_sigma = tf.exp(out_sigma)
return out_pi, out_sigma, out_mu
out_pi, out_sigma, out_mu = get_mixture_coef(output)
NSAMPLE = 2500
y_data = np.float32(np.random.uniform(-10.5, 10.5, (1, NSAMPLE))).T
r_data = np.float32(np.random.normal(size=(NSAMPLE,1))) # random noise
x_data = np.float32(np.sin(0.75*y_data)*7.0+y_data*0.5+r_data*1.0)
oneDivSqrtTwoPI = 1 / math.sqrt(2*math.pi) # normalisation factor for gaussian, not needed.
def tf_normal(y, mu, sigma):
result = tf.subtract(y, mu)
result = tf.multiply(result,tf.reciprocal(sigma))
result = -tf.square(result)/2
return tf.multiply(tf.exp(result),tf.reciprocal(sigma))*oneDivSqrtTwoPI
def get_lossfunc(out_pi, out_sigma, out_mu, y):
result = tf_normal(y, out_mu, out_sigma)
result = tf.multiply(result, out_pi)
result = tf.reduce_sum(result, 1, keep_dims=True)
result = -tf.log(result)
return tf.reduce_mean(result)
lossfunc = get_lossfunc(out_pi, out_sigma, out_mu, y)
train_op = tf.train.AdamOptimizer().minimize(lossfunc)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
NEPOCH = 10000
loss = np.zeros(NEPOCH) # store the training progress here.
for i in range(NEPOCH):
sess.run(train_op,feed_dict={x: x_data, y: y_data})
loss[i] = sess.run(lossfunc, feed_dict={x: x_data, y: y_data})
plt.figure(figsize=(8, 8))
plt.plot(np.arange(100, NEPOCH,1), loss[100:], 'r-')
plt.show()
x_test = np.float32(np.arange(-15,15,0.1))
NTEST = x_test.size
x_test = x_test.reshape(NTEST,1) # needs to be a matrix, not a vector
def get_pi_idx(x, pdf):
N = pdf.size
accumulate = 0
for i in range(0, N):
accumulate += pdf[i]
if (accumulate > x):
return i
print 'error with sampling ensemble'
return -1
def generate_ensemble(out_pi, out_mu, out_sigma, M = 10):
NTEST = x_test.size
result = np.random.rand(NTEST, M) # initially random [0, 1]
rn = np.random.randn(NTEST, M) # normal random matrix (0.0, 1.0)
mu = 0
std = 0
idx = 0
# transforms result into random ensembles
for j in range(0, M): # mixtures
for i in range(0, NTEST): # datapoints
idx = get_pi_idx(result[i, j], out_pi[i])
mu = out_mu[i, idx]
std = out_sigma[i, idx]
result[i, j] = mu + rn[i, j]*std
return result
out_pi_test, out_sigma_test, out_mu_test = sess.run(get_mixture_coef(output), feed_dict={x: x_test})
y_test = generate_ensemble(out_pi_test, out_mu_test, out_sigma_test)
plt.figure(figsize=(8, 8))
plt.plot(x_data,y_data,'ro', x_test,y_test,'bo',alpha=0.3)
plt.show()
#####========================================================================
# actual_offset = tf.slice(So,[0,0],[batch_size,2])
# actual_pen = tf.squeeze(tf.slice(So,[0,2],[batch_size,-1]))
# pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_multiplier)
# pred_pen = tf.squeeze(tf.slice(output,[0,2],[batch_size,-1]))
# offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
# pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
# labels = actual_pen,
# logits = pred_pen))
# loss = tf.add(tf.multiply(offset_weight,offset_loss),tf.multiply(1-offset_weight,pen_loss))
# # run backprop
# optimizer = tf.train.AdamOptimizer(learning_rate)
# train_op = optimizer.minimize(loss)
# # saver
# save = False
# saver = tf.train.Saver()
# # get predicted stroke vector
# strokes = tf.concat([pred_offset, tf.expand_dims(tf.round(tf.sigmoid(pred_pen_)+1),1)],axis=1)
# Strokes = []
# # run batches
# with tf.Session() as sess:
# tf.global_variables_initializer().run()
# for m,idx in get_minibatches(S_train.as_matrix().astype('float32')[:len(S_train)-1],batch_size,shuffle=True):
# Si_batch = m # batch of current strokes
# if (max(idx)<45040):
# So_batch = S_train.iloc[idx+1].as_matrix().astype('float32')
# updates = sess.run([offset_loss, pen_loss, loss, pred_offset, actual_pen, pred_pen, strokes], feed_dict={Si:Si_batch,So:So_batch})
# offset_loss_ = updates[0]
# pen_loss_ = updates[1]
# loss_ = updates[2]
# pred_offset_ = updates[3]
# actual_pen_ = updates[4]
# pred_pen_ = updates[5]
# strokes_ = updates[6]
# if epoch_num%200==0:
# print "Epoch: " + str(epoch_num) + " | Loss: " + str(loss_) + \
# " | Offset loss: " + str(offset_loss_) + " | Pen loss: " + str(pen_loss_)
# # save
# if save:
# saver.save(sess, 'checkpoints/pix2svg_train_svg2svg_0')
# # increment epoch number
# epoch_num += 1
```
### run rnn version
```
# RANDOM_SEED = 42
# tf.set_random_seed(RANDOM_SEED)
# # reset entire graph
# tf.reset_default_graph()
# # weight on offset loss
# offset_weight = 1000.
# # learning rate
# learning_rate = 0.01
# # set batch size
# batch_size = 10
# # epoch counter
# epoch_num = 0
# # max strokes
# max_strokes = 200
# # initialize variables
# F = tf.placeholder("float", shape=[None, 2048]) # features (input)
# S = tf.placeholder("float", shape=[None, 3]) # strokes (output)
# # layer sizes
# x_size = F.shape[1] # Number of input nodes: 2048 features and 1 bias
# h_size = 512 # Number of hidden nodes
# y_size = S.shape[1] # Number of outcomes (x,y,pen)
# # rnn hyperparameters
# rnn_hidden_size = 512 # number of rnn hidden units
# output = tf.placeholder("float", shape=[None,y_size])
# # convert to tensorflow tensor
# F = tf.cast(tf.stack(F,name='F'),tf.float32)
# S = tf.cast(tf.stack(S,name='S'),tf.float32)
# # Weight initializations
# W1 = tf.get_variable('W1', [x_size, h_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
# b1 = tf.get_variable('b1', [h_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# W2 = tf.get_variable('W2', [h_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
# b2 = tf.get_variable('b2', [y_size],initializer=tf.zeros_initializer(), dtype=tf.float32)
# # forward propagation
# # Run RNN and run linear layer to fit to correct size.
# rnn_input = tf.nn.xw_plus_b(F, W1, b1,name='rnn_input')
# cell = tf.contrib.rnn.BasicLSTMCell(rnn_hidden_size)
# starting_state = cell.zero_state(batch_size=batch_size, dtype=tf.float32)
# outputs, final_rnn_state = tf.contrib.rnn.static_rnn(cell,
# [rnn_input]*max_strokes,
# initial_state=starting_state,
# dtype=tf.float32)
# W_hy = tf.get_variable('W_hy', [rnn_hidden_size, y_size],initializer=tf.contrib.layers.xavier_initializer(), dtype=tf.float32)
# preds = []
# for output in outputs:
# preds.append(tf.matmul(outputs, W_hy))
# # output = tf.nn.xw_plus_b(fc1, W2, b2,name='output')
# # actual_offset = tf.slice(S,[0,0],[batch_size,2])
# # actual_pen = tf.slice(S,[0,2],[batch_size,-1])
# # pred_offset = tf.multiply(tf.slice(output,[0,0],[batch_size,2]),offset_weight)
# # pred_pen = tf.nn.softmax(tf.slice(output,[0,2],[batch_size,-1]))
# # offset_loss = tf.reduce_sum(tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(pred_offset,actual_offset)),axis=1)))
# # pen_loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
# # labels = actual_pen,
# # logits = pred_pen))
# # loss = tf.add(offset_loss,pen_loss)
# # # run backprop
# # optimizer = tf.train.AdamOptimizer(learning_rate)
# # train_op = optimizer.minimize(loss)
# # saver
# save = False
# saver = tf.train.Saver()
# # # get predicted stroke vector
# # strokes = tf.concat([pred_offset, pred_pen],axis=1)
# # run batches
# with tf.Session() as sess:
# tf.global_variables_initializer().run()
# for m in get_minibatches([F_train,S_train.as_matrix()],batch_size,shuffle=True):
# if m[0].shape[0]==batch_size:
# F_batch = m[0]
# S_batch = m[1]
# updates = sess.run([preds], feed_dict={F:F_batch,S:S_batch})
# preds_ = updates[0]
# if epoch_num%200==0:
# print "Epoch: " + str(epoch_num)
# # save
# if save:
# saver.save(sess, 'checkpoints/pix2svg_train_rnn_0')
# # increment epoch number
# epoch_num += 1
# for epoch in range(50):
# # Train with each examplea
# for i in range(len(F_batch)):
# sess.run(updates, feed_dict={X: F_batch[i: i + 1], y: S_batch[i: i + 1]})
# loss = sess.run(output, feed_dict={X: F_batch, y: S_batch})
fig = plt.figure()
im = plt.matshow(np.corrcoef(F_batch_array),vmin=0.5)
plt.show()
sess.close()
# get minibatch
batch_size = 1500
F_batch = F_train[:batch_size,:]
S_batch = S_train.head(n=batch_size)
# reserve numpy version
F_batch_array = F_batch
S_batch_array = S_batch.as_matrix()
plt.matshow(np.corrcoef(F_batch_array))
plt.show()
SF_ = SF[100:110,:]
plt.matshow(np.corrcoef(SF_))
plt.show()
PF_ = PF[:batch_size,:]
plt.matshow(np.corrcoef(PF_))
plt.show()
```
|
github_jupyter
|
# Project 3: Implement SLAM
---
## Project Overview
In this project, you'll implement SLAM for robot that moves and senses in a 2 dimensional, grid world!
SLAM gives us a way to both localize a robot and build up a map of its environment as a robot moves and senses in real-time. This is an active area of research in the fields of robotics and autonomous systems. Since this localization and map-building relies on the visual sensing of landmarks, this is a computer vision problem.
Using what you've learned about robot motion, representations of uncertainty in motion and sensing, and localization techniques, you will be tasked with defining a function, `slam`, which takes in six parameters as input and returns the vector `mu`.
> `mu` contains the (x,y) coordinate locations of the robot as it moves, and the positions of landmarks that it senses in the world
You can implement helper functions as you see fit, but your function must return `mu`. The vector, `mu`, should have (x, y) coordinates interlaced, for example, if there were 2 poses and 2 landmarks, `mu` will look like the following, where `P` is the robot position and `L` the landmark position:
```
mu = matrix([[Px0],
[Py0],
[Px1],
[Py1],
[Lx0],
[Ly0],
[Lx1],
[Ly1]])
```
You can see that `mu` holds the poses first `(x0, y0), (x1, y1), ...,` then the landmark locations at the end of the matrix; we consider a `nx1` matrix to be a vector.
## Generating an environment
In a real SLAM problem, you may be given a map that contains information about landmark locations, and in this example, we will make our own data using the `make_data` function, which generates a world grid with landmarks in it and then generates data by placing a robot in that world and moving and sensing over some numer of time steps. The `make_data` function relies on a correct implementation of robot move/sense functions, which, at this point, should be complete and in the `robot_class.py` file. The data is collected as an instantiated robot moves and senses in a world. Your SLAM function will take in this data as input. So, let's first create this data and explore how it represents the movement and sensor measurements that our robot takes.
---
## Create the world
Use the code below to generate a world of a specified size with randomly generated landmark locations. You can change these parameters and see how your implementation of SLAM responds!
`data` holds the sensors measurements and motion of your robot over time. It stores the measurements as `data[i][0]` and the motion as `data[i][1]`.
#### Helper functions
You will be working with the `robot` class that may look familiar from the first notebook,
In fact, in the `helpers.py` file, you can read the details of how data is made with the `make_data` function. It should look very similar to the robot move/sense cycle you've seen in the first notebook.
```
import numpy as np
from helpers import make_data
# your implementation of slam should work with the following inputs
# feel free to change these input values and see how it responds!
# world parameters
num_landmarks = 5 # number of landmarks
N = 20 # time steps
world_size = 100.0 # size of world (square)
# robot parameters
measurement_range = 50.0 # range at which we can sense landmarks
motion_noise = 2.0 # noise in robot motion
measurement_noise = 2.0 # noise in the measurements
distance = 20.0 # distance by which robot (intends to) move each iteratation
# make_data instantiates a robot, AND generates random landmarks for a given world size and number of landmarks
data = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
```
### A note on `make_data`
The function above, `make_data`, takes in so many world and robot motion/sensor parameters because it is responsible for:
1. Instantiating a robot (using the robot class)
2. Creating a grid world with landmarks in it
**This function also prints out the true location of landmarks and the *final* robot location, which you should refer back to when you test your implementation of SLAM.**
The `data` this returns is an array that holds information about **robot sensor measurements** and **robot motion** `(dx, dy)` that is collected over a number of time steps, `N`. You will have to use *only* these readings about motion and measurements to track a robot over time and find the determine the location of the landmarks using SLAM. We only print out the true landmark locations for comparison, later.
In `data` the measurement and motion data can be accessed from the first and second index in the columns of the data array. See the following code for an example, where `i` is the time step:
```
measurement = data[i][0]
motion = data[i][1]
```
```
# print out some stats about the data
time_step = 0
print('Example measurements: \n', data[time_step][0])
print('\n')
print('Example motion: \n', data[time_step][1])
```
Try changing the value of `time_step`, you should see that the list of measurements varies based on what in the world the robot sees after it moves. As you know from the first notebook, the robot can only sense so far and with a certain amount of accuracy in the measure of distance between its location and the location of landmarks. The motion of the robot always is a vector with two values: one for x and one for y displacement. This structure will be useful to keep in mind as you traverse this data in your implementation of slam.
## Initialize Constraints
One of the most challenging tasks here will be to create and modify the constraint matrix and vector: omega and xi. In the second notebook, you saw an example of how omega and xi could hold all the values the define the relationships between robot poses `xi` and landmark positions `Li` in a 1D world, as seen below, where omega is the blue matrix and xi is the pink vector.
<img src='images/motion_constraint.png' width=50% height=50% />
In *this* project, you are tasked with implementing constraints for a 2D world. We are referring to robot poses as `Px, Py` and landmark positions as `Lx, Ly`, and one way to approach this challenge is to add *both* x and y locations in the constraint matrices.
<img src='images/constraints2D.png' width=50% height=50% />
You may also choose to create two of each omega and xi (one for x and one for y positions).
### TODO: Write a function that initializes omega and xi
Complete the function `initialize_constraints` so that it returns `omega` and `xi` constraints for the starting position of the robot. Any values that we do not yet know should be initialized with the value `0`. You may assume that our robot starts out in exactly the middle of the world with 100% confidence (no motion or measurement noise at this point). The inputs `N` time steps, `num_landmarks`, and `world_size` should give you all the information you need to construct intial constraints of the correct size and starting values.
*Depending on your approach you may choose to return one omega and one xi that hold all (x,y) positions *or* two of each (one for x values and one for y); choose whichever makes most sense to you!*
```
def initialize_constraints(N, num_landmarks, world_size):
''' This function takes in a number of time steps N, number of landmarks, and a world_size,
and returns initialized constraint matrices, omega and xi.'''
## Recommended: Define and store the size (rows/cols) of the constraint matrix in a variable
num_poses = N
rows = (num_poses * 2) + (num_landmarks * 2)
cols = (num_poses * 2) + (num_landmarks * 2)
initial_x = world_size/2
initial_y = world_size/2
Px_initial = 0
Py_initial = 1
## TODO: Define the constraint matrix, Omega, with two initial "strength" values
## for the initial x, y location of our robot
# omega = [0]
omega = np.zeros(shape=(rows,cols))
omega[Px_initial][Px_initial] = 1
omega[Py_initial][Py_initial] = 1
## TODO: Define the constraint *vector*, xi
## you can assume that the robot starts out in the middle of the world with 100% confidence
# xi = [0]
xi = np.zeros(shape=(cols,1))
xi[Px_initial] = initial_x
xi[Py_initial] = initial_y
return omega, xi
```
### Test as you go
It's good practice to test out your code, as you go. Since `slam` relies on creating and updating constraint matrices, `omega` and `xi` to account for robot sensor measurements and motion, let's check that they initialize as expected for any given parameters.
Below, you'll find some test code that allows you to visualize the results of your function `initialize_constraints`. We are using the [seaborn](https://seaborn.pydata.org/) library for visualization.
**Please change the test values of N, landmarks, and world_size and see the results**. Be careful not to use these values as input into your final smal function.
This code assumes that you have created one of each constraint: `omega` and `xi`, but you can change and add to this code, accordingly. The constraints should vary in size with the number of time steps and landmarks as these values affect the number of poses a robot will take `(Px0,Py0,...Pxn,Pyn)` and landmark locations `(Lx0,Ly0,...Lxn,Lyn)` whose relationships should be tracked in the constraint matrices. Recall that `omega` holds the weights of each variable and `xi` holds the value of the sum of these variables, as seen in Notebook 2. You'll need the `world_size` to determine the starting pose of the robot in the world and fill in the initial values for `xi`.
```
# import data viz resources
import matplotlib.pyplot as plt
from pandas import DataFrame
import seaborn as sns
%matplotlib inline
# define a small N and world_size (small for ease of visualization)
N_test = 5
num_landmarks_test = 2
small_world = 10
# initialize the constraints
initial_omega, initial_xi = initialize_constraints(N_test, num_landmarks_test, small_world)
# define figure size
plt.rcParams["figure.figsize"] = (10,7)
# display omega
sns.heatmap(DataFrame(initial_omega), cmap='Blues', annot=True, linewidths=.5)
# define figure size
plt.rcParams["figure.figsize"] = (1,7)
# display xi
sns.heatmap(DataFrame(initial_xi), cmap='Oranges', annot=True, linewidths=.5)
```
---
## SLAM inputs
In addition to `data`, your slam function will also take in:
* N - The number of time steps that a robot will be moving and sensing
* num_landmarks - The number of landmarks in the world
* world_size - The size (w/h) of your world
* motion_noise - The noise associated with motion; the update confidence for motion should be `1.0/motion_noise`
* measurement_noise - The noise associated with measurement/sensing; the update weight for measurement should be `1.0/measurement_noise`
#### A note on noise
Recall that `omega` holds the relative "strengths" or weights for each position variable, and you can update these weights by accessing the correct index in omega `omega[row][col]` and *adding/subtracting* `1.0/noise` where `noise` is measurement or motion noise. `Xi` holds actual position values, and so to update `xi` you'll do a similar addition process only using the actual value of a motion or measurement. So for a vector index `xi[row][0]` you will end up adding/subtracting one measurement or motion divided by their respective `noise`.
### TODO: Implement Graph SLAM
Follow the TODO's below to help you complete this slam implementation (these TODO's are in the recommended order), then test out your implementation!
#### Updating with motion and measurements
With a 2D omega and xi structure as shown above (in earlier cells), you'll have to be mindful about how you update the values in these constraint matrices to account for motion and measurement constraints in the x and y directions. Recall that the solution to these matrices (which holds all values for robot poses `P` and landmark locations `L`) is the vector, `mu`, which can be computed at the end of the construction of omega and xi as the inverse of omega times xi: $\mu = \Omega^{-1}\xi$
**You may also choose to return the values of `omega` and `xi` if you want to visualize their final state!**
```
## TODO: Complete the code to implement SLAM
## slam takes in 6 arguments and returns mu,
## mu is the entire path traversed by a robot (all x,y poses) *and* all landmarks locations
def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise):
omega, xi = initialize_constraints(N, num_landmarks, world_size)
# Iterate through each time step in the data
for time_step in range(N-1):
# Retrieve all the motion and measurement data for this time_step
measurement = data[time_step][0]
motion = data[time_step][1]
dx = motion[0] # distance to be moved along x in this time_step
dy = motion[1] # distance to be moved along y in this time_step
'''Consider that the robot moves from (x0,y0) to (x1,y1) in this time_step'''
# even-numbered columns of omega correspond to x values
x0 = (time_step * 2) # x0 = 0,2,4,...
x1 = x0 + 2 # x0 = 2,4,6,...
# odd-numbered columns of omega correspond to y values
y0 = x0 + 1 # y0 = 1,3,5,...
y1 = y0 + 2 # y1 = 3,5,7,...
# Update omega and xi to account for all measurements
# Measurement noise taken into account
for landmark in measurement:
lm = landmark[0] # landmark id
dx_lm = landmark[1] # separation along x from current position
dy_lm = landmark[2] # separation along y from current position
Lx0 = (N * 2) + (lm * 2) # even-numbered columns have x values of landmarks
Ly0 = Lx0 + 1 # odd-numbered columns have y values of landmarks
# update omega values corresponding to measurement between x0 and Lx0
omega[ x0 ][ x0 ] += 1.0/measurement_noise
omega[ Lx0 ][ Lx0 ] += 1.0/measurement_noise
omega[ x0 ][ Lx0 ] += -1.0/measurement_noise
omega[ Lx0 ][ x0 ] += -1.0/measurement_noise
# update omega values corresponding to measurement between y0 and Ly0
omega[ y0 ][ y0 ] += 1.0/measurement_noise
omega[ Ly0 ][ Ly0 ] += 1.0/measurement_noise
omega[ y0 ][ Ly0 ] += -1.0/measurement_noise
omega[ Ly0 ][ y0 ] += -1.0/measurement_noise
# update xi values corresponding to measurement between x0 and Lx0
xi[x0] -= dx_lm/measurement_noise
xi[Lx0] += dx_lm/measurement_noise
# update xi values corresponding to measurement between y0 and Ly0
xi[y0] -= dy_lm/measurement_noise
xi[Ly0] += dy_lm/measurement_noise
# Update omega and xi to account for motion from (x0,y0) to (x1,y1)
# Motion noise taken into account
omega[x0][x0] += 1.0/motion_noise
omega[x1][x1] += 1.0/motion_noise
omega[x0][x1] += -1.0/motion_noise
omega[x1][x0] += -1.0/motion_noise
omega[y0][y0] += 1.0/motion_noise
omega[y1][y1] += 1.0/motion_noise
omega[y0][y1] += -1.0/motion_noise
omega[y1][y0] += -1.0/motion_noise
xi[x0] -= dx/motion_noise
xi[y0] -= dy/motion_noise
xi[x1] += dx/motion_noise
xi[y1] += dy/motion_noise
# Compute the best estimate of poses and landmark positions
# using the formula, omega_inverse * xi
omega_inv = np.linalg.inv(np.matrix(omega))
mu = omega_inv*xi
return mu # return `mu`
```
## Helper functions
To check that your implementation of SLAM works for various inputs, we have provided two helper functions that will help display the estimated pose and landmark locations that your function has produced. First, given a result `mu` and number of time steps, `N`, we define a function that extracts the poses and landmarks locations and returns those as their own, separate lists.
Then, we define a function that nicely print out these lists; both of these we will call, in the next step.
```
# a helper function that creates a list of poses and of landmarks for ease of printing
# this only works for the suggested constraint architecture of interlaced x,y poses
def get_poses_landmarks(mu, N):
# create a list of poses
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# create a list of landmarks
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# return completed lists
return poses, landmarks
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
```
## Run SLAM
Once you've completed your implementation of `slam`, see what `mu` it returns for different world sizes and different landmarks!
### What to Expect
The `data` that is generated is random, but you did specify the number, `N`, or time steps that the robot was expected to move and the `num_landmarks` in the world (which your implementation of `slam` should see and estimate a position for. Your robot should also start with an estimated pose in the very center of your square world, whose size is defined by `world_size`.
With these values in mind, you should expect to see a result that displays two lists:
1. **Estimated poses**, a list of (x, y) pairs that is exactly `N` in length since this is how many motions your robot has taken. The very first pose should be the center of your world, i.e. `[50.000, 50.000]` for a world that is 100.0 in square size.
2. **Estimated landmarks**, a list of landmark positions (x, y) that is exactly `num_landmarks` in length.
#### Landmark Locations
If you refer back to the printout of *exact* landmark locations when this data was created, you should see values that are very similar to those coordinates, but not quite (since `slam` must account for noise in motion and measurement).
```
# call your implementation of slam, passing in the necessary parameters
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# print out the resulting landmarks and poses
if(mu is not None):
# get the lists of poses and landmarks
# and print them out
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)
```
## Visualize the constructed world
Finally, using the `display_world` code from the `helpers.py` file (which was also used in the first notebook), we can actually visualize what you have coded with `slam`: the final position of the robot and the positon of landmarks, created from only motion and measurement data!
**Note that these should be very similar to the printed *true* landmark locations and final pose from our call to `make_data` early in this notebook.**
```
# import the helper function
from helpers import display_world
# Display the final world!
# define figure size
plt.rcParams["figure.figsize"] = (20,20)
# check if poses has been created
if 'poses' in locals():
# print out the last pose
print('Last pose: ', poses[-1])
# display the last position of the robot *and* the landmark positions
display_world(int(world_size), poses[-1], landmarks)
```
### Question: How far away is your final pose (as estimated by `slam`) compared to the *true* final pose? Why do you think these poses are different?
You can find the true value of the final pose in one of the first cells where `make_data` was called. You may also want to look at the true landmark locations and compare them to those that were estimated by `slam`. Ask yourself: what do you think would happen if we moved and sensed more (increased N)? Or if we had lower/higher noise parameters.
**Answer**: (Write your answer here.)
## Testing
To confirm that your slam code works before submitting your project, it is suggested that you run it on some test data and cases. A few such cases have been provided for you, in the cells below. When you are ready, uncomment the test cases in the next cells (there are two test cases, total); your output should be **close-to or exactly** identical to the given results. If there are minor discrepancies it could be a matter of floating point accuracy or in the calculation of the inverse matrix.
### Submit your project
If you pass these tests, it is a good indication that your project will pass all the specifications in the project rubric. Follow the submission instructions to officially submit!
```
# Here is the data and estimated outputs for test case 1
test_data1 = [[[[1, 19.457599255548065, 23.8387362100849], [2, -13.195807561967236, 11.708840328458608], [3, -30.0954905279171, 15.387879242505843]], [-12.2607279422326, -15.801093326936487]], [[[2, -0.4659930049620491, 28.088559771215664], [4, -17.866382374890936, -16.384904503932]], [-12.2607279422326, -15.801093326936487]], [[[4, -6.202512900833806, -1.823403210274639]], [-12.2607279422326, -15.801093326936487]], [[[4, 7.412136480918645, 15.388585962142429]], [14.008259661173426, 14.274756084260822]], [[[4, -7.526138813444998, -0.4563942429717849]], [14.008259661173426, 14.274756084260822]], [[[2, -6.299793150150058, 29.047830407717623], [4, -21.93551130411791, -13.21956810989039]], [14.008259661173426, 14.274756084260822]], [[[1, 15.796300959032276, 30.65769689694247], [2, -18.64370821983482, 17.380022987031367]], [14.008259661173426, 14.274756084260822]], [[[1, 0.40311325410337906, 14.169429532679855], [2, -35.069349468466235, 2.4945558982439957]], [14.008259661173426, 14.274756084260822]], [[[1, -16.71340983241936, -2.777000269543834]], [-11.006096015782283, 16.699276945166858]], [[[1, -3.611096830835776, -17.954019226763958]], [-19.693482634035977, 3.488085684573048]], [[[1, 18.398273354362416, -22.705102332550947]], [-19.693482634035977, 3.488085684573048]], [[[2, 2.789312482883833, -39.73720193121324]], [12.849049222879723, -15.326510824972983]], [[[1, 21.26897046581808, -10.121029799040915], [2, -11.917698965880655, -23.17711662602097], [3, -31.81167947898398, -16.7985673023331]], [12.849049222879723, -15.326510824972983]], [[[1, 10.48157743234859, 5.692957082575485], [2, -22.31488473554935, -5.389184118551409], [3, -40.81803984305378, -2.4703329790238118]], [12.849049222879723, -15.326510824972983]], [[[0, 10.591050242096598, -39.2051798967113], [1, -3.5675572049297553, 22.849456408289125], [2, -38.39251065320351, 7.288990306029511]], [12.849049222879723, -15.326510824972983]], [[[0, -3.6225556479370766, -25.58006865235512]], [-7.8874682868419965, -18.379005523261092]], [[[0, 1.9784503557879374, -6.5025974151499]], [-7.8874682868419965, -18.379005523261092]], [[[0, 10.050665232782423, 11.026385307998742]], [-17.82919359778298, 9.062000642947142]], [[[0, 26.526838150174818, -0.22563393232425621], [4, -33.70303936886652, 2.880339841013677]], [-17.82919359778298, 9.062000642947142]]]
## Test Case 1
##
# Estimated Pose(s):
# [50.000, 50.000]
# [37.858, 33.921]
# [25.905, 18.268]
# [13.524, 2.224]
# [27.912, 16.886]
# [42.250, 30.994]
# [55.992, 44.886]
# [70.749, 59.867]
# [85.371, 75.230]
# [73.831, 92.354]
# [53.406, 96.465]
# [34.370, 100.134]
# [48.346, 83.952]
# [60.494, 68.338]
# [73.648, 53.082]
# [86.733, 38.197]
# [79.983, 20.324]
# [72.515, 2.837]
# [54.993, 13.221]
# [37.164, 22.283]
# Estimated Landmarks:
# [82.679, 13.435]
# [70.417, 74.203]
# [36.688, 61.431]
# [18.705, 66.136]
# [20.437, 16.983]
### Uncomment the following three lines for test case 1 and compare the output to the values above ###
mu_1 = slam(test_data1, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_1, 20)
print_all(poses, landmarks)
# Here is the data and estimated outputs for test case 2
test_data2 = [[[[0, 26.543274387283322, -6.262538160312672], [3, 9.937396825799755, -9.128540360867689]], [18.92765331253674, -6.460955043986683]], [[[0, 7.706544739722961, -3.758467215445748], [1, 17.03954411948937, 31.705489938553438], [3, -11.61731288777497, -6.64964096716416]], [18.92765331253674, -6.460955043986683]], [[[0, -12.35130507136378, 2.585119104239249], [1, -2.563534536165313, 38.22159657838369], [3, -26.961236804740935, -0.4802312626141525]], [-11.167066095509824, 16.592065417497455]], [[[0, 1.4138633151721272, -13.912454837810632], [1, 8.087721200818589, 20.51845934354381], [3, -17.091723454402302, -16.521500551709707], [4, -7.414211721400232, 38.09191602674439]], [-11.167066095509824, 16.592065417497455]], [[[0, 12.886743222179561, -28.703968411636318], [1, 21.660953298391387, 3.4912891084614914], [3, -6.401401414569506, -32.321583037341625], [4, 5.034079343639034, 23.102207946092893]], [-11.167066095509824, 16.592065417497455]], [[[1, 31.126317672358578, -10.036784369535214], [2, -38.70878528420893, 7.4987265861424595], [4, 17.977218575473767, 6.150889254289742]], [-6.595520680493778, -18.88118393939265]], [[[1, 41.82460922922086, 7.847527392202475], [3, 15.711709540417502, -30.34633659912818]], [-6.595520680493778, -18.88118393939265]], [[[0, 40.18454208294434, -6.710999804403755], [3, 23.019508919299156, -10.12110867290604]], [-6.595520680493778, -18.88118393939265]], [[[3, 27.18579315312821, 8.067219022708391]], [-6.595520680493778, -18.88118393939265]], [[], [11.492663265706092, 16.36822198838621]], [[[3, 24.57154567653098, 13.461499960708197]], [11.492663265706092, 16.36822198838621]], [[[0, 31.61945290413707, 0.4272295085799329], [3, 16.97392299158991, -5.274596836133088]], [11.492663265706092, 16.36822198838621]], [[[0, 22.407381798735177, -18.03500068379259], [1, 29.642444125196995, 17.3794951934614], [3, 4.7969752441371645, -21.07505361639969], [4, 14.726069092569372, 32.75999422300078]], [11.492663265706092, 16.36822198838621]], [[[0, 10.705527984670137, -34.589764174299596], [1, 18.58772336795603, -0.20109708164787765], [3, -4.839806195049413, -39.92208742305105], [4, 4.18824810165454, 14.146847823548889]], [11.492663265706092, 16.36822198838621]], [[[1, 5.878492140223764, -19.955352450942357], [4, -7.059505455306587, -0.9740849280550585]], [19.628527845173146, 3.83678180657467]], [[[1, -11.150789592446378, -22.736641053247872], [4, -28.832815721158255, -3.9462962046291388]], [-19.841703647091965, 2.5113335861604362]], [[[1, 8.64427397916182, -20.286336970889053], [4, -5.036917727942285, -6.311739993868336]], [-5.946642674882207, -19.09548221169787]], [[[0, 7.151866679283043, -39.56103232616369], [1, 16.01535401373368, -3.780995345194027], [4, -3.04801331832137, 13.697362774960865]], [-5.946642674882207, -19.09548221169787]], [[[0, 12.872879480504395, -19.707592098123207], [1, 22.236710716903136, 16.331770792606406], [3, -4.841206109583004, -21.24604435851242], [4, 4.27111163223552, 32.25309748614184]], [-5.946642674882207, -19.09548221169787]]]
## Test Case 2
##
# Estimated Pose(s):
# [50.000, 50.000]
# [69.035, 45.061]
# [87.655, 38.971]
# [76.084, 55.541]
# [64.283, 71.684]
# [52.396, 87.887]
# [44.674, 68.948]
# [37.532, 49.680]
# [31.392, 30.893]
# [24.796, 12.012]
# [33.641, 26.440]
# [43.858, 43.560]
# [54.735, 60.659]
# [65.884, 77.791]
# [77.413, 94.554]
# [96.740, 98.020]
# [76.149, 99.586]
# [70.211, 80.580]
# [64.130, 61.270]
# [58.183, 42.175]
# Estimated Landmarks:
# [76.777, 42.415]
# [85.109, 76.850]
# [13.687, 95.386]
# [59.488, 39.149]
# [69.283, 93.654]
### Uncomment the following three lines for test case 2 and compare to the values above ###
mu_2 = slam(test_data2, 20, 5, 100.0, 2.0, 2.0)
poses, landmarks = get_poses_landmarks(mu_2, 20)
print_all(poses, landmarks)
```
|
github_jupyter
|
# Apply CNN Classifier to DESI Spectra and visualize results with gradCAM
Mini-SV2 tiles from February-March 2020:
- https://desi.lbl.gov/trac/wiki/TargetSelectionWG/miniSV2
See also the DESI tile picker with (limited) SV0 tiles from March 2020:
- https://desi.lbl.gov/svn/data/tiles/trunk/
- https://desi.lbl.gov/svn/data/tiles/trunk/SV0.html
```
import sys
sys.path.append('/global/homes/p/palmese/desi/timedomain/desitrip/py/') #Note:change this path as needed!
sys.path.append('/global/homes/p/palmese/desi/timedomain/timedomain/')
from desispec.io import read_spectra, write_spectra
from desispec.spectra import Spectra
from desispec.coaddition import coadd_cameras
from desitarget.cmx.cmx_targetmask import cmx_mask
from desitrip.preproc import rebin_flux, rescale_flux
from desitrip.deltamag import delta_mag
from astropy.io import fits
from astropy.table import Table, vstack, hstack
from glob import glob
from datetime import date
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from tensorflow import keras
mpl.rc('font', size=14)
# Set up BGS target bit selection.
cmx_bgs_bits = '|'.join([_ for _ in cmx_mask.names() if 'BGS' in _])
```
## Select a Date & Tile from matches files
```
matches_filename='matches_DECam.npy'
file_arr=np.load('matches_DECam.npy', allow_pickle=True)
obsdates = file_arr[:,0]
tile_ids = file_arr[:,1]
petal_ids = file_arr[:,2]
target_ids = file_arr[:,3]
tamuids = file_arr[:,6]
# Access redux folder.
zbfiles = []
cafiles = []
redux='/global/project/projectdirs/desi/spectro/redux/daily/tiles'
for tile_id, obsdate, petal_id, targetid in zip(tile_ids[:], obsdates[:], petal_ids[:], target_ids[:]):
tile_id = int(tile_id)
if obsdate < 20210301:
print('Skipping files')
continue
elif obsdate < 20210503:
prefix_in ='/'.join([redux, str(tile_id), str(obsdate)])
else:
prefix_in = '/'.join([redux, 'cumulative', str(tile_id),str(obsdate)])
#print(prefix_in)
if not os.path.isdir(prefix_in):
print('{} does not exist.'.format(prefix_in))
continue
# List zbest and coadd files.
# Data are stored by petal ID.
if obsdate < 20210503:
fileend = '-'.join((str(petal_id), str(tile_id), str(obsdate)))
cafile=sorted(glob('{}/coadd-'.format(prefix_in) + fileend + '*.fits'))
else:
fileend = '-'.join((str(petal_id), str(tile_id)))
cafile=sorted(glob('{}/spectra-'.format(prefix_in) + fileend + '*.fits'))
#print(fileend)
zbfile=sorted(glob('{}/zbest-'.format(prefix_in) + fileend + '*.fits'))
zbfiles.extend(zbfile)
cafiles.extend(cafile)
print(len(zbfiles))
print(len(cafiles))
print(len(tile_ids))
print(len(obsdates))
print(len(petal_ids))
```
## Load the Keras Model
Load a model trained on real or simulated data using the native Keras output format. In the future this could be updated to just load the Keras weights.
```
tfmodel = '/global/homes/l/lehsani/timedomain/desitrip/docs/nb/models_9label_first/6_b65_e200_9label/b65_e200_9label_model'
#tfmodel = '/global/homes/s/sybenzvi/desi/timedomain/desitrip/docs/nb/6label_cnn_restframe'
if os.path.exists(tfmodel):
classifier = keras.models.load_model(tfmodel)
else:
classifier = None
print('Sorry, could not find {}'.format(tfmodel))
if classifier is not None:
classifier.summary()
```
## Loop Through Spectra and Classify
```
# Loop through zbest and coadd files for each petal.
# Extract the fibermaps, ZBEST tables, and spectra.
# Keep only BGS targets passing basic event selection.
allzbest = None
allfmap = None
allwave = None
allflux = None
allivar = None
allmask = None
allres = None
handy_table = []
color_string = 'brz'
count = 0
for cafile, zbfile, targetid, obsdate in zip(cafiles, zbfiles, target_ids, obsdates): # rows[:-1] IS TEMPORARY
# Access data per petal.
print("Accessing file number ",count)
print(cafile,zbfile)
zbest = Table.read(zbfile, 'ZBEST')
idx_zbest = (zbest['TARGETID']==targetid)
targetids = zbest[idx_zbest]['TARGETID']
chi2 = zbest[idx_zbest]['CHI2']
pspectra = read_spectra(cafile)
if obsdate>20210503:
select_nite = pspectra.fibermap['NIGHT'] == obsdate
pspectra = pspectra[select_nite]
cspectra = coadd_cameras(pspectra)
fibermap = cspectra.fibermap
idx_fibermap = (fibermap['TARGETID'] == targetid)
ra = fibermap[idx_fibermap]['TARGET_RA'][0]
dec = fibermap[idx_fibermap]['TARGET_DEC'][0]
handy_table.append((targetid, tamuids[count], ra, dec, tile_ids[count], obsdate))
#print(pspectra.flux)S
# Apply standard event selection.
#isTGT = fibermap['OBJTYPE'] == 'TGT'
#isGAL = zbest['SPECTYPE'] == 'GALAXY'
#& isGAL #isTGT #& isBGS
#exp_id = fibermap['EXPID'] & select # first need to figure out all columns as this fails
#print(select)
count += 1
# Accumulate spectrum data.
if allzbest is None:
allzbest = zbest[idx_zbest]
allfmap = fibermap[idx_fibermap]
allwave = cspectra.wave[color_string]
allflux = cspectra.flux[color_string][idx_fibermap]
allivar = cspectra.ivar[color_string][idx_fibermap]
allmask = cspectra.mask[color_string][idx_fibermap]
allres = cspectra.resolution_data[color_string][idx_fibermap]
else:
allzbest = vstack([allzbest, zbest[idx_zbest]])
allfmap = vstack([allfmap, fibermap[idx_fibermap]])
allflux = np.vstack([allflux, cspectra.flux[color_string][idx_fibermap]])
allivar = np.vstack([allivar, cspectra.ivar[color_string][idx_fibermap]])
allmask = np.vstack([allmask, cspectra.mask[color_string][idx_fibermap]])
allres = np.vstack([allres, cspectra.resolution_data[color_string][idx_fibermap]])
# Apply the DESITRIP preprocessing to selected spectra.
rewave, reflux, reivar = rebin_flux(allwave, allflux, allivar, allzbest['Z'],
minwave=2500., maxwave=9500., nbins=150,
log=True, clip=True)
rsflux = rescale_flux(reflux)
# Run the classifier on the spectra.
# The output layer uses softmax activation to produce an array of label probabilities.
# The classification is based on argmax(pred).
pred = classifier.predict(rsflux)
allflux.shape
pred.shape
ymax = np.max(pred, axis=1)
#print(ymax)
#handy_table.pop(0)
print('targetid', '(ra, dec)', 'tileid', 'obsdate', 'row - prob', sep=", ")
for i in range(len(ymax)):
print(handy_table[i], "-", round(ymax[i],2)) #print(handy_table)
fig, ax = plt.subplots(1,1, figsize=(6,4), tight_layout=True)
ax.hist(ymax, bins=np.linspace(0,1,51))
ax.set(xlabel='$\max{(y_\mathrm{pred})}$',
ylabel='count');
#title='Tile {}, {}'.format(tile_id, obsdate));
```
### Selection on Classifier Output
To be conservative we can select only spectra where the classifier is very confident in its output, e.g., ymax > 0.99. See the [CNN training notebook](https://github.com/desihub/timedomain/blob/master/desitrip/docs/nb/cnn_multilabel-restframe.ipynb) for the motivation behind this cut.
```
idx = np.argwhere(ymax > 0.0) #0.99
labels = np.argmax(pred, axis=1)
idx.shape
label_names = ['Galaxy',
'SN Ia',
'SN Ib',
'SN Ib/c',
'SN Ic',
'SN IIn',
'SN IIL/P',
'SN IIP',
'KN']
```
### Save spectra and classification to file
```
# Save classification info to a table.
classification = Table()
classification['TARGETID'] = allfmap[idx]['TARGETID']
classification['CNNPRED'] = pred[idx]
classification['CNNLABEL'] = label_names_arr[labels[idx]]
# Merge the classification and redrock fit to the fibermap.
#Temporary fix for candidate mismatch
fmap = hstack([allfmap[idx], allzbest[idx], classification])
fmap['TARGETID_1'].name='TARGETID'
fmap.remove_columns(['TARGETID_2','TARGETID_3'])
# Pack data into Spectra and write to FITS.
cand_spectra = Spectra(bands=['brz'],
wave={'brz' : allwave},
flux={'brz' : allflux[idx]},
ivar={'brz' : allivar[idx]},
mask={'brz' : allmask[idx]},
resolution_data={'brz' : allres[idx]},
fibermap=fmap
)
outfits = 'DECam_transient_spectra.fits'
write_spectra(outfits, cand_spectra)
print('Output file saved in {}'.format(outfits))
```
### GradCAM action happens here
Adapting from https://keras.io/examples/vision/grad_cam/
```
import tensorflow as tf
last_conv_layer_name = "conv1d_23"
classifier_layer_names = [
"batch_normalization_23",
"activation_23",
"max_pooling1d_23",
"flatten_5",
"dense_5",
"dropout_5",
"Output_Classes"
]
def make_gradcam_heatmap(
img_array, model, last_conv_layer_name, classifier_layer_names
):
# First, we create a model that maps the input image to the activations
# of the last conv layer
last_conv_layer = model.get_layer(last_conv_layer_name)
last_conv_layer_model = keras.Model(model.inputs, last_conv_layer.output)
# Second, we create a model that maps the activations of the last conv
# layer to the final class predictions
classifier_input = keras.Input(shape=last_conv_layer.output.shape[1:])
x = classifier_input
for layer_name in classifier_layer_names:
#print(layer_name,x.shape)
x = model.get_layer(layer_name)(x)
classifier_model = keras.Model(classifier_input, x)
# Then, we compute the gradient of the top predicted class for our input image
# with respect to the activations of the last conv layer
with tf.GradientTape() as tape:
# Compute activations of the last conv layer and make the tape watch it
last_conv_layer_output = last_conv_layer_model(img_array)
tape.watch(last_conv_layer_output)
# Compute class predictions
preds = classifier_model(last_conv_layer_output)
top_pred_index = tf.argmax(preds[0])
top_class_channel = preds[:, top_pred_index]
# This is the gradient of the top predicted class with regard to
# the output feature map of the last conv layer
grads = tape.gradient(top_class_channel, last_conv_layer_output)
# This is a vector where each entry is the mean intensity of the gradient
# over a specific feature map channel
pooled_grads = tf.reduce_mean(grads, axis=(0, 1))
#print(grads.shape,pooled_grads.shape)
# We multiply each channel in the feature map array
# by "how important this channel is" with regard to the top predicted class
last_conv_layer_output = last_conv_layer_output.numpy()[0]
pooled_grads = pooled_grads.numpy()
for i in range(pooled_grads.shape[-1]):
last_conv_layer_output[:, i] *= pooled_grads[i]
# The channel-wise mean of the resulting feature map
# is our heatmap of class activation
heatmap = np.mean(last_conv_layer_output, axis=-1)
#We apply ReLU here and select only elements>0
# For visualization purpose, we will also normalize the heatmap between 0 & 1
heatmap = np.maximum(heatmap, 0) / np.max(heatmap)
return heatmap
```
### Apply GradCAM to all spectra classified as transients
```
#allzbest = allzbest[1:] #TEMP
#allzbest.pprint_all()
#print(labels.shape)
#print(labels)
#print(rewave.shape)
#print(rsflux.shape)
preprocess_input = keras.applications.xception.preprocess_input
decode_predictions = keras.applications.xception.decode_predictions
# Loop over all and create a bunch of 16x16 plots
fig, axes = plt.subplots(4,4, figsize=(15,10), sharex=True, sharey=True,
gridspec_kw={'wspace':0, 'hspace':0})
for j, ax in zip(selection[:16], axes.flatten()):
myarr=rsflux[j,:]
#print()
# Print what the top predicted class is
preds = classifier.predict(myarr)
#print("Predicted:", preds)
# Generate class activation heatmap
heatmap = make_gradcam_heatmap(
myarr, classifier, last_conv_layer_name, classifier_layer_names
)
color='blue'
rewave_nbin_inblock=rewave.shape[0]/float(heatmap.shape[0])
first_bin=0
for i in range(1,heatmap.shape[0]+1):
alpha=np.min([1,heatmap[i-1]+0.2])
last_bin=int(i*rewave_nbin_inblock)
if (i==1):
ax.plot(rewave[first_bin:last_bin+1], myarr[0,first_bin:last_bin+1],c=color,alpha=alpha,\
label = str(allzbest[j[0]]['TARGETID']) + "\n" +
label_names[labels[j[0]]] +
'\nz={:.2f}'.format(allzbest[j[0]]['Z']) +
'\ntype={}'.format(allzbest[j[0]]['SPECTYPE']) +
'\nprob={:.2f}'.format(ymax[j[0]]))
else:
ax.plot(rewave[first_bin:last_bin+1], myarr[0,first_bin:last_bin+1],c=color,alpha=alpha)
first_bin=last_bin
ax.legend(fontsize=10)
```
### Plot spectra of objects classified as transients
Plot observed spectra
```
testwave, testflux, testivar = rebin_flux(allwave, allflux, allivar,
minwave=2500., maxwave=9500., nbins=150,
log=True, clip=True)
fig, axes = plt.subplots(4,4, figsize=(15,10), sharex=True, sharey=True,
gridspec_kw={'wspace':0, 'hspace':0})
for j, ax in zip(selection, axes.flatten()):
ax.plot(testwave, testflux[j[0]], alpha=0.7, label='label: '+label_names[labels[j[0]]] +# Just this for single plot with [0] on testflux, label_names, allzbest
'\nz={:.2f}'.format(allzbest[j[0]]['Z'])) # +
#'\nobsdate={}'.format(obsdates[j[0]]) +
#'\ntile id: {}'.format(tile_ids[j[0]]) +
#'\npetal id: {}'.format(petal_ids[j[0]]))
ax.set(xlim=(3500,9900),ylim=(-0.1,4))
#ax.fill_between([5600,6000],[-0.1,-0.1],[4,4],alpha=0.1,color='blue')
#ax.fill_between([7400,7800],[-0.1,-0.1],[4,4],alpha=0.1,color='blue')
ax.legend(fontsize=10)
#for k in [0,1,2]:
# axes[k,0].set(ylabel=r'flux [erg s$^{-1}$ cm$^{-1}$ $\AA^{-1}$]')
# axes[2,k].set(xlabel=r'$\lambda_\mathrm{obs}$ [$\AA$]', xlim=(3500,9900))
fig.tight_layout();
#filename = "spectra_plots/all_spectra_TAMU_ylim"
#plt.savefig(filename)
```
### For plotting individual plots
```
# Save to FITS files rather than PNG, see cnn_classify_data.py
# See line 404 - 430, 'Save Classification info to file'
#https://github.com/desihub/timedomain/blob/ab7257a4ed232875f5769cbb11c21f483ceccc5e/cronjobs/cnn_classify_data.py#L404
for j in selection:
plt.plot(testwave, testflux[j[0]], alpha=0.7, label='label: '+ label_names[labels[j[0]]] + # Just this for single plot with [0] on testflux, label_names, allzbest
#'\nz={:.2f}'.format(allzbest[j[0]]['Z']) +
'\nprob={:.2f}'.format(ymax[j[0]]))
#'\nobsdate={}'.format(obsdates[j[0]]) +
#'\ntile id: {}'.format(tile_ids[j[0]]) +
#'\npetal id: {}'.format(petal_ids[j[0]]))
plt.xlim(3500, 9900)
#plt.ylim(-0.1, 50)
#ax.fill_between([5600,6000],[-0.1,-0.1],[4,4],alpha=0.1,color='blue')
#ax.fill_between([7400,7800],[-0.1,-0.1],[4,4],alpha=0.1,color='blue')
plt.legend(fontsize=10)
filename = "spectra_plots/"+"_".join(("TAMU", "spectra", str(allzbest[j[0]]['TARGETID']), str(obsdates[j[0]]), str(tile_ids[j[0]]), str(petal_ids[j[0]]), label_names[labels[j[0]]].replace(" ", "-").replace("/","-")))
#filename = "spectra_plots/"+"_".join(("TAMU", "spectra", str(obsdates[j[0]+1]), str(tile_ids[j[0]+1]), str(petal_ids[j[0]+1]), label_names[labels[j[0]]].replace(" ", "-"))) # temp
#plt.show();
#print(filename)
plt.savefig(filename)
plt.clf()
#for k in [0,1,2]:
# axes[k,0].set(ylabel=r'flux [erg s$^{-1}$ cm$^{-1}$ $\AA^{-1}$]')
# axes[2,k].set(xlabel=r'$\lambda_\mathrm{obs}$ [$\AA$]', xlim=(3500,9900))
#fig.tight_layout();
#filename = "spectra_plots/all_spectra_TAMU_ylim"
#filename = "_".join(("spectra", str(obsdate), str(tile_id), label_names[labels[0]].replace(" ", "-")))
#plt.savefig(filename)
```
### Reading files in parallel
Does not work
```
# Loop through zbest and coadd files for each petal.
# Extract the fibermaps, ZBEST tables, and spectra.
# Keep only BGS targets passing basic event selection.
allzbest = None
allfmap = None
allwave = None
allflux = None
allivar = None
allmask = None
allres = None
handy_table = []
from joblib import Parallel, delayed
njobs=40
color_string = 'brz'
def get_spectra(cafile, zbfile,targetid,tamuid,obsdate,tileid):
# Access data per petal.
print("Accessing file number ",count)
print(cafile,zbfile)
zbest = Table.read(zbfile, 'ZBEST')
idx_zbest = (zbest['TARGETID']==targetid)
targetids = zbest[idx_zbest]['TARGETID']
chi2 = zbest[idx_zbest]['CHI2']
pspectra = read_spectra(cafile)
if obsdate>20210503:
select_nite = pspectra.fibermap['NIGHT'] == obsdate
pspectra = pspectra[select_nite]
cspectra = coadd_cameras(pspectra)
fibermap = cspectra.fibermap
idx_fibermap = (fibermap['TARGETID'] == targetid)
ra = fibermap[idx_fibermap]['TARGET_RA'][0]
dec = fibermap[idx_fibermap]['TARGET_DEC'][0]
return allzbest,allfmap, allwave, allflux, allivar, allmask, allres
allzbest,allfmap, allwave, allflux, allivar, allmask, allres = \
Parallel(n_jobs=njobs)(delayed(get_spectra)(cafile, zbfile,targetid,tamuid,obsdate,tileid) \
for cafile, zbfile,targetid,tamuid,obsdate,tileid in zip(cafiles, zbfiles, target_ids,tamuids, obsdates,tile_ids))
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
import numpy as np, pandas as pd
import matplotlib.pyplot as plt, seaborn as sns
from tqdm import tqdm, tqdm_notebook
from pathlib import Path
# pd.set_option('display.max_columns', 1000)
# pd.set_option('display.max_rows', 400)
sns.set()
os.chdir('..')
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from project.ranker.ranker import RankingPredictor
%%time
rp = Pipeline([
('scale', StandardScaler()),
('estimator', RankingPredictor("ma_100", n_neighbors=15)),
])
df_mf, df_rank, df_scores, df_fold_scores = rp.named_steps['estimator'].get_data()
from sklearn.model_selection import train_test_split
X_train, _, y_train, _, y_scores_train, _ = train_test_split(df_mf.values,
df_rank.values,
df_scores.values,
test_size=0)
X_train.shape, y_train.shape
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
params = {'objective': 'lambdarank',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=10, random_state=42)
params = {'objective': 'lambdarank',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
from project.ranker.ltr_rankers import wide2long
X, y = wide2long(X_train, y_train)
X.shape, y.shape
from scipy.stats import rankdata
y_pred = np.array([rankdata(models[0].predict(wide2long(x_[None,:], y_[None,:])[0]),
method='ordinal') for x_, y_ in zip(X_train, y_train)])
y_pred.shape
13 - y_train[0] + 1
y_pred[0]
from scipy.stats import spearmanr
spearmanr(13 - y_train[0] + 1, y_pred[0])
```
## Ranking, Regression, Classification
```
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
params = {'objective': 'lambdarank',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
params = {'objective': 'regression',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
params = {'objective': 'binary',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
```
## 10 runs - 10 folds
```
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=10, random_state=42)
params = {'objective': 'lambdarank',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=10, random_state=42)
params = {'objective': 'regression',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=10, random_state=42)
params = {'objective': 'binary',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train.shape[1] - y_train + 1, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
# LambdaRank
Trn_Spearman: 0.3714 +/-0.0634 | Val_Spearman: 0.0922 +/-0.1403
Trn_ACCLoss: 0.0254 +/-0.0194 | Val_ACCLoss: 0.0921 +/-0.0564
Trn_NDCG: 0.7845 +/-0.0671 | Val_NDCG: 0.6157 +/-0.0555
# Regression
Trn_Spearman: 0.3531 +/-0.1215 | Val_Spearman: 0.1699 +/-0.1319
Trn_ACCLoss: 0.0847 +/-0.0324 | Val_ACCLoss: 0.1166 +/-0.0723
Trn_NDCG: 0.6294 +/-0.0510 | Val_NDCG: 0.5891 +/-0.0665
# Binary Classification
Trn_Spearman: -0.0821 +/-0.0170 | Val_Spearman: -0.0821 +/-0.1533
Trn_ACCLoss: 0.1172 +/-0.0064 | Val_ACCLoss: 0.1172 +/-0.0573
Trn_NDCG: 0.5275 +/-0.0054 | Val_NDCG: 0.5275 +/-0.0486
```
## New ranking
```
%%time
from sklearn.model_selection import train_test_split
rp = Pipeline([
('scale', StandardScaler()),
('estimator', RankingPredictor("ma_100", n_neighbors=15)),
])
df_mf, df_rank, df_scores, _ = rp.named_steps['estimator'].get_data()
df_mf = df_mf.sort_index()
df_rank = df_rank.sort_index()
df_scores = df_scores.sort_index()
X_train, _, y_train, _, y_scores_train, _ = train_test_split(df_mf.values,
df_rank.values,
df_scores.values,
test_size=0,
random_state=42)
print(X_train.shape, y_train.shape, y_scores_train.shape)
df_mf.head()
df_rank.head()
df_scores.head()
%%time
import lightgbm
from project.ranker.ltr_rankers import cv_lgbm
from sklearn.model_selection import RepeatedKFold
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
params = {'objective': 'lambdarank',
'metric': 'ndcg',
'learning_rate': 1e-3,
# 'num_leaves': 50,
'ndcg_at': y_train.shape[1],
'min_data_in_leaf': 3,
'min_sum_hessian_in_leaf': 1e-4}
results, models = cv_lgbm(lightgbm, X_train, y_train, y_scores_train, kfolds,
params, num_rounds=1000, early_stopping_rounds=50, verbose_eval=False)
from sklearn.model_selection import KFold
from project.ranker.ltr_rankers import cv_random
from project.ranker.ranker import RandomRankingPredictor
rr = RandomRankingPredictor()
kfolds = RepeatedKFold(10, n_repeats=2, random_state=42)
results = cv_random(rr, X_train, y_train, y_scores_train, kfolds)
lightgbm.plot_importance(models[0], figsize=(5,10))
from project.ranker.ltr_rankers import wide2long
X, y = wide2long(X_train, y_train)
X.shape, y.shape
X_train[0]
```
|
github_jupyter
|
# Codebuster STAT 535 Statistical Computing Project
## Movie recommendation recommendation pipeline
##### Patrick's comments 11/9
- Goal: Build a small real world deployment pipeline like it can be used in netflix / amazon
- build / test with movie recommendation data set (model fitting, data preprocessing, evaluation)
- Show that it also works with another dataset like product recommendation
- Find data on UCI repo, kaggle, google search
- Use scikit learn estimation: https://github.com/scikit-learn-contrib/project-template
## Literature
- https://users.ece.cmu.edu/~dbatra/publications/assets/goel_batra_netflix.pdf
- http://delivery.acm.org/10.1145/1460000/1454012/p11-park.pdf?ip=72.19.68.210&id=1454012&acc=ACTIVE%20SERVICE&key=73B3886B1AEFC4BB%2EB478147E31829731%2E4D4702B0C3E38B35%2E4D4702B0C3E38B35&__acm__=1543416754_7f92e0642e26e7ea732886879096c704
- https://www.kaggle.com/prajitdatta/movielens-100k-dataset/kernels
- https://medium.com/@james_aka_yale/the-4-recommendation-engines-that-can-predict-your-movie-tastes-bbec857b8223
- https://www.kaggle.com/c/predict-movie-ratings
- https://cseweb.ucsd.edu/classes/wi17/cse258-a/reports/a048.pdf
- https://github.com/neilsummers/predict_movie_ratings/blob/master/movieratings.py
- https://medium.com/@connectwithghosh/recommender-system-on-the-movielens-using-an-autoencoder-using-tensorflow-in-python-f13d3e8d600d
### A few more
- https://sci2s.ugr.es/keel/pdf/specific/congreso/xia_dong_06.pdf (Uses SMV for classification, then MF for recommendation)
- https://www.kaggle.com/rounakbanik/movie-recommender-systems (Employs at least three Modules for recommendation)
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.703.4954&rep=rep1&type=pdf (Close to what we need, but a little too involving)
- https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0165868 (Uses SVM and correlation matrices...I have already tried the correlation approach, looks quite good, but how to quantify accuracy?)
- https://www.quora.com/How-do-we-use-SVMs-in-a-collaborative-recommendation (A good thread on SVM)
-http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/ (A good tutorial on matrix factorizasion)
## Approach
##### User profile cases:
- ##### Case 0 rated movies: Supervised prediction with just user age, gender, and year of the movie
In case of cold-start: No user information available
- ##### Case < 20 rated movies: Content-based recommender system
Content-based recommendation information about users and their taste. As we can see in the preprocessing, most of the users only rated one to five movies, implying that we have incomplete user-profiles. I think content-based recommendation makes sense here, because we can recommend similar movies, but not other categories that a user might like because we can not identify similar users with an incomplete user profile.
- ##### Case >=20 rated movies: Collaborative recommender system
Collaborative filtering makes sense if you have a good user profile, which we assume we have if a user rated more or equal than 10 movies. With a good user profile we can identify similar users and make more sophisticated recommendations, e.g. movies from other genres.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from scipy import interp
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import linear_kernel
from sklearn.model_selection import cross_val_predict, cross_val_score, cross_validate, StratifiedKFold
from sklearn.metrics import classification_report,confusion_matrix, roc_curve, auc
```
## Data Understanding and Preprocessing
Get a feeling for the dataset, its problems and conduct helpful preprocessing
```
df = pd.read_csv("allData.tsv", sep='\t')
print(f"Shape: {df.shape}")
print(df.dtypes)
df.head()
df.age.value_counts()
```
##### Histogram: Number of movies are rated by users
Most users rated only up tp 5 movies
```
df.userID.value_counts().hist(bins=50)
```
##### Divide datasets for different recommendations (random forest, content based, collaborative based)
It can be useful to use content-based recommender systems for those users
```
df_split = df.copy()
df_split.set_index('userID', inplace=True)
# set for content based recommendation with #ratings < 10
df_content = df_split[df.userID.value_counts()<10]
# set for collaborative recommendation with #ratings >= 10
df_collaborative = df_split[df.userID.value_counts()>=10]
df_content.index.value_counts().hist(bins=50)
df_collaborative.index.value_counts().hist(bins=50)
```
##### Transform numerical rating to binary
- 1, if user rates movie 4 or 5
- 0, if user rates movie less than 4
```
df['rating'].mask(df['rating'] < 4, 0, inplace=True)
df['rating'].mask(df['rating'] > 3, 1, inplace=True)
```
##### Check rating distribution
```
df['rating'].hist()
```
## Recommendation
##### Cold start: Gradient Boosting Classifier
Logic: Treat every user as same, predicting rating over whole movie dataset
- ##### Case 0 rated movies: Supervised prediction with just user age, gender, and year of the movie
In case of cold-start: No user information available
```
# Cross Validation to test and anticipate overfitting problem
def crossvalidate(clf, X,y):
'''
Calculate precision, recall, and roc_auc for a 10-fold cross validation run with passed classifier
'''
scores1 = cross_val_score(clf, X, y, cv=10, scoring='precision')
scores2 = cross_val_score(clf, X, y, cv=10, scoring='recall')
scores3 = cross_val_score(clf, X, y, cv=10, scoring='roc_auc')
# The mean score and standard deviation of the score estimate
print("Cross Validation Precision: %0.2f (+/- %0.2f)" % (scores1.mean(), scores1.std()))
print("Cross Validation Recall: %0.2f (+/- %0.2f)" % (scores2.mean(), scores2.std()))
print("Cross Validation roc_auc: %0.2f (+/- %0.2f)" % (scores3.mean(), scores3.std()))
# Run classifier with cross-validation and plot ROC curves
# from http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc_crossval.html
def get_crossval_roc(clfname, classifier,X,y):
'''
Run classifier with cross-validation and plot ROC curves
'''
n_samples, n_features = X.shape
cv = StratifiedKFold(n_splits=6)
tprs = []
aucs = []
mean_fpr = np.linspace(0, 1, 100)
i = 0
for train, test in cv.split(X, y):
probas_ = classifier.fit(X[train], y[train]).predict_proba(X[test])
# Compute ROC curve and area the curve
fpr, tpr, thresholds = roc_curve(y[test], probas_[:, 1])
tprs.append(interp(mean_fpr, fpr, tpr))
tprs[-1][0] = 0.0
roc_auc = auc(fpr, tpr)
aucs.append(roc_auc)
plt.plot(fpr, tpr, lw=1, alpha=0.3,
label='ROC fold %d (AUC = %0.2f)' % (i, roc_auc))
i += 1
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',
label='Chance', alpha=.8)
mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(aucs)
plt.plot(mean_fpr, mean_tpr, color='b',
label=r'Mean ROC (AUC = %0.2f $\pm$ %0.2f)' % (mean_auc, std_auc),
lw=2, alpha=.8)
std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
plt.fill_between(mean_fpr, tprs_lower, tprs_upper, color='grey', alpha=.2,
label=r'$\pm$ 1 std. dev.')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
return
```
##### Preprocessing for boosted random forest classifier
```
# User information before any movie ratings
X = df[['age', 'gender', 'year', 'genre1', 'genre2', 'genre3']]
y = df['rating'].as_matrix()
# Preprocessing
# One hot encoding
dummyvars = pd.get_dummies(X[['gender', 'genre1', 'genre2', 'genre3']])
# append the dummy variables to df
X = pd.concat([X[['age', 'year']], dummyvars], axis = 1).as_matrix()
print("GradientBoostingClassifier")
gbclf = GradientBoostingClassifier(n_estimators=100)
gbclf.fit(X=X, y=y)
gbclf.predict()
#crossvalidate(gbclf,X,y)
#get_crossval_roc("gbclf",gbclf,X,y)
```
##### Content-based recommendation with tf-idf for user with <10 ratings
- ##### Case < 10 rated movies: Content-based recommender system
Content-based recommendation information about users and their taste. As we can see in the preprocessing, most of the users only rated one to five movies, implying that we have incomplete user-profiles. I think content-based recommendation makes sense here, because we can recommend similar movies, but not other categories that a user might like because we can not identify similar users with an incomplete user profile.
- Code inspired by: https://medium.com/@james_aka_yale/the-4-recommendation-engines-that-can-predict-your-movie-tastes-bbec857b8223
- Make recommendations based on similarity of movie genres, purely content based.
```
# import movies
movies = pd.read_csv("movies.tsv", sep='\t')
print(f"Shape: {df.shape}")
movies.head()
# Preprocessing
# Strip space at the end of string
movies['name'] = movies['name'].str.rstrip()
# Concat genres into one string
movies['genres_concat'] = movies[['genre1', 'genre2', 'genre3']].astype(str).apply(' '.join, axis=1)
# Remove nans in string and strip spaces at the end
movies['genres_concat'] = movies['genres_concat'].str.replace('nan','').str.rstrip()
movies.head()
# Function that get movie recommendations based on the cosine similarity score of movie genres
def content_based_recommendation(movies, name, number_recommendations):
'''
Recommends number of similar movie based on movie title and similarity to movies in movie database
@param movies: pandas dataframe with movie dataset with columns (movieID, name, genres_concat)
@param name: movie title as string
@param number_recommendations: number of recommendations returned as integer
'''
# Create tf_idf matrix sklearn TfidfVectorizer
tf = TfidfVectorizer(analyzer='word',ngram_range=(1, 2),min_df=0, stop_words='english')
tfidf_matrix = tf.fit_transform(movies['genres_concat'])
# calculate similarity matrix with cosine distance of tf_idf values
cosine_sim = linear_kernel(tfidf_matrix, tfidf_matrix)
# Build a 1-dimensional array with movie titles
indices = pd.Series(movies.index, index=movies['name'])
# Ranks movies according to similarity to requested movie
idx = indices[name]
sim_scores = list(enumerate(cosine_sim[idx]))
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
sim_scores = sim_scores[1:(number_recommendations+1)]
movie_indices = [i[0] for i in sim_scores]
return movies.name.iloc[movie_indices]
```
##### Test recommendations
```
content_based_recommendation(movies, 'Father of the Bride Part II', 5)
```
## Evaluation
## Ceate predictions for predict.csv
|
github_jupyter
|
```
from glob import glob
from os import path
import re
from skbio import DistanceMatrix
import pandas as pd
import numpy as np
from kwipexpt import *
%matplotlib inline
%load_ext rpy2.ipython
%%R
library(tidyr)
library(dplyr, warn.conflicts=F, quietly=T)
library(ggplot2)
```
Calculate performance of kWIP
=============================
The next bit of python code calculates the performance of kWIP against the distance between samples calulcated from the alignments of their genomes.
This code caluclates spearman's $\rho$ between the off-diagonal elements of the triagnular distance matrices.
```
expts = list(map(lambda fp: path.basename(fp.rstrip('/')), glob('data/*/')))
print("Expts:", *expts[:10], "...")
def process_expt(expt):
expt_results = []
def extract_info(filename):
return re.search(r'kwip/(\d\.?\d*)x-(0\.\d+)-(wip|ip).dist', filename).groups()
# dict of scale: distance matrix, populated as we go
truths = {}
for distfile in glob("data/{}/kwip/*.dist".format(expt)):
cov, scale, metric = extract_info(distfile)
if scale not in truths:
genome_dist_path = 'data/{ex}/all_genomes-{sc}.dist'.format(ex=expt, sc=scale)
truths[scale] = load_sample_matrix_to_runs(genome_dist_path)
exptmat = DistanceMatrix.read(distfile)
rho = spearmans_rho_distmats(exptmat, truths[scale])
expt_results.append({
"coverage": cov,
"scale": scale,
"metric": metric,
"rho": rho,
"seed": expt,
})
return expt_results
#process_expt('3662')
results = []
for res in map(process_expt, expts):
results.extend(res)
results = pd.DataFrame(results)
```
Statistical analysis
====================
Is done is R, as that's easier.
Below we see a summary and structure of the data
```
%%R -i results
results$coverage = as.numeric(as.character(results$coverage))
results$scale = as.numeric(as.character(results$scale))
print(summary(results))
str(results)
```
### Experiment design
Below we see the design of the experiment in terms of the two major variables.
We have a series (vertically) that, at 30x coverage, looks at the effect of genetic variation on performance. There is a second series that examines the effect of coverage at an average pairwise genetic distance of 0.001.
There are 100 replicates for each data point, performed as a separate bootstrap across the random creation of the tree and sampling of reads etc.
```
%%R
ggplot(results, aes(x=coverage, y=scale)) +
geom_point() +
scale_x_log10() +
scale_y_log10() +
theme_bw()
```
Effect of Coverage
------------------
Here we show the spread of data across the 100 reps as boxplots per metric and covreage level.
I note that the weighted product seems slightly more variable, particularly at higher coverage. Though the median is nearly always higher
```
%%R
dat = results %>%
filter(scale==0.001, coverage<=30) %>%
select(rho, metric, coverage)
dat$coverage = as.factor(dat$coverage)
ggplot(dat, aes(x=coverage, y=rho, fill=metric)) +
geom_boxplot(aes(fill=metric))
%%R
# AND AGAIN WITHOUT SUBSETTING
dat = results %>%
filter(scale==0.001) %>%
select(rho, metric, coverage)
dat$coverage = as.factor(dat$coverage)
ggplot(dat, aes(x=coverage, y=rho, fill=metric)) +
geom_boxplot(aes(fill=metric))
%%R
dat = subset(results, scale==0.001 & coverage <=15, select=-scale)
ggplot(dat, aes(x=coverage, y=rho, colour=seed, linetype=metric)) +
geom_line()
%%R
summ = results %>%
filter(scale==0.001, coverage <= 50) %>%
select(-scale) %>%
group_by(coverage, metric) %>%
summarise(rho_av=mean(rho), rho_err=sd(rho))
ggplot(summ, aes(x=coverage, y=rho_av, ymin=rho_av-rho_err, ymax=rho_av+rho_err, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Spearman's ", rho, " +- SD"))) +
scale_x_log10()+
ggtitle("Performance of WIP & IP") +
theme_bw()
%%R
sem <- function(x) sqrt(var(x,na.rm=TRUE)/length(na.omit(x)))
summ = results %>%
filter(scale==0.001) %>%
select(-scale) %>%
group_by(coverage, metric) %>%
summarise(rho_av=mean(rho), rho_err=sem(rho))
ggplot(summ, aes(x=coverage, y=rho_av, ymin=rho_av-rho_err, ymax=rho_av+rho_err, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Spearman's ", rho))) +
scale_x_log10()+
theme_bw()
%%R
cov_diff = results %>%
filter(scale==0.001) %>%
select(rho, metric, coverage, seed) %>%
spread(metric, rho) %>%
mutate(diff=wip-ip) %>%
select(coverage, seed, diff)
print(summary(cov_diff))
p = ggplot(cov_diff, aes(x=coverage, y=diff, colour=seed)) +
geom_line() +
scale_x_log10() +
ggtitle("Per expt difference in performance (wip - ip)")
print(p)
summ = cov_diff %>%
group_by(coverage) %>%
summarise(diff_av=mean(diff), diff_sd=sd(diff))
ggplot(summ, aes(x=coverage, y=diff_av, ymin=diff_av-diff_sd, ymax=diff_av+diff_sd)) +
geom_line() +
geom_ribbon(alpha=0.2) +
xlab('Genome Coverage') +
ylab(expression(paste("Improvment in Spearman's ", rho, " (wip - IP)"))) +
scale_x_log10() +
theme_bw()
%%R
var = results %>%
filter(coverage == 30) %>%
select(-coverage)
var$scale = as.factor(var$scale)
ggplot(var, aes(x=scale, y=rho, fill=metric)) +
geom_boxplot() +
xlab('Mean pairwise variation') +
ylab(expression(paste("Spearman's ", rho))) +
#scale_x_log10()+
theme_bw()
%%R
summ = results %>%
filter(coverage == 30) %>%
select(-coverage) %>%
group_by(scale, metric) %>%
summarise(rho_av=mean(rho), rho_sd=sd(rho))
ggplot(summ, aes(x=scale, y=rho_av, ymin=rho_av-rho_sd, ymax=rho_av+rho_sd, group=metric)) +
geom_line(aes(linetype=metric)) +
geom_ribbon(aes(fill=metric), alpha=0.2) +
xlab('Mean pairwise variation') +
ylab(expression(paste("Spearman's ", rho))) +
scale_x_log10()+
theme_bw()
```
|
github_jupyter
|
# Example from Image Processing
```
%matplotlib inline
import matplotlib.pyplot as plt
```
Here we'll take a look at a simple facial recognition example.
This uses a dataset available within scikit-learn consisting of a
subset of the [Labeled Faces in the Wild](http://vis-www.cs.umass.edu/lfw/)
data. Note that this is a relatively large download (~200MB) so it may
take a while to execute.
```
from sklearn import datasets
lfw_people = datasets.fetch_lfw_people(min_faces_per_person=70, resize=0.4,
data_home='datasets')
lfw_people.data.shape
```
If you're on a unix-based system such as linux or Mac OSX, these shell commands
can be used to see the downloaded dataset:
```
!ls datasets
!du -sh datasets/lfw_home
```
Once again, let's visualize these faces to see what we're working with:
```
fig = plt.figure(figsize=(8, 6))
# plot several images
for i in range(15):
ax = fig.add_subplot(3, 5, i + 1, xticks=[], yticks=[])
ax.imshow(lfw_people.images[i], cmap=plt.cm.bone)
import numpy as np
plt.figure(figsize=(10, 2))
unique_targets = np.unique(lfw_people.target)
counts = [(lfw_people.target == i).sum() for i in unique_targets]
plt.xticks(unique_targets, lfw_people.target_names[unique_targets])
locs, labels = plt.xticks()
plt.setp(labels, rotation=45, size=14)
_ = plt.bar(unique_targets, counts)
```
One thing to note is that these faces have already been localized and scaled
to a common size. This is an important preprocessing piece for facial
recognition, and is a process that can require a large collection of training
data. This can be done in scikit-learn, but the challenge is gathering a
sufficient amount of training data for the algorithm to work
Fortunately, this piece is common enough that it has been done. One good
resource is [OpenCV](http://opencv.willowgarage.com/wiki/FaceRecognition), the
*Open Computer Vision Library*.
We'll perform a Support Vector classification of the images. We'll
do a typical train-test split on the images to make this happen:
```
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
lfw_people.data, lfw_people.target, random_state=0)
print(X_train.shape, X_test.shape)
```
## Preprocessing: Principal Component Analysis
1850 dimensions is a lot for SVM. We can use PCA to reduce these 1850 features to a manageable
size, while maintaining most of the information in the dataset. Here it is useful to use a variant
of PCA called ``RandomizedPCA``, which is an approximation of PCA that can be much faster for large
datasets. We saw this method in the previous notebook, and will use it again here:
```
from sklearn import decomposition
pca = decomposition.RandomizedPCA(n_components=150, whiten=True,
random_state=1999)
pca.fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print(X_train_pca.shape)
print(X_test_pca.shape)
```
These projected components correspond to factors in a linear combination of
component images such that the combination approaches the original face. In general, PCA can be a powerful technique for preprocessing that can greatly improve classification performance.
## Doing the Learning: Support Vector Machines
Now we'll perform support-vector-machine classification on this reduced dataset:
```
from sklearn import svm
clf = svm.SVC(C=5., gamma=0.001)
clf.fit(X_train_pca, y_train)
```
Finally, we can evaluate how well this classification did. First, we might plot a
few of the test-cases with the labels learned from the training set:
```
fig = plt.figure(figsize=(8, 6))
for i in range(15):
ax = fig.add_subplot(3, 5, i + 1, xticks=[], yticks=[])
ax.imshow(X_test[i].reshape((50, 37)), cmap=plt.cm.bone)
y_pred = clf.predict(X_test_pca[i])[0]
color = 'black' if y_pred == y_test[i] else 'red'
ax.set_title(lfw_people.target_names[y_pred], fontsize='small', color=color)
```
The classifier is correct on an impressive number of images given the simplicity
of its learning model! Using a linear classifier on 150 features derived from
the pixel-level data, the algorithm correctly identifies a large number of the
people in the images.
Again, we can
quantify this effectiveness using ``clf.score``
```
print(clf.score(X_test_pca, y_test))
```
## Final Note
Here we have used PCA "eigenfaces" as a pre-processing step for facial recognition.
The reason we chose this is because PCA is a broadly-applicable technique, which can
be useful for a wide array of data types. For more details on the eigenfaces approach, see the original paper by [Turk and Penland, Eigenfaces for Recognition](http://www.face-rec.org/algorithms/PCA/jcn.pdf). Research in the field of facial recognition has moved much farther beyond this paper, and has shown specific feature extraction methods can be more effective. However, eigenfaces is a canonical example of machine learning "in the wild", and is a simple method with good results.
|
github_jupyter
|
```
import pandas as pd #pandas does things with matrixes
import numpy as np #used for sorting a matrix
import matplotlib.pyplot as plt #matplotlib is used for plotting data
import matplotlib.ticker as ticker #used for changing tick spacing
import datetime as dt #used for dates
import matplotlib.dates as mdates #used for dates, in a different way
import os #used for changes of directory
import warnings
warnings.filterwarnings("ignore")
from sklearn.preprocessing import MinMaxScaler # It scales the data between 0 and 1
import sys
sys.path.append('../')
from utils import simple_plot, simple_plot_by_date, hit_count
import torch
import torch.nn as nn
from torchvision.transforms import ToTensor
from torch.utils.data.dataloader import DataLoader
import torch.nn.functional as F
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
dataset_1yr = pd.read_csv("../../Data/all_stocks_5yr.csv")
dataset_1yr.head()
# Changing the date column to the datetime format (best format to work with time series)
dataset_1yr['Date'] = [dt.datetime.strptime(d,'%Y-%m-%d').date() for d in dataset_1yr['Date']]
dataset_1yr.head()
# Assigning a mid price column with the mean of the Highest and Lowest values
dataset_1yr['Mid'] = (dataset_1yr['High'] + dataset_1yr['Low'])/2
dataset_1yr.head()
# Getting rid of null columns
missing_data = pd.DataFrame(dataset_1yr.isnull().sum()).T
print(missing_data)
for index, column in enumerate(missing_data.columns):
if missing_data.loc[0][index] != 0:
dataset_1yr = dataset_1yr.drop(dataset_1yr.loc[dataset_1yr[column].isnull()].index)
missing_data = pd.DataFrame(dataset_1yr.isnull().sum()).T
print(missing_data)
# Let's analyze 3M stocks a bit deeper
MMM_stocks = dataset_1yr[dataset_1yr['Name'] == 'MMM']
MMM_stocks.head()
# Creating a percent change column related to the closing price
percent_change_closing_price = MMM_stocks['Close'].pct_change()
percent_change_closing_price.fillna(0, inplace=True)
MMM_stocks['PC_change'] = pd.DataFrame(percent_change_closing_price)
# As we want to predict the closing price, let's add the target column as the close price shifted by 1
MMM_stocks['Target'] = MMM_stocks['Close'].shift(-1)
MMM_stocks = MMM_stocks.drop(0, axis = 0)
MMM_stocks = MMM_stocks.drop('Name', axis = 1)
MMM_stocks = MMM_stocks.drop('Date', axis = 1)
MMM_stocks.head()
# Separating as Training and Testing
train_data = MMM_stocks.iloc[:1000,:]
train_data = train_data.drop('Target',axis=1)
test_data = MMM_stocks.iloc[1000:,:]
test_data = test_data.drop('Target',axis=1)
y_train = MMM_stocks.iloc[:1000,-1]
y_test = MMM_stocks.iloc[1000:,-1]
print(train_data.shape)
print(test_data.shape)
print(y_train.shape)
print(y_test.shape)
# Data still needs to be scaled.
# Training Data
scaler_closing_price = MinMaxScaler(feature_range = (0, 1))
scaler_closing_price.fit(np.array(train_data['Close']).reshape(-1,1))
scaler_dataframe = MinMaxScaler(feature_range = (0, 1))
training_set_scaled = pd.DataFrame(scaler_dataframe.fit_transform(train_data))
training_set_scaled.head()
y_set_scaled = pd.DataFrame(scaler_closing_price.transform(np.array(y_train).reshape(-1,1)))
# Testing Data
testing_set_scaled = pd.DataFrame(scaler_dataframe.fit_transform(test_data))
y_test_scaled = pd.DataFrame(scaler_closing_price.transform(np.array(y_test).reshape(-1,1)))
# Preparing data for the experiment with an univariate model
# Getting Closing Price and arranging lists for training/testing based on the sequence
def split_sequence(sequence, n_steps):
X, y = list(), list()
for i in range(len(sequence)):
# find the end of this pattern
end_ix = i + n_steps
# check if we are beyond the sequence
if end_ix > len(sequence)-1:
break
# gather input and output parts of the pattern
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
train_univariate, y_train_univariate = split_sequence(training_set_scaled[3], 5)
test_univariate, y_test_univariate = split_sequence(testing_set_scaled[3], 5)
def reshape_pandas_data(x, y, input_size):
x = torch.from_numpy(np.array(x)).type(torch.Tensor).view([-1, input_size])
y = torch.from_numpy(np.array(y)).type(torch.Tensor).view(-1)
return (x, y)
train_tensor, target = reshape_pandas_data(train_univariate, y_train_univariate, train_univariate.shape[1])
#train_tensor, target = reshape_pandas_data(train_data, y_train, train_data.shape[1])
print(train_tensor.shape)
#train_tensor = DataLoader(train_tensor, batch_size)
# Creating a device data loader in order to pass batches to device memory
def to_device(data, device):
''' Move tensor to chosen device'''
if isinstance(data, (list,tuple)):
return [to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class DeviceDataLoader():
def __init__(self, data, device):
self.data = data
self.device = device
def __iter__(self):
"Yield a batch of data after moving it to device"
for item in self.data:
yield to_device(item, self.device)
def __len__(self):
"Number of batches"
return len(self.data)
train_tensor = DeviceDataLoader(train_tensor, device)
#target = DeviceDataLoader(target, device)
# Recurrent neural network (many-to-one)
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1, num_classes=1):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
self.input_size = input_size
def forward(self, x):
print(x)
#x = x.reshape(-1, len(x), self.input_size)
# Set initial hidden and cell states
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
# Forward propagate LSTM
out, self.hidden = self.lstm(x, (h0, c0)) # out: tensor of shape (batch_size, seq_length, hidden_size)
# Decode the hidden state of the last time step
out = self.fc(out[:, -1, :])
return out
# Recurrent neural network (many-to-one)
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers=1, num_classes=1):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
self.input_size = input_size
def forward(self, x):
#x = x.reshape(-1, len(x), self.input_size)
# Set initial hidden and cell states
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
# Forward propagate LSTM
out, self.hidden = self.lstm(x, (h0, c0)) # out: tensor of shape (batch_size, seq_length, hidden_size)
# Decode the hidden state of the last time step
out = self.fc(out[:, -1, :])
return out
# Hyper-parameters
epochs = 50
input_size = 5
hidden_size = 128
num_layers = 2
num_classes = 1
learning_rate = 1e-3
model = RNN(input_size, hidden_size, num_layers, num_classes).to(device)
for t in model.parameters():
print(t.shape)
for index, tensor in enumerate(train_tensor):
y_pred = model(tensor)
loss += loss_fn(y_pred, target[index])
loss
hist = []
loss_fn = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
for epoch in range(epochs):
#model.zero_grad()
loss = []
for tensor, real_output in train_tensor, target:
y_pred = model(tensor)
loss += loss_fn(y_pred, real_output)
y_pred = model(train_tensor)
loss += loss_fn(y_pred, target.to(device))
hist.append(loss.mean())
loss.backward()
optimizer.step()
optimizer.zero_grad()
#if epoch+1 % 10 == 0:
print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, epochs, loss.item()))
plt.plot(hist, '-x')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.title('Accuracy vs Epoch');
class TimeSeriesRNNModel(nn.Module):
def __init__(self):
super(TimeSeriesRNNModel, self).__init__()
self.lstm1 = nn.LSTM(input_size=5, hidden_size=50, num_layers=1)
self.lstm2 = nn.LSTM(input_size=50, hidden_size=25, num_layers=1)
self.linear = nn.Linear(in_features=25, out_features=1)
self.h_t1 = None
self.c_t1 = None
self.h_t2 = None
self.c_t2 = None
def initialize_model(self, input_data):
self.h_t1 = torch.rand(1, 1, 50, dtype=torch.double).to(device)
self.c_t1 = torch.rand(1, 1, 50, dtype=torch.double).to(device)
self.h_t2 = torch.rand(1, 1, 25, dtype=torch.double).to(device)
self.c_t2 = torch.rand(1, 1, 25, dtype=torch.double).to(device)
def forward(self, input_data):
outputs = []
self.initialize_model(input_data)
input_data = input_data.reshape(-1, len(input_data), 5)
output = None
for _, input_t in enumerate(input_data.chunk(input_data.size(1), dim=1)):
self.h_t1, self.c_t1 = self.lstm1(input_t, (self.h_t1, self.c_t1))
self.h_t2, self.c_t2 = self.lstm2(self.h_t1, (self.h_t2, self.c_t2))
output = self.linear(self.h_t2)
outputs += [output]
outputs = torch.stack(outputs, 1).squeeze(2)
return outputs
# Hyper-parameters
epochs = 20
learning_rate = 1e-3
model = TimeSeriesRNNModel().to(device)
for t in model.parameters():
print(t.shape)
hist = []
loss_fn = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
for epoch in range(epochs):
#model.zero_grad()
y_pred = model(train_tensor.to(device))
loss = loss_fn(y_pred, target.to(device))
hist.append(loss.item())
loss.backward()
optimizer.step()
optimizer.zero_grad()
#if epoch+1 % 10 == 0:
print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, epochs, loss.item()))
```
|
github_jupyter
|
```
# 8.3.3. Natural Language Statistics
import random
import torch
from d2l import torch as d2l
tokens = d2l.tokenize(d2l.read_time_machine())
# Since each text line is not necessarily a sentence or a paragraph, we
# concatenate all text lines
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]
freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)', xscale='log',
yscale='log')
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]
trigram_tokens = [
triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
ylabel='frequency: n(x)', xscale='log', yscale='log',
legend=['unigram', 'bigram', 'trigram'])
# 8.3.4. Reading Long Sequence Data
# 8.3.4.1. Random Sampling
def seq_data_iter_random(corpus, batch_size, num_steps): #@save
"""Generate a minibatch of subsequences using random sampling."""
# Start with a random offset (inclusive of `num_steps - 1`) to partition a
# sequence
corpus = corpus[random.randint(0, num_steps - 1):]
# Subtract 1 since we need to account for labels
num_subseqs = (len(corpus) - 1) // num_steps
# The starting indices for subsequences of length `num_steps`
initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
# In random sampling, the subsequences from two adjacent random
# minibatches during iteration are not necessarily adjacent on the
# original sequence
random.shuffle(initial_indices)
def data(pos):
# Return a sequence of length `num_steps` starting from `pos`
return corpus[pos:pos + num_steps]
num_batches = num_subseqs // batch_size
for i in range(0, batch_size * num_batches, batch_size):
# Here, `initial_indices` contains randomized starting indices for
# subsequences
initial_indices_per_batch = initial_indices[i:i + batch_size]
X = [data(j) for j in initial_indices_per_batch]
Y = [data(j + 1) for j in initial_indices_per_batch]
yield torch.tensor(X), torch.tensor(Y)
my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
print('X: ', X, '\nY:', Y)
# 8.3.4.2. Sequential Partitioning
def seq_data_iter_sequential(corpus, batch_size, num_steps): #@save
"""Generate a minibatch of subsequences using sequential partitioning."""
# Start with a random offset to partition a sequence
offset = random.randint(0, num_steps)
num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
Xs = torch.tensor(corpus[offset:offset + num_tokens])
Ys = torch.tensor(corpus[offset + 1:offset + 1 + num_tokens])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
num_batches = Xs.shape[1] // num_steps
for i in range(0, num_steps * num_batches, num_steps):
X = Xs[:, i:i + num_steps]
Y = Ys[:, i:i + num_steps]
yield X, Y
for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):
print('X: ', X, '\nY:', Y)
class SeqDataLoader: #@save
"""An iterator to load sequence data."""
def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
if use_random_iter:
self.data_iter_fn = d2l.seq_data_iter_random
else:
self.data_iter_fn = d2l.seq_data_iter_sequential
self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
self.batch_size, self.num_steps = batch_size, num_steps
def __iter__(self):
return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)
def load_data_time_machine(batch_size, num_steps, #@save
use_random_iter=False, max_tokens=10000):
"""Return the iterator and the vocabulary of the time machine dataset."""
data_iter = SeqDataLoader(batch_size, num_steps, use_random_iter,
max_tokens)
return data_iter, data_iter.vocab
```
|
github_jupyter
|
## 7-3. HHLアルゴリズムを用いたポートフォリオ最適化
この節では論文[1]を参考に、過去の株価変動のデータから、最適なポートフォリオ(資産配分)を計算してみよう。
ポートフォリオ最適化は、[7-1節](7.1_quantum_phase_estimation_detailed.ipynb)で学んだHHLアルゴリズムを用いることで、従来より高速に解けることが期待されている問題の一つである。
今回は具体的に、GAFA (Google, Apple, Facebook, Amazon) の4社の株式に投資する際、どのような資産配分を行えば最も低いリスクで高いリターンを得られるかという問題を考える。
### 株価データ取得
まずは各社の株価データを取得する。
* GAFA 4社の日次データを用いる
* 株価データ取得のためにpandas_datareaderを用いてYahoo! Financeのデータベースから取得
* 株価はドル建ての調整後終値(Adj. Close)を用いる
```
# データ取得に必要なpandas, pandas_datareaderのインストール
# !pip install pandas pandas_datareader
import numpy as np
import pandas as pd
import pandas_datareader.data as web
import datetime
import matplotlib.pyplot as plt
# 銘柄選択
codes = ['GOOG', 'AAPL', 'FB', 'AMZN'] # GAFA
# 2017年の1年間のデータを使用
start = datetime.datetime(2017, 1, 1)
end = datetime.datetime(2017, 12, 31)
# Yahoo! Financeから日次の株価データを取得
data = web.DataReader(codes, 'yahoo', start, end)
df = data['Adj Close']
## 直近のデータの表示
display(df.tail())
## 株価をプロットしてみる
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 6))
df.loc[:,['AAPL', 'FB']].plot(ax=axes[0])
df.loc[:,['GOOG', 'AMZN']].plot(ax=axes[1])
```
※ここで、4つの銘柄を2つのグループに分けているのは、株価の値がそれぞれ近くプロット時に見やすいからであり、深い意味はない。
### データの前処理
次に、取得した株価を日次リターンに変換し、いくつかの統計量を求めておく。
#### 日次リターンへの変換
個別銘柄の日次リターン(変化率) $y_t$ ($t$は日付)は以下で定義される。
$$
y_t = \frac{P_t - P_{t-1}}{P_{t-1}}
$$
これは `pandas DataFrame` の `pct_change()` メソッドで得られる。
```
daily_return = df.pct_change()
display(daily_return.tail())
```
#### 期待リターン
銘柄ごとの期待リターン$\vec R$を求める。ここでは過去のリターンの算術平均を用いる:
$$
\vec R = \frac{1}{T} \sum_{t= 1}^{T} \vec y_t
$$
```
expected_return = daily_return.dropna(how='all').mean() * 252 # 年率換算のため年間の営業日数252を掛ける
print(expected_return)
```
#### 分散・共分散行列
リターンの標本不偏分散・共分散行列$\Sigma$は以下で定義される。
$$
\Sigma = \frac{1}{T-1} \sum_{t=1}^{T} ( \vec y_t -\vec R ) (\vec y_t -\vec R )^T
$$
```
cov = daily_return.dropna(how='all').cov() * 252 # 年率換算のため
display(cov)
```
### ポートフォリオ最適化
準備が整ったところで、ポートフォリオ最適化に取り組もう。
まず、ポートフォリオ(i.e., 資産配分)を4成分のベクトル $\vec{w} = (w_0,w_1,w_2,w_3)^T$ で表す。
これは各銘柄を持つ割合(ウェイト)を表しており、例えば $\vec{w}=(1,0,0,0)$ であれば Google 株に全資産の100%を投入しするポートフォリオを意味する。
以下の式を満たすようなポートフォリオを考えてみよう。
$$
\min_{\vec{w}} \frac{1}{2} \vec{w}^T \Sigma \vec{w} \:\:\: \text{s.t.} \:\: \vec R^T \vec w = \mu , \: \vec 1^T \vec w =1
$$
この式は
* 「ポートフォリオの期待リターン(リターンの平均値)が$\mu$ 」
* 「ポートフォリオに投資するウェイトの合計が1」($\vec 1 = (1,1,1,1)^T$)
という条件の下で、
* 「ポートフォリオのリターンの分散の最小化」
を行うことを意味している。つまり、将来的に $\mu$ だけのリターンを望む時に、なるべくその変動(リスク)を小さくするようなポートフォリオが最善だというわけである。このような問題設定は、[Markowitzの平均分散アプローチ](https://ja.wikipedia.org/wiki/現代ポートフォリオ理論)と呼ばれ、現代の金融工学の基礎となる考えの一つである。
ラグランジュの未定乗数法を用いると、上記の条件を満たす$\vec{w}$は、線形方程式
$$
\begin{gather}
W
\left(
\begin{array}{c}
\eta \\
\theta \\
\vec w
\end{array}
\right)
=
\left(
\begin{array}{c}
\mu \\
1 \\
\vec 0
\end{array}
\right), \tag{1}\\
W =
\left(
\begin{array}{ccc}
0 & 0 & \vec R^T \\
0 & 0 & \vec 1^T \\
\vec{R} &\vec 1 & \Sigma
\end{array}
\right)
\end{gather}
$$
を解くことで得られる事がわかる。
ここで $\eta, \theta$ はラグランジュの未定乗数法のパラメータである。
したがって、最適なポートフォリオ $\vec w$ を求めるためには、連立方程式(1)を $\vec w$ について解けば良いことになる。
これで、ポートフォリオ最適化問題をHHLアルゴリズムが使える線形一次方程式に帰着できた。
#### 行列Wの作成
```
R = expected_return.values
Pi = np.ones(4)
S = cov.values
row1 = np.append(np.zeros(2), R).reshape(1,-1)
row2 = np.append(np.zeros(2), Pi).reshape(1,-1)
row3 = np.concatenate([R.reshape(-1,1), Pi.reshape(-1,1), S], axis=1)
W = np.concatenate([row1, row2, row3])
np.set_printoptions(linewidth=200)
print(W)
## Wの固有値を確認 -> [-pi, pi] に収まっている
print(np.linalg.eigh(W)[0])
```
#### 右辺ベクトルの作成
以下でポートフォリオの期待リターン $\mu$ を指定すると、そのようなリターンをもたらす最もリスクの小さいポートフォリオを計算できる。$\mu$ は自由に設定できる。一般に期待リターンが大きいほどリスクも大きくなるが、ここでは例として10%としておく(GAFA株がガンガン上がっている時期なので、これはかなり弱気な方である)。
```
mu = 0.1 # ポートフォリオのリターン(手で入れるパラメータ)
xi = 1.0
mu_xi_0 = np.append(np.array([mu, xi]), np.zeros_like(R)) ## (1)式の右辺のベクトル
print(mu_xi_0)
```
#### 量子系で扱えるように行列を拡張する
$W$ は6次元なので、3量子ビットあれば量子系で計算可能である ($2^3 = 8$)。
そこで、拡張した2次元分を0で埋めた行列とベクトルも作っておく。
```
nbit = 3 ## 状態に使うビット数
N = 2**nbit
W_enl = np.zeros((N, N)) ## enl は enlarged の略
W_enl[:W.shape[0], :W.shape[1]] = W.copy()
mu_xi_0_enl = np.zeros(N)
mu_xi_0_enl[:len(mu_xi_0)] = mu_xi_0.copy()
```
以上で、連立方程式(1)を解く準備が整った。
### HHLアルゴリズムを用いた最小分散ポートフォリオ算出
それでは、HHL アルゴリズムを用いて、連立一次方程式(1)を解いていこう。
先ずはその下準備として、
* 古典データ $\mathbf{x}$ に応じて、量子状態を $|0\cdots0\rangle \to \sum_i x_i |i \rangle$ と変換する量子回路を返す関数 `input_state_gate` (本来は qRAM の考え方を利用して作るべきだが、シミュレータを使っているので今回は non-unitary なゲートとして実装してしまう。また、規格化は無視している)
* 制御位相ゲートを返す関数 `CPhaseGate`
* 量子フーリエ変換を行うゲートを返す関数 `QFT_gate`
を用意する。
```
# Qulacs のインストール
# !pip install qulacs
## Google Colaboratory / (Linux or Mac)のjupyter notebook 環境の場合にのみ実行してください。
## Qulacsのエラーが正常に出力されるようになります。
!pip3 install wurlitzer
%load_ext wurlitzer
import numpy as np
from qulacs import QuantumCircuit, QuantumState, gate
from qulacs.gate import merge, Identity, H, SWAP
def input_state_gate(start_bit, end_bit, vec):
"""
Making a quantum gate which transform |0> to \sum_i x[i]|i>m where x[i] is input vector.
!!! this uses 2**n times 2**n matrix, so it is quite memory-cosuming.
!!! this gate is not unitary (we assume that the input state is |0>)
Args:
int start_bit: first index of qubit which the gate applies
int end_bit: last index of qubit which the gate applies
np.ndarray vec: input vector.
Returns:
qulacs.QuantumGate
"""
nbit = end_bit - start_bit + 1
assert vec.size == 2**nbit
mat_0tox = np.eye(vec.size, dtype=complex)
mat_0tox[:,0] = vec
return gate.DenseMatrix(np.arange(start_bit, end_bit+1), mat_0tox)
def CPhaseGate(target, control, angle):
"""
Create controlled phase gate diag(1,e^{i*angle}) with controll. (Qulacs.gate is requried)
Args:
int target: index of target qubit.
int control: index of control qubit.
float64 angle: angle of phase gate.
Returns:
QuantumGateBase.DenseMatrix: diag(1, exp(i*angle)).
"""
CPhaseGate = gate.DenseMatrix(target, np.array( [[1,0], [0,np.cos(angle)+1.j*np.sin(angle)]]) )
CPhaseGate.add_control_qubit(control, 1)
return CPhaseGate
def QFT_gate(start_bit, end_bit, Inverse = False):
"""
Making a gate which performs quantum Fourier transfromation between start_bit to end_bit.
(Definition below is the case when start_bit = 0 and end_bit=n-1)
We associate an integer j = j_{n-1}...j_0 to quantum state |j_{n-1}...j_0>.
We define QFT as
|k> = |k_{n-1}...k_0> = 1/sqrt(2^n) sum_{j=0}^{2^n-1} exp(2pi*i*(k/2^n)*j) |j>.
then, |k_m > = 1/sqrt(2)*(|0> + exp(i*2pi*0.j_{n-1-m}...j_0)|1> )
When Inverse=True, the gate represents Inverse QFT,
|k> = |k_{n-1}...k_0> = 1/sqrt(2^n) sum_{j=0}^{2^n-1} exp(-2pi*i*(k/2^n)*j) |j>.
Args:
int start_bit: first index of qubits where we apply QFT.
int end_bit: last index of qubits where we apply QFT.
bool Inverse: When True, the gate perform inverse-QFT ( = QFT^{\dagger}).
Returns:
qulacs.QuantumGate: QFT gate which acts on a region between start_bit and end_bit.
"""
gate = Identity(start_bit) ## make empty gate
n = end_bit - start_bit + 1 ## size of QFT
## loop from j_{n-1}
for target in range(end_bit, start_bit-1, -1):
gate = merge(gate, H(target)) ## 1/sqrt(2)(|0> + exp(i*2pi*0.j_{target})|1>)
for control in range(start_bit, target):
gate = merge( gate, CPhaseGate(target, control, (-1)**Inverse * 2.*np.pi/2**(target-control+1)) )
## perform SWAP between (start_bit + s)-th bit and (end_bit - s)-th bit
for s in range(n//2): ## s runs 0 to n//2-1
gate = merge(gate, SWAP(start_bit + s, end_bit - s))
## return final circuit
return gate
```
まずはHHLアルゴリズムに必要なパラメータを設定する。
クロックレジスタ量子ビット数 `reg_nbit`を `7` とし、行列 $W$ のスケーリングに使う係数 `scale_fac` を`1` とする(つまり、スケールさせない)。
また、制御回転ゲートに使う係数 $c$ は、`reg_nbit` ビットで表せる非ゼロの最も小さい数の半分にとっておく。
```
# 位相推定に使うレジスタの数
reg_nbit = 7
## W_enl をスケールする係数
scale_fac = 1.
W_enl_scaled = scale_fac * W_enl
## W_enl_scaledの固有値として想定する最小の値
## 今回は射影が100%成功するので, レジスタで表せる最小値の定数倍でとっておく
C = 0.5*(2 * np.pi * (1. / 2**(reg_nbit) ))
```
HHLアルゴリズムの核心部分を書いていく。今回は、シミュレータ qulacs を使うので様々な簡略化を行なっている。
HHLアルゴリズムがどのように動作するのかについての感覚を知る実装と思っていただきたい。
* 入力状態 $|\mathbf{b}\rangle$ を用意する部分は簡略化
* 量子位相推定アルゴリズムで使う $e^{iA}$ の部分は、 $A$ を古典計算機で対角化したものを使う
* 逆数をとる制御回転ゲートも、古典的に行列を用意して実装
* 補助ビット $|0 \rangle{}_{S}$ への射影測定を行い、測定結果 `0` が得られた状態のみを扱う
(実装の都合上、制御回転ゲートの作用の定義を[7-1節](7.1_quantum_phase_estimation_detailed.ipynb)と逆にした)
```
from functools import reduce
## 対角化. AP = PD <-> A = P*D*P^dag
D, P = np.linalg.eigh(W_enl_scaled)
#####################################
### HHL量子回路を作る. 0番目のビットから順に、Aの作用する空間のbit達 (0番目 ~ nbit-1番目),
### register bit達 (nbit番目 ~ nbit+reg_nbit-1番目), conditional回転用のbit (nbit+reg_nbit番目)
### とする.
#####################################
total_qubits = nbit + reg_nbit + 1
total_circuit = QuantumCircuit(total_qubits)
## ------ 0番目~(nbit-1)番目のbitに入力するベクトルbの準備 ------
## 本来はqRAMのアルゴリズムを用いるべきだが, ここでは自作の入力ゲートを用いている.
## qulacsではstate.load(b_enl)でも実装可能.
state = QuantumState(total_qubits)
state.set_zero_state()
b_gate = input_state_gate(0, nbit-1, mu_xi_0_enl)
total_circuit.add_gate(b_gate)
## ------- レジスターbit に Hadamard gate をかける -------
for register in range(nbit, nbit+reg_nbit): ## from nbit to nbit+reg_nbit-1
total_circuit.add_H_gate(register)
## ------- 位相推定を実装 -------
## U := e^{i*A*t), その固有値をdiag( {e^{i*2pi*phi_k}}_{k=0, ..., N-1) )とおく.
## Implement \sum_j |j><j| exp(i*A*t*j) to register bits
for register in range(nbit, nbit+reg_nbit):
## U^{2^{register-nbit}} を実装.
## 対角化した結果を使ってしまう
U_mat = reduce(np.dot, [P, np.diag(np.exp( 1.j * D * (2**(register-nbit)) )), P.T.conj()] )
U_gate = gate.DenseMatrix(np.arange(nbit), U_mat)
U_gate.add_control_qubit(register, 1) ## control bitの追加
total_circuit.add_gate(U_gate)
## ------- Perform inverse QFT to register bits -------
total_circuit.add_gate(QFT_gate(nbit, nbit+reg_nbit-1, Inverse=True))
## ------- conditional rotation を掛ける -------
## レジスター |phi> に対応するA*tの固有値は l = 2pi * 0.phi = 2pi * (phi / 2**reg_nbit).
## conditional rotationの定義は (本文と逆)
## |phi>|0> -> C/(lambda)|phi>|0> + sqrt(1 - C^2/(lambda)^2)|phi>|1>.
## 古典シミュレーションなのでゲートをあらわに作ってしまう.
condrot_mat = np.zeros( (2**(reg_nbit+1), (2**(reg_nbit+1))), dtype=complex)
for index in range(2**reg_nbit):
lam = 2 * np.pi * (float(index) / 2**(reg_nbit) )
index_0 = index ## integer which represents |index>|0>
index_1 = index + 2**reg_nbit ## integer which represents |index>|1>
if lam >= C:
if lam >= np.pi: ## あらかじめ[-pi, pi]内に固有値をスケールしているので、[pi, 2pi] は 負の固有値に対応
lam = lam - 2*np.pi
condrot_mat[index_0, index_0] = C / lam
condrot_mat[index_1, index_0] = np.sqrt( 1 - C**2/lam**2 )
condrot_mat[index_0, index_1] = - np.sqrt( 1 - C**2/lam**2 )
condrot_mat[index_1, index_1] = C / lam
else:
condrot_mat[index_0, index_0] = 1.
condrot_mat[index_1, index_1] = 1.
## DenseGateに変換して実装
condrot_gate = gate.DenseMatrix(np.arange(nbit, nbit+reg_nbit+1), condrot_mat)
total_circuit.add_gate(condrot_gate)
## ------- Perform QFT to register bits -------
total_circuit.add_gate(QFT_gate(nbit, nbit+reg_nbit-1, Inverse=False))
## ------- 位相推定の逆を実装(U^\dagger = e^{-iAt}) -------
for register in range(nbit, nbit+reg_nbit): ## from nbit to nbit+reg_nbit-1
## {U^{\dagger}}^{2^{register-nbit}} を実装.
## 対角化した結果を使ってしまう
U_mat = reduce(np.dot, [P, np.diag(np.exp( -1.j* D * (2**(register-nbit)) )), P.T.conj()] )
U_gate = gate.DenseMatrix(np.arange(nbit), U_mat)
U_gate.add_control_qubit(register, 1) ## control bitの追加
total_circuit.add_gate(U_gate)
## ------- レジスターbit に Hadamard gate をかける -------
for register in range(nbit, nbit+reg_nbit):
total_circuit.add_H_gate(register)
## ------- 補助ビットを0に射影する. qulacsでは非ユニタリゲートとして実装されている -------
total_circuit.add_P0_gate(nbit+reg_nbit)
#####################################
### HHL量子回路を実行し, 結果を取り出す
#####################################
total_circuit.update_quantum_state(state)
## 0番目から(nbit-1)番目の bit が計算結果 |x>に対応
result = state.get_vector()[:2**nbit].real
x_HHL = result/C * scale_fac
```
HHL アルゴリズムによる解 `x_HHL` と、通常の古典計算の対角化による解 `x_exact` を比べると、概ね一致していることが分かる。(HHLアルゴリズムの精度を決めるパラメータはいくつかある(例えば`reg_nbit`)ので、それらを変えて色々試してみて頂きたい。)
```
## 厳密解
x_exact = np.linalg.lstsq(W_enl, mu_xi_0_enl, rcond=0)[0]
print("HHL: ", x_HHL)
print("exact:", x_exact)
rel_error = np.linalg.norm(x_HHL- x_exact) / np.linalg.norm(x_exact)
print("rel_error", rel_error)
```
実際のウェイトの部分だけ取り出すと
```
w_opt_HHL = x_HHL[2:6]
w_opt_exact = x_exact[2:6]
w_opt = pd.DataFrame(np.vstack([w_opt_exact, w_opt_HHL]).T, index=df.columns, columns=['exact', 'HHL'])
w_opt
w_opt.plot.bar()
```
※重みが負になっている銘柄は、「空売り」(株を借りてきて売ること。株価が下がる局面で利益が得られる手法)を表す。今回は目標リターンが10%と、GAFA株(単独で30〜40%の期待リターン)にしてはかなり小さい値を設定したため、空売りを行って全体の期待リターンを下げていると思われる。
### Appendix: バックテスト
過去のデータから得られた投資ルールを、それ以降のデータを用いて検証することを「バックテスト」と呼び、その投資ルールの有効性を測るために重要である。
ここでは以上のように2017年のデータから構築したポートフォリオに投資した場合に、翌年の2018年にどの程度資産価値が変化するかを観察する。
```
# 2018年の1年間のデータを使用
start = datetime.datetime(2017, 12, 30)
end = datetime.datetime(2018, 12, 31)
# Yahoo! Financeから日次の株価データを取得
data = web.DataReader(codes, 'yahoo', start, end)
df2018 = data['Adj Close']
display(df2018.tail())
## 株価をプロットしてみる
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15, 6))
df2018.loc[:,['AAPL', 'FB']].plot(ax=axes[0])
df2018.loc[:,['GOOG', 'AMZN']].plot(ax=axes[1])
# ポートフォリオの資産価値の推移
pf_value = df2018.dot(w_opt)
pf_value.head()
# exact と HHLで初期金額が異なることがありうるので、期初の値で規格化したリターンをみる。
pf_value.exact = pf_value.exact / pf_value.exact[0]
pf_value.HHL = pf_value.HHL / pf_value.HHL[0]
print(pf_value.tail())
pf_value.plot(figsize=(9, 6))
```
2018年はAmazon以外のGAFA各社の株式が軟調だったので、およそ-20%もの損が出ているが、exact解の方は多少マシであるようだ。。
ちなみに、元々行ったのはリスク最小化なので、この一年間のリスクも計算してみると、exact解の方が小さい結果となった。
```
pf_value.pct_change().std() * np.sqrt(252) ## 年率換算
```
### 参考文献
[1] P. Rebentrost and S. Lloyd, “Quantum computational finance: quantum algorithm for portfolio optimization“, https://arxiv.org/abs/1811.03975
|
github_jupyter
|
# Create redo records
This Jupyter notebook shows how to create a Senzing "redo record".
It assumes a G2 database that is empty.
Essentially the steps are to create very similar records under different data sources,
then delete one of the records. This produces a "redo record".
## G2Engine
### Senzing initialization
Create an instance of G2Engine, G2ConfigMgr, and G2Config.
```
from G2Engine import G2Engine
from G2ConfigMgr import G2ConfigMgr
from G2Config import G2Config
g2_engine = G2Engine()
try:
g2_engine_flags = G2Engine.G2_EXPORT_DEFAULT_FLAGS
g2_engine.initV2(
"pyG2EngineForRedoRecords",
senzing_config_json,
verbose_logging)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
g2_configuration_manager = G2ConfigMgr()
try:
g2_configuration_manager.initV2(
"pyG2ConfigMgrForRedoRecords",
senzing_config_json,
verbose_logging)
except G2Exception.G2ModuleGenericException as err:
print(g2_configuration_manager.getLastException())
g2_config = G2Config()
try:
g2_config.initV2(
"pyG2ConfigForRedoRecords",
senzing_config_json,
verbose_logging)
config_handle = g2_config.create()
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
### primeEngine
```
try:
g2_engine.primeEngine()
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Variable initialization
```
load_id = None
```
### Create add data source function
Create a data source with a name having the form `TEST_DATA_SOURCE_nnn`.
```
def add_data_source(datasource_suffix):
datasource_prefix = "TEST_DATA_SOURCE_"
datasource_id = "{0}{1}".format(datasource_prefix, datasource_suffix)
configuration_comment = "Added {}".format(datasource_id)
g2_config.addDataSource(config_handle, datasource_id)
configuration_bytearray = bytearray()
return_code = g2_config.save(config_handle, configuration_bytearray)
configuration_json = configuration_bytearray.decode()
configuration_id_bytearray = bytearray()
g2_configuration_manager.addConfig(configuration_json, configuration_comment, configuration_id_bytearray)
g2_configuration_manager.setDefaultConfigID(configuration_id_bytearray)
g2_engine.reinitV2(configuration_id_bytearray)
```
### Create add record function
Create a record with the id having the form `RECORD_nnn`.
**Note:** this is essentially the same record with only the `DRIVERS_LICENSE_NUMBER` modified slightly.
```
def add_record(record_id_suffix, datasource_suffix):
datasource_prefix = "TEST_DATA_SOURCE_"
record_id_prefix = "RECORD_"
datasource_id = "{0}{1}".format(datasource_prefix, datasource_suffix)
record_id = "{0}{1}".format(record_id_prefix, record_id_suffix)
data = {
"NAMES": [{
"NAME_TYPE": "PRIMARY",
"NAME_LAST": "Smith",
"NAME_FIRST": "John",
"NAME_MIDDLE": "M"
}],
"PASSPORT_NUMBER": "PP11111",
"PASSPORT_COUNTRY": "US",
"DRIVERS_LICENSE_NUMBER": "DL1{:04d}".format(record_id_suffix),
"SSN_NUMBER": "111-11-1111"
}
data_as_json = json.dumps(data)
g2_engine.addRecord(
datasource_id,
record_id,
data_as_json,
load_id)
```
## Redo record
### Print data sources
Print the list of currently defined data sources.
```
try:
datasources_bytearray = bytearray()
g2_config.listDataSources(config_handle, datasources_bytearray)
datasources_dictionary = json.loads(datasources_bytearray.decode())
print(datasources_dictionary)
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
### Add data sources and records
```
try:
add_data_source(1)
add_record(1,1)
add_record(2,1)
add_data_source(2)
add_record(3,2)
add_record(4,2)
add_data_source(3)
add_record(5,3)
add_record(6,3)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Delete record
Deleting a record will create a "redo record".
```
try:
g2_engine.deleteRecord("TEST_DATA_SOURCE_3", "RECORD_5", load_id)
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Count redo records
The `count_of_redo_records` will show how many redo records are in Senzing's queue of redo records.
```
try:
count_of_redo_records = g2_engine.countRedoRecords()
print("Number of redo records: {0}".format(count_of_redo_records))
except G2Exception.G2ModuleGenericException as err:
print(g2_engine.getLastException())
```
### Print data sources again
Print the list of currently defined data sources.
```
try:
datasources_bytearray = bytearray()
g2_config.listDataSources(config_handle, datasources_bytearray)
datasources_dictionary = json.loads(datasources_bytearray.decode())
print(datasources_dictionary)
except G2Exception.G2ModuleGenericException as err:
print(g2_config.getLastException())
```
|
github_jupyter
|
```
%matplotlib inline
```
Neural Transfer Using PyTorch
=============================
**Author**: `Alexis Jacq <https://alexis-jacq.github.io>`_
**Edited by**: `Winston Herring <https://github.com/winston6>`_
**Re-implemented by:** `Shubhajit Das <https://github.com/Shubhajitml>`
Introduction
------------
This tutorial explains how to implement the `Neural-Style algorithm <https://arxiv.org/abs/1508.06576>`__
developed by Leon A. Gatys, Alexander S. Ecker and Matthias Bethge.
Neural-Style, or Neural-Transfer, allows you to take an image and
reproduce it with a new artistic style. The algorithm takes three images,
an input image, a content-image, and a style-image, and changes the input
to resemble the content of the content-image and the artistic style of the style-image.
.. figure:: /_static/img/neural-style/neuralstyle.png
:alt: content1
Underlying Principle
--------------------
The principle is simple: we define two distances, one for the content
($D_C$) and one for the style ($D_S$). $D_C$ measures how different the content
is between two images while $D_S$ measures how different the style is
between two images. Then, we take a third image, the input, and
transform it to minimize both its content-distance with the
content-image and its style-distance with the style-image. Now we can
import the necessary packages and begin the neural transfer.
Importing Packages and Selecting a Device
-----------------------------------------
Below is a list of the packages needed to implement the neural transfer.
- ``torch``, ``torch.nn``, ``numpy`` (indispensables packages for
neural networks with PyTorch)
- ``torch.optim`` (efficient gradient descents)
- ``PIL``, ``PIL.Image``, ``matplotlib.pyplot`` (load and display
images)
- ``torchvision.transforms`` (transform PIL images into tensors)
- ``torchvision.models`` (train or load pre-trained models)
- ``copy`` (to deep copy the models; system package)
```
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
!ls
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from PIL import Image
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
import torchvision.models as models
import copy
```
Next, we need to choose which device to run the network on and import the
content and style images. Running the neural transfer algorithm on large
images takes longer and will go much faster when running on a GPU. We can
use ``torch.cuda.is_available()`` to detect if there is a GPU available.
Next, we set the ``torch.device`` for use throughout the tutorial. Also the ``.to(device)``
method is used to move tensors or modules to a desired device.
```
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
Loading the Images
------------------
Now we will import the style and content images. The original PIL images have values between 0 and 255, but when
transformed into torch tensors, their values are converted to be between
0 and 1. The images also need to be resized to have the same dimensions.
An important detail to note is that neural networks from the
torch library are trained with tensor values ranging from 0 to 1. If you
try to feed the networks with 0 to 255 tensor images, then the activated
feature maps will be unable sense the intended content and style.
However, pre-trained networks from the Caffe library are trained with 0
to 255 tensor images.
.. Note::
Here are links to download the images required to run the tutorial:
`picasso.jpg <https://pytorch.org/tutorials/_static/img/neural-style/picasso.jpg>`__ and
`dancing.jpg <https://pytorch.org/tutorials/_static/img/neural-style/dancing.jpg>`__.
Download these two images and add them to a directory
with name ``images`` in your current working directory.
```
# desired size of the output image
imsize = 512 if torch.cuda.is_available() else 128 # use small size if no gpu
loader = transforms.Compose([
transforms.Resize(imsize), # scale imported image
transforms.ToTensor()]) # transform it into a torch tensor
def image_loader(image_name):
image = Image.open(image_name)
# fake batch dimension required to fit network's input dimensions
image = loader(image).unsqueeze(0)
return image.to(device, torch.float)
style_img = image_loader("colorful.jpg")
content_img = image_loader("shubha.jpg")
assert style_img.size() == content_img.size(), \
"we need to import style and content images of the same size"
```
Now, let's create a function that displays an image by reconverting a
copy of it to PIL format and displaying the copy using
``plt.imshow``. We will try displaying the content and style images
to ensure they were imported correctly.
```
unloader = transforms.ToPILImage() # reconvert into PIL image
plt.ion()
def imshow(tensor, title=None):
image = tensor.cpu().clone() # we clone the tensor to not do changes on it
image = image.squeeze(0) # remove the fake batch dimension
image = unloader(image)
plt.imshow(image)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
plt.figure()
imshow(style_img, title='Style Image')
plt.figure()
imshow(content_img, title='Content Image')
```
Loss Functions
--------------
Content Loss
~~~~~~~~~~~~
The content loss is a function that represents a weighted version of the
content distance for an individual layer. The function takes the feature
maps $F_{XL}$ of a layer $L$ in a network processing input $X$ and returns the
weighted content distance $w_{CL}.D_C^L(X,C)$ between the image $X$ and the
content image $C$. The feature maps of the content image($F_{CL}$) must be
known by the function in order to calculate the content distance. We
implement this function as a torch module with a constructor that takes
$F_{CL}$ as an input. The distance $\|F_{XL} - F_{CL}\|^2$ is the mean square error
between the two sets of feature maps, and can be computed using ``nn.MSELoss``.
We will add this content loss module directly after the convolution
layer(s) that are being used to compute the content distance. This way
each time the network is fed an input image the content losses will be
computed at the desired layers and because of auto grad, all the
gradients will be computed. Now, in order to make the content loss layer
transparent we must define a ``forward`` method that computes the content
loss and then returns the layer’s input. The computed loss is saved as a
parameter of the module.
```
class ContentLoss(nn.Module):
def __init__(self, target,):
super(ContentLoss, self).__init__()
# we 'detach' the target content from the tree used
# to dynamically compute the gradient: this is a stated value,
# not a variable. Otherwise the forward method of the criterion
# will throw an error.
self.target = target.detach()
def forward(self, input):
self.loss = F.mse_loss(input, self.target)
return input
```
.. Note::
**Important detail**: although this module is named ``ContentLoss``, it
is not a true PyTorch Loss function. If you want to define your content
loss as a PyTorch Loss function, you have to create a PyTorch autograd function
to recompute/implement the gradient manually in the ``backward``
method.
Style Loss
~~~~~~~~~~
The style loss module is implemented similarly to the content loss
module. It will act as a transparent layer in a
network that computes the style loss of that layer. In order to
calculate the style loss, we need to compute the gram matrix $G_{XL}$. A gram
matrix is the result of multiplying a given matrix by its transposed
matrix. In this application the given matrix is a reshaped version of
the feature maps $F_{XL}$ of a layer $L$. $F_{XL}$ is reshaped to form $\hat{F}_{XL}$, a $K$\ x\ $N$
matrix, where $K$ is the number of feature maps at layer $L$ and $N$ is the
length of any vectorized feature map $F_{XL}^k$. For example, the first line
of $\hat{F}_{XL}$ corresponds to the first vectorized feature map $F_{XL}^1$.
Finally, the gram matrix must be normalized by dividing each element by
the total number of elements in the matrix. This normalization is to
counteract the fact that $\hat{F}_{XL}$ matrices with a large $N$ dimension yield
larger values in the Gram matrix. These larger values will cause the
first layers (before pooling layers) to have a larger impact during the
gradient descent. Style features tend to be in the deeper layers of the
network so this normalization step is crucial.
```
def gram_matrix(input):
a, b, c, d = input.size() # a=batch size(=1)
# b=number of feature maps
# (c,d)=dimensions of a f. map (N=c*d)
features = input.view(a * b, c * d) # resise F_XL into \hat F_XL
G = torch.mm(features, features.t()) # compute the gram product
# we 'normalize' the values of the gram matrix
# by dividing by the number of element in each feature maps.
return G.div(a * b * c * d)
```
Now the style loss module looks almost exactly like the content loss
module. The style distance is also computed using the mean square
error between $G_{XL}$ and $G_{SL}$.
```
class StyleLoss(nn.Module):
def __init__(self, target_feature):
super(StyleLoss, self).__init__()
self.target = gram_matrix(target_feature).detach()
def forward(self, input):
G = gram_matrix(input)
self.loss = F.mse_loss(G, self.target)
return input
```
Importing the Model
-------------------
Now we need to import a pre-trained neural network. We will use a 19
layer VGG network like the one used in the paper.
PyTorch’s implementation of VGG is a module divided into two child
``Sequential`` modules: ``features`` (containing convolution and pooling layers),
and ``classifier`` (containing fully connected layers). We will use the
``features`` module because we need the output of the individual
convolution layers to measure content and style loss. Some layers have
different behavior during training than evaluation, so we must set the
network to evaluation mode using ``.eval()``.
```
cnn = models.vgg19(pretrained=True).features.to(device).eval()
```
Additionally, VGG networks are trained on images with each channel
normalized by mean=[0.485, 0.456, 0.406] and std=[0.229, 0.224, 0.225].
We will use them to normalize the image before sending it into the network.
```
cnn_normalization_mean = torch.tensor([0.485, 0.456, 0.406]).to(device)
cnn_normalization_std = torch.tensor([0.229, 0.224, 0.225]).to(device)
# create a module to normalize input image so we can easily put it in a
# nn.Sequential
class Normalization(nn.Module):
def __init__(self, mean, std):
super(Normalization, self).__init__()
# .view the mean and std to make them [C x 1 x 1] so that they can
# directly work with image Tensor of shape [B x C x H x W].
# B is batch size. C is number of channels. H is height and W is width.
self.mean = torch.tensor(mean).view(-1, 1, 1)
self.std = torch.tensor(std).view(-1, 1, 1)
def forward(self, img):
# normalize img
return (img - self.mean) / self.std
```
A ``Sequential`` module contains an ordered list of child modules. For
instance, ``vgg19.features`` contains a sequence (Conv2d, ReLU, MaxPool2d,
Conv2d, ReLU…) aligned in the right order of depth. We need to add our
content loss and style loss layers immediately after the convolution
layer they are detecting. To do this we must create a new ``Sequential``
module that has content loss and style loss modules correctly inserted.
```
# desired depth layers to compute style/content losses :
content_layers_default = ['conv_4']
style_layers_default = ['conv_1', 'conv_2', 'conv_3', 'conv_4', 'conv_5']
def get_style_model_and_losses(cnn, normalization_mean, normalization_std,
style_img, content_img,
content_layers=content_layers_default,
style_layers=style_layers_default):
cnn = copy.deepcopy(cnn)
# normalization module
normalization = Normalization(normalization_mean, normalization_std).to(device)
# just in order to have an iterable access to or list of content/syle
# losses
content_losses = []
style_losses = []
# assuming that cnn is a nn.Sequential, so we make a new nn.Sequential
# to put in modules that are supposed to be activated sequentially
model = nn.Sequential(normalization)
i = 0 # increment every time we see a conv
for layer in cnn.children():
if isinstance(layer, nn.Conv2d):
i += 1
name = 'conv_{}'.format(i)
elif isinstance(layer, nn.ReLU):
name = 'relu_{}'.format(i)
# The in-place version doesn't play very nicely with the ContentLoss
# and StyleLoss we insert below. So we replace with out-of-place
# ones here.
layer = nn.ReLU(inplace=False)
elif isinstance(layer, nn.MaxPool2d):
name = 'pool_{}'.format(i)
elif isinstance(layer, nn.BatchNorm2d):
name = 'bn_{}'.format(i)
else:
raise RuntimeError('Unrecognized layer: {}'.format(layer.__class__.__name__))
model.add_module(name, layer)
if name in content_layers:
# add content loss:
target = model(content_img).detach()
content_loss = ContentLoss(target)
model.add_module("content_loss_{}".format(i), content_loss)
content_losses.append(content_loss)
if name in style_layers:
# add style loss:
target_feature = model(style_img).detach()
style_loss = StyleLoss(target_feature)
model.add_module("style_loss_{}".format(i), style_loss)
style_losses.append(style_loss)
# now we trim off the layers after the last content and style losses
for i in range(len(model) - 1, -1, -1):
if isinstance(model[i], ContentLoss) or isinstance(model[i], StyleLoss):
break
model = model[:(i + 1)]
return model, style_losses, content_losses
```
Next, we select the input image. You can use a copy of the content image
or white noise.
```
input_img = content_img.clone()
# if you want to use white noise instead uncomment the below line:
# input_img = torch.randn(content_img.data.size(), device=device)
# add the original input image to the figure:
plt.figure()
imshow(input_img, title='Input Image')
```
Gradient Descent
----------------
As Leon Gatys, the author of the algorithm, suggested `here <https://discuss.pytorch.org/t/pytorch-tutorial-for-neural-transfert-of-artistic-style/336/20?u=alexis-jacq>`__, we will use
L-BFGS algorithm to run our gradient descent. Unlike training a network,
we want to train the input image in order to minimise the content/style
losses. We will create a PyTorch L-BFGS optimizer ``optim.LBFGS`` and pass
our image to it as the tensor to optimize.
```
def get_input_optimizer(input_img):
# this line to show that input is a parameter that requires a gradient
optimizer = optim.LBFGS([input_img.requires_grad_()])
return optimizer
```
Finally, we must define a function that performs the neural transfer. For
each iteration of the networks, it is fed an updated input and computes
new losses. We will run the ``backward`` methods of each loss module to
dynamicaly compute their gradients. The optimizer requires a “closure”
function, which reevaluates the modul and returns the loss.
We still have one final constraint to address. The network may try to
optimize the input with values that exceed the 0 to 1 tensor range for
the image. We can address this by correcting the input values to be
between 0 to 1 each time the network is run.
```
def run_style_transfer(cnn, normalization_mean, normalization_std,
content_img, style_img, input_img, num_steps=500,
style_weight=1000000, content_weight=1):
"""Run the style transfer."""
print('Building the style transfer model..')
model, style_losses, content_losses = get_style_model_and_losses(cnn,
normalization_mean, normalization_std, style_img, content_img)
optimizer = get_input_optimizer(input_img)
print('Optimizing..')
run = [0]
while run[0] <= num_steps:
def closure():
# correct the values of updated input image
input_img.data.clamp_(0, 1)
optimizer.zero_grad()
model(input_img)
style_score = 0
content_score = 0
for sl in style_losses:
style_score += sl.loss
for cl in content_losses:
content_score += cl.loss
style_score *= style_weight
content_score *= content_weight
loss = style_score + content_score
loss.backward()
run[0] += 1
if run[0] % 50 == 0:
print("run {}:".format(run))
print('Style Loss : {:4f} Content Loss: {:4f}'.format(
style_score.item(), content_score.item()))
print()
return style_score + content_score
optimizer.step(closure)
# a last correction...
input_img.data.clamp_(0, 1)
return input_img
```
Finally, we can run the algorithm.
```
output = run_style_transfer(cnn, cnn_normalization_mean, cnn_normalization_std,
content_img, style_img, input_img)
plt.figure()
imshow(output, title='Output Image')
# sphinx_gallery_thumbnail_number = 4
plt.ioff()
plt.show()
```
|
github_jupyter
|
### Training a Graph Convolution Model
Now that we have the data appropriately formatted, we can use this data to train a Graph Convolution model. First we need to import the necessary libraries.
```
import deepchem as dc
from deepchem.models import GraphConvModel
import numpy as np
import sys
import pandas as pd
import seaborn as sns
from rdkit.Chem import PandasTools
from tqdm.auto import tqdm
```
Now let's define a function to create a GraphConvModel. In this case we will be creating a classification model. Since we will be apply the model later on a different dataset, it's a good idea to create a directory in which to store the model.
```
def generate_graph_conv_model():
batch_size = 128
model = GraphConvModel(1, batch_size=batch_size, mode='classification', model_dir="./model_dir")
return model
```
Now we will read in the dataset that we just created.
```
dataset_file = "dude_erk2_mk01.csv"
tasks = ["is_active"]
featurizer = dc.feat.ConvMolFeaturizer()
loader = dc.data.CSVLoader(tasks=tasks, feature_field="SMILES", featurizer=featurizer)
dataset = loader.create_dataset(dataset_file, shard_size=8192)
```
Now that we have the dataset loaded, let's build a model.
We will create training and test sets to evaluate the model's performance. In this case we will use the RandomSplitter(). DeepChem offers a number of other splitters such as the ScaffoldSplitter, which will divide the dataset by chemical scaffold or the ButinaSplitter which will first cluster the data then split the dataset so that different clusters will end up in the training and test sets.
```
splitter = dc.splits.RandomSplitter()
```
With the dataset split, we can train a model on the training set and test that model on the validation set.
At this point we can define some metrics and evaluate the performance of our model. In this case our dataset is unbalanced, we have a small number of active compounds and a large number of inactive compounds. Given this difference, we need to use a metric that reflects the performance on unbalanced datasets. One metric that is apporpriate for datasets like this is the Matthews correlation coefficient (MCC). Put more info about MCC here.
```
metrics = [dc.metrics.Metric(dc.metrics.matthews_corrcoef, np.mean)]
```
In order to evaluate the performance of our moldel, we will perform 10 folds of cross valiation, where we train a model on the training set and validate on the validation set.
```
training_score_list = []
validation_score_list = []
transformers = []
cv_folds = 10
for i in tqdm(range(0,cv_folds)):
model = generate_graph_conv_model()
train_dataset, valid_dataset, test_dataset = splitter.train_valid_test_split(dataset)
model.fit(train_dataset)
train_scores = model.evaluate(train_dataset, metrics, transformers)
training_score_list.append(train_scores["mean-matthews_corrcoef"])
validation_scores = model.evaluate(valid_dataset, metrics, transformers)
validation_score_list.append(validation_scores["mean-matthews_corrcoef"])
print(training_score_list)
print(validation_score_list)
```
To visualize the preformance of our models on the training and test data, we can make boxplots of the models' performance.
```
sns.boxplot(x=["training"]*cv_folds+["validation"]*cv_folds,y=training_score_list+validation_score_list);
```
It is also useful to visualize the result of our model. In order to do this, we will generate a set of predictions for a validation set.
```
pred = [x.flatten() for x in model.predict(valid_dataset)]
pred
```
**The results of predict on a GraphConv model are returned as a list of lists. Is this the intent? It doesn't seem consistent across models. RandomForest returns a list. For convenience, we will put our predicted results into a Pandas dataframe.**
```
pred_df = pd.DataFrame(pred,columns=["neg","pos"])
```
We can easily add the activity class (1 = active, 0 = inactive) and the SMILES string for our predicted moleculesto the dataframe. __Is the moleculed id retained as part of the DeepChem dataset? I can't find it__
```
pred_df["active"] = [int(x) for x in valid_dataset.y]
pred_df["SMILES"] = valid_dataset.ids
pred_df.head()
pred_df.sort_values("pos",ascending=False).head(25)
sns.boxplot(x=pred_df.active,y=pred_df.pos)
```
The performance of our model is very good, we can see a clear separation between the active and inactive compounds. It appears that only one of our active compounds receieved a low positive score. Let's look more closely.
```
false_negative_df = pred_df.query("active == 1 & pos < 0.5").copy()
PandasTools.AddMoleculeColumnToFrame(false_negative_df,"SMILES","Mol")
false_negative_df
false_positive_df = pred_df.query("active == 0 & pos > 0.5").copy()
PandasTools.AddMoleculeColumnToFrame(false_positive_df,"SMILES","Mol")
false_positive_df
```
Now that we've evaluated our model's performance we can retrain the model on the entire dataset and save it.
```
model.fit(dataset)
```
|
github_jupyter
|
# Transmission
```
%matplotlib inline
import numpy as np
np.seterr(divide='ignore') # Ignore divide by zero in log plots
from scipy import signal
import scipy.signal
from numpy.fft import fft, fftfreq
import matplotlib.pyplot as plt
#import skrf as rf # pip install scikit-rf if you want to run this one
```
First, let's set up a traditional, full-precision modulator and plot the spectrum of that as a baseline
```
def prbs(n=0, taps=[]):
state = [1]*n
shift = lambda s: [sum([s[i] for i in taps]) % 2] + s[0:-1]
out = []
for i in range(2**n - 1):
out.append(state[-1])
state = shift(state)
return out
prbs9 = lambda: prbs(n=9, taps=[4,8])
def make_carrier(freq=None, sample_rate=None, samples=None, phase=0):
t = (1/sample_rate)*np.arange(samples)
return np.real(np.exp(1j*(2*np.pi*freq*t - phase)))
def modulate_gmsk(bits, carrier_freq=2.402e9, sample_rate=5e9, baseband=False, phase_offset=0, include_phase=False):
symbol_rate = 1e6 # 1Mhz
BT = 0.5
bw = symbol_rate*BT/sample_rate
samples_per_symbol = int(sample_rate/symbol_rate)
# This looks scary but it's just a traditional gaussian distribution from wikipedia
kernel = np.array([(np.sqrt(2*np.pi/np.log(2))*bw)*np.exp(-(2/np.log(2))*np.power(np.pi*t*bw, 2)) for t in range(-5000,5000)])
kernel /= sum(kernel) # Normalize so things amplitude after convolution remains the same
rotation = np.repeat(bits, sample_rate/symbol_rate)*2.0 - 1.0
smoothed_rotation = np.convolve(rotation, kernel,mode='same')
angle_per_sample = (np.pi/2.0)/(samples_per_symbol)
current_angle = phase_offset
modulated = np.zeros((len(smoothed_rotation),), dtype=np.complex64) # Represents I and Q as a complex number
i = 0
for bit in smoothed_rotation:
current_angle += angle_per_sample*bit
modulated[i] = np.exp(1j*current_angle)
i += 1
if baseband:
return modulated
I = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(modulated), phase=0)
Q = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(modulated), phase=np.pi/2)
if include_phase:
return np.real(modulated)*I + np.imag(modulated)*Q, np.angle(modulated)
return np.real(modulated)*I + np.imag(modulated)*Q
```
Now let's look at the FFT of this...
```
sample_rate = 6e9
modulated = modulate_gmsk(prbs9(), sample_rate=sample_rate)
fftm = np.abs(fft(modulated))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(modulated), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.gca().set_ylim(-40, 0)
```
This is clean (as one would expect), now let's see what happens if we reduce things to 1-bit of precision by just rounding
# The Naive Approach (Rounding)
```
sample_rate=5e9
modulates_5g = modulated = np.sign(modulate_gmsk(prbs9(), sample_rate=sample_rate))
fftm = np.abs(fft(modulated))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(modulated), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
```
_Oof_ this is not pretty. What's happening here is that (I think) the aliases are mixing with each other to produce these interference paterns. In this case, it looks like the big subharmonics are spaced about 200Mhz which makes sense given the alias of 2.402ghz at 2.698ghz when sampling at 2.5ghz.
```
sample_rate = 6e9
modulated_6g = modulated = np.sign(modulate_gmsk(prbs9(), sample_rate=sample_rate))
fftm = np.abs(fft(modulated))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(modulated), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
plt.title("Unfiltered")
```
Ok, in this case, the alias is at `3 + (3 - 2.402) = 3.6ghz`. The difference between this and 2.402ghz is about 1.2ghz, which looking at the next big peak, looks to be about 1.2ghz, so this makes sense. From this math, we can intuit that it's a good idea for the sample rate to be a whole number multiple of the carrier frequency. In the ideal case, 4 times the carrier:
```
sample_rate = 2.402e9*4
modulated_4x = modulated = np.sign(modulate_gmsk(prbs9(), sample_rate=sample_rate))
fftm = np.abs(fft(modulated))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(modulated), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
```
There a couple of challenges here, however:
1. In order to get the clean(ish) spectrum, we have to clock the output frequency at a rate relative to the carrier frequency. If we only intended to use one frequency, this would be fine but Bluetooth (as an example) hops around frequency constantly by design. This might be doable, but it's kind of painful (this might require various SERDES resets which aren't instantaneous)
2. At 2.402ghz, 4x this would be... 9.6ghz, which is too fast for my (low-end-ish) SERDES which maxes out around 6ghz.
# Adding a Reconstruction Filter
In order to prevent a friendly visit from an unmarked FCC van, it's more or less mandatory that we filter noise outside of the band of interest. In our case, I have a tiny 2.4Ghz surface mount band pass filter that I've put onto a test board. This is the delightfully named "DEA252450BT-2027A1" which is a surface mount part which has a frequency response of:

To (more fully) characterize this filter, I hooked it up to a NanoVNA2 and saved its S parameters using a NanoVNA Saver:
```
# pip install scikit-rf if you want to run this one
# Note: running this before we've plotted anything, borks matplotlib
import skrf as rf
filter2_4 = rf.Network('2_4ghzfilter.s2p')
filter2_4.s21.plot_s_db()
```
Hey that's not too far off from data sheet (at least up to 4.4Ghz).
To turn this into a filter, we can use the scipy-rf to compute an impulse response which we can then convolve with our input data to see what the filtered output would be:
```
ts, ms = filter2_4.s21.impulse_response()
impulse_response = ms[list(ts).index(0):]
impulse_response = impulse_response/np.max(impulse_response)
tstep = ts[1] - ts[0]
print("Timestep {} seconds, frequency {:e} hz".format(tstep, 1/tstep))
plt.plot(impulse_response)
plt.gca().set_xlim(0, 300)
```
This is great and all but the impulse response is sampled at north of 30ghz (!). Our output serdes runs at around 6ghz so let's resample this to that rate
```
# Truncate the impulse response so we can get relatively close to 6ghz
trunc = impulse_response[:-4]
size = int((tstep*(len(trunc) - 1))/(1/6e9) + 1)
print(size)
impulse_response_6g = scipy.signal.resample(impulse_response, size)
plt.plot(impulse_response_6g)
plt.gca().set_xlim(0, 50)
```
Not quite as pretty, but it's what we need. Let's verify that this does "the thing" by filtering our 6ghz signal:
```
sample_rate=6e9
fftm = np.abs(fft(np.convolve(modulated_6g, impulse_response_6g, mode="same")))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(fftm), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.grid(b=True)
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
```
This looks better, but the passband for my filter is still super wide (hundreds of MHz, not surprising for a 50c filter, I should look at B39242B9413K610 which is a $1 surface acoustic wave filter). We see some nontrivial imaging up to -12db, which is... not great.
What to do?
# Delta Sigma Modulation
A way around this is to use something called Delta Sigma Modulation. The way to think about this conceptually is that we keep a running sum of values we've output (think of this as the error) and factor this into the value we decide to output (versus just blindly rounding the current value). Further, you can filter this feedback loop to "shape" the noise to different parts of the spectrum (that we can filter out elsewhere).
A good place to read about this is [Wikipedia](https://en.wikipedia.org/wiki/Delta-sigma_modulation#Oversampling). In [Novel Architectures for Flexible and Wideband All-digital Transmitters](https://ria.ua.pt/bitstream/10773/23875/1/Documento.pdf) by Rui Fiel Cordeiro, Rui proposes using a filter that has a zero at the carrier of interest, which looks like the following
```
def pwm2(sig, k=1.0):
z1 = 0.0
z2 = 0.0
out = np.zeros((len(sig,)))
for i in range(len(sig)):
v = sig[i] - (k*z1 + z2)
out[i] = np.sign(v)
z2 = z1
z1 = v - out[i]
return out
```
To be clear, `pwm2` is replacing `np.sign`
```
sample_rate = 6e9
modulated = modulate_gmsk(prbs9(), sample_rate=sample_rate)
modulatedsd5 = modulated = pwm2(modulated, k=-2.0*np.cos(2.0*np.pi*2.402e9/sample_rate))
fftm = np.abs(fft(np.sign(modulated)))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(modulated), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
plt.title("Second order Delta Sigma Modulation")
```
Now let's filter this with our output filter
```
fftm = np.abs(fft(np.convolve(modulatedsd5, impulse_response_6g, mode="same")))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(fftm), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.grid(b=True)
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
plt.title("Filtered Second Order Delta Sigma Modulation")
```
This is better in the immediate vicinity of our signal.
You'll notice on the wikipedia page that we can use increasing filter orders to increase the steepness of the valley around our signal of interest.
On one hand this is good, but because our filter is not very good (tm) this actually results in higher peaks than we'd like at around 2.2ghz.
Given that our filter is... not that good, can we design the filter in the modulator to compliment it?
# Filter-Aware Sigma Delta Modulator
I lay no claim to this awesome work by the folks who wrote pydsm, but it's great -- feed it an impulse response for a reconstruction filter and it will optimize a noise transfer function that matches it:
```
from pydsm.ir import impulse_response
from pydsm.delsig import synthesizeNTF, simulateDSM, evalTF
from pydsm.delsig import dbv, dbp
from pydsm.NTFdesign import quantization_noise_gain
from pydsm.NTFdesign.legacy import q0_from_filter_ir
from pydsm.NTFdesign.weighting import ntf_fir_from_q0
H_inf = 1.6 # This is out of band noise level in dB
q0 = q0_from_filter_ir(51, impulse_response_6g) # 51 is the number of filter coefficients
ntf_opti = ntf_fir_from_q0(q0, H_inf=H_inf)
```
Let's see how well we did. Anecdotally, this is not a _great_ solution (likely constrained by the low oversampling) but I'd wager this is because the oversampling rate is super low.
```
# Take the frequency response
samples = filter2_4.s21.s_db[:,0,0]
# Normalize the samples
ff = filter2_4.f/6e9
# Compute frequency response data
resp_opti = evalTF(ntf_opti, np.exp(1j*2*np.pi*ff))
# Plot the output filter,
plt.figure()
plt.plot(ff*6e9, dbv(resp_opti), 'r', label="Optimal NTF")
plt.plot(ff*6e9, samples, 'b', label="External Filter")
plt.plot(ff*6e9, dbv(resp_opti) + samples, 'g', label="Resulting Noise Shape")
plt.gca().set_xlim(0, 3e9)
plt.legend(loc="lower right")
plt.suptitle("Output filter and NTFs")
```
Ok, so it's not amazing but definitely an improvement. But now that we've got this monstrous 49 coefficient NTF, how do we modulate with it?
Fortunately we have the pydsm to the rescue!
```
sample_rate = 6e9
modulated = modulate_gmsk(prbs9(), sample_rate=sample_rate)
xx_opti = simulateDSM(modulated, ntf_opti)
fftm = np.abs(fft(np.convolve(xx_opti[0], impulse_response_6g, mode="same")))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(fftm), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.grid(b=True)
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
```
Ok, so we've basically "filled in the valley" with the peaks from eithe sides. We've cut the max spurs down by about 3db. Not amazing, but not bad!
After looking around at SAW filters I realized how impressive they can be in this frequency rance, so I tried to order one (CBPFS-2441) and try with that. Unfortunately, the datasheets only show _drawing_ of parameters (and only phase) and actual s2p files are impossible to find. This seems dumb. Nevertheless, https://apps.automeris.io/wpd/ exists which allow you to extimate a graph from an image.
```
import csv
from scipy.interpolate import interp1d
traced = np.array([(float(f), float(d)) for f,d in csv.reader(open('saw_filter_traced.csv'))])
# Interpolate to 600 equally spaced points (this means 1200 total, so 1200 * 5MHz -> 6GHz sampling rate)
x = traced[:,0]
y = -1*traced[:,1]
f = interp1d(x, y)
x = np.array(np.linspace(5, 3000, 600))
y = np.array(f(x))
x = np.concatenate((np.flip(x)*-1, np.array([0]), x))
# In FFT format
y_orig = 10**(np.concatenate((np.array([-70]), y, np.flip(y)))/10)
y = 10**(np.concatenate((np.flip(y), np.array([-70]), y))/10.0)
plt.plot(x, 10*np.log10(y))
```
Let's look at the impulse respponse quickly
```
impulse = np.fft.ifft(y_orig)
impulse_trunc = impulse[:300]
plt.plot(np.real(impulse_trunc))
```
**Update:** The filter finally arrived and I can characterize it, as shown below...
(the remaining code uses the measured filter response rather than the one trace from the image)
```
sawfilter = rf.Network('crysteksawfilter.s2p')
sawfilter.s21.plot_s_db()
filter2_4.s21.plot_s_db()
ts, ms = sawfilter.s21.impulse_response()
impulse_response = ms[list(ts).index(0):]
impulse_response = impulse_response/np.max(impulse_response)
tstep = ts[1] - ts[0]
print("Timestep {} seconds, frequency {:e} hz".format(tstep, 1/tstep))
plt.plot(impulse_response)
plt.gca().set_xlim(0, 600)
plt.show()
trunc = impulse_response[:-2]
size = int((tstep*(len(trunc) - 1))/(1/6e9) + 1)
print(size)
impulse_response_6g = scipy.signal.resample(impulse_response, size)
plt.plot(impulse_response_6g)
plt.gca().set_xlim(0, 400)
```
Wow that is a fair bit sharper.
```
H_inf = 1.5
q0 = q0_from_filter_ir(49, np.real(impulse_response_6g))
ntf_opti = ntf_fir_from_q0(q0, H_inf=H_inf)
# Take the frequency response
#samples = 10*np.log10(y)
# Normalize the samples
#ff = x*1e6/6e9
# Take the frequency response
samples = sawfilter.s21.s_db[:,0,0]
# Normalize the samples
ff = sawfilter.f/6e9
# Compute frequency response data
resp_opti = evalTF(ntf_opti, np.exp(1j*2*np.pi*ff))
# Plot the output filter,
plt.figure()
plt.plot(ff*6e9, dbv(resp_opti), 'r', label="Optimal NTF")
plt.plot(ff*6e9, samples, 'b', label="External Filter")
plt.plot(ff*6e9, dbv(resp_opti) + samples, 'g', label="Resulting Noise Shape")
plt.gca().set_xlim(0, 3e9)
plt.legend(loc="lower left")
plt.suptitle("Output filter and NTFs")
sample_rate = 6e9
modulated = modulate_gmsk(prbs9(), sample_rate=sample_rate)
xx_opti = simulateDSM(modulated, ntf_opti)
fftm = np.abs(fft(np.convolve(xx_opti[0], impulse_response_6g, mode="same")))
fftm = fftm/np.max(fftm)
fftbins = fftfreq(len(fftm), 1/sample_rate)
plt.figure(figsize=(10,6))
plt.plot(fftbins, 10*np.log10(fftm))
plt.grid(b=True)
plt.gca().set_ylim(-40, 0)
plt.gca().set_xlim(0, 3e9)
plt.title("Optimized Filtered Output")
```
Wow, the baseline noise level has dropped by almost 10db! Impressive!
# Symbol Dictionaries
Now that we've figured out how much noise we can stifle with this setup, we can begin to design our transmitter.
Now you may notice that the above noise transfer function filter is... quite expensive, clocking in at 51 coefficients. While we might be able to implement this on our FPGA, a better question is -- can we avoid it?
Given that we're transmitting digital data with a finite number of symbols, it turns out we can just pre-compute the symbols, store them in a dictionary and then play back the relevant pre-processed symbol when we need to transmit a given symbol. Simple!
Except, GMSK is not _quite_ that simple in this context because not only do we have to consider 1s and 0s but also where we currently are on a phase plot. If you think about GMSK visually on a constellation diagram, one symbols is recomended by a 90 degree arc on a unit circle that is either moving clockwise or counter clockwise. This is futher complicated by the fact that the gaussian smoothing, makes the velocity of the arc potentially slow down if the next bit is different from the current bit (because it needs to gradually change direction).
The result of this (if you enumerate out all the computations) is that we actually end up with a 32-symbol table. This is not the _only_ way to simplify these symbols, nor the most efficient, but it's simplest from an implementation perspective. I spent some time figuring out a train of bits that would iterate through each symbol. I'm sur ethere's a more optimal pattern, but efficiency is not hugely important when we only need to run this once when precomputing.
```
carrier_freq = 2.402e9
sample_rate = 6e9
symbol_rate = 1e6
samples_per_symbol = int(sample_rate/symbol_rate)
# Used to test that we've mapped things correctly.
# Note that this returns the phase angle, not the output bits
def demodulate_gmsk(sig, phase_offset=0):
I = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(sig), phase=0 + phase_offset)
Q = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(sig), phase=np.pi/2 + phase_offset)
# Mix down to (complex) baseband
down = sig*I + 1j*sig*Q
# Create a low pass filter at the symbol rate
sos = signal.butter(5, symbol_rate, 'low', fs=sample_rate, output='sos')
filtered_down = signal.sosfilt(sos, down)
# Take the phase angle of the baseband
return np.angle(filtered_down)
# The sequence of bits to modulate
seq = [0, 0, 0, 1, 1, 1,
0, 0, 1, 0, 1, 1,
0, 0,
1, 0, 1, 0, 1, 0,
0, 1,
1, 0, 1, 0, 0, 0]
# The relevant samples to pull out and store in the dictionary
samples = np.array([1, 4, 7, 10, 14, 17, 22, 25])
fig, axs = plt.subplots(4, 8, sharey=True, figsize=(24, 12))
dictionary = np.zeros((4*8, samples_per_symbol))
for q in range(4):
current_angle = [0, np.pi/2, np.pi, np.pi*3/2][q]
# Modulate the symbol with out optimized delta-sigma-modulator
modulated, angle = modulate_gmsk(seq, phase_offset=current_angle, sample_rate=sample_rate, include_phase=True)
modulated = simulateDSM(modulated, ntf_opti)[0]
demodulated = demodulate_gmsk(modulated, phase_offset=0)
n = 0
for i in samples:
iqsymbol = modulated[samples_per_symbol*i:samples_per_symbol*(i+1)]
dictionary[q*8 + n,:] = iqsymbol
axs[q, n].plot(np.unwrap(angle[samples_per_symbol*i:samples_per_symbol*(i+1)]))
n += 1
```
With these established, let's concatenate a few symbols together, demodulate to phase angle and make sure things look nice and smooth
```
def sim(out):
carrier=2.402e9
I = make_carrier(freq=carrier, sample_rate=sample_rate, samples=len(out), phase=0)
Q = make_carrier(freq=carrier, sample_rate=sample_rate, samples=len(out), phase=np.pi/2)
sos = signal.butter(2, symbol_rate, 'low', fs=sample_rate, output='sos')
rx_baseband = signal.sosfilt(sos, out*I + 1j*out*Q)
plt.plot(np.angle(rx_baseband))
sim(np.concatenate((dictionary[4,:], dictionary[5,:], dictionary[4,:], dictionary[5,:])))
sim(-1.0*np.concatenate((dictionary[13,:], dictionary[12,:], dictionary[13,:], dictionary[12,:])))
sim(np.concatenate((dictionary[21,:], dictionary[20,:], dictionary[21,:], dictionary[20,:])))
sim(-1.0*np.concatenate((dictionary[28,:], dictionary[29,:], dictionary[28,:], dictionary[29,:])))
```
Now, in order to synthesize this, we need a bit more logic to map between a bit stream and its respective symbols.
Note that there is additional state (i.e. the current phase offset) that factors into the symbol encoding beyond just the symbol value itself, which makes things a bit more complicate than most other forms of simple modulation. The code below keeps track of the starting phase angle at a given symbol as well as the before and after symbols to then output the right symbol.
```
idx = {
'000': 0,
'111': 1,
'001': 2,
'011': 3,
'010': 4,
'101': 5,
'110': 6,
'100': 7
}
start_q = [
[3, 2, 3, 2, 2, 3, 2, 3],
[0, 3, 0, 3, 3, 0, 3, 0],
[1, 0, 1, 0, 0, 1, 0, 1],
[2, 1, 2, 1, 1, 2, 1, 2]
]
def encode(bitstream):
out = np.zeros((len(bitstream)*samples_per_symbol,))
q = 0
prev = bitstream[0]
bitstream = bitstream + [bitstream[-1]] # Pad at the end so we can do a lookup
syms = []
for i in range(len(bitstream) - 1):
n = idx[str(prev) + str(bitstream[i]) + str(bitstream[i+1])]
d = -1
for j in range(4):
if start_q[j][n] == q:
d = j*8 + n
assert d != -1
syms.append(d)
out[i*samples_per_symbol:(i+1)*samples_per_symbol] = dictionary[d]
if bitstream[i]:
q = (q + 1) % 4
else:
q = (q + 4 - 1) % 4
prev = bitstream[i]
return out, syms
# Whitened bits from elsewhere
wbits = [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1]
out, syms = encode([1 - b for b in wbits])
# Let's look at the resulting symbol indexes
print(syms)
```
As a reminder, the dictionary is really just one bit of precision:
```
dictionary[0][:100]
```
Let's demodulate the encoded bits to check that things make sense (note that the filtering will delay the output a bit in time, but it demodulates correctly)
```
def demodulate_gmsk(sig):
carrier_freq=2.402e9
I = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(sig), phase=0)
Q = make_carrier(freq=carrier_freq, sample_rate=sample_rate, samples=len(sig), phase=np.pi/2)
# Mix down to (complex) baseband
down = sig*I + 1j*sig*Q
# Create a low pass filter at the symbol rate
sos = signal.butter(5, symbol_rate, 'low', fs=sample_rate, output='sos')
filtered_down = signal.sosfilt(sos, down)
# Take the phase angle of the baseband
angle = np.unwrap(np.angle(filtered_down))
# Take the derivative of the phase angle and hard limit it to 1:-1
return -(np.sign(angle[1:] - angle[:-1]) + 1.0)/2.0
plt.figure(figsize=(40,3))
plt.plot(demodulate_gmsk(out))
plt.plot(np.repeat(wbits, int(sample_rate/1e6)) + 1.5)
plt.gca().set_xlim(0, 0.6e6)
fftout = np.abs(fft(out))
fftout = fftout/np.max(fftout)
plt.figure(figsize=(10,6))
plt.plot(fftfreq(len(out), d=1/sample_rate), 10*np.log(fftout))
plt.gca().set_xlim(0, 3e9)
plt.gca().set_ylim(-80, 0)
plt.title("BLE Packet Before Reconstruction Filter")
plt.show()
fftm = np.abs(fft(np.convolve(out, impulse_response_6g, mode="same")))
fftm = fftm/np.max(fftm)
plt.figure(figsize=(10,6))
plt.plot(fftfreq(len(out), d=1/sample_rate), 10*np.log(fftm))
plt.gca().set_xlim(0, 3e9)
plt.gca().set_ylim(-80, 0)
plt.title("BLE Packet After Reconstruction Filter")
plt.show()
plt.figure(figsize=(10,6))
plt.plot(fftfreq(len(out), d=1/sample_rate), 10*np.log(fftm))
plt.gca().set_xlim(2.402e9 - 5e6, 2.402e9 + 5e6)
plt.gca().set_ylim(-80, 0)
plt.title("BLE Packet After Reconstruction Filter (10MHz span)")
```
The library used to generate the NTF filter uses a copyleft license, so rather than integrate that into the code, we save out the resulting symbol waveforms and use those directly.
```
np.save('../data/gmsk_2402e6_6e9.npy', dictionary)
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.