text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
<a href="https://colab.research.google.com/github/towardsai/tutorials/blob/master/random-number-generator/random_number_generator_tutorial.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Random Number Generator Tutorial with Python
* Tutorial: https://towardsai.net/p/data-science/random-number-generator-tutorial-with-python-3b35986132c7
* Github: https://github.com/towardsai/tutorials/tree/master/random-number-generator
## Generating pseudorandom numbers with Python's standard library
Python has a built-in module called random to generate a variety of pseudorandom numbers. Although it is recommended that this module should not be used for security purposes like cryptographic uses this will do for machine learning and data science. This module uses a PRNG called Mersenne Twister.
### Importing module: random
```
import random
```
### Random numbers within a range
```
#initialize the seed to 25
random.seed(25)
#generating random number between 10 and 20(both excluded)
print(random.randrange(10, 20))
#generating random number between 10 and 20(both included)
print(random.randint(10, 20))
```
### Random element from a sequence
```
#initialize the seed to 2
random.seed(2)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing an element from the sequence
random.choice(myseq)
```
### Multiple random selections with different possibilities
```
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#random selection of length 15
#10 time higher possibility of selecting 'Towards'
#5 time higher possibility of selecting 'AI'
#2 time higher possibility of selecting 'is'
#2 time higher possibility of selecting 1
random.choices(myseq, weights=[10, 5, 2, 2], k = 15)
```
### Random element from a sequence without replacement
```
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing an element from the sequence
random.sample(myseq, 2)
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing an element from the sequence
#you are trying to choose 5 random elements from a sequence of lenth 4
#since the selection is without replacement it is not possible and hence the error
random.sample(myseq, 35)
```
### Rearrange the sequence
```
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#rearranging the order of elements of the list
random.shuffle(myseq)
myseq
```
### Floating-point random number
```
#initialize the seed to 25
random.seed(25)
#random float number between 0 and 1
random.random()
```
### Real-valued distributions
```
#initialize the seed to 25
random.seed(25)
#random float number between 10 and 20 (both included)
print(random.uniform(10, 20))
#random float number mean 10 standard deviation 4
print(random.gauss(10, 4))
```
## Generating pseudorandom numbers with Numpy
```
#importing random module from numpy
import numpy as np
```
### Uniform distributed floating values
```
#initialize the seed to 25
np.random.seed(25)
#single uniformly distributed random number
np.random.rand()
#initialize the seed to 25
np.random.seed(25)
#uniformly distributed random numbers of length 10: 1-D array
np.random.rand(10)
#initialize the seed to 25
np.random.seed(25)
#uniformly distributed random numbers of 2 rows and 3 columns: 2-D array
np.random.rand(2, 3)
```
### Normal distributed floating values
```
#initialize the seed to 25
np.random.seed(25)
#single normally distributed random number
np.random.randn()
#initialize the seed to 25
np.random.seed(25)
#normally distributed random numbers of length 10: 1-D array
np.random.randn(10)
#initialize the seed to 25
np.random.seed(25)
#normally distributed random numbers of 2 rows and 3 columns: 2-D array
np.random.randn(2, 3)
```
### Uniformly distributed integers in a given range
```
#initialize the seed to 25
np.random.seed(25)
#single uniformly distributed random integer between 10 and 20
np.random.randint(10, 20)
#initialize the seed to 25
np.random.seed(25)
#uniformly distributed random integer between 0 to 100 of length 10: 1-D array
np.random.randint(100, size=(10))
#initialize the seed to 25
np.random.seed(25)
#uniformly distributed random integer between 0 to 100 of 2 rows and 3 columns: 2-D array
np.random.randint(100, size=(2, 3))
```
### Random elements from a defined list
```
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing an element from the sequence
np.random.choice(myseq)
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing elements from the sequence: 2-D array
np.random.choice(myseq, size=(2, 3))
#initialize the seed to 25
random.seed(25)
#setting up the sequence
myseq = ['Towards', 'AI', 'is', 1]
#randomly choosing elements from the sequence with defined probabilities
#The probability for the value to be 'Towards' is set to be 0.1
#The probability for the value to be 'AI' is set to be 0.6
#The probability for the value to be 'is' is set to be 0.05
#The probability for the value to be 1 is set to be 0.25
#0.1 + 0.6 + 0.05 + 0.25 = 1
np.random.choice(myseq, p=[0.1, 0.6, 0.05, 0.25], size=(2, 3))
```
### Binomial distributed values
```
#initialize the seed to 25
np.random.seed(25)
#10 number of trials with probability of 0.5 each
np.random.binomial(n=10, p=0.5, size=10)
```
### Poisson Distribution values
```
#initialize the seed to 25
np.random.seed(25)
#rate 2 and size 10
np.random.poisson(lam=2, size=10)
```
### Chi Square distribution
```
#initialize the seed to 25
np.random.seed(25)
#degree of freedom 2 and size (2, 3)
np.random.chisquare(df=2, size=(2, 3))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/daveshap/QuestionDetector/blob/main/QuestionDetector.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Compile Training Data
Note: Generate the raw data with [this notebook](https://github.com/daveshap/QuestionDetector/blob/main/DownloadGutenbergTop100.ipynb)
```
import re
import random
datafile = '/content/drive/My Drive/Gutenberg/sentence_data.txt'
corpusfile = '/content/drive/My Drive/Gutenberg/corpus_data.txt'
testfile = '/content/drive/My Drive/Gutenberg/test_data.txt'
sample_cnt = 3000
test_cnt = 30
questions = list()
exclamations = list()
other = list()
with open(datafile, 'r', encoding='utf-8') as infile:
body = infile.read()
sentences = re.split('\n\n', body)
for i in sentences:
if 'í' in i or 'á' in i:
continue
if '?' in i:
questions.append(i)
elif '!' in i:
exclamations.append(i)
else:
other.append(i)
def flatten_sentence(text):
text = text.lower()
fa = re.findall('[\w\s]',text)
return ''.join(fa)
def compose_corpus(data, count, label):
result = ''
random.seed()
subset = random.sample(data, count)
for i in subset:
result += '<|SENTENCE|> %s <|LABEL|> %s <|END|>\n\n' % (flatten_sentence(i), label)
return result
corpus = compose_corpus(questions, sample_cnt, 'question')
corpus += compose_corpus(exclamations, sample_cnt, 'other')
corpus += compose_corpus(other, sample_cnt, 'other')
with open(corpusfile, 'w', encoding='utf-8') as outfile:
outfile.write(corpus)
print('Done!', corpusfile)
corpus = compose_corpus(questions, test_cnt, 'question')
corpus += compose_corpus(exclamations, test_cnt, 'other')
corpus += compose_corpus(other, test_cnt, 'other')
with open(testfile, 'w', encoding='utf-8') as outfile:
outfile.write(corpus)
print('Done!', testfile)
```
# Finetune Model
Finetune GPT-2
```
!pip install tensorflow-gpu==1.15.0 --quiet
!pip install gpt-2-simple --quiet
import gpt_2_simple as gpt2
# note: manually mount your google drive in the file explorer to the left
model_dir = '/content/drive/My Drive/GPT2/models'
checkpoint_dir = '/content/drive/My Drive/GPT2/checkpoint'
#model_name = '124M'
model_name = '355M'
#model_name = '774M'
gpt2.download_gpt2(model_name=model_name, model_dir=model_dir)
print('\n\nModel is ready!')
run_name = 'QuestionDetector'
step_cnt = 4000
sess = gpt2.start_tf_sess()
gpt2.finetune(sess,
dataset=corpusfile,
model_name=model_name,
model_dir=model_dir,
checkpoint_dir=checkpoint_dir,
steps=step_cnt,
restore_from='fresh', # start from scratch
#restore_from='latest', # continue from last work
run_name=run_name,
print_every=50,
sample_every=1000,
save_every=1000
)
```
# Test Results
| Run | Model | Steps | Samples | Last Loss | Avg Loss | Accuracy |
|---|---|---|---|---|---|---|
| 01 | 124M | 2000 | 9000 | 0.07 | 0.69 | 71.4% |
| 02 | 355M | 2000 | 9000 | 0.24 | 1.63 | 66% |
| 03 | 355M | 4000 | 9000 | 0.06 | 0.83 | 58% |
| 04 | 355M | 4000 | 9000 | 0.11 | 0.68 | 74.4% |
Larger models seem to need more steps and/or data. Seems to perform very high on questions and less good on others. Test 04 was reduced to 2 classes.
```
right = 0
wrong = 0
print('Loading test set...')
with open(testfile, 'r', encoding='utf-8') as file:
test_set = file.readlines()
for t in test_set:
t = t.strip()
if t == '':
continue
prompt = t.split('<|LABEL|>')[0] + '<|LABEL|>'
expect = t.split('<|LABEL|>')[1].replace('<|END|>', '').strip()
#print('\nPROMPT:', prompt)
response = gpt2.generate(sess,
return_as_list=True,
length=30, # prevent it from going too crazy
prefix=prompt,
model_name=model_name,
model_dir=model_dir,
truncate='\n', # stop inferring here
include_prefix=False,
checkpoint_dir=checkpoint_dir,)[0]
response = response.strip()
if expect in response:
right += 1
else:
wrong += 1
print('right:', right, '\twrong:', wrong, '\taccuracy:', right / (right+wrong))
#print('RESPONSE:', response)
print('\n\nModel:', model_name)
print('Samples:', max_samples)
print('Steps:', step_cnt)
```
|
github_jupyter
|
# RadiusNeighborsClassifier with MinMaxScaler
This Code template is for the Classification task using a simple Radius Neighbor Classifier, with data being scaled by MinMaxScaler. It implements learning based on the number of neighbors within a fixed radius r of each training point, where r is a floating-point value specified by the user.
### Required Packages
```
!pip install imblearn
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from imblearn.over_sampling import RandomOverSampler
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import RadiusNeighborsClassifier
from sklearn.pipeline import make_pipeline
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X = df[features]
Y = df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), axis=-1, kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
#### Handling Target Imbalance
The challenge of working with imbalanced datasets is that most machine learning techniques will ignore, and in turn have poor performance on, the minority class, although typically it is performance on the minority class that is most important.
One approach to addressing imbalanced datasets is to oversample the minority class. The simplest approach involves duplicating examples in the minority class.We will perform overspampling using imblearn library.
```
x_train,y_train = RandomOverSampler(random_state=123).fit_resample(x_train, y_train)
```
### Model
RadiusNeighborsClassifier implements learning based on the number of neighbors within a fixed radius of each training point, where is a floating-point value specified by the user.
In cases where the data is not uniformly sampled, radius-based neighbors classification can be a better choice.
#### Tuning parameters
> **radius**: Range of parameter space to use by default for radius_neighbors queries.
> **algorithm**: Algorithm used to compute the nearest neighbors:
> **leaf_size**: Leaf size passed to BallTree or KDTree.
> **p**: Power parameter for the Minkowski metric.
> **metric**: the distance metric to use for the tree.
> **outlier_label**: label for outlier samples
> **weights**: weight function used in prediction.
For more information refer: [API](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.RadiusNeighborsClassifier.html)
#### Data Rescaling
MinMaxScaler subtracts the minimum value in the feature and then divides by the range, where range is the difference between the original maximum and original minimum.
```
# Build Model here
model = make_pipeline(MinMaxScaler(),RadiusNeighborsClassifier(n_jobs=-1))
model.fit(x_train, y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,x_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* **where**:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(x_test)))
```
#### Creator: Viraj Jayant, Github: [Profile](https://github.com/Viraj-Jayant/)
|
github_jupyter
|
# 03 - Stats Review: The Most Dangerous Equation
In his famous article of 2007, Howard Wainer writes about very dangerous equations:
"Some equations are dangerous if you know them, and others are dangerous if you do not. The first category may pose danger because the secrets within its bounds open doors behind which lies terrible peril. The obvious winner in this is Einstein’s ionic equation \\(E = MC^2\\), for it provides a measure of the enormous energy hidden within ordinary matter. \[...\] Instead I am interested in equations that unleash their danger not when we know about them, but rather when we do not. Kept close at hand, these equations allow us to understand things clearly, but their absence leaves us dangerously ignorant."
The equation he talks about is Moivre’s equation:
$
SE = \dfrac{\sigma}{\sqrt{n}}
$
where \\(SE\\) is the standard error of the mean, \\(\sigma\\) is the standard deviation and \\(n\\) is the sample size. Sounds like a piece of math the brave and true should master, so let's get to it.
To see why not knowing this equation is very dangerous, let's take a look at some education data. I've compiled data on ENEM scores (Brazilian standardised high school scores, similar to SAT) from different schools for a period of 3 years. I also did some cleaning on the data to keep only the information relevant to us. The original data can be downloaded in the [Inep website](http://portal.inep.gov.br/web/guest/microdados#).
If we look at the top performing school, something catches the eye: those schools have a fairly small number of students.
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from scipy import stats
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import style
style.use("fivethirtyeight")
df = pd.read_csv("./data/enem_scores.csv")
df.sort_values(by="avg_score", ascending=False).head(10)
```
Looking at it from another angle, we can separate only the 1% top schools and study them. What are they like? Perhaps we can learn something from the best and replicate it elsewhere. And sure enough, if we look at the top 1% schools, we figure out they have, on average, fewer students.
```
plot_data = (df
.assign(top_school = df["avg_score"] >= np.quantile(df["avg_score"], .99))
[["top_school", "number_of_students"]]
.query(f"number_of_students<{np.quantile(df['number_of_students'], .98)}")) # remove outliers
plt.figure(figsize=(6,6))
sns.boxplot(x="top_school", y="number_of_students", data=plot_data)
plt.title("Number of Students of 1% Top Schools (Right)");
```
One natural conclusion that follows is that small schools lead to higher academic performance. This makes intuitive sense, since we believe that less students per teacher allows the teacher to give focused attention to each student. But what does this have to do with Moivre’s equation? And why is it dangerous?
Well, it becomes dangerous once people start to make important and expensive decisions based on this information. In his article, Howard continues:
"In the 1990s, it became popular to champion reductions in the size of schools. Numerous philanthropic organisations and government agencies funded the division of larger schools based on the fact that students at small schools are over represented in groups with high test scores."
What people forgot to do was to look also at the bottom 1% of schools. If we do that, lo and behold! They also have very few students!
```
q_99 = np.quantile(df["avg_score"], .99)
q_01 = np.quantile(df["avg_score"], .01)
plot_data = (df
.sample(10000)
.assign(Group = lambda d: np.select([d["avg_score"] > q_99, d["avg_score"] < q_01],
["Top", "Bottom"], "Middle")))
plt.figure(figsize=(10,5))
sns.scatterplot(y="avg_score", x="number_of_students", hue="Group", data=plot_data)
plt.title("ENEM Score by Number of Students in the School");
```
What we are seeing above is exactly what is expected according to the Moivre’s equation. As the number of students grows, the average score becomes more and more precise. Schools with very few samples can have very high and very low scores simply due to chance. This is less likley to occur with large schools. Moivre’s equation talks about a fundamental fact about the reality of information and records in the form of data: it is always imprecise. The question then becomes how imprecise.
Statistics is the science that deals with these imprecisions so they don't catch us off-guard. As Taleb puts it in his book, Fooled by Randomness:
> Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance.
One way to quantify our uncertainty is the **variance of our estimates**. Variance tells us how much observation deviates from their central and most probably value. As indicated by Moivre’s equation, this uncertainty shrinks as the amount of data we observe increases. This makes sense, right? If we see lots and lots of students performing excellently at a school, we can be more confident that this is indeed a good school. However, if we see a school with only 10 students and 8 of them perform well, we need to be more suspicious. It could be that, by chance, that school got some above average students.
The beautiful triangular plot we see above tells exactly this story. It shows us how our estimates of the school performance has a huge variance when the sample sizes are small. It also shows that variance shrinks as the sample size increases. This is true for the average score in a school, but it is also true about any summary statistics that we have, including the ATE we so often want to estimate.
## The Standard Error of Our Estimates
Since this is just a review on statistics, I'll take the liberty to go a bit faster now. If you are not familiar with distributions, variance and standard errors, please, do read on, but keep in mind that you might need some additional resources. I suggest you google any MIT course on introduction to statistics. They are usually quite good.
In the previous section, we estimated the average treatment effect \\(E[Y_1-Y_0]\\) as the difference in the means between the treated and the untreated \\(E[Y|T=1]-E[Y|T=0]\\). As our motivating example, we figured out the \\(ATE\\) for online classes. We also saw that it was a negative impact, that is, online classes made students perform about 5 points worse than the students with face to face classes. Now, we get to see if this impact is statistically significant.
To do so, we need to estimate the \\(SE\\). We already have \\(n\\), our sample size. To get the estimate for the standard deviation we can do the following
$
\hat{\sigma}=\frac{1}{N-1}\sum_{i=0}^N (x-\bar{x})^2
$
where \\(\bar{x}\\) is the mean of \\(x\\). Fortunately for us, most programming software already implements this. In Pandas, we can use the method [std](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.std.html).
```
data = pd.read_csv("./data/online_classroom.csv")
online = data.query("format_ol==1")["falsexam"]
face_to_face = data.query("format_ol==0 & format_blended==0")["falsexam"]
def se(y: pd.Series):
return y.std() / np.sqrt(len(y))
print("SE for Online:", se(online))
print("SE for Face to Face:", se(face_to_face))
```
## Confidence Intervals
The standard error of our estimate is a measure of confidence. To understand exactly what it means, we need to go into turbulent and polemic statistical waters. For one view of statistics, the frequentist view, we would say that the data we have is nothing more than a manifestation of a true data generating process. This process is abstract and ideal. It is governed by true parameters that are unchanging but also unknown to us. In the context of the students test, if we could run multiple experiments and collect multiple datasets, all would resemble the true underlying data generating process, but wouldn't be exactly like it. This is very much like Plato's writing on the Forms:
> Each [of the essential forms] manifests itself in a great variety of combinations, with actions, with material things, and with one another, and each seems to be many
To better grasp this, let's suppose we have a true abstract distribution of students' test score. This is a normal distribution with true mean of 74 and true standard deviation of 2. From this distribution, we can run 10000 experiments. On each one, we collect 500 samples. Some experiment data will have a mean lower than the true one, some will be higher. If we plot them in a histogram, we can see that means of the experiments are distributed around the true mean.
```
true_std = 2
true_mean = 74
n = 500
def run_experiment():
return np.random.normal(true_mean,true_std, 500)
np.random.seed(42)
plt.figure(figsize=(8,5))
freq, bins, img = plt.hist([run_experiment().mean() for _ in range(10000)], bins=40, label="Experiment Means")
plt.vlines(true_mean, ymin=0, ymax=freq.max(), linestyles="dashed", label="True Mean", color="orange")
plt.legend();
```
Notice that we are talking about the mean of means here. So, by chance, we could have an experiment where the mean is somewhat below or above the true mean. This is to say that we can never be sure that the mean of our experiment matches the true platonic and ideal mean. However, **with the standard error, we can create an interval that will contain the true mean 95% of the time**.
In real life, we don't have the luxury of simulating the same experiment with multiple datasets. We often only have one. But we can draw on the intuition above to construct what we call **confidence intervals**. Confidence intervals come with a probability attached to them. The most common one is 95%. This probability tells us how many of the hypothetical confidence intervals we would build from different studies contain the true mean. For example, the 95% confidence intervals computed from many similar studies would contain the true mean 95% of the time.
To calculate the confidence interval, we use what is called the **central limit theorem**. This theorem states that **means of experiments are normally distributed**. From statistical theory, we know that 95% of the mass of a normal distribution is between 2 standard deviations above and below the mean. Technically, 1.96, but 2 is close enough.

The Standard Error of the mean serves as our estimate of the distribution of the experiment means. So, if we multiply it by 2 and add and subtract it from the mean of one of our experiments, we will construct a 95% confidence interval for the true mean.
```
np.random.seed(321)
exp_data = run_experiment()
exp_se = exp_data.std() / np.sqrt(len(exp_data))
exp_mu = exp_data.mean()
ci = (exp_mu - 2 * exp_se, exp_mu + 2 * exp_se)
print(ci)
x = np.linspace(exp_mu - 4*exp_se, exp_mu + 4*exp_se, 100)
y = stats.norm.pdf(x, exp_mu, exp_se)
plt.plot(x, y)
plt.vlines(ci[1], ymin=0, ymax=1)
plt.vlines(ci[0], ymin=0, ymax=1, label="95% CI")
plt.legend()
plt.show()
```
Of course, we don't need to restrict ourselves to the 95% confidence interval. We could generate the 99% interval by finding what we need to multiply the standard deviation by so the interval contains 99% of the mass of a normal distribution.
The function `ppf` in python gives us the inverse of the CDF. So, `ppf(0.5)` will return 0.0, saying that 50% of the mass of the standard normal distribution is below 0.0. By the same token, if we plug 99.5%, we will have the value `z`, such that 99.5% of the distribution mass falls below this value. In other words, 0.05% of the mass falls above this value. Instead of multiplying the standard error by 2 like we did to find the 95% CI, we will multiply it by `z`, which will result in the 99% CI.
```
from scipy import stats
z = stats.norm.ppf(.995)
print(z)
ci = (exp_mu - z * exp_se, exp_mu + z * exp_se)
ci
x = np.linspace(exp_mu - 4*exp_se, exp_mu + 4*exp_se, 100)
y = stats.norm.pdf(x, exp_mu, exp_se)
plt.plot(x, y)
plt.vlines(ci[1], ymin=0, ymax=1)
plt.vlines(ci[0], ymin=0, ymax=1, label="99% CI")
plt.legend()
plt.show()
```
Back to our classroom experiment, we can construct the confidence interval for the mean exam score for both the online and face to face students' group
```
def ci(y: pd.Series):
return (y.mean() - 2 * se(y), y.mean() + 2 * se(y))
print("95% CI for Online:", ci(online))
print("95% for Face to Face:", ci(face_to_face))
```
What we can see is that the 95% CI of the groups don't overlap. The lower end of the CI for Face to Face class is above the upper end of the CI for online classes. This is evidence that our result is not by chance, and that the true mean for students in face to face clases is higher than the true mean for students in online classes. In other words, there is a significant causal decrease in academic performance when switching from face to face to online classes.
As a recap, confidence intervals are a way to place uncertainty around our estimates. The smaller the sample size, the larger the standard error and the wider the confidence interval. Finally, you should always be suspicious of measurements without any uncertainty metric attached to it. Since they are super easy to compute, lack of confidence intervals signals either some bad intentions or simply lack of knowledge, which is equally concerning.

One final word of caution here. Confidence intervals are trickier to interpret than at first glance. For instance, I **shouldn't** say that this particular 95% confidence interval contains the true population mean with 95% chance. That's because in frequentist statistics, the one that uses confidence intervals, the population mean is regarded as a true population constant. So it either is or isn't in our particular confidence interval. In other words, our particular confidence interval either contains or doesn't contain the true mean. If it does, the chance of containing it would be 100%, not 95%. If it doesn't, the chance would be 0%. Rather, in confidence intervals, the 95% refers to the frequency that such confidence intervals, computed in many many studies, contain the true mean. 95% is our confidence in the algorithm used to compute the 95% CI, not on the particular interval itself.
Now, having said that, as an Economist (statisticians, please look away now), I think this purism is not very useful. In practice, you will see people saying that the particular confidence interval contains the true mean 95% of the time. Although wrong, this is not very harmful, as it still places a precise degree of uncertainty in our estimates. Moreover, if we switch to Bayesian statistics and use probable intervals instead of confidence intervals, we would be able to say that the interval contains the distribution mean 95% of the time. Also, from what I've seen in practice, with decent sample sizes, bayesian probability intervals are more similar to confidence intervals than both bayesian and frequentists would like to admit. So, if my word counts for anything, feel free to say whatever you want about your confidence interval. I don't care if you say they contain the true mean 95% of the time. Just, please, never forget to place them around your estimates, otherwise you will look silly.
## Hypothesis Testing
Another way to incorporate uncertainty is to state a hypothesis test: is the difference in means statistically different from zero (or any other value)? To do so, we will recall that the sum or difference of 2 normal distributions is also a normal distribution. The resulting mean will be the sum or difference between the two distributions, while the variance will always be the sum of the variance:
$
N(\mu_1, \sigma_1^2) - N(\mu_2, \sigma_2^2) = N(\mu_1 - \mu_2, \sigma_1^2 + \sigma_2^2)
$
$
N(\mu_1, \sigma_1^2) + N(\mu_2, \sigma_2^2) = N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)
$
If you don't recall, its OK. We can always use code and simulated data to check:
```
np.random.seed(123)
n1 = np.random.normal(4, 3, 30000)
n2 = np.random.normal(1, 4, 30000)
n_diff = n2 - n1
sns.distplot(n1, hist=False, label="N(4,3)")
sns.distplot(n2, hist=False, label="N(1,4)")
sns.distplot(n_diff, hist=False, label=f"N(4,3) - N(1,4) = N(-1, 5)")
plt.show()
```
If we take the distribution of the means of our 2 groups and subtract one from the other, we will have a third distribution. The mean of this final distribution will be the difference in the means and the standard deviation of this distribution will be the square root of the sum of the standard deviations.
$
\mu_{diff} = \mu_1 - \mu_2
$
$
SE_{diff} = \sqrt{SE_1 + SE_2} = \sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}
$
Let's return to our classroom example. We will construct this distribution of the difference. Of course, once we have it, building the 95% CI is very easy.
```
diff_mu = online.mean() - face_to_face.mean()
diff_se = np.sqrt(face_to_face.var()/len(face_to_face) + online.var()/len(online))
ci = (diff_mu - 1.96*diff_se, diff_mu + 1.96*diff_se)
print(ci)
x = np.linspace(diff_mu - 4*diff_se, diff_mu + 4*diff_se, 100)
y = stats.norm.pdf(x, diff_mu, diff_se)
plt.plot(x, y)
plt.vlines(ci[1], ymin=0, ymax=.05)
plt.vlines(ci[0], ymin=0, ymax=.05, label="95% CI")
plt.legend()
plt.show()
```
With this at hand, we can say that we are 95% confident that the true difference between the online and face to face group falls between -8.37 and -1.44. We can also construct a **z statistic** by dividing the difference in mean by the \\\(SE\\\\) of the differences.
$
z = \dfrac{\mu_{diff} - H_{0}}{SE_{diff}} = \dfrac{(\mu_1 - \mu_2) - H_{0}}{\sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}}
$
Where \\(H_0\\) is the value which we want to test our difference against.
The z statistic is a measure of how extreme the observed difference is. To test our hypothesis that the difference in the means is statistically different from zero, we will use contradiction. We will assume that the opposite is true, that is, we will assume that the difference is zero. This is called a null hypothesis, or \\(H_0\\). Then, we will ask ourselves "is it likely that we would observe such a difference if the true difference were indeed zero?" In statistical math terms, we can translate this question to checking how far from zero is our z statistic.
Under \\(H_0\\), the z statistic follows a standard normal distribution. So, if the difference is indeed zero, we would see the z statistic within 2 standard deviations of the mean 95% of the time. The direct consequence of this is that if z falls above or below 2 standard deviations, we can reject the null hypothesis with 95% confidence.
Let's see how this looks like in our classroom example.
```
z = diff_mu / diff_se
print(z)
x = np.linspace(-4,4,100)
y = stats.norm.pdf(x, 0, 1)
plt.plot(x, y, label="Standard Normal")
plt.vlines(z, ymin=0, ymax=.05, label="Z statistic", color="C1")
plt.legend()
plt.show()
```
This looks like a pretty extreme value. Indeed, it is above 2, which means there is less than a 5% chance that we would see such an extreme value if there were no difference in the groups. This again leads us to conclude that switching from face to face to online classes causes a statistically significant drop in academic performance.
One final interesting thing about hypothesis tests is that it is less conservative than checking if the 95% CI from the treated and untreated group overlaps. In other words, if the confidence intervals in the two groups overlap, it can still be the case that the result is statistically significant. For example, let's pretend that the face-to-face group has an average score of 74 and standard error of 7 and the online group has an average score of 71 with a standard error of 1.
```
cont_mu, cont_se = (71, 1)
test_mu, test_se = (74, 7)
diff_mu = test_mu - cont_mu
diff_se = np.sqrt(cont_se + cont_se)
print("Control 95% CI:", (cont_mu-1.96*cont_se, cont_mu+1.96*cont_se))
print("Test 95% CI:", (test_mu-1.96*test_se, test_mu+1.96*test_se))
print("Diff 95% CI:", (diff_mu-1.96*diff_se, diff_mu+1.96*diff_se))
```
If we construct the confidence intervals for these groups, they overlap. The upper bound for the 95% CI of the online group is 72.96 and the lower bound for the face-to-face group is 60.28. However, once we compute the 95% confidence interval for the difference between the groups, we can see that it does not contain zero. In summary, even though the individual confidence intervals overlap, the difference can still be statistically different from zero.
## P-values
I've said previously that there is less than 5% chance that we would observe such an extreme value if the difference between online and face to face groups were actually zero. But can we estimate exactly what is that chance? How likely are we to observe such an extreme value? Enters p-values!
Just like with confidence intervals (and most frequentist statistics, as a matter of fact) the true definition of p-values can be very confusing. So, to not take any risks, I'll copy the definition from Wikipedia: "the p-value is the probability of obtaining test results at least as extreme as the results actually observed during the test, assuming that the null hypothesis is correct".
To put it more succinctly, the p-value is the probability of seeing such data, given that the null-hypothesis is true. It measures how unlikely it is that you are seeing a measurement if the null-hypothesis is true. Naturally, this often gets confused with the probability of the null-hypothesis being true. Note the difference here. The p-value is NOT \\(P(H_0|data)\\), but rather \\(P(data|H_0)\\).
But don't let this complexity fool you. In practical terms, they are pretty straightforward to use.

To get the p-value, we need to compute the area under the standard normal distribution before or after the z statistic. Fortunately, we have a computer to do this calculation for us. We can simply plug the z statistic in the CDF of the standard normal distribution.
```
print("P-value:", stats.norm.cdf(z))
```
This means that there is only a 0.2% chance of observing this extreme z statistic if the difference was zero. Notice how the p-value is interesting because it avoids us having to specify a confidence level, like 95% or 99%. But, if we wish to report one, from the p-value, we know exactly at which confidence our test will pass or fail. For instance, with a p-value of 0.0027, we know that we have significance up to the 0.2% level. So, while the 95% CI and the 99% CI for the difference will neither contain zero, the 99.9% CI will.
```
diff_mu = online.mean() - face_to_face.mean()
diff_se = np.sqrt(face_to_face.var()/len(face_to_face) + online.var()/len(online))
print("95% CI:", (diff_mu - stats.norm.ppf(.975)*diff_se, diff_mu + stats.norm.ppf(.975)*diff_se))
print("99% CI:", (diff_mu - stats.norm.ppf(.995)*diff_se, diff_mu + stats.norm.ppf(.995)*diff_se))
print("99.9% CI:", (diff_mu - stats.norm.ppf(.9995)*diff_se, diff_mu + stats.norm.ppf(.9995)*diff_se))
```
## Keys Ideas
We've seen how important it is to know Moivre’s equation and we used it to place a degree of certainty around our estimates. Namely, we figured out that the online classes cause a decrease in academic performance compared to face to face classes. We also saw that this was a statistically significant result. We did it by comparing the Confidence Intervals of the means for the 2 groups, by looking at the confidence interval for the difference, by doing a hypothesis test and by looking at the p-value. Let's wrap everything up in a single function that does A/B testing comparison like the one we did above
```
def AB_test(test: pd.Series, control: pd.Series, confidence=0.95, h0=0):
mu1, mu2 = test.mean(), control.mean()
se1, se2 = test.std() / np.sqrt(len(test)), control.std() / np.sqrt(len(control))
diff = mu1 - mu2
se_diff = np.sqrt(test.var()/len(test) + control.var()/len(control))
z_stats = (diff-h0)/se_diff
p_value = stats.norm.cdf(z_stats)
def critial(se): return -se*stats.norm.ppf((1 - confidence)/2)
print(f"Test {confidence*100}% CI: {mu1} +- {critial(se1)}")
print(f"Control {confidence*100}% CI: {mu2} +- {critial(se2)}")
print(f"Test-Control {confidence*100}% CI: {diff} +- {critial(se_diff)}")
print(f"Z Statistic {z_stats}")
print(f"P-Value {p_value}")
AB_test(online, face_to_face)
```
Since our function is generic enough, we can test other null hypotheses. For instance, can we try to reject that the difference between online and face to face class performance is -1. With the results we get, we can say with 95% confidence that the difference is greater than -1. But we can't say it with 99% confidence:
```
AB_test(online, face_to_face, h0=-1)
```
## References
I like to think of this entire book as a tribute to Joshua Angrist, Alberto Abadie and Christopher Walters for their amazing Econometrics class. Most of the ideas here are taken from their classes at the American Economic Association. Watching them is what is keeping me sane during this tough year of 2020.
* [Cross-Section Econometrics](https://www.aeaweb.org/conference/cont-ed/2017-webcasts)
* [Mastering Mostly Harmless Econometrics](https://www.aeaweb.org/conference/cont-ed/2020-webcasts)
I'll also like to reference the amazing books from Angrist. They have shown me that Econometrics, or 'Metrics as they call it, is not only extremely useful but also profoundly fun.
* [Mostly Harmless Econometrics](https://www.mostlyharmlesseconometrics.com/)
* [Mastering 'Metrics](https://www.masteringmetrics.com/)
My final reference is Miguel Hernan and Jamie Robins' book. It has been my trustworthy companion in the most thorny causal questions I had to answer.
* [Causal Inference Book](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/)
In this particular section, I've also referenced The [Most Dangerous Equation](https://www.researchgate.net/publication/255612702_The_Most_Dangerous_Equation), by Howard Wainer.
Finally, if you are curious about the correct interpretation of the statistical concepts we've discussed here, I recommend reading the paper by Greenland et al, 2016: [Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations](https://link.springer.com/content/pdf/10.1007/s10654-016-0149-3.pdf).

## Contribute
Causal Inference for the Brave and True is an open-source material on causal inference, the statistics of science. It uses only free software, based in Python. Its goal is to be accessible monetarily and intellectually.
If you found this book valuable and you want to support it, please go to [Patreon](https://www.patreon.com/causal_inference_for_the_brave_and_true). If you are not ready to contribute financially, you can also help by fixing typos, suggesting edits or giving feedback on passages you didn't understand. Just go to the book's repository and [open an issue](https://github.com/matheusfacure/python-causality-handbook/issues). Finally, if you liked this content, please share it with others who might find it useful and give it a [star on GitHub](https://github.com/matheusfacure/python-causality-handbook/stargazers).
|
github_jupyter
|
# Gender Prediction, using Pre-trained Keras Model
Deep Neural Networks can be used to extract features in the input and derive higher level abstractions. This technique is used regularly in vision, speech and text analysis. In this exercise, we use a pre-trained model deep learning model that would identify low level features in texts containing people's names, and would be able to classify them in one of two categories - Male or Female.
## Network Architecture
The problem we are trying to solve is to predict whether a given name belongs to a male or female. We will use supervised learning, where the character sequence making up the names would be `X` variable, and the flag indicating **Male(M)** or **Female(F)** would be `Y` variable.
We use a stacked 2-Layer LSTM model and a final dense layer with softmax activation as our network architecture. We use categorical cross-entropy as loss function, with an Adam optimizer. We also add a 20% dropout layer is added for regularization to avoid over-fitting.
## Dependencies
* The model was built using Keras, therefore we need to include Keras deep learning library to build the network locally, in order to be able to test, prior to hosting the model.
* While running on SageMaker Notebook Instance, we choose conda_tensorflow kernel, so that Keras code is compiled to use tensorflow in the backend.
* If you choose P2 and P3 class of instances for your Notebook, using Tensorflow ensures the low level code takes advantage of all available GPUs. So further dependencies needs to be installed.
```
import os
import time
import numpy as np
import keras
from keras.models import load_model
import boto3
```
## Model testing
To test the validity of the model, we do some local testing.<p>
The model was built to be able to process one-hot encoded data representing names, therefore we need to do same pre-processing on our test data (one-hot encoding using the same character indices)<p>
We feed this one-hot encoded test data to the model, and the `predict` generates a vector, similar to the training labels vector we used before. Except in this case, it contains what model thinks the gender represented by each of the test records.<p>
To present data intutitively, we simply map it back to `Male` / `Female`, from the `0` / `1` flag.
```
!tar -zxvf ../pretrained-model/model.tar.gz -C ../pretrained-model/
model = load_model('../pretrained-model/lstm-gender-classifier-model.h5')
char_indices = np.load('../pretrained-model/lstm-gender-classifier-indices.npy').item()
max_name_length = char_indices['max_name_length']
char_indices.pop('max_name_length', None)
alphabet_size = len(char_indices)
print(char_indices)
print(max_name_length)
print(alphabet_size)
names_test = ["Tom","Allie","Jim","Sophie","John","Kayla","Mike","Amanda","Andrew"]
num_test = len(names_test)
X_test = np.zeros((num_test, max_name_length, alphabet_size))
for i,name in enumerate(names_test):
name = name.lower()
for t, char in enumerate(name):
X_test[i, t,char_indices[char]] = 1
predictions = model.predict(X_test)
for i,name in enumerate(names_test):
print("{} ({})".format(names_test[i],"M" if predictions[i][0]>predictions[i][1] else "F"))
```
## Model saving
In order to deploy the model behind an hosted endpoint, we need to save the model fileto an S3 location.<p>
We can obtain the name of the S3 bucket from the execution role we attached to this Notebook instance. This should work if the policies granting read permission to IAM policies was granted, as per the documentation.
If for some reason, it fails to fetch the associated bucket name, it asks the user to enter the name of the bucket. If asked, use the bucket that you created in Module-3, such as 'smworkshop-firstname-lastname'.<p>
It is important to ensure that this is the same S3 bucket, to which you provided access in the Execution role used while creating this Notebook instance.
```
sts = boto3.client('sts')
iam = boto3.client('iam')
caller = sts.get_caller_identity()
account = caller['Account']
arn = caller['Arn']
role = arn[arn.find("/AmazonSageMaker")+1:arn.find("/SageMaker")]
timestamp = role[role.find("Role-")+5:]
policyarn = "arn:aws:iam::{}:policy/service-role/AmazonSageMaker-ExecutionPolicy-{}".format(account, timestamp)
s3bucketname = ""
policystatements = []
try:
policy = iam.get_policy(
PolicyArn=policyarn
)['Policy']
policyversion = policy['DefaultVersionId']
policystatements = iam.get_policy_version(
PolicyArn = policyarn,
VersionId = policyversion
)['PolicyVersion']['Document']['Statement']
except Exception as e:
s3bucketname=input("Which S3 bucket do you want to use to host training data and model? ")
for stmt in policystatements:
action = ""
actions = stmt['Action']
for act in actions:
if act == "s3:ListBucket":
action = act
break
if action == "s3:ListBucket":
resource = stmt['Resource'][0]
s3bucketname = resource[resource.find(":::")+3:]
print(s3bucketname)
s3 = boto3.resource('s3')
s3.meta.client.upload_file('../pretrained-model/model.tar.gz', s3bucketname, 'model/model.tar.gz')
```
# Model hosting
Amazon SageMaker provides a powerful orchestration framework that you can use to productionize any of your own machine learning algorithm, using any machine learning framework and programming languages.<p>
This is possible because SageMaker, as a manager of containers, have standarized ways of interacting with your code running inside a Docker container. Since you are free to build a docker container using whatever code and depndency you like, this gives you freedom to bring your own machinery.<p>
In the following steps, we'll containerize the prediction code and host the model behind an API endpoint.<p>
This would allow us to use the model from web-application, and put it into real use.<p>
The boilerplate code, which we affectionately call the `Dockerizer` framework, was made available on this Notebook instance by the Lifecycle Configuration that you used. Just look into the folder and ensure the necessary files are available as shown.<p>
<home>
|
├── container
│
├── byoa
| |
│ ├── train
| |
│ ├── predictor.py
| |
│ ├── serve
| |
│ ├── nginx.conf
| |
│ └── wsgi.py
|
├── build_and_push.sh
│
├── Dockerfile.cpu
│
└── Dockerfile.gpu
```
os.chdir('../container')
os.getcwd()
!ls -Rl
```
* `Dockerfile` describes the container image and the accompanying script `build_and_push.sh` does the heavy lifting of building the container, and uploading it into an Amazon ECR repository
* Sagemaker containers that we'll be building serves prediction request using a Flask based application. `wsgi.py` is a wrapper to invoke the Flask application, while `nginx.conf` is the configuration for the nginx front end and `serve` is the program that launches the gunicorn server. These files can be used as-is, and are required to build the webserver stack serving prediction requests, following the architecture as shown:

<details>
<summary><strong>Request serving stack (expand to view diagram)</strong></summary><p>

</p></details>
* The file named `predictor.py` is where we need to package the code for generating inference using the trained model that was saved into an S3 bucket location by the training code during the training job run.<p>
* We'll write code into this file using Jupyter magic command - `writefile`.<p><br>
First part of the file would contain the necessary imports, as ususal.
```
%%writefile byoa/predictor.py
# This is the file that implements a flask server to do inferences. It's the file that you will modify to
# implement the scoring for your own algorithm.
from __future__ import print_function
import os
import json
import pickle
from io import StringIO
import sys
import signal
import traceback
import numpy as np
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import LSTM
from keras.models import load_model
import flask
import tensorflow as tf
import pandas as pd
from os import listdir, sep
from os.path import abspath, basename, isdir
from sys import argv
```
When run within an instantiated container, SageMaker makes the trained model available locally at `/opt/ml`
```
%%writefile -a byoa/predictor.py
prefix = '/opt/ml/'
model_path = os.path.join(prefix, 'model')
```
The machinery to produce inference is wrapped around in a Pythonic class structure, within a `Singleton` class, aptly named - `ScoringService`.<p>
We create `Class` variables in this class to hold loaded model, character indices, tensor-flow graph, and anything else that needs to be referenced while generating prediction.
```
%%writefile -a byoa/predictor.py
# A singleton for holding the model. This simply loads the model and holds it.
# It has a predict function that does a prediction based on the model and the input data.
class ScoringService(object):
model_type = None # Where we keep the model type, qualified by hyperparameters used during training
model = None # Where we keep the model when it's loaded
graph = None
indices = None # Where we keep the indices of Alphabet when it's loaded
```
Generally, we have to provide class methods to load the model and related artefacts from the model path as assigned by SageMaker within the running container.<p>
Notice here that SageMaker copies the artefacts from the S3 location (as defined during model creation) into the container local file system.
```
%%writefile -a byoa/predictor.py
@classmethod
def get_indices(cls):
#Get the indices for Alphabet for this instance, loading it if it's not already loaded
if cls.indices == None:
model_type='lstm-gender-classifier'
index_path = os.path.join(model_path, '{}-indices.npy'.format(model_type))
if os.path.exists(index_path):
cls.indices = np.load(index_path).item()
else:
print("Character Indices not found.")
return cls.indices
@classmethod
def get_model(cls):
#Get the model object for this instance, loading it if it's not already loaded
if cls.model == None:
model_type='lstm-gender-classifier'
mod_path = os.path.join(model_path, '{}-model.h5'.format(model_type))
if os.path.exists(mod_path):
cls.model = load_model(mod_path)
cls.model._make_predict_function()
cls.graph = tf.get_default_graph()
else:
print("LSTM Model not found.")
return cls.model
```
Finally, inside another clas method, named `predict`, we provide the code that we used earlier to generate prediction.<p>
Only difference with our previous test prediciton (in development notebook) is that in this case, the predictor will grab the data from the `input` variable, which in turn is obtained from the HTTP request payload.
```
%%writefile -a byoa/predictor.py
@classmethod
def predict(cls, input):
mod = cls.get_model()
ind = cls.get_indices()
result = {}
if mod == None:
print("Model not loaded.")
else:
if 'max_name_length' not in ind:
max_name_length = 15
alphabet_size = 26
else:
max_name_length = ind['max_name_length']
ind.pop('max_name_length', None)
alphabet_size = len(ind)
inputs_list = input.strip('\n').split(",")
num_inputs = len(inputs_list)
X_test = np.zeros((num_inputs, max_name_length, alphabet_size))
for i,name in enumerate(inputs_list):
name = name.lower().strip('\n')
for t, char in enumerate(name):
if char in ind:
X_test[i, t,ind[char]] = 1
with cls.graph.as_default():
predictions = mod.predict(X_test)
for i,name in enumerate(inputs_list):
result[name] = 'M' if predictions[i][0]>predictions[i][1] else 'F'
print("{} ({})".format(inputs_list[i],"M" if predictions[i][0]>predictions[i][1] else "F"))
return json.dumps(result)
```
With the prediction code captured, we move on to define the flask app, and provide a `ping`, which SageMaker uses to conduct health check on container instances that are responsible behind the hosted prediction endpoint.<p>
Here we can have the container return healthy response, with status code `200` when everythings goes well.<p>
For simplicity, we are only validating whether model has been loaded in this case. In practice, this provides opportunity extensive health check (including any external dependency check), as required.
```
%%writefile -a byoa/predictor.py
# The flask app for serving predictions
app = flask.Flask(__name__)
@app.route('/ping', methods=['GET'])
def ping():
#Determine if the container is working and healthy.
# Declare it healthy if we can load the model successfully.
health = ScoringService.get_model() is not None and ScoringService.get_indices() is not None
status = 200 if health else 404
return flask.Response(response='\n', status=status, mimetype='application/json')
```
Last but not the least, we define a `transformation` method that would intercept the HTTP request coming through to the SageMaker hosted endpoint.<p>
Here we have the opportunity to decide what type of data we accept with the request. In this particular example, we are accepting only `CSV` formatted data, decoding the data, and invoking prediction.<p>
The response is similarly funneled backed to the caller with MIME type of `CSV`.<p>
You are free to choose any or multiple MIME types for your requests and response. However if you choose to do so, it is within this method that we have to transform the back to and from the format that is suitable to passed for prediction.
```
%%writefile -a byoa/predictor.py
@app.route('/invocations', methods=['POST'])
def transformation():
#Do an inference on a single batch of data
data = None
# Convert from CSV to pandas
if flask.request.content_type == 'text/csv':
data = flask.request.data.decode('utf-8')
else:
return flask.Response(response='This predictor only supports CSV data', status=415, mimetype='text/plain')
print('Invoked with {} records'.format(data.count(",")+1))
# Do the prediction
predictions = ScoringService.predict(data)
result = ""
for prediction in predictions:
result = result + prediction
return flask.Response(response=result, status=200, mimetype='text/csv')
```
Note that in containerizing our custom LSTM Algorithm, where we used `Keras` as our framework of our choice, we did not have to interact directly with the SageMaker API, even though SageMaker API doesn't support `Keras`.<p>
This serves to show the power and flexibility offered by containerized machine learning pipeline on SageMaker.
## Container publishing
In order to host and deploy the trained model using SageMaker, we need to build the `Docker` containers, publish it to `Amazon ECR` repository, and then either use SageMaker console or API to created the endpoint configuration and deploy the stages.<p>
Conceptually, the steps required for publishing are:<p>
1. Make the`predictor.py` files executable
2. Create an ECR repository within your default region
3. Build a docker container with an identifieable name
4. Tage the image and publish to the ECR repository
<p><br>
All of these are conveniently encapsulated inside `build_and_push` script. We simply run it with the unique name of our production run.
```
run_type='cpu'
instance_class = "p3" if run_type.lower()=='gpu' else "c4"
instance_type = "ml.{}.8xlarge".format(instance_class)
pipeline_name = 'gender-classifier'
run=input("Enter run version: ")
run_name = pipeline_name+"-"+run
if run_type == "cpu":
!cp "Dockerfile.cpu" "Dockerfile"
if run_type == "gpu":
!cp "Dockerfile.gpu" "Dockerfile"
!sh build_and_push.sh $run_name
```
## Orchestration
At this point, we can head to ECS console, grab the ARN for the repository where we published the docker image, and use SageMaker console to create hosted model, and endpoint.<p>
However, it is often more convenient to automate these steps. In this notebook we do exactly that using `boto3 SageMaker` API.<p>
Following are the steps:<p>
* First we create a model hosting definition, by providing the S3 location to the model artifact, and ARN to the ECR image of the container.
* Using the model hosting definition, our next step is to create configuration of a hosted endpoint that will be used to serve prediciton generation requests.
* Creating the endpoint is the last step in the ML cycle, that prepares your model to serve client reqests from applications.
* We wait until the provision is completed and the endpoint in service. At this point we can send request to this endpoint and obtain gender predictions.
```
import sagemaker
sm_role = sagemaker.get_execution_role()
print("Using Role {}".format(sm_role))
acc = boto3.client('sts').get_caller_identity().get('Account')
reg = boto3.session.Session().region_name
sagemaker = boto3.client('sagemaker')
#Check if model already exists
model_name = "{}-model".format(run_name)
models = sagemaker.list_models(NameContains=model_name)['Models']
model_exists = False
if len(models) > 0:
for model in models:
if model['ModelName'] == model_name:
model_exists = True
break
#Delete model, if chosen
if model_exists == True:
choice = input("Model already exists, do you want to delete and create a fresh one (Y/N) ? ")
if choice.upper()[0:1] == "Y":
sagemaker.delete_model(ModelName = model_name)
model_exists = False
else:
print("Model - {} already exists".format(model_name))
if model_exists == False:
model_response = sagemaker.create_model(
ModelName=model_name,
PrimaryContainer={
'Image': '{}.dkr.ecr.{}.amazonaws.com/{}:latest'.format(acc, reg, run_name),
'ModelDataUrl': 's3://{}/model/model.tar.gz'.format(s3bucketname)
},
ExecutionRoleArn=sm_role,
Tags=[
{
'Key': 'Name',
'Value': model_name
}
]
)
print("{} Created at {}".format(model_response['ModelArn'],
model_response['ResponseMetadata']['HTTPHeaders']['date']))
#Check if endpoint configuration already exists
endpoint_config_name = "{}-endpoint-config".format(run_name)
endpoint_configs = sagemaker.list_endpoint_configs(NameContains=endpoint_config_name)['EndpointConfigs']
endpoint_config_exists = False
if len(endpoint_configs) > 0:
for endpoint_config in endpoint_configs:
if endpoint_config['EndpointConfigName'] == endpoint_config_name:
endpoint_config_exists = True
break
#Delete endpoint configuration, if chosen
if endpoint_config_exists == True:
choice = input("Endpoint Configuration already exists, do you want to delete and create a fresh one (Y/N) ? ")
if choice.upper()[0:1] == "Y":
sagemaker.delete_endpoint_config(EndpointConfigName = endpoint_config_name)
endpoint_config_exists = False
else:
print("Endpoint Configuration - {} already exists".format(endpoint_config_name))
if endpoint_config_exists == False:
endpoint_config_response = sagemaker.create_endpoint_config(
EndpointConfigName=endpoint_config_name,
ProductionVariants=[
{
'VariantName': 'default',
'ModelName': model_name,
'InitialInstanceCount': 1,
'InstanceType': instance_type,
'InitialVariantWeight': 1
},
],
Tags=[
{
'Key': 'Name',
'Value': endpoint_config_name
}
]
)
print("{} Created at {}".format(endpoint_config_response['EndpointConfigArn'],
endpoint_config_response['ResponseMetadata']['HTTPHeaders']['date']))
from ipywidgets import widgets
from IPython.display import display
#Check if endpoint already exists
endpoint_name = "{}-endpoint".format(run_name)
endpoints = sagemaker.list_endpoints(NameContains=endpoint_name)['Endpoints']
endpoint_exists = False
if len(endpoints) > 0:
for endpoint in endpoints:
if endpoint['EndpointName'] == endpoint_name:
endpoint_exists = True
break
#Delete endpoint, if chosen
if endpoint_exists == True:
choice = input("Endpoint already exists, do you want to delete and create a fresh one (Y/N) ? ")
if choice.upper()[0:1] == "Y":
sagemaker.delete_endpoint(EndpointName = endpoint_name)
print("Deleting Endpoint - {} ...".format(endpoint_name))
waiter = sagemaker.get_waiter('endpoint_deleted')
waiter.wait(EndpointName=endpoint_name,
WaiterConfig = {'Delay':1,'MaxAttempts':100})
endpoint_exists = False
print("Endpoint - {} deleted".format(endpoint_name))
else:
print("Endpoint - {} already exists".format(endpoint_name))
if endpoint_exists == False:
endpoint_response = sagemaker.create_endpoint(
EndpointName=endpoint_name,
EndpointConfigName=endpoint_config_name,
Tags=[
{
'Key': 'string',
'Value': endpoint_name
}
]
)
status='Creating'
sleep = 3
print("{} Endpoint : {}".format(status,endpoint_name))
bar = widgets.FloatProgress(min=0, description="Progress") # instantiate the bar
display(bar) # display the bar
while status != 'InService' and status != 'Failed' and status != 'OutOfService':
endpoint_response = sagemaker.describe_endpoint(
EndpointName=endpoint_name
)
status = endpoint_response['EndpointStatus']
time.sleep(sleep)
bar.value = bar.value + 1
if bar.value >= bar.max-1:
bar.max = int(bar.max*1.05)
if status != 'InService' and status != 'Failed' and status != 'OutOfService':
print(".", end='')
bar.max = bar.value
html = widgets.HTML(
value="<H2>Endpoint <b><u>{}</b></u> - {}</H2>".format(endpoint_response['EndpointName'], status)
)
display(html)
```
At the end we run a quick test to validate we are able to generate meaningful predicitions using the hosted endpoint, as we did locally using the model on the Notebbok instance.
```
!aws sagemaker-runtime invoke-endpoint --endpoint-name "$run_name-endpoint" --body 'Tom,Allie,Jim,Sophie,John,Kayla,Mike,Amanda,Andrew' --content-type text/csv outfile
!cat outfile
```
Head back to Module-3 of the workshop now, to the section titled - `Integration`, and follow the steps described.<p>
You'll need to copy the endpoint name from the output of the cell below, to use in the Lambda function that will send request to this hosted endpoint.
```
print(endpoint_response
['EndpointName'])
```
|
github_jupyter
|
# Carving Unit Tests
So far, we have always generated _system input_, i.e. data that the program as a whole obtains via its input channels. If we are interested in testing only a small set of functions, having to go through the system can be very inefficient. This chapter introduces a technique known as _carving_, which, given a system test, automatically extracts a set of _unit tests_ that replicate the calls seen during the unit test. The key idea is to _record_ such calls such that we can _replay_ them later – as a whole or selectively. On top, we also explore how to synthesize API grammars from carved unit tests; this means that we can _synthesize API tests without having to write a grammar at all._
**Prerequisites**
* Carving makes use of dynamic traces of function calls and variables, as introduced in the [chapter on configuration fuzzing](ConfigurationFuzzer.ipynb).
* Using grammars to test units was introduced in the [chapter on API fuzzing](APIFuzzer.ipynb).
```
import bookutils
import APIFuzzer
```
## Synopsis
<!-- Automatically generated. Do not edit. -->
To [use the code provided in this chapter](Importing.ipynb), write
```python
>>> from fuzzingbook.Carver import <identifier>
```
and then make use of the following features.
This chapter provides means to _record and replay function calls_ during a system test. Since individual function calls are much faster than a whole system run, such "carving" mechanisms have the potential to run tests much faster.
### Recording Calls
The `CallCarver` class records all calls occurring while it is active. It is used in conjunction with a `with` clause:
```python
>>> with CallCarver() as carver:
>>> y = my_sqrt(2)
>>> y = my_sqrt(4)
```
After execution, `called_functions()` lists the names of functions encountered:
```python
>>> carver.called_functions()
['my_sqrt', '__exit__']
```
The `arguments()` method lists the arguments recorded for a function. This is a mapping of the function name to a list of lists of arguments; each argument is a pair (parameter name, value).
```python
>>> carver.arguments('my_sqrt')
[[('x', 2)], [('x', 4)]]
```
Complex arguments are properly serialized, such that they can be easily restored.
### Synthesizing Calls
While such recorded arguments already could be turned into arguments and calls, a much nicer alternative is to create a _grammar_ for recorded calls. This allows to synthesize arbitrary _combinations_ of arguments, and also offers a base for further customization of calls.
The `CallGrammarMiner` class turns a list of carved executions into a grammar.
```python
>>> my_sqrt_miner = CallGrammarMiner(carver)
>>> my_sqrt_grammar = my_sqrt_miner.mine_call_grammar()
>>> my_sqrt_grammar
{'<start>': ['<call>'],
'<call>': ['<my_sqrt>'],
'<my_sqrt-x>': ['2', '4'],
'<my_sqrt>': ['my_sqrt(<my_sqrt-x>)']}
```
This grammar can be used to synthesize calls.
```python
>>> fuzzer = GrammarCoverageFuzzer(my_sqrt_grammar)
>>> fuzzer.fuzz()
'my_sqrt(4)'
```
These calls can be executed in isolation, effectively extracting unit tests from system tests:
```python
>>> eval(fuzzer.fuzz())
1.414213562373095
```
## System Tests vs Unit Tests
Remember the URL grammar introduced for [grammar fuzzing](Grammars.ipynb)? With such a grammar, we can happily test a Web browser again and again, checking how it reacts to arbitrary page requests.
Let us define a very simple "web browser" that goes and downloads the content given by the URL.
```
import urllib.parse
def webbrowser(url):
"""Download the http/https resource given by the URL"""
import requests # Only import if needed
r = requests.get(url)
return r.text
```
Let us apply this on [fuzzingbook.org](https://www.fuzzingbook.org/) and measure the time, using the [Timer class](Timer.ipynb):
```
from Timer import Timer
with Timer() as webbrowser_timer:
fuzzingbook_contents = webbrowser(
"http://www.fuzzingbook.org/html/Fuzzer.html")
print("Downloaded %d bytes in %.2f seconds" %
(len(fuzzingbook_contents), webbrowser_timer.elapsed_time()))
fuzzingbook_contents[:100]
```
A full webbrowser, of course, would also render the HTML content. We can achieve this using these commands (but we don't, as we do not want to replicate the entire Web page here):
```python
from IPython.display import HTML, display
HTML(fuzzingbook_contents)
```
Having to start a whole browser (or having it render a Web page) again and again means lots of overhead, though – in particular if we want to test only a subset of its functionality. In particular, after a change in the code, we would prefer to test only the subset of functions that is affected by the change, rather than running the well-tested functions again and again.
Let us assume we change the function that takes care of parsing the given URL and decomposing it into the individual elements – the scheme ("http"), the network location (`"www.fuzzingbook.com"`), or the path (`"/html/Fuzzer.html"`). This function is named `urlparse()`:
```
from urllib.parse import urlparse
urlparse('https://www.fuzzingbook.com/html/Carver.html')
```
You see how the individual elements of the URL – the _scheme_ (`"http"`), the _network location_ (`"www.fuzzingbook.com"`), or the path (`"//html/Carver.html"`) are all properly identified. Other elements (like `params`, `query`, or `fragment`) are empty, because they were not part of our input.
The interesting thing is that executing only `urlparse()` is orders of magnitude faster than running all of `webbrowser()`. Let us measure the factor:
```
runs = 1000
with Timer() as urlparse_timer:
for i in range(runs):
urlparse('https://www.fuzzingbook.com/html/Carver.html')
avg_urlparse_time = urlparse_timer.elapsed_time() / 1000
avg_urlparse_time
```
Compare this to the time required by the webbrowser
```
webbrowser_timer.elapsed_time()
```
The difference in time is huge:
```
webbrowser_timer.elapsed_time() / avg_urlparse_time
```
Hence, in the time it takes to run `webbrowser()` once, we can have _tens of thousands_ of executions of `urlparse()` – and this does not even take into account the time it takes the browser to render the downloaded HTML, to run the included scripts, and whatever else happens when a Web page is loaded. Hence, strategies that allow us to test at the _unit_ level are very promising as they can save lots of overhead.
## Carving Unit Tests
Testing methods and functions at the unit level requires a very good understanding of the individual units to be tested as well as their interplay with other units. Setting up an appropriate infrastructure and writing unit tests by hand thus is demanding, yet rewarding. There is, however, an interesting alternative to writing unit tests by hand. The technique of _carving_ automatically _converts system tests into unit tests_ by means of recording and replaying function calls:
1. During a system test (given or generated), we _record_ all calls into a function, including all arguments and other variables the function reads.
2. From these, we synthesize a self-contained _unit test_ that reconstructs the function call with all arguments.
3. This unit test can be executed (replayed) at any time with high efficiency.
In the remainder of this chapter, let us explore these steps.
## Recording Calls
Our first challenge is to record function calls together with their arguments. (In the interest of simplicity, we restrict ourself to arguments, ignoring any global variables or other non-arguments that are read by the function.) To record calls and arguments, we use the mechanism [we introduced for coverage](Coverage.ipynb): By setting up a tracer function, we track all calls into individual functions, also saving their arguments. Just like `Coverage` objects, we want to use `Carver` objects to be able to be used in conjunction with the `with` statement, such that we can trace a particular code block:
```python
with Carver() as carver:
function_to_be_traced()
c = carver.calls()
```
The initial definition supports this construct:
\todo{Get tracker from [dynamic invariants](DynamicInvariants.ipynb)}
```
import sys
class Carver(object):
def __init__(self, log=False):
self._log = log
self.reset()
def reset(self):
self._calls = {}
# Start of `with` block
def __enter__(self):
self.original_trace_function = sys.gettrace()
sys.settrace(self.traceit)
return self
# End of `with` block
def __exit__(self, exc_type, exc_value, tb):
sys.settrace(self.original_trace_function)
```
The actual work takes place in the `traceit()` method, which records all calls in the `_calls` attribute. First, we define two helper functions:
```
import inspect
def get_qualified_name(code):
"""Return the fully qualified name of the current function"""
name = code.co_name
module = inspect.getmodule(code)
if module is not None:
name = module.__name__ + "." + name
return name
def get_arguments(frame):
"""Return call arguments in the given frame"""
# When called, all arguments are local variables
arguments = [(var, frame.f_locals[var]) for var in frame.f_locals]
arguments.reverse() # Want same order as call
return arguments
class CallCarver(Carver):
def add_call(self, function_name, arguments):
"""Add given call to list of calls"""
if function_name not in self._calls:
self._calls[function_name] = []
self._calls[function_name].append(arguments)
# Tracking function: Record all calls and all args
def traceit(self, frame, event, arg):
if event != "call":
return None
code = frame.f_code
function_name = code.co_name
qualified_name = get_qualified_name(code)
arguments = get_arguments(frame)
self.add_call(function_name, arguments)
if qualified_name != function_name:
self.add_call(qualified_name, arguments)
if self._log:
print(simple_call_string(function_name, arguments))
return None
```
Finally, we need some convenience functions to access the calls:
```
class CallCarver(CallCarver):
def calls(self):
"""Return a dictionary of all calls traced."""
return self._calls
def arguments(self, function_name):
"""Return a list of all arguments of the given function
as (VAR, VALUE) pairs.
Raises an exception if the function was not traced."""
return self._calls[function_name]
def called_functions(self, qualified=False):
"""Return all functions called."""
if qualified:
return [function_name for function_name in self._calls.keys()
if function_name.find('.') >= 0]
else:
return [function_name for function_name in self._calls.keys()
if function_name.find('.') < 0]
```
### Recording my_sqrt()
Let's try out our new `Carver` class – first on a very simple function:
```
from Intro_Testing import my_sqrt
with CallCarver() as sqrt_carver:
my_sqrt(2)
my_sqrt(4)
```
We can retrieve all calls seen...
```
sqrt_carver.calls()
sqrt_carver.called_functions()
```
... as well as the arguments of a particular function:
```
sqrt_carver.arguments("my_sqrt")
```
We define a convenience function for nicer printing of these lists:
```
def simple_call_string(function_name, argument_list):
"""Return function_name(arg[0], arg[1], ...) as a string"""
return function_name + "(" + \
", ".join([var + "=" + repr(value)
for (var, value) in argument_list]) + ")"
for function_name in sqrt_carver.called_functions():
for argument_list in sqrt_carver.arguments(function_name):
print(simple_call_string(function_name, argument_list))
```
This is a syntax we can directly use to invoke `my_sqrt()` again:
```
eval("my_sqrt(x=2)")
```
### Carving urlparse()
What happens if we apply this to `webbrowser()`?
```
with CallCarver() as webbrowser_carver:
webbrowser("http://www.example.com")
```
We see that retrieving a URL from the Web requires quite some functionality:
```
function_list = webbrowser_carver.called_functions(qualified=True)
len(function_list)
print(function_list[:50])
```
Among several other functions, we also have a call to `urlparse()`:
```
urlparse_argument_list = webbrowser_carver.arguments("urllib.parse.urlparse")
urlparse_argument_list
```
Again, we can convert this into a well-formatted call:
```
urlparse_call = simple_call_string("urlparse", urlparse_argument_list[0])
urlparse_call
```
Again, we can re-execute this call:
```
eval(urlparse_call)
```
We now have successfully carved the call to `urlparse()` out of the `webbrowser()` execution.
## Replaying Calls
Replaying calls in their entirety and in all generality is tricky, as there are several challenges to be addressed. These include:
1. We need to be able to _access_ individual functions. If we access a function by name, the name must be in scope. If the name is not visible (for instance, because it is a name internal to the module), we must make it visible.
2. Any _resources_ accessed outside of arguments must be recorded and reconstructed for replay as well. This can be difficult if variables refer to external resources such as files or network resources.
3. _Complex objects_ must be reconstructed as well.
These constraints make carving hard or even impossible if the function to be tested interacts heavily with its environment. To illustrate these issues, consider the `email.parser.parse()` method that is invoked in `webbrowser()`:
```
email_parse_argument_list = webbrowser_carver.arguments("email.parser.parse")
```
Calls to this method look like this:
```
email_parse_call = simple_call_string(
"email.parser.parse",
email_parse_argument_list[0])
email_parse_call
```
We see that `email.parser.parse()` is part of a `email.parser.Parser` object and it gets a `StringIO` object. Both are non-primitive values. How could we possibly reconstruct them?
### Serializing Objects
The answer to the problem of complex objects lies in creating a _persistent_ representation that can be _reconstructed_ at later points in time. This process is known as _serialization_; in Python, it is also known as _pickling_. The `pickle` module provides means to create a serialized representation of an object. Let us apply this on the `email.parser.Parser` object we just found:
```
import pickle
parser_object = email_parse_argument_list[0][0][1]
parser_object
pickled = pickle.dumps(parser_object)
pickled
```
From this string representing the serialized `email.parser.Parser` object, we can recreate the Parser object at any time:
```
unpickled_parser_object = pickle.loads(pickled)
unpickled_parser_object
```
The serialization mechanism allows us to produce a representation for all objects passed as parameters (assuming they can be pickled, that is). We can now extend the `simple_call_string()` function such that it automatically pickles objects. Additionally, we set it up such that if the first parameter is named `self` (i.e., it is a class method), we make it a method of the `self` object.
```
def call_value(value):
value_as_string = repr(value)
if value_as_string.find('<') >= 0:
# Complex object
value_as_string = "pickle.loads(" + repr(pickle.dumps(value)) + ")"
return value_as_string
def call_string(function_name, argument_list):
"""Return function_name(arg[0], arg[1], ...) as a string, pickling complex objects"""
if len(argument_list) > 0:
(first_var, first_value) = argument_list[0]
if first_var == "self":
# Make this a method call
method_name = function_name.split(".")[-1]
function_name = call_value(first_value) + "." + method_name
argument_list = argument_list[1:]
return function_name + "(" + \
", ".join([var + "=" + call_value(value)
for (var, value) in argument_list]) + ")"
```
Let us apply the extended `call_string()` method to create a call for `email.parser.parse()`, including pickled objects:
```
call = call_string("email.parser.parse", email_parse_argument_list[0])
print(call)
```
With this call involvimng the pickled object, we can now re-run the original call and obtain a valid result:
```
eval(call)
```
### All Calls
So far, we have seen only one call of `webbrowser()`. How many of the calls within `webbrowser()` can we actually carve and replay? Let us try this out and compute the numbers.
```
import traceback
import enum
import socket
all_functions = set(webbrowser_carver.called_functions(qualified=True))
call_success = set()
run_success = set()
exceptions_seen = set()
for function_name in webbrowser_carver.called_functions(qualified=True):
for argument_list in webbrowser_carver.arguments(function_name):
try:
call = call_string(function_name, argument_list)
call_success.add(function_name)
result = eval(call)
run_success.add(function_name)
except Exception as exc:
exceptions_seen.add(repr(exc))
# print("->", call, file=sys.stderr)
# traceback.print_exc()
# print("", file=sys.stderr)
continue
print("%d/%d calls (%.2f%%) successfully created and %d/%d calls (%.2f%%) successfully ran" % (
len(call_success), len(all_functions), len(
call_success) * 100 / len(all_functions),
len(run_success), len(all_functions), len(run_success) * 100 / len(all_functions)))
```
About half of the calls succeed. Let us take a look into some of the error messages we get:
```
for i in range(10):
print(list(exceptions_seen)[i])
```
We see that:
* **A large majority of calls could be converted into call strings.** If this is not the case, this is mostly due to having unserialized objects being passed.
* **About half of the calls could be executed.** The error messages for the failing runs are varied; the most frequent being that some internal name is invoked that is not in scope.
Our carving mechanism should be taken with a grain of salt: We still do not cover the situation where external variables and values (such as global variables) are being accessed, and the serialization mechanism cannot recreate external resources. Still, if the function of interest falls among those that _can_ be carved and replayed, we can very effectively re-run its calls with their original arguments.
## Mining API Grammars from Carved Calls
So far, we have used carved calls to replay exactly the same invocations as originally encountered. However, we can also _mutate_ carved calls to effectively fuzz APIs with previously recorded arguments.
The general idea is as follows:
1. First, we record all calls of a specific function from a given execution of the program.
2. Second, we create a grammar that incorporates all these calls, with separate rules for each argument and alternatives for each value found; this allows us to produce calls that arbitrarily _recombine_ these arguments.
Let us explore these steps in the following sections.
### From Calls to Grammars
Let us start with an example. The `power(x, y)` function returns $x^y$; it is but a wrapper around the equivalent `math.pow()` function. (Since `power()` is defined in Python, we can trace it – in contrast to `math.pow()`, which is implemented in C.)
```
import math
def power(x, y):
return math.pow(x, y)
```
Let us invoke `power()` while recording its arguments:
```
with CallCarver() as power_carver:
z = power(1, 2)
z = power(3, 4)
power_carver.arguments("power")
```
From this list of recorded arguments, we could now create a grammar for the `power()` call, with `x` and `y` expanding into the values seen:
```
from Grammars import START_SYMBOL, is_valid_grammar, new_symbol, extend_grammar
POWER_GRAMMAR = {
"<start>": ["power(<x>, <y>)"],
"<x>": ["1", "3"],
"<y>": ["2", "4"]
}
assert is_valid_grammar(POWER_GRAMMAR)
```
When fuzzing with this grammar, we then get arbitrary combinations of `x` and `y`; aiming for coverage will ensure that all values are actually tested at least once:
```
from GrammarCoverageFuzzer import GrammarCoverageFuzzer
power_fuzzer = GrammarCoverageFuzzer(POWER_GRAMMAR)
[power_fuzzer.fuzz() for i in range(5)]
```
What we need is a method to automatically convert the arguments as seen in `power_carver` to the grammar as seen in `POWER_GRAMMAR`. This is what we define in the next section.
### A Grammar Miner for Calls
We introduce a class `CallGrammarMiner`, which, given a `Carver`, automatically produces a grammar from the calls seen. To initialize, we pass the carver object:
```
class CallGrammarMiner(object):
def __init__(self, carver, log=False):
self.carver = carver
self.log = log
```
#### Initial Grammar
The initial grammar produces a single call. The possible `<call>` expansions are to be constructed later:
```
import copy
class CallGrammarMiner(CallGrammarMiner):
CALL_SYMBOL = "<call>"
def initial_grammar(self):
return extend_grammar(
{START_SYMBOL: [self.CALL_SYMBOL],
self.CALL_SYMBOL: []
})
m = CallGrammarMiner(power_carver)
initial_grammar = m.initial_grammar()
initial_grammar
```
#### A Grammar from Arguments
Let us start by creating a grammar from a list of arguments. The method `mine_arguments_grammar()` creates a grammar for the arguments seen during carving, such as these:
```
arguments = power_carver.arguments("power")
arguments
```
The `mine_arguments_grammar()` method iterates through the variables seen and creates a mapping `variables` of variable names to a set of values seen (as strings, going through `call_value()`). In a second step, it then creates a grammar with a rule for each variable name, expanding into the values seen.
```
class CallGrammarMiner(CallGrammarMiner):
def var_symbol(self, function_name, var, grammar):
return new_symbol(grammar, "<" + function_name + "-" + var + ">")
def mine_arguments_grammar(self, function_name, arguments, grammar):
var_grammar = {}
variables = {}
for argument_list in arguments:
for (var, value) in argument_list:
value_string = call_value(value)
if self.log:
print(var, "=", value_string)
if value_string.find("<") >= 0:
var_grammar["<langle>"] = ["<"]
value_string = value_string.replace("<", "<langle>")
if var not in variables:
variables[var] = set()
variables[var].add(value_string)
var_symbols = []
for var in variables:
var_symbol = self.var_symbol(function_name, var, grammar)
var_symbols.append(var_symbol)
var_grammar[var_symbol] = list(variables[var])
return var_grammar, var_symbols
m = CallGrammarMiner(power_carver)
var_grammar, var_symbols = m.mine_arguments_grammar(
"power", arguments, initial_grammar)
var_grammar
```
The additional return value `var_symbols` is a list of argument symbols in the call:
```
var_symbols
```
#### A Grammar from Calls
To get the grammar for a single function (`mine_function_grammar()`), we add a call to the function:
```
class CallGrammarMiner(CallGrammarMiner):
def function_symbol(self, function_name, grammar):
return new_symbol(grammar, "<" + function_name + ">")
def mine_function_grammar(self, function_name, grammar):
arguments = self.carver.arguments(function_name)
if self.log:
print(function_name, arguments)
var_grammar, var_symbols = self.mine_arguments_grammar(
function_name, arguments, grammar)
function_grammar = var_grammar
function_symbol = self.function_symbol(function_name, grammar)
if len(var_symbols) > 0 and var_symbols[0].find("-self") >= 0:
# Method call
function_grammar[function_symbol] = [
var_symbols[0] + "." + function_name + "(" + ", ".join(var_symbols[1:]) + ")"]
else:
function_grammar[function_symbol] = [
function_name + "(" + ", ".join(var_symbols) + ")"]
if self.log:
print(function_symbol, "::=", function_grammar[function_symbol])
return function_grammar, function_symbol
m = CallGrammarMiner(power_carver)
function_grammar, function_symbol = m.mine_function_grammar(
"power", initial_grammar)
function_grammar
```
The additionally returned `function_symbol` holds the name of the function call just added:
```
function_symbol
```
#### A Grammar from all Calls
Let us now repeat the above for all function calls seen during carving. To this end, we simply iterate over all function calls seen:
```
power_carver.called_functions()
class CallGrammarMiner(CallGrammarMiner):
def mine_call_grammar(self, function_list=None, qualified=False):
grammar = self.initial_grammar()
fn_list = function_list
if function_list is None:
fn_list = self.carver.called_functions(qualified=qualified)
for function_name in fn_list:
if function_list is None and (function_name.startswith("_") or function_name.startswith("<")):
continue # Internal function
# Ignore errors with mined functions
try:
function_grammar, function_symbol = self.mine_function_grammar(
function_name, grammar)
except:
if function_list is not None:
raise
if function_symbol not in grammar[self.CALL_SYMBOL]:
grammar[self.CALL_SYMBOL].append(function_symbol)
grammar.update(function_grammar)
assert is_valid_grammar(grammar)
return grammar
```
The method `mine_call_grammar()` is the one that clients can and should use – first for mining...
```
m = CallGrammarMiner(power_carver)
power_grammar = m.mine_call_grammar()
power_grammar
```
...and then for fuzzing:
```
power_fuzzer = GrammarCoverageFuzzer(power_grammar)
[power_fuzzer.fuzz() for i in range(5)]
```
With this, we have successfully extracted a grammar from a recorded execution; in contrast to "simple" carving, our grammar allows us to _recombine_ arguments and thus to fuzz at the API level.
## Fuzzing Web Functions
Let us now apply our grammar miner on a larger API – the `urlparse()` function we already encountered during carving.
```
with CallCarver() as webbrowser_carver:
webbrowser("https://www.fuzzingbook.org")
webbrowser("http://www.example.com")
```
We can mine a grammar from the calls encountered:
```
m = CallGrammarMiner(webbrowser_carver)
webbrowser_grammar = m.mine_call_grammar()
```
This is a rather large grammar:
```
call_list = webbrowser_grammar['<call>']
len(call_list)
print(call_list[:20])
```
Here's the rule for the `urlsplit()` function:
```
webbrowser_grammar["<urlsplit>"]
```
Here are the arguments. Note that although we only passed `http://www.fuzzingbook.org` as a parameter, we also see the `https:` variant. That is because opening the `http:` URL automatically redirects to the `https:` URL, which is then also processed by `urlsplit()`.
```
webbrowser_grammar["<urlsplit-url>"]
```
There also is some variation in the `scheme` argument:
```
webbrowser_grammar["<urlsplit-scheme>"]
```
If we now apply a fuzzer on these rules, we systematically cover all variations of arguments seen, including, of course, combinations not seen during carving. Again, we are fuzzing at the API level here.
```
urlsplit_fuzzer = GrammarCoverageFuzzer(
webbrowser_grammar, start_symbol="<urlsplit>")
for i in range(5):
print(urlsplit_fuzzer.fuzz())
```
Just as seen with carving, running tests at the API level is orders of magnitude faster than executing system tests. Hence, this calls for means to fuzz at the method level:
```
from urllib.parse import urlsplit
from Timer import Timer
with Timer() as urlsplit_timer:
urlsplit('http://www.fuzzingbook.org/', 'http', True)
urlsplit_timer.elapsed_time()
with Timer() as webbrowser_timer:
webbrowser("http://www.fuzzingbook.org")
webbrowser_timer.elapsed_time()
webbrowser_timer.elapsed_time() / urlsplit_timer.elapsed_time()
```
But then again, the caveats encountered during carving apply, notably the requirement to recreate the original function environment. If we also alter or recombine arguments, we get the additional risk of _violating an implicit precondition_ – that is, invoking a function with arguments the function was never designed for. Such _false alarms_, resulting from incorrect invocations rather than incorrect implementations, must then be identified (typically manually) and wed out (for instance, by altering or constraining the grammar). The huge speed gains at the API level, however, may well justify this additional investment.
## Synopsis
This chapter provides means to _record and replay function calls_ during a system test. Since individual function calls are much faster than a whole system run, such "carving" mechanisms have the potential to run tests much faster.
### Recording Calls
The `CallCarver` class records all calls occurring while it is active. It is used in conjunction with a `with` clause:
```
with CallCarver() as carver:
y = my_sqrt(2)
y = my_sqrt(4)
```
After execution, `called_functions()` lists the names of functions encountered:
```
carver.called_functions()
```
The `arguments()` method lists the arguments recorded for a function. This is a mapping of the function name to a list of lists of arguments; each argument is a pair (parameter name, value).
```
carver.arguments('my_sqrt')
```
Complex arguments are properly serialized, such that they can be easily restored.
### Synthesizing Calls
While such recorded arguments already could be turned into arguments and calls, a much nicer alternative is to create a _grammar_ for recorded calls. This allows to synthesize arbitrary _combinations_ of arguments, and also offers a base for further customization of calls.
The `CallGrammarMiner` class turns a list of carved executions into a grammar.
```
my_sqrt_miner = CallGrammarMiner(carver)
my_sqrt_grammar = my_sqrt_miner.mine_call_grammar()
my_sqrt_grammar
```
This grammar can be used to synthesize calls.
```
fuzzer = GrammarCoverageFuzzer(my_sqrt_grammar)
fuzzer.fuzz()
```
These calls can be executed in isolation, effectively extracting unit tests from system tests:
```
eval(fuzzer.fuzz())
```
## Lessons Learned
* _Carving_ allows for effective replay of function calls recorded during a system test.
* A function call can be _orders of magnitude faster_ than a system invocation.
* _Serialization_ allows to create persistent representations of complex objects.
* Functions that heavily interact with their environment and/or access external resources are difficult to carve.
* From carved calls, one can produce API grammars that arbitrarily combine carved arguments.
## Next Steps
In the next chapter, we will discuss [how to reduce failure-inducing inputs](Reducer.ipynb).
## Background
Carving was invented by Elbaum et al. \cite{Elbaum2006} and originally implemented for Java. In this chapter, we follow several of their design choices (including recording and serializing method arguments only).
The combination of carving and fuzzing at the API level is described in \cite{Kampmann2018}.
## Exercises
### Exercise 1: Carving for Regression Testing
So far, during carving, we only have looked into reproducing _calls_, but not into actually checking the _results_ of these calls. This is important for _regression testing_ – i.e. checking whether a change to code does not impede existing functionality. We can build this by recording not only _calls_, but also _return values_ – and then later compare whether the same calls result in the same values. This may not work on all occasions; values that depend on time, randomness, or other external factors may be different. Still, for functionality that abstracts from these details, checking that nothing has changed is an important part of testing.
Our aim is to design a class `ResultCarver` that extends `CallCarver` by recording both calls and return values.
In a first step, create a `traceit()` method that also tracks return values by extending the `traceit()` method. The `traceit()` event type is `"return"` and the `arg` parameter is the returned value. Here is a prototype that only prints out the returned values:
```
class ResultCarver(CallCarver):
def traceit(self, frame, event, arg):
if event == "return":
if self._log:
print("Result:", arg)
super().traceit(frame, event, arg)
# Need to return traceit function such that it is invoked for return
# events
return self.traceit
with ResultCarver(log=True) as result_carver:
my_sqrt(2)
```
#### Part 1: Store function results
Extend the above code such that results are _stored_ in a way that associates them with the currently returning function (or method). To this end, you need to keep track of the _current stack of called functions_.
**Solution.** Here's a solution, building on the above:
```
class ResultCarver(CallCarver):
def reset(self):
super().reset()
self._call_stack = []
self._results = {}
def add_result(self, function_name, arguments, result):
key = simple_call_string(function_name, arguments)
self._results[key] = result
def traceit(self, frame, event, arg):
if event == "call":
code = frame.f_code
function_name = code.co_name
qualified_name = get_qualified_name(code)
self._call_stack.append(
(function_name, qualified_name, get_arguments(frame)))
if event == "return":
result = arg
(function_name, qualified_name, arguments) = self._call_stack.pop()
self.add_result(function_name, arguments, result)
if function_name != qualified_name:
self.add_result(qualified_name, arguments, result)
if self._log:
print(
simple_call_string(
function_name,
arguments),
"=",
result)
# Keep on processing current calls
super().traceit(frame, event, arg)
# Need to return traceit function such that it is invoked for return
# events
return self.traceit
with ResultCarver(log=True) as result_carver:
my_sqrt(2)
result_carver._results
```
#### Part 2: Access results
Give it a method `result()` that returns the value recorded for that particular function name and result:
```python
class ResultCarver(CallCarver):
def result(self, function_name, argument):
"""Returns the result recorded for function_name(argument"""
```
**Solution.** This is mostly done in the code for part 1:
```
class ResultCarver(ResultCarver):
def result(self, function_name, argument):
key = simple_call_string(function_name, arguments)
return self._results[key]
```
#### Part 3: Produce assertions
For the functions called during `webbrowser()` execution, create a set of _assertions_ that check whether the result returned is still the same. Test this for `urllib.parse.urlparse()` and `urllib.parse.urlsplit()`.
**Solution.** Not too hard now:
```
with ResultCarver() as webbrowser_result_carver:
webbrowser("http://www.example.com")
for function_name in ["urllib.parse.urlparse", "urllib.parse.urlsplit"]:
for arguments in webbrowser_result_carver.arguments(function_name):
try:
call = call_string(function_name, arguments)
result = webbrowser_result_carver.result(function_name, arguments)
print("assert", call, "==", call_value(result))
except Exception:
continue
```
We can run these assertions:
```
from urllib.parse import SplitResult, ParseResult, urlparse, urlsplit
assert urlparse(
url='http://www.example.com',
scheme='',
allow_fragments=True) == ParseResult(
scheme='http',
netloc='www.example.com',
path='',
params='',
query='',
fragment='')
assert urlsplit(
url='http://www.example.com',
scheme='',
allow_fragments=True) == SplitResult(
scheme='http',
netloc='www.example.com',
path='',
query='',
fragment='')
```
We can now add these carved tests to a _regression test suite_ which would be run after every change to ensure that the functionality of `urlparse()` and `urlsplit()` is not changed.
### Exercise 2: Abstracting Arguments
When mining an API grammar from executions, set up an abstraction scheme to widen the range of arguments to be used during testing. If the values for an argument, all conform to some type `T`. abstract it into `<T>`. For instance, if calls to `foo(1)`, `foo(2)`, `foo(3)` have been seen, the grammar should abstract its calls into `foo(<int>)`, with `<int>` being appropriately defined.
Do this for a number of common types: integers, positive numbers, floating-point numbers, host names, URLs, mail addresses, and more.
**Solution.** Left to the reader.
|
github_jupyter
|
```
# Import Module
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import h5py
# Read data, which has a size of N * 784 and N * 1
MNIST = h5py.File("..\MNISTdata.hdf5",'r')
x_train = np.float32(MNIST['x_train'][:])
x_test = np.float32(MNIST['x_test'][:])
y_train = np.int32(MNIST['y_train'][:,0])
y_test = np.int32(MNIST['y_test'][:,0])
# Reshape samples as 28 * 28 images
x_trainnew = np.reshape(x_train, (len(x_train),28,28))
x_testnew = np.reshape(x_test, (len(x_test),28,28))
# Build activate functions
relu = lambda x: x*(x>0)
# Input a m * n matrix, output a m * n matrix whose rows are transformed and normalized
def softmax(X):
Xexp = np.exp(X)
return Xexp / np.sum(Xexp,axis=1,keepdims=True)
# Initialize the parameters
def param_init(input_size, kernel_size, output_size):
lx = input_size # 2-dim
lk = kernel_size # 2-dim
lh = (lx[0]-lk[0]+1, lx[1]-lk[1]+1) # Hidden layer size, 2-dim
ly = output_size # 1-dim
K = np.random.randn(lk[0],lk[1]) / max(lx)
W = np.random.randn(ly,lh[0],lh[1]) / max(lx)
b = np.zeros(ly)
return K,W,b
K,W,b = param_init((28,28),(3,3),10)
# Build the forward step
# Model: Z = X * K → H = relu(Z) → U = WH + b → Yhat = softmax(U)
def Convolution(image, kernel):
d1,d2 = image.shape
k1,k2 = kernel.shape
output_a = d1 - k1 + 1
output_b = d2 - k2 + 1
conv = np.zeros((output_a,output_b))
for a in range(output_a):
for b in range(output_b):
conv[a,b] = np.sum(np.multiply(image[a:a+k1,b:b+k2], kernel))
return conv
def forward_prop(X,K,W,b):
# Input to Hidden layer
Z = Convolution(X,K) # Shape: (lx[0]-lk[0]+1, lx[1]-lk[1]+1)
H = relu(Z) # Shape: (lx[0]-lk[0]+1, lx[1]-lk[1]+1)
# Hidden layer to Output
U = np.sum(np.multiply(W,H), axis=(1,2)) + b # Shape: (1 * ly)
U.shape = (1,W.shape[0])
Yhat = softmax(U) # Shape: (1 * ly)
return Z, H, Yhat
N = x_trainnew.shape[0]
r = np.random.randint(N)
x_samp = x_trainnew[r,:,:]
Y_oh = np.array(pd.get_dummies(np.squeeze(y_train)))
y_samp = Y_oh[[r]]
Z, H, Yhat = forward_prop(x_samp,K,W,b)
# Build the back-propagation step
def back_prop(K,W,b,Z,H,Yhat,X,Y,alpha):
bDel = Y - Yhat # Length ly
bDel = np.squeeze(bDel)
WDel = np.tensordot(bDel, H, axes=0) # Shape (ly, lx[0]-lk[0]+1, lx[1]-lk[1]+1)
HDel = np.tensordot(bDel, W, axes=1) # Shape (lx[0]-lk[0]+1, lx[1]-lk[1]+1)
ZDel = np.multiply(HDel,(lambda x:(x>0))(Z)) # Shape (lx[0]-lk[0]+1, lx[1]-lk[1]+1)
KDel = Convolution(X,ZDel) # Shape: (lk[0], lk[1])
#KDel = np.zeros(KDel.shape)
#WDel = np.zeros(WDel.shape)
#bDel = np.zeros(bDel.shape)
bn = b + alpha * bDel # Length ly
Wn = W + alpha * WDel # Shape (ly, lx[0]-lk[0]+1, lx[1]-lk[1]+1)
Kn = K + alpha * KDel # Shape (1k[0], lk[1])
return Kn,Wn,bn
alpha = 0.01
bDel,WDel,KDel = back_prop(K,W,b,Z,H,Yhat,x_samp,y_samp,alpha)
# Build the complete Neural Network
def TwoLayer_CNN_train(X, Y, ChannelSize = (3,3), NumChannel = 1, OrigAlpha = 0.01, num_epochs = 10):
# Recode Y as One-Hot
Y_oh = np.array(pd.get_dummies(np.squeeze(Y)))
# Indicate number of units per layer
N = X.shape[0] # Number of samples
xsize = X.shape[1:] # Size of every sample
ksize = ChannelSize # Size of the channel
ysize = Y_oh.shape[1] # Number of classes
# Initialized the parameters
K,W,b = param_init(xsize,ksize,ysize)
# Run 20 train iterations, record the error every time
for epoch in range(num_epochs):
if epoch <= 5:
alpha = OrigAlpha
elif epoch <= 10:
alpha = OrigAlpha * 1e-1
elif epoch <= 15:
alpha = OrigAlpha * 1e-2
else:
alpha = OrigAlpha * 1e-3
total_cor = 0
for n in range(int(N/6)):
r = np.random.randint(N)
x_samp = X[r,:,:]
y_samp = Y_oh[[r]]
# Forward
Z, H, Yhat = forward_prop(x_samp,K,W,b)
pred = np.argmax(Yhat)
if pred==Y[r]:
total_cor += 1
# Backward
K,W,b = back_prop(K,W,b,Z,H,Yhat,x_samp,y_samp,alpha)
print("Training Accuracy: ",total_cor / np.float(N/6))
return K,W,b
K,W,b = TwoLayer_CNN_train(x_trainnew, y_train, OrigAlpha=0.01, num_epochs=10)
# For a given neural network, predict an input X
def predict_NN(X,K,W,b):
X_predprob = forward_prop(X,K,W,b)[2]
X_pred = X_predprob.argmax(axis=1) # Take the biggest probability as its choice
return X_pred
# Predict on test set
# Still has problems!
y_predtest = predict_NN(x_testnew,K,W,b)
np.sum(y_predtest == y_test) / x_testnew.shape[0]
Ut = np.array([1,2,3])
Ut.shape = (1,3)
Wt = np.array([[[1,1],[2,2]],[[3,3],[4,4]],[[5,5],[6,6]]])
Ht = np.array([[0.3,0.3],[0.4,0.4]])
kt = np.sum(np.multiply(Wt,Ht),axis=(1,2))
np.tensordot(Ut,Wt,axes=1)
```
|
github_jupyter
|
# Attention Basics
In this notebook, we look at how attention is implemented. We will focus on implementing attention in isolation from a larger model. That's because when implementing attention in a real-world model, a lot of the focus goes into piping the data and juggling the various vectors rather than the concepts of attention themselves.
We will implement attention scoring as well as calculating an attention context vector.
## Attention Scoring
### Inputs to the scoring function
Let's start by looking at the inputs we'll give to the scoring function. We will assume we're in the first step in the decoding phase. The first input to the scoring function is the hidden state of decoder (assuming a toy RNN with three hidden nodes -- not usable in real life, but easier to illustrate):
```
dec_hidden_state = [5,1,20]
```
Let's visualize this vector:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Let's visualize our decoder hidden state
plt.figure(figsize=(1.5, 4.5))
sns.heatmap(np.transpose(np.matrix(dec_hidden_state)), annot=True, cmap=sns.light_palette("purple", as_cmap=True), linewidths=1)
```
Our first scoring function will score a single annotation (encoder hidden state), which looks like this:
```
annotation = [3,12,45] #e.g. Encoder hidden state
# Let's visualize the single annotation
plt.figure(figsize=(1.5, 4.5))
sns.heatmap(np.transpose(np.matrix(annotation)), annot=True, cmap=sns.light_palette("orange", as_cmap=True), linewidths=1)
```
### IMPLEMENT: Scoring a Single Annotation
Let's calculate the dot product of a single annotation. NumPy's [dot()](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html) is a good candidate for this operation
```
def single_dot_attention_score(dec_hidden_state, enc_hidden_state):
# TODO: return the dot product of the two vectors
return
single_dot_attention_score(dec_hidden_state, annotation)
```
### Annotations Matrix
Let's now look at scoring all the annotations at once. To do that, here's our annotation matrix:
```
annotations = np.transpose([[3,12,45], [59,2,5], [1,43,5], [4,3,45.3]])
```
And it can be visualized like this (each column is a hidden state of an encoder time step):
```
# Let's visualize our annotation (each column is an annotation)
ax = sns.heatmap(annotations, annot=True, cmap=sns.light_palette("orange", as_cmap=True), linewidths=1)
```
### IMPLEMENT: Scoring All Annotations at Once
Let's calculate the scores of all the annotations in one step using matrix multiplication. Let's continue to use the dot scoring method
<img src="images/scoring_functions.png" />
To do that, we'll have to transpose `dec_hidden_state` and [matrix multiply](https://docs.scipy.org/doc/numpy/reference/generated/numpy.matmul.html) it with `annotations`.
```
def dot_attention_score(dec_hidden_state, annotations):
# TODO: return the product of dec_hidden_state transpose and annotations
return
attention_weights_raw = dot_attention_score(dec_hidden_state, annotations)
attention_weights_raw
```
Looking at these scores, can you guess which of the four vectors will get the most attention from the decoder at this time step?
## Softmax
Now that we have our scores, let's apply softmax:
<img src="images/softmax.png" />
```
def softmax(x):
x = np.array(x, dtype=np.float128)
e_x = np.exp(x)
return e_x / e_x.sum(axis=0)
attention_weights = softmax(attention_weights_raw)
attention_weights
```
Even when knowing which annotation will get the most focus, it's interesting to see how drastic softmax makes the end score become. The first and last annotation had the respective scores of 927 and 929. But after softmax, the attention they'll get is 0.12 and 0.88 respectively.
# Applying the scores back on the annotations
Now that we have our scores, let's multiply each annotation by its score to proceed closer to the attention context vector. This is the multiplication part of this formula (we'll tackle the summation part in the latter cells)
<img src="images/Context_vector.png" />
```
def apply_attention_scores(attention_weights, annotations):
# TODO: Multiple the annotations by their weights
return
applied_attention = apply_attention_scores(attention_weights, annotations)
applied_attention
```
Let's visualize how the context vector looks now that we've applied the attention scores back on it:
```
# Let's visualize our annotations after applying attention to them
ax = sns.heatmap(applied_attention, annot=True, cmap=sns.light_palette("orange", as_cmap=True), linewidths=1)
```
Contrast this with the raw annotations visualized earlier in the notebook, and we can see that the second and third annotations (columns) have been nearly wiped out. The first annotation maintains some of its value, and the fourth annotation is the most pronounced.
# Calculating the Attention Context Vector
All that remains to produce our attention context vector now is to sum up the four columns to produce a single attention context vector
```
def calculate_attention_vector(applied_attention):
return np.sum(applied_attention, axis=1)
attention_vector = calculate_attention_vector(applied_attention)
attention_vector
# Let's visualize the attention context vector
plt.figure(figsize=(1.5, 4.5))
sns.heatmap(np.transpose(np.matrix(attention_vector)), annot=True, cmap=sns.light_palette("Blue", as_cmap=True), linewidths=1)
```
Now that we have the context vector, we can concatenate it with the hidden state and pass it through a hidden layer to produce the the result of this decoding time step.
|
github_jupyter
|
# Seasonal Accuracy Assessment of Water Observations from Space (WOfS) Product in Africa<img align="right" src="../Supplementary_data/DE_Africa_Logo_Stacked_RGB_small.jpg">
## Description
Now that we have run WOfS classification for each AEZs in Africa, its time to conduct seasonal accuracy assessment for each AEZ in Africa which is already compiled and stored in the following folder:`Results/WOfS_Assessment/Point_Based/ValidPoints_Per_AEZ`.
Accuracy assessment for WOfS product in Africa includes generating a confusion error matrix for a WOFL binary classification.
The inputs for the estimating the accuracy of WOfS derived product are a binary classification WOFL layer showing water/non-water and a shapefile containing validation points collected by [Collect Earth Online](https://collect.earth/) tool. Validation points are the ground truth or actual data while the extracted value for each location from WOFL is the predicted value.
This notebook will explain how you can perform seasonal accuracy assessment for WOfS starting with `Western` AEZ using collected ground truth dataset. It will output a confusion error matrix containing overall, producer's and user's accuracy, along with the F1 score for each class.
## Getting started
To run this analysis, run all the cells in the notebook, starting with the "Load packages" cell.
### Load packages
Import Python packages that are used for the analysis.
```
%matplotlib inline
import sys
import os
import rasterio
import xarray
import glob
import numpy as np
import pandas as pd
import seaborn as sn
import geopandas as gpd
import matplotlib.pyplot as plt
import scipy, scipy.ndimage
import warnings
warnings.filterwarnings("ignore") #this will suppress the warnings for multiple UTM zones in your AOI
sys.path.append("../Scripts")
from geopandas import GeoSeries, GeoDataFrame
from shapely.geometry import Point
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn.metrics import plot_confusion_matrix, f1_score
from deafrica_plotting import map_shapefile,display_map, rgb
from deafrica_spatialtools import xr_rasterize
from deafrica_datahandling import wofs_fuser, mostcommon_crs,load_ard,deepcopy
from deafrica_dask import create_local_dask_cluster
```
### Analysis Parameters
- CEO : groundtruth points containing valid points in each AEZ containing WOfS assigned classes, WOfS clear observations and the labels identified by analyst in each calendar month
- input_data : dataframe for further analysis and accuracy assessment
### Load the Dataset
Validation points that are valid for each AEZ
```
#Read the valid ground truth data
CEO = 'Results/WOfS_Assessment/Point_Based/ValidPoints_Per_AEZ/ValidationPoints_Western.csv'
df = pd.read_csv(CEO,delimiter=",")
#explore the dataframe
df.columns
#rename a column in dataframe
input_data = df.drop(['Unnamed: 0'], axis=1)
input_data = input_data.rename(columns={'WATERFLAG':'ACTUAL'})
#The table contains each calendar month as well as CEO and WOfS lables for each validation points
input_data
#Counting the number of rows in valid points dataframe
count = input_data.groupby('PLOT_ID',as_index=False,sort=False).last()
count
```
From the table, choose those rows that are in Wet season and also choose those in Dry season, then save them in separate tables.
```
#setting the months that are identified as wet in the AEZ using Climatology dataset
WetMonth = [5,6,7,8,9,10]
#identifying the points that are in wet season and counting their numbers
Wet_Season = input_data[input_data['MONTH'].isin(WetMonth)]
count_Wet_Season = Wet_Season.groupby('PLOT_ID',as_index=False,sort=False).last()
count_Wet_Season
#setting the months that are identified as dry in the AEZ using Climatology dataset then counting the points that are in dry season
Dry_Season = input_data[~input_data['MONTH'].isin(WetMonth)]
count_Dry_Season = Dry_Season.groupby('PLOT_ID',as_index=False,sort=False).last()
count_Dry_Season
```
Some points are in both dry and wet seasons as the number of points show.
### Create a Confusion Matrix
```
confusion_matrix = pd.crosstab(Wet_Season['ACTUAL'],Wet_Season['PREDICTION'],rownames=['ACTUAL'],colnames=['PREDICTION'],margins=True)
confusion_matrix
```
`Producer's Accuracy` is the map-maker accuracy showing the probability that a certain class on the ground is classified. Producer's accuracy complements error of omission.
```
confusion_matrix["Producer's"] = [confusion_matrix.loc[0][0] / confusion_matrix.loc[0]['All'] * 100, confusion_matrix.loc[1][1] / confusion_matrix.loc[1]['All'] *100, np.nan]
confusion_matrix
```
`User's Accuracy` is the map-user accuracy showing how often the class on the map will actually be present on the ground. `User's accuracy` shows the reliability. It is calculated based on the total number of correct classification for a particular class over the total number of classified sites.
```
users_accuracy = pd.Series([confusion_matrix[0][0] / confusion_matrix[0]['All'] * 100,
confusion_matrix[1][1] / confusion_matrix[1]['All'] * 100]).rename("User's")
confusion_matrix = confusion_matrix.append(users_accuracy)
confusion_matrix
```
`Overal Accuracy` shows what proportion of reference(actual) sites mapped correctly.
```
confusion_matrix.loc["User's", "Producer's"] = (confusion_matrix[0][0] + confusion_matrix[1][1]) / confusion_matrix['All']['All'] * 100
confusion_matrix
input_data['PREDICTION'] = input_data['PREDICTION'] .astype(str).astype(int)
```
The F1 score is the harmonic mean of the precision and recall, where an F1 score reaches its best value at 1(perfect precision and recall), and is calculated as:
```
fscore = pd.Series([(2*(confusion_matrix.loc["User's"][0]*confusion_matrix.loc[0]["Producer's"]) / (confusion_matrix.loc["User's"][0] + confusion_matrix.loc[0]["Producer's"])) / 100,
f1_score(input_data['ACTUAL'],input_data['PREDICTION'])]).rename("F-score")
confusion_matrix = confusion_matrix.append(fscore)
confusion_matrix
confusion_matrix = confusion_matrix.round(decimals=2)
confusion_matrix = confusion_matrix.rename(columns={'0':'NoWater','1':'Water', 0:'NoWater',1:'Water','All':'Total'},index={'0':'NoWater','1':'Water',0:'NoWater',1:'Water','All':'Total'})
confusion_matrix
confusion_matrix.to_csv('../Results/WOfS_Assessment/Point_Based/ConfusionMatrix/Western_WetSeason_confusion_matrix.csv')
```
***
## Additional information
**License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
Digital Earth Africa data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
**Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/digitalearthafrica/deafrica-sandbox-notebooks).
**Last modified:** January 2020
**Compatible datacube version:**
## Tags
Browse all available tags on the DE Africa User Guide's [Tags Index](https://) (placeholder as this does not exist yet)
|
github_jupyter
|
# Residual Networks
Welcome to the second assignment of this week! You will learn how to build very deep convolutional networks, using Residual Networks (ResNets). In theory, very deep networks can represent very complex functions; but in practice, they are hard to train. Residual Networks, introduced by [He et al.](https://arxiv.org/pdf/1512.03385.pdf), allow you to train much deeper networks than were previously practically feasible.
**In this assignment, you will:**
- Implement the basic building blocks of ResNets.
- Put together these building blocks to implement and train a state-of-the-art neural network for image classification.
## <font color='darkblue'>Updates</font>
#### If you were working on the notebook before this update...
* The current notebook is version "2a".
* You can find your original work saved in the notebook with the previous version name ("v2")
* To view the file directory, go to the menu "File->Open", and this will open a new tab that shows the file directory.
#### List of updates
* For testing on an image, replaced `preprocess_input(x)` with `x=x/255.0` to normalize the input image in the same way that the model's training data was normalized.
* Refers to "shallower" layers as those layers closer to the input, and "deeper" layers as those closer to the output (Using "shallower" layers instead of "lower" or "earlier").
* Added/updated instructions.
This assignment will be done in Keras.
Before jumping into the problem, let's run the cell below to load the required packages.
```
import numpy as np
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from resnets_utils import *
from keras.initializers import glorot_uniform
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline
import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
```
## 1 - The problem of very deep neural networks
Last week, you built your first convolutional neural network. In recent years, neural networks have become deeper, with state-of-the-art networks going from just a few layers (e.g., AlexNet) to over a hundred layers.
* The main benefit of a very deep network is that it can represent very complex functions. It can also learn features at many different levels of abstraction, from edges (at the shallower layers, closer to the input) to very complex features (at the deeper layers, closer to the output).
* However, using a deeper network doesn't always help. A huge barrier to training them is vanishing gradients: very deep networks often have a gradient signal that goes to zero quickly, thus making gradient descent prohibitively slow.
* More specifically, during gradient descent, as you backprop from the final layer back to the first layer, you are multiplying by the weight matrix on each step, and thus the gradient can decrease exponentially quickly to zero (or, in rare cases, grow exponentially quickly and "explode" to take very large values).
* During training, you might therefore see the magnitude (or norm) of the gradient for the shallower layers decrease to zero very rapidly as training proceeds:
<img src="images/vanishing_grad_kiank.png" style="width:450px;height:220px;">
<caption><center> <u> <font color='purple'> **Figure 1** </u><font color='purple'> : **Vanishing gradient** <br> The speed of learning decreases very rapidly for the shallower layers as the network trains </center></caption>
You are now going to solve this problem by building a Residual Network!
## 2 - Building a Residual Network
In ResNets, a "shortcut" or a "skip connection" allows the model to skip layers:
<img src="images/skip_connection_kiank.png" style="width:650px;height:200px;">
<caption><center> <u> <font color='purple'> **Figure 2** </u><font color='purple'> : A ResNet block showing a **skip-connection** <br> </center></caption>
The image on the left shows the "main path" through the network. The image on the right adds a shortcut to the main path. By stacking these ResNet blocks on top of each other, you can form a very deep network.
We also saw in lecture that having ResNet blocks with the shortcut also makes it very easy for one of the blocks to learn an identity function. This means that you can stack on additional ResNet blocks with little risk of harming training set performance.
(There is also some evidence that the ease of learning an identity function accounts for ResNets' remarkable performance even more so than skip connections helping with vanishing gradients).
Two main types of blocks are used in a ResNet, depending mainly on whether the input/output dimensions are same or different. You are going to implement both of them: the "identity block" and the "convolutional block."
### 2.1 - The identity block
The identity block is the standard block used in ResNets, and corresponds to the case where the input activation (say $a^{[l]}$) has the same dimension as the output activation (say $a^{[l+2]}$). To flesh out the different steps of what happens in a ResNet's identity block, here is an alternative diagram showing the individual steps:
<img src="images/idblock2_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 3** </u><font color='purple'> : **Identity block.** Skip connection "skips over" 2 layers. </center></caption>
The upper path is the "shortcut path." The lower path is the "main path." In this diagram, we have also made explicit the CONV2D and ReLU steps in each layer. To speed up training we have also added a BatchNorm step. Don't worry about this being complicated to implement--you'll see that BatchNorm is just one line of code in Keras!
In this exercise, you'll actually implement a slightly more powerful version of this identity block, in which the skip connection "skips over" 3 hidden layers rather than 2 layers. It looks like this:
<img src="images/idblock3_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 4** </u><font color='purple'> : **Identity block.** Skip connection "skips over" 3 layers.</center></caption>
Here are the individual steps.
First component of main path:
- The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and its name should be `conv_name_base + '2a'`. Use 0 as the seed for the random initialization.
- The first BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2a'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Second component of main path:
- The second CONV2D has $F_2$ filters of shape $(f,f)$ and a stride of (1,1). Its padding is "same" and its name should be `conv_name_base + '2b'`. Use 0 as the seed for the random initialization.
- The second BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2b'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Third component of main path:
- The third CONV2D has $F_3$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and its name should be `conv_name_base + '2c'`. Use 0 as the seed for the random initialization.
- The third BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2c'`.
- Note that there is **no** ReLU activation function in this component.
Final step:
- The `X_shortcut` and the output from the 3rd layer `X` are added together.
- **Hint**: The syntax will look something like `Add()([var1,var2])`
- Then apply the ReLU activation function. This has no name and no hyperparameters.
**Exercise**: Implement the ResNet identity block. We have implemented the first component of the main path. Please read this carefully to make sure you understand what it is doing. You should implement the rest.
- To implement the Conv2D step: [Conv2D](https://keras.io/layers/convolutional/#conv2d)
- To implement BatchNorm: [BatchNormalization](https://faroit.github.io/keras-docs/1.2.2/layers/normalization/) (axis: Integer, the axis that should be normalized (typically the 'channels' axis))
- For the activation, use: `Activation('relu')(X)`
- To add the value passed forward by the shortcut: [Add](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: identity_block
def identity_block(X, f, filters, stage, block):
"""
Implementation of the identity block as defined in Figure 4
Arguments:
X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
f -- integer, specifying the shape of the middle CONV's window for the main path
filters -- python list of integers, defining the number of filters in the CONV layers of the main path
stage -- integer, used to name the layers, depending on their position in the network
block -- string/character, used to name the layers, depending on their position in the network
Returns:
X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
"""
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value. You'll need this later to add back to the main path.
X_shortcut = X
# First component of main path
X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
### START CODE HERE ###
# Second component of main path (≈3 lines)
X = Conv2D(filters = F2, kernel_size = (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
# Third component of main path (≈2 lines)
X = Conv2D(filters = F3, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
R = Add()([X_shortcut,X])
X = Activation('relu')(R)
### END CODE HERE ###
return X
tf.reset_default_graph()
with tf.Session() as test:
np.random.seed(1)
A_prev = tf.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = identity_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
```
**Expected Output**:
<table>
<tr>
<td>
**out**
</td>
<td>
[ 0.94822985 0. 1.16101444 2.747859 0. 1.36677003]
</td>
</tr>
</table>
## 2.2 - The convolutional block
The ResNet "convolutional block" is the second block type. You can use this type of block when the input and output dimensions don't match up. The difference with the identity block is that there is a CONV2D layer in the shortcut path:
<img src="images/convblock_kiank.png" style="width:650px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 4** </u><font color='purple'> : **Convolutional block** </center></caption>
* The CONV2D layer in the shortcut path is used to resize the input $x$ to a different dimension, so that the dimensions match up in the final addition needed to add the shortcut value back to the main path. (This plays a similar role as the matrix $W_s$ discussed in lecture.)
* For example, to reduce the activation dimensions's height and width by a factor of 2, you can use a 1x1 convolution with a stride of 2.
* The CONV2D layer on the shortcut path does not use any non-linear activation function. Its main role is to just apply a (learned) linear function that reduces the dimension of the input, so that the dimensions match up for the later addition step.
The details of the convolutional block are as follows.
First component of main path:
- The first CONV2D has $F_1$ filters of shape (1,1) and a stride of (s,s). Its padding is "valid" and its name should be `conv_name_base + '2a'`. Use 0 as the `glorot_uniform` seed.
- The first BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2a'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Second component of main path:
- The second CONV2D has $F_2$ filters of shape (f,f) and a stride of (1,1). Its padding is "same" and it's name should be `conv_name_base + '2b'`. Use 0 as the `glorot_uniform` seed.
- The second BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2b'`.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
Third component of main path:
- The third CONV2D has $F_3$ filters of shape (1,1) and a stride of (1,1). Its padding is "valid" and it's name should be `conv_name_base + '2c'`. Use 0 as the `glorot_uniform` seed.
- The third BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '2c'`. Note that there is no ReLU activation function in this component.
Shortcut path:
- The CONV2D has $F_3$ filters of shape (1,1) and a stride of (s,s). Its padding is "valid" and its name should be `conv_name_base + '1'`. Use 0 as the `glorot_uniform` seed.
- The BatchNorm is normalizing the 'channels' axis. Its name should be `bn_name_base + '1'`.
Final step:
- The shortcut and the main path values are added together.
- Then apply the ReLU activation function. This has no name and no hyperparameters.
**Exercise**: Implement the convolutional block. We have implemented the first component of the main path; you should implement the rest. As before, always use 0 as the seed for the random initialization, to ensure consistency with our grader.
- [Conv2D](https://keras.io/layers/convolutional/#conv2d)
- [BatchNormalization](https://keras.io/layers/normalization/#batchnormalization) (axis: Integer, the axis that should be normalized (typically the features axis))
- For the activation, use: `Activation('relu')(X)`
- [Add](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: convolutional_block
def convolutional_block(X, f, filters, stage, block, s = 2):
"""
Implementation of the convolutional block as defined in Figure 4
Arguments:
X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
f -- integer, specifying the shape of the middle CONV's window for the main path
filters -- python list of integers, defining the number of filters in the CONV layers of the main path
stage -- integer, used to name the layers, depending on their position in the network
block -- string/character, used to name the layers, depending on their position in the network
s -- Integer, specifying the stride to be used
Returns:
X -- output of the convolutional block, tensor of shape (n_H, n_W, n_C)
"""
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value
X_shortcut = X
##### MAIN PATH #####
# First component of main path
X = Conv2D(F1,kernel_size= (1, 1), strides = (s,s),padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
### START CODE HERE ###
# Second component of main path (≈3 lines)
X = Conv2D(F2,kernel_size= (f, f), strides = (1,1), name = conv_name_base + '2b',padding = 'same', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
# Third component of main path (≈2 lines)
X = Conv2D(F3,kernel_size= (1, 1), strides = (1,1),padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
##### SHORTCUT PATH #### (≈2 lines)
X_shortcut = Conv2D(F3,kernel_size= (1, 1), strides = (s,s),padding = 'valid', name = conv_name_base + '1', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
X_shortcut = BatchNormalization(axis = 3, name = bn_name_base + '1')(X_shortcut)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
X = Add()([X,X_shortcut])
X = Activation('relu')(X)
### END CODE HERE ###
return X
tf.reset_default_graph()
with tf.Session() as test:
np.random.seed(1)
A_prev = tf.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = convolutional_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
```
**Expected Output**:
<table>
<tr>
<td>
**out**
</td>
<td>
[ 0.09018463 1.23489773 0.46822017 0.0367176 0. 0.65516603]
</td>
</tr>
</table>
## 3 - Building your first ResNet model (50 layers)
You now have the necessary blocks to build a very deep ResNet. The following figure describes in detail the architecture of this neural network. "ID BLOCK" in the diagram stands for "Identity block," and "ID BLOCK x3" means you should stack 3 identity blocks together.
<img src="images/resnet_kiank.png" style="width:850px;height:150px;">
<caption><center> <u> <font color='purple'> **Figure 5** </u><font color='purple'> : **ResNet-50 model** </center></caption>
The details of this ResNet-50 model are:
- Zero-padding pads the input with a pad of (3,3)
- Stage 1:
- The 2D Convolution has 64 filters of shape (7,7) and uses a stride of (2,2). Its name is "conv1".
- BatchNorm is applied to the 'channels' axis of the input.
- MaxPooling uses a (3,3) window and a (2,2) stride.
- Stage 2:
- The convolutional block uses three sets of filters of size [64,64,256], "f" is 3, "s" is 1 and the block is "a".
- The 2 identity blocks use three sets of filters of size [64,64,256], "f" is 3 and the blocks are "b" and "c".
- Stage 3:
- The convolutional block uses three sets of filters of size [128,128,512], "f" is 3, "s" is 2 and the block is "a".
- The 3 identity blocks use three sets of filters of size [128,128,512], "f" is 3 and the blocks are "b", "c" and "d".
- Stage 4:
- The convolutional block uses three sets of filters of size [256, 256, 1024], "f" is 3, "s" is 2 and the block is "a".
- The 5 identity blocks use three sets of filters of size [256, 256, 1024], "f" is 3 and the blocks are "b", "c", "d", "e" and "f".
- Stage 5:
- The convolutional block uses three sets of filters of size [512, 512, 2048], "f" is 3, "s" is 2 and the block is "a".
- The 2 identity blocks use three sets of filters of size [512, 512, 2048], "f" is 3 and the blocks are "b" and "c".
- The 2D Average Pooling uses a window of shape (2,2) and its name is "avg_pool".
- The 'flatten' layer doesn't have any hyperparameters or name.
- The Fully Connected (Dense) layer reduces its input to the number of classes using a softmax activation. Its name should be `'fc' + str(classes)`.
**Exercise**: Implement the ResNet with 50 layers described in the figure above. We have implemented Stages 1 and 2. Please implement the rest. (The syntax for implementing Stages 3-5 should be quite similar to that of Stage 2.) Make sure you follow the naming convention in the text above.
You'll need to use this function:
- Average pooling [see reference](https://keras.io/layers/pooling/#averagepooling2d)
Here are some other functions we used in the code below:
- Conv2D: [See reference](https://keras.io/layers/convolutional/#conv2d)
- BatchNorm: [See reference](https://keras.io/layers/normalization/#batchnormalization) (axis: Integer, the axis that should be normalized (typically the features axis))
- Zero padding: [See reference](https://keras.io/layers/convolutional/#zeropadding2d)
- Max pooling: [See reference](https://keras.io/layers/pooling/#maxpooling2d)
- Fully connected layer: [See reference](https://keras.io/layers/core/#dense)
- Addition: [See reference](https://keras.io/layers/merge/#add)
```
# GRADED FUNCTION: ResNet50
def ResNet50(input_shape = (64, 64, 3), classes = 6):
"""
Implementation of the popular ResNet50 the following architecture:
CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
-> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> TOPLAYER
Arguments:
input_shape -- shape of the images of the dataset
classes -- integer, number of classes
Returns:
model -- a Model() instance in Keras
"""
# Define the input as a tensor with shape input_shape
X_input = Input(input_shape)
# Zero-Padding
X = ZeroPadding2D((3, 3))(X_input)
# Stage 1
X = Conv2D(64, (7, 7), strides = (2, 2), name = 'conv1', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = 'bn_conv1')(X)
X = Activation('relu')(X)
X = MaxPooling2D((3, 3), strides=(2, 2))(X)
# Stage 2
X = convolutional_block(X, f = 3, filters = [64, 64, 256], stage = 2, block='a', s = 1)
X = identity_block(X, 3, [64, 64, 256], stage=2, block='b')
X = identity_block(X, 3, [64, 64, 256], stage=2, block='c')
### START CODE HERE ###
#[128,128,512], "f" is 3, "s" is 2 and the block is "a".
#The 3 identity blocks use three sets of filters of size [128,128,512], "f" is 3 and the blocks are "b", "c" and "d".
# Stage 3 (≈4 lines)
X = convolutional_block(X,f=3,s=2,filters = [128,128,512],stage = 3,block = 'a')
X = identity_block(X,3,[128,128,512],stage = 3,block = 'b')
X = identity_block(X,3,[128,128,512],stage = 3,block = 'c')
X = identity_block(X,3,[128,128,512],stage = 3,block = 'd')
#The convolutional block uses three sets of filters of size [256, 256, 1024], "f" is 3, "s" is 2 and the block is "a".
#The 5 identity blocks use three sets of filters of size [256, 256, 1024], "f" is 3 and the blocks are "b", "c", "d", "e" and "f".
# Stage 4 (≈6 lines)
X = convolutional_block(X, f=3, filters=[256, 256, 1024], stage=4, block='a', s=2)
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='b')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='c')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='d')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='e')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='f')
# Stage 5 (≈3 lines)
X = X = convolutional_block(X, f=3, filters=[512, 512, 2048], stage=5, block='a', s=2)
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='b')
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='c')
# AVGPOOL (≈1 line). Use "X = AveragePooling2D(...)(X)"
X = AveragePooling2D(pool_size=(2, 2), padding='same')(X)
### END CODE HERE ###
# output layer
X = Flatten()(X)
X = Dense(classes, activation='softmax', name='fc' + str(classes), kernel_initializer = glorot_uniform(seed=0))(X)
# Create model
model = Model(inputs = X_input, outputs = X, name='ResNet50')
return model
```
Run the following code to build the model's graph. If your implementation is not correct you will know it by checking your accuracy when running `model.fit(...)` below.
```
model = ResNet50(input_shape = (64, 64, 3), classes = 6)
```
As seen in the Keras Tutorial Notebook, prior training a model, you need to configure the learning process by compiling the model.
```
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
```
The model is now ready to be trained. The only thing you need is a dataset.
Let's load the SIGNS Dataset.
<img src="images/signs_data_kiank.png" style="width:450px;height:250px;">
<caption><center> <u> <font color='purple'> **Figure 6** </u><font color='purple'> : **SIGNS dataset** </center></caption>
```
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
```
Run the following cell to train your model on 2 epochs with a batch size of 32. On a CPU it should take you around 5min per epoch.
```
model.fit(X_train, Y_train, epochs = 2, batch_size = 32)
```
**Expected Output**:
<table>
<tr>
<td>
** Epoch 1/2**
</td>
<td>
loss: between 1 and 5, acc: between 0.2 and 0.5, although your results can be different from ours.
</td>
</tr>
<tr>
<td>
** Epoch 2/2**
</td>
<td>
loss: between 1 and 5, acc: between 0.2 and 0.5, you should see your loss decreasing and the accuracy increasing.
</td>
</tr>
</table>
Let's see how this model (trained on only two epochs) performs on the test set.
```
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
```
**Expected Output**:
<table>
<tr>
<td>
**Test Accuracy**
</td>
<td>
between 0.16 and 0.25
</td>
</tr>
</table>
For the purpose of this assignment, we've asked you to train the model for just two epochs. You can see that it achieves poor performances. Please go ahead and submit your assignment; to check correctness, the online grader will run your code only for a small number of epochs as well.
After you have finished this official (graded) part of this assignment, you can also optionally train the ResNet for more iterations, if you want. We get a lot better performance when we train for ~20 epochs, but this will take more than an hour when training on a CPU.
Using a GPU, we've trained our own ResNet50 model's weights on the SIGNS dataset. You can load and run our trained model on the test set in the cells below. It may take ≈1min to load the model.
```
model = load_model('ResNet50.h5')
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
```
ResNet50 is a powerful model for image classification when it is trained for an adequate number of iterations. We hope you can use what you've learnt and apply it to your own classification problem to perform state-of-the-art accuracy.
Congratulations on finishing this assignment! You've now implemented a state-of-the-art image classification system!
## 4 - Test on your own image (Optional/Ungraded)
If you wish, you can also take a picture of your own hand and see the output of the model. To do this:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the following code
4. Run the code and check if the algorithm is right!
```
img_path = 'images/my_image.jpg'
img = image.load_img(img_path, target_size=(64, 64))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = x/255.0
print('Input image shape:', x.shape)
my_image = scipy.misc.imread(img_path)
imshow(my_image)
print("class prediction vector [p(0), p(1), p(2), p(3), p(4), p(5)] = ")
print(model.predict(x))
```
You can also print a summary of your model by running the following code.
```
model.summary()
```
Finally, run the code below to visualize your ResNet50. You can also download a .png picture of your model by going to "File -> Open...-> model.png".
```
plot_model(model, to_file='model.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))
```
## What you should remember
- Very deep "plain" networks don't work in practice because they are hard to train due to vanishing gradients.
- The skip-connections help to address the Vanishing Gradient problem. They also make it easy for a ResNet block to learn an identity function.
- There are two main types of blocks: The identity block and the convolutional block.
- Very deep Residual Networks are built by stacking these blocks together.
### References
This notebook presents the ResNet algorithm due to He et al. (2015). The implementation here also took significant inspiration and follows the structure given in the GitHub repository of Francois Chollet:
- Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun - [Deep Residual Learning for Image Recognition (2015)](https://arxiv.org/abs/1512.03385)
- Francois Chollet's GitHub repository: https://github.com/fchollet/deep-learning-models/blob/master/resnet50.py
|
github_jupyter
|
# Siamese Neural Network with Triplet Loss trained on MNIST
## Cameron Trotter
### [email protected]
This notebook builds an SNN to determine similarity scores between MNIST digits using a triplet loss function. The use of class prototypes at inference time is also explored.
This notebook is based heavily on the approach described in [this Coursera course](https://www.coursera.org/learn/siamese-network-triplet-loss-keras/), which in turn is based on the [FaceNet](https://arxiv.org/abs/1503.03832) paper. Any uses of open-source code are linked throughout where utilised.
For an in-depth guide to understand this code, and the theory behind it, please see LINK.
### Imports
```
# TF 1.14 gives lots of warnings for deprecations ready for the switch to TF 2.0
import warnings
warnings.filterwarnings('ignore')
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import random
import os
import glob
from datetime import datetime
from tensorflow.keras.models import model_from_json
from tensorflow.keras.callbacks import Callback, CSVLogger, ModelCheckpoint
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.layers import Activation, Input, concatenate
from tensorflow.keras.layers import Layer, BatchNormalization, MaxPooling2D, Concatenate, Lambda, Flatten, Dense
from tensorflow.keras.initializers import glorot_uniform, he_uniform
from tensorflow.keras.regularizers import l2
from tensorflow.keras.utils import multi_gpu_model
from sklearn.decomposition import PCA
from sklearn.metrics import roc_curve, roc_auc_score
import math
from pylab import dist
import json
from tensorflow.python.client import device_lib
import matplotlib.gridspec as gridspec
```
## Import the data and reshape for use with the SNN
The data loaded in must be in the same format as `tf.keras.datasets.mnist.load_data()`, that is `(x_train, y_train), (x_test, y_test)`
```
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
num_classes = len(np.unique(y_train))
x_train_w = x_train.shape[1] # (60000, 28, 28)
x_train_h = x_train.shape[2]
x_test_w = x_test.shape[1]
x_test_h = x_test.shape[2]
x_train_w_h = x_train_w * x_train_h # 28 * 28 = 784
x_test_w_h = x_test_w * x_test_h
x_train = np.reshape(x_train, (x_train.shape[0], x_train_w_h))/255. # (60000, 784)
x_test = np.reshape(x_test, (x_test.shape[0], x_test_w_h))/255.
```
### Plotting the triplets
```
def plot_triplets(examples):
plt.figure(figsize=(6, 2))
for i in range(3):
plt.subplot(1, 3, 1 + i)
plt.imshow(np.reshape(examples[i], (x_train_w, x_train_h)), cmap='binary')
plt.xticks([])
plt.yticks([])
plt.show()
plot_triplets([x_train[0], x_train[1], x_train[2]])
```
### Create triplet batches
Random batches are generated by `create_batch`. Semi-hard triplet batches are generated by `create_batch_hard`.
Semi-Hard: dist(A, P) < dist(A, N) < dist(A, P) + margin. Using only easy triplets will lead to no learning. Hard triplets generate high loss and have high impact on training parameters, but may cause any mislabelled data to cause too much of a weight change.
```
def create_batch(batch_size=256, split = "train"):
x_anchors = np.zeros((batch_size, x_train_w_h))
x_positives = np.zeros((batch_size, x_train_w_h))
x_negatives = np.zeros((batch_size, x_train_w_h))
if split =="train":
data = x_train
data_y = y_train
else:
data = x_test
data_y = y_test
for i in range(0, batch_size):
# We need to find an anchor, a positive example and a negative example
random_index = random.randint(0, data.shape[0] - 1)
x_anchor = data[random_index]
y = data_y[random_index]
indices_for_pos = np.squeeze(np.where(data_y == y))
indices_for_neg = np.squeeze(np.where(data_y != y))
x_positive = data[indices_for_pos[random.randint(0, len(indices_for_pos) - 1)]]
x_negative = data[indices_for_neg[random.randint(0, len(indices_for_neg) - 1)]]
x_anchors[i] = x_anchor
x_positives[i] = x_positive
x_negatives[i] = x_negative
return [x_anchors, x_positives, x_negatives]
def create_hard_batch(batch_size, num_hard, split = "train"):
x_anchors = np.zeros((batch_size, x_train_w_h))
x_positives = np.zeros((batch_size, x_train_w_h))
x_negatives = np.zeros((batch_size, x_train_w_h))
if split =="train":
data = x_train
data_y = y_train
else:
data = x_test
data_y = y_test
# Generate num_hard number of hard examples:
hard_batches = []
batch_losses = []
rand_batches = []
# Get some random batches
for i in range(0, batch_size):
hard_batches.append(create_batch(1, split))
A_emb = embedding_model.predict(hard_batches[i][0])
P_emb = embedding_model.predict(hard_batches[i][1])
N_emb = embedding_model.predict(hard_batches[i][2])
# Compute d(A, P) - d(A, N) for each selected batch
batch_losses.append(np.sum(np.square(A_emb-P_emb),axis=1) - np.sum(np.square(A_emb-N_emb),axis=1))
# Sort batch_loss by distance, highest first, and keep num_hard of them
hard_batch_selections = [x for _, x in sorted(zip(batch_losses,hard_batches), key=lambda x: x[0])]
hard_batches = hard_batch_selections[:num_hard]
# Get batch_size - num_hard number of random examples
num_rand = batch_size - num_hard
for i in range(0, num_rand):
rand_batch = create_batch(1, split)
rand_batches.append(rand_batch)
selections = hard_batches + rand_batches
for i in range(0, len(selections)):
x_anchors[i] = selections[i][0]
x_positives[i] = selections[i][1]
x_negatives[i] = selections[i][2]
return [x_anchors, x_positives, x_negatives]
```
### Create the Embedding Model
This model takes in input image and generates some `emb_size`-dimensional embedding for the image, plotted on some latent space.
The untrained model's embedding space is stored for later use when comparing clustering between the untrained and the trained model using PCA, based on [this notebook](https://github.com/AdrianUng/keras-triplet-loss-mnist/blob/master/Triplet_loss_KERAS_semi_hard_from_TF.ipynb).
```
def create_embedding_model(emb_size):
embedding_model = tf.keras.models.Sequential([
Dense(4096,
activation='relu',
kernel_regularizer=l2(1e-3),
kernel_initializer='he_uniform',
input_shape=(x_train_w_h,)),
Dense(emb_size,
activation=None,
kernel_regularizer=l2(1e-3),
kernel_initializer='he_uniform')
])
embedding_model.summary()
return embedding_model
```
### Create the SNN
This model takes a triplet image input, passes them to the embedding model for embedding, then concats them together for the loss function
```
def create_SNN(embedding_model):
input_anchor = tf.keras.layers.Input(shape=(x_train_w_h,))
input_positive = tf.keras.layers.Input(shape=(x_train_w_h,))
input_negative = tf.keras.layers.Input(shape=(x_train_w_h,))
embedding_anchor = embedding_model(input_anchor)
embedding_positive = embedding_model(input_positive)
embedding_negative = embedding_model(input_negative)
output = tf.keras.layers.concatenate([embedding_anchor, embedding_positive,
embedding_negative], axis=1)
siamese_net = tf.keras.models.Model([input_anchor, input_positive, input_negative],
output)
siamese_net.summary()
return siamese_net
```
### Create the Triplet Loss Function
```
def triplet_loss(y_true, y_pred):
anchor, positive, negative = y_pred[:,:emb_size], y_pred[:,emb_size:2*emb_size],y_pred[:,2*emb_size:]
positive_dist = tf.reduce_mean(tf.square(anchor - positive), axis=1)
negative_dist = tf.reduce_mean(tf.square(anchor - negative), axis=1)
return tf.maximum(positive_dist - negative_dist + alpha, 0.)
```
### Data Generator
This function creates hard batches for the network to train on. `y` is required by TF but not by our model, so just return a filler to keep TF happy.
```
def data_generator(batch_size=256, num_hard=50, split="train"):
while True:
x = create_hard_batch(batch_size, num_hard, split)
y = np.zeros((batch_size, 3*emb_size))
yield x, y
```
### Evaluation
Allows for the model's metrics to be visualised and evaluated. Based on [this Medium post](https://medium.com/@crimy/one-shot-learning-siamese-networks-and-triplet-loss-with-keras-2885ed022352) and [this GitHub notebook](https://github.com/asagar60/One-Shot-Learning/blob/master/Omniglot_data/One_shot_implementation.ipynb).
```
def compute_dist(a,b):
return np.linalg.norm(a-b)
def compute_probs(network,X,Y):
'''
Input
network : current NN to compute embeddings
X : tensor of shape (m,w,h,1) containing pics to evaluate
Y : tensor of shape (m,) containing true class
Returns
probs : array of shape (m,m) containing distances
'''
m = X.shape[0]
nbevaluation = int(m*(m-1)/2)
probs = np.zeros((nbevaluation))
y = np.zeros((nbevaluation))
#Compute all embeddings for all imgs with current embedding network
embeddings = embedding_model.predict(X)
k = 0
# For each img in the evaluation set
for i in range(m):
# Against all other images
for j in range(i+1,m):
# compute the probability of being the right decision : it should be 1 for right class, 0 for all other classes
probs[k] = -compute_dist(embeddings[i,:],embeddings[j,:])
if (Y[i]==Y[j]):
y[k] = 1
#print("{3}:{0} vs {1} : \t\t\t{2}\tSAME".format(i,j,probs[k],k, Y[i], Y[j]))
else:
y[k] = 0
#print("{3}:{0} vs {1} : {2}\tDIFF".format(i,j,probs[k],k, Y[i], Y[j]))
k += 1
return probs, y
def compute_metrics(probs,yprobs):
'''
Returns
fpr : Increasing false positive rates such that element i is the false positive rate of predictions with score >= thresholds[i]
tpr : Increasing true positive rates such that element i is the true positive rate of predictions with score >= thresholds[i].
thresholds : Decreasing thresholds on the decision function used to compute fpr and tpr. thresholds[0] represents no instances being predicted and is arbitrarily set to max(y_score) + 1
auc : Area Under the ROC Curve metric
'''
# calculate AUC
auc = roc_auc_score(yprobs, probs)
# calculate roc curve
fpr, tpr, thresholds = roc_curve(yprobs, probs)
return fpr, tpr, thresholds,auc
def draw_roc(fpr, tpr,thresholds, auc):
#find threshold
targetfpr=1e-3
_, idx = find_nearest(fpr,targetfpr)
threshold = thresholds[idx]
recall = tpr[idx]
# plot no skill
plt.plot([0, 1], [0, 1], linestyle='--')
# plot the roc curve for the model
plt.plot(fpr, tpr, marker='.')
plt.title('AUC: {0:.3f}\nSensitivity : {2:.1%} @FPR={1:.0e}\nThreshold={3})'.format(auc,targetfpr,recall,abs(threshold) ))
# show the plot
plt.show()
def find_nearest(array,value):
idx = np.searchsorted(array, value, side="left")
if idx > 0 and (idx == len(array) or math.fabs(value - array[idx-1]) < math.fabs(value - array[idx])):
return array[idx-1],idx-1
else:
return array[idx],idx
def draw_interdist(network, epochs):
interdist = compute_interdist(network)
data = []
for i in range(num_classes):
data.append(np.delete(interdist[i,:],[i]))
fig, ax = plt.subplots()
ax.set_title('Evaluating embeddings distance from each other after {0} epochs'.format(epochs))
ax.set_ylim([0,3])
plt.xlabel('Classes')
plt.ylabel('Distance')
ax.boxplot(data,showfliers=False,showbox=True)
locs, labels = plt.xticks()
plt.xticks(locs,np.arange(num_classes))
plt.show()
def compute_interdist(network):
'''
Computes sum of distances between all classes embeddings on our reference test image:
d(0,1) + d(0,2) + ... + d(0,9) + d(1,2) + d(1,3) + ... d(8,9)
A good model should have a large distance between all theses embeddings
Returns:
array of shape (num_classes,num_classes)
'''
res = np.zeros((num_classes,num_classes))
ref_images = np.zeros((num_classes, x_test_w_h))
#generates embeddings for reference images
for i in range(num_classes):
ref_images[i,:] = x_test[i]
ref_embeddings = network.predict(ref_images)
for i in range(num_classes):
for j in range(num_classes):
res[i,j] = dist(ref_embeddings[i],ref_embeddings[j])
return res
def DrawTestImage(network, images, refidx=0):
'''
Evaluate some pictures vs some samples in the test set
image must be of shape(1,w,h,c)
Returns
scores : result of the similarity scores with the basic images => (N)
'''
nbimages = images.shape[0]
#generates embedings for given images
image_embedings = network.predict(images)
#generates embedings for reference images
ref_images = np.zeros((num_classes,x_test_w_h))
for i in range(num_classes):
images_at_this_index_are_of_class_i = np.squeeze(np.where(y_test == i))
ref_images[i,:] = x_test[images_at_this_index_are_of_class_i[refidx]]
ref_embedings = network.predict(ref_images)
for i in range(nbimages):
# Prepare the figure
fig=plt.figure(figsize=(16,2))
subplot = fig.add_subplot(1,num_classes+1,1)
plt.axis("off")
plotidx = 2
# Draw this image
plt.imshow(np.reshape(images[i], (x_train_w, x_train_h)),vmin=0, vmax=1,cmap='Greys')
subplot.title.set_text("Test image")
for ref in range(num_classes):
#Compute distance between this images and references
dist = compute_dist(image_embedings[i,:],ref_embedings[ref,:])
#Draw
subplot = fig.add_subplot(1,num_classes+1,plotidx)
plt.axis("off")
plt.imshow(np.reshape(ref_images[ref, :], (x_train_w, x_train_h)),vmin=0, vmax=1,cmap='Greys')
subplot.title.set_text(("Class {0}\n{1:.3e}".format(ref,dist)))
plotidx += 1
def generate_prototypes(x_data, y_data, embedding_model):
classes = np.unique(y_data)
prototypes = {}
for c in classes:
#c = classes[0]
# Find all images of the chosen test class
locations_of_c = np.where(y_data == c)[0]
imgs_of_c = x_data[locations_of_c]
imgs_of_c_embeddings = embedding_model.predict(imgs_of_c)
# Get the median of the embeddings to generate a prototype for the class (reshaping for PCA)
prototype_for_c = np.median(imgs_of_c_embeddings, axis = 0).reshape(1, -1)
# Add it to the prototype dict
prototypes[c] = prototype_for_c
return prototypes
def test_one_shot_prototypes(network, sample_embeddings):
distances_from_img_to_test_against = []
# As the img to test against is in index 0, we compare distances between img@0 and all others
for i in range(1, len(sample_embeddings)):
distances_from_img_to_test_against.append(compute_dist(sample_embeddings[0], sample_embeddings[i]))
# As the correct img will be at distances_from_img_to_test_against index 0 (sample_imgs index 1),
# If the smallest distance in distances_from_img_to_test_against is at index 0,
# we know the one shot test got the right answer
is_min = distances_from_img_to_test_against[0] == min(distances_from_img_to_test_against)
is_max = distances_from_img_to_test_against[0] == max(distances_from_img_to_test_against)
return int(is_min and not is_max)
def n_way_accuracy_prototypes(n_val, n_way, network):
num_correct = 0
for val_step in range(n_val):
num_correct += load_one_shot_test_batch_prototypes(n_way, network)
accuracy = num_correct / n_val * 100
return accuracy
def load_one_shot_test_batch_prototypes(n_way, network):
labels = np.unique(y_test)
# Reduce the label set down from size n_classes to n_samples
labels = np.random.choice(labels, size = n_way, replace = False)
# Choose a class as the test image
label = random.choice(labels)
# Find all images of the chosen test class
imgs_of_label = np.where(y_test == label)[0]
# Randomly select a test image of the selected class, return it's index
img_of_label_idx = random.choice(imgs_of_label)
# Expand the array at the selected indexes into useable images
img_of_label = np.expand_dims(x_test[img_of_label_idx],axis=0)
sample_embeddings = []
# Get the anchor image embedding
anchor_prototype = network.predict(img_of_label)
sample_embeddings.append(anchor_prototype)
# Get the prototype embedding for the positive class
positive_prototype = prototypes[label]
sample_embeddings.append(positive_prototype)
# Get the negative prototype embeddings
# Remove the selected test class from the list of labels based on it's index
label_idx_in_labels = np.where(labels == label)[0]
other_labels = np.delete(labels, label_idx_in_labels)
# Get the embedding for each of the remaining negatives
for other_label in other_labels:
negative_prototype = prototypes[other_label]
sample_embeddings.append(negative_prototype)
correct = test_one_shot_prototypes(network, sample_embeddings)
return correct
def visualise_n_way_prototypes(n_samples, network):
labels = np.unique(y_test)
# Reduce the label set down from size n_classes to n_samples
labels = np.random.choice(labels, size = n_samples, replace = False)
# Choose a class as the test image
label = random.choice(labels)
# Find all images of the chosen test class
imgs_of_label = np.where(y_test == label)[0]
# Randomly select a test image of the selected class, return it's index
img_of_label_idx = random.choice(imgs_of_label)
# Get another image idx that we know is of the test class for the sample set
label_sample_img_idx = random.choice(imgs_of_label)
# Expand the array at the selected indexes into useable images
img_of_label = np.expand_dims(x_test[img_of_label_idx],axis=0)
label_sample_img = np.expand_dims(x_test[label_sample_img_idx],axis=0)
# Make the first img in the sample set the chosen test image, the second the other image
sample_imgs = np.empty((0, x_test_w_h))
sample_imgs = np.append(sample_imgs, img_of_label, axis=0)
sample_imgs = np.append(sample_imgs, label_sample_img, axis=0)
sample_embeddings = []
# Get the anchor embedding image
anchor_prototype = network.predict(img_of_label)
sample_embeddings.append(anchor_prototype)
# Get the prototype embedding for the positive class
positive_prototype = prototypes[label]
sample_embeddings.append(positive_prototype)
# Get the negative prototype embeddings
# Remove the selected test class from the list of labels based on it's index
label_idx_in_labels = np.where(labels == label)[0]
other_labels = np.delete(labels, label_idx_in_labels)
# Get the embedding for each of the remaining negatives
for other_label in other_labels:
negative_prototype = prototypes[other_label]
sample_embeddings.append(negative_prototype)
# Find all images of the other class
imgs_of_other_label = np.where(y_test == other_label)[0]
# Randomly select an image of the selected class, return it's index
another_sample_img_idx = random.choice(imgs_of_other_label)
# Expand the array at the selected index into useable images
another_sample_img = np.expand_dims(x_test[another_sample_img_idx],axis=0)
# Add the image to the support set
sample_imgs = np.append(sample_imgs, another_sample_img, axis=0)
distances_from_img_to_test_against = []
# As the img to test against is in index 0, we compare distances between img@0 and all others
for i in range(1, len(sample_embeddings)):
distances_from_img_to_test_against.append(compute_dist(sample_embeddings[0], sample_embeddings[i]))
# + 1 as distances_from_img_to_test_against doesn't include the test image
min_index = distances_from_img_to_test_against.index(min(distances_from_img_to_test_against)) + 1
return sample_imgs, min_index
def evaluate(embedding_model, epochs = 0):
probs,yprob = compute_probs(embedding_model, x_test[:500, :], y_test[:500])
fpr, tpr, thresholds, auc = compute_metrics(probs,yprob)
draw_roc(fpr, tpr, thresholds, auc)
draw_interdist(embedding_model, epochs)
for i in range(3):
DrawTestImage(embedding_model, np.expand_dims(x_train[i],axis=0))
```
### Model Training Setup
FaceNet, the original triplet batch paper, draws a large random sample of triplets respecting the class distribution then picks N/2 hard and N/2 random samples (N = batch size), along with an `alpha` of 0.2
Logs out to Tensorboard, callback adapted from https://stackoverflow.com/a/52581175.
Saves best model only based on a validation loss. Adapted from https://stackoverflow.com/a/58103272.
```
# Hyperparams
batch_size = 256
epochs = 100
steps_per_epoch = int(x_train.shape[0]/batch_size)
val_steps = int(x_test.shape[0]/batch_size)
alpha = 0.2
num_hard = int(batch_size * 0.5) # Number of semi-hard triplet examples in the batch
lr = 0.00006
optimiser = 'Adam'
emb_size = 10
with tf.device("/cpu:0"):
# Create the embedding model
print("Generating embedding model... \n")
embedding_model = create_embedding_model(emb_size)
print("\nGenerating SNN... \n")
# Create the SNN
siamese_net = create_SNN(embedding_model)
# Compile the SNN
optimiser_obj = Adam(lr = lr)
siamese_net.compile(loss=triplet_loss, optimizer= optimiser_obj)
# Store visualisations of the embeddings using PCA for display next to "after training" for comparisons
num_vis = 500 # Take only the first num_vis elements of the test set to visualise
embeddings_before_train = embedding_model.predict(x_test[:num_vis, :])
pca = PCA(n_components=2)
decomposed_embeddings_before = pca.fit_transform(embeddings_before_train)
# Display evaluation the untrained model
print("\nEvaluating the model without training for a baseline...\n")
evaluate(embedding_model)
# Set up logging directory
## Use date-time as logdir name:
#dt = datetime.now().strftime("%Y%m%dT%H%M")
#logdir = os.path.join("PATH/TO/LOGDIR",dt)
## Use a custom non-dt name:
name = "snn-example-run"
logdir = os.path.join("PATH/TO/LOGDIR",name)
if not os.path.exists(logdir):
os.mkdir(logdir)
## Callbacks:
# Create the TensorBoard callback
tensorboard = tf.keras.callbacks.TensorBoard(
log_dir = logdir,
histogram_freq=0,
batch_size=batch_size,
write_graph=True,
write_grads=True,
write_images = True,
update_freq = 'epoch',
profile_batch=0
)
# Training logger
csv_log = os.path.join(logdir, 'training.csv')
csv_logger = CSVLogger(csv_log, separator=',', append=True)
# Only save the best model weights based on the val_loss
checkpoint = ModelCheckpoint(os.path.join(logdir, 'snn_model-{epoch:02d}-{val_loss:.2f}.h5'),
monitor='val_loss', verbose=1,
save_best_only=True, save_weights_only=True,
mode='auto')
# Save the embedding mode weights based on the main model's val loss
# This is needed to reecreate the emebedding model should we wish to visualise
# the latent space at the saved epoch
class SaveEmbeddingModelWeights(Callback):
def __init__(self, filepath, monitor='val_loss', verbose=1):
super(Callback, self).__init__()
self.monitor = monitor
self.verbose = verbose
self.best = np.Inf
self.filepath = filepath
def on_epoch_end(self, epoch, logs={}):
current = logs.get(self.monitor)
if current is None:
warnings.warn("SaveEmbeddingModelWeights requires %s available!" % self.monitor, RuntimeWarning)
if current < self.best:
filepath = self.filepath.format(epoch=epoch + 1, **logs)
#if self.verbose == 1:
#print("Saving embedding model weights at %s" % filepath)
embedding_model.save_weights(filepath, overwrite = True)
self.best = current
# Save the embedding model weights if you save a new snn best model based on the model checkpoint above
emb_weight_saver = SaveEmbeddingModelWeights(os.path.join(logdir, 'emb_model-{epoch:02d}.h5'))
callbacks = [tensorboard, csv_logger, checkpoint, emb_weight_saver]
# Save model configs to JSON
model_json = siamese_net.to_json()
with open(os.path.join(logdir, "siamese_config.json"), "w") as json_file:
json_file.write(model_json)
json_file.close()
model_json = embedding_model.to_json()
with open(os.path.join(logdir, "embedding_config.json"), "w") as json_file:
json_file.write(model_json)
json_file.close()
hyperparams = {'batch_size' : batch_size,
'epochs' : epochs,
'steps_per_epoch' : steps_per_epoch,
'val_steps' : val_steps,
'alpha' : alpha,
'num_hard' : num_hard,
'optimiser' : optimiser,
'lr' : lr,
'emb_size' : emb_size
}
with open(os.path.join(logdir, "hyperparams.json"), "w") as json_file:
json.dump(hyperparams, json_file)
# Set the model to TB
tensorboard.set_model(siamese_net)
def delete_older_model_files(filepath):
model_dir = filepath.split("emb_model")[0]
# Get model files
model_files = os.listdir(model_dir)
# Get only the emb_model files
emb_model_files = [file for file in model_files if "emb_model" in file]
# Get the epoch nums of the emb_model_files
emb_model_files_epoch_nums = [int(file.split("-")[1].split(".h5")[0]) for file in emb_model_files]
# Find all the snn model files
snn_model_files = [file for file in model_files if "snn_model" in file]
# Sort, get highest epoch num
emb_model_files_epoch_nums.sort()
highest_epoch_num = str(emb_model_files_epoch_nums[-1]).zfill(2)
# Filter the emb_model and snn_model file lists to remove the highest epoch number ones
emb_model_files_without_highest = [file for file in emb_model_files if highest_epoch_num not in file]
snn_model_files_without_highest = [file for file in snn_model_files if ("-" + highest_epoch_num + "-") not in file]
# Delete the non-highest model files from the subdir
if len(emb_model_files_without_highest) != 0:
print("Deleting previous best model file")
for model_file_list in [emb_model_files_without_highest, snn_model_files_without_highest]:
for file in model_file_list:
os.remove(os.path.join(model_dir, file))
```
### Show example batches
Based on code found [here](https://zhangruochi.com/Create-a-Siamese-Network-with-Triplet-Loss-in-Keras/2020/08/11/).
```
# Display sample batches. This has to be performed after the embedding model is created
# as create_batch_hard utilises the model to see which batches are actually hard.
examples = create_batch(1)
print("Example triplet batch:")
plot_triplets(examples)
print("Example semi-hard triplet batch:")
ex_hard = create_hard_batch(1, 1, split="train")
plot_triplets(ex_hard)
```
### Training
Using `.fit(workers = 0)` fixes the error when using hard batches where TF can't predict on the embedding network whilst fitting the siamese network (see: https://github.com/keras-team/keras/issues/5511#issuecomment-427666222).
```
def get_num_gpus():
local_device_protos = device_lib.list_local_devices()
return len([x.name for x in local_device_protos if x.device_type == 'GPU'])
## Training:
#print("Logging out to Tensorboard at:", logdir)
print("Starting training process!")
print("-------------------------------------")
# Make the model work over the two GPUs we have
num_gpus = get_num_gpus()
parallel_snn = multi_gpu_model(siamese_net, gpus = num_gpus)
batch_per_gpu = int(batch_size / num_gpus)
parallel_snn.compile(loss=triplet_loss, optimizer= optimiser_obj)
siamese_history = parallel_snn.fit(
data_generator(batch_per_gpu, num_hard),
steps_per_epoch=steps_per_epoch,
epochs=epochs,
verbose=1,
callbacks=callbacks,
workers = 0,
validation_data = data_generator(batch_per_gpu, num_hard, split="test"),
validation_steps = val_steps)
print("-------------------------------------")
print("Training complete.")
```
### Evaluate the trained network
Load the best performing models. We need to load the weights and configs seperately rather than using model.load() as our custom loss function relies on the embedding length. As such, it is easier to load the weights and config seperately and build a model based on them.
```
def json_to_dict(json_src):
with open(json_src, 'r') as j:
return json.loads(j.read())
## Load in best trained SNN and emb model
# The best performing model weights has the higher epoch number due to only saving the best weights
highest_epoch = 0
dir_list = os.listdir(logdir)
for file in dir_list:
if file.endswith(".h5"):
epoch_num = int(file.split("-")[1].split(".h5")[0])
if epoch_num > highest_epoch:
highest_epoch = epoch_num
# Find the embedding and SNN weights src for the highest_epoch (best) model
for file in dir_list:
# Zfill ensure a leading 0 on number < 10
if ("-" + str(highest_epoch).zfill(2)) in file:
if file.startswith("emb"):
embedding_weights_src = os.path.join(logdir, file)
elif file.startswith("snn"):
snn_weights_src = os.path.join(logdir, file)
hyperparams = os.path.join(logdir, "hyperparams.json")
snn_config = os.path.join(logdir, "siamese_config.json")
emb_config = os.path.join(logdir, "embedding_config.json")
snn_config = json_to_dict(snn_config)
emb_config = json_to_dict(emb_config)
# json.dumps to make the dict a string, as required by model_from_json
loaded_snn_model = model_from_json(json.dumps(snn_config))
loaded_snn_model.load_weights(snn_weights_src)
loaded_emb_model = model_from_json(json.dumps(emb_config))
loaded_emb_model.load_weights(embedding_weights_src)
# Store visualisations of the embeddings using PCA for display next to "after training" for comparisons
embeddings_after_train = loaded_emb_model.predict(x_test[:num_vis, :])
pca = PCA(n_components=2)
decomposed_embeddings_after = pca.fit_transform(embeddings_after_train)
evaluate(loaded_emb_model, highest_epoch)
```
### Comparisons of the embeddings in the latent space
Based on [this notebook](https://github.com/AdrianUng/keras-triplet-loss-mnist/blob/master/Triplet_loss_KERAS_semi_hard_from_TF.ipynb).
```
step = 1 # Step = 1, take every element
dict_embeddings = {}
dict_gray = {}
test_class_labels = np.unique(np.array(y_test))
decomposed_embeddings_after = pca.fit_transform(embeddings_after_train)
fig = plt.figure(figsize=(16, 8))
for label in test_class_labels:
y_test_labels = y_test[:num_vis]
decomposed_embeddings_class_before = decomposed_embeddings_before[y_test_labels == label]
decomposed_embeddings_class_after = decomposed_embeddings_after[y_test_labels == label]
plt.subplot(1,2,1)
plt.scatter(decomposed_embeddings_class_before[::step, 1], decomposed_embeddings_class_before[::step, 0], label=str(label))
plt.title('Embedding Locations Before Training')
plt.legend()
plt.subplot(1,2,2)
plt.scatter(decomposed_embeddings_class_after[::step, 1], decomposed_embeddings_class_after[::step, 0], label=str(label))
plt.title('Embedding Locations After %d Training Epochs' % epochs)
plt.legend()
plt.show()
```
### Determine n_way_accuracy
```
prototypes = generate_prototypes(x_test, y_test, loaded_emb_model)
n_way_accuracy_prototypes(val_steps, num_classes, loaded_emb_model)
```
### Visualise support set inference
Based on code found [here](https://github.com/asagar60/One-Shot-Learning/blob/master/Omniglot_data/One_shot_implementation.ipynb).
```
n_samples = 10
sample_imgs, min_index = visualise_n_way_prototypes(n_samples, loaded_emb_model)
img_matrix = []
for index in range(1, len(sample_imgs)):
img_matrix.append(np.reshape(sample_imgs[index], (x_train_w, x_train_h)))
img_matrix = np.asarray(img_matrix)
img_matrix = np.vstack(img_matrix)
f, ax = plt.subplots(1, 3, figsize = (10, 12))
f.tight_layout()
ax[0].imshow(np.reshape(sample_imgs[0], (x_train_w, x_train_h)),vmin=0, vmax=1,cmap='Greys')
ax[0].set_title("Test Image")
ax[1].imshow(img_matrix ,vmin=0, vmax=1,cmap='Greys')
ax[1].set_title("Support Set (Img of same class shown first)")
ax[2].imshow(np.reshape(sample_imgs[min_index], (x_train_w, x_train_h)),vmin=0, vmax=1,cmap='Greys')
ax[2].set_title("Image most similar to Test Image in Support Set")
```
|
github_jupyter
|
# Multi-class Classification and Neural Networks
## 1. Multi-class Classification
In this exercise, we will use logistic regression and neural networks to recognize handwritten digits (from 0 to 9).
### 1.1 Dataset
The dataset ex3data1.mat contains 5000 training examples of handwritten digits. Each training example is a 20 pixel by 20 pixel grayscale image of the digit. Each pixel is represented by a floating point number indicating the grayscale intensity at that location (value between -1 and 1). The 20 by 20 grid of pixels are flattened into a 400 long vector. Each training example is a single row in data matrix X. This results in a 5000 by 400 matrix X where every row is a training example.
$$ X=\left[\matrix{-(x^{(1)})^T-\\ -(x^{(2)})^T-\\ \vdots\\ -(x^{(m)})^T-}\right]_{5000\times400} $$
The other dtat in the training set is a 5000 long vector y that contains labels for the training set. Since the data was prepared for MATLAB, in which index starts from 1, digits 0-9 have been converted to 1-10. Here, we will convert it back to using 0-9 as labels.
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline
from scipy.io import loadmat
data = loadmat('ex3data1.mat')
X = data["X"] # 5000x400 np array
y = data["y"] # 5000x1 np array (2d)
y = y.flatten() # change to (5000,) 1d array and
y[y==10] = 0 # convert to 0-9 scale from 1-10 scale
```
### 1.2 Visualizing the data
```
def displayData(X):
"""displays the 100 rows of digit image data stored in X in a nice grid.
It returns the figure handle fig, ax
"""
# form the big 10 x 10 matrix containing all 100 images data
# padding between 2 images
pad = 1
# initialize matrix with -1 (black)
wholeimage = -np.ones((20*10+9, 20*10+9))
# fill values
for i in range(10):
for j in range(10):
wholeimage[j*21:j*21+20, i*21:i*21+20] = X[10*i+j, :].reshape((20, 20))
fig, ax = plt.subplots(figsize=(6, 6))
ax.imshow(wholeimage.T, cmap=plt.cm.gray, vmin=-1, vmax=1)
ax.axis('off')
return fig, ax
x = X[3200:3300, :]
fig, ax = displayData(x)
ax.axis('off')
# randomly select 100 data points to display
rand_indices = np.random.randint(0, 5000, size=100)
sel = X[rand_indices, :]
# display images
fig, ax = displayData(sel)
```
### 1.3 Vectorizing Logistic Regression
Since it's already been vectorized in assignment 2, we will just copy the functions here, just renaming it to lrCostFunction(). This includes regularization.
```
def sigmoid(z):
"""sigmoid(z) computes the sigmoid of z. z can be a number,
vector, or matrix.
"""
g = 1 / (1 + np.exp(-z))
return g
def lrCostFucntion(theta, X, y, lmd):
"""computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
"""
m = len(y)
# prepare for matrix calculations
y = y[:, np.newaxis]
# to prevent error in scipy.optimize.minimize(method='CG')
# unroll theta first, make sure theta is (n+1) by 1 array
theta = theta.ravel()
theta = theta[:, np.newaxis]
# print('theta: {}'.format(theta.shape))
# print('X: {}'.format(X.shape))
# print('y: {}'.format(y.shape))
# cost
J = ([email protected](sigmoid(X@theta)))/m - ((1-y.T)@np.log(1-sigmoid(X@theta)))/m + (theta[1:].T@theta[1:])*lmd/(2*m)
# J = J[0, 0]
# gradient
grad = np.zeros(theta.shape)
# added newaxis in order to get 2d array instead of 1d array
grad[0] = X.T[0, np.newaxis, :]@(sigmoid(X@theta)-y)/m
grad[1:] = X.T[1:, :]@(sigmoid(X@theta)-y)/m + lmd*theta[1:]/m
return J, grad.flatten()
# Test lrCostFunction
theta_t = np.array([-2, -1, 1, 2])
X_t = np.concatenate((np.ones((5, 1)), np.arange(1, 16).reshape((5, 3), order='F')/10), axis=1)
y_t = np.array([1, 0, 1, 0, 1])
lambda_t = 3
J, grad = lrCostFucntion(theta_t, X_t, y_t, lambda_t)
print('Cost: {:.6f}'.format(J[0, 0]))
print('Expected: 2.534819')
print('Gradients: \n{}'.format(grad))
print('Expected: \n0.146561\n -0.548558\n 0.724722\n 1.398003\n')
```
### 1.4 One-vs-all Classification
Here, we implement one-vs-all classification by training multiple regularized logistic regression classifier, one for each of the K classes in our dataset. K=10 in this case.
```
from scipy.optimize import minimize
def oneVsAll(X, y, num_class, lmd):
"""trains num_labels logistic regression classifiers and returns each of these classifiers
% in a matrix all_theta, where the i-th row of all_theta corresponds
% to the classifier for label i
"""
# m is number of training samples, n is number of features + 1
m, n = X.shape
# store theta results
all_theta = np.zeros((num_class, n))
#print(all_theta.shape)
# initial conidition, 1d array
theta0 = np.zeros(n)
print(theta0.shape)
# train one theta at a time
for i in range(num_class):
# y should be either 0 or 1, representing true or false
ylabel = (y==i).astype(int)
# run optimization
result = minimize(lrCostFucntion, theta0, args=(X, ylabel, lmd), method='CG',
jac=True, options={'disp': True, 'maxiter':1000})
# print(result)
all_theta[i, :] = result.x
return all_theta
# prepare parameters
lmd = 0.1
m = len(y)
X_wb = np.concatenate((np.ones((m, 1)), X), axis=1)
num_class = 10 # 10 classes, digits 0 to 9
print(X_wb.shape)
print(y.shape)
# Run training
all_theta = oneVsAll(X_wb, y, num_class, lmd)
```
#### One-vs-all Prediction
```
def predictOneVsAll(all_theta, X):
"""will return a vector of predictions
% for each example in the matrix X. Note that X contains the examples in
% rows. all_theta is a matrix where the i-th row is a trained logistic
% regression theta vector for the i-th class. You should return column vector
% of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
% for 4 examples)
"""
# apply np.argmax to the output matrix to find the predicted label
# for that training sample
out = (all_theta @ X.T).T
#print(out[4000:4020, :])
return np.argmax(out, axis=1)
# prediction accuracy
pred = predictOneVsAll(all_theta, X_wb)
print(pred.shape)
accuracy = np.sum((pred==y).astype(int))/m*100
print('Training accuracy is {:.2f}%'.format(accuracy))
```
## 2. Neural Networks
In the previous part of this exercise, you implemented multi-class logistic re-
gression to recognize handwritten digits. However, logistic regression cannot
form more complex hypotheses as it is only a linear classifier.3
In this part of the exercise, you will implement a neural network to rec-
ognize handwritten digits using the same training set as before. The neural
network will be able to represent complex models that form non-linear hy-
potheses.
For this week, you will be using parameters from a neural network
that we have already trained. Your goal is to implement the feedforward
propagation algorithm to use our weights for prediction.
Our neural network is shown in Figure 2. It has 3 layers: an input layer, a
hidden layer and an output layer. Recall that our inputs are pixel values of
digit images. Since the images are of size 20x20, this gives us 400 input layer
units (excluding the extra bias unit which always outputs +1). As before,
the training data will be loaded into the variables X and y.
A set of pre-trained network parameters ($\Theta_{(1)},\Theta_{(2)}$) are provided and stored in ex3weights.mat. The neural network used contains 25 units in the 2nd layer and 10 output units (corresponding to 10 digit classes).

```
#from scipy.io import loadmat
data = loadmat('ex3weights.mat')
Theta1 = data["Theta1"] # 25x401 np array
Theta2 = data["Theta2"] # 10x26 np array (2d)
print(Theta1.shape, Theta2.shape)
```
### Vectorizing the forward propagation
Matrix dimensions:
$X_wb$: 5000 x 401
$\Theta^{(1)}$: 25 x 401
$\Theta^{(2)}$: 10 x 26
$a^{(2)}$: 5000 x 25 or 5000 x 26 after adding intercept terms
$a^{(3)}$: 5000 x 10
$$a^{(2)} = g(X_{wb}\Theta^{(1)^T})$$
$$a^{(3)} = g(a^{(2)}_{wb}\Theta^{(2)^T})$$
```
def predict(X, Theta1, Theta2):
""" predicts output given network parameters Theta1 and Theta2 in Theta.
The prediction from the neural network will be the label that has the largest output.
"""
a2 = sigmoid(X @ Theta1.T)
# add intercept terms to a2
m, n = a2.shape
a2_wb = np.concatenate((np.ones((m, 1)), a2), axis=1)
a3 = sigmoid(a2_wb @ Theta2.T)
# print(a3[:10, :])
# apply np.argmax to the output matrix to find the predicted label
# for that training sample
# correct for indexing difference between MATLAB and Python
p = np.argmax(a3, axis=1) + 1
p[p==10] = 0
return p # this is a 1d array
# prediction accuracy
pred = predict(X_wb, Theta1, Theta2)
print(pred.shape)
accuracy = np.sum((pred==y).astype(int))/m*100
print('Training accuracy is {:.2f}%'.format(accuracy))
# randomly show 10 images and corresponding results
# randomly select 10 data points to display
rand_indices = np.random.randint(0, 5000, size=10)
sel = X[rand_indices, :]
for i in range(10):
# Display predicted digit
print("Predicted {} for this image: ".format(pred[rand_indices[i]]))
# display image
fig, ax = plt.subplots(figsize=(2, 2))
ax.imshow(sel[i, :].reshape(20, 20).T, cmap=plt.cm.gray, vmin=-1, vmax=1)
ax.axis('off')
plt.show()
```
|
github_jupyter
|
```
import construction as cs
import matplotlib.pyplot as plt
### read font
from matplotlib import font_manager
font_dirs = ['Barlow/']
font_files = font_manager.findSystemFonts(fontpaths=font_dirs)
for font_file in font_files:
font_manager.fontManager.addfont(font_file)
# set font
plt.rcParams['font.family'] = 'Barlow'
import networkx as nx
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
%load_ext autoreload
%autoreload 2
```
# Load generated graphs
```
def load_origin_graph(file_name,gap=299):
data_in = cs.load_data("../Datasets/"+file_name+".dat")
gap = 299
graphs_in = cs.build_graphs(data_in,gap=gap)
return graphs_in
def load_ETNgen_graph(file_name):
path = "../Generated_graphs/Multiple_run/"+file_name+"/"
gap = 299
graphs = []
for i in os.listdir(path):
data_in = cs.load_data(path+i)
graphs_in = cs.build_graphs(data_in,gap=gap)
graphs.append(graphs_in)
return graphs
def load_dym_graph(file_name):
path = "../Competitors_generated_graphs/Dymond/Multiple_run/"+file_name+"/"
gap = 0
graphs = []
for i in os.listdir(path):
print(path+i)
data_in = cs.load_data(path+i)
graphs_in = cs.build_graphs(data_in,gap=gap)
graphs.append(graphs_in)
return graphs
def load_stm_graph(file_name):
path = "../Competitors_generated_graphs/STM/Multiple_run/"+file_name+"/"
gap = 0
graphs = []
for i in os.listdir(path):
print(path+i)
data_in = cs.load_data(path+i)
graphs_in = cs.build_graphs(data_in,gap=gap)
graphs.append(graphs_in)
return graphs
def load_tag_graph(file_name):
path = "../Competitors_generated_graphs/TagGen/Multiple_run/"+file_name+"/"
gap = 0
graphs = []
for i in os.listdir(path):
print(path+i)
data_in = cs.load_data(path+i)
graphs_in = cs.build_graphs(data_in,gap=gap)
graphs.append(graphs_in)
return graphs
import networkx as nx
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from topological_metrics import *
import os
```
# Compute and store topological distributions
```
file_name = "High_School11"
orig_graphs = load_origin_graph(file_name,gap=299)
etn_gen = load_ETNgen_graph(file_name)
dym_gen = load_dym_graph(file_name)
tag_gen = load_tag_graph(file_name)
stm_gen = load_stm_graph(file_name)
def comp_metric(graphs,metric):
metric_dist = []
for graph in graphs:
metric_dist.append(metric(graph))
return metric_dist
def compute_store_metrics(metrics,metrics_names,generator,file_name,graphs):
for i in range(len(metrics)):
metric = metrics[i]
metric_name = metrics_names[i]
met = comp_metric(graphs,metric)
np.save("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/"+metric_name,met)
def compute_store_metrics_original(metrics,metrics_names,file_name,graphs):
for i in range(len(metrics)):
metric = metrics[i]
metric_name = metrics_names[i]
met = comp_metric([graphs],metric)
np.save("topology_results/original_distributions/"+file_name+"/"+metric_name,met)
metrics = [density,global_clustering,average_shortest_path,dist_number_of_individuals,
dist_number_of_new_conversations,get_ass,s_metric,dist_frequency_of_interactions,
dist_strength_of_nodes,dist_duration]
metrics_names = ["density","clust","asp","nb_interactions",
"new_con","ass","s_metric","interacting_indiv",
"streng","dur"]
compute_store_metrics_original(metrics,metrics_names,file_name,orig_graphs)
compute_store_metrics(metrics,metrics_names,
"etngen",
file_name,
etn_gen)
compute_store_metrics(metrics,metrics_names,
"taggen",
file_name,
tag_gen)
compute_store_metrics(metrics,metrics_names,
"stmgen",
file_name,
stm_gen)
compute_store_metrics(metrics,metrics_names,
"dymgen",
file_name,
dym_gen)
```
# load distributions
```
labels
def load_topo_distributions(generator,file_name):
den = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/density.npy",allow_pickle=True)
clust = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/clust.npy",allow_pickle=True)
asp = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/asp.npy",allow_pickle=True)
nb_inter = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/nb_interactions.npy",allow_pickle=True)
new_conv = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/new_con.npy",allow_pickle=True)
ass = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/ass.npy",allow_pickle=True)
s_met = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/s_metric.npy",allow_pickle=True)
inter_indiv = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/interacting_indiv.npy",allow_pickle=True)
stren = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/streng.npy",allow_pickle=True)
durat = np.load("topology_results/"+generator+"/Multiple_run/distributions/"+file_name+"/dur.npy",allow_pickle=True)
return asp,ass,clust,stren,durat,s_met,new_conv,inter_indiv,den,nb_inter
def load_topo_original(file_name):
den = np.load("topology_results/original_distributions/"+file_name+"/density.npy",allow_pickle=True)
clust = np.load("topology_results/original_distributions/"+file_name+"/clust.npy",allow_pickle=True)
asp = np.load("topology_results/original_distributions/"+file_name+"/asp.npy",allow_pickle=True)
nb_inter = np.load("topology_results/original_distributions/"+file_name+"/nb_interactions.npy",allow_pickle=True)
new_conv = np.load("topology_results/original_distributions/"+file_name+"/new_con.npy",allow_pickle=True)
ass = np.load("topology_results/original_distributions/"+file_name+"/ass.npy",allow_pickle=True)
s_met = np.load("topology_results/original_distributions/"+file_name+"/s_metric.npy",allow_pickle=True)
inter_indiv = np.load("topology_results/original_distributions/"+file_name+"/interacting_indiv.npy",allow_pickle=True)
stren = np.load("topology_results/original_distributions/"+file_name+"/streng.npy",allow_pickle=True)
durat = np.load("topology_results/original_distributions/"+file_name+"/dur.npy",allow_pickle=True)
return asp,ass,clust,stren,durat,s_met,new_conv,inter_indiv,den,nb_inter
def compute_counts(ro,e):
counts = []
e = np.array(e)
for i in range(len(ro)-1):
r1 = ro[i]
r2 = ro[i+1]
ee = e[e>r1]
count = ee[ee<=r2]
counts.append(len(count))
return counts
def compute_multpile_counts(ranges,ee):
counts = []
for e in ee:
counts.append(compute_counts(ranges,e))
return counts
# example of calculating the kl divergence between two mass functions
from math import log2
# calculate the kl divergence
def kl_divergence_max(d2, d1):
max_len = max(len(d1),len(d2))
new_d1 = np.zeros(max_len)
new_d1[:len(d1)] = d1
new_d2 = np.zeros(max_len)
new_d2[:len(d2)] = d2
E = 0.0000001
new_d1 = new_d1 + E
new_d2 = new_d2 + E
res = 0
for i in range(max_len):
d1 = new_d1[i]
d2 = new_d2[i]
if (d1 != 0) and (d2 != 0):
res = res + (d1 * log2(d1/d2))
return res
```
```
def compute_ks_all_metrics(nb_bins,file_name):
res_etn = []
res_tag = []
res_stm = []
res_dym = []
o_in = load_topo_original(file_name)
e_in = load_topo_distributions("etngen",file_name)
t_in = load_topo_distributions("taggen",file_name)
d_in = load_topo_distributions("dymgen",file_name)
s_in = load_topo_distributions("stmgen",file_name)
all_res = []
for i in range(10):
o = o_in[i]
e = e_in[i]
t = t_in[i]
d = d_in[i]
s = s_in[i]
#if i == 1 or i == 5 or i == 6:
biggest_dist = o[0]
#else:
#biggest_dist = np.max(t)
tc,tranges = np.histogram(biggest_dist,bins=nb_bins)
oc = compute_counts(tranges,o)
ec = compute_multpile_counts(tranges,e)
dc = compute_multpile_counts(tranges,d)
tc = compute_multpile_counts(tranges,t)
sc = compute_multpile_counts(tranges,s)
oc = oc/np.sum(oc)
ec = [np.array(x)/sum(x) for x in ec]
dc = [np.array(x)/sum(x) for x in dc]
tc = [np.array(x)/sum(x) for x in tc]
sc = [np.array(x)/sum(x) for x in sc]
ec_kl = []
tc_kl = []
sc_kl = []
dc_kl = []
for i in ec:
ec_kl.append(kl_divergence_max(i,oc))
for i in tc:
tc_kl.append(kl_divergence_max(i,oc))
for i in dc:
dc_kl.append(kl_divergence_max(i,oc))
for i in sc:
sc_kl.append(kl_divergence_max(i,oc))
maximum_for_nome = max(np.nanmax(ec_kl),np.nanmax(tc_kl),np.nanmax(sc_kl),np.nanmax(dc_kl))
ec_kl = ec_kl/maximum_for_nome
tc_kl = tc_kl/maximum_for_nome
sc_kl = sc_kl/maximum_for_nome
dc_kl = dc_kl/maximum_for_nome
res = [[np.nanmean(ec_kl),np.nanstd(ec_kl)],[np.nanmean(tc_kl),np.nanstd(tc_kl)],
[np.nanmean(sc_kl),np.nanstd(sc_kl)],[np.nanmean(dc_kl),np.nanstd(dc_kl)]]
res_etn.append([np.nanmean(ec_kl),np.nanstd(ec_kl)])
res_tag.append([np.nanmean(tc_kl),np.nanstd(tc_kl)])
res_stm.append([np.nanmean(sc_kl),np.nanstd(sc_kl)])
res_dym.append([np.nanmean(dc_kl),np.nanstd(dc_kl)])
if False:
plt.figure(figsize=(15,5))
plt.subplot(1,5,1)
plt.bar(range(nb_bins),oc)
plt.title("orig")
plt.subplot(1,5,2)
plt.bar(range(nb_bins),ec[0])
plt.title("etn\n"+str(res[0])[0:5])
plt.subplot(1,5,3)
plt.bar(range(nb_bins),tc[0])
plt.title("tag\n"+str(res[1])[0:5])
plt.subplot(1,5,4)
plt.bar(range(nb_bins),sc[0])
plt.title("stm\n"+str(res[2])[0:5])
plt.subplot(1,5,5)
plt.bar(range(nb_bins),dc[0])
plt.title("diam\n"+str(res[3])[0:5])
plt.show()
#res2 = []
#ooo = o[0]/np.sum(o[0])
#eee = e[0]/np.sum(e[0])
#ttt = t[0]/np.sum(t[0])
#sss = s[0]/np.sum(s[0])
#ddd = d[0]/np.sum(d[0])
#res2.append(kl_divergence_max(ooo,eee))
#res2.append(kl_divergence_max(ooo,ttt))
#res2.append(kl_divergence_max(ooo,sss))
#res2.append(kl_divergence_max(ooo,ddd))
#if False:
# plt.figure(figsize=(15,5))
# plt.subplot(1,5,1)
# plt.hist(o[0],bins=10)
# plt.title("orig")
# plt.subplot(1,5,2)
# plt.hist(e[0],bins=10)
# plt.title("etn\n"+str(res2[0])[0:5])
# plt.subplot(1,5,3)
# plt.hist(t[0],bins=10)
# plt.title("tag\n"+str(res2[1])[0:5])
# plt.subplot(1,5,4)
# plt.hist(s[0],bins=10)
# plt.title("stm\n"+str(res2[2])[0:5])
# plt.subplot(1,5,5)
# plt.hist(d[0],bins=10)
# plt.title("diam\n"+str(res2[3])[0:5])
# plt.show()
return [np.array(res_etn),np.array(res_tag),np.array(res_stm),np.array(res_dym)]
ORIGINAL_COLOR = '#474747' #dark grey
ETN_COLOR = '#fb7041' #'#E5865E' # arancio
TAG_COLOR = '#96ccc8' # light blue
STM_COLOR = '#bad1f2' #8F2E27' # rosso
DYM_COLOR = '#559ca6' # teal
line_width = 1.5
idx =[2, 5, 1, 8, 9, 6, 4, 3, 0, 7]
tmp= ["Density",
"Global clustering \ncoefficient",
"Average shortest\npath length",
"Interacting\nindividuals",
"New conversations",
"Assortativity",
"S-metric",
"Number of interactions",
"Edge strength",
"Duration of contacts"]
tmp = np.array(tmp)
labels = tmp[idx]
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
nb_bins = 50
x1,x2,x3,x4 = compute_ks_all_metrics(nb_bins,"LH10")
x = np.arange(10) # the label locations
width = 0.2 # the width of the bars
fig, ax = plt.subplots(1,3,figsize=(12,10))
fig.tight_layout(pad=-4)
error_bar_style = dict(ecolor=ORIGINAL_COLOR, alpha=0.8, lw=1.5, capsize=3, capthick=1)
ax[0].title.set_text("Hospital")
rects1 = ax[0].barh(x + 0.3, x1[:,0], width, xerr=x1[:,1],label='ETN-gen',color=ETN_COLOR, error_kw=error_bar_style)
rects2 = ax[0].barh(x + 0.1, x2[:,0], width, xerr=x2[:,1],label='STM',color=STM_COLOR, error_kw=error_bar_style)
rects3 = ax[0].barh(x - 0.1, x3[:,0], width, xerr=x3[:,1],label='TagGen',color=TAG_COLOR, error_kw=error_bar_style)
rects4 = ax[0].barh(x - 0.3, x4[:,0], width, xerr=x4[:,1],label='Dymond',color=DYM_COLOR,error_kw=error_bar_style)
x1,x2,x3,x4 = compute_ks_all_metrics(nb_bins,"InVS13")
ax[1].title.set_text("Workplace")
rects1 = ax[1].barh(x + 0.3, x1[:,0], width, xerr=x1[:,1],label='ETN-gen',color=ETN_COLOR, error_kw=error_bar_style)
rects2 = ax[1].barh(x + 0.1, x2[:,0], width, xerr=x2[:,1],label='STM',color=STM_COLOR, error_kw=error_bar_style)
rects3 = ax[1].barh(x - 0.1, x3[:,0], width, xerr=x3[:,1],label='TagGen',color=TAG_COLOR, error_kw=error_bar_style)
rects4 = ax[1].barh(x - 0.3, x4[:,0], width, xerr=x4[:,1],label='Dymond',color=DYM_COLOR,error_kw=error_bar_style)
x1,x2,x3,x4 = compute_ks_all_metrics(nb_bins,"High_School11")
ax[2].title.set_text("High school")
rects1 = ax[2].barh(x + 0.3, x1[:,0], width, xerr=x1[:,1],label='ETN-gen',color=ETN_COLOR, error_kw=error_bar_style)
rects2 = ax[2].barh(x + 0.1, x2[:,0], width, xerr=x2[:,1],label='STM',color=STM_COLOR, error_kw=error_bar_style)
rects3 = ax[2].barh(x - 0.1, x3[:,0], width, xerr=x3[:,1],label='TagGen',color=TAG_COLOR, error_kw=error_bar_style)
rects4 = ax[2].barh(x - 0.3, x4[:,0], width, xerr=x4[:,1],label='Dymond',color=DYM_COLOR,error_kw=error_bar_style)
ax[0].set_yticklabels(labels)
ax[0].set_yticks(x)
ax[0].set_xlim(0,1)
ax[1].set_yticks(x)
ax[1].set_yticklabels([" "," "," "," "," "," "," "," "," "," "],rotation=0)
ax[1].set_xlim(0,1)
ax[2].set_yticks(x)
ax[2].set_xlim(0,1)
ax[2].set_yticklabels([" "," "," "," "," "," "," "," "," "," "],rotation=0)
ax[2].set_xticks([0,0.33,0.66,1])
ax[2].set_xticklabels(["0.0","0.33","0.66","1.0"])
ax[1].set_xticks([0,0.33,0.66,1])
ax[1].set_xticklabels(["0.0","0.33","0.66","1.0"])
ax[0].set_xticks([0,0.33,0.66,1])
ax[0].set_xticklabels(["0.0","0.33","0.66","1.0"])
ax[0].tick_params(bottom=True, right=False,left=False)
ax[0].set_axisbelow(True)
ax[0].xaxis.grid(True, color='#b3b3b3')
ax[0].yaxis.grid(False)
ax[1].tick_params(bottom=True, right=False,left=False)
ax[1].set_axisbelow(True)
ax[1].xaxis.grid(True, color='#b3b3b3')
ax[1].yaxis.grid(False)
ax[2].tick_params(bottom=True, right=False,left=False)
ax[2].set_axisbelow(True)
ax[2].xaxis.grid(True, color='#b3b3b3')
ax[2].yaxis.grid(False)
ax[0].spines['top'].set_visible(False)
ax[0].spines['right'].set_visible(False)
ax[0].spines['left'].set_visible(False)
ax[0].spines['bottom'].set_visible(False)
ax[1].spines['top'].set_visible(False)
ax[1].spines['right'].set_visible(False)
ax[1].spines['left'].set_visible(False)
ax[1].spines['bottom'].set_visible(False)
ax[2].spines['top'].set_visible(False)
ax[2].spines['right'].set_visible(False)
ax[2].spines['left'].set_visible(False)
ax[2].spines['bottom'].set_visible(False)
ax[0].legend(loc='upper right',ncol = 5,bbox_to_anchor=(1, -0.05))
fig.tight_layout()
plt.savefig("topology_main_kld_test1.pdf", bbox_inches = 'tight')
plt.show()
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.ensemble import *
from sklearn.linear_model import *
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_predict
### UTILITY FUNCTION FOR DATA GENERATION ###
def gen_sinusoidal(timesteps, amp, freq, noise):
X = np.arange(timesteps)
e = np.random.normal(0,noise, (timesteps,))
y = amp*np.sin(X*(2*np.pi/freq))+e
return y
def gen_randomwalk(timesteps, noise):
y = np.random.normal(0,noise, (timesteps,))
return y.cumsum()
### CREATE SYNTHETIC DATA ###
np.random.seed(0)
timesteps = 1000
data1 = gen_sinusoidal(timesteps=timesteps, amp=10, freq=24, noise=5)
data2 = gen_sinusoidal(timesteps=timesteps, amp=10, freq=24*7, noise=5)
data3 = gen_randomwalk(timesteps=timesteps, noise=1)
```
# STATIONARY DATA
```
### STORE DATA IN DF ###
data = data1 + data2
df = pd.DataFrame({
'X1':data1,
'X2':data2,
'Y':data
})
df.index = pd.date_range('2021', periods=timesteps, freq='H')
cols = df.columns
print(df.shape)
df.head()
### PLOT SYNTHETIC DATA ###
plt.figure(figsize=(16,4))
for i,c in enumerate(cols[:-1]):
plt.subplot(1,2,i+1)
df[c].plot(ax=plt.gca(), title=c, color='blue'); plt.xlabel(None)
plt.figure(figsize=(16,4))
df['Y'].plot(title='Y', color='red')
### CREATE ROLLING FEATURES ###
lags = [6, 12, 18, 24]
for l in lags:
for c in cols:
df[f"{c}_mean_t-{l}"] = df[c].rolling(l).mean()
df[f"{c}_std_t-{l}"] = df[c].rolling(l).std()
df['Y'] = df['Y'].shift(-1)
df.drop(cols[cols.str.startswith('X')], axis=1, inplace=True)
df.dropna(inplace=True)
### TRAIN TEST SPLIT ###
X_train, X_test, y_train, y_test = train_test_split(
df.drop('Y', axis=1), df['Y'],
test_size=24*7*2, shuffle=False)
X_train.shape, X_test.shape
### RANDOM FOREST TUNING ###
model = GridSearchCV(estimator=RandomForestRegressor(random_state=33),
param_grid={'max_depth': [8, 10, 12, None], 'n_estimators': [20, 30, 40]},
scoring='neg_mean_squared_error', cv=3, refit=True)
model.fit(X_train, y_train)
model.best_params_
### OUT-OF-FOLDS RESIDUAL DISTRIBUTION ###
pred_train = cross_val_predict(RandomForestRegressor(**model.best_params_, random_state=33),
X_train, y_train, cv=3)
res = y_train - pred_train
### PLOT RESIDUAL STATISTICS ###
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.title('Residuals Distribution')
plt.hist(res, bins=20)
plt.subplot(1,2,2)
plt.title('Residuals Autocorrelation')
plt.plot([res.autocorr(lag=dt) for dt in range(1,200)])
plt.ylim([-1,1]); plt.axhline(0, c='black', linestyle='--')
plt.ylabel('Autocorrelation'); plt.xlabel('Lags')
plt.show()
### BOOTSTRAPPED INTERVALS ###
alpha = 0.05
bootstrap = np.asarray([np.random.choice(res, size=res.shape) for _ in range(100)])
q_bootstrap = np.quantile(bootstrap, q=[alpha/2, 1-alpha/2], axis=0)
y_pred = pd.Series(model.predict(X_test), index=X_test.index)
y_lower = y_pred + q_bootstrap[0].mean()
y_upper = y_pred + q_bootstrap[1].mean()
### PLOT BOOTSTRAPPED PREDICTION INTERVALS ###
plt.figure(figsize=(10,6))
y_pred.plot(linewidth=3)
y_test.plot(style='.k', alpha=0.5)
plt.fill_between(y_pred.index, y_lower, y_upper, alpha=0.3)
plt.title('RandomForest test predictions')
### HOW MANY OUTLIERS IN TEST DATA ###
((y_test > y_upper).sum() + (y_test < y_lower).sum()) / y_test.shape[0]
### RIDGE TUNING ###
model = GridSearchCV(estimator=Ridge(), param_grid={'alpha': [3, 5, 10, 20, 50]},
scoring='neg_mean_squared_error', cv=3, refit=True)
model.fit(X_train, y_train)
model.best_params_
### OUT-OF-FOLDS RESIDUAL DISTRIBUTION ###
pred_train = cross_val_predict(Ridge(**model.best_params_), X_train, y_train, cv=3)
res = y_train - pred_train
### PLOT RESIDUAL STATISTICS ###
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.title('Residuals Distribution')
plt.hist(res, bins=20)
plt.subplot(1,2,2)
plt.title('Residuals Autocorrelation')
plt.plot([res.autocorr(lag=dt) for dt in range(1,200)])
plt.ylim([-1,1]); plt.axhline(0, c='black', linestyle='--')
plt.ylabel('Autocorrelation'); plt.xlabel('Lags')
plt.show()
### BOOTSTRAPPED INTERVALS ###
alpha = 0.05
bootstrap = np.asarray([np.random.choice(res, size=res.shape) for _ in range(100)])
q_bootstrap = np.quantile(bootstrap, q=[alpha/2, 1-alpha/2], axis=0)
y_pred = pd.Series(model.predict(X_test), index=X_test.index)
y_lower = y_pred + q_bootstrap[0].mean()
y_upper = y_pred + q_bootstrap[1].mean()
### PLOT BOOTSTRAPPED PREDICTION INTERVALS ###
plt.figure(figsize=(10,6))
y_pred.plot(linewidth=3)
y_test.plot(style='.k', alpha=0.5)
plt.fill_between(y_pred.index, y_lower, y_upper, alpha=0.3)
plt.title('Ridge test predictions')
### HOW MANY OUTLIERS IN TEST DATA ###
((y_test > y_upper).sum() + (y_test < y_lower).sum()) / y_test.shape[0]
```
# NOT STATIONARY DATA
```
### STORE DATA IN DF ###
data = data1 + data2 + data3
df = pd.DataFrame({
'X1':data1,
'X2':data2,
'X3':data3,
'Y':data
})
df.index = pd.date_range('2021', periods=timesteps, freq='H')
cols = df.columns
print(df.shape)
df.head()
### PLOT SYNTHETIC DATA ###
plt.figure(figsize=(16,11))
for i,c in enumerate(cols):
color = 'red' if c == 'Y' else 'blue'
plt.subplot(2,2,i+1)
df[c].plot(ax=plt.gca(), title=c, color=color); plt.xlabel(None)
### CREATE ROLLING FEATURES ###
lags = [6, 12, 18, 24]
for l in lags:
for c in cols:
df[f"{c}_mean_t-{l}"] = df[c].rolling(l).mean()
df[f"{c}_std_t-{l}"] = df[c].rolling(l).std()
df['Y'] = df['Y'].shift(-1)
df.drop(cols[cols.str.startswith('X')], axis=1, inplace=True)
df.dropna(inplace=True)
### TRAIN TEST SPLIT ###
X_train, X_test, y_train, y_test = train_test_split(
df.drop('Y', axis=1), df['Y'],
test_size=24*7*2, shuffle=False)
X_train.shape, X_test.shape
### RANDOM FOREST TUNING ###
model = GridSearchCV(estimator=RandomForestRegressor(random_state=33),
param_grid={'max_depth': [8, 10, 12, None], 'n_estimators': [20, 30, 40]},
scoring='neg_mean_squared_error', cv=3, refit=True)
model.fit(X_train, y_train)
model.best_params_
### OUT-OF-FOLDS RESIDUAL DISTRIBUTION ###
pred_train = cross_val_predict(RandomForestRegressor(**model.best_params_, random_state=33),
X_train, y_train, cv=3)
res = y_train - pred_train
### PLOT RESIDUAL STATISTICS ###
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.title('Residuals Distribution')
plt.hist(res, bins=20)
plt.subplot(1,2,2)
plt.title('Residuals Autocorrelation')
plt.plot([res.autocorr(lag=dt) for dt in range(1,200)])
plt.ylim([-1,1]); plt.axhline(0, c='black', linestyle='--')
plt.ylabel('Autocorrelation'); plt.xlabel('Lags')
plt.show()
### BOOTSTRAPPED INTERVALS ###
alpha = 0.05
bootstrap = np.asarray([np.random.choice(res, size=res.shape) for _ in range(100)])
q_bootstrap = np.quantile(bootstrap, q=[alpha/2, 1-alpha/2], axis=0)
y_pred = model.predict(X_test)
y_lower = y_pred + q_bootstrap[0].mean()
y_upper = y_pred + q_bootstrap[1].mean()
### HOW MANY OUTLIERS IN TEST DATA ###
((y_test > y_upper).sum() + (y_test < y_lower).sum()) / y_test.shape[0]
### RIDGE TUNING ###
model = GridSearchCV(estimator=Ridge(), param_grid={'alpha': [3, 5, 10, 20, 50]},
scoring='neg_mean_squared_error', cv=3, refit=True)
model.fit(X_train, y_train)
model.best_params_
### OUT-OF-FOLDS RESIDUAL DISTRIBUTION ###
pred_train = cross_val_predict(Ridge(**model.best_params_), X_train, y_train, cv=3)
res = y_train - pred_train
### PLOT RESIDUAL STATISTICS ###
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.title('Residuals Distribution')
plt.hist(res, bins=20)
plt.subplot(1,2,2)
plt.title('Residuals Autocorrelation')
plt.plot([res.autocorr(lag=dt) for dt in range(1,200)])
plt.ylim([-1,1]); plt.axhline(0, c='black', linestyle='--')
plt.ylabel('Autocorrelation'); plt.xlabel('Lags')
plt.show()
### BOOTSTRAPPED INTERVALS ###
alpha = 0.05
bootstrap = np.asarray([np.random.choice(res, size=res.shape) for _ in range(100)])
q_bootstrap = np.quantile(bootstrap, q=[alpha/2, 1-alpha/2], axis=0)
y_pred = pd.Series(model.predict(X_test), index=X_test.index)
y_lower = y_pred + q_bootstrap[0].mean()
y_upper = y_pred + q_bootstrap[1].mean()
### PLOT BOOTSTRAPPED PREDICTION INTERVALS ###
plt.figure(figsize=(10,6))
y_pred.plot(linewidth=3)
y_test.plot(style='.k', alpha=0.5)
plt.fill_between(y_pred.index, y_lower, y_upper, alpha=0.3)
plt.title('Ridge test predictions')
### HOW MANY OUTLIERS IN TEST DATA ###
((y_test > y_upper).sum() + (y_test < y_lower).sum()) / y_test.shape[0]
```
|
github_jupyter
|
# Plotting Categorical Data
In this section, we will:
- Plot distributions of data across categorical variables
- Plot aggregate/summary statistics across categorical variables
## Plotting Distributions Across Categories
We have seen how to plot distributions of data. Often, the distributions reveal new information when you plot them across categorical variables.
Let's see some examples.
```
# loading libraries and reading the data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# set seaborn theme if you prefer
sns.set(style="white")
# read data
market_df = pd.read_csv("./global_sales_data/market_fact.csv")
customer_df = pd.read_csv("./global_sales_data/cust_dimen.csv")
product_df = pd.read_csv("./global_sales_data/prod_dimen.csv")
shipping_df = pd.read_csv("./global_sales_data/shipping_dimen.csv")
orders_df = pd.read_csv("./global_sales_data/orders_dimen.csv")
```
### Boxplots
We had created simple boxplots such as the ones shown below. Now, let's plot multiple boxplots and see what they can tell us the distribution of variables across categories.
```
# boxplot of a variable
sns.boxplot(y=market_df['Sales'])
plt.yscale('log')
plt.show()
```
Now, let's say you want to **compare the (distribution of) sales of various product categories**. Let's first merge the product data into the main dataframe.
```
# merge the dataframe to add a categorical variable
df = pd.merge(market_df, product_df, how='inner', on='Prod_id')
df.head()
# boxplot of a variable across various product categories
sns.boxplot(x='Product_Category', y='Sales', data=df)
plt.yscale('log')
plt.show()
```
So this tells you that the sales of office supplies are, on an average, lower than the other two categories. The sales of technology and furniture categories seem much better. Note that each order can have multiple units of products sold, so Sales being higher/lower may be due to price per unit or the number of units.
Let's now plot the other important variable - Profit.
```
# boxplot of a variable across various product categories
sns.boxplot(x='Product_Category', y='Profit', data=df)
plt.show()
```
Profit clearly has some *outliers* due to which the boxplots are unreadable. Let's remove some extreme values from Profit (for the purpose of visualisation) and try plotting.
```
df = df[(df.Profit<1000) & (df.Profit>-1000)]
# boxplot of a variable across various product categories
sns.boxplot(x='Product_Category', y='Profit', data=df)
plt.show()
```
You can see that though the category 'Technology' has better sales numbers than others, it is also the one where the **most loss making transactions** happen. You can drill further down into this.
```
# adjust figure size
plt.figure(figsize=(10, 8))
# subplot 1: Sales
plt.subplot(1, 2, 1)
sns.boxplot(x='Product_Category', y='Sales', data=df)
plt.title("Sales")
plt.yscale('log')
# subplot 2: Profit
plt.subplot(1, 2, 2)
sns.boxplot(x='Product_Category', y='Profit', data=df)
plt.title("Profit")
plt.show()
```
Now that we've compared Sales and Profits across product categories, let's drill down further and do the same across **another categorical variable** - Customer_Segment.
We'll need to add the customer-related attributes (dimensions) to this dataframe.
```
# merging with customers df
df = pd.merge(df, customer_df, how='inner', on='Cust_id')
df.head()
# boxplot of a variable across various product categories
sns.boxplot(x='Customer_Segment', y='Profit', data=df)
plt.show()
```
You can **visualise the distribution across two categorical variables** using the ```hue= ``` argument.
```
# set figure size for larger figure
plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w', edgecolor='k')
# specify hue="categorical_variable"
sns.boxplot(x='Customer_Segment', y='Profit', hue="Product_Category", data=df)
plt.show()
```
Across all customer segments, the product category ```Technology``` seems to be doing fairly well, though ```Furniture``` is incurring losses across all segments.
Now say you are curious to know why certain orders are making huge losses. One of your hypothesis is that the *shipping cost is too high in some orders*. You can **plot derived variables** as well, such as *shipping cost as percentage of sales amount*.
```
# plot shipping cost as percentage of Sales amount
sns.boxplot(x=df['Product_Category'], y=100*df['Shipping_Cost']/df['Sales'])
plt.ylabel("100*(Shipping cost/Sales)")
plt.show()
```
## Plotting Aggregated Values across Categories
### Bar Plots - Mean, Median and Count Plots
Bar plots are used to **display aggregated values** of a variable, rather than entire distributions. This is especially useful when you have a lot of data which is difficult to visualise in a single figure.
For example, say you want to visualise and *compare the average Sales across Product Categories*. The ```sns.barplot()``` function can be used to do that.
```
# bar plot with default statistic=mean
sns.barplot(x='Product_Category', y='Sales', data=df)
plt.show()
```
Note that, **by default, seaborn plots the mean value across categories**, though you can plot the count, median, sum etc. Also, barplot computes and shows the confidence interval of the mean as well.
```
# Create 2 subplots for mean and median respectively
# increase figure size
plt.figure(figsize=(12, 6))
# subplot 1: statistic=mean
plt.subplot(1, 2, 1)
sns.barplot(x='Product_Category', y='Sales', data=df)
plt.title("Average Sales")
# subplot 2: statistic=median
plt.subplot(1, 2, 2)
sns.barplot(x='Product_Category', y='Sales', data=df, estimator=np.median)
plt.title("Median Sales")
plt.show()
```
Look at that! The mean and median sales across the product categories tell different stories. This is because of some outliers (extreme values) in the ```Furniture``` category, distorting the value of the mean.
You can add another categorical variable in the plot.
```
# set figure size for larger figure
plt.figure(num=None, figsize=(12, 8), dpi=80, facecolor='w', edgecolor='k')
# specify hue="categorical_variable"
sns.barplot(x='Customer_Segment', y='Profit', hue="Product_Category", data=df, estimator=np.median)
plt.show()
```
The plot neatly shows the median profit across product categories and customer segments. It says that:
- On an average, only Technology products in Small Business and Corporate (customer) categories are profitable.
- Furniture is incurring losses across all Customer Segments
Compare this to the boxplot we had created above - though the bar plots contains 'lesser information' than the boxplot, it is more revealing.
<hr>
When you want to visualise having a large number of categories, it is helpful to plot the categories across the y-axis. Let's now *drill down into product sub categories*.
```
# Plotting categorical variable across the y-axis
plt.figure(figsize=(10, 8))
sns.barplot(x='Profit', y="Product_Sub_Category", data=df, estimator=np.median)
plt.show()
```
The plot clearly shows which sub categories are incurring the heaviest losses - Copiers and Fax, Tables, Chairs and Chairmats are the most loss making categories.
You can also plot the **count of the observations** across categorical variables using ```sns.countplot()```.
```
# Plotting count across a categorical variable
plt.figure(figsize=(10, 8))
sns.countplot(y="Product_Sub_Category", data=df)
plt.show()
```
Note the most loss making category - Copiers and Fax - has a very few number of orders.
In the next section, we will see how to plot Time Series data.
## Additional Stuff on Plotting Categorical Variables
1. <a href="https://seaborn.pydata.org/tutorial/categorical.html">Seaborn official tutorial on categorical variables</a>
|
github_jupyter
|
# AWS Elastic Kubernetes Service (EKS) Deep MNIST
In this example we will deploy a tensorflow MNIST model in Amazon Web Services' Elastic Kubernetes Service (EKS).
This tutorial will break down in the following sections:
1) Train a tensorflow model to predict mnist locally
2) Containerise the tensorflow model with our docker utility
3) Send some data to the docker model to test it
4) Install and configure AWS tools to interact with AWS
5) Use the AWS tools to create and setup EKS cluster with Seldon
6) Push and run docker image through the AWS Container Registry
7) Test our Elastic Kubernetes deployment by sending some data
#### Let's get started! 🚀🔥
## Dependencies:
* Helm v3.0.0+
* A Kubernetes cluster running v1.13 or above (minkube / docker-for-windows work well if enough RAM)
* kubectl v1.14+
* EKS CLI v0.1.32
* AWS Cli v1.16.163
* Python 3.6+
* Python DEV requirements
## 1) Train a tensorflow model to predict mnist locally
We will load the mnist images, together with their labels, and then train a tensorflow model to predict the right labels
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
import tensorflow as tf
if __name__ == '__main__':
x = tf.placeholder(tf.float32, [None,784], name="x")
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x,W) + b, name="y")
y_ = tf.placeholder(tf.float32, [None, 10])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y_:mnist.test.labels}))
saver = tf.train.Saver()
saver.save(sess, "model/deep_mnist_model")
```
## 2) Containerise the tensorflow model with our docker utility
First you need to make sure that you have added the .s2i/environment configuration file in this folder with the following content:
```
!cat .s2i/environment
```
Now we can build a docker image named "deep-mnist" with the tag 0.1
```
!s2i build . seldonio/seldon-core-s2i-python36:1.3.0-dev deep-mnist:0.1
```
## 3) Send some data to the docker model to test it
We first run the docker image we just created as a container called "mnist_predictor"
```
!docker run --name "mnist_predictor" -d --rm -p 5000:5000 deep-mnist:0.1
```
Send some random features that conform to the contract
```
import matplotlib.pyplot as plt
# This is the variable that was initialised at the beginning of the file
i = [0]
x = mnist.test.images[i]
y = mnist.test.labels[i]
plt.imshow(x.reshape((28, 28)), cmap='gray')
plt.show()
print("Expected label: ", np.sum(range(0,10) * y), ". One hot encoding: ", y)
from seldon_core.seldon_client import SeldonClient
import math
import numpy as np
# We now test the REST endpoint expecting the same result
endpoint = "0.0.0.0:5000"
batch = x
payload_type = "ndarray"
sc = SeldonClient(microservice_endpoint=endpoint)
# We use the microservice, instead of the "predict" function
client_prediction = sc.microservice(
data=batch,
method="predict",
payload_type=payload_type,
names=["tfidf"])
for proba, label in zip(client_prediction.response.data.ndarray.values[0].list_value.ListFields()[0][1], range(0,10)):
print(f"LABEL {label}:\t {proba.number_value*100:6.4f} %")
!docker rm mnist_predictor --force
```
## 4) Install and configure AWS tools to interact with AWS
First we install the awscli
```
!pip install awscli --upgrade --user
```
#### Configure aws so it can talk to your server
(if you are getting issues, make sure you have the permmissions to create clusters)
```
%%bash
# You must make sure that the access key and secret are changed
aws configure << END_OF_INPUTS
YOUR_ACCESS_KEY
YOUR_ACCESS_SECRET
us-west-2
json
END_OF_INPUTS
```
#### Install EKCTL
*IMPORTANT*: These instructions are for linux
Please follow the official installation of ekctl at: https://docs.aws.amazon.com/eks/latest/userguide/getting-started-eksctl.html
```
!curl --silent --location "https://github.com/weaveworks/eksctl/releases/download/latest_release/eksctl_$(uname -s)_amd64.tar.gz" | tar xz
!chmod 755 ./eksctl
!./eksctl version
```
## 5) Use the AWS tools to create and setup EKS cluster with Seldon
In this example we will create a cluster with 2 nodes, with a minimum of 1 and a max of 3. You can tweak this accordingly.
If you want to check the status of the deployment you can go to AWS CloudFormation or to the EKS dashboard.
It will take 10-15 minutes (so feel free to go grab a ☕).
### IMPORTANT: If you get errors in this step...
It is most probably IAM role access requirements, which requires you to discuss with your administrator.
```
%%bash
./eksctl create cluster \
--name demo-eks-cluster \
--region us-west-2 \
--nodes 2
```
### Configure local kubectl
We want to now configure our local Kubectl so we can actually reach the cluster we've just created
```
!aws eks --region us-west-2 update-kubeconfig --name demo-eks-cluster
```
And we can check if the context has been added to kubectl config (contexts are basically the different k8s cluster connections)
You should be able to see the context as "...aws:eks:eu-west-1:27...".
If it's not activated you can activate that context with kubectlt config set-context <CONTEXT_NAME>
```
!kubectl config get-contexts
```
## Setup Seldon Core
Use the setup notebook to [Setup Cluster](../../seldon_core_setup.ipynb#Setup-Cluster) with [Ambassador Ingress](../../seldon_core_setup.ipynb#Ambassador) and [Install Seldon Core](../../seldon_core_setup.ipynb#Install-Seldon-Core). Instructions [also online](./seldon_core_setup.html).
## Push docker image
In order for the EKS seldon deployment to access the image we just built, we need to push it to the Elastic Container Registry (ECR).
If you have any issues please follow the official AWS documentation: https://docs.aws.amazon.com/AmazonECR/latest/userguide/docker-basics.html
### First we create a registry
You can run the following command, and then see the result at https://us-west-2.console.aws.amazon.com/ecr/repositories?#
```
!aws ecr create-repository --repository-name seldon-repository --region us-west-2
```
### Now prepare docker image
We need to first tag the docker image before we can push it
```
%%bash
export AWS_ACCOUNT_ID=""
export AWS_REGION="us-west-2"
if [ -z "$AWS_ACCOUNT_ID" ]; then
echo "ERROR: Please provide a value for the AWS variables"
exit 1
fi
docker tag deep-mnist:0.1 "$AWS_ACCOUNT_ID.dkr.ecr.$AWS_REGION.amazonaws.com/seldon-repository"
```
### We now login to aws through docker so we can access the repository
```
!`aws ecr get-login --no-include-email --region us-west-2`
```
### And push the image
Make sure you add your AWS Account ID
```
%%bash
export AWS_ACCOUNT_ID=""
export AWS_REGION="us-west-2"
if [ -z "$AWS_ACCOUNT_ID" ]; then
echo "ERROR: Please provide a value for the AWS variables"
exit 1
fi
docker push "$AWS_ACCOUNT_ID.dkr.ecr.$AWS_REGION.amazonaws.com/seldon-repository"
```
## Running the Model
We will now run the model.
Let's first have a look at the file we'll be using to trigger the model:
```
!cat deep_mnist.json
```
Now let's trigger seldon to run the model.
We basically have a yaml file, where we want to replace the value "REPLACE_FOR_IMAGE_AND_TAG" for the image you pushed
```
%%bash
export AWS_ACCOUNT_ID=""
export AWS_REGION="us-west-2"
if [ -z "$AWS_ACCOUNT_ID" ]; then
echo "ERROR: Please provide a value for the AWS variables"
exit 1
fi
sed 's|REPLACE_FOR_IMAGE_AND_TAG|'"$AWS_ACCOUNT_ID"'.dkr.ecr.'"$AWS_REGION"'.amazonaws.com/seldon-repository|g' deep_mnist.json | kubectl apply -f -
```
And let's check that it's been created.
You should see an image called "deep-mnist-single-model...".
We'll wait until STATUS changes from "ContainerCreating" to "Running"
```
!kubectl get pods
```
## Test the model
Now we can test the model, let's first find out what is the URL that we'll have to use:
```
!kubectl get svc ambassador -o jsonpath='{.status.loadBalancer.ingress[0].hostname}'
```
We'll use a random example from our dataset
```
import matplotlib.pyplot as plt
# This is the variable that was initialised at the beginning of the file
i = [0]
x = mnist.test.images[i]
y = mnist.test.labels[i]
plt.imshow(x.reshape((28, 28)), cmap='gray')
plt.show()
print("Expected label: ", np.sum(range(0,10) * y), ". One hot encoding: ", y)
```
We can now add the URL above to send our request:
```
from seldon_core.seldon_client import SeldonClient
import math
import numpy as np
host = "a68bbac487ca611e988060247f81f4c1-707754258.us-west-2.elb.amazonaws.com"
port = "80" # Make sure you use the port above
batch = x
payload_type = "ndarray"
sc = SeldonClient(
gateway="ambassador",
ambassador_endpoint=host + ":" + port,
namespace="default",
oauth_key="oauth-key",
oauth_secret="oauth-secret")
client_prediction = sc.predict(
data=batch,
deployment_name="deep-mnist",
names=["text"],
payload_type=payload_type)
print(client_prediction)
```
### Let's visualise the probability for each label
It seems that it correctly predicted the number 7
```
for proba, label in zip(client_prediction.response.data.ndarray.values[0].list_value.ListFields()[0][1], range(0,10)):
print(f"LABEL {label}:\t {proba.number_value*100:6.4f} %")
```
|
github_jupyter
|
```
import sys
sys.path.append('../transformers/')
import tensorflow as tf
import tensorflow_datasets as tfds
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import pickle
from tqdm import tqdm
from path_explain import utils
from plot.text import text_plot, matrix_interaction_plot, bar_interaction_plot
from model import cnn_model
from embedding_explainer import EmbeddingExplainerTF
utils.set_up_environment(visible_devices='3')
encoder = tfds.features.text.TokenTextEncoder.load_from_file('encoder')
model = tf.keras.models.load_model('model.h5')
interpret_model = cnn_model(encoder.vocab_size, for_interpretation=True)
interpret_model.load_weights('model.h5', by_name=True)
sentences = [
'This movie was bad',
'This movie was not bad',
'A movie',
'A bad movie',
'A bad, terrible movie',
'A bad, terrible, awful movie',
'A bad, terrible, awful, horrible movie'
]
ids_list = []
for sentence in sentences:
ids = encoder.encode(sentence)
ids = np.array(ids)
ids = np.pad(ids, pad_width=(0, max(0, 52 - len(ids))))
ids_list.append(ids)
ids_list = np.stack(ids_list, axis=0)
model(ids_list)
embedding_model = tf.keras.models.Model(model.input, model.layers[1].output)
embeddings = embedding_model(ids_list)
baseline_embedding = embedding_model(np.zeros((1, 52), dtype=np.float32))
explainer = EmbeddingExplainerTF(interpret_model)
attributions = explainer.attributions(inputs=embeddings,
baseline=baseline_embedding,
batch_size=128,
num_samples=256,
use_expectation=False,
output_indices=0,
verbose=True)
interactions = explainer.interactions(inputs=embeddings,
baseline=baseline_embedding,
batch_size=128,
num_samples=256,
use_expectation=False,
output_indices=0,
verbose=True)
encoder.decode(ids_list[i]).split(' ')
i = 1
text_plot('this movie was not bad'.split(' '), attributions[i], include_legend=True)
plt.savefig('movie_not_bad_cnn_text.pdf')
i = 1
matrix_interaction_plot(interactions[i, ids_list[i] != 0][:, :5], encoder.decode(ids_list[i]).split(' '))
plt.savefig('not_bad_cnn_matrix.pdf')
plot_all(0)
plot_all(1)
plot_all(2)
plot_all(3)
plot_all(4)
plot_all(5)
plot_all(6)
```
|
github_jupyter
|
# explore_data_gov_sg_api
## Purpose:
Explore the weather-related APIs at https://developers.data.gov.sg.
## History:
- 2017-05 - Benjamin S. Grandey
- 2017-05-29 - Moving from atmos-scripts repository to access-data-gov-sg repository, and renaming from data_gov_sg_explore.ipynb to explore_data_gov_sg_api.ipynb.
```
import matplotlib.pyplot as plt
import pandas as pd
import requests
import seaborn as sns
%matplotlib inline
# Get my API keys
from my_api_keys import my_api_dict
# Note: this module, containing my API keys, will not be shared via GitHub
# You can obtain your own API key(s) by registering at https://developers.data.gov.sg
my_key = my_api_dict['data.gov.sg'] # API key for data.gov.sg
```
## Meta-data for available meteorological APIs
[I added this section after exploring the wind-speed data - see below.]
```
# Meteorological variables
for variable in ['rainfall', 'wind-speed', 'wind-direction', 'air-temperature', 'relative-humidity']:
print(variable)
r = requests.get('https://api.data.gov.sg/v1/environment/{}'.format(variable),
headers={'api-key': my_key})
metadata = r.json()['metadata']
for key in metadata.keys():
if key != 'stations': # don't print information about stations
print(' {}: {}'.format(key, r.json()['metadata'][key]))
# 1hr PM2.5 data are also available
r = requests.get('https://api.data.gov.sg/v1/environment/{}'.format('pm25'),
headers={'api-key': my_key})
r.json()
```
## Wind-speed
```
# Query without specifying date_time - returns most recent data?
!date
r = requests.get('https://api.data.gov.sg/v1/environment/wind-speed',
headers={'api-key': my_key})
r.json()
# Re-organize data into DataFrame
df = pd.DataFrame(r.json()['items'][0]['readings'])
df = df.rename(columns={'value': 'wind-speed'})
df['timestamp (SGT)'] = pd.to_datetime(r.json()['items'][0]['timestamp'].split('+')[0])
df
# Get wind-speed for specific time in past
r = requests.get('https://api.data.gov.sg/v1/environment/wind-speed',
headers={'api-key': my_key},
params={'date_time': '2016-12-10T00:00:00'})
df = pd.DataFrame(r.json()['items'][0]['readings'])
df = df.rename(columns={'value': 'wind-speed'})
df['timestamp (SGT)'] = pd.to_datetime(r.json()['items'][0]['timestamp'].split('+')[0])
df
# Get wind-speed at 5-min intervals on a specific date
# Note: if 'date' is used instead of 'date_time', the API appears to timeout
wind_speed_df = pd.DataFrame(columns=['station_id', 'wind-speed', 'timestamp (SGT)'])
for dt in pd.date_range('2017-05-24', periods=(24*12+1), freq='5min'):
r = requests.get('https://api.data.gov.sg/v1/environment/wind-speed',
headers={'api-key': my_key},
params={'date_time': dt.strftime('%Y-%m-%dT%H:%M:%S')})
temp_df = pd.DataFrame(r.json()['items'][0]['readings'])
temp_df = temp_df.rename(columns={'value': 'wind-speed'})
temp_df['timestamp (SGT)'] = pd.to_datetime(r.json()['items'][0]['timestamp'].split('+')[0])
wind_speed_df = wind_speed_df.append(temp_df, ignore_index=True)
wind_speed_df.head(15)
wind_speed_df.info()
wind_speed_df.groupby('station_id').describe()
```
## Rainfall
```
# Get rainfall at 5-min intervals on a specific date
rainfall_df = pd.DataFrame(columns=['station_id', 'rainfall', 'timestamp (SGT)'])
for dt in pd.date_range('2017-05-24', periods=(24*12+1), freq='5min'): # I remember this was a wet day
r = requests.get('https://api.data.gov.sg/v1/environment/rainfall',
headers={'api-key': my_key},
params={'date_time': dt.strftime('%Y-%m-%dT%H:%M:%S')})
temp_df = pd.DataFrame(r.json()['items'][0]['readings'])
temp_df = temp_df.rename(columns={'value': 'rainfall'})
temp_df['timestamp (SGT)'] = pd.to_datetime(r.json()['items'][0]['timestamp'].split('+')[0])
rainfall_df = rainfall_df.append(temp_df, ignore_index=True)
rainfall_df.head(15)
rainfall_df.info()
rainfall_df['rainfall'] = rainfall_df['rainfall'].astype('float') # convert to float
rainfall_df.info()
```
## Merge wind-speed and rainfall DataFrames
```
# Union of wind-speed and rainfall data
outer_df = pd.merge(wind_speed_df, rainfall_df, how='outer', on=['station_id', 'timestamp (SGT)'])
outer_df.head(15)
outer_df.info()
# Intersection of wind-speed and rainfall data
inner_df = pd.merge(wind_speed_df, rainfall_df, how='inner', on=['station_id', 'timestamp (SGT)'])
inner_df.head(15)
inner_df.info()
inner_df.groupby('station_id').describe()
# Quick look at relationship between rainfall and wind-speed for one station and one day
# Information about station S50
r = requests.get('https://api.data.gov.sg/v1/environment/rainfall',
headers={'api-key': my_key},
params={'date_time': '2017-05-04T00:00:00'})
for d in r.json()['metadata']['stations']:
if d['device_id'] == 'S50':
print(d)
# Select data for station S50
s50_df = inner_df.loc[inner_df['station_id'] == 'S50']
# Plot
sns.jointplot(s50_df['rainfall'], s50_df['wind-speed'], kind='scatter')
```
|
github_jupyter
|
Before you turn this problem in, make sure everything runs as expected. First, **restart the kernel** (in the menubar, select Kernel$\rightarrow$Restart) and then **run all cells** (in the menubar, select Cell$\rightarrow$Run All).
Make sure you fill in any place that says `YOUR CODE HERE` or "YOUR ANSWER HERE", as well as your name and collaborators below:
```
NAME = ""
COLLABORATORS = ""
```
---
<!--NOTEBOOK_HEADER-->
*This notebook contains material from [PyRosetta](https://RosettaCommons.github.io/PyRosetta.notebooks);
content is available [on Github](https://github.com/RosettaCommons/PyRosetta.notebooks.git).*
<!--NAVIGATION-->
< [Practice: Analyzing energy between residues](http://nbviewer.jupyter.org/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/03.02-Analyzing-energy-between-residues.ipynb) | [Contents](toc.ipynb) | [Index](index.ipynb) | [Introduction to Folding](http://nbviewer.jupyter.org/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/04.00-Introduction-to-Folding.ipynb) ><p><a href="https://colab.research.google.com/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/03.03-Energies-and-the-PyMOLMover.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a>
# Energies and the PyMOL Mover
Keywords: send_energy(), label_energy(), send_hbonds()
```
# Notebook setup
import sys
if 'google.colab' in sys.modules:
!pip install pyrosettacolabsetup
import pyrosettacolabsetup
pyrosettacolabsetup.setup()
print ("Notebook is set for PyRosetta use in Colab. Have fun!")
from pyrosetta import *
from pyrosetta.teaching import *
init()
```
**Make sure you are in the directory with the pdb files:**
`cd google_drive/My\ Drive/student-notebooks/`
```
# From previous section:
ras = pyrosetta.pose_from_pdb("inputs/6Q21_A.pdb")
sfxn = get_fa_scorefxn()
```
The `PyMOLMover` class contains a method for sending score function information to PyMOL,
which will then color the structure based on relative residue energies.
Open up PyMOL. Instantiate a `PyMOLMover` object and use the `pymol_mover.send_energy(ras)` to send the coloring command to PyMOL.
```
pymol_mover = PyMOLMover()
pymol_mover.apply(ras)
print(sfxn(ras))
pymol_mover.send_energy(ras)
```
```
# YOUR CODE HERE
raise NotImplementedError()
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
from IPython import display
from pathlib import Path
gifPath = Path("./Media/PyMOL-send_energy.gif")
# Display GIF in Jupyter, CoLab, IPython
with open(gifPath,'rb') as f:
display.Image(data=f.read(), format='png',width='800')
```
What color is residue Proline34? What color is residue Alanine66? Which residue has lower energy?
```
# your response here
```
`pymol_mover.send_energy(ras, fa_atr)` will have PyMOL color only by the attractive van der Waals energy component. What color is residue 34 if colored by solvation energy, `fa_sol`?
```
# send specific energies to pymol
# YOUR CODE HERE
raise NotImplementedError()
```
You can have PyMOL label each Cα with the value of its residue’s specified energy using:
```
pymol_mover.label_energy(ras, "fa_atr")
```
```
# YOUR CODE HERE
raise NotImplementedError()
```
Finally, if you have scored the `pose` first, you can have PyMOL display all of the calculated hydrogen bonds for the structure:
```
pymol_mover.send_hbonds(ras)
```
```
# YOUR CODE HERE
raise NotImplementedError()
```
## References
This Jupyter notebook is an adapted version of "Workshop #3: Scoring" in the PyRosetta workbook: https://graylab.jhu.edu/pyrosetta/downloads/documentation/pyrosetta4_online_format/PyRosetta4_Workshop3_Scoring.pdf
<!--NAVIGATION-->
< [Practice: Analyzing energy between residues](http://nbviewer.jupyter.org/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/03.02-Analyzing-energy-between-residues.ipynb) | [Contents](toc.ipynb) | [Index](index.ipynb) | [Introduction to Folding](http://nbviewer.jupyter.org/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/04.00-Introduction-to-Folding.ipynb) ><p><a href="https://colab.research.google.com/github/RosettaCommons/PyRosetta.notebooks/blob/master/notebooks/03.03-Energies-and-the-PyMOLMover.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a>
|
github_jupyter
|
This model will cluster a set of data, first with KMeans and then with MiniBatchKMeans, and plot the results. It will also plot the points that are labelled differently between the two algorithms.
```
import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets import make_blobs
# Generate sample data
np.random.seed(0)
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]]
n_clusters = len(centers)
X, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7)
# Compute clustering with Means
k_means = KMeans(init="k-means++", n_clusters=3, n_init=10)
t0 = time.time()
k_means.fit(X)
t_batch = time.time() - t0
# Compute clustering with MiniBatchKMeans
mbk = MiniBatchKMeans(
init="k-means++",
n_clusters=3,
batch_size=batch_size,
n_init=10,
max_no_improvement=10,
verbose=0,
)
t0 = time.time()
mbk.fit(X)
t_mini_batch = time.time() - t0
# Plot result
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = ["#4EACC5", "#FF9C34", "#4E9A06"]
# We want to have the same colors for the same cluster from the
# MiniBatchKMeans and the KMeans algorithm. Let's pair the cluster centers per
# closest one.
k_means_cluster_centers = k_means.cluster_centers_
order = pairwise_distances_argmin(k_means.cluster_centers_, mbk.cluster_centers_)
mbk_means_cluster_centers = mbk.cluster_centers_[order]
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
# KMeans
ax = fig.add_subplot(1, 3, 1)
for k, col in zip(range(n_clusters), colors):
my_members = k_means_labels == k
cluster_center = k_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], "w", markerfacecolor=col, marker=".")
ax.plot(
cluster_center[0],
cluster_center[1],
"o",
markerfacecolor=col,
markeredgecolor="k",
markersize=6,
)
ax.set_title("KMeans")
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, "train time: %.2fs\ninertia: %f" % (t_batch, k_means.inertia_))
# MiniBatchKMeans
ax = fig.add_subplot(1, 3, 2)
for k, col in zip(range(n_clusters), colors):
my_members = mbk_means_labels == k
cluster_center = mbk_means_cluster_centers[k]
ax.plot(X[my_members, 0], X[my_members, 1], "w", markerfacecolor=col, marker=".")
ax.plot(
cluster_center[0],
cluster_center[1],
"o",
markerfacecolor=col,
markeredgecolor="k",
markersize=6,
)
ax.set_title("MiniBatchKMeans")
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, "train time: %.2fs\ninertia: %f" % (t_mini_batch, mbk.inertia_))
# Initialise the different array to all False
different = mbk_means_labels == 4
ax = fig.add_subplot(1, 3, 3)
for k in range(n_clusters):
different += (k_means_labels == k) != (mbk_means_labels == k)
identic = np.logical_not(different)
ax.plot(X[identic, 0], X[identic, 1], "w", markerfacecolor="#bbbbbb", marker=".")
ax.plot(X[different, 0], X[different, 1], "w", markerfacecolor="m", marker=".")
ax.set_title("Difference")
ax.set_xticks(())
ax.set_yticks(())
plt.show()
```
|
github_jupyter
|
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# `GiRaFFE_NRPy`: Source Terms
## Author: Patrick Nelson
<a id='intro'></a>
**Notebook Status:** <font color=green><b> Validated </b></font>
**Validation Notes:** This code produces the expected results for generated functions.
## This module presents the functionality of [GiRaFFE_NRPy_Source_Terms.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms.py).
## Introduction:
This writes and documents the C code that `GiRaFFE_NRPy` uses to compute the source terms for the right-hand sides of the evolution equations for the unstaggered prescription.
The equations themselves are already coded up in other functions; however, for the $\tilde{S}_i$ source term, we will need derivatives of the metric. It will be most efficient and accurate to take them using the interpolated metric values that we will have calculated anyway; however, we will need to write our derivatives in a nonstandard way within NRPy+ in order to take advantage of this, writing our own code for memory access.
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#stilde_source): The $\tilde{S}_i$ source term
1. [Step 2](#code_validation): Code Validation against original C code
1. [Step 3](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
```
# Step 0: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os,sys
nrpy_dir_path = os.path.join("..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
import cmdline_helper as cmd
outdir = os.path.join("GiRaFFE_NRPy","GiRaFFE_Ccode_validation","RHSs")
cmd.mkdir(outdir)
```
<a id='stilde_source'></a>
## Step 1: The $\tilde{S}_i$ source term \[Back to [top](#toc)\]
$$\label{stilde_source}$$
We start in the usual way - import the modules we need. We will also import the Levi-Civita symbol from `indexedexp.py` and use it to set the Levi-Civita tensor $\epsilon^{ijk} = [ijk]/\sqrt{\gamma}$.
```
# Step 1: The StildeD RHS *source* term
from outputC import outputC, outCfunction # NRPy+: Core C code output module
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import GRHD.equations as GRHD # NRPy+: Generate general relativistic hydrodynamics equations
import GRFFE.equations as GRFFE # NRPy+: Generate general relativistic force-free electrodynamics equations
thismodule = "GiRaFFE_NRPy_Source_Terms"
def generate_memory_access_code(gammaDD,betaU,alpha):
# There are several pieces of C code that we will write ourselves because we need to do things
# a little bit outside of what NRPy+ is built for.
# First, we will write general memory access. We will read in values from memory at a given point
# for each quantity we care about.
global general_access
general_access = ""
for var in ["GAMMADD00", "GAMMADD01", "GAMMADD02",
"GAMMADD11", "GAMMADD12", "GAMMADD22",
"BETAU0", "BETAU1", "BETAU2","ALPHA",
"BU0","BU1","BU2",
"VALENCIAVU0","VALENCIAVU1","VALENCIAVU2"]:
lhsvar = var.lower().replace("dd","DD").replace("u","U").replace("bU","BU").replace("valencia","Valencia")
# e.g.,
# const REAL gammaDD00dD0 = auxevol_gfs[IDX4S(GAMMA_FACEDD00GF,i0,i1,i2)];
general_access += "const REAL "+lhsvar+" = auxevol_gfs[IDX4S("+var+"GF,i0,i1,i2)];\n"
# This quick function returns a nearby point for memory access. We need this because derivatives are not local operations.
def idxp1(dirn):
if dirn==0:
return "i0+1,i1,i2"
if dirn==1:
return "i0,i1+1,i2"
if dirn==2:
return "i0,i1,i2+1"
# Next we evaluate needed derivatives of the metric, based on their values at cell faces
global metric_deriv_access
metric_deriv_access = []
# for dirn in range(3):
# metric_deriv_access.append("")
# for var in ["GAMMA_FACEDDdD00", "GAMMA_FACEDDdD01", "GAMMA_FACEDDdD02",
# "GAMMA_FACEDDdD11", "GAMMA_FACEDDdD12", "GAMMA_FACEDDdD22",
# "BETA_FACEUdD0", "BETA_FACEUdD1", "BETA_FACEUdD2","ALPHA_FACEdD"]:
# lhsvar = var.lower().replace("dddd","DDdD").replace("udd","UdD").replace("dd","dD").replace("u","U").replace("_face","")
# rhsvar = var.replace("dD","")
# # e.g.,
# # const REAL gammaDDdD000 = (auxevol_gfs[IDX4S(GAMMA_FACEDD00GF,i0+1,i1,i2)]-auxevol_gfs[IDX4S(GAMMA_FACEDD00GF,i0,i1,i2)])/dxx0;
# metric_deriv_access[dirn] += "const REAL "+lhsvar+str(dirn)+" = (auxevol_gfs[IDX4S("+rhsvar+"GF,"+idxp1(dirn)+")]-auxevol_gfs[IDX4S("+rhsvar+"GF,i0,i1,i2)])/dxx"+str(dirn)+";\n"
# metric_deriv_access[dirn] += "REAL Stilde_rhsD"+str(dirn)+";\n"
# For this workaround, instead of taking the derivative of the metric components and then building the
# four-metric, we build the four-metric and then take derivatives. Do this at i and i+1
for dirn in range(3):
metric_deriv_access.append("")
for var in ["GAMMA_FACEDD00", "GAMMA_FACEDD01", "GAMMA_FACEDD02",
"GAMMA_FACEDD11", "GAMMA_FACEDD12", "GAMMA_FACEDD22",
"BETA_FACEU0", "BETA_FACEU1", "BETA_FACEU2","ALPHA_FACE"]:
lhsvar = var.lower().replace("dd","DD").replace("u","U")
rhsvar = var
# e.g.,
# const REAL gammaDD00 = auxevol_gfs[IDX4S(GAMMA_FACEDD00GF,i0,i1,i2)];
metric_deriv_access[dirn] += "const REAL "+lhsvar+" = auxevol_gfs[IDX4S("+rhsvar+"GF,i0,i1,i2)];\n"
# Read in at the next grid point
for var in ["GAMMA_FACEDD00", "GAMMA_FACEDD01", "GAMMA_FACEDD02",
"GAMMA_FACEDD11", "GAMMA_FACEDD12", "GAMMA_FACEDD22",
"BETA_FACEU0", "BETA_FACEU1", "BETA_FACEU2","ALPHA_FACE"]:
lhsvar = var.lower().replace("dd","DD").replace("u","U").replace("_face","_facep1")
rhsvar = var
# e.g.,
# const REAL gammaDD00 = auxevol_gfs[IDX4S(GAMMA_FACEDD00GF,i0+1,i1,i2)];
metric_deriv_access[dirn] += "const REAL "+lhsvar+" = auxevol_gfs[IDX4S("+rhsvar+"GF,"+idxp1(dirn)+")];\n"
metric_deriv_access[dirn] += "REAL Stilde_rhsD"+str(dirn)+";\n"
import BSSN.ADMBSSN_tofrom_4metric as AB4m
AB4m.g4DD_ito_BSSN_or_ADM("ADM",gammaDD,betaU,alpha)
four_metric_vars = [
AB4m.g4DD[0][0],
AB4m.g4DD[0][1],
AB4m.g4DD[0][2],
AB4m.g4DD[0][3],
AB4m.g4DD[1][1],
AB4m.g4DD[1][2],
AB4m.g4DD[1][3],
AB4m.g4DD[2][2],
AB4m.g4DD[2][3],
AB4m.g4DD[3][3]
]
four_metric_names = [
"g4DD00",
"g4DD01",
"g4DD02",
"g4DD03",
"g4DD11",
"g4DD12",
"g4DD13",
"g4DD22",
"g4DD23",
"g4DD33"
]
global four_metric_C, four_metric_Cp1
four_metric_C = outputC(four_metric_vars,four_metric_names,"returnstring",params="outCverbose=False,CSE_sorting=none")
for ii in range(len(four_metric_names)):
four_metric_names[ii] += "p1"
four_metric_Cp1 = outputC(four_metric_vars,four_metric_names,"returnstring",params="outCverbose=False,CSE_sorting=none")
four_metric_C = four_metric_C.replace("gamma","gamma_face").replace("beta","beta_face").replace("alpha","alpha_face").replace("{","").replace("}","").replace("g4","const REAL g4").replace("tmp_","tmp_deriv")
four_metric_Cp1 = four_metric_Cp1.replace("gamma","gamma_facep1").replace("beta","beta_facep1").replace("alpha","alpha_facep1").replace("{","").replace("}","").replace("g4","const REAL g4").replace("tmp_","tmp_derivp")
global four_metric_deriv
four_metric_deriv = []
for dirn in range(3):
four_metric_deriv.append("")
for var in ["g4DDdD00", "g4DDdD01", "g4DDdD02", "g4DDdD03", "g4DDdD11",
"g4DDdD12", "g4DDdD13", "g4DDdD22", "g4DDdD23", "g4DDdD33"]:
lhsvar = var + str(dirn+1)
rhsvar = var.replace("dD","")
rhsvarp1 = rhsvar + "p1"
# e.g.,
# const REAL g44DDdD000 = (g4DD00p1 - g4DD00)/dxx0;
four_metric_deriv[dirn] += "const REAL "+lhsvar+" = ("+rhsvarp1+" - "+rhsvar+")/dxx"+str(dirn)+";\n"
# This creates the C code that writes to the Stilde_rhs direction specified.
global write_final_quantity
write_final_quantity = []
for dirn in range(3):
write_final_quantity.append("")
write_final_quantity[dirn] += "rhs_gfs[IDX4S(STILDED"+str(dirn)+"GF,i0,i1,i2)] += Stilde_rhsD"+str(dirn)+";"
def write_out_functions_for_StildeD_source_term(outdir,outCparams,gammaDD,betaU,alpha,ValenciavU,BU,sqrt4pi):
generate_memory_access_code(gammaDD,betaU,alpha)
# First, we declare some dummy tensors that we will use for the codegen.
gammaDDdD = ixp.declarerank3("gammaDDdD","sym01",DIM=3)
betaUdD = ixp.declarerank2("betaUdD","nosym",DIM=3)
alphadD = ixp.declarerank1("alphadD",DIM=3)
g4DDdD = ixp.declarerank3("g4DDdD","sym01",DIM=4)
# We need to rerun a few of these functions with the reset lists to make sure these functions
# don't cheat by using analytic expressions
GRHD.compute_sqrtgammaDET(gammaDD)
GRHD.u4U_in_terms_of_ValenciavU__rescale_ValenciavU_by_applying_speed_limit(alpha, betaU, gammaDD, ValenciavU)
GRFFE.compute_smallb4U(gammaDD, betaU, alpha, GRHD.u4U_ito_ValenciavU, BU, sqrt4pi)
GRFFE.compute_smallbsquared(gammaDD, betaU, alpha, GRFFE.smallb4U)
GRFFE.compute_TEM4UU(gammaDD,betaU,alpha, GRFFE.smallb4U, GRFFE.smallbsquared,GRHD.u4U_ito_ValenciavU)
# GRHD.compute_g4DD_zerotimederiv_dD(gammaDD,betaU,alpha, gammaDDdD,betaUdD,alphadD)
GRHD.compute_S_tilde_source_termD(alpha, GRHD.sqrtgammaDET,g4DDdD, GRFFE.TEM4UU)
for i in range(3):
desc = "Adds the source term to StildeD"+str(i)+"."
name = "calculate_StildeD"+str(i)+"_source_term"
outCfunction(
outfile = os.path.join(outdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,const REAL *auxevol_gfs, REAL *rhs_gfs",
body = general_access \
+metric_deriv_access[i]\
+four_metric_C\
+four_metric_Cp1\
+four_metric_deriv[i]\
+outputC(GRHD.S_tilde_source_termD[i],"Stilde_rhsD"+str(i),"returnstring",params=outCparams).replace("IDX4","IDX4S")\
+write_final_quantity[i],
loopopts ="InteriorPoints",
rel_path_to_Cparams=os.path.join("../"))
```
<a id='code_validation'></a>
# Step 2: Code Validation against original C code \[Back to [top](#toc)\]
$$\label{code_validation}$$
To validate the code in this tutorial we check for agreement between the files
1. that were written in this tutorial and
1. those that are stored in `GiRaFFE_NRPy/GiRaFFE_Ccode_library` or generated by `GiRaFFE_NRPy_A2B.py`
```
# Declare gridfunctions necessary to generate the C code:
gammaDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gammaDD","sym01",DIM=3)
betaU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","betaU",DIM=3)
alpha = gri.register_gridfunctions("AUXEVOL","alpha",DIM=3)
BU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","BU",DIM=3)
ValenciavU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","ValenciavU",DIM=3)
StildeD = ixp.register_gridfunctions_for_single_rank1("EVOL","StildeD",DIM=3)
# Declare this symbol:
sqrt4pi = par.Cparameters("REAL",thismodule,"sqrt4pi","sqrt(4.0*M_PI)")
# First, we generate the file using the functions written in this notebook:
outCparams = "outCverbose=False"
write_out_functions_for_StildeD_source_term(outdir,outCparams,gammaDD,betaU,alpha,ValenciavU,BU,sqrt4pi)
# Define the directory that we wish to validate against:
valdir = os.path.join("GiRaFFE_NRPy","GiRaFFE_Ccode_library","RHSs")
cmd.mkdir(valdir)
import GiRaFFE_NRPy.GiRaFFE_NRPy_Source_Terms as source
source.write_out_functions_for_StildeD_source_term(valdir,outCparams,gammaDD,betaU,alpha,ValenciavU,BU,sqrt4pi)
import difflib
import sys
print("Printing difference between original C code and this code...")
# Open the files to compare
files = ["calculate_StildeD0_source_term.h","calculate_StildeD1_source_term.h","calculate_StildeD2_source_term.h"]
for file in files:
print("Checking file " + file)
with open(os.path.join(valdir,file)) as file1, open(os.path.join(outdir,file)) as file2:
# Read the lines of each file
file1_lines = file1.readlines()
file2_lines = file2.readlines()
num_diffs = 0
for line in difflib.unified_diff(file1_lines, file2_lines, fromfile=os.path.join(valdir+file), tofile=os.path.join(outdir+file)):
sys.stdout.writelines(line)
num_diffs = num_diffs + 1
if num_diffs == 0:
print("No difference. TEST PASSED!")
else:
print("ERROR: Disagreement found with .py file. See differences above.")
sys.exit(1)
```
<a id='latex_pdf_output'></a>
# Step 3: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-GiRaFFE_NRPy_C_code_library-Source_Terms](TTutorial-GiRaFFE_NRPy_C_code_library-Source_Terms.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-GiRaFFE_NRPy-Source_Terms",location_of_template_file=os.path.join(".."))
```
|
github_jupyter
|
# Find Descriptors (Matching)
Similar to classification, VDMS supports feature vector search based on similariy matching as part of its API.
In this example, where we have a pre-load set of feature vectors and labels associated,
we can search for similar feature vectors, and query information related to it.
We will start by taking a new image, not seeing by VDMS before (FIX THIS),
find the faces on it, and run feature vector extraction, and finding images related to it:
```
import getDescriptors as g
imagePath = "images/1.jpg"
descriptors = g.get_descriptors(imagePath)
```
Now that we have the new faces and its feature vectors, we can ask VDMS to return the similar descriptors.
But first, let's connect to VDMS:
```
import vdms
db = vdms.vdms()
db.connect("localhost")
```
We can now search for similar descriptors by passing the descriptor of the face to VDMS as follows:
```
import numpy as np
import json
import util
who_is_this = descriptors[1] # Number 1 is Tom's face
blob_array = []
query = """
[
{
"FindDescriptor" : {
"set": "hike_mt_rainier",
"_ref": 33,
"k_neighbors": 4,
"results": {
"list": ["_distance", "_id", "_label"]
}
}
}
]
"""
blob_array.append(who_is_this)
response, images = db.query(query, [blob_array])
print (db.get_last_response_str())
```
Now that we can see this similar descriptors, let's go one step further and retrieve the images asociated with those descriptors:
```
blob_array = []
query = """
[
{
"FindDescriptor" : {
"set": "hike_mt_rainier",
"_ref": 33,
"k_neighbors": 5,
"results": {
"list": ["_distance", "_id"]
}
}
},
{
"FindImage" : {
"link": { "ref": 33 },
"operations": [
{
"type": "resize",
"height": 200,
"width": 200
}
],
"results": {
"list": ["name_file"]
}
}
}
]
"""
blob_array.append(who_is_this)
response, images = db.query(query, [blob_array])
util.display_images(images)
print ("Number of images:", len(images))
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
import vdms
import numpy as np
import json
db = vdms.vdms()
db.connect("localhost")
who_is_this = descriptors[1]
blob_array = []
query = """
[
{
"FindDescriptor" : {
"set": "hike_mt_rainier",
"_ref": 33,
"k_neighbors": 1,
"results": {
"list": ["_distance", "_id"]
}
}
},
{
"FindEntity" : {
"class": "Person",
"link": { "ref": 33 },
"_ref": 34,
"results": {
"list": ["name", "lastname"]
}
}
},
{
"FindImage" : {
"link": { "ref": 34 },
"operations": [
{
"type": "resize",
"height": 300,
"width": 300
}
],
"results": {
"list": ["name_file"]
}
}
}
]
"""
blob_array.append(who_is_this)
response, images = db.query(query, [blob_array])
util.display_images(images)
print ("Number of images:", len(images))
```
|
github_jupyter
|
```
!sudo nvidia-persistenced
!sudo nvidia-smi -ac 877,1530
from IPython.core.display import display, HTML
display(HTML("<style>.container {width:95% !important;}</style>"))
from core import *
from torch_backend import *
colors = ColorMap()
draw = lambda graph: display(DotGraph({p: ({'fillcolor': colors[type(v)], 'tooltip': repr(v)}, inputs) for p, (v, inputs) in graph.items() if v is not None}))
```
### Network definitions
```
batch_norm = partial(BatchNorm, weight_init=None, bias_init=None)
def res_block(c_in, c_out, stride, **kw):
block = {
'bn1': batch_norm(c_in, **kw),
'relu1': nn.ReLU(True),
'branch': {
'conv1': nn.Conv2d(c_in, c_out, kernel_size=3, stride=stride, padding=1, bias=False),
'bn2': batch_norm(c_out, **kw),
'relu2': nn.ReLU(True),
'conv2': nn.Conv2d(c_out, c_out, kernel_size=3, stride=1, padding=1, bias=False),
}
}
projection = (stride != 1) or (c_in != c_out)
if projection:
block['conv3'] = (nn.Conv2d(c_in, c_out, kernel_size=1, stride=stride, padding=0, bias=False), ['relu1'])
block['add'] = (Add(), [('conv3' if projection else 'relu1'), 'branch/conv2'])
return block
def DAWN_net(c=64, block=res_block, prep_bn_relu=False, concat_pool=True, **kw):
if isinstance(c, int):
c = [c, 2*c, 4*c, 4*c]
classifier_pool = {
'in': Identity(),
'maxpool': nn.MaxPool2d(4),
'avgpool': (nn.AvgPool2d(4), ['in']),
'concat': (Concat(), ['maxpool', 'avgpool']),
} if concat_pool else {'pool': nn.MaxPool2d(4)}
return {
'input': (None, []),
'prep': union({'conv': nn.Conv2d(3, c[0], kernel_size=3, stride=1, padding=1, bias=False)},
{'bn': batch_norm(c[0], **kw), 'relu': nn.ReLU(True)} if prep_bn_relu else {}),
'layer1': {
'block0': block(c[0], c[0], 1, **kw),
'block1': block(c[0], c[0], 1, **kw),
},
'layer2': {
'block0': block(c[0], c[1], 2, **kw),
'block1': block(c[1], c[1], 1, **kw),
},
'layer3': {
'block0': block(c[1], c[2], 2, **kw),
'block1': block(c[2], c[2], 1, **kw),
},
'layer4': {
'block0': block(c[2], c[3], 2, **kw),
'block1': block(c[3], c[3], 1, **kw),
},
'final': union(classifier_pool, {
'flatten': Flatten(),
'linear': nn.Linear(2*c[3] if concat_pool else c[3], 10, bias=True),
}),
'logits': Identity(),
}
def conv_bn(c_in, c_out, bn_weight_init=1.0, **kw):
return {
'conv': nn.Conv2d(c_in, c_out, kernel_size=3, stride=1, padding=1, bias=False),
'bn': batch_norm(c_out, bn_weight_init=bn_weight_init, **kw),
'relu': nn.ReLU(True)
}
def basic_net(channels, weight, pool, **kw):
return {
'input': (None, []),
'prep': conv_bn(3, channels['prep'], **kw),
'layer1': dict(conv_bn(channels['prep'], channels['layer1'], **kw), pool=pool),
'layer2': dict(conv_bn(channels['layer1'], channels['layer2'], **kw), pool=pool),
'layer3': dict(conv_bn(channels['layer2'], channels['layer3'], **kw), pool=pool),
'pool': nn.MaxPool2d(4),
'flatten': Flatten(),
'linear': nn.Linear(channels['layer3'], 10, bias=False),
'logits': Mul(weight),
}
def net(channels=None, weight=0.125, pool=nn.MaxPool2d(2), extra_layers=(), res_layers=('layer1', 'layer3'), **kw):
channels = channels or {'prep': 64, 'layer1': 128, 'layer2': 256, 'layer3': 512}
residual = lambda c, **kw: {'in': Identity(), 'res1': conv_bn(c, c, **kw), 'res2': conv_bn(c, c, **kw),
'add': (Add(), ['in', 'res2/relu'])}
n = basic_net(channels, weight, pool, **kw)
for layer in res_layers:
n[layer]['residual'] = residual(channels[layer], **kw)
for layer in extra_layers:
n[layer]['extra'] = conv_bn(channels[layer], channels[layer], **kw)
return n
remove_identity_nodes = lambda net: remove_by_type(net, Identity)
```
### Download and preprocess data
```
DATA_DIR = './data'
dataset = cifar10(DATA_DIR)
timer = Timer()
print('Preprocessing training data')
transforms = [
partial(normalise, mean=np.array(cifar10_mean, dtype=np.float32), std=np.array(cifar10_std, dtype=np.float32)),
partial(transpose, source='NHWC', target='NCHW'),
]
train_set = list(zip(*preprocess(dataset['train'], [partial(pad, border=4)] + transforms).values()))
print(f'Finished in {timer():.2} seconds')
print('Preprocessing test data')
test_set = list(zip(*preprocess(dataset['valid'], transforms).values()))
print(f'Finished in {timer():.2} seconds')
```
### Training loop
```
def train(model, lr_schedule, train_set, test_set, batch_size, num_workers=0):
train_batches = DataLoader(train_set, batch_size, shuffle=True, set_random_choices=True, num_workers=num_workers)
test_batches = DataLoader(test_set, batch_size, shuffle=False, num_workers=num_workers)
lr = lambda step: lr_schedule(step/len(train_batches))/batch_size
opts = [SGD(trainable_params(model).values(), {'lr': lr, 'weight_decay': Const(5e-4*batch_size), 'momentum': Const(0.9)})]
logs, state = Table(), {MODEL: model, LOSS: x_ent_loss, OPTS: opts}
for epoch in range(lr_schedule.knots[-1]):
logs.append(union({'epoch': epoch+1, 'lr': lr_schedule(epoch+1)},
train_epoch(state, Timer(torch.cuda.synchronize), train_batches, test_batches)))
return logs
```
### [Post 1: Baseline](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_1/) - DAWNbench baseline + no initial bn-relu+ efficient dataloading/augmentation, 1 dataloader process (301s)
```
lr_schedule = PiecewiseLinear([0, 15, 30, 35], [0, 0.1, 0.005, 0])
batch_size = 128
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device)
#convert all children including batch norms to half precision (triggering slow codepath!)
for v in model.children():
v.half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR()])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=1)
```
### [Post 1: Baseline](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_1/) - 0 dataloader processes (297s)
```
lr_schedule = PiecewiseLinear([0, 15, 30, 35], [0, 0.1, 0.005, 0])
batch_size = 128
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device)
#convert all children including batch norms to half precision (triggering slow codepath!)
for v in model.children():
v.half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR()])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 2: Mini-batches](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_2/) - batch size=512 (256s)
```
lr_schedule = PiecewiseLinear([0, 15, 30, 35], [0, 0.44, 0.005, 0])
batch_size = 512
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device)
#convert all children including batch norms to half precision (triggering slow codepath!)
for v in model.children():
v.half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR()])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 3: Regularisation](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_3/) - speed up batch norms (186s)
```
lr_schedule = PiecewiseLinear([0, 15, 30, 35], [0, 0.44, 0.005, 0])
batch_size = 512
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR()])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 3: Regularisation](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_3/) - cutout+30 epochs+batch_size=512 (161s)
```
lr_schedule = PiecewiseLinear([0, 8, 30], [0, 0.4, 0])
batch_size = 512
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 3: Regularisation](https://www.myrtle.ai/2018/09/24/how_to_train_your_resnet_3/) - batch_size=768 (154s)
```
lr_schedule = PiecewiseLinear([0, 8, 30], [0, 0.6, 0])
batch_size = 768
n = DAWN_net()
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone (36s; test acc 55.9%)
It seems reasonable to study how the shortest path through the network trains in isolation and to take steps to improve this before adding back the longer branches.
Eliminating the long branches yields the following backbone network in which all convolutions, except for the initial one, have a stride of two.
Training the shortest path network for 20 epochs yields an unimpressive test accuracy of 55.9% in 36 seconds.
```
def shortcut_block(c_in, c_out, stride, **kw):
block = {
'bn1': batch_norm(c_in, **kw),
'relu1': nn.ReLU(True),
}
projection = (stride != 1) or (c_in != c_out)
if projection:
block['conv3'] = (nn.Conv2d(c_in, c_out, kernel_size=1, stride=stride, padding=0, bias=False), ['relu1'])
return block
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = DAWN_net(block=shortcut_block)
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone, remove repeat bn-relu (32s; test acc 56.0%)
Removing the repeated batch norm-ReLU groups, reduces training time to 32s and leaves test accuracy approximately unchanged.
```
def shortcut_block(c_in, c_out, stride, **kw):
projection = (stride != 1) or (c_in != c_out)
if projection:
return {
'conv': nn.Conv2d(c_in, c_out, kernel_size=1, stride=stride, padding=0, bias=False),
'bn': batch_norm(c_out, **kw),
'relu': nn.ReLU(True),
}
else:
return {'id': Identity()}
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = DAWN_net(block=shortcut_block, prep_bn_relu=True)
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone, 3x3 convs (36s; test acc 85.6%)
A serious shortcoming of this network is that the downsampling convolutions have 1x1 kernels and a stride of two, so that rather than enlarging the receptive field they are simply discarding information.
If we replace these with 3x3 convolutions, things improve considerably and test accuracy after 20 epochs is 85.6% in a time of 36s.
```
def shortcut_block(c_in, c_out, stride, **kw):
projection = (stride != 1) or (c_in != c_out)
if projection:
return {
'conv': nn.Conv2d(c_in, c_out, kernel_size=3, stride=stride, padding=1, bias=False),
'bn': batch_norm(c_out, **kw),
'relu': nn.ReLU(True),
}
else:
return {'id': Identity()}
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = DAWN_net(block=shortcut_block, prep_bn_relu=True)
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone, maxpool downsampling (43s; test acc 89.7%)
We can further improve the downsampling stages by applying 3x3 convolutions of stride one followed by a pooling layer instead of using strided convolutions.
We choose max pooling with a 2x2 window size leading to a final test accuracy of 89.7% after 43s. Using average pooling gives a similar result but takes slightly longer.
```
def shortcut_block(c_in, c_out, stride, **kw):
projection = (stride != 1) or (c_in != c_out)
if projection:
return {
'conv': nn.Conv2d(c_in, c_out, kernel_size=3, stride=1, padding=1, bias=False),
'bn': batch_norm(c_out, **kw),
'relu': nn.ReLU(True),
'pool': nn.MaxPool2d(2),
}
else:
return {'id': Identity()}
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = DAWN_net(block=shortcut_block, prep_bn_relu=True)
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone, 2x output dim, global maxpool (47s; test acc 90.7%)
The final pooling layer before the classifier is a concatenation of global average pooling and max pooling layers, inherited from the original network.
We replace this with a more standard global max pooling layer and double the output dimension of the final convolution to compensate for the reduction in input dimension to the classifier, leading to a final test accuracy of 90.7% in 47s. Note that average pooling at this stage underperforms max pooling significantly.
```
def shortcut_block(c_in, c_out, stride, **kw):
projection = (stride != 1) or (c_in != c_out)
if projection:
return {
'conv': nn.Conv2d(c_in, c_out, kernel_size=3, stride=1, padding=1, bias=False),
'bn': batch_norm(c_out, **kw),
'relu': nn.ReLU(True),
'pool': nn.MaxPool2d(2),
}
else:
return {'id': Identity()}
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = DAWN_net(c=[64,128,256,512], block=shortcut_block, prep_bn_relu=True, concat_pool=False)
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - backbone, bn scale init=1, classifier weight=0.125 (47s; test acc 91.1%)
By default in PyTorch (0.4), initial batch norm scales are chosen uniformly at random from the interval [0,1]. Channels which are initialised near zero could be wasted so we replace this with a constant initialisation at 1.
This leads to a larger signal through the network and to compensate we introduce an overall constant multiplicative rescaling of the final classifier. A rough manual optimisation of this extra hyperparameter suggest that 0.125 is a reasonable value.
(The low value makes predictions less certain and appears to ease optimisation.)
With these changes in place, 20 epoch training reaches a test accuracy of 91.1% in 47s.
```
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = net(extra_layers=(), res_layers=())
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - double width, 60 epoch train! (321s; test acc 93.5%)
ne approach that doesn't seem particularly promising is to just add width.
If we double the channel dimensions and train for 60 epochs we can reach 93.5% test accuracy with a 5 layer network. This is nice but not efficient since training now takes 321s.
```
lr_schedule = PiecewiseLinear([0, 12, 60], [0, 0.4, 0])
batch_size = 512
c = 128
n = net(channels={'prep': c, 'layer1': 2*c, 'layer2': 4*c, 'layer3': 8*c}, extra_layers=(), res_layers=())
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - extra:L1+L2+L3 network, 60 epochs, cutout=12 (180s, 95.0% test acc)
```
lr_schedule = PiecewiseLinear([0, 12, 60], [0, 0.4, 0])
batch_size = 512
cutout=12
n = net(extra_layers=['layer1', 'layer2', 'layer3'], res_layers=())
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(cutout, cutout)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - final network Residual:L1+L3, 20 epochs (66s; test acc 93.7%)
```
lr_schedule = PiecewiseLinear([0, 4, 20], [0, 0.4, 0])
batch_size = 512
n = net()
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
### [Post 4: Architecture](https://www.myrtle.ai/2018/10/26/how_to_train_your_resnet_4/) - final network, 24 epochs (79s; test acc 94.1%)
```
lr_schedule = PiecewiseLinear([0, 5, 24], [0, 0.4, 0])
batch_size = 512
n = net()
draw(build_graph(n))
model = Network(n).to(device).half()
train_set_x = Transform(train_set, [Crop(32, 32), FlipLR(), Cutout(8,8)])
summary = train(model, lr_schedule, train_set_x, test_set, batch_size=batch_size, num_workers=0)
```
|
github_jupyter
|
# Radius and mean slip of rock patches failing in micro-seismic events
When stresses in a rock surpass its shear strength, the affected rock volume will fail to shearing.
Assume that we observe a circular patch with radius $r$ on, e.g. a fault, and that this patch is affected by a slip with an average slip distance $d$.
This slip is a response to increasing shear stresses, hence it reduces shear stresses by $\Delta \tau$.
These three parameters are linked by:
$$\Delta \tau = \frac{7 \, \pi \, \mu}{16 \, r} \, d $$
where $\mu$ is the shear modulus near the fault.
The seismic moment $M_0$, the energy to offset an area $A$ by a distance $d$, is defined by:
$$M_0 = \mu \, d \, A$$
$$ d = \frac{M_0}{\mu \, A} $$
with $A = \pi r^2$.
The [USGS definition](https://earthquake.usgs.gov/learn/glossary/?term=seismic%20moment) for the seismic moments is: *The seismic moment is a measure of the size of an earthquake based on the area of fault rupture, the average amount of slip, and the force that was required to overcome the friction sticking the rocks together that were offset by faulting. Seismic moment can also be calculated from the amplitude spectra of seismic waves.*
Putting the $d = ...$ equation in the first one and solving for the radius yields:
$$r = \bigg(\frac{7 \, M_0}{16 \, \Delta \tau}\bigg)^{1/3}$$
The following code leads to a plot which relates the influenced radius $r$ to the average displacement $d$ for micro-earthquakes. It shows that a larger area can be affected by smaller displacements for a small shear stress reduction $\Delta \tau$ to bigger displacements for smaller areas for larger shear stress reductions.
```
# import libraries
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style('ticks')
sns.set_context('talk')
def get_displacement(mu, dtau, m0):
r = ((7*m0)/(16*dtau))**(1./3.)
d = m0 / (mu*r**2 * np.pi)
# Alternatively:
# od = np.pi * mu * r * (7/(16*dtau*m0**2))**(1./3.)
# d = 1 / od
return r, d
# Parameters
dtau = np.arange(1,11)*1e6 # shear stress reduction
m0 = np.array([3.2e10, 1.0e12, 3.2e13]) # seismic moment
mu = 2.5e10 # shear modulus
# calculate displacements and radius
displacements = np.concatenate([get_displacement(mu, x, m0) for x in dtau])
# seperate arrays
disps = displacements[1::2,:]
rads = displacements[0::2,:]
# min tau and max tau
mitau = np.polyfit(disps[0,:], rads[0,:],1)
matau = np.polyfit(disps[-1,:], rads[-1,:],1)
dsim = np.linspace(0,0.033)
mirad = mitau[0]*dsim+mitau[1]
marad = matau[0]*dsim+matau[1]
# plot results
fig = plt.figure(figsize=[12,7])
plt.plot(disps[:,0]*1000, rads[:,0], '.', label='M$_w$1')
plt.plot(disps[:,1]*1000, rads[:,1], '^', label='M$_w$2')
plt.plot(disps[:,2]*1000, rads[:,2], 's', label='M$_w$3')
plt.plot(dsim*1000, mirad, '-', color='gray', alpha=.5)
plt.plot(dsim*1000, marad, '-', color='gray', alpha=.5)
plt.legend()
plt.ylim([0, 300])
plt.xlim([0, 0.033*1000])
plt.text(.8, 200, '$\Delta tau = 1$ MPa', fontsize=14)
plt.text(20, 55, '$\Delta tau = 10$ MPa', fontsize=14)
plt.xlabel('average displacement [mm]')
plt.ylabel('influenced radius [m]')
#fig.savefig('displacement_radius.png', dpi=300, bbox_inches='tight')
```
|
github_jupyter
|
# Color extraction from images with Lithops4Ray
In this tutorial we explain how to use Lithops4Ray to extract colors and [HSV](https://en.wikipedia.org/wiki/HSL_and_HSV) color range from the images persisted in the IBM Cloud Oject Storage. To experiment with this tutorial, you can use any public image dataset and upload it to your bucket in IBM Cloud Object Storage. For example follow [Stanford Dogs Dataset](http://vision.stanford.edu/aditya86/ImageNetDogs/) to download images. We also provide upload [script](https://github.com/project-codeflare/data-integration/blob/main/scripts/upload_to_ibm_cos.py) that can be used to upload local images to the IBM Cloud Object Storage
Our code is using colorthief package that need to be installed in the Ray cluster, both on head and worker nodes. You can edit `cluster.yaml` file and add
`- pip install colorthief`
To the `setup_commands` section. This will ensure that once Ray cluster is started required package will be installed automatically.
```
import lithops
import ray
```
We write function that extracts color from a single image. Once invoked, Lithops framework will inject a reserved parameter `obj` that points to the data stream of the image. More information on the reserved `obj` parameter can be found [here](https://github.com/lithops-cloud/lithops/blob/master/docs/data_processing.md#processing-data-from-a-cloud-object-storage-service)
```
def extract_color(obj):
from colorthief import ColorThief
body = obj.data_stream
dominant_color = ColorThief(body).get_color(quality=10)
return dominant_color, obj.key
```
We now write a Ray task that will return image name and HSV color range of the image. Instead of a direct call to extract_color function, Lithops is being used behind the scenes (through the data object) to call it only at the right moment.
```
@ray.remote
def identify_colorspace(data):
import colorsys
color, name = data.result()
hsv = colorsys.rgb_to_hsv(color[0], color[1], color[2])
val = hsv[0] * 180
return name, val
```
Now let's tie all together with a main method. By using Lithops allows us to remove all the boiler plate code required to list data from the object storage. It also inspects the data source by using the internal Lithops data partitioner and creates a lazy execution plan, where each entry maps an "extract_color" function to a single image. Moreover, Lithops creates a single authentication token that is used by all the tasks, instead of letting each task perform authentication. The parallelism is controlled by Ray and once Ray task is executed, it will call Lithops to execute the extract_color function directly in the context of the calling task. Thus, by using Lithops, we can allow code to access object storage data, without requiring additional coding effort from the user.
```
if __name__ == '__main__':
ray.init(ignore_reinit_error=True)
fexec = lithops.LocalhostExecutor(log_level=None)
my_data = fexec.map(extract_color, 'cos://<bucket>/<path to images>/')
results = [identify_colorspace.remote(d) for d in my_data]
for res in results:
value = ray.get(res)
print("Image: " + value[0] + ", dominant color HSV range: " + str(value[1]))
ray.shutdown()
```
|
github_jupyter
|
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables
features = torch.randn((1, 5))
# True weights for our data, random normal variables again
weights = torch.randn_like(features)
# and a true bias term
bias = torch.randn((1, 1))
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice benefits though such as GPU acceleration which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
y_hat = activation(torch.mm(features, weights.T) + bias)
print(y_hat)
```
You can do the multiplication and sum in the same operation using a matrix multiplication. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
```
### Stack them up!
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on the right) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
y_hat = activation(torch.mm(activation(torch.mm(features, W1) + B1), W2) + B2)
print(y_hat)
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a
b = torch.from_numpy(a)
b
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place
b.mul_(2)
# Numpy array matches new values from Tensor
a
```
|
github_jupyter
|
```
import nltk
import re
import operator
from collections import defaultdict
import numpy as np
import matplotlib.pyplot as plt
```
The idea is generate more common sentences according to their word tagging. So the sentences will have the real structure written by lovecraft and composed by a list of most common words in that kind of sentence.
The result should be a somewhat real phrase.
```
lovecraft = nltk.corpus.PlaintextCorpusReader("lovecraft", ".*")
class TaggedWord(object):
def __init__(self, words, count):
self.word_hash = {}
self.words = words
self.count = count
index = 0
for word in words:
self.word_hash[word] = index
index += 1
def update(self, word):
word_index = self.word_hash.get(word)
if word_index is not None:
self.count[word_index] += 1
else:
self.words.append(word)
self.count.append(1)
word_index = len(self.words) - 1
self.word_hash[word] = word_index
def get_random(self, seed):
np.random.seed(seed=seed)
total_count = sum(self.count)
probabilities = [word_count/total_count for word_count in self.count]
random_word_chose = np.random.multinomial(1, probabilities)
random_word_index = list(random_word_chose).index(1)
return self.words[random_word_index]
class Sentence(object):
def __init__(self, words, tags):
self.tags = tags
self.words = []
for word in words:
self.words.append(TaggedWord(words=[word.lower()], count=[1]))
def update(self, words):
word_index = 0
for word in words:
self.words[word_index].update(word.lower())
word_index += 1
def generate(self, seed):
return [word.get_random(seed) for word in self.words]
lovecraft_sentences = lovecraft.sents()
sentences = {}
sentence_count = defaultdict(int)
for tokenized_sentence in lovecraft_sentences:
sentence_with_tagged_words = nltk.pos_tag(tokenized_sentence)
sentence_words = list(zip(*sentence_with_tagged_words))[0]
sentence_tags = list(zip(*sentence_with_tagged_words))[1]
sentence_checksum = "-".join(sentence_tags)
if sentence_checksum in sentences:
sentences[sentence_checksum].update(sentence_words)
else:
sentences[sentence_checksum] = Sentence(words=sentence_words, tags=sentence_tags)
sentence_count[sentence_checksum] += 1
total_count = sum(sentence_count.values())
sentence_tags = [_sentence_tags for _sentence_tags in sentences.keys()]
sentence_probabilities = [sentence_count[sentence_tag]/total_count for sentence_tag in sentence_tags]
for i in range(0, 3):
random_sentence_chose = np.random.multinomial(1, sentence_probabilities)
random_sentence_index = list(random_sentence_chose).index(1)
print(sentences[sentence_tags[random_sentence_index]].generate(0))
```
The problem with that approach is that if the author uses a rich grammar (as it is the case of Lovecraft), not many phrases are gramatically repeated,
so we get many unique tagged sentences as it happens here.
```
print("{} sentences are available and there are {} unique sentences (almost all)".format(len(sentences), len([s for s, c in sentence_count.items() if c == 1])))
print("Sentences with more than one occurrence:")
for cs, count in sentence_count.items():
if count > 1:
print("{}: {} times".format(cs, count))
```
|
github_jupyter
|
# Tutorial - Evaluate DNBs additional Rules
This notebook contains a tutorial for the evaluation of DNBs additional Rules for the following Solvency II reports:
- Annual Reporting Solo (ARS); and
- Quarterly Reporting Solo (QRS)
Besides the necessary preparation, the tutorial consists of 6 steps:
1. Read possible datapoints
2. Read data
3. Clean data
4. Read additional rules
5. Evaluate rules
6. Save results
## 0. Preparation
### Import packages
```
import pandas as pd # dataframes
import numpy as np # mathematical functions, arrays and matrices
from os.path import join, isfile # some os dependent functionality
import data_patterns # evaluation of patterns
import regex as re # regular expressions
from pprint import pprint # pretty print
import logging
```
### Variables
```
# ENTRYPOINT: 'ARS' for 'Annual Reporting Solo' or 'QRS' for 'Quarterly Reporting Solo'
# INSTANCE: Name of the report you want to evaluate the additional rules for
ENTRYPOINT = 'ARS'
INSTANCE = 'ars_240_instance' # Test instances: ars_240_instance or qrs_240_instance
# DATAPOINTS_PATH: path to the excel-file containing all possible datapoints (simplified taxonomy)
# RULES_PATH: path to the excel-file with the additional rules
# INSTANCES_DATA_PATH: path to the source data
# RESULTS_PATH: path to the results
DATAPOINTS_PATH = join('..', 'data', 'datapoints')
RULES_PATH = join('..', 'solvency2-rules')
INSTANCES_DATA_PATH = join('..', 'data', 'instances', INSTANCE)
RESULTS_PATH = join('..', 'results')
# We log to rules.log in the data/instances path
logging.basicConfig(filename = join(INSTANCES_DATA_PATH, 'rules.log'),level = logging.INFO,
format='%(asctime)s - %(name)s - %(levelname)s - %(message)s')
```
## 1. Read possible datapoints
In the data/datapoints directory there is a file for both ARS and QRS in which all possible datapoints are listed (simplified taxonomy).
We will use this information to add all unreported datapoints to the imported data.
```
df_datapoints = pd.read_csv(join(DATAPOINTS_PATH, ENTRYPOINT.upper() + '.csv'), sep=";").fillna("") # load file to dataframe
df_datapoints.head()
```
## 2. Read data
We distinguish 2 types of tables:
- With a closed-axis, e.g. the balance sheet: an entity reports only 1 balance sheet per period
- With an open-axis, e.g. the list of assets: an entity reports several 'rows of data' in the relevant table
### General information
First we gather some general information:
- A list of all possible reported tables
- A list of all reported tables
- A list of all tables that have not been reported
```
tables_complete_set = df_datapoints.tabelcode.sort_values().unique().tolist()
tables_reported = [table for table in tables_complete_set if isfile(join(INSTANCES_DATA_PATH, table + '.pickle'))]
tables_not_reported = [table for table in tables_complete_set if table not in tables_reported]
```
### Closed-axis
Besides all separate tables, the 'Tutorial Convert XBRL-instance to CSV, HTML and pickles' also outputs a large dataframe with the data from all closed-axis tables combined.
We use this dataframe for evaluating the patterns on closed-axis tables.
```
df_closed_axis = pd.read_pickle(join(INSTANCES_DATA_PATH, INSTANCE + '.pickle'))
tables_closed_axis = sorted(list(set(x[:13] for x in df_closed_axis.columns)))
df_closed_axis.head()
```
### Open-axis
For open-axis tables we create a dictionary with all data per table.
Later we will evaluate the additional rules on each seperate table in this dictionary.
```
dict_open_axis = {}
tables_open_axis = [table for table in tables_reported if table not in tables_closed_axis]
for table in tables_open_axis:
df = pd.read_pickle(join(INSTANCES_DATA_PATH, table + '.pickle'))
# Identify which columns within the open-axis table make a table row unique (index-columns):
index_columns_open_axis = [col for col in list(df.index.names) if col not in ['entity','period']]
# Duplicate index-columns to data columns:
df.reset_index(level=index_columns_open_axis, inplace=True)
for i in range(len(index_columns_open_axis)):
df['index_col_' + str(i)] = df[index_columns_open_axis[i]].astype(str)
df.set_index(['index_col_' + str(i)], append=True, inplace=True)
dict_open_axis[table] = df
print("Open-axis tables:")
print(list(dict_open_axis.keys()))
```
## 3. Clean data
We have to make 2 modifications on the data:
1. Add unreported datapoints
so rules (partly) pointing to unreported datapoints can still be evaluated
2. Change string values to uppercase
because the additional rules are defined using capital letters for textual comparisons
```
all_datapoints = [x.replace(',,',',') for x in
list(df_datapoints['tabelcode'] + ',' + df_datapoints['rij'] + ',' + df_datapoints['kolom'])]
all_datapoints_closed = [x for x in all_datapoints if x[:13] in tables_closed_axis]
all_datapoints_open = [x for x in all_datapoints if x[:13] in tables_open_axis]
```
### Closed-axis tables
```
# add not reported datapoints to the dataframe with data from closed axis tables:
for col in [column for column in all_datapoints_closed if column not in list(df_closed_axis.columns)]:
df_closed_axis[col] = np.nan
df_closed_axis.fillna(0, inplace = True)
# string values to uppercase
df_closed_axis = df_closed_axis.applymap(lambda s:s.upper() if type(s) == str else s)
```
### Open-axis tables
```
for table in [table for table in dict_open_axis.keys()]:
all_datapoints_table = [x for x in all_datapoints_open if x[:13] == table]
for col in [column for column in all_datapoints_table if column not in list(dict_open_axis[table].columns)]:
dict_open_axis[table][col] = np.nan
dict_open_axis[table].fillna(0, inplace = True)
dict_open_axis[table] = dict_open_axis[table].applymap(lambda s:s.upper() if type(s) == str else s)
```
## 4. Read additional rules
DNBs additional validation rules are published as an Excel file on the DNB statistics website.
We included the Excel file in the project under data/downloaded files.
The rules are already converted to a syntax Python can interpret, using the notebook: 'Convert DNBs Additional Validation Rules to Patterns'.
In the next line of code we read these converted rules (patterns).
```
df_patterns = pd.read_excel(join(RULES_PATH, ENTRYPOINT.lower() + '_patterns_additional_rules.xlsx'), engine='openpyxl').fillna("").set_index('index')
```
## 5. Evaluate rules
### Closed-axis tables
To be able to evaluate the rules for closed-axis tables, we need to filter out:
- patterns for open-axis tables; and
- patterns pointing to tables that are not reported.
```
df_patterns_closed_axis = df_patterns.copy()
df_patterns_closed_axis = df_patterns_closed_axis[df_patterns_closed_axis['pandas ex'].apply(
lambda expr: not any(table in expr for table in tables_not_reported)
and not any(table in expr for table in tables_open_axis))]
df_patterns_closed_axis.head()
```
We now have:
- the data for closed-axis tables in a dataframe;
- the patterns for closed-axis tables in a dataframe.
To evaluate the patterns we need to create a 'PatternMiner' (part of the data_patterns package), and run the analyze function.
```
miner = data_patterns.PatternMiner(df_patterns=df_patterns_closed_axis)
df_results_closed_axis = miner.analyze(df_closed_axis)
df_results_closed_axis.head()
```
### Open-axis tables
First find the patterns defined for open-axis tables
```
df_patterns_open_axis = df_patterns.copy()
df_patterns_open_axis = df_patterns_open_axis[df_patterns_open_axis['pandas ex'].apply(
lambda expr: any(table in expr for table in tables_open_axis))]
```
Patterns involving multiple open-axis tables are not yet supported
```
df_patterns_open_axis = df_patterns_open_axis[df_patterns_open_axis['pandas ex'].apply(
lambda expr: len(set(re.findall('S.\d\d.\d\d.\d\d.\d\d',expr)))) == 1]
df_patterns_open_axis.head()
```
Next we loop through the open-axis tables en evaluate the corresponding patterns on the data
```
output_open_axis = {} # dictionary with input and results per table
for table in tables_open_axis: # loop through open-axis tables
if df_patterns_open_axis['pandas ex'].apply(lambda expr: table in expr).sum() > 0: # check if there are patterns
info = {}
info['data'] = dict_open_axis[table] # select data
info['patterns'] = df_patterns_open_axis[df_patterns_open_axis['pandas ex'].apply(
lambda expr: table in expr)] # select patterns
miner = data_patterns.PatternMiner(df_patterns=info['patterns'])
info['results'] = miner.analyze(info['data']) # evaluate patterns
output_open_axis[table] = info
```
Print results for the first table (if there are rules for tables with an open axis)
```
if len(output_open_axis.keys()) > 0:
display(output_open_axis[list(output_open_axis.keys())[0]]['results'].head())
```
## 6. Save results
### Combine results for closed- and open-axis tables
To output the results in a single file, we want to combine the results for closed-axis and open-axis tables
```
# Function to transform results for open-axis tables, so it can be appended to results for closed-axis tables
# The 'extra' index columns are converted to data columns
def transform_results_open_axis(df):
if df.index.nlevels > 2:
reset_index_levels = list(range(2, df.index.nlevels))
df = df.reset_index(level=reset_index_levels)
rename_columns={}
for x in reset_index_levels:
rename_columns['level_' + str(x)] = 'id_column_' + str(x - 1)
df.rename(columns=rename_columns, inplace=True)
return df
df_results = df_results_closed_axis.copy() # results for closed axis tables
for table in list(output_open_axis.keys()): # for all open axis tables with rules -> append and sort results
df_results = transform_results_open_axis(output_open_axis[table]['results']).append(df_results, sort=False).sort_values(by=['pattern_id']).sort_index()
```
Change column order so the dataframe starts with the identifying columns:
```
list_col_order = []
for i in range(1, len([col for col in list(df_results.columns) if col[:10] == 'id_column_']) + 1):
list_col_order.append('id_column_' + str(i))
list_col_order.extend(col for col in list(df_results.columns) if col not in list_col_order)
df_results = df_results[list_col_order]
df_results.head()
```
### Save results
The dataframe df_results contains all output of the evaluation of the validation rules.
```
# To save all results use df_results
# To save all exceptions use df_results['result_type']==False
# To save all confirmations use df_results['result_type']==True
# Here we save only the exceptions to the validation rules
df_results[df_results['result_type']==False].to_excel(join(RESULTS_PATH, "results.xlsx"))
```
### Example of an error in the report
```
# Get the pandas code from the first pattern and evaluate it
s = df_patterns.loc[4, 'pandas ex'].replace('df', 'df_closed_axis')
print('Pattern:', s)
display(eval(s)[re.findall('S.\d\d.\d\d.\d\d.\d\d,R\d\d\d\d,C\d\d\d\d',s)])
```
|
github_jupyter
|
# SST-2
# Simple Baselines using ``mean`` and ``last`` pooling
## Librairies
```
# !pip install transformers==4.8.2
# !pip install datasets==1.7.0
# !pip install ax-platform==0.1.20
import os
import sys
sys.path.insert(0, os.path.abspath("../..")) # comment this if library is pip installed
import io
import re
import pickle
from timeit import default_timer as timer
from tqdm.notebook import tqdm
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from datasets import load_dataset, Dataset, concatenate_datasets
from transformers import AutoTokenizer
from transformers import BertModel
from transformers.data.data_collator import DataCollatorWithPadding
from ax import optimize
from ax.plot.contour import plot_contour
from ax.plot.trace import optimization_trace_single_method
from ax.service.managed_loop import optimize
from ax.utils.notebook.plotting import render, init_notebook_plotting
import esntorch.core.reservoir as res
import esntorch.core.learning_algo as la
import esntorch.core.merging_strategy as ms
import esntorch.core.esn as esn
%config Completer.use_jedi = False
%load_ext autoreload
%autoreload 2
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
SEED = 42
```
## Global variables
```
CACHE_DIR = '~/Data/huggignface/' # put your path here
RESULTS_FILE = 'Results/Baselines_v2/sst-2_results_.pkl' # put your path here
```
## Dataset
```
# download dataset
# full train, mini train, and val sets
raw_datasets = load_dataset('glue', 'sst2', cache_dir=CACHE_DIR)
raw_datasets = raw_datasets.rename_column('sentence', 'text')
full_train_dataset = raw_datasets['train']
train_dataset = full_train_dataset.train_test_split(train_size=0.3, shuffle=True)['train']
val_dataset = raw_datasets['validation']
# special test set
test_dataset = load_dataset('gpt3mix/sst2', split='test', cache_dir=CACHE_DIR)
def clean(example):
example['text'] = example['text'].replace('-LRB-', '(').replace('-RRB-', ')').replace(r'\/', r'/')
example['label'] = np.abs(example['label'] - 1) # revert labels of test set
return example
test_dataset = test_dataset.map(clean)
# create dataset_d
dataset_d = {}
dataset_d = {
'full_train': full_train_dataset,
'train': train_dataset,
'val': val_dataset,
'test': test_dataset
}
dataset_d
# tokenize
tokenizer = AutoTokenizer.from_pretrained("bert-base-uncased")
def tokenize_function(examples):
return tokenizer(examples["text"], padding=False, truncation=True, return_length=True)
for k, v in dataset_d.items():
tmp = v.map(tokenize_function, batched=True)
tmp = tmp.rename_column('length', 'lengths')
tmp = tmp.sort("lengths")
tmp = tmp.rename_column('label', 'labels')
tmp.set_format(type='torch', columns=['input_ids', 'attention_mask', 'labels', 'lengths'])
dataset_d[k] = tmp
# dataloaders
dataloader_d = {}
for k, v in dataset_d.items():
dataloader_d[k] = torch.utils.data.DataLoader(v, batch_size=256, collate_fn=DataCollatorWithPadding(tokenizer))
dataset_d
```
## Optimization
```
baseline_params = {
'embedding_weights': 'bert-base-uncased', # TEXT.vocab.vectors,
'distribution' : 'uniform', # uniform, gaussian
'input_dim' : 768, # dim of encoding!
'reservoir_dim' : 0, # not used
'bias_scaling' : 0.0, # not used
'sparsity' : 0.0, # not used
'spectral_radius' : None,
'leaking_rate': 0.5, # not used
'activation_function' : 'tanh',
'input_scaling' : 0.1,
'mean' : 0.0,
'std' : 1.0,
'learning_algo' : None,
'criterion' : None,
'optimizer' : None,
'merging_strategy' : None,
'lexicon' : None,
'bidirectional' : False,
'mode' : 'no_layer', # simple baseline
'device' : device,
'seed' : 4
}
results_d = {}
for pooling_strategy in tqdm(['last', 'mean']):
results_d[pooling_strategy] = {}
for alpha in tqdm([0.1, 1.0, 10.0, 100.0]):
results_d[pooling_strategy][alpha] = []
# model
baseline_params['merging_strategy'] = pooling_strategy
baseline_params['mode'] = 'no_layer'
print(baseline_params)
ESN = esn.EchoStateNetwork(**baseline_params)
ESN.learning_algo = la.RidgeRegression(alpha=alpha)
ESN = ESN.to(device)
# train
t0 = timer()
LOSS = ESN.fit(dataloader_d["full_train"]) # full train set
t1 = timer()
acc = ESN.predict(dataloader_d["test"], verbose=False)[1].item() # full test set
# results
results_d[pooling_strategy][alpha].append([acc, t1 - t0])
# clean objects
del ESN.learning_algo
del ESN.criterion
del ESN.merging_strategy
del ESN
torch.cuda.empty_cache()
results_d
```
## Results
```
# save results
with open(RESULTS_FILE, 'wb') as fh:
pickle.dump(results_d, fh)
# # load results
# with open(os.path.join(RESULTS_PATH, RESULTS_FILE), 'rb') as fh:
# results_d = pickle.load(fh)
# results_d
```
|
github_jupyter
|
```
%run ./dlt
%run ./dlt_workflow_refactored
from pyspark.sql import Row
import unittest
from pyspark.sql.functions import lit
import datetime
timestamp = datetime.datetime.fromisoformat("2000-01-01T00:00:00")
def timestamp_provider():
return lit(timestamp)
from pyspark.sql.functions import when, col
from pyspark.sql import Row
class FunctionUnitTests(unittest.TestCase):
@classmethod
def setUpClass(cls):
container.register(
timestamp_provider=timestamp_provider
)
def test_add_ingest_columns(self):
df = spark.range(1)
df = df.transform(container.add_ingest_columns)
result = df.collect()
self.assertEqual(1, len(result), "Only one record expected")
self.assertIn("ingest_timestamp", df.columns, "Ingest timestamp column not present")
self.assertIn("ingest_source", df.columns, "Ingest source column not present")
self.assertEqual(url.split("/")[-1], result[0].ingest_source, "Ingest source not correct")
self.assertEqual(timestamp, result[0].ingest_timestamp, "Ingest timestamp not correct")
def test_add_processed_timestamp(self):
df = spark.range(1)
df = df.transform(container.add_processed_timestamp)
result = df.collect()
self.assertEqual(1, len(result), "Only one record expected")
self.assertIn("processed_timestamp", df.columns, "Processed timestamp column not present")
self.assertEqual(timestamp, result[0].processed_timestamp, "Processed timestamp not correct")
def test_add_null_index_array(self):
df = spark.createDataFrame([
Row(id=1, test_null=None),
Row(id=2, test_null=1)
])
df = df.transform(container.add_null_index_array)
result = df.collect()
self.assertEqual(2, len(result), "Two records are expected")
self.assertIn("nulls", df.columns, "Nulls column not present")
self.assertIsNone(result[0].test_null, "First record should contain null")
self.assertIsNotNone(result[1].test_null, "Second record should not contain null")
self.assertIn(1, result[0].nulls, "Nulls array should include 1")
self.assertIsNot(result[1].nulls, "Nulls array should be empty")
def test_filter_null_index_empty(self):
df = spark.createDataFrame([
Row(id=1, test_null=None, nulls=[1]),
Row(id=2, test_null=1, nulls=[])
])
df = df.transform(container.filter_null_index_empty)
result = df.collect()
self.assertEqual(1, len(result), "One record is expected")
self.assertNotIn("nulls", df.columns, "Nulls column not present")
def test_filter_null_index_not_empty(self):
df = spark.createDataFrame([
Row(id=1, test_null=None, nulls=[1]),
Row(id=2, test_null=1, nulls=[])
])
df = df.transform(container.filter_null_index_not_empty)
result = df.collect()
self.assertEqual(1, len(result), "One record is expected")
self.assertIn("nulls", df.columns, "Nulls column not present")
def test_agg_count_by_country(self):
df = spark.createDataFrame([
Row(country="Country0"),
Row(country="Country1"),
Row(country="Country0")
])
df = df.transform(container.agg_count_by_country)
result = df.collect()
self.assertEqual(2, len(result), "Two records expected")
self.assertIn("country", df.columns, "Country column not present")
self.assertIn("count", df.columns, "Count column not present")
d = {r[0]: r[1] for r in result}
self.assertEqual(2, d.get("Country0", -1), "Country0 count should be 2")
self.assertEqual(1, d.get("Country1", -1), "Country1 count should be 1")
```
|
github_jupyter
|
# T1056.004 - Input Capture: Credential API Hooking
Adversaries may hook into Windows application programming interface (API) functions to collect user credentials. Malicious hooking mechanisms may capture API calls that include parameters that reveal user authentication credentials.(Citation: Microsoft TrojanSpy:Win32/Ursnif.gen!I Sept 2017) Unlike [Keylogging](https://attack.mitre.org/techniques/T1056/001), this technique focuses specifically on API functions that include parameters that reveal user credentials. Hooking involves redirecting calls to these functions and can be implemented via:
* **Hooks procedures**, which intercept and execute designated code in response to events such as messages, keystrokes, and mouse inputs.(Citation: Microsoft Hook Overview)(Citation: Endgame Process Injection July 2017)
* **Import address table (IAT) hooking**, which use modifications to a process’s IAT, where pointers to imported API functions are stored.(Citation: Endgame Process Injection July 2017)(Citation: Adlice Software IAT Hooks Oct 2014)(Citation: MWRInfoSecurity Dynamic Hooking 2015)
* **Inline hooking**, which overwrites the first bytes in an API function to redirect code flow.(Citation: Endgame Process Injection July 2017)(Citation: HighTech Bridge Inline Hooking Sept 2011)(Citation: MWRInfoSecurity Dynamic Hooking 2015)
## Atomic Tests
```
#Import the Module before running the tests.
# Checkout Jupyter Notebook at https://github.com/cyb3rbuff/TheAtomicPlaybook to run PS scripts.
Import-Module /Users/0x6c/AtomicRedTeam/atomics/invoke-atomicredteam/Invoke-AtomicRedTeam.psd1 - Force
```
### Atomic Test #1 - Hook PowerShell TLS Encrypt/Decrypt Messages
Hooks functions in PowerShell to read TLS Communications
**Supported Platforms:** windows
Elevation Required (e.g. root or admin)
#### Dependencies: Run with `powershell`!
##### Description: T1056.004x64.dll must exist on disk at specified location (#{file_name})
##### Check Prereq Commands:
```powershell
if (Test-Path PathToAtomicsFolder\T1056.004\bin\T1056.004x64.dll) {exit 0} else {exit 1}
```
##### Get Prereq Commands:
```powershell
New-Item -Type Directory (split-path PathToAtomicsFolder\T1056.004\bin\T1056.004x64.dll) -ErrorAction ignore | Out-Null
Invoke-WebRequest "https://github.com/redcanaryco/atomic-red-team/raw/master/atomics/T1056.004/bin/T1056.004x64.dll" -OutFile "PathToAtomicsFolder\T1056.004\bin\T1056.004x64.dll"
```
```
Invoke-AtomicTest T1056.004 -TestNumbers 1 -GetPreReqs
```
#### Attack Commands: Run with `powershell`
```powershell
mavinject $pid /INJECTRUNNING PathToAtomicsFolder\T1056.004\bin\T1056.004x64.dll
curl https://www.example.com
```
```
Invoke-AtomicTest T1056.004 -TestNumbers 1
```
## Detection
Monitor for calls to the `SetWindowsHookEx` and `SetWinEventHook` functions, which install a hook procedure.(Citation: Microsoft Hook Overview)(Citation: Volatility Detecting Hooks Sept 2012) Also consider analyzing hook chains (which hold pointers to hook procedures for each type of hook) using tools(Citation: Volatility Detecting Hooks Sept 2012)(Citation: PreKageo Winhook Jul 2011)(Citation: Jay GetHooks Sept 2011) or by programmatically examining internal kernel structures.(Citation: Zairon Hooking Dec 2006)(Citation: EyeofRa Detecting Hooking June 2017)
Rootkits detectors(Citation: GMER Rootkits) can also be used to monitor for various types of hooking activity.
Verify integrity of live processes by comparing code in memory to that of corresponding static binaries, specifically checking for jumps and other instructions that redirect code flow. Also consider taking snapshots of newly started processes(Citation: Microsoft Process Snapshot) to compare the in-memory IAT to the real addresses of the referenced functions.(Citation: StackExchange Hooks Jul 2012)(Citation: Adlice Software IAT Hooks Oct 2014)
|
github_jupyter
|
```
#from lab2.utils import get_random_number_generator
class BoxWindow:
"""[summary]"""
def __init__(self, args):
"""initialize the box window with the bounding points
Args:
args (np.array([integer])): array of the bounding points of the box
"""
self.bounds = args
def __str__(self):
r"""BoxWindow: :math:`[a_1, b_1] \times [a_2, b_2] \times \cdots`
Returns:
str : give the bounds of the box
"""
mot=""
for k in range(len(self.bounds)):
mot = mot+'['+str(self.bounds[k][0])+', '+ str(self.bounds[k][0])+']'
if k != len(self.bounds)-1:
mot=mot+' x '
return ("BoxWindow: " + mot)
def __len__(self):
L=[]
for k in range(len(self.bounds)):
L.append(self.bounds[k][1]-self.bounds[k][0])
return L
def __contains__(self, args):
"""args: coordonnées de point"""
for p in range(len(args)):
if args[p]<self.bounds[p][1] and args[p]>self.bounds[p][0]:
continue
else:
return False
return True
# a=self.bounds[:,0]
# b=self.bounds[:,1]
# return all(np.logical_and(a<= point, point<=b))
def dimension(self):
"""[summary]"""
return (len(self.bounds))
def volume(self):
"""[summary]"""
vol=1
for p in self.__len__():
vol=vol*p
return vol
def indicator_function(self, args):
"""[summary]
Args:
args ([type]): [description]
"""
if self.__contains__(args)==True:
return (1)
else:
return (0)
def rand(self, n=1, rng=None):
"""Generate ``n`` points uniformly at random inside the :py:class:`BoxWindow`.
Args:
n (int, optional): [description]. Defaults to 1.
rng ([type], optional): [description]. Defaults to None.
"""
rng = get_random_number_generator(rng)
L=[]
for p in range(n):
L_petit=[]
for k in range(len(self.bounds)):
if self.bounds[k][0]==self.bounds[k][1]:
L_petit.append(self.bounds[k][0])
else:
L_petit.append(np.random.uniform(self.bounds[k][1]-self.bounds[k][0])+self.bounds[k][0])
L.append(L_petit)
return (L)
#heritage
class UnitBoxWindow(BoxWindow):
def __init__(self, center, dimension):
"""[summary]
Args:
dimension ([type]): [description]
center ([type], optional): [description]. Defaults to None.
"""
super(BoxWindow, self).__init__(args)
import numpy as np
def get_random_number_generator(seed):
"""Turn seed into a np.random.Generator instance."""
return np.random.default_rng(seed)
np.random.uniform(0)
import numpy as np
c=BoxWindow(np.array([[2.5, 2.5]]))
d=BoxWindow(np.array([[0, 5], [-1.45, 3.14], [-10, 10]]))
d.bounds.shape
d.bounds[0][1]
c.rand()
point1=[-1,1,1]
point2=[1,1,1]
d.__contains__(point1)
d.indicator_function(point1)
d.__len__()
d.volume()
d.__str__()
c.__str__()
```
|
github_jupyter
|
# Introduction to Data Science
## From correlation to supervised segmentation and tree-structured models
Spring 2018 - Profs. Foster Provost and Josh Attenberg
Teaching Assistant: Apostolos Filippas
***
### Some general imports
```
import os
import numpy as np
import pandas as pd
import math
import matplotlib.pylab as plt
import seaborn as sns
%matplotlib inline
sns.set(style='ticks', palette='Set2')
```
Recall the automobile MPG dataset from last week? Because its familiar, let's reuse it here.
```
url = "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data-original"
column_names = ['mpg', 'cylinders', 'displacement', 'horsepower', 'weight', 'acceleration',
'model', 'origin', 'car_name']
mpg_df = pd.read_csv(url,
delim_whitespace=True,
header=None,
names=column_names).dropna()
```
Rather than attempt to predict the MPG from the other aspects of a car, let's try a simple classification problem, whether a car gets good milage (high MPG) or not
```
mpg_df["mpg"].hist()
```
Arbitrarily, let's say that those cars with a MPG greater than the median get good miles per gallon.
```
median_mpg = mpg_df["mpg"].median()
print ("the median MPG is: %s" % median_mpg)
def is_high_mpg(mpg):
return 1 if mpg > median_mpg else 0
mpg_df["is_high_mpg"] = mpg_df["mpg"].apply(is_high_mpg)
```
We'd like to use information contained in the other automobile quantities to predict whether or not the car is efficient. Let's take a look at how well these observables "split" our data according to our target.
```
def visualize_split(df, target_column, info_column, color_one="red", color_two="blue"):
plt.rcParams['figure.figsize'] = [15.0, 2.0]
color = ["red" if x == 0 else "blue" for x in df[target_column]]
plt.scatter(df[info_column], df[target_column], c=color, s=50)
plt.xlabel(info_column)
plt.ylabel(target_column)
plt.show()
visualize_split(mpg_df, "is_high_mpg", "weight")
```
Above we see a scatter plot of all possible car weights and a color code that represents our target variable (is good mpg).
- Blue dots correspond to fuel efficient cars, red dots are fuel inefficient cars
- The horizontal position is the weight of the car
- The vertical position separates our two classes
Clearly car weight and high MPG-ness are correlated.
Looks like cars weighing more than 3000 lbs tend to be inefficient. How effective is this decision boundary? Let's quantify it!
***
**Entropy** ($H$) and **information gain** ($IG$) au useful tools for measuring the effectiveness of a split on the data. Entropy measures how random data is, information gain is a measure of the reduction in randomness after performing a split.
<table style="border: 0px">
<tr style="border: 0px">
<td style="border: 0px"><img src="images/dsfb_0304.png" height=80% width=80%>
Figure 3-4. Splitting the "write-off" sample into two segments, based on splitting the Balance attribute (account balance) at 50K.</td>
<td style="border: 0px; width: 30px"></td>
<td style="border: 0px"><img src="images/dsfb_0305.png" height=75% width=75%>
Figure 3-5. A classification tree split on the three-values Residence attribute.</td>
</tr>
</table>
Given the data, it is fairly straight forward to calculate both of these quantities.
##### Functions to get the entropy and IG
```
def entropy(target_column):
"""
computes -sum_i p_i * log_2 (p_i) for each i
"""
# get the counts of each target value
target_counts = target_column.value_counts().astype(float).values
total = target_column.count()
# compute probas
probas = target_counts/total
# p_i * log_2 (p_i)
entropy_components = probas * np.log2(probas)
# return negative sum
return - entropy_components.sum()
def information_gain(df, info_column, target_column, threshold):
"""
computes H(target) - H(target | info > thresh) - H(target | info <= thresh)
"""
data_above_thresh = df[df[info_column] > threshold]
data_below_thresh = df[df[info_column] <= threshold]
H = entropy(df[target_column])
entropy_above = entropy(data_above_thresh[target_column])
entropy_below = entropy(data_below_thresh[target_column])
ct_above = data_above_thresh.shape[0]
ct_below = data_below_thresh.shape[0]
tot = float(df.shape[0])
return H - entropy_above*ct_above/tot - entropy_below*ct_below/tot
```
Now that we have a way of calculating $H$ and $IG$, let's test our prior hunch, that using 3000 as a split on weight allows us to determine if a car is high MPG using $IG$.
```
threshold = 3000
prior_entropy = entropy(mpg_df["is_high_mpg"])
IG = information_gain(mpg_df, "weight", "is_high_mpg", threshold)
print ("IG of %.4f using a threshold of %.2f given a prior entropy of %.4f" % (IG, threshold, prior_entropy))
```
How good was our guess of 3000? Let's loop through all possible splits on weight and see what is the best!
```
def best_threshold(df, info_column, target_column, criteria=information_gain):
maximum_ig = 0
maximum_threshold = 0
for thresh in df[info_column]:
IG = criteria(df, info_column, target_column, thresh)
if IG > maximum_ig:
maximum_ig = IG
maximum_threshold = thresh
return (maximum_threshold, maximum_ig)
maximum_threshold, maximum_ig = best_threshold(mpg_df, "weight", "is_high_mpg")
print ("the maximum IG we can achieve splitting on weight is %.4f using a thresh of %.2f" % (maximum_ig, maximum_threshold))
```
Other observed features may also give us a strong clue about the efficiency of cars.
```
predictor_cols = ['cylinders', 'displacement', 'horsepower', 'weight', 'acceleration', 'model', 'origin']
for col in predictor_cols:
visualize_split(mpg_df, "is_high_mpg", col)
```
This now begs the question: what feature gives the most effective split?
```
def best_split(df, info_columns, target_column, criteria=information_gain):
maximum_ig = 0
maximum_threshold = 0
maximum_column = ""
for info_column in info_columns:
thresh, ig = best_threshold(df, info_column, target_column, criteria)
if ig > maximum_ig:
maximum_ig = ig
maximum_threshold = thresh
maximum_column = info_column
return maximum_column, maximum_threshold, maximum_ig
maximum_column, maximum_threshold, maximum_ig = best_split(mpg_df, predictor_cols, "is_high_mpg")
print ("The best column to split on is %s giving us a IG of %.4f using a thresh of %.2f" % (maximum_column, maximum_ig, maximum_threshold))
```
### The Classifier Tree: Recursive Splitting
Of course, splitting the data one time sometimes isn't enough to make accurate categorical predictions. However, we can continue to split the data recursively until we achieve acceptable results. This recursive splitting is the basis for a "decision tree classifier" or "classifier tree", a popular and powerful class of machine learning algorithm. In particular, this specific algorithm is known as ID3 for Iterative Dichotomizer.
What are some other ways you might consider splitting the data?
```
def Plot_Data(df, info_col_1, info_col_2, target_column, color1="red", color2="blue"):
# Make the plot square
plt.rcParams['figure.figsize'] = [12.0, 8.0]
# Color
color = [color1 if x == 0 else color2 for x in df[target_column]]
# Plot and label
plt.scatter(df[info_col_1], df[info_col_2], c=color, s=50)
plt.xlabel(info_col_1)
plt.ylabel(info_col_2)
plt.xlim([min(df[info_col_1]) , max(df[info_col_1]) ])
plt.ylim([min(df[info_col_2]) , max(df[info_col_2]) ])
plt.show()
plt.figure(figsize=[7,5])
Plot_Data(mpg_df, "acceleration", "weight","is_high_mpg")
```
Rather than build a classifier tree from scratch (think if you could now do this!) let's use sklearn's implementation which includes some additional functionality.
```
from sklearn.tree import DecisionTreeClassifier
# Let's define the model (tree)
decision_tree = DecisionTreeClassifier(max_depth=1, criterion="entropy") # Look at those 2 arguments !!!
# Let's tell the model what is the data
decision_tree.fit(mpg_df[predictor_cols], mpg_df["is_high_mpg"])
```
We now have a classifier tree, let's visualize the results!
```
from IPython.display import Image
from sklearn.tree import export_graphviz
def visualize_tree(decision_tree, feature_names, class_names, directory="./images", name="tree",proportion=True):
# Export our decision tree to graphviz format
dot_name = "%s/%s.dot" % (directory, name)
dot_file = export_graphviz(decision_tree, out_file=dot_name,
feature_names=feature_names, class_names=class_names,proportion=proportion)
# Call graphviz to make an image file from our decision tree
image_name = "%s/%s.png" % (directory, name)
os.system("dot -Tpng %s -o %s" % (dot_name, image_name))
# to get this part to actually work, you may need to open a terminal window in Jupyter and run the following command "sudo apt install graphviz"
# Return the .png image so we can see it
return Image(filename=image_name)
visualize_tree(decision_tree, predictor_cols, ["n", "y"])
```
Let's look at the `"acceleration"`, `"weight"`, including the **DECISION SURFACE!!**
More details for this graph: [sklearn decision surface](http://scikit-learn.org/stable/auto_examples/tree/plot_iris.html)
```
def Decision_Surface(data, col1, col2, target, model, probabilities=False):
# Get bounds
x_min, x_max = data[col1].min(), data[col1].max()
y_min, y_max = data[col2].min(), data[col2].max()
# Create a mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max,0.5), np.arange(y_min, y_max,0.5))
meshed_data = pd.DataFrame(np.c_[xx.ravel(), yy.ravel()])
tdf = data[[col1, col2]]
model.fit(tdf, target)
if probabilities:
Z = model.predict(meshed_data).reshape(xx.shape)
else:
Z = model.predict_proba(meshed_data)[:, 1].reshape(xx.shape)
plt.figure(figsize=[12,7])
plt.title("Decision surface")
plt.ylabel(col1)
plt.xlabel(col2)
if probabilities:
# Color-scale on the contour (surface = separator)
cs = plt.contourf(xx, yy, Z,cmap=plt.cm.coolwarm, alpha=0.4)
else:
# Only a curve/line on the contour (surface = separator)
cs = plt.contourf(xx, yy, Z, levels=[-1,0,1],cmap=plt.cm.coolwarm, alpha=0.4)
color = ["blue" if t == 0 else "red" for t in target]
plt.scatter(data[col1], data[col2], color=color )
plt.show()
tree_depth=1
Decision_Surface(mpg_df[predictor_cols], "acceleration", "weight", mpg_df["is_high_mpg"], DecisionTreeClassifier(max_depth=tree_depth, criterion="entropy"), True)
```
How good is our model? Let's compute accuracy, the percent of times where we correctly identified that a car was high MPG.
```
from sklearn import metrics
print ( "Accuracy = %.3f" % (metrics.accuracy_score(decision_tree.predict(mpg_df[predictor_cols]), mpg_df["is_high_mpg"])) )
```
What are some other ways we could classify the data? Last class we used linear regression, let's take a look to see how that partitions the data
```
from sklearn import linear_model
import warnings
warnings.filterwarnings('ignore')
Decision_Surface(mpg_df[predictor_cols], "acceleration", "weight", mpg_df["is_high_mpg"], linear_model.Lasso(alpha=0.01), True)
```
## Decision Tree Regression
Recall our problem from last time, trying to predict the real-valued MPG for each car. In data science, problems where one tries to predict a real-valued number is known as regression. As with classification, much of the intuition for splitting data based on values of known observables applies:
```
from mpl_toolkits.mplot3d import Axes3D
def plot_regression_data(df, info_col_1, info_col_2, target_column):
# Make the plot square
plt.rcParams['figure.figsize'] = [12.0, 8.0]
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_trisurf(df[info_col_1], df[info_col_2], df[target_column], cmap=plt.cm.viridis, linewidth=0.2)
ax.set_xlabel(info_col_1)
ax.set_ylabel(info_col_2)
ax.set_zlabel(target_column);
ax.view_init(60, 45)
plt.show()
plot_regression_data(mpg_df, "acceleration", "weight", "mpg")
```
At a high level, one could imagine splitting the data recursively, assigning an estimated MPG to each side of the split. On more thoughtful reflection, some questions emerge:
- how do predict a real number at a leaf node given the examples that "filter" to that node?
- how do we assess the effectiveness of a particular split?
As with decision tree classification, there are many valid answers to both of these questions. A typical approach involves collecting all nodes that filter to a leaf, computing the mean target value, and using this as a prediction. The effectiveness of a split can then be measured by computing the mean difference between all true values and this prediction.
As before, we can easily experiment with decison tree regression models using sklearn:
```
from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(max_depth=1, criterion="mse") # note the use of mse (mean squared error) as a criterion
regressor.fit(mpg_df[predictor_cols], mpg_df["mpg"])
visualize_tree(regressor, predictor_cols, ["n", "y"])
```
As before, we can also view the "regression surface"
```
def Regression_Surface(data, col1, col2, target, model):
# Get bounds
x_min, x_max = data[col1].min(), data[col1].max()
y_min, y_max = data[col2].min(), data[col2].max()
# Create a mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max,0.5), np.arange(y_min, y_max,0.5))
meshed_data = pd.DataFrame(np.c_[xx.ravel(), yy.ravel()])
tdf = data[[col1, col2]]
model.fit(tdf, target)
Z = model.predict(meshed_data).reshape(xx.shape)
plt.figure(figsize=[12,7])
plt.title("Decision surface")
plt.ylabel(col1)
plt.xlabel(col2)
cs = plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.coolwarm)
plt.scatter(data[col1], data[col2], c=target, cmap=plt.cm.coolwarm)
plt.show()
tree_depth=1
Regression_Surface(mpg_df[predictor_cols], "acceleration", "weight", mpg_df["mpg"], DecisionTreeRegressor(max_depth=tree_depth, criterion="mse"))
```
Let's also take a look using linear regression!
```
Regression_Surface(mpg_df[predictor_cols], "acceleration", "weight", mpg_df["mpg"], linear_model.LinearRegression())
```
How about a more complicated model? Let's try random forrest regression!
```
from sklearn.ensemble import RandomForestRegressor
Regression_Surface(mpg_df[predictor_cols], "acceleration", "weight", mpg_df["mpg"], RandomForestRegressor(n_estimators=10))
```
|
github_jupyter
|
This notebook was prepared by [Donne Martin](http://donnemartin.com). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Challenge Notebook
## Problem: Find the kth to last element of a linked list.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
* [Solution Notebook](#Solution-Notebook)
## Constraints
* Can we assume this is a non-circular, singly linked list?
* Yes
* Can we assume k is a valid integer?
* Yes
* If k = 0, does this return the last element?
* Yes
* What happens if k is greater than or equal to the length of the linked list?
* Return None
* Can you use additional data structures?
* No
* Can we assume we already have a linked list class that can be used for this problem?
* Yes
## Test Cases
* Empty list -> None
* k is >= the length of the linked list -> None
* One element, k = 0 -> element
* General case with many elements, k < length of linked list
## Algorithm
Refer to the [Solution Notebook](http://nbviewer.ipython.org/github/donnemartin/interactive-coding-challenges/blob/master/linked_lists/kth_to_last_elem/kth_to_last_elem_solution.ipynb). If you are stuck and need a hint, the solution notebook's algorithm discussion might be a good place to start.
## Code
```
%run ../linked_list/linked_list.py
%load ../linked_list/linked_list.py
class MyLinkedList(LinkedList):
def kth_to_last_elem(self, k):
# TODO: Implement me
pass
```
## Unit Test
**The following unit test is expected to fail until you solve the challenge.**
```
# %load test_kth_to_last_elem.py
import unittest
class Test(unittest.TestCase):
def test_kth_to_last_elem(self):
print('Test: Empty list')
linked_list = MyLinkedList(None)
self.assertEqual(linked_list.kth_to_last_elem(0), None)
print('Test: k >= len(list)')
self.assertEqual(linked_list.kth_to_last_elem(100), None)
print('Test: One element, k = 0')
head = Node(2)
linked_list = MyLinkedList(head)
self.assertEqual(linked_list.kth_to_last_elem(0), 2)
print('Test: General case')
linked_list.insert_to_front(1)
linked_list.insert_to_front(3)
linked_list.insert_to_front(5)
linked_list.insert_to_front(7)
self.assertEqual(linked_list.kth_to_last_elem(2), 3)
print('Success: test_kth_to_last_elem')
def main():
test = Test()
test.test_kth_to_last_elem()
if __name__ == '__main__':
main()
```
## Solution Notebook
Review the [Solution Notebook](http://nbviewer.ipython.org/github/donnemartin/interactive-coding-challenges/blob/master/linked_lists/kth_to_last_elem/kth_to_last_elem_solution.ipynb) for a discussion on algorithms and code solutions.
|
github_jupyter
|
## Distinction of solid liquid atoms and clustering
In this example, we will take one snapshot from a molecular dynamics simulation which has a solid cluster in liquid. The task is to identify solid atoms and cluster them. More details about the method can be found [here](https://pyscal.readthedocs.io/en/latest/solidliquid.html).
The first step is, of course, importing all the necessary module. For visualisation, we will use [Ovito](https://www.ovito.org/).

The above image shows a visualisation of the system using Ovito. Importing modules,
```
import pyscal.core as pc
```
Now we will set up a System with this input file, and calculate neighbors. Here we will use a cutoff method to find neighbors. More details about finding neighbors can be found [here](https://pyscal.readthedocs.io/en/latest/nearestneighbormethods.html#).
```
sys = pc.System()
sys.read_inputfile('cluster.dump')
sys.find_neighbors(method='cutoff', cutoff=3.63)
```
Once we compute the neighbors, the next step is to find solid atoms. This can be done using [System.find_solids](https://docs.pyscal.org/en/latest/pyscal.html#pyscal.core.System.find_solids) method. There are few parameters that can be set, which can be found in detail [here](https://docs.pyscal.org/en/latest/pyscal.html#pyscal.core.System.find_solids).
```
sys.find_solids(bonds=6, threshold=0.5, avgthreshold=0.6, cluster=False)
```
The above statement found all the solid atoms. Solid atoms can be identified by the value of the `solid` attribute. For that we first get the atom objects and select those with `solid` value as True.
```
atoms = sys.atoms
solids = [atom for atom in atoms if atom.solid]
len(solids)
```
There are 202 solid atoms in the system. In order to visualise in Ovito, we need to first write it out to a trajectory file. This can be done with the help of [to_file](https://docs.pyscal.org/en/latest/pyscal.html#pyscal.core.System.to_file) method of System. This method can help to save any attribute of the atom or ant Steinhardt parameter value.
```
sys.to_file('sys.solid.dat', custom = ['solid'])
```
We can now visualise this file in Ovito. After opening the file in Ovito, the modifier [compute property](https://ovito.org/manual/particles.modifiers.compute_property.html) can be selected. The `Output property` should be `selection` and in the expression field, `solid==0` can be selected to select all the non solid atoms. Applying a modifier [delete selected particles](https://ovito.org/manual/particles.modifiers.delete_selected_particles.html) can be applied to delete all the non solid particles. The system after removing all the liquid atoms is shown below.

### Clustering algorithm
You can see that there is a cluster of atom. The clustering functions that pyscal offers helps in this regard. If you used `find_clusters` with `cluster=True`, the clustering is carried out. Since we did used `cluster=False` above, we will rerun the function
```
sys.find_solids(bonds=6, threshold=0.5, avgthreshold=0.6, cluster=True)
```
You can see that the above function call returned the number of atoms belonging to the largest cluster as an output. In order to extract atoms that belong to the largest cluster, we can use the `largest_cluster` attribute of the atom.
```
atoms = sys.atoms
largest_cluster = [atom for atom in atoms if atom.largest_cluster]
len(largest_cluster)
```
The value matches that given by the function. Once again we will save this information to a file and visualise it in Ovito.
```
sys.to_file('sys.cluster.dat', custom = ['solid', 'largest_cluster'])
```
The system visualised in Ovito following similar steps as above is shown below.

It is clear from the image that the largest cluster of solid atoms was successfully identified. Clustering can be done over any property. The following example with the same system will illustrate this.
## Clustering based on a custom property
In pyscal, clustering can be done based on any property. The following example illustrates this. To find the clusters based on a custom property, the [System.clusters_atoms](https://docs.pyscal.org/en/latest/pyscal.html#pyscal.core.System.cluster_atoms) method has to be used. The simulation box shown above has the centre roughly at (25, 25, 25). For the custom clustering, we will cluster all atoms within a distance of 10 from the the rough centre of the box at (25, 25, 25). Let us define a function that checks the above condition.
```
def check_distance(atom):
#get position of atom
pos = atom.pos
#calculate distance from (25, 25, 25)
dist = ((pos[0]-25)**2 + (pos[1]-25)**2 + (pos[2]-25)**2)**0.5
#check if dist < 10
return (dist <= 10)
```
The above function would return True or False depending on a condition and takes the Atom as an argument. These are the two important conditions to be satisfied. Now we can pass this function to cluster. First, set up the system and find the neighbors.
```
sys = pc.System()
sys.read_inputfile('cluster.dump')
sys.find_neighbors(method='cutoff', cutoff=3.63)
```
Now cluster
```
sys.cluster_atoms(check_distance)
```
There are 242 atoms in the cluster! Once again we can check this, save to a file and visualise in ovito.
```
atoms = sys.atoms
largest_cluster = [atom for atom in atoms if atom.largest_cluster]
len(largest_cluster)
sys.to_file('sys.dist.dat', custom = ['solid', 'largest_cluster'])
```

This example illustrates that any property can be used to cluster the atoms!
|
github_jupyter
|
## Download the Fashion-MNIST dataset
```
import os
import numpy as np
from tensorflow.keras.datasets import fashion_mnist
(x_train, y_train), (x_val, y_val) = fashion_mnist.load_data()
os.makedirs("./data", exist_ok = True)
np.savez('./data/training', image=x_train, label=y_train)
np.savez('./data/validation', image=x_val, label=y_val)
!pygmentize fmnist-3.py
```
## Upload Fashion-MNIST data to S3
```
import sagemaker
print(sagemaker.__version__)
sess = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = sess.default_bucket()
prefix = 'keras2-fashion-mnist'
training_input_path = sess.upload_data('data/training.npz', key_prefix=prefix+'/training')
validation_input_path = sess.upload_data('data/validation.npz', key_prefix=prefix+'/validation')
output_path = 's3://{}/{}/output/'.format(bucket, prefix)
chk_path = 's3://{}/{}/checkpoints/'.format(bucket, prefix)
print(training_input_path)
print(validation_input_path)
print(output_path)
print(chk_path)
```
## Train with Tensorflow
```
from sagemaker.tensorflow import TensorFlow
tf_estimator = TensorFlow(entry_point='fmnist-3.py',
role=role,
instance_count=1,
instance_type='ml.p3.2xlarge',
framework_version='2.1.0',
py_version='py3',
hyperparameters={'epochs': 60},
output_path=output_path,
use_spot_instances=True,
max_run=3600,
max_wait=7200)
objective_metric_name = 'val_acc'
objective_type = 'Maximize'
metric_definitions = [
{'Name': 'val_acc', 'Regex': 'Best val_accuracy: ([0-9\\.]+)'}
]
from sagemaker.tuner import ContinuousParameter, IntegerParameter
hyperparameter_ranges = {
'learning_rate': ContinuousParameter(0.001, 0.2, scaling_type='Logarithmic'),
'batch-size': IntegerParameter(32,512)
}
from sagemaker.tuner import HyperparameterTuner
tuner = HyperparameterTuner(tf_estimator,
objective_metric_name,
hyperparameter_ranges,
metric_definitions=metric_definitions,
objective_type=objective_type,
max_jobs=60,
max_parallel_jobs=2,
early_stopping_type='Auto')
tuner.fit({'training': training_input_path, 'validation': validation_input_path})
from sagemaker.analytics import HyperparameterTuningJobAnalytics
exp = HyperparameterTuningJobAnalytics(
hyperparameter_tuning_job_name=tuner.latest_tuning_job.name)
jobs = exp.dataframe()
jobs.sort_values('FinalObjectiveValue', ascending=0)
```
## Deploy
```
import time
tf_endpoint_name = 'keras-tf-fmnist-'+time.strftime("%Y-%m-%d-%H-%M-%S", time.gmtime())
tf_predictor = tuner.deploy(
initial_instance_count=1,
instance_type='ml.m5.large',
endpoint_name=tf_endpoint_name)
```
## Predict
```
%matplotlib inline
import random
import matplotlib.pyplot as plt
num_samples = 5
indices = random.sample(range(x_val.shape[0] - 1), num_samples)
images = x_val[indices]/255
labels = y_val[indices]
for i in range(num_samples):
plt.subplot(1,num_samples,i+1)
plt.imshow(images[i].reshape(28, 28), cmap='gray')
plt.title(labels[i])
plt.axis('off')
payload = images.reshape(num_samples, 28, 28, 1)
response = tf_predictor.predict(payload)
prediction = np.array(response['predictions'])
predicted_label = prediction.argmax(axis=1)
print('Predicted labels are: {}'.format(predicted_label))
```
## Clean up
```
tf_predictor.delete_endpoint()
```
|
github_jupyter
|
```
import mackinac
import cobra
import pandas as pd
import json
import os
import numpy as np
# load ID's for each organisms genome
id_table = pd.read_table('../data/study_strain_subset_w_patric.tsv',sep='\t',dtype=str)
id_table = id_table.replace(np.nan, '', regex=True)
species_to_id = dict(zip(id_table["designation in screen"],id_table["PATRIC genome ID"]))
id_table
mackinac.get_token('gregmedlock_seed')
# grab and save a universal model to be used later for gapfilling. This is a public template available in Mike Mundy's workspace.
# The template says "gramneg", but there is no difference between the g+ and g- templates other than biomass composition,
# which will not be used during gapfilling (the GENREs will already have their own biomass function).
gramneg = mackinac.create_universal_model('/mmundy/public/modelsupport/templates/MicrobialNegativeResolved.modeltemplate')
cobra.io.save_json_model(gramneg,'../data/universal_mundy.json')
# save id's and both names in dictionary
name_to_recon_info = {}
name_to_gapfill_solution = {}
for species in species_to_id.keys():
# Check for an existing GENRE and make sure there is a PATRIC ID for the strain--
# if there is no PATRIC ID, the dictionary will have an empty string for that strain.
if species+'.json' not in os.listdir('../data/modelseed_models') and species_to_id[species]:
species_id = species_to_id[species]
# reconstruct model; function returns a dictionary with reconstruction info, NOT the model
print("Reconstructing GENRE for " + species)
recon_info = mackinac.create_patric_model(species_id,species)
name_to_recon_info[species] = recon_info
# Get the reactions contained in the gapfill solution. This is on complete media
name_to_gapfill_solution[species] = mackinac.get_patric_gapfill_solutions(species)[0]
# convert to a cobra model
model = mackinac.create_cobra_model_from_patric_model(species)
# Save model in json format
cobra.io.save_json_model(model, '../data/modelseed_models/'+species+'.json')
# Save the model with gapfilled reactions removed
gapfilled_reactions = name_to_gapfill_solution[species]['reactions'].keys()
model.remove_reactions(gapfilled_reactions, remove_orphans=True)
model.repair()
cobra.io.save_json_model(model, '../data/modelseed_models/'+species+'_gapfill_removed.json')
# save conversion dict for id:original_name:SEED_name mapping
with open('../data/patric_recon_info.json','w') as jsonfile:
json.dump(name_to_recon_info,jsonfile)
# save the gapfill solutions
with open('../data/patric_gapfill_solutions.json','w') as jsonfile:
json.dump(name_to_gapfill_solution,jsonfile)
species_to_id
```
|
github_jupyter
|
This script loads behavioral mice data (from `biasedChoiceWorld` protocol and, separately, the last three sessions of training) only from mice that pass a given (stricter) training criterion. For the `biasedChoiceWorld` protocol, only sessions achieving the `trained_1b` and `ready4ephysrig` training status are collected.
The data are slightly reformatted and saved as `.csv` files.
```
import datajoint as dj
dj.config['database.host'] = 'datajoint.internationalbrainlab.org'
from ibl_pipeline import subject, acquisition, action, behavior, reference, data
from ibl_pipeline.analyses.behavior import PsychResults, SessionTrainingStatus
from ibl_pipeline.utils import psychofit as psy
from ibl_pipeline.analyses import behavior as behavior_analysis
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import os
myPath = r"C:\Users\Luigi\Documents\GitHub\ibl-changepoint\data" # Write here your data path
os.chdir(myPath)
# Get list of mice that satisfy given training criteria (stringent trained_1b)
# Check query from behavioral paper:
# https://github.com/int-brain-lab/paper-behavior/blob/master/paper_behavior_functions.py
subj_query = (subject.Subject * subject.SubjectLab * reference.Lab * subject.SubjectProject
& 'subject_project = "ibl_neuropixel_brainwide_01"').aggr(
(acquisition.Session * behavior_analysis.SessionTrainingStatus())
# & 'training_status="trained_1a" OR training_status="trained_1b"',
# & 'training_status="trained_1b" OR training_status="ready4ephysrig"',
& 'training_status="trained_1b"',
'subject_nickname', 'sex', 'subject_birth_date', 'institution',
date_trained='min(date(session_start_time))')
subjects = (subj_query & 'date_trained < "2019-09-30"')
mice_names = sorted(subjects.fetch('subject_nickname'))
print(mice_names)
sess_train = ((acquisition.Session * behavior_analysis.SessionTrainingStatus) &
'task_protocol LIKE "%training%"' & 'session_start_time < "2019-09-30"')
sess_stable = ((acquisition.Session * behavior_analysis.SessionTrainingStatus) &
'task_protocol LIKE "%biased%"' & 'session_start_time < "2019-09-30"' &
('training_status="trained_1b" OR training_status="ready4ephysrig"'))
stable_mice_names = list()
# Perform at least this number of sessions
MinSessionNumber = 4
def get_mouse_data(df):
position_deg = 35. # Stimuli appear at +/- 35 degrees
# Create new dataframe
datamat = pd.DataFrame()
datamat['trial_num'] = df['trial_id']
datamat['session_num'] = np.cumsum(df['trial_id'] == 1)
datamat['stim_probability_left'] = df['trial_stim_prob_left']
signed_contrast = df['trial_stim_contrast_right'] - df['trial_stim_contrast_left']
datamat['contrast'] = np.abs(signed_contrast)
datamat['position'] = np.sign(signed_contrast)*position_deg
datamat['response_choice'] = df['trial_response_choice']
datamat.loc[df['trial_response_choice'] == 'CCW','response_choice'] = 1
datamat.loc[df['trial_response_choice'] == 'CW','response_choice'] = -1
datamat.loc[df['trial_response_choice'] == 'No Go','response_choice'] = 0
datamat['trial_correct'] = np.double(df['trial_feedback_type']==1)
datamat['reaction_time'] = df['trial_response_time'] - df['trial_stim_on_time'] # double-check
# Since some trials have zero contrast, need to compute the alleged position separately
datamat.loc[(datamat['trial_correct'] == 1) & (signed_contrast == 0),'position'] = \
datamat.loc[(datamat['trial_correct'] == 1) & (signed_contrast == 0),'response_choice']*position_deg
datamat.loc[(datamat['trial_correct'] == 0) & (signed_contrast == 0),'position'] = \
datamat.loc[(datamat['trial_correct'] == 0) & (signed_contrast == 0),'response_choice']*(-position_deg)
return datamat
# Loop over all mice
for mouse_nickname in mice_names:
mouse_subject = {'subject_nickname': mouse_nickname}
# Get mouse data for biased sessions
behavior_stable = (behavior.TrialSet.Trial & (subject.Subject & mouse_subject)) \
* sess_stable.proj('session_uuid','task_protocol','session_start_time','training_status') * subject.Subject.proj('subject_nickname') \
* subject.SubjectLab.proj('lab_name')
df = pd.DataFrame(behavior_stable.fetch(order_by='subject_nickname, session_start_time, trial_id', as_dict=True))
if len(df) > 0: # The mouse has performed in at least one stable session with biased blocks
datamat = get_mouse_data(df)
# Take mice that have performed a minimum number of sessions
if np.max(datamat['session_num']) >= MinSessionNumber:
# Should add 'N' to mice names that start with numbers?
# Save dataframe to CSV file
filename = mouse_nickname + '.csv'
datamat.to_csv(filename,index=False)
stable_mice_names.append(mouse_nickname)
# Get mouse last sessions of training data
behavior_train = (behavior.TrialSet.Trial & (subject.Subject & mouse_subject)) \
* sess_train.proj('session_uuid','task_protocol','session_start_time') * subject.Subject.proj('subject_nickname') \
* subject.SubjectLab.proj('lab_name')
df_train = pd.DataFrame(behavior_train.fetch(order_by='subject_nickname, session_start_time, trial_id', as_dict=True))
datamat_train = get_mouse_data(df_train)
Nlast = np.max(datamat_train['session_num']) - 3
datamat_final = datamat_train[datamat_train['session_num'] > Nlast]
# Save final training dataframe to CSV file
filename = mouse_nickname + '_endtrain.csv'
datamat_final.to_csv(filename,index=False)
print(stable_mice_names)
len(stable_mice_names)
```
|
github_jupyter
|
<h1>CI Midterm<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Q1-Simple-Linear-Regression" data-toc-modified-id="Q1-Simple-Linear-Regression-1">Q1 Simple Linear Regression</a></span></li><li><span><a href="#Q2-Fuzzy-Linear-Regression" data-toc-modified-id="Q2-Fuzzy-Linear-Regression-2">Q2 Fuzzy Linear Regression</a></span></li><li><span><a href="#Q3-Support-Vector-Regression" data-toc-modified-id="Q3-Support-Vector-Regression-3">Q3 Support Vector Regression</a></span></li><li><span><a href="#Q4-Single-layer-NN" data-toc-modified-id="Q4-Single-layer-NN-4">Q4 Single-layer NN</a></span><ul class="toc-item"><li><span><a href="#First-two-iterations-illustration" data-toc-modified-id="First-two-iterations-illustration-4.1">First two iterations illustration</a></span></li><li><span><a href="#Code" data-toc-modified-id="Code-4.2">Code</a></span></li></ul></li><li><span><a href="#Q5-Two-layer-NN" data-toc-modified-id="Q5-Two-layer-NN-5">Q5 Two-layer NN</a></span><ul class="toc-item"><li><span><a href="#First-two-iterations-illustration" data-toc-modified-id="First-two-iterations-illustration-5.1">First two iterations illustration</a></span></li><li><span><a href="#Code" data-toc-modified-id="Code-5.2">Code</a></span></li></ul></li><li><span><a href="#Q6-Re-do-Q1-Q5" data-toc-modified-id="Q6-Re-do-Q1-Q5-6">Q6 Re-do Q1-Q5</a></span><ul class="toc-item"><li><span><a href="#Simple-Linear-Regression" data-toc-modified-id="Simple-Linear-Regression-6.1">Simple Linear Regression</a></span></li><li><span><a href="#Fuzzy-Linear-Regression" data-toc-modified-id="Fuzzy-Linear-Regression-6.2">Fuzzy Linear Regression</a></span></li><li><span><a href="#Support-Vector-Regression" data-toc-modified-id="Support-Vector-Regression-6.3">Support Vector Regression</a></span></li><li><span><a href="#Single-layer-NN" data-toc-modified-id="Single-layer-NN-6.4">Single-layer NN</a></span><ul class="toc-item"><li><span><a href="#First-two-iterations-illustration" data-toc-modified-id="First-two-iterations-illustration-6.4.1">First two iterations illustration</a></span></li><li><span><a href="#Code" data-toc-modified-id="Code-6.4.2">Code</a></span></li></ul></li><li><span><a href="#Two-layer-NN" data-toc-modified-id="Two-layer-NN-6.5">Two-layer NN</a></span><ul class="toc-item"><li><span><a href="#First-two-iterations-illustration" data-toc-modified-id="First-two-iterations-illustration-6.5.1">First two iterations illustration</a></span></li><li><span><a href="#Code" data-toc-modified-id="Code-6.5.2">Code</a></span></li></ul></li></ul></li><li><span><a href="#Q7-Discussion" data-toc-modified-id="Q7-Discussion-7">Q7 Discussion</a></span><ul class="toc-item"><li><span><a href="#Discussion-of-Convergence-Issue" data-toc-modified-id="Discussion-of-Convergence-Issue-7.1">Discussion of Convergence Issue</a></span></li></ul></li><li><span><a href="#Q8-Bonus-Question" data-toc-modified-id="Q8-Bonus-Question-8">Q8 Bonus Question</a></span><ul class="toc-item"><li><span><a href="#Simple-Linear-Regression" data-toc-modified-id="Simple-Linear-Regression-8.1">Simple Linear Regression</a></span></li><li><span><a href="#Fuzzy-Linear-Regression" data-toc-modified-id="Fuzzy-Linear-Regression-8.2">Fuzzy Linear Regression</a></span></li><li><span><a href="#Support-Vector-Regression" data-toc-modified-id="Support-Vector-Regression-8.3">Support Vector Regression</a></span></li><li><span><a href="#Single-layer-NN" data-toc-modified-id="Single-layer-NN-8.4">Single-layer NN</a></span></li></ul></li></ul></div>
## Q1 Simple Linear Regression
First, the training data has been visualized as below.
```
%matplotlib inline
import numpy as np
import pandas as pd
import cvxpy as cp
import matplotlib.pyplot as plt
ar = np.array([[1, 1, 1, 1, 1, 1], # intercept
[1, 2, 3, 4, 5, 6], # x
[1, 2, 3, 4, 5, 6]]) # y
# plot the dot points
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.title('Visualization of training observations')
plt.axis('scaled')
plt.show()
```
The data has been processed and the optimization problem (least sum of square) has been formulated. The estimate of $a$ (the slope) is very close to 1 and $b$ (intercept) is very close to 0. The fitted line has been plotted above the training set as well.
```
# Data preprocessing
X_lp = ar[[0, 1], :].T # transpose the array before modeling
y_lp = ar[2].T
# Define and solve the CVXPY problem.
beta = cp.Variable(X_lp.shape[1]) # return num of cols, 2 in total
cost = cp.sum_squares(X_lp * beta - y_lp) # define cost function
obj = cp.Minimize(cost) # define objective function
prob = cp.Problem(obj)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe estimated of a (slope) is:", beta.value[1],
"\nThe estimate of b (intercept) is:", beta.value[0])
x = np.linspace(0, 10, 100)
y = beta.value[1] * x + beta.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = ax + b')
plt.title('Fitted line using simple LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
## Q2 Fuzzy Linear Regression
Same as HW2, the optimization problem has been formulated as below. Here I pick the threshold $\alpha$ as $0.5$ for spread calculation. Similar to Q1, The estimate of $A_1$ (the slope) is 1 and $A_0$ (intercept) is 0. The spread of $A_1$ and $A_0$ have both been calculated. As expected, both spreads are 0 since the regression line fits perfectly to the training data and there is no need of spreads to cover any errors between the estimate $\hat{y}$ and the true values $y$.
The fitted line has been plotted above the training set as well.
```
# Define threshold h (it has same meaning as the alpha in alpha-cut). Higher the h, wider the spread.
h = 0.5
# Define and solve the CVXPY problem.
c = cp.Variable(X_lp.shape[1]) # for spread variables, A0 and A1
alpha = cp.Variable(X_lp.shape[1]) # for center/core variables, A0 and A1
cost = cp.sum(X_lp * c) # define cost function
obj = cp.Minimize(cost) # define objective function
constraints = [c >= 0,
y_lp <= (1 - h) * abs(X_lp) * c + X_lp * alpha, # abs operate on each elements of X_lp
-y_lp <= (1 - h) * abs(X_lp) * c - X_lp * alpha]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe center of A1 (slope) is:", alpha.value[1],
"\nThe spread of A1 (slope) is:", c.value[1],
"\nThe center of A0 (intercept) is:", alpha.value[0],
"\nThe spread of A0 (intercept) is:", c.value[0])
x = np.linspace(0, 10, 100)
y = alpha.value[1] * x + alpha.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = A1x + A0')
plt.title('Fitted line using Fuzzy LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
## Q3 Support Vector Regression
In the course lecture, it was mentioned that the objective function of SVR is to ***minimize the sum of squares plus seek for flatness of the hyperplane.*** In $\epsilon$-SV regression, our goal is to find a function $f(x)$ that has at most $\epsilon$ deviation from the actually obtained targets $y_i$ for all the training data, and at the same time is as flat as possible. Flatness in the case means that one seeks a small $w$ and the approach here is to minimize the L2-norm. The problem can be written as a convex optimization problem:

Sometimes the convex optimization problem does not render feasible solution. We also may want to allow for some errors. Similarly to the loss function of “soft margin” in SVM, we introduce slack variables $ξ_i$, $ξ_i^*$ to cope with otherwise infeasible constraints of the optimization problem:

Here the constent $C$ should be $>0$ and determines the trade-off between the flatness of $f(x)$ and the amount up to which deviations larger than $\epsilon$ are tolerated. The optimization problem is formulated with slack variables and in the program below, I defined $C$ as $\frac{1}{N}$ where $N=6$ is the # of observations in the training set. The $\epsilon$ here has been set to 0.
From the output below, the estimated $w$ is very close to 1 and $b$ is very close to 0.
```
# The constant C, defines the trade-off between the flatness of f and the amount up to which deviations larger than ε are tolerated.
# When C gets bigger, the margin get softer. Here C is defined as 1/N. N is the # of observations.
C = 1 / len(ar[1])
epsilon = 0 # For this ε-SVR problem set ε=0
# Define and solve the CVXPY problem.
bw = cp.Variable(X_lp.shape[1]) # for b and w parameters in SVR. bw[0]=b, bw[1]=w
epsilon1 = cp.Variable(X_lp.shape[0]) # for slack variables ξi
epsilon2 = cp.Variable(X_lp.shape[0]) # for slack variables ξ*i
cost = 1 / 2 * bw[1] ** 2 + C * cp.sum(epsilon1 + epsilon2) # define cost function
obj = cp.Minimize(cost) # define objective function
constraints = [epsilon1 >= 0,
epsilon2 >= 0,
y_lp <= X_lp * bw + epsilon + epsilon1,
-y_lp <= -(X_lp * bw) + epsilon + epsilon2]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe estimate of w is:", bw.value[1],
"\nThe estimate of b is:", bw.value[0], )
```
The fitted line has been plotted above the training set as well:
```
x = np.linspace(0, 10, 100)
y = bw.value[1] * x + bw.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = wx + b')
plt.title('Fitted line using SVR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
## Q4 Single-layer NN
### First two iterations illustration
From the NN archiecture on Lecture 7 page 13, the network output $a$ can be denoted as:
$$a=f(x)=f(wp+b)$$
where
$$x=wp+b\quad f(x)=5x\quad \frac{\partial f}{\partial x}=5$$
Since $b=1$,
$$a=f(x)=f(wp+b)=5(wp+1)$$
Set the loss function $E$ as:
$$ E=\sum_{i=1}^N \frac{1}{2}(T_i-a_i)^2 $$
where $T_i$ is the target value for each input $i$ and $N$ is the number of observations in the training set.
We can find the gradient for $w$ by:
$$\frac{\partial E}{\partial w}=\frac{\partial E}{\partial a}\frac{\partial a}{\partial x}\frac{\partial x}{\partial w}$$
**For the 1st iteration**, with initial value $w=10$:
$$
\frac{\partial E}{\partial a}=a-T=5(wp_i+1)-T_i\\
\frac{\partial f}{\partial x}=5$$
$$\frac{\partial x_1}{\partial w}=p_1=1$$
$$\vdots$$
$$\frac{\partial x_6}{\partial w}=p_6=6$$
For $i=1$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*1+1)-1=54\\
\frac{\partial E}{\partial w}=54*5*1$$
For $i=2$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*2+1)-2=103\\
\frac{\partial E}{\partial w}=103*5*2$$
For $i=3$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*3+1)-3=152\\
\frac{\partial E}{\partial w}=152*5*3$$
For $i=4$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*4+1)-4=201\\
\frac{\partial E}{\partial w}=201*5*4$$
For $i=5$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*5+1)-5=250\\
\frac{\partial E}{\partial w}=250*5*5$$
For $i=6$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*6+1)-6=299\\
\frac{\partial E}{\partial w}=299*5*6$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w})=(54*1+103*2+152*3+201*4+250*5+299*6)*5=22820
$$
Average the sum of gradient by $N=6$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w})}{N}=380.333
$$.
The new $w$ and output $a$ is calculated:
$$w=10-380.333=-370.333\\
a=[-1846.667,-3698.333,-5550,-7401.667,-9253.333, -11105]
$$
**For the 2nd iteration:**
For $i=1$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*1+1)-1=-1847.667\\
\frac{\partial E}{\partial w}=-1847.667*5*1$$
For $i=2$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*2+1)-2=-3700.333\\
\frac{\partial E}{\partial w}=-3700.333*5*2$$
For $i=3$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*3+1)-3=-5553\\
\frac{\partial E}{\partial w}=-5553*5*3$$
For $i=4$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*4+1)-4=-7405.667\\
\frac{\partial E}{\partial w}=-7405.667*5*4$$
For $i=5$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*5+1)-5=-9258.333\\
\frac{\partial E}{\partial w}=-9258.333*5*5$$
For $i=6$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(-370.333*6+1)-6=-11111\\
\frac{\partial E}{\partial w}=-11111*5*6$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w})=(-1847.667*1+-3700.333*2+-5553*3+-7405.667*4+-9258.333*5+-11111*6)*5=-842438.333
$$
Average the sum of gradient by $N=6$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w})}{N}=-14040.639
$$.
The new $w$ and output $a$ is calculated:
$$w=-370.333-(-14040.638)=-13670.305\\
a=[68356.528, 136708.056, 205059.583, 273411.111, 341762.639, 410114.167]
$$
### Code
**We can tell from the above that throughout the first 2 iterations, the updated fit $a$ more and more far away from the actual value. This is because of the learning rate=0.1 was set to be too large and cause the result to be oscillating and won't be able to converge.** Further discussion has been made in Q7 to explore for a proper learning rate in this case.
From the code below, after 30 iterations the loss function value becomes larger and larger and won't be able to converge, which further proves the findings.
```
def single_layer_NN(lr, w, maxiteration):
"""lr - learning rate\n
w - initial value of w\n
maxiteration - define # of max iteration """
E0 = sum(0.5 * np.power((y_lp - 5 * (w * X_lp[:, 1] + 1)), 2)) # initialize Loss, before 1st iteration
for i in range(maxiteration):
if i > 0: # Starting 2nd iteration, E1 value give to E0
E0 = E1 # Loss before iteration
print("Iteration=", i, ",", "Loss value=", E0)
gradient = np.mean((5 * (w * X_lp[:, 1] + 1) - y_lp) * 5 * X_lp[:, 1]) # calculate gradient
step = gradient * lr # calculate step size
w = w - step # refresh the weight
E1 = sum(0.5 * np.power((5 * (w * X_lp[:, 1] + 1) - y_lp), 2)) # Loss after iteration
a = 5 * (w * X_lp[:, 1] + 1) # the refreshed output
if abs(E0 - E1) <= 0.0001:
print('Break out of the loop and end at Iteration=', i,
'\nThe value of loss is:', E1,
'\nThe value of w is:', w)
break
return w, a, gradient
w, a, gradient = single_layer_NN(lr=0.1, w=10, maxiteration=30)
```
## Q5 Two-layer NN
### First two iterations illustration

The above structure will be used to model Q5, with $b_1=b_2=1$ and initial values $w_1=w_2=1$. For $f_1$, the activation function is sigmoid activation function. Since the sample data implies linear relationship, for $f_2$, a linear activation function (specifically, an **identify activation function**) has been chosen. The loss function $E$ has been the same as Q4:
$$
E=\sum_{i=1}^N \frac{1}{2}(T_i-a_2)^2
$$
where $T_i$ is the target value for each input $i$ and $N$ is the number of observations in the training set.
The output $a_1$ and $a_2$ can be denoted as:
$$
a_1=f_1(w_1p+b) \quad a_2=f_2(w_2a_1+b)
$$
where
$$
f_1(x)=\frac{1}{1+e^{-x}} \quad \frac{\partial f_1}{\partial x}=f_1(1-f_1)\\
and \quad f_2(x)=x \quad \frac{\partial f_2}{\partial x}=1
$$
We can find the gradient for $w_1$ and $w_2$ by:
$$
\frac{\partial E}{\partial w_2}=\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial n_2}\frac{\partial n_2}{\partial w_2}=(w_2a_1+b-T)*1*a_1=(w_2a_1+1-T)a_1
\\
\frac{\partial E}{\partial w_1}=\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial a_1}\frac{\partial a_1}{\partial n_1}\frac{\partial n_1}{\partial w_1}=(w_2a_1+b-T)*w_2*a_1(1-a_1)*p\\=\frac{\partial E}{\partial w_2}*w_2*(1-a_1)*p
$$
where
$$
a_1=f_1(w_1p+b)=\frac{1}{1+e^{-(w_1p+1)}}
$$
**We can see that the gradient of $w_1$ can be calculated from the gradient of $w_2$ and the gradient of both weights ($w_1$ and $w_2$) only relate to the input and the initial values of the weights!**
**For the 1st iteration**,
$$
For\quad i=1, 2, 3, 4, 5, 6, \quad a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1\\
$$
For $i=1:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-1=10\\
\frac{\partial E}{\partial w_2}=10*1*1=10,\quad \frac{\partial E}{\partial w_1}=10*10*(1-1)*1=0
$$
For $i=2:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-2=9\\
\frac{\partial E}{\partial w_2}=9*1*1=9,\quad \frac{\partial E}{\partial w_1}=9*10*(1-1)*1=0
$$
For $i=3:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-3=8\\
\frac{\partial E}{\partial w_2}=8*1*1=8,\quad \frac{\partial E}{\partial w_1}=8*10*(1-1)*1=0
$$
For $i=4:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-4=7\\
\frac{\partial E}{\partial w_2}=7*1*1=7,\quad \frac{\partial E}{\partial w_1}=7*10*(1-1)*1=0
$$
For $i=5:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-5=6\\
\frac{\partial E}{\partial w_2}=6*1*1=6,\quad \frac{\partial E}{\partial w_1}=6*10*(1-1)*1=0
$$
For $i=6:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-6=5\\
\frac{\partial E}{\partial w_2}=5*1*1=5,\quad \frac{\partial E}{\partial w_1}=5*10*(1-1)*1=0
$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w_1})=0$$
$$\sum_{i}(\frac{\partial E}{\partial w_2})=10+9+8+7+6+5=45$$
Average the sum of gradient by $N=6$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_1})}{N}=0$$
$$s_2=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_2})}{N}=0.75$$
The new weight $w_1$, $w_2$ and output $a_1$ and $a_2$ can be calculated. The value of $a_1$ and $a_2$ are both for all 6 observations.
$$
w_1=w_1-s_1=10-0=10,\\
w_2=w_2-s_2=10-0.75=9.25\\
a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1, \quad i\in [1,2,3,4,5,6]\\
a_2=w_2a_1+b=9.25*1+1=10.25
$$
**For the 2nd iteration**,
$$
For\quad i=1, 2, 3, 4, 5, 6, \quad a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1\\
$$
For $i=1:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-1=9.25\\
\frac{\partial E}{\partial w_2}=9.25*1*1=9.25,\quad \frac{\partial E}{\partial w_1}=9.25*9.25*(1-1)*1=0
$$
For $i=2:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-2=8.25\\
\frac{\partial E}{\partial w_2}=8.25*1*1=8.25,\quad \frac{\partial E}{\partial w_1}=8.25*9.25*(1-1)*1=0
$$
For $i=3:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-3=7.25\\
\frac{\partial E}{\partial w_2}=7.25*1*1=7.25,\quad \frac{\partial E}{\partial w_1}=7.25*9.25*(1-1)*1=0
$$
For $i=4:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-4=6.25\\
\frac{\partial E}{\partial w_2}=6.25*1*1=6.25,\quad \frac{\partial E}{\partial w_1}=6.25*9.25*(1-1)*1=0
$$
For $i=5:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-5=5.25\\
\frac{\partial E}{\partial w_2}=5.25*1*1=5.25,\quad \frac{\partial E}{\partial w_1}=5.25*9.25*(1-1)*1=0
$$
For $i=6:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(9.25*1+1)-6=4.25\\
\frac{\partial E}{\partial w_2}=4.25*1*1=4.25,\quad \frac{\partial E}{\partial w_1}=4.25*9.25*(1-1)*1=0
$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w_1})=0$$
$$\sum_{i}(\frac{\partial E}{\partial w_2})=9.25+8.25+7.25+6.25+5.25+4.25=40.5$$
Average the sum of gradient by $N=6$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_1})}{N}=0$$
$$s_2=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_2})}{N}=0.675$$
The new weight $w_1$, $w_2$ and output $a_1$ and $a_2$ can be calculated, The value of $a_1$ and $a_2$ are both for all 6 observations:
$$
w_1=w_1-s_1=10-0=10,\\
w_2=w_2-s_2=9.25-0.675=8.575\\
a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1, \quad i\in [1,2,3,4,5,6]\\
a_2=w_2a_1+b=8.575*1+1=9.575
$$
### Code
Below is the code to estimate all weights using batch training, with the stopping criteria as change in loss function less than 0.0001. We can tell the iteration stopped at Iteration 62 and $w_1=10$ while $w_2=2.511$. We can tell that the $w_1$ hardly changes throughout the iterations. I did not show the first 60 iteration results since it makes the report wordy.
```
def linear_activation_NN(C, lr, w1, w2, maxiteration):
# C - set the slope of the f2: f2(x)=Cx
# lr - learning rate
# w1 - initial value of w1
# w2 - initial value of w2
# maxiteration - define # of max iteration
a1 = 1 / (1 + np.exp(-(w1 * X_lp[:, 1] + 1))) # initialize output1 - a1
a2 = C * (w2 * a1 + 1) # initialize output2 - a2
E0 = sum(0.5 * np.power(y_lp - a2, 2)) # initialize Loss, before 1st iteration
for i in range(maxiteration):
if i > 0: # Starting 2nd iteration, E1 value will give to E0
E0 = E1 # Loss before iteration
# print("Iteration=", i, ",", "Loss value=", E0)
gradient_2 = np.mean((w2 * a1 + 1 - y_lp) * C * a1) # calculate gradient for w2
gradient_1 = np.mean(
(w2 * a1 + 1 - y_lp) * C * w2 * a1 * (1 - a1) * X_lp[:, 1]) # use BP to calculate gradient for w1
# gradient_1 = np.mean(gradient_2 * w2 * (1 - a1) * X_lp[:, 1])
step_1 = gradient_1 * lr # calculate step size
step_2 = gradient_2 * lr
w1 = w1 - step_1 # refresh w1
w2 = w2 - step_2 # refresh w2
a1 = 1 / (1 + np.exp(-(w1 * X_lp[:, 1] + 1))) # refresh a1
a2 = C * (w2 * a1 + 1) # refresh a2
E1 = sum(0.5 * np.power(y_lp - a2, 2)) # Loss after iteration
if abs(E0 - E1) <= 0.0001:
print('Break out of the loop and the iteration converge at Iteration=', i,
'\nThe value of loss is:', E1,
'\nThe value of w1 is:', w1,
'\nThe value of w2 is:', w2)
break
return w1, w2, a1, a2, gradient_1, gradient_2
w1, w2, a1, a2, gradient_1, gradient_2 = linear_activation_NN(C=1, lr=0.1, w1=10, w2=10, maxiteration=100)
```
Below gives a plot on how the NN model fit to the current sample data points.
```
# plot the fit
x = np.linspace(-4, 10, 100)
y = w2 * (1 / (1 + np.exp(-(w1 * x + 1)))) + 1
# plt.close('all')
plt.plot(x, y, c='red', label='y = f(w2 * a1 + b)')
plt.title('Fitted line using two-layer NN')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.xlim((-5, 8))
plt.ylim((-2, 8))
plt.xlabel('x')
plt.ylabel('y')
plt.show()
```
## Q6 Re-do Q1-Q5
Two additional observations, (2, 3) and (3, 4) are added and below is the scatterplot showing how the data sample looks like.
```
ar = np.array([[1, 1, 1, 1, 1, 1, 1, 1], # intercept
[1, 2, 3, 4, 5, 6, 2, 3], # x
[1, 2, 3, 4, 5, 6, 3, 4]]) # y
# plot the dot points
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.title('Visualization of training observations')
plt.axis('scaled')
plt.show()
```
### Simple Linear Regression
The simple linear regression fit similar to Q1 has been conducted as below. The estimated $slope=0.923$ and estimated $intercept=0.5$.
```
# Data preprocessing
X_lp = ar[[0, 1], :].T # transpose the array before modeling
y_lp = ar[2].T
# Define and solve the CVXPY problem.
beta = cp.Variable(X_lp.shape[1]) # return num of cols, 2 in total
cost = cp.sum_squares(X_lp * beta - y_lp) # define cost function
obj = cp.Minimize(cost) # define objective function
prob = cp.Problem(obj)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe estimated of a (slope) is:", beta.value[1],
"\nThe estimate of b (intercept) is:", beta.value[0])
```
The regression line has been plotted:
```
# Plot the fit
x = np.linspace(0, 10, 100)
y = beta.value[1] * x + beta.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = ax + b')
plt.title('Fitted line using simple LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Fuzzy Linear Regression
The fuzzy linear regression fit similar to Q2 has been conducted as below. We can see that some spread was estimated for the intercept $A0$ because we are unable to fit the data perfectly this time and there will have to be some spread to cover the data points around the regression line.
```
# Define threshold h (it has same meaning as the alpha in alpha-cut). Higher the h, wider the spread.
h = 0.5
# Define and solve the CVXPY problem.
c = cp.Variable(X_lp.shape[1]) # for spread variables, A0 and A1
alpha = cp.Variable(X_lp.shape[1]) # for center/core variables, A0 and A1
cost = cp.sum(X_lp * c) # define cost function
obj = cp.Minimize(cost) # define objective function
constraints = [c >= 0,
y_lp <= (1 - h) * abs(X_lp) * c + X_lp * alpha, # abs operate on each elements of X_lp
-y_lp <= (1 - h) * abs(X_lp) * c - X_lp * alpha]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe center of A1 (slope) is:", alpha.value[1],
"\nThe spread of A1 (slope) is:", c.value[1],
"\nThe center of A0 (intercept) is:", alpha.value[0],
"\nThe spread of A0 (intercept) is:", c.value[0])
```
The regression line has been plotted, along with the fuzzy spread.
```
x = np.linspace(0, 10, 100)
y = alpha.value[1] * x + alpha.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = A1x + A0')
y = (alpha.value[1] + c.value[1]) * x + alpha.value[0] + c.value[0]
plt.plot(x, y, '--g', label='Fuzzy Spread')
y = (alpha.value[1] - c.value[1]) * x + alpha.value[0] - c.value[0]
plt.plot(x, y, '--g')
plt.title('Fitted line using Fuzzy LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Support Vector Regression
The support vector regression fit similar to Q3 has been conducted as below. Here a simpler version of SVR is used with $\epsilon$ has been set to 1:
$$
minimize \quad \frac{1}{2}||w||^2$$
$$
subject\, to=\left\{
\begin{aligned}
y_i-(w \cdot x_i)-b\le\epsilon\\
(w \cdot x_i)-b\le\epsilon-y_i\le\epsilon\\
\end{aligned}
\right.
$$
The fitted line and the hard margin has been plotted above the training set as well. The estimated $w=0.6$ and $b=1.4$.
```
# A simplified version without introducing the slack variables ξi and ξ*i
epsilon = 1
bw = cp.Variable(X_lp.shape[1]) # for b and w parameters in SVR. bw[0]=b, bw[1]=w
cost = 1 / 2 * bw[1] ** 2
obj = cp.Minimize(cost)
constraints = [
y_lp <= X_lp * bw + epsilon,
-y_lp <= -(X_lp * bw) + epsilon]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe estimate of w is:", bw.value[1],
"\nThe estimate of b is:", bw.value[0], )
upper = X_lp[:, 1] * bw.value[1] + bw.value[0] + epsilon # upper bound of the margin
lower = X_lp[:, 1] * bw.value[1] + bw.value[0] - epsilon # lower bound of the margin
plt.close('all')
x = np.linspace(.5, 6, 100)
y = bw.value[1] * x + bw.value[0]
plt.plot(x, y, c='red', label='y = wx + b')
x = [[min(X_lp[:, 1]), max(X_lp[:, 1])]]
y = [[min(lower), max(lower)]]
for i in range(len(x)):
plt.plot(x[i], y[i], '--g')
y = [[min(upper), max(upper)]]
for i in range(len(x)):
plt.plot(x[i], y[i], '--g', label='margin')
plt.title('Fitted line using SVR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Single-layer NN
#### First two iterations illustration
Similar to the Q4,
**For the 1st iteration**, with initial value $w=10$:
$$
\frac{\partial E}{\partial a}=a-T=5(wp_i+1)-T_i\\
\frac{\partial f}{\partial x}=5$$
$$\frac{\partial x_1}{\partial w}=p_1=1$$
$$\vdots$$
$$\frac{\partial x_6}{\partial w}=p_6=6$$
$$\frac{\partial x_7}{\partial w}=p_7=2$$
$$\frac{\partial x_8}{\partial w}=p_8=3$$
For $i=1$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*1+1)-1=54\\
\frac{\partial E}{\partial w}=54*5*1$$
For $i=2$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*2+1)-2=103\\
\frac{\partial E}{\partial w}=103*5*2$$
For $i=3$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*3+1)-3=152\\
\frac{\partial E}{\partial w}=152*5*3$$
For $i=4$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*4+1)-4=201\\
\frac{\partial E}{\partial w}=201*5*4$$
For $i=5$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*5+1)-5=250\\
\frac{\partial E}{\partial w}=250*5*5$$
For $i=6$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*6+1)-6=299\\
\frac{\partial E}{\partial w}=299*5*6$$
For $i=7$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*2+1)-3=102\\
\frac{\partial E}{\partial w}=102*5*2$$
For $i=8$,
$$
\frac{\partial E}{\partial a}=a_i-T_i=5(wp_i+1)-T_i=5(10*3+1)-4=151\\
\frac{\partial E}{\partial w}=151*5*3$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w})=26105
$$
Average the sum of gradient by $N=8$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w})}{N}=326.3125
$$.
The new $w$ and output $a$ is calculated:
$$w=10-326.3125=-316.3125\\
a=[-1576.562, -3158.125, -4739.688, -6321.25 , -7902.812, -9484.375, -3158.125, -4739.688]
$$
**For the 2nd iteration,** similar steps have been conducted as the 1st iteration and:
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w})=-822307.5
$$
Average the sum of gradient by $N=8$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w})}{N}=-10278.844
$$
The new $w$ and output $a$ is calculated:
$$w=-316.3125-(−10278.844)=9962.531\\
a=[49817.656, 99630.312, 149442.969, 199255.625, 249068.281, 298880.938, 99630.312, 149442.969]
$$
#### Code
Similar to Q4, **We can tell from the above that throughout the first 2 iterations, the updated fit $a$ more and more far away from the actual value. This is because of the learning rate=0.1 was set to be too large and cause the result to be oscillating and won't be able to converge.** Further discussion has been made in Q7 to explore for a proper learning rate in this case.
From the code below, after 30 iterations the loss function value becomes larger and larger and won't be able to converge, which further proves the findings.
```
w, a, gradient = single_layer_NN(lr=0.1, w=10, maxiteration=30)
```
### Two-layer NN
#### First two iterations illustration
The first two iterations calculation is enoughly similar to the Q5.
**For the 1st iteration**,
$$
For\quad i=1, 2, 3, 4, 5, 6, \quad a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1\\
$$
For $i=1:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-1=10\\
\frac{\partial E}{\partial w_2}=10*1*1=10,\quad \frac{\partial E}{\partial w_1}=10*10*(1-1)*1=0
$$
For $i=2:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-2=9\\
\frac{\partial E}{\partial w_2}=9*1*1=9,\quad \frac{\partial E}{\partial w_1}=9*10*(1-1)*1=0
$$
For $i=3:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-3=8\\
\frac{\partial E}{\partial w_2}=8*1*1=8,\quad \frac{\partial E}{\partial w_1}=8*10*(1-1)*1=0
$$
For $i=4:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-4=7\\
\frac{\partial E}{\partial w_2}=7*1*1=7,\quad \frac{\partial E}{\partial w_1}=7*10*(1-1)*1=0
$$
For $i=5:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-5=6\\
\frac{\partial E}{\partial w_2}=6*1*1=6,\quad \frac{\partial E}{\partial w_1}=6*10*(1-1)*1=0
$$
For $i=6:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-6=5\\
\frac{\partial E}{\partial w_2}=5*1*1=5,\quad \frac{\partial E}{\partial w_1}=5*10*(1-1)*1=0
$$
For $i=7:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-3=8\\
\frac{\partial E}{\partial w_2}=8*1*1=8,\quad \frac{\partial E}{\partial w_1}=5*10*(1-1)*1=0
$$
For $i=8:$
$$
\frac{\partial E}{\partial a_2}=a_2-T_i=(w_2a_1+1)-T_i=(10*1+1)-4=7\\
\frac{\partial E}{\partial w_2}=7*1*1=7,\quad \frac{\partial E}{\partial w_1}=5*10*(1-1)*1=0
$$
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w_1})=0$$
$$\sum_{i}(\frac{\partial E}{\partial w_2})=10+9+8+7+6+5+8+7=60$$
Average the sum of gradient by $N=8$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_1})}{N}=0$$
$$s_2=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_2})}{N}=0.75$$
The new weight $w_1$, $w_2$ and output $a_1$ and $a_2$ can be calculated. The value of $a_1$ and $a_2$ are both for all 6 observations.
$$
w_1=w_1-s_1=10-0=10,\\
w_2=w_2-s_2=10-0.75=9.25\\
a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1, \quad i\in [1,2,3,4,5,6]\\
a_2=w_2a_1+b=9.25*1+1=10.25
$$
**For the 1st iteration**, similar steps have been conducted as the 1st iteration and:
The sum of gradient for the batch training is:
$$\sum_{i}(\frac{\partial E}{\partial w_1})=0$$
$$\sum_{i}(\frac{\partial E}{\partial w_2})=54$$
Average the sum of gradient by $N=6$ and the step size (learning rate=0.1) can be calculated as:
$$s_1=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_1})}{N}=0$$
$$s_2=0.1*\frac{\sum_{i}(\frac{\partial E}{\partial w_2})}{N}=0.675$$
The new weight $w_1$, $w_2$ and output $a_1$ and $a_2$ can be calculated, The value of $a_1$ and $a_2$ are both for all 6 observations:
$$
w_1=w_1-s_1=10-0=10,\\
w_2=w_2-s_2=9.25-0.675=8.575\\
a_1=\frac{1}{1+e^{-(w_1p_i+1)}}\approx1, \quad i\in [1,2,3,4,5,6]\\
a_2=w_2a_1+b=8.575*1+1=9.575
$$
#### Code
Below is the code to estimate all weights using batch training, with the stopping criteria as change in loss function less than 0.0001. We can tell the iteration stopped at Iteration 62 and $w_1=10$ while $w_2=2.51$. We can tell that the $w_1$ hardly changes throughout the iterations. I did not show the first 60 iteration results since it makes the report wordy.
One thing we can tell is, comparing to Q5, the fitted $w_1$ and $w_2$ are almost the same even thought we added two more points to the training set. Also a plot has been given to see how well the 2-layer NN model fit to the 8 sample data points. As we see, they are not fitted well.
```
w1, w2, a1, a2, gradient_1, gradient_2 = linear_activation_NN(C=1, lr=0.1, w1=10, w2=10, maxiteration=100)
# plot the fit
x = np.linspace(-4, 10, 100)
y = w2 * (1 / (1 + np.exp(-(w1 * x + 1)))) + 1
# plt.close('all')
plt.plot(x, y, c='red', label='y = f(w2 * a1 + b)')
plt.title('Fitted line using two-layer NN')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.xlim((-5, 8))
plt.ylim((-2, 8))
plt.xlabel('x')
plt.ylabel('y')
plt.show()
```
## Q7 Discussion
The detailed comments for Q1, Q2, Q3, Q5 and Q6 have been made in each section respectively. Here the convergence issue in Q4 and Q6 (the Single-layer NN) will be discussed.
### Discussion of Convergence Issue
As mentioned in Q4, throughout the first 2 iterations, the updated fit $a$ more and more far away from the actual value. From the code after running 30 iterations, the loss function value becomes larger and larger and won't be able to converge. This is because of the learning rate=0.1 was set to be too large and cause the result to be oscillating and won't be able to converge. In below, the learning rate has been adjusted to 0.001 and the algorithm converged after 23 iterations with loss function value=`14.423`.
The fit has been plotted against the sample data points.
```
ar = np.array([[1, 1, 1, 1, 1, 1], # intercept
[1, 2, 3, 4, 5, 6], # x
[1, 2, 3, 4, 5, 6]]) # y
# Data preprocessing
X_lp = ar[[0, 1], :].T # transpose the array before modeling
y_lp = ar[2].T
# Learning rate has been adjusted to 0.001
w, a, gradient = single_layer_NN(lr=0.001, w=10, maxiteration=100)
# plot the fit
x = np.linspace(0, 10, 100)
y = 5 * w * x + 5
plt.close('all')
plt.plot(x, y, c='red', label='y = f(wx + b)')
plt.title('Fitted line using single-layer NN')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.show()
```
The same experiment has been conducted to the convergence issue in Q6 (single-layer NN). As mentioned in Q6, throughout the first 2 iterations, the updated fit $a$ more and more far away from the actual value. From the code after running 30 iterations, the loss function value becomes larger and larger and won't be able to converge. This is because of the learning rate=0.1 was set to be too large and cause the result to be oscillating and won't be able to converge. In below, the learning rate has been adjusted to 0.001 and the algorithm converged after 26 iterations with loss function value=`15.880`.
The fit has been plotted against the sample data points.
```
ar = np.array([[1, 1, 1, 1, 1, 1, 1, 1], # intercept
[1, 2, 3, 4, 5, 6, 2, 3], # x
[1, 2, 3, 4, 5, 6, 3, 4]]) # y
# Data preprocessing
X_lp = ar[[0, 1], :].T # transpose the array before modeling
y_lp = ar[2].T
# Learning rate has been adjusted to 0.001
w, a, gradient = single_layer_NN(lr=0.001, w=10, maxiteration=100)
# plot the fit
x = np.linspace(0, 10, 100)
y = 5 * w * x + 5
plt.close('all')
plt.plot(x, y, c='red', label='y = f(wx + b)')
plt.title('Fitted line using single-layer NN')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.show()
```
## Q8 Bonus Question
I attempt to add two points aiming at balancing out the effect of the two additional points added in Q6. The (2,1) and (3,2) have been added.
**All four models (Simple Linear Regression, Fuzzy Linear Regression, Support Vector Regression and Single-layer NN) all lead to the same fitted line and they give the same predictions for x = 1, 2, 3, 4, 5, and 6. The prediction results are y = 1, 2, 3, 4, 5, and 6 respectively.**
The training observations look like the graph below.
```
ar = np.array([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], # intercept
[1, 2, 3, 4, 5, 6, 2, 3, 2, 3], # x
[1, 2, 3, 4, 5, 6, 3, 4, 1, 2]]) # y
# plot the dot points
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.title('Visualization of training observations')
plt.axis('scaled')
plt.show()
X_lp = ar[[0, 1], :].T # transpose the array before modeling
y_lp = ar[2].T
```
### Simple Linear Regression
For Simple Linear Regression, the same model in Q1 is used. The estimated a is 1 and b is 0:
```
# Define and solve the CVXPY problem.
beta = cp.Variable(X_lp.shape[1]) # return num of cols, 2 in total
cost = cp.sum_squares(X_lp * beta - y_lp) # define cost function
obj = cp.Minimize(cost) # define objective function
prob = cp.Problem(obj)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe estimated of a (slope) is:", beta.value[1],
"\nThe estimate of b (intercept) is:", beta.value[0])
# Plot the fit
x = np.linspace(0, 10, 100)
y = beta.value[1] * x + beta.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = ax + b')
plt.title('Fitted line using simple LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Fuzzy Linear Regression
For Fuzzy Linear Regression, the same model has been used from Q6. The estimated $A0=0$ with spread=2 and $A1=1$ with spread=0.
```
# Define threshold h (it has same meaning as the alpha in alpha-cut). Higher the h, wider the spread.
h = 0.5
# Define and solve the CVXPY problem.
c = cp.Variable(X_lp.shape[1]) # for spread variables, A0 and A1
alpha = cp.Variable(X_lp.shape[1]) # for center/core variables, A0 and A1
cost = cp.sum(X_lp * c) # define cost function
obj = cp.Minimize(cost) # define objective function
constraints = [c >= 0,
y_lp <= (1 - h) * abs(X_lp) * c + X_lp * alpha, # abs operate on each elements of X_lp
-y_lp <= (1 - h) * abs(X_lp) * c - X_lp * alpha]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nThe optimal value of loss is:", prob.value)
print("\nThe center of A1 (slope) is:", alpha.value[1],
"\nThe spread of A1 (slope) is:", c.value[1],
"\nThe center of A0 (intercept) is:", alpha.value[0],
"\nThe spread of A0 (intercept) is:", c.value[0])
# Plot the FR fit
x = np.linspace(0, 10, 100)
y = alpha.value[1] * x + alpha.value[0]
plt.close('all')
plt.plot(x, y, c='red', label='y = A1x + A0')
y = (alpha.value[1] + c.value[1]) * x + alpha.value[0] + c.value[0]
plt.plot(x, y, '--g', label='Fuzzy Spread')
y = (alpha.value[1] - c.value[1]) * x + alpha.value[0] - c.value[0]
plt.plot(x, y, '--g')
plt.title('Fitted line using Fuzzy LR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Support Vector Regression
For Support Vector Regression, the same model has been used from Q6 with $\epsilon$ been set to 1. The estimated $w$ is 1 and $b$ is 0.
```
epsilon = 1
bw = cp.Variable(X_lp.shape[1]) # for b and w parameters in SVR. bw[0]=b, bw[1]=w
cost = 1 / 2 * bw[1] ** 2
obj = cp.Minimize(cost)
constraints = [
y_lp <= X_lp * bw + epsilon,
-y_lp <= -(X_lp * bw) + epsilon]
prob = cp.Problem(obj, constraints)
prob.solve(solver=cp.CPLEX, verbose=False)
# print("status:", prob.status)
print("\nSVR result:")
print("The estimate of w is:", bw.value[1],
"\nThe estimate of b is:", bw.value[0], )
# Plot the SVR fit
upper = X_lp[:, 1] * bw.value[1] + bw.value[0] + epsilon # upper bound of the margin
lower = X_lp[:, 1] * bw.value[1] + bw.value[0] - epsilon # lower bound of the margin
x = np.linspace(.5, 6, 100)
y = bw.value[1] * x + bw.value[0]
plt.plot(x, y, c='red', label='y = wx + b')
x = [[min(X_lp[:, 1]), max(X_lp[:, 1])]]
y = [[min(lower), max(lower)]]
for i in range(len(x)):
plt.plot(x[i], y[i], '--g')
y = [[min(upper), max(upper)]]
for i in range(len(x)):
plt.plot(x[i], y[i], '--g', label='margin')
plt.title('Fitted line using SVR')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
### Single-layer NN
For single-layer NN, I use the same structure in Q4 ***with the bias set to 0***. As discussed in Q7, I set the learning rate=0.001 and the algorithm converge at iteration 30. The estimated $w$ is 0.2. The fitted line with the training sample points are plotted.
```
def single_layer_NN(lr, w, maxiteration, bias=1):
"""lr - learning rate\n
w - initial value of w\n
maxiteration - define # of max iteration\n
bias - default is 1 """
E0 = sum(0.5 * np.power((y_lp - 5 * (w * X_lp[:, 1] + bias)), 2)) # initialize Loss, before 1st iteration
for i in range(maxiteration):
if i > 0: # Starting 2nd iteration, E1 value give to E0
E0 = E1 # Loss before iteration
print("Iteration=", i, ",", "Loss value=", E0)
gradient = np.mean((5 * (w * X_lp[:, 1] + bias) - y_lp) * 5 * X_lp[:, 1]) # calculate gradient
step = gradient * lr # calculate step size
w = w - step # refresh the weight
E1 = sum(0.5 * np.power((5 * (w * X_lp[:, 1] + bias) - y_lp), 2)) # Loss after iteration
a = 5 * (w * X_lp[:, 1] + 1) # the refreshed output
if abs(E0 - E1) <= 0.0001:
print('Break out of the loop and end at Iteration=', i,
'\nThe value of loss is:', E1,
'\nThe value of w is:', w)
break
return w, a, gradient
w, a, gradient = single_layer_NN(lr=0.001, w=10, maxiteration=40, bias=0)
# plot the NN fit
x = np.linspace(0, 10, 100)
y = 5 * w * x + 0
plt.close('all')
plt.plot(x, y, c='red', label='y = f(wx + b)')
plt.title('Fitted line using single-layer NN')
plt.legend(loc='upper left')
plt.scatter(x=ar[1], y=ar[2], c='blue')
plt.axis('scaled')
plt.show()
```
|
github_jupyter
|
```
# fetching data online
import os
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
if not os.path.isdir(housing_path):
os.makedirs(housing_path)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
%matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()
import numpy as np
def split_train_test (data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print(len(train_set))
print(len(test_set))
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio * 2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index() # adds an `index` column
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id")
#splitting using sciktlearn
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
housing['income_cat'].hist()
plt.show()
#stratifield splitting
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set["income_cat"].value_counts() / len(strat_test_set)
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)
housing = strat_train_set.copy()
housing.plot(kind="scatter", alpha =0.1, x="longitude", y="latitude")
plt.show()
corr_matrix = housing.corr()
corr_matrix
corr_matrix['median_house_value'].sort_values(ascending=False)
plt.subplot()
plt.plot(corr_matrix['median_house_value'], color ='red')
plt.show()
#using pandas's scatter matrix to check for correlation
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12,8))
plt.show()
housing.plot(kind='scatter', x='median_income', y="median_house_value", alpha=0.1)
plt.show()
housing["rooms_per_household"] = housing["total_rooms"] / housing["households"]
housing["population_per_household"] = housing["population"] / housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"] / housing["total_rooms"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)
#Prepare the Data for Machine Learning Algorithms
housing = strat_train_set.drop("median_house_value", axis=1)
housing_labels = strat_train_set["median_house_value"].copy()
median = housing["total_bedrooms"].median()
```
## Data Cleaning
- Most Machine Learning algorithms cannot work with missing features, so let’s create a few functions to take care of them.
You noticed earlier that the total_bedrooms
attribute has some missing values, so let’s fix this. You have three options:
- Get rid of the corresponding districts.
- Get rid of the whole attribute.
- Set the values to some value (zero, the mean, the median, etc.).
You can accomplish these easily using DataFrame’s dropna(), drop(), and fillna()
methods.
If you choose option 3, you should compute the median value on the training set, and
use it to fill the missing values in the training set, but also don’t forget to save the
median value that you have computed. You will need it later to replace missing values
in the test set when you want to evaluate your system, and also once the system goes
live to replace missing values in new data.
Scikit-Learn provides a handy class to take care of missing values: SimpleImputer.
Here is how to use it. First, you need to create a SimpleImputer instance, specifying
that you want to replace each attribute’s missing values with the median of that
attribute.
However, I won't be dealing with sklearn now because we are yet to treat the library
```
housing.dropna(subset=["total_bedrooms"]) # option 1
housing.drop("total_bedrooms", axis=1) # option 2
median = housing["total_bedrooms"].median() # option 3
housing["total_bedrooms"].fillna(median, inplace=True)
from sklearn.impute import SimpleImputer
housing["total_bedrooms"].fillna(median, inplace=True)
imputer = SimpleImputer(strategy="median")
#I made mistake in this code. I wrote simpler instead of simple
# imputer = SimplerImputer(strategy= "median")
#Since the median can only be computed on numerical attributes, we need to create a
#copy of the data without the text attribute ocean_proximity:
housing_num = housing.drop("ocean_proximity", axis=1)
print(imputer.fit(housing_num))
imputer
#I could have just treat only total_bedrooms attribute that has missing values rather than everything. But we can't be so sure of tomorrow's data
#so let's apply it to everywhere
imputer.statistics_
housing_num.median().values
#transform the values
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns)
housing_tr
#fit() and transform() what about fit_transform()?
#fit_transform() is saying fit then transform. Fit_transform() method sometimes run faster.
```
## Handling Text and Categorical Attributes
```
# let's us treat ocean_proximity attributes
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(15)
#check for the value counts
housing_cat.value_counts(sort=True)
```
# to convert text attribute to number because machine learning algorithms tends to work better with numbers, we use
- oneht encoding
- Scikit-Learn’s OrdinalEncoder class
- etc
```
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
ordinal_encoder
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded
ordinal_encoder.categories_
_
```
## Underscore (_) in Python
Difficulty Level : Medium
Last Updated : 22 Nov, 2020
Following are different places where _ is used in Python:
Single Underscore:
In Interpreter
After a name
Before a name
Double Underscore:
__leading_double_underscore
__before_after__
Single Underscore
In Interpreter:
_ returns the value of last executed expression value in Python Prompt/Interpreter
For ignoring values:
Multiple time we do not want return values at that time assign those values to Underscore. It used as throwaway variable.
# Ignore a value of specific location/index
for _ in range(10)
print ("Test")
# Ignore a value when unpacking
a,b,_,_ = my_method(var1)
After a name
Python has their by default keywords which we can not use as the variable name. To avoid such conflict between python keyword and variable we use underscore after name
- snake_case vs camelCase vs PascalCase
```
# One hot encoding
#Our ML algorithm from previous result, 0.,1.,..4. can think 0.1 and 0.2 are close
# to solve this problem, we do dummy variable. To achieve that, scikit- learn provides us with One hot encoding
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
# Using up tons of memory mostly to store zeros
# would be very wasteful, so instead a sparse matrix only stores the location of the non‐
# 70 | Chapter 2: End-to-End Machine Learning Project
# 21 See SciPy’s documentation for more details.
# zero elements. You can use it mostly like a normal 2D array,21 but if you really want to
# convert it to a (dense) NumPy array, just call the toarray() method:
# get list of categories
housing_cat_1hot.toarray()
```
# Feature Scaling
One of the most important transformations you need to apply to your data is feature
scaling. With few exceptions, Machine Learning algorithms don’t perform well when
the input numerical attributes have very different scales. This is the case for the hous‐
ing data: the total number of rooms ranges from about 6 to 39,320, while the median
incomes only range from 0 to 15. Note that scaling the target values is generally not
required.
There are two common ways to get all attributes to have the same scale: min-max
scaling and standardization.
Min-max scaling (many people call this normalization) is quite simple: values are
shifted and rescaled so that they end up ranging from 0 to 1.#
```
housing_cat
housing
housing.info()
housing.info()
housing["total_rooms"].value_counts().head(100)
housing["median_income"].value_counts().head(100)
```
## feature scaling
### types
- Min-Max /Normalization
- Standarzation
- Min-Max
Min-Max scaler: In this we subtract the Minimum from all values – thereby marking a scale from Min to Max. Then divide it by the difference between Min and Max. The result is that our values will go from zero to 1.
- Standardization is quite different: first it subtracts the mean value (so standardized
values always have a zero mean), and then it divides by the standard deviation so that
the resulting distribution has unit variance. Unlike min-max scaling, standardization
does not bound values to a specific range, which may be a problem for some algo‐
rithms (e.g., neural networks often expect an input value ranging from 0 to 1). How‐
ever, standardization is much less affected by outliers. For example, suppose a district
had a median income equal to 100 (by mistake). Min-max scaling would then crush
all the other values from 0–15 down to 0–0.15, whereas standardization would not be
much affected. Scikit-Learn provides a transformer called StandardScaler for stand‐
ardization.
#### scikit learn handling feature scaling
Scikit-Learn provides a
transformer called MinMaxScaler for this. It has a feature_range hyperparameter
that lets you change the range if you don’t want 0–1 for some reason.
# Transformation Pipelines
```
pip install scikit-learn==2.0
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder' , CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([('imputer', SimpleImputer(strategy="median")),
('attribs_adder',CombinedAttributesAdder() ),
('std_scaler', StandardScaler()),
])
from sklearn.compose import ColumnTransformer
housing_num
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
pip install scikit-learn==2.0
```
|
github_jupyter
|
# 2016 Olympics medal count acquisition
In this notebook, we acquire the current medal count from the web.
# 1. List of sports
```
from bs4 import BeautifulSoup
import urllib
r = urllib.urlopen('http://www.bbc.com/sport/olympics/rio-2016/medals/sports').read()
soup = BeautifulSoup(r,"lxml")
sports_span = soup.findAll("span",{"class","medals-table-by-sport__sport-name"})
sports_names = []
sports_names_format = []
for s in sports_span:
sports_names_format.append(str(s))
sports_names.append(str(s).lower().replace(" ","-")[48:-7])
print sports_names
```
# 2. HTMLs for each sport's medal table
```
# Save html for each sport
htmls = {}
for s in sports_names:
htmls[s] = urllib.urlopen('http://www.bbc.com/sport/olympics/rio-2016/medals/sports/'+s+'#'+s).read()
# Find table html for each sport
thtmls = {}
for s in sports_names:
soupsp = BeautifulSoup(htmls[s],"lxml")
thtmls[s] = soupsp.findAll("table",{"class","medals-table-by-sport__countries_table"})
```
# 3. Scrape medals for each country and sport
```
# For every sport, scrape medal data
import re
medal_names = ['gold','silver','bronze']
medals = {}
sports_countries = {}
all_countries_format = []
for s in sports_names:
print s
medals[s] = {}
h = str(thtmls[s])
if not thtmls[s]:
print 'no medals yet'
else:
# Find countries of interest
pattern = r"<abbr class=\"abbr-on medium-abbr-off\" title=\""
pmatch = re.finditer(pattern, h)
countries = []
for i,match in enumerate(pmatch):
country = h[int(match.end()):int(match.end())+200].rsplit('"')[0]
all_countries_format.append(country)
countries.append(country.lower().replace(" ","-"))
sports_countries[s] = countries
for c in sports_countries[s]:
if c == 'great-britain-&-n.-ireland':
ci1 = 'great-britain-and-northern-ireland'
medals[s][c] = {}
for m in medal_names:
pattern = r"<abbr class=\"abbr-on medium-abbr-off\" title=\".{,800}" + m + ".{,150}" + ci1 + "\">"
gendermatch = re.finditer(pattern, h)
for i,match in enumerate(gendermatch):
medals[s][c][m] = int(h[int(match.end()):int(match.end())+3])
else:
ci = c
medals[s][ci] = {}
for m in medal_names:
pattern = r"<abbr class=\"abbr-on medium-abbr-off\" title=\".{,500}" + m + ".{,150}" + ci + "\">"
gendermatch = re.finditer(pattern, h)
for i,match in enumerate(gendermatch):
medals[s][ci][m] = int(h[int(match.end()):int(match.end())+3])
print medals[s]
```
# Create dataframe of medals
```
import numpy as np
all_countries_format = list(np.unique(all_countries_format))
all_countries_format.remove('Great Britain & N. Ireland')
all_countries_format.append('Great Britain')
all_countries_format_list = list(np.unique(all_countries_format))
import pandas as pd
# Create an empty dataframe
columns = ['country','sport','medal','N']
df = pd.DataFrame(columns=columns)
# Identify all countries with at least 1 medal
countries_list = list(set(reduce(lambda x,y: x+y,sports_countries.values())))
countries_list = sorted(countries_list)
# Fill dataframe
for s in sports_names:
if thtmls[s]:
for i,c in enumerate(countries_list):
ci = all_countries_format_list[i]
for m in medal_names:
if c in sports_countries[s]:
rowtemp = [ci, s, m, medals[s][c][m]]
else:
rowtemp = [ci, s, m, 0]
dftemp = pd.DataFrame([rowtemp], columns=columns)
df =df.append(dftemp)
```
# Save dataframe
```
df.to_csv('now_medals.csv')
```
|
github_jupyter
|
```
import torch
from torch.nn import functional as F
from torch import nn
from pytorch_lightning.core.lightning import LightningModule
import pytorch_lightning as pl
import torch.optim as optim
import torchvision
import torchvision.datasets as datasets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from src.models import *
from src.dataloader import *
from src.utils import *
import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
import pickle
import json
```
## Train and Val
```
data_dir = '/home/jupyter/data/'
args = {'tigge_dir':data_dir + f'tigge/32km/',
'tigge_vars':['total_precipitation_ens10','total_column_water', '2m_temperature', 'convective_available_potential_energy', 'convective_inhibition'],
'mrms_dir':data_dir + f'mrms/4km/RadarOnly_QPE_06H/',
'rq_fn':data_dir + f'mrms/4km/RadarQuality.nc',
# 'const_fn':data_dir + 'tigge/32km/constants.nc',
# 'const_vars':['orog', 'lsm'],
'data_period':('2018-01', '2019-12'),
'val_days':1,
'split':'train',
# 'pure_sr_ratio':8,
'tp_log':0.01,
'scale':True,
'ensemble_mode':'stack_by_variable',
'pad_tigge':15,
'pad_tigge_channel': True,
'idx_stride': 8
}
save_dir = '/home/jupyter/data/data_patches/'
# dataset_name = 'ensemble_tp_x10_added_vars_TCW-T-CAPE-CIN_log_trans_padded_15_channel'
ds_train = TiggeMRMSDataset(**args)
# pickle.dump(args, open(save_dir+'train/configs/dataset_args.pkl', 'wb'))
#save_images(ds_train, save_dir, 'train')
pickle.dump(ds_train, open(data_dir + f"saved_datasets/traindataset_{dataset_name}.pkl", "wb"))
pickle.dump(args, open(data_dir + f"saved_datasets/traindataset_{dataset_name}_args.pkl", "wb"))
val_args = args
val_args['maxs'] = ds_train.maxs
val_args['mins'] = ds_train.mins
val_args['split'] = 'valid'
#ds_valid = TiggeMRMSDataset(**val_args)
pickle.dump(val_args, open(save_dir+'valid/configs/dataset_args.pkl', 'wb'))
len(ds_valid)
save_images(ds_valid, save_dir, 'valid')
#pickle.dump(ds_valid, open(data_dir + f"saved_datasets/validdataset_{dataset_name}.pkl", "wb"))
#pickle.dump(val_args, open(data_dir + f"saved_datasets/validdataset_{dataset_name}_args.pkl", "wb"))
val_args = pickle.load(open('/home/jupyter/data/data_patches/valid/configs/dataset_args.pkl', 'rb'))
test_args = args
test_args['href_dir'] = data_dir + 'hrefv2/4km/total_precipitation/2020*.nc'
test_args['maxs'] = val_args['maxs']
test_args['mins'] = val_args['mins']
test_args.pop('val_days')
test_args.pop('split')
test_args['first_days'] = 5
test_args['data_period'] = ('2020-01', '2020-12')
# test_dataset_name = dataset_name + f"_first_days_{test_args['first_days']}"
ds_test = TiggeMRMSHREFDataset(**test_args)
save_images(ds_test, save_dir, 'test')
pickle.dump(test_args, open(save_dir+'test/configs/dataset_args.pkl', 'wb'))
len(ds_test)
pickle.dump(ds_test, open(data_dir + f"saved_datasets/testdataset_{test_dataset_name}.pkl", "wb"))
pickle.dump(test_args, open(data_dir + f"saved_datasets/testdataset_{test_dataset_name}_args.pkl", "wb"))
print("check")
```
|
github_jupyter
|
**Chapter 7 – Ensemble Learning and Random Forests**
_This notebook contains all the sample code and solutions to the exercises in chapter 7._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/07_ensemble_learning_and_random_forests.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ensembles"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Voting classifiers
```
heads_proba = 0.51
coin_tosses = (np.random.rand(10000, 10) < heads_proba).astype(np.int32)
cumulative_heads_ratio = np.cumsum(coin_tosses, axis=0) / np.arange(1, 10001).reshape(-1, 1)
plt.figure(figsize=(8,3.5))
plt.plot(cumulative_heads_ratio)
plt.plot([0, 10000], [0.51, 0.51], "k--", linewidth=2, label="51%")
plt.plot([0, 10000], [0.5, 0.5], "k-", label="50%")
plt.xlabel("Number of coin tosses")
plt.ylabel("Heads ratio")
plt.legend(loc="lower right")
plt.axis([0, 10000, 0.42, 0.58])
save_fig("law_of_large_numbers_plot")
plt.show()
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
```
**Note**: to be future-proof, we set `solver="lbfgs"`, `n_estimators=100`, and `gamma="scale"` since these will be the default values in upcoming Scikit-Learn versions.
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
log_clf = LogisticRegression(solver="lbfgs", random_state=42)
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma="scale", random_state=42)
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='hard')
voting_clf.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
```
Soft voting:
```
log_clf = LogisticRegression(solver="lbfgs", random_state=42)
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma="scale", probability=True, random_state=42)
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='soft')
voting_clf.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
```
# Bagging ensembles
```
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
max_samples=100, bootstrap=True, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_tree))
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[-1.5, 2.45, -1, 1.5], alpha=0.5, contour=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", alpha=alpha)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
fix, axes = plt.subplots(ncols=2, figsize=(10,4), sharey=True)
plt.sca(axes[0])
plot_decision_boundary(tree_clf, X, y)
plt.title("Decision Tree", fontsize=14)
plt.sca(axes[1])
plot_decision_boundary(bag_clf, X, y)
plt.title("Decision Trees with Bagging", fontsize=14)
plt.ylabel("")
save_fig("decision_tree_without_and_with_bagging_plot")
plt.show()
```
# Random Forests
```
bag_clf = BaggingClassifier(
DecisionTreeClassifier(splitter="random", max_leaf_nodes=16, random_state=42),
n_estimators=500, max_samples=1.0, bootstrap=True, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)
np.sum(y_pred == y_pred_rf) / len(y_pred) # almost identical predictions
from sklearn.datasets import load_iris
iris = load_iris()
rnd_clf = RandomForestClassifier(n_estimators=500, random_state=42)
rnd_clf.fit(iris["data"], iris["target"])
for name, score in zip(iris["feature_names"], rnd_clf.feature_importances_):
print(name, score)
rnd_clf.feature_importances_
plt.figure(figsize=(6, 4))
for i in range(15):
tree_clf = DecisionTreeClassifier(max_leaf_nodes=16, random_state=42 + i)
indices_with_replacement = np.random.randint(0, len(X_train), len(X_train))
tree_clf.fit(X[indices_with_replacement], y[indices_with_replacement])
plot_decision_boundary(tree_clf, X, y, axes=[-1.5, 2.45, -1, 1.5], alpha=0.02, contour=False)
plt.show()
```
## Out-of-Bag evaluation
```
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
bootstrap=True, oob_score=True, random_state=40)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_
bag_clf.oob_decision_function_
from sklearn.metrics import accuracy_score
y_pred = bag_clf.predict(X_test)
accuracy_score(y_test, y_pred)
```
## Feature importance
```
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.target = mnist.target.astype(np.uint8)
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
rnd_clf.fit(mnist["data"], mnist["target"])
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.hot,
interpolation="nearest")
plt.axis("off")
plot_digit(rnd_clf.feature_importances_)
cbar = plt.colorbar(ticks=[rnd_clf.feature_importances_.min(), rnd_clf.feature_importances_.max()])
cbar.ax.set_yticklabels(['Not important', 'Very important'])
save_fig("mnist_feature_importance_plot")
plt.show()
```
# AdaBoost
```
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1), n_estimators=200,
algorithm="SAMME.R", learning_rate=0.5, random_state=42)
ada_clf.fit(X_train, y_train)
plot_decision_boundary(ada_clf, X, y)
m = len(X_train)
fix, axes = plt.subplots(ncols=2, figsize=(10,4), sharey=True)
for subplot, learning_rate in ((0, 1), (1, 0.5)):
sample_weights = np.ones(m)
plt.sca(axes[subplot])
for i in range(5):
svm_clf = SVC(kernel="rbf", C=0.05, gamma="scale", random_state=42)
svm_clf.fit(X_train, y_train, sample_weight=sample_weights)
y_pred = svm_clf.predict(X_train)
sample_weights[y_pred != y_train] *= (1 + learning_rate)
plot_decision_boundary(svm_clf, X, y, alpha=0.2)
plt.title("learning_rate = {}".format(learning_rate), fontsize=16)
if subplot == 0:
plt.text(-0.7, -0.65, "1", fontsize=14)
plt.text(-0.6, -0.10, "2", fontsize=14)
plt.text(-0.5, 0.10, "3", fontsize=14)
plt.text(-0.4, 0.55, "4", fontsize=14)
plt.text(-0.3, 0.90, "5", fontsize=14)
else:
plt.ylabel("")
save_fig("boosting_plot")
plt.show()
list(m for m in dir(ada_clf) if not m.startswith("_") and m.endswith("_"))
```
# Gradient Boosting
```
np.random.seed(42)
X = np.random.rand(100, 1) - 0.5
y = 3*X[:, 0]**2 + 0.05 * np.random.randn(100)
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X, y)
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X, y2)
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X, y3)
X_new = np.array([[0.8]])
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1, tree_reg2, tree_reg3))
y_pred
def plot_predictions(regressors, X, y, axes, label=None, style="r-", data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center", fontsize=16)
plt.axis(axes)
plt.figure(figsize=(11,11))
plt.subplot(321)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="g-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)
plt.subplot(322)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(323)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="g-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)
plt.subplot(324)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(325)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="g-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(326)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
save_fig("gradient_boosting_plot")
plt.show()
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3, learning_rate=1.0, random_state=42)
gbrt.fit(X, y)
gbrt_slow = GradientBoostingRegressor(max_depth=2, n_estimators=200, learning_rate=0.1, random_state=42)
gbrt_slow.fit(X, y)
fix, axes = plt.subplots(ncols=2, figsize=(10,4), sharey=True)
plt.sca(axes[0])
plot_predictions([gbrt], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="Ensemble predictions")
plt.title("learning_rate={}, n_estimators={}".format(gbrt.learning_rate, gbrt.n_estimators), fontsize=14)
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.sca(axes[1])
plot_predictions([gbrt_slow], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("learning_rate={}, n_estimators={}".format(gbrt_slow.learning_rate, gbrt_slow.n_estimators), fontsize=14)
plt.xlabel("$x_1$", fontsize=16)
save_fig("gbrt_learning_rate_plot")
plt.show()
```
## Gradient Boosting with Early stopping
```
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train, X_val, y_train, y_val = train_test_split(X, y, random_state=49)
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=120, random_state=42)
gbrt.fit(X_train, y_train)
errors = [mean_squared_error(y_val, y_pred)
for y_pred in gbrt.staged_predict(X_val)]
bst_n_estimators = np.argmin(errors) + 1
gbrt_best = GradientBoostingRegressor(max_depth=2, n_estimators=bst_n_estimators, random_state=42)
gbrt_best.fit(X_train, y_train)
min_error = np.min(errors)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.plot(errors, "b.-")
plt.plot([bst_n_estimators, bst_n_estimators], [0, min_error], "k--")
plt.plot([0, 120], [min_error, min_error], "k--")
plt.plot(bst_n_estimators, min_error, "ko")
plt.text(bst_n_estimators, min_error*1.2, "Minimum", ha="center", fontsize=14)
plt.axis([0, 120, 0, 0.01])
plt.xlabel("Number of trees")
plt.ylabel("Error", fontsize=16)
plt.title("Validation error", fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_best], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("Best model (%d trees)" % bst_n_estimators, fontsize=14)
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.xlabel("$x_1$", fontsize=16)
save_fig("early_stopping_gbrt_plot")
plt.show()
gbrt = GradientBoostingRegressor(max_depth=2, warm_start=True, random_state=42)
min_val_error = float("inf")
error_going_up = 0
for n_estimators in range(1, 120):
gbrt.n_estimators = n_estimators
gbrt.fit(X_train, y_train)
y_pred = gbrt.predict(X_val)
val_error = mean_squared_error(y_val, y_pred)
if val_error < min_val_error:
min_val_error = val_error
error_going_up = 0
else:
error_going_up += 1
if error_going_up == 5:
break # early stopping
print(gbrt.n_estimators)
print("Minimum validation MSE:", min_val_error)
```
## Using XGBoost
```
try:
import xgboost
except ImportError as ex:
print("Error: the xgboost library is not installed.")
xgboost = None
if xgboost is not None: # not shown in the book
xgb_reg = xgboost.XGBRegressor(random_state=42)
xgb_reg.fit(X_train, y_train)
y_pred = xgb_reg.predict(X_val)
val_error = mean_squared_error(y_val, y_pred) # Not shown
print("Validation MSE:", val_error) # Not shown
if xgboost is not None: # not shown in the book
xgb_reg.fit(X_train, y_train,
eval_set=[(X_val, y_val)], early_stopping_rounds=2)
y_pred = xgb_reg.predict(X_val)
val_error = mean_squared_error(y_val, y_pred) # Not shown
print("Validation MSE:", val_error) # Not shown
%timeit xgboost.XGBRegressor().fit(X_train, y_train) if xgboost is not None else None
%timeit GradientBoostingRegressor().fit(X_train, y_train)
```
# Exercise solutions
## 1. to 7.
See Appendix A.
## 8. Voting Classifier
Exercise: _Load the MNIST data and split it into a training set, a validation set, and a test set (e.g., use 50,000 instances for training, 10,000 for validation, and 10,000 for testing)._
The MNIST dataset was loaded earlier.
```
from sklearn.model_selection import train_test_split
X_train_val, X_test, y_train_val, y_test = train_test_split(
mnist.data, mnist.target, test_size=10000, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(
X_train_val, y_train_val, test_size=10000, random_state=42)
```
Exercise: _Then train various classifiers, such as a Random Forest classifier, an Extra-Trees classifier, and an SVM._
```
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.svm import LinearSVC
from sklearn.neural_network import MLPClassifier
random_forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
extra_trees_clf = ExtraTreesClassifier(n_estimators=100, random_state=42)
svm_clf = LinearSVC(random_state=42)
mlp_clf = MLPClassifier(random_state=42)
estimators = [random_forest_clf, extra_trees_clf, svm_clf, mlp_clf]
for estimator in estimators:
print("Training the", estimator)
estimator.fit(X_train, y_train)
[estimator.score(X_val, y_val) for estimator in estimators]
```
The linear SVM is far outperformed by the other classifiers. However, let's keep it for now since it may improve the voting classifier's performance.
Exercise: _Next, try to combine them into an ensemble that outperforms them all on the validation set, using a soft or hard voting classifier._
```
from sklearn.ensemble import VotingClassifier
named_estimators = [
("random_forest_clf", random_forest_clf),
("extra_trees_clf", extra_trees_clf),
("svm_clf", svm_clf),
("mlp_clf", mlp_clf),
]
voting_clf = VotingClassifier(named_estimators)
voting_clf.fit(X_train, y_train)
voting_clf.score(X_val, y_val)
[estimator.score(X_val, y_val) for estimator in voting_clf.estimators_]
```
Let's remove the SVM to see if performance improves. It is possible to remove an estimator by setting it to `None` using `set_params()` like this:
```
voting_clf.set_params(svm_clf=None)
```
This updated the list of estimators:
```
voting_clf.estimators
```
However, it did not update the list of _trained_ estimators:
```
voting_clf.estimators_
```
So we can either fit the `VotingClassifier` again, or just remove the SVM from the list of trained estimators:
```
del voting_clf.estimators_[2]
```
Now let's evaluate the `VotingClassifier` again:
```
voting_clf.score(X_val, y_val)
```
A bit better! The SVM was hurting performance. Now let's try using a soft voting classifier. We do not actually need to retrain the classifier, we can just set `voting` to `"soft"`:
```
voting_clf.voting = "soft"
voting_clf.score(X_val, y_val)
```
Nope, hard voting wins in this case.
_Once you have found one, try it on the test set. How much better does it perform compared to the individual classifiers?_
```
voting_clf.voting = "hard"
voting_clf.score(X_test, y_test)
[estimator.score(X_test, y_test) for estimator in voting_clf.estimators_]
```
The voting classifier only very slightly reduced the error rate of the best model in this case.
## 9. Stacking Ensemble
Exercise: _Run the individual classifiers from the previous exercise to make predictions on the validation set, and create a new training set with the resulting predictions: each training instance is a vector containing the set of predictions from all your classifiers for an image, and the target is the image's class. Train a classifier on this new training set._
```
X_val_predictions = np.empty((len(X_val), len(estimators)), dtype=np.float32)
for index, estimator in enumerate(estimators):
X_val_predictions[:, index] = estimator.predict(X_val)
X_val_predictions
rnd_forest_blender = RandomForestClassifier(n_estimators=200, oob_score=True, random_state=42)
rnd_forest_blender.fit(X_val_predictions, y_val)
rnd_forest_blender.oob_score_
```
You could fine-tune this blender or try other types of blenders (e.g., an `MLPClassifier`), then select the best one using cross-validation, as always.
Exercise: _Congratulations, you have just trained a blender, and together with the classifiers they form a stacking ensemble! Now let's evaluate the ensemble on the test set. For each image in the test set, make predictions with all your classifiers, then feed the predictions to the blender to get the ensemble's predictions. How does it compare to the voting classifier you trained earlier?_
```
X_test_predictions = np.empty((len(X_test), len(estimators)), dtype=np.float32)
for index, estimator in enumerate(estimators):
X_test_predictions[:, index] = estimator.predict(X_test)
y_pred = rnd_forest_blender.predict(X_test_predictions)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_pred)
```
This stacking ensemble does not perform as well as the voting classifier we trained earlier, it's not quite as good as the best individual classifier.
|
github_jupyter
|
# Using [vtreat](https://github.com/WinVector/pyvtreat) with Classification Problems
Nina Zumel and John Mount
November 2019
Note: this is a description of the [`Python` version of `vtreat`](https://github.com/WinVector/pyvtreat), the same example for the [`R` version of `vtreat`](https://github.com/WinVector/vtreat) can be found [here](https://github.com/WinVector/vtreat/blob/master/Examples/Classification/Classification.md).
## Preliminaries
Load modules/packages.
```
import pkg_resources
import pandas
import numpy
import numpy.random
import seaborn
import matplotlib.pyplot as plt
import vtreat
import vtreat.util
import wvpy.util
numpy.random.seed(2019)
```
Generate example data.
* `y` is a noisy sinusoidal function of the variable `x`
* `yc` is the output to be predicted: : whether `y` is > 0.5.
* Input `xc` is a categorical variable that represents a discretization of `y`, along some `NaN`s
* Input `x2` is a pure noise variable with no relationship to the output
```
def make_data(nrows):
d = pandas.DataFrame({'x': 5*numpy.random.normal(size=nrows)})
d['y'] = numpy.sin(d['x']) + 0.1*numpy.random.normal(size=nrows)
d.loc[numpy.arange(3, 10), 'x'] = numpy.nan # introduce a nan level
d['xc'] = ['level_' + str(5*numpy.round(yi/5, 1)) for yi in d['y']]
d['x2'] = numpy.random.normal(size=nrows)
d.loc[d['xc']=='level_-1.0', 'xc'] = numpy.nan # introduce a nan level
d['yc'] = d['y']>0.5
return d
d = make_data(500)
d.head()
outcome_name = 'yc' # outcome variable / column
outcome_target = True # value we consider positive
```
### Some quick data exploration
Check how many levels `xc` has, and their distribution (including `NaN`)
```
d['xc'].unique()
d['xc'].value_counts(dropna=False)
```
Find the prevalence of `yc == True` (our chosen notion of "positive").
```
numpy.mean(d[outcome_name] == outcome_target)
```
Plot of `yc` versus `x`.
```
seaborn.lineplot(x='x', y='yc', data=d)
```
## Build a transform appropriate for classification problems.
Now that we have the data, we want to treat it prior to modeling: we want training data where all the input variables are numeric and have no missing values or `NaN`s.
First create the data treatment transform object, in this case a treatment for a binomial classification problem.
```
transform = vtreat.BinomialOutcomeTreatment(
outcome_name=outcome_name, # outcome variable
outcome_target=outcome_target, # outcome of interest
cols_to_copy=['y'], # columns to "carry along" but not treat as input variables
)
```
Use the training data `d` to fit the transform and the return a treated training set: completely numeric, with no missing values.
Note that for the training data `d`: `transform.fit_transform()` is **not** the same as `transform.fit().transform()`; the second call can lead to nested model bias in some situations, and is **not** recommended.
For other, later data, not seen during transform design `transform.transform(o)` is an appropriate step.
```
d_prepared = transform.fit_transform(d, d['yc'])
```
Now examine the score frame, which gives information about each new variable, including its type, which original variable it is derived from, its (cross-validated) correlation with the outcome, and its (cross-validated) significance as a one-variable linear model for the outcome.
```
transform.score_frame_
```
Note that the variable `xc` has been converted to multiple variables:
* an indicator variable for each possible level (`xc_lev_level_*`)
* the value of a (cross-validated) one-variable model for `yc` as a function of `xc` (`xc_logit_code`)
* a variable that returns how prevalent this particular value of `xc` is in the training data (`xc_prevalence_code`)
* a variable indicating when `xc` was `NaN` in the original data (`xc_is_bad`, `x_is_bad`)
Any or all of these new variables are available for downstream modeling. `x` doesn't show as exciting a significance as `xc`, as we are only checking linear relations, and `x` is related to `y` in a very non-linear way.
The `recommended` column indicates which variables are non constant (`has_range` == True) and have a significance value smaller than `default_threshold`. See the section *Deriving the Default Thresholds* below for the reasoning behind the default thresholds. Recommended columns are intended as advice about which variables appear to be most likely to be useful in a downstream model. This advice attempts to be conservative, to reduce the possibility of mistakenly eliminating variables that may in fact be useful (although, obviously, it can still mistakenly eliminate variables that have a real but non-linear relationship to the output, as is the case with `x`, in our example).
Let's look at the variables that are and are not recommended:
```
# recommended variables
transform.score_frame_.loc[transform.score_frame_['recommended'], ['variable']]
# not recommended variables
transform.score_frame_.loc[~transform.score_frame_['recommended'], ['variable']]
```
Notice that `d_prepared` only includes recommended variables (along with `y` and `yc`):
```
d_prepared.head()
```
This is `vtreat`s default behavior; to include all variables in the prepared data, set the parameter `filter_to_recommended` to False, as we show later, in the *Parameters for `BinomialOutcomeTreatment`* section below.
## A Closer Look at `logit_code` variables
Variables of type `logit_code` are the outputs of a one-variable hierarchical logistic regression of a categorical variable (in our example, `xc`) against the centered output on the (cross-validated) treated training data.
Let's see whether `xc_logit_code` makes a good one-variable model for `yc`. It has a large AUC:
```
wvpy.util.plot_roc(prediction=d_prepared['xc_logit_code'],
istrue=d_prepared['yc'],
title = 'performance of xc_logit_code variable')
```
This indicates that `xc_logit_code` is strongly predictive of the outcome. Negative values of `xc_logit_code` correspond strongly to negative outcomes, and positive values correspond strongly to positive outcomes.
```
wvpy.util.dual_density_plot(probs=d_prepared['xc_logit_code'],
istrue=d_prepared['yc'])
```
The values of `xc_logit_code` are in "link space". We can often visualize the relationship a little better by converting the logistic score to a probability.
```
from scipy.special import expit # sigmoid
from scipy.special import logit
offset = logit(numpy.mean(d_prepared.yc))
wvpy.util.dual_density_plot(probs=expit(d_prepared['xc_logit_code'] + offset),
istrue=d_prepared['yc'])
```
Variables of type `logit_code` are useful when dealing with categorical variables with a very large number of possible levels. For example, a categorical variable with 10,000 possible values potentially converts to 10,000 indicator variables, which may be unwieldy for some modeling methods. Using a single numerical variable of type `logit_code` may be a preferable alternative.
## Using the Prepared Data in a Model
Of course, what we really want to do with the prepared training data is to fit a model jointly with all the (recommended) variables.
Let's try fitting a logistic regression model to `d_prepared`.
```
import sklearn.linear_model
import seaborn
not_variables = ['y', 'yc', 'prediction']
model_vars = [v for v in d_prepared.columns if v not in set(not_variables)]
fitter = sklearn.linear_model.LogisticRegression()
fitter.fit(d_prepared[model_vars], d_prepared['yc'])
# now predict
d_prepared['prediction'] = fitter.predict_proba(d_prepared[model_vars])[:, 1]
# look at the ROC curve (on the training data)
wvpy.util.plot_roc(prediction=d_prepared['prediction'],
istrue=d_prepared['yc'],
title = 'Performance of logistic regression model on training data')
```
Now apply the model to new data.
```
# create the new data
dtest = make_data(450)
# prepare the new data with vtreat
dtest_prepared = transform.transform(dtest)
# apply the model to the prepared data
dtest_prepared['prediction'] = fitter.predict_proba(dtest_prepared[model_vars])[:, 1]
wvpy.util.plot_roc(prediction=dtest_prepared['prediction'],
istrue=dtest_prepared['yc'],
title = 'Performance of logistic regression model on test data')
```
## Parameters for `BinomialOutcomeTreatment`
We've tried to set the defaults for all parameters so that `vtreat` is usable out of the box for most applications.
```
vtreat.vtreat_parameters()
```
**use_hierarchical_estimate:**: When True, uses hierarchical smoothing when estimating `logit_code` variables; when False, uses unsmoothed logistic regression.
**coders**: The types of synthetic variables that `vtreat` will (potentially) produce. See *Types of prepared variables* below.
**filter_to_recommended**: When True, prepared data only includes variables marked as "recommended" in score frame. When False, prepared data includes all variables. See the Example below.
**indicator_min_fraction**: For categorical variables, indicator variables (type `indicator_code`) are only produced for levels that are present at least `indicator_min_fraction` of the time. A consequence of this is that 1/`indicator_min_fraction` is the maximum number of indicators that will be produced for a given categorical variable. To make sure that *all* possible indicator variables are produced, set `indicator_min_fraction = 0`
**cross_validation_plan**: The cross validation method used by `vtreat`. Most people won't have to change this.
**cross_validation_k**: The number of folds to use for cross-validation
**user_transforms**: For passing in user-defined transforms for custom data preparation. Won't be needed in most situations, but see [here](https://github.com/WinVector/pyvtreat/blob/master/Examples/UserCoders/UserCoders.ipynb) for an example of applying a GAM transform to input variables.
**sparse_indicators**: When True, use a (Pandas) sparse representation for indicator variables. This representation is compatible with `sklearn`; however, it may not be compatible with other modeling packages. When False, use a dense representation.
**missingness_imputation** The function or value that `vtreat` uses to impute or "fill in" missing numerical values. The default is `numpy.mean()`. To change the imputation function or use different functions/values for different columns, see the [Imputation example](https://github.com/WinVector/pyvtreat/blob/master/Examples/Imputation/Imputation.ipynb).
### Example: Use all variables to model, not just recommended
```
transform_all = vtreat.BinomialOutcomeTreatment(
outcome_name='yc', # outcome variable
outcome_target=True, # outcome of interest
cols_to_copy=['y'], # columns to "carry along" but not treat as input variables
params = vtreat.vtreat_parameters({
'filter_to_recommended': False
})
)
transform_all.fit_transform(d, d['yc']).columns
transform_all.score_frame_
```
Note that the prepared data produced by `fit_transform()` includes all the variables, including those that were not marked as "recommended".
## Types of prepared variables
**clean_copy**: Produced from numerical variables: a clean numerical variable with no `NaNs` or missing values
**indicator_code**: Produced from categorical variables, one for each (common) level: for each level of the variable, indicates if that level was "on"
**prevalence_code**: Produced from categorical variables: indicates how often each level of the variable was "on"
**logit_code**: Produced from categorical variables: score from a one-dimensional model of the centered output as a function of the variable
**missing_indicator**: Produced for both numerical and categorical variables: an indicator variable that marks when the original variable was missing or `NaN`
**deviation_code**: not used by `BinomialOutcomeTreatment`
**impact_code**: not used by `BinomialOutcomeTreatment`
### Example: Produce only a subset of variable types
In this example, suppose you only want to use indicators and continuous variables in your model;
in other words, you only want to use variables of types (`clean_copy`, `missing_indicator`, and `indicator_code`), and no `logit_code` or `prevalence_code` variables.
```
transform_thin = vtreat.BinomialOutcomeTreatment(
outcome_name='yc', # outcome variable
outcome_target=True, # outcome of interest
cols_to_copy=['y'], # columns to "carry along" but not treat as input variables
params = vtreat.vtreat_parameters({
'filter_to_recommended': False,
'coders': {'clean_copy',
'missing_indicator',
'indicator_code',
}
})
)
transform_thin.fit_transform(d, d['yc']).head()
transform_thin.score_frame_
```
## Deriving the Default Thresholds
While machine learning algorithms are generally tolerant to a reasonable number of irrelevant or noise variables, too many irrelevant variables can lead to serious overfit; see [this article](http://www.win-vector.com/blog/2014/02/bad-bayes-an-example-of-why-you-need-hold-out-testing/) for an extreme example, one we call "Bad Bayes". The default threshold is an attempt to eliminate obviously irrelevant variables early.
Imagine that you have a pure noise dataset, where none of the *n* inputs are related to the output. If you treat each variable as a one-variable model for the output, and look at the significances of each model, these significance-values will be uniformly distributed in the range [0:1]. You want to pick a weakest possible significance threshold that eliminates as many noise variables as possible. A moment's thought should convince you that a threshold of *1/n* allows only one variable through, in expectation.
This leads to the general-case heuristic that a significance threshold of *1/n* on your variables should allow only one irrelevant variable through, in expectation (along with all the relevant variables). Hence, *1/n* used to be our recommended threshold, when we developed the R version of `vtreat`.
We noticed, however, that this biases the filtering against numerical variables, since there are at most two derived variables (of types *clean_copy* and *missing_indicator* for every numerical variable in the original data. Categorical variables, on the other hand, are expanded to many derived variables: several indicators (one for every common level), plus a *logit_code* and a *prevalence_code*. So we now reweight the thresholds.
Suppose you have a (treated) data set with *ntreat* different types of `vtreat` variables (`clean_copy`, `indicator_code`, etc).
There are *nT* variables of type *T*. Then the default threshold for all the variables of type *T* is *1/(ntreat nT)*. This reweighting helps to reduce the bias against any particular type of variable. The heuristic is still that the set of recommended variables will allow at most one noise variable into the set of candidate variables.
As noted above, because `vtreat` estimates variable significances using linear methods by default, some variables with a non-linear relationship to the output may fail to pass the threshold. Setting the `filter_to_recommended` parameter to False will keep all derived variables in the treated frame, for the data scientist to filter (or not) as they will.
## Conclusion
In all cases (classification, regression, unsupervised, and multinomial classification) the intent is that `vtreat` transforms are essentially one liners.
The preparation commands are organized as follows:
* **Regression**: [`Python` regression example](https://github.com/WinVector/pyvtreat/blob/master/Examples/Regression/Regression.md), [`R` regression example, fit/prepare interface](https://github.com/WinVector/vtreat/blob/master/Examples/Regression/Regression_FP.md), [`R` regression example, design/prepare/experiment interface](https://github.com/WinVector/vtreat/blob/master/Examples/Regression/Regression.md).
* **Classification**: [`Python` classification example](https://github.com/WinVector/pyvtreat/blob/master/Examples/Classification/Classification.md), [`R` classification example, fit/prepare interface](https://github.com/WinVector/vtreat/blob/master/Examples/Classification/Classification_FP.md), [`R` classification example, design/prepare/experiment interface](https://github.com/WinVector/vtreat/blob/master/Examples/Classification/Classification.md).
* **Unsupervised tasks**: [`Python` unsupervised example](https://github.com/WinVector/pyvtreat/blob/master/Examples/Unsupervised/Unsupervised.md), [`R` unsupervised example, fit/prepare interface](https://github.com/WinVector/vtreat/blob/master/Examples/Unsupervised/Unsupervised_FP.md), [`R` unsupervised example, design/prepare/experiment interface](https://github.com/WinVector/vtreat/blob/master/Examples/Unsupervised/Unsupervised.md).
* **Multinomial classification**: [`Python` multinomial classification example](https://github.com/WinVector/pyvtreat/blob/master/Examples/Multinomial/MultinomialExample.md), [`R` multinomial classification example, fit/prepare interface](https://github.com/WinVector/vtreat/blob/master/Examples/Multinomial/MultinomialExample_FP.md), [`R` multinomial classification example, design/prepare/experiment interface](https://github.com/WinVector/vtreat/blob/master/Examples/Multinomial/MultinomialExample.md).
Some `vtreat` common capabilities are documented here:
* **Score Frame** [score_frame_](https://github.com/WinVector/pyvtreat/blob/master/Examples/ScoreFrame/ScoreFrame.md), using the `score_frame_` information.
* **Cross Validation** [Customized Cross Plans](https://github.com/WinVector/pyvtreat/blob/master/Examples/CustomizedCrossPlan/CustomizedCrossPlan.md), controlling the cross validation plan.
These current revisions of the examples are designed to be small, yet complete. So as a set they have some overlap, but the user can rely mostly on a single example for a single task type.
|
github_jupyter
|
```
# Copyright 2019 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<a target="_blank" href="https://colab.research.google.com/github/GoogleCloudPlatform/keras-idiomatic-programmer/blob/master/workshops/Advanced_Convolutional_Neural_Networks/Idiomatic%20Programmer%20-%20handbook%201%20-%20Codelab%204.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# Idiomatic Programmer Code Labs
## Code Labs #4 - Get Familiar with Advanced CNN Designs
## Prerequistes:
1. Familiar with Python
2. Completed Handbook 1/Part 4: Advanced Convolutional Neural Networks
## Objectives:
1. Architecture Changes - Pre-stems
2. Dense connections across sublayers in DenseNet
3. Xception Redesigned Macro-Architecture for CNN
## Pre-Stems Groups for Handling Different Input Sizes
Let's create a pre-stem to handle an input size different than what the neural network was designed for.
We will use these approaches:
1. Calculate the difference in size between the expected input and the actual size of
the input (in our case we are assuming actual size less than expected size).
A. Expected = (230, 230, 3)
B. Actual = (224, 224, 3)
2. Pad the inputs to fit into the expected size.
You fill in the blanks (replace the ??), make sure it passes the Python interpreter, and then verify it's correctness with the summary output.
You will need to:
1. Set the padding of the image prior to the first convolution.
```
from keras import layers, Input
# Not the input shape expected by the stem (which is (230, 230, 3)
inputs = Input(shape=(224, 224, 3))
# Add a pre-stem and pad (224, 224, 3) to (230, 230, 3)
# HINT: Since the pad is on both sides (left/right, top/bottom) you want to divide the
# difference by two (half goes to the left, half goes to the right, etc)
inputs = layers.ZeroPadding2D(??)(inputs)
# This stem's expected shape is (230, 230, 3)
x = layers.Conv2D(64, (7, 7), strides=(2,2))(inputs)
X = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
```
## Verify that actual is padded to expected:
You should get the following output on the shape of the inputs and outputs
```
inputs (?, 230, 230, 3)
outputs (?, 112, 112, 64)
```
```
# this will output: (230, 230, 3)
print("inputs", inputs.shape)
# this will output: (?, 112, 112, 64)
print("outputs", x.shape)
```
## DenseNet as Function API
Let's create a DenseNet-121:
We will use these approaches:
1. Add a pre-stem step of padding by 1 pixel so a 230x230x3 input results in 7x7
feature maps at the global average (bottleneck) layer.
2. Use average pooling (subsamnpling) in transition blocks.
3. Accumulated feature maps through residual blocks by concatenting the input to the
output, and making that the new output.
4. Use compression to reduce feature map sizes between dense blocks.
You will need to:
1. Set the padding in the stem group.
2. Concatenate the input and output at each residual block.
3. Set the compression (reduction) of filters in the transition block.
4. Use average pooling in transition block.
```
from keras import layers, Input, Model
def stem(inputs):
""" The Stem Convolution Group
inputs : input tensor
"""
# First large convolution for abstract features for input 230 x 230 and output
# 112 x 112
x = layers.Conv2D(64, (7, 7), strides=2)(inputs)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Add padding so when downsampling we fit shape 56 x 56
# Hint: we want to pad one pixel all around.
x = layers.ZeroPadding2D(padding=(??, ??)(x)
x = layers.MaxPooling2D((3, 3), strides=2)(x)
return x
def dense_block(x, nblocks, nb_filters):
""" Construct a Dense Block
x : input layer
nblocks : number of residual blocks in dense block
nb_filters: number of filters in convolution layer in residual block
"""
# Construct a group of residual blocks
for _ in range(nblocks):
x = residual_block(x, nb_filters)
return x
def residual_block(x, nb_filters):
""" Construct Residual Block
x : input layer
nb_filters: number of filters in convolution layer in residual block
"""
shortcut = x # remember input tensor into residual block
# Bottleneck convolution, expand filters by 4 (DenseNet-B)
x = layers.Conv2D(4 * nb_filters, (1, 1), strides=(1, 1))(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# 3 x 3 convolution with padding=same to preserve same shape of feature maps
x = layers.Conv2D(nb_filters, (3, 3), strides=(1, 1), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Concatenate the input (identity) with the output of the residual block
# Concatenation (vs. merging) provides Feature Reuse between layers
# HINT: Use a list which includes the remembered input and the output from the residual block - which becomes the new output
x = layers.concatenate([??])
return x
def trans_block(x, reduce_by):
""" Construct a Transition Block
x : input layer
reduce_by: percentage of reduction of feature maps
"""
# Reduce (compression) the number of feature maps (DenseNet-C)
# shape[n] returns a class object. We use int() to cast it into the dimension
# size
# HINT: the compression is a percentage (~0.5) that was passed as a parameter to this function
nb_filters = int( int(x.shape[3]) * ?? )
# Bottleneck convolution
x = layers.Conv2D(nb_filters, (1, 1), strides=(1, 1))(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Use mean value (average) instead of max value sampling when pooling
# reduce by 75%
# HINT: instead of Max Pooling (downsampling) we use Average Pooling (subsampling)
x = layers.??Pooling2D((2, 2), strides=(2, 2))(x)
return x
inputs = Input(shape=(230, 230, 3))
# Create the Stem Convolution Group
x = stem(inputs)
# number of residual blocks in each dense block
blocks = [6, 12, 24, 16]
# pop off the list the last dense block
last = blocks.pop()
# amount to reduce feature maps by (compression) during transition blocks
reduce_by = 0.5
# number of filters in a convolution block within a residual block
nb_filters = 32
# Create the dense blocks and interceding transition blocks
for nblocks in blocks:
x = dense_block(x, nblocks, nb_filters)
x = trans_block(x, reduce_by)
# Add the last dense block w/o a following transition block
x = dense_block(x, last, nb_filters)
# Classifier
# Global Average Pooling will flatten the 7x7 feature maps into 1D feature maps
x = layers.GlobalAveragePooling2D()(x)
# Fully connected output layer (classification)
outputs = x = layers.Dense(1000, activation='softmax')(x)
model = Model(inputs, outputs)
```
### Verify the model architecture using summary method
It should look like below:
```
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_3 (InputLayer) (None, 230, 230, 3) 0
__________________________________________________________________________________________________
conv2d_241 (Conv2D) (None, 112, 112, 64) 9472 input_3[0][0]
__________________________________________________________________________________________________
batch_normalization_241 (BatchN (None, 112, 112, 64) 256 conv2d_241[0][0]
__________________________________________________________________________________________________
re_lu_241 (ReLU) (None, 112, 112, 64) 0 batch_normalization_241[0][0]
__________________________________________________________________________________________________
zero_padding2d_2 (ZeroPadding2D (None, 114, 114, 64) 0 re_lu_241[0][0]
__________________________________________________________________________________________________
max_pooling2d_3 (MaxPooling2D) (None, 56, 56, 64) 0 zero_padding2d_2[0][0]
__________________________________________________________________________________________________
conv2d_242 (Conv2D) (None, 56, 56, 128) 8320 max_pooling2d_3[0][0]
__________________________________________________________________________________________________
batch_normalization_242 (BatchN (None, 56, 56, 128) 512 conv2d_242[0][0]
__________________________________________________________________________________________________
re_lu_242 (ReLU) (None, 56, 56, 128) 0 batch_normalization_242[0][0]
__________________________________________________________________________________________________
conv2d_243 (Conv2D) (None, 56, 56, 32) 36896 re_lu_242[0][0]
__________________________________________________________________________________________________
batch_normalization_243 (BatchN (None, 56, 56, 32) 128 conv2d_243[0][0]
__________________________________________________________________________________________________
re_lu_243 (ReLU) (None, 56, 56, 32) 0 batch_normalization_243[0][0]
__________________________________________________________________________________________________
concatenate_117 (Concatenate) (None, 56, 56, 96) 0 max_pooling2d_3[0][0]
re_lu_243[0][0]
__________________________________________________________________________________________________
conv2d_244 (Conv2D) (None, 56, 56, 128) 12416 concatenate_117[0][0]
__________________________________________________________________________________________________
batch_normalization_244 (BatchN (None, 56, 56, 128) 512 conv2d_244[0][0]
__________________________________________________________________________________________________
re_lu_244 (ReLU) (None, 56, 56, 128) 0 batch_normalization_244[0][0]
__________________________________________________________________________________________________
conv2d_245 (Conv2D) (None, 56, 56, 32) 36896 re_lu_244[0][0]
__________________________________________________________________________________________________
batch_normalization_245 (BatchN (None, 56, 56, 32) 128 conv2d_245[0][0]
__________________________________________________________________________________________________
re_lu_245 (ReLU) (None, 56, 56, 32) 0 batch_normalization_245[0][0]
__________________________________________________________________________________________________
concatenate_118 (Concatenate) (None, 56, 56, 128) 0 concatenate_117[0][0]
re_lu_245[0][0]
__________________________________________________________________________________________________
conv2d_246 (Conv2D) (None, 56, 56, 128) 16512 concatenate_118[0][0]
__________________________________________________________________________________________________
batch_normalization_246 (BatchN (None, 56, 56, 128) 512 conv2d_246[0][0]
__________________________________________________________________________________________________
re_lu_246 (ReLU) (None, 56, 56, 128) 0 batch_normalization_246[0][0]
__________________________________________________________________________________________________
conv2d_247 (Conv2D) (None, 56, 56, 32) 36896 re_lu_246[0][0]
__________________________________________________________________________________________________
batch_normalization_247 (BatchN (None, 56, 56, 32) 128 conv2d_247[0][0]
__________________________________________________________________________________________________
re_lu_247 (ReLU) (None, 56, 56, 32) 0 batch_normalization_247[0][0]
__________________________________________________________________________________________________
concatenate_119 (Concatenate) (None, 56, 56, 160) 0 concatenate_118[0][0]
re_lu_247[0][0]
__________________________________________________________________________________________________
conv2d_248 (Conv2D) (None, 56, 56, 128) 20608 concatenate_119[0][0]
__________________________________________________________________________________________________
batch_normalization_248 (BatchN (None, 56, 56, 128) 512 conv2d_248[0][0]
__________________________________________________________________________________________________
re_lu_248 (ReLU) (None, 56, 56, 128) 0 batch_normalization_248[0][0]
__________________________________________________________________________________________________
conv2d_249 (Conv2D) (None, 56, 56, 32) 36896 re_lu_248[0][0]
__________________________________________________________________________________________________
batch_normalization_249 (BatchN (None, 56, 56, 32) 128 conv2d_249[0][0]
__________________________________________________________________________________________________
re_lu_249 (ReLU) (None, 56, 56, 32) 0 batch_normalization_249[0][0]
__________________________________________________________________________________________________
concatenate_120 (Concatenate) (None, 56, 56, 192) 0 concatenate_119[0][0]
re_lu_249[0][0]
__________________________________________________________________________________________________
conv2d_250 (Conv2D) (None, 56, 56, 128) 24704 concatenate_120[0][0]
__________________________________________________________________________________________________
batch_normalization_250 (BatchN (None, 56, 56, 128) 512 conv2d_250[0][0]
__________________________________________________________________________________________________
re_lu_250 (ReLU) (None, 56, 56, 128) 0 batch_normalization_250[0][0]
__________________________________________________________________________________________________
conv2d_251 (Conv2D) (None, 56, 56, 32) 36896 re_lu_250[0][0]
__________________________________________________________________________________________________
batch_normalization_251 (BatchN (None, 56, 56, 32) 128 conv2d_251[0][0]
__________________________________________________________________________________________________
re_lu_251 (ReLU) (None, 56, 56, 32) 0 batch_normalization_251[0][0]
__________________________________________________________________________________________________
concatenate_121 (Concatenate) (None, 56, 56, 224) 0 concatenate_120[0][0]
re_lu_251[0][0]
__________________________________________________________________________________________________
conv2d_252 (Conv2D) (None, 56, 56, 128) 28800 concatenate_121[0][0]
__________________________________________________________________________________________________
batch_normalization_252 (BatchN (None, 56, 56, 128) 512 conv2d_252[0][0]
__________________________________________________________________________________________________
re_lu_252 (ReLU) (None, 56, 56, 128) 0 batch_normalization_252[0][0]
__________________________________________________________________________________________________
conv2d_253 (Conv2D) (None, 56, 56, 32) 36896 re_lu_252[0][0]
__________________________________________________________________________________________________
batch_normalization_253 (BatchN (None, 56, 56, 32) 128 conv2d_253[0][0]
__________________________________________________________________________________________________
re_lu_253 (ReLU) (None, 56, 56, 32) 0 batch_normalization_253[0][0]
__________________________________________________________________________________________________
concatenate_122 (Concatenate) (None, 56, 56, 256) 0 concatenate_121[0][0]
re_lu_253[0][0]
__________________________________________________________________________________________________
conv2d_254 (Conv2D) (None, 56, 56, 128) 32896 concatenate_122[0][0]
__________________________________________________________________________________________________
batch_normalization_254 (BatchN (None, 56, 56, 128) 512 conv2d_254[0][0]
__________________________________________________________________________________________________
re_lu_254 (ReLU) (None, 56, 56, 128) 0 batch_normalization_254[0][0]
REMOVED for BREVITY ...
__________________________________________________________________________________________________
average_pooling2d_9 (AveragePoo (None, 7, 7, 512) 0 re_lu_328[0][0]
__________________________________________________________________________________________________
conv2d_329 (Conv2D) (None, 7, 7, 128) 65664 average_pooling2d_9[0][0]
__________________________________________________________________________________________________
batch_normalization_329 (BatchN (None, 7, 7, 128) 512 conv2d_329[0][0]
__________________________________________________________________________________________________
re_lu_329 (ReLU) (None, 7, 7, 128) 0 batch_normalization_329[0][0]
__________________________________________________________________________________________________
conv2d_330 (Conv2D) (None, 7, 7, 32) 36896 re_lu_329[0][0]
__________________________________________________________________________________________________
batch_normalization_330 (BatchN (None, 7, 7, 32) 128 conv2d_330[0][0]
__________________________________________________________________________________________________
re_lu_330 (ReLU) (None, 7, 7, 32) 0 batch_normalization_330[0][0]
__________________________________________________________________________________________________
concatenate_159 (Concatenate) (None, 7, 7, 544) 0 average_pooling2d_9[0][0]
re_lu_330[0][0]
__________________________________________________________________________________________________
conv2d_331 (Conv2D) (None, 7, 7, 128) 69760 concatenate_159[0][0]
__________________________________________________________________________________________________
batch_normalization_331 (BatchN (None, 7, 7, 128) 512 conv2d_331[0][0]
__________________________________________________________________________________________________
re_lu_331 (ReLU) (None, 7, 7, 128) 0 batch_normalization_331[0][0]
__________________________________________________________________________________________________
conv2d_332 (Conv2D) (None, 7, 7, 32) 36896 re_lu_331[0][0]
__________________________________________________________________________________________________
batch_normalization_332 (BatchN (None, 7, 7, 32) 128 conv2d_332[0][0]
__________________________________________________________________________________________________
re_lu_332 (ReLU) (None, 7, 7, 32) 0 batch_normalization_332[0][0]
__________________________________________________________________________________________________
concatenate_160 (Concatenate) (None, 7, 7, 576) 0 concatenate_159[0][0]
re_lu_332[0][0]
__________________________________________________________________________________________________
conv2d_333 (Conv2D) (None, 7, 7, 128) 73856 concatenate_160[0][0]
__________________________________________________________________________________________________
batch_normalization_333 (BatchN (None, 7, 7, 128) 512 conv2d_333[0][0]
__________________________________________________________________________________________________
re_lu_333 (ReLU) (None, 7, 7, 128) 0 batch_normalization_333[0][0]
__________________________________________________________________________________________________
conv2d_334 (Conv2D) (None, 7, 7, 32) 36896 re_lu_333[0][0]
__________________________________________________________________________________________________
batch_normalization_334 (BatchN (None, 7, 7, 32) 128 conv2d_334[0][0]
__________________________________________________________________________________________________
re_lu_334 (ReLU) (None, 7, 7, 32) 0 batch_normalization_334[0][0]
__________________________________________________________________________________________________
concatenate_161 (Concatenate) (None, 7, 7, 608) 0 concatenate_160[0][0]
re_lu_334[0][0]
__________________________________________________________________________________________________
conv2d_335 (Conv2D) (None, 7, 7, 128) 77952 concatenate_161[0][0]
__________________________________________________________________________________________________
batch_normalization_335 (BatchN (None, 7, 7, 128) 512 conv2d_335[0][0]
__________________________________________________________________________________________________
re_lu_335 (ReLU) (None, 7, 7, 128) 0 batch_normalization_335[0][0]
__________________________________________________________________________________________________
conv2d_336 (Conv2D) (None, 7, 7, 32) 36896 re_lu_335[0][0]
__________________________________________________________________________________________________
batch_normalization_336 (BatchN (None, 7, 7, 32) 128 conv2d_336[0][0]
__________________________________________________________________________________________________
re_lu_336 (ReLU) (None, 7, 7, 32) 0 batch_normalization_336[0][0]
__________________________________________________________________________________________________
concatenate_162 (Concatenate) (None, 7, 7, 640) 0 concatenate_161[0][0]
re_lu_336[0][0]
__________________________________________________________________________________________________
conv2d_337 (Conv2D) (None, 7, 7, 128) 82048 concatenate_162[0][0]
__________________________________________________________________________________________________
batch_normalization_337 (BatchN (None, 7, 7, 128) 512 conv2d_337[0][0]
__________________________________________________________________________________________________
re_lu_337 (ReLU) (None, 7, 7, 128) 0 batch_normalization_337[0][0]
__________________________________________________________________________________________________
conv2d_338 (Conv2D) (None, 7, 7, 32) 36896 re_lu_337[0][0]
__________________________________________________________________________________________________
batch_normalization_338 (BatchN (None, 7, 7, 32) 128 conv2d_338[0][0]
__________________________________________________________________________________________________
re_lu_338 (ReLU) (None, 7, 7, 32) 0 batch_normalization_338[0][0]
__________________________________________________________________________________________________
concatenate_163 (Concatenate) (None, 7, 7, 672) 0 concatenate_162[0][0]
re_lu_338[0][0]
__________________________________________________________________________________________________
conv2d_339 (Conv2D) (None, 7, 7, 128) 86144 concatenate_163[0][0]
__________________________________________________________________________________________________
batch_normalization_339 (BatchN (None, 7, 7, 128) 512 conv2d_339[0][0]
__________________________________________________________________________________________________
re_lu_339 (ReLU) (None, 7, 7, 128) 0 batch_normalization_339[0][0]
__________________________________________________________________________________________________
conv2d_340 (Conv2D) (None, 7, 7, 32) 36896 re_lu_339[0][0]
__________________________________________________________________________________________________
batch_normalization_340 (BatchN (None, 7, 7, 32) 128 conv2d_340[0][0]
__________________________________________________________________________________________________
re_lu_340 (ReLU) (None, 7, 7, 32) 0 batch_normalization_340[0][0]
__________________________________________________________________________________________________
concatenate_164 (Concatenate) (None, 7, 7, 704) 0 concatenate_163[0][0]
re_lu_340[0][0]
__________________________________________________________________________________________________
conv2d_341 (Conv2D) (None, 7, 7, 128) 90240 concatenate_164[0][0]
__________________________________________________________________________________________________
batch_normalization_341 (BatchN (None, 7, 7, 128) 512 conv2d_341[0][0]
__________________________________________________________________________________________________
re_lu_341 (ReLU) (None, 7, 7, 128) 0 batch_normalization_341[0][0]
__________________________________________________________________________________________________
conv2d_342 (Conv2D) (None, 7, 7, 32) 36896 re_lu_341[0][0]
__________________________________________________________________________________________________
batch_normalization_342 (BatchN (None, 7, 7, 32) 128 conv2d_342[0][0]
__________________________________________________________________________________________________
re_lu_342 (ReLU) (None, 7, 7, 32) 0 batch_normalization_342[0][0]
__________________________________________________________________________________________________
concatenate_165 (Concatenate) (None, 7, 7, 736) 0 concatenate_164[0][0]
re_lu_342[0][0]
__________________________________________________________________________________________________
conv2d_343 (Conv2D) (None, 7, 7, 128) 94336 concatenate_165[0][0]
__________________________________________________________________________________________________
batch_normalization_343 (BatchN (None, 7, 7, 128) 512 conv2d_343[0][0]
__________________________________________________________________________________________________
re_lu_343 (ReLU) (None, 7, 7, 128) 0 batch_normalization_343[0][0]
__________________________________________________________________________________________________
conv2d_344 (Conv2D) (None, 7, 7, 32) 36896 re_lu_343[0][0]
__________________________________________________________________________________________________
batch_normalization_344 (BatchN (None, 7, 7, 32) 128 conv2d_344[0][0]
__________________________________________________________________________________________________
re_lu_344 (ReLU) (None, 7, 7, 32) 0 batch_normalization_344[0][0]
__________________________________________________________________________________________________
concatenate_166 (Concatenate) (None, 7, 7, 768) 0 concatenate_165[0][0]
re_lu_344[0][0]
__________________________________________________________________________________________________
conv2d_345 (Conv2D) (None, 7, 7, 128) 98432 concatenate_166[0][0]
__________________________________________________________________________________________________
batch_normalization_345 (BatchN (None, 7, 7, 128) 512 conv2d_345[0][0]
__________________________________________________________________________________________________
re_lu_345 (ReLU) (None, 7, 7, 128) 0 batch_normalization_345[0][0]
__________________________________________________________________________________________________
conv2d_346 (Conv2D) (None, 7, 7, 32) 36896 re_lu_345[0][0]
__________________________________________________________________________________________________
batch_normalization_346 (BatchN (None, 7, 7, 32) 128 conv2d_346[0][0]
__________________________________________________________________________________________________
re_lu_346 (ReLU) (None, 7, 7, 32) 0 batch_normalization_346[0][0]
__________________________________________________________________________________________________
concatenate_167 (Concatenate) (None, 7, 7, 800) 0 concatenate_166[0][0]
re_lu_346[0][0]
__________________________________________________________________________________________________
conv2d_347 (Conv2D) (None, 7, 7, 128) 102528 concatenate_167[0][0]
__________________________________________________________________________________________________
batch_normalization_347 (BatchN (None, 7, 7, 128) 512 conv2d_347[0][0]
__________________________________________________________________________________________________
re_lu_347 (ReLU) (None, 7, 7, 128) 0 batch_normalization_347[0][0]
__________________________________________________________________________________________________
conv2d_348 (Conv2D) (None, 7, 7, 32) 36896 re_lu_347[0][0]
__________________________________________________________________________________________________
batch_normalization_348 (BatchN (None, 7, 7, 32) 128 conv2d_348[0][0]
__________________________________________________________________________________________________
re_lu_348 (ReLU) (None, 7, 7, 32) 0 batch_normalization_348[0][0]
__________________________________________________________________________________________________
concatenate_168 (Concatenate) (None, 7, 7, 832) 0 concatenate_167[0][0]
re_lu_348[0][0]
__________________________________________________________________________________________________
conv2d_349 (Conv2D) (None, 7, 7, 128) 106624 concatenate_168[0][0]
__________________________________________________________________________________________________
batch_normalization_349 (BatchN (None, 7, 7, 128) 512 conv2d_349[0][0]
__________________________________________________________________________________________________
re_lu_349 (ReLU) (None, 7, 7, 128) 0 batch_normalization_349[0][0]
__________________________________________________________________________________________________
conv2d_350 (Conv2D) (None, 7, 7, 32) 36896 re_lu_349[0][0]
__________________________________________________________________________________________________
batch_normalization_350 (BatchN (None, 7, 7, 32) 128 conv2d_350[0][0]
__________________________________________________________________________________________________
re_lu_350 (ReLU) (None, 7, 7, 32) 0 batch_normalization_350[0][0]
__________________________________________________________________________________________________
concatenate_169 (Concatenate) (None, 7, 7, 864) 0 concatenate_168[0][0]
re_lu_350[0][0]
__________________________________________________________________________________________________
conv2d_351 (Conv2D) (None, 7, 7, 128) 110720 concatenate_169[0][0]
__________________________________________________________________________________________________
batch_normalization_351 (BatchN (None, 7, 7, 128) 512 conv2d_351[0][0]
__________________________________________________________________________________________________
re_lu_351 (ReLU) (None, 7, 7, 128) 0 batch_normalization_351[0][0]
__________________________________________________________________________________________________
conv2d_352 (Conv2D) (None, 7, 7, 32) 36896 re_lu_351[0][0]
__________________________________________________________________________________________________
batch_normalization_352 (BatchN (None, 7, 7, 32) 128 conv2d_352[0][0]
__________________________________________________________________________________________________
re_lu_352 (ReLU) (None, 7, 7, 32) 0 batch_normalization_352[0][0]
__________________________________________________________________________________________________
concatenate_170 (Concatenate) (None, 7, 7, 896) 0 concatenate_169[0][0]
re_lu_352[0][0]
__________________________________________________________________________________________________
conv2d_353 (Conv2D) (None, 7, 7, 128) 114816 concatenate_170[0][0]
__________________________________________________________________________________________________
batch_normalization_353 (BatchN (None, 7, 7, 128) 512 conv2d_353[0][0]
__________________________________________________________________________________________________
re_lu_353 (ReLU) (None, 7, 7, 128) 0 batch_normalization_353[0][0]
__________________________________________________________________________________________________
conv2d_354 (Conv2D) (None, 7, 7, 32) 36896 re_lu_353[0][0]
__________________________________________________________________________________________________
batch_normalization_354 (BatchN (None, 7, 7, 32) 128 conv2d_354[0][0]
__________________________________________________________________________________________________
re_lu_354 (ReLU) (None, 7, 7, 32) 0 batch_normalization_354[0][0]
__________________________________________________________________________________________________
concatenate_171 (Concatenate) (None, 7, 7, 928) 0 concatenate_170[0][0]
re_lu_354[0][0]
__________________________________________________________________________________________________
conv2d_355 (Conv2D) (None, 7, 7, 128) 118912 concatenate_171[0][0]
__________________________________________________________________________________________________
batch_normalization_355 (BatchN (None, 7, 7, 128) 512 conv2d_355[0][0]
__________________________________________________________________________________________________
re_lu_355 (ReLU) (None, 7, 7, 128) 0 batch_normalization_355[0][0]
__________________________________________________________________________________________________
conv2d_356 (Conv2D) (None, 7, 7, 32) 36896 re_lu_355[0][0]
__________________________________________________________________________________________________
batch_normalization_356 (BatchN (None, 7, 7, 32) 128 conv2d_356[0][0]
__________________________________________________________________________________________________
re_lu_356 (ReLU) (None, 7, 7, 32) 0 batch_normalization_356[0][0]
__________________________________________________________________________________________________
concatenate_172 (Concatenate) (None, 7, 7, 960) 0 concatenate_171[0][0]
re_lu_356[0][0]
__________________________________________________________________________________________________
conv2d_357 (Conv2D) (None, 7, 7, 128) 123008 concatenate_172[0][0]
__________________________________________________________________________________________________
batch_normalization_357 (BatchN (None, 7, 7, 128) 512 conv2d_357[0][0]
__________________________________________________________________________________________________
re_lu_357 (ReLU) (None, 7, 7, 128) 0 batch_normalization_357[0][0]
__________________________________________________________________________________________________
conv2d_358 (Conv2D) (None, 7, 7, 32) 36896 re_lu_357[0][0]
__________________________________________________________________________________________________
batch_normalization_358 (BatchN (None, 7, 7, 32) 128 conv2d_358[0][0]
__________________________________________________________________________________________________
re_lu_358 (ReLU) (None, 7, 7, 32) 0 batch_normalization_358[0][0]
__________________________________________________________________________________________________
concatenate_173 (Concatenate) (None, 7, 7, 992) 0 concatenate_172[0][0]
re_lu_358[0][0]
__________________________________________________________________________________________________
conv2d_359 (Conv2D) (None, 7, 7, 128) 127104 concatenate_173[0][0]
__________________________________________________________________________________________________
batch_normalization_359 (BatchN (None, 7, 7, 128) 512 conv2d_359[0][0]
__________________________________________________________________________________________________
re_lu_359 (ReLU) (None, 7, 7, 128) 0 batch_normalization_359[0][0]
__________________________________________________________________________________________________
conv2d_360 (Conv2D) (None, 7, 7, 32) 36896 re_lu_359[0][0]
__________________________________________________________________________________________________
batch_normalization_360 (BatchN (None, 7, 7, 32) 128 conv2d_360[0][0]
__________________________________________________________________________________________________
re_lu_360 (ReLU) (None, 7, 7, 32) 0 batch_normalization_360[0][0]
__________________________________________________________________________________________________
concatenate_174 (Concatenate) (None, 7, 7, 1024) 0 concatenate_173[0][0]
re_lu_360[0][0]
__________________________________________________________________________________________________
global_average_pooling2d_3 (Glo (None, 1024) 0 concatenate_174[0][0]
__________________________________________________________________________________________________
dense_3 (Dense) (None, 1000) 1025000 global_average_pooling2d_3[0][0]
==================================================================================================
Total params: 7,946,408
Trainable params: 7,925,928
Non-trainable params: 20,480
__________________________________________________________________________________________________
```
```
model.summary()
```
## Xception Architecture using Functional API
Let's layout a CNN using the Xception architecture pattern.
We will use these approaches:
1. Decompose into a stem, entrance, middle and exit module.
2. Stem does the initial sequential convolutional layers for the input.
3. Entrance does the coarse filter learning.
4. Middle does the detail filter learning.
5. Exit does the classification.
We won't build a full Xception, just a mini-example to practice the layout.
You will need to:
1. Use a strided convolution in the stem group.
2. Set the number of residual blocks in the residual groups in the middle flow.
3. Use global averaging in the classifier.
4. Set the input to the project link in the residual blocks in the entry flow.
5. Remember the input to the residual blocks in the middle flow.
```
from keras import layers, Input, Model
def entryFlow(inputs):
""" Create the entry flow section
inputs : input tensor to neural network
"""
def stem(inputs):
""" Create the stem entry into the neural network
inputs : input tensor to neural network
"""
# The stem uses two 3x3 convolutions.
# The first one downsamples and the second one doubles the number of filters
# First convolution
x = layers.Conv2D(32, (3, 3), strides=(2, 2))(inputs)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Second convolution, double the number of filters (no downsampling)
# HINT: when stride > 1 you are downsampling (also known as strided convolution)
x = layers.Conv2D(??, (3, 3), strides=??)(inputs)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
return x
# Create the stem to the neural network
x = stem(inputs)
# Create three residual blocks
for nb_filters in [128, 256, 728]:
x = residual_block_entry(x, nb_filters)
return x
def middleFlow(x):
""" Create the middle flow section
x : input tensor into section
"""
# Create 8 residual blocks, each with 728 filters
for _ in range(8):
x = residual_block_middle(x, ??)
return x
def exitFlow(x):
""" Create the exit flow section
x : input tensor into section
"""
def classifier(x):
""" The output classifier
x : input tensor
"""
# Global Average Pooling will flatten the 10x10 feature maps into 1D
# feature maps
x = layers.??()(x)
# Fully connected output layer (classification)
x = layers.Dense(1000, activation='softmax')(x)
return x
shortcut = x
# First Depthwise Separable Convolution
x = layers.SeparableConv2D(728, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
# Second Depthwise Separable Convolution
x = layers.SeparableConv2D(1024, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Create pooled feature maps, reduce size by 75%
x = layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same')(x)
# Add strided convolution to identity link to double number of filters to
# match output of residual block for the add operation
shortcut = layers.Conv2D(1024, (1, 1), strides=(2, 2),
padding='same')(shortcut)
shortcut = layers.BatchNormalization()(shortcut)
x = layers.add([x, shortcut])
# Third Depthwise Separable Convolution
x = layers.SeparableConv2D(1556, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Fourth Depthwise Separable Convolution
x = layers.SeparableConv2D(2048, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Create classifier section
x = classifier(x)
return x
def residual_block_entry(x, nb_filters):
""" Create a residual block using Depthwise Separable Convolutions
x : input into residual block
nb_filters: number of filters
"""
shortcut = x
# First Depthwise Separable Convolution
x = layers.SeparableConv2D(nb_filters, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Second depthwise Separable Convolution
x = layers.SeparableConv2D(nb_filters, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Create pooled feature maps, reduce size by 75%
x = layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same')(x)
# Add strided convolution to identity link to double number of filters to
# match output of residual block for the add operation
# HINT: this is the identity branch, so what should be the input?
shortcut = layers.Conv2D(nb_filters, (1, 1), strides=(2, 2),
padding='same')(??)
shortcut = layers.BatchNormalization()(shortcut)
x = layers.add([x, shortcut])
return x
def residual_block_middle(x, nb_filters):
""" Create a residual block using Depthwise Separable Convolutions
x : input into residual block
nb_filters: number of filters
"""
# Remember to save the input for the identity link
# HINT: it's in the params!
shortcut = ??
# First Depthwise Separable Convolution
x = layers.SeparableConv2D(nb_filters, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Second depthwise Separable Convolution
x = layers.SeparableConv2D(nb_filters, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
# Third depthwise Separable Convolution
x = layers.SeparableConv2D(nb_filters, (3, 3), padding='same')(x)
x = layers.BatchNormalization()(x)
x = layers.ReLU()(x)
x = layers.add([x, shortcut])
return x
inputs = Input(shape=(299, 299, 3))
# Create entry section
x = entryFlow(inputs)
# Create the middle section
x = middleFlow(x)
# Create the exit section
outputs = exitFlow(x)
model = Model(inputs, outputs)
```
### Verify the model architecture using summary method
It should look (end) like below:
```
global_average_pooling2d_1 (Glo (None, 2048) 0 re_lu_37[0][0]
__________________________________________________________________________________________________
dense_1 (Dense) (None, 1000) 2049000 global_average_pooling2d_1[0][0]
==================================================================================================
Total params: 22,981,736
Trainable params: 22,927,232
Non-trainable params: 54,504
```
```
model.summary()
```
## End of Code Lab
|
github_jupyter
|
# Hypothesis Testing
```
set.seed(37)
```
## Student's t-test
The `Student's t-test` compares the means of two samples to see if they are different. Here is a `two-sided` Student's t-test.
```
x <- rnorm(1000, mean=0, sd=1)
y <- rnorm(1000, mean=1, sd=1)
r <- t.test(x, y, alternative='two.sided')
print(r)
```
Here is a directional Student's t-test to see if the mean of `x` is greater than the mean of `y`.
```
x <- rnorm(1000, mean=0, sd=1)
y <- rnorm(1000, mean=1, sd=1)
r <- t.test(x, y, alternative='greater')
print(r)
```
Here is a directional Student's t-test to see if the mean of `x` is less than the mean of `y`.
```
x <- rnorm(1000, mean=0, sd=1)
y <- rnorm(1000, mean=1, sd=1)
r <- t.test(x, y, alternative='less')
print(r)
```
We may also perform a `one-sample` Student's t-test.
```
x <- rnorm(1000, mean=0, sd=1)
r <- t.test(x, mu=5)
print(r)
```
If your data is in long format, you may use a formula to perform a Student's t-test.
```
data <- data.frame(
score = c(90, 89, 70, 99, 100, 77, 80, 67, 70),
gender = c(rep('girl', 5), rep('boy', 4))
)
r <- t.test(score ~ gender, data=data)
print(r)
```
## Wilcoxon U-Test
The `Wilcoxon U-Test` is non-parametric test used to compare two samples. The function `wilcox.text` behaves the same way as the `t.test` function.
```
x <- rnorm(1000, mean=0, sd=1)
y <- rnorm(1000, mean=0.5, sd=1)
r <- wilcox.test(x, y)
print(r)
```
## Correlation
May also compute correlation and test the it as well.
```
x <- seq(1, 1000)
y <- x * 2 + rnorm(1000, mean=5, sd=5)
c <- cor(x, y)
print(c)
```
We compute the covariance with the `cov` function.`
```
x <- seq(1, 1000)
y <- x * 2 + rnorm(1000, mean=5, sd=5)
c <- cov(x, y)
print(c)
```
We compute the significance with `cor.test`.
```
x <- seq(1, 1000)
y <- x * 2 + rnorm(1000, mean=5, sd=5)
r <- cor.test(x, y)
print(r)
```
## Chi-squared test
A `Chi-squared` test is used to test for association with contigency tables.
```
df <- data.frame(
rural = c(10, 15, 12),
urban = c(20, 30, 25),
row.names=c('DC', 'MD', 'VA')
)
r <- chisq.test(df)
print(r)
```
A `goodness of fit` test using the `Chi-squared test` is performed as follows.
```
df <- data.frame(
rural = c(10, 15, 12),
urban = c(20, 30, 25),
row.names=c('DC', 'MD', 'VA')
)
r <- chisq.test(df$rural, p=df$urban, rescale.p=TRUE)
print(r)
```
## Analysis of variance
### One-way analysis of variance
A one-way `analysis of variance` (`AOV`) may be conducted as follows.
```
library(tidyr)
df <- data.frame(
city = c('A', 'B', 'C', 'D', 'E'),
urban = c(20, 25, 22, 24, 21),
rural = c(10, 15, 12, 14, 11),
suburb = c(15, 18, 19, 20, 17)
)
df <- df %>% pivot_longer(-city, names_to='location', values_to='expense')
r <- aov(expense ~ location, data=df)
print(r)
print('-- summary below --')
print(summary(r))
```
#### Post-hoc test
We apply `Tukey's Honestly Significant Difference` (`HSD`) test to see which pairs differ.
```
t <- TukeyHSD(r)
print(t)
```
#### Obtaining the effects
```
e <- model.tables(r, type='effects')
print(e)
```
#### Obtaining the means
```
m <- model.tables(r, type='means')
print(m)
```
#### Visualizing the means
```
options(repr.plot.width=4, repr.plot.height=4)
boxplot(expense ~ location, data=df)
```
#### Visualizing the differences
```
options(repr.plot.width=5, repr.plot.height=3)
op = par(mar = c(5, 8, 4, 2))
plot(t, cex=0.2, las=1)
par(op)
```
### Two-way ANOVA
```
suppressMessages({
library('dplyr')
})
N = 5
a <- 5 + 20 * rnorm(N, mean=20, sd=1) + 4 * rnorm(N, mean=4, sd=1) # urban-high
b <- 5 + 18 * rnorm(N, mean=18, sd=1) + 2 * rnorm(N, mean=2, sd=1) # urban-low
c <- 5 + 10 * rnorm(N, mean=10, sd=1) + 4 * rnorm(N, mean=4, sd=1) # suburban-high
d <- 5 + 8 * rnorm(N, mean=8, sd=1) + 2 * rnorm(N, mean=2, sd=1) # suburban-low
e <- 5 + 5 * rnorm(N, mean=5, sd=1) + 4 * rnorm(N, mean=4, sd=1) # rural-high
f <- 5 + 3 * rnorm(N, mean=3, sd=1) + 2 * rnorm(N, mean=2, sd=1) # rural-low
df <- data.frame(
expense=c(a, b, c, d, e, f),
location=c(rep('urban', 2*N), rep('suburban', 2*N), rep('rural', 2*N)),
income=c(rep('high', N), rep('low', N), rep('high', N), rep('low', N), rep('high', N), rep('low', N)),
stringsAsFactors=TRUE
)
r <- aov(expense ~ location * income, data=df)
print(r)
print('-- summary below --')
print(summary(r))
```
#### Two-Way ANOVA post-hoc
```
t <- TukeyHSD(r)
print(t)
```
#### Two-Way ANOVA effects
```
e <- model.tables(r, type='effects')
print(e)
```
#### Two-Way ANOVA means
```
m <- model.tables(r, type='means')
print(m)
```
#### Two-Way ANOVA means visualization
```
options(repr.plot.width=5, repr.plot.height=5)
op = par(mar = c(8, 4, 4, 2))
boxplot(expense ~ location * income, data = df, cex.axis = 0.9, las=2, xlab='')
par(op)
```
#### Two-Way ANOVA differences visualization
```
options(repr.plot.width=5, repr.plot.height=3)
op = par(mar = c(5, 14, 4, 2))
plot(t, cex=0.2, las=1)
par(op)
```
#### Two-Way ANOVA interaction plot
```
options(repr.plot.width=5, repr.plot.height=5)
attach(df)
interaction.plot(location, income, expense)
detach(df)
```
|
github_jupyter
|
```
!pip install confluent-kafka==1.7.0
from confluent_kafka.admin import AdminClient, NewTopic, NewPartitions
from confluent_kafka import KafkaException
import sys
from uuid import uuid4
bootstrap_server = "kafka:9092" # Brokers act as cluster entripoints
conf = {'bootstrap.servers': bootstrap_server}
a = AdminClient(conf)
md = a.list_topics(timeout=10)
print(" {} topics:".format(len(md.topics)))
for t in iter(md.topics.values()):
if t.error is not None:
errstr = ": {}".format(t.error)
else:
errstr = ""
print(" \"{}\" with {} partition(s){}".format(t, len(t.partitions), errstr))
from confluent_kafka import SerializingProducer
from confluent_kafka.serialization import *
import time
topic = "RoboticArm"
def delivery_report(err, msg):
if err is not None:
print("Failed to deliver message: {}".format(err))
else:
print("Produced record to topic {} partition [{}] @ offset {}"
.format(msg.topic(), msg.partition(), msg.offset()))
producer_conf = {
'bootstrap.servers': bootstrap_server,
'key.serializer': StringSerializer('utf_8'),
'value.serializer': StringSerializer('utf_8')
}
producer = SerializingProducer(producer_conf)
```
## run the following cell to loop across the data
they are the same data as those in the EPL example only the time flows at half of the speed
```
import json
from IPython.display import clear_output
def send(value):
key = None
producer.produce(topic=topic, value=json.dumps(value), key=key, on_delivery=delivery_report)
print(value)
producer.poll(1)
clear_output(wait=True)
while True:
send({"id":"1", "status":"ready", "stressLevel": 0, "ts": int(time.time())})
time.sleep(2)
send({"id":"1", "status": "goodGrasped", "stressLevel": 1, "ts": int(time.time())})
time.sleep(2)
ts = int(time.time())
send({"id":"1", "status":"movingGood", "stressLevel": 7, "ts": ts})
send({"id":"2", "status":"ready", "stressLevel": 0, "ts": ts })
time.sleep(2)
send({"id":"2", "status":"goodGrasped", "stressLevel": 5, "ts": int(time.time()) })
time.sleep(1)
send({"id":"2", "status":"movingGood", "stressLevel": 9, "ts": int(time.time()) })
time.sleep(10)
ts = int(time.time())
send({"id":"1", "status":"placingGood", "stressLevel": 3, "ts": ts})
send({"id":"2", "status":"placingGood", "stressLevel": 3, "ts": ts })
time.sleep(8)
ts = int(time.time())
send({"id":"1", "status":"moving", "stressLevel": 2, "ts": ts})
send({"id":"2", "status":"moving", "stressLevel": 1, "ts": ts })
time.sleep(6)
ts = int(time.time())
send({"id":"1", "status":"ready", "stressLevel": 0, "ts": ts})
send({"id":"2", "status":"ready", "stressLevel": 0, "ts": ts })
time.sleep(2)
```
to interrupt the execution of the cell, prese the square icon in the bar or choose *interrupt kernel* from the *kernel* dropdown menu
|
github_jupyter
|
```
#default_exp dispatch
#export
from fastcore.imports import *
from fastcore.foundation import *
from fastcore.utils import *
from nbdev.showdoc import *
from fastcore.test import *
```
# Type dispatch
> Basic single and dual parameter dispatch
## Helpers
```
#exports
def type_hints(f):
"Same as `typing.get_type_hints` but returns `{}` if not allowed type"
return typing.get_type_hints(f) if isinstance(f, typing._allowed_types) else {}
#export
def anno_ret(func):
"Get the return annotation of `func`"
if not func: return None
ann = type_hints(func)
if not ann: return None
return ann.get('return')
#hide
def f(x) -> float: return x
test_eq(anno_ret(f), float)
def f(x) -> typing.Tuple[float,float]: return x
test_eq(anno_ret(f), typing.Tuple[float,float])
def f(x) -> None: return x
test_eq(anno_ret(f), NoneType)
def f(x): return x
test_eq(anno_ret(f), None)
test_eq(anno_ret(None), None)
#export
cmp_instance = functools.cmp_to_key(lambda a,b: 0 if a==b else 1 if issubclass(a,b) else -1)
td = {int:1, numbers.Number:2, numbers.Integral:3}
test_eq(sorted(td, key=cmp_instance), [numbers.Number, numbers.Integral, int])
#export
def _p2_anno(f):
"Get the 1st 2 annotations of `f`, defaulting to `object`"
hints = type_hints(f)
ann = [o for n,o in hints.items() if n!='return']
while len(ann)<2: ann.append(object)
return ann[:2]
def _f(a): pass
test_eq(_p2_anno(_f), (object,object))
def _f(a, b): pass
test_eq(_p2_anno(_f), (object,object))
def _f(a:None, b)->str: pass
test_eq(_p2_anno(_f), (NoneType,object))
def _f(a:str, b)->float: pass
test_eq(_p2_anno(_f), (str,object))
def _f(a:None, b:str)->float: pass
test_eq(_p2_anno(_f), (NoneType,str))
def _f(a:int, b:int)->float: pass
test_eq(_p2_anno(_f), (int,int))
def _f(self, a:int, b:int): pass
test_eq(_p2_anno(_f), (int,int))
def _f(a:int, b:str)->float: pass
test_eq(_p2_anno(_f), (int,str))
test_eq(_p2_anno(attrgetter('foo')), (object,object))
```
## TypeDispatch -
The following class is the basis that allows us to do type dipatch with type annotations. It contains a dictionary type -> functions and ensures that the proper function is called when passed an object (depending on its type).
```
#export
class _TypeDict:
def __init__(self): self.d,self.cache = {},{}
def _reset(self):
self.d = {k:self.d[k] for k in sorted(self.d, key=cmp_instance, reverse=True)}
self.cache = {}
def add(self, t, f):
"Add type `t` and function `f`"
if not isinstance(t,tuple): t=tuple(L(t))
for t_ in t: self.d[t_] = f
self._reset()
def all_matches(self, k):
"Find first matching type that is a super-class of `k`"
if k not in self.cache:
types = [f for f in self.d if k==f or (isinstance(k,type) and issubclass(k,f))]
self.cache[k] = [self.d[o] for o in types]
return self.cache[k]
def __getitem__(self, k):
"Find first matching type that is a super-class of `k`"
res = self.all_matches(k)
return res[0] if len(res) else None
def __repr__(self): return self.d.__repr__()
def first(self): return first(self.d.values())
#export
class TypeDispatch:
"Dictionary-like object; `__getitem__` matches keys of types using `issubclass`"
def __init__(self, funcs=(), bases=()):
self.funcs,self.bases = _TypeDict(),L(bases).filter(is_not(None))
for o in L(funcs): self.add(o)
self.inst = None
def add(self, f):
"Add type `t` and function `f`"
a0,a1 = _p2_anno(f)
t = self.funcs.d.get(a0)
if t is None:
t = _TypeDict()
self.funcs.add(a0, t)
t.add(a1, f)
def first(self): return self.funcs.first().first()
def returns(self, x): return anno_ret(self[type(x)])
def returns_none(self, x):
r = anno_ret(self[type(x)])
return r if r == NoneType else None
def _attname(self,k): return getattr(k,'__name__',str(k))
def __repr__(self):
r = [f'({self._attname(k)},{self._attname(l)}) -> {getattr(v, "__name__", v.__class__.__name__)}'
for k in self.funcs.d for l,v in self.funcs[k].d.items()]
return '\n'.join(r)
def __call__(self, *args, **kwargs):
ts = L(args).map(type)[:2]
f = self[tuple(ts)]
if not f: return args[0]
if self.inst is not None: f = MethodType(f, self.inst)
return f(*args, **kwargs)
def __get__(self, inst, owner):
self.inst = inst
return self
def __getitem__(self, k):
"Find first matching type that is a super-class of `k`"
k = L(k)
while len(k)<2: k.append(object)
r = self.funcs.all_matches(k[0])
for t in r:
o = t[k[1]]
if o is not None: return o
for base in self.bases:
res = base[k]
if res is not None: return res
return None
def f_col(x:typing.Collection): return x
def f_nin(x:numbers.Integral)->int: return x+1
def f_ni2(x:int): return x
def f_bll(x:(bool,list)): return x
def f_num(x:numbers.Number): return x
t = TypeDispatch([f_nin,f_ni2,f_num,f_bll,None])
t.add(f_ni2) #Should work even if we add the same function twice.
test_eq(t[int], f_ni2)
test_eq(t[np.int32], f_nin)
test_eq(t[str], None)
test_eq(t[float], f_num)
test_eq(t[bool], f_bll)
test_eq(t[list], f_bll)
t.add(f_col)
test_eq(t[str], f_col)
test_eq(t[np.int32], f_nin)
o = np.int32(1)
test_eq(t(o), 2)
test_eq(t.returns(o), int)
assert t.first() is not None
t
```
If `bases` is set to a collection of `TypeDispatch` objects, then they are searched matching functions if no match is found in this object.
```
def f_str(x:str): return x+'1'
t2 = TypeDispatch(f_str, bases=t)
test_eq(t2[int], f_ni2)
test_eq(t2[np.int32], f_nin)
test_eq(t2[float], f_num)
test_eq(t2[bool], f_bll)
test_eq(t2[str], f_str)
test_eq(t2('a'), 'a1')
test_eq(t2[np.int32], f_nin)
test_eq(t2(o), 2)
test_eq(t2.returns(o), int)
def m_nin(self, x:(str,numbers.Integral)): return str(x)+'1'
def m_bll(self, x:bool): self.foo='a'
def m_num(self, x:numbers.Number): return x
t = TypeDispatch([m_nin,m_num,m_bll])
class A: f = t
a = A()
test_eq(a.f(1), '11')
test_eq(a.f(1.), 1.)
test_is(a.f.inst, a)
a.f(False)
test_eq(a.foo, 'a')
test_eq(a.f(()), ())
def m_tup(self, x:tuple): return x+(1,)
t2 = TypeDispatch(m_tup, t)
class A2: f = t2
a2 = A2()
test_eq(a2.f(1), '11')
test_eq(a2.f(1.), 1.)
test_is(a2.f.inst, a2)
a2.f(False)
test_eq(a2.foo, 'a')
test_eq(a2.f(()), (1,))
def f1(x:numbers.Integral, y): return x+1
def f2(x:int, y:float): return x+y
t = TypeDispatch([f1,f2])
test_eq(t[int], f1)
test_eq(t[int,int], f1)
test_eq(t[int,float], f2)
test_eq(t[float,float], None)
test_eq(t[np.int32,float], f1)
test_eq(t(3,2.0), 5)
test_eq(t(3,2), 4)
test_eq(t('a'), 'a')
t
```
## typedispatch Decorator
```
#export
class DispatchReg:
"A global registry for `TypeDispatch` objects keyed by function name"
def __init__(self): self.d = defaultdict(TypeDispatch)
def __call__(self, f):
nm = f'{f.__qualname__}'
self.d[nm].add(f)
return self.d[nm]
typedispatch = DispatchReg()
@typedispatch
def f_td_test(x, y): return f'{x}{y}'
@typedispatch
def f_td_test(x:numbers.Integral, y): return x+1
@typedispatch
def f_td_test(x:int, y:float): return x+y
test_eq(f_td_test(3,2.0), 5)
test_eq(f_td_test(3,2), 4)
test_eq(f_td_test('a','b'), 'ab')
```
## Casting
Now that we can dispatch on types, let's make it easier to cast objects to a different type.
```
#export
_all_=['cast']
#export
def retain_meta(x, res):
"Call `res.set_meta(x)`, if it exists"
if hasattr(res,'set_meta'): res.set_meta(x)
return res
#export
def default_set_meta(self, x):
"Copy over `_meta` from `x` to `res`, if it's missing"
if hasattr(x, '_meta') and not hasattr(self, '_meta'): self._meta = x._meta
return self
#export
@typedispatch
def cast(x, typ):
"cast `x` to type `typ` (may also change `x` inplace)"
res = typ._before_cast(x) if hasattr(typ, '_before_cast') else x
if isinstance(res, ndarray): res = res.view(typ)
elif hasattr(res, 'as_subclass'): res = res.as_subclass(typ)
else:
try: res.__class__ = typ
except: res = typ(res)
return retain_meta(x, res)
```
This works both for plain python classes:...
```
mk_class('_T1', 'a')
class _T2(_T1): pass
t = _T1(a=1)
t2 = cast(t, _T2)
test_eq_type(_T2(a=1), t2)
```
...as well as for arrays and tensors.
```
class _T1(ndarray): pass
t = array([1])
t2 = cast(t, _T1)
test_eq(array([1]), t2)
test_eq(_T1, type(t2))
```
To customize casting for other types, define a separate `cast` function with `typedispatch` for your type.
```
#export
def retain_type(new, old=None, typ=None):
"Cast `new` to type of `old` or `typ` if it's a superclass"
# e.g. old is TensorImage, new is Tensor - if not subclass then do nothing
if new is None: return
assert old is not None or typ is not None
if typ is None:
if not isinstance(old, type(new)): return new
typ = old if isinstance(old,type) else type(old)
# Do nothing the new type is already an instance of requested type (i.e. same type)
if typ==NoneType or isinstance(new, typ): return new
return retain_meta(old, cast(new, typ))
class _T(tuple): pass
a = _T((1,2))
b = tuple((1,2))
test_eq_type(retain_type(b, typ=_T), a)
```
If `old` has a `_meta` attribute, its content is passed when casting `new` to the type of `old`.
```
class _A():
set_meta = default_set_meta
def __init__(self, t): self.t=t
class _B1(_A):
def __init__(self, t, a=1):
super().__init__(t)
self._meta = {'a':a}
x = _B1(1, a=2)
b = _A(1)
test_eq(retain_type(b, old=x)._meta, {'a': 2})
a = {L: [int, tuple]}
first(a.keys())
#export
def retain_types(new, old=None, typs=None):
"Cast each item of `new` to type of matching item in `old` if it's a superclass"
if not is_listy(new): return retain_type(new, old, typs)
if typs is not None:
if isinstance(typs, dict):
t = first(typs.keys())
typs = typs[t]
else: t,typs = typs,None
else: t = type(old) if old is not None and isinstance(old,type(new)) else type(new)
return t(L(new, old, typs).map_zip(retain_types, cycled=True))
class T(tuple): pass
t1,t2 = retain_types((1,(1,(1,1))), (2,T((2,T((3,4))))))
test_eq_type(t1, 1)
test_eq_type(t2, T((1,T((1,1)))))
t1,t2 = retain_types((1,(1,(1,1))), typs = {tuple: [int, {T: [int, {T: [int,int]}]}]})
test_eq_type(t1, 1)
test_eq_type(t2, T((1,T((1,1)))))
#export
def explode_types(o):
"Return the type of `o`, potentially in nested dictionaries for thing that are listy"
if not is_listy(o): return type(o)
return {type(o): [explode_types(o_) for o_ in o]}
test_eq(explode_types((2,T((2,T((3,4)))))), {tuple: [int, {T: [int, {T: [int,int]}]}]})
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
# Scalars
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
```
## Integers
### Binary representation of integers
```
format(16, '032b')
```
### Bit shifting
```
format(16 >> 2, '032b')
16 >> 2
format(16 << 2, '032b')
16 << 2
```
### Overflow
In general, the computer representation of integers has a limited range, and may overflow. The range depends on whether the integer is signed or unsigned.
For example, with 8 bits, we can represent at most $2^8 = 256$ integers.
- 0 to 255 unsigned
- -128 ti 127 signed
Signed integers
```
np.arange(130, dtype=np.int8)[-5:]
```
Unsigned integers
```
np.arange(130, dtype=np.uint8)[-5:]
np.arange(260, dtype=np.uint8)[-5:]
```
### Integer division
In Python 2 or other languages such as C/C++, be very careful when dividing as the division operator `/` performs integer division when both numerator and denominator are integers. This is rarely what you want. In Python 3 the `/` always performs floating point division, and you use `//` for integer division, removing a common source of bugs in numerical calculations.
```
%%python2
import numpy as np
x = np.arange(10)
print(x/10)
```
Python 3 does the "right" thing.
```
x = np.arange(10)
x/10
```
## Real numbers
Real numbers are represented as **floating point** numbers. A floating point number is stored in 3 pieces (sign bit, exponent, mantissa) so that every float is represetned as get +/- mantissa ^ exponent. Because of this, the interval between consecutive numbers is smallest (high precison) for numebrs close to 0 and largest for numbers close to the lower and upper bounds.
Because exponents have to be singed to represent both small and large numbers, but it is more convenint to use unsigned numbers here, the exponnent has an offset (also knwnn as the exponentn bias). For example, if the expoennt is an unsigned 8-bit number, it can rerpesent the range (0, 255). By using an offset of 128, it will now represent the range (-127, 128).

**Note**: Intervals between consecutive floating point numbers are not constant. In particular, the precision for small numbers is much larger than for large numbers. In fact, approximately half of all floating point numbers lie between -1 and 1 when using the `double` type in C/C++ (also the default for `numpy`).
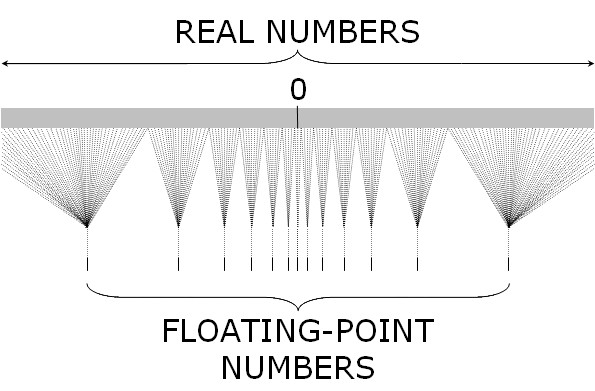
Because of this, if you are adding many numbers, it is more accurate to first add the small numbers before the large numbers.
#### IEEE 754 32-bit floating point representation

See [Wikipedia](https://en.wikipedia.org/wiki/Single-precision_floating-point_format) for how this binary number is evaluated to 0.15625.
```
from ctypes import c_int, c_float
s = c_int.from_buffer(c_float(0.15625)).value
s = format(s, '032b')
s
rep = {
'sign': s[:1],
'exponent' : s[1:9:],
'fraction' : s[9:]
}
rep
```
### Most base 10 real numbers are approximations
This is simply because numbers are stored in finite-precision binary format.
```
'%.20f' % (0.1 * 0.1 * 100)
```
### Never check for equality of floating point numbers
```
i = 0
loops = 0
while i != 1:
i += 0.1 * 0.1
loops += 1
if loops == 1000000:
break
i
i = 0
loops = 0
while np.abs(1 - i) > 1e-6:
i += 0.1 * 0.1
loops += 1
if loops == 1000000:
break
i
```
### Associative law does not necessarily hold
```
6.022e23 - 6.022e23 + 1
1 + 6.022e23 - 6.022e23
```
### Distributive law does not hold
```
a = np.exp(1)
b = np.pi
c = np.sin(1)
a*(b+c)
a*b + a*c
```
### Catastrophic cancellation
Consider calculating sample variance
$$
s^2= \frac{1}{n(n-1)}\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i)^2
$$
Be careful whenever you calculate the difference of potentially big numbers.
```
def var(x):
"""Returns variance of sample data using sum of squares formula."""
n = len(x)
return (1.0/(n*(n-1))*(n*np.sum(x**2) - (np.sum(x))**2))
```
### Underflow
```
np.warnings.filterwarnings('ignore')
np.random.seed(4)
xs = np.random.random(1000)
ys = np.random.random(1000)
np.prod(xs)/np.prod(ys)
```
#### Prevent underflow by staying in log space
```
x = np.sum(np.log(xs))
y = np.sum(np.log(ys))
np.exp(x - y)
```
### Overflow
```
np.exp(1000)
```
### Numerically stable algorithms
#### What is the sample variance for numbers from a normal distribution with variance 1?
```
np.random.seed(15)
x_ = np.random.normal(0, 1, int(1e6))
x = 1e12 + x_
var(x)
```
#### Use functions from numerical libraries where available
```
np.var(x)
```
There is also a variance function in the standard library, but it is slower for large arrays.
```
import statistics
statistics.variance(x)
```
Note that `numpy` uses does not use the asymptotically unbiased estimator by default. If you want the unbiased variance, set `ddof` to 1.
```
np.var([1,2,3,4], ddof=1)
statistics.variance([1,2,3,4])
```
### Useful numerically stable functions
Let's calculate
$$
\log(e^{1000} + e^{1000})
$$
Using basic algebra, we get the solution $\log(2) + 1000$.
\begin{align}
\log(e^{1000} + e^{1000}) &= \log(e^{0}e^{1000} + e^{0}e^{1000}) \\
&= \log(e^{100}(e^{0} + e^{0})) \\
&= \log(e^{1000}) + \log(e^{0} + e^{0}) \\
&= 1000 + \log(2)
\end{align}
**logaddexp**
```
x = np.array([1000, 1000])
np.log(np.sum(np.exp(x)))
np.logaddexp(*x)
```
**logsumexp**
This function generalizes `logaddexp` to an arbitrary number of addends and is useful in a variety of statistical contexts.
Suppose we need to calculate a probability distribution $\pi$ parameterized by a vector $x$
$$
\pi_i = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}
$$
Taking logs, we get
$$
\log(\pi_i) = x_i - \log{\sum_{j=1}^n e^{x_j}}
$$
```
x = 1e6*np.random.random(100)
np.log(np.sum(np.exp(x)))
from scipy.special import logsumexp
logsumexp(x)
```
**logp1 and expm1**
```
np.exp(np.log(1 + 1e-6)) - 1
np.expm1(np.log1p(1e-6))
```
**sinc**
```
x = 1
np.sin(x)/x
np.sinc(x)
x = np.linspace(0.01, 2*np.pi, 100)
plt.plot(x, np.sinc(x), label='Library function')
plt.plot(x, np.sin(x)/x, label='DIY function')
plt.legend()
pass
```
|
github_jupyter
|
#Introduction to the Research Environment
The research environment is powered by IPython notebooks, which allow one to perform a great deal of data analysis and statistical validation. We'll demonstrate a few simple techniques here.
##Code Cells vs. Text Cells
As you can see, each cell can be either code or text. To select between them, choose from the 'Cell Type' dropdown menu on the top left.
###This is a test
Oh, so amazing
Incluso se puede usar ${{LaTeX}}:$
$$x=\frac{-b \pm \sqrt{b^2 -4(a)(c)}}{2(a)}$$
$$\text{Incluso podemos escribir}$$
##Executing a Command
A code cell will be evaluated when you press play, or when you press the shortcut, shift-enter. Evaluating a cell evaluates each line of code in sequence, and prints the results of the last line below the cell.
```
2 + 2
6 + 6
```
Sometimes there is no result to be printed, as is the case with assignment.
```
X = 2
W = 10
```
Remember that only the result from the last line is printed.
```
2 + 2
3 + 3
6 + 6
7 + 7
```
However, you can print whichever lines you want using the `print` statement.
```
print (2 + 2)
3 + 3
print (4 + 4)
5 + 5
```
##Knowing When a Cell is Running
While a cell is running, a `[*]` will display on the left. When a cell has yet to be executed, `[ ]` will display. When it has been run, a number will display indicating the order in which it was run during the execution of the notebook `[5]`. Try on this cell and note it happening.
```
#Take some time to run something
c = 0
for i in range(10000000):
c = c + i
c
c = 1
for i in range(10):
c = c * (i+1)
c
```
##Importing Libraries
The vast majority of the time, you'll want to use functions from pre-built libraries. You can't import every library on Quantopian due to security issues, but you can import most of the common scientific ones. Here I import numpy and pandas, the two most common and useful libraries in quant finance. I recommend copying this import statement to every new notebook.
Notice that you can rename libraries to whatever you want after importing. The `as` statement allows this. Here we use `np` and `pd` as aliases for `numpy` and `pandas`. This is a very common aliasing and will be found in most code snippets around the web. The point behind this is to allow you to type fewer characters when you are frequently accessing these libraries.
```
import numpy as np
import pandas as pd
# This is a plotting library for pretty pictures.
import matplotlib.pyplot as plt
import cython as cy
import pandas_datareader as pdr
import datetime
import xarray as xa
```
##Tab Autocomplete
Pressing tab will give you a list of IPython's best guesses for what you might want to type next. This is incredibly valuable and will save you a lot of time. If there is only one possible option for what you could type next, IPython will fill that in for you. Try pressing tab very frequently, it will seldom fill in anything you don't want, as if there is ambiguity a list will be shown. This is a great way to see what functions are available in a library.
Try placing your cursor after the `.` and pressing tab.
```
np.random.normal
np.random.binomial
```
##Getting Documentation Help
Placing a question mark after a function and executing that line of code will give you the documentation IPython has for that function. It's often best to do this in a new cell, as you avoid re-executing other code and running into bugs.
```
np.random.normal?
np.test?
```
##Sampling
We'll sample some random data using a function from `numpy`.
```
# Sample 100 points with a mean of 0 and an std of 1. This is a standard normal distribution.
X = np.random.normal(0, 1, 100)
print(X)
W = np.random.lognormal(0,1,100)
print(W)
```
##Plotting
We can use the plotting library we imported as follows.
```
plt.plot(X)
plt.plot(W)
```
###Squelching Line Output
You might have noticed the annoying line of the form `[<matplotlib.lines.Line2D at 0x7f72fdbc1710>]` before the plots. This is because the `.plot` function actually produces output. Sometimes we wish not to display output, we can accomplish this with the semi-colon as follows.
```
plt.plot(X);
plt.plot(W);
```
###Adding Axis Labels
No self-respecting quant leaves a graph without labeled axes. Here are some commands to help with that.
```
X = np.random.normal(0, 1, 100)
X2 = np.random.normal(0, 1, 100)
plt.plot(X);
plt.plot(X2);
plt.xlabel('Time') # The data we generated is unitless, but don't forget units in general.
plt.ylabel('Returns')
plt.legend(['X', 'X2']);
W = np.random.lognormal(0, 1, 100)
W2 = np.random.lognormal(0, 1, 100)
plt.plot(W);
plt.plot(W2);
plt.xlabel('Time') # The data we generated is unitless, but don't forget units in general.
plt.ylabel('Returns')
plt.legend(['W', 'W2']);
```
##Generating Statistics
Let's use `numpy` to take some simple statistics.
```
np.mean(X)
np.std(X)
np.mean(W)
np.std(W)
```
##Getting Real Pricing Data
Randomly sampled data can be great for testing ideas, but let's get some real data. We can use `get_pricing` to do that. You can use the `?` syntax as discussed above to get more information on `get_pricing`'s arguments.
```
#No Funciona :c
#get_pricing?
#data = get_pricing('MSFT', start_date='2012-1-1', end_date='2015-6-1')
pdr.get_data_yahoo?
data = pdr.get_data_yahoo('MSFT', start=datetime.datetime(2020, 1, 1),
end=datetime.datetime(2021,1,1))
pdr.get_data_yahoo?
mi_ejemplo = pdr.get_data_yahoo('LNVGY', start=datetime.datetime(2020, 1, 1),
end=datetime.datetime(2021,1,1))
```
Our data is now a dataframe. You can see the datetime index and the colums with different pricing data.
```
data
mi_ejemplo
```
This is a pandas dataframe, so we can index in to just get price like this. For more info on pandas, please [click here](http://pandas.pydata.org/pandas-docs/stable/10min.html).
```
X = data['Close']
Y= mi_ejemplo['Close']
```
Because there is now also date information in our data, we provide two series to `.plot`. `X.index` gives us the datetime index, and `X.values` gives us the pricing values. These are used as the X and Y coordinates to make a graph.
```
plt.plot(X.index, X.values)
plt.ylabel('Price')
plt.legend(['MSFT']);
plt.plot(X.index, X.values)
plt.ylabel('Precio')
plt.legend(['LNVGY']);
```
We can get statistics again on real data.
```
np.mean(X)
np.mean(Y)
np.std(X)
np.std(Y)
```
##Getting Returns from Prices
We can use the `pct_change` function to get returns. Notice how we drop the first element after doing this, as it will be `NaN` (nothing -> something results in a NaN percent change).
```
R = X.pct_change()[1:]
T = Y.pct_change()[1:]
```
We can plot the returns distribution as a histogram.
```
plt.hist(R, bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['MSFT Returns']);
plt.hist(T, bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['LNVGY Returns']);
```
Get statistics again.
```
np.mean(R)
np.mean(T)
np.std(R)
np.std(T)
```
Now let's go backwards and generate data out of a normal distribution using the statistics we estimated from Microsoft's returns. We'll see that we have good reason to suspect Microsoft's returns may not be normal, as the resulting normal distribution looks far different.
```
plt.hist(np.random.normal(np.mean(R), np.std(R), 10000), bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['Normally Distributed Returns']);
plt.hist(np.random.normal(np.mean(T), np.std(T), 10000), bins=20)
plt.xlabel('Return')
plt.ylabel('Frequency')
plt.legend(['Normally Distributed Returns']);
```
##Generating a Moving Average
`pandas` has some nice tools to allow us to generate rolling statistics. Here's an example. Notice how there's no moving average for the first 60 days, as we don't have 60 days of data on which to generate the statistic.
```
##Rolling_mean ya se dejó de usar!!!!
# Take the average of the last 60 days at each timepoint.
#MAVG = pd.rolling_mean(X, window=60)
#plt.plot(X.index, X.values)
#plt.plot(MAVG.index, MAVG.values)
#plt.ylabel('Price')
#plt.legend(['MSFT', '60-day MAVG']);
MAVG = X.rolling(60).mean()
plt.plot(X.index, X.values)
plt.plot(MAVG.index, MAVG.values)
plt.ylabel('Price')
plt.legend(['MSFT', '60-day MAVG']);
SPRT = Y.rolling(60).mean()
plt.plot(Y.index, Y.values)
plt.plot(SPRT.index, SPRT.values)
plt.ylabel('Price')
plt.legend(['LNVGY', '60-day SPRT']);
```
This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.
|
github_jupyter
|
## GMLS-Nets: 1D Regression of Linear and Non-linear Operators $L[u]$.
__Ben J. Gross__, __Paul J. Atzberger__ <br>
http://atzberger.org/
Examples showing how GMLS-Nets can be used to perform regression for some basic linear and non-linear differential operators in 1D.
__Parameters:__</span> <br>
The key parameter terms to adjust are:<br>
``op_type``: The operator type.<br>
``flag_mlp_case``: The type of mapping unit to use.<br>
__Examples of Non-linear Operators ($u{u_x},u_x^2,u{u_{xx}},u_{xx}^2$) :__<br>
To run training for a non-linear operator like ``u*ux`` using MLP for the non-linear GMLS mapping unit, you can use:<br>
``op_type='u*ux';`` <br>
``flag_mlp_case = 'NonLinear1';`` <br>
You can obtain different performance by adjusting the mapping architecture and hyperparameters of the network.
__Examples of linear Operators ($u_x,u_{xx}$):__<br>
To run training for a linear operator like the 1d Laplacian ``uxx`` with a linear mapping unit, you can use<br>
``op_type='uxx';``<br>
``flag_mlp_case = 'Linear1';``<br>
These are organized for different combinations of these settings allowing for exploring the methods. The codes are easy to modify and adjust to also experiment with other operators. For example, see the dataset classes.
### Imports
```
import sys;
# setup path to location of gmlsnets_pytorch (if not install system-wide)
path_gmlsnets_pytorch = '../../';
sys.path.append(path_gmlsnets_pytorch);
import torch;
import torch.nn as nn;
import numpy as np;
import pickle;
import matplotlib.pyplot as plt;
import pdb
import time
import os
# setup gmlsnets package
import gmlsnets_pytorch as gmlsnets;
import gmlsnets_pytorch.nn;
import gmlsnets_pytorch.vis;
import gmlsnets_pytorch.dataset;
# dereference a few common items
MapToPoly_Function = gmlsnets.nn.MapToPoly_Function;
get_num_polys = MapToPoly_Function.get_num_polys;
weight_one_minus_r = MapToPoly_Function.weight_one_minus_r;
eval_poly = MapToPoly_Function.eval_poly;
print("Packages:");
print("torch.__version__ = " + str(torch.__version__));
print("numpy.__version__ = " + str(np.__version__));
print("gmlsnets.__version__ = " + str(gmlsnets.__version__));
```
### Parameters and basic setup
```
# Setup the parameters
batch_size = int(1e2);
flag_extend_periodic = False; # periodic boundaries
flag_dataset = 'diffOp1';
run_name = '%s_Test1'%flag_dataset;
base_dir = './output/regression_diff_op_1d/%s'%run_name;
flag_print_model = False;
print("Settings:");
print("flag_dataset = " + flag_dataset);
print("run_name = " + run_name);
print("base_dir = " + base_dir);
if not os.path.exists(base_dir):
os.makedirs(base_dir);
# Configure devices
if torch.cuda.is_available():
num_gpus = torch.cuda.device_count();
print("num_gpus = " + str(num_gpus));
if num_gpus >= 4:
device = torch.device('cuda:3');
else:
device = torch.device('cuda:0');
else:
device = torch.device('cpu');
print("device = " + str(device));
```
### Setup GMLS-Net for regressing differential operator
```
class gmlsNetRegressionDiffOp1(nn.Module):
"""Sets up a GMLS-Net for regression differential operator in 1D."""
def __init__(self,
flag_GMLS_type=None,
porder1=None,Nc=None,
pts_x1=None,layer1_epsilon=None,
weight_func1=None,weight_func1_params=None,
mlp_q1=None,pts_x2=None,
device=None,flag_verbose=0,
**extra_params):
super(gmlsNetRegressionDiffOp1, self).__init__();
self.layer_types = [];
if device is None:
device = torch.device('cpu'); # default
# --
Ncp1 = mlp_q1.channels_out; # number of channels out of the MLP-Pointwise layer
num_features1 = mlp_q1.channels_out; # number of channels out (16 typical)
GMLS_Layer = gmlsnets.nn.GMLS_Layer;
ExtractFromTuple = gmlsnets.nn.ExtractFromTuple;
PermuteLayer = gmlsnets.nn.PermuteLayer;
PdbSetTraceLayer = gmlsnets.nn.PdbSetTraceLayer;
# --- Layer 1
#flag_layer1 = 'standard_conv1';
flag_layer1 = 'gmls1d_1';
self.layer_types.append(flag_layer1);
if flag_layer1 == 'standard_conv1':
self.layer1 = nn.Sequential(
nn.Conv1d(in_channels=Nc,out_channels=num_features1,
kernel_size=5,stride=1,padding=2,bias=False),
).to(device);
elif flag_layer1 == 'gmls1d_1':
self.layer1 = nn.Sequential(
GMLS_Layer(flag_GMLS_type, porder1,
pts_x1, layer1_epsilon,
weight_func1, weight_func1_params,
mlp_q=mlp_q1, pts_x2=pts_x2, device=device,
flag_verbose=flag_verbose),
#PdbSetTraceLayer(),
ExtractFromTuple(index=0), # just get the forward output associated with the mapping and not pts_x2
#PdbSetTraceLayer(),
PermuteLayer((0,2,1))
).to(device);
else:
raise Exception('flag_layer1 type not recognized.');
def forward(self, x):
out = self.layer1(x);
return out;
```
### Setup the Model: Neural Network
```
# setup sample point locations
xj = torch.linspace(0,1.0,steps=101,device=device).unsqueeze(1);
xi = torch.linspace(0,1.0,steps=101,device=device).unsqueeze(1);
# make a numpy copy for plotting and some other routines
np_xj = xj.cpu().numpy(); np_xi = xi.cpu().numpy();
# setup parameters
Nc = 1; # scalar field
Nx = xj.shape[0]; num_dim = xj.shape[1];
porder = 2; num_polys = get_num_polys(porder,num_dim);
weight_func1 = MapToPoly_Function.weight_one_minus_r;
targ_kernel_width = 11.5; layer1_epsilon = 0.4*0.5*np.sqrt(2)*targ_kernel_width/Nx;
#targ_kernel_width = 21.5; layer1_epsilon = 0.4*0.5*np.sqrt(2)*targ_kernel_width/Nx;
weight_func1_params = {'epsilon': layer1_epsilon,'p':4};
color_input = (0.05,0.44,0.69);
color_output = (0.44,0.30,0.60);
color_predict = (0.05,0.40,0.5);
color_target = (221/255,103/255,103/255);
# print the current settings
print("GMLS Parameters:")
print("porder = " + str(porder));
print("num_dim = " + str(num_dim));
print("num_polys = " + str(num_polys));
print("layer1_epsilon = %.3e"%layer1_epsilon);
print("weight_func1 = " + str(weight_func1));
print("weight_func1_params = " + str(weight_func1_params));
print("xj.shape = " + str(xj.shape));
print("xi.shape = " + str(xi.shape));
# create an MLP for training the non-linear part of the GMLS Net
#flag_mlp_case = 'Linear1';flag_mlp_case = 'Nonlinear1'
flag_mlp_case = 'Nonlinear1';
if (flag_mlp_case == 'Linear1'):
layer_sizes = [];
num_depth = 0; # number of internal layers
num_hidden = -1; # number of hidden per layer
channels_in = Nc; # number of poly channels (matches input u channel size)
channels_out = 1; # number of output filters
layer_sizes.append(num_polys); # input
layer_sizes.append(1); # output, single channel always, for vectors, we use channels_out separate units.
mlp_q1 = gmlsnets.nn.MLP_Pointwise(layer_sizes,channels_in=channels_in,channels_out=channels_out,
flag_bias=False).to(device);
elif (flag_mlp_case == 'Nonlinear1'):
layer_sizes = [];
num_input = Nc*num_polys; # number of channels*num_polys, allows for cross-channel coupling
num_depth = 4; # number of internal layers
num_hidden = 100; # number of hidden per layer
num_out_channels = 16; # number of output filters
layer_sizes.append(num_polys);
for k in range(num_depth):
layer_sizes.append(num_hidden);
layer_sizes.append(1); # output, single channel always, for vectors, we use channels_out separate units.
mlp_q1 = gmlsnets.nn.MLP_Pointwise(layer_sizes,channels_out=num_out_channels,
flag_bias=True).to(device);
if flag_print_model:
print("mlp_q1:");
print(mlp_q1);
# Setup the Neural Network for Regression
flag_verbose = 0;
flag_case = 'standard';
# Setup the model
xi = xi.float();
xj = xj.float();
model = gmlsNetRegressionDiffOp1(flag_case,porder,Nc,xj,layer1_epsilon,
weight_func1,weight_func1_params,
mlp_q1=mlp_q1,pts_x2=xi,
device=device,
flag_verbose=flag_verbose);
if flag_print_model:
print("model:");
print(model);
```
## Setup the training and test data
```
### Generate Dataset
if flag_dataset == 'diffOp1':
# Use the FFT to represent differential operators for training data sets.
#
# Setup a data set of the following:
# To start let's do regression for the Laplacian (not inverse, just action of it, like finding FD)
#
#op_type = 'u*ux';op_type = 'ux*ux';op_type = 'uxx';op_type = 'u*uxx';op_type = 'uxx*uxx';
op_type = 'u*ux';
flag_verbose = 1;
num_training_samples = int(5e4);
nchannels = 1;
nx = np_xj.shape[0];
#alpha1 = 0.05;
alpha1 = 0.1;
scale_factor = 1e2;
train_dataset = gmlsnets.dataset.diffOp1(op_type=op_type,op_params=None,
gen_mode='exp1',gen_params={'alpha1':alpha1},
num_samples=num_training_samples,
nchannels=nchannels,nx=nx,
noise_factor=0,scale_factor=scale_factor,
flag_verbose=flag_verbose);
train_dataset = train_dataset.to(device);
if flag_verbose > 0:
print("done.");
num_test_samples = int(1e4);
scale_factor = 1e2;
test_dataset = gmlsnets.dataset.diffOp1(op_type=op_type,op_params=None,
gen_mode='exp1',gen_params={'alpha1':alpha1},
num_samples=num_test_samples,
nchannels=nchannels,nx=nx,
noise_factor=0,scale_factor=scale_factor,
flag_verbose=flag_verbose);
test_dataset = test_dataset.to(device);
if flag_verbose > 0:
print("done.");
# Put the data into the
#train_dataset and test_dataset structures for processing
else:
msg = "flag_dataset not recognized.";
msg += "flag_data_set = " + str(flag_data_set);
raise Exception(msg);
# Data loader
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,batch_size=batch_size,shuffle=True);
test_loader = torch.utils.data.DataLoader(dataset=test_dataset,batch_size=batch_size,shuffle=False);
%matplotlib inline
# plot sample of the training data
gmlsnets.vis.plot_dataset_diffOp1(train_dataset,np_xj,np_xi,rows=4,cols=6,
title="Data Samples: u, f=L[u], L = %s"%op_type);
```
## Train the Model
### Custom Functions
```
def custom_loss_least_squares(val1,val2):
r"""Computes the Mean-Square-Error (MSE) over the entire batch."""
diff_flat = (val1 - val2).flatten();
N = diff_flat.shape[0];
loss = torch.sum(torch.pow(diff_flat,2),-1)/N;
return loss;
def domain_periodic_repeat(Z):
r"""Extends the input periodically."""
Z_periodic = torch.cat((Z, Z, Z), 2);
return Z_periodic;
def domain_periodic_extract(Z_periodic):
r"""Extracts the middle unit cell portion of the extended data."""
nn = int(Z_periodic.shape[2]/3);
Z = Z_periodic[:,:,nn:2*nn];
return Z;
```
### Initialize
```
loss_list = np.empty(0); loss_step_list = np.empty(0);
save_skip = 1; step_count = 0;
```
### Train the network.
```
num_epochs = int(3e0); #int(1e4);
learning_rate = 1e-2;
print("Training the network with:");
print("");
print("model:");
print("model.layer_types = " + str(model.layer_types));
print("");
# setup the optimization method and loss function
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate);
#loss_func = nn.CrossEntropyLoss();
#loss_func = nn.MSELoss();
loss_func = custom_loss_least_squares;
print("num_epochs = %d"%num_epochs);
print("batch_size = %d"%batch_size);
print(" ");
# Train the model
flag_time_it = True;
if flag_time_it:
time_1 = time.time();
print("-"*80);
num_steps = len(train_loader);
for epoch in range(num_epochs):
for i, (input,target) in enumerate(train_loader):
input = input.to(device);
target = target.to(device);
if flag_extend_periodic:
# Extend input periodically
input_periodic = domain_periodic_repeat(input);
# Forward pass
output_periodic = model(input_periodic);
output = domain_periodic_extract(output_periodic);
else:
output = model(input);
# Compute loss
loss = loss_func(output,target);
# Display
if step_count % save_skip == 0:
np_loss = loss.cpu().detach().numpy();
loss_list = np.append(loss_list,np_loss);
loss_step_list = np.append(loss_step_list,step_count);
# Back-propagation for gradients and use to optimize
optimizer.zero_grad();
loss.backward();
optimizer.step();
step_count += 1;
if ((i + 1) % 100) == 0 or i == 0:
msg = 'epoch: [%d/%d]; '%(epoch+1,num_epochs);
msg += 'batch_step = [%d/%d]; '%(i + 1,num_steps);
msg += 'loss_MSE: %.3e.'%(loss.item());
print(msg);
if flag_time_it and i > 0:
msg = 'elapsed_time = %.4e secs \n'%(time.time() - time_1);
print(msg);
time_1 = time.time();
print("done training.")
print("-"*80);
```
### Plot Loss
```
%matplotlib inline
plt.figure(figsize=(8,6));
plt.plot(loss_step_list,loss_list,'b-');
plt.yscale('log');
plt.xlabel('step');
plt.ylabel('loss');
plt.title('Loss');
```
### Test the Neural Network Predictions
```
print("Testing predictions of the neural network:");
flag_save_tests = True;
if flag_save_tests:
test_data = {};
# Save the first few to show as examples of labeling
saved_test_input = [];
saved_test_target = [];
saved_test_output_pred = [];
count_batch = 0;
with torch.no_grad():
total = 0; II = 0;
avg_error = 0;
for input,target in test_loader: # loads data in batches and then sums up
if (II >= 1000):
print("tested on %d samples"%total);
II = 0;
input = input.to(device); target = target.to(device);
# Compute model
flag_extend_periodic = False;
if flag_extend_periodic:
# Extend input periodically
input_periodic = domain_periodic_repeat(input);
# Forward pass
output_periodic = model(input_periodic);
output = domain_periodic_extract(output_periodic);
else:
output = model(input);
# Compute loss
loss = loss_func(output,target);
# Record the results
avg_error += loss;
total += output.shape[0];
II += output.shape[0];
count_batch += 1;
NN = output.shape[0];
for k in range(min(NN,20)): # save first 10 images of each batch
saved_test_input.append(input[k]);
saved_test_target.append(target[k]);
saved_test_output_pred.append(output[k]);
print("");
print("Tested on a total of %d samples."%total);
print("");
# Compute RMSD error
test_accuracy = avg_error.cpu()/count_batch;
test_accuracy = np.sqrt(test_accuracy);
print("The neural network has RMSD error %.2e on the %d test samples."%(test_accuracy,total));
print("");
```
### Show a Sample of the Predictions
```
# collect a subset of the data to show and attach named labels
%matplotlib inline
num_prediction_samples = len(saved_test_input);
print("num_prediction_samples = " + str(num_prediction_samples));
#II = np.random.permutation(num_samples); # compute random collection of indices @optimize
II = np.arange(num_prediction_samples);
if flag_dataset == 'name-here' or 0 == 0:
u_list = []; f_list = []; f_pred_list = [];
for I in np.arange(0,min(num_prediction_samples,16)):
u_list.append(saved_test_input[II[I]].cpu());
f_list.append(saved_test_target[II[I]].cpu());
f_pred_list.append(saved_test_output_pred[II[I]].cpu());
# plot predictions against test data
gmlsnets.vis.plot_samples_u_f_fp_1d(u_list,f_list,f_pred_list,np_xj,np_xi,rows=4,cols=6,
title="Test Samples and Predictions: u, f=L[u], L = %s"%op_type);
```
### Save Model
```
model_filename = '%s/model.ckpt'%base_dir;
print("model_filename = " + model_filename);
torch.save(model.state_dict(), model_filename);
model_filename = "%s/model_state.pickle"%base_dir;
print("model_filename = " + model_filename);
f = open(model_filename,'wb');
pickle.dump(model.state_dict(),f);
f.close();
```
### Display the GMLS-Nets Learned Parameters
```
flag_run_cell = flag_print_model;
if flag_run_cell:
print("-"*80)
print("model.parameters():");
ll = model.parameters();
for l in ll:
print(l);
if flag_run_cell:
print("-"*80)
print("model.state_dict():");
print(model.state_dict());
print("-"*80)
```
### Done
|
github_jupyter
|
```
from moviepy.editor import *
postedByFontSize=25
replyFontSize=35
titleFontSize=100
cortinilla= VideoFileClip('assets for Channel/assets for video/transicion.mp4')
clip = ImageClip('assets for Channel/assets for video/background assets/fondo_preguntas.jpg').on_color((1920, 1080))
final= VideoFileClip('assets for Channel/assets for video/transicion.mp4')
def generate_video_of_reply(author,replyLines,replyaudio):
videoComponents=[]
textReply= []
postedBy = TextClip('Posted by /'+author, fontsize=postedByFontSize, color='white')
postedBy=postedBy.set_pos((162, 124))
index=0
yAxis=184
for replyLine in replyLines:
print('line '+str(index)+replyLine)
try:
replyline=TextClip(replyLine, fontsize=postedByFontSize, color='white')
replyline=replyline.set_pos((162,yAxis))
textReply.append(replyline)
except:
print('null line')
print(yAxis)
yAxis+=25
index+=1
videoComponents.append(clip)
videoComponents.append(postedBy)
videoComponents.extend(textReply)
replyVideo = CompositeVideoClip(videoComponents)
replyVideo = replyVideo.set_duration(replyaudio.duration)
replyVideo = replyVideo.set_audio(replyaudio)
return replyVideo
def generate_final_video(title,replies):
videoClips=[]
videoClips.append(generate_title(title))
index=0
for reply in replies:
audio=AudioFileClip('comment'+str(index)+'.mp3')
videoClips.append(generate_video_of_reply(reply['author'],reply['replyLines'],audio))
videoClips.append(cortinilla)
index+=1
videoClips.append(final)
finalVideo=concatenate_videoclips(videoClips)
finalVideo.fx(vfx.speedx, factor=1.3)
finalVideo.write_videofile("text.mp4", fps=24)
def generate_title(title):
videoComponents=[]
yAxisJumpInLine=80
maxCharsInLine=38
titleaudio=AudioFileClip('title.mp3')
titleline=TextClip(title, fontsize=titleFontSize, color='white')
titleline=titleline.set_pos((202,94))
#if(len(titleline)>38):
# sublines=[line[i:i+maxCharsInLine] for i in range(0, len(line), maxCharsInLine)]
# sublinesSize=len(sublines)
# for x in range(sublinesSize):
# index = len(sublines[x]) # calculate length of string and save in index
# while index > 0:
# if(sublines[x][ index - 1 ]==' '): # save the value of str[index-1] in reverseString
# index = index - 1
#if(' ' in sublines[x+1]):
videoComponents.append(clip)
videoComponents.append(titleline)
titleVideo = CompositeVideoClip(videoComponents)
titleVideo = titleVideo.set_duration(titleaudio.duration)
titleVideo = titleVideo.set_audio(titleaudio)
return titleVideo
```
|
github_jupyter
|
# PoissonRegressor with StandardScaler & Power Transformer
This Code template is for the regression analysis using Poisson Regressor, StandardScaler as feature rescaling technique and Power Transformer as transformer in a pipeline. This is a generalized Linear Model with a Poisson distribution.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.linear_model import PoissonRegressor
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler, PowerTransformer
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
### Model
Poisson regression is a generalized linear model form of regression used to model count data and contingency tables. It assumes the response variable or target variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown parameters. It is sometimes known as a log-linear model, especially when used to model contingency tables.
#### Model Tuning Parameters
> **alpha** -> Constant that multiplies the penalty term and thus determines the regularization strength. alpha = 0 is equivalent to unpenalized GLMs.
> **tol** -> Stopping criterion.
> **max_iter** -> The maximal number of iterations for the solver.
Feature Transformation
Power Transformers are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
Currently, <Code>PowerTransformer</Code> supports the Box-Cox transform and the Yeo-Johnson transform. The optimal parameter for stabilizing variance and minimizing skewness is estimated through maximum likelihood.
Refer [API](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html) for the parameters
```
model=make_pipeline(StandardScaler(),PowerTransformer(),PoissonRegressor())
model.fit(x_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Viraj Jayant , Github: [Profile](https://github.com/Viraj-Jayant)
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Build a Convolutional Neural Network using Estimators
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r1/tutorials/estimators/cnn.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r1/tutorials/estimators/cnn.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
> Note: This is an archived TF1 notebook. These are configured
to run in TF2's
[compatbility mode](https://www.tensorflow.org/guide/migrate)
but will run in TF1 as well. To use TF1 in Colab, use the
[%tensorflow_version 1.x](https://colab.research.google.com/notebooks/tensorflow_version.ipynb)
magic.
The `tf.layers` module provides a high-level API that makes
it easy to construct a neural network. It provides methods that facilitate the
creation of dense (fully connected) layers and convolutional layers, adding
activation functions, and applying dropout regularization. In this tutorial,
you'll learn how to use `layers` to build a convolutional neural network model
to recognize the handwritten digits in the MNIST data set.

The [MNIST dataset](http://yann.lecun.com/exdb/mnist/) comprises 60,000
training examples and 10,000 test examples of the handwritten digits 0–9,
formatted as 28x28-pixel monochrome images.
## Get Started
Let's set up the imports for our TensorFlow program:
```
import tensorflow.compat.v1 as tf
import numpy as np
tf.logging.set_verbosity(tf.logging.INFO)
```
## Intro to Convolutional Neural Networks
Convolutional neural networks (CNNs) are the current state-of-the-art model
architecture for image classification tasks. CNNs apply a series of filters to
the raw pixel data of an image to extract and learn higher-level features, which
the model can then use for classification. CNNs contains three components:
* **Convolutional layers**, which apply a specified number of convolution
filters to the image. For each subregion, the layer performs a set of
mathematical operations to produce a single value in the output feature map.
Convolutional layers then typically apply a
[ReLU activation function](https://en.wikipedia.org/wiki/Rectifier_\(neural_networks\)) to
the output to introduce nonlinearities into the model.
* **Pooling layers**, which
[downsample the image data](https://en.wikipedia.org/wiki/Convolutional_neural_network#Pooling_layer)
extracted by the convolutional layers to reduce the dimensionality of the
feature map in order to decrease processing time. A commonly used pooling
algorithm is max pooling, which extracts subregions of the feature map
(e.g., 2x2-pixel tiles), keeps their maximum value, and discards all other
values.
* **Dense (fully connected) layers**, which perform classification on the
features extracted by the convolutional layers and downsampled by the
pooling layers. In a dense layer, every node in the layer is connected to
every node in the preceding layer.
Typically, a CNN is composed of a stack of convolutional modules that perform
feature extraction. Each module consists of a convolutional layer followed by a
pooling layer. The last convolutional module is followed by one or more dense
layers that perform classification. The final dense layer in a CNN contains a
single node for each target class in the model (all the possible classes the
model may predict), with a
[softmax](https://en.wikipedia.org/wiki/Softmax_function) activation function to
generate a value between 0–1 for each node (the sum of all these softmax values
is equal to 1). We can interpret the softmax values for a given image as
relative measurements of how likely it is that the image falls into each target
class.
Note: For a more comprehensive walkthrough of CNN architecture, see Stanford University's [Convolutional Neural Networks for Visual Recognition course material](https://cs231n.github.io/convolutional-networks/).
## Building the CNN MNIST Classifier
Let's build a model to classify the images in the MNIST dataset using the
following CNN architecture:
1. **Convolutional Layer #1**: Applies 32 5x5 filters (extracting 5x5-pixel
subregions), with ReLU activation function
2. **Pooling Layer #1**: Performs max pooling with a 2x2 filter and stride of 2
(which specifies that pooled regions do not overlap)
3. **Convolutional Layer #2**: Applies 64 5x5 filters, with ReLU activation
function
4. **Pooling Layer #2**: Again, performs max pooling with a 2x2 filter and
stride of 2
5. **Dense Layer #1**: 1,024 neurons, with dropout regularization rate of 0.4
(probability of 0.4 that any given element will be dropped during training)
6. **Dense Layer #2 (Logits Layer)**: 10 neurons, one for each digit target
class (0–9).
The `tf.layers` module contains methods to create each of the three layer types
above:
* `conv2d()`. Constructs a two-dimensional convolutional layer. Takes number
of filters, filter kernel size, padding, and activation function as
arguments.
* `max_pooling2d()`. Constructs a two-dimensional pooling layer using the
max-pooling algorithm. Takes pooling filter size and stride as arguments.
* `dense()`. Constructs a dense layer. Takes number of neurons and activation
function as arguments.
Each of these methods accepts a tensor as input and returns a transformed tensor
as output. This makes it easy to connect one layer to another: just take the
output from one layer-creation method and supply it as input to another.
Add the following `cnn_model_fn` function, which
conforms to the interface expected by TensorFlow's Estimator API (more on this
later in [Create the Estimator](#create-the-estimator)). This function takes
MNIST feature data, labels, and mode (from
`tf.estimator.ModeKeys`: `TRAIN`, `EVAL`, `PREDICT`) as arguments;
configures the CNN; and returns predictions, loss, and a training operation:
```
def cnn_model_fn(features, labels, mode):
"""Model function for CNN."""
# Input Layer
input_layer = tf.reshape(features["x"], [-1, 28, 28, 1])
# Convolutional Layer #1
conv1 = tf.layers.conv2d(
inputs=input_layer,
filters=32,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu)
# Pooling Layer #1
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
# Convolutional Layer #2 and Pooling Layer #2
conv2 = tf.layers.conv2d(
inputs=pool1,
filters=64,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
# Dense Layer
pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64])
dense = tf.layers.dense(inputs=pool2_flat, units=1024, activation=tf.nn.relu)
dropout = tf.layers.dropout(
inputs=dense, rate=0.4, training=mode == tf.estimator.ModeKeys.TRAIN)
# Logits Layer
logits = tf.layers.dense(inputs=dropout, units=10)
predictions = {
# Generate predictions (for PREDICT and EVAL mode)
"classes": tf.argmax(input=logits, axis=1),
# Add `softmax_tensor` to the graph. It is used for PREDICT and by the
# `logging_hook`.
"probabilities": tf.nn.softmax(logits, name="softmax_tensor")
}
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)
# Calculate Loss (for both TRAIN and EVAL modes)
loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
# Configure the Training Op (for TRAIN mode)
if mode == tf.estimator.ModeKeys.TRAIN:
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001)
train_op = optimizer.minimize(
loss=loss,
global_step=tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode=mode, loss=loss, train_op=train_op)
# Add evaluation metrics (for EVAL mode)
eval_metric_ops = {
"accuracy": tf.metrics.accuracy(
labels=labels, predictions=predictions["classes"])
}
return tf.estimator.EstimatorSpec(
mode=mode, loss=loss, eval_metric_ops=eval_metric_ops)
```
The following sections (with headings corresponding to each code block above)
dive deeper into the `tf.layers` code used to create each layer, as well as how
to calculate loss, configure the training op, and generate predictions. If
you're already experienced with CNNs and [TensorFlow `Estimator`s](../../guide/custom_estimators.md),
and find the above code intuitive, you may want to skim these sections or just
skip ahead to ["Training and Evaluating the CNN MNIST Classifier"](#train_eval_mnist).
### Input Layer
The methods in the `layers` module for creating convolutional and pooling layers
for two-dimensional image data expect input tensors to have a shape of
<code>[<em>batch_size</em>, <em>image_height</em>, <em>image_width</em>,
<em>channels</em>]</code> by default. This behavior can be changed using the
<code><em>data_format</em></code> parameter; defined as follows:
* `batch_size` —Size of the subset of examples to use when performing
gradient descent during training.
* `image_height` —Height of the example images.
* `image_width` —Width of the example images.
* `channels` —Number of color channels in the example images. For color
images, the number of channels is 3 (red, green, blue). For monochrome
images, there is just 1 channel (black).
* `data_format` —A string, one of `channels_last` (default) or `channels_first`.
`channels_last` corresponds to inputs with shape
`(batch, ..., channels)` while `channels_first` corresponds to
inputs with shape `(batch, channels, ...)`.
Here, our MNIST dataset is composed of monochrome 28x28 pixel images, so the
desired shape for our input layer is <code>[<em>batch_size</em>, 28, 28,
1]</code>.
To convert our input feature map (`features`) to this shape, we can perform the
following `reshape` operation:
```
input_layer = tf.reshape(features["x"], [-1, 28, 28, 1])
```
Note that we've indicated `-1` for batch size, which specifies that this
dimension should be dynamically computed based on the number of input values in
`features["x"]`, holding the size of all other dimensions constant. This allows
us to treat `batch_size` as a hyperparameter that we can tune. For example, if
we feed examples into our model in batches of 5, `features["x"]` will contain
3,920 values (one value for each pixel in each image), and `input_layer` will
have a shape of `[5, 28, 28, 1]`. Similarly, if we feed examples in batches of
100, `features["x"]` will contain 78,400 values, and `input_layer` will have a
shape of `[100, 28, 28, 1]`.
### Convolutional Layer #1
In our first convolutional layer, we want to apply 32 5x5 filters to the input
layer, with a ReLU activation function. We can use the `conv2d()` method in the
`layers` module to create this layer as follows:
```
conv1 = tf.layers.conv2d(
inputs=input_layer,
filters=32,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu)
```
The `inputs` argument specifies our input tensor, which must have the shape
<code>[<em>batch_size</em>, <em>image_height</em>, <em>image_width</em>,
<em>channels</em>]</code>. Here, we're connecting our first convolutional layer
to `input_layer`, which has the shape <code>[<em>batch_size</em>, 28, 28,
1]</code>.
Note: `conv2d()` will instead accept a shape of `[<em>batch_size</em>, <em>channels</em>, <em>image_height</em>, <em>image_width</em>]` when passed the argument `data_format=channels_first`.
The `filters` argument specifies the number of filters to apply (here, 32), and
`kernel_size` specifies the dimensions of the filters as `[<em>height</em>,
<em>width</em>]</code> (here, <code>[5, 5]`).
<p class="tip"><b>TIP:</b> If filter height and width have the same value, you can instead specify a
single integer for <code>kernel_size</code>—e.g., <code>kernel_size=5</code>.</p>
The `padding` argument specifies one of two enumerated values
(case-insensitive): `valid` (default value) or `same`. To specify that the
output tensor should have the same height and width values as the input tensor,
we set `padding=same` here, which instructs TensorFlow to add 0 values to the
edges of the input tensor to preserve height and width of 28. (Without padding,
a 5x5 convolution over a 28x28 tensor will produce a 24x24 tensor, as there are
24x24 locations to extract a 5x5 tile from a 28x28 grid.)
The `activation` argument specifies the activation function to apply to the
output of the convolution. Here, we specify ReLU activation with
`tf.nn.relu`.
Our output tensor produced by `conv2d()` has a shape of
<code>[<em>batch_size</em>, 28, 28, 32]</code>: the same height and width
dimensions as the input, but now with 32 channels holding the output from each
of the filters.
### Pooling Layer #1
Next, we connect our first pooling layer to the convolutional layer we just
created. We can use the `max_pooling2d()` method in `layers` to construct a
layer that performs max pooling with a 2x2 filter and stride of 2:
```
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
```
Again, `inputs` specifies the input tensor, with a shape of
<code>[<em>batch_size</em>, <em>image_height</em>, <em>image_width</em>,
<em>channels</em>]</code>. Here, our input tensor is `conv1`, the output from
the first convolutional layer, which has a shape of <code>[<em>batch_size</em>,
28, 28, 32]</code>.
Note: As with <code>conv2d()</code>, <code>max_pooling2d()</code> will instead
accept a shape of <code>[<em>batch_size</em>, <em>channels</em>,
<em>image_height</em>, <em>image_width</em>]</code> when passed the argument
<code>data_format=channels_first</code>.
The `pool_size` argument specifies the size of the max pooling filter as
<code>[<em>height</em>, <em>width</em>]</code> (here, `[2, 2]`). If both
dimensions have the same value, you can instead specify a single integer (e.g.,
`pool_size=2`).
The `strides` argument specifies the size of the stride. Here, we set a stride
of 2, which indicates that the subregions extracted by the filter should be
separated by 2 pixels in both the height and width dimensions (for a 2x2 filter,
this means that none of the regions extracted will overlap). If you want to set
different stride values for height and width, you can instead specify a tuple or
list (e.g., `stride=[3, 6]`).
Our output tensor produced by `max_pooling2d()` (`pool1`) has a shape of
<code>[<em>batch_size</em>, 14, 14, 32]</code>: the 2x2 filter reduces height and width by 50% each.
### Convolutional Layer #2 and Pooling Layer #2
We can connect a second convolutional and pooling layer to our CNN using
`conv2d()` and `max_pooling2d()` as before. For convolutional layer #2, we
configure 64 5x5 filters with ReLU activation, and for pooling layer #2, we use
the same specs as pooling layer #1 (a 2x2 max pooling filter with stride of 2):
```
conv2 = tf.layers.conv2d(
inputs=pool1,
filters=64,
kernel_size=[5, 5],
padding="same",
activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
```
Note that convolutional layer #2 takes the output tensor of our first pooling
layer (`pool1`) as input, and produces the tensor `conv2` as output. `conv2`
has a shape of <code>[<em>batch_size</em>, 14, 14, 64]</code>, the same height and width as `pool1` (due to `padding="same"`), and 64 channels for the 64
filters applied.
Pooling layer #2 takes `conv2` as input, producing `pool2` as output. `pool2`
has shape <code>[<em>batch_size</em>, 7, 7, 64]</code> (50% reduction of height and width from `conv2`).
### Dense Layer
Next, we want to add a dense layer (with 1,024 neurons and ReLU activation) to
our CNN to perform classification on the features extracted by the
convolution/pooling layers. Before we connect the layer, however, we'll flatten
our feature map (`pool2`) to shape <code>[<em>batch_size</em>,
<em>features</em>]</code>, so that our tensor has only two dimensions:
```
pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64])
```
In the `reshape()` operation above, the `-1` signifies that the *`batch_size`*
dimension will be dynamically calculated based on the number of examples in our
input data. Each example has 7 (`pool2` height) * 7 (`pool2` width) * 64
(`pool2` channels) features, so we want the `features` dimension to have a value
of 7 * 7 * 64 (3136 in total). The output tensor, `pool2_flat`, has shape
<code>[<em>batch_size</em>, 3136]</code>.
Now, we can use the `dense()` method in `layers` to connect our dense layer as
follows:
```
dense = tf.layers.dense(inputs=pool2_flat, units=1024, activation=tf.nn.relu)
```
The `inputs` argument specifies the input tensor: our flattened feature map,
`pool2_flat`. The `units` argument specifies the number of neurons in the dense
layer (1,024). The `activation` argument takes the activation function; again,
we'll use `tf.nn.relu` to add ReLU activation.
To help improve the results of our model, we also apply dropout regularization
to our dense layer, using the `dropout` method in `layers`:
```
dropout = tf.layers.dropout(
inputs=dense, rate=0.4, training=mode == tf.estimator.ModeKeys.TRAIN)
```
Again, `inputs` specifies the input tensor, which is the output tensor from our
dense layer (`dense`).
The `rate` argument specifies the dropout rate; here, we use `0.4`, which means
40% of the elements will be randomly dropped out during training.
The `training` argument takes a boolean specifying whether or not the model is
currently being run in training mode; dropout will only be performed if
`training` is `True`. Here, we check if the `mode` passed to our model function
`cnn_model_fn` is `TRAIN` mode.
Our output tensor `dropout` has shape <code>[<em>batch_size</em>, 1024]</code>.
### Logits Layer
The final layer in our neural network is the logits layer, which will return the
raw values for our predictions. We create a dense layer with 10 neurons (one for
each target class 0–9), with linear activation (the default):
```
logits = tf.layers.dense(inputs=dropout, units=10)
```
Our final output tensor of the CNN, `logits`, has shape `[batch_size, 10]`.
### Generate Predictions {#generate_predictions}
The logits layer of our model returns our predictions as raw values in a
<code>[<em>batch_size</em>, 10]</code>-dimensional tensor. Let's convert these
raw values into two different formats that our model function can return:
* The **predicted class** for each example: a digit from 0–9.
* The **probabilities** for each possible target class for each example: the
probability that the example is a 0, is a 1, is a 2, etc.
For a given example, our predicted class is the element in the corresponding row
of the logits tensor with the highest raw value. We can find the index of this
element using the `tf.argmax`
function:
```
tf.argmax(input=logits, axis=1)
```
The `input` argument specifies the tensor from which to extract maximum
values—here `logits`. The `axis` argument specifies the axis of the `input`
tensor along which to find the greatest value. Here, we want to find the largest
value along the dimension with index of 1, which corresponds to our predictions
(recall that our logits tensor has shape <code>[<em>batch_size</em>,
10]</code>).
We can derive probabilities from our logits layer by applying softmax activation
using `tf.nn.softmax`:
```
tf.nn.softmax(logits, name="softmax_tensor")
```
Note: We use the `name` argument to explicitly name this operation `softmax_tensor`, so we can reference it later. (We'll set up logging for the softmax values in ["Set Up a Logging Hook"](#set-up-a-logging-hook)).
We compile our predictions in a dict, and return an `EstimatorSpec` object:
```
predictions = {
"classes": tf.argmax(input=logits, axis=1),
"probabilities": tf.nn.softmax(logits, name="softmax_tensor")
}
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)
```
### Calculate Loss {#calculating-loss}
For both training and evaluation, we need to define a
[loss function](https://en.wikipedia.org/wiki/Loss_function)
that measures how closely the model's predictions match the target classes. For
multiclass classification problems like MNIST,
[cross entropy](https://en.wikipedia.org/wiki/Cross_entropy) is typically used
as the loss metric. The following code calculates cross entropy when the model
runs in either `TRAIN` or `EVAL` mode:
```
loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits)
```
Let's take a closer look at what's happening above.
Our `labels` tensor contains a list of prediction indices for our examples, e.g. `[1,
9, ...]`. `logits` contains the linear outputs of our last layer.
`tf.losses.sparse_softmax_cross_entropy`, calculates the softmax crossentropy
(aka: categorical crossentropy, negative log-likelihood) from these two inputs
in an efficient, numerically stable way.
### Configure the Training Op
In the previous section, we defined loss for our CNN as the softmax
cross-entropy of the logits layer and our labels. Let's configure our model to
optimize this loss value during training. We'll use a learning rate of 0.001 and
[stochastic gradient descent](https://en.wikipedia.org/wiki/Stochastic_gradient_descent)
as the optimization algorithm:
```
if mode == tf.estimator.ModeKeys.TRAIN:
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001)
train_op = optimizer.minimize(
loss=loss,
global_step=tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode=mode, loss=loss, train_op=train_op)
```
Note: For a more in-depth look at configuring training ops for Estimator model functions, see ["Defining the training op for the model"](../../guide/custom_estimators.md#defining-the-training-op-for-the-model) in the ["Creating Estimations in tf.estimator"](../../guide/custom_estimators.md) tutorial.
### Add evaluation metrics
To add accuracy metric in our model, we define `eval_metric_ops` dict in EVAL
mode as follows:
```
eval_metric_ops = {
"accuracy": tf.metrics.accuracy(
labels=labels, predictions=predictions["classes"])
}
return tf.estimator.EstimatorSpec(
mode=mode, loss=loss, eval_metric_ops=eval_metric_ops)
```
<a id="train_eval_mnist"></a>
## Training and Evaluating the CNN MNIST Classifier
We've coded our MNIST CNN model function; now we're ready to train and evaluate
it.
### Load Training and Test Data
First, let's load our training and test data with the following code:
```
# Load training and eval data
((train_data, train_labels),
(eval_data, eval_labels)) = tf.keras.datasets.mnist.load_data()
train_data = train_data/np.float32(255)
train_labels = train_labels.astype(np.int32) # not required
eval_data = eval_data/np.float32(255)
eval_labels = eval_labels.astype(np.int32) # not required
```
We store the training feature data (the raw pixel values for 55,000 images of
hand-drawn digits) and training labels (the corresponding value from 0–9 for
each image) as [numpy
arrays](https://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html)
in `train_data` and `train_labels`, respectively. Similarly, we store the
evaluation feature data (10,000 images) and evaluation labels in `eval_data`
and `eval_labels`, respectively.
### Create the Estimator {#create-the-estimator}
Next, let's create an `Estimator` (a TensorFlow class for performing high-level
model training, evaluation, and inference) for our model. Add the following code
to `main()`:
```
# Create the Estimator
mnist_classifier = tf.estimator.Estimator(
model_fn=cnn_model_fn, model_dir="/tmp/mnist_convnet_model")
```
The `model_fn` argument specifies the model function to use for training,
evaluation, and prediction; we pass it the `cnn_model_fn` we created in
["Building the CNN MNIST Classifier."](#building-the-cnn-mnist-classifier) The
`model_dir` argument specifies the directory where model data (checkpoints) will
be saved (here, we specify the temp directory `/tmp/mnist_convnet_model`, but
feel free to change to another directory of your choice).
Note: For an in-depth walkthrough of the TensorFlow `Estimator` API, see the tutorial [Creating Estimators in tf.estimator](../../guide/custom_estimators.md).
### Set Up a Logging Hook {#set_up_a_logging_hook}
Since CNNs can take a while to train, let's set up some logging so we can track
progress during training. We can use TensorFlow's `tf.train.SessionRunHook` to create a
`tf.train.LoggingTensorHook`
that will log the probability values from the softmax layer of our CNN. Add the
following to `main()`:
```
# Set up logging for predictions
tensors_to_log = {"probabilities": "softmax_tensor"}
logging_hook = tf.train.LoggingTensorHook(
tensors=tensors_to_log, every_n_iter=50)
```
We store a dict of the tensors we want to log in `tensors_to_log`. Each key is a
label of our choice that will be printed in the log output, and the
corresponding label is the name of a `Tensor` in the TensorFlow graph. Here, our
`probabilities` can be found in `softmax_tensor`, the name we gave our softmax
operation earlier when we generated the probabilities in `cnn_model_fn`.
Note: If you don't explicitly assign a name to an operation via the `name` argument, TensorFlow will assign a default name. A couple easy ways to discover the names applied to operations are to visualize your graph on [TensorBoard](../../guide/graph_viz.md)) or to enable the [TensorFlow Debugger (tfdbg)](../../guide/debugger.md).
Next, we create the `LoggingTensorHook`, passing `tensors_to_log` to the
`tensors` argument. We set `every_n_iter=50`, which specifies that probabilities
should be logged after every 50 steps of training.
### Train the Model
Now we're ready to train our model, which we can do by creating `train_input_fn`
and calling `train()` on `mnist_classifier`. In the `numpy_input_fn` call, we pass the training feature data and labels to
`x` (as a dict) and `y`, respectively. We set a `batch_size` of `100` (which
means that the model will train on minibatches of 100 examples at each step).
`num_epochs=None` means that the model will train until the specified number of
steps is reached. We also set `shuffle=True` to shuffle the training data. Then train the model a single step and log the output:
```
# Train the model
train_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": train_data},
y=train_labels,
batch_size=100,
num_epochs=None,
shuffle=True)
# train one step and display the probabilties
mnist_classifier.train(
input_fn=train_input_fn,
steps=1,
hooks=[logging_hook])
```
Now—without logging each step—set `steps=1000` to train the model longer, but in a reasonable time to run this example. Training CNNs is computationally intensive. To increase the accuracy of your model, increase the number of `steps` passed to `train()`, like 20,000 steps.
```
mnist_classifier.train(input_fn=train_input_fn, steps=1000)
```
### Evaluate the Model
Once training is complete, we want to evaluate our model to determine its
accuracy on the MNIST test set. We call the `evaluate` method, which evaluates
the metrics we specified in `eval_metric_ops` argument in the `model_fn`.
Add the following to `main()`:
```
eval_input_fn = tf.estimator.inputs.numpy_input_fn(
x={"x": eval_data},
y=eval_labels,
num_epochs=1,
shuffle=False)
eval_results = mnist_classifier.evaluate(input_fn=eval_input_fn)
print(eval_results)
```
To create `eval_input_fn`, we set `num_epochs=1`, so that the model evaluates
the metrics over one epoch of data and returns the result. We also set
`shuffle=False` to iterate through the data sequentially.
## Additional Resources
To learn more about TensorFlow Estimators and CNNs in TensorFlow, see the
following resources:
* [Creating Estimators in tf.estimator](../../guide/custom_estimators.md)
provides an introduction to the TensorFlow Estimator API. It walks through
configuring an Estimator, writing a model function, calculating loss, and
defining a training op.
* [Advanced Convolutional Neural Networks](../../tutorials/images/deep_cnn.md) walks through how to build a MNIST CNN classification model
*without estimators* using lower-level TensorFlow operations.
|
github_jupyter
|
# This notebook helps you to do several things:
1) Find your optimal learning rate
https://docs.fast.ai/callbacks.html#LRFinder
2)
```
%reload_ext autoreload
%autoreload 2
import fastai
from fastai.callbacks import *
from torch.utils.data import Dataset, DataLoader
from models import UNet2d_assembled
import numpy as np
import torch
from fastai.vision import *
torch.backends.cudnn.benchmark = True
DEVICE = 'cuda'
OS = 'Windows'
# GET DATASET
class CMRIreconDataset(Dataset):
"""CMRIrecon dataset."""
def __init__(self, input_file_path, target_file_path):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.inputs = np.load(input_file_path)
self.targets = np.load(target_file_path)
def __len__(self):
# print("print length of inputs",len(self.inputs))
# print("print shape of inputs",np.shape(self.inputs))
return len(self.inputs)
def __getitem__(self, idx):
# sample = {'input': self.inputs[idx], 'target': self.targets[idx]}
X = self.inputs[idx].astype(np.float32)
Y = self.targets[idx].astype(np.float32)
return X, Y
if OS == 'Linux':
CMRIdataset = CMRIreconDataset(
input_file_path = \
'/home/nw92/reconproject_data/input_data.npy', \
target_file_path = \
'/home/nw92/reconproject_data/target_data.npy')
elif OS == 'Windows':
CMRIdataset = CMRIreconDataset(
input_file_path = \
'C:/Users/littl/Documents/PythonScripts/reconproject_data/input_data.npy', \
target_file_path = \
'C:/Users/littl/Documents/PythonScripts/reconproject_data/target_data.npy')
else:
print("Please use valid COMPUTER.\nOptions:\t\'Windows\'\t\'Linux\'")
# SPLIT DATASET INTO TRAIN, VAL AND TEST #####################################
# CMRIdataset = train_dataset + test_dataset
print("\nSplit dataset into train data (80%) and test data (20%)...\n")
train_size = int(0.8 * len(CMRIdataset))
test_size = len(CMRIdataset) - train_size
train_dataset, test_dataset = torch.utils.data.random_split(CMRIdataset, [train_size, test_size])
# train_dataset = train_dataset + val_dataset
print("\nSplit train data into train data (80%) and val data (20%)...\n")
train_size = int(0.8 * len(train_dataset))
val_size = len(train_dataset) - train_size
train_dataset, val_dataset = torch.utils.data.random_split(train_dataset, [train_size, val_size])
print("Load train_dl, val_dl and test_dl...")
# load train set
train_dl = DataLoader(train_dataset, batch_size=16,
shuffle=True, num_workers=0)
# load validation set
valid_dl = DataLoader(val_dataset, batch_size=16,
shuffle=True, num_workers=0)
# load test set
test_dl = DataLoader(test_dataset, batch_size=16,
shuffle=True, num_workers=0)
print("train_dl, val_dl and test_dl loaded!")
# # DEFINE DATABUNCH TO FEED THE MODEL
data = DataBunch(train_dl,
valid_dl,
test_dl,
device=DEVICE,
# dl_tfms:Optional[Collection[Callable]]=None,
# path:PathOrStr='.',
# collate_fn:Callable='data_collate',
# no_check:bool=False
)
# data.show_batch(rows=4)
# DEFINE LEARNER
loss_func = nn.MSELoss()
metrics = mean_absolute_error
model = UNet2d_assembled.UNet2D(20) #20 channels
learn = Learner(data = data,
model = model,
# opt_func:Callable='Adam',
loss_func = loss_func,
metrics = metrics,
# callback_fns=[CSVLogger],
# true_wd:bool=True,
# bn_wd:bool=True,
# wd:Floats=0.01,
# train_bn:bool=True,
# path:str=None,
# model_dir:PathOrStr='models',
# callback_fns:Collection[Callable]=None,
# callbacks:Collection[Callback]=<factory>,
# layer_groups:ModuleList=None,
# add_time:bool=True,
# silent:bool=None
)
# learn.summary()
learn.lr_find(start_lr=1e-07, end_lr=10)
# learn = cnn_learner(data, models.resnet18, metrics=accuracy)
# learn.fit(1)
learn.recorder.plot()
learn.recorder.plot()
lr = 1.5e-2
learn.fit_one_cycle(3, lr)
learn.recorder.plot_lr(show_moms=True)
learn = Learner(data = data,
model = model,
# opt_func:Callable='Adam',
loss_func = loss_func,
metrics = metrics,
callback_fns=[CSVLogger],
# true_wd:bool=True,
# bn_wd:bool=True,
# wd:Floats=0.01,
# train_bn:bool=True,
# path:str=None,
# model_dir:PathOrStr='models',
# callback_fns:Collection[Callable]=None,
# callbacks:Collection[Callback]=<factory>,
# layer_groups:ModuleList=None,
# add_time:bool=True,
# silent:bool=None
)
learn.fit(3)
learn.fit(3)
learn.fit(3, 1e-1)
learn.csv_logger.read_logged_file()
def fit_odd_shedule(learn, lr):
n = len(learn.data.train_dl)
phases = [TrainingPhase(n).schedule_hp('lr', lr, anneal=annealing_cos),
TrainingPhase(n*2).schedule_hp('lr', lr, anneal=annealing_poly(2))]
sched = GeneralScheduler(learn, phases)
learn.callbacks.append(sched)
total_epochs = 3
learn.fit(total_epochs)
learn = Learner(data = data,
model = model,
# opt_func:Callable='Adam',
loss_func = loss_func,
metrics = metrics,
# callback_fns=[CSVLogger],
# true_wd:bool=True,
# bn_wd:bool=True,
# wd:Floats=0.01,
# train_bn:bool=True,
# path:str=None,
# model_dir:PathOrStr='models',
# callback_fns:Collection[Callable]=None,
# callbacks:Collection[Callback]=<factory>,
# layer_groups:ModuleList=None,
# add_time:bool=True,
# silent:bool=None
)
fit_odd_shedule(learn, lr)
learn.recorder.plot_lr()
learn = Learner(data = data,
model = model,
# opt_func:Callable='Adam',
loss_func = loss_func,
metrics = metrics,
# callback_fns=[CSVLogger,
# SaveModelCallback(learn,
# every='epoch',
# monitor='valid_loss')],
# true_wd:bool=True,
# bn_wd:bool=True,
# wd:Floats=0.01,
# train_bn:bool=True,
# path:str=None,
# model_dir:PathOrStr='models',
# callback_fns:Collection[Callable]=None,
# callbacks:Collection[Callback]=<factory>,
# layer_groups:ModuleList=None,
# add_time:bool=True,
# silent:bool=None
)
learn.fit_one_cycle(3, lr,
callbacks=[fastai.callbacks.SaveModelCallback(learn, every='epoch', monitor='valid_loss')])
```
|
github_jupyter
|
## Sampling
You can get a randomly rows of the dataset. It is very usefull in training machine learning models.
We will use the dataset about movie reviewers obtained of [here](http://grouplens.org/datasets/movielens/100k/).
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# read a dataset of movie reviewers into a DataFrame
user_cols = ['user_id', 'age', 'gender', 'occupation', 'zip_code']
users = pd.read_csv('./dataset/u.user', sep='|', header=None, names=user_cols, index_col='user_id')
users.head()
# sample 3 rows from the DataFrame without replacement (new in pandas 0.16.1)
users.sample(n=3)
#use the 'random_state' parameter for reproducibility
users.sample(n=3, random_state=42)
# sample 75% of the DataFrame's rows without replacement
train = users.sample(frac=0.75, random_state=99)
# store the remaining 25% of the rows in another DataFrame
test = users.loc[~users.index.isin(train.index), :]
train.head()
test.head()
# detect duplicate zip codes: True if an item is identical to a previous item
users.zip_code.duplicated().tail()
# count the duplicate items (True becomes 1, False becomes 0)
users.zip_code.duplicated().sum()
# detect duplicate DataFrame rows: True if an entire row is identical to a previous row
users.duplicated().tail()
```
### Logic for duplicated:
+ keep='first' (default): Mark duplicates as True except for the first occurrence.
+ keep='last': Mark duplicates as True except for the last occurrence.
+ keep=False: Mark all duplicates as True.
```
# examine the duplicate rows (ignoring the first occurrence)
users.loc[users.duplicated(keep='first'), :]
# examine the duplicate rows (ignoring the last occurrence)
users.loc[users.duplicated(keep='last'), :]
# examine the duplicate rows (including all duplicates)
users.loc[users.duplicated(keep=False), :]
# only consider a subset of columns when identifying duplicates
users.duplicated(subset=['age', 'zip_code']).sum()
# drop the duplicate rows (inplace=False by default)
users.drop_duplicates(keep='first').shape
users.drop_duplicates(keep='last').shape
users.drop_duplicates(keep=False).shape
```
## Appending pandas Series
```
# Load 'sales-jan-2015.csv' into a DataFrame: jan
jan = pd.read_csv('./dataset/sales-jan-2015.csv', parse_dates=True, index_col='Date')
# Load 'sales-feb-2015.csv' into a DataFrame: feb
feb = pd.read_csv('./dataset/sales-feb-2015.csv', parse_dates=True, index_col='Date')
# Load 'sales-mar-2015.csv' into a DataFrame: mar
mar = pd.read_csv('./dataset/sales-mar-2015.csv', parse_dates=True, index_col='Date')
# Extract the 'Units' column from jan: jan_units
jan_units = pd.DataFrame(jan['Units'])
# Extract the 'Units' column from feb: feb_units
feb_units = pd.DataFrame(feb['Units'])
# Extract the 'Units' column from mar: mar_units
mar_units = pd.DataFrame(mar['Units'])
# Append feb_units and then mar_units to jan_units: quarter1
quarter1 = jan_units.append(feb_units).append(mar_units)
# Print the first slice from quarter1
print(quarter1.loc['jan 27, 2015':'feb 2, 2015'])
# Print the second slice from quarter1
print(quarter1.loc['feb 26, 2015':'mar 7, 2015'])
# Compute & print total sales in quarter1
print(quarter1.sum())
df_quarter= pd.DataFrame(quarter1, columns = ['Units'])
df_quarter
jan_units.reset_index(inplace = True)
feb_units.reset_index(inplace = True)
mar_units.reset_index(inplace = True)
quarter_columns = pd.concat([jan_units, feb_units, mar_units], axis= 1, ignore_index=False)
df_quarter_columns= pd.DataFrame(quarter_columns)
df_quarter_columns
```
## Reading multiple files to build a DataFrame
It is often convenient to build a large DataFrame by parsing many files as DataFrames and concatenating them all at once. You'll do this here with three files, but, in principle, this approach can be used to combine data from dozens or hundreds of files.
Here, you'll work with DataFrames compiled from The Guardian's Olympic medal dataset.
```
medals=[]
medal_types = ['gold','silver','bronze']
for medal in medal_types:
# Create the file name: file_name
file_name = "./dataset/olympic-medals/%s_top5.csv" % medal
# Create list of column names: columns
columns = ['Country', medal]
# Read file_name into a DataFrame: df
medal_df = pd.read_csv(file_name, header=0, index_col='Country', names=columns)
# Append medal_df to medals
medals.append(medal_df)
# Concatenate medals horizontally: medals
medals = pd.concat(medals, axis='columns', sort = True)
# Print medals
pd.DataFrame(medals)
```
## Concatenating vertically to get MultiIndexed rows
When stacking a sequence of DataFrames vertically, it is sometimes desirable to construct a MultiIndex to indicate the DataFrame from which each row originated. This can be done by specifying the keys parameter in the call to pd.concat(), which generates a hierarchical index with the labels from keys as the outermost index label. So you don't have to rename the columns of each DataFrame as you load it. Instead, only the Index column needs to be specified.
```
medals=[]
for medal in medal_types:
file_name = "./dataset/olympic-medals/%s_top5.csv" % medal
# Read file_name into a DataFrame: medal_df
medal_df = pd.read_csv(file_name, index_col='Country')
# Append medal_df to medals
medals.append(medal_df)
# Concatenate medals: medals
medals = pd.concat(medals, keys=['bronze', 'silver', 'gold'])
# Print medals
pd.DataFrame(medals)
```
## Concatenating DataFrames with inner join
```
medals=[]
for medal in medal_types:
file_name = "./dataset/olympic-medals/%s_top5.csv" % medal
# Read file_name into a DataFrame: medal_df
medal_df = pd.read_csv(file_name, index_col='Country')
# Append medal_df to medals
medals.append(medal_df)
# Concatenate medal_list horizontally using an inner join: medals
medals = pd.concat(medals, keys=['bronze', 'silver', 'gold'], axis=1, join='inner')
# Print medals
pd.DataFrame(medals)
```
## Slicing MultiIndexed DataFrames
```
# Sort the entries of medals
medals_sorted = medals.sort_index(level=0)
# Print the number of Bronze medals won by Germany
print(medals_sorted.loc[('bronze','Germany')])
# Print data about silver medals
print(medals_sorted.loc['silver'])
# Create alias for pd.IndexSlice: idx
idx = pd.IndexSlice
# Print all the data on medals won by the United Kingdom
print(medals_sorted.loc[idx[:,'United Kingdom'], :])
```
## Merging
```
user_usage = pd.read_csv("./dataset/merge/user_usage.csv")
user_device = pd.read_csv("./dataset/merge/user_device.csv")
devices = pd.read_csv("./dataset/merge/android_devices.csv")
user_usage.head()
user_device.head()
devices.head()
devices.rename(columns={"Retail Branding": "manufacturer"}, inplace=True)
devices.head()
```
## First merge
We're trying to get the average usage figures for different types of devices. So we need to get the user's device code from user_usage as a column on user_usage, and then get the device's manufacturer from devices as a column on the result.
First, we merge user_usage with user_device with "use_id" as our common column
```
result = pd.merge(user_usage,
user_device[['use_id', 'platform', 'device']],
on='use_id')
result.head()
```
An inner merge, (or inner join) keeps only the common values in both the left and right dataframes for the result. In our example above, only the rows that contain use_id values that are common between user_usage and user_device remain in the result dataset. We can validate this by looking at how many values are common:
```
print("user_usage dimensions: {}".format(user_usage.shape))
print("user_device dimensions: {}".format(user_device[['use_id', 'platform', 'device']].shape))
print("Result dimensions : {}".format(result.shape))
```
## Left merge example
A left merge, or left join, between two dataframes keeps all of the rows and values from the left dataframe, in this case "user_usage". Rows from the right dataframe will be kept in the result only where there is a match in the merge variable in the right dataframe, and NaN values will be in the result where not.
```
result = pd.merge(user_usage,
user_device[['use_id', 'platform', 'device']],
on='use_id', how='left')
print("user_usage dimensions: {}".format(user_usage.shape))
print("result dimensions: {}".format(result.shape))
print("There are {} missing values in the result.".format(
result['device'].isnull().sum()))
result.head()
```
## Right merge example
A right merge, or right join, between two dataframes keeps all of the rows and values from the right dataframe, in this case "user_device". Rows from the left dataframe will be kept where there is a match in the merge variable, and NaN values will be in the result where not.
```
result = pd.merge(user_usage,
user_device[['use_id', 'platform', 'device']],
on='use_id', how='right')
print("user_device dimensions: {}".format(user_device.shape))
print("result dimensions: {}".format(result.shape))
print("There are {} missing values in the 'monthly_mb' column in the result.".format(
result['monthly_mb'].isnull().sum()))
print("There are {} missing values in the 'platform' column in the result.".format(
result['platform'].isnull().sum()))
```
## Outer merge example
A full outer join, or outer merge, keeps all rows from the left and right dataframe in the result. Rows will be aligned where there is shared join values between the left and right, and rows with NaN values, in either the left-originating or right-originating columns will be, will be left in the result where there is no shared join value.
In the final result, a subset of rows should have no missing values. These rows are the rows where there was a match between the merge column in the left and right dataframes. These rows are the same values as found by our inner merge result before.
```
print("There are {} unique values of use_id in our dataframes.".format(
pd.concat([user_usage['use_id'], user_device['use_id']]).unique().shape[0]))
result = pd.merge(user_usage,
user_device[['use_id', 'platform', 'device']],
on='use_id', how='outer', indicator=True)
print("Outer merge result has {} rows.".format(result.shape))
print("There are {} rows with no missing values.".format(
(result.apply(lambda x: x.isnull().sum(), axis=1) == 0).sum()))
result.iloc[[0, 1, 200,201, 350,351]]
# First, add the platform and device to the user usage.
result = pd.merge(user_usage,
user_device[['use_id', 'platform', 'device']],
on='use_id',
how='left')
# Now, based on the "device" column in result, match the "Model" column in devices.
devices.rename(columns={"Retail Branding": "manufacturer"}, inplace=True)
result = pd.merge(result,
devices[['manufacturer', 'Model']],
left_on='device',
right_on='Model',
how='left')
result.head()
devices[devices.Device.str.startswith('GT')]
```
## Calculating statistics on final result
With merges complete, we can simply calculate statistics for users grouped by the manufacturer of their device.
```
result.groupby("manufacturer").agg({
"outgoing_mins_per_month": "mean",
"outgoing_sms_per_month": "mean",
"monthly_mb": "mean",
"use_id": "count"
})
```
|
github_jupyter
|
# Plots of the total distance covered by the particles as a function of their initial position
*Author: Miriam Sterl*
We plot the total distances covered by the particles during the simulation, as a function of their initial position. We do this for the FES, the GC and the GC+FES run.
```
from netCDF4 import Dataset
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import cartopy.mpl.ticker as cticker
File1 = '/science/projects/oceanparcels/output_data/data_Miriam/Results_TrackingFES.nc'
dataset1 = Dataset(File1)
lat1 = dataset1.variables['lat'][:]
lon1 = dataset1.variables['lon'][:]
time1 = dataset1.variables['time'][:]
dist1 = dataset1.variables['distance'][:]
lon1[lon1>180]-=360
lon1[lon1<-180]+=360
File2 = '/science/projects/oceanparcels/output_data/data_Miriam/Results_TrackingGC.nc'
dataset2 = Dataset(File2)
lat2 = dataset2.variables['lat'][:]
lon2 = dataset2.variables['lon'][:]
time2 = dataset2.variables['time'][:]
dist2 = dataset2.variables['distance'][:]
lon2[lon2>180]-=360
lon2[lon2<-180]+=360
File3 = '/science/projects/oceanparcels/output_data/data_Miriam/Results_TrackingGCFES.nc'
dataset3 = Dataset(File3)
lat3 = dataset3.variables['lat'][:]
lon3 = dataset3.variables['lon'][:]
time3 = dataset3.variables['time'][:]
dist3 = dataset3.variables['distance'][:]
lon3[lon3>180]-=360
lon3[lon3<-180]+=360
# Initial longitudes and latitudes (on 2002-01-01)
startLons = lon1[:,0]
startLats = lat1[:,0]
# Distance travelled by the particles between 2002-01-01 and 2015-01-01
finalDist = [dist1[:,-1], dist2[:,-1], dist3[:,-1]]
titles = ['(a) FES run', '(b) GC run', '(c) GC+FES run']
def DistancePlot(lons, lats, dist, fig, ax, vmin, vmax, titlenr, titlesize, labelnr, labelsize, colormap):
"""
Function that plots the total distance covered by particles during a certain period as a function of their initial position
"""
minLat = np.min(np.round(lats)) # the minimal (rounded) latitude
maxLat = np.max(np.round(lats)) # the maximal (rounded) latitude
minLon = np.min(np.round(lons)) # the minimal (rounded) longitude
maxLon = np.max(np.round(lons)) # the maximal (rounded) longitude
allLats = np.arange(minLat, maxLat+1) # the latitudinal grid
allLons = np.arange(minLon, maxLon+1) # the longitudinal grid
distances = np.zeros((len(allLons), len(allLats)))
for i in range(len(dist)):
distances[int(np.round(lons[i]-minLon)), int(np.round(lats[i]-minLat))] = dist[i]
# shift by minLon, minLat to get positive indices
maskedDist = np.ma.masked_where(distances==0.0, distances) # mask land points
Lat, Lon = np.meshgrid(allLats, allLons)
distplot = ax.pcolormesh(Lon, Lat, maskedDist/1e4, cmap = colormap, vmin=vmin, vmax=vmax)
ax.set_title(titles[titlenr], fontsize=titlesize,fontweight='bold')
ax.coastlines()
ax.add_feature(cfeature.LAND, zorder=0, edgecolor='black', facecolor=(0.6,0.6,0.6))
ax.set_xticks([-180, -150, -120, -90, -60, -30, 0, 30, 60, 90, 120, 150, 180], crs=ccrs.PlateCarree())
ax.set_xticklabels([-180, -150, -120, -90, -60, -30, 0, 30, 60, 90, 120, 150, 180], fontsize=labelsize)
ax.set_yticks([-90, -60, - 30, 0, 30, 60, 90], crs=ccrs.PlateCarree())
ax.set_yticklabels([-90, -60, - 30, 0, 30, 60, 90], fontsize=labelsize)
lon_formatter = cticker.LongitudeFormatter()
lat_formatter = cticker.LatitudeFormatter()
ax.xaxis.set_major_formatter(lon_formatter)
ax.yaxis.set_major_formatter(lat_formatter)
ax.grid(linewidth=2, color='black', alpha=0.25, linestyle=':')
return distplot
# Compare the three different runs after 13 years
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(28,16), subplot_kw={'projection': ccrs.PlateCarree()})
i=0
for ax in axes.flat:
distance = DistancePlot(startLons, startLats, finalDist[i], fig, ax,
vmin=1, vmax=10, titlenr = i, titlesize=18, labelnr = 0, labelsize=15, colormap='YlOrRd')
i = i+1
cbar = fig.colorbar(distance, ax=axes.ravel().tolist(), shrink=0.53, extend='both', anchor=(2.2,0.5))
cbar.set_label("Distance ($10^{4}$ km)", rotation=90, fontsize=15)
cbar.ax.tick_params(labelsize=12)
fig.suptitle('Total distance covered', x=0.835, y=1.02, fontsize=21, fontweight='bold')
plt.tight_layout()
#plt.savefig('DistanceComparison', bbox_inches='tight')
```
|
github_jupyter
|
# Data-Sitters Club 8: Just the Code
This notebook contains just the code (and a little bit of text) from the portions of *[DSC 8: Text-Comparison-Algorithm-Crazy-Quinn](https://datasittersclub.github.io/site/dsc8/)* for using Euclidean and cosine distance with word counts and word frequencies, and running TF-IDF for your texts.
This code assumes you've actually read the Data-Sitters Club book already. There's lots of pitfalls if you just try to apply the code without understanding what it's doing, or the effect caused by the various different options. Read first, then try!
## Load modules
```
#Installs seaborn
#You only need to run this cell the first time you run this notebook
import sys
!{sys.executable} -m pip install seaborn
#Imports the count vectorizer from Scikit-learn along with
from sklearn.feature_extraction.text import CountVectorizer
#Glob is used for finding path names
import glob
#We need these to format the data correctly
from scipy.spatial.distance import pdist, squareform
#In case you're starting to run the code just at this point, we'll need os again
import os
import numpy as np
#In case you're starting to run the code just at this point, we'll need pandas again
import pandas as pd
#Import matplotlib
import matplotlib.pyplot as plt
#Import seaborn
import seaborn as sns
```
## Set the file directory for your corpus
```
filedir = '/Users/qad/Documents/dsc_corpus_clean'
os.chdir(filedir)
```
# Word count vectorizer
This looks at just the top 1000 words, and doesn't use `max_df` to remove words that occur across all your texts. You can add it in between the input and the `max_features` parameters, separated by a comma (e.g. `input="filename", max_df=.7, max_features=1000`).
```
# Use the glob library to create a list of file names, sorted alphabetically
# Alphabetical sorting will get us the books in numerical order
filenames = sorted(glob.glob("*.txt"))
# Parse those filenames to create a list of file keys (ID numbers)
# You'll use these later on.
filekeys = [f.split('/')[-1].split('.')[0] for f in filenames]
# Create a CountVectorizer instance with the parameters you need
wordcountvectorizer = CountVectorizer(input="filename", max_features=1000)
# Run the vectorizer on your list of filenames to create your wordcounts
# Use the toarray() function so that SciPy will accept the results
wordcounts = wordcountvectorizer.fit_transform(filenames)
```
### Bonus: word count toy
The code below will display all the words that were included in the word count vectorizer, based on the parameters you've set.
```
sum_words = wordcounts.sum(axis=0)
words_freq = [(word, sum_words[0, idx]) for word, idx in wordcountvectorizer.vocabulary_.items()]
sorted(words_freq, key = lambda x: x[1], reverse=True)
```
## Euclidean distance for word count vectorizer
```
#Runs the Euclidean distance calculation, prints the output, and saves it as a CSV
euclidean_distances = pd.DataFrame(squareform(pdist(wordcounts)), index=filekeys, columns=filekeys)
euclidean_distances
```
### Euclidean distance visualization
```
#Defines the size of the image
plt.figure(figsize=(100, 100))
#Increases the label size so it's more legible
sns.set(font_scale=3)
#Generates the visualization using the data in the dataframe
ax = sns.heatmap(euclidean_distances)
#Displays the image
plt.show()
```
## Cosine distance for word count vectorizer
```
cosine_distances = pd.DataFrame(squareform(pdist(wordcounts, metric='cosine')), index=filekeys, columns=filekeys)
cosine_distances
```
### Cosine distance visualization
```
#Defines the size of the image
plt.figure(figsize=(100, 100))
#Increases the label size so it's more legible
sns.set(font_scale=3)
#Generates the visualization using the data in the dataframe
ax = sns.heatmap(cosine_distances)
#Displays the image
plt.show()
```
# Term frequency vectorizer
```
from sklearn.feature_extraction.text import TfidfVectorizer
# Use the glob library to create a list of file names, sorted alphabetically
# Alphabetical sorting will get us the books in numerical order
filenames = sorted(glob.glob("*.txt"))
# Parse those filenames to create a list of file keys (ID numbers)
# You'll use these later on.
filekeys = [f.split('/')[-1].split('.')[0] for f in filenames]
# Create a CountVectorizer instance with the parameters you need
freqvectorizer = TfidfVectorizer(input="filename", stop_words=None, use_idf=False, norm='l1', max_features=1000)
# Run the vectorizer on your list of filenames to create your wordcounts
# Use the toarray() function so that SciPy will accept the results
wordfreqs = freqvectorizer.fit_transform(filenames).toarray()
```
## Euclidean distance for term frequency vectorizer
```
euclidean_distances_freq = pd.DataFrame(squareform(pdist(wordfreqs, metric='euclidean')), index=filekeys, columns=filekeys)
euclidean_distances_freq
```
### Euclidean distance visualization
```
#Defines the size of the image
plt.figure(figsize=(100, 100))
#Increases the label size so it's more legible
sns.set(font_scale=3)
#Generates the visualization using the data in the dataframe
ax = sns.heatmap(euclidean_distances_freq)
#Displays the image
plt.show()
```
## Cosine distance for word count vectorizer
```
cosine_distances_freq = pd.DataFrame(squareform(pdist(wordfreqs, metric='cosine')), index=filekeys, columns=filekeys)
cosine_distances_freq
```
### Cosine distance visualization
```
#Defines the size of the image
plt.figure(figsize=(100, 100))
#Increases the label size so it's more legible
sns.set(font_scale=3)
#Generates the visualization using the data in the dataframe
ax = sns.heatmap(cosine_distances_freq)
#Displays the image
plt.show()
```
## TF-IDF
```
# Use the glob library to create a list of file names, sorted alphabetically
# Alphabetical sorting will get us the books in numerical order
filenames = sorted(glob.glob("*.txt"))
# Parse those filenames to create a list of file keys (ID numbers)
# You'll use these later on.
filekeys = [f.split('/')[-1].split('.')[0] for f in filenames]
# Create a CountVectorizer instance with the parameters you need
vectorizer = TfidfVectorizer(input="filename", stop_words=None, use_idf=True, norm=None, max_features=1000, max_df=.95)
# Run the vectorizer on your list of filenames to create your wordcounts
# Use the toarray() function so that SciPy will accept the results
transformed_documents = vectorizer.fit_transform(filenames)
transformed_documents_as_array = transformed_documents.toarray()
```
Create a CSV per text file with most distinctive terms.
```
# construct a list of output file paths using the previous list of text files the relative path for tf_idf_output
output_filenames = [str(txt_file).replace(".txt", ".csv") for txt_file in filenames]
# loop each item in transformed_documents_as_array, using enumerate to keep track of the current position
for counter, doc in enumerate(transformed_documents_as_array):
# construct a dataframe
tf_idf_tuples = list(zip(vectorizer.get_feature_names(), doc))
one_doc_as_df = pd.DataFrame.from_records(tf_idf_tuples, columns=['term', 'score']).sort_values(by='score', ascending=False).reset_index(drop=True)
# output to a csv using the enumerated value for the filename
one_doc_as_df.to_csv(output_filenames[counter])
```
## Suggested Citation
Dombrowski, Quinn. “DSC #8: Just the Code.” Jupyter Notebook. *The Data-Sitters Club*, October 21, 2020. https://github.com/datasittersclub/dsc8.
|
github_jupyter
|
# Politician Activity on Facebook by Political Affiliation
The parameters in the cell below can be adjusted to explore other political affiliations and time frames.
### How to explore other political affiliation?
The ***affiliation*** parameter can be use to aggregate politicians by their political affiliations. The column `affiliation` in this [this other notebook](../politicians.ipynb?autorun=true) show the politicians that belong each political affiliation.
***Alternatively***, you can direcly use the [politicians API](http://mediamonitoring.gesis.org/api/politicians/swagger/), or access it with the [SMM Wrapper](https://pypi.org/project/smm-wrapper/).
## A. Set Up parameters
```
# Parameters:
affiliation = 'Grüne'
from_date = '2017-09-01'
to_date = '2018-12-31'
aggregation = 'week'
```
## B. Using the SMM Politician API
```
import pandas as pd
# Create an instance to the smm wrapper
from smm_wrapper import SMMPoliticians
smm = SMMPoliticians()
#using the api to get the data
df = smm.dv.get_politicians()
# Filter the accounts by party, and valid ones (the ones that contain fb_ids)
party_df = df[(df['affiliation']==affiliation) & (df['fb_ids'].notnull())]
# query the Social Media Monitoring API
posts_by = pd.concat(smm.dv.posts_by(_id=organization_id, from_date=from_date, to_date=to_date, aggregate_by=aggregation)
for organization_id in party_df.index)
comments_by = pd.concat(smm.dv.comments_by(_id=organization_id, from_date=from_date, to_date=to_date, aggregate_by=aggregation)
for organization_id in party_df.index)
# aggregate posts and comments
total_posts_by = posts_by.groupby('date')[
'posts', 'replies', 'shares', 'reactions', 'likes'].sum()
total_comments_by = comments_by.groupby('date')[
'comments', 'replies', 'likes'].sum()
```
## C. Plotting
### C.1 Plot Facebook Post Activity
```
import plotly
from plotly import graph_objs as go
plotly.offline.init_notebook_mode(connected=True)
#plot for facebook posts activity
plotly.offline.iplot({
"data": [go.Scatter(x=total_posts_by.index.tolist(), y=total_posts_by['posts'], name='Posts', line_shape='spline'),
go.Scatter(x=total_posts_by.index.tolist(), y=total_posts_by['replies'], name='Replies',line_shape='spline'),
go.Scatter(x=total_posts_by.index.tolist(), y=total_posts_by['shares'], name='Shares', line_shape='spline'),
go.Scatter(x=total_posts_by.index.tolist(), y=total_posts_by['reactions'], name='Reactions', line_shape='spline'),
go.Scatter(x=total_posts_by.index.tolist(), y=total_posts_by['likes'], name='Likes', line_shape='spline')],
"layout": go.Layout(title='Facebook posts for {}'.format(affiliation), xaxis={'title':''}, yaxis={'title':'N'})
})
```
### C.2 Plot Facebook Comment Activity
```
# plot for facebook comments activity
plotly.offline.iplot({
"data": [go.Scatter(x=total_comments_by.index.tolist(), y=total_comments_by['comments'], name='Comments', line_shape='spline'),
go.Scatter(x=total_comments_by.index.tolist(), y=total_comments_by['replies'], name='Replies', line_shape='spline'),
go.Scatter(x=total_comments_by.index.tolist(), y=total_comments_by['likes'], name='Likes', line_shape='spline')],
"layout": go.Layout(title='Facebook comments for {}'.format(affiliation), xaxis={'title':''}, yaxis={'title':'N'})
})
```
|
github_jupyter
|
# 目的:了解Python基本語法
1. [資料型別](#01)
2. [for-loop](#02)
3. [while-loop](#03)
4. [清單(list)](#04)
5. [tuple是什麼?](#05)
6. [Python特殊的清單處理方式](#06)
7. [if的用法](#07)
8. [以if控制迴圈的break和continue](#08)
9. [函數:將計算結果直接於函數內印出或回傳(return)出函數外](#09)
10. [匿名函數](#10)
11. [物件導向範例](#11)
12. [NumPy (Python中用於處理numerical array的套件)](#12)
13. [一維序列](#13)
14. [二維矩陣](#14)
# 練習
* [運用range(5),for以及append()建立一清單,其內容為\[0,1,4,9,16\] ](#ex01)
* [運用range(5), if以及for建立一清單,其內容為\[0,4,16\] ](#ex02)
* [試輸出99乘法表](#ex1)
* [試輸出99乘法表(以清單表示)](#ex2)
* [寫一個函數factorial(n)。](#ex3)
* [建立一函數 f。輸入: 一個 2 維矩陣,輸出: 該2維矩陣內的所有數值加總。](#ex4)
---
## <a id="01"/>資料型別
### 整數(int)
```
a=1
type(a)
b=3
type(b)
```
兩整數相除,輸出結果為浮點數(float)。(備註:Python 3開始)
```
a/b
type(a/b)
```
在Python3,兩整數相除,需以//運算子來相除,方能真正用整數儲存該結果。
```
a//b
type(a//b)
```
兩整數相加,其輸出仍然為整數。
```
a+b
type(a+b)
```
### 浮點數(float)
Python不需宣告型別。一個數字將會被判別為整數(int)或浮點數(float),需看該數是否有小數點存在。
```
type(1)
type(1.)
type(1.E-5)
```
### 字串(str)
```
mystr='Hello World!'
type(mystr)
```
將該字串所有字變成大寫
```
mystr.upper()
```
將該字串所有字變成小寫
```
mystr.upper().lower()
```
取出該字串前三個字
```
mystr[0:3]
```
檢查某字串片段是否存在於該字串
```
'Wor' in mystr
'WOR' in mystr
'WOR' in mystr.upper()
```
以len()看字串長度
```
len(mystr)
mystr=' hi '
```
清除左右空白
```
mystr.strip()
```
清除左空白
```
mystr.lstrip()
```
清除右空白
```
mystr.rstrip()
```
置換字串內的h成f
```
mystr.replace('h','f')
```
### 布林(Boolean)
```
t=True #真
f=False #假
t==f #真等於假?
t==t #真等於真?
t!=f #真不等於假?
t==f or t!=f #真等於假 或是 真不等於假?
t==f and t!=f #真等於假 和 真不等於假?
not t #非真?
```
[回索引](#目的:了解Python基本語法)
## <a id="02"/>for-loop
```
for j in range(5):
print(j)
```
以上,我們使用了range()這個內建函數,它到底是什麼?
```
r=range(5)
print( type(r) )
```
用type()檢查變數r的型別,我們發現了r=range(5)是屬於'range'這個類別的一個物件。
接下來,我們以內建函數hasattr()去檢查range(5)這個物件是不是可疊代(iterable):
首先以help()函數檢查一下hasattr()的用法:
```
help(hasattr)
hasattr(range(5), '__iter__')
r=range(5).__iter__() # 取得range(5)的疊代器
print( r.__next__() ) # 進行疊代並印出
print( r.__next__() ) # 進行疊代並印出
print( r.__next__() ) # 進行疊代並印出
print( r.__next__() ) # 進行疊代並印出
print( r.__next__() ) # 進行疊代並印出
print( r.__next__() ) # 進行疊代並印出
```
### 小結
1. 若物件(object)為可疊代(iterable):
* 表示我們可用\_\_iter\_\_()以及\_\_next\_\_()來操控該物件,一個一個的去取得物件裡面的元素。
* 物件裡面的元素亦可簡單的以for迴圈來取得。
2. 複習以下函數的意義:hasattr(),\_\_iter\_\_(),\_\_next\_\_(),range()
[回索引](#目的:了解Python基本語法)
-----
## <a id="03"/> while-loop
```
i=0
while(i<5):
print(i)
i+=1 # i=i+1的簡寫
```
常用於不確定要跑幾次,要跑到直到條件滿足才跳出迴圈的情形。例如:嘗試擷取某網頁,直到失敗次數太多或是擷取成功為止。
[回索引](#目的:了解Python基本語法)
## <a id="04"/>清單(list)
定義:包含元素的一個集合。清單內的元素可重複,且每個元素都有一個索引(index)。
```
array=[1,2,2,3,4,5] #建立一個清單
print(array)
print(array[0]) #印出清單內的第一個元素
print(array[-1]) #印出清單內最後一個元素
type([1,2,2,3,4,5]) #以type查看清單型別,確定清單(list)的型別就是list。
hasattr([1,2,3,4,5],'__iter__') # 若是[1,2,3,4,5]為可疊代物件,那我們就可以用迴圈來疊代出清單內的所有元素。
for j in [1,2,3,4,5]:
print(j,j**2)
for j in [1,2.,'字串',3,range(10),5,[1,1,1,2,2,2]]:
print(j,'\t',type(j),'\t',hasattr(j,'__iter__'))
```
從以上得知:
1. 清單裡的元素可以有不同的型別(type)。
2. 字串(str)和清單(list)一樣,是可以疊代的物件。因此,他們可以用for迴圈來進行內容的提取,例如:
```
for j in 'Python':
print(j)
```
使用append()添加新元素至清單內
```
array=[1,2,3]
array.append(4)
print(array)
```
使用del 刪除清單內元素
```
print(array)
del array[2] #刪除清單內的第二個元素
print(array)
```
我們可使用len()去得知清單的長度
```
array=[10,20,30,40]
print(len(array))
```
使用enumerate()去列舉清單
```
enumerate(array)
type(enumerate(array))
hasattr(enumerate,'__iter__')
for j in enumerate(array):
print(j)
print( type( (0,10) ) )
```
[回索引](#目的:了解Python基本語法)
## <a id="05"/>tuple是什麼?
```
array=(1,2,3,"abc")
print(array)
del array[1]
array.append(5)
array[2]=0
```
結論:不可新增刪除覆蓋tuple內的元素,因此tuple可以被看做是唯讀的list。
list可以被取set()。
set的定義:集合內元素不允許重複,且集合內的元素無索引。
```
set([1,1,2,3,3,4,1,2,'alpha','beta'])
type( {1, 2, 3, 4, 'beta', 'alpha'} )
st={1,1,2,3,3,4,1,2,'alpha','beta'}
print(st)
print(hasattr(st,'__iter__'))
for j in st:
print(j)
print(st[0])
```
也就是先前說的,set內的元素並無索引。
[回索引](#目的:了解Python基本語法)
## <a id="06"/>Python特殊的清單處理方式
將range(5)裡面的東西抓出來,放到一清單叫做lst,可有各種寫法:
第一種
```
lst=[]
for j in range(5):
lst.append(j)
print(lst)
```
第二種
```
lst=[j for j in range(5)] #此是非常Python的寫法(Pythonic way of coding)
print(lst)
```
第三種
```
lst=list(range(5))
print(lst)
```
第四種
```
lst=[*range(5)]
print(lst)
```
## <a id="ex01" style='color:purple'/> 練習0-1. 運用range(5),for以及append()建立一清單,其內容為[0,1,4,9,16]
```
#法一:
lst=[]
for j in range(5):
#完成接下來的部分
#法二:
#提示: lst=[.....]
```
[回索引](#目的:了解Python基本語法)
## <a id="ex02" style='color:purple'/> 練習0-2. 運用range(5), if以及for建立一清單,其內容為[0,4,16]
```
# 法一:
lst=[]
for j in range(5):
#完成接下來的部分
#法二:
#提示: lst=[.....]
```
[回索引](#目的:了解Python基本語法)
## <a id="07"/>if的用法
### if...elif..else的使用 :
```
x=5
if(x==1):
print('x is 1')
elif(x==2):
print('x is 2')
else:
print('x is neither 1 nor 2.')
```
### 例:取range(10)內的偶數並印出:
法一
```
for j in range(10):
if(j%2==0):
print(j)
```
法二
```
[j for j in range(10) if j%2==0]
```
[回索引](#目的:了解Python基本語法)
## <a id="08"/>以if控制迴圈的break和continue
```
for j in range(5):
print(j)
if(j==2):
break #中斷,跳出迴圈
for j in range(5):
if(j==2):
continue #略過以下程式碼,並繼續疊代至下一個元素
print(j)
```
[回索引](#目的:了解Python基本語法)
## <a id="ex1" style='color:purple'/> 練習1. 試著輸出以下內容
```
#提示:使用for, range(),print()
for i in range(1,4):
#完成接下來的部分
```
[回索引](#目的:了解Python基本語法)
## <a id="ex2" style='color:purple'/> 練習2. 試著輸出以下內容
```
#提示:使用for, range(),print(),以及建立一個清單(list)
#完成接下來的部分
```
[回索引](#目的:了解Python基本語法)
## <a id="09"/>函數:將計算結果直接於函數內印出或回傳(return)出函數外
### 例一
```
def square(x):
print(x*x)
def square_return(x):
return(x**2)
```
square(x)將只會印出x, 而square_return(x)將會回傳x。
```
square(2)
square_return(2)
```
可另一變數res接收square_return(x)回傳的值。
```
res=square_return(2)
print(res)
```
需注意的是,square(x)並不會回傳值,因此res將接收到None(無)。
```
res=square(2)
print(res)
```
### 例二: 寫一個函數add(a, b)。其輸入為 a和b,輸出為 a+b。
```
def add(a,b):
return a+b
addResult=add(5,7)
print(addResult)
```
### 複習:Java函數寫法(輸入x,回傳x平方)
```
%%file testSquare.java
public class testSquare{
public static void main(String args[]){
int y=square(2);
System.out.println(y);
}
static int square(int x){
return x*x;
}
}
!javac testSquare.java
!java testSquare
```
[回索引](#目的:了解Python基本語法)
## <a id="ex3" style='color:purple'/> 練習3:寫一個函數factorial(n)。
其作用為:
輸入:$n$,輸出:$1*2*3*....*n$
```
# 修改以下程式碼,以完成函數factorial(n)
def factorial(n):
if(n==0):
return ???
if(n!=0):
return ???
```
[回索引](#目的:了解Python基本語法)
## <a id="10"/>匿名函數
一般函數寫法
```
def f(x,y):
return x+y
f(1,2)
```
使用匿名函數,並將匿名函數給予名稱f。此方法得到的函數等同於上述使用一般函數寫法的結果。
```
f=lambda x,y:x+y
f(1,2)
```
將匿名函數直接拿來使用,不給名稱,用完就丟。
```
(lambda x,y:x+y)(1,2) # 1+2=3
(lambda x:x*x)(7) # 7X7=49
```
[回索引](#目的:了解Python基本語法)
## <a id="11"/> 物件導向範例
範例:提款機
```
class Customer(object):
def __init__(self, name, balance=0.0):
self.name=name #當物件被新建立,姓名以及餘額兩個屬性將被初始化
self.balance=balance
def withdraw(self, amount): #提款
if amount > self.balance: #若要提取大於帳戶餘額的數目,將提出錯誤訊息
raise RuntimeError('Amount greater than available balance.')
self.balance -= amount
return self.balance
def deposit(self, amount): #存款
self.balance += amount
return self.balance
```
* 第1行:所有Python3類別都是object這個類別的子類別。
* 第2行:當物件產生時,初始子__init__()(等同Java中的建構子)將初始化屬於該物件的一些屬性。此範例中,屬於該物件的兩個屬性,也就是人名和帳戶餘額將被建立。
* 所有方法都要接收物件本身為第一個參數。依照慣例,大家將該物件本身稱作self。
```
a=Customer("Bill",100)
a.withdraw(70)
a.deposit(60)
a.withdraw(100)
```
[回索引](#目的:了解Python基本語法)
---
## <a id="12"/>NumPy (Python中用於處理numerical array的套件)
此套件用於建立數值陣列和做數值運算。
https://docs.scipy.org/doc/numpy/reference/index.html
```
import numpy as np
```
內建常數$\pi$
```
np.pi
```
計算根號$\pi$
```
np.sqrt(np.pi)
```
[回索引](#目的:了解Python基本語法)
## <a id="13"/>一維序列
用np.arange(n)建立一序列內容為[0 1 2 .....n-1]
```
np.arange(10)
```
用np.linspace(0,2.*np.pi,10)建立一個一維線性空間。起始為0,終點為 $\pi$ ,共10個點。
```
np.linspace(0,2.*np.pi,10)
```
將數列內所有數值+100
```
np.arange(10)+100
```
將數列內所有數值取平方
```
np.arange(10)**2
```
以np.mean()計算出算數平均
```
np.mean( np.arange(10) )
```
以np.std()計算出標準差
```
np.std( np.arange(10) )
```
檢驗Numpy序列和Python清單效能差異
```
a=np.random.normal(0,1,100000) # 100000個常態分佈亂數
b=np.random.normal(0,1,100000) # 100000個常態分佈亂數
list_a=list(a)
list_b=list(b)
%%timeit
res=a+b
%%timeit
res=[]
for j in range(len(list_a)):
res.append(list_a[j]+list_b[j])
```
NumPy較快,因
* 有做vectorization (能把資料一次餵給多個算數邏輯閘,以加快運算速度。)
* array裡的資料皆同型別,相加時不用一個個做型別判別。
[回索引](#目的:了解Python基本語法)
## <a id="14"/>二維矩陣
建立一矩陣
```
A=np.array([[1,2,3],[4,5,6],[7,8,9]])
A
```
將$A$轉置 ($A^{T}$)
```
A.T
```
$A\cdot A^{T}$
```
A.dot(A.T)
```
截取片段:清單方式:以A [index0][index1] 取出二維陣列$A$的部分片段。
```
A[0]
A[1:3]
A[1:3]
A[:][1:3]
```
截取片段:矩陣方式:以A [index0,index1] 取出二維陣列$A$的部分片段。(index0方向:垂直,index1方向:水平)
```
A
A[1:3,:]
A[:,1:3]
```
檢查一下A的形狀
```
A.shape
```
以條件找尋A裡面符合條件的數值
```
A>5
A[A>5]
```
[回索引](#目的:了解Python基本語法)
## <a id="ex4" style='color:purple'/>練習4: 建立一函數 f。輸入: 一個 2 維矩陣,輸出: 該2維矩陣內的所有數值加總。
```
A=np.array([[1,2,3],[4,5,6],[7,8,9]])
def f(A)
# 完成此函數
return ???
```
[回索引](#目的:了解Python基本語法)
|
github_jupyter
|
# SageMaker Batch Transform using an XgBoost Bring Your Own Container (BYOC)
In this notebook, we will walk through an end to end data science workflow demonstrating how to build your own custom XGBoost Container using Amazon SageMaker Studio. We will first process the data using SageMaker Processing, push an XGB algorithm container to ECR, train the model, and use Batch Transform to generate inferences from your model in batch or offline mode. Finally we will use SageMaker Experiments to capture the metadata and lineage associated with the trained model. This is a key differentiator of SageMaker Studio as the metadata captured is visible in the Experiments UI.
## The example
In this example we show how to package a custom XGBoost container with Amazon SageMaker studio with a Python example which works with the UCI Credit Card dataset. To use a different algorithm or a different dataset, you can easily change the Docker container and the xgboost folder attached with this code.
In this example, we use a single image to support training and hosting. This simplifies the procedure because we only need to manage one image for both tasks. Sometimes you may want separate images for training and hosting because they have different requirements. In this case, separate the parts discussed below into separate Dockerfiles and build two images. Choosing whether to use a single image or two images is a matter of what is most convenient for you to develop and manage.
If you're only using Amazon SageMaker for training or hosting, but not both, only the functionality used needs to be built into your container.
## The workflow
This notebook is divided into three parts: *exploring your data and feature engineering*, *building your contianer* and *using your container to train a model and generate inferences*
### The Dockerfile
The Dockerfile describes the image that we want to build. You can think of it as describing the complete operating system installation of the system that you want to run. A Docker container running is quite a bit lighter than a full operating system, however, because it takes advantage of Linux on the host machine for the basic operations.
For the Python science stack, we start from an official TensorFlow docker image and run the normal tools to install TensorFlow Serving. Then we add the code that implements our specific algorithm to the container and set up the right environment for it to run under.
For details on how BYOC works with SageMaker Notebook instances, see this example: https://github.com/awslabs/amazon-sagemaker-examples/blob/master/advanced_functionality/scikit_bring_your_own/scikit_bring_your_own.ipynb. Unlike SageMaker notebook instances, in SageMaker studio as we will see below, you will not need the build_and_push.sh script anymore. The studio-build CLI will handle pushing the container to ECR for you.
Let's look at the Dockerfile for this example.
```
!cat Dockerfile
```
### Step 1: Pre-requisites: Download the necessary libraries
```
import sys
#!{sys.executable} -m pip install "sagemaker-experiments"
#!{sys.executable} -m pip install "sagemaker-studio-image-build"
```
### Step 2: Ensure IAM Role has access to necessary services
The SageMaker Studio Image Build CLI uses Amazon Elastic Container Registry and AWS CodeBuild so we need to ensure that the role we provide as input to our CLI commands has the necessary policies and permissions attached.
Two scenarios are supported including:
* **Add IAM Permissions to SageMaker Execution Role**
This scenario includes updating the Execution Role attached to this notebook instance with the required permissions. In this scenario, you need to get the current execution role and ensure the trust policy and additional permissions are associated with the role.
* **Create/Utilize a secondary role with appropriate permissions attached**
This scenario include using a secondary role setup with the permissions below and identified in the --role argument when invoking the CLI (Example: *sm-docker build . --role build-cli-role*)
**Ensure the role that will be used has the following**
1) Trust policy with CodeBuild
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Principal": {
"Service": [
"codebuild.amazonaws.com"
]
},
"Action": "sts:AssumeRole"
}
]
}
2) Permissions attached to the execution role to execute a build in AWS CodeBuild, create ECR repository and push images to ECR
{
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Action": [
"codebuild:DeleteProject",
"codebuild:CreateProject",
"codebuild:BatchGetBuilds",
"codebuild:StartBuild"
],
"Resource": "arn:aws:codebuild:*:*:project/sagemaker-studio*"
},
{
"Effect": "Allow",
"Action": "logs:CreateLogStream",
"Resource": "arn:aws:logs:*:*:log-group:/aws/codebuild/sagemaker-studio*"
},
{
"Effect": "Allow",
"Action": [
"logs:GetLogEvents",
"logs:PutLogEvents"
],
"Resource": "arn:aws:logs:*:*:log-group:/aws/codebuild/sagemaker-studio*:log-stream:*"
},
{
"Effect": "Allow",
"Action": "logs:CreateLogGroup",
"Resource": "*"
},
{
"Effect": "Allow",
"Action": [
"ecr:CreateRepository",
"ecr:BatchGetImage",
"ecr:CompleteLayerUpload",
"ecr:DescribeImages",
"ecr:DescribeRepositories",
"ecr:UploadLayerPart",
"ecr:ListImages",
"ecr:InitiateLayerUpload",
"ecr:BatchCheckLayerAvailability",
"ecr:PutImage"
],
"Resource": "arn:aws:ecr:*:*:repository/sagemaker-studio*"
},
{
"Effect": "Allow",
"Action": "ecr:GetAuthorizationToken",
"Resource": "*"
},
{
"Effect": "Allow",
"Action": [
"s3:GetObject",
"s3:DeleteObject",
"s3:PutObject"
],
"Resource": "arn:aws:s3:::sagemaker-*/*"
},
{
"Effect": "Allow",
"Action": [
"s3:CreateBucket"
],
"Resource": "arn:aws:s3:::sagemaker*"
},
{
"Effect": "Allow",
"Action": [
"iam:GetRole",
"iam:ListRoles"
],
"Resource": "*"
},
{
"Effect": "Allow",
"Action": "iam:PassRole",
"Resource": "arn:aws:iam::*:role/*",
"Condition": {
"StringLikeIfExists": {
"iam:PassedToService": "codebuild.amazonaws.com"
}
}
}
]
}
### Restart Kernel
Once the libraries are installed, restart the kernel by clicking Kernel --> Restart and Running all the cells below.
```
# Let's inspect the role we have created for our notebook here:
import boto3
import sagemaker
from sagemaker import get_execution_role
role = get_execution_role()
sess = sagemaker.Session()
region = boto3.session.Session().region_name
print("Region = {}".format(region))
sm = boto3.Session().client("sagemaker")
```
### Complete Setup: Import libraries and set global definitions.
All needed libraries will come pre-installed with this notebook with the Lifecycle configuration scripts.
```
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import os
from time import sleep, gmtime, strftime
import json
import time
# Import SageMaker Experiments
from sagemaker.analytics import ExperimentAnalytics
from smexperiments.experiment import Experiment
from smexperiments.trial import Trial
from smexperiments.trial_component import TrialComponent
from smexperiments.tracker import Tracker
```
### Specify buckets for storing data
```
# Use our custom bucket here.
rawbucket = sess.default_bucket()
prefix = "sagemaker-modelmonitor" # use this prefix to store all files pertaining to this workshop.
dataprefix = prefix + "/data"
traindataprefix = prefix + "/train_data"
testdataprefix = prefix + "/test_data"
testdatanolabelprefix = prefix + "/test_data_no_label"
trainheaderprefix = prefix + "/train_headers"
```
### Step 3: Data Exploration
A key part of the data science lifecyle is data exploration, pre-processing and feature engineering. We will demonstrate how to use SM notebooks for data exploration and SM Processing for feature engineering and pre-processing data
### Download and Import the data
We will use the UCI Machine Learning Archive dataset on payment default for this example [https://archive.ics.uci.edu/ml/datasets/default+of+credit+card+client]. Here we have a number of common features such as payment histories from prior months, payments, bills etc to predict a binary outcome -- whether or not a user will default on their payment in the following month.
```
data = pd.read_excel("data.xls", header=1)
data = data.drop(columns=["ID"])
data.head()
data.rename(columns={"default payment next month": "Label"}, inplace=True)
lbl = data.Label
data = pd.concat([lbl, data.drop(columns=["Label"])], axis=1)
data.head()
COLS = data.columns
```
### Data Exploration
Once you have downloaded the dataset, the next step in the data science lifecycle is to explore the dataset. A correlation plot can indicate whether the features are correlated to one another and the label itself.
```
## Corr plot
f = plt.figure(figsize=(19, 15))
plt.matshow(data.corr(), fignum=f.number)
plt.xticks(range(data.shape[1]), data.columns, fontsize=14, rotation=45)
plt.yticks(range(data.shape[1]), data.columns, fontsize=14)
cb = plt.colorbar()
cb.ax.tick_params(labelsize=14)
plt.title("Correlation Matrix", fontsize=16);
from pandas.plotting import scatter_matrix
SCAT_COLUMNS = ["BILL_AMT1", "BILL_AMT2", "PAY_AMT1", "PAY_AMT2"]
scatter_matrix(data[SCAT_COLUMNS], figsize=(10, 10), diagonal="kde")
plt.show()
```
### Step 4: Secure Feature Processing pipeline using SageMaker Processing
While you can pre-process small amounts of data directly in a notebook SageMaker Processing offloads the heavy lifting of pre-processing larger datasets by provisioning the underlying infrastructure, downloading the data from an S3 location to the processing container, running the processing scripts, storing the processed data in an output directory in Amazon S3 and deleting the underlying transient resources needed to run the processing job. Once the processing job is complete, the infrastructure used to run the job is wiped, and any temporary data stored on it is deleted.
```
if not os.path.exists('rawdata/rawdata.csv'):
!mkdir rawdata
data.to_csv('rawdata/rawdata.csv', index=None)
else:
pass
# Upload the raw dataset
raw_data_location = sess.upload_data("rawdata", bucket=rawbucket, key_prefix=dataprefix)
print(raw_data_location)
## Use SageMaker Processing with Sk Learn. -- combine data into train and test at this stage if possible.
from sagemaker.sklearn.processing import SKLearnProcessor
sklearn_processor = SKLearnProcessor(
framework_version="0.20.0", role=role, instance_type="ml.c4.xlarge", instance_count=1
)
```
### Write a preprocessing script (same as above)
```
%%writefile preprocessing.py
import argparse
import os
import warnings
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.exceptions import DataConversionWarning
from sklearn.compose import make_column_transformer
warnings.filterwarnings(action="ignore", category=DataConversionWarning)
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("--train-test-split-ratio", type=float, default=0.3)
parser.add_argument("--random-split", type=int, default=0)
args, _ = parser.parse_known_args()
print("Received arguments {}".format(args))
input_data_path = os.path.join("/opt/ml/processing/input", "rawdata.csv")
print("Reading input data from {}".format(input_data_path))
df = pd.read_csv(input_data_path)
df.sample(frac=1)
COLS = df.columns
newcolorder = (
["PAY_AMT1", "BILL_AMT1"]
+ list(COLS[1:])[:11]
+ list(COLS[1:])[12:17]
+ list(COLS[1:])[18:]
)
split_ratio = args.train_test_split_ratio
random_state = args.random_split
X_train, X_test, y_train, y_test = train_test_split(
df.drop("Label", axis=1), df["Label"], test_size=split_ratio, random_state=random_state
)
preprocess = make_column_transformer(
(["PAY_AMT1"], StandardScaler()), (["BILL_AMT1"], MinMaxScaler()), remainder="passthrough"
)
print("Running preprocessing and feature engineering transformations")
train_features = pd.DataFrame(preprocess.fit_transform(X_train), columns=newcolorder)
test_features = pd.DataFrame(preprocess.transform(X_test), columns=newcolorder)
# concat to ensure Label column is the first column in dataframe
train_full = pd.concat(
[pd.DataFrame(y_train.values, columns=["Label"]), train_features], axis=1
)
test_full = pd.concat([pd.DataFrame(y_test.values, columns=["Label"]), test_features], axis=1)
print("Train data shape after preprocessing: {}".format(train_features.shape))
print("Test data shape after preprocessing: {}".format(test_features.shape))
train_features_headers_output_path = os.path.join(
"/opt/ml/processing/train_headers", "train_data_with_headers.csv"
)
train_features_output_path = os.path.join("/opt/ml/processing/train", "train_data.csv")
test_features_output_path = os.path.join("/opt/ml/processing/test", "test_data.csv")
print("Saving training features to {}".format(train_features_output_path))
train_full.to_csv(train_features_output_path, header=False, index=False)
print("Complete")
print("Save training data with headers to {}".format(train_features_headers_output_path))
train_full.to_csv(train_features_headers_output_path, index=False)
print("Saving test features to {}".format(test_features_output_path))
test_full.to_csv(test_features_output_path, header=False, index=False)
print("Complete")
# Copy the preprocessing code over to the s3 bucket
codeprefix = prefix + "/code"
codeupload = sess.upload_data("preprocessing.py", bucket=rawbucket, key_prefix=codeprefix)
print(codeupload)
train_data_location = rawbucket + "/" + traindataprefix
test_data_location = rawbucket + "/" + testdataprefix
print("Training data location = {}".format(train_data_location))
print("Test data location = {}".format(test_data_location))
```
Next we will execute the script above using the managed scikit-learn preprocessing container. This step may take a few minutes to execute.
```
from sagemaker.processing import ProcessingInput, ProcessingOutput
sklearn_processor.run(
code=codeupload,
inputs=[ProcessingInput(source=raw_data_location, destination="/opt/ml/processing/input")],
outputs=[
ProcessingOutput(
output_name="train_data",
source="/opt/ml/processing/train",
destination="s3://" + train_data_location,
),
ProcessingOutput(
output_name="test_data",
source="/opt/ml/processing/test",
destination="s3://" + test_data_location,
),
ProcessingOutput(
output_name="train_data_headers",
source="/opt/ml/processing/train_headers",
destination="s3://" + rawbucket + "/" + prefix + "/train_headers",
),
],
arguments=["--train-test-split-ratio", "0.2"],
)
preprocessing_job_description = sklearn_processor.jobs[-1].describe()
output_config = preprocessing_job_description["ProcessingOutputConfig"]
for output in output_config["Outputs"]:
if output["OutputName"] == "train_data":
preprocessed_training_data = output["S3Output"]["S3Uri"]
if output["OutputName"] == "test_data":
preprocessed_test_data = output["S3Output"]["S3Uri"]
```
# Part 2: Building the Container and Training the model
### Step 5: Set up SageMaker Experiments
In this notebook, we first build the Docker image by providing the Dockerfile discussed before and train a model using that Dockerfile
We use SageMaker Experiments for data scientists to track the lineage of the model from the raw data source to the preprocessing steps and the model training pipeline. With SageMaker Experiments, data scientists can compare, track and manage multiple diferent model training jobs, data processing jobs, hyperparameter tuning jobs and retain a lineage from the source data to the training job artifacts to the model hyperparameters and any custom metrics that they may want to monitor as part of the model training.
```
# Create a SageMaker Experiment
cc_experiment = Experiment.create(
experiment_name=f"CreditCardDefault-{int(time.time())}",
description="Predict credit card default from payments data",
sagemaker_boto_client=sm,
)
print(cc_experiment)
```
In addition to training, we want to track the lineage of the entire machine learing pipeline also including the processing job above.
```
# Start Tracking parameters used in the Pre-processing pipeline.
with Tracker.create(display_name="Preprocessing", sagemaker_boto_client=sm) as tracker:
tracker.log_parameters({"train_test_split_ratio": 0.2, "random_state": 0})
# we can log the s3 uri to the dataset we just uploaded
tracker.log_input(name="ccdefault-raw-dataset", media_type="s3/uri", value=raw_data_location)
tracker.log_input(
name="ccdefault-train-dataset", media_type="s3/uri", value=train_data_location
)
tracker.log_input(name="ccdefault-test-dataset", media_type="s3/uri", value=test_data_location)
```
### Step 6: Build XgBoost container for training
The code for the XGB container is already supplied with this notebook. We simply need to build this container and push it to ECR. The single line of code below will do it.
```
!sm-docker build .
```
### Step 7: Train the Model
The same security postures we applied previously during SM Processing apply to training jobs. We will also have SageMaker experiments track the training job and store metadata such as model artifact location, training/validation data location, model hyperparameters etc.
As shown above, your image URI has the following form:
Image URI: {account-id}.dkr.ecr.{region}.amazonaws.com/sagemaker-studio-{studioID}:{username}
```
account = sess.boto_session.client("sts").get_caller_identity()["Account"]
ecr = boto3.client("ecr")
domain_id = "sagemaker-studio-{}".format(sm.list_apps()["Apps"][0]["DomainId"])
image_tag = ecr.list_images(repositoryName=domain_id, filter={"tagStatus": "TAGGED"})["imageIds"][
0
]["imageTag"]
image = "{}.dkr.ecr.{}.amazonaws.com/{}:{}".format(account, region, domain_id, image_tag)
preprocessing_trial_component = tracker.trial_component
trial_name = f"cc-fraud-training-job-{int(time.time())}"
cc_trial = Trial.create(
trial_name=trial_name, experiment_name=cc_experiment.experiment_name, sagemaker_boto_client=sm
)
cc_trial.add_trial_component(preprocessing_trial_component)
cc_training_job_name = "cc-training-job-{}".format(int(time.time()))
xgb = sagemaker.estimator.Estimator(
image,
role,
instance_count=1,
instance_type="ml.m4.xlarge",
max_run=86400,
output_path="s3://{}/{}/models".format(rawbucket, prefix),
sagemaker_session=sess,
) # set to true for distributed training
xgb.set_hyperparameters(
max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
verbosity=0,
objective="binary:logistic",
num_round=100,
)
xgb.fit(
inputs={"training": "s3://" + train_data_location},
job_name=cc_training_job_name,
experiment_config={
"TrialName": cc_trial.trial_name, # log training job in Trials for lineage
"TrialComponentDisplayName": "Training",
},
wait=True,
)
time.sleep(2)
```
Having used SageMaker Experiments to track the training runs, we can now extract model metadata to get the entire lineage of the model from the source data to the model artifacts and the hyperparameters.
To do this, simply call the **describe_trial_component** API.
```
# Present the Model Lineage as a dataframe
from sagemaker.session import Session
session = boto3.Session()
lineage_table = ExperimentAnalytics(
sagemaker_session=Session(session, sm),
search_expression={
"Filters": [{"Name": "Parents.TrialName", "Operator": "Equals", "Value": trial_name}]
},
sort_by="CreationTime",
sort_order="Ascending",
)
lineagedf = lineage_table.dataframe()
lineagedf
# get detailed information about a particular trial
sm.describe_trial_component(TrialComponentName=lineagedf.TrialComponentName[1])
```
# Part 3: Using the trained model for inference
### Step 8: Inference using Batch Transform
Let's first use Batch Transform to generate inferences for the test dataset you pre-processed before.
```
s3 = boto3.client("s3")
s3.download_file(rawbucket, testdataprefix + "/test_data.csv", "test_data.csv")
newcolorder = (
["PAY_AMT1", "BILL_AMT1"] + list(COLS[1:])[:11] + list(COLS[1:])[12:17] + list(COLS[1:])[18:]
)
test_full = pd.read_csv("test_data.csv", names=["Label"] + newcolorder)
test_full.head()
test_data_no_label = test_full.drop(columns=["Label"], axis=1)
label = test_full["Label"]
test_data_no_label.to_csv("test_data_no_label.csv", index=False, header=False)
test_data_no_label.shape
sess = sagemaker.Session()
test_data_nohead_location = sess.upload_data(
"test_data_no_label.csv", bucket=rawbucket, key_prefix=testdatanolabelprefix
)
%%time
sm_transformer = xgb.transformer(1, "ml.m5.xlarge", accept="text/csv")
# start a transform job
sm_transformer.transform(test_data_nohead_location, split_type="Line", content_type="text/csv")
sm_transformer.wait()
import json
import io
from urllib.parse import urlparse
def get_csv_output_from_s3(s3uri, file_name):
parsed_url = urlparse(s3uri)
bucket_name = parsed_url.netloc
prefix = parsed_url.path[1:]
s3 = boto3.resource("s3")
obj = s3.Object(bucket_name, "{}/{}".format(prefix, file_name))
return obj.get()["Body"].read().decode("utf-8")
output = get_csv_output_from_s3(sm_transformer.output_path, "test_data_no_label.csv.out")
output_df = pd.read_csv(io.StringIO(output), sep=",", header=None)
output_df.head(8)
from sklearn.metrics import confusion_matrix, accuracy_score
1 - np.unique(data["Label"], return_counts=True)[1][1] / (len(data["Label"]))
print(
"Baseline Accuracy = {}".format(
1 - np.unique(data["Label"], return_counts=True)[1][1] / (len(data["Label"]))
)
)
print("Accuracy Score = {}".format(accuracy_score(label, output_df)))
output_df["Predicted"] = output_df.values
output_df["Label"] = label
confusion_matrix = pd.crosstab(
output_df["Predicted"],
output_df["Label"],
rownames=["Actual"],
colnames=["Predicted"],
margins=True,
)
confusion_matrix
```
### Step 9: Conclusions
In this notebook we demonstrated an end to end cycle of data exploration, data processing using SageMaker processing, model development using an XGBoost Bring Your Own Container which we pushed to ECR, model training and offline inference using Batch Transform. Finally we logged our training metadata using SageMaker Experiments.
You can use this notebook to experiment with end to end data science experimentation using SageMaker Studio.
Remember to delete your datasets in the Amazon S3 bucket you used for this notebook.
|
github_jupyter
|
# Operations on word vectors
Welcome to your first assignment of this week!
Because word embeddings are very computionally expensive to train, most ML practitioners will load a pre-trained set of embeddings.
**After this assignment you will be able to:**
- Load pre-trained word vectors, and measure similarity using cosine similarity
- Use word embeddings to solve word analogy problems such as Man is to Woman as King is to ______.
- Modify word embeddings to reduce their gender bias
Let's get started! Run the following cell to load the packages you will need.
```
import numpy as np
from w2v_utils import *
```
Next, lets load the word vectors. For this assignment, we will use 50-dimensional GloVe vectors to represent words. Run the following cell to load the `word_to_vec_map`.
```
words, word_to_vec_map = read_glove_vecs('data/glove.6B.50d.txt')
```
You've loaded:
- `words`: set of words in the vocabulary.
- `word_to_vec_map`: dictionary mapping words to their GloVe vector representation.
You've seen that one-hot vectors do not do a good job cpaturing what words are similar. GloVe vectors provide much more useful information about the meaning of individual words. Lets now see how you can use GloVe vectors to decide how similar two words are.
# 1 - Cosine similarity
To measure how similar two words are, we need a way to measure the degree of similarity between two embedding vectors for the two words. Given two vectors $u$ and $v$, cosine similarity is defined as follows:
$$\text{CosineSimilarity(u, v)} = \frac {u . v} {||u||_2 ||v||_2} = cos(\theta) \tag{1}$$
where $u.v$ is the dot product (or inner product) of two vectors, $||u||_2$ is the norm (or length) of the vector $u$, and $\theta$ is the angle between $u$ and $v$. This similarity depends on the angle between $u$ and $v$. If $u$ and $v$ are very similar, their cosine similarity will be close to 1; if they are dissimilar, the cosine similarity will take a smaller value.
<img src="images/cosine_sim.png" style="width:800px;height:250px;">
<caption><center> **Figure 1**: The cosine of the angle between two vectors is a measure of how similar they are</center></caption>
**Exercise**: Implement the function `cosine_similarity()` to evaluate similarity between word vectors.
**Reminder**: The norm of $u$ is defined as $ ||u||_2 = \sqrt{\sum_{i=1}^{n} u_i^2}$
```
# GRADED FUNCTION: cosine_similarity
def cosine_similarity(u, v):
"""
Cosine similarity reflects the degree of similariy between u and v
Arguments:
u -- a word vector of shape (n,)
v -- a word vector of shape (n,)
Returns:
cosine_similarity -- the cosine similarity between u and v defined by the formula above.
"""
distance = 0.0
### START CODE HERE ###
# Compute the dot product between u and v (≈1 line)
dot = np.dot(u,v)
# Compute the L2 norm of u (≈1 line)
norm_u = np.linalg.norm(u)
# Compute the L2 norm of v (≈1 line)
norm_v = np.linalg.norm(v)
# Compute the cosine similarity defined by formula (1) (≈1 line)
cosine_similarity = dot / (norm_u * norm_v)
### END CODE HERE ###
return cosine_similarity
father = word_to_vec_map["father"]
mother = word_to_vec_map["mother"]
ball = word_to_vec_map["ball"]
crocodile = word_to_vec_map["crocodile"]
france = word_to_vec_map["france"]
italy = word_to_vec_map["italy"]
paris = word_to_vec_map["paris"]
rome = word_to_vec_map["rome"]
print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother))
print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile))
print("cosine_similarity(france - paris, rome - italy) = ",cosine_similarity(france - paris, rome - italy))
```
**Expected Output**:
<table>
<tr>
<td>
**cosine_similarity(father, mother)** =
</td>
<td>
0.890903844289
</td>
</tr>
<tr>
<td>
**cosine_similarity(ball, crocodile)** =
</td>
<td>
0.274392462614
</td>
</tr>
<tr>
<td>
**cosine_similarity(france - paris, rome - italy)** =
</td>
<td>
-0.675147930817
</td>
</tr>
</table>
After you get the correct expected output, please feel free to modify the inputs and measure the cosine similarity between other pairs of words! Playing around the cosine similarity of other inputs will give you a better sense of how word vectors behave.
## 2 - Word analogy task
In the word analogy task, we complete the sentence <font color='brown'>"*a* is to *b* as *c* is to **____**"</font>. An example is <font color='brown'> '*man* is to *woman* as *king* is to *queen*' </font>. In detail, we are trying to find a word *d*, such that the associated word vectors $e_a, e_b, e_c, e_d$ are related in the following manner: $e_b - e_a \approx e_d - e_c$. We will measure the similarity between $e_b - e_a$ and $e_d - e_c$ using cosine similarity.
**Exercise**: Complete the code below to be able to perform word analogies!
```
# GRADED FUNCTION: complete_analogy
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
"""
Performs the word analogy task as explained above: a is to b as c is to ____.
Arguments:
word_a -- a word, string
word_b -- a word, string
word_c -- a word, string
word_to_vec_map -- dictionary that maps words to their corresponding vectors.
Returns:
best_word -- the word such that v_b - v_a is close to v_best_word - v_c, as measured by cosine similarity
"""
# convert words to lower case
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
### START CODE HERE ###
# Get the word embeddings v_a, v_b and v_c (≈1-3 lines)
e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b], word_to_vec_map[word_c]
### END CODE HERE ###
words = word_to_vec_map.keys()
max_cosine_sim = -100 # Initialize max_cosine_sim to a large negative number
best_word = None # Initialize best_word with None, it will help keep track of the word to output
# loop over the whole word vector set
for w in words:
# to avoid best_word being one of the input words, pass on them.
if w in [word_a, word_b, word_c] :
continue
### START CODE HERE ###
# Compute cosine similarity between the vector (e_b - e_a) and the vector ((w's vector representation) - e_c) (≈1 line)
cosine_sim = cosine_similarity(e_b-e_a, word_to_vec_map[w]-e_c)
# If the cosine_sim is more than the max_cosine_sim seen so far,
# then: set the new max_cosine_sim to the current cosine_sim and the best_word to the current word (≈3 lines)
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = w
### END CODE HERE ###
return best_word
```
Run the cell below to test your code, this may take 1-2 minutes.
```
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} :: {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))
```
**Expected Output**:
<table>
<tr>
<td>
**italy -> italian** ::
</td>
<td>
spain -> spanish
</td>
</tr>
<tr>
<td>
**india -> delhi** ::
</td>
<td>
japan -> tokyo
</td>
</tr>
<tr>
<td>
**man -> woman ** ::
</td>
<td>
boy -> girl
</td>
</tr>
<tr>
<td>
**small -> smaller ** ::
</td>
<td>
large -> larger
</td>
</tr>
</table>
Once you get the correct expected output, please feel free to modify the input cells above to test your own analogies. Try to find some other analogy pairs that do work, but also find some where the algorithm doesn't give the right answer: For example, you can try small->smaller as big->?.
### Congratulations!
You've come to the end of this assignment. Here are the main points you should remember:
- Cosine similarity a good way to compare similarity between pairs of word vectors. (Though L2 distance works too.)
- For NLP applications, using a pre-trained set of word vectors from the internet is often a good way to get started.
Even though you have finished the graded portions, we recommend you take a look too at the rest of this notebook.
Congratulations on finishing the graded portions of this notebook!
## 3 - Debiasing word vectors (OPTIONAL/UNGRADED)
In the following exercise, you will examine gender biases that can be reflected in a word embedding, and explore algorithms for reducing the bias. In addition to learning about the topic of debiasing, this exercise will also help hone your intuition about what word vectors are doing. This section involves a bit of linear algebra, though you can probably complete it even without being expert in linear algebra, and we encourage you to give it a shot. This portion of the notebook is optional and is not graded.
Lets first see how the GloVe word embeddings relate to gender. You will first compute a vector $g = e_{woman}-e_{man}$, where $e_{woman}$ represents the word vector corresponding to the word *woman*, and $e_{man}$ corresponds to the word vector corresponding to the word *man*. The resulting vector $g$ roughly encodes the concept of "gender". (You might get a more accurate representation if you compute $g_1 = e_{mother}-e_{father}$, $g_2 = e_{girl}-e_{boy}$, etc. and average over them. But just using $e_{woman}-e_{man}$ will give good enough results for now.)
```
g = word_to_vec_map['woman'] - word_to_vec_map['man']
print(g)
```
Now, you will consider the cosine similarity of different words with $g$. Consider what a positive value of similarity means vs a negative cosine similarity.
```
print ('List of names and their similarities with constructed vector:')
# girls and boys name
name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin']
for w in name_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
```
As you can see, female first names tend to have a positive cosine similarity with our constructed vector $g$, while male first names tend to have a negative cosine similarity. This is not suprising, and the result seems acceptable.
But let's try with some other words.
```
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
```
Do you notice anything surprising? It is astonishing how these results reflect certain unhealthy gender stereotypes. For example, "computer" is closer to "man" while "literature" is closer to "woman". Ouch!
We'll see below how to reduce the bias of these vectors, using an algorithm due to [Boliukbasi et al., 2016](https://arxiv.org/abs/1607.06520). Note that some word pairs such as "actor"/"actress" or "grandmother"/"grandfather" should remain gender specific, while other words such as "receptionist" or "technology" should be neutralized, i.e. not be gender-related. You will have to treat these two type of words differently when debiasing.
### 3.1 - Neutralize bias for non-gender specific words
The figure below should help you visualize what neutralizing does. If you're using a 50-dimensional word embedding, the 50 dimensional space can be split into two parts: The bias-direction $g$, and the remaining 49 dimensions, which we'll call $g_{\perp}$. In linear algebra, we say that the 49 dimensional $g_{\perp}$ is perpendicular (or "othogonal") to $g$, meaning it is at 90 degrees to $g$. The neutralization step takes a vector such as $e_{receptionist}$ and zeros out the component in the direction of $g$, giving us $e_{receptionist}^{debiased}$.
Even though $g_{\perp}$ is 49 dimensional, given the limitations of what we can draw on a screen, we illustrate it using a 1 dimensional axis below.
<img src="images/neutral.png" style="width:800px;height:300px;">
<caption><center> **Figure 2**: The word vector for "receptionist" represented before and after applying the neutralize operation. </center></caption>
**Exercise**: Implement `neutralize()` to remove the bias of words such as "receptionist" or "scientist". Given an input embedding $e$, you can use the following formulas to compute $e^{debiased}$:
$$e^{bias\_component} = \frac{e \cdot g}{||g||_2^2} * g\tag{2}$$
$$e^{debiased} = e - e^{bias\_component}\tag{3}$$
If you are an expert in linear algebra, you may recognize $e^{bias\_component}$ as the projection of $e$ onto the direction $g$. If you're not an expert in linear algebra, don't worry about this.
<!--
**Reminder**: a vector $u$ can be split into two parts: its projection over a vector-axis $v_B$ and its projection over the axis orthogonal to $v$:
$$u = u_B + u_{\perp}$$
where : $u_B = $ and $ u_{\perp} = u - u_B $
!-->
```
def neutralize(word, g, word_to_vec_map):
"""
Removes the bias of "word" by projecting it on the space orthogonal to the bias axis.
This function ensures that gender neutral words are zero in the gender subspace.
Arguments:
word -- string indicating the word to debias
g -- numpy-array of shape (50,), corresponding to the bias axis (such as gender)
word_to_vec_map -- dictionary mapping words to their corresponding vectors.
Returns:
e_debiased -- neutralized word vector representation of the input "word"
"""
### START CODE HERE ###
# Select word vector representation of "word". Use word_to_vec_map. (≈ 1 line)
e = word_to_vec_map[word]
# Compute e_biascomponent using the formula give above. (≈ 1 line)
e_biascomponent = np.multiply((np.dot(e, g) / np.linalg.norm(g)**2), g)
# Neutralize e by substracting e_biascomponent from it
# e_debiased should be equal to its orthogonal projection. (≈ 1 line)
e_debiased = e - e_biascomponent
### END CODE HERE ###
return e_debiased
e = "receptionist"
print("cosine similarity between " + e + " and g, before neutralizing: ", cosine_similarity(word_to_vec_map["receptionist"], g))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("cosine similarity between " + e + " and g, after neutralizing: ", cosine_similarity(e_debiased, g))
```
**Expected Output**: The second result is essentially 0, up to numerical roundof (on the order of $10^{-17}$).
<table>
<tr>
<td>
**cosine similarity between receptionist and g, before neutralizing:** :
</td>
<td>
0.330779417506
</td>
</tr>
<tr>
<td>
**cosine similarity between receptionist and g, after neutralizing:** :
</td>
<td>
-3.26732746085e-17
</tr>
</table>
### 3.2 - Equalization algorithm for gender-specific words
Next, lets see how debiasing can also be applied to word pairs such as "actress" and "actor." Equalization is applied to pairs of words that you might want to have differ only through the gender property. As a concrete example, suppose that "actress" is closer to "babysit" than "actor." By applying neutralizing to "babysit" we can reduce the gender-stereotype associated with babysitting. But this still does not guarantee that "actor" and "actress" are equidistant from "babysit." The equalization algorithm takes care of this.
The key idea behind equalization is to make sure that a particular pair of words are equi-distant from the 49-dimensional $g_\perp$. The equalization step also ensures that the two equalized steps are now the same distance from $e_{receptionist}^{debiased}$, or from any other work that has been neutralized. In pictures, this is how equalization works:
<img src="images/equalize10.png" style="width:800px;height:400px;">
The derivation of the linear algebra to do this is a bit more complex. (See Bolukbasi et al., 2016 for details.) But the key equations are:
$$ \mu = \frac{e_{w1} + e_{w2}}{2}\tag{4}$$
$$ \mu_{B} = \frac {\mu \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
\tag{5}$$
$$\mu_{\perp} = \mu - \mu_{B} \tag{6}$$
$$ e_{w1B} = \frac {e_{w1} \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
\tag{7}$$
$$ e_{w2B} = \frac {e_{w2} \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
\tag{8}$$
$$e_{w1B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w1B}} - \mu_B} {|(e_{w1} - \mu_{\perp}) - \mu_B)|} \tag{9}$$
$$e_{w2B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w2B}} - \mu_B} {|(e_{w2} - \mu_{\perp}) - \mu_B)|} \tag{10}$$
$$e_1 = e_{w1B}^{corrected} + \mu_{\perp} \tag{11}$$
$$e_2 = e_{w2B}^{corrected} + \mu_{\perp} \tag{12}$$
**Exercise**: Implement the function below. Use the equations above to get the final equalized version of the pair of words. Good luck!
```
def equalize(pair, bias_axis, word_to_vec_map):
"""
Debias gender specific words by following the equalize method described in the figure above.
Arguments:
pair -- pair of strings of gender specific words to debias, e.g. ("actress", "actor")
bias_axis -- numpy-array of shape (50,), vector corresponding to the bias axis, e.g. gender
word_to_vec_map -- dictionary mapping words to their corresponding vectors
Returns
e_1 -- word vector corresponding to the first word
e_2 -- word vector corresponding to the second word
"""
### START CODE HERE ###
# Step 1: Select word vector representation of "word". Use word_to_vec_map. (≈ 2 lines)
w1, w2 = None
e_w1, e_w2 = None
# Step 2: Compute the mean of e_w1 and e_w2 (≈ 1 line)
mu = None
# Step 3: Compute the projections of mu over the bias axis and the orthogonal axis (≈ 2 lines)
mu_B = None
mu_orth = None
# Step 4: Use equations (7) and (8) to compute e_w1B and e_w2B (≈2 lines)
e_w1B = None
e_w2B = None
# Step 5: Adjust the Bias part of e_w1B and e_w2B using the formulas (9) and (10) given above (≈2 lines)
corrected_e_w1B = None
corrected_e_w2B = None
# Step 6: Debias by equalizing e1 and e2 to the sum of their corrected projections (≈2 lines)
e1 = None
e2 = None
### END CODE HERE ###
return e1, e2
print("cosine similarities before equalizing:")
print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g))
print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g))
print()
e1, e2 = equalize(("man", "woman"), g, word_to_vec_map)
print("cosine similarities after equalizing:")
print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g))
print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))
```
**Expected Output**:
cosine similarities before equalizing:
<table>
<tr>
<td>
**cosine_similarity(word_to_vec_map["man"], gender)** =
</td>
<td>
-0.117110957653
</td>
</tr>
<tr>
<td>
**cosine_similarity(word_to_vec_map["woman"], gender)** =
</td>
<td>
0.356666188463
</td>
</tr>
</table>
cosine similarities after equalizing:
<table>
<tr>
<td>
**cosine_similarity(u1, gender)** =
</td>
<td>
-0.700436428931
</td>
</tr>
<tr>
<td>
**cosine_similarity(u2, gender)** =
</td>
<td>
0.700436428931
</td>
</tr>
</table>
Please feel free to play with the input words in the cell above, to apply equalization to other pairs of words.
These debiasing algorithms are very helpful for reducing bias, but are not perfect and do not eliminate all traces of bias. For example, one weakness of this implementation was that the bias direction $g$ was defined using only the pair of words _woman_ and _man_. As discussed earlier, if $g$ were defined by computing $g_1 = e_{woman} - e_{man}$; $g_2 = e_{mother} - e_{father}$; $g_3 = e_{girl} - e_{boy}$; and so on and averaging over them, you would obtain a better estimate of the "gender" dimension in the 50 dimensional word embedding space. Feel free to play with such variants as well.
### Congratulations
You have come to the end of this notebook, and have seen a lot of the ways that word vectors can be used as well as modified.
Congratulations on finishing this notebook!
**References**:
- The debiasing algorithm is from Bolukbasi et al., 2016, [Man is to Computer Programmer as Woman is to
Homemaker? Debiasing Word Embeddings](https://papers.nips.cc/paper/6228-man-is-to-computer-programmer-as-woman-is-to-homemaker-debiasing-word-embeddings.pdf)
- The GloVe word embeddings were due to Jeffrey Pennington, Richard Socher, and Christopher D. Manning. (https://nlp.stanford.edu/projects/glove/)
|
github_jupyter
|
# 16 - Regression Discontinuity Design
We don't stop to think about it much, but it is impressive how smooth nature is. You can't grow a tree without first getting a bud, you can't teleport from one place to another, a wound takes its time to heal. Even in the social realm, smoothness seems to be the norm. You can't grow a business in one day, consistency and hard work are required to build wealth and it takes years before you learn how linear regression works. Under normal circumstances, nature is very cohesive and doesn't jump around much.
> When the intelligent and animal souls are held together in one embrace, they can be kept from separating.
\- Tao Te Ching, Lao Tzu.
Which means that **when we do see jumps and spikes, they are probably artificial** and often man-made situations. These events are usually accompanied by counterfactuals to the normal way of things: if a weird thing happens, this gives us some insight into what would have happened if nature was to work in a different way. Exploring these artificial jumps is at the core of Regression Discontinuity Design.

The basic setup goes like this. Imagine that you have a treatment variable $T$ and potential outcomes $Y_0$ and $Y_1$. The treatment T is a discontinuous function of an observed running variable $R$ such that
$
D_i = \mathcal{1}\{R_i>c\}
$
In other words, this is saying that treatment is zero when $R$ is below a threshold $c$ and one otherwise. This means that we get to observe $Y_1$ when $R>c$ and $Y_0$ when $R<c$. To wrap our head around this, think about the potential outcomes as 2 functions that we can't observe entirely. Both $Y_0(R)$ and $Y_1(R)$ are there, we just can't see that. The threshold acts as a switch that allows us to see one or the other of those function, but never both, much like in the image below:

The idea of regression discontinuity is to compare the outcome just above and just below the threshold to identify the treatment effect at the threshold. This is called a **sharp RD** design, since the probability of getting the treatment jumps from 0 to 1 at the threshold, but we could also think about a **fuzzy RD** design, where the probability also jumps, but is a less dramatic manner.
## Is Alcohol Killing You?
A very relevant public policy question is what should be the minimal drinking age. Most countries, Brazil included, set it to be 18 year, but in the US (most states) it is currently 21. So, is it the case that the US is being overly prudent and that they should lower their minimal drinking age? Or is it the case that other countries should make their legal drinking age higher?
One way to look at this question is from a [mortality rate perspective (Carpenter and Dobkin, 2009)](https://www.aeaweb.org/articles?id=10.1257/app.1.1.164). From the public policy standpoint, one could argue that we should lower the mortality rate as much as possible. If alcohol consumption increases the mortality rate by a lot, we should avoid lowering the minimum drinking age. This would be consistent with the objective of lowering deaths caused by alcohol consumption.
To estimate the impacts of alcohol on death, we could use the fact that legal drinking age imposes a discontinuity on nature. In the US, those just under 21 years don't drink (or drink much less) while those just older than 21 do drink. This means that the probability of drinking jumps at 21 years and that is something we can explore with an RDD.
```
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
%matplotlib inline
style.use("fivethirtyeight")
```
To do so we can grab some mortality data aggregated by age. Each row is the average age of a group of people and the average mortality by all causes (`all`), by moving vehicle accident (`mva`) and by suicide (`suicide`).
```
drinking = pd.read_csv("./data/drinking.csv")
drinking.head()[["agecell", "all", "mva", "suicide"]]
```
Just to aid visibility (and for another important reason we will see later) we will centralize the running variable `agecell` at the threshold 21.
```
drinking["agecell"] -= 21
```
If we plot the multiple outcome variables (`all`, `mva`, `suicide`) with the runing variable on the x axis, we get some visual cue about some sort of jump in mortality as we cross the legal drinking age.
```
plt.figure(figsize=(8,8))
ax = plt.subplot(3,1,1)
drinking.plot.scatter(x="agecell", y="all", ax=ax)
plt.title("Death Cause by Age (Centered at 0)")
ax = plt.subplot(3,1,2, sharex=ax)
drinking.plot.scatter(x="agecell", y="mva", ax=ax)
ax = plt.subplot(3,1,3, sharex=ax)
drinking.plot.scatter(x="agecell", y="suicide", ax=ax);
```
There are some cues, but we need more than that. What exactly is the effect of drinking on mortality at the threshold? And what is the standard error on that estimate?
## RDD Estimation
The key assumption that RDD relies on is the smoothness of the potential outcome at the threshold. Formally, the limits of the potential outcomes as the running variable approaches the threshold from the right and from the left should be the same.
$$
\lim_{r \to c^-} E[Y_{ti}|R_i=r] = \lim_{r \to c^+} E[Y_{ti}|R_i=r]
$$
If this holds true, we can find the causal effect at the threshold
$$
\begin{align}
\lim_{r \to c^+} E[Y_{ti}|R_i=r] - \lim_{r \to c^-} E[Y_{ti}|R_i=r]=&\lim_{r \to c^+} E[Y_{1i}|R_i=r] - \lim_{r \to c^-} E[Y_{0i}|R_i=r] \\
=& E[Y_{1i}|R_i=r] - E[Y_{0i}|R_i=r] \\
=& E[Y_{1i} - Y_{0i}|R_i=r]
\end{align}
$$
This is, in its own way, a sort of Local Average Treatment Effect (LATE), since we can only know it at the threshold. In this setting, we can think of RDD as a local randomized trial. For those at the threshold, the treatment could have gone either way and, by chance, some people fell below the threshold, and some people fell above. In our example, at the same point in time, some people are just above 21 years and some people are just below 21. What determines this is if someone was born some days later or not, which is pretty random. For this reason, RDD provides a very compelling causal story. It is not the golden standard of RCT, but it is close.
Now, to estimate the treatment effect at the threshold, all we need to do is estimate both of the limits in the formula above and compare them. The simplest way to do that is by running a linear regression

To make it work, we interact a dummy for being above the threshold with the running variable
$
y_i = \beta_0 + \beta_1 r_i + \beta_2 \mathcal{1}\{r_i>c\} + \beta_3 \mathcal{1}\{r_i>c\} r_i
$
Essentially, this is the same as fitting a linear regression above the threshold and another below it. The parameter $\beta_0$ is the intercept of the regression below the threshold and $\beta_0+\beta_2$ is the intercept for the regression above the threshold.
Here is where the trick of centering the running variable at the threshold comes into play. After this pre-processing step, the threshold becomes zero. This causes the intercept $\beta_0$ to be the predicted value at the threshold, for the regression below it. In other words, $\beta_0=\lim_{r \to c^-} E[Y_{ti}|R_i=r]$. By the same reasoning, $\beta_0+\beta_2$ is the limit of the outcome from above. Wich means, that
$
\lim_{r \to c^+} E[Y_{ti}|R_i=r] - \lim_{r \to c^-} E[Y_{ti}|R_i=r]=\beta_2=E[ATE|R=c]
$
Here is what this looks like in code for the case where we want to estimate the effect of alcohol consumption on death by all causes at 21 years.
```
rdd_df = drinking.assign(threshold=(drinking["agecell"] > 0).astype(int))
model = smf.wls("all~agecell*threshold", rdd_df).fit()
model.summary().tables[1]
```
This model is telling us that mortality increases by 7.6627 points with the consumption of alcohol. Another way of putting this is that alcohol increases the chance of death by all causes by 8% ((7.6627+93.6184)/93.6184). Notice that this also gives us standard errors for our causal effect estimate. In this case, the effect is statistically significant, since the p-value is below 0.01.
If we want to verify this model visually, we can show the predicted values on the data that we have. You can see that it is as though we had 2 regression models: one for those above the threshold and one for below it.
```
ax = drinking.plot.scatter(x="agecell", y="all", color="C0")
drinking.assign(predictions=model.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title("Regression Discontinuity");
```
If we do the same for the other causes, this is what we get.
```
plt.figure(figsize=(8,8))
for p, cause in enumerate(["all", "mva", "suicide"], 1):
ax = plt.subplot(3,1,p)
drinking.plot.scatter(x="agecell", y=cause, ax=ax)
m = smf.wls(f"{cause}~agecell*threshold", rdd_df).fit()
ate_pct = 100*((m.params["threshold"] + m.params["Intercept"])/m.params["Intercept"] - 1)
drinking.assign(predictions=m.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title(f"Impact of Alcohol on Death: {np.round(ate_pct, 2)}%")
plt.tight_layout()
```
RDD is telling us that alcohol increases the chance of death by suicide and car accidents by 15%, which is a pretty significant amount. These results are compelling arguments to not lower the drinking age, if we want to minimize mortality rates.
### Kernel Weighting
Regression Discontinuity relies heavily on the extrapolations properties of linear regression. Since we are looking at the values at the beginning and end of 2 regression lines, we better get those limits right. What can happen is that regression might focus too much on fitting the other data points at the cost of a poor fit at the threshold. If this happens, we might get the wrong measure of the treatment effect.
One way to solve this is to give higher weights for the points that are closer to the threshold. There are many ways to do this, but a popular one is to reweight the samples with the **triangular kernel**
$
K(R, c, h) = \mathcal{1}\{|R-c| \leq h\} * \bigg(1-\frac{|R-c|}{h}\bigg)
$
The first part of this kernel is an indicator function to whether we are close to the threshold. How close? This is determined by a bandwidth parameter $h$. The second part of this kernel is a weighting function. As we move away from the threshold, the weights get smaller and smaller. These weights are divided by the bandwidth. If the bandwidth is large, the weights get smaller at a slower rate. If the bandwidth is small, the weights quickly go to zero.
To make it easier to understand, here is what the weights look like for this kernel applied to our problem. I've set the bandwidth to be 1 here, meaning we will only consider data from people that are no older than 22 years and no younger than 20 years.
```
def kernel(R, c, h):
indicator = (np.abs(R-c) <= h).astype(float)
return indicator * (1 - np.abs(R-c)/h)
plt.plot(drinking["agecell"], kernel(drinking["agecell"], c=0, h=1))
plt.xlabel("agecell")
plt.ylabel("Weight")
plt.title("Kernel Weight by Age");
```
If we apply these weights to our original problem, the impact of alcohol gets bigger, at least for all causes. It jumps from 7.6627 to 9.7004. The result remains very significant. Also, notice that I'm using `wls` instead of `ols`
```
model = smf.wls("all~agecell*threshold", rdd_df,
weights=kernel(drinking["agecell"], c=0, h=1)).fit()
model.summary().tables[1]
ax = drinking.plot.scatter(x="agecell", y="all", color="C0")
drinking.assign(predictions=model.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title("Regression Discontinuity (Local Regression)");
```
And here is what it looks like for the other causes of death. Notice how the regression on the right is more negatively sloped since it disconsiders the right most points.
```
plt.figure(figsize=(8,8))
weights = kernel(drinking["agecell"], c=0, h=1)
for p, cause in enumerate(["all", "mva", "suicide"], 1):
ax = plt.subplot(3,1,p)
drinking.plot.scatter(x="agecell", y=cause, ax=ax)
m = smf.wls(f"{cause}~agecell*threshold", rdd_df, weights=weights).fit()
ate_pct = 100*((m.params["threshold"] + m.params["Intercept"])/m.params["Intercept"] - 1)
drinking.assign(predictions=m.fittedvalues).plot(x="agecell", y="predictions", ax=ax, color="C1")
plt.title(f"Impact of Alcohol on Death: {np.round(ate_pct, 2)}%")
plt.tight_layout()
```
With the exception of suicide, it looks like adding the kernel weight made the negative impact on alcohol bigger. Once again, if we want to minimize the death rate, we should NOT recommend lowering the legal drinking age, since there is a clear impact of alcohol on the death rates.
This simple case covers what happens when regression discontinuity design works perfectly. Next, we will see some diagnostics that we should run in order to check how much we can trust RDD and talk about a topic that is very dear to our heart: the effect of education on earnings.
## Sheepskin Effect and Fuzzy RDD
When it comes to the effect of education on earnings, there are two major views in economics. The first one is the widely known argument that education increases human capital, increasing productivity and thus, earnings. In this view, education actually changes you for the better. Another view is that education is simply a signaling mechanism. It just puts you through all these hard tests and academic tasks. If you can make it, it signals to the market that you are a good employee. In this way, education doesn't make you more productive. It only tells the market how productive you have always been. What matters here is the diploma. If you have it, you will be paid more. We refer to this as the **sheepskin effect**, since diplomas were printed in sheepskin in the past.
To test this hypothesis, [Clark and Martorell](https://faculty.smu.edu/millimet/classes/eco7321/papers/clark%20martorell%202014.pdf) used regression discontinuity to measure the effect of graduating 12th grade on earnings. In order to do that, they had to think about some running variable where students that fall above it graduate and those who fall below it, don't. They found such data in the Texas education system.
In order to graduate in Texas, one has to pass an exam. Testing starts at 10th grade and students can do it multiple times, but eventually, they face a last chance exam at the end of 12th grade. The idea was to get data from students who took those last chance exams and compare those that had barely failed it to those that barely passed it. These students will have very similar human capital, but different signaling credentials. Namely, those that barely passed it, will receive a diploma.
```
sheepskin = pd.read_csv("./data/sheepskin.csv")[["avgearnings", "minscore", "receivehsd", "n"]]
sheepskin.head()
```
Once again, this data is grouped by the running variable. It contains not only the running variable (minscore, already centered at zero) and the outcome (avgearnings), but it also has the probability of receiving a diploma in that score cell and the size of the call (n). So, for example, out of the 12 students in the cell -30 below the score threshold, only 5 were able to get the diploma (12 * 0,416).
This means that there is some slippage in the treatment assignment. Some students that are below the passing threshold managed to get the diploma anyway. Here, the regression discontinuity is **fuzzy**, rather than sharp. Notice how the probability of getting the diploma doesn't jump from zero to one at the threshold. But it does jump from something like 50% to 90%.
```
sheepskin.plot.scatter(x="minscore", y="receivehsd", figsize=(10,5))
plt.xlabel("Test Scores Relative to Cut off")
plt.ylabel("Fraction Receiving Diplomas")
plt.title("Last-chance Exams");
```
We can think of fuzzy RD as a sort of non compliance. Passing the threshold should make everyone receive the diploma, but some students, the never takers, don’t get it. Likewise, being below the threshold should prevent you from getting a diploma, but some students, the always takers, manage to get it anyway.
Just like when we have the potential outcome, we have the potential treatment status in this situation. $T_1$ is the treatment everyone would have received had they been above the threshold. $T_0$ is the treatment everyone would have received had they been below the threshold. As you've might have noticed, we can think of the **threshold as an Instrumental Variable**. Just as in IV, if we naively estimate the treatment effect, it will be biased towards zero.

The probability of treatment being less than one, even above the threshold, makes the outcome we observe less than the true potential outcome $Y_1$. By the same token, the outcome we observe below the threshold is higher than the true potential outcome $Y_0$. This makes it look like the treatment effect at the threshold is smaller than it actually is and we will have to use IV techniques to correct for that.
Just like when we've assumed smoothness on the potential outcome, we now assume it for the potential treatment. Also, we need to assume monotonicity, just like in IV. In case you don't remember, it states that $T_{i1}>T_{i0} \ \forall i$. This means that crossing the threshold from the left to the right only increases your chance of getting a diploma (or that there are no defiers). With these 2 assumptions, we have a Wald Estimator for LATE.
$$
\dfrac{\lim_{r \to c^+} E[Y_i|R_i=r] - \lim_{r \to c^-} E[Y_i|R_i=r]}{\lim_{r \to c^+} E[T_i|R_i=r] - \lim_{r \to c^-} E[T_i|R_i=r]} = E[Y_{1i} - Y_{0i} | T_{1i} > T_{0i}, R_i=c]
$$
Notice how this is a local estimate in two senses. First, it is local because it only gives the treatment effect at the threshold $c$. This is the RD locality. Second, it is local because it only estimates the treatment effect for the compliers. This is the IV locality.
To estimate this, we will use 2 linear regression. The numerator can be estimated just like we've done before. To get the denominator, we simply replace the outcome with the treatment. But first, let's talk about a sanity check we need to run to make sure we can trust our RDD estimates.
### The McCrary Test
One thing that could break our RDD argument is if people can manipulate where they stand at the threshold. In the sheepskin example this could happen if students just below the threshold found a way around the system to increase their test score by just a bit. Another example is when you need to be below a certain income level to get a government benefit. Some families might lower their income on purpose, just to be just eligible for the program.
In these sorts of situations, we tend to see a phenomenon called bunching on the density of the running variable. This means that we will have a lot of entities just above or just below the threshold. To check for that, we can plot the density function of the running variable and see if there are any spikes around the threshold. For our case, the density is given by the `n` column in our data.
```
plt.figure(figsize=(8,8))
ax = plt.subplot(2,1,1)
sheepskin.plot.bar(x="minscore", y="n", ax=ax)
plt.title("McCrary Test")
plt.ylabel("Smoothness at the Threshold")
ax = plt.subplot(2,1,2, sharex=ax)
sheepskin.replace({1877:1977, 1874:2277}).plot.bar(x="minscore", y="n", ax=ax)
plt.xlabel("Test Scores Relative to Cut off")
plt.ylabel("Spike at the Threshold");
```
The first plot shows how our data density looks like. As we can see, there are no spikes around the threshold, meaning there is no bunching. Students are not manipulating where they fall on the threshold. Just for illustrative purposes, the second plot shows what bunching would look like if students could manipulate where they fall on the threshold. We would see a spike in the density for the cells just above the threshold, since many students would be on that cell, barely passing the exam.
Getting this out of the way, we can go back to estimate the sheepskin effect. As I've said before, the numerator of the Wald estimator can be estimated just like we did in the Sharp RD. Here, we will use as weight the kernel with a bandwidth of 15. Since we also have the cell size, we will multiply the kernel by the sample size to get a final weight for the cell.
```
sheepsking_rdd = sheepskin.assign(threshold=(sheepskin["minscore"]>0).astype(int))
model = smf.wls("avgearnings~minscore*threshold",
sheepsking_rdd,
weights=kernel(sheepsking_rdd["minscore"], c=0, h=15)*sheepsking_rdd["n"]).fit()
model.summary().tables[1]
```
This is telling us that the effect of a diploma is -97.7571, but this is not statistically significant (P-value of 0.5). If we plot these results, we get a very continuous line at the threshold. More educated people indeed make more money, but there isn't a jump at the point where they receive the 12th grade diploma. This is an argument in favor of the view that says that education increases earnings by making people more productive, rather than being just a signal to the marker. In other words, there is no sheepskin effect.
```
ax = sheepskin.plot.scatter(x="minscore", y="avgearnings", color="C0")
sheepskin.assign(predictions=model.fittedvalues).plot(x="minscore", y="predictions", ax=ax, color="C1", figsize=(8,5))
plt.xlabel("Test Scores Relative to Cutoff")
plt.ylabel("Average Earnings")
plt.title("Last-chance Exams");
```
However, as we know from the way non compliance bias works, this result is biased towards zero. To correct for that, we need to scale it by the first stage and get the Wald estimator. Unfortunately, there isn't a good Python implementation for this, so we will have to do it manually and use bootstrap to get the standard errors.
The code below runs the numerator of the Wald estimator just like we did before and also constructs the denominator by replacing the target variable with the treatment variable `receivehsd`. The final step just divides the numerator by the denominator.
```
def wald_rdd(data):
weights=kernel(data["minscore"], c=0, h=15)*data["n"]
denominator = smf.wls("receivehsd~minscore*threshold", data, weights=weights).fit()
numerator = smf.wls("avgearnings~minscore*threshold", data, weights=weights).fit()
return numerator.params["threshold"]/denominator.params["threshold"]
from joblib import Parallel, delayed
np.random.seed(45)
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(wald_rdd)(sheepsking_rdd.sample(frac=1, replace=True))
for _ in range(bootstrap_sample))
ates = np.array(ates)
```
With the bootstrap samples, we can plot the distribution of ATEs and see where the 95% confidence interval is.
```
sns.distplot(ates, kde=False)
plt.vlines(np.percentile(ates, 2.5), 0, 100, linestyles="dotted")
plt.vlines(np.percentile(ates, 97.5), 0, 100, linestyles="dotted", label="95% CI")
plt.title("ATE Bootstrap Distribution")
plt.xlim([-10000, 10000])
plt.legend();
```
As you can see, even when we scale the effect by the first stage, it is still not statistically different from zero. This means that education doesn't increase earnings by a simple sheepskin effect, but rather by increasing one's productivity.
## Key Ideas
We learned how to take advantage of artificial discontinuities to estimate causal effects. The idea is that we will have some artificial threshold that makes the probability of treatment jump. One example that we saw was how age makes the probability of drinking jump at 21 years. We could use that to estimate the impact of drinking on mortality rate. We use the fact that very close to the threshold, we have something close to a randomized trial. Entities very close to the threshold could have gone either way and what determines where they've landed is essentially random. With this, we can compare those just above and just below to get the treatment effect. We saw how we could do that with weighted linear regression using a kernel and how this even gave us, for free, standard errors for our ATE.
Then, we look at what would happen in the fuzzy RD design, where we have non compliance. We saw how we could approach the situation much like we did with IV.
## References
I like to think of this entire book as a tribute to Joshua Angrist, Alberto Abadie and Christopher Walters for their amazing Econometrics class. Most of the ideas here are taken from their classes at the American Economic Association. Watching them is what is keeping me sane during this tough year of 2020.
* [Cross-Section Econometrics](https://www.aeaweb.org/conference/cont-ed/2017-webcasts)
* [Mastering Mostly Harmless Econometrics](https://www.aeaweb.org/conference/cont-ed/2020-webcasts)
I'll also like to reference the amazing books from Angrist. They have shown me that Econometrics, or 'Metrics as they call it, is not only extremely useful but also profoundly fun.
* [Mostly Harmless Econometrics](https://www.mostlyharmlesseconometrics.com/)
* [Mastering 'Metrics](https://www.masteringmetrics.com/)
Other important reference is Miguel Hernan and Jamie Robins' book. It has been my trustworthy companion in the most thorny causal questions I had to answer.
* [Causal Inference Book](https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/)

## Contribute
Causal Inference for the Brave and True is an open-source material on causal inference, the statistics of science. It uses only free software, based in Python. Its goal is to be accessible monetarily and intellectually.
If you found this book valuable and you want to support it, please go to [Patreon](https://www.patreon.com/causal_inference_for_the_brave_and_true). If you are not ready to contribute financially, you can also help by fixing typos, suggesting edits or giving feedback on passages you didn't understand. Just go to the book's repository and [open an issue](https://github.com/matheusfacure/python-causality-handbook/issues). Finally, if you liked this content, please share it with others who might find it useful and give it a [star on GitHub](https://github.com/matheusfacure/python-causality-handbook/stargazers).
|
github_jupyter
|
```
# Import libraries and modules
import matplotlib.pyplot as plt
import numpy as np
import os
import tensorflow as tf
print(np.__version__)
print(tf.__version__)
np.set_printoptions(threshold=np.inf)
```
# Local Development
## Arguments
```
arguments = {}
# File arguments.
arguments["train_file_pattern"] = "gs://machine-learning-1234-bucket/gan/data/mnist/train*.tfrecord"
arguments["eval_file_pattern"] = "gs://machine-learning-1234-bucket/gan/data/mnist/test*.tfrecord"
arguments["output_dir"] = "gs://machine-learning-1234-bucket/gan/vanilla_gan/trained_model"
# Training parameters.
arguments["train_batch_size"] = 32
arguments["train_steps"] = 56250
arguments["save_summary_steps"] = 100
arguments["save_checkpoints_steps"] = 10000
arguments["keep_checkpoint_max"] = 10
arguments["input_fn_autotune"] = False
# Eval parameters.
arguments["eval_batch_size"] = 32
arguments["eval_steps"] = 100
arguments["start_delay_secs"] = 60000
arguments["throttle_secs"] = 60000
# Image parameters.
arguments["height"] = 28
arguments["width"] = 28
arguments["depth"] = 1
# Generator parameters.
arguments["latent_size"] = 512
arguments["generator_hidden_units"] = [256, 512, 1024]
arguments["generator_leaky_relu_alpha"] = 0.2
arguments["generator_final_activation"] = "tanh"
arguments["generator_l1_regularization_scale"] = 0.
arguments["generator_l2_regularization_scale"] = 0.
arguments["generator_optimizer"] = "Adam"
arguments["generator_learning_rate"] = 0.0002
arguments["generator_adam_beta1"] = 0.5
arguments["generator_adam_beta2"] = 0.999
arguments["generator_adam_epsilon"] = 1e-8
arguments["generator_clip_gradients"] = None
arguments["generator_train_steps"] = 1
# Discriminator hyperparameters.
arguments["discriminator_hidden_units"] = [1024, 512, 256]
arguments["discriminator_leaky_relu_alpha"] = 0.2
arguments["discriminator_l1_regularization_scale"] = 0.
arguments["discriminator_l2_regularization_scale"] = 0.
arguments["discriminator_optimizer"] = "Adam"
arguments["discriminator_learning_rate"] = 0.0002
arguments["discriminator_adam_beta1"] = 0.5
arguments["discriminator_adam_beta2"] = 0.999
arguments["discriminator_adam_epsilon"] = 1e-8
arguments["discriminator_clip_gradients"] = None
arguments["discriminator_train_steps"] = 1
arguments["label_smoothing"] = 0.9
```
## print_object.py
```
def print_obj(function_name, object_name, object_value):
"""Prints enclosing function, object name, and object value.
Args:
function_name: str, name of function.
object_name: str, name of object.
object_value: object, value of passed object.
"""
# pass
print("{}: {} = {}".format(function_name, object_name, object_value))
```
## input.py
```
def preprocess_image(image):
"""Preprocess image tensor.
Args:
image: tensor, input image with shape
[cur_batch_size, height, width, depth].
Returns:
Preprocessed image tensor with shape
[cur_batch_size, height, width, depth].
"""
func_name = "preprocess_image"
# Convert from [0, 255] -> [-1.0, 1.0] floats.
image = tf.cast(x=image, dtype=tf.float32) * (2. / 255) - 1.0
print_obj(func_name, "image", image)
return image
def decode_example(protos, params):
"""Decodes TFRecord file into tensors.
Given protobufs, decode into image and label tensors.
Args:
protos: protobufs from TFRecord file.
params: dict, user passed parameters.
Returns:
Image and label tensors.
"""
func_name = "decode_example"
# Create feature schema map for protos.
features = {
"image_raw": tf.io.FixedLenFeature(shape=[], dtype=tf.string),
"label": tf.io.FixedLenFeature(shape=[], dtype=tf.int64)
}
# Parse features from tf.Example.
parsed_features = tf.io.parse_single_example(
serialized=protos, features=features
)
print_obj("\n" + func_name, "features", features)
# Convert from a scalar string tensor (whose single string has
# length height * width * depth) to a uint8 tensor with shape
# [height * width * depth].
image = tf.io.decode_raw(
input_bytes=parsed_features["image_raw"], out_type=tf.uint8
)
print_obj(func_name, "image", image)
# Reshape flattened image back into normal dimensions.
image = tf.reshape(
tensor=image,
shape=[params["height"], params["width"], params["depth"]]
)
print_obj(func_name, "image", image)
# Preprocess image.
image = preprocess_image(image=image)
print_obj(func_name, "image", image)
# Convert label from a scalar uint8 tensor to an int32 scalar.
label = tf.cast(x=parsed_features["label"], dtype=tf.int32)
print_obj(func_name, "label", label)
return {"image": image}, label
def read_dataset(filename, mode, batch_size, params):
"""Reads TF Record data using tf.data, doing necessary preprocessing.
Given filename, mode, batch size, and other parameters, read TF Record
dataset using Dataset API, apply necessary preprocessing, and return an
input function to the Estimator API.
Args:
filename: str, file pattern that to read into our tf.data dataset.
mode: The estimator ModeKeys. Can be TRAIN or EVAL.
batch_size: int, number of examples per batch.
params: dict, dictionary of user passed parameters.
Returns:
An input function.
"""
def _input_fn():
"""Wrapper input function used by Estimator API to get data tensors.
Returns:
Batched dataset object of dictionary of feature tensors and label
tensor.
"""
# Create list of files that match pattern.
file_list = tf.data.Dataset.list_files(file_pattern=filename)
# Create dataset from file list.
if params["input_fn_autotune"]:
dataset = tf.data.TFRecordDataset(
filenames=file_list,
num_parallel_reads=tf.data.experimental.AUTOTUNE
)
else:
dataset = tf.data.TFRecordDataset(filenames=file_list)
# Shuffle and repeat if training with fused op.
if mode == tf.estimator.ModeKeys.TRAIN:
dataset = dataset.apply(
tf.data.experimental.shuffle_and_repeat(
buffer_size=50 * batch_size,
count=None # indefinitely
)
)
# Decode CSV file into a features dictionary of tensors, then batch.
if params["input_fn_autotune"]:
dataset = dataset.apply(
tf.data.experimental.map_and_batch(
map_func=lambda x: decode_example(
protos=x,
params=params
),
batch_size=batch_size,
num_parallel_calls=tf.data.experimental.AUTOTUNE
)
)
else:
dataset = dataset.apply(
tf.data.experimental.map_and_batch(
map_func=lambda x: decode_example(
protos=x,
params=params
),
batch_size=batch_size
)
)
# Prefetch data to improve latency.
if params["input_fn_autotune"]:
dataset = dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
else:
dataset = dataset.prefetch(buffer_size=1)
return dataset
return _input_fn
```
## generator.py
```
class Generator(object):
"""Generator that takes latent vector input and outputs image.
Fields:
name: str, name of `Generator`.
kernel_regularizer: `l1_l2_regularizer` object, regularizar for kernel
variables.
bias_regularizer: `l1_l2_regularizer` object, regularizar for bias
variables.
"""
def __init__(self, kernel_regularizer, bias_regularizer, name):
"""Instantiates and builds generator network.
Args:
kernel_regularizer: `l1_l2_regularizer` object, regularizar for
kernel variables.
bias_regularizer: `l1_l2_regularizer` object, regularizar for bias
variables.
name: str, name of generator.
"""
# Set name of generator.
self.name = name
# Regularizer for kernel weights.
self.kernel_regularizer = kernel_regularizer
# Regularizer for bias weights.
self.bias_regularizer = bias_regularizer
def get_fake_images(self, Z, params):
"""Creates generator network and returns generated images.
Args:
Z: tensor, latent vectors of shape [cur_batch_size, latent_size].
params: dict, user passed parameters.
Returns:
Generated image tensor of shape
[cur_batch_size, height * width * depth].
"""
func_name = "get_fake_images"
# Create the input layer to our DNN.
# shape = (cur_batch_size, latent_size)
network = Z
print_obj("\n" + func_name, "network", network)
# Dictionary containing possible final activations.
final_activation_dict = {
"sigmoid": tf.nn.sigmoid, "relu": tf.nn.relu, "tanh": tf.nn.tanh
}
with tf.compat.v1.variable_scope("generator", reuse=tf.compat.v1.AUTO_REUSE):
# Add hidden layers with given number of units/neurons per layer.
for i, units in enumerate(params["generator_hidden_units"]):
# shape = (cur_batch_size, generator_hidden_units[i])
network = tf.compat.v1.layers.dense(
inputs=network,
units=units,
activation=None,
kernel_regularizer=self.kernel_regularizer,
bias_regularizer=self.bias_regularizer,
name="layers_dense_{}".format(i)
)
print_obj(func_name, "network", network)
network = tf.nn.leaky_relu(
features=network,
alpha=params["generator_leaky_relu_alpha"],
name="leaky_relu_{}".format(i)
)
print_obj(func_name, "network", network)
# Final linear layer for outputs.
# shape = (cur_batch_size, height * width * depth)
generated_outputs = tf.compat.v1.layers.dense(
inputs=network,
units=params["height"] * params["width"] * params["depth"],
activation=final_activation_dict.get(
params["generator_final_activation"].lower(), None
),
kernel_regularizer=self.kernel_regularizer,
bias_regularizer=self.bias_regularizer,
name="layers_dense_generated_outputs"
)
print_obj(func_name, "generated_outputs", generated_outputs)
return generated_outputs
def get_generator_loss(self, fake_logits):
"""Gets generator loss.
Args:
fake_logits: tensor, shape of
[cur_batch_size, 1].
Returns:
Tensor of generator's total loss of shape [].
"""
func_name = "get_generator_loss"
# Calculate base generator loss.
generator_loss = tf.reduce_mean(
input_tensor=tf.nn.sigmoid_cross_entropy_with_logits(
logits=fake_logits,
labels=tf.ones_like(input=fake_logits)
),
name="generator_loss"
)
print_obj("\n" + func_name, "generator_loss", generator_loss)
# Get regularization losses.
generator_reg_loss = tf.compat.v1.losses.get_regularization_loss(
scope="generator",
name="generator_regularization_loss"
)
print_obj(func_name, "generator_reg_loss", generator_reg_loss)
# Combine losses for total losses.
generator_total_loss = tf.math.add(
x=generator_loss,
y=generator_reg_loss,
name="generator_total_loss"
)
print_obj(func_name, "generator_total_loss", generator_total_loss)
# # Add summaries for TensorBoard.
# tf.summary.scalar(
# name="generator_loss", tensor=generator_loss, family="losses"
# )
# tf.summary.scalar(
# name="generator_reg_loss",
# tensor=generator_reg_loss,
# family="losses"
# )
# tf.summary.scalar(
# name="generator_total_loss",
# tensor=generator_total_loss,
# family="total_losses"
# )
return generator_total_loss
```
## discriminator.py
```
class Discriminator(object):
"""Discriminator that takes image input and outputs logits.
Fields:
name: str, name of `Discriminator`.
kernel_regularizer: `l1_l2_regularizer` object, regularizar for kernel
variables.
bias_regularizer: `l1_l2_regularizer` object, regularizar for bias
variables.
"""
def __init__(self, kernel_regularizer, bias_regularizer, name):
"""Instantiates and builds discriminator network.
Args:
kernel_regularizer: `l1_l2_regularizer` object, regularizar for
kernel variables.
bias_regularizer: `l1_l2_regularizer` object, regularizar for bias
variables.
name: str, name of discriminator.
"""
# Set name of discriminator.
self.name = name
# Regularizer for kernel weights.
self.kernel_regularizer = kernel_regularizer
# Regularizer for bias weights.
self.bias_regularizer = bias_regularizer
def get_discriminator_logits(self, X, params):
"""Creates discriminator network and returns logits.
Args:
X: tensor, image tensors of shape
[cur_batch_size, height * width * depth].
params: dict, user passed parameters.
Returns:
Logits tensor of shape [cur_batch_size, 1].
"""
func_name = "get_discriminator_logits"
# Create the input layer to our DNN.
# shape = (cur_batch_size, height * width * depth)
network = X
print_obj("\n" + func_name, "network", network)
with tf.compat.v1.variable_scope("discriminator", reuse=tf.compat.v1.AUTO_REUSE):
# Add hidden layers with given number of units/neurons per layer.
for i, units in enumerate(params["discriminator_hidden_units"]):
# shape = (cur_batch_size, discriminator_hidden_units[i])
network = tf.compat.v1.layers.dense(
inputs=network,
units=units,
activation=None,
kernel_regularizer=self.kernel_regularizer,
bias_regularizer=self.bias_regularizer,
name="layers_dense_{}".format(i)
)
print_obj(func_name, "network", network)
network = tf.nn.leaky_relu(
features=network,
alpha=params["discriminator_leaky_relu_alpha"],
name="leaky_relu_{}".format(i)
)
print_obj(func_name, "network", network)
# Final linear layer for logits.
# shape = (cur_batch_size, 1)
logits = tf.compat.v1.layers.dense(
inputs=network,
units=1,
activation=None,
kernel_regularizer=self.kernel_regularizer,
bias_regularizer=self.bias_regularizer,
name="layers_dense_logits"
)
print_obj(func_name, "logits", logits)
return logits
def get_discriminator_loss(self, fake_logits, real_logits, params):
"""Gets discriminator loss.
Args:
fake_logits: tensor, shape of
[cur_batch_size, 1].
real_logits: tensor, shape of
[cur_batch_size, 1].
params: dict, user passed parameters.
Returns:
Tensor of discriminator's total loss of shape [].
"""
func_name = "get_discriminator_loss"
# Calculate base discriminator loss.
discriminator_real_loss = tf.reduce_mean(
input_tensor=tf.nn.sigmoid_cross_entropy_with_logits(
logits=real_logits,
labels=tf.multiply(
x=tf.ones_like(input=real_logits),
y=params["label_smoothing"]
)
),
name="discriminator_real_loss"
)
print_obj(
"\n" + func_name,
"discriminator_real_loss",
discriminator_real_loss
)
discriminator_fake_loss = tf.reduce_mean(
input_tensor=tf.nn.sigmoid_cross_entropy_with_logits(
logits=fake_logits,
labels=tf.zeros_like(input=fake_logits)
),
name="discriminator_fake_loss"
)
print_obj(
func_name, "discriminator_fake_loss", discriminator_fake_loss
)
discriminator_loss = tf.add(
x=discriminator_real_loss,
y=discriminator_fake_loss,
name="discriminator_loss"
)
print_obj(func_name, "discriminator_loss", discriminator_loss)
# Get regularization losses.
discriminator_reg_loss = tf.compat.v1.losses.get_regularization_loss(
scope="discriminator",
name="discriminator_reg_loss"
)
print_obj(func_name, "discriminator_reg_loss", discriminator_reg_loss)
# Combine losses for total losses.
discriminator_total_loss = tf.math.add(
x=discriminator_loss,
y=discriminator_reg_loss,
name="discriminator_total_loss"
)
print_obj(
func_name, "discriminator_total_loss", discriminator_total_loss
)
# # Add summaries for TensorBoard.
# tf.summary.scalar(
# name="discriminator_real_loss",
# tensor=discriminator_real_loss,
# family="losses"
# )
# tf.summary.scalar(
# name="discriminator_fake_loss",
# tensor=discriminator_fake_loss,
# family="losses"
# )
# tf.summary.scalar(
# name="discriminator_loss",
# tensor=discriminator_loss,
# family="losses"
# )
# tf.summary.scalar(
# name="discriminator_reg_loss",
# tensor=discriminator_reg_loss,
# family="losses"
# )
# tf.summary.scalar(
# name="discriminator_total_loss",
# tensor=discriminator_total_loss,
# family="total_losses"
# )
return discriminator_total_loss
```
## train_and_eval.py
```
def get_logits_and_losses(features, generator, discriminator, params):
"""Gets logits and losses for both train and eval modes.
Args:
features: dict, feature tensors from input function.
generator: instance of generator.`Generator`.
discriminator: instance of discriminator.`Discriminator`.
params: dict, user passed parameters.
Returns:
Real and fake logits and generator and discriminator losses.
"""
func_name = "get_logits_and_losses"
# Extract real images from features dictionary.
real_images = tf.reshape(
tensor=features["image"],
shape=[-1, params["height"] * params["width"] * params["depth"]]
)
print_obj("\n" + func_name, "real_images", real_images)
# Get dynamic batch size in case of partial batch.
cur_batch_size = tf.shape(
input=real_images,
out_type=tf.int32,
name="{}_cur_batch_size".format(func_name)
)[0]
# Create random noise latent vector for each batch example.
Z = tf.random.normal(
shape=[cur_batch_size, params["latent_size"]],
mean=0.0,
stddev=1.0,
dtype=tf.float32
)
print_obj(func_name, "Z", Z)
# Get generated image from generator network from gaussian noise.
print("\nCall generator with Z = {}.".format(Z))
fake_images = generator.get_fake_images(Z=Z, params=params)
# # Add summaries for TensorBoard.
# tf.summary.image(
# name="fake_images",
# tensor=tf.reshape(
# tensor=fake_images,
# shape=[-1, params["height"], params["width"], params["depth"]]
# ),
# max_outputs=5
# )
# Get fake logits from discriminator using generator's output image.
print("\nCall discriminator with fake_images = {}.".format(fake_images))
fake_logits = discriminator.get_discriminator_logits(
X=fake_images, params=params
)
# Get real logits from discriminator using real image.
print(
"\nCall discriminator with real_images = {}.".format(real_images)
)
real_logits = discriminator.get_discriminator_logits(
X=real_images, params=params
)
# Get generator total loss.
generator_total_loss = generator.get_generator_loss(
fake_logits=fake_logits
)
# Get discriminator total loss.
discriminator_total_loss = discriminator.get_discriminator_loss(
fake_logits=fake_logits, real_logits=real_logits, params=params
)
return (real_logits,
fake_logits,
generator_total_loss,
discriminator_total_loss)
```
## train.py
```
def get_variables_and_gradients(loss, scope):
"""Gets variables and their gradients wrt. loss.
Args:
loss: tensor, shape of [].
scope: str, the network's name to find its variables to train.
Returns:
Lists of variables and their gradients.
"""
func_name = "get_variables_and_gradients"
# Get trainable variables.
variables = tf.compat.v1.trainable_variables(scope=scope)
print_obj("\n{}_{}".format(func_name, scope), "variables", variables)
# Get gradients.
gradients = tf.gradients(
ys=loss,
xs=variables,
name="{}_gradients".format(scope)
)
print_obj("\n{}_{}".format(func_name, scope), "gradients", gradients)
# Add variable names back in for identification.
gradients = [
tf.identity(
input=g,
name="{}_{}_gradients".format(func_name, v.name[:-2])
)
if tf.is_tensor(x=g) else g
for g, v in zip(gradients, variables)
]
print_obj("\n{}_{}".format(func_name, scope), "gradients", gradients)
return variables, gradients
def create_variable_and_gradient_histogram_summaries(loss_dict, params):
"""Creates variable and gradient histogram summaries.
Args:
loss_dict: dict, keys are scopes and values are scalar loss tensors
for each network kind.
params: dict, user passed parameters.
"""
pass
# for scope, loss in loss_dict.items():
# # Get variables and their gradients wrt. loss.
# variables, gradients = get_variables_and_gradients(loss, scope)
# # Add summaries for TensorBoard.
# for g, v in zip(gradients, variables):
# tf.summary.histogram(
# name="{}".format(v.name[:-2]),
# values=v,
# family="{}_variables".format(scope)
# )
# if tf.is_tensor(x=g):
# tf.summary.histogram(
# name="{}".format(v.name[:-2]),
# values=g,
# family="{}_gradients".format(scope)
# )
def train_network(loss, global_step, params, scope):
"""Trains network and returns loss and train op.
Args:
loss: tensor, shape of [].
global_step: tensor, the current training step or batch in the
training loop.
params: dict, user passed parameters.
scope: str, the variables that to train.
Returns:
Loss tensor and training op.
"""
func_name = "train_network"
print_obj("\n" + func_name, "scope", scope)
# Create optimizer map.
optimizers = {
"Adam": tf.compat.v1.train.AdamOptimizer,
"Adadelta": tf.compat.v1.train.AdadeltaOptimizer,
"AdagradDA": tf.compat.v1.train.AdagradDAOptimizer,
"Adagrad": tf.compat.v1.train.AdagradOptimizer,
"Ftrl": tf.compat.v1.train.FtrlOptimizer,
"GradientDescent": tf.compat.v1.train.GradientDescentOptimizer,
"Momentum": tf.compat.v1.train.MomentumOptimizer,
"ProximalAdagrad": tf.compat.v1.train.ProximalAdagradOptimizer,
"ProximalGradientDescent": tf.compat.v1.train.ProximalGradientDescentOptimizer,
"RMSProp": tf.compat.v1.train.RMSPropOptimizer
}
# Get optimizer and instantiate it.
if params["{}_optimizer".format(scope)] == "Adam":
optimizer = optimizers[params["{}_optimizer".format(scope)]](
learning_rate=params["{}_learning_rate".format(scope)],
beta1=params["{}_adam_beta1".format(scope)],
beta2=params["{}_adam_beta2".format(scope)],
epsilon=params["{}_adam_epsilon".format(scope)],
name="{}_{}_optimizer".format(
scope, params["{}_optimizer".format(scope)].lower()
)
)
else:
optimizer = optimizers[params["{}_optimizer".format(scope)]](
learning_rate=params["{}_learning_rate".format(scope)],
name="{}_{}_optimizer".format(
scope, params["{}_optimizer".format(scope)].lower()
)
)
print_obj("{}_{}".format(func_name, scope), "optimizer", optimizer)
# Get gradients.
gradients = tf.gradients(
ys=loss,
xs=tf.compat.v1.trainable_variables(scope=scope),
name="{}_gradients".format(scope)
)
print_obj("\n{}_{}".format(func_name, scope), "gradients", gradients)
# Clip gradients.
if params["{}_clip_gradients".format(scope)]:
gradients, _ = tf.clip_by_global_norm(
t_list=gradients,
clip_norm=params["{}_clip_gradients".format(scope)],
name="{}_clip_by_global_norm_gradients".format(scope)
)
print_obj("\n{}_{}".format(func_name, scope), "gradients", gradients)
# Zip back together gradients and variables.
grads_and_vars = zip(gradients, tf.compat.v1.trainable_variables(scope=scope))
print_obj(
"{}_{}".format(func_name, scope), "grads_and_vars", grads_and_vars
)
# Create train op by applying gradients to variables and incrementing
# global step.
train_op = optimizer.apply_gradients(
grads_and_vars=grads_and_vars,
global_step=global_step,
name="{}_apply_gradients".format(scope)
)
return loss, train_op
def get_loss_and_train_op(
generator_total_loss, discriminator_total_loss, params):
"""Gets loss and train op for train mode.
Args:
generator_total_loss: tensor, scalar total loss of generator.
discriminator_total_loss: tensor, scalar total loss of discriminator.
params: dict, user passed parameters.
Returns:
Loss scalar tensor and train_op to be used by the EstimatorSpec.
"""
func_name = "get_loss_and_train_op"
# Get global step.
global_step = tf.compat.v1.train.get_or_create_global_step()
# Determine if it is time to train generator or discriminator.
cycle_step = tf.math.mod(
x=global_step,
y=tf.cast(
x=tf.add(
x=params["discriminator_train_steps"],
y=params["generator_train_steps"]
),
dtype=tf.int64
),
name="{}_cycle_step".format(func_name)
)
# Create choose discriminator condition.
condition = tf.less(
x=cycle_step, y=params["discriminator_train_steps"]
)
# Conditionally choose to train generator or discriminator subgraph.
loss, train_op = tf.cond(
pred=condition,
true_fn=lambda: train_network(
loss=discriminator_total_loss,
global_step=global_step,
params=params,
scope="discriminator"
),
false_fn=lambda: train_network(
loss=generator_total_loss,
global_step=global_step,
params=params,
scope="generator"
)
)
return loss, train_op
```
## eval_metrics.py
```
def get_eval_metric_ops(fake_logits, real_logits, params):
"""Gets eval metric ops.
Args:
fake_logits: tensor, shape of [cur_batch_size, 1] that came from
discriminator having processed generator's output image.
real_logits: tensor, shape of [cur_batch_size, 1] that came from
discriminator having processed real image.
params: dict, user passed parameters.
Returns:
Dictionary of eval metric ops.
"""
func_name = "get_eval_metric_ops"
# Concatenate discriminator logits and labels.
discriminator_logits = tf.concat(
values=[real_logits, fake_logits],
axis=0,
name="discriminator_concat_logits"
)
print_obj("\n" + func_name, "discriminator_logits", discriminator_logits)
discriminator_labels = tf.concat(
values=[
tf.ones_like(input=real_logits) * params["label_smoothing"],
tf.zeros_like(input=fake_logits)
],
axis=0,
name="discriminator_concat_labels"
)
print_obj(func_name, "discriminator_labels", discriminator_labels)
# Calculate discriminator probabilities.
discriminator_probabilities = tf.nn.sigmoid(
x=discriminator_logits, name="discriminator_probabilities"
)
print_obj(
func_name, "discriminator_probabilities", discriminator_probabilities
)
# Create eval metric ops dictionary.
eval_metric_ops = {
"accuracy": tf.compat.v1.metrics.accuracy(
labels=discriminator_labels,
predictions=discriminator_probabilities,
name="discriminator_accuracy"
),
"precision": tf.compat.v1.metrics.precision(
labels=discriminator_labels,
predictions=discriminator_probabilities,
name="discriminator_precision"
),
"recall": tf.compat.v1.metrics.recall(
labels=discriminator_labels,
predictions=discriminator_probabilities,
name="discriminator_recall"
),
"auc_roc": tf.compat.v1.metrics.auc(
labels=discriminator_labels,
predictions=discriminator_probabilities,
num_thresholds=200,
curve="ROC",
name="discriminator_auc_roc"
),
"auc_pr": tf.compat.v1.metrics.auc(
labels=discriminator_labels,
predictions=discriminator_probabilities,
num_thresholds=200,
curve="PR",
name="discriminator_auc_pr"
)
}
print_obj(func_name, "eval_metric_ops", eval_metric_ops)
return eval_metric_ops
```
## predict.py
```
def get_predictions_and_export_outputs(features, generator, params):
"""Gets predictions and serving export outputs.
Args:
features: dict, feature tensors from serving input function.
generator: instance of `Generator`.
params: dict, user passed parameters.
Returns:
Predictions dictionary and export outputs dictionary.
"""
func_name = "get_predictions_and_export_outputs"
# Extract given latent vectors from features dictionary.
Z = features["Z"]
print_obj("\n" + func_name, "Z", Z)
# Establish generator network subgraph.
fake_images = generator.get_fake_images(Z=Z, params=params)
print_obj(func_name, "fake_images", fake_images)
# Reshape into a rank 4 image.
generated_images = tf.reshape(
tensor=fake_images,
shape=[-1, params["height"], params["width"], params["depth"]]
)
print_obj(func_name, "generated_images", generated_images)
# Create predictions dictionary.
predictions_dict = {
"generated_images": generated_images
}
print_obj(func_name, "predictions_dict", predictions_dict)
# Create export outputs.
export_outputs = {
"predict_export_outputs": tf.estimator.export.PredictOutput(
outputs=predictions_dict)
}
print_obj(func_name, "export_outputs", export_outputs)
return predictions_dict, export_outputs
```
## vanilla_gan.py
```
def vanilla_gan_model(features, labels, mode, params):
"""Vanilla GAN custom Estimator model function.
Args:
features: dict, keys are feature names and values are feature tensors.
labels: tensor, label data.
mode: tf.estimator.ModeKeys with values of either TRAIN, EVAL, or
PREDICT.
params: dict, user passed parameters.
Returns:
Instance of `tf.estimator.EstimatorSpec` class.
"""
func_name = "vanilla_gan_model"
print_obj("\n" + func_name, "features", features)
print_obj(func_name, "labels", labels)
print_obj(func_name, "mode", mode)
print_obj(func_name, "params", params)
# Loss function, training/eval ops, etc.
predictions_dict = None
loss = None
train_op = None
eval_metric_ops = None
export_outputs = None
# Instantiate generator.
vanilla_generator = Generator(
kernel_regularizer=None,
# tf.contrib.layers.l1_l2_regularizer(
# scale_l1=params["generator_l1_regularization_scale"],
# scale_l2=params["generator_l2_regularization_scale"]
# ),
bias_regularizer=None,
name="generator"
)
# Instantiate discriminator.
vanilla_discriminator = Discriminator(
kernel_regularizer=None,
# tf.contrib.layers.l1_l2_regularizer(
# scale_l1=params["discriminator_l1_regularization_scale"],
# scale_l2=params["discriminator_l2_regularization_scale"]
# ),
bias_regularizer=None,
name="discriminator"
)
if mode == tf.estimator.ModeKeys.PREDICT:
# Get predictions and export outputs.
(predictions_dict,
export_outputs) = get_predictions_and_export_outputs(
features=features, generator=vanilla_generator, params=params
)
else:
# Get logits and losses from networks for train and eval modes.
(real_logits,
fake_logits,
generator_total_loss,
discriminator_total_loss) = get_logits_and_losses(
features=features,
generator=vanilla_generator,
discriminator=vanilla_discriminator,
params=params
)
if mode == tf.estimator.ModeKeys.TRAIN:
# Create variable and gradient histogram summaries.
create_variable_and_gradient_histogram_summaries(
loss_dict={
"generator": generator_total_loss,
"discriminator": discriminator_total_loss
},
params=params
)
# Get loss and train op for EstimatorSpec.
loss, train_op = get_loss_and_train_op(
generator_total_loss=generator_total_loss,
discriminator_total_loss=discriminator_total_loss,
params=params
)
else:
# Set eval loss.
loss = discriminator_total_loss
# Get eval metrics.
eval_metric_ops = get_eval_metric_ops(
real_logits=real_logits,
fake_logits=fake_logits,
params=params
)
# Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions_dict,
loss=loss,
train_op=train_op,
eval_metric_ops=eval_metric_ops,
export_outputs=export_outputs
)
```
## serving.py
```
def serving_input_fn(params):
"""Serving input function.
Args:
params: dict, user passed parameters.
Returns:
ServingInputReceiver object containing features and receiver tensors.
"""
func_name = "serving_input_fn"
# Create placeholders to accept data sent to the model at serving time.
# shape = (batch_size,)
feature_placeholders = {
"Z": tf.compat.v1.placeholder(
dtype=tf.float32,
shape=[None, params["latent_size"]],
name="serving_input_placeholder_Z"
)
}
print_obj("\n" + func_name, "feature_placeholders", feature_placeholders)
# Create clones of the feature placeholder tensors so that the SavedModel
# SignatureDef will point to the placeholder.
features = {
key: tf.identity(
input=value,
name="{}_identity_placeholder_{}".format(func_name, key)
)
for key, value in feature_placeholders.items()
}
print_obj(func_name, "features", features)
return tf.estimator.export.ServingInputReceiver(
features=features, receiver_tensors=feature_placeholders
)
```
## model.py
```
def train_and_evaluate(args):
"""Trains and evaluates custom Estimator model.
Args:
args: dict, user passed parameters.
Returns:
`Estimator` object.
"""
func_name = "train_and_evaluate"
print_obj("\n" + func_name, "args", args)
# Ensure filewriter cache is clear for TensorBoard events file.
# tf.summary.FileWriterCache.clear()
# Set logging to be level of INFO.
# tf.logging.set_verbosity(tf.logging.INFO)
# Create a RunConfig for Estimator.
config = tf.estimator.RunConfig(
model_dir=args["output_dir"],
save_summary_steps=args["save_summary_steps"],
save_checkpoints_steps=args["save_checkpoints_steps"],
keep_checkpoint_max=args["keep_checkpoint_max"]
)
# Create our custom estimator using our model function.
estimator = tf.estimator.Estimator(
model_fn=vanilla_gan_model,
model_dir=args["output_dir"],
config=config,
params=args
)
# Create train spec to read in our training data.
train_spec = tf.estimator.TrainSpec(
input_fn=read_dataset(
filename=args["train_file_pattern"],
mode=tf.estimator.ModeKeys.TRAIN,
batch_size=args["train_batch_size"],
params=args
),
max_steps=args["train_steps"]
)
# Create exporter to save out the complete model to disk.
exporter = tf.estimator.LatestExporter(
name="exporter",
serving_input_receiver_fn=lambda: serving_input_fn(args)
)
# Create eval spec to read in our validation data and export our model.
eval_spec = tf.estimator.EvalSpec(
input_fn=read_dataset(
filename=args["eval_file_pattern"],
mode=tf.estimator.ModeKeys.EVAL,
batch_size=args["eval_batch_size"],
params=args
),
steps=args["eval_steps"],
start_delay_secs=args["start_delay_secs"],
throttle_secs=args["throttle_secs"],
exporters=exporter
)
# Create train and evaluate loop to train and evaluate our estimator.
tf.estimator.train_and_evaluate(
estimator=estimator, train_spec=train_spec, eval_spec=eval_spec)
return estimator
```
## Run model
```
os.environ["OUTPUT_DIR"] = arguments["output_dir"]
%%bash
gsutil -m rm -rf ${OUTPUT_DIR}
estimator = train_and_evaluate(arguments)
```
## Prediction
```
!gsutil ls gs://machine-learning-1234-bucket/gan/vanilla_gan/trained_model/export/exporter
loaded = tf.saved_model.load(
export_dir=os.path.join(
arguments["output_dir"], "export", "exporter", "1595549661"
)
)
print(list(loaded.signatures.keys()))
infer = loaded.signatures["serving_default"]
print(infer.structured_outputs)
Z = tf.random.normal(shape=(10, 512))
predictions = infer(Z)
```
Convert image back to the original scale.
```
generated_images = np.clip(
a=tf.cast(
x=((tf.reshape(
tensor=predictions["generated_images"],
shape=[
-1,
arguments["height"],
arguments["width"],
arguments["depth"]
]
) + 1.0) * (255. / 2)),
dtype=tf.int32
),
a_min=0,
a_max=255
)
print(generated_images.shape)
def plot_images(images):
"""Plots images.
Args:
images: np.array, array of images of
[num_images, image_size, image_size, num_channels].
"""
num_images = len(images)
plt.figure(figsize=(20, 20))
for i in range(num_images):
image = images[i]
plt.subplot(1, num_images, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(
tf.reshape(image, image.shape[:-1]),
cmap="gray_r"
)
plt.show()
plot_images(generated_images)
```
|
github_jupyter
|
# Tidy Data
> Structuring datasets to facilitate analysis [(Wickham 2014)](http://www.jstatsoft.org/v59/i10/paper)
If there's one maxim I can impart it's that your tools shouldn't get in the way of your analysis. Your problem is already difficult enough, don't let the data or your tools make it any harder.
## The Rules
In a tidy dataset...
1. Each variable forms a column
2. Each observation forms a row
3. Each type of observational unit forms a table
We'll cover a few methods that help you get there.
Based on [this](http://stackoverflow.com/questions/22695680/python-pandas-timedelta-specific-rows) StackOverflow question.
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
pd.options.display.max_rows = 10
%matplotlib inline
```
Earlier, I fetched some data
```python
tables = pd.read_html("http://www.basketball-reference.com/leagues/NBA_2015_games.html")
games = tables[0]
games.to_csv('data/games.csv', index=False)
```
```
pd.read_html?
!head -n 2 data/games.csv
```
The Question:
> **How many days of rest did each team get between each game?**
Whether or not your dataset is tidy depends on your question. Given our question, what is an observation?
```
column_names = ['date', '_', 'away_team', 'away_points', 'home_team',
'home_points', 'n_ot', 'notes']
games = (pd.read_csv('data/games.csv', names=column_names, parse_dates=['date'],
skiprows=1)
.drop(['_', 'notes', 'n_ot'], axis='columns')
.set_index('date', append=True))
games.index.names = ['game_id', 'date']
games.head()
```
Is `games` a tidy dataset, given our question? No, we have multiple observations (teams) per row. We'll use `pd.melt` to fix that.
```
tidy = pd.melt(games.sort_index().reset_index(),
id_vars=['game_id', 'date'], value_vars=['away_team', 'home_team'],
value_name='team')
tidy.head()
```
Now the translation from question to operation is direct:
```
# For each team... get number of dates between games
tidy.groupby('team')['date'].diff().dt.days - 1
tidy['rest'] = tidy.sort('date').groupby('team').date.diff().dt.days - 1
tidy.dropna().head()
un = pd.pivot_table(tidy, values='rest',
index=['game_id', 'date'],
columns='variable').rename(
columns={'away_team': 'away_rest', 'home_team': 'home_rest'}
)
un.columns.name = None
un.dropna().head()
df = pd.concat([games, un], axis=1)
df
g = sns.FacetGrid(data=tidy.dropna(), col='team', col_wrap=5, hue='team')
g.map(sns.barplot, "variable", "rest");
delta = (un.home_rest - un.away_rest).dropna().astype(int)
(delta.value_counts()
.reindex(np.arange(delta.min(), delta.max() + 1), fill_value=0)
.sort_index().plot(kind='bar', color='k', width=.9, rot=0, figsize=(12, 6)))
```
# Stack / Unstack
An "observation" depends on the question. Home team advantage?
```
home_adv = games.home_points - games.away_points
ax = (home_adv).plot(kind='hist', bins=80, color='k', figsize=(10, 5))
ax.set_xlim(-40, 40)
mu = home_adv.mean()
ax.vlines(mu, *ax.get_ylim(), color='steelblue', linewidth=3)
print('Home win percent:', (home_adv > 0).mean())
```
# Team Strength
# Mini Project: Home Court Advantage?
What's the effect (in terms of probability to win) of being
the home team.
### Step 1: Calculate Win %
We need to create an indicator for whether the home team won.
Add it as a column called `home_win` in `games`.
```
games['home_win'] = ... # fill this in
#%load -r 1:4 solutions_tidy.py
```
### Step 2: Find the win percent for each team
Teams are split across two columns. It's easiest to calculate the number of wins and
number of games as away, and the number of wins and number of games as home. Then
combine those two results to get the win percent.
```
wins_as_home = games.groupby('').agg([])
# hint: use `~` to flip an array of booleans
wins_as_away = ...
wins_as_home.columns = ['n_wins', 'n_games']
wins_as_away.columns = ['n_wins', 'n_games']
%load -r 5:13 solutions_tidy.py
```
Now add `wins_as_home` and `wins_as_away` to get a DataFrame with
two columsn, `n_wins`, and `n_games` and one row per team.
Finally, calculate the win percent.
```
%load -r 14:20 solutions_tidy.py
strength.order().plot(kind='barh', figsize=(5, 12))
```
Bring the `strength` valuess in for each team, for each game.
```
games.head()
```
For SQL people
```sql
SELECT *
FROM games NATURAL JOIN strength
```
We just need to get the names worked out.
```
strength.head().reset_index().rename(columns=lambda x: 'away_' + x)
(pd.merge(games.reset_index(), strength.reset_index().add_prefix('away_'))
.pipe(pd.merge, strength.reset_index().add_prefix('home_'))
.set_index(['game_id', 'date']))
```
For python people
```
games = games.assign(away_strength=games.away_team.map(strength),
home_strength=games.home_team.map(strength))
games.head()
X = pd.concat([games, un], axis=1).set_index(['away_team', 'home_team'], append=True).dropna()
X.head()
X['home_win'] = X.home_win.astype(int) # for statsmodels
import statsmodels.api as sm
mod = sm.Logit.from_formula('home_win ~ home_strength + away_strength + home_rest + away_rest', X)
res = mod.fit()
res.summary()
mod = sm.Logit.from_formula('home_win ~ rest_difference',
X.assign(rest_difference=lambda df: df.home_rest - df.away_rest))
res = mod.fit()
res.summary()
mod = sm.OLS.from_formula('spread ~ home_strength + away_strength + rest_difference',
X.assign(rest_difference=lambda df: df.home_rest - df.away_rest,
spread=lambda df: df.home_points - df.away_points))
res = mod.fit()
res.summary()
```
# Recap
- Tidy data: one row per observation
- melt / stack: wide to long
- pivot_table / unstack: long to wide
|
github_jupyter
|
# Module 3 Graded Assessment
```
"""
1.Question 1
Fill in the blanks of this code to print out the numbers 1 through 7.
"""
number = 1
while number <= 7:
print(number, end=" ")
number +=1
"""
2.Question 2
The show_letters function should print out each letter of a word on a separate line.
Fill in the blanks to make that happen.
"""
def show_letters(word):
for letter in word:
print(letter)
show_letters("Hello")
# Should print one line per letter
"""
3.Question 3
Complete the function digits(n) that returns how many digits the number has.
For example: 25 has 2 digits and 144 has 3 digits. Tip: you can figure out the digits of a number by dividing
it by 10 once per digit until there are no digits left.
"""
def digits(n):
count = str(n)
return len(count)
print(digits(25)) # Should print 2
print(digits(144)) # Should print 3
print(digits(1000)) # Should print 4
print(digits(0)) # Should print 1
"""
4.Question 4
This function prints out a multiplication table (where each number is the result of multiplying the first number of its row by the number at the top of its column). Fill in the blanks so that calling multiplication_table(1, 3) will print out:
1 2 3
2 4 6
3 6 9
"""
def multiplication_table(start, stop):
for x in range(start,stop+1):
for y in range(start,stop+1):
print(str(x*y), end=" ")
print()
multiplication_table(1, 3)
# Should print the multiplication table shown above
"""
5.Question 5
The counter function counts down from start to stop when start is bigger than stop,
and counts up from start to stop otherwise.
Fill in the blanks to make this work correctly.
"""
def counter(start, stop):
x = start
if x>stop:
return_string = "Counting down: "
while x >= stop:
return_string += str(x)
if x>stop:
return_string += ","
x = x-1
else:
return_string = "Counting up: "
while x <= stop:
return_string += str(x)
if x<stop:
return_string += ","
x = x+1
return return_string
print(counter(1, 10)) # Should be "Counting up: 1,2,3,4,5,6,7,8,9,10"
print(counter(2, 1)) # Should be "Counting down: 2,1"
print(counter(5, 5)) # Should be "Counting up: 5"
"""
6.Question 6
The loop function is similar to range(), but handles the parameters somewhat differently: it takes in 3 parameters:
the starting point, the stopping point, and the increment step. When the starting point is greater
than the stopping point, it forces the steps to be negative. When, instead, the starting point is less
than the stopping point, it forces the step to be positive. Also, if the step is 0, it changes to 1 or -1.
The result is returned as a one-line, space-separated string of numbers. For example, loop(11,2,3)
should return 11 8 5 and loop(1,5,0) should return 1 2 3 4. Fill in the missing parts to make that happen.
"""
def loop(start, stop, step):
return_string = ""
if step == 0:
step=1
if start>stop:
step = abs(step) * -1
else:
step = abs(step)
for count in range(start, stop, step):
return_string += str(count) + " "
return return_string.strip()
print(loop(11,2,3)) # Should be 11 8 5
print(loop(1,5,0)) # Should be 1 2 3 4
print(loop(-1,-2,0)) # Should be -1
print(loop(10,25,-2)) # Should be 10 12 14 16 18 20 22 24
print(loop(1,1,1)) # Should be empty
#8.Question 8
#What is the value of x at the end of the following code?
for x in range(1, 10, 3):
print(x)
#7
#9.Question 9
#What is the value of y at the end of the following code?
for x in range(10):
for y in range(x):
print(y)
#8
```
|
github_jupyter
|
### Instructions
The lecture uses random forest to predict the state of the loan with data taken from Lending Club (2015). With minimal feature engineering, they were able to get an accuracy of 98% with cross validation. However, the accuracies had a lot of variance, ranging from 98% to 86%, indicating there are lots of useless features.
I am tasked with 1) removing as many features as possible without dropping the average below 90% accuracy in a 10 fold cross validation and 2) if the first task is possible without using anything related to payment amount or outstanding principal.
### 1 - Import Data
In this dataset, there are 420k+ rows and 110 features and the target variable (loan status).
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import ensemble
from sklearn.model_selection import cross_val_score
import warnings
warnings.filterwarnings('ignore')
df = pd.read_csv('LoanStats3d.csv', skipinitialspace=True, header=1)
df.info()
```
The the last two rows of the dataset holds no data, so these rows will be deleted.
```
df.tail()
df = df[:-2]
```
### 2 - Removing Features
In the lecture, they removed any columns with missing values. I'm not sure this is the best method, as there could be valuable information in the missing values. Instead, the method I employ is to identify the categorical features. If there are less than 30 unique values, then I create dummy variables out of them. If there are more than 30 unique values, I use panda's ability to map each unique value to a numeric value, allowing me to retain all columns and rows.
```
cat_col = [col for col in df.columns if df[col].dtype == 'object']
num_col = [col for col in df.columns if df[col].dtype != 'object']
cat_col.remove('loan_status')
dummy_df = pd.DataFrame()
for col in cat_col:
if df[col].nunique() < 30:
dummy_df = pd.concat([dummy_df, pd.get_dummies(df[col], prefix = col, drop_first=True)], axis = 1)
cat_col.remove(col)
```
For whatever reason, the id and interest rates are labeled as 'objects'. The following is to convert them into numeric features.
```
df['id'] = pd.to_numeric(df['id'], errors='coerce')
df['int_rate'] = pd.to_numeric(df['int_rate'].str.strip('%'), errors='coerce')
cat_col.remove('id')
cat_col.remove('int_rate')
```
Using Panda's codes function is as simple as converting the objects into categorical dtypes (instead of objects). Then add one to the codes as null values are given a value of -1, which random forest will not take.
```
for col in cat_col + ['loan_status']:
df[col] = df[col].astype('category')
df[col] = df[col].cat.codes+1
df_combined = pd.concat([df[cat_col+num_col], df['loan_status'], dummy_df], axis = 1)
combined_cols_lst = list(df_combined.columns)
combined_cols_lst.remove('loan_status')
```
At this point, I have 136 features. How do we remove the features that do not help predict the loan status? One way is to find the features that are highly correlated with the loan status. Below I've found 9 features that have a correlation of at least 0.15.
```
print('There are {} features.'.format(len(combined_cols_lst)))
important_cols = [col for col in combined_cols_lst if df_combined[[col, 'loan_status']].corr().abs()['loan_status'][0] > 0.15]
important_cols
```
### 3 - Random Forest Classifier
I'm finally ready to apply the data to a random forest classifier. I will be using a 10 fold cross validation, the same as the lecture for comparison. Recall that in the lecture, the average accuracy was ~97%, but it had a range of ~11%. **On the other hand, this model with only 9 features has an accuracy of ~97%, but a range of ~2.5%. **
```
rfc = ensemble.RandomForestClassifier()
X = df_combined[important_cols]
Y = df_combined['loan_status']
cv = cross_val_score(rfc, X, Y, cv = 10)
print('The cross validation score has a range of {:0.3f} and mean of {:0.3f}'.format(cv.max() - cv.min(), cv.mean()))
```
#### 3.1 - Removing Payment Amount and Outstanding Principal
The second question to answer is if is is possible to have an accuracy above 90% without using features related to payment amounts or outstanding principals. Looking at the features deemed 'important', there are only three that are not related to payment amount or principals. Of these three features, two of them have very low correlations. My guess is it will be pretty difficult to achieve 90% accuracy.
```
for col in important_cols:
print(col, df_combined[[col, 'loan_status']].corr().abs()['loan_status'][0])
important_cols_2 = ['total_rec_prncp',
'recoveries',
'collection_recovery_fee']
```
As expected, the average accuracy is ~86% and is not able to meet the target accuracy.
```
rfc2 = ensemble.RandomForestClassifier()
X2 = df_combined[important_cols_2]
Y2 = df_combined['loan_status']
cv2 = cross_val_score(rfc2, X2, Y2, cv = 10)
print('The cross validation score has a range of {:0.3f} and mean of {:0.3f}'.format(cv2.max() - cv2.min(), cv2.mean()))
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Rock, Paper & Scissors with TensorFlow Hub - TFLite
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/lmoroney/dlaicourse/blob/master/TensorFlow%20Deployment/Course%202%20-%20TensorFlow%20Lite/Week%203/Exercise/TFLite_Week3_Exercise.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/lmoroney/dlaicourse/blob/master/TensorFlow%20Deployment/Course%202%20-%20TensorFlow%20Lite/Week%203/Exercise/TFLite_Week3_Exercise.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
</table>
## Setup
```
try:
%tensorflow_version 2.x
except:
pass
import numpy as np
import matplotlib.pylab as plt
import tensorflow as tf
import tensorflow_hub as hub
from tqdm import tqdm
print("\u2022 Using TensorFlow Version:", tf.__version__)
print("\u2022 Using TensorFlow Hub Version: ", hub.__version__)
print('\u2022 GPU Device Found.' if tf.test.is_gpu_available() else '\u2022 GPU Device Not Found. Running on CPU')
```
## Select the Hub/TF2 Module to Use
Hub modules for TF 1.x won't work here, please use one of the selections provided.
```
module_selection = ("mobilenet_v2", 224, 1280) #@param ["(\"mobilenet_v2\", 224, 1280)", "(\"inception_v3\", 299, 2048)"] {type:"raw", allow-input: true}
handle_base, pixels, FV_SIZE = module_selection
MODULE_HANDLE ="https://tfhub.dev/google/tf2-preview/{}/feature_vector/4".format(handle_base)
IMAGE_SIZE = (pixels, pixels)
print("Using {} with input size {} and output dimension {}".format(MODULE_HANDLE, IMAGE_SIZE, FV_SIZE))
```
## Data Preprocessing
Use [TensorFlow Datasets](http://tensorflow.org/datasets) to load the cats and dogs dataset.
This `tfds` package is the easiest way to load pre-defined data. If you have your own data, and are interested in importing using it with TensorFlow see [loading image data](../load_data/images.ipynb)
```
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
```
The `tfds.load` method downloads and caches the data, and returns a `tf.data.Dataset` object. These objects provide powerful, efficient methods for manipulating data and piping it into your model.
Since `"cats_vs_dog"` doesn't define standard splits, use the subsplit feature to divide it into (train, validation, test) with 80%, 10%, 10% of the data respectively.
```
splits = tfds.Split.ALL.subsplit(weighted=(80, 10, 10))
# Go to the TensorFlow Dataset's website and search for the Rock, Paper, Scissors dataset and load it here
splits, info = tfds.load( # YOUR CODE HERE )
(train_examples, validation_examples, test_examples) = splits
num_examples = info.splits['train'].num_examples
num_classes = info.features['label'].num_classes
```
### Format the Data
Use the `tf.image` module to format the images for the task.
Resize the images to a fixes input size, and rescale the input channels
```
def format_image(image, label):
image = tf.image.resize(image, IMAGE_SIZE) / 255.0
return image, label
```
Now shuffle and batch the data
```
BATCH_SIZE = 32 #@param {type:"integer"}
# Prepare the examples by preprocessing the them and then batching them (and optionally prefetching them)
# If you wish you can shuffle train set here
train_batches = # YOUR CODE HERE
validation_batches = # YOUR CODE HERE
test_batches = # YOUR CODE HERE
```
Inspect a batch
```
for image_batch, label_batch in train_batches.take(1):
pass
image_batch.shape
```
## Defining the Model
All it takes is to put a linear classifier on top of the `feature_extractor_layer` with the Hub module.
For speed, we start out with a non-trainable `feature_extractor_layer`, but you can also enable fine-tuning for greater accuracy.
```
do_fine_tuning = False #@param {type:"boolean"}
feature_extractor = hub.KerasLayer(MODULE_HANDLE,
input_shape=IMAGE_SIZE + (3,),
output_shape=[FV_SIZE],
trainable=do_fine_tuning)
print("Building model with", MODULE_HANDLE)
model = tf.keras.Sequential([
feature_extractor,
tf.keras.layers.Dense(num_classes, activation='softmax')
])
model.summary()
#@title (Optional) Unfreeze some layers
NUM_LAYERS = 10 #@param {type:"slider", min:1, max:50, step:1}
if do_fine_tuning:
feature_extractor.trainable = True
for layer in model.layers[-NUM_LAYERS:]:
layer.trainable = True
else:
feature_extractor.trainable = False
```
## Training the Model
```
if do_fine_tuning:
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.002, momentum=0.9),
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
else:
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
EPOCHS = 5
hist = model.fit(train_batches,
epochs=EPOCHS,
validation_data=validation_batches)
```
## Export the Model
```
RPS_SAVED_MODEL = "rps_saved_model"
```
Export the SavedModel
```
# Use TensorFlow's SavedModel API to export the SavedModel from the trained Keras model
# YOUR CODE HERE
%%bash -s $RPS_SAVED_MODEL
saved_model_cli show --dir $1 --tag_set serve --signature_def serving_default
loaded = tf.saved_model.load(RPS_SAVED_MODEL)
print(list(loaded.signatures.keys()))
infer = loaded.signatures["serving_default"]
print(infer.structured_input_signature)
print(infer.structured_outputs)
```
## Convert Using TFLite's Converter
```
# Intialize the TFLite converter to load the SavedModel
converter = # YOUR CODE HERE
# Set the optimization strategy for 'size' in the converter
converter.optimizations = [# YOUR CODE HERE]
# Use the tool to finally convert the model
tflite_model = # YOUR CODE HERE
tflite_model_file = 'converted_model.tflite'
with open(tflite_model_file, "wb") as f:
f.write(tflite_model)
```
## Test the TFLite Model Using the Python Interpreter
```
# Load TFLite model and allocate tensors.
with open(tflite_model_file, 'rb') as fid:
tflite_model = fid.read()
interpreter = tf.lite.Interpreter(model_content=tflite_model)
interpreter.allocate_tensors()
input_index = interpreter.get_input_details()[0]["index"]
output_index = interpreter.get_output_details()[0]["index"]
# Gather results for the randomly sampled test images
predictions = []
test_labels, test_imgs = [], []
for img, label in tqdm(test_batches.take(10)):
interpreter.set_tensor(input_index, img)
interpreter.invoke()
predictions.append(interpreter.get_tensor(output_index))
test_labels.append(label.numpy()[0])
test_imgs.append(img)
#@title Utility functions for plotting
# Utilities for plotting
class_names = ['rock', 'paper', 'scissors']
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
img = np.squeeze(img)
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
print(type(predicted_label), type(true_label))
if predicted_label == true_label:
color = 'green'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]), color=color)
#@title Visualize the outputs { run: "auto" }
index = 0 #@param {type:"slider", min:0, max:9, step:1}
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(index, predictions, test_labels, test_imgs)
plt.show()
```
Create a file to save the labels.
```
with open('labels.txt', 'w') as f:
f.write('\n'.join(class_names))
```
If you are running this notebook in a Colab, you can run the cell below to download the model and labels to your local disk.
**Note**: If the files do not download when you run the cell, try running the cell a second time. Your browser might prompt you to allow multiple files to be downloaded.
```
try:
from google.colab import files
files.download('converted_model.tflite')
files.download('labels.txt')
except:
pass
```
# Prepare the Test Images for Download (Optional)
This part involves downloading additional test images for the Mobile Apps only in case you need to try out more samples
```
!mkdir -p test_images
from PIL import Image
for index, (image, label) in enumerate(test_batches.take(50)):
image = tf.cast(image * 255.0, tf.uint8)
image = tf.squeeze(image).numpy()
pil_image = Image.fromarray(image)
pil_image.save('test_images/{}_{}.jpg'.format(class_names[label[0]], index))
!ls test_images
!zip -qq rps_test_images.zip -r test_images/
```
If you are running this notebook in a Colab, you can run the cell below to download the Zip file with the images to your local disk.
**Note**: If the Zip file does not download when you run the cell, try running the cell a second time.
```
try:
files.download('rps_test_images.zip')
except:
pass
```
|
github_jupyter
|
論文<br>
https://arxiv.org/abs/2109.07161<br>
<br>
GitHub<br>
https://github.com/saic-mdal/lama<br>
<br>
<a href="https://colab.research.google.com/github/kaz12tech/ai_demos/blob/master/Lama_demo.ipynb" target="_blank"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 環境セットアップ
## GitHubからソースコードを取得
## ライブラリをインストール
```
%cd /content
!git clone https://github.com/saic-mdal/lama.git
!pip install -r lama/requirements.txt --quiet
!pip install wget --quiet
!pip install --upgrade webdataset==0.1.103
!pip uninstall opencv-python-headless -y --quiet
!pip install opencv-python-headless==4.1.2.30 --quiet
# torchtext 0.8.0をインストール
!pip uninstall torch torchvision torchaudio torchtext -y
!pip install torch==1.7.1+cu110 torchvision==0.8.2+cu110 torchaudio==0.7.2 torchtext -f https://download.pytorch.org/whl/torch_stable.html
# avoid AttributeError: 'builtin_function_or_method' object has no attribute 'rfftn'
!sed -E -i "15i import torch.fft" /content/lama/saicinpainting/training/modules/ffc.py
```
## 学習済みモデルのセットアップ
```
% cd /content/lama
!curl -L $(yadisk-direct https://disk.yandex.ru/d/ouP6l8VJ0HpMZg) -o big-lama.zip
!unzip big-lama.zip
```
## ライブラリをインポート
```
import base64, os
from IPython.display import HTML, Image
from google.colab.output import eval_js
from base64 import b64decode
import matplotlib.pyplot as plt
import numpy as np
import wget
from shutil import copyfile
import shutil
```
# Canvasのセットアップ
```
canvas_html = """
<style>
.button {
background-color: #4CAF50;
border: none;
color: white;
padding: 15px 32px;
text-align: center;
text-decoration: none;
display: inline-block;
font-size: 16px;
margin: 4px 2px;
cursor: pointer;
}
</style>
<canvas1 width=%d height=%d>
</canvas1>
<canvas width=%d height=%d>
</canvas>
<button class="button">Finish</button>
<script>
var canvas = document.querySelector('canvas')
var ctx = canvas.getContext('2d')
var canvas1 = document.querySelector('canvas1')
var ctx1 = canvas.getContext('2d')
ctx.strokeStyle = 'red';
var img = new Image();
img.src = "data:image/%s;charset=utf-8;base64,%s";
console.log(img)
img.onload = function() {
ctx1.drawImage(img, 0, 0);
};
img.crossOrigin = 'Anonymous';
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.lineWidth = %d
var button = document.querySelector('button')
var mouse = {x: 0, y: 0}
canvas.addEventListener('mousemove', function(e) {
mouse.x = e.pageX - this.offsetLeft
mouse.y = e.pageY - this.offsetTop
})
canvas.onmousedown = ()=>{
ctx.beginPath()
ctx.moveTo(mouse.x, mouse.y)
canvas.addEventListener('mousemove', onPaint)
}
canvas.onmouseup = ()=>{
canvas.removeEventListener('mousemove', onPaint)
}
var onPaint = ()=>{
ctx.lineTo(mouse.x, mouse.y)
ctx.stroke()
}
var data = new Promise(resolve=>{
button.onclick = ()=>{
resolve(canvas.toDataURL('image/png'))
}
})
</script>
"""
def draw(imgm, filename='drawing.png', w=400, h=200, line_width=1):
display(HTML(canvas_html % (w, h, w,h, filename.split('.')[-1], imgm, line_width)))
data = eval_js("data")
binary = b64decode(data.split(',')[1])
with open(filename, 'wb') as f:
f.write(binary)
```
# 画像のセットアップ
[使用画像1](https://www.pakutaso.com/shared/img/thumb/PAK85_oyakudachisimasu20140830_TP_V.jpg)<br>
[使用画像2](https://www.pakutaso.com/shared/img/thumb/TSU88_awaitoykyo_TP_V.jpg)<br>
[使用画像3](https://www.pakutaso.com/20211208341post-37933.html)
```
% cd /content/lama
from google.colab import files
files = files.upload()
fname = list(files.keys())[0]
shutil.rmtree('./data_for_prediction', ignore_errors=True)
! mkdir data_for_prediction
copyfile(fname, f'./data_for_prediction/{fname}')
os.remove(fname)
fname = f'./data_for_prediction/{fname}'
image64 = base64.b64encode(open(fname, 'rb').read())
image64 = image64.decode('utf-8')
print(f'Will use {fname} for inpainting')
img = np.array(plt.imread(f'{fname}')[:,:,:3])
```
# inpainting
```
mask_path = f".{fname.split('.')[1]}_mask.png"
draw(image64, filename=mask_path, w=img.shape[1], h=img.shape[0], line_width=0.04*img.shape[1])
with_mask = np.array(plt.imread(mask_path)[:,:,:3])
mask = (with_mask[:,:,0]==1)*(with_mask[:,:,1]==0)*(with_mask[:,:,2]==0)
plt.imsave(mask_path,mask, cmap='gray')
%cd /content/lama
!mkdir output/
copyfile(mask_path,os.path.join("./output/", os.path.basename(mask_path)))
!PYTHONPATH=. TORCH_HOME=$(pwd) python3 bin/predict.py \
model.path=$(pwd)/big-lama \
indir=$(pwd)/data_for_prediction \
outdir=/content/lama/output \
dataset.img_suffix={suffix}
plt.rcParams['figure.dpi'] = 200
plt.imshow(plt.imread(f"/content/lama/output/{fname.split('.')[1].split('/')[2]}_mask.png"))
_=plt.axis('off')
_=plt.title('inpainting result')
plt.show()
fname = None
```
|
github_jupyter
|
```
# assume you have openmm, pdbfixer and mdtraj installed.
# if not, you can follow the gudie here https://github.com/npschafer/openawsem
# import all using lines below
# from simtk.openmm.app import *
# from simtk.openmm import *
# from simtk.unit import *
from simtk.openmm.app import ForceField
# define atoms and residues.
forcefield = ForceField("cg.xml")
from pdbfixer import PDBFixer
from simtk.openmm.app import PDBFile
fixer = PDBFixer("1r69.pdb")
# more on pdbfixer, check:
# https://htmlpreview.github.io/?https://github.com/openmm/pdbfixer/blob/master/Manual.html
fixer.removeHeterogens(keepWater=False)
PDBFile.writeFile(fixer.topology, fixer.positions, open('1r69_cleaned.pdb', 'w'))
import mdtraj
pdb = mdtraj.load("1r69_cleaned.pdb")
keep_list = []
for atom in pdb.topology.atoms:
if atom.name == "CA":
keep_list.append(atom.index)
chosen = pdb.atom_slice(keep_list)
chosen.save("ca_only.pdb")
from simtk.openmm import HarmonicBondForce
def connect_term(system):
k_con= 10000
con = HarmonicBondForce()
n = system.getNumParticles()
for i in range(n-1):
con.addBond(i, i+1, 0.3816, k_con)
return con
from simtk.openmm import CustomBondForce
def connect_term_v2(system):
k_con= 10000
r0 = 0.3816
con = CustomBondForce(f"0.5*{k_con}*(r-r0)^2")
n = system.getNumParticles()
con.addPerBondParameter("r0")
for i in range(n-1):
con.addBond(i, i+1, [r0])
return con
from simtk.openmm import CustomCompoundBondForce
def connect_term_v3(system):
k_con= 10000
r0 = 0.3816
con = CustomCompoundBondForce(2, f"0.5*{k_con}*(distance(p1,p2)-r0)^2")
n = system.getNumParticles()
con.addPerBondParameter("r0")
for i in range(n-1):
con.addBond([i, i+1], [r0])
return con
# contact map
import numpy as np
from simtk.unit import *
pdb = PDBFile("ca_only.pdb")
pos = pdb.positions.value_in_unit(nanometer)
pos = np.array(pos)
dis = (((pos.reshape(1, -1, 3) - pos.reshape(-1, 1, 3))**2).sum(axis=-1))**0.5
import matplotlib.pylab as plt
%matplotlib inline
plt.figure(figsize=[10,10])
plt.imshow(dis < 0.8, origin="lower")
plt.colorbar()
n = dis.shape[0]
contact_threshold = 0.8 # in unit of nm
contact_list = []
for i in range(n):
for j in range(i+1, n):
dis_ij = dis[i][j]
if dis_ij < contact_threshold:
sigma_ij = 0.1*(j-i)**0.15
contact_list.append((i, j, (dis_ij, sigma_ij)))
len(contact_list)
from simtk.openmm import CustomBondForce
def structure_based_term(contact_list):
k = 10
structure_based = CustomBondForce(f"-{k}*exp(-(r-r_ijN)^2/(2*sigma_ij^2))")
# structure_based = CustomBondForce(f"-{k}")
structure_based.addPerBondParameter("r_ijN")
structure_based.addPerBondParameter("sigma_ij")
for contact in contact_list:
structure_based.addBond(*contact)
return structure_based
from simtk.openmm import LangevinIntegrator
from simtk.openmm import CustomIntegrator
from simtk.openmm.app import Simulation
from simtk.openmm.app import PDBReporter
from simtk.openmm.app import StateDataReporter
from simtk.openmm.app import DCDReporter
from sys import stdout
pdb = PDBFile("ca_only.pdb")
forcefield = ForceField("cg.xml")
print(pdb.topology)
system = forcefield.createSystem(pdb.topology)
system.removeForce(0) # remove the default force "CMotionRemover"
# connect = connect_term(system)
# system.addForce(connect)
# connect = connect_term_v2(system)
# system.addForce(connect)
connect = connect_term_v3(system)
system.addForce(connect)
structure_based = structure_based_term(contact_list)
system.addForce(structure_based)
print("Number of particles: ", system.getNumParticles())
print("Number of forces: ", system.getNumForces())
integrator = LangevinIntegrator(300*kelvin, 1/picosecond, 0.004*picoseconds)
simulation = Simulation(pdb.topology, system, integrator)
simulation.context.setPositions(pdb.positions)
simulation.reporters.append(PDBReporter('output.pdb', 1000))
simulation.reporters.append(StateDataReporter(stdout, 1000, step=True,
potentialEnergy=True, temperature=True))
simulation.step(10000)
integrator = CustomIntegrator(0.001)
simulation = Simulation(pdb.topology, system, integrator)
simulation.context.setPositions(pdb.positions)
simulation.reporters.append(DCDReporter('output.dcd', 1))
simulation.reporters.append(StateDataReporter(stdout, 1, step=True,
potentialEnergy=True, temperature=True))
simulation.step(int(1))
simulation.minimizeEnergy()
simulation.step(int(1))
integrator = LangevinIntegrator(300*kelvin, 1/picosecond, 0.004*picoseconds)
simulation = Simulation(pdb.topology, system, integrator)
simulation.context.setPositions(pdb.positions)
simulation.reporters.append(DCDReporter('output.dcd', 1000, append=True))
simulation.reporters.append(StateDataReporter(stdout, 1000, step=True,
potentialEnergy=True, temperature=True))
simulation.step(10000)
# conda install nglview -c conda-forge
# jupyter-nbextension enable nglview --py --sys-prefix
import nglview
view = nglview.show_pdbid("1r69") # load "3pqr" from RCSB PDB and display viewer widget
view
view = nglview.show_structure_file("ca_only.pdb")
view
traj = mdtraj.load_dcd("output.dcd", top="ca_only.pdb")
view = nglview.show_mdtraj(traj)
view
# Input: expects 3xN matrix of points
# Returns R,t
# R = 3x3 rotation matrix
# t = 3x1 column vector
def rigid_transform_3D(A, B, correct_reflection=True):
assert A.shape == B.shape
num_rows, num_cols = A.shape
if num_rows != 3:
raise Exception(f"matrix A is not 3xN, it is {num_rows}x{num_cols}")
num_rows, num_cols = B.shape
if num_rows != 3:
raise Exception(f"matrix B is not 3xN, it is {num_rows}x{num_cols}")
# find mean column wise
centroid_A = np.mean(A, axis=1)
centroid_B = np.mean(B, axis=1)
# ensure centroids are 3x1
centroid_A = centroid_A.reshape(-1, 1)
centroid_B = centroid_B.reshape(-1, 1)
# subtract mean
Am = A - centroid_A
Bm = B - centroid_B
H = Am @ np.transpose(Bm)
# sanity check
#if linalg.matrix_rank(H) < 3:
# raise ValueError("rank of H = {}, expecting 3".format(linalg.matrix_rank(H)))
# find rotation
U, S, Vt = np.linalg.svd(H)
R = Vt.T @ U.T
# special reflection case
if np.linalg.det(R) < 0 and correct_reflection:
print("det(R) < R, reflection detected!, correcting for it ...")
Vt[2,:] *= -1
R = Vt.T @ U.T
t = -R @ centroid_A + centroid_B
return R, t
target = traj.xyz[0].T
n = traj.xyz.shape[0]
for i in range(1, n):
current = traj.xyz[i].T
ret_R, ret_t = rigid_transform_3D(current, target, correct_reflection=False)
out = (ret_R@current) + ret_t
traj.xyz[i] = out.T.reshape(1, -1, 3)
view = nglview.show_mdtraj(traj, gui=True)
view
# energy evaluation.
pdb = PDBFile('ca_only.pdb')
traj = mdtraj.load_dcd("output.dcd", top='ca_only.pdb')
integrator = CustomIntegrator(0.001)
simulation = Simulation(pdb.topology, system, integrator)
for frame in range(traj.n_frames):
simulation.context.setPositions(traj.openmm_positions(frame))
state = simulation.context.getState(getEnergy=True)
termEnergy = state.getPotentialEnergy().value_in_unit(kilojoule_per_mole)
# termEnergy = state.getPotentialEnergy()
print(frame, f"{termEnergy:.3f} kJ/mol")
system = forcefield.createSystem(pdb.topology)
system.removeForce(0) # remove the default force "CMotionRemover"
connect = connect_term(system)
connect.setForceGroup(1)
system.addForce(connect)
connect = connect_term_v2(system)
connect.setForceGroup(2)
system.addForce(connect)
connect = connect_term_v3(system)
connect.setForceGroup(3)
system.addForce(connect)
structure_based = structure_based_term(contact_list)
structure_based.setForceGroup(4)
system.addForce(structure_based)
print("Number of particles: ", system.getNumParticles())
print("Number of forces: ", system.getNumForces())
integrator = LangevinIntegrator(300*kelvin, 1/picosecond, 0.004*picoseconds)
simulation = Simulation(pdb.topology, system, integrator)
simulation.context.setPositions(pdb.positions)
force_groups = {"con":1, "con_v2":2, "con_v3":3, "structure_based_term":4}
show_energy = ["con", "con_v2", "con_v3", "structure_based_term"]
integrator = CustomIntegrator(0.001)
simulation = Simulation(pdb.topology, system, integrator)
width = 15
line = "".join([f"{term:<15}" for term in ["frame"] + show_energy])
print(line)
for frame in range(traj.n_frames):
simulation.context.setPositions(traj.openmm_positions(frame))
all_energy = []
for term in show_energy:
group = force_groups[term]
state = simulation.context.getState(getEnergy=True, groups={group})
termEnergy = state.getPotentialEnergy().value_in_unit(kilojoule_per_mole)
all_energy.append(termEnergy)
line = "".join([f"{termEnergy:<15.3f}" for termEnergy in all_energy])
print(f"{frame:<15}{line}")
```
|
github_jupyter
|
# [NTDS'18] tutorial 2: build a graph from an edge list
[ntds'18]: https://github.com/mdeff/ntds_2018
[Benjamin Ricaud](https://people.epfl.ch/benjamin.ricaud), [EPFL LTS2](https://lts2.epfl.ch)
* Dataset: [Open Tree of Life](https://tree.opentreeoflife.org)
* Tools: [pandas](https://pandas.pydata.org), [numpy](http://www.numpy.org), [networkx](https://networkx.github.io), [gephi](https://gephi.org/)
## Tools
The below line is a [magic command](https://ipython.readthedocs.io/en/stable/interactive/magics.html) that allows plots to appear in the notebook.
```
%matplotlib inline
```
The first thing is always to import the packages we'll use.
```
import pandas as pd
import numpy as np
import networkx as nx
```
Tutorials on pandas can be found at:
* <https://pandas.pydata.org/pandas-docs/stable/10min.html>
* <https://pandas.pydata.org/pandas-docs/stable/tutorials.html>
Tutorials on numpy can be found at:
* <https://docs.scipy.org/doc/numpy/user/quickstart.html>
* <http://www.scipy-lectures.org/intro/numpy/index.html>
* <http://www.scipy-lectures.org/advanced/advanced_numpy/index.html>
A tutorial on networkx can be found at:
* <https://networkx.github.io/documentation/stable/tutorial.html>
## Import the data
We will play with a excerpt of the Tree of Life, that can be found together with this notebook. This dataset is reduced to the first 1000 taxons (starting from the root node). The full version is available here: [Open Tree of Life](https://tree.opentreeoflife.org/about/taxonomy-version/ott3.0).


```
tree_of_life = pd.read_csv('data/taxonomy_small.tsv', sep='\t\|\t?', encoding='utf-8', engine='python')
```
If you do not remember the details of a function:
```
pd.read_csv?
```
For more info on the separator, see [regex](https://docs.python.org/3.6/library/re.html).
Now, what is the object `tree_of_life`? It is a Pandas DataFrame.
```
tree_of_life
```
The description of the entries is given here:
https://github.com/OpenTreeOfLife/reference-taxonomy/wiki/Interim-taxonomy-file-format
## Explore the table
```
tree_of_life.columns
```
Let us drop some columns.
```
tree_of_life = tree_of_life.drop(columns=['sourceinfo', 'uniqname', 'flags','Unnamed: 7'])
tree_of_life.head()
```
Pandas infered the type of values inside each column (int, float, string and string). The parent_uid column has float values because there was a missing value, converted to `NaN`
```
print(tree_of_life['uid'].dtype, tree_of_life.parent_uid.dtype)
```
How to access individual values.
```
tree_of_life.iloc[0, 2]
tree_of_life.loc[0, 'name']
```
**Exercise**: Guess the output of the below line.
```
# tree_of_life.uid[0] == tree_of_life.parent_uid[1]
```
Ordering the data.
```
tree_of_life.sort_values(by='name').head()
```
## Operation on the columns
Unique values, useful for categories:
```
tree_of_life['rank'].unique()
```
Selecting only one category.
```
tree_of_life[tree_of_life['rank'] == 'species'].head()
```
How many species do we have?
```
len(tree_of_life[tree_of_life['rank'] == 'species'])
tree_of_life['rank'].value_counts()
```
## Building the graph
Let us build the adjacency matrix of the graph. For that we need to reorganize the data. First we separate the nodes and their properties from the edges.
```
nodes = tree_of_life[['uid', 'name','rank']]
edges = tree_of_life[['uid', 'parent_uid']]
```
When using an adjacency matrix, nodes are indexed by their row or column number and not by a `uid`. Let us create a new index for the nodes.
```
# Create a column for node index.
nodes.reset_index(level=0, inplace=True)
nodes = nodes.rename(columns={'index':'node_idx'})
nodes.head()
# Create a conversion table from uid to node index.
uid2idx = nodes[['node_idx', 'uid']]
uid2idx = uid2idx.set_index('uid')
uid2idx.head()
edges.head()
```
Now we are ready to use yet another powerful function of Pandas. Those familiar with SQL will recognize it: the `join` function.
```
# Add a new column, matching the uid with the node_idx.
edges = edges.join(uid2idx, on='uid')
# Do the same with the parent_uid.
edges = edges.join(uid2idx, on='parent_uid', rsuffix='_parent')
# Drop the uids.
edges = edges.drop(columns=['uid','parent_uid'])
edges.head()
```
The above table is a list of edges connecting nodes and their parents.
## Building the (weighted) adjacency matrix
We will use numpy to build this matrix. Note that we don't have edge weights here, so our graph is going to be unweighted.
```
n_nodes = len(nodes)
adjacency = np.zeros((n_nodes, n_nodes), dtype=int)
for idx, row in edges.iterrows():
if np.isnan(row.node_idx_parent):
continue
i, j = int(row.node_idx), int(row.node_idx_parent)
adjacency[i, j] = 1
adjacency[j, i] = 1
adjacency[:15, :15]
```
Congratulations, you have built the adjacency matrix!
## Graph visualization
To conclude, let us visualize the graph. We will use the python module networkx.
```
# A simple command to create the graph from the adjacency matrix.
graph = nx.from_numpy_array(adjacency)
```
In addition, let us add some attributes to the nodes:
```
node_props = nodes.to_dict()
for key in node_props:
# print(key, node_props[key])
nx.set_node_attributes(graph, node_props[key], key)
```
Let us check if it is correctly recorded:
```
graph.node[1]
```
Draw the graph with two different [layout algorithms](https://en.wikipedia.org/wiki/Graph_drawing#Layout_methods).
```
nx.draw_spectral(graph)
nx.draw_spring(graph)
```
Save the graph to disk in the `gexf` format, readable by gephi and other tools that manipulate graphs. You may now explore the graph using gephi and compare the visualizations.
```
nx.write_gexf(graph, 'tree_of_life.gexf')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/livjab/DS-Unit-2-Sprint-4-Practicing-Understanding/blob/master/module1-hyperparameter-optimization/LS_DS_241_Hyperparameter_Optimization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science — Practicing & Understanding Predictive Modeling_
# Hyperparameter Optimization
Today we'll use this process:
## "A universal workflow of machine learning"
_Excerpt from Francois Chollet, [Deep Learning with Python](https://github.com/fchollet/deep-learning-with-python-notebooks/blob/master/README.md), Chapter 4: Fundamentals of machine learning_
**1. Define the problem at hand and the data on which you’ll train.** Collect this data, or annotate it with labels if need be.
**2. Choose how you’ll measure success on your problem.** Which metrics will you monitor on your validation data?
**3. Determine your evaluation protocol:** hold-out validation? K-fold validation? Which portion of the data should you use for validation?
**4. Develop a first model that does better than a basic baseline:** a model with statistical power.
**5. Develop a model that overfits.** The universal tension in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it.
**6. Regularize your model and tune its hyperparameters, based on performance on the validation data.** Repeatedly modify your model, train it, evaluate on your validation data (not the test data, at this point), modify it again, and repeat, until the model is as good as it can get.
**Iterate on feature engineering: add new features, or remove features that don’t seem to be informative.**
Once you’ve developed a satisfactory model configuration, you can **train your final production model on all the available data (training and validation) and evaluate it one last time on the test set.**
## 1. Define the problem at hand and the data on which you'll train
We'll apply the workflow to a [project from _Python Data Science Handbook_](https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic) by Jake VanderPlas:
> **Predicting Bicycle Traffic**
> As an example, let's take a look at whether we can predict the number of bicycle trips across Seattle's Fremont Bridge based on weather, season, and other factors.
> We will join the bike data with another dataset, and try to determine the extent to which weather and seasonal factors—temperature, precipitation, and daylight hours—affect the volume of bicycle traffic through this corridor. Fortunately, the NOAA makes available their daily [weather station data](http://www.ncdc.noaa.gov/cdo-web/search?datasetid=GHCND) (I used station ID USW00024233) and we can easily use Pandas to join the two data sources.
> Let's start by loading the two datasets, indexing by date:
So this is a regression problem, not a classification problem. We'll define the target, choose an evaluation metric, and choose models that are appropriate for regression problems.
### Download data
```
!curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD
!wget https://raw.githubusercontent.com/jakevdp/PythonDataScienceHandbook/master/notebooks/data/BicycleWeather.csv
```
### Load data
```
# Modified from cells 15, 16, and 20, at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
import pandas as pd
# Download and join data into a dataframe
def load():
fremont_bridge = 'https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD'
bicycle_weather = 'https://raw.githubusercontent.com/jakevdp/PythonDataScienceHandbook/master/notebooks/data/BicycleWeather.csv'
counts = pd.read_csv(fremont_bridge, index_col='Date', parse_dates=True,
infer_datetime_format=True)
weather = pd.read_csv(bicycle_weather, index_col='DATE', parse_dates=True,
infer_datetime_format=True)
daily = counts.resample('d').sum()
daily['Total'] = daily.sum(axis=1)
daily = daily[['Total']] # remove other columns
weather_columns = ['PRCP', 'SNOW', 'SNWD', 'TMAX', 'TMIN', 'AWND']
daily = daily.join(weather[weather_columns], how='inner')
# Make a feature for yesterday's total
daily['Total_yesterday'] = daily.Total.shift(1)
daily = daily.drop(index=daily.index[0])
return daily
daily = load()
```
### First fast look at the data
- What's the shape?
- What's the date range?
- What's the target and the features?
```
# TODO
daily.shape
daily.head()
daily.tail()
```
Target
- Total : Daily total number of bicycle trips across Seattle's Fremont Bridge
Features
- Date (index) : from 2012-10-04 to 2015-09-01
- Total_yesterday : Total trips yesterday
- PRCP : Precipitation (1/10 mm)
- SNOW : Snowfall (1/10 mm)
- SNWD : Snow depth (1/10 mm)
- TMAX : Maximum temperature (1/10 Celsius)
- TMIN : Minimum temperature (1/10 Celsius)
- AWND : Average daily wind speed (1/10 meters per second)
## 2. Choose how you’ll measure success on your problem.
Which metrics will you monitor on your validation data?
This is a regression problem, so we need to choose a regression [metric](https://scikit-learn.org/stable/modules/model_evaluation.html#common-cases-predefined-values).
I'll choose mean absolute error.
```
# TODO
from sklearn.metrics import mean_absolute_error
```
## 3. Determine your evaluation protocol
We're doing model selection, hyperparameter optimization, and performance estimation. So generally we have two ideal [options](https://sebastianraschka.com/images/blog/2018/model-evaluation-selection-part4/model-eval-conclusions.jpg) to choose from:
- 3-way holdout method (train/validation/test split)
- Cross-validation with independent test set
I'll choose cross-validation with independent test set. Scikit-learn makes cross-validation convenient for us!
Specifically, I will use random shuffled cross validation to train and validate, but I will hold out an "out-of-time" test set, from the last 100 days of data:
```
# TODO
test = daily[-100:]
train = daily[:-100]
train.shape, test.shape
X_train = train.drop(columns="Total")
y_train = train["Total"]
X_test = test.drop(columns="Total")
y_test = test["Total"]
X_train.shape, y_train.shape, X_test.shape, y_test.shape
```
## 4. Develop a first model that does better than a basic baseline
### Look at the target's distribution and descriptive stats
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(y_train);
y_train.describe()
```
### Basic baseline 1
```
y_pred = [y_train.median()] * len(y_train)
mean_absolute_error(y_train, y_pred)
```
### Basic baseline 2
```
y_pred = X_train["Total_yesterday"]
mean_absolute_error(y_train, y_pred)
```
### First model that does better than a basic baseline
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html
```
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_validate
scores = cross_validate(LinearRegression(),
X_train,
y_train,
scoring="neg_mean_absolute_error",
cv=3,
return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
scores["test_score"].mean()
scores["estimator"][0].coef_
for i, model in enumerate(scores["estimator"]):
coefficients = model.coef_
intercept = model.intercept_
feature_names = X_train.columns
print(f'Model from cross-validation fols #{i}')
print("Intercept", intercept)
print(pd.Series(coefficients, feature_names).to_string())
print('\n')
```
## 5. Develop a model that overfits.
"The universal tension in machine learning is between optimization and generalization; the ideal model is one that stands right at the border between underfitting and overfitting; between undercapacity and overcapacity. To figure out where this border lies, first you must cross it." —Chollet
<img src="https://jakevdp.github.io/PythonDataScienceHandbook/figures/05.03-validation-curve.png">
Diagram Source: https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html#Validation-curves-in-Scikit-Learn
### Random Forest?
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html
```
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=100, max_depth=None, n_jobs=-1)
scores = cross_validate(model,
X_train,
y_train,
scoring="neg_mean_absolute_error",
cv=3,
return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
scores["test_score"].mean()
```
### Validation Curve
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.validation_curve.html
> Validation curve. Determine training and test scores for varying parameter values. This is similar to grid search with one parameter.
```
import numpy as np
# Modified from cell 13 at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.03-hyperparameters-and-model-validation.html#Validation-curves-in-Scikit-Learn
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
model = RandomForestRegressor(n_estimators=100)
depth = [2, 3, 4, 5, 6]
train_score, val_score = validation_curve(
model, X_train, y_train,
param_name='max_depth', param_range=depth,
scoring='neg_mean_absolute_error', cv=3)
plt.plot(depth, np.median(train_score, 1), color='blue', label='training score')
plt.plot(depth, np.median(val_score, 1), color='red', label='validation score')
plt.legend(loc='best')
plt.xlabel('depth');
```
### `RandomizedSearchCV`
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html
https://scikit-learn.org/stable/modules/grid_search.html
```
from sklearn.model_selection import RandomizedSearchCV
param_distributions = {
"n_estimators": [100, 200],
"max_depth": [4, 5],
"criterion": ["mse", "mae"]
}
gridsearch = RandomizedSearchCV(
RandomForestRegressor(n_jobs=-1, random_state=42),
param_distributions=param_distributions,
n_iter=8,
cv=3, scoring="neg_mean_absolute_error",
verbose=10,
return_train_score=True)
gridsearch.fit(X_train, y_train)
results = pd.DataFrame(gridsearch.cv_results_)
results.sort_values(by="rank_test_score")
gridsearch.best_estimator_
```
## FEATURE ENGINEERING!
Jake VanderPlas demonstrates this feature engineering:
https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
```
# Modified from code cells 17-21 at
# https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic
def jake_wrangle(X):
X = X.copy()
# patterns of use generally vary from day to day;
# let's add binary columns that indicate the day of the week:
days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']
for i, day in enumerate(days):
X[day] = (X.index.dayofweek == i).astype(float)
# we might expect riders to behave differently on holidays;
# let's add an indicator of this as well:
from pandas.tseries.holiday import USFederalHolidayCalendar
cal = USFederalHolidayCalendar()
holidays = cal.holidays('2012', '2016')
X = X.join(pd.Series(1, index=holidays, name='holiday'))
X['holiday'].fillna(0, inplace=True)
# We also might suspect that the hours of daylight would affect
# how many people ride; let's use the standard astronomical calculation
# to add this information:
def hours_of_daylight(date, axis=23.44, latitude=47.61):
"""Compute the hours of daylight for the given date"""
days = (date - pd.datetime(2000, 12, 21)).days
m = (1. - np.tan(np.radians(latitude))
* np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))
return 24. * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180.
X['daylight_hrs'] = list(map(hours_of_daylight, X.index))
# temperatures are in 1/10 deg C; convert to C
X['TMIN'] /= 10
X['TMAX'] /= 10
# We can also calcuate the average temperature.
X['Temp (C)'] = 0.5 * (X['TMIN'] + X['TMAX'])
# precip is in 1/10 mm; convert to inches
X['PRCP'] /= 254
# In addition to the inches of precipitation, let's add a flag that
# indicates whether a day is dry (has zero precipitation):
X['dry day'] = (X['PRCP'] == 0).astype(int)
# Let's add a counter that increases from day 1, and measures how many
# years have passed. This will let us measure any observed annual increase
# or decrease in daily crossings:
X['annual'] = (X.index - X.index[0]).days / 365.
return X
X_train = jake_wrangle(X_train)
```
### Linear Regression (with new features)
```
scores = cross_validate(LinearRegression(),
X_train,
y_train,
scoring="neg_mean_absolute_error",
cv=3,
return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
scores["test_score"].mean()
```
### Random Forest (with new features)
```
param_distributions = {
'n_estimators': [100],
'max_depth': [5, 10, 15, None],
'criterion': ["mae"]
}
gridsearch = RandomizedSearchCV(
RandomForestRegressor(n_jobs=-1, random_state=42),
param_distributions=param_distributions,
n_iter=2,
cv=3,
scoring="neg_mean_absolute_error",
verbose=10,
return_train_score=True)
gridsearch.fit(X_train, y_train)
gridsearch.best_estimator_
```
### Feature engineering, explained by Francois Chollet
> _Feature engineering_ is the process of using your own knowledge about the data and about the machine learning algorithm at hand to make the algorithm work better by applying hardcoded (nonlearned) transformations to the data before it goes into the model. In many cases, it isn’t reasonable to expect a machine-learning model to be able to learn from completely arbitrary data. The data needs to be presented to the model in a way that will make the model’s job easier.
> Let’s look at an intuitive example. Suppose you’re trying to develop a model that can take as input an image of a clock and can output the time of day.
> If you choose to use the raw pixels of the image as input data, then you have a difficult machine-learning problem on your hands. You’ll need a convolutional neural network to solve it, and you’ll have to expend quite a bit of computational resources to train the network.
> But if you already understand the problem at a high level (you understand how humans read time on a clock face), then you can come up with much better input features for a machine-learning algorithm: for instance, write a Python script to follow the black pixels of the clock hands and output the (x, y) coordinates of the tip of each hand. Then a simple machine-learning algorithm can learn to associate these coordinates with the appropriate time of day.
> You can go even further: do a coordinate change, and express the (x, y) coordinates as polar coordinates with regard to the center of the image. Your input will become the angle theta of each clock hand. At this point, your features are making the problem so easy that no machine learning is required; a simple rounding operation and dictionary lookup are enough to recover the approximate time of day.
> That’s the essence of feature engineering: making a problem easier by expressing it in a simpler way. It usually requires understanding the problem in depth.
> Before convolutional neural networks became successful on the MNIST digit-classification problem, solutions were typically based on hardcoded features such as the number of loops in a digit image, the height of each digit in an image, a histogram of pixel values, and so on.
> Neural networks are capable of automatically extracting useful features from raw data. Does this mean you don’t have to worry about feature engineering as long as you’re using deep neural networks? No, for two reasons:
> - Good features still allow you to solve problems more elegantly while using fewer resources. For instance, it would be ridiculous to solve the problem of reading a clock face using a convolutional neural network.
> - Good features let you solve a problem with far less data. The ability of deep-learning models to learn features on their own relies on having lots of training data available; if you have only a few samples, then the information value in their features becomes critical.
# ASSIGNMENT
**1.** Complete the notebook cells that were originally commented **`TODO`**.
**2.** Then, focus on feature engineering to improve your cross validation scores. Collaborate with your cohort on Slack. You could start with the ideas [Jake VanderPlas suggests:](https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html#Example:-Predicting-Bicycle-Traffic)
> Our model is almost certainly missing some relevant information. For example, nonlinear effects (such as effects of precipitation and cold temperature) and nonlinear trends within each variable (such as disinclination to ride at very cold and very hot temperatures) cannot be accounted for in this model. Additionally, we have thrown away some of the finer-grained information (such as the difference between a rainy morning and a rainy afternoon), and we have ignored correlations between days (such as the possible effect of a rainy Tuesday on Wednesday's numbers, or the effect of an unexpected sunny day after a streak of rainy days). These are all potentially interesting effects, and you now have the tools to begin exploring them if you wish!
**3.** Experiment with the Categorical Encoding notebook.
**4.** At the end of the day, take the last step in the "universal workflow of machine learning" — "You can train your final production model on all the available data (training and validation) and evaluate it one last time on the test set."
See the [`RandomizedSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html) documentation for the `refit` parameter, `best_estimator_` attribute, and `predict` method:
> **refit : boolean, or string, default=True**
> Refit an estimator using the best found parameters on the whole dataset.
> The refitted estimator is made available at the `best_estimator_` attribute and permits using `predict` directly on this `GridSearchCV` instance.
### STRETCH
**A.** Apply this lesson other datasets you've worked with, like Ames Housing, Bank Marketing, or others.
**B.** In additon to `RandomizedSearchCV`, scikit-learn has [`GridSearchCV`](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html). Another library called scikit-optimize has [`BayesSearchCV`](https://scikit-optimize.github.io/notebooks/sklearn-gridsearchcv-replacement.html). Experiment with these alternatives.
**C.** _[Introduction to Machine Learning with Python](http://shop.oreilly.com/product/0636920030515.do)_ discusses options for "Grid-Searching Which Model To Use" in Chapter 6:
> You can even go further in combining GridSearchCV and Pipeline: it is also possible to search over the actual steps being performed in the pipeline (say whether to use StandardScaler or MinMaxScaler). This leads to an even bigger search space and should be considered carefully. Trying all possible solutions is usually not a viable machine learning strategy. However, here is an example comparing a RandomForestClassifier and an SVC ...
The example is shown in [the accompanying notebook](https://github.com/amueller/introduction_to_ml_with_python/blob/master/06-algorithm-chains-and-pipelines.ipynb), code cells 35-37. Could you apply this concept to your own pipelines?
```
len(X_train.columns)
X_train.describe()
# Lets feature engineer a column determining if it rained yesterday.
# We can use the feature engineered by Jake VanderPlas called "dry day"
# to determine if there was rain on a given day
X_train["dry day"].value_counts()
X_train["yesterday dry day"] = X_train["dry day"].shift()
X_train[["dry day", "yesterday dry day"]].head(10)
# deal with Nan and change to int type
X_train["yesterday dry day"] = X_train["yesterday dry day"].fillna(value=1).astype(int)
# Let's try to make a column for the number of days since it was last sunny
X_train['rainy day streak'] = X_train.groupby( (X_train['dry day'] !=1)
.cumsum()).cumcount() + ( (X_train['dry day'] != 0)
.cumsum() == 0).astype(int)
X_train[["dry day", "rainy day streak"]].head(10)
# Let's make a feature for extreme cold/extreme heat
# Anything above about 80 degrees (F) and below 40 degrees (F) counts as extreme temp
# 80F = 26.67C, 40F = 4.44C
def extreme_temps(X_train):
if (X_train["Temp (C)"] > 26.67):
return 1
elif (X_train["Temp (C)"] < 4.44):
return 1
else:
return 0
X_train["extreme temp day"] = X_train.apply(extreme_temps, axis=1)
X_train["extreme temp day"].value_counts()
X_train[["Temp (C)", "extreme temp day"]].sort_values("Temp (C)").head()
X_train[["Temp (C)", "extreme temp day"]].sort_values("Temp (C)", ascending=False).head()
# linear regression with new added features
scores = cross_validate(LinearRegression(),
X_train,
y_train,
scoring="neg_mean_absolute_error",
cv=3,
return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
scores["test_score"].mean()
# random forest regression
param_distributions = {
'n_estimators': [100, 200, 300],
'max_depth': [5, 10, 15, None],
'criterion': ["mse", "mae"]
}
gridsearch = RandomizedSearchCV(
RandomForestRegressor(n_jobs=-1, random_state=42),
param_distributions=param_distributions,
cv=3,
scoring="neg_mean_absolute_error",
verbose=10,
return_train_score=True)
gridsearch.fit(X_train, y_train)
gridsearch.best_estimator_
scores = cross_validate(RandomForestRegressor(bootstrap=True,
criterion='mse',
max_depth=None,
max_features='auto',
max_leaf_nodes=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators=300,
n_jobs=-1,
oob_score=False,
random_state=42,
verbose=0,
warm_start=False),
X_train,
y_train,
scoring="neg_mean_absolute_error",
cv=3,
return_train_score=True,
return_estimator=True)
pd.DataFrame(scores)
scores["test_score"].mean()
pd.DataFrame(gridsearch.cv_results_).sort_values(by="rank_test_score")
```
|
github_jupyter
|
```
import fitsio as ft
import healpy as hp
import numpy as np
import matplotlib.pyplot as plt
import sys
sys.path.append('/users/PHS0336/medirz90/github/LSSutils')
from lssutils.utils import make_hp
from lssutils.lab import get_cl
from lssutils.extrn.galactic.hpmaps import logHI
from sklearn.linear_model import LinearRegression
from lssutils.dataviz import setup_color
setup_color()
def run_linear(xtrain, ytrain,
xtest, ytest,
x, ix):
reg2 = LinearRegression().fit(xtrain, ytrain)
npred = reg2.predict(xtest)
print(f'MSE: {((npred - ytest)**2).mean():.3f} MAE:{(abs(npred - ytest)).mean():.3f}')
sfun = reg2.predict(x)
return make_hp(1024, ix, sfun, True) / sfun.mean()
lh = logHI(nside_out=1024, path='/fs/ess/PHS0336/data/templates/NHI_HPX.fits')
df = ft.read('/fs/ess/PHS0336/data/rongpu/imaging_sys/tables/v3/nelg_features_bmzls_1024.fits')
loghi = lh.map[:, np.newaxis]
hi = 10**(loghi-20.)
ix = df['hpix']
frac = make_hp(1024, df['hpix'], df['fracgood'], True)
mask = np.isfinite(frac)
ngal = make_hp(1024, df['hpix'], df['label'], True)
print(mask.sum())
x1 = loghi #np.column_stack([loghi, loghi*loghi])
x2 = hi #np.column_stack([hi, hi*hi])
np.random.seed(85)
train_ix = np.random.choice(ix, size=int(0.8*ix.size), replace=False)
test_ix = np.setdiff1d(ix, train_ix)
sf_loghi = run_linear(x1[train_ix], ngal[train_ix],
x1[test_ix], ngal[test_ix],
x1[ix], ix)
sf_loghi *= (ngal[ix]/sf_loghi[ix]).sum() / ngal[ix].sum()
sf_hi = run_linear(x2[train_ix], ngal[train_ix],
x2[test_ix], ngal[test_ix],
x1[ix], ix)
sf_hi *= (ngal[ix]/sf_hi[ix]).sum() / ngal[ix].sum()
kw = dict(min=0.9, max=1.1, rot=-95, cmap=plt.cm.jet)
hp.mollview(sf_hi, **kw)
hp.mollview(sf_loghi, **kw)
hp.mollview(ngal/df['label'].mean(), **kw)
cl_null = get_cl(ngal, frac, mask, njack=0)
cl_hi = get_cl(ngal, frac, mask, njack=0, selection_fn=sf_hi)
cl_loghi = get_cl(ngal, frac, mask, njack=0, selection_fn=sf_loghi)
fg, ax = plt.subplots(nrows=2, figsize=(6, 8), sharex=True)
fg.subplots_adjust(hspace=0.0)
for n_i, cl_i in zip(['No weight', 'HI', 'logHI'],
[cl_null, cl_hi, cl_loghi]):
ln = ax[0].plot(1000*cl_i['cl_gg']['l']*cl_i['cl_gg']['cl'], alpha=0.8, label=n_i)
ax[1].plot(cl_i['cl_gg']['cl']/cl_null['cl_gg']['cl'], color=ln[0].get_color())
ax[0].legend()
ax[0].set(ylabel=r'$\ell C_{\ell}~[10^{-3}]$', xscale='log',)
ax[1].set(xlabel=r'$\ell$', ylim=(0.0, 1.45), ylabel='$C_{\ell} / Noweight$')
```
## Updated Galaxy Density Count
```
old = ft.read('/fs/ess/PHS0336/data/rongpu/imaging_sys/tables/v2/nelg_features_bmzls_1024_old.fits')
new = ft.read('/fs/ess/PHS0336/data/rongpu/imaging_sys/tables/v3/nelg_features_bmzls_1024.fits')
old.size, new.size
np.array_equal(old['hpix'], new['hpix'])
old['label'], new['label']
frac = make_hp(1024, new['hpix'], new['fracgood'], True)
mask = np.isfinite(frac)
mask.sum()
old['features'][:, 0]-new['features'][:, 0]
syst = make_hp(1024, new['hpix'], new['features'][:, 0])[:, np.newaxis]
syst.shape
nold = make_hp(1024, old['hpix'], old['label'])
nnew = make_hp(1024, new['hpix'], new['label'])
cl_old = get_cl(nold, frac, mask, systematics=syst, njack=0, cross_only=True)
cl_new = get_cl(nnew, frac, mask, systematics=syst, njack=0, cross_only=True)
plt.plot(cl_old['cl_gg']['cl'], label='Old')
plt.plot(cl_new['cl_gg']['cl'], label='New')
plt.legend()
# plt.xscale('log')
plt.yscale('log') #symlog', linthreshy=1.0e-6)
plt.ylim(ymin=8.0e-9)
plt.ylabel('C_gg')
plt.xlabel(r'$\ell$')
from lssutils.utils import histogram_cell
def plot(cl, **kw):
lb = np.arange(0, 3000, 100)
lb_, cl_ = histogram_cell(cl, bins=lb)
al = kw.pop('alpha')
lab = kw.pop('label')
ln = plt.plot(cl, alpha=al, **kw)
plt.plot(lb_, cl_, color=ln[0].get_color(),
label=lab, marker='o', mfc='w', **kw)
plot(cl_old['cl_sg'][0]['cl'], label='Old', alpha=0.5)
plot(cl_new['cl_sg'][0]['cl'], label='New', alpha=0.5)
plt.legend()
plt.axhline(0)
plt.ylim(-1.0e-8, 1.0e-8)
# plt.yscale('symlog', linthreshy=1.0e-9)
plt.ylabel('C_gs')
plt.xlabel(r'$\ell$')
```
|
github_jupyter
|
# Scroll down to get to the interesting tables...
# Construct list of properties of widgets
"Properties" here is one of:
+ `keys`
+ `traits()`
+ `class_own_traits()`
Common (i.e. uninteresting) properties are filtered out.
The dependency on astropy is for their Table. Replace it with pandas if you want...
```
import itertools
from ipywidgets import *
from IPython.display import display
from traitlets import TraitError
from astropy.table import Table, Column
```
# Function definitions
## Calculate "interesting" properties
```
def properties(widget, omit=None, source=None):
"""
Return a list of widget properties for a widget instance, omitting
common properties.
Parameters
----------
widget : ipywidgets.Widget instance
The widget for which the list of preoperties is desired.
omit : list, optional
List of properties to omit in the return value. Default is
``['layout', 'style', 'msg_throttle']``, and for `source='traits'
is extended to add ``['keys', 'comm']``.
source : str, one of 'keys', 'traits', 'class_own_traits', 'style_keys' optional
Source of property list for widget. Default is ``'keys'``.
"""
if source is None:
source = 'keys'
valid_sources = ('keys', 'traits', 'class_own_traits', 'style_keys')
if source not in valid_sources:
raise ValueError('source must be one of {}'.format(', '.join(valid_sources)))
if omit is None:
omit = ['layout', 'style', 'msg_throttle']
if source == 'keys':
props = widget.keys
elif source == 'traits':
props = widget.traits()
omit.extend(['keys', 'comm'])
elif source == 'class_own_traits':
props = widget.class_own_traits()
elif source == 'style_keys':
props = widget.style.keys
props = [k for k in props if not k.startswith('_')]
return [k for k in props if k not in omit]
```
## Create a table (cross-tab style) for which properties are available for which widgets
This is the only place astropy.table.Table is used, so delete if you want to.
```
def table_for_keys(keys, keys_info, source):
unique_keys = set()
for k in keys:
unique_keys.update(keys_info[k])
unique_keys = sorted(unique_keys)
string_it = lambda x: 'X' if x else ''
colnames = ['Property ({})'.format(source)] + keys
columns = [Column(name=colnames[0], data=unique_keys)]
for c in colnames[1:]:
column = Column(name=c, data=[string_it(k in key_dict[c]) for k in unique_keys])
columns.append(column)
return Table(columns)
```
## List of widget objects...
```
widget_list = [
IntSlider,
FloatSlider,
IntRangeSlider,
FloatRangeSlider,
IntProgress,
FloatProgress,
BoundedIntText,
BoundedFloatText,
IntText,
FloatText,
ToggleButton,
Checkbox,
Valid,
Dropdown,
RadioButtons,
Select,
SelectionSlider,
SelectionRangeSlider,
ToggleButtons,
SelectMultiple,
Text,
Textarea,
Label,
HTML,
HTMLMath,
Image,
Button,
Play,
DatePicker,
ColorPicker,
Box,
HBox,
VBox,
Accordion,
Tab
]
```
## ...and their names
```
names = [wd.__name__ for wd in widget_list]
```
## Figure out the properties for each widget
The `try`/`except` below is to catch a couple of classes that *require* that `options` be passed on intialization.
```
property_source = 'keys'
all_keys = []
for widget_class in widget_list:
try:
keys = properties(widget_class(), source=property_source)
except TraitError as e:
keys = properties(widget_class(options=(2,10)), source=property_source)
finally:
all_keys.append(keys)
```
Probably should have used a dict from the beginning...
```
key_dict = {k: v for k, v in zip(names, all_keys)}
```
## Define a few groups of widgets by widget interface type
This makes for nicer (i.e. more compact and readable) tables later on.
```
sliders = [k for k in key_dict.keys() if 'Slider' in k]
buttons = [k for k in key_dict.keys() if 'Button' in k]
containers = ['Box', 'VBox', 'HBox', 'Accordion', 'Tab']
texts = [k for k in names if 'text' in k or 'Text' in k] + [k for k in names if 'HTML' in k] + ['Label']
progress = [k for k in names if 'Progress' in k]
selects = ['Dropdown', 'Select', 'SelectMultiple']
all_so_far = sliders + buttons + texts + containers + progress + selects
others = [k for k in names if k not in all_so_far]
slider_keys = set()
```
# Tables of keys (synced properties)
## Sliders
```
table_for_keys(sliders, key_dict, source=property_source)
```
## Buttons
```
table_for_keys(buttons, key_dict, source=property_source)
```
## Containers
```
table_for_keys(containers, key_dict, source=property_source)
```
## Text
```
table_for_keys(texts, key_dict, source=property_source)
```
## Progress bars
```
table_for_keys(progress, key_dict, source=property_source)
```
# Select widgets
```
table_for_keys(selects, key_dict, source=property_source)
```
## Everything else
```
table_for_keys(others, key_dict, source=property_source)
property_source = 'style_keys'
style_keys = []
for widget_class in widget_list:
try:
keys = properties(widget_class(), source=property_source)
except TraitError as e:
keys = properties(widget_class(options=(2,10)), source=property_source)
except AttributeError:
keys=''
finally:
style_keys.append(keys)
for w, s in zip(names, style_keys):
print('{} has style keys: {}'.format(w, ', '.join(s)))
```
|
github_jupyter
|
# DJL BERT Inference Demo
## Introduction
In this tutorial, you walk through running inference using DJL on a [BERT](https://towardsdatascience.com/bert-explained-state-of-the-art-language-model-for-nlp-f8b21a9b6270) QA model trained with MXNet and PyTorch.
You can provide a question and a paragraph containing the answer to the model. The model is then able to find the best answer from the answer paragraph.
Example:
```text
Q: When did BBC Japan start broadcasting?
```
Answer paragraph:
```text
BBC Japan was a general entertainment channel, which operated between December 2004 and April 2006.
It ceased operations after its Japanese distributor folded.
```
And it picked the right answer:
```text
A: December 2004
```
One of the most powerful features of DJL is that it's engine agnostic. Because of this, you can run different backend engines seamlessly. We showcase BERT QA first with an MXNet pre-trained model, then with a PyTorch model.
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.6.0
%maven ai.djl.mxnet:mxnet-engine:0.6.0
%maven ai.djl.mxnet:mxnet-model-zoo:0.6.0
%maven ai.djl.pytorch:pytorch-engine:0.6.0
%maven ai.djl.pytorch:pytorch-model-zoo:0.6.0
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven net.java.dev.jna:jna:5.3.0
// See https://github.com/awslabs/djl/blob/master/mxnet/mxnet-engine/README.md
// and See https://github.com/awslabs/djl/blob/master/pytorch/pytorch-engine/README.md
// for more engine library selection options
%maven ai.djl.mxnet:mxnet-native-auto:1.7.0-b
%maven ai.djl.pytorch:pytorch-native-auto:1.5.0
```
### Import java packages by running the following:
```
import ai.djl.*;
import ai.djl.engine.*;
import ai.djl.modality.nlp.qa.*;
import ai.djl.repository.zoo.*;
import ai.djl.training.util.*;
import ai.djl.inference.*;
import ai.djl.repository.zoo.*;
```
Now that all of the prerequisites are complete, start writing code to run inference with this example.
## Load the model and input
**First, load the input**
```
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
```
Then load the model and vocabulary. Create a variable `model` by using the `ModelZoo` as shown in the following code.
```
Criteria<QAInput, String> criteria = Criteria.builder()
.optApplication(Application.NLP.QUESTION_ANSWER)
.setTypes(QAInput.class, String.class)
.optFilter("backbone", "bert")
.optEngine("MXNet") // For DJL to use MXNet engine
.optProgress(new ProgressBar()).build();
ZooModel<QAInput, String> model = ModelZoo.loadModel(criteria);
```
## Run inference
Once the model is loaded, you can call `Predictor` and run inference as follows
```
Predictor<QAInput, String> predictor = model.newPredictor();
String answer = predictor.predict(input);
answer
```
Running inference on DJL is that easy. Now, let's try the PyTorch engine by specifying PyTorch engine in Criteria.optEngine("PyTorch"). Let's rerun the inference code.
```
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
Criteria<QAInput, String> criteria = Criteria.builder()
.optApplication(Application.NLP.QUESTION_ANSWER)
.setTypes(QAInput.class, String.class)
.optFilter("backbone", "bert")
.optEngine("PyTorch") // Use PyTorch engine
.optProgress(new ProgressBar()).build();
ZooModel<QAInput, String> model = ModelZoo.loadModel(criteria);
Predictor<QAInput, String> predictor = model.newPredictor();
String answer = predictor.predict(input);
answer
```
## Summary
Suprisingly, there are no differences between the PyTorch code snippet and MXNet code snippet.
This is power of DJL. We define a unified API where you can switch to different backend engines on the fly.
Next chapter: Inference with your own BERT: [MXNet](mxnet/load_your_own_mxnet_bert.ipynb) [PyTorch](pytorch/load_your_own_pytorch_bert.ipynb).
|
github_jupyter
|
# Feature Engineering in Keras.
Let's start off with the Python imports that we need.
```
import os, json, math, shutil
import numpy as np
import tensorflow as tf
print(tf.__version__)
# Note that this cell is special. It's got a tag (you can view tags by clicking on the wrench icon on the left menu in Jupyter)
# These are parameters that we will configure so that we can schedule this notebook
DATADIR = '../data'
OUTDIR = './trained_model'
EXPORT_DIR = os.path.join(OUTDIR,'export/savedmodel')
NBUCKETS = 10 # for feature crossing
TRAIN_BATCH_SIZE = 32
NUM_TRAIN_EXAMPLES = 10000 * 5 # remember the training dataset repeats, so this will wrap around
NUM_EVALS = 5 # evaluate this many times
NUM_EVAL_EXAMPLES = 10000 # enough to get a reasonable sample, but no so much that it slows down
```
## Locating the CSV files
We will start with the CSV files that we wrote out in the [first notebook](../01_explore/taxifare.iypnb) of this sequence. Just so you don't have to run the notebook, we saved a copy in ../data
```
if DATADIR[:5] == 'gs://':
!gsutil ls $DATADIR/*.csv
else:
!ls -l $DATADIR/*.csv
```
## Use tf.data to read the CSV files
We wrote these cells in the [third notebook](../03_tfdata/input_pipeline.ipynb) of this sequence.
```
CSV_COLUMNS = ['fare_amount', 'pickup_datetime',
'pickup_longitude', 'pickup_latitude',
'dropoff_longitude', 'dropoff_latitude',
'passenger_count', 'key']
LABEL_COLUMN = 'fare_amount'
DEFAULTS = [[0.0],['na'],[0.0],[0.0],[0.0],[0.0],[0.0],['na']]
def features_and_labels(row_data):
for unwanted_col in ['key']: # keep the pickup_datetime!
row_data.pop(unwanted_col)
label = row_data.pop(LABEL_COLUMN)
return row_data, label # features, label
# load the training data
def load_dataset(pattern, batch_size=1, mode=tf.estimator.ModeKeys.EVAL):
pattern = '{}/{}'.format(DATADIR, pattern)
dataset = (tf.data.experimental.make_csv_dataset(pattern, batch_size, CSV_COLUMNS, DEFAULTS)
.map(features_and_labels) # features, label
.cache())
if mode == tf.estimator.ModeKeys.TRAIN:
print("Repeating training dataset indefinitely")
dataset = dataset.shuffle(1000).repeat()
dataset = dataset.prefetch(1) # take advantage of multi-threading; 1=AUTOTUNE
return dataset
import datetime
# Python 3.5 doesn't handle timezones of the form 00:00, only 0000
s = '2012-07-05 14:18:00+00:00'
print(s)
ts = datetime.datetime.strptime(s.replace(':',''), "%Y-%m-%d %H%M%S%z")
print(ts.weekday())
DAYS = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
print(DAYS[ts.weekday()])
s = tf.constant('2012-07-05 14:18:00+00:00').numpy().decode('utf-8')
print(s)
ts = datetime.datetime.strptime(s.replace(':',''), "%Y-%m-%d %H%M%S%z")
print(ts.weekday())
DAYS = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
print(DAYS[ts.weekday()])
## Add transformations
def euclidean(params):
lon1, lat1, lon2, lat2 = params
londiff = lon2 - lon1
latdiff = lat2 - lat1
return tf.sqrt(londiff*londiff + latdiff*latdiff)
DAYS = ['Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat']
def get_dayofweek(s):
# Python 3.5 doesn't handle timezones of the form 00:00, only 0000
s1 = s.numpy().decode('utf-8') # get Python string
ts = datetime.datetime.strptime(s1.replace(':',''), "%Y-%m-%d %H%M%S%z")
return DAYS[ts.weekday()]
def dayofweek(ts_in):
return tf.map_fn(
lambda s: tf.py_function(get_dayofweek, inp=[s], Tout=tf.string),
ts_in
)
def transform(inputs, NUMERIC_COLS, STRING_COLS):
transformed = inputs.copy()
print("BEFORE TRANSFORMATION")
print("INPUTS:", inputs.keys())
print(inputs['pickup_longitude'].shape)
feature_columns = {
colname: tf.feature_column.numeric_column(colname)
for colname in NUMERIC_COLS
}
# scale the lat, lon values to be in 0, 1
for lon_col in ['pickup_longitude', 'dropoff_longitude']: # in range -70 to -78
transformed[lon_col] = tf.keras.layers.Lambda(
lambda x: (x+78)/8.0,
name='scale_{}'.format(lon_col)
)(inputs[lon_col])
for lat_col in ['pickup_latitude', 'dropoff_latitude']: # in range 37 to 45
transformed[lat_col] = tf.keras.layers.Lambda(
lambda x: (x-37)/8.0,
name='scale_{}'.format(lat_col)
)(inputs[lat_col])
# add Euclidean distance. Doesn't have to be accurate calculation because NN will calibrate it
transformed['euclidean'] = tf.keras.layers.Lambda(euclidean, name='euclidean')([
inputs['pickup_longitude'],
inputs['pickup_latitude'],
inputs['dropoff_longitude'],
inputs['dropoff_latitude']
])
feature_columns['euclidean'] = tf.feature_column.numeric_column('euclidean')
# hour of day from timestamp of form '2010-02-08 09:17:00+00:00'
transformed['hourofday'] = tf.keras.layers.Lambda(
lambda x: tf.strings.to_number(tf.strings.substr(x, 11, 2), out_type=tf.dtypes.int32),
name='hourofday'
)(inputs['pickup_datetime'])
feature_columns['hourofday'] = tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_identity('hourofday', num_buckets=24))
# day of week is hard because there is no TensorFlow function for date handling
transformed['dayofweek'] = tf.keras.layers.Lambda(
lambda x: dayofweek(x),
name='dayofweek_pyfun'
)(inputs['pickup_datetime'])
transformed['dayofweek'] = tf.keras.layers.Reshape((), name='dayofweek')(transformed['dayofweek'])
feature_columns['dayofweek'] = tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_vocabulary_list(
'dayofweek', vocabulary_list = DAYS))
# featurecross lat, lon into nxn buckets, then embed
# b/135479527
#nbuckets = NBUCKETS
#latbuckets = np.linspace(0, 1, nbuckets).tolist()
#lonbuckets = np.linspace(0, 1, nbuckets).tolist()
#b_plat = tf.feature_column.bucketized_column(feature_columns['pickup_latitude'], latbuckets)
#b_dlat = tf.feature_column.bucketized_column(feature_columns['dropoff_latitude'], latbuckets)
#b_plon = tf.feature_column.bucketized_column(feature_columns['pickup_longitude'], lonbuckets)
#b_dlon = tf.feature_column.bucketized_column(feature_columns['dropoff_longitude'], lonbuckets)
#ploc = tf.feature_column.crossed_column([b_plat, b_plon], nbuckets * nbuckets)
#dloc = tf.feature_column.crossed_column([b_dlat, b_dlon], nbuckets * nbuckets)
#pd_pair = tf.feature_column.crossed_column([ploc, dloc], nbuckets ** 4 )
#feature_columns['pickup_and_dropoff'] = tf.feature_column.embedding_column(pd_pair, 100)
print("AFTER TRANSFORMATION")
print("TRANSFORMED:", transformed.keys())
print("FEATURES", feature_columns.keys())
return transformed, feature_columns
def rmse(y_true, y_pred):
return tf.sqrt(tf.reduce_mean(tf.square(y_pred - y_true)))
def build_dnn_model():
# input layer is all float except for pickup_datetime which is a string
STRING_COLS = ['pickup_datetime']
NUMERIC_COLS = set(CSV_COLUMNS) - set([LABEL_COLUMN, 'key']) - set(STRING_COLS)
print(STRING_COLS)
print(NUMERIC_COLS)
inputs = {
colname : tf.keras.layers.Input(name=colname, shape=(), dtype='float32')
for colname in NUMERIC_COLS
}
inputs.update({
colname : tf.keras.layers.Input(name=colname, shape=(), dtype='string')
for colname in STRING_COLS
})
# transforms
transformed, feature_columns = transform(inputs, NUMERIC_COLS, STRING_COLS)
dnn_inputs = tf.keras.layers.DenseFeatures(feature_columns.values())(transformed)
# two hidden layers of [32, 8] just in like the BQML DNN
h1 = tf.keras.layers.Dense(32, activation='relu', name='h1')(dnn_inputs)
h2 = tf.keras.layers.Dense(8, activation='relu', name='h2')(h1)
# final output would normally have a linear activation because this is regression
# However, we know something about the taxi problem (fares are +ve and tend to be below $60).
# Use that here. (You can verify by running this query):
# SELECT APPROX_QUANTILES(fare_amount, 100) FROM serverlessml.cleaned_training_data
# b/136476088
#fare_thresh = lambda x: 60 * tf.keras.activations.relu(x)
#output = tf.keras.layers.Dense(1, activation=fare_thresh, name='fare')(h2)
output = tf.keras.layers.Dense(1, name='fare')(h2)
model = tf.keras.models.Model(inputs, output)
model.compile(optimizer='adam', loss='mse', metrics=[rmse, 'mse'])
return model
model = build_dnn_model()
print(model.summary())
tf.keras.utils.plot_model(model, 'dnn_model.png', show_shapes=False, rankdir='LR')
```
## Train model
To train the model, call model.fit()
```
trainds = load_dataset('taxi-train*', TRAIN_BATCH_SIZE, tf.estimator.ModeKeys.TRAIN)
evalds = load_dataset('taxi-valid*', 1000, tf.estimator.ModeKeys.EVAL).take(NUM_EVAL_EXAMPLES//10000) # evaluate on 1/10 final evaluation set
steps_per_epoch = NUM_TRAIN_EXAMPLES // (TRAIN_BATCH_SIZE * NUM_EVALS)
shutil.rmtree('{}/checkpoints/'.format(OUTDIR), ignore_errors=True)
checkpoint_path = '{}/checkpoints/taxi'.format(OUTDIR)
cp_callback = tf.keras.callbacks.ModelCheckpoint(checkpoint_path,
save_weights_only=True,
verbose=1)
history = model.fit(trainds,
validation_data=evalds,
epochs=NUM_EVALS,
steps_per_epoch=steps_per_epoch,
callbacks=[cp_callback])
# plot
import matplotlib.pyplot as plt
nrows = 1
ncols = 2
fig = plt.figure(figsize=(10, 5))
for idx, key in enumerate(['loss', 'rmse']):
ax = fig.add_subplot(nrows, ncols, idx+1)
plt.plot(history.history[key])
plt.plot(history.history['val_{}'.format(key)])
plt.title('model {}'.format(key))
plt.ylabel(key)
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left');
```
## Evaluate over full validation dataset
Let's evaluate over the full validation dataset (provided the validation dataset is large enough).
```
evalds = load_dataset('taxi-valid*', 1000, tf.estimator.ModeKeys.EVAL).take(NUM_EVAL_EXAMPLES//1000)
model.evaluate(evalds)
```
Yippee! We are now at under 4 dollars RMSE!
## Predict with model
This is how to predict with this model:
```
model.predict({
'pickup_longitude': tf.convert_to_tensor([-73.982683]),
'pickup_latitude': tf.convert_to_tensor([40.742104]),
'dropoff_longitude': tf.convert_to_tensor([-73.983766]),
'dropoff_latitude': tf.convert_to_tensor([40.755174]),
'passenger_count': tf.convert_to_tensor([3.0]),
'pickup_datetime': tf.convert_to_tensor(['2010-02-08 09:17:00+00:00'], dtype=tf.string),
})
```
However, this is not realistic, because we can't expect client code to have a model object in memory. We'll have to export our model to a file, and expect client code to instantiate the model from that exported file.
## Export model
Let's export the model to a TensorFlow SavedModel format. Once we have a model in this format, we have lots of ways to "serve" the model, from a web application, from JavaScript, from mobile applications, etc.
```
export_dir = os.path.join(EXPORT_DIR, datetime.datetime.now().strftime('%Y%m%d%H%M%S'))
tf.keras.experimental.export_saved_model(model, export_dir)
print(export_dir)
# Recreate the exact same model
new_model = tf.keras.experimental.load_from_saved_model(export_dir)
# try predicting with this model
new_model.predict({
'pickup_longitude': tf.convert_to_tensor([-73.982683]),
'pickup_latitude': tf.convert_to_tensor([40.742104]),
'dropoff_longitude': tf.convert_to_tensor([-73.983766]),
'dropoff_latitude': tf.convert_to_tensor([40.755174]),
'passenger_count': tf.convert_to_tensor([3.0]),
'pickup_datetime': tf.convert_to_tensor(['2010-02-08 09:17:00+00:00'], dtype=tf.string),
})
```
In this notebook, we have looked at how to implement a custom Keras model using feature columns.
Copyright 2019 Google Inc.
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
|
github_jupyter
|
```
import os, numpy, warnings
import pandas as pd
os.environ['R_HOME'] = '/home/gdpoore/anaconda3/envs/tcgaAnalysisPythonR/lib/R'
warnings.filterwarnings('ignore')
%config InlineBackend.figure_format = 'retina'
%reload_ext rpy2.ipython
%%R
require(ggplot2)
require(snm)
require(limma)
require(edgeR)
require(dplyr)
require(edgeR)
require(pvca)
require(lme4)
require(ggsci)
require(cowplot)
require(doMC)
numCores <- detectCores()
registerDoMC(cores=numCores)
%%R
load("tcgaVbDataAndMetadataAndSNM.RData")
%%R
print(dim(vbDataBarnDFReconciled))
print(dim(vbDataBarnDFReconciledQC))
print(dim(metadataSamplesAllQC))
%%R
metadataSamplesAllQCAML <- droplevels(metadataSamplesAll[! (is.na(metadataSamplesAll$race) |
is.na(metadataSamplesAll$portion_is_ffpe) |
is.na(metadataSamplesAll$age_at_diagnosis)),])
# metadataSamplesAllQCAML <- droplevels(metadataSamplesAllQCAML[metadataSamplesAllQCAML$disease_type == "Acute Myeloid Leukemia",])
vbDataBarnDFReconciledQCAML <- vbDataBarnDFReconciled[rownames(metadataSamplesAllQCAML),]
print(dim(metadataSamplesAllQCAML))
print(dim(vbDataBarnDFReconciledQCAML))
%%R
qcMetadata <- metadataSamplesAllQC # metadataSamplesAllQCAML
qcData <- vbDataBarnDFReconciledQC # vbDataBarnDFReconciledQCAML
# Set up design matrix
covDesignNorm <- model.matrix(~0 + sample_type +
data_submitting_center_label +
platform +
experimental_strategy +
tissue_source_site_label +
portion_is_ffpe,
data = qcMetadata)
print(colnames(covDesignNorm))
colnames(covDesignNorm) <- gsub('([[:punct:]])|\\s+','',colnames(covDesignNorm))
print(colnames(covDesignNorm))
# Set up counts matrix
counts <- t(qcData) # DGEList object from a table of counts (rows=features, columns=samples)
# Normalize using edgeR and then plug into voom
dge <- DGEList(counts = counts)
keep <- filterByExpr(dge, covDesignNorm)
dge <- dge[keep,,keep.lib.sizes=FALSE]
print("Now normalizing data...")
dge <- calcNormFactors(dge, method = "TMM")
print("Now applying voom on normalized data...")
vdge <- voom(dge, design = covDesignNorm, plot = TRUE, save.plot = TRUE, normalize.method="none")
%%R
print(table(metadataSamplesAllQCAML$sample_type))
%%R
# Apply
bio.var.sample.type <- model.matrix(~sample_type, #sample_type, # histological_diagnosis_label and disease_type tried but cause function to fail
data=qcMetadata)
bio.var.gender <- model.matrix(~gender, #sample_type, # histological_diagnosis_label and disease_type tried but cause function to fail
data=qcMetadata)
adj.var <- model.matrix(~data_submitting_center_label +
platform +
experimental_strategy +
tissue_source_site_label +
portion_is_ffpe,
data=qcMetadata)
colnames(bio.var.sample.type) <- gsub('([[:punct:]])|\\s+','',colnames(bio.var.sample.type))
colnames(bio.var.gender) <- gsub('([[:punct:]])|\\s+','',colnames(bio.var.gender))
colnames(adj.var) <- gsub('([[:punct:]])|\\s+','',colnames(adj.var))
print(dim(adj.var))
print(dim(bio.var.sample.type))
print(dim(bio.var.gender))
print(dim(t(vdge$E)))
print(dim(covDesignNorm))
%%R
snmDataObjSampleTypeWithExpStrategyFA <- snm(raw.dat = vdge$E,
bio.var = bio.var.sample.type,
adj.var = adj.var,
rm.adj=TRUE,
verbose = TRUE,
diagnose = TRUE)
snmDataSampleTypeWithExpStrategyFA <- t(snmDataObjSampleTypeWithExpStrategyFA$norm.dat)
print(dim(snmDataSampleTypeWithExpStrategyFA))
%%R
save(snmDataSampleTypeWithExpStrategyFA, file = "snmDataSampleTypeWithExpStrategyFA.RData")
```
# PCA plotting to visually examine batch effects and batch correction
```
%%R
pcaPlotting <- function(pcaObject,pcChoices, dataLabels, factorString, titleString){
require(ggbiplot)
theme_update(plot.title = element_text(hjust = 0.5))
g <- ggbiplot(pcaObject,pcChoices, obs.scale = 1, var.scale = 1,
groups = dataLabels, ellipse = TRUE,
alpha = 0.2,
circle = TRUE,var.axes=FALSE) +
scale_color_nejm(name = factorString) +
theme_bw() +
#theme(legend.direction = "horizontal", legend.position = "top") +
ggtitle(titleString) + theme(plot.title = element_text(hjust = 0.5))
print(g)
}
%%R
unnormalizedPCAPlotFA <- pcaPlotting(pcaObject = prcomp(t(vdge$E)),
pcChoices = c(1,2),
dataLabels = qcMetadata$data_submitting_center_label,
factorString = "Batch",
titleString = "PCA w/o Batch Correction")
%%R
snmPCAPlotSampleTypeFA <- pcaPlotting(pcaObject = prcomp(snmDataSampleTypeWithExpStrategyFA),
pcChoices = c(1,2),
dataLabels = qcMetadata$data_submitting_center_label,
factorString = "Sequencing Center",
titleString = "PCA w/ SNM Correction\n(Target: Sample Type)")
# %%R
# snmPCAPlotGender <- pcaPlotting(pcaObject = prcomp(snmDataGenderWithAML),
# pcChoices = c(1,2),
# dataLabels = qcMetadata$data_submitting_center_label,
# factorString = "Sequencing Center",
# titleString = "PCA w/ SNM Correction\n(Target: Gender)")
%%R
ggsave(plot = unnormalizedPCAPlotFA,
filename = "unnormalizedPCAPlotFA_DecreasedOpacity_NEJM.png",
width = 16.2,
height = 5.29,
units = "in",
dpi = "retina")
ggsave(plot = snmPCAPlotSampleTypeFA,
filename = "snmPCAPlotSampleTypeFA_DecreasedOpacity_NEJM.png",
width = 16.2,
height = 5.29,
units = "in",
dpi = "retina")
# save(snmDataGenderWithAML, metadataSamplesAllQCAML,
# vbDataBarnDFReconciledQCAML,
# file = "amlVbDataAndMetadataAndSNMByGender.RData")
# %%R
# snmDataObjGenderWithAML <- snm(raw.dat = vdge$E,
# bio.var = bio.var.gender,
# adj.var = adj.var,
# rm.adj=TRUE,
# verbose = TRUE,
# diagnose = TRUE)
# snmDataGenderWithAML <- t(snmDataObjGenderWithAML$norm.dat)
# print(dim(snmDataGenderWithAML))
```
# PVCA using key filtered metadata features (i.e. narrowing down the extended version of this)
```
%%R
# Implement PVCA
# From extended model, remove variables that contribute very little if at all:
# ethnicity, gender, reference_genome
pct_threshold <- 0.8
metaPVCAExtendedFiltered <- metadataSamplesAllQC[,c("sample_type",
"disease_type",
"data_submitting_center_label",
"platform",
"experimental_strategy",
"tissue_source_site_label",
"portion_is_ffpe")]
print(dim(metaPVCAExtendedFiltered))
print(dim(snmDataSampleTypeWithExpStrategy))
print(dim(vbDataBarnDFReconciledQC))
%%R
pvcaVbRawNoVoomNoSNM_ExtendedFiltered_FA <- PVCA(counts = t(vbDataBarnDFReconciledQC),
meta = metaPVCAExtendedFiltered,
threshold = pct_threshold,
inter = FALSE)
save(pvcaVbRawNoVoomNoSNM_ExtendedFiltered_FA, file = "pvcaVbRawNoVoomNoSNM_ExtendedFiltered_FA.RData")
PlotPVCA(pvcaVbRawNoVoomNoSNM_ExtendedFiltered_FA, "Raw count data")
%%R
pvcaVoomNoSNM_ExtendedFiltered_FA <- PVCA(counts = vdge$E,
meta = metaPVCAExtendedFiltered,
threshold = pct_threshold,
inter = FALSE)
save(pvcaVoomNoSNM_ExtendedFiltered_FA, file = "pvcaVoomNoSNM_ExtendedFiltered_FA.RData")
PlotPVCA(pvcaVoomNoSNM_ExtendedFiltered_FA, "Voom Normalized")
%%R
pvcaSampleWithExpStrategySNM_ExtendedFiltered_FA <- PVCA(counts = t(snmDataSampleTypeWithExpStrategyFA),
meta = metaPVCAExtendedFiltered,
threshold = pct_threshold,
inter = FALSE)
save(pvcaSampleWithExpStrategySNM_ExtendedFiltered_FA,
file = "pvcnoaSampleWithExpStrategySNM_ExtendedFiltered_FA.RData")
PlotPVCA(pvcaSampleWithExpStrategySNM_ExtendedFiltered_FA,
"Voom Normalized & SNM Corrected Plus Exp Strategy (Target is Sample Type)")
%%R
1+2
```
# Examining sample and taxa ratio changes due to batch correction
```
%%R
require(ggplot2)
require(matrixStats)
divSNMDataSampleType <- snmDataSampleType / t(snmDataObjSampleType$raw.dat)
taxaMedians <- data.frame(Medians = colMedians(divSNMDataSampleType),
Taxa = colnames(divSNMDataSampleType),
pval = factor(ifelse(snmDataObjSampleType$pval <=0.05,
yes = "P-value <= 0.05", no = "P-value > 0.05")))
sampleMedians <- data.frame(Medians = rowMedians(divSNMDataSampleType),
Samples = rownames(divSNMDataSampleType),
SeqCenter = metadataSamplesAllQC$data_submitting_center_label,
SampleType = metadataSamplesAllQC$sample_type,
CancerType = metadataSamplesAllQC$disease_type)
gt <- ggplot(taxaMedians, aes(x = reorder(Taxa, -Medians), y = Medians, fill = pval)) +
geom_bar(stat = "identity") +
theme(axis.title.x=element_blank(), axis.text.x=element_blank(), axis.ticks.x=element_blank()) +
labs(y = "Median of Normalizing Ratios Per Taxa", x = "Samples", fill = "ANOVA Result Per Taxa")
gs <- ggplot(sampleMedians, aes(x = reorder(Samples, -Medians), y = Medians, fill = CancerType)) +
geom_bar(stat = "identity") + coord_flip() +
theme(axis.text.y=element_blank(), axis.ticks.y=element_blank()) +
scale_y_log10() + labs(y = "Median of Normalizing Ratios Per Sample", x = "Samples", fill='Cancer Type')
%%R
gt
%%R
ggsave(plot = gt,
filename = "snmNormMedianPerTaxaPval.png",
width = 8.5,
height = 6,
units = "in",
dpi = "retina")
%%R
require(pheatmap)
pheatmap(snmDataSampleTypeLMFit$coefficients,
clustering_distance_rows = "correlation",
clustering_distance_cols = "correlation",
show_rownames = FALSE,
show_colnames = FALSE,
filename = "snmLMFitCoefCorr.png")
# %%R
# save(snmDataObjPathStage, snmDataPathStage, metadataSamplesAllQCPath, file = "snmResultsPathBinned.RData")
```
|
github_jupyter
|

# <font color='Blue'> Ciência dos Dados na Prática</font>
# Sistemas de Recomendação

Cada empresa de consumo de Internet precisa um sistema de recomendação como **Netflix**, **Youtube**, **feed de notícias**, **Site de Viagens e passagens Aéreas**, **Hotéis**, **Mercado livre**, **Magalu**, **Olist**, etc. O que você deseja mostrar de uma grande variedade de itens é um sistema de recomendação.
## O que realmente é o Sistema de Recomendação?
Um mecanismo de recomendação é uma classe de aprendizado de máquina que oferece sugestões relevantes ao cliente. Antes do sistema de recomendação, a grande tendência para comprar era aceitar sugestões de amigos. Mas agora o Google sabe quais notícias você vai ler, o Youtube sabe que tipo de vídeos você vai assistir com base em seu histórico de pesquisa, histórico de exibição ou histórico de compra.
Um sistema de recomendação ajuda uma organização a criar clientes fiéis e construir a confiança deles nos produtos e serviços desejados para os quais vieram em seu site. Os sistemas de recomendação de hoje são tão poderosos que também podem lidar com o novo cliente que visitou o site pela primeira vez. Eles recomendam os produtos que estão em alta ou com alta classificação e também podem recomendar os produtos que trazem o máximo de lucro para a empresa.
Um sistema de recomendação de livros é um tipo de sistema de recomendação em que temos que recomendar livros semelhantes ao leitor com base em seu interesse. O sistema de recomendação de livros é usado por sites online que fornecem e-books como google play books, open library, good Read's, etc.
# 1° Problema de Negócio
Usaremos o método de **filtragem baseada em colaboração** para construir um sistema de recomendação de livros. Ou seja, precisamos construir uma máquina preditiva que, **com base nas escolhas de leituras de outras pessoas, o livro seja recomendado a outras pessoas com interesses semelhantes.**
Ex:
**Eduardo** leu e gostou dos livros A loja de Tudo e Elon Musk.
**Clarice** também leu e gostou desses dois livros

Agora o **Eduardo** leu e gostou do livro "StartUp de U$100" que não é lido pela **Clarice**.

Então **temos que recomendar o livro **"StartUp de U$100" para **Clarice**
## **Resultado**
Você concorda que se vc receber uma recomendação certeira, a chance de vc comprar o livro é muito maior?
Vc concorda que se mais pessoas comprarem, maior será o faturamento da empresa?
Vc concorda que os clientes vão ficar muito mais satisfeitos se o site demonstrar que conhece ela e que realmente só oferece produtos que realmente são relevantes p ela?
# 2° Análise Exploratória dos Dados
```
#Importação das Bibliotecas ou Pacotes
import numpy as np
import pandas as pd
from sklearn.neighbors import NearestNeighbors
```
Fonte de Dados:
https://www.kaggle.com/rxsraghavagrawal/book-recommender-system
#### Base de Livros
```
# Importação dos Dados Referentes aos Livros
books = pd.read_csv("BX-Books.csv", sep=';', encoding="latin-1", error_bad_lines= False)
books
```
#### Base de Usuários
```
# Importação dos Dados Referentes aos Usuários
users = pd.read_csv("BX-Users.csv", sep=';', encoding="latin-1", error_bad_lines= False)
users
```
#### Base de Ratings
```
# Importação dos Dados Referentes aos Ratings dados aos Livros (Avaliação do Usuário em relação ao Livro)
ratings = pd.read_csv("BX-Book-Ratings.csv", sep=';', encoding="latin-1", error_bad_lines= False)
ratings.info()
```
# 3° Pré-Processamento dos Dados
### Renomeando Colunas
Agora, no arquivo de livros, temos algumas colunas extras que não são necessárias para nossa tarefa, como URLs de imagens. E vamos renomear as colunas de cada arquivo, pois o nome da coluna contém espaço e letras maiúsculas, então faremos as correções para facilitar o uso.
```
# Rename de Colunas
books = books[['ISBN', 'Book-Title', 'Book-Author', 'Year-Of-Publication', 'Publisher']]
books.rename(columns = {'Book-Title':'title', 'Book-Author':'author', 'Year-Of-Publication':'year', 'Publisher':'publisher'}, inplace=True)
users.rename(columns = {'User-ID':'user_id', 'Location':'location', 'Age':'age'}, inplace=True)
ratings.rename(columns = {'User-ID':'user_id', 'Book-Rating':'rating'}, inplace=True)
books
#Quantidade de Ratings por Usuários
ratings['user_id'].value_counts()
# Livros que tenham mais de 200 avaliações
x = ratings['user_id'].value_counts() > 200
x
# Quantidade Usuários
# user_ids
y = x[x].index
print(y.shape)
y
```
#### *Decisão de Negócio*
```
# Trazendo ratings somente dos usuários q avaliaram mais de 200 livros
ratings = ratings[ratings['user_id'].isin(y)]
ratings
# Juntando tabelas (Join ou Merge)
rating_with_books = ratings.merge(books, on='ISBN')
rating_with_books.head()
#Quantidade de rating dos livros
number_rating = rating_with_books.groupby('title')['rating'].count().reset_index()
number_rating
#Renomeando coluna
number_rating.rename(columns= {'rating':'number_of_ratings'}, inplace=True)
number_rating
# Juntando a tabela de livros com os Ratings com a tabela de quantidade de ratings por livro
final_rating = rating_with_books.merge(number_rating, on='title')
final_rating
```
#### *Decisão de Negócio*
```
# Filtrar somente livros que tenham pelo menos 50 avaliações
final_rating = final_rating[final_rating['number_of_ratings'] >= 50]
final_rating.shape
# Vamos descartar os valores duplicados, porque se o mesmo usuário tiver avaliado o mesmo livro várias vezes, isso pode dar rúim.
final_rating.drop_duplicates(['user_id','title'], inplace=True)
final_rating.shape
final_rating
```
### Vamos fazer uma parada que é o seguinte:
Vamos transpor os **usuários** em **colunas**, ao invés de linhas, pois as avaliações dadas por eles serão as **variáveis** da máquina preditiva.
```
final_rating.info()
# Transposição de linhas(users_id) em colunas
book_pivot = final_rating.pivot_table(columns='user_id', index='title', values="rating")
book_pivot
book_pivot.shape
book_pivot.fillna(0, inplace=True)
book_pivot
```
Preparamos nosso conjunto de dados para modelagem. Usaremos o algoritmo de vizinhos mais próximos (nearest neighbors algorithm), que é usado para agrupamento com base na **distância euclidiana**.
**Nesta aula explicadim**:
https://www.youtube.com/watch?v=jD4AKp4-Tmo
Mas aqui na tabela dinâmica, temos muitos valores zero e no agrupamento, esse poder de computação aumentará para calcular a distância dos valores zero, portanto, converteremos a tabela dinâmica para a matriz esparsa e, em seguida, alimentaremos o modelo.
```
from scipy.sparse import csr_matrix
book_sparse = csr_matrix(book_pivot)
```
#4° Criação da Máquina Preditiva
https://scikit-learn.org/stable/modules/neighbors.html
```
from sklearn.neighbors import NearestNeighbors
model = NearestNeighbors(algorithm='brute')
model.fit(book_sparse)
```
## Novas Predições
```
#1984
distances, suggestions = model.kneighbors(book_pivot.iloc[0, :].values.reshape(1, -1))
book_pivot.head()
for i in range(len(suggestions)):
print(book_pivot.index[suggestions[i]])
#Hannibal
distances, suggestions = model.kneighbors(book_pivot.iloc[236, :].values.reshape(1, -1))
book_pivot.head(236)
for i in range(len(suggestions)):
print(book_pivot.index[suggestions[i]])
#Harry Potter
distances, suggestions = model.kneighbors(book_pivot.iloc[238, :].values.reshape(1, -1))
book_pivot.head(238)
for i in range(len(suggestions)):
print(book_pivot.index[suggestions[i]])
```
# Fim
## Valeu!
Fonte de Inspiração:
https://www.analyticsvidhya.com/blog/2021/06/build-book-recommendation-system-unsupervised-learning-project/
|
github_jupyter
|
# Transporter statistics and taxonomic profiles
## Overview
In this notebook some overview statistics of the datasets are computed and taxonomic profiles investigated. The notebook uses data produced by running the [01.process_data](01.process_data.ipynb) notebook.
```
import numpy as np
import pandas as pd
import seaborn as sns
import glob
import os
import matplotlib.pyplot as plt, matplotlib
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
plt.style.use('ggplot')
def make_tax_table(df,name="",rank="superkingdom"):
df_t = df.groupby(rank).sum()
df_tp = df_t.div(df_t.sum())*100
df_tp_mean = df_tp.mean(axis=1)
df_tp_max = df_tp.max(axis=1)
df_tp_min = df_tp.min(axis=1)
df_tp_sd = df_tp.std(axis=1)
table = pd.concat([df_tp_mean,df_tp_max,df_tp_min,df_tp_sd],axis=1)
table.columns = [name+" mean(%)",name+" max(%)",name+" min(%)",name+" std"]
table.rename(index=lambda x: x.split("_")[0], inplace=True)
return table
```
## Load the data
```
transinfo = pd.read_csv("selected_transporters_classified.tab", header=0, sep="\t", index_col=0)
transinfo.head()
```
Read gene abundance values with taxonomic annotations.
```
mg_cov = pd.read_table("data/mg/all_genes.tpm.taxonomy.tsv.gz", header=0, sep="\t", index_col=0)
mt_cov = pd.read_table("data/mt/all_genes.tpm.taxonomy.tsv.gz", header=0, sep="\t", index_col=0)
```
Read orf level transporter data.
```
mg_transcov = pd.read_table("results/mg/all_transporters.tpm.taxonomy.tsv.gz", header=0, sep="\t", index_col=0)
mt_transcov = pd.read_table("results/mt/all_transporters.tpm.taxonomy.tsv.gz", header=0, sep="\t", index_col=0)
mg_select_transcov = pd.read_table("results/mg/select_trans_genes.tpm.tsv", header=0, sep="\t", index_col=0)
mt_select_transcov = pd.read_table("results/mt/select_trans_genes.tpm.tsv", header=0, sep="\t", index_col=0)
```
Read transporter abundances.
```
mg_trans = pd.read_csv("results/mg/all_trans.tpm.tsv", header=0, sep="\t", index_col=0)
mt_trans = pd.read_csv("results/mt/all_trans.tpm.tsv", header=0, sep="\t", index_col=0)
```
## Generate taxonomic overview table
```
mg_tax_table = make_tax_table(mg_cov,name="MG ")
mg_tax_table_cyano = make_tax_table(mg_cov,name="MG ",rank="phylum").loc["Cyanobacteria"]
mg_tax_table = pd.concat([mg_tax_table,pd.DataFrame(mg_tax_table_cyano).T])
mg_tax_table
mt_tax_table = make_tax_table(mt_cov,name="MT ")
mt_tax_table_cyano = make_tax_table(mt_cov,name="MT ",rank="phylum").loc["Cyanobacteria"]
mt_tax_table = pd.concat([mt_tax_table,pd.DataFrame(mt_tax_table_cyano).T])
mt_tax_table
```
Concatenate overview tables. This is **Table 2** in the paper.
```
tax_table = pd.concat([mg_tax_table,mt_tax_table],axis=1).round(2)
tax_table.to_csv("results/Table2.tsv",sep="\t")
```
## Generate general overview of transporters
Make table with number of ORFs, ORFs classified as transporters, min, mean and max coverage for transporter ORFs.
```
num_genes = len(mg_cov)
gene_lengths = pd.read_table("data/mg/all_genes.tpm.tsv.gz", usecols=[1])
gene_lengths = np.round(gene_lengths.mean())
def generate_transporter_stats(df):
# Number of transporter genes (genes with sum > 0)
num_trans_genes = len(df.loc[df.groupby(level=0).sum().sum(axis=1)>0])
# Percent of transporter genes
num_trans_genes_p = np.round((num_trans_genes / float(num_genes))*100,2)
# Mean total coverage for transporter genes across the samples
transcov_mean = np.round(((df.groupby(level=0).sum().sum().mean()) / 1e6)*100,2)
# Minimum total coverage for transporter genes across the samples
transcov_min = np.round(((df.groupby(level=0).sum().sum().min()) / 1e6)*100,2)
# Maximum ...
transcov_max = np.round(((df.groupby(level=0).sum().sum().max()) / 1e6)*100,2)
# Standard dev
transcov_std = np.round(((df.groupby(level=0).sum().sum() / 1e6)*100).std(),2)
return num_trans_genes, num_trans_genes_p, transcov_mean, transcov_min, transcov_max, transcov_std
mg_num_trans_genes, mg_num_trans_genes_p, mg_transcov_mean, mg_transcov_min, mg_transcov_max, mg_transcov_std = generate_transporter_stats(mg_transcov)
mt_num_trans_genes, mt_num_trans_genes_p, mt_transcov_mean, mt_transcov_min, mt_transcov_max, mt_transcov_std = generate_transporter_stats(mt_transcov)
```
Create table with transporter statistics for MG and MT datasets (**Table 3** in the paper).
```
stats_df = pd.DataFrame(data={
"Transporter genes": ["{} ({}%)".format(mg_num_trans_genes,mg_num_trans_genes_p),"{} ({}%)".format(mt_num_trans_genes,mt_num_trans_genes_p)],
"Transporter mean": ["{}%".format(mg_transcov_mean),"{}%".format(mt_transcov_mean)],
"Transporter min": ["{}%".format(mg_transcov_min),"{}%".format(mt_transcov_min)],
"Transporter max": ["{}%".format(mg_transcov_max),"{}%".format(mt_transcov_max)],
"Transporter std": ["{}%".format(mg_transcov_std),"{}%".format(mt_transcov_std)]},index=["MG","MT"]).T
stats_df.to_csv("results/Table3.tsv",sep="\t")
stats_df
```
Do the same with the selected transporters.
```
mg_select_num_trans_genes, mg_select_num_trans_genes_p, mg_select_transcov_mean, mg_select_transcov_min, mg_select_transcov_max, mg_select_transcov_std = generate_transporter_stats(mg_select_transcov)
mt_select_num_trans_genes, mt_select_num_trans_genes_p, mt_select_transcov_mean, mt_select_transcov_min, mt_select_transcov_max, mt_select_transcov_std = generate_transporter_stats(mt_select_transcov)
select_stats_df = pd.DataFrame(data={
"Selected transporter genes": ["{} ({}%)".format(mg_select_num_trans_genes,mg_select_num_trans_genes_p),"{} ({}%)".format(mt_select_num_trans_genes,mt_select_num_trans_genes_p)],
"Selected transporter mean": ["{}%".format(mg_select_transcov_mean),"{}%".format(mt_select_transcov_mean)],
"Selected transporter min": ["{}%".format(mg_select_transcov_min),"{}%".format(mt_select_transcov_min)],
"Selected transporter max": ["{}%".format(mg_select_transcov_max),"{}%".format(mt_select_transcov_max)],
"Selected transporter std": ["{}%".format(mg_select_transcov_std),"{}%".format(mt_select_transcov_std)]},index=["mg_select","mt_select"]).T
select_stats_df.to_csv("results/selected_transporter_stats.tab",sep="\t")
select_stats_df
```
## Generate kingdom/phylum level taxonomic plots
```
def get_euk_taxa(taxa, df, rank):
euk_taxa = []
for t in taxa:
k = df.loc[df[rank]==t, "superkingdom"].unique()[0]
if k=="Eukaryota":
euk_taxa.append(t)
return euk_taxa
def set_euk_hatches(ax):
for patch in ax.patches:
t = color2taxmap[patch.properties()['facecolor'][0:-1]]
if t in euk_taxa:
patch.set_hatch("////")
```
Generate profiles for metagenomes.
```
# Get sum of abundances at superkingdom level
mg_k = mg_cov.groupby("superkingdom").sum()
# Normalize to %
mg_kn = mg_k.div(mg_k.sum())*100
mg_kn = mg_kn.loc[["Archaea","Bacteria","Eukaryota","Viruses","Unclassified.sequences","other sequences"]]
mg_kn = mg_kn.loc[mg_kn.sum(axis=1).sort_values(ascending=False).index]
# Swtich Proteobacterial classes to phylum
mg_cov.loc[mg_cov.phylum=="Proteobacteria","phylum"] = mg_cov.loc[mg_cov.phylum=="Proteobacteria","class"]
# Normalize at phylum level
mg_p = mg_cov.groupby("phylum").sum()
mg_pn = mg_p.div(mg_p.sum())*100
_ = mg_pn.mean(axis=1).sort_values(ascending=False)
_.loc[~_.index.str.contains("Unclassified")].head(8)
```
Create the taxonomic overview of the 7 most abundant phyla in the metagenomic dataset. This is **Figure 1** in the paper.
```
select_taxa = ["Verrucomicrobia","Actinobacteria","Alphaproteobacteria","Gammaproteobacteria","Cyanobacteria","Bacteroidetes","Betaproteobacteria"]
# Sort taxa by mean abundance
taxa_order = mg_pn.loc[select_taxa].mean(axis=1).sort_values(ascending=False).index
ax = mg_pn.loc[taxa_order].T.plot(kind="area",stacked=True)
ax.legend(bbox_to_anchor=(1,1))
ax.set_ylabel("% normalized abundance");
xticks = list(range(0,33))
ax.set_xticks(xticks);
ax.set_xticklabels(mg_pn.columns, rotation=90);
plt.savefig("results/Figure1.svg", bbox_inches="tight")
```
Generate profiles for metatranscriptomes.
```
# Get sum of abundances at superkingdom level
mt_k = mt_cov.groupby("superkingdom").sum()
# Normalize to %
mt_kn = mt_k.div(mt_k.sum())*100
mt_kn = mt_kn.loc[["Archaea","Bacteria","Eukaryota","Viruses","Unclassified.sequences","other sequences"]]
mt_kn = mt_kn.loc[mt_kn.sum(axis=1).sort_values(ascending=False).index]
# Swtich Proteobacterial classes to phylum
mt_cov.loc[mt_cov.phylum=="Proteobacteria","phylum"] = mt_cov.loc[mt_cov.phylum=="Proteobacteria","class"]
# Normalize at phylum level
mt_p = mt_cov.groupby("phylum").sum()
mt_pn = mt_p.div(mt_p.sum())*100
```
Get common taxa for both datasets by taking the union of the top 15 most abundant taxa
```
mg_taxa = mg_pn.mean(axis=1).sort_values(ascending=False).head(15).index
mt_taxa = mt_pn.mean(axis=1).sort_values(ascending=False).head(15).index
taxa = set(mg_taxa).union(set(mt_taxa))
```
Single out eukaryotic taxa
```
euk_taxa = get_euk_taxa(taxa, mg_cov, rank="phylum")
```
Sort the taxa by their mean abundance in the mg data
```
taxa_sort = mg_pn.loc[taxa].mean(axis=1).sort_values(ascending=False).index
taxa_colors = dict(zip(taxa_sort,(sns.color_palette("Set1",7)+sns.color_palette("Set2",7)+sns.color_palette("Dark2",5))))
color2taxmap = {}
for t, c in taxa_colors.items():
color2taxmap[c] = t
```
Plot metagenome profiles
```
fig,axes = plt.subplots(ncols=2,nrows=1, figsize=(12,4))
# Plot the kingdoms
ax1 = mg_kn.T.plot(kind="bar",stacked=True,ax=axes[0])
ax1.legend(loc="lower right",fontsize="small")
ax1.set_ylabel("%")
# Plot the phyla
ax2 = mg_pn.loc[taxa_sort].T.plot(kind="bar",stacked=True, color=[taxa_colors[tax] for tax in taxa_sort], legend=None,ax=axes[1])
set_euk_hatches(ax2)
ax2.set_ylabel("%")
ax2.legend(bbox_to_anchor=(1,1),fontsize="small");
```
Plot metatranscriptome profiles
```
fig,axes = plt.subplots(ncols=2,nrows=1, figsize=(12,4))
# Plot the kingdoms
ax1 = mt_kn.T.plot(kind="bar",stacked=True,ax=axes[0])
ax1.legend(loc="lower center",fontsize="small")
ax1.set_ylabel("%")
# Plot the phyla
ax2 = mt_pn.loc[taxa_sort].T.plot(kind="bar",stacked=True, color=[taxa_colors[tax] for tax in taxa_sort], legend=None,ax=axes[1])
set_euk_hatches(ax2)
ax2.set_ylabel("%")
ax2.legend(bbox_to_anchor=(1,1),fontsize="small");
```
Calculate total number of orders.
```
mg_ordersum = mg_cov.groupby("order").sum()
mg_total_orders = len(mg_ordersum.loc[mg_ordersum.sum(axis=1)>0])
print("{} orders in the entire mg dataset".format(mg_total_orders))
mg_trans_ordersum = mg_select_transcov.groupby("order").sum()
mg_trans_total_orders = len(mg_trans_ordersum.loc[mg_trans_ordersum.sum(axis=1)>0])
print("{} orders in the transporter mg dataset".format(mg_trans_total_orders))
mt_ordersum = mt_cov.groupby("order").sum()
mt_total_orders = len(mt_ordersum.loc[mt_ordersum.sum(axis=1)>0])
print("{} orders in the entire mt dataset".format(mt_total_orders))
mt_trans_ordersum = mt_select_transcov.groupby("order").sum()
mt_trans_total_orders = len(mt_trans_ordersum.loc[mt_trans_ordersum.sum(axis=1)>0])
print("{} orders in the transporter mt dataset".format(mt_trans_total_orders))
```
## Calculate and plot distributions per taxonomic subsets.
Extract ORFs belonging to each subset.
```
cya_orfs = mg_transcov.loc[mg_transcov.phylum=="Cyanobacteria"].index
bac_orfs = mg_transcov.loc[(mg_transcov.phylum!="Cyanobacteria")&(mg_transcov.superkingdom=="Bacteria")].index
euk_orfs = mg_transcov.loc[mg_transcov.superkingdom=="Eukaryota"].index
```
Calculate contribution of taxonomic subsets to the identified transporters.
```
taxgroup_df = pd.DataFrame(columns=["MG","MT"],index=["Bacteria","Cyanobacteria","Eukaryota"])
mg_all_transcov_info = pd.merge(transinfo,mg_transcov,left_index=True,right_on="transporter")
mg_bac_transcov_info = pd.merge(transinfo,mg_transcov.loc[bac_orfs],left_index=True,right_on="transporter")
mg_euk_transcov_info = pd.merge(transinfo,mg_transcov.loc[euk_orfs],left_index=True,right_on="transporter")
mg_cya_transcov_info = pd.merge(transinfo,mg_transcov.loc[cya_orfs],left_index=True,right_on="transporter")
mt_all_transcov_info = pd.merge(transinfo,mt_transcov,left_index=True,right_on="transporter")
mt_bac_transcov_info = pd.merge(transinfo,mt_transcov.loc[bac_orfs],left_index=True,right_on="transporter")
mt_euk_transcov_info = pd.merge(transinfo,mt_transcov.loc[euk_orfs],left_index=True,right_on="transporter")
mt_cya_transcov_info = pd.merge(transinfo,mt_transcov.loc[cya_orfs],left_index=True,right_on="transporter")
mg_cya_part = mg_cya_transcov_info.groupby("transporter").sum().sum().div(mg_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mg_cya_part.min(),mg_cya_part.max(),mg_cya_part.mean()
taxgroup_df.loc["Cyanobacteria","MG"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
mg_euk_part = mg_euk_transcov_info.groupby("transporter").sum().sum().div(mg_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mg_euk_part.min(),mg_euk_part.max(),mg_euk_part.mean()
taxgroup_df.loc["Eukaryota","MG"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
mg_bac_part = mg_bac_transcov_info.groupby("transporter").sum().sum().div(mg_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mg_bac_part.min(),mg_bac_part.max(),mg_bac_part.mean()
taxgroup_df.loc["Bacteria","MG"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
mt_cya_part = mt_cya_transcov_info.groupby("transporter").sum().sum().div(mt_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mt_cya_part.min(),mt_cya_part.max(),mt_cya_part.mean()
taxgroup_df.loc["Cyanobacteria","MT"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
mt_euk_part = mt_euk_transcov_info.groupby("transporter").sum().sum().div(mt_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mt_euk_part.min(),mt_euk_part.max(),mt_euk_part.mean()
taxgroup_df.loc["Eukaryota","MT"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
mt_bac_part = mt_bac_transcov_info.groupby("transporter").sum().sum().div(mt_all_transcov_info.groupby("transporter").sum().sum())*100
mi,ma,me = mt_bac_part.min(),mt_bac_part.max(),mt_bac_part.mean()
taxgroup_df.loc["Bacteria","MT"] = "{}% ({}-{}%)".format(round(me,2),round(mi,2),round(ma,2))
taxgroup_df
```
### Taxonomic subsets per substrate category
```
def calculate_mean_total_substrate_subset(df,df_sum,subset,var_name="Sample",value_name="%"):
cols = ["fam","transporter","substrate_category","name"]
# Sum to protein family
x = df.groupby(["fam","transporter","substrate_category","name"]).sum().reset_index()
cols.pop(cols.index("fam"))
# Calculate mean of transporters
x.groupby(cols).mean().reset_index()
xt = x.copy()
# Normalize to sum of all transporters
x.iloc[:,4:] = x.iloc[:,4:].div(df_sum)*100
# Sum percent to substrate category
x = x.groupby("substrate_category").sum()
# Melt dataframe and add subset column
x["substrate_category"] = x.index
xm = pd.melt(x,id_vars="substrate_category", var_name="Sample",value_name="%")
xm = xm.assign(Subset=pd.Series(data=subset,index=xm.index))
return xm,xt
# Get contribution of bacterial transporters to total for substrate category
mg_bac_cat_melt,mg_bac_cat = calculate_mean_total_substrate_subset(mg_bac_transcov_info,mg_trans.sum(),"Bacteria")
# Get contribution of eukaryotic transporters to total for substrate category
mg_euk_cat_melt,mg_euk_cat = calculate_mean_total_substrate_subset(mg_euk_transcov_info,mg_trans.sum(),"Eukaryota")
# Get contribution of cyanobacterial transporters to total for substrate category
mg_cya_cat_melt,mg_cya_cat = calculate_mean_total_substrate_subset(mg_cya_transcov_info,mg_trans.sum(),"Cyanobacteria")
# Get contribution of bacterial transporters to total for substrate category
mt_bac_cat_melt,mt_bac_cat = calculate_mean_total_substrate_subset(mt_bac_transcov_info,mt_trans.sum(),"Bacteria")
# Get contribution of eukaryotic transporters to total for substrate category
mt_euk_cat_melt,mt_euk_cat = calculate_mean_total_substrate_subset(mt_euk_transcov_info,mt_trans.sum(),"Eukaryota")
# Get contribution of cyanobacterial transporters to total for substrate category
mt_cya_cat_melt,mt_cya_cat = calculate_mean_total_substrate_subset(mt_cya_transcov_info,mt_trans.sum(),"Cyanobacteria")
# Concatenate dataframes for metagenomes
mg_subsets_cat = pd.concat([pd.concat([mg_bac_cat_melt,mg_euk_cat_melt]),mg_cya_cat_melt])
mg_subsets_cat = mg_subsets_cat.assign(dataset=pd.Series(data="MG",index=mg_subsets_cat.index))
# Concatenate dataframes for metagenomes
mt_subsets_cat = pd.concat([pd.concat([mt_bac_cat_melt,mt_euk_cat_melt]),mt_cya_cat_melt])
mt_subsets_cat = mt_subsets_cat.assign(dataset=pd.Series(data="MT",index=mt_subsets_cat.index))
```
**Concatenate MG and MT**
```
subsets_cat = pd.concat([mg_subsets_cat,mt_subsets_cat])
```
### Plot substrate category distributions
```
cats = transinfo.substrate_category.unique()
# Update Eukaryota subset label
subsets_cat.loc[subsets_cat.Subset=="Eukaryota","Subset"] = ["Picoeukaryota"]*len(subsets_cat.loc[subsets_cat.Subset=="Eukaryota","Subset"])
sns.set(font_scale=0.8)
ax = sns.catplot(kind="bar",data=subsets_cat.loc[subsets_cat.substrate_category.isin(cats)],hue="dataset",
y="substrate_category", x="%", col="Subset",
errwidth=1, height=3, palette="Set1", aspect=1)
ax.set_titles("{col_name}")
ax.set_axis_labels("% of normalized transporter abundance","Substrate category")
plt.savefig("results/Figure3A.svg", bbox_inches="tight")
_ = mg_transcov.groupby(["fam","transporter"]).sum().reset_index()
_ = _.groupby("transporter").mean()
_ = pd.merge(transinfo, _, left_index=True, right_index=True)
_ = _.loc[_.substrate_category=="Carbohydrate"].groupby("name").sum()
(_.div(_.sum())*100).mean(axis=1).sort_values(ascending=False).head(3).sum()
```
|
github_jupyter
|
```
import numpy as np
from keras.models import Sequential
from keras.models import load_model
from keras.models import model_from_json
from keras.layers.core import Dense, Activation
from keras.utils import np_utils
from keras.preprocessing.image import load_img, save_img, img_to_array
from keras.applications.imagenet_utils import preprocess_input
import matplotlib.pyplot as plt
from keras.preprocessing import image
#you can find the model at https://github.com/serengil/tensorflow-101/blob/master/model/facenet_model.json
model = model_from_json(open("C:/Users/IS96273/Desktop/facenet_model.json", "r").read())
#you can find the pre-trained weights at https://drive.google.com/file/d/1971Xk5RwedbudGgTIrGAL4F7Aifu7id1/view?usp=sharing
model.load_weights('C:/Users/IS96273/Desktop/facenet_weights.h5')
#both model and pre-trained weights are inspired from the work of David Sandberg (github.com/davidsandberg/facenet)
#and transformed by Sefik Serengil (sefiks.com)
#model.summary()
def preprocess_image(image_path):
img = load_img(image_path, target_size=(160, 160))
img = img_to_array(img)
img = np.expand_dims(img, axis=0)
img = preprocess_input(img)
return img
def l2_normalize(x):
return x / np.sqrt(np.sum(np.multiply(x, x)))
def findCosineSimilarity(source_representation, test_representation):
a = np.matmul(np.transpose(source_representation), test_representation)
b = np.sum(np.multiply(source_representation, source_representation))
c = np.sum(np.multiply(test_representation, test_representation))
return 1 - (a / (np.sqrt(b) * np.sqrt(c)))
def findEuclideanDistance(source_representation, test_representation):
euclidean_distance = source_representation - test_representation
euclidean_distance = np.sum(np.multiply(euclidean_distance, euclidean_distance))
euclidean_distance = np.sqrt(euclidean_distance)
return euclidean_distance
metric = "euclidean" #euclidean or cosine
threshold = 0
if metric == "euclidean":
threshold = 0.35
elif metric == "cosine":
threshold = 0.07
def verifyFace(img1, img2):
#produce 128-dimensional representation
img1_representation = model.predict(preprocess_image('C:/Users/IS96273/Desktop/trainset/%s' % (img1)))[0,:]
img2_representation = model.predict(preprocess_image('C:/Users/IS96273/Desktop/trainset/%s' % (img2)))[0,:]
if metric == "euclidean":
img1_representation = l2_normalize(img1_representation)
img2_representation = l2_normalize(img2_representation)
euclidean_distance = findEuclideanDistance(img1_representation, img2_representation)
print("euclidean distance (l2 norm): ",euclidean_distance)
if euclidean_distance < threshold:
print("verified... they are same person")
else:
print("unverified! they are not same person!")
elif metric == "cosine":
cosine_similarity = findCosineSimilarity(img1_representation, img2_representation)
print("cosine similarity: ",cosine_similarity)
if cosine_similarity < 0.07:
print("verified... they are same person")
else:
print("unverified! they are not same person!")
f = plt.figure()
f.add_subplot(1,2, 1)
plt.imshow(image.load_img('C:/Users/IS96273/Desktop/trainset/%s' % (img1)))
plt.xticks([]); plt.yticks([])
f.add_subplot(1,2, 2)
plt.imshow(image.load_img('C:/Users/IS96273/Desktop/trainset/%s' % (img2)))
plt.xticks([]); plt.yticks([])
plt.show(block=True)
print("-----------------------------------------")
#true positive
verifyFace("1.jpg", "5.jpg")
verifyFace("1.jpg", "7.jpg")
#true negative
verifyFace("1.jpg", "8.jpg")
verifyFace("1.jpg", "10.jpg")
#true positive
verifyFace("17.jpg", "8.jpg")
verifyFace("17.jpg", "9.jpg")
```
|
github_jupyter
|
## Prepare data
```
# mount google drive & set working directory
# requires auth (click on url & copy token into text box when prompted)
from google.colab import drive
drive.mount("/content/gdrive", force_remount=True)
import os
print(os.getcwd())
os.chdir('/content/gdrive/My Drive/Colab Notebooks/MidcurveNN')
!pwd
!pip install drawSVG
"""
Prepare Data: populating input images from raw profile data
Takes raw data from "data/raw/*" files for both, profile shape (shape.dat) as well as midcurve shape (shape.mid)
Generates raster image files from svg (simple vector graphics)
Multiple variations are populated using image transformations.
These images become input for further modeling (stored in "data/input/*")
"""
import os
import sys
import PIL
import json
import shutil
import numpy as np
import PIL.ImageOps
from random import shuffle
from keras.preprocessing.image import img_to_array, load_img, array_to_img
np.set_printoptions(threshold=sys.maxsize)
from PIL import Image
# working directory
#wdir = os.getcwd()
wdir = '/content/gdrive/My Drive/Colab Notebooks/MidcurveNN'
print("Working directory: ", wdir)
imdim = 100
#input_data_folder = wdir + "\\data\\sample"
#input_data_folder = wdir + "/data/newinput"
#print("input data dir: ", input_data_folder)
raw_data_folder = "data/new_shapes"
input_data_folder = "data/new_images"
pix2pix_data_folder = "/data/pix2pix/datasets/pix2pix"
def read_dat_files(datafolder=raw_data_folder):
profiles_dict_list = []
for file in os.listdir(datafolder):
if os.path.isdir(os.path.join(datafolder, file)):
continue
filename = file.split(".")[0]
profile_dict = get_profile_dict(filename,profiles_dict_list)
if file.endswith(".dat"):
with open(os.path.join(datafolder, file)) as f:
profile_dict['Profile'] = [tuple(map(float, i.split('\t'))) for i in f]
if file.endswith(".mid"):
with open(os.path.join(datafolder, file)) as f:
profile_dict['Midcurve'] = [tuple(map(float, i.split('\t'))) for i in f]
profiles_dict_list.append(profile_dict)
return profiles_dict_list
def get_profile_dict(shapename,profiles_dict_list):
for i in profiles_dict_list:
if i['ShapeName'] == shapename:
return i
profile_dict = {}
profile_dict['ShapeName'] = shapename
return profile_dict
import drawSvg as draw
def create_image_file(fieldname,profile_dict,datafolder=input_data_folder,imgsize=imdim, isOpenClose=True):
d = draw.Drawing(imgsize, imgsize, origin='center')
profilepoints = []
for tpl in profile_dict[fieldname]:
profilepoints.append(tpl[0])
profilepoints.append(tpl[1])
d.append(draw.Lines(profilepoints[0],profilepoints[1],*profilepoints,close=isOpenClose,fill='none',stroke='black'))
shape = profile_dict['ShapeName']
# d.saveSvg(datafolder+"/"+shape+'.svg')
# d.savePng(datafolder+"/"+shape+'_'+fieldname+'.png')
d.savePng(datafolder+"/"+shape+'_'+fieldname+'.png')
def get_original_png_files(datafolder=input_data_folder):
pngfilenames = []
for file in os.listdir(datafolder):
fullpath = os.path.join(datafolder, file)
if os.path.isdir(fullpath):
continue
if file.endswith(".png") and file.find("_rotated_") == -1 and file.find("_translated_")==-1 and file.find("_mirrored_")==-1:
pngfilenames.append(fullpath)
return pngfilenames
def mirror_images(pngfilenames, mode=PIL.Image.TRANSPOSE):
mirrored_filenames = []
for fullpath in pngfilenames:
picture= Image.open(fullpath)
newfilename = fullpath.replace(".png", "_mirrored_"+str(mode)+".png")
picture.transpose(mode).save(newfilename)
mirrored_filenames.append(newfilename)
return mirrored_filenames
def rotate_images(pngfilenames, angle=90):
for fullpath in pngfilenames:
picture= Image.open(fullpath)
newfilename = fullpath.replace(".png", "_rotated_"+str(angle)+".png")
picture.rotate(angle).save(newfilename)
def translate_images(pngfilenames, dx=1,dy=1):
for fullpath in pngfilenames:
picture= Image.open(fullpath)
x_shift = dx
y_shift = dy
a = 1
b = 0
c = x_shift #left/right (i.e. 5/-5)
d = 0
e = 1
f = y_shift #up/down (i.e. 5/-5)
translate = picture.transform(picture.size, Image.AFFINE, (a, b, c, d, e, f))
# # Calculate the size after cropping
# size = (translate.size[0] - x_shift, translate.size[1] - y_shift)
# # Crop to the desired size
# translate = translate.transform(size, Image.EXTENT, (0, 0, size[0], size[1]))
newfilename = fullpath.replace(".png", "_translated_"+str(dx)+"_"+str(dy)+".png")
translate.save(newfilename)
def generate_images(datafolder=input_data_folder):
if not os.path.exists(datafolder):
os.makedirs(datafolder)
else:
for file in os.listdir(datafolder):
if file.endswith(".png") and (file.find("_rotated_") != -1 or file.find("_translated_") !=-1):
print("files already present, not generating...")
return
print("transformed files not present, generating...")
profiles_dict_list = read_dat_files()
print(profiles_dict_list)
for profile_dict in profiles_dict_list:
create_image_file('Profile',profile_dict,datafolder,imdim,True)
create_image_file('Midcurve',profile_dict,datafolder,imdim,False)
pngfilenames = get_original_png_files(datafolder)
mirrored_filenames_left_right = mirror_images(pngfilenames, PIL.Image.FLIP_LEFT_RIGHT)
mirrored_filenames_top_bottom = mirror_images(pngfilenames, PIL.Image.FLIP_TOP_BOTTOM)
mirrored_filenames_transpose = mirror_images(pngfilenames, PIL.Image.TRANSPOSE)
files_list_list = [pngfilenames,mirrored_filenames_left_right,mirrored_filenames_top_bottom,mirrored_filenames_transpose]
for filelist in files_list_list:
for angle in range(30,360,30):
rotate_images(filelist,angle)
for dx in range(5,21,5):
for dy in range(5,21,5):
translate_images(filelist,dx,-dy)
generate_images()
# wait till all images are generated before executing the next cell
break
# move images to appropriate directories
# directory names follows the shape name
import os
import shutil
srcpath = input_data_folder
destpath = input_data_folder
for root, subFolders, files in os.walk(srcpath):
for file in files:
#print(file)
subFolder = os.path.join(destpath, file[:4])
if not os.path.isdir(subFolder):
os.makedirs(subFolder)
try:
shutil.move(os.path.join(root, file), subFolder)
except:
pass
print(wdir)
# move images from temporary directory to actual
# directory names follows the shape name
src_shapes = wdir + "/data/new_shapes/"
src_images = wdir + "/data/new_images/"
dest_shapes = wdir + "/data/shapes/"
dest_images = wdir + "/data/images/"
files = os.listdir(src_shapes)
for f in files:
shutil.move(src_shapes+f, dest_shapes)
files = os.listdir(src_images)
for f in files:
shutil.move(src_images+f, dest_images)
```
|
github_jupyter
|
```
import io
import os
import pandas as pd
data_path = 'E:\\BaiduYunDownload\\optiondata3\\'
```
## Definitions
* Underlying The stock, index, or ETF symbol
* Underlying_last The last traded price at the time of the option quote.
* Exchange The exchange of the quote – Asterisk(*) represents a consolidated price of all exchanges and is the most common value.*
* Optionsymbol The option symbol. Note that in the format starting 2010 this will be longer than 18 characters, depending on the length of the underlying. Blank This item is always blank, to preserve continuity with the older format. It is always blank. So if you are importing this into a database, either do not import this column, or make the field nullable.
* Optiontype Call or put Expiration The expiration date of the option.
* Expiration date The date of the expiration
* Quotedate The date and time of the quote. Most of the time, the time will be 4:00 PM. This only means that it is at the close, even though some options trade until 4:15 PM EST
* Strike The strike of the option
* Last The last traded price of the option which could even be from a previous day.
* Bid The bid price of the option
* Ask The ask price of the option
* Volume The number of contracts traded
* Open interest Open Interest – always a day behind. The OCC changes this number at 3:00AM every morning and the number does not change through the day
* BELOW THIS LINE, THESE COLUMNS NOT CONTAINED IN BARE BONES PRODUCTS
* Implied volatility The implied volatility (a measure of the estimate of how much the price could change. A high number means that traders believe the option could make a large change)
* Delta The delta. (a measure of how much the option price would change in relation to the underlying stock price. A delta of .50 means the option would change 50 cents for every 1 dollar the stock moves)
* Gamma The gamma. (a measure of how fast the Delta will change when the stock price changes. A high number means this is a very explosive option, and could gain or loss value quickly)
* Theta The theta (a measure of how fast the option is losing value per day due to time decay. As the expiration day arrives, the theta increases)
* Vega The vega (a measure of how sensitive the option price is to a change in the implied volatility. Options that are way out of the money, or have a long time until expiration are more sensitive to a change in implied volatility)
* Alias If possible, the old name of the option. Because of the 2010 OSI Symbology, it is important to know what the old symbol name was during the 2010 switch over. If this can be determined, it will list the old name, otherwise it will display the same value as the option symbol. The Alias column has no usage outside of 2010.
```
columns= ['UnderlyingSymbol','UnderlyingPrice','Exchange','OptionSymbol','Blank','Type','Expiration', 'DataDate','Strike','Last','Bid','Ask','Volume','OpenInterest','IV','Delta','Gamma','Theta','Vega','Alias']
print(columns)
test=pd.read_csv(data_path+"\\201801\\options_20180102.csv", header=None,
names=columns)
symbols = ['AMD', 'AMED', 'ATLC', 'BLFS', 'CROX', 'DXCM', 'FATE', 'FIVN',
'FRPT', 'HZNP', 'JYNT', 'LPSN', 'LULU', 'MRTX', 'NEO', 'NSTG',
'PCTY', 'PDEX', 'PTCT', 'QDEL', 'REGI', 'RGEN', 'SPSC', 'STAA',
'VCYT', 'VICR', 'WIX']#from 3 years data NASDAQ clustering
df= None
for path in os.listdir(data_path):
for file in os.listdir(data_path+'/'+path):
print('reading file'+file)
df_one = pd.read_csv(data_path+'/'+path+'/'+file,
header=None, names=columns)
df_one = df_one[df_one['UnderlyingSymbol'].isin(symbols)]
print(df_one.shape)
if df is None:
df= df_one
print(df.shape)
continue
#print(df_one.head())
df = pd.concat([df,df_one],axis=0)
print(df.shape)
df.shape
df.head()
df.to_csv(data_path+'/option_data_NASDAQ.csv',index = False)
```
|
github_jupyter
|
# Modeling Transmission Line Properties
## Table of Contents
* [Introduction](#introduction)
* [Propagation constant](#propagation_constant)
* [Interlude on attenuation units](#attenuation_units)
* [Modeling a loaded lossy transmission line using transmission line functions](#tline_functions)
* [Input impedances, reflection coefficients and SWR](#tline_impedances)
* [Voltages and Currents](#voltages_currents)
* [Modeling a loaded lossy transmission line by cascading Networks](#cascading_networks)
* [Determination of the propagation constant from the input impedance](#propagation_constant_from_zin)
## Introduction <a class="anchor" id="introduction"></a>
In this tutorial, `scikit-rf` is used to work with some classical transmission line situations, such as calculating impedances, reflection coefficients, standing wave ratios or voltages and currents. There is at least two way of performing these calculations, one using [transmission line functions](#tline_functions) or by [creating and cascading Networks](#cascading_networks)
Let's consider a lossy coaxial cable of characteristic impedance $Z_0=75 \Omega$ of length $d=12 m$. The coaxial cable has an attenuation of 0.02 Neper/m and a [velocity factor](https://en.wikipedia.org/wiki/Velocity_factor) VF=0.67 (This corresponds roughly to a [RG-6](https://en.wikipedia.org/wiki/RG-6) coaxial). The cable is loaded with a $Z_L=150 \Omega$ impedance. The RF frequency of interest is 250 MHz.
Please note that in `scikit-rf`, the line length is defined from the load, ie $z=0$ at the load and $z=d$ at the input of the transmission line:
<img src="transmission_line_properties.svg">
First, let's make the necessary Python import statements:
```
%matplotlib inline
import skrf as rf
from pylab import *
# skrf figure styling
rf.stylely()
```
And the constants of the problem:
```
freq = rf.Frequency(250, npoints=1, unit='MHz')
Z_0 = 75 # Ohm
Z_L = 150 # Ohm
d = 12 # m
VF = 0.67
att = 0.02 # Np/m. Equivalent to 0.1737 dB/m
```
Before going into impedance and reflection coefficient calculations, first we need to define the transmission line properties, in particular its propagation constant.
### Propagation constant <a class="anchor" id="propagation_constant"></a>
In order to get the RF parameters of the transmission line, it is necessary to derive the propagation constant of the line. The propagation constant $\gamma$ of the line is defined in `scikit-rf` as $\gamma=\alpha + j\beta$ where $\alpha$ is the attenuation (in Neper/m) and $\beta=\frac{2\pi}{\lambda}=\frac{\omega}{c}/\mathrm{VF}=\frac{\omega}{c}\sqrt{\epsilon_r}$ the phase constant.
First, the wavelength in the coaxial cable is $$\lambda=\frac{c}{f \sqrt{\epsilon_r}}=\frac{c}{f} \mathrm{VF} $$
```
lambd = rf.c/freq.f * VF
print('VF=', VF, 'and Wavelength:', lambd, 'm')
```
As the attenuation is already given in Np/m, the propagation constant is:
```
alpha = att # Np/m !
beta = freq.w/rf.c/VF
gamma = alpha + 1j*beta
print('Transmission line propagation constant: gamma = ', gamma, 'rad/m')
```
If the attenuation would have been given in other units, `scikit-rf` provides the necessary tools to convert units, as described below.
### Interlude: On Attenuation Units <a class="anchor" id="attenuation_units"></a>
Attenuation is generally provided (or expected) in various kind of units. `scikit-rf` provides convenience functions to manipulate line attenuation units.
For example, the cable attenuation given in Np/m, can be expressed in dB:
```
print('Attenuation dB/m:', rf.np_2_db(att))
```
Hence, the attenuation in dB/100m is:
```
print('Line attenuation in dB/100m:', rf.np_2_db(att)*100)
```
And in dB/100feet is:
```
print('Line attenuation in dB/100ft:', rf.np_2_db(att)*100*rf.feet_2_meter())
```
If the attenuation would have been given in imperial units, such as dB/100ft, the opposite conversions would have been:
```
rf.db_per_100feet_2_db_per_100meter(5.2949) # to dB/100m
rf.db_2_np(5.2949)/rf.feet_2_meter(100) # to Np/m
```
## Using transmission line functions <a class="anchor" id="tline_functions"></a>
`scikit-rf` brings few convenient functions to deal with transmission lines. They are detailed in the [transmission line functions](https://scikit-rf.readthedocs.io/en/latest/api/tlineFunctions.html) documentation pages.
### Input impedances, reflection coefficients and SWR <a class="anchor" id="tline_impedances"></a>
The reflection coefficient $\Gamma_L$ induced by the load is given by `zl_2_Gamma0()`:
```
Gamma0 = rf.zl_2_Gamma0(Z_0, Z_L)
print('|Gamma0|=', abs(Gamma0))
```
and its associated Standing Wave Ratio (SWR) is obtained from `zl_2_swr()`:
```
rf.zl_2_swr(Z_0, Z_L)
```
After propagating by a distance $d$ in the transmission line of propagation constant $\gamma$ (hence having travelled an electrical length $\theta=\gamma d$), the reflection coefficient at the line input is obtained from `zl_2_Gamma_in()`:
```
Gamma_in = rf.zl_2_Gamma_in(Z_0, Z_L, theta=gamma*d)
print('|Gamma_in|=', abs(Gamma_in), 'phase=', 180/rf.pi*angle(Gamma_in))
```
The input impedance $Z_{in}$ from `zl_2_zin()`:
```
Z_in = rf.zl_2_zin(Z_0, Z_L, gamma * d)
print('Input impedance Z_in=', Z_in)
```
Like previously, the SWR at the line input is:
```
rf.zl_2_swr(Z_0, Z_in)
```
The total line loss in dB is get from `zl_2_total_loss()`:
```
rf.mag_2_db10(rf.zl_2_total_loss(Z_0, Z_L, gamma*d))
```
### Voltages and Currents <a class="anchor" id="voltages_currents"></a>
Now assume that the previous circuit is excited by a source delivering a voltage $V=1 V$ associated to a source impedance $Z_s=100\Omega$ :
<img src="transmission_line_properties_vi.svg">
```
Z_s = 100 # Ohm
V_s = 1 # V
```
At the input of the transmission line, the voltage is a voltage divider circuit:
$$
V_{in} = V_s \frac{Z_{in}}{Z_s + Z_{in}}
$$
```
V_in = V_s * Z_in / (Z_s + Z_in)
print('Voltage at transmission line input : V_in = ', V_in, ' V')
```
and the current at the input of the transmission line is:
$$
I_{in} = \frac{V_s}{Z_s + Z_{in}}
$$
```
I_in = V_s / (Z_s + Z_in)
print('Current at transmission line input : I_in = ', I_in, ' A')
```
which represent a power of
$$
P_{in} = \frac{1}{2} \Re \left[V_{in} I_{in}^* \right]
$$
```
P_in = 1/2 * real(V_in * conj(I_in))
print('Input Power : P_in = ', P_in, 'W')
```
The reflected power is:
$$
P_r = |\Gamma_{in}|^2 P_{in}
$$
```
P_r = abs(Gamma_in)**2 * P_in
print('Reflected power : P_r = ', P_r, 'W')
```
The voltage and current at the load can be deduced from the ABCD parameters of the line of length $L$ :
```
V_out, I_out = rf.voltage_current_propagation(V_in, I_in, Z_0,theta= gamma*d)
print('Voltage at load: V_out = ', V_out, 'V')
print('Current at load: I_out = ', I_out, 'A')
```
Note that voltages and currents are expressed a peak values. RMS values are thus:
```
print(abs(V_out)/sqrt(2), abs(I_out)/sqrt(2))
```
The power delivered to the load is thus:
```
P_out = 1/2 * real(V_out * conj(I_out))
print('Power delivered to the load : P_out = ', P_out, ' W')
```
Voltage and current are plotted below against the transmission line length (pay attention to the sign of $d$ in the voltage and current propagation: as we go from source ($z=d$) to the load ($z=0$), $\theta$ goes in the opposite direction and should be inversed)
```
ds = linspace(0, d, num=1001)
thetas = - gamma*ds
v1 = np.full_like(ds, V_in)
i1 = np.full_like(ds, I_in)
v2, i2 = rf.voltage_current_propagation(v1, i1, Z_0, thetas)
fig, (ax_V, ax_I) = plt.subplots(2, 1, sharex=True)
ax_V.plot(ds, abs(v2), lw=2)
ax_I.plot(ds, abs(i2), lw=2, c='C1')
ax_I.set_xlabel('z [m]')
ax_V.set_ylabel('|V| [V]')
ax_I.set_ylabel('|I| [A]')
ax_V.axvline(0, c='k', lw=5)
ax_I.axvline(0, c='k', lw=5)
ax_V.text(d-2, 0.4, 'input')
ax_V.text(1, 0.6, 'load')
ax_V.axvline(d, c='k', lw=5)
ax_I.axvline(d, c='k', lw=5)
ax_I.set_title('Current')
ax_V.set_title('Voltage')
```
## Using `media` objects for transmission line calculations <a class="anchor" id="cascading_networks"></a>
`scikit-rf` also provides objects representing transmission line mediums. The `Media` object provides generic methods to produce Network’s for any transmission line medium, such as transmission line length (`line()`), lumped components (`resistor()`, `capacitor()`, `inductor()`, `shunt()`, etc.) or terminations (`open()`, `short()`, `load()`). For additional references, please see the [media documentation](https://scikit-rf.readthedocs.io/en/latest/api/media/).
Let's create a transmission line `media` object for our coaxial line of characteristic impedance $Z_0$ and propagation constant $\gamma$:
```
# if not passing the gamma parameter, it would assume that gamma = alpha + j*beta = 0 + j*1
coax_line = rf.media.DefinedGammaZ0(frequency=freq, Z0=Z_0, gamma=gamma)
```
In order to build the circuit illustrated by the figure above, all the circuit's Networks are created and then [cascaded](https://scikit-rf.readthedocs.io/en/latest/tutorials/Networks.html#Cascading-and-De-embedding) with the `**` operator:
<img src="transmission_line_properties_networks.svg">
* [transmission line](https://scikit-rf.readthedocs.io/en/latest/api/media/generated/skrf.media.media.Media.line.html) of length $d$ (from the media created above),
* a [resistor](https://scikit-rf.readthedocs.io/en/latest/api/media/generated/skrf.media.media.Media.resistor.html) of impedance $Z_L$,
* then terminated by a [short](https://scikit-rf.readthedocs.io/en/latest/api/media/generated/skrf.media.media.Media.short.html).
This results in a one-port network, which $Z$-parameter is then the input impedance:
```
ntw = coax_line.line(d, unit='m') ** coax_line.resistor(Z_L) ** coax_line.short()
ntw.z
```
Note that full Network can also be built with convenience functions [load](https://scikit-rf.readthedocs.io/en/latest/api/media/generated/skrf.media.media.Media.load.html):
```
ntw = coax_line.line(d, unit='m') ** coax_line.load(rf.zl_2_Gamma0(Z_0, Z_L))
ntw.z
```
or even more directly using or [delay_load](https://scikit-rf.readthedocs.io/en/latest/api/media/generated/skrf.media.media.Media.delay_load.html):
```
ntw = coax_line.delay_load(rf.zl_2_Gamma0(Z_0, Z_L), d, unit='m')
ntw.z
```
## Determination of the propagation constant from the input impedance <a class="anchor" id="propagation_constant_from_zin"></a>
Let's assume the input impedance of a short‐circuited lossy transmission line of length d=1.5 m and a characteristic impedance of $Z_0=$100 Ohm has been measured to $Z_{in}=40 - 280j \Omega$.
<img src="transmission_line_properties_propagation_constant.svg">
The transmission line propagation constant $\gamma$ is unknown and researched. Let see how to deduce its value using `scikit-rf`:
```
# input data
z_in = 20 - 140j
z_0 = 75
d = 1.5
Gamma_load = -1 # short
```
Since we know the input impedance, we can deduce the reflection coefficient at the input of the transmission line. Since there is a direction relationship between the reflection coefficient at the load and at the input of the line:
$$
\Gamma_{in} = \Gamma_L e^{- 2 \gamma d}
$$
we can deduce the propagation constant value $\gamma$ as:
$$
\gamma = -\frac{1}{2d} \ln \left( \frac{\Gamma_{in}}{\Gamma_l} \right)
$$
This is what the convenience function `reflection_coefficient_2_propagation_constant` is doing:
```
# reflection coefficient at input
Gamma_in = rf.zl_2_Gamma0(z_0, z_in)
# line propagation constant
gamma = rf.reflection_coefficient_2_propagation_constant(Gamma_in, Gamma_load, d)
print('Line propagation constant, gamma =', gamma, 'rad/m')
```
One can check the consistency of the result by making the reverse calculation: the input impedance at a distance $d$ from the load $Z_l$:
```
rf.zl_2_zin(z_0, zl=0, theta=gamma * d)
```
Which was indeed the value given as input of the example.
Now that the line propagation constant has been determined, one can replace the short by a load resistance:
```
rf.zl_2_zin(z_0, zl=50+50j, theta=gamma * d)
```
|
github_jupyter
|
# Ridge Regression
## Goal
Given a dataset with continuous inputs and corresponding outputs, the objective is to find a function that matches the two as accurately as possible. This function is usually called the target function.
In the case of a ridge regression, the idea is to modellize the target function as a linear sum of functions (that can be non linear and are generally not). Thus, with f the target function, $\phi_i$ a base function and $w_i$ its weight in the linear sum, we suppose that:
$$f(x) = \sum w_i \phi_i(x)$$
The parameters that must be found are the weights $w_i$ for each base function $\phi_i$. This is done by minimizing the [root mean square error](https://en.wikipedia.org/wiki/Root-mean-square_deviation).
There is a closed solution to this problem given by the following equation $W = (\Phi^T \Phi)^{-1} \Phi^T Y$ with:
- $d$ the number of base functions
- $W = (w_0, ..., w_d)$ the weight vector
- $Y$ the output vector
- $\Phi(X) = (\phi_0(X)^T, \phi_1(X)^T, ..., \phi_d(X)^T)$, $\phi_0(X) = \mathbf{1}$ and $\phi_i(X) = (\phi_i(X_1), ... \phi_i(X_n))$.
If you want more details, I find that the best explanation is the one given in the book [Pattern Recognition and Machine Learning](http://research.microsoft.com/en-us/um/people/cmbishop/PRML/) by C. Bishop.
## Implementation
The following implementation does exactly what is explained above and uses three different types of kernel:
- linear $f(x) = w_0 + w_1 x$
- polynomial $f(x) = \sum_{i=0}^d w_i x^i$ with d the degree of the polynome. Notice that d = 1 is the linear case.
- gaussian $f(x) = \sum w_i \exp(-\frac{x - b_i}{2 \sigma^2})$ with $b_i$ define the location of the base function number $i$ (they are usually taken at random within the dataset) and $\sigma$ a parameter tuning the width of the functions. Here the "width" is the same for all base function but you could make them different for each of them.
The steps are:
- normalization
- building the $\Phi$ matrix
- computing the weights $W$
- plotting the found function and the dataset
```
# to display plots within the notebook
%matplotlib inline
# to define the size of the plotted images
from pylab import rcParams
rcParams['figure.figsize'] = (15, 10)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from numpy.linalg import inv
from fct import normalize_pd
```
The X matrix correspond to the inputs and the Y matrix to the outputs to predict.
```
data = pd.read_csv('datasets/data_regression.csv')
X = data['X']
Y = data['Y']
# Normalization
X = np.asmatrix(normalize_pd(X)).T
Y = np.asmatrix(normalize_pd(Y)).T
```
## Linear regression
Here we have $\Phi(X) = X$. The function we look for has the form $f(x) = ax + b$.
```
def linear_regression(X, Y):
# Building the Phi matrix
Ones = np.ones((X.shape[0], 1))
phi_X = np.hstack((Ones, X))
# Calculating the weights
w = np.dot(np.dot(inv(np.dot(phi_X.T, phi_X)), phi_X.T), Y)
# Predicting the output values
Y_linear_reg = np.dot(phi_X, w)
return Y_linear_reg
Y_linear_reg = linear_regression(X, Y)
plt.plot(X, Y, '.')
plt.plot(X, Y_linear_reg, 'r')
plt.title('Linear Regression')
plt.legend(['Data', 'Linear Regression'])
```
The obtained solution does not represent the data very well. It is because the power of representation is too low compared to the target function. This is usually referred to as **underfitting**.
## Polynomial Regression
Now, we approximate the target function by a polynom $f(x) = w_0 + w_1 x + w_2 x^2 + ... + w_d x^d$ with $d$ the degree of the polynom.
We plotted the results obtained with different degrees.
```
def polynomial_regression(X, Y, degree):
# Building the Phi matrix
Ones = np.ones((X.shape[0], 1))
# Add a column of ones
phi_X = np.hstack((Ones, X))
# add a column of X elevated to all the powers from 2 to degree
for i in range(2, degree + 1):
# calculate the vector X to the power i and add it to the Phi matrix
X_power = np.array(X) ** i
phi_X = np.hstack((phi_X, np.asmatrix(X_power)))
# Calculating the weights
w = np.dot(np.dot(inv(np.dot(phi_X.T, phi_X)), phi_X.T), Y)
# Predicting the output values
Y_poly_reg = np.dot(phi_X, w)
return Y_poly_reg
# Degrees to plot you can change these values to
# see how the degree of the polynom affects the
# predicted function
degrees = [1, 2, 20]
legend = ['Data']
plt.plot(X, Y, '.')
for degree in degrees:
Y_poly_reg = polynomial_regression(X, Y, degree)
plt.plot(X, Y_poly_reg)
legend.append('degree ' + str(degree))
plt.legend(legend)
plt.title('Polynomial regression results depending on the degree of the polynome used')
```
The linear case is still underfitting but now, we see that the polynom of degree 20 is too sensitive to the data, especially around $[-2.5, -1.5]$. This phenomena is called **overfitting**: the model starts fitting the noise in the data as well and looses its capacity to generalize.
## Regression with kernel gaussian
Lastly, we look at function of the type $f(x) = \sum \phi_i(x)$ with $\phi_i(x) = \exp({-\frac{x - b_i}{\sigma^2}}$). $b_i$ is called the base and $\sigma$ is its width.
Usually, the $b_i$ are taken randomly within the dataset. That is what I did in the implementation with b the number of bases.
In the plot, there is the base function used to compute the regressed function and the latter.
```
def gaussian_regression(X, Y, b, sigma, return_base=True):
"""b is the number of bases to use, sigma is the variance of the
base functions."""
# Building the Phi matrix
Ones = np.ones((X.shape[0], 1))
# Add a column of ones
phi_X = np.hstack((Ones, X))
# Choose randomly without replacement b values from X
# to be the center of the base functions
X_array = np.array(X).reshape(1, -1)[0]
bases = np.random.choice(X_array, b, replace=False)
bases_function = []
for i in range(1, b):
base_function = np.exp(-0.5 * (((X_array - bases[i - 1] *
np.ones(len(X_array))) / sigma) ** 2))
bases_function.append(base_function)
phi_X = np.hstack((phi_X, np.asmatrix(base_function).T))
w = np.dot(np.dot(inv(np.dot(phi_X.T, phi_X)), phi_X.T), Y)
if return_base:
return np.dot(phi_X, w), bases_function
else:
return np.dot(phi_X, w)
# By changing this value, you will change the width of the base functions
sigma = 0.2
# b is the number of base functions used
b = 5
Y_gauss_reg, bases_function = gaussian_regression(X, Y, b, sigma)
# Plotting the base functions and the dataset
plt.plot(X, Y, '.')
plt.plot(X, Y_gauss_reg)
legend = ['Data', 'Regression result']
for i, base_function in enumerate(bases_function):
plt.plot(X, base_function)
legend.append('Base function n°' + str(i))
plt.legend(legend)
plt.title('Regression with gaussian base functions')
```
We can observe that here the sigma is too small. Some part of the dataset are too far away from the bases to be taken into accoutn.
If you change the <code>sigma</code> in the code to 0.5 and then 1. You will notice how the output function will get closer to the data.
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
train = pd.read_csv("/kaggle/input/30-days-of-ml/train.csv")
test = pd.read_csv("/kaggle/input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("/kaggle/input/30-days-of-ml/sample_submission.csv")
from pandas.plotting._misc import scatter_matrix
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import OrdinalEncoder
from sklearn.neighbors import KNeighborsRegressor
from mlxtend.regressor import StackingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
%matplotlib inline
train.head()
train.isnull().sum()
s = (train.dtypes == 'object')
object_cols = list(s[s].index)
ordinal_encoder = OrdinalEncoder()
train[object_cols] = ordinal_encoder.fit_transform(train[object_cols])
train.head()
X_Data= train.drop(['target'],axis=1)
Y_Data= train['target']
x_train,x_test,y_train,y_test = train_test_split(X_Data,Y_Data,test_size=.2)
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(x_train,y_train)
predicted=knn.predict(x_test)
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, predicted)))
tree_clf = DecisionTreeRegressor(max_depth=2,random_state=42)
tree_clf.fit(X_Data,Y_Data)
tree_clf.score(X_Data,Y_Data)
prediction = tree_clf.predict(x_test)
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, prediction)))
rnd = RandomForestRegressor(max_depth=10)
rnd.fit(x_train,y_train)
rnd.score(x_test,y_test)
prediction = rnd.predict(x_test)
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, prediction)))
dtc=DecisionTreeRegressor()
knnc=KNeighborsRegressor()
rfc=RandomForestRegressor()
stregr = StackingRegressor(regressors=[dtc,knnc,rfc],
meta_regressor=knnc)
stregr.fit(x_train,y_train)
stregr.score(x_test,y_test)
prediction = stregr.predict(x_test)
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, prediction)))
from sklearn import model_selection
train = pd.read_csv("../input/30-days-of-ml/train.csv")
test = pd.read_csv("../input/30-days-of-ml/test.csv")
print(train.shape,test.shape)
train['kfold']=-1
kfold = model_selection.KFold(n_splits=10, shuffle= True, random_state = 42)
for fold, (train_indicies, valid_indicies) in enumerate(kfold.split(X=train)):
train.loc[valid_indicies,'kfold'] = fold
print(train.kfold.value_counts())
train.to_csv("trainfold_10.csv",index=False)
train = pd.read_csv("./trainfold_10.csv")
test = pd.read_csv("../input/30-days-of-ml/test.csv")
sample_submission = pd.read_csv("../input/30-days-of-ml/sample_submission.csv")
print(train.shape,test.shape)
train.sample()
from sklearn import preprocessing
final_predictions = []
score= []
useful_features = [c for c in train.columns if c not in ("id","target","kfold")]
object_cols = [col for col in useful_features if 'cat' in col]
numerical_cols = [col for col in useful_features if 'cont' in col]
test = test[useful_features]
for fold in range(10):
xtrain = train[train.kfold != fold].reset_index(drop=True)
xvalid = train[train.kfold == fold].reset_index(drop=True)
xtest = test.copy()
ytrain = xtrain.target
yvalid = xvalid.target
xtrain = xtrain[useful_features]
xvalid = xvalid[useful_features]
ordinal_encoder = OrdinalEncoder()
xtrain[object_cols] = ordinal_encoder.fit_transform(xtrain[object_cols])
xvalid[object_cols] = ordinal_encoder.transform(xvalid[object_cols])
xtest[object_cols] = ordinal_encoder.transform(xtest[object_cols])
scaler = preprocessing.StandardScaler()
xtrain[numerical_cols] = scaler.fit_transform(xtrain[numerical_cols])
xvalid[numerical_cols] = scaler.transform(xvalid[numerical_cols])
xtest[numerical_cols] = scaler.transform(xtest[numerical_cols])
xgb_params = {
'learning_rate': 0.03628302216953097,
'subsample': 0.7875490025178,
'colsample_bytree': 0.11807135201147,
'max_depth': 3,
'booster': 'gbtree',
'reg_lambda': 0.0008746338866473539,
'reg_alpha': 23.13181079976304,
'random_state':40,
'n_estimators':10000
}
model= XGBRegressor()
model.fit(xtrain,ytrain,early_stopping_rounds=300,eval_set=[(xvalid,yvalid)],verbose=2000)
preds_valid = model.predict(xvalid)
test_pre = model.predict(xtest)
final_predictions.append(test_pre)
rms = mean_squared_error(yvalid,preds_valid,squared=False)
score.append(rms)
print(f"fold:{fold},rmse:{rms}")
print(np.mean(score),np.std(score))
preds = np.mean(np.column_stack(final_predictions),axis=1)
print(preds)
sample_submission.target = preds
sample_submission.to_csv("submission.csv",index=False)
print("success")
```
|
github_jupyter
|
```
%matplotlib inline
```
GroupLasso for linear regression with dummy variables
=====================================================
A sample script for group lasso with dummy variables
Setup
-----
```
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder
from group_lasso import GroupLasso
from group_lasso.utils import extract_ohe_groups
np.random.seed(42)
GroupLasso.LOG_LOSSES = True
```
Set dataset parameters
----------------------
```
num_categories = 30
min_options = 2
max_options = 10
num_datapoints = 10000
noise_std = 1
```
Generate data matrix
--------------------
```
X_cat = np.empty((num_datapoints, num_categories))
for i in range(num_categories):
X_cat[:, i] = np.random.randint(min_options, max_options, num_datapoints)
ohe = OneHotEncoder()
X = ohe.fit_transform(X_cat)
groups = extract_ohe_groups(ohe)
group_sizes = [np.sum(groups == g) for g in np.unique(groups)]
active_groups = [np.random.randint(0, 2) for _ in np.unique(groups)]
```
Generate coefficients
---------------------
```
w = np.concatenate(
[
np.random.standard_normal(group_size) * is_active
for group_size, is_active in zip(group_sizes, active_groups)
]
)
w = w.reshape(-1, 1)
true_coefficient_mask = w != 0
intercept = 2
```
Generate regression targets
---------------------------
```
y_true = X @ w + intercept
y = y_true + np.random.randn(*y_true.shape) * noise_std
```
View noisy data and compute maximum R^2
---------------------------------------
```
plt.figure()
plt.plot(y, y_true, ".")
plt.xlabel("Noisy targets")
plt.ylabel("Noise-free targets")
# Use noisy y as true because that is what we would have access
# to in a real-life setting.
R2_best = r2_score(y, y_true)
```
Generate pipeline and train it
------------------------------
```
pipe = pipe = Pipeline(
memory=None,
steps=[
(
"variable_selection",
GroupLasso(
groups=groups,
group_reg=0.1,
l1_reg=0,
scale_reg=None,
supress_warning=True,
n_iter=100000,
frobenius_lipschitz=False,
),
),
("regressor", Ridge(alpha=1)),
],
)
pipe.fit(X, y)
```
Extract results and compute performance metrics
-----------------------------------------------
```
# Extract from pipeline
yhat = pipe.predict(X)
sparsity_mask = pipe["variable_selection"].sparsity_mask_
coef = pipe["regressor"].coef_.T
# Construct full coefficient vector
w_hat = np.zeros_like(w)
w_hat[sparsity_mask] = coef
R2 = r2_score(y, yhat)
# Print performance metrics
print(f"Number variables: {len(sparsity_mask)}")
print(f"Number of chosen variables: {sparsity_mask.sum()}")
print(f"R^2: {R2}, best possible R^2 = {R2_best}")
```
Visualise regression coefficients
---------------------------------
```
for i in range(w.shape[1]):
plt.figure()
plt.plot(w[:, i], ".", label="True weights")
plt.plot(w_hat[:, i], ".", label="Estimated weights")
plt.figure()
plt.plot([w.min(), w.max()], [coef.min(), coef.max()], "gray")
plt.scatter(w, w_hat, s=10)
plt.ylabel("Learned coefficients")
plt.xlabel("True coefficients")
plt.show()
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import sys
import shutil
sys.path.append('../code/')
sys.path.append('../python/')
from pprint import pprint
from os import path
import scipy
import os
from matplotlib import pyplot as plt
from tqdm import tqdm
from argparse import Namespace
import pickle
import seaborn as sns
import torchvision
import torchvision.transforms as transforms
from sklearn.model_selection import train_test_split
# import seaborn as sns
import numpy as np
# import pandas as pd
import scipy
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
from metrics import ranking
# from sh import sh
import data
def get_numpy_data(dataloader):
x, y = [], []
for batch_x, batch_y in tqdm(iter(dataloader)):
x.append(batch_x.numpy())
y.append(batch_y.numpy())
x = np.vstack(x)
y = np.concatenate(y)
return x, y
def create_hashgan_train_test(x, y, db_size, query_size):
train_x, query_x, train_y, query_y = train_test_split(x, y, test_size = query_size, stratify = y)
train_x, db_x, train_y, db_y = train_test_split(train_x, train_y, test_size = db_size, stratify = train_y)
return train_x, train_y, query_x, query_y, db_x, db_y
def create_train_test(x, y, query_size):
"""Train and DB are using the same dataset: gallery"""
train_x, query_x, train_y, query_y = train_test_split(x, y, test_size = query_size, stratify = y)
return train_x, train_y, query_x, query_y, train_x, train_y
def get_cifar10_data(image_size, batch_size, dataroot='../data/', workers=2, data_transforms=None):
if data_transforms is None:
data_transforms = transforms.Compose([
transforms.Scale(image_size),
transforms.ToTensor()
# transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])
train_dataset = dset.CIFAR10(root=dataroot, download=True, train=True, transform=data_transforms)
train_dataloader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers)
test_dataset = dset.CIFAR10(root=dataroot, download=True, train=False, transform=data_transforms)
test_dataloader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers)
return train_dataloader, test_dataloader
def get_places365_dataloaders(image_size, batch_size, dataroot, workers=2, data_transforms=None):
if data_transforms is None:
data_transforms = transforms.Compose([
transforms.Resize(image_size),
transforms.ToTensor()
])
train_dataloader = torch.utils.data.DataLoader(dset.ImageFolder(
root=path.join(dataroot, 'train'),
transform=data_transforms
),
batch_size=batch_size, shuffle=False, num_workers=workers)
valid_dataloader = torch.utils.data.DataLoader(dset.ImageFolder(
root=path.join(dataroot, 'val'),
transform=data_transforms
),
batch_size=batch_size, shuffle=False, num_workers=workers)
return train_dataloader, valid_dataloader
def get_mnist_data(image_size, batch_size, dataroot='../data/', workers=2, data_transforms=None):
if data_transforms is None:
data_transforms = transforms.Compose([
transforms.Scale(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, ), (0.5, )),
])
train_dataset = dset.MNIST(root=dataroot, download=True, train=True, transform=data_transforms)
train_x, train_y = get_numpy_data(torch.utils.data.DataLoader(train_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers))
test_dataset = dset.MNIST(root=dataroot, download=True, train=False, transform=data_transforms)
test_x, test_y = get_numpy_data(torch.utils.data.DataLoader(test_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers))
x = np.vstack([train_x, test_x])
y = np.concatenate([train_y, test_y])
return x, y
def get_mnist_3c_data(image_size, batch_size, dataroot='../data/', workers=2, data_transforms=None):
if data_transforms is None:
data_transforms = transforms.Compose([
transforms.Scale(image_size),
transforms.Grayscale(3),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])
train_dataset = dset.MNIST(root=dataroot, download=True, train=True, transform=data_transforms)
train_x, train_y = get_numpy_data(torch.utils.data.DataLoader(train_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers))
test_dataset = dset.MNIST(root=dataroot, download=True, train=False, transform=data_transforms)
test_x, test_y = get_numpy_data(torch.utils.data.DataLoader(test_dataset, batch_size=batch_size,
shuffle=False, num_workers=workers))
x = np.vstack([train_x, test_x])
y = np.concatenate([train_y, test_y])
return x, y
def get_flickr_data(image_size, dataroot='../data/Flickr25K', workers=2, data_transforms=None):
data_transforms = transforms.Compose([
transforms.Scale(image_size),
transforms.ToTensor(),
transforms.Normalize((0.0, 0.0, 0.0), (1.0, 1.0, 1.0))])
dataset = torchvision.datasets.ImageFolder(dataroot, transform=data_transforms)
loader = torch.utils.data.DataLoader(dataset, batch_size=1, shuffle=True, num_workers=0)
test_x, test_y = get_numpy_data(loader)
x = np.vstack([train_x, test_x])
y = np.concatenate([train_y, test_y])
return x, y
def sample_files_from_list(basedir, file_list, n_per_class, seed, ignored_file_list=set()):
sampled_files = {}
permuted_indices = np.arange(len(file_list))
print('Setting seed {}'.format(seed))
np.random.seed(seed)
np.random.shuffle(permuted_indices)
selected_files = []
for idx in tqdm(permuted_indices):
filename = file_list[idx]
if filename not in ignored_file_list:
_, label, img_filename = filename.split('/')
if label not in sampled_files:
sampled_files[label] = []
if len(sampled_files[label]) < n_per_class:
sampled_files[label].append((img_filename, path.join(basedir, filename)))
selected_files.append(filename)
for label, img_list in sampled_files.items():
assert len(img_list) == n_per_class
return sampled_files, selected_files
def sample_train_db_data_from_dataloader(dataloader, num_train, num_db, seed):
x, y = get_numpy_data(dataloader)
assert (num_train + num_db) == x.shape[0]
print('Setting seed {}'.format(seed))
train_x, db_x, train_y, db_y = train_test_split(x, y, train_size = num_train, random_state=seed, stratify = y)
return train_x, train_y, db_x, db_y
def make_dir_if_not_exist(folder):
if not path.exists(folder):
# print('Creating folder: {}'.format(folder))
os.makedirs(folder)
def create_dataset_from_files(basedir, sampled_files):
if path.exists(basedir):
raise Exception('Directory already exists: {}'.format(basedir))
pbar = tqdm(sampled_files.items())
cnt = 0
try:
for label, img_list in pbar :
label_dir = path.join(basedir, label)
make_dir_if_not_exist(label_dir)
for img_filename, img_path in img_list:
cnt += 1
shutil.copyfile(img_path, path.join(label_dir, img_filename))
if cnt %500 == 0:
pbar.set_postfix(file_cnt=cnt)
pbar.set_postfix(file_cnt=cnt)
finally:
pbar.close()
def check_evenly_sampling(a):
cnts = np.sum(ranking.one_hot_label(a), axis=0)
for cnt in cnts:
assert cnt == cnts[0]
IMAGE_SIZE = 64
```
# MNIST-3C
MNIST data with 3 channels (stacking the same copy of the 1-channel)
```
all_x, all_y = get_mnist_3c_data(IMAGE_SIZE, 100, dataroot='../data/', workers=0)
dataset = 'mnist-3c'
NUM_IMAGES = all_x.shape[0]
print('Dataset: {} images'.format(NUM_IMAGES))
print('Data range: [{}, {}]'.format(all_x.min(), all_x.max()))
# DCW-AE paper
for seed, num_query in [
(9, 10000),
(19, 10000),
(29, 10000),
(39, 10000),
(49, 10000)
]:
num_train = num_db = NUM_IMAGES - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, db_y = train_x, train_y
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
# This is used in DistillHash, SSDH papers
for seed, num_train, num_query in [
(109, 5000, 10000),
(119, 5000, 10000),
(129, 5000, 10000),
(139, 5000, 10000),
(149, 5000, 10000),
]:
num_db = NUM_IMAGES - num_train - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, query_x, db_y, query_y = train_test_split(
query_x, query_y, train_size = num_db, random_state=seed, stratify = query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
```
# MNIST
```
all_x, all_y = get_mnist_data(IMAGE_SIZE, 100, dataroot='../data/', workers=0)
dataset = 'mnist'
NUM_IMAGES = all_x.shape[0]
print('Dataset: {} images'.format(NUM_IMAGES))
print('Data range: [{}, {}]'.format(all_x.min(), all_x.max()))
# DCW-AE paper
for seed, num_query in [
(9, 10000),
(19, 10000),
(29, 10000),
(39, 10000),
(49, 10000)
]:
num_train = num_db = NUM_IMAGES - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, db_y = train_x, train_y
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
# This is used in DistillHash, SSDH papers
for seed, num_train, num_query in [
(109, 5000, 10000),
(119, 5000, 10000),
(129, 5000, 10000),
(139, 5000, 10000),
(149, 5000, 10000),
]:
num_db = NUM_IMAGES - num_train - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, query_x, db_y, query_y = train_test_split(
query_x, query_y, train_size = num_db, random_state=seed, stratify = query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
```
# Flickr25k
```
dataset = 'flickr25k'
image_size=IMAGE_SIZE
dataroot='../data/Flickr25K/'
workers=0
data_transforms = transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
loader = torch.utils.data.DataLoader(torchvision.datasets.ImageFolder(dataroot, transform=data_transforms),
batch_size=100, shuffle=True, num_workers=0)
all_x, all_y = get_numpy_data(loader)
NUM_IMAGES = all_x.shape[0]
print('Dataset: {} images'.format(NUM_IMAGES))
print('Data range: [{}, {}]'.format(all_x.min(), all_x.max()))
# DCW-AE paper
for seed, num_query in [
(9, 5000),
(19, 5000),
(29, 5000),
(39, 5000),
(49, 5000)
]:
num_train = num_db = NUM_IMAGES - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, db_y = train_x, train_y
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
```
# CIFAR-10
```
dataset = 'cifar10'
train_dataloader, query_dataloader = get_cifar10_data(IMAGE_SIZE, 100, dataroot='../data/', workers=0)
train_x, train_y = get_numpy_data(train_dataloader)
query_x, query_y = get_numpy_data(query_dataloader)
all_x = np.vstack([train_x, query_x])
all_y = np.concatenate([train_y, query_y])
NUM_IMAGES = all_x.shape[0]
print('Dataset: {} images'.format(NUM_IMAGES))
print('Data range: [{}, {}]'.format(all_x.min(), all_x.max()))
# DCW-AE paper
for seed, num_query in [
(9, 10000),
(19, 10000),
(29, 10000),
(39, 10000),
(49, 10000)
]:
num_train = num_db = NUM_IMAGES - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, db_y = train_x, train_y
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
# This is used in DistillHash, SSDH papers
for seed, num_train, num_query in [
(109, 5000, 10000),
(119, 5000, 10000),
(129, 5000, 10000),
(139, 5000, 10000),
(149, 5000, 10000),
]:
num_db = NUM_IMAGES - num_train - num_query
output_dir = '../data/{}_isize{}_seed{}'.format(dataset, IMAGE_SIZE, seed)
print('Setting seed {}: {} train, {} query, {} db'.format(seed, num_train, num_query, num_db))
if path.exists(output_dir):
print('Deleting existing folder: {}'.format(output_dir))
shutil.rmtree(output_dir)
print('Will save in {}'.format(output_dir))
os.makedirs(output_dir)
train_x, query_x, train_y, query_y = train_test_split(
all_x, all_y, train_size = num_train, random_state=seed, stratify = all_y)
db_x, query_x, db_y, query_y = train_test_split(
query_x, query_y, train_size = num_db, random_state=seed, stratify = query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'query')), x = query_x, y=query_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'train')), x = train_x, y=train_y)
np.savez_compressed(path.join(output_dir, '{}_{}_manual_{}.npz'.format(dataset, IMAGE_SIZE, 'db')), x = db_x, y=db_y)
```
# END
|
github_jupyter
|
# Pair-wise Correlations
The purpose is to identify predictor variables strongly correlated with the sales price and with each other to get an idea of what variables could be good predictors and potential issues with collinearity.
Furthermore, Box-Cox transformations and linear combinations of variables are added where applicable or useful.
## "Housekeeping"
```
import warnings
import json
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import PowerTransformer
from tabulate import tabulate
from utils import (
ALL_VARIABLES,
CONTINUOUS_VARIABLES,
DISCRETE_VARIABLES,
NUMERIC_VARIABLES,
ORDINAL_VARIABLES,
TARGET_VARIABLES,
encode_ordinals,
load_clean_data,
print_column_list,
)
pd.set_option("display.max_columns", 100)
sns.set_style("white")
```
## Load the Data
Only a subset of the previously cleaned data is used in this analysis. In particular, it does not make sense to calculate correlations involving nominal variables.
Furthermore, ordinal variables are encoded as integers (with greater values indicating a higher sales price by "guts feeling"; refer to the [data documentation](https://www.amstat.org/publications/jse/v19n3/decock/DataDocumentation.txt) to see the un-encoded values) and take part in the analysis.
A `cleaned_df` DataFrame with the original data from the previous notebook is kept so as to restore the encoded ordinal labels again at the end of this notebook for correct storage.
```
cleaned_df = load_clean_data()
df = cleaned_df[NUMERIC_VARIABLES + ORDINAL_VARIABLES + TARGET_VARIABLES]
df = encode_ordinals(df)
df[NUMERIC_VARIABLES].head()
df[ORDINAL_VARIABLES].head()
```
## Linearly "dependent" Features
The "above grade (ground) living area" (= *Gr Liv Area*) can be split into 1st and 2nd floor living area plus some undefined rest.
```
assert not (
df["Gr Liv Area"]
!= (df["1st Flr SF"] + df["2nd Flr SF"] + df["Low Qual Fin SF"])
).any()
```
The various basement areas also add up.
```
assert not (
df["Total Bsmt SF"]
!= (df["BsmtFin SF 1"] + df["BsmtFin SF 2"] + df["Bsmt Unf SF"])
).any()
```
Calculate a variable for the total living area *Total SF* as this is the number communicated most often in housing ads.
```
df["Total SF"] = df["Gr Liv Area"] + df["Total Bsmt SF"]
new_variables = ["Total SF"]
CONTINUOUS_VARIABLES.append("Total SF")
```
The different porch areas are unified into a new variable *Total Porch SF*. This potentially helps making the presence of a porch in general relevant in the prediction.
```
df["Total Porch SF"] = (
df["3Ssn Porch"] + df["Enclosed Porch"] + df["Open Porch SF"]
+ df["Screen Porch"] + df["Wood Deck SF"]
)
new_variables.append("Total Porch SF")
CONTINUOUS_VARIABLES.append("Total Porch SF")
```
The various types of rooms "above grade" (i.e., *TotRms AbvGrd*, *Bedroom AbvGr*, *Kitchen AbvGr*, and *Full Bath*) do not add up (only in 29% of the cases they do). Therefore, no single unified variable can be used as a predictor.
```
round(
100
* (
df["TotRms AbvGrd"]
== (df["Bedroom AbvGr"] + df["Kitchen AbvGr"] + df["Full Bath"])
).sum()
/ df.shape[0]
)
```
Unify the number of various types of bathrooms into a single variable. Note that "half" bathrooms are counted as such.
```
df["Total Bath"] = (
df["Full Bath"] + 0.5 * df["Half Bath"]
+ df["Bsmt Full Bath"] + 0.5 * df["Bsmt Half Bath"]
)
new_variables.append("Total Bath")
DISCRETE_VARIABLES.append("Total Bath")
```
## Box-Cox Transformations
Only numeric columns with non-negative values are eligable for a Box-Cox transformation.
```
columns = CONTINUOUS_VARIABLES + TARGET_VARIABLES
transforms = df[columns].describe().T
transforms = list(transforms[transforms['min'] > 0].index)
print_column_list(transforms)
```
A common convention is to use Box-Cox transformations only if the found lambda value (estimated with Maximum Likelyhood Estimation) is in the range from -3 to +3.
Consequently, the only applicable transformation are for *SalePrice* and the new variable *Total SF*.
```
# Check the Box-Cox tranformations for each column seperately
# to decide if the optimal lambda value is in an acceptable range.
output = []
transformed_columns = []
for column in transforms:
X = df[[column]] # 2D array needed!
pt = PowerTransformer(method="box-cox", standardize=False)
# Suppress a weird but harmless warning from scipy
with warnings.catch_warnings():
warnings.simplefilter("ignore")
pt.fit(X)
# Check if the optimal lambda is ok.
lambda_ = pt.lambdas_[0].round(1)
if -3 <= lambda_ <= 3:
lambda_label = 0 if lambda_ <= 0.01 else lambda_ # to avoid -0.0
new_column = f"{column} (box-cox-{lambda_label})"
df[new_column] = (
np.log(X) if lambda_ <= 0.001 else (((X ** lambda_) - 1) / lambda_)
)
# Track the new column in the appropiate list.
new_variables.append(new_column)
if column in TARGET_VARIABLES:
TARGET_VARIABLES.append(new_column)
else:
CONTINUOUS_VARIABLES.append(new_column)
# To show only the transformed columns below.
transformed_columns.append(column)
transformed_columns.append(new_column)
output.append((
f"{column}:",
f"use lambda of {lambda_}",
))
else:
output.append((
f"{column}:",
f"lambda of {lambda_} not in realistic range",
))
print(tabulate(sorted(output), tablefmt="plain"))
df[transformed_columns].head()
```
## Correlations
The pair-wise correlations are calculated based on the type of the variables:
- **continuous** variables are assumed to be linearly related with the target and each other or not: use **Pearson's correlation coefficient**
- **discrete** (because of the low number of distinct realizations as seen in the data cleaning notebook) and **ordinal** (low number of distinct realizations as well) variables are assumed to be related in a monotonic way with the target and each other or not: use **Spearman's rank correlation coefficient**
Furthermore, for a **naive feature selection** a "rule of thumb" classification in *weak* and *strong* correlation is applied to the predictor variables. The identified variables will be used in the prediction modelling part to speed up the feature selection. A correlation between 0.33 and 0.66 is considered *weak* while a correlation above 0.66 is considered *strong* (these thresholds refer to the absolute value of the correlation). Correlations are calculated for **each** target variable (i.e., raw "SalePrice" and Box-Cox transformation thereof). Correlations below 0.1 are considered "uncorrelated".
```
strong = 0.66
weak = 0.33
uncorrelated = 0.1
```
Two heatmaps below (implemented in the reusable `plot_correlation` function) help visualize the correlations.
Obviously, many variables are pair-wise correlated. This could yield regression coefficients *inprecise* and not usable / interpretable. At the same time, this does not lower the predictive power of a model as a whole. In contrast to the pair-wise correlations, *multi-collinearity* is not checked here.
```
def plot_correlation(data, title):
"""Visualize a correlation matrix in a nice heatmap."""
fig, ax = plt.subplots(figsize=(12, 12))
ax.set_title(title, fontsize=24)
# Blank out the upper triangular part of the matrix.
mask = np.zeros_like(data, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
# Use a diverging color map.
cmap = sns.diverging_palette(240, 0, as_cmap=True)
# Adjust the labels' font size.
labels = data.columns
ax.set_xticklabels(labels, fontsize=10)
ax.set_yticklabels(labels, fontsize=10)
# Plot it.
sns.heatmap(
data, vmin=-1, vmax=1, cmap=cmap, center=0, linewidths=.5,
cbar_kws={"shrink": .5}, square=True, mask=mask, ax=ax
)
```
### Pearson
Pearson's correlation coefficient shows a linear relationship between two variables.
```
columns = CONTINUOUS_VARIABLES + TARGET_VARIABLES
pearson = df[columns].corr(method="pearson")
plot_correlation(pearson, "Pearson's Correlation")
```
Predictors weakly or strongly correlated with a target variable are collected.
```
pearson_weakly_correlated = set()
pearson_strongly_correlated = set()
pearson_uncorrelated = set()
# Iterate over the raw and transformed target.
for target in TARGET_VARIABLES:
corrs = pearson.loc[target].drop(TARGET_VARIABLES).abs()
pearson_weakly_correlated |= set(corrs[(weak < corrs) & (corrs <= strong)].index)
pearson_strongly_correlated |= set(corrs[(strong < corrs)].index)
pearson_uncorrelated |= set(corrs[(corrs < uncorrelated)].index)
# Show that no contradiction exists between the classifications.
assert pearson_weakly_correlated & pearson_strongly_correlated == set()
assert pearson_weakly_correlated & pearson_uncorrelated == set()
```
Show the continuous variables that are weakly and strongly correlated with the sales price or uncorrelated.
```
print_column_list(pearson_uncorrelated)
print_column_list(pearson_weakly_correlated)
print_column_list(pearson_strongly_correlated)
```
### Spearman
Spearman's correlation coefficient shows an ordinal rank relationship between two variables.
```
columns = sorted(DISCRETE_VARIABLES + ORDINAL_VARIABLES) + TARGET_VARIABLES
spearman = df[columns].corr(method="spearman")
plot_correlation(spearman, "Spearman's Rank Correlation")
```
Predictors weakly or strongly correlated with a target variable are collected.
```
spearman_weakly_correlated = set()
spearman_strongly_correlated = set()
spearman_uncorrelated = set()
# Iterate over the raw and transformed target.
for target in TARGET_VARIABLES:
corrs = spearman.loc[target].drop(TARGET_VARIABLES).abs()
spearman_weakly_correlated |= set(corrs[(weak < corrs) & (corrs <= strong)].index)
spearman_strongly_correlated |= set(corrs[(strong < corrs)].index)
spearman_uncorrelated |= set(corrs[(corrs < uncorrelated)].index)
# Show that no contradiction exists between the classifications.
assert spearman_weakly_correlated & spearman_strongly_correlated == set()
assert spearman_weakly_correlated & spearman_uncorrelated == set()
```
Show the discrete and ordinal variables that are weakly and strongly correlated with the sales price or uncorrelated.
```
print_column_list(spearman_uncorrelated)
print_column_list(spearman_weakly_correlated)
print_column_list(spearman_strongly_correlated)
```
## Save the Results
### Save the weakly and strongly correlated Variables
The subset of variables that have a correlation with the house price are saved in a simple JSON file for easy re-use.
```
with open("data/correlated_variables.json", "w") as file:
file.write(json.dumps({
"uncorrelated": sorted(
list(pearson_uncorrelated) + list(spearman_uncorrelated)
),
"weakly_correlated": sorted(
list(pearson_weakly_correlated) + list(spearman_weakly_correlated)
),
"strongly_correlated": sorted(
list(pearson_strongly_correlated) + list(spearman_strongly_correlated)
),
}))
```
### Save the Data
Sort the new variables into the unprocessed `cleaned_df` DataFrame with the targets at the end. This "restores" the ordinal labels again for storage.
```
for column in new_variables:
cleaned_df[column] = df[column]
for target in set(TARGET_VARIABLES) & set(new_variables):
new_variables.remove(target)
cleaned_df = cleaned_df[sorted(ALL_VARIABLES + new_variables) + TARGET_VARIABLES]
```
In totality, this notebook added two new linear combinations and one Box-Cox transformation to the previous 78 columns.
```
cleaned_df.shape
cleaned_df.head()
cleaned_df.to_csv("data/data_clean_with_transformations.csv")
```
|
github_jupyter
|
# This notebook shows an example where a set of electrodes are selected from a dataset and then LFP is extracted from those electrodes and then written to a new NWB file
```
import pynwb
import os
#DataJoint and DataJoint schema
import datajoint as dj
## We also import a bunch of tables so that we can call them easily
from nwb_datajoint.common import (RawPosition, HeadDir, Speed, LinPos, StateScriptFile, VideoFile,
DataAcquisitionDevice, CameraDevice, Probe,
DIOEvents,
ElectrodeGroup, Electrode, Raw, SampleCount,
LFPSelection, LFP, LFPBandSelection, LFPBand,
SortGroup, SpikeSorting, SpikeSorter, SpikeSorterParameters, SpikeSortingWaveformParameters, SpikeSortingParameters, SpikeSortingMetrics, CuratedSpikeSorting,\
FirFilter,
IntervalList, SortInterval,
Lab, LabMember, LabTeam, Institution,
BrainRegion,
SensorData,
Session, ExperimenterList,
Subject,
Task, TaskEpoch,
Nwbfile, AnalysisNwbfile, NwbfileKachery, AnalysisNwbfileKachery,
interval_list_contains,
interval_list_contains_ind,
interval_list_excludes,
interval_list_excludes_ind,
interval_list_intersect,
get_electrode_indices)
import warnings
warnings.simplefilter('ignore', category=DeprecationWarning)
warnings.simplefilter('ignore', category=ResourceWarning)
```
#### Next we select the NWB file, which corresponds to the dataset we want to extract LFP from
```
nwb_file_names = Nwbfile().fetch('nwb_file_name')
# take the first one for this demonstration
nwb_file_name = nwb_file_names[0]
print(nwb_file_name)
```
#### Create the standard LFP Filters. This only needs to be done once.
```
FirFilter().create_standard_filters()
```
#### Now we Select every 16th electrode for LFP or, below, a specific set of electrodes. Choose one
Note that this will delete the current selection, and all downstream LFP and LFPBand information (if it exists), but only for the current dataset. This is fine to do if you want to generate or regenerate the LFP
```
electrode_ids = (Electrode & {'nwb_file_name' : nwb_file_name}).fetch('electrode_id')
lfp_electrode_ids = electrode_ids[range(0, len(electrode_ids), 128)]
LFPSelection().set_lfp_electrodes(nwb_file_name, lfp_electrode_ids.tolist())
LFPSelection().LFPElectrode() & {'nwb_file_name' : nwb_file_name}
```
### Or select one electrode for LFP
```
LFPSelection().set_lfp_electrodes(nwb_file_name, [0, 1])
LFPSelection().LFPElectrode() & {'nwb_file_name':nwb_file_name}
```
### Populate the LFP table. Note that this takes 2 hours or so on a laptop if you use all electrodes
```
LFP().populate([LFPSelection & {'nwb_file_name':nwb_file_name}])
```
### Now that we've created the LFP object we can perform a second level of filtering for a band of interest, in this case the theta band
We first need to create the filter
```
lfp_sampling_rate = (LFP() & {'nwb_file_name' : nwb_file_name}).fetch1('lfp_sampling_rate')
filter_name = 'Theta 5-11 Hz'
FirFilter().add_filter(filter_name, lfp_sampling_rate, 'bandpass', [4, 5, 11, 12], 'theta filter for 1 Khz data')
FirFilter()
```
Next we add an entry for the LFP Band and the electrodes we want to filter
```
# assume that we've filtered these electrodes; change this if not
lfp_band_electrode_ids = [1]
# set the interval list name corresponding to the second epoch (a run session)
interval_list_name = '02_r1'
# set the reference to -1 to indicate no reference for all channels
ref_elect = [-1]
# desired sampling rate
lfp_band_sampling_rate = 100
LFPBandSelection().set_lfp_band_electrodes(nwb_file_name, lfp_band_electrode_ids, filter_name, interval_list_name, ref_elect, lfp_band_sampling_rate)
```
Check to make sure it worked
```
(LFPBandSelection() & {'nwb_file_name' : nwb_file_name})
LFPBand().populate(LFPBandSelection() & {'nwb_file_name' : nwb_file_name})
LFPBand()
```
### Now we can plot the original signal, the LFP filtered trace, and the theta filtered trace together.
Much of the code below could be replaced by a function calls that would return the data from each electrical series
```
import matplotlib.pyplot as plt
import numpy as np
#get the three electrical series objects and the indeces of the electrodes we band pass filtered
orig_eseries = (Raw() & {'nwb_file_name' : nwb_file_name}).fetch_nwb()[0]['raw']
orig_elect_indeces = get_electrode_indices(orig_eseries, lfp_band_electrode_ids)
lfp_eseries = (LFP() & {'nwb_file_name' : nwb_file_name}).fetch_nwb()[0]['lfp']
lfp_elect_indeces = get_electrode_indices(lfp_eseries, lfp_band_electrode_ids)
lfp_band_eseries = (LFPBand() & {'nwb_file_name' : nwb_file_name}).fetch_nwb()[0]['filtered_data']
lfp_band_elect_indeces = get_electrode_indices(lfp_band_eseries, lfp_band_electrode_ids)
# get a list of times for the first run epoch and then select a 2 second interval 100 seconds from the beginning
run1times = (IntervalList & {'nwb_file_name': nwb_file_name, 'interval_list_name' : '02_r1'}).fetch1('valid_times')
plottimes = [run1times[0][0] + 101, run1times[0][0] + 102]
# get the time indeces for each dataset
orig_time_ind = np.argwhere(np.logical_and(orig_eseries.timestamps > plottimes[0], orig_eseries.timestamps < plottimes[1]))
lfp_time_ind = np.argwhere(np.logical_and(lfp_eseries.timestamps > plottimes[0], lfp_eseries.timestamps < plottimes[1]))
lfp_band_time_ind = np.argwhere(np.logical_and(lfp_band_eseries.timestamps > plottimes[0], lfp_band_eseries.timestamps < plottimes[1]))
plt.plot(orig_eseries.timestamps[orig_time_ind], orig_eseries.data[orig_time_ind,orig_elect_indeces[0]], 'k-')
plt.plot(lfp_eseries.timestamps[lfp_time_ind], lfp_eseries.data[lfp_time_ind,lfp_elect_indeces[0]], 'b-')
plt.plot(lfp_band_eseries.timestamps[lfp_band_time_ind], lfp_band_eseries.data[lfp_band_time_ind,lfp_band_elect_indeces[0]], 'r-')
plt.xlabel('Time (sec)')
plt.ylabel('Amplitude (AD units)')
plt.show()
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Forecasting with an RNN
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/examples/blob/master/courses/udacity_intro_to_tensorflow_for_deep_learning/l08c06_forecasting_with_rnn.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/examples/blob/master/courses/udacity_intro_to_tensorflow_for_deep_learning/l08c06_forecasting_with_rnn.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# Use the %tensorflow_version magic if in colab.
%tensorflow_version 2.x
except Exception:
pass
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
keras = tf.keras
def plot_series(time, series, format="-", start=0, end=None, label=None):
plt.plot(time[start:end], series[start:end], format, label=label)
plt.xlabel("Time")
plt.ylabel("Value")
if label:
plt.legend(fontsize=14)
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def white_noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
def window_dataset(series, window_size, batch_size=32,
shuffle_buffer=1000):
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer)
dataset = dataset.map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
def model_forecast(model, series, window_size):
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(32).prefetch(1)
forecast = model.predict(ds)
return forecast
time = np.arange(4 * 365 + 1)
slope = 0.05
baseline = 10
amplitude = 40
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
noise_level = 5
noise = white_noise(time, noise_level, seed=42)
series += noise
plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
```
## Simple RNN Forecasting
```
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
window_size = 30
train_set = window_dataset(x_train, window_size, batch_size=128)
model = keras.models.Sequential([
keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
keras.layers.SimpleRNN(100, return_sequences=True),
keras.layers.SimpleRNN(100),
keras.layers.Dense(1),
keras.layers.Lambda(lambda x: x * 200.0)
])
lr_schedule = keras.callbacks.LearningRateScheduler(
lambda epoch: 1e-7 * 10**(epoch / 20))
optimizer = keras.optimizers.SGD(lr=1e-7, momentum=0.9)
model.compile(loss=keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(train_set, epochs=100, callbacks=[lr_schedule])
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-7, 1e-4, 0, 30])
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
window_size = 30
train_set = window_dataset(x_train, window_size, batch_size=128)
valid_set = window_dataset(x_valid, window_size, batch_size=128)
model = keras.models.Sequential([
keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
keras.layers.SimpleRNN(100, return_sequences=True),
keras.layers.SimpleRNN(100),
keras.layers.Dense(1),
keras.layers.Lambda(lambda x: x * 200.0)
])
optimizer = keras.optimizers.SGD(lr=1.5e-6, momentum=0.9)
model.compile(loss=keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
early_stopping = keras.callbacks.EarlyStopping(patience=50)
model_checkpoint = keras.callbacks.ModelCheckpoint(
"my_checkpoint", save_best_only=True)
model.fit(train_set, epochs=500,
validation_data=valid_set,
callbacks=[early_stopping, model_checkpoint])
model = keras.models.load_model("my_checkpoint")
rnn_forecast = model_forecast(
model,
series[split_time - window_size:-1],
window_size)[:, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast)
keras.metrics.mean_absolute_error(x_valid, rnn_forecast).numpy()
```
## Sequence-to-Sequence Forecasting
```
def seq2seq_window_dataset(series, window_size, batch_size=32,
shuffle_buffer=1000):
series = tf.expand_dims(series, axis=-1)
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size + 1, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size + 1))
ds = ds.shuffle(shuffle_buffer)
ds = ds.map(lambda w: (w[:-1], w[1:]))
return ds.batch(batch_size).prefetch(1)
for X_batch, Y_batch in seq2seq_window_dataset(tf.range(10), 3,
batch_size=1):
print("X:", X_batch.numpy())
print("Y:", Y_batch.numpy())
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
window_size = 30
train_set = seq2seq_window_dataset(x_train, window_size,
batch_size=128)
model = keras.models.Sequential([
keras.layers.SimpleRNN(100, return_sequences=True,
input_shape=[None, 1]),
keras.layers.SimpleRNN(100, return_sequences=True),
keras.layers.Dense(1),
keras.layers.Lambda(lambda x: x * 200)
])
lr_schedule = keras.callbacks.LearningRateScheduler(
lambda epoch: 1e-7 * 10**(epoch / 30))
optimizer = keras.optimizers.SGD(lr=1e-7, momentum=0.9)
model.compile(loss=keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(train_set, epochs=100, callbacks=[lr_schedule])
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-7, 1e-4, 0, 30])
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
window_size = 30
train_set = seq2seq_window_dataset(x_train, window_size,
batch_size=128)
valid_set = seq2seq_window_dataset(x_valid, window_size,
batch_size=128)
model = keras.models.Sequential([
keras.layers.SimpleRNN(100, return_sequences=True,
input_shape=[None, 1]),
keras.layers.SimpleRNN(100, return_sequences=True),
keras.layers.Dense(1),
keras.layers.Lambda(lambda x: x * 200.0)
])
optimizer = keras.optimizers.SGD(lr=1e-6, momentum=0.9)
model.compile(loss=keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
early_stopping = keras.callbacks.EarlyStopping(patience=10)
model.fit(train_set, epochs=500,
validation_data=valid_set,
callbacks=[early_stopping])
rnn_forecast = model_forecast(model, series[..., np.newaxis], window_size)
rnn_forecast = rnn_forecast[split_time - window_size:-1, -1, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast)
keras.metrics.mean_absolute_error(x_valid, rnn_forecast).numpy()
```
|
github_jupyter
|
# Introduction to TensorFlow v2 : Basics
### Importing and printing the versions
```
import tensorflow as tf
print("TensorFlow version: {}".format(tf.__version__))
print("Eager execution is: {}".format(tf.executing_eagerly()))
print("Keras version: {}".format(tf.keras.__version__))
```
### TensorFlow Variables
[Tensors](https://www.tensorflow.org/guide/tensor) are multi-dimensional arrays in TensorFlow. But, Tensors are immutable in nature. [Variables](https://www.tensorflow.org/guide/variable) are a way to store data which can be manipulated and changed easily. Variables are automatically placed on the fastest compatible device for it's datatype. For ex: If GPU is found, the tensors are automatically placed on GPU directly.
```
var = 1
# Defining a Tensorflow Variables
ten = tf.Variable(7)
another_tensor = tf.Variable([[1, 2],[3, 4]])
var, ten, another_tensor
```
### Creating new Variables
```
f1 = tf.Variable(100.6)
print(f1)
```
### Assigning values to existing Variables
```
# Assign and print the Data-Type
print(f1.assign(25))
print(f1.dtype)
f2 = tf.Variable(7, dtype = tf.float64)
print(f2.dtype)
# Creating a TensorFlow constant - Value cannot be changed in future
constant_var = tf.constant(10)
print(constant_var)
```
### Extracting the value from a Tensor and formatting like a Numpy array using .numpy()
```
constant_var.numpy()
```
### Rank and Shape of Tensor
About [Rank and Shape](https://www.tensorflow.org/guide/tensor#about_shapes) in TensorFlow
```
tf.rank(another_tensor)
tf.shape(another_tensor)
new_tensor = tf.Variable([ [ [0., 1., 2.], [3., 4., 5.] ], [ [6., 7., 8.], [9., 10., 11.] ] ])
print(new_tensor.shape)
print(tf.rank(new_tensor))
```
### Reshaping Tensors
```
new_reshape = tf.reshape(new_tensor, [2, 6])
recent_reshape = tf.reshape(new_tensor, [1, 12])
print(new_reshape)
print(recent_reshape)
```
### Broadcasting Feature
```
new_tensor + 4
new_tensor - 4
new_tensor * 4
```
### Matrix Multiplication
```
new_tensor * new_tensor
u = tf.constant([[5, 6, 7]])
v = tf.constant([[8, 9, 0]])
print('Matrix Multiplication - Transpose')
print(tf.matmul(u, tf.transpose(a=v)))
```
### Type Casting
```
int_tensor = tf.cast(ten, dtype=tf.float32)
print(int_tensor)
```
### Arithmetic Operations
```
a = tf.random.normal(shape=(2, 2))
b = tf.random.normal(shape=(2, 2))
c = a + b
d = tf.square(c)
e = tf.exp(d)
print('Addition - {}'.format(c))
print('Square Root - {}'.format(d))
print('Exponent - {}'.format(e))
```
# TensorFlow v2 Functions
### Squared Difference Function
```
#Squared Difference Function
x = [2, 4, 6, 8, 12]
y = 6
#(x-y)*(x-y)
result = tf.math.squared_difference(x, y)
result
```
### Reduce Mean
```
numbers = tf.constant([[6., 9.], [3., 5.]])
print(numbers)
tf.reduce_mean(input_tensor = numbers)
```
### Mean across columns
```
# Reduce rows -> Find mean across columns
#(6. + 3.)/2, (9. + 5.)/2
print(tf.reduce_mean(input_tensor = numbers, axis = 0))
# (6. + 3.)/2, (9. + 5.)/2
print(tf.reduce_mean(input_tensor = numbers, axis = 0, keepdims = True))
```
### Mean across rows
```
# Reduce columns -> Find mean across rows
#(6. + 9.)/2, (3. + 5.)/2
print(tf.reduce_mean(input_tensor = numbers, axis = 1))
# (6. + 9.)/2, (3. + 5.)/2
print(tf.reduce_mean(input_tensor = numbers, axis = 1, keepdims = True))
```
### Generating normal distribution in a tensor
```
print(tf.random.normal(shape = (3, 2), mean = 10, stddev = 2, dtype = tf.float32, seed = None, name = None))
```
### Generating uniform distribution in a tensor
```
tf.random.uniform(shape = (3, 2), minval = 0, maxval = 1, dtype = tf.float32, seed = None, name = None)
```
### Random Seed in Tensorflow
```
print('Random Seed - 11\n')
tf.random.set_seed(11)
random_1 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
random_2 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
print(random_1)
print(random_2)
print('\n')
print('Random Seed - 12\n')
tf.random.set_seed(12)
random_1 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
random_2 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
print(random_1)
print(random_2)
print('\n')
print('Random Seed - 11\n')
tf.random.set_seed(11)
random_1 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
random_2 = tf.random.uniform(shape = (2, 2), maxval = 7, dtype = tf.int32)
print(random_1)
print(random_2)
```
### Max, Min and Indices
```
tensor_m = tf.constant([2, 20, 15, 32, 77, 29, -16, -51, 29])
print(tensor_m)
# Max argument
index = tf.argmax(input = tensor_m)
print('Index of max: {}\n'.format(index))
print('Max element: {}'.format(tensor_m[index].numpy()))
print(tensor_m)
# Min argument
index = tf.argmin(input = tensor_m)
print('Index of minumum element: {}\n'.format(index))
print('Minimum element: {}'.format(tensor_m[index].numpy()))
```
# TensorFlow v2 : Advanced
### Computing gradients with GradientTape - Automatic Differentiation
TensorFlow v2 has this API for recording gradient values based on the values computed in the forward pass with respect to inputs. Since we need values to be remembered during the forward pass, the tf.GradientTape provides us a way to automatically differentiate a certain function wrt to the input variable specified. To read more on Auto Diiferentiation in TensorFlow v2 click [here]https://www.tensorflow.org/guide/autodiff).
```
x = tf.random.normal(shape=(2, 2))
y = tf.random.normal(shape=(2, 2))
with tf.GradientTape() as tape:
# Start recording the history of operations applied to x
tape.watch(x)
# Do some math using x and y
z = tf.sqrt(tf.square(x) + tf.square(y))
# What's the gradient of z with respect to x
dz = tape.gradient(z, x)
print(dz)
```
tf.GradientTape API automatically watches the function to be differentiated, no need to explicitly mention/run tape.watch()
```
x = tf.Variable(x)
with tf.GradientTape() as tape:
# Doing some calculations using x and y
z = tf.sqrt(tf.square(x) + tf.square(y))
# Getting the gradient of z wrt x
dz = tape.gradient(z, x)
print(dz)
```
We can perform differentiation in chains also, using two tapes!
```
with tf.GradientTape() as outer_tape:
with tf.GradientTape() as tape:
# Computation using x and y
z = tf.sqrt(tf.square(x) + tf.square(y))
# First differentiation of z wrt x
dz = tape.gradient(z, x)
# Second differentiation of z wrt x
dz2 = outer_tape.gradient(dz, x)
print(dz2)
```
### Tensorflow v2 Graph Function
Read [here](https://www.tensorflow.org/guide/intro_to_graphs) for more information on Computation Graphs and TensorFlow Functions of TensorFlow v1
```
#Normal Python function
def f1(x, y):
return tf.reduce_mean(input_tensor=tf.multiply(x ** 2, 5) + y**2)
#Converting that into Tensorflow Graph function
f2 = tf.function(f1)
x = tf.constant([7., -2.])
y = tf.constant([8., 6.])
#Funtion 1 and function 2 return the same value, but function 2 executes as a TensorFlow graph
assert f1(x,y).numpy() == f2(x,y).numpy()
ans = f1(x,y)
print(ans)
ans = f2(x,y)
print(ans)
```
# TensorFlow v2 : Linear Regression and tf.function
### Let's see what is the importance of tf.function with a small example of Linear Regression
```
input_dim = 2
output_dim = 1
learning_rate = 0.01
# This is our weight matrix
w = tf.Variable(tf.random.uniform(shape=(input_dim, output_dim)))
# This is our bias vector
b = tf.Variable(tf.zeros(shape=(output_dim,)))
def compute_predictions(features):
return tf.matmul(features, w) + b
def compute_loss(labels, predictions):
return tf.reduce_mean(tf.square(labels - predictions))
def train_on_batch(x, y):
with tf.GradientTape() as tape:
predictions = compute_predictions(x)
loss = compute_loss(y, predictions)
# Note that `tape.gradient` works with a list as well (w, b).
dloss_dw, dloss_db = tape.gradient(loss, [w, b])
w.assign_sub(learning_rate * dloss_dw)
b.assign_sub(learning_rate * dloss_db)
return loss
import numpy as np
import random
import matplotlib.pyplot as plt
%matplotlib inline
# Prepare a dataset.
num_samples = 10000
negative_samples = np.random.multivariate_normal(mean=[0, 3], cov=[[1, 0.5],[0.5, 1]], size=num_samples)
positive_samples = np.random.multivariate_normal(mean=[3, 0], cov=[[1, 0.5],[0.5, 1]], size=num_samples)
features = np.vstack((negative_samples, positive_samples)).astype(np.float32)
labels = np.vstack((np.zeros((num_samples, 1), dtype='float32'), np.ones((num_samples, 1), dtype='float32')))
plt.scatter(features[:, 0], features[:, 1], c=labels[:, 0])
# Shuffle the data.
indices = np.random.permutation(len(features))
features = features[indices]
labels = labels[indices]
# Create a tf.data.Dataset object for easy batched iteration
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
dataset = dataset.shuffle(buffer_size=1024).batch(256)
for epoch in range(10):
for step, (x, y) in enumerate(dataset):
loss = train_on_batch(x, y)
print('Epoch %d: last batch loss = %.4f' % (epoch, float(loss)))
predictions = compute_predictions(features)
plt.scatter(features[:, 0], features[:, 1], c=predictions[:, 0] > 0.5)
```
### Analysizing the code run time
TensorFlow v2 with Eager Execution
```
import time
t0 = time.time()
for epoch in range(20):
for step, (x, y) in enumerate(dataset):
loss = train_on_batch(x, y)
t_end = time.time() - t0
print('Time per epoch: %.3f s' % (t_end / 20,))
```
Adding the @tf.function to convert the function into a static graph (TensorFlow v1)
```
@tf.function
def train_on_batch_tf(x, y):
with tf.GradientTape() as tape:
predictions = compute_predictions(x)
loss = compute_loss(y, predictions)
dloss_dw, dloss_db = tape.gradient(loss, [w, b])
w.assign_sub(learning_rate * dloss_dw)
b.assign_sub(learning_rate * dloss_db)
return loss
```
Running using the Static Graph method
```
t0 = time.time()
for epoch in range(20):
for step, (x, y) in enumerate(dataset):
loss = train_on_batch_tf(x, y)
t_end = time.time() - t0
print('Time per epoch: %.3f s' % (t_end / 20,))
```
## There is a huge decrease in the time taken per epoch!!!
## Eager execution is great for debugging and printing results line-by-line, but when it's time to scale, static graphs are a researcher's best friends.
|
github_jupyter
|
```
%reload_ext autoreload
%autoreload 2
import sys
import os
BASE_DIR = os.path.abspath(os.path.join(os.path.dirname("__file__"), os.path.pardir))
sys.path.append(BASE_DIR)
import cv2
import time
import numpy as np
import matplotlib.pyplot as plt
import imgaug as ia
import imgaug.augmenters as iaa
import tensorflow as tf
from data_processor.data_loader import DataLoader, show_batch, DataLoaderWithoutCache
from models.dcgan import DCGAN, gen_random
os.environ["CUDA_VISIBLE_DEVICES"] = "1"
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
cpus = tf.config.experimental.list_physical_devices(device_type='CPU')
tf.config.experimental.set_virtual_device_configuration(
gpus[0],
[tf.config.experimental.VirtualDeviceConfiguration(memory_limit=1024*7.5)])
batch_size = 256
cache_size = 1024 * 64
nz = 100
glr = 2e-4
dlr = 2e-4
img_dir = 'data/faces/'
IMG_HEIGHT, IMG_WIDTH, IMG_CHANNELS = 64, 64, 3
def scale(img):
return (img - 127.5) / 127.5
def rescale(img):
return img * 127.5 + 127.5
sometimes = lambda aug: iaa.Sometimes(0.5, aug)
aug = iaa.Sequential(
[
iaa.Fliplr(0.5), # horizontally flip 50% of all images
sometimes(iaa.CropAndPad(
percent=(-0.05, 0.1),
pad_mode=ia.ALL,
pad_cval=(0, 255)
)),
sometimes(iaa.Affine(
scale={"x": (0.9, 1.1), "y": (0.9, 1.1)}, # scale images to 80-120% of their size, individually per axis
translate_percent={"x": (-0.1, 0.1), "y": (-0.1, 0.1)}, # translate by -20 to +20 percent (per axis)
rotate=(-10, 10), # rotate by -45 to +45 degrees
order=[0, 1], # use nearest neighbour or bilinear interpolation (fast)
cval=(0, 255), # if mode is constant, use a cval between 0 and 255
mode=ia.ALL # use any of scikit-image's warping modes (see 2nd image from the top for examples)
)),
],
random_order=True
)
data_loader = DataLoaderWithoutCache(data_dir=os.path.join(BASE_DIR, img_dir), img_shape=(IMG_HEIGHT, IMG_WIDTH, IMG_CHANNELS), cache_size=cache_size)
data_loader.scale(scale)\
.batch(batch_size)\
.augment(lambda x: aug(images=x))
img_batch = rescale(next(iter(data_loader)))
show_batch(img_batch)
num_examples_to_generate = 36
seed = gen_random((num_examples_to_generate, nz))
def show_generator(generator, seed):
predictions = generator(seed, training=False).numpy()
images = rescale(predictions).astype(np.uint8)
show_batch(images)
dcgan = DCGAN(image_shape=(IMG_HEIGHT, IMG_WIDTH, IMG_CHANNELS), dlr=dlr, glr=glr, nz=nz)
dcgan.summary()
show_generator(dcgan.generator, seed)
for epoch in range(500):
for batch_idx, img_batch in enumerate(data_loader):
dcgan.train_step(img_batch, num_iter_disc=1, num_iter_gen=1)
print(f'epoch: {epoch}, batch: {batch_idx} ', end='\r')
show_generator(dcgan.generator, seed)
img_batch = rescale(next(iter(data_loader)))
show_batch(img_batch)
show_generator(dcgan.generator, seed)
```
|
github_jupyter
|
# Statistics & Data Analysis
## Req
#### Import Requirements
##### HTML formatting
```
from IPython.display import HTML
HTML("""<style type="text/css">
table.dataframe td, table.dataframe th {
max-width: none;
</style>
""")
HTML("""<style type="text/css">
table.dataframe td, table.dataframe th {
max-width: none;
white-space: normal;
}
</style>
""")
HTML("""<style type="text/css">
table.dataframe td, table.dataframe th {
max-width: none;
white-space: normal;
line-height: normal;
}
</style>
""")
HTML("""<style type="text/css">
table.dataframe td, table.dataframe th {
max-width: none;
white-space: normal;
line-height: normal;
padding: 0.3em 0.5em;
}
</style>
""")
import numpy as np
import pandas as pd
import scipy
import matplotlib.pyplot as plt
from pandas.api.types import CategoricalDtype
from plotnine import *
from scipy.stats import *
import scikit_posthocs as sp
data = pd.read_csv("./NewCols.csv")
```
## Calculating the differences between the noremalized values.
```
data_control = data[data["treatment"] == "baseline"]
data_control.to_csv("./control.csv")
data_treatment = data[data["treatment"] == "intravenous LPS"]
data_control.to_csv("./lps.csv")
procData = data_treatment
procData['diff_AVAR2'] = (
np.array(data_treatment["AVAR2"]) - np.array(data_control["AVAR2"])).tolist()
procData["diff_CVAR2"] = (
np.array(data_treatment["CVAR2"]) - np.array(data_control["CVAR2"])).tolist()
procData["diff_AWT2"] = (np.array(data_treatment["AWT2"]) -
np.array(data_control["AWT2"])).tolist()
procData["diff_CWT2"] = (np.array(data_treatment["CWT2"]) -
np.array(data_control["CWT2"])).tolist()
procData["diff_total2"] = (
np.array(data_treatment["total2"]) - np.array(data_control["total2"])).tolist()
procData["diff_totalA"] = (
np.array(data_treatment["totalA"]) - np.array(data_control["totalA"])).tolist()
procData["diff_totalC"] = (
np.array(data_treatment["totalC"]) - np.array(data_control["totalC"])).tolist()
procData["diff_totalWT"] = (np.array(
data_treatment["totalWT"]) - np.array(data_control["totalWT"])).tolist()
procData["diff_totalVar"] = (np.array(
data_treatment["totalVar"]) - np.array(data_control["totalVar"])).tolist()
procData.to_csv("./procData.csv")
newDF= data_control[["testGroup","tg2"]]
newDF
newDF.rename(columns = {'testGroup':'c_tg','tg2':'c_tg2'}, inplace=True)
newDF
newDF.index = procData.index
procData= pd.concat([procData,newDF], axis=1)
```
#### Difference Table
```
pd.set_option('display.max_rows', procData.shape[0]+1)
diff_data = procData.loc[ :,"diff_AVAR2":"diff_totalVar" ]
diff_data.to_csv("./diffData.csv")
diff_data.describe()
diff_data.var()
diff_data.std()
diff_data.skew()
diff_data.kurtosis().tolist()
diff_data.kurtosis()
```
## Graph Data -
```
from plotnine import *
ggplot(data, aes(x='treatment', y='AWT2') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(data_control["AWT2"],data_treatment["AWT2"])
ggplot(data, aes(x='treatment', y='CWT2') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(data_control["CWT2"],data_treatment["CWT2"])
ggplot(data, aes(x='treatment', y='AVAR2') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(data_control["AVAR2"],data_treatment["AVAR2"])
ggplot(data, aes(x='treatment', y='CVAR2') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(data_control["CVAR2"],data_treatment["CVAR2"])
removed_outliers = data.total2.between(data.total2.quantile(.05), data.total2.quantile(.95))
data_total= data[removed_outliers]
ggplot(data_total, aes(x='treatment',y="total2" ), ) + geom_boxplot(outlier_shape = "") + geom_jitter(data_total,aes(y="total2",colour='treatment',shape='treatment') ) + ggtitle("QQ Plot of IRAK-1 expression per GbP") + xlab("Treatment") + ylab("Total IRAK-1 Levels per Gigabase pair") + ylim(data_total.total2.quantile(.05), data_total.total2.quantile(.95))
a = 0.05
wilcoxon(diff_data["diff_total2"])
removed_outliers_diffData = diff_data.diff_total2.between(diff_data.diff_total2.quantile(.05), diff_data.diff_total2.quantile(.95))
difftotalData=diff_data[removed_outliers_diffData]
ggplot(difftotalData, aes( x='0',y='diff_total2') ) + geom_boxplot() + geom_point(color="red") + ylim(difftotalData.diff_total2.quantile(.05), difftotalData.diff_total2.quantile(.95)) + ggtitle("QQ Plot of changes in IRAK-1 levels per Gbp") + xlab("Treatment") + ylab("Changes in IRAK-1 Levels per Gigabase pair")
data_plot = data_treatment
controlData = data_control['total2']
controlData
data_plot["ctrl_total2"]=controlData.to_list()
data_plot
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(data_plot.total2.to_numpy().reshape((-1, 1)), data_plot.ctrl_total2)
r_sq= model.score(data_plot.total2.to_numpy().reshape((-1, 1)), data_plot.ctrl_total2)
print('coefficient of determination:', r_sq)
print('intercept:', model.intercept_)
print('slope:', model.coef_)
ggplot(data_plot,aes(x='total2',y='ctrl_total2') ) + geom_point() + geom_smooth(method='lm')
from sklearn import linear_model
lm = linear_model.LinearRegression()
shapiro_test = shapiro(data_control['total2'])
shapiro_test
shapiro_test = shapiro(data_treatment['total2'])
shapiro_test
shapiro_test = shapiro(diff_data['diff_total2'])
shapiro_test
ggplot(data, aes(x='treatment', y='totalVar') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(diff_data["diff_totalVar"])
ggplot(data, aes(x='treatment', y='totalWT') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(diff_data["diff_totalWT"])
ggplot(data, aes(x='treatment', y='totalA') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(diff_data["diff_totalA"])
ggplot(data, aes(x='treatment', y='totalC') ) + geom_boxplot() + geom_jitter(data,aes(colour='treatment',shape='treatment'))
a = 0.05
wilcoxon(diff_data["diff_totalC"])
```
## Statistics
### Total 2 Comparison
#### Wilcoxon non-parametric
```
a = 0.05
w, p = wilcoxon(data_control["total2"],data_treatment["total2"])
print(w, p)
if (p < a):
print("As P"+str(p)+" is less than a: "+str(a))
print( "we reject the Null Hypothesis.")
print(". There is significant difference betwween the groups")
else:
print("As P"+p+" is larger than a: "+str(a))
print( "we FAIL TO reject the Null Hypothesis.")
print(". There is NOT a significant difference betwween the groups")
```
#### Freidman's Anova
```
sp.posthoc_nemenyi_friedman(diff_data)
```
Friedman Tes
### other
```
a = 0.05
w, p = wilcoxon((data_control["totalA"]/data_control["totalC"] ),(data_treatment["totalA"]/data_treatment["totalC"]))
print(w, p)
a = 0.05
w, p = wilcoxon((data_control["AVAR2"]/data_control["CVAR2"] ),(data_treatment["AVAR2"]/data_treatment["CVAR2"]))
print(w, p)
a = 0.05
w, p = wilcoxon((data_control["AWT2"]/data_control["CWT2"] ),(data_treatment["AWT2"]/data_treatment["CWT2"]))
print(w, p)
ggplot()+geom_histogram(procData,aes(x="tg2"))
ggplot()+geom_histogram(procData,aes(x="mutant"))
ggplot()+geom_bar(procData,aes(x="spliceVariant",fill="mutant"))
ggplot()+geom_col(procData,aes(x="spliceVariant",y="diff_totalA/diff_totalC",fill="mutant"))
a = 0.05
diff_data = procData[(data["totalC"] > 0 ) & (data["totalA"] > 0 )]
ggplot()+geom_histogram(diff_data,aes(x="tg2"))
w, p = wilcoxon((diff_data["totalC"] )/(diff_data["totalA"]))
print(w, p)
a = 0.05
w, p = wilcoxon(data_control["total2"],data_treatment["total2"])
print(w, p)
```
2 graphs
1. Do the Table
3. Black and white
3. Make sure its not sloppy
4.
control, LPS & Difference.
correlation plot for each patient - total 2 & diff_total2
Look for A/C ratios
ggplot(data_plot,aes(x='total2',y='ctrl_total2') ) + geom_point(colour) + geom_smooth(method='lm')
|
github_jupyter
|
```
import os
import numpy as np
import tensorflow as tf
from tensorflow.python.keras.datasets import mnist
from tensorflow.contrib.eager.python import tfe
# enable eager mode
tf.enable_eager_execution()
tf.set_random_seed(0)
np.random.seed(0)
if not os.path.exists('weights/'):
os.makedirs('weights/')
# constants
units = 64
batch_size = 256
epochs = 2
num_classes = 10
# dataset loading
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((-1, 28, 28)) # 28 timesteps, 28 inputs / timestep
x_test = x_test.reshape((-1, 28, 28)) # 28 timesteps, 28 inputs / timeste
# one hot encode the labels. convert back to numpy as we cannot use a combination of numpy
# and tensors as input to keras
y_train_ohe = tf.one_hot(y_train, depth=num_classes).numpy()
y_test_ohe = tf.one_hot(y_test, depth=num_classes).numpy()
print('x train', x_train.shape)
print('y train', y_train_ohe.shape)
print('x test', x_test.shape)
print('y test', y_test_ohe.shape)
```
# Bi-Directional LSTM
Writing a Bi-directional LSTM in keras is super simple with the Bidirectional wrapper. However the speed of such a model is slower than expected.
Some fixes for it are to use the GPU implementation for all the cells, and to unroll the entire RNN before hand. In normal Keras and Tensorflow, unrolling the RNN yields significant speed improvements since the symbolic loop is replaced with the unrolled graph representation of the RNN.
In Eager, I don't believe it is doing much to help with the speed.
```
class BiRNN(tf.keras.Model):
def __init__(self, units, num_classes, merge_mode='concat', num_layers=1):
super(BiRNN, self).__init__()
self.impl = 1 if tfe.num_gpus() == 0 else 2
self.cells = [tf.keras.layers.LSTMCell(units, implementation=self.impl) for _ in range(num_layers)]
self.rnn = tf.keras.layers.RNN(self.cells, unroll=True) # slower if not unrolled - probably because it is using K.rnn() internally.
self.bidirectional = tf.keras.layers.Bidirectional(self.rnn, merge_mode=merge_mode)
self.classifier = tf.keras.layers.Dense(num_classes)
def call(self, inputs, training=None, mask=None):
x = self.bidirectional(inputs)
output = self.classifier(x)
# softmax op does not exist on the gpu, so always use cpu
with tf.device('/cpu:0'):
output = tf.nn.softmax(output)
return output
device = '/cpu:0' if tfe.num_gpus() == 0 else '/gpu:0'
with tf.device(device):
# build model and optimizer
model = BiRNN(units, num_classes, num_layers=2)
model.compile(optimizer=tf.train.AdamOptimizer(0.01), loss='categorical_crossentropy',
metrics=['accuracy'])
# TF Keras tries to use entire dataset to determine shape without this step when using .fit()
# Fix = Use exactly one sample from the provided input dataset to determine input/output shape/s for the model
dummy_x = tf.zeros((1, 28, 28))
model._set_inputs(dummy_x)
# train
model.fit(x_train, y_train_ohe, batch_size=batch_size, epochs=epochs,
validation_data=(x_test, y_test_ohe), verbose=1)
# evaluate on test set
scores = model.evaluate(x_test, y_test_ohe, batch_size, verbose=1)
print("Final test loss and accuracy :", scores)
saver = tfe.Saver(model.variables)
saver.save('weights/07_01_bi_rnn/weights.ckpt')
```
|
github_jupyter
|
# ANCOM: WGS
```
library(tidyverse)
library(magrittr)
source("/Users/Cayla/ANCOM/scripts/ancom_v2.1.R")
```
## T2
```
t2 <- read_csv('https://github.com/bryansho/PCOS_WGS_16S_metabolome/raw/master/DESEQ2/WGS/T2/T2_filtered_greater_00001.csv')
head(t2,n=1)
t2.meta <- read_csv('https://github.com/bryansho/PCOS_WGS_16S_metabolome/raw/master/DESEQ2/WGS/T2/Deseq2_T2_mapping.csv')
head(t2.meta,n=1)
# subset data
t2.meta.PvL <- t2.meta %>% filter(Treatment == 'Placebo' | Treatment == 'Let')
t2.PvL <- t2 %>% select(X1, any_of(t2.meta.PvL$Sample)) %>% column_to_rownames('X1')
t2.meta.LvLCH <- t2.meta %>% filter(Treatment == 'Let' | Treatment == 'CoL')
t2.LvLCH <- t2 %>% select(X1, any_of(t2.meta.LvLCH$Sample)) %>% column_to_rownames('X1')
```
### Placebo vs. Let
```
# Data Preprocessing
# feature_table is a df/matrix with features as rownames and samples in columns
feature_table <- t2.PvL
# character vector/column containing sample IDs
sample_var <- "Sample"
# grouping variable to detect structural zeros and outliers
group_var <- "Treatment"
# 0 < fraction < 1. For each feature, observations with proportion of mixture
# distribution < out_cut will be detected as outlier zeros;
# > (1 - out_cut) will be detected as outlier values
out_cut <- 0.05
# 0 < fraction < 1. Features with proportion of zeros > zero_cut are removed.
zero_cut <- 0.90
# samples with library size < lib_cut will be excluded in the analysis
lib_cut <- 0
# TRUE indicates a taxon would be classified as a structural zero in the
# corresponding experimental group using its asymptotic lower bound. More
# specifically, ```neg_lb = TRUE``` indicates you are using both criteria
# stated in section 3.2 of [ANCOM-II]
# (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5682008/) to detect structural
# zeros; Otherwise, ```neg_lb = FALSE``` will only use the equation 1 in
# section 3.2 of [ANCOM-II](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5682008/)
# for declaring structural zeros.
neg_lb <- TRUE
prepro <- feature_table_pre_process(feature_table, t2.meta.PvL, sample_var, group_var,
out_cut, zero_cut, lib_cut, neg_lb)
# Preprocessed feature table
feature_table1 <- prepro$feature_table
# Preprocessed metadata
meta_data1 <- prepro$meta_data
# Structural zero info
struc_zero1 <- prepro$structure_zeros
# Run ANCOM
# name of the main variable of interest (character)
main_var <- "Treatment"
p_adj_method <- "BH" # number of taxa > 10, therefore use Benjamini-Hochberg correction
alpha <- 0.05
# character string representing the formula for adjustment
adj_formula <- NULL
# character string representing the formula for random effects in lme
rand_formula <- NULL
t_start <- Sys.time()
res <- ANCOM(feature_table1, meta_data1, struc_zero1, main_var, p_adj_method,
alpha, adj_formula, rand_formula)
t_end <- Sys.time()
t_end - t_start
# write output to file
# output contains the "W" statistic for each taxa - a count of the number of times
# the null hypothesis is rejected for each taxa
# detected_x are logicals indicating detection at specified FDR cut-off
write_csv(res$out, "2021-07-25_WGS_T2_PvL_ANCOM_data.csv")
n_taxa <- ifelse(is.null(struc_zero1), nrow(feature_table1), sum(apply(struc_zero1, 1, sum) == 0))
res$fig + scale_y_continuous(sec.axis = sec_axis(~ . * 100 / n_taxa, name = 'W proportion'))
ggsave(filename = paste(lubridate::today(),'volcano_WGS_T2_PvL.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina')
# to find most significant taxa, I will sort the data
# 1) y (W statistic)
# 2) according to the absolute value of CLR mean difference
sig <- res$fig$data %>%
mutate(taxa_id = str_split_fixed(res$fig$data$taxa_id, pattern='s_', n=2)[,2]) %>% # remove leading 's_'
arrange(desc(y), desc(abs(x))) %>%
filter(y >= (0.7*n_taxa), !is.na(taxa_id)) # keep significant taxa, remove unidentified taxa
write.csv(sig, paste(lubridate::today(),'SigFeatures_WGS_T2_PvL.csv',sep='_'))
# save features with W > 0
non.zero <- res$fig$data %>%
arrange(desc(y), desc(abs(x))) %>%
mutate(taxa_id = str_split_fixed(res$fig$data$taxa_id, pattern='s_', n=2)[,2], # remove leading 's_'
W.proportion = y/(n_taxa-1)) %>% # add W
filter(y > 0) %>%
rowid_to_column()
write.csv(non.zero, paste(lubridate::today(),'NonZeroW_Features_WGS_T2_PvL.csv',sep='_'))
# plot top 20 taxa
sig %>%
slice_head(n=20) %>%
ggplot(aes(x, taxa_id)) +
geom_point(aes(size = 1)) +
theme_bw(base_size = 16) +
guides(size = FALSE) +
labs(x = 'CLR Mean Difference', y = NULL)
ggsave(filename = paste(lubridate::today(),'Top20_WGS_T2_PvL.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina', width = 10)
```
### Let v Let-co-housed
```
# Data Preprocessing
feature_table <- t2.LvLCH
sample_var <- "Sample"
group_var <- "Treatment"
out_cut <- 0.05
zero_cut <- 0.90
lib_cut <- 0
neg_lb <- TRUE
prepro <- feature_table_pre_process(feature_table, t2.meta.LvLCH, sample_var, group_var,
out_cut, zero_cut, lib_cut, neg_lb)
# Preprocessed feature table
feature_table2 <- prepro$feature_table
# Preprocessed metadata
meta_data2 <- prepro$meta_data
# Structural zero info
struc_zero2 <- prepro$structure_zeros
# Run ANCOM
# name of the main variable of interest (character)
main_var <- "Treatment"
p_adj_method <- "BH" # number of taxa > 10, therefore use Benjamini-Hochberg correction
alpha <- 0.05
# character string representing the formula for adjustment
adj_formula <- NULL
# character string representing the formula for random effects in lme
rand_formula <- NULL
t_start <- Sys.time()
res2 <- ANCOM(feature_table2, meta_data2, struc_zero2, main_var, p_adj_method,
alpha, adj_formula, rand_formula)
t_end <- Sys.time()
t_end - t_start
# write output to file
# output contains the "W" statistic for each taxa - a count of the number of times
# the null hypothesis is rejected for each taxa
# detected_x are logicals indicating detection at specified FDR cut-off
write_csv(res2$out, "2021-07-25_WGS_T2_LvLCH_ANCOM_data.csv")
n_taxa <- ifelse(is.null(struc_zero2), nrow(feature_table2), sum(apply(struc_zero2, 1, sum) == 0))
res2$fig + scale_y_continuous(sec.axis = sec_axis(~ . * 100 / n_taxa, name = 'W proportion'))
ggsave(filename = paste(lubridate::today(),'volcano_WGS_T2_LvLCH.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina')
# save features with W > 0
non.zero <- res2$fig$data %>%
arrange(desc(y), desc(abs(x))) %>%
mutate(taxa_id = str_split_fixed(res2$fig$data$taxa_id, pattern='s_', n=2)[,2], # remove leading 's_'
W.proportion = y/(n_taxa-1)) %>% # add W
filter(y > 0) %>%
rowid_to_column()
write.csv(non.zero, paste(lubridate::today(),'NonZeroW_Features_WGS_T2_LvLCH.csv',sep='_'))
# to find most significant taxa, I will sort the data
# 1) y (W statistic)
# 2) according to the absolute value of CLR mean difference
sig <- res2$fig$data %>%
mutate(taxa_id = str_split_fixed(res2$fig$data$taxa_id, pattern='s_', n=2)[,2]) %>% # remove leading 's_'
arrange(desc(y), desc(abs(x))) %>%
filter(y >= (0.7*n_taxa), !is.na(taxa_id)) # keep significant taxa, remove unidentified taxa
write.csv(sig, paste(lubridate::today(),'SigFeatures_WGS_T2_LvLCH.csv',sep='_'))
# plot top 20 taxa
sig %>%
slice_head(n=20) %>%
ggplot(aes(x, taxa_id)) +
geom_point(aes(size = 1)) +
theme_bw(base_size = 16) +
guides(size = FALSE) +
labs(x = 'CLR Mean Difference', y = NULL)
ggsave(filename = paste(lubridate::today(),'Top20_WGS_T2_LvLCH.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina', width = 10)
```
## T5
```
t5 <- read_csv('https://github.com/bryansho/PCOS_WGS_16S_metabolome/raw/master/DESEQ2/WGS/T5/T5_filtered_greater_00001.csv')
head(t5,n=1)
t5.meta <- read_csv('https://github.com/bryansho/PCOS_WGS_16S_metabolome/raw/master/DESEQ2/WGS/T5/Deseq2_T5_mapping.csv')
head(t5.meta,n=1)
# subset data
t5.meta.PvL <- t5.meta %>% filter(Treatment == 'Placebo' | Treatment == 'Let')
t5.PvL <- t5 %>% select(X1, any_of(t5.meta.PvL$SampleID)) %>% column_to_rownames('X1')
t5.meta.LvLCH <- t5.meta %>% filter(Treatment == 'Let' | Treatment == 'CoL')
t5.LvLCH <- t5 %>% select(X1, any_of(t5.meta.LvLCH$SampleID)) %>% column_to_rownames('X1')
```
### Placebo v Let
```
# Data Preprocessing
feature_table <- t5.PvL
sample_var <- "SampleID"
group_var <- "Treatment"
out_cut <- 0.05
zero_cut <- 0.90
lib_cut <- 0
neg_lb <- TRUE
prepro <- feature_table_pre_process(feature_table, t5.meta.PvL, sample_var, group_var,
out_cut, zero_cut, lib_cut, neg_lb)
# Preprocessed feature table
feature_table3 <- prepro$feature_table
# Preprocessed metadata
meta_data3 <- prepro$meta_data
# Structural zero info
struc_zero3 <- prepro$structure_zeros
# Run ANCOM
# name of the main variable of interest (character)
main_var <- "Treatment"
p_adj_method <- "BH" # number of taxa > 10, therefore use Benjamini-Hochberg correction
alpha <- 0.05
# character string representing the formula for adjustment
adj_formula <- NULL
# character string representing the formula for random effects in lme
rand_formula <- NULL
t_start <- Sys.time()
res3 <- ANCOM(feature_table3, meta_data3, struc_zero3, main_var, p_adj_method,
alpha, adj_formula, rand_formula)
t_end <- Sys.time()
t_end - t_start
# write output to file
# output contains the "W" statistic for each taxa - a count of the number of times
# the null hypothesis is rejected for each taxa
# detected_x are logicals indicating detection at specified FDR cut-off
write_csv(res3$out, "2021-07-25_WGS_T5_PvL_ANCOM_data.csv")
n_taxa <- ifelse(is.null(struc_zero3), nrow(feature_table3), sum(apply(struc_zero3, 1, sum) == 0))
res3$fig + scale_y_continuous(sec.axis = sec_axis(~ . * 100 / n_taxa, name = 'W proportion'))
ggsave(filename = paste(lubridate::today(),'volcano_WGS_T5_PvL.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina')
# save features with W > 0
non.zero <- res3$fig$data %>%
arrange(desc(y), desc(abs(x))) %>%
mutate(taxa_id = str_split_fixed(res3$fig$data$taxa_id, pattern='s_', n=2)[,2], # remove leading 's_'
W.proportion = y/(n_taxa-1)) %>% # add W
filter(y > 0) %>%
rowid_to_column()
write.csv(non.zero, paste(lubridate::today(),'NonZeroW_Features_WGS_T5_PvL.csv',sep='_'))
# to find most significant taxa, I will sort the data
# 1) y (W statistic)
# 2) according to the absolute value of CLR mean difference
sig <- res3$fig$data %>%
mutate(taxa_id = str_split_fixed(res3$fig$data$taxa_id, pattern='s_', n=2)[,2]) %>% # remove leading 's_'
arrange(desc(y), desc(abs(x))) %>%
filter(y >= (0.7*n_taxa), !is.na(taxa_id)) # keep significant taxa, remove unidentified taxa
write.csv(sig, paste(lubridate::today(),'SigFeatures_WGS_T5_PvL.csv',sep='_'))
# plot top 20 taxa
sig %>%
slice_head(n=20) %>%
ggplot(aes(x, taxa_id)) +
geom_point(aes(size = 1)) +
theme_bw(base_size = 16) +
guides(size = FALSE) +
labs(x = 'CLR Mean Difference', y = NULL)
ggsave(filename = paste(lubridate::today(),'Top20_WGS_T5_PvL.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina', width = 10)
```
### Let v Let-co-housed
```
# Data Preprocessing
feature_table <- t5.LvLCH
sample_var <- "SampleID"
group_var <- "Treatment"
out_cut <- 0.05
zero_cut <- 0.90
lib_cut <- 0
neg_lb <- TRUE
prepro <- feature_table_pre_process(feature_table, t5.meta.LvLCH, sample_var, group_var,
out_cut, zero_cut, lib_cut, neg_lb)
# Preprocessed feature table
feature_table4 <- prepro$feature_table
# Preprocessed metadata
meta_data4 <- prepro$meta_data
# Structural zero info
struc_zero4 <- prepro$structure_zeros
# Run ANCOM
# name of the main variable of interest (character)
main_var <- "Treatment"
p_adj_method <- "BH" # number of taxa > 10, therefore use Benjamini-Hochberg correction
alpha <- 0.05
# character string representing the formula for adjustment
adj_formula <- NULL
# character string representing the formula for random effects in lme
rand_formula <- NULL
t_start <- Sys.time()
res4 <- ANCOM(feature_table4, meta_data4, struc_zero4, main_var, p_adj_method,
alpha, adj_formula, rand_formula)
t_end <- Sys.time()
t_end - t_start
# write output to file
# output contains the "W" statistic for each taxa - a count of the number of times
# the null hypothesis is rejected for each taxa
# detected_x are logicals indicating detection at specified FDR cut-off
write_csv(res4$out, "2021-07-25_WGS_T5_LvLCH_ANCOM_data.csv")
n_taxa <- ifelse(is.null(struc_zero4), nrow(feature_table4), sum(apply(struc_zero4, 1, sum) == 0))
res4$fig + scale_y_continuous(sec.axis = sec_axis(~ . * 100 / n_taxa, name = 'W proportion'))
ggsave(filename = paste(lubridate::today(),'volcano_WGS_T5_LvLCH.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina')
# save features with W > 0
non.zero <- res4$fig$data %>%
arrange(desc(y), desc(abs(x))) %>%
mutate(taxa_id = str_split_fixed(res4$fig$data$taxa_id, pattern='s_', n=2)[,2], # remove leading 's_'
W.proportion = y/(n_taxa-1)) %>% # add W
filter(y > 0) %>%
rowid_to_column()
write.csv(non.zero, paste(lubridate::today(),'NonZeroW_Features_WGS_T5_LvLCH.csv',sep='_'))
# to find most significant taxa, I will sort the data
# 1) y (W statistic)
# 2) according to the absolute value of CLR mean difference
sig <- res4$fig$data %>%
mutate(taxa_id = str_split_fixed(res4$fig$data$taxa_id, pattern='s_', n=2)[,2]) %>% # remove leading 's_'
arrange(desc(y), desc(abs(x))) %>%
filter(y >= (0.7*n_taxa), !is.na(taxa_id)) # keep significant taxa, remove unidentified taxa
write.csv(sig, paste(lubridate::today(),'SigFeatures_WGS_T5_LvLCH.csv',sep='_'))
# plot top 20 taxa
sig %>%
slice_head(n=20) %>%
ggplot(aes(x, taxa_id)) +
geom_point(aes(size = 1)) +
theme_bw(base_size = 16) +
guides(size = FALSE) +
labs(x = 'CLR Mean Difference', y = NULL)
ggsave(filename = paste(lubridate::today(),'Top20_WGS_T5_LvLCH.pdf',sep='_'), bg = 'transparent', device = 'pdf', dpi = 'retina', width=10)
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"></ul></div>
```
!pip install tensorflow-addons
!pip install lifelines
!pip install scikit-plot
import tensorflow as tf
import tensorflow_addons as tfa
from tensorflow import keras
from sklearn.model_selection import train_test_split
from keras import backend as K
from tensorflow.keras.layers import StringLookup
from tqdm.keras import TqdmCallback
from tqdm.auto import tqdm
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('default')
plt.style.use('seaborn-white')
models = tf.keras.models
layers = tf.keras.layers
preprocessing = tf.keras.preprocessing
tqdm.pandas()
def mse_nan(y_true, y_pred):
masked_true = tf.where(tf.math.is_nan(y_true), tf.zeros_like(y_true), y_true)
masked_pred = tf.where(tf.math.is_nan(y_true), tf.zeros_like(y_true), y_pred)
return K.mean(K.square(masked_pred - masked_true), axis=-1)
def get_optimizer():
optimizer = tf.keras.optimizers.Adam()
return optimizer
def get_model(num_shared=2, units=64, rate=0.3, loss_weights=None):
sm = layers.Input(shape=(100, ), name='D_Inp')
aa = layers.Input(shape=(1000, ), name='T_Inp')
emsm0 = layers.Embedding(53,
128,
trainable=True,
name='D_Emb',
mask_zero=True)(sm)
emaa0 = layers.Embedding(22,
128,
trainable=True,
name='T_Emb',
mask_zero=True)(aa)
cnvsm1 = layers.Conv1D(32, 3, name='D_L1')(emsm0)
cnvaa1 = layers.Conv1D(32, 3, name='T_L1')(emaa0)
cnvsm2 = layers.Conv1D(64, 3, name='D_L2')(cnvsm1)
cnvaa2 = layers.Conv1D(64, 3, name='T_L2')(cnvaa1)
cnvsm3 = layers.Conv1D(96, 3, name='D_L3')(cnvsm2)
cnvaa3 = layers.Conv1D(96, 3, name='T_L3')(cnvaa2)
gmpsm = layers.GlobalMaxPool1D(name='D_Gmp')(cnvsm2)
gmpaa = layers.GlobalMaxPool1D(name='T_Gmp')(cnvaa2)
C1 = layers.concatenate([gmpsm, gmpaa], axis=-1, name='C1')
S1 = layers.Dense(512, activation='relu', name='S1')(C1)
S1 = layers.Dropout(rate)(S1)
S2 = layers.Dense(512, activation='relu', name='S2')(S1)
S2 = layers.Dropout(rate)(S2)
S3 = layers.Dense(512, activation='relu', name='S3')(S2)
S3 = layers.Dropout(rate)(S3)
Kd = layers.Dense(units, activation='relu', name='S1_Kd')(S3)
Kd = layers.Dropout(rate)(Kd)
Ki = layers.Dense(units, activation='relu', name='S1_Ki')(S3)
Ki = layers.Dropout(rate)(Ki)
IC50 = layers.Dense(units, activation='relu', name='S1_IC50')(S3)
IC50 = layers.Dropout(rate)(IC50)
EC50 = layers.Dense(units, activation='relu', name='S1_EC50')(S3)
EC50 = layers.Dropout(rate)(EC50)
IA = layers.Dense(units, activation='relu', name='S1_IA')(S3)
IA = layers.Dropout(rate)(IA)
pH = layers.Dense(units, activation='relu', name='S1_pH')(S3)
pH = layers.Dropout(rate)(pH)
out1 = layers.Dense(1, activation='linear', name='Kd')(Kd)
out2 = layers.Dense(1, activation='linear', name='Ki')(Ki)
out3 = layers.Dense(1, activation='linear', name='IC50')(IC50)
out4 = layers.Dense(1, activation='linear', name='EC50')(EC50)
out5 = layers.Dense(1, activation='sigmoid', name='IA')(IA)
out6 = layers.Dense(1, activation='linear', name='pH')(pH)
model = models.Model(inputs=[sm, aa],
outputs=[out1, out2, out3, out4, out5, out6])
losses = {
"Kd": mse_nan,
"Ki": mse_nan,
"IC50": mse_nan,
"EC50": mse_nan,
"pH": mse_nan,
"IA": "binary_crossentropy",
}
metrics = {"IA": tf.keras.metrics.AUC()}
model.compile(loss=losses, optimizer=get_optimizer(), metrics=metrics, loss_weights=loss_weights)
model.summary()
return model
tf.keras.backend.clear_session()
np.random.seed(7)
tf.random.set_seed(7)
loss_weights = [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
model = get_model(rate=0.3, loss_weights=loss_weights)
tf.keras.utils.plot_model(model, rankdir='LR',
show_shapes=True,
show_layer_activations=True)
CHARPROTSET = dict([('A', 1), ('G', 2), ('L', 3), ('M', 4), ('S', 5), ('T', 6),
('E', 7), ('Q', 8), ('P', 9), ('F', 10), ('R', 11),
('V', 12), ('D', 13), ('I', 14), ('N', 15), ('Y', 16),
('H', 17), ('C', 18), ('K', 19), ('W', 20), ('X', 21)])
CHARCANSMISET = dict([(')', 1), ('(', 2), ('1', 3), ('C', 4), ('c', 5),
('O', 6), ('2', 7), ('N', 8), ('=', 9), ('n', 10),
('3', 11), ('-', 12), ('4', 13), ('F', 14), ('S', 15),
('[', 16), (']', 17), ('l', 18), ('H', 19), ('s', 20),
('#', 21), ('o', 22), ('5', 23), ('B', 24), ('r', 25),
('+', 26), ('6', 27), ('P', 28), ('.', 29), ('I', 30),
('7', 31), ('e', 32), ('i', 33), ('a', 34), ('8', 35),
('K', 36), ('A', 37), ('9', 38), ('T', 39), ('g', 40),
('R', 41), ('Z', 42), ('%', 43), ('0', 44), ('u', 45),
('V', 46), ('b', 47), ('t', 48), ('L', 49), ('*', 50),
('d', 51), ('W', 52)])
class Gen:
def __init__(self,
data,
map_smiles,
map_aa,
shuffle=True,
test_only=False,
len_drug=100,
len_target=1000,
window=False):
self.data = data
self.map_smiles = map_smiles
self.map_aa = map_aa
self.shuffle = shuffle
self.test_only = test_only
self.len_drug = len_drug
self.len_target = len_target
self.size = self.data.shape[0]
self.inds = list(range(self.size))
if self.shuffle:
random.shuffle(self.inds)
self.window = window
self.gen = self._get_inputs()
def _get_inputs(self):
seen = 0
while seen < self.size:
ind = self.inds[seen]
sample = self.data.iloc[ind, :].values.tolist()
sample[0] = self.map_smiles[sample[0]]
sample[1] = self.map_aa[sample[1]]
if self.window:
ld = max(0, (len(sample[0]) - self.len_drug))
lt = max(0, (len(sample[1]) - self.len_target))
dstart = random.randint(0, ld)
tstart = random.randint(0, lt)
sample[0] = sample[0][dstart:dstart + self.len_drug]
sample[1] = sample[1][tstart:dstart + self.len_target]
yield sample
seen += 1
if seen == self.size:
if self.shuffle:
random.shuffle(self.inds)
seen = 0
def get_batch(self, batch_size):
while True:
BATCH = []
for _ in range(batch_size):
sample = next(self.gen)
for k, value in enumerate(sample):
if len(BATCH) < (k+1):
BATCH.append([])
BATCH[k].append(value)
BATCH[0] = preprocessing.sequence.pad_sequences(BATCH[0], self.len_drug)
BATCH[1] = preprocessing.sequence.pad_sequences(BATCH[1], self.len_target)
for k in range(2, len(BATCH)):
BATCH[k] = np.array(BATCH[k]).flatten()
if not self.test_only:
yield [BATCH[0], BATCH[1]], [BATCH[k] for k in range(2, len(BATCH))]
else:
yield [BATCH[0], BATCH[1]], [BATCH[k]*0 for k in range(2, len(BATCH))]
data = pd.read_csv("data_full_05_pH.zip", compression='zip')
order = [
'smiles', 'target', 'p1Kd', 'p1Ki', 'p1IC50', 'p1EC50', 'is_active', 'pH'
]
data = data[order]
data = data.sample(frac=1, random_state = 7)
data.head()
data.dropna().shape
SMILES = {}
for smiles in tqdm(data['smiles'].unique()):
SMILES[smiles] = [CHARCANSMISET[s] for s in smiles]
AA = {}
for aa in tqdm(data['target'].unique()):
AA[aa] = [CHARPROTSET[a.upper()] for a in aa]
X_train, X_test = train_test_split(data, test_size=0.1, shuffle=True, random_state = 7, stratify=data['is_active'])
X_train, X_valid = train_test_split(X_train, test_size=0.1, shuffle=True, random_state = 7, stratify=X_train['is_active'])
X_train.shape[0], X_test.shape[0], X_valid.shape[0]
X_train.head()
batch_size = 128
trg = Gen(X_train, SMILES, AA)
trg = trg.get_batch(batch_size)
vag = Gen(X_valid, SMILES, AA)
vag = vag.get_batch(batch_size)
# for batch in trg:
# break
# batch
steps_per_epoch = X_train.shape[0] // batch_size
valid_steps = X_valid.shape[0] // batch_size
filepath = "{epoch:02d}-{val_loss:.2f}.h5"
checkpoint = tf.keras.callbacks.ModelCheckpoint(filepath,
monitor='val_loss',
verbose=1,
save_best_only=False,
mode='auto',
save_weights_only=True)
history = model.fit(trg,
validation_data=vag,
steps_per_epoch=steps_per_epoch,
validation_steps=valid_steps,
verbose=0,
callbacks=[TqdmCallback(), checkpoint],
epochs=50)
model.load_weights('45-5.30.h5')
# !rm *.h5 -r
# history.history
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='valid')
plt.xlabel('Epoch')
plt.title('Loss on train-valid subsets')
plt.legend()
def get_batch_size(S):
mbs = 1
for i in range(1, min(64, S)):
if S % i == 0:
mbs = i
assert S % mbs == 0
return mbs
mbs = get_batch_size(X_test.shape[0])
mbs
teg = Gen(X_test, SMILES, AA, shuffle=False, test_only=True)
teg = teg.get_batch(mbs)
prediction = model.predict(teg, steps=X_test.shape[0]//mbs, verbose=1)
from sklearn.metrics import mean_squared_error
from lifelines.utils import concordance_index
from scipy import stats
def get_scores(y_true, y_pred):
mse = np.round(mean_squared_error(y_true, y_pred), 3)
rmse = np.round(mse**0.5, 3)
ci = np.round(concordance_index(y_true, y_pred), 3)
pearson = np.round(stats.pearsonr(y_true, y_pred)[0], 3)
spearman = np.round(stats.spearmanr(y_true, y_pred)[0], 3)
res = f"rmse={rmse}, mse={mse},\npearson={pearson}, spearman={spearman},\nci={ci}"
return res
for k, col in enumerate(
['p1Kd', 'p1Ki', 'p1IC50', 'p1EC50', 'is_active', 'pH']):
plt.scatter(X_test[col], prediction[k], alpha=0.7, c='k')
plt.xlabel('true')
plt.ylabel('predicted')
y_true = X_test[col][X_test[col].notna()]
y_pred = prediction[k][X_test[col].notna()].ravel()
plt.title(col + ":\n" + get_scores(y_true, y_pred))
plt.show() # 74.6
import scikitplot as skplt
p = prediction[-2].ravel().tolist()
probas = np.zeros((len(p),2))
probas[:,1] = p
probas[:,0] = 1
probas[:,0] = probas[:,0] - p
skplt.metrics.plot_roc_curve(X_test['is_active'].values.ravel().tolist(), probas)
plt.show()
plt.hist(prediction[-2].ravel(), bins=32, edgecolor='w', color='k', alpha=0.7);
```
|
github_jupyter
|
# TensorFlow BYOM: Train with Custom Training Script, Compile with Neo, and Deploy on SageMaker
In this notebook you will compile a trained model using Amazon SageMaker Neo. This notebook is similar to the [TensorFlow MNIST training and serving notebook](https://github.com/aws/amazon-sagemaker-examples/blob/master/sagemaker-python-sdk/tensorflow_script_mode_training_and_serving/tensorflow_script_mode_training_and_serving.ipynb) in terms of its functionality. You will complete the same classification task, however this time you will compile the trained model using the SageMaker Neo API on the backend. SageMaker Neo will optimize your model to run on your choice of hardware. At the end of this notebook you will setup a real-time hosting endpoint in SageMaker for your SageMaker Neo compiled model using the TensorFlow Model Server. Note: This notebooks requires Sagemaker Python SDK v2.x.x or above.
### Set up the environment
```
import os
import sagemaker
from sagemaker import get_execution_role
sagemaker_session = sagemaker.Session()
role = get_execution_role()
```
### Download the MNIST dataset
```
import utils
from tensorflow.contrib.learn.python.learn.datasets import mnist
import tensorflow as tf
data_sets = mnist.read_data_sets("data", dtype=tf.uint8, reshape=False, validation_size=5000)
utils.convert_to(data_sets.train, "train", "data")
utils.convert_to(data_sets.validation, "validation", "data")
utils.convert_to(data_sets.test, "test", "data")
```
### Upload the data
We use the ```sagemaker.Session.upload_data``` function to upload our datasets to an S3 location. The return value inputs identifies the location -- we will use this later when we start the training job.
```
inputs = sagemaker_session.upload_data(path="data", key_prefix="data/DEMO-mnist")
```
# Construct a script for distributed training
Here is the full code for the network model:
```
!cat 'mnist.py'
```
The script here is and adaptation of the [TensorFlow MNIST example](https://github.com/tensorflow/models/blob/master/official/vision/image_classification/mnist_main.py). It provides a ```model_fn(features, labels, mode)```, which is used for training, evaluation and inference. See [TensorFlow MNIST training and serving notebook](https://github.com/aws/amazon-sagemaker-examples/blob/master/sagemaker-python-sdk/tensorflow_script_mode_training_and_serving/tensorflow_script_mode_training_and_serving.ipynb) for more details about the training script.
## Create a training job using the sagemaker.TensorFlow estimator
```
from sagemaker.tensorflow import TensorFlow
mnist_estimator = TensorFlow(
entry_point="mnist.py",
role=role,
framework_version="1.15.3",
py_version="py3",
training_steps=1000,
evaluation_steps=100,
instance_count=2,
instance_type="ml.c4.xlarge",
)
mnist_estimator.fit(inputs)
```
The **```fit```** method will create a training job in two **ml.c4.xlarge** instances. The logs above will show the instances doing training, evaluation, and incrementing the number of **training steps**.
In the end of the training, the training job will generate a saved model for TF serving.
# Deploy the trained model to prepare for predictions (the old way)
The deploy() method creates an endpoint which serves prediction requests in real-time.
```
mnist_predictor = mnist_estimator.deploy(initial_instance_count=1, instance_type="ml.m4.xlarge")
```
## Invoking the endpoint
```
import numpy as np
import json
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
for i in range(10):
data = mnist.test.images[i].tolist()
# Follow https://www.tensorflow.org/tfx/serving/api_rest guide to format input to the model server
predict_response = mnist_predictor.predict({"instances": np.asarray(data).tolist()})
print("========================================")
label = np.argmax(mnist.test.labels[i])
print("label is {}".format(label))
prediction = np.argmax(predict_response["predictions"])
print("prediction is {}".format(prediction))
```
## Deleting the endpoint
```
sagemaker.Session().delete_endpoint(mnist_predictor.endpoint)
```
# Deploy the trained model using Neo
Now the model is ready to be compiled by Neo to be optimized for our hardware of choice. We are using the ``TensorFlowEstimator.compile_model`` method to do this. For this example, our target hardware is ``'ml_c5'``. You can changed these to other supported target hardware if you prefer.
## Compiling the model
The ``input_shape`` is the definition for the model's input tensor and ``output_path`` is where the compiled model will be stored in S3. **Important. If the following command result in a permission error, scroll up and locate the value of execution role returned by `get_execution_role()`. The role must have access to the S3 bucket specified in ``output_path``.**
```
output_path = "/".join(mnist_estimator.output_path.split("/")[:-1])
optimized_estimator = mnist_estimator.compile_model(
target_instance_family="ml_c5",
input_shape={"data": [1, 784]}, # Batch size 1, 3 channels, 224x224 Images.
output_path=output_path,
framework="tensorflow",
framework_version="1.15.3",
)
```
## Set image uri (Temporarily required)
Image URI: aws_account_id.dkr.ecr.aws_region.amazonaws.com/sagemaker-inference-tensorflow:1.15.3-instance_type-py3
Refer to the table on the bottom [here](https://docs.aws.amazon.com/sagemaker/latest/dg/neo-deployment-hosting-services-container-images.html) to get aws account id and region mapping
```
optimized_estimator.image_uri = (
"301217895009.dkr.ecr.us-west-2.amazonaws.com/sagemaker-inference-tensorflow:1.15.3-cpu-py3"
)
```
## Deploying the compiled model
```
optimized_predictor = optimized_estimator.deploy(
initial_instance_count=1, instance_type="ml.c5.xlarge"
)
```
## Invoking the endpoint
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
for i in range(10):
data = mnist.test.images[i].tolist()
# Follow https://www.tensorflow.org/tfx/serving/api_rest guide to format input to the model server
predict_response = optimized_predictor.predict({"instances": np.asarray(data).tolist()})
print("========================================")
label = np.argmax(mnist.test.labels[i])
print("label is {}".format(label))
prediction = np.argmax(predict_response["predictions"])
print("prediction is {}".format(prediction))
```
## Deleting endpoint
```
sagemaker.Session().delete_endpoint(optimized_predictor.endpoint)
```
|
github_jupyter
|
# $$User\ Defined\ Metrics\ Tutorial$$
[](https://colab.research.google.com/github/catboost/tutorials/blob/master/custom_loss/custom_loss_and_metric_tutorial.ipynb)
# Contents
* [1. Introduction](#1.\-Introduction)
* [2. Classification](#2.\-Classification)
* [3. Regression](#3.\-Regression)
* [4. Multiclassification](#4.\-Multiclassification)
# 1. Introduction
CatBoost allows you to create and pass to model your own loss functions and metrics. To do this you should implement classes with specicial interfaces.
##### Interface for user defined objectives:
```
class UserDefinedObjective(object):
def calc_ders_range(self, approxes, targets, weights):
# approxes, targets, weights are indexed containers of floats
# (containers which have only __len__ and __getitem__ defined).
# weights parameter can be None.
#
# To understand what these parameters mean, assume that there is
# a subset of your dataset that is currently being processed.
# approxes contains current predictions for this subset,
# targets contains target values you provided with the dataset.
#
# This function should return a list of pairs (der1, der2), where
# der1 is the first derivative of the loss function with respect
# to the predicted value, and der2 is the second derivative.
pass
class UserDefinedMultiClassObjective(object):
def calc_ders_multi(self, approxes, target, weight):
# approxes - indexed container of floats with predictions
# for each dimension of single object
# target - contains a single expected value
# weight - contains weight of the object
#
# This function should return a tuple (der1, der2), where
# - der1 is a list-like object of first derivatives of the loss function with respect
# to the predicted value for each dimension.
# - der2 is a matrix of second derivatives.
pass
```
##### Interface for user defined metrics:
```
class UserDefinedMetric(object):
def is_max_optimal(self):
# Returns whether great values of metric are better
pass
def evaluate(self, approxes, target, weight):
# approxes is a list of indexed containers
# (containers with only __len__ and __getitem__ defined),
# one container per approx dimension.
# Each container contains floats.
# weight is a one dimensional indexed container.
# target is a one dimensional indexed container.
# weight parameter can be None.
# Returns pair (error, weights sum)
pass
def get_final_error(self, error, weight):
# Returns final value of metric based on error and weight
pass
```
Below we consider examples of user defined metrics for different types of tasks. We will use the following variables:
<center>$a$ - approx value</center>
<center>$p$ - probability</center>
<center>$t$ - target</center>
<center>$w$ - weight</center>
```
# import neccessary packages
from catboost import CatBoostClassifier, CatBoostRegressor
import numpy as np
from sklearn.datasets import make_classification, make_regression
from sklearn.model_selection import train_test_split
```
# 2. Classification
Note: for binary classification problems approxes are not equal to probabilities. Probabilities are calculated from approxes using sigmoid function.
<h4><center>$p=\frac{1}{1 + e^{-a}}=\frac{e^a}{1 + e^a}$</center></h4>
As an example, let's take Logloss metric which is defined by the following formula:
<h4><center>$Logloss_i = -{w_i * (t_i * log(p_i) + (1 - t_i) * log(1 - p_i))}$</center></h4>
<h4><center>$Logloss = \frac{\sum_{i=1}^{N}{Logloss_i}}{\sum_{i=1}^{N}{w_i}}$</center></h4>
This metric has derivative and can be used as objective. The derivatives of Logloss for single object are defined by the following formulas:
<h4><center>$\frac{\delta(Logloss_i)}{\delta(a)} = w_i * (t_i - p_i)$</center></h4>
<h4><center>$\frac{\delta^2(Logloss_i)}{\delta(a^2)} = -w_i * p_i * (1 - p_i)$</center></h4>
Below you can see implemented Logloss objective and metric.
```
class LoglossObjective(object):
def calc_ders_range(self, approxes, targets, weights):
assert len(approxes) == len(targets)
if weights is not None:
assert len(weights) == len(approxes)
result = []
for index in range(len(targets)):
e = np.exp(approxes[index])
p = e / (1 + e)
der1 = targets[index] - p
der2 = -p * (1 - p)
if weights is not None:
der1 *= weights[index]
der2 *= weights[index]
result.append((der1, der2))
return result
class LoglossMetric(object):
def get_final_error(self, error, weight):
return error / (weight + 1e-38)
def is_max_optimal(self):
return False
def evaluate(self, approxes, target, weight):
assert len(approxes) == 1
assert len(target) == len(approxes[0])
approx = approxes[0]
error_sum = 0.0
weight_sum = 0.0
for i in range(len(approx)):
e = np.exp(approx[i])
p = e / (1 + e)
w = 1.0 if weight is None else weight[i]
weight_sum += w
error_sum += -w * (target[i] * np.log(p) + (1 - target[i]) * np.log(1 - p))
return error_sum, weight_sum
```
Below there are examples of training with built-in Logloss function and our Logloss objective and metric. As we can see, the results are the same.
```
X, y = make_classification(n_classes=2, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model1 = CatBoostClassifier(iterations=10, loss_function='Logloss', eval_metric='Logloss',
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Gradient')
model1.fit(X_train, y_train, eval_set=(X_test, y_test))
model2 = CatBoostClassifier(iterations=10, loss_function=LoglossObjective(), eval_metric=LoglossMetric(),
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Gradient')
model2.fit(X_train, y_train, eval_set=(X_test, y_test))
```
# 3. Regression
For regression approxes don't need any transformations. As an example of regression loss function and metric we take well-known RMSE which is defined by the following formulas:
<h3><center>$RMSE = \sqrt{\frac{\sum_{i=1}^{N}{w_i * (t_i - a_i)^2}}{\sum_{i=1}^{N}{w_i}}}$</center></h3>
<h4><center>$\frac{\delta(RMSE_i)}{\delta(a)} = w_i * (t_i - a_i)$</center></h4>
<h4><center>$\frac{\delta^2(RMSE_i)}{\delta(a^2)} = -w_i$</center></h4>
```
class RmseObjective(object):
def calc_ders_range(self, approxes, targets, weights):
assert len(approxes) == len(targets)
if weights is not None:
assert len(weights) == len(approxes)
result = []
for index in range(len(targets)):
der1 = targets[index] - approxes[index]
der2 = -1
if weights is not None:
der1 *= weights[index]
der2 *= weights[index]
result.append((der1, der2))
return result
class RmseMetric(object):
def get_final_error(self, error, weight):
return np.sqrt(error / (weight + 1e-38))
def is_max_optimal(self):
return False
def evaluate(self, approxes, target, weight):
assert len(approxes) == 1
assert len(target) == len(approxes[0])
approx = approxes[0]
error_sum = 0.0
weight_sum = 0.0
for i in range(len(approx)):
w = 1.0 if weight is None else weight[i]
weight_sum += w
error_sum += w * ((approx[i] - target[i])**2)
return error_sum, weight_sum
```
Below there are examples of training with built-in RMSE function and our RMSE objective and metric. As we can see, the results are the same.
```
X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model1 = CatBoostRegressor(iterations=10, loss_function='RMSE', eval_metric='RMSE',
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Gradient')
model1.fit(X_train, y_train, eval_set=(X_test, y_test))
model2 = CatBoostRegressor(iterations=10, loss_function=RmseObjective(), eval_metric=RmseMetric(),
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Gradient')
model2.fit(X_train, y_train, eval_set=(X_test, y_test))
```
# 4. Multiclassification
Note: for multiclassification problems approxes are not equal to probabilities. Usually approxes are transformed to probabilities using Softmax function.
<h3><center>$p_{i,c} = \frac{e^{a_{i,c}}}{\sum_{j=1}^k{e^{a_{i,j}}}}$</center></h3>
<center>$p_{i,c}$ - the probability that $x_i$ belongs to class $c$</center>
<center>$k$ - number of classes</center>
<center>$a_{i,j}$ - approx for object $x_i$ for class $j$</center>
Let's implement MultiClass objective that is defined as follows:
<h3><center>$MultiClass_i = w_i * \log{p_{i,t_i}}$</center></h3>
<h3><center>$MultiClass = \frac{\sum_{i=1}^{N}Multiclass_i}{\sum_{i=1}^{N}w_i}$</center></h3>
<h3><center>$\frac{\delta(Multiclass_i)}{\delta{a_{i,c}}} = \begin{cases}
w_i-\frac{w_i*e^{a_{i,c}}}{\sum_{j=1}^{k}e^{a_{i,j}}}, & \mbox{if } c = t_i \\
-\frac{w_i*e^{a_{i,c}}}{\sum_{j=1}^{k}e^{a_{i,j}}}, & \mbox{if } c \neq t_i
\end{cases}$</center></h3>
<h3><center>$\frac{\delta^2(Multiclass_i)}{\delta{a_{i,c_1}}\delta{a_{i,c_2}}} = \begin{cases}
\frac{w_i*e^{2*a_{i,c_1}}}{(\sum_{j=1}^{k}e^{a_{i,j}})^2} - \frac{w_i*e^{a_{i, c_1}}}{\sum_{j=1}^{k}e^{a_{i,j}}}, & \mbox{if } c_1 = c_2 \\
\frac{w_i*e^{a_{i,c_1}+a_{i,c_2}}}{(\sum_{j=1}^{k}e^{a_{i,j}})^2}, & \mbox{if } c_1 \neq c_2
\end{cases}$</center></h3>
```
class MultiClassObjective(object):
def calc_ders_multi(self, approx, target, weight):
approx = np.array(approx) - max(approx)
exp_approx = np.exp(approx)
exp_sum = exp_approx.sum()
grad = []
hess = []
for j in range(len(approx)):
der1 = -exp_approx[j] / exp_sum
if j == target:
der1 += 1
hess_row = []
for j2 in range(len(approx)):
der2 = exp_approx[j] * exp_approx[j2] / (exp_sum**2)
if j2 == j:
der2 -= exp_approx[j] / exp_sum
hess_row.append(der2 * weight)
grad.append(der1 * weight)
hess.append(hess_row)
return (grad, hess)
class AccuracyMetric(object):
def get_final_error(self, error, weight):
return error / (weight + 1e-38)
def is_max_optimal(self):
return True
def evaluate(self, approxes, target, weight):
best_class = np.argmax(approxes, axis=0)
accuracy_sum = 0
weight_sum = 0
for i in range(len(target)):
w = 1.0 if weight is None else weight[i]
weight_sum += w
accuracy_sum += w * (best_class[i] == target[i])
return accuracy_sum, weight_sum
```
Below there are examples of training with built-in MultiClass function and our MultiClass objective. As we can see, the results are the same.
```
X, y = make_classification(n_samples=1000, n_features=50, n_informative=40, n_classes=5, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model1 = CatBoostClassifier(iterations=10, loss_function='MultiClass', eval_metric='Accuracy',
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Newton', classes_count=5)
model1.fit(X_train, y_train, eval_set=(X_test, y_test))
model2 = CatBoostClassifier(iterations=10, loss_function=MultiClassObjective(), eval_metric=AccuracyMetric(),
learning_rate=0.03, bootstrap_type='Bayesian', boost_from_average=False,
leaf_estimation_iterations=1, leaf_estimation_method='Newton', classes_count=5)
model2.fit(X_train, y_train, eval_set=(X_test, y_test))
```
|
github_jupyter
|
[Table of Contents](./table_of_contents.ipynb)
# The Extended Kalman Filter
```
from __future__ import division, print_function
%matplotlib inline
#format the book
import book_format
book_format.set_style()
```
We have developed the theory for the linear Kalman filter. Then, in the last two chapters we broached the topic of using Kalman filters for nonlinear problems. In this chapter we will learn the Extended Kalman filter (EKF). The EKF handles nonlinearity by linearizing the system at the point of the current estimate, and then the linear Kalman filter is used to filter this linearized system. It was one of the very first techniques used for nonlinear problems, and it remains the most common technique.
The EKF provides significant mathematical challenges to the designer of the filter; this is the most challenging chapter of the book. I do everything I can to avoid the EKF in favor of other techniques that have been developed to filter nonlinear problems. However, the topic is unavoidable; all classic papers and a majority of current papers in the field use the EKF. Even if you do not use the EKF in your own work you will need to be familiar with the topic to be able to read the literature.
## Linearizing the Kalman Filter
The Kalman filter uses linear equations, so it does not work with nonlinear problems. Problems can be nonlinear in two ways. First, the process model might be nonlinear. An object falling through the atmosphere encounters drag which reduces its acceleration. The drag coefficient varies based on the velocity the object. The resulting behavior is nonlinear - it cannot be modeled with linear equations. Second, the measurements could be nonlinear. For example, a radar gives a range and bearing to a target. We use trigonometry, which is nonlinear, to compute the position of the target.
For the linear filter we have these equations for the process and measurement models:
$$\begin{aligned}\dot{\mathbf x} &= \mathbf{Ax} + w_x\\
\mathbf z &= \mathbf{Hx} + w_z
\end{aligned}$$
Where $\mathbf A$ is the systems dynamic matrix. Using the state space methods covered in the **Kalman Filter Math** chapter these equations can be tranformed into
$$\begin{aligned}\bar{\mathbf x} &= \mathbf{Fx} \\
\mathbf z &= \mathbf{Hx}
\end{aligned}$$
where $\mathbf F$ is the *fundamental matrix*. The noise $w_x$ and $w_z$ terms are incorporated into the matrices $\mathbf R$ and $\mathbf Q$. This form of the equations allow us to compute the state at step $k$ given a measurement at step $k$ and the state estimate at step $k-1$. In earlier chapters I built your intuition and minimized the math by using problems describable with Newton's equations. We know how to design $\mathbf F$ based on high school physics.
For the nonlinear model the linear expression $\mathbf{Fx} + \mathbf{Bu}$ is replaced by a nonlinear function $f(\mathbf x, \mathbf u)$, and the linear expression $\mathbf{Hx}$ is replaced by a nonlinear function $h(\mathbf x)$:
$$\begin{aligned}\dot{\mathbf x} &= f(\mathbf x, \mathbf u) + w_x\\
\mathbf z &= h(\mathbf x) + w_z
\end{aligned}$$
You might imagine that we could proceed by finding a new set of Kalman filter equations that optimally solve these equations. But if you remember the charts in the **Nonlinear Filtering** chapter you'll recall that passing a Gaussian through a nonlinear function results in a probability distribution that is no longer Gaussian. So this will not work.
The EKF does not alter the Kalman filter's linear equations. Instead, it *linearizes* the nonlinear equations at the point of the current estimate, and uses this linearization in the linear Kalman filter.
*Linearize* means what it sounds like. We find a line that most closely matches the curve at a defined point. The graph below linearizes the parabola $f(x)=x^2-2x$ at $x=1.5$.
```
import kf_book.ekf_internal as ekf_internal
ekf_internal.show_linearization()
```
If the curve above is the process model, then the dotted lines shows the linearization of that curve for the estimate $x=1.5$.
We linearize systems by taking the derivative, which finds the slope of a curve:
$$\begin{aligned}
f(x) &= x^2 -2x \\
\frac{df}{dx} &= 2x - 2
\end{aligned}$$
and then evaluating it at $x$:
$$\begin{aligned}m &= f'(x=1.5) \\&= 2(1.5) - 2 \\&= 1\end{aligned}$$
Linearizing systems of differential equations is similar. We linearize $f(\mathbf x, \mathbf u)$, and $h(\mathbf x)$ by taking the partial derivatives of each to evaluate $\mathbf F$ and $\mathbf H$ at the point $\mathbf x_t$ and $\mathbf u_t$. We call the partial derivative of a matrix the [*Jacobian*](https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant). This gives us the the discrete state transition matrix and measurement model matrix:
$$
\begin{aligned}
\mathbf F
&= {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}} \\
\mathbf H &= \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
\end{aligned}
$$
This leads to the following equations for the EKF. I put boxes around the differences from the linear filter:
$$\begin{array}{l|l}
\text{linear Kalman filter} & \text{EKF} \\
\hline
& \boxed{\mathbf F = {\frac{\partial{f(\mathbf x_t, \mathbf u_t)}}{\partial{\mathbf x}}}\biggr|_{{\mathbf x_t},{\mathbf u_t}}} \\
\mathbf{\bar x} = \mathbf{Fx} + \mathbf{Bu} & \boxed{\mathbf{\bar x} = f(\mathbf x, \mathbf u)} \\
\mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q & \mathbf{\bar P} = \mathbf{FPF}^\mathsf{T}+\mathbf Q \\
\hline
& \boxed{\mathbf H = \frac{\partial{h(\bar{\mathbf x}_t)}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}} \\
\textbf{y} = \mathbf z - \mathbf{H \bar{x}} & \textbf{y} = \mathbf z - \boxed{h(\bar{x})}\\
\mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} & \mathbf{K} = \mathbf{\bar{P}H}^\mathsf{T} (\mathbf{H\bar{P}H}^\mathsf{T} + \mathbf R)^{-1} \\
\mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} & \mathbf x=\mathbf{\bar{x}} +\mathbf{K\textbf{y}} \\
\mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}} & \mathbf P= (\mathbf{I}-\mathbf{KH})\mathbf{\bar{P}}
\end{array}$$
We don't normally use $\mathbf{Fx}$ to propagate the state for the EKF as the linearization causes inaccuracies. It is typical to compute $\bar{\mathbf x}$ using a suitable numerical integration technique such as Euler or Runge Kutta. Thus I wrote $\mathbf{\bar x} = f(\mathbf x, \mathbf u)$. For the same reasons we don't use $\mathbf{H\bar{x}}$ in the computation for the residual, opting for the more accurate $h(\bar{\mathbf x})$.
I think the easiest way to understand the EKF is to start off with an example. Later you may want to come back and reread this section.
## Example: Tracking a Airplane
This example tracks an airplane using ground based radar. We implemented a UKF for this problem in the last chapter. Now we will implement an EKF for the same problem so we can compare both the filter performance and the level of effort required to implement the filter.
Radars work by emitting a beam of radio waves and scanning for a return bounce. Anything in the beam's path will reflects some of the signal back to the radar. By timing how long it takes for the reflected signal to get back to the radar the system can compute the *slant distance* - the straight line distance from the radar installation to the object.
The relationship between the radar's slant range distance $r$ and elevation angle $\epsilon$ with the horizontal position $x$ and altitude $y$ of the aircraft is illustrated in the figure below:
```
ekf_internal.show_radar_chart()
```
This gives us the equalities:
$$\begin{aligned}
\epsilon &= \tan^{-1} \frac y x\\
r^2 &= x^2 + y^2
\end{aligned}$$
### Design the State Variables
We want to track the position of an aircraft assuming a constant velocity and altitude, and measurements of the slant distance to the aircraft. That means we need 3 state variables - horizontal distance, horizonal velocity, and altitude:
$$\mathbf x = \begin{bmatrix}\mathtt{distance} \\\mathtt{velocity}\\ \mathtt{altitude}\end{bmatrix}= \begin{bmatrix}x \\ \dot x\\ y\end{bmatrix}$$
### Design the Process Model
We assume a Newtonian, kinematic system for the aircraft. We've used this model in previous chapters, so by inspection you may recognize that we want
$$\mathbf F = \left[\begin{array}{cc|c} 1 & \Delta t & 0\\
0 & 1 & 0 \\ \hline
0 & 0 & 1\end{array}\right]$$
I've partioned the matrix into blocks to show the upper left block is a constant velocity model for $x$, and the lower right block is a constant position model for $y$.
However, let's practice finding these matrices. We model systems with a set of differential equations. We need an equation in the form
$$\dot{\mathbf x} = \mathbf{Ax} + \mathbf{w}$$
where $\mathbf{w}$ is the system noise.
The variables $x$ and $y$ are independent so we can compute them separately. The differential equations for motion in one dimension are:
$$\begin{aligned}v &= \dot x \\
a &= \ddot{x} = 0\end{aligned}$$
Now we put the differential equations into state-space form. If this was a second or greater order differential system we would have to first reduce them to an equivalent set of first degree equations. The equations are first order, so we put them in state space matrix form as
$$\begin{aligned}\begin{bmatrix}\dot x \\ \ddot{x}\end{bmatrix} &= \begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\
\dot x\end{bmatrix} \\ \dot{\mathbf x} &= \mathbf{Ax}\end{aligned}$$
where $\mathbf A=\begin{bmatrix}0&1\\0&0\end{bmatrix}$.
Recall that $\mathbf A$ is the *system dynamics matrix*. It describes a set of linear differential equations. From it we must compute the state transition matrix $\mathbf F$. $\mathbf F$ describes a discrete set of linear equations which compute $\mathbf x$ for a discrete time step $\Delta t$.
A common way to compute $\mathbf F$ is to use the power series expansion of the matrix exponential:
$$\mathbf F(\Delta t) = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A \Delta t)^3}{3!} + ... $$
$\mathbf A^2 = \begin{bmatrix}0&0\\0&0\end{bmatrix}$, so all higher powers of $\mathbf A$ are also $\mathbf{0}$. Thus the power series expansion is:
$$
\begin{aligned}
\mathbf F &=\mathbf{I} + \mathbf At + \mathbf{0} \\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
\mathbf F &= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
\end{aligned}$$
This is the same result used by the kinematic equations! This exercise was unnecessary other than to illustrate finding the state transition matrix from linear differential equations. We will conclude the chapter with an example that will require the use of this technique.
### Design the Measurement Model
The measurement function takes the state estimate of the prior $\bar{\mathbf x}$ and turn it into a measurement of the slant range distance. We use the Pythagorean theorem to derive:
$$h(\bar{\mathbf x}) = \sqrt{x^2 + y^2}$$
The relationship between the slant distance and the position on the ground is nonlinear due to the square root. We linearize it by evaluating its partial derivative at $\mathbf x_t$:
$$
\mathbf H = \frac{\partial{h(\bar{\mathbf x})}}{\partial{\bar{\mathbf x}}}\biggr|_{\bar{\mathbf x}_t}
$$
The partial derivative of a matrix is called a Jacobian, and takes the form
$$\frac{\partial \mathbf H}{\partial \bar{\mathbf x}} =
\begin{bmatrix}
\frac{\partial h_1}{\partial x_1} & \frac{\partial h_1}{\partial x_2} &\dots \\
\frac{\partial h_2}{\partial x_1} & \frac{\partial h_2}{\partial x_2} &\dots \\
\vdots & \vdots
\end{bmatrix}
$$
In other words, each element in the matrix is the partial derivative of the function $h$ with respect to the $x$ variables. For our problem we have
$$\mathbf H = \begin{bmatrix}{\partial h}/{\partial x} & {\partial h}/{\partial \dot{x}} & {\partial h}/{\partial y}\end{bmatrix}$$
Solving each in turn:
$$\begin{aligned}
\frac{\partial h}{\partial x} &= \frac{\partial}{\partial x} \sqrt{x^2 + y^2} \\
&= \frac{x}{\sqrt{x^2 + y^2}}
\end{aligned}$$
and
$$\begin{aligned}
\frac{\partial h}{\partial \dot{x}} &=
\frac{\partial}{\partial \dot{x}} \sqrt{x^2 + y^2} \\
&= 0
\end{aligned}$$
and
$$\begin{aligned}
\frac{\partial h}{\partial y} &= \frac{\partial}{\partial y} \sqrt{x^2 + y^2} \\
&= \frac{y}{\sqrt{x^2 + y^2}}
\end{aligned}$$
giving us
$$\mathbf H =
\begin{bmatrix}
\frac{x}{\sqrt{x^2 + y^2}} &
0 &
&
\frac{y}{\sqrt{x^2 + y^2}}
\end{bmatrix}$$
This may seem daunting, so step back and recognize that all of this math is doing something very simple. We have an equation for the slant range to the airplane which is nonlinear. The Kalman filter only works with linear equations, so we need to find a linear equation that approximates $\mathbf H$. As we discussed above, finding the slope of a nonlinear equation at a given point is a good approximation. For the Kalman filter, the 'given point' is the state variable $\mathbf x$ so we need to take the derivative of the slant range with respect to $\mathbf x$. For the linear Kalman filter $\mathbf H$ was a constant that we computed prior to running the filter. For the EKF $\mathbf H$ is updated at each step as the evaluation point $\bar{\mathbf x}$ changes at each epoch.
To make this more concrete, let's now write a Python function that computes the Jacobian of $h$ for this problem.
```
from math import sqrt
def HJacobian_at(x):
""" compute Jacobian of H matrix at x """
horiz_dist = x[0]
altitude = x[2]
denom = sqrt(horiz_dist**2 + altitude**2)
return array ([[horiz_dist/denom, 0., altitude/denom]])
```
Finally, let's provide the code for $h(\bar{\mathbf x})$:
```
def hx(x):
""" compute measurement for slant range that
would correspond to state x.
"""
return (x[0]**2 + x[2]**2) ** 0.5
```
Now let's write a simulation for our radar.
```
from numpy.random import randn
import math
class RadarSim:
""" Simulates the radar signal returns from an object
flying at a constant altityude and velocity in 1D.
"""
def __init__(self, dt, pos, vel, alt):
self.pos = pos
self.vel = vel
self.alt = alt
self.dt = dt
def get_range(self):
""" Returns slant range to the object. Call once
for each new measurement at dt time from last call.
"""
# add some process noise to the system
self.vel = self.vel + .1*randn()
self.alt = self.alt + .1*randn()
self.pos = self.pos + self.vel*self.dt
# add measurement noise
err = self.pos * 0.05*randn()
slant_dist = math.sqrt(self.pos**2 + self.alt**2)
return slant_dist + err
```
### Design Process and Measurement Noise
The radar measures the range to a target. We will use $\sigma_{range}= 5$ meters for the noise. This gives us
$$\mathbf R = \begin{bmatrix}\sigma_{range}^2\end{bmatrix} = \begin{bmatrix}25\end{bmatrix}$$
The design of $\mathbf Q$ requires some discussion. The state $\mathbf x= \begin{bmatrix}x & \dot x & y\end{bmatrix}^\mathtt{T}$. The first two elements are position (down range distance) and velocity, so we can use `Q_discrete_white_noise` noise to compute the values for the upper left hand side of $\mathbf Q$. The third element of $\mathbf x$ is altitude, which we are assuming is independent of the down range distance. That leads us to a block design of $\mathbf Q$ of:
$$\mathbf Q = \begin{bmatrix}\mathbf Q_\mathtt{x} & 0 \\ 0 & \mathbf Q_\mathtt{y}\end{bmatrix}$$
### Implementation
`FilterPy` provides the class `ExtendedKalmanFilter`. It works similarly to the `KalmanFilter` class we have been using, except that it allows you to provide a function that computes the Jacobian of $\mathbf H$ and the function $h(\mathbf x)$.
We start by importing the filter and creating it. The dimension of `x` is 3 and `z` has dimension 1.
```python
from filterpy.kalman import ExtendedKalmanFilter
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)
```
We create the radar simulator:
```python
radar = RadarSim(dt, pos=0., vel=100., alt=1000.)
```
We will initialize the filter near the airplane's actual position:
```python
rk.x = array([radar.pos, radar.vel-10, radar.alt+100])
```
We assign the system matrix using the first term of the Taylor series expansion we computed above:
```python
dt = 0.05
rk.F = eye(3) + array([[0, 1, 0],
[0, 0, 0],
[0, 0, 0]])*dt
```
After assigning reasonable values to $\mathbf R$, $\mathbf Q$, and $\mathbf P$ we can run the filter with a simple loop. We pass the functions for computing the Jacobian of $\mathbf H$ and $h(x)$ into the `update` method.
```python
for i in range(int(20/dt)):
z = radar.get_range()
rk.update(array([z]), HJacobian_at, hx)
rk.predict()
```
Adding some boilerplate code to save and plot the results we get:
```
from filterpy.common import Q_discrete_white_noise
from filterpy.kalman import ExtendedKalmanFilter
from numpy import eye, array, asarray
import numpy as np
dt = 0.05
rk = ExtendedKalmanFilter(dim_x=3, dim_z=1)
radar = RadarSim(dt, pos=0., vel=100., alt=1000.)
# make an imperfect starting guess
rk.x = array([radar.pos-100, radar.vel+100, radar.alt+1000])
rk.F = eye(3) + array([[0, 1, 0],
[0, 0, 0],
[0, 0, 0]]) * dt
range_std = 5. # meters
rk.R = np.diag([range_std**2])
rk.Q[0:2, 0:2] = Q_discrete_white_noise(2, dt=dt, var=0.1)
rk.Q[2,2] = 0.1
rk.P *= 50
xs, track = [], []
for i in range(int(20/dt)):
z = radar.get_range()
track.append((radar.pos, radar.vel, radar.alt))
rk.update(array([z]), HJacobian_at, hx)
xs.append(rk.x)
rk.predict()
xs = asarray(xs)
track = asarray(track)
time = np.arange(0, len(xs)*dt, dt)
ekf_internal.plot_radar(xs, track, time)
```
## Using SymPy to compute Jacobians
Depending on your experience with derivatives you may have found the computation of the Jacobian difficult. Even if you found it easy, a slightly more difficult problem easily leads to very difficult computations.
As explained in Appendix A, we can use the SymPy package to compute the Jacobian for us.
```
import sympy
from IPython.display import display
sympy.init_printing(use_latex='mathjax')
x, x_vel, y = sympy.symbols('x, x_vel y')
H = sympy.Matrix([sympy.sqrt(x**2 + y**2)])
state = sympy.Matrix([x, x_vel, y])
J = H.jacobian(state)
display(state)
display(J)
```
This result is the same as the result we computed above, and with much less effort on our part!
## Robot Localization
It's time to try a real problem. I warn you that this section is difficult. However, most books choose simple, textbook problems with simple answers, and you are left wondering how to solve a real world problem.
We will consider the problem of robot localization. We already implemented this in the **Unscented Kalman Filter** chapter, and I recommend you read it now if you haven't already. In this scenario we have a robot that is moving through a landscape using a sensor to detect landmarks. This could be a self driving car using computer vision to identify trees, buildings, and other landmarks. It might be one of those small robots that vacuum your house, or a robot in a warehouse.
The robot has 4 wheels in the same configuration used by automobiles. It maneuvers by pivoting the front wheels. This causes the robot to pivot around the rear axle while moving forward. This is nonlinear behavior which we will have to model.
The robot has a sensor that measures the range and bearing to known targets in the landscape. This is nonlinear because computing a position from a range and bearing requires square roots and trigonometry.
Both the process model and measurement models are nonlinear. The EKF accommodates both, so we provisionally conclude that the EKF is a viable choice for this problem.
### Robot Motion Model
At a first approximation an automobile steers by pivoting the front tires while moving forward. The front of the car moves in the direction that the wheels are pointing while pivoting around the rear tires. This simple description is complicated by issues such as slippage due to friction, the differing behavior of the rubber tires at different speeds, and the need for the outside tire to travel a different radius than the inner tire. Accurately modeling steering requires a complicated set of differential equations.
For lower speed robotic applications a simpler *bicycle model* has been found to perform well. This is a depiction of the model:
```
ekf_internal.plot_bicycle()
```
In the **Unscented Kalman Filter** chapter we derived these equations:
$$\begin{aligned}
\beta &= \frac d w \tan(\alpha) \\
x &= x - R\sin(\theta) + R\sin(\theta + \beta) \\
y &= y + R\cos(\theta) - R\cos(\theta + \beta) \\
\theta &= \theta + \beta
\end{aligned}
$$
where $\theta$ is the robot's heading.
You do not need to understand this model in detail if you are not interested in steering models. The important thing to recognize is that our motion model is nonlinear, and we will need to deal with that with our Kalman filter.
### Design the State Variables
For our filter we will maintain the position $x,y$ and orientation $\theta$ of the robot:
$$\mathbf x = \begin{bmatrix}x \\ y \\ \theta\end{bmatrix}$$
Our control input $\mathbf u$ is the velocity $v$ and steering angle $\alpha$:
$$\mathbf u = \begin{bmatrix}v \\ \alpha\end{bmatrix}$$
### Design the System Model
We model our system as a nonlinear motion model plus noise.
$$\bar x = f(x, u) + \mathcal{N}(0, Q)$$
Using the motion model for a robot that we created above, we can expand this to
$$\bar{\begin{bmatrix}x\\y\\\theta\end{bmatrix}} = \begin{bmatrix}x\\y\\\theta\end{bmatrix} +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}$$
We find The $\mathbf F$ by taking the Jacobian of $f(x,u)$.
$$\mathbf F = \frac{\partial f(x, u)}{\partial x} =\begin{bmatrix}
\frac{\partial f_1}{\partial x} &
\frac{\partial f_1}{\partial y} &
\frac{\partial f_1}{\partial \theta}\\
\frac{\partial f_2}{\partial x} &
\frac{\partial f_2}{\partial y} &
\frac{\partial f_2}{\partial \theta} \\
\frac{\partial f_3}{\partial x} &
\frac{\partial f_3}{\partial y} &
\frac{\partial f_3}{\partial \theta}
\end{bmatrix}
$$
When we calculate these we get
$$\mathbf F = \begin{bmatrix}
1 & 0 & -R\cos(\theta) + R\cos(\theta+\beta) \\
0 & 1 & -R\sin(\theta) + R\sin(\theta+\beta) \\
0 & 0 & 1
\end{bmatrix}$$
We can double check our work with SymPy.
```
import sympy
from sympy.abc import alpha, x, y, v, w, R, theta
from sympy import symbols, Matrix
sympy.init_printing(use_latex="mathjax", fontsize='16pt')
time = symbols('t')
d = v*time
beta = (d/w)*sympy.tan(alpha)
r = w/sympy.tan(alpha)
fxu = Matrix([[x-r*sympy.sin(theta) + r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)- r*sympy.cos(theta+beta)],
[theta+beta]])
F = fxu.jacobian(Matrix([x, y, theta]))
F
```
That looks a bit complicated. We can use SymPy to substitute terms:
```
# reduce common expressions
B, R = symbols('beta, R')
F = F.subs((d/w)*sympy.tan(alpha), B)
F.subs(w/sympy.tan(alpha), R)
```
This form verifies that the computation of the Jacobian is correct.
Now we can turn our attention to the noise. Here, the noise is in our control input, so it is in *control space*. In other words, we command a specific velocity and steering angle, but we need to convert that into errors in $x, y, \theta$. In a real system this might vary depending on velocity, so it will need to be recomputed for every prediction. I will choose this as the noise model; for a real robot you will need to choose a model that accurately depicts the error in your system.
$$\mathbf{M} = \begin{bmatrix}\sigma_{vel}^2 & 0 \\ 0 & \sigma_\alpha^2\end{bmatrix}$$
If this was a linear problem we would convert from control space to state space using the by now familiar $\mathbf{FMF}^\mathsf T$ form. Since our motion model is nonlinear we do not try to find a closed form solution to this, but instead linearize it with a Jacobian which we will name $\mathbf{V}$.
$$\mathbf{V} = \frac{\partial f(x, u)}{\partial u} \begin{bmatrix}
\frac{\partial f_1}{\partial v} & \frac{\partial f_1}{\partial \alpha} \\
\frac{\partial f_2}{\partial v} & \frac{\partial f_2}{\partial \alpha} \\
\frac{\partial f_3}{\partial v} & \frac{\partial f_3}{\partial \alpha}
\end{bmatrix}$$
These partial derivatives become very difficult to work with. Let's compute them with SymPy.
```
V = fxu.jacobian(Matrix([v, alpha]))
V = V.subs(sympy.tan(alpha)/w, 1/R)
V = V.subs(time*v/R, B)
V = V.subs(time*v, 'd')
V
```
This should give you an appreciation of how quickly the EKF become mathematically intractable.
This gives us the final form of our prediction equations:
$$\begin{aligned}
\mathbf{\bar x} &= \mathbf x +
\begin{bmatrix}- R\sin(\theta) + R\sin(\theta + \beta) \\
R\cos(\theta) - R\cos(\theta + \beta) \\
\beta\end{bmatrix}\\
\mathbf{\bar P} &=\mathbf{FPF}^{\mathsf T} + \mathbf{VMV}^{\mathsf T}
\end{aligned}$$
This form of linearization is not the only way to predict $\mathbf x$. For example, we could use a numerical integration technique such as *Runge Kutta* to compute the movement
of the robot. This will be required if the time step is relatively large. Things are not as cut and dried with the EKF as for the Kalman filter. For a real problem you have to carefully model your system with differential equations and then determine the most appropriate way to solve that system. The correct approach depends on the accuracy you require, how nonlinear the equations are, your processor budget, and numerical stability concerns.
### Design the Measurement Model
The robot's sensor provides a noisy bearing and range measurement to multiple known locations in the landscape. The measurement model must convert the state $\begin{bmatrix}x & y&\theta\end{bmatrix}^\mathsf T$ into a range and bearing to the landmark. If $\mathbf p$
is the position of a landmark, the range $r$ is
$$r = \sqrt{(p_x - x)^2 + (p_y - y)^2}$$
The sensor provides bearing relative to the orientation of the robot, so we must subtract the robot's orientation from the bearing to get the sensor reading, like so:
$$\phi = \arctan(\frac{p_y - y}{p_x - x}) - \theta$$
Thus our measurement model $h$ is
$$\begin{aligned}
\mathbf z& = h(\bar{\mathbf x}, \mathbf p) &+ \mathcal{N}(0, R)\\
&= \begin{bmatrix}
\sqrt{(p_x - x)^2 + (p_y - y)^2} \\
\arctan(\frac{p_y - y}{p_x - x}) - \theta
\end{bmatrix} &+ \mathcal{N}(0, R)
\end{aligned}$$
This is clearly nonlinear, so we need linearize $h$ at $\mathbf x$ by taking its Jacobian. We compute that with SymPy below.
```
px, py = symbols('p_x, p_y')
z = Matrix([[sympy.sqrt((px-x)**2 + (py-y)**2)],
[sympy.atan2(py-y, px-x) - theta]])
z.jacobian(Matrix([x, y, theta]))
```
Now we need to write that as a Python function. For example we might write:
```
from math import sqrt
def H_of(x, landmark_pos):
""" compute Jacobian of H matrix where h(x) computes
the range and bearing to a landmark for state x """
px = landmark_pos[0]
py = landmark_pos[1]
hyp = (px - x[0, 0])**2 + (py - x[1, 0])**2
dist = sqrt(hyp)
H = array(
[[-(px - x[0, 0]) / dist, -(py - x[1, 0]) / dist, 0],
[ (py - x[1, 0]) / hyp, -(px - x[0, 0]) / hyp, -1]])
return H
```
We also need to define a function that converts the system state into a measurement.
```
from math import atan2
def Hx(x, landmark_pos):
""" takes a state variable and returns the measurement
that would correspond to that state.
"""
px = landmark_pos[0]
py = landmark_pos[1]
dist = sqrt((px - x[0, 0])**2 + (py - x[1, 0])**2)
Hx = array([[dist],
[atan2(py - x[1, 0], px - x[0, 0]) - x[2, 0]]])
return Hx
```
### Design Measurement Noise
It is reasonable to assume that the noise of the range and bearing measurements are independent, hence
$$\mathbf R=\begin{bmatrix}\sigma_{range}^2 & 0 \\ 0 & \sigma_{bearing}^2\end{bmatrix}$$
### Implementation
We will use `FilterPy`'s `ExtendedKalmanFilter` class to implement the filter. Its `predict()` method uses the standard linear equations for the process model. Ours is nonlinear, so we will have to override `predict()` with our own implementation. I'll want to also use this class to simulate the robot, so I'll add a method `move()` that computes the position of the robot which both `predict()` and my simulation can call.
The matrices for the prediction step are quite large. While writing this code I made several errors before I finally got it working. I only found my errors by using SymPy's `evalf` function. `evalf` evaluates a SymPy `Matrix` with specific values for the variables. I decided to demonstrate this technique to you, and used `evalf` in the Kalman filter code. You'll need to understand a couple of points.
First, `evalf` uses a dictionary to specify the values. For example, if your matrix contains an `x` and `y`, you can write
```python
M.evalf(subs={x:3, y:17})
```
to evaluate the matrix for `x=3` and `y=17`.
Second, `evalf` returns a `sympy.Matrix` object. Use `numpy.array(M).astype(float)` to convert it to a NumPy array. `numpy.array(M)` creates an array of type `object`, which is not what you want.
Here is the code for the EKF:
```
from filterpy.kalman import ExtendedKalmanFilter as EKF
from numpy import array, sqrt
class RobotEKF(EKF):
def __init__(self, dt, wheelbase, std_vel, std_steer):
EKF.__init__(self, 3, 2, 2)
self.dt = dt
self.wheelbase = wheelbase
self.std_vel = std_vel
self.std_steer = std_steer
a, x, y, v, w, theta, time = symbols(
'a, x, y, v, w, theta, t')
d = v*time
beta = (d/w)*sympy.tan(a)
r = w/sympy.tan(a)
self.fxu = Matrix(
[[x-r*sympy.sin(theta)+r*sympy.sin(theta+beta)],
[y+r*sympy.cos(theta)-r*sympy.cos(theta+beta)],
[theta+beta]])
self.F_j = self.fxu.jacobian(Matrix([x, y, theta]))
self.V_j = self.fxu.jacobian(Matrix([v, a]))
# save dictionary and it's variables for later use
self.subs = {x: 0, y: 0, v:0, a:0,
time:dt, w:wheelbase, theta:0}
self.x_x, self.x_y, = x, y
self.v, self.a, self.theta = v, a, theta
def predict(self, u):
self.x = self.move(self.x, u, self.dt)
self.subs[self.theta] = self.x[2, 0]
self.subs[self.v] = u[0]
self.subs[self.a] = u[1]
F = array(self.F_j.evalf(subs=self.subs)).astype(float)
V = array(self.V_j.evalf(subs=self.subs)).astype(float)
# covariance of motion noise in control space
M = array([[self.std_vel*u[0]**2, 0],
[0, self.std_steer**2]])
self.P = np.dot(F, self.P).dot(F.T) + np.dot(V, M).dot(V.T)
def move(self, x, u, dt):
hdg = x[2, 0]
vel = u[0]
steering_angle = u[1]
dist = vel * dt
if abs(steering_angle) > 0.001: # is robot turning?
beta = (dist / self.wheelbase) * tan(steering_angle)
r = self.wheelbase / tan(steering_angle) # radius
dx = np.array([[-r*sin(hdg) + r*sin(hdg + beta)],
[r*cos(hdg) - r*cos(hdg + beta)],
[beta]])
else: # moving in straight line
dx = np.array([[dist*cos(hdg)],
[dist*sin(hdg)],
[0]])
return x + dx
```
Now we have another issue to handle. The residual is notionally computed as $y = z - h(x)$ but this will not work because our measurement contains an angle in it. Suppose z has a bearing of $1^\circ$ and $h(x)$ has a bearing of $359^\circ$. Naively subtracting them would yield a angular difference of $-358^\circ$, whereas the correct value is $2^\circ$. We have to write code to correctly compute the bearing residual.
```
def residual(a, b):
""" compute residual (a-b) between measurements containing
[range, bearing]. Bearing is normalized to [-pi, pi)"""
y = a - b
y[1] = y[1] % (2 * np.pi) # force in range [0, 2 pi)
if y[1] > np.pi: # move to [-pi, pi)
y[1] -= 2 * np.pi
return y
```
The rest of the code runs the simulation and plots the results, and shouldn't need too much comment by now. I create a variable `landmarks` that contains the landmark coordinates. I update the simulated robot position 10 times a second, but run the EKF only once per second. This is for two reasons. First, we are not using Runge Kutta to integrate the differental equations of motion, so a narrow time step allows our simulation to be more accurate. Second, it is fairly normal in embedded systems to have limited processing speed. This forces you to run your Kalman filter only as frequently as absolutely needed.
```
from filterpy.stats import plot_covariance_ellipse
from math import sqrt, tan, cos, sin, atan2
import matplotlib.pyplot as plt
dt = 1.0
def z_landmark(lmark, sim_pos, std_rng, std_brg):
x, y = sim_pos[0, 0], sim_pos[1, 0]
d = np.sqrt((lmark[0] - x)**2 + (lmark[1] - y)**2)
a = atan2(lmark[1] - y, lmark[0] - x) - sim_pos[2, 0]
z = np.array([[d + randn()*std_rng],
[a + randn()*std_brg]])
return z
def ekf_update(ekf, z, landmark):
ekf.update(z, HJacobian=H_of, Hx=Hx,
residual=residual,
args=(landmark), hx_args=(landmark))
def run_localization(landmarks, std_vel, std_steer,
std_range, std_bearing,
step=10, ellipse_step=20, ylim=None):
ekf = RobotEKF(dt, wheelbase=0.5, std_vel=std_vel,
std_steer=std_steer)
ekf.x = array([[2, 6, .3]]).T # x, y, steer angle
ekf.P = np.diag([.1, .1, .1])
ekf.R = np.diag([std_range**2, std_bearing**2])
sim_pos = ekf.x.copy() # simulated position
# steering command (vel, steering angle radians)
u = array([1.1, .01])
plt.figure()
plt.scatter(landmarks[:, 0], landmarks[:, 1],
marker='s', s=60)
track = []
for i in range(200):
sim_pos = ekf.move(sim_pos, u, dt/10.) # simulate robot
track.append(sim_pos)
if i % step == 0:
ekf.predict(u=u)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='k', alpha=0.3)
x, y = sim_pos[0, 0], sim_pos[1, 0]
for lmark in landmarks:
z = z_landmark(lmark, sim_pos,
std_range, std_bearing)
ekf_update(ekf, z, lmark)
if i % ellipse_step == 0:
plot_covariance_ellipse(
(ekf.x[0,0], ekf.x[1,0]), ekf.P[0:2, 0:2],
std=6, facecolor='g', alpha=0.8)
track = np.array(track)
plt.plot(track[:, 0], track[:,1], color='k', lw=2)
plt.axis('equal')
plt.title("EKF Robot localization")
if ylim is not None: plt.ylim(*ylim)
plt.show()
return ekf
landmarks = array([[5, 10], [10, 5], [15, 15]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
print('Final P:', ekf.P.diagonal())
```
I have plotted the landmarks as solid squares. The path of the robot is drawn with a black line. The covariance ellipses for the predict step are light gray, and the covariances of the update are shown in green. To make them visible at this scale I have set the ellipse boundary at 6$\sigma$.
We can see that there is a lot of uncertainty added by our motion model, and that most of the error in in the direction of motion. We determine that from the shape of the blue ellipses. After a few steps we can see that the filter incorporates the landmark measurements and the errors improve.
I used the same initial conditions and landmark locations in the UKF chapter. The UKF achieves much better accuracy in terms of the error ellipse. Both perform roughly as well as far as their estimate for $\mathbf x$ is concerned.
Now let's add another landmark.
```
landmarks = array([[5, 10], [10, 5], [15, 15], [20, 5]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1)
plt.show()
print('Final P:', ekf.P.diagonal())
```
The uncertainly in the estimates near the end of the track are smaller. We can see the effect that multiple landmarks have on our uncertainty by only using the first two landmarks.
```
ekf = run_localization(
landmarks[0:2], std_vel=1.e-10, std_steer=1.e-10,
std_range=1.4, std_bearing=.05)
print('Final P:', ekf.P.diagonal())
```
The estimate quickly diverges from the robot's path after passing the landmarks. The covariance also grows quickly. Let's see what happens with only one landmark:
```
ekf = run_localization(
landmarks[0:1], std_vel=1.e-10, std_steer=1.e-10,
std_range=1.4, std_bearing=.05)
print('Final P:', ekf.P.diagonal())
```
As you probably suspected, one landmark produces a very bad result. Conversely, a large number of landmarks allows us to make very accurate estimates.
```
landmarks = array([[5, 10], [10, 5], [15, 15], [20, 5], [15, 10],
[10,14], [23, 14], [25, 20], [10, 20]])
ekf = run_localization(
landmarks, std_vel=0.1, std_steer=np.radians(1),
std_range=0.3, std_bearing=0.1, ylim=(0, 21))
print('Final P:', ekf.P.diagonal())
```
### Discussion
I said that this was a real problem, and in some ways it is. I've seen alternative presentations that used robot motion models that led to simpler Jacobians. On the other hand, my model of the movement is also simplistic in several ways. First, it uses a bicycle model. A real car has two sets of tires, and each travels on a different radius. The wheels do not grip the surface perfectly. I also assumed that the robot responds instantaneously to the control input. Sebastian Thrun writes in *Probabilistic Robots* that this simplified model is justified because the filters perform well when used to track real vehicles. The lesson here is that while you have to have a reasonably accurate nonlinear model, it does not need to be perfect to operate well. As a designer you will need to balance the fidelity of your model with the difficulty of the math and the CPU time required to perform the linear algebra.
Another way in which this problem was simplistic is that we assumed that we knew the correspondance between the landmarks and measurements. But suppose we are using radar - how would we know that a specific signal return corresponded to a specific building in the local scene? This question hints at SLAM algorithms - simultaneous localization and mapping. SLAM is not the point of this book, so I will not elaborate on this topic.
## UKF vs EKF
In the last chapter I used the UKF to solve this problem. The difference in implementation should be very clear. Computing the Jacobians for the state and measurement models was not trivial despite a rudimentary motion model. A different problem could result in a Jacobian which is difficult or impossible to derive analytically. In contrast, the UKF only requires you to provide a function that computes the system motion model and another for the measurement model.
There are many cases where the Jacobian cannot be found analytically. The details are beyond the scope of this book, but you will have to use numerical methods to compute the Jacobian. That undertaking is not trivial, and you will spend a significant portion of a master's degree at a STEM school learning techniques to handle such situations. Even then you'll likely only be able to solve problems related to your field - an aeronautical engineer learns a lot about Navier Stokes equations, but not much about modelling chemical reaction rates.
So, UKFs are easy. Are they accurate? In practice they often perform better than the EKF. You can find plenty of research papers that prove that the UKF outperforms the EKF in various problem domains. It's not hard to understand why this would be true. The EKF works by linearizing the system model and measurement model at a single point, and the UKF uses $2n+1$ points.
Let's look at a specific example. Take $f(x) = x^3$ and pass a Gaussian distribution through it. I will compute an accurate answer using a monte carlo simulation. I generate 50,000 points randomly distributed according to the Gaussian, pass each through $f(x)$, then compute the mean and variance of the result.
The EKF linearizes the function by taking the derivative to find the slope at the evaluation point $x$. This slope becomes the linear function that we use to transform the Gaussian. Here is a plot of that.
```
import kf_book.nonlinear_plots as nonlinear_plots
nonlinear_plots.plot_ekf_vs_mc()
```
The EKF computation is rather inaccurate. In contrast, here is the performance of the UKF:
```
nonlinear_plots.plot_ukf_vs_mc(alpha=0.001, beta=3., kappa=1.)
```
Here we can see that the computation of the UKF's mean is accurate to 2 decimal places. The standard deviation is slightly off, but you can also fine tune how the UKF computes the distribution by using the $\alpha$, $\beta$, and $\gamma$ parameters for generating the sigma points. Here I used $\alpha=0.001$, $\beta=3$, and $\gamma=1$. Feel free to modify them to see the result. You should be able to get better results than I did. However, avoid over-tuning the UKF for a specific test. It may perform better for your test case, but worse in general.
|
github_jupyter
|
```
import os
import sys
import random
import math
import re
import time
import numpy as np
import cv2
import matplotlib
import matplotlib.pyplot as plt
# Root directory of the project
ROOT_DIR = os.getenv("MRCNN_HOME", "/Mask_RCNN")
# Import Mask RCNN
sys.path.append(ROOT_DIR) # To find local version of the library
from mrcnn.config import Config
from mrcnn import utils
import mrcnn.model as modellib
from mrcnn import visualize
from mrcnn.model import log
%matplotlib inline
# Directory to save logs and trained model
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
# Local path to trained weights file
COCO_MODEL_PATH = os.path.join(ROOT_DIR, "mask_rcnn_coco.h5")
# Download COCO trained weights from Releases if needed
if not os.path.exists(COCO_MODEL_PATH):
utils.download_trained_weights(COCO_MODEL_PATH)
DATA_PATH = "/data/RCNNTanks256Train/Yanbu"
DATA_PATH = os.path.join("E:", os.sep, "RCNNTanks256Train")
IMG_SIZE = 256
# set tf backend to allow memory to grow, instead of claiming everything
import tensorflow as tf
import keras
def get_session():
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
return tf.Session(config=config)
# set the modified tf session as backend in keras
keras.backend.tensorflow_backend.set_session(get_session())
```
## Configurations
```
class MRConfig(Config):
"""Configuration for training on the Miami buildings dataset.
Derives from the base Config class and overrides values specific
to the toy shapes dataset.
"""
# Give the configuration a recognizable name
NAME = "tank"
BATCH_SIZE = 8
GPU_COUNT = 1
IMAGES_PER_GPU = 8
# Number of classes (including background)
NUM_CLASSES = 1 + 1
# Use small images for faster training. Set the limits of the small side
# the large side, and that determines the image shape.
IMAGE_MIN_DIM = IMG_SIZE
IMAGE_MAX_DIM = IMG_SIZE
# Use smaller anchors because our image and objects are small
RPN_ANCHOR_SCALES = (8, 16, 32, 64, 128)
# RPN_ANCHOR_SCALES = (10, 20, 40, 80, 160)
# Ratios of anchors at each cell (width/height)
# A value of 1 represents a square anchor, and 0.5 is a wide anchor
# RPN_ANCHOR_RATIOS = [0.25, 1, 4]
# Loss weights for more precise optimization.
# Can be used for R-CNN training setup.
# LOSS_WEIGHTS = {
# "rpn_class_loss": 1.,
# "rpn_bbox_loss": 1.,
# "mrcnn_class_loss": 1.,
# "mrcnn_bbox_loss": 1.,
# "mrcnn_mask_loss": 1.1
# }
# Reduce training ROIs per image because the images are small and have
# few objects. Aim to allow ROI sampling to pick 33% positive ROIs.
TRAIN_ROIS_PER_IMAGE = 256
# ROI_POSITIVE_RATIO = 0.5 #makes no positive effect
# Max number of final detections
DETECTION_MAX_INSTANCES = 100
# Maximum number of ground truth instances to use in one image
MAX_GT_INSTANCES = 100
# Use a small epoch since the data is simple
STEPS_PER_EPOCH = 100
# use small validation steps since the epoch is small
VALIDATION_STEPS = 1
# Image mean (RGB)
MEAN_PIXEL = np.array([131.84381436753546, 125.43039054432134, 113.32320930217874])
LEARNING_RATE = 1.e-4
WEIGHT_DECAY = 1.e-5
config = MRConfig()
config.display()
```
## Notebook Preferences
```
def get_ax(rows=1, cols=1, size=8):
fig, ax = plt.subplots(rows, cols, figsize=(size*cols, size*rows))
return ax, fig
import glob
import skimage
class MRDataset(utils.Dataset):
def load(self, dataset_dir):
# Add classes
self.add_class("tank", 1, "C_TankCompleted")
#loading images
self._image_dir = os.path.join(dataset_dir, "images/")
self._label_dir = os.path.join(dataset_dir, "labels/")
for i, f in enumerate(glob.glob(os.path.join(self._image_dir, "*.tif"))):
_, filename = os.path.split(f)
self.add_image("tank",
image_id=i,
path=f,
width=config.IMAGE_MAX_DIM,
height=config.IMAGE_MAX_DIM,
filename=filename)
def load_mask(self, image_id):
info = self.image_info[image_id]
fname = info["filename"]
masks = []
class_ids = []
#looping through all the classes, loading and processing corresponding masks
for ci in self.class_info:
class_name = ci["name"]
class_id = ci["id"]
try:
m_src = skimage.io.imread(os.path.join(self._label_dir, class_name, fname))
except:
#no file with masks of this class found
continue
#making individual masks for each instance
instance_ids = np.unique(m_src)
for i in instance_ids:
if i > 0:
m = np.zeros(m_src.shape)
m[m_src==i] = i
if np.any(m==i):
masks.append(m)
class_ids.append(class_id)
if len(masks) == 0:
masks.append(np.zeros(m_src.shape))
class_ids.append(1)
masks = np.stack(masks, axis=-1)
return masks.astype(np.bool), np.array(class_ids, dtype=np.int32)
def image_reference(self, image_id):
"""Return the shapes data of the image."""
info = self.image_info[image_id]
if info["source"] == "tank":
return info["path"]
else:
super(self.__class__).image_reference(self, image_id)
# Training dataset
dataset_train = MRDataset()
dataset_train.load(os.path.join(DATA_PATH, "Karachi20170515_060830"))
dataset_train.prepare()
# Validation dataset
dataset_val = MRDataset()
dataset_val.load(os.path.join(DATA_PATH, "Paradip20170210_043931"))
dataset_val.prepare()
# Test dataset
dataset_test = MRDataset()
dataset_test.load(os.path.join(DATA_PATH, "Karachi20170718_055349"))
dataset_test.prepare()
# Load and display random samples
dataset = dataset_test
image_ids = np.random.choice(dataset.image_ids, 4)
# for ii in dataset.image_info:
# if ii['filename'] == '000005160.tif':
# image_ids = [ii['id']]
# break
for image_id in image_ids:
image = dataset.load_image(image_id)
mask, class_ids = dataset.load_mask(image_id)
visualize.display_top_masks(image, mask, class_ids, dataset.class_names)
#print(dataset.image_info[image_id]["filename"])
#log("mask", mask)
#log("class_ids", class_ids)
#print(class_ids)
```
## Ceate Model
```
# Create model in training mode
model = modellib.MaskRCNN(mode="training",
config=config,
model_dir=MODEL_DIR)
# Which weights to start with?
init_with = "imagenet" # imagenet, coco, or last
if init_with == "imagenet":
model.load_weights(model.get_imagenet_weights(), by_name=True)
elif init_with == "coco":
# Load weights trained on MS COCO, but skip layers that
# are different due to the different number of classes
# See README for instructions to download the COCO weights
model.load_weights(COCO_MODEL_PATH, by_name=True,
exclude=["mrcnn_class_logits",
"mrcnn_bbox_fc",
"mrcnn_bbox",
"mrcnn_mask"])
elif init_with == "last":
# Load the last model you trained and continue training
model_path = model.find_last()
print("Loading weights from ", model_path)
model.load_weights(model_path, by_name=True)
```
## Training
Train in two stages:
1. Only the heads. Here we're freezing all the backbone layers and training only the randomly initialized layers (i.e. the ones that we didn't use pre-trained weights from MS COCO). To train only the head layers, pass `layers='heads'` to the `train()` function.
2. Fine-tune all layers. For this simple example it's not necessary, but we're including it to show the process. Simply pass `layers="all` to train all layers.
```
# Train the head branches
# Passing layers="heads" freezes all layers except the head
# layers. You can also pass a regular expression to select
# which layers to train by name pattern.
model.train(dataset_train,
dataset_val,
learning_rate=config.LEARNING_RATE,
epochs=10,
layers='heads')
# Fine tune all layers
# Passing layers="all" trains all layers. You can also
# pass a regular expression to select which layers to
# train by name pattern.
#image augmentation: https://github.com/aleju/imgaug
import imgaug as ia
from imgaug import augmenters as iaa
sometimes = lambda aug: iaa.Sometimes(0.5, aug)
seqAug = iaa.Sequential(
[
# apply the following augmenters to most images
iaa.Fliplr(0.5), # horizontally flip 50% of all images
iaa.Flipud(0.5), # vertically flip 20% of all images
# crop images by -10% to 10% of their height/width
# sometimes(iaa.CropAndPad( # !!! Looks like memory curruption is hapenning somewhere in this C++ impl
# percent=(-0.1, 0.1),
# pad_mode=ia.ALL,
# pad_cval=0
# )),
sometimes(iaa.Affine(
scale={"x": (0.8, 1.2), "y": (0.8, 1.2)}, # scale images to 80-120% of their size, individually per axis
translate_percent={"x": (-0.2, 0.2), "y": (-0.2, 0.2)}, # translate by -20 to +20 percent (per axis)
rotate=(-175, 175), # rotate by -175 to +175 degrees
shear=(-16, 16), # shear by -16 to +16 degrees
order=[0, 1], # use nearest neighbour or bilinear interpolation (fast)
cval=0, # if mode is constant, use a cval = 0
mode=ia.ALL # use any of scikit-image's warping modes (see 2nd image from the top for examples)
))
],
random_order=True
)
model.train(dataset_train, dataset_val,
learning_rate=config.LEARNING_RATE / 100.0,
epochs=180,
layers="all",
augmentation=seqAug
)
```
## Detection
```
class InferenceConfig(MRConfig):
GPU_COUNT = 1
IMAGES_PER_GPU = 1
DETECTION_MIN_CONFIDENCE = 0.9
DETECTION_NMS_THRESHOLD = 0.2
inference_config = InferenceConfig()
# Recreate the model in inference mode
model = modellib.MaskRCNN(mode="inference",
config=inference_config,
model_dir=MODEL_DIR)
# Get path to saved weights
# Either set a specific path or find last trained weights
model_path = model.find_last()
# model_path = os.path.join(ROOT_DIR, "./logs/r5_imgaug_roi1000_20180608T1627/mask_rcnn_r5_imgaug_roi1000__0570.h5")
# Load trained weights (fill in path to trained weights here)
assert model_path != "", "Provide path to trained weights"
print("Loading weights from ", model_path)
model.load_weights(model_path, by_name=True)
# Test on a random image
dataset = dataset_test
image_id = random.choice(dataset.image_ids)
# for ii in dataset.image_info:
# if ii['filename'] == '000005160.tif':
# image_id = ii['id']
# break
original_image, image_meta, gt_class_id, gt_bbox, gt_mask =\
modellib.load_image_gt(dataset, inference_config,
image_id, use_mini_mask=False)
# log("original_image", original_image)
# log("image_meta", image_meta)
# log("gt_class_id", gt_class_id)
# log("gt_bbox", gt_bbox)
# log("gt_mask", gt_mask)
# print("image_id: ", image_id)
# print(dataset.image_info[image_id])
results = model.detect([original_image], verbose=1)
r = results[0]
#if r["masks"].shape[2] > 0:
# log("masks", r["masks"])
ax, fig = get_ax(1,2)
visualize.display_instances(original_image, gt_bbox, gt_mask, gt_class_id,
dataset.class_names, ax=ax[0])
visualize.display_instances(original_image, r['rois'], r['masks'], r['class_ids'],
dataset.class_names, r['scores'], ax=ax[1])
AP, precisions, recalls, overlaps =\
utils.compute_ap(gt_bbox, gt_class_id, gt_mask,
r["rois"], r["class_ids"], r["scores"], r['masks'])
print(AP)
fig.savefig("tank1.png")
```
## Evaluation
```
# Compute VOC-Style mAP @ IoU=0.5
dataset = dataset_val
image_ids = dataset.image_ids
APs = []
pss = []
rcs = []
ops = []
for image_id in image_ids:
# Load image and ground truth data
image, image_meta, gt_class_id, gt_bbox, gt_mask =\
modellib.load_image_gt(dataset, inference_config,
image_id, use_mini_mask=False)
molded_images = np.expand_dims(modellib.mold_image(image, inference_config), 0)
# Run object detection
results = model.detect([image], verbose=0)
r = results[0]
# Compute AP
AP, precisions, recalls, overlaps =\
utils.compute_ap(gt_bbox, gt_class_id, gt_mask,
r["rois"], r["class_ids"], r["scores"], r['masks'])
APs.append(AP)
pss.append(precisions)
rcs.append(recalls)
ops.append(overlaps)
print("mAP: ", np.mean(APs))
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.