prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Demo-of-RISE-for-slides-with-Jupyter-notebooks-(Python)" data-toc-modified-id="Demo-of-RISE-for-slides-with-Jupyter-notebooks-(Python)-1"><span class="toc-item-num">1 </span>Demo of RISE for slides with Jupyter notebooks (Python)</a></span><ul class="toc-item"><li><span><a href="#Title-2" data-toc-modified-id="Title-2-1.1"><span class="toc-item-num">1.1 </span>Title 2</a></span><ul class="toc-item"><li><span><a href="#Title-3" data-toc-modified-id="Title-3-1.1.1"><span class="toc-item-num">1.1.1 </span>Title 3</a></span><ul class="toc-item"><li><span><a href="#Title-4" data-toc-modified-id="Title-4-1.1.1.1"><span class="toc-item-num">1.1.1.1 </span>Title 4</a></span></li></ul></li></ul></li><li><span><a href="#Text" data-toc-modified-id="Text-1.2"><span class="toc-item-num">1.2 </span>Text</a></span></li><li><span><a href="#Maths" data-toc-modified-id="Maths-1.3"><span class="toc-item-num">1.3 </span>Maths</a></span></li><li><span><a href="#And-code" data-toc-modified-id="And-code-1.4"><span class="toc-item-num">1.4 </span>And code</a></span></li></ul></li><li><span><a href="#More-demo-of-Markdown-code" data-toc-modified-id="More-demo-of-Markdown-code-2"><span class="toc-item-num">2 </span>More demo of Markdown code</a></span><ul class="toc-item"><li><span><a href="#Lists" data-toc-modified-id="Lists-2.1"><span class="toc-item-num">2.1 </span>Lists</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Images" data-toc-modified-id="Images-2.1.0.1"><span class="toc-item-num">2.1.0.1 </span>Images</a></span></li><li><span><a href="#And-Markdown-can-include-raw-HTML" data-toc-modified-id="And-Markdown-can-include-raw-HTML-2.1.0.2"><span class="toc-item-num">2.1.0.2 </span>And Markdown can include raw HTML</a></span></li></ul></li></ul></li></ul></li><li><span><a href="#End-of-this-demo" data-toc-modified-id="End-of-this-demo-3"><span class="toc-item-num">3 </span>End of this demo</a></span></li></ul></div>
# Demo of RISE for slides with Jupyter notebooks (Python)
- This document is an example of a slideshow, written in a [Jupyter notebook](https://www.jupyter.org/) with the [RISE extension](https://github.com/damianavila/RISE).
> By [Lilian Besson](http://perso.crans.org/besson/), Sept.2017.
---
## Title 2
### Title 3
#### Title 4
##### Title 5
##### Title 6
## Text
With text, *emphasis*, **bold**, ~~striked~~, `inline code` and
> *Quote.*
>
> -- By a guy.
## Maths
With inline math $\sin(x)^2 + \cos(x)^2 = 1$ and equations:
$$\sin(x)^2 + \cos(x)^2 = \left(\frac{\mathrm{e}^{ix} - \mathrm{e}^{-ix}}{2i}\right)^2 + \left(\frac{\mathrm{e}^{ix} + \mathrm{e}^{-ix}}{2}\right)^2 = \frac{-\mathrm{e}^{2ix}-\mathrm{e}^{-2ix}+2 \; ++\mathrm{e}^{2ix}+\mathrm{e}^{-2ix}+2}{4} = 1.$$
## And code
In Markdown:
```python
from sys import version
print(version)
```
And in a executable cell (with Python 3 kernel) :
```
from sys import version
print(version)
```
# More demo of Markdown code
## Lists
- Unordered
- lists
- are easy.
And
1. and ordered also ! Just
2. start lines by `1.`, `2.` etc
3. or simply `1.`, `1.`, ...
#### Images
With a HTML `<img/>` tag or the `` Markdown code:
<img width="100" src="agreg/images/dooku.jpg"/>

```
# https://gist.github.com/dm-wyncode/55823165c104717ca49863fc526d1354
"""Embed a YouTube video via its embed url into a notebook."""
from functools import partial
from IPython.display import display, IFrame
width, height = (560, 315, )
def _iframe_attrs(embed_url):
"""Get IFrame args."""
return (
('src', 'width', 'height'),
(embed_url, width, height, ),
)
def _get_args(embed_url):
"""Get args for type to create a class."""
iframe = dict(zip(*_iframe_attrs(embed_url)))
attrs = {
'display': partial(display, IFrame(**iframe)),
}
return ('YouTubeVideo', (object, ), attrs, )
def youtube_video(embed_url):
"""Embed YouTube video into a notebook.
Place this module into the same directory as the notebook.
>>> from embed import youtube_video
>>> youtube_video(url).display()
"""
YouTubeVideo = type(*_get_args(embed_url)) # make a class
return YouTubeVideo() # return an object
```
#### And Markdown can include raw HTML
<center><span style="color: green;">This is a centered span, colored in green.</span></center>
Iframes are disabled by default, but by using the IPython internals we can include let say a YouTube video:
```
youtube_video("https://www.youtube.com/embed/FNg5_2UUCNU").display()
print(2**2021)
```
# End of this demo
- See [here for more notebooks](https://github.com/Naereen/notebooks/)!
- This document, like my other notebooks, is distributed [under the MIT License](https://lbesson.mit-license.org/).
| true |
code
| 0.651632 | null | null | null | null |
|
# GSD: Rpb1 orthologs in 1011 genomes collection
This collects Rpb1 gene and protein sequences from a collection of natural isolates of sequenced yeast genomes from [Peter et al 2017](https://www.ncbi.nlm.nih.gov/pubmed/29643504), and then estimates the count of the heptad repeats. It builds directly on the notebook [here](GSD%20Rpb1_orthologs_in_PB_genomes.ipynb), which descends from [Searching for coding sequences in genomes using BLAST and Python](../Searching%20for%20coding%20sequences%20in%20genomes%20using%20BLAST%20and%20Python.ipynb). It also builds on the notebooks shown [here](https://nbviewer.jupyter.org/github/fomightez/cl_sq_demo-binder/blob/master/notebooks/GSD/GSD%20Add_Supplemental_data_info_to_nt_count%20data%20for%201011_cerevisiae_collection.ipynb) and [here](https://github.com/fomightez/patmatch-binder).
Reference for sequence data:
[Genome evolution across 1,011 Saccharomyces cerevisiae isolates. Peter J, De Chiara M, Friedrich A, Yue JX, Pflieger D, Bergström A, Sigwalt A, Barre B, Freel K, Llored A, Cruaud C, Labadie K, Aury JM, Istace B, Lebrigand K, Barbry P, Engelen S, Lemainque A, Wincker P, Liti G, Schacherer J. Nature. 2018 Apr;556(7701):339-344. doi: 10.1038/s41586-018-0030-5. Epub 2018 Apr 11. PMID: 29643504](https://www.ncbi.nlm.nih.gov/pubmed/29643504)
-----
## Overview

## Preparation
Get scripts and sequence data necessary.
**DO NOT 'RUN ALL'. AN INTERACTION IS NECESSARY AT CELL FIVE. AFTER THAT INTERACTION, THE REST BELOW IT CAN BE RUN.**
(Caveat: right now this is written for genes with no introns. Only a few hundred have in yeast and that is the organism in this example. Intron presence would only become important when trying to translate in late stages of this workflow.)
```
gene_name = "RPB1"
size_expected = 5202
get_seq_from_link = False
link_to_FASTA_of_gene = "https://gist.githubusercontent.com/fomightez/f46b0624f1d8e3abb6ff908fc447e63b/raw/625eaba76bb54e16032f90c8812350441b753a0c/uz_S288C_YOR270C_VPH1_coding.fsa"
#**Possible future enhancement would be to add getting the FASTA of the gene from Yeastmine with just systematic id**
```
Get the `blast_to_df` script by running this commands.
```
import os
file_needed = "blast_to_df.py"
if not os.path.isfile(file_needed):
!curl -O https://raw.githubusercontent.com/fomightez/sequencework/master/blast-utilities/blast_to_df.py
import pandas as pd
```
**Now to get the entire collection or a subset of the 1011 genomes, the next cell will need to be edited.** I'll probably leave it with a small set for typical running purposes. However, to make it run fast, try the 'super-tiny' set with just two.
```
# Method to get ALL the genomes. TAKES A WHILE!!!
# (ca. 1 hour and 15 minutes to download alone? + Extracting is a while.)
# Easiest way to minotor extracting step is to open terminal, cd to
# `GENOMES_ASSEMBLED`, & use `ls | wc -l` to count files extracted.
#!curl -O http://1002genomes.u-strasbg.fr/files/1011Assemblies.tar.gz
#!tar xzf 1011Assemblies.tar.gz
#!rm 1011Assemblies.tar.gz
# Small development set
!curl -OL https://www.dropbox.com/s/f42tiygq9tr1545/medium_setGENOMES_ASSEMBLED.tar.gz
!tar xzf medium_setGENOMES_ASSEMBLED.tar.gz
# Tiny development set
#!curl -OL https://www.dropbox.com/s/txufq2jflkgip82/tiny_setGENOMES_ASSEMBLED.tar.gz
#!tar xzf tiny_setGENOMES_ASSEMBLED.tar.gz
#!mv tiny_setGENOMES_ASSEMBLED GENOMES_ASSEMBLED
#define directory with genomes
genomes_dirn = "GENOMES_ASSEMBLED"
```
Before process the list of all of them, fix one that has an file name mismatch with what the description lines have.
Specifically, the assembly file name is `CDH.re.fa`, but the FASTA-entries inside begin `CDH-3`.
Simple file name mismatch. So next cell will change that file name to match.
```
import os
import sys
file_with_issues = "CDH.re.fa"
if os.path.isfile("GENOMES_ASSEMBLED/"+file_with_issues):
sys.stderr.write("\nFile with name non-matching entries ('{}') observed and"
" fixed.".format(file_with_issues))
!mv GENOMES_ASSEMBLED/CDH.re.fa GENOMES_ASSEMBLED/CDH_3.re.fa
#pause and then check if file with original name is there still because
# it means this was attempted too soon and need to start over.
import time
time.sleep(12) #12 seconds
if os.path.isfile("GENOMES_ASSEMBLED/"+file_with_issues):
sys.stderr.write("\n***PROBLEM. TRIED THIS CELL BEFORE FINISHED UPLOADING.\n"
"DELETE FILES ASSOCIATED AND START ALL OVER AGAIN WITH UPLOAD STEP***.")
else:
sys.stderr.write("\nFile '{}' not seen and so nothing done"
". Seems wrong.".format(file_with_issues))
sys.exit(1)
# Get SGD gene sequence in FASTA format to search for best matches in the genomes
import sys
gene_filen = gene_name + ".fsa"
if get_seq_from_link:
!curl -o {gene_filen} {link_to_FASTA_of_gene}
else:
!touch {gene_filen}
sys.stderr.write("\nEDIT THE FILE '{}' TO CONTAIN "
"YOUR GENE OF INTEREST (FASTA-FORMATTED)"
".".format(gene_filen))
sys.exit(0)
```
**I PUT CONTENTS OF FILE `S288C_YDL140C_RPO21_coding.fsa` downloaded from [here](https://www.yeastgenome.org/locus/S000002299/sequence) as 'RPB1.fsa'.**
Now you are prepared to run BLAST to search each PacBio-sequenced genomes for the best match to a gene from the Saccharomyces cerevisiae strain S288C reference sequence.
## Use BLAST to search the genomes for matches to the gene in the reference genome at SGD
SGD is the [Saccharomyces cerevisiae Genome Database site](http:yeastgenome.org) and the reference genome is from S288C.
This is going to go through each genome and make a database so it is searchable and then search for matches to the gene. The information on the best match will be collected. One use for that information will be collecting the corresponding sequences later.
Import the script that allows sending BLAST output to Python dataframes so that we can use it here.
```
from blast_to_df import blast_to_df
# Make a list of all `genome.fa` files, excluding `genome.fa.nhr` and `genome.fa.nin` and `genome.fansq`
# The excluding was only necessary because I had run some queries preliminarily in development. Normally, it would just be the `.re.fa` at the outset.
fn_to_check = "re.fa"
genomes = []
import os
import fnmatch
for file in os.listdir(genomes_dirn):
if fnmatch.fnmatch(file, '*'+fn_to_check):
if not file.endswith(".nhr") and not file.endswith(".nin") and not file.endswith(".nsq") :
# plus skip hidden files
if not file.startswith("._"):
genomes.append(file)
len(genomes)
```
Using the trick of putting `%%capture` on first line from [here](https://stackoverflow.com/a/23692951/8508004) to suppress the output from BLAST for many sequences from filling up cell.
(You can monitor the making of files ending in `.nhr` for all the FASTA files in `GENOMES_ASSEMBLED` to monitor progress'.)
```
%%time
%%capture
SGD_gene = gene_filen
dfs = []
for genome in genomes:
!makeblastdb -in {genomes_dirn}/{genome} -dbtype nucl
result = !blastn -query {SGD_gene} -db {genomes_dirn}/{genome} -outfmt "6 qseqid sseqid stitle pident qcovs length mismatch gapopen qstart qend sstart send qframe sframe frames evalue bitscore qseq sseq" -task blastn
from blast_to_df import blast_to_df
blast_df = blast_to_df(result.n)
dfs.append(blast_df.head(1))
# merge the dataframes in the list `dfs` into one dataframe
df = pd.concat(dfs)
#Save the df
filen_prefix = gene_name + "_orthologBLASTdf"
df.to_pickle(filen_prefix+".pkl")
df.to_csv(filen_prefix+'.tsv', sep='\t',index = False)
#df
```
Computationally check if any genomes missing from the BLAST results list?
```
subjids = df.sseqid.tolist()
#print (subjids)
#print (subjids[0:10])
subjids = [x.split("-")[0] for x in subjids]
#print (subjids)
#print (subjids[0:10])
len_genome_fn_end = len(fn_to_check) + 1 # plus one to accound for the period that will be
# between `fn_to_check` and strain_id`, such as `SK1.genome.fa`
genome_ids = [x[:-len_genome_fn_end] for x in genomes]
#print (genome_ids[0:10])
a = set(genome_ids)
#print (a)
print ("initial:",len(a))
r = set(subjids)
print("results:",len(r))
print ("missing:",len(a-r))
if len(a-r):
print("\n")
print("ids missing:",a-r)
#a - r
```
Sanity check: Report on how expected size compares to max size seen?
```
size_seen = df.length.max(0)
print ("Expected size of gene:", size_expected)
print ("Most frequent size of matches:", df.length.mode()[0])
print ("Maximum size of matches:", df.length.max(0))
```
## Collect the identified, raw sequences
Get the expected size centered on the best match, plus a little flanking each because they might not exactly cover the entire open reading frame. (Although, the example here all look to be full size.)
```
# Get the script for extracting based on position (and install dependency pyfaidx)
import os
file_needed = "extract_subsequence_from_FASTA.py"
if not os.path.isfile(file_needed):
!curl -O https://raw.githubusercontent.com/fomightez/sequencework/master/Extract_from_FASTA/extract_subsequence_from_FASTA.py
!pip install pyfaidx
```
For the next cell, I am going to use the trick of putting `%%capture` on first line from [here](https://stackoverflow.com/a/23692951/8508004) to suppress the output from the entire set making a long list of output.
For ease just monitor the progress in a launched terminal with the following code run in the directory where this notebook will be because the generated files only moved into the `raw` directory as last step of cell:
ls seq_extracted* | wc -l
(**NOTE: WHEN RUNNING WITH THE FULL SET, THIS CELL BELOW WILL REPORT AROUND A DOZEN `FileNotFoundError:`/Exceptions. HOWEVER, THEY DON'T CAUSE THE NOTEBOOK ITSELF TO CEASE TO RUN. SO DISREGARD THEM FOR THE TIME BEING.** )
```
%%capture
size_expected = size_expected # use value from above, or alter at this point.
#size_expected = df.length.max(0) #bp length of SGD coding sequence; should be equivalent and that way not hardcoded?
extra_add_to_start = 51 #to allow for 'fuzziness' at starting end
extra_add_to_end = 51 #to allow for 'fuzziness' at far end
genome_fn_end = "re.fa"
def midpoint(items):
'''
takes a iterable of items and returns the midpoint (integer) of the first
and second values
'''
return int((int(items[0])+int(items[1]))/2)
#midpoint((1,100))
def determine_pos_to_get(match_start,match_end):
'''
Take the start and end of the matched region.
Calculate midpoint between those and then
center expected size on that to determine
preliminary start and preliminary end to get.
Add the extra basepairs to get at each end
to allow for fuzziness/differences of actual
gene ends for orthologs.
Return the final start and end positions to get.
'''
center_of_match = midpoint((match_start,match_end))
half_size_expected = int(size_expected/2.0)
if size_expected % 2 != 0:
half_size_expected += 1
start_pos = center_of_match - half_size_expected
end_pos = center_of_match + half_size_expected
start_pos -= extra_add_to_start
end_pos += extra_add_to_end
# Because of getting some flanking sequences to account for 'fuzziness', it
# is possible the start and end can exceed possible. 'End' is not a problem
# because the `extract_subsequence_from_FASTA.py` script will get as much as
# it from the indicated sequence if a larger than possible number is
# provided. However,'start' can become negative and because the region to
# extract is provided as a string the dash can become a problem. Dealing
# with it here by making sequence positive only.
# Additionally, because I rely on center of match to position where to get,
# part being cut-off due to absence on sequence fragment will shift center
# of match away from what is actually center of gene and to counter-balance
# add twice the amount to the other end. (Actually, I feel I should adjust
# the start end likewise if the sequence happens to be shorter than portion
# I would like to capture but I don't know length of involved hit yet and
# that would need to be added to allow that to happen!<--TO DO)
if start_pos < 0:
raw_amount_missing_at_start = abs(start_pos)# for counterbalancing; needs
# to be collected before `start_pos` adjusted
start_pos = 1
end_pos += 2 * raw_amount_missing_at_start
return start_pos, end_pos
# go through the dataframe using information on each to come up with sequence file,
# specific indentifier within sequence file, and the start and end to extract
# store these valaues as a list in a dictionary with the strain identifier as the key.
extracted_info = {}
start,end = 0,0
for row in df.itertuples():
#print (row.length)
start_to_get, end_to_get = determine_pos_to_get(row.sstart, row.send)
posns_to_get = "{}-{}".format(start_to_get, end_to_get)
record_id = row.sseqid
strain_id = row.sseqid.split("-")[0]
seq_fn = strain_id + "." + genome_fn_end
extracted_info[strain_id] = [seq_fn, record_id, posns_to_get]
# Use the dictionary to get the sequences
for id_ in extracted_info:
#%run extract_subsequence_from_FASTA.py {*extracted_info[id_]} #unpacking doesn't seem to work here in `%run`
%run extract_subsequence_from_FASTA.py {genomes_dirn}/{extracted_info[id_][0]} {extracted_info[id_][1]} {extracted_info[id_][2]}
#package up the retrieved sequences
archive_file_name = gene_name+"_raw_ortholog_seqs.tar.gz"
# make list of extracted files using fnmatch
fn_part_to_match = "seq_extracted"
collected_seq_files_list = []
import os
import sys
import fnmatch
for file in os.listdir('.'):
if fnmatch.fnmatch(file, fn_part_to_match+'*'):
#print (file)
collected_seq_files_list.append(file)
!tar czf {archive_file_name} {" ".join(collected_seq_files_list)} # use the list for archiving command
sys.stderr.write("\n\nCollected RAW sequences gathered and saved as "
"`{}`.".format(archive_file_name))
# move the collected raw sequences to a folder in preparation for
# extracting encoding sequence from original source below
!mkdir raw
!mv seq_extracted*.fa raw
```
That archive should contain the "raw" sequence for each gene, even if the ends are a little different for each. At minimum the entire gene sequence needs to be there at this point; extra at each end is preferable at this point.
You should inspect them as soon as possible and adjust the extra sequence to add higher or lower depending on whether the ortholog genes vary more or less, respectively. The reason they don't need to be perfect yet though is because next we are going to extract the longest open reading frame, which presumably demarcates the entire gene. Then we can return to use that information to clean up the collected sequences to just be the coding sequence.
## Collect protein translations of the genes and then clean up "raw" sequences to just be coding
We'll assume the longest translatable frame in the collected "raw" sequences encodes the protein sequence for the gene orthologs of interest. Well base these steps on the [section '20.1.13 Identifying open reading frames'](http://biopython.org/DIST/docs/tutorial/Tutorial.html#htoc299) in the present version of the [Biopython Tutorial and Cookbook](http://biopython.org/DIST/docs/tutorial/Tutorial.html) (Last Update – 18 December 2018 (Biopython 1.73).
(First run the next cell to get a script needed for dealing with the strand during the translation and gathering of thge encoding sequence.)
```
import os
file_needed = "convert_fasta_to_reverse_complement.py"
if not os.path.isfile(file_needed):
!curl -O https://raw.githubusercontent.com/fomightez/sequencework/master/ConvertSeq/convert_fasta_to_reverse_complement.py
```
Now to perform the work described in the header to this section...
For the next cell, I am going to use the trick of putting `%%capture` on first line from [here](https://stackoverflow.com/a/23692951/8508004) to suppress the output from the entire set making a long list of output.
For ease just monitor the progress in a launched terminal with the following code run in the directory where this notebook will be:
ls *_ortholog_gene.fa | wc -l
```
%%capture
# find the featured open reading frame and collect presumed protein sequences
# Collect the corresponding encoding sequence from the original source
def len_ORF(items):
# orf is fourth item in the tuples
return len(items[3])
def find_orfs_with_trans(seq, trans_table, min_protein_length):
'''
adapted from the present section '20.1.13 Identifying open reading frames'
http://biopython.org/DIST/docs/tutorial/Tutorial.html#htoc299 in the
present version of the [Biopython Tutorial and Cookbook at
http://biopython.org/DIST/docs/tutorial/Tutorial.html
(Last Update – 18 December 2018 (Biopython 1.73)
Same as there except altered to sort on the length of the
open reading frame.
'''
answer = []
seq_len = len(seq)
for strand, nuc in [(+1, seq), (-1, seq.reverse_complement())]:
for frame in range(3):
trans = str(nuc[frame:].translate(trans_table))
trans_len = len(trans)
aa_start = 0
aa_end = 0
while aa_start < trans_len:
aa_end = trans.find("*", aa_start)
if aa_end == -1:
aa_end = trans_len
if aa_end-aa_start >= min_protein_length:
if strand == 1:
start = frame+aa_start*3
end = min(seq_len,frame+aa_end*3+3)
else:
start = seq_len-frame-aa_end*3-3
end = seq_len-frame-aa_start*3
answer.append((start, end, strand,
trans[aa_start:aa_end]))
aa_start = aa_end+1
answer.sort(key=len_ORF, reverse = True)
return answer
def generate_rcoutput_file_name(file_name,suffix_for_saving = "_rc"):
'''
from https://github.com/fomightez/sequencework/blob/master/ConvertSeq/convert_fasta_to_reverse_complement.py
Takes a file name as an argument and returns string for the name of the
output file. The generated name is based on the original file
name.
Specific example
=================
Calling function with
("sequence.fa", "_rc")
returns
"sequence_rc.fa"
'''
main_part_of_name, file_extension = os.path.splitext(
file_name) #from
#http://stackoverflow.com/questions/541390/extracting-extension-from-filename-in-python
if '.' in file_name: #I don't know if this is needed with the os.path.splitext method but I had it before so left it
return main_part_of_name + suffix_for_saving + file_extension
else:
return file_name + suffix_for_saving + ".fa"
def add_strand_to_description_line(file,strand="-1"):
'''
Takes a file and edits description line to add
strand info at end.
Saves the fixed file
'''
import sys
output_file_name = "temp.txt"
# prepare output file for saving so it will be open and ready
with open(output_file_name, 'w') as output_file:
# read in the input file
with open(file, 'r') as input_handler:
# prepare to give feeback later or allow skipping to certain start
lines_processed = 0
for line in input_handler:
lines_processed += 1
if line.startswith(">"):
new_line = line.strip() + "; {} strand\n".format(strand)
else:
new_line = line
# Send text to output
output_file.write(new_line)
# replace the original file with edited
!mv temp.txt {file}
# Feedback
sys.stderr.write("\nIn {}, strand noted.".format(file))
table = 1 #sets translation table to standard nuclear, see
# https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi
min_pro_len = 80 #cookbook had the standard `100`. Feel free to adjust.
prot_seqs_info = {} #collect as dictionary with strain_id as key. Values to
# be list with source id as first item and protein length as second and
# strand in source seq as third item, and start and end in source sequence as fourth and fifth,
# and file name of protein and gene as sixth and seventh.
# Example key and value pair: 'YPS138':['<source id>','<protein length>',-1,52,2626,'<gene file name>','<protein file name>']
gene_seqs_fn_list = []
prot_seqs_fn_list = []
from Bio import SeqIO
for raw_seq_filen in collected_seq_files_list:
#strain_id = raw_seq_filen[:-len_genome_fn_end] #if was dealing with source seq
strain_id = raw_seq_filen.split("-")[0].split("seq_extracted")[1]
record = SeqIO.read("raw/"+raw_seq_filen,"fasta")
raw_seq_source_fn = strain_id + "." + genome_fn_end
raw_seq_source_id = record.description.split(":")[0]
orf_list = find_orfs_with_trans(record.seq, table, min_pro_len)
orf_start, orf_end, strand, prot_seq = orf_list[0] #longest ORF seq for protein coding
location_raw_seq = record.description.rsplit(":",1)[1] #get to use in calculating
# the start and end position in original genome sequence.
raw_loc_parts = location_raw_seq.split("-")
start_from_raw_seq = int(raw_loc_parts[0])
end_from_raw_seq = int(raw_loc_parts[1])
length_extracted = len(record) #also to use in calculating relative original
#Fix negative value. (Somehow Biopython can report negative value when hitting
# end of sequence without encountering stop codon and negatives messes up
# indexing later it seems.)
if orf_start < 0:
orf_start = 0
# Trim back to the first Methionine, assumed to be the initiating MET.
# (THIS MIGHT BE A SOURCE OF EXTRA 'LEADING' RESIDUES IN SOME CASES & ARGUES
# FOR LIMITING THE AMOUNT OF FLANKING SEQUENCE ADDED TO ALLOW FOR FUZINESS.)
try:
amt_resi_to_trim = prot_seq.index("M")
except ValueError:
sys.stderr.write("**ERROR**When searching for initiating methionine,\n"
"no Methionine found in the traslated protein sequence.**ERROR**")
sys.exit(1)
prot_seq = prot_seq[amt_resi_to_trim:]
len_seq_trimmed = amt_resi_to_trim * 3
# Calculate the adjusted start and end values for the untrimmed ORF
adj_start = start_from_raw_seq + orf_start
adj_end = end_from_raw_seq - (length_extracted - orf_end)
# Adjust for trimming for appropriate strand.
if strand == 1:
adj_start += len_seq_trimmed
#adj_end += 3 # turns out stop codon is part of numbering biopython returns
elif strand == -1:
adj_end -= len_seq_trimmed
#adj_start -= 3 # turns out stop codon is part of numbering biopython returns
else:
sys.stderr.write("**ERROR**No strand match option detected!**ERROR**")
sys.exit(1)
# Collect the sequence for the actual gene encoding region from
# the original sequence. This way the original numbers will
# be put in the file.
start_n_end_str = "{}-{}".format(adj_start,adj_end)
%run extract_subsequence_from_FASTA.py {genomes_dirn}/{raw_seq_source_fn} {raw_seq_source_id} {start_n_end_str}
# rename the extracted subsequence a more distinguishing name and notify
g_output_file_name = strain_id +"_" + gene_name + "_ortholog_gene.fa"
!mv {raw_seq_filen} {g_output_file_name} # because the sequence saved happens to
# be same as raw sequence file saved previously, that name can be used to
# rename new file.
gene_seqs_fn_list.append(g_output_file_name)
sys.stderr.write("\n\nRenamed gene file to "
"`{}`.".format(g_output_file_name))
# Convert extracted sequence to reverse complement if translation was on negative strand.
if strand == -1:
%run convert_fasta_to_reverse_complement.py {g_output_file_name}
# replace original sequence file with the produced file
produced_fn = generate_rcoutput_file_name(g_output_file_name)
!mv {produced_fn} {g_output_file_name}
# add (after saved) onto the end of the description line for that `-1 strand`
# No way to do this in my current version of convert sequence. So editing descr line.
add_strand_to_description_line(g_output_file_name)
#When settled on actual protein encoding sequence, fill out
# description to use for saving the protein sequence.
prot_descr = (record.description.rsplit(":",1)[0]+ " "+ gene_name
+ "_ortholog"+ "| " +str(len(prot_seq)) + " aas | from "
+ raw_seq_source_id + " "
+ str(adj_start) + "-"+str(adj_end))
if strand == -1:
prot_descr += "; {} strand".format(strand)
# save the protein sequence as FASTA
chunk_size = 70 #<---amino acids per line to have in FASTA
prot_seq_chunks = [prot_seq[i:i+chunk_size] for i in range(
0, len(prot_seq),chunk_size)]
prot_seq_fa = ">" + prot_descr + "\n"+ "\n".join(prot_seq_chunks)
p_output_file_name = strain_id +"_" + gene_name + "_protein_ortholog.fa"
with open(p_output_file_name, 'w') as output:
output.write(prot_seq_fa)
prot_seqs_fn_list.append(p_output_file_name)
sys.stderr.write("\n\nProtein sequence saved as "
"`{}`.".format(p_output_file_name))
# at end store information in `prot_seqs_info` for later making a dataframe
# and then text table for saving summary
#'YPS138':['<source id>',<protein length>,-1,52,2626,'<gene file name>','<protein file name>']
prot_seqs_info[strain_id] = [raw_seq_source_id,len(prot_seq),strand,adj_start,adj_end,
g_output_file_name,p_output_file_name]
sys.stderr.write("\n******END OF A SET OF PROTEIN ORTHOLOG "
"AND ENCODING GENE********")
# use `prot_seqs_info` for saving a summary text table (first convert to dataframe?)
table_fn_prefix = gene_name + "_orthologs_table"
table_fn = table_fn_prefix + ".tsv"
pkl_table_fn = table_fn_prefix + ".pkl"
import pandas as pd
info_df = pd.DataFrame.from_dict(prot_seqs_info, orient='index',
columns=['descr_id', 'length', 'strand', 'start','end','gene_file','prot_file']) # based on
# https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.from_dict.html and
# note from Python 3.6 that `pd.DataFrame.from_items` is deprecated;
#"Please use DataFrame.from_dict"
info_df.to_pickle(pkl_table_fn)
info_df.to_csv(table_fn, sep='\t') # keep index is default
sys.stderr.write("Text file of associated details saved as '{}'.".format(table_fn))
# pack up archive of gene and protein sequences plus the table
seqs_list = gene_seqs_fn_list + prot_seqs_fn_list + [table_fn,pkl_table_fn]
archive_file_name = gene_name+"_ortholog_seqs.tar.gz"
!tar czf {archive_file_name} {" ".join(seqs_list)} # use the list for archiving command
sys.stderr.write("\nCollected gene and protein sequences"
" (plus table of details) gathered and saved as "
"`{}`.".format(archive_file_name))
```
Save the tarballed archive to your local machine.
-----
## Estimate the count of the heptad repeats
Make a table of the estimate of heptad repeats for each orthlogous protein sequence.
```
# get the 'patmatch results to dataframe' script
!curl -O https://raw.githubusercontent.com/fomightez/sequencework/master/patmatch-utilities/patmatch_results_to_df.py
```
Using the trick of putting `%%capture` on first line from [here](https://stackoverflow.com/a/23692951/8508004) to suppress the output from `patmatch_results_to_df` function from filling up cell.
```
%%time
%%capture
# Go through each protein sequence file and look for matches to heptad pattern
# LATER POSSIBLE IMPROVEMENT. Translate pasted gene sequence and add SGD REF S228C as first in list `prot_seqs_fn_list`. Because
# although this set of orthologs includes essentially S228C, other lists won't and best to have reference for comparing.
heptad_pattern = "[YF]SP[TG]SP[STAGN]" # will catch repeats#2 through #26 of S288C according to Corden, 2013 PMID: 24040939
from patmatch_results_to_df import patmatch_results_to_df
sum_dfs = []
raw_dfs = []
for prot_seq_fn in prot_seqs_fn_list:
!perl ../../patmatch_1.2/unjustify_fasta.pl {prot_seq_fn}
output = !perl ../../patmatch_1.2/patmatch.pl -p {heptad_pattern} {prot_seq_fn}.prepared
os.remove(os.path.join(prot_seq_fn+".prepared")) #delete file made for PatMatch
raw_pm_df = patmatch_results_to_df(output.n, pattern=heptad_pattern, name="CTD_heptad")
raw_pm_df.sort_values('hit_number', ascending=False, inplace=True)
sum_dfs.append(raw_pm_df.groupby('FASTA_id').head(1))
raw_dfs.append(raw_pm_df)
sum_pm_df = pd.concat(sum_dfs, ignore_index=True)
sum_pm_df.sort_values('hit_number', ascending=False, inplace=True)
sum_pm_df = sum_pm_df[['FASTA_id','hit_number']]
#make protein length into dictionary with ids as keys to map to FASTA_ids in
# order to add protein length as a column in summary table
length_info_by_id= dict(zip(info_df.descr_id,info_df.length))
sum_pm_df['prot_length'] = sum_pm_df['FASTA_id'].map(length_info_by_id)
sum_pm_df = sum_pm_df.reset_index(drop=True)
raw_pm_df = pd.concat(raw_dfs, ignore_index=True)
```
Because of use of `%%capture` to suppress output, need a separate cell to see results summary. (Only showing parts here because will add more useful information below.)
```
sum_pm_df.head() # don't show all yet since lots and want to make this dataframe more useful below
sum_pm_df.tail() # don't show all yet since lots and want to make this dataframe more useful below
```
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
WHAT ONES MISSING NOW?
Computationally check if any genomes missing from the list of orthologs?
```
subjids = df.sseqid.tolist()
#print (subjids)
#print (subjids[0:10])
subjids = [x.split("-")[0] for x in subjids]
#print (subjids)
#print (subjids[0:10])
len_genome_fn_end = len(fn_to_check) + 1 # plus one to accound for the period that will be
# between `fn_to_check` and strain_id`, such as `SK1.genome.fa`
genome_ids = [x[:-len_genome_fn_end] for x in genomes]
#print (genome_ids[0:10])
ortholg_ids = sum_pm_df.FASTA_id.tolist()
ortholg_ids = [x.split("-")[0] for x in ortholg_ids]
a = set(genome_ids)
#print (a)
print ("initial:",len(a))
r = set(subjids)
print("BLAST results:",len(r))
print ("missing from BLAST:",len(a-r))
if len(a-r):
#print("\n")
print("ids missing in BLAST results:",a-r)
#a - r
print ("\n\n=====POST-BLAST=======\n\n")
o = set(ortholg_ids)
print("orthologs extracted:",len(o))
print ("missing post-BLAST:",len(r-o))
if len(r-o):
print("\n")
print("ids lost post-BLAST:",r-o)
#r - o
print ("\n\n\n=====SUMMARY=======\n\n")
if len(a-r) and len(r-o):
print("\nAll missing in end:",(a-r) | (r-o))
```
## Make the Summarizing Dataframe more informative
Add information on whether a stretch of 'N's is present. Making the data suspect and fit to be filtered out. Distinguish between cases where it is in what corresponds to the last third of the protein vs. elsewhere, if possible. Plus whether stop codon is present at end of encoding sequence because such cases also probably should be filtered out.
Add information from the supplemental data table so possible patterns can be assessed more easily.
#### Add information about N stretches and stop codon
```
# Collect following information for each gene sequence:
# N stretch of at least two or more present in first 2/3 of gene sequence
# N stretch of at least two or more present in last 1/3 of gene sequence
# stop codon encoded at end of sequence?
import re
min_number_Ns_in_row_to_collect = 2
pattern_obj = re.compile("N{{{},}}".format(min_number_Ns_in_row_to_collect), re.I) # adpated from
# code worked out in `collapse_large_unknown_blocks_in_DNA_sequence.py`, which relied heavily on
# https://stackoverflow.com/a/250306/8508004
def longest_stretch2ormore_found(string, pattern_obj):
'''
Check if a string has stretches of Ns of length two or more.
If it does, return the length of longest stretch.
If it doesn't return zero.
Based on https://stackoverflow.com/a/1155805/8508004 and
GSD Assessing_ambiguous_nts_in_nuclear_PB_genomes.ipynb
'''
longest_match = ''
for m in pattern_obj.finditer(string):
if len(m.group()) > len(longest_match):
longest_match = m.group()
if longest_match == '':
return 0
else:
return len(longest_match)
def chunk(xs, n):
'''Split the list, xs, into n chunks;
from http://wordaligned.org/articles/slicing-a-list-evenly-with-python'''
L = len(xs)
assert 0 < n <= L
s, r = divmod(L, n)
chunks = [xs[p:p+s] for p in range(0, L, s)]
chunks[n-1:] = [xs[-r-s:]]
return chunks
n_stretch_last_third_by_id = {}
n_stretch_first_two_thirds_by_id = {}
stop_codons = ['TAA','TAG','TGA']
stop_codon_presence_by_id = {}
for fn in gene_seqs_fn_list:
# read in sequence without using pyfaidx because small and not worth making indexing files
lines = []
with open(fn, 'r') as seqfile:
for line in seqfile:
lines.append(line.strip())
descr_line = lines[0]
seq = ''.join(lines[1:])
gene_seq_id = descr_line.split(":")[0].split(">")[1]#first line parsed for all in front of ":" and without caret
# determine first two-thirds and last third
chunks = chunk(seq,3)
assert len(chunks) == 3, ("The sequence must be split in three parts'.")
first_two_thirds = chunks[0] + chunks[1]
last_third = chunks[-1]
# Examine each part
n_stretch_last_third_by_id[gene_seq_id] = longest_stretch2ormore_found(last_third,pattern_obj)
n_stretch_first_two_thirds_by_id[gene_seq_id] = longest_stretch2ormore_found(first_two_thirds,pattern_obj)
#print(gene_seq_id)
#print (seq[-3:] in stop_codons)
#stop_codon_presence_by_id[gene_seq_id] = seq[-3:] in stop_codons
stop_codon_presence_by_id[gene_seq_id] = "+" if seq[-3:] in stop_codons else "-"
# Add collected information to sum_pm_df
sum_pm_df['NstretchLAST_THIRD'] = sum_pm_df['FASTA_id'].map(n_stretch_last_third_by_id)
sum_pm_df['NstretchELSEWHERE'] = sum_pm_df['FASTA_id'].map(n_stretch_first_two_thirds_by_id)
sum_pm_df['stop_codon'] = sum_pm_df['FASTA_id'].map(stop_codon_presence_by_id)
# Safe to ignore any warnings about copy. I think because I swapped columns in and out
# of sum_pm_df earlier perhaps.
```
#### Add details on strains from the published supplemental information
This section is based on [this notebook entitled 'GSD: Add Supplemental data info to nt count data for 1011 cerevisiae collection'](https://github.com/fomightez/cl_sq_demo-binder/blob/master/notebooks/GSD/GSD%20Add_Supplemental_data_info_to_nt_count%20data%20for%201011_cerevisiae_collection.ipynb).
```
!curl -OL https://static-content.springer.com/esm/art%3A10.1038%2Fs41586-018-0030-5/MediaObjects/41586_2018_30_MOESM3_ESM.xls
!pip install xlrd
import pandas as pd
#sum_pm_TEST_df = sum_pm_df.copy()
supp_df = pd.read_excel('41586_2018_30_MOESM3_ESM.xls', sheet_name=0, header=3, skipfooter=31)
supp_df['Standardized name'] = supp_df['Standardized name'].str.replace('SACE_','')
suppl_info_dict = supp_df.set_index('Standardized name').to_dict('index')
#Make new column with simplified strain_id tags to use for relating to supplemental table
def add_id_tags(fasta_fn):
return fasta_fn[:3]
sum_pm_df["id_tag"] = sum_pm_df['FASTA_id'].apply(add_id_tags)
ploidy_dict_by_id = {x:suppl_info_dict[x]['Ploidy'] for x in suppl_info_dict}
aneuploidies_dict_by_id = {x:suppl_info_dict[x]['Aneuploidies'] for x in suppl_info_dict}
eco_origin_dict_by_id = {x:suppl_info_dict[x]['Ecological origins'] for x in suppl_info_dict}
clade_dict_by_id = {x:suppl_info_dict[x]['Clades'] for x in suppl_info_dict}
sum_pm_df['Ploidy'] = sum_pm_df.id_tag.map(ploidy_dict_by_id) #Pandas docs has `Index.map` (uppercase `I`) but only lowercase works.
sum_pm_df['Aneuploidies'] = sum_pm_df.id_tag.map(aneuploidies_dict_by_id)
sum_pm_df['Ecological origin'] = sum_pm_df.id_tag.map(eco_origin_dict_by_id)
sum_pm_df['Clade'] = sum_pm_df.id_tag.map(clade_dict_by_id)
# remove the `id_tag` column add for relating details from supplemental to summary df
sum_pm_df = sum_pm_df.drop('id_tag',1)
# use following two lines when sure want to see all and COMMENT OUT BOTTOM LINE
#with pd.option_context('display.max_rows', None, 'display.max_columns', None):
# display(sum_pm_df)
sum_pm_df
```
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
## Filter collected set to those that are 'complete'
For plotting and summarizing with a good set of information, best to remove any where the identified ortholog gene has stretches of 'N's or lacks a stop codon.
(Keep unfiltered dataframe around though.)
```
sum_pm_UNFILTEREDdf = sum_pm_df.copy()
#subset to those where there noth columns for Nstretch assessment are zero
sum_pm_df = sum_pm_df[(sum_pm_df[['NstretchLAST_THIRD','NstretchELSEWHERE']] == 0).all(axis=1)] # based on https://codereview.stackexchange.com/a/185390
#remove any where there isn't a stop codon
sum_pm_df = sum_pm_df.drop(sum_pm_df[sum_pm_df.stop_codon != '+'].index)
```
Computationally summarize result of filtering in comparison to previous steps:
```
subjids = df.sseqid.tolist()
#print (subjids)
#print (subjids[0:10])
subjids = [x.split("-")[0] for x in subjids]
#print (subjids)
#print (subjids[0:10])
len_genome_fn_end = len(fn_to_check) + 1 # plus one to accound for the period that will be
# between `fn_to_check` and strain_id`, such as `SK1.genome.fa`
genome_ids = [x[:-len_genome_fn_end] for x in genomes]
#print (genome_ids[0:10])
ortholg_ids = sum_pm_UNFILTEREDdf.FASTA_id.tolist()
ortholg_ids = [x.split("-")[0] for x in ortholg_ids]
filtered_ids = sum_pm_df.FASTA_id.tolist()
filtered_ids =[x.split("-")[0] for x in filtered_ids]
a = set(genome_ids)
#print (a)
print ("initial:",len(a))
r = set(subjids)
print("BLAST results:",len(r))
print ("missing from BLAST:",len(a-r))
if len(a-r):
#print("\n")
print("ids missing in BLAST results:",a-r)
#a - r
print ("\n\n=====POST-BLAST=======\n\n")
o = set(ortholg_ids)
print("orthologs extracted:",len(o))
print ("missing post-BLAST:",len(r-o))
if len(r-o):
print("\n")
print("ids lost post-BLAST:",r-o)
#r - o
print ("\n\n\n=====PRE-FILTERING=======\n\n")
print("\nNumber before filtering:",len(sum_pm_UNFILTEREDdf))
if len(a-r) and len(r-o):
print("\nAll missing in unfiltered:",(a-r) | (r-o))
print ("\n\n\n=====POST-FILTERING SUMMARY=======\n\n")
f = set(filtered_ids)
print("\nNumber left in filtered set:",len(sum_pm_df))
print ("Number removed by filtering:",len(o-f))
if len(a-r) and len(r-o) and len(o-f):
print("\nAll missing in filtered:",(a-r) | (r-o) | (o-f))
# use following two lines when sure want to see all and COMMENT OUT BOTTOM LINE
with pd.option_context('display.max_rows', None, 'display.max_columns', None):
display(sum_pm_df)
#sum_pm_df
```
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
#### Archive the 'Filtered' set of sequences
Above I saved all the gene and deduced protein sequences of the orthologs in a single archive. It might be useful to just have an archive of the 'filtered' set.
```
# pack up archive of gene and protein sequences for the 'filtered' set.
# Include the summary table too.
# This is different than the other sets I made because this 'filtering' was
# done using the dataframe and so I don't have the file associations. The file names
# though can be generated using the unfiltered file names for the genes and proteins
# and sorting which ones don't remain in the filtered set using 3-letter tags at
# the beginning of the entries in `FASTA_id` column to relate them.
# Use the `FASTA_id` column of sum_pm_df to make a list of tags that remain in filtered set
tags_remaining_in_filtered = [x[:3] for x in sum_pm_df.FASTA_id.tolist()]
# Go through the gene and protein sequence list and collect those where the first
# three letters match the tag
gene_seqs_FILTfn_list = [x for x in gene_seqs_fn_list if x[:3] in tags_remaining_in_filtered]
prot_seqs_FILTfn_list = [x for x in prot_seqs_fn_list if x[:3] in tags_remaining_in_filtered]
# Save the files in those two lists along with the sum_pm_df (as tabular data and pickled form)
patmatchsum_fn_prefix = gene_name + "_orthologs_patmatch_results_summary"
patmatchsum_fn = patmatchsum_fn_prefix + ".tsv"
pklsum_patmatch_fn = patmatchsum_fn_prefix + ".pkl"
import pandas as pd
sum_pm_df.to_pickle(pklsum_patmatch_fn)
sum_pm_df.to_csv(patmatchsum_fn, sep='\t') # keep index is default
FILTEREDseqs_n_df_list = gene_seqs_FILTfn_list + prot_seqs_FILTfn_list + [patmatchsum_fn,pklsum_patmatch_fn]
archive_file_name = gene_name+"_ortholog_seqsFILTERED.tar.gz"
!tar czf {archive_file_name} {" ".join(FILTEREDseqs_n_df_list)} # use the list for archiving command
sys.stderr.write("\nCollected gene and protein sequences"
" (plus table of details) for 'FILTERED' set gathered and saved as "
"`{}`.".format(archive_file_name))
```
Download the 'filtered' sequences to your local machine.
## Summarizing with filtered set
Plot distribution.
```
%matplotlib inline
import math
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
#Want an image file of the figure saved?
saveplot = True
saveplot_fn_prefix = 'heptad_repeat_distribution'
#sns.distplot(sum_pm_df["hit_number"], kde=False, bins = max(sum_pm_df["hit_number"]));
p= sns.countplot(sum_pm_df["hit_number"],
order = list(range(sum_pm_df.hit_number.min(),sum_pm_df.hit_number.max()+1)),
color="C0", alpha= 0.93)
#palette="Blues"); # `order` to get those categories with zero
# counts to show up from https://stackoverflow.com/a/45359713/8508004
p.set_xlabel("heptad repeats")
#add percent above bars, based on code in middle of https://stackoverflow.com/a/33259038/8508004
ncount = len(sum_pm_df)
for pat in p.patches:
x=pat.get_bbox().get_points()[:,0]
y=pat.get_bbox().get_points()[1,1]
# note that this check on the next line was necessary to add when I went back to cases where there's
# no counts for certain categories and so `y` was coming up `nan` for for thos and causing error
# about needing positive value for the y value; `math.isnan(y)` based on https://stackoverflow.com/a/944733/8508004
if not math.isnan(y):
p.annotate('{:.1f}%'.format(100.*y/(ncount)), (x.mean(), y), ha='center', va='bottom', size = 9, color='#333333')
if saveplot:
fig = p.get_figure() #based on https://stackoverflow.com/a/39482402/8508004
fig.savefig(saveplot_fn_prefix + '.png', bbox_inches='tight')
fig.savefig(saveplot_fn_prefix + '.svg');
```
However, with the entire 1011 collection, those at the bottom can not really be seen. The next plot shows this by limiting y-axis to 103.
It should be possible to make a broken y-axis plot for this eventually but not right now as there is no automagic way. So for now will need to composite the two plots together outside.
(Note that adding percents annotations makes height of this plot look odd in the notebook cell for now.)
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
#Want an image file of the figure saved?
saveplot = True
saveplot_fn_prefix = 'heptad_repeat_distributionLIMIT103'
#sns.distplot(sum_pm_df["hit_number"], kde=False, bins = max(sum_pm_df["hit_number"]));
p= sns.countplot(sum_pm_df["hit_number"],
order = list(range(sum_pm_df.hit_number.min(),sum_pm_df.hit_number.max()+1)),
color="C0", alpha= 0.93)
#palette="Blues"); # `order` to get those categories with zero
# counts to show up from https://stackoverflow.com/a/45359713/8508004
p.set_xlabel("heptad repeats")
plt.ylim(0, 103)
#add percent above bars, based on code in middle of https://stackoverflow.com/a/33259038/8508004
ncount = len(sum_pm_df)
for pat in p.patches:
x=pat.get_bbox().get_points()[:,0]
y=pat.get_bbox().get_points()[1,1]
# note that this check on the next line was necessary to add when I went back to cases where there's
# no counts for certain categories and so `y` was coming up `nan` for those and causing error
# about needing positive value for the y value; `math.isnan(y)` based on https://stackoverflow.com/a/944733/8508004
if not math.isnan(y):
p.annotate('{:.1f}%'.format(100.*y/(ncount)), (x.mean(), y), ha='center', va='bottom', size = 9, color='#333333')
if saveplot:
fig = p.get_figure() #based on https://stackoverflow.com/a/39482402/8508004
fig.savefig(saveplot_fn_prefix + '.png')
fig.savefig(saveplot_fn_prefix + '.svg');
```
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
```
%matplotlib inline
# above line works for JupyterLab which I was developing in. Try `%matplotlib notebook` for when in classic.
# Visualization
# This is loosely based on my past use of seaborn when making `plot_sites_position_across_chromosome.py` and related scripts.
# For example, see `GC-clusters relative mito chromosome and feature` where I ran
# `%run plot_sites_position_across_chromosome.py GC_df_for_merging.pkl -o strand_ofGCacross_mito_chrom`
# add the strain info for listing that without chr info & add species information for coloring on that
chromosome_id_prefix = "-"
def FASTA_id_to_strain(FAid):
'''
use FASTA_id column value to convert to strain_id
and then return the strain_id
'''
return FAid.split(chromosome_id_prefix)[0]
sum_pm_df_for_plot = sum_pm_df.copy()
sum_pm_df_for_plot['strain'] = sum_pm_df['FASTA_id'].apply(FASTA_id_to_strain)
# sum_pm_df['species'] = sum_pm_df['FASTA_id'].apply(strain_to_species) # since need species for label plot strips
# it is easier to add species column first and then use map instead of doing both at same with one `apply`
# of a function or both separately, both with `apply` of two different function.
# sum_pm_df['species'] = sum_pm_df['strain'].apply(strain_to_species)
sum_pm_df_for_plot['species'] = 'cerevisiae'
#Want an image file of the figure saved?
saveplot = True
saveplot_fn_prefix = 'heptad_repeats_by_strain'
import matplotlib.pyplot as plt
if len(sum_pm_df) > 60:
plt.figure(figsize=(8,232))
else:
plt.figure(figsize=(8,12))
import seaborn as sns
sns.set()
# Simple look - Comment out everything below to the next two lines to see it again.
p = sns.stripplot(x="hit_number", y="strain", data=sum_pm_df_for_plot, marker="h", size=7.5, alpha=.98, palette="tab20b")
p = sns.stripplot(x="hit_number", y="strain", data=sum_pm_df_for_plot, marker="D", size=9.5, alpha=.98, hue="Clade")
# NOTE CANNOT JUST USE ONE WITH `hue` by 'Clase' because several don't Clades assigned in the supplemental data
# and so those left off. This overlays the two and doesn't cause artifacts when size of first maker smaller.
p.set_xlabel("heptad repeats")
#p.set_xticklabels([" ","23"," ","24", " ", "25"]) # This was much easier than all the stuff I tried for `Adjusted` look below
# and the only complaint I have with the results is that what I assume are the `minor` tick lines show up; still ended up
# needing this when added `xticks = p.xaxis.get_major_ticks()` in order to not show decimals for ones I kept
#p.set(xticks=[]) # this works to remove the ticks entirely; however, I want to keep major ticks
'''
xticks = p.xaxis.get_major_ticks() #based on https://stackoverflow.com/q/50820043/8508004
for i in range(len(xticks)):
#print (i) # WAS FOR DEBUGGING
keep_ticks = [1,3,5] #harcoding essentially again, but at least it works
if i not in keep_ticks:
xticks[i].set_visible(False)
'''
'''
# Highly Adjusted look - Comment out default look parts above. Ended up going with simple above because still couldn't get
# those with highest number of repeats with combination I could come up with.
sum_pm_df_for_plot["repeats"] = sum_pm_df_for_plot["hit_number"].astype(str) # when not here (use `x="hit_number"` in plot) or
# tried `.astype('category')` get plotting of the 0.5 values too
sum_pm_df_for_plot.sort_values('hit_number', ascending=True, inplace=True) #resorting again was necessary when
# added `sum_pm_df["hit_number"].astype(str)` to get 'lower' to 'higher' as left to right for x-axis; otherwise
# it was putting the first rows on the left, which happened to be the 'higher' repeat values
#p = sns.catplot(x="repeats", y="strain", hue="species", data=sum_pm_df, marker="D", size=10, alpha=.98) #marker size ignored in catplot?
p = sns.stripplot(x="repeats", y="strain", hue="species", data=sum_pm_df, marker="D", size=10, alpha=.98)
#p = sns.stripplot(x="repeats", y="strain", hue="species", order = list(species_dict.keys()), data=sum_pm_df_for_plot, marker="D",
# size=10, alpha=.98) # not fond of essentially harcoding to strain order but makes more logical sense to have
# strains with most repeats at the top of the y-axis; adding `order` makes `sort` order be ignored
p.set_xlabel("heptad repeats")
sum_pm_df_for_plot.sort_values('hit_number', ascending=False, inplace=True) #revert to descending sort for storing df;
'''
if saveplot:
fig = p.get_figure() #based on https://stackoverflow.com/a/39482402/8508004
fig.savefig(saveplot_fn_prefix + '.png', bbox_inches='tight')
fig.savefig(saveplot_fn_prefix + '.svg');
```
(Hexagons are used for those without an assigned clade in [the supplemental data Table 1](https://www.nature.com/articles/s41586-018-0030-5) in the plot above.)
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
```
%matplotlib inline
# above line works for JupyterLab which I was developing in. Try `%matplotlib notebook` for when in classic.
# Visualization
# This is loosely based on my past use of seaborn when making `plot_sites_position_across_chromosome.py` and related scripts.
# For example, see `GC-clusters relative mito chromosome and feature` where I ran
# `%run plot_sites_position_across_chromosome.py GC_df_for_merging.pkl -o strand_ofGCacross_mito_chrom`
# add the strain info for listing that without chr info & add species information for coloring on that
chromosome_id_prefix = "-"
def FASTA_id_to_strain(FAid):
'''
use FASTA_id column value to convert to strain_id
and then return the strain_id
'''
return FAid.split(chromosome_id_prefix)[0]
sum_pm_df_for_plot = sum_pm_df.copy()
sum_pm_df_for_plot['strain'] = sum_pm_df['FASTA_id'].apply(FASTA_id_to_strain)
# sum_pm_df['species'] = sum_pm_df['FASTA_id'].apply(strain_to_species) # since need species for label plot strips
# it is easier to add species column first and then use map instead of doing both at same with one `apply`
# of a function or both separately, both with `apply` of two different function.
# sum_pm_df['species'] = sum_pm_df['strain'].apply(strain_to_species)
sum_pm_df_for_plot['species'] = 'cerevisiae'
#Want an image file of the figure saved?
saveplot = True
saveplot_fn_prefix = 'heptad_repeats_by_proteinlen'
import matplotlib.pyplot as plt
if len(sum_pm_df) > 60:
plt.figure(figsize=(8,232))
else:
plt.figure(figsize=(8,12))
import seaborn as sns
sns.set()
# Simple look - Comment out everything below to the next two lines to see it again.
#p = sns.stripplot(x="hit_number", y="strain", data=sum_pm_df_for_plot, marker="h", size=7.5, alpha=.98, palette="tab20b")
p = sns.stripplot(x="hit_number", y="strain", data=sum_pm_df_for_plot, marker="D", size=9.5, alpha=.98, hue="prot_length")
# NOTE CANNOT JUST USE ONE WITH `hue` by 'Clase' because several don't Clades assigned in the supplemental data
# and so those left off. This overlays the two and doesn't cause artifacts when size of first maker smaller.
p.set_xlabel("heptad repeats")
#p.set_xticklabels([" ","23"," ","24", " ", "25"]) # This was much easier than all the stuff I tried for `Adjusted` look below
# and the only complaint I have with the results is that what I assume are the `minor` tick lines show up; still ended up
# needing this when added `xticks = p.xaxis.get_major_ticks()` in order to not show decimals for ones I kept
#p.set(xticks=[]) # this works to remove the ticks entirely; however, I want to keep major ticks
'''
xticks = p.xaxis.get_major_ticks() #based on https://stackoverflow.com/q/50820043/8508004
for i in range(len(xticks)):
#print (i) # WAS FOR DEBUGGING
keep_ticks = [1,3,5] #harcoding essentially again, but at least it works
if i not in keep_ticks:
xticks[i].set_visible(False)
'''
'''
# Highly Adjusted look - Comment out default look parts above. Ended up going with simple above because still couldn't get
# those with highest number of repeats with combination I could come up with.
sum_pm_df_for_plot["repeats"] = sum_pm_df_for_plot["hit_number"].astype(str) # when not here (use `x="hit_number"` in plot) or
# tried `.astype('category')` get plotting of the 0.5 values too
sum_pm_df_for_plot.sort_values('hit_number', ascending=True, inplace=True) #resorting again was necessary when
# added `sum_pm_df["hit_number"].astype(str)` to get 'lower' to 'higher' as left to right for x-axis; otherwise
# it was putting the first rows on the left, which happened to be the 'higher' repeat values
#p = sns.catplot(x="repeats", y="strain", hue="species", data=sum_pm_df, marker="D", size=10, alpha=.98) #marker size ignored in catplot?
p = sns.stripplot(x="repeats", y="strain", hue="species", data=sum_pm_df, marker="D", size=10, alpha=.98)
#p = sns.stripplot(x="repeats", y="strain", hue="species", order = list(species_dict.keys()), data=sum_pm_df_for_plot, marker="D",
# size=10, alpha=.98) # not fond of essentially harcoding to strain order but makes more logical sense to have
# strains with most repeats at the top of the y-axis; adding `order` makes `sort` order be ignored
p.set_xlabel("heptad repeats")
sum_pm_df_for_plot.sort_values('hit_number', ascending=False, inplace=True) #revert to descending sort for storing df;
'''
if saveplot:
fig = p.get_figure() #based on https://stackoverflow.com/a/39482402/8508004
fig.savefig(saveplot_fn_prefix + '.png', bbox_inches='tight')
fig.savefig(saveplot_fn_prefix + '.svg');
```
I assume that '+ 2' should be added to the hit_number for each based on S288C according to [Corden, 2013](https://www.ncbi.nlm.nih.gov/pubmed/24040939) (or `+1` like [Hsin and Manley, 2012](https://www.ncbi.nlm.nih.gov/pubmed/23028141)); however, that is something that could be explored further.
## Make raw and summary data available for use elsewhere
All the raw data is there for each strain in `raw_pm_df`. For example, the next cell shows how to view the data associated with the summary table for isolate ADK_8:
```
ADK_8_raw = raw_pm_df[raw_pm_df['FASTA_id'] == 'ADK_8-20587'].sort_values('hit_number', ascending=True).reset_index(drop=True)
ADK_8_raw
```
The summary and raw data will be packaged up into one file in the cell below. One of the forms will be a tabular text data ('.tsv') files that can be opened in any spreadsheet software.
```
# save summary and raw results for use elsewhere (or use `.pkl` files for reloading the pickled dataframe into Python/pandas)
patmatch_fn_prefix = gene_name + "_orthologs_patmatch_results"
patmatchsum_fn_prefix = gene_name + "_orthologs_patmatch_results_summary"
patmatchsumFILTERED_fn_prefix = gene_name + "_orthologs_patmatch_results_summaryFILTERED"
patmatch_fn = patmatch_fn_prefix + ".tsv"
pkl_patmatch_fn = patmatch_fn_prefix + ".pkl"
patmatchsumUNF_fn = patmatchsumFILTERED_fn_prefix + ".tsv"
pklsum_patmatchUNF_fn = patmatchsumFILTERED_fn_prefix + ".pkl"
patmatchsum_fn = patmatchsum_fn_prefix + ".tsv"
pklsum_patmatch_fn = patmatchsum_fn_prefix + ".pkl"
import pandas as pd
sum_pm_df.to_pickle(pklsum_patmatch_fn)
sum_pm_df.to_csv(patmatchsum_fn, sep='\t') # keep index is default
sys.stderr.write("Text file of summary details after filtering saved as '{}'.".format(patmatchsum_fn))
sum_pm_UNFILTEREDdf.to_pickle(pklsum_patmatchUNF_fn)
sum_pm_UNFILTEREDdf.to_csv(patmatchsumUNF_fn, sep='\t') # keep index is default
sys.stderr.write("\nText file of summary details before filtering saved as '{}'.".format(patmatchsumUNF_fn))
raw_pm_df.to_pickle(pkl_patmatch_fn)
raw_pm_df.to_csv(patmatch_fn, sep='\t') # keep index is default
sys.stderr.write("\nText file of raw details saved as '{}'.".format(patmatchsum_fn))
# pack up archive dataframes
pm_dfs_list = [patmatch_fn,pkl_patmatch_fn,patmatchsumUNF_fn,pklsum_patmatchUNF_fn, patmatchsum_fn,pklsum_patmatch_fn]
archive_file_name = patmatch_fn_prefix+".tar.gz"
!tar czf {archive_file_name} {" ".join(pm_dfs_list)} # use the list for archiving command
sys.stderr.write("\nCollected pattern matching"
" results gathered and saved as "
"`{}`.".format(archive_file_name))
```
Download the tarballed archive of the files to your computer.
For now that archive doesn't include the figures generated from the plots because with a lot of strains they can get large. Download those if you want them. (Look for `saveplot_fn_prefix` settings in the code to help identify file names.)
----
```
import time
def executeSomething():
#code here
print ('.')
time.sleep(480) #60 seconds times 8 minutes
while True:
executeSomething()
```
| true |
code
| 0.331972 | null | null | null | null |
|
```
#pip install seaborn
```
# Import Libraries
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
```
# Read the CSV and Perform Basic Data Cleaning
```
# Raw dataset drop NA
df = pd.read_csv("../resources/train_predict.csv")
# Drop the null columns where all values are null
df1 = df.dropna(axis='columns', how='all')
df1.head()
#Reviewing the % of null values
100*df1.isnull().sum()/df.shape[0]
# Drop the null rows data cleaning, making all column headers lowercase
loan_df = df.dropna()
loan_df.columns=df.columns.str.lower()
loan_df.head()
#Update column names
loan_df.columns=['loan_id', 'gender', 'married', 'dependents', 'education','self_employed'
, 'income', 'co_income'
, 'loan_amount', 'loan_term', 'credit_history', 'property_area', 'loan_status']
#Test data_df after drop NAN
loan_df.dtypes
loan_df.shape
#Reviewing data
loan_df['dependents'].unique()
#Reviewing data
loan_df['self_employed'].unique()
#Reviewing data
loan_df['loan_term'].unique()
#Reviewing data
loan_df['credit_history'].unique()
loan_df.describe()
```
# Select your features (columns)
```
# Set features. This will also be used as your x values. Removed 'loan_id', 'property_area'
loan_features_df = loan_df[['gender', 'married', 'dependents', 'education','self_employed'
, 'income', 'co_income'
, 'loan_amount', 'loan_term', 'credit_history', 'loan_status']]
loan_features_df.head()
sns.countplot(y='gender', hue ='loan_status',data =loan_features_df)
sns.countplot(y='married', hue ='loan_status',data =loan_features_df)
sns.countplot(y='credit_history', hue ='loan_status',data =loan_features_df)
sns.countplot(y='loan_term', hue ='loan_status',data =loan_features_df)
```
# Create a Train Test Split
Use `loan_status` for the y values
```
y = loan_features_df[["loan_status"]]
X = loan_features_df.drop(columns=["loan_status"])
print(X.shape, y.shape)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1, stratify=y)
#code to numberic Hold-> ‘Urban’: 3, ‘Semiurban’: 2,’Rural’: 1,
code_numeric = {'Female': 1, 'Male': 2,'Yes': 1, 'No': 2,
'Graduate': 1, 'Not Graduate': 2, 'Y': 1, 'N': 0, '3+': 3}
loan_features_df = loan_features_df.applymap(lambda s: code_numeric.get(s) if s in code_numeric else s)
loan_features_df.info()
```
# Pre-processing
Scale the data and perform some feature selection
```
# Scale Data
from sklearn.preprocessing import StandardScaler
# Create a StandardScater model and fit it to the training data
X_scaler = StandardScaler().fit(X_train)
#y_scaler = StandardScaler().fit(y_train)
# to_categorical(y)
# StandardScaler().fit(X)
# Preprocessing
#from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.utils import to_categorical
# label_encoder = LabelEncoder()
# label_encoder.fit(y_train)
# encoded_y_train = label_encoder.transform(y_train)
# encoded_y_test = label_encoder.transform(y_test)
y_train_categorical = to_categorical(y_train)
y_test_categorical = to_categorical(y_test)
```
# Train the Model
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(units=500, activation='relu', input_dim=10))
# model.add(Dense(units=100, activation='relu'))
model.add(Dense(units=2, activation='softmax'))
model.summary()
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Fit the model to the training data
model.fit(
X_scaled,
y_train_categorical,
epochs=100,
shuffle=True,
verbose=2
)
from sklearn.svm import SVC
model = SVC(kernel='linear')
model.fit(X_train_scaled, y_train.values.ravel())
print(f"Training Data Score: {model.score(X_train_scaled, y_train)}")
print(f"Testing Data Score: {model.score(X_test_scaled, y_test)}")
from sklearn.metrics import classification_report
predictions = model.predict(X_test)
print(classification_report(y_test, predictions))
```
# Hyperparameter Tuning
Use `GridSearchCV` to tune the model's parameters
```
# Create the GridSearchCV model
from sklearn.model_selection import GridSearchCV
param_grid = {'C': [1, 2, 10, 50],
'gamma': [0.0001, 0.0005, 0.001, 0.005]}
grid = GridSearchCV(model, param_grid, verbose=3)
# Train the model with GridSearch
grid.fit(X_train, y_train.values.ravel())
#print params, scores
print(grid.best_params_)
print(grid.best_score_)
```
# Save the Model
```
import joblib
# save your model by updating "your_name" with your name
# and "your_model" with your model variable
# be sure to turn this in to BCS
# if joblib fails to import, try running the command to install in terminal/git-bash
filename = 'finalized_Plant_model1.sav'
joblib.dump(model, filename)
#To be done later
# load the model from disk
loaded_model = joblib.load(filename)
result = loaded_model.score(X_test, y_test_categorical)
print(result)
```
| true |
code
| 0.626438 | null | null | null | null |
|
# RadiusNeighborsRegressor with MinMaxScaler & Polynomial Features
**This Code template is for the regression analysis using a RadiusNeighbors Regression and the feature rescaling technique MinMaxScaler along with Polynomial Features as a feature transformation technique in a pipeline**
### Required Packages
```
import warnings as wr
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler,PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score,mean_absolute_error
wr.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path) #reading file
df.head()#displaying initial entries
print('Number of rows are :',df.shape[0], ',and number of columns are :',df.shape[1])
df.columns.tolist()
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
plt.figure(figsize = (15, 10))
corr = df.corr()
mask = np.triu(np.ones_like(corr, dtype = bool))
sns.heatmap(corr, mask = mask, linewidths = 1, annot = True, fmt = ".2f")
plt.show()
correlation = df[df.columns[1:]].corr()[target][:]
correlation
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
#spliting data into X(features) and Y(Target)
X=df[features]
Y=df[target]
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
#we can choose randomstate and test_size as over requerment
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 1) #performing datasplitting
```
### Data Scaling
**Used MinMaxScaler**
* Transform features by scaling each feature to a given range.
* This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g. between zero and one.
### Feature Transformation
**PolynomialFeatures :**
* Generate polynomial and interaction features.
* Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree.
## Model
**RadiusNeighborsRegressor**
RadiusNeighborsRegressor implements learning based on the neighbors within a fixed radius of the query point, where is a floating-point value specified by the user.
**Tuning parameters :-**
* **radius:** Range of parameter space to use by default for radius_neighbors queries.
* **algorithm:** Algorithm used to compute the nearest neighbors:
* **leaf_size:** Leaf size passed to BallTree or KDTree.
* **p:** Power parameter for the Minkowski metric.
* **metric:** the distance metric to use for the tree.
* **outlier_label:** label for outlier samples
* **weights:** weight function used in prediction.
```
#training the RadiusNeighborsRegressor
model = make_pipeline(MinMaxScaler(),PolynomialFeatures(),RadiusNeighborsRegressor(radius=1.5))
model.fit(X_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
#prediction on testing set
prediction=model.predict(X_test)
```
### Model evolution
**r2_score:** The r2_score function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
**MAE:** The mean abosolute error function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
**MSE:** The mean squared error function squares the error(penalizes the model for large errors) by our model.
```
print('Mean Absolute Error:', mean_absolute_error(y_test, prediction))
print('Mean Squared Error:', mean_squared_error(y_test, prediction))
print('Root Mean Squared Error:', np.sqrt(mean_squared_error(y_test, prediction)))
print("R-squared score : ",r2_score(y_test,prediction))
#ploting actual and predicted
red = plt.scatter(np.arange(0,80,5),prediction[0:80:5],color = "red")
green = plt.scatter(np.arange(0,80,5),y_test[0:80:5],color = "green")
plt.title("Comparison of Regression Algorithms")
plt.xlabel("Index of Candidate")
plt.ylabel("target")
plt.legend((red,green),('RadiusNeighborsRegressor', 'REAL'))
plt.show()
```
### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis. For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(10,6))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(X_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Vipin Kumar , Github: [Profile](https://github.com/devVipin01)
| true |
code
| 0.598957 | null | null | null | null |
|
# **CatBoost**
### За основу взят ноутбук из вебинара "CatBoost на больших данных", канал Karpov.Courses, ведущий вебинара Александр Савченко
Репозиторий с исходником: https://github.com/AlexKbit/pyspark-catboost-example
```
%%capture
!pip install pyspark==3.0.3
from pyspark.ml import Pipeline
from pyspark.ml.feature import VectorAssembler, StringIndexer
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.sql import SparkSession
from pyspark.sql import DataFrame
from pyspark.sql.functions import col
from pyspark.sql.types import StructField, StructType
spark = SparkSession.builder\
.master('local[*]')\
.appName('CatBoostWithSpark')\
.config("spark.jars.packages", "ai.catboost:catboost-spark_3.0_2.12:1.0.3")\
.config("spark.executor.cores", "2")\
.config("spark.task.cpus", "2")\
.config("spark.driver.memory", "2g")\
.config("spark.driver.memoryOverhead", "2g")\
.config("spark.executor.memory", "2g")\
.config("spark.executor.memoryOverhead", "2g")\
.getOrCreate()
spark
import catboost_spark
schema_dataset = "col1 String, col2 String, col3 Double, col4 Double, col5 Double, target Integer"
df = spark.read.csv('/content/data.csv',sep=',',header=True,schema = schema_dataset)
df.printSchema()
print(df.describe().show())
print(df.show(7))
TARGET_LABEL = 'target'
evaluator = MulticlassClassificationEvaluator(
labelCol=TARGET_LABEL,
predictionCol="prediction",
metricName='f1')
train_df, test_df = df.randomSplit([0.75, 0.25])
```
### Train CatBoost with Pool
```
col1_indexer = StringIndexer(inputCol='col1', outputCol="col1_index")
col2_indexer = StringIndexer(inputCol='col2', outputCol="col2_index")
features = ["col1_index", "col2_index", "col3", "col4", "col5"]
assembler = VectorAssembler(inputCols=features, outputCol='features')
def prepare_vector(df: DataFrame)-> DataFrame:
result_df = col1_indexer.fit(df).transform(df)
result_df = col2_indexer.fit(result_df).transform(result_df)
result_df = assembler.transform(result_df)
return result_df
train = prepare_vector(train_df)
test = prepare_vector(test_df)
print(train.show(7))
train_pool = catboost_spark.Pool(train.select(['features', TARGET_LABEL]))
train_pool.setLabelCol(TARGET_LABEL)
train_pool.setFeaturesCol('features')
classifier = catboost_spark.CatBoostClassifier(featuresCol='features', labelCol=TARGET_LABEL)
classifier.setIterations(50)
classifier.setDepth(5)
model = classifier.fit(train_pool)
predict = model.transform(test)
print(f'Model F1 = {evaluator.evaluate(predict)}')
print(predict.show(7))
model.saveNativeModel('catboost_native')
model.write().overwrite().save('catboost_spark')
```
### Pipeline model with CatBoost
```
col1_indexer = StringIndexer(inputCol='col1', outputCol="col1_index")
col2_indexer = StringIndexer(inputCol='col2', outputCol="col2_index")
features = ["col1_index", "col2_index", "col3", "col4", "col5"]
assembler = VectorAssembler(inputCols=features, outputCol='features')
classifier = catboost_spark.CatBoostClassifier(featuresCol='features', labelCol=TARGET_LABEL)
classifier.setIterations(50)
classifier.setDepth(5)
pipeline = Pipeline(stages=[col1_indexer, col2_indexer, assembler, classifier])
p_model = pipeline.fit(train_df)
print(test_df.show(7))
predictions = p_model.transform(test_df)
print(predictions.show(7))
print(f'Model F1 = {evaluator.evaluate(predictions)}')
type(p_model)
p_model.write().overwrite().save('catboost_pipeline')
```
| true |
code
| 0.417271 | null | null | null | null |
|
# PyTorch
# Intro to Neural Networks
Lets use some simple models and try to match some simple problems
```
import numpy as np
import torch
import torch.nn as nn
from tensorboardX import SummaryWriter
import matplotlib.pyplot as plt
```
### Data Loading
Before we dive deep into the nerual net, lets take a brief aside to discuss data loading.
Pytorch provides a Dataset class which is fairly easy to inherit from. We need only implement two methods for our data load:
9. __len__(self) -> return the size of our dataset
9. __getitem__(self, idx) -> return a data at a given index.
The *real* benefit of implimenting a Dataset class comes from using the DataLoader class.
For data sets which are too large to fit into memory (or more likely, GPU memory), the DataLoader class gives us two advantages:
9. Efficient shuffling and random sampling for batches
9. Data is loaded in a seperate *processes*.
Number (2) above is *important*. The Python interpretter is single threaded only, enforced with a GIL (Global Interpreter Lock). Without (2), we waste valuable (and potentially expensive) processing time shuffling and sampling and building tensors.
So lets invest a little time to build a Dataset and use the DataLoader.
In or example below, we are going to mock a dataset with a simple function, this time:
y = sin(x) + 0.01 * x^2
```
fun = lambda x: np.sin(x) + 0.01 * x * x
X = np.linspace(-3, 3, 100)
Y = fun(X)
plt.figure(figsize=(7,7))
plt.scatter(X,Y)
plt.legend()
plt.show()
```
### Our First Neural Net
Lets now build our first neural net.
In this case, we'll take a classic approach with 2 fully connected hidden layers and a fully connected output layer.
```
class FirstNet(nn.Module):
def __init__(self, input_size, hidden_size, num_classes):
super(FirstNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, num_classes)
def forward(self, x):
x = x.view(-1,1)
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
return out
net = FirstNet(input_size=1, hidden_size=64, num_classes=1)
print(net)
```
Lets look at a few key features of our net:
1) We have 2 fully connected layers, defined in our init function.
2) We define a *forward pass* method which is the prediction of the neural net given an input X
3) Note that we make a *view* of our input array. In our simple model, we expect a 1D X value, and we output a 1D Y value. For efficiency, we may wish to pass in *many* X values, particularly when training. Thus, we need to set up a *view* of our input array: Many 1D X values. -1 in this case indicates that the first dimension (number of X values) is inferred from the tensor's shape.
### Logging and Visualizing to TensorboardX
Lets track the progress of our training and visualize in tensorboard (using tensorboardX). We'll also add a few other useful functions to help visualize things.
To view the output, run:
`tensorboard --logdir nb/run`
```
tbwriter = SummaryWriter()
```
### Graph Visualization and Batching
We will begin by adding a graph visualization to tensorboard. To do this, we need a valid input to our network.
Our network is simple - floating point in, floating point out. *However*, pytorch expects us to *batch* our inputs - therefore it expects an *array* of inputs instead of a single input. There are many ways to work around this, I like "unsqueeze".
```
X = torch.FloatTensor([0.0])
tbwriter.add_graph(net, X)
```
### Cuda
IF you have a GPU available, your training will run much faster.
Moving data back and forth between the CPU and the GPU is fairly straightforward - although it can be easy to forget.
```
use_cuda = torch.cuda.is_available()
if use_cuda:
net = net.cuda()
def makeFig(iteration):
X = np.linspace(-3, 3, 100, dtype=np.float32)
X = torch.FloatTensor(X)
if use_cuda:
Y = net.forward(X.cuda()).cpu()
else:
Y = net.forward(X)
fig = plt.figure()
plt.plot(X.data.numpy(), Y.data.numpy())
plt.title('Prediciton at iter: {}'.format(iteration))
return fig
def showFig(iteration):
fig = makeFig(iteration)
plt.show()
plt.close()
def logFig(iteration):
fig = makeFig(iteration)
fig.canvas.draw()
raw = np.fromstring(fig.canvas.tostring_rgb(), dtype=np.uint8, sep='')
raw = raw.reshape(fig.canvas.get_width_height()[::-1] + (3,))
tbwriter.add_image('Prediction at iter: {}'.format(iteration), raw)
plt.close()
showFig(0)
```
Ok, we have a ways to go. Lets use our data loader and do some training. Here we will use MSE loss (mean squared error) and SGD optimizer.
```
%%time
learning_rate = 0.01
num_epochs = 4000
if use_cuda:
net = net.cuda()
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)
net.train()
X = np.linspace(-3, 3, 100)
Y = fun(X)
X = torch.FloatTensor(X)
Y = torch.FloatTensor(Y).view(-1,1)
if use_cuda:
X = X.cuda()
Y = Y.cuda()
for epoch in range(num_epochs):
pred = net.forward(X)
loss = criterion(pred, Y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
tbwriter.add_scalar("Loss", loss.data[0])
if (epoch % 100 == 99):
print("Epoch: {:>4} Loss: {}".format(epoch, loss.data[0]))
for name, param in net.named_parameters():
tbwriter.add_histogram(name, param.clone().cpu().data.numpy(), epoch)
logFig(epoch)
net.eval()
showFig(0)
```
## Conclusions
We've written our first network, take a moment and play with some of our models here.
Try inputting a different function into the functional dataset, such as:
dataset = FunctionalDataset(lambda x: 1.0 if x > 0 else -1.0
Try experimenting with the network - change the number of neurons in the layer, or add more layers.
Try changing the learning rate (and probably the number of epochs).
And lastly, try disabling cuda (if you have a gpu).
#### How well does the prediction match our input function?
#### How long does it take to train?
One last note: we are absolutely *over-fitting* our dataset here. In this example, that's ok. For real work, we will need to be more careful.
Speaking of real work, lets do some real work identifying customer cohorts.
| true |
code
| 0.840684 | null | null | null | null |
|
# Doom Deadly Corridor with Dqn
The purpose of this scenario is to teach the agent to navigate towards his fundamental goal (the vest) and make sure he survives at the same time.
### Enviroment
Map is a corridor with shooting monsters on both sides (6 monsters in total). A green vest is placed at the oposite end of the corridor.Reward is proportional (negative or positive) to change of the distance between the player and the vest. If player ignores monsters on the sides and runs straight for the vest he will be killed somewhere along the way.
### Action
- MOVE_LEFT
- MOVE_RIGHT
- ATTACK
- MOVE_FORWARD
- MOVE_BACKWARD
- TURN_LEFT
- TURN_RIGHT
### Rewards
- +dX for getting closer to the vest.
- -dX for getting further from the vest.
- -100 death penalty
## Step 1: Import the libraries
```
import numpy as np
import random # Handling random number generation
import time # Handling time calculation
import cv2
import torch
from vizdoom import * # Doom Environment
import matplotlib.pyplot as plt
from IPython.display import clear_output
from collections import namedtuple, deque
import math
%matplotlib inline
import sys
sys.path.append('../../')
from algos.agents import DQNAgent
from algos.models import DQNCnn
from algos.preprocessing.stack_frame import preprocess_frame, stack_frame
```
## Step 2: Create our environment
Initialize the environment in the code cell below.
```
def create_environment():
game = DoomGame()
# Load the correct configuration
game.load_config("doom_files/deadly_corridor.cfg")
# Load the correct scenario (in our case defend_the_center scenario)
game.set_doom_scenario_path("doom_files/deadly_corridor.wad")
# Here our possible actions
possible_actions = np.identity(7, dtype=int).tolist()
return game, possible_actions
game, possible_actions = create_environment()
# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print("Device: ", device)
```
## Step 3: Viewing our Enviroment
```
print("The size of frame is: (", game.get_screen_height(), ", ", game.get_screen_width(), ")")
print("No. of Actions: ", possible_actions)
game.init()
plt.figure()
plt.imshow(game.get_state().screen_buffer.transpose(1, 2, 0))
plt.title('Original Frame')
plt.show()
game.close()
```
### Execute the code cell below to play Pong with a random policy.
```
def random_play():
game.init()
game.new_episode()
score = 0
while True:
reward = game.make_action(possible_actions[np.random.randint(3)])
done = game.is_episode_finished()
score += reward
time.sleep(0.01)
if done:
print("Your total score is: ", score)
game.close()
break
random_play()
```
## Step 4:Preprocessing Frame
```
game.init()
plt.figure()
plt.imshow(preprocess_frame(game.get_state().screen_buffer.transpose(1, 2, 0), (0, -60, -40, 60), 84), cmap="gray")
game.close()
plt.title('Pre Processed image')
plt.show()
```
## Step 5: Stacking Frame
```
def stack_frames(frames, state, is_new=False):
frame = preprocess_frame(state, (0, -60, -40, 60), 84)
frames = stack_frame(frames, frame, is_new)
return frames
```
## Step 6: Creating our Agent
```
INPUT_SHAPE = (4, 84, 84)
ACTION_SIZE = len(possible_actions)
SEED = 0
GAMMA = 0.99 # discount factor
BUFFER_SIZE = 100000 # replay buffer size
BATCH_SIZE = 32 # Update batch size
LR = 0.0001 # learning rate
TAU = .1 # for soft update of target parameters
UPDATE_EVERY = 100 # how often to update the network
UPDATE_TARGET = 10000 # After which thershold replay to be started
EPS_START = 0.99 # starting value of epsilon
EPS_END = 0.01 # Ending value of epsilon
EPS_DECAY = 100 # Rate by which epsilon to be decayed
agent = DQNAgent(INPUT_SHAPE, ACTION_SIZE, SEED, device, BUFFER_SIZE, BATCH_SIZE, GAMMA, LR, TAU, UPDATE_EVERY, UPDATE_TARGET, DQNCnn)
```
## Step 7: Watching untrained agent play
```
# watch an untrained agent
game.init()
score = 0
state = stack_frames(None, game.get_state().screen_buffer.transpose(1, 2, 0), True)
while True:
action = agent.act(state, 0.01)
score += game.make_action(possible_actions[action])
done = game.is_episode_finished()
if done:
print("Your total score is: ", score)
break
else:
state = stack_frames(state, game.get_state().screen_buffer.transpose(1, 2, 0), False)
game.close()
```
## Step 8: Loading Agent
Uncomment line to load a pretrained agent
```
start_epoch = 0
scores = []
scores_window = deque(maxlen=20)
```
## Step 9: Train the Agent with DQN
```
epsilon_by_epsiode = lambda frame_idx: EPS_END + (EPS_START - EPS_END) * math.exp(-1. * frame_idx /EPS_DECAY)
plt.plot([epsilon_by_epsiode(i) for i in range(1000)])
def train(n_episodes=1000):
"""
Params
======
n_episodes (int): maximum number of training episodes
"""
game.init()
for i_episode in range(start_epoch + 1, n_episodes+1):
game.new_episode()
state = stack_frames(None, game.get_state().screen_buffer.transpose(1, 2, 0), True)
score = 0
eps = epsilon_by_epsiode(i_episode)
while True:
action = agent.act(state, eps)
reward = game.make_action(possible_actions[action])
done = game.is_episode_finished()
score += reward
if done:
agent.step(state, action, reward, state, done)
break
else:
next_state = stack_frames(state, game.get_state().screen_buffer.transpose(1, 2, 0), False)
agent.step(state, action, reward, next_state, done)
state = next_state
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
clear_output(True)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
print('\rEpisode {}\tAverage Score: {:.2f}\tEpsilon: {:.2f}'.format(i_episode, np.mean(scores_window), eps), end="")
game.close()
return scores
scores = train(5000)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
```
## Step 10: Watch a Smart Agent!
```
game.init()
score = 0
state = stack_frames(None, game.get_state().screen_buffer.transpose(1, 2, 0), True)
while True:
action = agent.act(state, 0.01)
score += game.make_action(possible_actions[action])
done = game.is_episode_finished()
if done:
print("Your total score is: ", score)
break
else:
state = stack_frames(state, game.get_state().screen_buffer.transpose(1, 2, 0), False)
game.close()
```
| true |
code
| 0.451931 | null | null | null | null |
|
# <font color='Purple'>Gravitational Wave Generation Array</font>
A Phase Array of dumbells can make a detectable signal...
#### To do:
1. Calculate the dumbell parameters for given mass and frequency
1. How many dumbells?
1. Far-field radiation pattern from many radiators.
1. Beamed GW won't be a plane wave. So what?
1. How much energy is lost to keep it spinning?
1. How do we levitate while spinning?
##### Related work on GW radiation
1. https://www.mit.edu/~iancross/8901_2019A/readings/Quadrupole-GWradiation-Ferrari.pdf
1. Wikipedia article on the GW Quadrupole formula (https://en.wikipedia.org/wiki/Quadrupole_formula)
1. MIT 8.901 lecture on GW radiation (http://www.mit.edu/~iancross/8901_2019A/lec005.pdf)
## <font color='Orange'>Imports, settings, and constants</font>
```
import numpy as np
#import matplotlib as mpl
import matplotlib.pyplot as plt
#import multiprocessing as mproc
#import scipy.signal as sig
import scipy.constants as scc
#import scipy.special as scsp
#import sys, time
from scipy.io import loadmat
# http://www.astropy.org/astropy-tutorials/Quantities.html
# http://docs.astropy.org/en/stable/constants/index.html
from astropy import constants as ascon
# Update the matplotlib configuration parameters:
plt.rcParams.update({'text.usetex': False,
'lines.linewidth': 4,
'font.family': 'serif',
'font.serif': 'Georgia',
'font.size': 22,
'xtick.direction': 'in',
'ytick.direction': 'in',
'xtick.labelsize': 'medium',
'ytick.labelsize': 'medium',
'axes.labelsize': 'medium',
'axes.titlesize': 'medium',
'axes.grid.axis': 'both',
'axes.grid.which': 'both',
'axes.grid': True,
'grid.color': 'xkcd:beige',
'grid.alpha': 0.253,
'lines.markersize': 12,
'legend.borderpad': 0.2,
'legend.fancybox': True,
'legend.fontsize': 'small',
'legend.framealpha': 0.8,
'legend.handletextpad': 0.5,
'legend.labelspacing': 0.33,
'legend.loc': 'best',
'figure.figsize': ((12, 8)),
'savefig.dpi': 140,
'savefig.bbox': 'tight',
'pdf.compression': 9})
def setGrid(ax):
ax.grid(which='major', alpha=0.6)
ax.grid(which='major', linestyle='solid', alpha=0.6)
cList = [(0, 0.1, 0.9),
(0.9, 0, 0),
(0, 0.7, 0),
(0, 0.8, 0.8),
(1.0, 0, 0.9),
(0.8, 0.8, 0),
(1, 0.5, 0),
(0.5, 0.5, 0.5),
(0.4, 0, 0.5),
(0, 0, 0),
(0.3, 0, 0),
(0, 0.3, 0)]
G = scc.G # N * m**2 / kg**2; gravitational constant
c = scc.c
```
## Terrestrial Dumbell (Current Tech)
```
sigma_yield = 9000e6 # Yield strength of annealed silicon [Pa]
m_dumb = 100 # mass of the dumbell end [kg]
L_dumb = 10 # Length of the dumbell [m]
r_dumb = 1 # radius of the dumbell rod [m]
rho_pb = 11.34e3 # density of lead [kg/m^3]
r_ball = ((m_dumb / rho_pb)/(4/3 * np.pi))**(1/3)
f_rot = 1e3 / 2
lamduh = c / f_rot
v_dumb = 2*np.pi*(L_dumb/2) * f_rot
a_dumb = v_dumb**2 / (L_dumb / 2)
F = a_dumb * m_dumb
stress = F / (np.pi * r_dumb**2)
print('Ball radius is ' + '{:0.2f}'.format(r_ball) + ' m')
print(r'Acceleration of ball = ' + '{:0.2g}'.format(a_dumb) + r' m/s^2')
print('Stress = ' + '{:0.2f}'.format(stress/sigma_yield) + 'x Yield Stress')
```
#### Futuristic Dumbell
```
sigma_yield = 5000e9 # ultimate tensile strength of ??? [Pa]
m_f = 1000 # mass of the dumbell end [kg]
L_f = 3000 # Length of the dumbell [m]
r_f = 40 # radius of the dumbell rod [m]
rho_pb = 11.34e3 # density of lead [kg/m^3]
r_b = ((m_dumb / rho_pb)/(4/3 * np.pi))**(1/3)
f_f = 37e3 / 2
lamduh_f = c / f_f
v_f = 2*np.pi*(L_f/2) * f_f
a_f = v_f**2 / (L_f / 2)
F = a_f * m_f
stress = F / (np.pi * r_f**2)
print('Ball radius = ' + '{:0.2f}'.format(r_f) + ' m')
print('Acceleration of ball = ' + '{:0.2g}'.format(a_f) + ' m/s**2')
print('Stress = ' + '{:0.2f}'.format(stress/sigma_yield) + 'x Yield Stress')
```
## <font color='Navy'>Radiation of a dumbell</font>
The dumbell is levitated from its middle point using a magnet. So we can spin it at any frequency without friction.
The quadrupole formula for the strain from this rotating dumbell is:
$\ddot{I} = \omega^2 \frac{M R^2}{2}$
$\ddot{I} = \frac{1}{2} \sigma_{yield}~A~(L_{dumb} / 2)$
The resulting strain is:
$h = \frac{2 G}{c^4 r} \ddot{I}$
```
def h_of_f(omega_rotor, M_ball, d_earth_alien, L_rotor):
I_ddot = 1/2 * M_ball * (L_rotor/2)**2 * (omega_rotor**2)
h = (2*G)/(c**4 * d_earth_alien) * I_ddot
return h
r = 2 * lamduh # take the distance to be 2 x wavelength
#h_2020 = (2*G)/(c**4 * r) * (1/2 * m_dumb * (L_dumb/2)**2) * (2*np.pi*f_rot)**2
w_rot = 2 * np.pi * f_rot
h_2020 = h_of_f(w_rot, m_dumb, r, L_dumb)
d_ref = c * 3600*24*365 * 1000 # 1000 light years [m]
d = 1 * d_ref
h_2035 = h_of_f(w_rot, m_dumb, d, L_dumb)
print('Strain from a single (2018) dumbell is {h:0.3g} at a distance of {r:0.1f} km'.format(h=h_2020, r=r/1000))
print('Strain from a single (2018) dumbell is {h:0.3g} at a distance of {r:0.1f} kilo lt-years'.format(h=h_2035, r=d/d_ref))
r = 2 * lamduh_f # take the distance to be 2 x wavelength
h_f = (2*G)/(c**4 * r) * (1/2 * m_f * (L_f/2)**2) * (2*np.pi*f_f)**2
h_2345 = h_of_f(2*np.pi*f_f, m_f, d, L_dumb)
N_rotors = 100e6
print("Strain from a single (alien) dumbell is {h:0.3g} at a distance of {r:0.1f} kilo lt-years".format(h=h_2345, r=d/d_ref))
print("Strain from many many (alien) dumbells is " + '{:0.3g}'.format(N_rotors*h_2345) + ' at ' + str(1) + ' k lt-yr')
```
## <font color='Navy'>Phased Array</font>
Beam pattern for a 2D grid of rotating dumbells
Treat them like point sources?
Make an array and add up all the spherical waves
| true |
code
| 0.483526 | null | null | null | null |
|
# Introduction to Linear Regression
*Adapted from Chapter 3 of [An Introduction to Statistical Learning](http://www-bcf.usc.edu/~gareth/ISL/)*
||continuous|categorical|
|---|---|---|
|**supervised**|**regression**|classification|
|**unsupervised**|dimension reduction|clustering|
## Motivation
Why are we learning linear regression?
- widely used
- runs fast
- easy to use (not a lot of tuning required)
- highly interpretable
- basis for many other methods
## Libraries
Will be using [Statsmodels](http://statsmodels.sourceforge.net/) for **teaching purposes** since it has some nice characteristics for linear modeling. However, we recommend that you spend most of your energy on [scikit-learn](http://scikit-learn.org/stable/) since it provides significantly more useful functionality for machine learning in general.
```
# imports
import pandas as pd
import matplotlib.pyplot as plt
# this allows plots to appear directly in the notebook
%matplotlib inline
```
## Example: Advertising Data
Let's take a look at some data, ask some questions about that data, and then use linear regression to answer those questions!
```
# read data into a DataFrame
data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
data.head()
```
What are the **features**?
- TV: advertising dollars spent on TV for a single product in a given market (in thousands of dollars)
- Radio: advertising dollars spent on Radio
- Newspaper: advertising dollars spent on Newspaper
What is the **response**?
- Sales: sales of a single product in a given market (in thousands of widgets)
```
# print the shape of the DataFrame
data.shape
```
There are 200 **observations**, and thus 200 markets in the dataset.
```
# visualize the relationship between the features and the response using scatterplots
fig, axs = plt.subplots(1, 3, sharey=True)
data.plot(kind='scatter', x='TV', y='Sales', ax=axs[0], figsize=(16, 8))
data.plot(kind='scatter', x='Radio', y='Sales', ax=axs[1])
data.plot(kind='scatter', x='Newspaper', y='Sales', ax=axs[2])
```
## Questions About the Advertising Data
Let's pretend you work for the company that manufactures and markets this widget. The company might ask you the following: On the basis of this data, how should we spend our advertising money in the future?
This general question might lead you to more specific questions:
1. Is there a relationship between ads and sales?
2. How strong is that relationship?
3. Which ad types contribute to sales?
4. What is the effect of each ad type of sales?
5. Given ad spending in a particular market, can sales be predicted?
We will explore these questions below!
## Simple Linear Regression
Simple linear regression is an approach for predicting a **quantitative response** using a **single feature** (or "predictor" or "input variable"). It takes the following form:
$y = \beta_0 + \beta_1x$
What does each term represent?
- $y$ is the response
- $x$ is the feature
- $\beta_0$ is the intercept
- $\beta_1$ is the coefficient for x
Together, $\beta_0$ and $\beta_1$ are called the **model coefficients**. To create your model, you must "learn" the values of these coefficients. And once we've learned these coefficients, we can use the model to predict Sales!
## Estimating ("Learning") Model Coefficients
Generally speaking, coefficients are estimated using the **least squares criterion**, which means we are find the line (mathematically) which minimizes the **sum of squared residuals** (or "sum of squared errors"):
<img src="08_estimating_coefficients.png">
What elements are present in the diagram?
- The black dots are the **observed values** of x and y.
- The blue line is our **least squares line**.
- The red lines are the **residuals**, which are the distances between the observed values and the least squares line.
How do the model coefficients relate to the least squares line?
- $\beta_0$ is the **intercept** (the value of $y$ when $x$=0)
- $\beta_1$ is the **slope** (the change in $y$ divided by change in $x$)
Here is a graphical depiction of those calculations:
<img src="08_slope_intercept.png">
Let's use **Statsmodels** to estimate the model coefficients for the advertising data:
```
# this is the standard import if you're using "formula notation" (similar to R)
import statsmodels.formula.api as smf
# create a fitted model in one line
lm = smf.ols(formula='Sales ~ TV', data=data).fit()
# print the coefficients
lm.params
```
## Interpreting Model Coefficients
How do we interpret the TV coefficient ($\beta_1$)?
- A "unit" increase in TV ad spending is **associated with** a 0.047537 "unit" increase in Sales.
- Or more clearly: An additional $1,000 spent on TV ads is **associated with** an increase in sales of 47.537 widgets.
Note that if an increase in TV ad spending was associated with a **decrease** in sales, $\beta_1$ would be **negative**.
## Using the Model for Prediction
Let's say that there was a new market where the TV advertising spend was **$50,000**. What would we predict for the Sales in that market?
$$y = \beta_0 + \beta_1x$$
$$y = 7.032594 + 0.047537 \times 50$$
```
# manually calculate the prediction
7.032594 + 0.047537*50
```
Thus, we would predict Sales of **9,409 widgets** in that market.
Of course, we can also use Statsmodels to make the prediction:
```
# you have to create a DataFrame since the Statsmodels formula interface expects it
X_new = pd.DataFrame({'TV': [50]})
X_new.head()
# use the model to make predictions on a new value
lm.predict(X_new)
```
## Plotting the Least Squares Line
Let's make predictions for the **smallest and largest observed values of x**, and then use the predicted values to plot the least squares line:
```
# create a DataFrame with the minimum and maximum values of TV
X_new = pd.DataFrame({'TV': [data.TV.min(), data.TV.max()]})
X_new.head()
# make predictions for those x values and store them
preds = lm.predict(X_new)
preds
# first, plot the observed data
data.plot(kind='scatter', x='TV', y='Sales')
# then, plot the least squares line
plt.plot(X_new, preds, c='red', linewidth=2)
```
## Confidence in our Model
**Question:** Is linear regression a high bias/low variance model, or a low bias/high variance model?
**Answer:** High bias/low variance. Under repeated sampling, the line will stay roughly in the same place (low variance), but the average of those models won't do a great job capturing the true relationship (high bias). Note that low variance is a useful characteristic when you don't have a lot of training data!
A closely related concept is **confidence intervals**. Statsmodels calculates 95% confidence intervals for our model coefficients, which are interpreted as follows: If the population from which this sample was drawn was **sampled 100 times**, approximately **95 of those confidence intervals** would contain the "true" coefficient.
```
# print the confidence intervals for the model coefficients
lm.conf_int()
```
Keep in mind that we only have a **single sample of data**, and not the **entire population of data**. The "true" coefficient is either within this interval or it isn't, but there's no way to actually know. We estimate the coefficient with the data we do have, and we show uncertainty about that estimate by giving a range that the coefficient is **probably** within.
Note that using 95% confidence intervals is just a convention. You can create 90% confidence intervals (which will be more narrow), 99% confidence intervals (which will be wider), or whatever intervals you like.
## Hypothesis Testing and p-values
Closely related to confidence intervals is **hypothesis testing**. Generally speaking, you start with a **null hypothesis** and an **alternative hypothesis** (that is opposite the null). Then, you check whether the data supports **rejecting the null hypothesis** or **failing to reject the null hypothesis**.
(Note that "failing to reject" the null is not the same as "accepting" the null hypothesis. The alternative hypothesis may indeed be true, except that you just don't have enough data to show that.)
As it relates to model coefficients, here is the conventional hypothesis test:
- **null hypothesis:** There is no relationship between TV ads and Sales (and thus $\beta_1$ equals zero)
- **alternative hypothesis:** There is a relationship between TV ads and Sales (and thus $\beta_1$ is not equal to zero)
How do we test this hypothesis? Intuitively, we reject the null (and thus believe the alternative) if the 95% confidence interval **does not include zero**. Conversely, the **p-value** represents the probability that the coefficient is actually zero:
```
# print the p-values for the model coefficients
lm.pvalues
```
If the 95% confidence interval **includes zero**, the p-value for that coefficient will be **greater than 0.05**. If the 95% confidence interval **does not include zero**, the p-value will be **less than 0.05**. Thus, a p-value less than 0.05 is one way to decide whether there is likely a relationship between the feature and the response. (Again, using 0.05 as the cutoff is just a convention.)
In this case, the p-value for TV is far less than 0.05, and so we **believe** that there is a relationship between TV ads and Sales.
Note that we generally ignore the p-value for the intercept.
## How Well Does the Model Fit the data?
The most common way to evaluate the overall fit of a linear model is by the **R-squared** value. R-squared is the **proportion of variance explained**, meaning the proportion of variance in the observed data that is explained by the model, or the reduction in error over the **null model**. (The null model just predicts the mean of the observed response, and thus it has an intercept and no slope.)
R-squared is between 0 and 1, and higher is better because it means that more variance is explained by the model. Here's an example of what R-squared "looks like":
<img src="08_r_squared.png">
You can see that the **blue line** explains some of the variance in the data (R-squared=0.54), the **green line** explains more of the variance (R-squared=0.64), and the **red line** fits the training data even further (R-squared=0.66). (Does the red line look like it's overfitting?)
Let's calculate the R-squared value for our simple linear model:
```
# print the R-squared value for the model
lm.rsquared
```
Is that a "good" R-squared value? It's hard to say. The threshold for a good R-squared value depends widely on the domain. Therefore, it's most useful as a tool for **comparing different models**.
## Multiple Linear Regression
Simple linear regression can easily be extended to include multiple features. This is called **multiple linear regression**:
$y = \beta_0 + \beta_1x_1 + ... + \beta_nx_n$
Each $x$ represents a different feature, and each feature has its own coefficient. In this case:
$y = \beta_0 + \beta_1 \times TV + \beta_2 \times Radio + \beta_3 \times Newspaper$
Let's use Statsmodels to estimate these coefficients:
```
# create a fitted model with all three features
lm = smf.ols(formula='Sales ~ TV + Radio + Newspaper', data=data).fit()
# print the coefficients
lm.params
```
How do we interpret these coefficients? For a given amount of Radio and Newspaper ad spending, an **increase of $1000 in TV ad spending** is associated with an **increase in Sales of 45.765 widgets**.
A lot of the information we have been reviewing piece-by-piece is available in the model summary output:
```
# print a summary of the fitted model
lm.summary()
```
What are a few key things we learn from this output?
- TV and Radio have significant **p-values**, whereas Newspaper does not. Thus we reject the null hypothesis for TV and Radio (that there is no association between those features and Sales), and fail to reject the null hypothesis for Newspaper.
- TV and Radio ad spending are both **positively associated** with Sales, whereas Newspaper ad spending is **slightly negatively associated** with Sales. (However, this is irrelevant since we have failed to reject the null hypothesis for Newspaper.)
- This model has a higher **R-squared** (0.897) than the previous model, which means that this model provides a better fit to the data than a model that only includes TV.
## Feature Selection
How do I decide **which features to include** in a linear model? Here's one idea:
- Try different models, and only keep predictors in the model if they have small p-values.
- Check whether the R-squared value goes up when you add new predictors.
What are the **drawbacks** to this approach?
- Linear models rely upon a lot of **assumptions** (such as the features being independent), and if those assumptions are violated (which they usually are), R-squared and p-values are less reliable.
- Using a p-value cutoff of 0.05 means that if you add 100 predictors to a model that are **pure noise**, 5 of them (on average) will still be counted as significant.
- R-squared is susceptible to **overfitting**, and thus there is no guarantee that a model with a high R-squared value will generalize. Below is an example:
```
# only include TV and Radio in the model
lm = smf.ols(formula='Sales ~ TV + Radio', data=data).fit()
lm.rsquared
# add Newspaper to the model (which we believe has no association with Sales)
lm = smf.ols(formula='Sales ~ TV + Radio + Newspaper', data=data).fit()
lm.rsquared
```
**R-squared will always increase as you add more features to the model**, even if they are unrelated to the response. Thus, selecting the model with the highest R-squared is not a reliable approach for choosing the best linear model.
There is alternative to R-squared called **adjusted R-squared** that penalizes model complexity (to control for overfitting), but it generally [under-penalizes complexity](http://scott.fortmann-roe.com/docs/MeasuringError.html).
So is there a better approach to feature selection? **Cross-validation.** It provides a more reliable estimate of out-of-sample error, and thus is a better way to choose which of your models will best **generalize** to out-of-sample data. There is extensive functionality for cross-validation in scikit-learn, including automated methods for searching different sets of parameters and different models. Importantly, cross-validation can be applied to any model, whereas the methods described above only apply to linear models.
## Linear Regression in scikit-learn
Let's redo some of the Statsmodels code above in scikit-learn:
```
# create X and y
feature_cols = ['TV', 'Radio', 'Newspaper']
X = data[feature_cols]
y = data.Sales
# follow the usual sklearn pattern: import, instantiate, fit
from sklearn.linear_model import LinearRegression
lm = LinearRegression()
lm.fit(X, y)
# print intercept and coefficients
print lm.intercept_
print lm.coef_
# pair the feature names with the coefficients
zip(feature_cols, lm.coef_)
# predict for a new observation
lm.predict([100, 25, 25])
# calculate the R-squared
lm.score(X, y)
```
Note that **p-values** and **confidence intervals** are not (easily) accessible through scikit-learn.
## Handling Categorical Predictors with Two Categories
Up to now, all of our predictors have been numeric. What if one of our predictors was categorical?
Let's create a new feature called **Size**, and randomly assign observations to be **small or large**:
```
import numpy as np
# set a seed for reproducibility
np.random.seed(12345)
# create a Series of booleans in which roughly half are True
nums = np.random.rand(len(data))
mask_large = nums > 0.5
# initially set Size to small, then change roughly half to be large
data['Size'] = 'small'
data.loc[mask_large, 'Size'] = 'large'
data.head()
```
For scikit-learn, we need to represent all data **numerically**. If the feature only has two categories, we can simply create a **dummy variable** that represents the categories as a binary value:
```
# create a new Series called IsLarge
data['IsLarge'] = data.Size.map({'small':0, 'large':1})
data.head()
```
Let's redo the multiple linear regression and include the **IsLarge** predictor:
```
# create X and y
feature_cols = ['TV', 'Radio', 'Newspaper', 'IsLarge']
X = data[feature_cols]
y = data.Sales
# instantiate, fit
lm = LinearRegression()
lm.fit(X, y)
# print coefficients
zip(feature_cols, lm.coef_)
```
How do we interpret the **IsLarge coefficient**? For a given amount of TV/Radio/Newspaper ad spending, being a large market is associated with an average **increase** in Sales of 57.42 widgets (as compared to a Small market, which is called the **baseline level**).
What if we had reversed the 0/1 coding and created the feature 'IsSmall' instead? The coefficient would be the same, except it would be **negative instead of positive**. As such, your choice of category for the baseline does not matter, all that changes is your **interpretation** of the coefficient.
## Handling Categorical Predictors with More than Two Categories
Let's create a new feature called **Area**, and randomly assign observations to be **rural, suburban, or urban**:
```
# set a seed for reproducibility
np.random.seed(123456)
# assign roughly one third of observations to each group
nums = np.random.rand(len(data))
mask_suburban = (nums > 0.33) & (nums < 0.66)
mask_urban = nums > 0.66
data['Area'] = 'rural'
data.loc[mask_suburban, 'Area'] = 'suburban'
data.loc[mask_urban, 'Area'] = 'urban'
data.head()
```
We have to represent Area numerically, but we can't simply code it as 0=rural, 1=suburban, 2=urban because that would imply an **ordered relationship** between suburban and urban (and thus urban is somehow "twice" the suburban category).
Instead, we create **another dummy variable**:
```
# create three dummy variables using get_dummies, then exclude the first dummy column
area_dummies = pd.get_dummies(data.Area, prefix='Area').iloc[:, 1:]
# concatenate the dummy variable columns onto the original DataFrame (axis=0 means rows, axis=1 means columns)
data = pd.concat([data, area_dummies], axis=1)
data.head()
```
Here is how we interpret the coding:
- **rural** is coded as Area_suburban=0 and Area_urban=0
- **suburban** is coded as Area_suburban=1 and Area_urban=0
- **urban** is coded as Area_suburban=0 and Area_urban=1
Why do we only need **two dummy variables, not three?** Because two dummies captures all of the information about the Area feature, and implicitly defines rural as the baseline level. (In general, if you have a categorical feature with k levels, you create k-1 dummy variables.)
If this is confusing, think about why we only needed one dummy variable for Size (IsLarge), not two dummy variables (IsSmall and IsLarge).
Let's include the two new dummy variables in the model:
```
# create X and y
feature_cols = ['TV', 'Radio', 'Newspaper', 'IsLarge', 'Area_suburban', 'Area_urban']
X = data[feature_cols]
y = data.Sales
# instantiate, fit
lm = LinearRegression()
lm.fit(X, y)
# print coefficients
zip(feature_cols, lm.coef_)
```
How do we interpret the coefficients?
- Holding all other variables fixed, being a **suburban** area is associated with an average **decrease** in Sales of 106.56 widgets (as compared to the baseline level, which is rural).
- Being an **urban** area is associated with an average **increase** in Sales of 268.13 widgets (as compared to rural).
**A final note about dummy encoding:** If you have categories that can be ranked (i.e., strongly disagree, disagree, neutral, agree, strongly agree), you can potentially use a single dummy variable and represent the categories numerically (such as 1, 2, 3, 4, 5).
## What Didn't We Cover?
- Detecting collinearity
- Diagnosing model fit
- Transforming predictors to fit non-linear relationships
- Interaction terms
- Assumptions of linear regression
- And so much more!
You could certainly go very deep into linear regression, and learn how to apply it really, really well. It's an excellent way to **start your modeling process** when working a regression problem. However, it is limited by the fact that it can only make good predictions if there is a **linear relationship** between the features and the response, which is why more complex methods (with higher variance and lower bias) will often outperform linear regression.
Therefore, we want you to understand linear regression conceptually, understand its strengths and weaknesses, be familiar with the terminology, and know how to apply it. However, we also want to spend time on many other machine learning models, which is why we aren't going deeper here.
## Resources
- To go much more in-depth on linear regression, read Chapter 3 of [An Introduction to Statistical Learning](http://www-bcf.usc.edu/~gareth/ISL/), from which this lesson was adapted. Alternatively, watch the [related videos](http://www.dataschool.io/15-hours-of-expert-machine-learning-videos/) or read my [quick reference guide](http://www.dataschool.io/applying-and-interpreting-linear-regression/) to the key points in that chapter.
- To learn more about Statsmodels and how to interpret the output, DataRobot has some decent posts on [simple linear regression](http://www.datarobot.com/blog/ordinary-least-squares-in-python/) and [multiple linear regression](http://www.datarobot.com/blog/multiple-regression-using-statsmodels/).
- This [introduction to linear regression](http://people.duke.edu/~rnau/regintro.htm) is much more detailed and mathematically thorough, and includes lots of good advice.
- This is a relatively quick post on the [assumptions of linear regression](http://pareonline.net/getvn.asp?n=2&v=8).
| true |
code
| 0.652546 | null | null | null | null |
|
# The Discrete Fourier Transform
*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Comunications Engineering, Universität Rostock. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Fast Convolution
The linear convolution of signals is a basic building block in many practical applications. The straightforward convolution of two finite-length signals $x[k]$ and $h[k]$ has considerable numerical complexity. This has led to the development of various algorithms that realize the convolution with lower complexity. The basic concept of the *fast convolution* is to exploit the [convolution theorem](theorems.ipynb#Convolution-Theorem) of the discrete Fourier transform (DFT). This theorem states that the periodic convolution of two signals is equal to a scalar multiplication of their spectra. The scalar multiplication has considerably less numerical operations that the convolution. The transformation of the signals can be performed efficiently by the [fast Fourier transform](fast_fourier_transform.ipynb) (FFT).
Since the scalar multiplication of the spectra realizes a periodic convolution, special care has to be taken to realize a linear convolution in the spectral domain. The equivalence between linear and periodic convolution is discussed in the following.
### Equivalence of Linear and Periodic Convolution
The [linear convolution](../discrete_systems/linear_convolution.ipynb#Finite-Length-Signals) of a causal signal $x_L[k]$ of length $L$ with a causal signal $h_N[k]$ of length $N$ reads
\begin{equation}
y[k] = x_L[k] * h_N[k] = \sum_{\kappa = 0}^{L-1} x_L[\kappa] \; h_N[k - \kappa] = \sum_{\kappa = 0}^{N-1} h_N[\kappa] \; x_L[k - \kappa]
\end{equation}
The resulting signal $y[k]$ is of finite length $M = N+L-1$. Without loss of generality it is assumed in the following that $N \leq L$. The computation of $y[k]$ for $k=0,1, \dots, M-1$ requires $M \cdot N$ multiplications and $M \cdot (N-1)$ additions. The computational complexity of the convolution is consequently [on the order of](https://en.wikipedia.org/wiki/Big_O_notation) $\mathcal{O}(M \cdot N)$.
The periodic convolution of the two signals $x_L[k]$ and $h_N[k]$ is defined as
\begin{equation}
x_L[k] \circledast_P h_N[k] = \sum_{\kappa = 0}^{N-1} h_N[\kappa] \cdot \tilde{x}[k-\kappa]
\end{equation}
where $\tilde{x}[k]$ denotes the periodic summation of $x_L[k]$ with period $P$
\begin{equation}
\tilde{x}[k] = \sum_{\nu = -\infty}^{\infty} x_L[k - \nu P]
\end{equation}
The result of the circular convolution is periodic with period $P$. To compute the linear convolution by a periodic convolution, one has to take care that the result of the linear convolution fits into one period of the periodic convolution. Hence, the periodicity has to be chosen as $P \geq M$ where $M = N+L-1$. This can be achieved by zero-padding of $x_L[k]$ to the total length $M$ resulting in the signal $x_M[k]$ of length $M$ which is defined as
\begin{equation}
x_M[k] = \begin{cases}
x_L[k] & \text{for } 0 \leq k < L \\
0 & \text{for } L \leq k < M
\end{cases}
\end{equation}
and similar for $h_N[k]$ resulting in the zero-padded signal $h_M[k]$ which is defined as
\begin{equation}
h_M[k] = \begin{cases}
h_N[k] & \text{for } 0 \leq k < N \\
0 & \text{for } N \leq k < M
\end{cases}
\end{equation}
Using these signals, the linear and periodic convolution are equivalent for the first $M$ samples $k = 0,1,\dots, M-1$
\begin{equation}
x_L[k] * h_N[k] = x_M[k] \circledast_M h_M[k]
\end{equation}
#### Example
The following example computes the linear, periodic and linear by periodic convolution of two signals $x[k] = \text{rect}_L[k]$ and $h[k] = \text{rect}_N[k]$.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from tools import cconv
L = 8 # length of signal x[k]
N = 10 # length of signal h[k]
P = 14 # periodicity of periodic convolution
# generate signals
x = np.ones(L)
h = np.ones(N)
# linear convolution
y1 = np.convolve(x, h, 'full')
# periodic convolution
y2 = cconv(x, h, P)
# linear convolution via periodic convolution
xp = np.append(x, np.zeros(N-1))
hp = np.append(h, np.zeros(L-1))
y3 = cconv(xp, hp, L+N-1)
# plot results
def plot_signal(x):
plt.stem(x)
plt.xlabel('$k$')
plt.ylabel('$y[k]$')
plt.xlim([0, N+L])
plt.gca().margins(y=0.1)
plt.figure(figsize = (10, 8))
plt.subplot(3,1,1)
plot_signal(y1)
plt.title('Linear convolution')
plt.subplot(3,1,2)
plot_signal(y2)
plt.title('Periodic convolution with period $P=%d$'%P)
plt.subplot(3,1,3)
plot_signal(y3)
plt.title('Linear convolution as periodic convolution')
plt.tight_layout()
```
**Exercise**
* Change the lengths `L`, `N` and `P` and check how the results for the different convolutions change.
### The Fast Convolution Algorithm
Using the above derived equality of the linear and periodic convolution one can express the linear convolution $y[k] = x_L[k] * h_N[k]$ by the DFT as
$$ y[k] = \text{IDFT}_M \{ \; \text{DFT}_M\{ x_M[k] \} \cdot \text{DFT}_M\{ h_M[k] \} \; \} $$
The resulting algorithm is composed of the following steps
1. Zero-padding of the two input signals $x_L[k]$ and $h_N[k]$ to at least a total length of $M \geq N+L-1$
2. Computation of the DFTs $X[\mu]$ and $H[\mu]$ using a FFT of length $M$
3. Multiplication of the spectra $Y[\mu] = X[\mu] \cdot H[\mu]$
4. Inverse DFT of $Y[\mu]$ using an inverse FFT of length $M$
The algorithm requires two DFTs of length $M$, $M$ complex multiplications and one IDFT of length $M$. On first sight this does not seem to be an improvement, since one DFT/IDFT requires $M^2$ complex multiplications and $M \cdot (M-1)$ complex additions. The overall numerical complexity is hence in the order of $\mathcal{O}(M^2)$. The DFT can be realized efficiently by the [fast Fourier transformation](fast_fourier_transform.ipynb) (FFT), which lowers the number of numerical operations for each DFT/IDFT significantly. The actual gain depends on the particular implementation of the FFT. Many FFTs are most efficient for lengths which are a power of two. It therefore can make sense, in terms of the number of numerical operations, to choose $M$ as a power of two instead of the shortest possible length $N+L-1$. In this case, the numerical complexity of the radix-2 algorithm is on the order of $\mathcal{O}(M \log_2 M)$.
The introduced algorithm is known as *fast convolution* due to its computational efficiency when realized by the FFT. For real valued signals $x[k] \in \mathbb{R}$ and $h[k] \in \mathbb{R}$ the number of numerical operations can be reduced further by using a real valued FFT.
#### Example
The implementation of the fast convolution algorithm is straightforward. In the following example the fast convolution of two real-valued signals $x[k] = \text{rect}_L[k]$ and $h[k] = \text{rect}_N[k]$ is shown. The real valued FFT/IFFT is consequently used. Most implementations of the FFT include the zero-padding to a given length $M$, e.g as in `numpy` by `numpy.fft.rfft(x, M)`.
```
L = 8 # length of signal x[k]
N = 10 # length of signal h[k]
# generate signals
x = np.ones(L)
h = np.ones(N)
# fast convolution
M = N+L-1
y = np.fft.irfft(np.fft.rfft(x, M)*np.fft.rfft(h, M))
# show result
plt.figure(figsize=(10, 3))
plt.stem(y)
plt.xlabel('k')
plt.ylabel('y[k]');
```
### Benchmark
It was already argued that the numerical complexity of the fast convolution is considerably lower due to the usage of the FFT. As measure, the gain in terms of execution time with respect to the linear convolution is evaluated in the following. Both algorithms are executed for the convolution of two real-valued signals $x_L[k]$ and $h_N[k]$ of length $L=N=2^n$ for $n \in \mathbb{N}$. The length of the FFTs/IFFT was chosen as $M=2^{n+1}$. The results depend heavily on the implementation of the FFT and the hardware used. Note that the execution of the following script may take some time.
```
import timeit
n = np.arange(17) # lengths = 2**n to evaluate
reps = 20 # number of repetitions for timeit
gain = np.zeros(len(n))
for N in n:
length = 2**N
# setup environment for timeit
tsetup = 'import numpy as np; from numpy.fft import rfft, irfft; \
x=np.random.randn(%d); h=np.random.randn(%d)' % (length, length)
# direct convolution
tc = timeit.timeit('np.convolve(x, x, "full")', setup=tsetup, number=reps)
# fast convolution
tf = timeit.timeit('irfft(rfft(x, %d) * rfft(h, %d))' % (2*length, 2*length), setup=tsetup, number=reps)
# speedup by using the fast convolution
gain[N] = tc/tf
# show the results
plt.figure(figsize = (15, 10))
plt.barh(n-.5, gain, log=True)
plt.plot([1, 1], [-1, n[-1]+1], 'r-')
plt.yticks(n, 2**n)
plt.xlabel('Gain of fast convolution')
plt.ylabel('Length of signals')
plt.title('Comparison of execution times between direct and fast convolution')
plt.grid()
```
**Exercise**
* For which lengths is the fast convolution faster than the linear convolution?
* Why is it slower below a given signal length?
* Is the trend of the gain as expected from above considerations?
**Copyright**
The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors.
| true |
code
| 0.706431 | null | null | null | null |
|
# Concise Implementation of Linear Regression
:label:`sec_linear_concise`
Broad and intense interest in deep learning for the past several years
has inspired companies, academics, and hobbyists
to develop a variety of mature open source frameworks
for automating the repetitive work of implementing
gradient-based learning algorithms.
In :numref:`sec_linear_scratch`, we relied only on
(i) tensors for data storage and linear algebra;
and (ii) auto differentiation for calculating gradients.
In practice, because data iterators, loss functions, optimizers,
and neural network layers
are so common, modern libraries implement these components for us as well.
In this section, (**we will show you how to implement
the linear regression model**) from :numref:`sec_linear_scratch`
(**concisely by using high-level APIs**) of deep learning frameworks.
## Generating the Dataset
To start, we will generate the same dataset as in :numref:`sec_linear_scratch`.
```
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
```
## Reading the Dataset
Rather than rolling our own iterator,
we can [**call upon the existing API in a framework to read data.**]
We pass in `features` and `labels` as arguments and specify `batch_size`
when instantiating a data iterator object.
Besides, the boolean value `is_train`
indicates whether or not
we want the data iterator object to shuffle the data
on each epoch (pass through the dataset).
```
def load_array(data_arrays, batch_size, is_train=True): #@save
"""Construct a PyTorch data iterator."""
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)
batch_size = 10
data_iter = load_array((features, labels), batch_size)
```
Now we can use `data_iter` in much the same way as we called
the `data_iter` function in :numref:`sec_linear_scratch`.
To verify that it is working, we can read and print
the first minibatch of examples.
Comparing with :numref:`sec_linear_scratch`,
here we use `iter` to construct a Python iterator and use `next` to obtain the first item from the iterator.
```
next(iter(data_iter))
```
## Defining the Model
When we implemented linear regression from scratch
in :numref:`sec_linear_scratch`,
we defined our model parameters explicitly
and coded up the calculations to produce output
using basic linear algebra operations.
You *should* know how to do this.
But once your models get more complex,
and once you have to do this nearly every day,
you will be glad for the assistance.
The situation is similar to coding up your own blog from scratch.
Doing it once or twice is rewarding and instructive,
but you would be a lousy web developer
if every time you needed a blog you spent a month
reinventing the wheel.
For standard operations, we can [**use a framework's predefined layers,**]
which allow us to focus especially
on the layers used to construct the model
rather than having to focus on the implementation.
We will first define a model variable `net`,
which will refer to an instance of the `Sequential` class.
The `Sequential` class defines a container
for several layers that will be chained together.
Given input data, a `Sequential` instance passes it through
the first layer, in turn passing the output
as the second layer's input and so forth.
In the following example, our model consists of only one layer,
so we do not really need `Sequential`.
But since nearly all of our future models
will involve multiple layers,
we will use it anyway just to familiarize you
with the most standard workflow.
Recall the architecture of a single-layer network as shown in :numref:`fig_single_neuron`.
The layer is said to be *fully-connected*
because each of its inputs is connected to each of its outputs
by means of a matrix-vector multiplication.
In PyTorch, the fully-connected layer is defined in the `Linear` class. Note that we passed two arguments into `nn.Linear`. The first one specifies the input feature dimension, which is 2, and the second one is the output feature dimension, which is a single scalar and therefore 1.
```
# `nn` is an abbreviation for neural networks
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))
```
## Initializing Model Parameters
Before using `net`, we need to (**initialize the model parameters,**)
such as the weights and bias in the linear regression model.
Deep learning frameworks often have a predefined way to initialize the parameters.
Here we specify that each weight parameter
should be randomly sampled from a normal distribution
with mean 0 and standard deviation 0.01.
The bias parameter will be initialized to zero.
As we have specified the input and output dimensions when constructing `nn.Linear`,
now we can access the parameters directly to specify their initial values.
We first locate the layer by `net[0]`, which is the first layer in the network,
and then use the `weight.data` and `bias.data` methods to access the parameters.
Next we use the replace methods `normal_` and `fill_` to overwrite parameter values.
```
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
```
## Defining the Loss Function
[**The `MSELoss` class computes the mean squared error (without the $1/2$ factor in :eqref:`eq_mse`).**]
By default it returns the average loss over examples.
```
loss = nn.MSELoss()
```
## Defining the Optimization Algorithm
Minibatch stochastic gradient descent is a standard tool
for optimizing neural networks
and thus PyTorch supports it alongside a number of
variations on this algorithm in the `optim` module.
When we (**instantiate an `SGD` instance,**)
we will specify the parameters to optimize over
(obtainable from our net via `net.parameters()`), with a dictionary of hyperparameters
required by our optimization algorithm.
Minibatch stochastic gradient descent just requires that
we set the value `lr`, which is set to 0.03 here.
```
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
```
## Training
You might have noticed that expressing our model through
high-level APIs of a deep learning framework
requires comparatively few lines of code.
We did not have to individually allocate parameters,
define our loss function, or implement minibatch stochastic gradient descent.
Once we start working with much more complex models,
advantages of high-level APIs will grow considerably.
However, once we have all the basic pieces in place,
[**the training loop itself is strikingly similar
to what we did when implementing everything from scratch.**]
To refresh your memory: for some number of epochs,
we will make a complete pass over the dataset (`train_data`),
iteratively grabbing one minibatch of inputs
and the corresponding ground-truth labels.
For each minibatch, we go through the following ritual:
* Generate predictions by calling `net(X)` and calculate the loss `l` (the forward propagation).
* Calculate gradients by running the backpropagation.
* Update the model parameters by invoking our optimizer.
For good measure, we compute the loss after each epoch and print it to monitor progress.
```
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad()
l.backward()
trainer.step()
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
```
Below, we [**compare the model parameters learned by training on finite data
and the actual parameters**] that generated our dataset.
To access parameters,
we first access the layer that we need from `net`
and then access that layer's weights and bias.
As in our from-scratch implementation,
note that our estimated parameters are
close to their ground-truth counterparts.
```
w = net[0].weight.data
print('error in estimating w:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('error in estimating b:', true_b - b)
```
## Summary
* Using PyTorch's high-level APIs, we can implement models much more concisely.
* In PyTorch, the `data` module provides tools for data processing, the `nn` module defines a large number of neural network layers and common loss functions.
* We can initialize the parameters by replacing their values with methods ending with `_`.
## Exercises
1. If we replace `nn.MSELoss(reduction='sum')` with `nn.MSELoss()`, how can we change the learning rate for the code to behave identically. Why?
1. Review the PyTorch documentation to see what loss functions and initialization methods are provided. Replace the loss by Huber's loss.
1. How do you access the gradient of `net[0].weight`?
[Discussions](https://discuss.d2l.ai/t/45)
| true |
code
| 0.778565 | null | null | null | null |
|
# Sonar - Decentralized Model Training Simulation (local)
DISCLAIMER: This is a proof-of-concept implementation. It does not represent a remotely product ready implementation or follow proper conventions for security, convenience, or scalability. It is part of a broader proof-of-concept demonstrating the vision of the OpenMined project, its major moving parts, and how they might work together.
# Getting Started: Installation
##### Step 1: install IPFS
- https://ipfs.io/docs/install/
##### Step 2: Turn on IPFS Daemon
Execute on command line:
> ipfs daemon
##### Step 3: Install Ethereum testrpc
- https://github.com/ethereumjs/testrpc
##### Step 4: Turn on testrpc with 1000 initialized accounts (each with some money)
Execute on command line:
> testrpc -a 1000
##### Step 5: install openmined/sonar and all dependencies (truffle)
##### Step 6: Locally Deploy Smart Contracts in openmined/sonar
From the OpenMined/Sonar repository root run
> truffle compile
> truffle migrate
you should see something like this when you run migrate:
```
Using network 'development'.
Running migration: 1_initial_migration.js
Deploying Migrations...
Migrations: 0xf06039885460a42dcc8db5b285bb925c55fbaeae
Saving successful migration to network...
Saving artifacts...
Running migration: 2_deploy_contracts.js
Deploying ConvertLib...
ConvertLib: 0x6cc86f0a80180a491f66687243376fde45459436
Deploying ModelRepository...
ModelRepository: 0xe26d32efe1c573c9f81d68aa823dcf5ff3356946
Linking ConvertLib to MetaCoin
Deploying MetaCoin...
MetaCoin: 0x6d3692bb28afa0eb37d364c4a5278807801a95c5
```
The address after 'ModelRepository' is something you'll need to copy paste into the code
below when you initialize the "ModelRepository" object. In this case the address to be
copy pasted is `0xe26d32efe1c573c9f81d68aa823dcf5ff3356946`.
##### Step 7: execute the following code
# The Simulation: Diabetes Prediction
In this example, a diabetes research center (Cure Diabetes Inc) wants to train a model to try to predict the progression of diabetes based on several indicators. They have collected a small sample (42 patients) of data but it's not enough to train a model. So, they intend to offer up a bounty of $5,000 to the OpenMined commmunity to train a high quality model.
As it turns out, there are 400 diabetics in the network who are candidates for the model (are collecting the relevant fields). In this simulation, we're going to faciliate the training of Cure Diabetes Inc incentivizing these 400 anonymous contributors to train the model using the Ethereum blockchain.
Note, in this simulation we're only going to use the sonar and syft packages (and everything is going to be deployed locally on a test blockchain). Future simulations will incorporate mine and capsule for greater anonymity and automation.
### Imports and Convenience Functions
```
import warnings
import numpy as np
import phe as paillier
from sonar.contracts import ModelRepository,Model
from syft.he.paillier.keys import KeyPair
from syft.nn.linear import LinearClassifier
from sklearn.datasets import load_diabetes
def get_balance(account):
return repo.web3.fromWei(repo.web3.eth.getBalance(account),'ether')
warnings.filterwarnings('ignore')
```
### Setting up the Experiment
```
# for the purpose of the simulation, we're going to split our dataset up amongst
# the relevant simulated users
diabetes = load_diabetes()
y = diabetes.target
X = diabetes.data
validation = (X[0:5],y[0:5])
anonymous_diabetes_users = (X[6:],y[6:])
# we're also going to initialize the model trainer smart contract, which in the
# real world would already be on the blockchain (managing other contracts) before
# the simulation begins
# ATTENTION: copy paste the correct address (NOT THE DEFAULT SEEN HERE) from truffle migrate output.
repo = ModelRepository('0x6c7a23081b37e64adc5500c12ee851894d9fd500', ipfs_host='localhost', web3_host='localhost') # blockchain hosted model repository
# we're going to set aside 10 accounts for our 42 patients
# Let's go ahead and pair each data point with each patient's
# address so that we know we don't get them confused
patient_addresses = repo.web3.eth.accounts[1:10]
anonymous_diabetics = list(zip(patient_addresses,
anonymous_diabetes_users[0],
anonymous_diabetes_users[1]))
# we're going to set aside 1 account for Cure Diabetes Inc
cure_diabetes_inc = repo.web3.eth.accounts[1]
```
## Step 1: Cure Diabetes Inc Initializes a Model and Provides a Bounty
```
pubkey,prikey = KeyPair().generate(n_length=1024)
diabetes_classifier = LinearClassifier(desc="DiabetesClassifier",n_inputs=10,n_labels=1)
initial_error = diabetes_classifier.evaluate(validation[0],validation[1])
diabetes_classifier.encrypt(pubkey)
diabetes_model = Model(owner=cure_diabetes_inc,
syft_obj = diabetes_classifier,
bounty = 1,
initial_error = initial_error,
target_error = 10000
)
model_id = repo.submit_model(diabetes_model)
```
## Step 2: An Anonymous Patient Downloads the Model and Improves It
```
model_id
model = repo[model_id]
diabetic_address,input_data,target_data = anonymous_diabetics[0]
repo[model_id].submit_gradient(diabetic_address,input_data,target_data)
```
## Step 3: Cure Diabetes Inc. Evaluates the Gradient
```
repo[model_id]
old_balance = get_balance(diabetic_address)
print(old_balance)
new_error = repo[model_id].evaluate_gradient(cure_diabetes_inc,repo[model_id][0],prikey,pubkey,validation[0],validation[1])
new_error
new_balance = get_balance(diabetic_address)
incentive = new_balance - old_balance
print(incentive)
```
## Step 4: Rinse and Repeat
```
model
for i,(addr, input, target) in enumerate(anonymous_diabetics):
try:
model = repo[model_id]
# patient is doing this
model.submit_gradient(addr,input,target)
# Cure Diabetes Inc does this
old_balance = get_balance(addr)
new_error = model.evaluate_gradient(cure_diabetes_inc,model[i+1],prikey,pubkey,validation[0],validation[1],alpha=2)
print("new error = "+str(new_error))
incentive = round(get_balance(addr) - old_balance,5)
print("incentive = "+str(incentive))
except:
"Connection Reset"
```
| true |
code
| 0.550305 | null | null | null | null |
|
# NSCI 801 - Quantitative Neuroscience
## Reproducibility, reliability, validity
Gunnar Blohm
### Outline
* statistical considerations
* multiple comparisons
* exploratory analyses vs hypothesis testing
* Open Science
* general steps toward transparency
* pre-registration / registered report
* Open science vs. patents
### Multiple comparisons
In [2009, Bennett et al.](https://teenspecies.github.io/pdfs/NeuralCorrelates.pdf) studies the brain of a salmon using fMRI and found and found significant activation despite the salmon being dead... (IgNobel Prize 2012)
Why did they find this?
They images 140 volumes (samples) of the brain and ran a standard preprocessing pipeline, including spatial realignment, co-registration of functional and anatomical volumes, and 8mm full-width at half maximum (FWHM) Gaussian smoothing.
They computed voxel-wise statistics.
<img style="float: center; width:750px;" src="stuff/salmon.png">
This is a prime example of what's known as the **multiple comparison problem**!
“the problem that occurs when one considers a set of statistical inferences simultaneously or infers a subset of parameters selected based on the observed values” (Wikipedia)
* problem that arises when implementing a large number of statistical tests in the same experiment
* the more tests we do, the higher probability of obtaining, at least, one test with statistical significance
### Probability(false positive) = f(number comparisons)
If you repeat a statistical test over and over again, the false positive ($FP$) rate ($P$) evolves as follows:
$$P(FP)=1-(1-\alpha)^N$$
* $\alpha$ is the confidence level for each individual test (e.g. 0.05)
* $N$ is the number of comparisons
Let's see how this works...
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
plt.style.use('dark_background')
```
Let's create some random data...
```
rvs = stats.norm.rvs(loc=0, scale=10, size=1000)
sns.displot(rvs)
```
Now let's run a t-test to see if it's different from 0
```
statistic, pvalue = stats.ttest_1samp(rvs, 0)
print(pvalue)
```
Now let's do this many times for different samples, e.g. different voxels of our salmon...
```
def t_test_function(alp, N):
"""computes t-test statistics on N random samples and returns number of significant tests"""
counter = 0
for i in range(N):
rvs = stats.norm.rvs(loc=0, scale=10, size=1000)
statistic, pvalue = stats.ttest_1samp(rvs, 0)
if pvalue <= alp:
counter = counter + 1
print(counter)
return counter
N = 100
counter = t_test_function(0.05, N)
print("The false positve rate was", counter/N*100, "%")
```
Well, we wanted a $\alpha=0.05$, so what's the problem?
The problem is that we have hugely increased the likelihood of finding something significant by chance! (**p-hacking**)
Take the above example:
* running 100 independent tests with $\alpha=0.05$ resulted in a few positives
* well, that's good right? Now we can see if there is astory here we can publish...
* dead salmon!
* remember, our data was just noise!!! There was NO signal!
This is why we have corrections for multiple comparisons that adjust the p-value so that the **overall chance** to find a false positive stays at $\alpha$!
Why does this matter?
### Exploratory analyses vs hypothesis testing
Why do we distinguish between them?
<img style="float: center; width:750px;" src="stuff/ExploreConfirm1.png">
But in science, confirmatory analyses that are hypothesis-driven are often much more valued.
There is a temptation to frame *exploratory* analyses and *confirmatory*...
**This leads to disaster!!!**
* science is not solid
* replication crisis (psychology, social science, medicine, marketing, economics, sports science, etc, etc...)
* shaken trust in science
<img style="float: center; width:750px;" src="stuff/crisis.jpeg">
([Baker 2016](https://www.nature.com/news/1-500-scientists-lift-the-lid-on-reproducibility-1.19970))
### Quick excursion: survivorship bias
"Survivorship bias or survival bias is the logical error of concentrating on the people or things that made it past some selection process and overlooking those that did not, typically because of their lack of visibility." (Wikipedia)
<img style="float: center; width:750px;" src="stuff/SurvivorshipBias.png">
**How does survivorship bias affect neuroscience?**
Think about it...
E.g.
* people select neurons to analyze
* profs say it's absolutely achievable to become a prof
Just keep it in mind...
### Open science - transparency
Open science can hugely help increasing transparency in many different ways so that findings and data can be evaluated for what they are:
* publish data acquisition protocol and code: increases data reproducibility & credibility
* publish data: data get second, third, etc... lives
* publish data processing / analyses: increases reproducibility of results
* publish figures code and stats: increases reproducibility and credibility of conclusions
* pre-register hypotheses and analyses: ensures *confirmatory* analyses are not *exploratory* (HARKing)
For more info, see NSCI800 lectures about Open Science: [OS1](http://www.compneurosci.com/NSCI800/OpenScienceI.pdf), [OS2](http://www.compneurosci.com/NSCI800/OpenScienceII.pdf)
### Pre-registration / registered reports
<img style="float:right; width:500px;" src="stuff/RR.png">
* IPA guarantees publication
* If original methods are followed
* Main conclusions need to come from originally proposed analyses
* Does not prevent exploratory analyses
* Need to be labeled as such
[https://Cos.io/rr](https://Cos.io/rr)
Please follow **Stage 1** instructions of [the registered report intrustions from eNeuro](https://www.eneuro.org/sites/default/files/additional_assets/pdf/eNeuro%20Registered%20Reports%20Author%20Guidelines.pdf) for the course evaluation...
Questions???
### Open science vs. patents
The goal of Open Science is to share all aspects of research with the public!
* because knowledge should be freely available
* because the public paid for the science to happen in the first place
However, this prevents from patenting scientific results!
* this is good for science, because patents obstruct research
* prevents full privitazation of research: companies driving research is biased by private interest
Turns out open science is good for business!
* more people contribute
* wider adoption
* e.g. Github = Microsoft, Android = Google, etc
* better for society
* e.g. nonprofit pharma
**Why are patents still a thing?**
Well, some people think it's an outdated and morally corrupt concept.
* goal: maximum profit
* enabler: capitalism
* victims: general public
Think about it abd decide for yourself what to do with your research!!!
### THANK YOU!!!
<img style="float:center; width:750px;" src="stuff/empower.jpg">
| true |
code
| 0.384479 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/krmiddlebrook/intro_to_deep_learning/blob/master/machine_learning/mini_lessons/image_data.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Processing Image Data
Computer vision is a field of machine learning that trains computers to interpret and understand the visual world. It is one of the most popular fields in deep learning (neural networks). In computer vision, it is common to use digital images from cameras and videos to train models to accurately identify and classify objects.
Before we can solve computer vision tasks, it is important to understand how to handle image data. To this end, we will demonstrate how to process (prepare) image data for machine learning models.
We will use the MNIST digits dataset, which is provided by Kera Datasets--a collection of ready-to-use datasets for machine learning. All datasets are available through the `tf.keras.datasets` API endpoint.
Here is the lesson roadmap:
- Load the dataset
- Visualize the data
- Transform the data
- Normalize the data
```
# TensorFlow and tf.keras and TensorFlow datasets
import tensorflow as tf
from tensorflow import keras
# Commonly used modules
import numpy as np
# Images, plots, display, and visualization
import matplotlib.pyplot as plt
```
# Load the dataset
When we want to solve a problem with machine learning methods, the first step is almost always to find a good dataset. As we mentioned above, we will retrieve the MNIST dataset using the `tf.keras.datasets` module.
The MNIST dataset contains 70k grayscale images of handwritten digits (i.e., numbers between 0 and 9). Let's load the dataset into our notebook.
```
# the data, split between train and test sets
(train_features, train_labels), (test_features, test_labels) = keras.datasets.mnist.load_data()
print(f"training set shape: {train_features.shape}")
print(f"test set shape: {test_features.shape}")
print(f'dtypes of training and test set tensors: {train_features.dtype}, {test_features.dtype}')
```
We see that TensorFlow Datasets takes care of most of the processing we need to do. The `training_features` object tells us that there are 60k training images, and the `test_features` indicates there are 10k test images, so 70k total. We also see that the images are tensors of shape ($28 \times 28$) with integers of type uint8.
## Visualize the dataset
Now that we have the dataset, let's visualize some samples.
We will use the matplotlib plotting framework to display the images. Here are the first 5 images in the training dataset.
```
plt.figure(figsize=(10, 10))
for i in range(5):
ax = plt.subplot(3, 3, i + 1)
plt.imshow(train_features[i], cmap=plt.cm.binary)
plt.title(int(train_labels[i]))
plt.axis("off")
```
The above images give us a sense of the data, including samples belonging to different classes.
# Transforming the data
Before we start transforming data, let's discuss *tensors*--a key part of the machine learning (ML) process, particularly for deep learning methods.
As we learned in previous lessons, data, whether it be categorical or numerical in nature, is converted to a numerical representation. This process makes the data useful for machine learning models. In deep learning (neural networks), the numerical data is often stored in objects called *tensors*. A tensor is a container that can house data in $N$ dimensions. ML researchers sometimes use the term "tensor" and "matrix" interchangeably because a matrix is a 2-dimensional tensor. But, tensors are generalizations of matrices to $N$-dimensional space.
<figure>
<img src='https://www.kdnuggets.com/wp-content/uploads/scalar-vector-matrix-tensor.jpg' width='75%'>
<figcaption>A scalar, vector ($2 \times 1$), matrix ($2 \times 1$), and tensor ($2 \times 2 \times 2$) .</figcaption>
</figure>
```
# a (2 x 2 x 2) tensor
my_tensor = np.array([
[[1, 2], [3, 2]],
[[1, 7],[5, 4]]
])
print('my_tensor shape:', my_tensor.shape)
```
Now let's discuss how images are stored in tensors. Computer screens are composed of pixels. Each pixel generates three colors of light (red, green, and blue) and the different colors we see are due to different combinations and intensities of these three primary colors.
<figure>
<img src='https://www.chem.purdue.edu/gchelp/cchem/RGBColors/BlackWhiteGray.gif' width='75%'>
<figcaption>The colors black, white, and gray with a sketch of a pixel from each.</figcaption>
</figure>
We use tensors to store the pixel intensities for a given image. Colorized pictures have 3 different *channels*. Each channel contains a matrix that represents the intensity values that correspond to the pixels of a particular color (red, green, and blue; RGB for short). For instance, consider a small colorized $28 \times 28$ pixel image of a dog. Because the dog image is colorize, it has 3 channels, so its tensor shape is ($28 \times 28 \times 3$).
Let's have a look at the shape of the images in the MNIST dataset.
```
train_features[0, :, :].shape
```
Using the `train_features.shape` method, we can extract the image shape and see that images are in the tensor shape $28 \times 28$. The returned shape has no 3rd dimension, this indicates that we are working with grayscale images. By grayscale, we mean the pixels don't have intensities for red, green, and blue channels but rather for one grayscale channel, which describes an image using combinations of various shades of gray. Pixel intensities range between $0$ and $255$, and in our case, they correspond to black $0$ to white $255$.
Now let's reshape the images into $784 \times 1$ dimensional tensors. We call converting an image into an $n \times 1$ tensor "flattening" the tensor.
```
# get a subset of 5 images from the dataset
original_shape = train_features.shape
# Flatten the images.
input_shape = (-1, 28*28)
train_features = train_features.reshape(input_shape)
test_features = test_features.reshape(input_shape)
print(f'original shape: {original_shape}, flattened shape: {train_features.shape}')
```
We flattened all the images by using the NumPy `reshape` method. Since one shape dimension can be -1, and we may not always know the number of samples in the dataset we used $(-1,784)$ as the parameters to `reshape`. In our example, this means that each $28 \times 28$ image gets flattened into a $28 \cdot 28 = 784$ feature array. Then the images are stacked (because of the -1) to produce a final large tensor with shape $(\text{num samples}, 784$).
# Normalize the data
Another important transformation technique is *normalization*. We normalize data before training the model with it to encourage the model to learn generalizable features, which should lead to better results on unseen data.
At a high level, normalization makes the data more, well...normal. There are various ways to normalize data. Perhaps the most common normalization approach for image data is to subtract the mean pixel value and divide by the standard deviation (this method is applied to every pixel).
Before we can do any normalization, we have to cast the "uint8" tensors to the "float32" numeric type.
```
# convert to float32 type
train_features = train_features.astype('float32')
test_features = test_features.astype('float32')
```
Now we can normalize the data. We should mention that you always use the training set data to calculate normalization statistics like mean, standard deviation, etc.. Consequently, the test set is always normalized with the training set statistics.
```
# normalize the reshaped images
mean = train_features.mean()
std = train_features.std()
train_features -= mean
train_features /= std
test_features -= mean
test_features /= std
print(f'pre-normalization mean and std: {round(mean, 4)}, {round(std, 4)}')
print(f'normalized images mean and std: {round(train_features.mean(), 4)}, {round(train_features.std(), 4)}')
```
As the output above indicates, the normalized pixel values are now centered around 0 (i.e., mean = 0) and have a standard deviation of 1.
# Summary
In this lesson we learned:
- Keras offers ready-to-use datasets.
- Images are represented by *tensors*
- Tensors can be transformed (reshaped) and normalized easily using NumPy (or any other frameworks that enable tensor operations).
```
```
| true |
code
| 0.671107 | null | null | null | null |
|
## <div style="text-align: center"> 20 ML Algorithms from start to Finish for Iris</div>
<div style="text-align: center"> I want to solve<b> iris problem</b> a popular machine learning Dataset as a comprehensive workflow with python packages.
After reading, you can use this workflow to solve other real problems and use it as a template to deal with <b>machine learning</b> problems.</div>

<div style="text-align:center">last update: <b>10/28/2018</b></div>
>###### you may be interested have a look at it: [**10-steps-to-become-a-data-scientist**](https://github.com/mjbahmani/10-steps-to-become-a-data-scientist)
---------------------------------------------------------------------
you can Fork and Run this kernel on Github:
> ###### [ GitHub](https://github.com/mjbahmani/Machine-Learning-Workflow-with-Python)
-------------------------------------------------------------------------------------------------------------
**I hope you find this kernel helpful and some <font color="red"><b>UPVOTES</b></font> would be very much appreciated**
-----------
## Notebook Content
* 1- [Introduction](#1)
* 2- [Machine learning workflow](#2)
* 2-1 [Real world Application Vs Competitions](#2)
* 3- [Problem Definition](#3)
* 3-1 [Problem feature](#4)
* 3-2 [Aim](#5)
* 3-3 [Variables](#6)
* 4-[ Inputs & Outputs](#7)
* 4-1 [Inputs ](#8)
* 4-2 [Outputs](#9)
* 5- [Installation](#10)
* 5-1 [ jupyter notebook](#11)
* 5-2[ kaggle kernel](#12)
* 5-3 [Colab notebook](#13)
* 5-4 [install python & packages](#14)
* 5-5 [Loading Packages](#15)
* 6- [Exploratory data analysis](#16)
* 6-1 [Data Collection](#17)
* 6-2 [Visualization](#18)
* 6-2-1 [Scatter plot](#19)
* 6-2-2 [Box](#20)
* 6-2-3 [Histogram](#21)
* 6-2-4 [Multivariate Plots](#22)
* 6-2-5 [Violinplots](#23)
* 6-2-6 [Pair plot](#24)
* 6-2-7 [Kde plot](#25)
* 6-2-8 [Joint plot](#26)
* 6-2-9 [Andrews curves](#27)
* 6-2-10 [Heatmap](#28)
* 6-2-11 [Radviz](#29)
* 6-3 [Data Preprocessing](#30)
* 6-4 [Data Cleaning](#31)
* 7- [Model Deployment](#32)
* 7-1[ KNN](#33)
* 7-2 [Radius Neighbors Classifier](#34)
* 7-3 [Logistic Regression](#35)
* 7-4 [Passive Aggressive Classifier](#36)
* 7-5 [Naive Bayes](#37)
* 7-6 [MultinomialNB](#38)
* 7-7 [BernoulliNB](#39)
* 7-8 [SVM](#40)
* 7-9 [Nu-Support Vector Classification](#41)
* 7-10 [Linear Support Vector Classification](#42)
* 7-11 [Decision Tree](#43)
* 7-12 [ExtraTreeClassifier](#44)
* 7-13 [Neural network](#45)
* 7-13-1 [What is a Perceptron?](#45)
* 7-14 [RandomForest](#46)
* 7-15 [Bagging classifier ](#47)
* 7-16 [AdaBoost classifier](#48)
* 7-17 [Gradient Boosting Classifier](#49)
* 7-18 [Linear Discriminant Analysis](#50)
* 7-19 [Quadratic Discriminant Analysis](#51)
* 7-20 [Kmeans](#52)
* 7-21 [Backpropagation](#53)
* 8- [Conclusion](#54)
* 10- [References](#55)
<a id="1"></a> <br>
## 1- Introduction
This is a **comprehensive ML techniques with python** , that I have spent for more than two months to complete it.
it is clear that everyone in this community is familiar with IRIS dataset but if you need to review your information about the dataset please visit this [link](https://archive.ics.uci.edu/ml/datasets/iris).
I have tried to help **beginners** in Kaggle how to face machine learning problems. and I think it is a great opportunity for who want to learn machine learning workflow with python completely.
I have covered most of the methods that are implemented for iris until **2018**, you can start to learn and review your knowledge about ML with a simple dataset and try to learn and memorize the workflow for your journey in Data science world.
## 1-1 Courses
There are alot of Online courses that can help you develop your knowledge, here I have just listed some of them:
1. [Machine Learning Certification by Stanford University (Coursera)](https://www.coursera.org/learn/machine-learning/)
2. [Machine Learning A-Z™: Hands-On Python & R In Data Science (Udemy)](https://www.udemy.com/machinelearning/)
3. [Deep Learning Certification by Andrew Ng from deeplearning.ai (Coursera)](https://www.coursera.org/specializations/deep-learning)
4. [Python for Data Science and Machine Learning Bootcamp (Udemy)](Python for Data Science and Machine Learning Bootcamp (Udemy))
5. [Mathematics for Machine Learning by Imperial College London](https://www.coursera.org/specializations/mathematics-machine-learning)
6. [Deep Learning A-Z™: Hands-On Artificial Neural Networks](https://www.udemy.com/deeplearning/)
7. [Complete Guide to TensorFlow for Deep Learning Tutorial with Python](https://www.udemy.com/complete-guide-to-tensorflow-for-deep-learning-with-python/)
8. [Data Science and Machine Learning Tutorial with Python – Hands On](https://www.udemy.com/data-science-and-machine-learning-with-python-hands-on/)
9. [Machine Learning Certification by University of Washington](https://www.coursera.org/specializations/machine-learning)
10. [Data Science and Machine Learning Bootcamp with R](https://www.udemy.com/data-science-and-machine-learning-bootcamp-with-r/)
5- [https://www.kaggle.com/startupsci/titanic-data-science-solutions](https://www.kaggle.com/startupsci/titanic-data-science-solutions)
I am open to getting your feedback for improving this **kernel**
<a id="2"></a> <br>
## 2- Machine Learning Workflow
Field of study that gives computers the ability to learn without being
explicitly programmed.
Arthur Samuel, 1959
If you have already read some [machine learning books](https://towardsdatascience.com/list-of-free-must-read-machine-learning-books-89576749d2ff). You have noticed that there are different ways to stream data into machine learning.
most of these books share the following steps (checklist):
* Define the Problem(Look at the big picture)
* Specify Inputs & Outputs
* Data Collection
* Exploratory data analysis
* Data Preprocessing
* Model Design, Training, and Offline Evaluation
* Model Deployment, Online Evaluation, and Monitoring
* Model Maintenance, Diagnosis, and Retraining
**You can see my workflow in the below image** :
<img src="http://s9.picofile.com/file/8338227634/workflow.png" />
**you should feel free to adapt this checklist to your needs**
## 2-1 Real world Application Vs Competitions
<img src="http://s9.picofile.com/file/8339956300/reallife.png" height="600" width="500" />
<a id="3"></a> <br>
## 3- Problem Definition
I think one of the important things when you start a new machine learning project is Defining your problem. that means you should understand business problem.( **Problem Formalization**)
Problem Definition has four steps that have illustrated in the picture below:
<img src="http://s8.picofile.com/file/8338227734/ProblemDefination.png">
<a id="4"></a> <br>
### 3-1 Problem Feature
we will use the classic Iris data set. This dataset contains information about three different types of Iris flowers:
* Iris Versicolor
* Iris Virginica
* Iris Setosa
The data set contains measurements of four variables :
* sepal length
* sepal width
* petal length
* petal width
The Iris data set has a number of interesting features:
1. One of the classes (Iris Setosa) is linearly separable from the other two. However, the other two classes are not linearly separable.
2. There is some overlap between the Versicolor and Virginica classes, so it is unlikely to achieve a perfect classification rate.
3. There is some redundancy in the four input variables, so it is possible to achieve a good solution with only three of them, or even (with difficulty) from two, but the precise choice of best variables is not obvious.
**Why am I using iris dataset:**
1- This is a good project because it is so well understood.
2- Attributes are numeric so you have to figure out how to load and handle data.
3- It is a classification problem, allowing you to practice with perhaps an easier type of supervised learning algorithm.
4- It is a multi-class classification problem (multi-nominal) that may require some specialized handling.
5- It only has 4 attributes and 150 rows, meaning it is small and easily fits into memory (and a screen or A4 page).
6- All of the numeric attributes are in the same units and the same scale, not requiring any special scaling or transforms to get started.[5]
7- we can define problem as clustering(unsupervised algorithm) project too.
<a id="5"></a> <br>
### 3-2 Aim
The aim is to classify iris flowers among three species (setosa, versicolor or virginica) from measurements of length and width of sepals and petals
<a id="6"></a> <br>
### 3-3 Variables
The variables are :
**sepal_length**: Sepal length, in centimeters, used as input.
**sepal_width**: Sepal width, in centimeters, used as input.
**petal_length**: Petal length, in centimeters, used as input.
**petal_width**: Petal width, in centimeters, used as input.
**setosa**: Iris setosa, true or false, used as target.
**versicolour**: Iris versicolour, true or false, used as target.
**virginica**: Iris virginica, true or false, used as target.
**<< Note >>**
> You must answer the following question:
How does your company expact to use and benfit from your model.
<a id="7"></a> <br>
## 4- Inputs & Outputs
<a id="8"></a> <br>
### 4-1 Inputs
**Iris** is a very popular **classification** and **clustering** problem in machine learning and it is such as "Hello world" program when you start learning a new programming language. then I decided to apply Iris on 20 machine learning method on it.
The Iris flower data set or Fisher's Iris data set is a **multivariate data set** introduced by the British statistician and biologist Ronald Fisher in his 1936 paper The use of multiple measurements in taxonomic problems as an example of linear discriminant analysis. It is sometimes called Anderson's Iris data set because Edgar Anderson collected the data to quantify the morphologic variation of Iris flowers in three related species. Two of the three species were collected in the Gaspé Peninsula "all from the same pasture, and picked on the same day and measured at the same time by the same person with the same apparatus".
The data set consists of 50 samples from each of three species of Iris (Iris setosa, Iris virginica, and Iris versicolor). Four features were measured from each sample: the length and the width of the sepals and petals, in centimeters. Based on the combination of these four features, Fisher developed a linear discriminant model to distinguish the species from each other.
As a result, **iris dataset is used as the input of all algorithms**.
<a id="9"></a> <br>
### 4-2 Outputs
the outputs for our algorithms totally depend on the type of classification or clustering algorithms.
the outputs can be the number of clusters or predict for new input.
**setosa**: Iris setosa, true or false, used as target.
**versicolour**: Iris versicolour, true or false, used as target.
**virginica**: Iris virginica, true or false, used as a target.
<a id="10"></a> <br>
## 5-Installation
#### Windows:
* Anaconda (from https://www.continuum.io) is a free Python distribution for SciPy stack. It is also available for Linux and Mac.
* Canopy (https://www.enthought.com/products/canopy/) is available as free as well as commercial distribution with full SciPy stack for Windows, Linux and Mac.
* Python (x,y) is a free Python distribution with SciPy stack and Spyder IDE for Windows OS. (Downloadable from http://python-xy.github.io/)
#### Linux
Package managers of respective Linux distributions are used to install one or more packages in SciPy stack.
For Ubuntu Users:
sudo apt-get install python-numpy python-scipy python-matplotlibipythonipythonnotebook
python-pandas python-sympy python-nose
<a id="11"></a> <br>
## 5-1 Jupyter notebook
I strongly recommend installing **Python** and **Jupyter** using the **[Anaconda Distribution](https://www.anaconda.com/download/)**, which includes Python, the Jupyter Notebook, and other commonly used packages for scientific computing and data science.
First, download Anaconda. We recommend downloading Anaconda’s latest Python 3 version.
Second, install the version of Anaconda which you downloaded, following the instructions on the download page.
Congratulations, you have installed Jupyter Notebook! To run the notebook, run the following command at the Terminal (Mac/Linux) or Command Prompt (Windows):
> jupyter notebook
>
<a id="12"></a> <br>
## 5-2 Kaggle Kernel
Kaggle kernel is an environment just like you use jupyter notebook, it's an **extension** of the where in you are able to carry out all the functions of jupyter notebooks plus it has some added tools like forking et al.
<a id="13"></a> <br>
## 5-3 Colab notebook
**Colaboratory** is a research tool for machine learning education and research. It’s a Jupyter notebook environment that requires no setup to use.
### 5-3-1 What browsers are supported?
Colaboratory works with most major browsers, and is most thoroughly tested with desktop versions of Chrome and Firefox.
### 5-3-2 Is it free to use?
Yes. Colaboratory is a research project that is free to use.
### 5-3-3 What is the difference between Jupyter and Colaboratory?
Jupyter is the open source project on which Colaboratory is based. Colaboratory allows you to use and share Jupyter notebooks with others without having to download, install, or run anything on your own computer other than a browser.
<a id="15"></a> <br>
## 5-5 Loading Packages
In this kernel we are using the following packages:
<img src="http://s8.picofile.com/file/8338227868/packages.png">
### 5-5-1 Import
```
from sklearn.cross_validation import train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from pandas import get_dummies
import plotly.graph_objs as go
from sklearn import datasets
import plotly.plotly as py
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib
import warnings
import sklearn
import scipy
import numpy
import json
import sys
import csv
import os
```
### 5-5-2 Print
```
print('matplotlib: {}'.format(matplotlib.__version__))
print('sklearn: {}'.format(sklearn.__version__))
print('scipy: {}'.format(scipy.__version__))
print('seaborn: {}'.format(sns.__version__))
print('pandas: {}'.format(pd.__version__))
print('numpy: {}'.format(np.__version__))
print('Python: {}'.format(sys.version))
#show plot inline
%matplotlib inline
```
<a id="16"></a> <br>
## 6- Exploratory Data Analysis(EDA)
In this section, you'll learn how to use graphical and numerical techniques to begin uncovering the structure of your data.
* Which variables suggest interesting relationships?
* Which observations are unusual?
By the end of the section, you'll be able to answer these questions and more, while generating graphics that are both insightful and beautiful. then We will review analytical and statistical operations:
* 5-1 Data Collection
* 5-2 Visualization
* 5-3 Data Preprocessing
* 5-4 Data Cleaning
<img src="http://s9.picofile.com/file/8338476134/EDA.png">
<a id="17"></a> <br>
## 6-1 Data Collection
**Data collection** is the process of gathering and measuring data, information or any variables of interest in a standardized and established manner that enables the collector to answer or test hypothesis and evaluate outcomes of the particular collection.[techopedia]
**Iris dataset** consists of 3 different types of irises’ (Setosa, Versicolour, and Virginica) petal and sepal length, stored in a 150x4 numpy.ndarray
The rows being the samples and the columns being: Sepal Length, Sepal Width, Petal Length and Petal Width.[6]
```
# import Dataset to play with it
dataset = pd.read_csv('../input/Iris.csv')
```
**<< Note 1 >>**
* Each row is an observation (also known as : sample, example, instance, record)
* Each column is a feature (also known as: Predictor, attribute, Independent Variable, input, regressor, Covariate)
After loading the data via **pandas**, we should checkout what the content is, description and via the following:
```
type(dataset)
```
<a id="18"></a> <br>
## 6-2 Visualization
**Data visualization** is the presentation of data in a pictorial or graphical format. It enables decision makers to see analytics presented visually, so they can grasp difficult concepts or identify new patterns.
With interactive visualization, you can take the concept a step further by using technology to drill down into charts and graphs for more detail, interactively changing what data you see and how it’s processed.[SAS]
In this section I show you **11 plots** with **matplotlib** and **seaborn** that is listed in the blew picture:
<img src="http://s8.picofile.com/file/8338475500/visualization.jpg" />
<a id="19"></a> <br>
### 6-2-1 Scatter plot
Scatter plot Purpose To identify the type of relationship (if any) between two quantitative variables
```
# Modify the graph above by assigning each species an individual color.
sns.FacetGrid(dataset, hue="Species", size=5) \
.map(plt.scatter, "SepalLengthCm", "SepalWidthCm") \
.add_legend()
plt.show()
```
<a id="20"></a> <br>
### 6-2-2 Box
In descriptive statistics, a **box plot** or boxplot is a method for graphically depicting groups of numerical data through their quartiles. Box plots may also have lines extending vertically from the boxes (whiskers) indicating variability outside the upper and lower quartiles, hence the terms box-and-whisker plot and box-and-whisker diagram.[wikipedia]
```
dataset.plot(kind='box', subplots=True, layout=(2,3), sharex=False, sharey=False)
plt.figure()
#This gives us a much clearer idea of the distribution of the input attributes:
# To plot the species data using a box plot:
sns.boxplot(x="Species", y="PetalLengthCm", data=dataset )
plt.show()
# Use Seaborn's striplot to add data points on top of the box plot
# Insert jitter=True so that the data points remain scattered and not piled into a verticle line.
# Assign ax to each axis, so that each plot is ontop of the previous axis.
ax= sns.boxplot(x="Species", y="PetalLengthCm", data=dataset)
ax= sns.stripplot(x="Species", y="PetalLengthCm", data=dataset, jitter=True, edgecolor="gray")
plt.show()
# Tweek the plot above to change fill and border color color using ax.artists.
# Assing ax.artists a variable name, and insert the box number into the corresponding brackets
ax= sns.boxplot(x="Species", y="PetalLengthCm", data=dataset)
ax= sns.stripplot(x="Species", y="PetalLengthCm", data=dataset, jitter=True, edgecolor="gray")
boxtwo = ax.artists[2]
boxtwo.set_facecolor('red')
boxtwo.set_edgecolor('black')
boxthree=ax.artists[1]
boxthree.set_facecolor('yellow')
boxthree.set_edgecolor('black')
plt.show()
```
<a id="21"></a> <br>
### 6-2-3 Histogram
We can also create a **histogram** of each input variable to get an idea of the distribution.
```
# histograms
dataset.hist(figsize=(15,20))
plt.figure()
```
It looks like perhaps two of the input variables have a Gaussian distribution. This is useful to note as we can use algorithms that can exploit this assumption.
```
dataset["PetalLengthCm"].hist();
```
<a id="22"></a> <br>
### 6-2-4 Multivariate Plots
Now we can look at the interactions between the variables.
First, let’s look at scatterplots of all pairs of attributes. This can be helpful to spot structured relationships between input variables.
```
# scatter plot matrix
pd.plotting.scatter_matrix(dataset,figsize=(10,10))
plt.figure()
```
Note the diagonal grouping of some pairs of attributes. This suggests a high correlation and a predictable relationship.
<a id="23"></a> <br>
### 6-2-5 violinplots
```
# violinplots on petal-length for each species
sns.violinplot(data=dataset,x="Species", y="PetalLengthCm")
```
<a id="24"></a> <br>
### 6-2-6 pairplot
```
# Using seaborn pairplot to see the bivariate relation between each pair of features
sns.pairplot(dataset, hue="Species")
```
From the plot, we can see that the species setosa is separataed from the other two across all feature combinations
We can also replace the histograms shown in the diagonal of the pairplot by kde.
```
# updating the diagonal elements in a pairplot to show a kde
sns.pairplot(dataset, hue="Species",diag_kind="kde")
```
<a id="25"></a> <br>
### 6-2-7 kdeplot
```
# seaborn's kdeplot, plots univariate or bivariate density estimates.
#Size can be changed by tweeking the value used
sns.FacetGrid(dataset, hue="Species", size=5).map(sns.kdeplot, "PetalLengthCm").add_legend()
plt.show()
```
<a id="26"></a> <br>
### 6-2-8 jointplot
```
# Use seaborn's jointplot to make a hexagonal bin plot
#Set desired size and ratio and choose a color.
sns.jointplot(x="SepalLengthCm", y="SepalWidthCm", data=dataset, size=10,ratio=10, kind='hex',color='green')
plt.show()
```
<a id="27"></a> <br>
### 6-2-9 andrews_curves
```
#In Pandas use Andrews Curves to plot and visualize data structure.
#Each multivariate observation is transformed into a curve and represents the coefficients of a Fourier series.
#This useful for detecting outliers in times series data.
#Use colormap to change the color of the curves
from pandas.tools.plotting import andrews_curves
andrews_curves(dataset.drop("Id", axis=1), "Species",colormap='rainbow')
plt.show()
# we will use seaborn jointplot shows bivariate scatterplots and univariate histograms with Kernel density
# estimation in the same figure
sns.jointplot(x="SepalLengthCm", y="SepalWidthCm", data=dataset, size=6, kind='kde', color='#800000', space=0)
```
<a id="28"></a> <br>
### 6-2-10 Heatmap
```
plt.figure(figsize=(7,4))
sns.heatmap(dataset.corr(),annot=True,cmap='cubehelix_r') #draws heatmap with input as the correlation matrix calculted by(iris.corr())
plt.show()
```
<a id="29"></a> <br>
### 6-2-11 radviz
```
# A final multivariate visualization technique pandas has is radviz
# Which puts each feature as a point on a 2D plane, and then simulates
# having each sample attached to those points through a spring weighted
# by the relative value for that feature
from pandas.tools.plotting import radviz
radviz(dataset.drop("Id", axis=1), "Species")
```
### 6-2-12 Bar Plot
```
dataset['Species'].value_counts().plot(kind="bar");
```
### 6-2-14 visualization with Plotly
```
import plotly.offline as py
import plotly.graph_objs as go
py.init_notebook_mode(connected=True)
from plotly import tools
import plotly.figure_factory as ff
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features.
Y = iris.target
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
trace = go.Scatter(x=X[:, 0],
y=X[:, 1],
mode='markers',
marker=dict(color=np.random.randn(150),
size=10,
colorscale='Viridis',
showscale=False))
layout = go.Layout(title='Training Points',
xaxis=dict(title='Sepal length',
showgrid=False),
yaxis=dict(title='Sepal width',
showgrid=False),
)
fig = go.Figure(data=[trace], layout=layout)
py.iplot(fig)
```
**<< Note >>**
**Yellowbrick** is a suite of visual diagnostic tools called “Visualizers” that extend the Scikit-Learn API to allow human steering of the model selection process. In a nutshell, Yellowbrick combines scikit-learn with matplotlib in the best tradition of the scikit-learn documentation, but to produce visualizations for your models!
### 6-2-13 Conclusion
we have used Python to apply data visualization tools to the Iris dataset. Color and size changes were made to the data points in scatterplots. I changed the border and fill color of the boxplot and violin, respectively.
<a id="30"></a> <br>
## 6-3 Data Preprocessing
**Data preprocessing** refers to the transformations applied to our data before feeding it to the algorithm.
Data Preprocessing is a technique that is used to convert the raw data into a clean data set. In other words, whenever the data is gathered from different sources it is collected in raw format which is not feasible for the analysis.
there are plenty of steps for data preprocessing and we just listed some of them :
* removing Target column (id)
* Sampling (without replacement)
* Making part of iris unbalanced and balancing (with undersampling and SMOTE)
* Introducing missing values and treating them (replacing by average values)
* Noise filtering
* Data discretization
* Normalization and standardization
* PCA analysis
* Feature selection (filter, embedded, wrapper)
## 6-3-1 Features
Features:
* numeric
* categorical
* ordinal
* datetime
* coordinates
find the type of features in titanic dataset
<img src="http://s9.picofile.com/file/8339959442/titanic.png" height="700" width="600" />
### 6-3-2 Explorer Dataset
1- Dimensions of the dataset.
2- Peek at the data itself.
3- Statistical summary of all attributes.
4- Breakdown of the data by the class variable.[7]
Don’t worry, each look at the data is **one command**. These are useful commands that you can use again and again on future projects.
```
# shape
print(dataset.shape)
#columns*rows
dataset.size
```
how many NA elements in every column
```
dataset.isnull().sum()
# remove rows that have NA's
dataset = dataset.dropna()
```
We can get a quick idea of how many instances (rows) and how many attributes (columns) the data contains with the shape property.
You should see 150 instances and 5 attributes:
for getting some information about the dataset you can use **info()** command
```
print(dataset.info())
```
you see number of unique item for Species with command below:
```
dataset['Species'].unique()
dataset["Species"].value_counts()
```
to check the first 5 rows of the data set, we can use head(5).
```
dataset.head(5)
```
to check out last 5 row of the data set, we use tail() function
```
dataset.tail()
```
to pop up 5 random rows from the data set, we can use **sample(5)** function
```
dataset.sample(5)
```
to give a statistical summary about the dataset, we can use **describe()
```
dataset.describe()
```
to check out how many null info are on the dataset, we can use **isnull().sum()
```
dataset.isnull().sum()
dataset.groupby('Species').count()
```
to print dataset **columns**, we can use columns atribute
```
dataset.columns
```
**<< Note 2 >>**
in pandas's data frame you can perform some query such as "where"
```
dataset.where(dataset ['Species']=='Iris-setosa')
```
as you can see in the below in python, it is so easy perform some query on the dataframe:
```
dataset[dataset['SepalLengthCm']>7.2]
# Seperating the data into dependent and independent variables
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
```
**<< Note >>**
>**Preprocessing and generation pipelines depend on a model type**
<a id="31"></a> <br>
## 6-4 Data Cleaning
When dealing with real-world data, dirty data is the norm rather than the exception. We continuously need to predict correct values, impute missing ones, and find links between various data artefacts such as schemas and records. We need to stop treating data cleaning as a piecemeal exercise (resolving different types of errors in isolation), and instead leverage all signals and resources (such as constraints, available statistics, and dictionaries) to accurately predict corrective actions.
The primary goal of data cleaning is to detect and remove errors and **anomalies** to increase the value of data in analytics and decision making. While it has been the focus of many researchers for several years, individual problems have been addressed separately. These include missing value imputation, outliers detection, transformations, integrity constraints violations detection and repair, consistent query answering, deduplication, and many other related problems such as profiling and constraints mining.[8]
```
cols = dataset.columns
features = cols[0:4]
labels = cols[4]
print(features)
print(labels)
#Well conditioned data will have zero mean and equal variance
#We get this automattically when we calculate the Z Scores for the data
data_norm = pd.DataFrame(dataset)
for feature in features:
dataset[feature] = (dataset[feature] - dataset[feature].mean())/dataset[feature].std()
#Show that should now have zero mean
print("Averages")
print(dataset.mean())
print("\n Deviations")
#Show that we have equal variance
print(pow(dataset.std(),2))
#Shuffle The data
indices = data_norm.index.tolist()
indices = np.array(indices)
np.random.shuffle(indices)
# One Hot Encode as a dataframe
from sklearn.cross_validation import train_test_split
y = get_dummies(y)
# Generate Training and Validation Sets
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=.3)
# Convert to np arrays so that we can use with TensorFlow
X_train = np.array(X_train).astype(np.float32)
X_test = np.array(X_test).astype(np.float32)
y_train = np.array(y_train).astype(np.float32)
y_test = np.array(y_test).astype(np.float32)
#Check to make sure split still has 4 features and 3 labels
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
```
<a id="32"></a> <br>
## 7- Model Deployment
In this section have been applied more than **20 learning algorithms** that play an important rule in your experiences and improve your knowledge in case of ML technique.
> **<< Note 3 >>** : The results shown here may be slightly different for your analysis because, for example, the neural network algorithms use random number generators for fixing the initial value of the weights (starting points) of the neural networks, which often result in obtaining slightly different (local minima) solutions each time you run the analysis. Also note that changing the seed for the random number generator used to create the train, test, and validation samples can change your results.
## Families of ML algorithms
There are several categories for machine learning algorithms, below are some of these categories:
* Linear
* Linear Regression
* Logistic Regression
* Support Vector Machines
* Tree-Based
* Decision Tree
* Random Forest
* GBDT
* KNN
* Neural Networks
-----------------------------
And if we want to categorize ML algorithms with the type of learning, there are below type:
* Classification
* k-Nearest Neighbors
* LinearRegression
* SVM
* DT
* NN
* clustering
* K-means
* HCA
* Expectation Maximization
* Visualization and dimensionality reduction:
* Principal Component Analysis(PCA)
* Kernel PCA
* Locally -Linear Embedding (LLE)
* t-distributed Stochastic Neighbor Embedding (t-SNE)
* Association rule learning
* Apriori
* Eclat
* Semisupervised learning
* Reinforcement Learning
* Q-learning
* Batch learning & Online learning
* Ensemble Learning
**<< Note >>**
> Here is no method which outperforms all others for all tasks
<a id="33"></a> <br>
## Prepare Features & Targets
First of all seperating the data into dependent(Feature) and independent(Target) variables.
**<< Note 4 >>**
* X==>>Feature
* y==>>Target
```
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
# Splitting the dataset into the Training set and Test set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
```
## Accuracy and precision
* **precision** :
In pattern recognition, information retrieval and binary classification, precision (also called positive predictive value) is the fraction of relevant instances among the retrieved instances,
* **recall** :
recall is the fraction of relevant instances that have been retrieved over the total amount of relevant instances.
* **F-score** :
the F1 score is a measure of a test's accuracy. It considers both the precision p and the recall r of the test to compute the score: p is the number of correct positive results divided by the number of all positive results returned by the classifier, and r is the number of correct positive results divided by the number of all relevant samples (all samples that should have been identified as positive). The F1 score is the harmonic average of the precision and recall, where an F1 score reaches its best value at 1 (perfect precision and recall) and worst at 0.
**What is the difference between accuracy and precision?
"Accuracy" and "precision" are general terms throughout science. A good way to internalize the difference are the common "bullseye diagrams". In machine learning/statistics as a whole, accuracy vs. precision is analogous to bias vs. variance.
<a id="33"></a> <br>
## 7-1 K-Nearest Neighbours
In **Machine Learning**, the **k-nearest neighbors algorithm** (k-NN) is a non-parametric method used for classification and regression. In both cases, the input consists of the k closest training examples in the feature space. The output depends on whether k-NN is used for classification or regression:
In k-NN classification, the output is a class membership. An object is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor.
In k-NN regression, the output is the property value for the object. This value is the average of the values of its k nearest neighbors.
k-NN is a type of instance-based learning, or lazy learning, where the function is only approximated locally and all computation is deferred until classification. The k-NN algorithm is among the simplest of all machine learning algorithms.
```
# K-Nearest Neighbours
from sklearn.neighbors import KNeighborsClassifier
Model = KNeighborsClassifier(n_neighbors=8)
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="34"></a> <br>
## 7-2 Radius Neighbors Classifier
Classifier implementing a **vote** among neighbors within a given **radius**
In scikit-learn **RadiusNeighborsClassifier** is very similar to **KNeighborsClassifier** with the exception of two parameters. First, in RadiusNeighborsClassifier we need to specify the radius of the fixed area used to determine if an observation is a neighbor using radius. Unless there is some substantive reason for setting radius to some value, it is best to treat it like any other hyperparameter and tune it during model selection. The second useful parameter is outlier_label, which indicates what label to give an observation that has no observations within the radius - which itself can often be a useful tool for identifying outliers.
```
from sklearn.neighbors import RadiusNeighborsClassifier
Model=RadiusNeighborsClassifier(radius=8.0)
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
#summary of the predictions made by the classifier
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_test,y_pred))
#Accouracy score
print('accuracy is ', accuracy_score(y_test,y_pred))
```
<a id="35"></a> <br>
## 7-3 Logistic Regression
Logistic regression is the appropriate regression analysis to conduct when the dependent variable is **dichotomous** (binary). Like all regression analyses, the logistic regression is a **predictive analysis**.
In statistics, the logistic model (or logit model) is a widely used statistical model that, in its basic form, uses a logistic function to model a binary dependent variable; many more complex extensions exist. In regression analysis, logistic regression (or logit regression) is estimating the parameters of a logistic model; it is a form of binomial regression. Mathematically, a binary logistic model has a dependent variable with two possible values, such as pass/fail, win/lose, alive/dead or healthy/sick; these are represented by an indicator variable, where the two values are labeled "0" and "1"
```
# LogisticRegression
from sklearn.linear_model import LogisticRegression
Model = LogisticRegression()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="36"></a> <br>
## 7-4 Passive Aggressive Classifier
```
from sklearn.linear_model import PassiveAggressiveClassifier
Model = PassiveAggressiveClassifier()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="37"></a> <br>
## 7-5 Naive Bayes
In machine learning, naive Bayes classifiers are a family of simple "**probabilistic classifiers**" based on applying Bayes' theorem with strong (naive) independence assumptions between the features.
```
# Naive Bayes
from sklearn.naive_bayes import GaussianNB
Model = GaussianNB()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="39"></a> <br>
## 7-7 BernoulliNB
Like MultinomialNB, this classifier is suitable for **discrete data**. The difference is that while MultinomialNB works with occurrence counts, BernoulliNB is designed for binary/boolean features.
```
# BernoulliNB
from sklearn.naive_bayes import BernoulliNB
Model = BernoulliNB()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="40"></a> <br>
## 7-8 SVM
The advantages of support vector machines are:
* Effective in high dimensional spaces.
* Still effective in cases where number of dimensions is greater than the number of samples.
* Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
* Versatile: different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.
The disadvantages of support vector machines include:
* If the number of features is much greater than the number of samples, avoid over-fitting in choosing Kernel functions and regularization term is crucial.
* SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation
```
# Support Vector Machine
from sklearn.svm import SVC
Model = SVC()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="41"></a> <br>
## 7-9 Nu-Support Vector Classification
> Similar to SVC but uses a parameter to control the number of support vectors.
```
# Support Vector Machine's
from sklearn.svm import NuSVC
Model = NuSVC()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="42"></a> <br>
## 7-10 Linear Support Vector Classification
Similar to **SVC** with parameter kernel=’linear’, but implemented in terms of liblinear rather than libsvm, so it has more flexibility in the choice of penalties and loss functions and should scale better to large numbers of samples.
```
# Linear Support Vector Classification
from sklearn.svm import LinearSVC
Model = LinearSVC()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="43"></a> <br>
## 7-11 Decision Tree
Decision Trees (DTs) are a non-parametric supervised learning method used for **classification** and **regression**. The goal is to create a model that predicts the value of a target variable by learning simple **decision rules** inferred from the data features.
```
# Decision Tree's
from sklearn.tree import DecisionTreeClassifier
Model = DecisionTreeClassifier()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="44"></a> <br>
## 7-12 ExtraTreeClassifier
An extremely randomized tree classifier.
Extra-trees differ from classic decision trees in the way they are built. When looking for the best split to separate the samples of a node into two groups, random splits are drawn for each of the **max_features** randomly selected features and the best split among those is chosen. When max_features is set 1, this amounts to building a totally random decision tree.
**Warning**: Extra-trees should only be used within ensemble methods.
```
# ExtraTreeClassifier
from sklearn.tree import ExtraTreeClassifier
Model = ExtraTreeClassifier()
Model.fit(X_train, y_train)
y_pred = Model.predict(X_test)
# Summary of the predictions made by the classifier
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
# Accuracy score
print('accuracy is',accuracy_score(y_pred,y_test))
```
<a id="45"></a> <br>
## 7-13 Neural network
I have used multi-layer Perceptron classifier.
This model optimizes the log-loss function using **LBFGS** or **stochastic gradient descent**.
## 7-13-1 What is a Perceptron?
There are many online examples and tutorials on perceptrons and learning. Here is a list of some articles:
- [Wikipedia on Perceptrons](https://en.wikipedia.org/wiki/Perceptron)
- Jurafsky and Martin (ed. 3), Chapter 8
This is an example that I have taken from a draft of the 3rd edition of Jurafsky and Martin, with slight modifications:
We import *numpy* and use its *exp* function. We could use the same function from the *math* module, or some other module like *scipy*. The *sigmoid* function is defined as in the textbook:
```
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
```
Our example data, **weights** $w$, **bias** $b$, and **input** $x$ are defined as:
```
w = np.array([0.2, 0.3, 0.8])
b = 0.5
x = np.array([0.5, 0.6, 0.1])
```
Our neural unit would compute $z$ as the **dot-product** $w \cdot x$ and add the **bias** $b$ to it. The sigmoid function defined above will convert this $z$ value to the **activation value** $a$ of the unit:
```
z = w.dot(x) + b
print("z:", z)
print("a:", sigmoid(z))
```
### The XOR Problem
The power of neural units comes from combining them into larger networks. Minsky and Papert (1969): A single neural unit cannot compute the simple logical function XOR.
The task is to implement a simple **perceptron** to compute logical operations like AND, OR, and XOR.
- Input: $x_1$ and $x_2$
- Bias: $b = -1$ for AND; $b = 0$ for OR
- Weights: $w = [1, 1]$
with the following activation function:
$$
y = \begin{cases}
\ 0 & \quad \text{if } w \cdot x + b \leq 0\\
\ 1 & \quad \text{if } w \cdot x + b > 0
\end{cases}
$$
We can define this activation function in Python as:
```
def activation(z):
if z > 0:
return 1
return 0
```
For AND we could implement a perceptron as:
```
w = np.array([1, 1])
b = -1
x = np.array([0, 0])
print("0 AND 0:", activation(w.dot(x) + b))
x = np.array([1, 0])
print("1 AND 0:", activation(w.dot(x) + b))
x = np.array([0, 1])
print("0 AND 1:", activation(w.dot(x) + b))
x = np.array([1, 1])
print("1 AND 1:", activation(w.dot(x) + b))
```
For OR we could implement a perceptron as:
```
w = np.array([1, 1])
b = 0
x = np.array([0, 0])
print("0 OR 0:", activation(w.dot(x) + b))
x = np.array([1, 0])
print("1 OR 0:", activation(w.dot(x) + b))
x = np.array([0, 1])
print("0 OR 1:", activation(w.dot(x) + b))
x = np.array([1, 1])
print("1 OR 1:", activation(w.dot(x) + b))
```
There is no way to implement a perceptron for XOR this way.
no see our prediction for iris
```
from sklearn.neural_network import MLPClassifier
Model=MLPClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
# Summary of the predictions
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_test,y_pred))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="46"></a> <br>
## 7-14 RandomForest
A random forest is a meta estimator that **fits a number of decision tree classifiers** on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
The sub-sample size is always the same as the original input sample size but the samples are drawn with replacement if bootstrap=True (default).
```
from sklearn.ensemble import RandomForestClassifier
Model=RandomForestClassifier(max_depth=2)
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="47"></a> <br>
## 7-15 Bagging classifier
A Bagging classifier is an ensemble **meta-estimator** that fits base classifiers each on random subsets of the original dataset and then aggregate their individual predictions (either by voting or by averaging) to form a final prediction. Such a meta-estimator can typically be used as a way to reduce the variance of a black-box estimator (e.g., a decision tree), by introducing randomization into its construction procedure and then making an ensemble out of it.
This algorithm encompasses several works from the literature. When random subsets of the dataset are drawn as random subsets of the samples, then this algorithm is known as Pasting . If samples are drawn with replacement, then the method is known as Bagging . When random subsets of the dataset are drawn as random subsets of the features, then the method is known as Random Subspaces . Finally, when base estimators are built on subsets of both samples and features, then the method is known as Random Patches .[http://scikit-learn.org]
```
from sklearn.ensemble import BaggingClassifier
Model=BaggingClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="48"></a> <br>
## 7-16 AdaBoost classifier
An AdaBoost classifier is a meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset but where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
This class implements the algorithm known as **AdaBoost-SAMME** .
```
from sklearn.ensemble import AdaBoostClassifier
Model=AdaBoostClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="49"></a> <br>
## 7-17 Gradient Boosting Classifier
GB builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions.
```
from sklearn.ensemble import GradientBoostingClassifier
Model=GradientBoostingClassifier()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="50"></a> <br>
## 7-18 Linear Discriminant Analysis
Linear Discriminant Analysis (discriminant_analysis.LinearDiscriminantAnalysis) and Quadratic Discriminant Analysis (discriminant_analysis.QuadraticDiscriminantAnalysis) are two classic classifiers, with, as their names suggest, a **linear and a quadratic decision surface**, respectively.
These classifiers are attractive because they have closed-form solutions that can be easily computed, are inherently multiclass, have proven to work well in practice, and have no **hyperparameters** to tune.
```
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
Model=LinearDiscriminantAnalysis()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="51"></a> <br>
## 7-19 Quadratic Discriminant Analysis
A classifier with a quadratic decision boundary, generated by fitting class conditional densities to the data and using Bayes’ rule.
The model fits a **Gaussian** density to each class.
```
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
Model=QuadraticDiscriminantAnalysis()
Model.fit(X_train,y_train)
y_pred=Model.predict(X_test)
print(classification_report(y_test,y_pred))
print(confusion_matrix(y_pred,y_test))
#Accuracy Score
print('accuracy is ',accuracy_score(y_pred,y_test))
```
<a id="52"></a> <br>
## 7-20 Kmeans
K-means clustering is a type of unsupervised learning, which is used when you have unlabeled data (i.e., data without defined categories or groups).
The goal of this algorithm is **to find groups in the data**, with the number of groups represented by the variable K. The algorithm works iteratively to assign each data point to one of K groups based on the features that are provided.
```
from sklearn.cluster import KMeans
iris_SP = dataset[['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm']]
# k-means cluster analysis for 1-15 clusters
from scipy.spatial.distance import cdist
clusters=range(1,15)
meandist=[]
# loop through each cluster and fit the model to the train set
# generate the predicted cluster assingment and append the mean
# distance my taking the sum divided by the shape
for k in clusters:
model=KMeans(n_clusters=k)
model.fit(iris_SP)
clusassign=model.predict(iris_SP)
meandist.append(sum(np.min(cdist(iris_SP, model.cluster_centers_, 'euclidean'), axis=1))
/ iris_SP.shape[0])
"""
Plot average distance from observations from the cluster centroid
to use the Elbow Method to identify number of clusters to choose
"""
plt.plot(clusters, meandist)
plt.xlabel('Number of clusters')
plt.ylabel('Average distance')
plt.title('Selecting k with the Elbow Method')
# pick the fewest number of clusters that reduces the average distance
# If you observe after 3 we can see graph is almost linear
```
<a id="53"></a> <br>
## 7-21- Backpropagation
Backpropagation is a method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network.It is commonly used to train deep neural networks,a term referring to neural networks with more than one hidden layer.
In this example we will use a very simple network to start with. The network will only have one input and one output layer. We want to make the following predictions from the input:
| Input | Output |
| ------ |:------:|
| 0 0 1 | 0 |
| 1 1 1 | 1 |
| 1 0 1 | 1 |
| 0 1 1 | 0 |
We will use **Numpy** to compute the network parameters, weights, activation, and outputs:
We will use the *[Sigmoid](http://ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html#sigmoid)* activation function:
```
def sigmoid(z):
"""The sigmoid activation function."""
return 1 / (1 + np.exp(-z))
```
We could use the [ReLU](http://ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html#activation-relu) activation function instead:
```
def relu(z):
"""The ReLU activation function."""
return max(0, z)
```
The [Sigmoid](http://ml-cheatsheet.readthedocs.io/en/latest/activation_functions.html#sigmoid) activation function introduces non-linearity to the computation. It maps the input value to an output value between $0$ and $1$.
<img src="http://s8.picofile.com/file/8339774900/SigmoidFunction1.png" style="max-width:100%; width: 30%; max-width: none">
The derivative of the sigmoid function is maximal at $x=0$ and minimal for lower or higher values of $x$:
<img src="http://s9.picofile.com/file/8339770650/sigmoid_prime.png" style="max-width:100%; width: 25%; max-width: none">
The *sigmoid_prime* function returns the derivative of the sigmoid for any given $z$. The derivative of the sigmoid is $z * (1 - z)$. This is basically the slope of the sigmoid function at any given point:
```
def sigmoid_prime(z):
"""The derivative of sigmoid for z."""
return z * (1 - z)
```
We define the inputs as rows in *X*. There are three input nodes (three columns per vector in $X$. Each row is one trainig example:
```
X = np.array([ [ 0, 0, 1 ],
[ 0, 1, 1 ],
[ 1, 0, 1 ],
[ 1, 1, 1 ] ])
print(X)
```
The outputs are stored in *y*, where each row represents the output for the corresponding input vector (row) in *X*. The vector is initiated as a single row vector and with four columns and transposed (using the $.T$ method) into a column vector with four rows:
```
y = np.array([[0,0,1,1]]).T
print(y)
```
To make the outputs deterministic, we seed the random number generator with a constant. This will guarantee that every time you run the code, you will get the same random distribution:
```
np.random.seed(1)
```
We create a weight matrix ($Wo$) with randomly initialized weights:
```
n_inputs = 3
n_outputs = 1
#Wo = 2 * np.random.random( (n_inputs, n_outputs) ) - 1
Wo = np.random.random( (n_inputs, n_outputs) ) * np.sqrt(2.0/n_inputs)
print(Wo)
```
The reason for the output weight matrix ($Wo$) to have 3 rows and 1 column is that it represents the weights of the connections from the three input neurons to the single output neuron. The initialization of the weight matrix is random with a mean of $0$ and a variance of $1$. There is a good reason for chosing a mean of zero in the weight initialization. See for details the section on Weight Initialization in the [Stanford course CS231n on Convolutional Neural Networks for Visual Recognition](https://cs231n.github.io/neural-networks-2/#init).
The core representation of this network is basically the weight matrix *Wo*. The rest, input matrix, output vector and so on are components that we need to learning and evaluation. The leraning result is stored in the *Wo* weight matrix.
We loop in the optimization and learning cycle 10,000 times. In the *forward propagation* line we process the entire input matrix for training. This is called **full batch** training. I do not use an alternative variable name to represent the input layer, instead I use the input matrix $X$ directly here. Think of this as the different inputs to the input neurons computed at once. In principle the input or training data could have many more training examples, the code would stay the same.
```
for n in range(10000):
# forward propagation
l1 = sigmoid(np.dot(X, Wo))
# compute the loss
l1_error = y - l1
#print("l1_error:\n", l1_error)
# multiply the loss by the slope of the sigmoid at l1
l1_delta = l1_error * sigmoid_prime(l1)
#print("l1_delta:\n", l1_delta)
#print("error:", l1_error, "\nderivative:", sigmoid(l1, True), "\ndelta:", l1_delta, "\n", "-"*10, "\n")
# update weights
Wo += np.dot(X.T, l1_delta)
print("l1:\n", l1)
```
The dots in $l1$ represent the lines in the graphic below. The lines represent the slope of the sigmoid in the particular position. The slope is highest with a value $x = 0$ (blue dot). It is rather shallow with $x = 2$ (green dot), and not so shallow and not as high with $x = -1$. All derivatives are between $0$ and $1$, of course, that is, no slope or a maximal slope of $1$. There is no negative slope in a sigmoid function.
<img src="http://s8.picofile.com/file/8339770734/sigmoid_deriv_2.png" style="max-width:100%; width: 50%; max-width: none">
The matrix $l1\_error$ is a 4 by 1 matrix (4 rows, 1 column). The derivative matrix $sigmoid\_prime(l1)$ is also a 4 by one matrix. The returned matrix of the element-wise product $l1\_delta$ is also the 4 by 1 matrix.
The product of the error and the slopes **reduces the error of high confidence predictions**. When the sigmoid slope is very shallow, the network had a very high or a very low value, that is, it was rather confident. If the network guessed something close to $x=0, y=0.5$, it was not very confident. Such predictions without confidence are updated most significantly. The other peripheral scores are multiplied with a number closer to $0$.
In the prediction line $l1 = sigmoid(np.dot(X, Wo))$ we compute the dot-product of the input vectors with the weights and compute the sigmoid on the sums.
The result of the dot-product is the number of rows of the first matrix ($X$) and the number of columns of the second matrix ($Wo$).
In the computation of the difference between the true (or gold) values in $y$ and the "guessed" values in $l1$ we have an estimate of the miss.
An example computation for the input $[ 1, 0, 1 ]$ and the weights $[ 9.5, 0.2, -0.1 ]$ and an output of $0.99$: If $y = 1$, the $l1\_error = y - l2 = 0.01$, and $l1\_delta = 0.01 * tiny\_deriv$:
<img src="http://s8.picofile.com/file/8339770792/toy_network_deriv.png" style="max-width:100%; width: 40%; max-width: none">
## 7-21-1 More Complex Example with Backpropagation
Consider now a more complicated example where no column has a correlation with the output:
| Input | Output |
| ------ |:------:|
| 0 0 1 | 0 |
| 0 1 1 | 1 |
| 1 0 1 | 1 |
| 1 1 1 | 0 |
The pattern here is our XOR pattern or problem: If there is a $1$ in either column $1$ or $2$, but not in both, the output is $1$ (XOR over column $1$ and $2$).
From our discussion of the XOR problem we remember that this is a *non-linear pattern*, a **one-to-one relationship between a combination of inputs**.
To cope with this problem, we need a network with another layer, that is a layer that will combine and transform the input, and an additional layer will map it to the output. We will add a *hidden layer* with randomized weights and then train those to optimize the output probabilities of the table above.
We will define a new $X$ input matrix that reflects the above table:
```
X = np.array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])
print(X)
```
We also define a new output matrix $y$:
```
y = np.array([[ 0, 1, 1, 0]]).T
print(y)
```
We initialize the random number generator with a constant again:
```
np.random.seed(1)
```
Assume that our 3 inputs are mapped to 4 hidden layer ($Wh$) neurons, we have to initialize the hidden layer weights in a 3 by 4 matrix. The outout layer ($Wo$) is a single neuron that is connected to the hidden layer, thus the output layer is a 4 by 1 matrix:
```
n_inputs = 3
n_hidden_neurons = 4
n_output_neurons = 1
Wh = np.random.random( (n_inputs, n_hidden_neurons) ) * np.sqrt(2.0/n_inputs)
Wo = np.random.random( (n_hidden_neurons, n_output_neurons) ) * np.sqrt(2.0/n_hidden_neurons)
print("Wh:\n", Wh)
print("Wo:\n", Wo)
```
We will loop now 60,000 times to optimize the weights:
```
for i in range(100000):
l1 = sigmoid(np.dot(X, Wh))
l2 = sigmoid(np.dot(l1, Wo))
l2_error = y - l2
if (i % 10000) == 0:
print("Error:", np.mean(np.abs(l2_error)))
# gradient, changing towards the target value
l2_delta = l2_error * sigmoid_prime(l2)
# compute the l1 contribution by value to the l2 error, given the output weights
l1_error = l2_delta.dot(Wo.T)
# direction of the l1 target:
# in what direction is the target l1?
l1_delta = l1_error * sigmoid_prime(l1)
Wo += np.dot(l1.T, l2_delta)
Wh += np.dot(X.T, l1_delta)
print("Wo:\n", Wo)
print("Wh:\n", Wh)
```
The new computation in this new loop is $l1\_error = l2\_delta.dot(Wo.T)$, a **confidence weighted error** from $l2$ to compute an error for $l1$. The computation sends the error across the weights from $l2$ to $l1$. The result is a **contribution weighted error**, because we learn how much each node value in $l1$ **contributed** to the error in $l2$. This step is called **backpropagation**. We update $Wh$ using the same steps we did in the 2 layer implementation.
```
from sklearn import datasets
iris = datasets.load_iris()
X_iris = iris.data
y_iris = iris.target
plt.figure('sepal')
colormarkers = [ ['red','s'], ['greenyellow','o'], ['blue','x']]
for i in range(len(colormarkers)):
px = X_iris[:, 0][y_iris == i]
py = X_iris[:, 1][y_iris == i]
plt.scatter(px, py, c=colormarkers[i][0], marker=colormarkers[i][1])
plt.title('Iris Dataset: Sepal width vs sepal length')
plt.legend(iris.target_names)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.figure('petal')
for i in range(len(colormarkers)):
px = X_iris[:, 2][y_iris == i]
py = X_iris[:, 3][y_iris == i]
plt.scatter(px, py, c=colormarkers[i][0], marker=colormarkers[i][1])
plt.title('Iris Dataset: petal width vs petal length')
plt.legend(iris.target_names)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.show()
```
-----------------
<a id="54"></a> <br>
# 8- Conclusion
In this kernel, I have tried to cover all the parts related to the process of **Machine Learning** with a variety of Python packages and I know that there are still some problems then I hope to get your feedback to improve it.
you can follow me on:
> #### [ GitHub](https://github.com/mjbahmani)
--------------------------------------
**I hope you find this kernel helpful and some <font color="red"><b>UPVOTES</b></font> would be very much appreciated**
<a id="55"></a> <br>
-----------
# 9- References
* [1] [Iris image](https://rpubs.com/wjholst/322258)
* [2] [IRIS](https://archive.ics.uci.edu/ml/datasets/iris)
* [3] [https://skymind.ai/wiki/machine-learning-workflow](https://skymind.ai/wiki/machine-learning-workflow)
* [4] [IRIS-wiki](https://archive.ics.uci.edu/ml/datasets/iris)
* [5] [Problem-define](https://machinelearningmastery.com/machine-learning-in-python-step-by-step/)
* [6] [Sklearn](http://scikit-learn.org/)
* [7] [machine-learning-in-python-step-by-step](https://machinelearningmastery.com/machine-learning-in-python-step-by-step/)
* [8] [Data Cleaning](http://wp.sigmod.org/?p=2288)
* [9] [competitive data science](https://www.coursera.org/learn/competitive-data-science/)
-------------
| true |
code
| 0.666375 | null | null | null | null |
|
# Simple Test between NumPy and Numba
$$
x = \exp(-\Gamma_s d)
$$
```
import numba
import cython
import numexpr
import numpy as np
%load_ext cython
from empymod import filters
from scipy.constants import mu_0 # Magn. permeability of free space [H/m]
from scipy.constants import epsilon_0 # Elec. permittivity of free space [F/m]
res = np.array([2e14, 0.3, 1, 50, 1]) # nlay
freq = np.arange(1, 201)/20. # nfre
off = np.arange(1, 101)*1000 # noff
lambd = filters.key_201_2009().base/off[:, None] # nwav
aniso = np.array([1, 1, 1.5, 2, 1])
epermH = np.array([1, 80, 9, 20, 1])
epermV = np.array([1, 40, 9, 10, 1])
mpermH = np.array([1, 1, 3, 5, 1])
etaH = 1/res + np.outer(2j*np.pi*freq, epermH*epsilon_0)
etaV = 1/(res*aniso*aniso) + np.outer(2j*np.pi*freq, epermV*epsilon_0)
zetaH = np.outer(2j*np.pi*freq, mpermH*mu_0)
Gam = np.sqrt((etaH/etaV)[:, None, :, None] * (lambd*lambd)[None, :, None, :] + (zetaH*etaH)[:, None, :, None])
```
## NumPy
Numpy version to check result and compare times
```
def test_numpy(lGam, d):
return np.exp(-lGam*d)
```
## Numba @vectorize
This is exactly the same function as with NumPy, just added the @vectorize decorater.
```
@numba.vectorize('c16(c16, f8)')
def test_numba_vnp(lGam, d):
return np.exp(-lGam*d)
@numba.vectorize('c16(c16, f8)', target='parallel')
def test_numba_v(lGam, d):
return np.exp(-lGam*d)
```
## Numba @njit
```
@numba.njit
def test_numba_nnp(lGam, d):
out = np.empty_like(lGam)
for nf in numba.prange(lGam.shape[0]):
for no in numba.prange(lGam.shape[1]):
for ni in numba.prange(lGam.shape[2]):
out[nf, no, ni] = np.exp(-lGam[nf, no, ni] * d)
return out
@numba.njit(nogil=True, parallel=True)
def test_numba_n(lGam, d):
out = np.empty_like(lGam)
for nf in numba.prange(lGam.shape[0]):
for no in numba.prange(lGam.shape[1]):
for ni in numba.prange(lGam.shape[2]):
out[nf, no, ni] = np.exp(-lGam[nf, no, ni] * d)
return out
```
## Run comparison for a small and a big matrix
```
lGam = Gam[:, :, 1, :]
d = 100
# Output shape
out_shape = (freq.size, off.size, filters.key_201_2009().base.size)
print(' Shape Test Matrix ::', out_shape, '; total # elements:: '+str(freq.size*off.size*filters.key_201_2009().base.size))
print('------------------------------------------------------------------------------------------')
print(' NumPy :: ', end='')
# Get NumPy result for comparison
numpy_result = test_numpy(lGam, d)
# Get runtime
%timeit test_numpy(lGam, d)
print(' Numba @vectorize :: ', end='')
# Ensure it agrees with NumPy
numba_vnp_result = test_numba_vnp(lGam, d)
if not np.allclose(numpy_result, numba_vnp_result, atol=0, rtol=1e-10):
print('\n * FAIL, DOES NOT AGREE WITH NumPy RESULT!')
# Get runtime
%timeit test_numba_vnp(lGam, d)
print(' Numba @vectorize par :: ', end='')
# Ensure it agrees with NumPy
numba_v_result = test_numba_v(lGam, d)
if not np.allclose(numpy_result, numba_v_result, atol=0, rtol=1e-10):
print('\n * FAIL, DOES NOT AGREE WITH NumPy RESULT!')
# Get runtime
%timeit test_numba_v(lGam, d)
print(' Numba @njit :: ', end='')
# Ensure it agrees with NumPy
numba_nnp_result = test_numba_nnp(lGam, d)
if not np.allclose(numpy_result, numba_nnp_result, atol=0, rtol=1e-10):
print('\n * FAIL, DOES NOT AGREE WITH NumPy RESULT!')
# Get runtime
%timeit test_numba_nnp(lGam, d)
print(' Numba @njit par :: ', end='')
# Ensure it agrees with NumPy
numba_n_result = test_numba_n(lGam, d)
if not np.allclose(numpy_result, numba_n_result, atol=0, rtol=1e-10):
print('\n * FAIL, DOES NOT AGREE WITH NumPy RESULT!')
# Get runtime
%timeit test_numba_n(lGam, d)
from empymod import versions
versions('HTML', add_pckg=[cython, numba], ncol=5)
```
| true |
code
| 0.274984 | null | null | null | null |
|
# Tracking Callbacks
```
from fastai.gen_doc.nbdoc import *
from fastai.vision import *
from fastai.callbacks import *
```
This module regroups the callbacks that track one of the metrics computed at the end of each epoch to take some decision about training. To show examples of use, we'll use our sample of MNIST and a simple cnn model.
```
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
show_doc(TerminateOnNaNCallback)
```
Sometimes, training diverges and the loss goes to nan. In that case, there's no point continuing, so this callback stops the training.
```
model = simple_cnn((3,16,16,2))
learn = Learner(data, model, metrics=[accuracy])
learn.fit_one_cycle(1,1e4)
```
Using it prevents that situation to happen.
```
model = simple_cnn((3,16,16,2))
learn = Learner(data, model, metrics=[accuracy], callbacks=[TerminateOnNaNCallback()])
learn.fit(2,1e4)
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(TerminateOnNaNCallback.on_batch_end)
show_doc(TerminateOnNaNCallback.on_epoch_end)
show_doc(EarlyStoppingCallback)
```
This callback tracks the quantity in `monitor` during the training of `learn`. `mode` can be forced to 'min' or 'max' but will automatically try to determine if the quantity should be the lowest possible (validation loss) or the highest possible (accuracy). Will stop training after `patience` epochs if the quantity hasn't improved by `min_delta`.
```
model = simple_cnn((3,16,16,2))
learn = Learner(data, model, metrics=[accuracy],
callback_fns=[partial(EarlyStoppingCallback, monitor='accuracy', min_delta=0.01, patience=3)])
learn.fit(50,1e-42)
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(EarlyStoppingCallback.on_train_begin)
show_doc(EarlyStoppingCallback.on_epoch_end)
show_doc(SaveModelCallback)
```
This callback tracks the quantity in `monitor` during the training of `learn`. `mode` can be forced to 'min' or 'max' but will automatically try to determine if the quantity should be the lowest possible (validation loss) or the highest possible (accuracy). Will save the model in `name` whenever determined by `every` ('improvement' or 'epoch'). Loads the best model at the end of training is `every='improvement'`.
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(SaveModelCallback.on_epoch_end)
show_doc(SaveModelCallback.on_train_end)
show_doc(ReduceLROnPlateauCallback)
```
This callback tracks the quantity in `monitor` during the training of `learn`. `mode` can be forced to 'min' or 'max' but will automatically try to determine if the quantity should be the lowest possible (validation loss) or the highest possible (accuracy). Will reduce the learning rate by `factor` after `patience` epochs if the quantity hasn't improved by `min_delta`.
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(ReduceLROnPlateauCallback.on_train_begin)
show_doc(ReduceLROnPlateauCallback.on_epoch_end)
show_doc(TrackerCallback)
show_doc(TrackerCallback.get_monitor_value)
```
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(TrackerCallback.on_train_begin)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.821044 | null | null | null | null |
|
```
%cd ../
from torchsignal.datasets import OPENBMI
from torchsignal.datasets.multiplesubjects import MultipleSubjects
from torchsignal.trainer.multitask import Multitask_Trainer
from torchsignal.model import MultitaskSSVEP
import numpy as np
import torch
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
config = {
"exp_name": "multitask-run1",
"seed": 12,
"segment_config": {
"window_len": 1,
"shift_len": 1000,
"sample_rate": 1000,
"add_segment_axis": True
},
"bandpass_config": {
"sample_rate": 1000,
"lowcut": 1,
"highcut": 40,
"order": 6
},
"train_subject_ids": {
"low": 1,
"high": 54
},
"test_subject_ids": {
"low": 1,
"high": 54
},
"root": "../data/openbmi",
"selected_channels": ['P7', 'P3', 'Pz', 'P4', 'P8', 'PO9', 'O1', 'Oz', 'O2', 'PO10'],
"sessions": [1,2],
"tsdata": False,
"num_classes": 4,
"num_channel": 10,
"batchsize": 256,
"learning_rate": 0.001,
"epochs": 100,
"patience": 5,
"early_stopping": 10,
"model": {
"n1": 4,
"kernel_window_ssvep": 59,
"kernel_window": 19,
"conv_3_dilation": 4,
"conv_4_dilation": 4
},
"gpu": 0,
"multitask": True,
"runkfold": 4,
"check_model": True
}
device = torch.device("cuda:"+str(config['gpu']) if torch.cuda.is_available() else "cpu")
print('device', device)
```
# Load Data - OPENBMI
```
subject_ids = list(np.arange(config['train_subject_ids']['low'], config['train_subject_ids']['high']+1, dtype=int))
openbmi_data = MultipleSubjects(
dataset=OPENBMI,
root=config['root'],
subject_ids=subject_ids,
sessions=config['sessions'],
selected_channels=config['selected_channels'],
segment_config=config['segment_config'],
bandpass_config=config['bandpass_config'],
one_hot_labels=True,
)
```
# Train-Test model - leave one subject out
```
train_loader, val_loader, test_loader = openbmi_data.leave_one_subject_out(selected_subject_id=1)
dataloaders_dict = {
'train': train_loader,
'val': val_loader
}
check_model = config['check_model'] if 'check_model' in config else False
if check_model:
x = torch.ones((20, 10, 1000)).to(device)
if config['tsdata'] == True:
x = torch.ones((40, config['num_channel'], config['segment_config']['window_len'] * config['bandpass_config']['sample_rate'])).to(device)
model = MultitaskSSVEP(num_channel=config['num_channel'],
num_classes=config['num_classes'],
signal_length=config['segment_config']['window_len'] * config['bandpass_config']['sample_rate'],
filters_n1= config['model']['n1'],
kernel_window_ssvep= config['model']['kernel_window_ssvep'],
kernel_window= config['model']['kernel_window'],
conv_3_dilation= config['model']['conv_3_dilation'],
conv_4_dilation= config['model']['conv_4_dilation'],
).to(device)
out = model(x)
print('output',out.shape)
def count_params(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print('model size',count_params(model))
del model
del out
model = MultitaskSSVEP(num_channel=config['num_channel'],
num_classes=config['num_classes'],
signal_length=config['segment_config']['window_len'] * config['bandpass_config']['sample_rate'],
filters_n1= config['model']['n1'],
kernel_window_ssvep= config['model']['kernel_window_ssvep'],
kernel_window= config['model']['kernel_window'],
conv_3_dilation= config['model']['conv_3_dilation'],
conv_4_dilation= config['model']['conv_4_dilation'],
).to(device)
epochs=config['epochs'] if 'epochs' in config else 50
patience=config['patience'] if 'patience' in config else 20
early_stopping=config['early_stopping'] if 'early_stopping' in config else 40
trainer = Multitask_Trainer(model, model_name="multitask", device=device, num_classes=config['num_classes'], multitask_learning=True, patience=patience, verbose=True)
trainer.fit(dataloaders_dict, num_epochs=epochs, early_stopping=early_stopping, topk_accuracy=1, save_model=False)
test_loss, test_acc, test_metric = trainer.validate(test_loader, 1)
print('test: {:.5f}, {:.5f}, {:.5f}'.format(test_loss, test_acc, test_metric))
```
# Train-Test model - k-fold and leave one subject out
```
subject_kfold_acc = {}
subject_kfold_f1 = {}
test_subject_ids = list(np.arange(config['test_subject_ids']['low'], config['test_subject_ids']['high']+1, dtype=int))
for subject_id in test_subject_ids:
print('Subject', subject_id)
kfold_acc = []
kfold_f1 = []
for k in range(config['runkfold']):
openbmi_data.split_by_kfold(kfold_k=k, kfold_split=config['runkfold'])
train_loader, val_loader, test_loader = openbmi_data.leave_one_subject_out(selected_subject_id=subject_id, dataloader_batchsize=config['batchsize'])
dataloaders_dict = {
'train': train_loader,
'val': val_loader
}
model = MultitaskSSVEP(num_channel=config['num_channel'],
num_classes=config['num_classes'],
signal_length=config['segment_config']['window_len'] * config['bandpass_config']['sample_rate'],
filters_n1= config['model']['n1'],
kernel_window_ssvep= config['model']['kernel_window_ssvep'],
kernel_window= config['model']['kernel_window'],
conv_3_dilation= config['model']['conv_3_dilation'],
conv_4_dilation= config['model']['conv_4_dilation'],
).to(device)
epochs=config['epochs'] if 'epochs' in config else 50
patience=config['patience'] if 'patience' in config else 20
early_stopping=config['early_stopping'] if 'early_stopping' in config else 40
trainer = Multitask_Trainer(model, model_name="Network064b_1-8sub", device=device, num_classes=config['num_classes'], multitask_learning=True, patience=patience, verbose=False)
trainer.fit(dataloaders_dict, num_epochs=epochs, early_stopping=early_stopping, topk_accuracy=1, save_model=True)
test_loss, test_acc, test_metric = trainer.validate(test_loader, 1)
# print('test: {:.5f}, {:.5f}, {:.5f}'.format(test_loss, test_acc, test_metric))
kfold_acc.append(test_acc)
kfold_f1.append(test_metric)
subject_kfold_acc[subject_id] = kfold_acc
subject_kfold_f1[subject_id] = kfold_f1
print('results')
print('subject_kfold_acc', subject_kfold_acc)
print('subject_kfold_f1', subject_kfold_f1)
# acc
subjects = []
acc = []
acc_min = 1.0
acc_max = 0.0
for subject_id in subject_kfold_acc:
subjects.append(subject_id)
avg_acc = np.mean(subject_kfold_acc[subject_id])
if avg_acc < acc_min:
acc_min = avg_acc
if avg_acc > acc_max:
acc_max = avg_acc
acc.append(avg_acc)
x_pos = [i for i, _ in enumerate(subjects)]
figure(num=None, figsize=(15, 3), dpi=80, facecolor='w', edgecolor='k')
plt.bar(x_pos, acc, color='skyblue')
plt.xlabel("Subject")
plt.ylabel("Accuracies")
plt.title("Average k-fold Accuracies by subjects")
plt.xticks(x_pos, subjects)
plt.ylim([acc_min-0.02, acc_max+0.02])
plt.show()
# f1
subjects = []
f1 = []
f1_min = 1.0
f1_max = 0.0
for subject_id in subject_kfold_f1:
subjects.append(subject_id)
avg_f1 = np.mean(subject_kfold_f1[subject_id])
if avg_f1 < f1_min:
f1_min = avg_f1
if avg_f1 > f1_max:
f1_max = avg_f1
f1.append(avg_f1)
x_pos = [i for i, _ in enumerate(subjects)]
figure(num=None, figsize=(15, 3), dpi=80, facecolor='w', edgecolor='k')
plt.bar(x_pos, f1, color='skyblue')
plt.xlabel("Subject")
plt.ylabel("Accuracies")
plt.title("Average k-fold F1 by subjects")
plt.xticks(x_pos, subjects)
plt.ylim([f1_min-0.02, f1_max+0.02])
plt.show()
print('Average acc:', np.mean(acc))
print('Average f1:', np.mean(f1))
```
| true |
code
| 0.644309 | null | null | null | null |
|
If you're opening this Notebook on colab, you will probably need to install 🤗 Transformers and 🤗 Datasets as well as other dependencies. Uncomment the following cell and run it.
```
#! pip install datasets transformers rouge-score nltk
```
If you're opening this notebook locally, make sure your environment has the last version of those libraries installed.
You can find a script version of this notebook to fine-tune your model in a distributed fashion using multiple GPUs or TPUs [here](https://github.com/huggingface/transformers/tree/master/examples/seq2seq).
# Fine-tuning a model on a summarization task
In this notebook, we will see how to fine-tune one of the [🤗 Transformers](https://github.com/huggingface/transformers) model for a summarization task. We will use the [XSum dataset](https://arxiv.org/pdf/1808.08745.pdf) (for extreme summarization) which contains BBC articles accompanied with single-sentence summaries.

We will see how to easily load the dataset for this task using 🤗 Datasets and how to fine-tune a model on it using the `Trainer` API.
```
model_checkpoint = "t5-small"
```
This notebook is built to run with any model checkpoint from the [Model Hub](https://huggingface.co/models) as long as that model has a sequence-to-sequence version in the Transformers library. Here we picked the [`t5-small`](https://huggingface.co/t5-small) checkpoint.
## Loading the dataset
We will use the [🤗 Datasets](https://github.com/huggingface/datasets) library to download the data and get the metric we need to use for evaluation (to compare our model to the benchmark). This can be easily done with the functions `load_dataset` and `load_metric`.
```
from datasets import load_dataset, load_metric
raw_datasets = load_dataset("xsum")
metric = load_metric("rouge")
```
The `dataset` object itself is [`DatasetDict`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasetdict), which contains one key for the training, validation and test set:
```
raw_datasets
```
To access an actual element, you need to select a split first, then give an index:
```
raw_datasets["train"][0]
```
To get a sense of what the data looks like, the following function will show some examples picked randomly in the dataset.
```
import datasets
import random
import pandas as pd
from IPython.display import display, HTML
def show_random_elements(dataset, num_examples=5):
assert num_examples <= len(dataset), "Can't pick more elements than there are in the dataset."
picks = []
for _ in range(num_examples):
pick = random.randint(0, len(dataset)-1)
while pick in picks:
pick = random.randint(0, len(dataset)-1)
picks.append(pick)
df = pd.DataFrame(dataset[picks])
for column, typ in dataset.features.items():
if isinstance(typ, datasets.ClassLabel):
df[column] = df[column].transform(lambda i: typ.names[i])
display(HTML(df.to_html()))
show_random_elements(raw_datasets["train"])
```
The metric is an instance of [`datasets.Metric`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasets.Metric):
```
metric
```
You can call its `compute` method with your predictions and labels, which need to be list of decoded strings:
```
fake_preds = ["hello there", "general kenobi"]
fake_labels = ["hello there", "general kenobi"]
metric.compute(predictions=fake_preds, references=fake_labels)
```
## Preprocessing the data
Before we can feed those texts to our model, we need to preprocess them. This is done by a 🤗 Transformers `Tokenizer` which will (as the name indicates) tokenize the inputs (including converting the tokens to their corresponding IDs in the pretrained vocabulary) and put it in a format the model expects, as well as generate the other inputs that the model requires.
To do all of this, we instantiate our tokenizer with the `AutoTokenizer.from_pretrained` method, which will ensure:
- we get a tokenizer that corresponds to the model architecture we want to use,
- we download the vocabulary used when pretraining this specific checkpoint.
That vocabulary will be cached, so it's not downloaded again the next time we run the cell.
```
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)
```
By default, the call above will use one of the fast tokenizers (backed by Rust) from the 🤗 Tokenizers library.
You can directly call this tokenizer on one sentence or a pair of sentences:
```
tokenizer("Hello, this one sentence!")
```
Depending on the model you selected, you will see different keys in the dictionary returned by the cell above. They don't matter much for what we're doing here (just know they are required by the model we will instantiate later), you can learn more about them in [this tutorial](https://huggingface.co/transformers/preprocessing.html) if you're interested.
Instead of one sentence, we can pass along a list of sentences:
```
tokenizer(["Hello, this one sentence!", "This is another sentence."])
```
To prepare the targets for our model, we need to tokenize them inside the `as_target_tokenizer` context manager. This will make sure the tokenizer uses the special tokens corresponding to the targets:
```
with tokenizer.as_target_tokenizer():
print(tokenizer(["Hello, this one sentence!", "This is another sentence."]))
```
If you are using one of the five T5 checkpoints we have to prefix the inputs with "summarize:" (the model can also translate and it needs the prefix to know which task it has to perform).
```
if model_checkpoint in ["t5-small", "t5-base", "t5-larg", "t5-3b", "t5-11b"]:
prefix = "summarize: "
else:
prefix = ""
```
We can then write the function that will preprocess our samples. We just feed them to the `tokenizer` with the argument `truncation=True`. This will ensure that an input longer that what the model selected can handle will be truncated to the maximum length accepted by the model. The padding will be dealt with later on (in a data collator) so we pad examples to the longest length in the batch and not the whole dataset.
```
max_input_length = 1024
max_target_length = 128
def preprocess_function(examples):
inputs = [prefix + doc for doc in examples["document"]]
model_inputs = tokenizer(inputs, max_length=max_input_length, truncation=True)
# Setup the tokenizer for targets
with tokenizer.as_target_tokenizer():
labels = tokenizer(examples["summary"], max_length=max_target_length, truncation=True)
model_inputs["labels"] = labels["input_ids"]
return model_inputs
```
This function works with one or several examples. In the case of several examples, the tokenizer will return a list of lists for each key:
```
preprocess_function(raw_datasets['train'][:2])
```
To apply this function on all the pairs of sentences in our dataset, we just use the `map` method of our `dataset` object we created earlier. This will apply the function on all the elements of all the splits in `dataset`, so our training, validation and testing data will be preprocessed in one single command.
```
tokenized_datasets = raw_datasets.map(preprocess_function, batched=True)
```
Even better, the results are automatically cached by the 🤗 Datasets library to avoid spending time on this step the next time you run your notebook. The 🤗 Datasets library is normally smart enough to detect when the function you pass to map has changed (and thus requires to not use the cache data). For instance, it will properly detect if you change the task in the first cell and rerun the notebook. 🤗 Datasets warns you when it uses cached files, you can pass `load_from_cache_file=False` in the call to `map` to not use the cached files and force the preprocessing to be applied again.
Note that we passed `batched=True` to encode the texts by batches together. This is to leverage the full benefit of the fast tokenizer we loaded earlier, which will use multi-threading to treat the texts in a batch concurrently.
## Fine-tuning the model
Now that our data is ready, we can download the pretrained model and fine-tune it. Since our task is of the sequence-to-sequence kind, we use the `AutoModelForSeq2SeqLM` class. Like with the tokenizer, the `from_pretrained` method will download and cache the model for us.
```
from transformers import AutoModelForSeq2SeqLM, DataCollatorForSeq2Seq, Seq2SeqTrainingArguments, Seq2SeqTrainer
model = AutoModelForSeq2SeqLM.from_pretrained(model_checkpoint)
```
Note that we don't get a warning like in our classification example. This means we used all the weights of the pretrained model and there is no randomly initialized head in this case.
To instantiate a `Seq2SeqTrainer`, we will need to define three more things. The most important is the [`Seq2SeqTrainingArguments`](https://huggingface.co/transformers/main_classes/trainer.html#transformers.Seq2SeqTrainingArguments), which is a class that contains all the attributes to customize the training. It requires one folder name, which will be used to save the checkpoints of the model, and all other arguments are optional:
```
batch_size = 16
args = Seq2SeqTrainingArguments(
"test-summarization",
evaluation_strategy = "epoch",
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
weight_decay=0.01,
save_total_limit=3,
num_train_epochs=1,
predict_with_generate=True,
fp16=True,
)
```
Here we set the evaluation to be done at the end of each epoch, tweak the learning rate, use the `batch_size` defined at the top of the cell and customize the weight decay. Since the `Seq2SeqTrainer` will save the model regularly and our dataset is quite large, we tell it to make three saves maximum. Lastly, we use the `predict_with_generate` option (to properly generate summaries) and activate mixed precision training (to go a bit faster).
Then, we need a special kind of data collator, which will not only pad the inputs to the maximum length in the batch, but also the labels:
```
data_collator = DataCollatorForSeq2Seq(tokenizer, model=model)
```
The last thing to define for our `Seq2SeqTrainer` is how to compute the metrics from the predictions. We need to define a function for this, which will just use the `metric` we loaded earlier, and we have to do a bit of pre-processing to decode the predictions into texts:
```
import nltk
import numpy as np
def compute_metrics(eval_pred):
predictions, labels = eval_pred
decoded_preds = tokenizer.batch_decode(predictions, skip_special_tokens=True)
# Replace -100 in the labels as we can't decode them.
labels = np.where(labels != -100, labels, tokenizer.pad_token_id)
decoded_labels = tokenizer.batch_decode(labels, skip_special_tokens=True)
# Rouge expects a newline after each sentence
decoded_preds = ["\n".join(nltk.sent_tokenize(pred.strip())) for pred in decoded_preds]
decoded_labels = ["\n".join(nltk.sent_tokenize(label.strip())) for label in decoded_labels]
result = metric.compute(predictions=decoded_preds, references=decoded_labels, use_stemmer=True)
# Extract a few results
result = {key: value.mid.fmeasure * 100 for key, value in result.items()}
# Add mean generated length
prediction_lens = [np.count_nonzero(pred != tokenizer.pad_token_id) for pred in predictions]
result["gen_len"] = np.mean(prediction_lens)
return {k: round(v, 4) for k, v in result.items()}
```
Then we just need to pass all of this along with our datasets to the `Seq2SeqTrainer`:
```
trainer = Seq2SeqTrainer(
model,
args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["validation"],
data_collator=data_collator,
tokenizer=tokenizer,
compute_metrics=compute_metrics
)
```
We can now finetune our model by just calling the `train` method:
```
trainer.train()
```
Don't forget to [upload your model](https://huggingface.co/transformers/model_sharing.html) on the [🤗 Model Hub](https://huggingface.co/models). You can then use it only to generate results like the one shown in the first picture of this notebook!
| true |
code
| 0.686449 | null | null | null | null |
|
# Quantum Counting
To understand this algorithm, it is important that you first understand both Grover’s algorithm and the quantum phase estimation algorithm. Whereas Grover’s algorithm attempts to find a solution to the Oracle, the quantum counting algorithm tells us how many of these solutions there are. This algorithm is interesting as it combines both quantum search and quantum phase estimation.
## Contents
1. [Overview](#overview)
1.1 [Intuition](#intuition)
1.2 [A Closer Look](#closer_look)
2. [The Code](#code)
2.1 [Initialising our Code](#init_code)
2.2 [The Controlled-Grover Iteration](#cont_grover)
2.3 [The Inverse QFT](#inv_qft)
2.4 [Putting it Together](#putting_together)
3. [Simulating](#simulating)
4. [Finding the Number of Solutions](#finding_m)
5. [Exercises](#exercises)
6. [References](#references)
## 1. Overview <a id='overview'></a>
### 1.1 Intuition <a id='intuition'></a>
In quantum counting, we simply use the quantum phase estimation algorithm to find an eigenvalue of a Grover search iteration. You will remember that an iteration of Grover’s algorithm, $G$, rotates the state vector by $\theta$ in the $|\omega\rangle$, $|s’\rangle$ basis:

The percentage number of solutions in our search space affects the difference between $|s\rangle$ and $|s’\rangle$. For example, if there are not many solutions, $|s\rangle$ will be very close to $|s’\rangle$ and $\theta$ will be very small. It turns out that the eigenvalues of the Grover iterator are $e^{\pm i\theta}$, and we can extract this using quantum phase estimation (QPE) to estimate the number of solutions ($M$).
### 1.2 A Closer Look <a id='closer_look'></a>
In the $|\omega\rangle$,$|s’\rangle$ basis we can write the Grover iterator as the matrix:
$$
G =
\begin{pmatrix}
\cos{\theta} && -\sin{\theta}\\
\sin{\theta} && \cos{\theta}
\end{pmatrix}
$$
The matrix $G$ has eigenvectors:
$$
\begin{pmatrix}
-i\\
1
\end{pmatrix}
,
\begin{pmatrix}
i\\
1
\end{pmatrix}
$$
With the aforementioned eigenvalues $e^{\pm i\theta}$. Fortunately, we do not need to prepare our register in either of these states, the state $|s\rangle$ is in the space spanned by $|\omega\rangle$, $|s’\rangle$, and thus is a superposition of the two vectors.
$$
|s\rangle = \alpha |\omega\rangle + \beta|s'\rangle
$$
As a result, the output of the QPE algorithm will be a superposition of the two phases, and when we measure the register we will obtain one of these two values! We can then use some simple maths to get our estimate of $M$.

## 2. The Code <a id='code'></a>
### 2.1 Initialising our Code <a id='init_code'></a>
First, let’s import everything we’re going to need:
```
import matplotlib.pyplot as plt
import numpy as np
import math
# importing Qiskit
import qiskit
from qiskit import IBMQ, Aer
from qiskit import QuantumCircuit, execute
# import basic plot tools
from qiskit.visualization import plot_histogram
```
In this guide will choose to ‘count’ on the first 4 qubits on our circuit (we call the number of counting qubits $t$, so $t = 4$), and to 'search' through the last 4 qubits ($n = 4$). With this in mind, we can start creating the building blocks of our circuit.
### 2.2 The Controlled-Grover Iteration <a id='cont_grover'></a>
We have already covered Grover iterations in the Grover’s algorithm section. Here is an example with an Oracle we know has 5 solutions ($M = 5$) of 16 states ($N = 2^n = 16$), combined with a diffusion operator:
```
def example_grover_iteration():
"""Small circuit with 5/16 solutions"""
# Do circuit
qc = QuantumCircuit(4)
# Oracle
qc.h([2,3])
qc.ccx(0,1,2)
qc.h(2)
qc.x(2)
qc.ccx(0,2,3)
qc.x(2)
qc.h(3)
qc.x([1,3])
qc.h(2)
qc.mct([0,1,3],2)
qc.x([1,3])
qc.h(2)
# Diffuser
qc.h(range(3))
qc.x(range(3))
qc.z(3)
qc.mct([0,1,2],3)
qc.x(range(3))
qc.h(range(3))
qc.z(3)
return qc
```
Notice the python function takes no input and returns a `QuantumCircuit` object with 4 qubits. In the past the functions you created might have modified an existing circuit, but a function like this allows us to turn the `QuantmCircuit` object into a single gate we can then control.
We can use `.to_gate()` and `.control()` to create a controlled gate from a circuit. We will call our Grover iterator `grit` and the controlled Grover iterator `cgrit`:
```
# Create controlled-Grover
grit = example_grover_iteration().to_gate()
cgrit = grit.control()
cgrit.label = "Grover"
```
### 2.3 The Inverse QFT <a id='inv_qft'></a>
We now need to create an inverse QFT. This code implements the QFT on n qubits:
```
def qft(n):
"""Creates an n-qubit QFT circuit"""
circuit = QuantumCircuit(4)
def swap_registers(circuit, n):
for qubit in range(n//2):
circuit.swap(qubit, n-qubit-1)
return circuit
def qft_rotations(circuit, n):
"""Performs qft on the first n qubits in circuit (without swaps)"""
if n == 0:
return circuit
n -= 1
circuit.h(n)
for qubit in range(n):
circuit.cu1(np.pi/2**(n-qubit), qubit, n)
qft_rotations(circuit, n)
qft_rotations(circuit, n)
swap_registers(circuit, n)
return circuit
```
Again, note we have chosen to return another `QuantumCircuit` object, this is so we can easily invert the gate. We create the gate with t = 4 qubits as this is the number of counting qubits we have chosen in this guide:
```
qft_dagger = qft(4).to_gate().inverse()
qft_dagger.label = "QFT†"
```
### 2.4 Putting it Together <a id='putting_together'></a>
We now have everything we need to complete our circuit! Let’s put it together.
First we need to put all qubits in the $|+\rangle$ state:
```
# Create QuantumCircuit
t = 4 # no. of counting qubits
n = 4 # no. of searching qubits
qc = QuantumCircuit(n+t, t) # Circuit with n+t qubits and t classical bits
# Initialise all qubits to |+>
for qubit in range(t+n):
qc.h(qubit)
# Begin controlled Grover iterations
iterations = 1
for qubit in range(t):
for i in range(iterations):
qc.append(cgrit, [qubit] + [*range(t, n+t)])
iterations *= 2
# Do inverse QFT on counting qubits
qc.append(qft_dagger, range(t))
# Measure counting qubits
qc.measure(range(t), range(t))
# Display the circuit
qc.draw()
```
Great! Now let’s see some results.
## 3. Simulating <a id='simulating'></a>
```
# Execute and see results
emulator = Aer.get_backend('qasm_simulator')
job = execute(qc, emulator, shots=2048 )
hist = job.result().get_counts()
plot_histogram(hist)
```
We can see two values stand out, having a much higher probability of measurement than the rest. These two values correspond to $e^{i\theta}$ and $e^{-i\theta}$, but we can’t see the number of solutions yet. We need to little more processing to get this information, so first let us get our output into something we can work with (an `int`).
We will get the string of the most probable result from our output data:
```
measured_str = max(hist, key=hist.get)
```
Let us now store this as an integer:
```
measured_int = int(measured_str,2)
print("Register Output = %i" % measured_int)
```
## 4. Finding the Number of Solutions (M) <a id='finding_m'></a>
We will create a function, `calculate_M()` that takes as input the decimal integer output of our register, the number of counting qubits ($t$) and the number of searching qubits ($n$).
First we want to get $\theta$ from `measured_int`. You will remember that QPE gives us a measured $\text{value} = 2^n \phi$ from the eigenvalue $e^{2\pi i\phi}$, so to get $\theta$ we need to do:
$$
\theta = \text{value}\times\frac{2\pi}{2^t}
$$
Or, in code:
```
theta = (measured_int/(2**t))*math.pi*2
print("Theta = %.5f" % theta)
```
You may remember that we can get the angle $\theta/2$ can from the inner product of $|s\rangle$ and $|s’\rangle$:

$$
\langle s'|s\rangle = \cos{\tfrac{\theta}{2}}
$$
And that the inner product of these vectors is:
$$
\langle s'|s\rangle = \sqrt{\frac{N-M}{N}}
$$
We can combine these equations, then use some trigonometry and algebra to show:
$$
N\sin^2{\frac{\theta}{2}} = M
$$
From the [Grover's algorithm](https://qiskit.org/textbook/ch-algorithms/grover.html) chapter, you will remember that a common way to create a diffusion operator, $U_s$, is actually to implement $-U_s$. This implementation is used in the Grover iteration provided in this chapter. In a normal Grover search, this phase is global and can be ignored, but now we are controlling our Grover iterations, this phase does have an effect. The result is that we have effectively searched for the states that are _not_ solutions, and our quantum counting algorithm will tell us how many states are _not_ solutions. To fix this, we simply calculate $N-M$.
And in code:
```
N = 2**n
M = N * (math.sin(theta/2)**2)
print("No. of Solutions = %.1f" % (N-M))
```
And we can see we have (approximately) the correct answer! We can approximately calculate the error in this answer using:
```
m = t - 1 # Upper bound: Will be less than this
err = (math.sqrt(2*M*N) + N/(2**(m-1)))*(2**(-m))
print("Error < %.2f" % err)
```
Explaining the error calculation is outside the scope of this article, but an explanation can be found in [1].
Finally, here is the finished function `calculate_M()`:
```
def calculate_M(measured_int, t, n):
"""For Processing Output of Quantum Counting"""
# Calculate Theta
theta = (measured_int/(2**t))*math.pi*2
print("Theta = %.5f" % theta)
# Calculate No. of Solutions
N = 2**n
M = N * (math.sin(theta/2)**2)
print("No. of Solutions = %.1f" % (N-M))
# Calculate Upper Error Bound
m = t - 1 #Will be less than this (out of scope)
err = (math.sqrt(2*M*N) + N/(2**(m-1)))*(2**(-m))
print("Error < %.2f" % err)
```
## 5. Exercises <a id='exercises'></a>
1. Can you create an oracle with a different number of solutions? How does the accuracy of the quantum counting algorithm change?
2. Can you adapt the circuit to use more or less counting qubits to get a different precision in your result?
## 6. References <a id='references'></a>
[1] Michael A. Nielsen and Isaac L. Chuang. 2011. Quantum Computation and Quantum Information: 10th Anniversary Edition (10th ed.). Cambridge University Press, New York, NY, USA.
```
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.570331 | null | null | null | null |
|
# CORD-19 overview
In this notebook, we provide an overview of publication medatata for CORD-19.
```
%matplotlib inline
import matplotlib.pyplot as plt
# magics and warnings
%load_ext autoreload
%autoreload 2
import warnings; warnings.simplefilter('ignore')
import os, random, codecs, json
import pandas as pd
import numpy as np
seed = 99
random.seed(seed)
np.random.seed(seed)
import nltk, sklearn
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="white")
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 2.5})
# load metadata
df_meta = pd.read_csv("datasets_output/df_pub.csv",compression="gzip")
df_datasource = pd.read_csv("datasets_output/sql_tables/datasource.csv",sep="\t",header=None,names=['datasource_metadata_id', 'datasource', 'url'])
df_pub_datasource = pd.read_csv("datasets_output/sql_tables/pub_datasource.csv",sep="\t",header=None,names=['pub_id','datasource_metadata_id'])
df_cord_meta = pd.read_csv("datasets_output/sql_tables/cord19_metadata.csv",sep="\t",header=None,names=[ 'cord19_metadata_id', 'source', 'license', 'ms_academic_id',
'who_covidence', 'sha', 'full_text', 'pub_id'])
df_meta.head()
df_meta.columns
df_datasource
df_pub_datasource.head()
df_cord_meta.head()
```
#### Select just CORD-19
```
df_meta = df_meta.merge(df_pub_datasource, how="inner", left_on="pub_id", right_on="pub_id")
df_meta = df_meta.merge(df_datasource, how="inner", left_on="datasource_metadata_id", right_on="datasource_metadata_id")
df_cord19 = df_meta[df_meta.datasource_metadata_id==0]
df_cord19 = df_cord19.merge(df_cord_meta, how="inner", left_on="pub_id", right_on="pub_id")
df_meta.shape
df_cord19.shape
df_cord19.head()
```
#### Publication years
```
import re
def clean_year(s):
if pd.isna(s):
return np.nan
if not (s>1900):
return np.nan
elif s>2020:
return 2020
return s
df_cord19["publication_year"] = df_cord19["publication_year"].apply(clean_year)
df_cord19.publication_year.describe()
sns.distplot(df_cord19.publication_year.tolist(), bins=60, kde=False)
plt.xlabel("Publication year", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
plt.tight_layout()
plt.savefig("figures/publication_year_all.pdf")
sns.distplot(df_cord19[(pd.notnull(df_cord19.publication_year)) & (df_cord19.publication_year > 2000)].publication_year.tolist(), bins=20, hist=True, kde=False)
plt.xlabel("Publication year", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
plt.tight_layout()
plt.savefig("figures/publication_year_2000.pdf")
which = "PMC"
sns.distplot(df_cord19[(pd.notnull(df_cord19.publication_year)) & (df_cord19.publication_year > 2000) & (df_cord19.source == which)].publication_year.tolist(), bins=20, hist=True, kde=False)
plt.xlabel("Publication year", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
plt.tight_layout()
# recent uptake
df_cord19[df_cord19.publication_year>2018].groupby([(df_cord19.publication_year),(df_cord19.publication_month)]).count().pub_id
```
#### Null values
```
df_cord19.shape
df_cord19["abstract_length"] = df_cord19.abstract.str.len()
df_cord19[df_cord19.abstract_length>0].shape
sum(pd.notnull(df_cord19.abstract))
sum(pd.notnull(df_cord19.doi))
sum(pd.notnull(df_cord19.pmcid))
sum(pd.notnull(df_cord19.pmid))
sum(pd.notnull(df_cord19.journal))
```
#### Journals
```
df_cord19.journal.value_counts()[:30]
df_sub = df_cord19[df_cord19.journal.isin(df_cord19.journal.value_counts()[:20].index.tolist())]
b = sns.countplot(y="journal", data=df_sub, order=df_sub['journal'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("Journal",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/journals.pdf")
```
#### Sources and licenses
```
# source
df_sub = df_cord19[df_cord19.source.isin(df_cord19.source.value_counts()[:10].index.tolist())]
b = sns.countplot(y="source", data=df_sub, order=df_sub['source'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("Source",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/sources.pdf")
# license
df_sub = df_cord19[df_cord19.license.isin(df_cord19.license.value_counts()[:30].index.tolist())]
b = sns.countplot(y="license", data=df_sub, order=df_sub['license'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("License",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/licenses.pdf")
```
#### Full text availability
```
df_cord19["has_full_text"] = pd.notnull(df_cord19.full_text)
df_cord19["has_full_text"].sum()
# full text x source
df_plot = df_cord19.groupby(['has_full_text', 'source']).size().reset_index().pivot(columns='has_full_text', index='source', values=0)
df_plot.plot(kind='bar', stacked=True)
plt.xlabel("Source", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
#plt.tight_layout()
plt.savefig("figures/source_ft.pdf")
# full text x journal
df_sub = df_cord19[df_cord19.journal.isin(df_cord19.journal.value_counts()[:20].index.tolist())]
df_plot = df_sub.groupby(['has_full_text', 'journal']).size().reset_index().pivot(columns='has_full_text', index='journal', values=0)
df_plot.plot(kind='bar', stacked=True)
plt.xlabel("Source", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
#plt.tight_layout()
plt.savefig("figures/journal_ft.pdf")
# full text x year
df_sub = df_cord19[(pd.notnull(df_cord19.publication_year)) & (df_cord19.publication_year > 2000)]
df_plot = df_sub.groupby(['has_full_text', 'publication_year']).size().reset_index().pivot(columns='has_full_text', index='publication_year', values=0)
df_plot.plot(kind='bar', stacked=True)
plt.xticks(np.arange(20), [int(x) for x in df_plot.index.values], rotation=45)
plt.xlabel("Publication year", fontsize=15)
plt.ylabel("Publication count", fontsize=15)
plt.tight_layout()
plt.savefig("figures/year_ft.pdf")
```
## Dimensions
```
# load Dimensions data (you will need to download it on your own!)
directory_name = "datasets_output/json_dimensions_cwts"
all_dimensions = list()
for root, dirs, files in os.walk(directory_name):
for file in files:
if ".json" in file:
all_data = codecs.open(os.path.join(root,file)).read()
for record in all_data.split("\n"):
if record:
all_dimensions.append(json.loads(record))
df_dimensions = pd.DataFrame.from_dict({
"id":[r["id"] for r in all_dimensions],
"publication_type":[r["publication_type"] for r in all_dimensions],
"doi":[r["doi"] for r in all_dimensions],
"pmid":[r["pmid"] for r in all_dimensions],
"issn":[r["journal"]["issn"] for r in all_dimensions],
"times_cited":[r["times_cited"] for r in all_dimensions],
"relative_citation_ratio":[r["relative_citation_ratio"] for r in all_dimensions],
"for_top":[r["for"][0]["first_level"]["name"] if len(r["for"])>0 else "" for r in all_dimensions],
"for_bottom":[r["for"][0]["second_level"]["name"] if len(r["for"])>0 else "" for r in all_dimensions],
"open_access_versions":[r["open_access_versions"] for r in all_dimensions]
})
df_dimensions.head()
df_dimensions.pmid = df_dimensions.pmid.astype(float)
df_dimensions.shape
df_joined_doi = df_cord19[pd.notnull(df_cord19.doi)].merge(df_dimensions[pd.notnull(df_dimensions.doi)], how="inner", left_on="doi", right_on="doi")
df_joined_doi.shape
df_joined_pmid = df_cord19[pd.isnull(df_cord19.doi) & pd.notnull(df_cord19.pmid)].merge(df_dimensions[pd.isnull(df_dimensions.doi) & pd.notnull(df_dimensions.pmid)], how="inner", left_on="pmid", right_on="pmid")
df_joined_pmid.shape
df_joined = pd.concat([df_joined_doi,df_joined_pmid])
# nearly all publications from CORD-19 are in Dimensions
df_joined.shape
df_cord19.shape
# publication type
df_sub = df_joined[df_joined.publication_type.isin(df_joined.publication_type.value_counts()[:10].index.tolist())]
b = sns.countplot(y="publication_type", data=df_sub, order=df_sub['publication_type'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("Publication type",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/dim_pub_type.pdf")
```
#### Citation counts
```
# scatter of citations vs time of publication
sns.scatterplot(df_joined.publication_year.to_list(),df_joined.times_cited.to_list())
plt.xlabel("Publication year", fontsize=15)
plt.ylabel("Citation count", fontsize=15)
plt.tight_layout()
plt.savefig("figures/dim_citations_year.png")
# most cited papers
df_joined[["title","times_cited","relative_citation_ratio","journal","publication_year","doi"]].sort_values("times_cited",ascending=False).head(20)
# same but in 2020; note that duplicates are due to SI or pre-prints with different PMIDs
df_joined[df_joined.publication_year>2019][["title","times_cited","relative_citation_ratio","journal","publication_year","doi"]].sort_values("times_cited",ascending=False).head(10)
# most cited journals
df_joined[['journal','times_cited']].groupby('journal').sum().sort_values('times_cited',ascending=False).head(20)
```
#### Categories
```
# FOR jeywords distribution, TOP
df_sub = df_joined[df_joined.for_top.isin(df_joined.for_top.value_counts()[:10].index.tolist())]
b = sns.countplot(y="for_top", data=df_sub, order=df_sub['for_top'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("FOR first level",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/dim_for_top.pdf")
# FOR jeywords distribution, TOP
df_sub = df_joined[df_joined.for_bottom.isin(df_joined.for_bottom.value_counts()[:10].index.tolist())]
b = sns.countplot(y="for_bottom", data=df_sub, order=df_sub['for_bottom'].value_counts().index)
#b.axes.set_title("Title",fontsize=50)
b.set_xlabel("Publication count",fontsize=15)
b.set_ylabel("FOR second level",fontsize=15)
b.tick_params(labelsize=12)
plt.tight_layout()
plt.savefig("figures/dim_for_bottom.pdf")
```
| true |
code
| 0.424173 | null | null | null | null |
|
### 2.2 CNN Models - Test Cases
The trained CNN model was performed to a hold-out test set with 10,873 images.
The network obtained 0.743 and 0.997 AUC-PRC on the hold-out test set for cored plaque and diffuse plaque respectively.
```
import time, os
import torch
torch.manual_seed(42)
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.optim import lr_scheduler
import torchvision
from torchvision import transforms
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
CSV_DIR = 'data/CSVs/test.csv'
MODEL_DIR = 'models/CNN_model_parameters.pkl'
IMG_DIR = 'data/tiles/hold-out/'
NEGATIVE_DIR = 'data/seg/negatives/'
SAVE_DIR = 'data/outputs/'
if not os.path.exists(SAVE_DIR):
os.makedirs(SAVE_DIR)
batch_size = 32
num_workers = 8
norm = np.load('utils/normalization.npy', allow_pickle=True).item()
from torch.utils.data import Dataset
from PIL import Image
class MultilabelDataset(Dataset):
def __init__(self, csv_path, img_path, transform=None):
"""
Args:
csv_path (string): path to csv file
img_path (string): path to the folder where images are
transform: pytorch transforms for transforms and tensor conversion
"""
self.data_info = pd.read_csv(csv_path)
self.img_path = img_path
self.transform = transform
c=torch.Tensor(self.data_info.loc[:,'cored'])
d=torch.Tensor(self.data_info.loc[:,'diffuse'])
a=torch.Tensor(self.data_info.loc[:,'CAA'])
c=c.view(c.shape[0],1)
d=d.view(d.shape[0],1)
a=a.view(a.shape[0],1)
self.raw_labels = torch.cat([c,d,a], dim=1)
self.labels = (torch.cat([c,d,a], dim=1)>0.99).type(torch.FloatTensor)
def __getitem__(self, index):
# Get label(class) of the image based on the cropped pandas column
single_image_label = self.labels[index]
raw_label = self.raw_labels[index]
# Get image name from the pandas df
single_image_name = str(self.data_info.loc[index,'imagename'])
# Open image
try:
img_as_img = Image.open(self.img_path + single_image_name)
except:
img_as_img = Image.open(NEGATIVE_DIR + single_image_name)
# Transform image to tensor
if self.transform is not None:
img_as_img = self.transform(img_as_img)
# Return image and the label
return (img_as_img, single_image_label, raw_label, single_image_name)
def __len__(self):
return len(self.data_info.index)
data_transforms = {
'test' : transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(norm['mean'], norm['std'])
])
}
image_datasets = {'test': MultilabelDataset(CSV_DIR, IMG_DIR,
data_transforms['test'])}
dataloaders = {x: torch.utils.data.DataLoader(image_datasets[x],
batch_size=batch_size,
shuffle=False,
num_workers=num_workers)
for x in ['test']}
dataset_sizes = {x: len(image_datasets[x]) for x in ['test']}
image_classes = ['cored','diffuse','CAA']
use_gpu = torch.cuda.is_available()
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array(norm['mean'])
std = np.array(norm['std'])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.figure()
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
# Get a batch of training data
inputs, labels, raw_labels, names = next(iter(dataloaders['test']))
# Make a grid from batch
out = torchvision.utils.make_grid(inputs)
imshow(out)
class Net(nn.Module):
def __init__(self, fc_nodes=512, num_classes=3, dropout=0.5):
super(Net, self).__init__()
def forward(self, x):
x = self.features(x)
x = x.view(x.size(0), -1)
x = self.classifier(x)
return x
def dev_model(model, criterion, phase='test', gpu_id=None):
phase = phase
since = time.time()
dataloaders = {x: torch.utils.data.DataLoader(image_datasets[x], batch_size=batch_size,
shuffle=False, num_workers=num_workers)
for x in [phase]}
model.train(False)
running_loss = 0.0
running_corrects = torch.zeros(len(image_classes))
running_preds = torch.Tensor(0)
running_predictions = torch.Tensor(0)
running_labels = torch.Tensor(0)
running_raw_labels = torch.Tensor(0)
# Iterate over data.
step = 0
for data in dataloaders[phase]:
step += 1
# get the inputs
inputs, labels, raw_labels, names = data
running_labels = torch.cat([running_labels, labels])
running_raw_labels = torch.cat([running_raw_labels, raw_labels])
# wrap them in Variable
if use_gpu:
inputs = Variable(inputs.cuda(gpu_id))
labels = Variable(labels.cuda(gpu_id))
else:
inputs, labels = Variable(inputs), Variable(labels)
# forward
outputs = model(inputs)
preds = F.sigmoid(outputs) #posibility for each class
#print(preds)
if use_gpu:
predictions = (preds>0.5).type(torch.cuda.FloatTensor)
else:
predictions = (preds>0.5).type(torch.FloatTensor)
loss = criterion(outputs, labels)
preds = preds.data.cpu()
predictions = predictions.data.cpu()
labels = labels.data.cpu()
# statistics
running_loss += loss.data[0]
running_corrects += torch.sum(predictions==labels, 0).type(torch.FloatTensor)
running_preds = torch.cat([running_preds, preds])
running_predictions = torch.cat([running_predictions, predictions])
epoch_loss = running_loss / dataset_sizes[phase]
epoch_acc = running_corrects / dataset_sizes[phase]
print('{} Loss: {:.4f}\n Cored: {:.4f} Diffuse: {:.4f} CAA: {:.4f}'.format(
phase, epoch_loss, epoch_acc[0], epoch_acc[1], epoch_acc[2]))
print()
time_elapsed = time.time() - since
print('Prediction complete in {:.0f}m {:.0f}s'.format(
time_elapsed // 60, time_elapsed % 60))
return epoch_acc, running_preds, running_predictions, running_labels
from sklearn.metrics import roc_curve, auc, precision_recall_curve
def plot_roc(preds, label, image_classes, size=20, path=None):
colors = ['pink','c','deeppink', 'b', 'g', 'm', 'y', 'r', 'k']
fig = plt.figure(figsize=(1.2*size, size))
ax = plt.axes()
for i in range(preds.shape[1]):
fpr, tpr, _ = roc_curve(label[:,i].ravel(), preds[:,i].ravel())
lw = 0.2*size
# Plot all ROC curves
ax.plot([0, 1], [0, 1], 'k--', lw=lw, label='random')
ax.plot(fpr, tpr,
label='ROC-curve of {}'.format(image_classes[i])+ '( area = {0:0.3f})'
''.format(auc(fpr, tpr)),
color=colors[(i+preds.shape[1])%len(colors)], linewidth=lw)
ax.set_xlim([0.0, 1.0])
ax.set_ylim([0.0, 1.05])
ax.set_xlabel('False Positive Rate', fontsize=1.8*size)
ax.set_ylabel('True Positive Rate', fontsize=1.8*size)
ax.set_title('Receiver operating characteristic Curve', fontsize=1.8*size, y=1.01)
ax.legend(loc=0, fontsize=1.5*size)
ax.xaxis.set_tick_params(labelsize=1.6*size, size=size/2, width=0.2*size)
ax.yaxis.set_tick_params(labelsize=1.6*size, size=size/2, width=0.2*size)
if path != None:
fig.savefig(path)
# plt.close(fig)
print('saved')
def plot_prc(preds, label, image_classes, size=20, path=None):
colors = ['pink','c','deeppink', 'b', 'g', 'm', 'y', 'r', 'k']
fig = plt.figure(figsize=(1.2*size,size))
ax = plt.axes()
for i in range(preds.shape[1]):
rp = (label[:,i]>0).sum()/len(label)
precision, recall, _ = precision_recall_curve(label[:,i].ravel(), preds[:,i].ravel())
lw=0.2*size
ax.plot(recall, precision,
label='PR-curve of {}'.format(image_classes[i])+ '( area = {0:0.3f})'
''.format(auc(recall, precision)),
color=colors[(i+preds.shape[1])%len(colors)], linewidth=lw)
ax.plot([0, 1], [rp, rp], 'k--', color=colors[(i+preds.shape[1])%len(colors)], lw=lw, label='random')
ax.set_xlim([0.0, 1.0])
ax.set_ylim([0.0, 1.05])
ax.set_xlabel('Recall', fontsize=1.8*size)
ax.set_ylabel('Precision', fontsize=1.8*size)
ax.set_title('Precision-Recall curve', fontsize=1.8*size, y=1.01)
ax.legend(loc="lower left", bbox_to_anchor=(0.01, 0.1), fontsize=1.5*size)
ax.xaxis.set_tick_params(labelsize=1.6*size, size=size/2, width=0.2*size)
ax.yaxis.set_tick_params(labelsize=1.6*size, size=size/2, width=0.2*size)
if path != None:
fig.savefig(path)
# plt.close(fig)
print('saved')
def auc_roc(preds, label):
aucroc = []
for i in range(preds.shape[1]):
fpr, tpr, _ = roc_curve(label[:,i].ravel(), preds[:,i].ravel())
aucroc.append(auc(fpr, tpr))
return aucroc
def auc_prc(preds, label):
aucprc = []
for i in range(preds.shape[1]):
precision, recall, _ = precision_recall_curve(label[:,i].ravel(), preds[:,i].ravel())
aucprc.append(auc(recall, precision))
return aucprc
criterion = nn.MultiLabelSoftMarginLoss(size_average=False)
model = torch.load(MODEL_DIR, map_location=lambda storage, loc: storage)
if use_gpu:
model = model.module.cuda()
# take 10s running on single GPU
try:
acc, pred, prediction, target = dev_model(model.module, criterion, phase='test', gpu_id=None)
except:
acc, pred, prediction, target = dev_model(model, criterion, phase='test', gpu_id=None)
label = target.numpy()
preds = pred.numpy()
output = {}
for i in range(3):
fpr, tpr, _ = roc_curve(label[:,i].ravel(), preds[:,i].ravel())
precision, recall, _ = precision_recall_curve(label[:,i].ravel(), preds[:,i].ravel())
output['{} fpr'.format(image_classes[i])] = fpr
output['{} tpr'.format(image_classes[i])] = tpr
output['{} precision'.format(image_classes[i])] = precision
output['{} recall'.format(image_classes[i])] = recall
outcsv = pd.DataFrame(dict([ (k,pd.Series(v)) for k,v in output.items() ]))
outcsv.to_csv(SAVE_DIR+'CNN_test_output.csv', index=False)
plot_roc(pred.numpy(), target.numpy(), image_classes, size=30)
plot_prc(pred.numpy(), target.numpy(), image_classes, size=30)
```
| true |
code
| 0.782953 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/araffin/rl-tutorial-jnrr19/blob/master/1_getting_started.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Stable Baselines Tutorial - Getting Started
Github repo: https://github.com/araffin/rl-tutorial-jnrr19
Stable-Baselines: https://github.com/hill-a/stable-baselines
Documentation: https://stable-baselines.readthedocs.io/en/master/
RL Baselines zoo: https://github.com/araffin/rl-baselines-zoo
Medium article: [https://medium.com/@araffin/stable-baselines-a-fork-of-openai-baselines-df87c4b2fc82](https://medium.com/@araffin/stable-baselines-a-fork-of-openai-baselines-df87c4b2fc82)
[RL Baselines Zoo](https://github.com/araffin/rl-baselines-zoo) is a collection of pre-trained Reinforcement Learning agents using Stable-Baselines.
It also provides basic scripts for training, evaluating agents, tuning hyperparameters and recording videos.
## Introduction
In this notebook, you will learn the basics for using stable baselines library: how to create a RL model, train it and evaluate it. Because all algorithms share the same interface, we will see how simple it is to switch from one algorithm to another.
## Install Dependencies and Stable Baselines Using Pip
List of full dependencies can be found in the [README](https://github.com/hill-a/stable-baselines).
```
sudo apt-get update && sudo apt-get install cmake libopenmpi-dev zlib1g-dev
```
```
pip install stable-baselines[mpi]
```
```
# Stable Baselines only supports tensorflow 1.x for now
%tensorflow_version 1.x
!apt-get install ffmpeg freeglut3-dev xvfb # For visualization
!pip install stable-baselines[mpi]==2.10.0
```
## Imports
Stable-Baselines works on environments that follow the [gym interface](https://stable-baselines.readthedocs.io/en/master/guide/custom_env.html).
You can find a list of available environment [here](https://gym.openai.com/envs/#classic_control).
It is also recommended to check the [source code](https://github.com/openai/gym) to learn more about the observation and action space of each env, as gym does not have a proper documentation.
Not all algorithms can work with all action spaces, you can find more in this [recap table](https://stable-baselines.readthedocs.io/en/master/guide/algos.html)
```
import gym
import numpy as np
```
The first thing you need to import is the RL model, check the documentation to know what you can use on which problem
```
from stable_baselines import PPO2
```
The next thing you need to import is the policy class that will be used to create the networks (for the policy/value functions).
This step is optional as you can directly use strings in the constructor:
```PPO2('MlpPolicy', env)``` instead of ```PPO2(MlpPolicy, env)```
Note that some algorithms like `SAC` have their own `MlpPolicy` (different from `stable_baselines.common.policies.MlpPolicy`), that's why using string for the policy is the recommened option.
```
from stable_baselines.common.policies import MlpPolicy
```
## Create the Gym env and instantiate the agent
For this example, we will use CartPole environment, a classic control problem.
"A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track. The system is controlled by applying a force of +1 or -1 to the cart. The pendulum starts upright, and the goal is to prevent it from falling over. A reward of +1 is provided for every timestep that the pole remains upright. "
Cartpole environment: [https://gym.openai.com/envs/CartPole-v1/](https://gym.openai.com/envs/CartPole-v1/)

We chose the MlpPolicy because the observation of the CartPole task is a feature vector, not images.
The type of action to use (discrete/continuous) will be automatically deduced from the environment action space
Here we are using the [Proximal Policy Optimization](https://stable-baselines.readthedocs.io/en/master/modules/ppo2.html) algorithm (PPO2 is the version optimized for GPU), which is an Actor-Critic method: it uses a value function to improve the policy gradient descent (by reducing the variance).
It combines ideas from [A2C](https://stable-baselines.readthedocs.io/en/master/modules/a2c.html) (having multiple workers and using an entropy bonus for exploration) and [TRPO](https://stable-baselines.readthedocs.io/en/master/modules/trpo.html) (it uses a trust region to improve stability and avoid catastrophic drops in performance).
PPO is an on-policy algorithm, which means that the trajectories used to update the networks must be collected using the latest policy.
It is usually less sample efficient than off-policy alorithms like [DQN](https://stable-baselines.readthedocs.io/en/master/modules/dqn.html), [SAC](https://stable-baselines.readthedocs.io/en/master/modules/sac.html) or [TD3](https://stable-baselines.readthedocs.io/en/master/modules/td3.html), but is much faster regarding wall-clock time.
```
env = gym.make('CartPole-v1')
model = PPO2(MlpPolicy, env, verbose=0)
```
We create a helper function to evaluate the agent:
```
def evaluate(model, num_episodes=100):
"""
Evaluate a RL agent
:param model: (BaseRLModel object) the RL Agent
:param num_episodes: (int) number of episodes to evaluate it
:return: (float) Mean reward for the last num_episodes
"""
# This function will only work for a single Environment
env = model.get_env()
all_episode_rewards = []
for i in range(num_episodes):
episode_rewards = []
done = False
obs = env.reset()
while not done:
# _states are only useful when using LSTM policies
action, _states = model.predict(obs)
# here, action, rewards and dones are arrays
# because we are using vectorized env
obs, reward, done, info = env.step(action)
episode_rewards.append(reward)
all_episode_rewards.append(sum(episode_rewards))
mean_episode_reward = np.mean(all_episode_rewards)
print("Mean reward:", mean_episode_reward, "Num episodes:", num_episodes)
return mean_episode_reward
```
Let's evaluate the un-trained agent, this should be a random agent.
```
# Random Agent, before training
mean_reward_before_train = evaluate(model, num_episodes=100)
```
Stable-Baselines already provides you with that helper:
```
from stable_baselines.common.evaluation import evaluate_policy
mean_reward, std_reward = evaluate_policy(model, env, n_eval_episodes=100)
print(f"mean_reward:{mean_reward:.2f} +/- {std_reward:.2f}")
```
## Train the agent and evaluate it
```
# Train the agent for 10000 steps
model.learn(total_timesteps=10000)
# Evaluate the trained agent
mean_reward, std_reward = evaluate_policy(model, env, n_eval_episodes=100)
print(f"mean_reward:{mean_reward:.2f} +/- {std_reward:.2f}")
```
Apparently the training went well, the mean reward increased a lot !
### Prepare video recording
```
# Set up fake display; otherwise rendering will fail
import os
os.system("Xvfb :1 -screen 0 1024x768x24 &")
os.environ['DISPLAY'] = ':1'
import base64
from pathlib import Path
from IPython import display as ipythondisplay
def show_videos(video_path='', prefix=''):
"""
Taken from https://github.com/eleurent/highway-env
:param video_path: (str) Path to the folder containing videos
:param prefix: (str) Filter the video, showing only the only starting with this prefix
"""
html = []
for mp4 in Path(video_path).glob("{}*.mp4".format(prefix)):
video_b64 = base64.b64encode(mp4.read_bytes())
html.append('''<video alt="{}" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{}" type="video/mp4" />
</video>'''.format(mp4, video_b64.decode('ascii')))
ipythondisplay.display(ipythondisplay.HTML(data="<br>".join(html)))
```
We will record a video using the [VecVideoRecorder](https://stable-baselines.readthedocs.io/en/master/guide/vec_envs.html#vecvideorecorder) wrapper, you will learn about those wrapper in the next notebook.
```
from stable_baselines.common.vec_env import VecVideoRecorder, DummyVecEnv
def record_video(env_id, model, video_length=500, prefix='', video_folder='videos/'):
"""
:param env_id: (str)
:param model: (RL model)
:param video_length: (int)
:param prefix: (str)
:param video_folder: (str)
"""
eval_env = DummyVecEnv([lambda: gym.make(env_id)])
# Start the video at step=0 and record 500 steps
eval_env = VecVideoRecorder(eval_env, video_folder=video_folder,
record_video_trigger=lambda step: step == 0, video_length=video_length,
name_prefix=prefix)
obs = eval_env.reset()
for _ in range(video_length):
action, _ = model.predict(obs)
obs, _, _, _ = eval_env.step(action)
# Close the video recorder
eval_env.close()
```
### Visualize trained agent
```
record_video('CartPole-v1', model, video_length=500, prefix='ppo2-cartpole')
show_videos('videos', prefix='ppo2')
```
## Bonus: Train a RL Model in One Line
The policy class to use will be inferred and the environment will be automatically created. This works because both are [registered](https://stable-baselines.readthedocs.io/en/master/guide/quickstart.html).
```
model = PPO2('MlpPolicy', "CartPole-v1", verbose=1).learn(1000)
```
## Train a DQN agent
In the previous example, we have used PPO, which one of the many algorithms provided by stable-baselines.
In the next example, we are going train a [Deep Q-Network agent (DQN)](https://stable-baselines.readthedocs.io/en/master/modules/dqn.html), and try to see possible improvements provided by its extensions (Double-DQN, Dueling-DQN, Prioritized Experience Replay).
The essential point of this section is to show you how simple it is to tweak hyperparameters.
The main advantage of stable-baselines is that it provides a common interface to use the algorithms, so the code will be quite similar.
DQN paper: https://arxiv.org/abs/1312.5602
Dueling DQN: https://arxiv.org/abs/1511.06581
Double-Q Learning: https://arxiv.org/abs/1509.06461
Prioritized Experience Replay: https://arxiv.org/abs/1511.05952
### Vanilla DQN: DQN without extensions
```
# Same as before we instantiate the agent along with the environment
from stable_baselines import DQN
# Deactivate all the DQN extensions to have the original version
# In practice, it is recommend to have them activated
kwargs = {'double_q': False, 'prioritized_replay': False, 'policy_kwargs': dict(dueling=False)}
# Note that the MlpPolicy of DQN is different from the one of PPO
# but stable-baselines handles that automatically if you pass a string
dqn_model = DQN('MlpPolicy', 'CartPole-v1', verbose=1, **kwargs)
# Random Agent, before training
mean_reward_before_train = evaluate(dqn_model, num_episodes=100)
# Train the agent for 10000 steps
dqn_model.learn(total_timesteps=10000, log_interval=10)
# Evaluate the trained agent
mean_reward = evaluate(dqn_model, num_episodes=100)
```
### DQN + Prioritized Replay
```
# Activate only the prioritized replay
kwargs = {'double_q': False, 'prioritized_replay': True, 'policy_kwargs': dict(dueling=False)}
dqn_per_model = DQN('MlpPolicy', 'CartPole-v1', verbose=1, **kwargs)
dqn_per_model.learn(total_timesteps=10000, log_interval=10)
# Evaluate the trained agent
mean_reward = evaluate(dqn_per_model, num_episodes=100)
```
### DQN + Prioritized Experience Replay + Double Q-Learning + Dueling
```
# Activate all extensions
kwargs = {'double_q': True, 'prioritized_replay': True, 'policy_kwargs': dict(dueling=True)}
dqn_full_model = DQN('MlpPolicy', 'CartPole-v1', verbose=1, **kwargs)
dqn_full_model.learn(total_timesteps=10000, log_interval=10)
mean_reward = evaluate(dqn_per_model, num_episodes=100)
```
In this particular example, the extensions does not seem to give any improvement compared to the simple DQN version.
They are several reasons for that:
1. `CartPole-v1` is a pretty simple environment
2. We trained DQN for very few timesteps, not enough to see any difference
3. The default hyperparameters for DQN are tuned for atari games, where the number of training timesteps is much larger (10^6) and input observations are images
4. We have only compared one random seed per experiment
## Conclusion
In this notebook we have seen:
- how to define and train a RL model using stable baselines, it takes only one line of code ;)
- how to use different RL algorithms and change some hyperparameters
```
```
| true |
code
| 0.62701 | null | null | null | null |
|
<img src="https://github.com/pmservice/ai-openscale-tutorials/raw/master/notebooks/images/banner.png" align="left" alt="banner">
# Working with Watson OpenScale - Custom Machine Learning Provider
This notebook should be run using with **Python 3.7.x** runtime environment. **If you are viewing this in Watson Studio and do not see Python 3.7.x in the upper right corner of your screen, please update the runtime now.** It requires service credentials for the following services:
* Watson OpenScale
* A Custom ML provider which is hosted in a VM that can be accessible from CPD PODs, specifically OpenScale PODs namely ML Gateway fairness, quality, drift, and explain.
* DB2 - as part of this notebook, we make use of an existing data mart.
The notebook will configure a OpenScale data mart subscription for Custom ML Provider deployment. We configure and execute the fairness, explain, quality and drift monitors.
## Custom Machine Learning Provider Setup
Following code can be used to start a gunicorn/flask application that can be hosted in a VM, such that it can be accessable from CPD system.
This code does the following:
* It wraps a Watson Machine Learning model that is deployed to a space.
* So the hosting application URL should contain the SPACE ID and the DEPLOYMENT ID. Then, the same can be used to talk to the target WML model/deployment.
* Having said that, this is only for this tutorial purpose, and you can define your Custom ML provider endpoint in any fashion you want, such that it wraps your own custom ML engine.
* The scoring request and response payload should confirm to the schema as described here at: https://dataplatform.cloud.ibm.com/docs/content/wsj/model/wos-frameworks-custom.html
* To start the application using the below code, make sure you install following python packages in your VM:
python -m pip install gunicorn
python -m pip install flask
python -m pip install numpy
python -m pip install pandas
python -m pip install requests
python -m pip install joblib==0.11
python -m pip install scipy==0.19.1
python -m pip install --user numpy scipy matplotlib ipython jupyter pandas sympy nose
python -m pip install ibm_watson_machine_learning
-----------------
```
from flask import Flask, request, abort, jsonify
import json
import base64
import requests, io
import pandas as pd
from ibm_watson_machine_learning import APIClient
app = Flask(__name__)
WML_CREDENTIALS = {
"url": "https://namespace1-cpd-namespace1.apps.xxxxx.os.fyre.ibm.com",
"username": "admin",
"password" : "xxxx",
"instance_id": "wml_local",
"version" : "3.5"
}
@app.route('/spaces/<space_id>/deployments/<deployment_id>/predictions', methods=['POST'])
def wml_scoring(space_id, deployment_id):
if not request.json:
abort(400)
wml_credentials = WML_CREDENTIALS
payload_scoring = {
"input_data": [
request.json
]
}
wml_client = APIClient(wml_credentials)
wml_client.set.default_space(space_id)
records_list=[]
scoring_response = wml_client.deployments.score(deployment_id, payload_scoring)
return jsonify(scoring_response["predictions"][0])
if __name__ == '__main__':
app.run(host='xxxx.fyre.ibm.com', port=9443, debug=True)
```
-----------------
# Setup <a name="setup"></a>
## Package installation
```
import warnings
warnings.filterwarnings('ignore')
!pip install --upgrade pyspark==2.4 --no-cache | tail -n 1
!pip install --upgrade pandas==0.25.3 --no-cache | tail -n 1
!pip install --upgrade requests==2.23 --no-cache | tail -n 1
!pip install numpy==1.16.4 --no-cache | tail -n 1
!pip install scikit-learn==0.20 --no-cache | tail -n 1
!pip install SciPy --no-cache | tail -n 1
!pip install lime --no-cache | tail -n 1
!pip install --upgrade ibm-watson-machine-learning --user | tail -n 1
!pip install --upgrade ibm-watson-openscale --no-cache | tail -n 1
!pip install --upgrade ibm-wos-utils --no-cache | tail -n 1
```
### Action: restart the kernel!
## Configure credentials
- WOS_CREDENTIALS (CP4D)
- WML_CREDENTIALS (CP4D)
- DATABASE_CREDENTIALS (DB2 on CP4D or Cloud Object Storage (COS))
- SCHEMA_NAME
```
#masked
WOS_CREDENTIALS = {
"url": "https://namespace1-cpd-namespace1.apps.xxxxx.os.fyre.ibm.com",
"username": "admin",
"password": "xxxxx",
"version": "3.5"
}
CUSTOM_ML_PROVIDER_SCORING_URL = 'https://xxxxx.fyre.ibm.com:9443/spaces/$SPACE_ID/deployments/$DEPLOYMENT_ID/predictions'
scoring_url = CUSTOM_ML_PROVIDER_SCORING_URL
label_column="Risk"
model_type = "binary"
import os
import base64
import json
import requests
from requests.auth import HTTPBasicAuth
```
## Save training data to Cloud Object Storage
### Cloud object storage details¶
In next cells, you will need to paste some credentials to Cloud Object Storage. If you haven't worked with COS yet please visit getting started with COS tutorial. You can find COS_API_KEY_ID and COS_RESOURCE_CRN variables in Service Credentials in menu of your COS instance. Used COS Service Credentials must be created with Role parameter set as Writer. Later training data file will be loaded to the bucket of your instance and used as training refecence in subsription. COS_ENDPOINT variable can be found in Endpoint field of the menu.
```
IAM_URL="https://iam.ng.bluemix.net/oidc/token"
# masked
COS_API_KEY_ID = "*****"
COS_RESOURCE_CRN = "*****"
COS_ENDPOINT = "https://s3.us.cloud-object-storage.appdomain.cloud" # Current list avaiable at https://control.cloud-object-storage.cloud.ibm.com/v2/endpoints
BUCKET_NAME = "*****"
FILE_NAME = "german_credit_data_biased_training.csv"
```
# Load and explore data
```
!rm german_credit_data_biased_training.csv
!wget https://raw.githubusercontent.com/pmservice/ai-openscale-tutorials/master/assets/historical_data/german_credit_risk/wml/german_credit_data_biased_training.csv
```
## Explore data
```
training_data_references = [
{
"id": "Credit Risk",
"type": "s3",
"connection": {
"access_key_id": COS_API_KEY_ID,
"endpoint_url": COS_ENDPOINT,
"resource_instance_id":COS_RESOURCE_CRN
},
"location": {
"bucket": BUCKET_NAME,
"path": FILE_NAME,
}
}
]
```
## Construct the scoring payload
```
import pandas as pd
df = pd.read_csv("german_credit_data_biased_training.csv")
df.head()
cols_to_remove = [label_column]
def get_scoring_payload(no_of_records_to_score = 1):
for col in cols_to_remove:
if col in df.columns:
del df[col]
fields = df.columns.tolist()
values = df[fields].values.tolist()
payload_scoring ={"fields": fields, "values": values[:no_of_records_to_score]}
return payload_scoring
#debug
payload_scoring = get_scoring_payload(1)
payload_scoring
```
## Method to perform scoring
```
def custom_ml_scoring():
header = {"Content-Type": "application/json", "x":"y"}
print(scoring_url)
scoring_response = requests.post(scoring_url, json=payload_scoring, headers=header, verify=False)
jsonify_scoring_response = scoring_response.json()
return jsonify_scoring_response
```
## Method to perform payload logging
```
import uuid
scoring_id = None
from ibm_watson_openscale.supporting_classes.payload_record import PayloadRecord
def payload_logging(payload_scoring, scoring_response):
scoring_id = str(uuid.uuid4())
records_list=[]
#manual PL logging for custom ml provider
pl_record = PayloadRecord(scoring_id=scoring_id, request=payload_scoring, response=scoring_response, response_time=int(460))
records_list.append(pl_record)
wos_client.data_sets.store_records(data_set_id = payload_data_set_id, request_body=records_list)
time.sleep(5)
pl_records_count = wos_client.data_sets.get_records_count(payload_data_set_id)
print("Number of records in the payload logging table: {}".format(pl_records_count))
return scoring_id
```
## Score the model and print the scoring response
### Sample Scoring
```
custom_ml_scoring()
```
# Configure OpenScale
The notebook will now import the necessary libraries and set up a Python OpenScale client.
```
from ibm_watson_openscale import APIClient
from ibm_watson_openscale.utils import *
from ibm_watson_openscale.supporting_classes import *
from ibm_watson_openscale.supporting_classes.enums import *
from ibm_watson_openscale.base_classes.watson_open_scale_v2 import *
from ibm_cloud_sdk_core.authenticators import CloudPakForDataAuthenticator
import json
import requests
import base64
from requests.auth import HTTPBasicAuth
import time
```
## Get a instance of the OpenScale SDK client
```
authenticator = CloudPakForDataAuthenticator(
url=WOS_CREDENTIALS['url'],
username=WOS_CREDENTIALS['username'],
password=WOS_CREDENTIALS['password'],
disable_ssl_verification=True
)
wos_client = APIClient(service_url=WOS_CREDENTIALS['url'],authenticator=authenticator)
wos_client.version
```
## Set up datamart
Watson OpenScale uses a database to store payload logs and calculated metrics. If database credentials were not supplied above, the notebook will use the free, internal lite database. If database credentials were supplied, the datamart will be created there unless there is an existing datamart and the KEEP_MY_INTERNAL_POSTGRES variable is set to True. If an OpenScale datamart exists in Db2 or PostgreSQL, the existing datamart will be used and no data will be overwritten.
Prior instances of the model will be removed from OpenScale monitoring.
```
wos_client.data_marts.show()
data_marts = wos_client.data_marts.list().result.data_marts
if len(data_marts) == 0:
raise Exception("Missing data mart.")
data_mart_id=data_marts[0].metadata.id
print('Using existing datamart {}'.format(data_mart_id))
data_mart_details = wos_client.data_marts.list().result.data_marts[0]
data_mart_details.to_dict()
wos_client.service_providers.show()
```
## Remove existing service provider connected with used WML instance.
Multiple service providers for the same engine instance are avaiable in Watson OpenScale. To avoid multiple service providers of used WML instance in the tutorial notebook the following code deletes existing service provder(s) and then adds new one.
```
SERVICE_PROVIDER_NAME = "Custom ML Provider Demo - All Monitors"
SERVICE_PROVIDER_DESCRIPTION = "Added by tutorial WOS notebook to showcase monitoring Fairness, Quality, Drift and Explainability against a Custom ML provider."
service_providers = wos_client.service_providers.list().result.service_providers
for service_provider in service_providers:
service_instance_name = service_provider.entity.name
if service_instance_name == SERVICE_PROVIDER_NAME:
service_provider_id = service_provider.metadata.id
wos_client.service_providers.delete(service_provider_id)
print("Deleted existing service_provider for WML instance: {}".format(service_provider_id))
```
## Add service provider
Watson OpenScale needs to be bound to the Watson Machine Learning instance to capture payload data into and out of the model.
Note: You can bind more than one engine instance if needed by calling wos_client.service_providers.add method. Next, you can refer to particular service provider using service_provider_id.
```
request_headers = {"Content-Type": "application/json", "Custom_header_X": "Custom_header_X_value_Y"}
MLCredentials = {}
added_service_provider_result = wos_client.service_providers.add(
name=SERVICE_PROVIDER_NAME,
description=SERVICE_PROVIDER_DESCRIPTION,
service_type=ServiceTypes.CUSTOM_MACHINE_LEARNING,
request_headers=request_headers,
operational_space_id = "production",
credentials=MLCredentials,
background_mode=False
).result
service_provider_id = added_service_provider_result.metadata.id
print(wos_client.service_providers.get(service_provider_id).result)
print('Data Mart ID : ' + data_mart_id)
print('Service Provider ID : ' + service_provider_id)
```
## Subscriptions
Remove existing credit risk subscriptions
This code removes previous subscriptions to the model to refresh the monitors with the new model and new data.
```
wos_client.subscriptions.show()
```
## Remove the existing subscription
```
SUBSCRIPTION_NAME = "Custom ML Subscription - All Monitors"
subscriptions = wos_client.subscriptions.list().result.subscriptions
for subscription in subscriptions:
if subscription.entity.asset.name == "[asset] " + SUBSCRIPTION_NAME:
sub_model_id = subscription.metadata.id
wos_client.subscriptions.delete(subscription.metadata.id)
print('Deleted existing subscription for model', sub_model_id)
```
This code creates the model subscription in OpenScale using the Python client API. Note that we need to provide the model unique identifier, and some information about the model itself.
```
feature_columns=["CheckingStatus","LoanDuration","CreditHistory","LoanPurpose","LoanAmount","ExistingSavings","EmploymentDuration","InstallmentPercent","Sex","OthersOnLoan","CurrentResidenceDuration","OwnsProperty","Age","InstallmentPlans","Housing","ExistingCreditsCount","Job","Dependents","Telephone","ForeignWorker"]
cat_features=["CheckingStatus","CreditHistory","LoanPurpose","ExistingSavings","EmploymentDuration","Sex","OthersOnLoan","OwnsProperty","InstallmentPlans","Housing","Job","Telephone","ForeignWorker"]
import uuid
asset_id = str(uuid.uuid4())
asset_name = '[asset] ' + SUBSCRIPTION_NAME
url = ''
asset_deployment_id = str(uuid.uuid4())
asset_deployment_name = asset_name
asset_deployment_scoring_url = scoring_url
scoring_endpoint_url = scoring_url
scoring_request_headers = {
"Content-Type": "application/json",
"Custom_header_X": "Custom_header_X_value_Y"
}
subscription_details = wos_client.subscriptions.add(
data_mart_id=data_mart_id,
service_provider_id=service_provider_id,
asset=Asset(
asset_id=asset_id,
name=asset_name,
url=url,
asset_type=AssetTypes.MODEL,
input_data_type=InputDataType.STRUCTURED,
problem_type=ProblemType.BINARY_CLASSIFICATION
),
deployment=AssetDeploymentRequest(
deployment_id=asset_deployment_id,
name=asset_deployment_name,
deployment_type= DeploymentTypes.ONLINE,
scoring_endpoint=ScoringEndpointRequest(
url=scoring_endpoint_url,
request_headers=scoring_request_headers
)
),
asset_properties=AssetPropertiesRequest(
label_column=label_column,
probability_fields=["probability"],
prediction_field="predictedLabel",
feature_fields = feature_columns,
categorical_fields = cat_features,
training_data_reference=TrainingDataReference(type="cos",
location=COSTrainingDataReferenceLocation(bucket = BUCKET_NAME,
file_name = FILE_NAME),
connection=COSTrainingDataReferenceConnection.from_dict({
"resource_instance_id": COS_RESOURCE_CRN,
"url": COS_ENDPOINT,
"api_key": COS_API_KEY_ID,
"iam_url": IAM_URL}))
)
).result
subscription_id = subscription_details.metadata.id
print('Subscription ID: ' + subscription_id)
import time
time.sleep(5)
payload_data_set_id = None
payload_data_set_id = wos_client.data_sets.list(type=DataSetTypes.PAYLOAD_LOGGING,
target_target_id=subscription_id,
target_target_type=TargetTypes.SUBSCRIPTION).result.data_sets[0].metadata.id
if payload_data_set_id is None:
print("Payload data set not found. Please check subscription status.")
else:
print("Payload data set id:", payload_data_set_id)
```
### Before the payload logging
wos_client.subscriptions.get(subscription_id).result.to_dict()
# Score the model so we can configure monitors
Now that the WML service has been bound and the subscription has been created, we need to send a request to the model before we configure OpenScale. This allows OpenScale to create a payload log in the datamart with the correct schema, so it can capture data coming into and out of the model.
```
no_of_records_to_score = 100
```
### Construct the scoring payload
```
payload_scoring = get_scoring_payload(no_of_records_to_score)
```
### Perform the scoring against the Custom ML Provider
```
scoring_response = custom_ml_scoring()
```
### Perform payload logging by passing the scoring payload and scoring response
```
scoring_id = payload_logging(payload_scoring, scoring_response)
```
### The scoring id, which would be later used for explanation of the randomly picked transactions
```
print('scoring_id: ' + str(scoring_id))
```
# Fairness configuration <a name="Fairness"></a>
The code below configures fairness monitoring for our model. It turns on monitoring for two features, sex and age. In each case, we must specify:
Which model feature to monitor One or more majority groups, which are values of that feature that we expect to receive a higher percentage of favorable outcomes One or more minority groups, which are values of that feature that we expect to receive a higher percentage of unfavorable outcomes The threshold at which we would like OpenScale to display an alert if the fairness measurement falls below (in this case, 80%) Additionally, we must specify which outcomes from the model are favourable outcomes, and which are unfavourable. We must also provide the number of records OpenScale will use to calculate the fairness score. In this case, OpenScale's fairness monitor will run hourly, but will not calculate a new fairness rating until at least 100 records have been added. Finally, to calculate fairness, OpenScale must perform some calculations on the training data, so we provide the dataframe containing the data.
### Create Fairness Monitor Instance
```
target = Target(
target_type=TargetTypes.SUBSCRIPTION,
target_id=subscription_id
)
parameters = {
"features": [
{"feature": "Sex",
"majority": ['male'],
"minority": ['female']
},
{"feature": "Age",
"majority": [[26, 75]],
"minority": [[18, 25]]
}
],
"favourable_class": ["No Risk"],
"unfavourable_class": ["Risk"],
"min_records": 100
}
thresholds = [{
"metric_id": "fairness_value",
"specific_values": [{
"applies_to": [{
"key": "feature",
"type": "tag",
"value": "Age"
}],
"value": 95
},
{
"applies_to": [{
"key": "feature",
"type": "tag",
"value": "Sex"
}],
"value": 95
}
],
"type": "lower_limit",
"value": 80.0
}]
fairness_monitor_details = wos_client.monitor_instances.create(
data_mart_id=data_mart_id,
background_mode=False,
monitor_definition_id=wos_client.monitor_definitions.MONITORS.FAIRNESS.ID,
target=target,
parameters=parameters,
thresholds=thresholds).result
fairness_monitor_instance_id = fairness_monitor_details.metadata.id
```
### Get Fairness Monitor Instance
```
wos_client.monitor_instances.show()
```
### Get run details
In case of production subscription, initial monitoring run is triggered internally. Checking its status
```
runs = wos_client.monitor_instances.list_runs(fairness_monitor_instance_id, limit=1).result.to_dict()
fairness_monitoring_run_id = runs["runs"][0]["metadata"]["id"]
run_status = None
while(run_status not in ["finished", "error"]):
run_details = wos_client.monitor_instances.get_run_details(fairness_monitor_instance_id, fairness_monitoring_run_id).result.to_dict()
run_status = run_details["entity"]["status"]["state"]
print('run_status: ', run_status)
if run_status in ["finished", "error"]:
break
time.sleep(10)
```
### Fairness run output
```
wos_client.monitor_instances.get_run_details(fairness_monitor_instance_id, fairness_monitoring_run_id).result.to_dict()
wos_client.monitor_instances.show_metrics(monitor_instance_id=fairness_monitor_instance_id)
```
# Configure Explainability <a name="explain"></a>
We provide OpenScale with the training data to enable and configure the explainability features.
```
target = Target(
target_type=TargetTypes.SUBSCRIPTION,
target_id=subscription_id
)
parameters = {
"enabled": True
}
explain_monitor_details = wos_client.monitor_instances.create(
data_mart_id=data_mart_id,
background_mode=False,
monitor_definition_id=wos_client.monitor_definitions.MONITORS.EXPLAINABILITY.ID,
target=target,
parameters=parameters
).result
explain_monitor_details.metadata.id
scoring_ids = []
sample_size = 2
import random
for i in range(0, sample_size):
n = random.randint(1,100)
scoring_ids.append(scoring_id + '-' + str(n))
print("Running explanations on scoring IDs: {}".format(scoring_ids))
explanation_types = ["lime", "contrastive"]
result = wos_client.monitor_instances.explanation_tasks(scoring_ids=scoring_ids, explanation_types=explanation_types).result
print(result)
```
### Explanation tasks
```
explanation_task_ids=result.metadata.explanation_task_ids
explanation_task_ids
```
### Wait for the explanation tasks to complete - all of them
```
import time
def finish_explanation_tasks():
finished_explanations = []
finished_explanation_task_ids = []
# Check for the explanation task status for finished status.
# If it is in-progress state, then sleep for some time and check again.
# Perform the same for couple of times, so that all tasks get into finished state.
for i in range(0, 5):
# for each explanation
print('iteration ' + str(i))
#check status for all explanation tasks
for explanation_task_id in explanation_task_ids:
if explanation_task_id not in finished_explanation_task_ids:
result = wos_client.monitor_instances.get_explanation_tasks(explanation_task_id=explanation_task_id).result
print(explanation_task_id + ' : ' + result.entity.status.state)
if (result.entity.status.state == 'finished' or result.entity.status.state == 'error') and explanation_task_id not in finished_explanation_task_ids:
finished_explanation_task_ids.append(explanation_task_id)
finished_explanations.append(result)
# if there is altest one explanation task that is not yet completed, then sleep for sometime,
# and check for all those tasks, for which explanation is not yet completeed.
if len(finished_explanation_task_ids) != sample_size:
print('sleeping for some time..')
time.sleep(10)
else:
break
return finished_explanations
```
### You may have to run the below multiple times till all explanation tasks are either finished or error'ed.
```
finished_explanations = finish_explanation_tasks()
len(finished_explanations)
def construct_explanation_features_map(feature_name, feature_weight):
if feature_name in explanation_features_map:
explanation_features_map[feature_name].append(feature_weight)
else:
explanation_features_map[feature_name] = [feature_weight]
explanation_features_map = {}
for result in finished_explanations:
print('\n>>>>>>>>>>>>>>>>>>>>>>\n')
print('explanation task: ' + str(result.metadata.explanation_task_id) + ', perturbed:' + str(result.entity.perturbed))
if result.entity.explanations is not None:
explanations = result.entity.explanations
for explanation in explanations:
if 'predictions' in explanation:
predictions = explanation['predictions']
for prediction in predictions:
predicted_value = prediction['value']
probability = prediction['probability']
print('prediction : ' + str(predicted_value) + ', probability : ' + str(probability))
if 'explanation_features' in prediction:
explanation_features = prediction['explanation_features']
for explanation_feature in explanation_features:
feature_name = explanation_feature['feature_name']
feature_weight = explanation_feature['weight']
if (feature_weight >= 0 ):
feature_weight_percent = round(feature_weight * 100, 2)
print(str(feature_name) + ' : ' + str(feature_weight_percent))
task_feature_weight_map = {}
task_feature_weight_map[result.metadata.explanation_task_id] = feature_weight_percent
construct_explanation_features_map(feature_name, feature_weight_percent)
print('\n>>>>>>>>>>>>>>>>>>>>>>\n')
explanation_features_map
import matplotlib.pyplot as plt
for key in explanation_features_map.keys():
#plot_graph(key, explanation_features_map[key])
values = explanation_features_map[key]
plt.title(key)
plt.ylabel('Weight')
plt.bar(range(len(values)), values)
plt.show()
```
# Quality monitoring and feedback logging <a name="quality"></a>
## Enable quality monitoring
The code below waits ten seconds to allow the payload logging table to be set up before it begins enabling monitors. First, it turns on the quality (accuracy) monitor and sets an alert threshold of 70%. OpenScale will show an alert on the dashboard if the model accuracy measurement (area under the curve, in the case of a binary classifier) falls below this threshold.
The second paramater supplied, min_records, specifies the minimum number of feedback records OpenScale needs before it calculates a new measurement. The quality monitor runs hourly, but the accuracy reading in the dashboard will not change until an additional 50 feedback records have been added, via the user interface, the Python client, or the supplied feedback endpoint.
```
import time
#time.sleep(10)
target = Target(
target_type=TargetTypes.SUBSCRIPTION,
target_id=subscription_id
)
parameters = {
"min_feedback_data_size": 90
}
thresholds = [
{
"metric_id": "area_under_roc",
"type": "lower_limit",
"value": .80
}
]
quality_monitor_details = wos_client.monitor_instances.create(
data_mart_id=data_mart_id,
background_mode=False,
monitor_definition_id=wos_client.monitor_definitions.MONITORS.QUALITY.ID,
target=target,
parameters=parameters,
thresholds=thresholds
).result
quality_monitor_instance_id = quality_monitor_details.metadata.id
quality_monitor_instance_id
```
## Feedback logging
The code below downloads and stores enough feedback data to meet the minimum threshold so that OpenScale can calculate a new accuracy measurement. It then kicks off the accuracy monitor. The monitors run hourly, or can be initiated via the Python API, the REST API, or the graphical user interface.
```
!rm additional_feedback_data_v2.json
!wget https://raw.githubusercontent.com/IBM/watson-openscale-samples/main/IBM%20Cloud/WML/assets/data/credit_risk/additional_feedback_data_v2.json
```
## Get feedback logging dataset ID
```
feedback_dataset_id = None
feedback_dataset = wos_client.data_sets.list(type=DataSetTypes.FEEDBACK,
target_target_id=subscription_id,
target_target_type=TargetTypes.SUBSCRIPTION).result
feedback_dataset_id = feedback_dataset.data_sets[0].metadata.id
if feedback_dataset_id is None:
print("Feedback data set not found. Please check quality monitor status.")
with open('additional_feedback_data_v2.json') as feedback_file:
additional_feedback_data = json.load(feedback_file)
wos_client.data_sets.store_records(feedback_dataset_id, request_body=additional_feedback_data, background_mode=False)
wos_client.data_sets.get_records_count(data_set_id=feedback_dataset_id)
run_details = wos_client.monitor_instances.run(monitor_instance_id=quality_monitor_instance_id, background_mode=False).result
wos_client.monitor_instances.show_metrics(monitor_instance_id=quality_monitor_instance_id)
```
# Drift configuration <a name="drift"></a>
# Drift detection model generation
Please update the score function which will be used forgenerating drift detection model which will used for drift detection . This might take sometime to generate model and time taken depends on the training dataset size. The output of the score function should be a 2 arrays 1. Array of model prediction 2. Array of probabilities
- User is expected to make sure that the data type of the "class label" column selected and the prediction column are same . For eg : If class label is numeric , the prediction array should also be numeric
- Each entry of a probability array should have all the probabities of the unique class lable .
For eg: If the model_type=multiclass and unique class labels are A, B, C, D . Each entry in the probability array should be a array of size 4 . Eg : [ [50,30,10,10] ,[40,20,30,10]...]
**Note:**
- *User is expected to add "score" method , which should output prediction column array and probability column array.*
- *The data type of the label column and prediction column should be same . User needs to make sure that label column and prediction column array should have the same unique class labels*
- **Please update the score function below with the help of templates documented [here](https://github.com/IBM-Watson/aios-data-distribution/blob/master/Score%20function%20templates%20for%20drift%20detection.md)**
```
import pandas as pd
df = pd.read_csv("german_credit_data_biased_training.csv")
df.head()
def score(training_data_frame):
#The data type of the label column and prediction column should be same .
#User needs to make sure that label column and prediction column array should have the same unique class labels
prediction_column_name = "predictedLabel"
probability_column_name = "probability"
feature_columns = list(training_data_frame.columns)
training_data_rows = training_data_frame[feature_columns].values.tolist()
payload_scoring_records = {
"fields": feature_columns,
"values": [x for x in training_data_rows]
}
header = {"Content-Type": "application/json", "x":"y"}
scoring_response_raw = requests.post(scoring_url, json=payload_scoring_records, headers=header, verify=False)
scoring_response = scoring_response_raw.json()
probability_array = None
prediction_vector = None
prob_col_index = list(scoring_response.get('fields')).index(probability_column_name)
predict_col_index = list(scoring_response.get('fields')).index(prediction_column_name)
if prob_col_index < 0 or predict_col_index < 0:
raise Exception("Missing prediction/probability column in the scoring response")
import numpy as np
probability_array = np.array([value[prob_col_index] for value in scoring_response.get('values')])
prediction_vector = np.array([value[predict_col_index] for value in scoring_response.get('values')])
return probability_array, prediction_vector
```
### Define the drift detection input
```
drift_detection_input = {
"feature_columns": feature_columns,
"categorical_columns": cat_features,
"label_column": label_column,
"problem_type": model_type
}
print(drift_detection_input)
```
### Generate drift detection model
```
!rm drift_detection_model.tar.gz
from ibm_wos_utils.drift.drift_trainer import DriftTrainer
drift_trainer = DriftTrainer(df,drift_detection_input)
if model_type != "regression":
#Note: batch_size can be customized by user as per the training data size
drift_trainer.generate_drift_detection_model(score,batch_size=df.shape[0])
#Note: Two column constraints are not computed beyond two_column_learner_limit(default set to 200)
#User can adjust the value depending on the requirement
drift_trainer.learn_constraints(two_column_learner_limit=200)
drift_trainer.create_archive()
!ls -al
filename = 'drift_detection_model.tar.gz'
```
### Upload the drift detection model to OpenScale subscription
```
wos_client.monitor_instances.upload_drift_model(
model_path=filename,
archive_name=filename,
data_mart_id=data_mart_id,
subscription_id=subscription_id,
enable_data_drift=True,
enable_model_drift=True
)
```
### Delete the existing drift monitor instance for the subscription
```
monitor_instances = wos_client.monitor_instances.list().result.monitor_instances
for monitor_instance in monitor_instances:
monitor_def_id=monitor_instance.entity.monitor_definition_id
if monitor_def_id == "drift" and monitor_instance.entity.target.target_id == subscription_id:
wos_client.monitor_instances.delete(monitor_instance.metadata.id)
print('Deleted existing drift monitor instance with id: ', monitor_instance.metadata.id)
target = Target(
target_type=TargetTypes.SUBSCRIPTION,
target_id=subscription_id
)
parameters = {
"min_samples": 100,
"drift_threshold": 0.1,
"train_drift_model": False,
"enable_model_drift": True,
"enable_data_drift": True
}
drift_monitor_details = wos_client.monitor_instances.create(
data_mart_id=data_mart_id,
background_mode=False,
monitor_definition_id=wos_client.monitor_definitions.MONITORS.DRIFT.ID,
target=target,
parameters=parameters
).result
drift_monitor_instance_id = drift_monitor_details.metadata.id
drift_monitor_instance_id
```
### Drift run
```
drift_run_details = wos_client.monitor_instances.run(monitor_instance_id=drift_monitor_instance_id, background_mode=False)
time.sleep(5)
wos_client.monitor_instances.show_metrics(monitor_instance_id=drift_monitor_instance_id)
```
## Summary
As part of this notebook, we have performed the following:
* Create a subscription to an custom ML end point
* Scored the custom ML provider with 100 records
* With the scored payload and also the scored response, we called the DataSets SDK method to store the payload logging records into the data mart. While doing so, we have set the scoring_id attribute.
* Configured the fairness monitor and executed it and viewed the fairness metrics output.
* Configured explainabilty monitor
* Randomly selected 5 transactions for which we want to get the prediction explanation.
* Submitted explainability tasks for the selected scoring ids, and waited for their completion.
* In the end, we composed a weight map of feature and its weight across transactions. And plotted the same.
* For example:
```
{'ForeignWorker': [33.29, 5.23],
'OthersOnLoan': [15.96, 19.97, 12.76],
'OwnsProperty': [15.43, 3.92, 4.44, 10.36],
'Dependents': [9.06],
'InstallmentPercent': [9.05],
'CurrentResidenceDuration': [8.74, 13.15, 12.1, 10.83],
'Sex': [2.96, 12.76],
'InstallmentPlans': [2.4, 5.67, 6.57],
'Age': [2.28, 8.6, 11.26],
'Job': [0.84],
'LoanDuration': [15.02, 10.87, 18.91, 12.72],
'EmploymentDuration': [14.02, 14.05, 12.1],
'LoanAmount': [9.28, 12.42, 7.85],
'Housing': [4.35],
'CreditHistory': [6.5]}
```
The understanding of the above map is like this:
* LoanDuration, CurrentResidenceDuration, OwnsProperty are the most contributing features across transactions for their respective prediction. Their weights for the respective prediction can also be seen.
* And the low contributing features are CreditHistory, Housing, Job, InstallmentPercent and Dependents, with their respective weights can also be seen as printed.
* We configured quality monitor and uploaded feedback data, and thereby ran the quality monitor
* For drift monitoring purposes, we created the drift detection model and uploaded to the OpenScale subscription.
* Executed the drift monitor.
Thank You! for working on tutorial notebook.
Author: Ravi Chamarthy ([email protected])
| true |
code
| 0.251395 | null | null | null | null |
|
# ETS models
The ETS models are a family of time series models with an underlying state space model consisting of a level component, a trend component (T), a seasonal component (S), and an error term (E).
This notebook shows how they can be used with `statsmodels`. For a more thorough treatment we refer to [1], chapter 8 (free online resource), on which the implementation in statsmodels and the examples used in this notebook are based.
`statmodels` implements all combinations of:
- additive and multiplicative error model
- additive and multiplicative trend, possibly dampened
- additive and multiplicative seasonality
However, not all of these methods are stable. Refer to [1] and references therein for more info about model stability.
[1] Hyndman, Rob J., and George Athanasopoulos. *Forecasting: principles and practice*, 3rd edition, OTexts, 2019. https://www.otexts.org/fpp3/7
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
from statsmodels.tsa.exponential_smoothing.ets import ETSModel
plt.rcParams['figure.figsize'] = (12, 8)
```
## Simple exponential smoothing
The simplest of the ETS models is also known as *simple exponential smoothing*. In ETS terms, it corresponds to the (A, N, N) model, that is, a model with additive errors, no trend, and no seasonality. The state space formulation of Holt's method is:
\begin{align}
y_{t} &= y_{t-1} + e_t\\
l_{t} &= l_{t-1} + \alpha e_t\\
\end{align}
This state space formulation can be turned into a different formulation, a forecast and a smoothing equation (as can be done with all ETS models):
\begin{align}
\hat{y}_{t|t-1} &= l_{t-1}\\
l_{t} &= \alpha y_{t-1} + (1 - \alpha) l_{t-1}
\end{align}
Here, $\hat{y}_{t|t-1}$ is the forecast/expectation of $y_t$ given the information of the previous step. In the simple exponential smoothing model, the forecast corresponds to the previous level. The second equation (smoothing equation) calculates the next level as weighted average of the previous level and the previous observation.
```
oildata = [
111.0091, 130.8284, 141.2871, 154.2278,
162.7409, 192.1665, 240.7997, 304.2174,
384.0046, 429.6622, 359.3169, 437.2519,
468.4008, 424.4353, 487.9794, 509.8284,
506.3473, 340.1842, 240.2589, 219.0328,
172.0747, 252.5901, 221.0711, 276.5188,
271.1480, 342.6186, 428.3558, 442.3946,
432.7851, 437.2497, 437.2092, 445.3641,
453.1950, 454.4096, 422.3789, 456.0371,
440.3866, 425.1944, 486.2052, 500.4291,
521.2759, 508.9476, 488.8889, 509.8706,
456.7229, 473.8166, 525.9509, 549.8338,
542.3405
]
oil = pd.Series(oildata, index=pd.date_range('1965', '2013', freq='AS'))
oil.plot()
plt.ylabel("Annual oil production in Saudi Arabia (Mt)");
```
The plot above shows annual oil production in Saudi Arabia in million tonnes. The data are taken from the R package `fpp2` (companion package to prior version [1]).
Below you can see how to fit a simple exponential smoothing model using statsmodels's ETS implementation to this data. Additionally, the fit using `forecast` in R is shown as comparison.
```
model = ETSModel(oil, error='add', trend='add', damped_trend=True)
fit = model.fit(maxiter=10000)
oil.plot(label='data')
fit.fittedvalues.plot(label='statsmodels fit')
plt.ylabel("Annual oil production in Saudi Arabia (Mt)");
# obtained from R
params_R = [0.99989969, 0.11888177503085334, 0.80000197, 36.46466837, 34.72584983]
yhat = model.smooth(params_R).fittedvalues
yhat.plot(label='R fit', linestyle='--')
plt.legend();
```
By default the initial states are considered to be fitting parameters and are estimated by maximizing log-likelihood. Additionally it is possible to only use a heuristic for the initial values. In this case this leads to better agreement with the R implementation.
```
model_heuristic = ETSModel(oil, error='add', trend='add', damped_trend=True,
initialization_method='heuristic')
fit_heuristic = model_heuristic.fit()
oil.plot(label='data')
fit.fittedvalues.plot(label='estimated')
fit_heuristic.fittedvalues.plot(label='heuristic', linestyle='--')
plt.ylabel("Annual oil production in Saudi Arabia (Mt)");
# obtained from R
params = [0.99989969, 0.11888177503085334, 0.80000197, 36.46466837, 34.72584983]
yhat = model.smooth(params).fittedvalues
yhat.plot(label='with R params', linestyle=':')
plt.legend();
```
The fitted parameters and some other measures are shown using `fit.summary()`. Here we can see that the log-likelihood of the model using fitted initial states is a bit lower than the one using a heuristic for the initial states.
Additionally, we see that $\beta$ (`smoothing_trend`) is at the boundary of the default parameter bounds, and therefore it's not possible to estimate confidence intervals for $\beta$.
```
fit.summary()
fit_heuristic.summary()
```
## Holt-Winters' seasonal method
The exponential smoothing method can be modified to incorporate a trend and a seasonal component. In the additive Holt-Winters' method, the seasonal component is added to the rest. This model corresponds to the ETS(A, A, A) model, and has the following state space formulation:
\begin{align}
y_t &= l_{t-1} + b_{t-1} + s_{t-m} + e_t\\
l_{t} &= l_{t-1} + b_{t-1} + \alpha e_t\\
b_{t} &= b_{t-1} + \beta e_t\\
s_{t} &= s_{t-m} + \gamma e_t
\end{align}
```
austourists_data = [
30.05251300, 19.14849600, 25.31769200, 27.59143700,
32.07645600, 23.48796100, 28.47594000, 35.12375300,
36.83848500, 25.00701700, 30.72223000, 28.69375900,
36.64098600, 23.82460900, 29.31168300, 31.77030900,
35.17787700, 19.77524400, 29.60175000, 34.53884200,
41.27359900, 26.65586200, 28.27985900, 35.19115300,
42.20566386, 24.64917133, 32.66733514, 37.25735401,
45.24246027, 29.35048127, 36.34420728, 41.78208136,
49.27659843, 31.27540139, 37.85062549, 38.83704413,
51.23690034, 31.83855162, 41.32342126, 42.79900337,
55.70835836, 33.40714492, 42.31663797, 45.15712257,
59.57607996, 34.83733016, 44.84168072, 46.97124960,
60.01903094, 38.37117851, 46.97586413, 50.73379646,
61.64687319, 39.29956937, 52.67120908, 54.33231689,
66.83435838, 40.87118847, 51.82853579, 57.49190993,
65.25146985, 43.06120822, 54.76075713, 59.83447494,
73.25702747, 47.69662373, 61.09776802, 66.05576122,
]
index = pd.date_range("1999-03-01", "2015-12-01", freq="3MS")
austourists = pd.Series(austourists_data, index=index)
austourists.plot()
plt.ylabel('Australian Tourists');
# fit in statsmodels
model = ETSModel(austourists, error="add", trend="add", seasonal="add",
damped_trend=True, seasonal_periods=4)
fit = model.fit()
# fit with R params
params_R = [
0.35445427, 0.03200749, 0.39993387, 0.97999997, 24.01278357,
0.97770147, 1.76951063, -0.50735902, -6.61171798, 5.34956637
]
fit_R = model.smooth(params_R)
austourists.plot(label='data')
plt.ylabel('Australian Tourists')
fit.fittedvalues.plot(label='statsmodels fit')
fit_R.fittedvalues.plot(label='R fit', linestyle='--')
plt.legend();
fit.summary()
```
## Predictions
The ETS model can also be used for predicting. There are several different methods available:
- `forecast`: makes out of sample predictions
- `predict`: in sample and out of sample predictions
- `simulate`: runs simulations of the statespace model
- `get_prediction`: in sample and out of sample predictions, as well as prediction intervals
We can use them on our previously fitted model to predict from 2014 to 2020.
```
pred = fit.get_prediction(start='2014', end='2020')
df = pred.summary_frame(alpha=0.05)
df
```
In this case the prediction intervals were calculated using an analytical formula. This is not available for all models. For these other models, prediction intervals are calculated by performing multiple simulations (1000 by default) and using the percentiles of the simulation results. This is done internally by the `get_prediction` method.
We can also manually run simulations, e.g. to plot them. Since the data ranges until end of 2015, we have to simulate from the first quarter of 2016 to the first quarter of 2020, which means 17 steps.
```
simulated = fit.simulate(anchor="end", nsimulations=17, repetitions=100)
for i in range(simulated.shape[1]):
simulated.iloc[:,i].plot(label='_', color='gray', alpha=0.1)
df["mean"].plot(label='mean prediction')
df["pi_lower"].plot(linestyle='--', color='tab:blue', label='95% interval')
df["pi_upper"].plot(linestyle='--', color='tab:blue', label='_')
pred.endog.plot(label='data')
plt.legend()
```
In this case, we chose "end" as simulation anchor, which means that the first simulated value will be the first out of sample value. It is also possible to choose other anchor inside the sample.
| true |
code
| 0.72964 | null | null | null | null |
|
## **Bootstrap Your Own Latent A New Approach to Self-Supervised Learning:** https://arxiv.org/pdf/2006.07733.pdf
```
# !pip install torch==1.6.0+cu101 torchvision==0.7.0+cu101 -f https://download.pytorch.org/whl/torch_stable.html
# !pip install -qqU fastai fastcore
# !pip install nbdev
import fastai, fastcore, torch
fastai.__version__ , fastcore.__version__, torch.__version__
from fastai.vision.all import *
```
### Sizes
Resize -> RandomCrop
320 -> 256 | 224 -> 192 | 160 -> 128
```
resize = 320
size = 256
```
## 1. Implementation Details (Section 3.2 from the paper)
### 1.1 Image Augmentations
Same as SimCLR with optional grayscale
```
import kornia
def get_aug_pipe(size, stats=imagenet_stats, s=.6):
"SimCLR augmentations"
rrc = kornia.augmentation.RandomResizedCrop((size, size), scale=(0.2, 1.0), ratio=(3/4, 4/3))
rhf = kornia.augmentation.RandomHorizontalFlip()
rcj = kornia.augmentation.ColorJitter(0.8*s, 0.8*s, 0.8*s, 0.2*s)
rgs = kornia.augmentation.RandomGrayscale(p=0.2)
tfms = [rrc, rhf, rcj, rgs, Normalize.from_stats(*stats)]
pipe = Pipeline(tfms)
pipe.split_idx = 0
return pipe
```
### 1.2 Architecture
```
def create_encoder(arch, n_in=3, pretrained=True, cut=None, concat_pool=True):
"Create encoder from a given arch backbone"
encoder = create_body(arch, n_in, pretrained, cut)
pool = AdaptiveConcatPool2d() if concat_pool else nn.AdaptiveAvgPool2d(1)
return nn.Sequential(*encoder, pool, Flatten())
class MLP(Module):
"MLP module as described in paper"
def __init__(self, dim, projection_size=256, hidden_size=2048):
self.net = nn.Sequential(
nn.Linear(dim, hidden_size),
nn.BatchNorm1d(hidden_size),
nn.ReLU(inplace=True),
nn.Linear(hidden_size, projection_size)
)
def forward(self, x):
return self.net(x)
class BYOLModel(Module):
"Compute predictions of v1 and v2"
def __init__(self,encoder,projector,predictor):
self.encoder,self.projector,self.predictor = encoder,projector,predictor
def forward(self,v1,v2):
q1 = self.predictor(self.projector(self.encoder(v1)))
q2 = self.predictor(self.projector(self.encoder(v2)))
return (q1,q2)
def create_byol_model(arch=resnet50, hidden_size=4096, pretrained=True, projection_size=256, concat_pool=False):
encoder = create_encoder(arch, pretrained=pretrained, concat_pool=concat_pool)
with torch.no_grad():
x = torch.randn((2,3,128,128))
representation = encoder(x)
projector = MLP(representation.size(1), projection_size, hidden_size=hidden_size)
predictor = MLP(projection_size, projection_size, hidden_size=hidden_size)
apply_init(projector)
apply_init(predictor)
return BYOLModel(encoder, projector, predictor)
```
### 1.3 BYOLCallback
```
def _mse_loss(x, y):
x = F.normalize(x, dim=-1, p=2)
y = F.normalize(y, dim=-1, p=2)
return 2 - 2 * (x * y).sum(dim=-1)
def symmetric_mse_loss(pred, *yb):
(q1,q2),z1,z2 = pred,*yb
return (_mse_loss(q1,z2) + _mse_loss(q2,z1)).mean()
x = torch.randn((64,256))
y = torch.randn((64,256))
test_close(symmetric_mse_loss((x,y),y,x), 0) # perfect
test_close(symmetric_mse_loss((x,y),x,y), 4, 1e-1) # random
```
Useful Discussions and Supportive Material:
- https://www.reddit.com/r/MachineLearning/comments/hju274/d_byol_bootstrap_your_own_latent_cheating/fwohtky/
- https://untitled-ai.github.io/understanding-self-supervised-contrastive-learning.html
```
import copy
class BYOLCallback(Callback):
"Implementation of https://arxiv.org/pdf/2006.07733.pdf"
def __init__(self, T=0.99, debug=True, size=224, **aug_kwargs):
self.T, self.debug = T, debug
self.aug1 = get_aug_pipe(size, **aug_kwargs)
self.aug2 = get_aug_pipe(size, **aug_kwargs)
def before_fit(self):
"Create target model"
self.target_model = copy.deepcopy(self.learn.model).to(self.dls.device)
self.T_sched = SchedCos(self.T, 1) # used in paper
# self.T_sched = SchedNo(self.T, 1) # used in open source implementation
def before_batch(self):
"Generate 2 views of the same image and calculate target projections for these views"
if self.debug: print(f"self.x[0]: {self.x[0]}")
v1,v2 = self.aug1(self.x), self.aug2(self.x.clone())
self.learn.xb = (v1,v2)
if self.debug:
print(f"v1[0]: {v1[0]}\nv2[0]: {v2[0]}")
self.show_one()
assert not torch.equal(*self.learn.xb)
with torch.no_grad():
z1 = self.target_model.projector(self.target_model.encoder(v1))
z2 = self.target_model.projector(self.target_model.encoder(v2))
self.learn.yb = (z1,z2)
def after_step(self):
"Update target model and T"
self.T = self.T_sched(self.pct_train)
with torch.no_grad():
for param_k, param_q in zip(self.target_model.parameters(), self.model.parameters()):
param_k.data = param_k.data * self.T + param_q.data * (1. - self.T)
def show_one(self):
b1 = self.aug1.normalize.decode(to_detach(self.learn.xb[0]))
b2 = self.aug1.normalize.decode(to_detach(self.learn.xb[1]))
i = np.random.choice(len(b1))
show_images([b1[i],b2[i]], nrows=1, ncols=2)
def after_train(self):
if self.debug: self.show_one()
def after_validate(self):
if self.debug: self.show_one()
```
## 2. Pretext Training
```
sqrmom=0.99
mom=0.95
beta=0.
eps=1e-4
opt_func = partial(ranger, mom=mom, sqr_mom=sqrmom, eps=eps, beta=beta)
bs=128
def get_dls(size, bs, workers=None):
path = URLs.IMAGEWANG_160 if size <= 160 else URLs.IMAGEWANG
source = untar_data(path)
files = get_image_files(source)
tfms = [[PILImage.create, ToTensor, RandomResizedCrop(size, min_scale=0.9)],
[parent_label, Categorize()]]
dsets = Datasets(files, tfms=tfms, splits=RandomSplitter(valid_pct=0.1)(files))
batch_tfms = [IntToFloatTensor]
dls = dsets.dataloaders(bs=bs, num_workers=workers, after_batch=batch_tfms)
return dls
dls = get_dls(resize, bs)
model = create_byol_model(arch=xresnet34, pretrained=False)
learn = Learner(dls, model, symmetric_mse_loss, opt_func=opt_func,
cbs=[BYOLCallback(T=0.99, size=size, debug=False), TerminateOnNaNCallback()])
learn.to_fp16();
learn.lr_find()
lr=1e-3
wd=1e-2
epochs=100
learn.unfreeze()
learn.fit_flat_cos(epochs, lr, wd=wd, pct_start=0.5)
save_name = f'byol_iwang_sz{size}_epc{epochs}'
learn.save(save_name)
torch.save(learn.model.encoder.state_dict(), learn.path/learn.model_dir/f'{save_name}_encoder.pth')
learn.load(save_name);
lr=1e-4
wd=1e-2
epochs=100
learn.unfreeze()
learn.fit_flat_cos(epochs, lr, wd=wd, pct_start=0.5)
save_name = f'byol_iwang_sz{size}_epc200'
learn.save(save_name)
torch.save(learn.model.encoder.state_dict(), learn.path/learn.model_dir/f'{save_name}_encoder.pth')
lr=1e-4
wd=1e-2
epochs=30
learn.unfreeze()
learn.fit_flat_cos(epochs, lr, wd=wd, pct_start=0.5)
save_name = f'byol_iwang_sz{size}_epc230'
learn.save(save_name)
torch.save(learn.model.encoder.state_dict(), learn.path/learn.model_dir/f'{save_name}_encoder.pth')
lr=5e-5
wd=1e-2
epochs=30
learn.unfreeze()
learn.fit_flat_cos(epochs, lr, wd=wd, pct_start=0.5)
save_name = f'byol_iwang_sz{size}_epc260'
learn.save(save_name)
torch.save(learn.model.encoder.state_dict(), learn.path/learn.model_dir/f'{save_name}_encoder.pth')
learn.recorder.plot_loss()
save_name
```
## 3. Downstream Task - Image Classification
```
def get_dls(size, bs, workers=None):
path = URLs.IMAGEWANG_160 if size <= 160 else URLs.IMAGEWANG
source = untar_data(path)
files = get_image_files(source, folders=['train', 'val'])
splits = GrandparentSplitter(valid_name='val')(files)
item_aug = [RandomResizedCrop(size, min_scale=0.35), FlipItem(0.5)]
tfms = [[PILImage.create, ToTensor, *item_aug],
[parent_label, Categorize()]]
dsets = Datasets(files, tfms=tfms, splits=splits)
batch_tfms = [IntToFloatTensor, Normalize.from_stats(*imagenet_stats)]
dls = dsets.dataloaders(bs=bs, num_workers=workers, after_batch=batch_tfms)
return dls
def do_train(epochs=5, runs=5, lr=2e-2, size=size, bs=bs, save_name=None):
dls = get_dls(size, bs)
for run in range(runs):
print(f'Run: {run}')
learn = cnn_learner(dls, xresnet34, opt_func=opt_func, normalize=False,
metrics=[accuracy,top_k_accuracy], loss_func=LabelSmoothingCrossEntropy(),
pretrained=False)
# learn.to_fp16()
if save_name is not None:
state_dict = torch.load(learn.path/learn.model_dir/f'{save_name}_encoder.pth')
learn.model[0].load_state_dict(state_dict)
print("Model loaded...")
learn.unfreeze()
learn.fit_flat_cos(epochs, lr, wd=wd)
```
### ImageWang Leaderboard
**sz-256**
**Contrastive Learning**
- 5 epochs: 67.70%
- 20 epochs: 70.03%
- 80 epochs: 70.71%
- 200 epochs: 71.78%
**BYOL**
- 5 epochs: 64.74%
- 20 epochs: **71.01%**
- 80 epochs: **72.58%**
- 200 epochs: **72.13%**
### 5 epochs
```
# we are using old pretrained model with size 192 for transfer learning
# link: https://github.com/KeremTurgutlu/self_supervised/blob/252269827da41b41091cf0db533b65c0d1312f85/nbs/byol_iwang_192.ipynb
save_name = 'byol_iwang_sz192_epc230'
lr = 1e-2
wd=1e-2
bs=128
epochs = 5
runs = 5
do_train(epochs, runs, lr=lr, bs=bs, save_name=save_name)
np.mean([0.657165,0.637312,0.631967,0.646729,0.664291])
```
### 20 epochs
```
lr=2e-2
epochs = 20
runs = 3
do_train(epochs, runs, lr=lr, save_name=save_name)
np.mean([0.711631, 0.705269, 0.713413])
```
### 80 epochs
```
epochs = 80
runs = 1
do_train(epochs, runs, save_name=save_name)
```
### 200 epochs
```
epochs = 200
runs = 1
do_train(epochs, runs, save_name=save_name)
```
| true |
code
| 0.784794 | null | null | null | null |
|
# R API Serving Examples
In this example, we demonstrate how to quickly compare the runtimes of three methods for serving a model from an R hosted REST API. The following SageMaker examples discuss each method in detail:
* **Plumber**
* Website: [https://www.rplumber.io/](https://www.rplumber.io)
* SageMaker Example: [r_serving_with_plumber](../r_serving_with_plumber)
* **RestRServe**
* Website: [https://restrserve.org](https://restrserve.org)
* SageMaker Example: [r_serving_with_restrserve](../r_serving_with_restrserve)
* **FastAPI** (reticulated from Python)
* Website: [https://fastapi.tiangolo.com](https://fastapi.tiangolo.com)
* SageMaker Example: [r_serving_with_fastapi](../r_serving_with_fastapi)
We will reuse the docker images from each of these examples. Each one is configured to serve a small XGBoost model which has already been trained on the classical Iris dataset.
## Building Docker Images for Serving
First, we will build each docker image from the provided SageMaker Examples.
### Plumber Serving Image
```
!cd .. && docker build -t r-plumber -f r_serving_with_plumber/Dockerfile r_serving_with_plumber
```
### RestRServe Serving Image
```
!cd .. && docker build -t r-restrserve -f r_serving_with_restrserve/Dockerfile r_serving_with_restrserve
```
### FastAPI Serving Image
```
!cd .. && docker build -t r-fastapi -f r_serving_with_fastapi/Dockerfile r_serving_with_fastapi
```
## Launch Serving Containers
Next, we will launch each search container. The containers will be launch on the following ports to avoid port collisions on your local machine or SageMaker Notebook instance:
```
ports = {
"plumber": 5000,
"restrserve": 5001,
"fastapi": 5002,
}
!bash launch.sh
!docker container list
```
## Define Simple Client
```
import requests
from tqdm import tqdm
import pandas as pd
def get_predictions(examples, instance=requests, port=5000):
payload = {"features": examples}
return instance.post(f"http://127.0.0.1:{port}/invocations", json=payload)
def get_health(instance=requests, port=5000):
instance.get(f"http://127.0.0.1:{port}/ping")
```
## Define Example Inputs
Next, we define a example inputs from the classical [Iris](https://archive.ics.uci.edu/ml/datasets/iris) dataset.
* Dua, D. and Graff, C. (2019). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.
```
column_names = ["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width", "Label"]
iris = pd.read_csv(
"s3://sagemaker-sample-files/datasets/tabular/iris/iris.data", names=column_names
)
iris_features = iris[["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"]]
example = iris_features.values[:1].tolist()
many_examples = iris_features.values[:100].tolist()
```
## Testing
Now it's time to test how each API server performs under stress.
We will test two use cases:
* **New Requests**: In this scenario, we test how quickly the server can respond with predictions when each client request establishes a new connection with the server. This simulates the server's ability to handle real-time requests. We could make this more realistic by creating an asynchronous environment that tests the server's ability to fulfill concurrent rather than sequential requests.
* **Keep Alive / Reuse Session**: In this scenario, we test how quickly the server can respond with predictions when each client request uses a session to keep its connection to the server alive between requests. This simulates the server's ability to handle sequential batch requests from the same client.
For each of the two use cases, we will test the performance on following situations:
* 1000 requests of a single example
* 1000 requests of 100 examples
* 1000 pings for health status
## New Requests
### Plumber
```
# verify the prediction output
get_predictions(example, port=ports["plumber"]).json()
for i in tqdm(range(1000)):
_ = get_predictions(example, port=ports["plumber"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, port=ports["plumber"])
for i in tqdm(range(1000)):
get_health(port=ports["plumber"])
```
### RestRserve
```
# verify the prediction output
get_predictions(example, port=ports["restrserve"]).json()
for i in tqdm(range(1000)):
_ = get_predictions(example, port=ports["restrserve"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, port=ports["restrserve"])
for i in tqdm(range(1000)):
get_health(port=ports["restrserve"])
```
### FastAPI
```
# verify the prediction output
get_predictions(example, port=ports["fastapi"]).json()
for i in tqdm(range(1000)):
_ = get_predictions(example, port=ports["fastapi"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, port=ports["fastapi"])
for i in tqdm(range(1000)):
get_health(port=ports["fastapi"])
```
## Keep Alive (Reuse Session)
Now, let's test how each one performs when each request reuses a session connection.
```
# reuse the session for each post and get request
instance = requests.Session()
```
### Plumber
```
for i in tqdm(range(1000)):
_ = get_predictions(example, instance=instance, port=ports["plumber"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, instance=instance, port=ports["plumber"])
for i in tqdm(range(1000)):
get_health(instance=instance, port=ports["plumber"])
```
### RestRserve
```
for i in tqdm(range(1000)):
_ = get_predictions(example, instance=instance, port=ports["restrserve"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, instance=instance, port=ports["restrserve"])
for i in tqdm(range(1000)):
get_health(instance=instance, port=ports["restrserve"])
```
### FastAPI
```
for i in tqdm(range(1000)):
_ = get_predictions(example, instance=instance, port=ports["fastapi"])
for i in tqdm(range(1000)):
_ = get_predictions(many_examples, instance=instance, port=ports["fastapi"])
for i in tqdm(range(1000)):
get_health(instance=instance, port=ports["fastapi"])
```
### Stop All Serving Containers
Finally, we will shut down the serving containers we launched for the tests.
```
!docker kill $(docker ps -q)
```
## Conclusion
In this example, we demonstrated how to conduct a simple performance benchmark across three R model serving solutions. We leave the choice of serving solution up to the reader since in some cases it might be appropriate to customize the benchmark in the following ways:
* Update the serving example to serve a specific model
* Perform the tests across multiple instances types
* Modify the serving example and client to test asynchronous requests.
* Deploy the serving examples to SageMaker Endpoints to test within an autoscaling environment.
For more information on serving your models in custom containers on SageMaker, please see our [support documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/your-algorithms-inference-main.html) for the latest updates and best practices.
| true |
code
| 0.353358 | null | null | null | null |
|
# KNN
Importing required python modules
---------------------------------
```
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import train_test_split
from sklearn import metrics
from sklearn.preprocessing import normalize,scale
from sklearn.cross_validation import cross_val_score
import numpy as np
import pandas as pd
```
The following libraries have been used :
* **Pandas** : pandas is an open source, BSD-licensed library providing high-performance, easy-to-use data structures and data analysis tools for the Python programming language.
* **Numpy** : NumPy is the fundamental package for scientific computing with Python.
* **Matplotlib** : matplotlib is a python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments .
* **Sklearn** : It features various classification, regression and clustering algorithms including support vector machines, random forests, gradient boosting, k-means and DBSCAN, and is designed to interoperate with the Python numerical and scientific libraries NumPy and SciPy.
Retrieving the dataset
----------------------
```
data = pd.read_csv('heart.csv', header=None)
df = pd.DataFrame(data)
x = df.iloc[:, 0:5]
x = x.drop(x.columns[1:3], axis=1)
x = pd.DataFrame(scale(x))
y = df.iloc[:, 13]
y = y-1
```
1. Dataset is imported.
2. The imported dataset is converted into a pandas DataFrame.
3. Attributes(x) and labels(y) are extracted.
```
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
```
Train/Test split is 0.4
Plotting the dataset
--------------------
```
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(x[1],x[2], c=y)
ax1.set_title("Original Data")
```
Matplotlib is used to plot the loaded pandas DataFrame.
Learning from the data
----------------------
```
model = KNeighborsClassifier(n_neighbors=5)
scores = cross_val_score(model, x, y, scoring='accuracy', cv=10)
print ("10-Fold Accuracy : ", scores.mean()*100)
model.fit(x_train,y_train)
print ("Testing Accuracy : ",model.score(x_test, y_test)*100)
predicted = model.predict(x)
```
Here **model** is an instance of KNeighborsClassifier method from sklearn.neighbors. 10 Fold Cross Validation is used to verify the results.
```
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(x[1],x[2], c=predicted)
ax2.set_title("KNearestNeighbours")
```
The learned data is plotted.
```
cm = metrics.confusion_matrix(y, predicted)
print (cm/len(y))
print (metrics.classification_report(y, predicted))
plt.show()
```
Compute confusion matrix to evaluate the accuracy of a classification and build a text report showing the main classification metrics.
| true |
code
| 0.645707 | null | null | null | null |
|
Universidade Federal do Rio Grande do Sul (UFRGS)
Programa de Pós-Graduação em Engenharia Civil (PPGEC)
# PEC00144: Experimental Methods in Civil Engineering
### Reading the serial port of an Arduino device
---
_Prof. Marcelo M. Rocha, Dr.techn._ [(ORCID)](https://orcid.org/0000-0001-5640-1020)
_Porto Alegre, RS, Brazil_
```
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import sys
import time
import serial
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from MRPy import MRPy
```
### 1. Setup serial communication
In order to run this notebook, the Python module ``pyserial`` must be installed.
To ensure the module availability, open a conda terminal and issue the command:
conda install -c anaconda pyserial
Before openning the serial port, verify with Arduino IDE which USB identifier the
board has be assigned (in Windows it has the form "COMxx", while in Linux it
it is something like "/dev/ttyXXXX").
```
#port = '/dev/ttyUSB0'
#baud = 9600
port = 'COM5' # change this address according to your computer
baud = 9600 # match this number with the Arduino's output baud rate
Ardn = serial.Serial(port, baud, timeout=1)
time.sleep(3) # this is important to give time for serial settling
```
### 2. Define function for reading one incoming line
```
def ReadSerial(nchar, nvar, nlines=1):
Ardn.write(str(nlines).encode())
data = np.zeros((nlines,nvar))
for k in range(nlines):
wait = True
while(wait):
if (Ardn.inWaiting() >= nchar):
wait = False
bdat = Ardn.readline()
sdat = bdat.decode()
sdat = sdat.replace('\n',' ').split()
data[k, :] = np.array(sdat[0:nvar], dtype='int')
return data
```
### 3. Acquire data lines from serial port
```
try:
data = ReadSerial(16, 2, nlines=64)
t = data[:,0]
LC = data[:,1]
Ardn.close()
print('Acquisition ok!')
except:
Ardn.close()
sys.exit('Acquisition failure!')
```
### 4. Create ``MRPy`` instance and save to file
```
ti = (t - t[0])/1000
LC = (LC + 1270)/2**23
data = MRPy.resampling(ti, LC)
data.to_file('read_HX711', form='excel')
print('Average sampling rate is {0:5.1f}Hz.'.format(data.fs))
print('Total record duration is {0:5.1f}Hz.'.format(data.Td))
print((2**23)*data.mean())
```
### 5. Data visualization
```
fig1 = data.plot_time(fig=1, figsize=(12,8), axis_t=[0, data.Td, -0.01, 0.01])
```
| true |
code
| 0.36352 | null | null | null | null |
|
```
import numpy as np
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
%matplotlib notebook
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
font = {'weight' : 'medium',
'size' : 13}
matplotlib.rc('font', **font)
import time
import concurrent.futures as cf
import warnings
warnings.filterwarnings("ignore")
import scipy.constants
mec2 = scipy.constants.value('electron mass energy equivalent in MeV')*1e6
c_light = scipy.constants.c
e_charge = scipy.constants.e
r_e = scipy.constants.value('classical electron radius')
```
### Parameters
```
gamma = 5000
rho = 1.5 # Bend radius in m
beta = (1-1/gamma**2)**(1/2)
sigma_x = 50e-6
sigma_z = 50e-6
# Entrance angle
phi = 0.1/rho
```
## code
```
from csr2d.core2 import psi_s, psi_x0_hat
import numpy as np
gamma = 5000
rho = 1.5 # Bend radius in m
beta = (1-1/gamma**2)**(1/2)
sigma_x = 50e-6
sigma_z = 50e-6
nz = 100
nx = 100
dz = (10*sigma_z) / (nz - 1)
dx = (10*sigma_x) / (nx - 1)
zvec = np.linspace(-5*sigma_z, 5*sigma_z, nz)
xvec = np.linspace(-5*sigma_x, 5*sigma_x, nx)
zm, xm = np.meshgrid(zvec, xvec, indexing='ij')
psi_s_grid = psi_s(zm, xm, beta)
psi_x_grid = psi_x0_hat(zm, xm, beta, dx)
from csr2d.core2 import psi_s, psi_x_hat, psi_x0_hat
from scipy.interpolate import RectBivariateSpline
from numba import njit, vectorize, float64
from csr2d.kick2 import green_meshes_hat, green_meshes
# Bypassing the beam, use smooth Gaussian distribution for testing
def lamb_2d(z,x):
return 1/(2*np.pi*sigma_x*sigma_z)* np.exp(-z**2 / 2 / sigma_z**2 - x**2 / 2 / sigma_x**2)
def lamb_2d_prime(z,x):
return 1/(2*np.pi*sigma_x*sigma_z)* np.exp(-z**2 / 2 / sigma_z**2 - x**2 / 2 / sigma_x**2) * (-z / sigma_z**2)
nz = 100
nx = 100
zvec = np.linspace(-5*sigma_z, 5*sigma_z, nz)
xvec = np.linspace(-5*sigma_x, 5*sigma_x, nx)
zm, xm = np.meshgrid(zvec, xvec, indexing='ij')
lambda_grid_filtered = lamb_2d(zm,xm)
lambda_grid_filtered_prime = lamb_2d_prime(zm,xm)
dz = (10*sigma_z) / (nz - 1)
dx = (10*sigma_x) / (nx - 1)
psi_s_grid = psi_s(zm, xm, beta)
psi_s_grid, psi_x_grid, zvec2, xvec2 = green_meshes_hat(nz, nx, dz, dx, rho=rho, beta=beta)
```
# Integral term code development
```
# Convolution for a specific observatino point only
@njit
def my_2d_convolve2(g1, g2, ix1, ix2):
d1, d2 = g1.shape
g2_flip = np.flip(g2)
g2_cut = g2_flip[d1-ix1:2*d1-ix1, d2-ix2:2*d2-ix2]
sums = 0
for i in range(d1):
for j in range(d2):
sums+= g1[i,j]*g2_cut[i,j]
return sums
#@njit
# njit doesn't like the condition grid and interpolation....
def transient_calc_lambda(phi, z_observe, x_observe, zvec, xvec, dz, dx, lambda_grid_filtered_prime, psi_s_grid, psi_x_grid):
x_observe_index = np.argmin(np.abs(xvec - x_observe))
#print('x_observe_index :', x_observe_index )
z_observe_index = np.argmin(np.abs(zvec - z_observe))
#print('z_observe_index :', z_observe_index )
# Boundary condition
temp = (x_observe - xvec)/rho
zi_vec = rho*( phi - beta*np.sqrt(temp**2 + 4*(1 + temp)*np.sin(phi/2)**2))
zo_vec = -beta*np.abs(x_observe - xvec)
condition_grid = np.array([(zvec > z_observe - zo_vec[i]) | (zvec < z_observe - zi_vec[i]) for i in range(len(xvec))])
lambda_grid_filtered_prime_bounded = np.where(condition_grid.T, 0, lambda_grid_filtered_prime)
conv_s = my_2d_convolve2(lambda_grid_filtered_prime_bounded, psi_s_grid, z_observe_index, x_observe_index)
conv_x = my_2d_convolve2(lambda_grid_filtered_prime_bounded, psi_x_grid, z_observe_index, x_observe_index)
##conv_s, conv_x = fftconvolve2(lambda_grid_filtered_prime_bounded, psi_s_grid, psi_x_grid)
#Ws_grid = (beta**2 / abs(rho)) * (conv_s) * (dz * dx)
#Wx_grid = (beta**2 / abs(rho)) * (conv_x) * (dz * dx)
#lambda_interp = RectBivariateSpline(zvec, xvec, lambda_grid_filtered) # lambda lives in the observation grid
#lambda_zi_vec = lambda_interp.ev( z_observe - zi_vec, xvec )
#psi_x_zi_vec = psi_x0(zi_vec/2/rho, temp, beta, dx)
#Wx_zi = (beta**2 / rho) * np.dot(psi_x_zi_vec, lambda_zi_vec)*dx
#lambda_zo_vec = lambda_interp.ev( z_observe - zo_vec, xvec )
#psi_x_zo_vec = psi_x0(zo_vec/2/rho, temp, beta, dx)
#Wx_zo = (beta**2 / rho) * np.dot(psi_x_zo_vec, lambda_zo_vec)*dx
#return Wx_grid[ z_observe_index ][ x_observe_index ], Wx_zi, Wx_zo
#return conv_x, Wx_zi, Wx_zo
return conv_x
#return condition_grid
@njit
def transient_calc_lambda_2(phi, z_observe, x_observe, zvec, xvec, dz, dx, lambda_grid_filtered_prime, psi_s_grid, psi_x_grid):
x_observe_index = np.argmin(np.abs(xvec - x_observe))
#print('x_observe_index :', x_observe_index )
z_observe_index = np.argmin(np.abs(zvec - z_observe))
#print('z_observe_index :', z_observe_index )
# Boundary condition
temp = (x_observe - xvec)/rho
zi_vec = rho*( phi - beta*np.sqrt(temp**2 + 4*(1 + temp)*np.sin(phi/2)**2))
zo_vec = -beta*np.abs(x_observe - xvec)
nz = len(zvec)
nx = len(xvec)
# Allocate array for histogrammed data
cond = np.zeros( (nz,nx) )
for i in range(nx):
cond[:,i] = (zvec > z_observe - zo_vec[i]) | (zvec < z_observe - zi_vec[i])
#condition_grid = np.array([(zvec < z_observe - zi_vec[i]) for i in range(len(xvec))])
#condition_grid = np.array([(zvec > z_observe - zo_vec[i]) | (zvec < z_observe - zi_vec[i]) for i in range(len(xvec))])
lambda_grid_filtered_prime_bounded = np.where(cond, 0, lambda_grid_filtered_prime)
conv_s = my_2d_convolve2(lambda_grid_filtered_prime_bounded, psi_s_grid, z_observe_index, x_observe_index)
conv_x = my_2d_convolve2(lambda_grid_filtered_prime_bounded, psi_x_grid, z_observe_index, x_observe_index)
return conv_x
```
# Applying the codes
### Note that numba-jitted code are slower the FIRST time
```
t1 = time.time()
r1 = transient_calc_lambda(phi, 2*sigma_z, sigma_x, zvec, xvec, dz, dx,lambda_grid_filtered_prime, psi_s_grid, psi_x_grid)
print(r1)
t2 = time.time()
print('Mapping takes:', t2-t1, 'sec')
t1 = time.time()
r1 = transient_calc_lambda_2(phi, 2*sigma_z, sigma_x, zvec, xvec, dz, dx,lambda_grid_filtered_prime, psi_s_grid, psi_x_grid)
print(r1)
t2 = time.time()
print('Mapping takes:', t2-t1, 'sec')
```
## super version for parallelism
```
def transient_calc_lambda_super(z_observe, x_observe):
return transient_calc_lambda(phi, z_observe, x_observe, zvec, xvec, dz, dx,lambda_grid_filtered_prime, psi_s_grid, psi_x_grid)
#@njit
@vectorize([float64(float64,float64)], target='parallel')
def transient_calc_lambda_2_super(z_observe, x_observe):
return transient_calc_lambda_2(phi, z_observe, x_observe, zvec, xvec, dz, dx,lambda_grid_filtered_prime, psi_s_grid, psi_x_grid)
t1 = time.time()
with cf.ProcessPoolExecutor(max_workers=20) as executor:
result = executor.map(transient_calc_lambda_super, zm.flatten(), xm.flatten())
g1 = np.array(list(result)).reshape(zm.shape)
t2 = time.time()
print('Mapping takes:', t2-t1, 'sec')
t1 = time.time()
g4 = transient_calc_lambda_boundary_super_new(zm,xm)
t2 = time.time()
print('Mapping takes:', t2-t1, 'sec')
fig, ax = plt.subplots(figsize=(8,8))
ax = plt.axes(projection='3d')
ax.plot_surface(zm*1e5, xm*1e5, yaya , cmap='inferno', zorder=1)
ax.set_xlabel(r'z $(10^{-5}m)$')
ax.set_ylabel(r'x $(10^{-5}m)$')
ax.set_zlabel(r'$W_x$ $(\times 10^3/m^2)$ ')
ax.zaxis.labelpad = 10
ax.set_title(r'$W_x$ benchmarking')
# To be fixed
from scipy.integrate import quad
def transient_calc_lambda_boundary_quad(phi, z_observe, x_observe, dx):
def integrand_zi(xp):
temp = (x_observe - xp)/rho
zi = rho*( phi - beta*np.sqrt(temp**2 + 4*(1 + temp)*np.sin(phi/2)**2))
#return psi_x_hat(zi/2/rho, temp, beta)*lamb_2d(z_observe - zi, xp)
return psi_x0_hat(zi/2/rho, temp, beta, dx)*lamb_2d(z_observe - zi, xp)
def integrand_zo(xp):
zo = -beta*np.abs(x_observe - xp)
#return psi_x_hat(zo/2/rho, temp, beta)*lamb_2d(z_observe - zo, xp)
return psi_x0_hat(zo/2/rho, temp, beta, dx)*lamb_2d(z_observe - zo, xp)
return quad(integrand_zi, -5*sigma_x, 5*sigma_x)[0]/dx
factor = (beta**2 / rho)*dx
diff = np.abs((g4.reshape(zm.shape) - g3.reshape(zm.shape))/g3.reshape(zm.shape) )* 100
diff = np.abs((g0 - g3.reshape(zm.shape))/g3.reshape(zm.shape)) * 100
g3.shape
fig, ax = plt.subplots(figsize=(8,8))
ax = plt.axes(projection='3d')
ax.plot_surface(zm*1e5, xm*1e5, factor*g3, cmap='inferno', zorder=1)
ax.set_xlabel(r'z $(10^{-5}m)$')
ax.set_ylabel(r'x $(10^{-5}m)$')
ax.set_zlabel(r'$W_x$ $(m^{-2}$) ')
ax.zaxis.labelpad = 10
ax.set_title(r'$W_x$ benchmarking')
fig, ax = plt.subplots(figsize=(8,8))
ax = plt.axes(projection='3d')
ax.plot_surface(zm*1e5, xm*1e5, diff, cmap='inferno', zorder=1)
ax.set_xlabel(r'z $(10^{-5}m)$')
ax.set_ylabel(r'x $(10^{-5}m)$')
ax.set_zlabel(r'$W_x$ $(\times 10^3/m^2)$ ')
ax.zaxis.labelpad = 10
ax.set_title(r'$W_x$ benchmarking')
ax.zaxis.set_scale('log')
plt.plot(diff[30:100,100])
```
| true |
code
| 0.423756 | null | null | null | null |
|
# 自动微分
:label:`sec_autograd`
正如我们在 :numref:`sec_calculus`中所说的那样,求导是几乎所有深度学习优化算法的关键步骤。
虽然求导的计算很简单,只需要一些基本的微积分。
但对于复杂的模型,手工进行更新是一件很痛苦的事情(而且经常容易出错)。
深度学习框架通过自动计算导数,即*自动微分*(automatic differentiation)来加快求导。
实际中,根据我们设计的模型,系统会构建一个*计算图*(computational graph),
来跟踪计算是哪些数据通过哪些操作组合起来产生输出。
自动微分使系统能够随后反向传播梯度。
这里,*反向传播*(backpropagate)意味着跟踪整个计算图,填充关于每个参数的偏导数。
## 一个简单的例子
作为一个演示例子,(**假设我们想对函数$y=2\mathbf{x}^{\top}\mathbf{x}$关于列向量$\mathbf{x}$求导**)。
首先,我们创建变量`x`并为其分配一个初始值。
```
import tensorflow as tf
x = tf.range(4, dtype=tf.float32)
x
```
[**在我们计算$y$关于$\mathbf{x}$的梯度之前,我们需要一个地方来存储梯度。**]
重要的是,我们不会在每次对一个参数求导时都分配新的内存。
因为我们经常会成千上万次地更新相同的参数,每次都分配新的内存可能很快就会将内存耗尽。
注意,一个标量函数关于向量$\mathbf{x}$的梯度是向量,并且与$\mathbf{x}$具有相同的形状。
```
x = tf.Variable(x)
```
(**现在让我们计算$y$。**)
```
# 把所有计算记录在磁带上
with tf.GradientTape() as t:
y = 2 * tf.tensordot(x, x, axes=1)
y
```
`x`是一个长度为4的向量,计算`x`和`x`的点积,得到了我们赋值给`y`的标量输出。
接下来,我们[**通过调用反向传播函数来自动计算`y`关于`x`每个分量的梯度**],并打印这些梯度。
```
x_grad = t.gradient(y, x)
x_grad
```
函数$y=2\mathbf{x}^{\top}\mathbf{x}$关于$\mathbf{x}$的梯度应为$4\mathbf{x}$。
让我们快速验证这个梯度是否计算正确。
```
x_grad == 4 * x
```
[**现在让我们计算`x`的另一个函数。**]
```
with tf.GradientTape() as t:
y = tf.reduce_sum(x)
t.gradient(y, x) # 被新计算的梯度覆盖
```
## 非标量变量的反向传播
当`y`不是标量时,向量`y`关于向量`x`的导数的最自然解释是一个矩阵。
对于高阶和高维的`y`和`x`,求导的结果可以是一个高阶张量。
然而,虽然这些更奇特的对象确实出现在高级机器学习中(包括[**深度学习中**]),
但当我们调用向量的反向计算时,我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。
这里(**,我们的目的不是计算微分矩阵,而是单独计算批量中每个样本的偏导数之和。**)
```
with tf.GradientTape() as t:
y = x * x
t.gradient(y, x) # 等价于y=tf.reduce_sum(x*x)
```
## 分离计算
有时,我们希望[**将某些计算移动到记录的计算图之外**]。
例如,假设`y`是作为`x`的函数计算的,而`z`则是作为`y`和`x`的函数计算的。
想象一下,我们想计算`z`关于`x`的梯度,但由于某种原因,我们希望将`y`视为一个常数,
并且只考虑到`x`在`y`被计算后发挥的作用。
在这里,我们可以分离`y`来返回一个新变量`u`,该变量与`y`具有相同的值,
但丢弃计算图中如何计算`y`的任何信息。
换句话说,梯度不会向后流经`u`到`x`。
因此,下面的反向传播函数计算`z=u*x`关于`x`的偏导数,同时将`u`作为常数处理,
而不是`z=x*x*x`关于`x`的偏导数。
```
# 设置persistent=True来运行t.gradient多次
with tf.GradientTape(persistent=True) as t:
y = x * x
u = tf.stop_gradient(y)
z = u * x
x_grad = t.gradient(z, x)
x_grad == u
```
由于记录了`y`的计算结果,我们可以随后在`y`上调用反向传播,
得到`y=x*x`关于的`x`的导数,即`2*x`。
```
t.gradient(y, x) == 2 * x
```
## Python控制流的梯度计算
使用自动微分的一个好处是:
[**即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度**]。
在下面的代码中,`while`循环的迭代次数和`if`语句的结果都取决于输入`a`的值。
```
def f(a):
b = a * 2
while tf.norm(b) < 1000:
b = b * 2
if tf.reduce_sum(b) > 0:
c = b
else:
c = 100 * b
return c
```
让我们计算梯度。
```
a = tf.Variable(tf.random.normal(shape=()))
with tf.GradientTape() as t:
d = f(a)
d_grad = t.gradient(d, a)
d_grad
```
我们现在可以分析上面定义的`f`函数。
请注意,它在其输入`a`中是分段线性的。
换言之,对于任何`a`,存在某个常量标量`k`,使得`f(a)=k*a`,其中`k`的值取决于输入`a`。
因此,我们可以用`d/a`验证梯度是否正确。
```
d_grad == d / a
```
## 小结
* 深度学习框架可以自动计算导数:我们首先将梯度附加到想要对其计算偏导数的变量上。然后我们记录目标值的计算,执行它的反向传播函数,并访问得到的梯度。
## 练习
1. 为什么计算二阶导数比一阶导数的开销要更大?
1. 在运行反向传播函数之后,立即再次运行它,看看会发生什么。
1. 在控制流的例子中,我们计算`d`关于`a`的导数,如果我们将变量`a`更改为随机向量或矩阵,会发生什么?
1. 重新设计一个求控制流梯度的例子,运行并分析结果。
1. 使$f(x)=\sin(x)$,绘制$f(x)$和$\frac{df(x)}{dx}$的图像,其中后者不使用$f'(x)=\cos(x)$。
[Discussions](https://discuss.d2l.ai/t/1757)
| true |
code
| 0.505615 | null | null | null | null |
|
# Rossman data preparation
To illustrate the techniques we need to apply before feeding all the data to a Deep Learning model, we are going to take the example of the [Rossmann sales Kaggle competition](https://www.kaggle.com/c/rossmann-store-sales). Given a wide range of information about a store, we are going to try predict their sale number on a given day. This is very useful to be able to manage stock properly and be able to properly satisfy the demand without wasting anything. The official training set was giving a lot of informations about various stores in Germany, but it was also allowed to use additional data, as long as it was made public and available to all participants.
We are going to reproduce most of the steps of one of the winning teams that they highlighted in [Entity Embeddings of Categorical Variables](https://arxiv.org/pdf/1604.06737.pdf). In addition to the official data, teams in the top of the leaderboard also used information about the weather, the states of the stores or the Google trends of those days. We have assembled all that additional data in one file available for download [here](http://files.fast.ai/part2/lesson14/rossmann.tgz) if you want to replicate those steps.
### A first look at the data
First things first, let's import everything we will need.
```
from fastai.tabular.all import *
```
If you have download the previous file and decompressed it in a folder named rossmann in the fastai data folder, you should see the following list of files with this instruction:
```
path = Config().data/'rossmann'
path.ls()
```
The data that comes from Kaggle is in 'train.csv', 'test.csv', 'store.csv' and 'sample_submission.csv'. The other files are the additional data we were talking about. Let's start by loading everything using pandas.
```
table_names = ['train', 'store', 'store_states', 'state_names', 'googletrend', 'weather', 'test']
tables = [pd.read_csv(path/f'{fname}.csv', low_memory=False) for fname in table_names]
train, store, store_states, state_names, googletrend, weather, test = tables
```
To get an idea of the amount of data available, let's just look at the length of the training and test tables.
```
len(train), len(test)
```
So we have more than one million records available. Let's have a look at what's inside:
```
train.head()
```
The `Store` column contains the id of the stores, then we are given the id of the day of the week, the exact date, if the store was open on that day, if there were any promotion in that store during that day, and if it was a state or school holiday. The `Customers` column is given as an indication, and the `Sales` column is what we will try to predict.
If we look at the test table, we have the same columns, minus `Sales` and `Customers`, and it looks like we will have to predict on dates that are after the ones of the train table.
```
test.head()
```
The other table given by Kaggle contains some information specific to the stores: their type, what the competition looks like, if they are engaged in a permanent promotion program, and if so since then.
```
store.head().T
```
Now let's have a quick look at our four additional dataframes. `store_states` just gives us the abbreviated name of the sate of each store.
```
store_states.head()
```
We can match them to their real names with `state_names`.
```
state_names.head()
```
Which is going to be necessary if we want to use the `weather` table:
```
weather.head().T
```
Lastly the googletrend table gives us the trend of the brand in each state and in the whole of Germany.
```
googletrend.head()
```
Before we apply the fastai preprocessing, we will need to join the store table and the additional ones with our training and test table. Then, as we saw in our first example in chapter 1, we will need to split our variables between categorical and continuous. Before we do that, though, there is one type of variable that is a bit different from the others: dates.
We could turn each particular day in a category but there are cyclical information in dates we would miss if we did that. We already have the day of the week in our tables, but maybe the day of the month also bears some significance. People might be more inclined to go shopping at the beggining or the end of the month. The number of the week/month is also important to detect seasonal influences.
Then we will try to exctract meaningful information from those dates. For instance promotions on their own are important inputs, but maybe the number of running weeks with promotion is another useful information as it will influence customers. A state holiday in itself is important, but it's more significant to know if we are the day before or after such a holiday as it will impact sales. All of those might seem very specific to this dataset, but you can actually apply them in any tabular data containing time information.
This first step is called feature-engineering and is extremely important: your model will try to extract useful information from your data but any extra help you can give it in advance is going to make training easier, and the final result better. In Kaggle Competitions using tabular data, it's often the way people prepared their data that makes the difference in the final leaderboard, not the exact model used.
### Feature Engineering
#### Merging tables
To merge tables together, we will use this little helper function that relies on the pandas library. It will merge the tables `left` and `right` by looking at the column(s) which names are in `left_on` and `right_on`: the information in `right` will be added to the rows of the tables in `left` when the data in `left_on` inside `left` is the same as the data in `right_on` inside `right`. If `left_on` and `right_on` are the same, we don't have to pass `right_on`. We keep the fields in `right` that have the same names as fields in `left` and add a `_y` suffix (by default) to those field names.
```
def join_df(left, right, left_on, right_on=None, suffix='_y'):
if right_on is None: right_on = left_on
return left.merge(right, how='left', left_on=left_on, right_on=right_on,
suffixes=("", suffix))
```
First, let's replace the state names in the weather table by the abbreviations, since that's what is used in the other tables.
```
weather = join_df(weather, state_names, "file", "StateName")
weather[['file', 'Date', 'State', 'StateName']].head()
```
To double-check the merge happened without incident, we can check that every row has a `State` with this line:
```
len(weather[weather.State.isnull()])
```
We can now safely remove the columns with the state names (`file` and `StateName`) since they we'll use the short codes.
```
weather.drop(columns=['file', 'StateName'], inplace=True)
```
To add the weather informations to our `store` table, we first use the table `store_states` to match a store code with the corresponding state, then we merge with our weather table.
```
store = join_df(store, store_states, 'Store')
store = join_df(store, weather, 'State')
```
And again, we can check if the merge went well by looking if new NaNs where introduced.
```
len(store[store.Mean_TemperatureC.isnull()])
```
Next, we want to join the `googletrend` table to this `store` table. If you remember from our previous look at it, it's not exactly in the same format:
```
googletrend.head()
```
We will need to change the column with the states and the columns with the dates:
- in the column `fil`, the state names contain `Rossmann_DE_XX` with `XX` being the code of the state, so we want to remove `Rossmann_DE`. We will do this by creating a new column containing the last part of a split of the string by '\_'.
- in the column `week`, we will extract the date corresponding to the beginning of the week in a new column by taking the last part of a split on ' - '.
In pandas, creating a new column is very easy: you just have to define them.
```
googletrend['Date'] = googletrend.week.str.split(' - ', expand=True)[0]
googletrend['State'] = googletrend.file.str.split('_', expand=True)[2]
googletrend.head()
```
Let's check everything went well by looking at the values in the new `State` column of our `googletrend` table.
```
store['State'].unique(),googletrend['State'].unique()
```
We have two additional values in the second (`None` and 'SL') but this isn't a problem since they'll be ignored when we join. One problem however is that 'HB,NI' in the first table is named 'NI' in the second one, so we need to change that.
```
googletrend.loc[googletrend.State=='NI', "State"] = 'HB,NI'
```
Why do we have a `None` in state? As we said before, there is a global trend for Germany that corresponds to `Rosmann_DE` in the field `file`. For those, the previous split failed which gave the `None` value. We will keep this global trend and put it in a new column.
```
trend_de = googletrend[googletrend.file == 'Rossmann_DE'][['Date', 'trend']]
```
Then we can merge it with the rest of our trends, by adding the suffix '\_DE' to know it's the general trend.
```
googletrend = join_df(googletrend, trend_de, 'Date', suffix='_DE')
```
Then at this stage, we can remove the columns `file` and `week`since they won't be useful anymore, as well as the rows where `State` is `None` (since they correspond to the global trend that we saved in another column).
```
googletrend.drop(columns=['file', 'week'], axis=1, inplace=True)
googletrend = googletrend[~googletrend['State'].isnull()]
```
The last thing missing to be able to join this with or store table is to extract the week from the date in this table and in the store table: we need to join them on week values since each trend is given for the full week that starts on the indicated date. This is linked to the next topic in feature engineering: extracting dateparts.
#### Adding dateparts
If your table contains dates, you will need to split the information there in several column for your Deep Learning model to be able to train properly. There is the basic stuff, such as the day number, week number, month number or year number, but anything that can be relevant to your problem is also useful. Is it the beginning or the end of the month? Is it a holiday?
To help with this, the fastai library as a convenience function called `add_datepart`. It will take a dataframe and a column you indicate, try to read it as a date, then add all those new columns. If we go back to our `googletrend` table, we now have gour columns.
```
googletrend.head()
```
If we add the dateparts, we will gain a lot more
```
googletrend = add_datepart(googletrend, 'Date', drop=False)
googletrend.head().T
```
We chose the option `drop=False` as we want to keep the `Date` column for now. Another option is to add the `time` part of the date, but it's not relevant to our problem here.
Now we can join our Google trends with the information in the `store` table, it's just a join on \['Week', 'Year'\] once we apply `add_datepart` to that table. Note that we only keep the initial columns of `googletrend` with `Week` and `Year` to avoid all the duplicates.
```
googletrend = googletrend[['trend', 'State', 'trend_DE', 'Week', 'Year']]
store = add_datepart(store, 'Date', drop=False)
store = join_df(store, googletrend, ['Week', 'Year', 'State'])
```
At this stage, `store` contains all the information about the stores, the weather on that day and the Google trends applicable. We only have to join it with our training and test table. We have to use `make_date` before being able to execute that merge, to convert the `Date` column of `train` and `test` to proper date format.
```
make_date(train, 'Date')
make_date(test, 'Date')
train_fe = join_df(train, store, ['Store', 'Date'])
test_fe = join_df(test, store, ['Store', 'Date'])
```
#### Elapsed times
Another feature that can be useful is the elapsed time before/after a certain event occurs. For instance the number of days since the last promotion or before the next school holiday. Like for the date parts, there is a fastai convenience function that will automatically add them.
One thing to take into account here is that you will need to use that function on the whole time series you have, even the test data: there might be a school holiday that takes place during the training data and it's going to impact those new features in the test data.
```
all_ftrs = train_fe.append(test_fe, sort=False)
```
We will consider the elapsed times for three events: 'Promo', 'StateHoliday' and 'SchoolHoliday'. Note that those must correspondon to booleans in your dataframe. 'Promo' and 'SchoolHoliday' already are (only 0s and 1s) but 'StateHoliday' has multiple values.
```
all_ftrs['StateHoliday'].unique()
```
If we refer to the explanation on Kaggle, 'b' is for Easter, 'c' for Christmas and 'a' for the other holidays. We will just converts this into a boolean that flags any holiday.
```
all_ftrs.StateHoliday = all_ftrs.StateHoliday!='0'
```
Now we can add, for each store, the number of days since or until the next promotion, state or school holiday. This will take a little while since the whole table is big.
```
all_ftrs = add_elapsed_times(all_ftrs, ['Promo', 'StateHoliday', 'SchoolHoliday'],
date_field='Date', base_field='Store')
```
It added a four new features. If we look at 'StateHoliday' for instance:
```
[c for c in all_ftrs.columns if 'StateHoliday' in c]
```
The column 'AfterStateHoliday' contains the number of days since the last state holiday, 'BeforeStateHoliday' the number of days until the next one. As for 'StateHoliday_bw' and 'StateHoliday_fw', they contain the number of state holidays in the past or future seven days respectively. The same four columns have been added for 'Promo' and 'SchoolHoliday'.
Now that we have added those features, we can split again our tables between the training and the test one.
```
train_df = all_ftrs.iloc[:len(train_fe)]
test_df = all_ftrs.iloc[len(train_fe):]
```
One last thing the authors of this winning solution did was to remove the rows with no sales, which correspond to exceptional closures of the stores. This might not have been a good idea since even if we don't have access to the same features in the test data, it can explain why we have some spikes in the training data.
```
train_df = train_df[train_df.Sales != 0.]
```
We will use those for training but since all those steps took a bit of time, it's a good idea to save our progress until now. We will just pickle those tables on the hard drive.
```
train_df.to_pickle(path/'train_clean')
test_df.to_pickle(path/'test_clean')
```
| true |
code
| 0.290352 | null | null | null | null |
|
* [1.0 - Introduction](#1.0---Introduction)
- [1.1 - Library imports and loading the data from SQL to pandas](#1.1---Library-imports-and-loading-the-data-from-SQL-to-pandas)
* [2.0 - Data Cleaning](#2.0---Data-Cleaning)
- [2.1 - Pre-cleaning, investigating data types](#2.1---Pre-cleaning,-investigating-data-types)
- [2.2 - Dealing with non-numerical values](#2.2---Dealing-with-non-numerical-values)
* [3.0 - Creating New Features](#)
- [3.1 - Creating the 'gender' column](#3.1---Creating-the-'gender'-column)
- [3.2 - Categorizing job titles](#3.2---Categorizing-job-titles)
* [4.0 - Data Analysis and Visualizations](#4.0---Data-Analysis-and-Visualizations)
- [4.1 - Overview of the gender gap](#4.1---Overview-of-the-gender-gap)
- [4.2 - Exploring the year column](#4.2---Exploring-the-year-column)
- [4.3 - Full time vs. part time employees](#4.3---Full-time-vs.-part-time-employees)
- [4.4 - Breaking down the total pay](#4.4---Breaking-down-the-total-pay)
- [4.5 - Breaking down the base pay by job category](#4.5---Breaking-down-the-base-pay-by-job-category)
- [4.6 - Gender representation by job category](#4.6---Gender-representation-by-job-category)
- [4.7 - Significance testing by exact job title](#4.7---Significance-testing-by-exact-job-title)
* [5.0 - San Francisco vs. Newport Beach](#5.0---San Francisco-vs.-Newport-Beach)
- [5.1 - Part time vs. full time workers](#5.1---Part-time-vs.-full-time-workers)
- [5.2 - Comparisons by job cateogry](#5.2---Comparisons-by-job-cateogry)
- [5.3 - Gender representation by job category](#5.3---Gender-representation-by-job-category)
* [6.0 - Conclusion](#6.0---Conclusion)
### 1.0 - Introduction
In this notebook, I will focus on data analysis and preprocessing for the gender wage gap. Specifically, I am going to focus on public jobs in the city of San Francisco and Newport Beach. This data set is publically available on [Kaggle](https://www.kaggle.com/kaggle/sf-salaries) and [Transparent California](https://transparentcalifornia.com/).
I also created a web application based on this dataset. You can play arround with it [here](https://gendergapvisualization.herokuapp.com/). For a complete list of requirements and files used for my web app, check out my GitHub repository [here](https://github.com/sengkchu/gendergapvisualization).
In this notebook following questions will be explored:
+ Is there an overall gender wage gap for public jobs in San Francisco?
+ Is the gender gap really 78 cents on the dollar?
+ Is there a gender wage gap for full time employees?
+ Is there a gender wage gap for part time employees?
+ Is there a gender wage gap if the employees were grouped by job categories?
+ Is there a gender wage gap if the employees were grouped by exact job title?
+ If the gender wage gap exists, is the data statistically significant?
+ If the gender wage gap exists, how does the gender wage gap in San Francisco compare with more conservative cities in California?
Lastly, I want to mention that I am not affiliated with any political group, everything I write in this project is based on my perspective of the data alone.
#### 1.1 - Library imports and loading the data from SQL to pandas
The SQL database is about 18 megabytes, which is small enough for my computer to handle. So I've decided to just load the entire database into memory using pandas. However, I created a function that takes in a SQL query and returns the result as a pandas dataframe just in case I need to use SQL queries.
```
import pandas as pd
import numpy as np
import sqlite3
import matplotlib.pyplot as plt
import seaborn as sns
import gender_guesser.detector as gender
import time
import collections
%matplotlib inline
sns.set(font_scale=1.5)
def run_query(query):
with sqlite3.connect('database.sqlite') as conn:
return pd.read_sql(query, conn)
#Read the data from SQL->Pandas
q1 = '''
SELECT * FROM Salaries
'''
data = run_query(q1)
data.head()
```
### 2.0 - Data Cleaning
Fortunately, this data set is already very clean. However, we should still look into every column. Specifically, we are interested in the data types of each column, and check for null values within the rows.
#### 2.1 - Pre-cleaning, investigating data types
Before we do anything to the dataframe, we are going to simply explore the data a little bit.
```
data.dtypes
data['JobTitle'].nunique()
```
There is no gender column, so we'll have to create one. In addition, we'll need to reduce the number of unique values in the `'JobTitle'` column. `'BasePay'`, `'OvertimePay'`, `'OtherPay'`, and `'Benefits'` are all object columns. We'll need to find a way to covert these into numeric values.
Let's take a look at the rest of the columns using the `.value_counts()` method.
```
data['Year'].value_counts()
data['Notes'].value_counts()
data['Agency'].value_counts()
data['Status'].value_counts()
```
It looks like the data is split into 4 years. The `'Notes'` column is empty for 148654 rows, so we should just remove it. The `'Agency'` column is also not useful, because we already know the data is for San Francisco.
The `'Status'` column shows a separation for full time employees and part time employees. We should leave that alone for now.
#### 2.2 - Dealing with non-numerical values
Let's tackle the object columns first, we are going to convert everything into integers using the `pandas.to_numeric()` function. If we run into any errors, the returned value will be NaN.
```
def process_pay(df):
cols = ['BasePay','OvertimePay', 'OtherPay', 'Benefits']
print('Checking for nulls:')
for col in cols:
df[col] = pd.to_numeric(df[col], errors ='coerce')
print(len(col)*'-')
print(col)
print(len(col)*'-')
print(df[col].isnull().value_counts())
return df
data = process_pay(data.copy())
```
Looking at our results above, we found 609 null values in `BasePay` and 36163 null values in `Benefits`. We are going to drop the rows with null values in `BasePay`. Not everyone will recieve benefits for their job, so it makes more sense to fill in the null values for `Benefits` with zeroes.
```
def process_pay2(df):
df['Benefits'] = df['Benefits'].fillna(0)
df = df.dropna()
print(df['BasePay'].isnull().value_counts())
return df
data = process_pay2(data)
```
Lastly, let's drop the `Agency` and `Notes` columns as they do not provide any information.
```
data = data.drop(columns=['Agency', 'Notes'])
```
### 3.0 - Creating New Features
Unfortunately, this data set does not include demographic information. Since this project is focused on investigating the gender wage gap, we need a way to classify a person's gender. Furthermore, the `JobTitle` column has 2159 unique values. We'll need to simplify this column.
#### 3.1 - Creating the 'gender' column
Due to the limitations of this data set. We'll have to assume the gender of the employee by using their first name. The `gender_guesser` library is very useful for this.
```
#Create the 'Gender' column based on employee's first name.
d = gender.Detector(case_sensitive=False)
data['FirstName'] = data['EmployeeName'].str.split().apply(lambda x: x[0])
data['Gender'] = data['FirstName'].apply(lambda x: d.get_gender(x))
data['Gender'].value_counts()
```
We are just going to remove employees with ambiguous or gender neutral first names from our analysis.
```
#Retain data with 'male' and 'female' names.
male_female_only = data[(data['Gender'] == 'male') | (data['Gender'] == 'female')].copy()
male_female_only['Gender'].value_counts()
```
#### 3.2 - Categorizing job titles
Next, we'll have to simplify the `JobTitles` column. To do this, we'll use the brute force method. I created an ordered dictionary with keywords and their associated job category. The generic titles are at the bottom of the dictionary, and the more specific titles are at the top of the dictionary. Then we are going to use a for loop in conjunction with the `.map()` method on the column.
I used the same labels as this [kernel](https://www.kaggle.com/mevanoff24/data-exploration-predicting-salaries) on Kaggle, but I heavily modified the code for readability.
```
def find_job_title2(row):
#Prioritize specific titles on top
titles = collections.OrderedDict([
('Police',['police', 'sherif', 'probation', 'sergeant', 'officer', 'lieutenant']),
('Fire', ['fire']),
('Transit',['mta', 'transit']),
('Medical',['anesth', 'medical', 'nurs', 'health', 'physician', 'orthopedic', 'pharm', 'care']),
('Architect', ['architect']),
('Court',['court', 'legal']),
('Mayor Office', ['mayoral']),
('Library', ['librar']),
('Public Works', ['public']),
('Attorney', ['attorney']),
('Custodian', ['custodian']),
('Gardener', ['garden']),
('Recreation Leader', ['recreation']),
('Automotive',['automotive', 'mechanic', 'truck']),
('Engineer',['engineer', 'engr', 'eng', 'program']),
('General Laborer',['general laborer', 'painter', 'inspector', 'carpenter', 'electrician', 'plumber', 'maintenance']),
('Food Services', ['food serv']),
('Clerk', ['clerk']),
('Porter', ['porter']),
('Airport Staff', ['airport']),
('Social Worker',['worker']),
('Guard', ['guard']),
('Assistant',['aide', 'assistant', 'secretary', 'attendant']),
('Analyst', ['analy']),
('Manager', ['manager'])
])
#Loops through the dictionaries
for group, keywords in titles.items():
for keyword in keywords:
if keyword in row.lower():
return group
return 'Other'
start_time = time.time()
male_female_only["Job_Group"] = male_female_only["JobTitle"].map(find_job_title2)
print("--- Run Time: %s seconds ---" % (time.time() - start_time))
male_female_only['Job_Group'].value_counts()
```
### 4.0 - Data Analysis and Visualizations
In this section, we are going to use the data to answer the questions stated in the [introduction section](#1.0---Introduction).
#### 4.1 - Overview of the gender gap
Let's begin by splitting the data set in half, one for females and one for males. Then we'll plot the overall income distribution using kernel density estimation based on the gausian function.
```
fig = plt.figure(figsize=(10, 5))
male_only = male_female_only[male_female_only['Gender'] == 'male']
female_only = male_female_only[male_female_only['Gender'] == 'female']
ax = sns.kdeplot(male_only['TotalPayBenefits'], color ='Blue', label='Male', shade=True)
ax = sns.kdeplot(female_only['TotalPayBenefits'], color='Red', label='Female', shade=True)
plt.yticks([])
plt.title('Overall Income Distribution')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay + Benefits ($)')
plt.xlim(0, 350000)
plt.show()
```
The income distribution plot is bimodal. In addition, we see a gender wage gap in favor of males in between the ~110000 and the ~275000 region. But, this plot doesn't capture the whole story. We need to break down the data some more. But first, let's explore the percentage of employees based on gender.
```
fig = plt.figure(figsize=(5, 5))
colors = ['#AFAFF5', '#EFAFB5']
labels = ['Male', 'Female']
sizes = [len(male_only), len(female_only)]
explode = (0.05, 0)
sns.set(font_scale=1.5)
ax = plt.pie(sizes, labels=labels, explode=explode, colors=colors, shadow=True, startangle=90, autopct='%1.f%%')
plt.title('Estimated Percentages of Employees: Overall')
plt.show()
```
Another key factor we have to consider is the number of employees. How do we know if there are simply more men working at higher paying jobs? How can we determine if social injustice has occured?
The chart above only tells us the total percentage of employees across all job categories, but it does give us an overview of the data.
#### 4.2 - Exploring the year column
The data set contain information on employees between 2011-2014. Let's take a look at an overview of the income based on the `Year` column regardless of gender.
```
data_2011 = male_female_only[male_female_only['Year'] == 2011]
data_2012 = male_female_only[male_female_only['Year'] == 2012]
data_2013 = male_female_only[male_female_only['Year'] == 2013]
data_2014 = male_female_only[male_female_only['Year'] == 2014]
plt.figure(figsize=(10,7.5))
ax = plt.boxplot([data_2011['TotalPayBenefits'].values, data_2012['TotalPayBenefits'].values, \
data_2013['TotalPayBenefits'].values, data_2014['TotalPayBenefits'].values])
plt.ylim(0, 350000)
plt.xticks([1, 2, 3, 4], ['2011', '2012', '2013', '2014'])
plt.xlabel('Year')
plt.ylabel('Total Pay + Benefits ($)')
plt.tight_layout()
```
From the boxplots, we see that the total pay is increasing for every year. We'll have to consider inflation in our analysis. In addition, it is very possible for an employee to stay at their job for multiple years. We don't want to double sample on these employees.
To simplify the data for the purpose of investigating the gender gap. It makes more sense to only choose only one year for our analysis. From our data exploration, we noticed that the majority of the `status` column was blank. Let's break the data down by year using the `.value_counts()` method.
```
years = ['2011', '2012', '2013', '2014']
all_data = [data_2011, data_2012, data_2013, data_2014]
for i in range(4):
print(len(years[i])*'-')
print(years[i])
print(len(years[i])*'-')
print(all_data[i]['Status'].value_counts())
```
The status of the employee is critical to our analysis, only year 2014 has this information. So it makes sense to focus on analysis on 2014.
```
data_2014_FT = data_2014[data_2014['Status'] == 'FT']
data_2014_PT = data_2014[data_2014['Status'] == 'PT']
```
#### 4.3 - Full time vs. part time employees
Let's take a look at the kernal density estimation plot for part time and full time employees.
```
fig = plt.figure(figsize=(10, 5))
ax = sns.kdeplot(data_2014_PT['TotalPayBenefits'], color = 'Orange', label='Part Time Workers', shade=True)
ax = sns.kdeplot(data_2014_FT['TotalPayBenefits'], color = 'Green', label='Full Time Workers', shade=True)
plt.yticks([])
plt.title('Part Time Workers vs. Full Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay + Benefits ($)')
plt.xlim(0, 350000)
plt.show()
```
If we split the data by employment status, we can see that the kernal distribution plot is no longer bimodal. Next, let's see how these two plots look if we seperate the data by gender.
```
fig = plt.figure(figsize=(10, 10))
fig.subplots_adjust(hspace=.5)
#Generate the top plot
male_only = data_2014_FT[data_2014_FT['Gender'] == 'male']
female_only = data_2014_FT[data_2014_FT['Gender'] == 'female']
ax = fig.add_subplot(2, 1, 1)
ax = sns.kdeplot(male_only['TotalPayBenefits'], color ='Blue', label='Male', shade=True)
ax = sns.kdeplot(female_only['TotalPayBenefits'], color='Red', label='Female', shade=True)
plt.title('Full Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay & Benefits ($)')
plt.xlim(0, 350000)
plt.yticks([])
#Generate the bottom plot
male_only = data_2014_PT[data_2014_PT['Gender'] == 'male']
female_only = data_2014_PT[data_2014_PT['Gender'] == 'female']
ax2 = fig.add_subplot(2, 1, 2)
ax2 = sns.kdeplot(male_only['TotalPayBenefits'], color ='Blue', label='Male', shade=True)
ax2 = sns.kdeplot(female_only['TotalPayBenefits'], color='Red', label='Female', shade=True)
plt.title('Part Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay & Benefits ($)')
plt.xlim(0, 350000)
plt.yticks([])
plt.show()
```
For part time workers, the KDE plot is nearly identical for both males and females.
For full time workers, we still see a gender gap. We'll need to break down the data some more.
#### 4.4 - Breaking down the total pay
We used total pay including benefits for the x-axis for the KDE plot in the previous section. Is this a fair way to analyze the data? What if men work more overtime hours than women? Can we break down the data some more?
```
male_only = data_2014_FT[data_2014_FT['Gender'] == 'male']
female_only = data_2014_FT[data_2014_FT['Gender'] == 'female']
fig = plt.figure(figsize=(10, 15))
fig.subplots_adjust(hspace=.5)
#Generate the top plot
ax = fig.add_subplot(3, 1, 1)
ax = sns.kdeplot(male_only['OvertimePay'], color ='Blue', label='Male', shade=True)
ax = sns.kdeplot(female_only['OvertimePay'], color='Red', label='Female', shade=True)
plt.title('Full Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Overtime Pay ($)')
plt.xlim(0, 60000)
plt.yticks([])
#Generate the middle plot
ax2 = fig.add_subplot(3, 1, 2)
ax2 = sns.kdeplot(male_only['Benefits'], color ='Blue', label='Male', shade=True)
ax2 = sns.kdeplot(female_only['Benefits'], color='Red', label='Female', shade=True)
plt.ylabel('Density of Employees')
plt.xlabel('Benefits Only ($)')
plt.xlim(0, 75000)
plt.yticks([])
#Generate the bottom plot
ax3 = fig.add_subplot(3, 1, 3)
ax3 = sns.kdeplot(male_only['BasePay'], color ='Blue', label='Male', shade=True)
ax3 = sns.kdeplot(female_only['BasePay'], color='Red', label='Female', shade=True)
plt.ylabel('Density of Employees')
plt.xlabel('Base Pay Only ($)')
plt.xlim(0, 300000)
plt.yticks([])
plt.show()
```
We see a gender gap for all three plots above. Looks like we'll have to dig even deeper and analyze the data by job cateogries.
But first, let's take a look at the overall correlation for the data set.
```
data_2014_FT.corr()
```
The correlation table above uses Pearson's R to determine the values. The `BasePay` and `Benefits` column are very closely related. We can visualize this relationship using a scatter plot.
```
fig = plt.figure(figsize=(10, 5))
ax = plt.scatter(data_2014_FT['BasePay'], data_2014_FT['Benefits'])
plt.ylabel('Benefits ($)')
plt.xlabel('Base Pay ($)')
plt.show()
```
This makes a lot of sense because an employee's benefits is based on a percentage of their base pay. The San Francisco Human Resources department includes this information on their website [here](http://sfdhr.org/benefits-overview).
As we move further into our analysis of the data, it makes the most sense to focus on the `BasePay` column. Both `Benefits` and `OvertimePay` are dependent of the `BasePay`.
#### 4.5 - Breaking down the base pay by job category
Next we'll analyze the base pay of full time workers by job category.
```
pal = sns.diverging_palette(0, 255, n=2)
ax = sns.factorplot(x='BasePay', y='Job_Group', hue='Gender', data=data_2014_FT,
size=10, kind="bar", palette=pal, ci=None)
plt.title('Full Time Workers')
plt.xlabel('Base Pay ($)')
plt.ylabel('Job Group')
plt.show()
```
At a glance, we can't really draw any conclusive statements about the gender wage gap. Some job categories favor females, some favor males. It really depends on what job group the employee is actually in. Maybe it makes more sense to calculate the the difference between these two bars.
```
salaries_by_group = pd.pivot_table(data = data_2014_FT,
values = 'BasePay',
columns = 'Job_Group', index='Gender',
aggfunc = np.mean)
count_by_group = pd.pivot_table(data = data_2014_FT,
values = 'Id',
columns = 'Job_Group', index='Gender',
aggfunc = len)
salaries_by_group
fig = plt.figure(figsize=(10, 15))
sns.set(font_scale=1.5)
differences = (salaries_by_group.loc['female'] - salaries_by_group.loc['male'])*100/salaries_by_group.loc['male']
labels = differences.sort_values().index
x = differences.sort_values()
y = [i for i in range(len(differences))]
palette = sns.diverging_palette(240, 10, n=28, center ='dark')
ax = sns.barplot(x, y, orient = 'h', palette = palette)
#Draws the two arrows
bbox_props = dict(boxstyle="rarrow,pad=0.3", fc="white", ec="black", lw=1)
t = plt.text(5.5, 12, "Higher pay for females", ha="center", va="center", rotation=0,
size=15,
bbox=bbox_props)
bbox_props2 = dict(boxstyle="larrow,pad=0.3", fc="white", ec="black", lw=1)
t = plt.text(-5.5, 12, "Higher pay for males", ha="center", va="center", rotation=0,
size=15,
bbox=bbox_props2)
#Labels each bar with the percentage of females
percent_labels = count_by_group[labels].iloc[0]*100 \
/(count_by_group[labels].iloc[0] + count_by_group[labels].iloc[1])
for i in range(len(ax.patches)):
p = ax.patches[i]
width = p.get_width()*1+1
ax.text(15,
p.get_y()+p.get_height()/2+0.3,
'{:1.0f}'.format(percent_labels[i])+' %',
ha="center")
ax.text(15, -1+0.3, 'Female Representation',
ha="center", fontname='Arial', rotation = 0)
plt.yticks(range(len(differences)), labels)
plt.title('Full Time Workers (Base Pay)')
plt.xlabel('Mean Percent Difference in Pay (Females - Males)')
plt.xlim(-11, 11)
plt.show()
```
I believe this is a better way to represent the gender wage gap. I calculated the mean difference between female and male pay based on job categories. Then I converted the values into a percentage by using this formula:
$$ \text{Mean Percent Difference} = \frac{\text{(Female Mean Pay - Male Mean Pay)*100}} {\text{Male Mean Pay}} $$
The theory stating that women makes 78 cents for every dollar men makes implies a 22% pay difference. None of these percentages were more than 10%, and not all of these percentage values showed favoritism towards males. However, we should keep in mind that this data set only applies to San Francisco public jobs. We should also keep in mind that we do not have access to job experience data which would directly correlate with base pay.
In addition, I included a short table of female representation for each job group on the right side of the graph. We'll dig further into this on the next section.
#### 4.6 - Gender representation by job category
```
contingency_table = pd.crosstab(
data_2014_FT['Gender'],
data_2014_FT['Job_Group'],
margins = True
)
contingency_table
#Assigns the frequency values
femalecount = contingency_table.iloc[0][0:-1].values
malecount = contingency_table.iloc[1][0:-1].values
totals = contingency_table.iloc[2][0:-1]
femalepercentages = femalecount*100/totals
malepercentages = malecount*100/totals
malepercentages=malepercentages.sort_values(ascending=True)
femalepercentages=femalepercentages.sort_values(ascending=False)
length = range(len(femalepercentages))
#Plots the bar chart
fig = plt.figure(figsize=(10, 12))
sns.set(font_scale=1.5)
p1 = plt.barh(length, malepercentages.values, 0.55, label='Male', color='#AFAFF5')
p2 = plt.barh(length, femalepercentages, 0.55, left=malepercentages, color='#EFAFB5', label='Female')
labels = malepercentages.index
plt.yticks(range(len(malepercentages)), labels)
plt.xticks([0, 25, 50, 75, 100], ['0 %', '25 %', '50 %', '75 %', '100 %'])
plt.xlabel('Percentage of Males')
plt.title('Gender Representation by Job Group')
plt.legend(bbox_to_anchor=(0, 1, 1, 0), loc=3,
ncol=2, mode="expand", borderaxespad=0)
plt.show()
```
The chart above does not include any information based on pay. I wanted to show an overview of gender representation based on job category. It is safe to say, women don't like working with automotives with <1% female representation. Where as female representation is highest for medical jobs at 73%.
#### 4.7 - Significance testing by exact job title
So what if breaking down the wage gap by job category is not good enough? Should we break down the gender gap by exact job title? Afterall, the argument is for equal pay for equal work. We can assume equal work if the job titles are exactly the same.
We can use hypothesis testing using the Welch's t-test to determine if there is a statistically significant result between male and female wages. The Welch's t-test is very robust as it doesn't assume equal variance and equal sample size. It does however, assume a normal distrbution which is well represented by the KDE plots. I talk about this in detail in my blog post [here](https://codingdisciple.com/hypothesis-testing-welch-python.html).
Let's state our null and alternative hypothesis:
$ H_0 : \text{There is no statistically significant relationship between gender and pay.} $
$ H_a : \text{There is a statistically significant relationship between gender and pay.} $
We are going to use only job titles with more than 100 employees, and job titles with more than 30 females and 30 males for this t-test. Using a for loop, we'll perform the Welch's t-test on every job title tat matches our criteria.
```
from scipy import stats
#Significance testing by job title
job_titles = data_2014['JobTitle'].value_counts(dropna=True)
job_titles_over_100 = job_titles[job_titles > 100 ]
t_scores = {}
for title,count in job_titles_over_100.iteritems():
male_pay = pd.to_numeric(male_only[male_only['JobTitle'] == title]['BasePay'])
female_pay = pd.to_numeric(female_only[female_only['JobTitle'] == title]['BasePay'])
if female_pay.shape[0] < 30:
continue
if male_pay.shape[0] < 30:
continue
t_scores[title] = stats.ttest_ind_from_stats(
mean1=male_pay.mean(), std1=(male_pay.std()), nobs1= male_pay.shape[0], \
mean2=female_pay.mean(), std2=(female_pay.std()), nobs2=female_pay.shape[0], \
equal_var=False)
for key, value in t_scores.items():
if value[1] < 0.05:
print(len(key)*'-')
print(key)
print(len(key)*'-')
print(t_scores[key])
print(' ')
print('Male: {}'.format((male_only[male_only['JobTitle'] == key]['BasePay']).mean()))
print('sample size: {}'.format(male_only[male_only['JobTitle'] == key].shape[0]))
print(' ')
print('Female: {}'.format((female_only[female_only['JobTitle'] == key]['BasePay']).mean()))
print('sample size: {}'.format(female_only[female_only['JobTitle'] == key].shape[0]))
len(t_scores)
```
Out of the 25 jobs that were tested using the Welch's t-test, 5 jobs resulted in a p-value of less than 0.05. However, not all jobs showed favoritism towards males. 'Registered Nurse' and 'Senior Clerk' both showed an average pay in favor of females. However, we should take the Welch's t-test results with a grain of salt. We do not have data on the work experience of the employees. Maybe female nurses have more work experience over males. Maybe male transit operators have more work experience over females. We don't actually know. Since `BasePay` is a function of work experience, without this critical piece of information, we can not make any conclusions based on the t-test alone. All we know is that a statistically significant difference exists.
### 5.0 - San Francisco vs. Newport Beach
Let's take a look at more a more conservative city such as Newport Beach. This data can be downloaded at Transparent California [here](https://transparentcalifornia.com/salaries/2016/newport-beach/).
We can process the data similar to the San Francisco data set. The following code performs the following:
+ Read the data using pandas
+ Create the `Job_Group` column
+ Create the `Gender` column
+ Create two new dataframes: one for part time workers and one for full time workers
```
#Reads in the data
nb_data = pd.read_csv('newport-beach-2016.csv')
#Creates job groups
def find_job_title_nb(row):
titles = collections.OrderedDict([
('Police',['police', 'sherif', 'probation', 'sergeant', 'officer', 'lieutenant']),
('Fire', ['fire']),
('Transit',['mta', 'transit']),
('Medical',['anesth', 'medical', 'nurs', 'health', 'physician', 'orthopedic', 'pharm', 'care']),
('Architect', ['architect']),
('Court',['court', 'legal']),
('Mayor Office', ['mayoral']),
('Library', ['librar']),
('Public Works', ['public']),
('Attorney', ['attorney']),
('Custodian', ['custodian']),
('Gardener', ['garden']),
('Recreation Leader', ['recreation']),
('Automotive',['automotive', 'mechanic', 'truck']),
('Engineer',['engineer', 'engr', 'eng', 'program']),
('General Laborer',['general laborer', 'painter', 'inspector', 'carpenter', 'electrician', 'plumber', 'maintenance']),
('Food Services', ['food serv']),
('Clerk', ['clerk']),
('Porter', ['porter']),
('Airport Staff', ['airport']),
('Social Worker',['worker']),
('Guard', ['guard']),
('Assistant',['aide', 'assistant', 'secretary', 'attendant']),
('Analyst', ['analy']),
('Manager', ['manager'])
])
#Loops through the dictionaries
for group, keywords in titles.items():
for keyword in keywords:
if keyword in row.lower():
return group
return 'Other'
start_time = time.time()
nb_data["Job_Group"]=data["JobTitle"].map(find_job_title_nb)
#Create the 'Gender' column based on employee's first name.
d = gender.Detector(case_sensitive=False)
nb_data['FirstName'] = nb_data['Employee Name'].str.split().apply(lambda x: x[0])
nb_data['Gender'] = nb_data['FirstName'].apply(lambda x: d.get_gender(x))
nb_data['Gender'].value_counts()
#Retain data with 'male' and 'female' names.
nb_male_female_only = nb_data[(nb_data['Gender'] == 'male') | (nb_data['Gender'] == 'female')]
nb_male_female_only['Gender'].value_counts()
#Seperates full time/part time data
nb_data_FT = nb_male_female_only[nb_male_female_only['Status'] == 'FT']
nb_data_PT = nb_male_female_only[nb_male_female_only['Status'] == 'PT']
nb_data_FT.head()
```
#### 5.1 - Part time vs. full time workers
```
fig = plt.figure(figsize=(10, 5))
nb_male_only = nb_data_PT[nb_data_PT['Gender'] == 'male']
nb_female_only = nb_data_PT[nb_data_PT['Gender'] == 'female']
ax = fig.add_subplot(1, 1, 1)
ax = sns.kdeplot(nb_male_only['Total Pay & Benefits'], color ='Blue', label='Male', shade=True)
ax = sns.kdeplot(nb_female_only['Total Pay & Benefits'], color='Red', label='Female', shade=True)
plt.title('Newport Beach: Part Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay + Benefits ($)')
plt.xlim(0, 400000)
plt.yticks([])
plt.show()
```
Similar to the KDE plot for San Francisco, the KDE plot is nearly identical for both males and females for part time workers.
Let's take a look at the full time workers.
```
fig = plt.figure(figsize=(10, 10))
fig.subplots_adjust(hspace=.5)
#Generate the top chart
nb_male_only = nb_data_FT[nb_data_FT['Gender'] == 'male']
nb_female_only = nb_data_FT[nb_data_FT['Gender'] == 'female']
ax = fig.add_subplot(2, 1, 1)
ax = sns.kdeplot(nb_male_only['Total Pay & Benefits'], color ='Blue', label='Male', shade=True)
ax = sns.kdeplot(nb_female_only['Total Pay & Benefits'], color='Red', label='Female', shade=True)
plt.title('Newport Beach: Full Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay + Benefits ($)')
plt.xlim(0, 400000)
plt.yticks([])
#Generate the bottom chart
male_only = data_2014_FT[data_2014_FT['Gender'] == 'male']
female_only = data_2014_FT[data_2014_FT['Gender'] == 'female']
ax2 = fig.add_subplot(2, 1, 2)
ax2 = sns.kdeplot(male_only['TotalPayBenefits'], color ='Blue', label='Male', shade=True)
ax2 = sns.kdeplot(female_only['TotalPayBenefits'], color='Red', label='Female', shade=True)
plt.title('San Francisco: Full Time Workers')
plt.ylabel('Density of Employees')
plt.xlabel('Total Pay + Benefits ($)')
plt.xlim(0, 400000)
plt.yticks([])
plt.show()
```
The kurtosis of the KDE plot for Newport Beach full time workers is lower than KDE plot for San Francisco full time workers. We can see a higher gender wage gap for Newport beach workers than San Francisco workers. However, these two plots do not tell us the full story. We need to break down the data by job category.
#### 5.2 - Comparisons by job cateogry
```
nb_salaries_by_group = pd.pivot_table(data = nb_data_FT,
values = 'Base Pay',
columns = 'Job_Group', index='Gender',
aggfunc = np.mean,)
nb_salaries_by_group
fig = plt.figure(figsize=(10, 7.5))
sns.set(font_scale=1.5)
differences = (nb_salaries_by_group.loc['female'] - nb_salaries_by_group.loc['male'])*100/nb_salaries_by_group.loc['male']
nb_labels = differences.sort_values().index
x = differences.sort_values()
y = [i for i in range(len(differences))]
nb_palette = sns.diverging_palette(240, 10, n=9, center ='dark')
ax = sns.barplot(x, y, orient = 'h', palette = nb_palette)
plt.yticks(range(len(differences)), nb_labels)
plt.title('Newport Beach: Full Time Workers (Base Pay)')
plt.xlabel('Mean Percent Difference in Pay (Females - Males)')
plt.xlim(-25, 25)
plt.show()
```
Most of these jobs shows a higher average pay for males. The only job category where females were paid higher on average was 'Manager'. Some of these job categories do not even have a single female within the category, so the difference cannot be calculated. We should create a contingency table to check the sample size of our data.
#### 5.3 - Gender representation by job category
```
nb_contingency_table = pd.crosstab(
nb_data_FT['Gender'],
nb_data_FT['Job_Group'],
margins = True
)
nb_contingency_table
```
The number of public jobs is much lower in Newport Beach compared to San Francisco. With only 3 female managers working full time in Newport Beach, we can't really say female managers make more money on average than male managers.
```
#Assigns the frequency values
nb_femalecount = nb_contingency_table.iloc[0][0:-1].values
nb_malecount = nb_contingency_table.iloc[1][0:-1].values
nb_totals = nb_contingency_table.iloc[2][0:-1]
nb_femalepercentages = nb_femalecount*100/nb_totals
nb_malepercentages = nb_malecount*100/nb_totals
nb_malepercentages=nb_malepercentages.sort_values(ascending=True)
nb_femalepercentages=nb_femalepercentages.sort_values(ascending=False)
nb_length = range(len(nb_malepercentages))
#Plots the bar chart
fig = plt.figure(figsize=(10, 10))
sns.set(font_scale=1.5)
p1 = plt.barh(nb_length, nb_malepercentages.values, 0.55, label='Male', color='#AFAFF5')
p2 = plt.barh(nb_length, nb_femalepercentages, 0.55, left=nb_malepercentages, color='#EFAFB5', label='Female')
labels = nb_malepercentages.index
plt.yticks(range(len(nb_malepercentages)), labels)
plt.xticks([0, 25, 50, 75, 100], ['0 %', '25 %', '50 %', '75 %', '100 %'])
plt.xlabel('Percentage of Males')
plt.title('Gender Representation by Job Group')
plt.legend(bbox_to_anchor=(0, 1, 1, 0), loc=3,
ncol=2, mode="expand", borderaxespad=0)
plt.show()
fig = plt.figure(figsize=(10, 5))
colors = ['#AFAFF5', '#EFAFB5']
labels = ['Male', 'Female']
sizes = [len(nb_male_only), len(nb_female_only)]
explode = (0.05, 0)
sns.set(font_scale=1.5)
ax = fig.add_subplot(1, 2, 1)
ax = plt.pie(sizes, labels=labels, explode=explode, colors=colors, shadow=True, startangle=90, autopct='%1.f%%')
plt.title('Newport Beach: Full Time')
sizes = [len(male_only), len(female_only)]
explode = (0.05, 0)
sns.set(font_scale=1.5)
ax2 = fig.add_subplot(1, 2, 2)
ax2 = plt.pie(sizes, labels=labels, explode=explode, colors=colors, shadow=True, startangle=90, autopct='%1.f%%')
plt.title('San Francisco: Full Time')
plt.show()
```
Looking at the plots above. There are fewer females working full time public jobs in Newport Beach compared to San Francisco.
### 6.0 - Conclusion
It is very easy for people to say there is a gender wage gap and make general statements about it. But the real concern is whether if there is social injustice and discrimination involved. Yes, there is an overall gender wage gap for both San Francisco and Newport Beach. In both cases, the income distribution for part time employees were nearly identical for both males and females.
For full time public positions in San Francisco, an overall gender wage gap can be observed. When the full time positions were broken down to job categories, the gender wage gap went both ways. Some jobs favored men, some favored women. For full time public positions in Newport Beach, the majority of the jobs favored men.
However, we were missing a critical piece of information in this entire analysis. We don't have any information on the job experience of the employees. Maybe the men just had more job experience in Newport Beach, we don't actually know. For San Francisco, we assumed equal experience by comparing employees with the same exact job titles. Only job titles with a size greater than 100 were chosen. Out of the 25 job titles that were selected, 5 of them showed a statistically significant result with the Welch's t-test. Two of those jobs showed an average base pay in favor of females.
Overall, I do not believe the '78 cents to a dollar' is a fair statement. It generalizes the data and oversimplifies the problem. There are many hidden factors that is not shown by the data. Maybe women are less likely to ask for a promotion. Maybe women perform really well in the medical world. Maybe the men's body is more suitable for the police officer role. Maybe women are more organized than men and make better libarians. The list goes on and on, the point is, we should always be skeptical of what the numbers tell us. The truth is, men and women are different on a fundamental level. Social injustices and gender discrimination should be analyzed on a case by case basis.
| true |
code
| 0.394901 | null | null | null | null |
|
Lambda School Data Science
*Unit 2, Sprint 3, Module 3*
---
# Permutation & Boosting
- Get **permutation importances** for model interpretation and feature selection
- Use xgboost for **gradient boosting**
### Setup
Run the code cell below. You can work locally (follow the [local setup instructions](https://lambdaschool.github.io/ds/unit2/local/)) or on Colab.
Libraries:
- category_encoders
- [**eli5**](https://eli5.readthedocs.io/en/latest/)
- matplotlib
- numpy
- pandas
- scikit-learn
- [**xgboost**](https://xgboost.readthedocs.io/en/latest/)
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
!pip install eli5
# If you're working locally:
else:
DATA_PATH = '../data/'
```
We'll go back to Tanzania Waterpumps for this lesson.
```
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# Merge train_features.csv & train_labels.csv
train = pd.merge(pd.read_csv(DATA_PATH+'waterpumps/train_features.csv'),
pd.read_csv(DATA_PATH+'waterpumps/train_labels.csv'))
# Read test_features.csv & sample_submission.csv
test = pd.read_csv(DATA_PATH+'waterpumps/test_features.csv')
sample_submission = pd.read_csv(DATA_PATH+'waterpumps/sample_submission.csv')
# Split train into train & val
train, val = train_test_split(train, train_size=0.80, test_size=0.20,
stratify=train['status_group'], random_state=42)
def wrangle(X):
"""Wrangle train, validate, and test sets in the same way"""
# Prevent SettingWithCopyWarning
X = X.copy()
# About 3% of the time, latitude has small values near zero,
# outside Tanzania, so we'll treat these values like zero.
X['latitude'] = X['latitude'].replace(-2e-08, 0)
# When columns have zeros and shouldn't, they are like null values.
# So we will replace the zeros with nulls, and impute missing values later.
# Also create a "missing indicator" column, because the fact that
# values are missing may be a predictive signal.
cols_with_zeros = ['longitude', 'latitude', 'construction_year',
'gps_height', 'population']
for col in cols_with_zeros:
X[col] = X[col].replace(0, np.nan)
X[col+'_MISSING'] = X[col].isnull()
# Drop duplicate columns
duplicates = ['quantity_group', 'payment_type']
X = X.drop(columns=duplicates)
# Drop recorded_by (never varies) and id (always varies, random)
unusable_variance = ['recorded_by', 'id']
X = X.drop(columns=unusable_variance)
# Convert date_recorded to datetime
X['date_recorded'] = pd.to_datetime(X['date_recorded'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['date_recorded'].dt.year
X['month_recorded'] = X['date_recorded'].dt.month
X['day_recorded'] = X['date_recorded'].dt.day
X = X.drop(columns='date_recorded')
# Engineer feature: how many years from construction_year to date_recorded
X['years'] = X['year_recorded'] - X['construction_year']
X['years_MISSING'] = X['years'].isnull()
# return the wrangled dataframe
return X
train = wrangle(train)
val = wrangle(val)
test = wrangle(test)
# Arrange data into X features matrix and y target vector
target = 'status_group'
X_train = train.drop(columns=target)
y_train = train[target]
X_val = val.drop(columns=target)
y_val = val[target]
X_test = test
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
print('Validation Accuracy', pipeline.score(X_val, y_val))
```
# Get permutation importances for model interpretation and feature selection
## Overview
Default Feature Importances are fast, but Permutation Importances may be more accurate.
These links go deeper with explanations and examples:
- Permutation Importances
- [Kaggle / Dan Becker: Machine Learning Explainability](https://www.kaggle.com/dansbecker/permutation-importance)
- [Christoph Molnar: Interpretable Machine Learning](https://christophm.github.io/interpretable-ml-book/feature-importance.html)
- (Default) Feature Importances
- [Ando Saabas: Selecting good features, Part 3, Random Forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/)
- [Terence Parr, et al: Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html)
There are three types of feature importances:
### 1. (Default) Feature Importances
Fastest, good for first estimates, but be aware:
>**When the dataset has two (or more) correlated features, then from the point of view of the model, any of these correlated features can be used as the predictor, with no concrete preference of one over the others.** But once one of them is used, the importance of others is significantly reduced since effectively the impurity they can remove is already removed by the first feature. As a consequence, they will have a lower reported importance. This is not an issue when we want to use feature selection to reduce overfitting, since it makes sense to remove features that are mostly duplicated by other features. But when interpreting the data, it can lead to the incorrect conclusion that one of the variables is a strong predictor while the others in the same group are unimportant, while actually they are very close in terms of their relationship with the response variable. — [Selecting good features – Part III: random forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/)
> **The scikit-learn Random Forest feature importance ... tends to inflate the importance of continuous or high-cardinality categorical variables.** ... Breiman and Cutler, the inventors of Random Forests, indicate that this method of “adding up the gini decreases for each individual variable over all trees in the forest gives a **fast** variable importance that is often very consistent with the permutation importance measure.” — [Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html)
```
# Get feature importances
rf = pipeline.named_steps['randomforestclassifier']
importances = pd.Series(rf.feature_importances_, X_train.columns)
# Plot feature importances
%matplotlib inline
import matplotlib.pyplot as plt
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances.sort_values()[-n:].plot.barh(color='grey');
```
### 2. Drop-Column Importance
The best in theory, but too slow in practice
```
column = 'quantity'
# Fit without column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train.drop(columns=column), y_train)
score_without = pipeline.score(X_val.drop(columns=column), y_val)
print(f'Validation Accuracy without {column}: {score_without}')
# Fit with column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='median'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
score_with = pipeline.score(X_val, y_val)
print(f'Validation Accuracy with {column}: {score_with}')
# Compare the error with & without column
print(f'Drop-Column Importance for {column}: {score_with - score_without}')
```
### 3. Permutation Importance
Permutation Importance is a good compromise between Feature Importance based on impurity reduction (which is the fastest) and Drop Column Importance (which is the "best.")
[The ELI5 library documentation explains,](https://eli5.readthedocs.io/en/latest/blackbox/permutation_importance.html)
> Importance can be measured by looking at how much the score (accuracy, F1, R^2, etc. - any score we’re interested in) decreases when a feature is not available.
>
> To do that one can remove feature from the dataset, re-train the estimator and check the score. But it requires re-training an estimator for each feature, which can be computationally intensive. ...
>
>To avoid re-training the estimator we can remove a feature only from the test part of the dataset, and compute score without using this feature. It doesn’t work as-is, because estimators expect feature to be present. So instead of removing a feature we can replace it with random noise - feature column is still there, but it no longer contains useful information. This method works if noise is drawn from the same distribution as original feature values (as otherwise estimator may fail). The simplest way to get such noise is to shuffle values for a feature, i.e. use other examples’ feature values - this is how permutation importance is computed.
>
>The method is most suitable for computing feature importances when a number of columns (features) is not huge; it can be resource-intensive otherwise.
### Do-It-Yourself way, for intuition
### With eli5 library
For more documentation on using this library, see:
- [eli5.sklearn.PermutationImportance](https://eli5.readthedocs.io/en/latest/autodocs/sklearn.html#eli5.sklearn.permutation_importance.PermutationImportance)
- [eli5.show_weights](https://eli5.readthedocs.io/en/latest/autodocs/eli5.html#eli5.show_weights)
- [scikit-learn user guide, `scoring` parameter](https://scikit-learn.org/stable/modules/model_evaluation.html#the-scoring-parameter-defining-model-evaluation-rules)
eli5 doesn't work with pipelines.
```
# Ignore warnings
```
### We can use importances for feature selection
For example, we can remove features with zero importance. The model trains faster and the score does not decrease.
# Use xgboost for gradient boosting
## Overview
In the Random Forest lesson, you learned this advice:
#### Try Tree Ensembles when you do machine learning with labeled, tabular data
- "Tree Ensembles" means Random Forest or **Gradient Boosting** models.
- [Tree Ensembles often have the best predictive accuracy](https://arxiv.org/abs/1708.05070) with labeled, tabular data.
- Why? Because trees can fit non-linear, non-[monotonic](https://en.wikipedia.org/wiki/Monotonic_function) relationships, and [interactions](https://christophm.github.io/interpretable-ml-book/interaction.html) between features.
- A single decision tree, grown to unlimited depth, will [overfit](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/). We solve this problem by ensembling trees, with bagging (Random Forest) or **[boosting](https://www.youtube.com/watch?v=GM3CDQfQ4sw)** (Gradient Boosting).
- Random Forest's advantage: may be less sensitive to hyperparameters. **Gradient Boosting's advantage:** may get better predictive accuracy.
Like Random Forest, Gradient Boosting uses ensembles of trees. But the details of the ensembling technique are different:
### Understand the difference between boosting & bagging
Boosting (used by Gradient Boosting) is different than Bagging (used by Random Forests).
Here's an excerpt from [_An Introduction to Statistical Learning_](http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Seventh%20Printing.pdf) Chapter 8.2.3, Boosting:
>Recall that bagging involves creating multiple copies of the original training data set using the bootstrap, fitting a separate decision tree to each copy, and then combining all of the trees in order to create a single predictive model.
>
>**Boosting works in a similar way, except that the trees are grown _sequentially_: each tree is grown using information from previously grown trees.**
>
>Unlike fitting a single large decision tree to the data, which amounts to _fitting the data hard_ and potentially overfitting, the boosting approach instead _learns slowly._ Given the current model, we fit a decision tree to the residuals from the model.
>
>We then add this new decision tree into the fitted function in order to update the residuals. Each of these trees can be rather small, with just a few terminal nodes. **By fitting small trees to the residuals, we slowly improve fˆ in areas where it does not perform well.**
>
>Note that in boosting, unlike in bagging, the construction of each tree depends strongly on the trees that have already been grown.
This high-level overview is all you need to know for now. If you want to go deeper, we recommend you watch the StatQuest videos on gradient boosting!
Let's write some code. We have lots of options for which libraries to use:
#### Python libraries for Gradient Boosting
- [scikit-learn Gradient Tree Boosting](https://scikit-learn.org/stable/modules/ensemble.html#gradient-boosting) — slower than other libraries, but [the new version may be better](https://twitter.com/amuellerml/status/1129443826945396737)
- Anaconda: already installed
- Google Colab: already installed
- [xgboost](https://xgboost.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://xiaoxiaowang87.github.io/monotonicity_constraint/)
- Anaconda, Mac/Linux: `conda install -c conda-forge xgboost`
- Windows: `conda install -c anaconda py-xgboost`
- Google Colab: already installed
- [LightGBM](https://lightgbm.readthedocs.io/en/latest/) — can accept missing values and enforce [monotonic constraints](https://blog.datadive.net/monotonicity-constraints-in-machine-learning/)
- Anaconda: `conda install -c conda-forge lightgbm`
- Google Colab: already installed
- [CatBoost](https://catboost.ai/) — can accept missing values and use [categorical features](https://catboost.ai/docs/concepts/algorithm-main-stages_cat-to-numberic.html) without preprocessing
- Anaconda: `conda install -c conda-forge catboost`
- Google Colab: `pip install catboost`
In this lesson, you'll use a new library, xgboost — But it has an API that's almost the same as scikit-learn, so it won't be a hard adjustment!
#### [XGBoost Python API Reference: Scikit-Learn API](https://xgboost.readthedocs.io/en/latest/python/python_api.html#module-xgboost.sklearn)
#### [Avoid Overfitting By Early Stopping With XGBoost In Python](https://machinelearningmastery.com/avoid-overfitting-by-early-stopping-with-xgboost-in-python/)
Why is early stopping better than a For loop, or GridSearchCV, to optimize `n_estimators`?
With early stopping, if `n_iterations` is our number of iterations, then we fit `n_iterations` decision trees.
With a for loop, or GridSearchCV, we'd fit `sum(range(1,n_rounds+1))` trees.
But it doesn't work well with pipelines. You may need to re-run multiple times with different values of other parameters such as `max_depth` and `learning_rate`.
#### XGBoost parameters
- [Notes on parameter tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html)
- [Parameters documentation](https://xgboost.readthedocs.io/en/latest/parameter.html)
### Try adjusting these hyperparameters
#### Random Forest
- class_weight (for imbalanced classes)
- max_depth (usually high, can try decreasing)
- n_estimators (too low underfits, too high wastes time)
- min_samples_leaf (increase if overfitting)
- max_features (decrease for more diverse trees)
#### Xgboost
- scale_pos_weight (for imbalanced classes)
- max_depth (usually low, can try increasing)
- n_estimators (too low underfits, too high wastes time/overfits) — Use Early Stopping!
- learning_rate (too low underfits, too high overfits)
For more ideas, see [Notes on Parameter Tuning](https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html) and [DART booster](https://xgboost.readthedocs.io/en/latest/tutorials/dart.html).
## Challenge
You will use your portfolio project dataset for all assignments this sprint. Complete these tasks for your project, and document your work.
- Continue to clean and explore your data. Make exploratory visualizations.
- Fit a model. Does it beat your baseline?
- Try xgboost.
- Get your model's permutation importances.
You should try to complete an initial model today, because the rest of the week, we're making model interpretation visualizations.
But, if you aren't ready to try xgboost and permutation importances with your dataset today, you can practice with another dataset instead. You may choose any dataset you've worked with previously.
| true |
code
| 0.50177 | null | null | null | null |
|
# Partial Correlation
The purpose of this notebook is to understand how to compute the [partial correlation](https://en.wikipedia.org/wiki/Partial_correlation) between two variables, $X$ and $Y$, given a third $Z$. In particular, these variables are assumed to be guassians (or, in general, multivariate gaussians).
Why is it important to estimate partial correlations? The primary reason for estimating a partial correlation is to use it to detect for [confounding](https://en.wikipedia.org/wiki/Confounding_variable) variables during causal analysis.
## Simulation
Let's start out by simulating 3 data sets. Graphically, these data sets comes from graphs represented by the following.
* $X \rightarrow Z \rightarrow Y$ (serial)
* $X \leftarrow Z \rightarrow Y$ (diverging)
* $X \rightarrow Z \leftarrow Y$ (converging)
```
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
import warnings
warnings.filterwarnings('ignore')
plt.style.use('ggplot')
def get_serial_graph():
g = nx.DiGraph()
g.add_node('X')
g.add_node('Y')
g.add_node('Z')
g.add_edge('X', 'Z')
g.add_edge('Z', 'Y')
return g
def get_diverging_graph():
g = nx.DiGraph()
g.add_node('X')
g.add_node('Y')
g.add_node('Z')
g.add_edge('Z', 'X')
g.add_edge('Z', 'Y')
return g
def get_converging_graph():
g = nx.DiGraph()
g.add_node('X')
g.add_node('Y')
g.add_node('Z')
g.add_edge('X', 'Z')
g.add_edge('Y', 'Z')
return g
g_serial = get_serial_graph()
g_diverging = get_diverging_graph()
g_converging = get_converging_graph()
p_serial = nx.nx_agraph.graphviz_layout(g_serial, prog='dot', args='-Kcirco')
p_diverging = nx.nx_agraph.graphviz_layout(g_diverging, prog='dot', args='-Kcirco')
p_converging = nx.nx_agraph.graphviz_layout(g_converging, prog='dot', args='-Kcirco')
fig, ax = plt.subplots(3, 1, figsize=(5, 5))
nx.draw(g_serial, pos=p_serial, with_labels=True, node_color='#e0e0e0', node_size=800, arrowsize=20, ax=ax[0])
nx.draw(g_diverging, pos=p_diverging, with_labels=True, node_color='#e0e0e0', node_size=800, arrowsize=20, ax=ax[1])
nx.draw(g_converging, pos=p_converging, with_labels=True, node_color='#e0e0e0', node_size=800, arrowsize=20, ax=ax[2])
ax[0].set_title('Serial')
ax[1].set_title('Diverging')
ax[2].set_title('Converging')
plt.tight_layout()
```
In the serial graph, `X` causes `Z` and `Z` causes `Y`. In the diverging graph, `Z` causes both `X` and `Y`. In the converging graph, `X` and `Y` cause `Z`. Below, the serial, diverging, and converging data sets are named S, D, and C, correspondingly.
Note that in the serial graph, the data is sampled as follows.
* $X \sim \mathcal{N}(0, 1)$
* $Z \sim 2 + 1.8 \times X$
* $Y \sim 5 + 2.7 \times Z$
In the diverging graph, the data is sampled as follows.
* $Z \sim \mathcal{N}(0, 1)$
* $X \sim 4.3 + 3.3 \times Z$
* $Y \sim 5.0 + 2.7 \times Z$
Lastly, in the converging graph, the data is sampled as follows.
* $X \sim \mathcal{N}(0, 1)$
* $Y \sim \mathcal{N}(5.5, 1)$
* $Z \sim 2.0 + 0.8 \times X + 1.2 \times Y$
Note the ordering of the sampling with the variables follows the structure of the corresponding graph.
```
import numpy as np
np.random.seed(37)
def get_error(N=10000, mu=0.0, std=0.2):
return np.random.normal(mu, std, N)
def to_matrix(X, Z, Y):
return np.concatenate([
X.reshape(-1, 1),
Z.reshape(-1, 1),
Y.reshape(-1, 1)], axis=1)
def get_serial(N=10000, e_mu=0.0, e_std=0.2):
X = np.random.normal(0, 1, N) + get_error(N, e_mu, e_std)
Z = 2 + 1.8 * X + get_error(N, e_mu, e_std)
Y = 5 + 2.7 * Z + get_error(N, e_mu, e_std)
return to_matrix(X, Z, Y)
def get_diverging(N=10000, e_mu=0.0, e_std=0.2):
Z = np.random.normal(0, 1, N) + get_error(N, e_mu, e_std)
X = 4.3 + 3.3 * Z + get_error(N, e_mu, e_std)
Y = 5 + 2.7 * Z + get_error(N, e_mu, e_std)
return to_matrix(X, Z, Y)
def get_converging(N=10000, e_mu=0.0, e_std=0.2):
X = np.random.normal(0, 1, N) + get_error(N, e_mu, e_std)
Y = np.random.normal(5.5, 1, N) + get_error(N, e_mu, e_std)
Z = 2 + 0.8 * X + 1.2 * Y + get_error(N, e_mu, e_std)
return to_matrix(X, Z, Y)
S = get_serial()
D = get_diverging()
C = get_converging()
```
## Computation
For the three datasets, `S`, `D`, and `C`, we want to compute the partial correlation between $X$ and $Y$ given $Z$. The way to do this is as follows.
* Regress $X$ on $Z$ and also $Y$ on $Z$
* $X = b_X + w_X * Z$
* $Y = b_Y + w_Y * Z$
* With the new weights $(b_X, w_X)$ and $(b_Y, w_Y)$, predict $X$ and $Y$.
* $\hat{X} = b_X + w_X * Z$
* $\hat{Y} = b_Y + w_Y * Z$
* Now compute the residuals between the true and predicted values.
* $R_X = X - \hat{X}$
* $R_Y = Y - \hat{Y}$
* Finally, compute the Pearson correlation between $R_X$ and $R_Y$.
The correlation between the residuals is the partial correlation and runs from -1 to +1. More interesting is the test of significance. If $p > \alpha$, where $\alpha \in [0.1, 0.05, 0.01]$, then assume independence. For example, assume $\alpha = 0.01$ and $p = 0.002$, then $X$ is conditionally independent of $Y$ given $Z$.
```
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from scipy.stats import pearsonr
from scipy import stats
def get_cond_indep_test(c_xy_z, N=10000, alpha=0.01):
point = stats.norm.ppf(1 - (alpha / 2.0))
z_transform = np.sqrt(N - 3) * np.abs(0.5 * np.log((1 + c_xy_z) / (1 - c_xy_z)))
return z_transform, point, z_transform > point
def get_partial_corr(M):
X = M[:, 0]
Z = M[:, 1].reshape(-1, 1)
Y = M[:, 2]
mXZ = LinearRegression()
mXZ.fit(Z, X)
pXZ = mXZ.predict(Z)
rXZ = X - pXZ
mYZ = LinearRegression()
mYZ.fit(Z, Y)
pYZ = mYZ.predict(Z)
rYZ = Y - pYZ
c_xy, p_xy = pearsonr(X, Y)
c_xy_z, p_xy_z = pearsonr(rXZ, rYZ)
return c_xy, p_xy, c_xy_z, p_xy_z
```
## Serial graph data
For $X \rightarrow Z \rightarrow Y$, note that the marginal correlation is high (0.99) and the correlation is significant (p < 0.01). However, the correlation between X and Y vanishes given Z to -0.01 (p > 0.01). Note the conditional independence test fails to reject the null hypothesis.
```
c_xy, p_xy, c_xy_z, p_xy_z = get_partial_corr(S)
print(f'corr_xy={c_xy:.5f}, p_xy={p_xy:.5f}')
print(f'corr_xy_z={c_xy_z:.5f}, p_xy_z={p_xy_z:.5f}')
print(get_cond_indep_test(c_xy_z))
```
## Diverging graph data
For $X \leftarrow Z \rightarrow Y$, note that the marginal correlation is high (0.99) and the correlation is significant (p < 0.01). However, the correlation between X and Y vanishes given Z to 0.01 (p > 0.01). Note the conditional independence test fails to reject the null hypothesis.
```
c_xy, p_xy, c_xy_z, p_xy_z = get_partial_corr(D)
print(f'corr_xy={c_xy:.5f}, p_xy={p_xy:.5f}')
print(f'corr_xy_z={c_xy_z:.5f}, p_xy_z={p_xy_z:.5f}')
print(get_cond_indep_test(c_xy_z))
```
## Converging graph data
For $X \rightarrow Z \leftarrow Y$, note that the correlation is low (-0.00) and the correlation is insignficiant (p > 0.01). However, the correlation between X and Y increases to -0.96 and becomes significant (p < 0.01)! Note the conditional independence test rejects the null hypothesis.
```
c_xy, p_xy, c_xy_z, p_xy_z = get_partial_corr(C)
print(f'corr_xy={c_xy:.5f}, p_xy={p_xy:.5f}')
print(f'corr_xy_z={c_xy_z:.5f}, p_xy_z={p_xy_z:.5f}')
print(get_cond_indep_test(c_xy_z))
```
## Statistically Distinguishable
The `serial` and `diverging` graphs are said to be `statistically indistingishable` since $X$ and $Y$ are both `conditionally independent` given $Z$. However, the `converging` graph is `statistically distinguishable` since it is the only graph where $X$ and $Y$ are `conditionally dependent` given $Z$.
| true |
code
| 0.484685 | null | null | null | null |
|
# Benchmarking the Permanent
This tutorial shows how to use the permanent function using The Walrus, which calculates the permanent using Ryser's algorithm
### The Permanent
The permanent of an $n$-by-$n$ matrix A = $a_{i,j}$ is defined as
$\text{perm}(A)=\sum_{\sigma\in S_n}\prod_{i=1}^n a_{i,\sigma(i)}.$
The sum here extends over all elements $\sigma$ of the symmetric group $S_n$; i.e. over all permutations of the numbers $1, 2, \ldots, n$. ([see Wikipedia](https://en.wikipedia.org/wiki/Permanent)).
The function `thewalrus.perm` implements [Ryser's algorithm](https://en.wikipedia.org/wiki/Computing_the_permanent#Ryser_formula) to calculate the permanent of an arbitrary matrix using [Gray code](https://en.wikipedia.org/wiki/Gray_code) ordering.
## Using the library
Once installed or compiled, one imports the library in the usual way:
```
from thewalrus import perm
```
To use it we need to pass square numpy arrays thus we also import NumPy:
```
import numpy as np
import time
```
The library provides functions to compute permanents of real and complex matrices. The functions take as arguments the matrix; the number of threads to be used to do the computation are determined using OpenMP.
```
size = 20
matrix = np.ones([size,size])
perm(matrix)
size = 20
matrix = np.ones([size,size], dtype=np.complex128)
perm(matrix)
```
Not surprisingly, the permanent of a matrix containing only ones equals the factorial of the dimension of the matrix, in our case $20!$.
```
from math import factorial
factorial(20)
```
### Benchmarking the performance of the code
For sizes $n=1,28$ we will generate random unitary matrices and measure the (average) amount of time it takes to calculate their permanent. The number of samples for each will be geometrically distirbuted with a 1000 samples for size $n=1$ and 10 samples for $n=28$. The unitaries will be random Haar distributed.
```
a0 = 1000.
anm1 = 10.
n = 28
r = (anm1/a0)**(1./(n-1))
nreps = [(int)(a0*(r**((i)))) for i in range(n)]
nreps
```
The following function generates random Haar unitaries of dimensions $n$
```
from scipy import diagonal, randn
from scipy.linalg import qr
def haar_measure(n):
'''A Random matrix distributed with Haar measure
See https://arxiv.org/abs/math-ph/0609050
How to generate random matrices from the classical compact groups
by Francesco Mezzadri '''
z = (randn(n,n) + 1j*randn(n,n))/np.sqrt(2.0)
q,r = qr(z)
d = diagonal(r)
ph = d/np.abs(d)
q = np.multiply(q,ph,q)
return q
```
Now let's bench mark the scaling of the calculation with the matrix size:
```
times = np.empty(n)
for ind, reps in enumerate(nreps):
#print(ind+1,reps)
start = time.time()
for i in range(reps):
size = ind+1
nth = 1
matrix = haar_measure(size)
res = perm(matrix)
end = time.time()
times[ind] = (end - start)/reps
print(ind+1, times[ind])
```
We can now plot the (average) time it takes to calculate the permanent vs. the size of the matrix:
```
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_formats=['svg']
plt.semilogy(np.arange(1,n+1),times,"+")
plt.xlabel(r"Matrix size $n$")
plt.ylabel(r"Time in seconds for 4 threads")
```
We can also fit to the theoretical scaling of $ c n 2^n$ and use it to extrapolate for larger sizes:
```
def fit(n,c):
return c*n*2**n
from scipy.optimize import curve_fit
popt, pcov = curve_fit(fit, np.arange(1,n+1)[15:-1],times[15:-1])
```
The scaling prefactor is
```
popt[0]
```
And we can use it to extrapolate the time it takes to calculate permanents of bigger dimensions
```
flags = [3600,3600*24*7, 3600*24*365, 3600*24*365*1000]
labels = ["1 hour", "1 week", "1 year", "1000 years"]
plt.semilogy(np.arange(1,n+1), times, "+", np.arange(1,61), fit(np.arange(1,61),popt[0]))
plt.xlabel(r"Matrix size $n$")
plt.ylabel(r"Time in seconds for single thread")
plt.hlines(flags,0,60,label="1 hr",linestyles=u'dotted')
for i in range(len(flags)):
plt.text(0,2*flags[i], labels[i])
```
The specs of the computer on which this benchmark was performed are:
```
!cat /proc/cpuinfo|head -19
```
| true |
code
| 0.469399 | null | null | null | null |
|
### Processing Echosounder Data from Ocean Observatories Initiative with `echopype`.
Downloading a file from the OOI website. We pick August 21, 2017 since this was the day of the solar eclipse which affected the traditional patterns of the marine life.
```
# downloading the file
!wget https://rawdata.oceanobservatories.org/files/CE04OSPS/PC01B/ZPLSCB102_10.33.10.143/OOI-D20170821-T163049.raw
filename = 'OOI-D20170821-T163049.raw'
```
**Converting from Raw to Standartized Netcdf Format**
```
# import as part of a submodule
from echopype.convert import ConvertEK60
data_tmp = ConvertEK60(filename)
data_tmp.raw2nc()
os.remove(filename)
```
**Calibrating, Denoising, Mean Volume Backscatter Strength**
```
from echopype.model import EchoData
data = EchoData(filename[:-4]+'.nc')
data.calibrate() # Calibration and echo-integration
data.remove_noise(save=True) # Save denoised Sv to FILENAME_Sv_clean.nc
data.get_MVBS(save=True)
```
**Visualizing the Result**
```
%matplotlib inline
data.MVBS.MVBS.sel(frequency=200000).plot(x='ping_time',cmap = 'jet')
```
**Processing Multiple Files**
To process multiple file from the OOI website we need to scrape the names of the existing files there. We will use the `Beautiful Soup`
package for that.
```
!conda install --yes beautifulsoup4
from bs4 import BeautifulSoup
from urllib.request import urlopen
path = 'https://rawdata.oceanobservatories.org/files/CE04OSPS/PC01B/ZPLSCB102_10.33.10.143/'
response = urlopen(path)
soup = BeautifulSoup(response.read(), "html.parser")
# urls = []
# for item in soup.find_all(text=True):
# if '.raw' in item:
# urls.append(path+'/'+item)
urls = [path+'/'+item for item in soup.find_all(text=True) if '.raw' in item]
# urls
from datetime import datetime
```
Specify range:
```
start_time = '20170821-T000000'
end_time = '20170822-T235959'
# convert the times to datetime format
start_datetime = datetime.strptime(start_time,'%Y%m%d-T%H%M%S')
end_datetime = datetime.strptime(end_time,'%Y%m%d-T%H%M%S')
# function to check if a date is in the date range
def in_range(date_str, start_time, end_time):
date_str = datetime.strptime(date_str,'%Y%m%d-T%H%M%S')
true = date_str >= start_datetime and date_str <= end_datetime
return(true)
# identify the list of urls in range
range_urls = []
for url in urls:
date_str = url[-20:-4]
if in_range(date_str, start_time, end_time):
range_urls.append(url)
range_urls
rawnames = [url.split('//')[-1] for url in range_urls]
ls
import os
```
**Downloading the Files**
```
# Download the files
import requests
rawnames = []
for url in range_urls:
r = requests.get(url, allow_redirects=True)
rawnames.append(url.split('//')[-1])
open(url.split('//')[-1], 'wb').write(r.content)
!pip install echopype
ls
```
**Converting from Raw to Standartized Netcdf Format**
```
# import as part of a submodule
from echopype.convert import ConvertEK60
for filename in rawnames:
data_tmp = ConvertEK60(filename)
data_tmp.raw2nc()
os.remove(filename)
#ls
```
**Calibrating, Denoising, Mean Volume Backscatter Strength**
```
# calibrate and denoise
from echopype.model import EchoData
for filename in rawnames:
data = EchoData(filename[:-4]+'.nc')
data.calibrate() # Calibration and echo-integration
data.remove_noise(save=False) # Save denoised Sv to FILENAME_Sv_clean.nc
data.get_MVBS(save=True)
os.remove(filename[:-4]+'.nc')
os.remove(filename[:-4]+'_Sv.nc')
```
**Opening and Visualizing the Results in Parallel**
No that all files are in an appropriate format, we can open them and visualize them in parallel. For that we will need to install the `dask` parallelization library.
```
!conda install --yes dask
import xarray as xr
res = xr.open_mfdataset('*MVBS.nc')
import matplotlib.pyplot as plt
plt.figure(figsize = (15,5))
res.MVBS.sel(frequency=200000).plot(x='ping_time',cmap = 'jet')
```
| true |
code
| 0.268725 | null | null | null | null |
|
# Hawaii - A Climate Analysis And Exploration
### For data between August 23, 2016 - August 23, 2017
---
```
# Import dependencies
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
```
## Reflect Tables into SQLAlchemy ORM
```
# Set up query engine. 'echo=True is the default - will keep a log of activities'
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# Reflect an existing database into a new model
Base = automap_base()
# Reflect the tables
Base.prepare(engine, reflect=True)
# We can view all of the classes that automap found
Base.classes.keys()
# Another way to get table names from SQL-lite
inspector = inspect(engine)
inspector.get_table_names()
```
## Exploratory Climate Analysis
```
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
# Display details of 'measurement' table
columns = inspector.get_columns('measurement')
for c in columns:
print(c['name'], c['type'])
# DISPLY number of line items measurement, and remove tuple form
result, = engine.execute('SELECT COUNT(*) FROM measurement').fetchall()[0]
print(result,)
# Display details of 'station' table
columns = inspector.get_columns('station')
for c in columns:
print(c['name'], c['type'])
# DISPLY number of line items station, and remove tuple form
result, = engine.execute('SELECT COUNT(*) FROM station').fetchall()[0]
print(result,)
# FULL INNTER JOIN BOTH THE MEASUREMENT AND STATION TABLE
# engine.execute('SELECT measurement.*, station.name, station.latitude FROM measurement INNER JOIN station ON measurement.station = station.station;').fetchall()
join_result = engine.execute('SELECT * FROM measurement INNER JOIN station ON measurement.station = station.station;').fetchall()
join_result
# Another way to PERFORM AN INNER JOIN ON THE MEASUREMENT AND STATION TABLES
engine.execute('SELECT measurement.*, station.* FROM measurement, station WHERE measurement.station=station.station;').fetchall()
# Query last date of the measurement file
last_date = session.query(Measurement.date).order_by(Measurement.date.desc()).first()[0]
print(last_date)
last_date_measurement = dt.date(2017, 8 ,23)
# Calculate the date 1 year delta of the "last date measurement"
one_year_ago = last_date_measurement - dt.timedelta(days=365)
print(one_year_ago)
# Plotting precipitation data from 1 year ago
date = dt.date(2016, 8, 23)
#sel = [Measurement.id, Measurement.station, Measurement.date, Measurement.prcp, Measurement.tobs]
sel = [Measurement.date, Measurement.prcp]
print(date)
# date = "2016-08-23"
result = session.query(Measurement.date, Measurement.prcp).\
filter(Measurement.date >= date).all()
# get the count / length of the list of tuples
print(len(result))
# Created a line plot and saved the figure
df = pd.DataFrame(result, columns=['Date', 'Precipitation'])
df.sort_values(by=['Date'])
df.set_index('Date', inplace=True)
s = df['Precipitation']
ax = s.plot(figsize=(8,6), use_index=True, title='Precipitation Data Between 8/23/2016 - 8/23/2017')
fig = ax.get_figure()
fig.savefig('./Images/precipitation_line.png')
# Use Pandas to calcualte the summary statistics for the precipitation data
df.describe()
# Design a query to show how many stations are available in this dataset?
session.query(Measurement.station).\
group_by(Measurement.station).count()
# Querying for the most active stations (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
engine.execute('SELECT DISTINCT station, COUNT(id) FROM measurement GROUP BY station ORDER BY COUNT(id) DESC').fetchall()
# Query for stations from the measurement table
session.query(Measurement.station).\
group_by(Measurement.station).all()
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature most active station?
sel = [func.min(Measurement.tobs), func.max(Measurement.tobs), func.avg(Measurement.tobs)]
session.query(*sel).\
filter(Measurement.station == 'USC00519281').all()
# Query the dates of the last 12 months of the most active station
last_date = session.query(Measurement.date).\
filter(Measurement.station == 'USC00519281').\
order_by(Measurement.date.desc()).first()[0]
print(last_date)
last_date_USC00519281 = dt.date(2017, 8 ,18)
last_year_USC00519281 = last_date_USC00519281 - dt.timedelta(days=365)
print(last_year_USC00519281)
# SET UP HISTOGRAM QUERY AND PLOT
sel_two = [Measurement.tobs]
results_tobs_hist = session.query(*sel_two).\
filter(Measurement.date >= last_year_USC00519281).\
filter(Measurement.station == 'USC00519281').all()
# HISTOGRAM Plot
df = pd.DataFrame(results_tobs_hist, columns=['tobs'])
ax = df.plot.hist(figsize=(8,6), bins=12, use_index=False, title='Hawaii - Temperature Histogram Between 8/23/2016 - 8/23/2017')
fig = ax.get_figure()
fig.savefig('./Images/temperature_histogram.png')
# Created a function called `calc_temps` that accepts a 'start date' and 'end date' in the format 'YYYY-MM-DD'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""Temp MIN,Temp AVG, and Temp MAX for a list of dates.
Args are:
start_date (string): A date string in the format YYYY-MM-DD
end_date (string): A date string in the format YYYY-MM-DD
Returns:
T-MIN, T-AVG, and T-MAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
print(calc_temps('2017-08-01', '2017-08-07'))
```
| true |
code
| 0.687263 | null | null | null | null |
|
<a id="title_ID"></a>
# JWST Pipeline Validation Testing Notebook: spec2, extract_2d step
<span style="color:red"> **Instruments Affected**</span>: NIRSpec
Tested on CV3 data
### Table of Contents
<div style="text-align: left">
<br> [Imports](#imports_ID) <br> [Introduction](#intro_ID) <br> [Testing Data Set](#data_ID) <br> [Run the JWST pipeline and assign_wcs validation tests](#pipeline_ID): [FS Full-Frame test](#FULLFRAME), [FS ALLSLITS test](#ALLSLITS), [MOS test](#MOS) <br> [About This Notebook](#about_ID)<br> [Results](#results) <br>
</div>
<a id="imports_ID"></a>
# Imports
The library imports relevant to this notebook are aready taken care of by importing PTT.
* astropy.io for opening fits files
* jwst.module.PipelineStep is the pipeline step being tested
* matplotlib.pyplot.plt to generate plot
NOTE: This notebook assumes that the pipeline version to be tested is already installed and its environment is activated.
To be able to run this notebook you need to install nptt.
If all goes well you will be able to import PTT.
[Top of Page](#title_ID)
```
# Create a temporary directory to hold notebook output, and change the working directory to that directory.
from tempfile import TemporaryDirectory
import os
import shutil
data_dir = TemporaryDirectory()
os.chdir(data_dir.name)
# Choose CRDS cache location
use_local_crds_cache = False
crds_cache_tempdir = False
crds_cache_notebook_dir = True
crds_cache_home = False
crds_cache_custom_dir = False
crds_cache_dir_name = ""
if use_local_crds_cache:
if crds_cache_tempdir:
os.environ['CRDS_PATH'] = os.path.join(os.getcwd(), "crds")
elif crds_cache_notebook_dir:
try:
os.environ['CRDS_PATH'] = os.path.join(orig_dir, "crds")
except Exception as e:
os.environ['CRDS_PATH'] = os.path.join(os.getcwd(), "crds")
elif crds_cache_home:
os.environ['CRDS_PATH'] = os.path.join(os.environ['HOME'], 'crds', 'cache')
elif crds_cache_custom_dir:
os.environ['CRDS_PATH'] = crds_cache_dir_name
import warnings
import psutil
from astropy.io import fits
# Only print a DeprecationWarning the first time it shows up, not every time.
with warnings.catch_warnings():
warnings.simplefilter("once", category=DeprecationWarning)
import jwst
from jwst.pipeline.calwebb_detector1 import Detector1Pipeline
from jwst.assign_wcs.assign_wcs_step import AssignWcsStep
from jwst.msaflagopen.msaflagopen_step import MSAFlagOpenStep
from jwst.extract_2d.extract_2d_step import Extract2dStep
# The latest version of NPTT is installed in the requirements text file at:
# /jwst_validation_notebooks/environment.yml
# import NPTT
import nirspec_pipe_testing_tool as nptt
# To get data from Artifactory
from ci_watson.artifactory_helpers import get_bigdata
# Print the versions used for the pipeline and NPTT
pipeline_version = jwst.__version__
nptt_version = nptt.__version__
print("Using jwst pipeline version: ", pipeline_version)
print("Using NPTT version: ", nptt_version)
```
<a id="intro_ID"></a>
# Test Description
We compared Institute's pipeline product of the assign_wcs step with our benchmark files, or with the intermediary products from the ESA pipeline, which is completely independent from the Institute's. The comparison file is referred to as 'truth'. We calculated the relative difference and expected it to be equal to or less than computer precision: relative_difference = absolute_value( (Truth - ST)/Truth ) <= 1x10^-7.
For the test to be considered PASSED, every single slit (for FS data), slitlet (for MOS data) or slice (for IFU data) in the input file has to pass. If there is any failure, the whole test will be considered as FAILED.
The code for this test can be obtained at: https://github.com/spacetelescope/nirspec_pipe_testing_tool/blob/master/nirspec_pipe_testing_tool/calwebb_spec2_pytests/auxiliary_code/check_corners_extract2d.py. Multi Object Spectroscopy (MOS), the code is in the same repository but is named ```compare_wcs_mos.py```, and for Integral Field Unit (IFU) data, the test is named ```compare_wcs_ifu.py```.
The input file is defined in the variable ```input_file``` (see section [Testing Data Set and Variable Setup](#data_ID)).
Step description: https://jwst-pipeline.readthedocs.io/en/latest/jwst/extract_2d/main.html
Pipeline code: https://github.com/spacetelescope/jwst/tree/master/jwst/extract_2d
### Results
If the test **PASSED** this means that all slits, slitlets, or slices individually passed the test. However, if ony one individual slit (for FS data), slitlet (for MOS data) or slice (for IFU data) test failed, the whole test will be reported as **FAILED**.
### Calibration WG Requested Algorithm:
A short description and link to the page:
https://outerspace.stsci.edu/display/JWSTCC/Vanilla+Path-Loss+Correction
### Defining Term
Acronymns used un this notebook:
pipeline: calibration pipeline
spec2: spectroscopic calibration pipeline level 2b
PTT: NIRSpec pipeline testing tool (https://github.com/spacetelescope/nirspec_pipe_testing_tool)
[Top of Page](#title_ID)
<a id="pipeline_ID"></a>
# Run the JWST pipeline and extract_2d validation tests
The pipeline can be run from the command line in two variants: full or per step.
Tu run the spec2 pipeline in full use the command:
$ strun jwst.pipeline.Spec2Pipeline jwtest_rate.fits
Tu only run the extract_2d step, use the command:
$ strun jwst.extract_2d.Extract2dStep jwtest_previous_step_output.fits
These options are also callable from a script with the testing environment active. The Python call for running the pipeline in full or by step are:
$\gt$ from jwst.pipeline.calwebb_spec2 import Spec2Pipeline
$\gt$ Spec2Pipeline.call(jwtest_rate.fits)
or
$\gt$ from jwst.extract_2d import Extract2dStep
$\gt$ Extract2dStep.call(jwtest_previous_step_output.fits)
PTT can run the spec2 pipeline either in full or per step, as well as the imaging pipeline in full. In this notebook we will use PTT to run the pipeline and the validation tests. To run PTT, follow the directions in the corresponding repo page.
[Top of Page](#title_ID)
<a id="data_ID"></a>
# Testing Data Set
All testing data is from the CV3 campaign. We chose these files because this is our most complete data set, i.e. all modes and filter-grating combinations.
Data used was for testing was only FS and MOS, since extract_2d is skipped for IFU. Data sets are:
- FS_PRISM_CLEAR
- FS_FULLFRAME_G395H_F290LP
- FS_ALLSLITS_G140H_F100LP
- MOS_G140M_LINE1
- MOS_PRISM_CLEAR
[Top of Page](#title_ID)
```
testing_data = {'fs_prism_clear':{
'uncal_file_nrs1': 'fs_prism_nrs1_uncal.fits',
'uncal_file_nrs2': 'fs_prism_nrs2_uncal.fits',
'truth_file_nrs1': 'fs_prism_nrs1_extract_2d_truth.fits',
'truth_file_nrs2': 'fs_prism_nrs2_extract_2d_truth.fits',
'msa_shutter_config': None },
'fs_fullframe_g395h_f290lp':{
'uncal_file_nrs1': 'fs_fullframe_g35h_f290lp_nrs1_uncal.fits',
'uncal_file_nrs2': 'fs_fullframe_g35h_f290lp_nrs2_uncal.fits',
'truth_file_nrs1': 'fs_fullframe_g35h_f290lp_nrs1_extract_2d_truth.fits',
'truth_file_nrs2': 'fs_fullframe_g35h_f290lp_nrs2_extract_2d_truth.fits',
'msa_shutter_config': None },
'fs_allslits_g140h_f100lp':{
'uncal_file_nrs1': 'fs_allslits_g140h_f100lp_nrs1_uncal.fits',
'uncal_file_nrs2': 'fs_allslits_g140h_f100lp_nrs2_uncal.fits',
'truth_file_nrs1': 'fs_allslits_g140h_f100lp_nrs1_extract_2d_truth.fits',
'truth_file_nrs2': 'fs_allslits_g140h_f100lp_nrs2_extract_2d_truth.fits',
'msa_shutter_config': None },
# Commented out because the pipeline is failing with this file
#'bots_g235h_f170lp':{
# 'uncal_file_nrs1': 'bots_g235h_f170lp_nrs1_uncal.fits',
# 'uncal_file_nrs2': 'bots_g235h_f170lp_nrs2_uncal.fits',
# 'truth_file_nrs1': 'bots_g235h_f170lp_nrs1_extract_2d_truth.fits',
# 'truth_file_nrs2': 'bots_g235h_f170lp_nrs2_extract_2d_truth.fits',
# 'msa_shutter_config': None },
'mos_prism_clear':{
'uncal_file_nrs1': 'mos_prism_nrs1_uncal.fits',
'uncal_file_nrs2': 'mos_prism_nrs2_uncal.fits',
'truth_file_nrs1': 'mos_prism_nrs1_extract_2d_truth.fits',
'truth_file_nrs2': None,
'msa_shutter_config': 'V0030006000104_msa.fits' },
'mos_g140m_f100lp':{
'uncal_file_nrs1': 'mos_g140m_line1_NRS1_uncal.fits',
'uncal_file_nrs2': 'mos_g140m_line1_NRS2_uncal.fits',
'truth_file_nrs1': 'mos_g140m_line1_nrs1_extract_2d_truth.fits',
'truth_file_nrs2': 'mos_g140m_line1_nrs2_extract_2d_truth.fits',
'msa_shutter_config': 'V8460001000101_msa.fits' },
}
# define function to pull data from Artifactory
def get_artifactory_file(data_set_dict, detector):
"""This function creates a list with all the files needed per detector to run the test.
Args:
data_set_dict: dictionary, contains inputs for a specific mode and configuration
detector: string, either nrs1 or nrs2
Returns:
data: list, contains all files needed to run test
"""
files2obtain = ['uncal_file_nrs1', 'truth_file_nrs1', 'msa_shutter_config']
data = []
for file in files2obtain:
data_file = None
try:
if '_nrs' in file and '2' in detector:
file = file.replace('_nrs1', '_nrs2')
data_file = get_bigdata('jwst_validation_notebooks',
'validation_data',
'nirspec_data',
data_set_dict[file])
except TypeError:
data.append(None)
continue
data.append(data_file)
return data
# Set common NPTT switches for NPTT and run the test for both detectors in each data set
# define benchmark (or 'truth') file
compare_assign_wcs_and_extract_2d_with_esa = False
# accepted threshold difference with respect to benchmark files
extract_2d_threshold_diff = 4
# define benchmark (or 'truth') file
esa_files_path, raw_data_root_file = None, None
compare_assign_wcs_and_extract_2d_with_esa = False
# Get the data
results_dict = {}
detectors = ['nrs1', 'nrs2']
for mode_config, data_set_dict in testing_data.items():
for det in detectors:
print('Testing files for detector: ', det)
data = get_artifactory_file(data_set_dict, det)
uncal_file, truth_file, msa_shutter_config = data
print('Working with uncal_file: ', uncal_file)
uncal_basename = os.path.basename(uncal_file)
# Make sure that there is an assign_wcs truth product to compare to, else skip this data set
if truth_file is None:
print('No truth file to compare to for this detector, skipping this file. \n')
skip_file = True
else:
skip_file = False
if not skip_file:
# Run the stage 1 pipeline
rate_object = Detector1Pipeline.call(uncal_file)
# Make sure the MSA shutter configuration file is set up correctly
if msa_shutter_config is not None:
msa_metadata = rate_object.meta.instrument.msa_metadata_file
print(msa_metadata)
if msa_metadata is None or msa_metadata == 'N/A':
rate_object.meta.instrument.msa_metadata_file = msa_shutter_config
# Run the stage 2 pipeline steps
pipe_object = AssignWcsStep.call(rate_object)
if 'mos' in uncal_basename.lower():
pipe_object = MSAFlagOpenStep.call(pipe_object)
extract_2d_object = Extract2dStep.call(pipe_object)
# Run the validation test
%matplotlib inline
if 'fs' in uncal_file.lower():
print('Running test for FS...')
result, _ = nptt.calwebb_spec2_pytests.auxiliary_code.check_corners_extract2d.find_FSwindowcorners(
extract_2d_object,
truth_file=truth_file,
esa_files_path=esa_files_path,
extract_2d_threshold_diff=extract_2d_threshold_diff)
if 'mos' in uncal_file.lower():
print('Running test for MOS...')
result, _ = nptt.calwebb_spec2_pytests.auxiliary_code.check_corners_extract2d.find_MOSwindowcorners(
extract_2d_object,
msa_shutter_config,
truth_file=truth_file,
esa_files_path=esa_files_path,
extract_2d_threshold_diff= extract_2d_threshold_diff)
else:
result = 'skipped'
# Did the test passed
print("Did assign_wcs validation test passed? ", result, "\n\n")
rd = {uncal_basename: result}
results_dict.update(rd)
# close all open files
psutil.Process().open_files()
closing_files = []
for fd in psutil.Process().open_files():
if data_dir.name in fd.path:
closing_files.append(fd)
for fd in closing_files:
try:
print('Closing file: ', fd)
open(fd.fd).close()
except:
print('File already closed: ', fd)
# Quickly see if the test passed
print('These are the final results of the tests: ')
for key, val in results_dict.items():
print(key, val)
```
<a id="about_ID"></a>
## About this Notebook
**Author:** Maria A. Pena-Guerrero, Staff Scientist II - Systems Science Support, NIRSpec
<br>**Updated On:** Mar/24/2021
[Top of Page](#title_ID)
<img style="float: right;" src="./stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="stsci_pri_combo_mark_horizonal_white_bkgd" width="200px"/>
| true |
code
| 0.502563 | null | null | null | null |
|
# Targeting Direct Marketing with Amazon SageMaker XGBoost
_**Supervised Learning with Gradient Boosted Trees: A Binary Prediction Problem With Unbalanced Classes**_
---
## Background
Direct marketing, either through mail, email, phone, etc., is a common tactic to acquire customers. Because resources and a customer's attention is limited, the goal is to only target the subset of prospects who are likely to engage with a specific offer. Predicting those potential customers based on readily available information like demographics, past interactions, and environmental factors is a common machine learning problem.
This notebook presents an example problem to predict if a customer will enroll for a term deposit at a bank, after one or more phone calls. The steps include:
* Preparing your Amazon SageMaker notebook
* Downloading data from the internet into Amazon SageMaker
* Investigating and transforming the data so that it can be fed to Amazon SageMaker algorithms
* Estimating a model using the Gradient Boosting algorithm
* Evaluating the effectiveness of the model
* Setting the model up to make on-going predictions
---
## Preparation
_This notebook was created and tested on an ml.m4.xlarge notebook instance._
Let's start by specifying:
- The S3 bucket and prefix that you want to use for training and model data. This should be within the same region as the Notebook Instance, training, and hosting.
- The IAM role arn used to give training and hosting access to your data. See the documentation for how to create these. Note, if more than one role is required for notebook instances, training, and/or hosting, please replace the boto regexp with a the appropriate full IAM role arn string(s).
```
# cell 01
import sagemaker
bucket=sagemaker.Session().default_bucket()
prefix = 'sagemaker/DEMO-xgboost-dm'
# Define IAM role
import boto3
import re
from sagemaker import get_execution_role
role = get_execution_role()
```
Now let's bring in the Python libraries that we'll use throughout the analysis
```
# cell 02
import numpy as np # For matrix operations and numerical processing
import pandas as pd # For munging tabular data
import matplotlib.pyplot as plt # For charts and visualizations
from IPython.display import Image # For displaying images in the notebook
from IPython.display import display # For displaying outputs in the notebook
from time import gmtime, strftime # For labeling SageMaker models, endpoints, etc.
import sys # For writing outputs to notebook
import math # For ceiling function
import json # For parsing hosting outputs
import os # For manipulating filepath names
import sagemaker
import zipfile # Amazon SageMaker's Python SDK provides many helper functions
```
---
## Data
Let's start by downloading the [direct marketing dataset](https://sagemaker-sample-data-us-west-2.s3-us-west-2.amazonaws.com/autopilot/direct_marketing/bank-additional.zip) from the sample data s3 bucket.
\[Moro et al., 2014\] S. Moro, P. Cortez and P. Rita. A Data-Driven Approach to Predict the Success of Bank Telemarketing. Decision Support Systems, Elsevier, 62:22-31, June 2014
```
# cell 03
!wget https://sagemaker-sample-data-us-west-2.s3-us-west-2.amazonaws.com/autopilot/direct_marketing/bank-additional.zip
with zipfile.ZipFile('bank-additional.zip', 'r') as zip_ref:
zip_ref.extractall('.')
```
Now lets read this into a Pandas data frame and take a look.
```
# cell 04
data = pd.read_csv('./bank-additional/bank-additional-full.csv')
pd.set_option('display.max_columns', 500) # Make sure we can see all of the columns
pd.set_option('display.max_rows', 20) # Keep the output on one page
data
```
We will store this natively in S3 to then process it with SageMaker Processing.
```
# cell 05
from sagemaker import Session
sess = Session()
input_source = sess.upload_data('./bank-additional/bank-additional-full.csv', bucket=bucket, key_prefix=f'{prefix}/input_data')
input_source
```
# Feature Engineering with Amazon SageMaker Processing
Amazon SageMaker Processing allows you to run steps for data pre- or post-processing, feature engineering, data validation, or model evaluation workloads on Amazon SageMaker. Processing jobs accept data from Amazon S3 as input and store data into Amazon S3 as output.
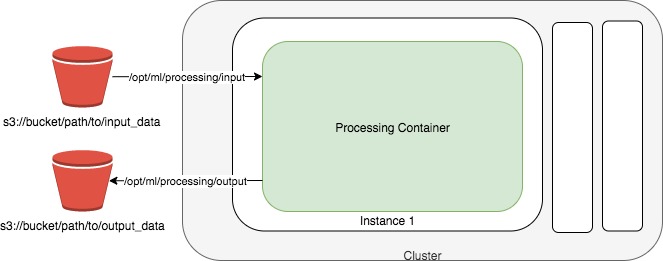
Here, we'll import the dataset and transform it with SageMaker Processing, which can be used to process terabytes of data in a SageMaker-managed cluster separate from the instance running your notebook server. In a typical SageMaker workflow, notebooks are only used for prototyping and can be run on relatively inexpensive and less powerful instances, while processing, training and model hosting tasks are run on separate, more powerful SageMaker-managed instances. SageMaker Processing includes off-the-shelf support for Scikit-learn, as well as a Bring Your Own Container option, so it can be used with many different data transformation technologies and tasks.
To use SageMaker Processing, simply supply a Python data preprocessing script as shown below. For this example, we're using a SageMaker prebuilt Scikit-learn container, which includes many common functions for processing data. There are few limitations on what kinds of code and operations you can run, and only a minimal contract: input and output data must be placed in specified directories. If this is done, SageMaker Processing automatically loads the input data from S3 and uploads transformed data back to S3 when the job is complete.
```
# cell 06
%%writefile preprocessing.py
import pandas as pd
import numpy as np
import argparse
import os
from sklearn.preprocessing import OrdinalEncoder
def _parse_args():
parser = argparse.ArgumentParser()
# Data, model, and output directories
# model_dir is always passed in from SageMaker. By default this is a S3 path under the default bucket.
parser.add_argument('--filepath', type=str, default='/opt/ml/processing/input/')
parser.add_argument('--filename', type=str, default='bank-additional-full.csv')
parser.add_argument('--outputpath', type=str, default='/opt/ml/processing/output/')
parser.add_argument('--categorical_features', type=str, default='y, job, marital, education, default, housing, loan, contact, month, day_of_week, poutcome')
return parser.parse_known_args()
if __name__=="__main__":
# Process arguments
args, _ = _parse_args()
# Load data
df = pd.read_csv(os.path.join(args.filepath, args.filename))
# Change the value . into _
df = df.replace(regex=r'\.', value='_')
df = df.replace(regex=r'\_$', value='')
# Add two new indicators
df["no_previous_contact"] = (df["pdays"] == 999).astype(int)
df["not_working"] = df["job"].isin(["student", "retired", "unemployed"]).astype(int)
df = df.drop(['duration', 'emp.var.rate', 'cons.price.idx', 'cons.conf.idx', 'euribor3m', 'nr.employed'], axis=1)
# Encode the categorical features
df = pd.get_dummies(df)
# Train, test, validation split
train_data, validation_data, test_data = np.split(df.sample(frac=1, random_state=42), [int(0.7 * len(df)), int(0.9 * len(df))]) # Randomly sort the data then split out first 70%, second 20%, and last 10%
# Local store
pd.concat([train_data['y_yes'], train_data.drop(['y_yes','y_no'], axis=1)], axis=1).to_csv(os.path.join(args.outputpath, 'train/train.csv'), index=False, header=False)
pd.concat([validation_data['y_yes'], validation_data.drop(['y_yes','y_no'], axis=1)], axis=1).to_csv(os.path.join(args.outputpath, 'validation/validation.csv'), index=False, header=False)
test_data['y_yes'].to_csv(os.path.join(args.outputpath, 'test/test_y.csv'), index=False, header=False)
test_data.drop(['y_yes','y_no'], axis=1).to_csv(os.path.join(args.outputpath, 'test/test_x.csv'), index=False, header=False)
print("## Processing complete. Exiting.")
```
Before starting the SageMaker Processing job, we instantiate a `SKLearnProcessor` object. This object allows you to specify the instance type to use in the job, as well as how many instances.
```
# cell 07
train_path = f"s3://{bucket}/{prefix}/train"
validation_path = f"s3://{bucket}/{prefix}/validation"
test_path = f"s3://{bucket}/{prefix}/test"
# cell 08
from sagemaker.sklearn.processing import SKLearnProcessor
from sagemaker.processing import ProcessingInput, ProcessingOutput
from sagemaker import get_execution_role
sklearn_processor = SKLearnProcessor(
framework_version="0.23-1",
role=get_execution_role(),
instance_type="ml.m5.large",
instance_count=1,
base_job_name='sm-immday-skprocessing'
)
sklearn_processor.run(
code='preprocessing.py',
# arguments = ['arg1', 'arg2'],
inputs=[
ProcessingInput(
source=input_source,
destination="/opt/ml/processing/input",
s3_input_mode="File",
s3_data_distribution_type="ShardedByS3Key"
)
],
outputs=[
ProcessingOutput(
output_name="train_data",
source="/opt/ml/processing/output/train",
destination=train_path,
),
ProcessingOutput(output_name="validation_data", source="/opt/ml/processing/output/validation", destination=validation_path),
ProcessingOutput(output_name="test_data", source="/opt/ml/processing/output/test", destination=test_path),
]
)
# cell 09
!aws s3 ls $train_path/
```
---
## End of Lab 1
---
## Training
Now we know that most of our features have skewed distributions, some are highly correlated with one another, and some appear to have non-linear relationships with our target variable. Also, for targeting future prospects, good predictive accuracy is preferred to being able to explain why that prospect was targeted. Taken together, these aspects make gradient boosted trees a good candidate algorithm.
There are several intricacies to understanding the algorithm, but at a high level, gradient boosted trees works by combining predictions from many simple models, each of which tries to address the weaknesses of the previous models. By doing this the collection of simple models can actually outperform large, complex models. Other Amazon SageMaker notebooks elaborate on gradient boosting trees further and how they differ from similar algorithms.
`xgboost` is an extremely popular, open-source package for gradient boosted trees. It is computationally powerful, fully featured, and has been successfully used in many machine learning competitions. Let's start with a simple `xgboost` model, trained using Amazon SageMaker's managed, distributed training framework.
First we'll need to specify the ECR container location for Amazon SageMaker's implementation of XGBoost.
```
# cell 10
container = sagemaker.image_uris.retrieve(region=boto3.Session().region_name, framework='xgboost', version='latest')
```
Then, because we're training with the CSV file format, we'll create `s3_input`s that our training function can use as a pointer to the files in S3, which also specify that the content type is CSV.
```
# cell 11
s3_input_train = sagemaker.inputs.TrainingInput(s3_data=train_path.format(bucket, prefix), content_type='csv')
s3_input_validation = sagemaker.inputs.TrainingInput(s3_data=validation_path.format(bucket, prefix), content_type='csv')
```
First we'll need to specify training parameters to the estimator. This includes:
1. The `xgboost` algorithm container
1. The IAM role to use
1. Training instance type and count
1. S3 location for output data
1. Algorithm hyperparameters
And then a `.fit()` function which specifies:
1. S3 location for output data. In this case we have both a training and validation set which are passed in.
```
# cell 12
sess = sagemaker.Session()
xgb = sagemaker.estimator.Estimator(container,
role,
instance_count=1,
instance_type='ml.m4.xlarge',
output_path='s3://{}/{}/output'.format(bucket, prefix),
sagemaker_session=sess)
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
silent=0,
objective='binary:logistic',
num_round=100)
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
---
## Hosting
Now that we've trained the `xgboost` algorithm on our data, let's deploy a model that's hosted behind a real-time endpoint.
```
# cell 13
xgb_predictor = xgb.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge')
```
---
## Evaluation
There are many ways to compare the performance of a machine learning model, but let's start by simply comparing actual to predicted values. In this case, we're simply predicting whether the customer subscribed to a term deposit (`1`) or not (`0`), which produces a simple confusion matrix.
First we'll need to determine how we pass data into and receive data from our endpoint. Our data is currently stored as NumPy arrays in memory of our notebook instance. To send it in an HTTP POST request, we'll serialize it as a CSV string and then decode the resulting CSV.
*Note: For inference with CSV format, SageMaker XGBoost requires that the data does NOT include the target variable.*
```
# cell 14
xgb_predictor.serializer = sagemaker.serializers.CSVSerializer()
```
Now, we'll use a simple function to:
1. Loop over our test dataset
1. Split it into mini-batches of rows
1. Convert those mini-batches to CSV string payloads (notice, we drop the target variable from our dataset first)
1. Retrieve mini-batch predictions by invoking the XGBoost endpoint
1. Collect predictions and convert from the CSV output our model provides into a NumPy array
```
# cell 15
!aws s3 cp $test_path/test_x.csv /tmp/test_x.csv
!aws s3 cp $test_path/test_y.csv /tmp/test_y.csv
# cell 16
def predict(data, predictor, rows=500 ):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep=',')
test_x = pd.read_csv('/tmp/test_x.csv', names=[f'{i}' for i in range(59)])
test_y = pd.read_csv('/tmp/test_y.csv', names=['y'])
predictions = predict(test_x.drop(test_x.columns[0], axis=1).to_numpy(), xgb_predictor)
```
Now we'll check our confusion matrix to see how well we predicted versus actuals.
```
# cell 17
pd.crosstab(index=test_y['y'].values, columns=np.round(predictions), rownames=['actuals'], colnames=['predictions'])
```
So, of the ~4000 potential customers, we predicted 136 would subscribe and 94 of them actually did. We also had 389 subscribers who subscribed that we did not predict would. This is less than desirable, but the model can (and should) be tuned to improve this. Most importantly, note that with minimal effort, our model produced accuracies similar to those published [here](http://media.salford-systems.com/video/tutorial/2015/targeted_marketing.pdf).
_Note that because there is some element of randomness in the algorithm's subsample, your results may differ slightly from the text written above._
## Automatic model Tuning (optional)
Amazon SageMaker automatic model tuning, also known as hyperparameter tuning, finds the best version of a model by running many training jobs on your dataset using the algorithm and ranges of hyperparameters that you specify. It then chooses the hyperparameter values that result in a model that performs the best, as measured by a metric that you choose.
For example, suppose that you want to solve a binary classification problem on this marketing dataset. Your goal is to maximize the area under the curve (auc) metric of the algorithm by training an XGBoost Algorithm model. You don't know which values of the eta, alpha, min_child_weight, and max_depth hyperparameters to use to train the best model. To find the best values for these hyperparameters, you can specify ranges of values that Amazon SageMaker hyperparameter tuning searches to find the combination of values that results in the training job that performs the best as measured by the objective metric that you chose. Hyperparameter tuning launches training jobs that use hyperparameter values in the ranges that you specified, and returns the training job with highest auc.
```
# cell 18
from sagemaker.tuner import IntegerParameter, CategoricalParameter, ContinuousParameter, HyperparameterTuner
hyperparameter_ranges = {'eta': ContinuousParameter(0, 1),
'min_child_weight': ContinuousParameter(1, 10),
'alpha': ContinuousParameter(0, 2),
'max_depth': IntegerParameter(1, 10)}
# cell 19
objective_metric_name = 'validation:auc'
# cell 20
tuner = HyperparameterTuner(xgb,
objective_metric_name,
hyperparameter_ranges,
max_jobs=20,
max_parallel_jobs=3)
# cell 21
tuner.fit({'train': s3_input_train, 'validation': s3_input_validation})
# cell 22
boto3.client('sagemaker').describe_hyper_parameter_tuning_job(
HyperParameterTuningJobName=tuner.latest_tuning_job.job_name)['HyperParameterTuningJobStatus']
# cell 23
# return the best training job name
tuner.best_training_job()
# cell 24
# Deploy the best trained or user specified model to an Amazon SageMaker endpoint
tuner_predictor = tuner.deploy(initial_instance_count=1,
instance_type='ml.m4.xlarge')
# cell 25
# Create a serializer
tuner_predictor.serializer = sagemaker.serializers.CSVSerializer()
# cell 26
# Predict
predictions = predict(test_x.to_numpy(),tuner_predictor)
# cell 27
# Collect predictions and convert from the CSV output our model provides into a NumPy array
pd.crosstab(index=test_y['y'].values, columns=np.round(predictions), rownames=['actuals'], colnames=['predictions'])
```
---
## Extensions
This example analyzed a relatively small dataset, but utilized Amazon SageMaker features such as distributed, managed training and real-time model hosting, which could easily be applied to much larger problems. In order to improve predictive accuracy further, we could tweak value we threshold our predictions at to alter the mix of false-positives and false-negatives, or we could explore techniques like hyperparameter tuning. In a real-world scenario, we would also spend more time engineering features by hand and would likely look for additional datasets to include which contain customer information not available in our initial dataset.
### (Optional) Clean-up
If you are done with this notebook, please run the cell below. This will remove the hosted endpoint you created and avoid any charges from a stray instance being left on.
```
# cell 28
xgb_predictor.delete_endpoint(delete_endpoint_config=True)
# cell 29
tuner_predictor.delete_endpoint(delete_endpoint_config=True)
```
| true |
code
| 0.517571 | null | null | null | null |
|
### Image Classification - Conv Nets -Pytorch
> Classifying if an image is a `bee` of an `ant` using `ConvNets` in pytorch
### Imports
```
import cv2
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
import torch
from torch import nn
import torch.nn.functional as F
import os
```
### Data Preparation
```
class Insect:
BEE = 'BEE'
ANT = "ANT"
BEES_IMAGES_PATH = 'data/colored/rgb/bees'
ANTS_IMAGES_PATH = 'data/colored/rgb/ants'
classes = {'bee': 0, 'ant' : 1}
classes =dict([(i, j) for (j, i) in classes.items()])
classes
os.path.exists(Insect.BEES_IMAGES_PATH)
insects = []
for path in os.listdir(Insect.BEES_IMAGES_PATH):
img_path = os.path.join(Insect.BEES_IMAGES_PATH, path)
image = np.array(cv2.imread(img_path, cv2.IMREAD_UNCHANGED), dtype='float32')
image = image / 255
insects.append([image, 0])
for path in os.listdir(Insect.ANTS_IMAGES_PATH):
img_path = os.path.join(Insect.ANTS_IMAGES_PATH, path)
image = np.array(cv2.imread(img_path, cv2.IMREAD_UNCHANGED), dtype='float32')
image = image / 255
insects.append([image, 1])
insects = np.array(insects)
np.random.shuffle(insects)
```
### Visualization
```
plt.imshow(insects[7][0], cmap="gray"), insects[10][0].shape
```
> Seperating Labels and features
```
X = np.array([insect[0] for insect in insects])
y = np.array([insect[1] for insect in insects])
X[0].shape
```
> Splitting the data into training and test.
```
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=.2)
X_train.shape, y_train.shape, y_test.shape, X_test.shape
```
> Converting the data into `torch` tensor.
```
X_train = torch.from_numpy(X_train.astype('float32'))
X_test = torch.from_numpy(X_test.astype('float32'))
y_train = torch.Tensor(y_train)
y_test = torch.Tensor(y_test)
```
### Model Creation
```
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels= 32, kernel_size=(3, 3))
self.conv2 = nn.Conv2d(32, 64, (3, 3))
self.conv3 = nn.Conv2d(64, 64, (3, 3))
self._to_linear = None # protected variable
self.x = torch.randn(3, 200, 200).view(-1, 3, 200, 200)
self.conv(self.x)
self.fc1 = nn.Linear(self._to_linear, 64)
self.fc2 = nn.Linear(64, 2)
def conv(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv3(x)), (2, 2))
if self._to_linear is None:
self._to_linear = x.shape[1] * x.shape[2] * x.shape[3]
return x
def forward(self, x):
x = self.conv(x)
x = x.view(-1, self._to_linear)
x = F.relu(self.fc1(x))
return x
net = Net()
net
optimizer = torch.optim.SGD(net.parameters(), lr=1e-3)
loss_function = nn.CrossEntropyLoss()
EPOCHS = 10
BATCH_SIZE = 5
for epoch in range(EPOCHS):
print(f'Epochs: {epoch+1}/{EPOCHS}')
for i in range(0, len(y_train), BATCH_SIZE):
X_batch = X_train[i: i+BATCH_SIZE].view(-1, 3, 200, 200)
y_batch = y_train[i: i+BATCH_SIZE].long()
net.zero_grad() ## or you can say optimizer.zero_grad()
outputs = net(X_batch)
loss = loss_function(outputs, y_batch)
loss.backward()
optimizer.step()
print("Loss", loss)
```
### Evaluating the model
### Test set
```
total, correct = 0, 0
with torch.no_grad():
for i in range(len(X_test)):
correct_label = torch.argmax(y_test[i])
prediction = torch.argmax(net(X_test[i].view(-1, 3, 200, 200))[0])
if prediction == correct_label:
correct+=1
total +=1
print(f"Accuracy: {correct/total}")
torch.argmax(net(X_test[1].view(-1, 3, 200, 200))), y_test[0]
```
### Train set
```
total, correct = 0, 0
with torch.no_grad():
for i in range(len(X_train)):
correct_label = torch.argmax(y_train[i])
prediction = torch.argmax(net(X_train[i].view(-1, 3, 200, 200))[0])
if prediction == correct_label:
correct+=1
total +=1
print(f"Accuracy: {correct/total}")
```
### Making Predictions
```
plt.imshow(X_test[12])
plt.title(classes[torch.argmax(net(X_test[12].view(-1, 3, 200, 200))).item()].title(), fontsize=16)
plt.show()
fig, ax = plt.subplots(nrows=3, ncols=3, figsize=(10, 10))
for row in ax:
for col in row:
col.imshow(X_test[2])
plt.show()
```
| true |
code
| 0.660775 | null | null | null | null |
|
# Using Models as Layers in Another Model
In this notebook, we show how you can use Keras models as Layers within a larger model and still perform pruning on that model.
```
# Import required packages
import tensorflow as tf
import mann
from sklearn.metrics import confusion_matrix, classification_report
# Load the data
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Convert images from grayscale to RGB
x_train = tf.image.grayscale_to_rgb(tf.Variable(x_train.reshape(-1, 28, 28, 1)))
x_test = tf.image.grayscale_to_rgb(tf.Variable(x_test.reshape(-1, 28, 28, 1)))
```
## Model Creation
In the following cells, we create two models and put them together to create a larger model. The first model, called the `preprocess_model`, takes in images, divides the pixel values by 255 to ensure all values are between 0 and 1, resized the image to a height and width of 40 pixels. It then performs training data augmentation by randomly flips some images across the y-axis, randomly rotates images, and randomly translates the images.
The second model, called the `true_model`, contains the logic for performing prediction on images. It contains blocks of convolutional layers followed by max pooling and dropout layers. The output of these blocks is flattened and passed through fully-connected layers to output predicted class probabilities.
These two models are combined in the `training_model` to be trained.
```
preprocess_model = tf.keras.models.Sequential()
preprocess_model.add(tf.keras.layers.Rescaling(1./255))
preprocess_model.add(tf.keras.layers.Resizing(40, 40, input_shape = (None, None, 3)))
preprocess_model.add(tf.keras.layers.RandomFlip('horizontal'))
preprocess_model.add(tf.keras.layers.RandomRotation(0.1))
preprocess_model.add(tf.keras.layers.RandomTranslation(0.1, 0.1))
true_model = tf.keras.models.Sequential()
true_model.add(mann.layers.MaskedConv2D(16, padding = 'same', input_shape = (40, 40, 3)))
true_model.add(mann.layers.MaskedConv2D(16, padding = 'same'))
true_model.add(tf.keras.layers.MaxPool2D())
true_model.add(tf.keras.layers.Dropout(0.2))
true_model.add(mann.layers.MaskedConv2D(32, padding = 'same', activation = 'relu'))
true_model.add(mann.layers.MaskedConv2D(32, padding = 'same', activation = 'relu'))
true_model.add(tf.keras.layers.MaxPool2D())
true_model.add(tf.keras.layers.Dropout(0.2))
true_model.add(mann.layers.MaskedConv2D(64, padding = 'same', activation = 'relu'))
true_model.add(mann.layers.MaskedConv2D(64, padding = 'same', activation = 'relu'))
true_model.add(tf.keras.layers.MaxPool2D())
true_model.add(tf.keras.layers.Dropout(0.2))
true_model.add(tf.keras.layers.Flatten())
true_model.add(mann.layers.MaskedDense(256, activation = 'relu'))
true_model.add(mann.layers.MaskedDense(256, activation = 'relu'))
true_model.add(mann.layers.MaskedDense(10, activation = 'softmax'))
training_input = tf.keras.layers.Input((None, None, 3))
training_x = preprocess_model(training_input)
training_output = true_model(training_x)
training_model = tf.keras.models.Model(
training_input,
training_output
)
training_model.compile(
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'],
optimizer = 'adam'
)
training_model.summary()
```
## Model Training
In this cell, we create the `ActiveSparsification` object to continually sparsify the model as it trains, and train the model.
```
callback = mann.utils.ActiveSparsification(
0.80,
sparsification_rate = 5
)
training_model.fit(
x_train,
y_train,
epochs = 200,
batch_size = 512,
validation_split = 0.2,
callbacks = [callback]
)
```
## Convert the model to not have masking layers
In the following cell, we configure the model to remove masking layers and replace them with non-masking native TensorFlow layers. We then perform prediction on the resulting model and present the results.
```
model = mann.utils.remove_layer_masks(training_model)
preds = model.predict(x_test).argmax(axis = 1)
print(confusion_matrix(y_test, preds))
print(classification_report(y_test, preds))
```
## Save only the model that performs prediction
Lastly, save only the part of the model that performs prediction
```
model.layers[2].save('ModelLayer.h5')
```
| true |
code
| 0.739005 | null | null | null | null |
|
# Transform JD text files into an LDA model and pyLDAvis visualization
### Steps:
1. Use spaCy phrase matching to identify skills
2. Parse the job descriptions. A full, readable job description gets turned into a bunch of newline-delimited skills.
3. Create a Gensim corpus and dictionary from the parsed skills
4. Train an LDA model using the corpus and dictionary
5. Visualize the LDA model
6. Compare user input to the LDA model; get out a list of relevant skills
```
# Modeling and visualization
import gensim
from gensim.corpora import Dictionary, MmCorpus
from gensim.models.ldamodel import LdaModel
import pyLDAvis
import pyLDAvis.gensim
# Utilities
import codecs
import pickle
import os
import warnings
# Black magic
import spacy
from spacy.matcher import Matcher
from spacy.attrs import *
nlp = spacy.load('en')
```
### 1. Use spaCy phrase matching to ID skills in job descriptions
**First, we read in a pickled dictionary that contains the word patterns we'll use to extract skills from JDs. Here's what the first few patterns look like:**
``` Python
{
0 : [{"lower": "after"}, {"lower": "effects"}],
1 : [{"lower": "amazon"}, {"lower": "web"}, {"lower": "services"}],
2 : [{"lower": "angular"}, {"lower": "js"}],
3 : [{"lower": "ansible"}],
4 : [{"lower": "bash"}, {"lower": "shell"}],
5 : [{"lower": "business"}, {"lower": "intelligence"}]
}
```
**We generated the pickled dictionary through some (rather heavy) preprocessing steps:**
1. Train a word2vec model on all of the job descriptions. Cluster the word embeddings, identify clusters associated with hard skills, and annotate all of the words in those clusters. Save those words as a "skill repository" (a text document that we'll use as the canonical list of hard tech skills).
2. Clean the skill repository. Inevitably, terms that are not hard skills made it into the word2vec "skill" clusters. Remove them. In this case, we defined a "skill" as "a tool, platform, or language that would make sense as a skill to learn or improve."
3. Use the skill repository to train an Named Entity Recognition model (in our case, using Prodigy). Use the training process to identify hard skills that we previously did not have in our repository. Add the new skills to the repository.
4. Create a Python dictionary of the skills. Format the dictionary so that the values can be ingested as spaCy language patterns.
See spaCy's [matcher documentation](https://spacy.io/api/matcher#init) for more details.
```
# read pickled dict() object
with open('skill_dict.pkl', 'rb') as f:
skill_dict = pickle.load(f)
%%time
# Read JDs into memory
import os
directory = os.fsencode('../local_data/')
jds = []
for file in os.listdir(directory):
filename = os.fsdecode(file)
path = '../local_data/' + filename
with open(path, 'r') as infile:
jds.append(infile.read())
print(len(jds), "JDs")
import sys
print(sys.getsizeof(jds)/1000000, "Megabytes")
```
### 2. Parse job descriptions
From each JD, generate a list of skills.
```
%%time
# Write skill-parsed JDs to file.
# This took about three hours for 106k jobs.
for idx, jd in enumerate(jds):
out_path = '../skill_parsed/'+ str(idx+1) + '.txt'
with open(out_path, 'w') as outfile:
# Creating a matcher object
doc = nlp(jd)
matcher = Matcher(nlp.vocab)
for label, pattern in skill_dict.items():
matcher.add(label, None, pattern)
matches = matcher(doc)
for match in matches:
# match object returns a tuple with (id, startpos, endpos)
output = str(doc[match[1]:match[2]]).replace(' ', '_').lower()
outfile.write(output)
outfile.write('\n')
```
### 3. Generate a Gensim corpus and dictionary from the parsed skill documents
```
%%time
# Load parsed items back into memory
directory = os.fsencode('skill_parsed//')
parsed_jds = []
for file in os.listdir(directory):
filename = os.fsdecode(file)
path = 'skill_parsed/' + filename
# Ran into an encoding issue; changing to latin-1 fixed it
with codecs.open(path, 'r', encoding='latin-1') as infile:
parsed_jds.append(infile.read())
%%time
'''
Gensim needs documents to be formatted as a list-of-lists, where the inner
lists are simply lists including the tokens (skills) from a given document.
It's important to note that any bigram or trigram skills are already tokenized
with underscores instead of spaces to preserve them as tokens.
'''
nested_dict_corpus = [text.split() for text in parsed_jds]
print(nested_dict_corpus[222:226])
from gensim.corpora import Dictionary, MmCorpus
gensim_skills_dict = Dictionary(nested_dict_corpus)
# save the dict
gensim_skills_dict.save('gensim_skills.dict')
corpus = [gensim_skills_dict.doc2bow(text) for text in nested_dict_corpus]
# Save the corpus
gensim.corpora.MmCorpus.serialize('skill_bow_corpus.mm', corpus, id2word=gensim_skills_dict)
# Load up the dictionary
gensim_skills_dict = Dictionary.load('gensim_skills.dict')
# Load the corpus
bow_corpus = MmCorpus('skill_bow_corpus.mm')
```
### 4. Create the LDA model using Gensim
```
%%time
with warnings.catch_warnings():
warnings.simplefilter('ignore')
lda_alpha_auto = LdaModel(bow_corpus,
id2word=gensim_skills_dict,
num_topics=20)
lda_alpha_auto.save('lda/skills_lda')
# load the finished LDA model from disk
lda = LdaModel.load('lda/skills_lda')
```
### 5. Visualize using pyLDAvis
```
LDAvis_data_filepath = 'lda/ldavis/ldavis'
%%time
LDAvis_prepared = pyLDAvis.gensim.prepare(lda, bow_corpus,
gensim_skills_dict)
with open(LDAvis_data_filepath, 'wb') as f:
pickle.dump(LDAvis_prepared, f)
# load the pre-prepared pyLDAvis data from disk
with open(LDAvis_data_filepath, 'rb') as f:
LDAvis_prepared = pickle.load(f)
pyLDAvis.display(LDAvis_prepared)
# Save the file as HTML
pyLDAvis.save_html(LDAvis_prepared, 'lda/html/lda.html')
```
### 6. Compare user input to the LDA model
Output the skills a user has and does not have from various topics.
```
# Look at the topics
def explore_topic(topic_number, topn=20):
"""
accept a topic number and print out a
formatted list of the top terms
"""
print(u'{:20} {}'.format(u'term', u'frequency') + u'')
for term, frequency in lda.show_topic(topic_number, topn=40):
print(u'{:20} {:.3f}'.format(term, round(frequency, 3)))
for i in range(20): # Same number as the types of jobs we scraped initially
print("\n\nTopic %s" % i)
explore_topic(topic_number=i)
# A stab at naming the topics
topic_names = {1: u'Data Engineering (Big Data Focus)',
2: u'Microsoft OOP Engineering (C, C++, .NET)',
3: u'Web Application Development (Ruby, Rails, JS, Databases)',
4: u'Linux/Unix, Software Engineering, and Scripting',
5: u'Database Administration',
6: u'Project Management (Agile Focus)',
7: u'Project Management (General Software)',
8: u'Product Management',
9: u'General Management & Productivity (Microsoft Office Focus)',
10: u'Software Program Management',
11: u'Project and Program Management',
12: u'DevOps and Cloud Computing/Infrastructure',
13: u'Frontend Software Engineering and Design',
14: u'Business Intelligence',
15: u'Analytics',
16: u'Quality Engineering, Version Control, & Build',
17: u'Big Data Analytics; Hardware & Scientific Computing',
18: u'Software Engineering',
19: u'Data Science, Machine Learning, and AI',
20: u'Design'}
```
#### Ingest user input & transform into list of skills
```
matcher = Matcher(nlp.vocab)
user_input = '''
My skills are Postgresql, and Python.
Experience with Chef Puppet and Docker required.
I also happen to know Blastoise and Charzard. Also NeuRal neTwOrk.
I use Git, Github, svn, Subversion, but not git, github or subversion.
Additionally, I can program using Perl, Java, and Haskell. But not perl, java, or haskell.'''
# Construct matcher object
doc = nlp(user_input)
for label, pattern in skill_dict.items():
matcher.add(label, None, pattern)
# Compare input to pre-defined skill patterns
user_skills = []
matches = matcher(doc)
for match in matches:
if match is not None:
# match object returns a tuple with (id, startpos, endpos)
output = str(doc[match[1]:match[2]]).lower()
user_skills.append(output)
print("*** User skills: *** ")
for skill in user_skills:
print(skill)
```
#### Compare user skills to the LDA model
```
def top_match_items(input_doc, lda_model, input_dictionary, num_terms=20):
"""
(1) parse input doc with spaCy, apply text pre-proccessing steps,
(3) create a bag-of-words representation (4) create an LDA representation
"""
doc_bow = gensim_skills_dict.doc2bow(input_doc)
# create an LDA representation
document_lda = lda_model[doc_bow]
# Sort in descending order
sorted_doc_lda = sorted(document_lda, key=lambda review_lda: -review_lda[1])
topic_number, freq = sorted_doc_lda[0][0], sorted_doc_lda[0][1]
highest_probability_topic = topic_names[topic_number+1]
top_topic_skills = []
for term, term_freq in lda.show_topic(topic_number, topn=num_terms):
top_topic_skills.append(term)
return highest_probability_topic, round(freq, 3), top_topic_skills
matched_topic, matched_freq, top_topic_skills = top_match_items(user_skills, lda, gensim_skills_dict)
def common_skills(top_topic_skills, user_skills):
return [item for item in top_topic_skills if item in user_skills]
def non_common_skills(top_topic_skills, user_skills):
return [item for item in top_topic_skills if item not in user_skills]
print("**** User's matched topic and percent match:")
print(matched_topic, matched_freq)
print("\n**** Skills user has in common with topic:")
for skill in common_skills(top_topic_skills, user_skills):
print(skill)
print("\n**** Skills user does NOT have in common with topic:")
for skill in non_common_skills(top_topic_skills, user_skills):
print(skill)
```
| true |
code
| 0.556279 | null | null | null | null |
|
# Unconstrainted optimization with NN models
In this tutorial we will go over type 1 optimization problem which entails nn.Module rerpesented cost function and __no constarint__ at all. This type of problem is often written as follows:
$$ \min_{x} f_{\theta}(x) $$
we can find Type1 problems quite easily. For instance assuming you are the manager of some manufactoring facilities, then your primary objective would be to maximize the yield of the manufactoring process. In industrial grade of manufactoring process the model of process is often __unknown__. hence we may need to learn the model through your favorite differentiable models such as neural networks and perform the graident based optimization to find the (local) optimums that minimize (or maximize) the yield.
### General problem solving tricks; Cast your problem into QP, approximately.
As far as I know, Convex optimization is the most general class of optmization problems where we have algorithms that can solve the problem optimally. Qudartic progamming (QP) is a type of convex optimization problems which is well developed in the side of theory and computations. We will heavily utilize QPs to solve the optimziation problems that have dependency with `torch` models.
Our general problem solving tricks are as follows:
1. Construct the cost or constraint models from the data
2. By utilizting `torch` automatic differentiation functionality, compute the jacobian or hessians of the moodels.
3. solve (possibley many times) QP with the estimated jacobian and hessians.
> It is noteworthy that even we locally cast the problem into QP, that doesn't mean our original problem is convex. Therefore, we cannot say that this approahces we will look over can find the global optimum.
```
import torch
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import TensorDataset, DataLoader
from src.utils import generate_y
from src.nn.MLP import MLP
```
## Generate training dataset
```
x_min, x_max = -4.0, 4.0
xs_linspace = torch.linspace(-4, 4, 2000).view(-1, 1)
ys_linspace = generate_y(xs_linspace)
# samples to construct training dataset
x_dist = torch.distributions.uniform.Uniform(-4.0, 4.0)
xs = x_dist.sample(sample_shape=(500, 1))
ys = generate_y(xs)
BS = 64 # Batch size
ds = TensorDataset(xs, ys)
loader = DataLoader(ds, batch_size=BS, shuffle=True)
input_dim, output_dim = 1, 1
m = MLP(input_dim, output_dim, num_neurons=[128, 128])
mse_criteria = torch.nn.MSELoss()
opt = torch.optim.Adam(m.parameters(), lr=1e-3)
n_update = 0
print_every = 500
epochs = 200
for _ in range(epochs):
for x, y in loader:
y_pred = m(x)
loss = mse_criteria(y_pred, y)
opt.zero_grad()
loss.backward()
opt.step()
n_update += 1
if n_update % print_every == 0:
print(n_update, loss.item())
# save model for the later usages
torch.save(m.state_dict(), './model.pt')
```
## Solve the unconstraint optimization problem
Let's solve the unconstraint optimization problem with torch estmiated graidents and simple gradient descent method.
```
def minimize_y(x_init, model, num_steps=15, step_size=1e-1):
def _grad(model, x):
return torch.autograd.functional.jacobian(model, x).squeeze()
x = x_init
xs = [x]
ys = [model(x)]
gs = [_grad(model, x)]
for _ in range(num_steps):
grad = _grad(model, x)
x = (x- step_size * grad).clone()
y = model(x)
xs.append(x)
ys.append(y)
gs.append(grad)
xs = torch.stack(xs).detach().numpy()
ys = torch.stack(ys).detach().numpy()
gs = torch.stack(gs).detach().numpy()
return xs, ys, gs
x_min, x_max = -4.0, 4.0
n_steps = 40
x_init = torch.tensor(np.random.uniform(x_min, x_max, 1)).float()
opt_xs, opt_ys, grad = minimize_y(x_init, m, n_steps)
pred_ys = m(xs_linspace).detach()
fig, axes = plt.subplots(1, 1, figsize=(10, 5))
axes.grid()
axes.plot(xs_linspace, ys_linspace, label='Ground truth')
axes.plot(xs_linspace, pred_ys, label='Model prediction')
axes.scatter(opt_xs[0], opt_ys[0], label='Opt start',
c='green', marker='*', s=100.0)
axes.scatter(opt_xs[1:], opt_ys[1:], label='NN opt', c='green')
_ = axes.legend()
```
| true |
code
| 0.720593 | null | null | null | null |
|
<!-- :Author: Arthur Goldberg <[email protected]> -->
<!-- :Date: 2020-08-02 -->
<!-- :Copyright: 2020, Karr Lab -->
<!-- :License: MIT -->
# DE-Sim: Ordering simultaneous events
DE-Sim makes it easy to build and simulate discrete-event models.
This notebook discusses DE-Sim's methods for controlling the execution order of simultaneous messages.
## Installation
Use `pip` to install `de_sim`.
## Scheduling events with equal simulation times
A discrete-event simulation may execute multiple events simultaneously, that is, at a particular simulation time.
To ensure that simulation runs are reproducible and deterministic, a simulator must provide mechanisms that deterministically control the execution order of simultaneous events.
Two types of situations arise, *local* and *global*.
A local situation arises when a simulation object receives multiple event messages simultaneously, while a global situation arises when multiple simulation objects execute events simultaneously.
Separate *local* and *global* mechanisms ensure that these situations are simulated deterministically.
The local mechanism ensures that simultaneous events are handled deterministically at a single simulation object, while the global mechanism ensures that simultaneous events are handled deterministically across all objects in a simulation.
### Local mechanism: simultaneous event messages at a simulation object
The local mechanism, called *event superposition* after the [physics concept of superposition](https://en.wikipedia.org/wiki/Superposition_principle), involves two components:
1. When a simulation object receives multiple event messages at the same time, the simulator passes all of the event messages to the object's event handler in a list.
(However, if simultaneous event messages have different handlers then the simulator raises a `SimulatorError` exception.)
2. The simulator sorts the events in the list so that any given list of events will always be arranged in the same order.
Event messages are sorted by the pair (event message priority, event message content).
Sorting costs O(n log n), but since simultaneous events are usually rare, sorting event lists is unlikely to slow down simulations.
```
""" This example illustrates the local mechanism that handles simultaneous
event messages received by a simulation object
"""
import random
import de_sim
from de_sim.event import Event
class Double(de_sim.EventMessage):
'Double value'
class Increment(de_sim.EventMessage):
'Increment value'
class IncrementThenDoubleSimObject(de_sim.SimulationObject):
""" Execute Increment before Double, demonstrating superposition """
def __init__(self, name):
super().__init__(name)
self.value = 0
def init_before_run(self):
self.send_events()
def handle_superposed_events(self, event_list):
""" Process superposed events in an event list
Each Increment message increments value, and each Double message doubles value.
Assumes that `event_list` contains an Increment event followed by a Double event.
Args:
event_list (:obj:`event_list` of :obj:`de_sim.Event`): list of events
"""
for event in event_list:
if isinstance(event.message, Increment):
self.value += 1
elif isinstance(event.message, Double):
self.value *= 2
self.send_events()
# The order of the message types in event_handlers, (Increment, Double), determines
# the sort order of messages in `event_list` received by `handle_superposed_events`
event_handlers = [(Increment, 'handle_superposed_events'),
(Double, 'handle_superposed_events')]
def send_events(self):
# To show that the simulator delivers event messages to `handle_superposed_events`
# sorted into the order (Increment, Double), send them in a random order.
if random.randrange(2):
self.send_event(1, self, Double())
self.send_event(1, self, Increment())
else:
self.send_event(1, self, Increment())
self.send_event(1, self, Double())
# Register the message types sent
messages_sent = (Increment, Double)
class TestSuperposition(object):
def increment_then_double_from_0(self, iterations):
v = 0
for _ in range(iterations):
v += 1
v *= 2
return v
def test_superposition(self, max_time):
simulator = de_sim.Simulator()
simulator.add_object(IncrementThenDoubleSimObject('name'))
simulator.initialize()
simulator.simulate(max_time)
for sim_obj in simulator.get_objects():
assert sim_obj.value, self.increment_then_double_from_0(max_time)
print(f'Simulation to {max_time} executed all messages in the order (Increment, Double).')
TestSuperposition().test_superposition(20)
```
This example shows how event superposition handles simultaneous events.
An `IncrementThenDoubleSimObject` simulation object stores an integer value.
It receives two events every time unit, one carrying an `Increment` message and another containing a `Double` message.
Executing an `Increment` event increments the value, while executing a `Double` message event doubles the value.
The design for `IncrementThenDoubleSimObject` requires that it increments before doubling.
Several features of DE-Sim and `IncrementThenDoubleSimObject` ensure this behavior:
1. The mapping between event message types and event handlers, stored in the list `event_handlers`, contains `Increment` before `Double`. This gives events containing an `Increment` message a higher priority than events containing `Double`.
2. Under the covers, when DE-Sim passes superposed events to a subclass of [`SimulationObject`](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.simulation_object.SimulationObject), it sorts the messages by their (event message priority, event message content), which sorts events with higher priority message types earlier.
3. The message handler `handle_superposed_events` receives a list of events and executes them in order.
To challenge and test this superposition mechanism, the `send_events()` method in `IncrementThenDoubleSimObject` randomizes the order in which it sends `Increment` and `Double` events.
Finally, `TestSuperposition().test_superposition()` runs a simulation of `IncrementThenDoubleSimObject` and asserts that the value it computes equals the correct value for a sequence of increment and double operations.
### Global mechanism: simultaneous event messages at multiple simulation objects
A *global* mechanism is needed to ensure that simultaneous events which occur at distinct objects in a simulation are executed in a deterministic order.
Otherwise, the discrete-event simulator might execute simultaneous events at distinct simulation objects in a different order in different simulation runs that use the same input.
When using a simulator that allows 0-delay event messages or global state shared between simulation objects -- both of which DE-Sim supports -- this can alter the simulation's predictions and thereby imperil debugging efforts, statistical analyses of predictions and other essential uses of simulation results.
The global mechanism employed by DE-Sim conceives of the simulation time as a pair -- the event time, and a *sub-time* which breaks event time ties.
Sub-time values within a particular simulation time must be distinct.
Given that constraint, many approaches for selecting the sub-time would achieve the objective.
DE-Sim creates a distinct sub-time from the state of the simulation object receiving an event.
The sub-time is a pair composed of a priority assigned to the simulation class and a unique identifier for each class instance.
Each simulation class defines a `class_priority` attribute that determines the relative execution order of simultaneous events by different simulation classes.
Among multiple instances of a simulation class, the attribute `event_time_tiebreaker`, which defaults to a simulation instance's unique name, breaks ties.
All classes have the same default priority of `LOW`. If class priorities are not set and `event_time_tiebreaker`s are not set for individual simulation objects, then an object's global priority is given by its name.
```
from de_sim.simulation_object import SimObjClassPriority
class ExampleMsg(de_sim.EventMessage):
'Example message'
class NoPrioritySimObj(de_sim.SimulationObject):
def init_before_run(self):
self.send_event(0., self, ExampleMsg())
# register the message types sent
messages_sent = (ExampleMsg, )
class LowPrioritySimObj(NoPrioritySimObj):
def handler(self, event):
print(f"{self.time}: LowPrioritySimObj {self.name} running")
self.send_event(1., self, ExampleMsg())
event_handlers = [(ExampleMsg, 'handler')]
# have `LowPrioritySimObj`s execute at low priority
class_priority = SimObjClassPriority.LOW
class MediumPrioritySimObj(NoPrioritySimObj):
def handler(self, event):
print(f"{self.time}: MediumPrioritySimObj {self.name} running")
self.send_event(1., self, ExampleMsg())
event_handlers = [(ExampleMsg, 'handler')]
# have `MediumPrioritySimObj`s execute at medium priority
class_priority = SimObjClassPriority.MEDIUM
simulator = de_sim.Simulator()
simulator.add_object(LowPrioritySimObj('A'))
simulator.add_object(MediumPrioritySimObj('B'))
simulator.initialize()
print(simulator.simulate(2).num_events, 'events executed')
```
This example illustrates the scheduling of simultaneous event messages.
`SimObjClassPriority` is an `IntEnum` that provides simulation object class priorities, including `LOW`, `MEDIUM`, and `HIGH`.
We create two classes, `LowPrioritySimObj` and `MediumPrioritySimObj`, with `LOW` and `MEDIUM` priorities, respectively, and execute them simultaneously at simulation times 0, 1, 2, ...
At each time, the `MediumPrioritySimObj` object runs before the `LowPrioritySimObj` one.
#### Execution order of objects without an assigned `class_priority`
The next example shows the ordering of simultaneous events executed by objects that don't have assigned priorities.
```
class DefaultPrioritySimObj(NoPrioritySimObj):
def handler(self, event):
print(f"{self.time}: DefaultPrioritySimObj {self.name} running")
self.send_event(1., self, ExampleMsg())
event_handlers = [(ExampleMsg, 'handler')]
simulator = de_sim.Simulator()
for name in random.sample(range(10), k=3):
sim_obj = DefaultPrioritySimObj(str(name))
print(f"{sim_obj.name} priority: {sim_obj.class_event_priority.name}")
simulator.add_object(sim_obj)
simulator.initialize()
print(simulator.simulate(2).num_events, 'events executed')
```
In this example, the [`SimulationObject`s](https://docs.karrlab.org/de_sim/master/source/de_sim.html#de_sim.simulation_object.SimulationObject) have no priorities assigned, so their default priorities are `LOW`. (The `class_event_priority` attribute of a simulation object is a `SimObjClassPriority`)
Three objects with names randomly selected from '0', '1', ..., '9', are created.
When they execute simultaneously, events are ordered by the sort order of the objects' names.
#### Execution order of instances of simulation object classes with relative priorities
Often, a modeler wants to control the *relative* simultaneous priorities of simulation objects, but does not care about their absolute priorities.
The next example shows how to specify relative priorities.
```
class FirstNoPrioritySimObj(NoPrioritySimObj):
def handler(self, event):
print(f"{self.time}: FirstNoPrioritySimObj {self.name} running")
self.send_event(1., self, ExampleMsg())
event_handlers = [(ExampleMsg, 'handler')]
class SecondNoPrioritySimObj(NoPrioritySimObj):
def handler(self, event):
print(f"{self.time}: SecondNoPrioritySimObj {self.name} running")
self.send_event(1., self, ExampleMsg())
event_handlers = [(ExampleMsg, 'handler')]
# Assign decreasing priorities to classes in [FirstNoPrioritySimObj, SecondNoPrioritySimObj]
SimObjClassPriority.assign_decreasing_priority([FirstNoPrioritySimObj,
SecondNoPrioritySimObj])
simulator = de_sim.Simulator()
simulator.add_object(SecondNoPrioritySimObj('A'))
simulator.add_object(FirstNoPrioritySimObj('B'))
for sim_obj in simulator.simulation_objects.values():
print(f"{type(sim_obj).__name__}: {sim_obj.name}; "
f"priority: {sim_obj.class_event_priority.name}")
simulator.initialize()
print(simulator.simulate(2).num_events, 'events executed')
```
The `assign_decreasing_priority` method of `SimObjClassPriority` takes an iterator over `SimulationObject` subclasses, and assigns them decreasing simultaneous event priorities.
The `FirstNoPrioritySimObj` instance therefore executes before the `SecondNoPrioritySimObj` instance at each discrete simulation time.
| true |
code
| 0.883261 | null | null | null | null |
|
# HandGestureDetection using OpenCV
This code template is for Hand Gesture detection in a video using OpenCV Library.
### Required Packages
```
!pip install opencv-python
!pip install mediapipe
import cv2
import mediapipe as mp
import time
```
### Hand Detection
For detecting hands in the image, we use the detectMultiScale() function.
It detects objects of different sizes in the input image. The detected objects are returned as a list of rectangles which can be then plotted around the hands.
####Tuning Parameters:
**image** - Matrix of the type CV_8U containing an image where objects are detected.
**objects** - Vector of rectangles where each rectangle contains the detected object, the rectangles may be partially outside the original image.
**scaleFactor** - Parameter specifying how much the image size is reduced at each image scale.
**minNeighbors** - Parameter specifying how many neighbors each candidate rectangle should have to retain it.
```
class handDetector():
def __init__(self, mode = False, maxHands = 2, detectionCon = 0.5, trackCon = 0.5):
self.mode = mode
self.maxHands = maxHands
self.detectionCon = detectionCon
self.trackCon = trackCon
self.mpHands = mp.solutions.hands
self.hands = self.mpHands.Hands(self.mode, self.maxHands, self.detectionCon, self.trackCon)
self.mpDraw = mp.solutions.drawing_utils
def findHands(self,img, draw = True):
imgRGB = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
self.results = self.hands.process(imgRGB)
# print(results.multi_hand_landmarks)
if self.results.multi_hand_landmarks:
for handLms in self.results.multi_hand_landmarks:
if draw:
self.mpDraw.draw_landmarks(img, handLms, self.mpHands.HAND_CONNECTIONS)
return img
def findPosition(self, img, handNo = 0, draw = True):
lmlist = []
if self.results.multi_hand_landmarks:
myHand = self.results.multi_hand_landmarks[handNo]
for id, lm in enumerate(myHand.landmark):
h, w, c = img.shape
cx, cy = int(lm.x * w), int(lm.y * h)
lmlist.append([id, cx, cy])
if draw:
cv2.circle(img, (cx, cy), 3, (255, 0, 255), cv2.FILLED)
return lmlist
```
To run the handDetector(), save this file with .py extension and allow your webcam to take a video. The co-ordinates will be outputted at the terminal.
```
pTime = 0
cTime = 0
cap = cv2.VideoCapture(0)
detector = handDetector()
while True:
success, img = cap.read()
img = detector.findHands(img)
lmlist = detector.findPosition(img)
if len(lmlist) != 0:
print(lmlist[4])
cTime = time.time()
fps = 1 / (cTime - pTime)
pTime = cTime
cv2.putText(img, str(int(fps)), (10, 70), cv2.FONT_HERSHEY_PLAIN, 3, (255, 0, 255), 3)
cv2.imshow("Image", img)
cv2.waitKey(1)
```
#### Creator: Ayush Gupta , Github: [Profile](https://github.com/guptayush179)
| true |
code
| 0.329105 | null | null | null | null |
|
# Similarity Encoders with Keras
## using the model definition from `simec.py`
```
from __future__ import unicode_literals, division, print_function, absolute_import
from builtins import range
import numpy as np
np.random.seed(28)
import matplotlib.pyplot as plt
from sklearn.manifold import Isomap
from sklearn.decomposition import KernelPCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import fetch_mldata, fetch_20newsgroups
import tensorflow as tf
tf.set_random_seed(28)
import keras
from keras.models import Sequential, Model
from keras.layers import Input, Dense, Activation
# https://github.com/cod3licious/nlputils
from nlputils.features import FeatureTransform, features2mat
from simec import SimilarityEncoder
from utils import center_K, check_embed_match, check_similarity_match
from utils_plotting import plot_mnist, plot_20news
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
### MNIST with Linear Kernel
```
# load digits
mnist = fetch_mldata('MNIST original', data_home='data')
X = mnist.data/255. # normalize to 0-1
y = np.array(mnist.target, dtype=int)
# subsample 10000 random data points
np.random.seed(42)
n_samples = 10000
n_test = 2000
rnd_idx = np.random.permutation(X.shape[0])[:n_samples]
X_test, y_test = X[rnd_idx[:n_test],:], y[rnd_idx[:n_test]]
X, y = X[rnd_idx[n_test:],:], y[rnd_idx[n_test:]]
ss = StandardScaler(with_std=False)
X = ss.fit_transform(X)
X_test = ss.transform(X_test)
n_train, n_features = X.shape
# centered linear kernel matrix
K_lin = center_K(np.dot(X, X.T))
# linear kPCA
kpca = KernelPCA(n_components=2, kernel='linear')
X_embed = kpca.fit_transform(X)
X_embed_test = kpca.transform(X_test)
plot_mnist(X_embed, y, X_embed_test, y_test, title='MNIST - linear Kernel PCA')
print("error similarity match: msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embed, K_lin))
# on how many target similarities you want to train - faster and works equally well than training on all
n_targets = 1000 # K_lin.shape[1]
# initialize the model
simec = SimilarityEncoder(X.shape[1], 2, n_targets, s_ll_reg=0.5, S_ll=K_lin[:n_targets,:n_targets])
# train the model to get an embedding with which the target similarities
# can be linearly approximated
simec.fit(X, K_lin[:,:n_targets], epochs=25)
# get the embeddings
X_embeds = simec.transform(X)
X_embed_tests = simec.transform(X_test)
plot_mnist(X_embeds, y, X_embed_tests, y_test, title='MNIST - SimEc (lin. kernel, linear)')
# correlation with the embedding produced by the spectral method should be high
print("correlation with lin kPCA : %f" % check_embed_match(X_embed, X_embeds)[1])
print("correlation with lin kPCA (test): %f" % check_embed_match(X_embed_test, X_embed_tests)[1])
# similarity match error should be similar to the one from kpca
print("error similarity match: msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embeds, K_lin))
```
### Non-linear MNIST embedding with isomap
```
# isomap
isomap = Isomap(n_neighbors=10, n_components=2)
X_embed = isomap.fit_transform(X)
X_embed_test = isomap.transform(X_test)
plot_mnist(X_embed, y, X_embed_test, y_test, title='MNIST - isomap')
# non-linear SimEc to approximate isomap solution
K_geod = center_K(-0.5*(isomap.dist_matrix_**2))
n_targets = 1000
# initialize the model
simec = SimilarityEncoder(X.shape[1], 2, n_targets, hidden_layers=[(20, 'tanh')], s_ll_reg=0.5,
S_ll=K_geod[:n_targets,:n_targets], opt=keras.optimizers.Adamax(lr=0.01))
# train the model to get an embedding with which the target similarities
# can be linearly approximated
simec.fit(X, K_geod[:,:n_targets], epochs=25)
# get the embeddings
X_embeds = simec.transform(X)
X_embed_tests = simec.transform(X_test)
plot_mnist(X_embeds, y, X_embed_tests, y_test, title='MNIST - SimEc (isomap, 1 h.l.)')
print("correlation with isomap : %f" % check_embed_match(X_embed, X_embeds)[1])
print("correlation with isomap (test): %f" % check_embed_match(X_embed_test, X_embed_tests)[1])
```
## 20newsgroups embedding
```
## load the data and transform it into a tf-idf representation
categories = [
"comp.graphics",
"rec.autos",
"rec.sport.baseball",
"sci.med",
"sci.space",
"soc.religion.christian",
"talk.politics.guns"
]
newsgroups_train = fetch_20newsgroups(subset='train', remove=(
'headers', 'footers', 'quotes'), data_home='data', categories=categories, random_state=42)
newsgroups_test = fetch_20newsgroups(subset='test', remove=(
'headers', 'footers', 'quotes'), data_home='data', categories=categories, random_state=42)
# store in dicts (if the text contains more than 3 words)
textdict = {i: t for i, t in enumerate(newsgroups_train.data) if len(t.split()) > 3}
textdict.update({i: t for i, t in enumerate(newsgroups_test.data, len(newsgroups_train.data)) if len(t.split()) > 3})
train_ids = [i for i in range(len(newsgroups_train.data)) if i in textdict]
test_ids = [i for i in range(len(newsgroups_train.data), len(textdict)) if i in textdict]
print("%i training and %i test samples" % (len(train_ids), len(test_ids)))
# transform into tf-idf features
ft = FeatureTransform(norm='max', weight=True, renorm='max')
docfeats = ft.texts2features(textdict, fit_ids=train_ids)
# organize in feature matrix
X, featurenames = features2mat(docfeats, train_ids)
X_test, _ = features2mat(docfeats, test_ids, featurenames)
print("%i features" % len(featurenames))
targets = np.hstack([newsgroups_train.target,newsgroups_test.target])
y = targets[train_ids]
y_test = targets[test_ids]
target_names = newsgroups_train.target_names
n_targets = 1000
# linear kPCA
kpca = KernelPCA(n_components=2, kernel='linear')
X_embed = kpca.fit_transform(X)
X_embed_test = kpca.transform(X_test)
plot_20news(X_embed, y, target_names, X_embed_test, y_test,
title='20newsgroups - linear Kernel PCA', legend=True)
# compute linear kernel and center
K_lin = center_K(X.dot(X.T).A)
K_lin_test = center_K(X_test.dot(X_test.T).A)
print("similarity approximation : msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embed, K_lin))
print("similarity approximation (test): msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embed_test, K_lin_test))
# project to 2d with linear similarity encoder
# careful: our input is sparse!!!
simec = SimilarityEncoder(X.shape[1], 2, n_targets, sparse_inputs=True, opt=keras.optimizers.SGD(lr=50.))
# train the model to get an embedding with which the target similarities
# can be linearly approximated
simec.fit(X, K_lin[:,:n_targets], epochs=25)
# get the embeddings
X_embeds = simec.transform(X)
X_embed_tests = simec.transform(X_test)
plot_20news(X_embeds, y, target_names, X_embed_tests, y_test,
title='20 newsgroups - SimEc (lin. kernel, linear)', legend=True)
print("correlation with lin kPCA : %f" % check_embed_match(X_embed, X_embeds)[1])
print("correlation with lin kPCA (test): %f" % check_embed_match(X_embed_test, X_embed_tests)[1])
print("similarity approximation : msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embeds, K_lin))
print("similarity approximation (test): msqe: %.10f ; r^2: %.10f ; rho: %.10f" % check_similarity_match(X_embed_tests, K_lin_test))
```
| true |
code
| 0.679285 | null | null | null | null |
|
** ----- IMPORTANT ------ **
The code presented here assumes that you're running TensorFlow v1.3.0 or higher, this was not released yet so the easiet way to run this is update your TensorFlow version to TensorFlow's master.
To do that go [here](https://github.com/tensorflow/tensorflow#installation) and then execute:
`pip install --ignore-installed --upgrade <URL for the right binary for your machine>`.
For example, considering a Linux CPU-only running python2:
`pip install --upgrade https://ci.tensorflow.org/view/Nightly/job/nightly-matrix-cpu/TF_BUILD_IS_OPT=OPT,TF_BUILD_IS_PIP=PIP,TF_BUILD_PYTHON_VERSION=PYTHON2,label=cpu-slave/lastSuccessfulBuild/artifact/pip_test/whl/tensorflow-1.2.1-cp27-none-linux_x86_64.whl`
## Here is walk-through to help getting started with tensorflow
1) Simple Linear Regression with low-level TensorFlow
2) Simple Linear Regression with a canned estimator
3) Playing with real data: linear regressor and DNN
4) Building a custom estimator to classify handwritten digits (MNIST)
### [What's next?](https://goo.gl/hZaLPA)
## Dependencies
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import collections
# tensorflow
import tensorflow as tf
print('Expected TensorFlow version is v1.3.0 or higher')
print('Your TensorFlow version:', tf.__version__)
# data manipulation
import numpy as np
import pandas as pd
# visualization
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
matplotlib.rcParams['figure.figsize'] = [12,8]
```
## 1) Simple Linear Regression with low-level TensorFlow
### Generating data
This function creates a noisy dataset that's roughly linear, according to the equation y = mx + b + noise.
Notice that the expected value for m is 0.1 and for b is 0.3. This is the values we expect the model to predict.
```
def make_noisy_data(m=0.1, b=0.3, n=100):
x = np.random.randn(n)
noise = np.random.normal(scale=0.01, size=len(x))
y = m * x + b + noise
return x, y
```
Create training data
```
x_train, y_train = make_noisy_data()
```
Plot the training data
```
plt.plot(x_train, y_train, 'b.')
```
### The Model
```
# input and output
x = tf.placeholder(shape=[None], dtype=tf.float32, name='x')
y_label = tf.placeholder(shape=[None], dtype=tf.float32, name='y_label')
# variables
W = tf.Variable(tf.random_normal([1], name="W")) # weight
b = tf.Variable(tf.random_normal([1], name="b")) # bias
# actual model
y = W * x + b
```
### The Loss and Optimizer
Define a loss function (here, squared error) and an optimizer (here, gradient descent).
```
loss = tf.reduce_mean(tf.square(y - y_label))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(loss)
```
### The Training Loop and generating predictions
```
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init) # initialize variables
for i in range(100): # train for 100 steps
sess.run(train, feed_dict={x: x_train, y_label:y_train})
x_plot = np.linspace(-3, 3, 101) # return evenly spaced numbers over a specified interval
# using the trained model to predict values for the training data
y_plot = sess.run(y, feed_dict={x: x_plot})
# saving final weight and bias
final_W = sess.run(W)
final_b = sess.run(b)
```
### Visualizing predictions
```
plt.scatter(x_train, y_train)
plt.plot(x_plot, y_plot, 'g')
```
### What is the final weight and bias?
```
print('W:', final_W, 'expected: 0.1')
print('b:', final_b, 'expected: 0.3')
```
## 2) Simple Linear Regression with a canned estimator
### Input Pipeline
```
x_dict = {'x': x_train}
train_input = tf.estimator.inputs.numpy_input_fn(x_dict, y_train,
shuffle=True,
num_epochs=None) # repeat forever
```
### Describe input feature usage
```
features = [tf.feature_column.numeric_column('x')] # because x is a real number
```
### Build and train the model
```
estimator = tf.estimator.LinearRegressor(features)
estimator.train(train_input, steps = 1000)
```
### Generating and visualizing predictions
```
x_test_dict = {'x': np.linspace(-5, 5, 11)}
data_source = tf.estimator.inputs.numpy_input_fn(x_test_dict, shuffle=False)
predictions = list(estimator.predict(data_source))
preds = [p['predictions'][0] for p in predictions]
for y in predictions:
print(y['predictions'])
plt.scatter(x_train, y_train)
plt.plot(x_test_dict['x'], preds, 'g')
```
## 3) Playing with real data: linear regressor and DNN
### Get the data
The Adult dataset is from the Census bureau and the task is to predict whether a given adult makes more than $50,000 a year based attributes such as education, hours of work per week, etc.
But the code here presented can be easilly aplicable to any csv dataset that fits in memory.
More about the data [here](https://archive.ics.uci.edu/ml/machine-learning-databases/adult/old.adult.names)
```
census_train_url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data'
census_train_path = tf.contrib.keras.utils.get_file('census.train', census_train_url)
census_test_url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.test'
census_test_path = tf.contrib.keras.utils.get_file('census.test', census_test_url)
```
### Load the data
```
column_names = [
'age', 'workclass', 'fnlwgt', 'education', 'education-num',
'marital-status', 'occupation', 'relationship', 'race', 'sex',
'capital-gain', 'capital-loss', 'hours-per-week', 'native-country',
'income'
]
census_train = pd.read_csv(census_train_path, index_col=False, names=column_names)
census_test = pd.read_csv(census_train_path, index_col=False, names=column_names)
census_train_label = census_train.pop('income') == " >50K"
census_test_label = census_test.pop('income') == " >50K"
census_train.head(10)
census_train_label[:20]
```
### Input pipeline
```
train_input = tf.estimator.inputs.pandas_input_fn(
census_train,
census_train_label,
shuffle=True,
batch_size = 32, # process 32 examples at a time
num_epochs=None,
)
test_input = tf.estimator.inputs.pandas_input_fn(
census_test,
census_test_label,
shuffle=True,
num_epochs=1)
features, labels = train_input()
features
```
### Feature description
```
features = [
tf.feature_column.numeric_column('hours-per-week'),
tf.feature_column.bucketized_column(tf.feature_column.numeric_column('education-num'), list(range(25))),
tf.feature_column.categorical_column_with_vocabulary_list('sex', ['male','female']),
tf.feature_column.categorical_column_with_hash_bucket('native-country', 1000),
]
estimator = tf.estimator.LinearClassifier(features, model_dir='census/linear',n_classes=2)
estimator.train(train_input, steps=5000)
```
### Evaluate the model
```
estimator.evaluate(test_input)
```
## DNN model
### Update input pre-processing
```
features = [
tf.feature_column.numeric_column('education-num'),
tf.feature_column.numeric_column('hours-per-week'),
tf.feature_column.numeric_column('age'),
tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_vocabulary_list('sex',['male','female'])),
tf.feature_column.embedding_column( # now using embedding!
tf.feature_column.categorical_column_with_hash_bucket('native-country', 1000), 10)
]
estimator = tf.estimator.DNNClassifier(hidden_units=[20,20],
feature_columns=features,
n_classes=2,
model_dir='census/dnn')
estimator.train(train_input, steps=5000)
estimator.evaluate(test_input)
```
## Custom Input Pipeline using Datasets API
### Read the data
```
def census_input_fn(path):
def input_fn():
dataset = (
tf.contrib.data.TextLineDataset(path)
.map(csv_decoder)
.shuffle(buffer_size=100)
.batch(32)
.repeat())
columns = dataset.make_one_shot_iterator().get_next()
income = tf.equal(columns.pop('income')," >50K")
return columns, income
return input_fn
csv_defaults = collections.OrderedDict([
('age',[0]),
('workclass',['']),
('fnlwgt',[0]),
('education',['']),
('education-num',[0]),
('marital-status',['']),
('occupation',['']),
('relationship',['']),
('race',['']),
('sex',['']),
('capital-gain',[0]),
('capital-loss',[0]),
('hours-per-week',[0]),
('native-country',['']),
('income',['']),
])
def csv_decoder(line):
parsed = tf.decode_csv(line, csv_defaults.values())
return dict(zip(csv_defaults.keys(), parsed))
```
### Try the input function
```
tf.reset_default_graph()
census_input = census_input_fn(census_train_path)
training_batch = census_input()
with tf.Session() as sess:
features, high_income = sess.run(training_batch)
print(features['education'])
print(features['age'])
print(high_income)
```
## 4) Building a custom estimator to classify handwritten digits (MNIST)
Image from: http://rodrigob.github.io/are_we_there_yet/build/images/mnist.png?1363085077
```
train,test = tf.contrib.keras.datasets.mnist.load_data()
x_train,y_train = train
x_test,y_test = test
mnist_train_input = tf.estimator.inputs.numpy_input_fn({'x':np.array(x_train, dtype=np.float32)},
np.array(y_train,dtype=np.int32),
shuffle=True,
num_epochs=None)
mnist_test_input = tf.estimator.inputs.numpy_input_fn({'x':np.array(x_test, dtype=np.float32)},
np.array(y_test,dtype=np.int32),
shuffle=True,
num_epochs=1)
```
### tf.estimator.LinearClassifier
```
estimator = tf.estimator.LinearClassifier([tf.feature_column.numeric_column('x',shape=784)],
n_classes=10,
model_dir="mnist/linear")
estimator.train(mnist_train_input, steps = 10000)
estimator.evaluate(mnist_test_input)
```
### Examine the results with [TensorBoard](http://0.0.0.0:6006)
$> tensorboard --logdir mnnist/DNN
```
estimator = tf.estimator.DNNClassifier(hidden_units=[256],
feature_columns=[tf.feature_column.numeric_column('x',shape=784)],
n_classes=10,
model_dir="mnist/DNN")
estimator.train(mnist_train_input, steps = 10000)
estimator.evaluate(mnist_test_input)
# Parameters
BATCH_SIZE = 128
STEPS = 10000
```
## A Custom Model
```
def build_cnn(input_layer, mode):
with tf.name_scope("conv1"):
conv1 = tf.layers.conv2d(inputs=input_layer,filters=32, kernel_size=[5, 5],
padding='same', activation=tf.nn.relu)
with tf.name_scope("pool1"):
pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2)
with tf.name_scope("conv2"):
conv2 = tf.layers.conv2d(inputs=pool1,filters=64, kernel_size=[5, 5],
padding='same', activation=tf.nn.relu)
with tf.name_scope("pool2"):
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
with tf.name_scope("dense"):
pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64])
dense = tf.layers.dense(inputs=pool2_flat, units=1024, activation=tf.nn.relu)
with tf.name_scope("dropout"):
is_training_mode = mode == tf.estimator.ModeKeys.TRAIN
dropout = tf.layers.dropout(inputs=dense, rate=0.4, training=is_training_mode)
logits = tf.layers.dense(inputs=dropout, units=10)
return logits
def model_fn(features, labels, mode):
# Describing the model
input_layer = tf.reshape(features['x'], [-1, 28, 28, 1])
tf.summary.image('mnist_input',input_layer)
logits = build_cnn(input_layer, mode)
# Generate Predictions
classes = tf.argmax(input=logits, axis=1)
predictions = {
'classes': classes,
'probabilities': tf.nn.softmax(logits, name='softmax_tensor')
}
if mode == tf.estimator.ModeKeys.PREDICT:
# Return an EstimatorSpec object
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)
with tf.name_scope('loss'):
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits)
loss = tf.reduce_sum(loss)
tf.summary.scalar('loss', loss)
with tf.name_scope('accuracy'):
accuracy = tf.cast(tf.equal(tf.cast(classes,tf.int32),labels),tf.float32)
accuracy = tf.reduce_mean(accuracy)
tf.summary.scalar('accuracy', accuracy)
# Configure the Training Op (for TRAIN mode)
if mode == tf.estimator.ModeKeys.TRAIN:
train_op = tf.contrib.layers.optimize_loss(
loss=loss,
global_step=tf.train.get_global_step(),
learning_rate=1e-4,
optimizer='Adam')
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions,
loss=loss, train_op=train_op)
# Configure the accuracy metric for evaluation
eval_metric_ops = {
'accuracy': tf.metrics.accuracy(
classes,
input=labels)
}
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions,
loss=loss, eval_metric_ops=eval_metric_ops)
```
## Runs estimator
```
# create estimator
run_config = tf.contrib.learn.RunConfig(model_dir='mnist/CNN')
estimator = tf.estimator.Estimator(model_fn=model_fn, config=run_config)
# train for 10000 steps
estimator.train(input_fn=mnist_train_input, steps=10000)
# evaluate
estimator.evaluate(input_fn=mnist_test_input)
# predict
preds = estimator.predict(input_fn=test_input_fn)
```
## Distributed tensorflow: using experiments
```
# Run an experiment
from tensorflow.contrib.learn.python.learn import learn_runner
# Enable TensorFlow logs
tf.logging.set_verbosity(tf.logging.INFO)
# create experiment
def experiment_fn(run_config, hparams):
# create estimator
estimator = tf.estimator.Estimator(model_fn=model_fn,
config=run_config)
return tf.contrib.learn.Experiment(
estimator,
train_input_fn=train_input_fn,
eval_input_fn=test_input_fn,
train_steps=STEPS
)
# run experiment
learn_runner.run(experiment_fn,
run_config=run_config)
```
### Examine the results with [TensorBoard](http://0.0.0.0:6006)
$> tensorboard --logdir mnist/CNN
| true |
code
| 0.723468 | null | null | null | null |
|
# Understanding the FFT Algorithm
Copy from http://jakevdp.github.io/blog/2013/08/28/understanding-the-fft/
*This notebook first appeared as a post by Jake Vanderplas on [Pythonic Perambulations](http://jakevdp.github.io/blog/2013/08/28/understanding-the-fft/). The notebook content is BSD-licensed.*
<!-- PELICAN_BEGIN_SUMMARY -->
The Fast Fourier Transform (FFT) is one of the most important algorithms in signal processing and data analysis. I've used it for years, but having no formal computer science background, It occurred to me this week that I've never thought to ask *how* the FFT computes the discrete Fourier transform so quickly. I dusted off an old algorithms book and looked into it, and enjoyed reading about the deceptively simple computational trick that JW Cooley and John Tukey outlined in their classic [1965 paper](http://www.ams.org/journals/mcom/1965-19-090/S0025-5718-1965-0178586-1/) introducing the subject.
The goal of this post is to dive into the Cooley-Tukey FFT algorithm, explaining the symmetries that lead to it, and to show some straightforward Python implementations putting the theory into practice. My hope is that this exploration will give data scientists like myself a more complete picture of what's going on in the background of the algorithms we use.
<!-- PELICAN_END_SUMMARY -->
## The Discrete Fourier Transform
The FFT is a fast, $\mathcal{O}[N\log N]$ algorithm to compute the Discrete Fourier Transform (DFT), which
naively is an $\mathcal{O}[N^2]$ computation. The DFT, like the more familiar continuous version of the Fourier transform, has a forward and inverse form which are defined as follows:
**Forward Discrete Fourier Transform (DFT):**
$$X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N}$$
**Inverse Discrete Fourier Transform (IDFT):**
$$x_n = \frac{1}{N}\sum_{k=0}^{N-1} X_k e^{i~2\pi~k~n~/~N}$$
The transformation from $x_n \to X_k$ is a translation from configuration space to frequency space, and can be very useful in both exploring the power spectrum of a signal, and also for transforming certain problems for more efficient computation. For some examples of this in action, you can check out Chapter 10 of our upcoming Astronomy/Statistics book, with figures and Python source code available [here](http://www.astroml.org/book_figures/chapter10/). For an example of the FFT being used to simplify an otherwise difficult differential equation integration, see my post on [Solving the Schrodinger Equation in Python](http://jakevdp.github.io/blog/2012/09/05/quantum-python/).
Because of the importance of the FFT in so many fields, Python contains many standard tools and wrappers to compute this. Both NumPy and SciPy have wrappers of the extremely well-tested FFTPACK library, found in the submodules ``numpy.fft`` and ``scipy.fftpack`` respectively. The fastest FFT I am aware of is in the [FFTW](http://www.fftw.org/) package, which is also available in Python via the [PyFFTW](https://pypi.python.org/pypi/pyFFTW) package.
For the moment, though, let's leave these implementations aside and ask how we might compute the FFT in Python from scratch.
## Computing the Discrete Fourier Transform
For simplicity, we'll concern ourself only with the forward transform, as the inverse transform can be implemented in a very similar manner. Taking a look at the DFT expression above, we see that it is nothing more than a straightforward linear operation: a matrix-vector multiplication of $\vec{x}$,
$$\vec{X} = M \cdot \vec{x}$$
with the matrix $M$ given by
$$M_{kn} = e^{-i~2\pi~k~n~/~N}.$$
With this in mind, we can compute the DFT using simple matrix multiplication as follows:
```
import numpy as np
def DFT_slow(x):
"""Compute the discrete Fourier Transform of the 1D array x"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
n = np.arange(N)
k = n.reshape((N, 1))
M = np.exp(-2j * np.pi * k * n / N)
return np.dot(M, x)
```
We can double-check the result by comparing to numpy's built-in FFT function:
```
x = np.random.random(1024)
np.allclose(DFT_slow(x), np.fft.fft(x))
```
Just to confirm the sluggishness of our algorithm, we can compare the execution times
of these two approaches:
```
%timeit DFT_slow(x)
%timeit np.fft.fft(x)
```
We are over 1000 times slower, which is to be expected for such a simplistic implementation. But that's not the worst of it. For an input vector of length $N$, the FFT algorithm scales as $\mathcal{O}[N\log N]$, while our slow algorithm scales as $\mathcal{O}[N^2]$. That means that for $N=10^6$ elements, we'd expect the FFT to complete in somewhere around 50 ms, while our slow algorithm would take nearly 20 hours!
So how does the FFT accomplish this speedup? The answer lies in exploiting symmetry.
## Symmetries in the Discrete Fourier Transform
One of the most important tools in the belt of an algorithm-builder is to exploit symmetries of a problem. If you can show analytically that one piece of a problem is simply related to another, you can compute the subresult
only once and save that computational cost. Cooley and Tukey used exactly this approach in deriving the FFT.
We'll start by asking what the value of $X_{N+k}$ is. From our above expression:
$$
\begin{align*}
X_{N + k} &= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~(N + k)~n~/~N}\\
&= \sum_{n=0}^{N-1} x_n \cdot e^{- i~2\pi~n} \cdot e^{-i~2\pi~k~n~/~N}\\
&= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N}
\end{align*}
$$
where we've used the identity $\exp[2\pi~i~n] = 1$ which holds for any integer $n$.
The last line shows a nice symmetry property of the DFT:
$$X_{N+k} = X_k.$$
By a simple extension,
$$X_{k + i \cdot N} = X_k$$
for any integer $i$. As we'll see below, this symmetry can be exploited to compute the DFT much more quickly.
## DFT to FFT: Exploiting Symmetry
Cooley and Tukey showed that it's possible to divide the DFT computation into two smaller parts. From
the definition of the DFT we have:
$$
\begin{align}
X_k &= \sum_{n=0}^{N-1} x_n \cdot e^{-i~2\pi~k~n~/~N} \\
&= \sum_{m=0}^{N/2 - 1} x_{2m} \cdot e^{-i~2\pi~k~(2m)~/~N} + \sum_{m=0}^{N/2 - 1} x_{2m + 1} \cdot e^{-i~2\pi~k~(2m + 1)~/~N} \\
&= \sum_{m=0}^{N/2 - 1} x_{2m} \cdot e^{-i~2\pi~k~m~/~(N/2)} + e^{-i~2\pi~k~/~N} \sum_{m=0}^{N/2 - 1} x_{2m + 1} \cdot e^{-i~2\pi~k~m~/~(N/2)}
\end{align}
$$
We've split the single Discrete Fourier transform into two terms which themselves look very similar to smaller Discrete Fourier Transforms, one on the odd-numbered values, and one on the even-numbered values. So far, however, we haven't saved any computational cycles. Each term consists of $(N/2)*N$ computations, for a total of $N^2$.
The trick comes in making use of symmetries in each of these terms. Because the range of $k$ is $0 \le k < N$, while the range of $n$ is $0 \le n < M \equiv N/2$, we see from the symmetry properties above that we need only perform half the computations for each sub-problem. Our $\mathcal{O}[N^2]$ computation has become $\mathcal{O}[M^2]$, with $M$ half the size of $N$.
But there's no reason to stop there: as long as our smaller Fourier transforms have an even-valued $M$, we can reapply this divide-and-conquer approach, halving the computational cost each time, until our arrays are small enough that the strategy is no longer beneficial. In the asymptotic limit, this recursive approach scales as $\mathcal{O}[N\log N]$.
This recursive algorithm can be implemented very quickly in Python, falling-back on our slow DFT code when the size of the sub-problem becomes suitably small:
```
def FFT(x):
"""A recursive implementation of the 1D Cooley-Tukey FFT"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
if N % 2 > 0:
raise ValueError("size of x must be a power of 2")
elif N <= 32: # this cutoff should be optimized
return DFT_slow(x)
else:
X_even = FFT(x[::2])
X_odd = FFT(x[1::2])
factor = np.exp(-2j * np.pi * np.arange(N) / N)
return np.concatenate([X_even + factor[:N / 2] * X_odd,
X_even + factor[N / 2:] * X_odd])
```
Here we'll do a quick check that our algorithm produces the correct result:
```
x = np.random.random(1024)
np.allclose(FFT(x), np.fft.fft(x))
```
And we'll time this algorithm against our slow version:
```
%timeit DFT_slow(x)
%timeit FFT(x)
%timeit np.fft.fft(x)
```
Our calculation is faster than the naive version by over an order of magnitude! What's more, our recursive algorithm is asymptotically $\mathcal{O}[N\log N]$: we've implemented the Fast Fourier Transform.
Note that we still haven't come close to the speed of the built-in FFT algorithm in numpy, and this is to be expected. The FFTPACK algorithm behind numpy's ``fft`` is a Fortran implementation which has received years of tweaks and optimizations. Furthermore, our NumPy solution involves both Python-stack recursions and the allocation of many temporary arrays, which adds significant computation time.
A good strategy to speed up code when working with Python/NumPy is to vectorize repeated computations where possible. We can do this, and in the process remove our recursive function calls, and make our Python FFT even more efficient.
## Vectorized Numpy Version
Notice that in the above recursive FFT implementation, at the lowest recursion level we perform $N~/~32$ identical matrix-vector products. The efficiency of our algorithm would benefit by computing these matrix-vector products all at once as a single matrix-matrix product. At each subsequent level of recursion, we also perform duplicate operations which can be vectorized. NumPy excels at this sort of operation, and we can make use of that fact to create this vectorized version of the Fast Fourier Transform:
```
def FFT_vectorized(x):
"""A vectorized, non-recursive version of the Cooley-Tukey FFT"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
if np.log2(N) % 1 > 0:
raise ValueError("size of x must be a power of 2")
# N_min here is equivalent to the stopping condition above,
# and should be a power of 2
N_min = min(N, 32)
# Perform an O[N^2] DFT on all length-N_min sub-problems at once
n = np.arange(N_min)
k = n[:, None]
M = np.exp(-2j * np.pi * n * k / N_min)
X = np.dot(M, x.reshape((N_min, -1)))
# build-up each level of the recursive calculation all at once
while X.shape[0] < N:
X_even = X[:, :X.shape[1] / 2]
X_odd = X[:, X.shape[1] / 2:]
factor = np.exp(-1j * np.pi * np.arange(X.shape[0])
/ X.shape[0])[:, None]
X = np.vstack([X_even + factor * X_odd,
X_even - factor * X_odd])
return X.ravel()
```
Though the algorithm is a bit more opaque, it is simply a rearrangement of the operations used in the recursive version with one exception: we exploit a symmetry in the ``factor`` computation and construct only half of the array. Again, we'll confirm that our function yields the correct result:
```
x = np.random.random(1024)
np.allclose(FFT_vectorized(x), np.fft.fft(x))
```
Because our algorithms are becoming much more efficient, we can use a larger array to compare the timings,
leaving out ``DFT_slow``:
```
x = np.random.random(1024 * 16)
%timeit FFT(x)
%timeit FFT_vectorized(x)
%timeit np.fft.fft(x)
```
We've improved our implementation by another order of magnitude! We're now within about a factor of 10 of the FFTPACK benchmark, using only a couple dozen lines of pure Python + NumPy. Though it's still no match computationally speaking, readibility-wise the Python version is far superior to the FFTPACK source, which you can browse [here](http://www.netlib.org/fftpack/fft.c).
So how does FFTPACK attain this last bit of speedup? Well, mainly it's just a matter of detailed bookkeeping. FFTPACK spends a lot of time making sure to reuse any sub-computation that can be reused. Our numpy version still involves an excess of memory allocation and copying; in a low-level language like Fortran it's easier to control and minimize memory use. In addition, the Cooley-Tukey algorithm can be extended to use splits of size other than 2 (what we've implemented here is known as the *radix-2* Cooley-Tukey FFT). Also, other more sophisticated FFT algorithms may be used, including fundamentally distinct approaches based on convolutions (see, e.g. Bluestein's algorithm and Rader's algorithm). The combination of the above extensions and techniques can lead to very fast FFTs even on arrays whose size is not a power of two.
Though the pure-Python functions are probably not useful in practice, I hope they've provided a bit of an intuition into what's going on in the background of FFT-based data analysis. As data scientists, we can make-do with black-box implementations of fundamental tools constructed by our more algorithmically-minded colleagues, but I am a firm believer that the more understanding we have about the low-level algorithms we're applying to our data, the better practitioners we'll be.
*This blog post was written entirely in the IPython Notebook. The full notebook can be downloaded
[here](http://jakevdp.github.io/downloads/notebooks/UnderstandingTheFFT.ipynb),
or viewed statically
[here](http://nbviewer.ipython.org/url/jakevdp.github.io/downloads/notebooks/UnderstandingTheFFT.ipynb).*
| true |
code
| 0.634685 | null | null | null | null |
|
```
# default_exp label
```
# Label
> A collection of functions to do label-based quantification
```
#hide
from nbdev.showdoc import *
```
## Label search
The label search is implemented based on the compare_frags from the search.
We have a fixed number of reporter channels and check if we find a respective peak within the search tolerance.
Useful resources:
- [IsobaricAnalyzer](https://abibuilder.informatik.uni-tuebingen.de/archive/openms/Documentation/nightly/html/TOPP_IsobaricAnalyzer.html)
- [TMT Talk from Hupo 2015](https://assets.thermofisher.com/TFS-Assets/CMD/Reference-Materials/PP-TMT-Multiplexed-Protein-Quantification-HUPO2015-EN.pdf)
```
#export
from numba import njit
from alphapept.search import compare_frags
import numpy as np
@njit
def label_search(query_frag: np.ndarray, query_int: np.ndarray, label: np.ndarray, reporter_frag_tol:float, ppm:bool)-> (np.ndarray, np.ndarray):
"""Function to search for a label for a given spectrum.
Args:
query_frag (np.ndarray): Array with query fragments.
query_int (np.ndarray): Array with query intensities.
label (np.ndarray): Array with label masses.
reporter_frag_tol (float): Fragment tolerance for search.
ppm (bool): Flag to use ppm instead of Dalton.
Returns:
np.ndarray: Array with intensities for the respective label channel.
np.ndarray: Array with offset masses.
"""
report = np.zeros(len(label))
off_mass = np.zeros_like(label)
hits = compare_frags(query_frag, label, reporter_frag_tol, ppm)
for idx, _ in enumerate(hits):
if _ > 0:
report[idx] = query_int[_-1]
off_mass[idx] = query_frag[_-1] - label[idx]
if ppm:
off_mass[idx] = off_mass[idx] / (query_frag[_-1] + label[idx]) *2 * 1e6
return report, off_mass
def test_label_search():
query_frag = np.array([1,2,3,4,5])
query_int = np.array([1,2,3,4,5])
label = np.array([1.0, 2.0, 3.0, 4.0, 5.0])
frag_tolerance = 0.1
ppm= False
assert np.allclose(label_search(query_frag, query_int, label, frag_tolerance, ppm)[0], query_int)
query_frag = np.array([1,2,3,4,6])
query_int = np.array([1,2,3,4,5])
assert np.allclose(label_search(query_frag, query_int, label, frag_tolerance, ppm)[0], np.array([1,2,3,4,0]))
query_frag = np.array([1,2,3,4,6])
query_int = np.array([5,4,3,2,1])
assert np.allclose(label_search(query_frag, query_int, label, frag_tolerance, ppm)[0], np.array([5,4,3,2,0]))
query_frag = np.array([1.1, 2.2, 3.3, 4.4, 6.6])
query_int = np.array([1,2,3,4,5])
frag_tolerance = 0.5
ppm= False
assert np.allclose(label_search(query_frag, query_int, label, frag_tolerance, ppm)[1], np.array([0.1, 0.2, 0.3, 0.4, 0.0]))
test_label_search()
#Example usage
query_frag = np.array([127, 128, 129.1, 132])
query_int = np.array([100, 200, 300, 400, 500])
label = np.array([127.0, 128.0, 129.0, 130.0])
frag_tolerance = 0.1
ppm = False
report, offset = label_search(query_frag, query_int, label, frag_tolerance, ppm)
print(f'Reported intensities {report}, Offset {offset}')
```
## MS2 Search
```
#export
from typing import NamedTuple
import alphapept.io
def search_label_on_ms_file(file_name:str, label:NamedTuple, reporter_frag_tol:float, ppm:bool):
"""Wrapper function to search labels on an ms_file and write results to the peptide_fdr of the file.
Args:
file_name (str): Path to ms_file:
label (NamedTuple): Label with channels, mod_name and masses.
reporter_frag_tol (float): Fragment tolerance for search.
ppm (bool): Flag to use ppm instead of Dalton.
"""
ms_file = alphapept.io.MS_Data_File(file_name, is_read_only = False)
df = ms_file.read(dataset_name='peptide_fdr')
label_intensities = np.zeros((len(df), len(label.channels)))
off_masses = np.zeros((len(df), len(label.channels)))
labeled = df['sequence'].str.startswith(label.mod_name).values
query_data = ms_file.read_DDA_query_data()
query_indices = query_data["indices_ms2"]
query_frags = query_data['mass_list_ms2']
query_ints = query_data['int_list_ms2']
for idx, query_idx in enumerate(df['raw_idx']):
query_idx_start = query_indices[query_idx]
query_idx_end = query_indices[query_idx + 1]
query_frag = query_frags[query_idx_start:query_idx_end]
query_int = query_ints[query_idx_start:query_idx_end]
query_frag_idx = query_frag < label.masses[-1]+1
query_frag = query_frag[query_frag_idx]
query_int = query_int[query_frag_idx]
if labeled[idx]:
label_int, off_mass = label_search(query_frag, query_int, label.masses, reporter_frag_tol, ppm)
label_intensities[idx, :] = label_int
off_masses[idx, :] = off_mass
df[label.channels] = label_intensities
df[[_+'_off_ppm' for _ in label.channels]] = off_masses
ms_file.write(df, dataset_name="peptide_fdr", overwrite=True) #Overwrite dataframe with label information
#export
import logging
import os
from alphapept.constants import label_dict
def find_labels(
to_process: dict,
callback: callable = None,
parallel:bool = False
) -> bool:
"""Wrapper function to search for labels.
Args:
to_process (dict): A dictionary with settings indicating which files are to be processed and how.
callback (callable): A function that accepts a float between 0 and 1 as progress. Defaults to None.
parallel (bool): If True, process multiple files in parallel.
This is not implemented yet!
Defaults to False.
Returns:
bool: True if and only if the label finding was succesful.
"""
index, settings = to_process
raw_file = settings['experiment']['file_paths'][index]
try:
base, ext = os.path.splitext(raw_file)
file_name = base+'.ms_data.hdf'
label = label_dict[settings['isobaric_label']['label']]
reporter_frag_tol = settings['isobaric_label']['reporter_frag_tolerance']
ppm = settings['isobaric_label']['reporter_frag_tolerance_ppm']
search_label_on_ms_file(file_name, label, reporter_frag_tol, ppm)
logging.info(f'Tag finding of file {file_name} complete.')
return True
except Exception as e:
logging.error(f'Tag finding of file {file_name} failed. Exception {e}')
return f"{e}" #Can't return exception object, cast as string
return True
#hide
from nbdev.export import *
notebook2script()
```
| true |
code
| 0.760018 | null | null | null | null |
|
# Explain Attacking BERT models using CAptum
Captum is a PyTorch library to explain neural networks
Here we show a minimal example using Captum to explain BERT models from TextAttack
[](https://colab.research.google.com/github/QData/TextAttack/blob/master/docs/2notebook/Example_5_Explain_BERT.ipynb)
[](https://github.com/QData/TextAttack/blob/master/docs/2notebook/Example_5_Explain_BERT.ipynb)
```
import torch
from copy import deepcopy
from textattack.datasets import HuggingFaceDataset
from textattack.models.tokenizers import AutoTokenizer
from textattack.models.wrappers import HuggingFaceModelWrapper
from textattack.models.wrappers import ModelWrapper
from transformers import AutoModelForSequenceClassification
from captum.attr import IntegratedGradients, LayerConductance, LayerIntegratedGradients, LayerDeepLiftShap, InternalInfluence, LayerGradientXActivation
from captum.attr import visualization as viz
device = torch.device("cuda:2" if torch.cuda.is_available() else "cpu")
print(device)
torch.cuda.set_device(device)
dataset = HuggingFaceDataset("ag_news", None, "train")
original_model = AutoModelForSequenceClassification.from_pretrained("textattack/bert-base-uncased-ag-news")
original_tokenizer = AutoTokenizer("textattack/bert-base-uncased-ag-news")
model = HuggingFaceModelWrapper(original_model,original_tokenizer)
def captum_form(encoded):
input_dict = {k: [_dict[k] for _dict in encoded] for k in encoded[0]}
batch_encoded = { k: torch.tensor(v).to(device) for k, v in input_dict.items()}
return batch_encoded
def get_text(tokenizer,input_ids,token_type_ids,attention_mask):
list_of_text = []
number = input_ids.size()[0]
for i in range(number):
ii = input_ids[i,].cpu().numpy()
tt = token_type_ids[i,]
am = attention_mask[i,]
txt = tokenizer.decode(ii, skip_special_tokens=True)
list_of_text.append(txt)
return list_of_text
sel =2
encoded = model.tokenizer.batch_encode([dataset[i][0]['text'] for i in range(sel)])
labels = [dataset[i][1] for i in range(sel)]
batch_encoded = captum_form(encoded)
clone = deepcopy(model)
clone.model.to(device)
def calculate(input_ids,token_type_ids,attention_mask):
#convert back to list of text
return clone.model(input_ids,token_type_ids,attention_mask)[0]
# x = calculate(**batch_encoded)
lig = LayerIntegratedGradients(calculate, clone.model.bert.embeddings)
# lig = InternalInfluence(calculate, clone.model.bert.embeddings)
# lig = LayerGradientXActivation(calculate, clone.model.bert.embeddings)
bsl = torch.zeros(batch_encoded['input_ids'].size()).type(torch.LongTensor).to(device)
labels = torch.tensor(labels).to(device)
attributions,delta = lig.attribute(inputs=batch_encoded['input_ids'],
baselines=bsl,
additional_forward_args=(batch_encoded['token_type_ids'], batch_encoded['attention_mask']),
n_steps = 10,
target = labels,
return_convergence_delta=True
)
atts = attributions.sum(dim=-1).squeeze(0)
atts = atts / torch.norm(atts)
# print(attributions.size())
atts = attributions.sum(dim=-1).squeeze(0)
atts = atts / torch.norm(atts)
from textattack.attack_recipes import PWWSRen2019
attack = PWWSRen2019.build(model)
results_iterable = attack.attack_dataset(dataset, indices=range(10))
viz_list = []
for n,result in enumerate(results_iterable):
orig = result.original_text()
pert = result.perturbed_text()
encoded = model.tokenizer.batch_encode([orig])
batch_encoded = captum_form(encoded)
x = calculate(**batch_encoded)
print(x)
print(dataset[n][1])
pert_encoded = model.tokenizer.batch_encode([pert])
pert_batch_encoded = captum_form(pert_encoded)
x_pert = calculate(**pert_batch_encoded)
attributions,delta = lig.attribute(inputs=batch_encoded['input_ids'],
# baselines=bsl,
additional_forward_args=(batch_encoded['token_type_ids'], batch_encoded['attention_mask']),
n_steps = 10,
target = torch.argmax(calculate(**batch_encoded)).item(),
return_convergence_delta=True
)
attributions_pert,delta_pert = lig.attribute(inputs=pert_batch_encoded['input_ids'],
# baselines=bsl,
additional_forward_args=(pert_batch_encoded['token_type_ids'], pert_batch_encoded['attention_mask']),
n_steps = 10,
target = torch.argmax(calculate(**pert_batch_encoded)).item(),
return_convergence_delta=True
)
orig = original_tokenizer.tokenizer.tokenize(orig)
pert = original_tokenizer.tokenizer.tokenize(pert)
atts = attributions.sum(dim=-1).squeeze(0)
atts = atts / torch.norm(atts)
atts_pert = attributions_pert.sum(dim=-1).squeeze(0)
atts_pert = atts_pert / torch.norm(atts)
all_tokens = original_tokenizer.tokenizer.convert_ids_to_tokens(batch_encoded['input_ids'][0])
all_tokens_pert = original_tokenizer.tokenizer.convert_ids_to_tokens(pert_batch_encoded['input_ids'][0])
v = viz.VisualizationDataRecord(
atts[:45].detach().cpu(),
torch.max(x).item(),
torch.argmax(x,dim=1).item(),
dataset[n][1],
2,
atts.sum().detach(),
all_tokens[:45],
delta)
v_pert = viz.VisualizationDataRecord(
atts_pert[:45].detach().cpu(),
torch.max(x_pert).item(),
torch.argmax(x_pert,dim=1).item(),
dataset[n][1],
2,
atts_pert.sum().detach(),
all_tokens_pert[:45],
delta_pert)
viz_list.append(v)
viz_list.append(v_pert)
# print(result.perturbed_text())
print(result.__str__(color_method='ansi'))
print('\033[1m', 'Visualizations For AG NEWS', '\033[0m')
viz.visualize_text(viz_list)
# reference for viz datarecord
# def __init__(
# self,
# word_attributions,
# pred_prob,
# pred_class,
# true_class,
# attr_class,
# attr_score,
# raw_input,
# convergence_score,
# ):
```
| true |
code
| 0.556761 | null | null | null | null |
|
```
%matplotlib inline
```
torchaudio Tutorial
===================
PyTorch is an open source deep learning platform that provides a
seamless path from research prototyping to production deployment with
GPU support.
Significant effort in solving machine learning problems goes into data
preparation. ``torchaudio`` leverages PyTorch’s GPU support, and provides
many tools to make data loading easy and more readable. In this
tutorial, we will see how to load and preprocess data from a simple
dataset.
For this tutorial, please make sure the ``matplotlib`` package is
installed for easier visualization.
```
import torch
import torchaudio
import matplotlib.pyplot as plt
```
Opening a file
-----------------
``torchaudio`` also supports loading sound files in the wav and mp3 format. We
call waveform the resulting raw audio signal.
```
filename = "../_static/img/steam-train-whistle-daniel_simon-converted-from-mp3.wav"
waveform, sample_rate = torchaudio.load(filename)
print("Shape of waveform: {}".format(waveform.size()))
print("Sample rate of waveform: {}".format(sample_rate))
plt.figure()
plt.plot(waveform.t().numpy())
```
When you load a file in ``torchaudio``, you can optionally specify the backend to use either
`SoX <https://pypi.org/project/sox/>`_ or `SoundFile <https://pypi.org/project/SoundFile/>`_
via ``torchaudio.set_audio_backend``. These backends are loaded lazily when needed.
``torchaudio`` also makes JIT compilation optional for functions, and uses ``nn.Module`` where possible.
Transformations
---------------
``torchaudio`` supports a growing list of
`transformations <https://pytorch.org/audio/transforms.html>`_.
- **Resample**: Resample waveform to a different sample rate.
- **Spectrogram**: Create a spectrogram from a waveform.
- **GriffinLim**: Compute waveform from a linear scale magnitude spectrogram using
the Griffin-Lim transformation.
- **ComputeDeltas**: Compute delta coefficients of a tensor, usually a spectrogram.
- **ComplexNorm**: Compute the norm of a complex tensor.
- **MelScale**: This turns a normal STFT into a Mel-frequency STFT,
using a conversion matrix.
- **AmplitudeToDB**: This turns a spectrogram from the
power/amplitude scale to the decibel scale.
- **MFCC**: Create the Mel-frequency cepstrum coefficients from a
waveform.
- **MelSpectrogram**: Create MEL Spectrograms from a waveform using the
STFT function in PyTorch.
- **MuLawEncoding**: Encode waveform based on mu-law companding.
- **MuLawDecoding**: Decode mu-law encoded waveform.
- **TimeStretch**: Stretch a spectrogram in time without modifying pitch for a given rate.
- **FrequencyMasking**: Apply masking to a spectrogram in the frequency domain.
- **TimeMasking**: Apply masking to a spectrogram in the time domain.
Each transform supports batching: you can perform a transform on a single raw
audio signal or spectrogram, or many of the same shape.
Since all transforms are ``nn.Modules`` or ``jit.ScriptModules``, they can be
used as part of a neural network at any point.
To start, we can look at the log of the spectrogram on a log scale.
```
specgram = torchaudio.transforms.Spectrogram()(waveform)
print("Shape of spectrogram: {}".format(specgram.size()))
plt.figure()
plt.imshow(specgram.log2()[0,:,:].numpy(), cmap='gray')
```
Or we can look at the Mel Spectrogram on a log scale.
```
specgram = torchaudio.transforms.MelSpectrogram()(waveform)
print("Shape of spectrogram: {}".format(specgram.size()))
plt.figure()
p = plt.imshow(specgram.log2()[0,:,:].detach().numpy(), cmap='gray')
```
We can resample the waveform, one channel at a time.
```
new_sample_rate = sample_rate/10
# Since Resample applies to a single channel, we resample first channel here
channel = 0
transformed = torchaudio.transforms.Resample(sample_rate, new_sample_rate)(waveform[channel,:].view(1,-1))
print("Shape of transformed waveform: {}".format(transformed.size()))
plt.figure()
plt.plot(transformed[0,:].numpy())
```
As another example of transformations, we can encode the signal based on
Mu-Law enconding. But to do so, we need the signal to be between -1 and
1. Since the tensor is just a regular PyTorch tensor, we can apply
standard operators on it.
```
# Let's check if the tensor is in the interval [-1,1]
print("Min of waveform: {}\nMax of waveform: {}\nMean of waveform: {}".format(waveform.min(), waveform.max(), waveform.mean()))
```
Since the waveform is already between -1 and 1, we do not need to
normalize it.
```
def normalize(tensor):
# Subtract the mean, and scale to the interval [-1,1]
tensor_minusmean = tensor - tensor.mean()
return tensor_minusmean/tensor_minusmean.abs().max()
# Let's normalize to the full interval [-1,1]
# waveform = normalize(waveform)
```
Let’s apply encode the waveform.
```
transformed = torchaudio.transforms.MuLawEncoding()(waveform)
print("Shape of transformed waveform: {}".format(transformed.size()))
plt.figure()
plt.plot(transformed[0,:].numpy())
```
And now decode.
```
reconstructed = torchaudio.transforms.MuLawDecoding()(transformed)
print("Shape of recovered waveform: {}".format(reconstructed.size()))
plt.figure()
plt.plot(reconstructed[0,:].numpy())
```
We can finally compare the original waveform with its reconstructed
version.
```
# Compute median relative difference
err = ((waveform-reconstructed).abs() / waveform.abs()).median()
print("Median relative difference between original and MuLaw reconstucted signals: {:.2%}".format(err))
```
Functional
---------------
The transformations seen above rely on lower level stateless functions for their computations.
These functions are available under ``torchaudio.functional``. The complete list is available
`here <https://pytorch.org/audio/functional.html>`_ and includes:
- **istft**: Inverse short time Fourier Transform.
- **gain**: Applies amplification or attenuation to the whole waveform.
- **dither**: Increases the perceived dynamic range of audio stored at a
particular bit-depth.
- **compute_deltas**: Compute delta coefficients of a tensor.
- **equalizer_biquad**: Design biquad peaking equalizer filter and perform filtering.
- **lowpass_biquad**: Design biquad lowpass filter and perform filtering.
- **highpass_biquad**:Design biquad highpass filter and perform filtering.
For example, let's try the `mu_law_encoding` functional:
```
mu_law_encoding_waveform = torchaudio.functional.mu_law_encoding(waveform, quantization_channels=256)
print("Shape of transformed waveform: {}".format(mu_law_encoding_waveform.size()))
plt.figure()
plt.plot(mu_law_encoding_waveform[0,:].numpy())
```
You can see how the output fron ``torchaudio.functional.mu_law_encoding`` is the same as
the output from ``torchaudio.transforms.MuLawEncoding``.
Now let's experiment with a few of the other functionals and visualize their output. Taking our
spectogram, we can compute it's deltas:
```
computed = torchaudio.functional.compute_deltas(specgram, win_length=3)
print("Shape of computed deltas: {}".format(computed.shape))
plt.figure()
plt.imshow(computed.log2()[0,:,:].detach().numpy(), cmap='gray')
```
We can take the original waveform and apply different effects to it.
```
gain_waveform = torchaudio.functional.gain(waveform, gain_db=5.0)
print("Min of gain_waveform: {}\nMax of gain_waveform: {}\nMean of gain_waveform: {}".format(gain_waveform.min(), gain_waveform.max(), gain_waveform.mean()))
dither_waveform = torchaudio.functional.dither(waveform)
print("Min of dither_waveform: {}\nMax of dither_waveform: {}\nMean of dither_waveform: {}".format(dither_waveform.min(), dither_waveform.max(), dither_waveform.mean()))
```
Another example of the capabilities in ``torchaudio.functional`` are applying filters to our
waveform. Applying the lowpass biquad filter to our waveform will output a new waveform with
the signal of the frequency modified.
```
lowpass_waveform = torchaudio.functional.lowpass_biquad(waveform, sample_rate, cutoff_freq=3000)
print("Min of lowpass_waveform: {}\nMax of lowpass_waveform: {}\nMean of lowpass_waveform: {}".format(lowpass_waveform.min(), lowpass_waveform.max(), lowpass_waveform.mean()))
plt.figure()
plt.plot(lowpass_waveform.t().numpy())
```
We can also visualize a waveform with the highpass biquad filter.
```
highpass_waveform = torchaudio.functional.highpass_biquad(waveform, sample_rate, cutoff_freq=2000)
print("Min of highpass_waveform: {}\nMax of highpass_waveform: {}\nMean of highpass_waveform: {}".format(highpass_waveform.min(), highpass_waveform.max(), highpass_waveform.mean()))
plt.figure()
plt.plot(highpass_waveform.t().numpy())
```
Migrating to torchaudio from Kaldi
----------------------------------
Users may be familiar with
`Kaldi <http://github.com/kaldi-asr/kaldi>`_, a toolkit for speech
recognition. ``torchaudio`` offers compatibility with it in
``torchaudio.kaldi_io``. It can indeed read from kaldi scp, or ark file
or streams with:
- read_vec_int_ark
- read_vec_flt_scp
- read_vec_flt_arkfile/stream
- read_mat_scp
- read_mat_ark
``torchaudio`` provides Kaldi-compatible transforms for ``spectrogram``,
``fbank``, ``mfcc``, and ``resample_waveform with the benefit of GPU support, see
`here <compliance.kaldi.html>`__ for more information.
```
n_fft = 400.0
frame_length = n_fft / sample_rate * 1000.0
frame_shift = frame_length / 2.0
params = {
"channel": 0,
"dither": 0.0,
"window_type": "hanning",
"frame_length": frame_length,
"frame_shift": frame_shift,
"remove_dc_offset": False,
"round_to_power_of_two": False,
"sample_frequency": sample_rate,
}
specgram = torchaudio.compliance.kaldi.spectrogram(waveform, **params)
print("Shape of spectrogram: {}".format(specgram.size()))
plt.figure()
plt.imshow(specgram.t().numpy(), cmap='gray')
```
We also support computing the filterbank features from waveforms,
matching Kaldi’s implementation.
```
fbank = torchaudio.compliance.kaldi.fbank(waveform, **params)
print("Shape of fbank: {}".format(fbank.size()))
plt.figure()
plt.imshow(fbank.t().numpy(), cmap='gray')
```
You can create mel frequency cepstral coefficients from a raw audio signal
This matches the input/output of Kaldi’s compute-mfcc-feats.
```
mfcc = torchaudio.compliance.kaldi.mfcc(waveform, **params)
print("Shape of mfcc: {}".format(mfcc.size()))
plt.figure()
plt.imshow(mfcc.t().numpy(), cmap='gray')
```
Available Datasets
-----------------
If you do not want to create your own dataset to train your model, ``torchaudio`` offers a
unified dataset interface. This interface supports lazy-loading of files to memory, download
and extract functions, and datasets to build models.
The datasets ``torchaudio`` currently supports are:
- **VCTK**: Speech data uttered by 109 native speakers of English with various accents
(`Read more here <https://homepages.inf.ed.ac.uk/jyamagis/page3/page58/page58.html>`_).
- **Yesno**: Sixty recordings of one individual saying yes or no in Hebrew; each
recording is eight words long (`Read more here <https://www.openslr.org/1/>`_).
- **Common Voice**: An open source, multi-language dataset of voices that anyone can use
to train speech-enabled applications (`Read more here <https://voice.mozilla.org/en/datasets>`_).
- **LibriSpeech**: Large-scale (1000 hours) corpus of read English speech (`Read more here <http://www.openslr.org/12>`_).
```
yesno_data = torchaudio.datasets.YESNO('./', download=True)
# A data point in Yesno is a tuple (waveform, sample_rate, labels) where labels is a list of integers with 1 for yes and 0 for no.
# Pick data point number 3 to see an example of the the yesno_data:
n = 3
waveform, sample_rate, labels = yesno_data[n]
print("Waveform: {}\nSample rate: {}\nLabels: {}".format(waveform, sample_rate, labels))
plt.figure()
plt.plot(waveform.t().numpy())
```
Now, whenever you ask for a sound file from the dataset, it is loaded in memory only when you ask for it.
Meaning, the dataset only loads and keeps in memory the items that you want and use, saving on memory.
Conclusion
----------
We used an example raw audio signal, or waveform, to illustrate how to
open an audio file using ``torchaudio``, and how to pre-process,
transform, and apply functions to such waveform. We also demonstrated how
to use familiar Kaldi functions, as well as utilize built-in datasets to
construct our models. Given that ``torchaudio`` is built on PyTorch,
these techniques can be used as building blocks for more advanced audio
applications, such as speech recognition, while leveraging GPUs.
| true |
code
| 0.756296 | null | null | null | null |
|
# Inference in Google Earth Engine + Colab
> Scaling up machine learning with GEE and Google Colab.
- toc: true
- badges: true
- author: Drew Bollinger
- comments: false
- hide: false
- sticky_rank: 11
# Inference in Google Earth Engine + Colab
Here we demonstrate how to take a trained model and apply to to imagery with Google Earth Engine + Colab + Tensorflow. This is adapted from an [Earth Engine <> TensorFlow demonstration notebook](https://developers.google.com/earth-engine/guides/tf_examples). We'll be taking the trained model from the [Deep Learning Crop Type Segmentation Model Example](https://developmentseed.org/sat-ml-training/DeepLearning_CropType_Segmentation).
# Setup software libraries
Authenticate and import as necessary.
```
# Import, authenticate and initialize the Earth Engine library.
import ee
ee.Authenticate()
ee.Initialize()
# Mount our Google Drive
from google.colab import drive
drive.mount('/content/drive')
# Add necessary libraries.
!pip install -q focal-loss
import os
from os import path as op
import tensorflow as tf
import folium
from focal_loss import SparseCategoricalFocalLoss
```
# Variables
Declare the variables that will be in use throughout the notebook.
```
# Specify names locations for outputs in Google Drive.
FOLDER = 'servir-inference-demo'
ROOT_DIR = '/content/drive/My Drive/'
# Specify inputs (Sentinel indexes) to the model.
BANDS = ['NDVI', 'WDRVI', 'SAVI']
# Specify the size and shape of patches expected by the model.
KERNEL_SIZE = 224
KERNEL_SHAPE = [KERNEL_SIZE, KERNEL_SIZE]
```
# Imagery
Gather and setup the imagery to use for inputs. It's important that we match the index inputs from the earlier analysis. This is a three-month Sentinel-2 composite. Display it in the notebook for a sanity check.
```
# Use Sentinel-2 data.
def add_indexes(img):
ndvi = img.expression(
'(nir - red) / (nir + red + a)', {
'a': 1e-5,
'nir': img.select('B8'),
'red': img.select('B4')
}
).rename('NDVI')
wdrvi = img.expression(
'(a * nir - red) / (a * nir + red)', {
'a': 0.2,
'nir': img.select('B8'),
'red': img.select('B4')
}
).rename('WDRVI')
savi = img.expression(
'1.5 * (nir - red) / (nir + red + 0.5)', {
'nir': img.select('B8'),
'red': img.select('B4')
}
).rename('SAVI')
return ee.Image.cat([ndvi, wdrvi, savi])
image = ee.ImageCollection('COPERNICUS/S2') \
.filterDate('2018-01-01', '2018-04-01') \
.filter(ee.Filter.lt('CLOUDY_PIXEL_PERCENTAGE', 20)) \
.map(add_indexes) \
.median()
# Use folium to visualize the imagery.
mapid = image.getMapId({'bands': BANDS, 'min': -1, 'max': 1})
map = folium.Map(location=[
-29.177943749121233,
30.55984497070313,
])
folium.TileLayer(
tiles=mapid['tile_fetcher'].url_format,
attr='Map Data © <a href="https://earthengine.google.com/">Google Earth Engine</a>',
overlay=True,
name='median composite',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
# Load our saved model
```
# Load a trained model.
MODEL_DIR = '/content/drive/Shared drives/servir-sat-ml/data/model_out/10062020/'
model = tf.keras.models.load_model(MODEL_DIR)
model.summary()
```
# Prediction
The prediction pipeline is:
1. Export imagery on which to do predictions from Earth Engine in TFRecord format to Google Drive.
2. Use the trained model to make the predictions.
3. Write the predictions to a TFRecord file in Google Drive.
4. Manually upload the predictions TFRecord file to Earth Engine.
The following functions handle this process. It's useful to separate the export from the predictions so that you can experiment with different models without running the export every time.
```
def doExport(out_image_base, shape, region):
"""Run the image export task. Block until complete.
"""
task = ee.batch.Export.image.toDrive(
image = image.select(BANDS),
description = out_image_base,
fileNamePrefix = out_image_base,
folder = FOLDER,
region = region.getInfo()['coordinates'],
scale = 30,
fileFormat = 'TFRecord',
maxPixels = 1e10,
formatOptions = {
'patchDimensions': shape,
'compressed': True,
'maxFileSize': 104857600
}
)
task.start()
# Block until the task completes.
print('Running image export to Google Drive...')
import time
while task.active():
time.sleep(30)
# Error condition
if task.status()['state'] != 'COMPLETED':
print('Error with image export.')
else:
print('Image export completed.')
def doPrediction(out_image_base, kernel_shape, region):
"""Perform inference on exported imagery.
"""
print('Looking for TFRecord files...')
# Get a list of all the files in the output bucket.
filesList = os.listdir(op.join(ROOT_DIR, FOLDER))
# Get only the files generated by the image export.
exportFilesList = [s for s in filesList if out_image_base in s]
# Get the list of image files and the JSON mixer file.
imageFilesList = []
jsonFile = None
for f in exportFilesList:
if f.endswith('.tfrecord.gz'):
imageFilesList.append(op.join(ROOT_DIR, FOLDER, f))
elif f.endswith('.json'):
jsonFile = f
# Make sure the files are in the right order.
imageFilesList.sort()
from pprint import pprint
pprint(imageFilesList)
print(jsonFile)
import json
# Load the contents of the mixer file to a JSON object.
with open(op.join(ROOT_DIR, FOLDER, jsonFile), 'r') as f:
mixer = json.load(f)
pprint(mixer)
patches = mixer['totalPatches']
# Get set up for prediction.
imageColumns = [
tf.io.FixedLenFeature(shape=kernel_shape, dtype=tf.float32)
for k in BANDS
]
imageFeaturesDict = dict(zip(BANDS, imageColumns))
def parse_image(example_proto):
return tf.io.parse_single_example(example_proto, imageFeaturesDict)
def toTupleImage(inputs):
inputsList = [inputs.get(key) for key in BANDS]
stacked = tf.stack(inputsList, axis=0)
stacked = tf.transpose(stacked, [1, 2, 0])
return stacked
# Create a dataset from the TFRecord file(s) in Cloud Storage.
imageDataset = tf.data.TFRecordDataset(imageFilesList, compression_type='GZIP')
imageDataset = imageDataset.map(parse_image, num_parallel_calls=5)
imageDataset = imageDataset.map(toTupleImage).batch(1)
# Perform inference.
print('Running predictions...')
predictions = model.predict(imageDataset, steps=patches, verbose=1)
# print(predictions[0])
print('Writing predictions...')
out_image_file = op.join(ROOT_DIR, FOLDER, f'{out_image_base}pred.TFRecord')
writer = tf.io.TFRecordWriter(out_image_file)
patches = 0
for predictionPatch in predictions:
print('Writing patch ' + str(patches) + '...')
predictionPatch = tf.argmax(predictionPatch, axis=2)
# Create an example.
example = tf.train.Example(
features=tf.train.Features(
feature={
'class': tf.train.Feature(
float_list=tf.train.FloatList(
value=predictionPatch.numpy().flatten()))
}
)
)
# Write the example.
writer.write(example.SerializeToString())
patches += 1
writer.close()
```
Now there's all the code needed to run the prediction pipeline, all that remains is to specify the output region in which to do the prediction, the names of the output files, where to put them, and the shape of the outputs.
```
# Base file name to use for TFRecord files and assets.
image_base = 'servir_inference_demo_'
# South Africa (near training data)
region = ee.Geometry.Polygon(
[[[
30.55984497070313,
-29.177943749121233
],
[
30.843429565429684,
-29.177943749121233
],
[
30.843429565429684,
-28.994928377910732
],
[
30.55984497070313,
-28.994928377910732
]]], None, False)
# Run the export.
doExport(image_base, KERNEL_SHAPE, region)
# Run the prediction.
doPrediction(image_base, KERNEL_SHAPE, region)
```
# Display the output
One the data has been exported, the model has made predictions and the predictions have been written to a file, we need to [manually import the TFRecord to Earth Engine](https://developers.google.com/earth-engine/guides/tfrecord#uploading-tfrecords-to-earth-engine). Then we can display our crop type predictions as an image asset
```
out_image = ee.Image('users/drew/servir_inference_demo_-mixer')
mapid = out_image.getMapId({'min': 0, 'max': 10, 'palette': ['00A600','63C600','E6E600','E9BD3A','ECB176','EFC2B3','F2F2F2']})
map = folium.Map(location=[
-29.177943749121233,
30.55984497070313,
])
folium.TileLayer(
tiles=mapid['tile_fetcher'].url_format,
attr='Map Data © <a href="https://earthengine.google.com/">Google Earth Engine</a>',
overlay=True,
name='predicted crop type',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
| true |
code
| 0.610512 | null | null | null | null |
|
<a href="https://cognitiveclass.ai"><img src = "https://ibm.box.com/shared/static/9gegpsmnsoo25ikkbl4qzlvlyjbgxs5x.png" width = 400> </a>
<h1 align=center><font size = 5>From Understanding to Preparation</font></h1>
## Introduction
In this lab, we will continue learning about the data science methodology, and focus on the **Data Understanding** and the **Data Preparation** stages.
## Table of Contents
<div class="alert alert-block alert-info" style="margin-top: 20px">
1. [Recap](#0)<br>
2. [Data Understanding](#2)<br>
3. [Data Preparation](#4)<br>
</div>
<hr>
# Recap <a id="0"></a>
In Lab **From Requirements to Collection**, we learned that the data we need to answer the question developed in the business understanding stage, namely *can we automate the process of determining the cuisine of a given recipe?*, is readily available. A researcher named Yong-Yeol Ahn scraped tens of thousands of food recipes (cuisines and ingredients) from three different websites, namely:
<img src = "https://ibm.box.com/shared/static/4fruwan7wmjov3gywiz3swlojw0srv54.png" width=500>
www.allrecipes.com
<img src = "https://ibm.box.com/shared/static/cebfdbr22fjxa47lltp0bs533r103g0z.png" width=500>
www.epicurious.com
<img src = "https://ibm.box.com/shared/static/epk727njg7xrz49pbkpkzd05cm5ywqmu.png" width=500>
www.menupan.com
For more information on Yong-Yeol Ahn and his research, you can read his paper on [Flavor Network and the Principles of Food Pairing](http://yongyeol.com/papers/ahn-flavornet-2011.pdf).
We also collected the data and placed it on an IBM server for your convenience.
------------
# Data Understanding <a id="2"></a>
<img src="https://ibm.box.com/shared/static/89geb3m0ge1z73s92hl8o8wdcpcrggtz.png" width=500>
<strong> Important note:</strong> Please note that you are not expected to know how to program in python. The following code is meant to illustrate the stages of data understanding and data preparation, so it is totally fine if you do not understand the individual lines of code. We have a full course on programming in python, <a href="http://cocl.us/PY0101EN_DS0103EN_LAB3_PYTHON">Python for Data Science</a>, so please feel free to complete the course if you are interested in learning how to program in python.
### Using this notebook:
To run any of the following cells of code, you can type **Shift + Enter** to excute the code in a cell.
Get the version of Python installed.
```
# check Python version
!python -V
```
Download the library and dependencies that we will need to run this lab.
```
import pandas as pd # import library to read data into dataframe
pd.set_option('display.max_columns', None)
import numpy as np # import numpy library
import re # import library for regular expression
```
Download the data from the IBM server and read it into a *pandas* dataframe.
```
recipes = pd.read_csv("https://ibm.box.com/shared/static/5wah9atr5o1akuuavl2z9tkjzdinr1lv.csv")
print("Data read into dataframe!") # takes about 30 seconds
```
Show the first few rows.
```
recipes.head()
```
Get the dimensions of the dataframe.
```
recipes.shape
```
So our dataset consists of 57,691 recipes. Each row represents a recipe, and for each recipe, the corresponding cuisine is documented as well as whether 384 ingredients exist in the recipe or not, beginning with almond and ending with zucchini.
We know that a basic sushi recipe includes the ingredients:
* rice
* soy sauce
* wasabi
* some fish/vegetables
Let's check that these ingredients exist in our dataframe:
```
ingredients = list(recipes.columns.values)
print([match.group(0) for ingredient in ingredients for match in [(re.compile(".*(rice).*")).search(ingredient)] if match])
print([match.group(0) for ingredient in ingredients for match in [(re.compile(".*(wasabi).*")).search(ingredient)] if match])
print([match.group(0) for ingredient in ingredients for match in [(re.compile(".*(soy).*")).search(ingredient)] if match])
```
Yes, they do!
* rice exists as rice.
* wasabi exists as wasabi.
* soy exists as soy_sauce.
So maybe if a recipe contains all three ingredients: rice, wasabi, and soy_sauce, then we can confidently say that the recipe is a **Japanese** cuisine! Let's keep this in mind!
----------------
# Data Preparation <a id="4"></a>
<img src="https://ibm.box.com/shared/static/lqc2j3r0ndhokh77mubohwjqybzf8dhk.png" width=500>
In this section, we will prepare data for the next stage in the data science methodology, which is modeling. This stage involves exploring the data further and making sure that it is in the right format for the machine learning algorithm that we selected in the analytic approach stage, which is decision trees.
First, look at the data to see if it needs cleaning.
```
recipes["country"].value_counts() # frequency table
```
By looking at the above table, we can make the following observations:
1. Cuisine column is labeled as Country, which is inaccurate.
2. Cuisine names are not consistent as not all of them start with an uppercase first letter.
3. Some cuisines are duplicated as variation of the country name, such as Vietnam and Vietnamese.
4. Some cuisines have very few recipes.
#### Let's fixes these problems.
Fix the name of the column showing the cuisine.
```
column_names = recipes.columns.values
column_names[0] = "cuisine"
recipes.columns = column_names
recipes
```
Make all the cuisine names lowercase.
```
recipes["cuisine"] = recipes["cuisine"].str.lower()
```
Make the cuisine names consistent.
```
recipes.loc[recipes["cuisine"] == "austria", "cuisine"] = "austrian"
recipes.loc[recipes["cuisine"] == "belgium", "cuisine"] = "belgian"
recipes.loc[recipes["cuisine"] == "china", "cuisine"] = "chinese"
recipes.loc[recipes["cuisine"] == "canada", "cuisine"] = "canadian"
recipes.loc[recipes["cuisine"] == "netherlands", "cuisine"] = "dutch"
recipes.loc[recipes["cuisine"] == "france", "cuisine"] = "french"
recipes.loc[recipes["cuisine"] == "germany", "cuisine"] = "german"
recipes.loc[recipes["cuisine"] == "india", "cuisine"] = "indian"
recipes.loc[recipes["cuisine"] == "indonesia", "cuisine"] = "indonesian"
recipes.loc[recipes["cuisine"] == "iran", "cuisine"] = "iranian"
recipes.loc[recipes["cuisine"] == "italy", "cuisine"] = "italian"
recipes.loc[recipes["cuisine"] == "japan", "cuisine"] = "japanese"
recipes.loc[recipes["cuisine"] == "israel", "cuisine"] = "jewish"
recipes.loc[recipes["cuisine"] == "korea", "cuisine"] = "korean"
recipes.loc[recipes["cuisine"] == "lebanon", "cuisine"] = "lebanese"
recipes.loc[recipes["cuisine"] == "malaysia", "cuisine"] = "malaysian"
recipes.loc[recipes["cuisine"] == "mexico", "cuisine"] = "mexican"
recipes.loc[recipes["cuisine"] == "pakistan", "cuisine"] = "pakistani"
recipes.loc[recipes["cuisine"] == "philippines", "cuisine"] = "philippine"
recipes.loc[recipes["cuisine"] == "scandinavia", "cuisine"] = "scandinavian"
recipes.loc[recipes["cuisine"] == "spain", "cuisine"] = "spanish_portuguese"
recipes.loc[recipes["cuisine"] == "portugal", "cuisine"] = "spanish_portuguese"
recipes.loc[recipes["cuisine"] == "switzerland", "cuisine"] = "swiss"
recipes.loc[recipes["cuisine"] == "thailand", "cuisine"] = "thai"
recipes.loc[recipes["cuisine"] == "turkey", "cuisine"] = "turkish"
recipes.loc[recipes["cuisine"] == "vietnam", "cuisine"] = "vietnamese"
recipes.loc[recipes["cuisine"] == "uk-and-ireland", "cuisine"] = "uk-and-irish"
recipes.loc[recipes["cuisine"] == "irish", "cuisine"] = "uk-and-irish"
recipes
```
Remove cuisines with < 50 recipes.
```
# get list of cuisines to keep
recipes_counts = recipes["cuisine"].value_counts()
cuisines_indices = recipes_counts > 50
cuisines_to_keep = list(np.array(recipes_counts.index.values)[np.array(cuisines_indices)])
rows_before = recipes.shape[0] # number of rows of original dataframe
print("Number of rows of original dataframe is {}.".format(rows_before))
recipes = recipes.loc[recipes['cuisine'].isin(cuisines_to_keep)]
rows_after = recipes.shape[0] # number of rows of processed dataframe
print("Number of rows of processed dataframe is {}.".format(rows_after))
print("{} rows removed!".format(rows_before - rows_after))
```
Convert all Yes's to 1's and the No's to 0's
```
recipes = recipes.replace(to_replace="Yes", value=1)
recipes = recipes.replace(to_replace="No", value=0)
```
#### Let's analyze the data a little more in order to learn the data better and note any interesting preliminary observations.
Run the following cell to get the recipes that contain **rice** *and* **soy** *and* **wasabi** *and* **seaweed**.
```
recipes.head()
check_recipes = recipes.loc[
(recipes["rice"] == 1) &
(recipes["soy_sauce"] == 1) &
(recipes["wasabi"] == 1) &
(recipes["seaweed"] == 1)
]
check_recipes
```
Based on the results of the above code, can we classify all recipes that contain **rice** *and* **soy** *and* **wasabi** *and* **seaweed** as **Japanese** recipes? Why?
Double-click __here__ for the solution.
<!-- The correct answer is:
No, because other recipes such as Asian and East_Asian recipes also contain these ingredients.
-->
Let's count the ingredients across all recipes.
```
# sum each column
ing = recipes.iloc[:, 1:].sum(axis=0)
# define each column as a pandas series
ingredient = pd.Series(ing.index.values, index = np.arange(len(ing)))
count = pd.Series(list(ing), index = np.arange(len(ing)))
# create the dataframe
ing_df = pd.DataFrame(dict(ingredient = ingredient, count = count))
ing_df = ing_df[["ingredient", "count"]]
print(ing_df.to_string())
```
Now we have a dataframe of ingredients and their total counts across all recipes. Let's sort this dataframe in descending order.
```
ing_df.sort_values(["count"], ascending=False, inplace=True)
ing_df.reset_index(inplace=True, drop=True)
print(ing_df)
```
#### What are the 3 most popular ingredients?
Double-click __here__ for the solution.
<!-- The correct answer is:
// 1. Egg with <strong>21,025</strong> occurrences.
// 2. Wheat with <strong>20,781</strong> occurrences.
// 3. Butter with <strong>20,719</strong> occurrences.
-->
However, note that there is a problem with the above table. There are ~40,000 American recipes in our dataset, which means that the data is biased towards American ingredients.
**Therefore**, let's compute a more objective summary of the ingredients by looking at the ingredients per cuisine.
#### Let's create a *profile* for each cuisine.
In other words, let's try to find out what ingredients Chinese people typically use, and what is **Canadian** food for example.
```
cuisines = recipes.groupby("cuisine").mean()
cuisines.head()
```
As shown above, we have just created a dataframe where each row is a cuisine and each column (except for the first column) is an ingredient, and the row values represent the percentage of each ingredient in the corresponding cuisine.
**For example**:
* *almond* is present across 15.65% of all of the **African** recipes.
* *butter* is present across 38.11% of all of the **Canadian** recipes.
Let's print out the profile for each cuisine by displaying the top four ingredients in each cuisine.
```
num_ingredients = 4 # define number of top ingredients to print
# define a function that prints the top ingredients for each cuisine
def print_top_ingredients(row):
print(row.name.upper())
row_sorted = row.sort_values(ascending=False)*100
top_ingredients = list(row_sorted.index.values)[0:num_ingredients]
row_sorted = list(row_sorted)[0:num_ingredients]
for ind, ingredient in enumerate(top_ingredients):
print("%s (%d%%)" % (ingredient, row_sorted[ind]), end=' ')
print("\n")
# apply function to cuisines dataframe
create_cuisines_profiles = cuisines.apply(print_top_ingredients, axis=1)
```
At this point, we feel that we have understood the data well and the data is ready and is in the right format for modeling!
-----------
### Thank you for completing this lab!
This notebook was created by [Alex Aklson](https://www.linkedin.com/in/aklson/). We hope you found this lab session interesting. Feel free to contact us if you have any questions!
This notebook is part of the free course on **Cognitive Class** called *Data Science Methodology*. If you accessed this notebook outside the course, you can take this free self-paced course, online by clicking [here](https://cocl.us/DS0103EN_LAB3_PYTHON).
<hr>
Copyright © 2018 [Cognitive Class](https://cognitiveclass.ai/?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu). This notebook and its source code are released under the terms of the [MIT License](https://bigdatauniversity.com/mit-license/).
| true |
code
| 0.237664 | null | null | null | null |
|
# Autoencoder (Semi-supervised)
```
%load_ext autoreload
%autoreload 2
# Seed value
# Apparently you may use different seed values at each stage
seed_value= 0
# 1. Set the `PYTHONHASHSEED` environment variable at a fixed value
import os
os.environ['PYTHONHASHSEED']=str(seed_value)
# 2. Set the `python` built-in pseudo-random generator at a fixed value
import random
random.seed(seed_value)
# 3. Set the `numpy` pseudo-random generator at a fixed value
import numpy as np
np.random.seed(seed_value)
# 4. Set the `tensorflow` pseudo-random generator at a fixed value
import tensorflow as tf
tf.set_random_seed(seed_value)
# 5. Configure a new global `tensorflow` session
from keras import backend as K
session_conf = tf.ConfigProto(intra_op_parallelism_threads=1, inter_op_parallelism_threads=1)
sess = tf.Session(graph=tf.get_default_graph(), config=session_conf)
K.set_session(sess)
import keras
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
# plt.style.use('fivethirtyeight')
sns.set_style("whitegrid")
sns.set_context("notebook")
DATA_PATH = '../data/'
VAL_SPLITS = 4
from plot_utils import plot_confusion_matrix
from cv_utils import run_cv_f1
from cv_utils import plot_cv_roc
from cv_utils import plot_cv_roc_prc
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import cross_validate
```
For this part of the project, we will only work with the training set, that we will split again into train and validation to perform the hyperparameter tuning.
We will save the test set for the final part, when we have already tuned our hyperparameters.
```
df = pd.read_csv(os.path.join(DATA_PATH,'df_train.csv'))
df.drop(columns= df.columns[0:2],inplace=True)
df.head()
```
## Preprocessing the data
Although we are always using cross validation with `VAL_SPLITS` folds, (in general, 4), here we are gonna set only one split in order to explore how the Autoencoder works and get intuition.
```
cv = StratifiedShuffleSplit(n_splits=1,test_size=0.15,random_state=0)
# In case we want to select a subset of features
# df_ = df[['Class','V9','V14','V16','V2','V3','V17']]
df_ = df[['Class','V4','V14','V16','V12','V3','V17']]
X = df_.drop(columns='Class').to_numpy()
y = df_['Class'].to_numpy()
for idx_t, idx_v in cv.split(X,y):
X_train = X[idx_t]
y_train = y[idx_t]
X_val = X[idx_v]
y_val = y[idx_v]
# Now we need to erase the FRAUD cases on the TRAINING set
X_train_normal = X_train[y_train==0]
```
## Defining the model
```
# this is the size of our encoded representations
ENCODED_DIM = 2
INPUT_DIM = X.shape[1]
from keras.layers import Input, Dense
from keras.models import Model
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import LeakyReLU
def create_encoder(input_dim, encoded_dim):
encoder = Sequential([
Dense(32, input_shape=(input_dim,)),
LeakyReLU(),
Dense(16),
LeakyReLU(),
Dense(8),
LeakyReLU(),
Dense(encoded_dim)
], name='encoder')
return encoder
def create_decoder(input_dim, encoded_dim):
decoder = Sequential([
Dense(8, input_shape=(encoded_dim,) ),
LeakyReLU(),
Dense(16),
LeakyReLU(),
Dense(8),
LeakyReLU(),
Dense(input_dim)
],name='decoder')
return decoder
def create_autoencoder(input_dim, encoded_dim, return_encoder = True):
encoder = create_encoder(input_dim,encoded_dim)
decoder = create_decoder(input_dim,encoded_dim)
inp = Input(shape=(INPUT_DIM,),name='Input_Layer')
# a layer instance is callable on a tensor, and returns a tensor
x_enc = encoder(inp)
x_out = decoder(x_enc)
# This creates a model that includes
# the Input layer and three Dense layers
autoencoder = Model(inputs=inp, outputs=x_out)
if return_encoder:
return autoencoder, encoder
else:
return autoencoder
autoencoder, encoder = create_autoencoder(INPUT_DIM,ENCODED_DIM)
print('ENCODER SUMMARY\n')
print(encoder.summary())
print('AUTOENCODER SUMMARY\n')
print(autoencoder.summary())
autoencoder.compile(optimizer='adam',
loss='mean_squared_error')
```
## Training the model
```
autoencoder.fit(x=X_train_normal, y= X_train_normal,
batch_size=512,epochs=40, validation_split=0.1) # starts training
```
## Testing
```
X_enc = encoder.predict(X_val)
X_enc_normal = X_enc[y_val==0]
X_enc_fraud = X_enc[y_val==1]
sns.scatterplot(x = X_enc_normal[:,0], y = X_enc_normal[:,1] ,label='Normal', alpha=0.5)
sns.scatterplot(x = X_enc_fraud[:,0], y = X_enc_fraud[:,1] ,label='Fraud')
X_out = autoencoder.predict(X_val)
print(X_out.shape)
X_val.shape
distances = np.sum((X_out-X_val)**2,axis=1)
bins = np.linspace(0,np.max(distances),40)
sns.distplot(distances[y_val==0],label='Normal',kde=False,
bins=bins, norm_hist=True, axlabel='Distance')
sns.distplot(distances[y_val==1],label='Fraud',kde=False, bins=bins, norm_hist=True)
bins = np.linspace(0,100,40)
sns.distplot(distances[y_val==0],label='Normal',kde=False,
bins=bins, norm_hist=True, axlabel='Distance')
sns.distplot(distances[y_val==1],label='Fraud',kde=False, bins=bins, norm_hist=True)
plt.xlim((0,100))
```
## Validating the model
```
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import cross_validate
from sklearn.metrics import f1_score
def clf_autoencoder(X,autoencoder,threshold):
"""
Classifier based in the autoencoder.
A datapoint is a nomaly if the distance of the original points
and the result of the autoencoder is greater than the threshold.
"""
X_out = autoencoder.predict(X)
distances = np.sum((X_out-X)**2,axis=1).reshape((-1,1))
# y_pred = 1 if it is anomaly
y_pred = 1.*(distances > threshold )
return y_pred
cv = StratifiedShuffleSplit(n_splits=VAL_SPLITS,test_size=0.15,random_state=0)
# Thresholds to validate
thresholds = np.linspace(0,100,100)
# List with the f1 of all the thresholds at each validation fold
f1_all = []
for i,(idx_t, idx_v) in enumerate(cv.split(X,y)):
X_train = X[idx_t]
y_train = y[idx_t]
X_val = X[idx_v]
y_val = y[idx_v]
# Now we need to erase the FRAUD cases on the TRAINING set
X_train_normal = X_train[y_train==0]
# Train the autoencoder
autoencoder, encoder = create_autoencoder(INPUT_DIM,ENCODED_DIM)
autoencoder.compile(optimizer='adam',
loss='mean_squared_error')
autoencoder.fit(x=X_train_normal, y= X_train_normal,
batch_size=512,epochs=30, shuffle=True,
verbose=0) # starts training
# Plot of the validation set in the embedding space
X_enc = encoder.predict(X_val)
X_enc_normal = X_enc[y_val==0]
X_enc_fraud = X_enc[y_val==1]
sns.scatterplot(x = X_enc_normal[:,0], y = X_enc_normal[:,1] ,label='Normal', alpha=0.5)
sns.scatterplot(x = X_enc_fraud[:,0], y = X_enc_fraud[:,1] ,label='Fraud')
plt.show()
# Transformation of the points through the autoencoder
# and calculate the predictions
y_preds=clf_autoencoder(X_val,autoencoder,thresholds)
metrics_f1 = np.array([ f1_score(y_val,y_pred) for y_pred in y_preds.T ])
f1_all.append(metrics_f1)
# Save the models into files for future use
autoencoder.save('models_autoencoder/autoencoder_fold_'+str(i+1)+'.h5')
encoder.save('models_autoencoder/encoder_fold_'+str(i+1)+'.h5')
del(autoencoder,encoder)
f1_mean = np.mean(f1_all,axis=0)
# Plot of F1-Threshold curves
for i,f1_fold in enumerate(f1_all):
sns.lineplot(thresholds,f1_fold, label='Fold '+str(i+1))
sns.scatterplot(thresholds,f1_mean,label='Mean')
plt.show()
f1_opt = f1_mean.max()
threshold_opt = thresholds[np.argmax(f1_mean)]
print('F1 max = {:.3f} at threshold = {:.3f}'.format(f1_opt,threshold_opt))
```
| true |
code
| 0.629604 | null | null | null | null |
|
# 2.4 Deep Taylor Decomposition Part 2.
## Tensorflow Walkthrough
### 1. Import Dependencies
I made a custom `Taylor` class for Deep Taylor Decomposition. If you are interested in the details, check out `models_3_2.py` in the models directory.
```
import os
import re
from tensorflow.examples.tutorials.mnist import input_data
from tensorflow.python.ops import nn_ops, gen_nn_ops
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
from models.models_2_4 import MNIST_CNN, Taylor
%matplotlib inline
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
images = mnist.train.images
labels = mnist.train.labels
logdir = './tf_logs/2_4_DTD/'
ckptdir = logdir + 'model'
if not os.path.exists(logdir):
os.mkdir(logdir)
```
### 2. Building Graph
```
with tf.name_scope('Classifier'):
# Initialize neural network
DNN = MNIST_CNN('CNN')
# Setup training process
X = tf.placeholder(tf.float32, [None, 784], name='X')
Y = tf.placeholder(tf.float32, [None, 10], name='Y')
activations, logits = DNN(X)
tf.add_to_collection('DTD', X)
for activation in activations:
tf.add_to_collection('DTD', activation)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=Y))
optimizer = tf.train.AdamOptimizer().minimize(cost, var_list=DNN.vars)
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
cost_summary = tf.summary.scalar('Cost', cost)
accuray_summary = tf.summary.scalar('Accuracy', accuracy)
summary = tf.summary.merge_all()
```
### 3. Training Network
This is the step where the DNN is trained to classify the 10 digits of the MNIST images. Summaries are written into the logdir and you can visualize the statistics using tensorboard by typing this command: `tensorboard --lodir=./tf_logs`
```
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())
# Hyper parameters
training_epochs = 15
batch_size = 100
for epoch in range(training_epochs):
total_batch = int(mnist.train.num_examples / batch_size)
avg_cost = 0
avg_acc = 0
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
_, c, a, summary_str = sess.run([optimizer, cost, accuracy, summary], feed_dict={X: batch_xs, Y: batch_ys})
avg_cost += c / total_batch
avg_acc += a / total_batch
file_writer.add_summary(summary_str, epoch * total_batch + i)
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost), 'accuracy =', '{:.9f}'.format(avg_acc))
saver.save(sess, ckptdir)
print('Accuracy:', sess.run(accuracy, feed_dict={X: mnist.test.images, Y: mnist.test.labels}))
sess.close()
```
### 4. Restoring Subgraph
Here we first rebuild the DNN graph from metagraph, restore DNN parameters from the checkpoint and then gather the necessary weight and biases for Deep Taylor Decomposition using the `tf.get_collection()` function.
```
tf.reset_default_graph()
sess = tf.InteractiveSession()
new_saver = tf.train.import_meta_graph(ckptdir + '.meta')
new_saver.restore(sess, tf.train.latest_checkpoint(logdir))
weights = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='CNN')
activations = tf.get_collection('DTD')
X = activations[0]
```
### 5. Attaching Subgraph for Calculating Relevance Scores
```
conv_ksize = [1, 3, 3, 1]
pool_ksize = [1, 2, 2, 1]
conv_strides = [1, 1, 1, 1]
pool_strides = [1, 2, 2, 1]
weights.reverse()
activations.reverse()
taylor = Taylor(activations, weights, conv_ksize, pool_ksize, conv_strides, pool_strides, 'Taylor')
Rs = []
for i in range(10):
Rs.append(taylor(i))
```
### 6. Calculating Relevance Scores $R(x_i)$
```
sample_imgs = []
for i in range(10):
sample_imgs.append(images[np.argmax(labels, axis=1) == i][3])
imgs = []
for i in range(10):
imgs.append(sess.run(Rs[i], feed_dict={X: sample_imgs[i][None,:]}))
```
### 7. Displaying Images
The relevance scores are visualized as heat maps. You can see which features/data points influenced the DNN most its decision making.
```
plt.figure(figsize=(15,15))
for i in range(5):
plt.subplot(5, 2, 2 * i + 1)
plt.imshow(np.reshape(imgs[2 * i], [28, 28]), cmap='hot_r')
plt.title('Digit: {}'.format(2 * i))
plt.colorbar()
plt.subplot(5, 2, 2 * i + 2)
plt.imshow(np.reshape(imgs[2 * i + 1], [28, 28]), cmap='hot_r')
plt.title('Digit: {}'.format(2 * i + 1))
plt.colorbar()
plt.tight_layout()
```
| true |
code
| 0.681793 | null | null | null | null |
|
```
# The usual preamble
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# Make the graphs a bit prettier, and bigger
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 5)
plt.rcParams['font.family'] = 'sans-serif'
# This is necessary to show lots of columns in pandas 0.12.
# Not necessary in pandas 0.13.
pd.set_option('display.width', 5000)
pd.set_option('display.max_columns', 60)
```
One of the main problems with messy data is: how do you know if it's messy or not?
We're going to use the NYC 311 service request dataset again here, since it's big and a bit unwieldy.
```
requests = pd.read_csv('data/311-service-requests.csv', low_memory=False)
```
# 7.1 How do we know if it's messy?
We're going to look at a few columns here. I know already that there are some problems with the zip code, so let's look at that first.
To get a sense for whether a column has problems, I usually use `.unique()` to look at all its values. If it's a numeric column, I'll instead plot a histogram to get a sense of the distribution.
When we look at the unique values in "Incident Zip", it quickly becomes clear that this is a mess.
Some of the problems:
* Some have been parsed as strings, and some as floats
* There are `nan`s
* Some of the zip codes are `29616-0759` or `83`
* There are some N/A values that pandas didn't recognize, like 'N/A' and 'NO CLUE'
What we can do:
* Normalize 'N/A' and 'NO CLUE' into regular nan values
* Look at what's up with the 83, and decide what to do
* Make everything strings
```
requests['Incident Zip'].unique()
```
# 7.2 Fixing the nan values and string/float confusion
We can pass a `na_values` option to `pd.read_csv` to clean this up a little bit. We can also specify that the type of Incident Zip is a string, not a float.
```
na_values = ['NO CLUE', 'N/A', '0']
requests = pd.read_csv('data/311-service-requests.csv', na_values=na_values, dtype={'Incident Zip': str})
requests['Incident Zip'].unique()
```
# 7.3 What's up with the dashes?
```
rows_with_dashes = requests['Incident Zip'].str.contains('-').fillna(False)
len(requests[rows_with_dashes])
requests[rows_with_dashes]
```
I thought these were missing data and originally deleted them like this:
`requests['Incident Zip'][rows_with_dashes] = np.nan`
But then my friend Dave pointed out that 9-digit zip codes are normal. Let's look at all the zip codes with more than 5 digits, make sure they're okay, and then truncate them.
```
long_zip_codes = requests['Incident Zip'].str.len() > 5
requests['Incident Zip'][long_zip_codes].unique()
```
Those all look okay to truncate to me.
```
requests['Incident Zip'] = requests['Incident Zip'].str.slice(0, 5)
```
Done.
Earlier I thought 00083 was a broken zip code, but turns out Central Park's zip code 00083! Shows what I know. I'm still concerned about the 00000 zip codes, though: let's look at that.
```
requests[requests['Incident Zip'] == '00000']
```
This looks bad to me. Let's set these to nan.
```
zero_zips = requests['Incident Zip'] == '00000'
requests.loc[zero_zips, 'Incident Zip'] = np.nan
```
Great. Let's see where we are now:
```
unique_zips = requests['Incident Zip'].unique()
unique_zips
```
Amazing! This is much cleaner. There's something a bit weird here, though -- I looked up 77056 on Google maps, and that's in Texas.
Let's take a closer look:
```
zips = requests['Incident Zip']
# Let's say the zips starting with '0' and '1' are okay, for now. (this isn't actually true -- 13221 is in Syracuse, and why?)
is_close = zips.str.startswith('0') | zips.str.startswith('1')
# There are a bunch of NaNs, but we're not interested in them right now, so we'll say they're False
is_far = ~(is_close) & zips.notnull()
zips[is_far]
requests[is_far][['Incident Zip', 'Descriptor', 'City']].sort_values(by='Incident Zip')
```
Okay, there really are requests coming from LA and Houston! Good to know. Filtering by zip code is probably a bad way to handle this -- we should really be looking at the city instead.
```
requests['City'].str.upper().value_counts()
```
It looks like these are legitimate complaints, so we'll just leave them alone.
# 7.4 Putting it together
Here's what we ended up doing to clean up our zip codes, all together:
```
na_values = ['NO CLUE', 'N/A', '0']
requests = pd.read_csv('data/311-service-requests.csv',
na_values=na_values,
dtype={'Incident Zip': str})
def fix_zip_codes(zips):
# Truncate everything to length 5
zips = zips.str.slice(0, 5)
# Set 00000 zip codes to nan
zero_zips = zips == '00000'
zips[zero_zips] = np.nan
return zips
requests['Incident Zip'] = fix_zip_codes(requests['Incident Zip'])
requests['Incident Zip'].unique()
```
<style>
@font-face {
font-family: "Computer Modern";
src: url('http://mirrors.ctan.org/fonts/cm-unicode/fonts/otf/cmunss.otf');
}
div.cell{
width:800px;
margin-left:16% !important;
margin-right:auto;
}
h1 {
font-family: Helvetica, serif;
}
h4{
margin-top:12px;
margin-bottom: 3px;
}
div.text_cell_render{
font-family: Computer Modern, "Helvetica Neue", Arial, Helvetica, Geneva, sans-serif;
line-height: 145%;
font-size: 130%;
width:800px;
margin-left:auto;
margin-right:auto;
}
.CodeMirror{
font-family: "Source Code Pro", source-code-pro,Consolas, monospace;
}
.text_cell_render h5 {
font-weight: 300;
font-size: 22pt;
color: #4057A1;
font-style: italic;
margin-bottom: .5em;
margin-top: 0.5em;
display: block;
}
.warning{
color: rgb( 240, 20, 20 )
}
| true |
code
| 0.397237 | null | null | null | null |
|
```
%load_ext autoreload
%autoreload 2
from IPython.display import Markdown, display
def printmd(string):
display(Markdown(string))
def colorize(string,color="red"):
return f"<span style=\"color:{color}\">{string}</span>"
```
# Problem description
### Subtask2: Detecting antecedent and consequence
Indicating causal insight is an inherent characteristic of counterfactual. To further detect the causal knowledge conveyed in counterfactual statements, subtask 2 aims to locate antecedent and consequent in counterfactuals.
According to (Nelson Goodman, 1947. The problem of counterfactual conditionals), a counterfactual statement can be converted to a contrapositive with a true antecedent and consequent. Consider example “Her post-traumatic stress could have been avoided if a combination of paroxetine and exposure therapy had been prescribed two months earlier”; it can be transposed into “because her post-traumatic stress was not avoided, (we know) a combination of paroxetine and exposure therapy was not prescribed”. Such knowledge can be not only used for analyzing the specific statement but also be accumulated across corpora to develop domain causal knowledge (e.g., a combination of paroxetine and exposure may help cure post-traumatic stress).
Please note that __in some cases there is only an antecedent part while without a consequent part in a counterfactual statement__. For example, "Frankly, I wish he had issued this order two years ago instead of this year", in this sentence we could only get the antecedent part. In our subtask2, when locating the antecedent and consequent part, please set '-1' as consequent starting index (character index) and ending index (character index) to refer that there is no consequent part in this sentence. For details, please refer to the 'Evaluation' on this website.
```
!ls
import pandas as pd
!pwd
df = pd.read_csv('../../.data/semeval2020_5/train_task2.csv')
```
We have this amount of data:
```
len(df)
import random
i = random.randint(0,len(df))
print(df.iloc[i])
print("-"*50)
print(df["sentence"].iloc[i])
print("-"*50)
print(df["antecedent"].iloc[i])
print("-"*50)
print(df["consequent"].iloc[i])
import random
i = random.randint(0,len(df))
s = df.loc[df["sentenceID"]==203483]
#print(s)
print("-"*50)
print(s["sentence"].iloc[0])
print("-"*50)
print(s["antecedent"].iloc[0])
print("-"*50)
print(s["consequent"].iloc[0])
df["antecedent"].iloc[0]
df["consequent"].iloc[0]
df["sentence"].iloc[0][df["consequent_startid"].iloc[0]:df["consequent_endid"].iloc[0]]
```
Check whether all indices fit the annotation
_Note: annotation indices are inclusive!_
```
for i in range(len(df)):
assert df["sentence"].iloc[i][df["antecedent_startid"].iloc[i]:df["antecedent_endid"].iloc[i]+1] \
== df["antecedent"].iloc[i]
if df["consequent_startid"].iloc[i]>0:
assert df["sentence"].iloc[i][df["consequent_startid"].iloc[i]:df["consequent_endid"].iloc[i]+1] \
== df["consequent"].iloc[i]
```
__Consequent part might not always exist!__
```
df.loc[df['consequent_startid'] == -1]
```
It does not exist in this number of cases
```
df_without_conseq = df.loc[df['consequent_startid'] == -1]
print(f"{len(df_without_conseq)} / {len(df)}")
```
Lets check what are the lengths of sentences, and how much sentences without consequent correlate with length.
```
all_lens = [len(s.split()) for s in df["sentence"].values.tolist()]
no_conseq_lens = [len(s.split()) for s in df_without_conseq["sentence"].values.tolist()]
all_lens
import matplotlib.pyplot as plt
values1 = all_lens
values2= no_conseq_lens
bins=100
_range=(0,max(all_lens))
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
ax.hist(values1, alpha=0.5, bins=bins, range=_range, color= 'b', label='All sentences')
ax.hist(values2, alpha=0.5, bins=bins, range=_range, color= 'r', label='Sentences without consequent')
ax.legend(loc='upper right', prop={'size':14})
plt.show()
```
Distribution is skewed a little bit toward smaller values, but there does not seem to be any big correlation here...
| true |
code
| 0.369969 | null | null | null | null |
|
# Stirlingの公式(対数近似)
* $\log n! \sim n\log n - n$
* $n!$はおおよそ$\left(\frac{n}{e}\right)^n$になる
* 参考: [スターリングの公式(対数近似)の導出](https://starpentagon.net/analytics/stirling_log_formula/)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## $\log n!$の上からの評価
```
MIN_X = 0.5
MAX_X = 10
x = np.linspace(MIN_X, MAX_X, 100)
y = np.log(x)
p = plt.plot(x, y, label='$\log x$')
p = plt.hlines([0], MIN_X, MAX_X)
p = plt.xlim(MIN_X, MAX_X-0.5)
p = plt.xticks(range(1, MAX_X+1))
p = plt.ylim([-0.2, 2.3])
# 面積log kの矩形を描画
for k in range(2, MAX_X):
p = plt.vlines(k, 0, np.log(k), linestyles='dashed')
p = plt.hlines(np.log(k), k, k+1, linestyles='dashed')
p = plt.legend()
plt.show(p)
```
## $\log n!$の下からの評価
```
MIN_X = 0.5
MAX_X = 10
x = np.linspace(MIN_X, MAX_X, 100)
y = np.log(x)
p = plt.plot(x, y, label='$\log x$')
p = plt.hlines([0], MIN_X, MAX_X)
p = plt.xlim(MIN_X, MAX_X-0.5)
p = plt.xticks(range(1, MAX_X+1))
p = plt.ylim([-0.2, 2.3])
# 面積log kの矩形を描画
for k in range(2, MAX_X):
p = plt.vlines(k-1, 0, np.log(k), linestyles='dashed')
p = plt.hlines(np.log(k), k-1, k, linestyles='dashed')
p = plt.vlines(MAX_X-1, 0, np.log(MAX_X), linestyles='dashed')
p = plt.legend()
plt.show(p)
```
## $n \log n - n$の近似精度
```
def log_factorial(n):
'''log n!を返す'''
val = 0.0
for i in range(1, n+1):
val += np.log(i)
return val
# test of log_factorial
eps = 10**-5
assert abs(log_factorial(1) - 0.0) < eps
assert abs(log_factorial(2) - np.log(2)) < eps
assert abs(log_factorial(5) - np.log(120)) < eps
def log_factorial_approx(n):
'''log n!の近似: n log n - nを返す'''
return n * np.log(n) - n
# test of log_factorial_approx
assert abs(log_factorial_approx(1) - (-1)) < eps
assert abs(log_factorial_approx(2) - (2 * np.log(2) - 2)) < eps
# log_factorial, log_factorial_approxをplot
n_list = range(1, 50+1)
y_fact = [log_factorial(n) for n in n_list]
y_approx = [log_factorial_approx(n) for n in n_list]
p = plt.plot(n_list, y_fact, label='$\log n!$')
p = plt.plot(n_list, y_approx, label='$n \log n - n$')
p = plt.legend()
plt.show(p)
# 近似精度を評価
n_list = [5, 10, 20, 50, 100, 1000]
approx_df = pd.DataFrame()
approx_df['n'] = n_list
approx_df['log n!'] = [log_factorial(n) for n in n_list]
approx_df['n log(n)-n'] = [log_factorial_approx(n) for n in n_list]
approx_df['error(%)'] = 100 * (approx_df['log n!'] - approx_df['n log(n)-n']) / approx_df['log n!']
pd.options.display.float_format = '{:.1f}'.format
approx_df
```
## $n!$と$\left(\frac{n}{e}\right)^n$の比較
```
n_list = [5, 10, 20, 50, 100]
approx_df = pd.DataFrame()
approx_df['n'] = n_list
approx_df['n!'] = [np.exp(log_factorial(n)) for n in n_list]
approx_df['(n/e)^n'] = [np.exp(log_factorial_approx(n)) for n in n_list]
approx_df['error(%)'] = 100 * (approx_df['n!'] - approx_df['(n/e)^n']) / approx_df['n!']
pd.options.display.float_format = None
pd.options.display.precision = 2
approx_df
```
| true |
code
| 0.335963 | null | null | null | null |
|
## Recursive Functions
A recursive function is a function that makes calls to itself. It works like the loops we described before, but sometimes it the situation is better to use recursion than loops.
Every recursive function has two components: a base case and a recursive step. The base case is usually the smallest input and has an easily verifiable solution. This is also the mechanism that stops the function from calling itself forever. The recursive step is the set of all cases where a recursive call, or a function call to itself, is made.
Consider the example of computing the factorial of a number. For example, the factorial of a number $n$ is given by $f(n) = 1 \ \times \ 2 \ \times \ 3 \ \times \ \dots \ \times \ (n-1) \ \times \ n$.
The recursive from of a factorial is
$$
f(n) = \left\{ \begin{array}{ll} 1 & if \ n=1 \\
n \ \times \ f(n-1) & otherwise\end{array} \right.
$$
which can be expressed in code as
```
def factorial_n(n):
assert type(n) == int, 'Input must be an integer'
if n == 1: #this is the base case
return 1
else: #this is the recursive step
return n * factorial_n(n-1)
factorial_n(1)
factorial_n(2)
factorial_n(5)
1*2*3*4*5
#We can use debbuging tools to understand the code
from pdb import set_trace
def factorial_n(n):
assert type(n) == int, 'Input must be an integer'
set_trace()
if n == 1: #this is the base case
return 1
else: #this is the recursive step
return n * factorial_n(n-1)
factorial_n(1)
factorial_n(3)
```
## mini challenge 1
Fibonacci numbers were originally developed to model the idealized population growth of rabbits. Since then, they have been found to be significant in any naturally occurring phenomena.
Use recursivity to compute the Fibonacci numbers.
The recursive form of the Fibonacci numbers.
$$
f(n) = \left\{ \begin{array}{ll} 1 & if \ n=1 \\
1 & if \ n=2 \\
f(n-1) + f(n-2) & otherwise\end{array} \right.
$$
```
#examples
fibonacci(1) = 1
fibonacci(2) = 1
fibonacci(3) = 2
fibonacci(4) = 3
fibonacci(5) = 5
fibonacci(35) = 9227465
def fibonacci(n) :
assert type(n) == int, 'Input must be an integer'
if n == 1:
return 1
if n == 2:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
```
## mini challenge 2
An integer number $n$ is said to be **prime** if is divisible only by itself and one. If $n$ is divisible by any other number between $1$ and $n$, the the number is not prime.
Write a recursive function to verify if a number n is prime.
```
def prime(N, div = 2):
if N == 1:
return True
else:
if N == 2:
return True
elif (N%div) == 0 :
return False
else:
prime(N,div+1)
return True
prime(7)
```
| true |
code
| 0.50769 | null | null | null | null |
|
```
from astropy.constants import G
import astropy.coordinates as coord
import astropy.table as at
import astropy.units as u
from astropy.time import Time
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from gala.units import galactic, UnitSystem
from twobody import TwoBodyKeplerElements, KeplerOrbit
from twobody.anomaly import mean_anomaly_from_eccentric_anomaly
usys = UnitSystem(1e12*u.Msun, u.kpc, u.Gyr, u.radian)
true_m31_sky_c = coord.SkyCoord(
10.64628564*u.deg,
41.23456631*u.deg
)
```
## Simulate some Keplerian data
```
M1 = 1.4e12 * u.Msun
M2 = 2.4e12 * u.Msun
M = M1 + M2
a = 511 * u.kpc
eta = 4.3 * u.rad
e = 0.981
mean_anomaly = mean_anomaly_from_eccentric_anomaly(eta, e)
elem = TwoBodyKeplerElements(
a=a, m1=M1, m2=M2, e=e,
omega=0*u.rad, i=90*u.deg,
M0=0.*u.rad, t0=0. * u.Gyr,
units=galactic
)
orb1 = KeplerOrbit(elem.primary)
orb2 = KeplerOrbit(elem.secondary)
Romega = coord.matrix_utilities.rotation_matrix(elem.secondary.omega, 'z')
xyz1 = orb1.orbital_plane(0. * u.Gyr)
xyz2 = orb2.orbital_plane(0. * u.Gyr).transform(Romega)
xyz1, xyz2
time = (elem.P * (mean_anomaly / (2*np.pi*u.rad))).to(u.Gyr)
xyz1 = orb1.orbital_plane(time)
xyz2 = orb2.orbital_plane(time).transform(Romega)
(xyz1.without_differentials()
- xyz2.without_differentials()).norm().to(u.kpc)
a * (1 - e * np.cos(eta))
times = np.linspace(0, 1, 1024) * elem.P
xyzs1 = orb1.orbital_plane(times)
xyzs2 = orb2.orbital_plane(times).transform(Romega)
rs = (xyzs1.without_differentials()
- xyzs2.without_differentials()).norm().to(u.kpc)
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
ax.plot(xyzs1.x, xyzs1.y, marker='')
ax.plot(xyzs2.x, xyzs2.y, marker='')
ax.plot(xyz1.x, xyz1.y, zorder=100, ms=10, color='tab:orange')
ax.plot(xyz2.x, xyz2.y, zorder=100, ms=10, color='tab:red')
ax.set_xlim(-2*a.value, 2*a.value)
ax.set_ylim(-2*a.value, 2*a.value)
plt.plot(times.value, rs.value)
dxs = xyzs1.without_differentials() - xyzs2.without_differentials()
dvs = xyzs1.differentials['s'] - xyzs2.differentials['s']
dx_cyl = dxs.represent_as(coord.CylindricalRepresentation)
dv_cyl = dvs.represent_as(coord.CylindricalDifferential, dxs)
vrads = dv_cyl.d_rho
vtans = (dx_cyl.rho * dv_cyl.d_phi).to(u.km/u.s, u.dimensionless_angles())
etas = np.linspace(0, 2*np.pi, 1024) * u.rad
mean_anoms = mean_anomaly_from_eccentric_anomaly(etas, e)
eq_times = elem.P * (mean_anoms / (2*np.pi*u.rad))
eq_vrad = np.sqrt(G * M / a) * (e * np.sin(etas)) / (1 - e * np.cos(etas))
eq_vtan = np.sqrt(G * M / a) * np.sqrt(1 - e**2) / (1 - e * np.cos(etas))
plt.plot(times.value, vrads.to_value(u.km/u.s))
plt.plot(times.value, vtans.to_value(u.km/u.s))
plt.plot(eq_times.value, eq_vrad.to_value(u.km/u.s))
plt.plot(eq_times.value, eq_vtan.to_value(u.km/u.s))
plt.ylim(-500, 500)
```
### Transform to ICRS
```
dx = xyz1.without_differentials() - xyz2.without_differentials()
dv = xyz1.differentials['s'] - xyz2.differentials['s']
dx_cyl = dx.represent_as(coord.CylindricalRepresentation)
dv_cyl = dv.represent_as(coord.CylindricalDifferential, dx)
vrad = dv_cyl.d_rho.to(u.km/u.s)
vtan = (dx_cyl.rho * dv_cyl.d_phi).to(u.km/u.s, u.dimensionless_angles())
r = dx.norm()
sun_galcen_dist = coord.Galactocentric().galcen_distance
gamma = coord.Galactocentric().galcen_coord.separation(true_m31_sky_c)
sun_m31_dist = (sun_galcen_dist * np.cos(gamma)) + np.sqrt(
r**2 - sun_galcen_dist**2 * np.sin(gamma)**2
)
r, sun_m31_dist
vscale = np.sqrt(G * M / a)
print(vscale.decompose(usys).value,
vrad.decompose(usys).value,
vtan.decompose(usys).value)
alpha = 32.4 * u.deg
galcen_pos = coord.SkyCoord(true_m31_sky_c.ra,
true_m31_sky_c.dec,
distance=sun_m31_dist)
galcen_pos = galcen_pos.transform_to(coord.Galactocentric())
# galcen_pos = coord.CartesianRepresentation(
# -375 * u.kpc, 605 * u.kpc, -279 * u.kpc)
# galcen_pos = coord.Galactocentric(galcen_pos / galcen_pos.norm() * r)
galcen_sph = galcen_pos.represent_as('spherical')
gc_Rz = coord.matrix_utilities.rotation_matrix(-galcen_sph.lon, 'z')
gc_Ry = coord.matrix_utilities.rotation_matrix(galcen_sph.lat, 'y')
gc_Rx = coord.matrix_utilities.rotation_matrix(alpha, 'x')
R = gc_Rz @ gc_Ry @ gc_Rx
fake_X = R @ [r.value, 0, 0] * r.unit
fake_V = R @ [vrad.to_value(u.km/u.s), vtan.to_value(u.km/u.s), 0.] * u.km/u.s
fake_galcen = coord.Galactocentric(*fake_X, *fake_V)
fake_icrs = fake_galcen.transform_to(coord.ICRS())
fake_icrs
```
## Check roundtripping
```
def tt_sph_to_xyz(r, lon, lat):
return [
r * np.cos(lon) * np.cos(lat),
r * np.sin(lon) * np.cos(lat),
r * np.sin(lat)
]
def tt_cross(a, b):
return np.array([
a[1]*b[2] - a[2]*b[1],
a[2]*b[0] - a[0]*b[2],
a[0]*b[1] - a[1]*b[0]
])
def tt_rotation_matrix(angle_rad, axis):
s = np.sin(angle_rad)
c = np.cos(angle_rad)
if axis == 'x':
R = np.array([
1., 0, 0,
0, c, s,
0, -s, c
])
elif axis == 'y':
R = np.array([
c, 0, -s,
0, 1., 0,
s, 0, c
])
elif axis == 'z':
R = np.array([
c, s, 0,
-s, c, 0,
0, 0, 1.
])
else:
raise ValueError('bork')
return np.reshape(R, (3, 3))
def ugh(m31_ra_rad, m31_dec_rad, m31_distance_kpc, r, vrad, vtan):
galcen_frame = coord.Galactocentric()
# tangent bases: ra, dec, r
M = np.array([
[-np.sin(m31_ra_rad), np.cos(m31_ra_rad), 0.],
[-np.sin(m31_dec_rad)*np.cos(m31_ra_rad), -np.sin(m31_dec_rad)*np.sin(m31_ra_rad), np.cos(m31_dec_rad)],
[np.cos(m31_dec_rad)*np.cos(m31_ra_rad), np.cos(m31_dec_rad)*np.sin(m31_ra_rad), np.sin(m31_dec_rad)]
])
# Matrix to go from ICRS to Galactocentric
R_I2G, offset_I2G = coord.builtin_frames.galactocentric.get_matrix_vectors(
galcen_frame, inverse=False)
dxyz_I2G = offset_I2G.xyz.to_value(usys['length'])
dvxyz_I2G = offset_I2G.differentials['s'].d_xyz.to_value(usys['velocity'])
# Matrix to go from Galactocentric to ICRS
R_G2I, offset_G2I = coord.builtin_frames.galactocentric.get_matrix_vectors(
galcen_frame, inverse=True)
dxyz_G2I = offset_G2I.xyz.to_value(usys['length'])
dvxyz_G2I = offset_G2I.differentials['s'].d_xyz.to_value(usys['velocity'])
m31_icrs_xyz = tt_sph_to_xyz(m31_distance_kpc,
m31_ra_rad, m31_dec_rad)
m31_galcen_xyz = np.dot(R_I2G, m31_icrs_xyz) + dxyz_I2G
m31_galcen_lon = np.arctan2(m31_galcen_xyz[1], m31_galcen_xyz[0])
m31_galcen_lat = np.arcsin(m31_galcen_xyz[2] / r)
xhat = m31_galcen_xyz / r
Rz = tt_rotation_matrix(-m31_galcen_lon, 'z')
print(gc_Ry)
Ry = tt_rotation_matrix(m31_galcen_lat, 'y')
print(Ry)
Rx = tt_rotation_matrix(alpha, 'x')
yhat = np.dot(np.dot(Rz, np.dot(Ry, Rx)), [0, 1, 0.])
zhat = tt_cross(xhat, yhat)
R_LGtoG = np.stack((xhat, yhat, zhat), axis=1)
print(R_LGtoG - R)
x_LG = np.array([r, 0., 0.])
v_LG = np.array([vrad, vtan, 0.])
x_I = np.dot(R_G2I, np.dot(R_LGtoG, x_LG)) + dxyz_G2I
v_I = np.dot(R_G2I, np.dot(R_LGtoG, v_LG)) + dvxyz_G2I
v_I_tangent_plane = np.dot(M, v_I) # alpha, delta, radial
shit1 = coord.CartesianRepresentation(*((R @ x_LG) * usys['length']))
shit2 = coord.CartesianDifferential(*((R @ v_LG) * usys['velocity']))
shit = coord.SkyCoord(shit1.with_differentials(shit2), frame=coord.Galactocentric())
return x_I, v_I, shit.transform_to(coord.ICRS()).velocity
ugh(fake_icrs.ra.radian, fake_icrs.dec.radian, fake_icrs.distance.to_value(u.kpc),
r.decompose(usys).value, vrad.decompose(usys).value, vtan.decompose(usys).value)
fake_icrs.velocity
def ugh2():
galcen_frame = coord.Galactocentric()
# Matrix to go from ICRS to Galactocentric
R_I2G, offset_I2G = coord.builtin_frames.galactocentric.get_matrix_vectors(
galcen_frame, inverse=False)
dxyz_I2G = offset_I2G.xyz.to_value(usys['length'])
dvxyz_I2G = offset_I2G.differentials['s'].d_xyz.to_value(usys['velocity'])
# Matrix to go from Galactocentric to ICRS
R_G2I, offset_G2I = coord.builtin_frames.galactocentric.get_matrix_vectors(
galcen_frame, inverse=True)
dxyz_G2I = offset_G2I.xyz.to_value(usys['length'])
dvxyz_G2I = offset_G2I.differentials['s'].d_xyz.to_value(usys['velocity'])
m31_icrs_xyz = tt_sph_to_xyz(m31_distance_kpc,
m31_ra_rad, m31_dec_rad)
m31_galcen_xyz = np.dot(R_I2G, m31_icrs_xyz) + dxyz_I2G
m31_galcen_lon = np.arctan2(m31_galcen_xyz[1], m31_galcen_xyz[0])
m31_galcen_lat = np.arcsin(m31_galcen_xyz[2] / r)
xhat = m31_galcen_xyz / r
Rz = tt_rotation_matrix(-m31_galcen_lon, 'z')
Ry = tt_rotation_matrix(m31_galcen_lat, 'y')
Rx = tt_rotation_matrix(alpha, 'x')
yhat = np.dot(np.dot(Rz, np.dot(Ry, Rx)), [0, 1, 0.])
zhat = tt_cross(xhat, yhat)
R_LGtoG = np.stack((xhat, yhat, zhat), axis=1)
x_LG = np.array([r, 0., 0.])
v_LG = np.array([vrad, vtan, 0.])
x_I = np.dot(R_G2I, np.dot(R_LGtoG, x_LG)) + dxyz_G2I
v_I = np.dot(R_G2I, np.dot(R_LGtoG, v_LG)) + dvxyz_G2I
v_I_tangent_plane = np.dot(M, v_I) # alpha, delta, radial
shit1 = coord.CartesianRepresentation(*((R @ x_LG) * usys['length']))
shit2 = coord.CartesianDifferential(*((R @ v_LG) * usys['velocity']))
shit = coord.SkyCoord(shit1.with_differentials(shit2), frame=coord.Galactocentric())
return x_I, v_I, shit.transform_to(coord.ICRS()).velocity
```
## Write data to files:
```
rng = np.random.default_rng(seed=42)
dist_err = 11. * u.kpc
pmra_err = 3 * u.microarcsecond / u.yr
pmdec_err = 4 * u.microarcsecond / u.yr
rv_err = 2. * u.km/u.s
t_err = 0.11 * u.Gyr
tbl = {}
tbl['ra'] = u.Quantity(fake_icrs.ra)
tbl['dec'] = u.Quantity(fake_icrs.dec)
tbl['distance'] = rng.normal(fake_icrs.distance.to_value(u.kpc),
dist_err.to_value(u.kpc)) * u.kpc
tbl['distance_err'] = dist_err
tbl['pm_ra_cosdec'] = rng.normal(
fake_icrs.pm_ra_cosdec.to_value(pmra_err.unit),
pmra_err.value) * pmra_err.unit
tbl['pm_ra_cosdec_err'] = pmra_err
tbl['pm_dec'] = rng.normal(
fake_icrs.pm_dec.to_value(pmdec_err.unit),
pmdec_err.value) * pmdec_err.unit
tbl['pm_dec_err'] = pmdec_err
tbl['radial_velocity'] = rng.normal(
fake_icrs.radial_velocity.to_value(rv_err.unit),
rv_err.value) * rv_err.unit
tbl['radial_velocity_err'] = rv_err
tbl['tperi'] = rng.normal(
time.to_value(t_err.unit),
t_err.value) * t_err.unit
tbl['tperi_err'] = t_err
t = at.QTable({k: [] * tbl[k].unit for k in tbl})
t.add_row(tbl)
t.meta['title'] = 'Simulated Two-body'
t.write('../datasets/apw-simulated.ecsv', overwrite=True)
rng = np.random.default_rng(seed=42)
dist_err = 1. * u.kpc
pmra_err = 0.1 * u.microarcsecond / u.yr
pmdec_err = 0.1 * u.microarcsecond / u.yr
rv_err = 0.1 * u.km/u.s
t_err = 0.02 * u.Gyr
tbl = {}
tbl['ra'] = u.Quantity(fake_icrs.ra)
tbl['dec'] = u.Quantity(fake_icrs.dec)
tbl['distance'] = rng.normal(fake_icrs.distance.to_value(u.kpc),
dist_err.to_value(u.kpc)) * u.kpc
tbl['distance_err'] = dist_err
tbl['pm_ra_cosdec'] = rng.normal(
fake_icrs.pm_ra_cosdec.to_value(pmra_err.unit),
pmra_err.value) * pmra_err.unit
tbl['pm_ra_cosdec_err'] = pmra_err
tbl['pm_dec'] = rng.normal(
fake_icrs.pm_dec.to_value(pmdec_err.unit),
pmdec_err.value) * pmdec_err.unit
tbl['pm_dec_err'] = pmdec_err
tbl['radial_velocity'] = rng.normal(
fake_icrs.radial_velocity.to_value(rv_err.unit),
rv_err.value) * rv_err.unit
tbl['radial_velocity_err'] = rv_err
tbl['tperi'] = rng.normal(
time.to_value(t_err.unit),
t_err.value) * t_err.unit
tbl['tperi_err'] = t_err
t = at.QTable({k: [] * tbl[k].unit for k in tbl})
t.add_row(tbl)
t.meta['title'] = 'Simulated Two-body - precise'
t.write('../datasets/apw-simulated-precise.ecsv', overwrite=True)
rng = np.random.default_rng(42)
tbl = {}
vrad_err = 1 * u.km/u.s
vtan_err = 1 * u.km/u.s
t_err = 0.1 * u.Gyr
r_err = 1 * u.kpc
tbl['vrad'] = rng.normal(
vrad.to_value(vrad_err.unit),
vrad_err.value) * vrad_err.unit
tbl['vrad_err'] = vrad_err
tbl['vtan'] = rng.normal(
vtan.to_value(vtan_err.unit),
vtan_err.value) * vtan_err.unit
tbl['vtan_err'] = vtan_err
tbl['r'] = rng.normal(
r.to_value(r_err.unit),
r_err.value) * r_err.unit
tbl['r_err'] = r_err
tbl['tperi'] = rng.normal(
time.to_value(t_err.unit),
t_err.value) * t_err.unit
tbl['tperi_err'] = t_err
t = at.QTable({k: [] * tbl[k].unit for k in tbl})
t.add_row(tbl)
t.meta['title'] = 'Simulated Two-body - simple vrad, vtan'
t.write('../datasets/apw-simulated-simple.ecsv', overwrite=True)
```
| true |
code
| 0.778944 | null | null | null | null |
|
Peakcalling Bam Stats and Filtering Report - Insert Sizes
================================================================
This notebook is for the analysis of outputs from the peakcalling pipeline
There are severals stats that you want collected and graphed (topics covered in this notebook in bold).
These are:
- how many reads input
- how many reads removed at each step (numbers and percentages)
- how many reads left after filtering
- inset size distribution pre filtering for PE reads
- how many reads mapping to each chromosome before filtering?
- how many reads mapping to each chromosome after filtering?
- X:Y reads ratio
- **inset size distribution after filtering for PE reads**
- samtools flags - check how many reads are in categories they shouldn't be
- picard stats - check how many reads are in categories they shouldn't be
This notebook takes the sqlite3 database created by cgat peakcalling_pipeline.py and uses it for plotting the above statistics
It assumes a file directory of:
location of database = project_folder/csvdb
location of this notebook = project_folder/notebooks.dir/
Firstly lets load all the things that might be needed
Insert size distribution
------------------------
This section get the size distribution of the fragements that have been sequeced in paired-end sequencing. The pipeline calculates the size distribution by caluculating the distance between the most 5' possition of both reads, for those mapping to the + stand this is the left-post possition, for those mapping to the - strand is the rightmost coordinate.
This plot is especially useful for ATAC-Seq experiments as good samples should show peaks with a period approximately equivelent to the length of a nucleosome (~ 146bp) a lack of this phasing might indicate poor quality samples and either over (if lots of small fragments) or under intergration (if an excess of large fragments) of the topoisomerase.
```
import sqlite3
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
#import cgatcore.pipeline as P
import os
import statistics
#import collections
#load R and the R packages required
#%load_ext rpy2.ipython
#%R require(ggplot2)
# use these functions to display tables nicely as html
from IPython.display import display, HTML
plt.style.use('ggplot')
#plt.style.available
```
This is where we are and when the notebook was run
```
!pwd
!date
```
First lets set the output path for where we want our plots to be saved and the database path and see what tables it contains
```
database_path = '../csvdb'
output_path = '.'
#database_path= "/ifs/projects/charlotteg/pipeline_peakcalling/csvdb"
```
This code adds a button to see/hide code in html
```
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')
```
The code below provides functions for accessing the project database and extract a table names so you can see what tables have been loaded into the database and are available for plotting. It also has a function for geting table from the database and indexing the table with the track name
```
def getTableNamesFromDB(database_path):
# Create a SQL connection to our SQLite database
con = sqlite3.connect(database_path)
cur = con.cursor()
# the result of a "cursor.execute" can be iterated over by row
cur.execute("SELECT name FROM sqlite_master WHERE type='table' ORDER BY name;")
available_tables = (cur.fetchall())
#Be sure to close the connection.
con.close()
return available_tables
db_tables = getTableNamesFromDB(database_path)
print('Tables contained by the database:')
for x in db_tables:
print('\t\t%s' % x[0])
#This function retrieves a table from sql database and indexes it with track name
def getTableFromDB(statement,database_path):
'''gets table from sql database depending on statement
and set track as index if contains track in column names'''
conn = sqlite3.connect(database_path)
df = pd.read_sql_query(statement,conn)
if 'track' in df.columns:
df.index = df['track']
return df
```
Insert Size Summary
====================
1) lets getthe insert_sizes table from database
Firsly lets look at the summary statistics that us the mean fragment size, sequencing type and mean read length. This table is produced using macs2 for PE data, or bamtools for SE data
If IDR has been run the insert_size table will contain entries for the pooled and pseudo replicates too - we don't really want this as it will duplicate the data from the origional samples so we subset this out
```
insert_df = getTableFromDB('select * from insert_sizes;',database_path)
insert_df = insert_df[insert_df["filename"].str.contains('pseudo')==False].copy()
insert_df = insert_df[insert_df["filename"].str.contains('pooled')==False].copy()
def add_expt_to_insertdf(dataframe):
''' splits track name for example HsTh1-RATotal-R1.star into expt
featues, expt, sample_treatment and replicate and adds these as
collumns to the dataframe'''
expt = []
treatment = []
replicate = []
for value in dataframe.filename:
x = value.split('/')[-1]
x = x.split('_insert')[0]
# split into design features
y = x.split('-')
expt.append(y[-3])
treatment.append(y[-2])
replicate.append(y[-1])
if len(expt) == len(treatment) and len(expt)== len(replicate):
print ('all values in list correctly')
else:
print ('error in loading values into lists')
#add collums to dataframe
dataframe['expt_name'] = expt
dataframe['sample_treatment'] = treatment
dataframe['replicate'] = replicate
return dataframe
insert_df = add_expt_to_insertdf(insert_df)
insert_df
```
lets graph the fragment length mean and tag size grouped by sample so we can see if they are much different
```
ax = insert_df.boxplot(column='fragmentsize_mean', by='sample_treatment')
ax.set_title('for mean fragment size',size=10)
ax.set_ylabel('mean fragment length')
ax.set_xlabel('sample treatment')
ax = insert_df.boxplot(column='tagsize', by='sample_treatment')
ax.set_title('for tag size',size=10)
ax.set_ylabel('tag size')
ax.set_xlabel('sample treatment')
ax.set_ylim(((insert_df.tagsize.min()-2),(insert_df.tagsize.max()+2)))
```
Ok now get get the fragment length distributiions for each sample and plot them
```
def getFraglengthTables(database_path):
'''Takes path to sqlite3 database and retrieves fraglengths tables for individual samples
, returns a dictionary where keys = sample table names, values = fraglengths dataframe'''
frag_tabs = []
db_tables = getTableNamesFromDB(database_path)
for table_name in db_tables:
if 'fraglengths' in str(table_name[0]):
tab_name = str(table_name[0])
statement ='select * from %s;' % tab_name
df = getTableFromDB(statement,database_path)
frag_tabs.append((tab_name,df))
print('detected fragment length distribution tables for %s files: \n' % len(frag_tabs))
for val in frag_tabs:
print(val[0])
return frag_tabs
def getDFofFragLengths(database_path):
''' this takes a path to database and gets a dataframe where length of fragments is the index,
each column is a sample and values are the number of reads that have that fragment length in that
sample
'''
fraglength_dfs_list = getFraglengthTables(database_path)
dfs=[]
for item in fraglength_dfs_list:
track = item[0].split('_filtered_fraglengths')[0]
df = item[1]
#rename collumns so that they are correct - correct this in the pipeline then delete this
#df.rename(columns={'frequency':'frag_length', 'frag_length':'frequency'}, inplace=True)
df.index = df.frag_length
df.drop('frag_length',axis=1,inplace=True)
df.rename(columns={'frequency':track},inplace=True)
dfs.append(df)
frag_length_df = pd.concat(dfs,axis=1)
frag_length_df.fillna(0, inplace=True)
return frag_length_df
#Note the frequency and fragment lengths are around the wrong way!
#frequency is actually fragment length, and fragement length is the frequency
#This gets the tables from db and makes master df of all fragment length frequencies
frag_length_df = getDFofFragLengths(database_path)
#plot fragment length frequencies
ax = frag_length_df.divide(1000).plot()
ax.set_ylabel('Number of fragments\n(thousands)')
ax.legend(loc=2,bbox_to_anchor=(1.05, 1),borderaxespad=0. )
ax.set_title('fragment length distribution')
ax.set_xlabel('fragment length (bp)')
ax.set_xlim()
```
Now lets zoom in on the interesting region of the plot (the default in the code looks at fragment lengths from 0 to 800bp - you can change this below by setting the tuple in the ax.set_xlim() function
```
ax = frag_length_df.divide(1000).plot(figsize=(9,9))
ax.set_ylabel('Number of fragments\n(thousands)')
ax.legend(loc=2,bbox_to_anchor=(1.05, 1),borderaxespad=0. )
ax.set_title('fragment length distribution')
ax.set_xlabel('fragment length (bp)')
ax.set_xlim((0,800))
```
it is a bit trickly to see differences between samples of different library sizes so lets look and see if the reads for each fragment length is similar
```
percent_frag_length_df = pd.DataFrame(index=frag_length_df.index)
for column in frag_length_df:
total_frags = frag_length_df[column].sum()
percent_frag_length_df[column] = frag_length_df[column].divide(total_frags)*100
ax = percent_frag_length_df.plot(figsize=(9,9))
ax.set_ylabel('Percentage of fragments')
ax.legend(loc=2,bbox_to_anchor=(1.05, 1),borderaxespad=0. )
ax.set_title('percentage fragment length distribution')
ax.set_xlabel('fragment length (bp)')
ax.set_xlim((0,800))
```
SUMMARISE HERE
==============
From these plots you should be able to tell wether there are any distinctive patterns in the size of the fragment lengths,this is especially important for ATAC-Seq data as in successful experiments you should be able to detect nucleosome phasing - it can also indicate over fragmentation or biases in cutting.
Lets looks at the picard insert size metrics also
```
insert_df = getTableFromDB('select * from picard_stats_insert_size_metrics;',database_path)
for c in insert_df.columns:
print (c)
insert_df
```
These metrics are actually quite different to the ones we calculate themselves - for some reason it seems to split the files into 2 and dives a distribution for smaller fragments and for larger fragments- not sure why at the moment
| true |
code
| 0.318459 | null | null | null | null |
|
```
import keras
from keras.models import Sequential, Model, load_model
from keras.layers import Dense, Dropout, Flatten, Input, Lambda, Concatenate
from keras.layers import Conv1D, MaxPooling1D
from keras.callbacks import ModelCheckpoint, EarlyStopping
from keras import backend as K
import keras.losses
import tensorflow as tf
import pandas as pd
import os
import numpy as np
import scipy.sparse as sp
import scipy.io as spio
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import isolearn.io as isoio
import isolearn.keras as iso
from scipy.stats import pearsonr
```
<h2>Load 5' Alternative Splicing Data</h2>
- Load a Pandas DataFrame + Matlab Matrix of measured Splicing Sequences<br/>
- isolearn.io loads all .csv and .mat files of a directory into memory as a dictionary<br/>
- The DataFrame has one column - padded_sequence - containing the splice donor sequence<br/>
- The Matrix contains RNA-Seq counts of measured splicing at each position across the sequence<br/>
```
#Load Splicing Data
splicing_dict = isoio.load('data/processed_data/splicing_5ss_data/splicing_5ss_data')
```
<h2>Create a Training and Test Set</h2>
- We create an index containing row numbers corresponding to training and test sequences<br/>
- Notice that we do not alter the underlying DataFrame, we only make lists of pointers to rows<br/>
```
#Generate training, validation and test set indexes
valid_set_size = 0.10
test_set_size = 0.10
data_index = np.arange(len(splicing_dict['df']), dtype=np.int)
train_index = data_index[:-int(len(data_index) * (valid_set_size + test_set_size))]
valid_index = data_index[train_index.shape[0]:-int(len(data_index) * test_set_size)]
test_index = data_index[train_index.shape[0] + valid_index.shape[0]:]
print('Training set size = ' + str(train_index.shape[0]))
print('Validation set size = ' + str(valid_index.shape[0]))
print('Test set size = ' + str(test_index.shape[0]))
```
<h2>Create Data Generators</h2>
- In Isolearn, we always build data generators that will encode and feed us the data on the fly<br/>
- Here, for example, we create a training and test generator separately (using list comprehension)<br/>
- First argument: The list of row indices (of data points) for this generator<br/>
- Second argument: Dictionary or data sources<br/>
- Third argument: Batch size for the data generator
- Fourth argument: List of inputs, where each input is specified as a dictionary of attributes<br/>
- Fifth argument: List of outputs<br/>
- Sixth argument: List of any randomizers (see description below)<br/>
- Seventh argument: Shuffle the dataset or not<br/>
- Eight argument: True if some data source matrices are in sparse format<br/>
- Ninth argument: In Keras, we typically want to specfiy the Outputs as Inputs when training. <br/>This argument achieves this by moving the outputs over to the input list and replaces the output with a dummy encoder.<br/>
In this example, we specify a One-Hot encoder as the input encoder for the entire splice donor sequence (centered on the splice donor).<br/>
We also specify the target output as the normalized RNA-Seq count at position 120 in the count matrix for each cell line (4 outputs).<br/>
Besides the canonical splice donor at position 120 in the sequence, there are many other splice donors inserted randomly at neighboring positions. If we wanted to learn a general model of splicing, it would be a lot better if we could stochastically "align" sequences on any of the possible splice donors, perturbing both the input sequence and the RNA-Seq count matrix that we estimate splice donor usage from.<br/>
This is achieved using the built-in CutAlignSampler class, which allows us to randomly sample a position in the sequence with supporting splice junction counts, and shift both the sequence and splice count vector to be centered around that position. In this example, we specfiy the sampling rate of splice donors to be 0.5 (p_pos) and the rate of sampling some other, non-splice-site, position at a rate of 0.5 (p_neg).<br/>
```
#Create a One-Hot data generator, to be used for a convolutional net to regress SD1 Usage
total_cuts = splicing_dict['hek_count'] + splicing_dict['hela_count'] + splicing_dict['mcf7_count'] + splicing_dict['cho_count']
shifter = iso.CutAlignSampler(total_cuts, 240, 120, [], 0.0, p_pos=0.5, p_neg=0.5, sparse_source=True)
splicing_gens = {
gen_id : iso.DataGenerator(
idx,
{
'df' : splicing_dict['df'],
'hek_count' : splicing_dict['hek_count'],
'hela_count' : splicing_dict['hela_count'],
'mcf7_count' : splicing_dict['mcf7_count'],
'cho_count' : splicing_dict['cho_count'],
},
batch_size=32,
inputs = [
{
'id' : 'seq',
'source_type' : 'dataframe',
'source' : 'df',
'extractor' : iso.SequenceExtractor('padded_sequence', start_pos=0, end_pos=240, shifter=shifter if gen_id == 'train' else None),
'encoder' : iso.OneHotEncoder(seq_length=240),
'dim' : (240, 4),
'sparsify' : False
}
],
outputs = [
{
'id' : cell_type + '_sd1_usage',
'source_type' : 'matrix',
'source' : cell_type + '_count',
'extractor' : iso.CountExtractor(start_pos=0, end_pos=240, static_poses=[-1], shifter=shifter if gen_id == 'train' else None, sparse_source=False),
'transformer' : lambda t: t[120] / np.sum(t)
} for cell_type in ['hek', 'hela', 'mcf7', 'cho']
],
randomizers = [shifter] if gen_id in ['train'] else [],
shuffle = True if gen_id in ['train'] else False,
densify_batch_matrices=True,
move_outputs_to_inputs=True if gen_id in ['train', 'valid'] else False
) for gen_id, idx in [('train', train_index), ('valid', valid_index), ('test', test_index)]
}
```
<h2>Keras Loss Functions</h2>
Here we specfiy a few loss function (Cross-Entropy and KL-divergence) to be used when optimizing our Splicing CNN.<br/>
```
#Keras loss functions
def sigmoid_entropy(inputs) :
y_true, y_pred = inputs
y_pred = K.clip(y_pred, K.epsilon(), 1. - K.epsilon())
return -K.sum(y_true * K.log(y_pred) + (1.0 - y_true) * K.log(1.0 - y_pred), axis=-1)
def mean_sigmoid_entropy(inputs) :
y_true, y_pred = inputs
y_pred = K.clip(y_pred, K.epsilon(), 1. - K.epsilon())
return -K.mean(y_true * K.log(y_pred) + (1.0 - y_true) * K.log(1.0 - y_pred), axis=-1)
def sigmoid_kl_divergence(inputs) :
y_true, y_pred = inputs
y_pred = K.clip(y_pred, K.epsilon(), 1. - K.epsilon())
y_true = K.clip(y_true, K.epsilon(), 1. - K.epsilon())
return K.sum(y_true * K.log(y_true / y_pred) + (1.0 - y_true) * K.log((1.0 - y_true) / (1.0 - y_pred)), axis=-1)
def mean_sigmoid_kl_divergence(inputs) :
y_true, y_pred = inputs
y_pred = K.clip(y_pred, K.epsilon(), 1. - K.epsilon())
y_true = K.clip(y_true, K.epsilon(), 1. - K.epsilon())
return K.mean(y_true * K.log(y_true / y_pred) + (1.0 - y_true) * K.log((1.0 - y_true) / (1.0 - y_pred)), axis=-1)
```
<h2>Splicing Model Definition</h2>
Here we specfiy the Keras Inputs that we expect to receive from the data generators.<br/>
We also define the model architecture (2 convolutional-layer CNN with MaxPooling).<br/>
```
#Splicing Model Definition (CNN)
#Inputs
seq_input = Input(shape=(240, 4))
#Outputs
true_usage_hek = Input(shape=(1,))
true_usage_hela = Input(shape=(1,))
true_usage_mcf7 = Input(shape=(1,))
true_usage_cho = Input(shape=(1,))
#Shared Model Definition (Applied to each randomized sequence region)
layer_1 = Conv1D(64, 8, padding='valid', activation='relu')
layer_1_pool = MaxPooling1D(pool_size=2)
layer_2 = Conv1D(128, 6, padding='valid', activation='relu')
def shared_model(seq_input) :
return Flatten()(
layer_2(
layer_1_pool(
layer_1(
seq_input
)
)
)
)
shared_out = shared_model(seq_input)
#Layers applied to the concatenated hidden representation
layer_dense = Dense(256, activation='relu')
layer_drop = Dropout(0.2)
dropped_dense_out = layer_drop(layer_dense(shared_out))
#Final cell-line specific regression layers
layer_usage_hek = Dense(1, activation='sigmoid', kernel_initializer='zeros')
layer_usage_hela = Dense(1, activation='sigmoid', kernel_initializer='zeros')
layer_usage_mcf7 = Dense(1, activation='sigmoid', kernel_initializer='zeros')
layer_usage_cho = Dense(1, activation='sigmoid', kernel_initializer='zeros')
pred_usage_hek = layer_usage_hek(dropped_dense_out)
pred_usage_hela = layer_usage_hela(dropped_dense_out)
pred_usage_mcf7 = layer_usage_mcf7(dropped_dense_out)
pred_usage_cho = layer_usage_cho(dropped_dense_out)
#Compile Splicing Model
splicing_model = Model(
inputs=[
seq_input
],
outputs=[
pred_usage_hek,
pred_usage_hela,
pred_usage_mcf7,
pred_usage_cho
]
)
```
<h2>Loss Model Definition</h2>
Here we specfiy our loss function, and we build it as a separate Keras Model.<br/>
In our case, our loss model averages the KL-divergence of predicted vs. true Splice Donor Usage across the 4 different cell types.<br/>
```
#Loss Model Definition
loss_hek = Lambda(sigmoid_kl_divergence, output_shape = (1,))([true_usage_hek, pred_usage_hek])
loss_hela = Lambda(sigmoid_kl_divergence, output_shape = (1,))([true_usage_hela, pred_usage_hela])
loss_mcf7 = Lambda(sigmoid_kl_divergence, output_shape = (1,))([true_usage_mcf7, pred_usage_mcf7])
loss_cho = Lambda(sigmoid_kl_divergence, output_shape = (1,))([true_usage_cho, pred_usage_cho])
total_loss = Lambda(
lambda l: (l[0] + l[1] + l[2] + l[3]) / 4.,
output_shape = (1,)
)(
[
loss_hek,
loss_hela,
loss_mcf7,
loss_cho
]
)
loss_model = Model([
#Inputs
seq_input,
#Target SD Usages
true_usage_hek,
true_usage_hela,
true_usage_mcf7,
true_usage_cho
], total_loss)
```
<h2>Optimize the Loss Model</h2>
Here we use SGD to optimize the Loss Model (defined in the previous notebook cell).<br/>
Since our Loss Model indirectly depends on predicted outputs from our CNN Splicing Model, SGD will optimize the weights of our CNN<br/>
<br/>
Note that we very easily pass the data generators, and run them in parallel, by simply calling Keras fit_generator.<br/>
```
#Optimize CNN with Keras using the Data Generators to stream genomic data features
opt = keras.optimizers.SGD(lr=0.1, decay=1e-6, momentum=0.9, nesterov=True)
loss_model.compile(loss=lambda true, pred: pred, optimizer=opt)
callbacks =[
EarlyStopping(monitor='val_loss', min_delta=0.001, patience=2, verbose=0, mode='auto')
]
loss_model.fit_generator(
generator=splicing_gens['train'],
validation_data=splicing_gens['valid'],
epochs=10,
use_multiprocessing=True,
workers=4,
callbacks=callbacks
)
#Save model
save_dir = os.path.join(os.getcwd(), 'saved_models')
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_name = 'splicing_cnn_perturbed_multicell.h5'
model_path = os.path.join(save_dir, model_name)
splicing_model.save(model_path)
print('Saved trained model at %s ' % model_path)
#Load model
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'splicing_cnn_perturbed_multicell.h5'
model_path = os.path.join(save_dir, model_name)
splicing_model = load_model(model_path)
```
<h2>Evaluate the Splicing CNN</h2>
Here we run our Splicing CNN on the Test set data generator (using Keras predict_generator).<br/>
We then compare our predictions of splice donor usage against the true RNA-Seq measurements.<br/>
```
#Evaluate predictions on test set
predictions = splicing_model.predict_generator(splicing_gens['test'], workers=4, use_multiprocessing=True)
pred_usage_hek, pred_usage_hela, pred_usage_mcf7, pred_usage_cho = [np.ravel(prediction) for prediction in predictions]
targets = zip(*[splicing_gens['test'][i][1] for i in range(len(splicing_gens['test']))])
true_usage_hek, true_usage_hela, true_usage_mcf7, true_usage_cho = [np.concatenate(list(target)) for target in targets]
cell_lines = [
('hek', (pred_usage_hek, true_usage_hek)),
('hela', (pred_usage_hela, true_usage_hela)),
('mcf7', (pred_usage_mcf7, true_usage_mcf7)),
('cho', (pred_usage_cho, true_usage_cho))
]
for cell_name, [y_true, y_pred] in cell_lines :
r_val, p_val = pearsonr(y_pred, y_true)
print("Test set R^2 = " + str(round(r_val * r_val, 2)) + ", p = " + str(p_val))
#Plot test set scatter
f = plt.figure(figsize=(4, 4))
plt.scatter(y_pred, y_true, color='black', s=5, alpha=0.05)
plt.xticks([0.0, 0.25, 0.5, 0.75, 1.0], fontsize=14)
plt.yticks([0.0, 0.25, 0.5, 0.75, 1.0], fontsize=14)
plt.xlabel('Predicted SD1 Usage', fontsize=14)
plt.ylabel('True SD1 Usage', fontsize=14)
plt.title(str(cell_name), fontsize=16)
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.tight_layout()
plt.show()
```
| true |
code
| 0.69181 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Matplotlib" data-toc-modified-id="Matplotlib-1"><span class="toc-item-num">1 </span>Matplotlib</a></span><ul class="toc-item"><li><span><a href="#Customization" data-toc-modified-id="Customization-1.1"><span class="toc-item-num">1.1 </span>Customization</a></span></li></ul></li><li><span><a href="#subplot" data-toc-modified-id="subplot-2"><span class="toc-item-num">2 </span>subplot</a></span></li></ul></div>
# Intermediate Python for Data Science
## Matplotlib
- source: https://www.datacamp.com/courses/intermediate-python-for-data-science
- color code: https://matplotlib.org/examples/color/named_colors.html
```
# Quick cheat sheet
# to change plot size
plt.figure(figsize=(20,8))
'''Line Plot'''
# Print the last item from years and populations
print(year[-1])
print(pop[-1])
# Import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
# Make a line plot: year on the x-axis, pop on the y-axis
plt.plot(year, pop)
# Display the plot with plt.show()
plt.show()
# Print the last item of gdp_cap and life_exp
print(gdp_cap[-1])
print(life_exp[-1])
# Make a line plot, gdp_cap on the x-axis, life_exp on the y-axis
plt.plot(gdp_cap, life_exp)
# Display the plot
plt.show()
'''Scatter Plot'''
# Change the line plot below to a scatter plot
plt.scatter(gdp_cap, life_exp)
# Put the x-axis on a logarithmic scale
plt.xscale('log')
# Show plot
plt.show()
'''Scatter Plot'''
# Import package
import matplotlib.pyplot as plt
# Build Scatter plot
plt.scatter(pop, life_exp)
# Show plot
plt.show()
'''Histogram'''
# Create histogram of life_exp data
plt.hist(life_exp)
# Display histogram
plt.show()
'''Histogram bins'''
# Build histogram with 5 bins
plt.hist(life_exp, bins = 5)
# Show and clear plot
plt.show()
plt.clf() # cleans it up again so you can start afresh.
# Build histogram with 20 bins
plt.hist(life_exp, bins = 20)
# Show and clear plot again
plt.show()
plt.clf()
'''Histogram compare'''
# Histogram of life_exp, 15 bins
plt.hist(life_exp, bins = 15)
# Show and clear plot
plt.show()
plt.clf()
# Histogram of life_exp1950, 15 bins
plt.hist(life_exp1950, bins = 15)
# Show and clear plot again
plt.show()
plt.clf()
```
### Customization
```
'''Label'''
# Basic scatter plot, log scale
plt.scatter(gdp_cap, life_exp)
plt.xscale('log')
# Strings
xlab = 'GDP per Capita [in USD]'
ylab = 'Life Expectancy [in years]'
title = 'World Development in 2007'
# Add axis labels
plt.xlabel(xlab)
plt.ylabel(ylab)
# Add title
plt.title(title)
# After customizing, display the plot
plt.show()
'''Ticks'''
# Scatter plot
plt.scatter(gdp_cap, life_exp)
# Previous customizations
plt.xscale('log')
plt.xlabel('GDP per Capita [in USD]')
plt.ylabel('Life Expectancy [in years]')
plt.title('World Development in 2007')
# Definition of tick_val and tick_lab
tick_val = [1000,10000,100000]
tick_lab = ['1k','10k','100k']
# Adapt the ticks on the x-axis
plt.xticks(tick_val, tick_lab)
# After customizing, display the plot
plt.show()
'''Sizes
Wouldn't it be nice if the size of the dots corresponds to the population?
'''
# Import numpy as np
import numpy as np
# Store pop as a numpy array: np_pop
np_pop = np.array(pop)
# Double np_pop
np_pop = np_pop * 2
# Update: set s argument to np_pop # s is size
plt.scatter(gdp_cap, life_exp, s = np_pop)
# Previous customizations
plt.xscale('log')
plt.xlabel('GDP per Capita [in USD]')
plt.ylabel('Life Expectancy [in years]')
plt.title('World Development in 2007')
plt.xticks([1000, 10000, 100000],['1k', '10k', '100k'])
# Display the plot
plt.show()
'''Colors
The next step is making the plot more colorful! To do this, a list col has been created for you. It's a list with a color for each corresponding country, depending on the continent the country is part of.
How did we make the list col you ask? The Gapminder data contains a list continent with the continent each country belongs to. A dictionary is constructed that maps continents onto colors:
'''
dict = {
'Asia':'red',
'Europe':'green',
'Africa':'blue',
'Americas':'yellow',
'Oceania':'black'
}
# c = color, alpha = opacity
# Specify c and alpha inside plt.scatter()
plt.scatter(x = gdp_cap, y = life_exp, s = np.array(pop) * 2, c = col, alpha = 0.8)
# Previous customizations
plt.xscale('log')
plt.xlabel('GDP per Capita [in USD]')
plt.ylabel('Life Expectancy [in years]')
plt.title('World Development in 2007')
plt.xticks([1000,10000,100000], ['1k','10k','100k'])
# Show the plot
plt.show()
'''Additional Customizations'''
# Scatter plot
plt.scatter(x = gdp_cap, y = life_exp, s = np.array(pop) * 2, c = col, alpha = 0.8)
# Previous customizations
plt.xscale('log')
plt.xlabel('GDP per Capita [in USD]')
plt.ylabel('Life Expectancy [in years]')
plt.title('World Development in 2007')
plt.xticks([1000,10000,100000], ['1k','10k','100k'])
# Additional customizations
plt.text(1550, 71, 'India')
plt.text(5700, 80, 'China')
# Add grid() call
plt.grid(True)
# Show the plot
plt.show()
from sklearn.datasets import load_iris
data = load_iris()
data.target[[10, 25, 50]]
list(data.target_names)
```
## subplot
source: https://matplotlib.org/examples/pylab_examples/subplot_demo.html
```
# subplot(nrows, ncols, plot_number)
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(0.0, 5.0)
x2 = np.linspace(0.0, 2.0)
y1 = np.cos(2 * np.pi * x1) * np.exp(-x1)
y2 = np.cos(2 * np.pi * x2)
plt.subplot(2, 1, 1)
plt.plot(x1, y1, 'ko-')
plt.title('A tale of 2 subplots')
plt.ylabel('Damped oscillation')
plt.subplot(2, 1, 2)
plt.plot(x2, y2, 'r.-')
plt.xlabel('time (s)')
plt.ylabel('Undamped')
plt.show()
plt.subplot(2, 1, 1)
plt.plot(x1, y1, 'ko-')
plt.title('A tale of 2 subplots')
plt.ylabel('Damped oscillation')
plt.subplot(2, 1, 2)
plt.plot(x2, y2, 'r.-')
plt.xlabel('time (s)')
plt.ylabel('Undamped')
plt.show()
plt.subplots(2, 2, sharex=True, sharey=True)
plt.show()
x = np.linspace(0, 2*np.pi, 400)
y = np.sin(x**2)
fig, axes = plt.subplots(1,2, sharey=True)
axes[0].plot(x, y)
axes[1].scatter(x, y)
plt.show()
# Two subplots, unpack the axes array immediately
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True)
ax1.plot(x, y)
ax1.set_title('Sharing Y axis')
ax2.scatter(x, y)
plt.show()
fig, axes = plt.subplots(1,3, sharey=True, sharex=True)
for i in range(3):
axes[i].scatter(center[i],xn)
axes[i].set_title('Cluster ' + str(i+1))
axes[i].grid(True)
plt.yticks(xn,var)
plt.subplots_adjust(wspace=0, hspace=0)
#plt.grid(True)
plt.show()
```
| true |
code
| 0.724371 | null | null | null | null |
|
# PyIndMach012: an example of user-model using DSS Python
This example runs a modified example from the OpenDSS distribution for the induction machine model with a sample PyIndMach012 implementation, written in Python, and the original, built-in IndMach012.
Check the `PyIndMach012.py` file for more comments. Comparing it to [the Pascal code for IndMach012](https://github.com/dss-extensions/dss_capi/blob/master/Version7/Source/PCElements/IndMach012.pas) can be useful to understand some of the inner workings of OpenDSS.
The user-model code in DSS Python is not stable yet but can be used to develop new ideas before commiting the final model in a traditional DLL user-model. Particularly, I (@PMeira) found some issues with callbacks with newer Version 8 COM DLLs, so changes related to that are expected.
```
%matplotlib inline
import os
import numpy as np
from matplotlib import pyplot as plt
from dss.UserModels import GenUserModel # used to get the DLL path
import PyIndMach012 # we need to import the model so it gets registered
```
## The model class
```
??PyIndMach012
```
## OpenDSS setup
For this example, we can use either COM or DSS Python (DSS C-API). The IndMach012 model in DSS C-API seems to have a bug somewhere though -- this is being tracked in [dss_capi#62](https://github.com/dss-extensions/dss_capi/issues/62).
```
original_dir = os.getcwd() # same the original working directory since the COM module messes with it
USE_COM = True # toggle this value to run with DSS C-API
if USE_COM:
from dss import patch_dss_com
import win32com.client
DSS = patch_dss_com(win32com.client.gencache.EnsureDispatch('OpenDSSengine.DSS'))
DSS.DataPath = original_dir
os.chdir(original_dir)
else:
from dss import DSS
DSS.Version
Text = DSS.Text
Monitors = DSS.ActiveCircuit.Monitors
```
## Using the model
To use a Python model for generators:
- the model class needs to be registered in advance
- create a generator with `model=6`
- pass a `usermodel="{dll_path}"` as in the following DSS command in the `run` function
- pass a `"pymodel=MODELNAME"` parameter in the userdata property, where MODELNAME is the name of the model class in Python
```
def run(pymodel):
Text.Command = 'redirect "master.dss"'
if pymodel:
# This uses our custom user-model in Python
Text.Command = 'New "Generator.Motor1" bus1=Bg2 kW=1200 conn=delta kVA=1500.000 H=6 model=6 kv=0.48 usermodel="{dll_path}" userdata=(pymodel=PyIndMach012 purs=0.048 puxs=0.075 purr=0.018 puxr=0.12 puxm=3.8 slip=0.02 SlipOption=variableslip)'.format(
dll_path=GenUserModel.dll_path,
)
Text.Command = 'New "Monitor.mfr2" element=Generator.Motor1 terminal=1 mode=3'
else:
# This uses the built-in model for comparison
Text.Command = 'New "IndMach012.Motor1" bus1=Bg2 kW=1200 conn=delta kVA=1500.000 H=6 purs=0.048 puxs=0.075 purr=0.018 puxr=0.12 puxm=3.8 slip=0.02 SlipOption=variableslip kv=0.48'
Text.Command = 'New "Monitor.mfr2" element=IndMach012.Motor1 terminal=1 mode=3'
# This will run a power-flow solution
Text.Command = 'Solve'
# This will toggle to the dynamics mode
Text.Command = 'Set mode=dynamics number=1 h=0.000166667'
# And finally run 5000 steps for the dynamic simulation
Text.Command = f'Solve number=5000'
# There are the channels from the Pascal/built-in IndMach012
channels_pas = (' Frequency', 'Theta (deg)', 'E1', 'dSpeed (deg/sec)', 'dTheta (deg)', 'Slip', 'Is1', 'Is2', 'Ir1', 'Ir2', 'Stator Losses', 'Rotor Losses', 'Shaft Power (hp)', 'Power Factor', 'Efficiency (%)')
# There are the channels from the Python module -- we define part of these and part come from the generator model itself
channels_py = (' Frequency', 'Theta (Deg)', 'E1_pu', 'dSpeed (Deg/sec)', 'dTheta (Deg)', 'Slip', 'Is1', 'Is2', 'Ir1', 'Ir2', 'StatorLosses', 'RotorLosses', 'ShaftPower_hp', 'PowerFactor', 'Efficiency_pct')
```
## Running and saving the outputs
Let's run the Pascal/built-in version of IndMach012 and our custom Python version for comparison:
```
run(False)
Monitors.Name = 'mfr2'
outputs_pas = {channel: Monitors.Channel(Monitors.Header.index(channel) + 1) for channel in channels_pas}
run(True)
Monitors.Name = 'mfr2'
outputs_py = {channel: Monitors.Channel(Monitors.Header.index(channel) + 1) for channel in channels_py}
time = np.arange(1, 5000 + 1) * 0.000166667
offset = int(0.1 / 0.000166667)
```
## Plotting the various output channels
The example circuit applies a fault at 0.3 s, isolating the machine at 0.4s (check `master.dss` for more details).
As we can see from the figures below, the outputs match very closely. After the induction machine is isolated, the efficiency and power factor values can misbehave as the power goes to zero, seem especially in the Pascal version.
```
for ch_pas, ch_py in zip(channels_pas, channels_py):
plt.figure(figsize=(8,4))
plt.plot(time, outputs_pas[ch_pas], label='IndMach012', lw=3)
plt.plot(time, outputs_py[ch_py], label='PyIndMach012', ls='--', lw=2)
plt.axvline(0.3, linestyle=':', color='k', alpha=0.5, label='Fault occurs')
plt.axvline(0.4, linestyle='--', color='r', alpha=0.5, label='Relays operate')
plt.legend()
plt.xlabel('Time (s)')
plt.ylabel(ch_pas)
if ch_pas == 'Efficiency (%)':
# Limit efficiency to 0-100
plt.ylim(0, 100)
plt.xlim(0, time[-1])
plt.tight_layout()
```
| true |
code
| 0.580471 | null | null | null | null |
|
# A Two-Level, Six-Factor Full Factorial Design
<br />
<br />
<br />
### Table of Contents
* [Introduction](#intro)
* Factorial Experimental Design:
* [Two-Level Six-Factor Full Factorial Design](#fullfactorial)
* [Variables and Variable Labels](#varlabels)
* [Computing Main and Interaction Effects](#computing_effects)
* Analysis of results:
* [Analyzing Effects](#analyzing_effects)
* [Quantile-Quantile Effects Plot](#quantile_effects)
* [Utilizing Degrees of Freedom](#dof)
* [Ordinary Least Squares Regression Model](#ols)
* [Goodness of Fit](#goodness_of_fit)
* [Distribution of Error](#distribution_of_error)
* [Aggregating Results](#aggregating)
* [Distribution of Variance](#dist_variance)
* [Residual vs. Response Plots](#residual)
<br />
<br />
<br />
<a name="intro"></a>
## Introduction
This notebook roughly follows content from Box and Draper's _Empirical Model-Building and Response Surfaces_ (Wiley, 1984). This content is covered by Chapter 4 of Box and Draper.
In this notebook, we'll carry out an anaylsis of a full factorial design, and show how we can obtain inforomation about a system and its responses, and a quantifiable range of certainty about those values. This is the fundamental idea behind empirical model-building and allows us to construct cheap and simple models to represent complex, nonlinear systems.
```
%matplotlib inline
import pandas as pd
import numpy as np
from numpy.random import rand, seed
import seaborn as sns
import scipy.stats as stats
from matplotlib.pyplot import *
seed(10)
```
<a name="fullfactorial"></a>
## Two-Level Six-Factor Full Factorial Design
Let's start with our six-factor factorial design example. Six factors means there are six input variables; this is still a two-level experiment, so this is now a $2^6$-factorial experiment.
Additionally, there are now three response variables, $(y_1, y_2, y_3)$.
To generate a table of the 64 experiments to be run at each factor level, we will use the ```itertools.product``` function below. This is all put into a DataFrame.
This example generates some random response data, by multiplying a vector of random numbers by the vector of input variable values. (Nothing too complicated.)
```
import itertools
# Create the inputs:
encoded_inputs = list( itertools.product([-1,1],[-1,1],[-1,1],[-1,1],[-1,1],[-1,1]) )
# Create the experiment design table:
doe = pd.DataFrame(encoded_inputs,columns=['x%d'%(i+1) for i in range(6)])
# "Manufacture" observed data y
doe['y1'] = doe.apply( lambda z : sum([ rand()*z["x%d"%(i)]+0.01*(0.5-rand()) for i in range(1,7) ]), axis=1)
doe['y2'] = doe.apply( lambda z : sum([ 5*rand()*z["x%d"%(i)]+0.01*(0.5-rand()) for i in range(1,7) ]), axis=1)
doe['y3'] = doe.apply( lambda z : sum([ 100*rand()*z["x%d"%(i)]+0.01*(0.5-rand()) for i in range(1,7) ]), axis=1)
print(doe[['y1','y2','y3']])
```
<a name="varlablels"></a>
## Defining Variables and Variable Labels
Next we'll define some containers for input variable labels, output variable labels, and any interaction terms that we'll be computing:
```
labels = {}
labels[1] = ['x1','x2','x3','x4','x5','x6']
for i in [2,3,4,5,6]:
labels[i] = list(itertools.combinations(labels[1], i))
obs_list = ['y1','y2','y3']
for k in labels.keys():
print(str(k) + " : " + str(labels[k]))
```
Now that we have variable labels for each main effect and interaction effect, we can actually compute those effects.
<a name="computing_effects"></a>
## Computing Main and Interaction Effects
We'll start by finding the constant effect, which is the mean of each response:
```
effects = {}
# Start with the constant effect: this is $\overline{y}$
effects[0] = {'x0' : [doe['y1'].mean(),doe['y2'].mean(),doe['y3'].mean()]}
print(effects[0])
```
Next, compute the main effect of each variable, which quantifies the amount the response changes by when the input variable is changed from the -1 to +1 level. That is, it computes the average effect of an input variable $x_i$ on each of the three response variables $y_1, y_2, y_3$.
```
effects[1] = {}
for key in labels[1]:
effects_result = []
for obs in obs_list:
effects_df = doe.groupby(key)[obs].mean()
result = sum([ zz*effects_df.ix[zz] for zz in effects_df.index ])
effects_result.append(result)
effects[1][key] = effects_result
effects[1]
```
Our next step is to crank through each variable interaction level: two-variable, three-variable, and on up to six-variable interaction effects. We compute interaction effects for each two-variable combination, three-variable combination, etc.
```
for c in [2,3,4,5,6]:
effects[c] = {}
for key in labels[c]:
effects_result = []
for obs in obs_list:
effects_df = doe.groupby(key)[obs].mean()
result = sum([ np.prod(zz)*effects_df.ix[zz]/(2**(len(zz)-1)) for zz in effects_df.index ])
effects_result.append(result)
effects[c][key] = effects_result
def printd(d):
for k in d.keys():
print("%25s : %s"%(k,d[k]))
for i in range(1,7):
printd(effects[i])
```
We've computed the main and interaction effects for every variable combination (whew!), but now we're at a point where we want to start doing things with these quantities.
<a name="analyzing_effects"></a>
## Analyzing Effects
The first and most important question is, what variable, or combination of variables, has the strongest effect on the three responses $y_1$? $y_2$? $y_3$?
To figure this out, we'll need to use the data we computed above. Python makes it easy to slice and dice data. In this case, we've constructed a nested dictionary, with the outer keys mapping to the number of variables and inner keys mapping to particular combinations of input variables. Its pretty easy to convert this to a flat data structure that we can use to sort by variable effects. We've got six "levels" of variable combinations, so we'll flatten ```effects``` by looping through all six dictionaries of variable combinations (from main effects to six-variable interaction effects), and adding each entry to a master dictionary.
The master dictionary will be a flat dictionary, and once we've populated it, we can use it to make a DataFrame for easier sorting, printing, manipulating, aggregating, and so on.
```
print(len(effects))
master_dict = {}
for nvars in effects.keys():
effect = effects[nvars]
for k in effect.keys():
v = effect[k]
master_dict[k] = v
master_df = pd.DataFrame(master_dict).T
master_df.columns = obs_list
y1 = master_df['y1'].copy()
y1.sort_values(inplace=True,ascending=False)
print("Top 10 effects for observable y1:")
print(y1[:10])
y2 = master_df['y2'].copy()
y2.sort_values(inplace=True,ascending=False)
print("Top 10 effects for observable y2:")
print(y2[:10])
y3 = master_df['y3'].copy()
y3.sort_values(inplace=True,ascending=False)
print("Top 10 effects for observable y3:")
print(y3[:10])
```
If we were only to look at the list of rankings of each variable, we would see that each response is affected by different input variables, listed below in order of descending importance:
* $y_1$: 136254
* $y_2$: 561234
* $y_3$: 453216
This is a somewhat mixed message that's hard to interpret - can we get rid of variable 2? We can't eliminate 1, 4, or 5, and probably not 3 or 6 either.
However, looking at the quantile-quantile plot of the effects answers the question in a more visual way.
<a name="quantile_effects"></a>
## Quantile-Quantile Effects Plot
We can examine the distribution of the various input variable effects using a quantile-quantile plot of the effects. Quantile-quantile plots arrange the effects in order from least to greatest, and can be applied in several contexts (as we'll see below, when assessing model fits). If the quantities plotted on a quantile-qantile plot are normally distributed, they will fall on a straight line; data that do not fall on the straight line indicate significant deviations from normal behavior.
In the case of a quantile-quantile plot of effects, non-normal behavior means the effect is paticularly strong. By identifying the outlier points on thse quantile-quantile plots (they're ranked in order, so they correspond to the lists printed above), we can identify the input variables most likely to have a strong impact on the responses.
We need to look both at the top (the variables that have the largest overall positive effect) and the bottom (the variables that have the largest overall negative effect) for significant outliers. When we find outliers, we can add them to a list of variabls that we have decided are important and will keep in our analysis.
```
# Quantify which effects are not normally distributed,
# to assist in identifying important variables
fig = figure(figsize=(14,4))
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
stats.probplot(y1, dist="norm", plot=ax1)
ax1.set_title('y1')
stats.probplot(y2, dist="norm", plot=ax2)
ax2.set_title('y2')
stats.probplot(y3, dist="norm", plot=ax3)
ax3.set_title('y3')
```
Normally, we would use the main effects that were computed, and their rankings, to eliminate any variables that don't have a strong effect on any of our variables. However, this analysis shows that sometimes we can't eliminate any variables.
All six input variables are depicted as the effects that fall far from the red line - indicating all have a statistically meaningful (i.e., not normally distributed) effect on all three response variables. This means we should keep all six factors in our analysis.
There is also a point on the $y_3$ graph that appears significant on the bottom. Examining the output of the lists above, this point represents the effect for the six-way interaction of all input variables. High-order interactions are highly unlikely (and in this case it is a numerical artifact of the way the responses were generated), so we'll keep things simple and stick to a linear model.
Let's continue our analysis without eliminating any of the six factors, since they are important to all of our responses.
<a name="dof"></a>
## Utilizing Degrees of Freedom
Our very expensive, 64-experiment full factorial design (the data for which maps $(x_1,x_2,\dots,x_6)$ to $(y_1,y_2,y_3)$) gives us 64 data points, and 64 degrees of freedom. What we do with those 64 degrees of freedom is up to us.
We _could_ fit an empirical model, or response surface, that has 64 independent parameters, and account for many of the high-order interaction terms - all the way up to six-variable interaction effects. However, high-order effects are rarely important, and are a waste of our degrees of freedom.
Alternatively, we can fit an empirical model with fewer coefficients, using up fewer degrees of freedom, and use the remaining degrees of freedom to characterize the error introduced by our approximate model.
To describe a model with the 6 variables listed above and no other variable interaction effects would use only 6 degrees of freedom, plus 1 degree of freedom for the constant term, leaving 57 degrees of freedom available to quantify error, attribute variance, etc.
Our goal is to use least squares to compute model equations for $(y_1,y_2,y_3)$ as functions of $(x_1,x_2,x_3,x_4,x_5,x_6)$.
```
xlabs = ['x1','x2','x3','x4','x5','x6']
ylabs = ['y1','y2','y3']
ls_data = doe[xlabs+ylabs]
import statsmodels.api as sm
import numpy as np
x = ls_data[xlabs]
x = sm.add_constant(x)
```
The first ordinary least squares linear model is created to predict values of the first variable, $y_1$, as a function of each of our input variables, the list of which are contained in the ```xlabs``` variable. When we perform the linear regression fitting, we see much of the same information that we found in the prior two-level three-factor full factorial design, but here, everything is done automatically.
The model is linear, meaning it's fitting the coefficients of the function:
$$
\hat{y} = a_0 + a_1 x_1 + a_2 x_2 + a_3 + x_3 + a_4 x_4 + a_5 x_5 + a_6 x_6
$$
(here, the variables $y$ and $x$ are vectors, with one component for each response; in our case, they are three-dimensional vectors.)
Because there are 64 observations and 7 coefficients, the 57 extra observations give us extra degrees of freedom with which to assess how good the model is. That analysis can be done with an ordinary least squares (OLS) model, available through the statsmodel library in Python.
<a name="ols"></a>
## Ordinary Least Squares Regression Model
This built-in OLS model will fit an input vector $(x_1,x_2,x_3,x_4,x_5,x_6)$ to an output vector $(y_1,y_2,y_3)$ using a linear model; the OLS model is designed to fit the model with more observations than coefficients, and utilize the remaining data to quantify the fit of the model.
Let's run through one of these, and analyze the results:
```
y1 = ls_data['y1']
est1 = sm.OLS(y1,x).fit()
print(est1.summary())
```
The StatsModel OLS object prints out quite a bit of useful information, in a nicely-formatted table. Starting at the top, we see a couple of important pieces of information: specifically, the name of the dependent variable (the response) that we're looking at, the number of observations, and the number of degrees of freedom.
We can see an $R^2$ statistic, which indicates how well this data is fit with our linear model, and an adjusted $R^2$ statistic, which accounts for the large nubmer of degrees of freedom. While an adjusted $R^2$ of 0.73 is not great, we have to remember that this linear model is trying to capture a wealth of complexity in six coefficients. Furthermore, the adjusted $R^2$ value is too broad to sum up how good our model actually is.
The table in the middle is where the most useful information is located. The `coef` column shows the coefficients $a_0, a_1, a_2, \dots$ for the model equation:
$$
\hat{y} = a_0 + a_1 x_1 + a_2 x_2 + a_3 + x_3 + a_4 x_4 + a_5 x_5 + a_6 x_6
$$
Using the extra degrees of freedom, an estime $s^2$ of the variance in the regression coefficients is also computed, and reported in the the `std err` column. Each linear term is attributed the same amount of variance, $\pm 0.082$.
```
y2 = ls_data['y2']
est2 = sm.OLS(y2,x).fit()
print(est2.summary())
y3 = ls_data['y3']
est3 = sm.OLS(y3,x).fit()
print(est3.summary())
```
<a name="goodness_of_fit"></a>
## Quantifying Model Goodness-of-Fit
We can now use these linear models to evaluate each set of inputs and compare the model response $\hat{y}$ to the actual observed response $y$. What we would expect to see, if our model does an adequate job of representing the underlying behavior of the model, is that in each of the 64 experiments, the difference between the model prediction $M$ and the measured data $d$, defined as the residual $r$,
$$
r = \left| d - M \right|
$$
should be comparable across all experiments. If the residuals appear to have functional dependence on the input variables, it is an indication that our model is missing important effects and needs more or different terms. The way we determine this, mathematically, is by looking at a quantile-quantile plot of our errors (that is, a ranked plot of our error magnitudes).
If the residuals are normally distributed, they will follow a straight line; if the plot shows the data have significant wiggle and do not follow a line, it is an indication that the errors are not normally distributed, and are therefore skewed (indicating terms missing from our OLS model).
```
%matplotlib inline
import seaborn as sns
import scipy.stats as stats
from matplotlib.pyplot import *
# Quantify goodness of fit
fig = figure(figsize=(14,4))
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
r1 = y1 - est1.predict(x)
r2 = y2 - est2.predict(x)
r3 = y3 - est3.predict(x)
stats.probplot(r1, dist="norm", plot=ax1)
ax1.set_title('Residuals, y1')
stats.probplot(r2, dist="norm", plot=ax2)
ax2.set_title('Residuals, y2')
stats.probplot(r3, dist="norm", plot=ax3)
ax3.set_title('Residuals, y3')
```
Determining whether significant trends are being missed by the model depends on how many points deviate from the red line, and how significantly. If there is a single point that deviates, it does not necessarily indicate a problem; but if there is significant wiggle and most points deviate significantly from the red line, it means that there is something about the relationship between the inputs and the outputs that our model is missing.
There are only a few points deviating from the red line. We saw from the effect quantile for $y_3$ that there was an interaction variable that was important to modeling the response $y_3$, and it is likely this interaction that is leading to noise at the tail end of these residuals. This indicates residual errors (deviations of the model from data) that do not follow a natural, normal distribution, which indicates there is a _pattern_ in the deviations - namely, the interaction effect.
The conclusion about the error from the quantile plots above is that there are only a few points deviation from the line, and no particularly significant outliers. Our model can use some improvement, but it's a pretty good first-pass model.
<a name="distribution_of_error"></a>
## Distribution of Error
Another thing we can look at is the normalized error: what are the residual errors (differences between our model prediction and our data)? How are their values distributed?
A kernel density estimate (KDE) plot, which is a smoothed histogram, shows the probability distribution of the normalized residual errors. As expected, they're bunched pretty close to zero. There are some bumps far from zero, corresponding to the outliers on the quantile-quantile plot of the errors above. However, they're pretty close to randomly distributed, and therefore it doesn't look like there is any systemic bias there.
```
fig = figure(figsize=(10,12))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)
axes = [ax1,ax2,ax3]
colors = sns.xkcd_palette(["windows blue", "amber", "faded green", "dusty purple","aqua blue"])
#resids = [r1, r2, r3]
normed_resids = [r1/y1, r2/y2, r3/y3]
for (dataa, axx, colorr) in zip(normed_resids,axes,colors):
sns.kdeplot(dataa, bw=1.0, ax=axx, color=colorr, shade=True, alpha=0.5);
ax1.set_title('Probability Distribution: Normalized Residual Error, y1')
ax2.set_title('Normalized Residual Error, y2')
ax3.set_title('Normalized Residual Error, y3')
```
Note that in these figures, the bumps at extreme value are caused by the fact that the interval containing the responses includes 0 and values close to 0, so the normalization factor is very tiny, leading to large values.
<a name="aggregating"></a>
## Aggregating Results
Let's next aggregate experimental results, by taking the mean over various variables to compute the mean effect for regressed varables. For example, we may want to look at the effects of variables 2, 3, and 4, and take the mean over the other three variables.
This is simple to do with Pandas, by grouping the data by each variable, and applying the mean function on all of the results. The code looks like this:
```
# Our original regression variables
xlabs = ['x2','x3','x4']
doe.groupby(xlabs)[ylabs].mean()
# If we decided to go for a different variable set
xlabs = ['x2','x3','x4','x6']
doe.groupby(xlabs)[ylabs].mean()
```
This functionality can also be used to determine the variance in all of the experimental observations being aggregated. For example, here we aggregate over $x_3 \dots x_6$ and show the variance broken down by $x_1, x_2$ vs $y_1, y_2, y_3$.
```
xlabs = ['x1','x2']
doe.groupby(xlabs)[ylabs].var()
```
Or even the number of experimental observations being aggregated!
```
doe.groupby(xlabs)[ylabs].count()
```
<a name="dist_variance"></a>
## Distributions of Variance
We can convert these dataframes of averages, variances, and counts into data for plotting. For example, if we want to make a histogram of every value in the groupby dataframe, we can use the ```.values``` method, so that this:
doe.gorupby(xlabs)[ylabs].mean()
becomes this:
doe.groupby(xlabs)[ylabs].mean().values
This $M \times N$ array can then be flattened into a vector using the ```ravel()``` method from numpy:
np.ravel( doe.groupby(xlabs)[ylabs].mean().values )
The resulting data can be used to generate histograms, as shown below:
```
# Histogram of means of response values, grouped by xlabs
xlabs = ['x1','x2','x3','x4']
print("Grouping responses by %s"%( "-".join(xlabs) ))
dat = np.ravel(doe.groupby(xlabs)[ylabs].mean().values) / np.ravel(doe.groupby(xlabs)[ylabs].var().values)
hist(dat, 10, normed=False, color=colors[3]);
xlabel(r'Relative Variance ($\mu$/$\sigma^2$)')
show()
# Histogram of variances of response values, grouped by xlabs
print("Grouping responses by %s"%( "-".join(xlabs) ))
dat = np.ravel(doe.groupby(xlabs)['y1'].var().values)
hist(dat, normed=True, color=colors[4])
xlabel(r'Variance in $y_{1}$ Response')
ylabel(r'Frequency')
show()
```
The distribution of variance looks _mostly_ normal, with some outliers. These are the same outliers that showed up in our quantile-quantile plot, and they'll show up in the plots below as well.
<a name="residual"></a>
## Residual vs. Response Plots
Another thing we can do, to look for uncaptured effects, is to look at our residuals vs. $\hat{y}$. This is a further effort to look for underlying functional relationships between $\hat{y}$ and the residuals, which would indicate that our system exhibits behavior not captured by our linear model.
```
# normal plot of residuals
fig = figure(figsize=(14,4))
ax1 = fig.add_subplot(131)
ax2 = fig.add_subplot(132)
ax3 = fig.add_subplot(133)
ax1.plot(y1,r1,'o',color=colors[0])
ax1.set_xlabel('Response value $y_1$')
ax1.set_ylabel('Residual $r_1$')
ax2.plot(y2,r2,'o',color=colors[1])
ax2.set_xlabel('Response value $y_2$')
ax2.set_ylabel('Residual $r_2$')
ax2.set_title('Response vs. Residual Plots')
ax3.plot(y1,r1,'o',color=colors[2])
ax3.set_xlabel('Response value $y_3$')
ax3.set_ylabel('Residual $r_3$')
show()
```
Notice that each plot is trending up and to the right - indicative of an underlying trend that our model $\hat{y}$ is not capturing. The trend is relatively weak, however, indicating that our linear model does a good job of capturing _most_ of the relevant effects of this system.
# Discussion
The analysis shows that there are some higher-order or nonlinear effects in the system that a purely linear model does not account for. Next steps would involve adding higher order points for a quadratic or higher order polynomial model to gather additional data to fit the higher-degree models.
| true |
code
| 0.394463 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/NikolaZubic/AppliedGameTheoryHomeworkSolutions/blob/main/domaci3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# TREĆI DOMAĆI ZADATAK iz predmeta "Primenjena teorija igara" (Applied Game Theory)
Razvoj bota za igranje igre Ajnc (BlackJack) koristeći "Q-learning" pristup.
# Potrebni import-i
```
import gym
import numpy as np
import matplotlib.pyplot as plt
from gym import spaces
import seaborn as sns
```
# Definisanje Ajnc okruženja koristeći "Open AI Gym" toolkit
```
class BlackJackEnvironment(gym.Env):
# Because of human-friendly output
metadata = {'render.modes':['human']}
def __init__(self):
"""
We will define possible number of states with observation_space.
Player's sum can go from 4 to 32: Now when the sum is 22, and the player chooses to hit, he may get a card with value 10, resulting in a sum of 32, and thus loosing the game.
Dealer's card can be from 1 to 10 and we have 2 actions.
Total number of states: 29 * 10 * 2 = 580
Total number of actions = 2 = len( {"HIT", "STAND"} )
"""
self.observation_space = spaces.Discrete(580)
self.action_space = spaces.Discrete(2)
self.step_count = 0 # at the beginning of the game we have 0 actions taken
def check_usable_ace(self,hand):
"""
If someone has an usable ace, we will replace that ace (1) with 11.
:param hand: player's or dealer's card
:return: True if we have usable ace, False otherwise
"""
temp_hand = hand.copy()
# Check if there is ace in hand
if np.any(temp_hand == 1):
# If we have any ace then replace it with 11, but if we have more than one ace replace the first one with 11
temp_hand[np.where(temp_hand == 1)[0][0]] = 11
# If the sum is less or equal than 21 then we can use it
if temp_hand.sum() <= 21:
return True
return False
def use_ace(self,hand):
"""
If there is usable ace in function above, then replace 1 with 11.
:param hand: player's or dealer's hand
:return: new hand where 1 is replaced with 11
"""
temp_hand = hand.copy()
temp_hand[np.where(temp_hand == 1)[0][0]] = 11
return temp_hand
def reset(self):
# Resets the environment after one game.
# Initialize player's hand
self.current_hand = np.random.choice(range(1,11),2)
# Initialize usable Ace to False, since we don't have it at the very beginning
self.usable_ace = False
self.dealer_stand, self.player_stand = False, False
# Replace usable ace in the player's hand
if self.check_usable_ace(self.current_hand):
self.usable_ace = True
self.current_hand = self.use_ace(self.current_hand)
# Player's current sum
self.current_sum = self.current_hand.sum()
# Dealer's hand
self.dealer_hand = np.random.choice(range(1,11),2)
# Dealer's sum
self.dealer_sum = self.dealer_hand.sum()
# First element of self.dealer_hand is the current showing card of dealer
self.dealer_showing_card = self.dealer_hand[0]
# Replace usable ace in the dealer's hand
if self.check_usable_ace(self.dealer_hand):
temp_dealer_hand = self.use_ace(self.dealer_hand)
self.dealer_sum = temp_dealer_hand.sum()
def take_turn(self, current_player):
"""
Play one turn for the player. This function will be called from step() function, directly depending on the game state.
We will take new random card, add it to the current_player hand.
:param player: {"player", "dealer"}
:return: None
"""
if current_player == 'dealer':
# Take new random card
new_card = np.random.choice(range(1,11))
# Add new card to the current_player hand
new_dealer_hand = np.array(self.dealer_hand.tolist() + [new_card])
# Check for usable ace and replace if found
if self.check_usable_ace(new_dealer_hand):
new_dealer_hand = self.use_ace(new_dealer_hand)
self.dealer_hand = new_dealer_hand
# Update his sum
self.dealer_sum = self.dealer_hand.sum()
if current_player == 'player':
new_card = np.random.choice(range(1,11))
new_player_hand = np.array(self.current_hand.tolist()+ [new_card])
if self.check_usable_ace(new_player_hand):
self.usable_ace = True
new_player_hand = self.use_ace(new_player_hand)
self.current_hand = new_player_hand
self.current_sum = self.current_hand.sum()
def check_game_status(self, mode = 'normal'):
"""
Check the current status of the game.
During the 'normal' we check after each turn whether we got in the terminal state.
In the 'compare' mode we compare the totals of both players (player vs dealer) in order to pronounce the winner.
:param mode: {'normal', 'compare'}
:return: dictionary with the winner, whether the game is finished and the reward of the game
"""
result = {'winner':'',
'is_done': False,
'reward':0}
if mode == 'normal':
if self.current_sum > 21:
result['winner'] = 'dealer'
result['is_done'] = True
result['reward'] = -1
elif self.dealer_sum > 21:
result['winner'] = 'player'
result['is_done'] = True
result['reward'] = 1
elif self.current_sum == 21:
result['winner'] = 'player'
result['is_done'] = True
result['reward'] = 1
elif self.dealer_sum == 21:
result['winner'] = 'dealer'
result['is_done'] = True
result['reward'] = -1
elif mode == 'compare':
result['is_done'] = True
diff_21_player = 21 - self.current_sum
diff_21_dealer = 21 - self.dealer_sum
if diff_21_player > diff_21_dealer:
result['reward'] = -1
result['winner'] = 'dealer'
elif diff_21_player < diff_21_dealer:
result['reward'] = 1
result['winner'] = 'player'
else:
result['reward'] = 0
result['winner'] = 'draw'
return result
return result
def step(self,action):
"""
Performs one action.
:param action:
:return: dictionary with the winner, whether the game is finished and the reward of the game
"""
# Increase number of actions that are taken during the game.
self.step_count += 1
result = {'winner':'',
'is_done': False,
'reward':0}
"""
Before taking the first step of the game, we need to ensure that there is no winning condition.
Check if the initial two cards of the players are 21. If anyone has 21, then that player wins.
If both players have 21, then the game is DRAW. Otherwise, we will continue with the game.
"""
if self.step_count == 1:
if self.check_usable_ace(self.current_hand):
self.current_hand = self.use_ace(self.current_hand)
if self.check_usable_ace(self.dealer_hand):
self.current_hand = self.use_ace(self.dealer_hand)
if self.current_sum == 21 and self.dealer_sum == 21:
result['is_done'] = True
result['reward'] = 0
result['winner'] = 'draw'
return result
elif self.current_sum == 21 and self.dealer_sum < 21:
result['is_done'] = True
result['reward'] = 1
result['winner'] = 'player'
return result
elif self.dealer_sum == 21 and self.current_sum < 21:
result['is_done'] = True
result['reward'] = -1
result['winner'] = 'dealer'
return result
if self.dealer_sum >= 17:
self.dealer_stand = True
# action = 0 means "HIT"
if action == 0:
self.take_turn('player')
result = self.check_game_status()
if result['is_done'] == True:
return result
# action = 1 means "STAND"
if action == 1:
if self.dealer_stand == True:
return self.check_game_status(mode = 'compare')
"""
If the dealer hasn't stand, he will hit unless his sum is greater than or equal to 17.
After that, he will stand.
"""
while self.dealer_sum < 17:
self.take_turn('dealer')
result = self.check_game_status()
# After dealer stands, check the game status.
if result['is_done'] == True:
return result
# If the game hasn't finished yet, we set dealer_stand to True, so the player will either HIT or STAND
self.dealer_stand = True
return result
def get_current_state(self):
"""
Get current state which is comprised of current player's sum, dealer's showing card and usable ace presence.
:return: return current state variables
"""
current_state = {}
current_state['current_sum'] = self.current_sum
current_state['dealer_showing_card'] = self.dealer_showing_card
current_state['usable_ace'] = self.usable_ace
return current_state
def render(self):
print("OBSERVABLE STATES")
print("Current player's sum: {}".format(self.current_sum))
print("Dealer's showing card: {}".format(self.dealer_showing_card))
print("Player has usable Ace: {}".format(self.usable_ace))
print("INFORMATION ABOUT CARDS AND DEALER'S SUM")
print("Player's hand: {}".format(self.current_hand))
print("Dealer's hand: {}".format(self.dealer_hand))
print("Dealer's sum: {}".format(self.dealer_sum))
```
# Pomoćne funkcije za Q-learning
```
# dictionaries used for converting the state values to indexes in the Q table
current_sum_to_index = dict(zip(np.arange(4,33),np.arange(29)))
dealer_showing_card_to_index = dict(zip(np.arange(1,11),np.arange(10)))
usable_ace_index = dict(zip([False,True],[0,1]))
action_index = dict(zip(['HIT','STAND'],[0,1]))
def get_state_q_indices(current_state):
"""
Get indexes of Q table for any given state.
:param current_state: comprised of current player's sum, dealer's showing card and usable ace presence.
:return: get table indexes for a state
"""
current_sum_idx = current_sum_to_index[current_state['current_sum']]
dealer_showing_card_idx = dealer_showing_card_to_index[current_state['dealer_showing_card']]
usable_ace_idx = usable_ace_index[current_state['usable_ace']]
return [current_sum_idx,dealer_showing_card_idx,usable_ace_idx]
def get_max_action(Q_sa, current_state):
"""
Get the action with the max Q-value for the given current state and the Q table.
:param Q_sa: given Q table
:param current_state: current state
:return: best action for given state and Q table
"""
state_q_idxs = get_state_q_indices(current_state)
action = Q_sa[state_q_idxs[0],state_q_idxs[1],state_q_idxs[2],:].argmax()
return action
def get_q_value(Q_sa, state, action):
"""
Get Q(s,a) value for state and action in certain Q table.
:param Q_sa: given Q table
:param state: given state
:param action: given action
:return: Q(s, a)
"""
state_q_idxs = get_state_q_indices(state)
q_value = Q_sa[state_q_idxs[0],state_q_idxs[1],state_q_idxs[2],action]
return q_value
```
# Q-learning
Inicijalizacija Q tabele.
```
"""
Player's current sum is ranging from 4 to 32 => 32 - 4 + 1 = 29
Dealer's showing card can be one from the following set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} => 10 values
Ace can be usable or not => 2
Actions are from the following set {"HIT", "STAND"} => 2
"""
Q = np.zeros((29,10,2,2))
```
Proces treniranja.
```
episode_count = 0
total_episodes = 2000000
# Discounting factor
gamma = 0.9
# Used for filtering q-values, learning rate
LAMBDA = 0.1
# Defined Black Jack Environment
environment = BlackJackEnvironment()
while episode_count < total_episodes:
environment.reset()
current_state = environment.get_current_state()
current_action = get_max_action(Q, current_state)
# Take action
step_result = environment.step(current_action)
# Get into next state and get the reward
next_state = environment.get_current_state()
next_max_action = get_max_action(Q, next_state)
immediate_reward = step_result['reward']
next_state_q_idxs = get_state_q_indices(next_state)
# Get the q-value for the next state and max action in the next state
q_max_s_a = get_q_value(Q, next_state, next_max_action)
td_target = immediate_reward + gamma * q_max_s_a
# Get the q-value for the current state and action
q_current_s_a = get_q_value(Q, current_state, current_action)
td_error = td_target - q_current_s_a
state_q_idxs = get_state_q_indices(current_state)
# Update the current Q(s, a)
Q[state_q_idxs[0],state_q_idxs[1],state_q_idxs[2],current_action] = q_current_s_a + LAMBDA * td_error
# get into the next state
current_state = next_state
if step_result['is_done']:
episode_count += 1
if episode_count % 100000 == 0:
print("Episode number: {}".format(episode_count))
```
# Diskusija rezultata
```
fig, ax = plt.subplots(ncols= 2,figsize=(16,8))
sns.heatmap(Q[:,:,0,0],cmap = sns.light_palette((210, 90, 60), input="husl"), ax = ax[0],
xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax[0].set_title("Usable Ace = False, Action = HIT")
ax[0].set_xlabel("Dealer's Showing Card")
ax[0].set_ylabel("Current Player's Sum")
sns.heatmap(Q[:,:,0,1],cmap = sns.light_palette((210, 90, 60), input="husl"), ax = ax[1],
xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax[1].set_title("Usable Ace = False, Action = STAND")
ax[1].set_xlabel("Dealer's Showing Card")
ax[1].set_ylabel("Current Player's Sum")
```
Na osnovu gornjih heatmapa možemo uočiti koje je to akcije dobro izvršiti u kojem stanju.
**Zaključak sa lijeve heatmape**: kada je ukupna suma igrača manja od 12, 13 onda je najbolje da se izvršava akcija "HIT".
**Zaključak sa desne heatmape**: Za veće vrijednosti otkrivene karte djelitelja i veće vrijednosti ukupne sume igrača bolje je izvršiti akciju "STAND".
```
fig, ax = plt.subplots(ncols = 2, figsize=(16,8))
sns.heatmap(Q[:,:,1,0],cmap = sns.light_palette((210, 90, 60), input="husl"), ax = ax[0],
xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax[0].set_title("Usable Ace = True, Action = HIT")
ax[0].set_xlabel("Dealer's Showing Card")
ax[0].set_ylabel("Current Player's Sum")
sns.heatmap(Q[:,:,1,1],cmap = sns.light_palette((210, 90, 60), input="husl"), ax = ax[1],
xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax[1].set_title("Usable Ace = True, Action = STAND")
ax[1].set_xlabel("Dealer's Showing Card")
ax[1].set_ylabel("Current Player's Sum")
```
U slučaju kad imamo iskoristiv kec, broj semplova je znatno manji, tako da paterni Q-vrijednosti nisu baš potpuno jasni, ali može se zaključiti da je najbolje izvršiti akciju **"HIT" u slučajevima kad je suma igrača oko 12**, dok se akcija **"STAND" izvršava u slučaju kada je igra pri kraju po pitanju sume igrača**.
Sada ćemo pogledati naučene politike (za slučaj pohlepne politike, jer želimo da naš igrač uvijek bira onako da najbolje igra).
**Sa crnim blokovima označeno je kada treba izvršiti akciju "HIT"**, a imamo 2 heatmape za slučaj kad nemamo i imamo iskoristiv kec.
```
fig, ax = plt.subplots(ncols= 1,figsize=(8,6))
sns.heatmap(np.argmax(Q[:17,:,0,:],axis=2),cmap = sns.cubehelix_palette(8, start=2, rot=0, dark=0, light=.95, reverse=True)\
,linewidths=1,xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax.set_title("Usable Ace = False")
ax.set_xlabel("Dealer's Showing Card")
ax.set_ylabel("Current Player's Sum")
fig, ax = plt.subplots(ncols= 1,figsize=(8,6))
sns.heatmap(np.argmax(Q[:17,:,1,:],axis=2),cmap = sns.cubehelix_palette(8, start=2, rot=0, dark=0, light=.95, reverse=True)\
,linewidths=1,xticklabels=np.arange(1,11),yticklabels=np.arange(4,33))
ax.set_title("Usable Ace = True")
ax.set_xlabel("Dealer's Showing Card")
ax.set_ylabel("Current Player's Sum")
```
# Na kraju, nakon 2 miliona iteracija treniranja, testiraćemo algoritam na 10 000 partija.
```
player_wins = 0
dealer_wins = 0
NUMBER_OF_GAMES = 10000
for i in range(NUMBER_OF_GAMES):
environment.reset()
while True:
current_state = environment.get_current_state()
current_action = get_max_action(Q, current_state)
# Take action
step_result = environment.step(current_action)
#environment.render()
next_state = environment.get_current_state()
current_state = next_state
if step_result['is_done']:
break
if step_result['winner'] == 'player':
player_wins += 1
elif step_result['winner'] == 'dealer':
dealer_wins += 1
print("Player wins: " + str(player_wins))
print("Dealer wins: " + str(dealer_wins))
print("Player wins percentage = " + str(round(100 * (player_wins / (player_wins + dealer_wins)), 2)) + "%")
```
| true |
code
| 0.609059 | null | null | null | null |
|
# DJL BERT Inference Demo
## Introduction
In this tutorial, you walk through running inference using DJL on a [BERT](https://towardsdatascience.com/bert-explained-state-of-the-art-language-model-for-nlp-f8b21a9b6270) QA model trained with MXNet.
You can provide a question and a paragraph containing the answer to the model. The model is then able to find the best answer from the answer paragraph.
Example:
```text
Q: When did BBC Japan start broadcasting?
```
Answer paragraph:
```text
BBC Japan was a general entertainment channel, which operated between December 2004 and April 2006.
It ceased operations after its Japanese distributor folded.
```
And it picked the right answer:
```text
A: December 2004
```
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
```
%maven ai.djl:api:0.2.0
%maven ai.djl.mxnet:mxnet-engine:0.2.0
%maven ai.djl:repository:0.2.0
%maven ai.djl.mxnet:mxnet-model-zoo:0.2.0
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven net.java.dev.jna:jna:5.3.0
```
### Include MXNet engine dependency
This tutorial uses MXNet engine as its backend. MXNet has different [build flavor](https://mxnet.apache.org/get_started?version=v1.5.1&platform=linux&language=python&environ=pip&processor=cpu) and it is platform specific.
Please read [here](https://github.com/awslabs/djl/blob/master/examples/README.md#engine-selection) for how to select MXNet engine flavor.
```
String classifier = System.getProperty("os.name").startsWith("Mac") ? "osx-x86_64" : "linux-x86_64";
%maven ai.djl.mxnet:mxnet-native-mkl:jar:${classifier}:1.6.0-a
```
### Import java packages by running the following:
```
import java.io.*;
import java.nio.charset.*;
import java.nio.file.*;
import java.util.*;
import com.google.gson.*;
import com.google.gson.annotations.*;
import ai.djl.*;
import ai.djl.inference.*;
import ai.djl.metric.*;
import ai.djl.mxnet.zoo.*;
import ai.djl.mxnet.zoo.nlp.qa.*;
import ai.djl.repository.zoo.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.training.util.*;
import ai.djl.translate.*;
import ai.djl.util.*;
```
Now that all of the prerequisites are complete, start writing code to run inference with this example.
## Load the model and input
The model requires three inputs:
- word indices: The index of each word in a sentence
- word types: The type index of the word. All Questions will be labelled with 0 and all Answers will be labelled with 1.
- sequence length: You need to limit the length of the input. In this case, the length is 384
- valid length: The actual length of the question and answer tokens
**First, load the input**
```
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument, 384);
```
Then load the model and vocabulary. Create a variable `model` by using the `ModelZoo` as shown in the following code.
```
Map<String, String> criteria = new ConcurrentHashMap<>();
criteria.put("backbone", "bert");
criteria.put("dataset", "book_corpus_wiki_en_uncased");
ZooModel<QAInput, String> model = MxModelZoo.BERT_QA.loadModel(criteria, new ProgressBar());
```
## Run inference
Once the model is loaded, you can call `Predictor` and run inference as follows
```
Predictor<QAInput, String> predictor = model.newPredictor();
String answer = predictor.predict(input);
answer
```
Running inference on DJL is that easy. In the example, you use a model from the `ModelZoo`. However, you can also load the model on your own and use custom classes as the input and output. The process for that is illustrated in greater detail later in this tutorial.
## Dive deep into Translator
Inference in deep learning is the process of predicting the output for a given input based on a pre-defined model.
DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
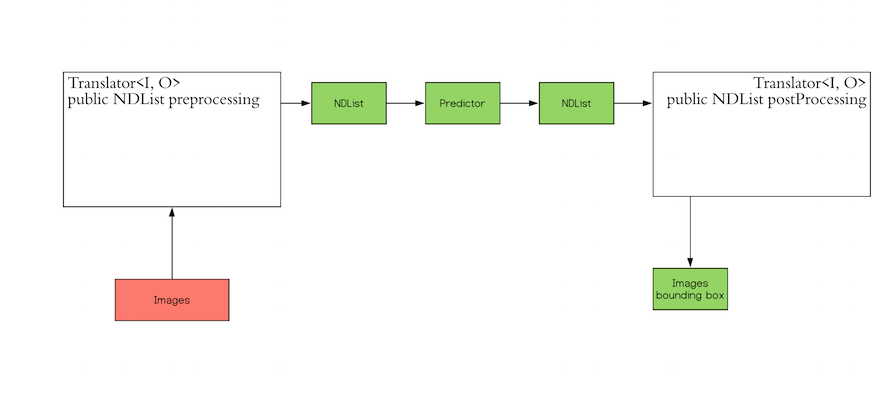
The red block ("Images") in the workflow is the input that DJL expects from you. The green block ("Images
bounding box") is the output that you expect. Because DJL does not know which input to expect and which output format that you prefer, DJL provides the `Translator` interface so you can define your own
input and output.
The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
`Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
format.
### Pre-processing
Now, you need to convert the sentences into tokens. You can use `BertDataParser.tokenizer` to convert questions and answers into tokens. Then, use `BertDataParser.formTokens` to create Bert-Formatted tokens. Once you have properly formatted tokens, use `parser.token2idx` to create the indices.
The following code block converts the question and answer defined earlier into bert-formatted tokens and creates word types for the tokens.
```
// Create token lists for question and answer
List<String> tokenQ = BertDataParser.tokenizer(question.toLowerCase());
List<String> tokenA = BertDataParser.tokenizer(resourceDocument.toLowerCase());
int validLength = tokenQ.size() + tokenA.size();
System.out.println("Question Token: " + tokenQ);
System.out.println("Answer Token: " + tokenA);
System.out.println("Valid length: " + validLength);
```
Normally, words/sentences are represented as indices instead of Strings for training. They typically work like a vector in a n-dimensional space. In this case, you need to map them into indices. The form tokens also pad the sentence to the required length.
```
// Create Bert-formatted tokens
List<String> tokens = BertDataParser.formTokens(tokenQ, tokenA, 384);
// Convert tokens into indices in the vocabulary
BertDataParser parser = model.getArtifact("vocab.json", BertDataParser::parse);
List<Integer> indices = parser.token2idx(tokens);
```
Finally, the model needs to understand which part is the Question and which part is the Answer. Mask the tokens as follows:
```
[Question tokens...AnswerTokens...padding tokens] => [000000...11111....0000]
```
```
// Get token types
List<Float> tokenTypes = BertDataParser.getTokenTypes(tokenQ, tokenA, 384);
```
To properly convert them into `float[]` for `NDArray` creation, here is the helper function:
```
/**
* Convert a List of Number to float array.
*
* @param list the list to be converted
* @return float array
*/
public static float[] toFloatArray(List<? extends Number> list) {
float[] ret = new float[list.size()];
int idx = 0;
for (Number n : list) {
ret[idx++] = n.floatValue();
}
return ret;
}
float[] indicesFloat = toFloatArray(indices);
float[] types = toFloatArray(tokenTypes);
```
Now that you have everything you need, you can create an NDList and populate all of the inputs you formatted earlier. You're done with pre-processing!
#### Construct `Translator`
You need to do this processing within an implementation of the `Translator` interface. `Translator` is designed to do pre-processing and post-processing. You must define the input and output objects. It contains the following two override classes:
- `public NDList processInput(TranslatorContext ctx, I)`
- `public String processOutput(TranslatorContext ctx, O)`
Every translator takes in input and returns output in the form of generic objects. In this case, the translator takes input in the form of `QAInput` (I) and returns output as a `String` (O). `QAInput` is just an object that holds questions and answer; We have prepared the Input class for you.
Armed with the needed knowledge, you can write an implementation of the `Translator` interface. `BertTranslator` uses the code snippets explained previously to implement the `processInput`method. For more information, see [`NDManager`](https://javadoc.djl.ai/api/0.2.0/ai/djl/ndarray/NDManager.html).
```
manager.create(Number[] data, Shape)
manager.create(Number[] data)
```
The `Shape` for `data0` and `data1` is (num_of_batches, sequence_length). For `data2` is just 1.
```
public class BertTranslator implements Translator<QAInput, String> {
private BertDataParser parser;
private List<String> tokens;
private int seqLength;
BertTranslator(BertDataParser parser) {
this.parser = parser;
this.seqLength = 384;
}
@Override
public Batchifier getBatchifier() {
return null;
}
@Override
public NDList processInput(TranslatorContext ctx, QAInput input) throws IOException {
BertDataParser parser = ctx.getModel().getArtifact("vocab.json", BertDataParser::parse);
// Pre-processing - tokenize sentence
// Create token lists for question and answer
List<String> tokenQ = BertDataParser.tokenizer(question.toLowerCase());
List<String> tokenA = BertDataParser.tokenizer(resourceDocument.toLowerCase());
// Calculate valid length (length(Question tokens) + length(resourceDocument tokens))
var validLength = tokenQ.size() + tokenA.size();
// Create Bert-formatted tokens
tokens = BertDataParser.formTokens(tokenQ, tokenA, 384);
if (tokens == null) {
throw new IllegalStateException("tokens is not defined");
}
// Convert tokens into indices in the vocabulary
List<Integer> indices = parser.token2idx(tokens);
// Get token types
List<Float> tokenTypes = BertDataParser.getTokenTypes(tokenQ, tokenA, 384);
NDManager manager = ctx.getNDManager();
// Using the manager created, create NDArrays for the indices, types, and valid length.
// in that order. The type of the NDArray should all be float
NDArray indicesNd = manager.create(toFloatArray(indices), new Shape(1, 384));
indicesNd.setName("data0");
NDArray typesNd = manager.create(toFloatArray(tokenTypes), new Shape(1, 384));
typesNd.setName("data1");
NDArray validLengthNd = manager.create(new float[]{validLength});
validLengthNd.setName("data2");
NDList list = new NDList(3);
list.add(indicesNd);
list.add(typesNd);
list.add(validLengthNd);
return list;
}
@Override
public String processOutput(TranslatorContext ctx, NDList list) {
NDArray array = list.singletonOrThrow();
NDList output = array.split(2, 2);
// Get the formatted logits result
NDArray startLogits = output.get(0).reshape(new Shape(1, -1));
NDArray endLogits = output.get(1).reshape(new Shape(1, -1));
// Get Probability distribution
NDArray startProb = startLogits.softmax(-1);
NDArray endProb = endLogits.softmax(-1);
int startIdx = (int) startProb.argMax(1).getFloat();
int endIdx = (int) endProb.argMax(1).getFloat();
return tokens.subList(startIdx, endIdx + 1).toString();
}
}
```
Congrats! You have created your first Translator! We have pre-filled the `processOutput()` that will process the `NDList` and return it in a desired format. `processInput()` and `processOutput()` offer the flexibility to get the predictions from the model in any format you desire.
With the Translator implemented, you need to bring up the predictor that uses your `Translator` to start making predictions. You can find the usage for `Predictor` in the [Predictor Javadoc](https://javadoc.djl.ai/api/0.2.0/ai/djl/inference/Predictor.html). Create a translator and use the `question` and `resourceDocument` provided previously.
```
String predictResult = null;
QAInput input = new QAInput(question, resourceDocument, 384);
BertTranslator translator = new BertTranslator(parser);
// Create a Predictor and use it to predict the output
try (Predictor<QAInput, String> predictor = model.newPredictor(translator)) {
predictResult = predictor.predict(input);
}
System.out.println(question);
System.out.println(predictResult);
```
Based on the input, the following result will be shown:
```
[december, 2004]
```
That's it!
You can try with more questions and answers. Here are the samples:
**Answer Material**
The Normans (Norman: Nourmands; French: Normands; Latin: Normanni) were the people who in the 10th and 11th centuries gave their name to Normandy, a region in France. They were descended from Norse ("Norman" comes from "Norseman") raiders and pirates from Denmark, Iceland and Norway who, under their leader Rollo, agreed to swear fealty to King Charles III of West Francia. Through generations of assimilation and mixing with the native Frankish and Roman-Gaulish populations, their descendants would gradually merge with the Carolingian-based cultures of West Francia. The distinct cultural and ethnic identity of the Normans emerged initially in the first half of the 10th century, and it continued to evolve over the succeeding centuries.
**Question**
Q: When were the Normans in Normandy?
A: 10th and 11th centuries
Q: In what country is Normandy located?
A: france
| true |
code
| 0.748573 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/yohanesnuwara/machine-learning/blob/master/06_simple_linear_regression/simple_linear_reg_algorithm.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# **Simple Linear Regression**
```
import numpy as np
import matplotlib.pyplot as plt
```
## Method 1 ("Traditional")
Calculate bias (or intercept $B_0$) and slope ($B_1$) using:
$$B_1 = \frac{\sum_{i=1}^{n}(x_i-mean(x))(y_i-mean(y))}{\sum_{i=1}^{n}(x_i-mean(x))^2}$$
$$B_0 = mean(y) - B_1 \cdot mean(x)$$
to construct simple linear regression model: $$y = B_0 + B_1 \cdot x$$
```
x = [1, 2, 4, 3, 5]
y = [1, 3, 3, 2, 5]
# visualize our data
plt.plot(x, y, 'o')
```
Calculate mean of data
```
mean_x = np.mean(x)
mean_y = np.mean(y)
print(mean_x, mean_y)
```
Calculate error
```
err_x = x - mean_x
err_y = y - mean_y
print(err_x)
print(err_y)
```
Multiply error of x and error of y
```
err_mult = err_x * err_y
print(err_mult)
```
Calculate numerator by summing up the errors
```
numerator = np.sum(err_mult)
numerator
```
Calculate denominator by squaring the x error and summing them up
```
err_x_squared = err_x**2
denominator = np.sum(err_x_squared)
print(denominator)
```
Calculate the **slope (B1)** !
```
B1 = numerator / denominator
print(B1)
```
And we can calculate the **intercept (c)** !
```
B0 = mean_y - B1 * mean_x
print(B0)
```
We now have the coefficents for our simple linear regression equation.
$$y = B_0 + B_1 x = 0.4 + 0.8 x$$
### Test the model to our training data
```
x_test = np.array([1, 2, 3, 4, 5])
y_predicted = B0 + B1 * x_test
p1 = plt.plot(x, y, 'o')
p2 = plt.plot(x_test, y_predicted, 'o-', color='r')
plt.legend((p1[0], p2[0]), (['y data', 'predicted y']))
```
### Estimating Error (Root Mean Squared Error)
$$RMSE = \sqrt{\frac{\sum_{i=1}^{n} (p_i - y_i)^2}{n}}$$
```
numerator = np.sum((y_predicted - y)**2)
denominator = len(y)
rmse = np.sqrt(numerator / denominator)
rmse
```
### Wrap all up
```
def simple_linear_regression_traditional(x, y, x_test):
import numpy as np
x = np.array(x); y = np.array(y); x_test = np.array(x_test)
mean_x = np.mean(x)
mean_y = np.mean(y)
err_x = x - mean_x
err_y = y - mean_y
err_mult = err_x * err_y
numerator = np.sum(err_mult)
err_x_squared = err_x**2
denominator = np.sum(err_x_squared)
B1 = numerator / denominator
B0 = mean_y - B1 * mean_x
y_predicted = B0 + B1 * x_test
return(B0, B1, y_predicted)
def linreg_error(y, y_predicted):
import numpy as np
y = np.array(y); y_predicted = np.array(y_predicted)
numerator = np.sum((y_predicted - y)**2)
denominator = len(y)
rmse = np.sqrt(numerator / denominator)
return(rmse)
```
## Method 2 ("Advanced")
Calculate bias (or intercept $B_0$) and slope ($B_1$) using:
$$B_1 = corr(x, y) \cdot \frac{stdev(y)}{stdev(x)}$$
Then, similar to **Method 1**.
$$B_0 = mean(y) - B_1 \cdot mean(x)$$
to construct simple linear regression model: $$y = B_0 + B_1 \cdot x$$
Calculate the **pearson's correlation coefficient $corr(x,y)$**. First, calculate mean and standard deviation.
```
import statistics as stat
mean_x = np.mean(x)
mean_y = np.mean(y)
stdev_x = stat.stdev(x)
stdev_y = stat.stdev(y)
print(stdev_x, stdev_y)
```
Calculate **covariance**. Covariance is the relationship that can be summarized between two variables. The sign of the covariance can be interpreted as whether the two variables change in the same direction (positive) or change in different directions (negative). A covariance value of zero indicates that both variables are completely independent.
```
cov_x_y = (np.sum((x - mean_x) * (y - mean_y))) * (1 / (len(x) - 1))
cov_x_y
```
Calculate **Pearson's Correlation Coefficient**. It summarizes the strength of the linear relationship between two data samples. It is the normalization of the covariance between the two variables. The coefficient returns a value between -1 and 1 that represents the limits of correlation from a full negative correlation to a full positive correlation. A value of 0 means no correlation. The value must be interpreted, where often a value below -0.5 or above 0.5 indicates a notable correlation, and values below those values suggests a less notable correlation.
```
corr_x_y = cov_x_y / (stdev_x * stdev_y)
corr_x_y
```
Calculate slope $B_1$
```
B1 = corr_x_y * (stdev_y / stdev_x)
B1
```
Next, is similar to **Method 1**.
```
B0 = mean_y - B1 * mean_x
x_test = np.array([1, 2, 3, 4, 5])
y_predicted = B0 + B1 * x_test
p1 = plt.plot(x, y, 'o')
p2 = plt.plot(x_test, y_predicted, 'o-', color='r')
plt.legend((p1[0], p2[0]), (['y data', 'predicted y']))
```
Calculate RMSE
```
rmse = linreg_error(y, y_predicted)
rmse
```
### Wrap all up
```
def simple_linear_regression_advanced(x, y, x_test):
import numpy as np
import statistics as stat
x = np.array(x); y = np.array(y); x_test = np.array(x_test)
mean_x = np.mean(x)
mean_y = np.mean(y)
stdev_x = stat.stdev(x)
stdev_y = stat.stdev(y)
cov_x_y = (np.sum((x - mean_x) * (y - mean_y))) * (1 / (len(x) - 1))
corr_x_y = cov_x_y / (stdev_x * stdev_y)
B1 = corr_x_y * (stdev_y / stdev_x)
B0 = mean_y - B1 * mean_x
y_predicted = B0 + B1 * x_test
return(B0, B1, y_predicted)
```
## Implement to Real Dataset
Simple linear regression to WTI and Brent Daily Oil Price (1980-2020)
```
!git clone https://www.github.com/yohanesnuwara/machine-learning
import pandas as pd
brent = pd.read_csv('/content/machine-learning/datasets/brent-daily_csv.csv')
wti = pd.read_csv('/content/machine-learning/datasets/wti-daily_csv.csv')
# Converting to Panda datetime
brent['Date'] = pd.to_datetime(brent['Date'], format='%Y-%m-%d') # depends on the data, format check web: https://strftime.org/
wti['Date'] = pd.to_datetime(wti['Date'], format='%Y-%m-%d') # depends on the data, format check web: https://strftime.org/
brent.head(10)
```
Visualize data
```
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()
plt.figure(figsize=(15, 6))
plt.plot(brent.Date, brent.Price, '.', color='blue')
plt.plot(wti.Date, wti.Price, '.', color='red')
plt.title('Daily Oil Price')
plt.xlabel('Year'); plt.ylabel('Price ($/bbl)')
# convert datetime to ordinal
import datetime as dt
brent_date = np.array(brent['Date'].map(dt.datetime.toordinal))
brent_price = brent.Price
brent_test = brent_date
B0_brent, B1_brent, brent_price_predicted = simple_linear_regression_advanced(brent_date, brent_price, brent_test)
wti_date = np.array(wti['Date'].map(dt.datetime.toordinal))
wti_price = wti.Price
wti_test = wti_date
B0_wti, B1_wti, wti_price_predicted = simple_linear_regression_advanced(wti_date, wti_price, wti_test)
plt.figure(figsize=(15, 6))
p1 = plt.plot(brent.Date, brent.Price, '.', color='blue')
p2 = plt.plot(wti.Date, wti.Price, '.', color='red')
p3 = plt.plot(brent_test, brent_price_predicted, color='blue')
p4 = plt.plot(wti_test, wti_price_predicted, color='red')
plt.legend((p1[0], p2[0], p3[0], p4[0]), (['Brent data', 'WTI data', 'Brent predicted', 'WTI predicted']))
plt.title('Daily Oil Price')
plt.xlabel('Year'); plt.ylabel('Price ($/bbl)')
```
| true |
code
| 0.560192 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
%matplotlib inline
import pickle
import numpy as np
from scipy.spatial.distance import pdist, squareform
with open('exp_features.p', 'rb') as f:
data = pickle.load(f)
```
## visualize
```
def get_continuous_quantile(x, y, n_interval=100, q=1):
"""
Take continuous x and y, bin the data according to the intervals of x
and then calculate the quantiles of y within this bin
Args:
x (list): array of x values
y (list): array of y values
n_interval (int): number of intervals on x
q (float): quantile value [0, 1]
"""
ind = np.argsort(x)
x = x[ind]
y = y[ind]
boundaries = np.linspace(x[0], x[-1], n_interval+1)
dx = boundaries[1] - boundaries[0]
x_center = np.linspace(x[0]+dx/2, x[-1]-dx/2, n_interval)
y_q = []
for x_min, x_max in zip(boundaries[:-1], boundaries[1:]):
ind = (x>=x_min) & (x<x_max)
ys = y[ind]
if len(ys) > 0:
y_q.append(np.quantile(ys, q))
else:
y_q.append(y_q[-1])
y_q = np.array(y_q)
return x_center, y_q
def visualize(key, n_interval=100, interval=5, alpha=0.5, data_file="100_0.xlsx"):
"""
Visualize the data specified by key.
Args:
key (str): key in data
n_interval (int): number of intervals for drawing the quantile bounds
interval (int): subsamping of the data. Sometimes the input data is too large for visualization
we just subsample the data
"""
keys = list(data['band_gap'].keys())
f = np.concatenate([data[key][i] for i in keys], axis=0)
values = np.array([data['band_gap'][i] for i in keys])
sort_index = np.argsort(values)
fscale = (f-np.min(f, axis=0)) / (np.max(f, axis=0) - np.min(f, axis=0))
d = pdist(fscale)
v_dist = pdist(values.reshape((-1, 1)))
ind = (d>0) & (d<1)
d_ = d[ind]
v_ = v_dist[ind]
#print(d_.shape, v_.shape)
x_center, y_q = get_continuous_quantile(d_, v_, n_interval=n_interval, q=1)
plt.rcParams['font.size'] = 22
plt.rcParams['font.family'] = 'Arial'
plt.figure(figsize=(5.7, 5.0 ))
d_ = d_[::interval]
v_ = v_[::interval]
print(v_.shape)
plt.plot(d_, v_, 'o', alpha=alpha, c='#21c277')
plt.plot(x_center, y_q, '--', c='#21c277', lw=2, alpha=0.5)
import pandas as pd
x = np.round(np.concatenate([d_, x_center]), 3)
y = np.round(np.concatenate([v_, y_q]), 3)
df = pd.DataFrame({"dF": x, "dEg": y})
with pd.ExcelWriter(data_file) as writer:
df.to_excel(writer)
plt.xlim([0, 1])
plt.ylim([0, 13])
plt.xticks(np.linspace(0, 1, 5))
plt.yticks(np.linspace(0, 12.5, 6))
plt.xlabel('$d_{F}$ (a.u.)')
plt.ylabel("$\Delta E_{g}$ (eV)")
plt.tight_layout()
visualize('100_0', n_interval=100, interval=15, alpha=0.08, data_file='100_0.xlsx')
plt.savefig("100_0.pdf")
visualize('100_41000', n_interval=100, interval=15, alpha=0.08, data_file='100_41000.xlsx')
plt.savefig("100_41000.pdf")
```
| true |
code
| 0.673809 | null | null | null | null |
|
# Deploy model
**Important**: Change the kernel to *PROJECT_NAME local*. You can do this from the *Kernel* menu under *Change kernel*. You cannot deploy the model using the *PROJECT_NAME docker* kernel.
```
from azureml.api.schema.dataTypes import DataTypes
from azureml.api.schema.sampleDefinition import SampleDefinition
from azureml.api.realtime.services import generate_schema
import pandas as pd
import numpy as np
import imp
import pickle
import os
import sys
import json
from azureml.logging import get_azureml_logger
run_logger = get_azureml_logger()
run_logger.log('amlrealworld.timeseries.deploy-model','true')
```
Enter the name of the model to deploy.
```
model_name = "linear_regression"
```
Load the test dataset and retain just one row. This record will be used to create and input schema for the web service. It will also allow us to simulate invoking the web service with features for one hour period and generating a demand forecast for this hour.
```
aml_dir = os.environ['AZUREML_NATIVE_SHARE_DIRECTORY']
test_df = pd.read_csv(os.path.join(aml_dir, 'nyc_demand_test.csv'), parse_dates=['timeStamp'])
test_df = test_df.drop(['demand', 'timeStamp'], axis=1).copy().iloc[[0]]
test_df
```
Load model from disk and transfer it to the working directory.
```
with open(os.path.join(aml_dir, model_name + '.pkl'), 'rb') as f:
mod = pickle.load(f)
with open('model_deploy.pkl', 'wb') as f:
pickle.dump(mod, f)
```
Check model object has loaded as expected.
```
mod
```
Apply model to predict test record
```
np.asscalar(mod.predict(test_df))
```
### Author a realtime web service
Create a score.py script which implements the scoring function to run inside the web service. Change model_name variable as required.
```
%%writefile score.py
# The init and run functions will load and score the input using the saved model.
# The score.py file will be included in the web service deployment package.
def init():
import pickle
import os
global model
with open('model_deploy.pkl', 'rb') as f:
model = pickle.load(f)
def run(input_df):
input_df = input_df[['precip', 'temp', 'hour', 'month', 'dayofweek',
'temp_lag1', 'temp_lag2', 'temp_lag3', 'temp_lag4', 'temp_lag5',
'temp_lag6', 'demand_lag1', 'demand_lag2', 'demand_lag3',
'demand_lag4', 'demand_lag5', 'demand_lag6']]
try:
if (input_df.shape != (1,17)):
return 'Bad imput: Expecting dataframe of shape (1,17)'
else:
pred = model.predict(input_df)
return int(pred)
except Exception as e:
return(str(e))
```
This script will be written to your current working directory:
```
os.getcwd()
```
#### Test the *init* and *run* functions
```
import score
imp.reload(score)
score.init()
score.run(test_df)
```
#### Create web service schema
The web service schema provides details on the required structure of the input data as well as the data types of each column.
```
inputs = {"input_df": SampleDefinition(DataTypes.PANDAS, test_df)}
generate_schema(run_func=score.run, inputs=inputs, filepath='service_schema.json')
```
#### Deploy the web service
The command below deploys a web service names "demandforecast", with input schema defined by "service_schema.json". The web service runs "score.py" which scores the input data using the model "model_deploy.pkl". This may take a few minutes.
```
!az ml service create realtime -f score.py -m model_deploy.pkl -s service_schema.json -n demandforecast -r python
```
Check web service is running.
```
!az ml service show realtime -i demandforecast
```
Test the web service is working by invoking it with a test record.
```
!az ml service run realtime -i demandforecast -d "{\"input_df\": [{\"hour\": 0, \"month\": 6, \"demand_lag3\": 7576.558, \"temp_lag5\": 77.36, \"temp\": 74.63, \"demand_lag1\": 6912.7, \"demand_lag5\": 7788.292, \"temp_lag6\": 80.92, \"temp_lag3\": 76.72, \"demand_lag6\": 8102.142, \"temp_lag4\": 75.85, \"precip\": 0.0, \"temp_lag2\": 75.72, \"demand_lag2\": 7332.625, \"temp_lag1\": 75.1, \"demand_lag4\": 7603.008, \"dayofweek\": 4}]}"
```
#### Delete the web service
```
!az ml service delete realtime --id=demandforecast
```
| true |
code
| 0.353693 | null | null | null | null |
|
# Tutorial 06: Networks from OpenStreetMap
In this tutorial, we discuss how networks that have been imported from OpenStreetMap can be integrated and run in Flow. This will all be presented via the Bay Bridge network, seen in the figure below. Networks from OpenStreetMap are commonly used in many traffic simulators for the purposes of replicating traffic in realistic traffic geometries. This is true in both SUMO and Aimsun (which are both supported in Flow), with each supporting several techniques for importing such network files. This process is further simplified and abstracted in Flow, with users simply required to specify the path to the osm file in order to simulate traffic in the network.
<img src="img/bay_bridge_osm.png" width=750>
<center> **Figure 1**: Snapshot of the Bay Bridge from OpenStreetMap </center>
Before we begin, let us import all relevant Flow parameters as we have done for previous tutorials. If you are unfamiliar with these parameters, you are encouraged to review tutorial 1.
```
# the TestEnv environment is used to simply simulate the network
from flow.envs import TestEnv
# the Experiment class is used for running simulations
from flow.core.experiment import Experiment
# all other imports are standard
from flow.core.params import VehicleParams
from flow.core.params import NetParams
from flow.core.params import InitialConfig
from flow.core.params import EnvParams
from flow.core.params import SumoParams
```
## 1. Running a Default Simulation
In order to create a network object in Flow with network features depicted from OpenStreetMap, we will use the base `Network` class. This class can sufficiently support the generation of any .osm file.
```
from flow.networks import Network
```
In order to recreate the network features of a specific osm file, the path to the osm file must be specified in `NetParams`. For this example, we will use an osm file extracted from the section of the Bay Bridge as depicted in Figure 1.
In order to specify the path to the osm file, simply fill in the `osm_path` attribute with the path to the .osm file as follows:
```
net_params = NetParams(
osm_path='networks/bay_bridge.osm'
)
```
Next, we create all other parameters as we have in tutorials 1 and 2. For this example, we will assume a total of 1000 are uniformly spread across the Bay Bridge. Once again, if the choice of parameters is unclear, you are encouraged to review Tutorial 1.
```
# create the remainding parameters
env_params = EnvParams()
sim_params = SumoParams(render=True)
initial_config = InitialConfig()
vehicles = VehicleParams()
vehicles.add('human', num_vehicles=100)
# create the network
network = Network(
name='bay_bridge',
net_params=net_params,
initial_config=initial_config,
vehicles=vehicles
)
```
We are finally ready to test our network in simulation. In order to do so, we create an `Experiment` object and run the simulation for a number of steps. This is done in the cell below.
```
# create the environment
env = TestEnv(
env_params=env_params,
sim_params=sim_params,
network=network
)
# run the simulation for 1000 steps
exp = Experiment(env=env)
exp.run(1, 1000)
```
## 2. Customizing the Network
While the above example does allow you to view the network within Flow, the simulation is limited for two reasons. For one, vehicles are placed on all edges within the network; if we wished to simulate traffic solely on the on the bridge and do not care about the artireols, for instance, this would result in unnecessary computational burdens. Next, as you may have noticed if you ran the above example to completion, routes in the base network class are defaulted to consist of the vehicles' current edges only, meaning that vehicles exit the network as soon as they reach the end of the edge they are originated on. In the next subsections, we discuss how the network can be modified to resolve these issues.
### 2.1 Specifying Traversable Edges
In order to limit the edges vehicles are placed on to the road sections edges corresponding to the westbound Bay Bridge, we define an `EDGES_DISTRIBUTION` variable. This variable specifies the names of the edges within the network that vehicles are permitted to originated in, and is assigned to the network via the `edges_distribution` component of the `InitialConfig` input parameter, as seen in the code snippet below. Note that the names of the edges can be identified from the .osm file or by right clicking on specific edges from the SUMO gui (see the figure below).
<img src="img/osm_edge_name.png" width=600>
<center> **Figure 2**: Name of an edge from SUMO </center>
```
# we define an EDGES_DISTRIBUTION variable with the edges within
# the westbound Bay Bridge
EDGES_DISTRIBUTION = [
"11197898",
"123741311",
"123741303",
"90077193#0",
"90077193#1",
"340686922",
"236348366",
"340686911#0",
"340686911#1",
"340686911#2",
"340686911#3",
"236348361",
"236348360#0",
"236348360#1"
]
# the above variable is added to initial_config
new_initial_config = InitialConfig(
edges_distribution=EDGES_DISTRIBUTION
)
```
### 2.2 Creating Custom Routes
Next, we choose to specify the routes of vehicles so that they can traverse the entire Bay Bridge, instead of the only the edge they are currently on. In order to this, we create a new network class that inherits all its properties from `Network` and simply redefine the routes by modifying the `specify_routes` variable. This method was originally introduced in Tutorial 07: Creating Custom Network. The new network class looks as follows:
```
# we create a new network class to specify the expected routes
class BayBridgeOSMNetwork(Network):
def specify_routes(self, net_params):
return {
"11197898": [
"11197898", "123741311", "123741303", "90077193#0", "90077193#1",
"340686922", "236348366", "340686911#0", "340686911#1",
"340686911#2", "340686911#3", "236348361", "236348360#0", "236348360#1",
],
"123741311": [
"123741311", "123741303", "90077193#0", "90077193#1", "340686922",
"236348366", "340686911#0", "340686911#1", "340686911#2",
"340686911#3", "236348361", "236348360#0", "236348360#1"
],
"123741303": [
"123741303", "90077193#0", "90077193#1", "340686922", "236348366",
"340686911#0", "340686911#1", "340686911#2", "340686911#3", "236348361",
"236348360#0", "236348360#1"
],
"90077193#0": [
"90077193#0", "90077193#1", "340686922", "236348366", "340686911#0",
"340686911#1", "340686911#2", "340686911#3", "236348361", "236348360#0",
"236348360#1"
],
"90077193#1": [
"90077193#1", "340686922", "236348366", "340686911#0", "340686911#1",
"340686911#2", "340686911#3", "236348361", "236348360#0", "236348360#1"
],
"340686922": [
"340686922", "236348366", "340686911#0", "340686911#1", "340686911#2",
"340686911#3", "236348361", "236348360#0", "236348360#1"
],
"236348366": [
"236348366", "340686911#0", "340686911#1", "340686911#2", "340686911#3",
"236348361", "236348360#0", "236348360#1"
],
"340686911#0": [
"340686911#0", "340686911#1", "340686911#2", "340686911#3", "236348361",
"236348360#0", "236348360#1"
],
"340686911#1": [
"340686911#1", "340686911#2", "340686911#3", "236348361", "236348360#0",
"236348360#1"
],
"340686911#2": [
"340686911#2", "340686911#3", "236348361", "236348360#0", "236348360#1"
],
"340686911#3": [
"340686911#3", "236348361", "236348360#0", "236348360#1"
],
"236348361": [
"236348361", "236348360#0", "236348360#1"
],
"236348360#0": [
"236348360#0", "236348360#1"
],
"236348360#1": [
"236348360#1"
]
}
```
### 2.3 Rerunning the SImulation
We are now ready to rerun the simulation with fully defined vehicle routes and a limited number of traversable edges. If we run the cell below, we can see the new simulation in action.
```
# create the network
new_network = BayBridgeOSMNetwork(
name='bay_bridge',
net_params=net_params,
initial_config=new_initial_config,
vehicles=vehicles,
)
# create the environment
env = TestEnv(
env_params=env_params,
sim_params=sim_params,
network=new_network
)
# run the simulation for 1000 steps
exp = Experiment(env=env)
exp.run(1, 10000)
```
## 3. Other Tips
This tutorial introduces how to incorporate OpenStreetMap files in Flow. This feature, however, does not negate other features that are introduced in other tutorials and documentation. For example, if you would like to not have vehicles be originated side-by-side within a network, this can still be done by specifying a "random" spacing for vehicles as follows:
initial_config = InitialConfig(
spacing="random",
edges_distribution=EDGES_DISTRIBUTION
)
In addition, inflows of vehicles can be added to networks imported from OpenStreetMap as they are for any other network (see the tutorial on adding inflows for more on this).
| true |
code
| 0.5119 | null | null | null | null |
|
# iMCSpec (iSpec+emcee)
iMCSpec is a tool which combines iSpec(https://www.blancocuaresma.com/s/iSpec) and emcee(https://emcee.readthedocs.io/en/stable/) into a single unit to perform Bayesian analysis of spectroscopic data to estimate stellar parameters. For more details on the individual code please refer to the links above. This code have been tested on Syntehtic dataset as well as GAIA BENCHMARK stars (https://www.blancocuaresma.com/s/benchmarkstars). The example shown here is for the grid genarated MARCS.GES_atom_hfs. If you want to use any other grid, just download it from the https://www.cfa.harvard.edu/~sblancoc/iSpec/grid/ and make the necessary changes in the line_regions.
Let us import all the necessary packages that are required for this analysis.
```
import os
import sys
import numpy as np
import pandas as pd
import emcee
from multiprocessing import Pool
import matplotlib.pyplot as plt
os.environ["OMP_NUM_THREADS"] = "1"
os.environ['QT_QPA_PLATFORM']='offscreen'
os.environ["NUMEXPR_MAX_THREADS"] = "8" #CHECK NUMBER OF CORES ON YOUR MACHINE AND CHOOSE APPROPRIATELY
ispec_dir = '/home/swastik/iSpec' #MENTION YOUR DIRECTORY WHERE iSPEC is present
sys.path.insert(0, os.path.abspath(ispec_dir))
import ispec
#np.seterr(all="ignore") #FOR MCMC THE WARNING COMES FOR RED BLUE MOVES WHEN ANY PARTICULAR WALKER VALUE DONOT LIE IN THE PARAMETER SPACE
```
Let us read the input spectra. Here I have the input spectrum in .txt format for reading the spectra. You can use the .fits format also for reading the spectra using Astropy (https://docs.astropy.org/en/stable/io/fits/). Please note that my input spectra is normalized and radial velocity (RV) corrected. For normalization and RV correction you can used iSpec or iraf.
```
df = pd.read_csv('/home/swastik/Downloads/test/HPArcturus.txt', sep ='\s+') #ENTER YOUR INPUT SPECTRA
df = df[df.flux != 0] #FOR SOME SPECTROGRAPH PARTS OF SPECTRA ARE MISSING AND THE CORRESPONDING FLUX VALUES ARE LABELLED AS ZEROS. WE WANT TO IGNORE SUCH POINTS
x = df['waveobs'].values
y = df['flux'].values
yerr = df['err'].values
df = np.array(df,dtype=[('waveobs', '<f8'), ('flux', '<f8'), ('err', '<f8')])
```
You can perform the analysis on the entire spectrum or choose specific regions/segments for which you want to perform the analysis for.
```
#--- Read lines with atomic data ------------------------------------------------
# line_regions = ispec.read_line_regions(ispec_dir + "/input/regions/47000_GES/grid_synth_good_for_params_all.txt") #CHANGE THIS ACCORDINGLY FOR THE INPUT GRID
# line_regions = ispec.adjust_linemasks(df, line_regions, max_margin=0.5)
# segments = ispec.create_segments_around_lines(line_regions, margin=0.5)
# ### Add also regions from the wings of strong lines:
# ## H beta
# hbeta_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/wings_Hbeta_segments.txt")
# #segments = hbeta_segments
# segments = np.hstack((segments, hbeta_segments))
# ## H ALPHA
# halpha_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/wings_Halpha_segments.txt")
# segments = np.hstack((segments, halpha_segments))
# ## MG TRIPLET
# mgtriplet_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/wings_MgTriplet_segments.txt")
# segments = np.hstack((segments, mgtriplet_segments))
##IRON
# fe_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/fe_lines_segments.txt")
# segments = np.hstack((segments, fe_segments))
##CALCIUM TRIPLET
# catriplet_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/Calcium_Triplet_segments.txt")
# segments = np.hstack((segments, catriplet_segments))
##Na doublet
# NaDoublet_segments = ispec.read_segment_regions(ispec_dir + "/input/regions/Calcium_Triplet_segments.txt")
# segments = np.hstack((segments, NaDoublet_segments_segments))
# for j in range(len(segments)):
# segments[j][0] = segments[j][0]+0.05
# segments[j][1] = segments[j][1]-0.05
#YOU CAN CHANGE THE STARTING AND ENDING POINTS OF THE SEGEMENT
```
I will create a mask all false values with the same dimension as my original spectra in 1D. I will keep only those values of wavelength and flux for which the value falls in the segments (i.e, Mask is True).
```
# mask =np.zeros(x.shape,dtype =bool)
# for i in range(len(segments)):
# mask|= (x>segments[i][0])&(x<segments[i][1])
# x = x[mask] #SELECTING THOSE VALUES ONLY FOR WHICH MASK VALUE IS TRUE
# y = y[mask]
# #yerr = yerr[mask]
yerr = y*0.0015 #IF ERROR IS NOT SPECIFIED YOU CAN CHOOSE ACCORDINGLY
```
Now let us interpolate the spectrum using iSpec. Here for simplicity I have considered only Teff, log g and [M/H] as free parameters. Vmic and Vmac are obtained from emperical relations by Jofre et al.2013 and Maria Bergemann
```
def synthesize_spectrum(theta):
teff ,logg ,MH = theta
# alpha = ispec.determine_abundance_enchancements(MH)
alpha =0.0
microturbulence_vel = ispec.estimate_vmic(teff, logg, MH)
macroturbulence = ispec.estimate_vmac(teff, logg, MH)
limb_darkening_coeff = 0.6
resolution = 47000
vsini = 1.6 #CHANGE HERE
code = "grid"
precomputed_grid_dir = ispec_dir + "/input/grid/SPECTRUM_MARCS.GES_GESv6_atom_hfs_iso.480_680nm/"
# precomputed_grid_dir = ispec_dir + "/input/grid/SPECTRUM_MARCS.GES_GESv6_atom_hfs_iso.480_680nm_light/"
# The light grid comes bundled with iSpec. It is just for testing purpose. Donot use it for Scientific purpose.
grid = ispec.load_spectral_grid(precomputed_grid_dir)
atomic_linelist = None
isotopes = None
modeled_layers_pack = None
solar_abundances = None
fixed_abundances = None
abundances = None
atmosphere_layers = None
regions = None
if not ispec.valid_interpolated_spectrum_target(grid, {'teff':teff, 'logg':logg, 'MH':MH, 'alpha':alpha, 'vmic': microturbulence_vel}):
msg = "The specified effective temperature, gravity (log g) and metallicity [M/H] \
fall out of the spectral grid limits."
print(msg)
# Interpolation
synth_spectrum = ispec.create_spectrum_structure(x)
synth_spectrum['flux'] = ispec.generate_spectrum(synth_spectrum['waveobs'], \
atmosphere_layers, teff, logg, MH, alpha, atomic_linelist, isotopes, abundances, \
fixed_abundances, microturbulence_vel = microturbulence_vel, \
macroturbulence=macroturbulence, vsini=vsini, limb_darkening_coeff=limb_darkening_coeff, \
R=resolution, regions=regions, verbose=1,
code=code, grid=grid)
return synth_spectrum
```
You can also synthesize the spectrum directly from various atmospheric models. A skeleton of the code taken from iSpec is shown below. For more details check example.py in iSpec.
```
# def synthesize_spectrum(theta,code="spectrum"):
# teff ,logg ,MH = theta
# resolution = 47000
# alpha = ispec.determine_abundance_enchancements(MH)
# microturbulence_vel = ispec.estimate_vmic(teff, logg, MH)
# macroturbulence = ispec.estimate_vmac(teff, logg, MH)
# limb_darkening_coeff = 0.6
# regions = None
# # Selected model amtosphere, linelist and solar abundances
# #model = ispec_dir + "/input/atmospheres/MARCS/"
# #model = ispec_dir + "/input/atmospheres/MARCS.GES/"
# #model = ispec_dir + "/input/atmospheres/MARCS.APOGEE/"
# #model = ispec_dir + "/input/atmospheres/ATLAS9.APOGEE/"
# model = ispec_dir + "/input/atmospheres/ATLAS9.Castelli/"
# #model = ispec_dir + "/input/atmospheres/ATLAS9.Kurucz/"
# #model = ispec_dir + "/input/atmospheres/ATLAS9.Kirby/"
# #atomic_linelist_file = ispec_dir + "/input/linelists/transitions/VALD.300_1100nm/atomic_lines.tsv"
# #atomic_linelist_file = ispec_dir + "/input/linelists/transitions/VALD.1100_2400nm/atomic_lines.tsv"
# atomic_linelist_file = ispec_dir + "/input/linelists/transitions/GESv6_atom_hfs_iso.420_920nm/atomic_lines.tsv"
# #atomic_linelist_file = ispec_dir + "/input/linelists/transitions/GESv6_atom_nohfs_noiso.420_920nm/atomic_lines.tsv"
# isotope_file = ispec_dir + "/input/isotopes/SPECTRUM.lst"
# atomic_linelist = ispec.read_atomic_linelist(atomic_linelist_file, wave_base=wave_base, wave_top=wave_top)
# atomic_linelist = atomic_linelist[atomic_linelist['theoretical_depth'] >= 0.01]
# isotopes = ispec.read_isotope_data(isotope_file)
# if "ATLAS" in model:
# solar_abundances_file = ispec_dir + "/input/abundances/Grevesse.1998/stdatom.dat"
# else:
# # MARCS
# solar_abundances_file = ispec_dir + "/input/abundances/Grevesse.2007/stdatom.dat"
# #solar_abundances_file = ispec_dir + "/input/abundances/Asplund.2005/stdatom.dat"
# #solar_abundances_file = ispec_dir + "/input/abundances/Asplund.2009/stdatom.dat"
# #solar_abundances_file = ispec_dir + "/input/abundances/Anders.1989/stdatom.dat"
# modeled_layers_pack = ispec.load_modeled_layers_pack(model)
# solar_abundances = ispec.read_solar_abundances(solar_abundances_file)
# ## Custom fixed abundances
# #fixed_abundances = ispec.create_free_abundances_structure(["C", "N", "O"], chemical_elements, solar_abundances)
# #fixed_abundances['Abund'] = [-3.49, -3.71, -3.54] # Abundances in SPECTRUM scale (i.e., x - 12.0 - 0.036) and in the same order ["C", "N", "O"]
# ## No fixed abundances
# fixed_abundances = None
# atmosphere_layers = ispec.interpolate_atmosphere_layers(modeled_layers_pack, {'teff':teff, 'logg':logg, 'MH':MH, 'alpha':alpha}, code=code)
# synth_spectrum = ispec.create_spectrum_structure(x)
# synth_spectrum['flux'] = ispec.generate_spectrum(synth_spectrum['waveobs'],
# atmosphere_layers, teff, logg, MH, alpha, atomic_linelist, isotopes, solar_abundances,
# fixed_abundances, microturbulence_vel = microturbulence_vel,
# macroturbulence=macroturbulence, vsini=vsini, limb_darkening_coeff=limb_darkening_coeff,
# R=resolution, regions=regions, verbose=0,
# code=code)
# return synth_spectrum
```
So far we have discussed about reading the input original spectra and interpolating the synthetic spectra from iSpec. Now the important part that comes into picture is to compare the original spectra and the interpolated spectra. For this we will use Montecarlo Markhov chain method to compare both the spectrums. For this we have used the emcee package by
Dan Foreman-Mackey.
```
walkers = eval(input("Enter Walkers: ")) #WALKER IMPLIES THE INDEPENDENT RANDOMLY SELECTED PARAMETER SETS. NOTE IT SHOULD HAVE ATLEAST TWICE THE VALUE OF AVAILABLE FREE PARAMETERS
Iter = eval(input("Enter Iterations: ")) #ITERATION IMPLIES NUMBER OF RUNS THE PARAMETERS WILL BE CHECKED FOR CONVERGENCE. FOR MOST CASES 250-300 SHOULD DO.
```
We will be creating four functions for this MCMC run. The first is straightforward, and is known as the model. The model function should take as an argument a list representing our θ vector, and return the model evaluated at that θ. For completion, your model function should also have your parameter array as an input. The form of this function comes from the Gaussian probability distribution P(x)dx.
```
def log_likelihood(theta):
model = synthesize_spectrum(theta) #GENARATING THE SPECTRUM FOR A GIVEN VALUE OF THETA
sigma2 = yerr ** 2 # FINDING THE Variance
return -0.5 * np.sum((y - (model['flux'])) ** 2/ sigma2) # returns the -chi^2/2 value
```
There is no unique way to set up your prior function. For the simplistic case we have choosen the log prior function returns zero if the input values genarated randomly lies wittin the specified ranges and -infinity if it doesnt(atleast one vale should satisty this criterion). You can choose your own prior function as well.
```
def log_prior(theta):
teff, logg, MH = theta
if 3200 < teff < 6900 and 1.1 < logg < 4.8 and -2.49 < MH <= 0.49 : #CHANGE HERE
return 0.0
return -np.inf
```
The last function we need to define is lnprob(). This function combines the steps above by running the lnprior function, and if the function returned -np.inf, passing that through as a return, and if not (if all priors are good), returning the lnlike for that model (by convention we say it’s the lnprior output + lnlike output, since lnprior’s output should be zero if the priors are good). lnprob needs to take as arguments theta,x,y,and yerr, since these get passed through to lnlike.
```
def log_probability(theta):
lp = log_prior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + log_likelihood(theta)
```
Select input guess values and create intial set of stellar parameters RANDOMLY
```
initial = np.array([4650,1.8,-0.7]) #INPUT GUESS VALUES
pos = initial + np.array([100,0.1,0.1])*np.random.randn(walkers, 3) # YOU CAN CHOOSE UNIFORM RANDOM FUNCTION OR GAUSSIAUN RANDOM NUMBER GENARATOR
nwalkers, ndim = pos.shape
```
Now we will run the EMCEE sampler to run the code. This will take some time depending on the your system. But don't worry :)
```
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_probability)
sampler.run_mcmc(pos,Iter, progress=True)
```
Let us plot the Walkers and Iterations. Check out for convergence in this plot. If you see the convergence you are good to go.
```
fig, axes = plt.subplots(3, figsize=(10, 7), sharex=True)
samples = sampler.get_chain()
accepted = sampler.backend.accepted.astype(bool) #Here accepted indicated that the lines for each parameter below have converged/moved at least one time.
labels = ["teff","logg","MH"]
for i in range(ndim):
ax = axes[i]
ax.plot(samples[:, :, i], "k", alpha=0.3)
ax.set_ylabel(labels[i])
ax.yaxis.set_label_coords(-0.1, 0.5)
axes[-1].set_xlabel("step number");
```
Let us check how good is the fitting.....
```
fig, ax = plt.subplots(1, figsize=(10, 7), sharex=True)
samples = sampler.flatchain
theta_max = samples[np.argmax(sampler.flatlnprobability)]
best_fit_model = synthesize_spectrum(theta_max)
ax.plot(x,y,alpha=0.3)
ax.plot(x,best_fit_model['flux'],alpha =0.3)
ax.plot(x,y-best_fit_model['flux'],alpha =0.3)
plt.savefig('t2.pdf') #CHANGE HERE
print(('Theta max: ',theta_max)) # Genarating the spectrum for the Maximum likelyhood function.
#NOTE THE SPIKES IN THE PLOT BELOW. THESE ARE DUE TO THE FACT THAT END POINTS OF THE SPECTRUMS ARE EXTRAPOLATED
```
Since the first few runs the walkers are exploring the parameter space and convergence have not yet been achived. We will ignore such runs. This is also known as "BURN-IN".
```
new_samples = sampler.get_chain(discard=100, thin=1, flat=False)
new_samples = new_samples[:,accepted,:] # WE ARE ONLY CHOOSING THE VALUES FOR WHICH THE WALKER HAVE MOVED ATLEAST ONCE DURING THE ENTIRE ITERATION. Stagnent walkers indicates that the prior function might have returned -inf.
```
Checking the Convergence after the BURN-IN... If it seems to be converged then it is DONE.
```
fig, axes = plt.subplots(3, figsize=(10, 7), sharex=True)
for i in range(ndim):
ax = axes[i]
ax.plot(new_samples[:, :, i], "k", alpha=0.3)
ax.set_ylabel(labels[i])
ax.yaxis.set_label_coords(-0.1, 0.5)
axes[-1].set_xlabel("step number")
plt.savefig('t3.pdf') #CHANGE HERE
flat_samples = new_samples.reshape(-1,new_samples.shape[2])
np.savetxt("RNtesto.txt",flat_samples,delimiter='\t') #CHANGE HERE
```
# DATA VISUALIZATION
Now after the final list of stellar parameters it is important to visualise the stellar parameter distribution. Also it is important to check for any correlation among the stellar parameters. Here I have shown two medhods by which you can do this. Note: I have taken very few points for analysis and for a proper plot you actually need a much larger dataset (40x300:150 Burns at minimum)
```
import corner
from pandas.plotting import scatter_matrix
df = pd.read_csv('/home/swastik/RNtesto.txt',delimiter='\t',header = None)
df.columns = ["$T_{eff}$", "logg", "[M/H]"]
df.hist() #Plotting Histogram for each individual stellar parameters. THIS NEED NOT BE A GAUSSIAN ONE
#df = df[df.logg < 4.451 ] #REMOVE ANY OUTLIER DISTRIBUTION
scatter_matrix(df, alpha=0.2, figsize=(6, 6), diagonal='kde') #PLOTTING THE SCATTER MATRIX. I HAVE USED A VERY LIGHT DATASET FOR TEST PURPOSE> YOU CAN USE A MORE WALKER X ITERATION FOR A BETTER RESULT
samples = np.vstack([df]) #IT IS NECESSARY TO STACK THE DATA VERTICALLY TO OBTAIN THE DISTRIBUTION FROM THE DATA FRAME
value2 = np.mean(samples, axis=0)
plt.rcParams["font.size"] = "10" #THIS CHANGES THE FONT SIZE OF THE LABELS(NOT LEGEND)
#FINALLY... MAKING THE CORNER PLOT>>>>
#fig = corner.corner(df,show_titles=True,plot_datapoints=True,quantiles=[0.16, 0.5, 0.84],color ='black',levels=(1-np.exp(-0.5),),label_kwargs=dict(fontsize=20,color = 'black'),hist_kwargs=dict(fill = True,color = 'dodgerblue'),alpha =0.2)
fig = corner.corner(df,show_titles=True,plot_datapoints=True,quantiles=[0.16, 0.5, 0.84],color ='black',label_kwargs=dict(fontsize=20,color = 'black'),hist_kwargs=dict(fill = True,color = 'dodgerblue'),alpha =0.2)
axes = np.array(fig.axes).reshape((3, 3))
for i in range(3):
ax = axes[i, i]
ax.axvline(value2[i], color="r",alpha =0.8)
for yi in range(3):
for xi in range(yi):
ax = axes[yi, xi]
ax.axvline(value2[xi], color="r",alpha =0.8,linestyle = 'dashed')
ax.axhline(value2[yi], color="r",alpha =0.8,linestyle = 'dashed')
ax.plot(value2[xi], value2[yi], "r")
# plt.tight_layout()
#THE CORNER PLOT DONOT LOOK GREAT>> THE REASON IS FEW NUMBER OF DATA POINTS AND SHARP CONVERGENCE
```
I would like to thank Sergi blanco-cuaresma for the valuable suggestions and feedbacks regarding the iSpec code and its intregation with emcee. I would also thank
Dan Foreman-Mackey for his insightful comments on using emcee. I would also like to thank Aritra Chakraborty and Dr.Ravinder Banyal for their comments and suggestion on improving the code which might have not been possible without their help.
| true |
code
| 0.334644 | null | null | null | null |
|
[@LorenaABarba](https://twitter.com/LorenaABarba)
12 steps to Navier–Stokes
=====
***
Did you experiment in Steps [1](./01_Step_1.ipynb) and [2](./02_Step_2.ipynb) using different parameter choices? If you did, you probably ran into some unexpected behavior. Did your solution ever blow up? (In my experience, CFD students *love* to make things blow up.)
You are probably wondering why changing the discretization parameters affects your solution in such a drastic way. This notebook complements our [interactive CFD lessons](https://github.com/barbagroup/CFDPython) by discussing the CFL condition. And learn more by watching Prof. Barba's YouTube lectures (links below).
Convergence and the CFL Condition
----
***
For the first few steps, we've been using the same general initial and boundary conditions. With the parameters we initially suggested, the grid has 41 points and the timestep is 0.25 seconds. Now, we're going to experiment with increasing the size of our grid. The code below is identical to the code we used in [Step 1](./01_Step_1.ipynb), but here it has been bundled up in a function so that we can easily examine what happens as we adjust just one variable: **the grid size**.
```
import numpy #numpy is a library for array operations akin to MATLAB
from matplotlib import pyplot #matplotlib is 2D plotting library
%matplotlib inline
def linearconv(nx):
dx = 2 / (nx - 1)
nt = 20 #nt is the number of timesteps we want to calculate
dt = .025 #dt is the amount of time each timestep covers (delta t)
c = 1
u = numpy.ones(nx) #defining a numpy array which is nx elements long with every value equal to 1.
u[int(.5/dx):int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s
un = numpy.ones(nx) #initializing our placeholder array, un, to hold the values we calculate for the n+1 timestep
for n in range(nt): #iterate through time
un = u.copy() ##copy the existing values of u into un
for i in range(1, nx):
u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])
pyplot.plot(numpy.linspace(0, 2, nx), u);
```
Now let's examine the results of our linear convection problem with an increasingly fine mesh.
```
linearconv(41) #convection using 41 grid points
```
This is the same result as our Step 1 calculation, reproduced here for reference.
```
linearconv(61)
```
Here, there is still numerical diffusion present, but it is less severe.
```
linearconv(71)
```
Here the same pattern is present -- the wave is more square than in the previous runs.
```
linearconv(85)
```
This doesn't look anything like our original hat function.
### What happened?
To answer that question, we have to think a little bit about what we're actually implementing in code.
In each iteration of our time loop, we use the existing data about our wave to estimate the speed of the wave in the subsequent time step. Initially, the increase in the number of grid points returned more accurate answers. There was less numerical diffusion and the square wave looked much more like a square wave than it did in our first example.
Each iteration of our time loop covers a time-step of length $\Delta t$, which we have been defining as 0.025
During this iteration, we evaluate the speed of the wave at each of the $x$ points we've created. In the last plot, something has clearly gone wrong.
What has happened is that over the time period $\Delta t$, the wave is travelling a distance which is greater than `dx`. The length `dx` of each grid box is related to the number of total points `nx`, so stability can be enforced if the $\Delta t$ step size is calculated with respect to the size of `dx`.
$$\sigma = \frac{u \Delta t}{\Delta x} \leq \sigma_{\max}$$
where $u$ is the speed of the wave; $\sigma$ is called the **Courant number** and the value of $\sigma_{\max}$ that will ensure stability depends on the discretization used.
In a new version of our code, we'll use the CFL number to calculate the appropriate time-step `dt` depending on the size of `dx`.
```
import numpy
from matplotlib import pyplot
def linearconv(nx):
dx = 2 / (nx - 1)
nt = 20 #nt is the number of timesteps we want to calculate
c = 1
sigma = .5
dt = sigma * dx
u = numpy.ones(nx)
u[int(.5/dx):int(1 / dx + 1)] = 2
un = numpy.ones(nx)
for n in range(nt): #iterate through time
un = u.copy() ##copy the existing values of u into un
for i in range(1, nx):
u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])
pyplot.plot(numpy.linspace(0, 2, nx), u)
linearconv(41)
linearconv(61)
linearconv(81)
linearconv(101)
linearconv(121)
```
Notice that as the number of points `nx` increases, the wave convects a shorter and shorter distance. The number of time iterations we have advanced the solution at is held constant at `nt = 20`, but depending on the value of `nx` and the corresponding values of `dx` and `dt`, a shorter time window is being examined overall.
Learn More
-----
***
It's possible to do rigurous analysis of the stability of numerical schemes, in some cases. Watch Prof. Barba's presentation of this topic in **Video Lecture 9** on You Tube.
```
from IPython.display import YouTubeVideo
YouTubeVideo('Yw1YPBupZxU')
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
| true |
code
| 0.529689 | null | null | null | null |
|
## 1-2. 量子ビットに対する基本演算
量子ビットについて理解が深まったところで、次に量子ビットに対する演算がどのように表されるかについて見ていこう。
これには、量子力学の性質が深く関わっている。
1. 線型性:
詳しくは第4章で学ぶのだが、量子力学では状態(量子ビット)の時間変化はつねに(状態の重ね合わせに対して)線型になっている。つまり、**量子コンピュータ上で許された操作は状態ベクトルに対する線型変換**ということになる
。1つの量子ビットの量子状態は規格化された2次元複素ベクトルとして表現されるのだったから、
1つの量子ビットに対する操作=線型演算は$2 \times 2$の**複素行列**によって表現される。
2. ユニタリ性:
さらに、確率の合計は常に1であるという規格化条件から、量子操作に表す線形演算(量子演算)に対してさらなる制限を導くことができる。まず、各測定結果を得る確率は複素確率振幅の絶対値の2乗で与えられるので、その合計は状態ベクトルの(自分自身との)内積と一致することに注目する:
$$
|\alpha|^2 + |\beta|^2 =
(\alpha^*, \beta^*)
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right) = 1.
$$
(アスタリスク $^*$ は複素共役を表す)
量子コンピュータで操作した後の状態は、量子演算に対応する線形変換(行列)を$U$とすると、
$$
U
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right)
$$
と書ける。この状態についても上記の規格化条件が成り立つ必要があるので、
$$
(\alpha^*, \beta^*)
U^\dagger U
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right) = 1
$$
が要請される。(ダガー $^\dagger$ は行列の転置と複素共役を両方適用したものを表し、エルミート共役という)
この関係式が任意の$\alpha$, $\beta$について成り立つ必要があるので、量子演算$U$は以下の条件を満たす**ユニタリー行列**に対応する:
$$
U^{\dagger} U = U U^{\dagger} = I.
$$
すなわち、**量子ビットに対する操作は、ユニタリー行列で表される**のである。
ここで、用語を整理しておく。量子力学では、状態ベクトルに対する線形変換のことを**演算子** (operator) と呼ぶ。単に演算子という場合は、ユニタリーとは限らない任意の線形変換を指す。それに対して、上記のユニタリー性を満たす線形変換のことを**量子演算** (quantum gate) と呼ぶ。量子演算は、量子状態に対する演算子のうち、(少なくとも理論的には)**物理的に実現可能なもの**と考えることができる。
### 1量子ビット演算の例:パウリ演算子
1つの量子ビットに作用する基本的な量子演算として**パウリ演算子**を導入する。
これは量子コンピュータを学んでいく上で最も重要な演算子であるので、定義を体に染み込ませておこう。
$$
\begin{eqnarray}
I&=&
\left(\begin{array}{cc}
1 & 0
\\
0 & 1
\end{array}
\right),\;\;\;
X=
\left(\begin{array}{cc}
0 & 1
\\
1 & 0
\end{array}
\right),\;\;\;
Y &=&
\left(\begin{array}{cc}
0 & -i
\\
i & 0
\end{array}
\right),\;\;\;
Z=
\left(\begin{array}{cc}
1 & 0
\\
0 & -1
\end{array}
\right).
\end{eqnarray}
$$
各演算子のイメージを説明する。
まず、$I$は恒等演算子で、要するに「何もしない」ことを表す。
$X$は古典ビットの反転(NOT)に対応し
$$X|0\rangle = |1\rangle, \;\;
X|1\rangle = |0\rangle
$$
のように作用する。(※ブラケット表記を用いた。下記コラムも参照。)
$Z$演算子は$|0\rangle$と$|1\rangle$の位相を反転させる操作で、
$$
Z|0\rangle = |0\rangle, \;\;
Z|1\rangle = -|1\rangle
$$
と作用する。
これは$|0\rangle$と$|1\rangle$の重ね合わせの「位相」という情報を保持できる量子コンピュータ特有の演算である。
例えば、
$$
Z \frac{1}{\sqrt{2}} ( |0\rangle + |1\rangle ) = \frac{1}{\sqrt{2}} ( |0\rangle - |1\rangle )
$$
となる。
$Y$演算子は$Y=iXZ$と書け、
位相の反転とビットの反転を組み合わせたもの(全体にかかる複素数$i$を除いて)であると考えることができる。
(詳細は Nielsen-Chuang の `1.3.1 Single qubit gates` を参照)
### SymPyを用いた一量子ビット演算
SymPyではよく使う基本演算はあらかじめ定義されている。
```
from IPython.display import Image, display_png
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
init_printing() # ベクトルや行列を綺麗に表示するため
# Google Colaboratory上でのみ実行してください
from IPython.display import HTML
def setup_mathjax():
display(HTML('''
<script>
if (!window.MathJax && window.google && window.google.colab) {
window.MathJax = {
'tex2jax': {
'inlineMath': [['$', '$'], ['\\(', '\\)']],
'displayMath': [['$$', '$$'], ['\\[', '\\]']],
'processEscapes': true,
'processEnvironments': true,
'skipTags': ['script', 'noscript', 'style', 'textarea', 'code'],
'displayAlign': 'center',
},
'HTML-CSS': {
'styles': {'.MathJax_Display': {'margin': 0}},
'linebreaks': {'automatic': true},
// Disable to prevent OTF font loading, which aren't part of our
// distribution.
'imageFont': null,
},
'messageStyle': 'none'
};
var script = document.createElement("script");
script.src = "https://colab.research.google.com/static/mathjax/MathJax.js?config=TeX-AMS_HTML-full,Safe";
document.head.appendChild(script);
}
</script>
'''))
get_ipython().events.register('pre_run_cell', setup_mathjax)
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP, CPHASE
```
演算子は何番目の量子ビットに作用するか、
というのを指定して `X(0)` のように定義する。
また、これを行列表示するときには、いくつの量子ビットの空間で表現するか
`nqubits`というのを指定する必要がある。
まだ、量子ビットは1つしかいないので、
`X(0)`、`nqubits=1`としておこう。
```
X(0)
represent(X(0),nqubits=1) # パウリX
```
同様に、`Y`, `Z`なども利用することができる。それに加え、アダマール演算 `H` や、位相演算 `S`、そして$\pi/4$の位相演算 `T` も利用することができる(これらもよく出てくる演算で、定義は各行列を見てほしい):
```
represent(H(0),nqubits=1)
represent(S(0),nqubits=1)
represent(T(0),nqubits=1)
```
これらの演算を状態に作用させるのは、
```
ket0 = Qubit('0')
S(0)*Y(0)*X(0)*H(0)*ket0
```
のように `*`で書くことができる。実際に計算をする場合は `qapply()`を利用する。
```
qapply(S(0)*Y(0)*X(0)*H(0)*ket0)
```
この列ベクトル表示が必要な場合は、
```
represent(qapply(S(0)*Y(0)*X(0)*H(0)*ket0))
```
のような感じで、SymPyは簡単な行列の計算はすべて自動的にやってくれる。
---
### コラム:ブラケット記法
ここで一旦、量子力学でよく用いられるブラケット記法というものについて整理しておく。ブラケット記法に慣れると非常に簡単に見通しよく計算を行うことができる。
列ベクトルは
$$
|\psi \rangle = \left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right)
$$
とかくのであった。これを**ケット**と呼ぶ。同様に、行ベクトルは
$$
\langle \psi | = ( |\psi \rangle ) ^{\dagger} = ( \alpha ^* , \beta ^*)
$$
とかき、これを**ブラ**と呼ぶ。${\dagger}$マークは転置と複素共役を取る操作で、列ベクトルを行ベクトルへと移す。
2つのベクトル、
$$
|\psi \rangle = \left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right), \;\;\;
|\phi \rangle = \left(
\begin{array}{c}
\gamma
\\
\delta
\end{array}
\right)
$$
があったとする。ブラとケットを抱き合わせると
$$
\langle \phi | \psi \rangle = (\gamma ^* , \delta ^* ) \left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right) = \gamma ^* \alpha + \delta ^* \beta
$$
となり、**内積**に対応する。行ベクトルと列ベクトルをそれぞれブラ・ケットと呼ぶのは、このように並べて内積を取ると「ブラケット」になるからである。
逆に、背中合わせにすると
$$
|\phi \rangle \langle \psi | = \left(
\begin{array}{c}
\gamma
\\
\delta
\end{array}
\right) (\alpha ^* , \beta ^*) = \left(
\begin{array}{cc}
\gamma \alpha ^* & \gamma \beta ^*
\\
\delta \alpha ^* & \delta \beta ^*
\end{array}
\right)
$$
となり、演算子となる。例えば、$X$演算子は
$$
X= \left(
\begin{array}{cc}
0 & 1
\\
1 & 0
\end{array}
\right)
=
|0\rangle \langle 1 | + |1\rangle \langle 0|
$$
のように書ける。このことを覚えておけば
$$
\langle 0| 0\rangle = \langle 1 | 1\rangle = 1, \;\;\; \langle 0 | 1 \rangle = \langle 1 | 0 \rangle = 0
$$
から
$$
X |0\rangle = |1\rangle
$$
を行列を書かずに計算できるようになる。
**量子情報の解析計算においては、実際にベクトルの要素を書き下して計算をすることはほとんどなく、このようにブラケットを使って形式的に書いて計算してしまう場合が多い**(古典計算機上で量子コンピュータをシミュレーションする場合はベクトルをすべて書き下すことになる)。
同様に、
$$
I = |0\rangle \langle 0 | + |1\rangle \langle 1| , \;\;\; Z = |0\rangle \langle 0| - |1\rangle \langle 1|
$$
も覚えておくと便利である。
| true |
code
| 0.389663 | null | null | null | null |
|
<center><h1>Improved Graph Laplacian via Geometric Self-Consistency</h1></center>
<center>Yu-Chia Chen, Dominique Perrault-Joncas, Marina Meilă, James McQueen. University of Washington</center> <br>
<center>Original paper: <a href=https://nips.cc/Conferences/2017/Schedule?showEvent=9223>Improved Graph Laplacian via Geometric Self-Consistency] on NIPS 2017 </a></center>
## The Task
1. Problem: Estimate the ``radius`` of heat kernel in manifold embedding
1. Formally: Optimize Laplacian w.r.t. parameters (e.g. ``radius``)
1. Previous work:
1. asymptotic rates depending on the (unknown) manifold [4]
1. Embedding dependent neighborhood reconstruction [6]
1. Challenge: it’s an unsupervised problem! What “target” to choose?
## The ``radius`` affects…
1. Quality of manifold embedding via neighborhood selection
1. Laplacian-based embedding and clustering via the kernel for computing similarities
1. Estimation of other geometric quantities that depend on the Laplacian (e.g Riemannian metric) or not (e.g intrinsic dimension).
1. Regression on manifolds via Gaussian Processes or Laplacian regularization.
All the reference is the same as the poster.
## Radius Estimation on hourglass dataset
In this tutorial, we are going to estimate the radius of a noisy hourglass data. The method we used is based on our NIPS 2017 paper "[Improved Graph Laplacian via Geometric Self-Consistency](https://nips.cc/Conferences/2017/Schedule?showEvent=9223)" (Perrault-Joncas et. al). Main idea is to find an estimated radius $\hat{r}_d$ given dimension $d$ that minimize the distorsion. The distorsion is evaluated by the riemannian metrics of local tangent space.
Below are some configurations that enables plotly to render Latex properly.
```
!yes | conda install --channel=conda-forge pip nose coverage gcc cython numpy scipy scikit-learn pyflann pyamg h5py plotly
!rm -rf megaman
!git clone https://github.com/mmp2/megaman.git
!cd megaman
import plotly
plotly.offline.init_notebook_mode(connected=True)
from IPython.core.display import display, HTML
display(HTML(
'<script>'
'var waitForPlotly = setInterval( function() {'
'if( typeof(window.Plotly) !== "undefined" ){'
'MathJax.Hub.Config({ SVG: { font: "STIX-Web" }, displayAlign: "center" });'
'MathJax.Hub.Queue(["setRenderer", MathJax.Hub, "SVG"]);'
'clearInterval(waitForPlotly);'
'}}, 250 );'
'</script>'
))
```
## Generate data
This dataset used in this tutorial has a shape of hourglass, with ``size = 10000`` and dimension be 13. The first three dimensions of the data is generated by adding gaussian noises onto the noise-free hourglass data, with ``sigma_primary = 0.1``, the variance of the noises added on hourglass data. We made ``addition_dims = 10``, which is the addition noises dimension to make the whole dataset has dimension 13, with ``sigmal_additional = 0.1``, which is the variance of additional dimension.
```
from plotly.offline import iplot
#import megaman
from megaman.datasets import *
data = generate_noisy_hourglass(size=10000, sigma_primary=0.1,
addition_dims=10, sigma_additional=0.1)
```
We can visualize dataset with the following plots:
```
from megaman.plotter.scatter_3d import scatter_plot3d_plotly
import plotly.graph_objs as go
t_data = scatter_plot3d_plotly(data,marker=dict(color='rgb(0, 102, 0)',opacity=0.5))
l_data = go.Layout(title='Noisy hourglass scatter plot for first 3 axis.')
f_data = go.Figure(data=t_data,layout=l_data)
iplot(f_data)
```
## Radius estimation
To estimate the ``radius``, we need to find the pairwise distance first.
To do so, we compute the adjacency matrix using the Geometry modules in megaman.
```
rmax=5
rmin=0.1
from megaman.geometry import Geometry
geom = Geometry(adjacency_method='brute',adjacency_kwds=dict(radius=rmax))
geom.set_data_matrix(data)
dist = geom.compute_adjacency_matrix()
```
For each data points, the distortion will be estimated. If the size $N$ used in estimating the distortion is large, it will be computationally expensive. We want to choose a sample with size $N'$ such that the average distion is well estimated. In our cases, we choose $N'=1000$. The error will be around $\frac{1}{\sqrt{1000}} \approx 0.03$.
In this example, we searched radius from the minimum pairwise distance ``rmin`` to the maximum distance between points ``rmax``. By doing so, the distance matrix will be dense. If the matrix is too large to fit in the memory, smaller maximum radius ``rmax`` can be chosen to make the distance matrix sparse.
Based on the discussion above, we run radius estimation with
1. sample size=1000 (created by choosing one data point out of every 10 of the original data.)
1. radius search from ``rmin=0.1`` to ``rmax=50``, with 50 points in logspace.
1. dimension ``d=1``
Specify run_parallel=True for searching the radius in parallel.
```
%%capture
# Using magic command %%capture for supressing the std out.
from megaman.utils.estimate_radius import run_estimate_radius
import numpy as np
# subsample by 10.
sample = np.arange(0,data.shape[0],10)
distorion_vs_rad_dim1 = run_estimate_radius(
data, dist, sample=sample, d=1, rmin=rmin, rmax=rmax,
ntry=50, run_parallel=True, search_space='logspace')
```
Run radius estimation same configurations as above except
1. dimension ``d=2``
```
%%capture
distorion_vs_rad_dim2 = run_estimate_radius(
data, dist, sample=sample, d=2, rmin=0.1, rmax=5,
ntry=50, run_parallel=True, search_space='logspace')
```
### Radius estimation result
The estimated radius is the minimizer of the distorsion, denoted as $\hat{r}_{d=1}$ and $\hat{r}_{d=2}$. (In the code, it's ``est_rad_dim1`` and ``est_rad_dim2``)
```
distorsion_dim1 = distorion_vs_rad_dim1[:,1].astype('float64')
distorsion_dim2 = distorion_vs_rad_dim2[:,1].astype('float64')
rad_search_space = distorion_vs_rad_dim1[:,0].astype('float64')
argmin_d1 = np.argmin(distorsion_dim1)
argmin_d2 = np.argmin(distorsion_dim2)
est_rad_dim1 = rad_search_space[argmin_d1]
est_rad_dim2 = rad_search_space[argmin_d2]
print ('Estimated radius with d=1 is: {:.4f}'.format(est_rad_dim1))
print ('Estimated radius with d=2 is: {:.4f}'.format(est_rad_dim2))
```
### Plot distorsions with different radii
```
t_distorsion = [go.Scatter(x=rad_search_space, y=distorsion_dim1, name='Dimension = 1'),
go.Scatter(x=rad_search_space, y=distorsion_dim2, name='Dimension = 2')]
l_distorsion = go.Layout(
title='Distorsions versus radii',
xaxis=dict(
title='$\\text{Radius } r$',
type='log',
autorange=True
),
yaxis=dict(
title='Distorsion',
type='log',
autorange=True
),
annotations=[
dict(
x=np.log10(est_rad_dim1),
y=np.log10(distorsion_dim1[argmin_d1]),
xref='x',
yref='y',
text='$\\hat{r}_{d=1}$',
font = dict(size = 30),
showarrow=True,
arrowhead=7,
ax=0,
ay=-30
),
dict(
x=np.log10(est_rad_dim2),
y=np.log10(distorsion_dim2[argmin_d2]),
xref='x',
yref='y',
text='$\\hat{r}_{d=2}$',
font = dict(size = 30),
showarrow=True,
arrowhead=7,
ax=0,
ay=-30
)
]
)
f_distorsion = go.Figure(data=t_distorsion,layout=l_distorsion)
iplot(f_distorsion)
```
## Application to dimension estimation
We followed the method proposed by [Chen et. al (2011)]((http://lcsl.mit.edu/papers/che_lit_mag_ros_2011.pdf) [5] to verify the estimated radius reflect the truth intrinsic dimension of the data. The basic idea is to find the largest gap of singular value of local PCA, which correspond to the dimension of the local structure.
We first plot the average singular values versus radii.
```
%%capture
from rad_est_utils import find_argmax_dimension, estimate_dimension
rad_search_space, singular_values = estimate_dimension(data, dist)
```
The singular gap is the different between two singular values. Since the intrinsic dimension is 2, we are interested in the region where the largest singular gap is the second. The region is:
```
singular_gap = -1*np.diff(singular_values,axis=1)
second_gap_is_max_range = (np.argmax(singular_gap,axis=1) == 1).nonzero()[0]
start_idx, end_idx = second_gap_is_max_range[0], second_gap_is_max_range[-1]+1
print ('The index which maximize the second singular gap is: {}'.format(second_gap_is_max_range))
print ('The start and end index of largest continuous range is {} and {}, respectively'.format(start_idx, end_idx))
```
### Averaged singular values with different radii
Plot the averaged singular values with different radii. The gray shaded area is the continous range in which the largest singular gap is the second, (local structure has dimension equals 2). And the purple shaded area denotes the second singular gap.
By hovering the line on this plot, you can see the value of the singular gap.
```
from rad_est_utils import plot_singular_values_versus_radius, generate_layouts
t_avg_singular = plot_singular_values_versus_radius(singular_values, rad_search_space, start_idx, end_idx)
l_avg_singular = generate_layouts(start_idx, end_idx, est_rad_dim1, est_rad_dim2, rad_search_space)
f_avg_singular = go.Figure(data=t_avg_singular,layout=l_avg_singular)
iplot(f_avg_singular)
```
### Histogram of estimated dimensions with estimated radius.
We first find out the estimated dimensions of each points in the data using the estimated radius $\hat{r}_{d=1}$ and $\hat{r}_{d=2}$.
```
dimension_freq_d1 = find_argmax_dimension(data,dist, est_rad_dim1)
dimension_freq_d2 = find_argmax_dimension(data,dist, est_rad_dim2)
```
The histogram of estimated dimensions with different optimal radius is shown as below:
```
t_hist_dim = [go.Histogram(x=dimension_freq_d1,name='d=1'),
go.Histogram(x=dimension_freq_d2,name='d=2')]
l_hist_dim = go.Layout(
title='Dimension histogram',
xaxis=dict(
title='Estimated dimension'
),
yaxis=dict(
title='Counts'
),
bargap=0.2,
bargroupgap=0.1
)
f_hist_dim = go.Figure(data=t_hist_dim,layout=l_hist_dim)
iplot(f_hist_dim)
```
## Conclusion
1. Choosing the correct radius/bound/scale is important in any non-linear dimension reduction task
1. The __Geometry Consistency (GC) Algorithm__ required minimal knowledge: maximum radius, minimum radius, (optionally: dimension $d$ of the manifold.)
1. The chosen radius can be used in
1. any embedding algorithm
1. semi-supervised learning with Laplacian Regularizer (see our NIPS 2017 paper)
1. estimating dimension $d$ (as shown here)
1. The megaman python package is __scalable__, and __efficient__
<img src=https://raw.githubusercontent.com/mmp2/megaman/master/doc/images/spectra_Halpha.png width=600 />
## __Try it:__
<div style="float:left;">All the functions are implemented by the manifold learning package <a href=https://github.com/mmp2/megaman>megaman.</a> </div><a style="float:left;" href="https://anaconda.org/conda-forge/megaman"><img src="https://anaconda.org/conda-forge/megaman/badges/downloads.svg" /></a>
## Reference
[1] R. R. Coifman, S. Lafon. Diffusion maps. Applied and Computational Harmonic Analysis, 2006. <br>
[2] D. Perrault-Joncas, M. Meila, Metric learning and manifolds: Preserving the intrinsic geometry , arXiv1305.7255 <br>
[3] X. Zhou, M. Belkin. Semi-supervised learning by higher order regularization. AISTAT, 2011 <br>
[4] A. Singer. From graph to manifold laplacian: the convergence rate. Applied and Computational Harmonic Analysis, 2006. <br>
[5] G. Chen, A. Little, M. Maggioni, L. Rosasco. Some recent advances in multiscale geometric analysis of point clouds. Wavelets and multiscale analysis. Springer, 2011. <br>
[6] L. Chen, A. Buja. Local Multidimensional Scaling for nonlinear dimension reduction, graph drawing and proximity analysis, JASA,2009. <br>
| true |
code
| 0.69259 | null | null | null | null |
|
# Road Following - Live demo
In this notebook, we will use model we trained to move jetBot smoothly on track.
### Load Trained Model
We will assume that you have already downloaded ``best_steering_model_xy.pth`` to work station as instructed in "train_model.ipynb" notebook. Now, you should upload model file to JetBot in to this notebooks's directory. Once that's finished there should be a file named ``best_steering_model_xy.pth`` in this notebook's directory.
> Please make sure the file has uploaded fully before calling the next cell
Execute the code below to initialize the PyTorch model. This should look very familiar from the training notebook.
```
import torchvision
import torch
model = torchvision.models.resnet18(pretrained=False)
model.fc = torch.nn.Linear(512, 2)
```
Next, load the trained weights from the ``best_steering_model_xy.pth`` file that you uploaded.
```
model.load_state_dict(torch.load('best_steering_model_xy.pth'))
```
Currently, the model weights are located on the CPU memory execute the code below to transfer to the GPU device.
```
device = torch.device('cuda')
model = model.to(device)
model = model.eval().half()
```
### Creating the Pre-Processing Function
We have now loaded our model, but there's a slight issue. The format that we trained our model doesnt exactly match the format of the camera. To do that, we need to do some preprocessing. This involves the following steps:
1. Convert from HWC layout to CHW layout
2. Normalize using same parameters as we did during training (our camera provides values in [0, 255] range and training loaded images in [0, 1] range so we need to scale by 255.0
3. Transfer the data from CPU memory to GPU memory
4. Add a batch dimension
```
import torchvision.transforms as transforms
import torch.nn.functional as F
import cv2
import PIL.Image
import numpy as np
mean = torch.Tensor([0.485, 0.456, 0.406]).cuda().half()
std = torch.Tensor([0.229, 0.224, 0.225]).cuda().half()
def preprocess(image):
image = PIL.Image.fromarray(image)
image = transforms.functional.to_tensor(image).to(device).half()
image.sub_(mean[:, None, None]).div_(std[:, None, None])
return image[None, ...]
```
Awesome! We've now defined our pre-processing function which can convert images from the camera format to the neural network input format.
Now, let's start and display our camera. You should be pretty familiar with this by now.
```
from IPython.display import display
import ipywidgets
import traitlets
from jetbot import Camera, bgr8_to_jpeg
camera = Camera()
image_widget = ipywidgets.Image()
traitlets.dlink((camera, 'value'), (image_widget, 'value'), transform=bgr8_to_jpeg)
display(image_widget)
```
We'll also create our robot instance which we'll need to drive the motors.
```
from jetbot import Robot
robot = Robot()
```
Now, we will define sliders to control JetBot
> Note: We have initialize the slider values for best known configurations, however these might not work for your dataset, therefore please increase or decrease the sliders according to your setup and environment
1. Speed Control (speed_gain_slider): To start your JetBot increase ``speed_gain_slider``
2. Steering Gain Control (steering_gain_sloder): If you see JetBot is woblling, you need to reduce ``steering_gain_slider`` till it is smooth
3. Steering Bias control (steering_bias_slider): If you see JetBot is biased towards extreme right or extreme left side of the track, you should control this slider till JetBot start following line or track in the center. This accounts for motor biases as well as camera offsets
> Note: You should play around above mentioned sliders with lower speed to get smooth JetBot road following behavior.
```
speed_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, description='speed gain')
steering_gain_slider = ipywidgets.FloatSlider(min=0.0, max=1.0, step=0.01, value=0.2, description='steering gain')
steering_dgain_slider = ipywidgets.FloatSlider(min=0.0, max=0.5, step=0.001, value=0.0, description='steering kd')
steering_bias_slider = ipywidgets.FloatSlider(min=-0.3, max=0.3, step=0.01, value=0.0, description='steering bias')
display(speed_gain_slider, steering_gain_slider, steering_dgain_slider, steering_bias_slider)
```
Next, let's display some sliders that will let us see what JetBot is thinking. The x and y sliders will display the predicted x, y values.
The steering slider will display our estimated steering value. Please remember, this value isn't the actual angle of the target, but simply a value that is
nearly proportional. When the actual angle is ``0``, this will be zero, and it will increase / decrease with the actual angle.
```
x_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='x')
y_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='y')
steering_slider = ipywidgets.FloatSlider(min=-1.0, max=1.0, description='steering')
speed_slider = ipywidgets.FloatSlider(min=0, max=1.0, orientation='vertical', description='speed')
display(ipywidgets.HBox([y_slider, speed_slider]))
display(x_slider, steering_slider)
```
Next, we'll create a function that will get called whenever the camera's value changes. This function will do the following steps
1. Pre-process the camera image
2. Execute the neural network
3. Compute the approximate steering value
4. Control the motors using proportional / derivative control (PD)
```
angle = 0.0
angle_last = 0.0
def execute(change):
global angle, angle_last
image = change['new']
xy = model(preprocess(image)).detach().float().cpu().numpy().flatten()
x = xy[0]
y = (0.5 - xy[1]) / 2.0
x_slider.value = x
y_slider.value = y
speed_slider.value = speed_gain_slider.value
angle = np.arctan2(x, y)
pid = angle * steering_gain_slider.value + (angle - angle_last) * steering_dgain_slider.value
angle_last = angle
steering_slider.value = pid + steering_bias_slider.value
robot.left_motor.value = max(min(speed_slider.value + steering_slider.value, 1.0), 0.0)
robot.right_motor.value = max(min(speed_slider.value - steering_slider.value, 1.0), 0.0)
execute({'new': camera.value})
```
Cool! We've created our neural network execution function, but now we need to attach it to the camera for processing.
We accomplish that with the observe function.
>WARNING: This code will move the robot!! Please make sure your robot has clearance and it is on Lego or Track you have collected data on. The road follower should work, but the neural network is only as good as the data it's trained on!
```
camera.observe(execute, names='value')
```
Awesome! If your robot is plugged in it should now be generating new commands with each new camera frame.
You can now place JetBot on Lego or Track you have collected data on and see whether it can follow track.
If you want to stop this behavior, you can unattach this callback by executing the code below.
```
camera.unobserve(execute, names='value')
robot.stop()
```
### Conclusion
That's it for this live demo! Hopefully you had some fun seeing your JetBot moving smoothly on track follwing the road!!!
If your JetBot wasn't following road very well, try to spot where it fails. The beauty is that we can collect more data for these failure scenarios and the JetBot should get even better :)
| true |
code
| 0.680693 | null | null | null | null |
|
# CNTK 201A Part A: CIFAR-10 Data Loader
This tutorial will show how to prepare image data sets for use with deep learning algorithms in CNTK. The CIFAR-10 dataset (http://www.cs.toronto.edu/~kriz/cifar.html) is a popular dataset for image classification, collected by Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. It is a labeled subset of the [80 million tiny images](http://people.csail.mit.edu/torralba/tinyimages/) dataset.
The CIFAR-10 dataset is not included in the CNTK distribution but can be easily downloaded and converted to CNTK-supported format
CNTK 201A tutorial is divided into two parts:
- Part A: Familiarizes you with the CIFAR-10 data and converts them into CNTK supported format. This data will be used later in the tutorial for image classification tasks.
- Part B: We will introduce image understanding tutorials.
If you are curious about how well computers can perform on CIFAR-10 today, Rodrigo Benenson maintains a [blog](http://rodrigob.github.io/are_we_there_yet/build/classification_datasets_results.html#43494641522d3130) on the state-of-the-art performance of various algorithms.
```
from __future__ import print_function
from PIL import Image
import getopt
import numpy as np
import pickle as cp
import os
import shutil
import struct
import sys
import tarfile
import xml.etree.cElementTree as et
import xml.dom.minidom
try:
from urllib.request import urlretrieve
except ImportError:
from urllib import urlretrieve
# Config matplotlib for inline plotting
%matplotlib inline
```
## Data download
The CIFAR-10 dataset consists of 60,000 32x32 color images in 10 classes, with 6,000 images per class.
There are 50,000 training images and 10,000 test images. The 10 classes are: airplane, automobile, bird,
cat, deer, dog, frog, horse, ship, and truck.
```
# CIFAR Image data
imgSize = 32
numFeature = imgSize * imgSize * 3
```
We first setup a few helper functions to download the CIFAR data. The archive contains the files data_batch_1, data_batch_2, ..., data_batch_5, as well as test_batch. Each of these files is a Python "pickled" object produced with cPickle. To prepare the input data for use in CNTK we use three oprations:
> `readBatch`: Unpack the pickle files
> `loadData`: Compose the data into single train and test objects
> `saveTxt`: As the name suggests, saves the label and the features into text files for both training and testing.
```
def readBatch(src):
with open(src, 'rb') as f:
if sys.version_info[0] < 3:
d = cp.load(f)
else:
d = cp.load(f, encoding='latin1')
data = d['data']
feat = data
res = np.hstack((feat, np.reshape(d['labels'], (len(d['labels']), 1))))
return res.astype(np.int)
def loadData(src):
print ('Downloading ' + src)
fname, h = urlretrieve(src, './delete.me')
print ('Done.')
try:
print ('Extracting files...')
with tarfile.open(fname) as tar:
tar.extractall()
print ('Done.')
print ('Preparing train set...')
trn = np.empty((0, numFeature + 1), dtype=np.int)
for i in range(5):
batchName = './cifar-10-batches-py/data_batch_{0}'.format(i + 1)
trn = np.vstack((trn, readBatch(batchName)))
print ('Done.')
print ('Preparing test set...')
tst = readBatch('./cifar-10-batches-py/test_batch')
print ('Done.')
finally:
os.remove(fname)
return (trn, tst)
def saveTxt(filename, ndarray):
with open(filename, 'w') as f:
labels = list(map(' '.join, np.eye(10, dtype=np.uint).astype(str)))
for row in ndarray:
row_str = row.astype(str)
label_str = labels[row[-1]]
feature_str = ' '.join(row_str[:-1])
f.write('|labels {} |features {}\n'.format(label_str, feature_str))
```
In addition to saving the images in the text format, we would save the images in PNG format. In addition we also compute the mean of the image. `saveImage` and `saveMean` are two functions used for this purpose.
```
def saveImage(fname, data, label, mapFile, regrFile, pad, **key_parms):
# data in CIFAR-10 dataset is in CHW format.
pixData = data.reshape((3, imgSize, imgSize))
if ('mean' in key_parms):
key_parms['mean'] += pixData
if pad > 0:
pixData = np.pad(pixData, ((0, 0), (pad, pad), (pad, pad)), mode='constant', constant_values=128)
img = Image.new('RGB', (imgSize + 2 * pad, imgSize + 2 * pad))
pixels = img.load()
for x in range(img.size[0]):
for y in range(img.size[1]):
pixels[x, y] = (pixData[0][y][x], pixData[1][y][x], pixData[2][y][x])
img.save(fname)
mapFile.write("%s\t%d\n" % (fname, label))
# compute per channel mean and store for regression example
channelMean = np.mean(pixData, axis=(1,2))
regrFile.write("|regrLabels\t%f\t%f\t%f\n" % (channelMean[0]/255.0, channelMean[1]/255.0, channelMean[2]/255.0))
def saveMean(fname, data):
root = et.Element('opencv_storage')
et.SubElement(root, 'Channel').text = '3'
et.SubElement(root, 'Row').text = str(imgSize)
et.SubElement(root, 'Col').text = str(imgSize)
meanImg = et.SubElement(root, 'MeanImg', type_id='opencv-matrix')
et.SubElement(meanImg, 'rows').text = '1'
et.SubElement(meanImg, 'cols').text = str(imgSize * imgSize * 3)
et.SubElement(meanImg, 'dt').text = 'f'
et.SubElement(meanImg, 'data').text = ' '.join(['%e' % n for n in np.reshape(data, (imgSize * imgSize * 3))])
tree = et.ElementTree(root)
tree.write(fname)
x = xml.dom.minidom.parse(fname)
with open(fname, 'w') as f:
f.write(x.toprettyxml(indent = ' '))
```
`saveTrainImages` and `saveTestImages` are simple wrapper functions to iterate through the data set.
```
def saveTrainImages(filename, foldername):
if not os.path.exists(foldername):
os.makedirs(foldername)
data = {}
dataMean = np.zeros((3, imgSize, imgSize)) # mean is in CHW format.
with open('train_map.txt', 'w') as mapFile:
with open('train_regrLabels.txt', 'w') as regrFile:
for ifile in range(1, 6):
with open(os.path.join('./cifar-10-batches-py', 'data_batch_' + str(ifile)), 'rb') as f:
if sys.version_info[0] < 3:
data = cp.load(f)
else:
data = cp.load(f, encoding='latin1')
for i in range(10000):
fname = os.path.join(os.path.abspath(foldername), ('%05d.png' % (i + (ifile - 1) * 10000)))
saveImage(fname, data['data'][i, :], data['labels'][i], mapFile, regrFile, 4, mean=dataMean)
dataMean = dataMean / (50 * 1000)
saveMean('CIFAR-10_mean.xml', dataMean)
def saveTestImages(filename, foldername):
if not os.path.exists(foldername):
os.makedirs(foldername)
with open('test_map.txt', 'w') as mapFile:
with open('test_regrLabels.txt', 'w') as regrFile:
with open(os.path.join('./cifar-10-batches-py', 'test_batch'), 'rb') as f:
if sys.version_info[0] < 3:
data = cp.load(f)
else:
data = cp.load(f, encoding='latin1')
for i in range(10000):
fname = os.path.join(os.path.abspath(foldername), ('%05d.png' % i))
saveImage(fname, data['data'][i, :], data['labels'][i], mapFile, regrFile, 0)
# URLs for the train image and labels data
url_cifar_data = 'http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz'
# Paths for saving the text files
data_dir = './data/CIFAR-10/'
train_filename = data_dir + '/Train_cntk_text.txt'
test_filename = data_dir + '/Test_cntk_text.txt'
train_img_directory = data_dir + '/Train'
test_img_directory = data_dir + '/Test'
root_dir = os.getcwd()
if not os.path.exists(data_dir):
os.makedirs(data_dir)
try:
os.chdir(data_dir)
trn, tst= loadData('http://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz')
print ('Writing train text file...')
saveTxt(r'./Train_cntk_text.txt', trn)
print ('Done.')
print ('Writing test text file...')
saveTxt(r'./Test_cntk_text.txt', tst)
print ('Done.')
print ('Converting train data to png images...')
saveTrainImages(r'./Train_cntk_text.txt', 'train')
print ('Done.')
print ('Converting test data to png images...')
saveTestImages(r'./Test_cntk_text.txt', 'test')
print ('Done.')
finally:
os.chdir("../..")
```
| true |
code
| 0.393647 | null | null | null | null |
|
# ONNX Runtime: Tutorial for STVM execution provider
This notebook shows a simple example for model inference with STVM EP.
#### Tutorial Roadmap:
1. Prerequistes
2. Accuracy check for STVM EP
3. Configuration options
## 1. Prerequistes
Make sure that you have installed all the necessary dependencies described in the corresponding paragraph of the documentation.
Also, make sure you have the `tvm` and `onnxruntime-stvm` packages in your pip environment.
If you are using `PYTHONPATH` variable expansion, make sure it contains the following paths: `<path_to_msft_onnxrt>/onnxruntime/cmake/external/tvm_update/python` and `<path_to_msft_onnxrt>/onnxruntime/build/Linux/Release`.
### Common import
These packages can be delivered from standard `pip`.
```
import onnx
import numpy as np
from typing import List, AnyStr
from onnx import ModelProto, helper, checker, mapping
```
### Specialized import
It is better to collect these packages from source code in order to clearly understand what is available to you right now.
```
import tvm.testing
from tvm.contrib.download import download_testdata
import onnxruntime.providers.stvm # nessesary to register tvm_onnx_import_and_compile and others
```
### Helper functions for working with ONNX ModelProto
This set of helper functions allows you to recognize the meta information of the models. This information is needed for more versatile processing of ONNX models.
```
def get_onnx_input_names(model: ModelProto) -> List[AnyStr]:
inputs = [node.name for node in model.graph.input]
initializer = [node.name for node in model.graph.initializer]
inputs = list(set(inputs) - set(initializer))
return sorted(inputs)
def get_onnx_output_names(model: ModelProto) -> List[AnyStr]:
return [node.name for node in model.graph.output]
def get_onnx_input_types(model: ModelProto) -> List[np.dtype]:
input_names = get_onnx_input_names(model)
return [
mapping.TENSOR_TYPE_TO_NP_TYPE[node.type.tensor_type.elem_type]
for node in sorted(model.graph.input, key=lambda node: node.name) if node.name in input_names
]
def get_onnx_input_shapes(model: ModelProto) -> List[List[int]]:
input_names = get_onnx_input_names(model)
return [
[dv.dim_value for dv in node.type.tensor_type.shape.dim]
for node in sorted(model.graph.input, key=lambda node: node.name) if node.name in input_names
]
def get_random_model_inputs(model: ModelProto) -> List[np.ndarray]:
input_shapes = get_onnx_input_shapes(model)
input_types = get_onnx_input_types(model)
assert len(input_types) == len(input_shapes)
inputs = [np.random.uniform(size=shape).astype(dtype) for shape, dtype in zip(input_shapes, input_types)]
return inputs
```
### Wrapper helper functions for Inference
Wrapper helper functions for running model inference using ONNX Runtime EP.
```
def get_onnxruntime_output(model: ModelProto, inputs: List, provider_name: AnyStr) -> np.ndarray:
output_names = get_onnx_output_names(model)
input_names = get_onnx_input_names(model)
assert len(input_names) == len(inputs)
input_dict = {input_name: input_value for input_name, input_value in zip(input_names, inputs)}
inference_session = onnxruntime.InferenceSession(model.SerializeToString(), providers=[provider_name])
output = inference_session.run(output_names, input_dict)
# Unpack output if there's only a single value.
if len(output) == 1:
output = output[0]
return output
def get_cpu_onnxruntime_output(model: ModelProto, inputs: List) -> np.ndarray:
return get_onnxruntime_output(model, inputs, "CPUExecutionProvider")
def get_stvm_onnxruntime_output(model: ModelProto, inputs: List) -> np.ndarray:
return get_onnxruntime_output(model, inputs, "StvmExecutionProvider")
```
### Helper function for checking accuracy
This function uses the TVM API to compare two output tensors. The tensor obtained using the `CPUExecutionProvider` is used as a reference.
If a mismatch is found between tensors, an appropriate exception will be thrown.
```
def verify_with_ort_with_inputs(
model,
inputs,
out_shape=None,
opset=None,
freeze_params=False,
dtype="float32",
rtol=1e-5,
atol=1e-5,
opt_level=1,
):
if opset is not None:
model.opset_import[0].version = opset
ort_out = get_cpu_onnxruntime_output(model, inputs)
stvm_out = get_stvm_onnxruntime_output(model, inputs)
for stvm_val, ort_val in zip(stvm_out, ort_out):
tvm.testing.assert_allclose(ort_val, stvm_val, rtol=rtol, atol=atol)
assert ort_val.dtype == stvm_val.dtype
```
### Helper functions for download models
These functions use the TVM API to download models from the ONNX Model Zoo.
```
BASE_MODEL_URL = "https://github.com/onnx/models/raw/master/"
MODEL_URL_COLLECTION = {
"ResNet50-v1": "vision/classification/resnet/model/resnet50-v1-7.onnx",
"ResNet50-v2": "vision/classification/resnet/model/resnet50-v2-7.onnx",
"SqueezeNet-v1.1": "vision/classification/squeezenet/model/squeezenet1.1-7.onnx",
"SqueezeNet-v1.0": "vision/classification/squeezenet/model/squeezenet1.0-7.onnx",
"Inception-v1": "vision/classification/inception_and_googlenet/inception_v1/model/inception-v1-7.onnx",
"Inception-v2": "vision/classification/inception_and_googlenet/inception_v2/model/inception-v2-7.onnx",
}
def get_model_url(model_name):
return BASE_MODEL_URL + MODEL_URL_COLLECTION[model_name]
def get_name_from_url(url):
return url[url.rfind("/") + 1 :].strip()
def find_of_download(model_name):
model_url = get_model_url(model_name)
model_file_name = get_name_from_url(model_url)
return download_testdata(model_url, model_file_name, module="models")
```
## 2. Accuracy check for STVM EP
This section will check the accuracy. The check will be to compare the output tensors for `CPUExecutionProvider` and `STVMExecutionProvider`. See the description of `verify_with_ort_with_inputs` function used above.
### Check for simple architectures
```
def get_two_input_model(op_name: AnyStr) -> ModelProto:
dtype = "float32"
in_shape = [1, 2, 3, 3]
in_type = mapping.NP_TYPE_TO_TENSOR_TYPE[np.dtype(dtype)]
out_shape = in_shape
out_type = in_type
layer = helper.make_node(op_name, ["in1", "in2"], ["out"])
graph = helper.make_graph(
[layer],
"two_input_test",
inputs=[
helper.make_tensor_value_info("in1", in_type, in_shape),
helper.make_tensor_value_info("in2", in_type, in_shape),
],
outputs=[
helper.make_tensor_value_info(
"out", out_type, out_shape
)
],
)
model = helper.make_model(graph, producer_name="two_input_test")
checker.check_model(model, full_check=True)
return model
onnx_model = get_two_input_model("Add")
inputs = get_random_model_inputs(onnx_model)
verify_with_ort_with_inputs(onnx_model, inputs)
print("****************** Success! ******************")
```
### Check for DNN architectures
```
def get_onnx_model(model_name):
model_path = find_of_download(model_name)
onnx_model = onnx.load(model_path)
return onnx_model
model_name = "ResNet50-v1"
onnx_model = get_onnx_model(model_name)
inputs = get_random_model_inputs(onnx_model)
verify_with_ort_with_inputs(onnx_model, inputs)
print("****************** Success! ******************")
```
## 3. Configuration options
This section shows how you can configure STVM EP using custom options. For more details on the options used, see the corresponding section of the documentation.
```
provider_name = "StvmExecutionProvider"
provider_options = dict(target="llvm -mtriple=x86_64-linux-gnu",
target_host="llvm -mtriple=x86_64-linux-gnu",
opt_level=3,
freeze_weights=True,
tuning_file_path="",
tuning_type="Ansor",
)
model_name = "ResNet50-v1"
onnx_model = get_onnx_model(model_name)
input_dict = {input_name: input_value for input_name, input_value in zip(get_onnx_input_names(onnx_model),
get_random_model_inputs(onnx_model))}
output_names = get_onnx_output_names(onnx_model)
stvm_session = onnxruntime.InferenceSession(onnx_model.SerializeToString(),
providers=[provider_name],
provider_options=[provider_options]
)
output = stvm_session.run(output_names, input_dict)[0]
print(f"****************** Output shape: {output.shape} ******************")
```
| true |
code
| 0.618147 | null | null | null | null |
|
<i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
<i>Licensed under the MIT License.</i>
# Hard Negative Sampling for Object Detection
You built an object detection model, evaluated it on a test set, and are happy with its accuracy. Now you deploy the model in a real-world application and you may find that the model over-fires heavily, i.e. it detects objects where none are.
This is a common problem in machine learning because our training set only contains a limited number of images, which is not sufficient to model the appearance of every object and every background in the world. Hard negative sampling (or hard negative mining) is a useful technique to address this problem. It is a way to make the model more robust to over-fitting by identifying images which are hard for the model and hence should be added to the training set.
The technique is widely used when one has a large number of negative images however adding all to the training set would cause (i) training to become too slow; and (ii) overwhelm training with too high a ratio of negatives to positives. For many negative images the model likely already performs well and hence adding them to the training set would not improve accuracy. Therefore, we try to identify those negative images where the model is incorrect.
Note that hard-negative mining is a special case of active learning where the task is to identify images which are hard for the model, annotate these images with the ground truth label, and to add them to the training set. *Hard* could be defined as the model being wrong, or as the model being uncertain about a prediction.
# Overview
In this notebook, we train our model on a training set <i>T</i> as usual, test the model on un-seen negative candidate images <i>U</i>, and see on which images in <i>U</i> the model over-fires. These images are then introduces into the training set <i>T</i> and the model is re-trained. As dataset, we use the *fridge objects* images (`watter_bottle`, `carton`, `can`, and `milk_bottle`), similar to the [01_training_introduction](./01_training_introduction.ipynb) notebook.
<img src="./media/hard_neg.jpg" width="600"/>
The overall hard negative mining process is as follows:
* First, prepare training set <i>T</i> and negative-candidate set <i>U</i>. A small proportion of both sets are set aside for evaluation.
* Second, load a pre-trained detection model.
* Next, mine hard negatives by following steps as shown in the figure:
1. Train the model on <i>T</i>.
2. Score the model on <i>U</i>.
3. Identify `NEGATIVE_NUM` images in <i>U</i> where the model is most incorrect and add to <i>T</i>.
* Finally, repeat these steps until the model stops improving.
```
import sys
sys.path.append("../../")
import os
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import scrapbook as sb
import torch
import torchvision
from torchvision import transforms
from utils_cv.classification.data import Urls as UrlsIC
from utils_cv.common.data import unzip_url
from utils_cv.common.gpu import which_processor, is_windows
from utils_cv.detection.data import Urls as UrlsOD
from utils_cv.detection.dataset import DetectionDataset, get_transform
from utils_cv.detection.model import DetectionLearner, get_pretrained_fasterrcnn
from utils_cv.detection.plot import plot_detections, plot_grid
# Change matplotlib backend so that plots are shown on windows machines
if is_windows():
plt.switch_backend('TkAgg')
print(f"TorchVision: {torchvision.__version__}")
which_processor()
# Ensure edits to libraries are loaded and plotting is shown in the notebook.
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
Default parameters. Choose `NEGATIVE_NUM` so that the number of negative images to be added at each iteration corresponds to roughly 10-20% of the total number of images in the training set. If `NEGATIVE_NUM` is too low, then too few hard negatives get added to make a noticeable difference.
```
# Path to training images, and to the negative images
DATA_PATH = unzip_url(UrlsOD.fridge_objects_path, exist_ok=True)
NEG_DATA_PATH = unzip_url(UrlsIC.fridge_objects_negatives_path, exist_ok=True)
# Number of negative images to add to the training set after each negative mining iteration.
# Here set to 10, but this value should be around 10-20% of the total number of images in the training set.
NEGATIVE_NUM = 10
# Model parameters corresponding to the "fast_inference" parameters in the 03_training_accuracy_vs_speed notebook.
EPOCHS = 10
LEARNING_RATE = 0.005
IM_SIZE = 500
BATCH_SIZE = 2
# Use GPU if available
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
print(f"Using torch device: {device}")
assert str(device)=="cuda", "Model evaluation requires CUDA capable GPU"
```
## 1. Prepare datasets
We prepare our datasets in the following way:
* Training images in `data.train_ds` which includes initially only *fridge objects* images, and after running hard-negative mining also negative images.
* Negative candidate images in `neg_data.train_ds`.
* Test images in `data.test_ds` to evaluate accuracy on *fridge objects* images, and in `neg_data.test_ds` to evaluate how often the model misfires on images which do not contain an object-of-interest.
```
# Model training dataset T, split into 75% training and 25% test
data = DetectionDataset(DATA_PATH, train_pct=0.75)
print(f"Positive dataset: {len(data.train_ds)} training images and {len(data.test_ds)} test images.")
# Negative images split into hard-negative mining candidates U, and a negative test set.
# Setting "allow_negatives=True" since the negative images don't have an .xml file with ground truth annotations
neg_data = DetectionDataset(NEG_DATA_PATH, train_pct=0.80, batch_size=BATCH_SIZE,
im_dir = "", allow_negatives = True,
train_transforms = get_transform(train=False))
print(f"Negative dataset: {len(neg_data.train_ds)} candidates for hard negative mining and {len(neg_data.test_ds)} test images.")
```
## 2. Prepare a model
Initialize a pre-trained Faster R-CNN model similar to the [01_training_introduction](./01_training_introduction.ipynb) notebook.
```
# Pre-trained Faster R-CNN model
detector = DetectionLearner(data, im_size=IM_SIZE)
# Record after each mining iteration the validation accuracy and how many objects were found in the negative test set
valid_accs = []
num_neg_detections = []
```
## 3. Train the model on *T*
<a id='train'></a>
Model training. As described at the start of this notebook, you likely need to repeat the steps from here until the end of the notebook several times to achieve optimal results.
```
# Fine-tune model. After each epoch prints the accuracy on the validation set.
detector.fit(EPOCHS, lr=LEARNING_RATE, print_freq=30)
```
Show the accuracy on the validation set for this and all previous mining iterations.
```
# Get validation accuracy on test set at IOU=0.5:0.95
acc = float(detector.ap[-1]["bbox"])
valid_accs.append(acc)
# Plot validation accuracy versus number of hard-negative mining iterations
from utils_cv.common.plot import line_graph
line_graph(
values=(valid_accs),
labels=("Validation"),
x_guides=range(len(valid_accs)),
x_name="Hard negative mining iteration",
y_name="[email protected]:0.95",
)
```
## 4. Score the model on *U*
Run inference on all negative candidate images. The images where the model is most incorrect will later be added as hard negatives to the training set.
```
detections = detector.predict_dl(neg_data.train_dl, threshold=0)
detections[0]
```
Count how many objects were detected in the negative test set. This number typically goes down dramatically after a few mining iterations, and is an indicator how much the model over-fires on unseen images.
```
# Count number of mis-detections on negative test set
test_detections = detector.predict_dl(neg_data.test_dl, threshold=0)
bbox_scores = [bbox.score for det in test_detections for bbox in det['det_bboxes']]
num_neg_detections.append(len(bbox_scores))
# Plot
from utils_cv.common.plot import line_graph
line_graph(
values=(num_neg_detections),
labels=("Negative test set"),
x_guides=range(len(num_neg_detections)),
x_name="Hard negative mining iteration",
y_name="Number of detections",
)
```
## 5. Hard negative mining
Use the negative candidate images where the model is most incorrect as hard negatives.
```
# For each image, get maximum score (i.e. confidence in the detection) over all detected bounding boxes in the image
max_scores = []
for idx, detection in enumerate(detections):
if len(detection['det_bboxes']) > 0:
max_score = max([d.score for d in detection['det_bboxes']])
else:
max_score = float('-inf')
max_scores.append(max_score)
# Use the n images with highest maximum score as hard negatives
hard_im_ids = np.argsort(max_scores)[::-1]
hard_im_ids = hard_im_ids[:NEGATIVE_NUM]
hard_im_scores =[max_scores[i] for i in hard_im_ids]
print(f"Indentified {len(hard_im_scores)} hard negative images with detection scores in range {min(hard_im_scores)} to {max(hard_im_scores):4.2f}")
```
Plot some of the identified hard negatives images. This will likely mistake objects which were not part of the training set as the objects-of-interest.
```
# Get image paths and ground truth boxes for the hard negative images
dataset_ids = [detections[i]['idx'] for i in hard_im_ids]
im_paths = [neg_data.train_ds.dataset.im_paths[i] for i in dataset_ids]
gt_bboxes = [neg_data.train_ds.dataset.anno_bboxes[i] for i in dataset_ids]
# Plot
def _grid_helper():
for i in hard_im_ids:
yield detections[i], neg_data, None, None
plot_grid(plot_detections, _grid_helper(), rows=1)
```
## 6. Add hard negatives to *T*
We now add the identified hard negative images to the training set.
```
# Add identified hard negatives to training set
data.add_images(im_paths, gt_bboxes, target = "train")
print(f"Added {len(im_paths)} hard negative images. Now: {len(data.train_ds)} training images and {len(data.test_ds)} test images")
print(f"Completed {len(valid_accs)} hard negative iterations.")
# Preserve some of the notebook outputs
sb.glue("valid_accs", valid_accs)
sb.glue("hard_im_scores", list(hard_im_scores))
```
## Repeat
Now, **repeat** all steps starting from "[3. Train the model on T](#train)" to re-train the model and the training set T with added and add more hard negative images to the training set. **Stop** once the accuracy `valid_accs` stopped improving and if the number of (mis)detections in the negative test set `num_neg_detections` stops decreasing.
| true |
code
| 0.520862 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/cxbxmxcx/EatNoEat/blob/master/Chapter_9_Build_Nutritionist.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Imports
```
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import os
import time
from PIL import Image
import pickle
```
Download Recipe Data
```
data_folder = 'data'
recipes_zip = tf.keras.utils.get_file('recipes.zip',
origin = 'https://www.dropbox.com/s/i1hvs96mnahozq0/Recipes5k.zip?dl=1',
extract = True)
print(recipes_zip)
data_folder = os.path.dirname(recipes_zip)
os.remove(recipes_zip)
print(data_folder)
```
Setup Folder Paths
```
!dir /root/.keras/datasets
data_folder = data_folder + '/Recipes5k/'
annotations_folder = data_folder + 'annotations/'
images_folder = data_folder + 'images/'
print(annotations_folder)
print(images_folder)
%ls /root/.keras/datasets/Recipes5k/images/
```
Extra Imports
```
from fastprogress.fastprogress import master_bar, progress_bar
from IPython.display import Image
from os import listdir
from pickle import dump
```
Setup Convnet Application
```
use_NAS = False
if use_NAS:
IMG_SIZE = 224 # 299 for Inception, 224 for NASNet
IMG_SHAPE = (IMG_SIZE, IMG_SIZE, 3)
else:
IMG_SIZE = 299 # 299 for Inception, 224 for NASNet
IMG_SHAPE = (IMG_SIZE, IMG_SIZE, 3)
def load_image(image_path):
img = tf.io.read_file(image_path)
img = tf.image.decode_jpeg(img, channels=3)
img = tf.image.resize(img, (IMG_SIZE, IMG_SIZE))
if use_NAS:
img = tf.keras.applications.nasnet.preprocess_input(img)
else:
img = tf.keras.applications.inception_v3.preprocess_input(img)
return img, image_path
foods_txt = tf.keras.utils.get_file('foods.txt',
origin = 'https://www.dropbox.com/s/xyukyq62g98dx24/foods_cat.txt?dl=1')
print(foods_txt)
def get_nutrient_array(fat, protein, carbs):
nutrients = np.array([float(fat)*4, float(protein)*4, float(carbs)*4])
nutrients /= np.linalg.norm(nutrients)
return nutrients
def get_category_array(keto, carbs, health):
return np.array([float(keto)-5, float(carbs)-5, float(health)-5])
import csv
def get_food_nutrients(nutrient_file):
foods = {}
with open(foods_txt) as csv_file:
csv_reader = csv.reader(csv_file, delimiter=',')
line_count = 0
for row in csv_reader:
if line_count == 0:
print(f'Column names are {", ".join(row)}')
line_count += 1
else:
categories = get_category_array(row[1],row[2],row[3])
foods[row[0]] = categories
line_count += 1
print(f'Processed {line_count} lines.')
return foods
food_nutrients = get_food_nutrients(foods_txt)
print(food_nutrients)
def load_images(food_w_nutrients, directory):
X = []
Y = []
i=0
mb = master_bar(listdir(directory))
for food_group in mb:
try:
for pic in progress_bar(listdir(directory + food_group),
parent=mb, comment='food = ' + food_group):
filename = directory + food_group + '/' + pic
image, img_path = load_image(filename)
if i < 5:
print(img_path)
i+=1
Y.append(food_w_nutrients[food_group])
X.append(image)
except:
continue
return X,Y
X, Y = load_images(food_nutrients, images_folder)
print(len(X), len(Y))
tf.keras.backend.clear_session()
if use_NAS:
# Create the base model from the pre-trained model
base_model = tf.keras.applications.NASNetMobile(input_shape=IMG_SHAPE,
include_top=False,
weights='imagenet')
else:
# Create the base model from the pre-trained model
base_model = tf.keras.applications.InceptionResNetV2(input_shape=IMG_SHAPE,
include_top=False,
weights='imagenet')
dataset = tf.data.Dataset.from_tensor_slices((X, Y))
dataset
batches = dataset.batch(64)
for image_batch, label_batch in batches.take(1):
pass
image_batch.shape
train_size = int(len(X)*.8)
test_size = int(len(X)*.2)
batches = batches.shuffle(test_size)
train_dataset = batches.take(train_size)
test_dataset = batches.skip(train_size)
test_dataset = test_dataset.take(test_size)
feature_batch = base_model(image_batch)
print(feature_batch.shape)
base_model.trainable = True
# Let's take a look to see how many layers are in the base model
print("Number of layers in the base model: ", len(base_model.layers))
# Fine-tune from this layer onwards
if use_NAS:
fine_tune_at = 100
else:
fine_tune_at = 550
# Freeze all the layers before the `fine_tune_at` layer
for layer in base_model.layers[:fine_tune_at]:
layer.trainable = False
base_model.summary()
```
Add Regression Head
```
global_average_layer = tf.keras.layers.GlobalAveragePooling2D()
feature_batch_average = global_average_layer(feature_batch)
print(feature_batch_average.shape)
prediction_layer = tf.keras.layers.Dense(3)
prediction_batch = prediction_layer(feature_batch_average)
print(prediction_batch.shape)
model = tf.keras.Sequential([
base_model,
global_average_layer,
prediction_layer
])
base_learning_rate = 0.0001
model.compile(optimizer=tf.keras.optimizers.Nadam(lr=base_learning_rate),
loss=tf.keras.losses.MeanAbsoluteError(),
metrics=['mae', 'mse', 'accuracy'])
model.summary()
from google.colab import drive
drive.mount('/content/gdrive')
folder = '/content/gdrive/My Drive/Models'
if os.path.isdir(folder) == False:
os.makedirs(folder)
# Include the epoch in the file name (uses `str.format`)
checkpoint_path = folder + "/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)
# Create a callback that saves the model's weights every 5 epochs
cp_callback = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_path,
verbose=1,
save_weights_only=True,
period=5)
history = model.fit(batches,epochs=25, callbacks=[cp_callback])
acc = history.history['accuracy']
loss = history.history['loss']
mae = history.history['mae']
mse = history.history['mse']
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.plot(acc, label='Accuracy')
plt.legend(loc='lower right')
plt.ylabel('Accuracy')
plt.ylim([min(plt.ylim()),1])
plt.title('Training Accuracy')
plt.subplot(2, 1, 2)
plt.plot(loss, label='Loss')
plt.legend(loc='upper right')
plt.ylabel('MAE')
plt.ylim([0,5.0])
plt.title('Training Loss')
plt.xlabel('epoch')
plt.show()
def get_test_images():
directory = '/content/'
images = []
for file in listdir(directory):
if file.endswith(".jpg"):
images.append(file)
return images
images = get_test_images()
print(images)
```
```
#@title Image Prediction { run: "auto", vertical-output: true, display-mode: "form" }
image_idx = 42 #@param {type:"slider", min:0, max:100, step:1}
cnt = len(images)
if cnt > 0:
image_idx = image_idx if image_idx < cnt else cnt - 1
image = images[image_idx]
x, _ = load_image(image)
img = x[np.newaxis, ...]
predict = model.predict(img)
print(predict+5)
print(image_idx,image)
plt.imshow(x)
```
| true |
code
| 0.614394 | null | null | null | null |
|
# Load and preprocess 2012 data
We will, over time, look over other years. Our current goal is to explore the features of a single year.
---
```
%pylab --no-import-all inline
import pandas as pd
```
## Load the data.
---
If this fails, be sure that you've saved your own data in the prescribed location, then retry.
```
file = "../data/interim/2012data.dta"
df_rawest = pd.read_stata(file)
good_columns = [#'campfin_limcorp', # "Should gov be able to limit corporate contributions"
'pid_x', # Your own party identification
'abortpre_4point', # Abortion
'trad_adjust', # Moral Relativism
'trad_lifestyle', # "Newer" lifetyles
'trad_tolerant', # Moral tolerance
'trad_famval', # Traditional Families
'gayrt_discstd_x', # Gay Job Discrimination
'gayrt_milstd_x', # Gay Military Service
'inspre_self', # National health insurance
'guarpr_self', # Guaranteed Job
'spsrvpr_ssself', # Services/Spending
'aa_work_x', # Affirmative Action ( Should this be aapost_hire_x? )
'resent_workway',
'resent_slavery',
'resent_deserve',
'resent_try',
]
df_raw = df_rawest[good_columns]
```
## Clean the data
---
```
def convert_to_int(s):
"""Turn ANES data entry into an integer.
>>> convert_to_int("1. Govt should provide many fewer services")
1
>>> convert_to_int("2")
2
"""
try:
return int(s.partition('.')[0])
except ValueError:
warnings.warn("Couldn't convert: "+s)
return np.nan
except AttributeError:
return s
def negative_to_nan(value):
"""Convert negative values to missing.
ANES codes various non-answers as negative numbers.
For instance, if a question does not pertain to the
respondent.
"""
return value if value >= 0 else np.nan
def lib1_cons2_neutral3(x):
"""Rearrange questions where 3 is neutral."""
return -3 + x if x != 1 else x
def liblow_conshigh(x):
"""Reorder questions where the liberal response is low."""
return -x
def dem_edu_special_treatment(x):
"""Eliminate negative numbers and {95. Other}"""
return np.nan if x == 95 or x <0 else x
df = df_raw.applymap(convert_to_int)
df = df.applymap(negative_to_nan)
df.abortpre_4point = df.abortpre_4point.apply(lambda x: np.nan if x not in {1, 2, 3, 4} else -x)
df.loc[:, 'trad_lifestyle'] = df.trad_lifestyle.apply(lambda x: -x) # 1: moral relativism, 5: no relativism
df.loc[:, 'trad_famval'] = df.trad_famval.apply(lambda x: -x) # Tolerance. 1: tolerance, 7: not
df.loc[:, 'spsrvpr_ssself'] = df.spsrvpr_ssself.apply(lambda x: -x)
df.loc[:, 'resent_workway'] = df.resent_workway.apply(lambda x: -x)
df.loc[:, 'resent_try'] = df.resent_try.apply(lambda x: -x)
df.rename(inplace=True, columns=dict(zip(
good_columns,
["PartyID",
"Abortion",
"MoralRelativism",
"NewerLifestyles",
"MoralTolerance",
"TraditionalFamilies",
"GayJobDiscrimination",
"GayMilitaryService",
"NationalHealthInsurance",
"StandardOfLiving",
"ServicesVsSpending",
"AffirmativeAction",
"RacialWorkWayUp",
"RacialGenerational",
"RacialDeserve",
"RacialTryHarder",
]
)))
print("Variables now available: df")
df_rawest.pid_x.value_counts()
df.PartyID.value_counts()
df.describe()
df.head()
df.to_csv("../data/processed/2012.csv")
```
| true |
code
| 0.527682 | null | null | null | null |
|
# Reinterpreting Tensors
Sometimes the data in tensors needs to be interpreted as if it had different type or shape. For example, reading a binary file into memory produces a flat tensor of byte-valued data, which the application code may want to interpret as an array of data of specific shape and possibly different type.
DALI provides the following operations which affect tensor metadata (shape, type, layout):
* reshape
* reinterpret
* squeeze
* expand_dims
Thsese operations neither modify nor copy the data - the output tensor is just another view of the same region of memory, making these operations very cheap.
## Fixed Output Shape
This example demonstrates the simplest use of the `reshape` operation, assigning a new fixed shape to an existing tensor.
First, we'll import DALI and other necessary modules, and define a utility for displaying the data, which will be used throughout this tutorial.
```
import nvidia.dali as dali
import nvidia.dali.fn as fn
from nvidia.dali import pipeline_def
import nvidia.dali.types as types
import numpy as np
def show_result(outputs, names=["Input", "Output"], formatter=None):
if not isinstance(outputs, tuple):
return show_result((outputs,))
outputs = [out.as_cpu() if hasattr(out, "as_cpu") else out for out in outputs]
for i in range(len(outputs[0])):
print(f"---------------- Sample #{i} ----------------")
for o, out in enumerate(outputs):
a = np.array(out[i])
s = "x".join(str(x) for x in a.shape)
title = names[o] if names is not None and o < len(names) else f"Output #{o}"
l = out.layout()
if l: l += ' '
print(f"{title} ({l}{s})")
np.set_printoptions(formatter=formatter)
print(a)
def rand_shape(dims, lo, hi):
return list(np.random.randint(lo, hi, [dims]))
```
Now let's define out pipeline - it takes data from an external source and returns it both in original form and reshaped to a fixed square shape `[5, 5]`. Additionally, output tensors' layout is set to HW
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example1(input_data):
np.random.seed(1234)
inp = fn.external_source(input_data, batch=False, dtype=types.INT32)
return inp, fn.reshape(inp, shape=[5, 5], layout="HW")
pipe1 = example1(lambda: np.random.randint(0, 10, size=[25], dtype=np.int32))
pipe1.build()
show_result(pipe1.run())
```
As we can see, the numbers from flat input tensors have been rearranged into 5x5 matrices.
## Reshape with Wildcards
Let's now consider a more advanced use case. Imagine you have some flattened array that represents a fixed number of columns, but the number of rows is free to vary from sample to sample. In that case, you can put a wildcard dimension by specifying its shape as `-1`. Whe using wildcards, the output is resized so that the total number of elements is the same as in the input.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example2(input_data):
np.random.seed(12345)
inp = fn.external_source(input_data, batch=False, dtype=types.INT32)
return inp, fn.reshape(inp, shape=[-1, 5])
pipe2 = example2(lambda: np.random.randint(0, 10, size=[5*np.random.randint(3, 10)], dtype=np.int32))
pipe2.build()
show_result(pipe2.run())
```
## Removing and Adding Unit Dimensions
There are two dedicated operators `squeeze` and `expand_dims` which can be used for removing and adding dimensions with unit extent. The following example demonstrates the removal of a redundant dimension as well as adding two new dimensions.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example_squeeze_expand(input_data):
np.random.seed(4321)
inp = fn.external_source(input_data, batch=False, layout="CHW", dtype=types.INT32)
squeezed = fn.squeeze(inp, axes=[0])
expanded = fn.expand_dims(squeezed, axes=[0, 3], new_axis_names="FC")
return inp, fn.squeeze(inp, axes=[0]), expanded
def single_channel_generator():
return np.random.randint(0, 10,
size=[1]+rand_shape(2, 1, 7),
dtype=np.int32)
pipe_squeeze_expand = example_squeeze_expand(single_channel_generator)
pipe_squeeze_expand.build()
show_result(pipe_squeeze_expand.run())
```
## Rearranging Dimensions
Reshape allows you to swap, insert or remove dimenions. The argument `src_dims` allows you to specify which source dimension is used for a given output dimension. You can also insert a new dimension by specifying -1 as a source dimension index.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example_reorder(input_data):
np.random.seed(4321)
inp = fn.external_source(input_data, batch=False, dtype=types.INT32)
return inp, fn.reshape(inp, src_dims=[1,0])
pipe_reorder = example_reorder(lambda: np.random.randint(0, 10,
size=rand_shape(2, 1, 7),
dtype=np.int32))
pipe_reorder.build()
show_result(pipe_reorder.run())
```
## Adding and Removing Dimensions
Dimensions can be added or removed by specifying `src_dims` argument or by using dedicated `squeeze` and `expand_dims` operators.
The following example reinterprets single-channel data from CHW to HWC layout by discarding the leading dimension and adding a new trailing dimension. It also specifies the output layout.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example_remove_add(input_data):
np.random.seed(4321)
inp = fn.external_source(input_data, batch=False, layout="CHW", dtype=types.INT32)
return inp, fn.reshape(inp,
src_dims=[1,2,-1], # select HW and add a new one at the end
layout="HWC") # specify the layout string
pipe_remove_add = example_remove_add(lambda: np.random.randint(0, 10, [1,4,3], dtype=np.int32))
pipe_remove_add.build()
show_result(pipe_remove_add.run())
```
## Relative Shape
The output shape may be calculated in relative terms, with a new extent being a multiple of a source extent.
For example, you may want to combine two subsequent rows into one - doubling the number of columns and halving the number of rows. The use of relative shape can be combined with dimension rearranging, in which case the new output extent is a multiple of a _different_ source extent.
The example below reinterprets the input as having twice as many _columns_ as the input had _rows_.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example_rel_shape(input_data):
np.random.seed(1234)
inp = fn.external_source(input_data, batch=False, dtype=types.INT32)
return inp, fn.reshape(inp,
rel_shape=[0.5, 2],
src_dims=[1,0])
pipe_rel_shape = example_rel_shape(
lambda: np.random.randint(0, 10,
[np.random.randint(1,7), 2*np.random.randint(1,5)],
dtype=np.int32))
pipe_rel_shape.build()
show_result(pipe_rel_shape.run())
```
## Reinterpreting Data Type
The `reinterpret` operation can view the data as if it was of different type. When a new shape is not specified, the innermost dimension is resized accordingly.
```
@pipeline_def(device_id=0, num_threads=4, batch_size=3)
def example_reinterpret(input_data):
np.random.seed(1234)
inp = fn.external_source(input_data, batch=False, dtype=types.UINT8)
return inp, fn.reinterpret(inp, dtype=dali.types.UINT32)
pipe_reinterpret = example_reinterpret(
lambda:
np.random.randint(0, 255,
[np.random.randint(1,7), 4*np.random.randint(1,5)],
dtype=np.uint8))
pipe_reinterpret.build()
def hex_bytes(x):
f = f"0x{{:0{2*x.nbytes}x}}"
return f.format(x)
show_result(pipe_reinterpret.run(), formatter={'int':hex_bytes})
```
| true |
code
| 0.524212 | null | null | null | null |
|
<img src='./img/LogoWekeo_Copernicus_RGB_0.png' align='right' width='20%'></img>
# Tutorial on basic land applications (data processing) Version 2
In this tutorial we will use the WEkEO Jupyterhub to access and analyse data from the Copernicus Sentinel-2 and products from the [Copernicus Land Monitoring Service (CLMS)](https://land.copernicus.eu/).
A region in northern Corsica has been selected as it contains representative landscape features and process elements which can be used to demonstrate the capabilities and strengths of Copernicus space component and services.
The tutorial comprises the following steps:
1. Search and download data: We will select and download a Sentinel-2 scene and the CLMS CORINE Land Cover (CLC) data from their original archive locations via WEkEO using the Harmonised Data Access (HAD) API.
2. [Read and view Sentinel-2 data](#load_sentinel2): Once downloaded, we will read and view the Sentinel-2 data in geographic coordinates as true colour image.
3. [Process and view Sentinel-2 data as a vegetation and other spectral indices](#sentinel2_ndvi): We will see how the vegetation density and health can be assessed from optical EO data to support crop and landscape management practices.
4. [Read and view the CLC data](#display_clc): Display the thematic CLC data with the correct legend.
5. [CLC2018 burnt area in the Sentinel-2 NDVI data](#CLC_burn_NDVI): The two products give different results, but they can be combined to provide more information.
NOTE - This Jupyter Notebook contains additonal processing to demonstrate further functionality during the training debrief.
<img src='./img/Intro_banner.jpg' align='center' width='100%'></img>
## <a id='load_sentinel2'></a>2. Load required Sentinel-2 bands and True Color image at 10 m spatial resolution
Before we begin we must prepare our environment. This includes importing the various python libraries that we will need.
### Load required libraries
```
import os
import rasterio as rio
from rasterio import plot
from rasterio.mask import mask
from rasterio.plot import show_hist
import matplotlib.pyplot as plt
import geopandas as gpd
from rasterio.plot import show
from rasterio.plot import plotting_extent
import zipfile
from matplotlib import rcParams
from pathlib import Path
import numpy as np
from matplotlib.colors import ListedColormap
from matplotlib import cm
from matplotlib import colors
import warnings
warnings.filterwarnings('ignore')
from IPython.core.display import HTML
from rasterio.warp import calculate_default_transform, reproject, Resampling
import scipy.ndimage
```
The Sentinel-2 Multiple Spectral Imager (MSI) records 13 spectral bands across the visible and infrared portions of the electromagnetic spectrum at different spatial resolutions from 10 m to 60 m depending on their operation and use. There are currently two Sentinel-2 satellites in suitably phased orbits to give a revisit period of 5 days at the Equator and 2-3 days at European latitudes. Being an optical sensor they are of course also affected by cloud cover and illumination conditions. The two satellites have been fully operational since 2017 and record continuously over land and the adjacent coastal sea areas. Their specification represents a continuation and upgrade of the US Landsat system which has archive data stretching back to the mid 1980s.
<img src='./img/S2_band_comp.png' align='center' width='50%'></img>
For this training session we will only need a composite true colour image (made up of the blue green and red bands) and the individual bands for red (665 nm) and near infrared (833 nm). The cell below loads the required data.
```
#Download folder
download_dir_path = os.path.join(os.getcwd(), 'data/from_wekeo')
data_path = os.path.join(os.getcwd(), 'data')
R10 = os.path.join(download_dir_path, 'S2A_MSIL2A_20170802T101031_N0205_R022_T32TNN_20170802T101051.SAFE/GRANULE/L2A_T32TNN_A011030_20170802T101051/IMG_DATA/R10m') #10 meters resolution folder
b3 = rio.open(R10+'/L2A_T32TNN_20170802T101031_B03_10m.jp2') #green
b4 = rio.open(R10+'/L2A_T32TNN_20170802T101031_B04_10m.jp2') #red
b8 = rio.open(R10+'/L2A_T32TNN_20170802T101031_B08_10m.jp2') #near infrared
TCI = rio.open(R10+'/L2A_T32TNN_20170802T101031_TCI_10m.jp2') #true color
```
### Display True Color and False Colour Infrared images
The true colour image for the Sentinel-2 data downloaded in the previous JN can be displayed as a plot to show we have the required area and assess other aspects such as the presence of cloud, cloud shadow, etc.
In this case we selected region of northern Corsica showing the area around Bastia and the Tyrrhenian Sea out to the Italian island of Elba in the east. The area has typical Mediterranean vegetation with mountainous semi natural habitats and urban and agricultural areas along the coasts.
The cell below displays the true colour image in its native WGS-84 coordinate reference system.
The right hand plot shows the same image in false colour infrared format (FCIR). In this format the green band is displayed as blue, red as green and near infrared as red. Vegetated areas appear red and water is black.
```
fig, (ax, ay) = plt.subplots(1,2, figsize=(21,7))
show(TCI.read(), ax=ax, transform=TCI.transform, title = "TRUE COLOR")
ax.set_ylabel("Northing (m)") # (WGS 84 / UTM zone 32N)
ax.set_xlabel("Easting (m)")
ax.ticklabel_format(axis = 'both', style = 'plain')
# Function to normalize false colour infrared image
def normalize(array):
"""Normalizes numpy arrays into scale 0.0 - 1.0"""
array_min, array_max = array.min(), array.max()
return ((array - array_min)/(array_max - array_min))
nir = b8.read(1)
red = b4.read(1)
green = b3.read(1)
nirn = normalize(scipy.ndimage.zoom(nir,0.5))
redn = normalize(scipy.ndimage.zoom(red,0.5))
greenn = normalize(scipy.ndimage.zoom(green,0.5))
FCIR = np.dstack((nirn, redn, greenn))
FCIR = np.moveaxis(FCIR.squeeze(),-1,0)
show(FCIR, ax=ay, transform=TCI.transform, title = "FALSE COLOR INFRARED")
ay.set_ylabel("Northing (m)") # (WGS 84 / UTM zone 32N)
ay.set_xlabel("Easting (m)")
ay.ticklabel_format(axis = 'both', style = 'plain')
```
## <a id='sentinel2_ndvi'></a>3. Process and view Sentinel-2 data as vegetation and other spectral indices
Vegetation status is a combination of a number of properties of the vegetation related to growth, density, health and environmental factors. By making measurements of surface reflectance in the red and near infrared (NIR) parts of the spectrum optical instruments can summarise crop status through a vegetation index. The red region is related to chlorophyll absorption and the NIR is related to multiple scattering within leaf structures, therefore low red and high NIR represent healthy / dense vegetation. These values are summarised in the commonly used Normalised Difference Vegetation Index (NDVI).
<img src='./img/ndvi.jpg' align='center' width='20%'></img>
We will examine a small subset of the full image were we know differences in vegetation will be present due to natural and anthropogenic processes and calculate the NDVI to show how its value changes.
We will also calculate a second spectral index, the Normalised Difference Water Index (NDWI), which emphasises water surfaces to compare to NDVI.
To do this we'll first load some vector datasets for an area of interest (AOI) and some field boundaries.
### Open Vector Data
```
path_shp = os.path.join(os.getcwd(), 'shp')
aoi = gpd.read_file(os.path.join(path_shp, 'WEkEO-Land-AOI-201223.shp'))
LPSI = gpd.read_file(os.path.join(path_shp, 'LPIS-AOI-201223.shp'))
```
### Check CRS of Vector Data
Before we can use the vector data we must check the coordinate reference system (CRS) and then transpose them to the same CRS as the Sentinel-2 data. In this case we require all the data to be in the WGS 84 / UTM zone 32N CRS with the EPSG code of 32632.
```
print(aoi.crs)
print(LPSI.crs)
aoi_proj = aoi.to_crs(epsg=32632) #convert to WGS 84 / UTM zone 32N (Sentinel-2 crs)
LPIS_proj = LPSI.to_crs(epsg=32632)
print("conversion to S2 NDVI crs:")
print(aoi_proj.crs)
print(LPIS_proj.crs)
```
### Calculate NDVI from red and near infrared bands
First step is to calculate the NDVI for the whole image using some straightforward band maths and write out the result to a geoTIFF file.
```
nir = b8.read()
red = b4.read()
ndvi = (nir.astype(float)-red.astype(float))/(nir+red)
meta = b4.meta
meta.update(driver='GTiff')
meta.update(dtype=rio.float32)
with rio.open(os.path.join(data_path, 'S2_NDVI.tif'), 'w', **meta) as dst:
dst.write(ndvi.astype(rio.float32))
```
### Calculate NDWI from green and near infrared bands
The new step is to calculate the NDWI for the whole image using some straightforward band maths and write out the result to a geoTIFF file.
```
nir = b8.read()
green = b3.read()
ndwi = (green.astype(float) - nir.astype(float))/(nir+green)
meta = b3.meta
meta.update(driver='GTiff')
meta.update(dtype=rio.float32)
with rio.open(os.path.join(data_path, 'S2_NDWI.tif'), 'w', **meta) as dst:
dst.write(ndwi.astype(rio.float32))
```
### Crop the extent of the NDVI and NDWI images to the AOI
The file produced in the previous step is then cropped using the AOI geometry.
```
with rio.open(os.path.join(data_path, "S2_NDVI.tif")) as src:
out_image, out_transform = mask(src, aoi_proj.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform})
with rio.open(os.path.join(data_path, "S2_NDVI_masked.tif"), "w", **out_meta) as dest:
dest.write(out_image)
with rio.open(os.path.join(data_path, "S2_NDWI.tif")) as src:
out_image, out_transform = mask(src, aoi_proj.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform})
with rio.open(os.path.join(data_path, "S2_NDWI_masked.tif"), "w", **out_meta) as dest:
dest.write(out_image)
```
### Display NDVI and NDWI for the AOI
The AOI represents an area of northern Corsica centred on the town of Bagnasca. To the west are mountains dominated by forests and woodlands of evergreen sclerophyll oaks which tend to give high values of NDVI intersperse by areas of grassland or bare ground occuring naturally or as a consequnce of forest fires. The patterns are more irregular and follow the terrain and hydrological features. The lowlands to east have been clear of forest for agriculture shown by a fine scale mosaic of regular geometric features representing crop fields with diffrerent NDVIs or the presence of vegetated boundary features. The lower values of NDVI (below zero) in the east are associated with the sea and the large lagoon of the Réserve naturelle de l'étang de Biguglia.
As expected the NDWI gives high values for the open sea and lagoon areas of the image. Interestingly there are relatively high values for some of the fields in the coastal plane suggesting they may be flooded or irrigated. The bare surfaces have NDWI values below zero and the vegetated areas are lower still.
The colour map used to display the NDVI uses a ramp from blue to green to emphasise the increasing density and vigour of vegetation at high NDVI values. If distinction are not so clear the cmap value can be change from "BuGn" or "RdBu" to something more appropriate with reference to the the available colour maps at [Choosing Colormaps in Matplotlib](https://matplotlib.org/3.1.0/tutorials/colors/colormaps.html).
```
ndvi_aoi = rio.open(os.path.join(data_path, 'S2_NDVI_masked.tif'))
fig, (az, ay) = plt.subplots(1,2, figsize=(21, 7))
# use imshow so that we have something to map the colorbar to
image_hidden_1 = az.imshow(ndvi_aoi.read(1),
cmap='BuGn')
# LPIS_proj.plot(ax=ax, facecolor='none', edgecolor='k')
image = show(ndvi_aoi, ax=az, cmap='BuGn', transform=ndvi_aoi.transform, title ="NDVI")
fig.colorbar(image_hidden_1, ax=az)
az.set_ylabel("Northing (m)") #(WGS 84 / UTM zone 32N)
az.set_xlabel("Easting (m)")
az.ticklabel_format(axis = 'both', style = 'plain')
ndwi_aoi = rio.open(os.path.join(data_path, 'S2_NDWI_masked.tif'))
# use imshow so that we have something to map the colorbar to
image_hidden_1 = ay.imshow(ndwi_aoi.read(1),
cmap='RdBu')
# LPIS_proj.plot(ax=ax, facecolor='none', edgecolor='k')
image = show(ndwi_aoi, ax=ay, cmap='RdBu', transform=ndwi_aoi.transform, title ="NDWI")
fig.colorbar(image_hidden_1, ax=ay)
ay.set_ylabel("Northing (m)") #(WGS 84 / UTM zone 32N)
ay.set_xlabel("Easting (m)")
ay.ticklabel_format(axis = 'both', style = 'plain')
```
### Histogram of NDVI values
If the NDVI values for the area are summarised as a histogram the two main levels of vegetation density / vigour become apprent. On the left of the plot there is a peak between NDVI values of -0.1 and 0.3 for the water and unvegetated areas together (with the water generally lower) and on the right the peak around an NDVI value of 0.8 is the dense forest and vigorous crops. The region in between shows spare vegetation, grassland and crops that are yet to mature.
In the NDWI histogram there are multiple peaks representing the sea and lagoons, bare surfaes and vegetation respectively. The NDVI and NDWI can be used in combination to characterise regons within satellite images.
```
fig, axhist = plt.subplots(1,1)
show_hist(ndvi_aoi, bins=100, masked=False, title='Histogram of NDVI values', facecolor = 'g', ax =axhist)
axhist.set_xlabel('NDVI')
axhist.set_ylabel('number of pixels')
plt.gca().get_legend().remove()
fig, axhist = plt.subplots(1,1)
show_hist(ndwi_aoi, bins=100, masked=False, title='Histogram of NDWI values', facecolor = 'b', ax =axhist)
axhist.set_xlabel('NDWI')
axhist.set_ylabel('number of pixels')
plt.gca().get_legend().remove()
```
### NDVI index on a cultivation pattern area
We can look in more detail at the agricultural area to see the patterns in the NDVI values caused by differential crop density and growth. As before we load a vector file containing an AOI, subset the original Sentinel-2 NDVI image. This time we over lay a set of field boundaries from the Land Parcel Information System (LPIS) which highlight some of the management units.
This analysis gives us a representation of the biophysical properties of the surface at the time of image acquisition.
```
#Load shapefile of the AOIs
cult_zoom = gpd.read_file(os.path.join(path_shp, 'complex_cultivation_patterns_zoom.shp'))
#Subset the Sentinel-2 NDVI image
with rio.open(os.path.join(data_path, "S2_NDVI.tif")) as src:
out_image, out_transform = mask(src, cult_zoom.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform})
with rio.open(os.path.join(data_path, "NDVI_cultivation_area.tif"), "w", **out_meta) as dest:
dest.write(out_image.astype(rio.float32))
#Display the results with the LPIS
rcParams['axes.titlepad'] = 20
src_cult = rio.open(os.path.join(data_path, "NDVI_cultivation_area.tif"))
fig, axg = plt.subplots(figsize=(21, 7))
image_hidden_1 = axg.imshow(src_cult.read(1),
cmap='BuGn')
LPIS_proj.plot(ax=axg, facecolor='none', edgecolor='k')
show(src_cult, ax=axg, cmap='BuGn', transform=src_cult.transform, title='NDVI - Complex cultivation patterns')
fig.colorbar(image_hidden_1, ax=axg)
axg.set_ylabel("Northing (m)") #(WGS 84 / UTM zone 32N)
axg.set_xlabel("Easting (m)")
plt.subplots_adjust(bottom=0.1, right=0.6, top=0.9)
axg.ticklabel_format(axis = 'both', style = 'plain')
```
## <a id='display_clc'></a>4. Read and view the CLC data
The CORINE Land Cover (CLC) inventory has been produced at a European level in 1990, 2000, 2006, 2012, and 2018. It records land cover and land use in 44 classes with a Minimum Mapping Unit (MMU) of 25 hectares (ha) and a minimum feature width of 100 m. The time series of status maps are complemented by change layers, which highlight changes between the land cover land use classes with an MMU of 5 ha. The Eionet network of National Reference Centres Land Cover (NRC/LC) produce the CLC databases at Member State level, which are coordinated and integrated by EEA. CLC is produced by the majority of countries by visual interpretation of high spatial resolution satellite imagery (10 - 30 m spatial resolution). In a few countries semi-automatic solutions are applied, using national in-situ data, satellite image processing, GIS integration and generalisation. CLC has a wide variety of applications, underpinning various policies in the domains of environment, but also agriculture, transport, spatial planning etc.
### Crop the extent of the Corine Land Cover 2018 (CLC 2018) to the AOI and display
As with the Sentinel-2 data it is necesasary to crop the pan-European CLC2018 dataset to be able to review it at the local level.
### Set up paths to data
```
#path to Corine land cover 2018
land_cover_dir = Path(os.path.join(download_dir_path,'u2018_clc2018_v2020_20u1_raster100m/DATA/'))
legend_dir = Path(os.path.join(download_dir_path,'u2018_clc2018_v2020_20u1_raster100m/Legend/'))
#path to the colormap
txt_filename = legend_dir/'CLC2018_CLC2018_V2018_20_QGIS.txt'
```
### Re-project vector files to the same coordinate system of the CLC 2018
```
aoi_3035 = aoi.to_crs(epsg=3035) # EPSG:3035 (ETRS89-extended / LAEA Europe)
```
### Write CLC 2018 subset
```
with rio.open(str(land_cover_dir)+'/U2018_CLC2018_V2020_20u1.tif') as src:
out_image, out_transform = mask(src, aoi_3035.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform,
"dtype": "int8",
"nodata":0
})
with rio.open("CLC_masked/Corine_masked.tif", "w", **out_meta) as dest:
dest.write(out_image)
```
### Set up the legend for the CLC data
As the CLC data is thematic in nature we must set up a legend to be displayed with the results showing the colour, code and definition of each land cover / land use class.
### Read CLC 2018 legend
A text file is availabe which contains the details of the CLC nomenclature for building the legend when displaying CLC.
```
### Create colorbar
def parse_line(line):
_, r, g, b, a, descr = line.split(',')
return (int(r), int(g), int(b), int(a)), descr.split('\n')[0]
with open(txt_filename, 'r') as txtf:
lines = txtf.readlines()
legend = {nline+1: parse_line(line) for nline, line in enumerate(lines[:-1])}
legend[0] = parse_line(lines[-1])
#print code and definition of each land cover / land use class
def parse_line_class_list(line):
class_id, r, g, b, a, descr = line.split(',')
return (int(class_id), int(r), int(g), int(b), int(a)), descr.split('\n')[0]
with open(txt_filename, 'r') as txtf:
lines = txtf.readlines()
legend_class = {nline+1: parse_line_class_list(line) for nline, line in enumerate(lines[:-1])}
legend_class[0] = parse_line_class_list(lines[-1])
print('Level 3 classes')
for k, v in sorted(legend_class.items()):
print(f'{v[0][0]}\t{v[1]}')
```
### Build the legend for the CLC 2018 in the area of interest
As less than half of the CLC classes are present in the AOI an area specific legend will be built to simplify interpretation.
```
#open CLC 2018 subset
cover_land = rio.open("CLC_masked/Corine_masked.tif")
array_rast = cover_land.read(1)
#Set no data value to 0
array_rast[array_rast == -128] = 0
class_aoi = list(np.unique(array_rast))
legend_aoi = dict((k, legend[k]) for k in class_aoi if k in legend)
classes_list =[]
number_list = []
for k, v in sorted(legend_aoi.items()):
#print(f'{k}:\t{v[1]}')
classes_list.append(v[1])
number_list.append(k)
class_dict = dict(zip(classes_list,number_list))
#create the colobar
corine_cmap_aoi= ListedColormap([np.array(v[0]).astype(float)/255.0 for k, v in sorted(legend_aoi.items())])
# Map the values in [0, 22]
new_dict = dict()
for i, v in enumerate(class_dict.items()):
new_dict[v[1]] = (v[0], i)
fun = lambda x : new_dict[x][1]
matrix = map(np.vectorize(fun), array_rast)
matrix = np.matrix(list(matrix))
```
### Display the CLC2018 data for the AOI
The thematic nature and the 100 m spatial resolution of the CLC2018 give a very different view of the landscape compared to the Sentinel-2 data. CLC2018 offers a greater information content as it is a combination of multiple images, ancillary data and human interpretation while Sentinel-2 offers great spatial information for one instance in time.
The separation of the mountains with woodland habitats and the coastal planes with agriculture can be clearly seen marked by a line of urban areas. The mountains are dominated by deciduous woodland, sclerophyllous vegetation and transitional scrub. The coastal planes consist of various types of agricultural land associated with small field farming practices.
The most striking feature of the CLC2018 data is a large burnt area which resulted from a major forest fire in July 2017.
```
#plot
fig2, axs2 = plt.subplots(figsize=(10,10),sharey=True)
show(matrix, ax=axs2, cmap=corine_cmap_aoi, transform = cover_land.transform, title = "Corine Land Cover 2018")
norm = colors.BoundaryNorm(np.arange(corine_cmap_aoi.N + 1), corine_cmap_aoi.N + 1)
cb = plt.colorbar(cm.ScalarMappable(norm=norm, cmap=corine_cmap_aoi), ax=axs2, fraction=0.03)
cb.set_ticks([x+.5 for x in range(-1,22)]) # move the marks to the middle
cb.set_ticklabels(list(class_dict.keys())) # label the colors
axs2.ticklabel_format(axis = 'both', style = 'plain')
axs2.set_ylabel("Northing (m)") #EPSG:3035 (ETRS89-extended / LAEA Europe)
axs2.set_xlabel("Easting (m)")
```
## <a id='CLC_burn_NDVI'></a>5. CLC2018 burnt area in the Sentinel-2 NDVI data
The area of the burn will have a very low NDVI compared to the surounding unburnt vegetation. The boundary of the burn can be easily seen as well as remnants of the original vegetation which have survived the burn.
```
#Load shapefile of the AOIs and check the crs
burnt_aoi = gpd.read_file(os.path.join(path_shp, 'burnt_area.shp'))
print("vector file crs:")
print(burnt_aoi.crs)
burnt_aoi_32632 = burnt_aoi.to_crs(epsg=32632) #Sentinel-2 NDVI crs
print("conversion to S2 NDVI crs:")
print(burnt_aoi_32632.crs)
```
### Crop the extent of the NDVI image for burnt area
```
with rio.open(os.path.join(data_path, 'S2_NDVI_masked.tif')) as src:
out_image, out_transform = mask(src, burnt_aoi_32632.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform})
with rio.open(os.path.join(data_path, "NDVI_burnt_area.tif"), "w", **out_meta) as dest:
dest.write(out_image)
```
### Crop the extent of the CLC 2018 for burnt area
```
#open CLC 2018 subset
cover_land = rio.open("CLC_masked/Corine_masked.tif")
print(cover_land.crs) #CLC 2018 crs
burn_aoi_3035 = burnt_aoi.to_crs(epsg=3035) #conversion to CLC 2018 crs
with rio.open(str(land_cover_dir)+'/U2018_CLC2018_V2020_20u1.tif') as src:
out_image, out_transform = mask(src, burn_aoi_3035.geometry,crop=True)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": out_image.shape[1],"width": out_image.shape[2],
"transform": out_transform,
"dtype": "int8",
"nodata":0
})
with rio.open("CLC_masked/Corine_burnt_area.tif", "w", **out_meta) as dest:
dest.write(out_image)
# Re-project S2 NDVI image to CLC 2018 crs
clc_2018_burnt_aoi = rio.open("CLC_masked/Corine_burnt_area.tif")
dst_crs = clc_2018_burnt_aoi.crs
with rio.open(os.path.join(data_path, "NDVI_burnt_area.tif")) as src:
transform, width, height = calculate_default_transform(
src.crs, dst_crs, src.width, src.height, *src.bounds)
kwargs = src.meta.copy()
kwargs.update({
'crs': dst_crs,
'transform': transform,
'width': width,
'height': height
})
with rio.open(os.path.join(data_path, "NDVI_burnt_area_EPSG_3035.tif"), 'w', **kwargs) as dst:
reproject(source=rio.band(src,1),
destination=rio.band(dst,1),
src_transform=src.transform,
src_crs=src.crs,
dst_transform=transform,
dst_crs=dst_crs,
resampling=Resampling.nearest)
```
### Display NDVI index on the AOIs
```
# Build the legend for the CLC 2018 in the area of interest
array_rast_b = clc_2018_burnt_aoi.read(1)
#Set no data value to 0
array_rast_b[array_rast_b == -128] = 0
class_aoi_b = list(np.unique(array_rast_b))
legend_aoi_b = dict((k, legend[k]) for k in class_aoi_b if k in legend)
classes_list_b =[]
number_list_b = []
for k, v in sorted(legend_aoi_b.items()):
#print(f'{k}:\t{v[1]}')
classes_list_b.append(v[1])
number_list_b.append(k)
class_dict_b = dict(zip(classes_list_b,number_list_b))
#create the colobar
corine_cmap_aoi_b= ListedColormap([np.array(v[0]).astype(float)/255.0 for k, v in sorted(legend_aoi_b.items())])
# Map the values in [0, 22]
new_dict_b = dict()
for i, v in enumerate(class_dict_b.items()):
new_dict_b[v[1]] = (v[0], i)
fun_b = lambda x : new_dict_b[x][1]
matrix_b = map(np.vectorize(fun_b), array_rast_b)
matrix_b = np.matrix(list(matrix_b))
#Plot
rcParams['axes.titlepad'] = 20
src_burnt = rio.open(os.path.join(data_path, "NDVI_burnt_area_EPSG_3035.tif"))
fig_b, (axr_b, axg_b) = plt.subplots(1,2, figsize=(25, 8))
image_hidden_1_b = axr_b.imshow(src_burnt.read(1),
cmap='BuGn')
show(src_burnt, ax=axr_b, cmap='BuGn', transform=src_burnt.transform, title='NDVI - Burnt area')
show(matrix_b, ax=axg_b, cmap=corine_cmap_aoi_b, transform=clc_2018_burnt_aoi.transform, title='CLC 2018 - Burnt area')
fig_b.colorbar(image_hidden_1_b, ax=axr_b)
plt.tight_layout(h_pad=1.0)
norm = colors.BoundaryNorm(np.arange(corine_cmap_aoi_b.N + 1), corine_cmap_aoi_b.N + 1)
cb = plt.colorbar(cm.ScalarMappable(norm=norm, cmap=corine_cmap_aoi_b), ax=axg_b, fraction=0.03)
cb.set_ticks([x+.5 for x in range(-1,6)]) # move the marks to the middle
cb.set_ticklabels(list(class_dict_b.keys())) # label the colors
axg_b.ticklabel_format(axis = 'both', style = 'plain')
axr_b.set_ylabel("Northing (m)") #(WGS 84 / UTM zone 32N)
axr_b.set_xlabel("Easting (m)")
axg_b.set_ylabel("Northing (m)") #(WGS 84 / UTM zone 32N)
axg_b.set_xlabel("Easting (m)")
axr_b.ticklabel_format(axis = 'both', style = 'plain')
axg_b.ticklabel_format(axis = 'both', style = 'plain')
plt.tight_layout(h_pad=1.0)
```
<hr>
<p><img src='./img/all_partners_wekeo_2.png' align='left' alt='Logo EU Copernicus' width='100%'></img></p>
| true |
code
| 0.513242 | null | null | null | null |
|
# Nonlinear Equations
We want to find a root of the nonlinear function $f$ using different methods.
1. Bisection method
2. Newton method
3. Chord method
4. Secant method
5. Fixed point iterations
```
%matplotlib inline
from numpy import *
from matplotlib.pyplot import *
import sympy as sym
t = sym.symbols('t')
f_sym = t/8. * (63.*t**4 - 70.*t**2. +15.) # Legendre polynomial of order 5
f_prime_sym = sym.diff(f_sym,t)
f = sym.lambdify(t, f_sym, 'numpy')
f_prime = sym.lambdify(t,f_prime_sym, 'numpy')
phi = lambda x : 63./70.*x**3 + 15./(70.*x)
#phi = lambda x : 70.0/15.0*x**3 - 63.0/15.0*x**5
#phi = lambda x : sqrt((63.*x**4 + 15.0)/70.)
# Let's plot
n = 1025
x = linspace(-1,1,n)
c = zeros_like(x)
_ = plot(x,f(x))
_ = plot(x,c)
_ = grid()
# Initial data for the variuos algorithms
# interval in which we seek the solution
a = 0.7
b = 1.
# initial points
x0 = (a+b)/2.0
x00 = b
# stopping criteria
eps = 1e-10
n_max = 1000
```
## Bisection method
$$
x^k = \frac{a^k+b^k}{2}
$$
```
if (f(a_k) * f(x_k)) < 0:
b_k1 = x_k
a_k1 = a_k
else:
a_k1 = x_k
b_k1 = b_k
```
```
def bisect(f,a,b,eps,n_max):
assert(f(a) * f(b) < 0)
a_new = a
b_new = b
x = mean([a,b])
err = eps + 1.
errors = [err]
it = 0
while (err > eps and it < n_max):
if ( f(a_new) * f(x) < 0 ):
# root in (a_new,x)
b_new = x
else:
# root in (x,b_new)
a_new = x
x_new = mean([a_new,b_new])
#err = 0.5 *(b_new -a_new)
err = abs(f(x_new))
#err = abs(x-x_new)
errors.append(err)
x = x_new
it += 1
semilogy(errors)
print(it)
print(x)
print(err)
return errors
errors_bisect = bisect(f,a,b,eps,n_max)
# is the number of iterations coherent with the theoretical estimation?
```
In order to find out other methods for solving non-linear equations, let's compute the Taylor's series of $f(x^k)$ up to the first order
$$
f(x^k) \simeq f(x^k) + (x-x^k)f^{\prime}(x^k)
$$
which suggests the following iterative scheme
$$
x^{k+1} = x^k - \frac{f(x^k)}{f^{\prime}(x^k)}
$$
The following methods are obtained applying the above scheme where
$$
f^{\prime}(x^k) \approx q^k
$$
## Newton's method
$$
q^k = f^{\prime}(x^k)
$$
$$
x^{k+1} = x^k - \frac{f(x^k)}{q^k}
$$
```
def newton(f,f_prime,x0,eps,n_max):
x_new = x0
err = eps + 1.
errors = [err]
it = 0
while (err > eps and it < n_max):
x_new = x_new - (f(x_new)/f_prime(x_new))
err = abs(f(x_new))
errors.append(err)
it += 1
semilogy(errors)
print(it)
print(x_new)
print(err)
return errors
%time errors_newton = newton(f,f_prime,1.0,eps,n_max)
```
## Chord method
$$
q^k \equiv q = \frac{f(b)-f(a)}{b-a}
$$
$$
x^{k+1} = x^k - \frac{f(x^k)}{q}
$$
```
def chord(f,a,b,x0,eps,n_max):
x_new = x0
err = eps + 1.
errors = [err]
it = 0
while (err > eps and it < n_max):
x_new = x_new - (f(x_new)/((f(b) - f(a)) / (b - a)))
err = abs(f(x_new))
errors.append(err)
it += 1
semilogy(errors)
print(it)
print(x_new)
print(err)
return errors
errors_chord = chord (f,a,b,x0,eps,n_max)
```
## Secant method
$$
q^k = \frac{f(x^k)-f(x^{k-1})}{x^k - x^{k-1}}
$$
$$
x^{k+1} = x^k - \frac{f(x^k)}{q^k}
$$
Note that this algorithm requirs **two** initial points
```
def secant(f,x0,x00,eps,n_max):
xk = x00
x_new = x0
err = eps + 1.
errors = [err]
it = 0
while (err > eps and it < n_max):
temp = x_new
x_new = x_new - (f(x_new)/((f(x_new)-f(xk))/(x_new - xk)))
xk = temp
err = abs(f(x_new))
errors.append(err)
it += 1
semilogy(errors)
print(it)
print(x_new)
print(err)
return errors
errors_secant = secant(f,x0,x00,eps,n_max)
```
## Fixed point iterations
$$
f(x)=0 \to x-\phi(x)=0
$$
$$
x^{k+1} = \phi(x^k)
$$
```
def fixed_point(phi,x0,eps,n_max):
x_new = x0
err = eps + 1.
errors = [err]
it = 0
while (err > eps and it < n_max):
x_new = phi(x_new)
err = abs(f(x_new))
errors.append(err)
it += 1
semilogy(errors)
print(it)
print(x_new)
print(err)
return errors
errors_fixed = fixed_point(phi,0.3,eps,n_max)
```
## Comparison
```
# plot the error convergence for the methods
loglog(errors_bisect, label='bisect')
loglog(errors_chord, label='chord')
loglog(errors_secant, label='secant')
loglog(errors_newton, label ='newton')
loglog(errors_fixed, label ='fixed')
_ = legend()
# Let's compare the scipy implmentation of Newton's method with our..
import scipy.optimize as opt
%time opt.newton(f, 1.0, f_prime, tol = eps)
```
We see that the scipy method is 1000 times slower than the `scipy` one
| true |
code
| 0.44571 | null | null | null | null |
|
Lambda School Data Science
*Unit 2, Sprint 3, Module 2*
---
# Permutation & Boosting
You will use your portfolio project dataset for all assignments this sprint.
## Assignment
Complete these tasks for your project, and document your work.
- [ ] If you haven't completed assignment #1, please do so first.
- [ ] Continue to clean and explore your data. Make exploratory visualizations.
- [ ] Fit a model. Does it beat your baseline?
- [ ] Try xgboost.
- [ ] Get your model's permutation importances.
You should try to complete an initial model today, because the rest of the week, we're making model interpretation visualizations.
But, if you aren't ready to try xgboost and permutation importances with your dataset today, that's okay. You can practice with another dataset instead. You may choose any dataset you've worked with previously.
The data subdirectory includes the Titanic dataset for classification and the NYC apartments dataset for regression. You may want to choose one of these datasets, because example solutions will be available for each.
## Reading
Top recommendations in _**bold italic:**_
#### Permutation Importances
- _**[Kaggle / Dan Becker: Machine Learning Explainability](https://www.kaggle.com/dansbecker/permutation-importance)**_
- [Christoph Molnar: Interpretable Machine Learning](https://christophm.github.io/interpretable-ml-book/feature-importance.html)
#### (Default) Feature Importances
- [Ando Saabas: Selecting good features, Part 3, Random Forests](https://blog.datadive.net/selecting-good-features-part-iii-random-forests/)
- [Terence Parr, et al: Beware Default Random Forest Importances](https://explained.ai/rf-importance/index.html)
#### Gradient Boosting
- [A Gentle Introduction to the Gradient Boosting Algorithm for Machine Learning](https://machinelearningmastery.com/gentle-introduction-gradient-boosting-algorithm-machine-learning/)
- _**[A Kaggle Master Explains Gradient Boosting](http://blog.kaggle.com/2017/01/23/a-kaggle-master-explains-gradient-boosting/)**_
- [_An Introduction to Statistical Learning_](http://www-bcf.usc.edu/~gareth/ISL/ISLR%20Seventh%20Printing.pdf) Chapter 8
- [Gradient Boosting Explained](http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html)
- _**[Boosting](https://www.youtube.com/watch?v=GM3CDQfQ4sw) (2.5 minute video)**_
```
# all imports needed for this sheet
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
import category_encoders as ce
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
from sklearn.feature_selection import f_regression, SelectKBest
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.model_selection import validation_curve
from sklearn.tree import DecisionTreeRegressor
import xgboost as xgb
%matplotlib inline
import seaborn as sns
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
pip install category_encoders
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
!pip install eli5
# If you're working locally:
else:
DATA_PATH = '../data/'
df = pd.read_excel(DATA_PATH+'/Unit_2_project_data.xlsx')
exit_reasons = ['Rental by client with RRH or equivalent subsidy',
'Rental by client, no ongoing housing subsidy',
'Staying or living with family, permanent tenure',
'Rental by client, other ongoing housing subsidy',
'Permanent housing (other than RRH) for formerly homeless persons',
'Staying or living with friends, permanent tenure',
'Owned by client, with ongoing housing subsidy',
'Rental by client, VASH housing Subsidy'
]
# pull all exit destinations from main data file and sum up the totals of each destination,
# placing them into new df for calculations
exits = df['3.12 Exit Destination'].value_counts()
# create target column (multiple types of exits to perm)
df['perm_leaver'] = df['3.12 Exit Destination'].isin(exit_reasons)
# base case
df['perm_leaver'].value_counts(normalize=True)
# replace spaces with underscore
df.columns = df.columns.str.replace(' ', '_')
# see size of df prior to dropping empties
df.shape
# drop rows with no exit destination (current guests at time of report)
df = df.dropna(subset=['3.12_Exit_Destination'])
# shape of df after dropping current guests
df.shape
# verify no NaN in exit destination feature
df['3.12_Exit_Destination'].isna().value_counts()
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
train = df
# Split train into train & val
train, val = train_test_split(train, train_size=0.80, test_size=0.20,
stratify=train['perm_leaver'], random_state=42)
def wrangle(X):
"""Wrangle train, validate, and test sets in the same way"""
# Prevent SettingWithCopyWarning
X = X.copy()
# drop any private information
X = X.drop(columns=['3.1_FirstName', '3.1_LastName', '3.2_SocSecNo',
'3.3_Birthdate', 'V5_Prior_Address'])
# drop unusable columns
X = X.drop(columns=['2.1_Organization_Name', '2.4_ProjectType',
'WorkSource_Referral_Most_Recent', 'YAHP_Referral_Most_Recent',
'SOAR_Enrollment_Determination_(Most_Recent)',
'R7_General_Health_Status', 'R8_Dental_Health_Status',
'R9_Mental_Health_Status', 'RRH_Date_Of_Move-In',
'RRH_In_Permanent_Housing', 'R10_Pregnancy_Due_Date',
'R10_Pregnancy_Status', 'R1_Referral_Source',
'R2_Date_Status_Determined', 'R2_Enroll_Status',
'R2_Reason_Why_No_Services_Funded', 'R2_Runaway_Youth',
'R3_Sexual_Orientation', '2.5_Utilization_Tracking_Method_(Invalid)',
'2.2_Project_Name', '2.6_Federal_Grant_Programs', '3.16_Client_Location',
'3.917_Stayed_Less_Than_90_Days',
'3.917b_Stayed_in_Streets,_ES_or_SH_Night_Before',
'3.917b_Stayed_Less_Than_7_Nights', '4.24_In_School_(Retired_Data_Element)',
'CaseChildren', 'ClientID', 'HEN-HP_Referral_Most_Recent',
'HEN-RRH_Referral_Most_Recent', 'Emergency_Shelter_|_Most_Recent_Enrollment',
'ProgramType', 'Days_Enrolled_Until_RRH_Date_of_Move-in',
'CurrentDate', 'Current_Age', 'Count_of_Bed_Nights_-_Entire_Episode',
'Bed_Nights_During_Report_Period'])
# drop rows with no exit destination (current guests at time of report)
X = X.dropna(subset=['3.12_Exit_Destination'])
# remove columns to avoid data leakage
X = X.drop(columns=['3.12_Exit_Destination', '5.9_Household_ID', '5.8_Personal_ID',
'4.2_Income_Total_at_Exit', '4.3_Non-Cash_Benefit_Count_at_Exit'])
# Drop needless feature
unusable_variance = ['Enrollment_Created_By', '4.24_Current_Status_(Retired_Data_Element)']
X = X.drop(columns=unusable_variance)
# Drop columns with timestamp
timestamp_columns = ['3.10_Enroll_Date', '3.11_Exit_Date',
'Date_of_Last_ES_Stay_(Beta)', 'Date_of_First_ES_Stay_(Beta)',
'Prevention_|_Most_Recent_Enrollment', 'PSH_|_Most_Recent_Enrollment',
'Transitional_Housing_|_Most_Recent_Enrollment', 'Coordinated_Entry_|_Most_Recent_Enrollment',
'Street_Outreach_|_Most_Recent_Enrollment', 'RRH_|_Most_Recent_Enrollment',
'SOAR_Eligibility_Determination_(Most_Recent)', 'Date_of_First_Contact_(Beta)',
'Date_of_Last_Contact_(Beta)', '4.13_Engagement_Date', '4.11_Domestic_Violence_-_When_it_Occurred',
'3.917_Homeless_Start_Date']
X = X.drop(columns=timestamp_columns)
# return the wrangled dataframe
return X
train = wrangle(train)
val = wrangle(val)
train.columns
# Assign to X, y to avoid data leakage
features = ['3.15_Relationship_to_HoH', 'CaseMembers',
'3.2_Social_Security_Quality', '3.3_Birthdate_Quality',
'Age_at_Enrollment', '3.4_Race', '3.5_Ethnicity', '3.6_Gender',
'3.7_Veteran_Status', '3.8_Disabling_Condition_at_Entry',
'3.917_Living_Situation', 'Length_of_Time_Homeless_(3.917_Approximate_Start)',
'3.917_Times_Homeless_Last_3_Years', '3.917_Total_Months_Homeless_Last_3_Years',
'V5_Last_Permanent_Address', 'V5_State', 'V5_Zip', 'Municipality_(City_or_County)',
'4.1_Housing_Status', '4.4_Covered_by_Health_Insurance', '4.11_Domestic_Violence',
'4.11_Domestic_Violence_-_Currently_Fleeing_DV?', 'Household_Type',
'R4_Last_Grade_Completed', 'R5_School_Status',
'R6_Employed_Status', 'R6_Why_Not_Employed', 'R6_Type_of_Employment',
'R6_Looking_for_Work', '4.2_Income_Total_at_Entry',
'4.3_Non-Cash_Benefit_Count', 'Barrier_Count_at_Entry',
'Chronic_Homeless_Status', 'Under_25_Years_Old',
'4.10_Alcohol_Abuse_(Substance_Abuse)', '4.07_Chronic_Health_Condition',
'4.06_Developmental_Disability', '4.10_Drug_Abuse_(Substance_Abuse)',
'4.08_HIV/AIDS', '4.09_Mental_Health_Problem',
'4.05_Physical_Disability'
]
target = 'perm_leaver'
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
# Arrange data into X features matrix and y target vector
target = 'perm_leaver'
X_train = train.drop(columns=target)
y_train = train[target]
X_val = val.drop(columns=target)
y_val = val[target]
from scipy.stats import randint, uniform
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import RandomizedSearchCV
param_distributions = {
'n_estimators': randint(5, 500, 5),
'max_depth': [10, 15, 20, 50, 'None'],
'max_features': [.5, 1, 1.5, 2, 2.5, 3, 'sqrt', None],
}
search = RandomizedSearchCV(
RandomForestRegressor(random_state=42),
param_distributions=param_distributions,
n_iter=20,
cv=5,
scoring='neg_mean_absolute_error',
verbose=10,
return_train_score=True,
n_jobs=-1,
random_state=42
)
search.fit(X_train, y_train);
import category_encoders as ce
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import GradientBoostingClassifier
# Make pipeline!
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=100, n_jobs=-1, max_features=None, random_state=42
)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_val)
print('Validation Accuracy', accuracy_score(y_val, y_pred))
# Get feature importances
rf = pipeline.named_steps['randomforestclassifier']
importances = pd.Series(rf.feature_importances_, X_train.columns)
# Plot feature importances
%matplotlib inline
import matplotlib.pyplot as plt
n = 20
plt.figure(figsize=(10,n/2))
plt.title(f'Top {n} features')
importances.sort_values()[-n:].plot.barh(color='grey');
# Make pipeline!
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
xgb.XGBClassifier(n_estimators=110, n_jobs=-1, num_parallel_tree=200,
random_state=42
)
)
# Fit on Train
pipeline.fit(X_train, y_train)
# Score on val
y_pred = pipeline.predict(X_val)
print('Validation Accuracy', accuracy_score(y_val, y_pred))
# cross validation
k = 3
scores = cross_val_score(pipeline, X_train, y_train, cv=k,
scoring='accuracy')
print(f'MAE for {k} folds:', -scores)
-scores.mean()
# get and plot feature importances
# Linear models have coefficients whereas decision trees have "Feature Importances"
import matplotlib.pyplot as plt
model = pipeline.named_steps['xgbclassifier']
encoder = pipeline.named_steps['ordinalencoder']
encoded_columns = encoder.transform(X_val).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
plt.figure(figsize=(10,30))
importances.sort_values().plot.barh(color='grey')
df['4.1_Housing_Status'].value_counts()
X_train.shape
X_train.columns
X_train.Days_Enrolled_in_Project.value_counts()
column = 'Days_Enrolled_in_Project'
# Fit without column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=250, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train.drop(columns=column), y_train)
score_without = pipeline.score(X_val.drop(columns=column), y_val)
print(f'Validation Accuracy without {column}: {score_without}')
# Fit with column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=250, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
score_with = pipeline.score(X_val, y_val)
print(f'Validation Accuracy with {column}: {score_with}')
# Compare the error with & without column
print(f'Drop-Column Importance for {column}: {score_with - score_without}')
column = 'Days_Enrolled_in_Project'
# Fit without column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=250, max_depth=7, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train.drop(columns=column), y_train)
score_without = pipeline.score(X_val.drop(columns=column), y_val)
print(f'Validation Accuracy without {column}: {score_without}')
# Fit with column
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=250, max_depth=7, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
score_with = pipeline.score(X_val, y_val)
print(f'Validation Accuracy with {column}: {score_with}')
# Compare the error with & without column
print(f'Drop-Column Importance for {column}: {score_with - score_without}')
# Fit with all the data
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
score_with = pipeline.score(X_val, y_val)
print(f'Validation Accuracy with {column}: {score_with}')
# Before: Sequence of features to be permuted
feature = 'Days_Enrolled_in_Project'
X_val[feature].head()
# Before: Distribution of quantity
X_val[feature].value_counts()
# Permute the dataset
X_val_permuted = X_val.copy()
X_val_permuted[feature] = np.random.permutation(X_val[feature])
# After: Sequence of features to be permuted
X_val_permuted[feature].head()
# Distribution hasn't changed!
X_val_permuted[feature].value_counts()
# Get the permutation importance
score_permuted = pipeline.score(X_val_permuted, y_val)
print(f'Validation Accuracy with {column} not permuted: {score_with}')
print(f'Validation Accuracy with {column} permuted: {score_permuted}')
print(f'Permutation Importance for {column}: {score_with - score_permuted}')
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent')
)
X_train_transformed = pipeline.fit_transform(X_train)
X_val_transformed = pipeline.transform(X_val)
model = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
model.fit(X_train_transformed, y_train)
pip install eli5
import eli5
from eli5.sklearn import PermutationImportance
permuter = PermutationImportance(
model,
scoring='accuracy',
n_iter=5,
random_state=42
)
permuter.fit(X_val_transformed, y_val)
permuter.feature_importances_
eli5.show_weights(
permuter,
top=None,
feature_names=X_val.columns.tolist()
)
print('Shape before removing features:', X_train.shape)
minimum_importance = 0
mask = permuter.feature_importances_ > minimum_importance
features = X_train.columns[mask]
X_train = X_train[features]
print('Shape after removing features:', X_train.shape)
X_val = X_val[features]
pipeline = make_pipeline(
ce.OrdinalEncoder(),
SimpleImputer(strategy='most_frequent'),
RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
print('Validation Accuracy:', pipeline.score(X_val, y_val))
from xgboost import XGBClassifier
pipeline = make_pipeline(
ce.OrdinalEncoder(),
XGBClassifier(n_estimators=100, random_state=42, n_jobs=-1)
)
# Fit on train, score on val
pipeline.fit(X_train, y_train)
print('Validation Accuracy:', pipeline.score(X_val, y_val))
encoder = ce.OrdinalEncoder()
X_train_encoded = encoder.fit_transform(X_train)
X_val_encoded = encoder.transform(X_val)
model = XGBClassifier(n_estimators=1000, # <= 1000 trees, early stopping depency
max_depth=7, # try deeper trees with high cardinality data
learning_rate=0.1, # try higher learning rate
random_state=42,
num_class=1,
n_jobs=-1)
eval_set = [(X_train_encoded, y_train),
(X_val_encoded, y_val)]
# Fit on train, score on val
model.fit(X_train_encoded, y_train,
eval_metric='auc',
eval_set=eval_set,
early_stopping_rounds=25)
from sklearn.metrics import mean_absolute_error as mae
results = model.evals_result()
train_error = results['validation_0']['auc']
val_error = results['validation_1']['auc']
iterations = range(1, len(train_error) + 1)
plt.figure(figsize=(10,7))
plt.plot(iterations, train_error, label='Train')
plt.plot(iterations, val_error, label='Validation')
plt.title('XGBoost Validation Curve')
plt.ylabel('Classification Error')
plt.xlabel('Model Complexity (n_estimators)')
plt.legend();
```
| true |
code
| 0.46557 | null | null | null | null |
|
Simulation Demonstration
=====================
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import soepy
```
In this notebook we present descriptive statistics of a series of simulated samples with the soepy toy model.
soepy is closely aligned to the model in Blundell et. al. (2016). Yet, we wish to use the soepy package for estimation based on the German SOEP. In this simulation demonstration, some parameter values are partially set close to the parameters estimated in the seminal paper of Blundell et. al. (2016). The remainder of the parameter values are altered such that simulated wage levels and employment choice probabilities (roughly) match the statistics observed in the SOEP Data.
- the constants in the wage process gamma_0 equal are set to ensure alignment with SOEP data.
- the returns to experience in the wage process gamma_1 are set close to the coefficient values on gamma0, Blundell Table VIII, p. 1733
- the part-time experience accumulation parameter is set close to the coefficient on g(P), Blundell Table VIII, p. 1733,
- the experience depreciation parameter delta is set close to the coefffient values on delta, Blundell Table VIII, p. 1733,
- the disutility of part-time work parameter theta_p is set to ensure alignment with SOEP data,
- the disutility of full-time work parameter theta_f is set to ensure alignment with SOEP data.
To ensure that some individuals also choose to be non-emplyed, we set the period wage for nonemployed to be equal to some fixed value, constant over all periods. We call this income in unemployment "benefits".
```
data_frame_baseline = soepy.simulate('toy_model_init_file_01_1000.yml')
data_frame_baseline.head(20)
#Determine the observed wage given period choice
def get_observed_wage (row):
if row['Choice'] == 2:
return row['Period Wage F']
elif row['Choice'] ==1:
return row['Period Wage P']
elif row['Choice'] ==0:
return row['Period Wage N']
else:
return np.nan
# Add to data frame
data_frame_baseline['Wage Observed'] = data_frame_baseline.apply(
lambda row: get_observed_wage (row),axis=1
)
# Determine the education level
def get_educ_level(row):
if row["Years of Education"] >= 10 and row["Years of Education"] < 12:
return 0
elif row["Years of Education"] >= 12 and row["Years of Education"] < 16:
return 1
elif row["Years of Education"] >= 16:
return 2
else:
return np.nan
data_frame_baseline["Educ Level"] = data_frame_baseline.apply(
lambda row: get_educ_level(row), axis=1
)
```
Descriptive statistics to look at:
- average part-time, full-time and nonemployment rate - ideally close to population rates
- frequency of each choice per period - ideally more often part-time in early periods, more full-time in later periods
- frequency of each choice over all periods for individuals with different levels of education - ideally, lower educated more often unemployed and in part-time jobs
- average period wages over all individuals - series for all periods
- average period individuals over all individuals - series for all periods
```
# Average non-employment, part-time, and full-time rates over all periods and individuals
data_frame_baseline['Choice'].value_counts(normalize=True).plot(kind = 'bar')
data_frame_baseline['Choice'].value_counts(normalize=True)
# Average non-employment, part-time, and full-time rates per period
data_frame_baseline.groupby(['Period'])['Choice'].value_counts(normalize=True).unstack().plot(kind = 'bar', stacked = True)
```
As far as the evolution of choices over all agents and periods is concerned, we first observe a declining tendency of individuals to be unemployed as desired in a perfectly calibrated simulation. Second, individuals in our simulation tend to choose full-time and non-employment less often in the later periods of the model. Rates of part-time employment increase for the same period.
```
# Average non-employment, part-time, and full-time rates for individuals with different level of education
data_frame_baseline.groupby(['Years of Education'])['Choice'].value_counts(normalize=True).unstack().plot(kind = 'bar', stacked = True)
```
As should be expected, the higher the education level of the individuals the lower the observed.
```
# Average wage for each period and choice
fig,ax = plt.subplots()
# Generate x axes values
period = np.arange(1,31)
# Generate plot lines
ax.plot(period,
data_frame_baseline[data_frame_baseline['Choice'] == 2].groupby(['Period'])['Period Wage F'].mean(),
color='green', label = 'F')
ax.plot(period,
data_frame_baseline[data_frame_baseline['Choice'] == 1].groupby(['Period'])['Period Wage P'].mean(),
color='orange', label = 'P')
ax.plot(period,
data_frame_baseline[data_frame_baseline['Choice'] == 0].groupby(['Period'])['Period Wage N'].mean(),
color='blue', label = 'N')
# Plot settings
ax.set_xlabel("period")
ax.set_ylabel("wage")
ax.legend(loc='best')
```
The period wage of non-employment actually refers to the unemployment benefits individuals receive. The amount of the benefits is constant over time. Part-time and full-time wages rise as individuals gather more experience.
```
# Average wages by period
data_frame_baseline.groupby(['Period'])['Wage Observed'].mean().plot()
```
Comparative Statics
------------------------
In the following, we discuss some comparative statics of the model.
While changing other parameter values we wish to assume that the parameters central to the part-time penalty phenomenon studied in Blundell (2016) stay the same as in the benchmark specification:
- part-time experience accumulation g_s1,2,3
- experience depreciation delta
Comparative statics:
Parameters in the systematic wage govern the choice between employment (either part-time, or full-time) and nonemployment. They do not determine the choice between part-time and full-time employment since the systematic wage is equal for both options.
- constnat in wage process gamma_0: lower/higher value of the coefficient implies that other components such as accumulated work experience and the productivity shock are relatively more/less important in determining the choice between employment and nonemployment. Decreasing the constant for individuals of a certain education level, e.g., low, results in these individuals choosing nonemployment more often.
- return to experience gamma_1: lower value of the coefficient implies that accumulated work experience is less relevant in determining the wage in comparison to other factors such as the constant or the productivity shock. Higher coefficients should lead to agents persistently choosing employment versus non-employment.
The productivity shock:
- productivity shock variances - the higher the variances, the more switching between occupational alternatives.
Risk aversion:
- risk aversion parameter mu: the more negative the risk aversion parameter, the more eager are agents to ensure themselves against productivity shoks through accumulation of experience. Therefore, lower values of the parameter are associated with higher rates of full-time employment.
The labor disutility parameters directly influence:
- benefits - for higher benefits individuals of all education levels would choose non-employment more often
- labor disutility for part-time theta_p - for a higher coefficient, individuals of all education levels would choose to work part-time more often
- labor disutility for full-time theta_f - for a higher coefficient, individuals of all education levels would choose to work part-time more often
Finally, we illustrate one of the changes discussed above. In the alternative specifications the return to experience coefficient gamma_1 for the individuals with medium level of educations is increased from 0.157 to 0.195. As a result, experience accumulation matters more in the utility maximization. Therefore, individuals with medium level of education choose to be employed more often. Consequently, also aggregate levels of nonemployment are lower in the model.
```
data_frame_alternative = soepy.simulate('toy_model_init_file_01_1000.yml')
# Average non-employment, part-time, and full-time rates for individuals with different level of education
[data_frame_alternative.groupby(['Years of Education'])['Choice'].value_counts(normalize=True),
data_frame_baseline.groupby(['Years of Education'])['Choice'].value_counts(normalize=True)]
# Average non-employment, part-time, and full-time rates for individuals with different level of education
data_frame_alternative.groupby(['Years of Education'])['Choice'].value_counts(normalize=True).unstack().plot(kind = 'bar', stacked = True)
# Average non-employment, part-time, and full-time rates over all periods and individuals
data_frame_alternative['Choice'].value_counts(normalize=True).plot(kind = 'bar')
data_frame_alternative['Choice'].value_counts(normalize=True)
```
| true |
code
| 0.650106 | null | null | null | null |
|
# Quickstart
In this tutorial, we will show how to solve a famous optimization problem, minimizing the Rosenbrock function, in simplenlopt. First, let's define the Rosenbrock function and plot it:
$$
f(x, y) = (1-x)^2+100(y-x^2)^2
$$
```
import numpy as np
def rosenbrock(pos):
x, y = pos
return (1-x)**2 + 100 * (y - x**2)**2
xgrid = np.linspace(-2, 2, 500)
ygrid = np.linspace(-1, 3, 500)
X, Y = np.meshgrid(xgrid, ygrid)
Z = (1 - X)**2 + 100 * (Y -X**2)**2
x0=np.array([-1.5, 2.25])
f0 = rosenbrock(x0)
#Plotly not rendering correctly on Readthedocs, but this shows how it is generated! Plot below is a PNG export
import plotly.graph_objects as go
fig = go.Figure(data=[go.Surface(z=Z, x=X, y=Y, cmax = 10, cmin = 0, showscale = False)])
fig.update_layout(
scene = dict(zaxis = dict(nticks=4, range=[0,10])))
fig.add_scatter3d(x=[1], y=[1], z=[0], mode = 'markers', marker=dict(size=10, color='green'), name='Optimum')
fig.add_scatter3d(x=[-1.5], y=[2.25], z=[f0], mode = 'markers', marker=dict(size=10, color='black'), name='Initial guess')
fig.show()
```

The crux of the Rosenbrock function is that the minimum indicated by the green dot is located in a very narrow, banana shaped valley with a small slope around the minimum. Local optimizers try to find the optimum by searching the parameter space starting from an initial guess. We place the initial guess shown in black on the other side of the banana.
In simplenlopt, local optimizers are called by the minimize function. It requires the objective function and a starting point. The algorithm is chosen by the method argument. Here, we will use the derivative-free Nelder-Mead algorithm. Objective functions must be of the form ``f(x, ...)`` where ``x`` represents a numpy array holding the parameters which are optimized.
```
import simplenlopt
def rosenbrock(pos):
x, y = pos
return (1-x)**2 + 100 * (y - x**2)**2
res = simplenlopt.minimize(rosenbrock, x0, method = 'neldermead')
print("Position of optimum: ", res.x)
print("Function value at Optimum: ", res.fun)
print("Number of function evaluations: ", res.nfev)
```
The optimization result is stored in a class whose main attributes are the position of the optimum and the function value at the optimum. The number of function evaluations is a measure of performance: the less function evaluations are required to find the minimum, the faster the optimization will be.
Next, let's switch to a derivative based solver. For better performance, we also supply the analytical gradient which is passed to the jac argument.
```
def rosenbrock_grad(pos):
x, y = pos
dx = 2 * x -2 - 400 * x * (y-x**2)
dy = 200 * (y-x**2)
return dx, dy
res_slsqp = simplenlopt.minimize(rosenbrock, x0, method = 'slsqp', jac = rosenbrock_grad)
print("Position of optimum: ", res_slsqp.x)
print("Function value at Optimum: ", res_slsqp.fun)
print("Number of function evaluations: ", res_slsqp.nfev)
```
As the SLSQP algorithm can use gradient information, it requires less function evaluations to find the minimum than the
derivative-free Nelder-Mead algorithm.
Unlike vanilla NLopt, simplenlopt automatically defaults to finite difference approximations of the gradient if it is
not provided:
```
res = simplenlopt.minimize(rosenbrock, x0, method = 'slsqp')
print("Position of optimum: ", res.x)
print("Function value at Optimum: ", res.fun)
print("Number of function evaluations: ", res.nfev)
```
As the finite differences are not as precise as the analytical gradient, the found optimal function value is higher than with analytical gradient information. In general, it is aways recommended to compute the gradient analytically or by automatic differentiation as the inaccuracies of finite differences can result in wrong results and bad performance.
For demonstration purposes, let's finally solve the problem with a global optimizer. Like in SciPy, each global optimizer is called by a dedicated function such as crs() for the Controlled Random Search algorithm. Instead of a starting point, the global optimizers require a region in which they seek to find the minimum. This region is provided as a list of (lower_bound, upper_bound) for each coordinate.
```
bounds = [(-2., 2.), (-2., 2.)]
res_crs = simplenlopt.crs(rosenbrock, bounds)
print("Position of optimum: ", res_crs.x)
print("Function value at Optimum: ", res_crs.fun)
print("Number of function evaluations: ", res_crs.nfev)
```
Note that using a global optimizer is overkill for a small problem like the Rosenbrock function: it requires many more function
evaluations than a local optimizer. Global optimization algorithms shine in case of complex, multimodal functions where local
optimizers converge to local minima instead of the global minimum. Check the Global Optimization page for such an example.
| true |
code
| 0.620938 | null | null | null | null |
|
# <img style="float: left; padding-right: 10px; width: 45px" src="https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png"> CS109B Data Science 2: Advanced Topics in Data Science
## Lecture 5.5 - Smoothers and Generalized Additive Models - Model Fitting
<div class="discussion"><b>JUST A NOTEBOOK</b></div>
**Harvard University**<br>
**Spring 2021**<br>
**Instructors:** Mark Glickman, Pavlos Protopapas, and Chris Tanner<br>
**Lab Instructor:** Eleni Kaxiras<br><BR>
*Content:* Eleni Kaxiras and Will Claybaugh
---
```
## RUN THIS CELL TO PROPERLY HIGHLIGHT THE EXERCISES
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2019-CS109B/master/content/styles/cs109.css").text
HTML(styles)
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
```
## Table of Contents
* 1 - Overview - A Top View of LMs, GLMs, and GAMs to set the stage
* 2 - A review of Linear Regression with `statsmodels`. Formulas.
* 3 - Splines
* 4 - Generative Additive Models with `pyGAM`
* 5 - Smooting Splines using `csaps`
## Overview

*image source: Dani Servén Marín (one of the developers of pyGAM)*
### A - Linear Models
First we have the **Linear Models** which you know from 109a. These models are linear in the coefficients. Very *interpretable* but suffer from high bias because let's face it, few relationships in life are linear. Simple Linear Regression (defined as a model with one predictor) as well as Multiple Linear Regression (more than one predictors) are examples of LMs. Polynomial Regression extends the linear model by adding terms that are still linear for the coefficients but non-linear when it somes to the predictiors which are now raised in a power or multiplied between them.

$$
\begin{aligned}
y = \beta{_0} + \beta{_1}{x_1} & \quad \mbox{(simple linear regression)}\\
y = \beta{_0} + \beta{_1}{x_1} + \beta{_2}{x_2} + \beta{_3}{x_3} & \quad \mbox{(multiple linear regression)}\\
y = \beta{_0} + \beta{_1}{x_1} + \beta{_2}{x_1^2} + \beta{_3}{x_3^3} & \quad \mbox{(polynomial multiple regression)}\\
\end{aligned}
$$
<div class="discussion"><b>Questions to think about</b></div>
- What does it mean for a model to be **interpretable**?
- Are linear regression models interpretable? Are random forests? What about Neural Networks such as Feed Forward?
- Do we always want interpretability? Describe cases where we do and cases where we do not care.
### B - Generalized Linear Models (GLMs)

**Generalized Linear Models** is a term coined in the early 1970s by Nelder and Wedderburn for a class of models that includes both Linear Regression and Logistic Regression. A GLM fits one coefficient per feature (predictor).
### C - Generalized Additive Models (GAMs)
Hastie and Tidshirani coined the term **Generalized Additive Models** in 1986 for a class of non-linear extensions to Generalized Linear Models.

$$
\begin{aligned}
y = \beta{_0} + f_1\left(x_1\right) + f_2\left(x_2\right) + f_3\left(x_3\right) \\
y = \beta{_0} + f_1\left(x_1\right) + f_2\left(x_2, x_3\right) + f_3\left(x_3\right) & \mbox{(with interaction terms)}
\end{aligned}
$$
In practice we add splines and regularization via smoothing penalties to our GLMs.
*image source: Dani Servén Marín*
### D - Basis Functions
In our models we can use various types of functions as "basis".
- Monomials such as $x^2$, $x^4$ (**Polynomial Regression**)
- Sigmoid functions (neural networks)
- Fourier functions
- Wavelets
- **Regression splines**
### 1 - Piecewise Polynomials a.k.a. Splines
Splines are a type of piecewise polynomial interpolant. A spline of degree k is a piecewise polynomial that is continuously differentiable k − 1 times.
Splines are the basis of CAD software and vector graphics including a lot of the fonts used in your computer. The name “spline” comes from a tool used by ship designers to draw smooth curves. Here is the letter $epsilon$ written with splines:

*font idea inspired by Chris Rycroft (AM205)*
If the degree is 1 then we have a Linear Spline. If it is 3 then we have a Cubic spline. It turns out that cubic splines because they have a continous 2nd derivative (curvature) at the knots are very smooth to the eye. We do not need higher order than that. The Cubic Splines are usually Natural Cubic Splines which means they have the added constrain of the end points' second derivative = 0.
We will use the CubicSpline and the B-Spline as well as the Linear Spline.
#### scipy.interpolate
See all the different splines that scipy.interpolate has to offer: https://docs.scipy.org/doc/scipy/reference/interpolate.html
Let's use the simplest form which is interpolate on a set of points and then find the points between them.
```
from scipy.interpolate import splrep, splev
from scipy.interpolate import BSpline, CubicSpline
from scipy.interpolate import interp1d
# define the range of the function
a = -1
b = 1
# define the number of knots
num_knots = 11
knots = np.linspace(a,b,num_knots)
# define the function we want to approximate
y = 1/(1+25*(knots**2))
# make a linear spline
linspline = interp1d(knots, y)
# sample at these points to plot
xx = np.linspace(a,b,1000)
yy = 1/(1+25*(xx**2))
plt.plot(knots,y,'*')
plt.plot(xx, yy, label='true function')
plt.plot(xx, linspline(xx), label='linear spline');
plt.legend();
```
<div class="exercise"><b>Exercise</b></div>
The Linear interpolation does not look very good. Fit a Cubic Spline and plot along the Linear to compare. Feel free to solve and then look at the solution.
```
# your answer here
# solution
# define the range of the function
a = -1
b = 1
# define the knots
num_knots = 10
x = np.linspace(a,b,num_knots)
# define the function we want to approximate
y = 1/(1+25*(x**2))
# make the Cubic spline
cubspline = CubicSpline(x, y)
print(f'Num knots in cubic spline: {num_knots}')
# OR make a linear spline
linspline = interp1d(x, y)
# plot
xx = np.linspace(a,b,1000)
yy = 1/(1+25*(xx**2))
plt.plot(xx, yy, label='true function')
plt.plot(x,y,'*', label='knots')
plt.plot(xx, linspline(xx), label='linear');
plt.plot(xx, cubspline(xx), label='cubic');
plt.legend();
```
<div class="discussion"><b>Questions to think about</b></div>
- Change the number of knots to 100 and see what happens. What would happen if we run a polynomial model of degree equal to the number of knots (a global one as in polynomial regression, not a spline)?
- What makes a spline 'Natural'?
```
# Optional and Outside of the scope of this class: create the `epsilon` in the figure above
x = np.array([1.,0.,-1.5,0.,-1.5,0.])
y = np.array([1.5,1.,2.5,3,4,5])
t = np.linspace(0,5,6)
f = interp1d(t,x,kind='cubic')
g = interp1d(t,y,kind='cubic')
tplot = np.linspace(0,5,200)
plt.plot(x,y, '*', f(tplot), g(tplot));
```
#### B-Splines (de Boor, 1978)
One way to construct a curve given a set of points is to *interpolate the points*, that is, to force the curve to pass through the points.
A B-splines (Basis Splines) is defined by a set of **control points** and a set of **basis functions** that fit the function between these points. By choosing to have no smoothing factor we force the final B-spline to pass though all the points. If, on the other hand, we set a smothing factor, our function is more of an approximation with the control points as "guidance". The latter produced a smoother curve which is prefferable for drawing software. For more on Splines see: https://en.wikipedia.org/wiki/B-spline)

We will use [`scipy.splrep`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.splrep.html#scipy.interpolate.splrep) to calulate the coefficients for the B-Spline and draw it.
#### B-Spline with no smooting
```
from scipy.interpolate import splev, splrep
x = np.linspace(0, 10, 10)
y = np.sin(x)
# (t,c,k) is a tuple containing the vector of knots, coefficients, degree of the spline
t,c,k = splrep(x, y)
x2 = np.linspace(0, 10, 200)
y2 = BSpline(t,c,k)
plt.plot(x, y, 'o', x2, y2(x2))
plt.show()
from scipy.interpolate import splrep
x = np.linspace(0, 10, 10)
y = np.sin(x)
t,c,k = splrep(x, y, k=3) # (tck) is a tuple containing the vector of knots, coefficients, degree of the spline
# define the points to plot on (x2)
print(f'Knots ({len(t)} of them): {t}\n')
print(f'B-Spline coefficients ({len(c)} of them): {c}\n')
print(f'B-Spline degree {k}')
x2 = np.linspace(0, 10, 100)
y2 = BSpline(t, c, k)
plt.figure(figsize=(10,5))
plt.plot(x, y, 'o', label='true points')
plt.plot(x2, y2(x2), label='B-Spline')
tt = np.zeros(len(t))
plt.plot(t, tt,'g*', label='knots eval by the function')
plt.legend()
plt.show()
```
<a id=splineparams></a>
#### What do the tuple values returned by `scipy.splrep` mean?
- The `t` variable is the array that contains the knots' position in the x axis. The length of this array is, of course, the number of knots.
- The `c` variable is the array that holds the coefficients for the B-Spline. Its length should be the same as `t`.
We have `number_of_knots - 1` B-spline basis elements to the spline constructed via this method, and they are defined as follows:<BR><BR>
$$
\begin{aligned}
B_{i, 0}(x) = 1, \textrm{if $t_i \le x < t_{i+1}$, otherwise $0$,} \\ \\
B_{i, k}(x) = \frac{x - t_i}{t_{i+k} - t_i} B_{i, k-1}(x)
+ \frac{t_{i+k+1} - x}{t_{i+k+1} - t_{i+1}} B_{i+1, k-1}(x)
\end{aligned}
$$
- t $\in [t_1, t_2, ..., t_]$ is the knot vector
- c : are the spline coefficients
- k : is the spline degree
#### B-Spline with smooting factor s
```
from scipy.interpolate import splev, splrep
x = np.linspace(0, 10, 5)
y = np.sin(x)
s = 0.5 # add smoothing factor
task = 0 # task needs to be set to 0, which represents:
# we are specifying a smoothing factor and thus only want
# splrep() to find the optimal t and c
t,c,k = splrep(x, y, task=task, s=s)
# draw the line segments
linspline = interp1d(x, y)
# define the points to plot on (x2)
x2 = np.linspace(0, 10, 200)
y2 = BSpline(t, c, k)
plt.plot(x, y, 'o', x2, y2(x2))
plt.plot(x2, linspline(x2))
plt.show()
```
#### B-Spline with given knots
```
x = np.linspace(0, 10, 100)
y = np.sin(x)
knots = np.quantile(x, [0.25, 0.5, 0.75])
print(knots)
# calculate the B-Spline
t,c,k = splrep(x, y, t=knots)
curve = BSpline(t,c,k)
curve
plt.scatter(x=x,y=y,c='grey', alpha=0.4)
yknots = np.sin(knots)
plt.scatter(knots, yknots, c='r')
plt.plot(x,curve(x))
plt.show()
```
### 2 - GAMs
https://readthedocs.org/projects/pygam/downloads/pdf/latest/
#### Classification in `pyGAM`
Let's get our (multivariate!) data, the `kyphosis` dataset, and the `LogisticGAM` model from `pyGAM` to do binary classification.
- kyphosis - wherther a particular deformation was present post-operation
- age - patient's age in months
- number - the number of vertebrae involved in the operation
- start - the number of the topmost vertebrae operated on
```
kyphosis = pd.read_csv("../data/kyphosis.csv")
display(kyphosis.head())
display(kyphosis.describe(include='all'))
display(kyphosis.dtypes)
# convert the outcome in a binary form, 1 or 0
kyphosis = pd.read_csv("../data/kyphosis.csv")
kyphosis["outcome"] = 1*(kyphosis["Kyphosis"] == "present")
kyphosis.describe()
from pygam import LogisticGAM, s, f, l
X = kyphosis[["Age","Number","Start"]]
y = kyphosis["outcome"]
kyph_gam = LogisticGAM().fit(X,y)
```
#### Outcome dependence on features
To help us see how the outcome depends on each feature, `pyGAM` has the `partial_dependence()` function.
```
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
```
For more on this see the : https://pygam.readthedocs.io/en/latest/api/logisticgam.html
```
res = kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(kyph_gam.terms):
if term.isintercept:
continue
XX = kyph_gam.generate_X_grid(term=i)
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
```
Notice that we did not specify the basis functions in the .fit(). `pyGAM` figures them out for us by using $s()$ (splines) for numerical variables and $f()$ for categorical features. If this is not what we want we can manually specify the basis functions, as follows:
```
kyph_gam = LogisticGAM(s(0)+s(1)+s(2)).fit(X,y)
res = kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(kyph_gam.terms):
if term.isintercept:
continue
XX = kyph_gam.generate_X_grid(term=i)
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
```
#### Regression in `pyGAM`
For regression problems, we can use a `linearGAM` model. For this part we will use the `wages` dataset.
https://pygam.readthedocs.io/en/latest/api/lineargam.html
#### The `wages` dataset
Let's inspect another dataset that is included in `pyGAM` that notes the wages of people based on their age, year of employment and education.
```
# from the pyGAM documentation
from pygam import LinearGAM, s, f
from pygam.datasets import wage
X, y = wage(return_X_y=True)
## model
gam = LinearGAM(s(0) + s(1) + f(2))
gam.gridsearch(X, y)
## plotting
plt.figure();
fig, axs = plt.subplots(1,3);
titles = ['year', 'age', 'education']
for i, ax in enumerate(axs):
XX = gam.generate_X_grid(term=i)
ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX))
ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX, width=.95)[1], c='r', ls='--')
if i == 0:
ax.set_ylim(-30,30)
ax.set_title(titles[i]);
```
### 3 - Smoothing Splines using csaps
**Note**: this is the spline model that minimizes <BR>
$MSE - \lambda\cdot\text{wiggle penalty}$ $=$ $\sum_{i=1}^N \left(y_i - f(x_i)\right)^2 - \lambda \int \left(f''(t)\right)^2 dt$, <BR>
across all possible functions $f$.
```
from csaps import csaps
np.random.seed(1234)
x = np.linspace(0,10,300000)
y = np.sin(x*2*np.pi)*x + np.random.randn(len(x))
xs = np.linspace(x[0], x[-1], 1000)
ys = csaps(x, y, xs, smooth=0.99)
print(ys.shape)
#plt.plot(x, y, 'o', xs, ys, '-')
plt.plot(x, y, 'o', xs, ys, '-')
plt.show()
```
### 4 - Data fitting using pyGAM and Penalized B-Splines
When we use a spline in pyGAM we are effectively using a penalized B-Spline with a regularization parameter $\lambda$. E.g.
```
LogisticGAM(s(0)+s(1, lam=0.5)+s(2)).fit(X,y)
```
Let's see how this smoothing works in `pyGAM`. We start by creating some arbitrary data and fitting them with a GAM.
```
X = np.linspace(0,10,500)
y = np.sin(X*2*np.pi)*X + np.random.randn(len(X))
plt.scatter(X,y);
# let's try a large lambda first and lots of splines
gam = LinearGAM(lam=1e6, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
```
We see that the large $\lambda$ forces a straight line, no flexibility. Let's see now what happens if we make it smaller.
```
# let's try a smaller lambda
gam = LinearGAM(lam=1e2, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
```
There is some curvature there but still not a good fit. Let's try no penalty. That should have the line fit exactly.
```
# no penalty, let's try a 0 lambda
gam = LinearGAM(lam=0, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3)
plt.plot(XX, gam.predict(XX))
```
Yes, that is good. Now let's see what happens if we lessen the number of splines. The fit should not be as good.
```
# no penalty, let's try a 0 lambda
gam = LinearGAM(lam=0, n_splines=10). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
```
| true |
code
| 0.777411 | null | null | null | null |
|
<h2>Quadratic Regression Dataset - Linear Regression vs XGBoost</h2>
Model is trained with XGBoost installed in notebook instance
In the later examples, we will train using SageMaker's XGBoost algorithm.
Training on SageMaker takes several minutes (even for simple dataset).
If algorithm is supported on Python, we will try them locally on notebook instance
This allows us to quickly learn an algorithm, understand tuning options and then finally train on SageMaker Cloud
In this exercise, let's compare XGBoost and Linear Regression for Quadratic regression dataset
```
# Install xgboost in notebook instance.
#### Command to install xgboost
!conda install -y -c conda-forge xgboost
import sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, mean_absolute_error
# XGBoost
import xgboost as xgb
# Linear Regression
from sklearn.linear_model import LinearRegression
df = pd.read_csv('quadratic_all.csv')
df.head()
plt.plot(df.x,df.y,label='Target')
plt.grid(True)
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.legend()
plt.title('Quadratic Regression Dataset')
plt.show()
train_file = 'quadratic_train.csv'
validation_file = 'quadratic_validation.csv'
# Specify the column names as the file does not have column header
df_train = pd.read_csv(train_file,names=['y','x'])
df_validation = pd.read_csv(validation_file,names=['y','x'])
df_train.head()
df_validation.head()
plt.scatter(df_train.x,df_train.y,label='Training',marker='.')
plt.scatter(df_validation.x,df_validation.y,label='Validation',marker='.')
plt.grid(True)
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.title('Quadratic Regression Dataset')
plt.legend()
plt.show()
X_train = df_train.iloc[:,1:] # Features: 1st column onwards
y_train = df_train.iloc[:,0].ravel() # Target: 0th column
X_validation = df_validation.iloc[:,1:]
y_validation = df_validation.iloc[:,0].ravel()
# Create an instance of XGBoost Regressor
# XGBoost Training Parameter Reference:
# https://github.com/dmlc/xgboost/blob/master/doc/parameter.md
regressor = xgb.XGBRegressor()
regressor
regressor.fit(X_train,y_train, eval_set = [(X_train, y_train), (X_validation, y_validation)])
eval_result = regressor.evals_result()
training_rounds = range(len(eval_result['validation_0']['rmse']))
plt.scatter(x=training_rounds,y=eval_result['validation_0']['rmse'],label='Training Error')
plt.scatter(x=training_rounds,y=eval_result['validation_1']['rmse'],label='Validation Error')
plt.grid(True)
plt.xlabel('Iteration')
plt.ylabel('RMSE')
plt.title('Training Vs Validation Error')
plt.legend()
plt.show()
xgb.plot_importance(regressor)
plt.show()
```
## Validation Dataset Compare Actual and Predicted
```
result = regressor.predict(X_validation)
result[:5]
plt.title('XGBoost - Validation Dataset')
plt.scatter(df_validation.x,df_validation.y,label='actual',marker='.')
plt.scatter(df_validation.x,result,label='predicted',marker='.')
plt.grid(True)
plt.legend()
plt.show()
# RMSE Metrics
print('XGBoost Algorithm Metrics')
mse = mean_squared_error(df_validation.y,result)
print(" Mean Squared Error: {0:.2f}".format(mse))
print(" Root Mean Square Error: {0:.2f}".format(mse**.5))
# Residual
# Over prediction and Under Prediction needs to be balanced
# Training Data Residuals
residuals = df_validation.y - result
plt.hist(residuals)
plt.grid(True)
plt.xlabel('Actual - Predicted')
plt.ylabel('Count')
plt.title('XGBoost Residual')
plt.axvline(color='r')
plt.show()
# Count number of values greater than zero and less than zero
value_counts = (residuals > 0).value_counts(sort=False)
print(' Under Estimation: {0}'.format(value_counts[True]))
print(' Over Estimation: {0}'.format(value_counts[False]))
# Plot for entire dataset
plt.plot(df.x,df.y,label='Target')
plt.plot(df.x,regressor.predict(df[['x']]) ,label='Predicted')
plt.grid(True)
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.legend()
plt.title('XGBoost')
plt.show()
```
## Linear Regression Algorithm
```
lin_regressor = LinearRegression()
lin_regressor.fit(X_train,y_train)
```
Compare Weights assigned by Linear Regression.
Original Function: 5*x**2 -23*x + 47 + some noise
Linear Regression Function: -15.08 * x + 709.86
Linear Regression Coefficients and Intercepts are not close to actual
```
lin_regressor.coef_
lin_regressor.intercept_
result = lin_regressor.predict(df_validation[['x']])
plt.title('LinearRegression - Validation Dataset')
plt.scatter(df_validation.x,df_validation.y,label='actual',marker='.')
plt.scatter(df_validation.x,result,label='predicted',marker='.')
plt.grid(True)
plt.legend()
plt.show()
# RMSE Metrics
print('Linear Regression Metrics')
mse = mean_squared_error(df_validation.y,result)
print(" Mean Squared Error: {0:.2f}".format(mse))
print(" Root Mean Square Error: {0:.2f}".format(mse**.5))
# Residual
# Over prediction and Under Prediction needs to be balanced
# Training Data Residuals
residuals = df_validation.y - result
plt.hist(residuals)
plt.grid(True)
plt.xlabel('Actual - Predicted')
plt.ylabel('Count')
plt.title('Linear Regression Residual')
plt.axvline(color='r')
plt.show()
# Count number of values greater than zero and less than zero
value_counts = (residuals > 0).value_counts(sort=False)
print(' Under Estimation: {0}'.format(value_counts[True]))
print(' Over Estimation: {0}'.format(value_counts[False]))
# Plot for entire dataset
plt.plot(df.x,df.y,label='Target')
plt.plot(df.x,lin_regressor.predict(df[['x']]) ,label='Predicted')
plt.grid(True)
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.legend()
plt.title('LinearRegression')
plt.show()
```
Linear Regression is showing clear symptoms of under-fitting
Input Features are not sufficient to capture complex relationship
<h2>Your Turn</h2>
You can correct this under-fitting issue by adding relavant features.
1. What feature will you add and why?
2. Complete the code and Test
3. What performance do you see now?
```
# Specify the column names as the file does not have column header
df_train = pd.read_csv(train_file,names=['y','x'])
df_validation = pd.read_csv(validation_file,names=['y','x'])
df = pd.read_csv('quadratic_all.csv')
```
# Add new features
```
# Place holder to add new features to df_train, df_validation and df
# if you need help, scroll down to see the answer
# Add your code
X_train = df_train.iloc[:,1:] # Features: 1st column onwards
y_train = df_train.iloc[:,0].ravel() # Target: 0th column
X_validation = df_validation.iloc[:,1:]
y_validation = df_validation.iloc[:,0].ravel()
lin_regressor.fit(X_train,y_train)
```
Original Function: -23*x + 5*x**2 + 47 + some noise (rewritten with x term first)
```
lin_regressor.coef_
lin_regressor.intercept_
result = lin_regressor.predict(X_validation)
plt.title('LinearRegression - Validation Dataset')
plt.scatter(df_validation.x,df_validation.y,label='actual',marker='.')
plt.scatter(df_validation.x,result,label='predicted',marker='.')
plt.grid(True)
plt.legend()
plt.show()
# RMSE Metrics
print('Linear Regression Metrics')
mse = mean_squared_error(df_validation.y,result)
print(" Mean Squared Error: {0:.2f}".format(mse))
print(" Root Mean Square Error: {0:.2f}".format(mse**.5))
print("***You should see an RMSE score of 30.45 or less")
df.head()
# Plot for entire dataset
plt.plot(df.x,df.y,label='Target')
plt.plot(df.x,lin_regressor.predict(df[['x','x2']]) ,label='Predicted')
plt.grid(True)
plt.xlabel('Input Feature')
plt.ylabel('Target')
plt.legend()
plt.title('LinearRegression')
plt.show()
```
## Solution for under-fitting
add a new X**2 term to the dataframe
syntax:
df_train['x2'] = df_train['x']**2
df_validation['x2'] = df_validation['x']**2
df['x2'] = df['x']**2
### Tree Based Algorithms have a lower bound and upper bound for predicted values
```
# True Function
def quad_func (x):
return 5*x**2 -23*x + 47
# X is outside range of training samples
# New Feature: Adding X^2 term
X = np.array([-100,-25,25,1000,5000])
y = quad_func(X)
df_tmp = pd.DataFrame({'x':X,'y':y,'x2':X**2})
df_tmp['xgboost']=regressor.predict(df_tmp[['x']])
df_tmp['linear']=lin_regressor.predict(df_tmp[['x','x2']])
df_tmp
plt.scatter(df_tmp.x,df_tmp.y,label='Actual',color='r')
plt.plot(df_tmp.x,df_tmp.linear,label='LinearRegression')
plt.plot(df_tmp.x,df_tmp.xgboost,label='XGBoost')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Input Outside Range')
plt.show()
# X is inside range of training samples
X = np.array([-15,-12,-5,0,1,3,5,7,9,11,15,18])
y = quad_func(X)
df_tmp = pd.DataFrame({'x':X,'y':y,'x2':X**2})
df_tmp['xgboost']=regressor.predict(df_tmp[['x']])
df_tmp['linear']=lin_regressor.predict(df_tmp[['x','x2']])
df_tmp
# XGBoost Predictions have an upper bound and lower bound
# Linear Regression Extrapolates
plt.scatter(df_tmp.x,df_tmp.y,label='Actual',color='r')
plt.plot(df_tmp.x,df_tmp.linear,label='LinearRegression')
plt.plot(df_tmp.x,df_tmp.xgboost,label='XGBoost')
plt.legend()
plt.xlabel('X')
plt.ylabel('y')
plt.title('Input within range')
plt.show()
```
<h2>Summary</h2>
1. In this exercise, we compared performance of XGBoost model and Linear Regression on a quadratic dataset
2. The relationship between input feature and target was non-linear.
3. XGBoost handled it pretty well; whereas, linear regression was under-fitting
4. To correct the issue, we had to add additional features for linear regression
5. With this change, linear regression performed much better
XGBoost can detect patterns involving non-linear relationship; whereas, algorithms like linear regression may need complex feature engineering
| true |
code
| 0.664431 | null | null | null | null |
|
# Example File:
In this package, we show three examples:
<ol>
<li>4 site XY model</li>
<li>4 site Transverse Field XY model with random coefficients</li>
<li><b> Custom Hamiltonian from OpenFermion </b> </li>
</ol>
## Clone and Install The Repo via command line:
```
git clone https://github.com/kemperlab/cartan-quantum-synthesizer.git
cd ./cartan-quantum-synthesizer/
pip install .
```
# Building Custom Hamiltonians
In this example, we will use OpenFermion to generate a Hubbard Model Hamiltonian, then use the Jordan-Wigner methods of OpenFermion and some custom functions to feed the output into the Cartan-Quantum-Synthesizer package
## Step 1: Build the Hamiltonian in OpenFermion
```
from CQS.methods import *
from CQS.util.IO import tuplesToMatrix
import openfermion
from openfermion import FermionOperator
t = 1
U = 8
mu = 1
systemSize = 4 #number of qubits neeed
#2 site, 1D lattice, indexed as |↑_0↑_1↓_2↓_3>
#Hopping terms
H = -t*(FermionOperator('0^ 1') + FermionOperator('1^ 0') + FermionOperator('2^ 3') + FermionOperator('3^ 2'))
#Coulomb Terms
H += U*(FermionOperator('0^ 0 2^ 2') + FermionOperator('1^ 1 3^ 3'))
#Chemical Potential
H += -mu*(FermionOperator('0^ 0') + FermionOperator('1^ 1') + FermionOperator('2^ 2') + FermionOperator('3^ 3'))
print(H)
#Jordan Wigner Transform
HPauli = openfermion.jordan_wigner(H)
print(HPauli)
#Custom Function to convert OpenFermion operators to a format readable by CQS:
#Feel free to use or modify this code, but it is not built into the CQS package
def OpenFermionToCQS(H, systemSize):
"""
Converts the Operators to a list of (PauliStrings)
Args:
H(obj): The OpenFermion Operator
systemSize (int): The number of qubits in the system
"""
stringToTuple = {
'X': 1,
'Y': 2,
'Z': 3
}
opList = []
coList = []
for op in H.terms.keys(): #Pulls the operator out of the QubitOperator format
coList.append(H.terms[op])
opIndexList = []
opTypeDict = {}
tempTuple = ()
for (opIndex, opType) in op:
opIndexList.append(opIndex)
opTypeDict[opIndex] = opType
for index in range(systemSize):
if index in opIndexList:
tempTuple += (stringToTuple[opTypeDict[index]],)
else:
tempTuple += (0,)
opList.append(tempTuple)
return (coList, opList)
#The new format looks like:
print(OpenFermionToCQS(HPauli, systemSize))
#Now, we can put all this together:
#Step 1: Create an Empty Hamiltonian Object
HubbardH = Hamiltonian(systemSize)
#Use Hamiltonian.addTerms to build the Hubbard model Hamiltonian:
HubbardH.addTerms(OpenFermionToCQS(HPauli, systemSize))
#This gives:
HubbardH.getHamiltonian(type='printText')
#There's an IIII term we would rather not deal with, so we can remove it like this:
HubbardH.removeTerm((0,0,0,0))
#This gives:
print('Idenity/Global Phase removed:')
HubbardH.getHamiltonian(type='printText')
#Be careful choosing an involution, because it might now decompose such that the Hamiltonian is in M:
try:
HubbardC = Cartan(HubbardH)
except Exception as e:
print('Default Even/Odd Involution does not work:')
print(e)
print('countY does work though. g = ')
HubbardC = Cartan(HubbardH, involution='countY')
print(HubbardC.g)
```
| true |
code
| 0.792946 | null | null | null | null |
|
Single-channel CSC (Constrained Data Fidelity)
==============================================
This example demonstrates solving a constrained convolutional sparse coding problem with a greyscale signal
$$\mathrm{argmin}_\mathbf{x} \sum_m \| \mathbf{x}_m \|_1 \; \text{such that} \; \left\| \sum_m \mathbf{d}_m * \mathbf{x}_m - \mathbf{s} \right\|_2 \leq \epsilon \;,$$
where $\mathbf{d}_{m}$ is the $m^{\text{th}}$ dictionary filter, $\mathbf{x}_{m}$ is the coefficient map corresponding to the $m^{\text{th}}$ dictionary filter, and $\mathbf{s}$ is the input image.
```
from __future__ import print_function
from builtins import input
import pyfftw # See https://github.com/pyFFTW/pyFFTW/issues/40
import numpy as np
from sporco import util
from sporco import signal
from sporco import plot
plot.config_notebook_plotting()
import sporco.metric as sm
from sporco.admm import cbpdn
```
Load example image.
```
img = util.ExampleImages().image('kodim23.png', scaled=True, gray=True,
idxexp=np.s_[160:416,60:316])
```
Highpass filter example image.
```
npd = 16
fltlmbd = 10
sl, sh = signal.tikhonov_filter(img, fltlmbd, npd)
```
Load dictionary and display it.
```
D = util.convdicts()['G:12x12x36']
plot.imview(util.tiledict(D), fgsz=(7, 7))
```
Set [admm.cbpdn.ConvMinL1InL2Ball](http://sporco.rtfd.org/en/latest/modules/sporco.admm.cbpdn.html#sporco.admm.cbpdn.ConvMinL1InL2Ball) solver options.
```
epsilon = 3.4e0
opt = cbpdn.ConvMinL1InL2Ball.Options({'Verbose': True, 'MaxMainIter': 200,
'HighMemSolve': True, 'LinSolveCheck': True,
'RelStopTol': 5e-3, 'AuxVarObj': False, 'rho': 50.0,
'AutoRho': {'Enabled': False}})
```
Initialise and run CSC solver.
```
b = cbpdn.ConvMinL1InL2Ball(D, sh, epsilon, opt)
X = b.solve()
print("ConvMinL1InL2Ball solve time: %.2fs" % b.timer.elapsed('solve'))
```
Reconstruct image from sparse representation.
```
shr = b.reconstruct().squeeze()
imgr = sl + shr
print("Reconstruction PSNR: %.2fdB\n" % sm.psnr(img, imgr))
```
Display low pass component and sum of absolute values of coefficient maps of highpass component.
```
fig = plot.figure(figsize=(14, 7))
plot.subplot(1, 2, 1)
plot.imview(sl, title='Lowpass component', fig=fig)
plot.subplot(1, 2, 2)
plot.imview(np.sum(abs(X), axis=b.cri.axisM).squeeze(), cmap=plot.cm.Blues,
title='Sparse representation', fig=fig)
fig.show()
```
Display original and reconstructed images.
```
fig = plot.figure(figsize=(14, 7))
plot.subplot(1, 2, 1)
plot.imview(img, title='Original', fig=fig)
plot.subplot(1, 2, 2)
plot.imview(imgr, title='Reconstructed', fig=fig)
fig.show()
```
Get iterations statistics from solver object and plot functional value, ADMM primary and dual residuals, and automatically adjusted ADMM penalty parameter against the iteration number.
```
its = b.getitstat()
fig = plot.figure(figsize=(20, 5))
plot.subplot(1, 3, 1)
plot.plot(its.ObjFun, xlbl='Iterations', ylbl='Functional', fig=fig)
plot.subplot(1, 3, 2)
plot.plot(np.vstack((its.PrimalRsdl, its.DualRsdl)).T,
ptyp='semilogy', xlbl='Iterations', ylbl='Residual',
lgnd=['Primal', 'Dual'], fig=fig)
plot.subplot(1, 3, 3)
plot.plot(its.Rho, xlbl='Iterations', ylbl='Penalty Parameter', fig=fig)
fig.show()
```
| true |
code
| 0.798756 | null | null | null | null |
|
# 六軸史都華平台模擬
```
import numpy as np
import pandas as pd
from sympy import *
init_printing(use_unicode=True)
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
import seaborn as sns
sns.set()
%matplotlib inline
```
### Stewart Func
```
α, β, γ = symbols('α β γ')
x, y, z = symbols('x y z')
r, R, w, W, t = symbols('r R w W t')
# x, y, z三軸固定軸旋轉矩陣
rotx = lambda θ : Matrix([[1, 0, 0],
[0, cos(θ), -sin(θ)],
[0, sin(θ), cos(θ)]])
roty = lambda θ : Matrix([[cos(θ), 0, sin(θ)],
[0, 1, 0],
[-sin(θ), 0, cos(θ)]])
rotz = lambda θ : Matrix([[cos(θ), -sin(θ), 0],
[sin(θ), cos(θ), 0],
[0, 0, 1]])
# 姿勢產生器 固定座標旋轉
def poses(α, β, γ):
return rotz(γ)*roty(β)*rotx(α)
# 質心位置產生器
def posit(x, y, z):
return Matrix([x, y, z])
# Basic 6 軸點設定
def basic(r, w):
b1 = Matrix([w/2, r, 0])
b2 = Matrix([-w/2, r, 0])
b3 = rotz(pi*2/3)*b1
b4 = rotz(pi*2/3)*b2
b5 = rotz(pi*2/3)*b3
b6 = rotz(pi*2/3)*b4
return [b1, b2, b3, b4, b5, b6]
# 平台 6 軸點設定
def plat(r, w, pos=poses(0, 0, 0), pit=posit(0, 0, 5)):
p1 = Matrix([-w/2, r, 0])
p1 = rotz(-pi/3)*p1
p2 = Matrix([[-1, 0, 0], [0, 1, 0], [0, 0, 1]])*p1
p3 = rotz(pi*2/3)*p1
p4 = rotz(pi*2/3)*p2
p5 = rotz(pi*2/3)*p3
p6 = rotz(pi*2/3)*p4
lst = [p1, p2, p3, p4, p5, p6]
for n in range(6):
lst[n] = (pos*lst[n]) + pit
return lst
# 六軸長度
def leng(a, b):
if a.ndim == 1:
return (((a - b)**2).sum())**0.5
else:
return (((a - b)**2).sum(1))**0.5
```
### Basic & plane
```
basic(R, W)
plat(r, w, poses(α, β, γ), posit(x, y, z))
```
### 設定α, β, γ, x, y, z 可設定為時間t的函數
```
pos = poses(sin(2*t), cos(t), 0)
pit = posit(x, y, z)
baspt = basic(R, W)
baspt = np.array(baspt)
pltpt = plat(r, w, pos, pit)
pltpt = np.array(pltpt)
```
### 6軸的長度 (示範軸1)
```
length = leng(baspt ,pltpt)
```
### 設定參數 r = 10, R = 5, w = 2, W = 2, x = 0, y = 0, z = 10
```
x1 = length[0].subs([(r, 10), (R, 5), (w, 2), (W, 2), (x, 0), (y, 0), (z, 10)])
x1
```
### 微分一次獲得速度變化
```
dx1 = diff(x1, t)
dx1
```
### 微分兩次獲得加速度變化
```
ddx1 = diff(dx1, t)
ddx1
```
### 畫圖
```
tline = np.linspace(0, 2*np.pi, 361)
xlst = lambdify(t, x1, 'numpy')
dxlst = lambdify(t, dx1, 'numpy')
ddxlst = lambdify(t, ddx1, 'numpy')
plt.rcParams['figure.figsize'] = [16, 6]
plt.plot(tline, xlst(tline), label = 'x')
plt.plot(tline, dxlst(tline), label = 'v')
plt.plot(tline, ddxlst(tline), label = 'a')
plt.ylabel('Length')
plt.xlabel('Time')
plt.legend()
```
| true |
code
| 0.520314 | null | null | null | null |
|
<h3>Implementation Of Doubly Linked List in Python</h3>
<p> It is similar to Single Linked List but the only Difference lies that it where in Single Linked List we had a link to the next data element ,In Doubly Linked List we also have the link to previous data element with addition to next link</p>
<ul> <b>It has three parts</b>
<li> Data Part :This stores the data element of the Node and also consists the reference of the address of the next and previous element </li>
<li>Next :This stores the address of the next pointer via links</li>
<li>Previous :This stores the address of the previous element/ pointer via links </li>
</ul>
```
from IPython.display import Image
Image(filename='C:/Users/prakhar/Desktop/Python_Data_Structures_and_Algorithms_Implementations/Images/DoublyLinkedList.png',width=800, height=400)
#save the images from github to your local machine and then give the absolute path of the image
class Node: # All the operation are similar to Single Linked List with just an addition of Previous which points towards the Prev address via links
def __init__(self, data=None, next=None, prev=None):
self.data = data
self.next = next
self.prev = prev
class Double_LL():
def __init__(self):
self.head = None
def print_forward(self):
if self.head is None:
print("Linked List is empty")
return
itr = self.head
llstr = ''
while itr:
llstr += str(itr.data) + ' --> '
itr = itr.next
print(llstr)
def print_backward(self):
if self.head is None:
print("Linked list is empty")
return
last_node = self.get_last_node()
itr = last_node
llstr = ''
while itr:
llstr += itr.data + '-->'
itr = itr.prev
print("Link list in reverse: ", llstr)
def get_last_node(self):
itr = self.head
while itr.next:
itr = itr.next
return itr
def get_length(self):
count = 0
itr = self.head
while itr:
count += 1
itr = itr.next
return count
def insert_at_begining(self, data):
if self.head == None:
node = Node(data, self.head, None)
self.head = node
else:
node = Node(data, self.head, None)
self.head.prev = node
self.head = node
def insert_at_end(self, data):
if self.head is None:
self.head = Node(data, None, None)
return
itr = self.head
while itr.next:
itr = itr.next
itr.next = Node(data, None, itr)
def insert_at(self, index, data):
if index < 0 or index > self.get_length():
raise Exception("Invalid Index")
if index == 0:
self.insert_at_begining(data)
return
count = 0
itr = self.head
while itr:
if count == index - 1:
node = Node(data, itr.next, itr)
if node.next:
node.next.prev = node
itr.next = node
break
itr = itr.next
count += 1
def remove_at(self, index):
if index < 0 or index >= self.get_length():
raise Exception("Invalid Index")
if index == 0:
self.head = self.head.next
self.head.prev = None
return
count = 0
itr = self.head
while itr:
if count == index:
itr.prev.next = itr.next
if itr.next:
itr.next.prev = itr.prev
break
itr = itr.next
count += 1
def insert_values(self, data_list):
self.head = None
for data in data_list:
self.insert_at_end(data)
from IPython.display import Image
Image(filename='C:/Users/prakhar/Desktop/Python_Data_Structures_and_Algorithms_Implementations/Images/DLL_insertion_at_beginning.png',width=800, height=400)
#save the images from github to your local machine and then give the absolute path of the image
```
<p> Insertion at Beginning</p>
```
from IPython.display import Image
Image(filename='C:/Users/prakhar/Desktop/Python_Data_Structures_and_Algorithms_Implementations/Images/DLL_insertion.png',width=800, height=400)
#save the images from github to your local machine and then give the absolute path of the image
```
<p>Inserting Node at Index</p>
```
if __name__ == '__main__':
ll = Double_LL()
ll.insert_values(["banana", "mango", "grapes", "orange"])
ll.print_forward()
ll.print_backward()
ll.insert_at_end("figs")
ll.print_forward()
ll.insert_at(0, "jackfruit")
ll.print_forward()
ll.insert_at(6, "dates")
ll.print_forward()
ll.insert_at(2, "kiwi")
ll.print_forward()
```
| true |
code
| 0.399226 | null | null | null | null |
|
# Ungraded Lab Part 2 - Consuming a Machine Learning Model
Welcome to the second part of this ungraded lab!
**Before going forward check that the server from part 1 is still running.**
In this notebook you will code a minimal client that uses Python's `requests` library to interact with your running server.
```
import os
import io
import cv2
import requests
import numpy as np
from IPython.display import Image, display
```
## Understanding the URL
### Breaking down the URL
After experimenting with the fastAPI's client you may have noticed that we made all requests by pointing to a specific URL and appending some parameters to it.
More concretely:
1. The server is hosted in the URL [http://localhost:8000/](http://localhost:8000/).
2. The endpoint that serves your model is the `/predict` endpoint.
Also you can specify the model to use: `yolov3` or`yolov3-tiny`. Let's stick to the tiny version for computational efficiency.
Let's get started by putting in place all this information.
```
base_url = 'http://localhost:8000'
endpoint = '/predict'
model = 'yolov3-tiny'
confidence = 0.1
```
To consume your model, you append the endpoint to the base URL to get the full URL. Notice that the parameters are absent for now.
```
url_with_endpoint_no_params = base_url + endpoint
url_with_endpoint_no_params
```
To set any of the expected parameters, the syntax is to add a "?" character followed by the name of the parameter and its value.
Let's do it and check how the final URL looks like:
```
full_url = url_with_endpoint_no_params + "?model=" + model + '&confidence=' + str(confidence)
full_url
```
This endpoint expects both a model's name and an image. But since the image is more complex it is not passed within the URL. Instead we leverage the `requests` library to handle this process.
# Sending a request to your server
### Coding the response_from_server function
As a reminder, this endpoint expects a POST HTTP request. The `post` function is part of the requests library.
To pass the file along with the request, you need to create a dictionary indicating the name of the file ('file' in this case) and the actual file.
`status code` is a handy command to check the status of the response the request triggered. **A status code of 200 means that everything went well.**
```
def response_from_server(url, image_file, verbose=True):
"""Makes a POST request to the server and returns the response.
Args:
url (str): URL that the request is sent to.
image_file (_io.BufferedReader): File to upload, should be an image.
verbose (bool): True if the status of the response should be printed. False otherwise.
Returns:
requests.models.Response: Response from the server.
"""
files = {'file': image_file}
response = requests.post(url, files=files)
status_code = response.status_code
if verbose:
msg = "Everything went well!" if status_code == 200 else "There was an error when handling the request."
print(msg)
return response
```
To test this function, open a file in your filesystem and pass it as a parameter alongside the URL:
```
with open("images/clock2.jpg", "rb") as image_file:
prediction = response_from_server(full_url, image_file)
```
Great news! The request was successful. However, you are not getting any information about the objects in the image.
To get the image with the bounding boxes and labels, you need to parse the content of the response into an appropriate format. This process looks very similar to how you read raw images into a cv2 image on the server.
To handle this step, let's create a directory called `images_predicted` to save the image to:
```
dir_name = "images_predicted"
if not os.path.exists(dir_name):
os.mkdir(dir_name)
```
### Creating the display_image_from_response function
```
def display_image_from_response(response):
"""Display image within server's response.
Args:
response (requests.models.Response): The response from the server after object detection.
"""
image_stream = io.BytesIO(response.content)
image_stream.seek(0)
file_bytes = np.asarray(bytearray(image_stream.read()), dtype=np.uint8)
image = cv2.imdecode(file_bytes, cv2.IMREAD_COLOR)
filename = "image_with_objects.jpeg"
cv2.imwrite(f'images_predicted/{filename}', image)
display(Image(f'images_predicted/{filename}'))
display_image_from_response(prediction)
```
Now you are ready to consume your object detection model through your own client!
Let's test it out on some other images:
```
image_files = [
'car2.jpg',
'clock3.jpg',
'apples.jpg'
]
for image_file in image_files:
with open(f"images/{image_file}", "rb") as image_file:
prediction = response_from_server(full_url, image_file, verbose=False)
display_image_from_response(prediction)
```
**Congratulations on finishing this ungraded lab!** Real life clients and servers have a lot more going on in terms of security and performance. However, the code you just experienced is close to what you see in real production environments.
Hopefully, this lab served the purpose of increasing your familiarity with the process of deploying a Deep Learning model, and consuming from it.
**Keep it up!**
#
## Optional Challenge - Adding the confidence level to the request
Let's expand on what you have learned so far. The next logical step is to extend the server and the client so that they can accommodate an additional parameter: the level of confidence of the prediction.
**To test your extended implementation you must perform the following steps:**
- Stop the server by interrupting the Kernel.
- Extend the `prediction` function in the server.
- Re run the cell containing your server code.
- Re launch the server.
- Extend your client.
- Test it with some images (either with your client or fastAPI's one).
Here are some hints that can help you out throughout the process:
#### Server side:
- The `prediction` function that handles the `/predict` endpoint needs an additional parameter to accept the confidence level. Add this new parameter before the `File` parameter. This is necessary because `File` has a default value and must be specified last.
- `cv.detect_common_objects` accepts the `confidence` parameter, which is a floating point number (type `float`in Python).
#### Client side:
- You can add a new parameter to the URL by extending it with an `&` followed by the name of the parameter and its value. The name of this new parameter must be equal to the name used within the `prediction` function in the server. An example would look like this: `myawesomemodel.com/predict?model=yolov3-tiny&newParam=value`
**You can do it!**
| true |
code
| 0.680719 | null | null | null | null |
|
```
!pip install -Uq catalyst gym
```
# Seminar. RL, DDPG.
Hi! It's a second part of the seminar. Here we are going to introduce another way to train bot how to play games. A new algorithm will help bot to work in enviroments with continuos actinon spaces. However, the algorithm have no small changes in bot-enviroment communication process. That's why a lot of code for DQN part are reused.
Let's code!
```
from collections import deque, namedtuple
import random
import numpy as np
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from catalyst import dl, utils
device = utils.get_device()
import numpy as np
from collections import deque, namedtuple
Transition = namedtuple(
'Transition',
field_names=[
'state',
'action',
'reward',
'done',
'next_state'
]
)
class ReplayBuffer:
def __init__(self, capacity: int):
self.buffer = deque(maxlen=capacity)
def append(self, transition: Transition):
self.buffer.append(transition)
def sample(self, size: int):
indices = np.random.choice(
len(self.buffer),
size,
replace=size > len(self.buffer)
)
states, actions, rewards, dones, next_states = \
zip(*[self.buffer[idx] for idx in indices])
states, actions, rewards, dones, next_states = (
np.array(states, dtype=np.float32),
np.array(actions, dtype=np.int64),
np.array(rewards, dtype=np.float32),
np.array(dones, dtype=np.bool),
np.array(next_states, dtype=np.float32)
)
return states, actions, rewards, dones, next_states
def __len__(self):
return len(self.buffer)
from torch.utils.data.dataset import IterableDataset
# as far as RL does not have some predefined dataset,
# we need to specify epoch lenght by ourselfs
class ReplayDataset(IterableDataset):
def __init__(self, buffer: ReplayBuffer, epoch_size: int = int(1e3)):
self.buffer = buffer
self.epoch_size = epoch_size
def __iter__(self):
states, actions, rewards, dones, next_states = \
self.buffer.sample(self.epoch_size)
for i in range(len(dones)):
yield states[i], actions[i], rewards[i], dones[i], next_states[i]
def __len__(self):
return self.epoch_size
```
The first difference is action normalization. Some enviroments have action space bounds, and model's actino have to lie in the bounds.
```
class NormalizedActions(gym.ActionWrapper):
def action(self, action):
low_bound = self.action_space.low
upper_bound = self.action_space.high
action = low_bound + (action + 1.0) * 0.5 * (upper_bound - low_bound)
action = np.clip(action, low_bound, upper_bound)
return action
def _reverse_action(self, action):
low_bound = self.action_space.low
upper_bound = self.action_space.high
action = 2 * (action - low_bound) / (upper_bound - low_bound) - 1
action = np.clip(action, low_bound, upper_bound)
return actions
```
Next difference is randomness. We can't just sample an action from action space. But we can add noise to generated action.
```
def get_action(env, network, state, sigma=None):
state = torch.tensor(state, dtype=torch.float32).to(device).unsqueeze(0)
action = network(state).detach().cpu().numpy()[0]
if sigma is not None:
action = np.random.normal(action, sigma)
return action
def generate_session(
env,
network,
sigma=None,
replay_buffer=None,
):
total_reward = 0
state = env.reset()
for t in range(env.spec.max_episode_steps):
action = get_action(env, network, state=state, sigma=sigma)
next_state, reward, done, _ = env.step(action)
if replay_buffer is not None:
transition = Transition(
state, action, reward, done, next_state)
replay_buffer.append(transition)
total_reward += reward
state = next_state
if done:
break
return total_reward, t
def generate_sessions(
env,
network,
sigma=None,
replay_buffer=None,
num_sessions=100,
):
sessions_reward, sessions_steps = 0, 0
for i_episone in range(num_sessions):
r, t = generate_session(
env=env,
network=network,
sigma=sigma,
replay_buffer=replay_buffer,
)
sessions_reward += r
sessions_steps += t
return sessions_reward, sessions_steps
def soft_update(target, source, tau):
"""Updates the target data with smoothing by ``tau``"""
for target_param, param in zip(target.parameters(), source.parameters()):
target_param.data.copy_(
target_param.data * (1.0 - tau) + param.data * tau
)
class GameCallback(dl.Callback):
def __init__(
self,
*,
env,
replay_buffer,
session_period,
sigma,
# sigma_k,
actor_key,
):
super().__init__(order=0)
self.env = env
self.replay_buffer = replay_buffer
self.session_period = session_period
self.sigma = sigma
# self.sigma_k = sigma_k
self.actor_key = actor_key
def on_stage_start(self, runner: dl.IRunner):
self.actor = runner.model[self.actor_key]
self.actor.eval()
generate_sessions(
env=self.env,
network=self.actor,
sigma=self.sigma,
replay_buffer=self.replay_buffer,
num_sessions=1000,
)
self.actor.train()
def on_epoch_start(self, runner: dl.IRunner):
self.session_counter = 0
self.session_steps = 0
def on_batch_end(self, runner: dl.IRunner):
if runner.global_batch_step % self.session_period == 0:
self.actor.eval()
session_reward, session_steps = generate_session(
env=self.env,
network=self.actor,
sigma=self.sigma,
replay_buffer=self.replay_buffer,
)
self.session_counter += 1
self.session_steps += session_steps
runner.batch_metrics.update({"s_reward": session_reward})
runner.batch_metrics.update({"s_steps": session_steps})
self.actor.train()
def on_epoch_end(self, runner: dl.IRunner):
num_sessions = 100
self.actor.eval()
valid_rewards, valid_steps = generate_sessions(
env=self.env,
network=self.actor,
num_sessions=num_sessions
)
self.actor.train()
valid_rewards /= float(num_sessions)
valid_steps /= float(num_sessions)
runner.epoch_metrics["_epoch_"]["num_samples"] = self.session_steps
runner.epoch_metrics["_epoch_"]["updates_per_sample"] = (
runner.loader_sample_step / self.session_steps
)
runner.epoch_metrics["_epoch_"]["v_reward"] = valid_rewards
```
And the main difference is that we have two networks! Look at the algorithm:

One network is used to generate action (Policy Network). Another judge network's action and predict current reward. Because we have two networks, we can train our model to act in a continues space. Let's code this algorithm in Runner train step.
```
class CustomRunner(dl.Runner):
def __init__(
self,
*,
gamma,
tau,
tau_period=1,
**kwargs,
):
super().__init__(**kwargs)
self.gamma = gamma
self.tau = tau
self.tau_period = tau_period
def on_stage_start(self, runner: dl.IRunner):
super().on_stage_start(runner)
soft_update(self.model["target_actor"], self.model["actor"], 1.0)
soft_update(self.model["target_critic"], self.model["critic"], 1.0)
def handle_batch(self, batch):
# model train/valid step
states, actions, rewards, dones, next_states = batch
actor, target_actor = self.model["actor"], self.model["target_actor"]
critic, target_critic = self.model["critic"], self.model["target_critic"]
actor_optimizer, critic_optimizer = self.optimizer["actor"], self.optimizer["critic"]
# get actions for the current state
pred_actions = actor(states)
# get q-values for the actions in current states
pred_critic_states = torch.cat([states, pred_actions], 1)
# use q-values to train the actor model
policy_loss = (-critic(pred_critic_states)).mean()
with torch.no_grad():
# get possible actions for the next states
next_state_actions = target_actor(next_states)
# get possible q-values for the next actions
next_critic_states = torch.cat([next_states, next_state_actions], 1)
next_state_values = target_critic(next_critic_states).detach().squeeze()
next_state_values[dones] = 0.0
# compute Bellman's equation value
target_state_values = next_state_values * self.gamma + rewards
# compute predicted values
critic_states = torch.cat([states, actions], 1)
state_values = critic(critic_states).squeeze()
# train the critic model
value_loss = self.criterion(
state_values,
target_state_values.detach()
)
self.batch_metrics.update({
"critic_loss": value_loss,
"actor_loss": policy_loss
})
if self.is_train_loader:
actor.zero_grad()
actor_optimizer.zero_grad()
policy_loss.backward()
actor_optimizer.step()
critic.zero_grad()
critic_optimizer.zero_grad()
value_loss.backward()
critic_optimizer.step()
if self.global_batch_step % self.tau_period == 0:
soft_update(target_actor, actor, self.tau)
soft_update(target_critic, critic, self.tau)
```
Prepare networks generator and train models!
```
def get_network_actor(env):
inner_fn = utils.get_optimal_inner_init(nn.ReLU)
outer_fn = utils.outer_init
network = torch.nn.Sequential(
nn.Linear(env.observation_space.shape[0], 400),
nn.ReLU(),
nn.Linear(400, 300),
nn.ReLU(),
)
head = torch.nn.Sequential(
nn.Linear(300, 1),
nn.Tanh()
)
network.apply(inner_fn)
head.apply(outer_fn)
return torch.nn.Sequential(network, head)
def get_network_critic(env):
inner_fn = utils.get_optimal_inner_init(nn.LeakyReLU)
outer_fn = utils.outer_init
network = torch.nn.Sequential(
nn.Linear(env.observation_space.shape[0] + 1, 400),
nn.LeakyReLU(0.01),
nn.Linear(400, 300),
nn.LeakyReLU(0.01),
)
head = nn.Linear(300, 1)
network.apply(inner_fn)
head.apply(outer_fn)
return torch.nn.Sequential(network, head)
# data
batch_size = 64
epoch_size = int(1e3) * batch_size
buffer_size = int(1e5)
# runner settings, ~training
gamma = 0.99
tau = 0.01
tau_period = 1
# callback, ~exploration
session_period = 1
sigma = 0.3
# optimization
lr_actor = 1e-4
lr_critic = 1e-3
# env_name = "LunarLanderContinuous-v2"
env_name = "Pendulum-v0"
env = NormalizedActions(gym.make(env_name))
replay_buffer = ReplayBuffer(buffer_size)
actor, target_actor = get_network_actor(env), get_network_actor(env)
critic, target_critic = get_network_critic(env), get_network_critic(env)
utils.set_requires_grad(target_actor, requires_grad=False)
utils.set_requires_grad(target_critic, requires_grad=False)
models = {
"actor": actor,
"critic": critic,
"target_actor": target_actor,
"target_critic": target_critic,
}
criterion = torch.nn.MSELoss()
optimizer = {
"actor": torch.optim.Adam(actor.parameters(), lr_actor),
"critic": torch.optim.Adam(critic.parameters(), lr=lr_critic),
}
loaders = {
"train": DataLoader(
ReplayDataset(replay_buffer, epoch_size=epoch_size),
batch_size=batch_size,
),
}
runner = CustomRunner(
gamma=gamma,
tau=tau,
tau_period=tau_period,
)
runner.train(
model=models,
criterion=criterion,
optimizer=optimizer,
loaders=loaders,
logdir="./logs_ddpg",
num_epochs=10,
verbose=True,
valid_loader="_epoch_",
valid_metric="v_reward",
minimize_valid_metric=False,
load_best_on_end=True,
callbacks=[
GameCallback(
env=env,
replay_buffer=replay_buffer,
session_period=session_period,
sigma=sigma,
actor_key="actor",
)
]
)
```
And we can watch how our model plays in the games!
\* to run cells below, you should update your python environment. Instruction depends on your system specification.
```
import gym.wrappers
env = gym.wrappers.Monitor(
gym.make(env_name),
directory="videos_ddpg",
force=True)
generate_sessions(
env=env,
network=runner.model["actor"],
num_sessions=100
)
env.close()
# show video
from IPython.display import HTML
import os
video_names = list(
filter(lambda s: s.endswith(".mp4"), os.listdir("./videos_ddpg/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/"+video_names[-1])) # this may or may not be _last_ video. Try other indices
```
| true |
code
| 0.839652 | null | null | null | null |
|
# VQE for Unitary Coupled Cluster using tket
In this tutorial, we will focus on:<br>
- building parameterised ansätze for variational algorithms;<br>
- compilation tools for UCC-style ansätze.
This example assumes the reader is familiar with the Variational Quantum Eigensolver and its application to electronic structure problems through the Unitary Coupled Cluster approach.<br>
<br>
To run this example, you will need `pytket` and `pytket-qiskit`, as well as `openfermion`, `scipy`, and `sympy`.<br>
<br>
We will start with a basic implementation and then gradually modify it to make it faster, more general, and less noisy. The final solution is given in full at the bottom of the notebook.<br>
<br>
Suppose we have some electronic configuration problem, expressed via a physical Hamiltonian. (The Hamiltonian and excitations in this example were obtained using `qiskit-aqua` version 0.5.2 and `pyscf` for H2, bond length 0.75A, sto3g basis, Jordan-Wigner encoding, with no qubit reduction or orbital freezing.)
```
from openfermion import QubitOperator
hamiltonian = (
-0.8153001706270075 * QubitOperator("")
+ 0.16988452027940318 * QubitOperator("Z0")
+ -0.21886306781219608 * QubitOperator("Z1")
+ 0.16988452027940323 * QubitOperator("Z2")
+ -0.2188630678121961 * QubitOperator("Z3")
+ 0.12005143072546047 * QubitOperator("Z0 Z1")
+ 0.16821198673715723 * QubitOperator("Z0 Z2")
+ 0.16549431486978672 * QubitOperator("Z0 Z3")
+ 0.16549431486978672 * QubitOperator("Z1 Z2")
+ 0.1739537877649417 * QubitOperator("Z1 Z3")
+ 0.12005143072546047 * QubitOperator("Z2 Z3")
+ 0.04544288414432624 * QubitOperator("X0 X1 X2 X3")
+ 0.04544288414432624 * QubitOperator("X0 X1 Y2 Y3")
+ 0.04544288414432624 * QubitOperator("Y0 Y1 X2 X3")
+ 0.04544288414432624 * QubitOperator("Y0 Y1 Y2 Y3")
)
nuclear_repulsion_energy = 0.70556961456
```
We would like to define our ansatz for arbitrary parameter values. For simplicity, let's start with a Hardware Efficient Ansatz.
```
from pytket import Circuit
```
Hardware efficient ansatz:
```
def hea(params):
ansatz = Circuit(4)
for i in range(4):
ansatz.Ry(params[i], i)
for i in range(3):
ansatz.CX(i, i + 1)
for i in range(4):
ansatz.Ry(params[4 + i], i)
return ansatz
```
We can use this to build the objective function for our optimisation.
```
from pytket.extensions.qiskit import AerBackend
from pytket.utils import expectation_from_counts
backend = AerBackend()
```
Naive objective function:
```
def objective(params):
energy = 0
for term, coeff in hamiltonian.terms.items():
if not term:
energy += coeff
continue
circ = hea(params)
circ.add_c_register("c", len(term))
for i, (q, pauli) in enumerate(term):
if pauli == "X":
circ.H(q)
elif pauli == "Y":
circ.V(q)
circ.Measure(q, i)
backend.compile_circuit(circ)
counts = backend.run_circuit(circ, n_shots=4000).get_counts()
energy += coeff * expectation_from_counts(counts)
return energy + nuclear_repulsion_energy
```
This objective function is then run through a classical optimiser to find the set of parameter values that minimise the energy of the system. For the sake of example, we will just run this with a single parameter value.
```
arg_values = [
-7.31158201e-02,
-1.64514836e-04,
1.12585591e-03,
-2.58367544e-03,
1.00006068e00,
-1.19551357e-03,
9.99963988e-01,
2.53283285e-03,
]
energy = objective(arg_values)
print(energy)
```
The HEA is designed to cram as many orthogonal degrees of freedom into a small circuit as possible to be able to explore a large region of the Hilbert space whilst the circuits themselves can be run with minimal noise. These ansätze give virtually-optimal circuits by design, but suffer from an excessive number of variational parameters making convergence slow, barren plateaus where the classical optimiser fails to make progress, and spanning a space where most states lack a physical interpretation. These drawbacks can necessitate adding penalties and may mean that the ansatz cannot actually express the true ground state.<br>
<br>
The UCC ansatz, on the other hand, is derived from the electronic configuration. It sacrifices efficiency of the circuit for the guarantee of physical states and the variational parameters all having some meaningful effect, which helps the classical optimisation to converge.<br>
<br>
This starts by defining the terms of our single and double excitations. These would usually be generated using the orbital configurations, so we will just use a hard-coded example here for the purposes of demonstration.
```
from pytket.pauli import Pauli, QubitPauliString
from pytket.circuit import Qubit
q = [Qubit(i) for i in range(4)]
xyii = QubitPauliString([q[0], q[1]], [Pauli.X, Pauli.Y])
yxii = QubitPauliString([q[0], q[1]], [Pauli.Y, Pauli.X])
iixy = QubitPauliString([q[2], q[3]], [Pauli.X, Pauli.Y])
iiyx = QubitPauliString([q[2], q[3]], [Pauli.Y, Pauli.X])
xxxy = QubitPauliString(q, [Pauli.X, Pauli.X, Pauli.X, Pauli.Y])
xxyx = QubitPauliString(q, [Pauli.X, Pauli.X, Pauli.Y, Pauli.X])
xyxx = QubitPauliString(q, [Pauli.X, Pauli.Y, Pauli.X, Pauli.X])
yxxx = QubitPauliString(q, [Pauli.Y, Pauli.X, Pauli.X, Pauli.X])
yyyx = QubitPauliString(q, [Pauli.Y, Pauli.Y, Pauli.Y, Pauli.X])
yyxy = QubitPauliString(q, [Pauli.Y, Pauli.Y, Pauli.X, Pauli.Y])
yxyy = QubitPauliString(q, [Pauli.Y, Pauli.X, Pauli.Y, Pauli.Y])
xyyy = QubitPauliString(q, [Pauli.X, Pauli.Y, Pauli.Y, Pauli.Y])
singles_a = {xyii: 1.0, yxii: -1.0}
singles_b = {iixy: 1.0, iiyx: -1.0}
doubles = {
xxxy: 0.25,
xxyx: -0.25,
xyxx: 0.25,
yxxx: -0.25,
yyyx: -0.25,
yyxy: 0.25,
yxyy: -0.25,
xyyy: 0.25,
}
```
Building the ansatz circuit itself is often done naively by defining the map from each term down to basic gates and then applying it to each term.
```
def add_operator_term(circuit: Circuit, term: QubitPauliString, angle: float):
qubits = []
for q, p in term.map.items():
if p != Pauli.I:
qubits.append(q)
if p == Pauli.X:
circuit.H(q)
elif p == Pauli.Y:
circuit.V(q)
for i in range(len(qubits) - 1):
circuit.CX(i, i + 1)
circuit.Rz(angle, len(qubits) - 1)
for i in reversed(range(len(qubits) - 1)):
circuit.CX(i, i + 1)
for q, p in term.map.items():
if p == Pauli.X:
circuit.H(q)
elif p == Pauli.Y:
circuit.Vdg(q)
```
Unitary Coupled Cluster Singles & Doubles ansatz:
```
def ucc(params):
ansatz = Circuit(4)
# Set initial reference state
ansatz.X(1).X(3)
# Evolve by excitations
for term, coeff in singles_a.items():
add_operator_term(ansatz, term, coeff * params[0])
for term, coeff in singles_b.items():
add_operator_term(ansatz, term, coeff * params[1])
for term, coeff in doubles.items():
add_operator_term(ansatz, term, coeff * params[2])
return ansatz
```
This is already quite verbose, but `pytket` has a neat shorthand construction for these operator terms using the `PauliExpBox` construction. We can then decompose these into basic gates using the `DecomposeBoxes` compiler pass.
```
from pytket.circuit import PauliExpBox
from pytket.passes import DecomposeBoxes
def add_excitation(circ, term_dict, param):
for term, coeff in term_dict.items():
qubits, paulis = zip(*term.map.items())
pbox = PauliExpBox(paulis, coeff * param)
circ.add_pauliexpbox(pbox, qubits)
```
UCC ansatz with syntactic shortcuts:
```
def ucc(params):
ansatz = Circuit(4)
ansatz.X(1).X(3)
add_excitation(ansatz, singles_a, params[0])
add_excitation(ansatz, singles_b, params[1])
add_excitation(ansatz, doubles, params[2])
DecomposeBoxes().apply(ansatz)
return ansatz
```
The objective function can also be simplified using a utility method for constructing the measurement circuits and processing for expectation value calculations.
```
from pytket.utils.operators import QubitPauliOperator
from pytket.utils import get_operator_expectation_value
hamiltonian_op = QubitPauliOperator.from_OpenFermion(hamiltonian)
```
Simplified objective function using utilities:
```
def objective(params):
circ = ucc(params)
return (
get_operator_expectation_value(circ, hamiltonian_op, backend, n_shots=4000)
+ nuclear_repulsion_energy
)
arg_values = [-3.79002933e-05, 2.42964799e-05, 4.63447157e-01]
energy = objective(arg_values)
print(energy)
```
This is now the simplest form that this operation can take, but it isn't necessarily the most effective. When we decompose the ansatz circuit into basic gates, it is still very expensive. We can employ some of the circuit simplification passes available in `pytket` to reduce its size and improve fidelity in practice.<br>
<br>
A good example is to decompose each `PauliExpBox` into basic gates and then apply `FullPeepholeOptimise`, which defines a compilation strategy utilising all of the simplifications in `pytket` that act locally on small regions of a circuit. We can examine the effectiveness by looking at the number of two-qubit gates before and after simplification, which tends to be a good indicator of fidelity for near-term systems where these gates are often slow and inaccurate.
```
from pytket import OpType
from pytket.passes import FullPeepholeOptimise
test_circuit = ucc(arg_values)
print("CX count before", test_circuit.n_gates_of_type(OpType.CX))
print("CX depth before", test_circuit.depth_by_type(OpType.CX))
FullPeepholeOptimise().apply(test_circuit)
print("CX count after FPO", test_circuit.n_gates_of_type(OpType.CX))
print("CX depth after FPO", test_circuit.depth_by_type(OpType.CX))
```
These simplification techniques are very general and are almost always beneficial to apply to a circuit if you want to eliminate local redundancies. But UCC ansätze have extra structure that we can exploit further. They are defined entirely out of exponentiated tensors of Pauli matrices, giving the regular structure described by the `PauliExpBox`es. Under many circumstances, it is more efficient to not synthesise these constructions individually, but simultaneously in groups. The `PauliSimp` pass finds the description of a given circuit as a sequence of `PauliExpBox`es and resynthesises them (by default, in groups of commuting terms). This can cause great change in the overall structure and shape of the circuit, enabling the identification and elimination of non-local redundancy.
```
from pytket.passes import PauliSimp
test_circuit = ucc(arg_values)
print("CX count before", test_circuit.n_gates_of_type(OpType.CX))
print("CX depth before", test_circuit.depth_by_type(OpType.CX))
PauliSimp().apply(test_circuit)
print("CX count after PS", test_circuit.n_gates_of_type(OpType.CX))
print("CX depth after PS", test_circuit.depth_by_type(OpType.CX))
FullPeepholeOptimise().apply(test_circuit)
print("CX count after PS+FPO", test_circuit.n_gates_of_type(OpType.CX))
print("CX depth after PS+FPO", test_circuit.depth_by_type(OpType.CX))
```
To include this into our routines, we can just add the simplification passes to the objective function. The `get_operator_expectation_value` utility handles compiling to meet the requirements of the backend, so we don't have to worry about that here.
Objective function with circuit simplification:
```
def objective(params):
circ = ucc(params)
PauliSimp().apply(circ)
FullPeepholeOptimise().apply(circ)
return (
get_operator_expectation_value(circ, hamiltonian_op, backend, n_shots=4000)
+ nuclear_repulsion_energy
)
```
These circuit simplification techniques have tried to preserve the exact unitary of the circuit, but there are ways to change the unitary whilst preserving the correctness of the algorithm as a whole.<br>
<br>
For example, the excitation terms are generated by trotterisation of the excitation operator, and the order of the terms does not change the unitary in the limit of many trotter steps, so in this sense we are free to sequence the terms how we like and it is sensible to do this in a way that enables efficient synthesis of the circuit. Prioritising collecting terms into commuting sets is a very beneficial heuristic for this and can be performed using the `gen_term_sequence_circuit` method to group the terms together into collections of `PauliExpBox`es and the `GuidedPauliSimp` pass to utilise these sets for synthesis.
```
from pytket.passes import GuidedPauliSimp
from pytket.utils import gen_term_sequence_circuit
def ucc(params):
singles_params = {qps: params[0] * coeff for qps, coeff in singles.items()}
doubles_params = {qps: params[1] * coeff for qps, coeff in doubles.items()}
excitation_op = QubitPauliOperator({**singles_params, **doubles_params})
reference_circ = Circuit(4).X(1).X(3)
ansatz = gen_term_sequence_circuit(excitation_op, reference_circ)
GuidedPauliSimp().apply(ansatz)
FullPeepholeOptimise().apply(ansatz)
return ansatz
```
Adding these simplification routines doesn't come for free. Compiling and simplifying the circuit to achieve the best results possible can be a difficult task, which can take some time for the classical computer to perform.<br>
<br>
During a VQE run, we will call this objective function many times and run many measurement circuits within each, but the circuits that are run on the quantum computer are almost identical, having the same gate structure but with different gate parameters and measurements. We have already exploited this within the body of the objective function by simplifying the ansatz circuit before we call `get_operator_expectation_value`, so it is only done once per objective calculation rather than once per measurement circuit.<br>
<br>
We can go even further by simplifying it once outside of the objective function, and then instantiating the simplified ansatz with the parameter values needed. For this, we will construct the UCC ansatz circuit using symbolic (parametric) gates.
```
from sympy import symbols
```
Symbolic UCC ansatz generation:
```
syms = symbols("p0 p1 p2")
singles_a_syms = {qps: syms[0] * coeff for qps, coeff in singles_a.items()}
singles_b_syms = {qps: syms[1] * coeff for qps, coeff in singles_b.items()}
doubles_syms = {qps: syms[2] * coeff for qps, coeff in doubles.items()}
excitation_op = QubitPauliOperator({**singles_a_syms, **singles_b_syms, **doubles_syms})
ucc_ref = Circuit(4).X(1).X(3)
ucc = gen_term_sequence_circuit(excitation_op, ucc_ref)
GuidedPauliSimp().apply(ucc)
FullPeepholeOptimise().apply(ucc)
```
Objective function using the symbolic ansatz:
```
def objective(params):
circ = ucc.copy()
sym_map = dict(zip(syms, params))
circ.symbol_substitution(sym_map)
return (
get_operator_expectation_value(circ, hamiltonian_op, backend, n_shots=4000)
+ nuclear_repulsion_energy
)
```
We have now got some very good use of `pytket` for simplifying each individual circuit used in our experiment and for minimising the amount of time spent compiling, but there is still more we can do in terms of reducing the amount of work the quantum computer has to do. Currently, each (non-trivial) term in our measurement hamiltonian is measured by a different circuit within each expectation value calculation. Measurement reduction techniques exist for identifying when these observables commute and hence can be simultaneously measured, reducing the number of circuits required for the full expectation value calculation.<br>
<br>
This is built in to the `get_operator_expectation_value` method and can be applied by specifying a way to partition the measuremrnt terms. `PauliPartitionStrat.CommutingSets` can greatly reduce the number of measurement circuits by combining any number of terms that mutually commute. However, this involves potentially adding an arbitrary Clifford circuit to change the basis of the measurements which can be costly on NISQ devices, so `PauliPartitionStrat.NonConflictingSets` trades off some of the reduction in circuit number to guarantee that only single-qubit gates are introduced.
```
from pytket.partition import PauliPartitionStrat
```
Objective function using measurement reduction:
```
def objective(params):
circ = ucc.copy()
sym_map = dict(zip(syms, params))
circ.symbol_substitution(sym_map)
return (
get_operator_expectation_value(
circ,
operator,
backend,
n_shots=4000,
partition_strat=PauliPartitionStrat.CommutingSets,
)
+ nuclear_repulsion_energy
)
```
At this point, we have completely transformed how our VQE objective function works, improving its resilience to noise, cutting the number of circuits run, and maintaining fast runtimes. In doing this, we have explored a number of the features `pytket` offers that are beneficial to VQE and the UCC method:<br>
- high-level syntactic constructs for evolution operators;<br>
- utility methods for easy expectation value calculations;<br>
- both generic and domain-specific circuit simplification methods;<br>
- symbolic circuit compilation;<br>
- measurement reduction for expectation value calculations.
For the sake of completeness, the following gives the full code for the final solution, including passing the objective function to a classical optimiser to find the ground state:
```
from openfermion import QubitOperator
from scipy.optimize import minimize
from sympy import symbols
from pytket.extensions.qiskit import AerBackend
from pytket.circuit import Circuit, Qubit
from pytket.partition import PauliPartitionStrat
from pytket.passes import GuidedPauliSimp, FullPeepholeOptimise
from pytket.pauli import Pauli, QubitPauliString
from pytket.utils import get_operator_expectation_value, gen_term_sequence_circuit
from pytket.utils.operators import QubitPauliOperator
```
Obtain electronic Hamiltonian:
```
hamiltonian = (
-0.8153001706270075 * QubitOperator("")
+ 0.16988452027940318 * QubitOperator("Z0")
+ -0.21886306781219608 * QubitOperator("Z1")
+ 0.16988452027940323 * QubitOperator("Z2")
+ -0.2188630678121961 * QubitOperator("Z3")
+ 0.12005143072546047 * QubitOperator("Z0 Z1")
+ 0.16821198673715723 * QubitOperator("Z0 Z2")
+ 0.16549431486978672 * QubitOperator("Z0 Z3")
+ 0.16549431486978672 * QubitOperator("Z1 Z2")
+ 0.1739537877649417 * QubitOperator("Z1 Z3")
+ 0.12005143072546047 * QubitOperator("Z2 Z3")
+ 0.04544288414432624 * QubitOperator("X0 X1 X2 X3")
+ 0.04544288414432624 * QubitOperator("X0 X1 Y2 Y3")
+ 0.04544288414432624 * QubitOperator("Y0 Y1 X2 X3")
+ 0.04544288414432624 * QubitOperator("Y0 Y1 Y2 Y3")
)
nuclear_repulsion_energy = 0.70556961456
hamiltonian_op = QubitPauliOperator.from_OpenFermion(hamiltonian)
```
Obtain terms for single and double excitations:
```
q = [Qubit(i) for i in range(4)]
xyii = QubitPauliString([q[0], q[1]], [Pauli.X, Pauli.Y])
yxii = QubitPauliString([q[0], q[1]], [Pauli.Y, Pauli.X])
iixy = QubitPauliString([q[2], q[3]], [Pauli.X, Pauli.Y])
iiyx = QubitPauliString([q[2], q[3]], [Pauli.Y, Pauli.X])
xxxy = QubitPauliString(q, [Pauli.X, Pauli.X, Pauli.X, Pauli.Y])
xxyx = QubitPauliString(q, [Pauli.X, Pauli.X, Pauli.Y, Pauli.X])
xyxx = QubitPauliString(q, [Pauli.X, Pauli.Y, Pauli.X, Pauli.X])
yxxx = QubitPauliString(q, [Pauli.Y, Pauli.X, Pauli.X, Pauli.X])
yyyx = QubitPauliString(q, [Pauli.Y, Pauli.Y, Pauli.Y, Pauli.X])
yyxy = QubitPauliString(q, [Pauli.Y, Pauli.Y, Pauli.X, Pauli.Y])
yxyy = QubitPauliString(q, [Pauli.Y, Pauli.X, Pauli.Y, Pauli.Y])
xyyy = QubitPauliString(q, [Pauli.X, Pauli.Y, Pauli.Y, Pauli.Y])
```
Symbolic UCC ansatz generation:
```
syms = symbols("p0 p1 p2")
singles_syms = {xyii: syms[0], yxii: -syms[0], iixy: syms[1], iiyx: -syms[1]}
doubles_syms = {
xxxy: 0.25 * syms[2],
xxyx: -0.25 * syms[2],
xyxx: 0.25 * syms[2],
yxxx: -0.25 * syms[2],
yyyx: -0.25 * syms[2],
yyxy: 0.25 * syms[2],
yxyy: -0.25 * syms[2],
xyyy: 0.25 * syms[2],
}
excitation_op = QubitPauliOperator({**singles_syms, **doubles_syms})
ucc_ref = Circuit(4).X(0).X(2)
ucc = gen_term_sequence_circuit(excitation_op, ucc_ref)
```
Circuit simplification:
```
GuidedPauliSimp().apply(ucc)
FullPeepholeOptimise().apply(ucc)
```
Connect to a simulator/device:
```
backend = AerBackend()
```
Objective function:
```
def objective(params):
circ = ucc.copy()
sym_map = dict(zip(syms, params))
circ.symbol_substitution(sym_map)
return (
get_operator_expectation_value(
circ,
hamiltonian_op,
backend,
n_shots=4000,
partition_strat=PauliPartitionStrat.CommutingSets,
)
+ nuclear_repulsion_energy
).real
```
Optimise against the objective function:
```
initial_params = [1e-4, 1e-4, 4e-1]
result = minimize(objective, initial_params, method="Nelder-Mead")
print("Final parameter values", result.x)
print("Final energy value", result.fun)
```
Exercises:<br>
- Replace the `get_operator_expectation_value` call with its implementation and use this to pull the analysis for measurement reduction outside of the objective function, so our circuits can be fully determined and compiled once. This means that the `symbol_substitution` method will need to be applied to each measurement circuit instead of just the state preparation circuit.<br>
- Use the `SpamCorrecter` class to add some mitigation of the measurement errors. Start by running the characterisation circuits first, before your main VQE loop, then apply the mitigation to each of the circuits run within the objective function.<br>
- Change the `backend` by passing in a `Qiskit` `NoiseModel` to simulate a noisy device. Compare the accuracy of the objective function both with and without the circuit simplification. Try running a classical optimiser over the objective function and compare the convergence rates with different noise models. If you have access to a QPU, try changing the `backend` to connect to that and compare the results to the simulator.
| true |
code
| 0.42937 | null | null | null | null |
|

# Sequences
In some cases, one may want to intersperse ideal unitary gates within a sequence of time-dependent operations. This is possible using an object called a [Sequence](../api/classes.rst#Sequence). A `Sequence` is essentially a list containing [PulseSequences](../api/classes.rst#PulseSequence), [Operations](../api/classes.rst#Operation), and unitary operators. When `Sequence.run(init_state)` is called, the `Sequence` iterates over its constituent `PulseSequences`, `Operations`, and unitaries, applying each to the resulting state of the last.
`Sequence` is designed to behave like a Python [list](https://docs.python.org/3/tutorial/datastructures.html), so it has the following methods defined:
- `append()`
- `extend()`
- `insert()`
- `pop()`
- `clear()`
- `__len__()`
- `__getitem__()`
- `__iter__()`
**Notes:**
- Just like a `PulseSequence` or `CompiledPulseSequence`, a `Sequence` must be associated with a `System`.
- Whereas `PulseSequence.run()` and `CompiledPulseSequence.run()` return an instance of `qutip.solver.Result`, `Sequence.run()` returns a [SequenceResult](../api/classes.rst#SequenceResult) object, which behaves just like `qutip.solver.Result`. `SequenceResult.states` stores the quantum `states` after each stage of the simulation (`states[0]` is `init_state` and `states[-1]` is the final state of the system).
```
%config InlineBackend.figure_formats = ['svg']
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import qutip
from sequencing import Transmon, Cavity, System, Sequence
qubit = Transmon('qubit', levels=3, kerr=-200e-3)
cavity = Cavity('cavity', levels=10, kerr=-10e-6)
system = System('system', modes=[qubit, cavity])
system.set_cross_kerr(cavity, qubit, chi=-2e-3)
qubit.gaussian_pulse.drag = 5
```
## Interleave pulses and unitaries
Here we perform a "$\pi$-pulse" composed of $20$ interleaved $\frac{\pi}{40}$-pulses and unitary rotations.
```
init_state = system.ground_state()
# calculate expectation value of |qubit=1, cavity=0>
e_ops = [system.fock_dm(qubit=1)]
n_rotations = 20
theta = np.pi / n_rotations
seq = Sequence(system)
for _ in range(n_rotations):
# Capture a PulseSequence
qubit.rotate_x(theta/2)
# # Alternatively, we can append an Operation
# operation = qubit.rotate_x(theta/2, capture=False)
# seq.append(operation)
# Append a unitary
seq.append(qubit.Rx(theta/2))
result = seq.run(init_state, e_ops=e_ops, full_evolution=True, progress_bar=True)
states = result.states
```
### Inspect the sequence
`Sequence.plot_coefficients()` plots Hamiltonian coefficients vs. time. Instantaneous unitary operations are represented by dashed vertical lines. If multiple unitaries occur at the same time, only a single dashed line is drawn.
```
fig, ax = seq.plot_coefficients(subplots=False)
ax.set_xlabel('Time [ns]')
ax.set_ylabel('Hamiltonian coefficient [GHz]')
fig.set_size_inches(8,4)
fig.tight_layout()
fig.subplots_adjust(top=0.9)
print('len(states):', len(states))
print(f'state fidelity: {qutip.fidelity(states[-1], qubit.Rx(np.pi) * init_state)**2:.4f}')
```
### Plot the results
```
e_pops = result.expect[0] # probability of measuring the state |qubit=1, cavity=0>
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(result.times, e_pops, '.')
ax.scatter(result.times[:1], e_pops[:1], marker='s', color='k', label='init_state')
# draw vertical lines at the location of each unitary rotation
for i in range(1, result.times.size // (2*n_rotations) + 1):
t = 2 * n_rotations * i - 1
label = 'unitaries' if i == 1 else None
ax.axvline(t, color='k', alpha=0.25, ls='--', lw=1.5, label=label)
ax.axhline(0, color='k', lw=1)
ax.axhline(1, color='k', lw=1)
ax.set_ylabel('$P(|e\\rangle)$')
ax.set_xlabel('Times [ns]')
ax.set_title('Interleaved pulses and unitaries')
ax.legend(loc=0);
print(result)
from qutip.ipynbtools import version_table
version_table()
```
| true |
code
| 0.710584 | null | null | null | null |
|
# recreating the paper with tiny imagenet
First we're going to take a stab at the most basic version of DeViSE: learning a mapping between image feature vectors and their corresponding labels' word vectors for imagenet classes. Doing this with the entirety of imagenet feels like overkill, so we'll start with tiny imagenet.
## tiny imagenet
Tiny imagenet is a subset of imagenet which has been preprocessed for the stanford computer vision course CS231N. It's freely available to download and ideal for putting together quick and easy tests and proof-of-concept work in computer vision. From [their website](https://tiny-imagenet.herokuapp.com/):
> Tiny Imagenet has 200 classes. Each class has 500 training images, 50 validation images, and 50 test images.
Images are also resized to 64x64px, making the whole dataset small and fast to load.
We'll use it to demo the DeViSE idea here. Lets load in a few of the packages we'll use in the project - plotting libraries, numpy, pandas etc, and pytorch, which we'll use to construct our deep learning models.
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("white")
plt.rcParams["figure.figsize"] = (20, 20)
import os
import io
import numpy as np
import pandas as pd
from PIL import Image
from scipy.spatial.distance import cdist
import torch
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
from torchvision import models, transforms
from tqdm._tqdm_notebook import tqdm_notebook as tqdm
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
base_path = "/mnt/efs/images/tiny-imagenet-200/"
```
# wordvectors
We're going to use the [fasttext](https://fasttext.cc/docs/en/english-vectors.html) word vectors trained on [common crawl](http://commoncrawl.org) as the target word vectors throughout this work. Let's load them into memory
```
wv_path = "/mnt/efs/nlp/word_vectors/fasttext/crawl-300d-2M.vec"
wv_file = io.open(wv_path, "r", encoding="utf-8", newline="\n", errors="ignore")
fasttext = {
line.split()[0]: np.array(line.split()[1:]).astype(np.float)
for line in tqdm(list(wv_file))
}
vocabulary = set(fasttext.keys())
```
# wordnet
We're also going to need to load the wordnet classes and ids from tiny-imagenet
```
clean = lambda x: x.lower().strip().replace(" ", "-").split(",-")
with open(base_path + "wnids.txt") as f:
wnids = np.array([id.strip() for id in f.readlines()])
wordnet = {}
with open(base_path + "words.txt") as f:
for line in f.readlines():
wnid, raw_words = line.split("\t")
words = [word for word in clean(raw_words) if word in vocabulary]
if wnid in wnids and len(words) > 0:
wordnet[wnid] = words
wnid_to_wordvector = {
wnid: (np.array([fasttext[word] for word in words]).mean(axis=0))
for wnid, words in wordnet.items()
}
wnids = list(wnid_to_wordvector.keys())
```
# example data
here's an example of what we've got inside tiny-imagenet: one tiny image and its corresponding class
```
wnid = np.random.choice(wnids)
image_path = base_path + "train/" + wnid + "/images/" + wnid + "_{}.JPEG"
print(" ".join(wordnet[wnid]))
Image.open(image_path.format(np.random.choice(500)))
```
# datasets and dataloaders
Pytorch allows you to explicitly write out how batches of data are assembled and fed to a network. Especially when dealing with images, I've found it's best to use a pandas dataframe of simple paths and pointers as the base structure for assembling data. Instead of loading all of the images and corresponding word vectors into memory at once, we can just store the paths to the images with their wordnet ids. Using pandas also gives us the opportunity to do all sorts of work to the structure of the data without having to use much memory.
Here's how that dataframe is put together:
```
df = {}
for wnid in wnids:
wnid_path = base_path + "train/" + wnid + "/images/"
image_paths = [wnid_path + file_name for file_name in os.listdir(wnid_path)]
for path in image_paths:
df[path] = wnid
df = pd.Series(df).to_frame().reset_index()
df.columns = ["path", "wnid"]
```
Pandas is great for working with this kind of structured data - we can quickly shuffle the dataframe:
```
df = df.sample(frac=1).reset_index(drop=True)
```
and split it into 80:20 train:test portions.
```
split_ratio = 0.8
train_size = int(split_ratio * len(df))
train_df = df.loc[:train_size]
test_df = df.loc[train_size:]
```
n.b. tiny-imagenet already has `train/`, `test/`, and `val/` directories set up which we could have used here instead. However, we're just illustrating the principle in this notebook so the data itself isn't important, and we'll use this kind of split later on when incorporating non-toy data.
Now we can define how our `Dataset` object will transform the initial, simple data when it's called on to produce a batch. Images are generated by giving a path to `PIL`, and word vectors are looked up in our `wnid_to_wordvector` dictionary. Both objects are then transformed into pytorch tensors and handed over to the network.
```
class ImageDataset(Dataset):
def __init__(self, dataframe, wnid_to_wordvector, transform=transforms.ToTensor()):
self.image_paths = dataframe["path"].values
self.wnids = dataframe["wnid"].values
self.wnid_to_wordvector = wnid_to_wordvector
self.transform = transform
def __getitem__(self, index):
image = Image.open(self.image_paths[index]).convert("RGB")
if self.transform is not None:
image = self.transform(image)
target = torch.Tensor(wnid_to_wordvector[self.wnids[index]])
return image, target
def __len__(self):
return len(self.wnids)
```
We can also apply transformations to the images as they move through the pipeline (see the `if` statement above in `__getitem__()`). The torchvision package provides lots of fast, intuitive utilities for this kind of thing which can be strung together as follows. Note that we're not applying any flips or grayscale to the test dataset - the test data should generally be left as raw as possible, with distortions applied at train time to increase the generality of the network's knowledge.
```
train_transform = transforms.Compose(
[
transforms.Resize(224),
transforms.RandomHorizontalFlip(),
transforms.RandomRotation(15),
transforms.RandomGrayscale(0.25),
transforms.ToTensor(),
]
)
test_transform = transforms.Compose([transforms.Resize(224), transforms.ToTensor()])
```
Now all we need to do is pass our dataframe, dictionary of word vectors, and the desired image transforms to the `ImageDataset` object to define our data pipeline for training and testing.
```
train_dataset = ImageDataset(train_df, wnid_to_wordvector, train_transform)
test_dataset = ImageDataset(test_df, wnid_to_wordvector, test_transform)
```
Pytorch then requires that you pass the `Dataset` through a `DataLoader` to handle the batching etc. The `DataLoader` manages the pace and order of the work, while the `Dataset` does the work itself. The structure of these things is very predictable, and we don't have to write anything custom at this point.
```
batch_size = 128
train_loader = DataLoader(
dataset=train_dataset, batch_size=batch_size, num_workers=5, shuffle=True
)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, num_workers=5)
```
# building the model
Our model uses a pre-trained backbone to extract feature vectors from the images. This biases our network to perform well on imagenet-style images and worse on others, but hey, we're searching on imagenet in this example! Later on, when working in some less imagenet-y images, we'll make some attempts to compensate for the backbone's biases.
```
backbone = models.vgg16_bn(pretrained=True).features
```
We don't want this backbone to be trainable, so we switch off the gradients for its weight and bias tensors.
```
for param in backbone.parameters():
param.requires_grad = False
```
Now we can put together the DeViSE network itself, which embeds image features into word vector space. The output of our backbone network is a $[512 \times 7 \times 7]$ tensor, which we then flatten into a 25088 dimensional vector. That vector is then fed through a few fully connected layers and ReLUs, while compressing the dimensionality down to our target size (300, to match the fasttext word vectors).
```
class DeViSE(nn.Module):
def __init__(self, backbone, target_size=300):
super(DeViSE, self).__init__()
self.backbone = backbone
self.head = nn.Sequential(
nn.Linear(in_features=(25088), out_features=target_size * 2),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(in_features=target_size * 2, out_features=target_size),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(in_features=target_size, out_features=target_size),
)
def forward(self, x):
x = self.backbone(x)
x = x.view(x.size(0), -1)
x = self.head(x)
x = x / x.max()
return x
devise_model = DeViSE(backbone, target_size=300).to(device)
```
# train loop
Pytorch requires that we write our own training loops - this is rough skeleton structure that I've got used to. For each batch, the inputs and target tensors are first passed to the GPU. The inputs are then passed through the network to generate a set of predictions, which are compared to the target using some appropriate loss function. Those losses are used to inform the backpropagation of tweaks to the network's weights and biases, before repeating the whole process with a new batch. We also display the network's current loss through in the progress bar which tracks the speed and progress of the training. We can also specify the number of epochs in the parameters for the train function.
```
losses = []
flags = torch.ones(batch_size).cuda()
def train(model, train_loader, loss_function, optimiser, n_epochs):
for epoch in range(n_epochs):
model.train()
loop = tqdm(train_loader)
for images, targets in loop:
images = images.cuda(non_blocking=True)
targets = targets.cuda(non_blocking=True)
optimiser.zero_grad()
predictions = model(images)
loss = loss_function(predictions, targets, flags)
loss.backward()
optimiser.step()
loop.set_description("Epoch {}/{}".format(epoch + 1, n_epochs))
loop.set_postfix(loss=loss.item())
losses.append(loss.item())
```
Here we define the optimiser, loss function and learning rate which we'll use.
```
trainable_parameters = filter(lambda p: p.requires_grad, devise_model.parameters())
loss_function = nn.CosineEmbeddingLoss()
optimiser = optim.Adam(trainable_parameters, lr=0.001)
```
Let's do some training!
```
train(
model=devise_model,
n_epochs=3,
train_loader=train_loader,
loss_function=loss_function,
optimiser=optimiser,
)
```
When that's done, we can take a look at how the losses are doing.
```
loss_data = pd.Series(losses).rolling(window=15).mean()
ax = loss_data.plot()
ax.set_xlim(
0,
)
ax.set_ylim(0, 1);
```
# evaluate on test set
The loop below is very similar to the training one above, but evaluates the network's loss against the test set and stores the predictions. Obviously we're only going to loop over the dataset once here as we're not training anything. The network only has to see an image once to process it.
```
preds = []
test_loss = []
flags = torch.ones(batch_size).cuda()
devise_model.eval()
with torch.no_grad():
test_loop = tqdm(test_loader)
for images, targets in test_loop:
images = images.cuda(non_blocking=True)
targets = targets.cuda(non_blocking=True)
predictions = devise_model(images)
loss = loss_function(predictions, targets, flags)
preds.append(predictions.cpu().data.numpy())
test_loss.append(loss.item())
test_loop.set_description("Test set")
test_loop.set_postfix(loss=np.mean(test_loss[-5:]))
preds = np.concatenate(preds).reshape(-1, 300)
np.mean(test_loss)
```
# run a search on the predictions
Now we're ready to use our network to perform image searches! Each of the test set's images has been assigned a position in word vector space which the network believes is a reasonable numeric description of its features. We can use the complete fasttext dictionary to find the position of new, unseen words, and then return the nearest images to our query.
```
def search(query, n=5):
image_paths = test_df["path"].values
distances = cdist(fasttext[query].reshape(1, -1), preds)
closest_n_paths = image_paths[np.argsort(distances)].squeeze()[:n]
close_images = [
np.array(Image.open(image_path).convert("RGB"))
for image_path in closest_n_paths
]
return Image.fromarray(np.concatenate(close_images, axis=1))
search("bridge")
```
It works! The network has never seen the word 'bridge', has never been told what a bridge might look like, and has never seen any of the test set's images, but thanks to the combined subtlety of the word vector space which we're embedding our images in and the dexterity with which a neural network can manipulate manifolds like these, the machine has enough knowledge to make a very good guess at what a bridge might be. This has been trained on a tiny, terribly grainy set of data but it's enough to get startlingly good results.
| true |
code
| 0.682256 | null | null | null | null |
|
Internet Resources:
[Python Programming.net - machine learning episodes 39-42](https://pythonprogramming.net/hierarchical-clustering-mean-shift-machine-learning-tutorial/)
```
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')
import numpy as np
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=25, centers=3, n_features=2, random_state=42)
##X = np.array([[1, 2],
## [1.5, 1.8],
## [5, 8],
## [8, 8],
## [1, 0.6],
## [9, 11],
## [8, 2],
## [10, 2],
## [9, 3]])
##plt.scatter(X[:, 0],X[:, 1], marker = "x", s=150, linewidths = 5, zorder = 10)
##plt.show()
#X = np.array([[-5, -4], [4,5], [3,-2], [-2,1]])
colors = 10*["g","r","c","b","k"]
plt.scatter(X[:,0], X[:,1], s=50)
plt.show()
```
The goal is to find clusters in the dataset. The first implementation of this algorithm still requires the user to input a radius parameter.
**Training algorithm for mean shift with fixed bandwitdth**
- 1. at start every data point is a centroid
Repeat until optimized:
for every centroid:
- 2. for every data point: calculate distance to centroid
- 3. new centroid = mean of all data points where distance of centroid and data point < radius
**Prediction**
- query is classified as class of nearest centroid

```
# mean shift without dynamic bandwidth
class Mean_Shift_With_Fixed_Bandwidth:
def __init__(self, radius):
self.radius = radius
def fit(self, data):
centroids = {}
# 1. every data point is initialized as centroid
for i in range(len(data)):
centroids[i] = data[i]
# Repeat until optimized
while True:
new_centroids = []
# for every centroid
for i in centroids: # i is centroid index
in_bandwidth = [] # list of all data points that are within a proximity of self.radius of centroid
centroid = centroids[i]
# 2. for every data point: calculate distance to centroid
for featureset in data:
if np.linalg.norm(featureset-centroid) < self.radius:
in_bandwidth.append(featureset)
# 3. new centroid = mean of all data points where distance of centroid and data point < self.radius
new_centroid = np.average(in_bandwidth,axis=0)
new_centroids.append(tuple(new_centroid)) # casts nparray to tuple
# get rid of any duplicate centroids
uniques = sorted(list(set(new_centroids)))
# need previous centroids to check if optimized
prev_centroids = dict(centroids)
# set new centroids (=uniques) as current centroids
centroids = {i:np.array(uniques[i]) for i in range(len(uniques))}
# is optimized if centroids are not moving anymore
optimized = True
for i in centroids:
if not np.array_equal(centroids[i], prev_centroids[i]):
optimized = False
if not optimized:
break
if optimized:
break
self.centroids = centroids
mean_shift = Mean_Shift_With_Fixed_Bandwidth(radius=3)
mean_shift.fit(X)
mean_shift_centroids = mean_shift.centroids
plt.scatter(X[:,0], X[:,1], s=150)
for c in mean_shift_centroids:
plt.scatter(mean_shift_centroids[c][0], mean_shift_centroids[c][1], color='k', marker='*', s=150)
plt.show()
```
Mean shift with dynamic bandwidth differs from the implementation with fixed bandwidth in that it no longer requires a set bandwidth from the user. Instead it estimates a fitting radius. Additionally when calculating new means, each data point is weighted depending how near or far its away from the current mean.
**Training algorithm for mean shift with dynamic bandwitdth**
- 1. at start every data point is a centroid
- 2. estimate radius:
radius = mean(distance of every datapoint to mean of entire dataset)
Repeat until optimized:
for every centroid:
- 3. for every data point: calculate distance to centroid and assign weight to it.
- 4. calculate new centroid: new centroid = mean of all weighted data points within radius
**Prediction:**
- query is classified as class of nearest centroid

```
class Mean_Shift_With_Dynamic_Bandwith:
def __init__(self, radius_norm_step = 100):
self.radius_norm_step = radius_norm_step # controls how many discrete wights are used
def fit(self,data,max_iter=1000, weight_fkt=lambda x : x**2): # weight_fkt: how to weight distances
# 1. every data point is a centroid
self.centroids = {i:data[i] for i in range(len(data))}
# 2. radius calculation
mean_of_entire_data = np.average(data,axis=0)
# all_distances= list of distances for ever data point to mean of entire date
all_distances = [np.linalg.norm(datapoint-mean_of_entire_data) for datapoint in data]
self.radius = np.mean(all_distances)
print("radius:", self.radius)
# list of discrete weights: let n = self.radius_norm_step -> weights = [n-1,n-2,n-3,...,2,1]
weights = [i for i in range(self.radius_norm_step)][::-1] # [::-1] inverts list
# do until convergence
for count in range(max_iter):
new_centroids = []
# for each centroid
for centroid_class in self.centroids:
centroid = self.centroids[centroid_class]
# 3. weigh data points
new_centroid_weights = []
for data_point in data:
weight_index = int(np.linalg.norm(data_point - centroid)/self.radius * self.radius_norm_step)
new_centroid_weights.append(weight_fkt(weights[min(weight_index, self.radius_norm_step)-1]))
# calculate new centroid
# w: weight, x: sample
new_centroid = np.sum([ w*x for w, x in zip(new_centroid_weights, data)], axis=0) / np.sum(new_centroid_weights)
new_centroids.append(tuple(new_centroid))
uniques = sorted(list(set(new_centroids)))
#remove non uniques
for i in uniques:
for ii in [i for i in uniques]:
# centroid is near enough to another centroid to merge
if not i == ii and np.linalg.norm(np.array(i)-np.array(ii)) <= self.radius/self.radius_norm_step:
uniques.remove(ii)
prev_centroids = dict(self.centroids)
self.centroids = {}
for i in range(len(uniques)):
self.centroids[i] = np.array(uniques[i])
# check if optimized
optimized = True
for i in self.centroids:
if not np.array_equal(self.centroids[i], prev_centroids[i]):
optimized = False
if optimized:
print("Converged @ iteration ", count)
break
# classify training data
self.classifications = {i:[] for i in range(len(self.centroids))}
for featureset in data:
#compare distance to either centroid
distances = [np.linalg.norm(featureset-self.centroids[centroid]) for centroid in self.centroids]
classification = (distances.index(min(distances)))
# featureset that belongs to that cluster
self.classifications[classification].append(featureset)
def predict(self,data):
#compare distance to either centroid
distances = [np.linalg.norm(data-self.centroids[centroid]) for centroid in self.centroids]
classification = (distances.index(min(distances)))
return classification
clf = Mean_Shift_With_Dynamic_Bandwith()
clf.fit(X)
centroids = clf.centroids
print(centroids)
colors = 10*['r','g','b','c','k','y']
for classification in clf.classifications:
color = colors[classification]
for featureset in clf.classifications[classification]:
plt.scatter(featureset[0],featureset[1], marker = "x", color=color, s=150, linewidths = 5, zorder = 10)
for c in centroids:
plt.scatter(centroids[c][0],centroids[c][1], color='k', marker = "*", s=150, linewidths = 5)
plt.show()
```
| true |
code
| 0.538012 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.