output
stringlengths 349
2.81k
| prompt
stringclasses 6
values | input
stringlengths 330
2.5k
| instruction
stringclasses 1
value |
|---|---|---|---|
#include <iostream>
using namespace std;
int main()
{
int l, n;
cin >> l >> n;
int mi = 0, ma = 0;
int cur;
for (int i = 0; i < n; i++)
{
cin >> cur;
// 更新cur的时候向左的计算出错
mi = max(mi, min(cur, l - cur + 1));
ma = max(ma, max(cur, l - cur + 1));
}
cout << mi << " " << ma;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <iostream>
using namespace std;
int main()
{
int l, n;
cin >> l >> n;
int mi = 0, ma = 0;
int cur;
for (int i = 0; i < n; i++)
{
cin >> cur;
mi = max(mi, min(cur + 1, l - cur + 1));
ma = max(ma, max(cur + 1, l - cur + 1));
}
cout << mi << " " << ma;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
// ----------------------------------------------------------------------------------------------------------
// #define int long long
#define ps push
#define pb push_back
#define PII pair<int, int>
#define PDD pair<double, double>
#define PSI pair<string, int>
#define PIS pair<int, string>
#define STI stack<int>
#define STS stack<string>
#define mm memset
#define EPS 1e-8
#define INF 0x7fffffff
// #define x first
// #define y second
#define rep(i, a, n) for (int i = a; i < n; i++)
#define per(i, a, n) for (int i = n - 1; i >= a; i--)
#define all(x) (x).begin(), (x).end()
#define endl "\n"
#define bl cout << "------------\n";
typedef long long LL;
// ----------------------------------------------------------------------------------------------------------
inline int read()
{
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9')
{ // ch 不是数字时
if (ch == '-')
w = -1; // 判断是否为负
ch = getchar(); // 继续读入
}
while (ch >= '0' && ch <= '9')
{ // ch 是数字时
x = x * 10 + (ch - '0'); // 将新读入的数字「加」在 x 的后面
// x 是 int 类型,char 类型的 ch 和 '0' 会被自动转为其对应的
// ASCII 码,相当于将 ch 转化为对应数字
// 此处也可以使用 (x<<3)+(x<<1) 的写法来代替 x*10
ch = getchar(); // 继续读入
}
return x * w; // 数字 * 正负号 = 实际数值
}
inline void write(int x)
{
static int sta[35];
int top = 0;
do
{
sta[top++] = x % 10, x /= 10;
} while (x);
while (top)
putchar(sta[--top] + 48); // 48 是 '0'
}
inline int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
inline int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
// ----------------------------------------------------------------------------------------------------------
const int N = 1e5 + 15;
int L;
int n;
int a[N];
void solve()
{
cin >> L;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
int ma = 0, mi = 0;
for (int i = 1; i <= n; i++)
{
// 修改maa和mii更新方式
int mii = min(abs(a[i] - 0), abs(a[i] - (L + 1)));
int maa = max(abs(a[i] - 0), abs(a[i] - (L + 1)));
ma = max(ma, maa);
mi = max(mi, mii);
}
// 更新输出
cout << mi << " " << ma << endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T;
// cin >> T;
T = 1;
while (T--)
{
solve();
}
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <bits/stdc++.h>
using namespace std;
// ----------------------------------------------------------------------------------------------------------
// #define int long long
#define ps push
#define pb push_back
#define PII pair<int, int>
#define PDD pair<double, double>
#define PSI pair<string, int>
#define PIS pair<int, string>
#define STI stack<int>
#define STS stack<string>
#define mm memset
#define EPS 1e-8
#define INF 0x7fffffff
// #define x first
// #define y second
#define rep(i, a, n) for (int i = a; i < n; i++)
#define per(i, a, n) for (int i = n - 1; i >= a; i--)
#define all(x) (x).begin(), (x).end()
#define endl "\n"
#define bl cout << "------------\n";
typedef long long LL;
// ----------------------------------------------------------------------------------------------------------
inline int read()
{
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9')
{ // ch 不是数字时
if (ch == '-')
w = -1; // 判断是否为负
ch = getchar(); // 继续读入
}
while (ch >= '0' && ch <= '9')
{ // ch 是数字时
x = x * 10 + (ch - '0'); // 将新读入的数字「加」在 x 的后面
// x 是 int 类型,char 类型的 ch 和 '0' 会被自动转为其对应的
// ASCII 码,相当于将 ch 转化为对应数字
// 此处也可以使用 (x<<3)+(x<<1) 的写法来代替 x*10
ch = getchar(); // 继续读入
}
return x * w; // 数字 * 正负号 = 实际数值
}
inline void write(int x)
{
static int sta[35];
int top = 0;
do
{
sta[top++] = x % 10, x /= 10;
} while (x);
while (top)
putchar(sta[--top] + 48); // 48 是 '0'
}
inline int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
inline int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
// ----------------------------------------------------------------------------------------------------------
const int N = 1e5 + 15;
int L;
int n;
int a[N];
void solve()
{
cin >> L;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
int ma = 0, mi = 0;
int maa = 0;
for (int i = 1; i <= n; i++)
{
maa = max(abs(a[i] - 0), maa);
maa = max(abs(a[i] - L), maa);
int mii = min(abs(a[i] - 0), abs(a[i] - (L)));
// cout <<abs(a[i]-0)<<" "<<abs(a[i]-(L))<<endl;
ma += maa;
// cout << mii << endl;
mi += mii;
}
cout << mi << " " << maa + 1 << endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int T;
// cin >> T;
T = 1;
while (T--)
{
solve();
}
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
const int N = 5e3;
int a[N];
// int s[N];
int main()
{
int l, n;
cin >> l >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
// 无用代码
// s[i] = s[i - 1] + a[i];
}
if (n == 0)
{
cout << 0 << " " << 0 << endl;
return 0;
}
// 思路错误,重写
// 更新min:使用max(min(两端的距离))
// 更新max:使用max(max(两端的距离))
sort(a + 1, a + n + 1);
// 初值
int min_ = 0, max_ = 0;
for (int i = 1; i <= n; i++)
{
min_ = max(min(l - a[i] + 1, a[i]), min_);
}
// 访问内存,边界条件
if (n)
max_ = max(l - a[1] + 1, a[n]);
cout << min_ << " " << max_;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <bits/stdc++.h>
using namespace std;
const int N = 5e3;
int a[N];
int s[N];
int main()
{
int l, n;
cin >> l >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
s[i] = s[i - 1] + a[i];
}
if (n == 0)
{
cout << 0 << " " << 0 << endl;
return 0;
}
int res = 1e9; // min
for (int i = 1; i <= n; i++)
{
if (s[i] + (n - i) * l - (s[n] - s[i]) < res)
{
res = s[i] + (n - i) * l - (s[n] - s[i]);
}
}
cout << res << endl;
if (n == 1)
{
cout << max(a[1], l - a[1]) << endl;
return 0;
}
else if (n & 1)
{ // 奇数个
res = 0;
for (int i = 2; i <= n; i += 2)
{
res += a[i] - a[i - 1] + l;
}
res += a[n];
}
else
{
res = 0;
for (int i = 2; i <= n; i += 2)
{
int t = a[i] + a[i - 1] >> 1;
res += a[i] - a[i - 1] + max(l - t, t);
}
}
cout << res << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int L, n;
int sol[N];
int main()
{
// min_res初值
int min_res = 0, max_res = 0;
cin >> L >> n;
for (int i = 0; i < n; i++)
{
cin >> sol[i];
min_res = max(min_res, min(sol[i], L + 1 - sol[i]));
}
sort(sol, sol + n);
// 边界条件
if (n)
max_res = max(L + 1 - sol[0], sol[n - 1]);
cout << min_res << " " << max_res;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int L, n;
int sol[N];
int main()
{
int min_res = 1e9, max_res = 0;
cin >> L >> n;
for (int i = 0; i < n; i++)
{
cin >> sol[i];
min_res = max(min_res, min(sol[i], L + 1 - sol[i]));
}
sort(sol, sol + n);
max_res = max(L + 1 - sol[0], sol[n - 1]);
cout << min_res << " " << max_res;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
int l;
cin >> l;
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + n + 1);
// 初值
int min_ = 0, max_ = 0;
for (int i = 1; i <= n; i++)
{
min_ = max(min(l - a[i] + 1, a[i]), min_);
}
// 访问内存,边界条件
if (n)
max_ = max(l - a[1] + 1, a[n]);
cout << min_ << " " << max_ << endl;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
int l;
cin >> l;
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + n + 1);
int min_, max_;
for (int i = 1; i <= n; i++)
{
min_ = max(min(l - a[i] + 1, a[i]), min_);
}
max_ = max(l - a[1] + 1, a[n]);
cout << min_ << " " << max_ << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int site[N];
int l, n, maxans = 0, minans = 0;
int main()
{
cin >> l >> n;
for (int i = 0; i < n; i++)
{
scanf("%d", &site[i]);
maxans = max(maxans, max(site[i], l + 1 - site[i]));
minans = max(minans, min(site[i], l + 1 - site[i]));
}
cout << minans << " " << maxans;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <iostream>
using namespace std;
const int N = 1e5 + 10;
int site[N];
int l, n, maxans = 0, minans = 0;
int main()
{
cin >> l >> n;
for (int i = 0; i < n; i++)
{
scanf("%d", &site[i]);
maxans = max(maxans, max(site[i], l + 1 - site[i]));
minans = max(minans, min(site[i], l + 1 - site[i]));
}
cout << maxans << " " << minans;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int M = 5e3 + 4;
typedef long long ll;
ll m[M];
int main()
{
ll L;
cin >> L;
ll n;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> m[i];
}
sort(m + 1, m + 1 + n);
ll minx = 0;
for (int i = 1; i <= n; i++)
{
minx = max(min(m[i], L - m[i] + 1), minx);
}
ll maxx = 0;
if (n >= 1)
{
maxx = max(m[n], L - m[1] + 1);
}
cout << minx << " " << maxx << endl;
return 0;
} | 这里是题目描述:# 独木桥
## 题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 $1$ 个人通过。假如有 $2$ 个人相向而行在桥上相遇,那么他们 $2$ 个人将无法绕过对方,只能有 $1$ 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
## 题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 $L$,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 $1$,但一个士兵某一时刻来到了坐标为 $0$ 或 $L+1$ 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
## 输入格式
第一行共一个整数 $L$,表示独木桥的长度。桥上的坐标为 $1, 2, \cdots, L$。
第二行共一个整数 $N$,表示初始时留在桥上的士兵数目。
第三行共有 $N$ 个整数,分别表示每个士兵的初始坐标。
## 输出格式
共一行,输出 $2$ 个整数,分别表示部队撤离独木桥的最小时间和最大时间。$2$ 个整数由一个空格符分开。
## 样例 #1
### 样例输入 #1
```
4
2
1 3
```
### 样例输出 #1
```
2 4
```
## 提示
对于 $100\%$ 的数据,满足初始时,没有两个士兵同在一个坐标,$1\le L\le5\times 10^3$,$0\le N\le5\times10^3$,且数据保证 $N\le L$。 下面是题目解析和做法:此题可以用排序做(高档一点的模拟)
核心思想:两个人相遇转身,相当于交换灵魂后继续走
最大值:最靠近端点两个人各自向对方走,时间较长的那个人的时间
最小值:所有人中走完桥最小值中的最大值
详细见代码:
```cpp
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size = 5005;
int a[size];
int main()
{
int L,N;
cin>>L>>N;
if (!N) //特判 N==0的情况
{
cout<<"0 0"<<endl;
return 0;
}
for (int i=1;i<=N;i++) cin>>a[i]; //输入
sort(a+1,a+N+1); //从小到大排序(算最长时间时可能方便一些)
int max_time,min_time;
for (int i=1;i<=N;i++)
min_time=max(min(a[i],L+1-a[i]),min_time); //最短时间就是所有人中走完桥最小值中的最大值
max_time=max(L+1-a[1],a[N]); //最长时间就是最靠近端点两个人各自向对方走,
//时间较长的那个人的时间 (排序的好处)
cout<<min_time<<' '<<max_time<<endl;
return 0;
}
``` 题目标签:排序 结论 | #include <iostream>
#include <cmath>
using namespace std;
const int M = 5e3 + 4;
typedef long long ll;
ll m[M];
int main()
{
ll L;
cin >> L;
ll n;
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> m[i];
}
ll minx = 0;
ll p = n;
for (int i = 1; i <= p; i++)
{
minx += min(m[i], L - m[p]);
if (m[i] > L - m[p])
{
p--;
i--;
}
}
ll maxx = 0;
p = n;
for (int i = 1; i <= p; i++)
{
maxx += max(m[i], L - m[p]);
if (m[i] < L - m[p])
{
p--;
i--;
}
}
cout << minx << " " << maxx << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
#define ll int
bool cmp(pair<ll, ll> &p, pair<ll, ll> &q)
{
return p.first < q.first;
}
int main()
{
ll n, k;
cin >> n >> k;
k = n - k;
vector<pair<ll, ll>> books(n + 1);
for (ll i = 1; i <= n; i++)
cin >> books[i].first >> books[i].second;
sort(books.begin() + 1, books.begin() + n + 1, cmp);
vector<vector<ll>> dp(n + 1, vector<ll>(k + 1, 0));
ll ans = INT_MAX;
for (ll i = 2; i <= n; i++)
{
for (ll j = 2; j <= min(i, k); j++)
{
dp[i][j] = INT_MAX;
for (ll h = j - 1; h < i; h++)
dp[i][j] = min(dp[i][j], dp[h][j - 1] + abs(books[i].second - books[h].second));
}
}
for (ll i = k; i <= n; i++)
ans = min(ans, dp[i][k]);
cout << ans << endl;
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
using namespace std;
#define ll int
bool cmp(pair<ll, ll> &p, pair<ll, ll> &q)
{
return p.first < q.first;
}
int main()
{
ll n, k;
cin >> n >> k;
k = n - k;
vector<pair<ll, ll>> books(n + 1);
for (ll i = 1; i <= n; i++)
cin >> books[i].first >> books[i].second;
sort(books.begin() + 1, books.begin() + n + 1, cmp);
vector<vector<ll>> dp(n + 1, vector<ll>(k + 1, 0));
ll ans = INT_MAX;
for (ll i = 2; i <= n; i++)
{
for (ll j = 2; j <= min(i, k); j++)
{
dp[i][j] = INT_MAX;
for (ll h = j - 1; h < i; h++)
dp[i][j] = min(dp[i][j], dp[i][j - 1] + abs(books[i].second - books[h].second));
}
}
for (ll i = k; i <= n; i++)
ans = min(ans, dp[i][k]);
cout << ans << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
#define all(a) a.begin(), a.end()
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
const int M = 4e6 + 10;
const int mod = 998244353;
const int mod1 = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f;
// const int P=10007;
// int dx[]={-1,-1,-1,0,0,1,1,1},dy[]={-1,0,1,-1,1,-1,0,1};
// int dx[]={0,1,-1,0},dy[]={1,0,0,-1};
PII a[N];
int dp[110][110];
void solve()
{
int n, m;
cin >> n >> m;
m = n - m;
for (int i = 1; i <= n; i++)
cin >> a[i].first >> a[i].second;
sort(a + 1, a + 1 + n);
memset(dp, 0x3f, sizeof dp);
for (int i = 1; i <= n; i++)
dp[i][1] = 0;
for (int i = 2; i <= n; i++)
{
for (int j = 1; j < i; j++)
{
for (int k = 2; k <= min(i, m); k++)
{
dp[i][k] = min(dp[i][k], dp[j][k - 1] + abs(a[i].second - a[j].second));
}
}
}
int ans = 1e9;
for (int i = m; i <= n; i++)
{
ans = min(ans, dp[i][m]);
}
cout << ans << '\n';
}
int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
#define all(a) a.begin(), a.end()
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
const int M = 4e6 + 10;
const int mod = 998244353;
const int mod1 = 1e9 + 7;
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f;
// const int P=10007;
// int dx[]={-1,-1,-1,0,0,1,1,1},dy[]={-1,0,1,-1,1,-1,0,1};
// int dx[]={0,1,-1,0},dy[]={1,0,0,-1};
PII a[N];
int dp[110][110];
void solve()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i].first >> a[i].second;
sort(a + 1, a + 1 + n);
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0, dp[1][0] = 0;
for (int i = 1; i <= n; i++)
dp[i][i] = dp[i][i - 1] = 0;
for (int i = 2; i <= n; i++)
dp[i][0] = dp[i - 1][0] + abs(a[i].second - a[i - 1].second);
for (int i = 2; i <= n; i++)
{
for (int k = 1; k <= m; k++)
{
for (int j = 1; j <= i; j++)
{
if (j == 1)
dp[i][k] = min(dp[i][k], dp[i][k - 1] - abs(a[2].second - a[1].second));
else if (j == i)
dp[i][k] = min(dp[i][k], dp[i][k - 1] - abs(a[i].second - a[i - 1].second));
else
{
dp[i][k] = min(dp[i][k], dp[i][k - 1] - abs(a[j].second - a[j - 1].second) - abs(a[j + 1].second - a[j].second) + abs(a[j + 1].second - a[j - 1].second));
}
}
}
}
cout << dp[n][m] << '\n';
}
int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define dd double
#define INF 0x3f3f3f3f
#define msin(a) memset(a, 0, sizeof(a))
#define msax(a) memset(a, INF, sizeof(a))
#define Road_Runner_ \
ios::sync_with_stdio(0); \
cin.tie(0); \
cout.tie(0);
using namespace std;
int dx[10] = {0, -1, 1, 0, 0, 1, -1, 1, -1};
int dy[10] = {0, 0, 0, -1, 1, 1, -1, -1, 1};
const int N = 205;
int lm = 9223372036854775807, im = 2147483647;
int T = 1;
int n, m, a[N], dp[N][N];
int minn = lm;
struct oo
{
int h;
int w;
} s[N];
bool cmp(oo x, oo y)
{
return x.h < y.h;
}
signed main()
{
Road_Runner_;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> s[i].h >> s[i].w;
}
sort(s + 1, s + 1 + n, cmp);
for (int i = 1; i <= n; i++)
{
a[i] = s[i].w;
// cout<<a[i]<<endl;
}
// dp[i][j]表示以a[i]结尾,去掉了j本书后的最小值
// 一次最多去掉m本书
msax(dp);
dp[1][0] = 0;
for (int i = 2; i <= n; i++)
{
dp[i][0] = dp[i - 1][0] + abs(a[i] - a[i - 1]);
dp[i][i - 1] = 0;
// cout<<i<<" "<<dp[i][0]<<endl;
}
dp[2][0] = abs(a[2] - a[1]);
dp[2][1] = 0;
for (int i = 3; i <= n; i++)
{ // 第i本书为结尾
for (int l = 1; l <= i - 1; l++)
{ // 之前的第l本书为结尾
for (int j = 0; j <= min(m + i - 1, m); j++)
{ // 去掉的总本数
for (int k = 0; k <= j; k++)
{ // 前半段用了k,后半段用了j-k
if (j - k + 1 == i - l)
{
dp[i][j] = min(dp[i][j], dp[l][k] + abs(a[i] - a[l]));
if (m - j == n - i)
{
minn = min(minn, dp[i][j]);
}
}
}
}
}
}
cout << minn << endl;
return 0;
}
| 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
#define endl '\n'
#define int long long
#define dd double
#define INF 0x3f3f3f3f
#define msin(a) memset(a, 0, sizeof(a))
#define msax(a) memset(a, INF, sizeof(a))
#define Road_Runner_ \
ios::sync_with_stdio(0); \
cin.tie(0); \
cout.tie(0);
using namespace std;
int dx[10] = {0, -1, 1, 0, 0, 1, -1, 1, -1};
int dy[10] = {0, 0, 0, -1, 1, 1, -1, -1, 1};
const int N = 205;
int lm = 9223372036854775807, im = 2147483647;
int T = 1;
int n, m, a[N], dp[N][N];
struct oo
{
int h;
int w;
} s[N];
bool cmp(oo x, oo y)
{
return x.h < y.h;
}
signed main()
{
Road_Runner_;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> s[i].h >> s[i].w;
}
sort(s + 1, s + 1 + n, cmp);
for (int i = 1; i <= n; i++)
{
a[i] = s[i].w;
// cout<<a[i]<<endl;
}
// dp[i][j]表示以a[i]结尾,去掉了j本书后的最小值
// 一次最多去掉m本书
msax(dp);
dp[1][0] = 0;
for (int i = 2; i <= n; i++)
{
dp[i][0] = dp[i - 1][0] + abs(a[i] - a[i - 1]);
dp[i][i - 1] = 0;
// cout<<i<<" "<<dp[i][0]<<endl;
}
dp[2][0] = abs(a[2] - a[1]);
dp[2][1] = 0;
for (int i = 3; i <= n; i++)
{ // 第i本书为结尾
for (int l = 1; l <= i - 1; l++)
{ // 之前的第l本书为结尾
for (int j = 0; j <= min(l - 1, m); j++)
{ // 去掉的总本数
for (int k = 0; k <= j; k++)
{ // 前半段用了k,后半段用了j-k
if (j - k + 1 == i - l)
{
dp[i][j] = min(dp[i][j], dp[l][k] + abs(a[i] - a[l]));
}
}
}
}
}
cout << dp[n][m] << endl;
return 0;
}
| 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
#define int long long
struct pos
{
int x, y;
} a[110];
int dp[110][110];
bool cmp(pos a1, pos a2)
{
return a1.x < a2.x;
}
signed main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i].x >> a[i].y;
}
// 需要增加排序才可以进行后续动态规划
sort(a + 1, a + 1 + n, cmp);
int mn = 1e9;
memset(dp, 0x3f, sizeof dp);
k = n - k;
for (int i = 1; i <= n; i++)
{
dp[i][1] = 0;
for (int j = 2; j <= i; j++)
{
for (int k1 = 1; k1 < i; k1++)
{
dp[i][j] = min(dp[i][j], dp[k1][j - 1] + abs(a[i].y - a[k1].y));
}
}
}
for (int i = 1; i <= n; i++)
mn = min(mn, dp[i][k]);
cout << mn << endl;
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
using namespace std;
#define int long long
struct pos
{
int x, y;
} a[110];
int dp[110][110];
signed main()
{
std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i].x >> a[i].y;
}
int mn = 1e9;
memset(dp, 0x3f, sizeof dp);
k = n - k;
for (int i = 1; i <= n; i++)
{
dp[i][1] = 0;
for (int j = 2; j <= i; j++)
{
for (int k1 = 1; k1 < i; k1++)
{
dp[i][j] = min(dp[i][j], dp[k1][j - 1] + abs(a[i].y - a[k1].y));
}
}
}
for (int i = 1; i <= n; i++)
mn = min(mn, dp[i][k]);
cout << mn << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int n, k, dp[20000];
struct node
{
int high, width;
} arr[20000];
bool priority(node x, node y)
{
return x.high < y.high;
}
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> arr[i].high >> arr[i].width;
}
sort(arr + 1, arr + 1 + n, priority);
for (int i = 2; i <= n - k; i++)
{
for (int j = n; j >= i; j--)
{
dp[j] = 1e9;
for (int l = i - 1; l <= j - 1; l++)
{
dp[j] = min(dp[j], dp[l] + abs(arr[j].width - arr[l].width));
}
}
}
int ans = 1e9;
for (int i = n - k; i <= n; i++)
{
ans = min(ans, dp[i]);
}
cout << ans;
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int n, k, dp[20000];
struct node
{
int high, width;
} arr[20000];
bool priority(node x, node y)
{
return x.high < y.high;
}
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> arr[i].high >> arr[i].width;
}
sort(arr + 1, arr + 1 + n, priority);
for (int i = 3; i <= n - k; i++)
{
for (int j = n; j >= i; j--)
{
dp[j] = 1e9;
for (int l = i - 1; l <= j - 1; l++)
{
dp[i] = min(dp[j], dp[l] + abs(arr[j].width - arr[l].width));
}
}
}
int ans = 1e9;
for (int i = n - k; i <= n; i++)
{
ans = min(ans, dp[i]);
}
cout << ans;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
struct book
{
int h, w;
} books[105];
int n, k;
int dp[501][501];
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; ++i)
{
cin >> books[i].h >> books[i].w;
}
auto cmp = [](const book &lhs, const book &rhs) -> bool
{
return lhs.h < rhs.h;
};
sort(books + 1, books + n + 1, cmp);
memset(dp, 0x3f, sizeof(dp));
for (int i = 1; i <= n; ++i)
{
dp[i][1] = 0;
}
for (int i = 2; i <= n; ++i)
{
for (int t = 1; t < i; ++t)
{
for (int j = 2; j <= i && j <= n - k; ++j)
{
dp[i][j] = std::min(dp[t][j - 1] + abs(books[t].w - books[i].w), dp[i][j]);
}
}
}
int ans = INT_MAX;
for (int i = n - k; i <= n; ++i)
{
ans = std::min(dp[i][n - k], ans);
}
cout << ans;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
using namespace std;
struct book
{
int h, w;
} books[105];
int n, k;
int dp[501][501];
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; ++i)
{
cin >> books[i].h >> books[i].w;
}
auto cmp = [](const book &lhs, const book &rhs) -> bool
{
return lhs.h < rhs.w;
};
sort(books + 1, books + n + 1, cmp);
memset(dp, 0x3f, sizeof(dp));
for (int i = 1; i <= n; ++i)
{
dp[i][1] = 0;
}
for (int i = 2; i <= n; ++i)
{
for (int t = 1; t < i; ++t)
{
for (int j = 2; j <= i && j <= n - k; ++j)
{
dp[i][j] = std::min(dp[t][j - 1] + abs(books[t].w - books[i].w), dp[i][j]);
}
}
}
int ans = INT_MAX;
for (int i = n - k; i <= n; ++i)
{
ans = std::min(dp[i][n - k], ans);
}
cout << ans;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stack>
#include <vector>
using namespace std;
struct book
{
int high;
int wide;
};
bool cmp(book a1, book a2)
{
return a1.high < a2.high;
}
int main()
{
int n, k;
cin >> n >> k;
k = n - k; // 转化为在n本书中取k本最整齐的书
book *a = new book[n];
for (int i = 0; i < n; i++)
cin >> a[i].high >> a[i].wide;
sort(a, a + n, cmp);
int **dp = new int *[n];
for (int i = 0; i < n; i++)
{
dp[i] = new int[k];
dp[i][0] = 0; // 只取1本书不整齐度一定为0
}
// dp[i-1][j-1]表示在前i本书中取j本书(且必须取第i本书)所构成的最小不整齐度(i>j>0)
for (int i = 1; i < n; i++)
for (int j = 1; j <= min(i, k - 1); j++)
{
dp[i][j] = 0x7fffffff;
for (int p = j - 1; p < i; p++)
{ // dp[p][j - 1]表示前p-1本书中取j-2本书且必须取第p-1本书的最小不整齐度
int add = abs(a[i].wide - a[p].wide);
dp[i][j] = min(dp[i][j], dp[p][j - 1] + add);
}
}
int ans = 0x7fffffff;
for (int i = k - 1; i < n; i++)
ans = min(ans, dp[i][k - 1]);
cout << ans;
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <iostream>
#include <string.h>
#include <algorithm>
#include <stack>
#include <vector>
using namespace std;
struct book
{
int high;
int wide;
};
bool cmp(book a1, book a2)
{
return a1.high < a2.high;
}
int main()
{
int n, k;
cin >> n >> k;
k = n - k; // 转化为在n本书中取k本最整齐的书
book *a = new book[n];
for (int i = 0; i < n; i++)
cin >> a[i].high >> a[i].wide;
// sort(a, a + n, cmp);
int **dp = new int *[n];
for (int i = 0; i < n; i++)
{
dp[i] = new int[k];
dp[i][0] = 0; // 只取1本书不整齐度一定为0
}
// dp[i-1][j-1]表示在前i本书中取j本书(且必须取第i本书)所构成的最小不整齐度(i>j>0)
for (int i = 1; i < n; i++)
for (int j = 1; j <= min(i, k - 1); j++)
{
dp[i][j] = 0x7fffffff;
for (int p = j - 1; p < i; p++)
{ // dp[p][j - 1]表示前p-1本书中取j-2本书且必须取第p-1本书的最小不整齐度
int add = abs(a[i].wide - a[p].wide);
dp[i][j] = min(dp[i][j], dp[p][j - 1] + add);
}
}
int ans = 0x7fffffff;
for (int i = k - 1; i < n; i++)
ans = min(ans, dp[i][k - 1]);
cout << ans;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
const int inf = INT_MAX;
int n, m;
int a[105], x, f[105][105];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> x;
a[i] <<= 18;
a[i] += x;
}
sort(a + 1, a + 1 + n);
for (int i = 1; i <= n; i++)
a[i] = a[i] & 0x0000FFFF;
memset(f, 0x3f, sizeof(f));
for (int i = 0; i <= n; i++)
f[i][1] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
for (int k = j - 1; k <= i - 1; k++)
f[i][j] = min(f[i][j], f[k][j - 1] + abs(a[i] - a[k]));
int ans = inf;
for (int i = n - m; i <= n; i++)
ans = min(ans, f[i][n - m]);
printf("%d\n", ans);
return 0l;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
using namespace std;
const int inf = INT_MAX;
int n, m;
int a[105], x, f[105][105];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> x;
a[i] <<= 18;
a[i] += x;
}
sort(a + 1, a + 1 + n);
memset(f, 0x3f, sizeof(f));
for (int i = 0; i <= n; i++)
f[i][1] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
for (int k = j - 1; k <= i - 1; k++)
f[i][j] = min(f[i][j], f[k][j - 1] + abs(a[i] - a[k]));
int ans = inf;
for (int i = n - m; i <= n; i++)
ans = min(ans, f[i][n - m]);
printf("%d\n", ans);
return 0l;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 1e2 + 5;
ll n, k, dp[MAXN][MAXN][2];
struct node
{
ll h;
ll w;
} a[MAXN];
bool cmp(node xx, node yy)
{
return xx.h < yy.h;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> k;
k = n - k;
for (int i = 1; i <= n; i++)
cin >> a[i].h >> a[i].w;
sort(a + 1, a + n + 1, cmp);
memset(dp, 0x3f, sizeof dp);
for (int i = 1; i <= n; i++)
dp[i][1][1] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= k; j++)
{
dp[i][j][0] = min({dp[i][j][0], dp[i - 1][j][1], dp[i - 1][j][0]});
for (int pwp = 1; pwp <= i - 1; pwp++)
{
dp[i][j][1] = min(dp[i][j][1], dp[pwp][j - 1][1] + abs(a[i].w - a[pwp].w));
}
}
}
cout << min(dp[n][k][1], dp[n][k][0]) << endl;
return 0;
} | 这里是题目描述:# 书本整理
## 题目描述
Frank 是一个非常喜爱整洁的人。他有一大堆书和一个书架,想要把书放在书架上。书架可以放下所有的书,所以 Frank 首先将书按高度顺序排列在书架上。但是 Frank 发现,由于很多书的宽度不同,所以书看起来还是非常不整齐。于是他决定从中拿掉k本书,使得书架可以看起来整齐一点。
书架的不整齐度是这样定义的:每两本书宽度的差的绝对值的和。例如有 $4$ 本书:
$1 \times 2$
$5 \times 3$
$2 \times 4$
$3 \times 1$
那么 Frank 将其排列整齐后是:
$1 \times 2$
$2 \times 4$
$3 \times 1$
$5 \times 3$
不整齐度就是 $2+3+2=7$。
已知每本书的高度都不一样,请你求出去掉 $k$ 本书后的最小的不整齐度。
## 输入格式
第一行两个数字 $n$ 和 $k$,代表书有几本,从中去掉几本($1 \le n \le 100, 1 \le k<n$)。
下面的 $n$ 行,每行两个数字表示一本书的高度和宽度,均小于等于 $200$。
保证高度不重复
## 输出格式
一行一个整数,表示书架的最小不整齐度。
## 样例 #1
### 样例输入 #1
```
4 1
1 2
2 4
3 1
5 3
```
### 样例输出 #1
```
3
``` 下面是题目解析和做法:## 先理解题意
对于给出的书本,`Frank`会先把它们按照高度排好序,接下来通过删去一些书本来达到宽度最整齐;不论怎么删去,都是在原有顺序的基础上抽走。
## 为我这种DP初学者的详细分析
(以下的“差”指的是差的绝对值)
“抽走”对于整齐度的影响是很奇怪的:减去自己与两旁书本宽度的差,再加上那两书本宽度的差。尽量转化为已学的模型:**从 $n$ 本书里面挑出 $n-k$ 本,按原顺序排列达到宽度最整齐。**
这是不是很熟悉?如果不,我们一本本地尝试加入,那么**“当前试着把哪一本加入”就是状态的一个维度**(至少要用 $f[i]$)。一步步推导出状态转移方程。
___
取第一本,不用花费(花费即增加“不整齐度”)。
___
第二本书,
1. 假如自顾自,成为一长串书本的队首(也就是忽略第一本,从第二本开始取),不用花费。
2. 可是如果接上第一本,要花费,好处是队列长度增加到 $2$ 了。发现了吗?**队列长度也是某个维度**(至少要用 $f[i][l]$)。
___
到第三本书,
1. 如果忽略前两本,不用花费,但是只取了这么一本书。$f[3][1] = 0$。
2. **如果从第一本或第二本接上,长度都会变成2,那么我们选择花费小的一种方式。$f[3][2] = min( f[1][1] + abs (a[3].w - a[1].w), f[2][1] + abs(a[3].w - a[2].w) )$。**
③:如果前两本都接上,队列成为 $1,2,3$。
___
尝试加入第四本书,
1. 也可以从自己开始取,$f[4][1] = 0$。
2. 也可以从 $1$ 或 $2$ 或 $3$ 其中一本接上,长度都会变成 $2$,择优。
3. 也可以从长度为 $2$ 的队列接上^,择优。
4. 也可以接上 $1,2,3$ 这个长度为 $3$ 的队列。
^**此时前三本中花费最小、长度为2的队列已经存储在 $f[2][2]$ 和 $f[3][2]$,为什么不直接用一个 $f[2]$ 存储?因为第四本与 $2,3$ 两本书相邻的代价是不同的**。不存在 $f[1][2]$,因为取到第一本的时候没有长度为 $2$ 的队列。
___
第五本,第六本依此类推。
```cpp
#include <bits/stdc++.h >using namespace std;
int n, k, m, Min = 0x7fffffff;
int f[501][501];
//f[i][l]:以i作末尾,选了l本书时的最小花费
struct info
{
int h, w;
}a[1001];
bool cmp(const info &x, const info &y)
{
return x.h <y.h;
}
int main()
{
cin >>n >>k;
m = n - k;//选取m本书
for(int i = 1; i <= n; i++)
scanf("%d %d ", &a[i].h, &a[i].w);
sort(a+1, a+n+1, cmp);//高度决定顺序
memset(f, 20, sizeof(f));//初始极大,能缩小就缩小
for(int i = 1; i <= n; i++)
f[i][1] = 0;
//单独选择任何书都不会有花费
for(int i = 2; i <= n; i++)//试着放第i本的时候
for(int j = 1; j <= i-1; j++)//尝试与前面第j本相邻
for(int l = 2; l <= min(i, m); l++)//放下第i本时,能从之前长1的队列继承为长2的队列,也能从之前长2的队列继承为长3的队列……l表示放下后的长度
//显然试到第i本时,长度不会超过i,也不会超过m,m是最终需要的长度
f[i][l] = min(f[i][l], f[j][l-1] + abs(a[i].w - a[j].w/*这是尝试相邻的书本*/));//放第i本继承到长度为l,总花费越小越好
for(int i = m; i <= n; i++)
Min = min(Min, f[i][m]);//i的循环的意思是:以m结尾的队列,可能最小,以m+1结尾的队列也可能的……以n结尾的队列也可能。
printf("%d\n ", Min);
return 0;
}
题目标签:动态规划 | #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MAXN = 1e2 + 5;
ll n, k, dp[MAXN][MAXN];
struct node
{
ll h;
ll w;
} a[MAXN];
bool cmp(node xx, node yy)
{
return xx.h < yy.h;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> k;
k = n - k;
for (int i = 1; i <= n; i++)
cin >> a[i].h >> a[i].w;
sort(a + 1, a + n + 1, cmp);
memset(dp, 0x3f, sizeof dp);
for (int i = 1; i <= n; i++)
dp[i][1] = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= k; j++)
{
for (int pwp = 1; pwp <= i - 1; pwp++)
{
dp[i][j] = min({dp[i][j], dp[i - 1][j], dp[pwp][j - 1] + abs(a[i].w - a[pwp].w)});
}
}
}
cout << dp[n][k] << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
#include <map>
#include <string>
using namespace std;
struct node
{
string s;
} f[12][12];
map<string, int> mp;
bool vis[12];
int is = 0;
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> f[i][j].s;
}
}
for (int i = 2; i <= n; i++)
{
string t = f[i][1].s;
int cnt = 0;
for (int j = 1; j <= n; j++)
{
if (f[i][j].s.size() == 2)
{
cnt++;
}
}
mp.insert({t, cnt});
vis[cnt] = true;
}
for (int i = 0; i <= n - 2; i++)
{
if (!vis[i])
{
is = 1;
break;
}
}
if (is == 1)
{
cout << "ERROR!" << endl;
}
else
{
int pp = 0;
for (int i = 2; i <= n; i++)
{
for (int j = 2; j <= n; j++)
{
int t1 = mp[f[i][1].s];
int t2 = mp[f[1][j].s];
int t;
if (f[i][j].s.size() == 2)
{
string s1;
string s2;
s1 += f[i][j].s[0];
s2 += f[i][j].s[1];
t = mp[s1] * n - 1 + mp[s2];
}
else
{
t = mp[f[i][j].s];
}
if (t != t1 + t2)
{
pp = 1;
break;
}
}
if (pp == 1)
{
break;
}
}
if (pp == 1)
{
cout << "ERROR!" << endl;
}
else
{
for (int i = 2; i <= n; i++)
{
if (i != n)
{
cout << f[i][1].s << "=" << mp[f[i][1].s] << " ";
}
else
{
cout << f[i][1].s << "=" << mp[f[i][1].s] << endl;
}
}
cout << n - 1 << endl;
}
}
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <iostream>
#include <map>
#include <string>
using namespace std;
struct node
{
string s;
} f[12][12];
map<string, int> mp;
bool vis[12];
int is = 0;
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> f[i][j].s;
}
}
for (int i = 2; i <= n; i++)
{
string t = f[i][1].s;
int cnt = 0;
for (int j = 1; j <= n; j++)
{
if (f[i][j].s.size() == 2)
{
cnt++;
}
}
mp.insert({t, cnt});
vis[cnt] = true;
}
for (int i = 0; i <= n - 2; i++)
{
if (!vis[i])
{
is = 1;
break;
}
}
if (is == 1)
{
cout << "ERROR!" << endl;
}
else
{
int pp = 0;
for (int i = 2; i <= n; i++)
{
for (int j = 2; j <= n; j++)
{
int t1 = mp[f[i][1].s];
int t2 = mp[f[1][j].s];
int t = mp[f[i][j].s];
if (t != t1 + t2)
{
pp = 1;
break;
}
}
if (pp == 1)
{
break;
}
}
if (pp == 1)
{
cout << "ERROR!" << endl;
}
else
{
for (int i = 2; i <= n; i++)
{
if (i != n)
{
cout << f[i][1].s << "=" << mp[f[i][1].s] << " ";
}
else
{
cout << f[i][1].s << "=" << mp[f[i][1].s] << endl;
}
}
cout << n - 1 << endl;
}
}
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
int n, m[100], p[15];
string s[15][15];
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
cin >> s[i][j];
}
for (int i = 1; i < n; ++i)
{
int sum = 0;
for (int j = 1; j < n; ++j)
sum += (s[i][j].size() == 2);
p[i] = sum;
m[s[i][0][0]] = sum;
}
for (int i = 1; i < n; ++i)
{
for (int j = 1; j < n; ++j)
{
int a = p[i], b = p[j], c = m[s[i][j][0]];
if (s[i][j].size() == 2)
c = c * (n - 1) + m[s[i][j][1]];
if (c != a + b)
{
cout << "ERROR!";
return 0;
}
}
}
for (int i = 1; i < n; ++i)
cout << s[i][0] << '=' << p[i] << ' ';
cout << '\n'
<< --n;
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <bits/stdc++.h>
using namespace std;
int n, m[100], p[15];
string s[15][15];
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
cin >> s[i][j];
}
for (int i = 1; i < n; ++i)
{
int sum = 0;
for (int j = 1; j < n; ++j)
sum += (s[i][j].size() == 2);
p[i] = sum;
m[s[i][0][0]] = sum;
}
for (int i = 1; i < n; ++i)
{
for (int j = 1; j < n; ++j)
{
int a = p[i], b = p[j], c = m[s[i][j][0]];
if (s[i][j].size() == 2)
c = c * (n - 1) + m[s[i][j][1]];
if (c != a + b)
{
cout << "ERROR!";
return 0;
}
}
}
for (int i = 1; i < n; ++i)
cout << s[i][1] << '=' << p[i] << ' ';
cout << '\n'
<< --n;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
int n, m[100], p[15];
string s[15][15];
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
cin >> s[i][j];
}
for (int i = 1; i < n; ++i)
{
int sum = 0;
for (int j = 1; j < n; ++j)
sum += (s[i][j].size() == 2);
p[i] = sum;
m[s[i][0][0]] = sum;
}
for (int i = 1; i < n; ++i)
{
for (int j = i; j < n; ++j)
{
int a = p[i], b = p[j], c = m[s[i][j][0]];
if (s[i][j].size() == 2)
c = c * (n - 1) + m[s[i][j][1]];
if (c != a + b)
{
cout << "ERROR!";
return 0;
}
}
}
for (int i = 1; i < n; ++i)
cout << s[i][0] << '=' << p[i] << ' ';
cout << '\n'
<< --n;
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <bits/stdc++.h>
using namespace std;
int n, m[100], p[15];
string s[15][15];
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
cin >> s[i][j];
}
for (int i = 1; i < n; ++i)
{
int sum = 0;
for (int j = 1; j < n; ++j)
sum += (s[i][j].size() == 2);
p[i] = sum;
m[s[i][0][0]] = sum;
}
for (int i = 1; i < n; ++i)
{
for (int j = i + 1; j < n; ++j)
{
int a = p[i], b = p[j], c = m[s[i][j][0]];
if (s[i][j].size() == 2)
c = c * (n - 1) + m[s[i][j][1]];
if (c != a + b)
{
cout << "ERROR!";
return 0;
}
}
}
for (int i = 1; i < n; ++i)
cout << s[i][0] << '=' << p[i] << ' ';
cout << '\n'
<< --n;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <iostream>
#include <map>
#define MAXN 10
using namespace std;
using i64 [[maybe_unused]] = long long;
string arr[MAXN][MAXN];
int ans[MAXN];
map<int, string> m;
signed main()
{
#ifdef LOCAL
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
int n;
cin >> n;
for (int j = 0; j < n; ++j)
{
cin >> arr[0][j];
}
for (int i = 1; i < n; ++i)
{
int cnt = 0;
for (int j = 0; j < n; ++j)
{
cin >> arr[i][j];
if (arr[i][j].length() > 1)
cnt++;
}
ans[i] = cnt;
m[cnt] = arr[0][i];
}
for (int i = 1; i < n; ++i)
{
for (int j = 1; j < n; ++j)
{
string s;
int p = ans[i] + ans[j];
if (p >= n - 1)
{
p -= n - 1;
s += m[1];
}
s += m[p];
if (s != arr[i][j])
{
cout << "ERROR!" << endl;
return 0;
}
}
}
for (int i = 1; i < n; ++i)
{
cout << arr[0][i] << "=" << ans[i] << " ";
}
cout << endl
<< n - 1 << endl;
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <iostream>
#include <map>
#define MAXN 10
using namespace std;
using i64 [[maybe_unused]] = long long;
string arr[MAXN][MAXN];
int ans[MAXN];
map<int, string> m;
signed main()
{
#ifdef LOCAL
freopen("test.in", "r", stdin);
freopen("test.out", "w", stdout);
#endif
int n;
cin >> n;
for (int j = 0; j < n; ++j)
{
cin >> arr[0][j];
}
for (int i = 1; i < n; ++i)
{
int cnt = 0;
for (int j = 0; j < n; ++j)
{
cin >> arr[i][j];
if (arr[i][j].length() > 1)
cnt++;
}
ans[i] = cnt;
m[cnt] = arr[0][i];
}
for (int i = 1; i < n; ++i)
{
for (int j = 1; j < n; ++j)
{
string s;
int p = ans[i] + ans[j];
if (p >= n - 1)
{
p -= n - 1;
s += m[1];
}
s += m[p];
if (s != arr[i][j])
{
cout << "ERROR!" << endl;
return 0;
}
}
}
for (int i = 0; i < n - 1; ++i)
{
cout << m[i] << "=" << i << " ";
}
cout << endl
<< n - 1 << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define all(a) a.begin(), a.end()
#define rep(i, l, r) for (int i = l; i < r; ++i)
#define per(i, r, l) for (int i = r - 1; i >= l; --i)
typedef long long ll;
typedef pair<int, int> PI;
typedef vector<int> VI;
typedef vector<ll> VL;
typedef vector<PI> VP;
template <typename T>
bool setmax(T &a, T b) { return (a < b ? a = b : false); }
template <typename T>
bool setmin(T &a, T b) { return (a > b ? a = b : false); }
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
vector<vector<string>> g(n, vector<string>(n));
unordered_map<char, int> mp;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> g[i][j];
if (!i)
mp[g[i][j][0]] = j; // debug("??", g[i][j][0], j);
}
}
bool ok = false;
VI cur(n), ans(n), vis(n);
auto dfs = [&](int u, auto &&dfs) -> void
{
if (ok)
return;
if (u == n)
{
auto check = [&]()
{
for (int i = 1; i < n; i++)
{
for (int j = 1; j < n; j++)
{
int val = 1, res = 0;
per(k, (int)g[i][j].size(), 0)
{
res += cur[mp[g[i][j][k]]] * val;
val *= (n - 1);
}
int p = cur[mp[g[0][j][0]]] + cur[mp[g[i][0][0]]];
// debug(g[i][j], p, res, cur[mp[g[0][j][0]]], mp[g[0][j][0]], g[0][j][0]);
if (res != p)
return false;
}
}
return true;
};
if (check())
ok = true;
ans = cur;
return;
}
for (int i = 0; i < n; i++)
{
if (!vis[i])
{
cur[u] = i;
vis[i] = 1;
dfs(u + 1, dfs);
vis[i] = 0;
cur[u] = 0;
}
}
};
dfs(1, dfs);
if (ok)
{
for (int i = 1; i < n; i++)
cout << g[0][i] << "=" << ans[i] << " ";
cout << '\n';
cout << n - 1 << '\n';
}
else
cout << "ERROR!\n";
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define all(a) a.begin(), a.end()
#define rep(i, l, r) for (int i = l; i < r; ++i)
#define per(i, r, l) for (int i = r - 1; i >= l; --i)
typedef long long ll;
typedef pair<int, int> PI;
typedef vector<int> VI;
typedef vector<ll> VL;
typedef vector<PI> VP;
template <typename T>
bool setmax(T &a, T b) { return (a < b ? a = b : false); }
template <typename T>
bool setmin(T &a, T b) { return (a > b ? a = b : false); }
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
vector<vector<string>> g(n, vector<string>(n));
unordered_map<char, int> mp;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> g[i][j];
if (!i)
mp[g[i][j][0]] = i;
}
}
bool ok = false;
VI cur(n), ans(n), vis(n);
auto dfs = [&](int u, auto &&dfs) -> void
{
if (ok)
return;
if (u == n)
{
auto check = [&]()
{
unordered_map<string, int> v;
for (int i = 1; i < n; i++)
{
for (int j = 1; j < n; j++)
{
int val = 1, res = 0;
per(k, (int)g[i][j].size(), 0)
{
res += cur[mp[g[i][j][k]]] * val;
val *= n;
}
if (v.count(g[i][j]) && v[g[i][j]] != res)
return false;
v[g[i][j]] = res;
}
}
return true;
};
if (check())
ok = true;
ans = cur;
return;
}
for (int i = 0; i < n; i++)
{
if (!vis[i])
{
cur[u] = i;
vis[i] = 1;
dfs(u + 1, dfs);
vis[i] = 0;
cur[u] = 0;
}
}
};
dfs(1, dfs);
if (ok)
{
for (int i = 1; i < n; i++)
cout << g[0][i] << "=" << ans[i] << " ";
cout << '\n';
cout << n - 1 << '\n';
}
else
cout << "ERROR!\n";
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <random>
#include <bits/stdc++.h>
#include <unistd.h>
using namespace std;
#define endl '\n'
#define ll long long
// ll是64位版本
#define bp __builtin_popcountll
#define gcd __gcd
typedef std::pair<ll, ll> pii;
const ll MOD = 1e9 + 7;
// const ll MOD = 998244353;
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
using namespace std;
int n;
string s[10][10];
map<string, int> m;
void solve()
{
cin >> n;
bool flag = true;
for (int i = 1; i <= n; i++)
{
int cnt = 0;
for (int j = 1; j <= n; j++)
{
cin >> s[i][j];
if (s[i][j].size() > 2)
{
flag = false;
}
else if (s[i][j].size() == 2)
{
cnt++;
}
}
if (i > 1)
{
m[s[i][1]] = cnt;
}
}
for (int i = 2; i <= n; i++)
{
for (int j = 2; j <= n; j++)
{
int target = m[s[i][1]] + m[s[1][j]];
int actual = 0;
if (s[i][j].size() == 1)
{
actual = m[s[i][j]];
}
else
{
actual = m[s[i][j].substr(0, 1)] * (n - 1) + m[s[i][j].substr(1, 1)];
}
if (target != actual)
{
// cout << i << " " << j << " t " << target << " " << actual<< endl;
flag = false;
}
}
}
if (!flag)
{
cout << "ERROR!" << endl;
return;
}
for (int i = 2; i <= n; i++)
{
cout << s[i][1] << "=";
cout << m[s[i][1]] << " ";
}
cout << endl;
cout << (n - 1) << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <random>
#include <bits/stdc++.h>
#include <unistd.h>
using namespace std;
#define endl '\n'
#define ll long long
// ll是64位版本
#define bp __builtin_popcountll
#define gcd __gcd
typedef std::pair<ll, ll> pii;
const ll MOD = 1e9 + 7;
// const ll MOD = 998244353;
#include <bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
using namespace std;
int n;
string s[10][10];
bool vis[10];
void solve()
{
cin >> n;
bool flag = true;
for (int i = 1; i <= n; i++)
{
int cnt = 0;
for (int j = 1; j <= n; j++)
{
cin >> s[i][j];
if (s[i][j].size() > 2)
{
flag = false;
}
else if (s[i][j].size() == 2)
{
cnt++;
}
}
if (i > 1)
{
if (vis[cnt])
{
flag = false;
}
else
{
vis[cnt] = true;
}
}
}
if (!flag)
{
cout << "ERROR!" << endl;
return;
}
for (int i = 2; i <= n; i++)
{
cout << s[i][1] << "=";
int cnt = 0;
for (int j = 2; j <= n; j++)
{
if (s[i][j].size() == 2)
{
cnt++;
}
}
cout << cnt << " ";
}
cout << endl;
cout << (n - 1) << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <cstdio>
using namespace std;
/*
int search(int n){
bool success = false;
return 0;
}*/
int find(char x, char know[])
{
for (int j = 0; j < 15; j++)
{
if (x == know[j])
{
return j;
}
}
return -1;
}
char get[15][15][5];
int main()
{
int n; // char ipt[50];
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
scanf("%s", get[i][j]);
}
}
/*for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
printf("%s ",get[i][j]);
}
printf("\n");
}*/
// search(n);
// find 0
char know[15] = {0};
for (int i = 1; i < n; i++)
{
if (get[1][i][0] == get[1][0][0] && get[1][i][1] == get[1][0][1])
{
know[0] = get[0][i][0];
break;
}
}
// find 10
bool success = false;
for (int i = 1; i < n; i++)
{
for (int j = n - 1; j >= 0; j--)
{
if (get[i][j][1] == know[0])
{
know[1] = get[i][j][0];
success = true;
}
}
if (success)
{
break;
}
}
int idx1;
// find 1_x
for (int i = 0; i < n; i++)
{
if (get[i][0][0] == know[1])
{
idx1 = i;
break;
}
}
char now = know[1];
// generate to n
for (int i = 2; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (get[0][j][0] == now)
{
now = get[idx1][j][0];
know[i] = now;
break;
}
}
}
// check
success = true;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - 1; j++)
{
int sum = 0;
if (get[i + 1][j + 1][1] == '\0')
{
sum += find(get[i + 1][j + 1][0], know);
}
else
{
sum += n;
sum += find(get[i + 1][j + 1][1], know);
}
if (find(get[0][j + 1][0], know) + find(get[0][i + 1][0], know) != sum && find(get[0][j + 1][0], know) + find(get[0][i + 1][0], know) != sum - 1)
{
success = false;
// printf("%d=%d+%d\n",sum-1,find(get[0][j+1][0],know),find(get[0][i+1][0],know));
}
}
}
if (!success)
{
printf("ERROR!");
return 0;
}
for (int i = 1; i < n; i++)
{
for (int j = 0; j < n - 1; j++)
{
if (get[0][i][0] == know[j])
{
printf("%c=%d ", know[j], j);
break;
}
}
}
printf("\n%d", n - 1);
return 0;
} | 这里是题目描述:# [NOIP1998 提高组] 进制位
## 题目描述
著名科学家卢斯为了检查学生对进位制的理解,他给出了如下的一张加法表,表中的字母代表数字。 例如:
$$
\def\arraystretch{2}
\begin{array}{c||c|c|c|c}
\rm + & \kern{.5cm} \rm \mathclap{L} \kern{.5cm} & \kern{.5cm} \rm \mathclap{K} \kern{.5cm} & \kern{.5cm} \rm \mathclap{V} \kern{.5cm} & \kern{.5cm} \rm \mathclap{E} \kern{.5cm} \\ \hline\hline
\rm L & \rm L & \rm K & \rm V & \rm E \\ \hline
\rm K & \rm K & \rm V & \rm E & \rm \mathclap{KL} \\ \hline
\rm V & \rm V & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} \\ \hline
\rm E & \rm E & \rm \mathclap{KL} & \rm \mathclap{KK} & \rm \mathclap{KV} \\
\end{array}$$
其含义为:
$L+L=L$,$L+K=K$,$L+V=V$,$L+E=E$
$K+L=K$,$K+K=V$,$K+V=E$,$K+E=KL$
$\cdots$
$E+E=KV$
根据这些规则可推导出:$L=0$,$K=1$,$V=2$,$E=3$。
同时可以确定该表表示的是 $4$ 进制加法。
## 输入格式
第一行一个整数 $n$($3\le n\le9$)表示行数。
以下 $n$ 行,每行包括 $n$ 个字符串,每个字符串间用空格隔开。)
若记 $s_{i,j}$ 表示第 $i$ 行第 $j$ 个字符串,数据保证 $s_{1,1}=\texttt +$,$s_{i,1}=s_{1,i}$,$|s_{i,1}|=1$,$s_{i,1}\ne s_{j,1}$ ($i\ne j$)。
保证至多有一组解。
## 输出格式
第一行输出各个字母表示什么数,格式如:`L=0 K=1` $\cdots$ 按给出的字母顺序排序。不同字母必须代表不同数字。
第二行输出加法运算是几进制的。
若不可能组成加法表,则应输出 `ERROR!`。
## 样例 #1
### 样例输入 #1
```
5
+ L K V E
L L K V E
K K V E KL
V V E KL KK
E E KL KK KV
```
### 样例输出 #1
```
L=0 K=1 V=2 E=3
4
```
## 提示
NOIP1998 提高组 第三题 下面是题目解析和做法:## 题意
给出一个加法表,一个字母代表一个数字。求加法的进制,以及每个大写字母代表的数字。
数字个数 $N\le 8$ 。(行数 $\le 9$)
## 题解
结论:
1. 一定是 $N$ 进制。
2. 每一行有几个二位数,这个数就是几。
---
证明:
因为有 $N$ 个不同的数,所以最少 $N$ 进制。
假设为 $N+1$ 进制,那么一定有一个数没有出现,假设为 $k$ 。
1. $k=0$ 或 $k=1$,而 $1+N=10$ ,矛盾。
2. $1 < k \le N$ ,而 $1+(k-1)=k$ ,矛盾。
其它 $> N$ 进制的情况同理,所以一定是 $N$ 进制,结论 $1$ 得证。
数字为 $0..N-1$ ,所以结论 $2$ 显然。
---
有上面的结论后这道题就很好做了。每个数的值都可以预处理出来,记为 $ans[]$ ;同时把字母与数字的对应关系记为 $mp[]$ 。
然后枚举每个数,检验有没有矛盾,如果有就直接输出 `ERROR` 。最后把 $ans[]$ 全部输出即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
char ch=getchar();
int f=1,x=0;
while (ch<'0' || ch>'9')
{
if (ch=='-') f=-1;
ch=getchar();
}
while (ch>='0' && ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return f*x;
}
int n,ans[15],mp[26];
char s[15][15][3];
inline bool check(int x,int y) //检验 (x,y)
{
int sum=ans[x]+ans[y]; //和
int cur=s[x][y][1]-'A'; //处理十位
if (sum>=n-1 && mp[cur]!=1) return 0; //如果和 >=n-1 但没有进位
if (sum>=n-1) sum-=n-1,cur=s[x][y][2]-'A'; //处理个位
if (mp[cur]!=sum) return 0; //不相等
return 1;
}
signed main()
{
n=read();
for (int j=1;j<=n;j++) scanf("%s",s[1][j]+1);
for (int i=2;i<=n;i++)
{
int cnt=0;
for (int j=1;j<=n;j++)
{
scanf("%s",s[i][j]+1);
cnt+=strlen(s[i][j]+1)>=2;
}
ans[i]=cnt;
mp[s[i][1][1]-'A']=cnt;
}
for (int i=2;i<=n;i++) for (int j=2;j<=n;j++) if (!check(i,j)) return 0&puts("ERROR!");
for (int i=2;i<=n;i++) printf("%c=%d ",s[i][1][1],ans[i]);
return !printf("\n%d",n-1);
}
``` 题目标签:搜索 | #include <cstdio>
using namespace std;
/*
int search(int n){
bool success = false;
return 0;
}*/
char get[15][15][5];
int main()
{
int n; // char ipt[50];
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
scanf("%s", get[i][j]);
}
}
/*for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
printf("%s ",get[i][j]);
}
printf("\n");
}*/
// search(n);
// find 0
char know[15] = {0};
for (int i = 1; i < n; i++)
{
if (get[1][i][0] == get[1][0][0] && get[1][i][1] == get[1][0][1])
{
know[0] = get[0][i][0];
break;
}
}
// find 10
bool success = false;
for (int i = 1; i < n; i++)
{
for (int j = n - 1; j >= 0; j--)
{
if (get[i][j][1] == know[0])
{
know[1] = get[i][j][0];
success = true;
}
}
if (success)
{
break;
}
}
int idx1;
// find 1_x
for (int i = 0; i < n; i++)
{
if (get[i][0][0] == know[1])
{
idx1 = i;
break;
}
}
char now = know[1];
// generate to n
for (int i = 2; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (get[0][j][0] == now)
{
now = get[idx1][j][0];
know[i] = now;
break;
}
}
}
for (int i = 0; i < n - 1; i++)
{
printf("%c=%d ", know[i], i);
}
printf("\n%d", n - 1);
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
#include <map>
#include <queue>
#include <set>
#include <vector>
#define int long long
#define ull unsigned long long
#define endl '\n'
#define all(s) s.begin(), s.end()
#define xx first
#define yy second
#define inf 0x3f3f3f3f3f3f3f3f
#define N 1000005
#define mod 1000000007 // 998244353
#define double long double
#define lowbit(x) ((x) & (-x))
#define ls(x) (x << 1)
#define rs(x) ((x << 1) | 1)
#define pll pair<int, int>
#define __lcm(a, b) (a / __gcd(a, b) * b)
const double pi = acos(-1);
const int P = 233333;
const int PP = 1313131;
const int mod1 = 1000001011;
const int mod2 = (1ll << 31) - 1;
using namespace std;
int arr[15][15];
int dp[15][15];
void show(int n)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
printf("%2lld ", dp[i][j]);
}
cout << endl;
}
cout << endl;
}
void move(int n)
{
map<int, pll> ma;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (!ma.count(dp[i][j]))
ma[dp[i][j]] = {i, j};
}
}
int x = n, y = n;
while (dp[x][y])
{
pll now = ma[dp[x][y]];
x = now.xx, y = now.yy;
arr[x][y] = 0;
if (dp[x - 1][y] > dp[x][y - 1])
x--;
else
y--;
}
}
void solve()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
arr[i][j] = 0;
}
for (int a, b, c; cin >> a >> b >> c && a && b && c;)
arr[a][b] = c;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = 0;
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + arr[i][j];
}
}
int ans = dp[n][n];
// show(n);
move(n);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = 0;
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + arr[i][j];
}
}
// show(n);
cout << dp[n][n] + ans << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int T = 1;
// cin>>T;
while (T--)
{
solve();
}
return 0;
} | 这里是题目描述:# [NOIP2000 提高组] 方格取数
## 题目背景
NOIP 2000 提高组 T4
## 题目描述
设有 $N \times N$ 的方格图 $(N \le 9)$,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 $0$。如下图所示(见样例):
某人从图的左上角的 $A$ 点出发,可以向下行走,也可以向右走,直到到达右下角的 $B$ 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 $0$)。
此人从 $A$ 点到 $B$ 点共走两次,试找出 $2$ 条这样的路径,使得取得的数之和为最大。
## 输入格式
输入的第一行为一个整数 $N$(表示 $N \times N$ 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。
## 输出格式
只需输出一个整数,表示 $2$ 条路径上取得的最大的和。
## 样例 #1
### 样例输入 #1
```
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
```
### 样例输出 #1
```
67
```
## 提示
数据范围:$1\le N\le 9$。 下面是题目解析和做法:第一份题解:
###深搜深搜
见都是动规的帖子,来来来,贴一个深搜的题解(手动滑稽)。。。
这道题深搜的最优方法就是两种方案同时从起点出发。因为如果记录完第一种方案,再计算第二种方案,不可控的因素太多了,大多都不是最优解→\_→,但两种方案同时执行就行,因为这可以根据当前的情况来判断最优。
总的来说,每走一步都会有四个分支(你理解成选择或者情况也可以):
1、两种都向下走
2、第一种向下走,第二种向右走
3、第一种向右走,第二种向下走
4、两种都向右走
每走一步走枚举一下这四种情况,因为在每个点的方案具有唯一性(也就是在某个点走到终点的取数方案只有一个最优解,自己理解一下),所以我们可以开一个数组来记录每一种情况,当重复枚举到一种情况时就直接返回(对,就是剪枝),大大节省了时间(不然会超时哦~)。深搜和动归的时间复杂度时一样的!
附代码:
```cpp
//方格取数~深搜 ~( ̄▽ ̄~)(~ ̄▽ ̄)~
#include <iostream >using namespace std;
int N=0;
int s[15][15],f[11][11][11][11];
int dfs(int x,int y,int x2,int y2)//两种方案同时执行,表示当第一种方案走到x,y,第二种方案走到x2,y2时到终点取得的最大数
{
if (f[x][y][x2][y2]!=-1) return f[x][y][x2][y2];//如果这种情况已经被记录过了,直接返回,节省时间
if (x==N &&y==N &&x2==N &&y2==N) return 0;//如果两种方案都走到了终点,返回结束
int M=0;
//如果两种方案都不在最后一列,就都往下走,统计取得的数,如果有重复,就减去一部分
if (x <N &&x2 <N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1 &&y==y2));
//如果第一种方案不在最后一行,第二种方案不在最后一列,第一种就向下走,第二种就向右走,
//统计取得的数,如果有重复,就减去一部分
if (x <N &&y2 <N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2 &&y==y2+1));
//如果第一种方案不在最后一列,第二种方案不在最后一行,第一种就向右走,第二种就向下走,
//统计取得的数,如果有重复,就减去一部分
if (y <N &&x2 <N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1 &&y+1==y2));
//如果第一种方案和第二种方案都不在最后一列,就都向右走,统计取得的数,如果有重复,就减去一部分
if (y <N &&y2 <N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2 &&y+1==y2+1));
//对最后那个 s[x][y+1]*(x==x2 &&y+1==y2+1))的解释:这个是用来判断两种方案是不是走到了同一格的
//如果是真,就返回1,否则返回0,如果是1的话,理所当然的可以减去s[x][y+1]*1,否则减去s[x][y+1]*0相当于
//不减,写得有点精简,省了4个if,见谅哈~
f[x][y][x2][y2]=M;//记录这种情况
return M;//返回最大值
}
int main()
{
cin >>N;
//将记录数组初始化成-1,因为可能出现取的数为0的情况,如果直接判断f[x][y][x2][y2]!=0(见dfs第一行)
//可能出现死循环而导致超时,细节问题
for(int a=0;a <=N;a++)
for(int b=0;b <=N;b++)
for(int c=0;c <=N;c++)
for(int d=0;d <=N;d++) f[a][b][c][d]=-1;
for(;;)//读入
{
int t1=0,t2=0,t3=0;
cin >>t1 >>t2 >>t3;
if(t1==0 &&t2==0 &&t3==0) break;
s[t1][t2]=t3;
}
cout <<dfs(1,1,1,1)+s[1][1];//输出,因为dfs中没有考虑第一格,即s[1][1],所以最后要加一下
return 0;
}
```
第二份题解:
一道典型的棋盘dp。
一共需要走两次,我们不妨同时处理这两条路径。这样,我们既可以方便地处理两条路径重合的情况,也可以减少代码的时间复杂度。
最朴素的想法是开一个四维数组$f[x_1][y_1][x_2][y_2]$表示当两条路径分别处理到$(x_1,y_1)$和$(x_2,y_2)$时能够获得的最大的累积和。但是,四维数组处理起来时间复杂度太大了,所以我们要想办法把它降成三维。
我们可以发现,每当我们走一步,那么x坐标和y坐标之间总会有一个数加$1$。所以,我们可以用k来表示x坐标和y坐标的和,从而通过y坐标来计算出x坐标。由于k对于两条同时处理的路径可以是公共的,所以我们可以用$f[k][y_1][y_2]$来表示当前状态。
特殊的,由于每一个方格的数只可以取一次,所以我们要判断i和j是否相当。
于是,我们就可以得到一个状态转移方程了:
$$f[k][i][j]=max(f[k-1][i][j],f[k-1][i-1][j]f[k-1][i][j-1]f[k-1][i-1][j-1])+[(i==j)?map[k-i+1][i]:map[k-i+1][i] + map[k-j+1][j]]$$
我们可以来看一下我们到底是通过哪些状态转移到当前状态的:
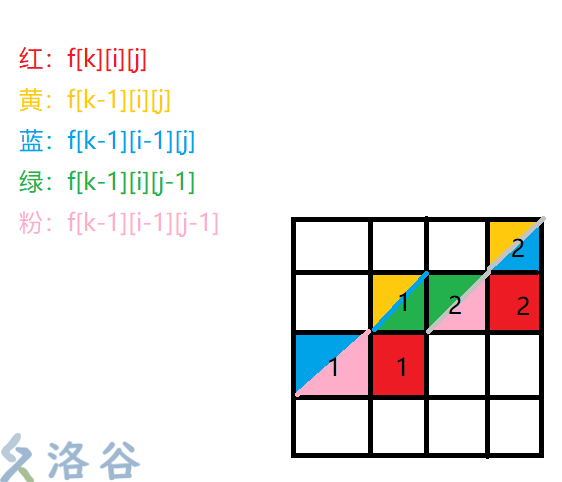
code:
```cpp
#include <iostream >#include <cstring >#include <cstdio >#include <cmath >#include <algorithm >#define ll long long
#define INF 0x7fffffff
#define re register
#define qwq printf("qwq\n ");
using namespace std;
int read()
{
register int x = 0,f = 1;register char ch;
ch = getchar();
while(ch >'9 '|| ch <'0 '){if(ch == '-') f = -f;ch = getchar();}
while(ch <= '9 '&&ch >= '0 '){x = x * 10 + ch - 48;ch = getchar();}
return x * f;
}
int n,m,map[205][205],f[205][205][205],x,y,v;
int cmp(int a,int b,int c,int d)
{
a = max(a,b);
c = max(c,d);
return max(a,c);
}
int main()
{
m = read();
n = m;
x = read(); y = read(); v = read();
while(x >0)
{
map[x][y] = v;
x = read(); y = read(); v = read();
}
for(int k = 1; k <= m + n; k++)
for(int i = 1; i <= min(k,n); i++)
for(int j = 1; j <= min(k,n); j++)
{
f[k][i][j] = cmp(f[k - 1][i][j],f[k - 1][i - 1][j],f[k - 1][i][j - 1],f[k - 1][i - 1][j - 1]) + map[k - i + 1][i] + map[k - j + 1][j];
if(i == j) f[k][i][j] -= map[k - i + 1][i];
}
f[n + m][n][n] = cmp(f[n + m - 1][n][n - 1],f[n + m - 1][n - 1][n],f[n + m - 1][n][n],f[n + m - 1][n - 1][n - 1]);
printf("%d\n ",f[n + m][n][n]);
return 0;
}
``` 题目标签:动 态 规 划 | #include <bits/stdc++.h>
#include <map>
#include <queue>
#include <set>
#include <vector>
#define int long long
#define ull unsigned long long
#define endl '\n'
#define all(s) s.begin(), s.end()
#define xx first
#define yy second
#define inf 0x3f3f3f3f3f3f3f3f
#define N 1000005
#define mod 1000000007 // 998244353
#define double long double
#define lowbit(x) ((x) & (-x))
#define ls(x) (x << 1)
#define rs(x) ((x << 1) | 1)
#define pll pair<int, int>
#define __lcm(a, b) (a / __gcd(a, b) * b)
const double pi = acos(-1);
const int P = 233333;
const int PP = 1313131;
const int mod1 = 1000001011;
const int mod2 = (1ll << 31) - 1;
using namespace std;
int arr[15][15];
int dp[15][15];
void show(int n)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
printf("%2lld ", dp[i][j]);
}
cout << endl;
}
cout << endl;
}
void move(int n)
{
map<int, pll> ma;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (!ma.count(dp[i][j]))
ma[dp[i][j]] = {i, j};
}
}
int x = n, y = n;
while (dp[x][y])
{
pll now = ma[dp[x][y]];
x = now.xx, y = now.yy;
arr[x][y] = 0;
x--, y--;
}
}
void solve()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
arr[i][j] = 0;
}
for (int a, b, c; cin >> a >> b >> c && a && b && c;)
arr[a][b] = c;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = 0;
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + arr[i][j];
}
}
int ans = dp[n][n];
// show(n);
move(n);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
dp[i][j] = 0;
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + arr[i][j];
}
}
cout << dp[n][n] + ans << endl;
}
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int T = 1;
// cin>>T;
while (T--)
{
solve();
}
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
int main()
{
int n;
std::cin >> n;
std::vector a(n + 5, std::vector<int>(n + 5, 0));
int i = 1, j, num;
while (i)
{
std::cin >> i >> j >> num;
a[i][j] = num;
}
std::vector dp(2 * n + 5, std::vector(n + 5, std::vector<int>(n + 5, 0)));
dp[0][1][1] = a[1][1];
for (int k = 1; k <= 2 * n - 2; k++)
{
for (int i = 1; i <= n && i <= k + 1; i++)
{
for (int j = 1; j <= n && j <= k + 1; j++)
{
if (k - i + 2 > n && k - j + 2 > n)
break;
int d = a[i][k - i + 2] + a[j][k - j + 2];
if (i == j)
d /= 2;
// if (a[i][k - i + 2]) std::cerr << i << ' ' << k - i + 2 << ' ' << a[i][k - i + 2] << '\n';
// if (a[j][k - j + 2]) std::cerr << j << ' ' << k - j + 2 << ' ' << a[j][k - j + 2] << '\n';
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i - 1][j - 1] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i][j - 1] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i - 1][j] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i][j] + d);
}
}
}
std::cout << dp[2 * n - 2][n][n];
} | 这里是题目描述:# [NOIP2000 提高组] 方格取数
## 题目背景
NOIP 2000 提高组 T4
## 题目描述
设有 $N \times N$ 的方格图 $(N \le 9)$,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 $0$。如下图所示(见样例):

某人从图的左上角的 $A$ 点出发,可以向下行走,也可以向右走,直到到达右下角的 $B$ 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 $0$)。
此人从 $A$ 点到 $B$ 点共走两次,试找出 $2$ 条这样的路径,使得取得的数之和为最大。
## 输入格式
输入的第一行为一个整数 $N$(表示 $N \times N$ 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。
## 输出格式
只需输出一个整数,表示 $2$ 条路径上取得的最大的和。
## 样例 #1
### 样例输入 #1
```
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
```
### 样例输出 #1
```
67
```
## 提示
数据范围:$1\le N\le 9$。 下面是题目解析和做法:第一份题解:
###深搜深搜
见都是动规的帖子,来来来,贴一个深搜的题解(手动滑稽)。。。
这道题深搜的最优方法就是两种方案同时从起点出发。因为如果记录完第一种方案,再计算第二种方案,不可控的因素太多了,大多都不是最优解→\_→,但两种方案同时执行就行,因为这可以根据当前的情况来判断最优。
总的来说,每走一步都会有四个分支(你理解成选择或者情况也可以):
1、两种都向下走
2、第一种向下走,第二种向右走
3、第一种向右走,第二种向下走
4、两种都向右走
每走一步走枚举一下这四种情况,因为在每个点的方案具有唯一性(也就是在某个点走到终点的取数方案只有一个最优解,自己理解一下),所以我们可以开一个数组来记录每一种情况,当重复枚举到一种情况时就直接返回(对,就是剪枝),大大节省了时间(不然会超时哦~)。深搜和动归的时间复杂度时一样的!
附代码:
```cpp
//方格取数~深搜 ~( ̄▽ ̄~)(~ ̄▽ ̄)~
#include <iostream >using namespace std;
int N=0;
int s[15][15],f[11][11][11][11];
int dfs(int x,int y,int x2,int y2)//两种方案同时执行,表示当第一种方案走到x,y,第二种方案走到x2,y2时到终点取得的最大数
{
if (f[x][y][x2][y2]!=-1) return f[x][y][x2][y2];//如果这种情况已经被记录过了,直接返回,节省时间
if (x==N &&y==N &&x2==N &&y2==N) return 0;//如果两种方案都走到了终点,返回结束
int M=0;
//如果两种方案都不在最后一列,就都往下走,统计取得的数,如果有重复,就减去一部分
if (x <N &&x2 <N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1 &&y==y2));
//如果第一种方案不在最后一行,第二种方案不在最后一列,第一种就向下走,第二种就向右走,
//统计取得的数,如果有重复,就减去一部分
if (x <N &&y2 <N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2 &&y==y2+1));
//如果第一种方案不在最后一列,第二种方案不在最后一行,第一种就向右走,第二种就向下走,
//统计取得的数,如果有重复,就减去一部分
if (y <N &&x2 <N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1 &&y+1==y2));
//如果第一种方案和第二种方案都不在最后一列,就都向右走,统计取得的数,如果有重复,就减去一部分
if (y <N &&y2 <N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2 &&y+1==y2+1));
//对最后那个 s[x][y+1]*(x==x2 &&y+1==y2+1))的解释:这个是用来判断两种方案是不是走到了同一格的
//如果是真,就返回1,否则返回0,如果是1的话,理所当然的可以减去s[x][y+1]*1,否则减去s[x][y+1]*0相当于
//不减,写得有点精简,省了4个if,见谅哈~
f[x][y][x2][y2]=M;//记录这种情况
return M;//返回最大值
}
int main()
{
cin >>N;
//将记录数组初始化成-1,因为可能出现取的数为0的情况,如果直接判断f[x][y][x2][y2]!=0(见dfs第一行)
//可能出现死循环而导致超时,细节问题
for(int a=0;a <=N;a++)
for(int b=0;b <=N;b++)
for(int c=0;c <=N;c++)
for(int d=0;d <=N;d++) f[a][b][c][d]=-1;
for(;;)//读入
{
int t1=0,t2=0,t3=0;
cin >>t1 >>t2 >>t3;
if(t1==0 &&t2==0 &&t3==0) break;
s[t1][t2]=t3;
}
cout <<dfs(1,1,1,1)+s[1][1];//输出,因为dfs中没有考虑第一格,即s[1][1],所以最后要加一下
return 0;
}
```
第二份题解:
一道典型的棋盘dp。
一共需要走两次,我们不妨同时处理这两条路径。这样,我们既可以方便地处理两条路径重合的情况,也可以减少代码的时间复杂度。
最朴素的想法是开一个四维数组$f[x_1][y_1][x_2][y_2]$表示当两条路径分别处理到$(x_1,y_1)$和$(x_2,y_2)$时能够获得的最大的累积和。但是,四维数组处理起来时间复杂度太大了,所以我们要想办法把它降成三维。
我们可以发现,每当我们走一步,那么x坐标和y坐标之间总会有一个数加$1$。所以,我们可以用k来表示x坐标和y坐标的和,从而通过y坐标来计算出x坐标。由于k对于两条同时处理的路径可以是公共的,所以我们可以用$f[k][y_1][y_2]$来表示当前状态。
特殊的,由于每一个方格的数只可以取一次,所以我们要判断i和j是否相当。
于是,我们就可以得到一个状态转移方程了:
$$f[k][i][j]=max(f[k-1][i][j],f[k-1][i-1][j]f[k-1][i][j-1]f[k-1][i-1][j-1])+[(i==j)?map[k-i+1][i]:map[k-i+1][i] + map[k-j+1][j]]$$
我们可以来看一下我们到底是通过哪些状态转移到当前状态的:

code:
```cpp
#include <iostream >#include <cstring >#include <cstdio >#include <cmath >#include <algorithm >#define ll long long
#define INF 0x7fffffff
#define re register
#define qwq printf("qwq\n ");
using namespace std;
int read()
{
register int x = 0,f = 1;register char ch;
ch = getchar();
while(ch >'9 '|| ch <'0 '){if(ch == '-') f = -f;ch = getchar();}
while(ch <= '9 '&&ch >= '0 '){x = x * 10 + ch - 48;ch = getchar();}
return x * f;
}
int n,m,map[205][205],f[205][205][205],x,y,v;
int cmp(int a,int b,int c,int d)
{
a = max(a,b);
c = max(c,d);
return max(a,c);
}
int main()
{
m = read();
n = m;
x = read(); y = read(); v = read();
while(x >0)
{
map[x][y] = v;
x = read(); y = read(); v = read();
}
for(int k = 1; k <= m + n; k++)
for(int i = 1; i <= min(k,n); i++)
for(int j = 1; j <= min(k,n); j++)
{
f[k][i][j] = cmp(f[k - 1][i][j],f[k - 1][i - 1][j],f[k - 1][i][j - 1],f[k - 1][i - 1][j - 1]) + map[k - i + 1][i] + map[k - j + 1][j];
if(i == j) f[k][i][j] -= map[k - i + 1][i];
}
f[n + m][n][n] = cmp(f[n + m - 1][n][n - 1],f[n + m - 1][n - 1][n],f[n + m - 1][n][n],f[n + m - 1][n - 1][n - 1]);
printf("%d\n ",f[n + m][n][n]);
return 0;
}
``` 题目标签:动 态 规 划 | #include <bits/stdc++.h>
int main()
{
int n;
std::cin >> n;
std::vector a(n + 5, std::vector<int>(n + 5, 0));
int i = 1, j, num;
while (i)
{
std::cin >> i >> j >> num;
a[i][j] = num;
}
std::vector dp(2 * n + 5, std::vector(n + 5, std::vector<int>(n + 5, 0)));
dp[0][1][1] = a[1][1];
for (int k = 1; k <= 2 * n - 2; k++)
{
for (int i = 1; i <= n && i <= k; i++)
{
for (int j = 1; j <= n && j <= k; j++)
{
if (k - i + 2 > n && k - j + 2 > n)
break;
int d = a[i][k - i + 2] + a[j][k - j + 2];
if (i == j)
d /= 2;
// if (a[i][k - i + 2]) std::cerr << i << ' ' << k - i + 2 << ' ' << a[i][k - i + 2] << '\n';
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i - 1][j - 1] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i][j - 1] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i - 1][j] + d);
dp[k][i][j] = std::max(dp[k][i][j], dp[k - 1][i][j] + d);
}
}
}
std::cout << dp[2 * n - 2][n][n];
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int n, grid[10][10], x, y, v, ans, dp[10][10][50];
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
while (true)
{
cin >> x >> y >> v;
if (x == y && y == v && v == 0)
break;
grid[x][y] = v;
}
for (int k = 1; k <= 2 * n; k++)
{
for (int i = 1; i <= min(k, n); i++)
{
for (int j = 1; j <= min(k, n); j++)
{
dp[i][j][k] = max({dp[i][j][k - 1], dp[i - 1][j][k - 1], dp[i][j - 1][k - 1], dp[i - 1][j - 1][k - 1]});
dp[i][j][k] += grid[i][k - i] + grid[j][k - j];
if (i == j)
dp[i][j][k] -= grid[i][k - i];
}
}
}
cout << dp[n][n][2 * n] << endl;
return 0;
} | 这里是题目描述:# [NOIP2000 提高组] 方格取数
## 题目背景
NOIP 2000 提高组 T4
## 题目描述
设有 $N \times N$ 的方格图 $(N \le 9)$,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 $0$。如下图所示(见样例):

某人从图的左上角的 $A$ 点出发,可以向下行走,也可以向右走,直到到达右下角的 $B$ 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 $0$)。
此人从 $A$ 点到 $B$ 点共走两次,试找出 $2$ 条这样的路径,使得取得的数之和为最大。
## 输入格式
输入的第一行为一个整数 $N$(表示 $N \times N$ 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。
## 输出格式
只需输出一个整数,表示 $2$ 条路径上取得的最大的和。
## 样例 #1
### 样例输入 #1
```
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
```
### 样例输出 #1
```
67
```
## 提示
数据范围:$1\le N\le 9$。 下面是题目解析和做法:第一份题解:
###深搜深搜
见都是动规的帖子,来来来,贴一个深搜的题解(手动滑稽)。。。
这道题深搜的最优方法就是两种方案同时从起点出发。因为如果记录完第一种方案,再计算第二种方案,不可控的因素太多了,大多都不是最优解→\_→,但两种方案同时执行就行,因为这可以根据当前的情况来判断最优。
总的来说,每走一步都会有四个分支(你理解成选择或者情况也可以):
1、两种都向下走
2、第一种向下走,第二种向右走
3、第一种向右走,第二种向下走
4、两种都向右走
每走一步走枚举一下这四种情况,因为在每个点的方案具有唯一性(也就是在某个点走到终点的取数方案只有一个最优解,自己理解一下),所以我们可以开一个数组来记录每一种情况,当重复枚举到一种情况时就直接返回(对,就是剪枝),大大节省了时间(不然会超时哦~)。深搜和动归的时间复杂度时一样的!
附代码:
```cpp
//方格取数~深搜 ~( ̄▽ ̄~)(~ ̄▽ ̄)~
#include <iostream >using namespace std;
int N=0;
int s[15][15],f[11][11][11][11];
int dfs(int x,int y,int x2,int y2)//两种方案同时执行,表示当第一种方案走到x,y,第二种方案走到x2,y2时到终点取得的最大数
{
if (f[x][y][x2][y2]!=-1) return f[x][y][x2][y2];//如果这种情况已经被记录过了,直接返回,节省时间
if (x==N &&y==N &&x2==N &&y2==N) return 0;//如果两种方案都走到了终点,返回结束
int M=0;
//如果两种方案都不在最后一列,就都往下走,统计取得的数,如果有重复,就减去一部分
if (x <N &&x2 <N) M=max(M,dfs(x+1,y,x2+1,y2)+s[x+1][y]+s[x2+1][y2]-s[x+1][y]*(x+1==x2+1 &&y==y2));
//如果第一种方案不在最后一行,第二种方案不在最后一列,第一种就向下走,第二种就向右走,
//统计取得的数,如果有重复,就减去一部分
if (x <N &&y2 <N) M=max(M,dfs(x+1,y,x2,y2+1)+s[x+1][y]+s[x2][y2+1]-s[x+1][y]*(x+1==x2 &&y==y2+1));
//如果第一种方案不在最后一列,第二种方案不在最后一行,第一种就向右走,第二种就向下走,
//统计取得的数,如果有重复,就减去一部分
if (y <N &&x2 <N) M=max(M,dfs(x,y+1,x2+1,y2)+s[x][y+1]+s[x2+1][y2]-s[x][y+1]*(x==x2+1 &&y+1==y2));
//如果第一种方案和第二种方案都不在最后一列,就都向右走,统计取得的数,如果有重复,就减去一部分
if (y <N &&y2 <N) M=max(M,dfs(x,y+1,x2,y2+1)+s[x][y+1]+s[x2][y2+1]-s[x][y+1]*(x==x2 &&y+1==y2+1));
//对最后那个 s[x][y+1]*(x==x2 &&y+1==y2+1))的解释:这个是用来判断两种方案是不是走到了同一格的
//如果是真,就返回1,否则返回0,如果是1的话,理所当然的可以减去s[x][y+1]*1,否则减去s[x][y+1]*0相当于
//不减,写得有点精简,省了4个if,见谅哈~
f[x][y][x2][y2]=M;//记录这种情况
return M;//返回最大值
}
int main()
{
cin >>N;
//将记录数组初始化成-1,因为可能出现取的数为0的情况,如果直接判断f[x][y][x2][y2]!=0(见dfs第一行)
//可能出现死循环而导致超时,细节问题
for(int a=0;a <=N;a++)
for(int b=0;b <=N;b++)
for(int c=0;c <=N;c++)
for(int d=0;d <=N;d++) f[a][b][c][d]=-1;
for(;;)//读入
{
int t1=0,t2=0,t3=0;
cin >>t1 >>t2 >>t3;
if(t1==0 &&t2==0 &&t3==0) break;
s[t1][t2]=t3;
}
cout <<dfs(1,1,1,1)+s[1][1];//输出,因为dfs中没有考虑第一格,即s[1][1],所以最后要加一下
return 0;
}
```
第二份题解:
一道典型的棋盘dp。
一共需要走两次,我们不妨同时处理这两条路径。这样,我们既可以方便地处理两条路径重合的情况,也可以减少代码的时间复杂度。
最朴素的想法是开一个四维数组$f[x_1][y_1][x_2][y_2]$表示当两条路径分别处理到$(x_1,y_1)$和$(x_2,y_2)$时能够获得的最大的累积和。但是,四维数组处理起来时间复杂度太大了,所以我们要想办法把它降成三维。
我们可以发现,每当我们走一步,那么x坐标和y坐标之间总会有一个数加$1$。所以,我们可以用k来表示x坐标和y坐标的和,从而通过y坐标来计算出x坐标。由于k对于两条同时处理的路径可以是公共的,所以我们可以用$f[k][y_1][y_2]$来表示当前状态。
特殊的,由于每一个方格的数只可以取一次,所以我们要判断i和j是否相当。
于是,我们就可以得到一个状态转移方程了:
$$f[k][i][j]=max(f[k-1][i][j],f[k-1][i-1][j]f[k-1][i][j-1]f[k-1][i-1][j-1])+[(i==j)?map[k-i+1][i]:map[k-i+1][i] + map[k-j+1][j]]$$
我们可以来看一下我们到底是通过哪些状态转移到当前状态的:

code:
```cpp
#include <iostream >#include <cstring >#include <cstdio >#include <cmath >#include <algorithm >#define ll long long
#define INF 0x7fffffff
#define re register
#define qwq printf("qwq\n ");
using namespace std;
int read()
{
register int x = 0,f = 1;register char ch;
ch = getchar();
while(ch >'9 '|| ch <'0 '){if(ch == '-') f = -f;ch = getchar();}
while(ch <= '9 '&&ch >= '0 '){x = x * 10 + ch - 48;ch = getchar();}
return x * f;
}
int n,m,map[205][205],f[205][205][205],x,y,v;
int cmp(int a,int b,int c,int d)
{
a = max(a,b);
c = max(c,d);
return max(a,c);
}
int main()
{
m = read();
n = m;
x = read(); y = read(); v = read();
while(x >0)
{
map[x][y] = v;
x = read(); y = read(); v = read();
}
for(int k = 1; k <= m + n; k++)
for(int i = 1; i <= min(k,n); i++)
for(int j = 1; j <= min(k,n); j++)
{
f[k][i][j] = cmp(f[k - 1][i][j],f[k - 1][i - 1][j],f[k - 1][i][j - 1],f[k - 1][i - 1][j - 1]) + map[k - i + 1][i] + map[k - j + 1][j];
if(i == j) f[k][i][j] -= map[k - i + 1][i];
}
f[n + m][n][n] = cmp(f[n + m - 1][n][n - 1],f[n + m - 1][n - 1][n],f[n + m - 1][n][n],f[n + m - 1][n - 1][n - 1]);
printf("%d\n ",f[n + m][n][n]);
return 0;
}
``` 题目标签:动 态 规 划 | #include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int n, grid[10][10], x, y, v, ans;
typedef struct
{
int x, y;
} node;
int dp[10][10], ind[10][10];
node lit[10][10][100];
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
while (true)
{
cin >> x >> y >> v;
if (x == y && y == v && v == 0)
break;
else
grid[x][y] = v;
}
for (int i = n; i >= 1; i--)
{
for (int j = n; j >= 1; j--)
{
if (grid[i][j])
{
lit[i][j][++ind[i][j]].x = i;
lit[i][j][ind[i][j]].y = j;
}
if (!(i < n && j < n))
continue;
dp[i][j] = max(dp[i + 1][j], dp[i][j + 1]) + grid[i][j];
if (dp[i][j + 1] >= dp[i + 1][j])
{
for (int k = 1; k <= ind[i][j + 1]; k++)
lit[i][j][++ind[i][j]] = lit[i][j + 1][k];
}
else
for (int k = 1; k <= ind[i + 1][j]; k++)
lit[i][j][++ind[i][j]] = lit[i + 1][j][k];
}
}
ans += dp[1][1];
for (int i = 1; i <= ind[1][1]; i++)
grid[lit[1][1][i].x][lit[1][1][i].y] = 0;
for (int i = n; i >= 1; i--)
{
for (int j = n; j >= 1; j--)
{
if (!(i < n && j < n))
continue;
dp[i][j] = max(dp[i + 1][j], dp[i][j + 1]) + grid[i][j];
}
}
ans += dp[1][1];
cout << ans << endl;
return 0;
} | 为我指出下面代码的问题,并修复它。下面是题目描述和题解 |
End of preview. Expand
in Dataset Viewer.
README.md exists but content is empty.
- Downloads last month
- 49