Spaces:
Running
Running
| title: MASE | |
| emoji: 🤗 | |
| colorFrom: blue | |
| colorTo: red | |
| sdk: gradio | |
| sdk_version: 3.19.1 | |
| app_file: app.py | |
| pinned: false | |
| tags: | |
| - evaluate | |
| - metric | |
| description: >- | |
| Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast on the training set. | |
| # Metric Card for MASE | |
| ## Metric Description | |
| Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast. For prediction $x_i$ and corresponding ground truth $y_i$ as well as training data $z_t$ with seasonality $p$ the metric is given by: | |
| 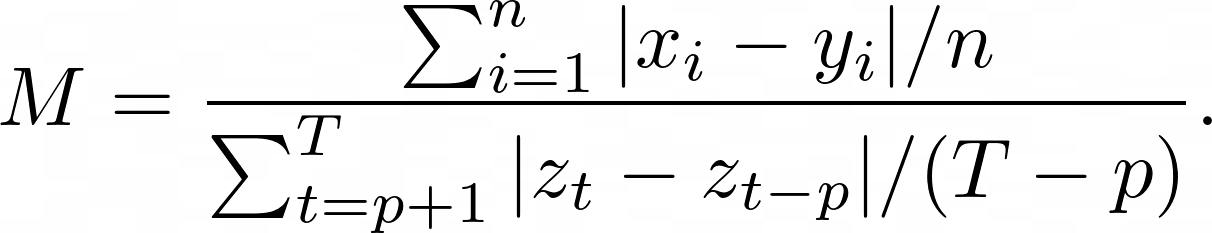 | |
| This metric is: | |
| * independent of the scale of the data; | |
| * has predictable behavior when predicted/ground-truth data is near zero; | |
| * symmetric; | |
| * interpretable, as values greater than one indicate that in-sample one-step forecasts from the naïve method perform better than the forecast values under consideration. | |
| ## How to Use | |
| At minimum, this metric requires predictions, references and training data as inputs. | |
| ```python | |
| >>> mase_metric = evaluate.load("mase") | |
| >>> predictions = [2.5, 0.0, 2, 8] | |
| >>> references = [3, -0.5, 2, 7] | |
| >>> training = [5, 0.5, 4, 6, 3, 5, 2] | |
| >>> results = mase_metric.compute(predictions=predictions, references=references, training=training) | |
| ``` | |
| ### Inputs | |
| Mandatory inputs: | |
| - `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values. | |
| - `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values. | |
| - `training`: numeric array-like of shape (`n_train_samples,`) or (`n_train_samples`, `n_outputs`), representing the in sample training data. | |
| Optional arguments: | |
| - `periodicity`: the seasonal periodicity of training data. The default is 1. | |
| - `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`. | |
| - `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`. | |
| - `raw_values` returns a full set of errors in case of multioutput input. | |
| - `uniform_average` means that the errors of all outputs are averaged with uniform weight. | |
| - the array-like value defines weights used to average errors. | |
| ### Output Values | |
| This metric outputs a dictionary, containing the mean absolute error score, which is of type: | |
| - `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned. | |
| - numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately. | |
| Each MASE `float` value ranges from `0.0` to `1.0`, with the best value being 0.0. | |
| Output Example(s): | |
| ```python | |
| {'mase': 0.5} | |
| ``` | |
| If `multioutput="raw_values"`: | |
| ```python | |
| {'mase': array([0.5, 1. ])} | |
| ``` | |
| #### Values from Popular Papers | |
| ### Examples | |
| Example with the `uniform_average` config: | |
| ```python | |
| >>> mase_metric = evaluate.load("mase") | |
| >>> predictions = [2.5, 0.0, 2, 8] | |
| >>> references = [3, -0.5, 2, 7] | |
| >>> training = [5, 0.5, 4, 6, 3, 5, 2] | |
| >>> results = mase_metric.compute(predictions=predictions, references=references, training=training) | |
| >>> print(results) | |
| {'mase': 0.1833...} | |
| ``` | |
| Example with multi-dimensional lists, and the `raw_values` config: | |
| ```python | |
| >>> mase_metric = evaluate.load("mase", "multilist") | |
| >>> predictions = [[0.5, 1], [-1, 1], [7, -6]] | |
| >>> references = [[0.1, 2], [-1, 2], [8, -5]] | |
| >>> training = [[0.5, 1], [-1, 1], [7, -6]] | |
| >>> results = mase_metric.compute(predictions=predictions, references=references, training=training) | |
| >>> print(results) | |
| {'mase': 0.1818...} | |
| >>> results = mase_metric.compute(predictions=predictions, references=references, training=training, multioutput='raw_values') | |
| >>> print(results) | |
| {'mase': array([0.1052..., 0.2857...])} | |
| ``` | |
| ## Limitations and Bias | |
| ## Citation(s) | |
| ```bibtex | |
| @article{HYNDMAN2006679, | |
| title = {Another look at measures of forecast accuracy}, | |
| journal = {International Journal of Forecasting}, | |
| volume = {22}, | |
| number = {4}, | |
| pages = {679--688}, | |
| year = {2006}, | |
| issn = {0169-2070}, | |
| doi = {https://doi.org/10.1016/j.ijforecast.2006.03.001}, | |
| url = {https://www.sciencedirect.com/science/article/pii/S0169207006000239}, | |
| author = {Rob J. Hyndman and Anne B. Koehler}, | |
| } | |
| ``` | |
| ## Further References | |
| - [Mean absolute scaled error - Wikipedia](https://en.wikipedia.org/wiki/Mean_absolute_scaled_errorr) | |