Spaces:
Running
A newer version of the Gradio SDK is available:
5.38.0
title: MASE
emoji: 🤗
colorFrom: blue
colorTo: red
sdk: gradio
sdk_version: 3.19.1
app_file: app.py
pinned: false
tags:
- evaluate
- metric
description: >-
Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast
values, divided by the mean absolute error of the in-sample one-step naive
forecast on the training set.
Metric Card for MASE
Metric Description
Mean Absolute Scaled Error (MASE) is the mean absolute error of the forecast values, divided by the mean absolute error of the in-sample one-step naive forecast. For prediction $x_i$ and corresponding ground truth $y_i$ as well as training data $z_t$ with seasonality $p$ the metric is given by:
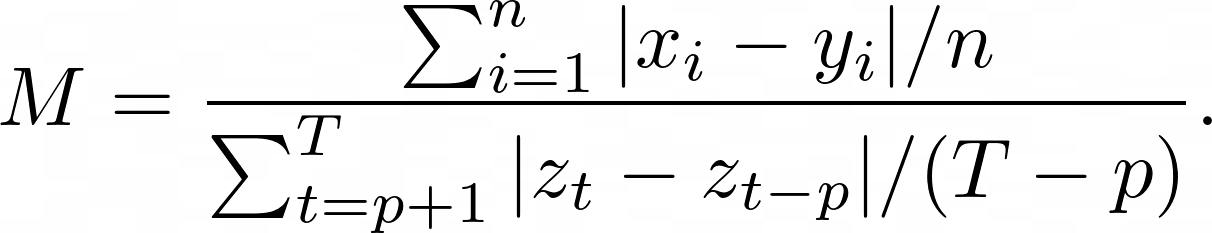
This metric is:
- independent of the scale of the data;
- has predictable behavior when predicted/ground-truth data is near zero;
- symmetric;
- interpretable, as values greater than one indicate that in-sample one-step forecasts from the naïve method perform better than the forecast values under consideration.
How to Use
At minimum, this metric requires predictions, references and training data as inputs.
>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
Inputs
Mandatory inputs:
predictions: numeric array-like of shape (n_samples,) or (n_samples,n_outputs), representing the estimated target values.references: numeric array-like of shape (n_samples,) or (n_samples,n_outputs), representing the ground truth (correct) target values.training: numeric array-like of shape (n_train_samples,) or (n_train_samples,n_outputs), representing the in sample training data.
Optional arguments:
periodicity: the seasonal periodicity of training data. The default is 1.sample_weight: numeric array-like of shape (n_samples,) representing sample weights. The default isNone.multioutput:raw_values,uniform_averageor numeric array-like of shape (n_outputs,), which defines the aggregation of multiple output values. The default value isuniform_average.raw_valuesreturns a full set of errors in case of multioutput input.uniform_averagemeans that the errors of all outputs are averaged with uniform weight.- the array-like value defines weights used to average errors.
Output Values
This metric outputs a dictionary, containing the mean absolute error score, which is of type:
float: if multioutput isuniform_averageor an ndarray of weights, then the weighted average of all output errors is returned.- numeric array-like of shape (
n_outputs,): if multioutput israw_values, then the score is returned for each output separately.
Each MASE float value ranges from 0.0 to 1.0, with the best value being 0.0.
Output Example(s):
{'mase': 0.5}
If multioutput="raw_values":
{'mase': array([0.5, 1. ])}
Values from Popular Papers
Examples
Example with the uniform_average config:
>>> mase_metric = evaluate.load("mase")
>>> predictions = [2.5, 0.0, 2, 8]
>>> references = [3, -0.5, 2, 7]
>>> training = [5, 0.5, 4, 6, 3, 5, 2]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1833...}
Example with multi-dimensional lists, and the raw_values config:
>>> mase_metric = evaluate.load("mase", "multilist")
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]]
>>> references = [[0.1, 2], [-1, 2], [8, -5]]
>>> training = [[0.5, 1], [-1, 1], [7, -6]]
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training)
>>> print(results)
{'mase': 0.1818...}
>>> results = mase_metric.compute(predictions=predictions, references=references, training=training, multioutput='raw_values')
>>> print(results)
{'mase': array([0.1052..., 0.2857...])}
Limitations and Bias
Citation(s)
@article{HYNDMAN2006679,
title = {Another look at measures of forecast accuracy},
journal = {International Journal of Forecasting},
volume = {22},
number = {4},
pages = {679--688},
year = {2006},
issn = {0169-2070},
doi = {https://doi.org/10.1016/j.ijforecast.2006.03.001},
url = {https://www.sciencedirect.com/science/article/pii/S0169207006000239},
author = {Rob J. Hyndman and Anne B. Koehler},
}