|
|
--- |
|
|
title: MSE |
|
|
emoji: 🤗 |
|
|
colorFrom: blue |
|
|
colorTo: red |
|
|
sdk: gradio |
|
|
sdk_version: 3.19.1 |
|
|
app_file: app.py |
|
|
pinned: false |
|
|
tags: |
|
|
- evaluate |
|
|
- metric |
|
|
description: >- |
|
|
Mean Squared Error(MSE) is the average of the square of difference between the predicted |
|
|
and actual values. |
|
|
--- |
|
|
|
|
|
# Metric Card for MSE |
|
|
|
|
|
|
|
|
## Metric Description |
|
|
|
|
|
Mean Squared Error(MSE) represents the average of the squares of errors -- i.e. the average squared difference between the estimated values and the actual values. |
|
|
|
|
|
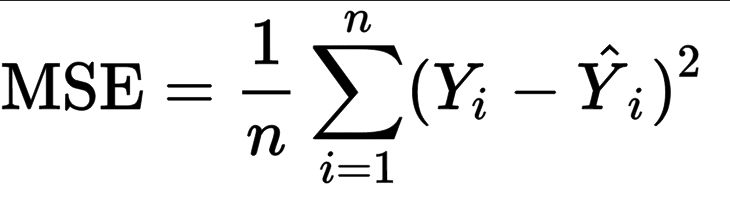 |
|
|
|
|
|
## How to Use |
|
|
|
|
|
At minimum, this metric requires predictions and references as inputs. |
|
|
|
|
|
```python |
|
|
>>> mse_metric = evaluate.load("mse") |
|
|
>>> predictions = [2.5, 0.0, 2, 8] |
|
|
>>> references = [3, -0.5, 2, 7] |
|
|
>>> results = mse_metric.compute(predictions=predictions, references=references) |
|
|
``` |
|
|
|
|
|
### Inputs |
|
|
|
|
|
Mandatory inputs: |
|
|
- `predictions`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the estimated target values. |
|
|
- `references`: numeric array-like of shape (`n_samples,`) or (`n_samples`, `n_outputs`), representing the ground truth (correct) target values. |
|
|
|
|
|
Optional arguments: |
|
|
- `sample_weight`: numeric array-like of shape (`n_samples,`) representing sample weights. The default is `None`. |
|
|
- `multioutput`: `raw_values`, `uniform_average` or numeric array-like of shape (`n_outputs,`), which defines the aggregation of multiple output values. The default value is `uniform_average`. |
|
|
- `raw_values` returns a full set of errors in case of multioutput input. |
|
|
- `uniform_average` means that the errors of all outputs are averaged with uniform weight. |
|
|
- the array-like value defines weights used to average errors. |
|
|
- `squared` (`bool`): If `True` returns MSE value, if `False` returns RMSE (Root Mean Squared Error). The default value is `True`. |
|
|
|
|
|
|
|
|
### Output Values |
|
|
This metric outputs a dictionary, containing the mean squared error score, which is of type: |
|
|
- `float`: if multioutput is `uniform_average` or an ndarray of weights, then the weighted average of all output errors is returned. |
|
|
- numeric array-like of shape (`n_outputs,`): if multioutput is `raw_values`, then the score is returned for each output separately. |
|
|
|
|
|
Each MSE `float` value ranges from `0.0` to `1.0`, with the best value being `0.0`. |
|
|
|
|
|
Output Example(s): |
|
|
```python |
|
|
{'mse': 0.5} |
|
|
``` |
|
|
|
|
|
If `multioutput="raw_values"`: |
|
|
```python |
|
|
{'mse': array([0.41666667, 1. ])} |
|
|
``` |
|
|
|
|
|
#### Values from Popular Papers |
|
|
|
|
|
|
|
|
### Examples |
|
|
|
|
|
Example with the `uniform_average` config: |
|
|
```python |
|
|
>>> mse_metric = evaluate.load("mse") |
|
|
>>> predictions = [2.5, 0.0, 2, 8] |
|
|
>>> references = [3, -0.5, 2, 7] |
|
|
>>> results = mse_metric.compute(predictions=predictions, references=references) |
|
|
>>> print(results) |
|
|
{'mse': 0.375} |
|
|
``` |
|
|
|
|
|
Example with `squared = True`, which returns the RMSE: |
|
|
```python |
|
|
>>> mse_metric = evaluate.load("mse") |
|
|
>>> predictions = [2.5, 0.0, 2, 8] |
|
|
>>> references = [3, -0.5, 2, 7] |
|
|
>>> rmse_result = mse_metric.compute(predictions=predictions, references=references, squared=False) |
|
|
>>> print(rmse_result) |
|
|
{'mse': 0.6123724356957945} |
|
|
``` |
|
|
|
|
|
Example with multi-dimensional lists, and the `raw_values` config: |
|
|
```python |
|
|
>>> mse_metric = evaluate.load("mse", "multilist") |
|
|
>>> predictions = [[0.5, 1], [-1, 1], [7, -6]] |
|
|
>>> references = [[0, 2], [-1, 2], [8, -5]] |
|
|
>>> results = mse_metric.compute(predictions=predictions, references=references, multioutput='raw_values') |
|
|
>>> print(results) |
|
|
{'mse': array([0.41666667, 1. ])} |
|
|
""" |
|
|
``` |
|
|
|
|
|
## Limitations and Bias |
|
|
MSE has the disadvantage of heavily weighting outliers -- given that it squares them, this results in large errors weighing more heavily than small ones. It can be used alongside [MAE](https://huggingface.co/metrics/mae), which is complementary given that it does not square the errors. |
|
|
|
|
|
## Citation(s) |
|
|
```bibtex |
|
|
@article{scikit-learn, |
|
|
title={Scikit-learn: Machine Learning in {P}ython}, |
|
|
author={Pedregosa, F. and Varoquaux, G. and Gramfort, A. and Michel, V. |
|
|
and Thirion, B. and Grisel, O. and Blondel, M. and Prettenhofer, P. |
|
|
and Weiss, R. and Dubourg, V. and Vanderplas, J. and Passos, A. and |
|
|
Cournapeau, D. and Brucher, M. and Perrot, M. and Duchesnay, E.}, |
|
|
journal={Journal of Machine Learning Research}, |
|
|
volume={12}, |
|
|
pages={2825--2830}, |
|
|
year={2011} |
|
|
} |
|
|
``` |
|
|
|
|
|
```bibtex |
|
|
@article{willmott2005advantages, |
|
|
title={Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance}, |
|
|
author={Willmott, Cort J and Matsuura, Kenji}, |
|
|
journal={Climate research}, |
|
|
volume={30}, |
|
|
number={1}, |
|
|
pages={79--82}, |
|
|
year={2005} |
|
|
} |
|
|
``` |
|
|
|
|
|
## Further References |
|
|
- [Mean Squared Error - Wikipedia](https://en.wikipedia.org/wiki/Mean_squared_error) |
|
|
|