title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
GCD && Median || C++ || Python || Greedy | make-k-subarray-sums-equal | 0 | 1 | # Intuition\nFor a simple problem of k==1, we need to make all elements equal to some number. That number will be median which can be understood with the help of number line and some intuition. For even length array n/2 and n/2+1 position both will give out same answer.\nSo now coming to this problem where we slide a k subarray window , observe that we can have equal sum in all subarrays only if the number going out and the number coming in the window are the same.\nFor this we need to get some kind of a pattern like consider the following pattern- x,y,z,x,y,z,x,y,z.... this pattern will be for gcd (n,k)=3 .\nAnd this is possible only if the length of the pattern is gcd of n and k. This is a necessary condition as we need to wrap the last array in a circular fashion.\nSo it all boils down to creating such a pattern where x is median(arr[0],arr[0+g],arr[0+2*g],...) , y is median(arr[1],arr[1+g],arr[1+2*g],...) and so on..\n\n# Approach\ncalculate all arrays for each index of gcd pattern and sort them to get the median and form the new result array. Take absolute difference of them and add it to answer.\n\n# Complexity\n- Time complexity:\nO(nlogn) in worst case\n\n- Space complexity:\nO(n)\n\n# Code\n# C++\n```\nclass Solution {\npublic:\n long long makeSubKSumEqual(vector<int>& arr, int k) {\n long long ans=0;\n long long n=arr.size();\n long long g=gcd(n,k);\n vector <long long> res;\n for (int i=0;i<g;i++){\n vector<long long> lol;\n for (int j=i;j<n;j+=g) lol.push_back(arr[j]);\n sort(lol.begin(),lol.end());\n res.push_back(lol[lol.size()/2]);\n }\n for (int i=0;i<n;i++) ans+=abs(res[i%g]-arr[i]);\n return ans;\n }\n};\n```\n# Python\n```\nclass Solution:\n def makeSubKSumEqual(self, arr: List[int], k: int) -> int:\n n=len(arr)\n g=gcd(n,k)\n ans=0\n nums=[]\n for i in range(g):\n lol=[]\n for j in range(i,n,g):\n lol.append(arr[j])\n lol.sort()\n nums.append(lol[len(lol)//2])\n for i in range(n):\n ans+=abs(nums[i%g]-arr[i])\n return ans\n \n \n\n \n \n\n``` | 3 | You are given a **0-indexed** integer array `arr` and an integer `k`. The array `arr` is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
* Pick any element from `arr` and increase or decrease it by `1`.
Return _the minimum number of operations such that the sum of each **subarray** of length_ `k` _is equal_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** arr = \[1,4,1,3\], k = 2
**Output:** 1
**Explanation:** we can do one operation on index 1 to make its value equal to 3.
The array after the operation is \[1,3,1,3\]
- Subarray starts at index 0 is \[1, 3\], and its sum is 4
- Subarray starts at index 1 is \[3, 1\], and its sum is 4
- Subarray starts at index 2 is \[1, 3\], and its sum is 4
- Subarray starts at index 3 is \[3, 1\], and its sum is 4
**Example 2:**
**Input:** arr = \[2,5,5,7\], k = 3
**Output:** 5
**Explanation:** we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5.
The array after the operations is \[5,5,5,5\]
- Subarray starts at index 0 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 1 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 2 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 3 is \[5, 5, 5\], and its sum is 15
**Constraints:**
* `1 <= k <= arr.length <= 105`
* `1 <= arr[i] <= 109` | null |
Python Union-Find without median or GCD | make-k-subarray-sums-equal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- starting from the question description, you may think of DP first. Good start but arr[i] is up to 10**9 so DP won\'t cut it. This pretty much means we have to find out mathematical/greedy way to solve it\n- then you make observation about the question and start to understand that for subarry `arr[i:i+k] == arr[i+1:i+k+1]` to happen, you need only `arr[i] == arr[i+k]`\n- then you observe that the array is circular meaning you can wrap it around so ultimately, starting from a index `i`, you want to find all the subsequent `i+k, i+k+k, ...` and make sure there are the same value \n- this is basically finding disjoint set in an undirected graph, use unionfind \n- Now this gives half of the solution, the other half, now that I know which items are in the same set, how to calculate their minimum cost\n- For two number a, b, the minimum cost to make them eqaul, regardless of what they end up being, is `abs(a-b)`, so we can sort the array within a set, and work from left and right towards the center\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- union find to find groups \n- sort the groups based on arr value \n- accumulate cost \n\n# Complexity\n- Time complexity: O(a(n) + nlogn), a(n) being the complexity for unionfind\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def makeSubKSumEqual(self, arr: List[int], k: int) -> int:\n\n parents = [i for i in range(len(arr))]\n def find(x): \n if parents[x] != x: \n parents[x] = find(parents[x])\n return parents[x]\n\n for u in range(len(arr)):\n v = (u + k) % len(arr)\n pu, pv = find(u), find(v)\n if pu != pv: \n parents[pv] = pu \n \n groups = [[] for _ in range(len(arr))]\n for u in range(len(arr)): \n pu = find(u)\n groups[pu].append(u) \n\n out = 0 \n for g in groups: \n # here g records indices \n # we need their values mapped back to arr\n g_val = sorted([arr[v] for v in g])\n l, r = 0, len(g_val) - 1\n while r > l:\n if g_val[r] == g_val[l]: \n break \n out += (g_val[r] - g_val[l])\n r -= 1\n l += 1\n\n return out \n``` | 0 | You are given a **0-indexed** integer array `arr` and an integer `k`. The array `arr` is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
* Pick any element from `arr` and increase or decrease it by `1`.
Return _the minimum number of operations such that the sum of each **subarray** of length_ `k` _is equal_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** arr = \[1,4,1,3\], k = 2
**Output:** 1
**Explanation:** we can do one operation on index 1 to make its value equal to 3.
The array after the operation is \[1,3,1,3\]
- Subarray starts at index 0 is \[1, 3\], and its sum is 4
- Subarray starts at index 1 is \[3, 1\], and its sum is 4
- Subarray starts at index 2 is \[1, 3\], and its sum is 4
- Subarray starts at index 3 is \[3, 1\], and its sum is 4
**Example 2:**
**Input:** arr = \[2,5,5,7\], k = 3
**Output:** 5
**Explanation:** we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5.
The array after the operations is \[5,5,5,5\]
- Subarray starts at index 0 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 1 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 2 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 3 is \[5, 5, 5\], and its sum is 15
**Constraints:**
* `1 <= k <= arr.length <= 105`
* `1 <= arr[i] <= 109` | null |
Make all elements k apart equal with explanation in comments — O(N) time and space | make-k-subarray-sums-equal | 0 | 1 | # Approach\nSee comments\n\n# Complexity\nLet `N = len(arr)`\n- Time complexity: `O(N)`\nCalculating the gcd is `O(log(N))`.\nSum of `len(group)` for all groups is `N` since they contain each element once. Calculating median is `O(len(group))`, so the the entire loop is `O(N)`.\n\n- Space complexity: `O(N)`\nBecause we\'re copying each element from `arr` into a new array.\n\n# Code\n```\nimport statistics\n\nclass Solution:\n def makeSubKSumEqual(self, arr: List[int], k: int) -> int:\n # All of the subarray sums are equal if the difference between all consecutive sums is 0\n # This is equivalent to all elements k apart being equal since the elements in between\n # cancel during the subtraction\n # This creates a group of elements that must be equal for each cycle of elements k apart\n # If the number of elements and k are co-prime there is only 1 group\n # Otherwise the number of groups is based on the gcd of k and the length of arr\n common_factor = gcd(k, len(arr))\n groups = [arr[i::common_factor] for i in range(common_factor)]\n\n ops = 0\n for group in groups:\n # The min number of ops to make all elements equal is to turn them all into the median\n med = int(statistics.median(group))\n for num in group:\n ops += abs(num - med)\n\n return ops\n``` | 0 | You are given a **0-indexed** integer array `arr` and an integer `k`. The array `arr` is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
* Pick any element from `arr` and increase or decrease it by `1`.
Return _the minimum number of operations such that the sum of each **subarray** of length_ `k` _is equal_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** arr = \[1,4,1,3\], k = 2
**Output:** 1
**Explanation:** we can do one operation on index 1 to make its value equal to 3.
The array after the operation is \[1,3,1,3\]
- Subarray starts at index 0 is \[1, 3\], and its sum is 4
- Subarray starts at index 1 is \[3, 1\], and its sum is 4
- Subarray starts at index 2 is \[1, 3\], and its sum is 4
- Subarray starts at index 3 is \[3, 1\], and its sum is 4
**Example 2:**
**Input:** arr = \[2,5,5,7\], k = 3
**Output:** 5
**Explanation:** we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5.
The array after the operations is \[5,5,5,5\]
- Subarray starts at index 0 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 1 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 2 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 3 is \[5, 5, 5\], and its sum is 15
**Constraints:**
* `1 <= k <= arr.length <= 105`
* `1 <= arr[i] <= 109` | null |
Simple Solution with Better Explanation | make-k-subarray-sums-equal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We have to restructure the array in such a way that it contains a pattern like, the element going out from the window is similar to the element comming into the window\n- (x, y, z, x, y, z, x, y, z) for window of size 3\n- pattern size must be equal to the gcd(n, k)\n- x_g = median(a[i], a[i + g], a[i + 2g], ....)\n- So the total number of operation for each element will be equal to abs(x_g - arr[i + g])\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: $$O(n)$$ -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: $$O(n)$$\nAdd your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def makeSubKSumEqual(self, arr: List[int], k: int) -> int:\n \n n = len(arr)\n g = gcd(n, k) # pattern_len\n ans = 0\n\n for i in range(g):\n \n # Finding the median of (a[i], a[i + g], a[i + 2g], ....)\n x_g = int(median(arr[i::g]))\n \n # Finding the total number of operation required to transform the current element to median\n ans += sum(abs(x_g - a) for a in arr[i::g])\n \n return ans\n\n```\n\nThanks\nhttps://leetcode.com/problems/make-k-subarray-sums-equal/solutions/3367499/gcd-median-c-python-greedy/ | 0 | You are given a **0-indexed** integer array `arr` and an integer `k`. The array `arr` is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
* Pick any element from `arr` and increase or decrease it by `1`.
Return _the minimum number of operations such that the sum of each **subarray** of length_ `k` _is equal_.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** arr = \[1,4,1,3\], k = 2
**Output:** 1
**Explanation:** we can do one operation on index 1 to make its value equal to 3.
The array after the operation is \[1,3,1,3\]
- Subarray starts at index 0 is \[1, 3\], and its sum is 4
- Subarray starts at index 1 is \[3, 1\], and its sum is 4
- Subarray starts at index 2 is \[1, 3\], and its sum is 4
- Subarray starts at index 3 is \[3, 1\], and its sum is 4
**Example 2:**
**Input:** arr = \[2,5,5,7\], k = 3
**Output:** 5
**Explanation:** we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5.
The array after the operations is \[5,5,5,5\]
- Subarray starts at index 0 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 1 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 2 is \[5, 5, 5\], and its sum is 15
- Subarray starts at index 3 is \[5, 5, 5\], and its sum is 15
**Constraints:**
* `1 <= k <= arr.length <= 105`
* `1 <= arr[i] <= 109` | null |
question on a tricky test case | shortest-cycle-in-a-graph | 0 | 1 | The overall idea is to apply bfs, and viewed a cycle as two different paths starting from start, and merge at a common node. \n\nFor this test case\n[[0,3],[0,5],[3,4],[4,5],[1,9],[1,11],[9,10],[11,10],[2,6],[2,8],[6,7],[8,7],[0,1],[0,2],[1,2]]\n\nCan some one help explain why.. it forms a very special graph if you draw it. I think immediately after we found a cycle, we can return its length already, but it would fail. See code comment below. Thanks!\n```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n graph = defaultdict(list)\n for i, j in edges:\n graph[i].append(j)\n graph[j].append(i)\n \n def dfs(start):\n # return shortest cycle staring at start\n # store (cur, parent)\n dq = deque([(start, -1)])\n dist = [float(\'inf\')] * n\n dist[start] = 0\n cur_min = float(\'inf\')\n while dq:\n cur, par = dq.popleft()\n for nei in graph[cur]:\n if dist[nei] == float(\'inf\'):\n dist[nei] = dist[cur] + 1\n dq.append((nei, cur))\n elif nei != par:\n cur_min = min(cur_min, dist[nei] + dist[cur] + 1)\n # if not comment out below 2 lines and return early, it will fail the list test case, why?? \n # I thought as long as it finds a cycle, it must be the shortest from this node due to bfs property?\n # if cur_min < float(\'inf\'):\n # return cur_min\n return cur_min\n \n ans = min([dfs(i) for i in range(n)])\n return ans if ans < float(\'inf\') else -1\n``` | 1 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
[Python3] BFS from all nodes | shortest-cycle-in-a-graph | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/1dc118daa80cfe1161dcee412e7c3536970ca60d) for solutions of biweely 101. \n\n```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u].append(v)\n graph[v].append(u)\n ans = inf \n for u in range(n): \n dist = {}\n queue = deque([(u, -1, 0)])\n while queue: \n u, p, d = queue.popleft()\n if u in dist: \n ans = min(ans, d + dist[u])\n break \n dist[u] = d \n for v in graph[u]: \n if v != p: queue.append((v, u, d+1))\n return ans if ans < inf else -1 \n``` | 5 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
Python | BFS from All Vertices | O(VE) | shortest-cycle-in-a-graph | 0 | 1 | # Code\n```\nfrom collections import defaultdict\nfrom collections import deque\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n G = defaultdict(list)\n for v, w in edges:\n G[v].append(w)\n G[w].append(v)\n self.res = float(\'inf\')\n def bfs(v):\n level = defaultdict(int)\n visited = set()\n que = deque([(v,0)])\n while que:\n v, d = que.popleft()\n if v in visited: continue\n visited.add(v)\n level[v] = d\n parents = set()\n for w in G[v]:\n if w in visited:\n if level[w] == d-1:\n parents.add(w)\n if len(parents) == 2:\n self.res = min(self.res, 2*d)\n return\n if level[w] == d:\n self.res = min(self.res, 2*d + 1)\n else:\n que.append((w,d+1))\n for v in range(n):\n bfs(v)\n return self.res if self.res != float(\'inf\') else -1\n \n \n \n \n``` | 2 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
[Java/Python 3] BFS within DFS. | shortest-cycle-in-a-graph | 1 | 1 | 1. Construct a graph to access each edge by vertex efficiently;\n2. Traverse all vertices, for each one, `i`, initialize the `dist` all as `MX` value except for `i`, set it as `0`; initialize `parent` all as `-1`;\n3. Use BFS to find the shortest cycle through current vertex `i`: if any offspring of `i` has never been visited, we set its `dist` value as `1 +` its parent\'s `dist`; If the offspring has already been visited and its parent is not the one we just visited, then a cycle found and update the mininum value `shortest`;\n4. Repeat 3 to find the final solution.\n\n```java\n private static final int MX = Integer.MAX_VALUE; \n public int findShortestCycle(int n, int[][] edges) {\n Map<Integer, Set<Integer>> g = new HashMap<>();\n for (int[] e : edges) {\n g.computeIfAbsent(e[0], s -> new HashSet<>()).add(e[1]);\n g.computeIfAbsent(e[1], s -> new HashSet<>()).add(e[0]);\n }\n int shortest = MX;\n for (int i = 0; i < n; ++i) {\n int[] dist = new int[n], parent = new int[n];\n Arrays.fill(dist, MX);\n Arrays.fill(parent, -1);\n Queue<Integer> q = new LinkedList<>();\n q.offer(i);\n dist[i] = 0;\n while (!q.isEmpty()) {\n int node = q.poll();\n for (int kid : g.getOrDefault(node, Collections.emptySet())) {\n if (dist[kid] == MX) {\n dist[kid] = dist[node] + 1;\n parent[kid] = node;\n q.offer(kid);\n }else if (parent[kid] != node && parent[node] != kid) {\n shortest = Math.min(shortest, dist[kid] + dist[node] + 1);\n }\n }\n }\n }\n return shortest == MX ? -1 : shortest;\n }\n```\n```python\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n g = defaultdict(set)\n for u, v in edges:\n g[u].add(v)\n g[v].add(u)\n shortest = inf\n for i in range(n):\n dq, dist, parent = deque([i]), [inf] * n, [-1] * n\n dist[i] = 0\n while dq:\n node = dq.popleft()\n for kid in g.get(node, set()):\n if dist[kid] == inf:\n dist[kid] = dist[node] + 1\n parent[kid] = node\n dq.append(kid)\n elif parent[kid] != node and parent[node] != kid:\n shortest = min(shortest, dist[node] + dist[kid] + 1)\n return -1 if shortest == inf else shortest \n```\n\n**Analysis:**\n\nTime: `O(n * (n + E))`, space: `O(n + E)`, where `E = edges.length.` | 10 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
[Python 3] [NOT CORRECT] | Will update soon | Topological Sort | BFS | shortest-cycle-in-a-graph | 0 | 1 | ```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n n = len(edges)\n g = defaultdict(list)\n indeg = Counter()\n inCycle = set(range(n))\n \n for i, j in edges:\n g[i].append(j)\n g[j].append(i)\n indeg[i] += 1\n indeg[j] += 1\n \n stack = [node for node in range(n) if indeg[node] <= 1]\n \n while stack:\n cur = stack.pop()\n inCycle.discard(cur)\n \n for nei in g[cur]:\n indeg[nei] -= 1\n if indeg[nei] == 1:\n stack.append(nei)\n \n \n def bfs(i):\n q = deque( [(i, 0, -1, {i})] )\n \n while q:\n cur, res, par, seen = q.popleft()\n \n for nei in g[cur]:\n if nei in seen and nei != par:\n return res + 1, seen\n if nei not in seen:\n q.append( (nei, res + 1, cur, seen | {nei}) )\n \n res = inf\n seen = set()\n \n for i in inCycle:\n if i not in seen:\n r, s = bfs(i)\n seen |= s\n res = min(res, r)\n \n return res if inCycle else -1\n``` | 2 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
Simple solution | shortest-cycle-in-a-graph | 0 | 1 | <!-- # Intuition -->\n<!-- - We have -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach\n- Fin -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n \n # Creating Graph\n G = [[] for _ in range(n)]\n for u, v in edges:\n G[u].append(v)\n G[v].append(u)\n\n ans = float(\'inf\')\n\n # Finding the minimum length cycle for each vertex\n for i in range(n):\n \n time = [-1] * n\n time[i] = 0\n \n Q = deque()\n Q.append(i)\n \n while Q:\n\n u = Q.popleft()\n for v in G[u]:\n \n # If we are visiting the node for the first time\n if time[v] == -1:\n time[v] = time[u] + 1\n Q.append(v)\n \n # If the node v is already visited then the len of the cycle will be\n # time_in[v] + time_in[u] + 1\n elif time[v] >= time[u]:\n ans = min(ans, time[v] + time[u] + 1)\n\n return -1 if ans == float(\'inf\') else ans\n``` | 1 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
[Python 3]DFS | shortest-cycle-in-a-graph | 0 | 1 | ```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n \n g = defaultdict(list)\n \n for a, b in edges:\n g[a].append(b)\n g[b].append(a)\n \n self.vis = set()\n \n def dfs(node, par, path):\n # if current path >= current shorteset cycle, then jump out of the recursion\n if len(path) >= self.res:\n return\n # keep track of visited nodes\n self.vis.add(node)\n \n for nei in g[node]:\n if nei == par: continue\n # cycle detected and involving more than three nodes \n\t\t\t\t\n\t\t\t\t# if nei in path and len(path) > 2: \n\t\t\t\tif nei in path:\n self.res = min(self.res, len(path) - path[nei])\n return\n # assign the visited order of vertex in the path\n new_path = path.copy()\n new_path[nei] = len(path)\n dfs(nei, node, new_path)\n \n \n self.res = float(\'inf\')\n for i in range(n):\n if i in self.vis: continue\n dfs(i, -1, {i: 0})\n \n return self.res if self.res < float(\'inf\') else -1\n```\nUpdates on 04/02/2023: Based on @WayWardCC, take out `len(path) > 2` | 1 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
💯✔ DAY 366 | [PYTHON/C++/JAVA] | EXPLAINED | algorithm || 100% BEATS | shortest-cycle-in-a-graph | 1 | 1 | # Please Upvote as it really motivates me\n##### \u2022\tThe problem statement is to find the length of the shortest cycle in an und graph. The approach used in this problem is to perform a breadth-first search (BFS) from each node in the graph and keep track of the distance from the starting node to each visited node. If a visited node is encountered again during the BFS, then a cycle has been found. The length of the cycle is the sum of the distances from the starting node to the two nodes that form the cycle, plus one.\n\n##### \u2022\tHere is the step-by-step algorithm:\n\n##### \u2022\tCreate an adjacency list to represent the graph.\n##### \u2022\tFor each node in the graph, perform a BFS starting from that node.\n##### \u2022\tDuring the BFS, keep track of the distance from the starting node to each visited node.\n##### \u2022\tIf a visited node is encountered again during the BFS, then a cycle has been found.\n##### \u2022\tCalculate the length of the cycle as the sum of the distances from the starting node to the two nodes that form the cycle, plus one.\n##### \u2022\tKeep track of the minimum cycle length found so far.\n##### \u2022\tReturn the minimum cycle length.\n##### \u2022\tThe intuition behind this approach is that by performing a BFS from each node in the graph, we can find all cycles in the graph. By keeping track of the distance from the starting node to each visited node, we can calculate the length of each cycle that is found. By keeping track of the minimum cycle length found so far, we can return the length of the shortest cycle in the graph.\n\n\n\n# Code\n```python []\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n adj = [[] for _ in range(n)]\n for u, v in edges:\n adj[u].append(v)\n adj[v].append(u)\n\n minCycle = float(\'inf\')\n for i in range(n):\n dist = [-1] * n\n q = deque()\n q.append(i)\n dist[i] = 0\n while q:\n u = q.popleft()\n for v in adj[u]:\n if dist[v] == -1:\n dist[v] = dist[u] + 1\n q.append(v)\n elif v != i and dist[v] >= dist[u]:\n minCycle = min(minCycle, dist[u] + dist[v] + 1)\n\n return -1 if minCycle == float(\'inf\') else minCycle\n```\n```c++ []\nclass Solution {\npublic:\n int findShortestCycle(int n, vector<vector<int>>& edges) {\n vector<vector<int>> adj(n);\n for (auto& edge : edges) {\n int u = edge[0];\n int v = edge[1];\n adj[u].push_back(v);\n adj[v].push_back(u);\n }\n\n int minCycle = INT_MAX;\n for (int i = 0; i < n; i++) {\n vector<int> dist(n, -1);\n queue<int> q;\n q.push(i);\n dist[i] = 0;\n while (!q.empty()) {\n int u = q.front();\n q.pop();\n for (int v : adj[u]) {\n if (dist[v] == -1) {\n dist[v] = dist[u] + 1;\n q.push(v);\n } else if (v != i && dist[v] >= dist[u]) {\n minCycle = min(minCycle, dist[u] + dist[v] + 1);\n }\n }\n }\n }\n\n return minCycle == INT_MAX ? -1 : minCycle;\n }\n};\n```\n```java []\nclass Solution {\n public int findShortestCycle(int n, int[][] edges) {\n List<Integer>[] adj = new List[n];\n for (int i = 0; i < n; i++) {\n adj[i] = new ArrayList<>();\n }\n for (int[] edge : edges) {\n int u = edge[0];\n int v = edge[1];\n adj[u].add(v);\n adj[v].add(u);\n }\n\n int minCycle = Integer.MAX_VALUE;\n for (int i = 0; i < n; i++) {\n int[] dist = new int[n];\n Arrays.fill(dist, -1);\n Queue<Integer> queue = new LinkedList<>();\n queue.offer(i);\n dist[i] = 0;\n while (!queue.isEmpty()) {\n int u = queue.poll();\n for (int v : adj[u]) {\n if (dist[v] == -1) {\n dist[v] = dist[u] + 1;\n queue.offer(v);\n } else if (v != i && dist[v] >= dist[u]) {\n minCycle = Math.min(minCycle, dist[u] + dist[v] + 1);\n }\n }\n }\n }\n\n return minCycle == Integer.MAX_VALUE ? -1 : minCycle;\n }\n}\n```\n\n\n\n# Complexity\n\n##### \u2022\tThe time complexity (TC) of this algorithm is O(n+2E), n is the number of nodes in the graph. This is because the algorithm performs a BFS starting from each node in the graph, and each BFS can visit up to n nodes. Therefore, the total number of nodes visited is O(n+2E).\n##### \u2022\tThe space complexity (SC) of this algorithm is O(n+2E), where n is the number of nodes in the graph. This is because the algorithm creates an adjacency list to represent the graph, which can have up to n+2E edges in the worst case. Additionally, the algorithm uses a queue to perform the BFS, which can have up to n nodes in the worst case. Finally, the algorithm uses an array to keep track of the distance from the starting node to each visited node, which can have up to n elements in the worst case. Therefore, the total space complexity is O(n+2E).\n\n##### \u2022\tPlease Upvote\uD83D\uDC4D\uD83D\uDC4D\n##### \u2022\tThanks for visiting my solution.\uD83D\uDE0A Keep Learning\n##### \u2022\tPlease give my solution an upvote! \uD83D\uDC4D\n##### \u2022\tIt\'s a simple way to show your appreciation and\n##### \u2022\tkeep me motivated. Thank you! \uD83D\uDE0A\n\n\n\nhttps://leetcode.com/problems/shortest-cycle-in-a-graph/solutions/3366865/day-366-python-c-java-explained-algorithm-100-beats/?orderBy=hot | 6 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
[Java/Python] | DFS | Runtime - 48ms | shortest-cycle-in-a-graph | 1 | 1 | 1. Idea is to start traverse from each unvisited node and try to find shortest length cycle.\n2. Here we are using map to store Map<Node,[distance,status]> , status means whether this node is part of current dfs call or not.\n2. If we have cycle like this\n\nand we start from node 1 , then it will evaluate cycle of length 4 --> 1,2,3,4,1 and of length 5 --> 1,2,3,4,5,1 , and it returns back to 1 and will go to node 4 for next iteration , here we will go to node-4 only if it is not in map which means it is not previously visited, or visited but has larger distance than current Distance + 1 , or it is forming cycle at node 4. this condition in code represent above line ` if it != par and (it not in hmap or hmap[it][0] > dist + 1 or hmap[it][1] == 1):`\n\n**Java**\n```\nclass Solution {\n private void dfs(int curr, int par, int dist, List<List<Integer>> graph, Map<Integer, int[]> hmap, Set<Integer> vis, int[] ans) {\n if (hmap.containsKey(curr) && hmap.get(curr)[1] == 1) { //checking for cycle and updating answer\n ans[0] = Math.min(ans[0], dist - hmap.get(curr)[0]);\n return;\n }\n vis.add(curr);\n hmap.put(curr, new int[]{dist, 1}); // marking status as 1 , means this node is part of current dfs call\n for (int it : graph.get(curr)) {\n if (it != par && (!hmap.containsKey(it) || hmap.get(it)[0] > dist + 1 || hmap.get(it)[1] == 1)) { //checking whether it is good to visit adjacent node to avoid TLE. \n dfs(it, curr, dist + 1, graph, hmap, vis, ans);\n }\n }\n hmap.put(curr, new int[]{dist, 0}); //marking status as 0 , means dfs call is completed for this node\n }\n public int findShortestCycle(int n, int[][] edges) {\n List<List<Integer>> graph = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n graph.add(new ArrayList<>());\n }\n int[] ans = new int[]{Integer.MAX_VALUE};\n for (int[] edge : edges) {\n int u = edge[0];\n int v = edge[1];\n graph.get(u).add(v);\n graph.get(v).add(u);\n }\n Map<Integer, int[]> hmap = new HashMap<>();\n Set<Integer> vis = new HashSet<>();\n for (int i = 0; i < n; i++) {\n if (!vis.contains(i)) {\n dfs(i, -1, 0, graph, hmap, vis, ans);\n }\n }\n return ans[0] == Integer.MAX_VALUE ? -1 : ans[0];\n }\n}\n```\n\n**Python3**\n\n```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n graph = [[] for i in range(n)]\n ans = math.inf\n for u,v in edges:\n graph[u].append(v)\n graph[v].append(u)\n def dfs(curr,par,dist):\n nonlocal ans\n if curr in hmap and hmap[curr][1] == 1: # checking for cycle and updating answer\n ans = min(ans,dist - hmap[curr][0])\n return\n vis.add(curr)\n hmap[curr] = [dist,1] # marking status as 1 , means this node is part of current dfs call\n for it in graph[curr]:\n if it != par and (it not in hmap or hmap[it][0] > dist + 1 or hmap[it][1] == 1): # checking whether it is good to visit adjacent node to avoid TLE. \n dfs(it,curr,dist+1)\n hmap[curr] = [dist,0] # marking status as 0 , means dfs call is completed for this node\n return\n vis = set()\n for i in range(n):\n if i not in vis:\n hmap = defaultdict(list)\n dfs(i,-1,0) \n if ans == math.inf:\n return -1\n else:\n return ans\n``` | 2 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
Python3 Solution | shortest-cycle-in-a-graph | 0 | 1 | \n```\nclass Solution:\n def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:\n G = [[] for _ in range(n)]\n for i, j in edges:\n G[i].append(j)\n G[j].append(i)\n def root(i):\n dis = [inf] * n\n fa = [-1] * n\n dis[i] = 0\n bfs = [i]\n for i in bfs:\n for j in G[i]:\n if dis[j] == inf:\n dis[j] = 1 + dis[i]\n fa[j] = i\n bfs.append(j)\n elif fa[i] != j and fa[j] != i:\n return dis[i] + dis[j] + 1\n return inf\n res = min(root(i) for i in range(n))\n return res if res < inf else -1\n \n``` | 1 | There is a **bi-directional** graph with `n` vertices, where each vertex is labeled from `0` to `n - 1`. The edges in the graph are represented by a given 2D integer array `edges`, where `edges[i] = [ui, vi]` denotes an edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return _the length of the **shortest** cycle in the graph_. If no cycle exists, return `-1`.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
**Example 1:**
**Input:** n = 7, edges = \[\[0,1\],\[1,2\],\[2,0\],\[3,4\],\[4,5\],\[5,6\],\[6,3\]\]
**Output:** 3
**Explanation:** The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
**Example 2:**
**Input:** n = 4, edges = \[\[0,1\],\[0,2\]\]
**Output:** -1
**Explanation:** There are no cycles in this graph.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= edges.length <= 1000`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no repeated edges. | null |
✅Python || Easy Approach | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n \n ans = 0\n zeroCnt = 0\n oneCnt = 0\n cnt = 0\n \n for i in range(len(s)):\n if s[i] == \'0\':\n if oneCnt == zeroCnt:\n ans = max(ans, oneCnt)\n oneCnt = 0\n zeroCnt += 1\n else:\n oneCnt += 1\n if oneCnt <= zeroCnt:\n ans = max(ans, oneCnt)\n if i + 1 < len(s) and s[i + 1] != s[i]:\n zeroCnt = 0\n \n return 2 * ans\n``` | 3 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
Well Explained Easy Python 3 solution | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | # Intuition\nTo find the longest balanced substring, we need to consider all possible substrings of the given binary string and check if each substring is balanced. To check if a substring is balanced, we need to count the number of zeroes and ones in the substring and check if they are equal. We can do this by maintaining a count of zeroes and ones and comparing them at each step. If the counts are equal, we have found a balanced substring.\n\n# Approach\nWe can use a sliding window approach to iterate over all possible substrings of the binary string s. We can maintain a count of zeroes and ones in the current window and update it as we slide the window. If the count of zeroes and ones is equal, we have found a balanced substring. We can keep track of the maximum length of a balanced substring seen so far and return it at the end.\n\n# Complexity\n- Time complexity:\nThe sliding window approach takes O(n) time to iterate over all possible substrings of the binary string s, where n is the length of the input string. Counting the number of zeroes and ones in each substring takes O(n) time in the worst case, giving us a total time complexity of O(n^2).\n\n- Space complexity:\nThe algorithm uses constant space to maintain the count of zeroes and ones in the current window, giving us a space complexity of O(1).\n\n# Code\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n res=0\n for i in range(1,len(s)):\n if s[i]==\'1\' and s[i-1]==\'0\':\n zero=1\n one=1\n for j in range(i-2,-1,-1):\n if s[j]==\'0\':\n zero+=1\n else:\n break\n for j in range(i+1,len(s)):\n if s[j]==\'1\':\n one+=1\n else:\n break\n res=max(res,min(one,zero)*2)\n return res\n``` | 2 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
Python || Java || C++ || Implemetation | find-the-longest-balanced-substring-of-a-binary-string | 1 | 1 | **Just check or ```01```, ```0011```, ```000111```....**\n```C++ []\nclass Solution {\npublic:\n int findTheLongestBalancedSubstring(string s) {\n int res = 0;\n string temp = "01";\n while(temp.size() <= s.size()){\n if(s.find(temp) != string::npos) \n res = temp.size();\n temp = \'0\' + temp + \'1\';\n }\n return res;\n }\n};\n```\n```python []\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n res, temp = 0, "01"\n while len(temp) <= len(s):\n if temp in s: \n res = len(temp)\n temp = \'0\' + temp + \'1\'\n return res\n```\n```Java []\nclass Solution {\n public int findTheLongestBalancedSubstring(String s) {\n int res = 0;\n String temp = "01";\n while(temp.length() <= s.length()){\n if(s.contains(temp))\n res = temp.length();\n temp = "0" + temp + "1";\n }\n return res;\n }\n}\n```\n | 97 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
simple python3 Solution T.C: O(N) | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | T.C = O(n),where n is the len of the binary string\nS.C = O(1)\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n res = 0\n it = 0\n while it < len(s):\n oCnt ,zCnt = 0 , 0\n while it < len(s) and s[it] == "0" :\n zCnt += 1\n it += 1\n while it < len(s) and s[it] == "1":\n oCnt += 1\n it += 1\n res = max(res,2*min(oCnt,zCnt))\n return res | 13 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
5 Lines of Code Super Logic with Python | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | \n\n# Base Condition is the basic Logic\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n count,temp=0,"01"\n while len(temp)<=len(s):\n if temp in s:count=len(temp)\n temp="0"+temp+"1"\n return count\n```\n# please upvote me it would encourage me alot\n | 2 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
stack ||O(n)||Easy approach | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n stack=[]\n count=0\n maxi=0\n flag=0\n fla=0\n for i in range(len(s)):\n maxi=max(count,maxi)\n if(s[i]=="0"):\n if(fla==1):\n stack=[]\n fla=0\n stack.append("0")\n flag=0\n maxi=max(count,maxi)\n count=0\n elif(s[i]=="1"):\n if(len(stack)!=0):\n stack.pop()\n count+=1\n fla=1\n \n maxi=max(maxi,count)\n return(maxi*2)\n``` | 2 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
Python | Easy Solution✅ | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n maxx, zero_count, one_count = 0, 0, 0 \n for index, digit in enumerate(s):\n if digit == \'0\':\n if one_count:\n maxx = max(maxx,min(zero_count,one_count)* 2) \n zero_count = 0\n one_count = 0\n zero_count +=1\n if zero_count and digit == \'1\':\n one_count += 1\n\n if index == len(s)-1:\n maxx = max(maxx,min(zero_count,one_count)*2)\n return maxx\n``` | 3 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
Soo simple. | find-the-longest-balanced-substring-of-a-binary-string | 1 | 1 | # Approach\nSimply traverse the string and count for the number of zeros and ones.\nAfter counting ones, reset the counters to 0.\nIf both (no. of zeros & no. of ones) are greater than zero, that means they are present.\nSome x no. of zeros followed by some y no. of ones.\nThis is to tackle cases like (11111)\nThen just take the minimum of x and y (because of cases like 0011111 or 0000111) so to take sufficient no. of either 0s or 1s to complete the pattern.\nMultiply it with 2 (because of both ones and zeros).\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int findTheLongestBalancedSubstring(string str) {\n int res = 0, i =0, n = str.size();\n while(i<n)\n {\n int zero = 0, one =0;\n if(str[i]==\'0\')\n {\n while(i< n && str[i] == \'0\')\n {\n i++;\n zero++;\n \n }\n }\n if(str[i] == \'1\')\n {\n while(i<n && str[i]==\'1\')\n {\n i++;\n one++;\n \n }\n }\n if(one>0 && zero>0){\n res = max(res, 2*(min(one,zero)));\n }\n \n }\n return res;\n }\n};\n```\n```Java []\npublic class Solution {\n public int findTheLongestBalancedSubstring(String str) {\n int res = 0, i = 0, n = str.length();\n while (i < n) {\n int zero = 0, one = 0;\n if (str.charAt(i) == \'0\') {\n while (i < n && str.charAt(i) == \'0\') {\n i++;\n zero++;\n }\n }\n if (str.charAt(i) == \'1\') {\n while (i < n && str.charAt(i) == \'1\') {\n i++;\n one++;\n }\n }\n if (one > 0 && zero > 0) {\n res = Math.max(res, 2 * (Math.min(one, zero)));\n }\n }\n return res;\n }\n}\n```\n```Python3 []\nclass Solution:\n def findTheLongestBalancedSubstring(self, str: str) -> int:\n res = 0\n i, n = 0, len(str)\n while i < n:\n zero, one = 0, 0\n if str[i] == \'0\':\n while i < n and str[i] == \'0\':\n i += 1\n zero += 1\n if str[i] == \'1\':\n while i < n and str[i] == \'1\':\n i += 1\n one += 1\n if one > 0 and zero > 0:\n res = max(res, 2 * min(one, zero))\n return res\n``` | 4 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
Python 3 || 5 lines, iteration, w/example || T/M: 100% / 100% | find-the-longest-balanced-substring-of-a-binary-string | 0 | 1 | ```\nclass Solution:\n def findTheLongestBalancedSubstring(self, s: str) -> int:\n\n string = \'\' # Example: "01000111101"\n\n for i in range(25): # i string s \n # \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\n string = \'0\'+ string + \'1\' # 0 "" "01000111101"\n if string not in s: return 2*i # 1 "01" "|01|00|01|111|01|"\n # 2 "0011" "010|0011|1101"\n return 50 # 3 "000111" "01|000111|101" \n \n # return 2*3 = 6\n```\n[https://leetcode.com/problems/find-the-longest-balanced-substring-of-a-binary-string/submissions/926762677/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 6 | You are given a binary string `s` consisting only of zeroes and ones.
A substring of `s` is considered balanced if **all zeroes are before ones** and the number of zeroes is equal to the number of ones inside the substring. Notice that the empty substring is considered a balanced substring.
Return _the length of the longest balanced substring of_ `s`.
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "01000111 "
**Output:** 6
**Explanation:** The longest balanced substring is "000111 ", which has length 6.
**Example 2:**
**Input:** s = "00111 "
**Output:** 4
**Explanation:** The longest balanced substring is "0011 ", which has length 4.
**Example 3:**
**Input:** s = "111 "
**Output:** 0
**Explanation:** There is no balanced substring except the empty substring, so the answer is 0.
**Constraints:**
* `1 <= s.length <= 50`
* `'0' <= s[i] <= '1'` | null |
✅Python || Easy Approach || Dictionary | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n \n from collections import defaultdict\n \n a = defaultdict(int)\n \n for w in nums:\n a[w] += 1\n \n ans = []\n for i in range(max(a.values())):\n res = []\n for k, v in a.items():\n if v != 0:\n a[k] -= 1\n res.append(k)\n ans.append(res)\n \n return ans\n``` | 4 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
O(N) Solution | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | # Summary\nIm sure there is a far better way to solve but I wasn\'t able to see any O(N) solutions available so decided to post. \n\n# Approach\nStep 1: Create a hashmap (mp1) to that maps elements of nums to their frequency and keep track of the maximum frequency (maxfreq). \n\nStep 2: Create another hashmap (mp2) that uses mp1 to map the frequency to a list of elements in nums\n\nStep 3: Since the maximum frequency is the amount of lists in the result array, fill it up with empty arrays\n\nStep 4: Append each list of \'num\' with the same frequency to the ith location in the result array. Trick behind what makes this part O(N) is that you will only iterate through a total of sum(frequency) times, i.e. the length of nums. To reiterate, the sum of all "freq" in mp2 will only be the length of nums ==> O(N)Time. \n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\n#O(N)Time O(infinity)Space\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n maxfreq, res, mp1, mp2 = -1, [], {}, {}\n for num in nums:\n mp1[num] = mp1.get(num, 0) +1\n maxfreq = max(mp1[num], maxfreq)\n for num in mp1:\n freq = mp1[num]\n mp2[freq] = mp2.get(freq, [])\n mp2[freq].append(num)\n for i in range(maxfreq):\n res.append([])\n for freq in mp2: #Step4 Explains why this is still O(N)\n for i in range(freq): \n res[i] += mp2[freq]\n return res\n\n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
[Python3] Hash Map/Counter - O(n * max(frequency) time, O(1) space | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | # Intuition\nWe create the 2D array map with the number of subarrays equal to max frequency that a number in `nums` can occur, representing the minimum rows that we have to have since we must have unique numbers in each row. For example, if the array is `[1,3,4,1,2,3,1]`, we must have at least 3 rows to accommodate all the 1s.\n\nHence, I chose to use `Counter` to solve this problem.\n\n# Approach\nI find the frequencies of each number in `nums`, using `Counter`. Then, I initialize the `result` to be the 2D array with `max(list(counter.values())` rows.\n\nThen, for each number, I spread it over each row to fulfill the unique numbers condition, and the decrementing its appearance along the way.\n\nThen, I return the `result` array.\n\n# Complexity\n- Time complexity: `O(n*max(frequencies))`\n- Space complexity: `O(n)` for the `counter` dictionary \n\n# Code\n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n counter = collections.Counter(nums)\n result = [[0] for _ in range(max(list(counter.values())))]\n\n for i in range(len(nums)):\n j = 0\n while counter[nums[i]] > 0:\n result[j].append(nums[i])\n j += 1\n counter[nums[i]] -= 1\n \n return [r[1:] for r in result]\n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
python3 Solution | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | \n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n ans=[]\n count=Counter(nums)\n while count:\n val=[]\n drop=[]\n for k,v in count.items():\n val.append(k)\n count[k]-=1\n if count[k]==0:\n drop.append(k)\n\n for k in drop:\n count.pop(k)\n\n ans.append(val)\n\n return ans \n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
Using Dictionaries Logic | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | \n# 1.Main Logic is Finding max Frequency\n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n dic=Counter(nums)\n list2=[]\n for i in range(max(dic.values())):\n list1=[]\n for key,freq in dic.items():\n if freq!=0:\n dic[key]-=1\n list1.append(key)\n list2.append(list1)\n return list2\n \n```\n# please upvote me it would encourage me alot\n | 3 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
Simple solution | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | # Code\n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n output = []\n\n while len(nums):\n output.append(list(set(nums)))\n for i in output[-1]:\n nums.pop(nums.index(i))\n \n return output\n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
Python3 | One-liner | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | ```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n return [[x for x in arr if x] for arr in zip_longest(*[(n,)*f for n, f in Counter(nums).items()], fillvalue=0)]\n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
Python3 Set | convert-an-array-into-a-2d-array-with-conditions | 0 | 1 | \n\n# Complexity \n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMatrix(self, nums: List[int]) -> List[List[int]]:\n res = []\n while len(nums) > 0:\n a = set(nums)\n res.append(list(a))\n for i in a:\n nums.remove(i)\n return res\n``` | 1 | You are given an integer array `nums`. You need to create a 2D array from `nums` satisfying the following conditions:
* The 2D array should contain **only** the elements of the array `nums`.
* Each row in the 2D array contains **distinct** integers.
* The number of rows in the 2D array should be **minimal**.
Return _the resulting array_. If there are multiple answers, return any of them.
**Note** that the 2D array can have a different number of elements on each row.
**Example 1:**
**Input:** nums = \[1,3,4,1,2,3,1\]
**Output:** \[\[1,3,4,2\],\[1,3\],\[1\]\]
**Explanation:** We can create a 2D array that contains the following rows:
- 1,3,4,2
- 1,3
- 1
All elements of nums were used, and each row of the 2D array contains distinct integers, so it is a valid answer.
It can be shown that we cannot have less than 3 rows in a valid array.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** \[\[4,3,2,1\]\]
**Explanation:** All elements of the array are distinct, so we can keep all of them in the first row of the 2D array.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= nums.length` | null |
✅Python || Easy Approach || Diff | mice-and-cheese | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def miceAndCheese(self, reward1: List[int], reward2: List[int], k: int) -> int:\n \n ans = 0\n diff = {}\n \n reward = [0] * len(reward1)\n \n for i in range(len(reward1)):\n diff[i] = reward1[i] - reward2[i]\n \n sortDiff = sorted(diff.items(), key = lambda x:x[1], reverse = True)\n \n for i in range(k):\n index = sortDiff[i][0]\n ans += reward1[index]\n \n for i in range(len(reward1) - k):\n index = sortDiff[i + k][0]\n ans += reward2[index]\n \n return ans \n``` | 2 | There are two mice and `n` different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index `i` (**0-indexed**) is:
* `reward1[i]` if the first mouse eats it.
* `reward2[i]` if the second mouse eats it.
You are given a positive integer array `reward1`, a positive integer array `reward2`, and a non-negative integer `k`.
Return _**the maximum** points the mice can achieve if the first mouse eats exactly_ `k` _types of cheese._
**Example 1:**
**Input:** reward1 = \[1,1,3,4\], reward2 = \[4,4,1,1\], k = 2
**Output:** 15
**Explanation:** In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese.
The total points are 4 + 4 + 3 + 4 = 15.
It can be proven that 15 is the maximum total points that the mice can achieve.
**Example 2:**
**Input:** reward1 = \[1,1\], reward2 = \[1,1\], k = 2
**Output:** 2
**Explanation:** In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese.
The total points are 1 + 1 = 2.
It can be proven that 2 is the maximum total points that the mice can achieve.
**Constraints:**
* `1 <= n == reward1.length == reward2.length <= 105`
* `1 <= reward1[i], reward2[i] <= 1000`
* `0 <= k <= n` | null |
Python max heap O(nlogn) | mice-and-cheese | 0 | 1 | ```\nclass Solution:\n def miceAndCheese(self, reward1: List[int], reward2: List[int], k: int) -> int:\n \n #build max heap, based on the extra we can get if we \n #choose reward1\n heap = []\n for i in range(0,len(reward1)):\n heap.append( [ -reward1[i]+reward2[i] ,i ])\n heapq.heapify(heap)\n\n #eat the ones where we get the most extra and store those\n #mark those visited\n visited ,res = {},0\n while(k):\n idx = heapq.heappop(heap)[1]\n res += reward1[idx]\n visited[idx] = 1\n k-=1\n\n # eat the remaining from the reward2 \n for i in range(0,len(reward2)):\n if(visited.get(i) != None ):\n continue\n res += reward2[i]\n return res \n``` | 1 | There are two mice and `n` different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index `i` (**0-indexed**) is:
* `reward1[i]` if the first mouse eats it.
* `reward2[i]` if the second mouse eats it.
You are given a positive integer array `reward1`, a positive integer array `reward2`, and a non-negative integer `k`.
Return _**the maximum** points the mice can achieve if the first mouse eats exactly_ `k` _types of cheese._
**Example 1:**
**Input:** reward1 = \[1,1,3,4\], reward2 = \[4,4,1,1\], k = 2
**Output:** 15
**Explanation:** In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese.
The total points are 4 + 4 + 3 + 4 = 15.
It can be proven that 15 is the maximum total points that the mice can achieve.
**Example 2:**
**Input:** reward1 = \[1,1\], reward2 = \[1,1\], k = 2
**Output:** 2
**Explanation:** In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese.
The total points are 1 + 1 = 2.
It can be proven that 2 is the maximum total points that the mice can achieve.
**Constraints:**
* `1 <= n == reward1.length == reward2.length <= 105`
* `1 <= reward1[i], reward2[i] <= 1000`
* `0 <= k <= n` | null |
Python || sort || O(n log n) | mice-and-cheese | 0 | 1 | 1. The first mice will eat exactly `k` types, and the second mice will eat others.\n2. Sort `reward1 - reward2` in descending order. Let the first mice eat those types with highest difference.\n```\nclass Solution:\n def miceAndCheese(self, reward1: List[int], reward2: List[int], k: int) -> int:\n diff = [[reward1[i] - reward2[i], i] for i in range(len(reward1))]\n diff.sort(reverse=True)\n ans = 0\n for i in range(k):\n ans += reward1[diff[i][1]]\n for i in range(k, len(reward1)):\n ans += reward2[diff[i][1]]\n return ans | 3 | There are two mice and `n` different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index `i` (**0-indexed**) is:
* `reward1[i]` if the first mouse eats it.
* `reward2[i]` if the second mouse eats it.
You are given a positive integer array `reward1`, a positive integer array `reward2`, and a non-negative integer `k`.
Return _**the maximum** points the mice can achieve if the first mouse eats exactly_ `k` _types of cheese._
**Example 1:**
**Input:** reward1 = \[1,1,3,4\], reward2 = \[4,4,1,1\], k = 2
**Output:** 15
**Explanation:** In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese.
The total points are 4 + 4 + 3 + 4 = 15.
It can be proven that 15 is the maximum total points that the mice can achieve.
**Example 2:**
**Input:** reward1 = \[1,1\], reward2 = \[1,1\], k = 2
**Output:** 2
**Explanation:** In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese.
The total points are 1 + 1 = 2.
It can be proven that 2 is the maximum total points that the mice can achieve.
**Constraints:**
* `1 <= n == reward1.length == reward2.length <= 105`
* `1 <= reward1[i], reward2[i] <= 1000`
* `0 <= k <= n` | null |
Streaming Solution Explained | No Sorting | O(N log k) | mice-and-cheese | 0 | 1 | # Intuition\nThe most important thing that matters is the advantage $$r_1[i]-r_2[i]$$ (the difference of rewards for mouse 1 and 2 respectively). We want to give mouse 1 the cheese whenever it has the greatest advantage and mouse 2 the cheese whenever it has greatest advantage. \n\n# Sorting Solution\n\nOne way to do this would be by sorting and giving mouse 1 the $$k$$ cheeses where it has the greatest advantage and mouse 2 the remaining cheese:\n```\nclass Solution:\n def miceAndCheese(self, r1: List[int], r2: List[int], k: int) -> int:\n adv = [(x-y,y) for x,y in zip(r1,r2)]\n adv.sort(reverse=True)\n r1 = sum(d+y for d,y in adv[:k])\n r2 = sum(y for _,y in adv[k:])\n return r1 + r2\n```\n\n##### Complexity of Sorting Solution\n- Time complexity: $$O(N \\log N)$$ \n- Space complexity: $$O(N)$$\n\n##### Drawbacks of Sorting Solution\nWe have to see all the data at least once before we can do anything. Additionally, the complexity is independent of $$k$$. As we shall see, we can improve both space and time complexity if we allow ourselves to take into account $$k$$ by using heaps.\n\n# Heap Solution (No Sorting)\n\nMouse 1 only needs the $$k$$ cheeses where it has the largest advantage. Let\'s exploit this. \n\nLet\'s build a min-heap where items are sorted by mouse 1\'s advantage $$r_1[i]-r_2[i]$$. We\'ll build this one reward pair at a time as we scan through `zip(r1,r2)`. We\'ll also attach the reward value to each item so we can tally up the points later.\n\nWe can limit heap size to $$k$$ and eject the smallest element if we need to make space for an incoming item. Every time we eject an item, that means mouse 2 will be getting that cheese, so we increment the tally by $$r_2[i]$$. \n\nAt the end, the heap contains precisely the $$k$$ cheeses where mouse 1 has the greatest advantage. We add mouse 1\'s rewards for those cheese to the final tally and we\'re done.\n\n```python\nfrom heapq import heappush as push, heappop as pop\nclass Solution:\n def miceAndCheese(self, r1: List[int], r2: List[int], k: int) -> int:\n heap, ans = [], 0\n for x,y in zip(r1, r2):\n push(heap, (x-y,y))\n if len(heap) > k:\n ans += pop(heap)[1]\n return ans + sum(d+y for d,y in heap)\n```\n##### Complexity of Heap Solution\nThe heap never gets larger than size $$k$$. Thus,\n\n- Time complexity: $$O(N \\log k)$$ \n- Space complexity: $$O(k)$$\n\nSince $$k\\leq n$$ this is better than the sorting solution when accounting for $$k$$. \n\n##### This is a streaming solution\n\nThis means that this will still solve the problem even if we are told the reward pairs one-by-one without knowledge of how many more rewards remain. In other words, this will work even if the reward pairs are generated on the fly. | 1 | There are two mice and `n` different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index `i` (**0-indexed**) is:
* `reward1[i]` if the first mouse eats it.
* `reward2[i]` if the second mouse eats it.
You are given a positive integer array `reward1`, a positive integer array `reward2`, and a non-negative integer `k`.
Return _**the maximum** points the mice can achieve if the first mouse eats exactly_ `k` _types of cheese._
**Example 1:**
**Input:** reward1 = \[1,1,3,4\], reward2 = \[4,4,1,1\], k = 2
**Output:** 15
**Explanation:** In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese.
The total points are 4 + 4 + 3 + 4 = 15.
It can be proven that 15 is the maximum total points that the mice can achieve.
**Example 2:**
**Input:** reward1 = \[1,1\], reward2 = \[1,1\], k = 2
**Output:** 2
**Explanation:** In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese.
The total points are 1 + 1 = 2.
It can be proven that 2 is the maximum total points that the mice can achieve.
**Constraints:**
* `1 <= n == reward1.length == reward2.length <= 105`
* `1 <= reward1[i], reward2[i] <= 1000`
* `0 <= k <= n` | null |
Python Heap | In-depth Explanation | mice-and-cheese | 0 | 1 | \n\nWe want to maximize the total reward by selecting \'k\' values from reward1 and everything remaining from reward2. To achieve this, we need to carefully choose values from reward1, as selecting an index in reward1 will make that index unavailable in reward2.\n\nTo determine the best selection, we first calculate the differences between the corresponding elements of reward2 and reward1. Then, we identify the \'k\' largest positive differences, which indicate the most optimal selections from reward1.\n\nConsider the example with reward1 = [4, 2, 1] and reward2 = [2, 5, 10]. The differences are calculated as follows: 2 - 4 = -2, 5 - 2 = 3, 10 - 1 = 9, resulting in the array [(-2, 0), (3, 1), (9, 2)]. Notice that we keep track of the index by storing tuples (value, index). In this case, if k = 2, we should select the values 4 and 2 from reward1, as they correspond to the largest positive differences. Next, we can take the remaining available value from reward2, which is 10.\n\nBy following this approach, we can achieve the maximum total reward, which is the sum of these values: 4 + 2 + 10 = 16.\n\n# Code\n```\nclass Solution:\n def miceAndCheese(self, reward1: List[int], reward2: List[int], k: int) -> int:\n output = 0\n n = len(reward1)\n heap = []\n for i in range(n):\n heap.append((reward2[i] - reward1[i], i))\n \n heapq.heapify(heap)\n visited = set()\n while k:\n k -= 1\n _, idx = heapq.heappop(heap)\n visited.add(idx)\n output += reward1[idx]\n \n # If there is anything left that has not been taken, we take it from reward2.\n for idx, val in enumerate(reward2):\n if idx in visited:\n continue\n output += val\n \n return output\n``` | 11 | There are two mice and `n` different types of cheese, each type of cheese should be eaten by exactly one mouse.
A point of the cheese with index `i` (**0-indexed**) is:
* `reward1[i]` if the first mouse eats it.
* `reward2[i]` if the second mouse eats it.
You are given a positive integer array `reward1`, a positive integer array `reward2`, and a non-negative integer `k`.
Return _**the maximum** points the mice can achieve if the first mouse eats exactly_ `k` _types of cheese._
**Example 1:**
**Input:** reward1 = \[1,1,3,4\], reward2 = \[4,4,1,1\], k = 2
**Output:** 15
**Explanation:** In this example, the first mouse eats the 2nd (0-indexed) and the 3rd types of cheese, and the second mouse eats the 0th and the 1st types of cheese.
The total points are 4 + 4 + 3 + 4 = 15.
It can be proven that 15 is the maximum total points that the mice can achieve.
**Example 2:**
**Input:** reward1 = \[1,1\], reward2 = \[1,1\], k = 2
**Output:** 2
**Explanation:** In this example, the first mouse eats the 0th (0-indexed) and 1st types of cheese, and the second mouse does not eat any cheese.
The total points are 1 + 1 = 2.
It can be proven that 2 is the maximum total points that the mice can achieve.
**Constraints:**
* `1 <= n == reward1.length == reward2.length <= 105`
* `1 <= reward1[i], reward2[i] <= 1000`
* `0 <= k <= n` | null |
Python3 | BFS w/o a queue beats 100% time and memory (Index math explained) | minimum-reverse-operations | 0 | 1 | # Index math\n\nA length-$N$ list has $N-k+1$ length-$k$ slices, one starting at each $i \\in [0, N-k]$.\n\nSuppose the set/on/one bit is currenlty at position $p \\in [0, N)$. Reverseing one of these slices, `bits[i:i+k]`, has no effect. if $p < i$ or $p \\geq i+k$; we should only consider reversing slices `bits[i:i+k]` s.t. $i \\leq p < i+k$. This gives us limits on $i$, the starting position of the slice: $p-k < i \\leftrightarrow p-k+1 \\leq i$ and $i \\leq p$, so $i \\in [p-k+1, p]$. Furthermore, we should make sure $0 \\leq i \\leq N-k$, so `i_lo = max(0, p-k+1)` and `i_hi = min(N-k, p)`.\n\nReversing `bits[i:i+k]` where the set bit is at position $p \\in [i, i+k]$ simply moves the set bit to posiiton $i+k-1-(p-i) = 2i+k-1-p$. Rather than iterating through the appropritate $i$s and calculating $2i+k-1-p$ for each $i$, we can just iterate throught `range(p_lo, p_hi+1, 2)` where `p_lo = 2*i_lo + k - 1 - p` and `p_hi = 2*i_hi + k - 1 - p`.\n\nSo given the position of the set bit, $p$, we can calculate the possible next positions. We do a BFS to identify all the possible positions in operations order, each time recording how many operations were necessary to reach said position.\n\n# Complexity\n- Time complexity: I think it\'s $O(N \\lg N)$.\n- Space complexity: $O(N)$\n\n# Code\n\nThis is an improvement on [awice\'s SortedList.irange soltuion](https://leetcode.com/problems/minimum-reverse-operations/solutions/3368819/python3-bfs-sortedlist-keep-track-of-remaining-nodes/).\n\n```\nIMPOSSIBLE = -1\nEVEN, ODD = 0, 1\nclass Solution:\n def minReverseOperations(self, N: int, p: int, banned: List[int], k: int) -> List[int]:\n if k == 1 or len(banned) == N-1:\n numOps = [IMPOSSIBLE] * N\n numOps[p] = 0\n return numOps\n \n numOps = [IMPOSSIBLE] * N\n numOps[p] = 0\n \n remaining = [[], []]\n banned = set(banned)\n for pos in range(0, N, 2):\n if pos != p and pos not in banned:\n remaining[EVEN].append(pos)\n pos += 1\n if pos != p and pos not in banned:\n remaining[ODD].append(pos)\n \n # BFS\n numOp = 1\n p0s = [p]\n while p0s:\n p1s = []\n for p0 in p0s:\n i_lo = max(0, p0+1-k)\n i_hi = min(N-k, p0)\n p1_lo = p1_hi = k-1-p0\n p1_lo += 2*i_lo\n p1_hi += 2*i_hi\n parity = p1_lo & 0b1\n rem = remaining[parity]\n lo = bisect_left(rem, p1_lo)\n hi = bisect_right(rem, p1_hi)\n\n # Alt 1\n for j in reversed(range(lo, hi)):\n p1 = rem.pop(j)\n numOps[p1] = numOp\n p1s.append(p1)\n\n # # Alt 2\n # for _ in range(hi - lo):\n # p1 = rem.pop(lo)\n # numOps[p1] = numOp\n # p1s.append(p1)\n \n p0s = p1s\n numOp += 1\n \n return numOps\n``` | 1 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
[Python3] BFS + SortedList, keep track of remaining nodes | minimum-reverse-operations | 0 | 1 | Evidently, we should start our investigation with the question: if there is a `1` at position `node`, what neighboring nodes `nei` could it reach in one move?\n\nLet `i_left = max(0, node - K + 1)`, `i_right = min(node + K - 1, n - 1) - (K - 1)` be the starting positions of the subarray to be reversed. Then, after reversing subarray `[i, i+K-1]` (for `i` in `[i_left, i_right]`), `node` goes to `nei = i + (i+K-1) - node`. In the end, `nei` is chosen from some interval `[lo, lo+2, ..., hi]`.\n\nArmed with this information, let\'s do a standard BFS. However, this is too slow as we are considering the same neighbors a lot.\n\nTo remedy this, let\'s keep track of which nodes haven\'t been reached by our BFS yet. We split these by parity into `remaining[0]` and `remaining[1]`. When we have some interval `[lo, lo+2, ..., hi]` of potential neigbhors, we can query the intersection (of this interval with unvisited nodes) quickly as we only consider each unvisited neighbor once.\n\n**Complexity**: Time $$O(N^2)$$, Space: $$O(N)$$. (`SortedList` dominates the complexity, and for general purposes it can be thought of as contributing $$\\approx O(N \\log N)$$, but the implementation is actually $$O(N^{\\frac{4}{3}})$$, assuming the load constant is chosen as $$m = N^{\\frac{1}{3}}$$.)\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def minReverseOperations(self, n, p, banned_vals, K):\n remaining = [SortedList(), SortedList()]\n banned = set(banned_vals)\n for u in range(n):\n if u != p and u not in banned:\n remaining[u & 1].add(u)\n\n queue = [p]\n dist = [-1] * n\n dist[p] = 0\n for node in queue:\n lo = max(node - K + 1, 0)\n lo = 2 * lo + K - 1 - node\n hi = min(node + K - 1, n - 1) - (K - 1)\n hi = 2 * hi + K - 1 - node\n\n for nei in list(remaining[lo % 2].irange(lo, hi)):\n queue.append(nei)\n dist[nei] = dist[node] + 1\n remaining[lo % 2].remove(nei)\n \n return dist\n``` | 35 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Python3 Solution | minimum-reverse-operations | 0 | 1 | # Intuition\nThis problem was hard to understand, and it has an $$O(K * N)$$ issue that needs to be addressed.\n\n# Approach\nThe basic algorithm is a breadth-first search of positions, where depth is a reversal operation.\n* Avoid set lookups by marking `banned` positions with a `-2` reduces the constant coefficient speed-up. This is not enough to avoid a TLE, however.\n* Every visited position has $$O(k)$$ potential target positions. On visiting a new position, the multiplicative cost can be avoided by updating `nextNode2s`, which originally points forward 2, to point beyond all target positions considered for that position.\n\n# Complexity\n- Time complexity: $$O(n + k)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:\n out = [-1] * n\n # To speed up iterations, mark banned positions differently; remember to\n # convert them to -1 at the end.\n for node in banned:\n out[node] = -2\n # Perform reversals in level-based breadth-first order.\n nodes = [p]\n depth = 0\n out[p] = depth\n step = k - 1\n \n # TLEs occur when n is large, k is large, and not to many are banned,\n # so that very O(N) points have O(N) possible post-reverse positions.\n # These O(N) post-reverse positions are 2 apart, but each only needs\n # to be visited once. We will nextNode2s dynamically to save work.\n nextNode2s = [i + 2 for i in range(n)] # might be out of range\n\n while nodes:\n depth += 1\n newNodes = []\n for node1 in nodes:\n # The post-reverse positions are every other node between\n # loNode2 and hiNode2, inclusive.\n loReverseStart = max(node1 - step, 0)\n hiReverseStart = min(node1, n - k) # Inclusive\n loNode2 = 2 * loReverseStart + k - 1 - node1\n hiNode2 = 2 * hiReverseStart + k - 1 - node1 # Inclusive\n # We will exclude the entire range from future iterations\n # by setting nextNode2s[node2] to hiNode2 + 2 for every\n # visited node2.\n postHiNode2 = hiNode2 + 2\n node2 = loNode2\n while node2 <= hiNode2:\n nextNode2 = nextNode2s[node2]\n nextNode2s[node2] = postHiNode2\n if node2 >= 0 and node2 < n and out[node2] == -1:\n newNodes.append(node2)\n out[node2] = depth\n node2 = nextNode2\n nodes = newNodes\n \n # Mark all banned positions as -1 (see above).\n for i in range(n):\n if out[i] == -2:\n out[i] = -1\n return out\n \n``` | 11 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Python || BFS, binary search || O(n log n) | minimum-reverse-operations | 0 | 1 | 1. Suppose we stand at `i1`, the widest range we can reach by one reverse is `i1-k+1`, `i1-k+3`, ..., `i1+k-3`, `i1+k-1`. The indices in the sequence are all even or all odd. \nBut we should be cautious when `i1 < k` or `i1 > n-k`. The starting index of the leftmost subarray containing `i1` is `max(0, i1-k+1)`, while the one of the rightmost subarray containing `i1` is `min(i1, n-k)`.\nFor a subarray containing `i1` with size `k`, say `[start:start+k]`, after reverse, `1` moved from `i1` to `i2 = 2*start-k-1-i1`.\nAssume the leftmost and rightmost indices we can reach are `le` and `ri`, respectively.\n2. During BFS, we would save indices not touched yet in `remain`. Because the possible indices in one step are all even/odd, we save even/odd indices seperately.\n3. To avoid TLE, use binary search to find the `intersection` of remaining indices(`remain[0]/remain[1]`) and `[le, ri]`.\n4. For each index `i2` in `intersection`, update `ans[i2]` and remove `i2` from `remain[0]/remain[1]`.\n```\nfrom collections import deque\nfrom bisect import bisect_left, bisect_right\n \nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:\n ans = [-1]*n\n ans[p] = 0\n banned = set(banned)\n remain_e = [i for i in range(n) if i not in banned and i != p and i&1 == 0]\n remain_o = [i for i in range(n) if i not in banned and i != p and i&1 == 1]\n remain = [remain_e, remain_o]\n \n cur = deque([p])\n step = 1\n while cur:\n for _ in range(len(cur)):\n i1 = cur.popleft()\n lm, rm = max(0, i1-k+1), min(i1, n-k)\n le = lm+lm+k-1-i1\n ri = rm+rm+k-1-i1\n i_l, i_r = bisect_left(remain[le&1], le), bisect_right(remain[le&1], ri)\n intersection = remain[le&1][i_l:i_r]\n for i2 in intersection:\n ans[i2] = step\n cur.append(i2)\n remain[le&1].pop(i_l)\n step += 1\n return ans | 2 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
[Python] Simple approach with SortedList + comments | minimum-reverse-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is formulated as a graph exploration problem, and the answer can be found by using BFS\n\nThe first complex issue is finding out to which other nodes I can go from a given node and a given k. Let\'s ignore cases too close to the margins for now. Notice that the furthest node we can go right is current_index + k - 1. This is done by using a subarray that starts at current_index and ends at current_index + k - 1. If we slide this subarray by one, making it start at current_index -1, and end at current_index + k - 2, the new position of the 1 is current_index + k - 3. So we slide to the left by 2 positions.\ncurrent_index + k - 1 => current_index + k - 3 => current_index + k - 5 etc.\n\nThis means that we maintain the parity of the index for a given iteration, if the first position that is attainable is even, then all subsequent attainable positions are even as well, same goes for odd. \n\nThe second complex issue is how to make the algorithm run fast enough.\nWe need to store the non visited and visitable indexes, these can be stored in a SortedList. This will make iterating over the attainable values easy and fast. Once we visited a node we can remove it from the list.\n\nThis is enough to have an AS.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nClassic BFS with a few twists:\n\n```\nstart at p\nwhile nodes to visit:\n visit node\n compute min attainable index, max attainable index and parity\n iterate over given indexes in the correct parity list:\n update res value\n add index to next node to visit\n remove nodes from non visited nodes\n```\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n log n), we visit each node once\neach visit is O(log n), computing lo and high is O(1), but finding the correct indices from the sorted list is O(log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\nwe simple store all the indexes we have not visited\n\n# Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:\n \n res = [-1 for _ in range(n)]\n res[p] = 0\n banned = set(banned)\n non_visited = [SortedList(), SortedList()]\n\n for i in range(n):\n if i not in banned and i != p:\n non_visited[i % 2].add(i)\n\n d = 0\n cand = set([p])\n\n while len(cand) > 0:\n\n next = set()\n d += 1\n \n for c in cand:\n #this is the position where the subarray can start, furthest down is c-k+1, unless it\'s smaller than 0 (subarray cannot start at index under 0)\n lo = max(c-k+1, 0)\n #once we have the lowest position the subarray can start at, easy to find new position of the 1, it\'s simply st_position + end_position - current_position\n low_po = lo + (lo +k-1) - c\n\n #this is the highest position the subarray can start at, it\'s c+k-1 unless it\'s bigger than n-1 (size of the array)\n hi = min(n-1, c+k-1)\n #once we have the lowest position the subarray can start at, easy to find new position of the 1, it\'s simply st_position + end_position - current_position\n hi_pos = (hi-k+1) + hi -c \n\n par = (c - k + 1) % 2\n\n #we store the values we want to iterate over in a separate list in memory\n #because in the loop we remove the values from the SortedList, and removing values from a list you are iterating over is bad\n iterations = list(non_visited[par].irange(low_po, hi_pos+1))\n for e in iterations:\n res[e] = d\n next.add(e)\n non_visited[par].remove(e)\n\n cand = next\n\n return res\n\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Minimum Reverse Operations to Move a Value in an Array | minimum-reverse-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to find the minimum number of reverse operations needed to move a value (represented as 1) to each position in an array, given certain positions are banned. The reverse operation can only be performed on a subarray of size k and the value should never go to any of the positions in banned.\n\nOur first thought is to use a breadth-first search (BFS) approach. We can start from the initial position of the value and try to move it to each position in the array using reverse operations. We need to keep track of the minimum number of reverse operations needed to move the value to each position.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use a breadth-first search (BFS) approach to solve this problem. We start from the initial position of the value and try to move it to each position in the array using reverse operations. We keep track of the minimum number of reverse operations needed to move the value to each position in a list out.\n\nFor each visited position, there are potentially O(k) target positions that can be reached through reverse operations. To avoid the multiplicative cost of iterating over all these potential positions, we update the nextNode2s array. This array initially points forward by 2, but it is updated dynamically to point beyond all the target positions considered for each visited position. This optimization helps improve the efficiency of the algorithm and avoids unnecessary computations.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is O(n), where n is the length of the array. This is because we visit each position in the array once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this approach is also O(n). This is because we need to store the minimum number of reverse operations needed to move the value to each position in a list, and we also need to store the next node for each position in an array.\n# Code\n```\nfrom collections import deque\nclass Solution:\n def minReverseOperations(self, n, p, banned, k):\n out = [-1]*n\n for node in banned:\n out[node] = -2\n nodes = [p]\n depth = 0\n out[p] = depth\n step = k - 1\n nextNode2s = [i+2 for i in range(n)]\n while nodes:\n depth += 1\n newNodes = []\n for node1 in nodes:\n loReverseStart = max(node1 - step, 0)\n hiReverseStart = min(node1, n - k)\n loNode2 = 2 * loReverseStart + k - 1 - node1\n hiNode2 = 2 * hiReverseStart + k - 1 - node1\n postHiNode2 = hiNode2 + 2\n node2 = loNode2\n while node2 <= hiNode2:\n nextNode2 = nextNode2s[node2]\n nextNode2s[node2] = postHiNode2\n if node2 >= 0 and node2 < n and out[node2] == -1:\n newNodes.append(node2)\n out[node2] = depth\n node2 = nextNode2\n nodes = newNodes\n for i in range(n):\n if out[i] == -2:\n out[i] = -1\n return out\n\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Doubly linked list, python | minimum-reverse-operations | 0 | 1 | \n# Code\n```\nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:\n right = [(i+2) % (n+4) for i in range(n+4)]\n left = [(i-2) for i in range(n+4)]\n distance = [-1] * n\n q = collections.deque(maxlen=n)\n\n def first(i):\n j = right[i]\n if left[j] == i:\n return i\n else:\n right[i] = first(j)\n return right[i]\n\n def drop(i):\n left[right[i]], right[left[i]] = left[i], right[i]\n\n def set_distance(i, d):\n distance[i] = d\n q.append(i)\n drop(i)\n\n for i in banned:\n drop(i)\n\n set_distance(p, 0)\n while q:\n i0 = q.popleft()\n s0 = abs(i0 - (k - 1))\n i = first(s0)\n if i < n:\n d = distance[i0] + 1\n s1 = min(i0+k-1, 2*n-k-1-i0)\n while i <= s1:\n set_distance(i, d)\n i = right[i]\n\n\n return distance\n\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
[Python] Beats 100% time with 14 lines, simple BFS idea | minimum-reverse-operations | 0 | 1 | # Intuition\n\nSome observations about the problem:\n\n* Each subarray reverse operation is just moving the position p of the single 1 in the array.\n* Therefore the current "state" after any number of reverses can be summarized by the current position `pos` of the 1, and the number of `moves` taken to get there.\n* The potential reversal operations at any state are limited by just two factors:\n * The banned positions: the 1 isn\'t allowed to be moved there by a subarray reversal\n * The boundaries of the array: the subarray being reversed should contain the 1 (otherwise there\'s no point), but it can\'t extend beyond the overall array.\n\n\n# Approach\n\nThe idea is to take a dynamic programming approach, sort of a breadth-first search from the starting point `pos=p` with `moves=0`.\n\nAt each step, we form an array `added` of the new positions that can be reached with one more reverse operation (i.e. `moves+1` steps).\n\nWhen the newly-reachable array `added` is empty, the search ends. We never add anything twice to this array.\n\nThe key observation for efficiency is that the **newly-reachable positions consist of all even or odd indexes within a sub-array**. That means that by just computing the left and right *boundaries* (called `lbound` and `rbound`) of what is newly-reachable, we have all the information we need. This saves a nested loop and makes the code much faster!\n\n# Complexity\n- Time complexity: $$O(n^2/k)$$. The bottleneck is the list comprehension to compute the next `added` set, which iterates over (half of) the integers in the range `[lbound..rbound]`. This outer while loop is then repeated $$O(n/k)$$ times in order to potentially reach from one side of the array to the other.\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned: List[int], k: int) -> List[int]:\n banda = [False] * n\n for i in banned: banda[i] = True\n ops = [-1] * n\n moves = 0\n added = [p]\n while added:\n lbound, rbound = n, -1\n for pos in added:\n ops[pos] = moves\n lbound = min(lbound, abs(pos - k + 1))\n rbound = max(rbound, n - 1 - abs(n - k - pos))\n added = [i for i in range(lbound, rbound+1, 2) if (ops[i] == -1 and not banda[i])]\n moves += 1\n return ops\n\n\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
[Python3] Without The Use Of Imports | minimum-reverse-operations | 0 | 1 | # Intuition\nI didn\'t really like how every other solution I saw involved some third party packages. I wanted to write a piece of code that works with python3 out of the box, no other packages or libraries.\n\n# Approach\nThe big piece I was missing was two fold:\n\n1. BFS alone is not fast enough. You need to track all elements that have not been queued yet. Since your step-width for every $$i$$ is $$2$$, it means it\'s most efficient to keep track of two lists with even and odd elements respectiveley.\n2. You shouldn\'t iterate other positions. Instead, you should iterate `lower` which is the lower bound of your reversing operation. Every reverse will flip the elements between `lower` and upper. \n\nI believe that most answers here get to the first realization so I want to expand on the second one in my own words. It\'s easy to see that the upper bound will be `lower + k - 1` for any lower and k. We now use the formular that translates a pre-flip position `i` into a post-flip `j` with `j = upper - (i - lower)` to be\n`j = 2 * lower + k - 1 - i`.\nThat was the last puzzle piece for me. With the observations above, we now need to go through all j\'s that have not previously been observed and are in the boundaries (inclusive)\n`[2 * lower_min + k - 1 - i, 2 * lower_max + k - 1 - i]`\nwhere\n`lower_min = max(0, i - k + 1)`\nand\n`lower_max = min(n - k, i)`\n\nTranslated back to plain english: Take all possible inversions, iterate over the lower index of that inversion, translate that iteration into an iteration over the new index j, and use the other observations to speed up that process by only looking at each j once.\n\n# Complexity\n- Time complexity:\nIt seems that all answers for this are $$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\ndef bisect_left(lst, num, lo=0, hi=None):\n if hi is None: hi = len(lst)\n while lo < hi:\n mid = (lo + hi) // 2\n if lst[mid] < num: lo = mid + 1\n else: hi = mid\n return lo\n\nclass Solution:\n def minReverseOperations(self, n: int, p: int, banned_: List[int], k: int) -> List[int]:\n banned = set(banned_)\n lists = [[], []]\n pos = [(0 if i == p else -1) for i in range(n)]\n for i in range(n):\n if i in banned or i == p:\n continue\n lists[i % 2].append(i)\n queue = [ p ]\n\n for i in queue:\n l = lists[(k - 1 - i) % 2]\n lower_min = max(0, i - k + 1)\n lower_max = min(n - k, i)\n j_lower_min = 2 * lower_min + k - 1 - i\n j_lower_max = 2 * lower_max + k - 1 - i\n j = bisect_left(l, j_lower_min)\n while j < len(l) and l[j] <= j_lower_max:\n queue.append(l[j])\n pos[l[j]] = pos[i] + 1\n del l[j]\n\n return pos\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Python (Simple BFS) | minimum-reverse-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minReverseOperations(self, n, p, banned, k):\n from sortedcontainers import SortedList\n\n remaining = [SortedList(),SortedList()]\n banned = set(banned)\n\n for i in range(n):\n if i!=p and i not in banned:\n remaining[i&1].add(i)\n\n stack = [p]\n dist = [-1]*n\n dist[p] = 0\n\n while stack:\n node = stack.pop(0)\n lo = max(node-k+1,0)\n lo = 2*lo + k - 1 - node\n hi = min(node+k-1,n-1) - (k-1)\n hi = 2*hi + k - 1 - node\n for neighbor in list(remaining[lo%2].irange(lo,hi)):\n stack.append(neighbor)\n dist[neighbor] = dist[node] + 1\n remaining[lo%2].remove(neighbor)\n\n return dist\n\n\n\n\n\n\n\n\n \n\n\n\n\n \n \n\n \n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Python3 - Optimized BFS Algorithm | minimum-reverse-operations | 0 | 1 | \n# Code\n```\nfrom bisect import bisect_left, bisect_right\nfrom collections import deque\n\nclass Solution:\n def minReverseOperations(self, n, p, banned_vals, K):\n remaining = [[], []]\n banned = set(banned_vals)\n for u in range(n):\n if u != p and u not in banned:\n remaining[u & 1].append(u)\n\n for i in range(2):\n remaining[i].sort()\n\n queue = deque([p])\n dist = [-1] * n\n dist[p] = 0\n while queue:\n node = queue.popleft()\n lo = max(node - K + 1, 0)\n lo = 2 * lo + K - 1 - node\n hi = min(node + K - 1, n - 1) - (K - 1)\n hi = 2 * hi + K - 1 - node\n\n idx_lo = bisect_left(remaining[lo % 2], lo)\n idx_hi = bisect_right(remaining[lo % 2], hi)\n\n for idx in range(idx_lo, idx_hi):\n nei = remaining[lo % 2][idx]\n queue.append(nei)\n dist[nei] = dist[node] + 1\n\n del remaining[lo % 2][idx_lo:idx_hi]\n \n return dist\n``` | 0 | You are given an integer `n` and an integer `p` in the range `[0, n - 1]`. Representing a **0-indexed** array `arr` of length `n` where all positions are set to `0`'s, except position `p` which is set to `1`.
You are also given an integer array `banned` containing some positions from the array. For the **i****th** position in `banned`, `arr[banned[i]] = 0`, and `banned[i] != p`.
You can perform **multiple** operations on `arr`. In an operation, you can choose a **subarray** with size `k` and **reverse** the subarray. However, the `1` in `arr` should never go to any of the positions in `banned`. In other words, after each operation `arr[banned[i]]` **remains** `0`.
_Return an array_ `ans` _where_ _for each_ `i` _from_ `[0, n - 1]`, `ans[i]` _is the **minimum** number of reverse operations needed to bring the_ `1` _to position_ `i` _in arr_, _or_ `-1` _if it is impossible_.
* A **subarray** is a contiguous **non-empty** sequence of elements within an array.
* The values of `ans[i]` are independent for all `i`'s.
* The **reverse** of an array is an array containing the values in **reverse order**.
**Example 1:**
**Input:** n = 4, p = 0, banned = \[1,2\], k = 4
**Output:** \[0,-1,-1,1\]
**Explanation:** In this case `k = 4` so there is only one possible reverse operation we can perform, which is reversing the whole array. Initially, 1 is placed at position 0 so the amount of operations we need for position 0 is `0`. We can never place a 1 on the banned positions, so the answer for positions 1 and 2 is `-1`. Finally, with one reverse operation we can bring the 1 to index 3, so the answer for position 3 is `1`.
**Example 2:**
**Input:** n = 5, p = 0, banned = \[2,4\], k = 3
**Output:** \[0,-1,-1,-1,-1\]
**Explanation:** In this case the 1 is initially at position 0, so the answer for that position is `0`. We can perform reverse operations of size 3. The 1 is currently located at position 0, so we need to reverse the subarray `[0, 2]` for it to leave that position, but reversing that subarray makes position 2 have a 1, which shouldn't happen. So, we can't move the 1 from position 0, making the result for all the other positions `-1`.
**Example 3:**
**Input:** n = 4, p = 2, banned = \[0,1,3\], k = 1
**Output:** \[-1,-1,0,-1\]
**Explanation:** In this case we can only perform reverse operations of size 1. So the 1 never changes its position.
**Constraints:**
* `1 <= n <= 105`
* `0 <= p <= n - 1`
* `0 <= banned.length <= n - 1`
* `0 <= banned[i] <= n - 1`
* `1 <= k <= n`
* `banned[i] != p`
* all values in `banned` are **unique** | null |
Python Elegant & Short | RegEx | number-of-valid-clock-times | 0 | 1 | ```\nimport re\n\n\nclass Solution:\n """\n Time: O(1)\n Memory: O(1)\n """\n\n def countTime(self, time: str) -> int:\n pattern = time.replace(\'?\', \'.\')\n return sum(\n re.fullmatch(pattern, f\'{hour:02}:{minute:02}\') is not None\n for hour in range(24)\n for minute in range(60)\n )\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n\n | 34 | You are given a string of length `5` called `time`, representing the current time on a digital clock in the format `"hh:mm "`. The **earliest** possible time is `"00:00 "` and the **latest** possible time is `"23:59 "`.
In the string `time`, the digits represented by the `?` symbol are **unknown**, and must be **replaced** with a digit from `0` to `9`.
Return _an integer_ `answer`_, the number of valid clock times that can be created by replacing every_ `?` _with a digit from_ `0` _to_ `9`.
**Example 1:**
**Input:** time = "?5:00 "
**Output:** 2
**Explanation:** We can replace the ? with either a 0 or 1, producing "05:00 " or "15:00 ". Note that we cannot replace it with a 2, since the time "25:00 " is invalid. In total, we have two choices.
**Example 2:**
**Input:** time = "0?:0? "
**Output:** 100
**Explanation:** Each ? can be replaced by any digit from 0 to 9, so we have 100 total choices.
**Example 3:**
**Input:** time = "??:?? "
**Output:** 1440
**Explanation:** There are 24 possible choices for the hours, and 60 possible choices for the minutes. In total, we have 24 \* 60 = 1440 choices.
**Constraints:**
* `time` is a valid string of length `5` in the format `"hh:mm "`.
* `"00 " <= hh <= "23 "`
* `"00 " <= mm <= "59 "`
* Some of the digits might be replaced with `'?'` and need to be replaced with digits from `0` to `9`. | null |
Structural pattern matching | number-of-valid-clock-times | 0 | 1 | Minutes are easy. For hours, we there could be be 1, 2, 3, 4, 10 or 24 combinations.\n\n**Python 3**\nJust for fun - using structural pattern matching.\n```python\nclass Solution:\n def countTime(self, t: str) -> int:\n mm = (6 if t[3] == \'?\' else 1) * (10 if t[4] == \'?\' else 1)\n match [t[0], t[1]]:\n case (\'?\', \'?\'):\n return mm * 24\n case (\'?\', (\'0\' | \'1\' | \'2\' | \'3\')):\n return mm * 3\n case (\'?\', _):\n return mm * 2\n case ((\'0\' | \'1\'), \'?\'):\n return mm * 10\n case (_, \'?\'):\n return mm * 4\n return mm\n```\n\n**C++**\n```cpp\nint countTime(string t) {\n int res = 1;\n if (t[0] == \'?\')\n res = t[1] == \'?\' ? 24 : t[1] < \'4\' ? 3 : 2;\n else if (t[1] == \'?\')\n res = t[0] < \'2\' ? 10 : 4; \n return res * (t[3] == \'?\' ? 6 : 1) * (t[4] == \'?\' ? 10 : 1);\n}\n``` | 25 | You are given a string of length `5` called `time`, representing the current time on a digital clock in the format `"hh:mm "`. The **earliest** possible time is `"00:00 "` and the **latest** possible time is `"23:59 "`.
In the string `time`, the digits represented by the `?` symbol are **unknown**, and must be **replaced** with a digit from `0` to `9`.
Return _an integer_ `answer`_, the number of valid clock times that can be created by replacing every_ `?` _with a digit from_ `0` _to_ `9`.
**Example 1:**
**Input:** time = "?5:00 "
**Output:** 2
**Explanation:** We can replace the ? with either a 0 or 1, producing "05:00 " or "15:00 ". Note that we cannot replace it with a 2, since the time "25:00 " is invalid. In total, we have two choices.
**Example 2:**
**Input:** time = "0?:0? "
**Output:** 100
**Explanation:** Each ? can be replaced by any digit from 0 to 9, so we have 100 total choices.
**Example 3:**
**Input:** time = "??:?? "
**Output:** 1440
**Explanation:** There are 24 possible choices for the hours, and 60 possible choices for the minutes. In total, we have 24 \* 60 = 1440 choices.
**Constraints:**
* `time` is a valid string of length `5` in the format `"hh:mm "`.
* `"00 " <= hh <= "23 "`
* `"00 " <= mm <= "59 "`
* Some of the digits might be replaced with `'?'` and need to be replaced with digits from `0` to `9`. | null |
beats 97.60% | number-of-valid-clock-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countTime(self, t: str) -> int:\n mm = (6 if t[3] == \'?\' else 1) * (10 if t[4] == \'?\' else 1)\n match [t[0],t[1]]:\n case (\'?\',\'?\'):\n return mm * 24\n case (\'?\', (\'0\'|\'1\'|\'2\'|\'3\')):\n return mm * 3\n case (\'?\',_):\n return mm * 2\n case ((\'0\'|\'1\', \'?\')):\n return mm * 10\n case (_, \'?\'):\n return mm * 4\n return mm\n``` | 1 | You are given a string of length `5` called `time`, representing the current time on a digital clock in the format `"hh:mm "`. The **earliest** possible time is `"00:00 "` and the **latest** possible time is `"23:59 "`.
In the string `time`, the digits represented by the `?` symbol are **unknown**, and must be **replaced** with a digit from `0` to `9`.
Return _an integer_ `answer`_, the number of valid clock times that can be created by replacing every_ `?` _with a digit from_ `0` _to_ `9`.
**Example 1:**
**Input:** time = "?5:00 "
**Output:** 2
**Explanation:** We can replace the ? with either a 0 or 1, producing "05:00 " or "15:00 ". Note that we cannot replace it with a 2, since the time "25:00 " is invalid. In total, we have two choices.
**Example 2:**
**Input:** time = "0?:0? "
**Output:** 100
**Explanation:** Each ? can be replaced by any digit from 0 to 9, so we have 100 total choices.
**Example 3:**
**Input:** time = "??:?? "
**Output:** 1440
**Explanation:** There are 24 possible choices for the hours, and 60 possible choices for the minutes. In total, we have 24 \* 60 = 1440 choices.
**Constraints:**
* `time` is a valid string of length `5` in the format `"hh:mm "`.
* `"00 " <= hh <= "23 "`
* `"00 " <= mm <= "59 "`
* Some of the digits might be replaced with `'?'` and need to be replaced with digits from `0` to `9`. | null |
Understandable If-Else python solution | number-of-valid-clock-times | 0 | 1 | ```\nclass Solution:\n def countTime(self, time: str) -> int:\n res = 1\n\t\t# split hour and minute digits\n h1, h2, _ , m1, m2 = time\n \n if h1 == "?" and h2 == "?":\n res*=24\n elif h1 == "?":\n if int(h2) >=4:\n res*=2\n else:\n res*=3\n \n elif h2 == "?":\n if int(h1) <= 1:\n res*=10\n elif h1 == "2":\n res*=4\n \n if m1 == "?" and m2 == "?":\n res*=60\n elif m1 == "?":\n res*=6\n elif m2 == "?":\n res*=10\n \n return res\n \n``` | 10 | You are given a string of length `5` called `time`, representing the current time on a digital clock in the format `"hh:mm "`. The **earliest** possible time is `"00:00 "` and the **latest** possible time is `"23:59 "`.
In the string `time`, the digits represented by the `?` symbol are **unknown**, and must be **replaced** with a digit from `0` to `9`.
Return _an integer_ `answer`_, the number of valid clock times that can be created by replacing every_ `?` _with a digit from_ `0` _to_ `9`.
**Example 1:**
**Input:** time = "?5:00 "
**Output:** 2
**Explanation:** We can replace the ? with either a 0 or 1, producing "05:00 " or "15:00 ". Note that we cannot replace it with a 2, since the time "25:00 " is invalid. In total, we have two choices.
**Example 2:**
**Input:** time = "0?:0? "
**Output:** 100
**Explanation:** Each ? can be replaced by any digit from 0 to 9, so we have 100 total choices.
**Example 3:**
**Input:** time = "??:?? "
**Output:** 1440
**Explanation:** There are 24 possible choices for the hours, and 60 possible choices for the minutes. In total, we have 24 \* 60 = 1440 choices.
**Constraints:**
* `time` is a valid string of length `5` in the format `"hh:mm "`.
* `"00 " <= hh <= "23 "`
* `"00 " <= mm <= "59 "`
* Some of the digits might be replaced with `'?'` and need to be replaced with digits from `0` to `9`. | null |
Python | Prefix Product | range-product-queries-of-powers | 0 | 1 | ```\nclass Solution:\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n MOD = (10**9)+7\n binary = bin(n)[2:]\n powers = []\n result = []\n for index, val in enumerate(binary[::-1]):\n if val == "1":\n powers.append(2**index)\n \n for index in range(1, len(powers)):\n powers[index] = powers[index] * powers[index - 1] \n \n for l,r in queries:\n if l == 0:\n result.append(powers[r]%MOD)\n else:\n result.append((powers[r]//powers[l-1])%MOD)\n \n return result\n \n``` | 8 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
Compute set bit power's | range-product-queries-of-powers | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nAs we\'ll know, we can any represent in it\'s power of 2\'s. \nHow to find which power of 2\'s is exactly required?\nChange the number to binary and the only the set-bit position will contribute to power. \nSo, Precompute all the required power. Here In number `n` check if i\'th bit is set or not and if it\'s then store it.\nNow, The max number of set bit can go up to 32(int) so run `l` to `r` every time to find the multiplication of the required range. \n\n* We can also process each query in log(n) time by calculating modulus inverse using fermat\'s little theorem(because the gcd(M,e) will always be 1 as it\'s case for fermat\'s) or Extended Euclidean algortihm.\n\n# Complexity\n- Time complexity: $$O(q * 31)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(31)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> productQueries(int n, vector<vector<int>>& queries) {\n const int M = 1e9+7, m = __builtin_popcount(n);\n vector<int> power(m),ans;\n int p = 0;\n for(int i=0,j=0; i<31; ++i){\n if(i == 0) p = 1;\n else p = ((p%M) * 2) % M;\n if((n>>i)&1) power[j++] = p;\n }\n for(auto q: queries){\n int x = 1;\n for(int i=q[0]; i<=q[1]; ++i) x = ((x%M) * 1ll * (power[i]%M)) % M;\n ans.push_back(x);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n M,power,p,ans = 10**9 + 7,[],0,[]\n for i in range(31):\n p = (p * 2) % M if i else 1\n if (n>>i)&1: power.append(p)\n\n for q in queries:\n x = 1\n for i in range(q[0], q[1] + 1): x = (x * power[i]) % M\n ans.append(x)\n\n return ans\n``` | 1 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
Python Elegant & Short | Prefix Sum | Binary Power | range-product-queries-of-powers | 0 | 1 | ```\nfrom itertools import accumulate\nfrom typing import List, Generator\n\n\nclass Solution:\n """\n Time: O(log(n) + m)\n Memory: O(log(n))\n\n where m - length of queries\n """\n\n MAX_POWER = 32\n MOD = 10 ** 9 + 7\n\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n cum_powers = list(accumulate(self._to_powers(n), initial=1))\n return [pow(2, cum_powers[r + 1] - cum_powers[l], self.MOD) for l, r in queries]\n\n @classmethod\n def _to_powers(cls, num: int) -> Generator:\n return (p for p in range(cls.MAX_POWER) if num & (1 << p) != 0)\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n | 11 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
✔ Python3 Solution | Prefix Sum | 2 Line Solution | range-product-queries-of-powers | 0 | 1 | ```\nclass Solution:\n def productQueries(self, n, Q):\n A = list(accumulate([i for i in range(31) if n & (1 << i)])) + [0]\n return [pow(2, A[r] - A[l - 1], 10 ** 9 + 7) for l, r in Q]\n``` | 2 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
fast python solution | range-product-queries-of-powers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:log(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:log(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n a=bin(n)[2:]\n # print(a)\n a=a[::-1]\n arr=[1]\n p=1\n for i in range(len(a)):\n if(a[i]=="1"):\n p*=2**i\n arr.append(p)\n ans=[]\n print(arr)\n for q in queries:\n p=arr[q[1]+1]//arr[q[0]]\n ans.append(p%(10**9+7))\n return ans\n``` | 5 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
Product prefix O(1) query / Product Segment tree O(logn) query | range-product-queries-of-powers | 0 | 1 | # Intuition\nThe problem is composed of two main parts:\n1. **Q1** determine which are the minimum powers of 2 which can be used to represents the given number N\n2. **Q2** compose an array created in increasing order of those powers\n3. **Q3** find product of values in the given query range relative to the previously found array(step 2.)\n\n#### Q1\nQ1 basically requires the binary representation of the given number N. Each bit set to one represents a positional power of two in the required array. Both solutions to Q1 have same time complexity. \nOne can do:\n- **Fenwick tree Bit trick** to get the largest power of two of given number(solution used in the code). This allows to get the largest bit set to one, whose smaller bits are all set to 0. This amount is then subtracted from the original value, and the rest is used to repeat the trick until 0 is attained.\n- **Simple solution**(n>>1 & 1) to see whether the least significant bit is set to one and then set n = n>>1 until n == 0, in order to extract all bits that are set to one. \nIf n>>1 & 1 is 1, then the corresponding power of two is 2**(number of done shifts up to now) otherwise just increase the counter without storing the current power of two.\n\n#### Q2\nThe array is naturally sorted in increasing order, as the first value that is found is the smallest bit set to 1 (e.g. the maximum smallest power of two that composes the given number).\n\n#### Q3\nTo answer range queries, a **product prefix array** or a **segment tree data** structure can be used. The former is more space optimized with no downside for this problem.\nThe **product prefix array** is defined with its elements $j$ as the product $\\prod_{i=0}^j nums[i]$ of all elements in the powers of 2 array up to the j-th.\n#### Product Prefix array\nTo obtain the answer with a **product prefix array** for a query $$[start, end]$$, one would simple get the value at a given $ans=prod\\_prefix[end]/prod\\_prefix[start-1]$, to obtain an equivalent prefix query to one of prefix sum arrays.\n\n#### Product Segment tree\nI have adapted a general purpose segment tree to fit the use case of computing the product of all numbers in any of the queries(generally they are seen for sum, min, max queries but are easily extensible).\nThe concept is the same of the prefix sum:\nwe want to compute a quantity over a given range, without having to recompute it for ranges that include each other.\n\nEach leaf node is an element of the powers array.\nThe non-leaf nodes represent the product of the numbers in a power of two range.\nThe only trick to note here is that to compute queries, one has to move to the neighboring node which represents a sub-range that is within the range query, if the current node represents a range larger than that required by the query. \nTo achieve this, the code of its **mul** function, in the provided data structure considers the case in which:\n- the sub-range that is considered by any given node exceeds with its left boundary the query range lower limit, hence we move to the node to its right\n- the sub-range that is considered by any given node exceeds with its right boundary the upper limit of the given query range, hence we move to the node to its left. \n\n# Product prefix Code (Optimal solution)\n###\nN is the number of found powers\n- Time complexity:\nO(N) to find powers\nO(1) to answer queries \n\n- Space complexity:\nO(N)\n```\ndef productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n MOD = 10**9 + 7\n k = n\n powers = []\n while k >0:\n val = k & (-k)\n powers.append(val)\n k -= val\n prodprefix = [1 for _ in range(len(powers))]\n prodprefix[0] = powers[0]\n for i in range(1,len(powers)):\n prodprefix[i] *= prodprefix[i-1]*powers[i]\n ans = []\n for start, end in queries:\n res = prodprefix[end]\n if start-1 >= 0:\n divider = prodprefix[start-1] \n res //= divider\n ans.append(res%MOD)\n \n return ans\n```\n# Product Segment Tree Code\nN is the number of found powers\n- Time complexity:\nO(N) to find powers\nO(log(N)) to answer queries \n\n- Space complexity:\nO(2*N)\n```python\nclass SegmentTree:\n\tdef __init__(self, array):\n\t\tN = len(array)\n\t\tk = 1\n\t\t\n\t\twhile k < N:\n\t\t\tk = k << 1\n\t\t\n\t\ttree = [0 for _ in range(2*k)]\n\t\tfor i in range(N):\n\t\t\ttree[k+i] = array[i]\n\t\tself.tree = tree\n\t\tself.tree_size = 2*k\n\t\twhile k > 1:\n\t\t\tj = k\n\n\t\t\twhile j < 2*k:\n\t\t\t\ttree[j//2] = tree[j] * tree[j+1]\n\t\t\t\tj += 2\n\t\t\tk = k//2\n\n\tdef mul(self, a, b):\n\t\ts = 1\n\t\ta += self.tree_size//2\n\t\tb += self.tree_size//2\n\t\twhile a <= b:\n\t\t\tif a%2 == 1:\n\t\t\t\ts *= self.tree[a]\n\t\t\t\ta += 1\n\t\t\tif b%2 == 0:\n\t\t\t\ts *= self.tree[b]\n\t\t\t\tb -= 1\n\n\t\t\ta = a//2\n\t\t\tb = b//2\n\t\treturn s\nclass Solution:\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n MOD = 10**9 + 7\n k = n\n powers = []\n while k >0:\n val = k & (-k)\n powers.append(val)\n k -= val\n segtree = SegmentTree(powers)\n ans = []\n for start, end in queries:\n res = segtree.mul(start, end)\n ans.append(res%MOD)\n \n return ans\n \n``` | 2 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
python || easy soln | range-product-queries-of-powers | 0 | 1 | ```\nclass Solution:\n def productQueries(self, n: int, queries: List[List[int]]) -> List[int]:\n def min_arr(x):\n k = bin(x)[2:]\n k = k[::-1]\n ans = []\n for i in range(0, len(k)):\n if (k[i] == \'1\'):\n ans.append(2**i)\n return ans\n nums = min_arr(n)\n prod = [1]\n for i in range(len(nums)):\n k = (prod[-1]*nums[i])\n prod.append(k)\n res = []\n for i in range(len(queries)):\n b = prod[queries[i][1]+1]\n a = prod[queries[i][0]]\n res.append((b//a))\n res[i] = res[i]%(10**9 + 7)\n return res \n```\t\t | 1 | Given a positive integer `n`, there exists a **0-indexed** array called `powers`, composed of the **minimum** number of powers of `2` that sum to `n`. The array is sorted in **non-decreasing** order, and there is **only one** way to form the array.
You are also given a **0-indexed** 2D integer array `queries`, where `queries[i] = [lefti, righti]`. Each `queries[i]` represents a query where you have to find the product of all `powers[j]` with `lefti <= j <= righti`.
Return _an array_ `answers`_, equal in length to_ `queries`_, where_ `answers[i]` _is the answer to the_ `ith` _query_. Since the answer to the `ith` query may be too large, each `answers[i]` should be returned **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 15, queries = \[\[0,1\],\[2,2\],\[0,3\]\]
**Output:** \[2,4,64\]
**Explanation:**
For n = 15, powers = \[1,2,4,8\]. It can be shown that powers cannot be a smaller size.
Answer to 1st query: powers\[0\] \* powers\[1\] = 1 \* 2 = 2.
Answer to 2nd query: powers\[2\] = 4.
Answer to 3rd query: powers\[0\] \* powers\[1\] \* powers\[2\] \* powers\[3\] = 1 \* 2 \* 4 \* 8 = 64.
Each answer modulo 109 + 7 yields the same answer, so \[2,4,64\] is returned.
**Example 2:**
**Input:** n = 2, queries = \[\[0,0\]\]
**Output:** \[2\]
**Explanation:**
For n = 2, powers = \[2\].
The answer to the only query is powers\[0\] = 2. The answer modulo 109 + 7 is the same, so \[2\] is returned.
**Constraints:**
* `1 <= n <= 109`
* `1 <= queries.length <= 105`
* `0 <= starti <= endi < powers.length` | null |
Python solution | minimize-maximum-of-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe previous element takes the fall for the bigger element.\nThe elements are getting equally distributed in a order.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCalculated average sum for every element in the given order.\nThe maximum average would be our answer.\n\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimizeArrayValue(self, nums: List[int]) -> int:\n s = 0\n ans = 0\n for i in range(len(nums)):\n s = s+nums[i]\n avg = s/(i+1)\n if avg > ans:\n ans = avg\n return ceil(ans)\n\n``` | 1 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
Python3 O(n) greedy solution. | minimize-maximum-of-array | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minimizeArrayValue(self, nums: List[int]) -> int:\n max_val = cur_sum = 0\n\n for ind, num in enumerate(nums): \n cur_sum += num\n\n if num > max_val:\n mid_float = cur_sum / (ind + 1)\n mid_int = int(-1 * mid_float // 1 * -1)\n max_val = max([max_val, mid_int])\n\n return max_val\n``` | 1 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
Python shortest 1-liner. Beats 100%. Functional programming. | minimize-maximum-of-array | 0 | 1 | # Approach\nTL;DR, Same as [Editorial Solution](https://leetcode.com/problems/minimize-maximum-of-array/editorial/) written in functional approach.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is length of nums`.\n\n# Code\n```python\nclass Solution:\n def minimizeArrayValue(self, nums: list[int]) -> int:\n return max(ceil(x / i) for i, x in enumerate(accumulate(nums), 1))\n\n\n``` | 2 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
✅✅Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand🔥 | minimize-maximum-of-array | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\n\n\n# Recursion Explained (How to think recursively)\n**Search \uD83D\uDC49`Recursion by Tech Wired` on YouTube**\n\n\n\n\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n# Approach:\n\n- Initialize total_sum and result to 0.\n- Loop through the nums array from index 0 to len(nums)-1.\n- For each index, add the value at that index to the total_sum.\n- Calculate the maximum of the current result and the division of total_sum and index+1 using integer division //.\n- Update the result with the maximum value.\n- Repeat steps 3-5 for all indices.\n- Return the result as the minimum maximum of the array.\n\n# Intuition:\n\n- The goal is to minimize the maximum of the array by dividing the array into subarrays and taking the sum of each subarray.\n- By dividing the array into subarrays and taking their sum, we can obtain the average value of each subarray.\n- The task is to find the maximum average value among all possible subarrays.\n- We can achieve this by iteratively calculating the sum of the array up to each index and dividing it by the number of elements up to that index.\n- We keep track of the maximum average value found so far and update it as we iterate through the array.\n- Finally, we return the maximum average value as the result, which represents the minimum maximum of the array. This is because a smaller average value indicates a smaller maximum value. By choosing the maximum average value, we are minimizing the maximum of the array.\n\n```Python []\nclass Solution:\n def minimizeArrayValue(self, nums):\n total_sum = 0\n result = 0\n for index in range(len(nums)):\n total_sum += nums[index]\n result = max(result, (total_sum + index) // (index + 1))\n return int(result)\n\n```\n```Java []\npublic class Solution {\n public int minimizeArrayValue(int[] nums) {\n long sum = 0;\n long result = 0;\n for (int index = 0; index < nums.length; ++index) {\n sum += nums[index];\n result = Math.max(result, (sum + index) / (index + 1));\n }\n return (int) result;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minimizeArrayValue(vector<int>& nums) {\n long long sum = 0;\n long long result = 0;\n for (int index = 0; index < nums.size(); ++index) {\n sum += nums[index];\n result = max(result, (sum + index) / (index + 1));\n }\n return (int) result;\n }\n};\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D | 126 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
Image Explanation🏆- [Brute -> Better O(nlogM) -> Optimal O(n) ] - C++/Java/Python | minimize-maximum-of-array | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Reducing Dishes` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n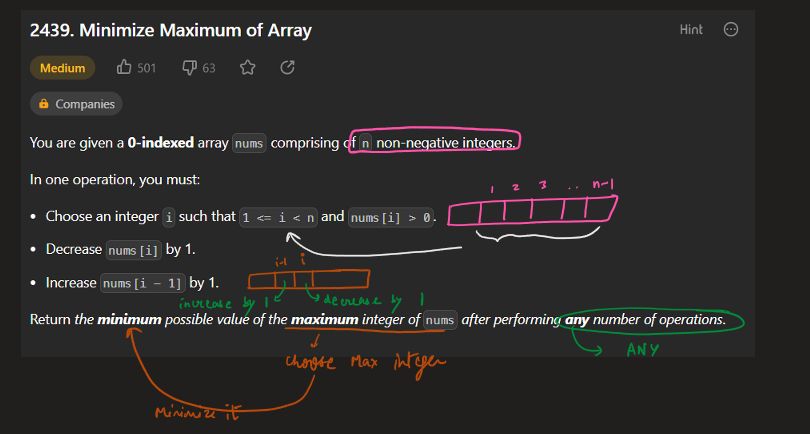\n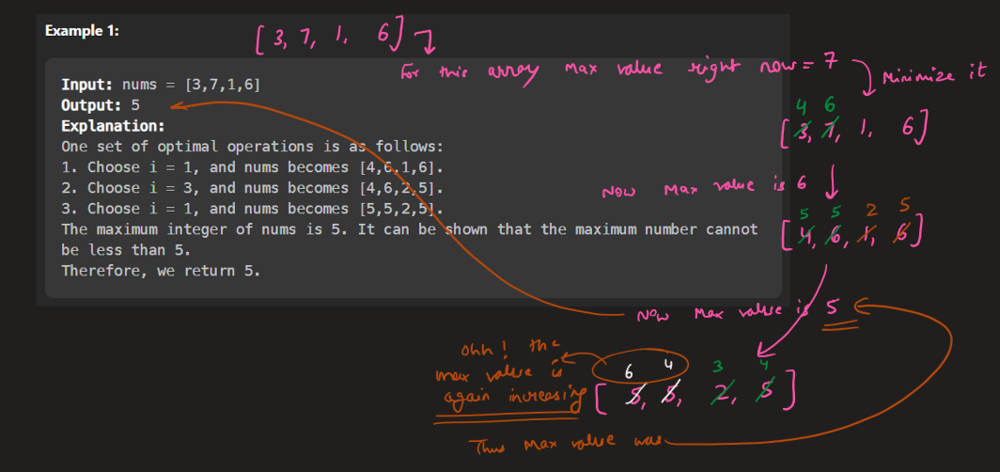\n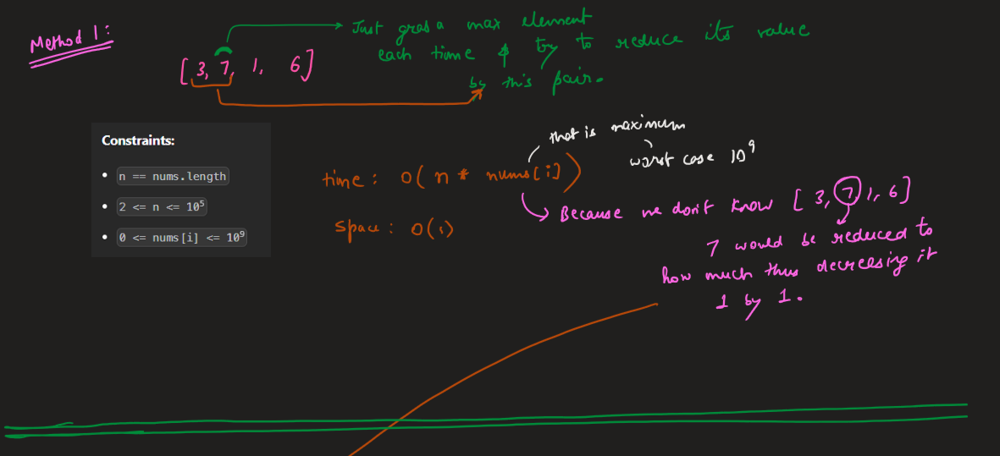\n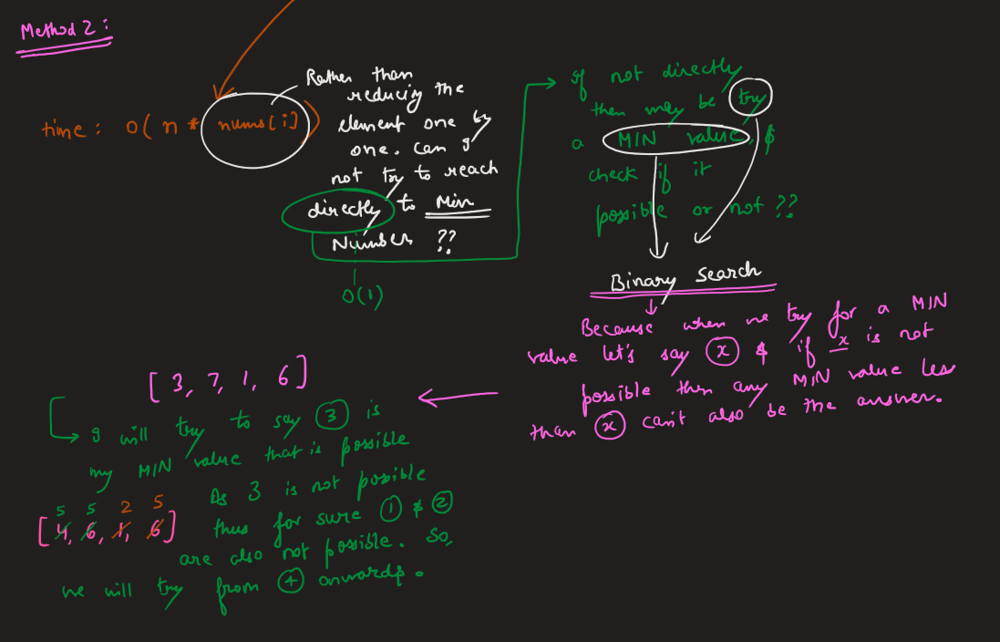\n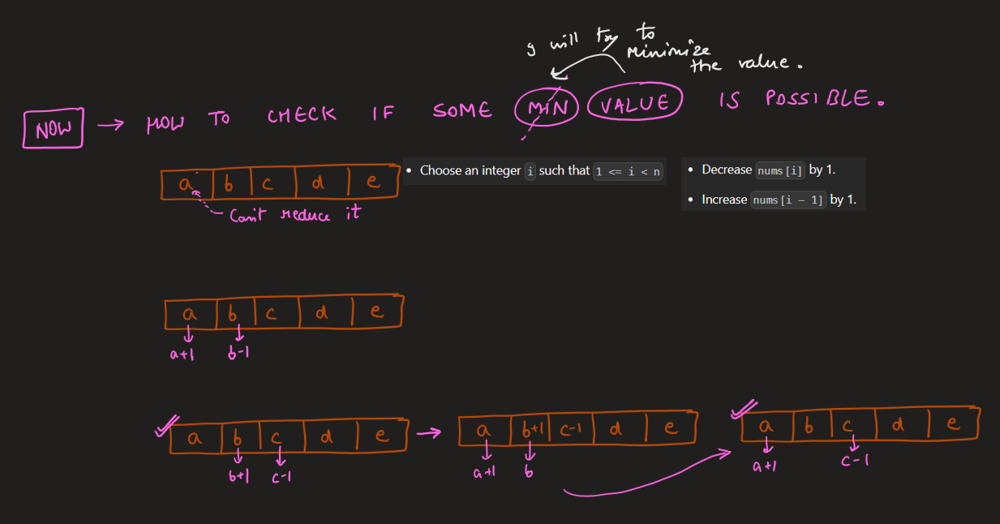\n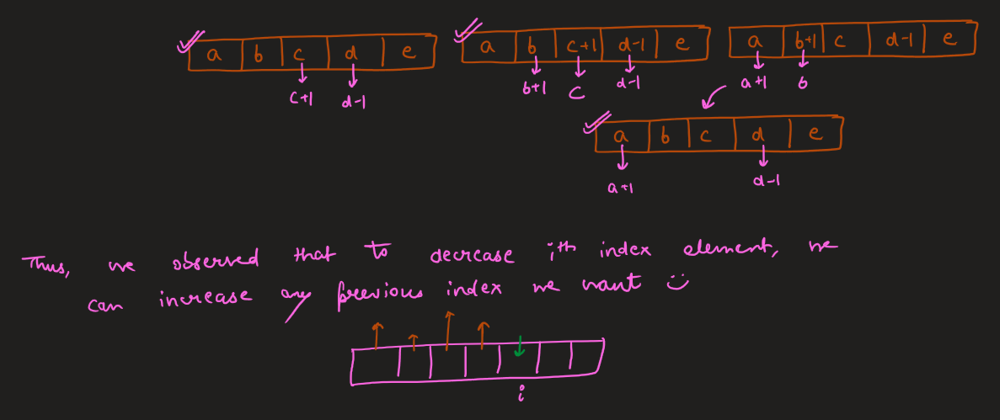\n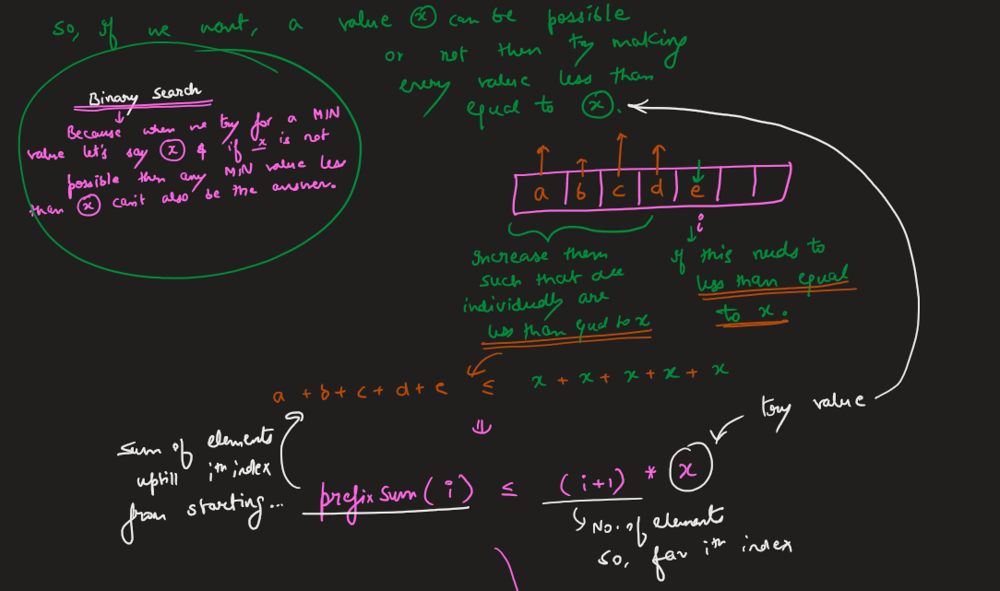\n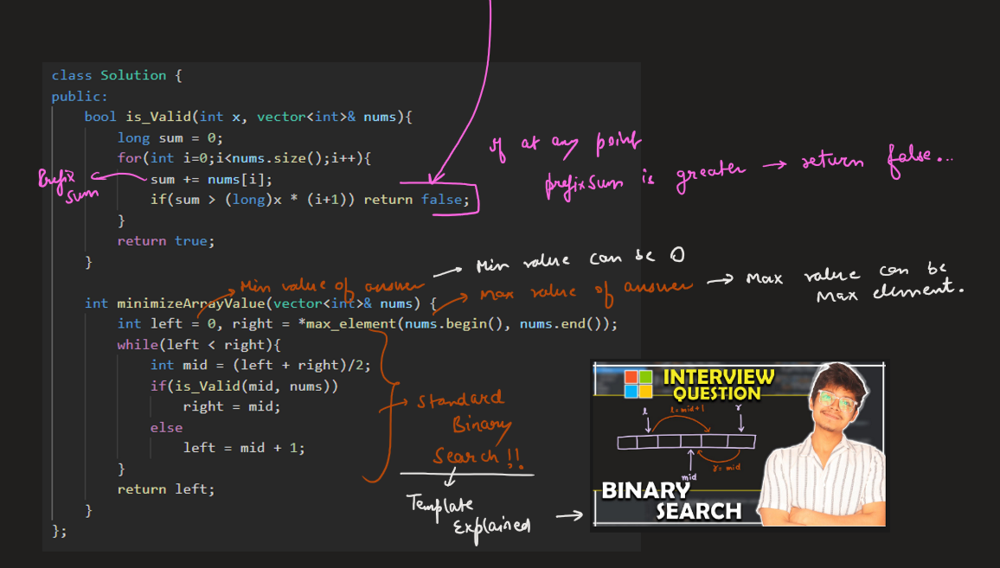\n\n\n\n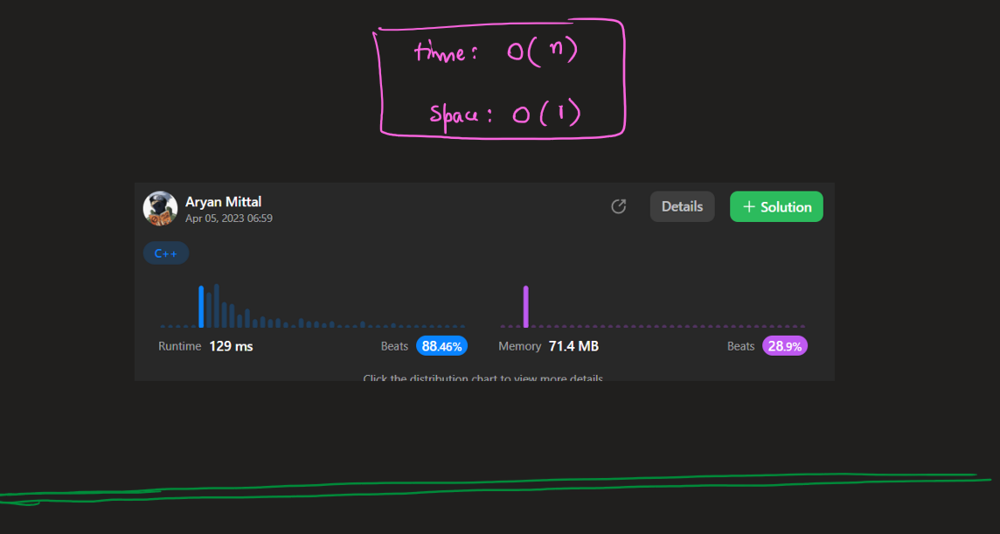\n\n\n# Optimal Code\n```C++ []\nclass Solution {\npublic:\n int minimizeArrayValue(vector<int>& A) {\n long sum = 0, res = 0;\n for (int i = 0; i < A.size(); ++i) {\n sum += A[i];\n res = max(res, (sum + i) / (i + 1));\n }\n return res;\n }\n};\n```\n```Java []\nclass Solution {\n public int minimizeArrayValue(int[] A) {\n long sum = 0, res = 0;\n for (int i = 0; i < A.length; ++i) {\n sum += A[i];\n res = Math.max(res, (sum + i) / (i + 1));\n }\n return (int)res;\n }\n}\n```\n```Python []\nclass Solution:\n def minimizeArrayValue(self, A: List[int]) -> int:\n return max((a + i) // (i + 1) for i,a in enumerate(accumulate(A)))\n```\n | 182 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
✔💯 DAY 370 | [JAVA/C++/PYTHON] | EXPLAINED |INTUITION | Approach | PROOF | minimize-maximum-of-array | 1 | 1 | \n\n\n# Please Upvote as it really motivates me\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n##### \u2022\tTo find the minimum maximum value of an array, we can use an iterative approach. \n##### \u2022\tFirst, we calculate the sum of the array up to each index and divide it by the number of elements up to that index. \n##### \u2022\tWe then keep track of the maximum average value found so far and update it as we iterate through the array. \n##### \u2022\tFinally, we return the maximum average value as the result, which represents the minimum maximum of the array. \n##### \u2022\tBy choosing the maximum average value, we are effectively minimizing the maximum value of the array.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tDefine a public method named "minimizeArrayValue" that takes an integer array "nums" as input and returns an integer value.\n##### \u2022\tInitialize two long variables "ans" and "sum" to 0.\n##### \u2022\tUse a for loop to iterate through the "nums" array from index 0 to the length of the array.\n##### \u2022\tInside the for loop, add the current element of the array to the "sum" variable and check if it is greater than the "ans" variable.\n##### \u2022\tIf the current element is greater than "ans", update "ans" to the maximum value between "ans" and the ceiling value of the sum of the current element and "sum" divided by the current index plus 1.\n##### \u2022\tReturn the integer value of "ans".\n\n\n# Code\n```c++ []\nint minimizeArrayValue(vector<int>& nums,long ans=0,long sum=0) {\n for(int i=0;i<nums.size();sum+=nums[i],i++)\n if(nums[i]>ans)ans=max(ans,(long )ceil((double)(sum+nums[i])/(i+1)));\n return (int)ans;\n }\n``` \n```java []\npublic int minimizeArrayValue(int[] nums) {\n long ans=0,sum=0;\n for(int i=0;i<nums.length;sum+=nums[i],i++)\n if(nums[i]>ans)ans=Math.max(ans,(long)Math.ceil((double)(sum+nums[i])/(i+1)));\n return (int)ans;\n }\n```\n```python []\ndef minimizeArrayValue(nums):\n ans = 0\n sum = 0\n for i in range(len(nums)):\n sum += nums[i]\n if nums[i] > ans:\n ans = max(ans, math.ceil((sum + nums[i]) / (i + 1)))\n return int(ans)\n```\n\n\n\n# Complexity\nTime Complexity: O(n), where n is the length of the input array "nums". This is because we are iterating through the array once.\n\nSpace Complexity: O(1), as we are only using a constant amount of extra space to store the variables "ans" and "sum".\n\n# 2nd way \n\n```python []\nclass Solution:\n def minimizeArrayValue(self, A: List[int]) -> int:\n return max((a + i) // (i + 1) for i,a in enumerate(accumulate(A)))\n```\n```c++ []\nint minimizeArrayValue(vector<int>& A) {\n long sum = 0, res = 0;\n for (int i = 0; i < A.size(); ++i) {\n sum += A[i];\n res = max(res, (sum + i) / (i + 1));\n }\n return res;\n }\n```\n```java []\npublic int minimizeArrayValue(int[] A) {\n long sum = 0, res = 0;\n for (int i = 0; i < A.length; ++i) {\n sum += A[i];\n res = Math.max(res, (sum + i) / (i + 1));\n }\n return (int)res;\n }\n```\n# DRY RUN \n##### \u2022\tWe have the input array nums = [3,7,1,6] and we need to find the minimum number of elements to be added to the array such that the maximum element in the array is less than or equal to the target value. \n##### \u2022\tWe start with an empty subarray and keep adding elements to it until the maximum element in the subarray is greater than the target value. Once this happens, we remove elements from the beginning of the subarray until the maximum element is less than or equal to the target value. We repeat this process until we reach the end of the array. \n##### \u2022\tAt each step, we keep track of the number of elements added to the array and return the minimum of all such values. \n##### \u2022\tLet\'s see how this works for the given input: Initially, we have an empty subarray and ans = 0 . \n##### \u2022\tWe add the first element 3 to the subarray and update sum = 3 . We add the second element 7 to the subarray and update sum = 10 . \n##### \u2022\tThe maximum element in the subarray is 7 , which is greater than the target value. So, we remove elements from the beginning of the subarray until the maximum element is less than or equal to the target value. \n##### \u2022\tWe remove the first element 3 and update sum = 7 . We add the third element 1 to the subarray and update sum = 8 . \n##### \u2022\tWe add the fourth element 6 to the subarray and update sum = 14 . \n##### \u2022\tThe maximum element in the subarray is 7 , which is less than or equal to the target value. So, we don\'t need to remove any elements. \n##### \u2022\tWe update ans to max(ans, ceil((sum + nums[i]) / (i + 1))) = max(0, ceil(14/4)) = 4 . We remove the first element 7 from the subarray and update sum = 7 . \n##### \u2022\tThe maximum element in the subarray is 6 , which is less than or equal to the target value. So, we don\'t need to remove any elements. \n##### \u2022\tWe update ans to max(ans, ceil((sum + nums[i]) / (i + 1))) = max(4, ceil(13/3)) = 5 . We remove the first element 1 from the subarray and update sum = 6 . \n##### \u2022\tThe maximum element in the subarray is 6 , which is less than or equal to the target value. So, we don\'t need to remove any elements. \n##### \u2022\tWe update ans to max(ans, ceil((sum + nums[i]) / (i + 1))) = max(5, ceil(12/2)) = 6 . We remove the first element 6 from the subarray and update sum = 6 . \n##### \u2022\tThe maximum element in the subarray is 6 , which is less than or equal to the target value. So, we don\'t need to remove any elements. \n##### \u2022\tWe update ans to max(ans, ceil((sum + nums[i]) / (i + 1))) = max(6, ceil(6/1)) = 6 . \n##### \u2022\tWe have reached the end of the array. \n##### \u2022\tThe minimum number of elements to be added to the array is ans = 6 . \n##### \u2022\tTherefore, the output is 6 .\n\n\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n\nhttps://leetcode.com/problems/minimize-maximum-of-array/solutions/3381606/day-370-java-c-python-explained-intuition-approach-proof/\n | 13 | You are given a **0-indexed** array `nums` comprising of `n` non-negative integers.
In one operation, you must:
* Choose an integer `i` such that `1 <= i < n` and `nums[i] > 0`.
* Decrease `nums[i]` by 1.
* Increase `nums[i - 1]` by 1.
Return _the **minimum** possible value of the **maximum** integer of_ `nums` _after performing **any** number of operations_.
**Example 1:**
**Input:** nums = \[3,7,1,6\]
**Output:** 5
**Explanation:**
One set of optimal operations is as follows:
1. Choose i = 1, and nums becomes \[4,6,1,6\].
2. Choose i = 3, and nums becomes \[4,6,2,5\].
3. Choose i = 1, and nums becomes \[5,5,2,5\].
The maximum integer of nums is 5. It can be shown that the maximum number cannot be less than 5.
Therefore, we return 5.
**Example 2:**
**Input:** nums = \[10,1\]
**Output:** 10
**Explanation:**
It is optimal to leave nums as is, and since 10 is the maximum value, we return 10.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `0 <= nums[i] <= 109` | null |
[Python3] post-order dfs | create-components-with-same-value | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/b09317beeb5fa2ae0b6d2537172ab52647a75cea) for solutions of biweekly 89. \n\n```\nclass Solution:\n def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:\n tree = [[] for _ in nums]\n for u, v in edges: \n tree[u].append(v)\n tree[v].append(u)\n \n def fn(u, p):\n """Post-order dfs."""\n ans = nums[u]\n for v in tree[u]: \n if v != p: ans += fn(v, u)\n return 0 if ans == cand else ans\n \n total = sum(nums)\n for cand in range(1, total//2+1): \n if total % cand == 0 and fn(0, -1) == 0: return total//cand-1\n return 0 \n``` | 12 | There is an undirected tree with `n` nodes labeled from `0` to `n - 1`.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
You are allowed to **delete** some edges, splitting the tree into multiple connected components. Let the **value** of a component be the sum of **all** `nums[i]` for which node `i` is in the component.
Return _the **maximum** number of edges you can delete, such that every connected component in the tree has the same value._
**Example 1:**
**Input:** nums = \[6,2,2,2,6\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The above figure shows how we can delete the edges \[0,1\] and \[3,4\]. The created components are nodes \[0\], \[1,2,3\] and \[4\]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.
**Example 2:**
**Input:** nums = \[2\], edges = \[\]
**Output:** 0
**Explanation:** There are no edges to be deleted.
**Constraints:**
* `1 <= n <= 2 * 104`
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= edges[i][0], edges[i][1] <= n - 1`
* `edges` represents a valid tree. | null |
[Python] Get factors of sum all nodes then check | create-components-with-same-value | 0 | 1 | # Intuition\n- Sum of each connected component must be values in factors of `sum(nums)`, and at least `max(nums)`.\n- So get factors of sum all nodes then check if we can split into connected component, where sum of each connected component is equal to factor.\n\n# Complexity\n- Time complexity: `O(sqrt(SUM_ALL_NODE) + N*log(SUM_ALL_NODE))`, where `SUM_ALL_NODE <= 10^6` is number of all nodes, `N <= 2*10^4` is number of nodes.\n - `factors` is up to `log(SUM_ALL_NODE)` elements.\n - `dfs()` function cost `O(N)`\n\n- Space complexity: `O(log(SUM_ALL_NODE) + N)`\n\n# Code\n```python\nclass Solution:\n def getFactors(self, x):\n factors = []\n for i in range(1, int(sqrt(x)) + 1):\n if x % i != 0: continue\n factors.append(i)\n if x // i != i: factors.append(x // i)\n return factors\n\n def componentValue(self, nums: List[int], edges: List[List[int]]) -> int:\n n = len(nums)\n graph = defaultdict(list)\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n\n self.cntRemainZero = 0\n def dfs(u, p, sumPerComponent): # return remain of the subtree with root `u`\n remain = nums[u]\n for v in graph[u]:\n if v == p: continue\n remain += dfs(v, u, sumPerComponent)\n \n remain %= sumPerComponent\n if remain == 0:\n self.cntRemainZero += 1\n \n return remain\n \n def isGood(sumPerComponent, expectedNumOfComponents):\n self.cntRemainZero = 0\n dfs(0, -1, sumPerComponent)\n return self.cntRemainZero == expectedNumOfComponents\n \n sumAllNodes, maxNum = sum(nums), max(nums)\n for sumPerComponent in sorted(self.getFactors(sumAllNodes)):\n if sumPerComponent < maxNum: continue # at least maxNum\n expectedNumOfComponents = sumAllNodes // sumPerComponent\n if isGood(sumPerComponent, expectedNumOfComponents):\n return expectedNumOfComponents - 1 # Need to cut `numOfComponent - 1` edges to make `numOfComponent` connected component\n \n return 0\n``` | 4 | There is an undirected tree with `n` nodes labeled from `0` to `n - 1`.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
You are allowed to **delete** some edges, splitting the tree into multiple connected components. Let the **value** of a component be the sum of **all** `nums[i]` for which node `i` is in the component.
Return _the **maximum** number of edges you can delete, such that every connected component in the tree has the same value._
**Example 1:**
**Input:** nums = \[6,2,2,2,6\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The above figure shows how we can delete the edges \[0,1\] and \[3,4\]. The created components are nodes \[0\], \[1,2,3\] and \[4\]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.
**Example 2:**
**Input:** nums = \[2\], edges = \[\]
**Output:** 0
**Explanation:** There are no edges to be deleted.
**Constraints:**
* `1 <= n <= 2 * 104`
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= edges[i][0], edges[i][1] <= n - 1`
* `edges` represents a valid tree. | null |
Python (Simple DFS) | create-components-with-same-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def componentValue(self, nums, edges):\n if not edges:\n return 0\n\n dict1, result = collections.defaultdict(list), sum(nums)\n\n for i,j in edges:\n dict1[i].append(j)\n dict1[j].append(i)\n\n def dfs(a,b):\n total = nums[a]\n\n for neighbor in dict1[a]:\n if neighbor != b:\n total += dfs(neighbor,a)\n\n return total if total != i else 0\n\n for i in range(max(nums),result//min(nums)):\n if result%i == 0 and dfs(0,len(nums)-1) == 0:\n return result//i - 1\n\n return 0\n\n``` | 0 | There is an undirected tree with `n` nodes labeled from `0` to `n - 1`.
You are given a **0-indexed** integer array `nums` of length `n` where `nums[i]` represents the value of the `ith` node. You are also given a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
You are allowed to **delete** some edges, splitting the tree into multiple connected components. Let the **value** of a component be the sum of **all** `nums[i]` for which node `i` is in the component.
Return _the **maximum** number of edges you can delete, such that every connected component in the tree has the same value._
**Example 1:**
**Input:** nums = \[6,2,2,2,6\], edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\]\]
**Output:** 2
**Explanation:** The above figure shows how we can delete the edges \[0,1\] and \[3,4\]. The created components are nodes \[0\], \[1,2,3\] and \[4\]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.
**Example 2:**
**Input:** nums = \[2\], edges = \[\]
**Output:** 0
**Explanation:** There are no edges to be deleted.
**Constraints:**
* `1 <= n <= 2 * 104`
* `nums.length == n`
* `1 <= nums[i] <= 50`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= edges[i][0], edges[i][1] <= n - 1`
* `edges` represents a valid tree. | null |
Python | Sorting + Two Pointers approach | 99.66% faster ✅ | largest-positive-integer-that-exists-with-its-negative | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach: Two Pointers, Sorting\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxK(self, nums: List[int]) -> int:\n nums.sort()\n if nums[0] >= 0:\n return -1\n i = 0\n j = len(nums)-1\n while i < j:\n if nums[i] >= 0:\n return -1\n if nums[i]*-1 == nums[j]:\n return nums[j]\n if nums[i]*-1 < nums[j]:\n j-=1\n else:\n i+=1\n return -1\n``` | 1 | Given an integer array `nums` that **does not contain** any zeros, find **the largest positive** integer `k` such that `-k` also exists in the array.
Return _the positive integer_ `k`. If there is no such integer, return `-1`.
**Example 1:**
**Input:** nums = \[-1,2,-3,3\]
**Output:** 3
**Explanation:** 3 is the only valid k we can find in the array.
**Example 2:**
**Input:** nums = \[-1,10,6,7,-7,1\]
**Output:** 7
**Explanation:** Both 1 and 7 have their corresponding negative values in the array. 7 has a larger value.
**Example 3:**
**Input:** nums = \[-10,8,6,7,-2,-3\]
**Output:** -1
**Explanation:** There is no a single valid k, we return -1.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0` | null |
largest-positive-integer-that-exists-with-its-negative | largest-positive-integer-that-exists-with-its-negative | 0 | 1 | \n\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n\n\n# Code\n```\nclass Solution:\n def findMaxK(self, nums: List[int]) -> int:\n nums=sorted(nums,reverse=True)\n s=set(nums)\n for i in range(len(nums)):\n if 0-nums[i] in s:\n return nums[i]\n return -1\n\n``` | 1 | Given an integer array `nums` that **does not contain** any zeros, find **the largest positive** integer `k` such that `-k` also exists in the array.
Return _the positive integer_ `k`. If there is no such integer, return `-1`.
**Example 1:**
**Input:** nums = \[-1,2,-3,3\]
**Output:** 3
**Explanation:** 3 is the only valid k we can find in the array.
**Example 2:**
**Input:** nums = \[-1,10,6,7,-7,1\]
**Output:** 7
**Explanation:** Both 1 and 7 have their corresponding negative values in the array. 7 has a larger value.
**Example 3:**
**Input:** nums = \[-10,8,6,7,-2,-3\]
**Output:** -1
**Explanation:** There is no a single valid k, we return -1.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0` | null |
Beginner-friendly || Simple solution with HashMap | largest-positive-integer-that-exists-with-its-negative | 0 | 1 | # Intuition\nLet\'s briefly explain, what problem is:\n- there\'s a list of `nums`\n- our goal is to find **the maximum**, that has a **negative integer of himself** (i.e., 2 and -2 etc)\n\nThe approach is **straighforward**: iterate over `nums` and at each step check, if a particular integer is **a maximum one**, and find it **negative version of himself**.\n\nIf this integer **doesn\'t exist**, simply return `-1`.\n\n# Approach\n1. declare `set` for effective indexing of a **negative version of a current maximum**\n2. declare `ans = -1`\n3. iterate over `nums` and **find a maximum**\n4. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**, for building a set and iterating over `nums`\n\n- Space complexity: **O(N)**, the same for storing `set`.\n\n# Code in Python3\n```\nclass Solution:\n def findMaxK(self, nums: List[int]) -> int:\n cache = set(nums)\n ans = -1\n\n for num in nums:\n if -num in cache and num > ans: ans = num\n \n return ans\n```\n# Code in TypeScript\n```\nfunction findMaxK(nums: number[]): number {\n const cache = new Set(nums)\n let ans = -1\n\n for (let i = 0; i < nums.length; i++) {\n const curMax = nums[i]\n\n if (cache.has(-curMax) && curMax > ans) ans = curMax\n }\n\n return ans\n};\n``` | 2 | Given an integer array `nums` that **does not contain** any zeros, find **the largest positive** integer `k` such that `-k` also exists in the array.
Return _the positive integer_ `k`. If there is no such integer, return `-1`.
**Example 1:**
**Input:** nums = \[-1,2,-3,3\]
**Output:** 3
**Explanation:** 3 is the only valid k we can find in the array.
**Example 2:**
**Input:** nums = \[-1,10,6,7,-7,1\]
**Output:** 7
**Explanation:** Both 1 and 7 have their corresponding negative values in the array. 7 has a larger value.
**Example 3:**
**Input:** nums = \[-10,8,6,7,-2,-3\]
**Output:** -1
**Explanation:** There is no a single valid k, we return -1.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-1000 <= nums[i] <= 1000`
* `nums[i] != 0` | null |
simple solution for beginners | count-number-of-distinct-integers-after-reverse-operations | 0 | 1 | \n# Code\n```\nclass Solution:\n def countDistinctIntegers(self, nums: List[int]) -> int:\n #copy the list to the variable num\n num=nums.copy()\n #reverse all the elements in nums and store it in the num list\n for x in nums:\n sum=0\n while x>0:\n digit=x%10\n sum=sum*10+digit\n x=x//10\n num.append(sum)\n #In the list num remove the duplicate values by using the set keyword and then return the length of the num\n return len(list(set(num)))\n```\n\n | 1 | You are given an array `nums` consisting of **positive** integers.
You have to take each integer in the array, **reverse its digits**, and add it to the end of the array. You should apply this operation to the original integers in `nums`.
Return _the number of **distinct** integers in the final array_.
**Example 1:**
**Input:** nums = \[1,13,10,12,31\]
**Output:** 6
**Explanation:** After including the reverse of each number, the resulting array is \[1,13,10,12,31,1,31,1,21,13\].
The reversed integers that were added to the end of the array are underlined. Note that for the integer 10, after reversing it, it becomes 01 which is just 1.
The number of distinct integers in this array is 6 (The numbers 1, 10, 12, 13, 21, and 31).
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Explanation:** After including the reverse of each number, the resulting array is \[2,2,2,2,2,2\].
The number of distinct integers in this array is 1 (The number 2).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
SIMPLE SOLUTION || T/S: O (N)/O(N) | count-number-of-distinct-integers-after-reverse-operations | 0 | 1 | ```\nclass Solution:\n def countDistinctIntegers(self, nums: List[int]) -> int:\n dct=defaultdict(lambda :0)\n for num in nums:\n dct[num]=1\n for num in nums:\n rev=int(str(num)[::-1])\n if dct[rev]!=1:\n dct[rev]=1\n return len(dct)\n``` | 1 | You are given an array `nums` consisting of **positive** integers.
You have to take each integer in the array, **reverse its digits**, and add it to the end of the array. You should apply this operation to the original integers in `nums`.
Return _the number of **distinct** integers in the final array_.
**Example 1:**
**Input:** nums = \[1,13,10,12,31\]
**Output:** 6
**Explanation:** After including the reverse of each number, the resulting array is \[1,13,10,12,31,1,31,1,21,13\].
The reversed integers that were added to the end of the array are underlined. Note that for the integer 10, after reversing it, it becomes 01 which is just 1.
The number of distinct integers in this array is 6 (The numbers 1, 10, 12, 13, 21, and 31).
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Explanation:** After including the reverse of each number, the resulting array is \[2,2,2,2,2,2\].
The number of distinct integers in this array is 1 (The number 2).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
Python BEATS 99.05% Easy | count-number-of-distinct-integers-after-reverse-operations | 0 | 1 | \n```\nclass Solution:\n def countDistinctIntegers(self, nums: List[int]) -> int:\n l=[]\n for i in nums:\n l.append(int(str(i)[::-1]))\n nums+=l\n #print(nums)\n return len(set(nums))\n``` | 2 | You are given an array `nums` consisting of **positive** integers.
You have to take each integer in the array, **reverse its digits**, and add it to the end of the array. You should apply this operation to the original integers in `nums`.
Return _the number of **distinct** integers in the final array_.
**Example 1:**
**Input:** nums = \[1,13,10,12,31\]
**Output:** 6
**Explanation:** After including the reverse of each number, the resulting array is \[1,13,10,12,31,1,31,1,21,13\].
The reversed integers that were added to the end of the array are underlined. Note that for the integer 10, after reversing it, it becomes 01 which is just 1.
The number of distinct integers in this array is 6 (The numbers 1, 10, 12, 13, 21, and 31).
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Explanation:** After including the reverse of each number, the resulting array is \[2,2,2,2,2,2\].
The number of distinct integers in this array is 1 (The number 2).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
✅✅✅ 90 % faster and one-line solution | count-number-of-distinct-integers-after-reverse-operations | 0 | 1 | \n\n```\nclass Solution:\n def countDistinctIntegers(self, nums: List[int]) -> int:\n return len(set([int(str(n)[::-1]) for n in nums] + nums))\n``` | 1 | You are given an array `nums` consisting of **positive** integers.
You have to take each integer in the array, **reverse its digits**, and add it to the end of the array. You should apply this operation to the original integers in `nums`.
Return _the number of **distinct** integers in the final array_.
**Example 1:**
**Input:** nums = \[1,13,10,12,31\]
**Output:** 6
**Explanation:** After including the reverse of each number, the resulting array is \[1,13,10,12,31,1,31,1,21,13\].
The reversed integers that were added to the end of the array are underlined. Note that for the integer 10, after reversing it, it becomes 01 which is just 1.
The number of distinct integers in this array is 6 (The numbers 1, 10, 12, 13, 21, and 31).
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Explanation:** After including the reverse of each number, the resulting array is \[2,2,2,2,2,2\].
The number of distinct integers in this array is 1 (The number 2).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
Easy Simple Approach In Python | count-number-of-distinct-integers-after-reverse-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\niterate over the given list and convert in string reverse it and add it end of the array if leading zeroes are present we used lstrip function to remove all the front zero.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countDistinctIntegers(self, nums: List[int]) -> int:\n lst=nums[:]\n for i in nums:\n if i%10==0:\n i=str(i)[::-1]\n a=i.lstrip(\'0\')\n lst.append(int(i))\n a=str(i)[::-1]\n lst.append(int(a))\n\n #print(lst)\n return len(set(lst))\n``` | 1 | You are given an array `nums` consisting of **positive** integers.
You have to take each integer in the array, **reverse its digits**, and add it to the end of the array. You should apply this operation to the original integers in `nums`.
Return _the number of **distinct** integers in the final array_.
**Example 1:**
**Input:** nums = \[1,13,10,12,31\]
**Output:** 6
**Explanation:** After including the reverse of each number, the resulting array is \[1,13,10,12,31,1,31,1,21,13\].
The reversed integers that were added to the end of the array are underlined. Note that for the integer 10, after reversing it, it becomes 01 which is just 1.
The number of distinct integers in this array is 6 (The numbers 1, 10, 12, 13, 21, and 31).
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Explanation:** After including the reverse of each number, the resulting array is \[2,2,2,2,2,2\].
The number of distinct integers in this array is 1 (The number 2).
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
sum-of-number-and-its-reverse | sum-of-number-and-its-reverse | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def sumOfNumberAndReverse(self, num: int) -> bool:\n i=1\n if num==0:\n return True\n while i<num:\n a=str(i)\n a=a[::-1]\n a=int(a)\n if a+i==num:\n return True\n i+=1\n return False\n \n``` | 1 | Given a **non-negative** integer `num`, return `true` _if_ `num` _can be expressed as the sum of any **non-negative** integer and its reverse, or_ `false` _otherwise._
**Example 1:**
**Input:** num = 443
**Output:** true
**Explanation:** 172 + 271 = 443 so we return true.
**Example 2:**
**Input:** num = 63
**Output:** false
**Explanation:** 63 cannot be expressed as the sum of a non-negative integer and its reverse so we return false.
**Example 3:**
**Input:** num = 181
**Output:** true
**Explanation:** 140 + 041 = 181 so we return true. Note that when a number is reversed, there may be leading zeros.
**Constraints:**
* `0 <= num <= 105` | null |
[Python3] Little Math, Time and Space: O(1) | sum-of-number-and-its-reverse | 0 | 1 | Probably could be optimized better and generalized to arbitrary length (or value)\n```python\nclass Solution:\n def sumOfNumberAndReverse(self, num: int) -> bool:\n if num <= 18:\n\t\t #Adding 1 digit number, a, and its reverse, also a: 2a\n if num % 2 == 0:\n return True\n\t\t\t#Adding 2 digit number, 10a+b, and its reverse, 10b+a: 11a+11b\n if num % 11 == 0:\n return True\n return False\n elif num <= 198:\n if num % 11 == 0:\n return True\n\t\t\t#Adding 3 digit number, 100a+10b+c, and its reverse, 100c+10b+a: 101a+20b+101c\n for b in range(10):\n newNum = (num - 20 * b)\n\t\t\t\t# checking last condition since a+c can be up to 18\n if newNum > 0 and newNum % 101 == 0 and newNum // 101 != 19: \n return True\n return False\n # rest follows similar pattern\n elif num <= 1998:\n for b in range(10):\n newNum = (num - 20 * b)\n if newNum > 0 and newNum % 101 == 0 and newNum // 101 != 19:\n return True\n for bc in range(19):\n newNum = (num - 110 * bc)\n if newNum > 0 and newNum % 1001 == 0 and newNum // 1001 != 19:\n return True \n return False\n elif num <= 19998:\n for c in range(10):\n for bd in range(19):\n newNum = (num - 200 *c - 1010 * bd)\n if newNum > 0 and newNum % 10001 == 0 and newNum // 10001 != 19:\n return True \n for bc in range(19):\n newNum = (num - 110 * bc)\n if newNum > 0 and newNum % 1001 == 0 and newNum // 1001 != 19:\n return True \n return False\n elif num <= 199998: # 10**5 - 2\n for c in range(10):\n for bd in range(19):\n newNum = (num - 200 *c - 1010 * bd)\n if newNum > 0 and newNum % 10001 == 0 and newNum // 10001 != 19:\n return True \n for cd in range(19):\n for be in range(19):\n newNum = (num - 100100 *cd - 100010 * be)\n if newNum > 0 and newNum % 100001 == 0 and newNum // 100001 != 19:\n return True \n return False\n``` | 1 | Given a **non-negative** integer `num`, return `true` _if_ `num` _can be expressed as the sum of any **non-negative** integer and its reverse, or_ `false` _otherwise._
**Example 1:**
**Input:** num = 443
**Output:** true
**Explanation:** 172 + 271 = 443 so we return true.
**Example 2:**
**Input:** num = 63
**Output:** false
**Explanation:** 63 cannot be expressed as the sum of a non-negative integer and its reverse so we return false.
**Example 3:**
**Input:** num = 181
**Output:** true
**Explanation:** 140 + 041 = 181 so we return true. Note that when a number is reversed, there may be leading zeros.
**Constraints:**
* `0 <= num <= 105` | null |
Detailed explanation of Python O(n) solution | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\nWe have to count all subarrays with certain properties. In such problems, a good pattern is to think about what happens when the subarrays end at a certain position. Let\'s iterate through the array and think about how to calculate the number of appropriate subarrays that end at a current position.\n\nnums = [1,3,5,2,7,5], minK = 1, maxK = 5\n\nHow many subarrays end at index 0, val - 1? -> 0 (no element equals maxK)\n\nHow many subarrays end at index 1, 3? -> 0 (no element equals maxK)\n\nHow many subarrays end at index 2, 5? -> 1 (the leftmost border can\'t be further than the last minK)\n\nHow many subarrays end at index 3, 2? -> 1 (the leftmost border can\'t be further than the last minK)\n\nHow many subarrays end at index 4, 7? -> 0 (7 is bigger than maxK)\n\nHow many subarrays end at index 5, 5? -> 0 (no element equals minK after the first element that can\'t be in the subarray (bigger than maxK or smaller than minK))\nthe answer is the suma of this values = 2\n\nIf the right border is fixed (current index inx in iteration) and we know the leftmost possible index of the left border "llb" and the rightmost possible left border "rlb" then the total number of subarrays that end at the current index is rlb-llb+1. So we can calculate the subarrays that end at all indexes, and the total number of subarrays is just the sum of all of them.\n\nThe rest is just figuring out how to calculate the leftmost left possible subarray border (llb) and rightmost left possible subarray border (rlb).\n\nFor rlb, it is simple. We always need maxK and minK elements, so let\'s just take the minimum of their indexes before the current index = min(lastmaxKinx, lastminKinx).\n\nThe only restriction for the llb is that it should be after any inappropriate element. When we encounter an element that is greater than maxK or smaller than minK, we can set llb = current index + 1.\n\nConsider the input array nums = [1,3,5,2,7,5] and the range constraints minK = 1, maxK = 5. Let\'s assume the right border is at index 3.\n\nIn this case, the leftmost left border(llb) is 1 at index 0 because there are no values between 1 and the right border that violate the constraints.\n\nTo calculate the rightmost left border(rlb), we need to find the index of the last minK or maxK element before the current index. In this case, the rightmost left border is also 1 because there is only one minK element and shifting the left border further right would exclude it.\n\nTherefore, the leftmost left border (llb) and rightmost left border (rlb) are both 0. The total number of subarrays ending at index 3 can be calculated as rlb-llb+1=0-0+1=1, which is correct.\n\n\n# Approach\n\nTo calculate the rlb, maintain the indices of the last occurrences of the minK and maxK in variables, "last_minK" and "last_maxK".\n\nMaintain left border (llb), the index of the next element AFTER the last element that violates the constraints in variable "left_most".\n\nIterate through the array and for each position, calculate the number of subarrays that end at that position: rlb-llb+1. \nSum them up to the variable called "count".\n\n# Complexity\n- Time complexity: O(n) - we iterate once through the array and perform a constant amount of work for each element.\n- Space complexity: O(1) - we only need a few variables to solve this problem.\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n count = 0 # total amount\n last_minK = None # at initialization we dont have such elements\n last_maxK = None # at initialization we don\'t have such elements\n left_most = 0 # we have no elements before wich violates constraints, llb value\n\n for inx, n in enumerate(nums):\n if n < minK or n > maxK: # this elements violates constraints\n # last_minK and last_maxK cant be included in any window after inx\n left_most = inx+1\n last_minK = None\n last_maxK = None\n else:\n if n == minK:\n last_minK = inx\n if n == maxK:\n last_maxK = inx\n # we have both maxK and minK so lets calculate the number of subarrays ended at inx\n if last_minK is not None and last_maxK is not None:\n right_most_left_border = min(last_minK, last_maxK)\n count += right_most_left_border-left_most+1\n\n\n return count\n\n``` | 2 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Awesome Logic Beginner Friendy Code in python | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n ans=0\n minindex=-1\n maxindex=-1\n culprit=-1\n for i in range(len(nums)):\n if nums[i]<minK or nums[i]>maxK:\n culprit=i\n if nums[i]==minK:\n minindex=i\n if nums[i]==maxK:\n maxindex=i\n \n smaller=min(minindex,maxindex)\n temp=smaller-culprit\n if temp<=0:\n ans+=0\n else:\n ans+=temp\n return ans\n\n \n\n\n \n\n``` | 2 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Formula based Problem | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n count=0\n minimum=maximum=nonelement=-1\n for ind,val in enumerate(nums):\n if val==minK:\n minimum=ind\n if val==maxK:\n maximum=ind\n if not minK<=val<=maxK:\n nonelement=ind\n count+=max(0,min(minimum,maximum)-nonelement)\n return count\n #please upvote me it would helping me alot\n \n``` | 2 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
📌📌Python3 || ⚡819 ms, faster than 97.11% of Python3 | count-subarrays-with-fixed-bounds | 0 | 1 | 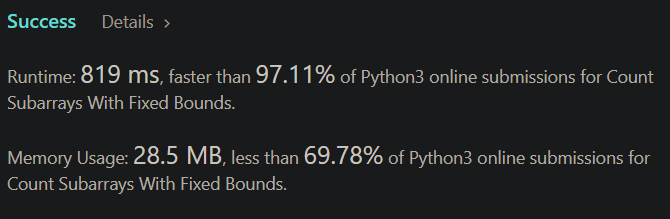\n```\ndef countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n count = last = 0\n min_index = max_index = -1\n for i, num in enumerate(nums):\n if num < minK or num > maxK:\n last = i + 1\n min_index = max_index = -1\n continue\n if num == minK:\n min_index = i\n if num == maxK:\n max_index = i\n if min_index != -1 and max_index != -1:\n count += min(max_index, min_index) - last + 1\n return count\n```\n\nThe given code is an implementation of a function called \'countSubarrays\' that takes in a list of integers \'nums\', and two integer values \'minK\' and \'maxK\' and returns the count of all contiguous subarrays in \'nums\' that have elements between \'minK\' and \'maxK\', inclusive. Here\'s a step-by-step explanation of the code:\n1. Define a function named \'countSubarrays\' that takes three input arguments: \'nums\' (a list of integers), \'minK\' (an integer), and \'maxK\' (an integer), and returns an integer.\n1. Initialize \'count\' and \'last\' variables to 0. Initialize \'min_index\' and \'max_index\' variables to -1.\n1. Loop through each index \'i\' and element \'num\' in the \'nums\' list:\n\t1. If the \'num\' is less than \'minK\' or greater than \'maxK\', set \'last\' to \'i+1\', \'min_index\' and \'max_index\' to -1 and continue to the next iteration.\n\t1. If the \'num\' is equal to \'minK\', set \'min_index\' to the current index \'i\'.\n\t1. If the \'num\' is equal to \'maxK\', set \'max_index\' to the current index \'i\'.\n\t1. If both \'min_index\' and \'max_index\' are not equal to -1, calculate the count of contiguous subarrays between the two indices, update the \'count\' variable and set \'last\' to the next index after the calculated subarray.\n1. Return the \'count\' variable.\n\nNote that the time complexity of this algorithm is O(n), where n is the length of the \'nums\' list. This is because we are traversing the list only once and performing a constant number of operations for each element. | 2 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Reverse Select - beating 100% in time | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCalculating the count of subarrays qualified is harder than calculating the opposite. Then do the opposite and subtract it from number of all possible subarrays.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWhenever there\'s a value outside interval [minK, maxK], do a calculation as the previous part does not impact later anymore. \nWithin each part, whenever there\'s a value == minK or maxK, we calculate the number of subarrays not qualified. \nIf minK == maxK, this corner case is even easier and we can take another measure. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n \n nums.append(maxK + 1)\n n = len(nums)\n \n if minK == maxK: \n cnt = 0\n res = 0\n for i in range(n): \n num = nums[i]\n if num == minK: \n cnt += 1\n else:\n res += cnt * (cnt + 1) // 2\n cnt = 0\n return res \n \n startidx = None\n prevminidx = None\n prevmaxidx = None\n offset = 0\n res = 0\n \n for i in range(n): \n num = nums[i]\n if num < minK or num > maxK: \n if prevminidx is not None and prevmaxidx is not None: \n llast1 = (i - 1) - (max(prevminidx, prevmaxidx) + 1) + 1\n llast2 = max(prevmaxidx, prevminidx) - (min(prevmaxidx, prevminidx) + 1) + 1\n ltotal = (i - 1) - startidx + 1\n offset += llast1 * (llast1 + 1) // 2 + llast1 * llast2\n res += ltotal * (ltotal + 1) // 2 - offset\n startidx = None\n prevminidx = None\n prevmaxidx = None\n offset = 0 \n continue\n else: \n if startidx is None: \n startidx = i\n if num == minK: \n if prevminidx is None and prevmaxidx is None: \n l = i - startidx + 1\n offset += l * (l + 1) // 2\n elif prevminidx is None: \n l1 = i - (prevmaxidx + 1) + 1\n l2 = prevmaxidx - startidx + 1\n offset += l1 * (l1 + 1) // 2 + (l1 - 1) * l2\n elif prevmaxidx is None:\n l1 = i - (prevminidx + 1) + 1\n l2 = prevminidx - startidx + 1\n offset += l1 * (l1 + 1) // 2 + l1 * l2\n else: \n if prevmaxidx >= prevminidx: \n l1 = i - (prevmaxidx + 1) + 1\n l2 = prevmaxidx - (prevminidx + 1) + 1\n offset += l1 * (l1 + 1) // 2 + (l1 - 1) * l2\n else: \n l1 = i - (prevminidx + 1) + 1\n l2 = prevminidx - (prevmaxidx + 1) + 1\n offset += l1 * (l1 + 1) // 2 + l1 * l2\n prevminidx = i\n elif num == maxK: \n if prevminidx is None and prevmaxidx is None: \n l = i - startidx + 1\n offset += l * (l + 1) // 2\n elif prevmaxidx is None: \n l1 = i - (prevminidx + 1) + 1\n l2 = prevminidx - startidx + 1\n offset += l1 * (l1 + 1) // 2 + (l1 - 1) * l2\n elif prevminidx is None: \n l1 = i - (prevmaxidx + 1) + 1\n l2 = prevmaxidx - startidx + 1\n offset += l1 * (l1 + 1) // 2 + l1 * l2\n else: \n if prevminidx >= prevmaxidx: \n l1 = i - (prevminidx + 1) + 1\n l2 = prevminidx - (prevmaxidx + 1) + 1\n offset += l1 * (l1 + 1) // 2 + (l1 - 1) * l2\n else: \n l1 = i - (prevmaxidx + 1) + 1\n l2 = prevmaxidx - (prevminidx + 1) + 1\n offset += l1 * (l1 + 1) // 2 + l1 * l2\n prevmaxidx = i \n \n return res \n \n``` | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
✅Python3 simple solution O(N)🔥🔥 | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Sliding window/two pointer method.**\n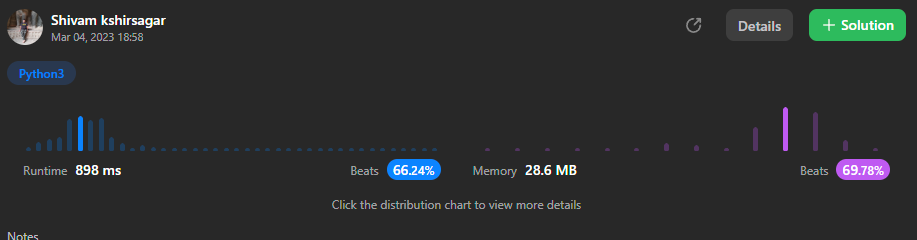\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- as per constraint as soon as we find minK and maxK in our subarray, update counter to 1.\n- now how we will keep track of this, with help of our vars **minI, maxI and end_of_ssI.**\n- these vars indicates indexes of found **minK, maxK** element and as well as when we encounter element less than or greater than provided we include it\'s index too.\n- **max(0, min(minI, maxI) - end_of_ssI)**: this ensures if till we have not found minK or maxK then update counter by 0, else update counter by 1.\n- when any of **minI** or **maxI** is **-1** this will always **result in 0.**\n- when we find both minK and maxK then **min(minI, maxI)** we take **because** it\'s **close to end_of_ssI** and will result in 1.\n- next time when minI and maxI gets updated counter will get updated to 1.\n- **return counter**. \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n minI = -1\n maxI = -1\n end_of_ssI = -1\n counter = 0\n for i in range(len(nums)):\n if minK <= nums[i] <= maxK:\n minI = i if nums[i] == minK else minI\n maxI = i if nums[i] == maxK else maxI\n counter += max(0, min(minI, maxI) - end_of_ssI)\n else:\n minI = -1\n maxI = -1\n end_of_ssI = i\n return counter\n```\n# Please like and comment below :-) | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Video Solution | Easiest Solution using Sliding Window | Python | count-subarrays-with-fixed-bounds | 0 | 1 | # Approach\nhttps://youtu.be/vwzal4jbEfw\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n minFound = False\n maxFound = False\n\n start = 0\n minStart = 0\n maxStart = 0\n count = 0\n\n for i, num in enumerate(nums):\n if num > maxK or num < minK:\n minFound = False\n maxFound = False\n start = i+1\n\n if num == minK:\n minStart = i\n minFound = True\n \n if num == maxK:\n maxStart = i\n maxFound = True\n\n if minFound and maxFound:\n count += min(minStart, maxStart) - start + 1\n\n return count\n \n\n \n``` | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
[Python] Divide and Expand | count-subarrays-with-fixed-bounds | 0 | 1 | **Solution**:\nSince a subarray must contains numbers between minK and maxK, any number outside such range will act as a divider and we can consider subarrays to the left and to the right of it independently.\n\nIterate through all numbers and find the count of valid subarrays ending at each number.\n \nFor a subarray starting from the divider and ending at some arbitrary number, we can shrink such subarray from the left and it will remain valid until it no longer includes minK or maxK. Thus, the count of valid subarrays is equal to the count of numbers starting from divider to the first of the last occurence of minK and maxK.\n \n**Complexity**:\n Time: O(n)\n Space: O(1)\n\n```\nclass Solution:\n def countSubarrays(self, nums: list[int], minK: int, maxK: int) -> int:\n\n # Initialize three variables to keep track of indices of latest divider, minK, maxK\n div, minLast, maxLast = 0, -1, -1\n\n # Initialize the result\n res = 0\n\n # Iterate through all numbers\n for i, num in enumerate(nums):\n\n # If the current number is a divider, we can disregard all numbers before it\n if not (minK <= num <= maxK):\n div, minLast, maxLast = i + 1, -1, -1\n continue\n\n # Update the latest indices of minK and maxK\n minLast, maxLast = (\n i if num == minK else minLast,\n i if num == maxK else maxLast,\n )\n\n # Update the result with the number of valid subarrays ending at the current number if we have seen minK and maxK\n res += (\n min(maxLast, minLast) - div + 1\n if minLast != -1 and maxLast != -1\n else 0\n )\n\n return res\n``` | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Time 100% Space 90% | Time O(n) Space O(1) | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLooking at a few base cases\n1, 5 [1,5] = 1\n1, 5 [2,1,5] = 2\n1, 5 [1,5,1] = 3\n1, 5 [2,1,5,1] = 5\nyou may notice that the count for a single pair of min and max is equal to `amount on left` * `amount on right`.\nFor multiple pairs, the number of substrings is the sum of single scores whenever we flip from minK to maxK, with updated bounds.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nEx: \n`minK = 1 `\n`maxK = 5 `\n`nums = [2,1,5,1] `\n`Expected Answer = 5`\n\nStart:\nLeft bound = 0\nRight bound = 3\ncount = 0\n\nFirst step:\n- First min/max value found: minK{1} @ i=1\n- Other value: maxK{5} @ i=2\n- Amount on left = (index of our first value - left bound + 1) = 2\n- Amount on right = (right bound - index of our first flip + 1) = 2\n- count += 2*2 // Count = 4\n- Update our left bound: Left Bound = 2 //Our first index + 1\n\nSecond step:\n- First min/max value found: maxK{5} @ i=2\n- Other value: minK{1} @ i=3\n- Amount on left = (index of our first value - left bound + 1) = 1\n- Amount on right = (right bound - index of our first flip + 1) = 1\n- count += 1*1 // Count = 5\n- Update our left bound: Left Bound = 2 //Our first index + 1\n\nThird step:\n- First min/max value found: minK{1} @ i=3\n- Other value: NOT FOUND. We\'re done with this string\n- Return count // 5, as expected!\n\n##### Now we repeat the above for each range of valid ints in nums and return the sum!\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n returnable = 0\n\n ### Handle special case where min and max are same\n if minK == maxK:\n started = False\n l = 0\n for i, n in enumerate(nums):\n if n == minK:\n if not started:\n started = True\n l = i\n else:\n if started:\n started = False\n c = i-l\n returnable += (c * (c+1)) // 2\n if started: # Finish it\n started = False\n c = i-l+1\n returnable += (c * (c+1)) // 2\n return returnable\n\n started = False\n l = r = -1\n\n ### Function to evaluate a single valid substring.\n ### - Must not contain invalid ints\n ### - Must contain minK and maxK \n def evaluate_substring(l, r):\n returnable = 0\n\n ### Get our first value, minK or maxK and its index\n for i in range(l, r+1):\n n = nums[i]\n if n == minK or n == maxK:\n curr_val = n\n curr_val_idx = i\n break\n\n ### Whenever we min or max and it\'s not equal to our current max, add score and flip our current value\n for i in range(curr_val_idx, r+1):\n n = nums[i]\n if n == minK or n == maxK:\n if n != curr_val:\n returnable += (curr_val_idx - l + 1) * (r - i + 1)\n l = curr_val_idx + 1\n curr_val_idx = i\n curr_val = n\n else: # n is current val\n curr_val_idx = i\n\n return returnable\n\n # Split substrings at invalid characters and add idx if we\'ve seen minK and maxK\n for i, n in enumerate(nums):\n if started:\n if minK <= n <= maxK:\n r = i\n min_found |= (n==minK)\n max_found |= (n==maxK)\n else: # End of a run\n started = False\n if min_found and max_found:\n returnable += evaluate_substring(l, r)\n else:\n if minK <= n <= maxK:\n started = True\n min_found = n == minK\n max_found = n == maxK\n l = i\n if started: # Finish last run\n if min_found and max_found:\n returnable += evaluate_substring(l, r)\n\n return returnable\n\n\n \n``` | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Python3 Solution using sliding window | count-subarrays-with-fixed-bounds | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find the number of subarrays in an array where the minimum element is at least minK and the maximum element is at most maxK.\nTo solve the problem, I used a sliding window approach.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI initialized three variables, lowest, highest, and inbetween, to -1. The lowest variable kept track of the last index where the minimum value was seen, the highest variable tracked the last index where the maximum value was seen, and the inbetween variable tracked the last index where a value outside the range of minK to maxK was seen.\n\nThen, I iterated through the array and updated these variables based on the current element\'s value. If the current element was outside the range of minK to maxK, I updated the inbetween variable. If the current element was equal to minK, I updated the lowest variable, and if it was equal to maxK, I updated the highest variable.\n\nFinally, for each index, I calculated the number of subarrays that end at that index and have a minimum value of at least minK and a maximum value of at most maxK. I did so by taking the minimum of lowest and highest and subtracting inbetween from it. If the result was greater than or equal to zero, I added it to the out variable, which represented the total number of subarrays that meet the criteria.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime Complexity of this solution is O(n), where n is the length of the input array nums. This is because the algorithm iterates through the array once and performs a constant number of operations at each index.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity of this solution is O(1), as it only uses a constant amount of extra space to store the three variables lowest, highest, and inbetween. The space used by the input array nums is not considered extra space as it is required by the problem statement. Therefore, the solution has a space complexity that is constant with respect to the size of the input array.\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:\n out, lowest, highest, inbetween = 0, -1, -1, -1\n for idx, num in enumerate(nums):\n if num < minK or num > maxK:\n inbetween = idx\n if num == minK:\n lowest = idx\n if num == maxK:\n highest = idx\n out += max(0, min(lowest, highest) - inbetween)\n return out\n``` | 1 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
Python short and clean. Functional programming. | count-subarrays-with-fixed-bounds | 0 | 1 | # Approach\nTLDR; Same as the [Official Solution](https://leetcode.com/problems/count-subarrays-with-fixed-bounds/editorial/).\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is the length of nums`.\n\n# Code\n```python\nclass Solution:\n def countSubarrays(self, nums: list[int], minK: int, maxK: int) -> int:\n indexes = lambda f: accumulate(range(len(nums)), lambda a, x: x if f(nums[x]) else a, initial=-1)\n\n left_bounds = indexes(lambda num: num < minK or num > maxK)\n maxs = indexes(lambda num: num == maxK)\n mins = indexes(lambda num: num == minK)\n\n count_fn = lambda lb, mx, mn: max(0, min(mx, mn) - lb)\n return sum(map(count_fn, left_bounds, maxs, mins))\n\n\n``` | 2 | You are given an integer array `nums` and two integers `minK` and `maxK`.
A **fixed-bound subarray** of `nums` is a subarray that satisfies the following conditions:
* The **minimum** value in the subarray is equal to `minK`.
* The **maximum** value in the subarray is equal to `maxK`.
Return _the **number** of fixed-bound subarrays_.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,3,5,2,7,5\], minK = 1, maxK = 5
**Output:** 2
**Explanation:** The fixed-bound subarrays are \[1,3,5\] and \[1,3,5,2\].
**Example 2:**
**Input:** nums = \[1,1,1,1\], minK = 1, maxK = 1
**Output:** 10
**Explanation:** Every subarray of nums is a fixed-bound subarray. There are 10 possible subarrays.
**Constraints:**
* `2 <= nums.length <= 105`
* `1 <= nums[i], minK, maxK <= 106` | null |
[Python3] 1-line | determine-if-two-events-have-conflict | 0 | 1 | \n```\nclass Solution:\n def haveConflict(self, event1: List[str], event2: List[str]) -> bool:\n return event1[0] <= event2[0] <= event1[1] or event2[0] <= event1[0] <= event2[1]\n``` | 8 | You are given two arrays of strings that represent two inclusive events that happened **on the same day**, `event1` and `event2`, where:
* `event1 = [startTime1, endTime1]` and
* `event2 = [startTime2, endTime2]`.
Event times are valid 24 hours format in the form of `HH:MM`.
A **conflict** happens when two events have some non-empty intersection (i.e., some moment is common to both events).
Return `true` _if there is a conflict between two events. Otherwise, return_ `false`.
**Example 1:**
**Input:** event1 = \[ "01:15 ", "02:00 "\], event2 = \[ "02:00 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect at time 2:00.
**Example 2:**
**Input:** event1 = \[ "01:00 ", "02:00 "\], event2 = \[ "01:20 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect starting from 01:20 to 02:00.
**Example 3:**
**Input:** event1 = \[ "10:00 ", "11:00 "\], event2 = \[ "14:00 ", "15:00 "\]
**Output:** false
**Explanation:** The two events do not intersect.
**Constraints:**
* `evnet1.length == event2.length == 2.`
* `event1[i].length == event2[i].length == 5`
* `startTime1 <= endTime1`
* `startTime2 <= endTime2`
* All the event times follow the `HH:MM` format. | null |
Python Elegant & Short | determine-if-two-events-have-conflict | 0 | 1 | ```\nclass Solution:\n """\n Time: O(1)\n Memory: O(1)\n """\n\n def haveConflict(self, a: List[str], b: List[str]) -> bool:\n a_start, a_end = a\n b_start, b_end = b\n return b_start <= a_start <= b_end or \\\n b_start <= a_end <= b_end or \\\n a_start <= b_start <= a_end or \\\n a_start <= b_end <= a_end\n```\n\nIf you like this solution remember to **upvote it** to let me know.\n | 6 | You are given two arrays of strings that represent two inclusive events that happened **on the same day**, `event1` and `event2`, where:
* `event1 = [startTime1, endTime1]` and
* `event2 = [startTime2, endTime2]`.
Event times are valid 24 hours format in the form of `HH:MM`.
A **conflict** happens when two events have some non-empty intersection (i.e., some moment is common to both events).
Return `true` _if there is a conflict between two events. Otherwise, return_ `false`.
**Example 1:**
**Input:** event1 = \[ "01:15 ", "02:00 "\], event2 = \[ "02:00 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect at time 2:00.
**Example 2:**
**Input:** event1 = \[ "01:00 ", "02:00 "\], event2 = \[ "01:20 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect starting from 01:20 to 02:00.
**Example 3:**
**Input:** event1 = \[ "10:00 ", "11:00 "\], event2 = \[ "14:00 ", "15:00 "\]
**Output:** false
**Explanation:** The two events do not intersect.
**Constraints:**
* `evnet1.length == event2.length == 2.`
* `event1[i].length == event2[i].length == 5`
* `startTime1 <= endTime1`
* `startTime2 <= endTime2`
* All the event times follow the `HH:MM` format. | null |
Python Solution (explanation and super fast) | determine-if-two-events-have-conflict | 0 | 1 | 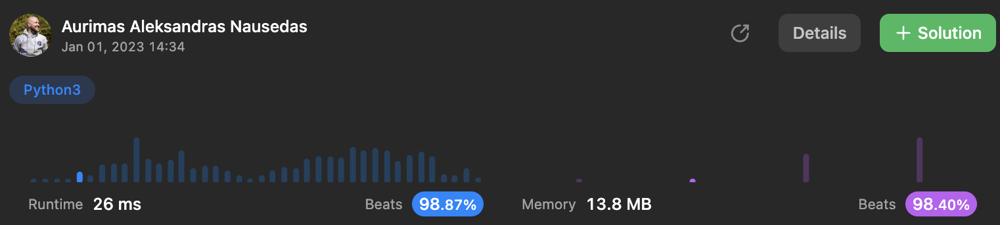\n\n```\nclass Solution:\n def haveConflict(self, event1: List[str], event2: List[str]) -> bool:\n\n event1Start = event1[0].split(\':\')\n event1End = event1[1].split(\':\')\n\n event2Start = event2[0].split(\':\')\n event2End = event2[1].split(\':\')\n\n return False if event2Start > event1End or event1Start > event2End else True \n```\n\n**Explanation**: changing **event1** and **event2** date strings by spliting to **single** **string** **date** **values** and then while comparing the **single date strings** return **True** if it is inbetween or **False** if it isn\'t.\n\nMore solutions of mine at https://github.com/aurimas13/SolutionsToProblems | 4 | You are given two arrays of strings that represent two inclusive events that happened **on the same day**, `event1` and `event2`, where:
* `event1 = [startTime1, endTime1]` and
* `event2 = [startTime2, endTime2]`.
Event times are valid 24 hours format in the form of `HH:MM`.
A **conflict** happens when two events have some non-empty intersection (i.e., some moment is common to both events).
Return `true` _if there is a conflict between two events. Otherwise, return_ `false`.
**Example 1:**
**Input:** event1 = \[ "01:15 ", "02:00 "\], event2 = \[ "02:00 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect at time 2:00.
**Example 2:**
**Input:** event1 = \[ "01:00 ", "02:00 "\], event2 = \[ "01:20 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect starting from 01:20 to 02:00.
**Example 3:**
**Input:** event1 = \[ "10:00 ", "11:00 "\], event2 = \[ "14:00 ", "15:00 "\]
**Output:** false
**Explanation:** The two events do not intersect.
**Constraints:**
* `evnet1.length == event2.length == 2.`
* `event1[i].length == event2[i].length == 5`
* `startTime1 <= endTime1`
* `startTime2 <= endTime2`
* All the event times follow the `HH:MM` format. | null |
[Python3] Straight-Forward, Clean & Concise | determine-if-two-events-have-conflict | 0 | 1 | ```\nclass Solution:\n def haveConflict(self, event1: List[str], event2: List[str]) -> bool:\n start1 = int(event1[0][:2]) * 60 + int(event1[0][3:])\n end1 = int(event1[1][:2]) * 60 + int(event1[1][3:])\n start2 = int(event2[0][:2]) * 60 + int(event2[0][3:])\n end2 = int(event2[1][:2]) * 60 + int(event2[1][3:])\n return True if start1 <= start2 <= end1 or start2 <= start1 <= end2 else False\n``` | 2 | You are given two arrays of strings that represent two inclusive events that happened **on the same day**, `event1` and `event2`, where:
* `event1 = [startTime1, endTime1]` and
* `event2 = [startTime2, endTime2]`.
Event times are valid 24 hours format in the form of `HH:MM`.
A **conflict** happens when two events have some non-empty intersection (i.e., some moment is common to both events).
Return `true` _if there is a conflict between two events. Otherwise, return_ `false`.
**Example 1:**
**Input:** event1 = \[ "01:15 ", "02:00 "\], event2 = \[ "02:00 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect at time 2:00.
**Example 2:**
**Input:** event1 = \[ "01:00 ", "02:00 "\], event2 = \[ "01:20 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect starting from 01:20 to 02:00.
**Example 3:**
**Input:** event1 = \[ "10:00 ", "11:00 "\], event2 = \[ "14:00 ", "15:00 "\]
**Output:** false
**Explanation:** The two events do not intersect.
**Constraints:**
* `evnet1.length == event2.length == 2.`
* `event1[i].length == event2[i].length == 5`
* `startTime1 <= endTime1`
* `startTime2 <= endTime2`
* All the event times follow the `HH:MM` format. | null |
Simple and Easy 2 lines[Python] | determine-if-two-events-have-conflict | 0 | 1 | Convert hours to minutes and compare\n```\nclass Solution:\n def haveConflict(self, event1: List[str], event2: List[str]) -> bool:\n \n arr = [[(int(event1[0][:2])*60)+int(event1[0][3:]) , (int(event1[1][:2])*60)+int(event1[1][3:])] ,\n [(int(event2[0][:2])*60)+int(event2[0][3:]) , (int(event2[1][:2])*60)+int(event2[1][3:])]]\n \n return (arr[0][0] <= arr[1][1] <= arr[0][1] or\n arr[1][0] <= arr[0][1] <= arr[1][1])\n``` | 2 | You are given two arrays of strings that represent two inclusive events that happened **on the same day**, `event1` and `event2`, where:
* `event1 = [startTime1, endTime1]` and
* `event2 = [startTime2, endTime2]`.
Event times are valid 24 hours format in the form of `HH:MM`.
A **conflict** happens when two events have some non-empty intersection (i.e., some moment is common to both events).
Return `true` _if there is a conflict between two events. Otherwise, return_ `false`.
**Example 1:**
**Input:** event1 = \[ "01:15 ", "02:00 "\], event2 = \[ "02:00 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect at time 2:00.
**Example 2:**
**Input:** event1 = \[ "01:00 ", "02:00 "\], event2 = \[ "01:20 ", "03:00 "\]
**Output:** true
**Explanation:** The two events intersect starting from 01:20 to 02:00.
**Example 3:**
**Input:** event1 = \[ "10:00 ", "11:00 "\], event2 = \[ "14:00 ", "15:00 "\]
**Output:** false
**Explanation:** The two events do not intersect.
**Constraints:**
* `evnet1.length == event2.length == 2.`
* `event1[i].length == event2[i].length == 5`
* `startTime1 <= endTime1`
* `startTime2 <= endTime2`
* All the event times follow the `HH:MM` format. | null |
[Python3] Brute Force + Early Stopping, Clean & Concise | number-of-subarrays-with-gcd-equal-to-k | 0 | 1 | **Implementation**\nWe use a nested for-loop to record the starting index `i` and ending index `j` for the subarray. Each time, when the GCD of subarray is smaller than `k`, we exit the inner for-loop.\n\n**Complexity**\nTime Complexity: `O(N^2logM)`, where `M <= 1e9` (worse case for GCD)\nSpace Complexity: `O(1)`\n \n **Solution**\n```\nclass Solution:\n def subarrayGCD(self, nums: List[int], k: int) -> int:\n n = len(nums)\n ans = 0\n for i in range(n):\n temp = nums[i]\n for j in range(i, n):\n temp = math.gcd(temp, nums[j])\n if temp == k:\n ans += 1\n elif temp < k:\n break\n return ans\n``` | 4 | Given an integer array `nums` and an integer `k`, return _the number of **subarrays** of_ `nums` _where the greatest common divisor of the subarray's elements is_ `k`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
The **greatest common divisor of an array** is the largest integer that evenly divides all the array elements.
**Example 1:**
**Input:** nums = \[9,3,1,2,6,3\], k = 3
**Output:** 4
**Explanation:** The subarrays of nums where 3 is the greatest common divisor of all the subarray's elements are:
- \[9,**3**,1,2,6,3\]
- \[9,3,1,2,6,**3**\]
- \[**9,3**,1,2,6,3\]
- \[9,3,1,2,**6,3**\]
**Example 2:**
**Input:** nums = \[4\], k = 7
**Output:** 0
**Explanation:** There are no subarrays of nums where 7 is the greatest common divisor of all the subarray's elements.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i], k <= 109` | null |
Python | brute force | number-of-subarrays-with-gcd-equal-to-k | 0 | 1 | # Complexity\n- Time complexity: O(n<sup>2</sup>)\n- Space complexity: O(1)\n\n# Code :\n```\nclass Solution:\n def subarrayGCD(self, nums: List[int], k: int) -> int:\n def gcd(n1, n2):\n if n2==0:\n return n1\n return gcd(n2, n1%n2)\n \n ans = 0\n n = len(nums)\n for i in range(n):\n curr_gcd = 0\n for j in range(i, n):\n curr_gcd = gcd(curr_gcd, nums[j])\n if curr_gcd == k:\n ans += 1\n \n return ans\n```\n\n----------------\n**Upvote the post if you find it helpful.\nHappy coding.** | 1 | Given an integer array `nums` and an integer `k`, return _the number of **subarrays** of_ `nums` _where the greatest common divisor of the subarray's elements is_ `k`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
The **greatest common divisor of an array** is the largest integer that evenly divides all the array elements.
**Example 1:**
**Input:** nums = \[9,3,1,2,6,3\], k = 3
**Output:** 4
**Explanation:** The subarrays of nums where 3 is the greatest common divisor of all the subarray's elements are:
- \[9,**3**,1,2,6,3\]
- \[9,3,1,2,6,**3**\]
- \[**9,3**,1,2,6,3\]
- \[9,3,1,2,**6,3**\]
**Example 2:**
**Input:** nums = \[4\], k = 7
**Output:** 0
**Explanation:** There are no subarrays of nums where 7 is the greatest common divisor of all the subarray's elements.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i], k <= 109` | null |
✔️ [Python3] Straightforward (っ•́。•́)♪♬, Explained | number-of-subarrays-with-gcd-equal-to-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter spending some time trying to use DP, you realize that it\'s usless here due to complexity reusing subproblems when calculationg GCD.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSimply check all possible subarrays and calculate GCD for all of them. Exploite the fact that:\n\n`GCD([el1, el2, el3]) = GCD(GCD([el1, el2]), el3)`\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import gcd\n\nclass Solution:\n def subarrayGCD(self, nums: List[int], k: int) -> int:\n L = len(nums)\n ans = 0\n for i in range(L):\n cur_gcd = nums[i]\n for j in range(i, L):\n cur_gcd = gcd(cur_gcd, nums[j])\n if cur_gcd == k:\n ans += 1\n if cur_gcd < k:\n break\n \n return ans\n\n``` | 0 | Given an integer array `nums` and an integer `k`, return _the number of **subarrays** of_ `nums` _where the greatest common divisor of the subarray's elements is_ `k`.
A **subarray** is a contiguous non-empty sequence of elements within an array.
The **greatest common divisor of an array** is the largest integer that evenly divides all the array elements.
**Example 1:**
**Input:** nums = \[9,3,1,2,6,3\], k = 3
**Output:** 4
**Explanation:** The subarrays of nums where 3 is the greatest common divisor of all the subarray's elements are:
- \[9,**3**,1,2,6,3\]
- \[9,3,1,2,6,**3**\]
- \[**9,3**,1,2,6,3\]
- \[9,3,1,2,**6,3**\]
**Example 2:**
**Input:** nums = \[4\], k = 7
**Output:** 0
**Explanation:** There are no subarrays of nums where 7 is the greatest common divisor of all the subarray's elements.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i], k <= 109` | null |
Binary_Search_Greedy.py | minimum-cost-to-make-array-equal | 0 | 1 | # Approach\n<h3>Binary Search</h1>\n\n# Complexity\n- Time complexity:\n $$O(N log N)$$\n\n- Space complexity:\n$$O(1)$$ \n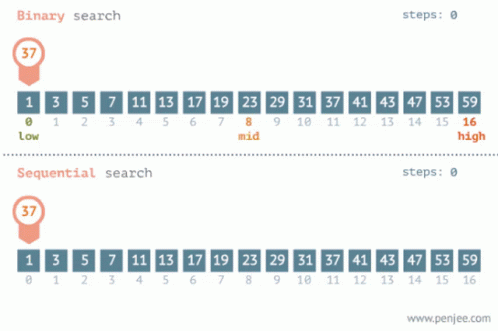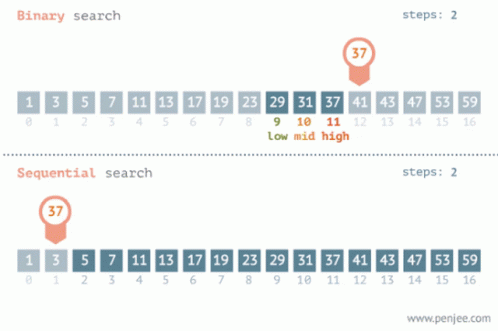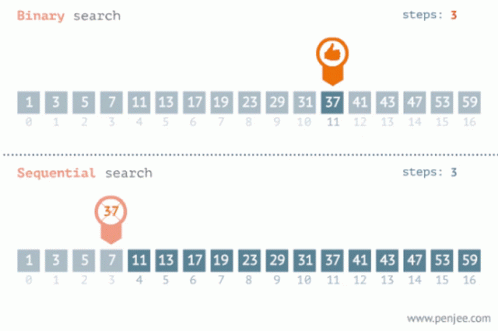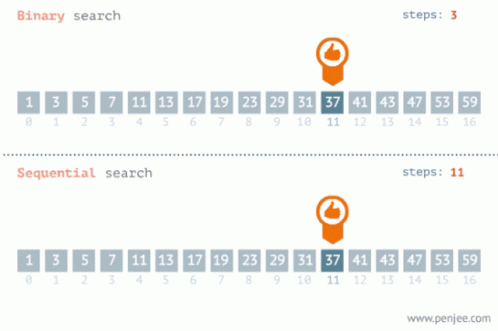\n\n# Code\n```\nclass Solution:\n def minCost(self, nums: List[int], cost: List[int]) -> int:\n ii,j=min(nums),max(nums)\n while ii<j:\n mid=(ii+j)//2\n total1,total2=0,0\n for i in range(len(nums)):\n total1+=abs(mid-nums[i])*cost[i]\n total2+=abs(mid+1-nums[i])*cost[i]\n if total1<total2:\n j=mid\n else:\n ii=mid+1\n ans=0\n for i in range(len(nums)):\n ans+=abs(ii-nums[i])*cost[i]\n return ans\n```\n\n | 3 | You are given two **0-indexed** arrays `nums` and `cost` consisting each of `n` **positive** integers.
You can do the following operation **any** number of times:
* Increase or decrease **any** element of the array `nums` by `1`.
The cost of doing one operation on the `ith` element is `cost[i]`.
Return _the **minimum** total cost such that all the elements of the array_ `nums` _become **equal**_.
**Example 1:**
**Input:** nums = \[1,3,5,2\], cost = \[2,3,1,14\]
**Output:** 8
**Explanation:** We can make all the elements equal to 2 in the following way:
- Increase the 0th element one time. The cost is 2.
- Decrease the 1st element one time. The cost is 3.
- Decrease the 2nd element three times. The cost is 1 + 1 + 1 = 3.
The total cost is 2 + 3 + 3 = 8.
It can be shown that we cannot make the array equal with a smaller cost.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], cost = \[4,2,8,1,3\]
**Output:** 0
**Explanation:** All the elements are already equal, so no operations are needed.
**Constraints:**
* `n == nums.length == cost.length`
* `1 <= n <= 105`
* `1 <= nums[i], cost[i] <= 106` | null |
4 lines only... without finding Median✅✅ | minimum-cost-to-make-array-equal | 0 | 1 | ```\nclass Solution:\n def minCost(self, nums: List[int], cost: List[int]) -> int:\n ll = sorted([[nums[i], cost[i]] for i in range(len(cost))])\n c = list(accumulate([ll[i][1] for i in range(len(cost))]))\n nc = list(accumulate([ll[i][0] * ll[i][1] for i in range(len(cost))]))\n return min([ll[i][0]*(2*c[i]-c[len(cost)-1]) + (nc[len(cost)-1]-2*nc[i]) for i in range(len(cost))])\n``` | 1 | You are given two **0-indexed** arrays `nums` and `cost` consisting each of `n` **positive** integers.
You can do the following operation **any** number of times:
* Increase or decrease **any** element of the array `nums` by `1`.
The cost of doing one operation on the `ith` element is `cost[i]`.
Return _the **minimum** total cost such that all the elements of the array_ `nums` _become **equal**_.
**Example 1:**
**Input:** nums = \[1,3,5,2\], cost = \[2,3,1,14\]
**Output:** 8
**Explanation:** We can make all the elements equal to 2 in the following way:
- Increase the 0th element one time. The cost is 2.
- Decrease the 1st element one time. The cost is 3.
- Decrease the 2nd element three times. The cost is 1 + 1 + 1 = 3.
The total cost is 2 + 3 + 3 = 8.
It can be shown that we cannot make the array equal with a smaller cost.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], cost = \[4,2,8,1,3\]
**Output:** 0
**Explanation:** All the elements are already equal, so no operations are needed.
**Constraints:**
* `n == nums.length == cost.length`
* `1 <= n <= 105`
* `1 <= nums[i], cost[i] <= 106` | null |
Easy Concise Python || Explanation || Without any Median like Hard Concept ✅ | minimum-cost-to-make-array-equal | 0 | 1 | # Approach\nHere is a simple example of my Approach:\nLet the nums[] be - `[a,b,c]` & cost[] be - `[x,y,z]`\nlet the number which the final nums[] be like - `n`(therefore, the nums[] will be `[n,n,n]`)\n\nThen the `res` will be: `(n-a)x + (n-b)y + (c-n)z`\n> here, assuming `x` is between `b` and `c`\n\nNow, solving this we get:\n`n(x+y-z) + (-(ax+by) + cz)` ...(1)\n\nNow, we can say that `x+y...` is a cummulative sum of `cost[]`\nand `ax+by...` is a cummulative sum of `cost[]*nums[]`\n\nThus we can calculate the value of this equation (1) everytime for `i`, `0 to n-1` and find the minimum of this value.\n\n\n<!-- Describe your approach to solving the problem. -->\n\n> Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, nums: List[int], cost: List[int]) -> int:\n n = len(cost)\n ll = sorted([[nums[i], cost[i]] for i in range(n)])\n c_cumm_sum = list(accumulate([ll[i][1] for i in range(n)]))\n nc_cumm_sum = list(accumulate([ll[i][0] * ll[i][1] for i in range(n)]))\n\n res = float(\'inf\')\n for i in range(n):\n res = min(res, ll[i][0] * (c_cumm_sum[i] - (c_cumm_sum[n-1] - c_cumm_sum[i]))\n + (-(nc_cumm_sum[i]) + (nc_cumm_sum[n-1] - nc_cumm_sum[i])))\n return res\n``` | 1 | You are given two **0-indexed** arrays `nums` and `cost` consisting each of `n` **positive** integers.
You can do the following operation **any** number of times:
* Increase or decrease **any** element of the array `nums` by `1`.
The cost of doing one operation on the `ith` element is `cost[i]`.
Return _the **minimum** total cost such that all the elements of the array_ `nums` _become **equal**_.
**Example 1:**
**Input:** nums = \[1,3,5,2\], cost = \[2,3,1,14\]
**Output:** 8
**Explanation:** We can make all the elements equal to 2 in the following way:
- Increase the 0th element one time. The cost is 2.
- Decrease the 1st element one time. The cost is 3.
- Decrease the 2nd element three times. The cost is 1 + 1 + 1 = 3.
The total cost is 2 + 3 + 3 = 8.
It can be shown that we cannot make the array equal with a smaller cost.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], cost = \[4,2,8,1,3\]
**Output:** 0
**Explanation:** All the elements are already equal, so no operations are needed.
**Constraints:**
* `n == nums.length == cost.length`
* `1 <= n <= 105`
* `1 <= nums[i], cost[i] <= 106` | null |
Fastest Solution Yet | minimum-cost-to-make-array-equal | 0 | 1 | # Intuition\nSince it asked to perform some operation (i.e. increasse/decrease elements by 1), it would be best to use mean of all elements belonging to `cost`. So using the hints we need to perform Iterative traversal and update\n\n# Approach\n1. Sort the elements.\n2. Determine the mean of `cost`.\n3. Create a new variable `count` and set it to `0`.\n4. Iterater through your 2D array containing nums and cost.\n5. Add the `cost[i]` to `count`.\n6. If `count>= mid`, return the positive value of `(target-n)*c` from the elements in array\n7. Repat Steps 5 and 6 till full traversal done\n\n# Complexity\n- Time complexity: $$O(nlog(n))$$ \n\n- Space complexity:$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minCost(self, nums: List[int], cost: List[int]) -> int:\n arr = sorted(zip(nums, cost))\n mid = sum(cost) / 2\n count = 0\n for target, co in arr:\n count += co\n if count >= mid:\n return sum(abs(target - n) * c for n, c in arr)\n \n``` | 1 | You are given two **0-indexed** arrays `nums` and `cost` consisting each of `n` **positive** integers.
You can do the following operation **any** number of times:
* Increase or decrease **any** element of the array `nums` by `1`.
The cost of doing one operation on the `ith` element is `cost[i]`.
Return _the **minimum** total cost such that all the elements of the array_ `nums` _become **equal**_.
**Example 1:**
**Input:** nums = \[1,3,5,2\], cost = \[2,3,1,14\]
**Output:** 8
**Explanation:** We can make all the elements equal to 2 in the following way:
- Increase the 0th element one time. The cost is 2.
- Decrease the 1st element one time. The cost is 3.
- Decrease the 2nd element three times. The cost is 1 + 1 + 1 = 3.
The total cost is 2 + 3 + 3 = 8.
It can be shown that we cannot make the array equal with a smaller cost.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], cost = \[4,2,8,1,3\]
**Output:** 0
**Explanation:** All the elements are already equal, so no operations are needed.
**Constraints:**
* `n == nums.length == cost.length`
* `1 <= n <= 105`
* `1 <= nums[i], cost[i] <= 106` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.