title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python Hard | count-number-of-possible-root-nodes | 0 | 1 | ```\nclass Solution:\n def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:\n lookup = defaultdict(list)\n\n N = len(edges) + 1\n\n for start, end in edges:\n lookup[start] += [end]\n lookup[end] += [start]\n\n\n guess = set()\n\n for start, end in guesses:\n guess.add((start, end))\n\n g = [0] * N\n\n def go(node, parent):\n\n best = 0\n\n arr = lookup[node]\n\n for nxt in arr:\n if nxt == parent:\n continue\n\n if (node, nxt) in guess:\n best += 1\n\n best += go(nxt, node)\n\n g[node] += best\n\n return best\n\n \n go(0, -1)\n\n # count -> number of edges against the grain of node\n def go2(node, parent, count):\n \n arr = lookup[node]\n\n for nxt in arr:\n if nxt == parent:\n continue\n\n c = count\n\n if (nxt, node) in guess:\n c += 1\n\n if (node, nxt) in guess:\n c -= 1\n \n\n go2(nxt, node, c - g[nxt] + g[node])\n\n g[node] += count\n \n go2(0, -1, 0)\n\n ans = 0\n\n for val in g:\n ans += (val >= k)\n\n return ans\n\n \n\n\n\n``` | 0 | Alice has an undirected tree with `n` nodes labeled from `0` to `n - 1`. The tree is represented as a 2D integer array `edges` of length `n - 1` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Alice wants Bob to find the root of the tree. She allows Bob to make several **guesses** about her tree. In one guess, he does the following:
* Chooses two **distinct** integers `u` and `v` such that there exists an edge `[u, v]` in the tree.
* He tells Alice that `u` is the **parent** of `v` in the tree.
Bob's guesses are represented by a 2D integer array `guesses` where `guesses[j] = [uj, vj]` indicates Bob guessed `uj` to be the parent of `vj`.
Alice being lazy, does not reply to each of Bob's guesses, but just says that **at least** `k` of his guesses are `true`.
Given the 2D integer arrays `edges`, `guesses` and the integer `k`, return _the **number of possible nodes** that can be the root of Alice's tree_. If there is no such tree, return `0`.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\],\[1,3\],\[4,2\]\], guesses = \[\[1,3\],\[0,1\],\[1,0\],\[2,4\]\], k = 3
**Output:** 3
**Explanation:**
Root = 0, correct guesses = \[1,3\], \[0,1\], \[2,4\]
Root = 1, correct guesses = \[1,3\], \[1,0\], \[2,4\]
Root = 2, correct guesses = \[1,3\], \[1,0\], \[2,4\]
Root = 3, correct guesses = \[1,0\], \[2,4\]
Root = 4, correct guesses = \[1,3\], \[1,0\]
Considering 0, 1, or 2 as root node leads to 3 correct guesses.
**Example 2:**
**Input:** edges = \[\[0,1\],\[1,2\],\[2,3\],\[3,4\]\], guesses = \[\[1,0\],\[3,4\],\[2,1\],\[3,2\]\], k = 1
**Output:** 5
**Explanation:**
Root = 0, correct guesses = \[3,4\]
Root = 1, correct guesses = \[1,0\], \[3,4\]
Root = 2, correct guesses = \[1,0\], \[2,1\], \[3,4\]
Root = 3, correct guesses = \[1,0\], \[2,1\], \[3,2\], \[3,4\]
Root = 4, correct guesses = \[1,0\], \[2,1\], \[3,2\]
Considering any node as root will give at least 1 correct guess.
**Constraints:**
* `edges.length == n - 1`
* `2 <= n <= 105`
* `1 <= guesses.length <= 105`
* `0 <= ai, bi, uj, vj <= n - 1`
* `ai != bi`
* `uj != vj`
* `edges` represents a valid tree.
* `guesses[j]` is an edge of the tree.
* `guesses` is unique.
* `0 <= k <= guesses.length` | null |
Python Easy Solution!! Easy to understand.. Successfully Passed | pass-the-pillow | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n3 conditons ==> \n1) when time is greater than n\n2) when time is lesser than n\n3) when time is equal to n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n rounds=time//(n-1)\n steps=rounds*(n-1)\n if time<n:\n result=time+1\n elif time>n:\n if rounds%2==0:\n result=(time-steps)+1\n else:\n result=n-((time-steps)+1)+1\n else:\n result=time-1\n return result\n``` | 1 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
Simple Solution || Python | pass-the-pillow | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n position = 0\n move = -1\n while time > 0:\n if position == n - 1 or position == 0:\n move *= -1\n position += move\n time -=1 \n \n return position + 1\n``` | 1 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
Easy Python Solution | pass-the-pillow | 0 | 1 | \n# Code\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n person=1\n c=0\n while time>0:\n if c==0:\n person+=1\n if person==n:\n c=-1\n elif c==-1:\n person-=1\n if person==1:\n c=0\n time-=1\n return person\n``` | 5 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
Python3 33ms faster than 100% | pass-the-pillow | 0 | 1 | \n\n\nAlongside the timer ,using a pointer to iterate from 1 to the n and if the pointer = n; n becomes negative and we iterate on the way back, and if time = 0 and the pointer is negative we multiply it by -1 and it will become positive.\n\nHere\'s the code:\n\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n p1 = 1\n p2 = -n\n while time != 0: \n p1 += 1\n time -= 1 \n if p1 == n:\n p1 = p2 \n elif p1 == -1:\n p1 = 1\n if p1 < 0:\n p1 = p1 * (-1)\n else:\n pass\n return p1\n``` | 1 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
Beats 99,70% speed Easy Python solution | pass-the-pillow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n a = [i for i in range(1, n+1)]\n b = [i for i in range(n-1, 1, -1)]\n c = (a + b)*(1 + time//n)\n return c[time]\n \n``` | 1 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
simple python solution | pass-the-pillow | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n\n if (math.ceil(time/(n-1)))%2==0:\n return n - (time - (n-1)*(math.ceil(time/(n-1)) - 1))\n else:\n return 1 + (time - (n-1)*(math.ceil(time/(n-1)) - 1))\n``` | 1 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
[Python3] math | pass-the-pillow | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e3093716659ec141e47ca013abcf405967592686) for solutions of weekly 335. \n\n**Intuition**\nIf the pillow is passed n-1 times, it will reached the end. After another n-1 times, it will reach the beginnig again. \nAs a result, there is a periodicity of 2*(n-1). So we can just focus on the the modulus time % 2*(n-1). \n\nIf it is passed less than or equal to n-1 times, it will reach index time. Otherwise, it will be at 2*(n-1) - time. Offset it by 1 will be the answer. \n**Implementation**\n```\nclass Solution:\n def passThePillow(self, n: int, time: int) -> int:\n time %= 2*(n-1)\n time -= 2*max(0, time-n+1)\n return time+1\n```\n**Complexity**\nTime `O(1)`\nSpace `O(1)` | 2 | There are `n` people standing in a line labeled from `1` to `n`. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
* For example, once the pillow reaches the `nth` person they pass it to the `n - 1th` person, then to the `n - 2th` person and so on.
Given the two positive integers `n` and `time`, return _the index of the person holding the pillow after_ `time` _seconds_.
**Example 1:**
**Input:** n = 4, time = 5
**Output:** 2
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2.
Afer five seconds, the pillow is given to the 2nd person.
**Example 2:**
**Input:** n = 3, time = 2
**Output:** 3
**Explanation:** People pass the pillow in the following way: 1 -> 2 -> 3.
Afer two seconds, the pillow is given to the 3rd person.
**Constraints:**
* `2 <= n <= 1000`
* `1 <= time <= 1000` | null |
Python 3 || BFS, queue || T/M: 94% / 86% | kth-largest-sum-in-a-binary-tree | 0 | 1 | ```\nclass Solution:\n def kthLargestLevelSum(self, root: TreeNode, k: int) -> int:\n\n queue, ans = deque([root]), []\n\n while len(queue) > 0:\n count = 0\n\n for _ in range(len(queue)):\n node = queue.popleft()\n\n if node.left : queue.append(node.left )\n if node.right: queue.append(node.right)\n\n count+= node.val\n\n ans.append(count)\n\n return sorted(ans)[-k] if k <= len(ans) else -1\n\n```\n[https://leetcode.com/problems/kth-largest-sum-in-a-binary-tree/submissions/1031896679/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 3 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
Kth Largest sum in a binary tree | kth-largest-sum-in-a-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n l=defaultdict(list)\n def traversal(root,h):\n if root is None:\n return\n l[h].append(root.val)\n traversal(root.left,h+1)\n traversal(root.right,h+1)\n traversal(root,1)\n res=[]\n for i in l.values():\n res.append(sum(i))\n res.sort(reverse=True)\n if k>len(res):\n return -1\n return res[k-1]\n\n``` | 1 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
Python3 BFS Easy Understanding | kth-largest-sum-in-a-binary-tree | 0 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n dq = collections.deque([root])\n a = []\n lvl = 1\n while dq:\n lvlsum = 0\n for i in range(len(dq)):\n n = dq.popleft()\n lvlsum += n.val\n if n.left: dq.append(n.left)\n if n.right: dq.append(n.right)\n a.append(lvlsum)\n lvl += 1\n a.sort(reverse=True)\n return a[k-1] if len(a) >= k else -1\n``` | 1 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
python/java bfs + heap | kth-largest-sum-in-a-binary-tree | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n minHeap = []\n curLevel = [root]\n while curLevel:\n nextLevel = []\n s = 0\n for node in curLevel:\n if node.left:\n nextLevel.append(node.left)\n if node.right:\n nextLevel.append(node.right)\n s += node.val\n heapq.heappush(minHeap, s)\n if len(minHeap) > k:\n heapq.heappop(minHeap)\n curLevel = nextLevel\n return minHeap[0] if len(minHeap) == k else -1\n\n\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public long kthLargestLevelSum(TreeNode root, int k) {\n Queue<Long> minHeap = new PriorityQueue<>();\n List<TreeNode> curLevel = new ArrayList<>();\n curLevel.add(root);\n while (!curLevel.isEmpty()) {\n List<TreeNode> nextLevel = new ArrayList<>();\n long s = 0;\n for (TreeNode node: curLevel) {\n if (node.left != null) {\n nextLevel.add(node.left);\n }\n if (node.right != null) {\n nextLevel.add(node.right);\n }\n s += node.val;\n }\n minHeap.offer(s);\n if (minHeap.size() > k) {\n minHeap.poll();\n }\n curLevel = nextLevel;\n }\n return minHeap.size() == k ? minHeap.peek() : -1;\n }\n}\n``` | 1 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
Simplest Python level-order | kth-largest-sum-in-a-binary-tree | 0 | 1 | \n# Code\n```\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n a = []\n \n def dfs(node, h):\n if not node: return\n if h == len(a):\n a.append([])\n a[h].append(node.val)\n dfs(node.left, h+1)\n dfs(node.right, h+1)\n \n dfs(root, 0)\n ans = []\n for i in range(len(a)):\n ans.append(sum(a[i]))\n \n return sorted(ans)[-k] if len(ans) >= k else -1\n \n``` | 3 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
Level Traversal || Python || Explained | kth-largest-sum-in-a-binary-tree | 0 | 1 | # Intuition\nPerform Level Traversal and find the value of all nodes values in current level and store in array\nSort the array in reverse order. why?\n`We are asked to return kth largest`\nReturn the val present at k - 1 in array (as array is 0-indexed based)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n levelMap = defaultdict(list)\n def dfs(node, level):\n if not node:\n return levelMap\n levelMap[level].append(node.val)\n dfs(node.left, level + 1)\n dfs(node.right, level + 1)\n dfs(root, 0)\n ans = []\n for i, v in levelMap.items():\n ans.append((sum(v)))\n \n ans = sorted(ans, reverse=True)\n # print(ans)\n if len(ans) < k:\n return -1\n return ans[k - 1]\n \n``` | 1 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
[Python3] dfs | kth-largest-sum-in-a-binary-tree | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e3093716659ec141e47ca013abcf405967592686) for solutions of weekly 335. \n\n**Intuition**\nWe can run either a BFS or DFS to collect sum of node values on each level. Here, I choose to do DFS. \nUpon collecting all such values, I sort the array to retrieve the kth element. \n**Implementation**\n```\nclass Solution:\n def kthLargestLevelSum(self, root: Optional[TreeNode], k: int) -> int:\n vals = []\n stack = [(root, 0)]\n while stack: \n node, i = stack.pop()\n if i == len(vals): vals.append(0)\n vals[i] += node.val \n if node.left: stack.append((node.left, i+1))\n if node.right: stack.append((node.right, i+1))\n return sorted(vals, reverse=True)[k-1] if len(vals) >= k else -1\n```\n**Complexity**\nTime `O(NlogN)`\nSpace `O(N)` | 7 | You are given the `root` of a binary tree and a positive integer `k`.
The **level sum** in the tree is the sum of the values of the nodes that are on the **same** level.
Return _the_ `kth` _**largest** level sum in the tree (not necessarily distinct)_. If there are fewer than `k` levels in the tree, return `-1`.
**Note** that two nodes are on the same level if they have the same distance from the root.
**Example 1:**
**Input:** root = \[5,8,9,2,1,3,7,4,6\], k = 2
**Output:** 13
**Explanation:** The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.
**Example 2:**
**Input:** root = \[1,2,null,3\], k = 1
**Output:** 3
**Explanation:** The largest level sum is 3.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= 106`
* `1 <= k <= n` | null |
[Python] A Short Solution that can pass | split-the-array-to-make-coprime-products | 0 | 1 | > This approach is just for fun, don\'t take it too serious\n> <s>It passes with a time about `9000ms`</s>\n> Now it is strictly TLE\n> View other post for optimal solution\n\n\n# Intuition\n\n1. We want to check the product of left array is coprime with the product of right array.\n2. This requirement is equivalent to all numbers of left array is coprime with all numbers of right array.\n3. This algorithm looks like brutforce $O(n^2)$ at first glance, but a lot of computation is redundant.\n4. It can be optimized by saving a potential answer, which is the the split point that all of number checked before coprime with all of number after the split point.\n5. The potential split point will be moved right monotonically.\n6. If the ans is at the last index, it is not possible, so return -1.\n\n# Complexity\n- Time complexity:$O(n^2)$ `:p` but it barely squeeze through during contest. \n\n- Space complexity:$O(1)$\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n ans = 0\n for i, a in enumerate(nums[:-1]):\n for j, b in enumerate(nums[ans:], ans):\n if gcd(a, b) != 1:\n ans = j\n if i == ans:\n return ans\n return -1\n\n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Prime factorization + merge intervals in Python with explanation | split-the-array-to-make-coprime-products | 0 | 1 | # Intuition\nFor each primes, if we know the first index (left) and last index (right) it can divide nums[index], then we know we cannot cut anywhere within [left, right) (can cut at index right, but cannot cut at left). \n\nThe problem then reduces to, we have a bunch of intervals, we cannot cut anywhere within the intervals, but we want to find the first cut position that doesn\'t fall into any of these intervals. This can be solved by greedy, similar to merge intervals. \n\n# Approach\nPrime factorization for each element (only need to check up to sqrt(n), which reduces factorizaiton for each element to 10^3). Record the first position (left) and last position (right) for each prime.\n\nNote that if we use seive method (which I failed during contest), that is, first to get all the primes that are less than max, it would lead to TLE in python, since there are 8*10^4 primes less than 10^6.\n\nA more efficient way involves only record the right most position for each prime using a map, we then can loop over nums, when we find that the right most index for all the primes we have encountered so far equals the current index in nums, it means we have found the smallest-postioned cut. For code see\nhttps://leetcode.com/problems/split-the-array-to-make-coprime-products/solutions/3258526/record-right-most-index-of-every-prime-factor-into-dictionary/\n\n# Complexity\n- Time complexity:\nsqrt(max) * len(nums), which is bounded by 10^7\n\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n n = len(nums)\n if n == 1:\n return -1\n # prime factorization for each elem\n # dict to record first and last pos for each prime: [left, right)\n mp = defaultdict(list)\n for i, v in enumerate(nums):\n d = 2\n while d * d <= v:\n if v % d == 0:\n # d is a prime factor\n if len(mp[d]) == 0:\n mp[d].append(i)\n elif len(mp[d]) == 1:\n mp[d].append(i)\n else:\n mp[d][1] = i\n v //= d\n while v % d == 0:\n v //= d\n d += 1\n if v > 1: # if remaining > 1, then it is a prime, e.g., 14 = 2 * 7, now v = 7\n if len(mp[v]) == 0:\n mp[v].append(i)\n elif len(mp[v]) == 1:\n mp[v].append(i)\n else:\n mp[v][1] = i\n\n intervals = []\n for k, v in mp.items():\n if len(v) == 2:\n intervals.append(v)\n # first and last index that can divide: cut at first not fine, cut at last is fine\n intervals = sorted(intervals)\n\n if not intervals or intervals[0][0] > 0:\n return 0\n \n mx = intervals[0][1]\n for i in range(1, len(intervals)):\n if intervals[i][0] > mx:\n return mx\n mx = max(mx, intervals[i][1])\n \n if mx < len(nums) - 1:\n return mx\n return -1\n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
It is a meduim question. Easy and Straightforward! | split-the-array-to-make-coprime-products | 0 | 1 | This solution is quite straightforward!\n\n1. Loop `i` from `0` to `n - 2`, `left = nums[i]`\n2. Loop `j` from` i + 1` to `n - 1` and check `gcd(left, nums[j]`. If `i` is the answer, return `i`\n3. Otherwise, If we find `gcd(num[i], nums[j]) > 1`, `i` and `j` should be put on one side for the splitting, then `i` should jump to `j`\n4. return `-1` if we cannot find such a `i`\n\n\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n n = len(nums)\n left = 1\n i = 0 \n while i < n - 1:\n left *= nums[i]\n j = i + 1\n while j < n and math.gcd(left, nums[j]) == 1:\n j += 1\n if j == n:\n return i\n left *= math.prod(nums[i + 1:j]) \n i = j \n return -1\n```\n | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Python | Count Prime Factor | split-the-array-to-make-coprime-products | 0 | 1 | ## For example [4,7,8,15,3,5]\nTotal Prime Count:\n2: 5\n3: 2\n5: 2\n7: 1\n\n### Spilt at index 1\n[4, 7] [8, 15, 3, 5]\nPrefix Prime Count:\n2: 2\n7: 1 (prepare to delet)\n\nSuffix (Total - Prefix) Prime Count:\n2: 3\n3: 2\n5: 2\n\nthen we delet prefix[7] because suffix don\'t any Prime 7 and perfix won\'t add any Prime 7\n\n## Split at index 2\n[4 7 8] [15, 3, 5]\nPrefix Prime Count:\n2: 5 (prepare to delet)\n\nSuffix (Total - Prefix) Prime Count:\n3: 2\n5: 2\n\nafter delet final key 2, len(prefix) == 0\n we get the index to fit the gcd(prefix, suffix) == 1 \n\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n def prime(n):\n divisor = 2\n factors = []\n while divisor * divisor <= n:\n if n % divisor:\n divisor += 1\n else:\n n //= divisor\n factors.append(divisor)\n \n if n > 1:\n factors.append(n)\n return factors\n \n total = Counter()\n for n in nums:\n for f in prime(n):\n total[f] += 1\n \n\n prefix = Counter()\n for i, n in enumerate(nums):\n if i == len(nums) - 1: return -1\n \n for f in prime(n):\n prefix[f] += 1\n total[f] -= 1\n if total[f] == 0:\n del prefix[f]\n if len(prefix) == 0:\n return i\n\n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
[Python 3] Interval Merge | split-the-array-to-make-coprime-products | 0 | 1 | # Intuition\nTrack [leftmost occurence index, rightmost occurence index] of all prime factors for values in nums to obtain an array of intervals. No need to sort, the array should be sorted by left indeices naturally.\n\nBegin merging them. If we found at a certain position merged end < next interval start, we can split at the merged end.\n\n1 is not a prime factor, so need to handle edge case below:\n [2,2,1,1,1,1,1] - Split at index 1.\n\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n @cache\n def get_pm(v):\n res = set()\n if v % 2 == 0:\n res.add(2)\n while v % 2 == 0:\n v = v // 2\n for i in range(3, int(sqrt(v)) + 1, 2):\n if v % i == 0:\n res.add(i)\n while v % i== 0:\n v = v // i\n if v > 2:\n res.add(v)\n return res\n \n n = len(nums)\n if n == 1:\n return -1\n \n arr = []\n idx = Counter()\n for i in range(n):\n tmp = get_pm(nums[i])\n for v in tmp:\n if v not in idx:\n idx[v] = len(arr)\n arr.append([i, i])\n else:\n arr[idx[v]][1] = i\n\n m = len(arr)\n if m:\n ss, ee = arr[0]\n for i in range(1, m):\n s, e = arr[i]\n if s <= ee:\n ee = max(e, ee)\n else:\n return ee\n ma = max(a[1] for a in arr)\n if ma < n - 1:\n return ma\n \n return -1\n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Python || Beats 100 % || Do Dry Run With Pen Paper To Understand 🔥 | split-the-array-to-make-coprime-products | 0 | 1 | # Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n n = len(nums)\n prod = nums[0]\n streak = 0\n prod2 = 1\n for i in range(1, n):\n num = nums[i]\n if gcd(prod, num) == 1:\n streak += 1\n prod2 *= num\n else:\n prod *= prod2\n prod *= num\n streak = 0\n prod2 = 1\n if streak == 0: return -1\n return n - streak - 1\n``` | 2 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Simple and Unique approach in Python!! | split-the-array-to-make-coprime-products | 0 | 1 | # Intuition\n- Let us consider a factor ***P*** to divide both prefix and suffix product.\n- Since P divides prefix product at the present index, **p** will divide the prefix product at all **j > i**.\n- And for all **j > i** that **P** divides the suffix product, the gcd will be greater than or equal to **P**.\n- So just check for when **P** does not divide the suffix product, and update P.\n- If **p == 1** thats you answer.\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n def gcd(a, b):\n a, b = min(a, b), max(a, b)\n \n if b%a == 0:\n return a\n return(gcd(b%a, a))\n \n #suffix product\n pro = 1\n for i in nums:\n pro *= i\n \n\n t = 1 # prefix product\n n = len(nums)\n\n prev_gcd = -1 #gcd of suffix_product\n \n for i in range(n - 1):\n t *= nums[i]\n pro = pro // nums[i]\n \n if prev_gcd == -1:\n prev_gcd = gcd(pro, t)\n \n if pro%prev_gcd == 0:\n continue\n \n prev_gcd = gcd(pro, t)\n \n if prev_gcd == 1:\n return i\n \n return -1\n```\n\n- Edit: Doesnt work after new test cases T_T.. | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Record right-most index of every prime factor into dictionary | split-the-array-to-make-coprime-products | 0 | 1 | # Intuition\nIf arr[0]==2, and if no factor "2" in the rest of the array, then arr[0] is the split point. If arr[5] also has prime factor "2", then it is not possible to split at arr[0\\~4]. The split index must be >=5. Also if all prime factors in arr[0~5] doesn\'t exist after arr[5], then the split point is arr[5], otherwise the split index is >5.\n\n# Approach\nWe record the right-most index of each prime factor into a dictionary. Then start from arr[0], we keep updating the right-most index **scanned so far**. If the current right-most index is "i" itself, then that means "i" is the smallest splitting point.\n\n# Code\n```python\nmx = 10**6\nspf = [i for i in range(mx+1)]\nfor i in range(2,int(math.sqrt(mx))+1):\n if spf[i]==i:\n for j in range(i*i,mx+1,i):\n spf[j]=min(spf[j],i)\ndef getPrimeFactors(x):\n while x!=1:\n yield spf[x]\n x//=spf[x]\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n fac_idx = defaultdict(int)\n for i,v in enumerate(nums):\n for fac in getPrimeFactors(v):\n fac_idx[fac] = i\n right_most = 0\n for i in range(len(nums)-1):\n for fac in getPrimeFactors(nums[i]):\n right_most = max(right_most,fac_idx[fac])\n if right_most==i:\n return i\n return -1\n``` | 31 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
[Python3] check common factors | split-the-array-to-make-coprime-products | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e3093716659ec141e47ca013abcf405967592686) for solutions of weekly 335. \n\n**Intuition**\nHere, we cannot actually compute the products as they can become astronomically large. Rather, we can collect prime factors and check if at any index no common prime factors were found in the prefix and suffix arrays. \n**Implementation**\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n freq = Counter()\n for x in nums: \n for p in range(2, isqrt(x)+1): \n while x % p == 0: \n freq[p] += 1\n x //= p \n if x > 1: freq[x] += 1\n ovlp = 0 \n prefix = Counter()\n for i, x in enumerate(nums): \n if i <= len(nums)-2: \n for p in range(2, isqrt(x)+1): \n if x % p == 0: \n if prefix[p] == 0: ovlp += 1\n while x % p == 0: \n prefix[p] += 1\n x //= p \n if prefix[p] == freq[p]: ovlp -= 1\n if x > 1: \n if prefix[x] == 0: ovlp += 1\n prefix[x] += 1\n if prefix[x] == freq[x]: ovlp -= 1\n if not ovlp: return i \n return -1 \n```\n**Complexity**\nTime `O(N\u221AN)`\nSpace `O(N)` | 11 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Oct., Day 6 - factors of prefix sum and suffix sum | split-the-array-to-make-coprime-products | 0 | 1 | # Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n n = len(nums)\n def getFactors(num):\n res = []\n for f in range(2, int(sqrt(num))+1):\n if num%f == 0:\n res.append(f)\n while num%f == 0:\n num //= f\n if num > 1:\n res.append(num)\n return res\n\n suffix = defaultdict(int)\n factors = []\n for num in nums:\n facs = getFactors(num)\n for x in facs:\n suffix[x] += 1\n factors.append(facs)\n\n prefix = defaultdict(int)\n for i in range(n-1): # check split at i\n if nums[i] == 1 and not prefix: return i\n \n for x in factors[i]:\n prefix[x] += 1\n suffix[x] -= 1\n\n for x in factors[i]:\n if suffix[x] == 0: # doesn\'t share factor x in both prefix and suffix anymore\n del prefix[x]\n if not prefix: return i\n return -1\n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
Python3 workable greedy approach | split-the-array-to-make-coprime-products | 0 | 1 | *Disclaimer: For what follows, `n = len(nums)`*\n\n# Complexity\n\n- **Time complexity**: Worst case `O(n ** 2)` (but somehow still passed).\n\n- **Space complexity**: If we regard the number of prime factors a number has is `O(1)` (as each number is bounded above by `10 ** 6`), then SC is `O(n)`.\n\n# Code\n```\nclass Solution:\n def findValidSplit(self, nums: List[int]) -> int:\n N = len(nums)\n if N == 1:\n return -1\n facs = [self.getPrimeFactors(num) for num in nums]\n i = 0\n pref = facs[i]\n used = set()\n while pref:\n p = pref.pop()\n used.add(p)\n j = N - 1\n while j > i:\n if p in facs[j]:\n if j == N - 1:\n return -1\n for k in range(i + 1, j + 1):\n pref |= facs[k]\n i = j\n pref -= used\n break\n j -= 1\n return i\n\n def getPrimeFactors(self, num):\n res = set()\n for i in range(2, 1002):\n if num == 1:\n return res\n if num % i == 0:\n res.add(i)\n while num % i == 0:\n num = num // i\n continue\n if i * i > num:\n res.add(num)\n return res\n\n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`.
A **split** at an index `i` where `0 <= i <= n - 2` is called **valid** if the product of the first `i + 1` elements and the product of the remaining elements are coprime.
* For example, if `nums = [2, 3, 3]`, then a split at the index `i = 0` is valid because `2` and `9` are coprime, while a split at the index `i = 1` is not valid because `6` and `3` are not coprime. A split at the index `i = 2` is not valid because `i == n - 1`.
Return _the smallest index_ `i` _at which the array can be split validly or_ `-1` _if there is no such split_.
Two values `val1` and `val2` are coprime if `gcd(val1, val2) == 1` where `gcd(val1, val2)` is the greatest common divisor of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[4,7,8,15,3,5\]
**Output:** 2
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
The only valid split is at index 2.
**Example 2:**
**Input:** nums = \[4,7,15,8,3,5\]
**Output:** -1
**Explanation:** The table above shows the values of the product of the first i + 1 elements, the remaining elements, and their gcd at each index i.
There is no valid split.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 104`
* `1 <= nums[i] <= 106` | null |
✔️ Python3 Solution | O(n * target) | 100% faster | DP | number-of-ways-to-earn-points | 0 | 1 | # Complexity\n- Time complexity: $$O(n * target)$$\n- Space complexity: $$O(target)$$\n\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, T, A):\n dp = [1] + [0] * T\n mod = 10 ** 9 + 7\n for c, m in A:\n for i in range(m, T + 1):\n dp[i] += dp[i - m]\n for i in range(T, (c + 1) * m - 1, -1):\n dp[i] = (dp[i] - dp[i - (c + 1) * m]) % mod\n return dp[-1] % mod\n``` | 1 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Python | Simple Top Down DP | number-of-ways-to-earn-points | 0 | 1 | # Code\n```\nfrom functools import cache\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n MOD = 10**9 + 7\n n = len(types)\n @cache\n def dfs(i, prev):\n if prev > target: return 0\n if prev == target: return 1\n if i == n: return 0\n count, mark = types[i]\n res = 0\n for j in range(count + 1):\n res = (res + dfs(i+1, prev + j*mark)) % MOD\n return res\n return dfs(0, 0)\n \n \n \n``` | 1 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
[C++, Java, Python3] Short Top Down DP explained | number-of-ways-to-earn-points | 1 | 1 | # Intuition\nSince the constraints are small we can explore a DP approach. Start with the `target` and then subtract combinations of question `types` from it. Our function definiton of the recursive function will have 2 variables, (target, i). `target` signifies the remaining `target` and `i` siginifies the ith question type.\n\n# Approach\nThe base cases for the `dfs` function are:\n* If the remaining `target` is 0, then return 1 as one way to reach the target has been found.\n* If the index `i` is greater than or equal to the number of `types` of questions or `target` is less than 0, then return 0 as no more ways to reach the `target` can be found.\n\nIn the recursive case, the `dfs` function calculates the sum of the number of ways to reach the target by considering different numbers of questions of the current type. It does this by iterating over j from 0 to the maximum number of questions of the current type (types[i][0]) and calling the `dfs` function with the updated `target` value `(target - j * types[i][1])` and the index of the next type of question `(i + 1)`. `types[i][1]` is the `value` of the ith question\n\nThe final result is the modulo `10^9 + 7` of the total number of ways to reach the target found by the `dfs` function.\n\nThe solution uses memoization to avoid redundant calculations and returns the answer modulo `10^9 + 7` to prevent integer overflow.\n\n\n# Complexity\n- Time complexity: `O(target * len(types) * max(count))`\n\n- Space complexity: `O(target * len(types))`\n\n# Code\n**Python3**:\n```\ndef waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n @cache\n def dfs(i, target):\n if target == 0: return 1\n if i >= len(types) or target < 0: return 0\n return sum(dfs(i + 1, target - j * types[i][1]) for j in range(types[i][0] + 1)) % 1000000007\n return dfs(0, target)\n```\n*Just for fun*\n```\ndef waysToReachTarget(self, target, T, mod = 1000000007):\n return (lambda dp: dp(dp, 0, target))(lru_cache(maxsize=None)(lambda f, i, t: 1 if t == 0 else 0 if i >= len(T) or t < 0 else sum(f(f, i+1, t-j*T[i][1]) for j in range(T[i][0]+1)) % mod))\n```\n\n**C++**:\n```\nint cache[1001][51] = {};\nint waysToReachTarget(int target, vector<vector<int>>& types) {\n memset(cache, -1, sizeof(cache)); // initialize cache with -1\n function<int(int, int)> dfs = [&](int i, int target) {\n if (target == 0) return 1;\n if (i >= types.size() || target < 0) return 0;\n if (cache[target][i] != -1) return cache[target][i];\n int ans = 0;\n for (int j = 0; j <= types[i][0]; j++)\n ans = (ans + dfs(i + 1, target - j * types[i][1])) % 1000000007;\n return cache[target][i] = ans;\n };\n return dfs(0, target);\n}\n```\n\n**Java**:\n```\nint[][] cache;\npublic int waysToReachTarget(int target, int[][] types) {\n cache = new int[target + 1][types.length + 1];\n Arrays.stream(cache).forEach(a -> Arrays.fill(a, -1)); // init cache with -1\n return dfs(0, target, types);\n}\nprivate int dfs(int i, int target, int[][] types) {\n if (target == 0) return 1;\n if (i >= types.length || target < 0) return 0;\n if (cache[target][i] != -1) return cache[target][i];\n int ans = 0;\n for (int j = 0; j <= types[i][0]; j++)\n ans = (ans + dfs(i + 1, target - j * types[i][1], types)) % 1000000007;\n cache[target][i] = ans;\n return ans;\n}\n``` | 31 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
python + dp explained | number-of-ways-to-earn-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI read some posts and had a hard time understanding some of the posted solutions. Then I figured out they are space optimized (if I am not understanding them incorrectly). I used a 2d dp here to kinda unfolded the things and to make it more easier to understand\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSay we have ``m`` types and the target is ``n``, initialize a 2d dp array of ``(m+1) * (n+1)``. ``dp[i][j]`` denotes the number of solutions to hit ``target = j`` using at most the first ``i`` types.\n\nSo at row ``0``, no question is available and we have exactly ``1`` way to hit ``target = 0`` and ``0`` way to hit any positve target. \n```\ndp[0][j] = 0 if j != 0 else 1\n```\n\nGiven ``dp[i][:]``, if we denote the number of available type ``i+1`` question by ``c``, the number of used question here can be any value between ``[0, c]`` and thus \n```\nfor j in range(target+1):\n for k in range(c+1):\n if j + k*v > target: break \n dp[i+1][j+k*v] = dp[i+1][j+k*v] + dp[i][j]\n\n```\n\nAnd it is easy to prove that no duplicate solutions are counted here (denoted by H). Suppose H is true for ``dp[i][:]`` (and ``dp[j][:]`` for ``j<i``). If there is a solution counted for multiploe times for ``dp[i+1][:]``, for example, it is counted in ``dp[i+1][j1]`` and ``do[i+1][j2]`` and ``j1 != j2``. And suppose for this solution (or trajectory), we used ``x`` type ``i+1`` quesitons, then there must be duplicate solutions (trajectories) in both ``dp[i][j1-x]`` and ``dp[i][j2-x]``, which violates our intial assumption. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(m\\*n\\*c)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m\\*n)\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n dp = [[0]*(target+1) for _ in range(len(types) + 1)]\n dp[0][0] = 1\n for i in range(len(types)):\n c, v = types[i]\n for j in range(target+1):\n for k in range(c+1):\n if j + k*v > target: break\n dp[i+1][j+k*v] = dp[i+1][j+k*v] + dp[i][j]\n return dp[-1][-1] % (10**9 + 7)\n``` | 1 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Python memoization | number-of-ways-to-earn-points | 0 | 1 | ```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n n = len(types)\n \n @lru_cache(None)\n def dfs(i, total):\n if total == target:\n return 1\n if i == n or total > target:\n return 0\n \n res = 0\n for j in range(types[i][0]):\n next_total = total + types[i][1] * (j + 1)\n if j == 0:\n res += dfs(i + 1, total) # cover case for no marks\n res += dfs(i + 1, next_total)\n \n return res\n \n return dfs(0, 0) % (10**9 + 7)\n``` | 2 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Simple Solution || Python | number-of-ways-to-earn-points | 0 | 1 | # Complexity\n- Time complexity:\n$$O(n * target * count)$$ \n\n\n\n- Space complexity:\n$$O(target)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n mod = 10**9 + 7\n dp = [0]*(target + 1)\n dp[0] = 1\n\n for count, mark in types:\n # Repeat in reverse order to avoid duplication \n for i in range(target, -1, -1):\n for j in range(1, count + 1):\n if i - mark*j >= 0:\n dp[i] += dp[i - mark*j]\n dp[i] %= mod\n \n return dp[target]\n``` | 3 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
[Python3] bottom-up dp | number-of-ways-to-earn-points | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e3093716659ec141e47ca013abcf405967592686) for solutions of weekly 335. \n\n**Intuition**\nDefine `dp[i][j]` as the number of ways to earn `i` points using questions starting from `j` forward. \n* The recurrence relationship is `dp[i][j] = dp[i-x*m][j+1]` for all `x = 0, 1, 2, ..., c` and `i-x*m >= 0` where `c` is count of questions of type `j` and `m` is mark of questions of type `j`. \n* What\'s asked is to compute `dp[target][0]`. \n\n**Implementation**\n```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n n = len(types)\n dp = [[0]*(1+n) for _ in range(target+1)]\n for j in range(n+1): dp[0][j] = 1\n for i in range(1, target+1): \n for j in range(n-1, -1, -1): \n c, m = types[j]\n for x in range(c+1): \n if i - x*m >= 0: dp[i][j] += dp[i-x*m][j+1]\n else: break \n dp[i][j] %= 1_000_000_007\n return dp[target][0]\n```\n**Complexity**\nTime `O(MN)`\nSpace `O(MN)` | 3 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Backtracking + Memoization = DP (😃) | number-of-ways-to-earn-points | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, target: int, arr: List[List[int]]) -> int:\n n = len(arr)\n mod = 10**9+7\n dp = {}\n def fun(ind,curr):\n if curr == target:\n return 1\n ans = 0\n if ind == n or curr>target:\n return ans\n if (ind,curr) in dp:\n return dp[(ind,curr)]\n c,m = arr[ind]\n for i in range(c+1):\n ans=(ans%mod + fun(ind+1,curr+(i*m))%mod)%mod\n dp[(ind,curr)] = ans\n return ans\n return fun(0,0)\n\n \n``` | 1 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Python || Recursion || Memoization | number-of-ways-to-earn-points | 0 | 1 | # Intuition\nThe idea is to consider 2 cases - one in which we include the current question and second if we don\'t include the current solution. \n\nIf we include the current solution, we can do it count times, and for each of these times we have to check for other ways in which we can reach the target. \n\nFor example for [[6,1], [2,2]] target=6, we include 1 mark question 1 time, and then check if we can reach remaining target 5 using [2,2]. Then we include it 2 times and check if we can reach remaining target 4 using [2,2].\n\n# Approach\nI wrote a plain recursion and optimized it by using memoization so that we don\'t solve the same problem again.\n\n\n\n# Code\n```\nmemo = None\n\nclass Solution:\n\n def waysRec(self, i, types, target):\n global memo \n\n if target == 0:\n return 1\n \n if i>=len(types) or target<0:\n return 0\n \n if memo[i][target]!=-1:\n return memo[i][target]\n\n count,marks = types[i]\n\n incl_ways = 0\n excl_ways = 0\n\n for j in range(1, count+1):\n curr_sum = target - (j*marks)\n\n if curr_sum<0:\n break\n \n incl_ways += self.waysRec(i+1, types, curr_sum)\n\n excl_ways = self.waysRec(i+1,types, target)\n\n memo[i][target]= (incl_ways+excl_ways)%1000000007\n return memo[i][target]\n\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n global memo\n memo = [[-1 for i in range(target+1)] for j in range(len(types))]\n return self.waysRec(0,types, target)\n \n``` | 0 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
python dp top down | number-of-ways-to-earn-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n mod = 10**9 + 7\n @functools.lru_cache(None)\n def dp(i, p):\n if p == 0:\n return 1\n elif p < 0:\n return 0\n\n if i == len(types):\n return 0\n ans = 0\n for n in range(types[i][0]+1):\n ans += dp(i+1, p-types[i][1]*n)\n \n \n return ans\n return dp(0, target) % mod\n\n``` | 0 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
python3 solution | number-of-ways-to-earn-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def waysToReachTarget(self, target: int, types: List[List[int]]) -> int:\n @lru_cache(None)\n def dfs(i,t):\n if t == target:\n return 1\n if t > target or i >= len(types):\n return 0\n res = 0\n for j in range(types[i][0]+1):\n res+=(dfs(i+1,t + j*types[i][1]))\n return res%(10**9+7)\n return dfs(0,0)\n \n``` | 0 | There is a test that has `n` types of questions. You are given an integer `target` and a **0-indexed** 2D integer array `types` where `types[i] = [counti, marksi]` indicates that there are `counti` questions of the `ith` type, and each one of them is worth `marksi` points.
Return _the number of ways you can earn **exactly**_ `target` _points in the exam_. Since the answer may be too large, return it **modulo** `109 + 7`.
**Note** that questions of the same type are indistinguishable.
* For example, if there are `3` questions of the same type, then solving the `1st` and `2nd` questions is the same as solving the `1st` and `3rd` questions, or the `2nd` and `3rd` questions.
**Example 1:**
**Input:** target = 6, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 7
**Explanation:** You can earn 6 points in one of the seven ways:
- Solve 6 questions of the 0th type: 1 + 1 + 1 + 1 + 1 + 1 = 6
- Solve 4 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 1 + 2 = 6
- Solve 2 questions of the 0th type and 2 questions of the 1st type: 1 + 1 + 2 + 2 = 6
- Solve 3 questions of the 0th type and 1 question of the 2nd type: 1 + 1 + 1 + 3 = 6
- Solve 1 question of the 0th type, 1 question of the 1st type and 1 question of the 2nd type: 1 + 2 + 3 = 6
- Solve 3 questions of the 1st type: 2 + 2 + 2 = 6
- Solve 2 questions of the 2nd type: 3 + 3 = 6
**Example 2:**
**Input:** target = 5, types = \[\[50,1\],\[50,2\],\[50,5\]\]
**Output:** 4
**Explanation:** You can earn 5 points in one of the four ways:
- Solve 5 questions of the 0th type: 1 + 1 + 1 + 1 + 1 = 5
- Solve 3 questions of the 0th type and 1 question of the 1st type: 1 + 1 + 1 + 2 = 5
- Solve 1 questions of the 0th type and 2 questions of the 1st type: 1 + 2 + 2 = 5
- Solve 1 question of the 2nd type: 5
**Example 3:**
**Input:** target = 18, types = \[\[6,1\],\[3,2\],\[2,3\]\]
**Output:** 1
**Explanation:** You can only earn 18 points by answering all questions.
**Constraints:**
* `1 <= target <= 1000`
* `n == types.length`
* `1 <= n <= 50`
* `types[i].length == 2`
* `1 <= counti, marksi <= 50` | null |
Easiest Python Solution | count-the-number-of-vowel-strings-in-range | 0 | 1 | # Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n v = [\'a\', \'e\', \'i\', \'o\', \'u\']\n ans = 0\n for i in words[left : right + 1]:\n if i[0] in v and i[-1] in v:\n ans += 1\n return ans\n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Simple python iterative approach | count-the-number-of-vowel-strings-in-range | 0 | 1 | # Intuition\nThis a simple string problem. We can solve it simple iterative approach.\n\n# Approach\nIterative approach.\n\n# Complexity\n- Time complexity: $$O(n)$$ - Linear Time\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ - Constant Time\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isVowel(self, char):\n return True if char in (\'A\', \'E\', \'I\', \'O\', \'U\', \'a\', \'e\', \'i\', \'o\', \'u\') else False\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n count = 0\n for i in range(left, right+1):\n wordLen = len(words[i])\n if self.isVowel(words[i][0]) and self.isVowel(words[i][-1]):\n count += 1 \n return count\n\n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Easy Solution Using For Loop in Python | count-the-number-of-vowel-strings-in-range | 0 | 1 | \n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n d=["a","e","i","o","u"]\n c=0\n for i in range(left,right+1):\n if(words[i][0] in d and words[i][-1] in d):\n c=c+1\n return c\n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Easy solution using python3 | count-the-number-of-vowel-strings-in-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\']\n count = 0\n for i in range(left, right+1):\n if words[i][0] in vowels and words[i][-1] in vowels:\n print(words[i],count)\n count += 1\n\n return count\n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Python3 Very Simple Solution | count-the-number-of-vowel-strings-in-range | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n ans=0\n vol="aeiou"\n\n for i in range(left,right+1):\n if words[i][0] in vol and words[i][-1] in vol:\n ans+=1\n return ans \n \n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Simple python3 O(n) solution | count-the-number-of-vowel-strings-in-range | 0 | 1 | \n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n res = 0\n for i in range(left, right + 1):\n if words[i][0] in \'aeiou\' and words[i][-1] in \'aeiou\':\n res += 1\n return res\n```\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Python3 Solution | count-the-number-of-vowel-strings-in-range | 0 | 1 | \n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n vowels=\'aeiouAEIOU\'\n count=0\n for i in range(left,right+1):\n if words[i][0] in vowels and words[i][-1] in vowels:\n count+=1\n\n return count \n``` | 2 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
2586: Solution with step by step explanation | count-the-number-of-vowel-strings-in-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function vowelStrings that takes a list of strings words and two integers left and right as input, and returns an integer.\n2. Initialize a variable vowels to the string \'aeiouAEIOU\', which contains all the vowels.\n3. Initialize a variable count to 0.\n4. Loop through the indices from left to right inclusive:\na. If the first character of the current word is a vowel and the last character of the current word is a vowel, increment count by 1.\n5. Return count.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n vowels = \'aeiouAEIOU\'\n count = 0\n for i in range(left, right+1):\n if words[i][0] in vowels and words[i][-1] in vowels:\n count += 1\n return count\n\n``` | 12 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Simple solution in Python3 | count-the-number-of-vowel-strings-in-range | 0 | 1 | # Intuition\nHere we have:\n- `words` list, `left` and `right` integers\n- we should find all of the **vowel** strings for `[left, right]` interval from `words`\n\n**Vowel strings** have the starting and the ending character as **vowel**. \n\n# Approach\n1. define `check` function to check if a character is a **vowel**\n2. declare `ans`\n3. iterate over `[left, right]` and find these strings with `check`\n4. return `ans`\n\n# Complexity\n- Time complexity: **O(N)**, to iterate over `words`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space.\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: list[str], left: int, right: int) -> int:\n def isVowelString(str):\n check = lambda char: char == \'a\' or char == \'e\' or char == \'i\' or char == \'o\' or char == \'u\'\n\n return check(str[0]) and check(str[-1])\n\n ans = 0\n\n for i in range(left, right + 1):\n ans += int(isVowelString(words[i]))\n\n return ans \n``` | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Easy to Understand Python Solution || Beats 90% of other solutions | count-the-number-of-vowel-strings-in-range | 0 | 1 | Please Upvote if you like it.\n```\nclass Solution:\n def vowelStrings(self, words: List[str], left: int, right: int) -> int:\n a = ["a","e","i","o","u"]\n count = 0\n for i in range(left,right+1):\n temp= words[i]\n if temp[0] in a and temp[-1] in a:\n count += 1\n return count | 1 | You are given a **0-indexed** array of string `words` and two integers `left` and `right`.
A string is called a **vowel string** if it starts with a vowel character and ends with a vowel character where vowel characters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
Return _the number of vowel strings_ `words[i]` _where_ `i` _belongs to the inclusive range_ `[left, right]`.
**Example 1:**
**Input:** words = \[ "are ", "amy ", "u "\], left = 0, right = 2
**Output:** 2
**Explanation:**
- "are " is a vowel string because it starts with 'a' and ends with 'e'.
- "amy " is not a vowel string because it does not end with a vowel.
- "u " is a vowel string because it starts with 'u' and ends with 'u'.
The number of vowel strings in the mentioned range is 2.
**Example 2:**
**Input:** words = \[ "hey ", "aeo ", "mu ", "ooo ", "artro "\], left = 1, right = 4
**Output:** 3
**Explanation:**
- "aeo " is a vowel string because it starts with 'a' and ends with 'o'.
- "mu " is not a vowel string because it does not start with a vowel.
- "ooo " is a vowel string because it starts with 'o' and ends with 'o'.
- "artro " is a vowel string because it starts with 'a' and ends with 'o'.
The number of vowel strings in the mentioned range is 3.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 10`
* `words[i]` consists of only lowercase English letters.
* `0 <= left <= right < words.length` | null |
Python 1 line - Easy | rearrange-array-to-maximize-prefix-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe must first put the positive numbers then zeros then negative numbers to get the most positives numbers in the accumulation\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst reverse sort the nums\nthen accumulate\nthen count the number of positive ones\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlog(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n return sum(x > 0 for x in accumulate(sorted(nums, reverse=True)))\n``` | 1 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
[Python] Count the number of negative numbers and zeros; Explained. | rearrange-array-to-maximize-prefix-score | 0 | 1 | We can count the number of negative numbers and zeros in the list.\n\nIf the sum of all the positive numbers is larger than 0 (i.e., we have positive prefix sum), we can first append zeros to the arranged list starting with all the positive numbers. After that, we append the negative numbers from the smallest so that we can get the longest prefix sum list.\n\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n negative_nums = []\n score, psum, zeros = 0, 0, 0\n for num in nums:\n if num > 0:\n score += 1\n psum += num\n elif num == 0:\n zeros += 1\n else:\n heapq.heappush(negative_nums, -num)\n \n if psum > 0:\n score += zeros\n \n while negative_nums:\n n = heapq.heappop(negative_nums)\n psum = psum - n\n if psum > 0:\n score += 1\n else:\n break\n return score\n``` | 1 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
Simple python3 O(nlog(n)) solution | rearrange-array-to-maximize-prefix-score | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n s = 0\n for i, n in enumerate(nums):\n s += n\n if s <= 0:\n return i\n return len(nums)\n \n```\n\n# Complexity\n- Time complexity: O(nlog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 1 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
Python simple solution | rearrange-array-to-maximize-prefix-score | 0 | 1 | # Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n pre = 0\n output = 0\n for i in range(len(nums)):\n pre += nums[i]\n if pre > 0:\n output += 1\n else:\n break\n \n return output\n``` | 1 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
Prefix Sum of Sorted Array | rearrange-array-to-maximize-prefix-score | 0 | 1 | **Python 3**\n```python\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n return sum(n > 0 for n in accumulate(sorted(nums, reverse=True)))\n```\n**C++**\n```cpp\nint maxScore(vector<int>& n) {\n sort(begin(n), end(n), greater<>());\n for (long long sum = 0, i = 0; i <= n.size(); sum += n[i++])\n if (i == n.size() || sum + n[i] <= 0)\n return i;\n return 0;\n}\n``` | 11 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
Easy PYTHON3 solution || O(nlogn) | rearrange-array-to-maximize-prefix-score | 0 | 1 | Simple use the sort function or use the 2 pointer approach to bring all the positive elements of the array in the front and pushing all the negative elementsof the array to the back.\n\n```\ndef maxScore(self, nums: List[int]) -> int:\n \n nums.sort(reverse =True)\n \n prefix = [nums[0]]\n \n for i in range(1,len(nums)):\n prefix.append(prefix[-1] + nums[i])\n \n count = 0\n \n for i in prefix:\n if i > 0:\n count +=1\n \n return count\n```\n\nediting the solution a bit and decreasing one for loop:\n```\n\t\tnums.sort(reverse =True)\n \n\t\tprefix = [nums[0]]\n count = 0\n count +=1 if prefix[-1] > 0 else 0\n \n for i in range(1,len(nums)):\n prefix.append(prefix[-1] + nums[i])\n if prefix[-1] > 0:\n count +=1\n \n return count\n``` | 1 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
2587: Solution with step by step explanation | rearrange-array-to-maximize-prefix-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function maxScore that takes a list of integers nums as input and returns an integer.\n2. Sort the input list nums in descending order.\n3. Initialize a list prefix_sums with a single element 0.\n4. Loop through the sorted list nums and compute the prefix sums, appending each sum to the list prefix_sums.\n5. Initialize a variable max_score to 0.\n6. Loop through the indices from 1 to the length of prefix_sums:\na. If the current prefix sum is greater than 0, update max_score to the current index.\n7. Return max_score.\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\nO(n),\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n prefix_sums = [0]\n for num in nums:\n prefix_sums.append(prefix_sums[-1] + num)\n max_score = 0\n for i in range(1, len(prefix_sums)):\n if prefix_sums[i] > 0:\n max_score = i\n return max_score\n\n``` | 9 | You are given a **0-indexed** integer array `nums`. You can rearrange the elements of `nums` to **any order** (including the given order).
Let `prefix` be the array containing the prefix sums of `nums` after rearranging it. In other words, `prefix[i]` is the sum of the elements from `0` to `i` in `nums` after rearranging it. The **score** of `nums` is the number of positive integers in the array `prefix`.
Return _the maximum score you can achieve_.
**Example 1:**
**Input:** nums = \[2,-1,0,1,-3,3,-3\]
**Output:** 6
**Explanation:** We can rearrange the array into nums = \[2,3,1,-1,-3,0,-3\].
prefix = \[2,5,6,5,2,2,-1\], so the score is 6.
It can be shown that 6 is the maximum score we can obtain.
**Example 2:**
**Input:** nums = \[-2,-3,0\]
**Output:** 0
**Explanation:** Any rearrangement of the array will result in a score of 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `-106 <= nums[i] <= 106` | null |
Python 3 || 2 lines, Counter and accumulate() || T/M: 975 ms / 36 MB | count-the-number-of-beautiful-subarrays | 0 | 1 | ```\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n \n ctr = Counter(accumulate(nums, xor, initial = 0))\n\n return sum (n*(n-1) for n in ctr.values())//2\n\n```\n[https://leetcode.com/problems/count-the-number-of-beautiful-subarrays/submissions/913653762/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*NlogN*) and space complexity is *O*(*N*).\n | 3 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
2588: Solution with step by step explanation | count-the-number-of-beautiful-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function beautifulSubarrays that takes a list of integers nums as input and returns an integer.\n2. Initialize a variable res to 0 to keep track of the number of beautiful subarrays.\n3. Get the length of the input list nums and store it in a variable n.\n4. Initialize a list pre_xor with n+1 elements and fill it with zeros.\n5. Set the first element of pre_xor to 0.\n6. Initialize a list cnt with (1<<20) elements and fill it with zeros. This list will be used to count the number of occurrences of each prefix xor value.\n7. Set the first element of cnt to 1, since the empty subarray has a prefix xor of 0.\n8. Loop through the indices i in the range [1, n]:\n 1. Compute the prefix xor value of the subarray nums[0:i] and store it in pre_xor[i].\n 2. Update the res variable by adding the value of cnt[pre_xor[i]].\n 3. Increment the value of cnt[pre_xor[i]].\n9. Return the value of res.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n res = 0\n n = len(nums)\n pre_xor = [0] * (n+1)\n pre_xor[0]=0\n cnt = [0]*(1<<20)\n cnt[0] = 1\n \n for i in range(1,n+1):\n pre_xor[i] = pre_xor[i-1] ^ nums[i-1]\n res += cnt[pre_xor[i]]\n cnt[pre_xor[i]] += 1\n\n return res\n\n``` | 9 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Simple python3 prefix dictionary solution | count-the-number-of-beautiful-subarrays | 0 | 1 | \n# Code\n```\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n prefixDict = defaultdict(list)\n prefixDict[0].append(-1)\n prefix = 0\n res = 0\n for i, num in enumerate(nums):\n p = 1\n while num > 0:\n if num % 2 == 1:\n if (prefix // p) % 2 == 1:\n prefix -= p\n else:\n prefix += p\n p *= 2\n num = num // 2\n res += len(prefixDict[prefix])\n prefixDict[prefix].append(i)\n return res\n \n```\n\n\n# Complexity\n- Time complexity: O(N * K)\n- Space complexity: O(N)\nN: length of nums, K: log(maximum number)\n | 1 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Go/Python O(n) time | O(1) space | count-the-number-of-beautiful-subarrays | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc beautifulSubarrays(nums []int) int64 {\n counter := make(map[int]int)\n counter[0] = 1\n answer := 0\n xor := 0\n for _,num := range(nums){\n xor^=num\n answer+=counter[xor]\n counter[xor]+=1\n }\n return int64(answer)\n}\n```\n```python []\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n counter = defaultdict(int)\n counter[0] = 1\n answer = 0\n xor = 0\n for num in nums:\n xor^=num\n answer+=counter[xor]\n counter[xor]+=1\n return answer\n``` | 2 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Can someone explain why [0,0] returns 3? | count-the-number-of-beautiful-subarrays | 0 | 1 | Since the i,j should be different, isn\'t the answer 1 instead of 3? | 3 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Count subarrays with zero XOR | count-the-number-of-beautiful-subarrays | 0 | 1 | \n\nBits in a beautiful subarray should appear even number of times. \n \nTherefore, XOR of elements of a beautiful subarray should be zero.\n \nCounting subarrays with a specific XOR in O(n) is a classic problem (you can find it by the name).\n\n**Python 3**\n```python\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n cnt = Counter({0: 1})\n for val in accumulate(nums, operator.xor):\n cnt[val] += 1\n return sum(v * (v - 1) // 2 for v in cnt.values())\n```\n\n**C++**\n```cpp\nlong long beautifulSubarrays(vector<int>& nums) {\n unordered_map<int, int> cnt{{0, 1}};\n partial_sum(begin(nums), end(nums), begin(nums), bit_xor<>());\n return accumulate(begin(nums), end(nums), 0LL, [&](long long s, int n){ return s + cnt[n]++; });\n} | 33 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Python | Easy to Understand | Beats 72% | O(n) | count-the-number-of-beautiful-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAn array is beautiful if xor sum of the array is zero\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe store all the encountered xor sums in a hash map. Whenever we encounter a xor sum which is present in the map, it means that the xor sum between the first encounter and now is zero. We just keep track of the count afterwards\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ for te xor sum mapxo\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n xorMap, xorSum, count = defaultdict(int), 0, 0\n xorMap[0] = 1\n for idx in range(len(nums)):\n xorSum ^= nums[idx]\n if xorSum in xorMap:\n count += xorMap[xorSum]\n xorMap[xorSum] += 1\n return count\n``` | 1 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
[Python3] | Count Subarrays with Zero Xor | count-the-number-of-beautiful-subarrays | 0 | 1 | ```\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n hmap = {0:1}\n x,ans = 0,0\n for i in nums:\n x ^= i\n if x in hmap:\n ans += hmap[x]\n hmap[x] += 1\n else:\n hmap[x] = 1\n return ans\n``` | 1 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Beats 100% | count-the-number-of-beautiful-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing Hashing\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStoring previous xor\'s with their count in hash\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(NlogN) - once iterating over the array and check for the x = xr^k in hash each time which might take logN time. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def beautifulSubarrays(self, arr: List[int]) -> int:\n xr = 0\n cnt = 0\n k =0\n hash = {0: 1}\n for i in range(len(arr)):\n xr = xr ^ arr[i]\n # looking for k\n x = xr ^ k\n cnt += hash.get(x, 0)\n if xr not in hash:\n hash[xr] = 1\n else:\n hash[xr] += 1\n return cnt\n\n\n\n\n\n\n``` | 0 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Python Solution with Intuition - Hash Table (Beats 95.98% in Time and 90.63% in Memory) | count-the-number-of-beautiful-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first step is to realize that **beautiful subarrays actually means the XOR of all the elements are `0`**. In each operation, we find a `1` bit in two elements and cancel them out. This is exactly what `XOR` does. If the `XOR` of two operations does not equal to `1`, there must be some bit `1` that cannot been cancelled out. Therefore, all we have to do is to find all the subarrays in `nums` that have accumulated `XOR` equal to `0`.\n\nThe brute-force solution resulting in $O(n^2)$ time leads to TLE. Thus, we need a more efficient solution. In summary, almost all the $O(n)$ algorithms for subarray problems fall in the two categories:\n- Sliding window\n- Prefix "sum" and hash table ("sum" can be replaced by other operations)\n\nIn this specific problem, sliding window does not apply because `XOR` is not *monotonic*, i.e., removing/adding elements do not certainly lead to a decrease/increase of `XOR`. We need to use prefix `XOR` and hash table.\n\n> If a value occurs twice (e.g., `i` and `j`) in `prefix`, that means `nums[i:j]` is a beautiful subarray.\n\nThe last thing to consider is how to contruct the *hash table*. Since we are only interested in the **counts** of beautiful arrays, we only need to store the frequency of each prefix XOR. When a value occurs `c` times in `prefix`, we can simply calculates `c choose 2`, i.e., $(c-1)c \\over 2$ to derive the number of beautiful subarrays.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Calculate the prefix `XOR` array `prefix`.\n2. Count the frequency of each value in `prefix`.\n3. For each value with frequency $> 1$, accumulate $(c-1)c \\over 2$ beautiful subarrays.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3\nfrom collections import Counter\n\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n prefix = [0]\n for v in nums:\n prefix.append(prefix[-1] ^ v)\n \n prefix_counter = Counter(prefix)\n\n cnt = 0\n for i, c in prefix_counter.items():\n if c > 1:\n cnt += (c - 1) * c // 2\n return cnt\n\n``` | 0 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Prefix Sum | count-the-number-of-beautiful-subarrays | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def beautifulSubarrays(self, nums: List[int]) -> int:\n prefToCnt = Counter({0: 1})\n result = 0\n summ = 0\n for num in nums:\n summ ^= num\n result += prefToCnt[summ]\n prefToCnt[summ] += 1\n\n return result\n``` | 0 | You are given a **0-indexed** integer array `nums`. In one operation, you can:
* Choose two different indices `i` and `j` such that `0 <= i, j < nums.length`.
* Choose a non-negative integer `k` such that the `kth` bit (**0-indexed**) in the binary representation of `nums[i]` and `nums[j]` is `1`.
* Subtract `2k` from `nums[i]` and `nums[j]`.
A subarray is **beautiful** if it is possible to make all of its elements equal to `0` after applying the above operation any number of times.
Return _the number of **beautiful subarrays** in the array_ `nums`.
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[4,3,1,2,4\]
**Output:** 2
**Explanation:** There are 2 beautiful subarrays in nums: \[4,3,1,2,4\] and \[4,3,1,2,4\].
- We can make all elements in the subarray \[3,1,2\] equal to 0 in the following way:
- Choose \[3, 1, 2\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[1, 1, 0\].
- Choose \[1, 1, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 0, 0\].
- We can make all elements in the subarray \[4,3,1,2,4\] equal to 0 in the following way:
- Choose \[4, 3, 1, 2, 4\] and k = 2. Subtract 22 from both numbers. The subarray becomes \[0, 3, 1, 2, 0\].
- Choose \[0, 3, 1, 2, 0\] and k = 0. Subtract 20 from both numbers. The subarray becomes \[0, 2, 0, 2, 0\].
- Choose \[0, 2, 0, 2, 0\] and k = 1. Subtract 21 from both numbers. The subarray becomes \[0, 0, 0, 0, 0\].
**Example 2:**
**Input:** nums = \[1,10,4\]
**Output:** 0
**Explanation:** There are no beautiful subarrays in nums.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 106` | null |
Take advantage of small time range - Greedy pickup | minimum-time-to-complete-all-tasks | 0 | 1 | Small time range allows tracking of all available time slots that can be greedily selected via sorting by earliest end time. \n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key = lambda x: x[1])\n tot = 0\n used = [0] * 2001\n for curr_task in tasks:\n s, e, d = curr_task\n up = sum(used[s:e + 1])\n remain = d - up\n if remain <= 0:\n continue\n else:\n for i in range(remain):\n while(used[e - i] == 1):\n e -= 1\n used[e-i] = 1\n return sum(used)\n``` | 3 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Simple python3 O(N^2) greedy solution | minimum-time-to-complete-all-tasks | 0 | 1 | \n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n runSet = set()\n tasks.sort(key = lambda x: [x[1], x[0], -x[2]])\n for i, v in enumerate(tasks):\n start, end, duration = v\n run = end\n while duration > 0:\n if run not in runSet:\n runSet.add(run)\n duration -= 1\n for j in range(i + 1, len(tasks)):\n if tasks[j][0] <= run:\n tasks[j][2] -= 1\n run -= 1\n return len(runSet)\n```\n\n\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 1 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
GREEDY Python | minimum-time-to-complete-all-tasks | 0 | 1 | # Intuition\nRun earlier task as late as you can which benefits later tasks.\n\n# Approach\nGREEDY\n\n# Complexity\n- Time complexity: $O(NT)$\n\n\n\n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x:x[1])\n on=[0]*2001\n for s,e,d in tasks:\n cr=sum(on[s:e+1])\n while cr<d:\n # Greedy: finish the task as late as you can which benefits later tasks\n if on[e]!=1:on[e]=1; cr+=1\n e-=1\n return sum(on)\n``` | 1 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Simple Diagram Explanation | minimum-time-to-complete-all-tasks | 1 | 1 | # Idea\n- The range for `start` and `end` is $$1$$ to $$2000$$ which is sizable to use a number line in the form of a list to represent it. \n- We put all previously ran tasks times onto the number line to know when intersection can occur. \n- Sort tasks by `end` times to maximize possible collisions. \n- Each time a new task collides with a recorded time on the number line, additional time is not needed to perform this task. \n- Remaining duration that does not collide must be added to number line starting from `end`.\n# Example\n- This is best understood through a simple example. \n- Consider a smaller range from $$1$$ to $$10$$ with the following tasks: `[1,6,3],[7,9,1],[2,5,2],[5,10,5]`\n\n\n\n\n\n- We mark from `end` to `start` because we sorted by `end` times.\n- Any intersection of tasks will be found starting from `end`.\n- We only mark spots not previously marked to get max number line coverage. \n\n\n\n\n\n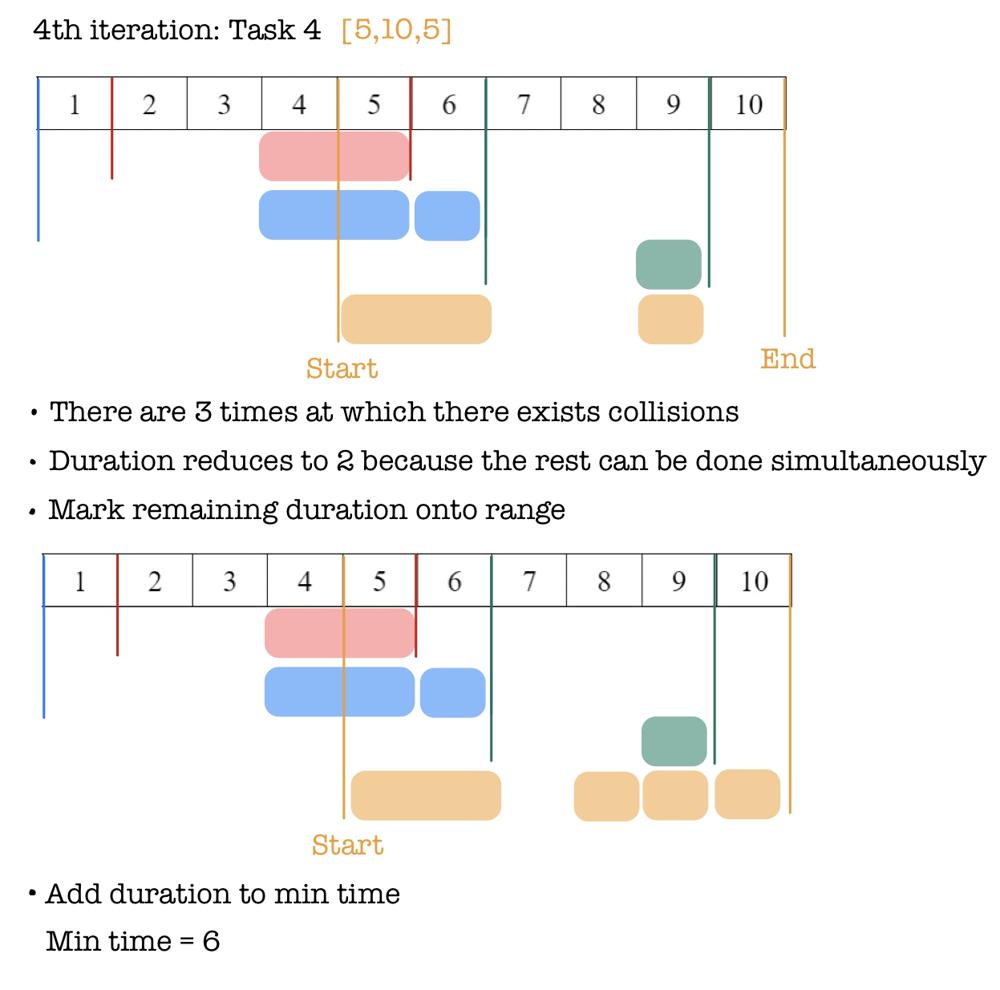\n\n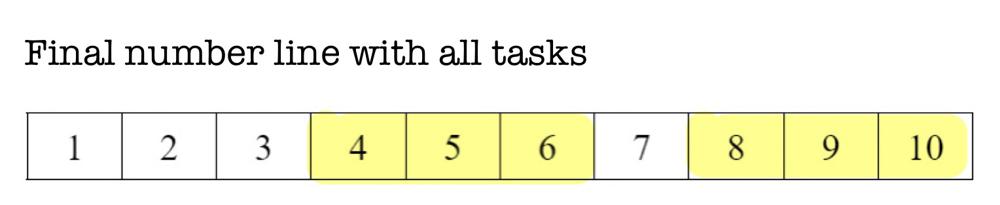\n\n# Code\n```\nint findMinimumTime(vector<vector<int>>& tasks) {\n int res = 0;\n // Determines whether work has been done before \n int range[2001] = {0};\n // Sort by interval end time \n sort(tasks.begin(), tasks.end(), [](auto& a, auto& b){return a[1] < b[1];});\n for (auto& t : tasks){\n int start = t[0], end = t[1], d = t[2];\n // If work has been done before, do it simultaneously\n for (int i = start; i <= end; i++){\n if (range[i]){\n d--;\n }\n if (d == 0){\n break;\n }\n }\n // For work that has not been done before \n while (d){ \n // duration is less than or equal to interval size\n // so no worry about going out of bound \n if (range[end] == 0){\n range[end]++;\n d--;\n res++;\n }\n end--;\n }\n }\n return res;\n}\n```\n- **Note:** Sorting by `end` times guarantees that the current interval has checked all possible collisions with the previous interval, whereas sorting by start times does not. Convince yourself by sorting with `start` times and testing it. \n#### Please leave an upvote if this helped! Thanks :) | 59 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python3 👍||⚡Easy solution🔥|| Greedy + sort + set || | minimum-time-to-complete-all-tasks | 0 | 1 | \n\n# Complexity\n- Time complexity:O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks = sorted(tasks,key=lambda x:x[1])\n chosen_set = set()\n for task in tasks:\n cur_start,cur_end,cur_duration = task[0],task[1],task[2]\n for time in chosen_set:\n if time >= cur_start and time <=cur_end:\n cur_duration-=1\n if cur_duration==0:\n break\n while cur_duration>0:\n if cur_end not in chosen_set:\n chosen_set.add(cur_end)\n cur_duration-=1\n cur_end-=1\n return len(chosen_set)\n \n \n \n``` | 4 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
[C++|Java|Python3] sweep line | minimum-time-to-complete-all-tasks | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/15456f4294fa2d2de5e056fc441f28872a0c2a71) for solutions of weekly 336. \n\n**C++**\n```\nclass Solution {\npublic:\n int findMinimumTime(vector<vector<int>>& tasks) {\n vector<int> line(2001); \n sort(tasks.begin(), tasks.end(), [](auto& lhs, auto& rhs) {return lhs[1] < rhs[1];}); \n for (auto& t : tasks) {\n int lo = t[0], hi = t[1], time = t[2], cnt = 0; \n for (int x = lo; x <= hi && time; ++x) time -= line[x]; \n for (int x = hi; x >= lo && time; --x) \n if (!line[x]) {\n line[x] = 1; \n --time; \n }\n }\n return accumulate(line.begin(), line.end(), 0); \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int findMinimumTime(int[][] tasks) {\n int[] line = new int[2001]; \n Arrays.sort(tasks, (a, b)->Integer.compare(a[1], b[1])); \n for (var t : tasks) {\n int lo = t[0], hi = t[1], time = t[2]; \n for (int x = lo; x <= hi && time > 0; ++x) time -= line[x]; \n for (int x = hi; x >= lo && time > 0; --x) {\n if (line[x] == 0) {\n line[x] = 1; \n --time; \n }\n }\n }\n return Arrays.stream(line).sum(); \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n line = [0]*2001\n for i, (lo, hi, time) in enumerate(sorted(tasks, key=lambda x: x[1])): \n cnt = sum(line[x] for x in range(lo, hi+1))\n time = max(0, time - cnt)\n for x in range(hi, lo-1, -1): \n if time and not line[x]: \n line[x] = 1\n time -= 1\n return sum(line)\n``` | 7 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Add Replace or Ignore (I didn't fully understand why but got AC ;) | minimum-time-to-complete-all-tasks | 0 | 1 | # Approach\nFor every time `t`, you can either select it, ignore it or replace a previous selected time with it.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^3)\n\n- Space complexity: O(n^2)\n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n n = len(tasks)\n L = min(tasks)[0]\n R = max(tasks, key = lambda xx : xx[1])[1]\n x = [0] * n\n xt = [None] * (R + 1)\n for t in range(L, R + 1):\n xt[t] = []\n for i in range(n):\n if t >= tasks[i][0] and t <= tasks[i][1]:\n xt[t].append(i)\n times = set()\n nonReplacable = set()\n for t in range(L, R + 1):\n # Add when no other choice\n add = 0\n for i in range(n):\n if t >= tasks[i][0] and t <= tasks[i][1] and x[i] + tasks[i][1] - t + 1 == tasks[i][2]:\n add = 1\n break\n if add == 1:\n for i in xt[t]:\n x[i] += 1\n nonReplacable.add(t)\n continue\n # Replace\n # xt[t] - xt[? in times] >= 0 or x + xt[t] - xt[? in times] >= tasks[i][2]\n rep = None\n for replace in times:\n z = set(xt[t])\n f = 1\n for i in xt[replace]:\n if i in z:\n z.remove(i)\n elif x[i] <= tasks[i][2]:\n f = 0\n break\n else:\n z.add(-i-1)\n if f:\n rep = replace\n break\n if rep != None:\n times.remove(rep)\n times.add(t)\n for i in z:\n if i < 0:\n x[-(i+1)] -= 1\n else:\n x[i] += 1\n else:\n # Ignore\n pass\n # print(times)\n return len(times) + len(nonReplacable)\n``` | 1 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Go/Python O(n*max(end)-min(start)) time | O(max(end)-min(start)) | minimum-time-to-complete-all-tasks | 0 | 1 | # Complexity\n- Time complexity: $$O(n*max(end)-min(start))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(max(end)-min(start))$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc findMinimumTime(tasks [][]int) int {\n sort.SliceStable(tasks, func(i, j int) bool {return tasks[i][1] < tasks[j][1]})\n min_start := math.MaxInt\n for _,task := range(tasks){\n min_start = min(min_start,task[0])\n }\n max_end := tasks[len(tasks)-1][1]\n time := make([]int, max_end-min_start+1)\n for _,task := range(tasks){\n start := task[0]-min_start\n end := task[1]-min_start\n duration := task[2]\n used := sum(&time,start,end+1)\n duration-=used\n for duration > 0{\n if time[end] == 0{\n time[end] = 1\n duration-=1\n }\n end-=1\n }\n }\n return sum(&time)\n}\n\nfunc sum(array *[]int, args ...int) int{\n left := 0\n right := len(*array)\n if len(args) == 2 {\n left = args[0]\n right = args[1]\n }\n item_sum := 0\n for i:=left;i<right;i++{\n item_sum+=(*array)[i]\n }\n return item_sum\n}\n\nfunc min(a,b int) int{\n if a<b{\n return a\n }\n return b\n}\n```\n```python []\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key = lambda x : x[1])\n min_start = float("inf")\n for task in tasks:\n min_start = min(min_start,task[0])\n max_end = tasks[-1][1]\n time = [0 for _ in range(max_end-min_start+1)]\n for task in tasks:\n start = task[0]-min_start\n end = task[1]-min_start\n duration = task[2]\n used = sum(time[start:end+1])\n duration-=used\n while duration > 0:\n if time[end] == 0:\n time[end] = 1\n duration-=1\n end-=1\n return sum(time) \n``` | 1 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
[Python] 100%, simple greedy, what to learn from this | minimum-time-to-complete-all-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis problem was eye opening for me for several reasons.\n\nThis is an overlapping intervals problem. We are going to calculate the minimum number of seconds the computer needs to be turned on to complete all of the tasks.\n\nThe two main insights I had after solving this problem were:\n\n1) when the problem gives us a confusing example, we should first create a brand new example ourselves. The example was purposely confusing so you wouldn\'t notice the optimal patterns. Also using longer intervals and durations will give you more data points and room to consider possibilities to assess how exploitable your strategy is. Intervals of length 3 and duration of 1 or 2 just isn\'t enough to really form much of an opinion on what a good strategy is.\n\n2) in any interval problem, we should always check if sorting by the start time or the end time will allow us to have a greedy solution. And we should do so with a few good examples.\n\nSorting by start point is a bad strategy for the simple example:\n\n[1,5,1],[2,3,1]\n\nwe\'d prefer to turn on the computer at time 2 or 3, but we can\'t know to do that when looking at [1,5,1]. However, if we sort by end point, you can see if we turn it on at 2 or 3, task 1 is also completed. \n\nTo test whether we could sort by endpoint, I created a second example.\n\nHere\'s the example i created to convince myself this strategy is good:\n[15,20,3],[10,25,5],[6,30,7]\n\n[15,20,3], overlaps: none duration = 3 times used: **20,19,18**\n\nHow do we know we want the computer turned on at times 18,19,20?\nThe only way we would want it turned on earlier is if we had a task with an end time before 18. Maybe a task like [13,16,2]. Because we sorted by end point, we will never see this task after [15,20,3]. We will see it before.\n\n[10,25,9], what overlaps? 18,19,20 duration (5-3)=2 \nnew used: **25,24** + old used 18,19,20\n\n[6,30,7]\n what overlaps? 18,19,20,24,25. duration = (7-5)\n new used: **30,29** + old used\n\nIf the computer is already on during a time in our interval, we would want to use that time to run the computer for one second. So first we iterate through and see which times in our interval the computer is on, and subtract one from duration for this task. Then, if we still have any duration left, we will turn it on at the latest second possible so we are most likely to overlap with the next task. The next task has an end point greater than the current task. It has an unknown starting point. \nWhen we choose the latest second possible we minimize our computer usage in all cases. \n\nSo keep a boolean array and iterate through. \nSum the times array to count the number of times used.\n\n\n1<= start,end <= 2000\n\n- Time complexity: O(N^2)\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n \n tasks.sort(key = lambda x:(x[1],x[0]))\n \n times = [False]*2001\n \n for start, end, duration in tasks:\n dur,e = duration,end\n for s in range(start,end+1):\n if times[s]:\n dur -= 1\n \n while dur > 0:\n if not times[e]:\n times[e] = True\n dur -= 1\n e -= 1\n \n return sum(times)\n \n\n``` | 4 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python3 Greedy O(n * n) no Sort solution | minimum-time-to-complete-all-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition is greedy.The time slot we say [x, x] needs to choose only if there is a task. If you don\'t start at time x, you won\'t make it on time. And since we know we need to turn on the machine at time x. Every task can use this time slot use this time slot. We test from the minimum start time of all task to the maximum end time. Keep updating the duration. Since these are constraint in 1~2000. We use it as our range.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse **check** function to test if time slot [x,x] (x = time in our code) need to choose.\nIf [time, time] needs to choose. We substract all duration which is legal 1 in func **elimtate**.\nAnd test from 1 ~ 2000 and count.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ for each check func.\n$$O(n)$$ for each elimtate func.\n$$O(n^2)$$ for total.\nn is 2000 in this case.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nConstant extra space.\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n def check(time, tasks):\n # check if time needs to turn on only need to turn on if there is a task task[2] != 0 and task[1] - task[2] == time\n # open time to time + 1\n for task in tasks:\n if task[2] and (task[1] - time + 1 == task[2]):\n return True\n return False\n \n def elimtate(time, tasks):\n for i in range(len(tasks)):\n if tasks[i][0] <= time and tasks[i][2] > 0:\n tasks[i][2] -= 1 \n ans = 0\n for i in range(1,2001):\n if check(i, tasks):\n #print(i)\n ans += 1\n elimtate(i, tasks)\n return ans\n``` | 2 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python Hard Line Sweep | minimum-time-to-complete-all-tasks | 0 | 1 | ```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n line = [0] * 2001\n\n tasks.sort(key = lambda x: x[1])\n\n for start, end, time in tasks:\n count = sum(line[x] for x in range(start, end+1))\n time = max(0, time - count)\n \n for i in range(end, start - 1, -1):\n \n if time and not line[i]:\n line[i] = 1\n time -= 1\n\n\n return sum(line)\n\n\n\n\n\n``` | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python Solution Easy to understand | minimum-time-to-complete-all-tasks | 0 | 1 | # Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x:[x[1],-x[2],x[1]])\n done=[]\n for a,b,c in tasks:\n for a1,b1 in done[::-1]:\n if(b1>=a and c!=0):\n c=max(c-(b1-max(a1,a)+1),0)\n else:\n break\n if(c!=0):\n done.append([b-c+1,b])\n i=len(done)-1\n j=i-1\n while(j>=0):\n if(done[j][1]>=done[i][0]):\n r=done[j][1]-done[i][0]+1\n done[i][0]+=r\n done[j][0]-=r\n else:\n break\n i-=1\n j-=1\n totalTime=0\n for a,b in done:\n totalTime+=(b-a+1)\n return totalTime\n``` | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Simple solution in Python3 with explanation, faster than 93% | minimum-time-to-complete-all-tasks | 0 | 1 | The goal is to minimize the total number of working time slots. Thus, my approach is to maximize the overlap of all tasks. \nThe tasks are first sorted by their end timestamps. \nI try to allocate the time slots that are already on for each task. \nIf the already on time slots in its [start, end] window is less than its duration, additional time slots should be set to on for it. \nIn this sitatuion, the later the time slot is better to choose because the coming tasks in the future, whose end timestamp will be greater or equal to that of the current task. \n\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x: (x[1], x[0]))\n slots = [0] * (tasks[-1][1]+1)\n for s, e, d in tasks:\n d -= sum(slots[s:e+1])\n for i in range(e, s-1, -1):\n if d <= 0:\n break\n if slots[i] == 0:\n slots[i] = 1\n d -= 1\n return sum(slots)\n | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python || greedy || O(n^2) | minimum-time-to-complete-all-tasks | 0 | 1 | 1. Consider the example `tasks = [[1,3,2],[2,5,3],[5,6,2]]`.\nImagine we list all tasks on schedule, like following:\n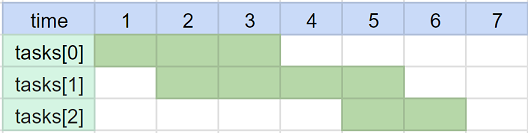\n1-1. As time increasing, at `time=3`, `tasks[0]` reaches its deadline. At this moment, we have `tasks[0]` and `tasks[1]` waiting, and we want to finish `tasks[0]`. \nThe later we run, more processes can be done. In this case, we choose to run `time=2` and `time=3`, so `tasks[0]` is done, and `tasks[1]` has 1 process left.\n1-2. Then we go on. At `time=5`, `tasks[1]` reaches its deadline. We choose to run `time=5` to finish `tasks[1]`, and `tasks[2]` has 1 process left.\n1-3. Finally we stop at `time=6`. To finish `tasks[2]`, we can only run `time=6`.\n2. Sort `tasks` by end time to ensure that all tasks can be finished in order.\n3. We use array `activated` to record time units used . For each task, go back from its `end`, and search for time units not used yet. When we finish the task, we can go on.\n4. After all tasks are done, the total number of time units used would be the answer.\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x: x[1])\n \n activated = [0]*(tasks[-1][1]+1)\n for s, e, d in tasks:\n d -= activated[s:e+1].count(1)\n idx = e\n while d > 0:\n if activated[idx] == 0:\n activated[idx] = 1\n d -= 1\n idx -= 1\n return sum(activated) | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Using SegmentTree | minimum-time-to-complete-all-tasks | 0 | 1 | \n\n# Code\n```\nclass SegmentTree:\n\n def __init__(self, arr, operator, operationIdentity) -> None:\n self.arrLength = len(arr)\n self.arr = arr\n self.modifiedNumberOfChildren = 2**(math.ceil(math.log(self.arrLength, 2)))\n self.segmentTreeLength = 2*self.modifiedNumberOfChildren - 1\n self.segmentTree = [None for i in range(self.segmentTreeLength)]\n self.operationIdentity = operationIdentity\n self.operation = operator\n self.buildSegmentTree(0,self.modifiedNumberOfChildren-1, 0)\n \n \n def buildSegmentTree(self, start, end, index):\n if(start == end): \n self.segmentTree[index] = self.arr[start] if(start < self.arrLength) else self.operationIdentity\n return self.segmentTree[index]\n \n mid = start + (end - start)//2\n leftSegmentValue = self.buildSegmentTree(start, mid, 2*index+1)\n rightSegmentValue = self.buildSegmentTree(mid+1, end, 2*index+2)\n self.segmentTree[index] = self.operation(leftSegmentValue, rightSegmentValue)\n return self.segmentTree[index]\n\n\n def query(self, start, end):\n\n def queryHelper(qstart, qend, start, end, index):\n if(qstart>end or qend<start): return self.operationIdentity\n if(qstart == start and qend == end): return self.segmentTree[index]\n\n mid = start + (end - start)//2\n return self.operation(queryHelper(qstart, min(qend, mid), start, mid, 2*index + 1), \n queryHelper(max(qstart, mid+1), qend, mid+1, end, 2*index + 2))\n\n return queryHelper(start, end, 0, self.modifiedNumberOfChildren-1, 0)\n \n def update(self, index, newValue):\n\n def updateHelper(start, end, segIndex, index, newValue):\n if(start == end == index): \n self.segmentTree[segIndex] = newValue\n return\n\n mid = start + (end - start)//2\n if(start <= index <= mid): updateHelper(start, mid, 2*segIndex+1, index, newValue)\n else: updateHelper(mid+1, end, 2*segIndex+2, index, newValue)\n\n self.segmentTree[segIndex] = self.operation(self.segmentTree[2*segIndex+1], self.segmentTree[2*segIndex+2])\n \n self.arr[index] = newValue\n updateHelper(0, self.modifiedNumberOfChildren -1, 0, index, newValue)\n \n def fillhelper(self, num, rstart, rend, fillNum, segstart, segend, index):\n if(num == 0 or fillNum == 0): return\n if(segend<rstart or rend<segstart): return\n \n # leaf node \n if(segstart == segend and num == 1): \n self.segmentTree[index] = fillNum\n return\n\n mid = segstart + (segend - segstart)//2\n rightSum = self.query(max(mid+1, rstart), rend)\n numEmptyToRight = (rend - max(mid+1, rstart)) + 1 - rightSum\n if(numEmptyToRight<0): numEmptyToRight = 0\n \n # enough to fill only right segment\n if(numEmptyToRight >= num): self.fillhelper(num, mid+1, rend, fillNum, mid+1, segend, 2*index+2)\n else:\n # have to fill in both segments\n self.fillhelper(numEmptyToRight, mid+1, rend, fillNum, mid+1, segend, 2*index+2)\n self.fillhelper(num - numEmptyToRight, rstart, min(mid, rend), fillNum, segstart, mid, 2*index+1)\n \n self.segmentTree[index] = self.operation(self.segmentTree[2*index+1], self.segmentTree[2*index+2])\n \n def rightfill(self, num, start, end, fillNum = None): \n if(not fillNum): fillNum = self.operationIdentity \n self.fillhelper(num, start, end, fillNum, 0, self.modifiedNumberOfChildren-1, 0)\n\n\n\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n tasks.sort(key=lambda x: (x[1], x[0], x[-1]))\n timeline = SegmentTree([0 for i in range(2001)], operator=lambda x, y : x+y, operationIdentity=0)\n ans = 0\n for start, end, duration in tasks:\n onTime = timeline.query(start, end)\n if(onTime >= duration): continue\n\n remaining = duration - onTime\n ans += remaining\n timeline.rightfill(remaining, start, end, fillNum = 1)\n \n return ans\n \n``` | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
Python solution + explanation | minimum-time-to-complete-all-tasks | 0 | 1 | # Approach\n1. Sort the tasks by the end time.\n```\n tasks.sort(key = (lambda x: x[1]))\n```\n2. We want to use list "work" to store times when the computer is on.\nFor each of the tasks we first check if the computer has already been designed to be working during the appropriate time to execute the task. We decrease the task duration accordingly.\n```\n for s,e,d in tasks:\n i = -1\n while work[i] >= s:\n d -=1\n i -=1\n if d == 0: break\n```\n3. Now if we have any remaining duration to perform we want to book the latest possible time on the computer. So we insert d points into "work", which represent the latest possible times to run the current task. However, we need to check if the selected times have not been inserted yet. If so, we shift the range of inserted times.\n```\n end = len(work)-1\n i = 0\n while i < d:\n if work[end] != e-i: work.insert(end+1,e-i)\n else:\n d+=1\n end -=1\n i +=1\n```\n\n\n# Code\n```\nclass Solution:\n def findMinimumTime(self, tasks: List[List[int]]) -> int:\n\n tasks.sort(key = (lambda x: x[1]))\n work = [-inf]\n for s,e,d in tasks:\n i = -1\n while work[i] >= s:\n d -=1\n i -=1\n if d == 0: break\n end = len(work)-1\n i = 0\n while i < d:\n if work[end] != e-i: work.insert(end+1,e-i)\n else:\n d+=1\n end -=1\n i +=1\n\n return len(work)-1\n\n``` | 0 | There is a computer that can run an unlimited number of tasks **at the same time**. You are given a 2D integer array `tasks` where `tasks[i] = [starti, endi, durationi]` indicates that the `ith` task should run for a total of `durationi` seconds (not necessarily continuous) within the **inclusive** time range `[starti, endi]`.
You may turn on the computer only when it needs to run a task. You can also turn it off if it is idle.
Return _the minimum time during which the computer should be turned on to complete all tasks_.
**Example 1:**
**Input:** tasks = \[\[2,3,1\],\[4,5,1\],\[1,5,2\]\]
**Output:** 2
**Explanation:**
- The first task can be run in the inclusive time range \[2, 2\].
- The second task can be run in the inclusive time range \[5, 5\].
- The third task can be run in the two inclusive time ranges \[2, 2\] and \[5, 5\].
The computer will be on for a total of 2 seconds.
**Example 2:**
**Input:** tasks = \[\[1,3,2\],\[2,5,3\],\[5,6,2\]\]
**Output:** 4
**Explanation:**
- The first task can be run in the inclusive time range \[2, 3\].
- The second task can be run in the inclusive time ranges \[2, 3\] and \[5, 5\].
- The third task can be run in the two inclusive time range \[5, 6\].
The computer will be on for a total of 4 seconds.
**Constraints:**
* `1 <= tasks.length <= 2000`
* `tasks[i].length == 3`
* `1 <= starti, endi <= 2000`
* `1 <= durationi <= endi - starti + 1` | null |
One By One Distribute || python3 || simple approach | distribute-money-to-maximum-children | 0 | 1 | \n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int: \n if money < children: return -1 \n ans = 0 \n for j in range(1,children+1):\n leftmoney = money - 8 # if current child gets 8$\n leftchildren = children - j\n if leftmoney >= leftchildren: \n money = leftmoney \n ans += 1 \n else: \n leftchildren = children - j + 1 # 1 is added because current child \n # has not gotten any dollar yet\n if leftchildren == 1 and money == 4:\n ans -= 1\n money = 0\n break\n if money > 0: # if some money is left to distribute\n ans -= 1\n return ans\n \n``` | 8 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
2591. Simple solution in Python | distribute-money-to-maximum-children | 0 | 1 | # Code\n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n if children > money: return -1\n elif children == money: return 0\n count, rem = money//8, money%8\n while count >= 0:\n if count + rem >= children:\n if children == count + 1 and rem == 4: return count - 1\n if count == children and rem != 0: return count - 1\n elif count > children:\n count -= 1\n rem += 8\n else:\n return count \n else:\n count -= 1\n rem += 8\n return -1\n``` | 1 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Python 3 || 5 lines, w/ explanation || T/M: 39 ms / 13.8 MB | distribute-money-to-maximum-children | 0 | 1 | ```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n\n if money < children: return -1 # <-- More children than dollars\n\n n = 8 * children - money # <-- Enough dollars for all children \n # to get at least 8 dollars; one\n if n <= 0: return children - (n < 0) # child may get more than 8 dollars \n \n ans, rem = divmod(money-children,7) # <-- Every child gets a dollar, then ans\n # children get an additional 7 dollars \n\n return ans - ((ans, rem) == (children - 1, 3))\n # <-- Decrement the ans if only one child \n # gets less than 8 dollars and that \n # child gets exactly 4 dollars\n```\n[https://leetcode.com/problems/distribute-money-to-maximum-children/submissions/917769198/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1).\n | 5 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
[Python 3] Modulo 7 | distribute-money-to-maximum-children | 0 | 1 | This *easy* question is actually tricky.\n\n# Approach\nFirst, we need to check if it is possible to distribute the money:\n```\nif money<children: return -1\n```\nSince *everyone must receive at least 1 dollar*, we give 1 dollar to each person:\n```\nmoney -= children\n```\nTo *maximize the number of children who may receive exactly 8 dollars*, we use the rest of money and try giving each person 7 dollars:\n```\nd,m = divmod(money,7)\n```\nConsider different cases of d,m (note that nobody receives 4 dollars), we can reach the solution:\n```\n if d>=children:\n if d==children and m==0:\n return children\n else:\n return children - 1\n else:\n if m==3:\n if d<children-1:\n return d\n else:\n return d - 1\n else:\n return d\n```\n# Code\n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n if money<children: return -1\n money -= children\n d,m = divmod(money,7)\n if d>=children:\n if d==children and m==0:\n return children\n else:\n return children - 1\n else:\n if m==3:\n if d<children-1:\n return d\n else:\n return d - 1\n else:\n return d\n``` | 5 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Python O(n) Just do what question says | distribute-money-to-maximum-children | 0 | 1 | \n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n if 8*children==money:\n return children\n \n if money<children:\n return -1\n\n #Give every child 1 dollar\n arr=[1]*children\n money-=children \n\n #------ Try making 8 now -----\n #remove if first child can\'t be made 8\n if money<7:\n return 0\n \n # Check how many can receive 7?\n # 3 cases:\n # last value can be greater than 8\n # some value in middle can be less than 8 and remaining are 1\n # just add 7 and keep making exact 8 values\n\n for i in range(children):\n if money>7 and i==children-1:\n arr[i]+=money\n break\n elif money<7 and i<=children-1:\n arr[i]+=money\n break\n else:\n arr[i]+=7\n money-=7\n\n # Check for 4 in array which will be at last\n # if 4 is in middle we can adjust its value with other 1\'s\n\n return arr.count(8)-arr.count(4) if arr[-1]==4 else arr.count(8)\n \n\n\n\n``` | 3 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Simple approach for the most toughest easy question :) | distribute-money-to-maximum-children | 0 | 1 | # Intuition\nTry to distribute the money keeping the conditions in mind.\n\n# Approach\nThink of each child as an element in a list.Initially each child value is 1 now we try to calculate how many children can get an additional 7.Here \'c\' calculates the no.of children who can get 8$ each without keeping any conditions in mind.The later conditional statements are applied to satisfy with the rules.\nIts largely an intutional problem and pretty hard for an easy question.\n\n# Complexity\n- Time complexity:\nIDK about that,still learning. Beats 89.65 %\n\n- Space complexity:\nIDK how to determine it, but the memory beats is 60% :(\n\n# Code\n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n #money left after distributing 1$ to each child\n money=money-children\n c=0\n if money>=0:\n while money>=7:\n money-=7 \n #addition of 7$ more to each child will make it 8$\n c+=1 \n if money==3 and c==children-1:\n c-=1 #because 1+3=4$\n elif c==children and money>0:\n c-=1 #all the remaining money is taken up by one child\n elif c>children:\n c=children-1 #all the remaining money is given to one child\n return c\n else:\n return -1\n``` | 2 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
O(1) Beats 98% Python | distribute-money-to-maximum-children | 0 | 1 | # Python \n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n if children>money:\n return -1\n if money>8*children:\n return children-1\n money-=children\n if children-money//7==1 and money%7==3:\n return money//7-1\n return money//7\n``` | 2 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Python3 Case by Case Solution | distribute-money-to-maximum-children | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n # cannot give 1 to every child\n if money < children: return -1\n # have more than enough, all child have 8 except 1 child have more\n if money > 8 * children: return children - 1\n # give 1 to every child first\n money -= children\n # find the number of child to reach 8 and the excess amount\n res, extra = divmod(money, 7)\n # if amount is 3 and only one child is not 8, we need two child to seperate money to avoid child having 4\n if extra == 3 and res + 1 == children: return res - 1\n # return the result\n return res\n \n``` | 8 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Python if-else | distribute-money-to-maximum-children | 0 | 1 | ```\nclass Solution:\n def distMoney(self, money: int, children: int) -> int:\n res = (money-children)//7\n if children>money:\n return -1\n elif res==children-1 and (money-children)%7==3:\n return res-1\n elif res==children and (money-children)%7>0:\n return res-1\n elif res>children:\n return children-1\n return res | 3 | You are given an integer `money` denoting the amount of money (in dollars) that you have and another integer `children` denoting the number of children that you must distribute the money to.
You have to distribute the money according to the following rules:
* All money must be distributed.
* Everyone must receive at least `1` dollar.
* Nobody receives `4` dollars.
Return _the **maximum** number of children who may receive **exactly**_ `8` _dollars if you distribute the money according to the aforementioned rules_. If there is no way to distribute the money, return `-1`.
**Example 1:**
**Input:** money = 20, children = 3
**Output:** 1
**Explanation:**
The maximum number of children with 8 dollars will be 1. One of the ways to distribute the money is:
- 8 dollars to the first child.
- 9 dollars to the second child.
- 3 dollars to the third child.
It can be proven that no distribution exists such that number of children getting 8 dollars is greater than 1.
**Example 2:**
**Input:** money = 16, children = 2
**Output:** 2
**Explanation:** Each child can be given 8 dollars.
**Constraints:**
* `1 <= money <= 200`
* `2 <= children <= 30` | null |
Python Elegant & Short | Sorting | Two pointers | maximize-greatness-of-an-array | 0 | 1 | ```\nclass Solution:\n def maximizeGreatness(self, nums: List[int]) -> int:\n nums.sort()\n i = 0\n\n for num in nums:\n if nums[i] < num:\n i += 1\n\n return i\n\n``` | 1 | You are given a 0-indexed integer array `nums`. You are allowed to permute `nums` into a new array `perm` of your choosing.
We define the **greatness** of `nums` be the number of indices `0 <= i < nums.length` for which `perm[i] > nums[i]`.
Return _the **maximum** possible greatness you can achieve after permuting_ `nums`.
**Example 1:**
**Input:** nums = \[1,3,5,2,1,3,1\]
**Output:** 4
**Explanation:** One of the optimal rearrangements is perm = \[2,5,1,3,3,1,1\].
At indices = 0, 1, 3, and 4, perm\[i\] > nums\[i\]. Hence, we return 4.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We can prove the optimal perm is \[2,3,4,1\].
At indices = 0, 1, and 2, perm\[i\] > nums\[i\]. Hence, we return 3.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
Greedy || Count Duplicates || Sorting | maximize-greatness-of-an-array | 1 | 1 | # Intuition\nThe test case : $$[1,2,3,4]$$ gives an idea to solve this problem. It\'s answer is $$3$$, or something to do with **the sorted array** arrangement. If the array had no duplicate elements, the answer would always be= **the number of elements -1** .Simple logic being, the greatest number[$$4$$ in the above array considered] in the array cannot be matched with any number, but everybody else can be. That is how we arrive to our answer.\n\n# Approach\nConsider the arrays: \n-$$[1,1,1,1,1,2,3,4]$$\nThe answer is $$3$$. The addition of additional $$1s$$ does not affect our answer, as we can match each $$1$$ with a $$1$$\n\n---\n\n\nConsider the array in test case 1 in sorted order:\n$$[1,1,1,2,3,3,5]$$ and notice that it has the same arrangement:\n$$[3,3,5]$$, which has an answer of $$2$$. The benefit in this case is though, we get an additional $$3$$ that we can match with one of the $$1$$ in the array. That is how the presence of duplicates will give us a greater answer than just the number of distinct elements in the array. \n\nIf we **sort** the array, we will always have this subproblem: \n$$[x,x,x,x,x,x+1,]$$ \n# It is akin to an array of $$[x,x+1]$$, we just get spare elements(x) that we can use to match with duplicates of numbers smaller than x\n\nOr if you **keep a count of numbers** that are greater than $$x$$, you can tabulate your result. \n\n# Complexity\n- Time complexity:\n$$O(n log n)$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code\n```Java []\nclass Solution {\n public int maximizeGreatness(int[] nums) {\n Arrays.sort(nums);\n int n=nums.length;\n int ans=0;\n int rem=0; //Numbers greater than the current number\n int curem=0; //Numbers equal to the current number\n int comp= nums[n-1]; //The last greatest number we have encountered so far\n for(int i=n-2;i>=0;i--){\n if(nums[i]<comp){ //[3,4] we are checking 3 here\n comp=nums[i]; //found a new guy\n rem+=curem; //include the number of 3s in our\n //numbers greater than nums[i] counter\n curem=0; //Reset the count of numbers same as nums[i]\n ans++;\n }\n else if(nums[i]==nums[i+1]) { \n if(rem>0){ //if there is a spare number above, incrememnt sum \n rem--;\n ans++;\n }\n curem++; //this number cannot be paired, but we can use it later\n }\n }\n return ans;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maximizeGreatness(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int n=nums.size();\n int ans=0;\n int rem=0; //Numbers greater than the current number\n int curem=0; //Numbers equal to the current number\n int comp= nums[n-1]; //The last greatest number we have encountered so far\n for(int i=n-2;i>=0;i--){\n if(nums[i]<comp){ //[3,4] we are checking 3 here\n comp=nums[i]; //found a new guy\n rem+=curem; //include the number of 3s in our\n //numbers greater than nums[i] counter\n curem=0; //Reset the count of numbers same as nums[i]\n ans++;\n }\n else if(nums[i]==nums[i+1]) { \n if(rem>0){ //if there is a spare number above, incrememnt sum \n rem--;\n ans++;\n }\n curem++; //this number cannot be paired, but we can use it later\n }\n }\n return ans;\n }\n};\n\n```\n```Python3 []\nclass Solution:\n def maximizeGreatness(self, nums: List[int]) -> int:\n nums.sort()\n n=len(nums)\n ans=0\n rem=0 #Numbers greater than the current number\n curem=0 #Numbers equal to the current number\n comp= nums[n-1] #The last greatest number we have encountered so far\n for i in range(n-2,-1,-1):\n if(nums[i]<comp): #[3,4] we are checking 3 here\n comp=nums[i] #found a new guy\n rem+=curem #include the number of 3s in our numbers greater than nums[i] counter\n curem=0 #Reset the count of numbers same as nums[i]\n ans+=1\n elif(nums[i]==nums[i+1]): \n if(rem>0): #if there is a spare number above, incrememnt sum \n rem-=1\n ans+=1\n curem+=1 #this number cannot be paired, but we can use it later\n return ans\n\n```\n | 1 | You are given a 0-indexed integer array `nums`. You are allowed to permute `nums` into a new array `perm` of your choosing.
We define the **greatness** of `nums` be the number of indices `0 <= i < nums.length` for which `perm[i] > nums[i]`.
Return _the **maximum** possible greatness you can achieve after permuting_ `nums`.
**Example 1:**
**Input:** nums = \[1,3,5,2,1,3,1\]
**Output:** 4
**Explanation:** One of the optimal rearrangements is perm = \[2,5,1,3,3,1,1\].
At indices = 0, 1, 3, and 4, perm\[i\] > nums\[i\]. Hence, we return 4.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We can prove the optimal perm is \[2,3,4,1\].
At indices = 0, 1, and 2, perm\[i\] > nums\[i\]. Hence, we return 3.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
[Java/Python 3] Sort then 2 pointers. | maximize-greatness-of-an-array | 1 | 1 | Sort then start from index `0` to check how many pairs of `nums[ans] < nums[j] (num in the code)` we can have.\n\n```java\n public int maximizeGreatness(int[] nums) {\n Arrays.sort(nums);\n int ans = 0;\n for (int num : nums) {\n if (nums[ans] < num) {\n ++ans;\n }\n }\n return ans;\n }\n```\n\n```python\n def maximizeGreatness(self, nums: List[int]) -> int:\n nums.sort()\n ans = 0\n for num in nums:\n if nums[ans] < num:\n ans += 1\n return ans\n```\n\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(sorting space)`, where `n = nums.length`. | 15 | You are given a 0-indexed integer array `nums`. You are allowed to permute `nums` into a new array `perm` of your choosing.
We define the **greatness** of `nums` be the number of indices `0 <= i < nums.length` for which `perm[i] > nums[i]`.
Return _the **maximum** possible greatness you can achieve after permuting_ `nums`.
**Example 1:**
**Input:** nums = \[1,3,5,2,1,3,1\]
**Output:** 4
**Explanation:** One of the optimal rearrangements is perm = \[2,5,1,3,3,1,1\].
At indices = 0, 1, 3, and 4, perm\[i\] > nums\[i\]. Hence, we return 4.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We can prove the optimal perm is \[2,3,4,1\].
At indices = 0, 1, and 2, perm\[i\] > nums\[i\]. Hence, we return 3.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
python3 Solution | maximize-greatness-of-an-array | 0 | 1 | \n```\nclass Solution:\n def maximizeGreatness(self, nums: List[int]) -> int:\n nums.sort()\n ans=0\n for num in nums:\n if num>nums[ans]:\n ans+=1\n\n return ans \n``` | 4 | You are given a 0-indexed integer array `nums`. You are allowed to permute `nums` into a new array `perm` of your choosing.
We define the **greatness** of `nums` be the number of indices `0 <= i < nums.length` for which `perm[i] > nums[i]`.
Return _the **maximum** possible greatness you can achieve after permuting_ `nums`.
**Example 1:**
**Input:** nums = \[1,3,5,2,1,3,1\]
**Output:** 4
**Explanation:** One of the optimal rearrangements is perm = \[2,5,1,3,3,1,1\].
At indices = 0, 1, 3, and 4, perm\[i\] > nums\[i\]. Hence, we return 4.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We can prove the optimal perm is \[2,3,4,1\].
At indices = 0, 1, and 2, perm\[i\] > nums\[i\]. Hence, we return 3.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
sorting || python3 || easiest solution | maximize-greatness-of-an-array | 0 | 1 | \n```\nclass Solution:\n def maximizeGreatness(self, nums: List[int]) -> int: \n nums.sort() \n count = 0\n j = i = 0 \n while j < len(nums):\n if nums[i] < nums[j]:\n count+=1 \n i+=1\n j+=1 \n return count\n \n \n``` | 4 | You are given a 0-indexed integer array `nums`. You are allowed to permute `nums` into a new array `perm` of your choosing.
We define the **greatness** of `nums` be the number of indices `0 <= i < nums.length` for which `perm[i] > nums[i]`.
Return _the **maximum** possible greatness you can achieve after permuting_ `nums`.
**Example 1:**
**Input:** nums = \[1,3,5,2,1,3,1\]
**Output:** 4
**Explanation:** One of the optimal rearrangements is perm = \[2,5,1,3,3,1,1\].
At indices = 0, 1, 3, and 4, perm\[i\] > nums\[i\]. Hence, we return 4.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 3
**Explanation:** We can prove the optimal perm is \[2,3,4,1\].
At indices = 0, 1, and 2, perm\[i\] > nums\[i\]. Hence, we return 3.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109` | null |
python3 Solution | find-score-of-an-array-after-marking-all-elements | 0 | 1 | \n```\nclass Solution:\n def findScore(self, nums: List[int]) -> int:\n look=[0]*(len(nums)+1)\n ans=0\n for a,i in sorted([a,i] for i,a in enumerate(nums)):\n if look[i]:\n continue\n\n ans+=a\n look[i]=look[i-1]=look[i+1]=1\n\n return ans \n``` | 2 | You are given an array `nums` consisting of positive integers.
Starting with `score = 0`, apply the following algorithm:
* Choose the smallest integer of the array that is not marked. If there is a tie, choose the one with the smallest index.
* Add the value of the chosen integer to `score`.
* Mark **the chosen element and its two adjacent elements if they exist**.
* Repeat until all the array elements are marked.
Return _the score you get after applying the above algorithm_.
**Example 1:**
**Input:** nums = \[2,1,3,4,5,2\]
**Output:** 7
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,1,3,4,5,2\].
- 2 is the smallest unmarked element, so we mark it and its left adjacent element: \[2,1,3,4,5,2\].
- 4 is the only remaining unmarked element, so we mark it: \[2,1,3,4,5,2\].
Our score is 1 + 2 + 4 = 7.
**Example 2:**
**Input:** nums = \[2,3,5,1,3,2\]
**Output:** 5
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,3,5,1,3,2\].
- 2 is the smallest unmarked element, since there are two of them, we choose the left-most one, so we mark the one at index 0 and its right adjacent element: \[2,3,5,1,3,2\].
- 2 is the only remaining unmarked element, so we mark it: \[2,3,5,1,3,2\].
Our score is 1 + 2 + 2 = 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
✔️ Python3 Solution | Sorting | find-score-of-an-array-after-marking-all-elements | 0 | 1 | # Approach\nsort the array for `index`, and traverse to the index with the smallest element, check if you marked it or not in `dp`, if it is not marked mark its adjacent element and add its `value` to the `score`.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python\nclass Solution:\n def findScore(self, A: List[int]) -> int:\n n = len(A)\n dp = [False] * n\n score = 0\n for v, k in sorted((i, e) for e, i in enumerate(A)):\n if dp[k]: continue\n if k > 0: dp[k - 1] = True\n if k < n - 1: dp[k + 1] = True\n score += v\n return score\n``` | 1 | You are given an array `nums` consisting of positive integers.
Starting with `score = 0`, apply the following algorithm:
* Choose the smallest integer of the array that is not marked. If there is a tie, choose the one with the smallest index.
* Add the value of the chosen integer to `score`.
* Mark **the chosen element and its two adjacent elements if they exist**.
* Repeat until all the array elements are marked.
Return _the score you get after applying the above algorithm_.
**Example 1:**
**Input:** nums = \[2,1,3,4,5,2\]
**Output:** 7
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,1,3,4,5,2\].
- 2 is the smallest unmarked element, so we mark it and its left adjacent element: \[2,1,3,4,5,2\].
- 4 is the only remaining unmarked element, so we mark it: \[2,1,3,4,5,2\].
Our score is 1 + 2 + 4 = 7.
**Example 2:**
**Input:** nums = \[2,3,5,1,3,2\]
**Output:** 5
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,3,5,1,3,2\].
- 2 is the smallest unmarked element, since there are two of them, we choose the left-most one, so we mark the one at index 0 and its right adjacent element: \[2,3,5,1,3,2\].
- 2 is the only remaining unmarked element, so we mark it: \[2,3,5,1,3,2\].
Our score is 1 + 2 + 2 = 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
Python | Heap | find-score-of-an-array-after-marking-all-elements | 0 | 1 | # Code\n```\nfrom heapq import heapify, heappush, heappop\nclass Solution:\n def findScore(self, nums: List[int]) -> int:\n n = len(nums)\n visited = set()\n h = [(num, i) for i,num in enumerate(nums)]\n heapify(h)\n res = 0\n while h:\n num, i = heappop(h)\n if i not in visited:\n res += num\n if i-1>=0:\n visited.add(i-1)\n if i+1<n:\n visited.add(i+1)\n visited.add(i)\n return res\n \n \n``` | 1 | You are given an array `nums` consisting of positive integers.
Starting with `score = 0`, apply the following algorithm:
* Choose the smallest integer of the array that is not marked. If there is a tie, choose the one with the smallest index.
* Add the value of the chosen integer to `score`.
* Mark **the chosen element and its two adjacent elements if they exist**.
* Repeat until all the array elements are marked.
Return _the score you get after applying the above algorithm_.
**Example 1:**
**Input:** nums = \[2,1,3,4,5,2\]
**Output:** 7
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,1,3,4,5,2\].
- 2 is the smallest unmarked element, so we mark it and its left adjacent element: \[2,1,3,4,5,2\].
- 4 is the only remaining unmarked element, so we mark it: \[2,1,3,4,5,2\].
Our score is 1 + 2 + 4 = 7.
**Example 2:**
**Input:** nums = \[2,3,5,1,3,2\]
**Output:** 5
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,3,5,1,3,2\].
- 2 is the smallest unmarked element, since there are two of them, we choose the left-most one, so we mark the one at index 0 and its right adjacent element: \[2,3,5,1,3,2\].
- 2 is the only remaining unmarked element, so we mark it: \[2,3,5,1,3,2\].
Our score is 1 + 2 + 2 = 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
[Java/Python 3] TreeSet. | find-score-of-an-array-after-marking-all-elements | 1 | 1 | **Method 1: Use only TreeSet/SortedSet.**\n\n```java\n public long findScore(int[] nums) {\n TreeSet<List<Integer>> valIndex = new TreeSet<>(\n Comparator.comparingLong(l -> l.get(0) * 1_000_001L + l.get(1))\n );\n for (int i = 0; i < nums.length; ++i) {\n valIndex.add(Arrays.asList(nums[i], i));\n }\n long score = 0;\n while (!valIndex.isEmpty()) {\n var l = valIndex.pollFirst();\n int key = l.get(0), index = l.get(1);\n for (int neighborIndex : new int[]{index - 1, index + 1}) {\n if (0 <= neighborIndex && neighborIndex < nums.length) {\n valIndex.remove(Arrays.asList(nums[neighborIndex], neighborIndex));\n }\n }\n score += key;\n }\n return score;\n }\n```\n\n```python\nfrom sortedcontainers import *\n\nclass Solution:\n def findScore(self, nums: List[int]) -> int:\n val_index, score = SortedSet(), 0\n for i, num in enumerate(nums):\n val_index.add((num, i))\n while len(val_index) > 0:\n key, idx = val_index.pop(0)\n score += key\n for neighbor_index in idx - 1, idx + 1: \n if 0 <= neighbor_index < len(nums):\n val_index.discard((nums[neighbor_index], neighbor_index))\n return score\n```\n**Method 2: TreeMap + TreeSet**\n\n1. Traverse the input `nums`, use each value as the key of TreeMap, and put the corresponding index into TreeSet as the value of the TreeMap.\n2. Add to the score the first key of the TreeMap, remove the smallest index of the first key; Then remove the neighbors (if any) of the index;\n3. Repeat 2. till the TreeMap is empty, and return the score.\n \n```java\n public long findScore(int[] nums) {\n TreeMap<Integer, TreeSet<Integer>> indices = new TreeMap<>();\n for (int i = 0; i < nums.length; ++i) {\n indices.computeIfAbsent(nums[i], s -> new TreeSet<>()).add(i);\n }\n long score = 0;\n while (!indices.isEmpty()) {\n int key = indices.firstKey();\n int index = indices.get(key).pollFirst();\n removeIfEmpty(indices, key);\n for (int neighborIndex : new int[]{index - 1, index + 1}) {\n if (0 <= neighborIndex && neighborIndex < nums.length) {\n int neighborValue = nums[neighborIndex];\n if (indices.containsKey(neighborValue)) {\n indices.get(neighborValue).remove(neighborIndex);\n removeIfEmpty(indices, neighborValue);\n }\n }\n }\n score += key;\n }\n return score;\n }\n private void removeIfEmpty(TreeMap<Integer, TreeSet<Integer>> indices, int key) {\n if (indices.get(key).isEmpty()) {\n indices.remove(key);\n }\n }\n```\n\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)`, where `n = nums.length`. | 8 | You are given an array `nums` consisting of positive integers.
Starting with `score = 0`, apply the following algorithm:
* Choose the smallest integer of the array that is not marked. If there is a tie, choose the one with the smallest index.
* Add the value of the chosen integer to `score`.
* Mark **the chosen element and its two adjacent elements if they exist**.
* Repeat until all the array elements are marked.
Return _the score you get after applying the above algorithm_.
**Example 1:**
**Input:** nums = \[2,1,3,4,5,2\]
**Output:** 7
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,1,3,4,5,2\].
- 2 is the smallest unmarked element, so we mark it and its left adjacent element: \[2,1,3,4,5,2\].
- 4 is the only remaining unmarked element, so we mark it: \[2,1,3,4,5,2\].
Our score is 1 + 2 + 4 = 7.
**Example 2:**
**Input:** nums = \[2,3,5,1,3,2\]
**Output:** 5
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,3,5,1,3,2\].
- 2 is the smallest unmarked element, since there are two of them, we choose the left-most one, so we mark the one at index 0 and its right adjacent element: \[2,3,5,1,3,2\].
- 2 is the only remaining unmarked element, so we mark it: \[2,3,5,1,3,2\].
Our score is 1 + 2 + 2 = 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
Heap || Easiest Solution || python3 | find-score-of-an-array-after-marking-all-elements | 0 | 1 | \n```\nclass Solution:\n def findScore(self, nums: List[int]) -> int: \n heap = [(nums[i],i) for i in range(len(nums))] \n marked = {} \n score = 0\n heapq.heapify(heap) \n for i in range(len(nums)):\n mini,ind = heapq.heappop(heap) \n if ind not in marked:\n score += mini \n marked[ind] = 1 \n marked[ind-1] = marked[ind+1] = 1 \n return score\n \n \n \n \n``` | 3 | You are given an array `nums` consisting of positive integers.
Starting with `score = 0`, apply the following algorithm:
* Choose the smallest integer of the array that is not marked. If there is a tie, choose the one with the smallest index.
* Add the value of the chosen integer to `score`.
* Mark **the chosen element and its two adjacent elements if they exist**.
* Repeat until all the array elements are marked.
Return _the score you get after applying the above algorithm_.
**Example 1:**
**Input:** nums = \[2,1,3,4,5,2\]
**Output:** 7
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,1,3,4,5,2\].
- 2 is the smallest unmarked element, so we mark it and its left adjacent element: \[2,1,3,4,5,2\].
- 4 is the only remaining unmarked element, so we mark it: \[2,1,3,4,5,2\].
Our score is 1 + 2 + 4 = 7.
**Example 2:**
**Input:** nums = \[2,3,5,1,3,2\]
**Output:** 5
**Explanation:** We mark the elements as follows:
- 1 is the smallest unmarked element, so we mark it and its two adjacent elements: \[2,3,5,1,3,2\].
- 2 is the smallest unmarked element, since there are two of them, we choose the left-most one, so we mark the one at index 0 and its right adjacent element: \[2,3,5,1,3,2\].
- 2 is the only remaining unmarked element, so we mark it: \[2,3,5,1,3,2\].
Our score is 1 + 2 + 2 = 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 106` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.