title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
python3 Solution | maximize-win-from-two-segments | 0 | 1 | \n```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n dp=[0]*(len(prizePositions)+1)\n res=0\n j=0\n for i,a in enumerate(prizePositions):\n while prizePositions[j]<prizePositions[i]-k:\n j+=1\n dp[i+1]=max(dp[i],i-j+1)\n res=max(res,i-j+1+dp[j])\n \n return res \n \n \n \n``` | 3 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Solution Using Binary Search | maximize-win-from-two-segments | 0 | 1 | # Code\n```\nfrom bisect import bisect_right,bisect_left\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n ans=prv=0\n for i,item in enumerate(prizePositions):\n j1=bisect_left(prizePositions,item-k)\n j2=bisect_right(prizePositions,item+k)\n ans=max(ans,j2-j1,prv+j2-i)\n prv=max(prv,i-j1+1)\n return ans\n``` | 2 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
maximize win from two segments | maximize-win-from-two-segments | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n\n intval=[]\n max_before=[]\n start=0\n count=0\n\n for index,pos in enumerate(prizePositions):\n count+=1\n while pos-k>prizePositions[start]:\n count-=1\n start+=1\n intval.append((count,pos))\n if not max_before or max_before[-1][0]<count:\n max_before.append((count,pos))\n\n max_sol=0\n while intval:\n count,pos=intval.pop()\n while max_before and max_before[-1][-1]>=pos-k:\n max_before.pop()\n\n candidate=count+(0 if not max_before else max_before[-1][0])\n max_sol=max(candidate,max_sol)\n\n return max_sol\n\n \n \n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Medium | maximize-win-from-two-segments | 0 | 1 | ```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n\n N = len(prizePositions)\n\n dp = [0] * (N + 1)\n\n l = 0\n\n ans = 0\n\n for r in range(N):\n\n while prizePositions[l] + k < prizePositions[r]:\n l += 1\n\n dp[r + 1] = max(dp[r], r - l + 1)\n\n ans = max(ans, dp[l] + r - l + 1)\n \n\n return ans\n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Sliding Window O(N). Clean Code + Intuition + Similar problem | maximize-win-from-two-segments | 0 | 1 | # Intuition\nThis is the same problem as:\nhttps://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/editorial, Approach 1: Bidirectional Dynamic Programming, where you want a max to the left of i and a max to the right of i.\n\n# Approach\n1. Use a counter to get a num -> count mapping so the distance to iterate becomes less\n2. Make an array in_span_l which is the maximum possible score making a span to the left of this index. Use a sliding window to compute this, tracking all numbers within k span of the index. \n3. Similarly, make an array in_span_r is the maximum possible to the right of this index. \n4. The max is max(in_span_l[i] + in_span_r[i + 1]) for any i \n```\n1 2 3 5 7 num\n2 2 2 1 2 count of num\n2 4 6 6 6 in_span_l\n6 4 3 3 2 in_span_r\n```\n\n# Code\n```\n\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n\n counts = Counter(prizePositions)\n counts_arr = [(num, count) for num, count in counts.items()]\n if len(counts_arr) == 1:\n return counts_arr[0][1]\n num_ind = list(counts.keys())\n in_span = []\n rolling_count = 0\n j = 0\n pre = -inf\n for i in range(len(counts_arr)):\n rolling_count += counts_arr[i][1]\n while num_ind[i] - num_ind[j] > k:\n rolling_count -= counts_arr[j][1]\n j += 1\n in_span.append(max(rolling_count, pre))\n pre = max(rolling_count, pre)\n\n in_span_r = []\n rolling_count = 0\n j = len(counts_arr) - 1\n pre = -inf\n for i in range(len(counts_arr) - 1, -1, -1):\n rolling_count += counts_arr[i][1]\n while num_ind[j] - num_ind[i] > k:\n rolling_count -= counts_arr[j][1]\n j -= 1\n in_span_r.append(max(rolling_count, pre))\n pre = max(rolling_count, pre)\n in_span_r = list(reversed(in_span_r))\n # print(list(range(len(counts_arr))), \'i\')\n # print(list(counts.keys()), \'num\')\n # print(list(counts.values()), \'count of num\')\n # print(in_span, \'span_l\')\n # print(in_span_r, \'span_r\')\n max_all = -inf\n for i in range(len(in_span) - 1):\n max_all = max(max_all, in_span[i] + in_span_r[i + 1])\n return max_all\n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python3 Dynamic programming | maximize-win-from-two-segments | 0 | 1 | # Approach\n- Need to choose at most two segment, the dfs function should go through all index or run out of two segments.\n- There are two states in each index, pick or not pick\n- If pick the idx, skip the value less or equal than the value plus k. \n ex: `prize[idx] = 1 and k = 2`\n It can cover from value 1 to 3, so find the next first index larger than 3, using binary search to find next index\n- If skip the index, skip all the index with the same value.\n ex: `prize = [1,1,1,1,2,2,2,3,3]`\n If skip index 0, should also skip other index with the same value `1`, it won\'t bring larget answer, using binary search to find the next first index of value larger than 1d\n\n# Complexity\n- Time complexity:\nO( n * log(n) *2)\n\n- Space complexity:\nO( n )\n\n# Code\n```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n @cache\n def dfs(idx, n):\n if idx==len(prizePositions) or n==0:\n return 0\n left = bisect.bisect_right(prizePositions, prizePositions[idx]+k)\n i = bisect.bisect_right(prizePositions, prizePositions[idx])\n a = dfs(left, n-1)+left-idx\n b = dfs(i, n)\n return max(a,b)\n return dfs(0, 2)\n```\n\nIterator\n```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n dp = [0 for _ in range(len(prizePositions)+1)]\n ans = 0\n for i in range(len(prizePositions)):\n if i>0:\n dp[i] = max(dp[i], dp[i-1])\n left = bisect.bisect_right(prizePositions, prizePositions[i]+k)\n dp[left] = max(dp[left], left-i)\n ans = max(ans, dp[i]+left-i)\n return ans\n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Use two points cleverly | maximize-win-from-two-segments | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximizeWin(self, p: List[int], k: int) -> int:\n i,n = 0,len(p)\n if p[-1] - p[0] <= k:\n return n\n pre = [0]\n i = 0\n for j in range(1,n):\n if p[j] - p[i] > k:\n i += 1\n else:\n pre.append(j)\n sub = [n-1]\n j = n-1\n for i in range(n-2,-1,-1):\n if p[j] - p[i] > k:\n j -= 1\n else:\n sub.append(i)\n \n sub = sub[::-1]\n i,j = 0,0\n ans = -len(sub)\n while i < len(pre) and j < len(sub):\n if pre[i] >= sub[j]:\n j += 1\n else:\n ans = max(i-j,ans)\n i += 1\n return ans + len(sub) + 1\n\n\n\n \n \n\n \n\n\n\n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python (Simple DP + Sliding Window) | maximize-win-from-two-segments | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximizeWin(self, prizePositions, k):\n n = len(prizePositions)\n\n left, dp, max_val = 0, [0]*(n+1), 0\n\n for right in range(n):\n while prizePositions[right] - prizePositions[left] > k:\n left += 1\n\n dp[right+1] = max(dp[right],right-left+1)\n\n max_val = max(max_val,dp[left] + right - left + 1)\n\n return max_val\n\n\n\n\n\n \n``` | 0 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
✅ Clever Diagonals with Diagram Explanation ✅ | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Overview\n- The brute force solution would be to search the grid for every $$1$$ that can be flipped. However, this solution would lead to TLE. \n - Instead, we can do this problem in $$O(mn)$$. Precisely 3 iterations of the entire grid. \n - All we need is $$O(m+n)$$ extra space for a list of diagonals. \n- It is important to know that the path only has ****2 directions****: down and right. This is an important constraint that makes this solution work. \n- First, we prune the possible paths so that our grid is simplified.\n- We keep track of **diagonal counts** (see example) which determine whether or not a graph can be disconnected. \n\n# Example\n\n- Let us take a look at the given **Example 1:**\n- The first two steps are used to [prune](https://en.wikipedia.org/wiki/Decision_tree_pruning#:~:text=Pruning%20is%20a%20data%20compression,and%20redundant%20to%20classify%20instances.) our grid so that useless $$1$$\'s are removed from our grid. \n\n\n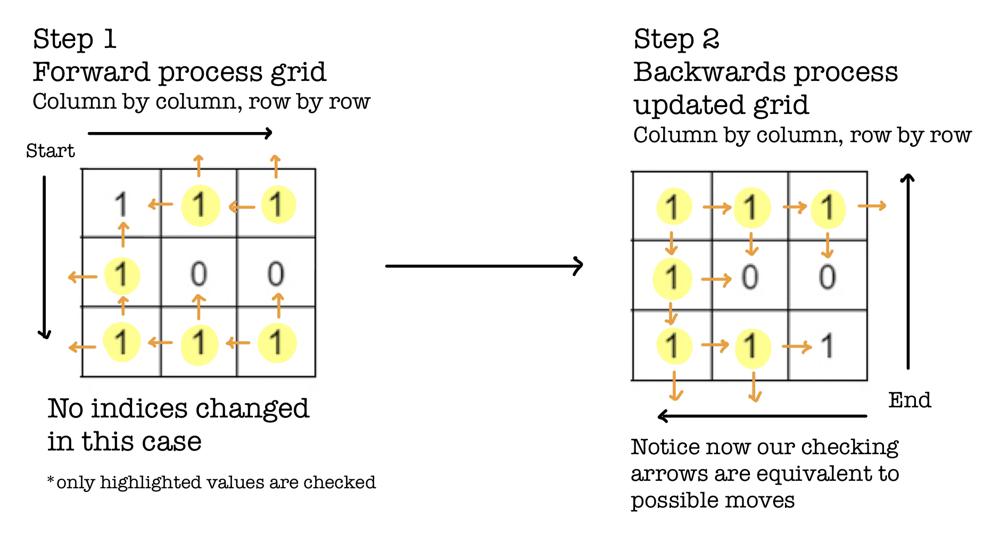\n- The first step prunes the tree by looking at all possible previous steps to that index. So we look at the index above and to the left. \n- The second step prunes the tree by looking at all possible moves for that index. So we look at the index below and to the right. \n\n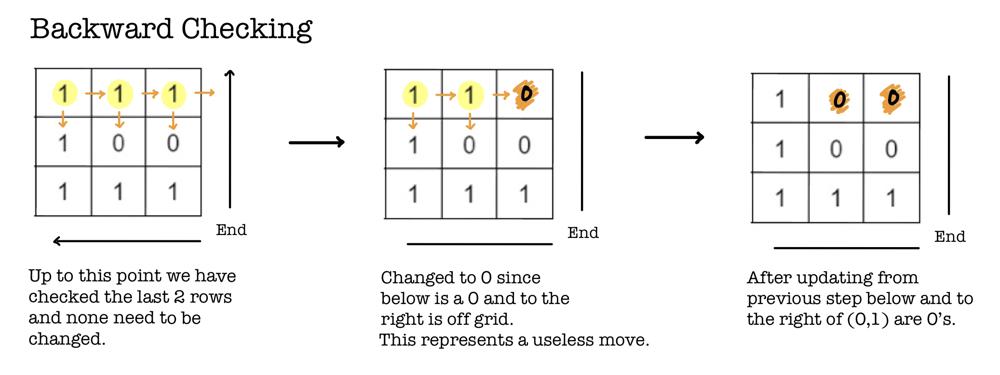\n- These two steps require us to iterate through our grid twice. \n- Now that we have pruned our grid, we will pass this result to the next step which involves diagonal counting. \n- *Note: motivation for pruning is given at the end of solution.*\n\n\n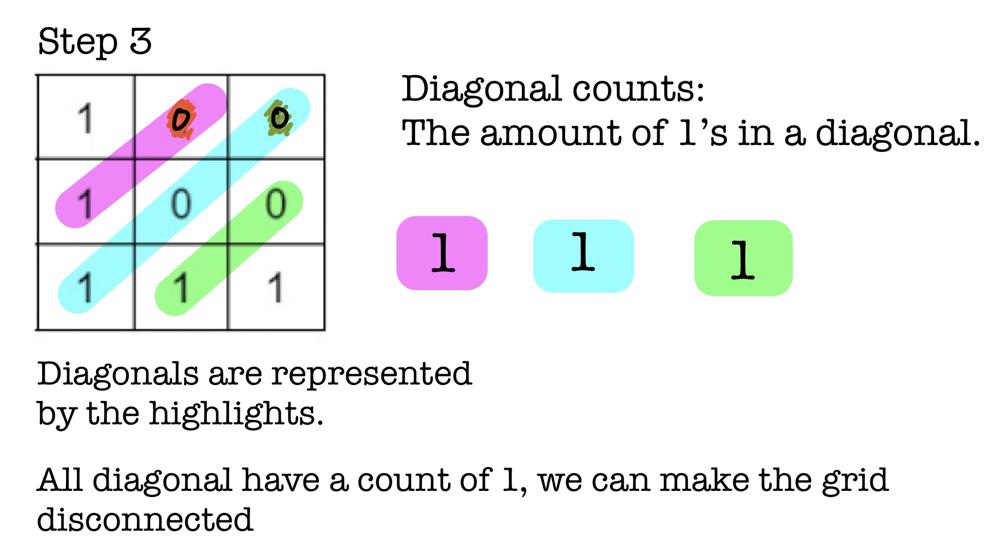\n\n- Notice we do not care about diagonal count for the begin and end. \n\n\n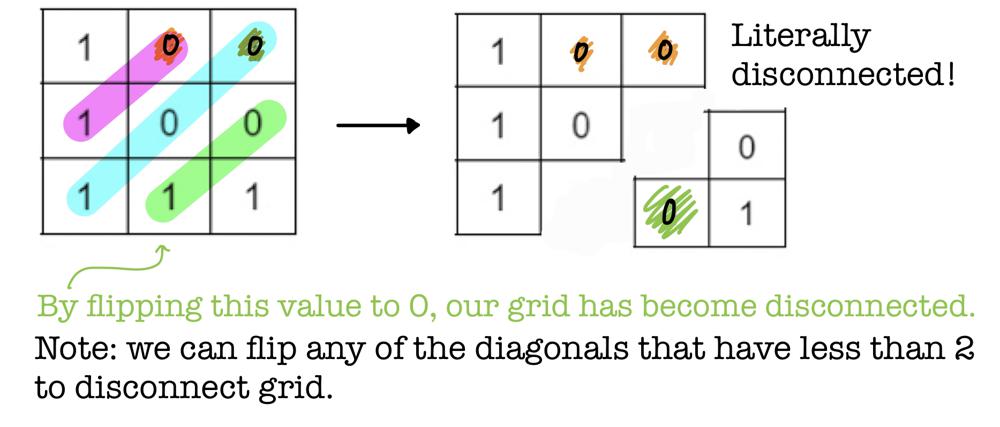\n\n- Think of the diagonals as gates: $$1$$\'s represent gate openings and $$0$$\'s represent closed gates. \n- **If a diagonal does not contain at least 2 openings then it can be disconnected.** \n- The reason is because if there are 0 openings then there are no paths to $$(n-1, m-1)$$ without any flips. If there is exactly 1 opening for that diagonal, then it can be flipped to make it 0 openings. \n- What make diagonals special is that the sum of their column and row indices are equivalent. Thus, `diagonals[i+j]` is the same for all that belong in the same diagonal. \n# Code\n\n```C++ []\nbool isPossibleToCutPath(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n // Initial pruning\n // Forward checking\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; j++){\n if (i == 0 && j == 0 || grid[i][j] == 0) continue;\n if ((i == 0 || grid[i-1][j] == 0) && (j == 0 || grid[i][j-1] == 0)){\n grid[i][j] = 0;\n }\n }\n }\n\n // Backwards checking\n for (int i = m-1; i >= 0; i--){\n for (int j = n-1; j >= 0; j--){\n if (i == m-1 && j == n-1 || grid[i][j] == 0) continue;\n if ((i == m-1 || grid[i+1][j] == 0) && (j == n-1 || grid[i][j+1] == 0)){\n grid[i][j] = 0;\n }\n }\n }\n\n // Diagonal counting\n vector<int> diagonal(m+n-1);\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; j++){\n if (grid[i][j]) diagonal[i+j]++;\n }\n }\n\n // Final count check\n for (int i = 1; i < m+n-2; i++){ \n if (diagonal[i] < 2) return true;\n }\n return false;\n}\n```\n```python3 []\ndef isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n # Forward checking\n for i in range(m):\n for j in range(n):\n if (i == 0 and j == 0) or (grid[i][j] == 0):\n continue\n if (i == 0 or grid[i-1][j] == 0) and (j == 0 or grid[i][j-1] == 0):\n grid[i][j] = 0\n\n # Backward checking\n for i in range(m-1, -1, -1):\n for j in range(n-1, -1, -1):\n if (i == m-1 and j == n-1) or (grid[i][j] == 0):\n continue\n if (i == m-1 or grid[i+1][j] == 0) and (j == n-1 or grid[i][j+1] == 0):\n grid[i][j] = 0\n \n # Diagonal counting\n diagonal = [0] * (m + n - 1)\n for i in range(m):\n for j in range(n):\n if (grid[i][j] != 0):\n diagonal[i + j] += 1\n\n # Final check\n for i in range(1, m + n - 2):\n if (diagonal[i] < 2):\n return True\n return False\n```\n\n\nAdditional note: If you skip pruning, solution will still AC. That is because cases such as the ones below are not being tested. \n\n# Motivation for Pruning\n\n- Consider the example below: \n- `[[1,1,1,0,1],[1,0,1,0,0],[1,1,0,1,1],[0,0,1,0,1],[1,0,1,1,1]]`\n\n\n - In this case, the grid is already disconnected. Due to the arrangement of the $$0$$\'s, diagonal counting will not catch any issues since each diagonal would have 2 openings. \n - Example where forward and backward are needed:\n - `[[1,1,0,0,1],[1,1,1,1,0],[1,1,0,1,1],[1,0,1,1,1],[1,1,0,1,1]]`\n \n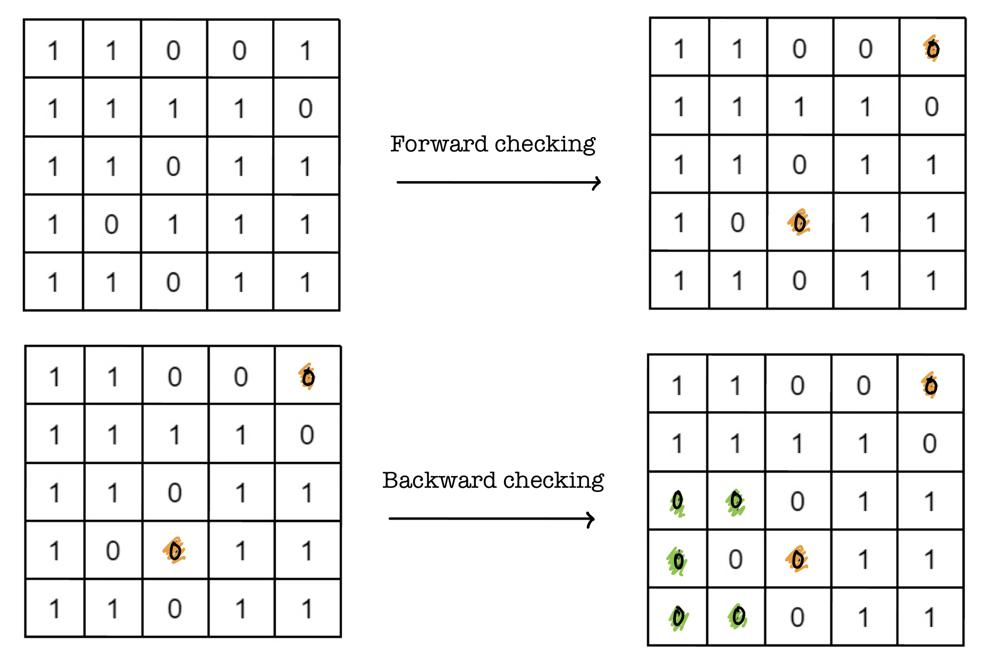\n- Notice that after forward checking our grid is still not acceptable for diagonal counting. Only after backward checking is it good. \n\n\n### Please upvote if this helped. Thanks!\n | 43 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
DP | Count number of path | Simple solution | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\nIf there exist a point `(i, j)` which is not `(0, 0)` or `(m-1, n-1)`, such that the number of the paths from `(0, 0)` to `(m-1, n-1)` go through `(i, j)`equals the number of paths from `(0, 0)` to `(m-1, n-1)` without any constraint, return True.\n\n# Approach\n\nTo count the numbers of paths go through `(i, j)`. We just calculate number of paths from `(0, 0)` to `(i, j)` and number of paths from `(i, j)` to `(m-1, n-1)`, then multiply them up.\n\n# Complexity\n- Time complexity:\n$O(n*m)$\n- Space complexity:\n$O(n*m)$\n\n# Code\n```python\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n\n # number of paths from (0, 0) to (i, j)\n dp1 = [[0] * (n+1) for _ in range(m + 1)]\n dp1[1][1] = 1\n for i in range(1, m + 1):\n for j in range(1, n + 1):\n if grid[i-1][j-1]:\n dp1[i][j] += dp1[i-1][j] + dp1[i][j-1]\n \n # number of paths from (i, j) to (m-1, n-1) \n dp2 = [[0] * (n+1) for _ in range(m + 1)]\n dp2[-2][-2] = 1\n for i in range(m - 1, -1, -1):\n for j in range(n - 1, -1, -1):\n if grid[i][j]:\n dp2[i][j] += dp2[i+1][j] + dp2[i][j+1]\n \n # number of paths from (0, 0) to (m-1, n-1) \n target = dp1[-1][-1]\n\n for i in range(m):\n for j in range(n):\n if (i!=0 or j!=0) and (i!=m-1 or j!=n-1):\n if dp1[i+1][j+1] * dp2[i][j] == target: \n return True\n return False\n``` | 52 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
[Python🐍] Simple DFS - remember the path and remove the path | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nGeneral approach is simple: 3 steps\n\n#1\ndo a DFS to reach the end (M-1,N-1) and remember the path.\n\n#2\nRemove the path by setting 0 all the way.\n\n#3\nTry DFS again to see if there is still a connected path.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(M*N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(M*N)\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n \n M = len(grid)\n N = len(grid[0])\n\n #visited set, to not visit the same nodes again\n v= set()\n\n dirs=[[0,1],[1,0]]\n\n path = set()\n \n v.add((0,0))\n path.add((0,0))\n \n def dfs(x,y):\n \n if x == M -1 and y == N -1:\n return True\n \n for d in dirs:\n nx = x + d[0]\n ny = y + d[1]\n \n if nx < M and ny < N and (nx,ny) not in v and grid[nx][ny] == 1:\n v.add((nx,ny))\n path.add((nx,ny))\n if dfs(nx,ny):\n return True\n path.remove((nx,ny))\n return False\n\n # 1 do a dfs from (0,0) to (M-1,N-1) \n res = dfs(0,0)\n \n # if there is no path the it\'s already disconnectd, return True\n if not res:\n return True\n \n # remove the first and last node from the path\n if (0,0) in path:\n path.remove((0,0))\n if (M-1,N-1) in path:\n path.remove((M-1,N-1))\n \n # 2 remove the path from the grid\n for p in path:\n grid[p[0]][p[1]] = 0\n \n #reset the visited set\n v= set()\n v.add((0,0))\n\n # 3 try again DFS, if it\'s not connected, return True\n return not dfs(0,0)\n \n``` | 17 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
[Python 3] DFS + BFS - Simple | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(M * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M * N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. DFS + BFS\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n dirs = [(-1, 0), (0, -1)]\n def dfs(i: int, j: int) -> None:\n grid[i][j] = 2\n for di, dj in dirs:\n if 0 <= i + di < m and 0 <= j + dj < n and grid[i + di][j + dj] == 1: dfs(i + di, j + dj)\n \n dfs(m - 1, n - 1)\n \n dq = collections.deque([(0, 0)])\n grid[0][0] = 0\n dirs = [(1, 0), (0, 1)]\n while dq:\n l = len(dq)\n for _ in range(l):\n i, j = dq.popleft()\n if i == m - 1 and j == n - 1: return False\n for di, dj in dirs:\n if 0 <= i + di < m and 0 <= j + dj < n and grid[i + di][j + dj] == 2: \n dq.append((i + di, j + dj))\n grid[i + di][j + dj] = 0\n\n\n if len(dq) == 1 and dq[0] != (m - 1, n - 1): return True\n\n return True\n``` | 3 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
【C++||Java||Python】DP and then count diagonals | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n\n# Intuition\n1. Immediately it comes to mind that we have no reason to change $0$ to $1$.\n2. Note that only from left to right or from top to bottom, dynamic programming could be considered at first.\n2. Using DP we can get the connectivity from $(0,0)$ to $(i,j)$ and from $(i,j)$ to $(m-1,n-1)$, but it\'s hard to handle the remove operation.\n3. It seems that all graphs that can be cut off satisfy a property: **all paths must pass through the same point**.\n4. **Notice that at the same distance on each path, the candidate points are distributed on the same diagonal.**:\n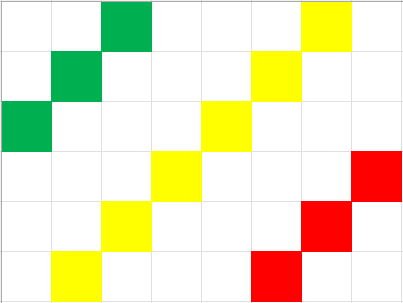\n *The 3rd point of each path must be chosen from green points.*\n *The 7th point of each path must be chosen from yellow points.*\n *The 11th point of each path must be chosen from red points.*\n\n5. If you find that there is a distance which has less than two candidate points, this single one will be the removed point, so return true; otherwise if you can\'t find this point, return false.\n\n# Approach\n1. First, using dynamic programming to get two tables which `vis1[i+1][j+1]` means if there is at least one path from $(0,0)$ to $(i,j)$, and `vis2[i+1][j+1]` means if there is at least one path from $(i,j)$ to $(m-1,n-1)$.\n2. Count how much points can be occuried on distant $i$, saved in an array `cnt`.\n3. Find if there has $1$ in `cnt[1:m+n-2]`.\n\n# Complexity\n- Time complexity: $O(mn)$\n- Space complexity: $O(mn)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n bool isPossibleToCutPath(vector<vector<int>>& a) {\n int m = a.size(), n = a[0].size();\n vector<int> cnt(m+n, 0);\n vector<vector<bool>> vis1(m+2, vector<bool>(n+2, false));\n vector<vector<bool>> vis2(m+2, vector<bool>(n+2, false));\n vis1[0][1] = true, vis2[m+1][n] = true;\n for (int i = 1; i <= m; ++i) {\n for (int j = 1; j <= n; ++j) {\n vis1[i][j] = a[i-1][j-1] && (vis1[i-1][j] || vis1[i][j-1]);\n }\n }\n for (int i = m; i >= 1; --i) {\n for (int j = n; j >= 1; --j) {\n vis2[i][j] = a[i-1][j-1] && (vis2[i+1][j] || vis2[i][j+1]);\n cnt[i+j-2] += vis1[i][j] && vis2[i][j];\n }\n }\n for (int i = 1; i < m+n-2; ++i) {\n if (cnt[i] <= 1) return true;\n }\n return false;\n }\n};\n```\n``` Java []\nclass Solution {\n public boolean isPossibleToCutPath(int[][] a) {\n int m = a.length, n = a[0].length;\n boolean [][]vis1 = new boolean[m+2][n+2];\n boolean [][]vis2 = new boolean[m+2][n+2];\n vis1[0][1] = true;\n vis2[m+1][n] = true;\n int []cnt = new int[m+n];\n for (int i = 1; i <= m; ++i) {\n for (int j = 1; j <= n; ++j) {\n vis1[i][j] = a[i-1][j-1] == 1 && (vis1[i-1][j] || vis1[i][j-1]);\n }\n }\n for (int i = m; i >= 1; --i) {\n for (int j = n; j >= 1; --j) {\n vis2[i][j] = a[i-1][j-1] == 1 && (vis2[i+1][j] || vis2[i][j+1]);\n if (vis1[i][j] && vis2[i][j]) cnt[i+j-2]++;\n }\n }\n for (int i = 1; i < m+n-2; ++i) {\n if (cnt[i] <= 1) return true;\n }\n return false;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def isPossibleToCutPath(self, a: List[List[int]]) -> bool:\n m, n = len(a), len(a[0])\n vis1 = [[0 for i in range(n+2)] for j in range(m+2)]\n vis2 = [[0 for i in range(n+2)] for j in range(m+2)]\n vis1[0][1], vis2[m][n+1] = 1, 1\n cnt = [0] * (m+n-1)\n for i in range(1, m+1):\n for j in range(1, n+1):\n vis1[i][j] = a[i-1][j-1] and (vis1[i-1][j] or vis1[i][j-1])\n for i in range(m, 0, -1):\n for j in range(n, 0, -1):\n vis2[i][j] = a[i-1][j-1] and (vis2[i+1][j] or vis2[i][j+1])\n cnt[i+j-2] += vis1[i][j] and vis2[i][j]\n return any(cnt[i] < 2 for i in range(1, n + m - 2))\n``` | 17 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
[Python] Diagonal Trick. Simple and intuitive solution. | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\nNotice that every path has to go through one of the antidiagonals (those that go from the bottom left to the top right). So if we can block at least one of these diagonals, a.k.a. assign zeros to all of its elements, there won\'t be any path.\n\n# Approach\nCount the number of ones for each antidiagonal. Then just check if there is at least one diagonal with at most one value $1$. If it\'s the case, we can flip this value to $0$, and there won\'t be any path. Also, take into account that we don\'t count the topmost $(0, 0)$ and the bottommost $(m - 1, n - 1)$ diagonals as they always consist of one value $1$ each and shouldn\'t be counted.\n\n# Complexity\n- Time complexity: $O(mn)$\n\n- Space complexity: $O(m + n)$ - to store all the antidiagonals.\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, M: list[list[int]]) -> bool:\n m, n = len(M), len(M[0])\n diag = Counter()\n\n for i in range(m):\n for j in range(n):\n if i + j not in (0, m + n - 2):\n diag[i + j] += M[i][j]\n\n return any(c < 2 for c in diag.values())\n``` | 1 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
DFS | Python3 | O(m*n) Time | O(1) Space | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we need to disconnect them then we just need to block the node which we visit. If still we can reach the end node more than once, then we can not disconnect them in a single flip.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse DFS to traverse the graph and block the point once visited by setting it to zero.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*m)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n if m == 1 and n == 2:\n return False\n \n \n def dfs(i=0,j=0):\n if i == m-1 and j == n-1:\n return True\n \n if i >= m or j >= n or grid[i][j]==0:\n return False\n \n grid[i][j]=0 #Blocking the point. So we do not visit it later.\n \n if (i, j) != (0, 0):\n #If we are not at start, we need to only check that whether this path leads to the end or not. We do not need to check whether more than one path leads to the end or not because if we flip this point, all the paths will be blocked going through the point.\n if dfs(i+1, j):\n return True\n return dfs(i, j+1)\n\n #In case of start, if only one path leads to end, we can flip that so to be impossible in one flip both the paths must go to the end.\n return not(dfs(i+1, j) and dfs(i, j+1))\n \n return dfs()\n \n``` | 5 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
Python 3 | Greedy, DFS | Explanation | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\n- If there are two paths that \n - can reach from top-left to bottom-right\n - has no overlap (except starting & ending point)\n- Then, it\'s not possible to disconnect the graph with one flip\n\n# Approach\n- The intuition is straight forward, but how do we do that? \n - Find out all paths and compare is definitely not possible with scale given\n- But note this, **if there is a valid `path A`, then any other paths `B` that share any points with `path A` are not what we are looking for.**\n- We can achieve this by using DFS with modifying the original matrix\n - We will make sure that each point (except starting & ending points) are fliped for `paht A`\n - Then do the same DFS again\n - If this DFS is able to find a `path B`, then it\'s not possible to disconnect graph with one flip, thus return `False`\n - Otherwise, we know that all possible `path B` share at least some points (if appliable) with `path A`. There will be some critical points can be fliped on `path A`, thus return `True`\n\n# Complexity\n- Time complexity:\n`O(m*n)`\n\n- Space complexity:\n`O(m*n)` for stack used\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n def dfs(x, y):\n nonlocal m, n, grid\n if not grid[x][y]:\n return False\n if x == m-1 and y == n-1:\n return True\n grid[x][y] = 0 \n if x + 1 < m and dfs(x + 1, y):\n return True\n if y + 1 < n and dfs(x, y + 1):\n return True\n return False\n dfs(0, 0) # destroy one path\n grid[0][0] = 1 # reset origin\n return not dfs(0, 0) # try to find another path, if not possible, then such a point exists\n \n``` | 2 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
Python DFS solution | Number of independent paths | Beats 96% | O(n*m) | O(1) | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n # Count the number of independent non-overlapping paths from s->d\n\n # define prior base cases \n if grid[0][0]==0 or grid[-1][-1]==0:return True\n if grid==[[1]] or grid==[[1,1]] or grid==[[1],[1]]:return False\n\n m,n=len(grid),len(grid[0])\n #Will return possible paths which can be either (0,1,2 at max from s->d)\n def dfs(r,c):\n if r==m-1 and c==n-1:\n return 1\n if r>=m or c>=n:\n return 0\n if grid[r][c]==1:\n grid[r][c]=2 # marked visited\n if (r,c)==(0,0):\n # only place where 2 independent paths\n return dfs(r+1,c) + dfs(r,c+1) \n else:\n # return 1 as if we make this cell 0 then \n # any number of paths from here will be unreachable \n return dfs(r+1,c) or dfs(r,c+1) \n else:\n return 0\n paths=dfs(0,0)\n # If paths is leff than 2 return True\n return paths<2\n\n \n \n``` | 0 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
DFS For Two Paths | disconnect-path-in-a-binary-matrix-by-at-most-one-flip | 0 | 1 | # Approach\nWe can\'t make matrix disconnected in case when two independent paths from (0, 0) to (m-1, n-1) exist.\n\n# Complexity\n- Time complexity: $$O(m*n)$$.\n\n- Space complexity: $$O(m+n)$$.\n\n# Code\n```\nclass Solution:\n def isPossibleToCutPath(self, grid: List[List[int]]) -> bool:\n m, n = len(grid), len(grid[0])\n if m == 1 and n > 2 or m > 2 and n == 1:\n return True\n elif grid[0][0] == 0 or grid[m-1][n-1] == 0:\n return True\n elif m <= 2 and n == 1 or m == 1 and n <= 2:\n return False\n\n def dfs(i, j, d1, d2, path):\n if (i, j) == (m-1, n-1):\n return True\n elif not (0 <= i < m and 0 <= j < n) or grid[i][j] == 0:\n return False\n\n path.add((i, j))\n if dfs(i+d1, j+d2, d1, d2, path):\n return True\n elif dfs(i+d2, j+d1, d1, d2, path):\n return True\n path.remove((i, j))\n\n return False\n \n pathHigh, pathLow = set(), set()\n if not dfs(0, 1, 0, 1, pathHigh):\n return True\n if not dfs(1, 0, 1, 0, pathLow):\n return True\n\n return pathHigh & pathLow\n``` | 0 | You are given a **0-indexed** `m x n` **binary** matrix `grid`. You can move from a cell `(row, col)` to any of the cells `(row + 1, col)` or `(row, col + 1)` that has the value `1`. The matrix is **disconnected** if there is no path from `(0, 0)` to `(m - 1, n - 1)`.
You can flip the value of **at most one** (possibly none) cell. You **cannot flip** the cells `(0, 0)` and `(m - 1, n - 1)`.
Return `true` _if it is possible to make the matrix disconnect or_ `false` _otherwise_.
**Note** that flipping a cell changes its value from `0` to `1` or from `1` to `0`.
**Example 1:**
**Input:** grid = \[\[1,1,1\],\[1,0,0\],\[1,1,1\]\]
**Output:** true
**Explanation:** We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** false
**Explanation:** It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 1` | null |
Python | 100% Faster | Easy Solution✅ | take-gifts-from-the-richest-pile | 0 | 1 | # Code\u2705\n```\nimport math\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n i = 0\n while i < k:\n gifts = sorted(gifts)\n sqrt = math.floor(math.sqrt(gifts[-1]))\n gifts[-1] = sqrt\n i +=1\n return sum(gifts)\n```\n\n | 9 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
5 lines simplest code You ever found.Python3 | take-gifts-from-the-richest-pile | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#heap approach\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n list1 = [-x for x in gifts]\n heapq.heapify(list1)\n for i in range(k):\n x = -heapq.heappop(list1)\n heapq.heappush(list1,-int(math.sqrt(x)))\n return abs(sum(list1)\n```\n```\n#normal approach\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n for i in range(k):\n x=max(gifts)\n gifts.remove(x)\n gifts.append(int(sqrt(x)))\n return sum(gifts)\n``` | 1 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
Easy | Python Solution | Heap | take-gifts-from-the-richest-pile | 0 | 1 | # Code\n```\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n res = [-i for i in gifts]\n heapq.heapify(res)\n for i in range(k):\n temp = -heapq.heappop(res)\n temp = int(math.sqrt(temp))\n heapq.heappush(res, -temp)\n ans = [-i for i in res]\n return int(sum(ans)) \n```\nDo upvote if you like the Solution :) | 1 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
Python 3 || 6 lines, heap, w/ example || T/M: 32 ms / 14.0 MB | take-gifts-from-the-richest-pile | 0 | 1 | "$$heapq.heappushpop(heap, item)$$: Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop." -- [https://docs.python.org/3/library/heapq.html]()"\n```\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n\n heap = [] # Example: gifts = [25,64,9,4,100] ; k = 4\n\n for g in gifts: heappush(heap,-g) # heap = [-100,-64,-25, -9,-4]\n \n # g isqrt(g) heap\n g = -heappop(heap) # \u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\n # 100 10 [-64,-25, -9, -4]\n for _ in range(k): # 64 8 [-25,-10, -9, -4] \n g = -heappushpop(heap, -isqrt(g)) # 10 3 [-10,- 8, -9, -4]\n # 9 [- 8, -4, -5, -3]\n \n return g - sum(heap) # return 9 - sum(- 8, -4,-5,-3) = 29\n```\n[https://leetcode.com/problems/take-gifts-from-the-richest-pile/submissions/892067623/](http://) | 4 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
[ Python ] ✅✅ Simple Python Solution | 100 % Faster🥳✌👍 | take-gifts-from-the-richest-pile | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 155 ms, faster than 100.00% of Python3 online submissions for Take Gifts From the Richest Pile.\n# Memory Usage: 14 MB, less than 100.00% of Python3 online submissions for Take Gifts From the Richest Pile.\n\n\n\n\n\tclass Solution:\n\t\tdef pickGifts(self, gifts: List[int], k: int) -> int:\n\n\t\t\twhile k > 0:\n\n\t\t\t\tmax_pile = max(gifts)\n\t\t\t\tindex = gifts.index(max_pile)\n\n\t\t\t\tgifts[index] = int(math.sqrt(max_pile))\n\n\t\t\t\tk = k - 1\n\n\t\t\treturn sum(gifts)\n\t\t\t\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 3 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
Easy to Understand Python Solution (100% faster and memory efficient) | take-gifts-from-the-richest-pile | 0 | 1 | \n\n# Complexity\n- Time complexity: O(nk)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n counter = 0\n while counter < k:\n gifts.sort(reverse = True)\n maxPile = gifts[0]\n maxPile = math.floor(maxPile**0.5)\n gifts[0] = maxPile\n counter+=1\n return sum(gifts) \n \n \n \n``` | 1 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
Python Solution Using Heap || Easy to Understand for beginners | take-gifts-from-the-richest-pile | 0 | 1 | ```\nfrom heapq import heapify,heappush,heappop\nclass Solution:\n def pickGifts(self, gifts: List[int], k: int) -> int:\n\t\t# python stores element as min heap so 1 will be popped out first instead of 2 to do it reverse multiply each\n\t\t# elements by -1 so -2 will be popped out first\n gifts = [-gift for gift in gifts]\n\t\t\n\t\t# heapify the new array\n heapify(gifts)\n\t\t\n\t\t# iterate till k>0\n while k:\n\t\t\t\n\t\t\t# pop the element from heap and negative it so that -(-2) => 2\n a = -heappop(gifts)\n\t\t\t\n\t\t\t# push floor of its square root and add it to the heap (remember to add negative sign)\n heappush(gifts,-int(a**0.5))\n\t\t\t\n k -= 1\n\t\t\t\n\t\t# return the final sum\n return -sum(gifts)\n``` | 1 | You are given an integer array `gifts` denoting the number of gifts in various piles. Every second, you do the following:
* Choose the pile with the maximum number of gifts.
* If there is more than one pile with the maximum number of gifts, choose any.
* Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return _the number of gifts remaining after_ `k` _seconds._
**Example 1:**
**Input:** gifts = \[25,64,9,4,100\], k = 4
**Output:** 29
**Explanation:**
The gifts are taken in the following way:
- In the first second, the last pile is chosen and 10 gifts are left behind.
- Then the second pile is chosen and 8 gifts are left behind.
- After that the first pile is chosen and 5 gifts are left behind.
- Finally, the last pile is chosen again and 3 gifts are left behind.
The final remaining gifts are \[5,8,9,4,3\], so the total number of gifts remaining is 29.
**Example 2:**
**Input:** gifts = \[1,1,1,1\], k = 4
**Output:** 4
**Explanation:**
In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile.
That is, you can't take any pile with you.
So, the total gifts remaining are 4.
**Constraints:**
* `1 <= gifts.length <= 103`
* `1 <= gifts[i] <= 109`
* `1 <= k <= 103` | null |
Python straightforward solution with prefix sum | count-vowel-strings-in-ranges | 0 | 1 | \n# Code\n```python\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n vowels = \'aeiou\'\n counts = [0] * len(words)\n for i, word in enumerate(words):\n if word[0] in vowels and word[-1] in vowels:\n counts[i] = 1\n acc = list(accumulate(counts, initial=0))\n res = []\n for l, r in queries:\n res.append(acc[r + 1] - acc[l])\n return res\n``` | 2 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
python 3 100% beats | count-vowel-strings-in-ranges | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n d={}\n for x in range(97,123):\n d[chr(x)]=0\n d["a"]=1\n d["e"]=1\n d["i"]=1\n d["o"]=1\n d[\'u\']=1\n le=len(words)\n l=[0]*len(words)\n y=0\n for x in words:\n if d[x[0]]==1 and d[x[-1]]==1:\n l[y]=1\n y+=1\n p_sum=[0]*len(words)\n prefix=0\n for x in range(len(l)):\n prefix+=l[x]\n p_sum[x]=prefix\n print(p_sum)\n l=[]\n for x in range(0,len(queries)):\n c=queries[x][1]\n d=queries[x][0]\n if queries[x][0]==0:\n l.append(p_sum[c])\n else:\n l.append(p_sum[c]-p_sum[d-1])\n return l\n\n \n\n\n \n \n\n \n \n``` | 2 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
Python Easy Solution || Beats 96.95% Solutions || Prefix Sum | count-vowel-strings-in-ranges | 0 | 1 | # Python Easy Solution||Prefix Sum||Beats 96.95% Solutions\n\n# Approach\nPreProcess and create the prefix sum array of count of valid words.Valid Words are those words which starts with vowel and ends with vowel.\n\nThen Easily iterate through given queries array and calculate the count of valid words in given range using prefix sum array.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n ##### PreProcessing:- Creating prefix sum array of count of valid words\n \n d={"a":1,"e":1,"i":1,"o":1,"u":1}\n preProcess=[0]*(len(words)+1)\n count=0\n for i in range(len(words)):\n if words[i][0] in d and words[i][-1] in d:\n count+=1\n preProcess[i+1]=count \n \n #### Main Method #####\n\n ans=[]\n for i in range(len(queries)):\n start=queries[i][0]\n end=queries[i][1]\n count=preProcess[end+1]-preProcess[start]\n ans.append(count)\n return ans \n``` | 3 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
prefixSum | count-vowel-strings-in-ranges | 0 | 1 | **Cpp**\n```\nclass Solution {\npublic:\n \n bool isVowel(char ch) {\n \n return (ch == \'a\' or ch == \'e\' or ch == \'i\' or ch == \'o\' or ch == \'u\');\n }\n \n vector<int> vowelStrings(vector<string>& words, vector<vector<int>>& queries) {\n \n int n(size(words));\n vector<int> prefix(n, 0);\n \n for (int i=0; i<n; i++) {\n prefix[i] = (i ? prefix[i-1] : 0) + (isVowel(words[i].front()) and isVowel(words[i].back()));\n }\n \n vector<int> ans;\n for (auto q : queries) {\n \n int x(q[0]), y(q[1]);\n ans.push_back((x == 0) ? prefix[y] : prefix[y]-prefix[x-1]);\n }\n return ans;\n }\n};\n```\n**Python**\n```\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n \n n = len(words)\n prefix = [0]*n\n\t\tvowels = [\'a\', \'e\', \'i\', \'o\', \'u\']\n \n for i in range(n):\n prefix[i] = (prefix[i-1] if i>0 else 0) + (words[i][0] in vowels and words[i][-1] in vowels)\n \n ans = []\n \n for q in queries:\n \n x, y = q[0], q[1]; \n ans.append(prefix[y] if (x == 0) else prefix[y]-prefix[x-1]);\n \n return ans;\n \n``` | 2 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
✔ Python3 Solution | Prefix Sum | count-vowel-strings-in-ranges | 0 | 1 | # Intution\nIt is a standard range query question which can be solved using `Prefix Sum`\n\n# Approach\nAt index `i` of Array `A` , it contains the no. of words which have first and last character vowel upto `i`. To find the no. of such words we need to subtract the no. words upto `l` from `r`.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n n = len(words)\n A = [0] * (n + 1)\n vowel = \'aeiou\'\n ans = []\n for i in range(n):\n A[i + 1] = A[i] + (1 if words[i][0] in vowel and words[i][-1] in vowel else 0)\n for l, r in queries:\n ans.append(A[r + 1] - A[l])\n return ans\n``` | 6 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
Python Solution || Easy to Understand for beginners || Prefix sum | count-vowel-strings-in-ranges | 0 | 1 | ```\nclass Solution:\n def vowelStrings(self, words: List[str], queries: List[List[int]]) -> List[int]:\n ans = []\n vowels = {\'a\',\'e\',\'i\',\'o\',\'u\'}\n for word in words:\n if word[0] in vowels and word[-1] in vowels:\n ans.append(1)\n else:\n ans.append(0)\n for i in range(len(ans)-1):\n ans[i+1] += ans[i]\n mans = []\n for q in queries:\n p = ans[q[1]]-ans[q[0]]\n if words[q[0]][0] in vowels and words[q[0]][-1] in vowels:\n p += 1\n mans.append(p)\n return mans\n``` | 1 | You are given a **0-indexed** array of strings `words` and a 2D array of integers `queries`.
Each query `queries[i] = [li, ri]` asks us to find the number of strings present in the range `li` to `ri` (both **inclusive**) of `words` that start and end with a vowel.
Return _an array_ `ans` _of size_ `queries.length`_, where_ `ans[i]` _is the answer to the_ `i`th _query_.
**Note** that the vowel letters are `'a'`, `'e'`, `'i'`, `'o'`, and `'u'`.
**Example 1:**
**Input:** words = \[ "aba ", "bcb ", "ece ", "aa ", "e "\], queries = \[\[0,2\],\[1,4\],\[1,1\]\]
**Output:** \[2,3,0\]
**Explanation:** The strings starting and ending with a vowel are "aba ", "ece ", "aa " and "e ".
The answer to the query \[0,2\] is 2 (strings "aba " and "ece ").
to query \[1,4\] is 3 (strings "ece ", "aa ", "e ").
to query \[1,1\] is 0.
We return \[2,3,0\].
**Example 2:**
**Input:** words = \[ "a ", "e ", "i "\], queries = \[\[0,2\],\[0,1\],\[2,2\]\]
**Output:** \[3,2,1\]
**Explanation:** Every string satisfies the conditions, so we return \[3,2,1\].
**Constraints:**
* `1 <= words.length <= 105`
* `1 <= words[i].length <= 40`
* `words[i]` consists only of lowercase English letters.
* `sum(words[i].length) <= 3 * 105`
* `1 <= queries.length <= 105`
* `0 <= li <= ri < words.length` | null |
python3 Solution | house-robber-iv | 0 | 1 | \n```\nclass Solution:\n def minCapability(self, nums: List[int], k: int) -> int:\n n=len(nums)\n def good(target):\n count=0\n i=0\n\n while i<n:\n if nums[i]<=target:\n i+=2\n count+=1\n continue\n\n i+=1\n\n return count>=k\n\n left=0\n right=10**12\n while left<right:\n mid=(left+right)//2\n if good(mid):\n right=mid\n\n else:\n left=mid+1\n\n\n return left \n``` | 1 | There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he **refuses to steal from adjacent homes**.
The **capability** of the robber is the maximum amount of money he steals from one house of all the houses he robbed.
You are given an integer array `nums` representing how much money is stashed in each house. More formally, the `ith` house from the left has `nums[i]` dollars.
You are also given an integer `k`, representing the **minimum** number of houses the robber will steal from. It is always possible to steal at least `k` houses.
Return _the **minimum** capability of the robber out of all the possible ways to steal at least_ `k` _houses_.
**Example 1:**
**Input:** nums = \[2,3,5,9\], k = 2
**Output:** 5
**Explanation:**
There are three ways to rob at least 2 houses:
- Rob the houses at indices 0 and 2. Capability is max(nums\[0\], nums\[2\]) = 5.
- Rob the houses at indices 0 and 3. Capability is max(nums\[0\], nums\[3\]) = 9.
- Rob the houses at indices 1 and 3. Capability is max(nums\[1\], nums\[3\]) = 9.
Therefore, we return min(5, 9, 9) = 5.
**Example 2:**
**Input:** nums = \[2,7,9,3,1\], k = 2
**Output:** 2
**Explanation:** There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums\[0\], nums\[4\]) = 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= (nums.length + 1)/2` | null |
Python3 - Binary Search | house-robber-iv | 0 | 1 | # Intuition\nI got stuck in the same rabbit hole others did\n\nI started with DP - got a TLE\nThen I tried BFS - still got a TLE\nI tried a tweak optimizing for houses you wanted to take from... waan\'t happening\nThen I switched to binary search\n\nThe idea is basically you decide ahead of time how \'bad\' your result will be and see if that is possible and keep iterating til you find the lowest value and return that\n\nThis works because there is no reason NOT to take from a house if it is lower value than the amount you have agreed you are going to take. \n\n# Code\n```\nclass Solution:\n def minCapability(self, nums: List[int], k: int) -> int:\n def possible(v, r):\n i = 0\n while i < len(nums) and r > 0:\n if nums[i] <= v:\n r -= 1\n i += 2\n else:\n i += 1\n return r==0\n items = list(sorted(set(nums)))\n lo, hi = 0, len(items) - 1\n while lo < hi:\n m = (lo + hi) // 2\n if possible(items[m], k):\n hi = m\n else:\n lo = m + 1\n return items[lo]\n\n\n``` | 1 | There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he **refuses to steal from adjacent homes**.
The **capability** of the robber is the maximum amount of money he steals from one house of all the houses he robbed.
You are given an integer array `nums` representing how much money is stashed in each house. More formally, the `ith` house from the left has `nums[i]` dollars.
You are also given an integer `k`, representing the **minimum** number of houses the robber will steal from. It is always possible to steal at least `k` houses.
Return _the **minimum** capability of the robber out of all the possible ways to steal at least_ `k` _houses_.
**Example 1:**
**Input:** nums = \[2,3,5,9\], k = 2
**Output:** 5
**Explanation:**
There are three ways to rob at least 2 houses:
- Rob the houses at indices 0 and 2. Capability is max(nums\[0\], nums\[2\]) = 5.
- Rob the houses at indices 0 and 3. Capability is max(nums\[0\], nums\[3\]) = 9.
- Rob the houses at indices 1 and 3. Capability is max(nums\[1\], nums\[3\]) = 9.
Therefore, we return min(5, 9, 9) = 5.
**Example 2:**
**Input:** nums = \[2,7,9,3,1\], k = 2
**Output:** 2
**Explanation:** There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums\[0\], nums\[4\]) = 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= (nums.length + 1)/2` | null |
[Python 3] Binary search with simple check | house-robber-iv | 0 | 1 | \n\n# Complexity\n- Time complexity: O(Nlog(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCapability(self, nums: List[int], k: int) -> int:\n def check(cap):\n count=taken=0\n for x in nums:\n if taken:\n taken=False\n elif x<=cap:\n count+=1\n taken=True\n return count>=k\n l,r=min(nums),max(nums)\n while l<=r:\n mid=l+(r-l)//2\n if check(mid):\n res=mid\n r=mid-1\n else:\n l=mid+1\n return res \n```\n\nAnother Problem that does not strike as binary search-https://leetcode.com/problems/kth-smallest-number-in-multiplication-table/\n | 3 | There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he **refuses to steal from adjacent homes**.
The **capability** of the robber is the maximum amount of money he steals from one house of all the houses he robbed.
You are given an integer array `nums` representing how much money is stashed in each house. More formally, the `ith` house from the left has `nums[i]` dollars.
You are also given an integer `k`, representing the **minimum** number of houses the robber will steal from. It is always possible to steal at least `k` houses.
Return _the **minimum** capability of the robber out of all the possible ways to steal at least_ `k` _houses_.
**Example 1:**
**Input:** nums = \[2,3,5,9\], k = 2
**Output:** 5
**Explanation:**
There are three ways to rob at least 2 houses:
- Rob the houses at indices 0 and 2. Capability is max(nums\[0\], nums\[2\]) = 5.
- Rob the houses at indices 0 and 3. Capability is max(nums\[0\], nums\[3\]) = 9.
- Rob the houses at indices 1 and 3. Capability is max(nums\[1\], nums\[3\]) = 9.
Therefore, we return min(5, 9, 9) = 5.
**Example 2:**
**Input:** nums = \[2,7,9,3,1\], k = 2
**Output:** 2
**Explanation:** There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums\[0\], nums\[4\]) = 2.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109`
* `1 <= k <= (nums.length + 1)/2` | null |
Python 3 || 10 lines, Counter, w/example || T/M: 85% / 50% | rearranging-fruits | 0 | 1 | ```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n\n # Example: [4, 4, 4, 4, 3] [5, 5, 5, 5, 3]\n\n c1, c2 = Counter(basket1), Counter(basket2) # c1, c2 = {3:1, 4:4}, {3:1, 5:4}\n c = c1 + c2 # c = {3:2, 4:4, 5:4} \n #\n for n in c: # c[3] = 2//2 = 1\n c[n], r = divmod(c[n],2) # c[4] = 4//2 = 2\n if r: return -1 # c[5] = 4//2 = 2\n\n mn = min(c) # mn = 3\n c1-= c # c1 = {4: 2}\n c2-= c # c2 = {5: 2}\n\n arr = sorted(list(c1.elements()) # arr = sorted([4,4]+[5,5]) = [4,4,5,5] \n + list(c2.elements()))\n\n return sum(min(2*mn, arr[i]) # return sum(min(6,4), min(6,4)) = 8\n for i in range(len(arr)//2))\n```\n[https://leetcode.com/problems/rearranging-fruits/submissions/896231451/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*NlogN*) and space complexity is *O*(*N*).\n | 3 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
[Python3] Use 3-Way Swap to Achieve Smaller Cost | rearranging-fruits | 0 | 1 | # Approach\n1. Count the excess elements in `basket1` and `basket2` that needs to be swapped. Record them in `move1` and `move2`.\n2. Sort `move1` and `move2`, respectively.\n3. The optimal strategy to achieve minimal cost is to take the minimum cost comparing (1) the direct "head/tail" swap using `move1` and `move2` with (2) a three-way swap using the overall smallest element in `basket1` and `basket2` twice.\n\n# Complexity\n- Time complexity: $$O(n\\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n cnt1, cnt2 = Counter(basket1), Counter(basket2)\n minCost = min(min(basket1), min(basket2)) * 2\n move1, move2 = [], []\n for fruit in cnt1:\n if (cnt1[fruit] + cnt2[fruit]) % 2 != 0:\n return -1\n avgFruit = (cnt1[fruit] + cnt2[fruit]) // 2\n if cnt1[fruit] > avgFruit:\n move1 += [fruit] * (cnt1[fruit] - avgFruit)\n for fruit in cnt2:\n if (cnt1[fruit] + cnt2[fruit]) % 2 != 0:\n return -1\n avgFruit = (cnt1[fruit] + cnt2[fruit]) // 2\n if cnt2[fruit] > avgFruit:\n move2 += [fruit] * (cnt2[fruit] - avgFruit)\n move1.sort()\n move2.sort()\n ans, m = 0, len(move1)\n for i in range(m):\n ans += min(min(move1[i], move2[m - 1 - i]), minCost)\n return ans\n``` | 1 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
[Python] Simple Solution | Image Explanation | rearranging-fruits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI start this problem from a simple test case.\n\n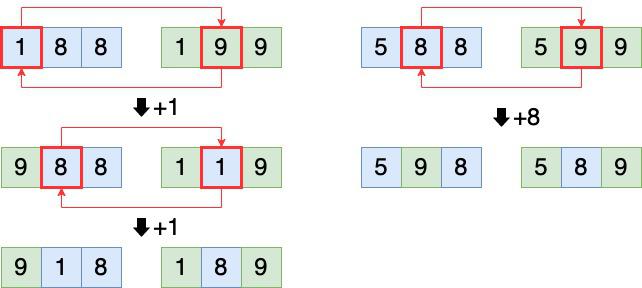\n\n\nGiven two baskets [1, 8, 8] and [1, 9, 9], we have two choices to make them equal.\n1. Use the minimum number, that is 1 in this example, to swap to a 9 in second basket, and then swap back to a 8 in the first basket, with $$cost = 2 * \\min(baskets) = 2 * 1 = 2$$. \n2. Swap 8 and 9 simultaneously with $$cost = \\min(8, 9) = 8$$.\n\nIt\'s obvious that we should swap the numbers using 1 with smaller cost 2, but when should we choose the second choice? Now maybe you got the idea. When the cost to swap two numbers (minimum of two numbers) is smaller than twice the minimum number in baskets, then we should swap them direcly. Othewise we use the minimum number to swap between two baskets.\n\nGiven two baskets [5, 8, 8] and [5, 9, 9], the minimum number is 5, so the costs of two choices will be:\n1. $$2 * min(baskets) = 2 * 5 = 10$$\n2. $$\\min(8, 9) = 8$$\n\nAs a result, we should swap 8 and 9 directly.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe first count every number in two baskets. All the occurrences in two baskets should be even, otherwise it is impossible to make two baskets equal.\n\nThen we make an array to store the numbers which should be swapped. The array is sorted increasingly, and only the first half of array will be took into account (they are smaller numbers than the second half). We don\'t care where are the numbers from in the first half because we can always find a bigger number from a different basket in the second half, e.g. if there are 3 numbers from basket1 and 2 numbers from basket2 in the first half, then there are 2 numbers from basket1 and 3 numbers from basket2 in the second half.\n\nFor example, [1,1,2,2,2,3] and [2,3,3,3,3,3], the array will be [1,2,2,3]. We will swap [1,2] and [2,3], so only 1 and 2 are took into cost consideration.\n\nFinally, we compare the cost between twice the minimum number and pair costs. Accumulate them as our final answer.\n\n# Complexity\n- Time complexity $$O(sort)$$:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(sort)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Python\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n counter1 = Counter(basket1)\n counter2 = Counter(basket2)\n total_counter = counter1 + counter2\n \n arr = []\n for key, count in sorted(total_counter.items()):\n if count % 2:\n return -1\n arr.extend([key] * (count // 2 - min(counter1[key], counter2[key])))\n \n res = 0\n min_cost = 2 * min(total_counter.keys())\n for c in arr[:len(arr) // 2]:\n res += min(c, min_cost)\n return res\n``` | 1 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
✅ Python || Hashtable || Heap. | rearranging-fruits | 0 | 1 | \n# Approach\n1. We compare the count of each element in both baskets and store the differences in a heap. \n1. If the difference is odd, we return -1 because it means we can\'t match the fruits. \n2. If the difference is even, we add half of the difference to the heap, representing the number of unmatched fruit pairs. \n3. Finally, we calculate the minimum cost by popping the smallest element from the heap and adding the minimum of its value and double the absolute minimum value of all fruits. (Take it or use absolute minimum twice to balance mismatch) \n\n\n# Complexity\n- Time complexity:\n$$O(n\\log n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n``` {python}\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n C1, C2 = Counter(basket1), Counter(basket2)\n abs_min = min(min(basket1), min(basket2))\n h = []\n for i in C1.keys():\n if C1[i] > C2[i]:\n diff = C1[i] - C2[i]\n if diff % 2:\n return -1\n for _ in range(diff//2):\n heappush(h, i)\n for i in C2.keys():\n if C2[i] > C1[i]:\n diff = C2[i] - C1[i]\n if diff % 2:\n return -1\n for _ in range(diff//2):\n heappush(h, i)\n n, ans = len(h), 0\n for _ in range(n//2):\n ans += min(2*abs_min, heappop(h))\n return ans\n \n \n```\nSubmission:\n\n\n | 1 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
[PYTHON] O(N log N) Count & Sorting Solution | rearranging-fruits | 0 | 1 | # Intuition\nWe can check each elements using counter.\n\nYou can easily come up with exchange two fruits as cheap as possibile.\n\nTo achieve this, the simple idea is to exchage larger value fruits and smaller value fruits.\n\nBut be careful, you have to check the way to exchange via the cheapest fruits. \n\nYou can see that code here\n\n```\n for v1,v2 in zip(c1,c2):\n ans += min(v1,v2, min_v*2)\n```\n\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n b1 = dict(Counter(basket1))\n b2 = dict(Counter(basket2))\n \n tot = Counter(basket1 + basket2)\n \n c1 = []\n c2 = []\n for k, v in tot.items():\n if v % 2 != 0:\n return -1\n b1c = b1.get(k, 0)\n b2c = b2.get(k, 0)\n if b1c == b2c:\n continue\n if b1c > b2c:\n for i in range((b1c - b2c) // 2):\n c1.append(k)\n else:\n for i in range((b2c - b1c) // 2):\n c2.append(k)\n c1 = sorted(c1)\n c2 = sorted(c2, reverse=True)\n ans = 0\n min_v = min(basket1 + basket2)\n for v1,v2 in zip(c1,c2):\n ans += min(v1,v2, min_v*2)\n return ans\n```\n# Q&A\n\n### Why min(v1, v2) is not working?\n\nLet\'s assume we have to exchange $basket1=[1, 100, 100], c2=[1, 200, 200]$\nThen, our array $c1=[100]$ and $c2=[200]$ \nThe simpleast way is exchange 100 and 200.\nBut there are more smart solution.\nThat is to exchange using fruit 1.\nThe step is follow\n 1. Exchange [100, 1]. \n - Then $basket1=[1, 1, 100]$ $basket2=[100, 200, 200]$ and cost is 1\n 2. Exchange [1, 200]. \n - Then $basket1=[1, 200, 100]$ $basket2=[100, 1, 200]$ and cost is 1\n\nThen we can solve this problem with total cost 2.\n\n | 9 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
【C++||Java||Python3】Count and match pairs, O(n) time complexity with quickselect | rearranging-fruits | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n\n# Intuition\n1. If the frequency of each number in the two input arrays is even, then you can always find a way to swap the two arrays to become the same. On the contrary, it must be impossible.\n2. Find a way to find out the numbers in each array that need to be given to the other, so you get two lists. The exchanged pair must form a one-to-one correspondence between the two lists.\n3. **Within each pair, there are two exchange methods**:\n - Direct exchange, the cost is the smaller number.\n - Indirect exchange, choose another small number $x$ as the "intermediate", swap "$a_{i}$ with $x$" and "$x$ with $b_{j}$", the cost is $2x$.\n4. **In order to minimize the result, be sure to make full use of "small numbers"**. \n5. So put all the elements of the two arrays that need to be exchanged together and sort them. **Choose the first half as the "costs"**.\n6. Choose to use "direct exchange" or "indirect exchange" each time according to the situation. Because the choice of which number is free, **the smallest number in the two arrays can be greedily selected as the intermediate**. (If $x$ is one of $a[i]$ or $b[j]$, the indirect way $2x$ will always greater than direct way $x$, so no need to think of this condition).\n7. Find the first half can easily use sort with $O(n\\log{n})$ time complexity, or use [quickselect](https://en.wikipedia.org/wiki/Quickselect) with $O(n)$ time complexity.\n\n# Complexity\n- Time complexity: $O(n\\log{n})$ or $O(n)$\n- Space complexity: $O(n)$\n\n# Code\nThanks for [Gang-Li\'s JavaScript solution](https://leetcode.com/problems/rearranging-fruits/solutions/3144240/based-on-realfan-s-solution-improve-the-space-usage-by-not-using-array-in-the-last-step/?orderBy=most_votes)!\n``` C++ []\nclass Solution {\npublic:\n long long minCost(vector<int>& basket1, vector<int>& basket2) {\n unordered_map<int, int> cnt;\n for (auto c: basket1) cnt[c]++;\n for (auto c: basket2) cnt[c]--;\n vector<int> last;\n for (auto &[k, v]: cnt) {\n // if v is odd, an even distribution is never possible\n if (v % 2) return -1;\n // the count of transferred k is |v|/2\n for (int i = 0; i < abs(v) / 2; ++i)\n last.push_back(k);\n }\n // find the min of two input arrays as the intermediate\n int minx = min(*min_element(basket1.begin(), basket1.end()),\n *min_element(basket2.begin(), basket2.end()));\n // sort(last.begin(), last.end()) can be used as well\n nth_element(last.begin(), last.begin() + last.size() / 2, last.end());\n return accumulate(last.begin(), last.begin() + last.size() / 2, 0ll, \n [&](long long s, int x) -> long long { return s + min(2*minx, x); }\n );\n }\n};\n```\n``` Java []\nclass Solution {\n public long minCost(int[] basket1, int[] basket2) {\n Map<Integer, Integer> cnt = new HashMap<>();\n for (int c: basket1) \n cnt.put(c, cnt.getOrDefault(c, 0) + 1);\n for (int c: basket2) \n cnt.put(c, cnt.getOrDefault(c, 0) - 1);\n List<Integer> last = new ArrayList<>();\n for (Map.Entry<Integer, Integer> e: cnt.entrySet()) {\n int v = e.getValue();\n // if v is odd, an even distribution is never possible\n if (v % 2 != 0) return -1;\n // the count of transferred k is |v|/2\n for (int i = 0; i < Math.abs(v) / 2; ++i)\n last.add(e.getKey());\n }\n // find the min of two input arrays as the intermediate\n int minx = Math.min(Arrays.stream(basket1).min().getAsInt(),\n Arrays.stream(basket2).min().getAsInt());\n // Use quickselect instead of sort can get a better complexity\n Collections.sort(last);\n long res = 0;\n // The first half may be the cost\n for (int i = 0; i < last.size() / 2; ++i) \n res += Math.min(last.get(i), minx * 2);\n return res;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n cnt = Counter(basket1)\n for x in basket2: cnt[x] -= 1\n last = []\n for k, v in cnt.items():\n # if v is odd, an even distribution is never possible\n if v % 2 != 0:\n return -1\n # the count of transferred k is |v|/2\n last += [k] * abs(v // 2)\n # find the min of two input arrays as the intermediate\n minx = min(basket1 + basket2)\n # Use quickselect instead of sort can get a better complexity\n last.sort()\n # The first half may be the cost\n return sum(min(2*minx, x) for x in last[0:len(last)//2])\n``` | 73 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Python Frequency Map Approach | Greedy | Easy to Understand | Optimal | rearranging-fruits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFrequency maps were the way to go\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a frequency map where we increment the occurence of instances for the first basket and decrement for the second one so that the possible elements to be exchanged have non-zero frequencies. Here, we check for odd total frequency for a fruit and if found, we return -1. Else, we take half of those non-zero fruits and store them in an array `toBeExchanged`. Then, sorting `toBeExchanged` ensures that we consider minimum element first while we traverse through the array\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n fruitsCount, minFruits = defaultdict(int), min(min(basket1), min(basket2))\n for fruit in basket1:\n fruitsCount[fruit] += 1\n for fruit in basket2:\n fruitsCount[fruit] -= 1\n toBeExchanged, cost = [], 0\n for fruit in fruitsCount:\n if fruitsCount[fruit] % 2:\n return -1\n for num in range(abs(fruitsCount[fruit]) // 2):\n toBeExchanged.append(fruit)\n toBeExchanged.sort()\n for idx in range(len(toBeExchanged) // 2):\n cost += min(minFruits * 2, toBeExchanged[idx])\n return cost\n``` | 2 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Simple O(n * log (n)) runtime solution using sorting [Python] | rearranging-fruits | 0 | 1 | # Intuition\nI reread the problem a few times and it seemed simple enough. Just make swaps so that you eventually have to "identical" sets.\n\n# Approach\nI first reasoned about when we couldn\'t have a solution. The only scenario is if I added up all the frequencies of each fruit, that some fruits counts were not divisible by 2, in other words, I cannot evenly "split" a fruit. Then I reasoned about if we can always reach a solution, given that the fruit counts were fine. If I swap two elements that are in the wrong basket, I always move to a more "solved" state. So this naturally gave way to the reasoning that if I can find all the fruits that are in the wrong place, then I can employ some strategy to swap them all. The simplest thing to do would be to get a list of all the "out-of-place" elements and then slowly process it. \n\nThe complexity arises from the fact that we need to solve the state in the cheapest way. If we have two "out-of-place" items, then one optimization is obviously if we have a super cheap item and a super expensive item, it makes sense to pair those together than any other combo, because we optimize the cost of the swap. What I didn\'t consider (and consequently spent a bunch of time on this problem) was that we can actually sometimes take advantage of the globally cheapest element to do a swap of two super expensive items. It doesn\'t matter which is swapped first, because the globally cheapest item bears the cost of the swap. When I finally discovered this, the algorithm was pretty straightforward, which you can read in the solution provided. The only complex part of algorithm, to me, is the decision to consider the bottom-half cheapest elements in the master set of "out-of-place" elements. The reasoning is that we greedily make swaps (pair every element swapped with another), so if we are done with the bottom-half cheapest elements, the top half are implicitly solved. There is no reason whatsoever not to do this, as you only incur more costs from taking elements **out** of their correct position. \n\nImportant thing to prove:\n1. You can prove that in a solveable state, the elements in the wrong basket in basket1\'s cardinality equals that of basket2\'s. The reason being that if these sets were of different cardinality, the system would be impossible to solve. \n2. You can prove that in any shuffled system, there is at most (n/2) out of place pairs. In other words, "master"\'s length is at most n. \n\n# Complexity\n- Time complexity:\nO(nlogn) from sorting the list "master", which contains the set of all "out-of-place" elements. This list\'s cardinality is at most 2 * (n / 2) ~ assuming WC (n) unique elements. \n\n- Space complexity:\nO(n) - master\'s size is at most 2 * (n / 2), the dictionaries "d" and "basket1d" are O(n), at most n unique keys. \n\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n # count up all the fruits in both baskets\n d = {}\n for num in basket1:\n d[num] = d.get(num, 0) + 1\n for num in basket2:\n d[num] = d.get(num, 0) + 1\n\n # solveable if the counts are all even\n for val in d.values():\n if val % 2 != 0:\n return -1\n \n # I only really need to know the extraneous items of one basket (use complement of "d" for others)\n basket1d = {}\n for num in basket1:\n basket1d[num] = basket1d.get(num, 0) + 1\n\n # get the absolute minimum\n mini = min(min(basket1), min(basket2))\n\n master = [] # set of all fruits that need to be "solved" (swapped to other basket)\n\n # populate master\n for key in d.keys():\n if key in basket1d:\n diff = basket1d[key] - (d[key] // 2)\n for _ in range(abs(diff)):\n master.append(key)\n else:\n for _ in range(d[key] // 2):\n master.append(key)\n\n master.sort()\n cost = 0\n N = len(master) // 2 # we only need to look at the bottom half of master\n for i in range(N):\n # set cur to the smallest element in master\n cur = master[i]\n\n # determine the cost of "solving" cur\n if cur == mini:\n cost += mini # cur is the smallest element == absolute cheapest swap\n elif mini * 2 <= cur: \n cost += 2 * mini # abuse cur to swap two expensive items\n else:\n cost += cur # abusing cur has no benefit, so swap to incur the cost of the cheapest expensive item\n \n return cost\n\n``` | 0 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
python3 solution for beginners | rearranging-fruits | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n basket1.sort()\n basket2.sort()\n c1 = Counter(basket1)\n c2 = Counter(basket2)\n \n for c in set(basket1):\n x = c1[c]\n if c in c2:\n y = c2[c]\n else:\n y=0\n if (x + y) % 2 != 0:\n\n return -1\n \n c = c1 + c2\n # print(c)\n m = min(c)\n # print(m)\n c3 = c1\n c1 = c1 - c2\n c2 = c2 - c3\n print(c1,c2)\n a = sorted(list(c1.elements()) + list(c2.elements()))\n res = 0\n # print(a)\n for i in range(len(a)//2):\n res+=min(2*m,a[i])\n return res //2\n\n\n \n \n\n\n``` | 0 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Simple 100% Fastest Solution | rearranging-fruits | 0 | 1 | # Intuition\nTwo baskets can be made equal if each of them contains several pairs of fruits that are missing in the other. \nThe number of missing pairs in the two baskets is the same.\nSince the cost of swap depends only on the cheap fruit in the pair, you can swap cheap fruits with expensive ones.\nIn addition, you can swap the cheapest fruit in the basket with the one that is missing, and then swap this cheap fruit back. In this case, the cost of swap will be two times the cost of the cheapest fruit.\nIn each case we can choose which way to make the baskets equal.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(len(basket1)+len(basket2))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(len(basket1)+len(basket2))$$\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n db1 = Counter(basket1)\n db12 = Counter(basket2)+db1\n if any(v for v in db12.values() if v % 2) : return -1\n min_frt = min(db12.keys())\n exch = []\n for key,v12 in db12.items() :\n dv = (v12 >>1) - db1[key]\n if dv ==0: continue\n exch.extend(repeat(key,abs(dv)))\n exch.sort()\n return sum(min(fr, 2 * min_frt) for fr in exch[:len(exch) >>1])\n\n``` | 0 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Python Hard | rearranging-fruits | 0 | 1 | ```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n N = len(basket1)\n \n \n d = defaultdict(int)\n \n for val in basket1:\n d[val] += 1\n \n for val in basket2:\n d[val] += 1\n \n for key in d:\n if d[key] % 2:\n return -1\n \n \n \n \n basket1.sort()\n basket2.sort()\n \n\n \n \n c = Counter(basket1)\n d = Counter(basket2)\n \n ans = []\n \n for key in c:\n if c[key] != 0 and c[key] > d[key]:\n ans.append([c[key] - d[key], key])\n \n for key in d:\n if d[key] != 0 and d[key] > c[key]:\n ans.append([d[key] - c[key], key])\n \n \n ans.sort(key = lambda x: x[1])\n \n l, r = 0, len(ans) - 1\n \n res = 0\n \n \n \n tmp = min(min(basket1), min(basket2))\n\n print(ans)\n \n while l <= r:\n amount, val = ans[l]\n amount2, val2 = ans[r]\n \n \n if amount <= 0:\n l += 1\n continue\n \n if amount2 <= 0:\n r -= 1\n continue\n \n \n ans[l][0] -= 2\n ans[r][0] -= 2\n res += min(val, tmp * 2)\n \n \n\n return res\n \n \n \n \n \n \n \n \n \n \n``` | 0 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Python Faster than 100% Stack + HashMap | rearranging-fruits | 0 | 1 | # Intuition\nWe either swap with the min element indirectly or swap with greedily.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, basket1: List[int], basket2: List[int]) -> int:\n b1f, b2f = collections.Counter(basket1), collections.Counter(basket2)\n tc = collections.Counter(basket1 + basket2)\n if any(tc[f] % 2 == 1 for f in tc): return -1\n\n b1_min, b2_min = min(b1f), min(b2f)\n min_element = min(b1_min, b2_min)\n\n b1_swap, b2_swap = [], []\n total = 0\n for key in tc:\n b1_count, b2_count = b1f[key], b2f[key]\n if b1_count == b2_count: continue\n \n swap_count = abs(b1_count - b2_count) // 2\n\n if b1_count > b2_count: b1_swap.append((key, swap_count))\n else: b2_swap.append((key, swap_count))\n\n b1_swap.sort()\n b2_swap.sort(reverse=True)\n\n total = 0\n while b1_swap and b2_swap:\n b1_cost, b1_amount = b1_swap[-1]\n b2_cost, b2_amount = b2_swap[-1]\n\n swap_both = min(b1_cost, b2_cost) * min(b1_amount, b2_amount)\n swap_via_min = 2 * min_element * min(b1_amount, b2_amount)\n\n if swap_both < swap_via_min:\n total += swap_both\n else:\n total += swap_via_min\n if b1_amount == b2_amount:\n b1_swap.pop(); b2_swap.pop()\n elif b1_amount > b2_amount:\n b2_swap.pop()\n b1_swap[-1] = (b1_cost, b1_amount - b2_amount)\n else:\n b1_swap.pop()\n b2_swap[-1] = (b2_cost, b2_amount - b1_amount)\n \n return total\n``` | 0 | You have two fruit baskets containing `n` fruits each. You are given two **0-indexed** integer arrays `basket1` and `basket2` representing the cost of fruit in each basket. You want to make both baskets **equal**. To do so, you can use the following operation as many times as you want:
* Chose two indices `i` and `j`, and swap the `ith` fruit of `basket1` with the `jth` fruit of `basket2`.
* The cost of the swap is `min(basket1[i],basket2[j])`.
Two baskets are considered equal if sorting them according to the fruit cost makes them exactly the same baskets.
Return _the minimum cost to make both the baskets equal or_ `-1` _if impossible._
**Example 1:**
**Input:** basket1 = \[4,2,2,2\], basket2 = \[1,4,1,2\]
**Output:** 1
**Explanation:** Swap index 1 of basket1 with index 0 of basket2, which has cost 1. Now basket1 = \[4,1,2,2\] and basket2 = \[2,4,1,2\]. Rearranging both the arrays makes them equal.
**Example 2:**
**Input:** basket1 = \[2,3,4,1\], basket2 = \[3,2,5,1\]
**Output:** -1
**Explanation:** It can be shown that it is impossible to make both the baskets equal.
**Constraints:**
* `basket1.length == bakste2.length`
* `1 <= basket1.length <= 105`
* `1 <= basket1[i],basket2[i] <= 109` | null |
Easy Python Solution using 2 pointers | find-the-array-concatenation-value | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n left=0\n right=len(nums)-1\n total=0\n while left<=right:\n if left<right:\n total+=int(str(nums[left])+str(nums[right]))\n else:\n total+=nums[left]\n left+=1\n right-=1\n return total\n``` | 2 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
BEGINNER FRIENDLY PYTHON PROGRAM [ BEATS 88% OF USERS ] | find-the-array-concatenation-value | 0 | 1 | # Intuition\nUsing for loop and string slicing\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe use for loop to iterate over the list and take the 1st and last elements as string and concatenate\n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n ls=[]\n x=-1\n l=len(nums)//2\n \n \n for i in range(l):\n \n ls.append(int(str(nums[i])+str(nums[x])))\n x-=1\n \n if len(nums)%2==0:\n return sum(ls)\n else:\n return sum(ls)+nums[l]\n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Easy Solution Using While Loop in Python | find-the-array-concatenation-value | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n i=0\n c=0\n j=len(nums)-1\n while(i<=j):\n if(i==j):\n c=c+nums[i]\n break\n s=str(nums[i])+str(nums[j])\n c=c+int(s)\n i=i+1\n j=j-1\n return c\n \n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
[Python3] simulation | find-the-array-concatenation-value | 0 | 1 | \n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 0 \n for i in range((n+1)//2): \n if i == n-1-i: ans += nums[i]\n else: ans += int(str(nums[i]) + str(nums[n-1-i]))\n return ans \n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Solution easy to understand || super easy solution | find-the-array-concatenation-value | 0 | 1 | ```\nclass Solution:\n def findTheArrayConcVal(self, num: List[int]) -> int:\n\t\t# to store final sum\n ans = 0\n\t\t# traverse the num array untill its empty\n while num:\n\t\t\t# pop the first element out convert it to string\n p = str(num.pop(0))\n q = ""\n\t\t\t\n\t\t\t# if array is non empty pop the last element out\n if num:\n q=str(num.pop())\n\t\t\t\n\t\t\t# concate the string and add it to final answer\n ans += int(p+q)\n return ans\n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
✅Python3 || C++✅ Beats 100% | find-the-array-concatenation-value | 0 | 1 | \n\n# Please UPVOTE \uD83D\uDE0A\n\n## Python3\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n ans=0\n if len(nums)%2==1:\n ans=nums[len(nums)//2]\n for i in range(len(nums)//2):\n ans+=int(str(nums[i])+str(nums[len(nums)-1-i]))\n return ans\n \n```\n## C++\n```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long int n=nums.size(),ans=0;\n if(n%2){\n ans=nums[n/2];\n }\n for(int i=0;i<n/2;i++){\n int y=nums[n-1-i],x=nums[i];\n while(y){\n x*=10;\n y/=10;\n }\n x+=nums[n-i-1];\n ans+=x;\n }\n return ans;\n\n }\n};\n```\n\n | 24 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Two pointers Python 3 solution | find-the-array-concatenation-value | 0 | 1 | \n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n result = 0\n\n p1 = 0\n p2 = len(nums) - 1\n\n while p1 <= p2:\n if p1 == p2:\n result += int(nums[p1])\n\n else:\n result += int(str(nums[p1]) + str(nums[p2]))\n\n p1 += 1\n p2 -= 1\n\n return result\n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Beats 100% Speed easy Python solution | find-the-array-concatenation-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n summary = 0\n a = nums.copy()\n for i in nums[:len(a) // 2]:\n summary += int(str(i) + str(nums[-1]))\n nums.pop(-1)\n return summary if len(a)%2 == 0 else summary + nums[-1] \n \n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **concatenation** of two numbers is the number formed by concatenating their numerals.
* For example, the concatenation of `15`, `49` is `1549`.
The **concatenation value** of `nums` is initially equal to `0`. Perform this operation until `nums` becomes empty:
* If there exists more than one number in `nums`, pick the first element and last element in `nums` respectively and add the value of their concatenation to the **concatenation value** of `nums`, then delete the first and last element from `nums`.
* If one element exists, add its value to the **concatenation value** of `nums`, then delete it.
Return _the concatenation value of the `nums`_.
**Example 1:**
**Input:** nums = \[7,52,2,4\]
**Output:** 596
**Explanation:** Before performing any operation, nums is \[7,52,2,4\] and concatenation value is 0.
- In the first operation:
We pick the first element, 7, and the last element, 4.
Their concatenation is 74, and we add it to the concatenation value, so it becomes equal to 74.
Then we delete them from nums, so nums becomes equal to \[52,2\].
- In the second operation:
We pick the first element, 52, and the last element, 2.
Their concatenation is 522, and we add it to the concatenation value, so it becomes equal to 596.
Then we delete them from the nums, so nums becomes empty.
Since the concatenation value is 596 so the answer is 596.
**Example 2:**
**Input:** nums = \[5,14,13,8,12\]
**Output:** 673
**Explanation:** Before performing any operation, nums is \[5,14,13,8,12\] and concatenation value is 0.
- In the first operation:
We pick the first element, 5, and the last element, 12.
Their concatenation is 512, and we add it to the concatenation value, so it becomes equal to 512.
Then we delete them from the nums, so nums becomes equal to \[14,13,8\].
- In the second operation:
We pick the first element, 14, and the last element, 8.
Their concatenation is 148, and we add it to the concatenation value, so it becomes equal to 660.
Then we delete them from the nums, so nums becomes equal to \[13\].
- In the third operation:
nums has only one element, so we pick 13 and add it to the concatenation value, so it becomes equal to 673.
Then we delete it from nums, so nums become empty.
Since the concatenation value is 673 so the answer is 673.
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 104`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
[Python] A Clean and Short Method Using Binary Search | count-the-number-of-fair-pairs | 0 | 1 | \n# Code\n```\nimport bisect\nclass Solution: \n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n sortingData=[nums[-1]]\n n=len(nums)\n answer=0\n for i in range(n-2, -1, -1):\n l=bisect.bisect_left(sortingData, lower-nums[i])\n u=bisect.bisect_right(sortingData, upper-nums[i]) \n answer+=(u-l)\n bisect.insort_left(sortingData, nums[i])\n return answer\n``` | 3 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Sorting + Binary Search --- Python simple solution | count-the-number-of-fair-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n cnt = 0\n for i in range(len(nums)-1, -1, -1):\n x = nums[i]\n lo = bisect_left(nums, lower - x, 0, i)\n hi = bisect_right(nums, upper - x, 0, i)\n cnt += hi - lo\n return cnt \n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
The simplest solution. Binary search with intervals. Python. | count-the-number-of-fair-pairs | 0 | 1 | ****Bold****# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport bisect\n\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n n = len(nums)\n\n ans = 0\n for i in range(n):\n l = bisect.bisect_left(nums, lower-nums[i], i+1, n)\n r = bisect.bisect_right(nums, upper-nums[i], i+1, n)\n\n ans += r-l\n\n return ans\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Pop tail before each binary search, O(n log n) | count-the-number-of-fair-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBinary search lower, and upper\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPop tail, so it will not count itself.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n A = nums\n A.sort()\n n = len(A)\n ans = 0\n\n for i in range(n-1, -1, -1):\n v = A.pop()\n a = bisect_left(A, lower - v)\n b = bisect_right(A, upper - v)\n\n ans += b - a\n \n return ans\n```\n\nThe version without pop(), or virtual pop. :)\n\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n A = nums\n A.sort()\n print(A)\n n = len(A)\n ans = 0\n for i in range(n-1, -1, -1):\n v = A[i]\n a = bisect_left(A, lower - v, lo=0, hi=i)\n b = bisect_right(A, upper - v, lo=0, hi=i)\n\n ans += b - a\n \n return ans\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Two Pointers * 2 | count-the-number-of-fair-pairs | 1 | 1 | Because `nums[i] + nums[j] == nums[j] + nums[i]` the `i < j` condition degrades to `i != j`.\n\nSo, we can sort the array, and use the two-pointer approach to count pairs less than a certain value.\n\nWe do it twice for `uppper` and `lower`, and return the difference.\n\nTime complexity: O(sort)\n\n**C++**\n```cpp\nlong long countLess(vector<int>& nums, int val) {\n long long res = 0;\n for (int i = 0, j = nums.size() - 1; i < j; ++i) {\n while(i < j && nums[i] + nums[j] > val)\n --j;\n res += j - i;\n } \n return res;\n}\nlong long countFairPairs(vector<int>& nums, int lower, int upper) {\n sort(begin(nums), end(nums));\n return countLess(nums, upper) - countLess(nums, lower - 1);\n}\n```\n**Python 3**\n```python\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n def countLess(val: int) -> int:\n res, j = 0, len(nums) - 1\n for i in range(len(nums)):\n while i < j and nums[i] + nums[j] > val:\n j -= 1\n res += max(0, j - i)\n return res\n nums.sort()\n return countLess(upper) - countLess(lower - 1)\n```\n**Java**\n```java\nlong countLess(int[] nums, int val) {\n long res = 0;\n for (int i = 0, j = nums.length - 1; i < j; ++i) {\n while(i < j && nums[i] + nums[j] > val)\n --j;\n res += j - i;\n } \n return res; \n}\npublic long countFairPairs(int[] nums, int lower, int upper) {\n Arrays.sort(nums);\n return countLess(nums, upper) - countLess(nums, lower - 1);\n}\n``` | 135 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Simple and Easy Approach with Explanation | count-the-number-of-fair-pairs | 0 | 1 | # Approach:-\n```\nCase 1:- if nums[left] + nums[right] > upper:\nChecking all the cases where sum is greater than upper then simply decrement right by one. If less or equal to the upper value then it satisfy for all case between right to left so add count += right - left and increment in left.\n```\n```\nCase 2:- if nums[left] + nums[right] > lower -1:\nChecking all the cases where sum is greater than lower - 1 then simply decrement right by one. If less or equal to the upper value then it satisfy for all case between right to left so add count += right - left and increment in left.\n\n```\n# Time Complexity And Space Complexity:-\n\nThe time complexity of the code using the two pointer approach is O(n log n), where n is the size of the input array nums. This is because the sorting of the array takes O(n log n) time and the two while loops take O(n) time each, so the total time complexity is O(n log n) + 2 * O(n) = O(n log n).\n\nThe space complexity of this algorithm is O(1), because it does not use any additional data structures other than the input array nums. The sorting is done in-place, so no additional space is used for sorting. The only extra space used is a few variables for storing intermediate values, such as left, right, and count, which have a constant space complexity of O(1).\n\n\n# Code:-\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n left , right = 0 , len(nums)-1\n count = 0\n while left < right:\n if nums[left] + nums[right] > upper:\n right -= 1\n else:\n count += right - left\n left += 1\n left , right = 0 , len(nums)-1\n while left < right:\n if nums[left] + nums[right] > lower - 1:\n right -= 1\n else:\n count -= right - left\n left += 1\n return count\n \n```\n# ___________PLEASE UPVOTE___________\n\n\n\n\n | 3 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Python (Simple Two Pointers) | count-the-number-of-fair-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countFairPairs(self, nums, lower, upper):\n nums.sort()\n\n total, i, j = 0, 0, len(nums)-1\n\n while i < j:\n if nums[i] + nums[j] > upper:\n j -= 1\n else:\n total += j-i\n i += 1\n\n i, j = 0, len(nums)-1\n\n while i < j:\n if nums[i] + nums[j] > lower-1:\n j -= 1\n else:\n total -= j-i\n i += 1\n\n return total\n\n\n``` | 4 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
✅C++ || Python3✅ sorting , lower and upper | count-the-number-of-fair-pairs | 0 | 1 | # Please Upvote \uD83D\uDE07\n# C++\n```\nclass Solution {\npublic:\n long long countFairPairs(vector<int>& v, int first_val, int last_val) {\n deque<int>vc;\n sort(v.begin(),v.end());\n for(auto i:v) vc.push_back(i);\n long long int ans=0;\n for(int i=0;i<v.size();i++)\n {\n vc.pop_front();\n int lower=first_val-v[i],upper=last_val-v[i];\n auto left=lower_bound(vc.begin(),vc.end(),lower);\n auto right=upper_bound(vc.begin(),vc.end(),upper);\n ans+=(right-left);\n }\n return ans;\n }\n};\n```\n# Python3\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n ans=0\n for i in range(len(nums)-1, -1, -1):\n v = nums[i]\n a = bisect_left(nums, lower - v, lo=0, hi=i)\n b = bisect_right(nums, upper - v, lo=0, hi=i)\n ans += b - a\n return ans \n``` | 53 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Easy Python solution (with comments) with 2 binary searches. | count-the-number-of-fair-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n ln(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n # First, note that the answer does not change if we sort the array\n nums.sort()\n fairCtr = 0\n for i in range(len(nums)):\n # For each index find the left and right elements for which the sums lie between lower and upper\n l = bisect_left(nums, lower - nums[i])\n r = bisect_right(nums, upper - nums[i])\n fairCtr += (r - l)\n # check if index i lies in the interval, subtract one (we don\'t want to double count index i)\n if l <= i < r:\n fairCtr -= 1\n return fairCtr // 2\n``` | 6 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
[Python3] two pointers | count-the-number-of-fair-pairs | 0 | 1 | \n```\nclass Solution:\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n ans = 0 \n lo = hi = len(nums)-1\n for i, x in enumerate(nums): \n while 0 <= hi and x + nums[hi] > upper: hi -= 1\n while 0 <= lo and x + nums[lo] >= lower: lo -= 1\n ans += hi - lo \n if lo < i <= hi: ans -= 1\n return ans//2\n``` | 8 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Python Elegant & Short | Two lines | Bisect | In-place | count-the-number-of-fair-pairs | 0 | 1 | ```\nfrom bisect import bisect, bisect_left\nfrom typing import List\n\n\nclass Solution:\n """\n Time: O(sort)\n Memory: O(1)\n """\n\n def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:\n nums.sort()\n return sum(\n bisect(nums, upper - num, hi=i) - bisect_left(nums, lower - num, hi=i)\n for i, num in enumerate(nums)\n )\n\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
Python 3 || 3 lines, sort and bisect || T/M: 706 ms / 24 MB | count-the-number-of-fair-pairs | 0 | 1 | ```\nclass Solution:\n def countFairPairs(self, nums: list[int], lower: int, upper: int) -> int:\n\n f = lambda x: sum(bisect_right(nums, x - num, hi=i)\n for i, num in enumerate(nums))\n nums.sort()\n\n return f(upper) - f(lower - 1)\n``` | 5 | Given a **0-indexed** integer array `nums` of size `n` and two integers `lower` and `upper`, return _the number of fair pairs_.
A pair `(i, j)` is **fair** if:
* `0 <= i < j < n`, and
* `lower <= nums[i] + nums[j] <= upper`
**Example 1:**
**Input:** nums = \[0,1,7,4,4,5\], lower = 3, upper = 6
**Output:** 6
**Explanation:** There are 6 fair pairs: (0,3), (0,4), (0,5), (1,3), (1,4), and (1,5).
**Example 2:**
**Input:** nums = \[1,7,9,2,5\], lower = 11, upper = 11
**Output:** 1
**Explanation:** There is a single fair pair: (2,3).
**Constraints:**
* `1 <= nums.length <= 105`
* `nums.length == n`
* `-109 <= nums[i] <= 109`
* `-109 <= lower <= upper <= 109` | null |
[Python3] preprocessing | substring-xor-queries | 0 | 1 | \n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n seen = {}\n for i, ch in enumerate(s):\n if ch == \'1\': \n val = 0\n for j in range(i, min(len(s), i+30)): \n val <<= 1\n if s[j] == \'1\': val ^= 1\n seen.setdefault(val, [i, j])\n else: seen.setdefault(0, [i, i])\n return [seen.get(x^y, [-1, -1]) for x, y in queries]\n``` | 2 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python clean solution | substring-xor-queries | 0 | 1 | use a dict to store numbers we can get from s\n- number 10^9 can be represent with 30 bit\n- for each index i, only need to look forward at most 30 bits\n- for each number, store the shortest substring index\n\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n dt, n = {}, len(s)\n for i in range(n):\n t = 0\n for j in range(i, min(i + 30, n)):\n t = (t << 1) | int(s[j])\n if t not in dt or dt[t][1] - dt[t][0] > j - i:\n dt[t] = [i, j]\n \n return [dt.get(fir ^ sec, [-1, -1]) for fir, sec in queries]\n``` | 1 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python Logical Solution | substring-xor-queries | 0 | 1 | # Approach\na^b=c => b^c=a\n\n\n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, q: List[List[int]]) -> List[List[int]]:\n ot=[]\n n=len(q)\n for i in range(n) :\n het=q[i][0]^q[i][1]\n # print(q[i][0],q[i][1],het)\n x=bin(het)[2:]\n # print(het,x)\n if x in s :\n gojo=s.find(x)\n # print(gojo)\n ot.append([gojo,gojo+len(str(x))-1])\n else :\n ot.append([-1,-1])\n return ot\n``` | 1 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python 3 || 6 lines, XOR algebra, w/explanation and example || T/M: 1467 ms / 79 MB | substring-xor-queries | 0 | 1 | Properties of the XOR binary operation:\n```\n \u2022 Associative: (a^b)^c = a^(b^c)\n \u2022 Identity: a^0 = a`\n \u2022 Inverse: a^a = 0\n```\nThese properties imply that the number`val`such that`first^val == second` is `first^second`:\n```\n first^val == second`\n first^(first^val) == `first^second \n (first^first)^val == `first^second (Associative)\n 0^val == `first^second (Inverse)\n val == `first^second (Identity)\n```\nThus, this problem reduces to finding the first occurrence of the binary representation of `first^second`in the string`s`. \n\nBefore we answer the queries, we build a`dict`to contain that first occurrence, if it exists. We then answer each query with`d[val]`. \n# The Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n \n d, ans, n = defaultdict(lambda:[-1,-1]), [], len(s) \n # Example:\n for j in range(min(32,n)): # s= \'101101\' queries = [[0,5],[1,2]]\n for i in range(n-j):\n # d = {1:[0,0], 0:[1,1], 2:[0,1], 3:[2,3], 5:[0,2],\n num = int(s[i:i+j+1], 2) # 6:[2,4], 11:[0,3], 13:[2,5], 22:[0,4], 45:[0,5]}\n if num not in d: d[num] = [i, i+j]\n\n return [d[a^b] for a, b in queries] # return [d[0^5], d[1^2]] = [d[5], d[3]] \n # = [[0,2], [2,3]]\n```\n[https://leetcode.com/problems/substring-xor-queries/submissions/896697049/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*). | 4 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
[PYTHON] Simple preprocessing & hashing solution O(N * 32) | substring-xor-queries | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe solution string length can\'t be over 32($2^{32}$).\nThe approach is simple. Just preprocess all the bit string under 32 length.\n\n## Why can we calculate the answer like `a^b` ?\n$$ A \\oplus X = B $$ \n$$ X = A \\oplus B $$ \n\n## Note that we must process reversely\nAnd we must process reversely because of description `there are multiple answers, choose the one with the minimum left.`\n# Complexity\n- Time complexity: $O(N \\times 32) $\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(N \\times 32) $\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n finder = defaultdict(lambda: [-1, -1])\n for l in range(33, 0, -1):\n for i in range(len(s)-l, -1, -1):\n finder[int(s[i:i+l], 2)] = [i, i+l-1]\n ans = []\n for a, b in queries:\n ans.append(finder[a^b])\n return ans\n \n``` | 5 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python3 XOR and dict(map) | substring-xor-queries | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, v: List[List[int]]) -> List[List[int]]:\n def cmp():\n return -2\n ans=[]\n mp=defaultdict(cmp)\n for i in v:\n x=bin((i[0]^i[1]))[2:]\n if mp[x]!=-2:\n if mp[x]==-1:\n ans+=[[-1,-1]]\n else:\n ans+=[[mp[x],mp[x]+len(x)-1]]\n continue \n y=s.find(x)\n if y==-1:\n ans+=[[-1,-1]]\n else:\n ans+=[[y,y+len(x)-1]]\n mp[x]=y\n return ans\n``` | 10 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python3 clean solution beginner friendly | substring-xor-queries | 0 | 1 | # Intuition\n- Any 10^9 number can be represented by 30 bits, hence we only need to look forward 30 number\n- We can get the target binary to fulfil the query by XOR-ing first and second.\n- Since len(queries) > len(s) by alot it is better to preprocess S into a dict of possible values\n\n# Approach\n- I iterated s from the back so if multiple string produces the same decimal number, the left most one would be taken\n- I skipped `s[i] == \'0\'` so that the binary generated will not start with a 0\n- int(value,2) converts the String value with base 2 into a decimal integer\n\n# Complexity\n- Time complexity:\nO(n*30)\n\n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n df = {}\n n = len(s)\n for i in range(n-1, -1, -1):\n if s[i] == \'0\':\n df[0] = [i,i]\n continue\n for j in range(min(n,i+30), i, -1):\n df[int(s[i:j],2)] = [i,j-1]\n\n return [df.get(a^b,[-1,-1]) for a,b in queries]\n``` | 0 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python | Beats 100% | O(n) solution | substring-xor-queries | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n pos = {}\n n = len(s)\n for i in range(n):\n if s[i] == \'0\':\n if 0 not in pos:\n pos[0] = i\n continue\n num = 0\n for j in range(i, min(i+32, n)):\n if s[j] == \'1\': num = (num<<1) | 1\n else: num <<= 1\n if num not in pos:\n pos[num] = i\n # print(pos)\n ans = []\n for f, s in queries:\n n = f^s\n # print(f,s,n)\n p = pos.get(n)\n if p is None:\n ans.append((-1, -1))\n else:\n l = math.floor(math.log2(n)) if n else 0\n ans.append((p, p+l))\n \n return ans\n``` | 0 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
Python | substring-xor-queries | 0 | 1 | \n# Code\n```\nclass Solution:\n def substringXorQueries(self, s: str, queries: List[List[int]]) -> List[List[int]]:\n mp = {}\n res = []\n for sub in range(1,31):\n i,j=0,sub\n while j<=len(s):\n mp.setdefault(int(s[i:j],2),(i,j-1))\n i+=1\n j+=1\n \n for first,second in queries:\n k = first^second\n if k in mp:\n res.append(mp[k])\n else:\n res.append([-1,-1])\n \n return res\n \n \n``` | 0 | You are given a **binary string** `s`, and a **2D** integer array `queries` where `queries[i] = [firsti, secondi]`.
For the `ith` query, find the **shortest substring** of `s` whose **decimal value**, `val`, yields `secondi` when **bitwise XORed** with `firsti`. In other words, `val ^ firsti == secondi`.
The answer to the `ith` query is the endpoints (**0-indexed**) of the substring `[lefti, righti]` or `[-1, -1]` if no such substring exists. If there are multiple answers, choose the one with the **minimum** `lefti`.
_Return an array_ `ans` _where_ `ans[i] = [lefti, righti]` _is the answer to the_ `ith` _query._
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "101101 ", queries = \[\[0,5\],\[1,2\]\]
**Output:** \[\[0,2\],\[2,3\]\]
**Explanation:** For the first query the substring in range `[0,2]` is ** "101 "** which has a decimal value of **`5`**, and **`5 ^ 0 = 5`**, hence the answer to the first query is `[0,2]`. In the second query, the substring in range `[2,3]` is ** "11 ",** and has a decimal value of **3**, and **3 `^ 1 = 2`**. So, `[2,3]` is returned for the second query.
**Example 2:**
**Input:** s = "0101 ", queries = \[\[12,8\]\]
**Output:** \[\[-1,-1\]\]
**Explanation:** In this example there is no substring that answers the query, hence `[-1,-1] is returned`.
**Example 3:**
**Input:** s = "1 ", queries = \[\[4,5\]\]
**Output:** \[\[0,0\]\]
**Explanation:** For this example, the substring in range `[0,0]` has a decimal value of **`1`**, and **`1 ^ 4 = 5`**. So, the answer is `[0,0]`.
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` is either `'0'` or `'1'`.
* `1 <= queries.length <= 105`
* `0 <= firsti, secondi <= 109` | null |
【C++ || Java || Python3】 Binary search in value range | subsequence-with-the-minimum-score | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n\n# Intuition\n1. **Clearly, "remove all" is no worse than "remove some" for selected subsequences.**\n2. Furthermore, if deleting a short string can make $t$ a subsequence of $s$, then it must also be true to expand on the basis of this short string.\n3. Therefore, the answer is dichotomous in the value domain, and binary search can be considered.\n4. In each sample, check whether each substring of length $x$ meets the requirements after deletion. If any one is found, the result of $x$ is true, otherwise it is false.\n5. Note that when enumerating each substring, $t$ will be cut into two segments, so it is only necessary to check whether the $left + right$ is a subsequence of $s$.\n6. For the left part, greedily match the left side of $s$, and record $t[0...i]$ that can become the smallest $j$ of a subsequence of $s[0...j]$. The same is true for the right part, the record $t[i...n]$ can become the largest $j$ of the subsequence of $s[j...m]$.\n7. In this way, it is enough to scan one round and check whether there is a qualified substring.\n\n# Approach\n1. \n\n# Complexity\n- Time complexity: $O(m + n\\log{n})$\n- Space complexity: $O(m+n)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n int minimumScore(string s, string t) {\n int m = s.size(), n = t.size();\n vector<int> left(n+2, -1), right(n+2, m);\n int p = 0;\n for (int i = 0; i < n; ++i) {\n while (p < m && s[p] != t[i]) p++;\n left[i+1] = p++;\n }\n p = m - 1;\n for (int i = n - 1; i >= 0; --i) {\n while (p >= 0 && s[p] != t[i]) p--;\n right[i+1] = p--;\n }\n auto check = [&](int x) -> bool {\n for (int i = 0; i + x - 1 < n; ++i) {\n if (left[i] < right[i+x+1]) \n return true;\n }\n return false;\n };\n int l = 0, r = n;\n while (l <= r) {\n int x = (l + r) / 2;\n if (check(x)) r = x - 1;\n else l = x + 1;\n }\n return l;\n }\n};\n```\n``` Java []\nclass Solution {\n public int minimumScore(String s, String t) {\n int m = s.length(), n = t.length();\n int []left = new int[n+2];\n int []right = new int[n+2];\n int p = 0;\n for (int i = 0; i < n; ++i) {\n while (p < m && s.charAt(p) != t.charAt(i)) p++;\n left[i+1] = p++;\n }\n left[0] = -1;\n p = m - 1;\n for (int i = n - 1; i >= 0; --i) {\n while (p >= 0 && s.charAt(p) != t.charAt(i)) p--;\n right[i+1] = p--;\n }\n right[n+1] = m;\n\n int l = 0, r = n;\n while (l <= r) {\n int x = (l + r) / 2;\n boolean flag = false;\n for (int i = 0; i + x - 1 < n; ++i) {\n if (left[i] < right[i+x+1]) \n flag = true;\n }\n if (flag) r = x - 1;\n else l = x + 1;\n }\n return l;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n m, n = len(s), len(t)\n left, right = [-1] * (n+2), [m] * (n+2)\n p = 0\n for i in range(n):\n while p < m and s[p] != t[i]: p += 1\n left[i+1] = p\n p += 1\n p = m - 1\n for i in range(n-1, -1, -1):\n while p >= 0 and s[p] != t[i]: p -= 1\n right[i+1] = p\n p -= 1\n\n def check(x): \n for i in range(n + 1 - x):\n if left[i] < right[i+x+1]:\n return True\n return False\n\n l, r = 0, n\n while l <= r:\n x = (l + r) // 2;\n if (check(x)): r = x - 1\n else: l = x + 1\n return l\n``` | 1 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
Python | Iterate from both sides | Explanation and Comment | subsequence-with-the-minimum-score | 0 | 1 | First, we consider that given `left` that `t[:left]` is a substring of `s[:sleft]`, how can we find the best `right`?\nOf course, `right` should be as small as possible. Even we delete a ton of character inside `t` but `t[len(t)-1]` is not deleted, the score is still `len(t) - left`.\nThus, we should start with the last character of `t` to find if there\'s a character equals to it in `s[sleft:]`. Every time we find, we should choose the rightest index and we can decrease `right`. Until we cannot decrease `right`, then we should decrease `left` by one to make `sleft` smaller for giving more characters for `t[right]` to match.\n\n\n# Code\n```Python[]\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n sl = 0\n sr = len(s) - 1\n tl = 0\n tr = len(t) - 1\n k = {}\n for tl in range(len(t)):\n while sl < len(s) and s[sl] != t[tl]:\n sl += 1\n if sl == len(s):\n tl -= 1\n break\n # save smallest sleft for all left\n k[tl] = sl\n sl += 1\n \n # we set left = -1, when we don\'t use left\n k[-1] = -1\n ans = tr - tl\n # iterate every left by decreasing one\n # releave the limitation of s[sleft:]\n for ntl in range(tl, -2, -1):\n # every time we decrease left, check if right can be decreased\n while tr > ntl and sr > k[ntl]:\n if s[sr] != t[tr]:\n sr -= 1\n elif s[sr] == t[tr]:\n sr -= 1\n tr -= 1\n ans = min(tr - ntl, ans)\n return ans\n``` | 1 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
Python 3 || 10 lines, two passes || T/M: 174 ms / 18 MB | subsequence-with-the-minimum-score | 0 | 1 | ```\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n\n m, n = len(s), len(t)\n suff, j = [0]*m, n\n\n for i in range(m)[::-1]:\n\n if j > 0 and s[i] == t[j-1]: j -= 1\n suff[i] = j-1\n\n ans, j = j, 0\n\n for i in range(m):\n\n ans = min(ans, max(0, suff[i] - j + 1))\n if j < n and s[i] == t[j]: j += 1\n\n return min(ans, n-j)\n```\n[https://leetcode.com/problems/subsequence-with-the-minimum-score/submissions/896781999](http://) | 4 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
[Python3] forward & backward | subsequence-with-the-minimum-score | 0 | 1 | \n```\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n suffix = [-1]*len(s)\n j = len(t)-1\n for i in reversed(range(len(s))): \n if 0 <= j and s[i] == t[j]: j -= 1\n suffix[i] = j \n ans = j + 1\n j = 0 \n for i, ch in enumerate(s): \n ans = min(ans, max(0, suffix[i] - j + 1))\n if j < len(t) and s[i] == t[j]: j += 1\n return min(ans, len(t)-j)\n``` | 11 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
O(n) time and space solution using a queue and a stack | subsequence-with-the-minimum-score | 0 | 1 | # Intuition\n\nMy initial thought was that this should be a dynamic programming problem as it superficially sounds related to the classic longest subsequence problem (e.g., see Cormen\'s Algorithms Text, DP Chapter). However, upon closer inspection, the problem is asking for something much simpler: the minimum distance between the first index that must be removed and the last index that must be removed to make the second string a subsequence of the first.\n\nNote that this is actually not equivalent to the LCS problem. As an example:\n\nLeft: complain\nRight: paning\n\nThe lonest common subsequence is "pain"; however, the subsequence that solves the problem is actually "pan" ("ing" get removed, which gives a minimum score of 3).\n\nThe correct way to think about it is to really focus on delaying the first character that should be removed while similtaneously considering its impact on the last character that should be removed.\n\nThe best way to explain the intuition behind my algorithm is with an example. Consider again:\n\nLeft: complain\nRight: paningoman\n\nThe minimum score is the minimum value of (maxRemove - minRemove). To maximimize minRemove (which reduces the score), we need to maximize the length of the prefix of "paning" that occurs in "complain". Note that \'p\' occurs at index 3 in complain, \'a\' occurs at index 5 (must be at an index greater than 3 to preserve subsequence order), \'n\' occurs at index 7, and then \'i\' can not longer exist in the subsequence of "comPlAiN" (where capitical letters should how the prefix "pan" becomes a subsequence of "complain"). Note that if we select "pan" as our subsequence, it means that we must remove all character of the suffix "ingoman", which gives us a score of 7.\n\nWe could also work backwards to minimize maxRemove by considering how much of the suffix of "paningoman" we can turn into a subsequence of "complain". Note that the last \'n\' occurs at index 7 in "complain", \'a\' occurs at index 5, \'m\' occurs at index 2, and \'o\' occurs at index 1. If we select "oman" as our subsequence, then we would need to remove the prefix "paning", which results in a score of 6 (which is better than 7).\n\nWe can also consider a hybrid of what is described in the last two paragraphs. We can simultaneosly select a prefix and a suffix of "paningoman" that attempts to increase minRemove and decrease maxRemove in a way that minimizes the overall score.\n\nNote that the prefixes of "paningoman" that fit as a subsequence in "complain" occur at indices:\n\n3, 5, 7 (this will be a queue as we will read element FIFO)\n\nNow traversing backwards through the two input strings, we note that the suffixes of "paningoman" that fit as a subsequence in "complain" occur at indices:\n\n1, 2, 5, 7 (this will be a stack as we will read elements LIFO)\n\nWe will refer to the first queue as `leftCand` or candidates that we will incrementally add to a prefix of "paningoman" that will exist in our optimal subsequence. We will refer to the second stack as `rightUsed`, which reflects the suffix of "paningoman" that will exist in our optimal subsequence. We will incrementally remove elements from `rightUsed` as we add elements of `leftCand`.\n\nThe first subsequence we will consider will be the characters at indices\n\n1, 2, 5, 7\n\nwhich is exactly equal to `rightUsed`. This corresponds to "oman". The score is 6 since we must remove "paning".\n\nNext, we want to add the first 3 from `leftCand` into our subsequence. But to do this, we must remove the 1 and 2 (since they occur before 3 and we need to maintain the subsequence property). This gives us\n\n3, 5, 7\n\nThis corresponds to "pan", which removes the substring "aningom", which gives us a score of 7 (not minimal, so 6 is still the best).\n\nNext, we want to add the second 5 from `leftCand` into our subsequence. But to do this, we have to remove the existing 5, again, since we want to preserve the subsequence property. This gives us\n\n3, 5, 7\n\nwhich is identical to the previous case. It turns out we will also get 3, 5, 7 when we insert the last 7 from `leftCand` and remove the 7 from `rightUsed`.\n\nThe final answer is that the minimum score is 6.\n\n\n# Approach\n\n1. Generate a queue `leftCand` consisting of the indices in `leftString` corresponding to the first n consecutive characters (i.e., prefix) of `rightString`. Note that this queue can be empty if the first character of `rightString` does not exist.\n2. Generate a stack `rightUsed` consisting of the indices in `leftString` corresponding to the last n consecutive character (i.e., suffix) of `rightString`. Note that elements being removed from this stack should be ascending order. Also, note that this stack can be empty if the last chacter of `leftString` does not exist in `rightString`.\n3. First calculate the score based on the subsequence implied by `rightUsed`. If there are no elements in `leftCand`, this this will be the minimum score.\n4. While `leftCand` is non-empty, pop the next element from the queue. Remove any indices from `rightUsed` that are less than or equal to the element popped off of `leftCand`. The list of all elements popped off of `leftCand` so far and the remaining (non-popped) elements of `rightUsed` for the next candidate subsequence. Calculate its score and check if it is minimal.\n5. Return the minimum score found.\n\n\n# Complexity\nAssume that the left string has length n and the right string has length m.\n\n**Time complexity:** \nCreating the `leftCand` queue and `rightString` stack both require a single full pass of the left string, which requires O(n) steps.\n\nThe main loop requires `|leftCand| + |rightUsed|` steps which is maximally O(2 x min(n, m)) = O(n).\n\nThe overall time complexity is O(n).\n\n**Space complexity:**\nThe only addition space created are from the queue `leftCand` and the stack `rightUsed`. This will be O(1) in the best case and O(n) in the worst case.\n\n# Code\nThe following python3 code passed all test cases. It uses the `deque` class to create the necessary queue and stack.\n\n```\nfrom collections import deque\n\nclass Solution:\n \n def getLeftIndices(leftString, rightString):\n rightIdx = 0\n leftCand = deque()\n for idx, letter in enumerate(leftString):\n if letter == rightString[rightIdx]:\n leftCand.append(idx)\n rightIdx += 1\n if rightIdx >= len(rightString):\n break\n return leftCand\n\n def getRightIndices(leftString, rightString):\n rightIdx = len(rightString) - 1\n rightCand = deque()\n for idx, letter in enumerate(leftString[::-1]):\n if letter == rightString[rightIdx]:\n rightCand.appendleft(len(leftString) - 1 - idx)\n rightIdx -= 1\n if rightIdx < 0:\n break\n return rightCand\n\n def minimumScore(self, s: str, t: str) -> int:\n leftCand = Solution.getLeftIndices(s, t)\n rightUsed = Solution.getRightIndices(s, t)\n\n minRemove = 0\n maxRemove = len(t) - 1 - len(rightUsed)\n minScore = maxRemove - minRemove + 1\n\n score = minScore\n while minScore > 0 and len(leftCand) > 0: \n if len(rightUsed) == 0 or leftCand[0] < rightUsed[0]:\n minRemove += 1\n leftCand.popleft()\n else:\n maxRemove += 1\n rightUsed.popleft()\n score = maxRemove - minRemove + 1\n minScore = min(score, minScore)\n\n return minScore\n\n``` | 2 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
simple binary search using prefix and suffix arrays O(nlogn) Python 3 | subsequence-with-the-minimum-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n s = \'0\'+s+\'0\'\n t = \'0\'+s+\'0\'\n prefix_arr = [-1 for _ in range(len(t))]\n suffix_arr = [-1 for _ in range(len(t))]\n \n cur_ind = 0\n for i in range(len(s)):\n if cur_ind >= len(t):\n break\n if s[i]==t[cur_ind]:\n prefix_arr[cur_ind] = i\n cur_ind += 1\n\n cur_ind = len(suffix_arr)-1\n for i in reversed(range(len(s))):\n if cur_ind < 0:\n break\n if s[i] == t[cur_ind]:\n suffix_arr[cur_ind] = i\n cur_ind -= 1\n min_score = len(t)\n for i in range(len(prefix_arr)):\n if prefix_arr[i] == -1:\n break\n low = i+1\n high = len(suffix_arr)\n while low < high:\n mid = int((low+high)/2)\n if suffix_arr[mid] == -1 or suffix_arr[mid]<=prefix_arr[i]:\n low = mid+1\n else:\n min_score = min(min_score, mid-i-1)\n high = mid \n return min_score\n``` | 0 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
Left and Right O(n) -- Python version | subsequence-with-the-minimum-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nLeft pass once for each index i in t, find the smallest index j in s such that t[: i+1] is a subsequence of s[: j+1]. Store the answer in an array (leftArr).\nIf such j does not exist for some i, then by default leftArr[i] = -1.\n\nSimilarly, right pass once for each i in t, find the largest index j in s such that t[i: ] is a subsequence of s[j: ]. Store the answer in an array (rightArr).\nIf such j does not exist for some i, then by default rightArr[i] = -1.\n\nFinally, pass t from right to left, for each index $right$ satisfying $rightArr[right]!=-1$, look for the largest index $left$ of t, such that $leftArr[left]!=-1$ and $leftArr[left] < rightArr[right]$.\nAbove can guarantee that t[ :left] + t[right: ] is a subsequence of s. \nWe simply need to find the $(left, right)$ pair which minimizes (right-1-left).\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n m = len(s)\n n = len(t)\n rightArr = [-1 for _ in range(n)]\n leftArr = [-1 for _ in range(n)]\n\n j = 0 \n for i in range(n):\n if j >= m:\n break\n while j < m and s[j] != t[i]:\n j+=1\n if j < m:\n leftArr[i] = j\n j += 1\n \n j = m-1\n for i in reversed(range(n)):\n if j < 0:\n break\n while j >= 0 and s[j] != t[i]:\n j -= 1\n if j >= 0:\n rightArr[i] = j\n j -= 1\n\n right = n\n left = -1\n for i in range(n):\n if leftArr[i] == -1:\n break\n left = i\n res = right-1-left\n right = n-1\n while right >= 0 and (rightArr[right]!= -1):\n boundary = rightArr[right]\n left = min(left, right-1)\n while left>=0 and leftArr[left] >= boundary:\n left -= 1\n res = min(res, right-1-left)\n right -= 1\n return res\n\n \n\n``` | 0 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
Python Solution Using Binary Search | subsequence-with-the-minimum-score | 0 | 1 | # Code\n```\nfrom bisect import bisect_right,bisect_left\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n d=[[] for _ in range(26)]\n for i in range(len(s)):\n d[ord(s[i])-97].append(i)\n j=len(s)\n dp=[-1 for _ in range(len(t))]\n for i in range(len(t)-1,-1,-1):\n arr=d[ord(t[i])-97]\n tem=bisect_left(arr,j)\n if(tem==0):\n break\n else:\n dp[i]=arr[tem-1]\n j=dp[i]\n else:\n return 0\n j=i\n i=0\n r=-1\n ans=len(t)\n while(i<len(t)):\n arr=d[ord(t[i])-97]\n tem=bisect_right(arr,r)\n if(tem>=len(arr)):\n ans=min(ans,j-i+1)\n break\n tem=arr[tem]\n if(j+1>=len(t) or dp[j+1]>tem):\n r=tem\n i+=1\n else:\n ans=min(ans,j-i+1)\n while(j<len(t)-1 and ( dp[j+1]<=tem)):\n j+=1\n r=tem\n i+=1\n return ans\n\n``` | 0 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
2 pointer LEFT - RIGHT | subsequence-with-the-minimum-score | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nlongest increasing prefix+suffix\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom copy import deepcopy\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n left=[-1]*len(t)\n right=[-1]*len(t)\n ind=defaultdict(deque)\n ind2=defaultdict(deque)\n for i in range(len(s)):\n ind[s[i]].append(i)\n ind2[s[i]].append(i)\n for i in range(len(t)):\n if ind[t[i]]:\n while i and ind[t[i]] and ind[t[i]][0]<left[i-1]:\n ind[t[i]].popleft()\n if ind[t[i]]:\n left[i]=ind[t[i]].popleft()\n ind=ind2\n ans=len(t)\n cnt=0\n for i in range(len(t)-1,-1,-1):\n cnt+=1\n if ind2[t[i]]:\n while i+1<len(t) and ind[t[i]] and ind[t[i]][-1]>right[i+1]:\n ind[t[i]].pop()\n if ind[t[i]]:\n right[i]=ind[t[i]].pop()\n ans=min(ans,len(t)-cnt)\n if i+1<len(t) and right[i+1]<right[i]:\n right[i]=-1\n break\n hi=len(left)-1\n for i in range(len(left)):\n if left[i]==-1:\n break\n l=i\n while right[hi]<left[l]:\n if hi+1<len(left):\n hi+=1\n else:\n break\n while hi>l and right[hi]!=-1 and right[hi]>left[l]:\n th=hi-1\n hi=th\n ans=min(ans,hi-l)\n \n return max(ans,0)\n``` | 0 | You are given two strings `s` and `t`.
You are allowed to remove any number of characters from the string `t`.
The score of the string is `0` if no characters are removed from the string `t`, otherwise:
* Let `left` be the minimum index among all removed characters.
* Let `right` be the maximum index among all removed characters.
Then the score of the string is `right - left + 1`.
Return _the minimum possible score to make_ `t` _a subsequence of_ `s`_._
A **subsequence** of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., `"ace "` is a subsequence of `"abcde "` while `"aec "` is not).
**Example 1:**
**Input:** s = "abacaba ", t = "bzaa "
**Output:** 1
**Explanation:** In this example, we remove the character "z " at index 1 (0-indexed).
The string t becomes "baa " which is a subsequence of the string "abacaba " and the score is 1 - 1 + 1 = 1.
It can be proven that 1 is the minimum score that we can achieve.
**Example 2:**
**Input:** s = "cde ", t = "xyz "
**Output:** 3
**Explanation:** In this example, we remove characters "x ", "y " and "z " at indices 0, 1, and 2 (0-indexed).
The string t becomes " " which is a subsequence of the string "cde " and the score is 2 - 0 + 1 = 3.
It can be proven that 3 is the minimum score that we can achieve.
**Constraints:**
* `1 <= s.length, t.length <= 105`
* `s` and `t` consist of only lowercase English letters. | null |
StraightForward solution | maximum-difference-by-remapping-a-digit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2*n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n0(2*n)\n\n# Code\n```\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n mmax = \'0\'\n mmin = \'0\'\n # temp = set(list(str(num)))\n # if set(list(str(num))) == {\'9\'}:\n # mmax = str(num)\n # else:\n # for index,ele in enumerate(str(num)):\n # if ele != \'9\':\n # mmax = str(num).replace(ele,\'9\')\n # mmin = str(num).replace(str(num)[0],\'0\')\n # return int(mmax) - int(mmin)\n for index,ele in enumerate(str(num)):\n if ele != \'9\':\n mmax = str(num).replace(ele,\'9\')\n break\n else:\n mmax += ele\n for index,ele in enumerate(str(num)):\n if ele != \'0\':\n mmin = str(num).replace(ele,\'0\')\n break\n else:\n mmin += ele\n \n return int(mmax) - int(mmin)\n``` | 1 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
🚀 Simple🚀 Greedy🚀 Math 🚀Easy 🚀 Python 🚀Python3 🚀 | maximum-difference-by-remapping-a-digit | 0 | 1 | ### Please Upvote if you find this useful \uD83D\uDE0A\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n lst = list(str(num))\n minN = lst[0]\n maxN = lst[0]\n num1 = list()\n num2 = list()\n \n for i in lst:\n if i != \'9\':\n minN = i\n break\n\n for i in range(len(lst)):\n if lst[i] == minN:\n num2.append(\'9\')\n else:\n num2.append(lst[i])\n if lst[i] == maxN:\n num1.append(\'0\')\n else:\n num1.append(lst[i])\n\n return int("".join(num2)) - int("".join(num1))\n```\n\n### Please Upvote if you find this useful \uD83D\uDE0A\n | 1 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
Simple Python3 solution | maximum-difference-by-remapping-a-digit | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n string_num = str(num)\n maximum_number = int(string_num)\n minimium_number = 0\n\n for i in string_num:\n if int(i) < 9:\n maximum_number = int(string_num.replace(i, "9"))\n break\n\n for i in string_num:\n if int(i) > 0:\n minimum_number = int(string_num.replace(i, "0"))\n break\n\n return maximum_number - minimum_number\n \n``` | 1 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
Python short and clean. | maximum-difference-by-remapping-a-digit | 0 | 1 | # Approach\nWe are allowed to replace one of the 10 possible digits to other.\n\n1. Min number can be formed by replacing the `first digit`, and all other occurences of it, with `0`.\n\n2. Max number can be formed by replacing the `first non 9 digit`, and all other occurences of it with `9`.\n\n3. Return the difference between max and min possible numbers.\n\n# Complexity\n- Time complexity: $$O(k)$$\n\n- Space complexity: $$O(k)$$\n\nwhere, `k is number of digits in num`.\n\n# Code\n```python\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n s_num = str(num)\n\n ch = s_num[0]\n min_num = int(s_num.replace(ch, \'0\'))\n\n ch = next((x for x in s_num if x != \'9\'), \'0\')\n max_num = int(s_num.replace(ch, \'9\'))\n\n return max_num - min_num\n\n\n``` | 2 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
Python | 5 lines of code | maximum-difference-by-remapping-a-digit | 0 | 1 | # Approach\nFor minimal value we always just replace first digit into zero:\n`int(num.replace(num[0], "0")`.\n\nFor maximum value - find first non-9 digit and replace it into 9.\n\n\n# Complexity\n- Time complexity: $$O(1)$$ as we only interate over string with maximum 8 chars. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n num = str(num)\n i = 0\n while num[i] == "9" and i < len(num)-1:\n i += 1\n\n return int(num.replace(num[i], "9")) - int(num.replace(num[0], "0"))\n \n``` | 22 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
🐍 Super simple Python3 🌟 | EASY, short and sweet 🍫 | O(1) TC and SC | maximum-difference-by-remapping-a-digit | 0 | 1 | # Intuition\nWe will switch the number over to string to make use of python\'s easy string replace. \n\n# Approach\nFor minimal value, always replace the first digit\'s all occurances with \'0\'s.\n\nFor maximal value, replace the first non-\'9\' digit with \'9\'.\n\n# Complexity\nThe lenght of `s` is `log(num, 10)`. As per the problem statement, `1 <= num <= 10^8`, so `log(num, 10) <= 8`.\n- Time complexity: `O(log num)`, which is constant `O(1)`.\n\n- Space complexity: `O(1)` Same as TC, because we allocate space for the string `s`.\n\n# Code\n```\nclass Solution:\n def minMaxDifference(self, num: int) -> int:\n s = str(num)\n v_min = int(s.replace(s[0], \'0\'))\n for c in s:\n if c != \'9\':\n s = s.replace(c, \'9\')\n break\n v_max = int(s)\n return v_max - v_min\n``` | 5 | You are given an integer `num`. You know that Danny Mittal will sneakily **remap** one of the `10` possible digits (`0` to `9`) to another digit.
Return _the difference between the maximum and minimum_ _values Danny can make by remapping **exactly** **one** digit_ _in_ `num`.
**Notes:**
* When Danny remaps a digit d1 to another digit d2, Danny replaces all occurrences of `d1` in `num` with `d2`.
* Danny can remap a digit to itself, in which case `num` does not change.
* Danny can remap different digits for obtaining minimum and maximum values respectively.
* The resulting number after remapping can contain leading zeroes.
* We mentioned "Danny Mittal " to congratulate him on being in the top 10 in Weekly Contest 326.
**Example 1:**
**Input:** num = 11891
**Output:** 99009
**Explanation:**
To achieve the maximum value, Danny can remap the digit 1 to the digit 9 to yield 99899.
To achieve the minimum value, Danny can remap the digit 1 to the digit 0, yielding 890.
The difference between these two numbers is 99009.
**Example 2:**
**Input:** num = 90
**Output:** 99
**Explanation:**
The maximum value that can be returned by the function is 99 (if 0 is replaced by 9) and the minimum value that can be returned by the function is 0 (if 9 is replaced by 0).
Thus, we return 99.
**Constraints:**
* `1 <= num <= 108` | null |
✅ 2 Lines of Code || Explaination💯 | minimum-score-by-changing-two-elements | 0 | 1 | First we will sort the list so we can easily access minimum and maximum values.\n\nThere are total 3 ways in which we can get answer.\n1. By changing First two values - In this case we will chage first two values to make difference zero. Now lowest value we have is nums[2] and largest is nums[-1].\n2. By changing Last two values - In this case we will chage last two values to to make difference zero. Now lowest value we have is nums[0] and largest is nums[-3].\n3. By changing Last value and First Values - In this case we will chage first value and last value to make difference zero. Now lowest value is nums[1] and largest is nums[-2].\n\nWe will select minimum from this three values.\n\n**Plot - We really dont need two change these values, we will calculate difference between values in which we are interested.**\n# Code\n```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n nums.sort()\n return min(nums[-1] - nums[2], nums[-2] - nums[1], nums[-3] - nums[0])\n \n \n``` | 1 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Simple Diagram Explanation | minimum-score-by-changing-two-elements | 1 | 1 | # Idea\n- Sort `nums` so that we can easily access maximum and minimum values\n- We will always make the low score $$0$$ by creating duplicate values\n- Now we have changed the question to finding the minimum maximum value difference by changing two values\n- We have three options:\n - Change the two largest values to the third largest value. Third largest value now becomes the max value.\n - Change the two smallest values to the third smallest value. Third smallest value now becomes the min value.\n - Change largest value to second largest value and smallest value to second smallest value. Second largest becomes max value and second smallest becomes min value.\n- It must be one of these three options because we have to create duplicates to satisfy the low score constraint and the high score always deals with difference between maximum and minimum.\n\n\n# Example\n\n- Let us use `nums = [1,4,7,8,5]`\n\n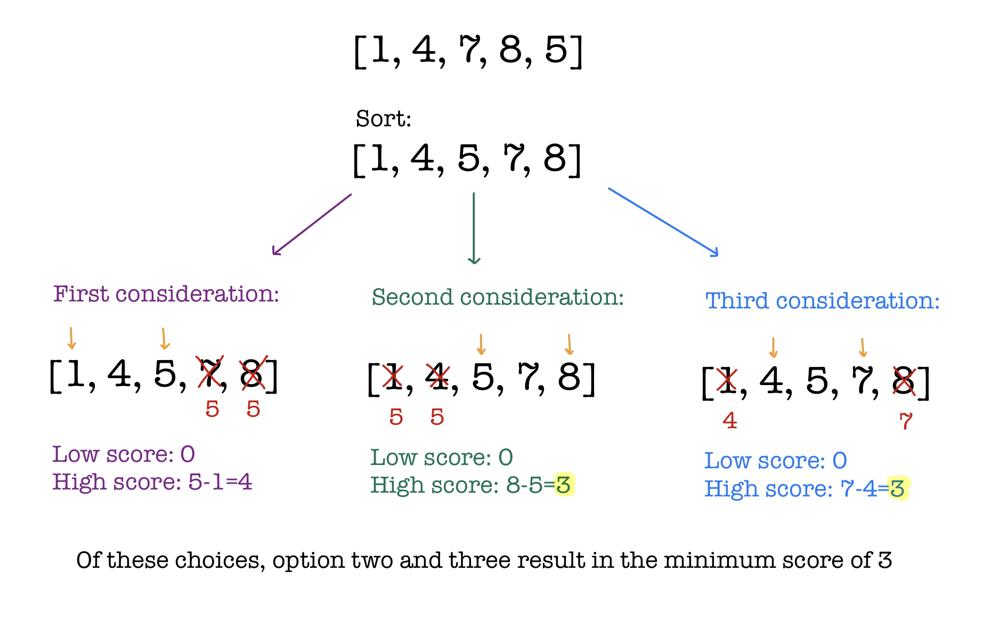\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int minimizeSum(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n return min(nums[n-1]-nums[2], min(nums[n-2]-nums[1], nums[n-3]-nums[0]));\n }\n};\n```\n- Notice from the code that we do not actually need to change the values, we just need to compare the elements of interest by the three options.\n#### If this helped please leave an upvote. Thanks! | 49 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python short and clean. Beats 100%. 2 solutions. Sorting and Heap. | minimum-score-by-changing-two-elements | 0 | 1 | # Approach 1: Sort\n1. Sort `nums` to `s_nums` for random access to maxes and mins.\n\n2. If there were `0` changes allowed:\n There\'s nothing to do.\n The best we can do is: `s_nums[n - 1] - s_nums[0]`.\n \n Note: Abbriviating `s_num[a] - s_num[b]` as `|a, b|` from henceforth.\n Hence the above becomes `|n - 1, 0|`\n\n3. If there were `1` change allowed:\n We can change the first or the last number to the adjacent one.\n The best we can do is:\n `min(|n - 1, 1| (changing the first), |n - 2, 0| (changing the last)`.\n\n4. If there were `2` change allowed:\n The best we can do is:\n `min(|n - 1, 2|, |n - 2, 1|, |n - 3, 0|)`\n\n5. Extending the same, If there were `k` changes allowed:\n The best we can do is:\n `min(|n - 1, k|, |n - 2, k - 1|, ...., |n - k - 1, 0|)`\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is the length of nums`.\n\n# Code\n```python\nclass Solution:\n def minimizeSum(self, nums: list[int]) -> int:\n s_nums = sorted(nums)\n k = 2\n return min(\n s_nums[i] - s_nums[j]\n for i, j in zip(range(-1, -k - 2, -1), range(k, -1, -1))\n )\n\n\n```\n\n---\n\n# Approach 2: Heap\nSince we only need first `k` minimum and first `k` maximum elements in `nums`, given atmost `k` changes allowed, we can use a `min heap` and `max heap` respectively.\n\nThis allows to reduce the time complexity from $$n + n * log(n)$$ to $$n + k * log(n)$$.\n\n# Complexity\n- Time complexity: $$O(n + k * log(n))$$\nFor given question, `k = 2`, `=>` $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is the length of nums`,\n`k is the number of number of values that can be changed`.\n\n# Code\n```python\nclass Solution:\n def minimizeSum(self, nums: list[int]) -> int:\n k, n = 2, len(nums)\n min_hq, max_hq = list(nums), list(map(neg, nums))\n heapify(min_hq); heapify(max_hq)\n\n maxs = tuple(-heappop(max_hq) for _ in range(min(k + 1, n)))\n mins = tuple( heappop(min_hq) for _ in range(min(k + 1, n)))\n\n return min(map(sub, maxs, reversed(mins)))\n\n\n``` | 2 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python 3 || 2 lines, w/ a terse explanation || T/M: 83% / 100% | minimum-score-by-changing-two-elements | 0 | 1 | ```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n\n nums.sort()\n\n return min(nums[-1] - nums[2], # [a,b,c, ..., x,y,z] => [c,c,c, ..., x,y,z]\n nums[-2] - nums[1], # [a,b,c, ..., x,y,z] => [b,b,c, ..., x,y,y] \n nums[-3] - nums[0]) # [a,b,c, ..., x,y,z] => [a,b,c, ..., x,x,x]\n\n # Return min((z-c)+(c-c), (x-a)+(x-x), (y-b)+(b-b))\n```\n[https://leetcode.com/problems/minimum-score-by-changing-two-elements/submissions/901346564/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*NlogN*) and space complexity is *O*(1).\n | 4 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python Solution || 2 lines || Easy to understand | minimum-score-by-changing-two-elements | 0 | 1 | ```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n n,_ = len(nums),nums.sort()\n return min([nums[n-1]-nums[0],nums[n-3]-nums[0],nums[n-1]-nums[2],nums[n-2]-nums[1]])\n``` | 1 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[Python] ✅🔥 2-line Solution w/ Explanation! | minimum-score-by-changing-two-elements | 0 | 1 | ## **Please upvote/favourite/comment if you like this solution!**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis question reduces to minimizing the range of `nums` by changing 2 elements in `nums`. We can minimize the range by doing one of 3 options:\n1. Increase the smallest two numbers. Therefore, the range in this option will be `largest - third smallest`.\n2. Increase the smallest number and decrease the largest number. Therefore, the range in this option will be `second largest - second smallest`.\n3. Decrease the largest two numbers. Therefore, the range in this option will be `third largest - smallest`.\n\nWe return the minimum of these three options to find the minimum score possible.\n\n# Code\n```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n nums.sort()\n return min(nums[-1]-nums[2],nums[-2]-nums[1],nums[-3]-nums[0]) \n```\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 8 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python | minimum-score-by-changing-two-elements | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n nums.sort()\n return min(nums[-2] - nums[1],\n nums[-1] - nums[2],\n nums[-3] - nums[0])\n \n``` | 4 | You are given a **0-indexed** integer array `nums`.
* The **low** score of `nums` is the minimum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **high** score of `nums` is the maximum value of `|nums[i] - nums[j]|` over all `0 <= i < j < nums.length`.
* The **score** of `nums` is the sum of the **high** and **low** scores of nums.
To minimize the score of `nums`, we can change the value of **at most two** elements of `nums`.
Return _the **minimum** possible **score** after changing the value of **at most two** elements o_f `nums`.
Note that `|x|` denotes the absolute value of `x`.
**Example 1:**
**Input:** nums = \[1,4,3\]
**Output:** 0
**Explanation:** Change value of nums\[1\] and nums\[2\] to 1 so that nums becomes \[1,1,1\]. Now, the value of `|nums[i] - nums[j]|` is always equal to 0, so we return 0 + 0 = 0.
**Example 2:**
**Input:** nums = \[1,4,7,8,5\]
**Output:** 3
**Explanation:** Change nums\[0\] and nums\[1\] to be 6. Now nums becomes \[6,6,7,8,5\].
Our low score is achieved when i = 0 and j = 1, in which case |`nums[i] - nums[j]`| = |6 - 6| = 0.
Our high score is achieved when i = 3 and j = 4, in which case |`nums[i] - nums[j]`| = |8 - 5| = 3.
The sum of our high and low score is 3, which we can prove to be minimal.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[Python] Simple solution of just checking power of two numbers; Explained | minimum-impossible-or | 0 | 1 | A number can be expressed by some power of two numbers. Thus, we only need to check the power of two numbers in the list, and find the minimum missing one.\n\nTo check the power of two, we can simply do:\n\n`num == num & (-num)`\n\n\n\n```\nclass Solution:\n def minImpossibleOR(self, nums: List[int]) -> int:\n bit_set = set()\n for num in nums:\n if num == num & (-num):\n bit_set.add(num)\n \n i = 1\n while i in bit_set:\n i = i << 1\n return i\n``` | 2 | You are given a **0-indexed** integer array `nums`.
We say that an integer x is **expressible** from `nums` if there exist some integers `0 <= index1 < index2 < ... < indexk < nums.length` for which `nums[index1] | nums[index2] | ... | nums[indexk] = x`. In other words, an integer is expressible if it can be written as the bitwise OR of some subsequence of `nums`.
Return _the minimum **positive non-zero integer** that is not_ _expressible from_ `nums`.
**Example 1:**
**Input:** nums = \[2,1\]
**Output:** 4
**Explanation:** 1 and 2 are already present in the array. We know that 3 is expressible, since nums\[0\] | nums\[1\] = 2 | 1 = 3. Since 4 is not expressible, we return 4.
**Example 2:**
**Input:** nums = \[5,3,2\]
**Output:** 1
**Explanation:** We can show that 1 is the smallest number that is not expressible.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python | Simple Solution | minimum-impossible-or | 0 | 1 | # Code\n```\nfrom collections import defaultdict\nclass Solution:\n def minImpossibleOR(self, nums: List[int]) -> int:\n nums = set(nums)\n for i in range(32):\n if (1<<i) not in nums:\n return 1<<i\n \n``` | 1 | You are given a **0-indexed** integer array `nums`.
We say that an integer x is **expressible** from `nums` if there exist some integers `0 <= index1 < index2 < ... < indexk < nums.length` for which `nums[index1] | nums[index2] | ... | nums[indexk] = x`. In other words, an integer is expressible if it can be written as the bitwise OR of some subsequence of `nums`.
Return _the minimum **positive non-zero integer** that is not_ _expressible from_ `nums`.
**Example 1:**
**Input:** nums = \[2,1\]
**Output:** 4
**Explanation:** 1 and 2 are already present in the array. We know that 3 is expressible, since nums\[0\] | nums\[1\] = 2 | 1 = 3. Since 4 is not expressible, we return 4.
**Example 2:**
**Input:** nums = \[5,3,2\]
**Output:** 1
**Explanation:** We can show that 1 is the smallest number that is not expressible.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python | Mathematical Induction | Explained | minimum-impossible-or | 0 | 1 | Consider if we don\'t have `1` in `nums`, then the answer is `1` because you cannot use anything larger than `1` to form `1`.\nConsider if we don\'t have `2` in `nums`, then the answer is `2` because you cannot use `1` and anything larger than `2` to form `2`.\nBut if we have [1, 2] in `nums`, we can form `3`.\nSo, by Mathematical Induction, we know that if we have $1, 2, 2^2, 2^3,...,2^n$ in `nums`, we can form every number in $[1, 2^{n+1}-1]$. If we further have $2^{n+1}$ in `nums`, we can form every number in $[1, 2^{n+2}-1]$. If we don\'t have $2^{n+1}$ in `nums`, then the minimum unexpressible number is $2^{n+1}$.\n\n# Code\n```python []\nclass Solution:\n def minImpossibleOR(self, nums: List[int]) -> int:\n nums = set(nums)\n for i in range(33):\n if 1 << i not in nums:\n return 1 << i\n \n``` | 4 | You are given a **0-indexed** integer array `nums`.
We say that an integer x is **expressible** from `nums` if there exist some integers `0 <= index1 < index2 < ... < indexk < nums.length` for which `nums[index1] | nums[index2] | ... | nums[indexk] = x`. In other words, an integer is expressible if it can be written as the bitwise OR of some subsequence of `nums`.
Return _the minimum **positive non-zero integer** that is not_ _expressible from_ `nums`.
**Example 1:**
**Input:** nums = \[2,1\]
**Output:** 4
**Explanation:** 1 and 2 are already present in the array. We know that 3 is expressible, since nums\[0\] | nums\[1\] = 2 | 1 = 3. Since 4 is not expressible, we return 4.
**Example 2:**
**Input:** nums = \[5,3,2\]
**Output:** 1
**Explanation:** We can show that 1 is the smallest number that is not expressible.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.