title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[C++|Java|Python3] counter | find-consecutive-integers-from-a-data-stream | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7360be4d63ffa8b13518401baa628a6f6800d326) for solutions of weekly 95. \n\n**Intuition**\nHere we can use a counter to count the number of occurrence of `num` as of now. \n**Implementation**\n**C++**\n```\nclass DataStream {\n int value = 0, k = 0, cnt = 0; \npublic:\n DataStream(int value, int k) : value(value), k(k) {}\n \n bool consec(int num) {\n if (value == num) ++cnt; \n else cnt = 0; \n return cnt >= k; \n }\n};\n```\n**Java**\n```\nclass DataStream {\n private int value = 0, k = 0, cnt = 0; \n\n public DataStream(int value, int k) {\n this.value = value; \n this.k = k; \n }\n \n public boolean consec(int num) {\n if (value == num) ++cnt; \n else cnt = 0; \n return cnt >= k; \n }\n}\n```\n**Python3**\n```\nclass DataStream:\n\n def __init__(self, value: int, k: int):\n self.value = value\n self.k = k \n self.cnt = 0\n\n def consec(self, num: int) -> bool:\n if num == self.value: self.cnt += 1\n else: self.cnt = 0 \n return self.cnt >= self.k \n```\n**Complexity**\nTime `O(1)` \nSpace `O(1)` | 2 | For a stream of integers, implement a data structure that checks if the last `k` integers parsed in the stream are **equal** to `value`.
Implement the **DataStream** class:
* `DataStream(int value, int k)` Initializes the object with an empty integer stream and the two integers `value` and `k`.
* `boolean consec(int num)` Adds `num` to the stream of integers. Returns `true` if the last `k` integers are equal to `value`, and `false` otherwise. If there are less than `k` integers, the condition does not hold true, so returns `false`.
**Example 1:**
**Input**
\[ "DataStream ", "consec ", "consec ", "consec ", "consec "\]
\[\[4, 3\], \[4\], \[4\], \[4\], \[3\]\]
**Output**
\[null, false, false, true, false\]
**Explanation**
DataStream dataStream = new DataStream(4, 3); //value = 4, k = 3
dataStream.consec(4); // Only 1 integer is parsed, so returns False.
dataStream.consec(4); // Only 2 integers are parsed.
// Since 2 is less than k, returns False.
dataStream.consec(4); // The 3 integers parsed are all equal to value, so returns True.
dataStream.consec(3); // The last k integers parsed in the stream are \[4,4,3\].
// Since 3 is not equal to value, it returns False.
**Constraints:**
* `1 <= value, num <= 109`
* `1 <= k <= 105`
* At most `105` calls will be made to `consec`. | null |
Beginner friendly Python Code | find-consecutive-integers-from-a-data-stream | 0 | 1 | # Code\n```\nclass DataStream:\n\n def __init__(self, value: int, k: int):\n self.val = value\n self.k = k\n self.i = 0\n \n\n def consec(self, num: int) -> bool:\n if(num == self.val):\n self.i += 1\n if(num != self.val):\n self.i = 0\n if((self.i == self.k or self.i > self.k) and num == self.val):\n return True\n else:\n return False\n \n\n\n# Your DataStream object will be instantiated and called as such:\n# obj = DataStream(value, k)\n# param_1 = obj.consec(num)\n```\n\n# Explanation\n\n1) Every time if the current num is equal to value, just increment the count\n\n2) If current num is not equal to value, then just re-set it to 0, to count again freshly\n\n3) Once if count is equal or greater than k, just return True or else return False.\n\n### As simple as that!\n\n\n\n##### If you find my solution helpful and worthy, please consider upvoting my solution. Upvotes play a crucial role in ensuring that this valuable content reaches others and helps them as well.\n\n##### Only your support motivates me to continue contributing more solutions and assisting the community further.\n\n##### Thank You for spending your valuable time.\n\n | 0 | For a stream of integers, implement a data structure that checks if the last `k` integers parsed in the stream are **equal** to `value`.
Implement the **DataStream** class:
* `DataStream(int value, int k)` Initializes the object with an empty integer stream and the two integers `value` and `k`.
* `boolean consec(int num)` Adds `num` to the stream of integers. Returns `true` if the last `k` integers are equal to `value`, and `false` otherwise. If there are less than `k` integers, the condition does not hold true, so returns `false`.
**Example 1:**
**Input**
\[ "DataStream ", "consec ", "consec ", "consec ", "consec "\]
\[\[4, 3\], \[4\], \[4\], \[4\], \[3\]\]
**Output**
\[null, false, false, true, false\]
**Explanation**
DataStream dataStream = new DataStream(4, 3); //value = 4, k = 3
dataStream.consec(4); // Only 1 integer is parsed, so returns False.
dataStream.consec(4); // Only 2 integers are parsed.
// Since 2 is less than k, returns False.
dataStream.consec(4); // The 3 integers parsed are all equal to value, so returns True.
dataStream.consec(3); // The last k integers parsed in the stream are \[4,4,3\].
// Since 3 is not equal to value, it returns False.
**Constraints:**
* `1 <= value, num <= 109`
* `1 <= k <= 105`
* At most `105` calls will be made to `consec`. | null |
Python3 - O(n) | find-xor-beauty-of-array | 0 | 1 | All the numbers will get cancelled out because of XOR, except the numbers themselves.\n\nSo, XOR of the numbers will give the answer\n\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n\t\n s = 0\n for x in nums:\n s^=x\n return s | 3 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python Simple 1-liner | Simplify the Expression | Faster than 100% | find-xor-beauty-of-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTried to simplify the expression\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe key observation is that the triplets ```((nums[i] | nums[j]) & nums[k])``` occurs in pairs except when $$i=j=k$$.\n\nWhen $$i=j=k$$, the result ```((nums[i] | nums[j]) & nums[k])``` is the the number itself.\n\nWhen $$i=j$$ but $$i\u2260k$$, we would have ```nums[i] & nums[k]``` and ```nums[k] & nums[i]``` be valid triplets for each pair of number in ```nums```. XORing them would give 0. Otherwise, for each ```nums[k]```, ```((nums[i] | nums[j]) & nums[k])``` and ```((nums[j] | nums[i]) & nums[k])``` would both be a valid triplets and be considered in the final result. Obviously they are the same and XORing them in the last step would make them 0.\nHence, the result is just the XOR of all numbers in the array.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n return reduce(operator.xor, nums)\n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[C++|Java|Python3] math | find-xor-beauty-of-array | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7360be4d63ffa8b13518401baa628a6f6800d326) for solutions of weekly 95. \n\n**Intuition**\nMath! The final answer is `(v|v) & v` where `v` is the xor of all numbers. \n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int xorBeauty(vector<int>& nums) {\n int val = 0; \n for (auto& x : nums) val ^= x; \n return val; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int xorBeauty(int[] nums) {\n int val = 0; \n for (int x : nums) val ^= x; \n return val; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n return reduce(xor, nums)\n```\n**Complexity**\nTime `O(N)`\nSpace `O(1)` | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python - one line | find-xor-beauty-of-array | 0 | 1 | # Intuition\nWhen you read it, it acutally asks to xor all elements\n\n# Approach\nWhen you read it, it acutally asks to xor all elements\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nfrom functools import reduce\nfrom operator import xor\n\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n return reduce(xor, nums)\n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[python3] Iteration solution for reference. | find-xor-beauty-of-array | 0 | 1 | ```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n N = len(nums)\n\n OR = 0 \n for i in range(N):\n OR = OR | nums[i]\n \n for i in range(N):\n nums[i] &= OR\n \n ans = 0 \n \n for i in nums:\n ans ^= i\n \n return ans | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
[Python3] One Liner with Formal Proof | find-xor-beauty-of-array | 0 | 1 | # Intuition\nMany of you may get accepted during contest by guessing the answer (the bitwise XOR of all `num` in `nums`). Here we provide a formal proof.\n\n# Key Observations:\n1. Fully utilize the symmetry between `i, j, k`.\n2. `a ^ a = 0` (the property of bitwise XOR).\n\n# Proof: \n\n1. First, note that by symmetry of `i` and `j`, we know that the value of `((nums[i] | nums[j]) & nums[k])` and `((nums[j] | nums[i]) & nums[k])` are equal. Which then implies that for a pair of `(i, j)` where `i != j`, the bitwise XOR of `((nums[i] | nums[j]) & nums[k])` and `((nums[j] | nums[i]) & nums[k])` is 0. Thus, we only need to deal with the triplets `(i, j, k)` where `i == j`.\n\n2. Now we only need to consider the triplets `(i, j, k)` where `i == j`, so that `((nums[i] | nums[j]) & nums[k]) = ((nums[i] | nums[i]) & nums[k]) = nums[i] & nums[k]`. By symmetry of `i` and `k`, we know that the value of `nums[i] & nums[k]` and `nums[k] & nums[i]` are equal. Which then implies that for a pair of `(i, k)` where `i != k`, the bitwise XOR of `nums[i] & nums[k]` and `nums[k] & nums[i]` is 0. Thus, we only need to deal with the case of `i == k`.\n\n3. Therefore, we only need to consider the triplets `(i, j, k)` where `i == j == k`, and the final answer reduces to the bitwise XOR of `((nums[i] | nums[j]) & nums[k]) = ((nums[i] | nums[i]) & nums[i]) = nums[i]`.\n\n# Complexity\n- Time complexity: `O(N)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n return reduce(xor, nums) \n``` | 76 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python3 | find-xor-beauty-of-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n return reduce(xor, nums) \n``` | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python 3 || 1 line, w/ explanation and example || T/M: 350 ms / 27.8 MB | find-xor-beauty-of-array | 0 | 1 | Here\'s the analysis:\n- We start with an identity:\n`A^A^B =B [Proof: `A^A^B = (A^A)^B = (0)^B = B `] \n\nHere\'s an example of how this identity works:\n `1^2^3^2^2^1 = 1^1 ^ 2^2 ^ 2 ^ 3 = 0^0^2^3 = 2^3 = 1`\n\n- In Example 1:\n```\nBeauty = (1|4)&1)^(4|1)&1) ^ (1|4)&4)^(4|1)&4) ^ (1|1)&4) ^ (4|4)&1) ^ (1|1)&1) ^ (4|4)&4)\n \\ / \\ / \n (5&1 5&1) (5&4 5&4)\n```\n\n- We can use the identity to discard the two pairs in parentheses. Note we are left only with elements in the form `(A|A)&B`, where `A` and `B` are not nescessarily distinct.\n```\nBeauty = (1|1)&4)^(4|4)&1) ^ (1|1)&1) ^ (4|4)&4)\n \\ / \n (1&4 4&1)\n``` \n \n- We can apply the identity again to discard the pair in parentheses to arrive at\n```\n Beauty = (1|1)&1) ^ (4|4)&4) = 1&1 ^ 4&4 = 1 ^ 4 = 5\n | | \n 1&4 4&1\n```\nNote we are now left only with elements in the form `(A|A)&A` for all `A` in`nums`, and note that `(A|A)&A = A`.\n\nBottom line: We can generalize from this example; the solution is simply XOR(`nums`) \n\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n\n return reduce(xor, nums)\n\n```\n[https://leetcode.com/problems/find-xor-beauty-of-array/submissions/873591810/](http://)\n\nI could be wrong, but I think that time complexity is *O*(1) and space complexity is *O*(1).\n | 5 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python | No Magic | find-xor-beauty-of-array | 0 | 1 | # Intuition\n\nI\'ll tell you what to do if you haven\'t noticed symmetries in the formula.\n\n# Approach\n\nFirst of all, contributions of different bits are independent, which is a common pattern in such questions. For each bit and each of the 8 possible combinations of bits in $$x, y, z$$, we can calculate how many triples $$(i, j, k)$$ yield this combination.\n\nThis technique is useful in formulas that are not that easy to simplify, the formulas that involve sums instead of xor-sums, and also in formulas that consider only ordered indices, like `i < j < k`.\n\nNote: I used `math.floor(math.log2(max(nums))) + 1` to calculate the number of bits, but you may as well hardcode `30` in this problem.\n\nNote: I used `itertools.product((0, 1), repeat=3)` to generate all 8 combinations `(0, 0, 0), (0, 0, 1), (0, 1, 0), ...` because I don\'t want to write three nested loops, but you can say `for x in (0, 1): for y in (0, 1): for z in (0, 1):`.\n\n# Complexity\n\n- Time complexity: $$O(n \\log \\max)$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n\n[Submission link](https://leetcode.com/problems/find-xor-beauty-of-array/submissions/873943705/)\n\n```python\nimport collections\nimport itertools\nimport math\n\n\nclass Solution:\n def xorBeauty(self, nums: list[int]) -> int:\n beauty = 0\n\n for bit in range(math.floor(math.log2(max(nums))) + 1):\n cnt = collections.Counter((num >> bit) & 1 for num in nums)\n\n for i, j, k in itertools.product((0, 1), repeat=3):\n if (cnt[i] * cnt[j] * cnt[k]) & 1:\n beauty ^= ((i | j) & k) << bit\n\n return beauty\n```\n\n | 7 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Python solution beats 100% time and space complexity, it's super easy :-) | find-xor-beauty-of-array | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n* Disclaimer : This question is meduim to understand but super easy to solve. Iterate over the array once doing xor of all elements and simply return it.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorBeauty(self, nums: List[int]) -> int:\n ans = 0\n for i in nums:\n ans ^= i\n return ans | 1 | You are given a **0-indexed** integer array `nums`.
The **effective value** of three indices `i`, `j`, and `k` is defined as `((nums[i] | nums[j]) & nums[k])`.
The **xor-beauty** of the array is the XORing of **the effective values of all the possible triplets** of indices `(i, j, k)` where `0 <= i, j, k < n`.
Return _the xor-beauty of_ `nums`.
**Note** that:
* `val1 | val2` is bitwise OR of `val1` and `val2`.
* `val1 & val2` is bitwise AND of `val1` and `val2`.
**Example 1:**
**Input:** nums = \[1,4\]
**Output:** 5
**Explanation:**
The triplets and their corresponding effective values are listed below:
- (0,0,0) with effective value ((1 | 1) & 1) = 1
- (0,0,1) with effective value ((1 | 1) & 4) = 0
- (0,1,0) with effective value ((1 | 4) & 1) = 1
- (0,1,1) with effective value ((1 | 4) & 4) = 4
- (1,0,0) with effective value ((4 | 1) & 1) = 1
- (1,0,1) with effective value ((4 | 1) & 4) = 4
- (1,1,0) with effective value ((4 | 4) & 1) = 0
- (1,1,1) with effective value ((4 | 4) & 4) = 4
Xor-beauty of array will be bitwise XOR of all beauties = 1 ^ 0 ^ 1 ^ 4 ^ 1 ^ 4 ^ 0 ^ 4 = 5.
**Example 2:**
**Input:** nums = \[15,45,20,2,34,35,5,44,32,30\]
**Output:** 34
**Explanation:** `The xor-beauty of the given array is 34.`
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | null |
Binary Search | Python | NlogN | maximize-the-minimum-powered-city | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nkey points-\n -optimization problem\n -"at max some k"\n\nSo I thought binary search could work\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBinary search on answer, this solution is weird because we are copying the whole array, but it\'s still O(n), so it works.\n\nUse sliding window to calculate the range sum.\nIn the check function, we greedly update the rightmost index in the sliding window if current sum is less than the selected mid \'m\'.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nLog(n))$$ - binary search \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ - copy the array Log(n) times\n# Code\n```\nclass Solution:\n def maxPower(self, nums: List[int], r: int, k: int) -> int:\n def check(m):\n res=0\n temp = nums.copy()\n curr = sum(temp[:r])\n for i in range(n):\n if i+r < n:\n curr+=temp[i+r]\n if i-r-1 > -1:\n curr-=temp[i-r-1]\n if curr<m:\n diff = m-curr\n rr = min(i+r,n-1)\n curr+=diff #wasted 1 hour because i forgot this\n temp[rr]+=diff\n res+=diff\n return res<=k\n \n n = len(nums)\n s,e = 0,sum(nums)+k\n while s<e:\n m = s+e+1>>1\n if check(m):\n s=m\n else:\n e=m-1\n return s\n \n``` | 1 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[Python3] Binary Search on the Answer and Sliding Window | maximize-the-minimum-powered-city | 0 | 1 | # Approach\nWe perform a binary search on the possible answer space by checking whether the given `target` (maximum possible minimum power) is valid or not. For each given `target`, we utilize a sliding window algorithm to check its validity in linear time.\n\n# Complexity\n- Time complexity: `O(NlogA)`, where `A` is the range of `[min(stations), sum(stations) + k]`.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(N)`, for the use of a hashmap to record the addition of new stations temporarily.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n start, end = min(stations), sum(stations) + k\n while start + 1 < end:\n mid = (start + end) // 2\n if self.check(stations, r, k, mid):\n start = mid\n else:\n end = mid\n if self.check(stations, r, k, end):\n return end\n else:\n return start\n \n def check(self, stations, r, k, target):\n n = len(stations)\n ans = True\n newStations = defaultdict(int)\n power = sum(stations[ : r])\n for i in range(n):\n if i + r < n:\n power += stations[i + r]\n if i - r - 1 >= 0:\n power -= stations[i - r - 1]\n if power >= target:\n continue\n elif power + k < target:\n ans = False\n break\n else:\n diff = target - power\n power = target\n stations[min(i + r, n - 1)] += diff\n k -= diff\n newStations[min(i + r, n - 1)] += diff\n for i in newStations:\n stations[i] -= newStations[i]\n return ans\n``` | 1 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[C++|Java|Python3] Binary search | maximize-the-minimum-powered-city | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7360be4d63ffa8b13518401baa628a6f6800d326) for solutions of weekly 95. \n\n**Intuition**\nBinary search for the desired answer. \n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n long long maxPower(vector<int>& stations, int r, int k) {\n int n = stations.size(); \n long long lo = 0, hi = 2e10; \n while (lo < hi) {\n long long mid = lo + (hi-lo+1)/2, prefix = 0; \n\t\t\tint kk = k; \n\t\t\tbool ok = true; \n\t\t\tvector<int> ss = stations; \n for (int i = 0; i < n+r; ++i) {\n if (i < n) prefix += ss[i]; \n if (i >= 2*r+1) prefix -= ss[i-2*r-1]; \n if (i >= r && prefix < mid) {\n if (kk < mid - prefix) {\n\t\t\t\t\t\tok = false; \n\t\t\t\t\t\tbreak; \n\t\t\t\t\t}\t\t\t\t\t\t\n kk -= mid - prefix; \n if (i < n) ss[i] += mid - prefix; \n prefix = mid; \n }\n }\n if (ok) lo = mid; \n else hi = mid-1; \n }\n return lo; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public long maxPower(int[] stations, int r, int k) {\n int n = stations.length; \n long lo = 0, hi = k + Arrays.stream(stations).asLongStream().sum();\n while (lo < hi) {\n long mid = lo + (hi-lo+1)/2, prefix = 0; \n int kk = k; \n int[] ss = stations.clone(); \n boolean ok = true; \n for (int i = 0; i < n+r; ++i) {\n if (i < n) prefix += ss[i]; \n if (i >= 2*r+1) prefix -= ss[i-2*r-1]; \n if (i >= r && prefix < mid) {\n if (kk < mid - prefix) {\n ok = false; \n break; \n }\n kk -= mid - prefix; \n if (i < n) ss[i] += mid - prefix; \n prefix = mid; \n }\n }\n if (ok) lo = mid; \n else hi = mid - 1; \n }\n return lo; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n n = len(stations)\n lo, hi = 0, sum(stations)+k\n while lo < hi: \n mid = lo + hi + 1 >> 1\n ok = True \n kk = k \n ss = stations.copy()\n prefix = 0 \n for i in range(n+r): \n if i < n: prefix += ss[i]\n if i >= 2*r+1: prefix -= ss[i-2*r-1]\n if i >= r and prefix < mid: \n if kk < mid - prefix: \n ok = False\n break \n kk -= mid - prefix \n if i < n: ss[i] += mid - prefix\n prefix = mid\n if ok: lo = mid\n else: hi = mid - 1\n return lo\n```\n**Complexity**\nTime `O(NlogN)`\nSpace `O(N)` | 3 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[C++/Python] Binary Search & Sliding Window & Greedy - Clear explanation | maximize-the-minimum-powered-city | 0 | 1 | # Intuition\n- We can see that:\n - If we **increase** the minimum power among cities, then we need **more** additional power stations (Given that we have up to `k` additional power stations).\n - If we **decrease** the minimum power among cities, then we need **less** additional power stations (Given that we have up to `k` additional power stations).\n- So we can **binary search** to find the maximum value of `minimum power among cities` as long as we can use up to `k` additional power stations.\n- We need to build a function `isGood(minPowerRequired, additionalStations = k)` to test if it\'s good if we set the minium power among cities are `minPowerRequired`?\n - We just iterate on each city, calculate its power, test if the power of all cities are at least `minPowerRequired` given that we have `additionalStations` additional power stations.\n - To calculate the power of each city fast, we keep window value to store sum of power stations of cities `[i-r...i+r]`, then just sliding window to calculate for all cities.\n - When calculate power of `ith` city, if it\'s not enough powers then we need some additional powers. \n - If `additionalStations` is not enough then `minPowerRequired` is invalid!\n - Else it\'s better to plant additional power station to `i+r`th city **(GREEDY)**, so it cover as much as cities as possible.\n\n# Complexity\n- Time complexity: `O(N * log(SUM_STATION + k))`, where `N <= 10^5` is the number of cities, `SUM_STATION <= 10^10` is sum of stations, `k <= 10^9` is the number of additional power stations.\n- Space complexity: `O(N)`\n\n# Code\n<iframe src="https://leetcode.com/playground/K2GRasqU/shared" frameBorder="0" width="100%" height="1000"></iframe> | 99 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[C++||Java||Python3] Binary search + sliding window, with comment | maximize-the-minimum-powered-city | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n\n# Intuition\n1. Notice "Maximize the Minimum", obviously binary searching on the value domain should be considered.\n2. When checking, traverse from $0$ to $n-1$ and count how many power stations are missing for each city.\n3. Obviously, if a city is found to lack a power station, it should be greedily placed in the rightmost city which can heat it.\n\n# Approach\n1. Binary search for result. Notice the maximum possible value will not exceed $k+\\sum_{i=0}^{n-1}stations[i]$, binary search in this range. Each time, check if $k$ is sufficient.\n2. Use a sliding window to maintain the number of power stations the current city has.\n3. Each time, city $i+r$ may be added, while city $i-r-1$ may be removed. \n\n**Additional, I found that the same Python code accepted in [LeetCode CN](https://leetcode.cn/problems/maximize-the-minimum-powered-city/submissions/393714497/), but TLE in [LeetCode US](https://leetcode.com/contest/biweekly-contest-95/submissions/detail/873396839/).** \n\n**Interesting.**\n\n# Complexity\n- Time complexity: $O(n \\log (k+\\sum_{i=0}^{n-1}stations[i]))$\n- Space complexity: $O(n)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n long long maxPower(vector<int>& stations, int r, int k) {\n int n = stations.size();\n long long left = 0;\n long long right = k + accumulate(stations.begin(), stations.end(), 0ll);\n // v is the stations after adding\n vector<long long> v(n);\n while (left <= right) {\n long long x = (left + right) / 2;\n for (int i = 0; i < n; ++i) v[i] = stations[i];\n long long use = 0;\n // s maintains the power of city i\n // at first, it record the sum of v[0,r)\n long long s = accumulate(stations.begin(), stations.begin() + r, 0ll);\n for (int i = 0; i < n; ++i) {\n // add to t if needed\n int t = min(n - 1, i + r);\n // update s\n // find a city should be added\n if (i + r < n) s += v[i + r];\n // find a city should be removed\n if (i - r > 0) s -= v[i - r - 1];\n // mising power stations\n long long diff = max(0ll, x - s);\n v[t] += diff;\n s += diff;\n use += diff;\n }\n if (use <= k) left = x + 1;\n else right = x - 1;\n }\n return right;\n }\n};\n```\n``` Java []\nclass Solution {\n public long maxPower(int[] stations, int r, int k) {\n int n = stations.length;\n long left = 0, right = k;\n for (int x: stations)\n right += x;\n // v is the stations after adding\n long []v = new long[n];\n while (left <= right) {\n long x = (left + right) / 2;\n for (int i = 0; i < n; ++i) \n v[i] = stations[i];\n // s means the power of city i\n // at first, it record the sum of v[0,r)\n long s = 0, use = 0;\n for (int i = 0; i < r; ++i) \n s += v[i];\n for (int i = 0; i < n; ++i) {\n // add to t if needed\n int t = Math.min(n - 1, i + r);\n // update s\n // find a city should be added\n if (i + r < n) s += v[i + r];\n // find a city should be removed\n if (i - r > 0) s -= v[i - r - 1];\n // mising power stations\n long diff = Math.max(0, x - s);\n v[t] += diff;\n s += diff;\n use += diff;\n }\n if (use <= k) left = x + 1;\n else right = x - 1;\n }\n return right;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n n = len(stations)\n left, right = 0, k + sum(stations)\n while left <= right:\n x = (left + right) // 2\n use = 0\n # v is the stations after adding\n v = stations.copy()\n # s means the power of city i\n # at first, it record the sum of v[0,r)\n s = sum(stations[0: r])\n for i in range(n):\n # add to t if needed\n t = n - 1 if n - 1 < i + r else i + r\n # update s\n # find a city should be added\n if i + r < n: s += v[i+r]\n # find a city should be removed\n if i - r > 0: s -= v[i-r-1]\n # mising power stations\n diff = x - s if x - s > 0 else 0 \n v[t] += diff\n s += diff\n use += diff\n \n if use <= k:\n left = x + 1\n else:\n right = x - 1\n return right\n``` | 16 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
Python - Binary Search - Video Solution | maximize-the-minimum-powered-city | 0 | 1 | I have explained the complete solution [here](https://youtu.be/E6aEq7V9TDk).\n\n# Intuition\nThis is a problem to maximize, so Binary Search is a candidate pattern.\nGiven an answer, we can reverse cross-check too if it is valid or not.\n\n# Logic\n**Min ans** can obviously be the min. of array\n\n**Max ans** can be `sum(stations) + K`\n\nSince, the power of a city is a range from `city - r` to `city + r`, we can keep a Sliding Window.\n\nFor handling, corner cases, so as not to exceed length of array, \nlet\'s add bunch of `0s` to both left & right.\n\n`stations = [0]*r + stations + [0]*r`\n\nInitially, our window will be sum of stations (`0` to `r-1`)\n\nWe\'ll start from stations `0` ( currently index `r` in array) and add `station[ind+r` to the window.\n\nWe\'ll see if there is a deficiency we\'ll try to use stations from our `available` stations and decrease the `available` accordingly.\n\nIt makes sense, to add the power to `ind+r` because, hence it will be available for the next `2r` cities. This is the most optimal.\n\nWe also have to keep track that `diff` was added to the `ind+r` city.\nSo, when this city goes out of range, we decrease it from `window`.\n\n**Time:** `O(N.log(sum(N))`\n**Space:** `O(N)`\n\nIf this was helpful, please Upvote, like the video and subscribe to the channel.\n\nCheers.\n\n```\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n lo = min(stations)\n hi = max(stations) * len(stations) + k\n \n # Adding bunch of (r+1) 0s to left, and (r) 0s to right for handling corner cases.\n stations = [0]*(r) + stations + [0]*r\n res = lo\n \n def check(med):\n available = k\n ind = r # ind of our first city\n \n window = sum(stations[:2*r]) # Sliding window will store power of stations for city\n # initially it will have values from 0th station to (r-1) stn\n \n\t\t\t# This will store, in which city we have added station because of deficiency. \n\t\t\t# Because we need to remove that val when that city is out of range.\n added = defaultdict(int) \n \n while ind < len(stations)-r:\n window += stations[ind + r]\n \n if window < med:\n diff = med-window\n if diff>available:\n return False\n window+=diff\n added[ind+r]=diff \n available-=diff\n\t\t\t\t\t\n window -= (stations[ind - r] + added[ind-r])\n ind+=1\n return True\n \n while lo<=hi: # Typical Binary Search\n m = (lo + hi )//2\n if check(m):\n res = m\n lo = m + 1\n else:\n hi = m-1\n return res | 7 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[Python 3] Work on the left bounary, binary search + line sweep | maximize-the-minimum-powered-city | 0 | 1 | If we can distribute k power stations to bring minimun power level to x, power level x - 1 is also achieveable. Intuitively, the problem can be solved by binary search of the maximum minimum power level.\n\nFirst we use a size 2 * r + 1 sliding window to find the current power level. Left and right bounds for binary search is the min(current power level) and max(current power level) + k.\n\nFor each target power level mid = (left + right + 1) // 2, we want to check whether mid can be realized. At each city, we can calculate the gap between the city\'s current power and mid, then, we start to place new stations to fill the gaps. At the stage, we sweep from 0 to n - 1, if a non-zero gap[i] encountered, we greedily place a new station such that **the left boundary of influence of the new station is at [i]** as a result, all cities in [i to i + 2 * r inclusively] are powered (gap reduced). Implementation-wise, we do not want to update the the city gaps [i to i + 2 * r inclusively], which will TLE, instead, we use a diffiential array to track the right bounary of influence of the new station, and use a cumulative vairable `c` to represent influences of the new stations. See function `check` below for details.\n\n# Code\n```\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n n = len(stations)\n pw = [0] * n\n pw[0] = sum(stations[0:r + 1])\n for i in range(1, n): # sliding window to obtain current power level\n pw[i] = pw[i - 1] \\\n - (stations[i - r - 1] if i - r - 1 >= 0 else 0) \\\n + (stations[i + r] if i + r < n else 0)\n \n def check(mid, k):\n gap = [max(0, mid - p) for p in pw]\n diff = [0] * (n + 1 + r * 2) # differential array for stations our of range\n c = 0\n for i in range(n):\n c += diff[i] # remove the stations out of range\n if gap[i] <= c:\n continue\n if gap[i] - c > k: # unachievable, return False\n return False\n else:\n x = gap[i] - c # number of stations to build where i is the left boundary of influence\n k -= x\n c += x # influence of the new stations\n diff[i + 1 + r * 2] -= x # track end of the influence\n return True\n \n mi, ma = min(pw), max(pw)\n le, ri = mi, ma + k\n while le < ri: # binary search\n mid = (le + ri + 1) // 2\n if check(mid, k):\n le = mid\n else:\n ri = mid - 1\n return le\n``` | 2 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
Difference Array + Binary Search | maximize-the-minimum-powered-city | 0 | 1 | \n# Code\n```\nclass Solution:\n # \u5DEE\u5206:[0, |0, 0, 0|, 0] -> \u533A\u95F4\u52A0k [0, k, 0, 0, -k] -> \u524D\u7F00\u548C[0, k, k, k, 0]\u4E3A\u53D8\u5316\u540E\u7684\u6570\u7EC4\n # \u521D\u59CB\u6570\u76EE [3, 7, 11, 9, 5]: s[i] = prefix[max(n, i + r + 1)] - prefix[min(0, i - r)]\n # \u5DEE\u5206\u6570\u7EC4: min_power, \u9700\u8981\u989D\u5916\u4FEE\u5EFA min_power - s[i], \u8D2A\u5FC3\u5EFA\u5728 min(i + r, n - 1) \u80FD\u6700\u5927\u5F71\u54CD, \u5F71\u54CD\u7684\u8303\u56F4\u662F(i, min(n-1, i + 2r)), \u6BCF\u4E00\u6B21\u9700\u8981\u989D\u5916\u4FEE\u5EFA\u90FD\u4F1A\u8BA9\u540E\u9762\u5F71\u54CD\u8303\u56F4\u5185\u7684\u6570\u7EC4\u90FD+delta, \u7528sum_diff\u7528\u6765\u8BB0\u5F55\u7D2F\u8BA1\u7684\u5DEE\u5206\u503C\u7528\u6765\u66F4\u65B0\u6570\u7EC4\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n prefix, n = [0], len(stations)\n for station in stations:\n prefix.append(prefix[-1] + station)\n \n # \u521D\u59CB\u6570\u7EC4\n for i in range(len(stations)):\n stations[i] = prefix[min(n, i + r + 1)] - prefix[max(0, i - r)]\n \n # check each answer min_power valid or not\n def check(min_power):\n sum_diff, extra = 0, 0\n diff = [0] * n\n for i, power in enumerate(stations):\n sum_diff += diff[i]\n cur_power = power + sum_diff\n d = min_power - cur_power \n if d > 0: # current need more d station\n extra += d # acc to the total extra\n if extra > k:\n return False\n sum_diff += d\n if i + 2 * r + 1 < n:\n diff[i + 2 * r + 1] -= d\n return True\n \n #\u4E8C\u5206\u7B54\u6848\n left, right = 0, prefix[n] + k + 1\n while left <= right:\n mid = left + (right - left) // 2\n if check(mid):\n left = mid + 1\n else:\n right = mid - 1\n return left - 1\n \n``` | 0 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
[Python3] Binary Search with Sliding Window to Determine Possibility | maximize-the-minimum-powered-city | 0 | 1 | ```python\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n """We know this is a binary search problem from the start, but the\n implementation has still evaded me for a quite a while.\n\n First, we need to obtain the current power level for each station. I\n tried to use a sliding window for this, but it was kind of complicated.\n Thus, I opted for a simpler prefix sum.\n\n Then, we do the binary search. The trick is to find a way to check\n whether the current power level can be reached given r and k.\n\n A simple case is when the lowest powered station requires much more\n power than k. We can immediately consider this case impossible.\n\n Otherwise, we need to go station by station that is currently lower\n than the desired power level. An implementation of sliding window and\n dynamically updated how much power is allowed to add to the current\n station thanks to the powers added in its previous neighbors wihtin the\n r range.\n\n The rest is formality for binary search.\n\n O(Nlog(sum of stations + k)), 4459 ms, faster than 49.77%\n """\n N = len(stations)\n prestations = list(accumulate(stations))\n powers = []\n for i in range(N):\n lo, hi = i - r - 1, min(i + r, N - 1)\n powers.append(prestations[hi] - (prestations[lo] if lo >= 0 else 0))\n \n min_power = min(powers)\n lo, hi = min_power, max(powers) + k + 1\n while lo < hi:\n mid = (lo + hi) // 2\n if mid - min_power > k:\n hi = mid\n else:\n added_power = deque()\n # total_added is the total power added so far. We use this to\n # check against k.\n # allowed_to_add is the power allowed to be added for the\n # current station. allowed_to_add is updated dynamically,\n # because when the current station falls outside the range, any\n # added power at the beginning of added_power deque must be\n # removed from allowed_to_add.\n total_added = allowed_to_add = 0\n for i, p in ((i, p) for i, p in enumerate(powers) if p < mid):\n while added_power and i - added_power[0][0] > 2 * r:\n # current station is outside the influence of the first\n # station in the dequa that gets additional power,\n # thus it cannot take the additional power from the\n # first station\n _, pp = added_power.popleft()\n allowed_to_add -= pp\n to_add = max(0, mid - p - allowed_to_add)\n total_added += to_add\n if total_added > k:\n break\n allowed_to_add += to_add\n added_power.append((i, to_add))\n else:\n lo = mid + 1\n continue\n hi = mid\n return lo - 1\n``` | 0 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
Binary search | Explanation | maximize-the-minimum-powered-city | 0 | 1 | # Intuition\n\nThere are 2 key points:\n1. We have a function `canAchieve` which determind if we can achieve **provided** minimum power by adding `k` stations. In other words we assume that we know a possible answer and try to check if it\'s true.\n2. We have a binary search from `min(stations)` to `sum(stations) + k`. `min(stations)` is a minimum possible answer if we cannot increase a power of minimum city. `sum(stations) + k` is a maximum possible answer if `r` >= `n`.\n\n`canAchieve` function logic:\n1. Go though all cities and calculate a power of `i` city.\n2. If the power is bigger or equals to the provided minimum power we do nothing.\n3. If the power is less then the provided minimum power we put needed count of stations to `i + r` city. Previous cities are meet minimum requiring power and more reasonable is covering as much next stations as we can. That\'s why we set all of them to `i + r` city.\n4. If we can make all cities have power more or equals to a provided minimum power we store the provided power untill we get a better answer.\n\n# Approach\n\n\n\n# Code\n```\nclass Solution:\n def maxPower(self, stations: List[int], r: int, k: int) -> int:\n left = min(stations)\n right = sum(stations) + k\n result = left\n while left <= right:\n m = left + (right - left) // 2\n if self.canAchieve(stations[:], r, k, m):\n left = m + 1\n result = m\n else:\n right = m - 1\n return result\n\n def canAchieve(self, stations: List[int], r: int, k: int, minV: int) -> bool:\n currentSum = sum(stations[:r])\n n = len(stations)\n for i in range(n):\n if r == 0:\n currentSum = stations[i]\n else:\n if i - r - 1 >= 0:\n currentSum -= stations[i - 1 - r]\n if i + r < n:\n currentSum += stations[i + r]\n if currentSum < minV:\n delta = minV - currentSum\n stations[min(n - 1, i + r)] += delta\n currentSum += delta\n k -= delta\n if k < 0:\n return False\n return True\n``` | 0 | You are given a **0-indexed** integer array `stations` of length `n`, where `stations[i]` represents the number of power stations in the `ith` city.
Each power station can provide power to every city in a fixed **range**. In other words, if the range is denoted by `r`, then a power station at city `i` can provide power to all cities `j` such that `|i - j| <= r` and `0 <= i, j <= n - 1`.
* Note that `|x|` denotes **absolute** value. For example, `|7 - 5| = 2` and `|3 - 10| = 7`.
The **power** of a city is the total number of power stations it is being provided power from.
The government has sanctioned building `k` more power stations, each of which can be built in any city, and have the same range as the pre-existing ones.
Given the two integers `r` and `k`, return _the **maximum possible minimum power** of a city, if the additional power stations are built optimally._
**Note** that you can build the `k` power stations in multiple cities.
**Example 1:**
**Input:** stations = \[1,2,4,5,0\], r = 1, k = 2
**Output:** 5
**Explanation:**
One of the optimal ways is to install both the power stations at city 1.
So stations will become \[1,4,4,5,0\].
- City 0 is provided by 1 + 4 = 5 power stations.
- City 1 is provided by 1 + 4 + 4 = 9 power stations.
- City 2 is provided by 4 + 4 + 5 = 13 power stations.
- City 3 is provided by 5 + 4 = 9 power stations.
- City 4 is provided by 5 + 0 = 5 power stations.
So the minimum power of a city is 5.
Since it is not possible to obtain a larger power, we return 5.
**Example 2:**
**Input:** stations = \[4,4,4,4\], r = 0, k = 3
**Output:** 4
**Explanation:**
It can be proved that we cannot make the minimum power of a city greater than 4.
**Constraints:**
* `n == stations.length`
* `1 <= n <= 105`
* `0 <= stations[i] <= 105`
* `0 <= r <= n - 1`
* `0 <= k <= 109` | null |
Easy Python Solution using filter() method🚀🚀 | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Approach:\nThe filter() method filters the given sequence with the help of a function that tests each element in the sequence to be true or not. \n\nThus using filter() the code has become more easier and effective\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n l1 = list(filter(lambda x: x>0, nums))\n l2 = list(filter(lambda x: x<0, nums))\n return max(len(l1),len(l2))\n``` | 2 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python || 2 diff method || 1 line code || simple code | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | \n# Code\n# bisect method\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n return max(bisect_left(nums,0), len(nums)-bisect_left(nums,1))\n```\n> # count approach\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n ne = 0 \n po = 0\n for ele in nums:\n if ele > 0:\n po += 1\n elif ele < 0:\n ne += 1\n return max(po,ne)\n\n \n \n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Extra simple solution in Python3/TypeScript | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a list of `nums`\n- and goal is to find a maximum between count of **negative** and **positive integers**\n\n# Approach\n1. initialize `neg` and `pos`\n2. iterate over `nums`\n3. increment `pos`, if `nums[i] > 0`\n4. increment `neg`, if `nums[i] < 0`\n5. return the **maximum** between `pos` and `neg` \n\n# Complexity\n- Time complexity: **O(n)**, to iterate over `nums`\n\n- Space complexity: **O(1)**, we don\'t allocate extra space.\n\n# Code in Python3\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n neg, pos = 0, 0\n\n for num in nums:\n if num > 0:\n pos += 1\n elif num < 0:\n neg += 1\n\n return max(neg, pos)\n```\n# Code in TypeScript\n```\nfunction maximumCount(nums: number[]): number {\n let neg = 0\n let pos = 0\n\n for (let i = 0; i < nums.length; i++) {\n if (nums[i] > 0) pos++\n else if (nums[i] < 0) neg++\n }\n\n return Math.max(neg, pos)\n};\n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python3| readable solution | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n a = []\n for i in nums:\n if i < 0:\n a.append(0)\n elif i > 0:\n a.append(1)\n return max(a.count(0),a.count(1))\n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Simple and Easy | 100% Faster Solution | C++ | Java | Python | maximum-count-of-positive-integer-and-negative-integer | 1 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Keeping two variables for storing count of negative `\nneg` and positive `\npos\n`integers in an array.\n2. Traversing array from 0 to n-1 `\nfor(auto i:nums)\n`\n - if element is less than 0 `i < 0`\n - increment `neg` counter\n - if element is greater than 0 `i > 0`\n - increment `pos` counter\n3. Return maximum of `pos` and `neg` as an answer.\n\n---\n# Point to Remember\n\n0 is neither negative nor positive so you have to write two `if` conditions instead of using `else` in `loop`.\n\n---\n\n\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n\n# Code\nC++\n```\nclass Solution {\npublic:\n int maximumCount(vector<int>& nums) {\n int neg=0,pos=0;\n for(auto i:nums)\n {\n if(i<0)neg++;\n if(i>0)pos++;\n }\n return pos > neg? pos : neg;\n }\n};\n```\n\nJava\n```\nclass Solution {\n public int maximumCount(int[] nums) {\n int neg=0,pos=0;\n for(int i:nums)\n {\n if(i<0)neg++;\n if(i>0)pos++;\n }\n return pos > neg ? pos : neg;\n }\n}\n```\nPython\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n neg=0\n pos=0\n for i in nums:\n if i>0:\n pos+=1\n if i<0:\n neg+=1\n\n return pos if pos > neg else neg\n```\n\n\n | 2 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
python ONE LINE solution!!! | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use the filter method to create a list of negative and a list of positive numbers\n2. Compare their length.\n3. Return max length\n# Complexity\n- Time complexity:$$O(2n)$$ \n<!-- Add your time complexity here, e.g. -->\n\n- Space complexity:$$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n return max(len(list(filter(lambda x: x<0, nums))), len(list(filter(lambda x: x>0, nums))))\n \n```\n# Please UPVOTE !!!! | 0 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
с использованием фильтра | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n l1 = list(filter(lambda x: x>0, nums))\n l2 = list(filter(lambda x: x<0, nums))\n return max(len(l1),len(l2))\n``` | 0 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python3 Simple solution || Beats 90+% ||💻🤖🧑💻 | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n pos=0\n neg=0\n for i in nums:\n if i <0 :\n neg +=1\n elif i>0:\n pos+=1\n return max(pos,neg)\n \n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python3 || Easy solution. | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Please upvote if you find the solution helpful guys!\n# Code:\n**Beats 92.46%**\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n neg_count=0\n pos_count = 0\n for i in nums:\n if i<0:\n neg_count += 1\n elif i>0:\n pos_count += 1\n return max(pos_count,neg_count) \n```\n | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python | Very easy counting solution | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Approach\nJust count positive and negative numbers (except zeros) in array and maximum of them \n\n# Complexity\n- Time complexity: $$O(N)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n pos, neg = 0, 0\n for num in nums:\n if num == 0:\n continue\n elif num < 0:\n neg += 1\n else: pos += 1\n return max(pos, neg)\n \n``` | 3 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
A solution that is better than 91% in speed | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n num_negative = len(list(filter(lambda x: x < 0, nums)))\n num_positive = len(list(filter(lambda x: x > 0, nums)))\n return max([num_negative, num_positive])\n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Python3 | maximum-count-of-positive-integer-and-negative-integer | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n c=0\n d=0\n for i in range(len(nums)):\n if nums[i]>0:\n c+=1\n elif nums[i]<0:\n d+=1\n return c if c>d else d\n``` | 1 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
[C++|Java|Python3] binary search | maximum-count-of-positive-integer-and-negative-integer | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/cd738c7122f758231c4f575936d09271343de490) for solutions of weekly 327. \n\n**Intuition**\nWe binary search for the number of negative numbers and positive numbers in the array. \n\n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int maximumCount(vector<int>& nums) {\n int neg = lower_bound(nums.begin(), nums.end(), 0) - nums.begin(), pos = nums.end() - upper_bound(nums.begin(), nums.end(), 0); \n return max(neg, pos); \n }\n};\n```\n**Java**\n```\nclass Solution {\n private static int bisect_left(int[] nums, int target) {\n int lo = 0, hi = nums.length; \n while (lo < hi) {\n int mid = lo + (hi - lo)/2; \n if (nums[mid] < target) lo = mid+1; \n else hi = mid; \n }\n return lo; \n }\n \n public int maximumCount(int[] nums) {\n int neg = bisect_left(nums, 0), pos = nums.length - bisect_left(nums, 1); \n return Math.max(neg, pos); \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def maximumCount(self, nums: List[int]) -> int:\n neg = bisect_left(nums, 0)\n pos = len(nums) - bisect_right(nums, 0)\n return max(neg, pos)\n```\n**Complexity**\nTime `O(logN)`\nSpace `O(1)` | 44 | Given an array `nums` sorted in **non-decreasing** order, return _the maximum between the number of positive integers and the number of negative integers._
* In other words, if the number of positive integers in `nums` is `pos` and the number of negative integers is `neg`, then return the maximum of `pos` and `neg`.
**Note** that `0` is neither positive nor negative.
**Example 1:**
**Input:** nums = \[-2,-1,-1,1,2,3\]
**Output:** 3
**Explanation:** There are 3 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 2:**
**Input:** nums = \[-3,-2,-1,0,0,1,2\]
**Output:** 3
**Explanation:** There are 2 positive integers and 3 negative integers. The maximum count among them is 3.
**Example 3:**
**Input:** nums = \[5,20,66,1314\]
**Output:** 4
**Explanation:** There are 4 positive integers and 0 negative integers. The maximum count among them is 4.
**Constraints:**
* `1 <= nums.length <= 2000`
* `-2000 <= nums[i] <= 2000`
* `nums` is sorted in a **non-decreasing order**.
**Follow up:** Can you solve the problem in `O(log(n))` time complexity? | null |
Easy-understanding solution! (Heap) | maximal-score-after-applying-k-operations | 0 | 1 | ```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n nums = [-n for n in nums]\n res = 0\n heap = heapq.heapify(nums)\n for _ in range(k):\n a = heapq.heappop(nums) * -1\n res += a\n heapq.heappush(nums, -math.ceil(a/3))\n return res\n``` | 2 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
[Python 3] MaxHeap | maximal-score-after-applying-k-operations | 0 | 1 | ```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n nums = [-i for i in nums]\n heapify(nums)\n \n res = 0\n for i in range(k):\n t = -heappop(nums)\n res += t\n heappush(nums, -ceil(t / 3))\n \n return res\n``` | 2 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
Python solution using Max Heap | maximal-score-after-applying-k-operations | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n \n heap=[-val for val in nums]\n\n heapify(heap)\n ans=0\n \n while k:\n mx=-heappop(heap)\n ans+=mx\n heappush(heap,-math.ceil(mx/3))\n k-=1\n return ans\n \n \n \n \n``` | 1 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
Python Solution using Priority Queue | maximal-score-after-applying-k-operations | 0 | 1 | ```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n score = 0\n pq = []\n for num in nums:\n heapq.heappush(pq, (-num, num))\n while k > 0:\n max_element = heapq.heappop(pq)[1]\n score += max_element\n updated_value = max_element // 3 + (max_element % 3 != 0)\n heapq.heappush(pq, (-updated_value, updated_value))\n k -= 1\n return score\n \n``` | 1 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
[Python] | Priority Queue | maximal-score-after-applying-k-operations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can solve this problem greedily, each time taking the max number from the array. However taking the max number from an array take 0(n) time and doing this k times makes the time complexity k * 0(n) time. As this approach requires taking the max each time we can use a priotity queue to optimise time complexity.\n\n# Code\n```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n \'\'\'\n #brute force TLE\n res = 0\n for i in range(k):\n m = max(nums)\n idx = nums.index(m)\n res += m\n nums.pop(idx)\n nums.append(ceil(m / 3))\n return res\n \'\'\'\n heap = []\n heapify(heap)\n for i in nums:\n heappush(heap, -1 * i)\n res = 0\n for i in range(k):\n max_num = heappop(heap) * -1\n res += max_num\n heappush(heap, ceil(max_num / 3) * -1)\n return res\n\n \n``` | 1 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
Python3 | Similar to 1962. Remove Stones to Minimize the Total | In-built Max Heap | maximal-score-after-applying-k-operations | 0 | 1 | This problem is similar to [1962. Remove Stones to Minimize the Total](https://leetcode.com/problems/remove-stones-to-minimize-the-total/)\n\nHere is the python3 solution using max heap.\n```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n heapq._heapify_max(nums)\n ans=0\n for _ in range(k):\n ans += nums[0]\n heapq._heapreplace_max(nums, (nums[0]+2)//3)\n return ans\n```\n\nIf you have any doubt, ask here in comment. | 1 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
Python - Heap - Video Solution | maximal-score-after-applying-k-operations | 0 | 1 | I have explained the whole solution [here](https://youtu.be/WxtI_i3JfaM).\n\n```\nclass Solution:\n def maxKelements(self, nums: List[int], k: int) -> int:\n res = 0\n h = [-v for v in nums]\n \n heapq.heapify(h)\n \n for i in range(k):\n x = -heapq.heappop(h)\n res += x\n x = math.ceil(x/3)\n heapq.heappush(h, -x)\n \n return res\n``` | 4 | You are given a **0-indexed** integer array `nums` and an integer `k`. You have a **starting score** of `0`.
In one **operation**:
1. choose an index `i` such that `0 <= i < nums.length`,
2. increase your **score** by `nums[i]`, and
3. replace `nums[i]` with `ceil(nums[i] / 3)`.
Return _the maximum possible **score** you can attain after applying **exactly**_ `k` _operations_.
The ceiling function `ceil(val)` is the least integer greater than or equal to `val`.
**Example 1:**
**Input:** nums = \[10,10,10,10,10\], k = 5
**Output:** 50
**Explanation:** Apply the operation to each array element exactly once. The final score is 10 + 10 + 10 + 10 + 10 = 50.
**Example 2:**
**Input:** nums = \[1,10,3,3,3\], k = 3
**Output:** 17
**Explanation:** You can do the following operations:
Operation 1: Select i = 1, so nums becomes \[1,**4**,3,3,3\]. Your score increases by 10.
Operation 2: Select i = 1, so nums becomes \[1,**2**,3,3,3\]. Your score increases by 4.
Operation 3: Select i = 2, so nums becomes \[1,1,**1**,3,3\]. Your score increases by 3.
The final score is 10 + 4 + 3 = 17.
**Constraints:**
* `1 <= nums.length, k <= 105`
* `1 <= nums[i] <= 109` | null |
✅ Python3 | Brute Force | O(26 * 26) | make-number-of-distinct-characters-equal | 0 | 1 | # Approach\n**Brute Force:**\n- iterate over all possible iterations (i.e., 2 `for` loops)\n- if both the letters exists (i.e., their count != 0)\n- Swap\n- Check for Validity\n- Restore\n\n# Complexity\n- Time complexity: $$O(26*26)$$\n\n# Code\n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n cnt1, cnt2 = [0 for i in range(26)], [0 for i in range(26)]\n for i in range(len(word1)):\n cnt1[ord(word1[i]) - ord(\'a\')] += 1\n for i in range(len(word2)):\n cnt2[ord(word2[i]) - ord(\'a\')] += 1\n for i in range(26):\n for j in range(26):\n if cnt1[i] != 0 and cnt2[j] != 0:\n # Swap\n cnt1[j] += 1\n cnt2[j] -= 1\n cnt1[i] -= 1\n cnt2[i] += 1\n # Check Validity\n if self.isValid(cnt1, cnt2):\n return True\n # Restore\n cnt1[j] -= 1\n cnt2[j] += 1\n cnt1[i] += 1\n cnt2[i] -= 1\n return False\n \n def isValid(self, c1, c2):\n d1, d2 = 0, 0\n for i in range(26):\n if c1[i] != 0:\n d1 += 1\n if c2[i] != 0:\n d2 += 1\n return d1 == d2\n``` | 1 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
[Python] Very interesting solution, take advantage of nested loops (115 ms) | make-number-of-distinct-characters-equal | 0 | 1 | We do not mess with `Counter` directly, we play with constant numbers here.\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe know swapping can have the following possible results:\n1. `word1[i] == word2[j]`\n2. `word1[i]` not in `word2`\n3. `word2[j]` not in `word1`\n4. `word1[i]` appears only once\n5. `word2[j]` appears only once\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use `collections.Counter` to make our lives easier:\n`Counter` for `word1` is `cnt1`\n`Counter` for `word2` is `cnt2`.\n\nThere\'s one interesting thing we need to pay attention to: we\'d better not use `del cnt1` stuff, b/c doing so in loops will be given: "RuntimeError: dictionary changed size during iteration". So, I recommend record their length before loops: `m, n = len(cnt1), len(cnt2)`.\n\nFor each possible results above:\n1. we continue here, b/c swapping the same letters does not contribute anything to (# of distinct letters);\n2. `cnt2` will have a new key, `word1[i]`. So `n+=1`;\n3. very similar as above "2", `m+=1`;\n4. deleting this letter will result in (# of keys in `cnt1` be decremented by 1): `m-=1`;\n5. very similar as above "2", `n-=1`;\n\nAfter these checks, we restore the values for `m` and `n`.\n\nAnother thing we need to pay attention to is: \nb/c we continue when `word1[i] == word2[j]`, so when we have two strings: `aaaaaaaaa` and `aaaaaa`, we should still `return True`. \n**Thus, we need to check if the (# of checked letters) is the same as `m*n` (as we have a nested loop, the total number of checked letters is exactly `m*n`). If less than that, we retun False; return True otherwise.**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`O(max(26*26, len(word1), len(word2)))`\nb/c the nested for loop costs `max(m, n) <= 26`, and `Counter`s cost `O(max(len(word1), len(word2)))`. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`O(26)`\nb/c `Counter`s can have at most 26 keys.\n\n# Code\n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n cnt1, cnt2 = Counter(word1), Counter(word2)\n m, n = len(cnt1), len(cnt2)\n cnt = 0\n for i in cnt1:\n for j in cnt2:\n if i == j: \n cnt += 1\n continue\n t1, t2 = m, n\n if cnt1[i] == 1: m -= 1\n if cnt2[j] == 1: n -= 1\n if i not in cnt2: n += 1\n if j not in cnt1: m += 1\n if m == n: return True\n m, n = t1, t2\n return False if cnt < m * n else True\n \n```\n\nHope you enjoy!\n\nIf you have any question, or suggestion, please comment \uD83D\uDC47\n | 3 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
✅ [Java/ C++/Python] Detailed Explanation, fully commented, Try all combs O(N+M) time | make-number-of-distinct-characters-equal | 1 | 1 | **Intution:**\nSince we can choose **any** indices from both strings to swap and at the end we just need both to have same number of distinct characters. The only thing that matters is which alphabet (\'a\',\'b\', \'c\',...) we choose from word1 and which alphabet (\'a\',\'b\', \'c\',...) we choose from word2 to swap. Since, only lowercase(26 alphabets) are there. We can try swapping all possible alphabet pairs between the two. \n\n**Method:**\n\n1. Create two maps to store frequency of characters of the strings.\n2. Try swapping all possible pairs of alphabets between word1 and word2.\n\n\n\tHow do we try swapping all possible pairs of alphabets between word1 and word2?\n\t\t2.1 Create two for loops iterating c1: \'a\' to \'z\', c2: \'a\' to \'z\'\n\t\t2.2 When char c1 is in word1 and char c2 is in word2\n\t\t2.3 Remove c1 and put c2 in word1\'s map\n\t\t2.4 Remove c2 and put c1 in word2\'s map\n\t\t \n3. Now check the sizes of maps. If the maps\' sizes are same means both words now have equal distinct characters. So, return true \n4. If map sizes are not same then reset the maps back.\n\n\tHow do we reset the maps?\n\t\t4.1 Remove c2 and put back c1 in word1\'s map (opposite of 2.3)\n\t\t4.2 Remove c1 and put back c2 in word2\'s map (opposite of 2.4)\n\n<br>\n\nSince we have are doing frequent insertion and removal from map. A helper function has been made to make the code simpler and concise. \n\n\n```\nvoid insertAndRemove(unordered_map<char,int>&mp, char toInsert, char toRemove){\n```\nIt takes 3 arguments. First is the map (unordered_map, HashMap, dictionary) which stores the char frequency of the word . Second is the character to insert and Third is the character to remove.\n\n**IMP to Note:**\nWhenever a character is removed from word i.e. when we substract map value by 1. In that case, if map value reaches 0 then we have to remove that key too from map\n```\nmp[c]--; // After we have done this\nif(mp[c]==0) mp.erase(c); // Need to do this too\n```\n\n<br>\n\n**C++:**\n\n```\nclass Solution {\npublic:\n \n void insertAndRemove(unordered_map<char,int>&mp, char toInsert, char toRemove){ // made this helper fxn for easy insert/ removal from map\n mp[toInsert]++; // increment freq for char to be inserted\n mp[toRemove]--; // decrement freq for char to be removed\n if(mp[toRemove]==0) mp.erase(toRemove); // if freq of that char reaches zero, then remove the key from map\n }\n\t\n\t// Remember to pass map as address in C++ " & mp "\n \n bool isItPossible(string word1, string word2) {\n unordered_map<char,int> mp1, mp2;\n \n for(char w1: word1) mp1[w1]++; // store freq of chars in word1 in mp1\n for(char w2: word2) mp2[w2]++; // store freq of chars in word2 in mp2\n\n for(char c1=\'a\'; c1<=\'z\'; c1++){\n for(char c2=\'a\'; c2<=\'z\'; c2++){\n if(mp1.count(c1)==0 || mp2.count(c2)==0) continue; // if any of the char is not present then skip\n\t\t\t\t\n insertAndRemove(mp1, c2, c1); // insert c2 to word1 and remove c1 from word1\n insertAndRemove(mp2, c1, c2); // insert c1 to word2 and remove c2 from word2\n \n if(mp1.size()==mp2.size()) return true; // if size of both maps are equal then possible return true\n\t\t\t\t\n // reset back the maps\n insertAndRemove(mp1, c1, c2); // insert c1 back to word1 and remove c2 from word1 \n insertAndRemove(mp2, c2, c1); // insert c2 back to word2 and remove c1 from word2\n \n }\n }\n \n return false;\n }\n};\n```\n\n\n**Java:**\n\n```\nclass Solution {\n \n public void insertAndRemove(Map<Character, Integer> mp, char toInsert, char toRemove){ // made this helper fxn for easy removal from hashmap\n mp.put(toInsert, mp.getOrDefault(toInsert, 0) + 1); // increment freq for char to be inserted\n mp.put(toRemove, mp.getOrDefault(toRemove, 0) - 1); // decrement freq for char to be removed\n if(mp.get(toRemove)==0) mp.remove(toRemove); // if freq of that char reaches zero, then remove the key from hashmap\n\n }\n \n public boolean isItPossible(String word1, String word2) {\n Map<Character, Integer> mp1 = new HashMap<>();\n Map<Character, Integer> mp2 = new HashMap<>();\n \n for (char w1: word1.toCharArray()) { // store freq of chars in word1 in mp1\n mp1.put(w1, mp1.getOrDefault(w1, 0) + 1);\n }\n for (char w2: word2.toCharArray()) { // store freq of chars in word2 in mp2\n mp2.put(w2, mp2.getOrDefault(w2, 0) + 1);\n }\n\n \n for(char c1=\'a\'; c1<=\'z\'; c1++){\n for(char c2=\'a\'; c2<=\'z\'; c2++){\n\n if(!mp1.containsKey(c1) || !mp2.containsKey(c2)) continue; // if any of the char is not present then skip\n\t\t\t\t\n insertAndRemove(mp1, c2, c1); // insert c2 to word1 and remove c1 from word1\n insertAndRemove(mp2, c1, c2); // insert c1 to word2 and remove c2 from word2\n \n if(mp1.size()==mp2.size()) return true; // if size of both maps are equal then possible return true\n\t\t\t\t\n // reset back the maps\n insertAndRemove(mp1, c1, c2); // insert c1 back to word1 and remove c2 from word1 \n insertAndRemove(mp2, c2, c1); // insert c2 back to word2 and remove c1 from word2\n }\n }\n \n return false;\n }\n}\n```\n\n\n**Python:**\n```\nclass Solution:\n \n def insertAndRemove(self, mp, toInsert, toRemove): \n mp[toInsert]+=1\n mp[toRemove]-=1\n \n if(mp[toRemove]==0):\n del mp[toRemove] # if freq of that char reaches zero, then remove the key from dict\n \n \n def isItPossible(self, word1: str, word2: str) -> bool:\n \n mp1, mp2 = Counter(word1), Counter(word2) # Get freq of chars using Counter\n\t\n """\n # If you are not familiar with Counters, you can simply do this:\n mp1=defaultdict(int)\n mp2=defaultdict(int)\n\n for w1 in word1:\n mp1[w1]+=1; #store freq of chars in word1 in mp1\n\n for w2 in word2:\n mp2[w2]+=1; #store freq of chars in word2 in mp2\n """\n\t\t\n for c1 in string.ascii_lowercase: # this for loop iterates through c1=\'a\' to c1=\'z\'\n for c2 in string.ascii_lowercase: # this for loop iterates through c2=\'a\' to c2=\'z\'\n \n if c1 not in mp1 or c2 not in mp2: # if any of the char is not present then skip\n continue\n\n self.insertAndRemove(mp1, c2, c1); # insert c2 to word1 and remove c1 from word1\n self.insertAndRemove(mp2, c1, c2); # insert c1 to word2 and remove c2 from word2\n \n if len(mp1)== len(mp2): # if size of both dicts are equal then possible return true\n return True\n\t\t\t\t\n # reset back the maps\n self.insertAndRemove(mp1, c1, c2); # insert c1 back to word1 and remove c2 from word1 \n self.insertAndRemove(mp2, c2, c1); # insert c2 back to word2 and remove c1 from word2 \n return False\n```\n\n**Complexity Analysis:**\nTime: O(N+M+26\\*26) i.e. O(N+M) : where N is the size of word1 and M is the size of word2 . We iterated both strings once, and a fixed 26\\*26 for loop (This 26*26 is constant, doesn\'t depend on input variables i.e. string sizes N or M)\nSpace: O(26) i.e O(1) : Since word1 and word2 consist of only lowercase English letters, so both map can have 26 elements only at max\n\n**Please upvote if you liked it.** | 109 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
[C++|Java|Python3] freq table | make-number-of-distinct-characters-equal | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/cd738c7122f758231c4f575936d09271343de490) for solutions of weekly 327. \n\n**Intuition**\nWe attempt each character pair (`a`, `a`), (`a`, `b`), ..., (`z`, `z`) and see if any swap can result in equal number of unique characters. \n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n bool isItPossible(string word1, string word2) {\n unordered_map<int, int> freq1, freq2; \n for (auto& ch : word1) ++freq1[ch]; \n for (auto& ch : word2) ++freq2[ch]; \n int sz1 = freq1.size(), sz2 = freq2.size(); \n for (char c1 = \'a\'; c1 <= \'z\'; ++c1) \n for (char c2 = \'a\'; c2 <= \'z\'; ++c2) \n if (freq1[c1] && freq2[c2]) \n if (c1 == c2) {\n if (sz1 == sz2) return true; \n } else {\n int cnt1 = sz1, cnt2 = sz2; \n if (freq1[c1] == 1) --cnt1; \n if (freq1[c2] == 0) ++cnt1; \n if (freq2[c1] == 0) ++cnt2; \n if (freq2[c2] == 1) --cnt2; \n if (cnt1 == cnt2) return true; \n }\n return false; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public boolean isItPossible(String word1, String word2) {\n HashMap<Character, Integer> freq1 = new HashMap(), freq2 = new HashMap(); \n for (var ch : word1.toCharArray()) freq1.merge(ch, 1, Integer::sum); \n for (var ch : word2.toCharArray()) freq2.merge(ch, 1, Integer::sum); \n int sz1 = freq1.size(), sz2 = freq2.size(); \n for (char c1 = \'a\'; c1 <= \'z\'; ++c1) \n for (char c2 = \'a\'; c2 <= \'z\'; ++c2) \n if (freq1.getOrDefault(c1, 0) > 0 && freq2.getOrDefault(c2, 0) > 0) \n if (c1 == c2) {\n if (sz1 == sz2) return true; \n } else {\n int cnt1 = sz1, cnt2 = sz2; \n if (freq1.getOrDefault(c1, 0) == 1) --cnt1; \n if (freq1.getOrDefault(c2, 0) == 0) ++cnt1; \n if (freq2.getOrDefault(c1, 0) == 0) ++cnt2; \n if (freq2.getOrDefault(c2, 0) == 1) --cnt2; \n if (cnt1 == cnt2) return true; \n }\n return false; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n freq1 = Counter(word1)\n freq2 = Counter(word2)\n sz1, sz2 = len(freq1), len(freq2)\n for c1 in ascii_lowercase: \n for c2 in ascii_lowercase: \n if freq1[c1] and freq2[c2]: \n if c1 == c2: \n if sz1 == sz2: return True \n else: \n cnt1, cnt2 = sz1, sz2 \n if freq1[c1] == 1: cnt1 -= 1\n if freq1[c2] == 0: cnt1 += 1\n if freq2[c1] == 0: cnt2 += 1\n if freq2[c2] == 1: cnt2 -= 1\n if cnt1 == cnt2: return True \n return False \n```\n**Complexity**\nTime `O(M+N)`\nSpace `O(1)` | 16 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
Python, using set operation, beats 100% time | make-number-of-distinct-characters-equal | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nI try to discuss how the number of character changes after the operation.\nThe time beats 100%, but it take me about an hour to cover all the cases.... So my ranking in the contest is bad :(\n\nThis might be not that efficient to cover all the cases, advices are welcome!\n\nLet x be the final equivalent number:\n#### Case 1: len(big) = len(small)\nThe only way to be `True` is that (x, x) -> (x-1+1, x+1-1)\n\n#### Case 2: len(big) - len(small) = 1\nType 2-1: (x+1, x) -> (x, x), means the bigger set decrease one element\nType 2-2: (x, x-1) -> (x, x), means the smaller set increase one element\n\n\n#### Case 3: len(big) - len(small) = 2\nType 3-1: (x+1, x-1) -> (x, x)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n \n count1 = collections.Counter(word1)\n count2 = collections.Counter(word2)\n\n word1 = set(word1)\n word2 = set(word2)\n d1 = len(word1)\n d2 = len(word2)\n \n \n if d1 == d2:\n \n a_diff_one = set()\n b_diff_one = set()\n a_diff_b = word1.difference(word2)\n b_diff_a = word2.difference(word1)\n \n \n for ch in list(a_diff_b):\n if count1[ch] == 1:\n a_diff_one.add(ch)\n \n for ch in list(b_diff_a):\n if count2[ch] == 1:\n b_diff_one.add(ch)\n \n if a_diff_one and b_diff_one:\n \n return True\n elif not a_diff_one and not b_diff_one:\n return True\n else:\n return False\n \n \n \n if abs(d1 - d2) > 2:\n return False\n \n intersec = word1.intersection(word2)\n \n if d1 > d2:\n big, small = word1, word2\n bigCount, smallCount = count1, count2\n else:\n big, small = word2, word1\n bigCount, smallCount = count2, count1\n \n diff = big.difference(small)\n \n big_intersecOnlyOne = set()\n big_intersecBigger = set()\n small_intersecBigger = set()\n small_intersecOnlyOne = set()\n big_diffOnlyOne = set()\n big_diffBigger = set()\n \n for ch in list(intersec):\n if smallCount[ch] > 1:\n small_intersecBigger.add(ch)\n elif smallCount[ch] == 1:\n small_intersecOnlyOne.add(ch)\n\n \n for ch in list(diff):\n if bigCount[ch] > 1:\n big_diffBigger.add(ch)\n elif bigCount[ch] == 1:\n big_diffOnlyOne.add(ch)\n \n\n if abs(d1 - d2) == 1:\n\n #type 1\n for ch in list(intersec):\n if bigCount[ch] == 1:\n big_intersecOnlyOne.add(ch)\n if big_intersecOnlyOne and small_intersecBigger and len(big_intersecOnlyOne.difference(small_intersecBigger)) != 0:\n \n return True\n if small_intersecOnlyOne and big_diffOnlyOne and len(big_diffOnlyOne.difference(small_intersecOnlyOne)) != 0:\n return True\n \n #type 2\n if big_diffBigger and small_intersecBigger and len(big_diffBigger.difference(small_intersecBigger)) != 0:\n return True\n \n\n\n \n elif abs(d1 - d2) == 2:\n \n if big_diffOnlyOne and small_intersecBigger and len(big_diffOnlyOne.difference(small_intersecBigger)) != 0:\n return True\n \n \n \n return False\n \n``` | 6 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
Python3 solution | make-number-of-distinct-characters-equal | 0 | 1 | # Code\n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n temp1, temp2 = [0] * 26, [0] * 26\n for i in range(len(word1)):\n temp1[ord(word1[i]) - ord(\'a\')] += 1\n for i in range(len(word2)):\n temp2[ord(word2[i]) - ord(\'a\')] += 1\n\n for i in range(ord(\'a\'), ord(\'z\')+1):\n for j in range(ord(\'a\'), ord(\'z\')+1):\n if temp1[i - ord(\'a\')] <= 0 or temp2[j - ord(\'a\')] <= 0:\n continue\n temp1[i - ord(\'a\')], temp2[j - ord(\'a\')] = temp1[i - ord(\'a\')]-1, temp2[j - ord(\'a\')]-1\n temp2[i - ord(\'a\')], temp1[j - ord(\'a\')] = temp2[i - ord(\'a\')]+1, temp1[j - ord(\'a\')]+1\n a, b = 0, 0\n for it in temp1:\n if it > 0:\n a += 1\n for it in temp2:\n if it > 0:\n b += 1\n if a == b:\n return True\n temp1[i - ord(\'a\')], temp2[j - ord(\'a\')] = temp1[i - ord(\'a\')]+1, temp2[j - ord(\'a\')]+1\n temp1[j - ord(\'a\')], temp2[i - ord(\'a\')] = temp1[j - ord(\'a\')]-1, temp2[i - ord(\'a\')]-1\n return False\n``` | 1 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
python3 Solution | make-number-of-distinct-characters-equal | 0 | 1 | \n```\nclass Solution:\n def isItPossible(self, word1: str, word2: str) -> bool:\n c1=collections.Counter(word1)\n c2=collections.Counter(word2)\n c1k=list(c1.keys())\n c2k=list(c2.keys())\n for x in c1k:\n for y in c2k:\n c1[y]+=1\n c1[x]-=1\n c2[x]+=1\n c2[y]-=1\n \n if c1[x]==0:\n del c1[x]\n \n if c2[y]==0:\n del c2[y]\n \n if len(c1)==len(c2):\n return True\n c2[y]+=1\n c2[x]-=1\n c1[x]+=1\n c1[y]-=1\n if c2[x]==0:\n del c2[x]\n \n if c1[y]==0:\n del c1[y]\n \n return False \n``` | 2 | You are given two **0-indexed** strings `word1` and `word2`.
A **move** consists of choosing two indices `i` and `j` such that `0 <= i < word1.length` and `0 <= j < word2.length` and swapping `word1[i]` with `word2[j]`.
Return `true` _if it is possible to get the number of distinct characters in_ `word1` _and_ `word2` _to be equal with **exactly one** move._ Return `false` _otherwise_.
**Example 1:**
**Input:** word1 = "ac ", word2 = "b "
**Output:** false
**Explanation:** Any pair of swaps would yield two distinct characters in the first string, and one in the second string.
**Example 2:**
**Input:** word1 = "abcc ", word2 = "aab "
**Output:** true
**Explanation:** We swap index 2 of the first string with index 0 of the second string. The resulting strings are word1 = "abac " and word2 = "cab ", which both have 3 distinct characters.
**Example 3:**
**Input:** word1 = "abcde ", word2 = "fghij "
**Output:** true
**Explanation:** Both resulting strings will have 5 distinct characters, regardless of which indices we swap.
**Constraints:**
* `1 <= word1.length, word2.length <= 105`
* `word1` and `word2` consist of only lowercase English letters. | null |
[Python3] Heap-Based Simulation | time-to-cross-a-bridge | 0 | 1 | Credit to @Yawn_Sean for this incredible solution (for self-learning purpose).\n\n# Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n ans = 0\n left = [[-t[0]-t[2], -i] for i, t in enumerate(time)]\n right = []\n save = []\n heapify(left)\n cnt = note = tmstamp = 0\n while cnt < n:\n if len(left) == len(right) == 0 and save[0][0] > tmstamp:\n tmstamp = save[0][0]\n while save and save[0][0] <= tmstamp:\n t, eff, idx, direction = heappop(save)\n if direction == 1:\n heappush(left, [eff, idx])\n else:\n heappush(right, [eff, idx])\n flag = True\n if note == n:\n while len(right) == 0:\n t, eff, idx, direction = heappop(save)\n tmstamp = t\n if direction == 0: heappush(right, [eff, idx])\n elif len(right) == 0: flag = False\n cnt += flag\n if flag:\n eff, idx = heappop(right)\n tmstamp += time[-idx][2]\n heappush(save, [tmstamp + time[-idx][3], eff, idx, 1])\n else:\n eff, idx = heappop(left)\n tmstamp += time[-idx][0]\n heappush(save, [tmstamp + time[-idx][1], eff, idx, 0])\n note += 1\n return tmstamp\n``` | 1 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Simulation with 3 queues (bridge left/right side and events queue) | time-to-cross-a-bridge | 0 | 1 | # Intuition/Ideas\nSimulate with 3 queues:\n- Time-series queue (based on timestamp)\n- Bridge left and right side waiting queue (based on their efficiency)\n\nDefine 4 events\n- waitL: complete putNew and join bridge left side queue\n- waitR: complete pickOld and join bridge right side queue\n- reachL: complete rightToLeft and start putNew\n- reachR: complete leftToRight and start pick old\n\nProcess each event accordingly, needs to be careful that when processing the time series, we need to process all the events happened at the same timestamp at once.\n\n#### Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n priority = [(time[i][0] + time[i][2], i) for i in range(k)]\n priority.sort()\n efficiency = [0] * k\n for i in range(k):\n efficiency[priority[i][1]] = -i\n \n left_queue, right_queue = [], []\n for i in range(k):\n heappush(left_queue, (efficiency[i], i))\n \n # Events: "waitL, waitR, reachL, reachR"\n time_series = []\n collected_box = [0, 0] # pending_box, total_box counts\n occupied = False\n timing = 0\n \n def process_bridge(timing):\n occupied = True\n if right_queue:\n _, worker = heappop(right_queue)\n heappush(time_series, (timing + time[worker][2], 2, worker))\n elif left_queue and collected_box[0] < n:\n collected_box[0] += 1\n _, worker = heappop(left_queue)\n heappush(time_series, (timing + time[worker][0], 3, worker))\n else:\n occupied = False\n return occupied\n \n def process_time_series(timing, events, worker, occupied):\n # print(timing, "waitL, waitR, reachL, reachR".split(\', \')[events], worker)\n if events == 0:\n heappush(left_queue, (efficiency[worker], worker))\n elif events == 1:\n heappush(right_queue, (efficiency[worker], worker))\n elif events == 2:\n collected_box[1] += 1\n if collected_box[1] == n:\n return True, occupied\n heappush(time_series, (timing + time[worker][3], 0, worker))\n else:\n heappush(time_series, (timing + time[worker][1], 1, worker))\n if events >= 2:\n occupied = process_bridge(timing)\n return False, occupied\n \n while True:\n if not occupied:\n occupied = process_bridge(timing)\n\n if time_series:\n timing, events, worker = heappop(time_series)\n complete, occupied = process_time_series(timing, events, worker, occupied)\n if complete:\n return timing\n while time_series:\n ctiming, events, worker = heappop(time_series)\n if ctiming == timing:\n complete, occupied = process_time_series(timing, events, worker, occupied)\n if complete:\n return timing\n else:\n heappush(time_series, (ctiming, events, worker))\n break\n \n return -1\n \n \n \n``` | 4 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[C++|Java|Python3] simulation | time-to-cross-a-bridge | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/cd738c7122f758231c4f575936d09271343de490) for solutions of weekly 327. \n\n**Intuition**\nHere, we maintain 4 prioirty queues. \n1) `l` ready to join the queue `ll` once the time allows\n2) `ll` ready to cross the bridge from left to right \n3) `r` ready to join the queue `rr` once the time allows \n4) `rr` ready to cross the bridge from right to left \n\n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int findCrossingTime(int n, int k, vector<vector<int>>& time) {\n int ans = 0, free = 0; \n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> l, r; \n priority_queue<pair<int, int>> ll, rr; \n for (int i = 0; i < time.size(); ++i) \n ll.emplace(time[i][0]+time[i][2], i); \n while (n || r.size() || rr.size()) {\n if (rr.empty() && (r.empty() || r.top().first>free) && (!n || ll.empty() && (l.empty() || l.top().first>free))) {\n int cand = INT_MAX; \n if (n && l.size()) cand = min(cand, l.top().first); \n if (r.size()) cand = min(cand, r.top().first); \n free = cand; \n }\n while (l.size() && l.top().first <= free) {\n auto [_, i] = l.top(); l.pop(); \n ll.emplace(time[i][0]+time[i][2], i); \n }\n while (r.size() && r.top().first <= free) {\n auto [_, i] = r.top(); r.pop(); \n rr.emplace(time[i][0]+time[i][2], i); \n }\n if (rr.size()) {\n auto [_, i] = rr.top(); rr.pop(); \n free += time[i][2]; \n if (n) l.emplace(free+time[i][3], i); \n else ans = max(ans, free); \n } else {\n auto [_, i] = ll.top(); ll.pop();\n free += time[i][0]; \n r.emplace(free+time[i][1], i); \n --n; \n }\n }\n return ans; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int findCrossingTime(int n, int k, int[][] time) {\n int ans = 0, free = 0; \n PriorityQueue<int[]> l = new PriorityQueue<>((a, b)->(a[0]-b[0])); \n PriorityQueue<int[]> r = new PriorityQueue<>((a, b)->(a[0]-b[0])); \n PriorityQueue<int[]> ll = new PriorityQueue<>((a, b)->(a[0] != b[0] ? b[0]-a[0] : b[1]-a[1]));\n PriorityQueue<int[]> rr = new PriorityQueue<>((a, b)->(a[0] != b[0] ? b[0]-a[0] : b[1]-a[1])); \n for (int i = 0; i < time.length; ++i) \n ll.add(new int[]{time[i][0]+time[i][2], i}); \n while (n > 0 || r.size() > 0 || rr.size() > 0) {\n if (rr.isEmpty() && (r.isEmpty() || r.peek()[0] > free) && (n == 0 || ll.isEmpty() && (l.isEmpty() || l.peek()[0] > free))) {\n int cand = Integer.MAX_VALUE; \n if (n > 0 && l.size() > 0) cand = Math.min(cand, l.peek()[0]); \n if (r.size() > 0) cand = Math.min(cand, r.peek()[0]); \n free = cand; \n }\n while (l.size() > 0 && l.peek()[0] <= free) {\n int i = l.poll()[1]; \n ll.add(new int[] {time[i][0] + time[i][2], i}); \n }\n while (r.size() > 0 && r.peek()[0] <= free) {\n int i = r.poll()[1]; \n rr.add(new int[] {time[i][0] + time[i][2], i}); \n }\n if (rr.size() > 0) {\n int i = rr.poll()[1]; \n free += time[i][2]; \n if (n > 0) l.add(new int[] {free+time[i][3], i}); \n else ans = Math.max(ans, free); \n } else {\n int i = ll.poll()[1]; \n free += time[i][0]; \n r.add(new int[] {free+time[i][1], i}); \n --n; \n }\n }\n return ans; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n ans = free = 0 \n l, ll = [], []\n r, rr = [], []\n for i, (x, _, y, _) in enumerate(time): heappush(ll, (-x-y, -i))\n while n or r or rr: \n if not rr and (not r or r[0][0] > free) and (not n or not ll and (not l or l[0][0] > free)): \n cand = inf \n if n and l: cand = min(cand, l[0][0])\n if r: cand = min(cand, r[0][0])\n free = cand\n \n while r and r[0][0] <= free: \n _, i = heappop(r)\n heappush(rr, (-time[i][0] - time[i][2], -i))\n\n while l and l[0][0] <= free: \n _, i = heappop(l)\n heappush(ll, (-time[i][0] - time[i][2], -i))\n \n if rr: \n _, i = heappop(rr)\n free += time[-i][2]\n if n: heappush(l, (free + time[-i][3], -i))\n else: ans = max(ans, free)\n else: \n _, i = heappop(ll)\n free += time[-i][0]\n heappush(r, (free + time[-i][1], -i))\n n -= 1\n return ans \n``` | 22 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[Python 3] Priority Queue (Heap) with Thought Process and Full Explanation | time-to-cross-a-bridge | 0 | 1 | This is a really hard and interesting problem, which took me many hours to solve. I could only get the final code (with all the conditions) after multiple attemps. The hardest part is to get all the right conditions (other posted solutions do not seem to give explanations for their conditions).\n\nMy first solution is easier to come up with and has less conditions, but it gives TLE. I will present it first, then my final accepted solution.\n\n# TLE Solution\n\n**Variables:**\n+ *timing*: keep track of the progress.\n+ *left*: heap to store info of workers on the left of the bridge\n+ *right*: heap to store info of workers on the right of the bridge\n\nInfo of each worker in *left* and *right* is the tuple (availableTime,-efficiency,-index), where *availableTime* is the time instance when the workers are ready to cross the bridge. *availableTime* is placed first so that heap will choose workers by the time workers are ready to cross the bridge before considering their efficiency and indices. For example, when the current time instance *timing* = 5, there are 2 workers on the right of the bridge: worker 0 is ready to cross at time instance 6 and worker 1 is ready at 5, then worker 1 will be chosen to cross the bridge, i.e. *availableTime* should be considered before efficiency and indices.\n\nThe variables are initialized as follows (which is straightforward):\n```\nleft,right = [],[] # (availableTime,-efficiency,-index)\nfor i in range(k):\n heapq.heappush(left,(0,-time[i][0]-time[i][2],-i))\ntiming = 0\n```\n**Approach**\nObviously, we need a variable (*timing*) to keep track of time progress.\nThere are 2 main processes for the workers (which should occur in the order listed below): \n+ crossing the bridge from left to right (when there are workers on the left, i.e. *left* is not null; and there are boxes in the old warehouse, i.e. *n>0*; and there is no woker waiting on the right, i.e. there is no worker on the right (*right* is null) or the time instance the workers on the right ready to cross the bridge is greater than the current time instance (*timing<right[0][0])*), with the secondary process of picking up boxes from the old warehouse. This process is reflected by the code below:\n```\nwhile left and n>0 and (not right or timing<right[0][0]):\n# all the workers with availableTime<=timing are ready to cross \n# the bridge and should be chosen by their efficiency, thus \n# we need to update their availableTime to the current time \n# instance (timing) so that the heap will work correctly \n# by the next while loop.\n while left and left[0][0]<timing:\n _,effi,i = heapq.heappop(left)\n heapq.heappush(left,(timing,effi,i))\n avail,effi,i = heapq.heappop(left)\n# we will need max(avail,timing) to update timing because, \n# for example, the current time instance timing = 10 (note that, \n# timing will only record the time instances workers finishing \n# crossing bridge) and there is only one worker 0 but worker 0 \n# is ready to cross the bridge from left to right at 11. \n# timing will be updated to the time instance workers finish \n# crossing bridge from left to right\n timing = max(avail,timing)+time[-i][0]\n# push the workers to right with availableTime to cross bridge \n# from right to left after picking up boxes\n heapq.heappush(right,(timing+time[-i][1],effi,i))\n n -= 1\n```\n+ crossing the bridge from right to left (when there are workers on the right, i.e. *right* is not null; and the workers on the right are waiting (*timing>=right[0][0]*) or there is no box left in the old warehouse (*n==0*) or there is no worker on the left (*left* is null)), with the secondary process of putting boxes in the new warehouse. This process is reflected by the code below:\n```\nwhile right and (timing>=right[0][0] or n==0 or not left):\n# similar to the previous process, we need to \n# update their availableTime.\n while right and right[0][0]<timing:\n _,effi,i = heapq.heappop(right)\n heapq.heappush(right,(timing,effi,i))\n avail,effi,i = heapq.heappop(right)\n# timing will be updated to the time instance workers finish \n# crossing bridge from right to left, using max(avail,timing)\n# similar to the previous process\n timing = max(avail,timing)+time[-i][2]\n# push the workers to left with availableTime to cross bridge \n# from left after putting boxes\n heapq.heappush(left,(timing+time[-i][3],effi,i))\n```\n*timing* will record the time instances workers finishing crossing bridge (left to right as well as right to left). It would record the instance of time at which the last worker reaches the left bank of the river after all n boxes have been taken from the old warehouse, thus we return *timing*.\n\n# TLE Python 3 Code\n```\nclass Solution:\n def findCrossingTime(self, n, k, time):\n left,right = [],[] # (availableTime,-efficiency,-index)\n for i in range(k):\n heapq.heappush(left,(0,-time[i][0]-time[i][2],-i))\n timing = 0\n while n>0:\n while left and n>0 and (not right or timing<right[0][0]):\n while left and left[0][0]<timing:\n _,effi,i = heapq.heappop(left)\n heapq.heappush(left,(timing,effi,i))\n avail,effi,i = heapq.heappop(left)\n timing = max(avail,timing)+time[-i][0]\n heapq.heappush(right,(timing+time[-i][1],effi,i))\n n -= 1\n while right and (timing>=right[0][0] or n==0 or not left):\n while right and right[0][0]<timing:\n _,effi,i = heapq.heappop(right)\n heapq.heappush(right,(timing,effi,i))\n avail,effi,i = heapq.heappop(right)\n timing = max(avail,timing)+time[-i][2]\n heapq.heappush(left,(timing+time[-i][3],effi,i))\n return timing\n```\n\nThe previous code gives TLE because of the third nested while loops (inside the main while loop). To improve time complexity and avoid TLE, we need to get rid of the third while loop.\n\n# Accepted Solution\n**Variables:**\n+ *timing*: keep track of the progress.\n+ *left*: heap to store info of workers on the left of bridge ready to cross the bridge\n+ *right*: heap to store info of workers on the right of bridge ready to cross the bridge\n\nDifferent from the TLE code, *left* and *right* only contain workers who are ready and waiting to cross the bridge, i.e. *availableTime<=Timing* (in the previous code, *left* and *right* contain all the workers). Info of each worker in *left* and *right* is the tuple (-efficiency,-index,availableTime), where *availableTime* is now placed last. Since the workers in *left* and *right* are all ready to cross the bridge, they will be chosen by their efficiency then indices.\n\n+ *left0*: heap to reserve info of workers on the left of bridge after they put boxes in the new warehouse. When they are ready to cross the bridge, i.e. *availableTime<=timing*, they will be pushed to *left* and wait to cross the bridge.\n+ *right0*: heap to reserve info of workers on the right of bridge after they pick up boxes from the old warehouse. When they are ready to cross the bridge, i.e. *availableTime<=timing*, they will be pushed to *right* and wait to cross the bridge.\n\nInfo of each worker in *left0* and *right0* is the tuple (availableTime,-index).\n\nThe variables are initialized as follows:\n```\nleft,right = [],[] # (-efficiency,-index,availableTime)\nfor i in range(k):\n heapq.heappush(left,(-time[i][0]-time[i][2],-i,0))\nleft0,right0 = [],[] # (availableTime,-index)\ntiming = 0\n```\n**Approach**\nThe 2 main processes are implemented by the codes as follows:\n+ crossing the bridge from left to right: conditions of the first process is similar to the TLE code. Note that, here, right is always null due to the condition of the (while right:) loop in the next process.\n```\nwhile left and n>0 and (not right0 or timing<right0[0][0]):\n _,i,avail = heapq.heappop(left)\n timing = max(avail,timing)+time[-i][0]\n heapq.heappush(right0,(timing+time[-i][1],i))\n n -= 1\n# we need to update left for each new time instance timing, \n# i.e. move the workers who are ready from left0 to left. \n# Function updateLeft will be explained later. \n self.updateLeft(timing,left,right,left0,right0,time,n)\n```\n+ crossing the bridge from right to left: \n```\n# we update right for the new time instance, i.e. \n# move workers who are ready from right0 to right. \n# Function updateRight will be explained later. \nself.updateRight(timing,left,right,left0,right0,time,n)\n# compare to the TLE code, condition (timing>=right[0][0] or n==0 or not left) \n# is not used in the (while right:) loop because it is used in \n# function updateRight. Note that, because of condition (while right:), \n# right will always be null at start of each main loop (while n>0:).\nwhile right:\n _,i,avail = heapq.heappop(right)\n timing = max(avail,timing)+time[-i][2]\n heapq.heappush(left0,(timing+time[-i][3],i))\n# we need to update right for each new time instance. Note that, \n# we need to update left before updating right.\n self.updateLeft(timing,left,right,left0,right0,time,n)\n self.updateRight(timing,left,right,left0,right0,time,n)\n```\n+ *updateLeft*: this function pushes workers from *left0* to *left* if they are ready to cross the bridge from the left of the bridge, i.e. *left0[0][0]<=timing*, in addition to the case when *left0[0][0]>timing* but *left* and *right* are null while: *right0* is null (there is no worker other than workers reserved in *left0*), or *right0* is not null and *left0[0][0]<right0[0][0]* (there are only workers reserved in *left0* and *right0*, and workers in *left0* are ready to cross the bridge earlier than workers in *right0*).\n```\ndef updateLeft(self,timing,left,right,left0,right0,time,n):\n while left0 and (left0[0][0]<=timing or (not left and not right and not right0) or (not left and not right and right0 and left0[0][0]<right0[0][0])):\n avail,i = heapq.heappop(left0)\n heapq.heappush(left,(-time[-i][0]-time[-i][2],i,max(avail,timing)))\n```\n+ *updateRight*: this function pushes workers from *right0* to *right* if they are ready to cross the bridge from the right of the bridge, i.e. *right0[0][0]<=timing*, in addition to the case when *right0[0][0]>timing* but *right* is null while: *n==0* (there is no box at the old warehouse and no worker is required to cross the bridge from left side), or *left* is null (there is no worker waiting to cross the bridge from left side at the current time instance).\n```\ndef updateRight(self,timing,left,right,left0,right0,time,n):\n while right0 and (right0[0][0]<=timing or (not right and (n==0 or not left))):\n avail,i = heapq.heappop(right0)\n heapq.heappush(right,(-time[-i][0]-time[-i][2],i,max(avail,timing)))\n```\n# Accepted Python 3 Code\n```\nclass Solution:\n def findCrossingTime(self, n, k, time):\n left,right = [],[] # (-efficiency,-index,availableTime)\n for i in range(k):\n heapq.heappush(left,(-time[i][0]-time[i][2],-i,0))\n left0,right0 = [],[] # (availableTime,-index)\n timing = 0\n while n>0:\n while left and n>0 and (not right0 or timing<right0[0][0]):\n _,i,avail = heapq.heappop(left)\n timing = max(avail,timing)+time[-i][0]\n heapq.heappush(right0,(timing+time[-i][1],i))\n n -= 1\n self.updateLeft(timing,left,right,left0,right0,time,n)\n self.updateRight(timing,left,right,left0,right0,time,n)\n while right:\n _,i,avail = heapq.heappop(right)\n timing = max(avail,timing)+time[-i][2]\n heapq.heappush(left0,(timing+time[-i][3],i))\n self.updateLeft(timing,left,right,left0,right0,time,n)\n self.updateRight(timing,left,right,left0,right0,time,n)\n return timing\n\n def updateLeft(self,timing,left,right,left0,right0,time,n):\n while left0 and (left0[0][0]<=timing or (not left and not right and right0 and left0[0][0]<right0[0][0]) or (not left and not right and not right0)):\n avail,i = heapq.heappop(left0)\n heapq.heappush(left,(-time[-i][0]-time[-i][2],i,max(avail,timing)))\n\n def updateRight(self,timing,left,right,left0,right0,time,n):\n while right0 and (right0[0][0]<=timing or (not right and (n==0 or not left))):\n avail,i = heapq.heappop(right0)\n heapq.heappush(right,(-time[-i][0]-time[-i][2],i,max(avail,timing)))\n```\n\n**Notes:**\nPlease note that the problem description is somewhat misleading. It states that: "... after all n boxes have been put in the new warehouse", but it actually should be (as shown by the examples): "... after all n boxes have been taken from the old warehouse". | 2 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Python simulation | time-to-cross-a-bridge | 0 | 1 | Use 2 priority queues (based on the efficiency) to simulate workers queuing on both sides of the bridge (l and r).\n\nUse 2 priority queues (based on the time) to simulate workers in the warehouses (ll and rr).\n\nFinally, t defines the time of the last crossing.\n\nWe "wait" till the bridge is available.\n- We move workers to the bridge queue.\n- We pick the next worker to cross the bridge from bridge queues:\n- We advance the time of the last crossing.\n- If the worker is moving right-to-left, we decrease the number of boxes needed.\n- We move the worker into the warehouse queue (with added time) on the opposite side.\n\n\n# Code\n```\nclass Solution:\n # l: (-(leftToRight + rightToLeft), -i), waiting on the left side, sort by efficiency\n # r: (-(leftToRight + rightToLeft), -i), waiting on the right side, sort by efficiency\n # ll: (time, i), on what time can move to l from new warehouse\n # rr: (time, i), on what time can move to r from old warehouse\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n ll, l, r, rr = list(), list(), list(), list()\n for i, (a, _, c, _) in enumerate(time):\n heapq.heappush(l, (-a - c, -i))\n\n t = 0\n while n:\n while ll and ll[0][0] <= t:\n _, i = heapq.heappop(ll)\n heapq.heappush(l, (-time[i][0] - time[i][2], -i))\n while rr and rr[0][0] <= t:\n _, i = heapq.heappop(rr)\n heapq.heappush(r, (-time[i][0] - time[i][2], -i))\n\n if r:\n _, i = heapq.heappop(r)\n t += time[-i][2]\n heapq.heappush(ll, (t + time[-i][3], -i))\n n -= 1\n elif l and n > len(r) + len(rr):\n _, i = heapq.heappop(l)\n t += time[-i][0]\n heapq.heappush(rr, (t + time[-i][1], -i))\n else:\n x = ll[0][0] if ll and n > len(r) + len(rr) else float(\'inf\')\n y = rr[0][0] if rr else float(\'inf\')\n t = min(x, y)\n return t\n``` | 8 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[Python] Simple & Organized Heap Queue | time-to-cross-a-bridge | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nMaintain 4 minimum Heap queue to record workers at different situation:\n* Waiting at **left side** of bridge\n* Waiting at **right side** of bridge\n* **Picking** box\n* **Putting** box\n\nWorker jump amount these 4 queue as time pass.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThere is a priority amount the 4 queues.\n1. Based on question, `rightSide` has the highest priority.\n2. If no person are waiting on `rightSide` and other work are busy, the `leftSide` can pass.\n3. If no one use bridge, we shall just move forward the time with the worker who finish `putting` or `picking` next.\n\nTo summarize, the priority amount the 4 queues is `rightSide -> leftSide -> Picking -> putting`.\n\n# Complexity\n- Time complexity: $$O(k + n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n leftSide = []\n rightSide = []\n picking = []\n putting = []\n for i, worker in enumerate(time):\n heapq.heappush(leftSide, [-(worker[0] + worker[2]), -i])\n t = 0\n while n or rightSide or picking or putting:\n if rightSide: # right to left passing\n worker = heapq.heappop(rightSide)\n t += time[-worker[1]][2]\n heapq.heappush(putting, [t + time[-worker[1]][3], worker])\n elif n and leftSide: # left to right passing\n worker = heapq.heappop(leftSide)\n t += time[-worker[1]][0]\n n -= 1\n heapq.heappush(picking, [t + time[-worker[1]][1], worker])\n # No one uses bridge, so move forward with the next worker who either picking or putting\n else:\n if not n and not picking:\n # Ending Case\n return t\n nextTime = []\n if picking:\n nextTime.append(picking[0][0])\n if putting:\n nextTime.append(putting[0][0])\n t = min(nextTime)\n\n # Put all worker back to bridge queue if they finish at current time\n while putting and putting[0][0] <= t:\n _, worker = heapq.heappop(putting)\n heapq.heappush(leftSide, worker)\n while picking and picking[0][0] <= t:\n _, worker = heapq.heappop(picking)\n heapq.heappush(rightSide, worker)\n return t\n``` | 1 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[Python3] Simulate CPU Scheduler with Four Priority Queues | time-to-cross-a-bridge | 0 | 1 | ```python\nclass Solution:\n def cross(self, wait, cpu, time, tick, is_left_to_right) -> int:\n cur = heapq.heappop(wait)\n i = 0 if is_left_to_right else 2\n tick += time[-cur[2]][i]\n cur[0] = tick + time[-cur[2]][i + 1]\n heapq.heappush(cpu, cur)\n return tick\n\n def check_cpu(self, cpu, wait, tick) -> None:\n while cpu and cpu[0][0] <= tick:\n cur = heapq.heappop(cpu)\n cur[0] = 0\n heapq.heappush(wait, cur)\n\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n """This is basically a CPU scheduler. We have two tasks, one on the left\n and the other on the right. When a task is done, the worker needs to\n wait for his turn to cross the bridge. Thus, we create four heaps.\n\n l_wait: left wait queue. Workers here have completed their tasks and\n wait for cross.\n l_cpu: left CPU queue. Workers here are actively doing the task\n r_wait: same as l_wait, but for the workers waiting on the right\n r_cpu: same as l_cpu, but for the workers doing the task on the right\n\n A worker is represented by an array\n\n [available_time_tick, efficiency, idx]\n\n available_time_tick is the time tick at which the worker finishes the\n task and is able to join l_wait or r_wait. Note that all the workers in\n the wait queue have available_time_tick equal to 0\n\n efficiency is the sum of left to right time and right to left time. In\n the implementation, efficiency must be the negative of the sum.\n\n idx is the index of the worker. In the implementation, idx must be\n negative as well.\n\n Thus, in the heap, the worker with the smallest available_time_tick,\n i.e., the worker who will finish the earlieset gets to the top. If the\n available_time_tick are the same (e.g. in the wait queue), the worker\n with the larger negative efficiency, i.e., lower efficiency, gets to\n the top. If the efficiency are the same, the worker with the larger\n negative index, gets to the top.\n\n We also use a variable tick to keep track of the current time.\n\n The work flow goes like this. First, we need to check if anyone on the\n CPU queue has completed their tasks. The check is to compare the current\n tick with available_time_tick on each worker. If the tick is larger\n than available_time_tick, the worker has completed the task and shall\n join the wait queue. We do this for both l_cpu and r_cpu\n\n Then, we grab workers from the wait queue. If only l_wait is available,\n as in the case at the beginning, we pop the worker from there and have\n him cross the bridge. The time spent crossing the bridge is the time\n everyone has to wait. We update tick for that. Once the worker is on the\n right side, we compute its available_time_tick as current tick plus the\n time needed for him to complete the task on the right. Then we put him\n in r_cpu.\n\n If r_wait is available, then regardless of whether l_wait is available,\n we always pop workers from r_wait, and have him cross the bridge from\n right to left. We update tick for the current time, and compute the\n available_time_tick for the worker working on the task on the left. Then\n we put him in l_cpu.\n\n Last case, if neither l_wait nor r_wait is available, that means the\n current tick is smaller than available_time_tick from the top worker on\n both l_cpu and r_cpu. Then we need to fast forward tick to the smaller\n of the two and then repeat the process.\n\n One complication is that once all jobs have been picked up, we need to\n terminate the process above. At this point, there are still workers on\n r_cpu, but we don\'t care about l_cpu or l_wait anymore. We just want to\n get workers from r_cpu to r_wait to crossing the bridge.\n\n O(NlogK), 731 ms, faster than 35.31%\n """\n l_wait, l_cpu, r_wait, r_cpu = [], [], [], []\n # All workers on l_wait at the beginning\n for i in range(k):\n heapq.heappush(l_wait, [0, -time[i][0] - time[i][2], -i])\n tick = 0\n while n:\n self.check_cpu(l_cpu, l_wait, tick)\n self.check_cpu(r_cpu, r_wait, tick)\n if l_wait and not r_wait:\n tick = self.cross(l_wait, r_cpu, time, tick, True)\n n -= 1\n elif r_wait:\n tick = self.cross(r_wait, l_cpu, time, tick, False)\n else: # l_wait and r_wait both empty\n tick = min(l_cpu[0][0] if l_cpu else math.inf, r_cpu[0][0] if r_cpu else math.inf)\n\n # Move all remaining workers from right to left\n while r_cpu or r_wait:\n self.check_cpu(r_cpu, r_wait, tick)\n tick = self.cross(r_wait, l_cpu, time, tick, False) if r_wait else r_cpu[0][0]\n return tick\n``` | 1 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[C++ || Python] Big Simulation | time-to-cross-a-bridge | 0 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n\n> **Vote welcome if this solution helped.**\n---\n\n# Intuition\n1. Notice that either answer or main logic are about the bridge, so we should mainly track the "events" of getting on and off the bridge.\n2. Usually, one worker should get on the bridge as soon as another worker gets off. Of course, there are special circumstances where everyone is working and the bridge is idle.\n3. Tracking time of "events". Now we must choose a data structure to **quickly "select a highest priority" and "remove it"**. That is heap.\n\n# Approach\n1. Notice we only care about the "events", which is the instants of up bridge and down bridge. As a result, **in these instances we can guarantee that nobody is on the bridge**.\n2. So the workers have only four states: waiting in leftside, working in leftside, waiting in rightside and working in rightside.\n3. Use four heaps to maintain them, then simulate.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $O(n \\log k)$\n- Space complexity: $O(k)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n typedef pair<int, int> pii;\n int findCrossingTime(int n, int k, vector<vector<int>>& time) {\n // After sorting, the order of the indexes is the order of selection\n stable_sort(time.begin(), time.end(), [](auto& x, auto& y) -> bool {\n return x[0] + x[2] < y[0] + y[2];\n });\n priority_queue<int> lwait, rwait;\n for (int i = 0; i < k; ++i) lwait.push(i);\n // Maintain the finish time and index\n priority_queue<pii, vector<pii>, greater<pii>> lwork, rwork;\n int t = 0;\n while (n || rwait.size() || rwork.size()) {\n // Before t, these workers have finished their work\n // Collect them and insert into waitlist\n while (lwork.size() && lwork.top().first <= t) {\n lwait.push(lwork.top().second);\n lwork.pop();\n }\n while (rwork.size() && rwork.top().first <= t) {\n rwait.push(rwork.top().second);\n rwork.pop();\n }\n\n if (rwait.size() > 0) {\n // Choose the rightside workers at first\n int c = rwait.top();\n rwait.pop();\n // Restart to wait after cross and work\n lwork.push(pii(t + time[c][2] + time[c][3], c));\n // Bridge return to idle after worker crossed\n t += time[c][2];\n }\n else {\n // Nobody waiting in rightside, choose leftside workers\n if (n == 0) {\n // No need to schedule leftside worker\n // Advance directly to the next worker to complete\n t = rwork.top().first; \n }\n else {\n if (lwait.size() > 0) {\n // There are workers waiting in leftside \n int c = lwait.top();\n lwait.pop();\n // Restart to wait after cross and work\n rwork.push(pii(t + time[c][0] + time[c][1], c));\n // Bridge return to idle after worker crossed\n t += time[c][0];\n n--;\n }\n else {\n // Choose the earlier complete time\n int u = lwork.size() ? lwork.top().first : INT_MAX;\n int v = rwork.size() ? rwork.top().first : INT_MAX;\n t = min(u, v);\n }\n }\n }\n }\n return t;\n }\n};\n```\n``` Python3 []\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n # After sorting, the order of the indexes is the order of selection\n time = sorted(time[::-1], key=lambda x: -x[0]-x[2])\n lwait, rwait, lwork, rwork = [i for i in range(k)], [], [], []\n heapify(lwait)\n t = 0\n while n or len(rwait) or len(rwork):\n # Before t, these workers have finished their work\n # Collect them and insert into waitlist\n while len(lwork) and lwork[0][0] <= t:\n heappush(lwait, heappop(lwork)[1])\n while len(rwork) and rwork[0][0] <= t:\n heappush(rwait, heappop(rwork)[1])\n if len(rwait):\n # Choose the rightside workers at first\n c = heappop(rwait)\n # Restart to wait after cross and work\n heappush(lwork, (t + time[c][2] + time[c][3], c))\n # Bridge return to idle after worker crossed\n t += time[c][2]\n else:\n # Nobody waiting in rightside, choose leftside workers\n if n == 0: \n # No need to schedule leftside worker\n # Advance directly to the next worker to complete\n t = rwork[0][0]\n else:\n if len(lwait):\n # There are workers waiting in leftside \n c = heappop(lwait)\n # Restart to wait after cross and work\n heappush(rwork, (t + time[c][0] + time[c][1], c))\n # Bridge return to idle after worker crossed\n t += time[c][0]\n n -= 1\n else:\n # Choose the earlier complete time\n u = lwork[0][0] if len(lwork) else 1e9\n v = rwork[0][0] if len(rwork) else 1e9\n t = min(u, v)\n return t\n``` | 2 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Python solution using 4 priority queues | time-to-cross-a-bridge | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n # workers putting new boxes\n put_new = [(0, i) for i in range(k)] # [(available_at, i)] waiting to put new\n heapq.heapify(put_new)\n # workers waiting on left bank of bridge\n bridge_left = [] # [(eff, i)] ready to cross river left to right\n # workers picking old boxes\n pick_old = [] # [(available_at, i)] waiting to pick old\n # workers waiting on right bank of bridge\n bridge_right = [] # [(eff, i)] ready to cross river right to left\n box_left = 0\n box_right = n\n \n def eff(i):\n return (-time[i][0]-time[i][2], -i)\n \n t = 0 \n while box_left < n:\n while put_new and put_new[0][0] <= t:\n _, i = heapq.heappop(put_new)\n heapq.heappush(bridge_left, (eff(i), i))\n while pick_old and pick_old[0][0] <= t:\n _, i = heapq.heappop(pick_old)\n heapq.heappush(bridge_right, (eff(i), i))\n \n if bridge_right:\n _, i = heapq.heappop(bridge_right)\n t += time[i][2]\n box_left += 1\n heapq.heappush(put_new, (t+time[i][3], i))\n elif bridge_left and box_right > 0:\n _, i = heapq.heappop(bridge_left)\n t += time[i][0]\n box_right -= 1\n heapq.heappush(pick_old, (t+time[i][1], i))\n elif put_new or pick_old:\n t = 2**31\n if put_new:\n t = min(t, put_new[0][0])\n if pick_old:\n t = min(t, pick_old[0][0]) \n return t\n \n``` | 0 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
[Python] Simulation with 4 priority queues; Explained | time-to-cross-a-bridge | 0 | 1 | We are using 4 priority queues to track the workers at four different points:\n(1) the new site on left bank of river;\n(2) the old site on right bank of river;\n(3) the left end of bridge;\n(4) the right end of bridge.\n\nqueue (1) and (2) are ordered based on the finishing time;\nqueue (3) and (4) are ordered based on the efficiency defined in the problem\n\nSince only one worker is allowed crossing the bridage, and workers on the right bank should cross first. We can use the bridge crossing event as the time control event and advance the time.\n\nThere are a few cases we need to pay attention and advance time accordingly. Othervise, we may enter infinite loop:\n1) both end of the bridge is empty --> no waiting workers: we need to advance time based on the first complete time in warehouse;\n2) we have already sent enough workers to old warehouse, and no workers is waiting on the right end of the bridge: --> we just need to advance time based on the complete time in old warehouse.\n\n```\nclass Solution:\n def findCrossingTime(self, n, k, time):\n self.time = time\n # one queue to track the workers putting down boxes at new site\n self.new_site_workers = []\n # one queue to track the workers picking up boxes at old site\n self.old_site_workers = []\n # two queues to track the workers waiting at two side of the bridge\n self.bridge_left_workers = []\n self.bridge_right_workers = []\n\n # initailly all the workers are at left side of river\n for idx, worker_time in enumerate(time):\n heapq.heappush(self.bridge_left_workers, (-(worker_time[0] + worker_time[2]), -idx))\n\n # start simulation\n moved_box = 0\n left_box = n\n t = 0\n while True:\n while self.bridge_right_workers:\n _, widx = heapq.heappop(self.bridge_right_workers)\n widx = -widx\n # advance time\n t += time[widx][2]\n # update status\n heapq.heappush(self.new_site_workers, (t + time[widx][3], widx))\n # one box is moved to new site\n moved_box += 1\n if moved_box == n:\n return t\n self.status_update(t)\n\n if not self.bridge_left_workers and not self.bridge_right_workers:\n # no workers are waiting at the bridge\n t_old, t_new = float(\'inf\'), float(\'inf\')\n if self.old_site_workers:\n t_old = self.old_site_workers[0][0]\n if self.new_site_workers:\n t_new = self.new_site_workers[0][0]\n t = min(t_old, t_new)\n self.status_update(t)\n\n if left_box == 0 and not self.bridge_right_workers:\n t = self.old_site_workers[0][0]\n self.status_update(t)\n\n # no more workers are waiting on the right side of the river\n if left_box and self.bridge_left_workers:\n _, widx = heapq.heappop(self.bridge_left_workers)\n widx = -widx\n # advance time\n t += time[widx][0]\n # update status\n heapq.heappush(self.old_site_workers, (t + time[widx][1], widx))\n self.status_update(t)\n left_box -= 1\n\n def status_update(self, t):\n while self.new_site_workers and self.new_site_workers[0][0] <= t:\n _, widx = heapq.heappop(self.new_site_workers)\n # adding this worker to the waiting queue at left side of river\n wt = self.time[widx]\n heapq.heappush(self.bridge_left_workers, (-(wt[0] + wt[2]), -widx))\n\n while self.old_site_workers and self.old_site_workers[0][0] <= t:\n _, widx = heapq.heappop(self.old_site_workers)\n # adding this worker to the waiting queue at right side of river\n wt = self.time[widx]\n heapq.heappush(self.bridge_right_workers, (-(wt[0] + wt[2]), -widx))\n``` | 0 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
python simple solution | time-to-cross-a-bridge | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n ll, l, r, rr = list(), list(), list(), list()\n for i, (a, _, c, _) in enumerate(time):\n heapq.heappush(l, (-a - c, -i))\n\n t = 0\n while n:\n while ll and ll[0][0] <= t:\n _, i = heapq.heappop(ll)\n heapq.heappush(l, (-time[i][0] - time[i][2], -i))\n while rr and rr[0][0] <= t:\n _, i = heapq.heappop(rr)\n heapq.heappush(r, (-time[i][0] - time[i][2], -i))\n\n if r:\n _, i = heapq.heappop(r)\n t += time[-i][2]\n heapq.heappush(ll, (t + time[-i][3], -i))\n n -= 1\n elif l and n > len(r) + len(rr):\n _, i = heapq.heappop(l)\n t += time[-i][0]\n heapq.heappush(rr, (t + time[-i][1], -i))\n else:\n x = ll[0][0] if ll and n > len(r) + len(rr) else float(\'inf\')\n y = rr[0][0] if rr else float(\'inf\')\n t = min(x, y)\n return t\n\n``` | 0 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Simulation | Explanation | time-to-cross-a-bridge | 0 | 1 | # Intuition\n\nThere are 4 queues:\n1. Workers waiting on the left side `left_q`\n2. Workers with box waiting on the right side `right_q`\n3. Workers picking box `right_box_q`\n4. Workers putting box `left_box_q`\n\n**Waiting queues** contain tubles `(x, y)` where `x` is a worker efficiency miltipled by `-1`. Doing that the biggest values becomes the smallest. And `y` is a worker index miltipled by `-1` for the same purpose: bigger index will be later in priopity queue. It helps meating regulation rule on the bridge.\n\n**Box queues** contain tubles `(x, y)` where `x` is a time when the worker `y` would pick/put a box (get ready to cross the bridge).\n\nI also count a number of workers left to send (initialy `n`) to avoid sending workers for nothing.\n\n# Approach\n\nReserve a number `current_time` to know where workers on a timeline.\nDo while there are some boxes on the right side or any worker somewhere on the right side.\n1. Check **box** queues if some worker is ready to go to **waiting** queue. Move them: `right_box_q` -> `right_q` or `left_box_q` -> `left_q`.\n2. Workers on the right side go first. One worker from the right queue can cross the bridge. Pick the one with lowest efficiency and "move" him to the left side: increase `current_time` and put him to `left_box_q` (which means he will be putting box until `x` from tuple `(x, y)` in `left_box_q`).\n3. If nobody waiting on the right side one worker from left queue can cross the bridge: increase `current_time` and move him from `left_q` to `right_box_q`. Decrease `workers_to_send` count.\n4. If both **waiting** queues are empty and we still in loop that means all workers are picking/putting boxes. In that case move the `current_time` to the closes time when any of workers will be ready to cross the bridge.\n\n# Complexity\n- Time complexity: $$O(n * k)$$ ?\n\n# Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n ef = []\n left_q = [] # queue waiting on the left side\n for i in range(k):\n ef.append(-(time[i][0] + time[i][2]))\n heapq.heappush(left_q, (ef[i], -i))\n workers_to_send = n # boxes to care minus workers in progress\n current_time = 0\n right_q = [] # queue waiting on the right side\n left_box_q = [] # queue for taking boxes\n right_box_q = [] # queue for putting boxes\n # box queues are sorted by the time when worker will be ready with picking boxes\n # waiting queues are sorted by efficiency\n while len(right_q) > 0 or len(right_box_q) > 0 or workers_to_send > 0:\n while len(right_box_q) > 0 and right_box_q[0][0] <= current_time: # check if smbd\'s picked a box\n _, with_box = heapq.heappop(right_box_q)\n # move him to the right queue\n heapq.heappush(right_q, (ef[with_box], -with_box))\n while len(left_box_q) and left_box_q[0][0] <= current_time: # check if smbd\'s put a box\n _, without_box = heapq.heappop(left_box_q)\n # move him to the right queue\n heapq.heappush(left_q, (ef[without_box], -without_box))\n if len(right_q) > 0: # the 1st from right to left go first\n _, next_to_left = heapq.heappop(right_q) # get with the lowest efficient\n next_to_left = -next_to_left\n current_time += time[next_to_left][2] # he crosses the bridge and putting a box\n heapq.heappush(left_box_q, (current_time + time[next_to_left][3], next_to_left))\n # when right queue is empty 1 from left queue can cross if some boxes left\n elif len(left_q) > 0 and workers_to_send > 0:\n _, next_to_right = heapq.heappop(left_q) # get with the lowest efficient\n next_to_right = -next_to_right\n current_time += time[next_to_right][0] # he crosses the bridge and picking a box\n heapq.heappush(right_box_q, (current_time + time[next_to_right][1], next_to_right))\n workers_to_send -= 1 # decrease a count of workers to send\n else: # both queues are empty (left queue we consider as empty if we dont need more workers)\n if len(right_box_q) == 0 and workers_to_send == 0: # nobody in a new warehouse and nobody to send\n return current_time # we\'ve done\n # take the smallest value from left_box_q and right_box_q and shift time\n right_box_time = sys.maxsize if len(right_box_q) == 0 else right_box_q[0][0]\n left_box_time = sys.maxsize if len(left_box_q) == 0 else left_box_q[0][0]\n # worker will get to a queue on the next iteration\n current_time = min(right_box_time, left_box_time)\n return current_time\n``` | 0 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Rephrasing the problem + Python O(nlogk) with descriptive comments | time-to-cross-a-bridge | 0 | 1 | # Rephrasing the Problem\nThis problem is very verbose and has some flaws in the wording. I\'ll re-explain it quickly, but I won\'t be as technical.\n\nThere are $$k$$ workers at the new warehouse and $$n$$ boxes in the old warehouse. The workers need to cross a bridge to the old warehouse, pick up a box, cross the bridge back to the new warehouse and put the box down. Each of these actions takes a certain amount of time for each worker (the ```ith``` entry of ```time```).\n\nCrossing the bridge is a blocking operation. Only one person can be on the bridge at a time (I guess imagine an old rickety bridge that will collapse if two people are on it).\n\nHowever, picking up and putting down the boxes are non-blocking and can be done concurrently.\n\nTo choose who can cross the bridge we need to consider 2 cases:\n1. Someone ready to bring a box to the new warehouse. I.e. they already finished picking up a box at the old warehouse.\n\nIn this case, we should send the slowest walker (highest total time to cross both directions (take higher index on tie)) who has a box.\n\n2. There are no box carriers ready to cross, but there is someone ready to cross from the new warehouse to the old warehouse and there is a box for them to pick up there.\n\nIn this case, we should send the slowest walker from the new warehouse.\n\nWe want to know the time at which the last box finishes crossing the bridge. (NOT when all boxes are have been put in the new warehouse)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Intuition\nJust by looking at the examples you should be able to tell that there isn\'t much you can do to reframe the problem into something simple. The state has many different possibilities and each next state heavily depends on the previous state. This indicates that we probably need to simulate it.\n\nWe first recognize that the bridge bottlenecks the process, and we don\'t need to make any decisions about who should cross the bridge until the current worker finishes crossing the bridge. So we can skip the current time to when the worker we choose to cross finishes and then see which workers would be done picking up/putting down boxes so we can consider them next time we choose who should cross.\n\nIt\'s also important to consider the case where no one is ready to cross. In this case, we should move time to when at least one person will be to cross.\n\nIt\'s not unreasonable to consider trying to find a cycle, but it will take a considerable amount of time to hash the state each time. If $$n>>k$$ or the limits on each worker\'s time cost were much closer to 1 (which would limit the number of concurrent workers picking up/putting down boxes and thus reduce the number of possible states), it would be a good idea to try to find a cycle. However, the constraints do not meet either of these requirements, so we will just simulate.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBefore solving this problem generally, we should consider the case where $$k==1$$. In this case, we don\'t actually need to simulate since we don\'t need to make any bridge crossing choices. The answer will simply be the time it takes for the worker to do all tasks multiplied by the number of boxes minus the time it takes to put down the last box (since that isn\'t counted).\n\nTo solve this problem, we will maintain 4 heaps. It is probably a bit more concise to only use 2 heaps, but in my opinion 4 heaps is more readable. (This is also the solution I thought of before being influenced by other solutions)\n\nThe 4 heaps are as follows:\n1. ```left```. This is a max heap for workers trying to cross from the new warehouse to the old warehouse. The items are a tuple of total crossing time and the index.\n2. ```right```. This is a max heap for workers trying to cross from the old warehouse to the new warehouse. The items are the same as ```left```.\n3. ```picking```. This is a min heap for workers picking up boxes in the old warehouse. The items are a tuple of time when finished picking up and the index.\n4. ```putting```. This is a min heap for workers putting down boxes in the new warehouse. The items are a tuple of time when finished putting down and the index.\n\nThroughout the simulation, we will move the workers between the heaps. Each heap feeds into exactly one heap:\n1. ```left``` feeds into ```picking```\n2. ```picking``` feeds into ```right```\n3. ```right``` feeds into ```putting```\n4. ```putting``` feeds into ```left```\n\nWe begin the simulation with all workers in the ```left``` heap.\n\nWe then loop until we run out of boxes to pick up (```n```), all workers picking up boxes are done (```picking```), and all workers trying to cross from the right are done crossing (```right```).\n\nIn each loop iteration we will do the following:\n1. If someone is ready to cross from the right:\n a. Get the slowest walker from ```right```.\n b. Add the time for them to cross to the total time.\n c. Push the worker onto ```putting```.\n2. Else if someone is ready to cross on the left and there is a box for them to pick up:\n a. Get the slowest walker from ```left```.\n b. Add the time for them to cross to the total time.\n c. Push the worker onto ```picking```.\n3. Else:\n a. Update the total time to when the next person is done picking up or putting down a box.\n4. Add all people done putting boxes down to ```left```.\n5. Add all people done picking boxes up to ```right```.\n\nAt the end of this loop, the total time will be the answer.\n\n# Complexity\n- Time complexity: $$O(nlogk)$$\nPushing/popping from heaps takes $$O(logk)$$ time where $$k$$ is the number of workers. A worker will enter and exit each of the 4 heaps once for each of the $$n$$ boxes. Therefore the total time complexity is $$O(nlogk)$$. Note that if $$k==1$$, we can determine the answer in $$O(1)$$ time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(k)$$\nThe number of workers, $$k$$, never changes and each worker will be in exactly one heap at any given time. Therefore the total amount of space taken up by the heaps will be proportional to $$k$$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:\n # left = new, right = old\n # 0 1 2 3\n # time[i] = [leftToRight, pickOld, rightToLeft, putNew]\n\n # if only one worker answer can be found in constant time\n # (simulation would still work for k==1, this is just faster)\n if k==1:\n # Don\'t count the last put by subtracting it\n return sum(time[0]) * n - time[0][3]\n\n # start with everyone on left side of bridge, trying to cross to old factory\n # left and right are max heaps based on efficiency\n left = [(-(time[i][0] + time[i][2]), -i) for i in range(k)]\n heapify(left)\n right = []\n # picking and putting are min heaps based on the timestamp that the worker will finish picking up/putting down a box\n picking = []\n putting = []\n\n total_time = 0\n\n # Since we are not counting the time to put down the last box(es), don\'t check if putting is non-empty\n # To adjust this so it counts the final put time, add "or putting" to while condition\n while n or right or picking:\n # try to have someone cross bridge, update total_time to the when they will finish crossing\n # add worker to corresponding picking/putting heap with the time they will be done at\n if right:\n efficiency, i = heappop(right)\n i *= -1\n total_time += time[i][2]\n heappush(putting, (total_time + time[i][3], i))\n elif left and n:\n efficiency, i = heappop(left)\n i *= -1\n total_time += time[i][0]\n heappush(picking, (total_time + time[i][1], i))\n n -= 1\n # If no one is trying to cross, update time to the first person to finish their current task\n else:\n total_time = min(putting[0][0] if putting else inf, picking[0][0] if picking else inf)\n # Now move anyone done picking or putting boxes back in corresponding heaps to cross the bridge\n while putting and putting[0][0] <= total_time:\n t, i = heappop(putting)\n heappush(left, (-(time[i][0] + time[i][2]), -i))\n while picking and picking[0][0] <= total_time:\n t, i = heappop(picking)\n heappush(right, (-(time[i][0] + time[i][2]), -i))\n\n return total_time\n``` | 0 | There are `k` workers who want to move `n` boxes from an old warehouse to a new one. You are given the two integers `n` and `k`, and a 2D integer array `time` of size `k x 4` where `time[i] = [leftToRighti, pickOldi, rightToLefti, putNewi]`.
The warehouses are separated by a river and connected by a bridge. The old warehouse is on the right bank of the river, and the new warehouse is on the left bank of the river. Initially, all `k` workers are waiting on the left side of the bridge. To move the boxes, the `ith` worker (**0-indexed**) can :
* Cross the bridge from the left bank (new warehouse) to the right bank (old warehouse) in `leftToRighti` minutes.
* Pick a box from the old warehouse and return to the bridge in `pickOldi` minutes. Different workers can pick up their boxes simultaneously.
* Cross the bridge from the right bank (old warehouse) to the left bank (new warehouse) in `rightToLefti` minutes.
* Put the box in the new warehouse and return to the bridge in `putNewi` minutes. Different workers can put their boxes simultaneously.
A worker `i` is **less efficient** than a worker `j` if either condition is met:
* `leftToRighti + rightToLefti > leftToRightj + rightToLeftj`
* `leftToRighti + rightToLefti == leftToRightj + rightToLeftj` and `i > j`
The following rules regulate the movement of the workers through the bridge :
* If a worker `x` reaches the bridge while another worker `y` is crossing the bridge, `x` waits at their side of the bridge.
* If the bridge is free, the worker waiting on the right side of the bridge gets to cross the bridge. If more than one worker is waiting on the right side, the one with **the lowest efficiency** crosses first.
* If the bridge is free and no worker is waiting on the right side, and at least one box remains at the old warehouse, the worker on the left side of the river gets to cross the bridge. If more than one worker is waiting on the left side, the one with **the lowest efficiency** crosses first.
Return _the instance of time at which the last worker **reaches the left bank** of the river after all n boxes have been put in the new warehouse_.
**Example 1:**
**Input:** n = 1, k = 3, time = \[\[1,1,2,1\],\[1,1,3,1\],\[1,1,4,1\]\]
**Output:** 6
**Explanation:**
From 0 to 1: worker 2 crosses the bridge from the left bank to the right bank.
From 1 to 2: worker 2 picks up a box from the old warehouse.
From 2 to 6: worker 2 crosses the bridge from the right bank to the left bank.
From 6 to 7: worker 2 puts a box at the new warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Example 2:**
**Input:** n = 3, k = 2, time = \[\[1,9,1,8\],\[10,10,10,10\]\]
**Output:** 50
**Explanation:**
From 0 to 10: worker 1 crosses the bridge from the left bank to the right bank.
From 10 to 20: worker 1 picks up a box from the old warehouse.
From 10 to 11: worker 0 crosses the bridge from the left bank to the right bank.
From 11 to 20: worker 0 picks up a box from the old warehouse.
From 20 to 30: worker 1 crosses the bridge from the right bank to the left bank.
From 30 to 40: worker 1 puts a box at the new warehouse.
From 30 to 31: worker 0 crosses the bridge from the right bank to the left bank.
From 31 to 39: worker 0 puts a box at the new warehouse.
From 39 to 40: worker 0 crosses the bridge from the left bank to the right bank.
From 40 to 49: worker 0 picks up a box from the old warehouse.
From 49 to 50: worker 0 crosses the bridge from the right bank to the left bank.
From 50 to 58: worker 0 puts a box at the new warehouse.
The whole process ends after 58 minutes. We return 50 because the problem asks for the instance of time at which the last worker reaches the left bank.
**Constraints:**
* `1 <= n, k <= 104`
* `time.length == k`
* `time[i].length == 4`
* `1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000` | null |
Element Sum and Digit Sum in Python | difference-between-element-sum-and-digit-sum-of-an-array | 0 | 1 | # Code\n```\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n element_sum = sum(nums)\n digit_sum = 0\n for i in nums:\n for character in str(i):\n digit_sum += int(character)\n\n return abs(element_sum - digit_sum)\n``` | 1 | You are given a positive integer array `nums`.
* The **element sum** is the sum of all the elements in `nums`.
* The **digit sum** is the sum of all the digits (not necessarily distinct) that appear in `nums`.
Return _the **absolute** difference between the **element sum** and **digit sum** of_ `nums`.
**Note** that the absolute difference between two integers `x` and `y` is defined as `|x - y|`.
**Example 1:**
**Input:** nums = \[1,15,6,3\]
**Output:** 9
**Explanation:**
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:**
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
**Constraints:**
* `1 <= nums.length <= 2000`
* `1 <= nums[i] <= 2000` | null |
PYTHON3 SOLUTION FOR BEGINNERS | difference-between-element-sum-and-digit-sum-of-an-array | 0 | 1 | PLEASE UPVOTE :)\n\n# Code\n```\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n sum1 = sum(nums)\n sum2 = 0\n for i in nums:\n for j in str(i):\n sum2 += int(j)\n return abs(sum1 - sum2)\n``` | 1 | You are given a positive integer array `nums`.
* The **element sum** is the sum of all the elements in `nums`.
* The **digit sum** is the sum of all the digits (not necessarily distinct) that appear in `nums`.
Return _the **absolute** difference between the **element sum** and **digit sum** of_ `nums`.
**Note** that the absolute difference between two integers `x` and `y` is defined as `|x - y|`.
**Example 1:**
**Input:** nums = \[1,15,6,3\]
**Output:** 9
**Explanation:**
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:**
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
**Constraints:**
* `1 <= nums.length <= 2000`
* `1 <= nums[i] <= 2000` | null |
Python - one liner | difference-between-element-sum-and-digit-sum-of-an-array | 0 | 1 | # Complexity\n- Time complexity: O(n<sup>2</sup>)\n- Space complexity: O(n)\n\n# Code (one liner)\n```\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n return abs(sum(nums) - sum([sum([int(j) for j in list(str(i))]) for i in nums]))\n```\n# Code (expanded)\n```\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n s = sum(nums)\n ds = 0\n for i in nums:\n ds += sum([int(j) for j in list(str(i))])\n return abs(s-ds)\n```\n\n---------------\n**Upvote the post if you find it helpful.\nHappy coding.** | 1 | You are given a positive integer array `nums`.
* The **element sum** is the sum of all the elements in `nums`.
* The **digit sum** is the sum of all the digits (not necessarily distinct) that appear in `nums`.
Return _the **absolute** difference between the **element sum** and **digit sum** of_ `nums`.
**Note** that the absolute difference between two integers `x` and `y` is defined as `|x - y|`.
**Example 1:**
**Input:** nums = \[1,15,6,3\]
**Output:** 9
**Explanation:**
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:**
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
**Constraints:**
* `1 <= nums.length <= 2000`
* `1 <= nums[i] <= 2000` | null |
[C++] [Python] Brute Force Approach || Too Easy || Fully Explained | difference-between-element-sum-and-digit-sum-of-an-array | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. `digiSum(int num)`:\n - This function calculates the sum of the digits of an integer `num`.\n - It initializes a variable `sum` to 0.\n - It enters a `while` loop that continues as long as `num` is not equal to 0.\n - In each iteration, it calculates the remainder of `num` divided by 10 (`num % 10`) to get the last digit of `num` and adds it to the `sum`.\n - It then updates `num` by dividing it by 10 (`num /= 10`) to move to the next digit.\n - Finally, it returns the computed `sum`, which represents the sum of the digits of `num`.\n\n2. `arSum(vector<int>& nums)`:\n - This function calculates the sum of elements in a vector of integers `nums`.\n - It initializes a variable `sum` to 0.\n - It uses a `for` loop to iterate through the elements of the `nums` vector and adds each element to the `sum`.\n - After iterating through all elements, it returns the computed `sum`, which represents the sum of the elements in `nums`.\n\n3. `differenceOfSum(vector<int>& nums)`:\n - This function calculates the difference between the sum of elements in a vector `nums` and the sum of the digits of each element in the vector using the previously defined functions.\n - It initializes a variable `diSum` to 0 to store the sum of digits.\n - It uses a `for` loop to iterate through the elements of the `nums` vector.\n - In each iteration, it calculates the sum of digits for the current element using the `digiSum` function and adds it to `diSum`.\n - Finally, it returns the difference between the sum of elements in `nums` (computed using `arSum(nums)`) and `diSum`.\n\n# Complexity\n- Time complexity:$$O(n * log(nums))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n int digiSum(int num){\n int sum = 0; \n while(num != 0){\n sum += num % 10;\n num /= 10;\n }\n return sum;\n }\n int arSum(vector<int>& nums){\n int sum = 0;\n for(int i = 0; i < nums.size(); i++){\n sum += nums[i];\n }\n return sum;\n }\n int differenceOfSum(vector<int>& nums) {\n int diSum = 0;\n for(int i = 0; i < nums.size(); i++){\n diSum += digiSum(nums[i]);\n }\n return arSum(nums) - diSum;\n }\n};\n```\n``` Python []\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n dSum = 0\n aSum = 0\n for i in nums:\n aSum += i\n while(i != 0):\n dSum += i % 10\n i = i // 10\n return aSum - dSum\n``` | 2 | You are given a positive integer array `nums`.
* The **element sum** is the sum of all the elements in `nums`.
* The **digit sum** is the sum of all the digits (not necessarily distinct) that appear in `nums`.
Return _the **absolute** difference between the **element sum** and **digit sum** of_ `nums`.
**Note** that the absolute difference between two integers `x` and `y` is defined as `|x - y|`.
**Example 1:**
**Input:** nums = \[1,15,6,3\]
**Output:** 9
**Explanation:**
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:**
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
**Constraints:**
* `1 <= nums.length <= 2000`
* `1 <= nums[i] <= 2000` | null |
Python/Python3 easy solution | difference-between-element-sum-and-digit-sum-of-an-array | 0 | 1 | \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n * log10(nums[i]))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def differenceOfSum(self, nums: List[int]) -> int:\n el_sum = d_sum = 0\n for i in nums:\n el_sum += i\n d_sum += self.digit_sum(i)\n return abs(el_sum - d_sum)\n \n def digit_sum(self, n: int) -> int:\n sum = 0\n while n:\n sum += int(n % 10)\n n //= 10\n return sum\n \n \n``` | 3 | You are given a positive integer array `nums`.
* The **element sum** is the sum of all the elements in `nums`.
* The **digit sum** is the sum of all the digits (not necessarily distinct) that appear in `nums`.
Return _the **absolute** difference between the **element sum** and **digit sum** of_ `nums`.
**Note** that the absolute difference between two integers `x` and `y` is defined as `|x - y|`.
**Example 1:**
**Input:** nums = \[1,15,6,3\]
**Output:** 9
**Explanation:**
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:**
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
**Constraints:**
* `1 <= nums.length <= 2000`
* `1 <= nums[i] <= 2000` | null |
Easy | Python Solution | Numpy | increment-submatrices-by-one | 0 | 1 | # Code\n```\nimport numpy as np\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n mat = [[0 for _ in range(n)] for _ in range(n)]\n mat = np.array(mat)\n for vals in queries:\n x1, x2, y1, y2 = vals[0], vals[1], vals[2], vals[3]\n mat[x1:y1+1, x2:y2+1] += 1\n return mat\n```\nDo upvote if you like the solution :) | 11 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
PREFIX SUM APPROACH || BEATS 100% SUBMISSIONS || JAVA || INTUITIVE | increment-submatrices-by-one | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPREFIX SUM APPROACH IMPLEMENTED FOR EACH QUERY WHICH DRASTICALLY REDUCES THE TC.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBRUTE FORCE APPROACH WONT WORK FOR C++ SUNMISSIONS . SO GO AHEAD WITH THIS PREFIX SUM APPROACH WHICH IS MUCH FASTER. IMPLEMENT THE PREFIX SUM CALCULATION FOR EACH QUERY THEN FORM THE FINAL 2D MATRIX BY ADDING THE CONTENT OF EACH ROW WHICH FINALLY FORMS THE ARRAY.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(q*N) + O(N^2)\n\nMUCH FASTER THAN BRUTE FORCE !\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nN*N MATRX IS ALL YOU NEED!\n\n# Code\n```\nclass Solution {\n public int[][] rangeAddQueries(int n, int[][] queries) {\n int[][] ans = new int[n][n];\n for (int[] q : queries) {\n int row1 = q[0], col1 = q[1], row2 = q[2], col2 = q[3];\n for (int i = row1; i <= row2; i++) \n {\n ans[i][col1] +=1; //MARK THE BEGINNING OF QUERY WITH +1\n if ((col2 +1) < n ) //CHECK IF THE POSITION LIES WITHIN THAT COL IN THE ARRAY\n {\n ans[i][col2 +1] -=1; //IF THE POS EXISTS, MARK IT WITH -1 ... DRY RUN IT FOR BETTER UNDERSTANDING.\n }\n }\n }\n for(int i=0;i<n;i++)\n {\n for(int j=1;j<n;j++)\n {\n ans[i][j] += ans[i][j-1]; //FINALLY TRAVERSE THE ARRAY AND ADD THE CONTENT OF EACH ROW IN IT.\n }\n }\n return ans;\n }\n}\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
Simple Python Solution Faster than 100% | increment-submatrices-by-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n grid = [[0]*n for _ in range(n)]\n \n for row1,col1, row2, col2 in queries:\n grid[row1][col1] += 1\n\n if row2+ 1< n:\n grid[row2+1][col1] -= 1\n if col2 + 1 < n:\n grid[row1][col2+1] -= 1\n\n if row2 + 1 < n and col2 + 1< n:\n grid[row2+1][col2+1] += 1\n\n for i in range(1,n):\n for j in range(n):\n grid[i][j] += grid[i-1][j]\n for i in range(n):\n for j in range(1,n):\n grid[i][j] += grid[i][j-1]\n return grid\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python3] Difference Array | Postfix Sum | increment-submatrices-by-one | 0 | 1 | The strategy is to keep track of the changes made to each cell at the boundaries, instead of maintaining the final value of each cell.\n\nInitially, we initialize the matrix with all zeroes. For each query, we add 1 to the top-left corner cell ($r_{start}, c_{start}$) and subtract 1 from the cells at ($r_{start}, c_{end+1}$) and ($r_{end+1}, c_{start}$). However, in the nature of prefix computation, this leads to a duplicate cost by subtracting both row and column boundaries. Therefore, we balance this out by adding 1 to the cell after the bottom-right corner of the sub-matrix ($r_{end+1}, c_{end+1}$). Afterwards, we use the prefix sum technique to update the final matrix by adding the differences from the previous cells.\n\nThis approach enables us to update the matrix in constant time for each query, without the need to iterate through the entire matrix for each query.\n\n# Complexity\nTime `O(q+n^2)`\nSpace `O(1)`\n\n# Code\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n mat = [[0]*n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n mat[r1][c1] += 1\n if r2 < n-1:\n mat[r2+1][c1] -= 1\n if c2 < n-1:\n mat[r1][c2+1] -= 1\n if r2 < n-1 and c2 < n-1:\n mat[r2+1][c2+1] += 1\n for i in range(1, n):\n mat[0][i] += mat[0][i-1]\n mat[i][0] += mat[i-1][0]\n for i in range(1, n):\n for j in range(1, n):\n mat[i][j] = mat[i][j] + mat[i-1][j] + mat[i][j-1] - mat[i-1][j-1]\n return mat\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python🤫🐍🐍🐍] Simple Clean Hashmap Counter Solution | increment-submatrices-by-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a HM that tells you how much to add to the counter for each row when you reach (i,j)\nUse a second HM that tells you how much to remove from the counter when you reach (i,j)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2 + q*n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n# Code\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n \n out = [ [0]*n for i in range(n)]\n\n #When we reach hms with key [i,j] we increment counter by hms[i,j]\n hms = defaultdict(int)\n #When we reach hme with key [i,j] we increment counter by hme[i,j]\n hme = defaultdict(int)\n \n for q in queries:\n \n for i in range(q[0],q[2]+1):\n hms[(i,q[1])] += 1\n hme[(i,q[3]+1)] += 1\n\n for i in range(n):\n count = 0\n for j in range(n):\n count += hms[(i,j)]\n count -= hme[(i,j)]\n out[i][j] = count\n return out\n\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python3] prefix sum | increment-submatrices-by-one | 0 | 1 | \n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n ans = [[0]*n for _ in range(n)]\n for i, j, ii, jj in queries: \n ans[i][j] += 1\n if ii+1 < n: ans[ii+1][j] -= 1\n if jj+1 < n: ans[i][jj+1] -= 1\n if ii+1 < n and jj+1 < n: ans[ii+1][jj+1] += 1\n for i in range(n): \n prefix = 0 \n for j in range(n): \n prefix += ans[i][j]\n ans[i][j] = prefix \n if i: ans[i][j] += ans[i-1][j]\n return ans \n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
Python3 | Prefix-Sum-Difference Array- Accepted Solutions | increment-submatrices-by-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing the difference array to solve the problem\n# Approach\nThe method is applying prefix sum to each row. we only need to mark the start and end position\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n O(N * N), because we are going through the entire matrix at the end\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1) if we do not count the output size\n\n# Code\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n mat = [[0] * n for _ in range(n)]\n for row1, col1, row2, col2 in queries:\n for r in range(row1, row2 + 1):\n mat[r][col1] += 1\n if col2 + 1 < n:\n mat[r][col2 + 1] -= 1\n for r in mat:\n for i in range(1, len(r)):\n r[i] += r[i - 1]\n return mat\n \n \n``` | 2 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python3] Sweep Line (Range Addition w/ Visualization), Clean & Concise | increment-submatrices-by-one | 0 | 1 | # Na\xEFve Approach\nFollowing the description of this problem, for each query, we update the every element covered in the submatrix defined by `(r1, c1)` and `(r2, c2)`. However, it is pretty clear to know that the time complexity for this approach is $$O(n^2q)$$, which could be up to $$500 \\times 500 \\times 10^4 = 2.5 \\times 10^9$$ and result in TLE.\n\nSo, how can we come up with a better algorithm with improved time complexity?\n\n# Intuition\nThis problem is the 2-D version of [LC 370. Range Addition](https://leetcode.com/problems/range-addition/). Essentially, we are doing range addition for each query.\n\n# Visualization\nConsider the 1-D Range Addition problem and suppose we have `n = 5` and `queries = [[1,3],[2,4],[0,2]]`. Below is the visual illustration on the technique of `Range Caching`.\n\n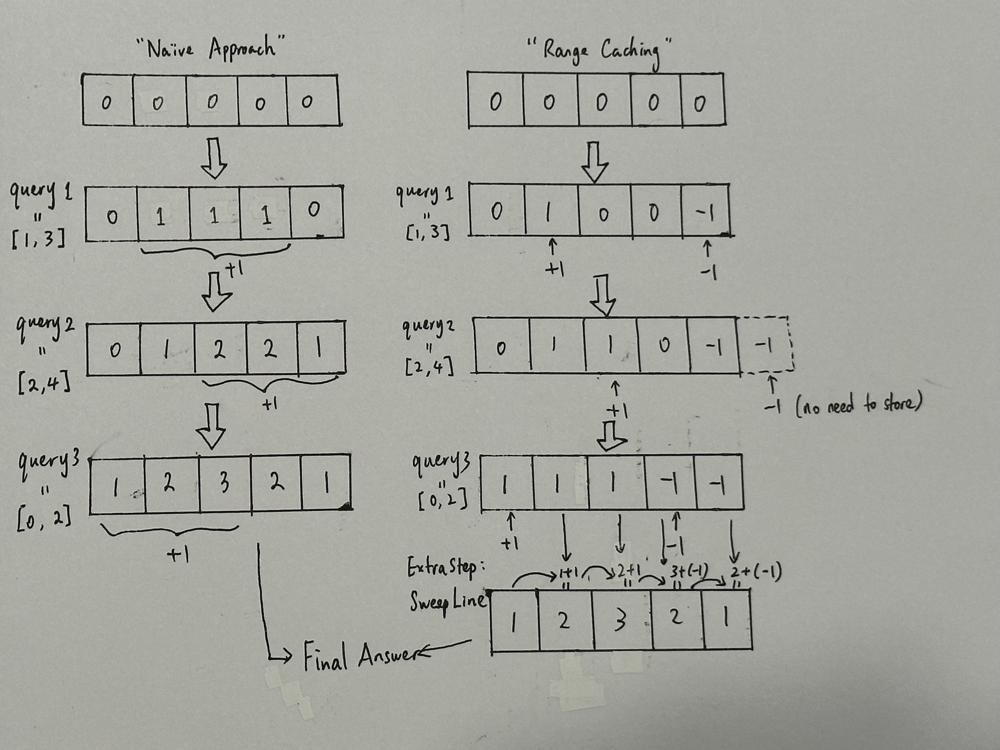\n\n\n# Approach\nFor each query, denoted as `(r1, c1, r2, c2)`, we perform a preprocessing (range caching) on each row involved. Specifically, for each row within `[r1, r2]`, we add 1 at column `c1` and subtract 1 at the next column of `c2`.\n\nAfter preprocessing, we calculate the output by performing range addition (sweeping line) on all elements of the matrix, and output the answer.\n\n# Complexity\n- Time complexity: $$O(n^2 + nq) \\approx O(nq)$$, if $$q \\gg n$$;\n\n- Space complexity: $$O(1)$$, if not including the $$O(n^2)$$ space for output.\n\n**Please upvote if you find this solution helpful. Thanks!**\n\n# Solution (Range Caching)\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n ans = [[0] * n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n for r in range(r1, r2 + 1):\n ans[r][c1] += 1\n if c2 + 1 < n: ans[r][c2 + 1] -= 1\n for r in range(n):\n for c in range(1, n):\n ans[r][c] += ans[r][c - 1]\n return ans\n```\n\n# Follow-up (Bonus)\nNow we know the concept of range caching technique to solve this problem, is there a even better solution to further improve the overall time complexity?\n\nThe answer is **yes** and the idea is straightforward as visualized below:\n\n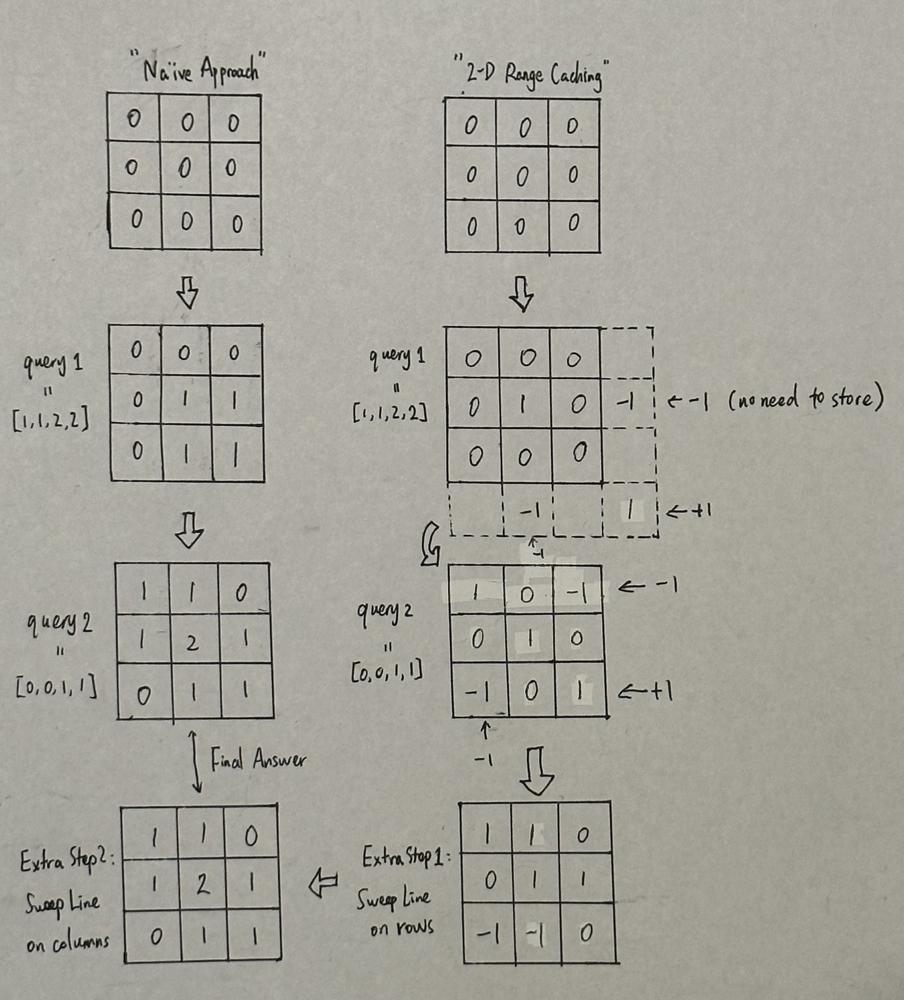\n\n\nIn brief, we can directly use 2-D range caching (previously we were using 1-D range caching in this 2-D problem). The difference here is that for each query, we now need to (1) cache the value at 4 cells (instead of 2 cells at each row); and (2) calculate the output by going through the full matrix twice, one by row and one by column (instead of once).\n\n- Time complexity: $$O(n^2 + q)$$, which is better than the solution above;\n\n- Space complexity: $$O(1)$$, if not including the $$O(n^2)$$ space for output.\n\n**Remark:** Personally, I feel that 2-D range caching is bit trickier to digest, but using 1-D range caching applied to this problem would be sufficient and easier to think & code.\n\n# Improved Solution (2-D Range Caching)\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n ans = [[0] * n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n ans[r1][c1] += 1\n if r2 + 1 < n: ans[r2 + 1][c1] -= 1\n if c2 + 1 < n: ans[r1][c2 + 1] -= 1\n if r2 + 1 < n and c2 + 1 < n: ans[r2 + 1][c2 + 1] += 1\n for r in range(1, n):\n for c in range(n):\n ans[r][c] += ans[r - 1][c]\n for r in range(n):\n for c in range(1, n):\n ans[r][c] += ans[r][c - 1]\n return ans\n``` | 193 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
✔ Python3 Solution | 100% faster | O(n * n) | increment-submatrices-by-one | 0 | 1 | # Complexity\n- Time complexity: $$O(n * n)$$\n- Space complexity: $$O(n * n)$$\n\n# Code\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n mat = [[0] * n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n mat[r1][c1] += 1\n if r2 + 1 < n: mat[r2 + 1][c1] -= 1\n if c2 + 1 < n: mat[r1][c2 + 1] -= 1\n if r2 + 1 < n and c2 + 1 < n: mat[r2 + 1][c2 + 1] += 1\n for i in range(n):\n for j in range(1, n):\n mat[i][j] += mat[i][j - 1]\n for i in range(1, n):\n for j in range(n):\n mat[i][j] += mat[i - 1][j]\n return mat\n``` | 9 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python 3] Sweep Line - Simple | increment-submatrices-by-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. 1-D sweep line\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n ans = [[0] * n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n for r in range(r1, r2 + 1):\n ans[r][c1] += 1\n if c2 + 1 < n: ans[r][c2 + 1] -= 1\n for r in range(n):\n for c in range(1, n):\n ans[r][c] += ans[r][c - 1]\n return ans\n```\n- TC: $$O(N^2 + NQ)$$\n- SC: $$O(1)$$ if not including space for answer\n\n2. 2-D Sweep line\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n ans = [[0] * n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n ans[r1][c1] += 1\n if r2 + 1 < n: ans[r2 + 1][c1] -= 1\n if c2 + 1 < n: ans[r1][c2 + 1] -= 1\n if r2 + 1 < n and c2 + 1 < n: ans[r2 + 1][c2 + 1] += 1\n for r in range(1, n):\n for c in range(n):\n ans[r][c] += ans[r - 1][c]\n for r in range(n):\n for c in range(1, n):\n ans[r][c] += ans[r][c - 1]\n return ans\n```\n- TC: $$O(N^2 + Q)$$\n- SC: $$O(1)$$ if not including space for answer | 4 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
Accepeted in Java but got TLE in C++ & Python !! | increment-submatrices-by-one | 1 | 1 | Java Brute Force Solution got accepted\n ```\nclass Solution {\n public int[][] rangeAddQueries(int n, int[][] queries) {\n int[][] mat = new int[n][n];\n for (int[] q : queries) {\n int row1 = q[0], col1 = q[1], row2 = q[2], col2 = q[3];\n for (int i = row1; i <= row2; i++) {\n for (int j = col1; j <= col2; j++) {\n mat[i][j]++;\n }\n }\n }\n return mat;\n }\n}\n```\n\nBut same C++ Solution gets Time Limit Exceeded on TestCase 18\n ```\nclass Solution {\npublic:\n vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {\n vector<vector<int>> mat(n, vector<int>(n, 0)) ;\n for (auto &q : queries) {\n int row1 = q[0], col1 = q[1], row2 = q[2], col2 = q[3];\n for (int i = row1; i <= row2; i++) {\n for (int j = col1; j <= col2; j++) {\n mat[i][j]++;\n }\n }\n }\n return mat;\n }\n};\n```\n\nPlease fix the issue as many participants got penalty because of this issue. | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
C++ and Python 70% Faster Code | Prefix Sum | Range Caching Behaviour | increment-submatrices-by-one | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nPrefix Sum\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**C++ Solution:-**\n```\nclass Solution {\npublic:\n vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {\n vector<vector<int>> mat(n, vector<int>(n,0));\n for(auto &it:queries) {\n int r1 = it[0];\n int c1 = it[1];\n int r2 = it[2];\n int c2 = it[3];\n for(int i=r1; i<=r2; i++) {\n mat[i][c1] += 1;\n if(c2+1<n) mat[i][c2+1] -= 1;\n }\n }\n for(int r=0; r<n; r++) {\n for(int c=1; c<n; c++) {\n mat[r][c] += mat[r][c-1];\n }\n }\n return mat;\n }\n};\n```\n**Python Solution:-**\n```\nclass Solution:\n def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:\n mat = [[0]*n for _ in range(n)]\n for r1, c1, r2, c2 in queries:\n for r in range(r1, r2+1):\n mat[r][c1] += 1\n if c2+1 < n:\n mat[r][c2+1] -= 1\n for row in range(n):\n for col in range(1, n):\n mat[row][col] += mat[row][col-1]\n return mat\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
[Python] Evolving Linear-time Sweep (3 Approaches), The Best | increment-submatrices-by-one | 0 | 1 | # Intuition\nApproach 1: Sort the queries, then for each result row scan the queries and maintain a min-heap of query right columns. This puts the solution in slowest 5%, narrowly avoiding TLE.\n\nApproach 2: Get rid of sorting and min-heap, and instead scan the queries for each row, adding $$1$$ at left column and $$-1$$ after right column. Then, recreate the result of previous approach by scanning each row. This puts the solution at roughly top 33%\u201350% running time.\n\nApproach 3: Instead of scanning queries per row, scan them once, adding $$1$$ at first row and $$-1$$ below last row. Then, recreate the prerequisites of previous approach by scanning each column. This puts the solution at top 5% running time.\n\nFinal variation: Compactify code lines a bit at some expense of running time. :)\n\nThe Best!\n\n# Complexity\n- Time complexity: $$O(n^2+m)$$\n- Space complexity: $$O(1)$$ extra space\n\n# Code\nApproach 1: $$O(n^2+nm\\log m)$$ / $$O(m)$$\n```py\ndef rangeAddQueries(self, n: int, queries: list[list[int]]) -> list[list[int]]:\n queries.sort(key=lambda q: q[1])\n res, qlen = [[0]*n for row in range(n)], len(queries)\n for row in range(n):\n ends, qidx = [], 0\n for col in range(n):\n while qidx < qlen and col == queries[qidx][1]:\n (r1, c1, r2, c2), qidx = queries[qidx], qidx+1\n if r1 <= row <= r2:\n heapq.heappush(ends, c2)\n while ends and col > ends[0]:\n heapq.heappop(ends)\n res[row][col] = len(ends)\n return res\n```\n\nApproach 2: $$O(n^2 + nm)$$ / $$O(1)$$\n```py\ndef rangeAddQueries(self, n: int, queries: list[list[int]]) -> list[list[int]]:\n res = [[0]*n for row in range(n)]\n for r1, c1, r2, c2 in queries:\n for row in range(r1, r2+1):\n res[row][c1] += 1\n if c2 != n-1:\n for row in range(r1, r2+1):\n res[row][c2+1] -= 1\n for row in range(n):\n ins = 0\n for col in range(n):\n res[row][col] = ins = ins + res[row][col]\n return res\n```\n\nApproach 3: $$O(n^2+m)$$ / $$O(1)$$\n```py\ndef rangeAddQueries(self, n: int, queries: list[list[int]]) -> list[list[int]]:\n res = [[0]*n for row in range(n)]\n for r1, c1, r2, c2 in queries:\n res[r1][c1] += 1\n if c2 != n-1:\n res[r1][c2+1] -= 1\n if r2 != n-1:\n res[r2+1][c1] -= 1\n if c2 != n-1:\n res[r2+1][c2+1] += 1\n for row in range(n):\n for col in range(n):\n res[row][col] += res[row-1][col] if row else 0\n for row in range(n):\n for col in range(n):\n res[row][col] += res[row][col-1] if col else 0\n return res\n```\n\nFinal variation: $$O(n^2+m)$$ / $$O(1)$$\n```py\ndef rangeAddQueries(self, n: int, queries: list[list[int]]) -> list[list[int]]:\n res = [[0]*n for row in range(n)]\n for r1, c1, r2, c2 in queries:\n res[r1][c1] += 1\n res[r1][min(c2+1, n-1)] -= c2 != n-1\n res[min(r2+1, n-1)][c1] -= r2 != n-1\n res[min(r2+1, n-1)][min(c2+1, n-1)] += max(r2, c2) != n-1\n for row in range(n):\n for col in range(n):\n res[row][col] += res[row-1][col] if row else 0\n for row in range(n):\n for col in range(n):\n res[row][col] += res[row][col-1] if col else 0\n return res\n``` | 1 | You are given a positive integer `n`, indicating that we initially have an `n x n` **0-indexed** integer matrix `mat` filled with zeroes.
You are also given a 2D integer array `query`. For each `query[i] = [row1i, col1i, row2i, col2i]`, you should do the following operation:
* Add `1` to **every element** in the submatrix with the **top left** corner `(row1i, col1i)` and the **bottom right** corner `(row2i, col2i)`. That is, add `1` to `mat[x][y]` for all `row1i <= x <= row2i` and `col1i <= y <= col2i`.
Return _the matrix_ `mat` _after performing every query._
**Example 1:**
**Input:** n = 3, queries = \[\[1,1,2,2\],\[0,0,1,1\]\]
**Output:** \[\[1,1,0\],\[1,2,1\],\[0,1,1\]\]
**Explanation:** The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).
**Example 2:**
**Input:** n = 2, queries = \[\[0,0,1,1\]\]
**Output:** \[\[1,1\],\[1,1\]\]
**Explanation:** The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.
**Constraints:**
* `1 <= n <= 500`
* `1 <= queries.length <= 104`
* `0 <= row1i <= row2i < n`
* `0 <= col1i <= col2i < n` | null |
Very Short Python solution | Sliding Window | count-the-number-of-good-subarrays | 0 | 1 | ```\nclass Solution:\n def countGood(self, nums: List[int], k: int) -> int:\n res, cnt, l = 0, 0, 0\n hm = defaultdict(int)\n for r, v in enumerate(nums):\n hm[v] += 1\n cnt += hm[v] - 1\n while cnt >= k:\n hm[nums[l]] -= 1\n cnt -= hm[nums[l]]\n l += 1\n res += r - l + 1\n return (len(nums) + 1) * len(nums) // 2 - res\n \n``` | 1 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
detailed Intuition,concise solution and python | count-the-number-of-good-subarrays | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs my usual blogs i am partioning this blog into 3 parts\n1. prerequisites\n2. intuition\n3. code\n\n*Read as much as you want*\n#### prerequisites(optional)\n1. subsequences hold some properties which will be used in the solution, i mean what is wrong in learning new stuff.\nbut just 1 thing before we start - **subsequence is a sequence with some elements remove at any index**\nif we want to know unique comparisions in a sequence it is n(n+1)/2,you don\'t need to have a proof just create an array of size 4 you will get it or visit the solution attached below.\neach element when added into a sequence opens a possibilty of comparision with each element in the sequence with this element,if we consider that during the time of addition we are making these comparisions we are assured that last inserted element is already compared so if after insertion array size is n nth element must compare with n-1 elements.\n2. sliding window.\n# Intution\n<!-- Describe your approach to solving the problem. -->\nwe can expand a window size until we find pair_count>=k and start shrinking as soon pair_count increases k,as elements are allowed to make pair with elements of same value our window can have any number of elements in the left,right or in the middle of elments participating in pair formation till condition is met(pair_count>=k)\nTo check all these possibilities in one pass we can use sliding window.\ncondition:pair_count>=k\nour window can start from one edge of array and can expand until condition is met as soon as condition is met we can start shrinking the shrinking phase consist of two parts\n1. finding the ending index - if we observe we can generate new subsequences by keep on appending elements and each appended element generates a new sequence,the number of these sequences can be 1+ size of sequence - ending_index_of_window here 1 is the current sequence without appending any value as it is also valid it should also be added.\n2. now we start shrinking from starting end of window,here a thing worth consideration is that the element we have at starting may be just not the one corresponding to pair formation but will be the one corresponding to sequence generation each removed element will generate a sequance shifted left(a new sequence) we remove elements till we have enough pair to hold our condition we don\'t have to check the remaining pairs as we are doing in the case of last elements by adding just 1+ size of sequence - ending_index_of_window and never questioning why it should work.\n**here is a blog with examples** *https://leetcode.com/problems/count-the-number-of-good-subarrays/solutions/3055134/intuitive-sliding-window-o-n-python-solution/?languageTags=python*\nRest i will clear in comments section.\n# Code\n```\nclass Solution(object):\n def countGood(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n elements_in_current_window=dict()\n pair_count=0\n start=0\n end=0\n ans=0\n while(end<len(nums)):\n if(elements_in_current_window.has_key(nums[end])):\n elements_in_current_window[nums[end]]+=1 #incrementing \n else:\n elements_in_current_window[nums[end]]=1 #initializing entry in the dictionary\n pair_count+=elements_in_current_window[nums[end]]-1 #counting number of pairs\n while pair_count>=k: #The shrinking phase\n ans+=1+len(nums)-end-1 #the number of new sequences\n elements_in_current_window[nums[start]]-=1 #remove the element at the starting of the window\n pair_count-=elements_in_current_window[nums[start]]\n start+=1\n end+=1 \n return ans \n \n \n``` | 3 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
Python - 2 pointers with counting | count-the-number-of-good-subarrays | 0 | 1 | # Intuition\nJust count frequency, add up pairs, when enough account to result current plus everything after (if condition is met then adding every element one by one after are also solutions), then move left pointer until rule is broken and not enough pairs.\nRepeat this till end.\n\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfrom collections import Counter\n\nclass Solution:\n def countGood(self, A: List[int], k: int) -> int:\n N, count = len(A), Counter()\n L = result = pair_count = 0\n\n for i, v in enumerate(A):\n pair_count += count[v]\n count[v] += 1\n while L < i and pair_count >= k:\n result += N - i\n count[A[L]] -= 1\n pair_count -= count[A[L]]\n L += 1\n return result\n``` | 1 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
Python 3 || 11 lines, two pointers, dict || T/M: 689 ms / 31.7 MB | count-the-number-of-good-subarrays | 0 | 1 | Here\'s the plan:\n1. We increment`right` and use a dict `d` to keep track of the count of each integer in `nums[:right+1]`.\n2. Once the number of pairs reaches`k`, we add the count of subarrays with subarray `[right+1]`to`ans`].\n3. We increment`left`and adjust`d`. If we still have`k`pairs, we add a similar count to `ans`and increment `left`again. If not, we iterate`right`and start again.\n4. Once`right`iterates`nums`completely and`left`increments so that pairs are less than`k`, we return `ans`. \n```\nclass Solution:\n def countGood(self, nums: List[int], k: int) -> int:\n\n left = ans = tally = 0\n n, d = len(nums), defaultdict(int)\n\n for right,num in enumerate(nums): # <-- 1\n tally += d[num]\n d[num] += 1\n \n while tally >= k: # <-- 2 \n ans+= n - right\n d[nums[left]] -= 1 # <-- 3\n tally -= d[nums[left]]\n left += 1\n \n return ans # <-- 4\n```\n[https://leetcode.com/problems/count-the-number-of-good-subarrays/submissions/878498085/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is worst case *O*(*N*). | 10 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
Intuitive Sliding Window O(n) Python Solution | count-the-number-of-good-subarrays | 0 | 1 | ### Sliding Window\nEasy read on [LeetCode Weekly Contest Medium (Sliding Window) 2537. Count the Number of Good Subarrays \u2014 Hung, Chien-Hsiang | Blog (chienhsiang-hung.github.io)](https://chienhsiang-hung.github.io/blog/posts/2023/leetcode-weekly-contest-medium-sliding-window-2537.-count-the-number-of-good-subarrays/)\n\nIntuitive Sliding Window O(n) Python Solution \n\nDry run some examples with sliding window technique.\n\n\nNotice. You need to make sure the left most window, mid-window, and the right most window all collected. With the trend we found below:\n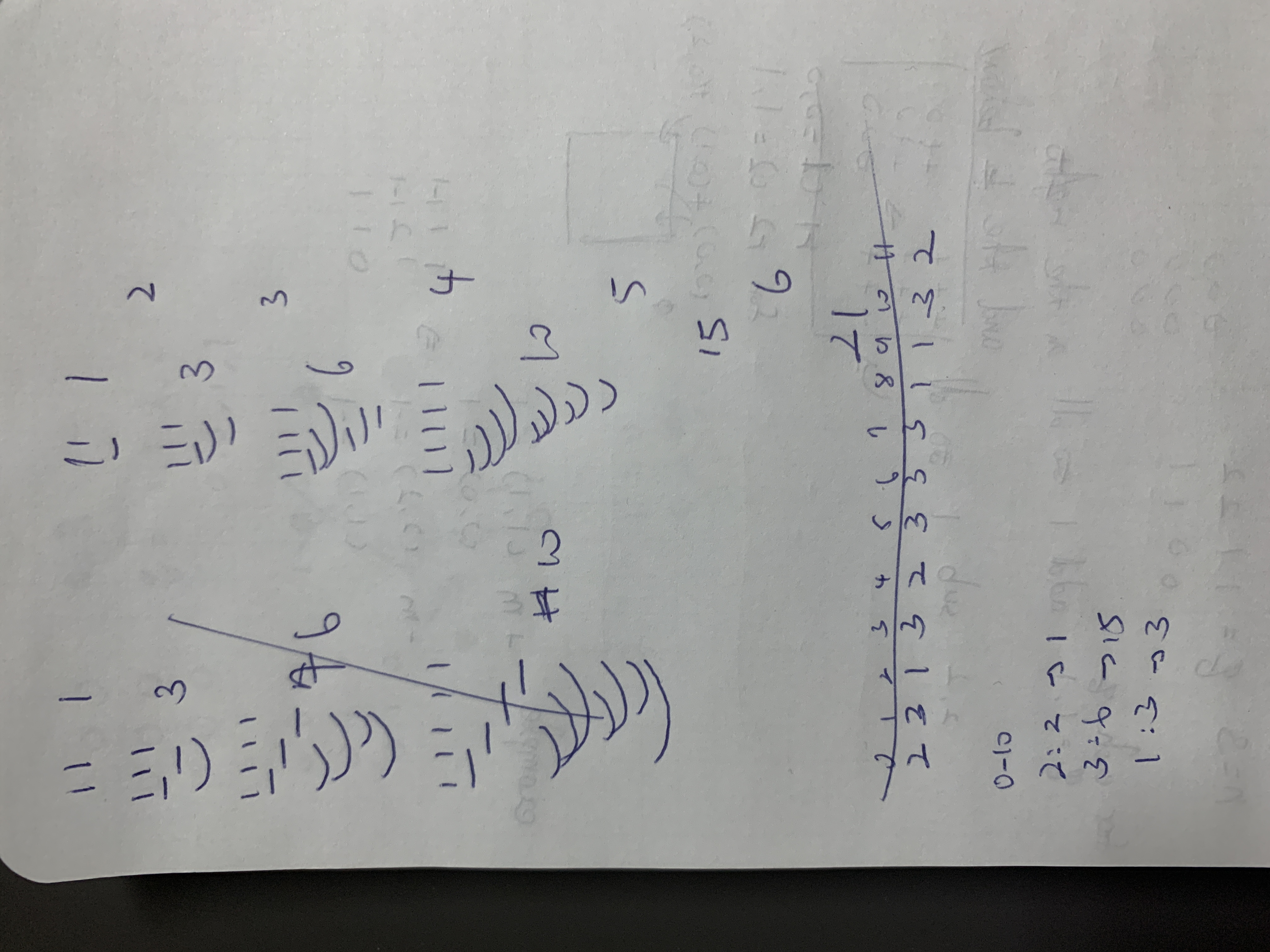\n\nCombine them to implement the solution.\n```python []\nclass Solution:\n def countGood(self, nums: List[int], k: int) -> int:\n right = left = 0\n window = defaultdict(int)\n pairs_count = defaultdict(int)\n ans = 0\n while left < len(nums)-1:\n # extend window\n if right < len(nums):\n window[nums[right]] += 1\n if window[nums[right]] >= 2:\n pairs_count[nums[right]] += window[nums[right]]-1\n\n while sum([v for v in pairs_count.values()]) >= k:\n ans += len(nums)-right if len(nums)-right else 1\n # shrink window\n window[nums[left]] -= 1\n if window[nums[left]] >= 1:\n pairs_count[nums[left]] -= window[nums[left]]\n left += 1\n continue\n\n if right < len(nums):\n right += 1\n else:\n left += 1\n return ans\n``` | 4 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
✔ Python3 Solution | 100% faster | Sliding Window | count-the-number-of-good-subarrays | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def countGood(self, A: List[int], k: int) -> int:\n D = defaultdict(int)\n ans = cnt = l = 0\n for i in A:\n cnt += D[i]\n D[i] += 1\n while cnt >= k:\n D[A[l]] -= 1\n cnt -= D[A[l]]\n l += 1\n ans += l\n return ans\n``` | 2 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
[Python3] sliding window | count-the-number-of-good-subarrays | 0 | 1 | \n```\nclass Solution:\n def countGood(self, nums: List[int], k: int) -> int:\n freq = Counter()\n ans = ii = total = 0 \n for x in nums: \n total += freq[x]\n freq[x] += 1\n while total >= k: \n freq[nums[ii]] -= 1\n total -= freq[nums[ii]]\n ii += 1\n ans += ii \n return ans \n``` | 4 | Given an integer array `nums` and an integer `k`, return _the number of **good** subarrays of_ `nums`.
A subarray `arr` is **good** if it there are **at least** `k` pairs of indices `(i, j)` such that `i < j` and `arr[i] == arr[j]`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], k = 10
**Output:** 1
**Explanation:** The only good subarray is the array nums itself.
**Example 2:**
**Input:** nums = \[3,1,4,3,2,2,4\], k = 2
**Output:** 4
**Explanation:** There are 4 different good subarrays:
- \[3,1,4,3,2,2\] that has 2 pairs.
- \[3,1,4,3,2,2,4\] that has 3 pairs.
- \[1,4,3,2,2,4\] that has 2 pairs.
- \[4,3,2,2,4\] that has 2 pairs.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i], k <= 109` | null |
damn just need one more line to get AK this week 😭 | difference-between-maximum-and-minimum-price-sum | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nuse dfs to build max price of each node\ndon\'t look at my code, its too complex and not elegant\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n n2n = defaultdict(set)\n for a, b in edges:\n n2n[a].add(b)\n n2n[b].add(a)\n \n nodeandway2path = dict()\n visited = set()\n \n \n def dfs1(node):\n rtn = 0\n for nxt in n2n[node]:\n if nxt not in visited:\n visited.add(nxt)\n maxprice = dfs1(nxt)\n nodeandway2path[(node, nxt)] = maxprice + price[node]\n rtn = max(rtn, maxprice)\n return rtn + price[node]\n \n visited.add(0) \n dfs1(0)\n \n visited = set()\n \n def dfs2(node, father):\n if father != None:\n maxfatherprice = price[father]\n for nxt in n2n[father]:\n if nxt != node:\n maxfatherprice = max(nodeandway2path[(father, nxt)], maxfatherprice)\n nodeandway2path[(node, father)] = maxfatherprice + price[node]\n for nxt in n2n[node]:\n if nxt not in visited:\n visited.add(nxt)\n dfs2(nxt, node)\n visited.add(0)\n dfs2(0, None)\n \n \n res = 0\n for node in range(n):\n maxprice = 0\n for nxt in n2n[node]:\n maxprice = max(nodeandway2path[(node, nxt)], maxprice)\n res = max(res, maxprice - price[node])\n return res\n \n``` | 1 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
[Python] 2 DFS | difference-between-maximum-and-minimum-price-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n # 1 <= price[i] <= 10^^5\n # min value is value of the root itself\n # find max value from the root to any leaf\n \n \n graph = defaultdict(list)\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n \n rtl = [[] for _ in range(n)]\n # first traversal to find the node to leaf path from each of the node (assume 0 is the root)\n def traverse1(node, parent):\n for nei in graph[node]:\n if nei == parent: continue\n traverse1(nei, node)\n \n child = rtl[nei][-1] # the max entry\n rtl[node].append(child + price[node])\n \n if not rtl[node]:\n rtl[node].append(price[node])\n \n rtl[node].sort()\n rtl[node] = rtl[node][-2:] # keep at most 2 entry, we dont need more\n \n traverse1(0, -1)\n \n ans = 0\n # second traversal to compute the result from the parent, max parent path that not going through the current node\n def traverse2(node, parent):\n if parent != -1:\n if len(rtl[parent]) == 1: # only 1 path\n rtl[node].append(price[parent] + price[node])\n else:\n if rtl[node][-1] + price[parent] == rtl[parent][-1]: # this is the longest path, we take the next longest\n rtl[node].append(rtl[parent][-2] + price[node])\n else:\n rtl[node].append(rtl[parent][-1] + price[node])\n \n rtl[node].sort()\n for nei in graph[node]:\n if nei == parent:\n continue\n \n traverse2(nei, node)\n \n traverse2(0, -1)\n return max(rtl[i][-1] - price[i] for i in range(n))\n \n \n \n \n \n``` | 1 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
[Python3] dfs | difference-between-maximum-and-minimum-price-sum | 0 | 1 | \n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n tree = [[] for _ in range(n)]\n for u, v in edges: \n tree[u].append(v)\n tree[v].append(u)\n \n def dfs(u, p): \n """Return """\n nonlocal ans\n include = [] # include leaf value \n exclude = [] # exclude leaf value\n for v in tree[u]:\n if v != p: \n x, y = dfs(v, u)\n include.append((x+price[u], v))\n exclude.append((y+price[u], v))\n if not include: \n include = [(price[u], u)]\n exclude = [(0, u)]\n if len(include) == 1: ans = max(ans, include[0][0] - price[u], exclude[0][0])\n else: \n include.sort(reverse=True)\n for e, v in exclude: \n if v != include[0][1]: cand = e + include[0][0] - price[u]\n else: cand = e + include[1][0] - price[u]\n ans = max(ans, cand)\n return include[0][0], max(exclude)[0]\n \n ans = 0 \n dfs(0, -1)\n return ans \n``` | 1 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
[Python] DFS traverse, similar to the maximum path sum problem; Explained | difference-between-maximum-and-minimum-price-sum | 0 | 1 | This problem is similar to the "maximum path sum" problem.\n\nWe pick any node, and DFS traverse the graph.\n\nFor each of the visiting node, we need to get **(1) the maximum path sum with the end node value; and (2) the maximum path sum without the end value**.\n\nSee the details in code:\n\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n # it is the same problem as the finding the maximum path sum of a tree\n \n # step 1, build the graph\n self.G = collections.defaultdict(list)\n for s, e in edges:\n self.G[s].append(e)\n self.G[e].append(s)\n\n self.visited = set()\n self.price = price\n self.ans = 0\n\n # step 2, start from a random node and DFS traverse the graph\n # the maximum path sum will be updated during the traversal, and we can\n # return the result after the traversal is done.\n self.dfs(0)\n \n # Since we are using the min heap to track the maximum, we need to return - self.ans\n return -self.ans\n\n \n def dfs(self, idx):\n self.visited.add(idx)\n\n ps_f_list, ps_p_list = [], []\n\n for nidx in self.G[idx]:\n # for each visiting child we need to get:\n # (1) the maximum path sum with the end node\n # (2) the maximum path sum without the end node\n # We are calculating the difference between maximum path sum and minimum path sum,\n # the price is always postive, therefore, the minimum path sum is always the root value. When we find a path sum, the maximum difference is the path sum - root value.\n # The root value can be at any end of this path.\n # Thus, we need to track two path sum: one is with the end node value, one is not.\n if nidx not in self.visited:\n ps_full, ps_partial = self.dfs(nidx)\n heapq.heappush(ps_f_list, (ps_full, nidx))\n heapq.heappush(ps_p_list, (ps_partial, nidx))\n\n max_val = 0\n if len(ps_f_list) == 1:\n ps_f_max, _ = heapq.heappop(ps_f_list)\n ps_p_max, _ = heapq.heappop(ps_p_list)\n max_val = min(ps_f_max, ps_p_max - self.price[idx])\n fp_max, pp_max = ps_f_max - self.price[idx], ps_p_max - self.price[idx]\n elif len(ps_f_list) > 1:\n ps_f_max, fm_idx = heapq.heappop(ps_f_list)\n ps_p_max, pm_idx = heapq.heappop(ps_p_list)\n if fm_idx != pm_idx:\n max_val = ps_f_max + ps_p_max - self.price[idx]\n fp_max, pp_max = ps_f_max - self.price[idx], ps_p_max - self.price[idx]\n else:\n # get the second bigest price\n ps_f_max_2, _ = heapq.heappop(ps_f_list)\n ps_p_max_2, _ = heapq.heappop(ps_p_list)\n max_val = min(ps_f_max + ps_p_max_2, ps_f_max_2 + ps_p_max) - self.price[idx]\n fp_max, pp_max = ps_f_max - self.price[idx], ps_p_max - self.price[idx]\n else:\n fp_max, pp_max = -self.price[idx], 0\n\n if max_val < self.ans:\n self.ans = max_val\n\n return fp_max, pp_max\n``` | 2 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
Python 3 || 14 lines dfs (updated) || T/M: 90 % / 100% | difference-between-maximum-and-minimum-price-sum | 0 | 1 | My original submission was weak, and with the recently added test case, it went TLE. The comment below (thank you [@user7784J](/user7784J)) included a link from which I got the idea for a better way to approach the problem.\n\nWe assign a three-uple`state`to each node. the root and each leaf gets `(0,price,0)`, and each other link\'s`state` is determined by the recurence relation in`dfs`. The figure below is for Example 1 in the problem\'s description.\n\nBest way to figure it out is to trace it from the recurence relation. The correct answer is`24`, which is `state[0]` for `node 1`. BTW, if you start from a root other than`0`, the `state` for some nodes may change, but the answer doesn\'t.\n\n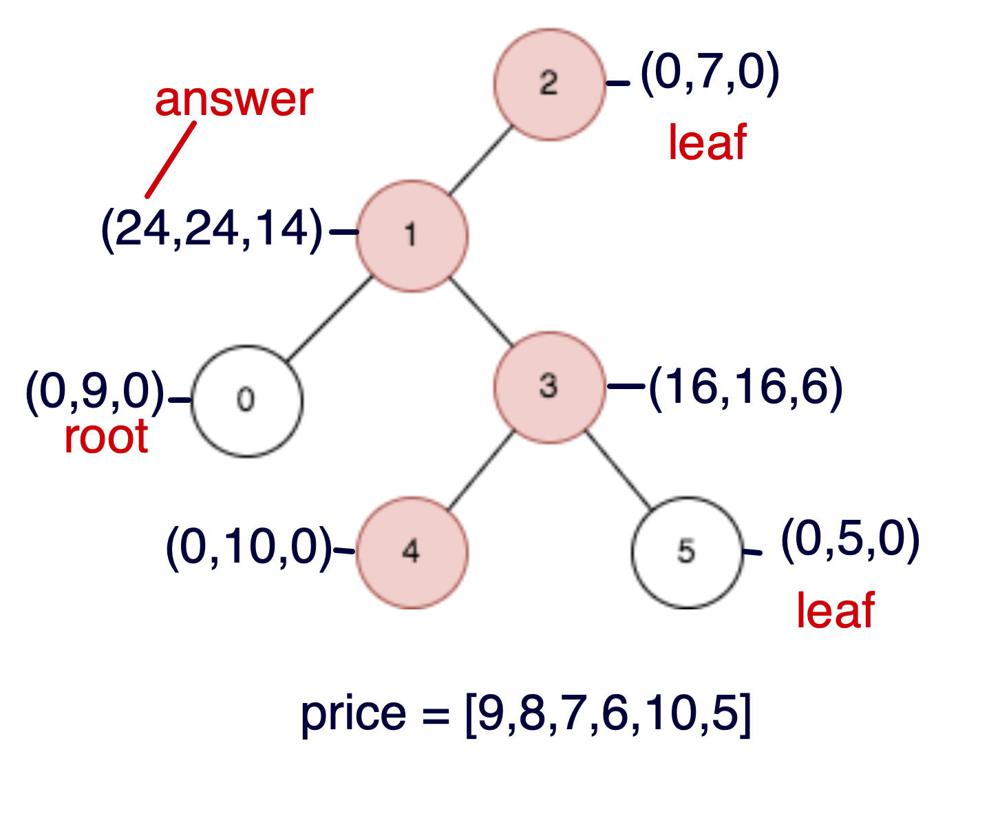\n\n\n\n\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n\n g = defaultdict(list)\n for a, b in edges: g[a].append(b) ; g[b].append(a)\n\n def dfs(node1, node2 =-1):\n p = price[node1]\n state = (0, p, 0)\n\n for n in g[node1]:\n if n == node2: continue\n\n (a1, a2, a3), (b1, b2, b3) = state, dfs(n, node1)\n \n state = (max(a1, b1, a2 + b3, a3 + b2),\n max(a2, b2 + p),\n max(a3, b3 + p))\n\n return state\n\n if n <= 2: return sum(price) - min(price)\n\n for node in range(n):\n if len(g[node]) > 1:\n return dfs(node)[0]\n\n```\n[https://leetcode.com/problems/difference-between-maximum-and-minimum-price-sum/submissions/880805710/]()\n```\n```\nOriginal post: \n\nI think this might be computing things twice (once each way); if so, I might work on it a little more later. Right now it barely squeaks through.\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n \n g = defaultdict(set) # construct the graph\n for a, b in edges: g[a].add(b) ; g[b].add(a)\n\n @lru_cache(None)\n def dfs(node1, node2): # recurse the tree node1 to node2\n\n return max((dfs(n, node1) for n in g[node1]\n if n != node2), default = 0) + price[node1]\n\n return max(dfs(node, -1) - price[node] for node in range(n)) \n # eval each node as root for max answer \n```\n[https://leetcode.com/problems/difference-between-maximum-and-minimum-price-sum/submissions/878829009/](http://)\n\n\n\n\n\nI think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*), but I\'m usually wrong when it comes to recursion. | 3 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
✅ 🔥 O(n) Python3 || ⚡ solution | difference-between-maximum-and-minimum-price-sum | 0 | 1 | ```\nfrom typing import List\nfrom collections import defaultdict\n\n\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n graph = defaultdict(list)\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n\n def dfs(node, parent=-1):\n current_price = price[node]\n max_output = (0, current_price, 0)\n\n for neighbor in graph[node]:\n if neighbor == parent:\n continue\n\n neighbor_output = dfs(neighbor, node)\n combined_output = (\n max(\n max_output[0],\n neighbor_output[0],\n max_output[1] + neighbor_output[2],\n max_output[2] + neighbor_output[1],\n ),\n max(max_output[1], neighbor_output[1] + current_price),\n max(max_output[2], neighbor_output[2] + current_price),\n )\n\n max_output = combined_output\n\n return max_output\n\n if n <= 2:\n return sum(price) - min(price)\n\n for node in range(n):\n if len(graph[node]) > 1:\n return dfs(node)[0]\n\n``` | 1 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
Very simple DFS + DP Explained | difference-between-maximum-and-minimum-price-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAssuming any of the nodes can be root, we will check for each node.\nFor any node:\n Mininum sum= node.val (as -ve numbers are not present)\n Maximum sum= node.val + max of all the paths through children ie. Maximum Sum (child) \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThe tree can be though of as an undirected graph, with no cycle (only 2-way parent child relationship). We can create an adjacency list using the edges.\n\nWe can calculate the maximum sum recursively through DFS.\nBut as this DFS will be called for each nodes, so the time comlexity will increase to O(n)*TC(DFS)=O(n)*O(n)\n\nTo reduce this, we can use caching or DP Memoization as there will be repeated subproblems. This will bring down the time complexity to O(n)\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:\n #DP+DFS\n adj_list=collections.defaultdict(list)\n for x,y in edges:\n adj_list[x].append(y)\n adj_list[y].append(x)\n \n dp={}\n def dfs(node,par)->int:\n if (node,par) in dp:\n return dp[(node,par)]\n \n sumC=0\n for child in adj_list[node]:\n if child!=par:\n sumC=max(sumC,dfs(child,node))\n dp[(node,par)]=sumC+price[node]\n return dp[(node,par)]\n \n cost=0 \n for key in adj_list:\n maxV=dfs(key,-1)\n minV=price[key]\n cost=max(cost,maxV-minV)\n return cost\n \n```\n\nPlease UPVOTE if this post helps.\n | 2 | There exists an undirected and initially unrooted tree with `n` nodes indexed from `0` to `n - 1`. You are given the integer `n` and a 2D integer array `edges` of length `n - 1`, where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Each node has an associated price. You are given an integer array `price`, where `price[i]` is the price of the `ith` node.
The **price sum** of a given path is the sum of the prices of all nodes lying on that path.
The tree can be rooted at any node `root` of your choice. The incurred **cost** after choosing `root` is the difference between the maximum and minimum **price sum** amongst all paths starting at `root`.
Return _the **maximum** possible **cost**_ _amongst all possible root choices_.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[1,2\],\[1,3\],\[3,4\],\[3,5\]\], price = \[9,8,7,6,10,5\]
**Output:** 24
**Explanation:** The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[2,1,3,4\]: the prices are \[7,8,6,10\], and the sum of the prices is 31.
- The second path contains the node \[2\] with the price \[7\].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1\],\[1,2\]\], price = \[1,1,1\]
**Output:** 2
**Explanation:** The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes \[0,1,2\]: the prices are \[1,1,1\], and the sum of the prices is 3.
- The second path contains node \[0\] with a price \[1\].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.
**Constraints:**
* `1 <= n <= 105`
* `edges.length == n - 1`
* `0 <= ai, bi <= n - 1`
* `edges` represents a valid tree.
* `price.length == n`
* `1 <= price[i] <= 105` | null |
✅ Explained - Simple and Clear Python3 Code✅ | minimum-common-value | 0 | 1 | # Intuition\nThe intuition behind the solution is that since the arrays are sorted in non-decreasing order, the minimum common integer must be the smallest value that appears in both arrays. Therefore, by comparing the first elements of both arrays, we can determine if they are equal, smaller in nums1, or smaller in nums2, and accordingly, we can move the pointers to the next elements in the respective arrays.\n\n\n# Approach\nThe solution iterates over the arrays using a while loop, and as long as both arrays have elements remaining, it compares the first elements of both arrays. If they are equal, it means that the minimum common integer has been found, so it is returned. If the element in nums1 is smaller, it means that the minimum common integer must be greater than that element, so the pointer in nums1 is moved to the next element. Similarly, if the element in nums2 is smaller, the pointer in nums2 is moved to the next element. If the loop finishes without finding a common integer, it means that there is no common integer, so -1 is returned.\n\n\n# Complexity\n- Time complexity:\nThe time complexity of the solution is determined by the length of the shorter array between nums1 and nums2. In the worst case, the while loop will iterate until one of the arrays is exhausted. Therefore, the time complexity is O(min(N, M)), where N and M are the lengths of nums1 and nums2, respectively.\n\n\n- Space complexity:\nThe space complexity of the solution is O(1) since it only uses a constant amount of additional space to store the indices and temporary variables for comparisons.\n\n\n\n\n\n# Code\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n while len(nums1)>0 and len(nums2)>0:\n if nums1[0]==nums2[0]:\n return nums1[0]\n elif nums1[0]<nums2[0]:\n nums1.pop(0)\n else:\n nums2.pop(0)\n return -1\n``` | 5 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Simplest Python two-liner | minimum-common-value | 0 | 1 | # Code\n```\nclass Solution(object):\n def getCommon(self, nums1, nums2):\n st = set(nums1) & set(nums2)\n return min(st) if len(st) else -1\n```\nWe can also return a one liner solution just for fun which is basically the same code:\n```\nclass Solution(object):\n def getCommon(self, nums1, nums2):\n return min(set(nums1) & set(nums2)) if len(set(nums1) & set(nums2)) else -1\n``` | 1 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
[C++|Java|Python3] 2-pointer | minimum-common-value | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7c339707e031611c80809107e7a667b2c6b6f7f0) for solutions of biweekly 96. \n\n**C++**\n```\nclass Solution {\npublic:\n int getCommon(vector<int>& nums1, vector<int>& nums2) {\n for (int i = 0, ii = 0; i < nums1.size() && ii < nums2.size(); ) {\n if (nums1[i] < nums2[ii]) ++i; \n else if (nums1[i] == nums2[ii]) return nums1[i]; \n else ++ii; \n }\n return -1; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int getCommon(int[] nums1, int[] nums2) {\n for (int i = 0, ii = 0; i < nums1.length && ii < nums2.length; ) {\n if (nums1[i] < nums2[ii]) ++i;\n else if (nums1[i] == nums2[ii]) return nums1[i]; \n else ++ii; \n }\n return -1; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n i = ii = 0 \n while i < len(nums1) and ii < len(nums2): \n if nums1[i] < nums2[ii]: i += 1\n elif nums1[i] == nums2[ii]: return nums1[i]\n else: ii += 1\n return -1 \n``` | 2 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Python | Easy Solution✅ | minimum-common-value | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n nums1, nums2 = set(nums1), set(nums2)\n common = sorted(list(nums1.intersection(nums2))) # sorted(list(nums1 & nums2)) will also work\n return -1 if not len(common) else common[0]\n \n``` | 5 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Python 3 || 5 lines, loop and ptr, w/ example || T/M: 98% / 95% | minimum-common-value | 0 | 1 | My first thought was`sets`, but now I see that also was true for most of you, so here\'s my second thought.\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n\n i, len2 = 0, len(nums2) # Example: nums1 = [ 2, 4, 8, 13] \n for n1 in nums1: # nums2 = [1, 1, 3, 6, 8, 9]\n \n while i < len2 and nums2[i] < n1: i += 1 # n1 nums2[i]\n # \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \n if i < len2 and n1 == nums2[i]: return n1 # 2 1\n # 1 \n return -1 # 3 <-- 2 < 3\n # 4 3\n # 6 <-- 4 < 6\n # 8 6\n # 8 <-- return 8\n```\n[https://leetcode.com/problems/minimum-common-value/submissions/882567303/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1). | 5 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Fastest beats 100% | minimum-common-value | 0 | 1 | # Upvote it :)\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n n = set(nums1).intersection(set(nums2))\n return min(n) if n else -1\n``` | 4 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.