title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
BEATS 95.59% OF USERS || BEGINNER FRIENDLY APPROACH 🔥🔥🔥✅✅✅ | minimum-common-value | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBy converting the given list into set and finding intersection we could find all common elements, and then by using min function we could find the minimum value and solve this problem.\n\n\n\n# Code\n```\n\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n snum1=set(nums1)\n snum2=set(nums2)\n try:\n return min(snum1.intersection(snum2))\n except ValueError:\n return -1\n```\n\n | 3 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Beat 97.56% 443ms Set Operation | minimum-common-value | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n if max(nums1) < min(nums2): return -1\n else:\n return min(set(nums1) & set(nums2)) if(set(nums1) & set(nums2)) else -1\n``` | 1 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
[ Python ] ✅✅ Simple Python Solution Using Binary Search🥳✌👍 | minimum-common-value | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 2298 ms, faster than 12.50% of Python3 online submissions for Minimum Common Value.\n# Memory Usage: 32.4 MB, less than 100.00% of Python3 online submissions for Minimum Common Value.\n\n\tclass Solution:\n\t\tdef getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n\n\t\t\tdef BinarySearch(start, end, target):\n\n\t\t\t\twhile start <= end:\n\n\t\t\t\t\tmid = (start + end) // 2\n\n\t\t\t\t\tif target == nums2[mid]:\n\t\t\t\t\t\treturn True\n\t\t\t\t\telif nums2[mid] < target:\n\t\t\t\t\t\tstart = mid + 1\n\t\t\t\t\telse:\n\t\t\t\t\t\tend = mid - 1\n\n\t\t\t\treturn False\n\n\t\t\tstart = 0\n\t\t\tend = len(nums2)\n\n\t\t\tfor num in nums1:\n\n\t\t\t\tif BinarySearch(start, end, num) == True:\n\t\t\t\t\treturn num\n\n\t\t\treturn -1\n\t\t\t\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 1 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
[Python] Two Pointers ✅ | minimum-common-value | 0 | 1 | # Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n\n l, r = 0, 0\n\n while l < len(nums1) and r < len(nums2):\n if nums1[l] < nums2[r]:\n l += 1\n elif nums1[l] > nums2[r]:\n r += 1\n else:\n return nums1[l]\n \n return -1\n``` | 1 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
[Python3] - Two Pointer + Binary Search - easy to understand | minimum-common-value | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTwo arrays are sorted, so we can just compare two like merge function in merge sort to find the min similar number start from the left\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nmaintain 2 pointer and do binary search with it\n\n# Complexity\n- Time complexity: $$O(m + n)$$ - m, n are length of nums1, nums2, respectively.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n i, j = 0, 0\n while i < len(nums1) and j < len(nums2):\n if nums1[i] == nums2[j]:\n return nums1[i]\n if nums1[i] < nums2[j]:\n i += 1\n else:\n j += 1\n return -1\n``` | 4 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Python3 one-liner + Rust three-liner O(n) | minimum-common-value | 0 | 1 | # Approach\nCreate sets of `nums1` and `nums2`, get the intersection and get the minimum of this set. If the intersection is empty return the default -1.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n## Python3\nRuntime 457 ms\n```\nclass Solution:\n def getCommon(self, nums1: List[int], nums2: List[int]) -> int:\n return min(set(nums1) & set(nums2), default=-1)\n```\n\n## Rust\nRuntime 16 ms\n```\nuse std::collections::HashSet;\nimpl Solution {\n pub fn get_common(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {\n let nums1: HashSet<_> = nums1.into_iter().collect();\n let nums2: HashSet<_> = nums2.into_iter().collect();\n *nums1.intersection(&nums2).min().unwrap_or(&-1)\n }\n}\n```\n | 2 | Given two integer arrays `nums1` and `nums2`, sorted in non-decreasing order, return _the **minimum integer common** to both arrays_. If there is no common integer amongst `nums1` and `nums2`, return `-1`.
Note that an integer is said to be **common** to `nums1` and `nums2` if both arrays have **at least one** occurrence of that integer.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4\]
**Output:** 2
**Explanation:** The smallest element common to both arrays is 2, so we return 2.
**Example 2:**
**Input:** nums1 = \[1,2,3,6\], nums2 = \[2,3,4,5\]
**Output:** 2
**Explanation:** There are two common elements in the array 2 and 3 out of which 2 is the smallest, so 2 is returned.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 105`
* `1 <= nums1[i], nums2[j] <= 109`
* Both `nums1` and `nums2` are sorted in **non-decreasing** order. | null |
Python - simple greedy one linear run | minimum-operations-to-make-array-equal-ii | 0 | 1 | # Intuition\nFind equilibrum if possible following 3 simple rules:\n1. If k is 0, then difference between all positions in nums1 and nums2 should 0, no steps needed.\n2. If any position diference is not divisible with k then it is not possbile to level up with k size increase or decrease work.\n3. to reach equilibrum, sum of all diferences should be zero.\nIf all these passes sum up positive difference divided by k, this is amount of steps need to reach equilibrum.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n s = result = 0\n for a, b in zip(nums1, nums2):\n if k == 0: \n if a-b: return -1\n elif abs(a-b) % k != 0: return -1\n else:\n s += a-b\n if a-b > 0: result += (a-b) // k\n\n return -1 if s != 0 else result\n``` | 1 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
[Java/Python 3] Modulos and balance check w/ brief explanation and analysis. | minimum-operations-to-make-array-equal-ii | 1 | 1 | \n1. Traverse `nums1` and `nums2` and check if each of the corresponding difference is divisible by `k`; If not, impossible to make the two arrays equal; \n2. If yes, accumulate the difference to `bal`, which will be `0` after traversal if it is possible to make the two arrays equal;\n3. Accumulate the times of the positive difference of `k`, and return it if `bal == 0`.\n\n```java\n public long minOperations(int[] nums1, int[] nums2, int k) {\n if (k == 0) {\n return Arrays.equals(nums1, nums2) ? 0 : -1;\n }\n long ops = 0, bal = 0;\n for (int i = 0; i < nums1.length; ++i) {\n int diff = nums1[i] - nums2[i];\n if (diff % k != 0) {\n return -1;\n }\n if (diff > 0) {\n ops += diff / k;\n }\n bal += diff;\n } \n return bal == 0 ? ops : -1; \n }\n```\n```python\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n if k == 0:\n return 0 if nums1 == nums2 else -1\n ops = bal = 0\n for a, b in zip(nums1, nums2):\n if (a - b) % k != 0:\n return -1\n bal += a - b\n if a > b:\n ops += (a - b) // k\n return ops if bal == 0 else -1 \n```\n\n**Analysis**\n\nTime: `O(n)`, space: `O(1)`. | 26 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
[C++|Java|Python3] difference | minimum-operations-to-make-array-equal-ii | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7c339707e031611c80809107e7a667b2c6b6f7f0) for solutions of biweekly 96. \n\n**C++**\n```\nclass Solution {\npublic:\n long long minOperations(vector<int>& nums1, vector<int>& nums2, int k) {\n long long ans = 0, total = 0; \n for (int i = 0; i < nums1.size(); ++i) {\n int diff = nums1[i] - nums2[i]; \n if (k == 0 && diff || k && diff % k) return -1; \n if (k) ans += abs(diff) / k; \n total += diff; \n }\n return total == 0 ? ans/2 : -1; \n }\n}; \n```\n**Java**\n```\nclass Solution {\n public long minOperations(int[] nums1, int[] nums2, int k) {\n long ans = 0, total = 0; \n for (int i = 0; i < nums1.length; ++i) {\n int diff = nums1[i] - nums2[i]; \n if (k == 0 && diff > 0 || k > 0 && diff % k != 0) return -1; \n if (k > 0) ans += Math.abs(diff) / k; \n total += diff; \n }\n return total == 0 ? ans/2 : -1; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n ans = total = 0 \n for x, y in zip(nums1, nums2): \n diff = x-y\n if k == 0 and diff or k and abs(diff) % k: return -1 \n if k: ans += abs(diff)//k\n total += diff\n return ans//2 if total == 0 else -1 \n``` | 2 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
🔥Python3🔥Very EASY Solution | minimum-operations-to-make-array-equal-ii | 0 | 1 | - Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n s=0\n c=0\n if k==0:\n if nums1==nums2:\n return 0\n return -1\n for i in range(len(nums1)):\n if abs(nums1[i]-nums2[i])%k!=0:\n return -1\n if nums1[i]>nums2[i]:\n c+=abs(nums1[i]-nums2[i])\n else:\n s+=abs(nums1[i]-nums2[i])\n if s!=c:\n return -1\n return s//k\n \n \n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 9 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
✅ Python| One iteration. | minimum-operations-to-make-array-equal-ii | 0 | 1 | Check if the sum of the elements in nums1 is equal to the sum of the elements in nums2, and if not, return -1.\n\nThe approach is to iterate through the elements of nums1 and nums2 in parallel using the zip function and check if the absolute difference between the elements is divisible by k, and add to count. If it is not, return -1.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$ \n\n# Code\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n if sum(nums1) != sum(nums2): \n return -1\n count = 0\n for num1, num2 in zip(nums1, nums2):\n if k == 0:\n if num1 != num2: \n return -1 \n else:\n if abs(num1 - num2) % k: \n return -1\n else:\n count += abs(num1 - num2) // k\n return count //2\n \n \n``` | 1 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
Python | O(n) | [EXPLAINED] | minimum-operations-to-make-array-equal-ii | 0 | 1 | # Approach\n- We can modify one array while keeping the other one same.\n- But here won\'t modify any array just simulate the modification and count number of operations.\n- Suppose we will modify second array to convert it into first one.\n- Iterate through the array and find difference between elements at i<sup>th</sup> position in both arrays.\n- This difference should be divisible by k, if it is not then conversion is not possible.\n- simultaneously we will maintain two variables for increment `p` and for decrement `m`.\n- Accordingly for each element we will update `p` and `m` variables.\n- now according to the question we will perform both increment and decrement in one operation, that means values of `p` and `m` should be equal.\n- If it is equal then return (p+m)/2\n- Else it is not possible, return -1.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums1: List[int], nums2: List[int], k: int) -> int:\n if k == 0:\n if nums1 == nums2:\n return 0\n else:\n return -1\n \n p = m = 0\n for i in range(len(nums1)):\n if abs(nums1[i]-nums2[i])%k==0:\n if nums1[i]>nums2[i]:\n p += (abs(nums1[i]-nums2[i])//k)\n elif nums1[i]<nums2[i]:\n m += (abs(nums1[i]-nums2[i])//k)\n else:\n continue\n else:\n return -1\n \n if p == m:\n return (p+m)//2\n else:\n return -1\n```\n-------------------------\n**Upvote the post if you find it helpful.\nHappy coding.** | 1 | You are given two integer arrays `nums1` and `nums2` of equal length `n` and an integer `k`. You can perform the following operation on `nums1`:
* Choose two indexes `i` and `j` and increment `nums1[i]` by `k` and decrement `nums1[j]` by `k`. In other words, `nums1[i] = nums1[i] + k` and `nums1[j] = nums1[j] - k`.
`nums1` is said to be **equal** to `nums2` if for all indices `i` such that `0 <= i < n`, `nums1[i] == nums2[i]`.
Return _the **minimum** number of operations required to make_ `nums1` _equal to_ `nums2`. If it is impossible to make them equal, return `-1`.
**Example 1:**
**Input:** nums1 = \[4,3,1,4\], nums2 = \[1,3,7,1\], k = 3
**Output:** 2
**Explanation:** In 2 operations, we can transform nums1 to nums2.
1st operation: i = 2, j = 0. After applying the operation, nums1 = \[1,3,4,4\].
2nd operation: i = 2, j = 3. After applying the operation, nums1 = \[1,3,7,1\].
One can prove that it is impossible to make arrays equal in fewer operations.
**Example 2:**
**Input:** nums1 = \[3,8,5,2\], nums2 = \[2,4,1,6\], k = 1
**Output:** -1
**Explanation:** It can be proved that it is impossible to make the two arrays equal.
**Constraints:**
* `n == nums1.length == nums2.length`
* `2 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 109`
* `0 <= k <= 105` | null |
EASY PYTHON SOLN USING SORTING AND HEAP SORT | maximum-subsequence-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def maxScore(self, nums1: List[int], nums2: List[int], k: int) -> int:\n lst=list(zip(nums2,nums1))\n lst.sort(key=lambda x:(-x[0],-x[1]))\n flst=[]\n heapq.heapify(flst)\n i=0\n sm=0\n ef=float("infinity")\n prd=float("-infinity")\n while i<k:\n x=lst.pop(0)\n heapq.heappush(flst,x[1])\n ef=min(ef,x[0])\n sm+=x[1]\n i+=1\n prd=max(prd,sm*ef)\n while lst:\n x=heapq.heappop(flst)\n sm-=x\n y=lst.pop(0)\n heapq.heappush(flst,y[1])\n ef=min(ef,y[0])\n sm+=y[1]\n prd=max(prd,sm*ef)\n return prd\n\n``` | 1 | You are given two **0-indexed** integer arrays `nums1` and `nums2` of equal length `n` and a positive integer `k`. You must choose a **subsequence** of indices from `nums1` of length `k`.
For chosen indices `i0`, `i1`, ..., `ik - 1`, your **score** is defined as:
* The sum of the selected elements from `nums1` multiplied with the **minimum** of the selected elements from `nums2`.
* It can defined simply as: `(nums1[i0] + nums1[i1] +...+ nums1[ik - 1]) * min(nums2[i0] , nums2[i1], ... ,nums2[ik - 1])`.
Return _the **maximum** possible score._
A **subsequence** of indices of an array is a set that can be derived from the set `{0, 1, ..., n-1}` by deleting some or no elements.
**Example 1:**
**Input:** nums1 = \[1,3,3,2\], nums2 = \[2,1,3,4\], k = 3
**Output:** 12
**Explanation:**
The four possible subsequence scores are:
- We choose the indices 0, 1, and 2 with score = (1+3+3) \* min(2,1,3) = 7.
- We choose the indices 0, 1, and 3 with score = (1+3+2) \* min(2,1,4) = 6.
- We choose the indices 0, 2, and 3 with score = (1+3+2) \* min(2,3,4) = 12.
- We choose the indices 1, 2, and 3 with score = (3+3+2) \* min(1,3,4) = 8.
Therefore, we return the max score, which is 12.
**Example 2:**
**Input:** nums1 = \[4,2,3,1,1\], nums2 = \[7,5,10,9,6\], k = 1
**Output:** 30
**Explanation:**
Choosing index 2 is optimal: nums1\[2\] \* nums2\[2\] = 3 \* 10 = 30 is the maximum possible score.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 105`
* `1 <= k <= n` | null |
[Python3] Heap + similar questions || beats 94% || 810ms | maximum-subsequence-score | 0 | 1 | ```\nclass Solution:\n def maxScore(self, nums1: List[int], nums2: List[int], k: int) -> int:\n res, prefixSum, minHeap = 0, 0, []\n \n for a, b in sorted(list(zip(nums1, nums2)), key=itemgetter(1), reverse=True):\n prefixSum += a\n heappush(minHeap, a)\n if len(minHeap) == k:\n res = max(res, prefixSum * b)\n prefixSum -= heappop(minHeap) \n \n return res\n```\n\n\n## Similar questions:\n[857. Minimum Cost to Hire K Workers](https://leetcode.com/problems/minimum-cost-to-hire-k-workers/description/)\n\n```\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n res, qualitySum, maxHeap = float(\'inf\'), 0, []\n\n for ration, q in sorted([(w / q, q) for w, q in zip(wage, quality)]):\n qualitySum += q\n heappush(maxHeap, -q)\n if len(maxHeap) == k:\n res = min(res, qualitySum * ration)\n qualitySum -= -heappop(maxHeap)\n \n return res\n```\n[1383. Maximum Performance of a Team](https://leetcode.com/problems/maximum-performance-of-a-team/description/)\n\n```\nclass Solution:\n def maxPerformance(self, n: int, speed: List[int], efficiency: List[int], k: int) -> int:\n res, speedSum, minHeap = 0, 0, []\n \n for ef, sp in sorted(zip(efficiency, speed), reverse=True):\n speedSum += sp\n heappush(minHeap, sp)\n res = max(res, speedSum * ef)\n if len(minHeap) == k:\n speedSum -= heappop(minHeap)\n \n return res % (10**9 + 7)\n```\n\n | 29 | You are given two **0-indexed** integer arrays `nums1` and `nums2` of equal length `n` and a positive integer `k`. You must choose a **subsequence** of indices from `nums1` of length `k`.
For chosen indices `i0`, `i1`, ..., `ik - 1`, your **score** is defined as:
* The sum of the selected elements from `nums1` multiplied with the **minimum** of the selected elements from `nums2`.
* It can defined simply as: `(nums1[i0] + nums1[i1] +...+ nums1[ik - 1]) * min(nums2[i0] , nums2[i1], ... ,nums2[ik - 1])`.
Return _the **maximum** possible score._
A **subsequence** of indices of an array is a set that can be derived from the set `{0, 1, ..., n-1}` by deleting some or no elements.
**Example 1:**
**Input:** nums1 = \[1,3,3,2\], nums2 = \[2,1,3,4\], k = 3
**Output:** 12
**Explanation:**
The four possible subsequence scores are:
- We choose the indices 0, 1, and 2 with score = (1+3+3) \* min(2,1,3) = 7.
- We choose the indices 0, 1, and 3 with score = (1+3+2) \* min(2,1,4) = 6.
- We choose the indices 0, 2, and 3 with score = (1+3+2) \* min(2,3,4) = 12.
- We choose the indices 1, 2, and 3 with score = (3+3+2) \* min(1,3,4) = 8.
Therefore, we return the max score, which is 12.
**Example 2:**
**Input:** nums1 = \[4,2,3,1,1\], nums2 = \[7,5,10,9,6\], k = 1
**Output:** 30
**Explanation:**
Choosing index 2 is optimal: nums1\[2\] \* nums2\[2\] = 3 \* 10 = 30 is the maximum possible score.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 105`
* `1 <= k <= n` | null |
heap + sort + one step check | maximum-subsequence-score | 0 | 1 | # Intuition\nimprove a little after reading lee215\'s solution https://leetcode.com/problems/maximum-subsequence-score/solutions/3082106/java-c-python-priority-queue/?orderBy=most_votes\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nheap + sort, but adding a check to see whether we are heap poping the element we just heap pushed. If we are, then take the second smallest nums2[i] instead since the current smallest one nums2[i] is not usable anymoe\n\n# Code\n```\nclass Solution:\n def maxScore(self, nums1: List[int], nums2: List[int], k: int) -> int:\n array = []\n for b, a in zip(nums2, nums1):\n array.append([b, a])\n\n array.sort(reverse = True)\n \n heap = []\n total = 0\n ans = 0\n candidB = []\n for i, (b, a) in enumerate(array):\n heapq.heappush(heap, a)\n \n total += a\n\n check = False\n insertB = True\n if len(heap) > k:\n aa = heapq.heappop(heap)\n total -= aa\n if aa == a and len(heap) == k:\n insertB = False\n ans = max(ans, total * candidB[0])\n check = True\n\n if not check and len(heap) == k:\n ans = max(ans, total * b)\n if insertB:\n heapq.heappush(candidB, b)\n\n return ans\n \n\n``` | 1 | You are given two **0-indexed** integer arrays `nums1` and `nums2` of equal length `n` and a positive integer `k`. You must choose a **subsequence** of indices from `nums1` of length `k`.
For chosen indices `i0`, `i1`, ..., `ik - 1`, your **score** is defined as:
* The sum of the selected elements from `nums1` multiplied with the **minimum** of the selected elements from `nums2`.
* It can defined simply as: `(nums1[i0] + nums1[i1] +...+ nums1[ik - 1]) * min(nums2[i0] , nums2[i1], ... ,nums2[ik - 1])`.
Return _the **maximum** possible score._
A **subsequence** of indices of an array is a set that can be derived from the set `{0, 1, ..., n-1}` by deleting some or no elements.
**Example 1:**
**Input:** nums1 = \[1,3,3,2\], nums2 = \[2,1,3,4\], k = 3
**Output:** 12
**Explanation:**
The four possible subsequence scores are:
- We choose the indices 0, 1, and 2 with score = (1+3+3) \* min(2,1,3) = 7.
- We choose the indices 0, 1, and 3 with score = (1+3+2) \* min(2,1,4) = 6.
- We choose the indices 0, 2, and 3 with score = (1+3+2) \* min(2,3,4) = 12.
- We choose the indices 1, 2, and 3 with score = (3+3+2) \* min(1,3,4) = 8.
Therefore, we return the max score, which is 12.
**Example 2:**
**Input:** nums1 = \[4,2,3,1,1\], nums2 = \[7,5,10,9,6\], k = 1
**Output:** 30
**Explanation:**
Choosing index 2 is optimal: nums1\[2\] \* nums2\[2\] = 3 \* 10 = 30 is the maximum possible score.
**Constraints:**
* `n == nums1.length == nums2.length`
* `1 <= n <= 105`
* `0 <= nums1[i], nums2[j] <= 105`
* `1 <= k <= n` | null |
[C++|Java|Python3] gcd | check-if-point-is-reachable | 1 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7c339707e031611c80809107e7a667b2c6b6f7f0) for solutions of biweekly 96. \n\n**C++**\n```\nclass Solution {\npublic:\n bool isReachable(int targetX, int targetY) {\n int g = gcd(targetX, targetY); \n return (g & (g-1)) == 0; \n }\n};\n```\n**Java**\n```\nimport java.math.BigInteger; \n\nclass Solution {\n public boolean isReachable(int targetX, int targetY) {\n int g = BigInteger.valueOf(targetX).gcd(BigInteger.valueOf(targetY)).intValue();\n return (g & (g-1)) == 0; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n g = gcd(targetX, targetY)\n return g & (g-1) == 0\n``` | 1 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
One-liner Python | check-if-point-is-reachable | 0 | 1 | \n# Code\n```\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n return (1 << 32) % gcd(targetX, targetY) == 0\n \n``` | 1 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
🔥Python3🔥only GCD | check-if-point-is-reachable | 0 | 1 | - Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(log(n))$$\n\n# Code\n```\nclass Solution:\n def isReachable(self, x: int, y: int) -> bool:\n a=gcd(x,y)\n while a%2==0:\n a//=2\n return a==1\n \n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 10 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
[Java/Python 3] Check if the GCD has only factor 2 w/ explanation and analysis. | check-if-point-is-reachable | 1 | 1 | **Intuition**\n\nNotice there is double operations for either `x` or `y`- coordinates and the corresponding result must be even. Therefore, if the target coordinates is odd, we can only have `1` option: `+/-`. \n\nHence we can simplify the operation if we return from target to source.\n\nAlso the following operation hint Euclidean Algorithm:\n`(x, y - x)`\n`(x - y, y)`\nor\n`(x, y + x)`\n`(x + y, y)`\n\nBased on the above we can implement the following algorithm.\n\n----\nLet us **reverse the procedure and start from target to source**, if either of the target coordinates is divisible by `2`, remove all factor `2`s from it then check if they are co-prime now; If yes, return `true`, otherwise return `false`.\n\nWe also can compute the `GCD` first, then check if it has only factor `2`s, and this makes code shorter.\n\n```java\n public boolean isReachable(int x, int y) {\n while (y != 0) {\n int tmp = x % y;\n x = y;\n y = tmp;\n }\n while (x % 2 == 0) {\n x /= 2;\n }\n return x == 1;\n }\n```\n```python\n def isReachable(self, x: int, y: int) -> bool:\n g = gcd(x, y)\n while g % 2 == 0:\n g //= 2\n return g == 1\n```\n\nOr further simplify the above as follows: \n```java\n public boolean isReachable(int x, int y) {\n while (y != 0) {\n int tmp = x % y;\n x = y;\n y = tmp;\n }\n return Integer.bitCount(x) == 1;\n }\n```\n```python\n def isReachable(self, x: int, y: int) -> bool:\n return gcd(x, y).bit_count() == 1\n```\n\n**Analysis:**\n\nBoth the dividing `2` and `gcd`(Euclidean Algorithm) operations cost time `O(log(max(x, y)))`, therefore\n\nTime: `O(log(max(x, y)))`, space: `O(1)`.\n\n----\n\n**Q & A**\n*Q1*: You have reversed 2*x by x//2. Then why (x-y) is still holding good? Shouldn\'t it be x+y?\n*A1*: Actually, *x + y* or *x - y* will NOT change their `GCD`. It is because `gcd(x + m * y, y) = gcd(x, n * x + y) = gcd(x, y)`, where `m` and `n` are both integers that can be positive, negative or zero.\n\n*Proof:*\n\nUse contradiction to prove `gcd(x + m * y, y) = gcd(x, y)` as follow:\n\nLet `g = gcd(x, y)`, then `x = a * g, y = b * g` and `a` and `b` co-prime.\n\n`x + m * y = a * g + m * b * g = (a + m * b) * g`\n`y = b * g `\n\nif `gcd(a + m * b, b) = g\' > 1`, then `a + m * b = p * g\'` and`b = q * g\'`, therefore `a + m * b = a + m * q * g\' = p * g\'`, so `a = (p - m * q) * g\'`, which indicates that `a` and `b` have a `GCD` of `g\' > 1` and hece `a` and `b` not co-prime, which contradicts the previous assumption `a` and `b` co-prime.\n\nSimilarly we can prove that `gcd(x, n * x + y) = gcd(x, y)`\n\n**End of Q & A** | 15 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
1 line solution that beats 100% | check-if-point-is-reachable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(logn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nfrom math import gcd\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n return bin(gcd(targetX, targetY)).count(\'1\') == 1\n``` | 1 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
Simple recursive approach | check-if-point-is-reachable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> The `isReachable` function uses a recursive approach to determine if it is possible to reach the target point `(targetX, targetY)` from the starting point `(1, 1)` using the given steps.\n\nThe function first checks if the current position is `(1, 1)`, in which case it returns `True` as the target has been reached. If either `targetX` or `targetY` is less than 1, it returns `False` as it is not possible to reach a negative coordinate.\n\nIf neither of these conditions is met, the function checks if either `targetX` or `targetY` is divisible by 2. If `targetX` is divisible by 2, it means that the previous step must have been to double the value of `x`, so the function calls itself recursively with the new position `(targetX // 2, targetY)` to undo this step. Similarly, if `targetY` is divisible by 2, it means that the previous step must have been to double the value of `y`, so the function calls itself recursively with the new position `(targetX, targetY // 2)` to undo this step.\n\nIf neither `targetX` nor `targetY` is divisible by 2, it means that the previous step must have been to either subtract `y` from `x` or subtract `x` from `y`. In this case, the function tries both possible moves by calling itself recursively with the new positions `(targetX - targetY, targetY)` and `(targetX, targetY - targetX)`.\n\nThis recursive approach continues until either the target position is reached or it is determined that it is not possible to reach the target position using the given steps. The function returns `True` if it is possible to reach the target position and `False` otherwise.\n\nI hope this explanation helps you understand the approach.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n if targetX == 1 and targetY == 1:\n return True\n if targetX < 1 or targetY < 1:\n return False\n if targetX % 2 == 0:\n return self.isReachable(targetX // 2, targetY)\n elif targetY % 2 == 0:\n return self.isReachable(targetX, targetY // 2)\n else:\n return self.isReachable(targetX - targetY, targetY) or self.isReachable(targetX, targetY - targetX)\n \n``` | 1 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
🔥Python3🔥 math, number theory | check-if-point-is-reachable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf x or y is a power of two, it means there is an exact solution. This is definitely a special case.\nIf the GCD of x and y is a power of two, then there is a solution. A very easy solution.\n\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(log(n))$$\n\n# Code\n```\nclass Solution:\n def isReachable(self, x: int, y: int) -> bool:\n bl=True\n a=x\n while a%2==0:\n a//=2\n if(a==1):\n return True\n a=y\n while a%2==0:\n a//=2\n if(a==1):\n return True\n while x>0 and y>0:\n x%=y\n if x==1:\n return True\n x,y=y,x\n a=x\n while a%2==0:\n a//=2\n if(a==1):\n return True\n return False\n \n \n \n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 8 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
Proof-based solution, now with correct proof | check-if-point-is-reachable | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition is quite straightforward: a pair (a, b) is accessible if and only if the greatest common divisor of a and b, gcd(a, b), is a power of 2.\nThe difficulty is proving this, which fortunately was not required during the contest. Anyway, here is the proof.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn one direction, note that all four operations preserve this property. The starting pair (1, 1) has it since $gcd(1, 1)=1=2^0$, the first two operations preserve the gcd, and the last two operations can multiply the gcd by 2 (or not). Thus, gcd(a, b) can only be a power of 2.\n\nConversely, starting from (1, 1) and multiplying the first term repeatedly by 2 we can obtain any pair of the form $(2^n, 1)$, then subtracting $1$ from $2^n$ repeatedly we can obtain any pair of the form $(n, 1)$.\n\nMultiplying the second term by 2 repeatedly we can obtain any pair of the form $(n, 2^m)$, then by subtracting $n$ from $2^m$ repeatedly we can obtain any pair of the form $(n,\\ 2^m \\mod n)$.\n\nSuppose we want to obtain the pair (n, k), where k<n and gcd(n, k)=1. Consider the infinite arithmetic progression (n, n+k, n+2k, ...). By Dirichlet\'s theorem, this progression contains infinitely many primes. Consider one of them: p=n+jk for some $j \\geq 0$.\n\nBy a slight generalization of [Artin\'s conjecture](https://mathworld.wolfram.com/ArtinsConjecture.html) (the generalization may need proof, but Artin\'s conjecture was proved by Christopher Hooley, ["On Artin\'s Conjecture"](https://eudml.org/doc/150785), in 1967, assuming the [Generalized Riemann Hypothesis](https://en.wikipedia.org/wiki/Generalized_Riemann_hypothesis)), there are infinitely many such p for which 2 is a primitive root of unity modulo p, meaning that $2^{p-1} \\equiv 1 \\mod p$ and $2^{k} \\not \\equiv 1 \\mod p$ for $0<k<p-1$.\n\nWe know we can obtain any pair of the form $(p,\\ 2^m \\mod p)$. Since p is prime, the multiplicative group $\\mathbb Z_p^*$ is cyclic. Since 2 is a generator (its order is equal to the order of the group), we can obtain any pair (p, k) where $1 \\leq k <p$ using powers of 2 modulo p, including the k we want.\n\nBut this is the same as (n+jk, k) and then by repeatedly subtracting k from n+jk we can obtain (n, k), as desired.\n\nBy symmetry (doing the same thing in reverse if necessary), we can obtain any pair (n, m) where gcd(m, n)=1. Finally, multiplying m and n by (possibly different) arbitrary powers of 2 we can obtain any pair whose gcd is a power of two.\n\nEdited: The initial proof was wrong and I corrected it.\n\n# Complexity\n- Time complexity: Logarithmic: $O(\\max(\\log a, \\log b))$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n def gcd(a, b):\n while b:\n a, b=b, a%b\n return a\n d=gcd(targetX, targetY)\n while d!=1:\n if d&1:\n return False\n d>>=1\n return True\n \n``` | 8 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
[Python] One-liner Math, Now with Proof, The Best | check-if-point-is-reachable | 0 | 1 | # Intuition\nThe possible generalized transformations of $$(x, y)$$ into $$(x, y-kx)$$ and $$(x-ky, y)$$ are reminiscent of coefficients computation in Extended Euclidean Algorithm. The other two generalized transformations into $$(2^kx, y)$$ and $$(x, 2^ky)$$ suggest that powers-of-$$2$$ are also related.\n\nLooking at the two examples provided, I guessed that $$\\gcd(x, y)=2^k$$ for some $$k$$ is the answer, and it worked.\n\nThe Best!\n\n# Proof\nWe will show that all and only points $$(x,y)$$ with $$\\gcd(x,y)=2^k$$ for $$k\\geqslant 0$$ are reachable from $$(1,1)$$, under the assumption that only $$x,y\\geqslant 1$$ are legal (the problem statement is unclear on this assumption, and it doesn\'t really matter).\n\nShowing that only points with $$\\gcd(x,y)=2^k$$ are reachable is simple: going from $$(x,y)$$ to $$(x,y-x)$$ or $$(x-y,y)$$ doesn\'t change the GCD, and doubling $$x$$ or $$y$$ also doubles the GCD or leaves it unchanged.\n\nShowing that all points with $$\\gcd(x,y)=2^k$$ are reachable is equivalent to showing that $$(1,1)$$ is reachable from such points using the reverse steps.\n\nDefine the following transformation on $$(x,y)\\neq(1,1)$$ with $$\\gcd(x,y)=2^k$$, always repeating the first applicable step:\n1. If $$x$$ is even, go to $$(\\frac{x}{2},y)$$.\n2. If $$y$$ is even, go to $$(x,\\frac{y}{2})$$.\n3. If $$x<y$$, go to $$\\left(x, \\frac{x+y}{2}\\right)$$.\n4. If $$x>y$$, go to $$\\left(\\frac{x+y}{2},y\\right)$$.\n\nBy induction on $$\\max(x,y)$$ with induction invariant $$\\gcd(x,y)=2^k$$, we can see that $$(x,y)$$ always reaches $$(1,1)$$ in finite number of steps:\n1. All steps reduce $$\\max(x,y)$$.\n2. All steps reduce the exponent $$k$$ in $$\\gcd(x,y)=2^k$$ or leave it unchanged (see Euclidean algorithm), maintaining the induction invariant.\n3. The only possibility not covered by the steps is odd $$x=y$$, in which case $$\\gcd(x,y)=2^0=1$$, resulting in $$(x,y)=(1,1)$$, the induction base.$$\\quad\\square$$\n\n# Complexity\n- Time complexity: $$O(\\log x)$$ for $$x \\geqslant y$$\n- Space complexity: $$O(1)$$\n\n# Code\n```py\ndef isReachable(self, x: int, y: int) -> bool:\n return (g := math.gcd(x, y)) & (g-1) == 0\n``` | 2 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
No GCD or other math magic! Simple intuition with explanation | check-if-point-is-reachable | 0 | 1 | # Intuition\n\nGo from the target to the start.\n\nIf `x` or `y` can reach `1`, then both coordinates can reach `1` (by subtracting `1` from the other coordinate).\n\nDecrease `x` and `y` greedily until any coordinate reaches `1`, or the process stucks in the same state.\n\n# Approach\n\nWhen you go backwards, there are only 2 operations possible:\n\n1. Divide a coordinate by 2\n2. Sum the coordinates and replace one of the coordinates with the sum\n\nDriven by the greed, we divide any coordinate by 2 whenever it\'s even.\n\nThen sum the coordinates together and replace the greatest coordinate with the sum (we don\'t try replacing the smallest one because we are greedy). Since the coordinates were odd, the sum is even, so it can be divided by 2 further, thus the process can continue in a cycle.\n\nThe process can\'t continue when the coordinates are equal. `(a + a) / 2 = a`, i.e. the state doesn\'t change. It means that the start can\'t be reached.\n\n# Code\n\n```python\nclass Solution:\n def isReachable(self, targetX: int, targetY: int) -> bool:\n x = self.decrease(targetX)\n y = self.decrease(targetY)\n\n while True:\n if x == 1 or y == 1:\n return True\n\n if x == y:\n return False # The coordinates won\'t change, we are stuck\n\n newCoordinate = self.decrease(x + y)\n \n # Putting the new coordinate to the place of the biggest current coordinate\n if x < y:\n y = newCoordinate\n else:\n x = newCoordinate\n\n def decrease(self, value):\n while value % 2 == 0:\n value = value >> 1 # This means division by 2\n return value\n``` | 9 | There exists an infinitely large grid. You are currently at point `(1, 1)`, and you need to reach the point `(targetX, targetY)` using a finite number of steps.
In one **step**, you can move from point `(x, y)` to any one of the following points:
* `(x, y - x)`
* `(x - y, y)`
* `(2 * x, y)`
* `(x, 2 * y)`
Given two integers `targetX` and `targetY` representing the X-coordinate and Y-coordinate of your final position, return `true` _if you can reach the point from_ `(1, 1)` _using some number of steps, and_ `false` _otherwise_.
**Example 1:**
**Input:** targetX = 6, targetY = 9
**Output:** false
**Explanation:** It is impossible to reach (6,9) from (1,1) using any sequence of moves, so false is returned.
**Example 2:**
**Input:** targetX = 4, targetY = 7
**Output:** true
**Explanation:** You can follow the path (1,1) -> (1,2) -> (1,4) -> (1,8) -> (1,7) -> (2,7) -> (4,7).
**Constraints:**
* `1 <= targetX, targetY <= 109` | null |
Countering Logic | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n count=0\n n=str(n)\n for i in range(len(n)):\n if i%2==0:\n count+=int(n[i])\n else:\n count-=int(n[i])\n return count\n``` | 2 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Simple solution | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n s=str(n)\n o=0\n e=0\n for i in range(len(s)):\n if i%2==0:\n o += int(s[i])\n else:\n e = e+ (int(s[i]) * -1)\n return o+e\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python 2 Approach Math + String || Simple Code | alternating-digit-sum | 0 | 1 | \n# Code\n> # Math Approach\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n nums = []\n while n > 0:\n nums.append(n%10)\n n = n//10\n\n nums.reverse()\n ans = 0\n\n for i in range(len(nums)):\n if i%2 == 0: #even place digit -> add\n ans += nums[i]\n else: #odd place digit -> Sub\n ans -= nums[i]\n return ans\n \n \n```\n\n> # String Approach\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n s = str(n)\n ans = 0\n for i in range(len(s)):\n if i%2 == 0: #even place digit -> add\n ans += int(s[i])\n else: #odd place digit -> Sub\n ans -= int(s[i])\n return ans\n\n#\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
simple approach wit python | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n result=str(n)\n sum=0\n for i in range(len(result)):\n if i%2 ==0:\n sum=sum+int(result[i])\n else: \n sum=sum-int(result[i]) \n return sum \n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
EASY and in less time complexity | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n result=str(n)\n ans=0\n for i in range(len(result)):\n if i%2==0:\n ans=ans+int(result[i])\n else:\n ans=ans-int(result[i])\n return ans\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Easy Solution with best approach | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n res=str(n)\n ans=0\n for i in range(len(res)):\n if i%2==0:\n ans=ans+int(res[i])\n else:\n ans=ans-int(res[i])\n return ans\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Simple | alternating-digit-sum | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n a=str(n)\n ans=0\n k=0\n for i in a:\n if k&1==0:\n ans+=int(i)\n else:\n ans-=int(i)\n k+=1\n return ans\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Sweetest code this side of the Mississippi | alternating-digit-sum | 1 | 1 | # Java\n\n## Using a basic loop:\n\n```java\nclass Solution {\n public int alternateDigitSum(int n) {\n String[] digits = Integer.toString(n).split("");\n\n int res = 0;\n for (int i = 0; i < digits.length; ++i) {\n res += Integer.parseInt(digits[i]) * (i % 2 == 0 ? 1 : -1);\n }\n return res;\n }\n}\n```\n\n## Using streams:\n\n```java\nclass Solution {\n public int alternateDigitSum(int n) {\n String[] digits = Integer.toString(n).split("");\n return IntStream.range(0, digits.length)\n .map(i -> Integer.parseInt(digits[i]) * (i % 2 == 0 ? 1 : -1))\n .sum();\n }\n}\n```\n\n# JavaScript / TypeScript\n\n(To get the pure JavaScript version, strip out the TypeScript type annotations.)\n\n## As one expression:\n\n```typescript\nfunction alternateDigitSum(n: number): string {\n return [...`${n}`]\n .map(Number)\n .map((d, i) => d * (i % 2 === 0 ? 1 : -1))\n .reduce((a, b) => a + b);\n}\n```\n\n## Using a basic loop:\n\n```typescript\nfunction alternateDigitSum(n: number): string {\n const digits = `${n}`;\n\n let res = 0;\n for (let i = 0; i < digits.length; ++i) {\n res += Number(digits[i]) * (i % 2 === 0 ? 1 : -1);\n }\n return res;\n}\n```\n\n# Ruby\n\n```ruby\ndef alternate_digit_sum(n)\n digits = n.digits.reverse\n digits.each_with_index.map { |d, i| d * (i.even? ? 1 : -1) }.sum\nend\n```\n\n# Python 3 / Python 2\n\n(To get the Python 2 version, strip out the type annotations.)\n\n## As one expression, using list comprehensions:\n\n```python\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n return sum(\n int(d) * (1 if i % 2 == 0 else -1)\n for i, d in enumerate(str(n))\n )\n```\n\n## Using a basic loop:\n\n```python\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n res = 0\n for i, d in enumerate(str(n)):\n res += int(d) * (1 if i % 2 == 0 else -1)\n return res\n```\n\n# C++\n\n## Using a basic loop:\n\n```c++\nclass Solution {\npublic:\n int alternateDigitSum(int n) {\n auto s = to_string(n);\n\n int res = 0;\n for (string::size_type i = 0; i < s.size(); ++i) {\n res += (s[i] - \'0\') * (i % 2 == 0 ? 1 : -1);\n }\n return res;\n }\n};\n```\n\n## Using iterators:\n\n```c++\nclass Solution {\npublic:\n int alternateDigitSum(int n) {\n auto s = to_string(n);\n\n int res = 0;\n int index = 0;\n for_each(s.cbegin(), s.cend(), [&index, &res](const char &d) {\n res += (d - \'0\') * (index++ % 2 == 0 ? 1 : -1);\n });\n return res;\n }\n};\n```\n\n# C\n\n```c\nint alternateDigitSum(int n) {\n // Reserve a buffer of size one more than what\'s needed for the maximum input.\n char digits[11];\n sprintf(digits, "%d", n);\n\n int res = 0;\n for (int i = 0; digits[i]; ++i) {\n res += (digits[i] - \'0\') * (i % 2 == 0 ? 1 : -1);\n }\n return res;\n}\n```\n | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Amazing speed 100% | alternating-digit-sum | 0 | 1 | # Intuition\n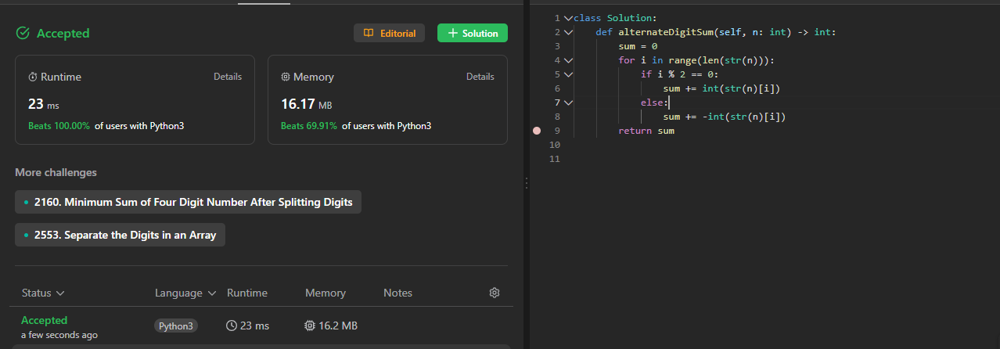\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n sum = 0\n for i in range(len(str(n))):\n if i % 2 == 0:\n sum += int(str(n)[i])\n else:\n sum += -int(str(n)[i])\n return sum\n\n \n``` | 2 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Beats 96.19% || Alternating digit sum | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n sum=0\n num1=0\n i=0\n while n!=0:\n num1=(n%10)+num1*10\n n//=10\n while num1!=0:\n rem=num1%10\n if i%2==0:\n sum+=rem\n i+=1\n print(sum)\n else:\n sum-=rem\n i+=1\n print(sum)\n num1//=10\n return sum\n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python Easy Solution || 100% || | alternating-digit-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def alternateDigitSum(self, n: int) -> int:\n sm_e=0\n sm_o=0\n sn=str(n)\n for i in range(len(sn)):\n if i&1==0:\n sm_e+=int(sn[i])\n else:\n sm_o+=int(sn[i])\n return sm_e-sm_o\n \n``` | 1 | You are given a positive integer `n`. Each digit of `n` has a sign according to the following rules:
* The **most significant digit** is assigned a **positive** sign.
* Each other digit has an opposite sign to its adjacent digits.
Return _the sum of all digits with their corresponding sign_.
**Example 1:**
**Input:** n = 521
**Output:** 4
**Explanation:** (+5) + (-2) + (+1) = 4.
**Example 2:**
**Input:** n = 111
**Output:** 1
**Explanation:** (+1) + (-1) + (+1) = 1.
**Example 3:**
**Input:** n = 886996
**Output:** 0
**Explanation:** (+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0.
**Constraints:**
* `1 <= n <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
✅ 91% || Python3 || 2 Lines || ⭐️ Sort and Lambda ⭐️ | sort-the-students-by-their-kth-score | 0 | 1 | # Intuition\n\n\n# Approach\nSort() funct iterate each list and sort according to the given specific index in lambda \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sortTheStudents(self, score: list[list[int]], k: int) -> list[list[int]]:\n score.sort(key=lambda x: x[k], reverse=True)\n return score\n\n\n\n\n\n\n```\n\n\n\n | 1 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
Easy | Python Solution | Hashmap | sort-the-students-by-their-kth-score | 0 | 1 | # Code\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n hashmap = defaultdict(list)\n refer = {}\n ans = []\n for i in range(len(score)):\n hashmap[i].append(score[i])\n refer[i] = score[i][k]\n sorted_ans = [k for k, v in sorted(refer.items(), key=lambda a:a[1], reverse=True)]\n for k in sorted_ans:\n ans += hashmap[k]\n return ans\n```\nDo upvote if you like the solution :) | 1 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
🔥Python3🔥 EASY Solution | sort-the-students-by-their-kth-score | 0 | 1 | \n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*log(n))$$\n# Python3\n```\nclass Solution:\n def sortTheStudents(self, a: List[List[int]], k: int) -> List[List[int]]:\n v=[]\n \n for i in range(len(a)):\n v+=[[a[i][k],a[i]]]\n print(v)\n def cmp(a):\n return a[0]\n v=sorted(v,key=cmp)[::-1]\n print(v)\n ans=[]\n for i in range(len(v)):\n a[i]=v[i][1]\n return a\n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 14 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
Simple solution with Sorting in Python3 / TypeScript | sort-the-students-by-their-kth-score | 0 | 1 | # Intuition\nHere we have:\n- `score` list of integers, and `k`\n- our goal is to sort `score` by `k` column\n\n# Approach\nJust simply sort by `k`-th column in **decreasing** order.\n\n# Complexity\n- Time complexity: **O(N log N)**\n\n- Space complexity: **O(1)**, **O(N)** for Python3 `sorted`, since it create **new** list\n\n# Code in Python3\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n return sorted(score, key=lambda x: x[k])[::-1]\n \n```\n# Code in TypeScript\n```\nfunction sortTheStudents(score: number[][], k: number): number[][] {\n return score.sort((a, b) => b[k] - a[k])\n};\n``` | 1 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
Very easy one linerb code | sort-the-students-by-their-kth-score | 0 | 1 | # One liner code\n\n# Code\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n return sorted(score,reverse=True, key=lambda x:x[k])\n``` | 1 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
PYTHON3 || SORTING || DICTIONARY || BEGINNER-FRIENDLY | sort-the-students-by-their-kth-score | 0 | 1 | # PYTHON3 || SORTING || DICTIONARY || BEGINNER-FRIENDLY\n\n# Approach\n Used Simple Approach first storing the values of k position element in new array. Then used that array element parallelly with score array then created Key-Value Pair like: \n {11: [7,5,11,2], 9: [10,6,9,1],3: [4,8,3,15]}\nThen sorted reversely dictionary by keys. Then append values in new answer array.\n\n\n# Code\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n\n ans=[]\n dicc={}\n arr=[]\n\n for i in range(len(score)):\n arr.append(score[i][k])\n\n for j in range(len(score)):\n dicc[arr[j]]=score[j]\n\n for kk in sorted(dicc.keys(),reverse=True):\n ans.append(dicc[kk])\n \n return ans\n\n``` | 2 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
🔥🔥2 Linear Python Solution🔥🔥Up vote Please😊 | sort-the-students-by-their-kth-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->we can solve the problem through sorting.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe have to add the total row to the kth element in the dictionary and sort the dictionary then add the rows to the new list and finally reverse the matrix\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n x={score[i][k]:score[i] for i in range(len(score))}\n return [x[i] for i in sorted(x)[::-1]]\n``` | 1 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
One liner python solutions | using Lambda | sort-the-students-by-their-kth-score | 0 | 1 | \n# Code\n```\nclass Solution:\n def sortTheStudents(self, score: List[List[int]], k: int) -> List[List[int]]:\n return sorted(score, key=lambda x:x[k],reverse=True)\n``` | 2 | There is a class with `m` students and `n` exams. You are given a **0-indexed** `m x n` integer matrix `score`, where each row represents one student and `score[i][j]` denotes the score the `ith` student got in the `jth` exam. The matrix `score` contains **distinct** integers only.
You are also given an integer `k`. Sort the students (i.e., the rows of the matrix) by their scores in the `kth` (**0-indexed**) exam from the highest to the lowest.
Return _the matrix after sorting it._
**Example 1:**
**Input:** score = \[\[10,6,9,1\],\[7,5,11,2\],\[4,8,3,15\]\], k = 2
**Output:** \[\[7,5,11,2\],\[10,6,9,1\],\[4,8,3,15\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 11 in exam 2, which is the highest score, so they got first place.
- The student with index 0 scored 9 in exam 2, which is the second highest score, so they got second place.
- The student with index 2 scored 3 in exam 2, which is the lowest score, so they got third place.
**Example 2:**
**Input:** score = \[\[3,4\],\[5,6\]\], k = 0
**Output:** \[\[5,6\],\[3,4\]\]
**Explanation:** In the above diagram, S denotes the student, while E denotes the exam.
- The student with index 1 scored 5 in exam 0, which is the highest score, so they got first place.
- The student with index 0 scored 3 in exam 0, which is the lowest score, so they got second place.
**Constraints:**
* `m == score.length`
* `n == score[i].length`
* `1 <= m, n <= 250`
* `1 <= score[i][j] <= 105`
* `score` consists of **distinct** integers.
* `0 <= k < n` | null |
2 LINES PYTHON SOLUTION | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n if \'1\' in s and \'1\' not in target or (\'1\' in target and \'1\' not in s):\n return False\n return True\n \n``` | 1 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
[Java/Python 3] Analysis results short codes. | apply-bitwise-operations-to-make-strings-equal | 1 | 1 | **If a string contains no `1`, then there is no way to change it any longer; If a string contains at least a `1`, there is no way to change it to an all-zero string, under the rules of the problem.**\n\nOtherwise, we can always change `s` to `target`.\n\n```java\n public boolean makeStringsEqual(String s, String target) {\n if (!s.contains("1") || !target.contains("1")) {\n return s.equals(target);\n }\n return true;\n }\n```\n\n```python\n def makeStringsEqual(self, s: str, target: str) -> bool:\n if (\'1\' not in s) or (\'1\' not in target):\n return s == target\n return True\n```\n\nIn case you are interested one liners:\n\n```java\n public boolean makeStringsEqual(String s, String target) {\n return s.equals(target) || s.contains("1") && target.contains("1");\n }\n```\n```python\n def makeStringsEqual(self, s: str, target: str) -> bool:\n return s == target or (\'1\' in s) and (\'1\' in target)\n```\nor \n```java\n public boolean makeStringsEqual(String s, String target) {\n return s.contains("1") == target.contains("1");\n }\n```\n```python\n def makeStringsEqual(self, s: str, target: str) -> bool:\n return max(s) == max(target)\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`. | 12 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
Didn't realise that 1 has so much power 💪|| Easy Approach explained💡 || | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | # Approach\uD83E\uDDE0\n<!-- Describe your approach to solving the problem. -->\n- Case 1 :\'1\' in s and \'0\' in target\n\n1.If we have \'1\' in s and \'0\' in target we can take help from another \'1\' in s to place \'0\' .\n```\ni.e (1^1=0) & (1|1=1) .\n```\n\n2.If there is no \'1\' available we can create an additional \'1\' by using \'0\' as below\n```\ni.e (1^0=1) & (1|0=1) .\n```\nand then using that \'1\' as in first point .\nHere if the target is string containing all \'0\' then we cannot make s and target equal as there would always be one \'1\' in s .\n\n\n- Case 2 :\'0\' in s and \'1\' in target\n\n1.If we have \'0\' in s and \'1\' in target we can take help from a \'1\' in s to place \'1\' .\n```\ni.e (0^1=1) & (0|1=1) .\n```\n2.If there is no \'1\' available we cannot make s and target equal .\nbecause : (0^0=0) && (0|0=0) .(s is string containing all \'0\' in this situation)\n\n\n#### \uD83C\uDF1FSo only thing we need to check is either number of \'1\' in both s and target is 0 \n\'OR\' \n#### both s and target should have atleast one \'1\'.\n\n----\n\n# Complexity\u231B\n## - Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n## - Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n----\n# Code \n## *C++ :*\n```\nclass Solution {\npublic:\n bool makeStringsEqual(string s, string target) {\n int n=s.size();\n bool chk1=0,chk2=0;\n for(int i=0 ; i<n; i++){\n if(s[i]&1){\n chk1=true;\n break;\n }\n }\n for(int i=0 ; i<n; i++){\n if(target[i]&1){\n chk2=true;\n break;\n }\n }\n return (chk1==chk2);\n }\n};\n```\n\n# Code \n## *Python3 :*\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n c1=False\n c2=False\n for i in s :\n if(i==\'1\') :\n c1=True\n break\n for i in target :\n if(i==\'1\') :\n c2=True\n break\n return c1==c2\n```\n# Code \n## *Javascript :*\n```\n/**\n * @param {string} s\n * @param {string} target\n * @return {boolean}\n */\nvar makeStringsEqual = function(s, target) {\n let n=s.length;\n let c1=false,c2=false;\n for(let i=0 ; i<n; i++){\n if(s[i]&1){\n c1=true;\n break;\n }\n }\n for(let i=0 ; i<n; i++){\n if(target[i]&1){\n c2=true;\n break;\n }\n }\n return c1==c2;\n};\n```\n### DO UPOTE if it helped you .\n\n | 1 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
Python 1 liner solution super easy to understand altho its an easy question :-) | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | # what should i even say, all testcases have been passed using this simple code!\n# Code\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n return max(s) == max(target)\n``` | 3 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
✅One Liner and Easy to Understand | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n return s==target or (int(target)>0 and int(s)>0)\n \n \n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 11 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
Python 3 || 2 lines, w/ explanation || T/M: 45 ms / 15 MB | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | From the table below, one can see that:\n- If`s` has a `1`, then any other digit in`s`can be flipped, but there will remain at least one`1` in`s`, no matter how many oprations are performed.\n- If`s` has no `1`s, then no other digit in`s`can be flipped.\n\n\n\n\n\nThese two conditions imply the two stuations in which we will return`True`:\n- The two strings as given are equal; or\n- Each string has at least one `1`.\n\nAll other situations return `False`.\n\n\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n\n if s == target: return True\n \n return int(s,2)*int(target,2)\n\n```\n[https://leetcode.com/problems/apply-bitwise-operations-to-make-strings-equal/submissions/883262113/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1).\n | 4 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
[Python3/Golang/Rust] Count one | apply-bitwise-operations-to-make-strings-equal | 0 | 1 | We have to check if one of the strings contains 1 and the other does not, and vice versa. If both have it, then we can bring our string s equal to the target.\n\n**Python3**:\n```\nclass Solution:\n def makeStringsEqual(self, s: str, target: str) -> bool:\n return \'1\' in s and \'1\' in target or \'1\' not in target and \'1\' not in s\n```\n\n**Golang**:\n```\nfunc makeStringsEqual(s string, target string) bool {\n s_check, target_check := strings.Contains(s, "1"), strings.Contains(target, "1")\n \n if (s_check == true && target_check == false) || (s_check == false && target_check == true) {\n return false\n } else {\n return true\n }\n}\n```\n\n**Rust**:\n```\nimpl Solution {\n pub fn make_strings_equal(s: String, target: String) -> bool {\n return (!s.contains("1") && !target.contains("1")) || (s.contains("1") && target.contains("1"))\n }\n}\n``` | 1 | You are given two **0-indexed binary** strings `s` and `target` of the same length `n`. You can do the following operation on `s` **any** number of times:
* Choose two **different** indices `i` and `j` where `0 <= i, j < n`.
* Simultaneously, replace `s[i]` with (`s[i]` **OR** `s[j]`) and `s[j]` with (`s[i]` **XOR** `s[j]`).
For example, if `s = "0110 "`, you can choose `i = 0` and `j = 2`, then simultaneously replace `s[0]` with (`s[0]` **OR** `s[2]` = `0` **OR** `1` = `1`), and `s[2]` with (`s[0]` **XOR** `s[2]` = `0` **XOR** `1` = `1`), so we will have `s = "1110 "`.
Return `true` _if you can make the string_ `s` _equal to_ `target`_, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1010 ", target = "0110 "
**Output:** true
**Explanation:** We can do the following operations:
- Choose i = 2 and j = 0. We have now s = "**0**0**1**0 ".
- Choose i = 2 and j = 1. We have now s = "0**11**0 ".
Since we can make s equal to target, we return true.
**Example 2:**
**Input:** s = "11 ", target = "00 "
**Output:** false
**Explanation:** It is not possible to make s equal to target with any number of operations.
**Constraints:**
* `n == s.length == target.length`
* `2 <= n <= 105`
* `s` and `target` consist of only the digits `0` and `1`. | null |
🔥Python3 || C++🔥 ✅ EASY Dynamic Programming with Dict(Map) | minimum-cost-to-split-an-array | 0 | 1 | \nAn initial value would be needed in this solution. \nTo that I added an element to the front of the array that is not in the array (nums=[-1]+nums) and since it is not in the array before, \ndp[0]=0 (it has no price).\nThen I started from the 1-index of the array because the 0-index has -1 and calculated the minimum cost up to each element.\nwhen I go to each index, I go back from it (to index 1).\nThe goal is to find the best answer.\nA good answer for j-index is in dp[j].\n$$for(j=i;j>0;j--)$$\n$$ans=min(ans,dp[j-1]+s)$$\n$$s=trimmed(nums[j:i+1])$$\nAnd at the end of the work dp[i]=ans+k. Because after adding one element, it is split by adding it, and k is added to it.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\nIf You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Python3\n```\nclass Solution:\n def minCost(self, nums: List[int], k: int) -> int:\n dp=[0]\n nums=[-1]+nums\n def main(i):\n mp=defaultdict(int)\n s=0\n ans=10000000000000\n while i>0:\n if mp[nums[i]]>0:\n s+=1\n if mp[nums[i]]==1:\n s+=1\n mp[nums[i]]+=1\n ans=min(dp[i-1]+s,ans)\n i-=1\n return ans+k\n \n \n for i in range(1,len(nums)):\n dp.append(main(i))\n return dp[-1]\n```\n# C++\n```\nclass Solution {\npublic:\n int minCost(vector<int>& nums, int k) {\n vector<int>dp(nums.size()+1,0);\n reverse(nums.begin(),nums.end());\n nums.push_back(-1);\n reverse(nums.begin(),nums.end());\n for(int i=1;i<nums.size();i++)\n {\n \tint s=0,ans=1e8;\n \tunordered_map<int,int>mp;\n \tfor(int j=i;j>0;j--)\n \t{\n \t\tif(mp[nums[j]]>0)\n \t\t{\n \t\t\ts++;\n \t\t\tif(mp[nums[j]]==1)\n \t\t\t{\n \t\t\t\ts++;\n \t\t\t}\n \t\t}\n \t\tmp[nums[j]]++;\n \t\tans=min(ans,dp[j-1]+s);\n \t}\n \tdp[i]=ans+k;\n }\n return dp[nums.size()-1];\n }\n};\n```\nPlease UPVOTE if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 23 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
✔ Python3 Solution | 100% faster | DP | minimum-cost-to-split-an-array | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def minCost(self, A, K):\n n = len(A)\n dp = [0] + [float(\'inf\')] * n\n for i in range(n):\n C = [0] * n\n val = K\n for j in range(i, -1, -1):\n val += (C[A[j]] >= 1) + (C[A[j]] == 1)\n C[A[j]] += 1\n dp[i + 1] = min(dp[i + 1], dp[j] + val)\n return dp[-1]\n``` | 1 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
SIMPLE PYTHON DP SOLUTION | minimum-cost-to-split-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,prev,nums,k,dct):\n if i>=len(nums):\n return 0\n if (i,prev) in dct:\n return dct[(i,prev)]\n x=float("infinity")\n sm=0\n cnt=defaultdict(lambda :0)\n for j in range(i,len(nums)):\n cnt[nums[j]]+=1\n if cnt[nums[j]]==2:\n sm+=2\n elif cnt[nums[j]]>2:\n sm+=1\n z=self.dp(j+1,j,nums,k,dct)+k+sm\n x=min(x,z)\n dct[(i,prev)]=x\n return x\n \n def minCost(self, nums: List[int], k: int) -> int:\n return self.dp(0,0,nums,k,{})\n \n``` | 1 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python 3 || 11 lines, w/ example || T/M: 5373 ms / 20 MB | minimum-cost-to-split-an-array | 0 | 1 | ```\nclass Solution: # Example: nums = [1, 2, 1, 2] 5\n def minCost(self, nums: List[int], k: int) -> int: #\n # left right tmp ans nums[left,right+1]\n @lru_cache(None) # \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \n def dp(left, n = len(nums)): # 0 3 9 9 <-- [1, 2, 1, 2]\n # 0 2 7 10 [1, 2, 1]\n if left == n: return 0 # 0 1 5 10 [1, 2]\n # 0 0 5 12 [1]\n tmp, ans,d = k, inf, defaultdict(int) # 1 3 7 7 [2, 1, 2]\n # 1 2 5 10 [2, 1]\n for right, num in enumerate( # 1 1 5 10 [2]\n nums[left:], start = left): # 2 3 5 5 [1, 2]\n # 2 2 5 10 [1]\n d[num]+= 1 # 3 3 5 5 [2]\n tmp+= (d[num] > 1) + (d[num] == 2)\n ans = min(ans, tmp + dp(right+1))\n \n return ans\n\n return dp(0) \n```\n[https://leetcode.com/problems/minimum-cost-to-split-an-array/submissions/883318213/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*). | 4 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
[Python🐍] Simple DP with Dict (Hashmap) 15 Lines of code | minimum-cost-to-split-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDP Memorization Approach where `i` is the index of the current number and returning the minimum cost starting at index `i`.\nKeep a Hashmap called `hm` to remember the count of each number in the subarray.\nKeep a count called `count` of numbers that are not unique in the subarray starting at `i`.\nKeep a current minimum cost value called `min_cost` for subarray starting the subarray at `i` and ending at `len(nums)` by adding `dp(j+1)` to `k + count`.\nReturn the minimum `dp` value starting at index 0.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def minCost(self, nums: List[int], k: int) -> int:\n \n # store the past dp results in a memory cache\n @cache\n def dp(i):\n\n # i reached the end of nums\n if i == len(nums):\n return 0\n\n # declare a hm, min_cost (minimum) and count of pairs\n min_cost = float(\'inf\')\n hm = defaultdict(int)\n count = 0\n\n for j in range(i,len(nums)):\n hm[nums[j]] += 1\n \n # one pair found, add both numbers\n if hm[nums[j]] == 2:\n count += 2\n \n # add the extra number to count\n elif hm[nums[j]] > 2:\n count += 1\n\n importance_value = k + count\n\n #optimization to return early since importance_value keeps increasing and we want to minimum\n if importance_value >= min_cost :\n break\n\n min_cost = min( importance_value + dp(j+1) , min_cost )\n \n return min_cost\n\n return dp(0) \n``` | 14 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
python3 Solution | minimum-cost-to-split-an-array | 0 | 1 | \n```\nclass Solution:\n def minCost(self, nums: List[int], k: int) -> int:\n n = len(nums)\n dp = [inf]*(n+1)\n dp[-1] = 0 \n for i in range(n-1, -1, -1): \n val = 0 \n freq = Counter()\n for ii in range(i, n): \n freq[nums[ii]] += 1\n if freq[nums[ii]] == 2: val += 2\n elif freq[nums[ii]] > 2: val += 1\n dp[i] = min(dp[i], k + val + dp[ii+1])\n return dp[0]\n``` | 1 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
[C++ || Java || Python] Easy dp | minimum-cost-to-split-an-array | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n\n> **Vote welcome if this solution helped.**\n---\n\n# Intuition\n1. The value range of length is no more than 1000, so an $O(n^{2})$ algorithm can be considered.\n2. Notice the subarray is consecutive, immediately think of enumerating all the potential start position $i$ for all the end position $j$.\n3. As a result, the answer of $i-1$ can easily transfer to the answer of $j$.\n4. Another question is to calculate the trimmed length. The trimmed length equals to the total length $j-i+1$ minus removed count. The removed count can be traced with $i$ moved from right to left.\n\n# Approach\n\n- Linear dynamic programming, define $dp[i]$ as the result of $nums[0...i]$, easily to write the transfer equation:\n$dp[j] = \\min_{i={0}} ^{j} {\\{ dp[i-1] + k+(j-i+1 -removed)\\}}$\n\n- Use a counter `mp` to record the count of each number, and an integer `rm` to record the removed count. \nOnce find a new number, the `rm` should add one; if find a new value has been removed, it should be returned, so the `rm` should be minus 1.\n\n# Complexity\n- Time complexity: $O(n ^ {2})$\n- Space complexity: $O(n)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n int minCost(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> dp(n+1, k+n+1);\n dp[0] = 0;\n for (int j = 1; j <= n; ++j) {\n vector<int> mp(n+1, 0);\n int rm = 0;\n for (int i = j; i >= 1; --i) {\n // update the removed number\n rm += (mp[nums[i-1]] == 0) - (mp[nums[i-1]] == 1);\n mp[nums[i-1]]++;\n dp[j] = min(dp[j], dp[i-1] + k + j - i + 1 - rm);\n }\n }\n return dp[n];\n }\n};\n```\n``` Java []\nclass Solution {\n public int minCost(int[] nums, int k) {\n int n = nums.length;\n int []dp = new int[n+1];\n for (int i = 0; i <= n; ++i) dp[i] = k + n + 1;\n dp[0] = 0;\n int []mp = new int[n+1];\n for (int j = 1; j <= n; ++j) {\n for (int i = 0; i <= n; ++i) mp[i] = 0;\n int rm = 0;\n for (int i = j; i >= 1; --i) {\n // update the removed number\n if (mp[nums[i-1]] == 0) rm++;\n else if (mp[nums[i-1]] == 1) rm--;\n mp[nums[i-1]]++;\n dp[j] = Math.min(dp[j], dp[i-1] + k + j - i + 1 - rm);\n }\n }\n return dp[n];\n }\n}\n```\n``` Python3 []\nclass Solution:\n def minCost(self, nums: List[int], k: int) -> int:\n n = len(nums)\n dp = [0] + [n+k+1] * n\n for j in range(1, n+1):\n mp = [0] * (n+1)\n rm = 0\n for i in range(j, 0, -1):\n # update the removed number\n rm += (mp[nums[i-1]] == 0) - (mp[nums[i-1]] == 1)\n mp[nums[i-1]] += 1\n last = dp[i-1] + k + j - i + 1 - rm\n if last < dp[j]: dp[j] = last\n return dp[n]\n``` | 9 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python easy to read and understand | dp | minimum-cost-to-split-an-array | 0 | 1 | ```\nclass Solution:\n def solve(self, nums, index, dp, k):\n if index == len(nums):\n return 0\n if index in dp:\n return dp[index]\n mn = float("inf")\n cnt = 0\n d = collections.defaultdict(int)\n for i in range(index, len(nums)):\n d[nums[i]] += 1\n if d[nums[i]] == 2:\n cnt += 2\n elif d[nums[i]] > 2:\n cnt += 1\n value = k + cnt\n mn = min(mn, value + self.solve(nums, i+1, dp, k))\n dp[index] = mn\n return mn\n \n def minCost(self, nums: List[int], k: int) -> int:\n dp = {}\n return self.solve(nums, 0, dp, k) | 0 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
DP approach with Question Explaination in Simple Language | minimum-cost-to-split-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe Questions asks you to add any number of particians such that cost of each partition on both side k+ how many int comes more than once in currently operated array\nkey thinking aproach such that we can add any number of particians not limited to just 2 particians \n# Approach\n<!-- Describe your approach to solving the problem. -->\nDynamic Programming with Memoization\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*n)\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minCost(self, nums: List[int], k: int) -> int:\n @lru_cache(1000)\n def do(pos):\n if(pos==len(nums)):\n return 0\n a={}\n t=0\n ans=float(\'inf\')\n for i in range(pos,len(nums)):\n a[nums[i]]=a.get(nums[i],0)+1\n if(a[nums[i]]==2):\n t+=2\n elif(a[nums[i]]>2):\n t+=1\n ans=min(ans,t+k+do(i+1))\n return min(ans,t+k)\n return do(0)\n``` | 0 | You are given an integer array `nums` and an integer `k`.
Split the array into some number of non-empty subarrays. The **cost** of a split is the sum of the **importance value** of each subarray in the split.
Let `trimmed(subarray)` be the version of the subarray where all numbers which appear only once are removed.
* For example, `trimmed([3,1,2,4,3,4]) = [3,4,3,4].`
The **importance value** of a subarray is `k + trimmed(subarray).length`.
* For example, if a subarray is `[1,2,3,3,3,4,4]`, then trimmed(`[1,2,3,3,3,4,4]) = [3,3,3,4,4].`The importance value of this subarray will be `k + 5`.
Return _the minimum possible cost of a split of_ `nums`.
A **subarray** is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,1,3,3\], k = 2
**Output:** 8
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1,3,3\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1,3,3\] is 2 + (2 + 2) = 6.
The cost of the split is 2 + 6 = 8. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 2:**
**Input:** nums = \[1,2,1,2,1\], k = 2
**Output:** 6
**Explanation:** We split nums to have two subarrays: \[1,2\], \[1,2,1\].
The importance value of \[1,2\] is 2 + (0) = 2.
The importance value of \[1,2,1\] is 2 + (2) = 4.
The cost of the split is 2 + 4 = 6. It can be shown that this is the minimum possible cost among all the possible splits.
**Example 3:**
**Input:** nums = \[1,2,1,2,1\], k = 5
**Output:** 10
**Explanation:** We split nums to have one subarray: \[1,2,1,2,1\].
The importance value of \[1,2,1,2,1\] is 5 + (3 + 2) = 10.
The cost of the split is 10. It can be shown that this is the minimum possible cost among all the possible splits.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < nums.length`
* `1 <= k <= 109`
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Python3 | count-distinct-numbers-on-board | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n return n-1 if n>1 else 1\n``` | 1 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Python3 || Oneliner | count-distinct-numbers-on-board | 0 | 1 | # Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n return n-1 if n>1 else n\n```\n# Please do upvote if you like the solution | 2 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
ONE LINER | count-distinct-numbers-on-board | 0 | 1 | \n# Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n if n == 1:\n return 1\n else:\n return n - 1\n \n``` | 2 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Python solutoin beats 99% in time and space complexity | count-distinct-numbers-on-board | 0 | 1 | # Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n return n - 1 or 1\n \n``` | 1 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Easy to Understand Python3 Solution | count-distinct-numbers-on-board | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(1)\n\n\n- Space complexity: O(1)\n\n\n# Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n if n==1:\n return 1\n return n-1\n \n``` | 1 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Python one-liner solution | count-distinct-numbers-on-board | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n return [n - 1, 1][n == 1]\n``` | 4 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Python | Easy Solution✅ | count-distinct-numbers-on-board | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def distinctIntegers(self, n: int) -> int:\n return n if n<=1 else n-1\n``` | 5 | You are given a positive integer `n`, that is initially placed on a board. Every day, for `109` days, you perform the following procedure:
* For each number `x` present on the board, find all numbers `1 <= i <= n` such that `x % i == 1`.
* Then, place those numbers on the board.
Return _the number of **distinct** integers present on the board after_ `109` _days have elapsed_.
**Note:**
* Once a number is placed on the board, it will remain on it until the end.
* `%` stands for the modulo operation. For example, `14 % 3` is `2`.
**Example 1:**
**Input:** n = 5
**Output:** 4
**Explanation:** Initially, 5 is present on the board.
The next day, 2 and 4 will be added since 5 % 2 == 1 and 5 % 4 == 1.
After that day, 3 will be added to the board because 4 % 3 == 1.
At the end of a billion days, the distinct numbers on the board will be 2, 3, 4, and 5.
**Example 2:**
**Input:** n = 3
**Output:** 2
**Explanation:**
Since 3 % 2 == 1, 2 will be added to the board.
After a billion days, the only two distinct numbers on the board are 2 and 3.
**Constraints:**
* `1 <= n <= 100` | null |
Very clear explanation | Straightforward solution | Explanation case missed | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | First of all, think that each monkey has two options to move. So this ends in them having `2^n` possible arrangements. \n\nThe only way the monkeys don\'t collide is if all of them go or clockwise or anticlockwise. In any other case there is at least one pair that ends in the same vertex. \n\nSo the raw solution would be `(2**n - 2) % 1000000007`.\n\nA little detail I had to face is that since the number of vertices is up to `1000000000`, you require to optimize the way you calculate the value `2**n`, and this is basically making a power exponentiation. For that part I would suggest reading and solving the [problem 50](https://leetcode.com/problems/powx-n/).\n\n## EDIT: \nIf someone checks one of [my attempts](https://leetcode.com/contest/weekly-contest-330/submissions/detail/887215331/), there is one that is related to the topic in other posts, about the answer `2**n-4` when `n` is even. I think the statement of the problem is wrong and that\'s why this case is not considered, but in case someone cares about why this result is a possible answer, the idea is: \n\nYou can swap between neighbors to avoid the possible overlap between monkeys **in a vertex**. So when you have an even number you can arrange them as\n\n```\nB\u2500\u2500\u2500\u2500B\n\u2502 \u2502\n\u2502 \u2502\nA\u2500\u2500\u2500\u2500A\n```\nor\n\n```\nA\u2500\u2500\u2500\u2500B\n\u2502 \u2502\n\u2502 \u2502\n\u2502 \u2502\nA\u2500\u2500\u2500\u2500B\n```\nAnd making one pair defines the other pairs. This generates the two missing cases that should be removed together with the full clockwise and anticlockwise cases.\n\nIn the case of odd `n` you will have one missing number that won\'t have partner, and this one will require to enter in one of the sites of his neighbors, but since those will be occupied by the other neighbors of its neighbors, this last monkey will overlap with one of the neighbors of distance `2` implying that in this case the pairs case is not considered as possible:\n\n```\n\u250C\u2500\u25BAB\u2500\u2500\u2500\u2500B\n\u2502 \u2502\nA \u2502\n\u2502 \u2502\n\u2514\u2500\u25BAC\u2500\u2500\u2500\u2500C\n```\n\n# Code\n```\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n modulo = 1_000_000_007\n answer = 1\n exponent = 2\n while n:\n if n&1:\n answer *= exponent \n exponent = (exponent*exponent) % modulo\n n >>= 1\n answer += modulo - 2\n answer %= modulo \n return answer\n\n``` | 7 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
✔ Python3 Solution | 1 linear | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | # Intuition\nEach monkey can move to left or right, So there are 2 possible ways a single monkey can move. For `n` number of monkeys there are `2 ^ n` possibilities. Out of which only `2` possible ways where no monkey can collide when all of them move to either left or right.\nTherefore, `ans = 2 ^ n - 2`\n\n# Complexity\n- Time complexity: $$O(pow(2, n))$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n mod = 10 ** 9 + 7\n return (pow(2, n, mod) + mod - 2) % mod\n``` | 3 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
Mod Pow | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | There are only 2 moves when no monkey collides - everyone goes clockwise or counter-clockwise.\n\nAlso, a pair of monkeys could swap places, but LeetCode added "... or intersect on an edge" after the contest to clarify that it would also cause a collision.\n\nThe total number of moves is 2 ^ n, so the result is 2 ^ n - 2. Note that we need to use Mod Pow, and Python has it.\n\n**Python 3**\n```python\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n mod = 10 ** 9 + 7\n return (mod + pow(2, n, mod) - 2) % mod\n``` | 2 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
[Python] Just math; Explained | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | This is a math problem. \nEach monkey can have two directions to move. Therefore, there are total `2 ** n` moving cases if there are n monkeys.\n\nAmong the 2 ** n cases, only 2 cases that no collision happens.\n\nTLE solutions\n```\nclass Solution: \n def monkeyMove(self, n: int) -> int:\n return (2 ** n - 2) % 1000000007\n```\n\nWe can use python internal function `pow()` to easily solve the TLE issue\n```\nclass Solution: \n def monkeyMove(self, n: int) -> int:\n return (pow(2, n, 1000000007) - 2) % 1000000007\n```\n\nHere is another way without using the `pow()` function. You can pick other numbers rather than the 1000000.\n```\nclass Solution: \n def monkeyMove(self, n: int) -> int:\n if n <= 1000000:\n return (2 ** n - 2) % 1000000007\n else:\n mul = 1\n while n > 1000000:\n mul *= self.calModeN(1000000)\n n = n - 1000000\n mul *= self.calModeN(n)\n return (mul % 1000000007 - 2) % 1000000007\n \n @cache\n def calModeN(self, n):\n return (2 ** n) % (1000000007)\n``` | 1 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
python3 Solution | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | \n\n```\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n return (pow(2,n,10**9+7)-2)%(10**9+7)\n``` | 1 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
[JavaScript / Python] solutions | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | ```javascript []\nconst monkeyMove = function (n) {\n const mod = BigInt(10 ** 9 + 7);\n let [base, res] = [2n, 1n];\n while (n > 0) {\n if (n % 2) res = (res * base) % mod;\n base = (base * base) % mod;\n n >>= 1;\n }\n return Number((res - 2n + mod) % mod);\n};\n```\n```python []\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n mod = 10**9 + 7\n return (pow(2, n, mod) + mod - 2) % mod\n```\n | 2 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
pow() Going on Lenthgs in Explanation and Experience | count-collisions-of-monkeys-on-a-polygon | 0 | 1 | ## Initial Thoughts\n\nI remember at the beginning of starting to confront LeetCode problems I made these judgments based on my ability that something was more difficult than it seemed. And problems with diagrams like this, I\'d go "Jesus Christ" a lot of times for. But once you get pass that and actually judge a problem by what it really is, you are going to discover a lot of verbose problems being actually quite simple, and a lot others being the total opposite lol.\n\nThe context in which the problem is discussed is basically graphs. They talk about edges and vertices.\n\nI noticed early on that you are able to visualize this like a binary string, where each position in the string can take either a 1 or a 0.\n\nThe monkeys can each one make one movement. They can go left or right, or we can think of it as they can go 1 or they can go 0. There has to be one decision for each monkey. So the absolute possible total of combinations of monkey movements in a n-vertex polygon will be the total combinations that you get with n positions in the binary string.\n\nBecause there are n positions and each one of the positions can take two values, either a 1 or a 0 you basically have **2<sup>n</sup>** combinations.\n\nNow the problem becomes (which was actually the only hint this problem had) counting the combinations that don\'t produce collisions in order to subtract it from that value of total possible combinations of movements which I know now to be **2<sup>n</sup>**.\n\n## Past Experiences\n\nVertices and edges are basic nomenclature that you deal with on problems that make use of graphs of any kind. But I could also, interestingly enough, relate this to even elementary level mathematics or geometry, where they talk about vertices and edges. Everything goes full circle one way or another.\n\nThere are a lot of problems that make you think about edges and vertices. I remember a lot of times being confused of what they meant by vertices and edges and kind of like mistaking one for the other. But now it\'s quite fast to understand what people are talking about in my head while I read. I guess the reading comprehension in regards to that kind of context and vocabulary has improved in me.\n\nAnd yeah, there\'s a lot of problems about that. So if at the beginning you feel kind of slow with them or their nomenclature, keep grinding, is not that they get easier, but you actually get harder.\n\nThere are also a lot of problems about basically having to surround or enumerate possibilities. Actually, there\'s a literal Enumeration tag where you have to discover and list each one of the problem\'s edge cases and decide how to handle them explicitly.\n\nIn this case it is conceptually kind of similar because you discover that each monkey can move one direction or the other in one step. They can\'t go any further at once. So those options of movements are the cases that we enumerate, account for and handle in our code. Then we have to think about the possible combinations of that.\n\nIf there\'s not only one monkey, but it\'s two monkeys or three monkeys or four, and the number of monkeys depends on the number of vertices in the polygon and each have the ability to make one decision or another, that together make a set of combinations of final decisions accounting for what each monkey decides to do.\n\nSo, in summary, confronting LeetCode I\'ve found, problems about both graphs, and things that have to do with enumeration and explicitly with binary stuff: binary strings and bit manipulation, other common ones. The first even if it\'s just geometric problems that are easy like this or complex problems that you still have to think abstractly about graphs and edges while working with arrays. \n\nAnd the second for an actual wide and varied range of use cases.\n\n## ChatGPT interaction\n\nI didn\'t use ChatGPT this time around. Neither this time, nor the time I approached the problem for the first time back in April.\n\nI actually started using it more heavily right after this when I purchased the GPT-Plus and decided to use it as an instructor.\n\nBut this second time I approached this problem, I can definitely see how my discussions with it regarding Bit Manipulation, Enumeration, and Graphs, particularly the vocabulary around graphs, has remarkably eased the difficulty of reading problem statements. And narrowing down the possible solutions.\n\nI actually find myself making less inappropriate assumptions. And this not only happens with problems I\'ve seen. I still find, with new problems that I confront, that I have a narrower and more targeted set of possibilities of assumptions to make about them, and that I\'m each time more likely to get them right.\n\nSo I find that my assumptions, first of all, are each and each time more accurate. And I think it\'s to a great degree due to how ChatGPT and I have interacted in the context of solving other problems ranging in topics and difficulty on LeetCode with this approach high level approach first.\n\n## Discoveries.\n\nReviewing this problem, having confronted it already before, It\'s difficult to tell if I came up with a solution by myself just now.\n\nI mean, probably every short-term memory queue that was left from the first time that I saw it is erased enough, but maybe far back into the longer-term memory part of my brain there may still be some pattern established only from that time that I suffered in frustration trying to come up with a solution to the problem. \n\nI think about this, because this time I actually found the solution to be super straightforward.\n\nWhat I mean is, I do know I have now further insights on how to verify that the assumption I made about the correct solution is correct, but it is difficult to know if making that right assumption was directly influenced by having encountered and remembering somehow the patterns in the solution the first time around.\n\nIn any case, there was a big moment of realization when I understood, first of all, what I explained earlier about understanding this as Bit Strings: the combinations of decisions that are possible for all the monkeys to make. The second one was discovering that as the great majority of the combinations would produce collisions, I had to worry about counting the ones where no collisions happened.\n\nAnd so I did, and I discovered the only way that not have collisions, neither on vertices nor edges, happen is by having all the monkeys moving in the same direction, which can be either clockwise or the other way around.\n\nWhich means subtracting 2 from the total possible combination of decisions that they can possibly make.\n\n## Solution\n\n```Python\nclass Solution:\n def monkeyMove(self, n: int) -> int:\n mod = 10 ** 9 + 7\n return (pow(2, n, mod) - 2) % mod\n```\n\n## Tricky parts\n\nRemember how I just talked about how sometimes rather verbose problems would be super easy and the other way around? well, that\'s basically what I just got into trying to understand in depth what we need to be doing with the modular operation.\n\nAnd we don\'t need to go so far back. The only thing that we need to know is that if we have a set of numbers that we want to evaluate and the result after the evaluation is going to be super big, one way we can set a boundary for what those values can be is using the modulus operation.\n\nBasically if you apply modulus to any value, you force the result to be inside a range from zero to the value you are applying the mod with `[0, mod]`, which makes all the results of doing modulo on some number non-negative and up until modulo, including it. And if you evaluate over modulo a number that\'s bigger than that, it\'s going to give you a result that is in that range.\n\nSo the modulo operation is a lot of times, including this one, used to make values fit into a range.\n\nAnd in the case of our problem, it effectively gives us a bound for values that could be huge. In this case, we can\'t directly calculate 2<sup>n</sup> and then just subtract 2 from it because n could be super huge, and the result even bigger.\n\nOr it can also be small and when we substract 2 from it could make it negative, so applying module again brings it back to somewhere in `[0, mod]`.\n\nAnd if I remember correctly, all of those modular arithmetic considerations for optimization are intrinsic to the way the pow function in Python works.\n\n## Optimization\n\nThis is of the type of LeetCode problems that on the way to the only test-passing solution you optimize most of it. The runtime rankings are pretty tight and would through my code answer around the whole percentile spectrums.\n\nSo in summary, we know pow is optimized to get the power of a number like crazy, and us handling the mod to get to the solution makes us use it optimally.\n\n## What I learned\n\nReturning solutions modulo a number is a fairly common pattern. Particularly in competitive programming questions of this type just by the nature of such high number returning problems and us wanting to give boundary to them. Both on the problem statement design and coming up with a solution ends.\n\nThe question has a tag recursion that I barely see how applies. I guess there could be another way to solve the problem that uses it, maybe to generate and count combinations but the Math solution gives a more straightforward approach.\n\nIn my experience, modular arithmetic in general has a wide range of applications and in a lot of problems they are touched upon but as secondary to the main topics of a question. So to a great degree is one of topics not tagged on LeetCode but still basic and assumed to have some familiarity with.\n\n## Further\n\n[ChatGPT](https://chat.openai.com/share/b2ada5c5-145e-4a2e-9bfd-db562f541321) got me in touch with the rabbit hole of modular arithmetic I could get into if I wanted. But I got out once I had more clarity on the nature of using module, how to use it, and why they commonly use it on some problem questions. Also the value `10**9 + 7` in relation to that.\n\nAnother common pattern is finding solution post from user lee215 and so I did review [his](https://leetcode.com/problems/count-collisions-of-monkeys-on-a-polygon/solutions/3111664/java-c-python-should-be-pow-2-n-4/) this time to get some insight and curious of if there were further improvements which could be made to the solution I came up with. | 0 | There is a regular convex polygon with `n` vertices. The vertices are labeled from `0` to `n - 1` in a clockwise direction, and each vertex has **exactly one monkey**. The following figure shows a convex polygon of `6` vertices.
Each monkey moves simultaneously to a neighboring vertex. A neighboring vertex for a vertex `i` can be:
* the vertex `(i + 1) % n` in the clockwise direction, or
* the vertex `(i - 1 + n) % n` in the counter-clockwise direction.
A **collision** happens if at least two monkeys reside on the same vertex after the movement or intersect on an edge.
Return _the number of ways the monkeys can move so that at least **one collision**_ _happens_. Since the answer may be very large, return it modulo `109 + 7`.
**Note** that each monkey can only move once.
**Example 1:**
**Input:** n = 3
**Output:** 6
**Explanation:** There are 8 total possible movements.
Two ways such that they collide at some point are:
- Monkey 1 moves in a clockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 2 collide.
- Monkey 1 moves in an anticlockwise direction; monkey 2 moves in an anticlockwise direction; monkey 3 moves in a clockwise direction. Monkeys 1 and 3 collide.
It can be shown 6 total movements result in a collision.
**Example 2:**
**Input:** n = 4
**Output:** 14
**Explanation:** It can be shown that there are 14 ways for the monkeys to collide.
**Constraints:**
* `3 <= n <= 109` | null |
Python 1-liner. Heap (PriorityQueue). Functional programming. | put-marbles-in-bags | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/put-marbles-in-bags/editorial/) but written functionally and using heaps instead of sorting.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def putMarbles(self, weights: list[int], k: int) -> int:\n return (lambda xs: sum(nlargest(k - 1, xs)) - sum(nsmallest(k - 1, xs)))(tuple(map(sum, pairwise(weights))))\n\n\n``` | 1 | You have `k` bags. You are given a **0-indexed** integer array `weights` where `weights[i]` is the weight of the `ith` marble. You are also given the integer `k.`
Divide the marbles into the `k` bags according to the following rules:
* No bag is empty.
* If the `ith` marble and `jth` marble are in a bag, then all marbles with an index between the `ith` and `jth` indices should also be in that same bag.
* If a bag consists of all the marbles with an index from `i` to `j` inclusively, then the cost of the bag is `weights[i] + weights[j]`.
The **score** after distributing the marbles is the sum of the costs of all the `k` bags.
Return _the **difference** between the **maximum** and **minimum** scores among marble distributions_.
**Example 1:**
**Input:** weights = \[1,3,5,1\], k = 2
**Output:** 4
**Explanation:**
The distribution \[1\],\[3,5,1\] results in the minimal score of (1+1) + (3+1) = 6.
The distribution \[1,3\],\[5,1\], results in the maximal score of (1+3) + (5+1) = 10.
Thus, we return their difference 10 - 6 = 4.
**Example 2:**
**Input:** weights = \[1, 3\], k = 2
**Output:** 0
**Explanation:** The only distribution possible is \[1\],\[3\].
Since both the maximal and minimal score are the same, we return 0.
**Constraints:**
* `1 <= k <= weights.length <= 105`
* `1 <= weights[i] <= 109` | null |
Python Elegant & Short | Two Lines | put-marbles-in-bags | 0 | 1 | # Complexity\n- Time complexity: $$O(n * log_{2} n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def putMarbles(self, weights: List[int], k: int) -> int:\n cost = [l + r for l, r in pairwise(weights)]\n return sum(nlargest(k - 1, cost)) - sum(nsmallest(k - 1, cost))\n```\n | 1 | You have `k` bags. You are given a **0-indexed** integer array `weights` where `weights[i]` is the weight of the `ith` marble. You are also given the integer `k.`
Divide the marbles into the `k` bags according to the following rules:
* No bag is empty.
* If the `ith` marble and `jth` marble are in a bag, then all marbles with an index between the `ith` and `jth` indices should also be in that same bag.
* If a bag consists of all the marbles with an index from `i` to `j` inclusively, then the cost of the bag is `weights[i] + weights[j]`.
The **score** after distributing the marbles is the sum of the costs of all the `k` bags.
Return _the **difference** between the **maximum** and **minimum** scores among marble distributions_.
**Example 1:**
**Input:** weights = \[1,3,5,1\], k = 2
**Output:** 4
**Explanation:**
The distribution \[1\],\[3,5,1\] results in the minimal score of (1+1) + (3+1) = 6.
The distribution \[1,3\],\[5,1\], results in the maximal score of (1+3) + (5+1) = 10.
Thus, we return their difference 10 - 6 = 4.
**Example 2:**
**Input:** weights = \[1, 3\], k = 2
**Output:** 0
**Explanation:** The only distribution possible is \[1\],\[3\].
Since both the maximal and minimal score are the same, we return 0.
**Constraints:**
* `1 <= k <= weights.length <= 105`
* `1 <= weights[i] <= 109` | null |
Explain Partition||C++/Python greedy||sort vs priority queue | put-marbles-in-bags | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[Please turn on english subtitles if neccessary]\n[https://youtu.be/XMOqSMrbz_Q](https://youtu.be/XMOqSMrbz_Q)\n# What is the essential meaning for a partition?\n\nA partition refers to dividing something, such as a set or array, into separate sections or subsets.\n\n# Can you explain how to find k-1 pairs based on the weights in a partition?\n\nTo find k-1 pairs based on the weights in a partition, we need to determine the end index for each subarray in the partition. For each i-th subarray, denoted by P[i], we look at the weights[P[i]] and weights[P[i]+1] elements. We continue this process for all the subarrays in the partition.\n\n\n# What is the score of a partition?\n\nThe score of a partition, denoted as score(P), is calculated by summing certain weights. We start with weights[0] and weights[n-1], and then for each subarray i, we add the weights[P[i]] and weights[P[i]+1] together. This sum is repeated for all subarrays in the partition.\n\n$$\nscore(P)=\\\\(weights[0]+weights[P[0]])+(weights[P[0]+1]+weights[P[1]])+\\\\ \\cdots\n+(weights[P[i-1]+1]+weights[P[i]])+\\\\\n\\cdots+(weights[P[k-2]+1]+weights[n-1])\n\\\\\n=weights[0]+weights[n-1]+\\sum_i (weights[P[i]]+weights[P[i]+1])\n$$\n\nLook at this example. Let "|" denote the partition. Since k=4, there are exactly 3 partitions.\n[54,6,34,66,63|52,39,62,46,75,28,65,18,37,18|13,33,69,19,40,13|10,43,61,72] \n\nP[0]=4, weights[P[0]]=63, weights[P[0]+1]=52 partition[0]=63+52\np[1]=14, weights[P[1]]=18, weights[P[1]+1]=13, partition[1]=18+13\n# What is the desired answer in terms of the scores of different partitions?\n\nThe desired answer is the difference between the maximum score of all partitions ($\\max_P score(P)$) and the minimum score of all partitions ($\\min_P score(P)$).\n\n# How many partitions are there at most?\n\nThere can be at most $n-1$ partitions.\n\n# How can you find the maximum and minimum scores of all partitions?\n\nTo find the maximum and minimum scores of all partitions, you can either sort the partition scores (partition[i] = weights[i] + weights[i+1]) or use heaps (a data structure). Once the scores are sorted or stored in a heap, it becomes easy to identify the maximum and minimum scores.\n\n<!-- Describe your approach to solving the problem. -->\ntest case\n```\n[54,6,34,66,63,52,39,62,46,75,28,65,18,37,18,13,33,69,19,40,13,10,43,61,72]\n4\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n \\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n\n```C++ []\nclass Solution {\npublic:\n long long putMarbles(vector<int>& weights, int k) {\n int n=weights.size();\n if (n<=2 || n==k) return 0;\n vector<int> P(n-1, 0);\n for (int i=0; i<n-1; i++)\n P[i]=weights[i]+weights[i+1];\n \n sort(P.begin(), P.end());\n\n // without weights[0]+weights[n-1]\n long long minP=accumulate(P.begin(), P.begin()+(k-1), 0LL), \n maxP=accumulate(P.begin()+(n-k), P.end(), 0LL);\n \n return maxP-minP;\n }\n};\n```\n```python []\nclass Solution:\n def putMarbles(self, weights: List[int], k: int) -> int:\n n=len(weights)\n if n<=2 or n==k:\n return 0\n partition=[0]*(n-1)\n for i in range(n-1):\n partition[i]=weights[i]+weights[i+1]\n\n partition.sort()\n\n maxP=sum(partition[n-k:]) #without weights[0]+weights[n-1]\n minP=sum(partition[:k-1])\n return maxP-minP\n```\n\n# 2nd Approach using priority queue is slower but theoretically faster time complexity O(n log k)\n```\nclass Solution {\npublic:\n long long putMarbles(vector<int>& weights, int k) {\n int n=weights.size();\n if (n<=2) return 0;\n\n priority_queue<int> maxHeap;\n priority_queue<int, vector<int>, greater<int> > minHeap;\n long long maxP=0, minP=0;\n for (int i=0; i<k-1; i++){\n int partition=weights[i]+weights[i+1];\n maxP+=partition;\n maxHeap.push(partition);\n minHeap.push(partition);\n }\n minP=maxP; \n\n //without weights[0]+weights[n-1]\n for(int i=k-1; i<n-1; i++){\n int partition=weights[i]+weights[i+1];\n maxHeap.push(partition);\n minP+=partition-maxHeap.top();\n maxHeap.pop();\n minHeap.push(partition);\n maxP+=partition-minHeap.top();\n minHeap.pop();\n }\n return maxP-minP;\n }\n};\n```\n\n | 10 | You have `k` bags. You are given a **0-indexed** integer array `weights` where `weights[i]` is the weight of the `ith` marble. You are also given the integer `k.`
Divide the marbles into the `k` bags according to the following rules:
* No bag is empty.
* If the `ith` marble and `jth` marble are in a bag, then all marbles with an index between the `ith` and `jth` indices should also be in that same bag.
* If a bag consists of all the marbles with an index from `i` to `j` inclusively, then the cost of the bag is `weights[i] + weights[j]`.
The **score** after distributing the marbles is the sum of the costs of all the `k` bags.
Return _the **difference** between the **maximum** and **minimum** scores among marble distributions_.
**Example 1:**
**Input:** weights = \[1,3,5,1\], k = 2
**Output:** 4
**Explanation:**
The distribution \[1\],\[3,5,1\] results in the minimal score of (1+1) + (3+1) = 6.
The distribution \[1,3\],\[5,1\], results in the maximal score of (1+3) + (5+1) = 10.
Thus, we return their difference 10 - 6 = 4.
**Example 2:**
**Input:** weights = \[1, 3\], k = 2
**Output:** 0
**Explanation:** The only distribution possible is \[1\],\[3\].
Since both the maximal and minimal score are the same, we return 0.
**Constraints:**
* `1 <= k <= weights.length <= 105`
* `1 <= weights[i] <= 109` | null |
[Python3] SortedList/bisect.insort Solution Clean & Concise | count-increasing-quadruplets | 0 | 1 | # Approach\nWe break the quadruple into `(i, j)` and `(k, l)`, and use a `SortedList` data structure in Python to maintain the ongoing subarray up to `j`.\n\nFor each current element `nums[j]` (maintained using a for loop from left to right), we loop through the possible value of `nums[k]` from right to left, and count\n\n(1) how many element on the left of `j` that satisfies `nums[k] > nums[i]`, this can be achieved using a binary search;\n(2) how many element on the right of `k` has the value `nums[l] > nums[j]`, this can be achieved by comparing the value of `nums[k]` with `nums[j]` each time;\n\nand add the product from (1) and (2) to the final `ans`.\n\n# Complexity\n- Time complexity: $$O(n^2\\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def countQuadruplets(self, nums: List[int]) -> int:\n n = len(nums)\n sl = SortedList([nums[0]])\n ans = 0\n for j in range(1, n):\n sl.add(nums[j])\n cnt = 1 if nums[j] < nums[-1] else 0\n for k in range(n - 2, j, -1):\n if nums[j] < nums[k]:\n cnt += 1\n continue\n ans += sl.bisect_left(nums[k]) * cnt\n return ans\n```\n\n# Updated Code (02/08/2023)\nIt has come to my attention that LC recently included additional long test cases that will make the above solution TLE (thanks to [noniero](https://leetcode.com/nonieno/) for pointing it out). Using the same algorithm but with the built-in `bisect.insort` method, we have the following `Accepted` solution (thanks to [chestnut890123](https://leetcode.com/chestnut890123/)).\n```\nclass Solution:\n def countQuadruplets(self, nums: List[int]) -> int:\n n = len(nums)\n sl = [nums[0]]\n ans = 0\n for j in range(1, n):\n bisect.insort(sl, nums[j])\n cnt = 1 if nums[j] < nums[-1] else 0\n for k in range(n - 2, j, -1):\n if nums[j] < nums[k]:\n cnt += 1\n continue\n ans += bisect_left(sl, nums[k]) * cnt\n return ans\n``` | 7 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
naive O(n^2 logn) solution python | count-increasing-quadruplets | 0 | 1 | the idea similar to 132 pattern\n\nbut now we have 1324 words\nwe keep the 3 as middle \n- first get the distribution of left hand side -> smaller\n- then check right hand side:\n - if bigger than 3 -> might be 4\n - if smaller than 3 -> count into 2\n\n\n```\nclass Solution:\n # Time: O(n^2 * logn)\n # Space: O(n)\n def countQuadruplets(self, nums: List[int]) -> int:\n # dp\n dp = [0] * len(nums)\n \n ans = 0\n for idx in range(1, len(nums)-1):\n num = nums[idx]\n # forward, get small distribution\n smaller = []\n for j in range(idx):\n if num > nums[j]:\n smaller.append(nums[j])\n if not smaller:\n continue\n smaller = sorted(smaller)\n\n # backward\n bigger = []\n for j in range(idx+1, len(nums)):\n # O(logn)\n if num > nums[j]:\n dp[idx] += bisect_left(smaller, nums[j])\n \n elif num < nums[j]:\n ans += dp[idx]\n\n return ans\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
[C++|Java|Python3] Cleanest Code with Clarification O(n^2) | count-increasing-quadruplets | 1 | 1 | # Intuition\n\nThe crux of this problem is to identify and count increasing quadruplets. To simplify the problem, let\'s break it down to count the **132 triplets** first, then leverage them to count **1324 quadruplets**.\n\n1. **132 Triplet**: A triplet (i, j, k) that satisfies the condition `i < j < k` and `nums[i] < nums[k] < nums[j]`.\n\n2. **1324 Quadruplet**: A quadruplet (i, j, k, l) that meets the criteria `i < j < k < l` and `nums[i] < nums[k] < nums[j] < nums[l]`.\n\n## Approach\n\nWe maintain an array `cnt` where `cnt[j]` stores the **count** of 132 triplets that using the current index number as the role `3` (index `j`) to construct 132 triplets. (*For example: if we have a array [1, 3, 2], there is only one 132 triplets in the list, the cnt array should looks like [0, 1, 0].*)\n\nAssume we have already constructed a `cnt` for a prefix subarray of the `nums` array, we can introduce a new value `l` in `num` immidiately after the prefix, then iterate all previous stored `cnt[j]` (132 pattern counts); if `nums[l] > nums[j]`, they can form valid 1324 quadruplet patterns, thus we add `cnt[j]` into total 1324 counts.\n\nTo finalize our approach, we will iteratively introduce a new value `l` and works on the prefix array before it to count 1324 patterns. While iterating the index `j`, we also update `cnt[j]` by keeping track of the amount of numbers smaller than the current new value (`l`) in front of `j`, defined as `previous_small`. If `nums[l] < nums[j]`, the new value (`l`) is a potential `k` for `j` to form 132 triplets, and `previous_small` is the number of unique 132 triplets they can form together, so add `previous_small` to `cnt[j]`.\n\nNote that in code, $i$ is actually `j`, $j$ is actually `l`, relate to above explanation.\n\n# Complexity\n\n- Time complexity: $O(n^2)$\n\n- Space complexity: $O(n)$\n\n# Code\n```python []\nclass Solution:\n def countQuadruplets(self, nums: List[int]) -> int:\n n = len(nums)\n cnt = [0] * n\n ans = 0\n for j in range(n):\n prev_small = 0\n for i in range(j):\n if nums[j] > nums[i]:\n prev_small += 1\n ans += cnt[i]\n elif nums[j] < nums[i]:\n cnt[i] += prev_small\n return ans\n```\n```java []\nclass Solution {\n public long countQuadruplets(int[] nums) {\n int n = nums.length;\n long[] cnt = new long[n];\n long ans = 0;\n for (int j = 0; j < n; j++) {\n int prev_small = 0;\n for (int i = 0; i < j; i++) {\n if (nums[j] > nums[i]) {\n prev_small++;\n ans += cnt[i];\n } else if (nums[j] < nums[i]) {\n cnt[i] += prev_small;\n }\n }\n }\n return ans;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n long long countQuadruplets(vector<int>& nums) {\n long long ans=0;\n int n=nums.size();\n long long prev_small=0;\n vector<long long> cnt(n,0);\n for(int i=0 ; i<n ; i++){\n prev_small=0;\n for(int j=0 ; j<i ; j++){\n if(nums[i]>nums[j]){\n prev_small++;\n ans+=cnt[j];\n }\n else if(nums[i]<nums[j]){\n cnt[j]+=prev_small;\n }\n }\n }\n return ans; \n }\n};\n```\n```Javascript []\nvar countQuadruplets = function (nums) {\n const N = nums.length;\n let ans = 0;\n let cnt = Array(N).fill(0);\n\n for (let j = 0; j < N; j++) {\n let prev_small = 0;\n for (let i = 0; i < j; i++) {\n if (nums[j] > nums[i]) {\n prev_small++;\n ans += cnt[i];\n } else if (nums[j] < nums[i]) {\n cnt[i] += prev_small;\n }\n }\n }\n return ans;\n};\n```\n\nC++ is contributed by @Manan_Jain_4, Java is contributed by @ibmtp380, Javascript is contributed by @Gang-Li.\n\n# Lets do some Simulation\n\n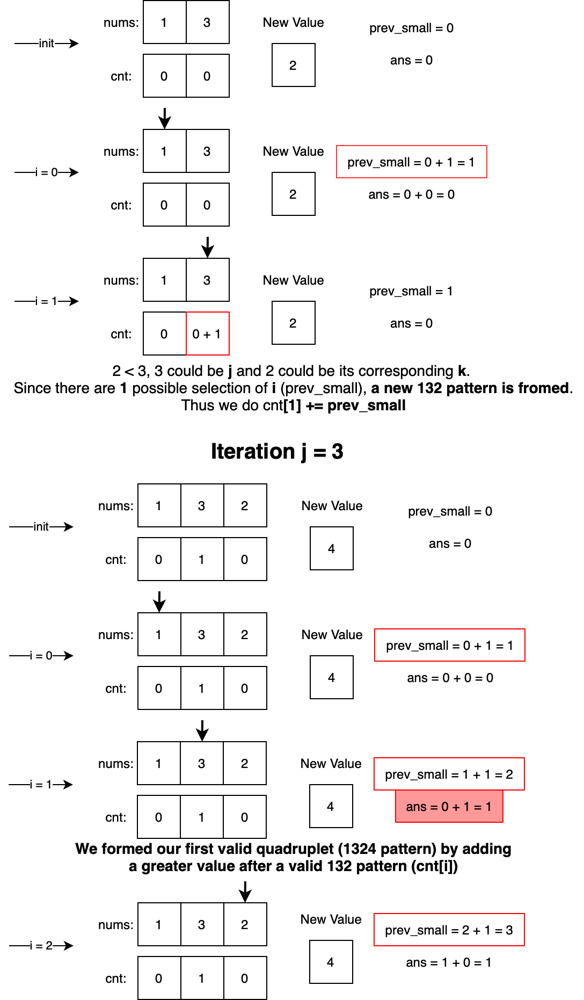\n\n\n\n# Please Vote Up if this helps ;D | 165 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
O(N^2) python code | count-increasing-quadruplets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countQuadruplets(self, nums: List[int]) -> int:\n n = len(nums)\n peakCount = [0] * n\n ans = 0\n for i in range(n):\n smaller = 0\n for j in range(i):\n if nums[j] < nums[i]:\n smaller += 1\n ans += peakCount[j]\n else:\n peakCount[j] += smaller\n return ans\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
【C++||Java||Python】Enumerate All (j,k) Pairs, with O(n²) Complexity | count-increasing-quadruplets | 1 | 1 | > **I know almost nothing about English, pointing out the mistakes in my article would be much appreciated.**\n\n> **In addition, I\'m too weak, please be critical of my ideas.**\n---\n\nThis is an [Better answer](https://leetcode.com/problems/count-increasing-quadruplets/solutions/3111697/python3-clean-dp-with-clarification-o-n-2/)!\n\n# Intuition\n1. The data range is no greater than $4000$, so we can consider an angorithm with around $O(n^2)$ time complexity.\n2. This problem seems like [LeetCode 493](https://leetcode.com/problems/reverse-pairs/) and [LeetCode 2179](https://leetcode.com/problems/count-good-triplets-in-an-array/), a direct idea is enumerating all the middle pairs, and count how many numbers could be the $i$ and $l$ for each $j$ and $k$.\n3. A simple way to count is to use a [Binary Index Tree](https://en.wikipedia.org/wiki/Fenwick_tree), which allows for fast point updates and range sums.\n4. But notice that the range of $a[i]$ will never greater than $n$, so we can generate two tables:\n - $left[i][j]$ records "from $0$ to $i-1$, the count of $< j$"\n - $right[i][j]$ records "from $n-1$ to $i+1$, the count of $>j$".\n5. Enumerate all the $jk$ pairs, the answer can be obtained using the [Rule of product](https://en.wikipedia.org/wiki/Rule_of_product).\n\n# Complexity\n- Time complexity: $O(n^2)$\n- Space complexity: $O(n^2)$\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n long long countQuadruplets(vector<int>& a) {\n long long res = 0;\n int n = a.size();\n vector<vector<int>> left(n, vector<int>(n+1, 0));\n vector<vector<int>> right(n, vector<int>(n+1, 0));\n for (int i = 1; i < n; ++i) {\n // new array will based on the old array\n left[i] = left[i-1];\n // update all the elements greater than a[i-1]\n for (int j = a[i-1] + 1; j <= n; ++j)\n left[i][j]++;\n }\n for (int i = n-2; i >= 0; --i) {\n right[i] = right[i+1];\n for (int j = 0; j < a[i+1]; ++j)\n right[i][j]++;\n }\n for (int j = 0; j < n; ++j) {\n for (int k = j+1; k < n; ++k) {\n if (a[j] <= a[k]) continue;\n // left[j][a[k]] is the count of feasible i\n // right[k][a[j]] is the count of feasible l\n res += left[j][a[k]] * right[k][a[j]];\n }\n }\n return res;\n }\n};\n```\n``` Java []\nclass Solution {\n public long countQuadruplets(int[] a) {\n long res = 0;\n int n = a.length;\n int [][]left = new int[n][n+1];\n int [][]right = new int[n][n+1];\n for (int i = 1; i < n; ++i) {\n // new array will based on the old array\n for (int j = 0; j <= n; ++j) \n left[i][j] = left[i-1][j];\n // update all the elements greater than a[i-1]\n for (int j = a[i-1] + 1; j <= n; ++j)\n left[i][j]++;\n }\n for (int i = n-2; i >= 0; --i) {\n for (int j = 0; j <= n; ++j) \n right[i][j] = right[i+1][j];\n for (int j = 0; j < a[i+1]; ++j) \n right[i][j]++;\n }\n for (int j = 0; j < n; ++j) {\n for (int k = j+1; k < n; ++k) {\n if (a[j] <= a[k]) continue;\n // left[j][a[k]] is the count of feasible i\n // right[k][a[j]] is the count of feasible l\n res += left[j][a[k]] * right[k][a[j]];\n }\n }\n return res;\n }\n}\n```\n``` Python3 []\nclass Solution:\n def countQuadruplets(self, a: List[int]) -> int:\n res, n = 0, len(a)\n left = [None for j in range(n)]\n right = [None for j in range(n)]\n left[0] = [0 for i in range(n+1)]\n right[-1] = [0 for i in range(n+1)]\n for i in range(1, n):\n # new array will based on the old array\n left[i] = left[i-1].copy()\n # update all the elements greater than a[i-1]\n for j in range(a[i-1] + 1, n + 1):\n left[i][j] += 1\n for i in range(n-2, -1, -1):\n right[i] = right[i+1].copy()\n for j in range(a[i+1]):\n right[i][j] += 1\n for j in range(n):\n for k in range(j+1, n):\n # left[j][a[k]] is the count of feasible i\n # right[k][a[j]] is the count of feasible l\n if a[j] > a[k]:\n res += left[j][a[k]] * right[k][a[j]]\n return res\n``` | 51 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
2 Pass counting 132 nums and then using them to build 1324 nums | count-increasing-quadruplets | 0 | 1 | # Code\n```\nclass Solution:\n # T = O(N^2)\n # S = O(N)\n def countQuadruplets(self, nums: List[int]) -> int:\n # https://leetcode.com/problems/count-increasing-quadruplets/solutions/3111697/c-java-python3-cleanest-code-with-clarification-o-n-2/\n # This is an extension of 132 triplets \n # For i < j < k < l\n # 1 3 2 4 \n # Num: a[i] < a[k] < a[j] < a[l]\n n = len(nums)\n # Counts number of 132 triplets from jth index with rest of numbers before after it.\n trips = [0] * n\n \n ans = 0\n\n for k in range(n):\n lessThanK = 0\n for i in range(k):\n\n if nums[i] < nums[k]:\n lessThanK += 1\n\n # Since nums[i] < nums[k]\n # k might be at l and i at j\n # We could have found the j, l pair\n # trips[i] gives number of triplets where i is the jth number\n # So now we have the 4rth element so ans += trips[i]\n # trips[i] will get a non zero value only when we actually find triplets \n # So before that trips[i] will be 0 as trips[i] cant have non zero value \n # without we first encountering a nums[i] > nums[k] case, which will not \n # happen in ascending sequences \n ans += trips[i]\n # we have a potential triplet (since n[i] > n[k])\n # in this case all nums unique so only else is also okay, but does not matter\n elif nums[i] > nums[k]: \n # we were counting less than n[k] nums and now we found a n[i] > n[k]\n # so ther num triplets will be lessThanK! \n # 1 2 3 10 <6> 8 16: At 6 we will first get a triplet\n # before that we just counted nums less than 6 (3)\n # When at 10 now we have 3 triplets!\n trips[i] += lessThanK\n \n # I/P: [1, 2, 3, 7, 6, 8, 4, 5, 9]\n # Trips: [0, 0, 0, 9, 6, 6, 0, 0, 0]\n # For 6: [1,6,4], [1,6,5], [2,6,4], [2,6,5], [3,6,4], [3,6,5]\n # For 7: [1,7,6], [1,7,4], [1,7,5], [2,7,6], [2,7,4], [2,7,5], [3,7,6], [3,7,4], [3,7,5]\n # For 8: [1,8,4], [1,8,5], [2,8,4], [2,8,5], [3,8,4], [3,8,5]\n return ans\n\n\n\n``` | 0 | Given a **0-indexed** integer array `nums` of size `n` containing all numbers from `1` to `n`, return _the number of increasing quadruplets_.
A quadruplet `(i, j, k, l)` is increasing if:
* `0 <= i < j < k < l < n`, and
* `nums[i] < nums[k] < nums[j] < nums[l]`.
**Example 1:**
**Input:** nums = \[1,3,2,4,5\]
**Output:** 2
**Explanation:**
- When i = 0, j = 1, k = 2, and l = 3, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
- When i = 0, j = 1, k = 2, and l = 4, nums\[i\] < nums\[k\] < nums\[j\] < nums\[l\].
There are no other quadruplets, so we return 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** 0
**Explanation:** There exists only one quadruplet with i = 0, j = 1, k = 2, l = 3, but since nums\[j\] < nums\[k\], we return 0.
**Constraints:**
* `4 <= nums.length <= 4000`
* `1 <= nums[i] <= nums.length`
* All the integers of `nums` are **unique**. `nums` is a permutation. | null |
✅ Explained - Simple and Clear Python3 Code✅ | separate-the-digits-in-an-array | 0 | 1 | # Intuition\nThe given problem requires separating the digits of positive integers in an array and returning the digits in the same order they appear in the original numbers.\n\n\n# Approach\nThe provided solution uses a function named separateDigits within a class named Solution. The function takes an input parameter nums, which is a list of positive integers. The function returns a list res containing the separated digits.\n\nTo separate the digits of each integer, the solution iterates over each number x in the input array nums. For each number, it initializes an empty list t. It then enters a while loop that continues until the number x becomes zero.\n\nWithin the while loop, the solution calculates the remainder of x divided by 10 using the modulo operator %, which gives the last digit of the number. This digit is then inserted at the beginning of the list t using the insert method with an index of 0.\n\nAfter inserting the digit, the solution updates x by performing an integer division x // 10, which removes the last digit from the number. This process is repeated until all the digits of x are separated.\n\nOnce all the digits of x are separated and stored in the list t, the solution appends the contents of t to the result list res using the += operator. This ensures that the digits of each number are added in the order they appear in the input array.\n\nFinally, when all numbers in the input array have been processed, the function returns the resulting list res.\n\n\n\n# Complexity\n- Time complexity:\nthe time complexity of this solution depends on the total number of digits in all the integers present in the input array. If there are a total of n digits, the solution will iterate over each digit once, resulting in a time complexity of O(n).\n\n- Space complexity:\nThe space complexity of the solution is also dependent on the number of digits. It uses additional space to store the separated digits of each number in the list t and the final result in the list res. Therefore, the space complexity is also O(n), where n represents the total number of digits in the input array.\n\n\n\n\n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n res=[]\n for x in nums:\n t=[]\n while x>0:\n t.insert(0,x%10)\n x=x//10\n res+=t\n return res\n``` | 5 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Python Solution Without Data Conv. || Easy to Understand | separate-the-digits-in-an-array | 0 | 1 | # Intuition\n\n---\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, you can use the simple **digit extraction method** to get the required output without converting data type which makes the program runtime **slower**.\n\n# Approach\n\n---\n\n\n<!-- Describe your approach to solving the problem. -->\nIn this solution, the **getDigits()** function takes an integer **n** and returns a list of its digits. It uses a while loop to extract digits from the number by repeatedly dividing it by **10** and adding the remainder to the list. The **insert(0, digit)** is used to maintain the order of digits.\n\nThe **separateDigits()** function then iterates through the input array nums, calls the **getDigits()** function for each number, and **extends** the answer list with the extracted digits. This way, you can achieve the desired result without using **data conversion to strings**.\n\n---\n\n\n\n\n# Code\n\n---\n\n\n```\nclass Solution(object):\n def separateDigits(self, nums):\n def getDigits(n):\n digits = []\n while n > 0:\n digit = n % 10\n digits.insert(0, digit)\n n = n // 10\n return digits\n \n answer = []\n for num in nums:\n digits = getDigits(num)\n answer.extend(digits)\n \n return answer\n``` | 1 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Easy python for beginners | separate-the-digits-in-an-array | 0 | 1 | \n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n answer = []\n hash_map = {}\n i = 0\n for num in nums:\n x = [int(y) for y in str(num)]\n for number in x:\n hash_map[i] = number\n i += 1 \n for value in hash_map.values():\n answer.append(value)\n return answer\n``` | 1 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Python 3 || Bit Operation || Reuse Input List | separate-the-digits-in-an-array | 0 | 1 | # Intuition\nMost solutions create a new list to return the result. This solution is based on reusing the input list by using bitwise operations.\n\n# Approach\nThe idea is to traverse the list and, if necessary, storing two values in one number. The maximum number is $$10^5$$, for which at most 17 bits are required. All other bits can be used to store the new values.\n\nWe split each number into its individual digits and store them one by one at the correct indices ```ptr``` in the list. To do this, we append the new number to the left of the original number ```int(num)<<17 | nums[ptr]```. If all elements of the list are already filled with a second value, the element is appended to the list. Finally, we remove the original value and set the new value by shifting ```nums[i] >>= 17```.\n\n\n```\nmax_number: 100000 (decimal) = 00000000 00000001 10000110 10100000 (binary)\nmask numbers: 00000000 00000001 11111111 11111111 (2^17-1)\nusable numbers: 11111111 11111110 00000000 00000000\n```\n\n# Code\n```Python3\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n ptr = 0\n n = len(nums)\n mask = 2**17-1\n for i in range(n):\n for num in str(nums[i]&mask):\n if ptr<n:\n nums[ptr] = int(num)<<17 | nums[ptr]\n ptr += 1\n else:\n nums.append(int(num))\n nums[i] >>= 17\n return nums\n```\n\n# Complexity\n- Time complexity: $$O(n)$$\n - Outer loop\n Each number is visited once\n - Inner loop\n For each number, we iterate all digits (at most 6 digits because max_number=$$10^5$$)\n - Worst case: $$O(6*n)=O(n)$$\n\n- Space complexity: $$O(n)$$ \n - Worst case\n Input list contains max_number=$$10^5$$ n times. List must be increased by 5 additional entries for each element => $$O(6*n)=O(n)$$\n\n | 4 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Python Easy Solution || 100% || | separate-the-digits-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n res=[]\n for i in nums:\n for j in str(i):\n res.append(int(j))\n return res\n``` | 1 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Easy | separate-the-digits-in-an-array | 0 | 1 | \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n res = []\n for i in range(0,len(nums)):\n if(len(str(nums[i]))> 1):\n j = str(nums[i])\n for k in j:\n res.append(int(k))\n else:\n res.append(int(nums[i]))\n return res\n``` | 1 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Easy to understand READABLE Python code | separate-the-digits-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n\n string_sep = []\n\n for num in nums:\n for s in str(num):\n string_sep.append(int(s))\n\n return string_sep\n \n```\nBy using List Comprehension:\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n ans = []\n for num in nums:\n ans.extend([int(s) for s in str(num)])\n return ans\n```\nJUST FOR FUN A FEW ONE LINERS:\n\nOne liner using List Comprehension:\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n return [int(s) for num in nums for s in str(num)]\n \n```\nOne liner using itertools.chain:\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n return map(int, chain(*map(str, nums)))\n``` | 2 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
[ Python ] ✅✅ Simple Python Solution Using Maths🥳✌👍 | separate-the-digits-in-an-array | 0 | 1 | # If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 123 ms, faster than 6.15% of Python3 online submissions for Separate the Digits in an Array.\n# Memory Usage: 14.6 MB, less than 27.41% of Python3 online submissions for Separate the Digits in an Array.\n\n\tclass Solution:\n\t\tdef separateDigits(self, nums: List[int]) -> List[int]:\n\n\t\t\tresult = []\n\n\t\t\tfor num in nums:\n\n\t\t\t\tcurrent_result = []\n\n\t\t\t\twhile num > 0:\n\t\t\t\t\tcurrent_result.append(num % 10)\n\t\t\t\t\tnum = num // 10\n\n\t\t\t\tresult = result + current_result[::-1]\n\n\t\t\treturn result\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D | 3 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Easy Python Solution - separateDigits | separate-the-digits-in-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n l = []\n for i in nums:\n s = str(i)\n for j in s:\n l.append(int(j))\n return l\n``` | 2 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Beats 98.88%. Python solution | separate-the-digits-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->Here\'s a easier method to solve this.\nAll you have to do is iterate\n\n# Approach\n<!-- Describe your approach to solving the problem. -->We first iterate the list.\nThen we iterate the numbers in the list as a string and append them into a list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n55ms\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->16.88mb\n\n# Code\n```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n l=[]\n for i in nums:\n for j in str(i):\n l.append(int(j))\n return l\n \n```\n\n | 0 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
Python Solution || Easy to understand | separate-the-digits-in-an-array | 0 | 1 | ```\nclass Solution:\n def separateDigits(self, nums: List[int]) -> List[int]:\n ans = []\n\t\t\n\t\t# iterating numbers one by one\n for num in nums:\n\t\t\n\t\t\t# iterating digit of num via converting it to string\n for dig in str(num):\n\t\t\t\n\t\t\t\t# adding each digit to ans array\n ans.append(int(dig))\n return ans\n``` | 1 | Given an array of positive integers `nums`, return _an array_ `answer` _that consists of the digits of each integer in_ `nums` _after separating them in **the same order** they appear in_ `nums`.
To separate the digits of an integer is to get all the digits it has in the same order.
* For example, for the integer `10921`, the separation of its digits is `[1,0,9,2,1]`.
**Example 1:**
**Input:** nums = \[13,25,83,77\]
**Output:** \[1,3,2,5,8,3,7,7\]
**Explanation:**
- The separation of 13 is \[1,3\].
- The separation of 25 is \[2,5\].
- The separation of 83 is \[8,3\].
- The separation of 77 is \[7,7\].
answer = \[1,3,2,5,8,3,7,7\]. Note that answer contains the separations in the same order.
**Example 2:**
**Input:** nums = \[7,1,3,9\]
**Output:** \[7,1,3,9\]
**Explanation:** The separation of each integer in nums is itself.
answer = \[7,1,3,9\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 105` | null |
[Python 3] Brute-force | maximum-number-of-integers-to-choose-from-a-range-i | 0 | 1 | ```python3 []\nclass Solution:\n def maxCount(self, banned: List[int], n: int, maxSum: int) -> int:\n res, s, b = 0, 0, set(banned)\n for i in range(1, n+1):\n if s + i > maxSum: break\n if i not in b:\n s += i\n res += 1\n\n return res\n```\n | 1 | You are given an integer array `banned` and two integers `n` and `maxSum`. You are choosing some number of integers following the below rules:
* The chosen integers have to be in the range `[1, n]`.
* Each integer can be chosen **at most once**.
* The chosen integers should not be in the array `banned`.
* The sum of the chosen integers should not exceed `maxSum`.
Return _the **maximum** number of integers you can choose following the mentioned rules_.
**Example 1:**
**Input:** banned = \[1,6,5\], n = 5, maxSum = 6
**Output:** 2
**Explanation:** You can choose the integers 2 and 4.
2 and 4 are from the range \[1, 5\], both did not appear in banned, and their sum is 6, which did not exceed maxSum.
**Example 2:**
**Input:** banned = \[1,2,3,4,5,6,7\], n = 8, maxSum = 1
**Output:** 0
**Explanation:** You cannot choose any integer while following the mentioned conditions.
**Example 3:**
**Input:** banned = \[11\], n = 7, maxSum = 50
**Output:** 7
**Explanation:** You can choose the integers 1, 2, 3, 4, 5, 6, and 7.
They are from the range \[1, 7\], all did not appear in banned, and their sum is 28, which did not exceed maxSum.
**Constraints:**
* `1 <= banned.length <= 104`
* `1 <= banned[i], n <= 104`
* `1 <= maxSum <= 109` | null |
Python Easy to Understand Approach !! | maximum-number-of-integers-to-choose-from-a-range-i | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is important to keep banned as set otherwise in PYTHON it gives TLE(Time Limit Exceeded)\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def maxCount(self, banned: List[int], n: int, maxSum: int) -> int:\n cnt = 0\n total = 0\n banned = set(banned)\n \n for i in range(1,n+1):\n if i not in banned and maxSum>=total+i:\n cnt+=1\n total+=i\n return cnt\n``` | 1 | You are given an integer array `banned` and two integers `n` and `maxSum`. You are choosing some number of integers following the below rules:
* The chosen integers have to be in the range `[1, n]`.
* Each integer can be chosen **at most once**.
* The chosen integers should not be in the array `banned`.
* The sum of the chosen integers should not exceed `maxSum`.
Return _the **maximum** number of integers you can choose following the mentioned rules_.
**Example 1:**
**Input:** banned = \[1,6,5\], n = 5, maxSum = 6
**Output:** 2
**Explanation:** You can choose the integers 2 and 4.
2 and 4 are from the range \[1, 5\], both did not appear in banned, and their sum is 6, which did not exceed maxSum.
**Example 2:**
**Input:** banned = \[1,2,3,4,5,6,7\], n = 8, maxSum = 1
**Output:** 0
**Explanation:** You cannot choose any integer while following the mentioned conditions.
**Example 3:**
**Input:** banned = \[11\], n = 7, maxSum = 50
**Output:** 7
**Explanation:** You can choose the integers 1, 2, 3, 4, 5, 6, and 7.
They are from the range \[1, 7\], all did not appear in banned, and their sum is 28, which did not exceed maxSum.
**Constraints:**
* `1 <= banned.length <= 104`
* `1 <= banned[i], n <= 104`
* `1 <= maxSum <= 109` | null |
Python 3 || 7 lines, brute force || T/M: 1142 ms / 16 MB | maximum-number-of-integers-to-choose-from-a-range-i | 0 | 1 | ```\nclass Solution:\n def maxCount(self, banned: List[int], n: int, maxSum: int) -> int:\n\n ans, banned = -1, set(banned)\n\n for i in range(1,n+1):\n if i not in banned:\n maxSum-= i\n ans+= 1\n\n if maxSum < 0: return ans\n\n return ans+1\n```\n[https://leetcode.com/problems/maximum-number-of-integers-to-choose-from-a-range-i/submissions/892114641/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | You are given an integer array `banned` and two integers `n` and `maxSum`. You are choosing some number of integers following the below rules:
* The chosen integers have to be in the range `[1, n]`.
* Each integer can be chosen **at most once**.
* The chosen integers should not be in the array `banned`.
* The sum of the chosen integers should not exceed `maxSum`.
Return _the **maximum** number of integers you can choose following the mentioned rules_.
**Example 1:**
**Input:** banned = \[1,6,5\], n = 5, maxSum = 6
**Output:** 2
**Explanation:** You can choose the integers 2 and 4.
2 and 4 are from the range \[1, 5\], both did not appear in banned, and their sum is 6, which did not exceed maxSum.
**Example 2:**
**Input:** banned = \[1,2,3,4,5,6,7\], n = 8, maxSum = 1
**Output:** 0
**Explanation:** You cannot choose any integer while following the mentioned conditions.
**Example 3:**
**Input:** banned = \[11\], n = 7, maxSum = 50
**Output:** 7
**Explanation:** You can choose the integers 1, 2, 3, 4, 5, 6, and 7.
They are from the range \[1, 7\], all did not appear in banned, and their sum is 28, which did not exceed maxSum.
**Constraints:**
* `1 <= banned.length <= 104`
* `1 <= banned[i], n <= 104`
* `1 <= maxSum <= 109` | null |
Easy O(n) Solution using Set ✅ | maximum-number-of-integers-to-choose-from-a-range-i | 0 | 1 | \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n) , for traversing from 1 to n.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n) , where n is the number of elements in the banned list to make set for faster access.\n\n\n# Code\n```\nclass Solution:\n def maxCount(self, banned: List[int], n: int, maxSum: int) -> int:\n st=set(banned)\n summ=0\n ans=0\n for i in range(1,n+1):\n if summ+i<=maxSum and i not in st:\n ans+=1\n summ+=i\n return ans\n \n\n``` | 3 | You are given an integer array `banned` and two integers `n` and `maxSum`. You are choosing some number of integers following the below rules:
* The chosen integers have to be in the range `[1, n]`.
* Each integer can be chosen **at most once**.
* The chosen integers should not be in the array `banned`.
* The sum of the chosen integers should not exceed `maxSum`.
Return _the **maximum** number of integers you can choose following the mentioned rules_.
**Example 1:**
**Input:** banned = \[1,6,5\], n = 5, maxSum = 6
**Output:** 2
**Explanation:** You can choose the integers 2 and 4.
2 and 4 are from the range \[1, 5\], both did not appear in banned, and their sum is 6, which did not exceed maxSum.
**Example 2:**
**Input:** banned = \[1,2,3,4,5,6,7\], n = 8, maxSum = 1
**Output:** 0
**Explanation:** You cannot choose any integer while following the mentioned conditions.
**Example 3:**
**Input:** banned = \[11\], n = 7, maxSum = 50
**Output:** 7
**Explanation:** You can choose the integers 1, 2, 3, 4, 5, 6, and 7.
They are from the range \[1, 7\], all did not appear in banned, and their sum is 28, which did not exceed maxSum.
**Constraints:**
* `1 <= banned.length <= 104`
* `1 <= banned[i], n <= 104`
* `1 <= maxSum <= 109` | null |
Python Solution || Easy to Understand for beginners | maximum-number-of-integers-to-choose-from-a-range-i | 0 | 1 | ```\nclass Solution:\n def maxCount(self, banned: List[int], n: int, maxSum: int) -> int:\n\t\t# making set of banned values because search in set is faster\n banned = set(banned)\n\t\t\n\t\t# cnt variable is use to store the count of minimum number required\n\t\t# ans stores the sum till current number\n cnt,ans = 0,0\n\t\t\n\t\t# greedily choose all number from 1 to n+1 that are not in banned till current sum exceeds the maxSum\n\t\t# it is always optimal to choose smaller number\n for i in range(1,n+1):\n if i not in banned:\n ans += i\n cnt += 1\n\t\t\t\t\n if ans > maxSum:\n\t\t\t\t# as current sum exceed we need not the last element so remove it.\n cnt -= 1\n break\n return cnt\n``` | 1 | You are given an integer array `banned` and two integers `n` and `maxSum`. You are choosing some number of integers following the below rules:
* The chosen integers have to be in the range `[1, n]`.
* Each integer can be chosen **at most once**.
* The chosen integers should not be in the array `banned`.
* The sum of the chosen integers should not exceed `maxSum`.
Return _the **maximum** number of integers you can choose following the mentioned rules_.
**Example 1:**
**Input:** banned = \[1,6,5\], n = 5, maxSum = 6
**Output:** 2
**Explanation:** You can choose the integers 2 and 4.
2 and 4 are from the range \[1, 5\], both did not appear in banned, and their sum is 6, which did not exceed maxSum.
**Example 2:**
**Input:** banned = \[1,2,3,4,5,6,7\], n = 8, maxSum = 1
**Output:** 0
**Explanation:** You cannot choose any integer while following the mentioned conditions.
**Example 3:**
**Input:** banned = \[11\], n = 7, maxSum = 50
**Output:** 7
**Explanation:** You can choose the integers 1, 2, 3, 4, 5, 6, and 7.
They are from the range \[1, 7\], all did not appear in banned, and their sum is 28, which did not exceed maxSum.
**Constraints:**
* `1 <= banned.length <= 104`
* `1 <= banned[i], n <= 104`
* `1 <= maxSum <= 109` | null |
Beats 100% by speed and memory, Python simple solution. | maximize-win-from-two-segments | 0 | 1 | # Intuition\nLet\'s iterate through the array and for each position, calculate the count of prizes in the interval if the interval ends at the current position and store the count and the position in the "intervals" list.\n```\nintervals = [(count of prizes, end pos), (count of prizes, end pos)]\n```\n\nLet\'s also store the interval which covers the maximum count of prizes that ends before some position, the "max stack for the intervals," in the "max_before".\n```\nmax_before = [(max count of prizes, end pos1), (max count of prizes, end pos2)]\nend pos1 <= end pos2 <= end pos3 <= end pos4 ....\ncount1 <= count2 <= count3 <= count4 ...\n```\n\nThe solution is then straightforward and is based on two key ideas:\n\n1. If we have two intervals, we can make them non-intersecting by moving the first of them, as the second will cover the same prizes. So we need only consider the non-intersecting intervals.\n\n2. The solution must have the last interval. To find the solution, we pop intervals from the "intervals" list one by one and calculate the solution if the current interval is the last one. Then, find the maximum among these solutions.\n\nTo implement this, we pop the next interval from the "intervals" list - the current last interval.\nThen, pop all intervals from the "max_before" list that do not end before the current interval.\nThe top of the "max_before" list will then have the interval with the maximum prize count before the current interval.\nThe current best candidate solution for the current last interval is the count of prizes for the current last interval plus the top of the "max_before" interval.\n```\ncandidate = count+(0 if not max_beffore else max_beffore[-1][0])\n```\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def maximizeWin(self, prizePositions: List[int], k: int) -> int:\n # count of prizes for all intervals\n # (count, end position of interval) \n intervals = []\n # max stack of intervals\n # (count, end position of interval),\n # There can\'t be interval with bigger count before the interval\n max_beffore = []\n start_inx = 0 # start index of the current interval\n count = 0 # count of the current interval\n for inx, pos in enumerate(prizePositions):\n count += 1\n # subtract prizes from the current interval if they are not covered by the interval\n while pos-k > prizePositions[start_inx]:\n count -= 1\n start_inx += 1\n intervals.append((count, pos))\n if not max_beffore or max_beffore[-1][0] < count:\n max_beffore.append((count, pos))\n\n max_solution = 0\n while intervals:\n # the last interval for the current solution\n count, pos = intervals.pop()\n # max_beffore stores only intervals before the last interval,\n # max_beffore is a max stack,\n # so the top of the max possible has the max count among all values in the max_beffore\n while max_beffore and max_beffore[-1][1] >= pos-k:\n max_beffore.pop()\n # The soluthon if the current last interval is the last\n candidate = count+(0 if not max_beffore else max_beffore[-1][0])\n # we need to find maximum among all candidates\n max_solution = max(candidate, max_solution)\n return max_solution\n \n``` | 3 | There are some prizes on the **X-axis**. You are given an integer array `prizePositions` that is **sorted in non-decreasing order**, where `prizePositions[i]` is the position of the `ith` prize. There could be different prizes at the same position on the line. You are also given an integer `k`.
You are allowed to select two segments with integer endpoints. The length of each segment must be `k`. You will collect all prizes whose position falls within at least one of the two selected segments (including the endpoints of the segments). The two selected segments may intersect.
* For example if `k = 2`, you can choose segments `[1, 3]` and `[2, 4]`, and you will win any prize i that satisfies `1 <= prizePositions[i] <= 3` or `2 <= prizePositions[i] <= 4`.
Return _the **maximum** number of prizes you can win if you choose the two segments optimally_.
**Example 1:**
**Input:** prizePositions = \[1,1,2,2,3,3,5\], k = 2
**Output:** 7
**Explanation:** In this example, you can win all 7 prizes by selecting two segments \[1, 3\] and \[3, 5\].
**Example 2:**
**Input:** prizePositions = \[1,2,3,4\], k = 0
**Output:** 2
**Explanation:** For this example, **one choice** for the segments is `[3, 3]` and `[4, 4],` and you will be able to get `2` prizes.
**Constraints:**
* `1 <= prizePositions.length <= 105`
* `1 <= prizePositions[i] <= 109`
* `0 <= k <= 109`
* `prizePositions` is sorted in non-decreasing order.
.spoilerbutton {display:block; border:dashed; padding: 0px 0px; margin:10px 0px; font-size:150%; font-weight: bold; color:#000000; background-color:cyan; outline:0; } .spoiler {overflow:hidden;} .spoiler > div {-webkit-transition: all 0s ease;-moz-transition: margin 0s ease;-o-transition: all 0s ease;transition: margin 0s ease;} .spoilerbutton\[value="Show Message"\] + .spoiler > div {margin-top:-500%;} .spoilerbutton\[value="Hide Message"\] + .spoiler {padding:5px;} | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.