title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Unleashing the Power of Dynamic Programming | concatenated-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- To check if a word can be formed by concatenating other words from the input list, we can use dynamic programming.\n- We will use a boolean array dp where dp[i] will be True if a word can be formed from the substring word[0:i].\n- We will iterate through the word and check for all possible combinations of substrings that are present in words_set, if present we will mark dp[i] as True.\n- At the end, if dp[-1] is true, that means the word can be formed using other words from the list and we will add it to concatenated_words list.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create a set of input words for fast lookup.\n- Initialize an empty list called concatenated_words.\n- Iterate through each word in the input list.\n- If a word is empty, skip it.\n- Initialize a boolean array dp of size len(word) + 1 with all elements set to False.\n- Set dp[0] to True.\n- For each index i in the range 0 to len(word).\n- If dp[i] is False, skip this index.\n- For each index j in the range i+1 to len(word) + 1.\n- If j - i < len(word) and substring word[i:j] is present in words_set Mark dp[j] as True.\n- If dp[-1] is True, that means the word can be formed using other words from the list, so add it to concatenated_words list.\n- Return concatenated_words list\n\n# Complexity\n- Time complexity: $$O(n*m)$$ where n is the number of words and m is the average length of a word\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n+m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n # Create a set of input words for fast lookup\n words_set = set(words)\n # Initialize an empty list to store concatenated words\n concatenated_words = []\n\n # Iterate through each word in the input list\n for word in words:\n # Skip empty words\n if len(word) == 0:\n continue\n\n # Initialize a boolean array dp of size len(word) + 1 with all elements set to False\n dp = [False] * (len(word) + 1)\n # Set dp[0] to True, as an empty string is always a valid word\n dp[0] = True\n\n # Iterate through each index i in the range 0 to len(word)\n for i in range(len(word)):\n # If dp[i] is False, it means that the substring word[0:i] cannot be formed by\n #concatenating other words\n # So we can skip checking the substrings that start at this index\n if not dp[i]:\n continue\n\n # Iterate through each index j in the range i+1 to len(word) + 1\n for j in range(i+1, len(word) + 1):\n # If j - i < len(word), it means that the substring word[i:j] is not the entire word\n # If substring word[i:j] is present in words_set, it means that this substring is a valid word\n # So we can mark dp[j] as True, as the substring word[0:j] can be formed by\n # concatenating valid words\n if j - i < len(word) and word[i:j] in words_set:\n dp[j] = True\n\n # If dp[-1] is True, it means that the word can be formed by concatenating other words from\n # the input list\n if dp[-1]:\n \n # So we add it to the concatenated_words list\n concatenated_words.append(word)\n\n # Return the concatenated_words list\n return concatenated_words\n``` | 1 | Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105` | null |
Clean Codes🔥🔥|| Full Explanation✅|| Trie & DFS✅|| C++|| Java || Python3 | concatenated-words | 1 | 1 | # Intuition :\n- We can use the data structure trie to store the words. Then for each word in the list of words, we use depth first search to see whether it is a concatenation of two or more words from the list.\n\n- We first build a trie structure that stores the list of words. In every trie node, we use an array of length 26 to store possible next trie node, and a flag to indicate whether the trie node is the last letter of a word in the dictionary.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- Suppose we have a list of words like this, words = [\u201Ccat\u201D, \u201Ccats\u201D, \u201Ccatsdogcats\u201D, \u201Cdog\u201D, \u201Cdogcatsdog\u201D, \u201Chippopotamuses\u201D, \u201Crat\u201D, \u201Cratcatdogcat\u201D]. The trie structure we build looks like the following. If the node is an end of a word, there is a * next to it.\n```\n c d h r\n | | | |\n a o i a\n | | | |\n t* g* p t*\n | | | |\n s* c p c\n | | | |\n d a o a\n | | | |\n o t p t\n | | | |\n g s o d\n | | | |\n c d t o\n | | | |\n a o a g\n | | | |\n t g* m c\n | | |\n s* u a\n | |\n s t*\n |\n e\n |\n s*\n```\n- Next, for each word in the sentence, we search whether the word is a concatenation of two or more other words from the list. We can use depth first search here.\n\n- For each word, we start from the root node of the trie and the first letter of the word. If the letter is not null in the current trie node, we go to the next trie node of that letter. We keep searching until the trie node is an end of a word (with a * in the above graph). \n\n- We increase the count of words the comprise the current word. Then we start from the root node of the trie again, and keep on searching until we reach the end of the current word. If we cannot find the letter in the trie, we go backtrack to the last run of trie nodes and continue the search.\n\n- If we can find a concatenation of words that reaches the end of the current word, we check how many words are concatenated. If it is greater than 2, we put the current word to the final answer\n<!-- Describe your approach to solving the problem. -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes for above Explained Approach :\n```C++ []\nclass Solution {\nstruct TrieNode {\n TrieNode* arr[26];\n bool is_end;\n TrieNode() {\n for (int i = 0; i < 26; i ++) arr[i] = NULL;\n is_end = false;\n } \n};\n\nvoid insert(TrieNode* root, string key) {\n TrieNode* curr = root;\n for (int i = 0; i < key.size(); i ++) {\n int idx = key[i] - \'a\';\n if (curr->arr[idx] == NULL)\n curr->arr[idx] = new TrieNode();\n curr = curr->arr[idx];\n }\n curr->is_end = true;\n}\n\nbool dfs(TrieNode* root, string key, int index, int count) {\n if (index >= key.size())\n return count > 1;\n TrieNode* curr = root;\n for (int i = index; i < key.size(); i ++) {\n int p = key[i] - \'a\';\n if (curr->arr[p] == NULL) {\n return false;\n }\n curr = curr->arr[p];\n if (curr->is_end) {\n if (dfs(root, key, i+1, count+1))\n return true;\n }\n }\n return false;\n}\npublic:\nvector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n TrieNode* root = new TrieNode();\n for (int i = 0; i < words.size(); i ++) {\n insert(root, words[i]);\n }\n vector<string> ans;\n for (int i = 0; i < words.size(); i ++) {\n if (dfs(root, words[i], 0, 0))\n ans.push_back(words[i]);\n }\n return ans; \n}\n};\n```\n```Java []\nimport java.util.List;\nimport java.util.ArrayList;\n\nclass Solution {\n class TrieNode {\n TrieNode[] arr = new TrieNode[26];\n boolean is_end;\n TrieNode() {\n for (int i = 0; i < 26; i ++) arr[i] = null;\n is_end = false;\n } \n };\n\n void insert(TrieNode root, String key) {\n TrieNode curr = root;\n for (int i = 0; i < key.length(); i ++) {\n int idx = key.charAt(i) - \'a\';\n if (curr.arr[idx] == null)\n curr.arr[idx] = new TrieNode();\n curr = curr.arr[idx];\n }\n curr.is_end = true;\n }\n\n boolean dfs(TrieNode root, String key, int index, int count) {\n if (index >= key.length())\n return count > 1;\n TrieNode curr = root;\n for (int i = index; i < key.length(); i ++) {\n int p = key.charAt(i) - \'a\';\n if (curr.arr[p] == null) {\n return false;\n }\n curr = curr.arr[p];\n if (curr.is_end) {\n if (dfs(root, key, i+1, count+1))\n return true;\n }\n }\n return false;\n }\n public List<String> findAllConcatenatedWordsInADict(String[] words) {\n TrieNode root = new TrieNode();\n for (int i = 0; i < words.length; i ++) {\n insert(root, words[i]);\n }\n List<String> ans = new ArrayList<String>();\n for (int i = 0; i < words.length; i ++) {\n if (dfs(root, words[i], 0, 0))\n ans.add(words[i]);\n }\n return ans; \n }\n}\n```\n```Python3 []\nclass TrieNode:\n def __init__(self):\n self.children = [None] * 26\n self.is_end = False\n\nclass Solution:\n def __init__(self):\n self.root = TrieNode()\n \n def insert(self, root, key):\n curr = root\n for i in range(len(key)):\n idx = ord(key[i]) - ord(\'a\')\n if not curr.children[idx]:\n curr.children[idx] = TrieNode()\n curr = curr.children[idx]\n curr.is_end = True\n\n def dfs(self, root, key, index, count):\n if index >= len(key):\n return count > 1\n curr = root\n for i in range(index, len(key)):\n p = ord(key[i]) - ord(\'a\')\n if not curr.children[p]:\n return False\n curr = curr.children[p]\n if curr.is_end:\n if self.dfs(root, key, i+1, count+1):\n return True\n return False\n\n def findAllConcatenatedWordsInADict(self, words):\n for i in range(len(words)):\n self.insert(self.root, words[i])\n ans = []\n for i in range(len(words)):\n if self.dfs(self.root, words[i], 0, 0):\n ans.append(words[i])\n return ans\n```\n# For the 42/43 test case passing issue in C++ : Use this code\n```\nclass Solution {\nprivate:\n struct Trie\n {\n vector<Trie*> children{26};\n bool end{false};\n };\n \n Trie* root;\n \n void insert(string& s)\n {\n if (s.empty()) return;\n Trie* cur = root;\n for (char c:s)\n {\n if (cur->children[c-\'a\'] == nullptr)\n cur->children[c-\'a\'] = new Trie();\n cur = cur->children[c-\'a\'];\n }\n cur->end = true;\n }\n \n bool dfs(Trie* root, Trie* node, string& word, int idx, int count)\n {\n if (!node)\n return false;\n \n if (idx >= word.size())\n {\n if (node->end && count >=1 )\n return true;\n else\n return false;\n }\n \n if (node->end && dfs(root, root, word, idx, count+1))\n return true;\n return dfs(root, node->children[word[idx]-\'a\'], word, idx+1, count);\n }\n \npublic:\n vector<string> findAllConcatenatedWordsInADict(vector<string>& words) {\n sort(words.begin(), words.end(), [](const string& w1, const string& w2) {\n return w1.size() < w2.size();\n });\n \n vector<string> ret;\n root = new Trie();\n \n for(auto &w: words)\n {\n if (w.empty()) continue;\n if(dfs(root, root, w, 0, 0)) \n ret.push_back(w);\n else \n insert(w);\n }\n \n return ret;\n }\n};\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n\n | 38 | Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105` | null |
📌📌Python3 || ⚡347 ms, faster than 91.39% of Python3 | concatenated-words | 0 | 1 | ```\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n result = []\n def dfs(word, wordset):\n if word == "":\n return True\n for i in range(len(word)):\n if word[:i+1] in wordset:\n if dfs(word[i+1:], wordset):\n return True\n return False\n for word in words:\n wordset.remove(word)\n if dfs(word, wordset):\n result.append(word)\n wordset.add(word)\n return result\n``` | 4 | Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105` | null |
python3 Solution | concatenated-words | 0 | 1 | \n```\nclass Solution:\n def findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n wordset = set(words)\n \n @cache\n def f(word,i):\n if i >= len(word):\n return True\n j = i+1\n while j <= len(word):\n if word[i:j] in wordset and j-i != len(word) and f(word,j):\n return True\n j += 1\n return False\n \n return [word for word in words if any(word) and f(word,0)]\n``` | 1 | Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105` | null |
O(N*L) | O(N*L) | Python Solution | Explained | concatenated-words | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we want to return all non duplicated `concatenated words`\n\nThis problem has the same logic as `139. Word Break`. This problem has its differences though because we want only words that are concatenated by 2 or more other words\n\nWe can use `Dynamic Programming` to break the problem down and try to form a single word by using words in our array.\n\n### Dynamic Programming\n\n1) Iterate over our given array and try to form a word by checking if each given word is a `concatenation` of other words\n\n2) If we found a word that is a concatenation of other words, we will add it to our result\n\n\n\n### Code\n```\ndef findAllConcatenatedWordsInADict(self, words: List[str]) -> List[str]:\n \n words_set = set(words)\n \n result = []\n \n def dfs(word):\n for i in range(len(word)):\n \n if word[:i+1] in words_set and word[i+1:] in words_set:\n return True\n\t\t\t\t\t\n if word[:i+1] in words_set and dfs(word[i+1:]):\n return True\n\n return False\n \n for word in words:\n if dfs(word):\n result.append(word)\n return result\n```\n\n#### Time Complexity: O(N*L)\n#### Space Complexity: O(N*L)\n\n\n***Upvote if this tenno\'s discussion helped you in some type of way***\n \n***Warframe\'s short pvp clip of the day***\n\n | 4 | Given an array of strings `words` (**without duplicates**), return _all the **concatenated words** in the given list of_ `words`.
A **concatenated word** is defined as a string that is comprised entirely of at least two shorter words (not necesssarily distinct) in the given array.
**Example 1:**
**Input:** words = \[ "cat ", "cats ", "catsdogcats ", "dog ", "dogcatsdog ", "hippopotamuses ", "rat ", "ratcatdogcat "\]
**Output:** \[ "catsdogcats ", "dogcatsdog ", "ratcatdogcat "\]
**Explanation:** "catsdogcats " can be concatenated by "cats ", "dog " and "cats ";
"dogcatsdog " can be concatenated by "dog ", "cats " and "dog ";
"ratcatdogcat " can be concatenated by "rat ", "cat ", "dog " and "cat ".
**Example 2:**
**Input:** words = \[ "cat ", "dog ", "catdog "\]
**Output:** \[ "catdog "\]
**Constraints:**
* `1 <= words.length <= 104`
* `1 <= words[i].length <= 30`
* `words[i]` consists of only lowercase English letters.
* All the strings of `words` are **unique**.
* `1 <= sum(words[i].length) <= 105` | null |
💡💡 Neatly coded and brilliantly structured backtracking solution | matchsticks-to-square | 0 | 1 | # Intuition behind the approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use backtracking to get the different combinations with a few overheads before backtracking so that the runtime does not exceed the limit.\nWe sort the array in reverse order so that if any matchstick is greater than the sq varible, the backtracing function return False in the very beginning. \nThe rest of the algorithm is pretty understandable. \nI personally really liked the structure and the writing of the program, so I\'ve added the video I referred to. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(4^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) + stack space\n\n# Note\n> Credits to Neetcode https://www.youtube.com/watch?v=hUe0cUKV-YY&list=PLot-Xpze53lf5C3HSjCnyFghlW0G1HHXo&index=17\n\n# Code\n```\nclass Solution:\n def makesquare(self, matchsticks: List[int]) -> bool:\n\n if sum(matchsticks) % 4 != 0:\n return False\n squ = sum(matchsticks) // 4\n sides = [0] * 4\n matchsticks.sort(reverse = True)\n\n def bt(i):\n if i == len(matchsticks):\n return True\n \n for idx in range(4):\n if sides[idx] + matchsticks[i] <= squ:\n sides[idx] += matchsticks[i]\n if bt(i+1):\n return True\n sides[idx] -= matchsticks[i]\n return False\n \n return bt(0)\n``` | 1 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
[Python 3]DP + Bitmask | matchsticks-to-square | 0 | 1 | ```\nclass Solution:\n def makesquare(self, arr: List[int]) -> bool:\n\t\t# no way to make the square if total length not divisble by 4\n if sum(arr) % 4:\n return False\n \n\t\t# target side length\n side = sum(arr) // 4\n \n @lru_cache(None)\n def dp(k, mask, s):\n\t\t\t# finish all four sides\n if k == 4:\n return True\n\t\t\t# move on to next side if current one finished\n if not s:\n return dp(k+1, mask, side)\n \n for i in range(len(arr)):\n\t\t\t\t# if current matchstick used or longer than remaining side length to fill then skip\n if mask & (1 << i) or s < arr[i]: continue\n if dp(k, mask ^ (1 << i), s - arr[i]):\n return True\n return False\n \n return dp(0, 0, side)\n```\n\nCould drop one dimension of the dp\n\n```\n def makesquare(self, arr: List[int]) -> bool:\n if sum(arr) % 4:\n return False\n \n side = sum(arr) // 4\n n = len(arr)\n \n @lru_cache(None)\n def dp(mask, s):\n if mask == (1 << n) - 1:\n return True\n if not s:\n return dp(mask, side)\n \n for i in range(n):\n if mask & (1 << i) or s < arr[i]: continue\n if dp(mask ^ (1 << i), s - arr[i]):\n return True\n return False\n \n return dp(0, side)\n``` | 6 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
Cleanest Python3 code with explanation / Generalized partitioning into k-buckets | matchsticks-to-square | 0 | 1 | ### Breakdown\n1. Few basic checks are needed \u2013\xA0there should be at least 4 matchsticks, the sum of matchstick lengths should be divisble by 4, and none of the matchstick length should exceed the side length of the square.\n2. To partition a list of nums (matchsticks) into k-buckets (4 sides in our case), we use backtracking to place each number into each bucket, ensuring that bucket sum doesn\'t exceed the target sum.\n3. Pruning \u2013\xA0Since buckets are filled from left to right, if any bucket remains empty (i.e. no combination of elements sum up to target), then all buckets to the right of it will also be empty.\n\n### Code\n```\nclass Solution:\n def makesquare(self, matchsticks: List[int]) -> bool:\n # There should be at least 4 matchsticks.\n if len(matchsticks) < 4:\n return False\n \n # Sum of matchstick lengths should be divisble by four.\n side_length, remainder = divmod(sum(matchsticks), 4)\n if remainder != 0:\n return False\n \n # There shouldn\'t be any single matchstick with length greater than side_length.\n if max(matchsticks) > side_length:\n return False\n \n # Check if partitioning is possible.\n return self.can_partition(matchsticks, 4, side_length)\n \n def can_partition(self, nums, k, target):\n buckets = [0] * k\n nums.sort(reverse=True) # pruning\n \n def backtrack(idx):\n # If all elements have been used, check if all are equal.\n if idx == len(nums):\n return len(set(buckets)) == 1\n \n # Try placing numbers in each bucket.\n for b in range(k):\n buckets[b] += nums[idx]\n if buckets[b] <= target and backtrack(idx + 1):\n return True\n buckets[b] -= nums[idx]\n \n # Pruning: Buckets are filled from left to right. If any bucket remains empty,\n # then all buckets to the right of it will also be empty.\n if buckets[b] == 0:\n break\n \n return False\n \n return backtrack(0)\n``` | 2 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
Python | 380ms Faster than 78% | Soln w/ Explanation | 86% Less Memory | matchsticks-to-square | 0 | 1 | ```\ndef makesquare(self, matchsticks: List[int]) -> bool:\n\ttotal = sum(matchsticks)\n\n\tif total % 4: # if total isn\'t perfectly divisible by 4 then we can\'t make a square\n\t\treturn False\n\n\treqLen = total // 4 # calculate length of each side we require\n\tsides = [0] * 4\n\tmatchsticks.sort(reverse = True) # sort in reverse so if biggest value is greater than reqLen we can return False\n\n\tdef recurse(i):\n\t\tif i == len(matchsticks):\n\t\t\treturn True\n\n\t\tfor j in range(4):\n\t\t\tif sides[j] + matchsticks[i] <= reqLen:\n\t\t\t\tsides[j] += matchsticks[i]\n\n\t\t\t\tif recurse(i + 1):\n\t\t\t\t\treturn True\n\n\t\t\t\tsides[j] -= matchsticks[i]\n\n\t\t\t\t# Important line, otherwise function will give TLE\n\t\t\t\tif sides[j] == 0:\n\t\t\t\t\tbreak\n\n\t\t\t\t"""\n\t\t\t\tExplanation:\n\t\t\t\tIf sides[j] = 0, it means this is the first time we\'ve added values to that side.\n\t\t\t\tIf the backtrack search fails when adding the values to sides[j] and it remains 0, it will also fail for all sides from sides[j+1:].\n\t\t\t\tBecause we are simply going through the previous recursive tree again for a different j+1 position.\n\t\t\t\tSo we can effectively break from the for loop or directly return False.\n\t\t\t\t"""\n\n\t\treturn False\n\n\treturn recurse(0)\n```\n\n\n | 13 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
473: Solution with step by step explanation | matchsticks-to-square | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Calculate the total length of all matchsticks in the input list matchsticks.\n2. If the total length is not divisible by 4 or if the length of the longest matchstick is greater than total_length // 4, return False as it\'s impossible to form a square using the given matchsticks.\n3. Calculate the target length of each side of the square by dividing total_length by 4.\n4. Sort the matchsticks list in decreasing order so that we can consider the larger matchsticks first while forming the sides of the square.\n5. Define a recursive function form_sides(i, sides) that takes two arguments - the index i of the current matchstick being considered, and a tuple sides representing the current lengths of each side of the square.\n6. If we\'ve considered all matchsticks and all sides of the square are of equal length, return True as we\'ve successfully formed a square using the matchsticks.\n7. For each of the 4 sides, check if adding the current matchstick\'s length to the side\'s length results in a length less than or equal to the target length. If yes, create a new list new_sides by updating the length of that side with the sum of its current length and the current matchstick\'s length.\n8. Recursively call the form_sides function with the updated index i+1 and the updated new_sides tuple as arguments. If this recursive call returns True, return True as well, since we\'ve successfully formed a square.\n9. If none of the recursive calls from step 8 returned True, return False, as it\'s not possible to form a square using the given matchsticks.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def makesquare(self, matchsticks: List[int]) -> bool:\n total_length = sum(matchsticks)\n if total_length % 4 != 0 or max(matchsticks) > total_length // 4:\n return False\n target_length = total_length // 4\n matchsticks.sort(reverse=True)\n \n def form_sides(i, sides):\n if i == len(matchsticks) and all(side == target_length for side in sides):\n return True\n \n for j in range(4):\n if sides[j] + matchsticks[i] <= target_length:\n new_sides = list(sides)\n new_sides[j] += matchsticks[i]\n if form_sides(i+1, tuple(new_sides)):\n return True\n \n return False\n \n return form_sides(0, (0, 0, 0, 0))\n``` | 4 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
python | using Backtracking | Faster than 99% | matchsticks-to-square | 0 | 1 | ```\nclass Solution:\n def makesquare(self, matchsticks: List[int]) -> bool:\n target,m=divmod(sum(matchsticks),4)\n if m:return False\n targetLst=[0]*4\n length=len(matchsticks)\n matchsticks.sort(reverse=True)\n def bt(i):\n if i==length:\n return len(set(targetLst))==1\n for j in range(4):\n if matchsticks[i]+targetLst[j]>target:\n continue\n targetLst[j]+=matchsticks[i]\n if bt(i+1):\n return True\n targetLst[j]-=matchsticks[i]\n if not targetLst[j]:break\n return False\n return matchsticks[0]<=target and bt(0)\n``` | 1 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
Python Backtracking | matchsticks-to-square | 0 | 1 | ```\nclass Solution:\n def makesquare(self, matchsticks: List[int]) -> bool:\n \n \n sides = [0]*4\n if sum(matchsticks)%4!=0:\n return False\n s = sum(matchsticks)//4\n \n matchsticks.sort(reverse=True)\n \n def helper(i):\n if i == len(matchsticks):\n return True\n \n for j in range(4):\n \n if sides[j]+matchsticks[i]<=s:\n sides[j]+=matchsticks[i]\n if helper(i+1):\n return True\n sides[j]-=matchsticks[i]\n return False\n \n return helper(0) | 1 | You are given an integer array `matchsticks` where `matchsticks[i]` is the length of the `ith` matchstick. You want to use **all the matchsticks** to make one square. You **should not break** any stick, but you can link them up, and each matchstick must be used **exactly one time**.
Return `true` if you can make this square and `false` otherwise.
**Example 1:**
**Input:** matchsticks = \[1,1,2,2,2\]
**Output:** true
**Explanation:** You can form a square with length 2, one side of the square came two sticks with length 1.
**Example 2:**
**Input:** matchsticks = \[3,3,3,3,4\]
**Output:** false
**Explanation:** You cannot find a way to form a square with all the matchsticks.
**Constraints:**
* `1 <= matchsticks.length <= 15`
* `1 <= matchsticks[i] <= 108` | Treat the matchsticks as an array. Can we split the array into 4 equal halves? Every matchstick can belong to either of the 4 sides. We don't know which one. Maybe try out all options! For every matchstick, we have to try out each of the 4 options i.e. which side it can belong to. We can make use of recursion for this. We don't really need to keep track of which matchsticks belong to a particular side during recursion. We just need to keep track of the length of each of the 4 sides. When all matchsticks have been used we simply need to see the length of all 4 sides. If they're equal, we have a square on our hands! |
Python Easy DP 2 approaches | ones-and-zeroes | 0 | 1 | \n1. ##### **Memoization(Top Down)**\n\n```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n counter=[[s.count("0"), s.count("1")] for s in strs]\n \n @cache\n def dp(i,j,idx):\n if i<0 or j<0:\n return -math.inf\n \n if idx==len(strs):\n return 0\n \n return max(dp(i,j,idx+1), 1 + dp(i-counter[idx][0], j-counter[idx][1], idx+1))\n return dp(m,n,0)\n```\n\n\n**Time - O(l * m * n)** - where `l` is length of `strs`\n**Space - O(l * m * n)** - memo table\n\n\n----\n\n2. ##### **Tabulation(Bottom Up)**\n\n```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int: \n dp = [[0] * (n+1) for _ in range(m+1)]\n counter=[[s.count("0"), s.count("1")] for s in strs]\n \n for zeroes, ones in counter:\n for i in range(m, zeroes-1, -1):\n for j in range(n, ones-1, -1): \n dp[i][j] = max(dp[i][j], 1+dp[i-zeroes][j-ones])\n \n return dp[-1][-1]\n```\n\n**Time - O(l * m * n)** - where `l` is length of `strs`\n**Space - O(m * n)**\n\n---\n\n***Please upvote if you find it useful*** | 83 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
beat 99.9%, extremely fast | ones-and-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCounter to count \'0\' and \'1\' size\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDP\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n # Counter for every element of strs to record 0, 1 size\n count = []\n for i in strs:\n d_temp = {\'0\': 0, "1": 0}\n for j in i: d_temp[j]+=1\n count.append((d_temp[\'0\'], d_temp[\'1\']))\n \n # merge elements in count to a list with the same \'0\' size\n # And combine those lists to a list called \'new\'\n list_0 = sorted(list(set([i[0] for i in count])))\n d_temp = {} # list_0[index]: index\n for i in range(len(list_0)): d_temp[list_0[i]] = i\n\n new = [[] for i in list_0] # the new list\n for i in count: new[d_temp[i[0]]].append(i)\n for i in new: i.sort(key = lambda x: x[1]) # sort the element in new according to \'1\' size\n\n\n # dp(loc of new, m, n)\n def dp(loc, m, n):\n if loc == 0: # exit\n start, cnt = 0, 0\n while (m>=0 and n>=0) and start<len(new[loc]):\n curr_m, curr_n = new[loc][start]\n m = m-curr_m\n n = n-curr_n\n if m>=0 and n>=0: cnt+=1\n start+=1\n return cnt\n \n start, cnt, res = 0, 0, [0]*(len(new[loc])+1)\n res[0] = dp(loc-1, m, n)\n while (m>=0 and n>=0) and start<len(new[loc]):\n curr_m, curr_n = new[loc][start]\n m = m-curr_m\n n = n-curr_n\n if m>=0 and n>=0: \n cnt+=1\n res[cnt] = dp(loc-1, m, n)+cnt\n start+=1\n return max(res)\n\n return dp(len(list_0)-1, m, n)\n \n\n\n\n\n\n \n\n\n \n\n\n\n\n \n``` | 1 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
[Python] DP Solution explained with example | ones-and-zeroes | 0 | 1 | ```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n ## RC ##\n\t\t## APPROACH : DP ##\n\t\t## Similar to Leetcode 416. partition equal subset sum ##\n\t\t## LOGIC ##\n\t\t#\t1. This problem can be decomposed to 0/1 Knapsack Problem, where you have n items with each having its own weight w and own profit p, \n # We have a limitation on maximum weight of the items that we can carry in a bag, so what is the maximum profit that can be achieved within the weight limit of the bag.\n\t\t#\t2. m, n are the similar to limitations of the bag, strings being with items with weight w\n\t\t#\t3. Each cell in DP indicates the number of strings that can be achieved with i zeros and j ones. We iterate with all strings and fill the matrix\n \n\t\t## TIME COMPLEXITY : O(Nx(mxn)) ##\n\t\t## SPACE COMPLEXITY : O(mxn) ##\n\n ## EXAMPLE ["10","0001","111001","1","0"] 5 3 ##\n ## STACK TRACE ##\n # [[0, 0, 0, 0], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 1, 1]]\n # [[0, 0, 0, 0], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 2, 2], [0, 1, 2, 2]]\n # [[0, 0, 0, 0], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 1, 1], [0, 1, 2, 2], [0, 1, 2, 2]]\n # [[0, 1, 1, 1], [0, 1, 2, 2], [0, 1, 2, 2], [0, 1, 2, 2], [0, 1, 2, 3], [0, 1, 2, 3]]\n # [[0, 1, 1, 1], [1, 2, 2, 2], [1, 2, 3, 3], [1, 2, 3, 3], [1, 2, 3, 3], [1, 2, 3, 4]]\n \n ## WATCH OUT FOR LOOPS,\n ## 1. We are traversing reverse to prevent sub problem overlapping, consider string "01" and m = 5, n = 3 and draw matrix from normal order and in reverse order, you\'ll understand\n ## 2. The lower limit is number of zeros and ones, coz before that you wont find any match\n dp = [[ 0 ] * (n+1) for _ in range(m+1)]\n for s in strs:\n zeros, ones = s.count("0"), s.count("1")\n for i in range(m, zeros - 1, -1):\n for j in range(n, ones - 1, -1):\n # dp[i][j] indicates it has i zeros and j ones, can this string be formed with those ?\n dp[i][j] = max( 1 + dp[i - zeros][j- ones], dp[i][j] )\n # print(dp)\n return dp[-1][-1]\n \n```\nPLEASE UPVOTE IF YOU LIKE MY SOLUTION | 47 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
Python || Easy Recursion || DP | ones-and-zeroes | 0 | 1 | ```\nclass Solution(object):\n def findMaxForm(self, strs, m, n):\n """\n :type strs: List[str]\n :type m: int\n :type n: int\n :rtype: int\n """\n #dp dict to store the computations\n dp={}\n \n \n def A(curm,curn,ind):\n \n if (curm,curn,ind) in dp:\n return dp[(curm,curn,ind)]\n #if it is less than the capacity return -1\n if curm<0 or curn<0:\n return -1\n #if the ind reached end of the array\n if ind==len(strs):\n return 0\n \n ans1,ans2=0,0\n \n #skip \n ans1=A(curm,curn,ind+1)\n \n #include \n ans2=1+A(curm-(strs[ind].count(\'0\')),curn-(strs[ind].count(\'1\')),ind+1)\n \n #store the value\n dp[(curm,curn,ind)]=max(ans1,ans2)\n\t\t\t\n #return the value\n return max(ans1,ans2)\n \n return A(m,n,0)\n \n \n``` | 2 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
Accepted Greedy Solution with Counterexample | ones-and-zeroes | 0 | 1 | # Overview\nGreedily take strings based on some sorted order. 4 orders were examined: sorting by (# of 0\'s, # of 1\'s), sorting by (# of 1\'s, # of 0\'s), sorting (combined length, # of 0\'s, # of 1\'s), (combined length, # of 1\'s, # of 0\'s).\n\n# Code\n```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n d = []\n for s in strs:\n cnts = [0,0]\n for char in s:\n if char == \'0\': \n cnts[0] +=1\n else:\n cnts[1] += 1\n if cnts[0] <= m and cnts[1] <= n:\n d.append(cnts)\n sorted_d3 = sorted(d, key=lambda x:(x[0]+x[1], x[0], x[1]))\n m_left, n_left = m, n\n ans3 = 0\n while sorted_d3:\n subset = sorted_d3.pop(0)\n if m_left-subset[0] >= 0 and n_left-subset[1] >= 0:\n ans3 += 1\n m_left = m_left-subset[0]\n n_left = n_left-subset[1]\n sorted_d4 = sorted(d, key=lambda x:(x[0]+x[1], x[1], x[0]))\n m_left, n_left = m, n\n ans4 = 0\n while sorted_d4:\n subset = sorted_d4.pop(0)\n if m_left-subset[0] >= 0 and n_left-subset[1] >= 0:\n ans4 += 1\n m_left = m_left-subset[0]\n n_left = n_left-subset[1]\n m_left, n_left = m, n\n sorted_d1 = sorted(d, key=lambda x:(x[0], x[1]))\n ans1 = 0\n while sorted_d1:\n subset = sorted_d1.pop(0)\n if m_left-subset[0] >= 0 and n_left-subset[1] >= 0:\n ans1 += 1\n m_left = m_left-subset[0]\n n_left = n_left-subset[1]\n m_left, n_left = m, n\n sorted_d2 = sorted(d, key=lambda x:(x[1], x[0]))\n ans2 = 0\n while sorted_d2:\n subset = sorted_d2.pop(0)\n if m_left-subset[0] >= 0 and n_left-subset[1] >= 0:\n ans2 += 1\n m_left = m_left-subset[0]\n n_left = n_left-subset[1]\n return max(ans1, ans2, ans3, ans4)\n```\n\nPasses all current test cases, but fails on this test:\n["0000", "1110", "1100", "1100"]\nm = 4, n = 4 | 3 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
✔ Python3 Solution | Knapsack | DP | ones-and-zeroes | 0 | 1 | # Complexity\n- Time complexity: $$O(n * m * s.length)$$\n- Space complexity: $$O(n * m)$$\n\n# Code\n```Python\nclass Solution:\n def findMaxForm(self, S, M, N):\n dp = [[0] * (M + 1) for _ in range(N + 1)]\n for s in S:\n x, y = s.count(\'1\'), s.count(\'0\')\n for i in range(N - x, -1, -1):\n for j in range(M - y, -1, -1):\n dp[i + x][j + y] = max(dp[i + x][j + y], dp[i][j] + 1)\n return dp[-1][-1]\n``` | 3 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
474: Solution with step by step explanation | ones-and-zeroes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a 2D array, dp, with m+1 rows and n+1 columns, filled with 0\'s. The purpose of this array is to keep track of the maximum subset size for each combination of zeros and ones that can be formed with the current set of strings.\n\n2. Iterate through each string in strs.\n\n3. For the current string, count the number of 0\'s and 1\'s it contains, and store these values in zero_count and one_count, respectively.\n\n4. Starting from the last row and last column of dp, iterate through each possible (i, j) combination such that i is greater than or equal to zero_count and j is greater than or equal to one_count. This is because we can only form a subset using a string if there are enough zeros and ones available to do so.\n\n5. For each (i, j) combination, update the value of dp[i][j] to be the maximum value of dp[i][j] and dp[i-zero_count][j-one_count] + 1. The first term represents the maximum subset size that can be formed without using the current string, while the second term represents the maximum subset size that can be formed by using the current string. By adding 1 to the latter, we include the current string in the subset.\n\n6. After iterating through all the strings in strs, return dp[m][n], which represents the maximum subset size that can be formed using at most m zeros and n ones.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n # Initialize dp with 0\'s\n dp = [[0] * (n+1) for _ in range(m+1)]\n \n # Iterate through each string in strs\n for s in strs:\n zero_count = s.count(\'0\')\n one_count = s.count(\'1\')\n \n # Update dp for each possible (i, j)\n for i in range(m, zero_count-1, -1):\n for j in range(n, one_count-1, -1):\n dp[i][j] = max(dp[i][j], dp[i-zero_count][j-one_count] + 1)\n \n return dp[m][n]\n\n``` | 5 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
Python | Easy DP | ones-and-zeroes | 0 | 1 | ```\nclass Solution:\n def findMaxForm(self, strs: List[str], m: int, n: int) -> int:\n \n dp = [[0 for i in range(m+1)] for i in range(n+1)]\n \n for s in strs:\n ones = s.count("1")\n zeros = s.count("0")\n \n for i in range(n,ones-1,-1):\n for j in range(m,zeros-1,-1):\n dp[i][j] = max(dp[i][j],dp[i-ones][j-zeros]+1)\n \n return dp[n][m]\n```\n\n**Please upvote if you find it useful** | 6 | You are given an array of binary strings `strs` and two integers `m` and `n`.
Return _the size of the largest subset of `strs` such that there are **at most**_ `m` `0`_'s and_ `n` `1`_'s in the subset_.
A set `x` is a **subset** of a set `y` if all elements of `x` are also elements of `y`.
**Example 1:**
**Input:** strs = \[ "10 ", "0001 ", "111001 ", "1 ", "0 "\], m = 5, n = 3
**Output:** 4
**Explanation:** The largest subset with at most 5 0's and 3 1's is { "10 ", "0001 ", "1 ", "0 "}, so the answer is 4.
Other valid but smaller subsets include { "0001 ", "1 "} and { "10 ", "1 ", "0 "}.
{ "111001 "} is an invalid subset because it contains 4 1's, greater than the maximum of 3.
**Example 2:**
**Input:** strs = \[ "10 ", "0 ", "1 "\], m = 1, n = 1
**Output:** 2
**Explanation:** The largest subset is { "0 ", "1 "}, so the answer is 2.
**Constraints:**
* `1 <= strs.length <= 600`
* `1 <= strs[i].length <= 100`
* `strs[i]` consists only of digits `'0'` and `'1'`.
* `1 <= m, n <= 100` | null |
Binary Search Python Explained | heaters | 0 | 1 | # Intuition\nset the left and right pointer over heater arrays and for every house in house array find the nearest heater present near it.\nFor each house we are supposed to find the nearest array located to it.\nFrom that found locations return the maximum distance as the max radius required by any one of the heater to reach a house.\nThree cases\n`1. curr house has heater itself -> radius req = 0 for that house`\n`2. the heater[mid] < currHouse thus shift left pointer to find if nearer heater exits in right`\n`3. heater[mid] > currHouse shift right pointer`\nreturn the maxSeenRadius among them as your ans.\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n maxRadiusSeen = 0\n heaters.sort()\n for i in range(len(houses)):\n left = 0\n right = len(heaters) - 1\n radiusReq = float(\'inf\')\n while left < right:\n mid = (left + right) // 2\n if heaters[mid] == houses[i]:\n radiusReq = 0\n break\n elif heaters[mid] < houses[i]:\n radiusReq = min(radiusReq, abs(heaters[mid] - houses[i]))\n left = mid + 1\n else:\n radiusReq = min(radiusReq, abs(heaters[mid] - houses[i]))\n right = mid\n radiusReq = min(radiusReq, abs(heaters[left] - houses[i]))\n maxRadiusSeen = max(maxRadiusSeen, radiusReq)\n return(maxRadiusSeen)\n \n\n\n``` | 1 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Simple loop | heaters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(Number of houses+ Number of heaters)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n heaters.sort()\n houses.sort()\n ans = 0\n j = 0\n for i in range(len(heaters)):\n if i == 0:\n mini = houses[0]\n else:\n mini = (heaters[i-1] + heaters[i])//2\n if i == len(heaters)-1:\n maxi = houses[-1]\n else:\n maxi = (heaters[i+1] + heaters[i])//2\n while j < len(houses) and mini <= houses[j] <= maxi:\n ans = max(ans,abs(heaters[i] - houses[j]))\n j += 1\n return ans \n``` | 1 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Python Two Pointers and Binary Search Solution | heaters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n houses.sort()\n heaters.sort()\n \n def can_cover_all(radius):\n i, j = 0, 0\n while i < len(houses) and j < len(heaters):\n if abs(houses[i] - heaters[j]) <= radius:\n i += 1\n else:\n j += 1\n return i == len(houses)\n \n left, right = 0, max(houses[-1], heaters[-1])\n \n while left < right:\n mid = left + (right - left) // 2\n if can_cover_all(mid):\n right = mid\n else:\n left = mid + 1\n \n return left\n``` | 2 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
python 99.84% speed O(1) memory | heaters | 0 | 1 | # Intuition\nmax min problem\n\n# Approach\nSort all of the lists.\nChecking for every house closest heater and solving max min problem.\nFor example:\n-1 = heater\n1 = house\n\n1|1|1|1|-1|1|1|1|1|-1|1|1|1|1\nHere we should try for every house find closest heater. Compare it to max value, which we already have, save if it\'s necessary. Go next.\n\n# Complexity\n- Time complexity:\n$$O(nlog(n))$$ - worst/average case\n$$O(n)$$ - best case\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n houses.sort()\n heaters.sort()\n\n if len(heaters) == 1:\n return max(abs(houses[0] - heaters[0]), abs(houses[-1] - heaters[0]))\n\n m_value = -1\n f, s, ind_heat = heaters[0], heaters[1], 2\n for i in range(len(houses)):\n while houses[i] > s and ind_heat < len(heaters):\n f, s = s, heaters[ind_heat]\n ind_heat += 1\n m_value = max(m_value, min(abs(houses[i] - f), abs(houses[i] - s)))\n return m_value\n \n\n\n \n \n``` | 3 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Python3, Binary search | heaters | 0 | 1 | # Intuition\n\nSince the heaters array cannot be empty, every house would have a heater that is the closest one to that house. The goal is to calculate the distance to the closest heater for every house and then return the maximum among them. By doing this we will fulfill the requirement of the problem to have every house covered by heaters.\n\n# Approach\n\nA brute force solution for this problem is to iterate over array `houses`, calculate the distance between every heater and the house and take the minimum value among them. After that take the maximum value among the minimums. \nThis solution, thought, will exceed the time limit. How can we improve it?\nInstead of iterating through the whole `heaters` array, we could use Binary Search to find the heater that is the closest to the house.\nTo perform Binary Search, we need array `heaters` to be sorted. After finding the closest heater, we subtract value of the house from it to get the minimum distance, and then we update maximum distance.\nAfter the iteration over houses is done, maximum distance would be the answer.\n\n# Complexity\n- Time complexity:\n\nTo have array `heaters` sorted, we would need $$O(n *log(n))$$ time (Timsort)\nTo perform binary search for every element in array `houses` we need $$O(m*log(n))$$ time\nTotal time complexity would be $$O((n+m)*log(n))$$, where `n` is the length of array `heaters` and `m` is the length of array `houses`\n\n- Space complexity:\n\nTo have array `heaters` sorted, we would need $$O(n)$$ space (Timsort)\nTo perform binary search we only need $$O(1)$$ space\nTotal space complexity would be $$O(n)$$, where `n` is the length of array `heaters`\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n abs_dist = float("-inf")\n n = len(heaters)\n heaters.sort()\n for i in houses:\n cur_dist = abs(self.findClosest(heaters, n, i) - i)\n abs_dist = max(abs_dist, cur_dist)\n return abs_dist\n\n def findClosest(self, arr, n, target):\n if (target <= arr[0]):\n return arr[0]\n if (target >= arr[n - 1]):\n return arr[n - 1]\n \n i = 0\n j = n\n mid = 0\n while (i < j):\n mid = (i + j) // 2\n if (arr[mid] == target):\n return arr[mid]\n if (target < arr[mid]):\n if (mid > 0 and target > arr[mid - 1]):\n return self.getClosest(arr[mid - 1], arr[mid], target)\n j = mid\n else:\n if (mid < n - 1 and target < arr[mid + 1]):\n return self.getClosest(arr[mid], arr[mid + 1], target)\n i = mid + 1\n\n return arr[mid]\n\n def getClosest(self, val1, val2, target):\n if (target - val1 >= val2 - target):\n return val2\n else:\n return val1\n``` | 7 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
[Python] - Greedy - O(nlogn) runtime and O(1) extra space | heaters | 0 | 1 | ```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n houses.sort()\n heaters.sort()\n \n max_r = 0\n heater = 0\n \n for i,house in enumerate(houses):\n # Greedy: check if the next heater will shorter the radius compared to the current one\n # it will always improve the max_r as the later index houses will stay on the RHS of current house\n\t\t\t# and if the next heater will reduce the radius, therefore next heater will also reduce the radius for later house\n while heater + 1 < len(heaters) and abs(heaters[heater] - house) >= abs(heaters[heater+1] - house):\n heater+=1\n max_r = max(max_r, abs(heaters[heater] - house))\n return max_r\n``` | 1 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
475: Solution with step by step explanation | heaters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Sort the houses and heaters in ascending order.\n2. Initialize a variable result to 0.\n3. For each house, find the closest heater to the left and right using binary search (i.e. use bisect.bisect_right to find the first heater to the right of the house, then subtract 1 to get the closest heater to the left. Do the same with bisect.bisect_left to find the closest heater to the right).\n4. If the house is to the left of all heaters, use the closest heater to the left and calculate the distance between the house and the heater.\n5. If the house is to the right of all heaters, use the closest heater to the right and calculate the distance between the house and the heater.\n6. If the house is between two heaters, use the closer of the two and calculate the distance between the house and the closer heater.\n7. Update the result variable with the maximum distance calculated so far.\n8. Return the result variable as the minimum radius of the heaters required to cover all houses.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n # Sort the houses and heaters\n houses.sort()\n heaters.sort()\n\n # Initialize the result to 0\n result = 0\n\n # For each house, find the closest heater to the left and the right\n for house in houses:\n left = bisect.bisect_right(heaters, house) - 1\n right = bisect.bisect_left(heaters, house)\n\n # If the house is to the left of all heaters, use the closest heater to the left\n if left < 0:\n result = max(result, heaters[0] - house)\n # If the house is to the right of all heaters, use the closest heater to the right\n elif right >= len(heaters):\n result = max(result, house - heaters[-1])\n # If the house is between two heaters, use the closer of the two\n else:\n result = max(result, min(house - heaters[left], heaters[right] - house))\n\n # Return the result\n return result\n\n``` | 4 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Beats Space complexity 99.8% SIMPLE PYTHON SOLUTION | heaters | 0 | 1 | \n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n c=0\n houses.sort()\n heaters.sort()\n dist=[]\n for i in houses:\n res=bisect_left(heaters,i)\n if(res==0):\n dist.append(abs(heaters[res]-i))\n elif (res>= len(heaters)):\n dist.append(abs(heaters[-1]-i))\n else:\n dist.append(min(abs(heaters[res]-i),abs(heaters[res-1]-i)))\n \n return max(dist)\n``` | 1 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Easy python solution with 90% SC and 50% TC | heaters | 0 | 1 | ```\ndef findRadius(self, houses: List[int], heaters: List[int]) -> int:\n\tdef isValid(rad):\n\t\th = 0\n\t\ti = 0\n\t\twhile(i < len(houses)):\n\t\t\tif(abs(houses[i] - heaters[h]) <= rad):\n\t\t\t\ti += 1\n\t\t\telse:\n\t\t\t\th += 1\n\t\t\tif(h == len(heaters)):\n\t\t\t\treturn 0\n\t\treturn 1\n\thouses.sort()\n\theaters.sort()\n\ti, j = 0, 1000000000\n\tans = 0\n\twhile(i <= j):\n\t\tmid = i+(j-i)//2\n\t\tif(isValid(mid)):\n\t\t\tj = mid-1\n\t\t\tans = mid\n\t\telse:\n\t\t\ti = mid+1\n\treturn ans\n``` | 1 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Binary Search - Python | heaters | 0 | 1 | \n```\nIn a anutshell, \n\tFor each house, we find the distance to the nearest heater.\nMax of the above distances, is the result.\n\nFor eg:\n\nhouses 1 2 3 4 5\nheaters h. h\n\nfor house 1,\n\tnearest heater is at distance 1, i.e at position 2\nfor house 2,\n\tnearest heater is at distance 0, i.e at position 2\nfor house 3,\n\tnearest heater is at distance 1, i.e at position 2\nfor house 4,\n\tnearest heater is at distance 1, i.e at position 5\nfor house 5,\n\tnearest heater is at distance 0, i.e at position 5\n\nthe maximum of all the above distances = max(1, 0, 1, 1, 0) = 1 (answer)\n\nFor finding nearest heater, we can use binary search ( O(logn) time complexity )\n\n```\n\n\n\n\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n \n heaters.sort() # so that we can use binary search\n result = float("-inf")\n for house in houses:\n distanceToNearestHeater = self.bs(house, heaters)\n result = max(result, distanceToNearestHeater)\n return result\n \n def bs(self, house, heaters):\n if len(heaters) == 1: # if only 1 heater present, then its obvious\n return abs(house - heaters[0])\n \n left = 0\n right = len(heaters) - 1\n justGreater, justSmaller = -1, -1\n \n while left <= right:\n mid = (left + right) // 2\n \n if house == heaters[mid]: # if heater at position of house, 0 distance\n return 0\n \n if house < heaters[mid]:\n justGreater = heaters[mid]\n right = mid - 1\n else:\n justSmaller = heaters[mid]\n left = mid + 1\n \n # if we have 2 heaters available, return min of, distance from house to those heaters.\n if justGreater != -1 and justSmaller != -1: \n return min(abs(house - justGreater), abs(house - justSmaller))\n \n # if we dont have a heater towards right, return distance from house to nearest left heater\n if justGreater == -1:\n return abs(house - justSmaller)\n # if we dont have a heater towards left, return distance from house to nearest right heater\n else:\n return abs(house - justGreater)\n```\n\nTime Complexity - O(nlogn)\nSpace Complexity - O(1)\n\n | 2 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Python easy-understanding greedy solution. | heaters | 0 | 1 | ```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n houses.sort()\n heaters.sort()\n res = 0\n heater = 0\n \n for h in houses:\n while heater + 1 < len(heaters) and heaters[heater + 1] == heaters[heater]: # Avoid duplicates\n heater += 1\n while heater + 1 < len(heaters) and abs(heaters[heater + 1] - h) < abs(heaters[heater] - h): # If using next heater is more efficient\n heater += 1 # Then use next heater\n \n res = max(res, abs(heaters[heater] - h)) # Update its range to house\n \n return res | 3 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
[Python3] greedy | heaters | 0 | 1 | \n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n heaters.sort()\n ans = k = 0 \n for x in sorted(houses):\n while k < len(heaters) and heaters[k] < x: k += 1\n cand = inf \n if k < len(heaters): cand = min(cand, heaters[k] - x)\n if k: cand = min(cand, x - heaters[k-1])\n ans = max(ans, cand)\n return ans\n``` | 2 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Binary Search | heaters | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nBinary search using build-in method bisect_right in Python\n# Complexity\n- Time complexity: *MlogM + NlogN where (*MlogM depend on sorting of programing language\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n heaters.sort()\n ans = 0\n n = len(heaters)\n\n for house in houses:\n iRight = bisect_right(heaters, house)\n minRadius = math.inf\n if iRight < n:\n minRadius = heaters[iRight] - house\n \n iLeft = iRight - 1\n if iLeft >= 0:\n minRadius = min(house - heaters[iLeft], minRadius)\n \n ans = max(ans, minRadius)\n\n return ans\n \n``` | 0 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Python | Looping binary search | heaters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom bisect import bisect_left\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n\n\n houses.sort()\n heaters.sort()\n H=len(heaters)\n def cond(mid):\n flag=True\n for i in houses:\n local=False\n k=bisect_left(heaters,i)\n if k-1>=0:\n if i-heaters[k-1]<=mid:\n local=True\n if k<H:\n \n if heaters[k]-i<=mid:\n local=True\n if not local:\n flag=False\n break\n return flag\n left,right=0,max(max(houses),max(heaters))\n while left<right:\n mid=left+(right-left)//2\n if cond(mid):\n right=mid\n else:\n left=mid+1\n return left\n\n``` | 0 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
Python3 Simple Binary Search | heaters | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntial idea is to search through all of the heaters and find the closest heater to the a house. we do this for every house and the heater that is the furthest from any house becomes our minimum required radius so that all homes are heated by a heater. The thing we have to realize here is that we should preprocess the heater data by sorting it once it is sorted we can use a modified binary search to find the closest heater and improve our time complexity. and pass all test case :) \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) sort the heaters array\n2) use binary search to find the closest heater. if house_position - heater_position is less than zero we know the heater is potentially to far to the right and thus all values further to the right will only increase the distance. the inverse is also true. if the value of house_position - heater_position is greater than 0 we know that our current heater is potentially to far to the left we update our left pointer acordingly. we repeat this process until our left pointer passes our right pointer. at every iteration we update the min_distance.\n\n \n# Complexity\n- Time complexity:$$O(M*logN)$$ \n- where M is the number of houses and N is the number of heaters\n\n- Space complexity: $$O(N^2)$$ \n- since python\'s built in sorting algorithm uses squared space complexity\n\n# Possible Improvements \nIf M is substantially larger than N it will be better to use binary search on the houses to find the closest house to to a heater. \n\n\n# Code\n```\nclass Solution:\n def findRadius(self, houses: List[int], heaters: List[int]) -> int:\n \'\'\'\n This method finds the closest heater to the home and keeps track of the largest radius ie abs(heater_position - house_position)\n The largest radius is thus the smallest radius required to heat up all of the homes.\n the Time Complexity of this algorithm is O(M * logN) Where M is the number of houses and N is the number of heaters \n The Space complexity of this algorithm is O(N^2) where N is the number of heaters since pythons default sorting algorithm uses N^2 space and thus dominates the space complexity of this algo\n \'\'\'\n #sort the heaters\n #sorting in python is O(nlogN) Time and O(N^2) Space \n heaters.sort()\n max_radius = float("-inf")\n\n for house in houses:\n max_radius = max(max_radius,self.find_closest_heater_binary(house, heaters))\n \n return max_radius\n\n # max_radius = float("-inf")\n # for house in houses:\n # min_radius = float(\'inf\')\n\n # max_radius = max(max_radius, self.find_closest_heater(house, heaters))\n\n # return max_radius\n \n\n # Time Complexity - O(N) \n # Space Complexity - O(1) \n # note - when we use this linear search method our overall time complexity is to M*N where M is the number of Houses and N is the number of heaters and overall space complexity is O(1) \n def find_closest_heater(self, target, heaters):\n\n \'\'\'\n The main idea here is to search the entire array and find the closest heater to the house \n note than in this approach the overall space complexity of our algorithm is O(1) since we don\'t use sorting \n \'\'\'\n\n min_distance = float(\'inf\')\n\n for heater in heaters:\n min_distance = min(min_distance, abs(target - heater))\n\n return min_distance\n\n # Time Complexity O(logN) where N is the number of heaters when we use this method our overall Time complexity is O(M*logN) where M is the number of Houses and N is the number of Heaters \n # Space Complexity O(1) since we are only using pointers and constants \n def find_closest_heater_binary(self, target, heaters):\n \'\'\'\n The main Idea of this algorithm is to realize that if house - heater < 0 it means that the heater is potentially to far and thus we can eliminate any heaters whose position is greater\n than the current heater. The inverse is also true where if house - heater > 0 we know that the heater is potential to far to the left of the house. \n for every value we compare it to the min_distance since we are minimizing the distance between the house and the heater. the smallest distance is thus the closest heater\n we return this result. \n \'\'\'\n l = 0 \n r = len(heaters) -1 \n min_distance = float(\'inf\')\n\n while l <= r:\n\n mid = (l + r) // 2\n\n curr_val = heaters[mid]\n curr_radius = abs(target - curr_val)\n \n if curr_radius == 0:\n return 0\n\n min_distance = min(min_distance, curr_radius)\n\n if target - curr_val < 0:\n r = mid -1 \n \n elif target:\n l = mid +1 \n \n\n return min_distance\n\n\n \n \n\n\n``` | 0 | Winter is coming! During the contest, your first job is to design a standard heater with a fixed warm radius to warm all the houses.
Every house can be warmed, as long as the house is within the heater's warm radius range.
Given the positions of `houses` and `heaters` on a horizontal line, return _the minimum radius standard of heaters so that those heaters could cover all houses._
**Notice** that all the `heaters` follow your radius standard, and the warm radius will the same.
**Example 1:**
**Input:** houses = \[1,2,3\], heaters = \[2\]
**Output:** 1
**Explanation:** The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
**Example 2:**
**Input:** houses = \[1,2,3,4\], heaters = \[1,4\]
**Output:** 1
**Explanation:** The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
**Example 3:**
**Input:** houses = \[1,5\], heaters = \[2\]
**Output:** 3
**Constraints:**
* `1 <= houses.length, heaters.length <= 3 * 104`
* `1 <= houses[i], heaters[i] <= 109` | null |
python3 code with O(n) time and space complexity | number-complement | 0 | 1 | # Intuition\nThe code first converts the given integer into binary using the built-in bin() function. Then, it iterates over each bit in the binary string and checks if it is 0 or 1. If it is 0, it appends 1 to a list, and if it is 1, it appends 0 to the list.\n\nAfter iterating over all bits in the binary string, the list of flipped bits is joined to form a new binary string. Finally, this new binary string is converted back to an integer using the int() function with the base 2 and returned as the complement of the input integer.\n\n# Approach\nThis code defines a class Solution with a method findComplement that takes an integer argument \'num\' and returns its complement.\n\nThe approach used in this code is to first convert the integer into binary using the built-in bin() function. Then, each digit in the binary string is checked and if it is 0, it is replaced with 1, and if it is 1, it is replaced with 0. Finally, the modified binary string is converted back to an integer using int() function with the base 2 (binary) and returned as the complement of the input integer.\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n s = bin(num)[2:]\n v = str(s)\n l=[]\n for i in v:\n if(i==\'0\'):\n l.append(\'1\')\n else:\n l.append(\'0\')\n v=\'\'.join(l)\n b = int(v,2)\n return b\n\n \n``` | 1 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
[Python3] | Rumtime > 97%| Simple Solution | number-complement | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n com = \'\'\n while num > 0 :\n \n if num % 2 == 1:\n com += \'0\'\n else:\n com += \'1\'\n num = num // 2\n return int(com[::-1],2)\n \n\n``` | 1 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
476: Solution with step by step explanation | number-complement | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Convert the given integer \'num\' to its binary string representation using the built-in \'bin()\' function in Python.\n2. Flip all bits in the binary string obtained in step 1 to obtain the binary string representation of its complement. This can be done by iterating over each bit in the binary string and replacing each \'0\' with \'1\' and vice versa.\n3. Convert the binary string obtained in step 2 back to its decimal integer representation using the built-in \'int()\' function in Python with base 2.\n4. Return the integer obtained in step 3 as the result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n # Convert num to binary string\n binary = bin(num)[2:]\n\n # Flip all bits in the binary string\n flipped_binary = \'\'.join([\'0\' if bit == \'1\' else \'1\' for bit in binary])\n\n # Convert the flipped binary string back to an integer\n if flipped_binary:\n return int(flipped_binary, 2)\n else:\n return 1\n\n``` | 4 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Solution | number-complement | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findComplement(int num) {\n int n = 0;\n int a = num;\n while(num > 0){\n num >>= 1;\n n ++;\n }\n cout << n;\n n = pow(2, n ) - 1;\n return n - a;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findComplement(self, num: int) -> int:\n count = 0\n temp = num\n while temp > 0:\n count += 1\n temp >>= 1\n return num ^ (2**count - 1)\n```\n\n```Java []\nclass Solution {\n public int findComplement(int num) {\n int s=0;\n int i=0;\n while(num!=0)\n {\n if((num&1)!=1)\n {\n s=s + (int)Math.pow(2,i);\n }\n i++;\n num=(num>>1); \n }\n return s;\n }\n}\n```\n | 2 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
[Python3] Easy One line Code -with Explanation | number-complement | 0 | 1 | Here\'s the code:\n```python\nclass Solution:\n def findComplement(self, num: int) -> int:\n return num^(2**(len(bin(num)[2:]))-1)\n```\nWhat does it mean?\nThe complement of a number is computable by "flipping" all the bits in his binary form.\nIn other words, that\'s nothing more than a **bitwise XOR with all 1**.\n\nFollowing the truth table:\n\n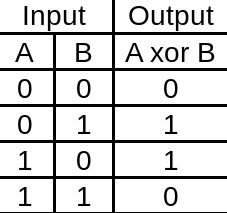\n\nWe can easily notice what I said before.\n\nSo, now?\nNow the idea is to **transform in binary** form the input number, taking the number of bit necessary for his representation. That\'s done with `len(bin(num)[2:])`, [2:] cause the bin() function in Python3 add also an initial \'0b\' (ex: `bin(5) = \'0b101\'`, but `bin(5)[2:] = \'101\'`).\n\nAfter taking the len, **compute** `2**len` taking the first pow of 2 that is >= our number, and finally compute the `-1`.\nReasoning: doing `2**len` we get a number with leading 1 and all zeros, subtracting 1 we finally get the number with the same len of our input, formed by all 1.\n\nReturn the XOR of input and this number, and **win**!\n\n-That\'s my first post, feel free to ask and upvote :D | 40 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Python 3 one-line solution beats 42% | number-complement | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nConvert to binary and replace the 1\'s with 2 and 0 with 1 and 2 with 0 then convert back to an integer.\n\n# Code\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n return int(bin(num)[2:].replace(\'1\', \'2\').replace(\'0\', \'1\').replace(\'2\', \'0\'), 2)\n \n``` | 1 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
✔️ [Python3] BITWISE OPERATORS •͡˘㇁•͡˘, Explained | number-complement | 0 | 1 | The idea is to shift all bits of the given integer to the right in the loop until it turns into `0`. Every time we do a shift we use a mask to check what is in the right-most bit of the number. If bit is `0` we add `2**n` to the result where `n` is the current number of shifts. Example:\n```\nn=0, num=1010, bit=0 => res += 2**0\nn=1, num=0101, bit=1 => res += 0\nn=2, num=0010, bit=0 => res += 2**2\nn=3, num=0001, bit=1 => res += 0\n num=0000 => break the loop\n```\n\nRuntime: 24 ms, faster than **94.85%** of Python3 online submissions for Number Complement.\nMemory Usage: 14.2 MB, less than **68.47%** of Python3 online submissions for Number Complement.\n\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n res, n = 0, 0\n while num:\n if not num & 1:\n res += 2**n\n \n num >>= 1\n n += 1\n \n return res\n``` | 8 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Python O( lg n ) sol. by XOR masking. 85%+ [ With explanation ] | number-complement | 0 | 1 | Python O( log n ) sol. based on XOR masking. \n\n---\n\nExample explanation\n\n---\nExample_#1\n\ninput: **5**\n\n5 = 0b **101**\n**bits length** of 5 = **3**\n**masking** = **2^3 -1** = 8 - 1 = **7** = 0b **111**\n\n5 = 0b **101**\n3 = 0b **111** ( **XOR** )\n\u2014\u2014\u2014\u2014\u2014\u2014\u2014\u2014\u2014\n**2** = 0b **010**\n\noutput: **2**\n\n---\nExample_#2\n\ninput: **9**\n\n9 = 0b **1001**\n**bits length** of 2 = **4**\n**masking** = **2^4 -1** = 16 - 1 = **15** = 0b **1111**\n\n09 = 0b **1001**\n15 = 0b **1111** ( **XOR** )\n\u2014\u2014\u2014\u2014\u2014\u2014\u2014\u2014\u2014\n**06** = 0b **0110**\n\noutput: **6**\n\n---\n**Implementation** with bit length calculation:\n```\nfrom math import floor\nfrom math import log\n\nclass Solution:\n def findComplement(self, num: int) -> int:\n \n bits_length = floor( log(num, 2) + 1)\n \n return num^( 2**bits_length - 1 )\n```\n\n---\n\n**Implementation** with python built-in method, **[.bit_length()](https://docs.python.org/3/library/stdtypes.html#int.bit_length)**,of integer:\n\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n \n bit_mask = 2**num.bit_length() -1 \n \n return ( num ^ bit_mask )\n```\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #1009 Complement of Base 10 Integer](https://leetcode.com/problems/complement-of-base-10-integer/) | 19 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Explained | Easy to understand | Faster than 99.58% | Simple | Bit manipulation | Python Solution | number-complement | 0 | 1 | ##### Later I found that this solution correponds to the second approach mentioned in the solution\n\nHere, in this soution, we are just making another bit variable to be full of 1\'s upto the length of bits in num and then simply returning the XOR of two\nnum = 5 = 101\nbit ===== 111\nAns ==== 010 = 2\n\n```\ndef findComplement(self, num: int) -> int:\n bit = 0\n todo = num\n while todo:\n bit = bit << 1\n bit = bit ^ 1\n todo = todo >> 1\n return bit ^ num\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38 | 17 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Python3 | 1 liner | xor logic | number-complement | 0 | 1 | First solved it with the array/list approach to individually inverse the elements. Then, thought of how to implement a not gate using other bitwise operators and realised A xor 1 = not A.\n1*len(bin(num) is for creating the same length of 1\'s to xor each element with and [2:] slicing is to discard the \'0b\' representing that the string is a binary of a number.\n```\nclass Solution:\n def findComplement(self, num: int) -> int:\n return num^int(\'1\'*len(bin(num)[2:]), 2)\n``` | 3 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
99.20% faster python MUCH easy solution. | number-complement | 0 | 1 | ```\nclass Solution:\n def findComplement(self, num: int) -> int:\n complement=""\n for i in bin(num)[2:]:\n if i is "0":\n complement+="1"\n else:\n complement+="0"\n \n return int(complement,2)\n``` | 7 | The **complement** of an integer is the integer you get when you flip all the `0`'s to `1`'s and all the `1`'s to `0`'s in its binary representation.
* For example, The integer `5` is `"101 "` in binary and its **complement** is `"010 "` which is the integer `2`.
Given an integer `num`, return _its complement_.
**Example 1:**
**Input:** num = 5
**Output:** 2
**Explanation:** The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.
**Example 2:**
**Input:** num = 1
**Output:** 0
**Explanation:** The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.
**Constraints:**
* `1 <= num < 231`
**Note:** This question is the same as 1009: [https://leetcode.com/problems/complement-of-base-10-integer/](https://leetcode.com/problems/complement-of-base-10-integer/) | null |
Python 3 | Bit Manipulation O(N) | Explanations | total-hamming-distance | 0 | 1 | ### Explanation\n- For each bit, count how many numbers have 0 or 1 on that bit; the total difference on that bit is `zero * one`\n\t- `zero`: the amount of numbers which have `0` on bit `i`\n\t- `one`: the amount of numbers which have `1` on bit `i`\n- Sum up each bit, then we got the answer\n- Time Complexity: `O(32*N) -> O(N)`\n\n### Implementation\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n ans = 0\n for i in range(32):\n zero = one = 0\n mask = 1 << i\n for num in nums:\n if mask & num: one += 1\n else: zero += 1 \n ans += one * zero \n return ans \n``` | 33 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
One-line Python solution beats 98% | total-hamming-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought on how to solve this problem was to find the Hamming Distance between each pair of integers in the given list. The Hamming Distance between two integers is the number of positions at which the corresponding bits are different.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach to solving this problem is to first convert each integer in the given list to its binary representation, which will be a string of 32 characters. Then use zip() function and map() function to pair each bit of the integers, count the number of \'0\' and \'1\' in each pair. Multiply the count of \'0\' and \'1\' and sum them up, this will give the total Hamming distance between all integers.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n return sum(b.count(\'0\')*b.count(\'1\') for b in zip(*map(\'{:032b}\'.format,nums)))\n\n``` | 2 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Easy python solution | total-hamming-distance | 0 | 1 | # Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n ans=0\n for i in range(32):\n cnt=0\n for j in range(len(nums)):\n cnt+=(nums[j]>>i&1)\n ans+=(len(nums)-cnt)*cnt\n return ans\n``` | 4 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
477: Solution with step by step explanation | total-hamming-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function named totalHammingDistance that takes a list of integers nums as input and returns an integer as output.\n2. Get the length of the nums list and store it in a variable n.\n3. Initialize a variable result to zero.\n4. Loop through each bit position i from 0 to 29:\n 1. Initialize a variable count to zero.\n 2. Loop through each integer num in nums:\n 1. Right-shift num by i positions and bitwise AND the result with 1 to get the value of the bit at position i.\n 2. If the value is 1, increment count by 1.\n 3. Compute the Hamming distance for position i by multiplying count by (n - count) and add the result to result.\n5. Return the final value of result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n n = len(nums)\n result = 0\n for i in range(30):\n count = 0\n for num in nums:\n count += (num >> i) & 1\n result += count * (n - count)\n return result\n\n``` | 3 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Easy and Clear Solution Python 3 | total-hamming-distance | 0 | 1 | ```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n res=0\n getbinary = lambda x, n: format(x, \'b\').zfill(n)\n bi=[]\n for i in range(len(nums)):\n a=getbinary(nums[i], 32)\n bi.append(a)\n for i in range (32):\n zero=0\n one=0\n for b in bi:\n if b[i]==\'1\':\n one+=1\n else:\n zero+=1\n res=res+ zero*one\n return res\n``` | 1 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Python 3, TC: O(n) | total-hamming-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n res = 0\n for i in range(32):\n bit = 1<<i\n count_1 = 0\n for x in nums:\n if x & bit != 0:\n count_1 += 1\n res += (len(nums) - count_1) * count_1\n return res\n \n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
easy solution || python3 | total-hamming-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n a=[]\n b=max(nums)\n s=len(bin(b)[2:])\n for i in nums:\n b=bin(i)[2:]\n if len(b)<s:\n b=\'0\'*(s-len(b))+b\n a.append(b)\n count=0\n for i in range(len(a[0])):\n count1=0\n for j in range(len(a)):\n if a[j][i]==\'1\':\n count1+=1\n count+=count1*(len(a)-count1)\n return count\n \n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Bit manuplation | Easy | total-hamming-distance | 0 | 1 | # Intuition\nThe "Total Hamming Distance" problem involves calculating the sum of Hamming distances between all pairs of integers in the given list `nums`. The Hamming distance between two integers is defined as the number of differing bits in their binary representations. Our initial thoughts are to find a way to efficiently compute the Hamming distance for all pairs.\n\n# Approach\nTo solve this problem, we adopt the following approach:\n\n1. Initialize a variable `res` to 0, which will store the total Hamming distance.\n\n2. Get the length of the `nums` list and store it in `n`.\n\n3. Iterate through each bit position from the least significant bit (LSB) to the most significant bit (MSB). For each bit position (30 bits in this case for a 32-bit integer), we perform the following steps:\n\n - Initialize a variable `count` to 0, which will count the number of set bits (1) at the current bit position.\n\n - Iterate through each integer `num` in the `nums` list.\n - Right shift the integer `num` by the current bit position using `(num >> i) & 1`. This operation extracts the bit at the current position, and we check if it\'s 1.\n - Increment the `count` by 1 for each set bit encountered in the `nums` list.\n\n - Calculate the number of unset bits (0) at the current bit position by subtracting `count` from the total number of integers `n`. This gives us the count of 0s at the current position.\n\n - Update the `res` by adding the product of the counts of 0s and 1s at the current bit position. This represents the Hamming distance contribution of this bit position.\n\n4. After iterating through all bit positions, the `res` will contain the total Hamming distance between all pairs of integers in the `nums` list.\n\n5. Return the `res` as the total Hamming distance.\n\n# Complexity\n- Time complexity: The time complexity is O(30 * n) = O(n) because we perform 30 iterations for each of the 30 bits, and in each iteration, we iterate through all the integers in the `nums` list, which has a length of `n`.\n- Space complexity: The space complexity is O(1) because we use a constant amount of extra space.\n\n# Code\n```python\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n res = 0\n n = len(nums)\n for i in range(30):\n count = 0\n for num in nums:\n count += (num >> i) & 1\n zeros = n - count\n res += zeros * count\n return res\n```\n | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Simple and clear python3 solutions | Bit manipulation | total-hamming-distance | 0 | 1 | # Complexity\n- Time complexity: $$O(n \\cdot k) = O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k) = O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nwhere `n = nums.length` and `k = log2(max(nums)) = log2(10^9) ~ 30 = O(1)`\n# Code\n``` python3 []\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n n = len(nums)\n\n ones = Counter()\n for elem in nums:\n position = 0\n while elem:\n if elem % 2:\n ones[position] += 1\n elem //= 2\n position += 1\n \n return sum(\n one * (n - one)\n for one in ones.values()\n )\n\n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Better solution! | total-hamming-distance | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: list[int]) -> int:\n total_distance = 0\n num_elements = len(nums)\n for bit in range(32):\n count_1 = sum(((num >> bit) & 1) for num in nums)\n total_distance += count_1 * (num_elements - count_1)\n return total_distance\n\n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Simple step by step explanation , in Python | total-hamming-distance | 0 | 1 | # Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n # Can calculate ans ==> count of given integers whose ith it is set\n # if x of them has ith bit as set \n """\n ==> 1*(n-x) + 1*(n-x)+........x times.\n \n ==> x*(n-x)\n """\n\n lst = []\n\n for ele in nums:\n temp = bin(ele)[2:]\n temp = "0"*(32-len(temp)) + temp\n lst += [temp]\n \n ans , n = 0 , len(lst)\n\n for x in range(32):\n count_1 = 0\n for i in range(n):\n if lst[i][x] == "1":\n count_1 += 1\n\n ans += (count_1)*(n-count_1)\n return ans\n \n # Using XOR = TLE\n \n n = len(nums)\n\n ans = 0\n \n for i in range(n):\n for j in range(i , n):\n\n val = nums[i] ^ nums[j] # XOR operation \n\n count_1 = bin(val).count("1")\n\n ans += count_1\n \n return ans\n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Easy Python Solution | total-hamming-distance | 0 | 1 | \n# Code\n```\nclass Solution:\n def totalHammingDistance(self, nums: List[int]) -> int:\n arr=[]\n l=0\n if len(nums)<2:\n return 0\n for i in range(len(nums)):\n l=max(l, len(bin(nums[i])[2:]))\n arr.append(bin(nums[i])[2:])\n for i in range(len(arr)):\n arr[i]=\'0\'*(l-len(arr[i]))+arr[i]\n c=0\n for i in range(len(arr[1])):\n z=0\n o=0\n for j in range(len(arr)):\n if arr[j][i]==\'0\':\n z+=1\n else:\n o+=1\n c+=(z*o)\n return c\n``` | 0 | The [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two integers is the number of positions at which the corresponding bits are different.
Given an integer array `nums`, return _the sum of **Hamming distances** between all the pairs of the integers in_ `nums`.
**Example 1:**
**Input:** nums = \[4,14,2\]
**Output:** 6
**Explanation:** In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just
showing the four bits relevant in this case).
The answer will be:
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
**Example 2:**
**Input:** nums = \[4,14,4\]
**Output:** 4
**Constraints:**
* `1 <= nums.length <= 104`
* `0 <= nums[i] <= 109`
* The answer for the given input will fit in a **32-bit** integer. | null |
Solution | generate-random-point-in-a-circle | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n double r, x, y;\npublic:\n Solution(double radius, double x_center, double y_center) {\n r = radius;\n x = x_center;\n y = y_center;\n }\n double random(){\n return (double) rand() / RAND_MAX;\n }\n vector<double> randPoint() {\n double a = random() * 2 * M_PI;\n double smallR = sqrt(random()) * r;\n return {x + smallR * cos(a), y + smallR * sin(a)};\n }\n};\n```\n\n```Python3 []\nfrom random import random\nfrom math import sin,cos\n\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x=x_center\n self.y=y_center\n self.r=radius\n \n def randPoint(self) -> List[float]:\n a = random()*6.28318530718\n r = sqrt(random())*self.r\n return [self.x+r*cos(a),self.y+r*sin(a)]\n```\n\n```Java []\nclass Solution {\n double radius;\n double x_center;\n double y_center;\n\n public Solution(double radius, double x_center, double y_center) {\n this.radius = radius;\n this.x_center = x_center;\n this.y_center = y_center; \n }\n public double[] randPoint() {\n \n double ang = Math.random() * 2 * Math.PI,\n r = Math.sqrt(Math.random()) * radius;\n \n return new double[]{r*Math.cos(ang)+x_center,r*Math.sin(ang)+y_center};\n }\n}\n```\n | 1 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
Solution | generate-random-point-in-a-circle | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n double r, x, y;\npublic:\n Solution(double radius, double x_center, double y_center) {\n r = radius;\n x = x_center;\n y = y_center;\n }\n double random(){\n return (double) rand() / RAND_MAX;\n }\n vector<double> randPoint() {\n double a = random() * 2 * M_PI;\n double smallR = sqrt(random()) * r;\n return {x + smallR * cos(a), y + smallR * sin(a)};\n }\n};\n```\n\n```Python3 []\nfrom random import random\nfrom math import sin,cos\n\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x=x_center\n self.y=y_center\n self.r=radius\n \n def randPoint(self) -> List[float]:\n a = random()*6.28318530718\n r = sqrt(random())*self.r\n return [self.x+r*cos(a),self.y+r*sin(a)]\n```\n\n```Java []\nclass Solution {\n double radius;\n double x_center;\n double y_center;\n\n public Solution(double radius, double x_center, double y_center) {\n this.radius = radius;\n this.x_center = x_center;\n this.y_center = y_center; \n }\n public double[] randPoint() {\n \n double ang = Math.random() * 2 * Math.PI,\n r = Math.sqrt(Math.random()) * radius;\n \n return new double[]{r*Math.cos(ang)+x_center,r*Math.sin(ang)+y_center};\n }\n}\n```\n | 1 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
Python3 Solution | generate-random-point-in-a-circle | 0 | 1 | \tclass Solution:\n\n\t\tdef __init__(self, radius: float, x_center: float, y_center: float):\n\t\t\tself.r = radius\n\t\t\tself.x, self.y = x_center, y_center\n \n\n\t\tdef randPoint(self) -> List[float]:\n\t\t\ttheta = uniform(0,2*pi)\n\t\t\tR = sqrt(uniform(0,self.r**2))\n\t\t\treturn [self.x+R*cos(theta), self.y+R*sin(theta)] | 3 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
Python3 Solution | generate-random-point-in-a-circle | 0 | 1 | \tclass Solution:\n\n\t\tdef __init__(self, radius: float, x_center: float, y_center: float):\n\t\t\tself.r = radius\n\t\t\tself.x, self.y = x_center, y_center\n \n\n\t\tdef randPoint(self) -> List[float]:\n\t\t\ttheta = uniform(0,2*pi)\n\t\t\tR = sqrt(uniform(0,self.r**2))\n\t\t\treturn [self.x+R*cos(theta), self.y+R*sin(theta)] | 3 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
478: Solution with step by step explanation | generate-random-point-in-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the class with radius, x_center, and y_center as instance variables.\n2. When randPoint() is called, generate a random length between 0 and radius using random.uniform(0, self.radius**2).\n3. Generate a random angle in radians between 0 and 2*pi using random.uniform(0, 1) * 2 * math.pi.\n4. Compute the x and y coordinates of the random point using the formulas:\nx = x_center + length * cos(angle)\ny = y_center + length * sin(angle)\n5. Return the coordinates as a list [x, y].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.radius = radius\n self.x_center = x_center\n self.y_center = y_center\n\n def randPoint(self) -> List[float]:\n length = math.sqrt(random.uniform(0, self.radius**2))\n degree = random.uniform(0, 1) * 2 * math.pi\n x = self.x_center + length * math.cos(degree)\n y = self.y_center + length * math.sin(degree)\n return [x, y]\n\n``` | 3 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
478: Solution with step by step explanation | generate-random-point-in-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the class with radius, x_center, and y_center as instance variables.\n2. When randPoint() is called, generate a random length between 0 and radius using random.uniform(0, self.radius**2).\n3. Generate a random angle in radians between 0 and 2*pi using random.uniform(0, 1) * 2 * math.pi.\n4. Compute the x and y coordinates of the random point using the formulas:\nx = x_center + length * cos(angle)\ny = y_center + length * sin(angle)\n5. Return the coordinates as a list [x, y].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.radius = radius\n self.x_center = x_center\n self.y_center = y_center\n\n def randPoint(self) -> List[float]:\n length = math.sqrt(random.uniform(0, self.radius**2))\n degree = random.uniform(0, 1) * 2 * math.pi\n x = self.x_center + length * math.cos(degree)\n y = self.y_center + length * math.sin(degree)\n return [x, y]\n\n``` | 3 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
Python easy - understanding solution with detailed explanation. | generate-random-point-in-a-circle | 0 | 1 | The idea is finding random angle and random radius, combining them together to get a random point on 2D circle.\nAt first, I really stuck for a long time with this code:\n```\nr = random.random() * self.r # Get wrong answer with test 7. Because it won\'t distribute evenly on circle.\n```\nAnd yeh, finally I found it easier to understand by taking probability into consideration.\nConsidering two circle:\nA: with radius 1\nB: with radius 0.5\n\nThe chance for randomly flying darts to hit target for A : B is 4 : 1 right?\nSo with the random.random() function, we know that the chance for getting number in range(0, 1) is 4 times the chance getting number in range(0, 0.25). \n\nHere\'s the table: Radius vs. the range of random.random() and the chance to hit :\n```\nRadius range chance\n1 [0, 1] 100%\n0.75 [0, 0.5625] 56%\n0.5 [0, 0.25] 25%\n0.25 [0, 0.0625] 6%\n```\nBy induction, we see that if we get random number by taking advantage of random.random(), the random number shoud be modified by sqrt() to conform to radius.\n\n\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x = x_center\n self.y = y_center\n self.r = radius\n\n def randPoint(self) -> List[float]:\n r = sqrt(random.random()) * self.r\n angle = random.uniform(0, 2*pi)\n return [self.x + r * math.cos(angle), self.y + r *math.sin(angle)] | 3 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
Python easy - understanding solution with detailed explanation. | generate-random-point-in-a-circle | 0 | 1 | The idea is finding random angle and random radius, combining them together to get a random point on 2D circle.\nAt first, I really stuck for a long time with this code:\n```\nr = random.random() * self.r # Get wrong answer with test 7. Because it won\'t distribute evenly on circle.\n```\nAnd yeh, finally I found it easier to understand by taking probability into consideration.\nConsidering two circle:\nA: with radius 1\nB: with radius 0.5\n\nThe chance for randomly flying darts to hit target for A : B is 4 : 1 right?\nSo with the random.random() function, we know that the chance for getting number in range(0, 1) is 4 times the chance getting number in range(0, 0.25). \n\nHere\'s the table: Radius vs. the range of random.random() and the chance to hit :\n```\nRadius range chance\n1 [0, 1] 100%\n0.75 [0, 0.5625] 56%\n0.5 [0, 0.25] 25%\n0.25 [0, 0.0625] 6%\n```\nBy induction, we see that if we get random number by taking advantage of random.random(), the random number shoud be modified by sqrt() to conform to radius.\n\n\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x = x_center\n self.y = y_center\n self.r = radius\n\n def randPoint(self) -> List[float]:\n r = sqrt(random.random()) * self.r\n angle = random.uniform(0, 2*pi)\n return [self.x + r * math.cos(angle), self.y + r *math.sin(angle)] | 3 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
Python, wrong test cases? | generate-random-point-in-a-circle | 0 | 1 | Quick answer: No, they are fine. Check out the answer by @mallikab. I\'ll let this post stand because of the discussion it has generated, but otherwise, both the solution presented below and the assumption of test cases being wrong is false.\n\n# UPD: Wrong claim, because 0.01 > 0.002:\nThe case below is wrong, the expected output is off the circle `-73839.10208 < -73839.101` and `-3289891.30206 < -3289891.301`. This is perhaps due to precision issues with floating point numbers. If I\'m missing something, please let me know.\n```\nInput: [0.01, -73839.1, -3289891.3],\nExpected output: [-73839.10208,-3289891.30206]\n```\n\n# UPD: The solution below is incorrect, see the comments to know why\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x = x_center\n self.y = y_center\n self.radius = radius\n\n def randPoint(self) -> List[float]:\n first = random.uniform(-self.radius, self.radius)\n secondmax = (self.radius ** 2 - first ** 2) ** 0.5\n second = random.uniform(-secondmax, secondmax)\n return [self.x + first, self.y + second]\n``` | 4 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
Python, wrong test cases? | generate-random-point-in-a-circle | 0 | 1 | Quick answer: No, they are fine. Check out the answer by @mallikab. I\'ll let this post stand because of the discussion it has generated, but otherwise, both the solution presented below and the assumption of test cases being wrong is false.\n\n# UPD: Wrong claim, because 0.01 > 0.002:\nThe case below is wrong, the expected output is off the circle `-73839.10208 < -73839.101` and `-3289891.30206 < -3289891.301`. This is perhaps due to precision issues with floating point numbers. If I\'m missing something, please let me know.\n```\nInput: [0.01, -73839.1, -3289891.3],\nExpected output: [-73839.10208,-3289891.30206]\n```\n\n# UPD: The solution below is incorrect, see the comments to know why\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.x = x_center\n self.y = y_center\n self.radius = radius\n\n def randPoint(self) -> List[float]:\n first = random.uniform(-self.radius, self.radius)\n secondmax = (self.radius ** 2 - first ** 2) ** 0.5\n second = random.uniform(-secondmax, secondmax)\n return [self.x + first, self.y + second]\n``` | 4 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
Python Solution O(n) | generate-random-point-in-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to randomly generate points within a circle of radius radius and center point (x_center, y_center).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to use the built-in random.uniform(a, b) function which generates a random float number between a and b. We use this function to generate x and y coordinates for the point. We then check if the point is within the circle by checking if the point\'s distance from the center of the circle is less than or equal to the radius. If it is, we return the point. If not, we continue generating new points until we find one that is within the circle.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.radius = radius\n self.x_center = x_center\n self.y_center = y_center\n self.x = x_center\n self.y = y_center\n self.r = radius\n\n def randPoint(self) -> List[float]:\n while True:\n x = random.uniform(self.x - self.r, self.x + self.r)\n y = random.uniform(self.y - self.r, self.y + self.r)\n if (x - self.x) ** 2 + (y - self.y) ** 2 <= self.r ** 2:\n return [x, y]\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(radius, x_center, y_center)\n# param_1 = obj.randPoint()\n``` | 2 | Given the radius and the position of the center of a circle, implement the function `randPoint` which generates a uniform random point inside the circle.
Implement the `Solution` class:
* `Solution(double radius, double x_center, double y_center)` initializes the object with the radius of the circle `radius` and the position of the center `(x_center, y_center)`.
* `randPoint()` returns a random point inside the circle. A point on the circumference of the circle is considered to be in the circle. The answer is returned as an array `[x, y]`.
**Example 1:**
**Input**
\[ "Solution ", "randPoint ", "randPoint ", "randPoint "\]
\[\[1.0, 0.0, 0.0\], \[\], \[\], \[\]\]
**Output**
\[null, \[-0.02493, -0.38077\], \[0.82314, 0.38945\], \[0.36572, 0.17248\]\]
**Explanation**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint(); // return \[-0.02493, -0.38077\]
solution.randPoint(); // return \[0.82314, 0.38945\]
solution.randPoint(); // return \[0.36572, 0.17248\]
**Constraints:**
* `0 < radius <= 108`
* `-107 <= x_center, y_center <= 107`
* At most `3 * 104` calls will be made to `randPoint`. | null |
Python Solution O(n) | generate-random-point-in-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to randomly generate points within a circle of radius radius and center point (x_center, y_center).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to use the built-in random.uniform(a, b) function which generates a random float number between a and b. We use this function to generate x and y coordinates for the point. We then check if the point is within the circle by checking if the point\'s distance from the center of the circle is less than or equal to the radius. If it is, we return the point. If not, we continue generating new points until we find one that is within the circle.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, radius: float, x_center: float, y_center: float):\n self.radius = radius\n self.x_center = x_center\n self.y_center = y_center\n self.x = x_center\n self.y = y_center\n self.r = radius\n\n def randPoint(self) -> List[float]:\n while True:\n x = random.uniform(self.x - self.r, self.x + self.r)\n y = random.uniform(self.y - self.r, self.y + self.r)\n if (x - self.x) ** 2 + (y - self.y) ** 2 <= self.r ** 2:\n return [x, y]\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(radius, x_center, y_center)\n# param_1 = obj.randPoint()\n``` | 2 | Given an integer array `nums`, partition it into two (contiguous) subarrays `left` and `right` so that:
* Every element in `left` is less than or equal to every element in `right`.
* `left` and `right` are non-empty.
* `left` has the smallest possible size.
Return _the length of_ `left` _after such a partitioning_.
Test cases are generated such that partitioning exists.
**Example 1:**
**Input:** nums = \[5,0,3,8,6\]
**Output:** 3
**Explanation:** left = \[5,0,3\], right = \[8,6\]
**Example 2:**
**Input:** nums = \[1,1,1,0,6,12\]
**Output:** 4
**Explanation:** left = \[1,1,1,0\], right = \[6,12\]
**Constraints:**
* `2 <= nums.length <= 105`
* `0 <= nums[i] <= 106`
* There is at least one valid answer for the given input. | null |
✅✅ Beats 100% || RUBY || Easy to understand || 🔥🔥 || | largest-palindrome-product | 0 | 1 | # Ruby\n```\n# @param {Integer} n\n# @return {Integer}\ndef largest_palindrome(n)\n return 9 if n == 1\n upper = (10.pow(n)) - 1 \n lower = 10.pow(n-1)\n i = upper\n (lower).times do\n i = i - 1\n s = i.to_s\n pal = (s + s.reverse).to_i\n lPal = ((pal.pow(0.5))-1).to_i\n j= upper\n (lPal).times do\n j = j-1\n if pal % j == 0 && ((pal / j).to_s).length == n\n return pal % 1337\n end\n end\n end\n return -1 \nend\n```\n# Pythone3\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n == 1:\n return 9\n upper = pow(10, n) - 1\n lower = pow(10, n - 1)\n for i in range(upper, lower-1, -1):\n s = str(i)\n pal = int(s + s[::-1])\n for j in range(upper, int(pow(pal, 0.5))-1, -1):\n if pal % j == 0 and len(str(pal//j)) == n:\n return pal % 1337\n return -1\n``` | 1 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Solution | largest-palindrome-product | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int flip(int n){\n auto str = to_string(n);\n std::reverse(str.begin(), str.end());\n return atoi(str.c_str());\n }\n bool isInteger(double v){\n double tmp;\n return std::modf(v, &tmp) == 0.0;\n }\n int largestPalindrome(int n) {\n if (n == 1) return 9;\n const long max = pow(10, n);\n for (int z = 2; z < max -1; z++){\n const long left = max -z;\n const long right = flip(left);\n const double sqrt_term = z*z - 4*right;\n \n if (sqrt_term < 0.0){ continue; }\n \n const double root1 = 0.5*(z + sqrt(sqrt_term));\n const double root2 = 0.5*(z - sqrt(sqrt_term));\n \n if (isInteger(root1) || isInteger(root2)){\n return (max*left + right) % 1337;\n }\n }\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n return [0, 9, 987, 123, 597, 677, 1218, 877, 475][n] \n def isPalindrome(x):\n return str(x) == str(x)[::-1]\n def solve(n):\n best = 0\n for i in range(10**n-1, 0, -1):\n for j in range(max(i, (best-1)//i+1), 10**n):\n if isPalindrome(i*j):\n best = i*j\n return best\n```\n\n```Java []\nclass Solution {\n public int largestPalindrome(int n) {\n if(n==1)\n return 9;\n if(n==2)\n return 987;\n if(n==3)\n return 123;\n if(n==4)return 597;\n if(n==5)return 677;\n if(n==6)return 1218;\n if(n==7)return 877;\n if(n==8)return 475;\n return 0;\n }\n}\n```\n | 2 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
[Python3] Solution with explanation | largest-palindrome-product | 0 | 1 | ```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n # just to forget about 1-digit case\n if n == 1:\n return 9\n \n # min number with n digits (for ex. for n = 4, min_num = 1000)\n min_num = 10 ** (n - 1)\n \n # max number with n digits (for ex. 9999)\n max_num = 10 ** n - 1 \n \n max_pal = 0\n \n # step is equal to 2, because we have to get a number, the 1st digit of which is 9, so we have to \n\t\t# iterate only over odd numbers\n for i in range(max_num, min_num - 1, -2): \n \n # since we are looking for the maximum palindrome number, it makes no sense to iterate over the \n # product less than the max_pal obtained from the last iteration\n if i * i < max_pal:\n break\n \n for j in range(max_num, i - 1, -2):\n product = i * j\n \n # since a palindrome with an even number of digits must be mod 11 == 0 and we have no reason to \n # check the product which less or equal than max_pal\n if product % 11 != 0 and product >= max_pal:\n continue\n \n # check if product is a palindrome then update the max_pal\n if str(product) == str(product)[::-1]:\n max_pal = product\n\n return max_pal % 1337\n```\n\nPalindrome with an even number of digits satisfies the criteria for divisibility by 11:\n1) If the number of digits is even, add the first and subtract the last digit from the rest. The result must be divisible by 11:\nFor example: 9966006699\n96600669 + 9 - 9 = 96600669,\n96600669 / 11 = 8781879\n2) Form the alternating sum of the digits. The result must be divisible by 11:\nabs(9 + 6 + 0 + 6 + 9) - abs(9 + 6 + 0 + 6 +9) = 0, \n0 is a multiple of 11 | 12 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
479: Solution with step by step explanation | largest-palindrome-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. If n is 1, return 9.\n2. Set upper to the largest n-digit number (10^n - 1) and lower to the smallest n-digit number (10^(n-1)).\n3. Starting from upper, iterate through all possible n-digit numbers i in descending order.\n4. Construct a palindrome number pal by concatenating the string of i and its reversed string.\n5. Starting from upper, iterate through all possible n-digit numbers j in descending order until j is less than the square root of pal.\n6. Check if pal is divisible by j without any remainder and if the quotient of pal divided by j is an n-digit number.\n7. If pal is divisible by j without any remainder and the quotient is an n-digit number, return the result of pal modulo 1337.\n8. If no palindrome product is found, return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n == 1:\n return 9\n \n upper = pow(10, n) - 1\n lower = pow(10, n - 1)\n \n for i in range(upper, lower-1, -1):\n s = str(i)\n # construct the palindrome number from its first half\n pal = int(s + s[::-1])\n # check if the palindrome number is the product of two n-digit numbers\n for j in range(upper, int(pow(pal, 0.5))-1, -1):\n if pal % j == 0 and len(str(pal//j)) == n:\n return pal % 1337\n return -1 # no palindrome product found\n``` | 3 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
✅Python Fast. Swift 100% faster 100% less memory. No cheating.🔥 | largest-palindrome-product | 0 | 1 | This is a very efficient solution for solving the problem; turns out to be a very straightforward way. Hint: it\'s about solving quadratic equations.\n```\nproduct = multiplicand * multiplier\nNow for an n-digit number, the maximum a multiplicand or a multiplier can be is (10\u207F - 1). So,\nproduct = \n = (10\u207F - x) * (10\u207F - y) (where x, y > 0); n = no. of digits\n = 10\xB2\u207F - 10\u207Fx - 10\u207Fy + xy\n = 10\xB2\u207F - 10\u207F(x + y) + xy\n = 10\u207F * (10\u207F - (x + y)) + xy\n = 10\u207F * left + right (let left = 10\u207F - (x + y) and right = xy)\n```\n\t\t \nNow, we\'ve\n```\n right = xy\n let z = x + y\n \u2234 right = x(z - x)\n \u2234 right = zx - x\xB2\n \u2234 x\xB2 - zx + right = 0\n\nWhich is a quadratic equation!\n\tax\xB2 + bx + c = 0\n\t\tx = -b \xB1 \u221A(b\xB2 - 4ac)\n\t\t\t----------------\n\t\t\t\t 2a\n\twhere; a = 1\n\t\t b = -z\n\t\t c = right\n```\nThus our problem is now reduced to solving a quadratic equation.\n**Python**\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n == 1:\n return 9\n maxi = 10 ** n # store the value of 10\u207F \n for z in range(2, maxi): # since both x, y > 0 and z = x + y; which implies that z has a minimum value of 2\n left = maxi - z\n right = int(str(left)[::-1]) # reverese number\n \n discriminant = z ** 2 - 4 * right # b\xB2 - 4ac\n if discriminant < 0: # no root\n continue\n else: # there exists at least one real solution; so calculate the roots\n root_1 = (z + discriminant ** 0.5) / 2\n root_2 = (z - discriminant ** 0.5) / 2\n if root_1.is_integer() or root_2.is_integer():\n return (maxi * left + right) % 1337\n```\n\n**PS: Don\'t get daunted by the program, it\'s difficult only syntactically!!**\nKindly ignore the ```isInt()``` and ```power()``` methods!!\n```\nclass Solution {\n private func isInt(_ num: Double) -> Bool {\n return num.truncatingRemainder(dividingBy: 1) == 0\n }\n private func power(_ num: Int, raisedTo: Int) -> Int {\n guard raisedTo != 0 else { return 0 }\n guard raisedTo != 1 else { return num }\n var ans = num\n for _ in 2...raisedTo {\n ans *= num\n }\n return ans\n }\n func largestPalindrome(_ n: Int) -> Int {\n if n == 1 { \n return 9 \n }\n let max = power(10, raisedTo: n) // store the value of 10\u207F \n for z in 2..<max { // since both x, y > 0 and z = x + y; which implies that z has a minimum value of 2\n let left = max - z \n let right = Int(String(String(left).reversed()))! // reverese number\n let discriminant = power(z, raisedTo: 2) - 4 * right // b\xB2 - 4ac\n \n if discriminant < 0 { // no root\n continue\n } else { // there exists at least one real solution\n // calculate the roots\n let roots = (first: 0.5 * (Double(z) + Double(discriminant).squareRoot()),\n second: 0.5 * (Double(z) - Double(discriminant).squareRoot()))\n if isInt(roots.first) || isInt(roots.second) {\n return (max * left + right) % 1337\n }\n }\n }\n return 0\n }\n}\n```\n\nReference: https://medium.com/@d_dchris/largest-palindrome-product-problem-brilliant-approach-using-mathematics-python3-leetcode-479-b3f2dd91b1aa | 6 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Short(est), Intuitive, Fast Solution (Python) | largest-palindrome-product | 0 | 1 | \n# Code\nSee explanation below!\n```py\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n == 1:\n return 9\n\n max_num = 10 ** n - 1\n min_num = 10 ** (n - 1)\n\n for num in range(int(max_num), int(min_num) - 1, -1):\n # Construct a palindrome by joining num with its reverse\n palindrome = int(str(num) + str(num)[::-1])\n\n # Check if this palindrome can be represented as the product of two n-digit integers\n for i in range(max_num, int(palindrome ** 0.5) - 1, -1):\n if palindrome % i == 0 and palindrome // i <= max_num:\n return palindrome % 1337\n```\n# Explanation\nTo solve this problem we need to minimize the number of steps we take and to a certain extent "think in reverse." Because the answer $9$ is so trivial to solve for $n=1$, I treated it as a base case to simply the following explanation.\n\nWhat we know: we are trying to find a palindrome (mod $1337$). This palindrome must be the product of two n-digit integers.\n\nFirst we should find the minimum and maximum values that our two n-digit integers can be. This mathematically can be represented as $min=10^{(n-1)}$ and $max = 10^n-1$\n\nFor $n=2$, our minimum and maximum 2-digit numbers are of course $10$ ($10^{2-1}$) and $99$ ($10^2-1$).\n\nWe can put this in our code as:\n```py\nmax_num = 10 ** n - 1\nmin_num = 10 ** (n - 1)\n```\n\nIncidently, using our `max_num` and `min_num` and some string manipulation we can construct our palindromes as the product of any n-digit numbers is 2n-digits long. We should do this going from our `max_num` down to our `min_num`, because we want to maximimzie the value of the palindrome. \n\n```py\nfor num in range(int(max_num), int(min_num) - 1, -1):\n # Construct a palindrome by joining num with its reverse\n palindrome = int(str(num) + str(num)[::-1])\n```\n\nAfter constructing our palindrome, we can check if it\'s divisible by any two digit integers. \n\nIn any pair of factors for a number $n$, one number has to be bigger than $\\sqrt{n}$ and the other has to be smaller, unless they are both exactly $\\sqrt{n}$. (Don\'t get lost on the math talk, just think about it). \n\nKnowing this fact, we know we only have to check $\\sqrt{n}$ factors. We want to check for factors from $max_num$ down to the $\\sqrt{n}$ (`-1` in our code to correctly index the array), since we want to ensure that our palindrome has large factors. If you reverse the check order you don\'t get the correct answers. To check if the factor completes a pair, we make sure that it evenly divides our palindrome by using `palindrome % i` and then we need to make sure that the other factor is 2-digits by using ``palindrome // i <= max_num``\n\n```py\n # Check if this palindrome can be represented as the product of two n-digit integers\n for i in range(max_num, int(palindrome ** 0.5) - 1, -1):\n if palindrome % i == 0 and palindrome // i <= max_num:\n return palindrome % 1337\n```\nFinally, if all our conditions are met we can return our palindrome modulo 1337. | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Meh | largest-palindrome-product | 0 | 1 | \n# Code\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n == 1:\n return 9\n \n upper = 10 ** n - 1\n lower = 10 ** (n - 1)\n \n left_half = str(upper)[:n]\n \n while True:\n palindrome = int(left_half + left_half[::-1])\n \n for i in range(upper, lower - 1, -1):\n if palindrome // i > upper:\n break\n if palindrome % i == 0:\n return palindrome % 1337\n \n left_half = str(int(left_half) - 1)\n \n return -1\n\n``` | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
PYTHON3. SIMPLE. WELL-COMMENTED. | largest-palindrome-product | 0 | 1 | # Intuition\nwell commented code, follow along. Comment any doubts! \n\n\n\n# Code\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n if n== 1: # case if n = 1\n return 9\n upper = (10 ** n) -1 # for everything else. easy to cacluate upper and lower bound values.\n lower = 10 ** (n-1)\n res = 0 # the variable to store our result\n\n for i in range(upper, lower-1, -2): # we only need odd elements (increment= -2), as the first digit of the largest pallindrome will be 9\n # so the last digit should be 9 also. no even numbers multiplied will give 9 in the unit\'s place.\n if i * i < res:\n return res%1337 # if our current res is bigger than the biggest number possible for the next iteration, we can simply returnt the\n # current res.\n for j in range(upper, i-1, -2):\n temp = i* j\n if temp % 11 != 0 and temp > res: # all even numbered digit pallinfomes are multiples of 11\n continue\n if (str(temp)[::-1] == str(temp)): # make sure it is a pallindrome\n res = temp\n \n\n return res%1337 # return!\n\n\n``` | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Commented and Explained, With Example 1 print log | Math Explained | Long Read | largest-palindrome-product | 0 | 1 | # Example One Print Log \ntotal boundary is 100\nCurrent upper boundary is 99\nCurrent lower boundary is 99\nResult of base squared minus 4 times lower boundary is -395\nCurrently not passing check one, as it has a value of -395\nRepeating with base value of 2\nCurrent upper boundary is 98\nCurrent lower boundary is 89\nResult of base squared minus 4 times lower boundary is -352\nCurrently not passing check one, as it has a value of -352\nRepeating with base value of 3\nCurrent upper boundary is 97\nCurrent lower boundary is 79\nResult of base squared minus 4 times lower boundary is -307\nCurrently not passing check one, as it has a value of -307\nRepeating with base value of 4\nCurrent upper boundary is 96\nCurrent lower boundary is 69\nResult of base squared minus 4 times lower boundary is -260\nCurrently not passing check one, as it has a value of -260\nRepeating with base value of 5\nCurrent upper boundary is 95\nCurrent lower boundary is 59\nResult of base squared minus 4 times lower boundary is -211\nCurrently not passing check one, as it has a value of -211\nRepeating with base value of 6\nCurrent upper boundary is 94\nCurrent lower boundary is 49\nResult of base squared minus 4 times lower boundary is -160\nCurrently not passing check one, as it has a value of -160\nRepeating with base value of 7\nCurrent upper boundary is 93\nCurrent lower boundary is 39\nResult of base squared minus 4 times lower boundary is -107\nCurrently not passing check one, as it has a value of -107\nRepeating with base value of 8\nCurrent upper boundary is 92\nCurrent lower boundary is 29\nResult of base squared minus 4 times lower boundary is -52\nCurrently not passing check one, as it has a value of -52\nRepeating with base value of 9\nCurrent upper boundary is 91\nCurrent lower boundary is 19\nResult of base squared minus 4 times lower boundary is 5\nSimple square root result is 2.23606797749979\nInteger square root is 2\nCheck two result is False\nBase is too low, incrementing base to 10\nCurrent upper boundary is 90\nCurrent lower boundary is 9\nResult of base squared minus 4 times lower boundary is 64\nSimple square root result is 8.0\nInteger square root is 8\nCheck two result is True\nPasses check one and two, product of upper boundary and total boundary is 9000\nAfter incrementing by lower boundary, the result is 9009\nFinal value after use of modular arithmetic is 987\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy use of modular arithmetic, we can continually set an upper and lower boundary value where we move the upper and lower as the total boundary minus a base value and the reversed integer cast of the string form of the upper boundary. This has the advantage of moving upper and lower in steps of approximately 10 for the lower as can be seen above. This eventually finds a base value where we can multiply the upper boundary and add the lower boundary to get our result. This is true in all cases and is based on the same modular arithmetic used in finding the correct key for message passing securely. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIncluded in the approach for ease of calculation is the print statements used to produce example 1\'s output for your own analysis benefits. \n\nSet up your modulo as requested \nIf n is 1, return 9 by default as provided in example 2 \nSet a total boundary of 10 to the power of n, as alluded to by values seen in examples 1 and 2. \n\nSet base = 1 \n\nWhile base is less than total boundary \n- calc upper boundary as total boundary - base \n- calc lower boundary as flip of upper boundary as a string \n- check if base squared minus 4 times lower boundary is positive, storing this in check one \n - if it is not positive, base is not yet big enough to give non-complex valuation \n - this is because of the base squared - 4 * 1 * c being related to the quadratic formula here \n - if it is not positive, increment base by 1 and continue \n - otherwise, we proceed to check two \n- if we proceeded to check two, set up a simple square root result of check one\'s value and an integer cast square root of this value \n- if these two values are the same, we have arrived at a modulo that is similar to one another, and as such the base is correct \n- if not, we can proceed to increment base and continue \n- if we do have success though \n - the product of upper boundary and total boundary gives us our multiple result without the lower boundary \n - we increase this by adding lower boundary to the result \n - then we can do modulo to arrive at the correct value and return it \n\n# Math Explained \nOur palindrome number at end is 10**n * a + b \nIf we let n = 2 for the first example then \n- palindrome number = 100 * (100-base) + b \n- factor this out to get 100 * 100 - 100*base + b \n- rearranging this, we can see (100 - c) * (100 - d) \n - where c + d = base \n - where c * d = b \n- expanding this gives us \n - 100**2 - 100 * c - 100 * d + c * d \n - 100**2 -`100(c + d) + c * d \n - 100 * (100 - base) + b \n - which if you notice is our factored out form, showing our correctness\n- now that we know we can do that, we can set up our equations as \n - 100 * (100 - base) + b = (100 - c) * (100 - d) \n - 100 ** 2 - 100 * base + b = 100 ** 2 - 100 * c+d + c*d\n - remove the 100 ** 2 from both sides, add 100 * c + d to the left \n - -100*(base) + 100*(c+d) = c*d - b \n - factor the 100 side \n - 100 ((c+d) - base) = c*d - b \n - from our above definitions of where this is true, we can see that we have a quadratic equation situation, such that we can use \n - (c-d) ** 2 = base ** 2 - 4 * b \n - if we let temp = base ** 2 - 4 * b \n - then we can say that c - d = sqrt(temp)\n - based on this, so long as temp is positive, the result of c - d is real\n - based on that, if temp square rooted is also integer square root of temp, we know that we have a temp that is a whole number, a requirement for our initial finding of a palindrome number \n - Then, if temp is positive, and temp\'s square root is the same as the integer square root of temp \n - 100 * (100 - base) + b is our palindrome number \n - BUT WHAT OF b?! \n - To find the correct b, we want the greatest such lower bound that satisfies these conditions. To check run the print statements on a test case with n = 3. Additionally, based on this we can also find this greatest such satisfying lower bound by moving in steps of 10 ** n - 1 where n is in this case where start, but if base gets large enough, might move down one in size. This could be found through repeated binary searching, but can also be found by having the lower boundary move based on the upper boundary string form reverse valuation. \n - This lets us have the lower range set itself appropriately, and based on the result for n = 1, means it will always find at least such a number at the boudning of 1. By showing the same for n = 2 above, we show that such is doable for all n in range, as we will move down appropriately. However something interesting would happen if you tried it on 9, so it is worth an investigation if you feel it. \n\n# Complexity\n- Time complexity: O(log(n))\n - Though base is incrementing by 1, that is not the true point of loop termination. The loop termination is based on lower and upper boundaries relationship, which moves in step sizes of approximately 10 ** (n-1). Thus, we can say that the loop actually terminates in log (n) time. \n\n\n- Space complexity: O(1)\n - No additional storage is used \n\n# Code\n```\nclass Solution:\n def largestPalindrome(self, n: int) -> int:\n # set up mod \n self.mod = 1337\n # deal with edge case \n if n == 1 : \n return 9 \n\n # set up base \n base = 1 \n # set up total boundary on palindromic size \n # intuition is from example case, where for n = 1 and n = 2 \n # we can see that the value of 10 ** n is greater than the answers \n # checked via print statements that can be reinitialized if desired \n total_boundary = 10**n\n # print(f\'total boundary is {total_boundary}\')\n\n # loop in range \n while base < total_boundary :\n # calculate upper boundary \n upper_boundary = total_boundary - base\n # print(f\'Current upper boundary is {upper_boundary}\') \n # calculate lowewr boundary as the reversed form of upper boundary \n lower_boundary = int(str(upper_boundary)[::-1]) \n # print(f\'Current lower boundary is {lower_boundary}\')\n # first check is if base squared - 4 * lower boundary is greater than 0 \n # if no, keep going on incrementing base \n check_one = base**2 - 4*lower_boundary\n # print(f\'Result of base squared minus 4 times lower boundary is {check_one}\')\n # if not in range \n if check_one < 0 :\n # print(f\'Currently not passing check one, as it has a value of {check_one}\')\n # print(f\'Repeating with base value of {base+1}\')\n base += 1 \n continue \n # if we pass check one, check second condition, which is that you have a prime value \n # if you have a prime value, then you can for sure use this \n simple_square_root = check_one**0.5\n # print(f\'Simple square root result is {simple_square_root}\')\n integer_square_root = int(simple_square_root)\n # print(f\'Integer square root is {integer_square_root}\')\n check_two = simple_square_root == integer_square_root\n # print(f\'Check two result is {check_two}\')\n # if check one and check two \n if check_one and check_two : \n product = upper_boundary * total_boundary\n # print(f\'Passes check one and two, product of upper boundary and total boundary is {product}\')\n product += lower_boundary\n # print(f\'After incrementing by lower boundary, the result is {product}\')\n # print(f\'Final value after use of modular arithmetic is {product % self.mod}\')\n return product % self.mod \n # print(f\'Base is too low, incrementing base to {base+1}\')\n base += 1 \n\n``` | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Python (Simple Maths) | largest-palindrome-product | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestPalindrome(self, n):\n if n == 1: return 9\n\n a = 1\n\n while a < 10**n:\n upper = 10**n-a\n lower = int(str(upper)[::-1])\n if a**2-lower*4 >= 0 and (a**2-lower*4)**0.5 == int((a**2-lower*4)**0.5):\n return (upper*10**n+lower)%1337\n a += 1\n\n \n\n\n\n\n\n \n\n \n``` | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
42ms (luck-based) solution Python | largest-palindrome-product | 0 | 1 | # Code\n```\nclass Solution:\n def largestPalindrome(self, n: int):\n if n == 1: return 9\n for i in range(1, 99999999):\n left = str(10**n - 2*i)\n right = left[::-1]\n if i**2 > int(right) \\\n and sqrt(i**2 - int(right)).is_integer():\n return int(left + right) % 1337\n``` | 0 | Given an integer n, return _the **largest palindromic integer** that can be represented as the product of two `n`\-digits integers_. Since the answer can be very large, return it **modulo** `1337`.
**Example 1:**
**Input:** n = 2
**Output:** 987
Explanation: 99 x 91 = 9009, 9009 % 1337 = 987
**Example 2:**
**Input:** n = 1
**Output:** 9
**Constraints:**
* `1 <= n <= 8` | null |
Solution | sliding-window-median | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<double> medianSlidingWindow(vector<int>& nums, int k) {\n vector<double> medians;\n unordered_map<int, int> hashTable;\n priority_queue<int> lo;\n priority_queue<int, vector<int>, greater<int>> hi;\n\n int i = 0;\n\n while(i < k){\n lo.push(nums[i++]);\n }\n for(int j = 0; j < k / 2; ++j){\n hi.push(lo.top());\n lo.pop();\n }\n\n while(true){\n medians.push_back(k & 1 ? lo.top() : ((double)lo.top() + (double)hi.top()) * 0.5);\n\n if(i >= nums.size()) break;\n\n int outNum = nums[i - k];\n int inNum = nums[i++];\n int balance = 0;\n\n balance += outNum <= lo.top() ? -1 : 1;\n hashTable[outNum]++;\n\n if(!lo.empty() && inNum <= lo.top()){\n balance++;\n lo.push(inNum);\n }\n else{\n balance--;\n hi.push(inNum);\n }\n\n if(balance < 0){\n lo.push(hi.top());\n hi.pop();\n balance++;\n }\n if(balance > 0){\n hi.push(lo.top());\n lo.pop();\n balance--;\n }\n\n while(hashTable[lo.top()]){\n hashTable[lo.top()]--;\n lo.pop();\n }\n\n while(!hi.empty() && hashTable[hi.top()]){\n hashTable[hi.top()]--;\n hi.pop();\n }\n }\n return medians;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n if k == 1:\n return nums\n if k == 2:\n return [(p + q) / 2 for p,q in pairwise(nums)]\n kodd = k % 2\n ref = sorted(nums[:k])\n hl = [-x for x in ref[:k//2]]\n hl.reverse()\n hr = ref[k//2:]\n if kodd:\n out = [hr[0]]\n else:\n out = [(hr[0] - hl[0]) / 2]\n hrd = []\n hld = []\n def cleanr():\n while hrd and hrd[0] == hr[0]:\n heappop(hrd)\n heappop(hr)\n def cleanl():\n while hld and hld[0] == hl[0]:\n heappop(hld)\n heappop(hl)\n for idx,x in enumerate(nums[k:]):\n y = nums[idx]\n mid = hr[0]\n if y >= mid:\n if x < mid:\n x = -heappushpop(hl, -x)\n cleanl()\n heappush(hr, x)\n heappush(hrd, y)\n cleanr()\n else:\n if x >= mid:\n x = heappushpop(hr, x)\n cleanr()\n heappush(hl, -x)\n heappush(hld, -y)\n cleanl()\n if kodd:\n out.append(hr[0])\n else:\n out.append((hr[0] - hl[0]) / 2)\n return out\n```\n\n```Java []\nclass Solution {\n public double[] medianSlidingWindow(int[] nums, int k) {\n if (nums == null || nums.length == 0)\n return new double[0];\n \n Node root = null;\n for (int i = 0; i < k; i++) {\n root = insert(root, nums[i]);\n }\n \n double[] r = new double[nums.length - k + 1];\n boolean even = k % 2 == 0;\n int j = 0;\n for (int i = k; i <= nums.length; i++) {\n double sum = 0.0;\n if (even)\n sum = (findSmallest(root, k/2).val + findSmallest(root, k/2 + 1).val) / 2.0;\n else\n sum = findSmallest(root, k/2 + 1).val;\n r[j++] = sum;\n if (i < nums.length) {\n root = insert(root, nums[i]);\n root = delete(root, nums[i - k]);\n }\n }\n \n return r;\n }\n \n private Node findSmallest(Node root, int k) {\n int s = countWith(root.left) + 1;\n if (s == k)\n return root;\n if (s > k) {\n return findSmallest(root.left, k);\n }\n return findSmallest(root.right, k - s);\n } \n \n private Node delete(Node root, long val) {\n if (root == null)\n return null;\n else if (val > root.val) \n root.right = delete(root.right, val);\n else if (val < root.val)\n root.left = delete(root.left, val);\n else {\n if (root.left == null)\n root = root.right;\n else if (root.right == null)\n root = root.left;\n else {\n Node t = findMin(root.right);\n root.val = t.val;\n root.right = delete(root.right, t.val);\n }\n }\n \n return updateNode(root);\n }\n \n private Node findMin(Node root) {\n if (root.left != null)\n return findMin(root.left);\n return root;\n }\n\n private Node insert(Node root, long val)\n {\n if (root == null)\n {\n return new Node(val);\n }\n if (val >= root.val)\n {\n root.right = insert(root.right, val);\n }\n else\n {\n root.left = insert(root.left, val);\n }\n \n return updateNode(root);\n }\n \n private Node updateNode(Node root) {\n int b = balance(root); \t\t\n if (b == 2 && balance(root.left) < 0)\n {\n root.left = leftRotate(root.left);\n root = rightRotate(root);\n }\n else if (b == -2 && balance(root.right) > 0)\n {\n root.right = rightRotate(root.right);\n root = leftRotate(root);\n }\n else if (b == 2)\n {\n root = rightRotate(root);\n }\n else if (b == -2)\n {\n root = leftRotate(root);\n }\n update(root);\n return root;\n }\n\n private Node leftRotate(Node n)\n {\n Node r = n.right;\n n.right = r.left;\n r.left = n;\n update(n);\n update(r);\n return r;\n }\n\n private Node rightRotate(Node n)\n {\n Node l = n.left;\n n.left = l.right;\n l.right = n;\n update(n);\n update(l);\n return l;\n }\n\n private int balance(Node n)\n {\n if (n==null)return 0;\n return height(n.left) - height(n.right);\n }\n\n private void update(Node n)\n {\n if (n==null)return;\n n.height = Math.max(height(n.left), height(n.right)) + 1;\n n.count = n.left != null ? n.left.count + 1 : 0;\n n.count += n.right != null ? n.right.count + 1 : 0;\n }\n\n private int height(Node n)\n {\n return n != null ? n.height : 0;\n }\n\n private int countWith(Node n)\n {\n return n != null ? n.count + 1 : 0;\n }\n\n static class Node\n {\n Node left;\n Node right;\n long val;\n int count;\n int height;\n\n Node(long val)\n {\n this.val = val;\n }\n }\n}\n```\n | 206 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
Two Heaps, Lazy removals, Python3 | sliding-window-median | 0 | 1 | # Intuition\nWant to use somehow changed version of MedianFinder from problem 295.\n\n# Approach\nThe class maintains a balance variable, which indicates the size difference between the two heaps. A negative balance\nindicates that the `small` heap has more elements, while a positive balance indicates that the `large` heap has more.\n\n\n# Complexity\n- Time complexity:\n$$O(n * log(k))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass MedianFinder:\n def __init__(self):\n self.small, self.large = [], []\n self.lazy = collections.defaultdict(int)\n self.balance = 0\n \n def add(self, num):\n if not self.small or num <= -self.small[0]:\n heapq.heappush(self.small, -num)\n self.balance -= 1\n else:\n heapq.heappush(self.large, num)\n self.balance += 1\n \n self.rebalance()\n \n def remove(self, num):\n self.lazy[num] += 1\n if num <= -self.small[0]:\n self.balance += 1\n else:\n self.balance -= 1\n \n self.rebalance()\n self.lazy_remove()\n \n def find_median(self):\n if self.balance == 0:\n return (-self.small[0] + self.large[0]) / 2\n elif self.balance < 0:\n return -self.small[0]\n else:\n return self.large[0]\n\n def rebalance(self):\n while self.balance < 0:\n heapq.heappush(self.large, -heapq.heappop(self.small))\n self.balance += 2\n \n while self.balance > 0:\n heapq.heappush(self.small, -heapq.heappop(self.large))\n self.balance -= 2\n \n def lazy_remove(self):\n while self.small and self.lazy[-self.small[0]] > 0:\n self.lazy[-self.small[0]] -= 1\n heapq.heappop(self.small)\n \n while self.large and self.lazy[self.large[0]] > 0:\n self.lazy[self.large[0]] -= 1\n heapq.heappop(self.large)\n\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n res = []\n median_finder = MedianFinder()\n for i, num in enumerate(nums):\n median_finder.add(num)\n\n if i >= k:\n median_finder.remove(nums[i - k])\n \n if i >= k - 1:\n res.append(median_finder.find_median())\n \n return res\n``` | 8 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
Treap solution O(nlogk) time O(k) space | sliding-window-median | 0 | 1 | \n\n```\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n tree = None\n ans = []\n for i, x in enumerate(nums):\n tree = insert(tree, x)\n if size(tree) > k:\n tree = remove(tree, nums[i - k])\n if size(tree) == k:\n if k % 2 == 1:\n ans.append(get(tree, k // 2 + 1))\n else:\n ans.append((get(tree, k // 2) + get(tree, k // 2 + 1)) / 2)\n return ans\n\n\n\nclass Node:\n __slots__ = [\'val\', \'count\', \'weight\', \'size\', \'left\', \'right\']\n def __init__(self, val):\n self.val = val\n self.count = 1\n self.weight = random.random()\n self.size = 1\n self.left = self.right = None\n\n\ndef touch(root):\n if not root:\n return\n root.size = root.count + size(root.left) + size(root.right)\n\n\ndef size(root):\n if not root:\n return 0\n return root.size\n\n\ndef insert(root, val):\n t1, r, t2 = split(root, val)\n if not r:\n r = Node(val)\n else:\n r.count += 1\n touch(r)\n t2 = join(r, t2)\n return join(t1, t2)\n\n\ndef remove(root, val):\n t1, r, t2 = split(root, val)\n if r and r.count > 1:\n r.count -= 1\n touch(r)\n t2 = join(r, t2)\n return join(t1, t2)\n\n\ndef split(root, val):\n if not root:\n return None, None, None\n elif root.val < val:\n a, b, c = split(root.right, val)\n root.right = a\n touch(root)\n return root, b, c\n elif root.val > val:\n a, b, c = split(root.left, val)\n root.left = c\n touch(root)\n return a, b, root\n else:\n a, c = root.left, root.right\n root.left = root.right = None\n touch(root)\n return a, root, c\n\n\ndef join(t1, t2):\n if not t1:\n return t2\n elif not t2:\n return t1\n elif t1.weight < t2.weight:\n t1.right = join(t1.right, t2)\n touch(t1)\n return t1\n else:\n t2.left = join(t1, t2.left)\n touch(t2)\n return t2\n\n\ndef get(root, index):\n if size(root.left) < index <= size(root.left) + root.count:\n return root.val\n elif size(root.left) + root.count < index:\n return get(root.right, index - root.count - size(root.left))\n else:\n return get(root.left, index)\n\n``` | 1 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
✅ Easiest Python O(n log k) Two Heaps (Lazy Removal), 96.23% | sliding-window-median | 0 | 1 | How to understand this solution:\n1) After we build our window, the length of window will ALWAYS be the same (now we will keep the length of valid elements in max_heap and min_heap the same too)\n2) Based on this, when we slide our window, the balance variable can be equal to 0, 2 or -2. It will NEVER be -1 or 1.\nExamples:\n0 -> when we remove an element from max_heap and then add a new one back to max_heap (or the same for min_heap)\n-2 -> when we remove an element from max_heap and then add a new one to min_heap (max_heap will have two less elements)\n2 -> when we remove an element from min_heap and then add a new one to max_heap (min_heap will have two less elements)\n3) Based on this - it is enough for us to move 1 element from one heap to another when the balance variable is equal to 2 or -2\n\nIf some points are not clear - Approach 2 in leetcode solutions should help. Best Regards!\n```\nclass Solution:\n # TC - O((n - k)*log(k))\n # SC - O(k)\n\t# 121 ms, faster than 96.23%\n\n def find_median(self, max_heap, min_heap, heap_size):\n if heap_size % 2 == 1:\n return -max_heap[0]\n else:\n return (-max_heap[0] + min_heap[0]) / 2\n\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n max_heap = []\n min_heap = []\n heap_dict = defaultdict(int)\n result = []\n \n for i in range(k):\n heappush(max_heap, -nums[i])\n heappush(min_heap, -heappop(max_heap))\n if len(min_heap) > len(max_heap):\n heappush(max_heap, -heappop(min_heap))\n \n median = self.find_median(max_heap, min_heap, k)\n result.append(median)\n \n for i in range(k, len(nums)):\n prev_num = nums[i - k]\n heap_dict[prev_num] += 1\n\n balance = -1 if prev_num <= median else 1\n \n if nums[i] <= median:\n balance += 1\n heappush(max_heap, -nums[i])\n else:\n balance -= 1\n heappush(min_heap, nums[i])\n \n if balance < 0:\n heappush(max_heap, -heappop(min_heap))\n elif balance > 0:\n heappush(min_heap, -heappop(max_heap))\n\n while max_heap and heap_dict[-max_heap[0]] > 0:\n heap_dict[-max_heap[0]] -= 1\n heappop(max_heap)\n \n while min_heap and heap_dict[min_heap[0]] > 0:\n heap_dict[min_heap[0]] -= 1\n heappop(min_heap)\n\n median = self.find_median(max_heap, min_heap, k)\n result.append(median)\n \n return result\n``` | 31 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
Python real O(nlogk) solution - easy to understand | sliding-window-median | 0 | 1 | **Solution 1: `O(nk)`**\nMaitain a sorted window. We can use binary search for remove and insert. \nBecause insert takes `O(k)`, the overall time complexity is `O(nk)`.\n\n**Solution 2: `O(nk)`**\nSimilar with LC 295, we need to maintain two heaps in the window, leftHq and rightHq. \nTo slide one step is actually to do two things: \n- Step 1: add a number, which is exactly the same as that in LC 295, which is `O(logk)`\n- Step 2: remove the number that is outside the window; there is not a remove method in heapq, so it takes ```\nO(k)\n```. So overall the heapq solution will take `O(nk)`.\n\n**Solution 3: O(nlogk)**\nUse a SortedList structure, which was implemented using self-balanced tree. \nSortedList enables `O(logk)` add and `O(logk)` remove. So the total time complexity is `O(nlogk)`.\n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n lst = SortedList() # maintain a sorted list\n \n res = []\n for i in range(len(nums)):\n lst.add(nums[i]) # O(logk)\n if len(lst) > k:\n lst.remove(nums[i-k]) # if we use heapq here, it will take O(k), but for sortedList, it takes O(logk)\n if len(lst) == k:\n median = lst[k//2] if k%2 == 1 else (lst[k//2-1] + lst[k//2]) / 2\n res.append(median)\n\n return res\n``` | 51 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
python solution using sliding window+bisect | sliding-window-median | 0 | 1 | Beats 98,2% Runtime and 56,77% Memory\n\n# Code\n```\nimport bisect\n\ndef medianaordenada(arr):\n d = len(arr)\n pos0 = (d - 1) // 2\n if d%2 == 0:\n return (arr[pos0]+arr[pos0+1])/2\n else:\n return arr[pos0]\n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n if len(nums) < k:\n return 0 \n cnt = 0\n roll = sorted(nums[:k])\n md = medianaordenada(roll)\n lmed = [md]\n\n for i,k in enumerate(nums[k:]):\n del roll[bisect.bisect_left(roll, nums[i])]\n if k >= 2*md:\n cnt+=1\n if k >= md:\n bisect.insort_right(roll, k)\n else:\n bisect.insort_left(roll, k)\n lmed.append(medianaordenada(roll))\n return lmed \n \n``` | 1 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
480: Solution with step by step explanation | sliding-window-median | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if the list is empty or the window size is greater than the list length. If either of these conditions is true, return an empty list.\n\n2. Create a helper function to calculate the median of a given subarray. If the length of the subarray is odd, return the middle element. If the length of the subarray is even, return the mean of the two middle elements.\n\n3. Create a deque to store the current window.\n\n4. Create an empty list to store the medians.\n\n5. Iterate over each element in the list. For each element:\na. Add the element to the deque.\nb. If the deque has reached the size of the window, calculate the median of the current window using the helper function and append it to the list of medians.\nc. Remove the leftmost element from the deque to maintain the window size.\n\n6. Return the list of medians.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n n = len(nums)\n # edge case: empty list or window size greater than list length\n if n == 0 or k > n:\n return []\n \n # helper function to get median of a subarray\n def get_median(arr):\n n = len(arr)\n # if length is odd, return middle element\n if n % 2 == 1:\n return arr[n // 2]\n # if length is even, return mean of middle elements\n return (arr[n // 2] + arr[n // 2 - 1]) / 2\n \n # initialize deque to store current window\n window = collections.deque()\n # initialize result list to store medians\n res = []\n \n # iterate over each element in nums\n for i, x in enumerate(nums):\n # add element to window\n window.append(x)\n # if window size is reached, get median and append to res\n if len(window) == k:\n res.append(get_median(sorted(window)))\n # remove leftmost element from window\n window.popleft()\n \n return res\n``` | 3 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
Python - Easy to understand using 2 heap | sliding-window-median | 0 | 1 | ```\nimport heapq\n\nclass Solution:\n def getMedian(self, maxHeap: List[int], minHeap: List[int]) -> float:\n # minHeap stores larger half and maxHeap stores small half elements\n # So data is like -> [maxHeap] + [minHeap]\n # if total no of element is odd, then maxHeap contains more elements than minHeap\n if len(maxHeap)==0: return 0\n elif len(maxHeap)!=len(minHeap): return -maxHeap[0]\n else: return (-maxHeap[0]+minHeap[0])/2\n\n def adjustHeapSize(self, maxHeap: List[int], minHeap: List[int]) -> None:\n while len(maxHeap)<len(minHeap) or len(maxHeap)>len(minHeap)+1:\n if len(maxHeap)>len(minHeap)+1:\n removedMaxHeapItem = -heapq.heappop(maxHeap)\n heapq.heappush(minHeap, removedMaxHeapItem)\n else:\n removedMaxHeapItem = heapq.heappop(minHeap)\n heapq.heappush(maxHeap, -removedMaxHeapItem)\n\n def addElement(self, maxHeap: List[int], minHeap: List[int], num: int, k: int) -> None:\n median = self.getMedian(maxHeap, minHeap)\n if num<=median: #Insert to maxHeap\n heapq.heappush(maxHeap, -num)\n else:\n heapq.heappush(minHeap, num)\n #print(num, maxHeap, minHeap, \'Before add adjust\')\n self.adjustHeapSize(maxHeap, minHeap)\n\n def removeElement(self, maxHeap: List[int], minHeap: List[int], num: int) -> None:\n median = self.getMedian(maxHeap, minHeap)\n #print(num, "Remove", maxHeap, minHeap, median)\n if num<=median: #Insert to maxHeap\n maxHeap.remove(-num)\n heapq.heapify(maxHeap)\n else:\n minHeap.remove(num)\n heapq.heapify(minHeap)\n #print(num, maxHeap, minHeap, \'Before remove adjust\')\n self.adjustHeapSize(maxHeap, minHeap)\n\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n maxHeap, minHeap, output = [], [], []\n for i in range(len(nums)):\n self.addElement(maxHeap, minHeap, nums[i], k)\n #print(maxHeap, minHeap, \'Added\', nums[i])\n if i>=k-1:\n output.append(self.getMedian(maxHeap, minHeap))\n #print(nums, i, i-k+1)\n self.removeElement(maxHeap, minHeap, nums[i-k+1])\n #print(maxHeap, minHeap, \'Removed\', nums[i-k+1])\n return output\n``` | 3 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
Python3 O(nlogk) heap with intuitive lazy deletion - Sliding Window Median | sliding-window-median | 0 | 1 | ```\nimport heapq\n\nclass Heap:\n def __init__(self, indices: List[int], nums: List[int], max=False) -> None:\n self.max = max\n self.heap = [[-nums[i], i] if self.max else [nums[i],i] for i in indices]\n self.indices = set(indices)\n heapq.heapify(self.heap)\n \n def __len__(self) -> int:\n return len(self.indices)\n \n def remove(self, index: int) -> None:\n if index in self.indices:\n self.indices.remove(index)\n \n def pop(self) -> List[int]:\n while self.heap and self.heap[0][1] not in self.indices:\n heapq.heappop(self.heap)\n item = heapq.heappop(self.heap)\n self.indices.remove(item[1])\n return [-item[0], item[1]] if self.max else item\n \n def push(self, item: List[int]) -> None:\n self.indices.add(item[1])\n heapq.heappush(self.heap, [-item[0], item[1]] if self.max else item)\n \n def peek(self) -> int:\n while self.heap and self.heap[0][1] not in self.indices:\n heapq.heappop(self.heap)\n v, _ = self.heap[0]\n return -v if self.max else v\n \n\nclass Solution:\n def medianSlidingWindow(self, nums: List[int], k: int) -> List[float]:\n indices = sorted(range(k), key=lambda x:nums[x])\n minheap = Heap(indices[(k+1)//2:], nums)\n maxheap = Heap(indices[:(k+1)//2], nums, max=True)\n median = ((lambda: maxheap.peek()) if k % 2 else \n\t\t (lambda: (minheap.peek() + maxheap.peek()) / 2))\n ans = []\n ans.append(median())\n for i in range(k, len(nums)):\n v = nums[i]\n minheap.remove(i-k)\n maxheap.remove(i-k)\n maxheap.push([v, i])\n minheap.push(maxheap.pop())\n if len(minheap) > len(maxheap):\n maxheap.push(minheap.pop())\n ans.append(median())\n return ans\n``` | 15 | The **median** is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle values.
* For examples, if `arr = [2,3,4]`, the median is `3`.
* For examples, if `arr = [1,2,3,4]`, the median is `(2 + 3) / 2 = 2.5`.
You are given an integer array `nums` and an integer `k`. There is a sliding window of size `k` which is moving from the very left of the array to the very right. You can only see the `k` numbers in the window. Each time the sliding window moves right by one position.
Return _the median array for each window in the original array_. Answers within `10-5` of the actual value will be accepted.
**Example 1:**
**Input:** nums = \[1,3,-1,-3,5,3,6,7\], k = 3
**Output:** \[1.00000,-1.00000,-1.00000,3.00000,5.00000,6.00000\]
**Explanation:**
Window position Median
--------------- -----
\[**1 3 -1**\] -3 5 3 6 7 1
1 \[**3 -1 -3**\] 5 3 6 7 -1
1 3 \[**\-1 -3 5**\] 3 6 7 -1
1 3 -1 \[**\-3 5 3**\] 6 7 3
1 3 -1 -3 \[**5 3 6**\] 7 5
1 3 -1 -3 5 \[**3 6 7**\] 6
**Example 2:**
**Input:** nums = \[1,2,3,4,2,3,1,4,2\], k = 3
**Output:** \[2.00000,3.00000,3.00000,3.00000,2.00000,3.00000,2.00000\]
**Constraints:**
* `1 <= k <= nums.length <= 105`
* `-231 <= nums[i] <= 231 - 1` | The simplest of solutions comes from the basic idea of finding the median given a set of numbers. We know that by definition, a median is the center element (or an average of the two center elements). Given an unsorted list of numbers, how do we find the median element? If you know the answer to this question, can we extend this idea to every sliding window that we come across in the array? Is there a better way to do what we are doing in the above hint? Don't you think there is duplication of calculation being done there? Is there some sort of optimization that we can do to achieve the same result? This approach is merely a modification of the basic approach except that it simply reduces duplication of calculations once done. The third line of thought is also based on this same idea but achieving the result in a different way. We obviously need the window to be sorted for us to be able to find the median. Is there a data-structure out there that we can use (in one or more quantities) to obtain the median element extremely fast, say O(1) time while having the ability to perform the other operations fairly efficiently as well? |
481. Magical String | magical-string | 0 | 1 | ```\nclass Solution:\n def magicalString(self, n: int) -> int:\n arr, i = [1,2,2], 2\n \n while len(arr) < n:\n arr.extend([arr[-1]^3]*arr[i])\n i += 1\n \n return arr[:n].count(1) | 3 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Easy python solution with explanation | magical-string | 0 | 1 | 1. We have to create the magic string upto length n.\n2. We will do that by using the string itself.\n3. So, one pointer will be telling us the count of the latest adding to the string.\n4. I hope that\'s well clear to you. If not then once again. If it is 2, then it\'s telling that something is in the count of 2, it could be either 1 or 2, whatever...., but it\'s count is 2.\n5. Now what that should be. Let\'s try any number, lets say 1. But accidentally, even the num at last index was 1. Which means now the consecutive count of 1 is not what we wished for, but atleast 1 more than that.\n6. So, that whatever will not be the one, last in the current string, but the other one.\n7. So just keep following this until the length of your string crosses/touches n. :)\n```\ndef magicalString(self, n: int) -> int:\n\ts = ["1", "2", "2"]\n\tfor i in range(2, n):\n\t\tp = s[-1] == "2"\n\t\tif(s[-1] == \'2\'):\n\t\t\ts += ["1"] * int(s[i])\n\t\telse:\n\t\t\ts += ["2"] * int(s[i])\n\t\tif(len(s) > n): break\n\treturn s[:n].count(\'1\')\n``` | 3 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
481: Solution with step by step explanation | magical-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Check if input n is 0, if so, return 0 as the output.\n\n2. Initialize the magical string s with the first three elements, which are 1, 2, 2.\n\n3. Initialize a variable i to 2, which will be used to keep track of the index of the current number in s.\n\n4. Start a while loop that continues until the length of s is less than n.\n\n5. Inside the while loop, append to s the next number in the sequence, which is 3 minus the previous number in s.\n\n6. The number of times to append the next number in the sequence is given by the value at index i in s.\n\n7. Increment i by 1.\n\n8. Once the while loop is finished, return the number of 1\'s in the first n elements of s by counting how many times 1 appears in the sublist s[:n].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def magicalString(self, n: int) -> int:\n if n == 0:\n return 0\n s = [1, 2, 2]\n i = 2\n while len(s) < n:\n s += [3 - s[-1]] * s[i]\n i += 1\n return s[:n].count(1)\n``` | 3 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Two Pointer | One pass | magical-string | 0 | 1 | ```\nclass Solution:\n def magicalString(self, n: int) -> int:\n if n in [1,2,3]:\n return 1\n s, p1, p2, curr, count = \'122\', 2, 3, \'1\', 1\n while p2 < n:\n s += curr * int(s[p1])\n p2 += int(s[p1])\n if curr == \'1\':\n if p2 > n:\n count += p2 - n \n return count\n count += int(s[p1])\n curr = \'1\' if curr == \'2\' else \'2\'\n p1 += 1\n return count\n``` | 1 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Magical String | magical-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def magicalString(self, n: int) -> int:\n s="12"\n if n==1 or n==2:\n return 1\n i=0\n while len(s)<=n:\n k=""\n for i in range(len(s)):\n if i%2==0:\n for i in range(int(s[i])):\n k=k+"1"\n else:\n for i in range(int(s[i])):\n k=k+"2"\n s=k\n s=s[:n:]\n print(s)\n return s.count("1")\n``` | 0 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Python 3 Solution | magical-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. The idea is to construct the string first upto the constraint\n 2. Return the count of 1 in string upto n\n\n# Code\n```\n# Below is the construction of string upto constraint\n\ns = "122"\ni = 2\n\nwhile len(s) < 10 ** 5:\n current = "1" if s[-1] == "2" else "2"\n s += int(s[i]) * current\n i += 1\n\nclass Solution:\n def magicalString(self, n: int) -> int:\n return s[:n].count("1")\n``` | 0 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Faster than 100% of the Submissions (python, 77ms) | magical-string | 0 | 1 | # Intuition\nThere are about the same amount of 1\'s and 2\'s in the string (at least for long strings). This means the number of Packs $$p$$ is approximately $$p=\\frac{2}{1+2}\\cdot n\\approx0.667 \\cdot n$$ in a string of the length $$n$$.\n\n# Approach\nKnowing the relation of Packs $$p$$ to Digits $$n$$ allows us approximate the amount of Packs we have to generate beforehand. \n\nThis means we can use a simple for loop without any control flow to generate the (slightly to long) magical string. \n\n>NOTE: This does not change the Time or Space complexity but is still a sigificant improvement since we eliminate the need for a `while` loop checking `len(s) < n` on every revolution.\n\nWe use a padding of $$2$$ above the approximate pack count.\nTbh this is lucky numbered but works reliable since for greater $$n$$ the padding grows larger because of the approximation $$0.667$$.\n \n\n# Complexity\n- Time complexity:\n$$O(n)$$ because the loop runs $$\\lfloor0.667 \\cdot n\\rfloor +2$$ times\n\n- Space complexity:\n$$O(n)$$ because the array `s` holds around $$1.5 \\cdot n$$ elements\n\n# Code\n```python\nclass Solution(object):\n def magicalString(self, n):\n s = [1, 2, 2]\n for i in range(2, int(0.667*n)+2):\n s += [i % 2 + 1] * s[i]\n return s[:n].count(1)\n```\n\n# Proof 100% faster\n\n | 0 | A magical string `s` consists of only `'1'` and `'2'` and obeys the following rules:
* The string s is magical because concatenating the number of contiguous occurrences of characters `'1'` and `'2'` generates the string `s` itself.
The first few elements of `s` is `s = "1221121221221121122...... "`. If we group the consecutive `1`'s and `2`'s in `s`, it will be `"1 22 11 2 1 22 1 22 11 2 11 22 ...... "` and the occurrences of `1`'s or `2`'s in each group are `"1 2 2 1 1 2 1 2 2 1 2 2 ...... "`. You can see that the occurrence sequence is `s` itself.
Given an integer `n`, return the number of `1`'s in the first `n` number in the magical string `s`.
**Example 1:**
**Input:** n = 6
**Output:** 3
**Explanation:** The first 6 elements of magical string s is "122112 " and it contains three 1's, so return 3.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 105` | null |
Reverse traversing || Simple logic | license-key-formatting | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n s = s.replace(\'-\', \'\').upper()\n new_key , dup = \'\' , k\n\n for i in range(len(s)-1,-1,-1):\n if k!=0:\n new_key = s[i] + new_key\n k -= 1\n\n if k == 0 and i != 0:\n new_key = \'-\' + new_key\n k = dup\n\n return new_key\n``` | 2 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Python3 Solution using replace | license-key-formatting | 0 | 1 | # Intuition\n##### To solve this problem, we need to format the **license key** by grouping the characters into groups of \'k\' separated by hyphens and converting all characters to upper case. The approach can be to first remove all hyphens from the input string, convert it to upper case, and then iterate over the characters of the string, adding them to a new string while keeping track of the length of each group. When the length of a group reaches \'k\' , a hyphen can be added to separate it from the next group. The resulting string can then be returned as the formatted license key.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n\nThe time complexity of the licenseKeyFormatting function is O(n), where n is the length of the input string s. This is because the function performs a constant number of operations for each character in the string.\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the function is also O(n), because it creates a new string st of the same length as the input string, and may create additional strings during the execution of the function. However, the amount of additional space used by the function is proportional to the size of the groups, which is at most k, so the space complexity can be considered O(k).\n\n# Code\n```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n st=""\n s=s.replace("-","").upper()\n s=s[::-1]\n \n for i in range(0,len(s),k):\n st+=s[i:i+k]\n st+="-"\n sts=st[::-1]\n \n sts=sts.replace("-","",1)\n return sts\n\n\n \n \n``` | 2 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Python/JS/C++ O(n) by string operation. [w/ Explanation] | license-key-formatting | 0 | 1 | O(n) by string operation.\n\n---\n\n**Explanation**:\n\nFirst, eliminate all dashes.\n\nSecond, start **grouping with size = K**,\nRemember to make a special handle for first group in case that len(S) is not divisible by K.\n\nThird, link each group togetger, separated by dash, \'-\', at the junction point.\n\nFinally, return the result in **uppercase**.\n\n---\n**Implementation**:\n\n**Python**:\n\n```\nclass Solution:\n def licenseKeyFormatting(self, S: str, K: int) -> str:\n \n # Eliminate all dashes\n S = S.replace(\'-\', \'\')\n \n head = len(S) % K\n \n grouping = []\n \n # Special handle for first group\n if head:\n grouping.append( S[:head] )\n \n # General case:\n for index in range(head, len(S), K ):\n grouping.append( S[ index : index+K ] )\n \n \n # Link each group togetger and separated by dash \'-\'\n return \'-\'.join( grouping ).upper()\n```\n\n---\n\n**Javascript**:\n\n```\nvar licenseKeyFormatting = function(s, k) {\n \n // Eliminate all dashes\n const regex = /\\-/g;\n s = s.replace(regex, "");\n \n let head = s.length % k;\n \n let grouping = [];\n \n // Special handle for first group\n if( head ){\n grouping.push( s.substring(0, head) );\n }\n \n // General cases:\n for( let i = head ; i < s.length ; i += k ){\n grouping.push( s.substring(i, i+k) );\n }\n \n return grouping.join("-").toUpperCase();\n \n \n};\n```\n\n---\n\n**C++**\n\n```\nclass Solution {\npublic:\n string licenseKeyFormatting(string s, int k) {\n \n // Eliminate all dashes\n s = std::regex_replace(s, std::regex("\\-"), "");\n \n int head = s.length() % k;\n \n vector<string> grouping;\n \n // Special handle for first group\n if( head ){\n grouping.emplace_back( s.substr(0, head) );\n }\n \n // General cases\n for( int i = head ; i < s.length() ; i += k ){\n grouping.emplace_back( s.substr(i, k) );\n }\n \n // Link each group togetger and separated by dash \'-\'\n s = join(grouping, "-");\n \n // to uppercase\n transform(s.begin(), s.end(), s.begin(), [](unsigned char c){ return std::toupper(c); } );\n return s;\n }\n \nprivate:\n string join(const std::vector<string> &lst, const string &delim)\n {\n std::string ret;\n for(const auto &s : lst) {\n if(!ret.empty())\n ret += delim;\n ret += s;\n }\n return ret;\n }\n \n};\n```\n\n----\n\nReference:\n\n[1] [Python official docs about slicing syntax [ start : end : step ]](https://docs.python.org/3/whatsnew/2.3.html?highlight=slicing#extended-slices)\n\n[2] [Python official docs about str.join( ... )](https://docs.python.org/3/library/stdtypes.html?highlight=join#str.join)\n\n[3] [Python official docs about str.upper( )](https://docs.python.org/3/library/stdtypes.html?highlight=join#str.upper) | 45 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.