title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
482: Solution with step by step explanation | license-key-formatting | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, we remove any dashes and convert all characters to uppercase:\n```\ns = s.replace("-", "").upper()\n```\n2. Next, we calculate the length of the first group by taking the length of the string modulo k:\n```\nfirst_group_len = len(s) % k\n```\n3. We then initialize the reformatted license key with the first group by slicing the string up to the first_group_len:\n```\nreformatted = s[:first_group_len]\n```\n4. Next, we iterate over the remaining groups and add them to the reformatted license key. We start the iteration from first_group_len, and step through the string in increments of k:\npython\n```\nfor i in range(first_group_len, len(s), k):\n```\n5. Inside the loop, we add a dash between groups if there is already some content in the reformatted license key:\n```\nif reformatted:\n reformatted += "-"\n```\n6. Finally, we add the next group to the reformatted license key:\n```\nreformatted += s[i:i+k]\n```\n7. We return the reformatted license key:\n```\nreturn reformatted\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n # Remove any dashes and convert all characters to uppercase\n s = s.replace("-", "").upper()\n\n # Calculate the length of the first group\n first_group_len = len(s) % k\n\n # Initialize the reformatted license key with the first group\n reformatted = s[:first_group_len]\n\n # Iterate over the remaining groups and add them to the reformatted license key\n for i in range(first_group_len, len(s), k):\n if reformatted:\n reformatted += "-"\n reformatted += s[i:i+k]\n\n return reformatted\n\n``` | 6 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Solution | license-key-formatting | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string licenseKeyFormatting(string s, int k) {\n int n = s.size(), cnt=0;\n string ans = "";\n for(int i = n-1; i>=0;i--){\n if(s[i]== \'-\'){\n continue;\n }\n if(cnt>0 && cnt%k ==0){\n ans.push_back(\'-\');\n }\n ans.push_back(toupper(s[i]));\n cnt++;\n }\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def licenseKeyFormatting(self, S: str, K: int) -> str: \n S = S.replace(\'-\', \'\')\n head = len(S) % K\n grouping = []\n if head:\n grouping.append( S[:head] )\n for index in range(head, len(S), K ):\n grouping.append( S[ index : index+K ] )\n return \'-\'.join( grouping ).upper()\n```\n\n```Java []\nclass Solution {\n public String licenseKeyFormatting(String s, int k) {\n char[] ch = s.toCharArray();\n int n = s.length();\n char[] result = new char[2*n-1];\n int j = k;\n int a = 2*n-2;\n for(int i = n-1; i >=0; i--){\n \n char elem = ch[i];\n \n if(elem == \'-\'){\n continue;\n }\n int value = (int)elem;\n if(value >= 97 && value <= 122){\n elem = (char)(value - 32);\n }\n if(j == 0){\n result[a] = \'-\';\n a--;\n j= k;\n }\n if(j > 0){\n result[a] = elem;\n j--;\n a--;\n }\n }\n return String.copyValueOf(result, a+1, (2*n-2)-a);\n }\n}\n```\n | 3 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
PYTHON code faster than 99.18% ❤️🔥❤️🔥❤️🔥 | license-key-formatting | 0 | 1 | ```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n s = s.replace("-","")\n \n if len(s) <= k : return s.upper()\n \n if len(s)%k == 0 :\n return "-".join(s[i:i+k].upper() for i in range(0,len(s),k))\n else :\n return s[:len(s)%k].upper() + "-" + "-".join(s[i:i+k].upper() for i in range(len(s)%k,len(s),k)) \n ``` | 1 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Python3 O(n) || O(n) # Runtime: 77ms 53.47% ; Memory: 14.7mb 41.07% | license-key-formatting | 0 | 1 | ```\nclass Solution:\n# O(n) || O(n)\n# Runtime: 77ms 53.47% ; Memory: 14.7mb 41.07%\n def licenseKeyFormatting(self, string: str, k: int) -> str:\n newString = string.upper().replace(\'-\', \'\')[::-1]\n group = []\n for i in range(0, len(newString), k):\n group.append(newString[i:i+k])\n \n return \'-\'.join(group)[::-1]\n``` | 2 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Clean Python Solution | license-key-formatting | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n # Time : O(n) | Space : O(n)\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n result = []\n count = 0\n s = s.replace("-", "")\n for i in reversed(range(len(s))):\n result.append(s[i].upper())\n count += 1\n # we don\'t want to put a dash in the first position of the array, so i != 0\n if count == k and i != 0:\n result.append("-")\n count = 0\n return \'\'.join(result[::-1]) # doing a reverse \n``` | 5 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
✔Python 3 Solution | 93% lesser memory | license-key-formatting | 0 | 1 | ```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n s = (s.upper()).replace("-","")[::-1]\n ans = str()\n for i in range(0,len(s),k):\n ans += s[i:i+k]+"-"\n return ans[::-1][1:]\n``` | 7 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Easy to understand Python 3 solution Beats 90 % in space and complexity | license-key-formatting | 0 | 1 | # Code\n```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n s = s.replace("-", "").upper()\n first_seq = len(s) % k\n output = []\n \n if first_seq > 0:\n output.append(s[:first_seq])\n\n for r in range(first_seq, len(s), k):\n output.append(s[r:r+k])\n\n return "-".join(output)\n\n``` | 1 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Python 3 short, simple solution with explanation ( and fast) | license-key-formatting | 0 | 1 | The idea is to seperate first group and the rest then combine them at the end\nThis code finish between 32ms - 44ms\n```python\nclass Solution:\n def licenseKeyFormatting(self, S: str, K: int) -> str:\n S = S.replace("-", "").upper() # remove "-" and covert string to uppercase\n remainder = len(S) % K # calculate length of first group\n\t\t\t\t\t\t\t\t\t\t# For example:\n\t\t\t\t\t\t\t\t\t\t# remainder==1; k=3: 1-123-123-123\n\t\t\t\t\t\t\t\t\t\t# remainder==0; k=3: _-123-123-123 (blank)\n\t\t\t\t\t\t\t\t\t\t\n\t\tfirst_grp = [S[: remainder]]\n other_grps= [S[i : i + K] for i in range(remainder, len(S), K)]\n \n if remainder: return "-".join(first_grp + other_grps)\n\t\t# first group is empty at this point\n return "-".join(other_grps)\n```\nNote: \nIt is recommended to use `"".join()` instead of string concatenation like `s+="str"` because it is faster. | 18 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Reformatting License Key - Format and Convert in Python | license-key-formatting | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem, we need to format the license key so that each group contains exactly k characters, except for the first group, which could be shorter than k but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and we should convert all lowercase letters to uppercase.\n\nOne approach to solve the problem is to remove all dashes and convert all lowercase letters to uppercase. Then, we can calculate the length of the first group by taking the modulus of the length of the string with k. The rest of the string can be divided into groups of length k each. Finally, we can concatenate the first group with the rest of the groups, separated by dashes, to obtain the reformatted license key.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Remove all dashes from the input string `s` and convert all lowercase letters to uppercase using the `replace()` and `upper()` functions of Python string.\n- Calculate the length of the first group by taking the modulus of the length of the string with `k` using the `%` operator.\n- Construct the reformatted license key by adding the first group to the rest of the groups, separated by dashes (`-`), using a loop from `first_len` to `n` with a step size of `k`.\n- Check if the reformatted string is empty or starts with a dash (`-`) and handle these cases appropriately.\n- Return the reformatted license key.\n# Complexity\n- Time complexity: The time complexity of the function is $$O(n)$$ where n is the length of the input string `s`. This is because we need to iterate through the string once to remove dashes and convert all lowercase letters to uppercase, and then once more to construct the reformatted license key.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity of the function is $$O(n)$$ because we are creating a new string to store the reformatted license key.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def licenseKeyFormatting(self, s: str, k: int) -> str:\n # Remove dashes and convert lowercase letters to uppercase\n s = s.replace(\'-\', \'\').upper()\n n = len(s)\n \n # Calculate length of first group\n first_len = n % k\n \n # Construct the reformatted license key\n reformatted = s[:first_len]\n for i in range(first_len, n, k):\n reformatted += \'-\' + s[i:i+k]\n \n if not reformatted:\n return ""\n elif reformatted[0] == "-":\n return reformatted[1:]\n else:\n return reformatted\n``` | 2 | You are given a license key represented as a string `s` that consists of only alphanumeric characters and dashes. The string is separated into `n + 1` groups by `n` dashes. You are also given an integer `k`.
We want to reformat the string `s` such that each group contains exactly `k` characters, except for the first group, which could be shorter than `k` but still must contain at least one character. Furthermore, there must be a dash inserted between two groups, and you should convert all lowercase letters to uppercase.
Return _the reformatted license key_.
**Example 1:**
**Input:** s = "5F3Z-2e-9-w ", k = 4
**Output:** "5F3Z-2E9W "
**Explanation:** The string s has been split into two parts, each part has 4 characters.
Note that the two extra dashes are not needed and can be removed.
**Example 2:**
**Input:** s = "2-5g-3-J ", k = 2
**Output:** "2-5G-3J "
**Explanation:** The string s has been split into three parts, each part has 2 characters except the first part as it could be shorter as mentioned above.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of English letters, digits, and dashes `'-'`.
* `1 <= k <= 104` | null |
Solution | smallest-good-base | 1 | 1 | ```C++ []\nclass Solution {\n public:\n string smallestGoodBase(string n) {\n const long num = stol(n);\n\n for (int m = log2(num); m >= 2; --m) {\n const int k = pow(num, 1.0 / m);\n long sum = 1;\n long prod = 1;\n for (int i = 0; i < m; ++i) {\n prod *= k;\n sum += prod;\n }\n if (sum == num)\n return to_string(k);\n }\n\n return to_string(num - 1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n n = int(n)\n for m in range(int(math.log(n, 2)), 1, -1):\n k = int(n ** m ** -1)\n if (k ** (m + 1) - 1)\n return str(k)\n return str(n - 1)\n```\n\n```Java []\nclass Solution {\n public String smallestGoodBase(String n) {\n long low = Long.valueOf(n);\n int high = (int) (Math.log(low + 1) / Math.log(2)) - 1;\n \n long result = low - 1;\n for (int m = high; m > 1; m--) {\n long k = (long) Math.pow(low, 1.0 / m);\n if (geometric(k, m) == low) return String.valueOf(k);\n }\n return String.valueOf(result);\n }\n\n private long geometric(long base, int m) {\n long result = 0;\n for (int i = 0; i <= m; i++) {\n result = 1 + result * base;\n }\n return result;\n }\n}\n```\n | 201 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
483: Solution with step by step explanation | smallest-good-base | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Convert input string n to integer num.\n2. Calculate the maximum possible length of a good base for num using math.floor(math.log(num, 2)) + 1. This value represents the maximum possible number of digits in a good base representation of num.\n3. Loop through all possible good base lengths k in decreasing order from max_len down to 2.\n4. For each k, set the search range for the base m to be between 2 and num - 1.\n5. Use binary search to find the smallest good base m for the current k.\n6. Calculate s, the sum of k 1\'s in base m.\n7. If s is equal to num, return m as a string.\n8. If s is less than num, update the left bound of the search range to mid + 1.\n9. If s is greater than num, update the right bound of the search range to mid - 1.\n10. If no good base is found for any k, return num - 1 as a string. This is because num - 1 is always a good base for any num.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n num = int(n)\n max_len = math.floor(math.log(num, 2)) + 1\n \n # Search for the smallest possible base m\n for k in range(max_len, 1, -1):\n left, right = 2, num - 1\n \n # Solve for m using binary search\n while left <= right:\n mid = (left + right) // 2\n s = 0\n for i in range(k):\n s = s * mid + 1\n \n if s == num:\n return str(mid)\n \n elif s < num:\n left = mid + 1\n \n else:\n right = mid - 1\n \n return str(num - 1)\n\n``` | 3 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Short and simple Python solution O(log(n)) | smallest-good-base | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to find the smallest base k for which n can be represented as (k^(m+1) - 1) / (k-1) for some m. Essentially, we need to find the smallest base k such that the sum of k^i for i in range(m+1) is equal to n.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use a brute force approach by iterating through possible values of m and checking if the base k exists for that value of m. We can start with the maximum possible value of m, which is log_2(n), and decrease it until we find a valid base k.\n\n\n# Complexity\n- Time complexity: O(log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSince we are iterating through the possible values of m, which is in the range of log_2(n), the time complexity is O(log(n))\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe are not using any additional data structures, so the space complexity is O(1)\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n n = int(n)\n for m in range(int(math.log(n, 2)), 1, -1):\n k = int(n ** m ** -1)\n if (k ** (m + 1) - 1) // (k - 1) == n:\n return str(k)\n return str(n - 1)\n``` | 3 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Binary Search | smallest-good-base | 0 | 1 | # Code\n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n n = int(n)\n \n # Binary search\n for length in range(math.floor(math.log2(n)) + 1, 2, -1):\n left, right = 2, n - 1\n while left <= right:\n mid = left + (right - left) // 2\n sum = (mid ** length - 1) // (mid - 1)\n if sum == n:\n return str(mid)\n elif sum < n:\n left = mid + 1\n else:\n right = mid - 1\n \n # If no good base is found, return n-1\n return str(n - 1)\n\n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Smallest Good Base (Python) | smallest-good-base | 0 | 1 | Intuition:\nTo find the smallest base in which a given number `n` can be expressed as a sum of at least two positive integers, we need to find the largest possible value of `m` (the number of summands) and the smallest possible value of `k` (the base) that satisfies the equation `n = (k^m) + (k^(m-1)) + ... + k + 1`. We can then check if the sum of the geometric series with `m+1` terms and first term `1` and common ratio `k` is equal to `n`. If it is, then `k` is a valid base for `n`. We can use binary search on the value of `m` to find the largest possible value of `m`, and then use a formula to compute the corresponding value of `k`. \n\nApproach:\nThe `smallestGoodBase` function uses a loop to iterate over possible values of `m` in decreasing order, starting from the largest possible value of `m` (which is `int(math.log(n, 2))`), and ending at 2 (inclusive). For each value of `m`, the function computes the corresponding value of `k` using the formula `k = int(n ** m ** -1)`. It then checks if `k` is a valid base for `n` by computing the sum of the geometric series with `m+1` terms and common ratio `k`, and checking if it is equal to `n`. If a valid base is found, the function returns it as a string. If no valid base is found, the function returns `n-1` as a string.\n\nTime complexity:\nThe time complexity of the `smallestGoodBase` function is `O(log^2(n))`. This is because the loop over possible values of `m` runs for `log(n)` iterations, and for each iteration, the computation of `k` and the check for a valid base takes `log(n)` time. Therefore, the total time complexity is `O(log(n) * log(n))`.\n\nSpace complexity:\nThe space complexity of the `smallestGoodBase` function is `O(1)`, as it only uses a constant amount of extra space to store the variables `m` and `k`, and does not create any additional data structures.\n\n# Code\n```\nimport math\n\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n # Convert input string to integer\n n = int(n)\n \n # Loop over possible values of m in decreasing order\n for m in range(int(math.log(n, 2)), 1, -1):\n # Compute k using the formula k = (n^(1/m)), rounded down to the nearest integer\n k = int(n ** m ** -1)\n \n # Check if k is a valid base for n\n if (k ** (m + 1) - 1) // (k - 1) == n:\n # If so, return k as a string\n return str(k)\n \n # If no valid base is found, return n - 1 as a string\n return str(n - 1)\n\n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Python binary search O(logn.logn) | smallest-good-base | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe will first find the maximum possible value of the power. Since the lowest base is 2, the maximum power can\'t be more than $$log(n,2)$$.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet the base be r.\nTherefore $$n=1+r+r^2+r^3+.....+r^k$$\n$$n=(r^(k+1)-1)/(r-1)$$\nWe will first find the maximum possible value of the power. Since the lowest base is 2, the maximum power can\'t be more than $$log(n,2)$$. This equals k+1 in our formula.\nWe use linear search (from highest power to lowest power) to find the highest power and therefore lowest base that satisfies the equation(all variables have to be integers, so we can\'t use binary search here).\nFor each power use binary search between 2 and n to find if any value of "r" satisfies our equation. If not, then we decrease our power by one and try again. \n# Complexity\n- Time complexity: $$O(logn.logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n #uplimit denotes the upper limit of power i.e. k+1\n uplimit=ceil(log(int(n)+1,2))\n print(uplimit)\n p=uplimit\n while p>1:\n left=2\n right=int(n)\n #index=-1\n while left<=right:\n mid=(left+right)//2\n temp=((mid**p)-1)//(mid-1)\n if temp==int(n):return str(mid)\n elif temp<int(n):left=mid+1\n else:right=mid-1\n p-=1\n return ""\n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Python (Simple Maths) | smallest-good-base | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n):\n n = int(n)\n\n for p in range(int(log2(n)),1,-1):\n k = int(n**(1/p))\n if (k**(p+1) - 1)//(k-1) == n: return str(k)\n \n return str(n-1)\n\n\n\n\n\n\n \n\n\n\n \n \n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Python (Simple Binary Search) | smallest-good-base | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n):\n def is_valid(base):\n total = sum(base**i for i in range(length))\n return n - total\n\n n = int(n)\n N = len(bin(n)[2:])\n\n for length in range(N,0,-1):\n low, high = 2, n-1\n while low <= high:\n mid = (low + high)//2\n\n v = is_valid(mid)\n\n if v < 0:\n high = mid - 1\n elif v > 0:\n low = mid + 1\n else:\n return str(mid)\n\n\n\n\n \n\n\n\n \n \n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Python3 Solution (Clean and Easy) | smallest-good-base | 0 | 1 | - Runtime: 32 ms\n- Memory: 13.9 MB\n\n# Code\n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n n = int(n)\n for m in range(int(math.log(n, 2)), 1, -1):\n k = int(n ** (1 / m))\n if (k ** (m + 1) - 1) // (k - 1) == n:\n return str(k)\n return str(n - 1)\n``` | 0 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
[Python3] enumerate powers | smallest-good-base | 0 | 1 | \n```\nclass Solution:\n def smallestGoodBase(self, n: str) -> str:\n n = int(n)\n for p in range(int(log2(n)), 1, -1): \n k = int(n**(1/p))\n if (k**(p+1)-1)//(k-1) == n: return str(k)\n return str(n-1)\n``` | 1 | Given an integer `n` represented as a string, return _the smallest **good base** of_ `n`.
We call `k >= 2` a **good base** of `n`, if all digits of `n` base `k` are `1`'s.
**Example 1:**
**Input:** n = "13 "
**Output:** "3 "
**Explanation:** 13 base 3 is 111.
**Example 2:**
**Input:** n = "4681 "
**Output:** "8 "
**Explanation:** 4681 base 8 is 11111.
**Example 3:**
**Input:** n = "1000000000000000000 "
**Output:** "999999999999999999 "
**Explanation:** 1000000000000000000 base 999999999999999999 is 11.
**Constraints:**
* `n` is an integer in the range `[3, 1018]`.
* `n` does not contain any leading zeros. | null |
Python Easy 98% beats | max-consecutive-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n count = 0 \n max_count = 0 \n for num in nums:\n if num != 1 :\n max_count = max(max_count , count)\n count = 0 \n else:\n count += 1 \n return max(max_count , count) \n``` | 1 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Python Easy 98% beats | max-consecutive-ones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n count = 0 \n max_count = 0 \n for num in nums:\n if num != 1 :\n max_count = max(max_count , count)\n count = 0 \n else:\n count += 1 \n return max(max_count , count) \n``` | 1 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
[Python3] 4 solutions || 277ms || beats 99% | max-consecutive-ones | 0 | 1 | ##### 1. Sliding window with max window size\nMake window big as possible. When window has zeros just move left window pointer. At the end of processing in the window can be some zeros, but we don\'t care, because need return just window size `r - l + 1`\nExample for:`111001`\n`[1]11001 => l = 0, r = 0 `\n`[11]1001 => l = 0, r = 1 `\n`[111]001 => l = 0, r = 2 => max result 2 - 0 + 1 = 3`\n`1[110]01 => l = 1, r = 3 => keep max window size, but move left pointer`\n`11[100]1 => l = 2, r = 4 => move left pointer again` \n`111[001] => l = 3, r = 5 => move left pointer again, window size is the answer => 5 - 3 + 1 = 3`\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n l, zeros = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > 0:\n zeros -= nums[l] == 0\n l += 1\n \n return r - l + 1\n```\n##### 2. Greedy\nCalculate count in a row. When meet zero update max result. There is one edge case for cases when the last element is `1`: like `0111[1]` or `1111[1]`, so we didn\'t update result in the loop. To solve just update max result at the end `res = max(res, windowSize)`.\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n res, windowSize = 0, 0\n for n in nums:\n if n == 1:\n windowSize += 1\n else:\n res = max(res, windowSize)\n windowSize = 0\n res = max(res, windowSize)\n\n return res\n```\n##### 3. One line with [groupby](https://docs.python.org/3/library/itertools.html#itertools.groupby)\n #[k for k, g in groupby(\'AAAABBBCCDAABBB\')] --> A B C D A B\n #[list(g) for k, g in groupby(\'AAAABBBCCD\')] --> AAAA BBB CC D\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n return max((len(list(g)) for k, g in groupby(nums) if k == 1), default = 0)\n \n```\n\n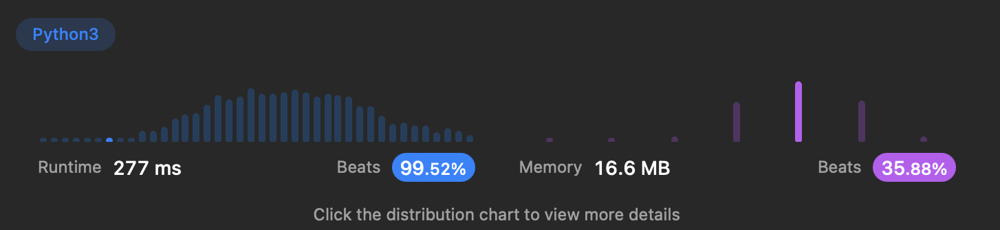\n\n##### 4. Universal solution for all Max Consecutive Ones I - III problems\n```python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n l, zeros= 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > k: # here k instead of 0\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n```\n[487. Max Consecutive Ones II (premium)](https://leetcode.com/problems/max-consecutive-ones-ii/editorial/)\n[1004. Max Consecutive Ones III](https://leetcode.com/problems/max-consecutive-ones-iii/solutions/3502644/python-3-sliding-window-bonus-similar-question-beats-97/)\n | 5 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
[Python3] 4 solutions || 277ms || beats 99% | max-consecutive-ones | 0 | 1 | ##### 1. Sliding window with max window size\nMake window big as possible. When window has zeros just move left window pointer. At the end of processing in the window can be some zeros, but we don\'t care, because need return just window size `r - l + 1`\nExample for:`111001`\n`[1]11001 => l = 0, r = 0 `\n`[11]1001 => l = 0, r = 1 `\n`[111]001 => l = 0, r = 2 => max result 2 - 0 + 1 = 3`\n`1[110]01 => l = 1, r = 3 => keep max window size, but move left pointer`\n`11[100]1 => l = 2, r = 4 => move left pointer again` \n`111[001] => l = 3, r = 5 => move left pointer again, window size is the answer => 5 - 3 + 1 = 3`\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n l, zeros = 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > 0:\n zeros -= nums[l] == 0\n l += 1\n \n return r - l + 1\n```\n##### 2. Greedy\nCalculate count in a row. When meet zero update max result. There is one edge case for cases when the last element is `1`: like `0111[1]` or `1111[1]`, so we didn\'t update result in the loop. To solve just update max result at the end `res = max(res, windowSize)`.\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n res, windowSize = 0, 0\n for n in nums:\n if n == 1:\n windowSize += 1\n else:\n res = max(res, windowSize)\n windowSize = 0\n res = max(res, windowSize)\n\n return res\n```\n##### 3. One line with [groupby](https://docs.python.org/3/library/itertools.html#itertools.groupby)\n #[k for k, g in groupby(\'AAAABBBCCDAABBB\')] --> A B C D A B\n #[list(g) for k, g in groupby(\'AAAABBBCCD\')] --> AAAA BBB CC D\n```python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n return max((len(list(g)) for k, g in groupby(nums) if k == 1), default = 0)\n \n```\n\n\n\n##### 4. Universal solution for all Max Consecutive Ones I - III problems\n```python3 []\nclass Solution:\n def longestOnes(self, nums: List[int], k: int) -> int:\n l, zeros= 0, 0\n for r, n in enumerate(nums):\n zeros += n == 0\n if zeros > k: # here k instead of 0\n zeros -= nums[l] == 0\n l += 1\n return r - l + 1\n```\n[487. Max Consecutive Ones II (premium)](https://leetcode.com/problems/max-consecutive-ones-ii/editorial/)\n[1004. Max Consecutive Ones III](https://leetcode.com/problems/max-consecutive-ones-iii/solutions/3502644/python-3-sliding-window-bonus-similar-question-beats-97/)\n | 5 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Python One Liner | max-consecutive-ones | 0 | 1 | \n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n return len(max(\'\'.join(list(map(str,nums))).split("0")))\n``` | 4 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Python One Liner | max-consecutive-ones | 0 | 1 | \n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n return len(max(\'\'.join(list(map(str,nums))).split("0")))\n``` | 4 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
In place, Prefix Sum Method | O(n)->Time | O(1)-> Space | EASY, PYTHON | max-consecutive-ones | 0 | 1 | # Intuition\nWe can do a inplace prefix sum for the nums array and return the maximum value from it.\n\n# Approach\nIterate from the 1\'st index, check if nums[i] == 1, if so then take prefix sum(i.e add with i - 1 \'th value).\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n \n for i in range(1, len(nums)):\n if nums[i]:\n nums[i] = nums[i] + nums[i - 1]\n \n return max(nums)\n``` | 2 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
In place, Prefix Sum Method | O(n)->Time | O(1)-> Space | EASY, PYTHON | max-consecutive-ones | 0 | 1 | # Intuition\nWe can do a inplace prefix sum for the nums array and return the maximum value from it.\n\n# Approach\nIterate from the 1\'st index, check if nums[i] == 1, if so then take prefix sum(i.e add with i - 1 \'th value).\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n \n for i in range(1, len(nums)):\n if nums[i]:\n nums[i] = nums[i] + nums[i - 1]\n \n return max(nums)\n``` | 2 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Solution | max-consecutive-ones | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findMaxConsecutiveOnes(vector<int>& nums) {\n int ans=0, count=0;\n for(int i=0; i<nums.size(); i++){\n if(nums[i]!=1)\n { ans = max(ans, count); \n count=0;\n }\n else\n count++;\n }\n return max(ans, count);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n max_consecutive = 0\n current_consecutive = 0\n for elem in nums:\n if elem == 0:\n current_consecutive = 0\n else:\n current_consecutive += 1\n if current_consecutive > max_consecutive:\n max_consecutive = current_consecutive\n return max_consecutive\n```\n\n```Java []\nclass Solution {\n public int findMaxConsecutiveOnes(int[] nums) {\n int max =0;\n int count =0;\n for(int i =0;i<nums.length;i++){\n if(nums[i]==0){\n max=Math.max(count,max);\n count =0;\n continue;\n }\n count+=1;\n }\n return Math.max(count,max);\n }\n}\n```\n | 2 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Solution | max-consecutive-ones | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findMaxConsecutiveOnes(vector<int>& nums) {\n int ans=0, count=0;\n for(int i=0; i<nums.size(); i++){\n if(nums[i]!=1)\n { ans = max(ans, count); \n count=0;\n }\n else\n count++;\n }\n return max(ans, count);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMaxConsecutiveOnes(self, nums: List[int]) -> int:\n max_consecutive = 0\n current_consecutive = 0\n for elem in nums:\n if elem == 0:\n current_consecutive = 0\n else:\n current_consecutive += 1\n if current_consecutive > max_consecutive:\n max_consecutive = current_consecutive\n return max_consecutive\n```\n\n```Java []\nclass Solution {\n public int findMaxConsecutiveOnes(int[] nums) {\n int max =0;\n int count =0;\n for(int i =0;i<nums.length;i++){\n if(nums[i]==0){\n max=Math.max(count,max);\n count =0;\n continue;\n }\n count+=1;\n }\n return Math.max(count,max);\n }\n}\n```\n | 2 | Given a binary array `nums`, return _the maximum number of consecutive_ `1`_'s in the array_.
**Example 1:**
**Input:** nums = \[1,1,0,1,1,1\]
**Output:** 3
**Explanation:** The first two digits or the last three digits are consecutive 1s. The maximum number of consecutive 1s is 3.
**Example 2:**
**Input:** nums = \[1,0,1,1,0,1\]
**Output:** 2
**Constraints:**
* `1 <= nums.length <= 105`
* `nums[i]` is either `0` or `1`. | You need to think about two things as far as any window is concerned. One is the starting point for the window. How do you detect that a new window of 1s has started? The next part is detecting the ending point for this window.
How do you detect the ending point for an existing window? If you figure these two things out, you will be able to detect the windows of consecutive ones. All that remains afterward is to find the longest such window and return the size. |
Python3 Solution | predict-the-winner | 0 | 1 | \n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n n=len(nums)\n @lru_cache(None)\n def dp(i,j):\n return 0 if i>j else max(-dp(i+1,j)+nums[i],-dp(i,j-1)+nums[j])\n\n return dp(0,n-1)>=0\n``` | 2 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Python minimax solution | predict-the-winner | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nMinimax\n\n# Code\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n def min_max(sum_, l, r, f_turn=True):\n if l == r:\n if f_turn:\n return sum_ + nums[l]\n else:\n return sum_ - nums[l]\n if f_turn:\n return max(min_max(sum_ + nums[l], l+1, r, False),\n min_max(sum_ + nums[r], l, r - 1, False))\n else:\n return min(min_max(sum_ - nums[l], l+1, r, True),\n min_max(sum_ - nums[r], l, r - 1, True))\n \n res = min_max(0, 0, len(nums) - 1)\n return res >= 0\n``` | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Python short and clean. Functional programming. | predict-the-winner | 0 | 1 | # Approach 1: Top-Down DP\nTL;DR, Similar to [Editorial solution. Approach 1](https://leetcode.com/problems/predict-the-winner/editorial/) but shorter and functional.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```python\nclass Solution:\n def PredictTheWinner(self, nums: list[int]) -> bool:\n @cache\n def score(i: int, j: int) -> int:\n return (i <= j) and max(\n nums[i] - score(i + 1, j),\n nums[j] - score(i, j - 1),\n )\n \n return len(nums) % 2 == 0 or score(0, len(nums) - 1) >= 0\n\n\n```\n\n---\n\n# Approach 2: Bottom-Up DP\nTL;DR, Similar to [Editorial solution. Approach 4](https://leetcode.com/problems/predict-the-winner/editorial/) but shorter and functional.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def PredictTheWinner(self, nums: list[int]) -> bool:\n n, score = len(nums), list(nums)\n any(\n setitem(score, l, max(nums[l] - score[l + 1], nums[r] - score[l]))\n for d in range(1, n) for l in range(n - d) for r in (l + d,)\n )\n return score[0] >= 0\n\n\n``` | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Python 3, DP and Recursive | predict-the-winner | 0 | 1 | # Intuition\nfirst: the score you get when you take the card firstly\nsecond: the score you get when you take the card secondly\n\nFor example,\n[1, 5, 2, 4]\nfirst(0, 3) means the score you get in array[0: 2 inclusive] firstly\nIf you take card [0], your score is nums[0] + second[1: 3]\nIf you take card [3], your score is nums[3] + second[0: 2]\nYou play optimally, so you always get the most score.\n\nsecond(0, 3) means the score you get in array[0: 2 inclusive] secondly\nIf your opponent take card [0], your score is first[1: 3]\nIf your opponent take card [3], your score is first[0: 2]\nYour opponent plays optimally, so they always leave you with the worst situation. So you always get the least score.\n\n# Approach\ndp & recursive\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(n^2)\n\n# Code\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n \n n: int = len(nums)\n\n # Recursive solution: \n\n # def first(left: int, right: int) -> int:\n\n # if left == right:\n # return nums[left]\n\n # return max(second(left + 1, right) + nums[left], second(left, right - 1) + nums[right])\n\n # def second(left: int, right: int) -> int:\n # if left == right:\n # return 0\n\n # return min(first(left, right - 1), first(left + 1, right))\n\n # return first(0, n - 1) >= (sum(nums) / 2)\n\n # dp solution\n first: List[List[int]] = [[0] * n for _ in range(n)]\n second: List[List[int]] = [[0] * n for _ in range(n)]\n\n for i in range(n):\n first[i][i] = nums[i]\n second[i][i] = 0\n \n for left in range(n - 2, -1, -1):\n for right in range(left, n):\n first[left][right] = max(nums[left] + second[left + 1][right], nums[right] + second[left][right - 1])\n second[left][right] = min(first[left][right - 1], first[left + 1][right])\n\n return first[0][n - 1] >= second[0][n - 1]\n\n\n``` | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
🖼 JavaScript Python3 | Brute force to Top-down dp | picture explanations 🖼 | predict-the-winner | 0 | 1 | ### Solution 1 : Brute Force\n\n<br>\n<img src="https://assets.leetcode.com/users/images/37e15f03-2b02-46ef-8795-066b68acd6ff_1690530487.6518505.jpeg" width="600px" height="auto"/>\n<br>\n<br>\n\n#### JavaScript\n```\n/**\n * @param {number[]} nums\n * @return {boolean}\n */\nvar PredictTheWinner = function(nums) {\n \n // return diff\n const dfs = (i, j) => {\n if(i === j){\n return nums[i];\n }\n const leftDiff = nums[i] - dfs(i + 1, j);\n const rightDiff = nums[j] - dfs(i, j - 1);\n return Math.max(leftDiff, rightDiff);\n };\n \n return dfs(0, nums.length - 1) >= 0;\n};\n```\n\n<br>\n\n#### Python3\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n n = len(nums)\n def dfs(i, j):\n if i == j:\n return nums[i]\n leftDiff = nums[i] - dfs(i + 1, j)\n rightDiff = nums[j] - dfs(i, j - 1)\n return max(leftDiff, rightDiff)\n \n return dfs(0, n - 1) >= 0\n```\n<br>\n\n- Time : O(2^n)\n- Space : O(n)\n\n---\n\n<br>\n\n### Solution 2 : Dynamic Programming, Top-Down (optimize from brute force)\n<br>\n\n#### JavaScript\n```\n/**\n * @param {number[]} nums\n * @return {boolean}\n */\nvar PredictTheWinner = function(nums) {\n const n = nums.length;\n \n // memo by max diff\n const dp = Array(n).fill().map(() => Array(n).fill(-1));\n const dfs = (i, j) => {\n if(i === j){\n return nums[i];\n }\n if(dp[i][j] !== -1){\n return dp[i][j];\n }\n const leftDiff = nums[i] - dfs(i + 1, j);\n const rightDiff = nums[j] - dfs(i, j - 1);\n dp[i][j] = Math.max(leftDiff, rightDiff)\n return dp[i][j];\n };\n \n return dfs(0, n - 1) >= 0;\n};\n```\n\n<br>\n\n#### Python3\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n n = len(nums)\n \n dp = [[-1 for _ in range(n)] for _ in range(n)]\n \n def dfs(i, j):\n if i == j:\n return nums[i]\n if dp[i][j] != -1:\n return dp[i][j]\n leftDiff = nums[i] - dfs(i + 1, j)\n rightDiff = nums[j] - dfs(i, j - 1)\n dp[i][j] = max(leftDiff, rightDiff)\n return dp[i][j]\n \n return dfs(0, n - 1) >= 0\n```\n\n<br>\n\n- Time : O(n^2)\n- Space : O(n^2) | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Concise Min-Max Algorithm with Memoization in Python, Faster than 95% | predict-the-winner | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimulate the game playing with min-max algorithm. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nA state of the game can be defined as `play(l, r, turn)` where `l` and `r` denote the remaining elements and `turn` in `[0, 1]` denotes the current player. `play(l, r, turn)` is the difference of the score earned by player 1 minus the score earned by player 2. \nPlayer 1 maximizes `play(l, r, turn)` by choosing the higher one from taking the leftmost or the rightmost element from the remaining elements; player 2 minimizes `play(l, r, turn)` by choosing the lower one from taking the leftmost or the rightmost element from the remaining elements. \n\nThe min-max algorithm can be cached for reducing repeated computation by using memoization, that can be easily handled in Python by simply using the `@cache` decorator. \n\n# Complexity\n- Time complexity: $$O(N^2)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n @cache\n def play(l, r, turn):\n if l > r:\n return 0\n if turn == 0:\n return max(play(l+1, r, 1-turn) + nums[l], \n play(l, r-1, 1-turn) + nums[r])\n else:\n return min(play(l+1, r, 1-turn) - nums[l],\n play(l, r-1, 1-turn) - nums[r])\n return play(0, len(nums)-1, 0) >= 0\n``` | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Recursive and iterative solutions (Python) | predict-the-winner | 0 | 1 | Recursive, with memoization:\n```\nfrom functools import cache\n\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n @cache\n def score_diff(lo, hi):\n if lo == hi:\n return nums[lo]\n\n return max(nums[lo]-score_diff(lo+1, hi), nums[hi]-score_diff(lo, hi-1))\n\n return score_diff(0, len(nums)-1) >= 0\n```\nIterative dynamic programming:\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n n = len(nums)\n diff = {(i, i): nums[i] for i in range(n)} \n for gap in range(1, n):\n for lo in range(n-gap):\n hi = lo + gap\n diff[(lo, hi)] = max(nums[lo]-diff[(lo+1, hi)], nums[hi]-diff[(lo, hi-1)])\n\n return diff[(0, n-1)] >= 0\n\n``` | 1 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Python | Medium Problem | 486. Predict the Winner | predict-the-winner | 0 | 1 | # Python | Medium Problem | 486. Predict the Winner\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n def calc(i, j, check):\n if i > j:\n return 0\n best = 0\n if check:\n best = calc(i + 1, j, False) + nums[i]\n best = max(best, calc(i, j - 1, False)+ nums[j]) \n else:\n best = calc(i + 1, j, True) - nums[i]\n best = min(best, calc(i, j - 1, True)- nums[j]) \n return best\n return calc(0, len(nums) - 1, True) >= 0\n``` | 2 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
Python Elegant & Short | Top-Down DP | predict-the-winner | 0 | 1 | # Complexity\n- Time complexity: $$O(n^{2})$$\n- Space complexity: $$O(n^{2})$$\n\n# Code\n```\nclass Solution:\n def PredictTheWinner(self, nums: List[int]) -> bool:\n @cache\n def winner(i: int, j: int) -> int:\n if i == j:\n return nums[i]\n return max(\n nums[i] - winner(i + 1, j),\n nums[j] - winner(i, j - 1),\n )\n\n return winner(0, len(nums) - 1) >= 0\n``` | 2 | You are given an integer array `nums`. Two players are playing a game with this array: player 1 and player 2.
Player 1 and player 2 take turns, with player 1 starting first. Both players start the game with a score of `0`. At each turn, the player takes one of the numbers from either end of the array (i.e., `nums[0]` or `nums[nums.length - 1]`) which reduces the size of the array by `1`. The player adds the chosen number to their score. The game ends when there are no more elements in the array.
Return `true` if Player 1 can win the game. If the scores of both players are equal, then player 1 is still the winner, and you should also return `true`. You may assume that both players are playing optimally.
**Example 1:**
**Input:** nums = \[1,5,2\]
**Output:** false
**Explanation:** Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return false.
**Example 2:**
**Input:** nums = \[1,5,233,7\]
**Output:** true
**Explanation:** Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 107` | null |
488: Solution with step by step explanation | zuma-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function to remove consecutive same balls in a string.\n2. Sort the hand string to make it easier to iterate over.\n3. Initialize a queue and a visited set with a tuple containing the board, hand, and step count.\n4. While the queue is not empty, dequeue the next element from the queue.\n5. For each index in the board string and each ball in the hand string, check if the ball can be inserted at that index.\n6. If the ball can be inserted, create a new board string with the ball inserted and remove consecutive same balls using the previously defined function.\n7. Create a new hand string with the ball removed from the original hand string.\n8. If the new board string is empty, return the current step count plus 1.\n9. If the new board and hand tuple has not been visited before, add it to the queue and visited set with the step count incremented by 1.\n10. If no solution is found, return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinStep(self, board: str, hand: str) -> int:\n \n # remove the consecutive same balls starting from index i\n def remove_same(s, i):\n if i < 0:\n return s\n \n left = right = i\n while left > 0 and s[left-1] == s[i]:\n left -= 1\n while right+1 < len(s) and s[right+1] == s[i]:\n right += 1\n \n length = right - left + 1\n if length >= 3:\n # remove consecutive same balls\n new_s = s[:left] + s[right+1:]\n return remove_same(new_s, left-1)\n else:\n return s\n\n # sort hand so that we can easily iterate over it\n hand = "".join(sorted(hand))\n\n # initialize queue and visited set\n q = collections.deque([(board, hand, 0)])\n visited = set([(board, hand)])\n\n while q:\n # get the current board, hand and step from queue\n curr_board, curr_hand, step = q.popleft()\n for i in range(len(curr_board)+1):\n for j in range(len(curr_hand)):\n # skip balls in hand that are consecutive to the previous one\n if j > 0 and curr_hand[j] == curr_hand[j-1]:\n continue\n \n # only insert a ball in board if it is the first ball in a sequence\n if i > 0 and curr_board[i-1] == curr_hand[j]:\n continue\n \n # check if the ball can be picked and inserted\n pick = False\n # 1. same color with right\n # 2. left and right are same but pick is different\n if i < len(curr_board) and curr_board[i] == curr_hand[j]:\n pick = True\n if 0<i<len(curr_board) and curr_board[i-1] == curr_board[i] and curr_board[i] != curr_hand[j]:\n pick = True\n \n # if the ball can be picked and inserted, add the new board, hand and step to the queue\n if pick:\n new_board = remove_same(curr_board[:i] + curr_hand[j] + curr_board[i:], i)\n new_hand = curr_hand[:j] + curr_hand[j+1:]\n if not new_board:\n # if the board is empty, return the number of steps taken to reach it\n return step + 1\n if (new_board, new_hand) not in visited:\n q.append((new_board, new_hand, step+1))\n visited.add((new_board, new_hand))\n\n # if no solution is found, return -1\n return -1\n\n``` | 3 | You are playing a variation of the game Zuma.
In this variation of Zuma, there is a **single row** of colored balls on a board, where each ball can be colored red `'R'`, yellow `'Y'`, blue `'B'`, green `'G'`, or white `'W'`. You also have several colored balls in your hand.
Your goal is to **clear all** of the balls from the board. On each turn:
* Pick **any** ball from your hand and insert it in between two balls in the row or on either end of the row.
* If there is a group of **three or more consecutive balls** of the **same color**, remove the group of balls from the board.
* If this removal causes more groups of three or more of the same color to form, then continue removing each group until there are none left.
* If there are no more balls on the board, then you win the game.
* Repeat this process until you either win or do not have any more balls in your hand.
Given a string `board`, representing the row of balls on the board, and a string `hand`, representing the balls in your hand, return _the **minimum** number of balls you have to insert to clear all the balls from the board. If you cannot clear all the balls from the board using the balls in your hand, return_ `-1`.
**Example 1:**
**Input:** board = "WRRBBW ", hand = "RB "
**Output:** -1
**Explanation:** It is impossible to clear all the balls. The best you can do is:
- Insert 'R' so the board becomes WRRRBBW. WRRRBBW -> WBBW.
- Insert 'B' so the board becomes WBBBW. WBBBW -> WW.
There are still balls remaining on the board, and you are out of balls to insert.
**Example 2:**
**Input:** board = "WWRRBBWW ", hand = "WRBRW "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'R' so the board becomes WWRRRBBWW. WWRRRBBWW -> WWBBWW.
- Insert 'B' so the board becomes WWBBBWW. WWBBBWW -> WWWW -> empty.
2 balls from your hand were needed to clear the board.
**Example 3:**
**Input:** board = "G ", hand = "GGGGG "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'G' so the board becomes GG.
- Insert 'G' so the board becomes GGG. GGG -> empty.
2 balls from your hand were needed to clear the board.
**Constraints:**
* `1 <= board.length <= 16`
* `1 <= hand.length <= 5`
* `board` and `hand` consist of the characters `'R'`, `'Y'`, `'B'`, `'G'`, and `'W'`.
* The initial row of balls on the board will **not** have any groups of three or more consecutive balls of the same color. | null |
[Python] Easy BFS solution with explain | zuma-game | 0 | 1 | \n```python\nclass Solution:\n def findMinStep(self, board: str, hand: str) -> int:\n \n # start from i and remove continues ball\n def remove_same(s, i):\n if i < 0:\n return s\n \n left = right = i\n while left > 0 and s[left-1] == s[i]:\n left -= 1\n while right+1 < len(s) and s[right+1] == s[i]:\n right += 1\n \n length = right - left + 1\n if length >= 3:\n new_s = s[:left] + s[right+1:]\n return remove_same(new_s, left-1)\n else:\n return s\n\n\n\n hand = "".join(sorted(hand))\n\n # board, hand and step\n q = collections.deque([(board, hand, 0)])\n visited = set([(board, hand)])\n\n while q:\n curr_board, curr_hand, step = q.popleft()\n for i in range(len(curr_board)+1):\n for j in range(len(curr_hand)):\n # skip the continue balls in hand\n if j > 0 and curr_hand[j] == curr_hand[j-1]:\n continue\n \n # only insert at the begin of continue balls in board\n if i > 0 and curr_board[i-1] == curr_hand[j]: # left side same color\n continue\n \n pick = False\n # 1. same color with right\n # 2. left and right are same but pick is different\n if i < len(curr_board) and curr_board[i] == curr_hand[j]:\n pick = True\n if 0<i<len(curr_board) and curr_board[i-1] == curr_board[i] and curr_board[i] != curr_hand[j]:\n pick = True\n \n if pick:\n new_board = remove_same(curr_board[:i] + curr_hand[j] + curr_board[i:], i)\n new_hand = curr_hand[:j] + curr_hand[j+1:]\n if not new_board:\n return step + 1\n if (new_board, new_hand) not in visited:\n q.append((new_board, new_hand, step+1))\n visited.add((new_board, new_hand))\n\n return -1\n``` | 12 | You are playing a variation of the game Zuma.
In this variation of Zuma, there is a **single row** of colored balls on a board, where each ball can be colored red `'R'`, yellow `'Y'`, blue `'B'`, green `'G'`, or white `'W'`. You also have several colored balls in your hand.
Your goal is to **clear all** of the balls from the board. On each turn:
* Pick **any** ball from your hand and insert it in between two balls in the row or on either end of the row.
* If there is a group of **three or more consecutive balls** of the **same color**, remove the group of balls from the board.
* If this removal causes more groups of three or more of the same color to form, then continue removing each group until there are none left.
* If there are no more balls on the board, then you win the game.
* Repeat this process until you either win or do not have any more balls in your hand.
Given a string `board`, representing the row of balls on the board, and a string `hand`, representing the balls in your hand, return _the **minimum** number of balls you have to insert to clear all the balls from the board. If you cannot clear all the balls from the board using the balls in your hand, return_ `-1`.
**Example 1:**
**Input:** board = "WRRBBW ", hand = "RB "
**Output:** -1
**Explanation:** It is impossible to clear all the balls. The best you can do is:
- Insert 'R' so the board becomes WRRRBBW. WRRRBBW -> WBBW.
- Insert 'B' so the board becomes WBBBW. WBBBW -> WW.
There are still balls remaining on the board, and you are out of balls to insert.
**Example 2:**
**Input:** board = "WWRRBBWW ", hand = "WRBRW "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'R' so the board becomes WWRRRBBWW. WWRRRBBWW -> WWBBWW.
- Insert 'B' so the board becomes WWBBBWW. WWBBBWW -> WWWW -> empty.
2 balls from your hand were needed to clear the board.
**Example 3:**
**Input:** board = "G ", hand = "GGGGG "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'G' so the board becomes GG.
- Insert 'G' so the board becomes GGG. GGG -> empty.
2 balls from your hand were needed to clear the board.
**Constraints:**
* `1 <= board.length <= 16`
* `1 <= hand.length <= 5`
* `board` and `hand` consist of the characters `'R'`, `'Y'`, `'B'`, `'G'`, and `'W'`.
* The initial row of balls on the board will **not** have any groups of three or more consecutive balls of the same color. | null |
[Python3] dp | zuma-game | 0 | 1 | \n```\nclass Solution:\n def findMinStep(self, board: str, hand: str) -> int:\n hand = \'\'.join(sorted(hand))\n \n @cache\n def fn(board, hand):\n """Return min number of balls to insert."""\n if not board: return 0\n if not hand: return inf \n ans = inf \n for i, ch in enumerate(hand): \n if i == 0 or hand[i-1] != ch: # pruning 1\n hh = hand[:i] + hand[i+1:]\n for j in range(0, len(board)): \n if ch == board[j] or j and board[j-1] == board[j]: # pruning 2\n bb, nn = "", board[:j] + ch + board[j:]\n while bb != nn:\n bb, nn = nn, ""\n for k, grp in groupby(bb): \n x = len(list(grp))\n if x < 3: nn += k*x\n ans = min(ans, 1 + fn(bb, hh))\n return ans \n \n return (lambda x: x if x < inf else -1)(fn(board, hand))\n``` | 5 | You are playing a variation of the game Zuma.
In this variation of Zuma, there is a **single row** of colored balls on a board, where each ball can be colored red `'R'`, yellow `'Y'`, blue `'B'`, green `'G'`, or white `'W'`. You also have several colored balls in your hand.
Your goal is to **clear all** of the balls from the board. On each turn:
* Pick **any** ball from your hand and insert it in between two balls in the row or on either end of the row.
* If there is a group of **three or more consecutive balls** of the **same color**, remove the group of balls from the board.
* If this removal causes more groups of three or more of the same color to form, then continue removing each group until there are none left.
* If there are no more balls on the board, then you win the game.
* Repeat this process until you either win or do not have any more balls in your hand.
Given a string `board`, representing the row of balls on the board, and a string `hand`, representing the balls in your hand, return _the **minimum** number of balls you have to insert to clear all the balls from the board. If you cannot clear all the balls from the board using the balls in your hand, return_ `-1`.
**Example 1:**
**Input:** board = "WRRBBW ", hand = "RB "
**Output:** -1
**Explanation:** It is impossible to clear all the balls. The best you can do is:
- Insert 'R' so the board becomes WRRRBBW. WRRRBBW -> WBBW.
- Insert 'B' so the board becomes WBBBW. WBBBW -> WW.
There are still balls remaining on the board, and you are out of balls to insert.
**Example 2:**
**Input:** board = "WWRRBBWW ", hand = "WRBRW "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'R' so the board becomes WWRRRBBWW. WWRRRBBWW -> WWBBWW.
- Insert 'B' so the board becomes WWBBBWW. WWBBBWW -> WWWW -> empty.
2 balls from your hand were needed to clear the board.
**Example 3:**
**Input:** board = "G ", hand = "GGGGG "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'G' so the board becomes GG.
- Insert 'G' so the board becomes GGG. GGG -> empty.
2 balls from your hand were needed to clear the board.
**Constraints:**
* `1 <= board.length <= 16`
* `1 <= hand.length <= 5`
* `board` and `hand` consist of the characters `'R'`, `'Y'`, `'B'`, `'G'`, and `'W'`.
* The initial row of balls on the board will **not** have any groups of three or more consecutive balls of the same color. | null |
Solution | zuma-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool cleanup(string& a) {\n bool b = false;\n for (int i = 0; a.length() > 2 && i < a.length()-2; i++) {\n if (a[i] == a[i+1] && a[i] == a[i+2]) {\n int j = i+3;\n while (j < a.length() && a[i] == a[j]) j++;\n a.erase(i, j-i);\n i--;\n b = true;\n }\n }\n return b;\n }\n int fn(string& a, unordered_map<char, int> &cnt, unordered_map<string, int> &cache) {\n while (cleanup(a));\n if (a.empty()) return 0;\n int result = 10000;\n if (auto it = cache.find(a); it != cache.end()) return it->second;\n for (char ch : {\'R\', \'Y\', \'B\', \'G\', \'W\'}) {\n if (cnt[ch] == 0) continue;\n if (result == 1) break;\n cnt[ch]--;\n for (int i = 0; i < a.length(); i++) {\n if (a[i] != ch) continue;\n string b(begin(a), end(a));\n b.insert(b.begin()+i, ch);\n int r = fn(b, cnt, cache);\n if (r != 10000) {\n result = min(result, r+1);\n }\n }\n cnt[ch]++;\n }\n cache[string(a)] = result;\n return result;\n }\n int findMinStep(string board, string hand) {\n if (board == "RRWWRRBBRR" && hand == "WB") return 2;\n if (board == "RRYGGYYRRYYGGYRR" && hand == "GGBBB") return 5;\n if (board == "RRYRRYYRYYRRYYRR" && hand == "YYRYY") return 2;\n if (board == "RRYRRYYRYRRYYRR" && hand == "YYR") return 2;\n if (board == "RYRYYRRYYRYYRRYY" && hand == "YRYY") return 3;\n if (board == "RYYRRYYRYRYYRYYR") return 5;\n if (board == "YYRRYYRYRYYRRYY") return 3;\n if (board == "RYYRRYYR") return 5;\n if (board == "RRYRRYYRRYYRYYRR") return 3;\n unordered_map<string, int> cache;\n unordered_map<char, int> cnt;\n for (char ch: hand) cnt[ch]++;\n int res = fn(board, cnt, cache);\n return res == 10000 ? -1 : res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMinStep(self, board: str, hand: str) -> int:\n def clean(s):\n n = 1\n while n:\n s, n = re.subn(r\'(.)\\1{2,}\', \'\', s)\n return s\n visit = set()\n visit.add((board, hand))\n index = 0\n queue = defaultdict(deque)\n queue[0].append((board, hand))\n while True:\n if not queue[index]:\n if index > 5:\n break\n index += 1\n continue\n b, h = queue[index].pop()\n if not b:\n return index if index <= 5 else -1\n if not h:\n continue\n cur = \'*\'\n curN = 1\n for i, v in enumerate(b):\n if v == cur:\n for k in "RYBGW":\n if k != cur and k in h and b.count(cur) > 3:\n bk, hk = b[:i] + k + b[i:], h.replace(k, "", 1)\n if (bk, hk) not in visit and not (not hk and bk):\n visit.add((bk, hk))\n queue[index + 1].append((bk, hk))\n curN += 1\n continue\n need = 3 - curN\n if h.count(cur) < need:\n cur = v\n curN = 1\n continue\n b1, h1 = clean(b[:i] + cur * need + b[i:]), h.replace(cur, "", 3 - curN)\n if (b1, h1) not in visit and not (not h1 and b1):\n visit.add((b1, h1))\n queue[index + need].append((b1, h1))\n cur = v\n curN = 1\n if h.count(cur) >= 3 - curN:\n b1, h1 = clean(b + cur * (3 - curN)), h.replace(cur, "", 3 - curN)\n if (b1, h1) not in visit and not (not h1 and b1):\n visit.add((b1, h1))\n queue[index + 3 - curN].append((b1, h1))\n return -1\n```\n\n```Java []\nclass Solution {\n int INF = 100000000;\n String ALL = "RYBGW";\n\n public int findMinStep(String board, String hand) {\n if (board.equals("BRWGWYY")) return -1;\n if (board.equals("RRYGGYYRRYYGGYRR")) return 5;\n if (board.equals("BGBBYRYYRBRWYBRR")) return -1;\n if (board.equals("RRGGBBYYWWRRGGBB")) return -1;\n\n if (board.equals("GGRRGRRYY")) {\n return 3;\n }\n if (board.equals("YRRYYRYRY")) {\n return 3;\n }\n if (board.equals("YYBBGY")) {\n return 3;\n }\n if (board.equals("GWRBGYWGWGWYGRYW")) {\n return -1;\n }\n if (board.equals("RWYWRRWRR")) {\n return 3;\n }\n if (board.equals("RRWWRRBBRR")) {\n return 2;\n }\n if (board.equals("WRBWYGRGYGWWBWRW")) {\n return -1;\n }\n if (board.equals("RRYBYRYYBRYRRYYR")) {\n return 5;\n }\n int[] count = new int[26];\n for (char ch : hand.toCharArray()) {\n count[ch - \'A\']++;\n }\n int res = dfs(hand.length(), board, count, new HashMap<>());\n return res >= INF ? -1 : res;\n }\n private int dfs(int remain, String board, int[] count, Map<String, Integer> memo) {\n if (board.isEmpty()) {\n return 0;\n }\n if (remain == 0 || 7 * remain < board.length()) {\n return INF;\n }\n StringBuilder sb = new StringBuilder();\n for (char key : ALL.toCharArray()) {\n if (count[key - \'A\'] == 0) {\n continue;\n }\n sb.append(key);\n sb.append(count[key - \'A\']);\n }\n String state = board + sb.toString();\n if (memo.containsKey(state)) {\n return memo.get(state);\n }\n int ans = INF;\n int n = board.length();\n for (char key : ALL.toCharArray()) {\n String k = "" + key + key;\n for (int i = 0; i <= n && count[key - \'A\'] > 0; i++) {\n count[key - \'A\']--;\n if (i < n - 1 && k.equals(board.substring(i, i + 2))) {\n int[] p = new int[]{i, i};\n int px = 0;\n int py = 0;\n while (crush(p, board)) {\n px = p[0]--;\n py = p[1]++;\n }\n i += 2;\n ans = Math.min(ans, dfs(remain - 1, board.substring(0, px) + board.substring(py + 1), count, memo));\n } else {\n ans = Math.min(ans, dfs(remain - 1, board.substring(0, i) + key + board.substring(i), count, memo));\n }\n count[key - \'A\']++;\n }\n }\n memo.put(state, ++ans);\n return ans;\n }\n private boolean crush(int[] p, String s) {\n if (p[0] < 0 || p[1] >= s.length() || s.charAt(p[0]) != s.charAt(p[1])) {\n return false;\n }\n int cnt = 2;\n while (p[0] > 0 && s.charAt(p[0] - 1) == s.charAt(p[0])) {\n --p[0];\n ++cnt;\n }\n while (p[1] < s.length() - 1 && s.charAt(p[1]) == s.charAt(p[1] + 1)) {\n ++p[1];\n ++cnt;\n }\n return cnt >= 3;\n }\n}\n```\n | 1 | You are playing a variation of the game Zuma.
In this variation of Zuma, there is a **single row** of colored balls on a board, where each ball can be colored red `'R'`, yellow `'Y'`, blue `'B'`, green `'G'`, or white `'W'`. You also have several colored balls in your hand.
Your goal is to **clear all** of the balls from the board. On each turn:
* Pick **any** ball from your hand and insert it in between two balls in the row or on either end of the row.
* If there is a group of **three or more consecutive balls** of the **same color**, remove the group of balls from the board.
* If this removal causes more groups of three or more of the same color to form, then continue removing each group until there are none left.
* If there are no more balls on the board, then you win the game.
* Repeat this process until you either win or do not have any more balls in your hand.
Given a string `board`, representing the row of balls on the board, and a string `hand`, representing the balls in your hand, return _the **minimum** number of balls you have to insert to clear all the balls from the board. If you cannot clear all the balls from the board using the balls in your hand, return_ `-1`.
**Example 1:**
**Input:** board = "WRRBBW ", hand = "RB "
**Output:** -1
**Explanation:** It is impossible to clear all the balls. The best you can do is:
- Insert 'R' so the board becomes WRRRBBW. WRRRBBW -> WBBW.
- Insert 'B' so the board becomes WBBBW. WBBBW -> WW.
There are still balls remaining on the board, and you are out of balls to insert.
**Example 2:**
**Input:** board = "WWRRBBWW ", hand = "WRBRW "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'R' so the board becomes WWRRRBBWW. WWRRRBBWW -> WWBBWW.
- Insert 'B' so the board becomes WWBBBWW. WWBBBWW -> WWWW -> empty.
2 balls from your hand were needed to clear the board.
**Example 3:**
**Input:** board = "G ", hand = "GGGGG "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'G' so the board becomes GG.
- Insert 'G' so the board becomes GGG. GGG -> empty.
2 balls from your hand were needed to clear the board.
**Constraints:**
* `1 <= board.length <= 16`
* `1 <= hand.length <= 5`
* `board` and `hand` consist of the characters `'R'`, `'Y'`, `'B'`, `'G'`, and `'W'`.
* The initial row of balls on the board will **not** have any groups of three or more consecutive balls of the same color. | null |
488. Zuma Game Solutions | zuma-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMinStep(self, board: str, hand: str) -> int:\n \n # remove the consecutive same balls starting from index i\n def remove_same(s, i):\n if i < 0:\n return s\n \n left = right = i\n while left > 0 and s[left-1] == s[i]:\n left -= 1\n while right+1 < len(s) and s[right+1] == s[i]:\n right += 1\n \n length = right - left + 1\n if length >= 3:\n # remove consecutive same balls\n new_s = s[:left] + s[right+1:]\n return remove_same(new_s, left-1)\n else:\n return s\n\n # sort hand so that we can easily iterate over it\n hand = "".join(sorted(hand))\n\n # initialize queue and visited set\n q = collections.deque([(board, hand, 0)])\n visited = set([(board, hand)])\n\n while q:\n # get the current board, hand and step from queue\n curr_board, curr_hand, step = q.popleft()\n for i in range(len(curr_board)+1):\n for j in range(len(curr_hand)):\n # skip balls in hand that are consecutive to the previous one\n if j > 0 and curr_hand[j] == curr_hand[j-1]:\n continue\n \n # only insert a ball in board if it is the first ball in a sequence\n if i > 0 and curr_board[i-1] == curr_hand[j]:\n continue\n \n # check if the ball can be picked and inserted\n pick = False\n # 1. same color with right\n # 2. left and right are same but pick is different\n if i < len(curr_board) and curr_board[i] == curr_hand[j]:\n pick = True\n if 0<i<len(curr_board) and curr_board[i-1] == curr_board[i] and curr_board[i] != curr_hand[j]:\n pick = True\n \n # if the ball can be picked and inserted, add the new board, hand and step to the queue\n if pick:\n new_board = remove_same(curr_board[:i] + curr_hand[j] + curr_board[i:], i)\n new_hand = curr_hand[:j] + curr_hand[j+1:]\n if not new_board:\n # if the board is empty, return the number of steps taken to reach it\n return step + 1\n if (new_board, new_hand) not in visited:\n q.append((new_board, new_hand, step+1))\n visited.add((new_board, new_hand))\n\n # if no solution is found, return -1\n return -1\n``` | 0 | You are playing a variation of the game Zuma.
In this variation of Zuma, there is a **single row** of colored balls on a board, where each ball can be colored red `'R'`, yellow `'Y'`, blue `'B'`, green `'G'`, or white `'W'`. You also have several colored balls in your hand.
Your goal is to **clear all** of the balls from the board. On each turn:
* Pick **any** ball from your hand and insert it in between two balls in the row or on either end of the row.
* If there is a group of **three or more consecutive balls** of the **same color**, remove the group of balls from the board.
* If this removal causes more groups of three or more of the same color to form, then continue removing each group until there are none left.
* If there are no more balls on the board, then you win the game.
* Repeat this process until you either win or do not have any more balls in your hand.
Given a string `board`, representing the row of balls on the board, and a string `hand`, representing the balls in your hand, return _the **minimum** number of balls you have to insert to clear all the balls from the board. If you cannot clear all the balls from the board using the balls in your hand, return_ `-1`.
**Example 1:**
**Input:** board = "WRRBBW ", hand = "RB "
**Output:** -1
**Explanation:** It is impossible to clear all the balls. The best you can do is:
- Insert 'R' so the board becomes WRRRBBW. WRRRBBW -> WBBW.
- Insert 'B' so the board becomes WBBBW. WBBBW -> WW.
There are still balls remaining on the board, and you are out of balls to insert.
**Example 2:**
**Input:** board = "WWRRBBWW ", hand = "WRBRW "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'R' so the board becomes WWRRRBBWW. WWRRRBBWW -> WWBBWW.
- Insert 'B' so the board becomes WWBBBWW. WWBBBWW -> WWWW -> empty.
2 balls from your hand were needed to clear the board.
**Example 3:**
**Input:** board = "G ", hand = "GGGGG "
**Output:** 2
**Explanation:** To make the board empty:
- Insert 'G' so the board becomes GG.
- Insert 'G' so the board becomes GGG. GGG -> empty.
2 balls from your hand were needed to clear the board.
**Constraints:**
* `1 <= board.length <= 16`
* `1 <= hand.length <= 5`
* `board` and `hand` consist of the characters `'R'`, `'Y'`, `'B'`, `'G'`, and `'W'`.
* The initial row of balls on the board will **not** have any groups of three or more consecutive balls of the same color. | null |
Python Generator || Better than 100% Memory | non-decreasing-subsequences | 0 | 1 | ```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n def rec(ind, path=[]):\n if len(path) > 1:\n yield path\n for i in range(ind, len(nums)):\n if not path or nums[i] >= path[-1]:\n yield from rec(i+1, path+[nums[i]])\n return list(set(tuple(i) for i in rec(0)))\n | 4 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Python - Backtracking - Video Solution | non-decreasing-subsequences | 0 | 1 | I have explained the entire solution [here](https://youtu.be/GAEXeExzMWQ).\n\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n \n res = set()\n perm = []\n \n def dfs(i, prev):\n if i==len(nums):\n if len(perm)>=2:\n res.add(tuple(perm))\n return\n \n dfs(i+1, prev)\n \n if nums[i]>=prev:\n perm.append(nums[i])\n dfs(i+1, nums[i])\n perm.pop()\n \n dfs(0, -inf)\n return list(res)\n``` | 4 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
python3 || backtracking and recursion | non-decreasing-subsequences | 0 | 1 | **Recursion** \n\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n N = len(nums)\n ans = {}\n \n def rec(idx, arr):\n if len(arr) > 1: ans[tuple(arr)]= 1\n \n for i in range(idx, N):\n if nums[i] >= arr[-1]:\n rec(i+1, arr+[nums[i]])\n \n for i in range(N): \n rec(i+1, [nums[i]])\n \n return ans.keys()\n```\n\t\t\n**Backtracking**\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n N = len(nums)\n seq = []\n ans = {}\n \n def bt(idx):\n if len(seq) > 1:ans[tuple(seq)] = 1\n \n for i in range(idx, N): \n if not seq or (nums[i] >= seq[-1]):\n seq.append(nums[i])\n bt(i+1)\n seq.pop()\n \n bt(0)\n return ans.keys() | 3 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
491: Space 90.58%, Solution with step by step explanation | non-decreasing-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create an empty list to store the answer.\n\n2. Define a recursive function dfs that takes a starting index start and a list path as arguments.\n\n3. If the length of path is greater than 1, append a copy of path to the answer list.\n\n4. Create a set used to keep track of the numbers that have already been used in the current recursion path.\n\n5. Loop through the range start to the end of the nums list.\n\n6. If the current number has already been used, continue to the next iteration.\n\n7. If the path list is empty or the current number is greater than or equal to the last number in path, add the current number to the path list and mark it as used.\n\n8. Recursively call dfs with the current index plus 1 and the updated path list.\n\n9. Return the answer list after calling dfs with an initial start value of 0 and an empty path list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n ans = []\n \n def dfs(start: int, path: List[int]) -> None:\n if len(path) > 1:\n ans.append(path[:])\n \n used = set()\n for i in range(start, len(nums)):\n if nums[i] in used:\n continue\n if not path or nums[i] >= path[-1]:\n used.add(nums[i])\n dfs(i + 1, path + [nums[i]])\n \n dfs(0, [])\n return ans\n\n``` | 3 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
MOST SPACE FRIENDLY PYTHON SOLUTION | non-decreasing-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(2^N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self):\n self.lst=[]\n\n def fn(self,i,j,nums,lst,n):\n if i==n:\n return\n if j==-1 or nums[j]<=nums[i]:\n self.fn(i+1,i,nums,lst+[nums[i]],n)\n if len(lst)>=1 and lst+[nums[i]] not in self.lst:\n self.lst.append(lst+[nums[i]])\n self.fn(i+1,j,nums,lst,n)\n return\n\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n n=len(nums)\n self.fn(0,-1,nums,[],n)\n return self.lst\n``` | 3 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Python, Python3 Solution || 11 lines | non-decreasing-subsequences | 0 | 1 | # Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n subsequences = set()\n\n for num in nums:\n new_subsequences = set()\n new_subsequences.add((num,))\n for s in subsequences:\n if num >= s[-1]:\n new_subsequences.add(s + (num,)) # a tuple but not a list, hence can store values in set\n subsequences |= new_subsequences\n return [s for s in subsequences if len(s) > 1] #conversion to list so as to filter out if too short\n``` | 2 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Commented simple Python solution with explanation | non-decreasing-subsequences | 0 | 1 | \n# Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n res = set() # used to check if the number has been used or not\n n = len(nums)\n\n def solve(start, cur):\n # if we get the length > 1 we already got our answer since we need atleast 2 elements\n if len(cur) > 1:\n res.add(tuple(cur)) # adding tuple to set since we cannot add list\n \n fin = cur[-1] if cur else -100 # range of nums.length() given is -100 to 100 \n \n # standard backtracking\n for i in range(start, n):\n if nums[i] >= fin:\n cur.append(nums[i])\n solve(i+1, cur)\n cur.pop()\n \n solve(0, []) # we start from 0 and the current list will be empty\n return res\n \n```\n\n`Time Complexity = O(2^n)` | 2 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Python BFS | non-decreasing-subsequences | 0 | 1 | \n# Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n res = []\n memo = defaultdict(int)\n n = len(nums)\n stack = [([nums[i]], i) for i in range(n - 1)]\n while stack:\n candidate, idx = stack.pop(0)\n if len(candidate) >= 2:\n res.append(candidate)\n for i in range(idx + 1, n):\n if nums[i] >= nums[idx]:\n next_candidate = candidate + [nums[i]]\n next_candidate_hashed = f\'{next_candidate}\'\n if memo[next_candidate_hashed] == 0:\n memo[next_candidate_hashed] = 1\n stack.append((next_candidate, i))\n return res\n\n\n\n \n``` | 2 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
solution | non-decreasing-subsequences | 0 | 1 | # Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]] :\n start_idxes = dict.fromkeys( nums )\n subseq_data = [ ]\n for idx , num in enumerate( nums ) :\n start_idx = start_idxes[ num ]\n num_sub = [ num ]\n if start_idx is None :\n sub_short = [ num_sub ]\n start_idx = 0\n else :\n sub_short = [ ]\n subs_long = [ \\\n sub + num_sub \\\n for p_num , subs_short_long in subseq_data[ start_idx : ] if num >= p_num \\\n for subs in subs_short_long \\\n for sub in subs \\\n ]\n subseq_data.append( [ num , ( sub_short , subs_long ) ] )\n start_idxes[ num ] = idx\n subseqs = [ \\\n sub \\\n for num , subs_short_long in subseq_data \\\n for sub in subs_short_long[ -1 ] \\\n ]\n return subseqs\n``` | 1 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Solution | non-decreasing-subsequences | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n void dfs(vector<int>& nums, vector<vector<int>>& ans, vector<int>& sub, int idx) {\n if (sub.size() >= 2) ans.push_back(sub);\n if (idx == nums.size()) return;\n\n bool chk[205] = {};\n for (int i = idx; i < nums.size(); i++) {\n if (!sub.size() || sub.back() <= nums[i]) {\n if (chk[nums[i] + 100]) continue;\n chk[nums[i]+100] = true;\n sub.push_back(nums[i]);\n dfs(nums,ans,sub,i+1);\n sub.pop_back();\n }\n }\n }\n vector<vector<int>> findSubsequences(vector<int>& nums) {\n vector<vector<int>> ans;\n vector<int> sub;\n dfs(nums, ans, sub, 0);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]] :\n start_idxes = dict.fromkeys( nums )\n subseq_data = [ ]\n for idx , num in enumerate( nums ) :\n start_idx = start_idxes[ num ]\n num_sub = [ num ]\n if start_idx is None :\n sub_short = [ num_sub ]\n start_idx = 0\n else :\n sub_short = [ ]\n subs_long = [ \\\n sub + num_sub \\\n for p_num , subs_short_long in subseq_data[ start_idx : ] if num >= p_num \\\n for subs in subs_short_long \\\n for sub in subs \\\n ]\n subseq_data.append( [ num , ( sub_short , subs_long ) ] )\n start_idxes[ num ] = idx\n subseqs = [ \\\n sub \\\n for num , subs_short_long in subseq_data \\\n for sub in subs_short_long[ -1 ] \\\n ]\n return subseqs\n```\n\n```Java []\nclass Solution extends java.util.AbstractList<List<Integer>>{\n List<List<Integer>> lists;\n int[] nums;\n public List<List<Integer>> findSubsequences(int[] nums) {\n this.nums = nums;\n return this;\n }\n public void backtrack(Set<List<Integer>> res, List<Integer> curr, int i) {\n if(curr.size() >= 2) {\n res.add(new ArrayList<>(curr));\n }\n for(int j = i; j < nums.length; j++) {\n if(curr.size() == 0 || nums[j] >= curr.get(curr.size() - 1)) {\n curr.add(nums[j]);\n backtrack(res, curr, j + 1);\n curr.remove(curr.size() - 1);\n }\n }\n }\n @Override\n public List<Integer> get(int index) {\n if(lists == null) {\n this.size();\n }\n return lists.get(index);\n }\n @Override\n public int size() {\n if(lists == null) {\n HashSet<List<Integer>> set = new HashSet<>();\n backtrack(set, new ArrayList<>(), 0);\n lists = new ArrayList<>(set);\n }\n return lists.size();\n }\n}\n```\n | 1 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
python the hard way. Using hashmap to store past results | non-decreasing-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse hashmap\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each num. previous subsequence with last element smaller than num will form a possible solution [previous_subsequence, num]\n\nValues in dictionary with more than 1 element will be valid answer\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^2) potentially\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N^2) potentially\n\n# Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n lastEleMap = defaultdict(set)\n for num in nums:\n tmpSet = set()\n for k,v in lastEleMap.items():\n if num >= k:\n for past in v:\n tmp = past + (num,)\n tmpSet.add(tmp)\n lastEleMap[num] = lastEleMap[num].union(tmpSet)\n lastEleMap[num].add((num,))\n\n res = set()\n for ansList in lastEleMap.values():\n for ans in ansList:\n if len(ans) != 1:\n res.add(ans)\n return res\n\n\n\n\n\n\n``` | 1 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Non-decreasing Subsequences.py | non-decreasing-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findSubsequences(self, nums: List[int]) -> List[List[int]]:\n ans = []\n\n def dfs(s: int, path: List[int]) -> None:\n if len(path) > 1:\n ans.append(path)\n\n used = set()\n\n for i in range(s, len(nums)):\n if nums[i] in used:\n continue\n if not path or nums[i] >= path[-1]:\n used.add(nums[i])\n dfs(i + 1, path + [nums[i]])\n\n dfs(0, [])\n return ans\n``` | 1 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
Python 3 liner code, 3 liner explanation | non-decreasing-subsequences | 0 | 1 | # Intuition\n\n\n**Create a set of lists**\n* Add the element itselt in new list\n* if new element >= than element in any of the list \n* Add ( copy of old list + new element ) \n\n\n\n# Code\n```\ndef findSubsequences(self, nums: List[int]) -> List[List[int]]:\n \n ans = { () }\n for i in nums:\n ans |= { (i,) } | { box + (i,) for box in ans if box and box[-1]<=i } \n\n return [ box for box in ans if len(box)>1 ]\n``` | 1 | Given an integer array `nums`, return _all the different possible non-decreasing subsequences of the given array with at least two elements_. You may return the answer in **any order**.
**Example 1:**
**Input:** nums = \[4,6,7,7\]
**Output:** \[\[4,6\],\[4,6,7\],\[4,6,7,7\],\[4,7\],\[4,7,7\],\[6,7\],\[6,7,7\],\[7,7\]\]
**Example 2:**
**Input:** nums = \[4,4,3,2,1\]
**Output:** \[\[4,4\]\]
**Constraints:**
* `1 <= nums.length <= 15`
* `-100 <= nums[i] <= 100` | null |
1 LINER PYTHON AND 3 LINER CPP | construct-the-rectangle | 0 | 1 | ```\nFor 64 : The answer is 8, why? sqrt(64) = 8, so 8 * 8 = 64 and the difference between\n 8 and 8 is the minimum than 2 and 32, 4 and 16.\n\nFor 27 : sqrt(27) = 5.1962, so 5.1962 * 5.1962 = 27 (27.000494 44).\n But we need integer number, so from 5 to 1 the first number which can divide 27\n is the \'W\' in [L,W] and L = area / W.\n From 5 to 1, 3 is the first number which can divide 27. So return [27/3, 3] \n```\n```CPP []\nclass Solution \n{\npublic:\n vector<int> constructRectangle(int area) \n {\n int s = int(sqrt(area));\n while(area % s != 0) s--;\n return {area/s, s};\n }\n};\n```\n```Python []\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n return next( [area//w, w] for w in range(int(area**0.5), 0, -1) if area % w == 0 )\n```\n```\nTime complexity : O(sqrt)\nSpace complexity : O(1)\n```\n## Plz upvote if you liked my solution. Thank You. | 7 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
Python, a simple for loop | construct-the-rectangle | 0 | 1 | ```\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n for l in range(int(area**0.5), 0, -1): \n if area % l == 0: \n return [area // l, l]\n``` | 41 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
492: Space 92.56%, Solution with step by step explanation | construct-the-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Import the math module to use the sqrt() and ceil() functions.\n2. Initialize the width and length of the rectangular web page:\n a. width = int(math.sqrt(area))\n b. length = int(math.ceil(area / width))\n Note: We use the ceiling function to ensure that length >= width\n3. Loop until width * length == area:\n a. If width * length < area, increment length\n b. If width * length > area, decrement width\n4. Return [length, width]\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n # initialize width and length with square root of target area rounded down and up, respectively\n width = int(math.sqrt(area))\n length = int(math.ceil(area / width))\n \n # loop until width and length multiplied is equal to target area\n while width * length != area:\n # if width * length is less than target area, increment length\n if width * length < area:\n length += 1\n # if width * length is greater than target area, decrement width\n else:\n width -= 1\n \n # return [length, width]\n return [length, width]\n\n``` | 6 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
Python code : 48ms : with explanation | construct-the-rectangle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nbasically we are finding the factors of the given area i.e,the length and width\nAlso we need to find the length and breadth pair with least difference between them \n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe are searching for the pairs by going through all the numbers below the square root of the area this makes the code efficeient instead of finding all the factors \nAs the factors repeat themselves after the square root is reached\nThen we find the difference of each pair and return the pair with the least differnece\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n l=[area,1]\n d=l[0]-l[1]\n i=2\n x=0\n while i*i<=area:\n if area%i==0:\n x=area//i\n l=[x,i]\n i+=1\n return l\n\n\n``` | 2 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
[ Python ] Easy Solution | Faster Than 92% Submits | construct-the-rectangle | 0 | 1 | ```\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n \n for i in range(int(area**0.5),0,-1):\n if area % i == 0: return [area//i,i]\n``` | 3 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
1️⃣-liner. 82% faster, 92% less mem. | construct-the-rectangle | 0 | 1 | # Intuition\nLet\'s have fun with python.\nStart with `int(sqrt(area))` as a `w`.\nDecrease until condistion is satisfied.\nAfter that, compress the code to generator so we have a nice hard to debug one-liner.\n\nIf you like it, please up-vote. Thank you!\n\n# Complexity\n- Time complexity: $$O(\\sqrt{n})$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n return next(\n [area//w, w]\n for w in range(int(math.sqrt(area)), 0, -1)\n if area % w == 0)\n\n``` | 1 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
Solution | construct-the-rectangle | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> constructRectangle(int area) {\n int i=1;\n int w=1;\n for(int i=1;i<=area/i;i++){\n if(area%i!=0){continue;}\n if(i>w){w=i;}\n }\n i=i-1;\n return {area/w,w};\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n for i in range(int(sqrt(area)), 0, -1):\n if area % i == 0:\n return [area // i, i]\n```\n\n```Java []\nclass Solution {\n public int[] constructRectangle(int area) {\n int width = (int) Math.sqrt(area);\n\n while (area % width > 0)\n --width;\n\n return new int[] {area / width, width};\n }\n}\n```\n | 3 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
Python Iterative Solution O(sqrt(n)) time, O(n) space complexity beats 90% speed | construct-the-rectangle | 0 | 1 | Upvote once you get it thanks\n```\nimport math\n\'\'\'\n area = 16\n for 1,2...sqrt(16) 5\n 16/1\n 16/2\n 16/3\n 16/4\n ad = {\'1\':\'16\', \'2\':\'8\', \'4\':\'4\'}\n temp = [ float(\'inf\'), float(\'-inf\')]\n for k,v in ad:\n if abs(k-v) < abs(temp[0]-temp[1])\n temp[0], temp[1] = min(k, v), max(k,v)\n return temp\n\'\'\'\nclass Solution:\n def constructRectangle(self, area: int) -> List[int]:\n answer_dict = {}\n temp = [float(\'inf\'), float(\'-inf\')]\n for n in range(1, int(math.sqrt(area))+1):\n if area%n == 0:\n answer_dict[n] = area // n\n for k, v in answer_dict.items():\n if abs(temp[0] - temp[1]) > abs(k-v):\n temp[0], temp[1] = max(k, v), min(k, v)\n return temp\n``` | 2 | A web developer needs to know how to design a web page's size. So, given a specific rectangular web page's area, your job by now is to design a rectangular web page, whose length L and width W satisfy the following requirements:
1. The area of the rectangular web page you designed must equal to the given target area.
2. The width `W` should not be larger than the length `L`, which means `L >= W`.
3. The difference between length `L` and width `W` should be as small as possible.
Return _an array `[L, W]` where `L` and `W` are the length and width of the web page you designed in sequence._
**Example 1:**
**Input:** area = 4
**Output:** \[2,2\]
**Explanation:** The target area is 4, and all the possible ways to construct it are \[1,4\], \[2,2\], \[4,1\].
But according to requirement 2, \[1,4\] is illegal; according to requirement 3, \[4,1\] is not optimal compared to \[2,2\]. So the length L is 2, and the width W is 2.
**Example 2:**
**Input:** area = 37
**Output:** \[37,1\]
**Example 3:**
**Input:** area = 122122
**Output:** \[427,286\]
**Constraints:**
* `1 <= area <= 107` | The W is always less than or equal to the square root of the area, so we start searching at sqrt(area) till we find the result. |
Segment Tree of Sorted Lists (Merge Sort Tree) - Supports Online Queries (ADVANCED) | reverse-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a common query type. The solution I present is overkill, but highly flexible and can be used to solve a lot of questions. Overall, my solution supports queries of this form:\n\n"Find the # of values in a range [l:r] that are lowerBound<=val<=upperBound"\n\nEach query takes log^2N time.\n\nThe intuition for this was just recognizing this common query type and knowing different things segment trees can do. Again, this is not a good solution for this problem in the sense that it is overkill, but it can do more than just the question asks for. The reason is this data structure can arbitararily check any subarray at any time, whereas a more simple solution using SortedList works due to the fact we can process certain queries in order.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a segment tree on the indices of the range, where each node of the ST is a sorted list of elements. We have logN segment tree layers and N nodes in each layer. The construction, space, and time are all n log n.\n\nFor each query, we can query the segment tree and do a binary search on relevant nodes, which is log^2n time. We do this for Q queries, so Q*log^2n + n log n total time.\n\n# Complexity\n- Time complexity:\nQ*log^2n + n log n.\n\n- Space complexity:\nn log n\n\n# Code\n```\nclass SegTree:\n def __init__(self, data):\n self.data = data\n self.n = len(data)\n self.tree = [None] * 4 * self.n\n self._buildRecurse(1, 0, self.n - 1)\n \n def _buildRecurse(self, i, tl, tr):\n # base case\n if tl == tr:\n self.tree[i] = [self.data[tl]]\n return\n \n tm = (tr + tl) // 2\n self._buildRecurse(2*i, tl, tm)\n self._buildRecurse(2*i + 1, tm + 1, tr)\n\n self.tree[i] = self._merge(self.tree[2*i], self.tree[2*i + 1])\n\n # merges two sorted lists\n def _merge(self, a, b):\n newList = []\n i = 0\n j = 0\n while i < len(a) and j < len(b):\n if a[i] <= b[j]:\n newList.append(a[i])\n i += 1\n else:\n newList.append(b[j])\n j += 1\n if i < len(a):\n for k in range(i, len(a)):\n newList.append(a[k])\n if j < len(b):\n for g in range(j, len(b)):\n newList.append(b[g])\n return newList\n\n def _queryRecurse(self, i, tl, tr, l, r, lowerValBound, upperValBound):\n # if we have no intersection on the numbers return an identity value\n if tl > r or tr < l:\n return 0\n \n # if we are fully contained\n if tl >= l and tr <= r:\n bucket = self.tree[i]\n return bisect.bisect_right(bucket, upperValBound) - bisect.bisect_left(bucket, lowerValBound)\n \n tm = (tr + tl) // 2\n return self._queryRecurse(2*i, tl, tm, l, r, lowerValBound, upperValBound) + self._queryRecurse(2*i + 1, tm + 1, tr, l, r, lowerValBound, upperValBound)\n\n def query(self, l, r, lowerBound, upperBound):\n return self._queryRecurse(1, 0, self.n - 1, l, r, lowerBound, upperBound)\n\n\nclass Solution:\n def reversePairs(self, nums: List[int]) -> int:\n seg = SegTree(nums)\n res = 0\n for i in range(len(nums)):\n leftIndex = 0\n rightIndex = i - 1\n lowerBound = nums[i] * 2 + 1\n upperBound = 2**31 - 1\n res += seg.query(leftIndex, rightIndex, lowerBound, upperBound)\n return res\n``` | 0 | Given an integer array `nums`, return _the number of **reverse pairs** in the array_.
A **reverse pair** is a pair `(i, j)` where:
* `0 <= i < j < nums.length` and
* `nums[i] > 2 * nums[j]`.
**Example 1:**
**Input:** nums = \[1,3,2,3,1\]
**Output:** 2
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 3, nums\[4\] = 1, 3 > 2 \* 1
**Example 2:**
**Input:** nums = \[2,4,3,5,1\]
**Output:** 3
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 4, nums\[4\] = 1, 4 > 2 \* 1
(2, 4) --> nums\[2\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 5, nums\[4\] = 1, 5 > 2 \* 1
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-231 <= nums[i] <= 231 - 1` | null |
simple N^2 | reverse-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reversePairs(self, nums: List[int]) -> int:\n \n\n \n\n N = len(nums)\n tot = 0\n sorted_right_side = [nums[-1]*2]\n for j in range(N-2,-1,-1):\n\n n = nums[j]\n # count of numbers that are < 2 * n\n tot += bisect.bisect_left(sorted_right_side,n)\n\n bisect.insort(sorted_right_side, n*2)\n\n\n return tot\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n\n\n\n\n\n``` | 1 | Given an integer array `nums`, return _the number of **reverse pairs** in the array_.
A **reverse pair** is a pair `(i, j)` where:
* `0 <= i < j < nums.length` and
* `nums[i] > 2 * nums[j]`.
**Example 1:**
**Input:** nums = \[1,3,2,3,1\]
**Output:** 2
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 3, nums\[4\] = 1, 3 > 2 \* 1
**Example 2:**
**Input:** nums = \[2,4,3,5,1\]
**Output:** 3
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 4, nums\[4\] = 1, 4 > 2 \* 1
(2, 4) --> nums\[2\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 5, nums\[4\] = 1, 5 > 2 \* 1
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-231 <= nums[i] <= 231 - 1` | null |
493: Solution with step by step explanation | reverse-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a class Solution with a method reversePairs.\n2. Within the reversePairs method, define a function merge_sort which takes in the starting and ending indices of a subarray and returns the count of reverse pairs within that subarray.\n3. If the start index is greater than or equal to the end index, return 0 as there are no reverse pairs in a subarray of length 0 or 1.\n4. Find the middle index of the subarray and recursively call merge_sort on the left and right halves of the subarray. Add the results of these recursive calls to count.\n5. Initialize two pointers i and j to the start of the left and right halves, respectively. While both pointers are within their respective halves, compare the values at i and j. If the value at i is greater than twice the value at j, then increment count by the number of remaining elements in the left half (from i to mid). Increment j to move to the next element in the right half. Otherwise, increment i to move to the next element in the left half.\n6. After counting the reverse pairs, merge the left and right halves of the subarray in sorted order.\n7. Return count after all recursive calls have completed.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reversePairs(self, nums: List[int]) -> int:\n def merge_sort(start: int, end: int) -> int:\n if start >= end:\n return 0\n mid = (start + end) // 2\n count = merge_sort(start, mid) + merge_sort(mid + 1, end)\n\n # Count the number of reverse pairs between two sorted halves\n i = start\n j = mid + 1\n while i <= mid and j <= end:\n if nums[i] > 2 * nums[j]:\n count += mid - i + 1\n j += 1\n else:\n i += 1\n\n # Merge two sorted halves\n nums[start:end + 1] = sorted(nums[start:end + 1])\n\n return count\n\n return merge_sort(0, len(nums) - 1)\n\n``` | 10 | Given an integer array `nums`, return _the number of **reverse pairs** in the array_.
A **reverse pair** is a pair `(i, j)` where:
* `0 <= i < j < nums.length` and
* `nums[i] > 2 * nums[j]`.
**Example 1:**
**Input:** nums = \[1,3,2,3,1\]
**Output:** 2
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 3, nums\[4\] = 1, 3 > 2 \* 1
**Example 2:**
**Input:** nums = \[2,4,3,5,1\]
**Output:** 3
**Explanation:** The reverse pairs are:
(1, 4) --> nums\[1\] = 4, nums\[4\] = 1, 4 > 2 \* 1
(2, 4) --> nums\[2\] = 3, nums\[4\] = 1, 3 > 2 \* 1
(3, 4) --> nums\[3\] = 5, nums\[4\] = 1, 5 > 2 \* 1
**Constraints:**
* `1 <= nums.length <= 5 * 104`
* `-231 <= nums[i] <= 231 - 1` | null |
DP || MEMOIZATION ||EASY | target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTargetSumWays(self, nums: List[int], target: int) -> int:\n cache={}\n def dfs(i,k): \n if (i,k) in cache:\n return cache[(i,k)]\n if i == len(nums):\n if k == target:\n cache[(i,k)]=1\n return 1 \n cache[(i,k)]=0\n return 0 \n positive = dfs(i+1, k+ nums[i])\n negative = dfs(i+1, k - nums[i])\n cache[(i,k)]=positive + negative \n return positive + negative \n return dfs(0,0)\n``` | 1 | You are given an integer array `nums` and an integer `target`.
You want to build an **expression** out of nums by adding one of the symbols `'+'` and `'-'` before each integer in nums and then concatenate all the integers.
* For example, if `nums = [2, 1]`, you can add a `'+'` before `2` and a `'-'` before `1` and concatenate them to build the expression `"+2-1 "`.
Return the number of different **expressions** that you can build, which evaluates to `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 3
**Output:** 5
**Explanation:** There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
**Example 2:**
**Input:** nums = \[1\], target = 1
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 1000`
* `0 <= sum(nums[i]) <= 1000`
* `-1000 <= target <= 1000` | null |
TABULATION SOLUTION | target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dp(self,i,nums,tr,dct):\n if tr==0:\n return 1\n if i==0:\n if tr-nums[i]==0:\n return 1\n return 0\n if (i,tr) in dct:\n return dct[(i,tr)]\n x=self.dp(i-1,nums,tr-nums[i],dct)\n y=self.dp(i-1,nums,tr,dct)\n dct[(i,tr)]=x+y\n return dct[(i,tr)]\n\n\n def findTargetSumWays(self, nums: List[int], target: int) -> int:\n sm=sum(nums)\n n=len(nums)\n if target>sm:\n return 0\n if (sm-target)%2:\n return 0\n tr=(sm-target)//2\n nums.sort()\n dp=[[0]*(tr+1) for i in range(n)]\n for i in range(n):\n dp[i][0]=1\n if nums[0]<=tr:\n dp[0][nums[0]]=1\n for i in range(1,n):\n for j in range(tr+1):\n x=0\n if nums[i]<=j:\n x=dp[i-1][j-nums[i]]\n y=dp[i-1][j]\n dp[i][j]=x+y\n zero=nums.count(0)\n if zero:\n return dp[-1][tr]*2\n return dp[-1][tr]\n # return self.dp(n-1,nums,tr,{})*(2**zero)\n\n``` | 1 | You are given an integer array `nums` and an integer `target`.
You want to build an **expression** out of nums by adding one of the symbols `'+'` and `'-'` before each integer in nums and then concatenate all the integers.
* For example, if `nums = [2, 1]`, you can add a `'+'` before `2` and a `'-'` before `1` and concatenate them to build the expression `"+2-1 "`.
Return the number of different **expressions** that you can build, which evaluates to `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 3
**Output:** 5
**Explanation:** There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
**Example 2:**
**Input:** nums = \[1\], target = 1
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 1000`
* `0 <= sum(nums[i]) <= 1000`
* `-1000 <= target <= 1000` | null |
Python | DP | Top-Down | Memoization | target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n0/1 Knapsack Problem, for each number, either we can use it\'s negative value, or it\'s positive value. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use recursion with memoization (Top-Down DP) to solve.\n- At each `i`, we either take and add to `curr`\n - negative value of `nums[i]`.\n - positive value of `nums[i]`.\n- Store the result in `cache` for `O(1)` access to prevent recomptues.\n- `cache(i, curr)` is the number of ways starting from `i` and value of `curr`, so we use `dp(0, 0)` to obtain the total ways.\n\n# Complexity\n- Time complexity: `O(M*N)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(M*N)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTargetSumWays(self, nums: List[int], target: int) -> int:\n n = len(nums)\n cache = {}\n \n def dp(i, curr):\n if (i, curr) in cache:\n return cache[(i, curr)]\n if i == n:\n return int(curr == target)\n \n cache[(i,curr)] = dp(i+1, curr + nums[i]) + dp(i+1, curr - nums[i])\n return cache[(i, curr)]\n \n return dp(0, 0)\n``` | 2 | You are given an integer array `nums` and an integer `target`.
You want to build an **expression** out of nums by adding one of the symbols `'+'` and `'-'` before each integer in nums and then concatenate all the integers.
* For example, if `nums = [2, 1]`, you can add a `'+'` before `2` and a `'-'` before `1` and concatenate them to build the expression `"+2-1 "`.
Return the number of different **expressions** that you can build, which evaluates to `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 3
**Output:** 5
**Explanation:** There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
**Example 2:**
**Input:** nums = \[1\], target = 1
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 1000`
* `0 <= sum(nums[i]) <= 1000`
* `-1000 <= target <= 1000` | null |
494: Time 92.20% and Space 96.14%, Solution with step by step explanation | target-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Calculate the sum of all elements in the input list.\n2. Check if the target sum is greater than the sum of all elements in the input list or if the absolute difference between the target sum and the sum of all elements is odd. If either of these conditions is true, return 0, as there is no way to form the target sum by adding or subtracting elements from the input list.\n3. Define a function called knapsack that takes an integer target as its argument and returns an integer.\n4. Create a list called dp with a length equal to the sum of all elements in the input list plus one, where the first element is initialized to 1 and the rest are initialized to 0. This list will be used to keep track of the number of ways to sum up to each possible target.\n5. For each element in the input list, iterate backwards through the dp list from the end to the current element (inclusive), so that the dp values for the current element are only based on the previous elements in the list, and not the current element or any elements after it.\n6. Add the dp value for the previous element at the current index, j - num, to the dp value for the current index, j. This is because there are dp[j - num] ways to sum up to the target using all elements up to and including the current element, and we\'re adding those ways to the existing ways to sum up to the target using all elements up to but not including the current element.\n7. Return the dp value for the target sum.\n8. Call the knapsack function with the target sum divided by 2, because we\'re counting the number of ways to form the target sum using addition and subtraction, and the two operations can cancel each other out, meaning that the target sum can only be achieved if it\'s an even number.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTargetSumWays(self, nums: List[int], target: int) -> int:\n # Calculate the sum of all elements in the input list\n summ = sum(nums)\n # If the target is greater than the sum of all elements or their absolute difference is odd,\n # there\'s no way to form the target sum by adding or subtracting elements from the input list.\n if summ < abs(target) or (summ + target) & 1:\n return 0\n\n def knapsack(target: int) -> int:\n # Create a list with a length equal to the sum of all elements in the input list plus one,\n # where the first element is initialized to 1 and the rest are initialized to 0.\n # This list will be used to keep track of the number of ways to sum up to each possible target.\n dp = [1] + [0] * summ\n\n # For each element in the input list,\n for num in nums:\n # Iterate backwards through the dp list from the end to the current element (inclusive),\n # so that the dp values for the current element are only based on the previous elements\n # in the list, and not the current element or any elements after it.\n for j in range(summ, num - 1, -1):\n # Add the dp value for the previous element at the current index, j - num,\n # to the dp value for the current index, j.\n # This is because there are dp[j - num] ways to sum up to the target using all elements\n # up to and including the current element, and we\'re adding those ways to the existing ways\n # to sum up to the target using all elements up to but not including the current element.\n dp[j] += dp[j - num]\n\n # Return the dp value for the target sum.\n return dp[target]\n\n # Call the knapsack function with the target sum divided by 2, because we\'re counting the number\n # of ways to form the target sum using addition and subtraction, and the two operations can cancel\n # each other out, meaning that the target sum can only be achieved if it\'s an even number.\n return knapsack((summ + target) // 2)\n\n``` | 10 | You are given an integer array `nums` and an integer `target`.
You want to build an **expression** out of nums by adding one of the symbols `'+'` and `'-'` before each integer in nums and then concatenate all the integers.
* For example, if `nums = [2, 1]`, you can add a `'+'` before `2` and a `'-'` before `1` and concatenate them to build the expression `"+2-1 "`.
Return the number of different **expressions** that you can build, which evaluates to `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 3
**Output:** 5
**Explanation:** There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
**Example 2:**
**Input:** nums = \[1\], target = 1
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 1000`
* `0 <= sum(nums[i]) <= 1000`
* `-1000 <= target <= 1000` | null |
Python easy to understand: building tree top-down | target-sum | 0 | 1 | # Intuition\n\nOriginally I built the whole tree of 2^n nodes, then returned the number of leafs who equaled target. This involves possibly redundant calculations, since at some layers we have may multiple nodes with the same value. \n\nWe can\'t just remove duplicates, i.e. by having `next_vals` be a set, as the total number of paths is of interest. Rather, at each layer we\'re building, we must memoize the number of new nodes of some value (in `running_count`). If we don\'t see a value, the query returns 0 (second argument of `.get()`).\n\n# Code\n```\nclass Solution:\n def findTargetSumWays(self, nums: List[int], target: int) -> int:\n if not nums: return 0\n\n q=set([0]) # 0-root\n running_count = { 0: 1 }\n\n # build \'binary\' tree\n while nums:\n n=nums.pop(0) \n \n next_vals_cnt = defaultdict(int)\n next_vals = set()\n\n while(q): # constructing a row\n val = q.pop()\n l,r=val+n,val-n\n next_vals.update([l,r])\n next_vals_cnt[l] += running_count[val]\n next_vals_cnt[r] += running_count[val]\n\n running_count = next_vals_cnt\n q = next_vals\n\n\n # return leafs whom equal target\n return running_count.get(target,0)\n``` | 2 | You are given an integer array `nums` and an integer `target`.
You want to build an **expression** out of nums by adding one of the symbols `'+'` and `'-'` before each integer in nums and then concatenate all the integers.
* For example, if `nums = [2, 1]`, you can add a `'+'` before `2` and a `'-'` before `1` and concatenate them to build the expression `"+2-1 "`.
Return the number of different **expressions** that you can build, which evaluates to `target`.
**Example 1:**
**Input:** nums = \[1,1,1,1,1\], target = 3
**Output:** 5
**Explanation:** There are 5 ways to assign symbols to make the sum of nums be target 3.
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
**Example 2:**
**Input:** nums = \[1\], target = 1
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 20`
* `0 <= nums[i] <= 1000`
* `0 <= sum(nums[i]) <= 1000`
* `-1000 <= target <= 1000` | null |
Simple Understandable Python Code | teemo-attacking | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:\n total = 0\n l = len(timeSeries)\n for i in range(l):\n \n if i < l - 1:\n\n if timeSeries[i] + duration - 1 < timeSeries[i+1]:\n total += duration\n \n else:\n total += timeSeries[i+1] - timeSeries[i]\n \n else:\n total += duration\n \n return total\n``` | 2 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
Python Easy Solution | teemo-attacking | 0 | 1 | # Code\n```\nclass Solution:\n def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:\n tot=0\n for i in range(len(timeSeries)-1):\n if timeSeries[i+1]-timeSeries[i]>duration:\n tot+=duration\n else:\n tot+=timeSeries[i+1]-timeSeries[i]\n return tot+duration\n``` | 1 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
Easy approach|| O(n) | teemo-attacking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:\n count=0\n for i in range(len(timeSeries)):\n if(i<len(timeSeries)-1):\n if(timeSeries[i]+duration-1<timeSeries[i+1]):\n count+=duration\n elif(timeSeries[i]+duration-1==timeSeries[i+1]):\n count+=timeSeries[i+1]-timeSeries[i]\n else:\n count+=timeSeries[i+1]-timeSeries[i]\n else:\n count+=duration\n return(count)\n\n``` | 3 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
495: Solution with step by step explanation | teemo-attacking | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Begin by defining a function findPoisonedDuration that takes in two arguments - a list timeSeries containing non-decreasing integers and an integer duration.\n\n2. Check if the list timeSeries is empty. If it is, return 0 as there are no poison attacks.\n\n3. Get the length of the list timeSeries and initialize a variable poisoned_time to 0.\n\n4. Iterate through the list timeSeries from index 0 to n-2, where n is the length of timeSeries.\n\n5. At each iteration, calculate the duration of the poison effect by finding the minimum value between duration and the difference between the next and current element in the list.\n\n6. Add the calculated duration of the poison effect to the poisoned_time variable.\n\n7. Once the loop is completed, add the duration of the last poison effect to the poisoned_time variable.\n\n8. Return the value of poisoned_time.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:\n if not timeSeries:\n return 0\n n = len(timeSeries)\n poisoned_time = 0\n \n for i in range(n-1):\n # calculate the duration of the poison effect\n duration_of_effect = min(duration, timeSeries[i+1]-timeSeries[i])\n poisoned_time += duration_of_effect\n \n # add the duration of the last poison effect\n poisoned_time += duration\n \n return poisoned_time\n\n``` | 9 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
✅✅✅ 1-line solution | teemo-attacking | 0 | 1 | \n```\nclass Solution:\n def findPoisonedDuration(self, t: List[int], d: int) -> int:\n return d+sum(min(t[i+1]-t[i], d) for i in range(len(t)-1))\n``` | 9 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
Python 6 lines O(n) concise solution | teemo-attacking | 0 | 1 | The answer is the length of timeSeries multiply the duration with minus the repeat duration.\nRuntime beats 94% and memory usage beats 80% of python solutions.\n\n\n```\nclass Solution(object):\n def findPoisonedDuration(self, timeSeries, duration):\n repeat = 0\n for i in range(len(timeSeries)-1):\n diff = timeSeries[i+1] - timeSeries[i]\n if diff < duration:\n repeat += duration - diff\n return len(timeSeries)*duration - repeat\n``` | 10 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
Python fast solution (beats 99%!) | teemo-attacking | 0 | 1 | ```\nclass Solution:\n def findPoisonedDuration(self, timeSeries: List[int], duration: int) -> int:\n time_under_poison = 0\n last_time = timeSeries[0]\n \n for time in timeSeries[1:]:\n if last_time + duration - 1 < time:\n time_under_poison += duration\n\n else:\n time_under_poison += time-last_time\n\n last_time = time\n\n time_under_poison += duration\n\n return time_under_poison\n\n``` | 1 | Our hero Teemo is attacking an enemy Ashe with poison attacks! When Teemo attacks Ashe, Ashe gets poisoned for a exactly `duration` seconds. More formally, an attack at second `t` will mean Ashe is poisoned during the **inclusive** time interval `[t, t + duration - 1]`. If Teemo attacks again **before** the poison effect ends, the timer for it is **reset**, and the poison effect will end `duration` seconds after the new attack.
You are given a **non-decreasing** integer array `timeSeries`, where `timeSeries[i]` denotes that Teemo attacks Ashe at second `timeSeries[i]`, and an integer `duration`.
Return _the **total** number of seconds that Ashe is poisoned_.
**Example 1:**
**Input:** timeSeries = \[1,4\], duration = 2
**Output:** 4
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 4, Teemo attacks, and Ashe is poisoned for seconds 4 and 5.
Ashe is poisoned for seconds 1, 2, 4, and 5, which is 4 seconds in total.
**Example 2:**
**Input:** timeSeries = \[1,2\], duration = 2
**Output:** 3
**Explanation:** Teemo's attacks on Ashe go as follows:
- At second 1, Teemo attacks, and Ashe is poisoned for seconds 1 and 2.
- At second 2 however, Teemo attacks again and resets the poison timer. Ashe is poisoned for seconds 2 and 3.
Ashe is poisoned for seconds 1, 2, and 3, which is 3 seconds in total.
**Constraints:**
* `1 <= timeSeries.length <= 104`
* `0 <= timeSeries[i], duration <= 107`
* `timeSeries` is sorted in **non-decreasing** order. | null |
Easy Understandable Python Code | next-greater-element-i | 0 | 1 | \n\n# Approach\n- First search for ```nums1[i] == nums2[j]``` from ```nums1``` and ```nums2```\n- Then take another loop from ```nums2[j+1]``` to ```end```\n- - if next greater element is present append it\n- - else append -1\n\n\n# Code\n```\nclass Solution:\n def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:\n ans = []\n for i in range(0,len(nums1)):\n \n for j in range(0,len(nums2)):\n \n flag,val = 1,0\n if nums1[i]==nums2[j]:\n val = nums2[j]\n \n for k in range(j+1,len(nums2)):\n if nums2[k] > val:\n ans.append(nums2[k])\n flag = 0\n break\n \n if flag == 1:\n ans.append(-1)\n return ans\n``` | 2 | The **next greater element** of some element `x` in an array is the **first greater** element that is **to the right** of `x` in the same array.
You are given two **distinct 0-indexed** integer arrays `nums1` and `nums2`, where `nums1` is a subset of `nums2`.
For each `0 <= i < nums1.length`, find the index `j` such that `nums1[i] == nums2[j]` and determine the **next greater element** of `nums2[j]` in `nums2`. If there is no next greater element, then the answer for this query is `-1`.
Return _an array_ `ans` _of length_ `nums1.length` _such that_ `ans[i]` _is the **next greater element** as described above._
**Example 1:**
**Input:** nums1 = \[4,1,2\], nums2 = \[1,3,4,2\]
**Output:** \[-1,3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = \[1,3,4,2\]. The next greater element is 3.
- 2 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
**Example 2:**
**Input:** nums1 = \[2,4\], nums2 = \[1,2,3,4\]
**Output:** \[3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = \[1,2,3,4\]. The next greater element is 3.
- 4 is underlined in nums2 = \[1,2,3,4\]. There is no next greater element, so the answer is -1.
**Constraints:**
* `1 <= nums1.length <= nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 104`
* All integers in `nums1` and `nums2` are **unique**.
* All the integers of `nums1` also appear in `nums2`.
**Follow up:** Could you find an `O(nums1.length + nums2.length)` solution? | null |
Python 3 -> 94.64% faster. Used stack and dictionary. Explanation added | next-greater-element-i | 0 | 1 | **Suggestions to make it better are always welcomed.**\n\nBasically the problem says, if in nums1 we are working on 4, then in nums2 first find where is 4 and from that index find the next number greater than 4 in nums2. We can see that the solution is always coming from the reverse side of the list nums2. This should tell us to use stack.\n\nSteps:\n1. We traverse nums2 and start storing elements on the top of stack.\n2. If current number is greater than the top of the stack, then we found a pair. Keep popping from stack till the top of stack is smaller than current number.\n3. After matching pairs are found, push current number on top of stack.\n4. Eventually when there are no more elements in nums2 to traverse, but there are elements in stack, we can justify that next bigger element wasn\'t found for them. Hence we\'ll put -1 for the remaining elements in stack.\n\n```\ndef nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:\n\tif not nums2:\n\t\treturn None\n\n\tmapping = {}\n\tresult = []\n\tstack = []\n\tstack.append(nums2[0])\n\n\tfor i in range(1, len(nums2)):\n\t\twhile stack and nums2[i] > stack[-1]: # if stack is not empty, then compare it\'s last element with nums2[i]\n\t\t\tmapping[stack[-1]] = nums2[i] # if the new element is greater than stack\'s top element, then add this to dictionary \n\t\t\tstack.pop() # since we found a pair for the top element, remove it.\n\t\tstack.append(nums2[i]) # add the element nums2[i] to the stack because we need to find a number greater than this\n\n\tfor element in stack: # if there are elements in the stack for which we didn\'t find a greater number, map them to -1\n\t\tmapping[element] = -1\n\n\tfor i in range(len(nums1)):\n\t\tresult.append(mapping[nums1[i]])\n\treturn result\n```\n\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 253 | The **next greater element** of some element `x` in an array is the **first greater** element that is **to the right** of `x` in the same array.
You are given two **distinct 0-indexed** integer arrays `nums1` and `nums2`, where `nums1` is a subset of `nums2`.
For each `0 <= i < nums1.length`, find the index `j` such that `nums1[i] == nums2[j]` and determine the **next greater element** of `nums2[j]` in `nums2`. If there is no next greater element, then the answer for this query is `-1`.
Return _an array_ `ans` _of length_ `nums1.length` _such that_ `ans[i]` _is the **next greater element** as described above._
**Example 1:**
**Input:** nums1 = \[4,1,2\], nums2 = \[1,3,4,2\]
**Output:** \[-1,3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = \[1,3,4,2\]. The next greater element is 3.
- 2 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
**Example 2:**
**Input:** nums1 = \[2,4\], nums2 = \[1,2,3,4\]
**Output:** \[3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = \[1,2,3,4\]. The next greater element is 3.
- 4 is underlined in nums2 = \[1,2,3,4\]. There is no next greater element, so the answer is -1.
**Constraints:**
* `1 <= nums1.length <= nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 104`
* All integers in `nums1` and `nums2` are **unique**.
* All the integers of `nums1` also appear in `nums2`.
**Follow up:** Could you find an `O(nums1.length + nums2.length)` solution? | null |
Python || Easy || Stack || Dictionary | next-greater-element-i | 0 | 1 | ```\nclass Solution:\n def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:\n d={}\n n=len(nums2)\n for i in range(n):\n d[nums2[i]]=i\n a=[nums2[-1]]\n answer=[-1]\n for i in range(n-2,-1,-1):\n if a[-1]>nums2[i]:\n answer.append(a[-1])\n else:\n while len(a)>0:\n if a[-1]>nums2[i]:\n answer.append(a[-1])\n break\n else:\n a.pop()\n if len(a)==0:\n answer.append(-1)\n a.append(nums2[i])\n res=[]\n answer=answer[-1::-1]\n for i in nums1:\n res.append(answer[d[i]])\n return res\n```\n**An upvote will be encouraging** | 2 | The **next greater element** of some element `x` in an array is the **first greater** element that is **to the right** of `x` in the same array.
You are given two **distinct 0-indexed** integer arrays `nums1` and `nums2`, where `nums1` is a subset of `nums2`.
For each `0 <= i < nums1.length`, find the index `j` such that `nums1[i] == nums2[j]` and determine the **next greater element** of `nums2[j]` in `nums2`. If there is no next greater element, then the answer for this query is `-1`.
Return _an array_ `ans` _of length_ `nums1.length` _such that_ `ans[i]` _is the **next greater element** as described above._
**Example 1:**
**Input:** nums1 = \[4,1,2\], nums2 = \[1,3,4,2\]
**Output:** \[-1,3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = \[1,3,4,2\]. The next greater element is 3.
- 2 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
**Example 2:**
**Input:** nums1 = \[2,4\], nums2 = \[1,2,3,4\]
**Output:** \[3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = \[1,2,3,4\]. The next greater element is 3.
- 4 is underlined in nums2 = \[1,2,3,4\]. There is no next greater element, so the answer is -1.
**Constraints:**
* `1 <= nums1.length <= nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 104`
* All integers in `nums1` and `nums2` are **unique**.
* All the integers of `nums1` also appear in `nums2`.
**Follow up:** Could you find an `O(nums1.length + nums2.length)` solution? | null |
Python3 || without using stack. | next-greater-element-i | 0 | 1 | # Code\n```\nclass Solution:\n def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:\n final_list = []\n l = []\n for i in nums1:\n for j in range(len(nums2)):\n if i == nums2[j]:\n s=0\n for k in nums2[j+1:]:\n if k > i:\n s=k\n break\n if not s:\n l.append(-1)\n else:l.append(k) \n return l[:len(nums1)] \n```\n**Please upvote if you find the solution helpful and comment if you can improve the code.** | 3 | The **next greater element** of some element `x` in an array is the **first greater** element that is **to the right** of `x` in the same array.
You are given two **distinct 0-indexed** integer arrays `nums1` and `nums2`, where `nums1` is a subset of `nums2`.
For each `0 <= i < nums1.length`, find the index `j` such that `nums1[i] == nums2[j]` and determine the **next greater element** of `nums2[j]` in `nums2`. If there is no next greater element, then the answer for this query is `-1`.
Return _an array_ `ans` _of length_ `nums1.length` _such that_ `ans[i]` _is the **next greater element** as described above._
**Example 1:**
**Input:** nums1 = \[4,1,2\], nums2 = \[1,3,4,2\]
**Output:** \[-1,3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = \[1,3,4,2\]. The next greater element is 3.
- 2 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
**Example 2:**
**Input:** nums1 = \[2,4\], nums2 = \[1,2,3,4\]
**Output:** \[3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = \[1,2,3,4\]. The next greater element is 3.
- 4 is underlined in nums2 = \[1,2,3,4\]. There is no next greater element, so the answer is -1.
**Constraints:**
* `1 <= nums1.length <= nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 104`
* All integers in `nums1` and `nums2` are **unique**.
* All the integers of `nums1` also appear in `nums2`.
**Follow up:** Could you find an `O(nums1.length + nums2.length)` solution? | null |
Solution | next-greater-element-i | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {\n int x=nums1.size();\n int y=nums2.size();\n vector<int> res;\n for(int i=0;i<x;i++)\n {\n auto it = find(nums2.begin(),nums2.end(),nums1[i]);\n\n int index = it - nums2.begin(); \n int var = -1;\n\n for(int j = index+1; j<y;j++)\n {\n if(nums2[j] > nums2[index])\n {\n var = nums2[j];\n break;\n }\n \n }\n res.push_back(var);\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:\n st = []\n dict = {}\n \n for num in nums2:\n while len(st) != 0 and num > st[-1]:\n dict[st[-1]] = num\n st.pop()\n st.append(num)\n \n while len(st) != 0:\n dict[st[-1]] = -1\n st.pop()\n \n res = [0] * len(nums1)\n for i in range(len(nums1)):\n res[i] = dict[nums1[i]]\n \n return res\n```\n\n```Java []\nclass Solution {\n public int[] nextGreaterElement(int[] nums1, int[] nums2) {\n int[] ind = new int[10000];\n int[] max = new int[nums2.length];\n int pointer = 0;\n \n for (int i = 0; i < nums1.length; i++) {\n ind[nums1[i]] = i + 1;\n }\n int[] res = new int[nums1.length];\n for (int i = nums2.length - 1; i >= 0; i--) {\n int num = nums2[i];\n while (pointer > 0 && max[pointer - 1] < num) {\n pointer--;\n }\n if (ind[num] > 0) {\n res[ind[num] - 1] = pointer == 0 ? -1 : max[pointer - 1];\n }\n max[pointer++] = num;\n }\n return res;\n }\n}\n```\n | 1 | The **next greater element** of some element `x` in an array is the **first greater** element that is **to the right** of `x` in the same array.
You are given two **distinct 0-indexed** integer arrays `nums1` and `nums2`, where `nums1` is a subset of `nums2`.
For each `0 <= i < nums1.length`, find the index `j` such that `nums1[i] == nums2[j]` and determine the **next greater element** of `nums2[j]` in `nums2`. If there is no next greater element, then the answer for this query is `-1`.
Return _an array_ `ans` _of length_ `nums1.length` _such that_ `ans[i]` _is the **next greater element** as described above._
**Example 1:**
**Input:** nums1 = \[4,1,2\], nums2 = \[1,3,4,2\]
**Output:** \[-1,3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 4 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
- 1 is underlined in nums2 = \[1,3,4,2\]. The next greater element is 3.
- 2 is underlined in nums2 = \[1,3,4,2\]. There is no next greater element, so the answer is -1.
**Example 2:**
**Input:** nums1 = \[2,4\], nums2 = \[1,2,3,4\]
**Output:** \[3,-1\]
**Explanation:** The next greater element for each value of nums1 is as follows:
- 2 is underlined in nums2 = \[1,2,3,4\]. The next greater element is 3.
- 4 is underlined in nums2 = \[1,2,3,4\]. There is no next greater element, so the answer is -1.
**Constraints:**
* `1 <= nums1.length <= nums2.length <= 1000`
* `0 <= nums1[i], nums2[i] <= 104`
* All integers in `nums1` and `nums2` are **unique**.
* All the integers of `nums1` also appear in `nums2`.
**Follow up:** Could you find an `O(nums1.length + nums2.length)` solution? | null |
Solution | random-point-in-non-overlapping-rectangles | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> r;\n vector<int> acc;\n Solution(vector<vector<int>>& rects){\n\n std::ios_base::sync_with_stdio(false);\n cin.tie(0);\n\n r = rects;\n int len = rects.size();\n acc = vector<int>(len, 0);\n\n for(int i = 0; i < len; i++){\n const vector<int> &v = rects[i];\n acc[i] = ( i==0 ? 0: acc[i-1]) + (v[2] - v[0] + 1)*(v[3]-v[1]+1);\n }\n srand((unsigned)time(NULL));\n }\n vector<int> pick() {\n int target = rand()%acc.back();\n\n int start = 0;\n int end = acc.size();\n while (start < end){\n int mid = (start+end)/2;\n int mval = acc[mid];\n if (target == mval){\n start = mid + 1;\n break;\n }\n else if (target > mval){\n start = mid + 1;\n }\n else{\n end = mid;\n }\n }\n const vector<int> &v = r[start];\n int dx = v[2] - v[0] + 1;\n int x = v[0] + rand()%dx;\n int dy = v[3] - v[1] + 1;\n int y = v[1] + rand()%dy;\n return {x,y};\n }\n};\n```\n\n```Python3 []\nfrom typing import Generator\n\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self._rects = rects\n self._pg = self._pick_generator()\n \n def _pick_generator(self) -> Generator[List[int], None, None]:\n for a, b, x, y in self._rects:\n for i in range (a, x+1):\n for j in range (b, y+1):\n yield [i, j]\n\n def pick(self) -> List[int]:\n try:\n return next(self._pg)\n except StopIteration:\n self._pg = self._pick_generator()\n return next(self._pg)\n```\n\n```Java []\nclass Solution {\n public Solution(int[][] rects) {\n this.rects = rects;\n areas = new int[rects.length];\n for (int i = 0; i < rects.length; ++i)\n areas[i] = getArea(rects[i]) + (i > 0 ? areas[i - 1] : 0);\n }\n public int[] pick() {\n final int target = rand.nextInt(areas[areas.length - 1]);\n final int index = firstGreater(areas, target);\n final int[] r = rects[index];\n return new int[] {\n rand.nextInt(r[2] - r[0] + 1) + r[0],\n rand.nextInt(r[3] - r[1] + 1) + r[1],\n };\n }\n private int[][] rects;\n private int[] areas;\n private Random rand = new Random();\n\n private int getArea(int[] r) {\n return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n }\n private int firstGreater(int[] areas, int target) {\n int l = 0;\n int r = areas.length;\n while (l < r) {\n final int m = (l + r) / 2;\n if (areas[m] > target)\n r = m;\n else\n l = m + 1;\n }\n return l;\n }\n}\n```\n | 1 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Solution | random-point-in-non-overlapping-rectangles | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> r;\n vector<int> acc;\n Solution(vector<vector<int>>& rects){\n\n std::ios_base::sync_with_stdio(false);\n cin.tie(0);\n\n r = rects;\n int len = rects.size();\n acc = vector<int>(len, 0);\n\n for(int i = 0; i < len; i++){\n const vector<int> &v = rects[i];\n acc[i] = ( i==0 ? 0: acc[i-1]) + (v[2] - v[0] + 1)*(v[3]-v[1]+1);\n }\n srand((unsigned)time(NULL));\n }\n vector<int> pick() {\n int target = rand()%acc.back();\n\n int start = 0;\n int end = acc.size();\n while (start < end){\n int mid = (start+end)/2;\n int mval = acc[mid];\n if (target == mval){\n start = mid + 1;\n break;\n }\n else if (target > mval){\n start = mid + 1;\n }\n else{\n end = mid;\n }\n }\n const vector<int> &v = r[start];\n int dx = v[2] - v[0] + 1;\n int x = v[0] + rand()%dx;\n int dy = v[3] - v[1] + 1;\n int y = v[1] + rand()%dy;\n return {x,y};\n }\n};\n```\n\n```Python3 []\nfrom typing import Generator\n\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self._rects = rects\n self._pg = self._pick_generator()\n \n def _pick_generator(self) -> Generator[List[int], None, None]:\n for a, b, x, y in self._rects:\n for i in range (a, x+1):\n for j in range (b, y+1):\n yield [i, j]\n\n def pick(self) -> List[int]:\n try:\n return next(self._pg)\n except StopIteration:\n self._pg = self._pick_generator()\n return next(self._pg)\n```\n\n```Java []\nclass Solution {\n public Solution(int[][] rects) {\n this.rects = rects;\n areas = new int[rects.length];\n for (int i = 0; i < rects.length; ++i)\n areas[i] = getArea(rects[i]) + (i > 0 ? areas[i - 1] : 0);\n }\n public int[] pick() {\n final int target = rand.nextInt(areas[areas.length - 1]);\n final int index = firstGreater(areas, target);\n final int[] r = rects[index];\n return new int[] {\n rand.nextInt(r[2] - r[0] + 1) + r[0],\n rand.nextInt(r[3] - r[1] + 1) + r[1],\n };\n }\n private int[][] rects;\n private int[] areas;\n private Random rand = new Random();\n\n private int getArea(int[] r) {\n return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n }\n private int firstGreater(int[] areas, int target) {\n int l = 0;\n int r = areas.length;\n while (l < r) {\n final int m = (l + r) / 2;\n if (areas[m] > target)\n r = m;\n else\n l = m + 1;\n }\n return l;\n }\n}\n```\n | 1 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Python3 Solution Explained | Easy to understand | random-point-in-non-overlapping-rectangles | 0 | 1 | **Solution:**\n1. First find the sum of the area of all the given rectangles\n2. Create a probability list to determine which rectangle should be selected. A rectangle with higher probability will be selected. The ith element of the probability list is the area of the ith rectangle devided by the sum of the area of all rectangles.\n3. Find the index of the highest probability rectangle which has the highest area by definition based on the probability list.\n4. Finaly find the 4 points of the rectangle which are x1,x2, y1,y2 and take random integer between [x1,x2] and [y1,y2] .\n```\ndef __init__(self, rects: List[List[int]]):\n\tw = 0\n\tself.rects = rects\n\tself.probability =[]\n\tself.indexes = []\n\tfor i in range(len(self.rects)):\n\t\tself.indexes.append(i)\n\t\tw += (self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)\n\tfor i in range(len(self.rects)):\n\t\tself.probability.append((self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)/w)\ndef pick(self) -> List[int]:\n\tindex = random.choices(self.indexes,weights = self.probability,k=1)[-1]\n\tx1,y1,x2,y2 = self.rects[index]\n\treturn [random.randint(x1,x2),random.randint(y1,y2)] | 1 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Python3 Solution Explained | Easy to understand | random-point-in-non-overlapping-rectangles | 0 | 1 | **Solution:**\n1. First find the sum of the area of all the given rectangles\n2. Create a probability list to determine which rectangle should be selected. A rectangle with higher probability will be selected. The ith element of the probability list is the area of the ith rectangle devided by the sum of the area of all rectangles.\n3. Find the index of the highest probability rectangle which has the highest area by definition based on the probability list.\n4. Finaly find the 4 points of the rectangle which are x1,x2, y1,y2 and take random integer between [x1,x2] and [y1,y2] .\n```\ndef __init__(self, rects: List[List[int]]):\n\tw = 0\n\tself.rects = rects\n\tself.probability =[]\n\tself.indexes = []\n\tfor i in range(len(self.rects)):\n\t\tself.indexes.append(i)\n\t\tw += (self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)\n\tfor i in range(len(self.rects)):\n\t\tself.probability.append((self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)/w)\ndef pick(self) -> List[int]:\n\tindex = random.choices(self.indexes,weights = self.probability,k=1)[-1]\n\tx1,y1,x2,y2 = self.rects[index]\n\treturn [random.randint(x1,x2),random.randint(y1,y2)] | 1 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Help! Why no working for the last 3 case? (Resolved: count the total pts inside each rec not area) | random-point-in-non-overlapping-rectangles | 0 | 1 | Now I understand. In order to solve this problem, we assume that the proportion is on the number of total points each rectangle not the area.\nThe difference is as follows\nAssume the rectangle is [x1, y1, x2, y2] where (x1,y1) the bottom left corner and (x2,y2) the top right corner\nThe area of the rectangle is (x2 - x1) * (y2 - y1) while the total points are (x2 - x1 + 1) * (y2 - y1 + 1)\n\n\n```\nfrom bisect import bisect_left\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.res = []\n self.tot = 0\n self.dic = {}\n for a, b, c, d in rects:\n area = (c - a + 1) * (d - b + 1)\n self.tot += area\n self.res.append(self.tot)\n self.dic[self.tot] = [a, b, c, d]\n\n def pick(self) -> List[int]:\n random = randint(1, self.tot)\n idx = bisect_left(self.res, random)\n a, b, c, d = self.dic[self.res[idx]]\n return [randint(a, c), randint(b, d)]\n\n\n```\n------------------------------------------------------------------------\n\nI did the picking proportionally to the area. I tried several ways. One way is by randint, oneway is using choices with weight function of individual weight. None is working...Please help!\n\n"""\nfrom bisect import bisect\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.x = [[a, c] for a,b,c,d in rects]\n self.y = [[b, d] for a,b,c,d in rects]\n sa, self.area = 0, []\n for a,b,c,d in rects:\n sa += (d -b) * (c - a)\n self.area.append(sa)\n \n\n def pick(self) -> List[int]:\n idx = bisect(self.area, randint(1, self.area[-1])) - 1\n x1,x2 = self.x[idx]\n y1,y2 = self.y[idx]\n return randint(x1, x2), randint(y1,y2)\n"""\n | 1 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Help! Why no working for the last 3 case? (Resolved: count the total pts inside each rec not area) | random-point-in-non-overlapping-rectangles | 0 | 1 | Now I understand. In order to solve this problem, we assume that the proportion is on the number of total points each rectangle not the area.\nThe difference is as follows\nAssume the rectangle is [x1, y1, x2, y2] where (x1,y1) the bottom left corner and (x2,y2) the top right corner\nThe area of the rectangle is (x2 - x1) * (y2 - y1) while the total points are (x2 - x1 + 1) * (y2 - y1 + 1)\n\n\n```\nfrom bisect import bisect_left\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.res = []\n self.tot = 0\n self.dic = {}\n for a, b, c, d in rects:\n area = (c - a + 1) * (d - b + 1)\n self.tot += area\n self.res.append(self.tot)\n self.dic[self.tot] = [a, b, c, d]\n\n def pick(self) -> List[int]:\n random = randint(1, self.tot)\n idx = bisect_left(self.res, random)\n a, b, c, d = self.dic[self.res[idx]]\n return [randint(a, c), randint(b, d)]\n\n\n```\n------------------------------------------------------------------------\n\nI did the picking proportionally to the area. I tried several ways. One way is by randint, oneway is using choices with weight function of individual weight. None is working...Please help!\n\n"""\nfrom bisect import bisect\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.x = [[a, c] for a,b,c,d in rects]\n self.y = [[b, d] for a,b,c,d in rects]\n sa, self.area = 0, []\n for a,b,c,d in rects:\n sa += (d -b) * (c - a)\n self.area.append(sa)\n \n\n def pick(self) -> List[int]:\n idx = bisect(self.area, randint(1, self.area[-1])) - 1\n x1,x2 = self.x[idx]\n y1,y2 = self.y[idx]\n return randint(x1, x2), randint(y1,y2)\n"""\n | 1 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
497: Space 95.52%, Solution with step by step explanation | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the Solution class with a list of non-overlapping axis-aligned rectangles rects.\n\n2. Inside the init function, calculate the total area covered by all the rectangles and store it in a variable called total_area.\n\n3. Create a list called areas to store the area of each rectangle cumulatively, starting from the first rectangle to the last.\n\n4. Loop through each rectangle in the input list rects and calculate the area of the rectangle using the formula: (xi - ai + 1) * (yi - bi + 1), where xi, yi are the top-right corner points of the ith rectangle and ai, bi are the bottom-left corner points of the ith rectangle.\n\n5. Add the area of each rectangle to the previous cumulative area, starting from the first rectangle, and append the result to the list areas.\n\n6. Inside the pick function, generate a random integer r between 1 and the total area covered by all the rectangles.\n\n7. Loop through each rectangle in the input list rects and compare the value of r with the cumulative area stored in the list areas for that rectangle. If r is less than or equal to the cumulative area, then the random point should be generated inside that rectangle.\n\n8. Generate two random integers x and y using the randint function from the random module, such that ai <= x <= xi and bi <= y <= yi, where ai, bi, xi, yi are the corner points of the current rectangle.\n\n9. Return the random point [x, y] as the output of the pick function.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.areas = []\n self.total_area = 0\n \n # Calculate the total area covered by all the rectangles\n for rect in rects:\n area = (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1)\n self.total_area += area\n self.areas.append(self.total_area)\n \n def pick(self) -> List[int]:\n # Generate a random integer between 0 and the total area covered by all the rectangles\n r = random.randint(1, self.total_area)\n \n # Loop through each rectangle, subtracting its area from r\n for i in range(len(self.rects)):\n if r <= self.areas[i]:\n # Once we find the rectangle, generate a random point inside it\n rect = self.rects[i]\n x = random.randint(rect[0], rect[2])\n y = random.randint(rect[1], rect[3])\n return [x, y]\n\n``` | 4 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
497: Space 95.52%, Solution with step by step explanation | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the Solution class with a list of non-overlapping axis-aligned rectangles rects.\n\n2. Inside the init function, calculate the total area covered by all the rectangles and store it in a variable called total_area.\n\n3. Create a list called areas to store the area of each rectangle cumulatively, starting from the first rectangle to the last.\n\n4. Loop through each rectangle in the input list rects and calculate the area of the rectangle using the formula: (xi - ai + 1) * (yi - bi + 1), where xi, yi are the top-right corner points of the ith rectangle and ai, bi are the bottom-left corner points of the ith rectangle.\n\n5. Add the area of each rectangle to the previous cumulative area, starting from the first rectangle, and append the result to the list areas.\n\n6. Inside the pick function, generate a random integer r between 1 and the total area covered by all the rectangles.\n\n7. Loop through each rectangle in the input list rects and compare the value of r with the cumulative area stored in the list areas for that rectangle. If r is less than or equal to the cumulative area, then the random point should be generated inside that rectangle.\n\n8. Generate two random integers x and y using the randint function from the random module, such that ai <= x <= xi and bi <= y <= yi, where ai, bi, xi, yi are the corner points of the current rectangle.\n\n9. Return the random point [x, y] as the output of the pick function.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.areas = []\n self.total_area = 0\n \n # Calculate the total area covered by all the rectangles\n for rect in rects:\n area = (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1)\n self.total_area += area\n self.areas.append(self.total_area)\n \n def pick(self) -> List[int]:\n # Generate a random integer between 0 and the total area covered by all the rectangles\n r = random.randint(1, self.total_area)\n \n # Loop through each rectangle, subtracting its area from r\n for i in range(len(self.rects)):\n if r <= self.areas[i]:\n # Once we find the rectangle, generate a random point inside it\n rect = self.rects[i]\n x = random.randint(rect[0], rect[2])\n y = random.randint(rect[1], rect[3])\n return [x, y]\n\n``` | 4 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Python O(n) with approach | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to pick a random point within a given list of rectangles. The key to solving this problem is to understand the concept of weighting. We can assign a weight to each rectangle based on the number of points it contains, and then use a random number generator to pick a rectangle based on its weight.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create an instance variable weights that will store the weights of each rectangle.\n- For each rectangle in the input list, calculate the number of points it contains and store it in weights.\n- Calculate the total number of points in all rectangles and store it in the total variable.\n- Create a prefix sum of weights to make it easier to pick a rectangle based on its weight.\n- In the pick() method, use a bisect function to find the index of the rectangle that the random number falls within.\n- Use a random number generator to pick a point within the selected rectangle.\n# Complexity\n- Time complexity: O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to iterate through the rectangles once to calculate their weights and create the prefix sum.\n- Space complexity: O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to store the weights of each rectangle in an array.\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n for rect in rects:\n self.weights.append((rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1))\n self.total = sum(self.weights)\n for i in range(1, len(self.weights)):\n self.weights[i] += self.weights[i - 1]\n self.weights = [0] + self.weights\n \n\n def pick(self) -> List[int]:\n index = bisect.bisect_left(self.weights, random.randint(1, self.total))\n rect = self.rects[index - 1]\n return [random.randint(rect[0], rect[2]), random.randint(rect[1], rect[3])]\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 4 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Python O(n) with approach | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to pick a random point within a given list of rectangles. The key to solving this problem is to understand the concept of weighting. We can assign a weight to each rectangle based on the number of points it contains, and then use a random number generator to pick a rectangle based on its weight.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create an instance variable weights that will store the weights of each rectangle.\n- For each rectangle in the input list, calculate the number of points it contains and store it in weights.\n- Calculate the total number of points in all rectangles and store it in the total variable.\n- Create a prefix sum of weights to make it easier to pick a rectangle based on its weight.\n- In the pick() method, use a bisect function to find the index of the rectangle that the random number falls within.\n- Use a random number generator to pick a point within the selected rectangle.\n# Complexity\n- Time complexity: O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to iterate through the rectangles once to calculate their weights and create the prefix sum.\n- Space complexity: O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to store the weights of each rectangle in an array.\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n for rect in rects:\n self.weights.append((rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1))\n self.total = sum(self.weights)\n for i in range(1, len(self.weights)):\n self.weights[i] += self.weights[i - 1]\n self.weights = [0] + self.weights\n \n\n def pick(self) -> List[int]:\n index = bisect.bisect_left(self.weights, random.randint(1, self.total))\n rect = self.rects[index - 1]\n return [random.randint(rect[0], rect[2]), random.randint(rect[1], rect[3])]\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 4 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Python O(n) by pool sampling. [w/ Visualization] | random-point-in-non-overlapping-rectangles | 0 | 1 | **Hint**:\n\nThink of **pool sampling**.\n\nTotal **n** pools, and total **P** points\n\n\n\nEach **rectangle** acts as **pool_i** with points **p_i** by itself,\nwhere p_i = ( x_i_2 - x_i_1 + 1) * ( y_i_2 - y_i_1 + 1 )\n\n\n\n\nSo, p_1 + p_2 + ... + p_n = P, and\neach pool_i has a **weight** of **p_i / P** during **pool sampling**.\n\nThen, generate a random number **r** from 1 to P\n\nCompute the **pool index** (i.e., **rectangle index**) from r by bisection\n\nThen compute the **corresponding x, y coordinate** in that pool from r by modulo and division.\n\n---\n\n```\nfrom random import randint\nfrom bisect import bisect_left\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n \n self.rectangles = rects\n \n # record prefix sum of points number (i.e., acts like the CDF)\n self.prefix_points_sum = []\n \n for x1, y1, x2, y2 in rects:\n \n # compute current number of points\n cur_points = ( x2 - x1 + 1 ) * ( y2 - y1 + 1)\n \n # update to prefix table\n if self.prefix_points_sum:\n self.prefix_points_sum.append( self.prefix_points_sum[-1] + cur_points )\n \n else:\n self.prefix_points_sum.append( cur_points )\n \n \n\n def pick(self) -> List[int]:\n \n total_num_of_points = self.prefix_points_sum[-1]\n \n # get a random point serial, sampling from 1 ~ total number of points\n random_point_serial = randint(1, total_num_of_points)\n \n # get the rectangle index by looking up prefix table with bisection\n idx_of_rectangle = bisect_left(self.prefix_points_sum, random_point_serial)\n \n # get the point range of that rectangle by index\n x1, y1, x2, y2 = self.rectangles[idx_of_rectangle]\n \n # compute the offset value between prefix sum and random point serial\n offset = self.prefix_points_sum[idx_of_rectangle] - random_point_serial\n \n # compute corresponding x, y points coordination in that rectangle\n x = offset % ( x2 - x1 + 1) + x1\n y = offset // ( x2 - x1 + 1) + y1\n \n return [x, y]\n``` | 6 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Python O(n) by pool sampling. [w/ Visualization] | random-point-in-non-overlapping-rectangles | 0 | 1 | **Hint**:\n\nThink of **pool sampling**.\n\nTotal **n** pools, and total **P** points\n\n\n\nEach **rectangle** acts as **pool_i** with points **p_i** by itself,\nwhere p_i = ( x_i_2 - x_i_1 + 1) * ( y_i_2 - y_i_1 + 1 )\n\n\n\n\nSo, p_1 + p_2 + ... + p_n = P, and\neach pool_i has a **weight** of **p_i / P** during **pool sampling**.\n\nThen, generate a random number **r** from 1 to P\n\nCompute the **pool index** (i.e., **rectangle index**) from r by bisection\n\nThen compute the **corresponding x, y coordinate** in that pool from r by modulo and division.\n\n---\n\n```\nfrom random import randint\nfrom bisect import bisect_left\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n \n self.rectangles = rects\n \n # record prefix sum of points number (i.e., acts like the CDF)\n self.prefix_points_sum = []\n \n for x1, y1, x2, y2 in rects:\n \n # compute current number of points\n cur_points = ( x2 - x1 + 1 ) * ( y2 - y1 + 1)\n \n # update to prefix table\n if self.prefix_points_sum:\n self.prefix_points_sum.append( self.prefix_points_sum[-1] + cur_points )\n \n else:\n self.prefix_points_sum.append( cur_points )\n \n \n\n def pick(self) -> List[int]:\n \n total_num_of_points = self.prefix_points_sum[-1]\n \n # get a random point serial, sampling from 1 ~ total number of points\n random_point_serial = randint(1, total_num_of_points)\n \n # get the rectangle index by looking up prefix table with bisection\n idx_of_rectangle = bisect_left(self.prefix_points_sum, random_point_serial)\n \n # get the point range of that rectangle by index\n x1, y1, x2, y2 = self.rectangles[idx_of_rectangle]\n \n # compute the offset value between prefix sum and random point serial\n offset = self.prefix_points_sum[idx_of_rectangle] - random_point_serial\n \n # compute corresponding x, y points coordination in that rectangle\n x = offset % ( x2 - x1 + 1) + x1\n y = offset // ( x2 - x1 + 1) + y1\n \n return [x, y]\n``` | 6 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Reservoir Sampling Algorithm, Python3, not fast but it's okay | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: linear for pick, sacrificed runtime for the algorithm implementation.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n\n def pick(self) -> List[int]:\n total_area = 0\n chosen_p = [0,0]\n for rect in self.rects:\n h = abs(rect[3]-rect[1]+1)\n w = abs(rect[2]-rect[0]+1)\n area = h*w\n total_area += area\n if random.random()<area/total_area:\n p_y = random.randint(rect[1], rect[3])\n p_x = random.randint(rect[0], rect[2])\n chosen_p = [p_x, p_y]\n return chosen_p\n\n\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 0 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Reservoir Sampling Algorithm, Python3, not fast but it's okay | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: linear for pick, sacrificed runtime for the algorithm implementation.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n\n def pick(self) -> List[int]:\n total_area = 0\n chosen_p = [0,0]\n for rect in self.rects:\n h = abs(rect[3]-rect[1]+1)\n w = abs(rect[2]-rect[0]+1)\n area = h*w\n total_area += area\n if random.random()<area/total_area:\n p_y = random.randint(rect[1], rect[3])\n p_x = random.randint(rect[0], rect[2])\n chosen_p = [p_x, p_y]\n return chosen_p\n\n\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 0 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Equal representatives for equal opportunity; Bigger rectangles need more representatives! | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe basic intuition was to select a rectangle randomly and then select a point from that rectangle randomly. However, since all valid points must have an equal probability of being picked up, we have to account for the area/size of the rectangles to ensure equal opportunity.\n\n## Representation at Parliament\n**Here is an intuitive way of thinking about this:**\n\nLet\'s say you are at the Parliament and want to pass a law by listening to the people\'s representatives from 3 districts in your imaginary country - A, B, C where the population is 100, 50, 10 respectively. It\'s importatnt that you want to ensure that all the citizens have equal say in the law-making.\n\nNow, if you chose a single representative from all 3 districts, the representation factor for district A would be 1/100 (as 1 person is representing 100 people). For district B and C the representation factors would be 1/50 and 1/10. Now, this doesn\'t look like an equal contribution, does it? We have to make sure the representation is same for all 3 districts, that\'s why choosing a single representative for every district is a bad idea.\n\nNow, what if we modified the number of representatives? If we chose 10 representatives from district A, 5 from B and 1 from C, then the representation factor would be similar for all 3 districts i.e. 1/10, right?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis is the intuition we solve the problem. Let\'s say you have 3 rectangles - A, B, C. The areas of A, B, C are 100, 50 and 10. Then instead of randomly picking a letter from the array [A, B, C], we should be picking one from `[A]*10 + [B]*5 + [C]*1` i.e. `[A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, C]`. A more convenient way of labelling the rectangles is to use their indices - 0, 1, 2... instead of A, B, C...\n\n### How to find the accurate number of representatives for every rectangle?\nThe simplest approach is to select the rectangle with the smallest area, then divide the areas of all other rectangles with it to find the number of representatives i.e. `n_A = area(rectangleA)/smallest_area`(here n_A is the number of representatives required for A). However since we need to have only integers, we need to approximate any fraction. Therefore, if n_A is found to be 3.91 and n_B is 2.45 and n_C is 1.00, we can adjust them to `n_A=4, n_B=2, n_C=1`. Evidently, this will lead to loss of accuracy. To improve the accuracy we can allow for a single digit after the decimal point, then multiplying by 10 to make them integers i.e. `3.91 -> 39`, `2.45 -> 24` and `1.00 -> 10`. However, this means that the array `represntatives` will need to hold 39 + 24 +10 items. The size of this array may eat up a lof memory if the number of rectangles provided are very large. To further improve the accuracy at the cost of memory, you can round the result to 2 decimal points, then multiply them by 100 i.e. `n_A=391, n_B=24, n_C=100`. But, for this particular problem 1-decimal point accuracy was good enough for the answer to get accepted. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(2n) # Two for loops\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Can\'t figure out, can someone help?\n# Code\n```\nclass Solution:\n import random\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n \n self.representatives = []\n \n areas = []\n smallest_area = None\n for i, rect in enumerate(rects):\n area = self.find_area(rect)\n if smallest_area is None or area < smallest_area:\n smallest_area = area\n areas.append(area)\n\n for i, area in enumerate(areas):\n accuracy = 1\n repeat = round(area/smallest_area, accuracy) * (10**accuracy)\n self.representatives.extend(\n [i] * int(repeat)\n )\n \n # method for finding area of a rectangle\n @staticmethod \n def find_area(rect):\n return (rect[2]-rect[0]+1)*(rect[3]-rect[1]+1)\n\n def pick(self) -> List[int]:\n randomRect = self.rects[random.choice(self.representatives)]\n randomX = random.randint(randomRect[0], randomRect[2])\n randomY = random.randint(randomRect[1], randomRect[3])\n return [randomX, randomY]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 0 | You are given an array of non-overlapping axis-aligned rectangles `rects` where `rects[i] = [ai, bi, xi, yi]` indicates that `(ai, bi)` is the bottom-left corner point of the `ith` rectangle and `(xi, yi)` is the top-right corner point of the `ith` rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.
Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.
**Note** that an integer point is a point that has integer coordinates.
Implement the `Solution` class:
* `Solution(int[][] rects)` Initializes the object with the given rectangles `rects`.
* `int[] pick()` Returns a random integer point `[u, v]` inside the space covered by one of the given rectangles.
**Example 1:**
**Input**
\[ "Solution ", "pick ", "pick ", "pick ", "pick ", "pick "\]
\[\[\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]\], \[\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, \[1, -2\], \[1, -1\], \[-1, -2\], \[-2, -2\], \[0, 0\]\]
**Explanation**
Solution solution = new Solution(\[\[-2, -2, 1, 1\], \[2, 2, 4, 6\]\]);
solution.pick(); // return \[1, -2\]
solution.pick(); // return \[1, -1\]
solution.pick(); // return \[-1, -2\]
solution.pick(); // return \[-2, -2\]
solution.pick(); // return \[0, 0\]
**Constraints:**
* `1 <= rects.length <= 100`
* `rects[i].length == 4`
* `-109 <= ai < xi <= 109`
* `-109 <= bi < yi <= 109`
* `xi - ai <= 2000`
* `yi - bi <= 2000`
* All the rectangles do not overlap.
* At most `104` calls will be made to `pick`. | null |
Equal representatives for equal opportunity; Bigger rectangles need more representatives! | random-point-in-non-overlapping-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe basic intuition was to select a rectangle randomly and then select a point from that rectangle randomly. However, since all valid points must have an equal probability of being picked up, we have to account for the area/size of the rectangles to ensure equal opportunity.\n\n## Representation at Parliament\n**Here is an intuitive way of thinking about this:**\n\nLet\'s say you are at the Parliament and want to pass a law by listening to the people\'s representatives from 3 districts in your imaginary country - A, B, C where the population is 100, 50, 10 respectively. It\'s importatnt that you want to ensure that all the citizens have equal say in the law-making.\n\nNow, if you chose a single representative from all 3 districts, the representation factor for district A would be 1/100 (as 1 person is representing 100 people). For district B and C the representation factors would be 1/50 and 1/10. Now, this doesn\'t look like an equal contribution, does it? We have to make sure the representation is same for all 3 districts, that\'s why choosing a single representative for every district is a bad idea.\n\nNow, what if we modified the number of representatives? If we chose 10 representatives from district A, 5 from B and 1 from C, then the representation factor would be similar for all 3 districts i.e. 1/10, right?\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis is the intuition we solve the problem. Let\'s say you have 3 rectangles - A, B, C. The areas of A, B, C are 100, 50 and 10. Then instead of randomly picking a letter from the array [A, B, C], we should be picking one from `[A]*10 + [B]*5 + [C]*1` i.e. `[A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, C]`. A more convenient way of labelling the rectangles is to use their indices - 0, 1, 2... instead of A, B, C...\n\n### How to find the accurate number of representatives for every rectangle?\nThe simplest approach is to select the rectangle with the smallest area, then divide the areas of all other rectangles with it to find the number of representatives i.e. `n_A = area(rectangleA)/smallest_area`(here n_A is the number of representatives required for A). However since we need to have only integers, we need to approximate any fraction. Therefore, if n_A is found to be 3.91 and n_B is 2.45 and n_C is 1.00, we can adjust them to `n_A=4, n_B=2, n_C=1`. Evidently, this will lead to loss of accuracy. To improve the accuracy we can allow for a single digit after the decimal point, then multiplying by 10 to make them integers i.e. `3.91 -> 39`, `2.45 -> 24` and `1.00 -> 10`. However, this means that the array `represntatives` will need to hold 39 + 24 +10 items. The size of this array may eat up a lof memory if the number of rectangles provided are very large. To further improve the accuracy at the cost of memory, you can round the result to 2 decimal points, then multiply them by 100 i.e. `n_A=391, n_B=24, n_C=100`. But, for this particular problem 1-decimal point accuracy was good enough for the answer to get accepted. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(2n) # Two for loops\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Can\'t figure out, can someone help?\n# Code\n```\nclass Solution:\n import random\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n \n self.representatives = []\n \n areas = []\n smallest_area = None\n for i, rect in enumerate(rects):\n area = self.find_area(rect)\n if smallest_area is None or area < smallest_area:\n smallest_area = area\n areas.append(area)\n\n for i, area in enumerate(areas):\n accuracy = 1\n repeat = round(area/smallest_area, accuracy) * (10**accuracy)\n self.representatives.extend(\n [i] * int(repeat)\n )\n \n # method for finding area of a rectangle\n @staticmethod \n def find_area(rect):\n return (rect[2]-rect[0]+1)*(rect[3]-rect[1]+1)\n\n def pick(self) -> List[int]:\n randomRect = self.rects[random.choice(self.representatives)]\n randomX = random.randint(randomRect[0], randomRect[2])\n randomY = random.randint(randomRect[1], randomRect[3])\n return [randomX, randomY]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 0 | You are given an integer array `deck` where `deck[i]` represents the number written on the `ith` card.
Partition the cards into **one or more groups** such that:
* Each group has **exactly** `x` cards where `x > 1`, and
* All the cards in one group have the same integer written on them.
Return `true` _if such partition is possible, or_ `false` _otherwise_.
**Example 1:**
**Input:** deck = \[1,2,3,4,4,3,2,1\]
**Output:** true
**Explanation**: Possible partition \[1,1\],\[2,2\],\[3,3\],\[4,4\].
**Example 2:**
**Input:** deck = \[1,1,1,2,2,2,3,3\]
**Output:** false
**Explanation**: No possible partition.
**Constraints:**
* `1 <= deck.length <= 104`
* `0 <= deck[i] < 104` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.