title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | sliding-puzzle | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string target = "123450";\n vector<vector<int>> dir{{1,3},{0,2,4},{1,5},{0,4},{1,3,5},{2,4}};\n int slidingPuzzle(vector<vector<int>>& board) \n {\n int m = board.size(),n = board[0].size();\n string first = "";\n for(int i=0; i<m; i++)\n {\n for(int j=0; j<n; j++)\n {\n first += to_string(board[i][j]);\n }\n }\n queue<pair<string,int>> q;\n unordered_set<string> visited;\n q.push({first,0});\n visited.insert(first);\n while(!q.empty())\n {\n int sz = q.size();\n while(sz--)\n {\n auto cur = q.front();\n q.pop();\n \n string s = cur.first;\n int count = cur.second;\n \n if(s == target)\n {\n return count;\n }\n int indx = s.find(\'0\');\n for(auto &x: dir[indx])\n {\n string temp = s;\n \n swap(temp[x],temp[indx]);\n \n if(!visited.count(temp))\n {\n visited.insert(temp);\n \n q.push({temp,count+1});\n }\n }\n }\n }\n return -1;\n \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def slidingPuzzle(self, board: List[List[int]]) -> int:\n\n src = ""\n zero = 0\n for i in range(len(board)):\n for j in range(len(board[i])):\n src += str(board[i][j])\n if board[i][j] == 0:\n zero = len(src)-1\n\n target = "123450"\n step = {0:[1, 3], 1:[0, 2, 4], 2:[ 1, 5], 3:[0, 4], 4:[3, 1, 5], 5:[4, 2]}\n\n q = collections.deque()\n q.append((src, 0, zero))\n visit = set()\n visit.add(src)\n\n while q:\n for _ in range(len(q)):\n arr, count, pos = q.popleft()\n if arr == target:\n return count\n for adj_index in step[pos]:\n n_arr = list(arr)\n n_arr[pos], n_arr[adj_index] = n_arr[adj_index], n_arr[pos]\n n_arr = "".join(n_arr)\n if n_arr not in visit:\n visit.add(n_arr)\n q.append(( n_arr, count+1, adj_index))\n return -1\n```\n\n```Java []\nclass Solution {\n int min = Integer.MAX_VALUE;\n int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n\n public int slidingPuzzle(int[][] board) {\n int[] zero = {-1, -1};\n outer:\n for (int i = 0; i < 2; i++) {\n for (int j = 0; j < 3; j++) {\n if (board[i][j] == 0) {\n zero = new int[]{i, j};\n break outer;\n }\n }\n }\n helper_backtrack(board, 0, new int[]{-1, -1}, zero);\n return min == Integer.MAX_VALUE ? -1 : min;\n }\n public void helper_backtrack(int[][] board, int moves, int[] last, int[] curr) {\n if (moves >= 20) return;\n if (helper_isDone(board)) {\n min = Math.min(min, moves);\n return;\n }\n for (int[] dir : dirs) {\n int i = curr[0] + dir[0];\n int j = curr[1] + dir[1];\n if (i < 0 || i >= 2 || j < 0 || j >= 3 || (last[0] == i && last[1] == j)) continue;\n int[] newMove = {i, j};\n helper_flip(board, curr, newMove);\n helper_backtrack(board, moves + 1, curr, newMove);\n helper_flip(board, curr, newMove);\n }\n }\n public void helper_flip(int[][] board, int[] f, int[] s) {\n int temp = board[f[0]][f[1]];\n board[f[0]][f[1]] = board[s[0]][s[1]];\n board[s[0]][s[1]] = temp;\n }\n public boolean helper_isDone(int[][] board) {\n for (int i = 0; i < 2; i++) {\n for (int j = 0; j < 3; j++) {\n if (i == 1 && j == 2) return true;\n if (board[i][j] != 3 * i + j + 1) return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**. | null |
Solution | sliding-puzzle | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string target = "123450";\n vector<vector<int>> dir{{1,3},{0,2,4},{1,5},{0,4},{1,3,5},{2,4}};\n int slidingPuzzle(vector<vector<int>>& board) \n {\n int m = board.size(),n = board[0].size();\n string first = "";\n for(int i=0; i<m; i++)\n {\n for(int j=0; j<n; j++)\n {\n first += to_string(board[i][j]);\n }\n }\n queue<pair<string,int>> q;\n unordered_set<string> visited;\n q.push({first,0});\n visited.insert(first);\n while(!q.empty())\n {\n int sz = q.size();\n while(sz--)\n {\n auto cur = q.front();\n q.pop();\n \n string s = cur.first;\n int count = cur.second;\n \n if(s == target)\n {\n return count;\n }\n int indx = s.find(\'0\');\n for(auto &x: dir[indx])\n {\n string temp = s;\n \n swap(temp[x],temp[indx]);\n \n if(!visited.count(temp))\n {\n visited.insert(temp);\n \n q.push({temp,count+1});\n }\n }\n }\n }\n return -1;\n \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def slidingPuzzle(self, board: List[List[int]]) -> int:\n\n src = ""\n zero = 0\n for i in range(len(board)):\n for j in range(len(board[i])):\n src += str(board[i][j])\n if board[i][j] == 0:\n zero = len(src)-1\n\n target = "123450"\n step = {0:[1, 3], 1:[0, 2, 4], 2:[ 1, 5], 3:[0, 4], 4:[3, 1, 5], 5:[4, 2]}\n\n q = collections.deque()\n q.append((src, 0, zero))\n visit = set()\n visit.add(src)\n\n while q:\n for _ in range(len(q)):\n arr, count, pos = q.popleft()\n if arr == target:\n return count\n for adj_index in step[pos]:\n n_arr = list(arr)\n n_arr[pos], n_arr[adj_index] = n_arr[adj_index], n_arr[pos]\n n_arr = "".join(n_arr)\n if n_arr not in visit:\n visit.add(n_arr)\n q.append(( n_arr, count+1, adj_index))\n return -1\n```\n\n```Java []\nclass Solution {\n int min = Integer.MAX_VALUE;\n int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n\n public int slidingPuzzle(int[][] board) {\n int[] zero = {-1, -1};\n outer:\n for (int i = 0; i < 2; i++) {\n for (int j = 0; j < 3; j++) {\n if (board[i][j] == 0) {\n zero = new int[]{i, j};\n break outer;\n }\n }\n }\n helper_backtrack(board, 0, new int[]{-1, -1}, zero);\n return min == Integer.MAX_VALUE ? -1 : min;\n }\n public void helper_backtrack(int[][] board, int moves, int[] last, int[] curr) {\n if (moves >= 20) return;\n if (helper_isDone(board)) {\n min = Math.min(min, moves);\n return;\n }\n for (int[] dir : dirs) {\n int i = curr[0] + dir[0];\n int j = curr[1] + dir[1];\n if (i < 0 || i >= 2 || j < 0 || j >= 3 || (last[0] == i && last[1] == j)) continue;\n int[] newMove = {i, j};\n helper_flip(board, curr, newMove);\n helper_backtrack(board, moves + 1, curr, newMove);\n helper_flip(board, curr, newMove);\n }\n }\n public void helper_flip(int[][] board, int[] f, int[] s) {\n int temp = board[f[0]][f[1]];\n board[f[0]][f[1]] = board[s[0]][s[1]];\n board[s[0]][s[1]] = temp;\n }\n public boolean helper_isDone(int[][] board) {\n for (int i = 0; i < 2; i++) {\n for (int j = 0; j < 3; j++) {\n if (i == 1 && j == 2) return true;\n if (board[i][j] != 3 * i + j + 1) return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
BFS APPROACH | sliding-puzzle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is that this problem can be solved using a breadth-first search (BFS) algorithm, where we start with the initial board state and explore all possible moves (by swapping the empty space with its neighboring tiles) until we reach the desired board state.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach to solving this problem is to use a BFS algorithm to explore all possible moves from the initial board state. The function starts by initializing a queue and adding the initial board state and the number of moves (0) to the queue. It also initializes a set to keep track of the board states that have already been seen. The function then enters a while loop that continues until the queue is empty. In each iteration, the function takes the first board state and move count from the queue, and checks if the board state is the desired state. If it is, the function returns the number of moves. If not, the function uses a helper function get_neighbors to find all possible moves (by swapping the empty space with its neighboring tiles) and adds them to the queue. The function also adds the new board states to the set of seen states. If the queue becomes empty, the function returns -1 indicating that the desired board state was not reached.\n\n\n# Complexity\n- Time complexity: $$O(mn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(mn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slidingPuzzle(self, board: List[List[int]]) -> int:\n def get_neighbors(board):\n neighbors = []\n r, c = 0, 0\n for i in range(2):\n for j in range(3):\n if board[i][j] == 0:\n r, c = i, j\n for i, j in [(0, 1), (1, 0), (0, -1), (-1, 0)]:\n new_r, new_c = r + i, c + j\n if 0 <= new_r < 2 and 0 <= new_c < 3:\n new_board = [row[:] for row in board]\n new_board[r][c] = new_board[new_r][new_c]\n new_board[new_r][new_c] = 0\n neighbors.append(new_board)\n return neighbors\n\n queue = deque()\n queue.append((board, 0))\n seen = set()\n seen.add(tuple(tuple(row) for row in board))\n\n while queue:\n board, moves = queue.popleft()\n if board == [[1, 2, 3], [4, 5, 0]]:\n return moves\n for neighbor in get_neighbors(board):\n if tuple(tuple(row) for row in neighbor) not in seen:\n queue.append((neighbor, moves + 1))\n seen.add(tuple(tuple(row) for row in neighbor))\n return -1\n``` | 2 | On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**. | null |
BFS APPROACH | sliding-puzzle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought is that this problem can be solved using a breadth-first search (BFS) algorithm, where we start with the initial board state and explore all possible moves (by swapping the empty space with its neighboring tiles) until we reach the desired board state.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach to solving this problem is to use a BFS algorithm to explore all possible moves from the initial board state. The function starts by initializing a queue and adding the initial board state and the number of moves (0) to the queue. It also initializes a set to keep track of the board states that have already been seen. The function then enters a while loop that continues until the queue is empty. In each iteration, the function takes the first board state and move count from the queue, and checks if the board state is the desired state. If it is, the function returns the number of moves. If not, the function uses a helper function get_neighbors to find all possible moves (by swapping the empty space with its neighboring tiles) and adds them to the queue. The function also adds the new board states to the set of seen states. If the queue becomes empty, the function returns -1 indicating that the desired board state was not reached.\n\n\n# Complexity\n- Time complexity: $$O(mn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(mn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def slidingPuzzle(self, board: List[List[int]]) -> int:\n def get_neighbors(board):\n neighbors = []\n r, c = 0, 0\n for i in range(2):\n for j in range(3):\n if board[i][j] == 0:\n r, c = i, j\n for i, j in [(0, 1), (1, 0), (0, -1), (-1, 0)]:\n new_r, new_c = r + i, c + j\n if 0 <= new_r < 2 and 0 <= new_c < 3:\n new_board = [row[:] for row in board]\n new_board[r][c] = new_board[new_r][new_c]\n new_board[new_r][new_c] = 0\n neighbors.append(new_board)\n return neighbors\n\n queue = deque()\n queue.append((board, 0))\n seen = set()\n seen.add(tuple(tuple(row) for row in board))\n\n while queue:\n board, moves = queue.popleft()\n if board == [[1, 2, 3], [4, 5, 0]]:\n return moves\n for neighbor in get_neighbors(board):\n if tuple(tuple(row) for row in neighbor) not in seen:\n queue.append((neighbor, moves + 1))\n seen.add(tuple(tuple(row) for row in neighbor))\n return -1\n``` | 2 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
Cool!!! | sliding-puzzle | 0 | 1 | \n# Code\n```\nclass Solution:\n\n \n def slidingPuzzle(self, board: List[List[int]]) -> int:\n board = tuple(board[0]+board[1])\n graph_step_history = { (1, 4, 3, 5, 2, 0): 14,\n (4, 0, 2, 5, 1, 3): 6,\n (5, 4, 1, 3, 0, 2): 11,\n (1, 0, 2, 4, 5, 3): 2,\n (4, 5, 1, 2, 0, 3): 9,\n (1, 2, 5, 0, 3, 4): 10,\n (3, 5, 1, 0, 4, 2): 14,\n (1, 3, 2, 0, 5, 4): 14,\n (5, 2, 3, 0, 1, 4): 10,\n (1, 4, 0, 2, 3, 5): 17,\n (4, 0, 1, 5, 3, 2): 8,\n (2, 5, 4, 0, 1, 3): 10,\n (5, 0, 4, 2, 1, 3): 12,\n (5, 3, 1, 2, 4, 0): 16,\n (1, 4, 3, 0, 5, 2): 16,\n (2, 3, 1, 0, 4, 5): 16,\n (0, 3, 5, 1, 4, 2): 7,\n (5, 0, 1, 3, 4, 2): 12,\n (2, 4, 5, 0, 3, 1): 12,\n (1, 2, 5, 3, 4, 0): 12,\n (2, 4, 5, 3, 0, 1): 13,\n (1, 5, 3, 0, 2, 4): 12,\n (3, 2, 1, 0, 5, 4): 20,\n (5, 4, 3, 2, 0, 1): 13,\n (3, 2, 0, 1, 5, 4): 13,\n (3, 5, 0, 4, 2, 1): 13,\n (0, 5, 4, 2, 1, 3): 11,\n (3, 1, 2, 4, 5, 0): 14,\n (3, 5, 2, 1, 4, 0): 10,\n (5, 3, 2, 4, 0, 1): 17,\n (4, 0, 3, 2, 1, 5): 6,\n (3, 1, 4, 5, 2, 0): 16,\n (3, 1, 0, 5, 2, 4): 17,\n (3, 5, 4, 2, 1, 0): 12,\n (5, 3, 2, 4, 1, 0): 18,\n (5, 1, 0, 3, 4, 2): 13,\n (4, 5, 3, 0, 1, 2): 18,\n (1, 0, 4, 2, 3, 5): 16,\n (0, 3, 4, 5, 1, 2): 13,\n (0, 1, 2, 5, 3, 4): 15,\n (3, 4, 1, 0, 2, 5): 14,\n (0, 1, 3, 4, 2, 5): 3,\n (3, 0, 2, 5, 4, 1): 18,\n (0, 3, 4, 2, 5, 1): 15,\n (0, 5, 2, 3, 1, 4): 13,\n (0, 2, 4, 3, 1, 5): 15,\n (4, 5, 3, 1, 2, 0): 20,\n (0, 3, 1, 2, 4, 5): 15,\n (2, 4, 1, 0, 5, 3): 10,\n (4, 0, 1, 2, 5, 3): 8,\n (1, 5, 2, 0, 4, 3): 4,\n (0, 4, 2, 3, 5, 1): 15,\n (2, 3, 5, 0, 1, 4): 8,\n (2, 1, 5, 4, 0, 3): 17,\n (2, 1, 3, 5, 4, 0): 14,\n (4, 3, 5, 2, 1, 0): 8,\n (0, 4, 3, 5, 2, 1): 11,\n (3, 2, 0, 4, 1, 5): 15,\n (4, 0, 5, 3, 1, 2): 10,\n (1, 0, 5, 4, 3, 2): 6,\n (0, 5, 1, 4, 2, 3): 11,\n (0, 2, 1, 4, 3, 5): 15,\n (5, 4, 0, 3, 2, 1): 13,\n (0, 1, 3, 5, 4, 2): 17,\n (4, 3, 0, 5, 2, 1): 11,\n (2, 5, 1, 3, 4, 0): 16,\n (1, 5, 2, 4, 3, 0): 4,\n (4, 3, 0, 2, 1, 5): 7,\n (5, 1, 0, 2, 3, 4): 15,\n (3, 1, 2, 0, 4, 5): 16,\n (3, 4, 1, 2, 0, 5): 15,\n (2, 4, 3, 0, 1, 5): 6,\n (4, 0, 2, 1, 3, 5): 18,\n (4, 2, 1, 3, 0, 5): 13,\n (1, 5, 0, 3, 2, 4): 13,\n (2, 0, 5, 4, 1, 3): 16,\n (0, 5, 4, 1, 3, 2): 11,\n (1, 5, 3, 2, 4, 0): 14,\n (3, 1, 2, 4, 0, 5): 15,\n (5, 2, 0, 4, 3, 1): 15,\n (3, 2, 4, 1, 5, 0): 14,\n (2, 4, 0, 5, 3, 1): 13,\n (0, 3, 2, 5, 4, 1): 19,\n (4, 0, 5, 2, 3, 1): 10,\n (3, 1, 0, 4, 5, 2): 13,\n (0, 5, 4, 3, 2, 1): 15,\n (4, 1, 2, 5, 3, 0): 6,\n (5, 3, 0, 2, 4, 1): 15,\n (1, 2, 4, 5, 3, 0): 12,\n (4, 5, 1, 0, 2, 3): 10,\n (1, 5, 4, 3, 2, 0): 14,\n (2, 3, 5, 1, 4, 0): 6,\n (1, 4, 5, 2, 0, 3): 17,\n (2, 0, 5, 3, 4, 1): 14,\n (2, 1, 4, 3, 5, 0): 18,\n (4, 5, 1, 2, 3, 0): 10,\n (1, 2, 5, 3, 0, 4): 11,\n (0, 4, 1, 2, 5, 3): 9,\n (1, 3, 2, 5, 0, 4): 15,\n (1, 3, 5, 0, 4, 2): 6,\n (1, 3, 5, 4, 0, 2): 5,\n (5, 0, 2, 1, 4, 3): 6,\n (4, 3, 0, 1, 5, 2): 19,\n (0, 4, 1, 3, 2, 5): 13,\n (4, 3, 1, 5, 0, 2): 9,\n (2, 0, 3, 5, 1, 4): 12,\n (5, 3, 4, 1, 0, 2): 11,\n (1, 0, 4, 5, 2, 3): 12,\n (4, 1, 3, 0, 2, 5): 4,\n (3, 0, 2, 4, 1, 5): 16,\n (0, 5, 2, 1, 4, 3): 5,\n (5, 1, 4, 2, 0, 3): 13,\n (1, 3, 0, 4, 2, 5): 3,\n (4, 5, 0, 2, 3, 1): 11,\n (2, 0, 1, 4, 3, 5): 16,\n (5, 2, 0, 1, 4, 3): 7,\n (3, 5, 2, 0, 1, 4): 12,\n (5, 0, 3, 4, 1, 2): 16,\n (5, 3, 0, 4, 1, 2): 17,\n (1, 4, 2, 3, 0, 5): 15,\n (3, 0, 1, 5, 2, 4): 18,\n (5, 0, 1, 4, 2, 3): 12,\n (5, 4, 0, 1, 3, 2): 9,\n (2, 3, 0, 5, 1, 4): 13,\n (2, 1, 3, 0, 5, 4): 14,\n (2, 1, 4, 3, 0, 5): 17,\n (5, 2, 3, 1, 4, 0): 8,\n (1, 4, 5, 2, 3, 0): 18,\n (0, 4, 2, 1, 3, 5): 17,\n (0, 2, 3, 5, 1, 4): 11,\n (4, 2, 5, 0, 1, 3): 18,\n (0, 2, 3, 4, 5, 1): 11,\n (4, 3, 2, 0, 1, 5): 18,\n (5, 4, 0, 2, 1, 3): 13,\n (3, 5, 4, 0, 2, 1): 14,\n (2, 0, 5, 1, 3, 4): 8,\n (3, 0, 5, 4, 2, 1): 12,\n (3, 1, 5, 0, 2, 4): 12,\n (1, 0, 4, 3, 5, 2): 14,\n (0, 4, 5, 2, 3, 1): 11,\n (1, 2, 4, 0, 5, 3): 10,\n (0, 3, 2, 4, 1, 5): 17,\n (2, 1, 4, 0, 3, 5): 18,\n (3, 2, 4, 1, 0, 5): 13,\n (3, 1, 4, 0, 5, 2): 16,\n (2, 3, 1, 4, 5, 0): 14,\n (5, 2, 0, 3, 1, 4): 15,\n (0, 1, 4, 3, 5, 2): 15,\n (3, 4, 2, 0, 5, 1): 16,\n (3, 2, 5, 4, 0, 1): 13,\n (0, 5, 1, 3, 4, 2): 13,\n (3, 2, 1, 5, 0, 4): 19,\n (3, 0, 2, 1, 5, 4): 12,\n (2, 3, 4, 5, 1, 0): 14,\n (1, 4, 2, 0, 3, 5): 16,\n (2, 5, 3, 4, 0, 1): 13,\n (5, 0, 4, 3, 2, 1): 14,\n (5, 4, 2, 1, 0, 3): 7,\n (3, 4, 1, 2, 5, 0): 16,\n (2, 3, 4, 0, 5, 1): 16,\n (3, 0, 5, 1, 4, 2): 8,\n (3, 4, 5, 1, 2, 0): 10,\n (4, 3, 2, 1, 5, 0): 20,\n (0, 3, 1, 4, 5, 2): 11,\n (1, 3, 4, 2, 5, 0): 16,\n (1, 0, 5, 2, 4, 3): 16,\n (2, 4, 0, 3, 1, 5): 15,\n (4, 2, 0, 3, 5, 1): 15,\n (2, 1, 0, 4, 3, 5): 17,\n (3, 1, 5, 2, 0, 4): 11,\n (2, 1, 3, 5, 0, 4): 13,\n (5, 4, 3, 0, 2, 1): 12,\n (0, 4, 2, 5, 1, 3): 7,\n (4, 0, 1, 3, 2, 5): 12,\n (0, 4, 3, 1, 5, 2): 17,\n (3, 5, 1, 4, 0, 2): 13,\n (1, 2, 3, 4, 5, 0): 0,\n (5, 4, 1, 3, 2, 0): 12,\n (0, 1, 2, 4, 5, 3): 3,\n (2, 5, 3, 4, 1, 0): 14,\n (2, 4, 1, 5, 0, 3): 11,\n (2, 0, 4, 3, 1, 5): 16,\n (0, 2, 5, 4, 1, 3): 17,\n (1, 5, 0, 2, 4, 3): 15,\n (4, 1, 3, 2, 5, 0): 6,\n (4, 5, 2, 3, 0, 1): 13,\n (0, 1, 4, 5, 2, 3): 13,\n (3, 5, 0, 2, 1, 4): 11,\n (3, 1, 4, 5, 0, 2): 15,\n (1, 4, 5, 0, 2, 3): 18,\n (5, 0, 1, 2, 3, 4): 16,\n (5, 3, 4, 0, 1, 2): 12,\n (4, 3, 5, 2, 0, 1): 9,\n (5, 4, 2, 1, 3, 0): 8,\n (0, 5, 2, 4, 3, 1): 15,\n (5, 3, 2, 0, 4, 1): 18,\n (1, 0, 5, 3, 2, 4): 12,\n (0, 1, 4, 2, 3, 5): 17,\n (5, 2, 1, 0, 4, 3): 14,\n (1, 4, 0, 5, 2, 3): 13,\n (4, 2, 0, 1, 3, 5): 19,\n (0, 2, 4, 1, 5, 3): 9,\n (1, 2, 0, 4, 5, 3): 1,\n (3, 4, 5, 0, 1, 2): 10,\n (4, 3, 2, 1, 0, 5): 19,\n (1, 3, 4, 2, 0, 5): 15,\n (5, 3, 0, 1, 2, 4): 11,\n (1, 2, 3, 4, 0, 5): 1,\n (2, 4, 3, 1, 5, 0): 6,\n (4, 1, 0, 3, 2, 5): 11,\n (4, 3, 1, 0, 5, 2): 10,\n (2, 3, 0, 4, 5, 1): 13,\n (0, 1, 2, 3, 4, 5): 15,\n (4, 2, 1, 0, 3, 5): 14,\n (4, 3, 1, 5, 2, 0): 10,\n (1, 0, 3, 5, 4, 2): 16,\n (1, 2, 4, 5, 0, 3): 11,\n (5, 1, 0, 4, 2, 3): 13,\n (4, 1, 2, 5, 0, 3): 5,\n (5, 2, 1, 4, 3, 0): 14,\n (1, 0, 3, 2, 5, 4): 14,\n (2, 4, 1, 5, 3, 0): 12,\n (3, 5, 4, 2, 0, 1): 13,\n (2, 5, 0, 1, 3, 4): 9,\n (5, 1, 2, 3, 0, 4): 15,\n (4, 2, 0, 5, 1, 3): 7,\n (3, 4, 0, 2, 5, 1): 15,\n (4, 1, 2, 0, 5, 3): 4,\n (4, 1, 5, 0, 3, 2): 8,\n (1, 0, 3, 4, 2, 5): 2,\n (0, 5, 3, 4, 1, 2): 17,\n (4, 2, 5, 1, 0, 3): 19,\n (1, 3, 0, 5, 4, 2): 17,\n (2, 1, 5, 0, 4, 3): 18,\n (1, 2, 3, 0, 4, 5): 2,\n (2, 3, 0, 1, 4, 5): 5,\n (4, 1, 3, 2, 0, 5): 5,\n (5, 3, 1, 0, 2, 4): 18,\n (4, 3, 5, 0, 2, 1): 10,\n (3, 4, 5, 1, 0, 2): 9,\n (4, 2, 3, 5, 1, 0): 8,\n (3, 2, 5, 0, 4, 1): 14,\n (0, 2, 3, 1, 4, 5): 3,\n (2, 0, 1, 3, 5, 4): 18,\n (0, 3, 5, 4, 2, 1): 11,\n (4, 5, 2, 0, 3, 1): 14,\n (1, 0, 2, 3, 4, 5): 14,\n (2, 0, 3, 4, 5, 1): 12,\n (5, 0, 2, 4, 3, 1): 16,\n (1, 5, 4, 0, 3, 2): 12,\n (1, 5, 4, 3, 0, 2): 13,\n (2, 0, 3, 1, 4, 5): 4,\n (1, 3, 2, 5, 4, 0): 16,\n (5, 2, 4, 3, 1, 0): 16,\n (3, 5, 0, 1, 4, 2): 9,\n (2, 0, 4, 5, 3, 1): 14,\n (0, 3, 4, 1, 2, 5): 13,\n (3, 2, 4, 0, 1, 5): 14,\n (5, 0, 3, 2, 4, 1): 14,\n (5, 1, 3, 4, 2, 0): 14,\n (0, 1, 5, 2, 4, 3): 17,\n (3, 1, 0, 2, 4, 5): 13,\n (0, 2, 5, 3, 4, 1): 15,\n (2, 1, 5, 4, 3, 0): 18,\n (1, 5, 0, 4, 3, 2): 5,\n (3, 2, 1, 5, 4, 0): 20,\n (2, 5, 0, 4, 1, 3): 15,\n (5, 1, 2, 0, 3, 4): 16,\n (5, 1, 4, 0, 2, 3): 14,\n (5, 2, 3, 1, 0, 4): 9,\n (0, 1, 5, 3, 2, 4): 13,\n (4, 0, 3, 1, 5, 2): 18,\n (4, 2, 5, 1, 3, 0): 20,\n (0, 5, 1, 2, 3, 4): 17,\n (4, 0, 5, 1, 2, 3): 20,\n (1, 3, 5, 4, 2, 0): 4,\n (2, 1, 0, 5, 4, 3): 13,\n (3, 0, 5, 2, 1, 4): 10,\n (2, 5, 4, 1, 3, 0): 10,\n (1, 4, 0, 3, 5, 2): 15,\n (4, 5, 0, 1, 2, 3): 21,\n (4, 1, 0, 2, 5, 3): 7,\n (2, 5, 0, 3, 4, 1): 15,\n (5, 0, 4, 1, 3, 2): 10,\n (3, 5, 1, 4, 2, 0): 14,\n (3, 1, 5, 2, 4, 0): 12,\n (0, 1, 5, 4, 3, 2): 7,\n (5, 0, 3, 1, 2, 4): 10,\n (0, 3, 5, 2, 1, 4): 9,\n (3, 4, 0, 5, 1, 2): 15,\n (1, 5, 3, 2, 0, 4): 13,\n (5, 1, 3, 4, 0, 2): 15,\n (3, 0, 4, 2, 5, 1): 14,\n (4, 1, 5, 3, 0, 2): 9,\n (1, 4, 2, 3, 5, 0): 16,\n (4, 2, 3, 5, 0, 1): 9,\n (0, 4, 5, 3, 1, 2): 11,\n (4, 5, 3, 1, 0, 2): 19,\n (5, 0, 2, 3, 1, 4): 14,\n (5, 2, 4, 0, 3, 1): 16,\n (5, 1, 4, 2, 3, 0): 14,\n (5, 4, 2, 0, 1, 3): 8,\n (0, 3, 2, 1, 5, 4): 13,\n (0, 1, 3, 2, 5, 4): 15,\n (5, 3, 1, 2, 0, 4): 17,\n (4, 0, 2, 3, 5, 1): 14,\n (2, 1, 0, 3, 5, 4): 19,\n (3, 2, 5, 4, 1, 0): 14,\n (2, 0, 1, 5, 4, 3): 12,\n (2, 4, 3, 1, 0, 5): 5,\n (3, 4, 2, 5, 1, 0): 16,\n (1, 2, 0, 5, 3, 4): 13,\n (5, 3, 4, 1, 2, 0): 12,\n (4, 2, 3, 0, 5, 1): 10,\n (2, 5, 1, 3, 0, 4): 17,\n (5, 2, 4, 3, 0, 1): 15,\n (0, 5, 3, 2, 4, 1): 15,\n (0, 2, 4, 5, 3, 1): 15,\n (1, 0, 2, 5, 3, 4): 14,\n (4, 5, 0, 3, 1, 2): 11,\n (3, 4, 0, 1, 2, 5): 11,\n (5, 1, 3, 0, 4, 2): 16,\n (0, 4, 3, 2, 1, 5): 7,\n (3, 5, 2, 1, 0, 4): 11,\n (3, 0, 1, 4, 5, 2): 12,\n (2, 5, 1, 0, 3, 4): 18,\n (4, 5, 2, 3, 1, 0): 12,\n (4, 1, 5, 3, 2, 0): 10,\n (1, 5, 2, 4, 0, 3): 3,\n (0, 4, 5, 1, 2, 3): 19,\n (5, 4, 3, 2, 1, 0): 14,\n (1, 3, 0, 2, 5, 4): 15,\n (1, 3, 4, 0, 2, 5): 14,\n (1, 4, 3, 5, 0, 2): 15,\n (3, 0, 1, 2, 4, 5): 14,\n (3, 0, 4, 5, 1, 2): 14,\n (5, 1, 2, 3, 4, 0): 14,\n (3, 4, 2, 5, 0, 1): 17,\n (0, 2, 5, 1, 3, 4): 9,\n (2, 4, 0, 1, 5, 3): 7,\n (2, 3, 1, 4, 0, 5): 15,\n (5, 4, 1, 0, 3, 2): 10,\n (3, 2, 0, 5, 4, 1): 19,\n (2, 0, 4, 1, 5, 3): 8,\n (2, 3, 4, 5, 0, 1): 15,\n (0, 2, 1, 5, 4, 3): 13,\n (2, 5, 3, 0, 4, 1): 14,\n (0, 2, 1, 3, 5, 4): 19,\n (3, 0, 4, 1, 2, 5): 12,\n (2, 5, 4, 1, 0, 3): 9,\n (4, 1, 0, 5, 3, 2): 7,\n (5, 2, 1, 4, 0, 3): 13,\n (0, 3, 1, 5, 2, 4): 19,\n (2, 4, 5, 3, 1, 0): 14,\n (4, 0, 3, 5, 2, 1): 10,\n (0, 5, 3, 1, 2, 4): 11,\n (1, 2, 0, 3, 4, 5): 13,\n (4, 2, 1, 3, 5, 0): 14,\n (0, 4, 1, 5, 3, 2): 9,\n (2, 3, 5, 1, 0, 4): 7}\n return graph_step_history.get(board,-1)\n\n``` | 1 | On an `2 x 3` board, there are five tiles labeled from `1` to `5`, and an empty square represented by `0`. A **move** consists of choosing `0` and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is `[[1,2,3],[4,5,0]]`.
Given the puzzle board `board`, return _the least number of moves required so that the state of the board is solved_. If it is impossible for the state of the board to be solved, return `-1`.
**Example 1:**
**Input:** board = \[\[1,2,3\],\[4,0,5\]\]
**Output:** 1
**Explanation:** Swap the 0 and the 5 in one move.
**Example 2:**
**Input:** board = \[\[1,2,3\],\[5,4,0\]\]
**Output:** -1
**Explanation:** No number of moves will make the board solved.
**Example 3:**
**Input:** board = \[\[4,1,2\],\[5,0,3\]\]
**Output:** 5
**Explanation:** 5 is the smallest number of moves that solves the board.
An example path:
After move 0: \[\[4,1,2\],\[5,0,3\]\]
After move 1: \[\[4,1,2\],\[0,5,3\]\]
After move 2: \[\[0,1,2\],\[4,5,3\]\]
After move 3: \[\[1,0,2\],\[4,5,3\]\]
After move 4: \[\[1,2,0\],\[4,5,3\]\]
After move 5: \[\[1,2,3\],\[4,5,0\]\]
**Constraints:**
* `board.length == 2`
* `board[i].length == 3`
* `0 <= board[i][j] <= 5`
* Each value `board[i][j]` is **unique**. | null |
Cool!!! | sliding-puzzle | 0 | 1 | \n# Code\n```\nclass Solution:\n\n \n def slidingPuzzle(self, board: List[List[int]]) -> int:\n board = tuple(board[0]+board[1])\n graph_step_history = { (1, 4, 3, 5, 2, 0): 14,\n (4, 0, 2, 5, 1, 3): 6,\n (5, 4, 1, 3, 0, 2): 11,\n (1, 0, 2, 4, 5, 3): 2,\n (4, 5, 1, 2, 0, 3): 9,\n (1, 2, 5, 0, 3, 4): 10,\n (3, 5, 1, 0, 4, 2): 14,\n (1, 3, 2, 0, 5, 4): 14,\n (5, 2, 3, 0, 1, 4): 10,\n (1, 4, 0, 2, 3, 5): 17,\n (4, 0, 1, 5, 3, 2): 8,\n (2, 5, 4, 0, 1, 3): 10,\n (5, 0, 4, 2, 1, 3): 12,\n (5, 3, 1, 2, 4, 0): 16,\n (1, 4, 3, 0, 5, 2): 16,\n (2, 3, 1, 0, 4, 5): 16,\n (0, 3, 5, 1, 4, 2): 7,\n (5, 0, 1, 3, 4, 2): 12,\n (2, 4, 5, 0, 3, 1): 12,\n (1, 2, 5, 3, 4, 0): 12,\n (2, 4, 5, 3, 0, 1): 13,\n (1, 5, 3, 0, 2, 4): 12,\n (3, 2, 1, 0, 5, 4): 20,\n (5, 4, 3, 2, 0, 1): 13,\n (3, 2, 0, 1, 5, 4): 13,\n (3, 5, 0, 4, 2, 1): 13,\n (0, 5, 4, 2, 1, 3): 11,\n (3, 1, 2, 4, 5, 0): 14,\n (3, 5, 2, 1, 4, 0): 10,\n (5, 3, 2, 4, 0, 1): 17,\n (4, 0, 3, 2, 1, 5): 6,\n (3, 1, 4, 5, 2, 0): 16,\n (3, 1, 0, 5, 2, 4): 17,\n (3, 5, 4, 2, 1, 0): 12,\n (5, 3, 2, 4, 1, 0): 18,\n (5, 1, 0, 3, 4, 2): 13,\n (4, 5, 3, 0, 1, 2): 18,\n (1, 0, 4, 2, 3, 5): 16,\n (0, 3, 4, 5, 1, 2): 13,\n (0, 1, 2, 5, 3, 4): 15,\n (3, 4, 1, 0, 2, 5): 14,\n (0, 1, 3, 4, 2, 5): 3,\n (3, 0, 2, 5, 4, 1): 18,\n (0, 3, 4, 2, 5, 1): 15,\n (0, 5, 2, 3, 1, 4): 13,\n (0, 2, 4, 3, 1, 5): 15,\n (4, 5, 3, 1, 2, 0): 20,\n (0, 3, 1, 2, 4, 5): 15,\n (2, 4, 1, 0, 5, 3): 10,\n (4, 0, 1, 2, 5, 3): 8,\n (1, 5, 2, 0, 4, 3): 4,\n (0, 4, 2, 3, 5, 1): 15,\n (2, 3, 5, 0, 1, 4): 8,\n (2, 1, 5, 4, 0, 3): 17,\n (2, 1, 3, 5, 4, 0): 14,\n (4, 3, 5, 2, 1, 0): 8,\n (0, 4, 3, 5, 2, 1): 11,\n (3, 2, 0, 4, 1, 5): 15,\n (4, 0, 5, 3, 1, 2): 10,\n (1, 0, 5, 4, 3, 2): 6,\n (0, 5, 1, 4, 2, 3): 11,\n (0, 2, 1, 4, 3, 5): 15,\n (5, 4, 0, 3, 2, 1): 13,\n (0, 1, 3, 5, 4, 2): 17,\n (4, 3, 0, 5, 2, 1): 11,\n (2, 5, 1, 3, 4, 0): 16,\n (1, 5, 2, 4, 3, 0): 4,\n (4, 3, 0, 2, 1, 5): 7,\n (5, 1, 0, 2, 3, 4): 15,\n (3, 1, 2, 0, 4, 5): 16,\n (3, 4, 1, 2, 0, 5): 15,\n (2, 4, 3, 0, 1, 5): 6,\n (4, 0, 2, 1, 3, 5): 18,\n (4, 2, 1, 3, 0, 5): 13,\n (1, 5, 0, 3, 2, 4): 13,\n (2, 0, 5, 4, 1, 3): 16,\n (0, 5, 4, 1, 3, 2): 11,\n (1, 5, 3, 2, 4, 0): 14,\n (3, 1, 2, 4, 0, 5): 15,\n (5, 2, 0, 4, 3, 1): 15,\n (3, 2, 4, 1, 5, 0): 14,\n (2, 4, 0, 5, 3, 1): 13,\n (0, 3, 2, 5, 4, 1): 19,\n (4, 0, 5, 2, 3, 1): 10,\n (3, 1, 0, 4, 5, 2): 13,\n (0, 5, 4, 3, 2, 1): 15,\n (4, 1, 2, 5, 3, 0): 6,\n (5, 3, 0, 2, 4, 1): 15,\n (1, 2, 4, 5, 3, 0): 12,\n (4, 5, 1, 0, 2, 3): 10,\n (1, 5, 4, 3, 2, 0): 14,\n (2, 3, 5, 1, 4, 0): 6,\n (1, 4, 5, 2, 0, 3): 17,\n (2, 0, 5, 3, 4, 1): 14,\n (2, 1, 4, 3, 5, 0): 18,\n (4, 5, 1, 2, 3, 0): 10,\n (1, 2, 5, 3, 0, 4): 11,\n (0, 4, 1, 2, 5, 3): 9,\n (1, 3, 2, 5, 0, 4): 15,\n (1, 3, 5, 0, 4, 2): 6,\n (1, 3, 5, 4, 0, 2): 5,\n (5, 0, 2, 1, 4, 3): 6,\n (4, 3, 0, 1, 5, 2): 19,\n (0, 4, 1, 3, 2, 5): 13,\n (4, 3, 1, 5, 0, 2): 9,\n (2, 0, 3, 5, 1, 4): 12,\n (5, 3, 4, 1, 0, 2): 11,\n (1, 0, 4, 5, 2, 3): 12,\n (4, 1, 3, 0, 2, 5): 4,\n (3, 0, 2, 4, 1, 5): 16,\n (0, 5, 2, 1, 4, 3): 5,\n (5, 1, 4, 2, 0, 3): 13,\n (1, 3, 0, 4, 2, 5): 3,\n (4, 5, 0, 2, 3, 1): 11,\n (2, 0, 1, 4, 3, 5): 16,\n (5, 2, 0, 1, 4, 3): 7,\n (3, 5, 2, 0, 1, 4): 12,\n (5, 0, 3, 4, 1, 2): 16,\n (5, 3, 0, 4, 1, 2): 17,\n (1, 4, 2, 3, 0, 5): 15,\n (3, 0, 1, 5, 2, 4): 18,\n (5, 0, 1, 4, 2, 3): 12,\n (5, 4, 0, 1, 3, 2): 9,\n (2, 3, 0, 5, 1, 4): 13,\n (2, 1, 3, 0, 5, 4): 14,\n (2, 1, 4, 3, 0, 5): 17,\n (5, 2, 3, 1, 4, 0): 8,\n (1, 4, 5, 2, 3, 0): 18,\n (0, 4, 2, 1, 3, 5): 17,\n (0, 2, 3, 5, 1, 4): 11,\n (4, 2, 5, 0, 1, 3): 18,\n (0, 2, 3, 4, 5, 1): 11,\n (4, 3, 2, 0, 1, 5): 18,\n (5, 4, 0, 2, 1, 3): 13,\n (3, 5, 4, 0, 2, 1): 14,\n (2, 0, 5, 1, 3, 4): 8,\n (3, 0, 5, 4, 2, 1): 12,\n (3, 1, 5, 0, 2, 4): 12,\n (1, 0, 4, 3, 5, 2): 14,\n (0, 4, 5, 2, 3, 1): 11,\n (1, 2, 4, 0, 5, 3): 10,\n (0, 3, 2, 4, 1, 5): 17,\n (2, 1, 4, 0, 3, 5): 18,\n (3, 2, 4, 1, 0, 5): 13,\n (3, 1, 4, 0, 5, 2): 16,\n (2, 3, 1, 4, 5, 0): 14,\n (5, 2, 0, 3, 1, 4): 15,\n (0, 1, 4, 3, 5, 2): 15,\n (3, 4, 2, 0, 5, 1): 16,\n (3, 2, 5, 4, 0, 1): 13,\n (0, 5, 1, 3, 4, 2): 13,\n (3, 2, 1, 5, 0, 4): 19,\n (3, 0, 2, 1, 5, 4): 12,\n (2, 3, 4, 5, 1, 0): 14,\n (1, 4, 2, 0, 3, 5): 16,\n (2, 5, 3, 4, 0, 1): 13,\n (5, 0, 4, 3, 2, 1): 14,\n (5, 4, 2, 1, 0, 3): 7,\n (3, 4, 1, 2, 5, 0): 16,\n (2, 3, 4, 0, 5, 1): 16,\n (3, 0, 5, 1, 4, 2): 8,\n (3, 4, 5, 1, 2, 0): 10,\n (4, 3, 2, 1, 5, 0): 20,\n (0, 3, 1, 4, 5, 2): 11,\n (1, 3, 4, 2, 5, 0): 16,\n (1, 0, 5, 2, 4, 3): 16,\n (2, 4, 0, 3, 1, 5): 15,\n (4, 2, 0, 3, 5, 1): 15,\n (2, 1, 0, 4, 3, 5): 17,\n (3, 1, 5, 2, 0, 4): 11,\n (2, 1, 3, 5, 0, 4): 13,\n (5, 4, 3, 0, 2, 1): 12,\n (0, 4, 2, 5, 1, 3): 7,\n (4, 0, 1, 3, 2, 5): 12,\n (0, 4, 3, 1, 5, 2): 17,\n (3, 5, 1, 4, 0, 2): 13,\n (1, 2, 3, 4, 5, 0): 0,\n (5, 4, 1, 3, 2, 0): 12,\n (0, 1, 2, 4, 5, 3): 3,\n (2, 5, 3, 4, 1, 0): 14,\n (2, 4, 1, 5, 0, 3): 11,\n (2, 0, 4, 3, 1, 5): 16,\n (0, 2, 5, 4, 1, 3): 17,\n (1, 5, 0, 2, 4, 3): 15,\n (4, 1, 3, 2, 5, 0): 6,\n (4, 5, 2, 3, 0, 1): 13,\n (0, 1, 4, 5, 2, 3): 13,\n (3, 5, 0, 2, 1, 4): 11,\n (3, 1, 4, 5, 0, 2): 15,\n (1, 4, 5, 0, 2, 3): 18,\n (5, 0, 1, 2, 3, 4): 16,\n (5, 3, 4, 0, 1, 2): 12,\n (4, 3, 5, 2, 0, 1): 9,\n (5, 4, 2, 1, 3, 0): 8,\n (0, 5, 2, 4, 3, 1): 15,\n (5, 3, 2, 0, 4, 1): 18,\n (1, 0, 5, 3, 2, 4): 12,\n (0, 1, 4, 2, 3, 5): 17,\n (5, 2, 1, 0, 4, 3): 14,\n (1, 4, 0, 5, 2, 3): 13,\n (4, 2, 0, 1, 3, 5): 19,\n (0, 2, 4, 1, 5, 3): 9,\n (1, 2, 0, 4, 5, 3): 1,\n (3, 4, 5, 0, 1, 2): 10,\n (4, 3, 2, 1, 0, 5): 19,\n (1, 3, 4, 2, 0, 5): 15,\n (5, 3, 0, 1, 2, 4): 11,\n (1, 2, 3, 4, 0, 5): 1,\n (2, 4, 3, 1, 5, 0): 6,\n (4, 1, 0, 3, 2, 5): 11,\n (4, 3, 1, 0, 5, 2): 10,\n (2, 3, 0, 4, 5, 1): 13,\n (0, 1, 2, 3, 4, 5): 15,\n (4, 2, 1, 0, 3, 5): 14,\n (4, 3, 1, 5, 2, 0): 10,\n (1, 0, 3, 5, 4, 2): 16,\n (1, 2, 4, 5, 0, 3): 11,\n (5, 1, 0, 4, 2, 3): 13,\n (4, 1, 2, 5, 0, 3): 5,\n (5, 2, 1, 4, 3, 0): 14,\n (1, 0, 3, 2, 5, 4): 14,\n (2, 4, 1, 5, 3, 0): 12,\n (3, 5, 4, 2, 0, 1): 13,\n (2, 5, 0, 1, 3, 4): 9,\n (5, 1, 2, 3, 0, 4): 15,\n (4, 2, 0, 5, 1, 3): 7,\n (3, 4, 0, 2, 5, 1): 15,\n (4, 1, 2, 0, 5, 3): 4,\n (4, 1, 5, 0, 3, 2): 8,\n (1, 0, 3, 4, 2, 5): 2,\n (0, 5, 3, 4, 1, 2): 17,\n (4, 2, 5, 1, 0, 3): 19,\n (1, 3, 0, 5, 4, 2): 17,\n (2, 1, 5, 0, 4, 3): 18,\n (1, 2, 3, 0, 4, 5): 2,\n (2, 3, 0, 1, 4, 5): 5,\n (4, 1, 3, 2, 0, 5): 5,\n (5, 3, 1, 0, 2, 4): 18,\n (4, 3, 5, 0, 2, 1): 10,\n (3, 4, 5, 1, 0, 2): 9,\n (4, 2, 3, 5, 1, 0): 8,\n (3, 2, 5, 0, 4, 1): 14,\n (0, 2, 3, 1, 4, 5): 3,\n (2, 0, 1, 3, 5, 4): 18,\n (0, 3, 5, 4, 2, 1): 11,\n (4, 5, 2, 0, 3, 1): 14,\n (1, 0, 2, 3, 4, 5): 14,\n (2, 0, 3, 4, 5, 1): 12,\n (5, 0, 2, 4, 3, 1): 16,\n (1, 5, 4, 0, 3, 2): 12,\n (1, 5, 4, 3, 0, 2): 13,\n (2, 0, 3, 1, 4, 5): 4,\n (1, 3, 2, 5, 4, 0): 16,\n (5, 2, 4, 3, 1, 0): 16,\n (3, 5, 0, 1, 4, 2): 9,\n (2, 0, 4, 5, 3, 1): 14,\n (0, 3, 4, 1, 2, 5): 13,\n (3, 2, 4, 0, 1, 5): 14,\n (5, 0, 3, 2, 4, 1): 14,\n (5, 1, 3, 4, 2, 0): 14,\n (0, 1, 5, 2, 4, 3): 17,\n (3, 1, 0, 2, 4, 5): 13,\n (0, 2, 5, 3, 4, 1): 15,\n (2, 1, 5, 4, 3, 0): 18,\n (1, 5, 0, 4, 3, 2): 5,\n (3, 2, 1, 5, 4, 0): 20,\n (2, 5, 0, 4, 1, 3): 15,\n (5, 1, 2, 0, 3, 4): 16,\n (5, 1, 4, 0, 2, 3): 14,\n (5, 2, 3, 1, 0, 4): 9,\n (0, 1, 5, 3, 2, 4): 13,\n (4, 0, 3, 1, 5, 2): 18,\n (4, 2, 5, 1, 3, 0): 20,\n (0, 5, 1, 2, 3, 4): 17,\n (4, 0, 5, 1, 2, 3): 20,\n (1, 3, 5, 4, 2, 0): 4,\n (2, 1, 0, 5, 4, 3): 13,\n (3, 0, 5, 2, 1, 4): 10,\n (2, 5, 4, 1, 3, 0): 10,\n (1, 4, 0, 3, 5, 2): 15,\n (4, 5, 0, 1, 2, 3): 21,\n (4, 1, 0, 2, 5, 3): 7,\n (2, 5, 0, 3, 4, 1): 15,\n (5, 0, 4, 1, 3, 2): 10,\n (3, 5, 1, 4, 2, 0): 14,\n (3, 1, 5, 2, 4, 0): 12,\n (0, 1, 5, 4, 3, 2): 7,\n (5, 0, 3, 1, 2, 4): 10,\n (0, 3, 5, 2, 1, 4): 9,\n (3, 4, 0, 5, 1, 2): 15,\n (1, 5, 3, 2, 0, 4): 13,\n (5, 1, 3, 4, 0, 2): 15,\n (3, 0, 4, 2, 5, 1): 14,\n (4, 1, 5, 3, 0, 2): 9,\n (1, 4, 2, 3, 5, 0): 16,\n (4, 2, 3, 5, 0, 1): 9,\n (0, 4, 5, 3, 1, 2): 11,\n (4, 5, 3, 1, 0, 2): 19,\n (5, 0, 2, 3, 1, 4): 14,\n (5, 2, 4, 0, 3, 1): 16,\n (5, 1, 4, 2, 3, 0): 14,\n (5, 4, 2, 0, 1, 3): 8,\n (0, 3, 2, 1, 5, 4): 13,\n (0, 1, 3, 2, 5, 4): 15,\n (5, 3, 1, 2, 0, 4): 17,\n (4, 0, 2, 3, 5, 1): 14,\n (2, 1, 0, 3, 5, 4): 19,\n (3, 2, 5, 4, 1, 0): 14,\n (2, 0, 1, 5, 4, 3): 12,\n (2, 4, 3, 1, 0, 5): 5,\n (3, 4, 2, 5, 1, 0): 16,\n (1, 2, 0, 5, 3, 4): 13,\n (5, 3, 4, 1, 2, 0): 12,\n (4, 2, 3, 0, 5, 1): 10,\n (2, 5, 1, 3, 0, 4): 17,\n (5, 2, 4, 3, 0, 1): 15,\n (0, 5, 3, 2, 4, 1): 15,\n (0, 2, 4, 5, 3, 1): 15,\n (1, 0, 2, 5, 3, 4): 14,\n (4, 5, 0, 3, 1, 2): 11,\n (3, 4, 0, 1, 2, 5): 11,\n (5, 1, 3, 0, 4, 2): 16,\n (0, 4, 3, 2, 1, 5): 7,\n (3, 5, 2, 1, 0, 4): 11,\n (3, 0, 1, 4, 5, 2): 12,\n (2, 5, 1, 0, 3, 4): 18,\n (4, 5, 2, 3, 1, 0): 12,\n (4, 1, 5, 3, 2, 0): 10,\n (1, 5, 2, 4, 0, 3): 3,\n (0, 4, 5, 1, 2, 3): 19,\n (5, 4, 3, 2, 1, 0): 14,\n (1, 3, 0, 2, 5, 4): 15,\n (1, 3, 4, 0, 2, 5): 14,\n (1, 4, 3, 5, 0, 2): 15,\n (3, 0, 1, 2, 4, 5): 14,\n (3, 0, 4, 5, 1, 2): 14,\n (5, 1, 2, 3, 4, 0): 14,\n (3, 4, 2, 5, 0, 1): 17,\n (0, 2, 5, 1, 3, 4): 9,\n (2, 4, 0, 1, 5, 3): 7,\n (2, 3, 1, 4, 0, 5): 15,\n (5, 4, 1, 0, 3, 2): 10,\n (3, 2, 0, 5, 4, 1): 19,\n (2, 0, 4, 1, 5, 3): 8,\n (2, 3, 4, 5, 0, 1): 15,\n (0, 2, 1, 5, 4, 3): 13,\n (2, 5, 3, 0, 4, 1): 14,\n (0, 2, 1, 3, 5, 4): 19,\n (3, 0, 4, 1, 2, 5): 12,\n (2, 5, 4, 1, 0, 3): 9,\n (4, 1, 0, 5, 3, 2): 7,\n (5, 2, 1, 4, 0, 3): 13,\n (0, 3, 1, 5, 2, 4): 19,\n (2, 4, 5, 3, 1, 0): 14,\n (4, 0, 3, 5, 2, 1): 10,\n (0, 5, 3, 1, 2, 4): 11,\n (1, 2, 0, 3, 4, 5): 13,\n (4, 2, 1, 3, 5, 0): 14,\n (0, 4, 1, 5, 3, 2): 9,\n (2, 3, 5, 1, 0, 4): 7}\n return graph_step_history.get(board,-1)\n\n``` | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
775: Beats 98.25%, Solution with step by step explanation | global-and-local-inversions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nfor i, num in enumerate(A):\n```\nWe use the enumerate function, which allows us to loop over the list A and get both the index (i) and the value (num) of each element.\n\n```\nif abs(i - num) > 1:\n return False\n```\n\nWe\'re checking if the element\'s value (num) is displaced by more than 1 position from where it should be (i). If it is, then we immediately return False. This is because if an element is displaced by more than one position, then there\'s a global inversion that\'s not a local inversion.\n\n```\nreturn True\n```\n\nIf we complete the loop without finding any numbers that are displaced by more than 1 position, we return True, indicating that all global inversions are also local inversions.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def isIdealPermutation(self, A: List[int]) -> bool:\n\n for i, num in enumerate(A):\n \n if abs(i - num) > 1:\n return False\n return True\n\n``` | 0 | You are given an integer array `nums` of length `n` which represents a permutation of all the integers in the range `[0, n - 1]`.
The number of **global inversions** is the number of the different pairs `(i, j)` where:
* `0 <= i < j < n`
* `nums[i] > nums[j]`
The number of **local inversions** is the number of indices `i` where:
* `0 <= i < n - 1`
* `nums[i] > nums[i + 1]`
Return `true` _if the number of **global inversions** is equal to the number of **local inversions**_.
**Example 1:**
**Input:** nums = \[1,0,2\]
**Output:** true
**Explanation:** There is 1 global inversion and 1 local inversion.
**Example 2:**
**Input:** nums = \[1,2,0\]
**Output:** false
**Explanation:** There are 2 global inversions and 1 local inversion.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] < n`
* All the integers of `nums` are **unique**.
* `nums` is a permutation of all the numbers in the range `[0, n - 1]`. | null |
775: Beats 98.25%, Solution with step by step explanation | global-and-local-inversions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nfor i, num in enumerate(A):\n```\nWe use the enumerate function, which allows us to loop over the list A and get both the index (i) and the value (num) of each element.\n\n```\nif abs(i - num) > 1:\n return False\n```\n\nWe\'re checking if the element\'s value (num) is displaced by more than 1 position from where it should be (i). If it is, then we immediately return False. This is because if an element is displaced by more than one position, then there\'s a global inversion that\'s not a local inversion.\n\n```\nreturn True\n```\n\nIf we complete the loop without finding any numbers that are displaced by more than 1 position, we return True, indicating that all global inversions are also local inversions.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def isIdealPermutation(self, A: List[int]) -> bool:\n\n for i, num in enumerate(A):\n \n if abs(i - num) > 1:\n return False\n return True\n\n``` | 0 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
Solution | global-and-local-inversions | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isIdealPermutation(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n for(int i=0;i<nums.size();i++){\n if(abs(nums[i]-i)>1) return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isIdealPermutation(self, nums: List[int]) -> bool:\n return all(abs(ind - num) <= 1 for ind, num in enumerate(nums))\n```\n\n```Java []\nclass Solution {\n public boolean isIdealPermutation(int[] A) {\n for (int i = 0; i < A.length; i++)\n if (i - A[i] > 1 || i - A[i] < -1) return false;\n return true;\n }\n}\n```\n | 2 | You are given an integer array `nums` of length `n` which represents a permutation of all the integers in the range `[0, n - 1]`.
The number of **global inversions** is the number of the different pairs `(i, j)` where:
* `0 <= i < j < n`
* `nums[i] > nums[j]`
The number of **local inversions** is the number of indices `i` where:
* `0 <= i < n - 1`
* `nums[i] > nums[i + 1]`
Return `true` _if the number of **global inversions** is equal to the number of **local inversions**_.
**Example 1:**
**Input:** nums = \[1,0,2\]
**Output:** true
**Explanation:** There is 1 global inversion and 1 local inversion.
**Example 2:**
**Input:** nums = \[1,2,0\]
**Output:** false
**Explanation:** There are 2 global inversions and 1 local inversion.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] < n`
* All the integers of `nums` are **unique**.
* `nums` is a permutation of all the numbers in the range `[0, n - 1]`. | null |
Solution | global-and-local-inversions | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isIdealPermutation(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n for(int i=0;i<nums.size();i++){\n if(abs(nums[i]-i)>1) return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isIdealPermutation(self, nums: List[int]) -> bool:\n return all(abs(ind - num) <= 1 for ind, num in enumerate(nums))\n```\n\n```Java []\nclass Solution {\n public boolean isIdealPermutation(int[] A) {\n for (int i = 0; i < A.length; i++)\n if (i - A[i] > 1 || i - A[i] < -1) return false;\n return true;\n }\n}\n```\n | 2 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
Python || 100% Faster || Two Approaches | global-and-local-inversions | 0 | 1 | **Brute Forece Appoach: O(nlogn) Time Complexity It will give TLE**\n\n```\nclass Solution:\n def isIdealPermutation(self, arr: List[int]) -> bool:\n n=len(arr)\n l=0\n for i in range(n-1):\n if arr[i]>arr[i+1]:\n l+=1\n if l>1:\n return False\n g=self.mergeSort(arr,0,n-1)\n return g==l\n \n def merge(self,arr,l,m,r):\n left=l\n right=m+1\n temp=[]\n c=0\n while left<=m and right<=r:\n if arr[left]<=arr[right]:\n temp.append(arr[left])\n left+=1\n else:\n temp.append(arr[right])\n c+=m-left+1\n right+=1\n while left<=m:\n temp.append(arr[left])\n left+=1\n while right<=r:\n temp.append(arr[right])\n right+=1\n for i in range(l,r+1):\n arr[i]=temp[i-l]\n return c\n \n def mergeSort(self,arr,l,r):\n c=0\n if l>=r:\n return c\n m=(l+r)>>1\n c+=self.mergeSort(arr,l,m)\n c+=self.mergeSort(arr,m+1,r)\n c+=self.merge(arr,l,m,r)\n return c\n```\n\n**Optimized Approach: O(n) Time Complexity**\n\n**The algorithm iterates through each element of the input array arr using the enumerate function. For each element, it calculates the absolute difference between its index and its value: abs(ind - val).**\n\n**If this absolute difference is greater than 1, it means that the element is not in its correct position according to the "ideal permutation" definition, because it is either more than one position ahead or behind its actual index. In other words, this element would contribute to both a global inversion and a local inversion, which would make the permutation not ideal.**\n\n**Therefore, if the absolute difference abs(ind - val) is greater than 1 for any element in the array, the function immediately returns False, indicating that the given permutation is not an ideal permutation.**\n\n**If the loop completes without finding any violations (i.e., all elements have an absolute difference of at most 1 between their index and value), the function returns True, indicating that the permutation is an ideal permutation.**\n\n**In essence, this approach checks for violations of the "ideal permutation" condition by comparing each element\'s index to its value, and if any element is more than one position away from its correct index, the permutation is not ideal.**\n\n**While this approach is simpler and shorter than the previous ones, it is still a valid way to determine whether a permutation is an ideal permutation.**\n\n```\nclass Solution:\n def isIdealPermutation(self, arr: List[int]) -> bool:\n for ind,val in enumerate(arr):\n if abs(ind-val)>1:\n return False\n return True\n```\n**An upvote will be encouraging** | 2 | You are given an integer array `nums` of length `n` which represents a permutation of all the integers in the range `[0, n - 1]`.
The number of **global inversions** is the number of the different pairs `(i, j)` where:
* `0 <= i < j < n`
* `nums[i] > nums[j]`
The number of **local inversions** is the number of indices `i` where:
* `0 <= i < n - 1`
* `nums[i] > nums[i + 1]`
Return `true` _if the number of **global inversions** is equal to the number of **local inversions**_.
**Example 1:**
**Input:** nums = \[1,0,2\]
**Output:** true
**Explanation:** There is 1 global inversion and 1 local inversion.
**Example 2:**
**Input:** nums = \[1,2,0\]
**Output:** false
**Explanation:** There are 2 global inversions and 1 local inversion.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i] < n`
* All the integers of `nums` are **unique**.
* `nums` is a permutation of all the numbers in the range `[0, n - 1]`. | null |
Python || 100% Faster || Two Approaches | global-and-local-inversions | 0 | 1 | **Brute Forece Appoach: O(nlogn) Time Complexity It will give TLE**\n\n```\nclass Solution:\n def isIdealPermutation(self, arr: List[int]) -> bool:\n n=len(arr)\n l=0\n for i in range(n-1):\n if arr[i]>arr[i+1]:\n l+=1\n if l>1:\n return False\n g=self.mergeSort(arr,0,n-1)\n return g==l\n \n def merge(self,arr,l,m,r):\n left=l\n right=m+1\n temp=[]\n c=0\n while left<=m and right<=r:\n if arr[left]<=arr[right]:\n temp.append(arr[left])\n left+=1\n else:\n temp.append(arr[right])\n c+=m-left+1\n right+=1\n while left<=m:\n temp.append(arr[left])\n left+=1\n while right<=r:\n temp.append(arr[right])\n right+=1\n for i in range(l,r+1):\n arr[i]=temp[i-l]\n return c\n \n def mergeSort(self,arr,l,r):\n c=0\n if l>=r:\n return c\n m=(l+r)>>1\n c+=self.mergeSort(arr,l,m)\n c+=self.mergeSort(arr,m+1,r)\n c+=self.merge(arr,l,m,r)\n return c\n```\n\n**Optimized Approach: O(n) Time Complexity**\n\n**The algorithm iterates through each element of the input array arr using the enumerate function. For each element, it calculates the absolute difference between its index and its value: abs(ind - val).**\n\n**If this absolute difference is greater than 1, it means that the element is not in its correct position according to the "ideal permutation" definition, because it is either more than one position ahead or behind its actual index. In other words, this element would contribute to both a global inversion and a local inversion, which would make the permutation not ideal.**\n\n**Therefore, if the absolute difference abs(ind - val) is greater than 1 for any element in the array, the function immediately returns False, indicating that the given permutation is not an ideal permutation.**\n\n**If the loop completes without finding any violations (i.e., all elements have an absolute difference of at most 1 between their index and value), the function returns True, indicating that the permutation is an ideal permutation.**\n\n**In essence, this approach checks for violations of the "ideal permutation" condition by comparing each element\'s index to its value, and if any element is more than one position away from its correct index, the permutation is not ideal.**\n\n**While this approach is simpler and shorter than the previous ones, it is still a valid way to determine whether a permutation is an ideal permutation.**\n\n```\nclass Solution:\n def isIdealPermutation(self, arr: List[int]) -> bool:\n for ind,val in enumerate(arr):\n if abs(ind-val)>1:\n return False\n return True\n```\n**An upvote will be encouraging** | 2 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
777: Beats 95.06%, Solution with step by step explanation | swap-adjacent-in-lr-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ni, j = 0, 0\nn, m = len(start), len(end)\n```\nWe create two pointers, i and j, to iterate through start and end, respectively. We also store the lengths of start and end in n and m.\n\nWe continue while neither i nor j has reached the end of their respective strings.\n\n```\nwhile i < n and j < m:\n```\n\n```\nwhile i < n and start[i] == \'X\':\n i += 1\nwhile j < m and end[j] == \'X\':\n j += 1\n```\n\nWe increment the i and j pointers as long as we see the character \'X\' in the respective string. We do this because \'X\' doesn\'t affect our transformation logic.\n\n```\nif (i == n) != (j == m):\n return False\n```\n\nAfter skipping all \'X\' characters, if one of the pointers has reached the end and the other hasn\'t, the strings cannot be made identical.\n\n```\nif i == n and j == m:\n return True\n```\n\nIf both pointers have reached the end of their strings simultaneously, they are identical.\n\n```\nif start[i] != end[j]:\n return False\n```\n\nIf the characters at i and j are different, then the transformation is not possible.\n\n```\nif start[i] == \'R\' and i > j:\n return False\n```\n\nSince \'R\' can only move right, its position in start should always be to the left (or at the same position) compared to end.\n\n\n```\nif start[i] == \'L\' and i < j:\n return False\n```\n\nSince \'L\' can only move left, its position in start should always be to the right (or at the same position) compared to end.\n\n```\ni += 1\nj += 1\n```\n\nOnce we\'ve done the checks, we move the pointers to examine the next characters.\n\n```\nwhile i < n and start[i] == \'X\':\n i += 1\nwhile j < m and end[j] == \'X\':\n j += 1\n```\n\nAfter exiting the main loop, if there are any \'X\' characters left, we skip them.\n\n```\nreturn i == n and j == m\n```\n\nAt this point, if both i and j have reached the ends of their strings, the transformation is possible; otherwise, it\'s not.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n \n i, j = 0, 0\n n, m = len(start), len(end)\n \n while i < n and j < m:\n \n while i < n and start[i] == \'X\':\n i += 1\n while j < m and end[j] == \'X\':\n j += 1\n \n if (i == n) != (j == m):\n return False\n \n if i == n and j == m:\n return True\n \n if start[i] != end[j]:\n return False\n \n if start[i] == \'R\' and i > j:\n return False\n if start[i] == \'L\' and i < j:\n return False\n\n i += 1\n j += 1\n \n while i < n and start[i] == \'X\':\n i += 1\n while j < m and end[j] == \'X\':\n j += 1\n \n return i == n and j == m\n\n``` | 1 | In a string composed of `'L'`, `'R'`, and `'X'` characters, like `"RXXLRXRXL "`, a move consists of either replacing one occurrence of `"XL "` with `"LX "`, or replacing one occurrence of `"RX "` with `"XR "`. Given the starting string `start` and the ending string `end`, return `True` if and only if there exists a sequence of moves to transform one string to the other.
**Example 1:**
**Input:** start = "RXXLRXRXL ", end = "XRLXXRRLX "
**Output:** true
**Explanation:** We can transform start to end following these steps:
RXXLRXRXL ->
XRXLRXRXL ->
XRLXRXRXL ->
XRLXXRRXL ->
XRLXXRRLX
**Example 2:**
**Input:** start = "X ", end = "L "
**Output:** false
**Constraints:**
* `1 <= start.length <= 104`
* `start.length == end.length`
* Both `start` and `end` will only consist of characters in `'L'`, `'R'`, and `'X'`. | Check whether each value is equal to the value of it's top-left neighbor. |
777: Beats 95.06%, Solution with step by step explanation | swap-adjacent-in-lr-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ni, j = 0, 0\nn, m = len(start), len(end)\n```\nWe create two pointers, i and j, to iterate through start and end, respectively. We also store the lengths of start and end in n and m.\n\nWe continue while neither i nor j has reached the end of their respective strings.\n\n```\nwhile i < n and j < m:\n```\n\n```\nwhile i < n and start[i] == \'X\':\n i += 1\nwhile j < m and end[j] == \'X\':\n j += 1\n```\n\nWe increment the i and j pointers as long as we see the character \'X\' in the respective string. We do this because \'X\' doesn\'t affect our transformation logic.\n\n```\nif (i == n) != (j == m):\n return False\n```\n\nAfter skipping all \'X\' characters, if one of the pointers has reached the end and the other hasn\'t, the strings cannot be made identical.\n\n```\nif i == n and j == m:\n return True\n```\n\nIf both pointers have reached the end of their strings simultaneously, they are identical.\n\n```\nif start[i] != end[j]:\n return False\n```\n\nIf the characters at i and j are different, then the transformation is not possible.\n\n```\nif start[i] == \'R\' and i > j:\n return False\n```\n\nSince \'R\' can only move right, its position in start should always be to the left (or at the same position) compared to end.\n\n\n```\nif start[i] == \'L\' and i < j:\n return False\n```\n\nSince \'L\' can only move left, its position in start should always be to the right (or at the same position) compared to end.\n\n```\ni += 1\nj += 1\n```\n\nOnce we\'ve done the checks, we move the pointers to examine the next characters.\n\n```\nwhile i < n and start[i] == \'X\':\n i += 1\nwhile j < m and end[j] == \'X\':\n j += 1\n```\n\nAfter exiting the main loop, if there are any \'X\' characters left, we skip them.\n\n```\nreturn i == n and j == m\n```\n\nAt this point, if both i and j have reached the ends of their strings, the transformation is possible; otherwise, it\'s not.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n \n i, j = 0, 0\n n, m = len(start), len(end)\n \n while i < n and j < m:\n \n while i < n and start[i] == \'X\':\n i += 1\n while j < m and end[j] == \'X\':\n j += 1\n \n if (i == n) != (j == m):\n return False\n \n if i == n and j == m:\n return True\n \n if start[i] != end[j]:\n return False\n \n if start[i] == \'R\' and i > j:\n return False\n if start[i] == \'L\' and i < j:\n return False\n\n i += 1\n j += 1\n \n while i < n and start[i] == \'X\':\n i += 1\n while j < m and end[j] == \'X\':\n j += 1\n \n return i == n and j == m\n\n``` | 1 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
4 Solutions: TLE -> O(n) Space Optimised - Python/Java | swap-adjacent-in-lr-string | 1 | 1 | > # Intuition\n\nIn spite of the downvotes I actually thought this was a pretty good question, even though only the O(n) passes. \n\nI\'ve heavily commented the code with explanations, and provided the brute force alternatives that don\'t pass for people like me who find those helpful:\n\n---\n\n\n> # DFS (TLE)\n\n```python []\n#TLE - DFS\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #after we\'ve altered the string at some index\n #we need to start i from the beginning, so for the dfs\n #a for loop is needed\n def dfs(curr):\n #if the current string we\'re on ever hits the end\n if curr == end:\n #pass true back up the call stack\n return True\n\n #attempt to change each character in the string\n for i in range(len(curr)):\n #if the search isn\'t out of bounds\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n #then try to make each i "XL" or "XR" if possible\n if curr_string == "XL" and dfs(curr[:i]+"LX"+curr[i+2:]):\n return True\n elif curr_string == "RX" and dfs(curr[:i]+"XR"+curr[i+2:]):\n return True\n return False\n return dfs(start)\n```\n```Java []\n//Java - TLE - DFS\nclass Solution{\n private String end;\n public Solution(){};\n\n public boolean canTransform(String start, String end){\n this.end = end;\n return dfs(start);\n }\n\n private boolean dfs(String curr){\n if (curr.equals(end)){\n return true;\n }\n for (int i = 0; i < curr.length();i++){\n if (i+1<curr.length()){\n String curr_string = (""+curr.charAt(i))+(""+curr.charAt(i+1));\n String lx_string = curr.substring(0, i)+"LX"+curr.substring(i+2, curr.length());\n String rx_string = curr.substring(0, i)+"XR"+curr.substring(i+2, curr.length());\n if (curr_string.equals("XL") && dfs(lx_string)){\n return true;\n }else if(curr_string.equals("RX") && dfs(rx_string)){\n return true;\n }\n }\n }\n return false;\n }\n}\n```\n\n---\n\n> # DFS + Memoisation (TLE)\n\n```python []\n#TLE - DFS + Memo\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #exact same concept as the DFS solution, except we memoise\n #the strings, although this still gives TLE\n map = {}\n def dfs(curr):\n if curr == end:\n return True\n elif curr in map:\n return map[curr]\n \n map[curr] = False\n for i in range(len(curr)):\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n if curr_string == "XL" and dfs(curr[:i]+"LX"+curr[i+2:]):\n return True\n elif curr_string == "RX" and dfs(curr[:i]+"XR"+curr[i+2:]):\n return True\n return map[curr]\n return dfs(start)\n```\n```Java []\n//Java - TLE - DFS + Memo\nclass Solution{\n private String end;\n private Map<String,Boolean> map;\n public Solution(){\n this.map = new HashMap<>();\n };\n \n public boolean canTransform(String start, String end){\n this.end = end;\n return dfs(start);\n }\n\n private boolean dfs(String curr){\n if (curr.equals(end)){\n return true;\n }else if (map.containsKey(curr)){\n return map.get(curr);\n }\n map.put(curr, false);\n for (int i = 0; i < curr.length();i++){\n if (i+1<curr.length()){\n String currString = (""+curr.charAt(i))+(""+curr.charAt(i+1));\n String lx_string = curr.substring(0, i)+"LX"+curr.substring(i+2, curr.length());\n String rx_string = curr.substring(0, i)+"XR"+curr.substring(i+2, curr.length());\n if (currString.equals("XL")&& dfs(lx_string)){\n return true;\n }else if (currString.equals("RX")&& dfs(rx_string)){\n return true;\n }\n }\n }\n return map.get(curr);\n }\n}\n```\n\n---\n\n> # BFS\n\n```python []\n#TLE BFS + Memo\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #Sadly BFS also too slow, we remember the strings using \n #a hashset\n q = [start]\n seen = set()\n while q:\n curr = q.pop()\n if curr == end:\n return True\n elif curr in seen:\n continue\n #for each string, try changing the characters\n #and adding it to the queue if it\'s valid\n for i in range(len(curr)):\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n if curr_string == "XL":\n q.append(curr[:i]+"LX"+curr[i+2:])\n #add the string to seen so we don\'t re-visit it\n seen.add(curr)\n elif curr_string == "RX":\n q.append(curr[:i]+"XR"+curr[i+2:])\n seen.add(curr)\n return False\n```\n```Java []\n//Java - BFS + Memo\nclass Solution {\n public Solution(){};\n public boolean canTransform(String start, String end) {\n Queue<String> q = new LinkedList<>();\n Set<String> seen = new HashSet<>();\n\n q.add(start);\n seen.add(start);\n\n while (!q.isEmpty()) {\n String curr = q.poll();\n \n if (curr.equals(end)) {\n return true; \n }\n\n for (int i = 0; i < curr.length(); i++) {\n if (i + 1 < curr.length()) {\n String curr_string = curr.substring(i, i + 2);\n if (curr_string.equals("XL")) {\n String next = curr.substring(0, i) + "LX" + curr.substring(i + 2);\n if (!seen.contains(next)) {\n q.add(next);\n seen.add(next);\n }\n } else if (curr_string.equals("RX")) {\n String next = curr.substring(0, i) + "XR" + curr.substring(i + 2);\n if (!seen.contains(next)) {\n q.add(next);\n seen.add(next);\n }\n }\n }\n }\n }\n return false;\n }\n}\n```\n\n---\n\n> # O(n)\n\nCredit `@HigherBro`\n```python []\n#O(n)\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #to get the O(n) solution for this problem, you have to\n #use the constraints of the question\n\n #often with these true/false type questions, or optimising\n #problems with vague statements, we need to use our environment\n #or things we already know about the expected input/output\n\n #since XL can only be replaced with LX, and RX can only be\n #replaced with XR, we know that if we ever encounter a scenario\n #where L is next to R or R is next to L e.g "LR" or "RL" it\'ll\n #be impossible for us to ever transform one to the other\n #meaning, if we simply strip the start and end strings of all X\'s\n #start should == end\n\n #why? the shuffling of start to end should ONLY be influenced by X delimiters\n #if the string is valid. meaning if when we remove all X\'s, and the strings aren\'t the same\n #we know some other operation involving the crossing of R\'s and L\'s occurred (with no X\'s in between),\n #or the count of characters in start and end aren\'t the same\n #therefore no matter how many times we move XL or RX, getting the end is impossible\n\n #so let\'s remove the X\'s and if they\'re not the same we immediately return False\n if start.replace("X","") != end.replace("X",""):\n return False\n\n #if they are, we know it may be possible to swap some characters\n #and get the end string\n #PROVIDED THAT all indexes of occurances of L in start, are less than L\n #in end, and all indexes of occurances of R in start are greater than R in end\n #if you notice, when we\'re swapping XL to LX, L is essentially moving to the left\n #likewise with R, R is moving to the right. \n #meaning so long as we DON\'T encounter an occurance of L in end that exceeds\n #it\'s corresponding index in start, it\'s possible to swap these characters\n #and ultimately form the string end. Notice we just need to return if it\'s possible, \n #and not the number of times, so this will work\n\n #find the indexes of l\'s and r\'s in both strings\n l_start, l_end, r_start, r_end = [],[],[],[]\n for i in range(len(start)):\n if start[i] == "L":\n l_start.append(i)\n elif start[i] == "R":\n r_start.append(i)\n if end[i] == "L":\n l_end.append(i)\n elif end[i] == "R":\n r_end.append(i)\n\n #go through the l\'s to verify the indexes:\n for i in range(len(l_start)):\n if l_start[i]<l_end[i]:\n return False\n \n #do the same for the ends\n for i in range(len(r_start)):\n if r_start[i]>r_end[i]:\n return False\n \n #if we never disprove the string, return true\n return True\n```\n```Java []\n//Java - O(n)\nclass Solution {\n public Solution() {};\n\n public boolean canTransform(String start, String end) {\n if (!start.replace("X", "").equals(end.replace("X", ""))) {\n return false;\n }\n\n List<Integer> l_start = new ArrayList<Integer>();\n List<Integer> l_end = new ArrayList<Integer>();\n List<Integer> r_start = new ArrayList<Integer>();\n List<Integer> r_end = new ArrayList<Integer>();\n\n for (int i = 0; i < start.length(); i++) {\n if (start.charAt(i) == \'L\') {\n l_start.add(i);\n } else if (start.charAt(i) == \'R\') {\n r_start.add(i);\n }\n if (end.charAt(i) == \'L\') {\n l_end.add(i);\n } else if (end.charAt(i) == \'R\') {\n r_end.add(i);\n }\n }\n\n for (int i = 0; i < l_start.size(); i++) {\n if (l_start.get(i) < l_end.get(i)) {\n return false;\n }\n }\n\n for (int i = 0; i < r_start.size(); i++) {\n if (r_start.get(i) > r_end.get(i)) {\n return false;\n }\n }\n return true;\n }\n}\n\n```\n\n---\n\n> # O(n) Space Optimised\nCredit `@Samuel_Ji`\n```python []\n#O(n) less space\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #we can optimise the O(n) to use less space by using two pointers\n \n #we still need to ensure the strings possess the same characters \n #this in essence serves two purposes\n # 1. ensure the strings possess the same count of characters for each distinct character\n # 2. ensures if they have the same characters, that they\'re in the same order\n # to avoid situations like "LR" and "RL" \n if start.replace("X","") != end.replace("X",""):\n #we can have cases such as:\n #start = "RXR"\n #end = "XXR"\n #here start actually has more R\'s than end, so it\'s impossible to make it into XXR\n return False\n\n #p1 and p2 begin at the start of both strings\n p1,p2 = 0,0\n\n #we stay in the loop while at least 1 pointer is less\n #than it\'s respective string\n while p1 < len(start) and p2 < len(end):\n #based on the previous O(n) solution, we know the X\'s\n #are largely irrelevant for this problem, so lets just increment the pointers\n #and skip them. We still need their presence in the strings however, in order\n #to track indexes for p1 and p2\n while p1 < len(start) and start[p1] == "X":\n p1+=1 \n while p2 < len(end) and end[p2] == "X":\n p2+=1 \n \n #if both have hit the end of the string at this point\n if p1 == len(start) and p2 == len(end):\n #then it\'s transformable\n return True\n #if one has, and one hasn\'t\n elif p1 == len(start) or p2 == len(end):\n #we know it\'s not transformable\n return False\n else:\n #if we\'ve made it this far the characters are valid\n #so we just now need to ensure the start index exceeds the end in the case of L\n #and the start preceeds end in the case of R\n if (start[p1] == "L" and p1 < p2) or (start[p1] == "R" and p1>p2):\n return False\n #if none of the above are triggered move on to the next character\n p1 +=1\n p2 +=1\n #if we make it out\n return True\n```\n```Java []\n//Java - O(n) less space\nclass Solution {\n public Solution() {}\n public boolean canTransform(String start, String end) {\n if (!start.replace("X", "").equals(end.replace("X", ""))) {\n return false;\n }\n\n int p1 = 0;\n int p2 = 0;\n\n while (p1 < start.length() && p2 < end.length()) {\n while (p1 < start.length() && start.charAt(p1) == \'X\') {\n p1 += 1;\n }\n\n while (p2 < end.length() && end.charAt(p2) == \'X\') {\n p2 += 1;\n }\n\n if (p1 == start.length() && p2 == end.length()) {\n return true;\n } else if (p1 == start.length() || p2 == end.length()) {\n return false;\n } else {\n if ((start.charAt(p1) == \'L\' && p1 < p2) || (start.charAt(p1) == \'R\' && p1 > p2)) {\n return false;\n }\n }\n p1 += 1;\n p2 += 1;\n }\n return true;\n }\n}\n```\n\n\n | 1 | In a string composed of `'L'`, `'R'`, and `'X'` characters, like `"RXXLRXRXL "`, a move consists of either replacing one occurrence of `"XL "` with `"LX "`, or replacing one occurrence of `"RX "` with `"XR "`. Given the starting string `start` and the ending string `end`, return `True` if and only if there exists a sequence of moves to transform one string to the other.
**Example 1:**
**Input:** start = "RXXLRXRXL ", end = "XRLXXRRLX "
**Output:** true
**Explanation:** We can transform start to end following these steps:
RXXLRXRXL ->
XRXLRXRXL ->
XRLXRXRXL ->
XRLXXRRXL ->
XRLXXRRLX
**Example 2:**
**Input:** start = "X ", end = "L "
**Output:** false
**Constraints:**
* `1 <= start.length <= 104`
* `start.length == end.length`
* Both `start` and `end` will only consist of characters in `'L'`, `'R'`, and `'X'`. | Check whether each value is equal to the value of it's top-left neighbor. |
4 Solutions: TLE -> O(n) Space Optimised - Python/Java | swap-adjacent-in-lr-string | 1 | 1 | > # Intuition\n\nIn spite of the downvotes I actually thought this was a pretty good question, even though only the O(n) passes. \n\nI\'ve heavily commented the code with explanations, and provided the brute force alternatives that don\'t pass for people like me who find those helpful:\n\n---\n\n\n> # DFS (TLE)\n\n```python []\n#TLE - DFS\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #after we\'ve altered the string at some index\n #we need to start i from the beginning, so for the dfs\n #a for loop is needed\n def dfs(curr):\n #if the current string we\'re on ever hits the end\n if curr == end:\n #pass true back up the call stack\n return True\n\n #attempt to change each character in the string\n for i in range(len(curr)):\n #if the search isn\'t out of bounds\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n #then try to make each i "XL" or "XR" if possible\n if curr_string == "XL" and dfs(curr[:i]+"LX"+curr[i+2:]):\n return True\n elif curr_string == "RX" and dfs(curr[:i]+"XR"+curr[i+2:]):\n return True\n return False\n return dfs(start)\n```\n```Java []\n//Java - TLE - DFS\nclass Solution{\n private String end;\n public Solution(){};\n\n public boolean canTransform(String start, String end){\n this.end = end;\n return dfs(start);\n }\n\n private boolean dfs(String curr){\n if (curr.equals(end)){\n return true;\n }\n for (int i = 0; i < curr.length();i++){\n if (i+1<curr.length()){\n String curr_string = (""+curr.charAt(i))+(""+curr.charAt(i+1));\n String lx_string = curr.substring(0, i)+"LX"+curr.substring(i+2, curr.length());\n String rx_string = curr.substring(0, i)+"XR"+curr.substring(i+2, curr.length());\n if (curr_string.equals("XL") && dfs(lx_string)){\n return true;\n }else if(curr_string.equals("RX") && dfs(rx_string)){\n return true;\n }\n }\n }\n return false;\n }\n}\n```\n\n---\n\n> # DFS + Memoisation (TLE)\n\n```python []\n#TLE - DFS + Memo\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #exact same concept as the DFS solution, except we memoise\n #the strings, although this still gives TLE\n map = {}\n def dfs(curr):\n if curr == end:\n return True\n elif curr in map:\n return map[curr]\n \n map[curr] = False\n for i in range(len(curr)):\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n if curr_string == "XL" and dfs(curr[:i]+"LX"+curr[i+2:]):\n return True\n elif curr_string == "RX" and dfs(curr[:i]+"XR"+curr[i+2:]):\n return True\n return map[curr]\n return dfs(start)\n```\n```Java []\n//Java - TLE - DFS + Memo\nclass Solution{\n private String end;\n private Map<String,Boolean> map;\n public Solution(){\n this.map = new HashMap<>();\n };\n \n public boolean canTransform(String start, String end){\n this.end = end;\n return dfs(start);\n }\n\n private boolean dfs(String curr){\n if (curr.equals(end)){\n return true;\n }else if (map.containsKey(curr)){\n return map.get(curr);\n }\n map.put(curr, false);\n for (int i = 0; i < curr.length();i++){\n if (i+1<curr.length()){\n String currString = (""+curr.charAt(i))+(""+curr.charAt(i+1));\n String lx_string = curr.substring(0, i)+"LX"+curr.substring(i+2, curr.length());\n String rx_string = curr.substring(0, i)+"XR"+curr.substring(i+2, curr.length());\n if (currString.equals("XL")&& dfs(lx_string)){\n return true;\n }else if (currString.equals("RX")&& dfs(rx_string)){\n return true;\n }\n }\n }\n return map.get(curr);\n }\n}\n```\n\n---\n\n> # BFS\n\n```python []\n#TLE BFS + Memo\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #Sadly BFS also too slow, we remember the strings using \n #a hashset\n q = [start]\n seen = set()\n while q:\n curr = q.pop()\n if curr == end:\n return True\n elif curr in seen:\n continue\n #for each string, try changing the characters\n #and adding it to the queue if it\'s valid\n for i in range(len(curr)):\n if i+1<len(curr):\n curr_string = curr[i]+curr[i+1]\n if curr_string == "XL":\n q.append(curr[:i]+"LX"+curr[i+2:])\n #add the string to seen so we don\'t re-visit it\n seen.add(curr)\n elif curr_string == "RX":\n q.append(curr[:i]+"XR"+curr[i+2:])\n seen.add(curr)\n return False\n```\n```Java []\n//Java - BFS + Memo\nclass Solution {\n public Solution(){};\n public boolean canTransform(String start, String end) {\n Queue<String> q = new LinkedList<>();\n Set<String> seen = new HashSet<>();\n\n q.add(start);\n seen.add(start);\n\n while (!q.isEmpty()) {\n String curr = q.poll();\n \n if (curr.equals(end)) {\n return true; \n }\n\n for (int i = 0; i < curr.length(); i++) {\n if (i + 1 < curr.length()) {\n String curr_string = curr.substring(i, i + 2);\n if (curr_string.equals("XL")) {\n String next = curr.substring(0, i) + "LX" + curr.substring(i + 2);\n if (!seen.contains(next)) {\n q.add(next);\n seen.add(next);\n }\n } else if (curr_string.equals("RX")) {\n String next = curr.substring(0, i) + "XR" + curr.substring(i + 2);\n if (!seen.contains(next)) {\n q.add(next);\n seen.add(next);\n }\n }\n }\n }\n }\n return false;\n }\n}\n```\n\n---\n\n> # O(n)\n\nCredit `@HigherBro`\n```python []\n#O(n)\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #to get the O(n) solution for this problem, you have to\n #use the constraints of the question\n\n #often with these true/false type questions, or optimising\n #problems with vague statements, we need to use our environment\n #or things we already know about the expected input/output\n\n #since XL can only be replaced with LX, and RX can only be\n #replaced with XR, we know that if we ever encounter a scenario\n #where L is next to R or R is next to L e.g "LR" or "RL" it\'ll\n #be impossible for us to ever transform one to the other\n #meaning, if we simply strip the start and end strings of all X\'s\n #start should == end\n\n #why? the shuffling of start to end should ONLY be influenced by X delimiters\n #if the string is valid. meaning if when we remove all X\'s, and the strings aren\'t the same\n #we know some other operation involving the crossing of R\'s and L\'s occurred (with no X\'s in between),\n #or the count of characters in start and end aren\'t the same\n #therefore no matter how many times we move XL or RX, getting the end is impossible\n\n #so let\'s remove the X\'s and if they\'re not the same we immediately return False\n if start.replace("X","") != end.replace("X",""):\n return False\n\n #if they are, we know it may be possible to swap some characters\n #and get the end string\n #PROVIDED THAT all indexes of occurances of L in start, are less than L\n #in end, and all indexes of occurances of R in start are greater than R in end\n #if you notice, when we\'re swapping XL to LX, L is essentially moving to the left\n #likewise with R, R is moving to the right. \n #meaning so long as we DON\'T encounter an occurance of L in end that exceeds\n #it\'s corresponding index in start, it\'s possible to swap these characters\n #and ultimately form the string end. Notice we just need to return if it\'s possible, \n #and not the number of times, so this will work\n\n #find the indexes of l\'s and r\'s in both strings\n l_start, l_end, r_start, r_end = [],[],[],[]\n for i in range(len(start)):\n if start[i] == "L":\n l_start.append(i)\n elif start[i] == "R":\n r_start.append(i)\n if end[i] == "L":\n l_end.append(i)\n elif end[i] == "R":\n r_end.append(i)\n\n #go through the l\'s to verify the indexes:\n for i in range(len(l_start)):\n if l_start[i]<l_end[i]:\n return False\n \n #do the same for the ends\n for i in range(len(r_start)):\n if r_start[i]>r_end[i]:\n return False\n \n #if we never disprove the string, return true\n return True\n```\n```Java []\n//Java - O(n)\nclass Solution {\n public Solution() {};\n\n public boolean canTransform(String start, String end) {\n if (!start.replace("X", "").equals(end.replace("X", ""))) {\n return false;\n }\n\n List<Integer> l_start = new ArrayList<Integer>();\n List<Integer> l_end = new ArrayList<Integer>();\n List<Integer> r_start = new ArrayList<Integer>();\n List<Integer> r_end = new ArrayList<Integer>();\n\n for (int i = 0; i < start.length(); i++) {\n if (start.charAt(i) == \'L\') {\n l_start.add(i);\n } else if (start.charAt(i) == \'R\') {\n r_start.add(i);\n }\n if (end.charAt(i) == \'L\') {\n l_end.add(i);\n } else if (end.charAt(i) == \'R\') {\n r_end.add(i);\n }\n }\n\n for (int i = 0; i < l_start.size(); i++) {\n if (l_start.get(i) < l_end.get(i)) {\n return false;\n }\n }\n\n for (int i = 0; i < r_start.size(); i++) {\n if (r_start.get(i) > r_end.get(i)) {\n return false;\n }\n }\n return true;\n }\n}\n\n```\n\n---\n\n> # O(n) Space Optimised\nCredit `@Samuel_Ji`\n```python []\n#O(n) less space\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n #we can optimise the O(n) to use less space by using two pointers\n \n #we still need to ensure the strings possess the same characters \n #this in essence serves two purposes\n # 1. ensure the strings possess the same count of characters for each distinct character\n # 2. ensures if they have the same characters, that they\'re in the same order\n # to avoid situations like "LR" and "RL" \n if start.replace("X","") != end.replace("X",""):\n #we can have cases such as:\n #start = "RXR"\n #end = "XXR"\n #here start actually has more R\'s than end, so it\'s impossible to make it into XXR\n return False\n\n #p1 and p2 begin at the start of both strings\n p1,p2 = 0,0\n\n #we stay in the loop while at least 1 pointer is less\n #than it\'s respective string\n while p1 < len(start) and p2 < len(end):\n #based on the previous O(n) solution, we know the X\'s\n #are largely irrelevant for this problem, so lets just increment the pointers\n #and skip them. We still need their presence in the strings however, in order\n #to track indexes for p1 and p2\n while p1 < len(start) and start[p1] == "X":\n p1+=1 \n while p2 < len(end) and end[p2] == "X":\n p2+=1 \n \n #if both have hit the end of the string at this point\n if p1 == len(start) and p2 == len(end):\n #then it\'s transformable\n return True\n #if one has, and one hasn\'t\n elif p1 == len(start) or p2 == len(end):\n #we know it\'s not transformable\n return False\n else:\n #if we\'ve made it this far the characters are valid\n #so we just now need to ensure the start index exceeds the end in the case of L\n #and the start preceeds end in the case of R\n if (start[p1] == "L" and p1 < p2) or (start[p1] == "R" and p1>p2):\n return False\n #if none of the above are triggered move on to the next character\n p1 +=1\n p2 +=1\n #if we make it out\n return True\n```\n```Java []\n//Java - O(n) less space\nclass Solution {\n public Solution() {}\n public boolean canTransform(String start, String end) {\n if (!start.replace("X", "").equals(end.replace("X", ""))) {\n return false;\n }\n\n int p1 = 0;\n int p2 = 0;\n\n while (p1 < start.length() && p2 < end.length()) {\n while (p1 < start.length() && start.charAt(p1) == \'X\') {\n p1 += 1;\n }\n\n while (p2 < end.length() && end.charAt(p2) == \'X\') {\n p2 += 1;\n }\n\n if (p1 == start.length() && p2 == end.length()) {\n return true;\n } else if (p1 == start.length() || p2 == end.length()) {\n return false;\n } else {\n if ((start.charAt(p1) == \'L\' && p1 < p2) || (start.charAt(p1) == \'R\' && p1 > p2)) {\n return false;\n }\n }\n p1 += 1;\n p2 += 1;\n }\n return true;\n }\n}\n```\n\n\n | 1 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Solution | swap-adjacent-in-lr-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool canTransform(string st, string tar) {\n int n=tar.length();\n int i=0,j=0;\n while(i<=n && j<=n){\n while(i<n && tar[i]==\'X\') i++;\n while(j<n && st[j]==\'X\') j++;\n if(i==n || j==n)\n return i==n && j==n;\n if(tar[i]!=st[j] || (tar[i]==\'L\' && j<i) || (tar[i]==\'R\' && i<j)) return false;\n i++,j++;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n countR = countL = 0\n for i in range(len(start)):\n if start[i]==\'R\':\n if countL > 0:\n return False\n countR += 1\n if end[i]==\'R\':\n countR -= 1\n if countR < 0:\n return False\n if end[i]==\'L\':\n if countR > 0:\n return False\n countL+=1\n if start[i]==\'L\':\n countL -= 1\n if countL < 0:\n return False\n if countR or countL:\n return False\n return True \n```\n\n```Java []\nclass Solution {\n public boolean canTransform(String start, String end) {\n int i = 0;\n int j = 0;\n char[] s = start.toCharArray();\n char[] e = end.toCharArray();\n while (i < s.length || j < e.length)\n {\n while (i<s.length && s[i] == \'X\') { \n i++; \n }\n while (j<e.length && e[j] == \'X\') {\n j++; \n }\n if (i == s.length || j == e.length) {\n break; \n }\n if (s[i] != e[j] || (s[i] == \'R\' && i > j) || (s[i] == \'L\' && i < j)) {\n return false; \n }\n i++;\n j++;\n }\n return i == j;\n }\n}\n```\n | 2 | In a string composed of `'L'`, `'R'`, and `'X'` characters, like `"RXXLRXRXL "`, a move consists of either replacing one occurrence of `"XL "` with `"LX "`, or replacing one occurrence of `"RX "` with `"XR "`. Given the starting string `start` and the ending string `end`, return `True` if and only if there exists a sequence of moves to transform one string to the other.
**Example 1:**
**Input:** start = "RXXLRXRXL ", end = "XRLXXRRLX "
**Output:** true
**Explanation:** We can transform start to end following these steps:
RXXLRXRXL ->
XRXLRXRXL ->
XRLXRXRXL ->
XRLXXRRXL ->
XRLXXRRLX
**Example 2:**
**Input:** start = "X ", end = "L "
**Output:** false
**Constraints:**
* `1 <= start.length <= 104`
* `start.length == end.length`
* Both `start` and `end` will only consist of characters in `'L'`, `'R'`, and `'X'`. | Check whether each value is equal to the value of it's top-left neighbor. |
Solution | swap-adjacent-in-lr-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool canTransform(string st, string tar) {\n int n=tar.length();\n int i=0,j=0;\n while(i<=n && j<=n){\n while(i<n && tar[i]==\'X\') i++;\n while(j<n && st[j]==\'X\') j++;\n if(i==n || j==n)\n return i==n && j==n;\n if(tar[i]!=st[j] || (tar[i]==\'L\' && j<i) || (tar[i]==\'R\' && i<j)) return false;\n i++,j++;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n countR = countL = 0\n for i in range(len(start)):\n if start[i]==\'R\':\n if countL > 0:\n return False\n countR += 1\n if end[i]==\'R\':\n countR -= 1\n if countR < 0:\n return False\n if end[i]==\'L\':\n if countR > 0:\n return False\n countL+=1\n if start[i]==\'L\':\n countL -= 1\n if countL < 0:\n return False\n if countR or countL:\n return False\n return True \n```\n\n```Java []\nclass Solution {\n public boolean canTransform(String start, String end) {\n int i = 0;\n int j = 0;\n char[] s = start.toCharArray();\n char[] e = end.toCharArray();\n while (i < s.length || j < e.length)\n {\n while (i<s.length && s[i] == \'X\') { \n i++; \n }\n while (j<e.length && e[j] == \'X\') {\n j++; \n }\n if (i == s.length || j == e.length) {\n break; \n }\n if (s[i] != e[j] || (s[i] == \'R\' && i > j) || (s[i] == \'L\' && i < j)) {\n return false; \n }\n i++;\n j++;\n }\n return i == j;\n }\n}\n```\n | 2 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Python 3 || Priority Queue | swim-in-rising-water | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Question similar to "Path with Minimum Effort" \nclass Solution:\n def swimInWater(self, grid: List[List[int]]) -> int:\n\n # Getting rows and cols\n r=len(grid)\n c=len(grid[0])\n\n # 2D array to store minimum elevation to reach there\n cache=[[math.inf for _ in range(c)] for _ in range(r)]\n\n # Directions to traverse\n directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]\n\n # Minheap storing (elevation,x co-ordinat, y co-ordinate)\n minheap=[(grid[0][0],0,0)]\n\n # Remains same, as this is start postion\n cache[0][0] = grid[0][0]\n\n while minheap:\n # Popping position with miniumm elevation\n elevation,i,j=heapq.heappop(minheap)\n\n # Base case to reach end\n if i==(r-1) and j==(c-1):\n return elevation\n \n # Traversing 4 directions\n for dx, dy in directions:\n nx, ny = i + dx, j + dy\n \n if 0 <= nx < r and 0 <= ny < c:\n\n # "new_elevation" keeping track of max encountered till now\n new_elevation=max(grid[nx][ny],elevation)\n\n # Update it in cache as well as add in heap if "new_elevation" is less\n # than one in cache\n if new_elevation < cache[nx][ny]:\n cache[nx][ny] = new_elevation\n heappush(minheap, (new_elevation, nx, ny))\n\n \n \n``` | 2 | You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
**Example 1:**
**Input:** grid = \[\[0,2\],\[1,3\]\]
**Output:** 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
**Example 2:**
**Input:** grid = \[\[0,1,2,3,4\],\[24,23,22,21,5\],\[12,13,14,15,16\],\[11,17,18,19,20\],\[10,9,8,7,6\]\]
**Output:** 16
**Explanation:** The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] < n2`
* Each value `grid[i][j]` is **unique**. | Alternate placing the most common letters. |
Python3 | Min Heap | Simple Solution | swim-in-rising-water | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe Brute force approach is to start from (0,0) traverse through every item in grid and return the smallest elevation value when we reach n-1,n-1. However this approach could possibly take O(N^N). \n\nhence we need a way to take smallest route at any point in time. Using a priority queue instead of a normal queue help us with that\n\n# Approach\n\n- maintain a priority queue to pick up the smallest elevation point.\n- maintain a reference of highest elevation value seen for each (x,y), initialize the reference to inf.\n- start from n-1, n-1 and traverse up to 0,0.\n- as the traversal is 4-directional,it is possible that we may visit the same (x,y) coordinates again. we should avoid it. we can avoid it by a condition that we step into a x,y only if reference value is greater than the biggest elevation seen in a path. this means we reach a x,y with a lesser elevation value than before. \n- push the neighbours of the x,y if they are valid\n- keep updating the reference until we reach 0,0\n- the first time we reach (0,0), that is the smallest elevation point we could achieve, hence we dont have to traverse any further.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nComplexity to maintain min heap - $$O(n^2 log(n^2))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nreference is a 2D grid as same as size of input array, hence $$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def swimInWater(self, grid: List[List[int]]) -> int:\n ROWS = len(grid)\n COLS = len(grid[0])\n ref = [[float("inf") for i in range(COLS)] for j in range(ROWS)]\n hq = [[(grid[ROWS-1][COLS-1]),ROWS-1,COLS-1]]\n iter = [[-1,0],[1,0],[0,-1],[0,1]]\n while hq:\n curr_big,idx_x,idx_y = heapq.heappop(hq)\n if ref[idx_x][idx_y]>curr_big:\n ref[idx_x][idx_y] = curr_big\n for x1,y1 in iter:\n x,y = idx_x+x1,idx_y+y1\n if x>=0 and x<ROWS and y>=0 and y<COLS:\n if (x,y)==(0,0):\n print(f\'reached\')\n return max(curr_big,grid[x][y])\n \n if ref[x][y]>curr_big:\n heapq.heappush(hq,[max(curr_big,grid[x][y]),x,y])\n return ref[0][0] \n``` | 1 | You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
**Example 1:**
**Input:** grid = \[\[0,2\],\[1,3\]\]
**Output:** 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
**Example 2:**
**Input:** grid = \[\[0,1,2,3,4\],\[24,23,22,21,5\],\[12,13,14,15,16\],\[11,17,18,19,20\],\[10,9,8,7,6\]\]
**Output:** 16
**Explanation:** The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] < n2`
* Each value `grid[i][j]` is **unique**. | Alternate placing the most common letters. |
EASY PYTHON SOLUTION USING HEAPSORT AND BFS | swim-in-rising-water | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(m*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def swimInWater(self, grid: List[List[int]]) -> int:\n m=len(grid)\n n=len(grid[0])\n vis=[[0]*n for _ in range(m)]\n queue=[(grid[0][0],0,0)]\n heapq.heapify(queue)\n vis[0][0]=1\n while queue:\n mx,x,y=heapq.heappop(queue)\n if x==m-1 and y==n-1:\n return mx\n row=[0,0,-1,1]\n col=[1,-1,0,0]\n for i in range(4):\n if 0<=x+row[i]<m and 0<=y+col[i]<n:\n if vis[x+row[i]][y+col[i]]==0:\n heapq.heappush(queue,(max(mx,grid[x+row[i]][y+col[i]]),x+row[i],y+col[i]))\n vis[x+row[i]][y+col[i]]=1\n\n \n``` | 2 | You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
**Example 1:**
**Input:** grid = \[\[0,2\],\[1,3\]\]
**Output:** 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
**Example 2:**
**Input:** grid = \[\[0,1,2,3,4\],\[24,23,22,21,5\],\[12,13,14,15,16\],\[11,17,18,19,20\],\[10,9,8,7,6\]\]
**Output:** 16
**Explanation:** The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] < n2`
* Each value `grid[i][j]` is **unique**. | Alternate placing the most common letters. |
Easy to follow python3 solutoon | swim-in-rising-water | 0 | 1 | Do please comment if the complexity analysis needs correction, I am more than happy to hear it.\n\n```\nclass Solution:\n # O(max(n^2, m)) time, h --> the highest elevation in the grid\n # O(n^2) space,\n # Approach: BFS, Priority queue\n # I wld advise to do task scheduler question, it\'s pretty similar\n # except that u apply bfs to traverse the grid 4 directionally\n def swimInWater(self, grid: List[List[int]]) -> int:\n n = len(grid)\n if n == 1:\n return 0\n \n def getNeighbours(coord: Tuple) -> List[Tuple]:\n i, j = coord\n n = len(grid)\n neighbours = []\n \n if i < n-1:\n neighbours.append((i+1, j))\n if i > 0:\n neighbours.append((i-1, j))\n if j < n-1:\n neighbours.append((i, j+1))\n if j > 0:\n neighbours.append((i, j-1))\n \n return neighbours\n \n qu = deque()\n waiting_qu = []\n vstd = set()\n waiting_qu.append([grid[0][0], (0, 0)])\n vstd.add((0, 0))\n time = 0\n \n while waiting_qu:\n time +=1\n while waiting_qu and waiting_qu[0][0] <= time:\n qu.append(heapq.heappop(waiting_qu)[1])\n \n while qu:\n cell = qu.popleft()\n if cell == (n-1, n-1):\n return time\n nbrs = getNeighbours(cell)\n for nb in nbrs:\n if nb in vstd: continue\n x, y = nb\n elevation = grid[x][y]\n vstd.add(nb)\n if elevation > time:\n heapq.heappush(waiting_qu, [elevation, nb])\n else:\n qu.append(nb)\n \n return -1\n``` | 1 | You are given an `n x n` integer matrix `grid` where each value `grid[i][j]` represents the elevation at that point `(i, j)`.
The rain starts to fall. At time `t`, the depth of the water everywhere is `t`. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most `t`. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return _the least time until you can reach the bottom right square_ `(n - 1, n - 1)` _if you start at the top left square_ `(0, 0)`.
**Example 1:**
**Input:** grid = \[\[0,2\],\[1,3\]\]
**Output:** 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.
**Example 2:**
**Input:** grid = \[\[0,1,2,3,4\],\[24,23,22,21,5\],\[12,13,14,15,16\],\[11,17,18,19,20\],\[10,9,8,7,6\]\]
**Output:** 16
**Explanation:** The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] < n2`
* Each value `grid[i][j]` is **unique**. | Alternate placing the most common letters. |
C/C++/Python recursion independent of n->one-line||0ms beats 100% | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat is the meaning for the contraint for `1 <= n <= 30`? There are exactly $2^{n-1}$ elements in n-th row! Let\'s try write out the first some rows to find the possible pattern\n```\n0\n01\n0110\n01101001\n.....\n```\nNow could you find the pattern? If not, write it out more!!\n\nLook at when n=4, the second half can be obtained by the following\n```1001=~(0110)```\nwhere `0110` is first half of the 4th row.\n\nIn fact the pattern does not depend on n, but only on k.\nIf $k=2^b$ for some $b$ then return $b\\pmod{2}$ which uses `bL&1` to compute.\n\nThe value for $k$-th position is just the different symbol for the one on the position $k-2^b$ where \n$b$=`(int)log2(k)=31-__builtin_clz(k)`\n\nA recurrence solution is done.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/PqbPjFAry1w?si=xykUQaSQR-cbj1Sf](https://youtu.be/PqbPjFAry1w?si=xykUQaSQR-cbj1Sf)\n\nWhen `k` is changed into 0-indexed, i.e. $k\'$=`k-1`, an iterative version is not hard to derive. And from the loop exclusive-or sum, it is nothing else than the hamming weight $hw(k\')$ of $k\'$ modulo 2. So 1 line solution is possible.\n\nLet\'s consider firstly the specail case when $k=2^b ( k\'=2^b-1$ for 0-indexed). \n$\nf(2^b)=b\\pmod{2}=hw(k\')\\pmod{2}=$`__builtin_popcount(k-1) &1`\n\nFor general $k$, say \n$k\'=B[b]2^b+B[b-1]2^{b-1}\\cdots +B[1]2+B[0]$ \nwhere $B[i]=0, 1$ One has\n$$\nf(k)=\\sum_{i=0}^b B[i] \\pmod{2} \\\\\n=hw(k\') \\pmod{2}\\\\\n=$$`__builtin_popcount(k-1) &1`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(\\log k)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(\\log k)$$ for system stack\n# C++ recursion independent of n running 0ms & beats 100%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (k==1) return 0; // Base case\n\n int bL=31-__builtin_clz(k); //Calculate log2(k)\n if (k==1<<bL) return bL&1;\n //invert the symbol \n else return 1-kthGrammar(n, k-(1<<bL)); \n }\n};\n```\n# Python solution\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n def f(k):\n if k==1: return 0\n b=(int)(math.log2(k)) # same as b=k.bit_length()-1\n if k==1<<b: return b%2\n else: return 1-f(k-(1<<b))\n return f(k)\n \n```\n# Code of iterative Version\n```\n int kthGrammar(int n, int k) {\n k--; // Adjust k to be 0-based\n int f=0;\n \n for (int i = 0; i < 31; i++) {\n f^=(k & (1<<i))?1:0;\n }\n return f;\n }\n```\n\n# Code uses 1 line\n```\nint kthGrammar(int n, int k){\n return __builtin_popcount(k-1) &1 ;\n}\n``` | 9 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
C/C++/Python recursion independent of n->one-line||0ms beats 100% | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat is the meaning for the contraint for `1 <= n <= 30`? There are exactly $2^{n-1}$ elements in n-th row! Let\'s try write out the first some rows to find the possible pattern\n```\n0\n01\n0110\n01101001\n.....\n```\nNow could you find the pattern? If not, write it out more!!\n\nLook at when n=4, the second half can be obtained by the following\n```1001=~(0110)```\nwhere `0110` is first half of the 4th row.\n\nIn fact the pattern does not depend on n, but only on k.\nIf $k=2^b$ for some $b$ then return $b\\pmod{2}$ which uses `bL&1` to compute.\n\nThe value for $k$-th position is just the different symbol for the one on the position $k-2^b$ where \n$b$=`(int)log2(k)=31-__builtin_clz(k)`\n\nA recurrence solution is done.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n[Please turn on English subtitles if necessary]\n[https://youtu.be/PqbPjFAry1w?si=xykUQaSQR-cbj1Sf](https://youtu.be/PqbPjFAry1w?si=xykUQaSQR-cbj1Sf)\n\nWhen `k` is changed into 0-indexed, i.e. $k\'$=`k-1`, an iterative version is not hard to derive. And from the loop exclusive-or sum, it is nothing else than the hamming weight $hw(k\')$ of $k\'$ modulo 2. So 1 line solution is possible.\n\nLet\'s consider firstly the specail case when $k=2^b ( k\'=2^b-1$ for 0-indexed). \n$\nf(2^b)=b\\pmod{2}=hw(k\')\\pmod{2}=$`__builtin_popcount(k-1) &1`\n\nFor general $k$, say \n$k\'=B[b]2^b+B[b-1]2^{b-1}\\cdots +B[1]2+B[0]$ \nwhere $B[i]=0, 1$ One has\n$$\nf(k)=\\sum_{i=0}^b B[i] \\pmod{2} \\\\\n=hw(k\') \\pmod{2}\\\\\n=$$`__builtin_popcount(k-1) &1`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(\\log k)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(\\log k)$$ for system stack\n# C++ recursion independent of n running 0ms & beats 100%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (k==1) return 0; // Base case\n\n int bL=31-__builtin_clz(k); //Calculate log2(k)\n if (k==1<<bL) return bL&1;\n //invert the symbol \n else return 1-kthGrammar(n, k-(1<<bL)); \n }\n};\n```\n# Python solution\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n def f(k):\n if k==1: return 0\n b=(int)(math.log2(k)) # same as b=k.bit_length()-1\n if k==1<<b: return b%2\n else: return 1-f(k-(1<<b))\n return f(k)\n \n```\n# Code of iterative Version\n```\n int kthGrammar(int n, int k) {\n k--; // Adjust k to be 0-based\n int f=0;\n \n for (int i = 0; i < 31; i++) {\n f^=(k & (1<<i))?1:0;\n }\n return f;\n }\n```\n\n# Code uses 1 line\n```\nint kthGrammar(int n, int k){\n return __builtin_popcount(k-1) &1 ;\n}\n``` | 9 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
【Video】Give me 8 minutes - How we think about solution - Python, JavaScript, Java, C++ | k-th-symbol-in-grammar | 1 | 1 | # Intuition\nCheck parent and position of a target pair.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/cCN38sMai-c\n\n\u25A0 Timeline of the video\n`0:04` Important Rules\n`0:17` How can you find the answer\n`1:13` How can you find the parent of the target pair\n`3:05` How can you know 0 or 1 in the target pair\n`3:40` How can you calculate the first position and the second position in the target pair\n`5:34` Coding\n`7:56` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,821\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nFirst of all, we have patterns.\n\n---\n\nRules\nIf we find `0`, then `0` creates `01` in the next row\nIf we find `1`, then `1` creates `10` in the next row\n\n---\n\nLet\'s think about this example.\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 1 0 \u2192 row 3\n```\n\nLet\'s find this\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 [1] 0 \u2192 row 3\n```\n\nWhere did `[1]` come from? The answer is `1` in `row 2`\nHow about this?\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 [1] 1 0 \u2192 row 3\n```\nWhere did `[1]` come from? The answer is `0` in `row 2`\n\nLet\'s look at `row 3`.\n\nThe first two numbers `01` is created by `0` in `row2`.\nThe later two numbers `10` is created by `1` in `row2`.\n\nThey are kind of pairs. So key points here are\n\n---\n\n\u2B50\uFE0F\u3000Points\n\n- If we know parent of the target pair\n- If we know a position in the target pair\n\nWe can find the answer.\n\n---\n\n- How can we find parent?\n\nLet\'s focus on `row 2` and `row 3`\n\n```\n 0(k1) 1(k2) \u2192 row 2\n 0(k1) 1(k2) 1(k3) 0(k4) \u2192 row 3\n```\n\n`k1` in `row2` creates `k1` and `k2` in `row3`\n`k2` in `row2` creates `k3` and `k4` in `row3`\n\nSo, we have a pattern.\n\n---\n\n\u2B50\uFE0F Points\n\nBy dividing the value of `k` in `row 3` by `2` and then rounding it up, you can obtain the value of `k` for the parent in `row 2`.\n\nFor example,\n\nk2 in row 3: `2 / 2 = 1`, 1 is k1 in row2\nk3 in row 3: `3 / 2 = 2 (1.5 \u2192 2)`, 2 is k2 in row2\n\n\n---\n\n- How can we know `0` or `1` in the target pair?\n\nNow we can know parent of the pair, so my answer for this qeustion is very simple.\n\nAgain, \n```\nIf we find 0, then 0 creates 01 in the next row\nIf we find 1, then 1 creates 10 in the next row\n```\n\nSo,\n\n---\n\n\u2B50\uFE0F Points\n\nIf we have `0 parent` then the first position of the target pair is `0`, if not, `1`\n\nIf we have `1 parent` then the first position of the target pair is `1`, if not, `0`\n\n---\n\n- How can we calculate the first postion or the second position?\n\nLook at this again.\n\n```\n 0(k1) 1(k2) \u2192 row 2\n 0(k1) 1(k2) 1(k3) 0(k4) \u2192 row 3\n```\n---\n\n\u2B50\uFE0F Points\n\nSeems like we can use `odd or even of k`. The first position of pairs is `odd k value` and the second position is `even k value`.\n\n if (parent == 1) {\n return is_odd ? 1 : 0;\n } else {\n return is_odd ? 0 : 1;\n } \n\n---\n\nNow I hope you understand main idea.\nLet\'s see a real algorithm!\n\n\n### Algorithm Overview:\n- The code recursively calculates the value of the k-th symbol in the n-th row of a binary pattern.\n\n- It uses a recursive function that considers the parent symbol and the position in the previous row to determine the current symbol.\n\n### Detailed Explanation:\n1. Start with the given row number `n` and position `k`.\n\n2. Check if `n` is equal to 1. If it is, return 0, as the first row always contains a single \'0\'. This serves as the base case of the recursion.\n\n3. If `n` is greater than 1, calculate the `parent` value by recursively calling the `kthGrammar` function for the previous row, which is `n - 1`. For the position in the previous row, use `ceil(k / 2.0)` to determine the corresponding position. This recursive step effectively moves up one row and adjusts the position in that row based on whether `k` is even or odd.\n\n4. Determine whether the current position `k` is an odd or even position in the current row by checking if `k % 2` is equal to 1. If it\'s 1, then `isOdd` is set to true; otherwise, it\'s set to false. This step helps decide how the symbol in the current row is related to the parent symbol.\n\n5. Check the `parent` value obtained from the previous row. If it is 1, return 1 if `isOdd` is true (indicating that the parent symbol is 1 and the current symbol should be flipped), or 0 if `isOdd` is false (indicating that the parent symbol is 1 and the current symbol should match it). This step simulates the pattern changes based on the parent symbol.\n\n6. If the `parent` value is 0, return 0 if `isOdd` is true (indicating that the parent symbol is 0 and the current symbol should match it), or 1 if `isOdd` is false (indicating that the parent symbol is 0 and the current symbol should be flipped). This step also simulates the pattern changes based on the parent symbol.\n\nThe algorithm recursively calculates the symbol in the `n`-th row and the `k`-th position based on the parent symbol and whether the current position is odd or even. It continues this process until it reaches the first row (base case), at which point it returns 0.\n\n\n---\n\n\n\n# How it works\n\n```\nN = 3, K = 3\n\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 [1] 0 \u2192 row 3\n```\n\nFirst of all, Let\'s find parent, call the same function recursively until `N = 1`.\n\nSee Python solution code.\n```\nparent = self.kthGrammar(N-1, math.ceil(K/2))\n\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\nparent = self.kthGrammar(1, 1), When N = 2, K = 2\n\nThen, we meet if N == 1: return 0, get back to When N = 2, K = 2\n```\nThe first parent is `0`. `k = 2`.\n```\nparent = 0 (= return value from previous call)\nK = 2 (= When N = 2, K = 2)\nis_odd = False\n\nCheck this\n\nif parent == 1:\n return 1 if is_odd else 0\nelse:\n return 0 if is_odd else [1] \u2190 meet 1\n```\nWe get `1` as a parent for the next row below.\n\nNow\n```\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\nparent = self.kthGrammar(1, 1), When N = 2, K = 2 (Done, return 1)\n\nNow rest of stack should be\n\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\n```\n\n```\nparent = 1 (= return value from previous call)\nK = 3 (= When N = 3, K = 3)\nis_odd = True\n\nCheck this\n\nif parent == 1:\n return [1] if is_odd else 0 \u2190 meet 1\nelse:\n return 0 if is_odd else 1\n```\n\nNow\n```\nparent = self.kthGrammar(2, 2), When N = 3, K = 3 (Done, return 1)\nparent = self.kthGrammar(1, 1), When N = 2, K = 2 (Done, return 1)\n\n```\nNow nothing in stack.\n```\nOutput: 1\n```\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n log k)$$\n$$O(log k)$$ oeration for each row and we have `n` rows\n\n- Space complexity: $$O(n)$$\nStack space for recursion.\n\n\n```python []\nclass Solution:\n def kthGrammar(self, N: int, K: int) -> int:\n\n if N == 1:\n return 0\n \n parent = self.kthGrammar(N-1, math.ceil(K/2))\n is_odd = K % 2 == 1\n \n if parent == 1:\n return 1 if is_odd else 0\n else:\n return 0 if is_odd else 1\n```\n```javascript []\nvar kthGrammar = function(n, k) {\n if (n === 1) {\n return 0;\n }\n\n const parent = kthGrammar(n - 1, Math.ceil(k / 2));\n const isOdd = k % 2 === 1;\n\n if (parent === 1) {\n return isOdd ? 1 : 0;\n } else {\n return isOdd ? 0 : 1;\n }\n};\n```\n```java []\nclass Solution {\n public int kthGrammar(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int parent = kthGrammar(n - 1, (int) Math.ceil(k / 2.0));\n boolean isOdd = k % 2 == 1;\n\n if (parent == 0) {\n return isOdd ? 0 : 1;\n } else {\n return isOdd ? 1 : 0;\n } \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int parent = kthGrammar(n - 1, ceil(k / 2.0));\n bool isOdd = k % 2 == 1;\n\n if (parent == 1) {\n return isOdd ? 1 : 0;\n } else {\n return isOdd ? 0 : 1;\n } \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-trees-with-factors/solutions/4209156/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-largest-value-in-each-tree-row/solutions/4205395/video-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/0fnMZvFM4p8\n\n\u25A0 Timeline of the video\n`0:05` Two difficulties\n`0:29` How can you keep max value at a single level? (the first difficulty)\n`1:10` Points of the first difficulty\n`1:32` How can you keep nodes at the next down level (the second difficulty)\n`2:09` Demonstrate how it works\n`6:23` Points of the second difficulty\n`6:45` What if we use normal array instead of deque\n`7:35` Coding with BFS\n`9:31` Time Complexity and Space Complexity\n`10:25` Explain DFS solution briefly\n\n | 29 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
【Video】Give me 8 minutes - How we think about solution - Python, JavaScript, Java, C++ | k-th-symbol-in-grammar | 1 | 1 | # Intuition\nCheck parent and position of a target pair.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/cCN38sMai-c\n\n\u25A0 Timeline of the video\n`0:04` Important Rules\n`0:17` How can you find the answer\n`1:13` How can you find the parent of the target pair\n`3:05` How can you know 0 or 1 in the target pair\n`3:40` How can you calculate the first position and the second position in the target pair\n`5:34` Coding\n`7:56` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,821\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution\n\nFirst of all, we have patterns.\n\n---\n\nRules\nIf we find `0`, then `0` creates `01` in the next row\nIf we find `1`, then `1` creates `10` in the next row\n\n---\n\nLet\'s think about this example.\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 1 0 \u2192 row 3\n```\n\nLet\'s find this\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 [1] 0 \u2192 row 3\n```\n\nWhere did `[1]` come from? The answer is `1` in `row 2`\nHow about this?\n\n```\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 [1] 1 0 \u2192 row 3\n```\nWhere did `[1]` come from? The answer is `0` in `row 2`\n\nLet\'s look at `row 3`.\n\nThe first two numbers `01` is created by `0` in `row2`.\nThe later two numbers `10` is created by `1` in `row2`.\n\nThey are kind of pairs. So key points here are\n\n---\n\n\u2B50\uFE0F\u3000Points\n\n- If we know parent of the target pair\n- If we know a position in the target pair\n\nWe can find the answer.\n\n---\n\n- How can we find parent?\n\nLet\'s focus on `row 2` and `row 3`\n\n```\n 0(k1) 1(k2) \u2192 row 2\n 0(k1) 1(k2) 1(k3) 0(k4) \u2192 row 3\n```\n\n`k1` in `row2` creates `k1` and `k2` in `row3`\n`k2` in `row2` creates `k3` and `k4` in `row3`\n\nSo, we have a pattern.\n\n---\n\n\u2B50\uFE0F Points\n\nBy dividing the value of `k` in `row 3` by `2` and then rounding it up, you can obtain the value of `k` for the parent in `row 2`.\n\nFor example,\n\nk2 in row 3: `2 / 2 = 1`, 1 is k1 in row2\nk3 in row 3: `3 / 2 = 2 (1.5 \u2192 2)`, 2 is k2 in row2\n\n\n---\n\n- How can we know `0` or `1` in the target pair?\n\nNow we can know parent of the pair, so my answer for this qeustion is very simple.\n\nAgain, \n```\nIf we find 0, then 0 creates 01 in the next row\nIf we find 1, then 1 creates 10 in the next row\n```\n\nSo,\n\n---\n\n\u2B50\uFE0F Points\n\nIf we have `0 parent` then the first position of the target pair is `0`, if not, `1`\n\nIf we have `1 parent` then the first position of the target pair is `1`, if not, `0`\n\n---\n\n- How can we calculate the first postion or the second position?\n\nLook at this again.\n\n```\n 0(k1) 1(k2) \u2192 row 2\n 0(k1) 1(k2) 1(k3) 0(k4) \u2192 row 3\n```\n---\n\n\u2B50\uFE0F Points\n\nSeems like we can use `odd or even of k`. The first position of pairs is `odd k value` and the second position is `even k value`.\n\n if (parent == 1) {\n return is_odd ? 1 : 0;\n } else {\n return is_odd ? 0 : 1;\n } \n\n---\n\nNow I hope you understand main idea.\nLet\'s see a real algorithm!\n\n\n### Algorithm Overview:\n- The code recursively calculates the value of the k-th symbol in the n-th row of a binary pattern.\n\n- It uses a recursive function that considers the parent symbol and the position in the previous row to determine the current symbol.\n\n### Detailed Explanation:\n1. Start with the given row number `n` and position `k`.\n\n2. Check if `n` is equal to 1. If it is, return 0, as the first row always contains a single \'0\'. This serves as the base case of the recursion.\n\n3. If `n` is greater than 1, calculate the `parent` value by recursively calling the `kthGrammar` function for the previous row, which is `n - 1`. For the position in the previous row, use `ceil(k / 2.0)` to determine the corresponding position. This recursive step effectively moves up one row and adjusts the position in that row based on whether `k` is even or odd.\n\n4. Determine whether the current position `k` is an odd or even position in the current row by checking if `k % 2` is equal to 1. If it\'s 1, then `isOdd` is set to true; otherwise, it\'s set to false. This step helps decide how the symbol in the current row is related to the parent symbol.\n\n5. Check the `parent` value obtained from the previous row. If it is 1, return 1 if `isOdd` is true (indicating that the parent symbol is 1 and the current symbol should be flipped), or 0 if `isOdd` is false (indicating that the parent symbol is 1 and the current symbol should match it). This step simulates the pattern changes based on the parent symbol.\n\n6. If the `parent` value is 0, return 0 if `isOdd` is true (indicating that the parent symbol is 0 and the current symbol should match it), or 1 if `isOdd` is false (indicating that the parent symbol is 0 and the current symbol should be flipped). This step also simulates the pattern changes based on the parent symbol.\n\nThe algorithm recursively calculates the symbol in the `n`-th row and the `k`-th position based on the parent symbol and whether the current position is odd or even. It continues this process until it reaches the first row (base case), at which point it returns 0.\n\n\n---\n\n\n\n# How it works\n\n```\nN = 3, K = 3\n\n 0 \u2192 row 1\n 0 1 \u2192 row 2\n 0 1 [1] 0 \u2192 row 3\n```\n\nFirst of all, Let\'s find parent, call the same function recursively until `N = 1`.\n\nSee Python solution code.\n```\nparent = self.kthGrammar(N-1, math.ceil(K/2))\n\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\nparent = self.kthGrammar(1, 1), When N = 2, K = 2\n\nThen, we meet if N == 1: return 0, get back to When N = 2, K = 2\n```\nThe first parent is `0`. `k = 2`.\n```\nparent = 0 (= return value from previous call)\nK = 2 (= When N = 2, K = 2)\nis_odd = False\n\nCheck this\n\nif parent == 1:\n return 1 if is_odd else 0\nelse:\n return 0 if is_odd else [1] \u2190 meet 1\n```\nWe get `1` as a parent for the next row below.\n\nNow\n```\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\nparent = self.kthGrammar(1, 1), When N = 2, K = 2 (Done, return 1)\n\nNow rest of stack should be\n\nparent = self.kthGrammar(2, 2), When N = 3, K = 3\n```\n\n```\nparent = 1 (= return value from previous call)\nK = 3 (= When N = 3, K = 3)\nis_odd = True\n\nCheck this\n\nif parent == 1:\n return [1] if is_odd else 0 \u2190 meet 1\nelse:\n return 0 if is_odd else 1\n```\n\nNow\n```\nparent = self.kthGrammar(2, 2), When N = 3, K = 3 (Done, return 1)\nparent = self.kthGrammar(1, 1), When N = 2, K = 2 (Done, return 1)\n\n```\nNow nothing in stack.\n```\nOutput: 1\n```\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n log k)$$\n$$O(log k)$$ oeration for each row and we have `n` rows\n\n- Space complexity: $$O(n)$$\nStack space for recursion.\n\n\n```python []\nclass Solution:\n def kthGrammar(self, N: int, K: int) -> int:\n\n if N == 1:\n return 0\n \n parent = self.kthGrammar(N-1, math.ceil(K/2))\n is_odd = K % 2 == 1\n \n if parent == 1:\n return 1 if is_odd else 0\n else:\n return 0 if is_odd else 1\n```\n```javascript []\nvar kthGrammar = function(n, k) {\n if (n === 1) {\n return 0;\n }\n\n const parent = kthGrammar(n - 1, Math.ceil(k / 2));\n const isOdd = k % 2 === 1;\n\n if (parent === 1) {\n return isOdd ? 1 : 0;\n } else {\n return isOdd ? 0 : 1;\n }\n};\n```\n```java []\nclass Solution {\n public int kthGrammar(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int parent = kthGrammar(n - 1, (int) Math.ceil(k / 2.0));\n boolean isOdd = k % 2 == 1;\n\n if (parent == 0) {\n return isOdd ? 0 : 1;\n } else {\n return isOdd ? 1 : 0;\n } \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int parent = kthGrammar(n - 1, ceil(k / 2.0));\n bool isOdd = k % 2 == 1;\n\n if (parent == 1) {\n return isOdd ? 1 : 0;\n } else {\n return isOdd ? 0 : 1;\n } \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-trees-with-factors/solutions/4209156/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-largest-value-in-each-tree-row/solutions/4205395/video-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/0fnMZvFM4p8\n\n\u25A0 Timeline of the video\n`0:05` Two difficulties\n`0:29` How can you keep max value at a single level? (the first difficulty)\n`1:10` Points of the first difficulty\n`1:32` How can you keep nodes at the next down level (the second difficulty)\n`2:09` Demonstrate how it works\n`6:23` Points of the second difficulty\n`6:45` What if we use normal array instead of deque\n`7:35` Coding with BFS\n`9:31` Time Complexity and Space Complexity\n`10:25` Explain DFS solution briefly\n\n | 29 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
🚀 100% || Easy Iterative Approach || Explained Intuition 🚀 | k-th-symbol-in-grammar | 1 | 1 | # Porblem Description\n\nThe task is **constructing** a table consisting of `n` rows, with each row generated from the row immediately above it according to a specific **rule**. \nThe rule involves **replacing** each `0` with `01` and each `1` with `10` in the **previous** row. \nThe task is to **determine** the value of the `kth` element (1-indexed) in the `nth` row of this table.\n\n- **Constraints:**\n - `1 <= n <= 30`\n - `1 <= k <= 2e(n - 1)`\n\n\n---\n\n\n# Intuition\n\nHello there,\uD83D\uDE04\n\nLet\'s zoom\uD83D\uDD0E in and examine the details in our today\'s problem.\nThe problem today wants us to calculate what is the `k-th` element in the `n-th` level of some tower.\uD83E\uDD28\n- We have some rule to calculate current tower from previous one by:\n - Replace each `0` with `01`\n - Replace each `1` with `10`\n - First level is only `0`\n\n**First** solution we will think of is our savior in all situations, **Brute Force** by **iterating** `n` loops and replace characters in each loop.\nUnfortunately, It won\'t work. Let\'s see why.\uD83D\uDE22\n\n```\nFirst Level -> 1 element\n0\n```\n```\nSecond Level -> 2 element\n01\n```\n```\nThird Level -> 4 element\n0110\n```\n```\nFourth Level -> 8 element\n01101001\n```\n```\nFifth Level -> 16 element\n0110100110010110\n```\n```\nSixth Level -> 32 element\n01101001100101101001011001101001\n```\n\nWe can see that the levels are growing **exponentially** and by the `30-th` row we will have `2^(n - 1)` element. which will eventually give us **TLE**.\uD83D\uDE14\n\nCan we do better ?\uD83E\uDD14\nThere is some **observation**, did you see it ?\uD83E\uDD2F\nEach time we hop from a row to the next row we only add the **inverse** of the elements of **previous** row. how?\n```\nFirst Level\n0\n```\n```\nSecond Level\n0 | 1\n```\n```\nThird Level\n01 | 10\n```\n```\nFourth Level\n0110 | 1001\n```\n```\nFifth Level\n01101001 | 10010110\n```\n\n- We can see that we have **two halves** in each level -except level one- where: \n - **first** element of **second half** is **inverse** of **first** element of **first half**.\n - **second** element of **second half** is inverse of **second** element of **first half**.\n - **third** element of **second half** is inverse of **third** element of **first half**.\n - And so on so forth.\nAnd the first half of some level **exact** is the level before it.\uD83E\uDD2F\n```\nThird Level\n0110\n\nFourth Level\n0110 | 1001\n```\n```\nFourth Level\n01101001\n\nFifth Level\n01101001 | 10010110\n```\n\nHow can we utilize these great **observations** ?\uD83E\uDD29\n- Since we want the `k-th` element why don\'t we look where it is in the row, the first half or second half.\uD83E\uDD28\n - If it in the **first half** then great we can proceed to the previous level since the `k-th` element in it will be the **exact** `k-th` element we are looking for.\n - If it in the **second half** then it is the **inverse** of the `(k - half elements in the row)` element in the first half then it is the inverse of `(k - half elements in the row)` element in the previous level.\nUntil we reach **level one** which is only `0`.\n\nLet\'s this example where `n = 4` and `K = 6`.\n\n**fourth** level:\n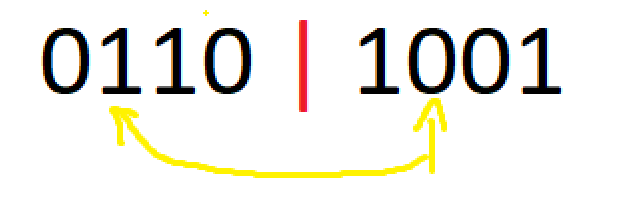\n`6-th` element is the **inverse** of the `second` element of the first half and previous level.\n\n**third** level:\n\n`second` element is the `second` element of the first half and previous level.\n\n**second** level:\n\n`second` element is the **inverse** of the `first` element of the first half and previous level.\nThe previous level is **first level** which is only `0`.\n\nSince we **inversed** **two times**, then the `k-th` element is the **same** of the **first row** which is `0`.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n1. Initialize a boolean flag, `areValuesSame`, to **track** if the values of `k` and the **first** element in the row are the same.\n2. Calculate the total **number** of elements in the `nth` row using the formula `2^(n-1)`.\n3. Enter a **loop** that continues until you reach the **first** row (where `n` equals `1` and its element is `0`):\n - **Halve** the number of elements in the row by dividing `n` by 2.\n - **Check** if `k` is in the **second half** of the current row by comparing it to `n`.\n - If `k` is in the second half, **adjust** its value by **subtracting** new `n`, and **toggle** the value of `areValuesSame` (if it was `true`, make it `false`, and vice versa).\n4. **Return** `0` if the `areValuesSame` flag indicates that the values are the same; otherwise, return `1`.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are start looping with $2^n$ elements and in each loop we divide `n` by two so the complexity is $O(log(2^N))$ which is $O(N)$.\n- **Space complexity:** $O(1)$\nSince we are using constant variables.\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and first element are the same.\n bool areValuesSame = true; \n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return ((areValuesSame) ? 0 : 1) ;\n }\n};\n```\n```Java []\npublic class Solution {\n public int kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and the first element are the same.\n boolean areValuesSame = true;\n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = (int) Math.pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return (areValuesSame ? 0 : 1);\n }\n}\n```\n```Python []\nclass Solution:\n def kthGrammar(self, n, k):\n # Initialize a flag to track if the values of k and the first element are the same.\n are_values_same = True\n\n # Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = 2**(n - 1)\n\n # Continue until we reach the first row.\n while n != 1:\n # Halve the number of elements in the row.\n n //= 2\n\n # If k is in the second half of the row, adjust k and toggle the flag.\n if k > n:\n k -= n\n are_values_same = not are_values_same\n\n # Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return 0 if are_values_same else 1\n```\n```C []\nint kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and the first element are the same.\n bool areValuesSame = true;\n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = (int)pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return (areValuesSame) ? 0 : 1;\n}\n```\n\n\n---\n\n## Edit\nA good note from our friend [@kenlau](/kenlau).\n\nInstead of using `pow(2, n - 1)` we can simply use shifting operation `1 << (n - 1)`.\n`pow(2, n - 1)` has complexity of `O(log(N))` and `1 << (n - 1)` has complexity of `O(1)`.\nsimply `1 << (n - 1)` means that put `1` and shift it `n - 1` positions in its binary representation. \n| Operation | Binary Representation | Integer | \n| :--- | :---:| :---: | \n| 1 << 0 | 00001 | 1 | \n| 1 << 1 | 00010 | 2 | \n| 1 << 2 | 00100 | 4 | \n| 1 << 3 | 01000 | 8 | \n| 1 << 4 | 10000 | 16 | \n\n\n | 172 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
🚀 100% || Easy Iterative Approach || Explained Intuition 🚀 | k-th-symbol-in-grammar | 1 | 1 | # Porblem Description\n\nThe task is **constructing** a table consisting of `n` rows, with each row generated from the row immediately above it according to a specific **rule**. \nThe rule involves **replacing** each `0` with `01` and each `1` with `10` in the **previous** row. \nThe task is to **determine** the value of the `kth` element (1-indexed) in the `nth` row of this table.\n\n- **Constraints:**\n - `1 <= n <= 30`\n - `1 <= k <= 2e(n - 1)`\n\n\n---\n\n\n# Intuition\n\nHello there,\uD83D\uDE04\n\nLet\'s zoom\uD83D\uDD0E in and examine the details in our today\'s problem.\nThe problem today wants us to calculate what is the `k-th` element in the `n-th` level of some tower.\uD83E\uDD28\n- We have some rule to calculate current tower from previous one by:\n - Replace each `0` with `01`\n - Replace each `1` with `10`\n - First level is only `0`\n\n**First** solution we will think of is our savior in all situations, **Brute Force** by **iterating** `n` loops and replace characters in each loop.\nUnfortunately, It won\'t work. Let\'s see why.\uD83D\uDE22\n\n```\nFirst Level -> 1 element\n0\n```\n```\nSecond Level -> 2 element\n01\n```\n```\nThird Level -> 4 element\n0110\n```\n```\nFourth Level -> 8 element\n01101001\n```\n```\nFifth Level -> 16 element\n0110100110010110\n```\n```\nSixth Level -> 32 element\n01101001100101101001011001101001\n```\n\nWe can see that the levels are growing **exponentially** and by the `30-th` row we will have `2^(n - 1)` element. which will eventually give us **TLE**.\uD83D\uDE14\n\nCan we do better ?\uD83E\uDD14\nThere is some **observation**, did you see it ?\uD83E\uDD2F\nEach time we hop from a row to the next row we only add the **inverse** of the elements of **previous** row. how?\n```\nFirst Level\n0\n```\n```\nSecond Level\n0 | 1\n```\n```\nThird Level\n01 | 10\n```\n```\nFourth Level\n0110 | 1001\n```\n```\nFifth Level\n01101001 | 10010110\n```\n\n- We can see that we have **two halves** in each level -except level one- where: \n - **first** element of **second half** is **inverse** of **first** element of **first half**.\n - **second** element of **second half** is inverse of **second** element of **first half**.\n - **third** element of **second half** is inverse of **third** element of **first half**.\n - And so on so forth.\nAnd the first half of some level **exact** is the level before it.\uD83E\uDD2F\n```\nThird Level\n0110\n\nFourth Level\n0110 | 1001\n```\n```\nFourth Level\n01101001\n\nFifth Level\n01101001 | 10010110\n```\n\nHow can we utilize these great **observations** ?\uD83E\uDD29\n- Since we want the `k-th` element why don\'t we look where it is in the row, the first half or second half.\uD83E\uDD28\n - If it in the **first half** then great we can proceed to the previous level since the `k-th` element in it will be the **exact** `k-th` element we are looking for.\n - If it in the **second half** then it is the **inverse** of the `(k - half elements in the row)` element in the first half then it is the inverse of `(k - half elements in the row)` element in the previous level.\nUntil we reach **level one** which is only `0`.\n\nLet\'s this example where `n = 4` and `K = 6`.\n\n**fourth** level:\n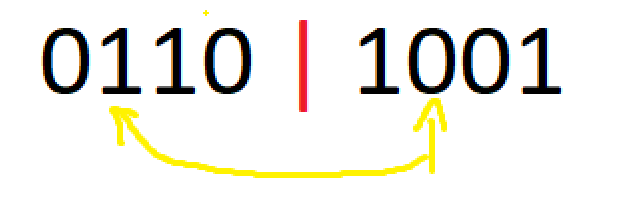\n`6-th` element is the **inverse** of the `second` element of the first half and previous level.\n\n**third** level:\n\n`second` element is the `second` element of the first half and previous level.\n\n**second** level:\n\n`second` element is the **inverse** of the `first` element of the first half and previous level.\nThe previous level is **first level** which is only `0`.\n\nSince we **inversed** **two times**, then the `k-th` element is the **same** of the **first row** which is `0`.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n1. Initialize a boolean flag, `areValuesSame`, to **track** if the values of `k` and the **first** element in the row are the same.\n2. Calculate the total **number** of elements in the `nth` row using the formula `2^(n-1)`.\n3. Enter a **loop** that continues until you reach the **first** row (where `n` equals `1` and its element is `0`):\n - **Halve** the number of elements in the row by dividing `n` by 2.\n - **Check** if `k` is in the **second half** of the current row by comparing it to `n`.\n - If `k` is in the second half, **adjust** its value by **subtracting** new `n`, and **toggle** the value of `areValuesSame` (if it was `true`, make it `false`, and vice versa).\n4. **Return** `0` if the `areValuesSame` flag indicates that the values are the same; otherwise, return `1`.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we are start looping with $2^n$ elements and in each loop we divide `n` by two so the complexity is $O(log(2^N))$ which is $O(N)$.\n- **Space complexity:** $O(1)$\nSince we are using constant variables.\n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and first element are the same.\n bool areValuesSame = true; \n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return ((areValuesSame) ? 0 : 1) ;\n }\n};\n```\n```Java []\npublic class Solution {\n public int kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and the first element are the same.\n boolean areValuesSame = true;\n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = (int) Math.pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return (areValuesSame ? 0 : 1);\n }\n}\n```\n```Python []\nclass Solution:\n def kthGrammar(self, n, k):\n # Initialize a flag to track if the values of k and the first element are the same.\n are_values_same = True\n\n # Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = 2**(n - 1)\n\n # Continue until we reach the first row.\n while n != 1:\n # Halve the number of elements in the row.\n n //= 2\n\n # If k is in the second half of the row, adjust k and toggle the flag.\n if k > n:\n k -= n\n are_values_same = not are_values_same\n\n # Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return 0 if are_values_same else 1\n```\n```C []\nint kthGrammar(int n, int k) {\n // Initialize a flag to track if the values of k and the first element are the same.\n bool areValuesSame = true;\n\n // Calculate the total number of elements in the nth row, which is 2^(n-1).\n n = (int)pow(2, n - 1);\n\n // Continue until we reach the first row.\n while (n != 1) {\n // Halve the number of elements in the row.\n n /= 2;\n\n // If k is in the second half of the row, adjust k and toggle the flag.\n if (k > n) {\n k -= n;\n areValuesSame = !areValuesSame;\n }\n }\n\n // Return 0 if the flag indicates that the values are the same; otherwise, return 1.\n return (areValuesSame) ? 0 : 1;\n}\n```\n\n\n---\n\n## Edit\nA good note from our friend [@kenlau](/kenlau).\n\nInstead of using `pow(2, n - 1)` we can simply use shifting operation `1 << (n - 1)`.\n`pow(2, n - 1)` has complexity of `O(log(N))` and `1 << (n - 1)` has complexity of `O(1)`.\nsimply `1 << (n - 1)` means that put `1` and shift it `n - 1` positions in its binary representation. \n| Operation | Binary Representation | Integer | \n| :--- | :---:| :---: | \n| 1 << 0 | 00001 | 1 | \n| 1 << 1 | 00010 | 2 | \n| 1 << 2 | 00100 | 4 | \n| 1 << 3 | 01000 | 8 | \n| 1 << 4 | 10000 | 16 | \n\n\n | 172 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
✅ 100% Recursive & Bit Count | k-th-symbol-in-grammar | 1 | 1 | # Solution 1: Recursive Approach\n\n## Intuition\nThe initial thought on solving the problem revolves around understanding the pattern of sequence generation as described in the problem statement. As the sequence grows by replacing 0 with 01 and 1 with 10, we can observe a recursive relationship between the nth row and the (n-1)th row.\n\n## Live Coding with Comments\nhttps://youtu.be/gYuvglDHXlU?si=owdAdZx3wrRb49NM\n\n## Approach\nOur approach is to leverage the recursive pattern observed. The length of the nth row is double the length of the (n-1)th row. If k is in the first half of the nth row, the symbol at position k in the nth row is the same as the symbol at position k in the (n-1)th row. If k is in the second half of the nth row, the symbol at position k in the nth row is the opposite of the symbol at position (k - length of (n-1)th row) in the (n-1)th row.\n\n## Complexity\n- Time complexity: The time complexity is O(n) as there is a single recursive call for every level of n.\n- Space complexity: The space complexity is also O(n) due to the stack space used by the recursive calls.\n\n## Code\n```python []\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n if n == 1:\n return 0\n length = 2 ** (n - 2)\n if k <= length:\n return self.kthGrammar(n - 1, k)\n else:\n return 1 - self.kthGrammar(n - 1, k - length)\n```\n``` Rust []\nimpl Solution {\n pub fn kth_grammar(n: i32, k: i32) -> i32 {\n if n == 1 { return 0; }\n let length = 1 << (n - 2);\n if k <= length { Solution::kth_grammar(n - 1, k) }\n else { 1 - Solution::kth_grammar(n - 1, k - length) }\n }\n}\n```\n``` Go []\nfunc kthGrammar(n int, k int) int {\n if n == 1 {\n return 0\n }\n length := 1 << (n - 2)\n if k <= length {\n return kthGrammar(n - 1, k)\n } else {\n return 1 - kthGrammar(n - 1, k - length)\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n }\n};\n```\n``` Java []\nclass Solution {\n public int kthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n }\n}\n```\n``` C# []\npublic class Solution {\n public int KthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return KthGrammar(n - 1, k);\n else return 1 - KthGrammar(n - 1, k - length);\n }\n}\n```\n``` JS []\nvar kthGrammar = function(n, k) {\n if (n === 1) return 0;\n let length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @param Integer $k\n * @return Integer\n */\n function kthGrammar($n, $k) {\n if ($n == 1) return 0;\n $length = 1 << ($n - 2);\n if ($k <= $length) return $this->kthGrammar($n - 1, $k);\n else return 1 - $this->kthGrammar($n - 1, $k - $length);\n }\n}\n```\n\n## Performance\n\n| Language | Execution Time (ms) | Memory Usage |\n|----------|---------------------|--------------|\n| Rust | 0 ms | 2 MB |\n| Java | 0 ms | 39 MB |\n| C++ | 0 ms | 6.2 MB |\n| Go | 1 ms | 1.9 MB |\n| PHP | 13 ms | 18.8 MB |\n| C# | 20 ms | 26.8 MB |\n| Python3 | 30 ms | 16.4 MB |\n| JavaScript| 34 ms | 41.6 MB |\n\n\n\n\n# Solution 2: Bit Count Approach\n\n## Intuition\nThe second approach is derived from the observation that the kth symbol in the nth row is determined by the parity (odd or even nature) of the count of 1-bits in the binary representation of (k-1).\n\n## Approach\nConvert the index (k-1) to its binary representation and count the number of 1-bits. If the count is even, the kth symbol is 0; if the count is odd, the kth symbol is 1. This approach leverages bitwise operation and avoids the need for recursion, making it more efficient.\n\n## Complexity\n- Time complexity: The time complexity is O(log k) as the time taken to convert the number to binary and count the 1-bits is logarithmic with respect to k.\n- Space complexity: The space complexity is O(1) as no extra space is used apart from the input and output variables.\n\n## Code\n```python []\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n return bin(k - 1).count(\'1\') % 2\n```\n\n## What did we learn?\n - We learned that recognizing patterns and relationships between different parts of the problem can lead to efficient solutions.\n - Recursive relationships can sometimes be optimized further by using mathematical or bitwise operations.\n## Why does it work?\n - The recursive approach works because of the defined recursive relationship between the nth row and the (n-1)th row.\n - The bit count approach works due to the observed correlation between the count of 1-bits in (k-1) and the kth symbol in the nth row.\n## Logic behind solutions?\n - The logic behind the recursive solution is the direct application of the recursive relationship between successive rows as defined in the problem.\n - The logic behind the bit count solution is derived from analyzing the pattern of symbol generation and correlating it with bitwise properties of the index k. | 67 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
✅ 100% Recursive & Bit Count | k-th-symbol-in-grammar | 1 | 1 | # Solution 1: Recursive Approach\n\n## Intuition\nThe initial thought on solving the problem revolves around understanding the pattern of sequence generation as described in the problem statement. As the sequence grows by replacing 0 with 01 and 1 with 10, we can observe a recursive relationship between the nth row and the (n-1)th row.\n\n## Live Coding with Comments\nhttps://youtu.be/gYuvglDHXlU?si=owdAdZx3wrRb49NM\n\n## Approach\nOur approach is to leverage the recursive pattern observed. The length of the nth row is double the length of the (n-1)th row. If k is in the first half of the nth row, the symbol at position k in the nth row is the same as the symbol at position k in the (n-1)th row. If k is in the second half of the nth row, the symbol at position k in the nth row is the opposite of the symbol at position (k - length of (n-1)th row) in the (n-1)th row.\n\n## Complexity\n- Time complexity: The time complexity is O(n) as there is a single recursive call for every level of n.\n- Space complexity: The space complexity is also O(n) due to the stack space used by the recursive calls.\n\n## Code\n```python []\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n if n == 1:\n return 0\n length = 2 ** (n - 2)\n if k <= length:\n return self.kthGrammar(n - 1, k)\n else:\n return 1 - self.kthGrammar(n - 1, k - length)\n```\n``` Rust []\nimpl Solution {\n pub fn kth_grammar(n: i32, k: i32) -> i32 {\n if n == 1 { return 0; }\n let length = 1 << (n - 2);\n if k <= length { Solution::kth_grammar(n - 1, k) }\n else { 1 - Solution::kth_grammar(n - 1, k - length) }\n }\n}\n```\n``` Go []\nfunc kthGrammar(n int, k int) int {\n if n == 1 {\n return 0\n }\n length := 1 << (n - 2)\n if k <= length {\n return kthGrammar(n - 1, k)\n } else {\n return 1 - kthGrammar(n - 1, k - length)\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int kthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n }\n};\n```\n``` Java []\nclass Solution {\n public int kthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n }\n}\n```\n``` C# []\npublic class Solution {\n public int KthGrammar(int n, int k) {\n if (n == 1) return 0;\n int length = 1 << (n - 2);\n if (k <= length) return KthGrammar(n - 1, k);\n else return 1 - KthGrammar(n - 1, k - length);\n }\n}\n```\n``` JS []\nvar kthGrammar = function(n, k) {\n if (n === 1) return 0;\n let length = 1 << (n - 2);\n if (k <= length) return kthGrammar(n - 1, k);\n else return 1 - kthGrammar(n - 1, k - length);\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer $n\n * @param Integer $k\n * @return Integer\n */\n function kthGrammar($n, $k) {\n if ($n == 1) return 0;\n $length = 1 << ($n - 2);\n if ($k <= $length) return $this->kthGrammar($n - 1, $k);\n else return 1 - $this->kthGrammar($n - 1, $k - $length);\n }\n}\n```\n\n## Performance\n\n| Language | Execution Time (ms) | Memory Usage |\n|----------|---------------------|--------------|\n| Rust | 0 ms | 2 MB |\n| Java | 0 ms | 39 MB |\n| C++ | 0 ms | 6.2 MB |\n| Go | 1 ms | 1.9 MB |\n| PHP | 13 ms | 18.8 MB |\n| C# | 20 ms | 26.8 MB |\n| Python3 | 30 ms | 16.4 MB |\n| JavaScript| 34 ms | 41.6 MB |\n\n\n\n\n# Solution 2: Bit Count Approach\n\n## Intuition\nThe second approach is derived from the observation that the kth symbol in the nth row is determined by the parity (odd or even nature) of the count of 1-bits in the binary representation of (k-1).\n\n## Approach\nConvert the index (k-1) to its binary representation and count the number of 1-bits. If the count is even, the kth symbol is 0; if the count is odd, the kth symbol is 1. This approach leverages bitwise operation and avoids the need for recursion, making it more efficient.\n\n## Complexity\n- Time complexity: The time complexity is O(log k) as the time taken to convert the number to binary and count the 1-bits is logarithmic with respect to k.\n- Space complexity: The space complexity is O(1) as no extra space is used apart from the input and output variables.\n\n## Code\n```python []\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n return bin(k - 1).count(\'1\') % 2\n```\n\n## What did we learn?\n - We learned that recognizing patterns and relationships between different parts of the problem can lead to efficient solutions.\n - Recursive relationships can sometimes be optimized further by using mathematical or bitwise operations.\n## Why does it work?\n - The recursive approach works because of the defined recursive relationship between the nth row and the (n-1)th row.\n - The bit count approach works due to the observed correlation between the count of 1-bits in (k-1) and the kth symbol in the nth row.\n## Logic behind solutions?\n - The logic behind the recursive solution is the direct application of the recursive relationship between successive rows as defined in the problem.\n - The logic behind the bit count solution is derived from analyzing the pattern of symbol generation and correlating it with bitwise properties of the index k. | 67 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 2 Approaches || EXPLAINED🔥 | k-th-symbol-in-grammar | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Binary Tree)***\n1. **depthFirstSearch(int n, int k, int rootVal):** This is a recursive function that calculates the kth symbol in the nth row of the sequence. It takes three parameters:\n\n - **n:**The current row number.\n - **k:** The position of the symbol within the row.\n - **rootVal:** The value (0 or 1) of the root node of the current subtree.\n1. **The base case:** If `n` is 1, it means we\'ve reached the first row, and the result is simply the `rootVal` (0 or 1).\n\n1. `totalNodes` is calculated as 2^(n-1), representing the total number of nodes in the current row.\n\n1. If `k` is greater than (`totalNodes / 2`), it means the target node is in the right half of the current subtree. In this case:\n\n - `nextRootVal` is updated to the opposite of the current `rootVal` (0 becomes 1, and 1 becomes 0).\n - `k` is adjusted to be relative to the right half, which is `k - (totalNodes / 2)`.\n - The function is called recursively with the updated values.\n1. If `k` is not greater than `(totalNodes / 2)`, it means the target node is in the left half of the current subtree. In this case:\n\n - `nextRootVal` remains the same as the current `rootVal`.\n - `k` is kept unchanged.\n - The function is called recursively with the updated values.\n1. **kthGrammar(int n, int k):** This is the main function that calls `depthFirstSearch` with the initial values of `n` (the desired row) and `k` (the target position) and an initial `rootVal` of 0.\n\n1. The result of the `depthFirstSearch` function is returned as the kth symbol in the nth row of the sequence.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n }\n\n int kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n }\n};\n\n```\n\n```C []\n#include <math.h>\n\nint depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n}\n\nint kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n}\n\nint main() {\n int n = 4; // Replace with your values for n and k\n int k = 5;\n int result = kthGrammar(n, k);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = (int) Math.pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n }\n\n public int kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def depthFirstSearch(self, n: int, k: int, rootVal: int) -> int:\n if n == 1:\n return rootVal\n\n totalNodes = 2 ** (n - 1)\n\n # Target node will be present in the right half sub-tree of the current root node.\n if k > (totalNodes / 2):\n nextRootVal = 1 if rootVal == 0 else 0\n return self.depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal)\n # Otherwise, the target node is in the left sub-tree of the current root node.\n else:\n nextRootVal = 0 if rootVal == 0 else 1\n return self.depthFirstSearch(n - 1, k, nextRootVal)\n\n def kthGrammar(self, n: int, k: int) -> int:\n return self.depthFirstSearch(n, k, 0)\n\n```\n\n```javascript []\nlet depthFirstSearch = (n, k, rootVal) => {\n if (n === 1) {\n return rootVal;\n }\n\n let totalNodes = Math.pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > totalNodes / 2) {\n let nextRootVal = (rootVal === 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n let nextRootVal = (rootVal === 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n};\n\nlet kthGrammar = function(n, k) {\n return depthFirstSearch(n, k, 0);\n};\n\n```\n\n---\n#### ***Approach 2(Recursion)***\n1. **recursion(int n, int k):** This recursive function calculates the k-th symbol in the nth row of the sequence. It takes two parameters:\n\n - **n:** The current row number.\n - **k:** The position of the symbol within the row.\n1. **The base case:** If `n` is 1, it means we\'ve reached the first row, which consists of only one symbol, \'0\'. Therefore, it returns 0.\n\n1. `totalElements` is calculated as 2^(n-1), representing the total number of elements in the current row.\n\n1. `halfElements` is calculated as `totalElements / 2`, representing the number of elements in the left half of the current row.\n\n1. If `k` is greater than `halfElements`, it means the target symbol is in the right half of the current row. In this case:\n\n - It calculates the symbol in the corresponding left half by subtracting `halfElements` from `k`.\n - It returns the negation of the symbol in the left half, which is found by calling `kthGrammar` recursively with the same `n` and the modified `k`.\n1. If `k` is not greater than `halfElements`, it means the target symbol is in the left half of the current row. In this case:\n\n - It switches to the previous row by calling `recursion` recursively with `n - 1` and the same `k`.\n1. **kthGrammar(int n, int k):** This is the main function that calls `recursion` with the initial values of `n` and `k`.\n\n1. The result of the `recursion` function is returned as the k-th symbol in the nth row of the sequence.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int recursion(int n, int k) {\n // First row will only have one symbol \'0\'.\n if (n == 1) {\n return 0;\n }\n\n int totalElements = pow(2, (n - 1));\n int halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - kthGrammar(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n }\n\n int kthGrammar(int n, int k) {\n return recursion(n, k);\n }\n};\n\n```\n\n```C []\n#include <stdio.h>\n#include <math.h>\n\nint recursion(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int totalElements = (int)pow(2, n - 1);\n int halfElements = totalElements / 2;\n\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n return recursion(n - 1, k);\n}\n\nint kthGrammar(int n, int k) {\n return recursion(n, k);\n}\n\nint main() {\n int n = 4;\n int k = 5;\n int result = kthGrammar(n, k);\n printf("The k-th grammar symbol at row %d, position %d is: %d\\n", n, k, result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int recursion(int n, int k) {\n // First row will only have one symbol \'0\'.\n if (n == 1) {\n return 0;\n }\n\n int totalElements = (int) Math.pow(2, (n - 1));\n int halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n }\n\n public int kthGrammar(int n, int k) {\n return recursion(n, k);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def recursion(self, n: int, k: int) -> int:\n # First row will only have one symbol \'0\'.\n if n == 1:\n return 0\n\n total_elements = 2 ** (n - 1)\n half_elements = total_elements // 2\n\n # If the target is present in the right half, we switch to the respective left half symbol.\n if k > half_elements:\n return 1 - self.recursion(n, k - half_elements)\n\n # Otherwise, we switch to the previous row.\n return self.recursion(n - 1, k)\n\n def kthGrammar(self, n: int, k: int) -> int:\n return self.recursion(n, k)\n\n```\n\n```javascript []\nlet recursion = (n, k) => {\n // First row will only have one symbol \'0\'.\n if (n === 1) {\n return 0;\n }\n\n const totalElements = Math.pow(2, n - 1);\n const halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n}\n\nlet kthGrammar = function(n, k) {\n return recursion(n, k);\n};\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 2 Approaches || EXPLAINED🔥 | k-th-symbol-in-grammar | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Binary Tree)***\n1. **depthFirstSearch(int n, int k, int rootVal):** This is a recursive function that calculates the kth symbol in the nth row of the sequence. It takes three parameters:\n\n - **n:**The current row number.\n - **k:** The position of the symbol within the row.\n - **rootVal:** The value (0 or 1) of the root node of the current subtree.\n1. **The base case:** If `n` is 1, it means we\'ve reached the first row, and the result is simply the `rootVal` (0 or 1).\n\n1. `totalNodes` is calculated as 2^(n-1), representing the total number of nodes in the current row.\n\n1. If `k` is greater than (`totalNodes / 2`), it means the target node is in the right half of the current subtree. In this case:\n\n - `nextRootVal` is updated to the opposite of the current `rootVal` (0 becomes 1, and 1 becomes 0).\n - `k` is adjusted to be relative to the right half, which is `k - (totalNodes / 2)`.\n - The function is called recursively with the updated values.\n1. If `k` is not greater than `(totalNodes / 2)`, it means the target node is in the left half of the current subtree. In this case:\n\n - `nextRootVal` remains the same as the current `rootVal`.\n - `k` is kept unchanged.\n - The function is called recursively with the updated values.\n1. **kthGrammar(int n, int k):** This is the main function that calls `depthFirstSearch` with the initial values of `n` (the desired row) and `k` (the target position) and an initial `rootVal` of 0.\n\n1. The result of the `depthFirstSearch` function is returned as the kth symbol in the nth row of the sequence.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n }\n\n int kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n }\n};\n\n```\n\n```C []\n#include <math.h>\n\nint depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n}\n\nint kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n}\n\nint main() {\n int n = 4; // Replace with your values for n and k\n int k = 5;\n int result = kthGrammar(n, k);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int depthFirstSearch(int n, int k, int rootVal) {\n if (n == 1) {\n return rootVal;\n }\n\n int totalNodes = (int) Math.pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > (totalNodes / 2)) {\n int nextRootVal = (rootVal == 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n int nextRootVal = (rootVal == 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n }\n\n public int kthGrammar(int n, int k) {\n return depthFirstSearch(n, k, 0);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def depthFirstSearch(self, n: int, k: int, rootVal: int) -> int:\n if n == 1:\n return rootVal\n\n totalNodes = 2 ** (n - 1)\n\n # Target node will be present in the right half sub-tree of the current root node.\n if k > (totalNodes / 2):\n nextRootVal = 1 if rootVal == 0 else 0\n return self.depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal)\n # Otherwise, the target node is in the left sub-tree of the current root node.\n else:\n nextRootVal = 0 if rootVal == 0 else 1\n return self.depthFirstSearch(n - 1, k, nextRootVal)\n\n def kthGrammar(self, n: int, k: int) -> int:\n return self.depthFirstSearch(n, k, 0)\n\n```\n\n```javascript []\nlet depthFirstSearch = (n, k, rootVal) => {\n if (n === 1) {\n return rootVal;\n }\n\n let totalNodes = Math.pow(2, n - 1);\n\n // Target node will be present in the right half sub-tree of the current root node.\n if (k > totalNodes / 2) {\n let nextRootVal = (rootVal === 0) ? 1 : 0;\n return depthFirstSearch(n - 1, k - (totalNodes / 2), nextRootVal);\n }\n // Otherwise, the target node is in the left sub-tree of the current root node.\n else {\n let nextRootVal = (rootVal === 0) ? 0 : 1;\n return depthFirstSearch(n - 1, k, nextRootVal);\n }\n};\n\nlet kthGrammar = function(n, k) {\n return depthFirstSearch(n, k, 0);\n};\n\n```\n\n---\n#### ***Approach 2(Recursion)***\n1. **recursion(int n, int k):** This recursive function calculates the k-th symbol in the nth row of the sequence. It takes two parameters:\n\n - **n:** The current row number.\n - **k:** The position of the symbol within the row.\n1. **The base case:** If `n` is 1, it means we\'ve reached the first row, which consists of only one symbol, \'0\'. Therefore, it returns 0.\n\n1. `totalElements` is calculated as 2^(n-1), representing the total number of elements in the current row.\n\n1. `halfElements` is calculated as `totalElements / 2`, representing the number of elements in the left half of the current row.\n\n1. If `k` is greater than `halfElements`, it means the target symbol is in the right half of the current row. In this case:\n\n - It calculates the symbol in the corresponding left half by subtracting `halfElements` from `k`.\n - It returns the negation of the symbol in the left half, which is found by calling `kthGrammar` recursively with the same `n` and the modified `k`.\n1. If `k` is not greater than `halfElements`, it means the target symbol is in the left half of the current row. In this case:\n\n - It switches to the previous row by calling `recursion` recursively with `n - 1` and the same `k`.\n1. **kthGrammar(int n, int k):** This is the main function that calls `recursion` with the initial values of `n` and `k`.\n\n1. The result of the `recursion` function is returned as the k-th symbol in the nth row of the sequence.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int recursion(int n, int k) {\n // First row will only have one symbol \'0\'.\n if (n == 1) {\n return 0;\n }\n\n int totalElements = pow(2, (n - 1));\n int halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - kthGrammar(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n }\n\n int kthGrammar(int n, int k) {\n return recursion(n, k);\n }\n};\n\n```\n\n```C []\n#include <stdio.h>\n#include <math.h>\n\nint recursion(int n, int k) {\n if (n == 1) {\n return 0;\n }\n\n int totalElements = (int)pow(2, n - 1);\n int halfElements = totalElements / 2;\n\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n return recursion(n - 1, k);\n}\n\nint kthGrammar(int n, int k) {\n return recursion(n, k);\n}\n\nint main() {\n int n = 4;\n int k = 5;\n int result = kthGrammar(n, k);\n printf("The k-th grammar symbol at row %d, position %d is: %d\\n", n, k, result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nclass Solution {\n public int recursion(int n, int k) {\n // First row will only have one symbol \'0\'.\n if (n == 1) {\n return 0;\n }\n\n int totalElements = (int) Math.pow(2, (n - 1));\n int halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n }\n\n public int kthGrammar(int n, int k) {\n return recursion(n, k);\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def recursion(self, n: int, k: int) -> int:\n # First row will only have one symbol \'0\'.\n if n == 1:\n return 0\n\n total_elements = 2 ** (n - 1)\n half_elements = total_elements // 2\n\n # If the target is present in the right half, we switch to the respective left half symbol.\n if k > half_elements:\n return 1 - self.recursion(n, k - half_elements)\n\n # Otherwise, we switch to the previous row.\n return self.recursion(n - 1, k)\n\n def kthGrammar(self, n: int, k: int) -> int:\n return self.recursion(n, k)\n\n```\n\n```javascript []\nlet recursion = (n, k) => {\n // First row will only have one symbol \'0\'.\n if (n === 1) {\n return 0;\n }\n\n const totalElements = Math.pow(2, n - 1);\n const halfElements = totalElements / 2;\n\n // If the target is present in the right half, we switch to the respective left half symbol.\n if (k > halfElements) {\n return 1 - recursion(n, k - halfElements);\n }\n\n // Otherwise, we switch to the previous row.\n return recursion(n - 1, k);\n}\n\nlet kthGrammar = function(n, k) {\n return recursion(n, k);\n};\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
🐱 Find parity of bits in k - 1. One Liner ! | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nImagine that we are building a binary tree starting from the root node with key `0`. \n\n1. **The key of the left child is same as the parent whereas the key of the right child is different than the parent.**\n\nIn mathematical terms, $left.val = root.val$ and $right.val = root.val \\: xor \\: 1$\n\nAlso, we can associate a bit for every move we make. When we go left, we will treat it as `0` and for every right we will treat it as a `1`.\n\nPicture depicting the same:\n\n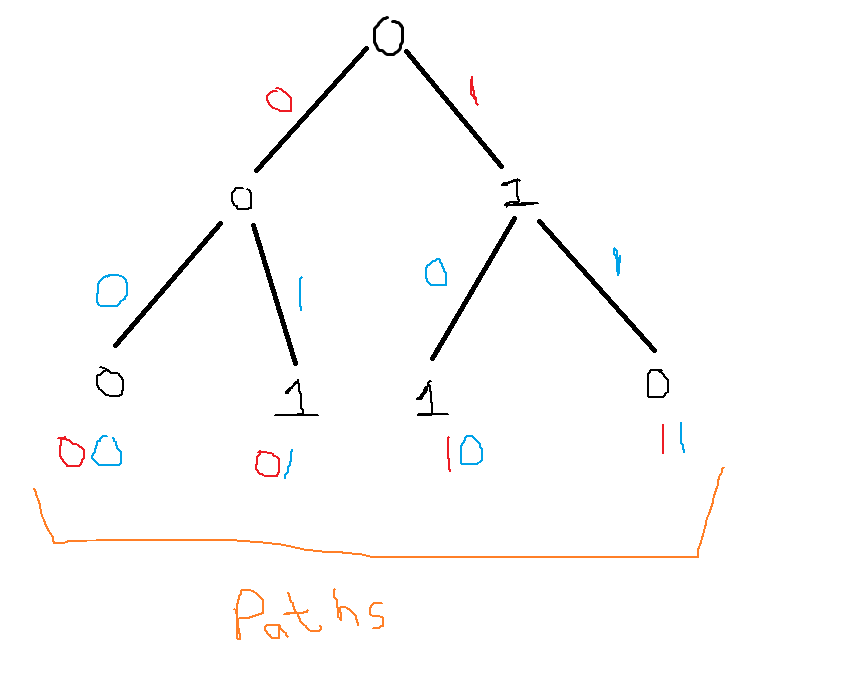\n\n\nNow, if you look at the leaf nodes in the third row, you can see an interesting pattern. \n\n2. **The sequence of directions we have taken to reach a particular node at `kth` index in `nth` row is the same as the n-bit binary representation of `k-1`.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. From our first observation, we can see that everytime we move right, the bit gets flipped.\n\n2. From our second observation, we can notice that we move right the same number times as the number of bits in the binary representation of `k - 1`.\n\nHence, we can conclude that we just need to find the parity of bits in `k - 1`!\n\n# Complexity\n- Time complexity: $O(log_2(k - 1))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(log_2(k - 1))$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n return bin(k - 1).count(\'1\') & 1\n```\n\n## Have a great day! | 3 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
🐱 Find parity of bits in k - 1. One Liner ! | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nImagine that we are building a binary tree starting from the root node with key `0`. \n\n1. **The key of the left child is same as the parent whereas the key of the right child is different than the parent.**\n\nIn mathematical terms, $left.val = root.val$ and $right.val = root.val \\: xor \\: 1$\n\nAlso, we can associate a bit for every move we make. When we go left, we will treat it as `0` and for every right we will treat it as a `1`.\n\nPicture depicting the same:\n\n\n\n\nNow, if you look at the leaf nodes in the third row, you can see an interesting pattern. \n\n2. **The sequence of directions we have taken to reach a particular node at `kth` index in `nth` row is the same as the n-bit binary representation of `k-1`.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. From our first observation, we can see that everytime we move right, the bit gets flipped.\n\n2. From our second observation, we can notice that we move right the same number times as the number of bits in the binary representation of `k - 1`.\n\nHence, we can conclude that we just need to find the parity of bits in `k - 1`!\n\n# Complexity\n- Time complexity: $O(log_2(k - 1))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(log_2(k - 1))$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n return bin(k - 1).count(\'1\') & 1\n```\n\n## Have a great day! | 3 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
Recursion | k-th-symbol-in-grammar | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(2^n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n if n == 1:\n return 0\n midpoint = 2 ** (n - 2)\n if k <= midpoint:\n return self.kthGrammar(n - 1, k)\n else:\n return 1 - self.kthGrammar(n - 1, k - midpoint)\n``` | 5 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
Recursion | k-th-symbol-in-grammar | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO(2^n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n if n == 1:\n return 0\n midpoint = 2 ** (n - 2)\n if k <= midpoint:\n return self.kthGrammar(n - 1, k)\n else:\n return 1 - self.kthGrammar(n - 1, k - midpoint)\n``` | 5 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
Python 3: Simple Iterative Solution | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n \n # start with 0\n # 0 turns 01\n # 1 turns 10\n\n # if k is odd, get 0th from the cur str\n stack = [0 if k % 2 else 1] \n\n while n > 1:\n k = (k + 1) // 2\n stack.append(0 if k % 2 else 1)\n n -= 1\n \n cur = "0"\n while stack:\n idx = stack.pop()\n cur = "01" if cur == "0" else "10"\n cur = cur[idx]\n \n return int(cur)\n``` | 1 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
Python 3: Simple Iterative Solution | k-th-symbol-in-grammar | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthGrammar(self, n: int, k: int) -> int:\n \n # start with 0\n # 0 turns 01\n # 1 turns 10\n\n # if k is odd, get 0th from the cur str\n stack = [0 if k % 2 else 1] \n\n while n > 1:\n k = (k + 1) // 2\n stack.append(0 if k % 2 else 1)\n n -= 1\n \n cur = "0"\n while stack:\n idx = stack.pop()\n cur = "01" if cur == "0" else "10"\n cur = cur[idx]\n \n return int(cur)\n``` | 1 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
Solution | reaching-points | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool reachingPoints(int sx, int sy, int tx, int ty) {\n while(sx < tx && sy < ty){\n if(tx > ty) tx = tx%ty;\n else ty = ty%tx;\n }\n if(sx == tx && sy<= ty && (ty-sy)%sx == 0) return true;\n if(sy == ty && sx <= tx && (tx-sx)%sy == 0) return true;\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n if tx==0 or ty==0: return (sx, sy)==(tx, ty)\n while not (sx==tx and sy==ty):\n if sx>tx or sy>ty: return False\n elif tx==ty: return ((0, ty)==(sx, sy) or (tx, 0)==(sx, sy))\n \n if ty>tx: \n if tx==sx: return (ty-sy)%sx==0\n ty%=tx\n else: \n if ty==sy: return (tx-sx)%sy==0\n tx%=ty\n \n return True\n```\n\n```Java []\nclass Solution {\n public boolean reachingPoints(int sx, int sy, int tx, int ty) {\n while (tx >= sx && ty >= sy) {\n if (tx == ty) break;\n if (tx > ty) {\n if (ty > sy) tx %= ty;\n else return (tx - sx) % ty == 0;\n } else {\n if (tx > sx) ty %= tx;\n else return (ty - sy) % tx == 0;\n }\n }\n return (tx == sx && ty == sy);\n }\n}\n```\n | 2 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Solution | reaching-points | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool reachingPoints(int sx, int sy, int tx, int ty) {\n while(sx < tx && sy < ty){\n if(tx > ty) tx = tx%ty;\n else ty = ty%tx;\n }\n if(sx == tx && sy<= ty && (ty-sy)%sx == 0) return true;\n if(sy == ty && sx <= tx && (tx-sx)%sy == 0) return true;\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n if tx==0 or ty==0: return (sx, sy)==(tx, ty)\n while not (sx==tx and sy==ty):\n if sx>tx or sy>ty: return False\n elif tx==ty: return ((0, ty)==(sx, sy) or (tx, 0)==(sx, sy))\n \n if ty>tx: \n if tx==sx: return (ty-sy)%sx==0\n ty%=tx\n else: \n if ty==sy: return (tx-sx)%sy==0\n tx%=ty\n \n return True\n```\n\n```Java []\nclass Solution {\n public boolean reachingPoints(int sx, int sy, int tx, int ty) {\n while (tx >= sx && ty >= sy) {\n if (tx == ty) break;\n if (tx > ty) {\n if (ty > sy) tx %= ty;\n else return (tx - sx) % ty == 0;\n } else {\n if (tx > sx) ty %= tx;\n else return (ty - sy) % tx == 0;\n }\n }\n return (tx == sx && ty == sy);\n }\n}\n```\n | 2 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python 3 || 4 lines, GCD, iteration || T/M: 95% / 97% | reaching-points | 0 | 1 | Pretty much the same plan as many others posted, but with one addtional twist. If `True`, then `tx` and `ty` must each be linear combinations of `sx` and `sy`, which in turn implies that `gcd(sx,sy)` and `gcd(tx,ty)` must be equal.\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n \n if (g:=gcd(sx,sy)) != gcd(tx,ty): return False\n (sx, sy), (tx, ty) = (sx//g, sy//g), (tx//g, ty//g)\n\n while tx > sx and ty > sy: (tx, ty) = (tx%ty, ty%tx)\n\n return ((tx, ty%sx) == (sx, sy%sx) and ty >= sy) or (\n (tx%sy, ty) == (sx%sy, sy) and tx >= sx)\n```\n[https://leetcode.com/problems/reaching-points/submissions/1011705374/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `max(tx, ty)`. | 5 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python 3 || 4 lines, GCD, iteration || T/M: 95% / 97% | reaching-points | 0 | 1 | Pretty much the same plan as many others posted, but with one addtional twist. If `True`, then `tx` and `ty` must each be linear combinations of `sx` and `sy`, which in turn implies that `gcd(sx,sy)` and `gcd(tx,ty)` must be equal.\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n \n if (g:=gcd(sx,sy)) != gcd(tx,ty): return False\n (sx, sy), (tx, ty) = (sx//g, sy//g), (tx//g, ty//g)\n\n while tx > sx and ty > sy: (tx, ty) = (tx%ty, ty%tx)\n\n return ((tx, ty%sx) == (sx, sy%sx) and ty >= sy) or (\n (tx%sy, ty) == (sx%sy, sy) and tx >= sx)\n```\n[https://leetcode.com/problems/reaching-points/submissions/1011705374/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `max(tx, ty)`. | 5 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
[Python3] [Impossible not to understand] Intuitive Method with Detailed Explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, we want to understand that it\'s faster to go from the target to the source because we can only subtract the smaller number from the larger to get a non-negative number.\n\nSecond, we want to optimize this "subtraction loop" because if the smaller number is too small and the larger number is too large, the loop takes too long. So we use modulo instead of substraction. But the question is that "**When should we stop subtracting?**"\n\nThe answer is: **we want to make sure the target number is not smaller than the source number**. So take `tx = 3, ty = 5, sx = 1, sy = 1` as an example:\n1. `tx < ty`, so we subtract `tx` from `ty`, til when? Til `ty >= sy`, so we break `ty` into two parts `ty = sy + Q` i.e. `5 = 1 + 4`, we can safely subtract `tx` from `Q` because we can gaurantee the remainder is at least `sy`, **thus as many `tx`s will be subtracted from `Q`, we use modulo so `ty = sy + (ty - sy) % tx`, as a result `tx = 3, ty = 1 + (5 - 1) % 3 = 2`**\n2. `ty < tx`, use the same logic, `tx = sx + Q`, `tx = sx + (tx - sx) % ty = 1 + (3 - 1) % 2 = 1, ty = 2`\n3. `tx < ty`, `tx = 1, ty = 1`, you can try the equation in 1\n4. **Now, we cannot do anything because `tx < sx + ty` and `ty < sy + tx`, meaning that we cannot subtract any `ty` from `tx` or any `tx` from `ty` to make sure the resulting `tx >= sx` or `ty >= sy`.** So we need to quit the loop.\n5. We check if target is exactly the same as source, because we cannot make any further move.\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while tx >= sx + ty or ty >= sy + tx: # make sure we can still make substractions\n if tx > ty:\n tx = sx + (tx - sx) % ty # the smallest we can get by deducting ty from tx\n else:\n ty = sy + (ty - sy) % tx # the smallest we can get by subtracting tx from ty\n\n return tx == sx and ty == sy\n``` | 9 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
[Python3] [Impossible not to understand] Intuitive Method with Detailed Explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, we want to understand that it\'s faster to go from the target to the source because we can only subtract the smaller number from the larger to get a non-negative number.\n\nSecond, we want to optimize this "subtraction loop" because if the smaller number is too small and the larger number is too large, the loop takes too long. So we use modulo instead of substraction. But the question is that "**When should we stop subtracting?**"\n\nThe answer is: **we want to make sure the target number is not smaller than the source number**. So take `tx = 3, ty = 5, sx = 1, sy = 1` as an example:\n1. `tx < ty`, so we subtract `tx` from `ty`, til when? Til `ty >= sy`, so we break `ty` into two parts `ty = sy + Q` i.e. `5 = 1 + 4`, we can safely subtract `tx` from `Q` because we can gaurantee the remainder is at least `sy`, **thus as many `tx`s will be subtracted from `Q`, we use modulo so `ty = sy + (ty - sy) % tx`, as a result `tx = 3, ty = 1 + (5 - 1) % 3 = 2`**\n2. `ty < tx`, use the same logic, `tx = sx + Q`, `tx = sx + (tx - sx) % ty = 1 + (3 - 1) % 2 = 1, ty = 2`\n3. `tx < ty`, `tx = 1, ty = 1`, you can try the equation in 1\n4. **Now, we cannot do anything because `tx < sx + ty` and `ty < sy + tx`, meaning that we cannot subtract any `ty` from `tx` or any `tx` from `ty` to make sure the resulting `tx >= sx` or `ty >= sy`.** So we need to quit the loop.\n5. We check if target is exactly the same as source, because we cannot make any further move.\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while tx >= sx + ty or ty >= sy + tx: # make sure we can still make substractions\n if tx > ty:\n tx = sx + (tx - sx) % ty # the smallest we can get by deducting ty from tx\n else:\n ty = sy + (ty - sy) % tx # the smallest we can get by subtracting tx from ty\n\n return tx == sx and ty == sy\n``` | 9 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
[Python3] Only Solution You'll Need || 30ms, 80% faster | reaching-points | 0 | 1 | Trust me when I say you should really just read this solution and you would understand it:\n\n**Optimized: Bottom Up Solution**:\n\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\t\n while (tx >= sx and ty >= sy):\n # check if we have reached ends\n if tx == sx:\n return (ty-sy) % tx == 0\n if ty == sy:\n return (tx-sx) % ty == 0\n \n # step\n if ty > tx:\n ty = ty%tx\n else:\n tx = tx%ty\n \n return False\n```\n\n**Explanation**\n\nImagine you\'re at a starting point on a grid, and you want to reach another point on the same grid. You can only move in two ways: either left or down. The question is, can you reach your destination using only these moves?\n\n\n```\n while (tx >= sx and ty >= sy):\n```\n\nWe start a loop that continues as long as two conditions are true: (1) tx is greater than or equal to sx, and (2) ty is greater than or equal to sy. These conditions mean we can still make moves.\n\n```\n if tx == sx:\n return (ty-sy) % tx == 0\n```\n\nIf tx becomes equal to sx, it means we can\'t move left anymore. In this case, we check if the difference between ty and sy (how far we need to go down) is divisible by tx (how many steps we can take down at once). If it\'s divisible (no remainder), we can reach the destination, so we return "yes" (True).\n\n```\n if ty == sy:\n return (tx-sx) % ty == 0\n```\n\nSimilarly, if ty becomes equal to sy, it means we can\'t move down anymore. We check if the difference between tx and sx (how far we need to go left) is divisible by ty (how many steps we can take left at once). If it\'s divisible (no remainder), we can reach the destination, so we return "yes" (True).\n\n```\n if ty > tx:\n ty = ty % tx\n else:\n tx = tx % ty\n```\n\nIf we haven\'t reached either of the "can\'t move anymore" situations, we decide on one of two moves:\n\n- If ty is greater than tx, we move down. We do this by finding out how many steps we can take down at once (ty % tx), and we update ty to that value.\n- If tx is greater than or equal to ty, we move left. We find out how many steps we can take left at once (tx % ty), and we update tx to that value.\n\nWe keep repeating these moves until one of the "can\'t move anymore" situations is reached.\n\n```\n return False\n```\n\nIf we\'ve gone through the loop without reaching one of the "can\'t move anymore" situations, we return "no" (False), indicating that it\'s not possible to reach the destination from the starting point using these moves.\n\nIn simple terms, this code figures out if you can reach a point on a grid by only moving left or down and tells you "yes" or "no." | 2 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
[Python3] Only Solution You'll Need || 30ms, 80% faster | reaching-points | 0 | 1 | Trust me when I say you should really just read this solution and you would understand it:\n\n**Optimized: Bottom Up Solution**:\n\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\t\n while (tx >= sx and ty >= sy):\n # check if we have reached ends\n if tx == sx:\n return (ty-sy) % tx == 0\n if ty == sy:\n return (tx-sx) % ty == 0\n \n # step\n if ty > tx:\n ty = ty%tx\n else:\n tx = tx%ty\n \n return False\n```\n\n**Explanation**\n\nImagine you\'re at a starting point on a grid, and you want to reach another point on the same grid. You can only move in two ways: either left or down. The question is, can you reach your destination using only these moves?\n\n\n```\n while (tx >= sx and ty >= sy):\n```\n\nWe start a loop that continues as long as two conditions are true: (1) tx is greater than or equal to sx, and (2) ty is greater than or equal to sy. These conditions mean we can still make moves.\n\n```\n if tx == sx:\n return (ty-sy) % tx == 0\n```\n\nIf tx becomes equal to sx, it means we can\'t move left anymore. In this case, we check if the difference between ty and sy (how far we need to go down) is divisible by tx (how many steps we can take down at once). If it\'s divisible (no remainder), we can reach the destination, so we return "yes" (True).\n\n```\n if ty == sy:\n return (tx-sx) % ty == 0\n```\n\nSimilarly, if ty becomes equal to sy, it means we can\'t move down anymore. We check if the difference between tx and sx (how far we need to go left) is divisible by ty (how many steps we can take left at once). If it\'s divisible (no remainder), we can reach the destination, so we return "yes" (True).\n\n```\n if ty > tx:\n ty = ty % tx\n else:\n tx = tx % ty\n```\n\nIf we haven\'t reached either of the "can\'t move anymore" situations, we decide on one of two moves:\n\n- If ty is greater than tx, we move down. We do this by finding out how many steps we can take down at once (ty % tx), and we update ty to that value.\n- If tx is greater than or equal to ty, we move left. We find out how many steps we can take left at once (tx % ty), and we update tx to that value.\n\nWe keep repeating these moves until one of the "can\'t move anymore" situations is reached.\n\n```\n return False\n```\n\nIf we\'ve gone through the loop without reaching one of the "can\'t move anymore" situations, we return "no" (False), indicating that it\'s not possible to reach the destination from the starting point using these moves.\n\nIn simple terms, this code figures out if you can reach a point on a grid by only moving left or down and tells you "yes" or "no." | 2 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python recursive solution runtime beats 98.91 % | reaching-points | 0 | 1 | ```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n if sx > tx or sy > ty: return False\n if sx == tx: return (ty-sy)%sx == 0 # only change y\n if sy == ty: return (tx-sx)%sy == 0\n if tx > ty: \n return self.reachingPoints(sx, sy, tx%ty, ty) # make sure tx%ty < ty\n elif tx < ty: \n return self.reachingPoints(sx, sy, tx, ty%tx)\n else:\n return False\n``` | 20 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python recursive solution runtime beats 98.91 % | reaching-points | 0 | 1 | ```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n if sx > tx or sy > ty: return False\n if sx == tx: return (ty-sy)%sx == 0 # only change y\n if sy == ty: return (tx-sx)%sy == 0\n if tx > ty: \n return self.reachingPoints(sx, sy, tx%ty, ty) # make sure tx%ty < ty\n elif tx < ty: \n return self.reachingPoints(sx, sy, tx, ty%tx)\n else:\n return False\n``` | 20 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python Modulo from the End 38ms | reaching-points | 0 | 1 | ```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx <= tx and sy <= ty:\n if tx == sx and ty == sy: return True\n if tx == ty: break\n if tx > ty:\n tx %= ty\n elif ty > tx:\n ty %= tx\n \n if tx == sx: # only change ty\n if (ty-sy) % sx ==0:\n return True\n else:\n return False \n \n if ty == sy: # only change tx\n if (tx-sx) % sy == 0:\n return True\n else:\n return False \n return False \n``` | 3 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python Modulo from the End 38ms | reaching-points | 0 | 1 | ```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx <= tx and sy <= ty:\n if tx == sx and ty == sy: return True\n if tx == ty: break\n if tx > ty:\n tx %= ty\n elif ty > tx:\n ty %= tx\n \n if tx == sx: # only change ty\n if (ty-sy) % sx ==0:\n return True\n else:\n return False \n \n if ty == sy: # only change tx\n if (tx-sx) % sy == 0:\n return True\n else:\n return False \n return False \n``` | 3 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python3 Beats 99% | reaching-points | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(log(max(tx, ty)))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while tx >= sx and ty >= sy:\n if tx == sx and ty == sy:\n return True\n if tx > ty:\n tx -= max((tx - sx) // ty, 1) * ty\n else:\n ty -= max((ty - sy) // tx, 1) * tx\n return False\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python3 Beats 99% | reaching-points | 0 | 1 | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(log(max(tx, ty)))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while tx >= sx and ty >= sy:\n if tx == sx and ty == sy:\n return True\n if tx > ty:\n tx -= max((tx - sx) // ty, 1) * ty\n else:\n ty -= max((ty - sy) // tx, 1) * tx\n return False\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python Simple Solution | reaching-points | 0 | 1 | # Approach\nBacktracking\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n\n return (\n sx <= tx\n and sy <= ty\n and (ty - sy) % tx == 0\n and (tx - sx) % ty == 0\n )\n\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python Simple Solution | reaching-points | 0 | 1 | # Approach\nBacktracking\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n\n return (\n sx <= tx\n and sy <= ty\n and (ty - sy) % tx == 0\n and (tx - sx) % ty == 0\n )\n\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
[Python] O(log(n)) solution using iteration and modulo operator | reaching-points | 0 | 1 | I\'m just doing a quick-submit this time, so I\'m leaving the code below without any commentary up here. If you have any questions, please ask me in the comments and I\'ll fill out more information over time. Thanks!\n\n# Complexity\n- Time complexity: O(log(n)) where n is max(tx,ty)\n- Space complexity: O(1)\n\n# Code\n```py\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\n if sx > tx or sy > ty: return False\n cx, cy = tx, ty\n\n while cx >= sx and cy >= sy:\n\n if (cx == sx and cy == sy): return True\n if cx == cy: return False\n \n if cx > cy:\n if (cx - sx) % cy == 0 and cy == sy:\n return True\n cx = cx % cy\n if cx == 0: cx = cy\n else:\n if (cy - sy) % cx == 0 and cx == sx:\n return True\n cy = cy % cx\n if cy == 0: cy = cx\n \n return False\n \n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
[Python] O(log(n)) solution using iteration and modulo operator | reaching-points | 0 | 1 | I\'m just doing a quick-submit this time, so I\'m leaving the code below without any commentary up here. If you have any questions, please ask me in the comments and I\'ll fill out more information over time. Thanks!\n\n# Complexity\n- Time complexity: O(log(n)) where n is max(tx,ty)\n- Space complexity: O(1)\n\n# Code\n```py\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\n if sx > tx or sy > ty: return False\n cx, cy = tx, ty\n\n while cx >= sx and cy >= sy:\n\n if (cx == sx and cy == sy): return True\n if cx == cy: return False\n \n if cx > cy:\n if (cx - sx) % cy == 0 and cy == sy:\n return True\n cx = cx % cy\n if cx == 0: cx = cy\n else:\n if (cy - sy) % cx == 0 and cx == sx:\n return True\n cy = cy % cx\n if cy == 0: cy = cx\n \n return False\n \n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Solution of leetcode 780 | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\n\n while tx >= sx and ty >= sy:\n if tx==sx and ty==sy:\n return True\n \n if tx > ty:\n tx %= ty\n else:\n ty %= tx\n \n if tx == sx: #then only need to change ty\n if (ty-sy) % tx == 0:\n return True\n else:\n return False\n \n if ty == sy: #then only need to change tx\n if (tx-sx) % ty == 0:\n return True\n else:\n return False\n \n return False \n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Solution of leetcode 780 | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n\n\n while tx >= sx and ty >= sy:\n if tx==sx and ty==sy:\n return True\n \n if tx > ty:\n tx %= ty\n else:\n ty %= tx\n \n if tx == sx: #then only need to change ty\n if (ty-sy) % tx == 0:\n return True\n else:\n return False\n \n if ty == sy: #then only need to change tx\n if (tx-sx) % ty == 0:\n return True\n else:\n return False\n \n return False \n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Python3 easy solution | reaching-points | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n # in such questions start from the target and move to the source, as \n #that contains only one path\n #going from source to target instead has many paths\n #visualize this in the form of a tree\n """\n Logic - question similar to GCD\n bring down the bigger number as much as you can using the mod operation\n once you have made one of the coordinates same, you need to make the other same\n """\n while tx > sx and ty > sy:\n if tx >= ty: tx %= ty\n elif ty > tx: ty %= tx\n\n if tx == sx and ty >= sy: return (ty-sy)%tx == 0\n elif ty == sy and tx >= sx: return (tx-sx)%ty == 0\n return False\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Python3 easy solution | reaching-points | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n # in such questions start from the target and move to the source, as \n #that contains only one path\n #going from source to target instead has many paths\n #visualize this in the form of a tree\n """\n Logic - question similar to GCD\n bring down the bigger number as much as you can using the mod operation\n once you have made one of the coordinates same, you need to make the other same\n """\n while tx > sx and ty > sy:\n if tx >= ty: tx %= ty\n elif ty > tx: ty %= tx\n\n if tx == sx and ty >= sy: return (ty-sy)%tx == 0\n elif ty == sy and tx >= sx: return (tx-sx)%ty == 0\n return False\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
780: Solution with step by step explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n```\n\nHere, we are using a while loop to reduce the tx and ty values. If both tx and ty are greater than their starting counterparts, then the target point can still be reduced. The modulo operation ensures that we\'re effectively taking the reverse step of the operations allowed. The operation is similar to subtracting smaller from the larger until we get them close to sx and sy.\n\n```\nreturn sx == tx and sy <= ty and (ty - sy) % sx == 0 or \\\n sy == ty and sx <= tx and (tx - sx) % sy == 0\n```\nThis line checks if we\'ve successfully reversed from (tx, ty) to (sx, sy).\n\nsx == tx: Checks if the x coordinates match.\nsy <= ty: The y coordinate of the starting point must be less than or equal to the target\'s y.\n(ty - sy) % sx == 0: If the above conditions are met, then this condition checks if the y difference can be formed by repeatedly adding sx.\n\nSimilarly, the conditions sy == ty, sx <= tx, and (tx - sx) % sy == 0 check for the y coordinates matching and the x difference being formed by repeatedly adding sy.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n\n return sx == tx and sy <= ty and (ty - sy) % sx == 0 or \\\n sy == ty and sx <= tx and (tx - sx) % sy == 0\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
780: Solution with step by step explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n```\n\nHere, we are using a while loop to reduce the tx and ty values. If both tx and ty are greater than their starting counterparts, then the target point can still be reduced. The modulo operation ensures that we\'re effectively taking the reverse step of the operations allowed. The operation is similar to subtracting smaller from the larger until we get them close to sx and sy.\n\n```\nreturn sx == tx and sy <= ty and (ty - sy) % sx == 0 or \\\n sy == ty and sx <= tx and (tx - sx) % sy == 0\n```\nThis line checks if we\'ve successfully reversed from (tx, ty) to (sx, sy).\n\nsx == tx: Checks if the x coordinates match.\nsy <= ty: The y coordinate of the starting point must be less than or equal to the target\'s y.\n(ty - sy) % sx == 0: If the above conditions are met, then this condition checks if the y difference can be formed by repeatedly adding sx.\n\nSimilarly, the conditions sy == ty, sx <= tx, and (tx - sx) % sy == 0 check for the y coordinates matching and the x difference being formed by repeatedly adding sy.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n\n return sx == tx and sy <= ty and (ty - sy) % sx == 0 or \\\n sy == ty and sx <= tx and (tx - sx) % sy == 0\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Magic solution with pure maths | reaching-points | 0 | 1 | # Intuition\nThe problem involves reaching a target point `(tx, ty)` starting from an initial point `(sx, sy)` while subtracting one coordinate from the other until one of them matches. We need to determine if it\'s possible to reach the target point using this method.\n\n# Approach\nWe use a while loop to iteratively update `(tx, ty)` by calculating their remainders when divided by the other value. This approach is based on the observation that when `x < u` and `y < v`, you can transform `(x, y)` into `(u, v)` by repeatedly subtracting the smaller value from the larger one until one of them becomes equal to the corresponding coordinate in `(u, v)`.\n\nAfter the loop, we check two conditions to verify if it\'s possible to reach the target point:\n1. If `sx` is equal to `tx` and `sy` is less than or equal to `ty`, it\'s possible to reach `(tx, ty)` if `(ty - sy) % sx == 0`.\n2. If `sy` is equal to `ty` and `sx` is less than or equal to `tx`, it\'s possible to reach `(tx, ty)` if `(tx - sx) % sy == 0`.\n\n# Complexity\n- Time complexity: O(log(max(tx, ty)). The while loop iterates until one coordinate becomes zero, which happens when one coordinate is the remainder of the other.\n- Space complexity: O(1), as we use only a constant amount of extra space.\n\n# Code\n```python\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n return (sx == tx and sy <= ty and (ty - sy) % sx == 0) or (sy == ty and sx <= tx and (tx - sx) % sy == 0)\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Magic solution with pure maths | reaching-points | 0 | 1 | # Intuition\nThe problem involves reaching a target point `(tx, ty)` starting from an initial point `(sx, sy)` while subtracting one coordinate from the other until one of them matches. We need to determine if it\'s possible to reach the target point using this method.\n\n# Approach\nWe use a while loop to iteratively update `(tx, ty)` by calculating their remainders when divided by the other value. This approach is based on the observation that when `x < u` and `y < v`, you can transform `(x, y)` into `(u, v)` by repeatedly subtracting the smaller value from the larger one until one of them becomes equal to the corresponding coordinate in `(u, v)`.\n\nAfter the loop, we check two conditions to verify if it\'s possible to reach the target point:\n1. If `sx` is equal to `tx` and `sy` is less than or equal to `ty`, it\'s possible to reach `(tx, ty)` if `(ty - sy) % sx == 0`.\n2. If `sy` is equal to `ty` and `sx` is less than or equal to `tx`, it\'s possible to reach `(tx, ty)` if `(tx - sx) % sy == 0`.\n\n# Complexity\n- Time complexity: O(log(max(tx, ty)). The while loop iterates until one coordinate becomes zero, which happens when one coordinate is the remainder of the other.\n- Space complexity: O(1), as we use only a constant amount of extra space.\n\n# Code\n```python\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n while sx < tx and sy < ty:\n tx, ty = tx % ty, ty % tx\n return (sx == tx and sy <= ty and (ty - sy) % sx == 0) or (sy == ty and sx <= tx and (tx - sx) % sy == 0)\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Solution with explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n # we just want to shift back from tx, ty -> sx, sy\n while tx != sx or ty != sy:\n # if we already shift to zero or minus zero, then return False\n if tx <= 0 or ty <= 0:\n return False\n if tx > ty:\n # we shift back, but we should keep tx still greater than sx, if it is not a constraint then reduce ty as much as possible, to tx % ty\n txn = max((tx - sx) % ty + sx, tx % ty)\n # because the (tx - sx) % ty + sx can be greater or equal to tx, we need to comfirm the loop is not a dead loop, we only do this shift when txn < tx\n if tx <= txn:\n return False\n else:\n tx = txn\n\n elif tx < ty:\n tyn = max((ty - sy) % tx + sy, ty % tx)\n if ty <= tyn:\n return False\n else:\n ty = tyn\n\n else:\n return False\n\n return True\n\n``` | 0 | Given four integers `sx`, `sy`, `tx`, and `ty`, return `true` _if it is possible to convert the point_ `(sx, sy)` _to the point_ `(tx, ty)` _through some operations__, or_ `false` _otherwise_.
The allowed operation on some point `(x, y)` is to convert it to either `(x, x + y)` or `(x + y, y)`.
**Example 1:**
**Input:** sx = 1, sy = 1, tx = 3, ty = 5
**Output:** true
**Explanation:**
One series of moves that transforms the starting point to the target is:
(1, 1) -> (1, 2)
(1, 2) -> (3, 2)
(3, 2) -> (3, 5)
**Example 2:**
**Input:** sx = 1, sy = 1, tx = 2, ty = 2
**Output:** false
**Example 3:**
**Input:** sx = 1, sy = 1, tx = 1, ty = 1
**Output:** true
**Constraints:**
* `1 <= sx, sy, tx, ty <= 109` | The first chunk can be found as the smallest k for which A[:k+1] == [0, 1, 2, ...k]; then we repeat this process. |
Solution with explanation | reaching-points | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachingPoints(self, sx: int, sy: int, tx: int, ty: int) -> bool:\n # we just want to shift back from tx, ty -> sx, sy\n while tx != sx or ty != sy:\n # if we already shift to zero or minus zero, then return False\n if tx <= 0 or ty <= 0:\n return False\n if tx > ty:\n # we shift back, but we should keep tx still greater than sx, if it is not a constraint then reduce ty as much as possible, to tx % ty\n txn = max((tx - sx) % ty + sx, tx % ty)\n # because the (tx - sx) % ty + sx can be greater or equal to tx, we need to comfirm the loop is not a dead loop, we only do this shift when txn < tx\n if tx <= txn:\n return False\n else:\n tx = txn\n\n elif tx < ty:\n tyn = max((ty - sy) % tx + sy, ty % tx)\n if ty <= tyn:\n return False\n else:\n ty = tyn\n\n else:\n return False\n\n return True\n\n``` | 0 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
Clear solution with comments (Java, Python) | rabbits-in-forest | 1 | 1 | # Intuition\n* If a rabbit says there are $n$ other rabbits of the same color, we can infer there is a group of $n+1$ rabbits that are the same color.\n* If $n+2$ rabbits say they are in a group with $n$ other rabbits of the same color, we need to add another $n+1$ rabbits to our total count.\n\n# Plan\n1. Create a hashtable counts\n2. Set sum = 0 \n3. For each answer in answers \n 1. If answer == 0, sum += 1 \n 2. Else if answer not in counts:\n 1. counts[answer] = 1 \n 2. sum += answer + 1\n 3. Else \n 1. counts[answer] += 1\n 2. if counts[answer] > answer,\n counts[answer] = 0\n4. Return sum\n\n\n# Complexity\n- Time complexity: $$O(n)$$, where $n$ is the number of answers\n\n- Space complexity: $$O(a)$$, where $a$ is the number of distinct answers; $$O(a) \\le O(n)$$\n\n# Python Code\n```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n counts = {}\n count = 0\n\n for answer in answers:\n if answer == 0:\n # This must be the only rabbit of its color.\n count += 1\n elif answer not in counts or counts[answer] == 0:\n # This is the first time the color appears.\n counts[answer] = 1\n # Add all rabbits having this new color.\n count += answer + 1\n else:\n # Add one to how many times answer occurred.\n counts[answer] += 1\n if counts[answer] > answer:\n # If n+1 rabbits have said n,\n # this color group is complete.\n counts[answer] = 0\n \n return count\n```\n\n# Java Code\n```\nclass Solution {\n public int numRabbits(int[] answers) {\n Map<Integer, Integer> counts = new HashMap<>();\n int count = 0;\n\n for (int answer : answers) {\n if (answer == 0) {\n // This must be the only rabbit of its color.\n count++;\n } else if (counts.getOrDefault(answer, 0) == 0) {\n // This is the first time the color appears.\n counts.put(answer, 1);\n // Add all rabbits having this color.\n count += answer + 1;\n } else {\n // Add one to how many times answer occurred.\n counts.put(answer, counts.get(answer) + 1);\n if (counts.get(answer) > answer) {\n // n+1 rabbits have said n, so color done.\n counts.put(answer, 0);\n }\n }\n }\n return count;\n }\n}\n``` | 2 | There is a forest with an unknown number of rabbits. We asked n rabbits **"How many rabbits have the same color as you? "** and collected the answers in an integer array `answers` where `answers[i]` is the answer of the `ith` rabbit.
Given the array `answers`, return _the minimum number of rabbits that could be in the forest_.
**Example 1:**
**Input:** answers = \[1,1,2\]
**Output:** 5
**Explanation:**
The two rabbits that answered "1 " could both be the same color, say red.
The rabbit that answered "2 " can't be red or the answers would be inconsistent.
Say the rabbit that answered "2 " was blue.
Then there should be 2 other blue rabbits in the forest that didn't answer into the array.
The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't.
**Example 2:**
**Input:** answers = \[10,10,10\]
**Output:** 11
**Constraints:**
* `1 <= answers.length <= 1000`
* `0 <= answers[i] < 1000` | One way is with a Polynomial class. For example,
* `Poly:add(this, that)` returns the result of `this + that`.
* `Poly:sub(this, that)` returns the result of `this - that`.
* `Poly:mul(this, that)` returns the result of `this * that`.
* `Poly:evaluate(this, evalmap)` returns the polynomial after replacing all free variables with constants as specified by `evalmap`.
* `Poly:toList(this)` returns the polynomial in the correct output format.
* `Solution::combine(left, right, symbol)` returns the result of applying the binary operator represented by `symbol` to `left` and `right`.
* `Solution::make(expr)` makes a new `Poly` represented by either the constant or free variable specified by `expr`.
* `Solution::parse(expr)` parses an expression into a new `Poly`. |
Clear solution with comments (Java, Python) | rabbits-in-forest | 1 | 1 | # Intuition\n* If a rabbit says there are $n$ other rabbits of the same color, we can infer there is a group of $n+1$ rabbits that are the same color.\n* If $n+2$ rabbits say they are in a group with $n$ other rabbits of the same color, we need to add another $n+1$ rabbits to our total count.\n\n# Plan\n1. Create a hashtable counts\n2. Set sum = 0 \n3. For each answer in answers \n 1. If answer == 0, sum += 1 \n 2. Else if answer not in counts:\n 1. counts[answer] = 1 \n 2. sum += answer + 1\n 3. Else \n 1. counts[answer] += 1\n 2. if counts[answer] > answer,\n counts[answer] = 0\n4. Return sum\n\n\n# Complexity\n- Time complexity: $$O(n)$$, where $n$ is the number of answers\n\n- Space complexity: $$O(a)$$, where $a$ is the number of distinct answers; $$O(a) \\le O(n)$$\n\n# Python Code\n```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n counts = {}\n count = 0\n\n for answer in answers:\n if answer == 0:\n # This must be the only rabbit of its color.\n count += 1\n elif answer not in counts or counts[answer] == 0:\n # This is the first time the color appears.\n counts[answer] = 1\n # Add all rabbits having this new color.\n count += answer + 1\n else:\n # Add one to how many times answer occurred.\n counts[answer] += 1\n if counts[answer] > answer:\n # If n+1 rabbits have said n,\n # this color group is complete.\n counts[answer] = 0\n \n return count\n```\n\n# Java Code\n```\nclass Solution {\n public int numRabbits(int[] answers) {\n Map<Integer, Integer> counts = new HashMap<>();\n int count = 0;\n\n for (int answer : answers) {\n if (answer == 0) {\n // This must be the only rabbit of its color.\n count++;\n } else if (counts.getOrDefault(answer, 0) == 0) {\n // This is the first time the color appears.\n counts.put(answer, 1);\n // Add all rabbits having this color.\n count += answer + 1;\n } else {\n // Add one to how many times answer occurred.\n counts.put(answer, counts.get(answer) + 1);\n if (counts.get(answer) > answer) {\n // n+1 rabbits have said n, so color done.\n counts.put(answer, 0);\n }\n }\n }\n return count;\n }\n}\n``` | 2 | Given a directed acyclic graph (**DAG**) of `n` nodes labeled from `0` to `n - 1`, find all possible paths from node `0` to node `n - 1` and return them in **any order**.
The graph is given as follows: `graph[i]` is a list of all nodes you can visit from node `i` (i.e., there is a directed edge from node `i` to node `graph[i][j]`).
**Example 1:**
**Input:** graph = \[\[1,2\],\[3\],\[3\],\[\]\]
**Output:** \[\[0,1,3\],\[0,2,3\]\]
**Explanation:** There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
**Example 2:**
**Input:** graph = \[\[4,3,1\],\[3,2,4\],\[3\],\[4\],\[\]\]
**Output:** \[\[0,4\],\[0,3,4\],\[0,1,3,4\],\[0,1,2,3,4\],\[0,1,4\]\]
**Constraints:**
* `n == graph.length`
* `2 <= n <= 15`
* `0 <= graph[i][j] < n`
* `graph[i][j] != i` (i.e., there will be no self-loops).
* All the elements of `graph[i]` are **unique**.
* The input graph is **guaranteed** to be a **DAG**. | null |
Python3 intuitive solution (98.43% Runtime, 100% Memory) | rabbits-in-forest | 0 | 1 | ```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n d = {}\n count = 0\n for i in answers:\n\t\t# add 1 if rabbit says 0 other rabbits have same color\n if i == 0:\n count+=1\n else:\n\t\t\t# check if i is present in dictionary or not \n\t\t\t# and also check whether the frequency of i and value of i is same or not\n\t\t\t# For example [2,2,2] and [2,2] has the same result (i.e) 3 but [2,2,2,2] should \n\t\t\t# be seperated into two groups and the result will be 6\n # So we are again initializing the i value to 0\n if i not in d or i == d[i]:\n d[i] = 0\n count+=1 + i\n else:\n d[i] += 1\n \n return count\n``` | 21 | There is a forest with an unknown number of rabbits. We asked n rabbits **"How many rabbits have the same color as you? "** and collected the answers in an integer array `answers` where `answers[i]` is the answer of the `ith` rabbit.
Given the array `answers`, return _the minimum number of rabbits that could be in the forest_.
**Example 1:**
**Input:** answers = \[1,1,2\]
**Output:** 5
**Explanation:**
The two rabbits that answered "1 " could both be the same color, say red.
The rabbit that answered "2 " can't be red or the answers would be inconsistent.
Say the rabbit that answered "2 " was blue.
Then there should be 2 other blue rabbits in the forest that didn't answer into the array.
The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't.
**Example 2:**
**Input:** answers = \[10,10,10\]
**Output:** 11
**Constraints:**
* `1 <= answers.length <= 1000`
* `0 <= answers[i] < 1000` | One way is with a Polynomial class. For example,
* `Poly:add(this, that)` returns the result of `this + that`.
* `Poly:sub(this, that)` returns the result of `this - that`.
* `Poly:mul(this, that)` returns the result of `this * that`.
* `Poly:evaluate(this, evalmap)` returns the polynomial after replacing all free variables with constants as specified by `evalmap`.
* `Poly:toList(this)` returns the polynomial in the correct output format.
* `Solution::combine(left, right, symbol)` returns the result of applying the binary operator represented by `symbol` to `left` and `right`.
* `Solution::make(expr)` makes a new `Poly` represented by either the constant or free variable specified by `expr`.
* `Solution::parse(expr)` parses an expression into a new `Poly`. |
Python3 intuitive solution (98.43% Runtime, 100% Memory) | rabbits-in-forest | 0 | 1 | ```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n d = {}\n count = 0\n for i in answers:\n\t\t# add 1 if rabbit says 0 other rabbits have same color\n if i == 0:\n count+=1\n else:\n\t\t\t# check if i is present in dictionary or not \n\t\t\t# and also check whether the frequency of i and value of i is same or not\n\t\t\t# For example [2,2,2] and [2,2] has the same result (i.e) 3 but [2,2,2,2] should \n\t\t\t# be seperated into two groups and the result will be 6\n # So we are again initializing the i value to 0\n if i not in d or i == d[i]:\n d[i] = 0\n count+=1 + i\n else:\n d[i] += 1\n \n return count\n``` | 21 | Given a directed acyclic graph (**DAG**) of `n` nodes labeled from `0` to `n - 1`, find all possible paths from node `0` to node `n - 1` and return them in **any order**.
The graph is given as follows: `graph[i]` is a list of all nodes you can visit from node `i` (i.e., there is a directed edge from node `i` to node `graph[i][j]`).
**Example 1:**
**Input:** graph = \[\[1,2\],\[3\],\[3\],\[\]\]
**Output:** \[\[0,1,3\],\[0,2,3\]\]
**Explanation:** There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
**Example 2:**
**Input:** graph = \[\[4,3,1\],\[3,2,4\],\[3\],\[4\],\[\]\]
**Output:** \[\[0,4\],\[0,3,4\],\[0,1,3,4\],\[0,1,2,3,4\],\[0,1,4\]\]
**Constraints:**
* `n == graph.length`
* `2 <= n <= 15`
* `0 <= graph[i][j] < n`
* `graph[i][j] != i` (i.e., there will be no self-loops).
* All the elements of `graph[i]` are **unique**.
* The input graph is **guaranteed** to be a **DAG**. | null |
W | rabbits-in-forest | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n\n rabbits = 0\n\n ans_dict = Counter(answers)\n\n for a in ans_dict:\n value = ans_dict[a]\n \n rabbits += math.ceil(value / (a+1)) * (a+1)\n\n return rabbits \n \n\n\n\n\n\n\n\n\n\n\n\n\n \n \n``` | 0 | There is a forest with an unknown number of rabbits. We asked n rabbits **"How many rabbits have the same color as you? "** and collected the answers in an integer array `answers` where `answers[i]` is the answer of the `ith` rabbit.
Given the array `answers`, return _the minimum number of rabbits that could be in the forest_.
**Example 1:**
**Input:** answers = \[1,1,2\]
**Output:** 5
**Explanation:**
The two rabbits that answered "1 " could both be the same color, say red.
The rabbit that answered "2 " can't be red or the answers would be inconsistent.
Say the rabbit that answered "2 " was blue.
Then there should be 2 other blue rabbits in the forest that didn't answer into the array.
The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't.
**Example 2:**
**Input:** answers = \[10,10,10\]
**Output:** 11
**Constraints:**
* `1 <= answers.length <= 1000`
* `0 <= answers[i] < 1000` | One way is with a Polynomial class. For example,
* `Poly:add(this, that)` returns the result of `this + that`.
* `Poly:sub(this, that)` returns the result of `this - that`.
* `Poly:mul(this, that)` returns the result of `this * that`.
* `Poly:evaluate(this, evalmap)` returns the polynomial after replacing all free variables with constants as specified by `evalmap`.
* `Poly:toList(this)` returns the polynomial in the correct output format.
* `Solution::combine(left, right, symbol)` returns the result of applying the binary operator represented by `symbol` to `left` and `right`.
* `Solution::make(expr)` makes a new `Poly` represented by either the constant or free variable specified by `expr`.
* `Solution::parse(expr)` parses an expression into a new `Poly`. |
W | rabbits-in-forest | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n\n rabbits = 0\n\n ans_dict = Counter(answers)\n\n for a in ans_dict:\n value = ans_dict[a]\n \n rabbits += math.ceil(value / (a+1)) * (a+1)\n\n return rabbits \n \n\n\n\n\n\n\n\n\n\n\n\n\n \n \n``` | 0 | Given a directed acyclic graph (**DAG**) of `n` nodes labeled from `0` to `n - 1`, find all possible paths from node `0` to node `n - 1` and return them in **any order**.
The graph is given as follows: `graph[i]` is a list of all nodes you can visit from node `i` (i.e., there is a directed edge from node `i` to node `graph[i][j]`).
**Example 1:**
**Input:** graph = \[\[1,2\],\[3\],\[3\],\[\]\]
**Output:** \[\[0,1,3\],\[0,2,3\]\]
**Explanation:** There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
**Example 2:**
**Input:** graph = \[\[4,3,1\],\[3,2,4\],\[3\],\[4\],\[\]\]
**Output:** \[\[0,4\],\[0,3,4\],\[0,1,3,4\],\[0,1,2,3,4\],\[0,1,4\]\]
**Constraints:**
* `n == graph.length`
* `2 <= n <= 15`
* `0 <= graph[i][j] < n`
* `graph[i][j] != i` (i.e., there will be no self-loops).
* All the elements of `graph[i]` are **unique**.
* The input graph is **guaranteed** to be a **DAG**. | null |
Solution with explaination | rabbits-in-forest | 0 | 1 | # Intuition\nWe notice two things:\n1. two rabbits with different answers belong to two diffent groups.\n2. two rabbits with the same answer may or may not belong to the same group.\n\n# Approach\nUsing the first notice, with answers occuring once, the number of rabbits is the sum of these answers plus 1. For example: with answers [1, 2, 3, 4], the number of rabbits is: (1 + 1) + (2 + 1) + (3 + 1) + (4 + 1)\n\nUsing the second notice, suppose that there are K rabbits with the answer A. Each (A + 1) rabbits belong to the same group. So the number of rabbits: ceil(K / (A + 1)) * (A + 1)\n\n# Complexity\n- Time complexity:\nO(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n freq = {}\n for a in answers:\n freq[a] = freq.get(a, 0) + 1\n rs = 0\n for a, k in freq.items():\n if k == 1:\n rs += a + 1\n else:\n rs += math.ceil(k / (a + 1)) * (a + 1)\n return rs\n``` | 0 | There is a forest with an unknown number of rabbits. We asked n rabbits **"How many rabbits have the same color as you? "** and collected the answers in an integer array `answers` where `answers[i]` is the answer of the `ith` rabbit.
Given the array `answers`, return _the minimum number of rabbits that could be in the forest_.
**Example 1:**
**Input:** answers = \[1,1,2\]
**Output:** 5
**Explanation:**
The two rabbits that answered "1 " could both be the same color, say red.
The rabbit that answered "2 " can't be red or the answers would be inconsistent.
Say the rabbit that answered "2 " was blue.
Then there should be 2 other blue rabbits in the forest that didn't answer into the array.
The smallest possible number of rabbits in the forest is therefore 5: 3 that answered plus 2 that didn't.
**Example 2:**
**Input:** answers = \[10,10,10\]
**Output:** 11
**Constraints:**
* `1 <= answers.length <= 1000`
* `0 <= answers[i] < 1000` | One way is with a Polynomial class. For example,
* `Poly:add(this, that)` returns the result of `this + that`.
* `Poly:sub(this, that)` returns the result of `this - that`.
* `Poly:mul(this, that)` returns the result of `this * that`.
* `Poly:evaluate(this, evalmap)` returns the polynomial after replacing all free variables with constants as specified by `evalmap`.
* `Poly:toList(this)` returns the polynomial in the correct output format.
* `Solution::combine(left, right, symbol)` returns the result of applying the binary operator represented by `symbol` to `left` and `right`.
* `Solution::make(expr)` makes a new `Poly` represented by either the constant or free variable specified by `expr`.
* `Solution::parse(expr)` parses an expression into a new `Poly`. |
Solution with explaination | rabbits-in-forest | 0 | 1 | # Intuition\nWe notice two things:\n1. two rabbits with different answers belong to two diffent groups.\n2. two rabbits with the same answer may or may not belong to the same group.\n\n# Approach\nUsing the first notice, with answers occuring once, the number of rabbits is the sum of these answers plus 1. For example: with answers [1, 2, 3, 4], the number of rabbits is: (1 + 1) + (2 + 1) + (3 + 1) + (4 + 1)\n\nUsing the second notice, suppose that there are K rabbits with the answer A. Each (A + 1) rabbits belong to the same group. So the number of rabbits: ceil(K / (A + 1)) * (A + 1)\n\n# Complexity\n- Time complexity:\nO(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\nO(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRabbits(self, answers: List[int]) -> int:\n freq = {}\n for a in answers:\n freq[a] = freq.get(a, 0) + 1\n rs = 0\n for a, k in freq.items():\n if k == 1:\n rs += a + 1\n else:\n rs += math.ceil(k / (a + 1)) * (a + 1)\n return rs\n``` | 0 | Given a directed acyclic graph (**DAG**) of `n` nodes labeled from `0` to `n - 1`, find all possible paths from node `0` to node `n - 1` and return them in **any order**.
The graph is given as follows: `graph[i]` is a list of all nodes you can visit from node `i` (i.e., there is a directed edge from node `i` to node `graph[i][j]`).
**Example 1:**
**Input:** graph = \[\[1,2\],\[3\],\[3\],\[\]\]
**Output:** \[\[0,1,3\],\[0,2,3\]\]
**Explanation:** There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
**Example 2:**
**Input:** graph = \[\[4,3,1\],\[3,2,4\],\[3\],\[4\],\[\]\]
**Output:** \[\[0,4\],\[0,3,4\],\[0,1,3,4\],\[0,1,2,3,4\],\[0,1,4\]\]
**Constraints:**
* `n == graph.length`
* `2 <= n <= 15`
* `0 <= graph[i][j] < n`
* `graph[i][j] != i` (i.e., there will be no self-loops).
* All the elements of `graph[i]` are **unique**.
* The input graph is **guaranteed** to be a **DAG**. | null |
Solution | transform-to-chessboard | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int movesToChessboard(vector<vector<int>>& board) {\n int n = board.size();\n int row_counter = 0, col_counter = 0;\n for(int r = 0; r < n; r++){\n row_counter += board[r][0] ? 1 : -1;\n for(int c = 0; c < n; c++){\n if(r == 0) col_counter += board[r][c] ? 1 : -1;\n if((board[r][0] ^ board[0][0]) ^ (board[r][c] ^ board[0][c])) return -1; \n }\n }\n if(abs(row_counter) > 1 || abs(col_counter) > 1) return -1;\n int row_swap_count = 0, col_swap_count = 0, row_0_count = 0, col_0_count = 0;\n for(int i = 0; i < n; i++){\n if(i & 1){\n row_swap_count += board[i][0];\n col_swap_count += board[0][i];\n }\n row_0_count += board[i][0] == 0, col_0_count += board[0][i] == 0; \n }\n int odd_position_count = n/2; \n if(n & 1){ \n row_swap_count = row_0_count == odd_position_count ? row_swap_count : (odd_position_count - row_swap_count);\n col_swap_count = col_0_count == odd_position_count ? col_swap_count : (odd_position_count - col_swap_count);\n }\n else{\n row_swap_count = min(row_swap_count, odd_position_count - row_swap_count);\n col_swap_count = min(col_swap_count, odd_position_count - col_swap_count); \n }\n return row_swap_count + col_swap_count;\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def check_even(self, count) : \n if len(count) != 2 or sorted(count.values()) != self.balanced : \n return -1 \n return 1\n\n def all_opposite(self, line1, line2) : \n if not all (line1_value ^ line2_value for line1_value, line2_value in zip(line1, line2)) : \n return -1 \n return 1 \n \n def set_sums_of_lists_of_values(self) : \n self.sums_of_lists_of_values = [sum(list_of_values) for list_of_values in self.lists_of_values]\n\n def update_number_of_swaps(self) : \n self.number_of_swaps += min(self.sums_of_lists_of_values) // 2\n\n def set_lists_of_values(self, line1) : \n self.lists_of_values = []\n for start in self.starts : \n new_list = []\n for index, value in enumerate(line1, start) : \n new_list.append((index-value) % 2)\n self.lists_of_values.append(new_list)\n\n def set_starting_values(self, line1) : \n self.starts = [+(line1.count(1) * 2 > self.n)] if self.n & 1 else [0, 1]\n\n def process_line(self, line1) : \n self.set_starting_values(line1)\n self.set_lists_of_values(line1) \n self.set_sums_of_lists_of_values()\n self.update_number_of_swaps()\n\n def process_board(self, board) : \n for count in (collections.Counter(map(tuple, board)), collections.Counter(zip(*board))) : \n if self.check_even(count) == -1 : \n return -1 \n line1, line2 = count\n if self.all_opposite(line1, line2) == -1 : \n return -1 \n self.process_line(line1)\n return self.number_of_swaps\n\n def set_up_for_processing_board(self, n) : \n self.n = n \n self.number_of_swaps = 0\n self.balanced = [n//2, (n+1)//2]\n \n def movesToChessboard(self, board: List[List[int]]) -> int:\n self.set_up_for_processing_board(len(board))\n return self.process_board(board)\n```\n\n```Java []\nclass Solution {\n public int movesToChessboard(int[][] board) {\n int N = board.length, rowSum = 0, colSum = 0, rowSwap = 0, colSwap = 0;\n for (int r = 0; r < N; ++r)\n for (int c = 0; c < N; ++c) {\n if ((board[0][0] ^ board[r][0] ^ board[0][c] ^ board[r][c]) == 1)\n return -1;\n }\n for (int i = 0; i < N; ++i) {\n rowSum += board[0][i];\n colSum += board[i][0];\n rowSwap += board[i][0] == i % 2 ? 1 : 0;\n colSwap += board[0][i] == i % 2 ? 1 : 0;\n }\n if (N / 2 > rowSum || rowSum > (N + 1) / 2) return -1;\n if (N / 2 > colSum || colSum > (N + 1) / 2) return -1;\n if (N % 2 == 1) {\n if (colSwap % 2 == 1) colSwap = N - colSwap;\n if (rowSwap % 2 == 1) rowSwap = N - rowSwap;\n } else {\n colSwap = Math.min(N - colSwap, colSwap);\n rowSwap = Math.min(N - rowSwap, rowSwap);\n }\n return (colSwap + rowSwap) / 2;\n }\n}\n```\n | 1 | You are given an `n x n` binary grid `board`. In each move, you can swap any two rows with each other, or any two columns with each other.
Return _the minimum number of moves to transform the board into a **chessboard board**_. If the task is impossible, return `-1`.
A **chessboard board** is a board where no `0`'s and no `1`'s are 4-directionally adjacent.
**Example 1:**
**Input:** board = \[\[0,1,1,0\],\[0,1,1,0\],\[1,0,0,1\],\[1,0,0,1\]\]
**Output:** 2
**Explanation:** One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
**Example 2:**
**Input:** board = \[\[0,1\],\[1,0\]\]
**Output:** 0
**Explanation:** Also note that the board with 0 in the top left corner, is also a valid chessboard.
**Example 3:**
**Input:** board = \[\[1,0\],\[1,0\]\]
**Output:** -1
**Explanation:** No matter what sequence of moves you make, you cannot end with a valid chessboard.
**Constraints:**
* `n == board.length`
* `n == board[i].length`
* `2 <= n <= 30`
* `board[i][j]` is either `0` or `1`. | For each stone, check if it is a jewel. |
Solution | transform-to-chessboard | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int movesToChessboard(vector<vector<int>>& board) {\n int n = board.size();\n int row_counter = 0, col_counter = 0;\n for(int r = 0; r < n; r++){\n row_counter += board[r][0] ? 1 : -1;\n for(int c = 0; c < n; c++){\n if(r == 0) col_counter += board[r][c] ? 1 : -1;\n if((board[r][0] ^ board[0][0]) ^ (board[r][c] ^ board[0][c])) return -1; \n }\n }\n if(abs(row_counter) > 1 || abs(col_counter) > 1) return -1;\n int row_swap_count = 0, col_swap_count = 0, row_0_count = 0, col_0_count = 0;\n for(int i = 0; i < n; i++){\n if(i & 1){\n row_swap_count += board[i][0];\n col_swap_count += board[0][i];\n }\n row_0_count += board[i][0] == 0, col_0_count += board[0][i] == 0; \n }\n int odd_position_count = n/2; \n if(n & 1){ \n row_swap_count = row_0_count == odd_position_count ? row_swap_count : (odd_position_count - row_swap_count);\n col_swap_count = col_0_count == odd_position_count ? col_swap_count : (odd_position_count - col_swap_count);\n }\n else{\n row_swap_count = min(row_swap_count, odd_position_count - row_swap_count);\n col_swap_count = min(col_swap_count, odd_position_count - col_swap_count); \n }\n return row_swap_count + col_swap_count;\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def check_even(self, count) : \n if len(count) != 2 or sorted(count.values()) != self.balanced : \n return -1 \n return 1\n\n def all_opposite(self, line1, line2) : \n if not all (line1_value ^ line2_value for line1_value, line2_value in zip(line1, line2)) : \n return -1 \n return 1 \n \n def set_sums_of_lists_of_values(self) : \n self.sums_of_lists_of_values = [sum(list_of_values) for list_of_values in self.lists_of_values]\n\n def update_number_of_swaps(self) : \n self.number_of_swaps += min(self.sums_of_lists_of_values) // 2\n\n def set_lists_of_values(self, line1) : \n self.lists_of_values = []\n for start in self.starts : \n new_list = []\n for index, value in enumerate(line1, start) : \n new_list.append((index-value) % 2)\n self.lists_of_values.append(new_list)\n\n def set_starting_values(self, line1) : \n self.starts = [+(line1.count(1) * 2 > self.n)] if self.n & 1 else [0, 1]\n\n def process_line(self, line1) : \n self.set_starting_values(line1)\n self.set_lists_of_values(line1) \n self.set_sums_of_lists_of_values()\n self.update_number_of_swaps()\n\n def process_board(self, board) : \n for count in (collections.Counter(map(tuple, board)), collections.Counter(zip(*board))) : \n if self.check_even(count) == -1 : \n return -1 \n line1, line2 = count\n if self.all_opposite(line1, line2) == -1 : \n return -1 \n self.process_line(line1)\n return self.number_of_swaps\n\n def set_up_for_processing_board(self, n) : \n self.n = n \n self.number_of_swaps = 0\n self.balanced = [n//2, (n+1)//2]\n \n def movesToChessboard(self, board: List[List[int]]) -> int:\n self.set_up_for_processing_board(len(board))\n return self.process_board(board)\n```\n\n```Java []\nclass Solution {\n public int movesToChessboard(int[][] board) {\n int N = board.length, rowSum = 0, colSum = 0, rowSwap = 0, colSwap = 0;\n for (int r = 0; r < N; ++r)\n for (int c = 0; c < N; ++c) {\n if ((board[0][0] ^ board[r][0] ^ board[0][c] ^ board[r][c]) == 1)\n return -1;\n }\n for (int i = 0; i < N; ++i) {\n rowSum += board[0][i];\n colSum += board[i][0];\n rowSwap += board[i][0] == i % 2 ? 1 : 0;\n colSwap += board[0][i] == i % 2 ? 1 : 0;\n }\n if (N / 2 > rowSum || rowSum > (N + 1) / 2) return -1;\n if (N / 2 > colSum || colSum > (N + 1) / 2) return -1;\n if (N % 2 == 1) {\n if (colSwap % 2 == 1) colSwap = N - colSwap;\n if (rowSwap % 2 == 1) rowSwap = N - rowSwap;\n } else {\n colSwap = Math.min(N - colSwap, colSwap);\n rowSwap = Math.min(N - rowSwap, rowSwap);\n }\n return (colSwap + rowSwap) / 2;\n }\n}\n```\n | 1 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
[Python3] alternating numbers | transform-to-chessboard | 0 | 1 | \n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n \n def fn(vals): \n """Return min moves to transform to chessboard."""\n total = odd = 0 \n for i, x in enumerate(vals): \n if vals[0] == x: \n total += 1\n if i&1: odd += 1\n elif vals[0] ^ x != (1 << n) - 1: return inf\n ans = inf \n if len(vals) <= 2*total <= len(vals)+1: ans = min(ans, odd)\n if len(vals)-1 <= 2*total <= len(vals): ans = min(ans, total - odd)\n return ans \n \n rows, cols = [0]*n, [0]*n\n for i in range(n): \n for j in range(n): \n if board[i][j]: \n rows[i] ^= 1 << j \n cols[j] ^= 1 << i\n ans = fn(rows) + fn(cols)\n return ans if ans < inf else -1 \n``` | 8 | You are given an `n x n` binary grid `board`. In each move, you can swap any two rows with each other, or any two columns with each other.
Return _the minimum number of moves to transform the board into a **chessboard board**_. If the task is impossible, return `-1`.
A **chessboard board** is a board where no `0`'s and no `1`'s are 4-directionally adjacent.
**Example 1:**
**Input:** board = \[\[0,1,1,0\],\[0,1,1,0\],\[1,0,0,1\],\[1,0,0,1\]\]
**Output:** 2
**Explanation:** One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
**Example 2:**
**Input:** board = \[\[0,1\],\[1,0\]\]
**Output:** 0
**Explanation:** Also note that the board with 0 in the top left corner, is also a valid chessboard.
**Example 3:**
**Input:** board = \[\[1,0\],\[1,0\]\]
**Output:** -1
**Explanation:** No matter what sequence of moves you make, you cannot end with a valid chessboard.
**Constraints:**
* `n == board.length`
* `n == board[i].length`
* `2 <= n <= 30`
* `board[i][j]` is either `0` or `1`. | For each stone, check if it is a jewel. |
[Python3] alternating numbers | transform-to-chessboard | 0 | 1 | \n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n \n def fn(vals): \n """Return min moves to transform to chessboard."""\n total = odd = 0 \n for i, x in enumerate(vals): \n if vals[0] == x: \n total += 1\n if i&1: odd += 1\n elif vals[0] ^ x != (1 << n) - 1: return inf\n ans = inf \n if len(vals) <= 2*total <= len(vals)+1: ans = min(ans, odd)\n if len(vals)-1 <= 2*total <= len(vals): ans = min(ans, total - odd)\n return ans \n \n rows, cols = [0]*n, [0]*n\n for i in range(n): \n for j in range(n): \n if board[i][j]: \n rows[i] ^= 1 << j \n cols[j] ^= 1 << i\n ans = fn(rows) + fn(cols)\n return ans if ans < inf else -1 \n``` | 8 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
782: Beats 98.8%, Solution with step by step explanation | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n n = len(board)\n```\n\nGet the size of the board.\n\n```\n for i in range(n):\n for j in range(n):\n if board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j]:\n return -1\n```\n\nFor every possible 2x2 square in the board (formed by picking cells (0, 0), (i, 0), (0, j), (i, j)), if the four cells are neither all the same nor all different, we instantly return -1 because it\'s impossible to form a chessboard in this situation. The ^ operator is a bitwise XOR operation that will return 1 if two bits are different and 0 if they\'re the same.\n\n```\n row_sum = sum(board[0])\n```\n\nCount the number of ones in the first row.\n\n```\n col_sum = sum(board[i][0] for i in range(n))\n```\n\nCount the number of ones in the first column.\n\n```\n if not n//2 <= row_sum <= (n+1)//2:\n return -1\n if not n//2 <= col_sum <= (n+1)//2:\n return -1\n```\n\nCheck if the number of ones in the first row and column is valid. A valid chessboard will have almost equal number of ones and zeros in the first row and column. Depending on whether the board size n is even or odd, we ensure that the number of ones lies in the acceptable range.\n\n```\n row_swaps = sum(board[i][0] == i % 2 for i in range(n))\n```\n\nCalculate how many rows in the board have their starting bit different from their row index modulo 2. This will help determine how many rows we need to swap to get the desired alternating pattern.\n\n```\n col_swaps = sum(board[0][i] == i % 2 for i in range(n))\n```\n\nSimilarly, calculate how many columns have their starting bit different from their column index modulo 2.\n\n```\n if n % 2:\n```\n\nIf the size of the board n is odd\n\n```\n if row_swaps % 2:\n row_swaps = n - row_swaps\n```\n\nIf the number of row swaps is odd, you adjust it because you can\'t make an odd number of swaps to achieve the desired configuration. It becomes the complement, i.e., the difference from the total number of rows.\n\n```\n if col_swaps % 2:\n col_swaps = n - col_swaps\n```\n\nSimilarly, adjust column swaps if it\'s odd.\n\n```\n else:\n row_swaps = min(row_swaps, n - row_swaps)\n col_swaps = min(col_swaps, n - col_swaps)\n```\n\nIf n is even, for both rows and columns, choose the minimum between the calculated swaps and its complement. This ensures you always take the minimum number of swaps required.\n\n```\n return (row_swaps + col_swaps) // 2\n```\n\nFinally, return the total number of swaps required. We divide by 2 because for every two moves, we fix one position in both rows and columns.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n \n for i in range(n):\n for j in range(n):\n if board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j]:\n return -1\n \n row_sum = sum(board[0])\n col_sum = sum(board[i][0] for i in range(n))\n\n if not n//2 <= row_sum <= (n+1)//2:\n return -1\n if not n//2 <= col_sum <= (n+1)//2:\n return -1\n\n row_swaps = sum(board[i][0] == i % 2 for i in range(n))\n col_swaps = sum(board[0][i] == i % 2 for i in range(n))\n\n if n % 2:\n if row_swaps % 2:\n row_swaps = n - row_swaps\n if col_swaps % 2:\n col_swaps = n - col_swaps\n else:\n row_swaps = min(row_swaps, n - row_swaps)\n col_swaps = min(col_swaps, n - col_swaps)\n \n return (row_swaps + col_swaps) // 2\n\n``` | 0 | You are given an `n x n` binary grid `board`. In each move, you can swap any two rows with each other, or any two columns with each other.
Return _the minimum number of moves to transform the board into a **chessboard board**_. If the task is impossible, return `-1`.
A **chessboard board** is a board where no `0`'s and no `1`'s are 4-directionally adjacent.
**Example 1:**
**Input:** board = \[\[0,1,1,0\],\[0,1,1,0\],\[1,0,0,1\],\[1,0,0,1\]\]
**Output:** 2
**Explanation:** One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
**Example 2:**
**Input:** board = \[\[0,1\],\[1,0\]\]
**Output:** 0
**Explanation:** Also note that the board with 0 in the top left corner, is also a valid chessboard.
**Example 3:**
**Input:** board = \[\[1,0\],\[1,0\]\]
**Output:** -1
**Explanation:** No matter what sequence of moves you make, you cannot end with a valid chessboard.
**Constraints:**
* `n == board.length`
* `n == board[i].length`
* `2 <= n <= 30`
* `board[i][j]` is either `0` or `1`. | For each stone, check if it is a jewel. |
782: Beats 98.8%, Solution with step by step explanation | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n n = len(board)\n```\n\nGet the size of the board.\n\n```\n for i in range(n):\n for j in range(n):\n if board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j]:\n return -1\n```\n\nFor every possible 2x2 square in the board (formed by picking cells (0, 0), (i, 0), (0, j), (i, j)), if the four cells are neither all the same nor all different, we instantly return -1 because it\'s impossible to form a chessboard in this situation. The ^ operator is a bitwise XOR operation that will return 1 if two bits are different and 0 if they\'re the same.\n\n```\n row_sum = sum(board[0])\n```\n\nCount the number of ones in the first row.\n\n```\n col_sum = sum(board[i][0] for i in range(n))\n```\n\nCount the number of ones in the first column.\n\n```\n if not n//2 <= row_sum <= (n+1)//2:\n return -1\n if not n//2 <= col_sum <= (n+1)//2:\n return -1\n```\n\nCheck if the number of ones in the first row and column is valid. A valid chessboard will have almost equal number of ones and zeros in the first row and column. Depending on whether the board size n is even or odd, we ensure that the number of ones lies in the acceptable range.\n\n```\n row_swaps = sum(board[i][0] == i % 2 for i in range(n))\n```\n\nCalculate how many rows in the board have their starting bit different from their row index modulo 2. This will help determine how many rows we need to swap to get the desired alternating pattern.\n\n```\n col_swaps = sum(board[0][i] == i % 2 for i in range(n))\n```\n\nSimilarly, calculate how many columns have their starting bit different from their column index modulo 2.\n\n```\n if n % 2:\n```\n\nIf the size of the board n is odd\n\n```\n if row_swaps % 2:\n row_swaps = n - row_swaps\n```\n\nIf the number of row swaps is odd, you adjust it because you can\'t make an odd number of swaps to achieve the desired configuration. It becomes the complement, i.e., the difference from the total number of rows.\n\n```\n if col_swaps % 2:\n col_swaps = n - col_swaps\n```\n\nSimilarly, adjust column swaps if it\'s odd.\n\n```\n else:\n row_swaps = min(row_swaps, n - row_swaps)\n col_swaps = min(col_swaps, n - col_swaps)\n```\n\nIf n is even, for both rows and columns, choose the minimum between the calculated swaps and its complement. This ensures you always take the minimum number of swaps required.\n\n```\n return (row_swaps + col_swaps) // 2\n```\n\nFinally, return the total number of swaps required. We divide by 2 because for every two moves, we fix one position in both rows and columns.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n \n for i in range(n):\n for j in range(n):\n if board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j]:\n return -1\n \n row_sum = sum(board[0])\n col_sum = sum(board[i][0] for i in range(n))\n\n if not n//2 <= row_sum <= (n+1)//2:\n return -1\n if not n//2 <= col_sum <= (n+1)//2:\n return -1\n\n row_swaps = sum(board[i][0] == i % 2 for i in range(n))\n col_swaps = sum(board[0][i] == i % 2 for i in range(n))\n\n if n % 2:\n if row_swaps % 2:\n row_swaps = n - row_swaps\n if col_swaps % 2:\n col_swaps = n - col_swaps\n else:\n row_swaps = min(row_swaps, n - row_swaps)\n col_swaps = min(col_swaps, n - col_swaps)\n \n return (row_swaps + col_swaps) // 2\n\n``` | 0 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
Time: O(n2)O(n2) Space: O(1)O(1) | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n\n if any(board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j] for i in range(n) for j in range(n)):\n return -1\n\n rowSum = sum(board[0])\n colSum = sum(board[i][0] for i in range(n))\n\n if rowSum != n // 2 and rowSum != (n + 1) // 2:\n return -1\n if colSum != n // 2 and colSum != (n + 1) // 2:\n return -1\n\n rowSwaps = sum(board[i][0] == (i & 1) for i in range(n))\n colSwaps = sum(board[0][i] == (i & 1) for i in range(n))\n\n if n & 1:\n if rowSwaps & 1:\n rowSwaps = n - rowSwaps\n if colSwaps & 1:\n colSwaps = n - colSwaps\n else:\n rowSwaps = min(rowSwaps, n - rowSwaps)\n colSwaps = min(colSwaps, n - colSwaps)\n\n return (rowSwaps + colSwaps) // 2\n\n``` | 0 | You are given an `n x n` binary grid `board`. In each move, you can swap any two rows with each other, or any two columns with each other.
Return _the minimum number of moves to transform the board into a **chessboard board**_. If the task is impossible, return `-1`.
A **chessboard board** is a board where no `0`'s and no `1`'s are 4-directionally adjacent.
**Example 1:**
**Input:** board = \[\[0,1,1,0\],\[0,1,1,0\],\[1,0,0,1\],\[1,0,0,1\]\]
**Output:** 2
**Explanation:** One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
**Example 2:**
**Input:** board = \[\[0,1\],\[1,0\]\]
**Output:** 0
**Explanation:** Also note that the board with 0 in the top left corner, is also a valid chessboard.
**Example 3:**
**Input:** board = \[\[1,0\],\[1,0\]\]
**Output:** -1
**Explanation:** No matter what sequence of moves you make, you cannot end with a valid chessboard.
**Constraints:**
* `n == board.length`
* `n == board[i].length`
* `2 <= n <= 30`
* `board[i][j]` is either `0` or `1`. | For each stone, check if it is a jewel. |
Time: O(n2)O(n2) Space: O(1)O(1) | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def movesToChessboard(self, board: List[List[int]]) -> int:\n n = len(board)\n\n if any(board[0][0] ^ board[i][0] ^ board[0][j] ^ board[i][j] for i in range(n) for j in range(n)):\n return -1\n\n rowSum = sum(board[0])\n colSum = sum(board[i][0] for i in range(n))\n\n if rowSum != n // 2 and rowSum != (n + 1) // 2:\n return -1\n if colSum != n // 2 and colSum != (n + 1) // 2:\n return -1\n\n rowSwaps = sum(board[i][0] == (i & 1) for i in range(n))\n colSwaps = sum(board[0][i] == (i & 1) for i in range(n))\n\n if n & 1:\n if rowSwaps & 1:\n rowSwaps = n - rowSwaps\n if colSwaps & 1:\n colSwaps = n - colSwaps\n else:\n rowSwaps = min(rowSwaps, n - rowSwaps)\n colSwaps = min(colSwaps, n - colSwaps)\n\n return (rowSwaps + colSwaps) // 2\n\n``` | 0 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
Solid Principles | Dimension Independence | Commented and Explained | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOur main insight into the problem is that there must be a balance of either exactly the same or alternating by 1 number of chess piece locations in two rows based on the idea that we have two rows next to each other (think of a 2 by 2 grid as the easiest case, then a 3 x 3, and so on), which you can convince yourself of by building up by 2 x 2 to 3 x 3 to 4 x 4 to 5 x 5 chess grids. \n\nThis implies two stopping early conditions we can exploit. These are that there are more than two types of lines based on the frequencies of values between the two rows, or if there are not a balanced valuation of frequencies for the two rows. If we encounter any case with this, we will never be able to swap our chess board (until someone out there decides to invent a fiendish version where we can swap items on one row with items far away on another! That\'d be horrid!). Similarly, if in our our processing of the two rows, we find that there are not exactly xor sequences when placed on top of each other and doing an xor summation, then we also know that this is not possible for our consideration at all. \n\nOnce we have these two cases, we need to figure out what to do in the meantime if we find two rows that are compatabile at some point. \n\nTo do so, we will need to determine what the line can start with. \nIn the case of an even number of items, we obviously need to only start with 0 and 1. But on the case of an odd length row (5 x 5 grid for example) we will need to start with some amalgatation of the count of line1\'s 1s being 2 times greater than our length of n. This will place us as either 0 and 1 or 1 and 0 depending on the row indice we currently occupy. \n\nOnce we know what we can start with, we want the sum of the lists of values that we currently have, namely the value of index - value mod 2 for each index in our row and value in our row depending on if we start with index 0 or index 1. \n\nThese then are summed up as two separate valuations in our list of sums of lists of values\n\nWe take the minimal account of these by half, and that is our update to our number of swaps. We can do this by half, since we will be swapping two items positions in a maximally advantageous way, and we only need to get the minimal number in order, since once they are in order the maximal are as well. \n\nTo process our board then, we need to first set up a bit. We will need of course a size of the board dimensions, n, a number of swaps holder, 0, and a way to know if wwe are balanced, a list of [n//2 and (n+1)//2] \n\nWhen we process we then want to take the counter of the map of the tuples of the board with the counter of the zipped board columns \nThis necessarily gives us row and column independent comparisons\nIn such a case, \n- For count in our independent spaces \n - if our count is not even (2 types of lines and sorted version of the line values are the balanced ones) we can return -1 \n - if our two lines do not form up an alternating pair (xor of one and the others values all the way across) we can return -1 \n - otherwise, we need to process a line, including updating our number of swaps accordingly \nWhen done, if we never returned, we now return our number of swaps \n\nTo calculate our moves to chessboard then, we simply call set up for processing board, passing the length of the board and then return the value of the call to process board passing the board. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAn object oriented approach using solid design principles was the focus of this work. The goal was to limit responsibility of each function to a singular purpose within the problem space. \n\n# Complexity\n- Time complexity: O(N * N) \n - We end up exploring the entire board, so it is the size of the board as the limit on time \n\n- Space complexity: O(N) \n - Count ends up storing N items for line1 and N items for line2, so total is 2N which reduces to N \n\n# Code\n```\nclass Solution:\n # check if there are two types of lines or that the sorted values are not the balanced form \n # on fail, return -1 \n # on pass, return 1 \n def check_even(self, count) : \n if len(count) != 2 or sorted(count.values()) != self.balanced : \n return -1 \n return 1\n\n # check if all are alternating row by row \n # if so, alternate is good, if not, not possible, return -1 \n def all_opposite(self, line1, line2) : \n if not all (line1_value ^ line2_value for line1_value, line2_value in zip(line1, line2)) : \n return -1 \n return 1 \n \n # set your sums of lists of values based on your current lists of values \n def set_sums_of_lists_of_values(self) : \n self.sums_of_lists_of_values = [sum(list_of_values) for list_of_values in self.lists_of_values]\n\n # update your number of swaps using your current sums of lists of values \n def update_number_of_swaps(self) : \n self.number_of_swaps += min(self.sums_of_lists_of_values) // 2\n\n def set_lists_of_values(self, line1) : \n self.lists_of_values = []\n for start in self.starts : \n new_list = []\n for index, value in enumerate(line1, start) : \n new_list.append((index-value) % 2)\n self.lists_of_values.append(new_list)\n\n def set_starting_values(self, line1) : \n self.starts = [+(line1.count(1) * 2 > self.n)] if self.n & 1 else [0, 1]\n\n def process_line(self, line1) : \n # starts is the starting value of line 1 \n # starts gets added to an empty list the value of \n # the number of 1s found multipled by 2 is greater than n if n is odd \n # this is to deal with the one off 1 factor on odd boards alternating \n # otherwise, it gets only 0 and 1 \n self.set_starting_values(line1)\n # use starts and line1 to build the list \n self.set_lists_of_values(line1) \n # use the lists of values to build the sums of lists of values \n self.set_sums_of_lists_of_values()\n # use those to update the number of swaps \n self.update_number_of_swaps()\n\n def process_board(self, board) : \n # get the count as the pair of tuples of the board as frequencies with the zip of the rows \n for count in (collections.Counter(map(tuple, board)), collections.Counter(zip(*board))) : \n # if there are more than 2 kinds of lines or they are not balanced \n if self.check_even(count) == -1 : \n return -1 \n line1, line2 = count\n # if the values of the two lines when zipped are not always alternating, also false\n # this can be checked with exclusive or of the values in line1 and line 2 as l1v and l2v\n if self.all_opposite(line1, line2) == -1 : \n return -1 \n # pass the line which is the first item in count \n self.process_line(line1)\n # if you haven\'t returned yet, return now \n return self.number_of_swaps\n\n def set_up_for_processing_board(self, n) : \n # n by n board \n self.n = n \n # number of swaps needed \n self.number_of_swaps = 0\n # balanced form for chess board \n self.balanced = [n//2, (n+1)//2]\n \n def movesToChessboard(self, board: List[List[int]]) -> int:\n # set up for processing \n self.set_up_for_processing_board(len(board))\n # then process it \n return self.process_board(board)\n\n``` | 0 | You are given an `n x n` binary grid `board`. In each move, you can swap any two rows with each other, or any two columns with each other.
Return _the minimum number of moves to transform the board into a **chessboard board**_. If the task is impossible, return `-1`.
A **chessboard board** is a board where no `0`'s and no `1`'s are 4-directionally adjacent.
**Example 1:**
**Input:** board = \[\[0,1,1,0\],\[0,1,1,0\],\[1,0,0,1\],\[1,0,0,1\]\]
**Output:** 2
**Explanation:** One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.
**Example 2:**
**Input:** board = \[\[0,1\],\[1,0\]\]
**Output:** 0
**Explanation:** Also note that the board with 0 in the top left corner, is also a valid chessboard.
**Example 3:**
**Input:** board = \[\[1,0\],\[1,0\]\]
**Output:** -1
**Explanation:** No matter what sequence of moves you make, you cannot end with a valid chessboard.
**Constraints:**
* `n == board.length`
* `n == board[i].length`
* `2 <= n <= 30`
* `board[i][j]` is either `0` or `1`. | For each stone, check if it is a jewel. |
Solid Principles | Dimension Independence | Commented and Explained | transform-to-chessboard | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOur main insight into the problem is that there must be a balance of either exactly the same or alternating by 1 number of chess piece locations in two rows based on the idea that we have two rows next to each other (think of a 2 by 2 grid as the easiest case, then a 3 x 3, and so on), which you can convince yourself of by building up by 2 x 2 to 3 x 3 to 4 x 4 to 5 x 5 chess grids. \n\nThis implies two stopping early conditions we can exploit. These are that there are more than two types of lines based on the frequencies of values between the two rows, or if there are not a balanced valuation of frequencies for the two rows. If we encounter any case with this, we will never be able to swap our chess board (until someone out there decides to invent a fiendish version where we can swap items on one row with items far away on another! That\'d be horrid!). Similarly, if in our our processing of the two rows, we find that there are not exactly xor sequences when placed on top of each other and doing an xor summation, then we also know that this is not possible for our consideration at all. \n\nOnce we have these two cases, we need to figure out what to do in the meantime if we find two rows that are compatabile at some point. \n\nTo do so, we will need to determine what the line can start with. \nIn the case of an even number of items, we obviously need to only start with 0 and 1. But on the case of an odd length row (5 x 5 grid for example) we will need to start with some amalgatation of the count of line1\'s 1s being 2 times greater than our length of n. This will place us as either 0 and 1 or 1 and 0 depending on the row indice we currently occupy. \n\nOnce we know what we can start with, we want the sum of the lists of values that we currently have, namely the value of index - value mod 2 for each index in our row and value in our row depending on if we start with index 0 or index 1. \n\nThese then are summed up as two separate valuations in our list of sums of lists of values\n\nWe take the minimal account of these by half, and that is our update to our number of swaps. We can do this by half, since we will be swapping two items positions in a maximally advantageous way, and we only need to get the minimal number in order, since once they are in order the maximal are as well. \n\nTo process our board then, we need to first set up a bit. We will need of course a size of the board dimensions, n, a number of swaps holder, 0, and a way to know if wwe are balanced, a list of [n//2 and (n+1)//2] \n\nWhen we process we then want to take the counter of the map of the tuples of the board with the counter of the zipped board columns \nThis necessarily gives us row and column independent comparisons\nIn such a case, \n- For count in our independent spaces \n - if our count is not even (2 types of lines and sorted version of the line values are the balanced ones) we can return -1 \n - if our two lines do not form up an alternating pair (xor of one and the others values all the way across) we can return -1 \n - otherwise, we need to process a line, including updating our number of swaps accordingly \nWhen done, if we never returned, we now return our number of swaps \n\nTo calculate our moves to chessboard then, we simply call set up for processing board, passing the length of the board and then return the value of the call to process board passing the board. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAn object oriented approach using solid design principles was the focus of this work. The goal was to limit responsibility of each function to a singular purpose within the problem space. \n\n# Complexity\n- Time complexity: O(N * N) \n - We end up exploring the entire board, so it is the size of the board as the limit on time \n\n- Space complexity: O(N) \n - Count ends up storing N items for line1 and N items for line2, so total is 2N which reduces to N \n\n# Code\n```\nclass Solution:\n # check if there are two types of lines or that the sorted values are not the balanced form \n # on fail, return -1 \n # on pass, return 1 \n def check_even(self, count) : \n if len(count) != 2 or sorted(count.values()) != self.balanced : \n return -1 \n return 1\n\n # check if all are alternating row by row \n # if so, alternate is good, if not, not possible, return -1 \n def all_opposite(self, line1, line2) : \n if not all (line1_value ^ line2_value for line1_value, line2_value in zip(line1, line2)) : \n return -1 \n return 1 \n \n # set your sums of lists of values based on your current lists of values \n def set_sums_of_lists_of_values(self) : \n self.sums_of_lists_of_values = [sum(list_of_values) for list_of_values in self.lists_of_values]\n\n # update your number of swaps using your current sums of lists of values \n def update_number_of_swaps(self) : \n self.number_of_swaps += min(self.sums_of_lists_of_values) // 2\n\n def set_lists_of_values(self, line1) : \n self.lists_of_values = []\n for start in self.starts : \n new_list = []\n for index, value in enumerate(line1, start) : \n new_list.append((index-value) % 2)\n self.lists_of_values.append(new_list)\n\n def set_starting_values(self, line1) : \n self.starts = [+(line1.count(1) * 2 > self.n)] if self.n & 1 else [0, 1]\n\n def process_line(self, line1) : \n # starts is the starting value of line 1 \n # starts gets added to an empty list the value of \n # the number of 1s found multipled by 2 is greater than n if n is odd \n # this is to deal with the one off 1 factor on odd boards alternating \n # otherwise, it gets only 0 and 1 \n self.set_starting_values(line1)\n # use starts and line1 to build the list \n self.set_lists_of_values(line1) \n # use the lists of values to build the sums of lists of values \n self.set_sums_of_lists_of_values()\n # use those to update the number of swaps \n self.update_number_of_swaps()\n\n def process_board(self, board) : \n # get the count as the pair of tuples of the board as frequencies with the zip of the rows \n for count in (collections.Counter(map(tuple, board)), collections.Counter(zip(*board))) : \n # if there are more than 2 kinds of lines or they are not balanced \n if self.check_even(count) == -1 : \n return -1 \n line1, line2 = count\n # if the values of the two lines when zipped are not always alternating, also false\n # this can be checked with exclusive or of the values in line1 and line 2 as l1v and l2v\n if self.all_opposite(line1, line2) == -1 : \n return -1 \n # pass the line which is the first item in count \n self.process_line(line1)\n # if you haven\'t returned yet, return now \n return self.number_of_swaps\n\n def set_up_for_processing_board(self, n) : \n # n by n board \n self.n = n \n # number of swaps needed \n self.number_of_swaps = 0\n # balanced form for chess board \n self.balanced = [n//2, (n+1)//2]\n \n def movesToChessboard(self, board: List[List[int]]) -> int:\n # set up for processing \n self.set_up_for_processing_board(len(board))\n # then process it \n return self.process_board(board)\n\n``` | 0 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
Easy Explanation | TC: O(N) and SC: O(H) | Python and C++ | minimum-distance-between-bst-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is that in a BST, the difference between adjacent values is always the smallest. Therefore, if we traverse the BST in a sorted order, we can compare adjacent values and find the smallest difference. By keeping track of the previously visited node, we can calculate the absolute difference between any two distinct nodes in the tree. Finally, we can take the minimum of all such differences to get the minimum distance between nodes in the BST.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach to finding the minimum distance between nodes in a binary search tree (BST) involves using an in-order traversal to visit the nodes in sorted order, and keeping track of the previously visited node to calculate the absolute difference between any two distinct nodes in the tree. The minimum of all such differences is the minimum distance between nodes in the BST.\n\nHere is the step-by-step approach to solve the problem:\n\n* Initialize a variable ```prev``` to ```None```, and a variable ```min_diff``` to ```infinity```.\n* Perform an in-order traversal of the BST, visiting each node in sorted order.\n* For each node visited, calculate the absolute difference between its value and the value of the previously visited node (if any), and update the min_diff variable if the difference is smaller than the current value of ```min_diff```.\n* Update the ```prev``` variable to the current node after processing it.\n* After the traversal is complete, return the value of ```min_diff```.\n\nIn the code [below], we define a class TreeNode to represent the nodes in the BST. The ```minDiffInBST``` method takes the root of the BST as an input and returns the minimum distance between nodes. We initialize the previously visited node to None, the minimum difference to infinity, and call the ```in_order_traversal``` method to traverse the BST.\n\nThe ```in_order_traversal``` method recursively visits the left child, processes the current node by calculating the absolute difference with the previously visited node, updates the minimum difference, and updates the previously visited node. Finally, it visits the right child.\n\nAfter the traversal is complete, the min_diff variable will contain the minimum distance between nodes in the BST.\n\n# Complexity\n- Time complexity: $$O(N)$$, where $$N$$ is the number of nodes in the tree.\n\n- Space complexity: $$O(H)$$, where $$H$$ is the height of the tree.\n\n# Code\n\n```py\n# PYTHON SOLUTION\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def in_order_traversal(self, node: TreeNode) -> None:\n if node is None:\n return\n self.in_order_traversal(node.left)\n if self.prev is not None:\n self.min_diff = min(self.min_diff, abs(node.val - self.prev.val))\n self.prev = node\n self.in_order_traversal(node.right)\n\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n self.prev = None\n self.min_diff = float(\'inf\')\n self.in_order_traversal(root)\n return self.min_diff\n```\n\n```cpp\n// CPP SOLUTION\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n void in_order_traversal(TreeNode* node, TreeNode*& prev, int& min_diff) {\n if (node == nullptr) {\n return;\n }\n in_order_traversal(node->left, prev, min_diff);\n if (prev != nullptr) {\n min_diff = std::min(min_diff, abs(node->val - prev->val));\n }\n prev = node;\n in_order_traversal(node->right, prev, min_diff);\n }\n int minDiffInBST(TreeNode* root) {\n TreeNode* prev = nullptr;\n int min_diff = INT_MAX;\n in_order_traversal(root, prev, min_diff);\n return min_diff;\n }\n};\n``` | 2 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Easy Explanation | TC: O(N) and SC: O(H) | Python and C++ | minimum-distance-between-bst-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is that in a BST, the difference between adjacent values is always the smallest. Therefore, if we traverse the BST in a sorted order, we can compare adjacent values and find the smallest difference. By keeping track of the previously visited node, we can calculate the absolute difference between any two distinct nodes in the tree. Finally, we can take the minimum of all such differences to get the minimum distance between nodes in the BST.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach to finding the minimum distance between nodes in a binary search tree (BST) involves using an in-order traversal to visit the nodes in sorted order, and keeping track of the previously visited node to calculate the absolute difference between any two distinct nodes in the tree. The minimum of all such differences is the minimum distance between nodes in the BST.\n\nHere is the step-by-step approach to solve the problem:\n\n* Initialize a variable ```prev``` to ```None```, and a variable ```min_diff``` to ```infinity```.\n* Perform an in-order traversal of the BST, visiting each node in sorted order.\n* For each node visited, calculate the absolute difference between its value and the value of the previously visited node (if any), and update the min_diff variable if the difference is smaller than the current value of ```min_diff```.\n* Update the ```prev``` variable to the current node after processing it.\n* After the traversal is complete, return the value of ```min_diff```.\n\nIn the code [below], we define a class TreeNode to represent the nodes in the BST. The ```minDiffInBST``` method takes the root of the BST as an input and returns the minimum distance between nodes. We initialize the previously visited node to None, the minimum difference to infinity, and call the ```in_order_traversal``` method to traverse the BST.\n\nThe ```in_order_traversal``` method recursively visits the left child, processes the current node by calculating the absolute difference with the previously visited node, updates the minimum difference, and updates the previously visited node. Finally, it visits the right child.\n\nAfter the traversal is complete, the min_diff variable will contain the minimum distance between nodes in the BST.\n\n# Complexity\n- Time complexity: $$O(N)$$, where $$N$$ is the number of nodes in the tree.\n\n- Space complexity: $$O(H)$$, where $$H$$ is the height of the tree.\n\n# Code\n\n```py\n# PYTHON SOLUTION\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def in_order_traversal(self, node: TreeNode) -> None:\n if node is None:\n return\n self.in_order_traversal(node.left)\n if self.prev is not None:\n self.min_diff = min(self.min_diff, abs(node.val - self.prev.val))\n self.prev = node\n self.in_order_traversal(node.right)\n\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n self.prev = None\n self.min_diff = float(\'inf\')\n self.in_order_traversal(root)\n return self.min_diff\n```\n\n```cpp\n// CPP SOLUTION\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n void in_order_traversal(TreeNode* node, TreeNode*& prev, int& min_diff) {\n if (node == nullptr) {\n return;\n }\n in_order_traversal(node->left, prev, min_diff);\n if (prev != nullptr) {\n min_diff = std::min(min_diff, abs(node->val - prev->val));\n }\n prev = node;\n in_order_traversal(node->right, prev, min_diff);\n }\n int minDiffInBST(TreeNode* root) {\n TreeNode* prev = nullptr;\n int min_diff = INT_MAX;\n in_order_traversal(root, prev, min_diff);\n return min_diff;\n }\n};\n``` | 2 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
simple solution for beginners | minimum-distance-between-bst-nodes | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n res=[]\n def helper(node):\n if node is not None:\n res.append(node.val)\n helper(node.left)\n helper(node.right)\n helper(root)\n res=sorted(res)\n temp=float(\'inf\')\n print(res)\n for i in range(1,len(res)):\n temp=min(temp,abs(res[i-1]-res[i]))\n return temp\n \n\n``` | 1 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
simple solution for beginners | minimum-distance-between-bst-nodes | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n res=[]\n def helper(node):\n if node is not None:\n res.append(node.val)\n helper(node.left)\n helper(node.right)\n helper(root)\n res=sorted(res)\n temp=float(\'inf\')\n print(res)\n for i in range(1,len(res)):\n temp=min(temp,abs(res[i-1]-res[i]))\n return temp\n \n\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Python3 | DFS | Easy | minimum-distance-between-bst-nodes | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ recursive stack space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n minSoFar = float(\'inf\')\n prev = float(\'-inf\')\n\n def recur(node):\n nonlocal minSoFar\n nonlocal prev\n \n if not node:\n return \n \n recur(node.left)\n minSoFar = min(minSoFar, node.val - prev)\n prev = node.val\n recur(node.right)\n\n recur(root)\n return minSoFar\n``` | 1 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Python3 | DFS | Easy | minimum-distance-between-bst-nodes | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ recursive stack space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDiffInBST(self, root: Optional[TreeNode]) -> int:\n minSoFar = float(\'inf\')\n prev = float(\'-inf\')\n\n def recur(node):\n nonlocal minSoFar\n nonlocal prev\n \n if not node:\n return \n \n recur(node.left)\n minSoFar = min(minSoFar, node.val - prev)\n prev = node.val\n recur(node.right)\n\n recur(root)\n return minSoFar\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Beginner-friendly || Simple solution with Backracking in Python3 / TypeScript | letter-case-permutation | 0 | 1 | # Intuition\nHere\'s the brief explanation of a problem:\n- there\'s a string `s`, \n- this consists with **alphabetical characters** (English letters and digits)\n- our goal is to get **all** the possible variations of this string by swapping letters in different cases\n\nThere\'re **2 cases** - **lowerCase and upperCase.**\nThe approach is straightforward - **swap each letter** into different case and store this string.\n\n```\ns = \'a1b2\'\n\n# Possible variations are [\'a1b2\',\'A1b2\',\'a1B2\',\'A1B2\']\n```\n\nThis could be solved with [Backtracking](https://en.wikipedia.org/wiki/Backtracking).\n\n# Approach\n1. declare `ans` to store swappings\n2. declare `backtrack` function, that accepts `i` as index and accumulated `path`\n3. if a string has all of the characters such `i == len(s)`, store it into `ans`\n4. backtrack each letter(twice) and digit(once) via checking type of `s`\n5. return `ans`\n\n# Complexity\n- Time complexity: **O(N * 2^N)**, for iterating over `s` and backtrack all possible swappings\n\n- Space complexity: **O(N * 2^N)**, the same for storing\n# Code in Python3\n```\nclass Solution:\n def letterCasePermutation(self, s: str) -> List[str]:\n ans = []\n\n def backtrack(i, path):\n if i == len(s):\n ans.append("".join(path))\n return \n\n path.append(s[i].lower())\n backtrack(i + 1, path)\n path.pop()\n\n if s[i].isalpha():\n path.append(s[i].upper())\n backtrack(i + 1, path)\n path.pop()\n\n backtrack(0, [])\n\n return ans\n```\n# Code in TypeScript\n```\nfunction letterCasePermutation(s: string): string[] {\n const ans = []\n\n const backtrack = (i: number, path: string[]): void => {\n if (i === s.length) {\n ans.push(path.join(\'\'))\n return\n }\n\n path.push(s[i].toLowerCase())\n backtrack(i + 1, path)\n path.pop()\n\n if (Number.isNaN(+s[i])) {\n path.push(s[i].toUpperCase())\n backtrack(i + 1, path)\n path.pop()\n }\n }\n\n backtrack(0, [])\n\n return ans\n};\n``` | 1 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Solution | letter-case-permutation | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<string> letterCasePermutation(string s) {\n vector<string> result;\n int length=s.length();\n letterCasePermutationRec(s,result,length,0);\n return result;\n }\n void letterCasePermutationRec(string& s,vector<string>& result,int length,int index){\n if(length==0){\n result.push_back(s);\n }else if(isalpha(s[index])){\n s[index]=toupper(s[index]);\n letterCasePermutationRec(s,result,length-1,index+1);\n s[index]=tolower(s[index]);\n letterCasePermutationRec(s,result,length-1,index+1);\n }else{\n letterCasePermutationRec(s,result,length-1,index+1);\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def letterCasePermutation(self, s: str) -> List[str]:\n record = []\n for ch in s:\n record.append([ch] if ch.isdigit() else [ch.lower(), ch.upper()])\n\n return [\'\'.join(v) for v in product(*record)]\n```\n\n```Java []\nclass Solution {\n private List<String> ans = new ArrayList<>();\n private char[] t;\n\n public List<String> letterCasePermutation(String s) {\n t = s.toCharArray();\n dfs(0);\n return ans;\n }\n private void dfs(int i) {\n if (i >= t.length) {\n ans.add(String.valueOf(t));\n return;\n }\n dfs(i + 1);\n if (t[i] >= \'A\') {\n t[i] ^= 32;\n dfs(i + 1);\n }\n }\n}\n```\n | 1 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Python clear solution | letter-case-permutation | 0 | 1 | ```\nclass Solution(object):\n def letterCasePermutation(self, S):\n """\n :type S: str\n :rtype: List[str]\n """\n def backtrack(sub="", i=0):\n if len(sub) == len(S):\n res.append(sub)\n else:\n if S[i].isalpha():\n backtrack(sub + S[i].swapcase(), i + 1)\n backtrack(sub + S[i], i + 1)\n \n res = []\n backtrack()\n return res\n```\nExample of handling an input "hey":\n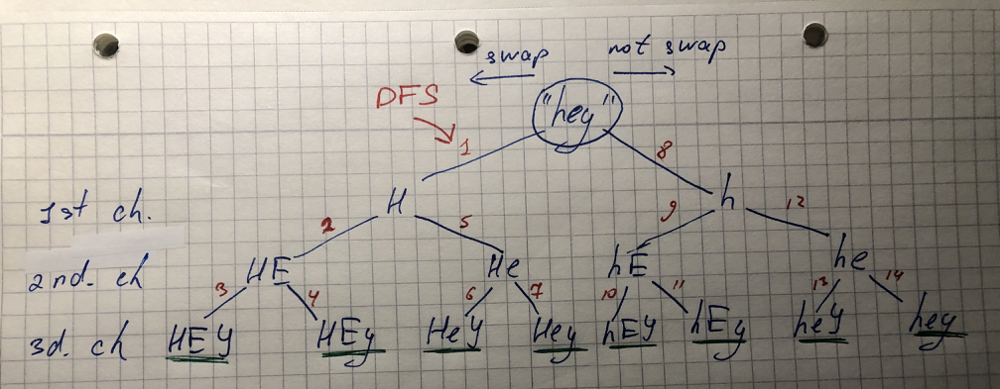 | 191 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
「Python3」🧼Clean w/ explain || O(2^N) || Beats "94.11%" || ⏫Thanks for reading & upvt | letter-case-permutation | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe see a `number`, we add it to every string in the `permutation[]`.\n\nWe see a `letter`, we add it 1st time **(lowercase)** to every string `permutation[]` + 2nd time **(uppercase)** to every string `permutation[]`.\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n```\n> Case: "a1b2", permutation[] = [""]\n\n-> a = alphabet\n[""] * 2 \n-> ["", ""] -> (+a 1st half, +A 2nd half)\n-> ["a", "A"] \n\n-> 1 = number\n["a", "A"] \n-> ["a1", "A1"]\n\n-> b = alphabet\n["a1", "A1"] * 2 \n-> ["a1", "A1", "a1", "A1"] -> (+b 1st half, +B 2nd half)\n-> ["a1b", "A1b", "a1B", "A1B"] \n\n-> 2 = number\n["a1b", "A1b", "a1B", "A1B"] \n-> ["a1b2", "A1b2", "a1B2", "A1B2"]\n\n```\n1. For every character in `s` we check if it is a `number` or a `letter`.\n2. If `s[i]` = `number`, we replace original string `permutation[p] = permutation[p] + (s[i])`in the `permutation[]`\n3. If `s[i]` = `letter`, we double the `permutation[]`: 1 - replace 1st half `permutation[p] = permutation[p] + (s[i].lower())` 2 - replace 2nd half `permutation[p] = permutation[p] + (s[i].upper())`\n\n# Complexity\n- \u2705\u231B Time complexity: $$O(2^N)$$\u231B --> The worst case scenario is where every character is a `letter`, as you double the `permutation[]`, you will have `2x` more permutations = adding (`1x` for lowercase + `1x` for uppercase).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- \u2705\uD83D\uDCBE Space complexity: $$O(2^N)$$ \uD83D\uDCBE --> Storing `2^N` all letters of different permutations.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# \uD83E\uDDFCCode\uD83E\uDDFC\n```\nclass Solution:\n def letterCasePermutation(self, s: str) -> List[str]:\n permutation = [""]\n\n for i in range(len(s)):\n # number #\n if s[i].isnumeric():\n for p in range(len(permutation)):\n permutation[p] = permutation[p] + (s[i])\n \n # alphabet #\n if s[i].isalpha():\n permutation = permutation * 2\n \n for p in range(len(permutation)):\n if (p*2 < len(permutation)):\n permutation[p] = permutation[p] + (s[i].lower())\n else:\n permutation[p] = permutation[p] + (s[i].upper())\n \n return permutation\n\n``` | 3 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
✅ 🔥 Python3 || ⚡very easy solution uwu | letter-case-permutation | 0 | 1 | ```\nclass Solution:\n def letterCasePermutation(self, S: str) -> List[str]:\n res = []\n def backtrack(i, curr):\n if i == len(S):\n res.append(curr)\n return\n if S[i].isalpha():\n backtrack(i+1, curr+S[i].upper())\n backtrack(i+1, curr+S[i].lower())\n else:\n backtrack(i+1, curr+S[i])\n backtrack(0, "")\n return res\n``` | 4 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Python || 99.36% Faster || Recursion || Easy | letter-case-permutation | 0 | 1 | ```\nclass Solution:\n def letterCasePermutation(self, s: str) -> List[str]:\n ans=[]\n def solve(ip,op):\n if ip==\'\':\n ans.append(op)\n return \n if ip[0].isalpha():\n op1=op+ip[0].lower()\n op2=op+ip[0].upper()\n solve(ip[1:],op1)\n solve(ip[1:],op2)\n else:\n solve(ip[1:],op+ip[0]) #if its not a character then we need not to take two cases for it\n solve(s,\'\')\n return ans\n```\n**An upvote will be encouraging** | 1 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
BFS Approach || Python || Easy to Understand | is-graph-bipartite | 0 | 1 | # Complexity\n- Time complexity:\nO(E+V)\n\n- Space complexity:\nO(V)\n\n# Code\n```\nfrom collections import deque\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color=[-1]*len(graph)\n def bfs(start,graph,color):\n q=deque()\n color[start]=0\n q.append(start)\n while(len(q)!=0):\n element=q.popleft()\n for ele in graph[element]:\n if(color[ele]==-1):\n if(color[element]==0):\n color[ele]=1\n q.append(ele)\n else:\n color[ele]=0\n q.append(ele)\n else:\n if(color[ele]==color[element]):\n return False \n return True\n for i in range(len(graph)):\n if(color[i]==-1):\n if(bfs(i,graph,color)==False):\n return False\n return True\n``` | 1 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
BFS Approach || Python || Easy to Understand | is-graph-bipartite | 0 | 1 | # Complexity\n- Time complexity:\nO(E+V)\n\n- Space complexity:\nO(V)\n\n# Code\n```\nfrom collections import deque\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color=[-1]*len(graph)\n def bfs(start,graph,color):\n q=deque()\n color[start]=0\n q.append(start)\n while(len(q)!=0):\n element=q.popleft()\n for ele in graph[element]:\n if(color[ele]==-1):\n if(color[element]==0):\n color[ele]=1\n q.append(ele)\n else:\n color[ele]=0\n q.append(ele)\n else:\n if(color[ele]==color[element]):\n return False \n return True\n for i in range(len(graph)):\n if(color[i]==-1):\n if(bfs(i,graph,color)==False):\n return False\n return True\n``` | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Python3 Solution | is-graph-bipartite | 0 | 1 | \n```\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n n=len(graph)\n col=[-1]*n\n for i in range(n):\n if col[i]!=-1:\n continue\n\n q=deque()\n q.append((i,0))\n while q:\n node,color=q.popleft()\n if col[node]==-1:\n col[node]=color\n for nx in graph[node]:\n q.append((nx,color^1))\n\n\n if col[node]!=color:\n return False\n\n return True \n``` | 1 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
Python3 Solution | is-graph-bipartite | 0 | 1 | \n```\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n n=len(graph)\n col=[-1]*n\n for i in range(n):\n if col[i]!=-1:\n continue\n\n q=deque()\n q.append((i,0))\n while q:\n node,color=q.popleft()\n if col[node]==-1:\n col[node]=color\n for nx in graph[node]:\n q.append((nx,color^1))\n\n\n if col[node]!=color:\n return False\n\n return True \n``` | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.