title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
793: Beats 96.08%, Solution with step by step explanation | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nStep 1: Calculate trailing zeros for a given number\nTo understand how many trailing zeros a number\'s factorial has, we need to count the number of times 5 appears as a factor in all numbers leading up to it.\n\nIf n is 0, return 0 because 0! has no trailing zeros.\n\n```\nreturn 0 if n == 0 \n```\n\nElse, count how many numbers up to n are divisible by 5 and recursively do the same for n/5.\n\n```\nelse n // 5 + trailing_zeroes(n // 5)\n```\n\nStep 2: Binary search for the largest number with up to k trailing zeros in its factorial\nThe idea here is to determine the largest number whose factorial has up to k trailing zeros.\n\nInitiate the search space between 0 and an upper limit. The number 5 * k + 4 is a heuristic to ensure our search includes the number with exactly k trailing zeros.\n\n```\nleft, right = 0, 5 * k + 4 \n```\n\nConduct binary search:\n\nCalculate the middle number of the current range.\n\n```\nmid = (left + right) // 2\n```\n\nCheck how many trailing zeros the factorial of mid has.\n\n```\nzeros = trailing_zeroes(mid)\n```\n\nIf this number is less than or equal to k, then a number with exactly k trailing zeros must be on the right side.\n\n```\nif zeros <= k:\n left = mid + 1\n```\n\nElse, it\'s on the left side.\n\n```\nelse:\n right = mid - 1\n```\n\nOnce the binary search concludes, right will point to the largest number whose factorial results in up to k zeros.\n\n```\nreturn right\n```\n\nStep 3: Find the count of numbers with k trailing zeros\nDeduct the count of numbers having "up to k-1 zeros" from those having "up to k zeros" to get numbers with exactly k zeros.\n\n```\nreturn largest_num_with_zeroes(k) - largest_num_with_zeroes(k - 1)\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n \n def trailing_zeroes(n: int) -> int:\n return 0 if n == 0 else n // 5 + trailing_zeroes(n // 5)\n\n def largest_num_with_zeroes(k: int) -> int:\n left, right = 0, 5 * k + 4\n while left <= right:\n mid = (left + right) // 2\n if trailing_zeroes(mid) <= k:\n left = mid + 1\n else:\n right = mid - 1\n return right\n\n return largest_num_with_zeroes(k) - largest_num_with_zeroes(k - 1)\n\n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
793: Beats 96.08%, Solution with step by step explanation | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nStep 1: Calculate trailing zeros for a given number\nTo understand how many trailing zeros a number\'s factorial has, we need to count the number of times 5 appears as a factor in all numbers leading up to it.\n\nIf n is 0, return 0 because 0! has no trailing zeros.\n\n```\nreturn 0 if n == 0 \n```\n\nElse, count how many numbers up to n are divisible by 5 and recursively do the same for n/5.\n\n```\nelse n // 5 + trailing_zeroes(n // 5)\n```\n\nStep 2: Binary search for the largest number with up to k trailing zeros in its factorial\nThe idea here is to determine the largest number whose factorial has up to k trailing zeros.\n\nInitiate the search space between 0 and an upper limit. The number 5 * k + 4 is a heuristic to ensure our search includes the number with exactly k trailing zeros.\n\n```\nleft, right = 0, 5 * k + 4 \n```\n\nConduct binary search:\n\nCalculate the middle number of the current range.\n\n```\nmid = (left + right) // 2\n```\n\nCheck how many trailing zeros the factorial of mid has.\n\n```\nzeros = trailing_zeroes(mid)\n```\n\nIf this number is less than or equal to k, then a number with exactly k trailing zeros must be on the right side.\n\n```\nif zeros <= k:\n left = mid + 1\n```\n\nElse, it\'s on the left side.\n\n```\nelse:\n right = mid - 1\n```\n\nOnce the binary search concludes, right will point to the largest number whose factorial results in up to k zeros.\n\n```\nreturn right\n```\n\nStep 3: Find the count of numbers with k trailing zeros\nDeduct the count of numbers having "up to k-1 zeros" from those having "up to k zeros" to get numbers with exactly k zeros.\n\n```\nreturn largest_num_with_zeroes(k) - largest_num_with_zeroes(k - 1)\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n \n def trailing_zeroes(n: int) -> int:\n return 0 if n == 0 else n // 5 + trailing_zeroes(n // 5)\n\n def largest_num_with_zeroes(k: int) -> int:\n left, right = 0, 5 * k + 4\n while left <= right:\n mid = (left + right) // 2\n if trailing_zeroes(mid) <= k:\n left = mid + 1\n else:\n right = mid - 1\n return right\n\n return largest_num_with_zeroes(k) - largest_num_with_zeroes(k - 1)\n\n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
math + binary search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key here is simply knowing a mathematical formula for the numer of trailing zeroes of a factorial. It\'s well known from math contests that this is just k = floor(n/5) + floor(n/25) + floor(n/125) + ....\n\nImportantly, this is monotonically increasing in n, so binary search is pretty intuitive. What\'s next is to come up with some upper and lower bounds.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nClearly, k < n/5 + n/25 + n/125 + ... < n/4 by infinite geometric series. Similarly, k > n/5 - 1 (very crude upper bound.) This gives 4k < n < 5k + 6. Now, just binary search LOLZ.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nTo compute the number of zeroes using the formula is log n. You have to do it log n times. So, our time complexity is O(log^2 n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1). didn\'t take up any space\n# Code\n```\nclass Solution:\n def factorialSize(self, n: int) -> int:\n power = 1\n res = 0\n while n//(5**power) > 0:\n res += (n//(5**power))\n power +=1\n return res\n def preimageSizeFZF(self, k: int) -> int:\n #note either 0 or 5 -> just check if possible to make or not\n #k = floor(n/5) + floor(n/25) + floor(n/125) + ... < n/4 \n #n > 4k, n < 5k + 6\n lo, hi = 4*k, 5*k + 6\n #binary search\n while lo < hi:\n med = (lo + hi)//2\n #print(lo, med, hi)\n num = self.factorialSize(med)\n if num < k: lo = med+1\n elif num == k: return 5\n else: hi = med\n return 0\n #O(logn^2)\n\n \n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
math + binary search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key here is simply knowing a mathematical formula for the numer of trailing zeroes of a factorial. It\'s well known from math contests that this is just k = floor(n/5) + floor(n/25) + floor(n/125) + ....\n\nImportantly, this is monotonically increasing in n, so binary search is pretty intuitive. What\'s next is to come up with some upper and lower bounds.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nClearly, k < n/5 + n/25 + n/125 + ... < n/4 by infinite geometric series. Similarly, k > n/5 - 1 (very crude upper bound.) This gives 4k < n < 5k + 6. Now, just binary search LOLZ.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nTo compute the number of zeroes using the formula is log n. You have to do it log n times. So, our time complexity is O(log^2 n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1). didn\'t take up any space\n# Code\n```\nclass Solution:\n def factorialSize(self, n: int) -> int:\n power = 1\n res = 0\n while n//(5**power) > 0:\n res += (n//(5**power))\n power +=1\n return res\n def preimageSizeFZF(self, k: int) -> int:\n #note either 0 or 5 -> just check if possible to make or not\n #k = floor(n/5) + floor(n/25) + floor(n/125) + ... < n/4 \n #n > 4k, n < 5k + 6\n lo, hi = 4*k, 5*k + 6\n #binary search\n while lo < hi:\n med = (lo + hi)//2\n #print(lo, med, hi)\n num = self.factorialSize(med)\n if num < k: lo = med+1\n elif num == k: return 5\n else: hi = med\n return 0\n #O(logn^2)\n\n \n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python Easy to Understand solution. Binary Search step by step explanation | preimage-size-of-factorial-zeroes-function | 0 | 1 | - Number of zeroes for a given number n = min(n//5, n//2)+n//10\n- n//2 gives the number of 2 factors and n//5 gives the number of 5 factors. \n- n//5 isn\'t accurance. Taking 1.2.3......125, we get 5,10,15,...125 and 25, 50, 75, 100, 125 and 125\n- The total isn\'t n//5. It is n//5 + n//25 + n//125\n- We also don\'t need n/10, It is taken care by n//5....\n- 2*5 makes a 10, so the number of 2s or 5s whichever are lesser determine the number of 0s\n- But we can be sure that 5 is the determining factor(since n//5 is going to yield a smaller number always)\n- We know that n//5 is an increasing function\n- So We can do a binary search on n\n- THe upper bound on what we should look for should contain k number of zeros. so 5*(k) has atleast (k) 0s. Since 5*(k)//10 = k. For 0 case, we need to find number till 10. So 5*(k+1) is a good option\n\n# Code\n```python []\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def num_zeros(n):\n ret = 0\n fac = 5\n while fac <= n:\n ret += n//fac\n fac *= 5\n return ret\n dp = defaultdict(int)\n mini = 0\n maxi = 5*(k+1)\n #Find the smallest number that has k number of zeros\n lo = mini\n hi = maxi\n # minimum number for which there are k zeros \n min_num = -1\n # Maximum number for which there are k zeros\n max_num = -1\n\n while lo <= hi:\n mid = (lo+hi)//2\n #number of zeros\n nz = num_zeros(mid)\n if nz == k:\n min_num = mid\n hi = mid-1\n elif nz>k:\n hi = mid-1\n else:\n lo = mid+1\n if min_num == -1:\n return 0\n lo = mini\n hi = maxi\n while lo <= hi:\n mid = (lo+hi)//2\n #number of zeros\n nz = num_zeros(mid)\n if nz == k:\n max_num = mid\n lo = mid+1\n elif nz>k:\n hi = mid-1\n else:\n lo = mid+1\n # print(min_num, max_num)\n return max_num-min_num+1\n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Python Easy to Understand solution. Binary Search step by step explanation | preimage-size-of-factorial-zeroes-function | 0 | 1 | - Number of zeroes for a given number n = min(n//5, n//2)+n//10\n- n//2 gives the number of 2 factors and n//5 gives the number of 5 factors. \n- n//5 isn\'t accurance. Taking 1.2.3......125, we get 5,10,15,...125 and 25, 50, 75, 100, 125 and 125\n- The total isn\'t n//5. It is n//5 + n//25 + n//125\n- We also don\'t need n/10, It is taken care by n//5....\n- 2*5 makes a 10, so the number of 2s or 5s whichever are lesser determine the number of 0s\n- But we can be sure that 5 is the determining factor(since n//5 is going to yield a smaller number always)\n- We know that n//5 is an increasing function\n- So We can do a binary search on n\n- THe upper bound on what we should look for should contain k number of zeros. so 5*(k) has atleast (k) 0s. Since 5*(k)//10 = k. For 0 case, we need to find number till 10. So 5*(k+1) is a good option\n\n# Code\n```python []\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def num_zeros(n):\n ret = 0\n fac = 5\n while fac <= n:\n ret += n//fac\n fac *= 5\n return ret\n dp = defaultdict(int)\n mini = 0\n maxi = 5*(k+1)\n #Find the smallest number that has k number of zeros\n lo = mini\n hi = maxi\n # minimum number for which there are k zeros \n min_num = -1\n # Maximum number for which there are k zeros\n max_num = -1\n\n while lo <= hi:\n mid = (lo+hi)//2\n #number of zeros\n nz = num_zeros(mid)\n if nz == k:\n min_num = mid\n hi = mid-1\n elif nz>k:\n hi = mid-1\n else:\n lo = mid+1\n if min_num == -1:\n return 0\n lo = mini\n hi = maxi\n while lo <= hi:\n mid = (lo+hi)//2\n #number of zeros\n nz = num_zeros(mid)\n if nz == k:\n max_num = mid\n lo = mid+1\n elif nz>k:\n hi = mid-1\n else:\n lo = mid+1\n # print(min_num, max_num)\n return max_num-min_num+1\n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python O(log(n)^2) - Binary Search using problem 172 | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Note: it might be helpful to complete https://leetcode.com/problems/factorial-trailing-zeroes/description/ beforehand to get a nice helper function\n- To recap\n - The number of 0\'s following a factorial come from the number of 2\'s and 5\'s in its prime factorization\n - Because there are always more 2\'s than 5\'s in a factorial prime factorization, the number of 0\'s in a factorial is equal to the number of 5\'s in its prime factorization\n - Note that 5\'s contribute one 0, 25\'s contribute two, 125\'s contribute three, etc.\n- Given a function that returns the number of 0\'s in a factorial, we can check whether the number of 0\'s trailing a factorial is valid by using binary search\n - Set l = 0\n - Set r to a factorial that will surely generate more than k zeros, e.g. 10k (factorials gain a zero slightly more often than every 5 numbers, so 10 should suffice)\n - Search until we can confirm/rule out the desired number of 0\'s\n - For each amount of trailing 0\'s, there are five factorials that have that amount of trailing 0\'s\n\n# Complexity\n- Time complexity: $O(log_5(n)log_2(n)) = O(kln(n)ln(n)) = O(ln(n)^2)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def zeros(self, n: int) -> int:\n total = 0\n base = 5\n while base <= n:\n total += n // base\n base *= 5\n return total\n\n def preimageSizeFZF(self, k: int) -> int:\n if k == 0: return 5\n l = 0\n r = k*10\n while l < r:\n mid = (l + r)//2\n if self.zeros(mid) == k:\n return 5\n elif self.zeros(mid) < k:\n l = mid + 1\n elif self.zeros(mid) > k:\n r = mid - 1\n\n return 0\n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Python O(log(n)^2) - Binary Search using problem 172 | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Note: it might be helpful to complete https://leetcode.com/problems/factorial-trailing-zeroes/description/ beforehand to get a nice helper function\n- To recap\n - The number of 0\'s following a factorial come from the number of 2\'s and 5\'s in its prime factorization\n - Because there are always more 2\'s than 5\'s in a factorial prime factorization, the number of 0\'s in a factorial is equal to the number of 5\'s in its prime factorization\n - Note that 5\'s contribute one 0, 25\'s contribute two, 125\'s contribute three, etc.\n- Given a function that returns the number of 0\'s in a factorial, we can check whether the number of 0\'s trailing a factorial is valid by using binary search\n - Set l = 0\n - Set r to a factorial that will surely generate more than k zeros, e.g. 10k (factorials gain a zero slightly more often than every 5 numbers, so 10 should suffice)\n - Search until we can confirm/rule out the desired number of 0\'s\n - For each amount of trailing 0\'s, there are five factorials that have that amount of trailing 0\'s\n\n# Complexity\n- Time complexity: $O(log_5(n)log_2(n)) = O(kln(n)ln(n)) = O(ln(n)^2)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def zeros(self, n: int) -> int:\n total = 0\n base = 5\n while base <= n:\n total += n // base\n base *= 5\n return total\n\n def preimageSizeFZF(self, k: int) -> int:\n if k == 0: return 5\n l = 0\n r = k*10\n while l < r:\n mid = (l + r)//2\n if self.zeros(mid) == k:\n return 5\n elif self.zeros(mid) < k:\n l = mid + 1\n elif self.zeros(mid) > k:\n r = mid - 1\n\n return 0\n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Solution using Binary search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\nIt is easy to calcuate f(x) given an integer x. The problem changes to find the left bound and the right bound of $f(x) = k$ which could be solved by binary search. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ $$n = $$ range of unsigned long\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def f(x):\n ans = 0\n divider = 5\n while divider<=x:\n ans = ans+ x//divider\n divider = divider*5\n return ans\n \n def left_bound(k):\n left = 0\n right = int(5e9)+1\n while left<right:\n mid = left+(right-left)//2\n if f(mid)<k:\n left = mid+1\n else:\n right = mid\n return left\n \n def right_bound(k):\n left = 0\n right = int(5e9)+1\n while left<right:\n mid = left+(right-left)//2\n if f(mid)<=k:\n left = mid+1\n else:\n right = mid\n\n return left\n return right_bound(k)-left_bound(k)\n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Solution using Binary search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\nIt is easy to calcuate f(x) given an integer x. The problem changes to find the left bound and the right bound of $f(x) = k$ which could be solved by binary search. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ $$n = $$ range of unsigned long\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def f(x):\n ans = 0\n divider = 5\n while divider<=x:\n ans = ans+ x//divider\n divider = divider*5\n return ans\n \n def left_bound(k):\n left = 0\n right = int(5e9)+1\n while left<right:\n mid = left+(right-left)//2\n if f(mid)<k:\n left = mid+1\n else:\n right = mid\n return left\n \n def right_bound(k):\n left = 0\n right = int(5e9)+1\n while left<right:\n mid = left+(right-left)//2\n if f(mid)<=k:\n left = mid+1\n else:\n right = mid\n\n return left\n return right_bound(k)-left_bound(k)\n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Modular and Extensible Python Solution - Beats 90% | valid-tic-tac-toe-state | 0 | 1 | O(1) time complexity, O(1) space complesity\n\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n n = 3\n rows = [0] * n\n cols = [0] * n\n diag = antidiag = balance = 0\n \n def win(v):\n if v in rows or v in cols or v in [diag, antidiag]: return True\n return False\n \n for i in range(n):\n for j in range(n):\n if board[i][j] != " ":\n balance += 1 if board[i][j] == "X" else -1\n rows[i] += 1 if board[i][j] == "X" else -1\n cols[j] += 1 if board[i][j] == "X" else -1\n if i == j: diag += 1 if board[i][j] == "X" else -1\n if i + j == n - 1: antidiag += 1 if board[i][j] == "X" else -1\n \n if not 0 <= balance <= 1: return False\n \n if balance == 0 and win(n): return False\n if balance == 1 and win(-n): return False\n \n return True | 4 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Modular and Extensible Python Solution - Beats 90% | valid-tic-tac-toe-state | 0 | 1 | O(1) time complexity, O(1) space complesity\n\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n n = 3\n rows = [0] * n\n cols = [0] * n\n diag = antidiag = balance = 0\n \n def win(v):\n if v in rows or v in cols or v in [diag, antidiag]: return True\n return False\n \n for i in range(n):\n for j in range(n):\n if board[i][j] != " ":\n balance += 1 if board[i][j] == "X" else -1\n rows[i] += 1 if board[i][j] == "X" else -1\n cols[j] += 1 if board[i][j] == "X" else -1\n if i == j: diag += 1 if board[i][j] == "X" else -1\n if i + j == n - 1: antidiag += 1 if board[i][j] == "X" else -1\n \n if not 0 <= balance <= 1: return False\n \n if balance == 0 and win(n): return False\n if balance == 1 and win(-n): return False\n \n return True | 4 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Solution | valid-tic-tac-toe-state | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool validTicTacToe(vector<string>& board) \n {\n int turn = 0, diag = 0, adg = 0, i, j;\n bool xwin = false, owin = false;\n vector<int> row(3), col(3);\n for(i = 0; i < 3; i ++)\n {\n for(j = 0; j < 3; j ++)\n {\n if(\'X\' == board[i][j])\n {\n turn ++;\n row[i] ++;\n col[j] ++;\n \n if(i == j)\n {\n diag ++;\n }\n if(i + j == 2)\n {\n adg ++;\n }\n }\n else if(\'O\' == board[i][j])\n {\n turn --;\n row[i] --;\n col[j] --;\n \n if(i == j)\n {\n diag --;\n }\n if(i + j == 2)\n {\n adg --;\n }\n }\n }\n }\n for(i = 0; i < 3; i ++)\n {\n if(3 == row[i] || 3 == col[i])\n {\n xwin = true;\n }\n if(-3 == row[i] || -3 == col[i])\n {\n owin = true;\n }\n }\n if(3 == diag || 3 == adg)\n {\n xwin = true;\n }\n if(-3 == diag || -3 == adg)\n {\n owin = true;\n }\n if(xwin && owin)\n {\n return false;\n }\n if(turn != 0 && turn != 1)\n {\n return false;\n }\n if((xwin && turn != 1) || (owin && turn != 0))\n {\n return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n rows, cols, diag1, diag2 = [0]*3, [0]*3, 0, 0 \n o, x = 0, 0\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == "O":\n o+=1\n rows[i]+=1\n cols[j]+=1\n if i == j:\n diag1+=1\n if i+j == 2:\n diag2+=1\n if board[i][j] == "X":\n x+=1\n rows[i]-=1\n cols[j]-=1\n if i == j:\n diag1-=1\n if i+j == 2:\n diag2-=1\n \n player1 = 3 in rows or 3 in cols or diag1 == 3 or diag2 == 3\n player2 = -3 in rows or -3 in cols or diag1 == -3 or diag2 == -3\n \n if o != x and x-o != 1: return False\n if player1 and player2: return False\n if player1: return o == x\n if player2: return x-o == 1\n\n return True\n```\n\n```Java []\nclass Solution {\n public boolean validTicTacToe(String[] board) {\n if (board == null || board.length == 0) {\n return false;\n }\n\n int n = board.length;\n int diag1 = 0;\n int diag2 = 0;\n int turnsDiff = 0;\n boolean xWin = false;\n boolean oWin = false;\n char c;\n\n for (int i = 0; i < n; i++) {\n int row = 0;\n int col = 0;\n for (int j = 0; j < n; j++) {\n c = board[i].charAt(j);\n if (c == \'X\') {\n row++;\n turnsDiff++;\n } else if (c == \'O\') {\n row--;\n turnsDiff--;\n }\n c = board[j].charAt(i);\n if (c == \'X\') {\n col++;\n } else if (c == \'O\') {\n col--;\n }\n }\n c = board[i].charAt(i);\n if (c == \'X\') {\n diag1++;\n } else if (c == \'O\') {\n diag1--;\n }\n c = board[i].charAt(n - 1 - i);\n if (c == \'X\') {\n diag2++;\n } else if (c == \'O\') {\n diag2--;\n }\n if (row == n || col == n || diag1 == n || diag2 == n) {\n if (oWin) {\n return false;\n }\n xWin = true;\n }\n if (row == -n || col == -n || diag1 == -n || diag2 == -n) {\n if (xWin) {\n return false;\n }\n oWin = true;\n }\n }\n if (turnsDiff < 0 || turnsDiff > 1) {\n return false;\n }\n if ((turnsDiff == 0 && xWin) || (turnsDiff == 1 && oWin)) {\n return false;\n }\n return true;\n }\n}\n```\n | 2 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Solution | valid-tic-tac-toe-state | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool validTicTacToe(vector<string>& board) \n {\n int turn = 0, diag = 0, adg = 0, i, j;\n bool xwin = false, owin = false;\n vector<int> row(3), col(3);\n for(i = 0; i < 3; i ++)\n {\n for(j = 0; j < 3; j ++)\n {\n if(\'X\' == board[i][j])\n {\n turn ++;\n row[i] ++;\n col[j] ++;\n \n if(i == j)\n {\n diag ++;\n }\n if(i + j == 2)\n {\n adg ++;\n }\n }\n else if(\'O\' == board[i][j])\n {\n turn --;\n row[i] --;\n col[j] --;\n \n if(i == j)\n {\n diag --;\n }\n if(i + j == 2)\n {\n adg --;\n }\n }\n }\n }\n for(i = 0; i < 3; i ++)\n {\n if(3 == row[i] || 3 == col[i])\n {\n xwin = true;\n }\n if(-3 == row[i] || -3 == col[i])\n {\n owin = true;\n }\n }\n if(3 == diag || 3 == adg)\n {\n xwin = true;\n }\n if(-3 == diag || -3 == adg)\n {\n owin = true;\n }\n if(xwin && owin)\n {\n return false;\n }\n if(turn != 0 && turn != 1)\n {\n return false;\n }\n if((xwin && turn != 1) || (owin && turn != 0))\n {\n return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n rows, cols, diag1, diag2 = [0]*3, [0]*3, 0, 0 \n o, x = 0, 0\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == "O":\n o+=1\n rows[i]+=1\n cols[j]+=1\n if i == j:\n diag1+=1\n if i+j == 2:\n diag2+=1\n if board[i][j] == "X":\n x+=1\n rows[i]-=1\n cols[j]-=1\n if i == j:\n diag1-=1\n if i+j == 2:\n diag2-=1\n \n player1 = 3 in rows or 3 in cols or diag1 == 3 or diag2 == 3\n player2 = -3 in rows or -3 in cols or diag1 == -3 or diag2 == -3\n \n if o != x and x-o != 1: return False\n if player1 and player2: return False\n if player1: return o == x\n if player2: return x-o == 1\n\n return True\n```\n\n```Java []\nclass Solution {\n public boolean validTicTacToe(String[] board) {\n if (board == null || board.length == 0) {\n return false;\n }\n\n int n = board.length;\n int diag1 = 0;\n int diag2 = 0;\n int turnsDiff = 0;\n boolean xWin = false;\n boolean oWin = false;\n char c;\n\n for (int i = 0; i < n; i++) {\n int row = 0;\n int col = 0;\n for (int j = 0; j < n; j++) {\n c = board[i].charAt(j);\n if (c == \'X\') {\n row++;\n turnsDiff++;\n } else if (c == \'O\') {\n row--;\n turnsDiff--;\n }\n c = board[j].charAt(i);\n if (c == \'X\') {\n col++;\n } else if (c == \'O\') {\n col--;\n }\n }\n c = board[i].charAt(i);\n if (c == \'X\') {\n diag1++;\n } else if (c == \'O\') {\n diag1--;\n }\n c = board[i].charAt(n - 1 - i);\n if (c == \'X\') {\n diag2++;\n } else if (c == \'O\') {\n diag2--;\n }\n if (row == n || col == n || diag1 == n || diag2 == n) {\n if (oWin) {\n return false;\n }\n xWin = true;\n }\n if (row == -n || col == -n || diag1 == -n || diag2 == -n) {\n if (xWin) {\n return false;\n }\n oWin = true;\n }\n }\n if (turnsDiff < 0 || turnsDiff > 1) {\n return false;\n }\n if ((turnsDiff == 0 && xWin) || (turnsDiff == 1 && oWin)) {\n return false;\n }\n return true;\n }\n}\n```\n | 2 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Python3 || int array, 7 lines, w/ explanation || T/M: 98%/ 49% | valid-tic-tac-toe-state | 0 | 1 | ```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n # The two criteria for a valid board are:\n # 1) num of Xs - num of Os is 0 or 1\n # 2) X is not a winner if the # of moves is even, and\n # O is not a winner if the # of moves is odd.\n\n d = {\'X\': 1, \'O\': -1, \' \': 0} # transform the 1x3 str array to a 1x9 int array\n s = [d[ch] for ch in \'\'.join(board)] # Ex: ["XOX"," X "," "] --> [1,-1,1,0,1,0,0,0,0]\n sm = sum(s)\n\n if sm>>1: return False # <-- criterion 1\n \n n = -3 if sm == 1 else 3 # <-- criterion 2.\n if n in {s[0]+s[1]+s[2], s[3]+s[4]+s[5], s[6]+s[7]+s[8], \n s[0]+s[3]+s[6], s[1]+s[4]+s[7], s[2]+s[5]+s[8], # the elements of the set are \n s[0]+s[4]+s[8], s[2]+s[4]+s[6]}: return False # the rows, cols, and diags\n \n return True # <-- both criteria are true | 7 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Python3 || int array, 7 lines, w/ explanation || T/M: 98%/ 49% | valid-tic-tac-toe-state | 0 | 1 | ```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n # The two criteria for a valid board are:\n # 1) num of Xs - num of Os is 0 or 1\n # 2) X is not a winner if the # of moves is even, and\n # O is not a winner if the # of moves is odd.\n\n d = {\'X\': 1, \'O\': -1, \' \': 0} # transform the 1x3 str array to a 1x9 int array\n s = [d[ch] for ch in \'\'.join(board)] # Ex: ["XOX"," X "," "] --> [1,-1,1,0,1,0,0,0,0]\n sm = sum(s)\n\n if sm>>1: return False # <-- criterion 1\n \n n = -3 if sm == 1 else 3 # <-- criterion 2.\n if n in {s[0]+s[1]+s[2], s[3]+s[4]+s[5], s[6]+s[7]+s[8], \n s[0]+s[3]+s[6], s[1]+s[4]+s[7], s[2]+s[5]+s[8], # the elements of the set are \n s[0]+s[4]+s[8], s[2]+s[4]+s[6]}: return False # the rows, cols, and diags\n \n return True # <-- both criteria are true | 7 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
concise code beat 100% python solution with explanation | valid-tic-tac-toe-state | 0 | 1 | There is only four situation that Tic-Tac-Toe is invalid:\n1. two players are not taking turns making move\n2. "O" player makes move before "X" player\n3. "X" player wins but "O" player continues to make move\n4. "O" player wins but "X" player continues to make move\n\n```\nclass Solution(object):\n def validTicTacToe(self, board):\n def win(s): # return True if the player who use s wins\n if board[0][0]==s and board[0][1]==s and board[0][2]==s: return True\n if board[1][0]==s and board[1][1]==s and board[1][2]==s: return True\n if board[2][0]==s and board[2][1]==s and board[2][2]==s: return True\n if board[0][0]==s and board[1][0]==s and board[2][0]==s: return True\n if board[0][1]==s and board[1][1]==s and board[2][1]==s: return True\n if board[0][2]==s and board[1][2]==s and board[2][2]==s: return True\n if board[0][0]==s and board[1][1]==s and board[2][2]==s: return True\n if board[0][2]==s and board[1][1]==s and board[2][0]==s: return True\n return False\n \n xNo, oNo=0, 0\n for row in board:\n xNo+=row.count(\'X\')\n oNo+=row.count(\'O\')\n if oNo>xNo or xNo-oNo>=2: # "X" not making move first or not taking turns making move\n return False\n if xNo>=3:\n if xNo==oNo and win(\'X\'): # put another "O" after "X" player winning\n return False\n if xNo!=oNo and win(\'O\'): # put another "X" after "O" player winning\n return False\n return True\n```\n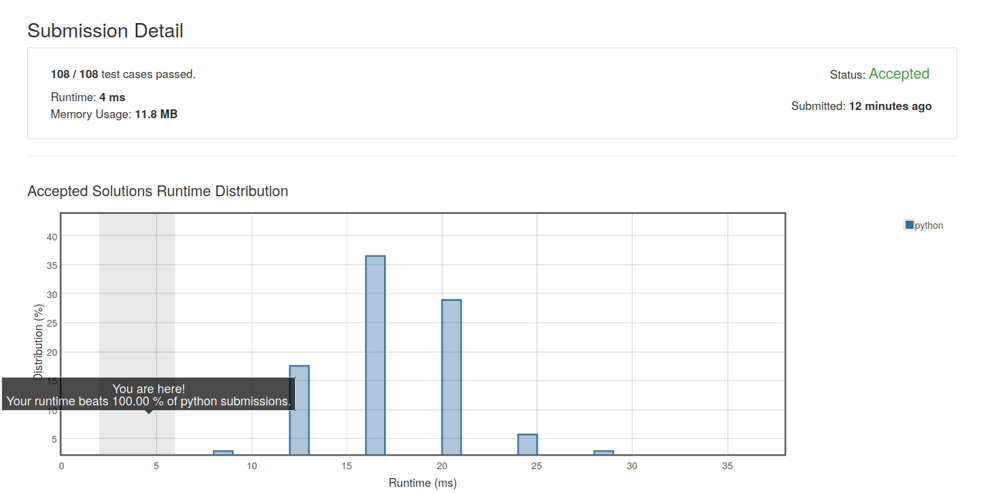\n | 12 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
concise code beat 100% python solution with explanation | valid-tic-tac-toe-state | 0 | 1 | There is only four situation that Tic-Tac-Toe is invalid:\n1. two players are not taking turns making move\n2. "O" player makes move before "X" player\n3. "X" player wins but "O" player continues to make move\n4. "O" player wins but "X" player continues to make move\n\n```\nclass Solution(object):\n def validTicTacToe(self, board):\n def win(s): # return True if the player who use s wins\n if board[0][0]==s and board[0][1]==s and board[0][2]==s: return True\n if board[1][0]==s and board[1][1]==s and board[1][2]==s: return True\n if board[2][0]==s and board[2][1]==s and board[2][2]==s: return True\n if board[0][0]==s and board[1][0]==s and board[2][0]==s: return True\n if board[0][1]==s and board[1][1]==s and board[2][1]==s: return True\n if board[0][2]==s and board[1][2]==s and board[2][2]==s: return True\n if board[0][0]==s and board[1][1]==s and board[2][2]==s: return True\n if board[0][2]==s and board[1][1]==s and board[2][0]==s: return True\n return False\n \n xNo, oNo=0, 0\n for row in board:\n xNo+=row.count(\'X\')\n oNo+=row.count(\'O\')\n if oNo>xNo or xNo-oNo>=2: # "X" not making move first or not taking turns making move\n return False\n if xNo>=3:\n if xNo==oNo and win(\'X\'): # put another "O" after "X" player winning\n return False\n if xNo!=oNo and win(\'O\'): # put another "X" after "O" player winning\n return False\n return True\n```\n\n | 12 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Python | Straightforward Solution | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\njust validate against the rules\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n n = len(board)\n cntx = cnto = 0\n rows = [0] * n\n cols = [0] * n\n diagonals = [0] * 2\n for i in range(n):\n for j in range(n):\n ch = board[i][j]\n score = 0\n if ch == \'X\':\n cntx += 1\n score = 1\n elif ch == \'O\':\n cnto += 1\n score = -1\n\n rows[i] += score\n cols[j] += score\n if i == j:\n diagonals[0] += score\n if i + j == n - 1:\n diagonals[1] += score\n \n def winning(k):\n return any([r == k for r in rows]) or \\\n any([c == k for c in cols]) or \\\n any([d == k for d in diagonals])\n\n winning_x = winning(n)\n winning_o = winning(-n)\n\n if winning_x and winning_o:\n return False\n elif winning_x:\n return cntx - cnto == 1\n elif winning_o:\n return cntx == cnto\n else:\n return 0 <= cntx - cnto <= 1\n\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Python | Straightforward Solution | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\njust validate against the rules\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n n = len(board)\n cntx = cnto = 0\n rows = [0] * n\n cols = [0] * n\n diagonals = [0] * 2\n for i in range(n):\n for j in range(n):\n ch = board[i][j]\n score = 0\n if ch == \'X\':\n cntx += 1\n score = 1\n elif ch == \'O\':\n cnto += 1\n score = -1\n\n rows[i] += score\n cols[j] += score\n if i == j:\n diagonals[0] += score\n if i + j == n - 1:\n diagonals[1] += score\n \n def winning(k):\n return any([r == k for r in rows]) or \\\n any([c == k for c in cols]) or \\\n any([d == k for d in diagonals])\n\n winning_x = winning(n)\n winning_o = winning(-n)\n\n if winning_x and winning_o:\n return False\n elif winning_x:\n return cntx - cnto == 1\n elif winning_o:\n return cntx == cnto\n else:\n return 0 <= cntx - cnto <= 1\n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Python3 | Easy To Understand | valid-tic-tac-toe-state | 0 | 1 | # Code\n```\nclass Solution:\n\n def win_check(self, arr, char):\n matches = [[0, 1, 2], [3, 4, 5],\n [6, 7, 8], [0, 3, 6],\n [1, 4, 7], [2, 5, 8],\n [0, 4, 8], [2, 4, 6]]\n \n for i in range(8):\n if(arr[int((matches[i][0])/3)][(matches[i][0])%3] == char and\n arr[int((matches[i][1])/3)][(matches[i][1])%3] == char and\n arr[int((matches[i][2])/3)][(matches[i][2])%3] == char):\n return True\n return False\n\n def validTicTacToe(self, board: List[str]) -> bool:\n if not board:\n return False\n\n countX = board[0].count(\'X\')\n countO = board[0].count(\'O\')\n countX += board[1].count(\'X\')\n countO += board[1].count(\'O\')\n countX += board[2].count(\'X\')\n countO += board[2].count(\'O\')\n\n if(countX != countO and countX != countO + 1):\n return False\n\n xWins = self.win_check(board, \'X\')\n oWins = self.win_check(board, \'O\')\n\n if(xWins and oWins or (xWins and countX != countO + 1) or (oWins and countX != countO)):\n return False\n\n return True\n\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Python3 | Easy To Understand | valid-tic-tac-toe-state | 0 | 1 | # Code\n```\nclass Solution:\n\n def win_check(self, arr, char):\n matches = [[0, 1, 2], [3, 4, 5],\n [6, 7, 8], [0, 3, 6],\n [1, 4, 7], [2, 5, 8],\n [0, 4, 8], [2, 4, 6]]\n \n for i in range(8):\n if(arr[int((matches[i][0])/3)][(matches[i][0])%3] == char and\n arr[int((matches[i][1])/3)][(matches[i][1])%3] == char and\n arr[int((matches[i][2])/3)][(matches[i][2])%3] == char):\n return True\n return False\n\n def validTicTacToe(self, board: List[str]) -> bool:\n if not board:\n return False\n\n countX = board[0].count(\'X\')\n countO = board[0].count(\'O\')\n countX += board[1].count(\'X\')\n countO += board[1].count(\'O\')\n countX += board[2].count(\'X\')\n countO += board[2].count(\'O\')\n\n if(countX != countO and countX != countO + 1):\n return False\n\n xWins = self.win_check(board, \'X\')\n oWins = self.win_check(board, \'O\')\n\n if(xWins and oWins or (xWins and countX != countO + 1) or (oWins and countX != countO)):\n return False\n\n return True\n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Beats 99% | valid-tic-tac-toe-state | 0 | 1 | # Approach\nFirst check who the winner(s) on the board are, then check if its possible to reach that state by counting the number of "X"s and "O"s on the board\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n def checkwinner(board):\n winners = \'\'\n\n # check rows:\n for row in board:\n if row == \'XXX\':\n winners += \'X\'\n if row == \'OOO\':\n winners += \'O\'\n\n # check columns:\n transposed = list(map(list, zip(*board)))\n for col in transposed:\n print(col)\n if col == [\'X\', \'X\', \'X\']:\n winners += \'X\'\n if col == [\'O\', \'O\', \'O\']:\n winners += \'O\'\n\n #check diagonals:\n diag1 = [board[0][0], board[1][1], board[2][2]]\n diag2 = [board[2][0], board[1][1], board[0][2]]\n if diag1 == [\'X\', \'X\', \'X\'] or diag2 == [\'X\', \'X\', \'X\']:\n winners += \'X\'\n elif diag1 == [\'O\', \'O\', \'O\'] or diag2 == [\'O\', \'O\', \'O\']:\n winners += \'O\'\n\n return winners\n \n winner = checkwinner(board)\n print(\'winner:\',winner)\n flattened = \'\'.join(row for row in board)\n if len(winner) > 1:\n if winner == \'XX\':\n return (flattened.count(\'O\') == flattened.count(\'X\') - 1)\n else:\n return False\n if winner == \'O\':\n return flattened.count(\'X\') == flattened.count(\'O\')\n elif winner == \'X\':\n return flattened.count(\'O\') == flattened.count(\'X\') - 1\n else:\n return (flattened.count(\'O\') == flattened.count(\'X\') - 1) or (flattened.count(\'X\') == flattened.count(\'O\'))\n\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Beats 99% | valid-tic-tac-toe-state | 0 | 1 | # Approach\nFirst check who the winner(s) on the board are, then check if its possible to reach that state by counting the number of "X"s and "O"s on the board\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n def checkwinner(board):\n winners = \'\'\n\n # check rows:\n for row in board:\n if row == \'XXX\':\n winners += \'X\'\n if row == \'OOO\':\n winners += \'O\'\n\n # check columns:\n transposed = list(map(list, zip(*board)))\n for col in transposed:\n print(col)\n if col == [\'X\', \'X\', \'X\']:\n winners += \'X\'\n if col == [\'O\', \'O\', \'O\']:\n winners += \'O\'\n\n #check diagonals:\n diag1 = [board[0][0], board[1][1], board[2][2]]\n diag2 = [board[2][0], board[1][1], board[0][2]]\n if diag1 == [\'X\', \'X\', \'X\'] or diag2 == [\'X\', \'X\', \'X\']:\n winners += \'X\'\n elif diag1 == [\'O\', \'O\', \'O\'] or diag2 == [\'O\', \'O\', \'O\']:\n winners += \'O\'\n\n return winners\n \n winner = checkwinner(board)\n print(\'winner:\',winner)\n flattened = \'\'.join(row for row in board)\n if len(winner) > 1:\n if winner == \'XX\':\n return (flattened.count(\'O\') == flattened.count(\'X\') - 1)\n else:\n return False\n if winner == \'O\':\n return flattened.count(\'X\') == flattened.count(\'O\')\n elif winner == \'X\':\n return flattened.count(\'O\') == flattened.count(\'X\') - 1\n else:\n return (flattened.count(\'O\') == flattened.count(\'X\') - 1) or (flattened.count(\'X\') == flattened.count(\'O\'))\n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
794: Beats 97.22%, Solution with step by step explanation | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nx_count = sum(row.count(\'X\') for row in board)\no_count = sum(row.count(\'O\') for row in board)\n```\n\nBefore proceeding with other checks, it\'s vital to understand that since \'X\' always starts the game, there should either be an equal number of \'X\'s and \'O\'s or at most one extra \'X\'.\n\n```\ndef win(player):\n for i in range(3):\n if all([cell == player for cell in board[i]]): return True\n if all([board[j][i] == player for j in range(3)]): return True\n if board[0][0] == board[1][1] == board[2][2] == player: return True\n if board[0][2] == board[1][1] == board[2][0] == player: return True\n return False\n```\n\nThese conditions ensure:\na. \'O\' count is never greater than \'X\', and \'X\' count is at most one greater than \'O\' count.\nb. If \'X\' has won, there must be one more \'X\' than \'O\'.\nc. If \'O\' has won, there must be an equal number of \'X\'s and \'O\'s.\n\n\nDetailed Explanation:\nCounting Characters:\nThe very first step is to count the characters since it helps in understanding the order of moves. As \'X\' always plays first, there cannot be more \'O\'s than \'X\'s on the board. And at most, there can be only one more \'X\' than \'O\'.\n\nChecking for Win:\nTo determine if a game is over and if a player has won, you need to check if any player has three of their characters in a row. This means checking each row, column, and the two diagonals to see if they contain the same character.\n\nFinal Validation:\nUsing the win conditions and character counts, you can conclude:\n\n\'X\' cannot win if there are an equal number of \'X\'s and \'O\'s since \'X\' always goes first.\n\'O\' cannot win if there are more \'X\'s than \'O\'s.\nThe board is invalid if there are more \'O\'s than \'X\'s or if there are more than one \'X\' compared to \'O\'.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n x_count = sum(row.count(\'X\') for row in board)\n o_count = sum(row.count(\'O\') for row in board)\n \n def win(player):\n for i in range(3):\n if all([cell == player for cell in board[i]]): return True\n if all([board[j][i] == player for j in range(3)]): return True\n if board[0][0] == board[1][1] == board[2][2] == player: return True\n if board[0][2] == board[1][1] == board[2][0] == player: return True\n return False\n \n if o_count > x_count or x_count > o_count + 1: return False\n if win(\'X\') and x_count <= o_count: return False\n if win(\'O\') and x_count != o_count: return False\n \n return True\n\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
794: Beats 97.22%, Solution with step by step explanation | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nx_count = sum(row.count(\'X\') for row in board)\no_count = sum(row.count(\'O\') for row in board)\n```\n\nBefore proceeding with other checks, it\'s vital to understand that since \'X\' always starts the game, there should either be an equal number of \'X\'s and \'O\'s or at most one extra \'X\'.\n\n```\ndef win(player):\n for i in range(3):\n if all([cell == player for cell in board[i]]): return True\n if all([board[j][i] == player for j in range(3)]): return True\n if board[0][0] == board[1][1] == board[2][2] == player: return True\n if board[0][2] == board[1][1] == board[2][0] == player: return True\n return False\n```\n\nThese conditions ensure:\na. \'O\' count is never greater than \'X\', and \'X\' count is at most one greater than \'O\' count.\nb. If \'X\' has won, there must be one more \'X\' than \'O\'.\nc. If \'O\' has won, there must be an equal number of \'X\'s and \'O\'s.\n\n\nDetailed Explanation:\nCounting Characters:\nThe very first step is to count the characters since it helps in understanding the order of moves. As \'X\' always plays first, there cannot be more \'O\'s than \'X\'s on the board. And at most, there can be only one more \'X\' than \'O\'.\n\nChecking for Win:\nTo determine if a game is over and if a player has won, you need to check if any player has three of their characters in a row. This means checking each row, column, and the two diagonals to see if they contain the same character.\n\nFinal Validation:\nUsing the win conditions and character counts, you can conclude:\n\n\'X\' cannot win if there are an equal number of \'X\'s and \'O\'s since \'X\' always goes first.\n\'O\' cannot win if there are more \'X\'s than \'O\'s.\nThe board is invalid if there are more \'O\'s than \'X\'s or if there are more than one \'X\' compared to \'O\'.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n x_count = sum(row.count(\'X\') for row in board)\n o_count = sum(row.count(\'O\') for row in board)\n \n def win(player):\n for i in range(3):\n if all([cell == player for cell in board[i]]): return True\n if all([board[j][i] == player for j in range(3)]): return True\n if board[0][0] == board[1][1] == board[2][2] == player: return True\n if board[0][2] == board[1][1] == board[2][0] == player: return True\n return False\n \n if o_count > x_count or x_count > o_count + 1: return False\n if win(\'X\') and x_count <= o_count: return False\n if win(\'O\') and x_count != o_count: return False\n \n return True\n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Python simplely list all case beats 94.33% | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nList all condition then we\'ll check it from item to item\n1.In any case, the count of O will be either count of X or count of X-1\n2.If X win, the count of O must equal the count of X -1\n3.If O win, the count of O must equal the count of X\n4.Can\'t form more than one lines without cross \n(that mean there won\'t have more than once horizontal line/Vertical line )\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n id={\'X\':0,\'O\':1}\n cnts=[0,0]\n serial=[0,0]\n \n for row in board:\n for c in row:\n serial[0]<<=1\n serial[1]<<=1\n if c==\' \':\n continue\n cnts[id[c]]+=1\n serial[id[c]]+=1\n if cnts[0]!=cnts[1] and cnts[0]!=cnts[1]+1:\n return False\n \n lines=[[0b111000000,0b000111000,0b000000111],[0b100100100,0b010010010,0b001001001],[0b100010001,0b001010100]]\n checkLines=[]\n for serial in serial:\n checkLines.append([])\n for types in lines:\n checkLines[-1].append(0)\n for line in types:\n if serial&line==line:\n checkLines[-1][-1]+=1\n if checkLines[0][0]+checkLines[1][0]>1:\n return False\n if checkLines[0][1]+checkLines[1][1]>1:\n return False\n if checkLines[0][0]+checkLines[0][1]+checkLines[0][2]>0 and cnts[0]==cnts[1]:\n return False\n if checkLines[1][0]+checkLines[1][1]+checkLines[1][2]>0 and cnts[0]==cnts[1]+1:\n return False\n return True\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
Python simplely list all case beats 94.33% | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nList all condition then we\'ll check it from item to item\n1.In any case, the count of O will be either count of X or count of X-1\n2.If X win, the count of O must equal the count of X -1\n3.If O win, the count of O must equal the count of X\n4.Can\'t form more than one lines without cross \n(that mean there won\'t have more than once horizontal line/Vertical line )\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n id={\'X\':0,\'O\':1}\n cnts=[0,0]\n serial=[0,0]\n \n for row in board:\n for c in row:\n serial[0]<<=1\n serial[1]<<=1\n if c==\' \':\n continue\n cnts[id[c]]+=1\n serial[id[c]]+=1\n if cnts[0]!=cnts[1] and cnts[0]!=cnts[1]+1:\n return False\n \n lines=[[0b111000000,0b000111000,0b000000111],[0b100100100,0b010010010,0b001001001],[0b100010001,0b001010100]]\n checkLines=[]\n for serial in serial:\n checkLines.append([])\n for types in lines:\n checkLines[-1].append(0)\n for line in types:\n if serial&line==line:\n checkLines[-1][-1]+=1\n if checkLines[0][0]+checkLines[1][0]>1:\n return False\n if checkLines[0][1]+checkLines[1][1]>1:\n return False\n if checkLines[0][0]+checkLines[0][1]+checkLines[0][2]>0 and cnts[0]==cnts[1]:\n return False\n if checkLines[1][0]+checkLines[1][1]+checkLines[1][2]>0 and cnts[0]==cnts[1]+1:\n return False\n return True\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
[Python3] Good enough | valid-tic-tac-toe-state | 0 | 1 | ``` Python3 []\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n xs = \'\'.join(board).count(\'X\')\n os = \'\'.join(board).count(\'O\')\n if xs-os not in (0,1):\n return False\n \n seen = {}\n\n if \'\'.join(board[0]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[0])] = seen.get(\'\'.join(board[0]),0)+1\n if \'\'.join(board[1]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[1])] = seen.get(\'\'.join(board[1]),0)+1\n if \'\'.join(board[2]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[2])] = seen.get(\'\'.join(board[2]),0)+1\n\n col = \'\'.join([board[0][0],board[1][0],board[2][0]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n col = \'\'.join([board[0][1],board[1][1],board[2][1]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n col = \'\'.join([board[0][2],board[1][2],board[2][2]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n\n diag = \'\'.join([board[0][0],board[1][1],board[2][2]])\n if diag in (\'XXX\',\'OOO\'): seen[diag] = seen.get(diag,0)+1\n diag = \'\'.join([board[0][2],board[1][1],board[2][0]])\n if diag in (\'XXX\',\'OOO\'): seen[diag] = seen.get(diag,0)+1\n\n return not seen or (len(seen)==1 and list(seen.values())[0]<=2 and xs-(1 if \'XXX\' in seen else 0)==os)\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
[Python3] Good enough | valid-tic-tac-toe-state | 0 | 1 | ``` Python3 []\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool:\n xs = \'\'.join(board).count(\'X\')\n os = \'\'.join(board).count(\'O\')\n if xs-os not in (0,1):\n return False\n \n seen = {}\n\n if \'\'.join(board[0]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[0])] = seen.get(\'\'.join(board[0]),0)+1\n if \'\'.join(board[1]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[1])] = seen.get(\'\'.join(board[1]),0)+1\n if \'\'.join(board[2]) in (\'XXX\',\'OOO\'): seen[\'\'.join(board[2])] = seen.get(\'\'.join(board[2]),0)+1\n\n col = \'\'.join([board[0][0],board[1][0],board[2][0]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n col = \'\'.join([board[0][1],board[1][1],board[2][1]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n col = \'\'.join([board[0][2],board[1][2],board[2][2]])\n if col in (\'XXX\',\'OOO\'): seen[col] = seen.get(col,0)+1\n\n diag = \'\'.join([board[0][0],board[1][1],board[2][2]])\n if diag in (\'XXX\',\'OOO\'): seen[diag] = seen.get(diag,0)+1\n diag = \'\'.join([board[0][2],board[1][1],board[2][0]])\n if diag in (\'XXX\',\'OOO\'): seen[diag] = seen.get(diag,0)+1\n\n return not seen or (len(seen)==1 and list(seen.values())[0]<=2 and xs-(1 if \'XXX\' in seen else 0)==os)\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
TicTacToe Lab Intro | Commented and Explained | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is serving as a lab walkthrough for my intro to python class. If just reviewing for your own purposes, you can skip to the approach. \n\nIn computer science we are concerned most often with presenting something of value to a user, whether that be a graphical user interface, up to the second calculation, or a description of some status or reading. One of the key ideas for this is that of the model view and controller. This allows computer scientists to split the work of interfacing with a user into three separate but minimally connected components. \n\nWhy minimally connected? The reason is quite simple with an analogy. Consider a basic automobile. If I want to drive my automobile, it\'s probably a good idea to make sure that the engine is able to start. Let\'s call that a minimal connection.\n\nMinimal Connection Example : if try to drive car, car must be able to start\n\nOn the other hand, if I want to drive my car, it doesn\'t ACTUALLY matter if I can\'t use the radio (though it is nice!). Let\'s call this a non-minimal connection. \n\nNon-minimal connection example : if try to drive car, radio must work\n\nThe second one obviously has no real bearing or implication on the first, and can be seen as a non-minimal connection. \n\nAs we move into the design of classes and objects as more advanced forms of data structures, it is necessary to consider what our connections are between classes and whether or not they are minimally connected. \n\nWith that in mind, let\'s return to our game of tic tac toe. \nTo play tic tac toe in an interactive manner we want to \n- be able to see the board \n- be able to choose a move \n- be able to know when I have won or lost \n- be able to know when it\'s a tie \n\nTo keep things simple, we\'ll start by playing against ourselves or a friend. Later in the course we\'ll add a computer opponent, first for this, then checkers, then other games. \n\nTo be able to see the board, we need a way to view it. This is one of your first tasks is to implement a way to easily see all positions that are marked or can be marked. \n\nTask 1 : \n- part a : Make a board class object that can print out a boards current view using a to string like method for the object \n- part b : Make a view class object that takes in a board as an argument and can produce a print out of the board when requested \n\nOnce you can see the board and have a view object that can print out one, we need some interaction. \n\nTask 2 : \n- Add a choose move option to the board. Make it player proof so they cannot choose where someone already is, and cannot go out of bounds. How you do this is up to you, but a game that won\'t crash everytime I make a wrong move is probably one I\'ll play more! \n\nAlright, by now you have a board and can make valid moves! Now we need to know who the winner is and who the winner is not! Before we get there, we\'re going to move some functionality around though \n\nTask 3 : \n- Part a : Make a controller class. It\'ll take in a view and a model, and then pass over control to a play method inside of it. \n- Part b : Within the play class method of the controller, have the view object of the controller display the current screen. Then, have the controller receive from the view the succesful choice of move. \n- Part c : Have the controller send to the model object the value from the move in a method called update board, passing in the board, player, and row and col as well. \n\nWell, you likely have a number of red line errors at this point! To help you out, complete task 4, and it\'ll make a bit more sense. \n\nTask 4 : \n- Part a : Make a model class. It does not take in any arguments, but it has fields set up much of the code below. Feel free to take some of the ideas there, as they may prove useful. \n- Part b : Make a update board method, where you are passed a board, a row and col within the board, and a mark to make. \n- Part c : In your update board method, change the appropriate row and col within the board to the mark, then, check your board status. If there\'s a winner, you\'ll want to report out who won. If there\'s a tie, report that too. Otherwise, report that the game continues and update who\'s move it is. Return the updated board, status, and if there is someones turn, say whos turn it is. \n\nBack to the controller now! \n\nTask 5 : \n- Part a : Have the controller point where we send to the model object our value from the move method receive the appropriate values from the model. Then, have the controller send these to the view by having the view call display move result using the updated board, game status, and if there is another player a new player message. Store the result of this function call in controller next step. \n- Part b : Now that we have something coming back to the view, we can \n - print the updated board in the view \n - display game status \n - if the game is over \n - ask the player if they want to play again \n - if they do not want to play again, \n - print the game over message and send the instruction to quit back to the controller \n - otherwise, get the next move and send it back to the controller \n - this method can run inside the view \n\nTask 6 : \n- Final part! When the controller receives a value from the view next it is either : \n - a new move in the current game -> continue the game by going to top of game loop current \n - a new game -> start a new game by recalling the play game method with a wiped board. \n - a desire to end play -> set status to game over and quit the play method. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nTo determine if we are in a valid state, we should \n- check the size of the board (for class you will need to modify for your board\'s representation potentially!)\n- check the board status (have we made a valid number of moves for each? How can you guard against this for class without crashing the game?)\n- check if the game is over (currently only determines if game ended succesfully, you\'ll need to modify to find out WHO won WHEN and WHY)\n\nIf we are a correctly sized board, and we have a status that is valid, and we do not have a winner and are not in an invalid state of play, then, return True. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool :\n if not self.check_board_sizing(board) : \n return False \n elif not self.check_board_status(board) : \n return False \n else : \n return self.check_winner(board)\n \n def check_board_sizing(self, board) -> bool :\n if len(board) == 3 : \n for row in board : \n if len(row) != 3 : \n return False \n return True \n return False \n\n def check_board_status(self, board : List[str]) -> bool : \n self.counts = collections.defaultdict(int)\n for row in board : \n for cell in row : \n self.counts[cell] += 1 \n return (self.counts["O"] <= self.counts["X"]) and (self.counts["X"] - self.counts["O"] <= 1)\n\n def check_winner(self, board : List[str]) -> bool : \n # statuses by row for x and o \n x_statuses = [False, False, False, False]\n o_statuses = [False, False, False, False]\n # sums by row, sums by col, and diagonals up and down \n x_sums = [[0, 0, 0], [0, 0, 0], [0, 0]]\n o_sums = [[0, 0, 0], [0, 0, 0], [0, 0]]\n\n # get row sum for x\'s and o\'s and if 3 set status 0 for each \n for row_index, row in enumerate(board) : \n x_sums[0][row_index] = sum([int(r_i == "X") for r_i in row])\n o_sums[0][row_index] = sum([int(r_i == "O") for r_i in row])\n x_statuses[0] = True if x_sums[0][row_index] == 3 else x_statuses[0]\n o_statuses[0] = True if o_sums[0][row_index] == 3 else o_statuses[0]\n\n # col major order since we can\'t unpack strings in python \n # if sum of col is 3 update status at 1 otherwise remain same \n for col in range(3) : \n for row in range(3) : \n cell = board[row][col]\n x_sums[1][col] += cell == \'X\'\n o_sums[1][col] += cell == \'O\'\n x_statuses[1] = True if x_sums[1][col] == 3 else x_statuses[1]\n o_statuses[1] = True if o_sums[1][col] == 3 else o_statuses[1]\n \n # for board index in range 3 \n # 0 cell diag down 1 cell diag up \n for b_i in range(3) : \n x_sums[2][0] += board[b_i][0+b_i] == "X"\n x_sums[2][1] += board[b_i][2-b_i] == "X"\n o_sums[2][0] += board[b_i][0+b_i] == "O"\n o_sums[2][1] += board[b_i][2-b_i] == "O"\n x_statuses[2] = x_sums[2][0] == 3 \n x_statuses[3] = x_sums[2][1] == 3 \n o_statuses[2] = o_sums[2][0] == 3 \n o_statuses[3] = o_sums[2][1] == 3 \n\n # if we have an x win and do not have one more x than o, False \n # similarly, if we have an o win, and have any more or less moves, False \n if sum(x_statuses) > 0 and (self.counts["X"] - self.counts["O"] != 1) : \n return False \n elif sum(o_statuses) > 0 and (self.counts["X"] - self.counts["O"] != 0) : \n return False \n else : \n # in all other cases, valid win, but we don\'t know who! \n # assignment for class is to modify this and return who won in a separate function\n return True \n\n``` | 0 | Given a Tic-Tac-Toe board as a string array `board`, return `true` if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.
The board is a `3 x 3` array that consists of characters `' '`, `'X'`, and `'O'`. The `' '` character represents an empty square.
Here are the rules of Tic-Tac-Toe:
* Players take turns placing characters into empty squares `' '`.
* The first player always places `'X'` characters, while the second player always places `'O'` characters.
* `'X'` and `'O'` characters are always placed into empty squares, never filled ones.
* The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
* The game also ends if all squares are non-empty.
* No more moves can be played if the game is over.
**Example 1:**
**Input:** board = \[ "O ", " ", " "\]
**Output:** false
**Explanation:** The first player always plays "X ".
**Example 2:**
**Input:** board = \[ "XOX ", " X ", " "\]
**Output:** false
**Explanation:** Players take turns making moves.
**Example 3:**
**Input:** board = \[ "XOX ", "O O ", "XOX "\]
**Output:** true
**Constraints:**
* `board.length == 3`
* `board[i].length == 3`
* `board[i][j]` is either `'X'`, `'O'`, or `' '`. | Use either Dijkstra's, or binary search for the best time T for which you can reach the end if you only step on squares at most T. |
TicTacToe Lab Intro | Commented and Explained | valid-tic-tac-toe-state | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is serving as a lab walkthrough for my intro to python class. If just reviewing for your own purposes, you can skip to the approach. \n\nIn computer science we are concerned most often with presenting something of value to a user, whether that be a graphical user interface, up to the second calculation, or a description of some status or reading. One of the key ideas for this is that of the model view and controller. This allows computer scientists to split the work of interfacing with a user into three separate but minimally connected components. \n\nWhy minimally connected? The reason is quite simple with an analogy. Consider a basic automobile. If I want to drive my automobile, it\'s probably a good idea to make sure that the engine is able to start. Let\'s call that a minimal connection.\n\nMinimal Connection Example : if try to drive car, car must be able to start\n\nOn the other hand, if I want to drive my car, it doesn\'t ACTUALLY matter if I can\'t use the radio (though it is nice!). Let\'s call this a non-minimal connection. \n\nNon-minimal connection example : if try to drive car, radio must work\n\nThe second one obviously has no real bearing or implication on the first, and can be seen as a non-minimal connection. \n\nAs we move into the design of classes and objects as more advanced forms of data structures, it is necessary to consider what our connections are between classes and whether or not they are minimally connected. \n\nWith that in mind, let\'s return to our game of tic tac toe. \nTo play tic tac toe in an interactive manner we want to \n- be able to see the board \n- be able to choose a move \n- be able to know when I have won or lost \n- be able to know when it\'s a tie \n\nTo keep things simple, we\'ll start by playing against ourselves or a friend. Later in the course we\'ll add a computer opponent, first for this, then checkers, then other games. \n\nTo be able to see the board, we need a way to view it. This is one of your first tasks is to implement a way to easily see all positions that are marked or can be marked. \n\nTask 1 : \n- part a : Make a board class object that can print out a boards current view using a to string like method for the object \n- part b : Make a view class object that takes in a board as an argument and can produce a print out of the board when requested \n\nOnce you can see the board and have a view object that can print out one, we need some interaction. \n\nTask 2 : \n- Add a choose move option to the board. Make it player proof so they cannot choose where someone already is, and cannot go out of bounds. How you do this is up to you, but a game that won\'t crash everytime I make a wrong move is probably one I\'ll play more! \n\nAlright, by now you have a board and can make valid moves! Now we need to know who the winner is and who the winner is not! Before we get there, we\'re going to move some functionality around though \n\nTask 3 : \n- Part a : Make a controller class. It\'ll take in a view and a model, and then pass over control to a play method inside of it. \n- Part b : Within the play class method of the controller, have the view object of the controller display the current screen. Then, have the controller receive from the view the succesful choice of move. \n- Part c : Have the controller send to the model object the value from the move in a method called update board, passing in the board, player, and row and col as well. \n\nWell, you likely have a number of red line errors at this point! To help you out, complete task 4, and it\'ll make a bit more sense. \n\nTask 4 : \n- Part a : Make a model class. It does not take in any arguments, but it has fields set up much of the code below. Feel free to take some of the ideas there, as they may prove useful. \n- Part b : Make a update board method, where you are passed a board, a row and col within the board, and a mark to make. \n- Part c : In your update board method, change the appropriate row and col within the board to the mark, then, check your board status. If there\'s a winner, you\'ll want to report out who won. If there\'s a tie, report that too. Otherwise, report that the game continues and update who\'s move it is. Return the updated board, status, and if there is someones turn, say whos turn it is. \n\nBack to the controller now! \n\nTask 5 : \n- Part a : Have the controller point where we send to the model object our value from the move method receive the appropriate values from the model. Then, have the controller send these to the view by having the view call display move result using the updated board, game status, and if there is another player a new player message. Store the result of this function call in controller next step. \n- Part b : Now that we have something coming back to the view, we can \n - print the updated board in the view \n - display game status \n - if the game is over \n - ask the player if they want to play again \n - if they do not want to play again, \n - print the game over message and send the instruction to quit back to the controller \n - otherwise, get the next move and send it back to the controller \n - this method can run inside the view \n\nTask 6 : \n- Final part! When the controller receives a value from the view next it is either : \n - a new move in the current game -> continue the game by going to top of game loop current \n - a new game -> start a new game by recalling the play game method with a wiped board. \n - a desire to end play -> set status to game over and quit the play method. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nTo determine if we are in a valid state, we should \n- check the size of the board (for class you will need to modify for your board\'s representation potentially!)\n- check the board status (have we made a valid number of moves for each? How can you guard against this for class without crashing the game?)\n- check if the game is over (currently only determines if game ended succesfully, you\'ll need to modify to find out WHO won WHEN and WHY)\n\nIf we are a correctly sized board, and we have a status that is valid, and we do not have a winner and are not in an invalid state of play, then, return True. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validTicTacToe(self, board: List[str]) -> bool :\n if not self.check_board_sizing(board) : \n return False \n elif not self.check_board_status(board) : \n return False \n else : \n return self.check_winner(board)\n \n def check_board_sizing(self, board) -> bool :\n if len(board) == 3 : \n for row in board : \n if len(row) != 3 : \n return False \n return True \n return False \n\n def check_board_status(self, board : List[str]) -> bool : \n self.counts = collections.defaultdict(int)\n for row in board : \n for cell in row : \n self.counts[cell] += 1 \n return (self.counts["O"] <= self.counts["X"]) and (self.counts["X"] - self.counts["O"] <= 1)\n\n def check_winner(self, board : List[str]) -> bool : \n # statuses by row for x and o \n x_statuses = [False, False, False, False]\n o_statuses = [False, False, False, False]\n # sums by row, sums by col, and diagonals up and down \n x_sums = [[0, 0, 0], [0, 0, 0], [0, 0]]\n o_sums = [[0, 0, 0], [0, 0, 0], [0, 0]]\n\n # get row sum for x\'s and o\'s and if 3 set status 0 for each \n for row_index, row in enumerate(board) : \n x_sums[0][row_index] = sum([int(r_i == "X") for r_i in row])\n o_sums[0][row_index] = sum([int(r_i == "O") for r_i in row])\n x_statuses[0] = True if x_sums[0][row_index] == 3 else x_statuses[0]\n o_statuses[0] = True if o_sums[0][row_index] == 3 else o_statuses[0]\n\n # col major order since we can\'t unpack strings in python \n # if sum of col is 3 update status at 1 otherwise remain same \n for col in range(3) : \n for row in range(3) : \n cell = board[row][col]\n x_sums[1][col] += cell == \'X\'\n o_sums[1][col] += cell == \'O\'\n x_statuses[1] = True if x_sums[1][col] == 3 else x_statuses[1]\n o_statuses[1] = True if o_sums[1][col] == 3 else o_statuses[1]\n \n # for board index in range 3 \n # 0 cell diag down 1 cell diag up \n for b_i in range(3) : \n x_sums[2][0] += board[b_i][0+b_i] == "X"\n x_sums[2][1] += board[b_i][2-b_i] == "X"\n o_sums[2][0] += board[b_i][0+b_i] == "O"\n o_sums[2][1] += board[b_i][2-b_i] == "O"\n x_statuses[2] = x_sums[2][0] == 3 \n x_statuses[3] = x_sums[2][1] == 3 \n o_statuses[2] = o_sums[2][0] == 3 \n o_statuses[3] = o_sums[2][1] == 3 \n\n # if we have an x win and do not have one more x than o, False \n # similarly, if we have an o win, and have any more or less moves, False \n if sum(x_statuses) > 0 and (self.counts["X"] - self.counts["O"] != 1) : \n return False \n elif sum(o_statuses) > 0 and (self.counts["X"] - self.counts["O"] != 0) : \n return False \n else : \n # in all other cases, valid win, but we don\'t know who! \n # assignment for class is to modify this and return who won in a separate function\n return True \n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Number of Subarrays with Bounded Maximum || Simple Python Sliding Window | number-of-subarrays-with-bounded-maximum | 0 | 1 | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n windowStart=0\n count=0\n curr=0\n \n for windowEnd, num in enumerate(nums):\n if left <= num <= right:\n curr = windowEnd - windowStart + 1\n elif num > right:\n curr = 0\n windowStart = windowEnd + 1\n \n count += curr\n return count\n``` | 4 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
Number of Subarrays with Bounded Maximum || Simple Python Sliding Window | number-of-subarrays-with-bounded-maximum | 0 | 1 | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n windowStart=0\n count=0\n curr=0\n \n for windowEnd, num in enumerate(nums):\n if left <= num <= right:\n curr = windowEnd - windowStart + 1\n elif num > right:\n curr = 0\n windowStart = windowEnd + 1\n \n count += curr\n return count\n``` | 4 | A website domain `"discuss.leetcode.com "` consists of various subdomains. At the top level, we have `"com "`, at the next level, we have `"leetcode.com "` and at the lowest level, `"discuss.leetcode.com "`. When we visit a domain like `"discuss.leetcode.com "`, we will also visit the parent domains `"leetcode.com "` and `"com "` implicitly.
A **count-paired domain** is a domain that has one of the two formats `"rep d1.d2.d3 "` or `"rep d1.d2 "` where `rep` is the number of visits to the domain and `d1.d2.d3` is the domain itself.
* For example, `"9001 discuss.leetcode.com "` is a **count-paired domain** that indicates that `discuss.leetcode.com` was visited `9001` times.
Given an array of **count-paired domains** `cpdomains`, return _an array of the **count-paired domains** of each subdomain in the input_. You may return the answer in **any order**.
**Example 1:**
**Input:** cpdomains = \[ "9001 discuss.leetcode.com "\]
**Output:** \[ "9001 leetcode.com ", "9001 discuss.leetcode.com ", "9001 com "\]
**Explanation:** We only have one website domain: "discuss.leetcode.com ".
As discussed above, the subdomain "leetcode.com " and "com " will also be visited. So they will all be visited 9001 times.
**Example 2:**
**Input:** cpdomains = \[ "900 google.mail.com ", "50 yahoo.com ", "1 intel.mail.com ", "5 wiki.org "\]
**Output:** \[ "901 mail.com ", "50 yahoo.com ", "900 google.mail.com ", "5 wiki.org ", "5 org ", "1 intel.mail.com ", "951 com "\]
**Explanation:** We will visit "google.mail.com " 900 times, "yahoo.com " 50 times, "intel.mail.com " once and "wiki.org " 5 times.
For the subdomains, we will visit "mail.com " 900 + 1 = 901 times, "com " 900 + 50 + 1 = 951 times, and "org " 5 times.
**Constraints:**
* `1 <= cpdomain.length <= 100`
* `1 <= cpdomain[i].length <= 100`
* `cpdomain[i]` follows either the `"repi d1i.d2i.d3i "` format or the `"repi d1i.d2i "` format.
* `repi` is an integer in the range `[1, 104]`.
* `d1i`, `d2i`, and `d3i` consist of lowercase English letters. | null |
Python | Two pointer technique | Easy solution | number-of-subarrays-with-bounded-maximum | 0 | 1 | ***Do hit like button if helpful!!!!***\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n start,end = -1, -1\n res = 0\n for i in range(len(nums)):\n if nums[i] > right:\n start = end = i\n continue\n \n if nums[i] >= left:\n end = i\n \n res += end - start\n return res\n``` | 4 | Given an integer array `nums` and two integers `left` and `right`, return _the number of contiguous non-empty **subarrays** such that the value of the maximum array element in that subarray is in the range_ `[left, right]`.
The test cases are generated so that the answer will fit in a **32-bit** integer.
**Example 1:**
**Input:** nums = \[2,1,4,3\], left = 2, right = 3
**Output:** 3
**Explanation:** There are three subarrays that meet the requirements: \[2\], \[2, 1\], \[3\].
**Example 2:**
**Input:** nums = \[2,9,2,5,6\], left = 2, right = 8
**Output:** 7
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 109`
* `0 <= left <= right <= 109` | Try to represent the current (N, K) in terms of some (N-1, prevK). What is prevK ? |
Python | Two pointer technique | Easy solution | number-of-subarrays-with-bounded-maximum | 0 | 1 | ***Do hit like button if helpful!!!!***\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n start,end = -1, -1\n res = 0\n for i in range(len(nums)):\n if nums[i] > right:\n start = end = i\n continue\n \n if nums[i] >= left:\n end = i\n \n res += end - start\n return res\n``` | 4 | A website domain `"discuss.leetcode.com "` consists of various subdomains. At the top level, we have `"com "`, at the next level, we have `"leetcode.com "` and at the lowest level, `"discuss.leetcode.com "`. When we visit a domain like `"discuss.leetcode.com "`, we will also visit the parent domains `"leetcode.com "` and `"com "` implicitly.
A **count-paired domain** is a domain that has one of the two formats `"rep d1.d2.d3 "` or `"rep d1.d2 "` where `rep` is the number of visits to the domain and `d1.d2.d3` is the domain itself.
* For example, `"9001 discuss.leetcode.com "` is a **count-paired domain** that indicates that `discuss.leetcode.com` was visited `9001` times.
Given an array of **count-paired domains** `cpdomains`, return _an array of the **count-paired domains** of each subdomain in the input_. You may return the answer in **any order**.
**Example 1:**
**Input:** cpdomains = \[ "9001 discuss.leetcode.com "\]
**Output:** \[ "9001 leetcode.com ", "9001 discuss.leetcode.com ", "9001 com "\]
**Explanation:** We only have one website domain: "discuss.leetcode.com ".
As discussed above, the subdomain "leetcode.com " and "com " will also be visited. So they will all be visited 9001 times.
**Example 2:**
**Input:** cpdomains = \[ "900 google.mail.com ", "50 yahoo.com ", "1 intel.mail.com ", "5 wiki.org "\]
**Output:** \[ "901 mail.com ", "50 yahoo.com ", "900 google.mail.com ", "5 wiki.org ", "5 org ", "1 intel.mail.com ", "951 com "\]
**Explanation:** We will visit "google.mail.com " 900 times, "yahoo.com " 50 times, "intel.mail.com " once and "wiki.org " 5 times.
For the subdomains, we will visit "mail.com " 900 + 1 = 901 times, "com " 900 + 50 + 1 = 951 times, and "org " 5 times.
**Constraints:**
* `1 <= cpdomain.length <= 100`
* `1 <= cpdomain[i].length <= 100`
* `cpdomain[i]` follows either the `"repi d1i.d2i.d3i "` format or the `"repi d1i.d2i "` format.
* `repi` is an integer in the range `[1, 104]`.
* `d1i`, `d2i`, and `d3i` consist of lowercase English letters. | null |
📌 MAANG One Liner 💥😯 | rotate-string | 1 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool rotateString(string s, string goal) {\n return (s.size()==goal.size()) && (s+s).find(goal) != string::npos;\n }\n};\n``` | 5 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
📌 MAANG One Liner 💥😯 | rotate-string | 1 | 1 | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool rotateString(string s, string goal) {\n return (s.size()==goal.size()) && (s+s).find(goal) != string::npos;\n }\n};\n``` | 5 | Given an array of points on the **X-Y** plane `points` where `points[i] = [xi, yi]`, return _the area of the largest triangle that can be formed by any three different points_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[0,0\],\[0,1\],\[1,0\],\[0,2\],\[2,0\]\]
**Output:** 2.00000
**Explanation:** The five points are shown in the above figure. The red triangle is the largest.
**Example 2:**
**Input:** points = \[\[1,0\],\[0,0\],\[0,1\]\]
**Output:** 0.50000
**Constraints:**
* `3 <= points.length <= 50`
* `-50 <= xi, yi <= 50`
* All the given points are **unique**. | null |
✅ | python3 | ONE LINE | FASTER THAN 99% | 🔥💪 | rotate-string | 0 | 1 | ```\nclass Solution:\n def rotateString(self, s: str, goal: str) -> bool:\n return len(s) == len(goal) and s in goal+goal \n```\n\nEnjoy :) | 47 | Given two strings `s` and `goal`, return `true` _if and only if_ `s` _can become_ `goal` _after some number of **shifts** on_ `s`.
A **shift** on `s` consists of moving the leftmost character of `s` to the rightmost position.
* For example, if `s = "abcde "`, then it will be `"bcdea "` after one shift.
**Example 1:**
**Input:** s = "abcde", goal = "cdeab"
**Output:** true
**Example 2:**
**Input:** s = "abcde", goal = "abced"
**Output:** false
**Constraints:**
* `1 <= s.length, goal.length <= 100`
* `s` and `goal` consist of lowercase English letters. | null |
✅ | python3 | ONE LINE | FASTER THAN 99% | 🔥💪 | rotate-string | 0 | 1 | ```\nclass Solution:\n def rotateString(self, s: str, goal: str) -> bool:\n return len(s) == len(goal) and s in goal+goal \n```\n\nEnjoy :) | 47 | Given an array of points on the **X-Y** plane `points` where `points[i] = [xi, yi]`, return _the area of the largest triangle that can be formed by any three different points_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** points = \[\[0,0\],\[0,1\],\[1,0\],\[0,2\],\[2,0\]\]
**Output:** 2.00000
**Explanation:** The five points are shown in the above figure. The red triangle is the largest.
**Example 2:**
**Input:** points = \[\[1,0\],\[0,0\],\[0,1\]\]
**Output:** 0.50000
**Constraints:**
* `3 <= points.length <= 50`
* `-50 <= xi, yi <= 50`
* All the given points are **unique**. | null |
python3, simple DFS | all-paths-from-source-to-target | 0 | 1 | ERROR: type should be string, got "https://leetcode.com/accounts/login/?next=/submissions/detail/868289908/ \\n```\\nRuntime: 93 ms, faster than 98.56% of Python3 online submissions for All Paths From Source to Target.\\nMemory Usage: 15.6 MB, less than 78.47% of Python3 online submissions for All Paths From Source to Target.\\n```\\n```\\nclass Solution:\\n def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:\\n target = len(graph) - 1\\n paths, targets = [[0]], []\\n while paths:\\n path = paths.pop(0)\\n edges = graph[path[-1]]\\n if not edges: \\n continue\\n for edge in edges:\\n if edge==target:\\n targets.append(path+[edge])\\n else:\\n paths = [path+[edge]] + paths\\n return targets \\n```" | 2 | Given a directed acyclic graph (**DAG**) of `n` nodes labeled from `0` to `n - 1`, find all possible paths from node `0` to node `n - 1` and return them in **any order**.
The graph is given as follows: `graph[i]` is a list of all nodes you can visit from node `i` (i.e., there is a directed edge from node `i` to node `graph[i][j]`).
**Example 1:**
**Input:** graph = \[\[1,2\],\[3\],\[3\],\[\]\]
**Output:** \[\[0,1,3\],\[0,2,3\]\]
**Explanation:** There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
**Example 2:**
**Input:** graph = \[\[4,3,1\],\[3,2,4\],\[3\],\[4\],\[\]\]
**Output:** \[\[0,4\],\[0,3,4\],\[0,1,3,4\],\[0,1,2,3,4\],\[0,1,4\]\]
**Constraints:**
* `n == graph.length`
* `2 <= n <= 15`
* `0 <= graph[i][j] < n`
* `graph[i][j] != i` (i.e., there will be no self-loops).
* All the elements of `graph[i]` are **unique**.
* The input graph is **guaranteed** to be a **DAG**. | null |
python3, simple DFS | all-paths-from-source-to-target | 0 | 1 | ERROR: type should be string, got "https://leetcode.com/accounts/login/?next=/submissions/detail/868289908/ \\n```\\nRuntime: 93 ms, faster than 98.56% of Python3 online submissions for All Paths From Source to Target.\\nMemory Usage: 15.6 MB, less than 78.47% of Python3 online submissions for All Paths From Source to Target.\\n```\\n```\\nclass Solution:\\n def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:\\n target = len(graph) - 1\\n paths, targets = [[0]], []\\n while paths:\\n path = paths.pop(0)\\n edges = graph[path[-1]]\\n if not edges: \\n continue\\n for edge in edges:\\n if edge==target:\\n targets.append(path+[edge])\\n else:\\n paths = [path+[edge]] + paths\\n return targets \\n```" | 2 | You are given an integer array `nums` and an integer `k`. You can partition the array into **at most** `k` non-empty adjacent subarrays. The **score** of a partition is the sum of the averages of each subarray.
Note that the partition must use every integer in `nums`, and that the score is not necessarily an integer.
Return _the maximum **score** you can achieve of all the possible partitions_. Answers within `10-6` of the actual answer will be accepted.
**Example 1:**
**Input:** nums = \[9,1,2,3,9\], k = 3
**Output:** 20.00000
**Explanation:**
The best choice is to partition nums into \[9\], \[1, 2, 3\], \[9\]. The answer is 9 + (1 + 2 + 3) / 3 + 9 = 20.
We could have also partitioned nums into \[9, 1\], \[2\], \[3, 9\], for example.
That partition would lead to a score of 5 + 2 + 6 = 13, which is worse.
**Example 2:**
**Input:** nums = \[1,2,3,4,5,6,7\], k = 4
**Output:** 20.50000
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i] <= 104`
* `1 <= k <= nums.length` | null |
Solution | smallest-rotation-with-highest-score | 1 | 1 | ```C++ []\nint cnt[100000];\nint speedup = []{ios::sync_with_stdio(0); cin.tie(0); return 0;}();\n\nclass Solution {\npublic:\n int bestRotation(vector<int>& nums) {\n int n = size(nums);\n memset(cnt, 0, sizeof(int) * n);\n for (int i = 0; i < n; ++i) {\n int v = nums[i], i2 = i-v;\n if (v > i) i2 += n;\n ++cnt[i]; --cnt[i2];\n }\n int best = -1, s = 0, bs = 0;\n for (int i = 0; i < n; ++i) if ((s += cnt[i]) > bs) bs = s, best = i;\n return best+1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n N = len(nums)\n change = [1] * N\n for i in range(N): change[(i - nums[i] + 1) % N] -= 1\n change = list(itertools.accumulate(change))\n return change.index(max(change))\n```\n\n```Java []\nclass Solution {\n public int bestRotation(int[] nums) {\n final int size = nums.length;\n int[] rsc = new int[size];\n for(int i = 0; i < size - 1; i++) {\n int value = nums[i];\n int downPos = (i + 1 + size - value) % size;\n rsc[downPos]--;\n }\n int value = nums[size-1];\n if( value != 0 ) rsc[size - value]--;\n int bestk = 0;\n int bestscore = rsc[0];\n int score = rsc[0];\n for(int i = 1; i < nums.length; i++) {\n score += rsc[i] + 1;\n if( score > bestscore ) {\n bestk = i;\n bestscore = score;\n }\n }\n return bestk;\n }\n}\n```\n | 1 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
Solution | smallest-rotation-with-highest-score | 1 | 1 | ```C++ []\nint cnt[100000];\nint speedup = []{ios::sync_with_stdio(0); cin.tie(0); return 0;}();\n\nclass Solution {\npublic:\n int bestRotation(vector<int>& nums) {\n int n = size(nums);\n memset(cnt, 0, sizeof(int) * n);\n for (int i = 0; i < n; ++i) {\n int v = nums[i], i2 = i-v;\n if (v > i) i2 += n;\n ++cnt[i]; --cnt[i2];\n }\n int best = -1, s = 0, bs = 0;\n for (int i = 0; i < n; ++i) if ((s += cnt[i]) > bs) bs = s, best = i;\n return best+1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n N = len(nums)\n change = [1] * N\n for i in range(N): change[(i - nums[i] + 1) % N] -= 1\n change = list(itertools.accumulate(change))\n return change.index(max(change))\n```\n\n```Java []\nclass Solution {\n public int bestRotation(int[] nums) {\n final int size = nums.length;\n int[] rsc = new int[size];\n for(int i = 0; i < size - 1; i++) {\n int value = nums[i];\n int downPos = (i + 1 + size - value) % size;\n rsc[downPos]--;\n }\n int value = nums[size-1];\n if( value != 0 ) rsc[size - value]--;\n int bestk = 0;\n int bestscore = rsc[0];\n int score = rsc[0];\n for(int i = 1; i < nums.length; i++) {\n score += rsc[i] + 1;\n if( score > bestscore ) {\n bestk = i;\n bestscore = score;\n }\n }\n return bestk;\n }\n}\n```\n | 1 | Given the `root` of a binary tree, return _the same tree where every subtree (of the given tree) not containing a_ `1` _has been removed_.
A subtree of a node `node` is `node` plus every node that is a descendant of `node`.
**Example 1:**
**Input:** root = \[1,null,0,0,1\]
**Output:** \[1,null,0,null,1\]
**Explanation:**
Only the red nodes satisfy the property "every subtree not containing a 1 ".
The diagram on the right represents the answer.
**Example 2:**
**Input:** root = \[1,0,1,0,0,0,1\]
**Output:** \[1,null,1,null,1\]
**Example 3:**
**Input:** root = \[1,1,0,1,1,0,1,0\]
**Output:** \[1,1,0,1,1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 200]`.
* `Node.val` is either `0` or `1`. | null |
✔ Python3 Solution | Prefix Sum | smallest-rotation-with-highest-score | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python\nclass Solution:\n def bestRotation(self, A):\n n = len(A)\n P = [1] * n\n for i in range(n):\n P[(i - A[i] + 1) % n] -= 1\n P = list(accumulate(P))\n return P.index(max(P))\n``` | 2 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
✔ Python3 Solution | Prefix Sum | smallest-rotation-with-highest-score | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```Python\nclass Solution:\n def bestRotation(self, A):\n n = len(A)\n P = [1] * n\n for i in range(n):\n P[(i - A[i] + 1) % n] -= 1\n P = list(accumulate(P))\n return P.index(max(P))\n``` | 2 | Given the `root` of a binary tree, return _the same tree where every subtree (of the given tree) not containing a_ `1` _has been removed_.
A subtree of a node `node` is `node` plus every node that is a descendant of `node`.
**Example 1:**
**Input:** root = \[1,null,0,0,1\]
**Output:** \[1,null,0,null,1\]
**Explanation:**
Only the red nodes satisfy the property "every subtree not containing a 1 ".
The diagram on the right represents the answer.
**Example 2:**
**Input:** root = \[1,0,1,0,0,0,1\]
**Output:** \[1,null,1,null,1\]
**Example 3:**
**Input:** root = \[1,1,0,1,1,0,1,0\]
**Output:** \[1,1,0,1,1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 200]`.
* `Node.val` is either `0` or `1`. | null |
798: Solution with step by step explanation | smallest-rotation-with-highest-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nn = len(nums)\nchange = [1] * n\n```\n\nHere, we find the length n of the nums array.\nWe initialize a change list of the same length filled with ones. This list represents the difference in scores for each rotation k.\n\n```\nfor i, num in enumerate(nums):\n change[(i - num + 1) % n] -= 1\n```\n\nWe iterate over each number num at index i in nums.\nIf a number num at index i is rotated to the first position (index 0), it would need i + 1 rotations. Hence, to represent the change in score when num is moved to index 0, we access change at position (i - num + 1) % n and decrement it by 1.\n\n```\nfor i in range(1, n):\n change[i] += change[i - 1]\n```\n\nHere, we are using the prefix sum technique to accumulate the score changes for each rotation. So, the change list now represents the total score for each rotation k.\n\n```\nreturn change.index(max(change))\n```\n\nFinally, we return the index k (rotation) that gives the maximum score.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n\n n = len(nums)\n change = [1] * n\n \n for i, num in enumerate(nums):\n change[(i - num + 1) % n] -= 1\n \n for i in range(1, n):\n change[i] += change[i - 1]\n \n return change.index(max(change))\n\n``` | 0 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
798: Solution with step by step explanation | smallest-rotation-with-highest-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nn = len(nums)\nchange = [1] * n\n```\n\nHere, we find the length n of the nums array.\nWe initialize a change list of the same length filled with ones. This list represents the difference in scores for each rotation k.\n\n```\nfor i, num in enumerate(nums):\n change[(i - num + 1) % n] -= 1\n```\n\nWe iterate over each number num at index i in nums.\nIf a number num at index i is rotated to the first position (index 0), it would need i + 1 rotations. Hence, to represent the change in score when num is moved to index 0, we access change at position (i - num + 1) % n and decrement it by 1.\n\n```\nfor i in range(1, n):\n change[i] += change[i - 1]\n```\n\nHere, we are using the prefix sum technique to accumulate the score changes for each rotation. So, the change list now represents the total score for each rotation k.\n\n```\nreturn change.index(max(change))\n```\n\nFinally, we return the index k (rotation) that gives the maximum score.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n\n n = len(nums)\n change = [1] * n\n \n for i, num in enumerate(nums):\n change[(i - num + 1) % n] -= 1\n \n for i in range(1, n):\n change[i] += change[i - 1]\n \n return change.index(max(change))\n\n``` | 0 | Given the `root` of a binary tree, return _the same tree where every subtree (of the given tree) not containing a_ `1` _has been removed_.
A subtree of a node `node` is `node` plus every node that is a descendant of `node`.
**Example 1:**
**Input:** root = \[1,null,0,0,1\]
**Output:** \[1,null,0,null,1\]
**Explanation:**
Only the red nodes satisfy the property "every subtree not containing a 1 ".
The diagram on the right represents the answer.
**Example 2:**
**Input:** root = \[1,0,1,0,0,0,1\]
**Output:** \[1,null,1,null,1\]
**Example 3:**
**Input:** root = \[1,1,0,1,1,0,1,0\]
**Output:** \[1,1,0,1,1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 200]`.
* `Node.val` is either `0` or `1`. | null |
Python 32% | score range parsing, but not prefix-sum | smallest-rotation-with-highest-score | 0 | 1 | # Intuition\r\nRather than using prefix-sum, I began with the awareness that this problem can be broken into two subproblems:\r\n1. for each number in array, what\'s the range of k? so that in the end this number can score?\r\n2. given certain intervals, find out the very first index that has the most intervals covering it.\r\n\r\nIt\'s not very fast compare to prefix-sum solution, but it got a steady 32% time consume outcome\r\n# Approach\r\n1. parse through nums, get score range of k for each number\r\n2. building two smallest heaps of range start-index and end-indes\r\n3. imaging using a vertical line scanning through number axis from 0 to L-1, every time you meet a start-index, you get 1 point, loss 1 if you meet end-index, keep updating max_points and corresponding k\r\n4. voila~ \r\n\r\n# Code\r\n```\r\nfrom heapq import heappop, heappush\r\n\r\nclass Solution:\r\n def bestRotation(self, nums):\r\n L = len(nums)\r\n\r\n score_ranges = [] # range of k that will get a score\r\n for idx, val in enumerate(nums): # score_idx in [val, L-1]\r\n if idx >= val: score_ranges.append((0, idx - val)) # idx left\r\n if idx < L - 1: score_ranges.append((idx + 1, min(L - 1, (L - val) + idx))) # idx right\r\n\r\n starts, ends = [], [] # notice these are possible k\'s\r\n for start, end in score_ranges:\r\n heappush(starts, start)\r\n heappush(ends, end)\r\n\r\n max_k, max_points, point = 0, 0, 0\r\n while starts: # chance to get higher score\r\n if starts[0] <= ends[0]: # score before loss points\r\n point += 1\r\n if point > max_points:\r\n max_k, max_points = starts[0], point\r\n heappop(starts)\r\n else:\r\n point -= 1\r\n heappop(ends)\r\n\r\n return max_k\r\n``` | 0 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
Python 32% | score range parsing, but not prefix-sum | smallest-rotation-with-highest-score | 0 | 1 | # Intuition\r\nRather than using prefix-sum, I began with the awareness that this problem can be broken into two subproblems:\r\n1. for each number in array, what\'s the range of k? so that in the end this number can score?\r\n2. given certain intervals, find out the very first index that has the most intervals covering it.\r\n\r\nIt\'s not very fast compare to prefix-sum solution, but it got a steady 32% time consume outcome\r\n# Approach\r\n1. parse through nums, get score range of k for each number\r\n2. building two smallest heaps of range start-index and end-indes\r\n3. imaging using a vertical line scanning through number axis from 0 to L-1, every time you meet a start-index, you get 1 point, loss 1 if you meet end-index, keep updating max_points and corresponding k\r\n4. voila~ \r\n\r\n# Code\r\n```\r\nfrom heapq import heappop, heappush\r\n\r\nclass Solution:\r\n def bestRotation(self, nums):\r\n L = len(nums)\r\n\r\n score_ranges = [] # range of k that will get a score\r\n for idx, val in enumerate(nums): # score_idx in [val, L-1]\r\n if idx >= val: score_ranges.append((0, idx - val)) # idx left\r\n if idx < L - 1: score_ranges.append((idx + 1, min(L - 1, (L - val) + idx))) # idx right\r\n\r\n starts, ends = [], [] # notice these are possible k\'s\r\n for start, end in score_ranges:\r\n heappush(starts, start)\r\n heappush(ends, end)\r\n\r\n max_k, max_points, point = 0, 0, 0\r\n while starts: # chance to get higher score\r\n if starts[0] <= ends[0]: # score before loss points\r\n point += 1\r\n if point > max_points:\r\n max_k, max_points = starts[0], point\r\n heappop(starts)\r\n else:\r\n point -= 1\r\n heappop(ends)\r\n\r\n return max_k\r\n``` | 0 | Given the `root` of a binary tree, return _the same tree where every subtree (of the given tree) not containing a_ `1` _has been removed_.
A subtree of a node `node` is `node` plus every node that is a descendant of `node`.
**Example 1:**
**Input:** root = \[1,null,0,0,1\]
**Output:** \[1,null,0,null,1\]
**Explanation:**
Only the red nodes satisfy the property "every subtree not containing a 1 ".
The diagram on the right represents the answer.
**Example 2:**
**Input:** root = \[1,0,1,0,0,0,1\]
**Output:** \[1,null,1,null,1\]
**Example 3:**
**Input:** root = \[1,1,0,1,1,0,1,0\]
**Output:** \[1,1,0,1,1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 200]`.
* `Node.val` is either `0` or `1`. | null |
[Python3] difference array | smallest-rotation-with-highest-score | 0 | 1 | \n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n diff = [0]*(len(nums) + 1)\n for i, x in enumerate(nums): \n diff[i+1] += 1\n if x <= i: diff[0] += 1\n diff[(i-x)%len(nums) + 1] -= 1\n \n ans = prefix = 0 \n mx = -inf \n for i, x in enumerate(diff): \n prefix += x\n if prefix > mx: mx, ans = prefix, i\n return ans \n```\n\n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n diff = [1] * len(nums)\n for i, x in enumerate(nums): \n diff[(i-x+1) % len(nums)] -= 1\n prefix = list(accumulate(diff))\n return prefix.index(max(prefix))\n``` | 1 | You are given an array `nums`. You can rotate it by a non-negative integer `k` so that the array becomes `[nums[k], nums[k + 1], ... nums[nums.length - 1], nums[0], nums[1], ..., nums[k-1]]`. Afterward, any entries that are less than or equal to their index are worth one point.
* For example, if we have `nums = [2,4,1,3,0]`, and we rotate by `k = 2`, it becomes `[1,3,0,2,4]`. This is worth `3` points because `1 > 0` \[no points\], `3 > 1` \[no points\], `0 <= 2` \[one point\], `2 <= 3` \[one point\], `4 <= 4` \[one point\].
Return _the rotation index_ `k` _that corresponds to the highest score we can achieve if we rotated_ `nums` _by it_. If there are multiple answers, return the smallest such index `k`.
**Example 1:**
**Input:** nums = \[2,3,1,4,0\]
**Output:** 3
**Explanation:** Scores for each k are listed below:
k = 0, nums = \[2,3,1,4,0\], score 2
k = 1, nums = \[3,1,4,0,2\], score 3
k = 2, nums = \[1,4,0,2,3\], score 3
k = 3, nums = \[4,0,2,3,1\], score 4
k = 4, nums = \[0,2,3,1,4\], score 3
So we should choose k = 3, which has the highest score.
**Example 2:**
**Input:** nums = \[1,3,0,2,4\]
**Output:** 0
**Explanation:** nums will always have 3 points no matter how it shifts.
So we will choose the smallest k, which is 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] < nums.length` | null |
[Python3] difference array | smallest-rotation-with-highest-score | 0 | 1 | \n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n diff = [0]*(len(nums) + 1)\n for i, x in enumerate(nums): \n diff[i+1] += 1\n if x <= i: diff[0] += 1\n diff[(i-x)%len(nums) + 1] -= 1\n \n ans = prefix = 0 \n mx = -inf \n for i, x in enumerate(diff): \n prefix += x\n if prefix > mx: mx, ans = prefix, i\n return ans \n```\n\n```\nclass Solution:\n def bestRotation(self, nums: List[int]) -> int:\n diff = [1] * len(nums)\n for i, x in enumerate(nums): \n diff[(i-x+1) % len(nums)] -= 1\n prefix = list(accumulate(diff))\n return prefix.index(max(prefix))\n``` | 1 | Given the `root` of a binary tree, return _the same tree where every subtree (of the given tree) not containing a_ `1` _has been removed_.
A subtree of a node `node` is `node` plus every node that is a descendant of `node`.
**Example 1:**
**Input:** root = \[1,null,0,0,1\]
**Output:** \[1,null,0,null,1\]
**Explanation:**
Only the red nodes satisfy the property "every subtree not containing a 1 ".
The diagram on the right represents the answer.
**Example 2:**
**Input:** root = \[1,0,1,0,0,0,1\]
**Output:** \[1,null,1,null,1\]
**Example 3:**
**Input:** root = \[1,1,0,1,1,0,1,0\]
**Output:** \[1,1,0,1,1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 200]`.
* `Node.val` is either `0` or `1`. | null |
🚀98.73% || Dynamic Programming || Commented Code🚀 | champagne-tower | 1 | 1 | # Problem Description\nStack drink glasses in a **pyramid** structure, starting with one glass in the first row and **incrementing** by one glass in each subsequent row, up to the `100th` row. Pour drink into the top glass, any excess spills equally to the **adjacent** `left` and `right` glasses. \nDetermine the levels of drink in a **specific** glasses for a given number of poured cups, considering the cascading effect.\n\n\n\n- **Constraints:**\n - `0 <= poured <= 10e9`\n - `0 <= query_glass <= query_row < 100`\n\n\n\n---\n\n\n# Intuition\nHello There,\uD83D\uDE00\n\nIn our today\'s interesting problem, We have a remarkable **structure**.\uD83E\uDD29\nThat the problem is like a **pyramid**.\uD83D\uDD3A\nHow can that help us?\uD83E\uDD14\nIf you solved **Pascal\'s Triangle** before, this problem has the same structure that can be solved with.\n\nActually the solution is **simple**, Only a simulation game.\uD83E\uDD2F\nStart from the **top** row and process the later rows **one by one** until you reach the **target** row.\nIn each row, we iterate over all the glasses then we compute if the glass has an extra drink that can be poured to the adjacent glasses in the next row or not until we reach the target row.\n\n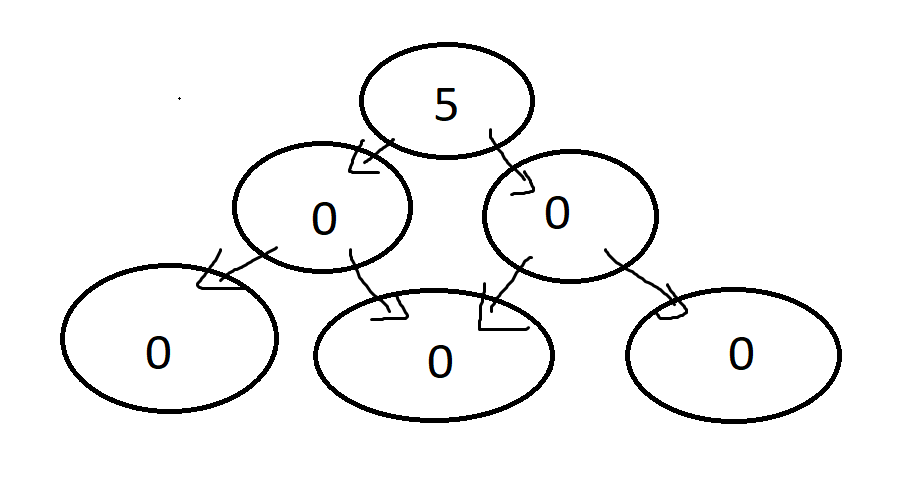\n\n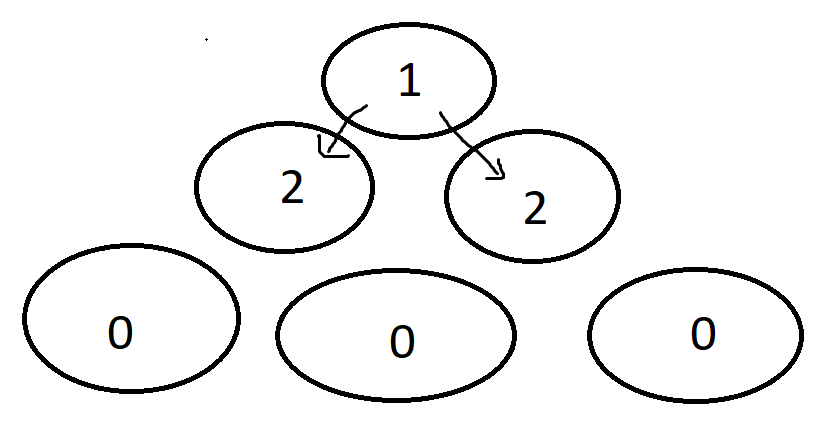\n\n\n\n\n\nBut where is the use of **Dynamic Programming** here?\uD83E\uDD14\nWe can **store** all of the rows to use them later to build the current row we are processing but since we need the row **before** the current row then we can only store **one row** which is the previous row.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n# Approach\n1. Start by **initializing** the **first** level with the `poured` amount in the top glass.\n2. For each row up to the `target` row:\n - Create a **new level** with the appropriate number of glasses for the current row.\n - **Traverse** each glass in the **current** level.\n - Calculate the **overflow of drink** and **distribute** it equally to adjacent glasses in the next level.\n - **Update** the current level with the next level for the next iteration.\n5. Return the drink level in the `target` glass, **clamped** to `1.0` if overflowed (**because** when we are iterating only to the row **before** the target row so we are not distributing the drink in the target row to the **next** row).\n\n# Complexity\n- **Time complexity:** $$O(N ^ 2)$$\nSince we have two for loops each for loop will iterate at most ``N`` iterations.\n- **Space complexity:** $$O(N)$$\nSince we are only storing row by row in our pyramid, then the complexity is `O(N)` where `N` is the number of the `target row`. Remember that the glasses in row `N` equal `N + 1` if `N` is 0-indexed.\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n // Initialize the current level with the poured amount in the top glass\n std::vector<double> currentLevel(1, poured);\n \n // Traverse each row up to the target row\n for (int row = 0; row < query_row; row++) {\n // Initialize the next level with the appropriate number of glasses for the current row\n std::vector<double> nextLevel(row + 2, 0.0);\n \n // Traverse each glass in the current level\n for (int glass = 0; glass < currentLevel.size(); glass++) {\n // Calculate overflow and distribute it to the adjacent glasses in the next level\n double overflow = (currentLevel[glass] - 1.0) / 2.0;\n if (overflow > 0.0) {\n nextLevel[glass] += overflow;\n nextLevel[glass + 1] += overflow;\n }\n }\n \n // Update the current level with the next level for the next iteration\n currentLevel = nextLevel;\n }\n \n // Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return std::min(1.0, currentLevel[query_glass]);\n }\n};\n```\n```Java []\n\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n // Initialize the current level with the poured amount in the top glass\n double[] currentLevel = { poured };\n \n // Traverse each row up to the target row\n for (int row = 0; row < query_row; row++) {\n // Initialize the next level with the appropriate number of glasses for the current row\n double[] nextLevel = new double[row + 2];\n Arrays.fill(nextLevel, 0.0);\n \n // Traverse each glass in the current level\n for (int glass = 0; glass < currentLevel.length; glass++) {\n // Calculate overflow and distribute it to the adjacent glasses in the next level\n double overflow = (currentLevel[glass] - 1.0) / 2.0;\n if (overflow > 0.0) {\n nextLevel[glass] += overflow;\n nextLevel[glass + 1] += overflow;\n }\n }\n \n // Update the current level with the next level for the next iteration\n currentLevel = nextLevel;\n }\n \n // Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return Math.min(1.0, currentLevel[query_glass]);\n }\n}\n```\n```Python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n # Initialize the current level with the poured amount in the top glass\n current_level = [poured]\n \n # Traverse each row up to the target row\n for row in range(query_row):\n # Initialize the next level with the appropriate number of glasses for the current row\n next_level = [0.0] * (row + 2)\n \n # Traverse each glass in the current level\n for glass in range(len(current_level)):\n # Calculate overflow and distribute it to the adjacent glasses in the next level\n overflow = (current_level[glass] - 1.0) / 2.0\n if overflow > 0.0:\n next_level[glass] += overflow\n next_level[glass + 1] += overflow\n \n # Update the current level with the next level for the next iteration\n current_level = next_level\n \n # Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return min(1.0, current_level[query_glass])\n```\n\n\n\n | 22 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
🚀98.73% || Dynamic Programming || Commented Code🚀 | champagne-tower | 1 | 1 | # Problem Description\nStack drink glasses in a **pyramid** structure, starting with one glass in the first row and **incrementing** by one glass in each subsequent row, up to the `100th` row. Pour drink into the top glass, any excess spills equally to the **adjacent** `left` and `right` glasses. \nDetermine the levels of drink in a **specific** glasses for a given number of poured cups, considering the cascading effect.\n\n\n\n- **Constraints:**\n - `0 <= poured <= 10e9`\n - `0 <= query_glass <= query_row < 100`\n\n\n\n---\n\n\n# Intuition\nHello There,\uD83D\uDE00\n\nIn our today\'s interesting problem, We have a remarkable **structure**.\uD83E\uDD29\nThat the problem is like a **pyramid**.\uD83D\uDD3A\nHow can that help us?\uD83E\uDD14\nIf you solved **Pascal\'s Triangle** before, this problem has the same structure that can be solved with.\n\nActually the solution is **simple**, Only a simulation game.\uD83E\uDD2F\nStart from the **top** row and process the later rows **one by one** until you reach the **target** row.\nIn each row, we iterate over all the glasses then we compute if the glass has an extra drink that can be poured to the adjacent glasses in the next row or not until we reach the target row.\n\n\n\n\n\n\n\n\n\nBut where is the use of **Dynamic Programming** here?\uD83E\uDD14\nWe can **store** all of the rows to use them later to build the current row we are processing but since we need the row **before** the current row then we can only store **one row** which is the previous row.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n# Approach\n1. Start by **initializing** the **first** level with the `poured` amount in the top glass.\n2. For each row up to the `target` row:\n - Create a **new level** with the appropriate number of glasses for the current row.\n - **Traverse** each glass in the **current** level.\n - Calculate the **overflow of drink** and **distribute** it equally to adjacent glasses in the next level.\n - **Update** the current level with the next level for the next iteration.\n5. Return the drink level in the `target` glass, **clamped** to `1.0` if overflowed (**because** when we are iterating only to the row **before** the target row so we are not distributing the drink in the target row to the **next** row).\n\n# Complexity\n- **Time complexity:** $$O(N ^ 2)$$\nSince we have two for loops each for loop will iterate at most ``N`` iterations.\n- **Space complexity:** $$O(N)$$\nSince we are only storing row by row in our pyramid, then the complexity is `O(N)` where `N` is the number of the `target row`. Remember that the glasses in row `N` equal `N + 1` if `N` is 0-indexed.\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n // Initialize the current level with the poured amount in the top glass\n std::vector<double> currentLevel(1, poured);\n \n // Traverse each row up to the target row\n for (int row = 0; row < query_row; row++) {\n // Initialize the next level with the appropriate number of glasses for the current row\n std::vector<double> nextLevel(row + 2, 0.0);\n \n // Traverse each glass in the current level\n for (int glass = 0; glass < currentLevel.size(); glass++) {\n // Calculate overflow and distribute it to the adjacent glasses in the next level\n double overflow = (currentLevel[glass] - 1.0) / 2.0;\n if (overflow > 0.0) {\n nextLevel[glass] += overflow;\n nextLevel[glass + 1] += overflow;\n }\n }\n \n // Update the current level with the next level for the next iteration\n currentLevel = nextLevel;\n }\n \n // Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return std::min(1.0, currentLevel[query_glass]);\n }\n};\n```\n```Java []\n\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n // Initialize the current level with the poured amount in the top glass\n double[] currentLevel = { poured };\n \n // Traverse each row up to the target row\n for (int row = 0; row < query_row; row++) {\n // Initialize the next level with the appropriate number of glasses for the current row\n double[] nextLevel = new double[row + 2];\n Arrays.fill(nextLevel, 0.0);\n \n // Traverse each glass in the current level\n for (int glass = 0; glass < currentLevel.length; glass++) {\n // Calculate overflow and distribute it to the adjacent glasses in the next level\n double overflow = (currentLevel[glass] - 1.0) / 2.0;\n if (overflow > 0.0) {\n nextLevel[glass] += overflow;\n nextLevel[glass + 1] += overflow;\n }\n }\n \n // Update the current level with the next level for the next iteration\n currentLevel = nextLevel;\n }\n \n // Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return Math.min(1.0, currentLevel[query_glass]);\n }\n}\n```\n```Python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n # Initialize the current level with the poured amount in the top glass\n current_level = [poured]\n \n # Traverse each row up to the target row\n for row in range(query_row):\n # Initialize the next level with the appropriate number of glasses for the current row\n next_level = [0.0] * (row + 2)\n \n # Traverse each glass in the current level\n for glass in range(len(current_level)):\n # Calculate overflow and distribute it to the adjacent glasses in the next level\n overflow = (current_level[glass] - 1.0) / 2.0\n if overflow > 0.0:\n next_level[glass] += overflow\n next_level[glass + 1] += overflow\n \n # Update the current level with the next level for the next iteration\n current_level = next_level\n \n # Return the drink level in the target glass (clamped to 1.0 if overflowed)\n return min(1.0, current_level[query_glass])\n```\n\n\n\n | 22 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
[Python3] 1-liner Top-down Dynamic Programming Solution | champagne-tower | 0 | 1 | # Approach\nTop-down DP in one line\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min((lambda func: lambda a, b, c: func(func, a, b, c))((functools.lru_cache(maxsize=None))(lambda champagneTower_, poured_, query_row_, query_glass_: poured_ if query_row_ == 0 else (max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_-1) - 1, 0) / 2 if query_glass_ == query_row_ else (max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_) - 1, 0) / 2 if query_glass_ == 0 else max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_-1) - 1, 0) / 2 + max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_) - 1, 0) / 2))))(poured, query_row, query_glass), 1.0)\n```\n\nDecompressed Version:\n```\nfrom functools import lru_cache\n\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min(self.champagneTower_(float(poured), query_row, query_glass), 1.0)\n\n @lru_cache(maxsize=None)\n def champagneTower_(self, poured, query_row, query_glass):\n if query_row == 0:\n return poured\n elif query_glass == query_row:\n return max(self.champagneTower_(poured, query_row-1, query_glass-1) - 1, 0) / 2\n elif query_glass == 0:\n return max(self.champagneTower_(poured, query_row-1, query_glass) - 1, 0) / 2\n else:\n return max(self.champagneTower_(poured, query_row-1, query_glass-1) - 1, 0) / 2 + max(self.champagneTower_(poured, query_row-1, query_glass) - 1, 0) / 2\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
[Python3] 1-liner Top-down Dynamic Programming Solution | champagne-tower | 0 | 1 | # Approach\nTop-down DP in one line\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min((lambda func: lambda a, b, c: func(func, a, b, c))((functools.lru_cache(maxsize=None))(lambda champagneTower_, poured_, query_row_, query_glass_: poured_ if query_row_ == 0 else (max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_-1) - 1, 0) / 2 if query_glass_ == query_row_ else (max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_) - 1, 0) / 2 if query_glass_ == 0 else max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_-1) - 1, 0) / 2 + max(champagneTower_(champagneTower_, poured_, query_row_-1, query_glass_) - 1, 0) / 2))))(poured, query_row, query_glass), 1.0)\n```\n\nDecompressed Version:\n```\nfrom functools import lru_cache\n\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min(self.champagneTower_(float(poured), query_row, query_glass), 1.0)\n\n @lru_cache(maxsize=None)\n def champagneTower_(self, poured, query_row, query_glass):\n if query_row == 0:\n return poured\n elif query_glass == query_row:\n return max(self.champagneTower_(poured, query_row-1, query_glass-1) - 1, 0) / 2\n elif query_glass == 0:\n return max(self.champagneTower_(poured, query_row-1, query_glass) - 1, 0) / 2\n else:\n return max(self.champagneTower_(poured, query_row-1, query_glass-1) - 1, 0) / 2 + max(self.champagneTower_(poured, query_row-1, query_glass) - 1, 0) / 2\n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Python greedy | champagne-tower | 0 | 1 | # Intuition\n`poured` in a `glass[i][j]` fall into `glass[i+1][j]` and `glass[i+1][j+1]`\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n A = [poured]\n row_index = 0\n while any(A):\n if row_index == query_row:\n return min(A[query_glass], 1)\n _A = list(A)\n A = [0] * (len(_A) + 1)\n for i, a in enumerate(_A):\n if (left := a - 1) > 0:\n A[i] += left / 2\n A[i+1] += left / 2\n row_index += 1\n return 0\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Python greedy | champagne-tower | 0 | 1 | # Intuition\n`poured` in a `glass[i][j]` fall into `glass[i+1][j]` and `glass[i+1][j+1]`\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n A = [poured]\n row_index = 0\n while any(A):\n if row_index == query_row:\n return min(A[query_glass], 1)\n _A = list(A)\n A = [0] * (len(_A) + 1)\n for i, a in enumerate(_A):\n if (left := a - 1) > 0:\n A[i] += left / 2\n A[i+1] += left / 2\n row_index += 1\n return 0\n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
easy solution | champagne-tower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n arr=[poured]\n\n for i in range(query_row):\n newarr=[0]\n for a in arr:\n if(a>1):\n newarr[-1]+=(a-1)/2\n newarr.append((a-1)/2)\n else:\n newarr.append(0)\n arr=newarr\n # print(arr)\n x=arr[query_glass]\n if(x>1):\n return 1\n else:\n return x\n\n \n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
easy solution | champagne-tower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n arr=[poured]\n\n for i in range(query_row):\n newarr=[0]\n for a in arr:\n if(a>1):\n newarr[-1]+=(a-1)/2\n newarr.append((a-1)/2)\n else:\n newarr.append(0)\n arr=newarr\n # print(arr)\n x=arr[query_glass]\n if(x>1):\n return 1\n else:\n return x\n\n \n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Solved it after 1 hour , i am improving . | champagne-tower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n a = [[0]*(i+1) for i in range(query_row+1)]\n a[0][0] = poured\n\n for i in range(query_row):\n for j in range(len(tower[i])):\n excess = (tower[i][j]-1.0)/2.0\n if excess > 0:\n a[i+1][j] += excess\n a[i+1][j+1] += excess \n \n return min(1.0,a[query_row][query_glass])\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Solved it after 1 hour , i am improving . | champagne-tower | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n a = [[0]*(i+1) for i in range(query_row+1)]\n a[0][0] = poured\n\n for i in range(query_row):\n for j in range(len(tower[i])):\n excess = (tower[i][j]-1.0)/2.0\n if excess > 0:\n a[i+1][j] += excess\n a[i+1][j+1] += excess \n \n return min(1.0,a[query_row][query_glass])\n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
[Python]Easy One, But Also Easy to Get It Wrong! | champagne-tower | 0 | 1 | # Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n if poured == 0:\n return 0\n states = {(0,0):(1,poured-1)}\n\n def getRe(query_row:int, query_glass:int):\n if states.__contains__((query_row,query_glass)):\n return states[(query_row,query_glass)][0]\n re = 0.0\n if query_glass>0 and query_glass<query_row:\n if getRe(query_row-1,query_glass)==1:\n re += (states[(query_row-1,query_glass)][1]/2.0)\n if getRe(query_row-1,query_glass-1)==1:\n re += (states[(query_row-1,query_glass-1)][1]/2.0)\n elif query_glass==0:\n if getRe(query_row-1,0)==1:\n re += (states[(query_row-1,0)][1]/2.0)\n else:\n if getRe(query_row-1,query_row-1)==1:\n re += (states[(query_row-1,query_row-1)][1]/2.0)\n \n if re >= 1:\n states[(query_row,query_glass)] = (1,re-1)\n else:\n states[(query_row,query_glass)] = (re,0)\n return states[(query_row,query_glass)][0]\n\n return getRe(query_row,query_glass)\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
[Python]Easy One, But Also Easy to Get It Wrong! | champagne-tower | 0 | 1 | # Code\n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n if poured == 0:\n return 0\n states = {(0,0):(1,poured-1)}\n\n def getRe(query_row:int, query_glass:int):\n if states.__contains__((query_row,query_glass)):\n return states[(query_row,query_glass)][0]\n re = 0.0\n if query_glass>0 and query_glass<query_row:\n if getRe(query_row-1,query_glass)==1:\n re += (states[(query_row-1,query_glass)][1]/2.0)\n if getRe(query_row-1,query_glass-1)==1:\n re += (states[(query_row-1,query_glass-1)][1]/2.0)\n elif query_glass==0:\n if getRe(query_row-1,0)==1:\n re += (states[(query_row-1,0)][1]/2.0)\n else:\n if getRe(query_row-1,query_row-1)==1:\n re += (states[(query_row-1,query_row-1)][1]/2.0)\n \n if re >= 1:\n states[(query_row,query_glass)] = (1,re-1)\n else:\n states[(query_row,query_glass)] = (re,0)\n return states[(query_row,query_glass)][0]\n\n return getRe(query_row,query_glass)\n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Python3 Solution | champagne-tower | 0 | 1 | \n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glasses=[poured]\n for i in range(query_row):\n temp=[0]*(len(glasses)+1)\n for i in range(len(glasses)):\n pour=max(0,glasses[i]-1)/2\n temp[i]+=pour\n temp[i+1]+=pour\n glasses=temp\n return min(1,glasses[query_glass]) \n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Python3 Solution | champagne-tower | 0 | 1 | \n```\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glasses=[poured]\n for i in range(query_row):\n temp=[0]*(len(glasses)+1)\n for i in range(len(glasses)):\n pour=max(0,glasses[i]-1)/2\n temp[i]+=pour\n temp[i+1]+=pour\n glasses=temp\n return min(1,glasses[query_glass]) \n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Solution | champagne-tower | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n double dp[101][101] = {0.00000};\n dp[0][0] = (double)poured;\n for(int i = 0; i <= query_row; i++){\n for(int j = 0; j <= i; j++){\n if(dp[i][j] > 1){\n dp[i+1][j] += (dp[i][j] - 1.00000)/2.00000;\n dp[i+1][j+1] += (dp[i][j] - 1.00000)/2.00000; \n dp[i][j] = 1.00000;\n }\n }\n }\n return min(1.00000, dp[query_row][query_glass]);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glasses = [poured]\n for _ in range(query_row):\n nxt = [0]*(len(glasses)+1)\n for key, value in enumerate(glasses):\n if value <= 1:\n continue\n move = (glasses[key]-1)/2.0\n nxt[key] += move\n nxt[key+1] += move\n glasses[key] = 1\n glasses = nxt\n return min(1, glasses[query_glass])\n```\n\n```Java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n \tdouble[][] cur = new double[query_row + 1][query_glass + 2];\n \tcur[0][0] = poured;\n \tfor (int i = 0; i < query_row; i++)\n \t\tfor (int j = 0; j <= query_glass; j++)\n\t \t\tif (cur[i][j] > 1) {\n\t \t\t\tdouble drop = (cur[i][j] - 1) / 2;\n\t \t\t\tcur[i + 1][j] += drop;\n\t \t\t\tcur[i + 1][j + 1] += drop;\n\t \t\t}\n \treturn cur[query_row][query_glass] < 1 ? cur[query_row][query_glass] : 1;\n }\n}\n```\n | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Solution | champagne-tower | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n double dp[101][101] = {0.00000};\n dp[0][0] = (double)poured;\n for(int i = 0; i <= query_row; i++){\n for(int j = 0; j <= i; j++){\n if(dp[i][j] > 1){\n dp[i+1][j] += (dp[i][j] - 1.00000)/2.00000;\n dp[i+1][j+1] += (dp[i][j] - 1.00000)/2.00000; \n dp[i][j] = 1.00000;\n }\n }\n }\n return min(1.00000, dp[query_row][query_glass]);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glasses = [poured]\n for _ in range(query_row):\n nxt = [0]*(len(glasses)+1)\n for key, value in enumerate(glasses):\n if value <= 1:\n continue\n move = (glasses[key]-1)/2.0\n nxt[key] += move\n nxt[key+1] += move\n glasses[key] = 1\n glasses = nxt\n return min(1, glasses[query_glass])\n```\n\n```Java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n \tdouble[][] cur = new double[query_row + 1][query_glass + 2];\n \tcur[0][0] = poured;\n \tfor (int i = 0; i < query_row; i++)\n \t\tfor (int j = 0; j <= query_glass; j++)\n\t \t\tif (cur[i][j] > 1) {\n\t \t\t\tdouble drop = (cur[i][j] - 1) / 2;\n\t \t\t\tcur[i + 1][j] += drop;\n\t \t\t\tcur[i + 1][j + 1] += drop;\n\t \t\t}\n \treturn cur[query_row][query_glass] < 1 ? cur[query_row][query_glass] : 1;\n }\n}\n```\n | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
🚀Beats 100% Acceptance📈 of runtime and memory with optimisation | Detailed and easy explanation | champagne-tower | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem models the pouring of champagne into a pyramid of glasses. The goal is to find the champagne level in a specific glass at a given row. The key insight is that champagne flows from higher rows to lower rows, and any excess champagne from a glass at row r and position c flows equally to the glasses at row r+1, positions c and c+1. We can simulate this process row by row.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a vector currentRow of size query_row + 1 to store the champagne levels for the current row. Set the first glass in currentRow with the poured amount of champagne.\n2. Use a loop to simulate the pouring process for each row from the top (row 0) to the target row (query_row).\n3. In each row, create a vector nextRow to store the champagne levels for the next row.\n4. For each glass in the current row, calculate the excess champagne by subtracting 1.0 (the maximum capacity) and divide it by 2.0 (to distribute equally to the left and right glasses). If there is excess, update nextRow accordingly.\n5. Check if the champagne level in the target glass (currentRow[query_glass]) becomes less than or equal to 1.0. If it does, there\'s no need to continue the simulation, and we can return the current value immediately.\n6. Swap currentRow and nextRow to update the current row for the next iteration.\n7. After the loop, return the minimum of 1.0 and the champagne level in the specified glass (currentRow[query_glass]).\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(query_row^2) because we iterate over each row up to query_row, and for each row, we perform a linear loop over the glasses in that row. In the worst case, we perform this process for each row.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(query_row) because we use two vectors (currentRow and nextRow) of size query_row + 1 to store champagne levels for the current and next rows. The space complexity is proportional to the number of rows we need to simulate, which is at most query_row.\n# Code\n```\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<double> currentRow(query_row + 1, 0.0); // Store champagne levels for the current row\n currentRow[0] = static_cast<double>(poured);\n\n for (int row = 0; row < query_row; ++row) {\n vector<double> nextRow(query_row + 1, 0.0);\n\n for (int glass = 0; glass <= row; ++glass) {\n double excess = (currentRow[glass] - 1.0) / 2.0;\n if (excess > 0) {\n nextRow[glass] += excess;\n nextRow[glass + 1] += excess;\n }\n }\n\n swap(currentRow, nextRow); // Update current row\n }\n\n return min(1.0, currentRow[query_glass]);\n }\n};\n\n``` | 3 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
🚀Beats 100% Acceptance📈 of runtime and memory with optimisation | Detailed and easy explanation | champagne-tower | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem models the pouring of champagne into a pyramid of glasses. The goal is to find the champagne level in a specific glass at a given row. The key insight is that champagne flows from higher rows to lower rows, and any excess champagne from a glass at row r and position c flows equally to the glasses at row r+1, positions c and c+1. We can simulate this process row by row.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a vector currentRow of size query_row + 1 to store the champagne levels for the current row. Set the first glass in currentRow with the poured amount of champagne.\n2. Use a loop to simulate the pouring process for each row from the top (row 0) to the target row (query_row).\n3. In each row, create a vector nextRow to store the champagne levels for the next row.\n4. For each glass in the current row, calculate the excess champagne by subtracting 1.0 (the maximum capacity) and divide it by 2.0 (to distribute equally to the left and right glasses). If there is excess, update nextRow accordingly.\n5. Check if the champagne level in the target glass (currentRow[query_glass]) becomes less than or equal to 1.0. If it does, there\'s no need to continue the simulation, and we can return the current value immediately.\n6. Swap currentRow and nextRow to update the current row for the next iteration.\n7. After the loop, return the minimum of 1.0 and the champagne level in the specified glass (currentRow[query_glass]).\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(query_row^2) because we iterate over each row up to query_row, and for each row, we perform a linear loop over the glasses in that row. In the worst case, we perform this process for each row.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(query_row) because we use two vectors (currentRow and nextRow) of size query_row + 1 to store champagne levels for the current and next rows. The space complexity is proportional to the number of rows we need to simulate, which is at most query_row.\n# Code\n```\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<double> currentRow(query_row + 1, 0.0); // Store champagne levels for the current row\n currentRow[0] = static_cast<double>(poured);\n\n for (int row = 0; row < query_row; ++row) {\n vector<double> nextRow(query_row + 1, 0.0);\n\n for (int glass = 0; glass <= row; ++glass) {\n double excess = (currentRow[glass] - 1.0) / 2.0;\n if (excess > 0) {\n nextRow[glass] += excess;\n nextRow[glass + 1] += excess;\n }\n }\n\n swap(currentRow, nextRow); // Update current row\n }\n\n return min(1.0, currentRow[query_glass]);\n }\n};\n\n``` | 3 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
✅98.44%🔥Dynamic Programming & Iterative Approach🔥 | champagne-tower | 1 | 1 | # Problem\n#### This problem can be viewed as a dynamic programming problem where you are pouring champagne into glasses arranged in a pyramid shape and need to find out how much champagne each glass contains after a certain amount of pouring. The key idea is to track the amount of champagne in each glass by simulating the pouring process row by row.\n---\n# Solution\n\n##### 1. Initialize a 2D array tower to represent the champagne glasses. The size of this array is determined by query_row + 1 rows, where each row contains i + 1 glasses, and all glasses are initially set to 0.\n\n##### 2. Pour the initial amount of champagne into the topmost glass, which is tower[0][0] = poured.\n\n##### 3. Iterate through each row from the top to the query_row:\n\n- For each glass in the current row, calculate the excess champagne that overflows from it. This is done by subtracting 1 (a full glass) from the current glass\'s content and dividing it by 2.0.\n\n- If there is excess champagne (excess > 0), distribute it equally to the two glasses in the next row below. Increase the content of the glasses in the next row accordingly (tower[row + 1][glass] += excess and tower[row + 1][glass + 1] += excess).\n\n##### 4. After simulating the pouring process, you\'ll have the amount of champagne in each glass. To find the amount of champagne in the query_glass of the query_row, simply access tower[query_row][query_glass].\n\n##### 5. Return the minimum of 1.0 and the content of the query_glass in the query_row. This is because the content of a glass cannot exceed 1.0, so if it\'s more than 1.0, we return 1.0.\n\n---\n\n# Code\n```Python3 []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n tower = [[0] * (i + 1) for i in range(query_row + 1)]\n tower[0][0] = poured\n\n for row in range(query_row):\n for glass in range(len(tower[row])):\n excess = (tower[row][glass] - 1) / 2.0\n if excess > 0:\n tower[row + 1][glass] += excess\n tower[row + 1][glass + 1] += excess\n\n return min(1.0, tower[query_row][query_glass])\n\n```\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n tower = [[0] * (i + 1) for i in range(query_row + 1)]\n tower[0][0] = poured\n\n for row in range(query_row):\n for glass in range(len(tower[row])):\n excess = (tower[row][glass] - 1) / 2.0\n if excess > 0:\n tower[row + 1][glass] += excess\n tower[row + 1][glass + 1] += excess\n\n return min(1.0, tower[query_row][query_glass])\n\n```\n```C# []\npublic class Solution {\n public double ChampagneTower(int poured, int query_row, int query_glass) {\n double[][] tower = new double[query_row + 1][];\n for (int i = 0; i <= query_row; i++) {\n tower[i] = new double[i + 1];\n }\n \n tower[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass < tower[row].Length; glass++) {\n double excess = (tower[row][glass] - 1) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.Min(1.0, tower[query_row][query_glass]);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n std::vector<std::vector<double>> tower(query_row + 1, std::vector<double>(query_row + 1, 0.0));\n tower[0][0] = static_cast<double>(poured);\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return std::min(1.0, tower[query_row][query_glass]);\n }\n};\n\n```\n```Java []\npublic class Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[][] tower = new double[query_row + 1][query_row + 1];\n tower[0][0] = (double) poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.min(1.0, tower[query_row][query_glass]);\n }\n}\n\n```\n```JavaScript []\nvar champagneTower = function(poured, query_row, query_glass) {\n const tower = new Array(query_row + 1).fill(0).map(() => new Array(query_row + 1).fill(0));\n tower[0][0] = poured;\n\n for (let row = 0; row < query_row; row++) {\n for (let glass = 0; glass <= row; glass++) {\n const excess = (tower[row][glass] - 1) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.min(1, tower[query_row][query_glass]);\n};\n```\n```C []\ndouble champagneTower(int poured, int query_row, int query_glass) {\n double tower[101][101] = {0};\n tower[0][0] = (double)poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return tower[query_row][query_glass] > 1.0 ? 1.0 : tower[query_row][query_glass];\n}\n```\n | 55 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
✅98.44%🔥Dynamic Programming & Iterative Approach🔥 | champagne-tower | 1 | 1 | # Problem\n#### This problem can be viewed as a dynamic programming problem where you are pouring champagne into glasses arranged in a pyramid shape and need to find out how much champagne each glass contains after a certain amount of pouring. The key idea is to track the amount of champagne in each glass by simulating the pouring process row by row.\n---\n# Solution\n\n##### 1. Initialize a 2D array tower to represent the champagne glasses. The size of this array is determined by query_row + 1 rows, where each row contains i + 1 glasses, and all glasses are initially set to 0.\n\n##### 2. Pour the initial amount of champagne into the topmost glass, which is tower[0][0] = poured.\n\n##### 3. Iterate through each row from the top to the query_row:\n\n- For each glass in the current row, calculate the excess champagne that overflows from it. This is done by subtracting 1 (a full glass) from the current glass\'s content and dividing it by 2.0.\n\n- If there is excess champagne (excess > 0), distribute it equally to the two glasses in the next row below. Increase the content of the glasses in the next row accordingly (tower[row + 1][glass] += excess and tower[row + 1][glass + 1] += excess).\n\n##### 4. After simulating the pouring process, you\'ll have the amount of champagne in each glass. To find the amount of champagne in the query_glass of the query_row, simply access tower[query_row][query_glass].\n\n##### 5. Return the minimum of 1.0 and the content of the query_glass in the query_row. This is because the content of a glass cannot exceed 1.0, so if it\'s more than 1.0, we return 1.0.\n\n---\n\n# Code\n```Python3 []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n tower = [[0] * (i + 1) for i in range(query_row + 1)]\n tower[0][0] = poured\n\n for row in range(query_row):\n for glass in range(len(tower[row])):\n excess = (tower[row][glass] - 1) / 2.0\n if excess > 0:\n tower[row + 1][glass] += excess\n tower[row + 1][glass + 1] += excess\n\n return min(1.0, tower[query_row][query_glass])\n\n```\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n tower = [[0] * (i + 1) for i in range(query_row + 1)]\n tower[0][0] = poured\n\n for row in range(query_row):\n for glass in range(len(tower[row])):\n excess = (tower[row][glass] - 1) / 2.0\n if excess > 0:\n tower[row + 1][glass] += excess\n tower[row + 1][glass + 1] += excess\n\n return min(1.0, tower[query_row][query_glass])\n\n```\n```C# []\npublic class Solution {\n public double ChampagneTower(int poured, int query_row, int query_glass) {\n double[][] tower = new double[query_row + 1][];\n for (int i = 0; i <= query_row; i++) {\n tower[i] = new double[i + 1];\n }\n \n tower[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass < tower[row].Length; glass++) {\n double excess = (tower[row][glass] - 1) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.Min(1.0, tower[query_row][query_glass]);\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n std::vector<std::vector<double>> tower(query_row + 1, std::vector<double>(query_row + 1, 0.0));\n tower[0][0] = static_cast<double>(poured);\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return std::min(1.0, tower[query_row][query_glass]);\n }\n};\n\n```\n```Java []\npublic class Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[][] tower = new double[query_row + 1][query_row + 1];\n tower[0][0] = (double) poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.min(1.0, tower[query_row][query_glass]);\n }\n}\n\n```\n```JavaScript []\nvar champagneTower = function(poured, query_row, query_glass) {\n const tower = new Array(query_row + 1).fill(0).map(() => new Array(query_row + 1).fill(0));\n tower[0][0] = poured;\n\n for (let row = 0; row < query_row; row++) {\n for (let glass = 0; glass <= row; glass++) {\n const excess = (tower[row][glass] - 1) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return Math.min(1, tower[query_row][query_glass]);\n};\n```\n```C []\ndouble champagneTower(int poured, int query_row, int query_glass) {\n double tower[101][101] = {0};\n tower[0][0] = (double)poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double excess = (tower[row][glass] - 1.0) / 2.0;\n if (excess > 0) {\n tower[row + 1][glass] += excess;\n tower[row + 1][glass + 1] += excess;\n }\n }\n }\n\n return tower[query_row][query_glass] > 1.0 ? 1.0 : tower[query_row][query_glass];\n}\n```\n | 55 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
【Video】How we think about a solution - DP Solution with 1D and 2D - Python, JavaScript, Java and C++ | champagne-tower | 1 | 1 | Welcome to my article! This artcle starts with "How we think about a solution". In other words, that is my thought process to solve the question. This article explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope this aricle is helpful for someone.\n\n# Intuition\n\nTo solve the question, we employ a simulation-based approach. The problem involves pouring champagne into a pyramid of glasses in a row-wise fashion. The goal is to find out how much champagne a specific glass in a particular row will contain after pouring.\n\nWe start by initializing a data structure, such as a 2D array or a list, to represent the champagne poured into each glass. The first glass at the top of the pyramid receives the initially poured amount of champagne.\n\nWe then simulate the pouring process, row by row, calculating the overflow of champagne from each glass to its adjacent glasses below. The overflow is calculated based on the amount of champagne in each glass. If there\'s an overflow, we distribute it equally to the left and right adjacent glasses in the current row.\n\nWe repeat this simulation for each row, updating the champagne amounts in each glass accordingly. Finally, we determine the amount of champagne in the specified glass in the desired row and return the minimum of 1.0 and the calculated amount, as each glass can hold a maximum of 1 cup of champagne. This ensures that the solution adheres to the problem constraints and accurately computes the champagne content in the specified glass.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/_yk6zri9a24\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Champagne Tower\n`1:33` How we think about a solution\n`3:28` Coding with 2D\n`7:09` Time Complexity and Space Complexity with 2D\n`7:49` Coding with 1D\n`10:49` Time Complexity and Space Complexity with 1D\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,456\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe can pour champagne from top of the tower and when the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it.\n\nSo, question is how we can calculate overflow.\n\nSince the description says "Each glass holds one cup of champagne", so we can say like\n\n```\noverflow = amount of champagne in current glass - 1.0\n```\n\nif `amount of champagne in current glass` is over `1.0`, that is overflow champagne. And the description says above `any excess liquid poured will fall equally to the glass immediately to the left and right of it` which means exact overflow amount for the next left and right glasses is\n\n```\noverflow = (amount of champagne in current glass - 1.0) / 2.0\n```\n\nAfter we calculate overflow, we just add amount of overflow to next left and right glasses.\n\nIn the end, we return like this.\n\n```\nreturn min(1.0, tower[query_glass])\n```\n\nThe calculation return min(1.0, tower[query_glass]) is determining the amount of champagne at the specified glass position (query_glass). However, this amount is capped at a maximum of 1.0, representing the maximum amount of champagne a single glass can hold. The min(1.0, tower[query_glass]) ensures that we return either the amount of champagne in the glass or 1.0, whichever is smaller, to respect the glass\'s maximum capacity.\n\nLet\'s see real algorithm with 2D and 1D solutions\n\n## 2D Solution\n\n**Algorithm Overview:**\n\n1. Initialize a pyramid to represent champagne glasses with 0.0 poured champagne.\n2. Iterate through each row of the pyramid up to the specified query_row.\n3. For each glass in a row, calculate the overflow of champagne and distribute it to the glasses below if there\'s overflow.\n4. Return the amount of champagne in the specified glass of the query_row.\n\n**Detailed Explanation:**\n\n1. Initialize a 2D array `pyramid` to represent the champagne glasses. The length of each row is determined by the variable `k` which ranges from 1 to 100.\n\n2. Set the first glass of the pyramid (`pyramid[0][0]`) to the poured amount of champagne.\n\n3. Iterate through each row up to the `query_row`.\n\n4. For each glass in the current row, calculate the overflow of champagne based on the formula: `overflow = (pyramid[row][glass] - 1.0) / 2.0`.\n\n5. If there\'s overflow (overflow > 0), distribute the overflow equally to the two glasses below in the next row (`pyramid[row + 1][glass]` and `pyramid[row + 1][glass + 1]`).\n\n6. Return the amount of champagne in the specified glass of the query_row, ensuring it does not exceed 1.0.\n\n## Complexity\nTime Complexity: O(1)\nLooks like O(n^2) but this is fixed with 100, so it doesn\'t grow, so we can say O(1).\n\nSpace Complexity: O(1)\nThe same reason above.\n\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n pyramid = [[0.0] * k for k in range(1, 101)]\n pyramid[0][0] = poured\n\n for row in range(query_row):\n for glass in range(row + 1):\n overflow = (pyramid[row][glass] - 1.0) / 2.0\n if overflow > 0:\n pyramid[row + 1][glass] += overflow\n pyramid[row + 1][glass + 1] += overflow\n \n return min(1.0, pyramid[query_row][query_glass])\n```\n```javascript []\n/**\n * @param {number} poured\n * @param {number} query_row\n * @param {number} query_glass\n * @return {number}\n */\nvar champagneTower = function(poured, query_row, query_glass) {\n const pyramid = Array.from({ length: 101 }, (_, k) => Array(k + 1).fill(0.0));\n pyramid[0][0] = poured;\n\n for (let row = 0; row < query_row; row++) {\n for (let glass = 0; glass <= row; glass++) {\n const overflow = Math.max(0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return Math.min(1.0, pyramid[query_row][query_glass]); \n};\n```\n```java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[][] pyramid = new double[101][];\n for (int i = 0; i < 101; i++)\n pyramid[i] = new double[i + 1];\n pyramid[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double overflow = Math.max(0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return Math.min(1.0, pyramid[query_row][query_glass]); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<vector<double>> pyramid(101, vector<double>(101, 0.0));\n pyramid[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double overflow = max(0.0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return min(1.0, pyramid[query_row][query_glass]); \n }\n};\n```\n\n\n\n---\n\n# 1D Solution\n\nSure, let\'s break down the algorithm step by step.\n\n**Algorithm Overview:**\n\n1. Initialize an array `glass_levels` to represent the champagne levels in each glass, with a maximum of 100 glasses. Set the first glass to the poured amount of champagne.\n2. Iterate through each row up to the specified row:\n a. Initialize an array `next_levels` to store the champagne levels for the next row.\n b. Iterate through each glass in the current row:\n - Calculate the overflow of champagne for the current glass based on its level.\n - Distribute the overflow equally to the current glass and the next glass.\n c. Update `glass_levels` with the champagne levels for the next row.\n3. Return the amount of champagne in the specified glass.\n\n**Detailed Explanation:**\n\n1. Initialize an array `glass_levels` of size 100 to represent the champagne levels in each glass. Set the first glass\'s level to the poured amount of champagne.\n2. Iterate through each row up to the specified row (`query_row`):\n - For each row:\n a. Initialize an array `next_levels` to store the champagne levels for the next row of glasses.\n b. Iterate through each glass in the current row (`cur_row`):\n - Calculate the overflow by finding the excess amount of champagne in the current glass beyond capacity.\n - Distribute this overflow equally to the current glass and the adjacent glass on the right (`cur_glass + 1`).\n c. Update `glass_levels` with the champagne levels for the next row, which are stored in the `next_levels` array.\n3. After iterating through all the rows, return the minimum value between 1.0 and the champagne level in the specified glass (`query_glass`). This ensures the value does not exceed 1.0 (representing a full glass).\n\n## Complexity\n\nTime Complexity: O(1)\nLooks like O(n^2) but this is fixed with 100 which means it doesn\'t grow, so we can say O(1)\n\nSpace Complexity: O(1)\nThe same reason above.\n\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glass_levels = [0.0] * 100\n glass_levels[0] = poured\n\n for cur_row in range(query_row):\n next_levels = [0.0] * 100\n\n for cur_glass in range(cur_row + 1):\n overflow = max(0, (glass_levels[cur_glass] - 1.0) / 2.0)\n next_levels[cur_glass] += overflow\n next_levels[cur_glass + 1] += overflow\n \n glass_levels = next_levels\n \n return min(1.0, glass_levels[query_glass]) \n```\n```javascript []\n/**\n * @param {number} poured\n * @param {number} query_row\n * @param {number} query_glass\n * @return {number}\n */\nvar champagneTower = function(poured, query_row, query_glass) {\n let glassLevels = Array(100).fill(0.0);\n glassLevels[0] = poured;\n\n for (let curRow = 0; curRow < query_row; curRow++) {\n let nextLevels = Array(100).fill(0.0);\n\n for (let curGlass = 0; curGlass <= curRow; curGlass++) {\n let overflow = Math.max(0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return Math.min(1.0, glassLevels[query_glass]); \n};\n```\n```java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[] glassLevels = new double[100];\n glassLevels[0] = poured;\n\n for (int curRow = 0; curRow < query_row; curRow++) {\n double[] nextLevels = new double[100];\n\n for (int curGlass = 0; curGlass <= curRow; curGlass++) {\n double overflow = Math.max(0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return Math.min(1.0, glassLevels[query_glass]); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<double> glassLevels(100, 0.0);\n glassLevels[0] = poured;\n\n for (int curRow = 0; curRow < query_row; curRow++) {\n vector<double> nextLevels(100, 0.0);\n\n for (int curGlass = 0; curGlass <= curRow; curGlass++) {\n double overflow = max(0.0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return min(1.0, glassLevels[query_glass]); \n }\n};\n```\n\n\n---\n\n\n\nThank you for reading such a long post. Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 25th, 2023\nhttps://leetcode.com/problems/find-the-difference/solutions/4086661/video-how-we-think-about-a-solution-python-javascript-java-c/\n\nHave a nice day!\n | 30 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
【Video】How we think about a solution - DP Solution with 1D and 2D - Python, JavaScript, Java and C++ | champagne-tower | 1 | 1 | Welcome to my article! This artcle starts with "How we think about a solution". In other words, that is my thought process to solve the question. This article explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope this aricle is helpful for someone.\n\n# Intuition\n\nTo solve the question, we employ a simulation-based approach. The problem involves pouring champagne into a pyramid of glasses in a row-wise fashion. The goal is to find out how much champagne a specific glass in a particular row will contain after pouring.\n\nWe start by initializing a data structure, such as a 2D array or a list, to represent the champagne poured into each glass. The first glass at the top of the pyramid receives the initially poured amount of champagne.\n\nWe then simulate the pouring process, row by row, calculating the overflow of champagne from each glass to its adjacent glasses below. The overflow is calculated based on the amount of champagne in each glass. If there\'s an overflow, we distribute it equally to the left and right adjacent glasses in the current row.\n\nWe repeat this simulation for each row, updating the champagne amounts in each glass accordingly. Finally, we determine the amount of champagne in the specified glass in the desired row and return the minimum of 1.0 and the calculated amount, as each glass can hold a maximum of 1 cup of champagne. This ensures that the solution adheres to the problem constraints and accurately computes the champagne content in the specified glass.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/_yk6zri9a24\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Champagne Tower\n`1:33` How we think about a solution\n`3:28` Coding with 2D\n`7:09` Time Complexity and Space Complexity with 2D\n`7:49` Coding with 1D\n`10:49` Time Complexity and Space Complexity with 1D\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,456\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe can pour champagne from top of the tower and when the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it.\n\nSo, question is how we can calculate overflow.\n\nSince the description says "Each glass holds one cup of champagne", so we can say like\n\n```\noverflow = amount of champagne in current glass - 1.0\n```\n\nif `amount of champagne in current glass` is over `1.0`, that is overflow champagne. And the description says above `any excess liquid poured will fall equally to the glass immediately to the left and right of it` which means exact overflow amount for the next left and right glasses is\n\n```\noverflow = (amount of champagne in current glass - 1.0) / 2.0\n```\n\nAfter we calculate overflow, we just add amount of overflow to next left and right glasses.\n\nIn the end, we return like this.\n\n```\nreturn min(1.0, tower[query_glass])\n```\n\nThe calculation return min(1.0, tower[query_glass]) is determining the amount of champagne at the specified glass position (query_glass). However, this amount is capped at a maximum of 1.0, representing the maximum amount of champagne a single glass can hold. The min(1.0, tower[query_glass]) ensures that we return either the amount of champagne in the glass or 1.0, whichever is smaller, to respect the glass\'s maximum capacity.\n\nLet\'s see real algorithm with 2D and 1D solutions\n\n## 2D Solution\n\n**Algorithm Overview:**\n\n1. Initialize a pyramid to represent champagne glasses with 0.0 poured champagne.\n2. Iterate through each row of the pyramid up to the specified query_row.\n3. For each glass in a row, calculate the overflow of champagne and distribute it to the glasses below if there\'s overflow.\n4. Return the amount of champagne in the specified glass of the query_row.\n\n**Detailed Explanation:**\n\n1. Initialize a 2D array `pyramid` to represent the champagne glasses. The length of each row is determined by the variable `k` which ranges from 1 to 100.\n\n2. Set the first glass of the pyramid (`pyramid[0][0]`) to the poured amount of champagne.\n\n3. Iterate through each row up to the `query_row`.\n\n4. For each glass in the current row, calculate the overflow of champagne based on the formula: `overflow = (pyramid[row][glass] - 1.0) / 2.0`.\n\n5. If there\'s overflow (overflow > 0), distribute the overflow equally to the two glasses below in the next row (`pyramid[row + 1][glass]` and `pyramid[row + 1][glass + 1]`).\n\n6. Return the amount of champagne in the specified glass of the query_row, ensuring it does not exceed 1.0.\n\n## Complexity\nTime Complexity: O(1)\nLooks like O(n^2) but this is fixed with 100, so it doesn\'t grow, so we can say O(1).\n\nSpace Complexity: O(1)\nThe same reason above.\n\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n pyramid = [[0.0] * k for k in range(1, 101)]\n pyramid[0][0] = poured\n\n for row in range(query_row):\n for glass in range(row + 1):\n overflow = (pyramid[row][glass] - 1.0) / 2.0\n if overflow > 0:\n pyramid[row + 1][glass] += overflow\n pyramid[row + 1][glass + 1] += overflow\n \n return min(1.0, pyramid[query_row][query_glass])\n```\n```javascript []\n/**\n * @param {number} poured\n * @param {number} query_row\n * @param {number} query_glass\n * @return {number}\n */\nvar champagneTower = function(poured, query_row, query_glass) {\n const pyramid = Array.from({ length: 101 }, (_, k) => Array(k + 1).fill(0.0));\n pyramid[0][0] = poured;\n\n for (let row = 0; row < query_row; row++) {\n for (let glass = 0; glass <= row; glass++) {\n const overflow = Math.max(0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return Math.min(1.0, pyramid[query_row][query_glass]); \n};\n```\n```java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[][] pyramid = new double[101][];\n for (int i = 0; i < 101; i++)\n pyramid[i] = new double[i + 1];\n pyramid[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double overflow = Math.max(0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return Math.min(1.0, pyramid[query_row][query_glass]); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<vector<double>> pyramid(101, vector<double>(101, 0.0));\n pyramid[0][0] = poured;\n\n for (int row = 0; row < query_row; row++) {\n for (int glass = 0; glass <= row; glass++) {\n double overflow = max(0.0, (pyramid[row][glass] - 1.0) / 2.0);\n if (overflow > 0) {\n pyramid[row + 1][glass] += overflow;\n pyramid[row + 1][glass + 1] += overflow;\n }\n }\n }\n\n return min(1.0, pyramid[query_row][query_glass]); \n }\n};\n```\n\n\n\n---\n\n# 1D Solution\n\nSure, let\'s break down the algorithm step by step.\n\n**Algorithm Overview:**\n\n1. Initialize an array `glass_levels` to represent the champagne levels in each glass, with a maximum of 100 glasses. Set the first glass to the poured amount of champagne.\n2. Iterate through each row up to the specified row:\n a. Initialize an array `next_levels` to store the champagne levels for the next row.\n b. Iterate through each glass in the current row:\n - Calculate the overflow of champagne for the current glass based on its level.\n - Distribute the overflow equally to the current glass and the next glass.\n c. Update `glass_levels` with the champagne levels for the next row.\n3. Return the amount of champagne in the specified glass.\n\n**Detailed Explanation:**\n\n1. Initialize an array `glass_levels` of size 100 to represent the champagne levels in each glass. Set the first glass\'s level to the poured amount of champagne.\n2. Iterate through each row up to the specified row (`query_row`):\n - For each row:\n a. Initialize an array `next_levels` to store the champagne levels for the next row of glasses.\n b. Iterate through each glass in the current row (`cur_row`):\n - Calculate the overflow by finding the excess amount of champagne in the current glass beyond capacity.\n - Distribute this overflow equally to the current glass and the adjacent glass on the right (`cur_glass + 1`).\n c. Update `glass_levels` with the champagne levels for the next row, which are stored in the `next_levels` array.\n3. After iterating through all the rows, return the minimum value between 1.0 and the champagne level in the specified glass (`query_glass`). This ensures the value does not exceed 1.0 (representing a full glass).\n\n## Complexity\n\nTime Complexity: O(1)\nLooks like O(n^2) but this is fixed with 100 which means it doesn\'t grow, so we can say O(1)\n\nSpace Complexity: O(1)\nThe same reason above.\n\n```python []\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n glass_levels = [0.0] * 100\n glass_levels[0] = poured\n\n for cur_row in range(query_row):\n next_levels = [0.0] * 100\n\n for cur_glass in range(cur_row + 1):\n overflow = max(0, (glass_levels[cur_glass] - 1.0) / 2.0)\n next_levels[cur_glass] += overflow\n next_levels[cur_glass + 1] += overflow\n \n glass_levels = next_levels\n \n return min(1.0, glass_levels[query_glass]) \n```\n```javascript []\n/**\n * @param {number} poured\n * @param {number} query_row\n * @param {number} query_glass\n * @return {number}\n */\nvar champagneTower = function(poured, query_row, query_glass) {\n let glassLevels = Array(100).fill(0.0);\n glassLevels[0] = poured;\n\n for (let curRow = 0; curRow < query_row; curRow++) {\n let nextLevels = Array(100).fill(0.0);\n\n for (let curGlass = 0; curGlass <= curRow; curGlass++) {\n let overflow = Math.max(0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return Math.min(1.0, glassLevels[query_glass]); \n};\n```\n```java []\nclass Solution {\n public double champagneTower(int poured, int query_row, int query_glass) {\n double[] glassLevels = new double[100];\n glassLevels[0] = poured;\n\n for (int curRow = 0; curRow < query_row; curRow++) {\n double[] nextLevels = new double[100];\n\n for (int curGlass = 0; curGlass <= curRow; curGlass++) {\n double overflow = Math.max(0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return Math.min(1.0, glassLevels[query_glass]); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n double champagneTower(int poured, int query_row, int query_glass) {\n vector<double> glassLevels(100, 0.0);\n glassLevels[0] = poured;\n\n for (int curRow = 0; curRow < query_row; curRow++) {\n vector<double> nextLevels(100, 0.0);\n\n for (int curGlass = 0; curGlass <= curRow; curGlass++) {\n double overflow = max(0.0, (glassLevels[curGlass] - 1.0) / 2.0);\n nextLevels[curGlass] += overflow;\n nextLevels[curGlass + 1] += overflow;\n }\n\n glassLevels = nextLevels;\n }\n\n return min(1.0, glassLevels[query_glass]); \n }\n};\n```\n\n\n---\n\n\n\nThank you for reading such a long post. Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 25th, 2023\nhttps://leetcode.com/problems/find-the-difference/solutions/4086661/video-how-we-think-about-a-solution-python-javascript-java-c/\n\nHave a nice day!\n | 30 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Python 1-liner. Functional programming. | champagne-tower | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/champagne-tower/editorial/?envType=daily-question&envId=2023-09-24) but shorter and functional.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is query_row`.\n\n# Code\nImperative multi-liner:\n```python\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n row = (poured,)\n\n for _ in range(query_row):\n xs = chain((0,), (max(x - 1, 0) / 2 for x in row), (0,))\n row = map(sum, pairwise(xs))\n \n return min(list(row)[query_glass], 1)\n\n\n```\n\nDeclarative and Functional 1-liner:\n```python\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min(list(reduce(\n lambda row, _: map(sum, pairwise(\n chain((0,), (max(x - 1, 0) / 2 for x in row), (0,))\n )),\n range(query_row),\n (poured,),\n ))[query_glass], 1)\n\n\n``` | 1 | We stack glasses in a pyramid, where the **first** row has `1` glass, the **second** row has `2` glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.
Now after pouring some non-negative integer cups of champagne, return how full the `jth` glass in the `ith` row is (both `i` and `j` are 0-indexed.)
**Example 1:**
**Input:** poured = 1, query\_row = 1, query\_glass = 1
**Output:** 0.00000
**Explanation:** We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
**Example 2:**
**Input:** poured = 2, query\_row = 1, query\_glass = 1
**Output:** 0.50000
**Explanation:** We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
**Example 3:**
**Input:** poured = 100000009, query\_row = 33, query\_glass = 17
**Output:** 1.00000
**Constraints:**
* `0 <= poured <= 109`
* `0 <= query_glass <= query_row < 100` | null |
Python 1-liner. Functional programming. | champagne-tower | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/champagne-tower/editorial/?envType=daily-question&envId=2023-09-24) but shorter and functional.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is query_row`.\n\n# Code\nImperative multi-liner:\n```python\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n row = (poured,)\n\n for _ in range(query_row):\n xs = chain((0,), (max(x - 1, 0) / 2 for x in row), (0,))\n row = map(sum, pairwise(xs))\n \n return min(list(row)[query_glass], 1)\n\n\n```\n\nDeclarative and Functional 1-liner:\n```python\nclass Solution:\n def champagneTower(self, poured: int, query_row: int, query_glass: int) -> float:\n return min(list(reduce(\n lambda row, _: map(sum, pairwise(\n chain((0,), (max(x - 1, 0) / 2 for x in row), (0,))\n )),\n range(query_row),\n (poured,),\n ))[query_glass], 1)\n\n\n``` | 1 | You are given an array `routes` representing bus routes where `routes[i]` is a bus route that the `ith` bus repeats forever.
* For example, if `routes[0] = [1, 5, 7]`, this means that the `0th` bus travels in the sequence `1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ...` forever.
You will start at the bus stop `source` (You are not on any bus initially), and you want to go to the bus stop `target`. You can travel between bus stops by buses only.
Return _the least number of buses you must take to travel from_ `source` _to_ `target`. Return `-1` if it is not possible.
**Example 1:**
**Input:** routes = \[\[1,2,7\],\[3,6,7\]\], source = 1, target = 6
**Output:** 2
**Explanation:** The best strategy is take the first bus to the bus stop 7, then take the second bus to the bus stop 6.
**Example 2:**
**Input:** routes = \[\[7,12\],\[4,5,15\],\[6\],\[15,19\],\[9,12,13\]\], source = 15, target = 12
**Output:** -1
**Constraints:**
* `1 <= routes.length <= 500`.
* `1 <= routes[i].length <= 105`
* All the values of `routes[i]` are **unique**.
* `sum(routes[i].length) <= 105`
* `0 <= routes[i][j] < 106`
* `0 <= source, target < 106` | null |
Solution | minimum-swaps-to-make-sequences-increasing | 1 | 1 | ```C++ []\nconst int ZERO = []() {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n return 0;\n}();\nclass Solution {\npublic:\n int minSwap(vector<int>& a, vector<int>& b) {\n int n = static_cast<int>(a.size());\n vector<int> swaps(n, n);\n vector<int> noswaps(n, n);\n swaps[0] = 1;\n noswaps[0] = 0;\n for (int i = 1; i < n; ++i) {\n if (a[i] > a[i-1] && b[i] > b[i-1]) {\n swaps[i] = swaps[i-1] + 1;\n noswaps[i] = noswaps[i-1];\n }\n if (a[i] > b[i-1] && b[i] > a[i-1]) {\n swaps[i] = min(swaps[i], noswaps[i-1] + 1);\n noswaps[i] = min(noswaps[i], swaps[i-1]);\n }\n }\n return min(swaps.back(), noswaps.back());\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y):\n ans += min(sm, lg)\n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n```\n\n```Java []\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n int swapRecord = 1, fixRecord = 0;\n for (int i = 1; i < A.length; i++) {\n if (A[i - 1] >= B[i] || B[i - 1] >= A[i]) {\n swapRecord++;\n } else if (A[i - 1] >= A[i] || B[i - 1] >= B[i]) {\n int temp = swapRecord;\n swapRecord = fixRecord + 1;\n fixRecord = temp;\n } else {\n int min = Math.min(swapRecord, fixRecord);\n swapRecord = min + 1;\n fixRecord = min;\n }\n }\n return Math.min(swapRecord, fixRecord);\n }\n}\n```\n | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Solution | minimum-swaps-to-make-sequences-increasing | 1 | 1 | ```C++ []\nconst int ZERO = []() {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n return 0;\n}();\nclass Solution {\npublic:\n int minSwap(vector<int>& a, vector<int>& b) {\n int n = static_cast<int>(a.size());\n vector<int> swaps(n, n);\n vector<int> noswaps(n, n);\n swaps[0] = 1;\n noswaps[0] = 0;\n for (int i = 1; i < n; ++i) {\n if (a[i] > a[i-1] && b[i] > b[i-1]) {\n swaps[i] = swaps[i-1] + 1;\n noswaps[i] = noswaps[i-1];\n }\n if (a[i] > b[i-1] && b[i] > a[i-1]) {\n swaps[i] = min(swaps[i], noswaps[i-1] + 1);\n noswaps[i] = min(noswaps[i], swaps[i-1]);\n }\n }\n return min(swaps.back(), noswaps.back());\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y):\n ans += min(sm, lg)\n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n```\n\n```Java []\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n int swapRecord = 1, fixRecord = 0;\n for (int i = 1; i < A.length; i++) {\n if (A[i - 1] >= B[i] || B[i - 1] >= A[i]) {\n swapRecord++;\n } else if (A[i - 1] >= A[i] || B[i - 1] >= B[i]) {\n int temp = swapRecord;\n swapRecord = fixRecord + 1;\n fixRecord = temp;\n } else {\n int min = Math.min(swapRecord, fixRecord);\n swapRecord = min + 1;\n fixRecord = min;\n }\n }\n return Math.min(swapRecord, fixRecord);\n }\n}\n```\n | 1 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
✅ [Python3] DP Solution O(n) Time | minimum-swaps-to-make-sequences-increasing | 0 | 1 | ```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [[-1]*2 for i in range(len(nums1))]\n \n def solve(prev1, prev2, i, swaped):\n if i >= len(nums1): return 0\n if dp[i][swaped] != -1: return dp[i][swaped]\n \n ans = 2**31\n \n # No Swap\n if nums1[i] > prev1 and nums2[i] > prev2:\n ans = solve(nums1[i], nums2[i], i+1, 0) \n \n # Swap\n if nums1[i] > prev2 and nums2[i] > prev1:\n ans = min(ans, 1 + solve(nums2[i], nums1[i], i+1, 1)) \n \n dp[i][swaped] = ans\n return ans\n \n return solve(-1, -1, 0, 0) \n``` | 4 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
✅ [Python3] DP Solution O(n) Time | minimum-swaps-to-make-sequences-increasing | 0 | 1 | ```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [[-1]*2 for i in range(len(nums1))]\n \n def solve(prev1, prev2, i, swaped):\n if i >= len(nums1): return 0\n if dp[i][swaped] != -1: return dp[i][swaped]\n \n ans = 2**31\n \n # No Swap\n if nums1[i] > prev1 and nums2[i] > prev2:\n ans = solve(nums1[i], nums2[i], i+1, 0) \n \n # Swap\n if nums1[i] > prev2 and nums2[i] > prev1:\n ans = min(ans, 1 + solve(nums2[i], nums1[i], i+1, 1)) \n \n dp[i][swaped] = ans\n return ans\n \n return solve(-1, -1, 0, 0) \n``` | 4 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
[Python 3] O(n) Time, O(1) Space, Detailed Explanation | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are 3 different cases to consider when looking at the border between two pairs of numbers (a pair being numbers in nums1 and nums2 with the same index):\n1. The numbers are increasing, and if either pair was flipped they would still be increasing (ex. nums1 = [1, 3] and nums2 = [2, 4])\n2. The numbers are increasing, but if either pair flipped they would not be increasing (ex. nums1 = [1, 2] and nums2 = [3, 4])\n3. The numbers are not increasing (since there is a guaranteed solution this means that if either pair is flipped they will be increasing, ex. nums1 = [6, 5] and nums2 = [4, 7])\n\nTwo observations that lead to this approach:\n1. In the first case above, these borders can be used to divide the problem into independent subproblems, as the chosen flips of each will not affect the other\n2. Within each subsection, Every boundary between numbers now falls into the second or third case above. As a result, there are only two sets of flips that are valid, and they are mirrors of each other.\n\nIf the second observation is confusing, try drawing out some examples to build intuition. Think of every flippable pair as being "aligned" a certain direction and all pairs needing to be "aligned" the same way for both arrays to be increasing\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThese two observations give us a relatively straightforward solution:\n1. Divide the problem into sections on borders where the arrays are increasing no matter whether the numbers are flipped or not\n2. In each subsection, take a greedy approach and flip any pair of numbers when necessary, counting the number of flips needed to make the subsection strictly increasing.\n3. After making all necessary flips in a subsection, add the count to the total. Note that the exact opposite set of flips would also results in an increasing subsection, so the real count is min(count, length of subsection - count)\n\nThe code below keeps track of each subsection as it goes, allowing the algorithm to be completed in one pass and without any extra memory.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n sectionSwaps = 0\n sectionLength = 1\n minSwaps = 0\n for x in range(0, len(nums1) - 1):\n # If the end of the subsection has been reached,\n # add the minimum number of steps to the total\n if max(nums1[x], nums2[x]) < min(nums1[x + 1], nums2[x + 1]):\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n sectionLength = 1\n sectionSwaps = 0\n continue\n sectionLength += 1\n # Flip the next pair if it does not align with the current one\n if nums1[x] >= nums1[x + 1] or nums2[x] >= nums2[x + 1]:\n sectionSwaps += 1\n temp = nums1[x + 1]\n nums1[x + 1] = nums2[x + 1]\n nums2[x + 1] = temp\n # The last subsection is not handled in the for loop\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n return minSwaps\n``` | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
[Python 3] O(n) Time, O(1) Space, Detailed Explanation | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are 3 different cases to consider when looking at the border between two pairs of numbers (a pair being numbers in nums1 and nums2 with the same index):\n1. The numbers are increasing, and if either pair was flipped they would still be increasing (ex. nums1 = [1, 3] and nums2 = [2, 4])\n2. The numbers are increasing, but if either pair flipped they would not be increasing (ex. nums1 = [1, 2] and nums2 = [3, 4])\n3. The numbers are not increasing (since there is a guaranteed solution this means that if either pair is flipped they will be increasing, ex. nums1 = [6, 5] and nums2 = [4, 7])\n\nTwo observations that lead to this approach:\n1. In the first case above, these borders can be used to divide the problem into independent subproblems, as the chosen flips of each will not affect the other\n2. Within each subsection, Every boundary between numbers now falls into the second or third case above. As a result, there are only two sets of flips that are valid, and they are mirrors of each other.\n\nIf the second observation is confusing, try drawing out some examples to build intuition. Think of every flippable pair as being "aligned" a certain direction and all pairs needing to be "aligned" the same way for both arrays to be increasing\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThese two observations give us a relatively straightforward solution:\n1. Divide the problem into sections on borders where the arrays are increasing no matter whether the numbers are flipped or not\n2. In each subsection, take a greedy approach and flip any pair of numbers when necessary, counting the number of flips needed to make the subsection strictly increasing.\n3. After making all necessary flips in a subsection, add the count to the total. Note that the exact opposite set of flips would also results in an increasing subsection, so the real count is min(count, length of subsection - count)\n\nThe code below keeps track of each subsection as it goes, allowing the algorithm to be completed in one pass and without any extra memory.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n sectionSwaps = 0\n sectionLength = 1\n minSwaps = 0\n for x in range(0, len(nums1) - 1):\n # If the end of the subsection has been reached,\n # add the minimum number of steps to the total\n if max(nums1[x], nums2[x]) < min(nums1[x + 1], nums2[x + 1]):\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n sectionLength = 1\n sectionSwaps = 0\n continue\n sectionLength += 1\n # Flip the next pair if it does not align with the current one\n if nums1[x] >= nums1[x + 1] or nums2[x] >= nums2[x + 1]:\n sectionSwaps += 1\n temp = nums1[x + 1]\n nums1[x + 1] = nums2[x + 1]\n nums2[x + 1] = temp\n # The last subsection is not handled in the for loop\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n return minSwaps\n``` | 1 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
[Python3] two counters | minimum-swaps-to-make-sequences-increasing | 0 | 1 | Algo \nThis solution is different from the mainstream solutions. Given that we know a solution exists, if we put larger of `A[i]` and `B[i]` to `A` and smaller of `A[i]` and `B[i]` to `B`. The resulting sequence satisfies the requirement of increasing `A` and increasing `B`. In the spirit of this idea, we can count the occurrence of `A[i] < B[i]` in `sm` and count the occurrence of `A[i] > B[i]` in `lg`. The minimum of `sm` and `lg` gives enough swap to get two increasing sequences. The issue is that it is more than enough as there can be cases where `max(A[i-1], B[i-1]) < min(A[i], B[i])`. In such a case, we treat the array as two subarrays ending at `i-1` and starting at `i`. The sum of all such pieces gives the correct answer. \n\nImplementation (72ms, 99.18%)\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y): # prev max < current min\n ans += min(sm, lg) # update answer & reset \n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n``` | 9 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
[Python3] two counters | minimum-swaps-to-make-sequences-increasing | 0 | 1 | Algo \nThis solution is different from the mainstream solutions. Given that we know a solution exists, if we put larger of `A[i]` and `B[i]` to `A` and smaller of `A[i]` and `B[i]` to `B`. The resulting sequence satisfies the requirement of increasing `A` and increasing `B`. In the spirit of this idea, we can count the occurrence of `A[i] < B[i]` in `sm` and count the occurrence of `A[i] > B[i]` in `lg`. The minimum of `sm` and `lg` gives enough swap to get two increasing sequences. The issue is that it is more than enough as there can be cases where `max(A[i-1], B[i-1]) < min(A[i], B[i])`. In such a case, we treat the array as two subarrays ending at `i-1` and starting at `i`. The sum of all such pieces gives the correct answer. \n\nImplementation (72ms, 99.18%)\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y): # prev max < current min\n ans += min(sm, lg) # update answer & reset \n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n``` | 9 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Clear Python o(n) Time, o(n) Space solution with comments | minimum-swaps-to-make-sequences-increasing | 0 | 1 | bottom up dp python solution with comments\n\nTime: o(n)\nSpace: o(n)\n\n\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n \n n = len(A)\n \n # In this problem, we have two states that we need to keep track at element i; \n # what happens if we swap or do not swap at i?\n \n # min number of swaps to get ascending order if we SWAP at i \n swap = [0] * n\n \n # min number of swaps to get ascending order if we do NOT SWAP at i\n noswap = [0] * n\n \n # base case: swapping 0th element\n swap[0] = 1\n\n for i in range(1, n):\n strictly_increasing = A[i] > A[i-1] and B[i] > B[i-1]\n strictly_xincreasing = A[i] > B[i-1] and B[i] > A[i-1]\n \n # we can swap here, but we also do not have too\n if strictly_increasing and strictly_xincreasing: \n \n # if we decide to swap at i, we can consider the state of either swapping or not swapping i-1, since doing either\n # will not break out strictly increasing for either array rule\n swap[i] = min(noswap[i-1], swap[i-1]) + 1\n \n # we chose not to swap at i, so we can consider states if we swap at i - 1 or not swap, since again we will not break the strictly increasing rule\n noswap[i] = min(noswap[i-1], swap[i-1])\n \n \n # we can not swap at i, since we know that A[i] is not greater than B[i-1], or that B[i] is not greater than A[i-1]\n elif strictly_increasing:\n \n \n \n # if we swap at i, then to keep increasing condition, we must also swap at i-1, we are essentially just swapping both i and i-1 and get the same thing \n swap[i] = swap[i-1] + 1\n \n # if we do not swap at i, then we must also chose to not swap at i-1 to keep the problem conditions true\n noswap[i] = noswap[i-1]\n \n \n # we must swap, since A[i] is not greater than A[i-1], or B[i] is not greater than B[i-1]\n # but we know that A[i] > B[i-1] and that B[i] > A[i-1]\n elif strictly_xincreasing:\n\n # if we swap at i, then we must have not swapped at i-1\n swap[i] = noswap[i-1] + 1\n \n # if we do not swap at i, then we must have swapped at i-1 for the problem conditions to be true\n noswap[i] = swap[i-1]\n \n \n \n # take min of both state paths to see who holds the better result\n return min(noswap[n-1], swap[n-1])\n\n\n``` | 11 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Clear Python o(n) Time, o(n) Space solution with comments | minimum-swaps-to-make-sequences-increasing | 0 | 1 | bottom up dp python solution with comments\n\nTime: o(n)\nSpace: o(n)\n\n\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n \n n = len(A)\n \n # In this problem, we have two states that we need to keep track at element i; \n # what happens if we swap or do not swap at i?\n \n # min number of swaps to get ascending order if we SWAP at i \n swap = [0] * n\n \n # min number of swaps to get ascending order if we do NOT SWAP at i\n noswap = [0] * n\n \n # base case: swapping 0th element\n swap[0] = 1\n\n for i in range(1, n):\n strictly_increasing = A[i] > A[i-1] and B[i] > B[i-1]\n strictly_xincreasing = A[i] > B[i-1] and B[i] > A[i-1]\n \n # we can swap here, but we also do not have too\n if strictly_increasing and strictly_xincreasing: \n \n # if we decide to swap at i, we can consider the state of either swapping or not swapping i-1, since doing either\n # will not break out strictly increasing for either array rule\n swap[i] = min(noswap[i-1], swap[i-1]) + 1\n \n # we chose not to swap at i, so we can consider states if we swap at i - 1 or not swap, since again we will not break the strictly increasing rule\n noswap[i] = min(noswap[i-1], swap[i-1])\n \n \n # we can not swap at i, since we know that A[i] is not greater than B[i-1], or that B[i] is not greater than A[i-1]\n elif strictly_increasing:\n \n \n \n # if we swap at i, then to keep increasing condition, we must also swap at i-1, we are essentially just swapping both i and i-1 and get the same thing \n swap[i] = swap[i-1] + 1\n \n # if we do not swap at i, then we must also chose to not swap at i-1 to keep the problem conditions true\n noswap[i] = noswap[i-1]\n \n \n # we must swap, since A[i] is not greater than A[i-1], or B[i] is not greater than B[i-1]\n # but we know that A[i] > B[i-1] and that B[i] > A[i-1]\n elif strictly_xincreasing:\n\n # if we swap at i, then we must have not swapped at i-1\n swap[i] = noswap[i-1] + 1\n \n # if we do not swap at i, then we must have swapped at i-1 for the problem conditions to be true\n noswap[i] = swap[i-1]\n \n \n \n # take min of both state paths to see who holds the better result\n return min(noswap[n-1], swap[n-1])\n\n\n``` | 11 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Mark my solution | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n nums1.append(float("-inf"))\n nums2.append(float("-inf"))\n f = [0] * 2\n for i in range(n):\n n1_1, n2_1, n1, n2 = nums1[i - 1], nums2[i - 1], nums1[i], nums2[i]\n old_0, old_1 = f\n incr = 1 if n1 != n2 else 0\n if n1_1 >= n1 or n2_1 >= n2:\n f[0] = old_1 \n f[1] = old_0 + incr\n continue\n f[1] += incr\n if n2_1 >= n1 or n1_1 >= n2:\n continue \n if f[0] > old_1:\n f[0] = old_1\n if f[1] > old_0 + incr:\n f[1] = old_0 + incr\n return f[0] if f[0] < f[1] else f[1]\n\n``` | 0 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Mark my solution | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n nums1.append(float("-inf"))\n nums2.append(float("-inf"))\n f = [0] * 2\n for i in range(n):\n n1_1, n2_1, n1, n2 = nums1[i - 1], nums2[i - 1], nums1[i], nums2[i]\n old_0, old_1 = f\n incr = 1 if n1 != n2 else 0\n if n1_1 >= n1 or n2_1 >= n2:\n f[0] = old_1 \n f[1] = old_0 + incr\n continue\n f[1] += incr\n if n2_1 >= n1 or n1_1 >= n2:\n continue \n if f[0] > old_1:\n f[0] = old_1\n if f[1] > old_0 + incr:\n f[1] = old_0 + incr\n return f[0] if f[0] < f[1] else f[1]\n\n``` | 0 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
801: Solution with step by step explanation | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nBefore we start processing the arrays, we need to initialize our DP arrays:\n\n```\nkeep = [float(\'inf\')] * n \nswap = [float(\'inf\')] * n \nkeep[0] = 0 \nswap[0] = 1 \n```\nWe will loop over each index starting from 1 (since we have already considered the 0th index in initialization):\n\n```\nfor i in range(1, n):\n```\nWithin the loop, we have to make decisions based on the current and previous elements:\n\n```\nif nums1[i] > nums1[i - 1] and nums2[i] > nums2[i - 1]:\n keep[i] = keep[i - 1]\n swap[i] = swap[i - 1] + 1\n\nif nums1[i] > nums2[i - 1] and nums2[i] > nums1[i - 1]:\n keep[i] = min(keep[i], swap[i - 1])\n swap[i] = min(swap[i], keep[i - 1] + 1)\n```\nAfter the loop, the answer will be the minimum value at the last index of either keep or swap array:\n\n```\nreturn min(keep[-1], swap[-1])\n```\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n\n keep = [float(\'inf\')] * n\n swap = [float(\'inf\')] * n\n\n keep[0] = 0\n swap[0] = 1\n\n for i in range(1, n):\n if nums1[i] > nums1[i - 1] and nums2[i] > nums2[i - 1]:\n keep[i] = keep[i - 1]\n swap[i] = swap[i - 1] + 1\n if nums1[i] > nums2[i - 1] and nums2[i] > nums1[i - 1]:\n keep[i] = min(keep[i], swap[i - 1])\n swap[i] = min(swap[i], keep[i - 1] + 1)\n\n return min(keep[-1], swap[-1])\n\n``` | 0 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
801: Solution with step by step explanation | minimum-swaps-to-make-sequences-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nBefore we start processing the arrays, we need to initialize our DP arrays:\n\n```\nkeep = [float(\'inf\')] * n \nswap = [float(\'inf\')] * n \nkeep[0] = 0 \nswap[0] = 1 \n```\nWe will loop over each index starting from 1 (since we have already considered the 0th index in initialization):\n\n```\nfor i in range(1, n):\n```\nWithin the loop, we have to make decisions based on the current and previous elements:\n\n```\nif nums1[i] > nums1[i - 1] and nums2[i] > nums2[i - 1]:\n keep[i] = keep[i - 1]\n swap[i] = swap[i - 1] + 1\n\nif nums1[i] > nums2[i - 1] and nums2[i] > nums1[i - 1]:\n keep[i] = min(keep[i], swap[i - 1])\n swap[i] = min(swap[i], keep[i - 1] + 1)\n```\nAfter the loop, the answer will be the minimum value at the last index of either keep or swap array:\n\n```\nreturn min(keep[-1], swap[-1])\n```\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n n = len(nums1)\n\n keep = [float(\'inf\')] * n\n swap = [float(\'inf\')] * n\n\n keep[0] = 0\n swap[0] = 1\n\n for i in range(1, n):\n if nums1[i] > nums1[i - 1] and nums2[i] > nums2[i - 1]:\n keep[i] = keep[i - 1]\n swap[i] = swap[i - 1] + 1\n if nums1[i] > nums2[i - 1] and nums2[i] > nums1[i - 1]:\n keep[i] = min(keep[i], swap[i - 1])\n swap[i] = min(swap[i], keep[i - 1] + 1)\n\n return min(keep[-1], swap[-1])\n\n``` | 0 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
topological sort | find-eventual-safe-states | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nstart with nodes that have no outgoing edges.These are terminal nodes.\n\n\n# Approach\n```\n1.mark all nodes with no outgoing edges. --->term\n2.store the count of outgoing edges from each node.-->d1\n3.create an adjacency list with reversed directed edges -->d\n4. start from terminal edges and apply topological sort.\n5. reduce the outdegree of nodes every time its parent appears.this is done from the adjacency list d .\n6. when the outdegree becomes 0. add the node to term(ans)., and to the queue. outdegree 0 means that starting from this node all the paths lead to a safe node.\n7. sort the answer as asked by the problem\n```\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:O(n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n d=defaultdict(list)\n term =set() #set of nodes in ans \n n =len(graph)\n d1=defaultdict(int)\n for i in range(n):\n c=0\n for j in graph[i]:\n c+=1\n d[j].append(i) #reversing the direction of the edge , to find from which edges we can reach to a particular edge \n d1[i]=c\n if c==0: #if the node is a terminal node \n term.add(i)\n \n \n ans =[]\n ret=[]\n \n q=list(term)\n while(q):\n x=q.pop(0)\n for node in d[x]:\n if node not in term:\n d1[node]-=1 #if all the paths starting from here have reached to a safe node \n if d1[node]==0:\n q.append(node)\n term.add(node)\n ans =list(term)\n ans.sort() #answer to be sorted \n return ans \n``` | 3 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
topological sort | find-eventual-safe-states | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nstart with nodes that have no outgoing edges.These are terminal nodes.\n\n\n# Approach\n```\n1.mark all nodes with no outgoing edges. --->term\n2.store the count of outgoing edges from each node.-->d1\n3.create an adjacency list with reversed directed edges -->d\n4. start from terminal edges and apply topological sort.\n5. reduce the outdegree of nodes every time its parent appears.this is done from the adjacency list d .\n6. when the outdegree becomes 0. add the node to term(ans)., and to the queue. outdegree 0 means that starting from this node all the paths lead to a safe node.\n7. sort the answer as asked by the problem\n```\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:O(n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n d=defaultdict(list)\n term =set() #set of nodes in ans \n n =len(graph)\n d1=defaultdict(int)\n for i in range(n):\n c=0\n for j in graph[i]:\n c+=1\n d[j].append(i) #reversing the direction of the edge , to find from which edges we can reach to a particular edge \n d1[i]=c\n if c==0: #if the node is a terminal node \n term.add(i)\n \n \n ans =[]\n ret=[]\n \n q=list(term)\n while(q):\n x=q.pop(0)\n for node in d[x]:\n if node not in term:\n d1[node]-=1 #if all the paths starting from here have reached to a safe node \n if d1[node]==0:\n q.append(node)\n term.add(node)\n ans =list(term)\n ans.sort() #answer to be sorted \n return ans \n``` | 3 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Python3 Solution | find-eventual-safe-states | 0 | 1 | \n```\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n=len(graph)\n safe={}\n ans=[]\n def dfs(i):\n if i in safe:\n return safe[i]\n\n safe[i]=False\n for nei in graph[i]:\n if not dfs(nei):\n return safe[i]\n\n safe[i]=True\n return safe[i]\n\n for i in range(n):\n if dfs(i):\n ans.append(i)\n\n return ans \n``` | 16 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python3 Solution | find-eventual-safe-states | 0 | 1 | \n```\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n=len(graph)\n safe={}\n ans=[]\n def dfs(i):\n if i in safe:\n return safe[i]\n\n safe[i]=False\n for nei in graph[i]:\n if not dfs(nei):\n return safe[i]\n\n safe[i]=True\n return safe[i]\n\n for i in range(n):\n if dfs(i):\n ans.append(i)\n\n return ans \n``` | 16 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Python short and clean. Topological sort. Functional programming. | find-eventual-safe-states | 0 | 1 | # Complexity\n- Time complexity: $$O(n + e)$$\n\n- Space complexity: $$O(n + e)$$\n\nwhere,\n`n is number of nodes in graph`,\n`e is number of edges in graph`.\n\n# Code\n```python\nclass Solution:\n def eventualSafeNodes(self, graph: list[list[int]]) -> list[int]:\n DiGraph = list[list[int]]\n\n def flip_dir(g: DiGraph) -> DiGraph:\n r_graph = [[] for _ in range(len(graph))]\n r_edges = ((v, u) for u, vs in enumerate(graph) for v in vs)\n for u, v in r_edges: r_graph[u].append(v)\n return r_graph\n \n safeness = [False] * len(graph)\n out_degrees = {u: len(vs) for u, vs in enumerate(graph)}\n\n r_graph = flip_dir(graph)\n\n terminals = (u for u, d in out_degrees.items() if d == 0)\n frontier = deque(terminals)\n\n while frontier:\n u = frontier.popleft()\n safeness[u] = True\n for v in r_graph[u]: out_degrees[v] -= 1\n frontier.extend(filterfalse(out_degrees.get, r_graph[u]))\n \n return [u for u, is_safe in enumerate(safeness) if is_safe]\n\n\n``` | 1 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python short and clean. Topological sort. Functional programming. | find-eventual-safe-states | 0 | 1 | # Complexity\n- Time complexity: $$O(n + e)$$\n\n- Space complexity: $$O(n + e)$$\n\nwhere,\n`n is number of nodes in graph`,\n`e is number of edges in graph`.\n\n# Code\n```python\nclass Solution:\n def eventualSafeNodes(self, graph: list[list[int]]) -> list[int]:\n DiGraph = list[list[int]]\n\n def flip_dir(g: DiGraph) -> DiGraph:\n r_graph = [[] for _ in range(len(graph))]\n r_edges = ((v, u) for u, vs in enumerate(graph) for v in vs)\n for u, v in r_edges: r_graph[u].append(v)\n return r_graph\n \n safeness = [False] * len(graph)\n out_degrees = {u: len(vs) for u, vs in enumerate(graph)}\n\n r_graph = flip_dir(graph)\n\n terminals = (u for u, d in out_degrees.items() if d == 0)\n frontier = deque(terminals)\n\n while frontier:\n u = frontier.popleft()\n safeness[u] = True\n for v in r_graph[u]: out_degrees[v] -= 1\n frontier.extend(filterfalse(out_degrees.get, r_graph[u]))\n \n return [u for u, is_safe in enumerate(safeness) if is_safe]\n\n\n``` | 1 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
BEATS 99.12% IN SPACE OPTIMIZATION || EASY PYTHON SOLUTION | find-eventual-safe-states | 0 | 1 | # Code\n```\nclass Solution:\n def soln(self,node,graph,lst,visited):\n visited[node]=0\n ans=1\n for i in graph[node]:\n if visited[i]==-1:\n ans&=self.soln(i,graph,lst,visited)\n else:\n ans&=visited[i]\n # print(node,ans)\n visited[node]=ans\n if ans==1:\n lst.append(node)\n return 1\n return 0\n\n\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n=len(graph)\n visited=[-1]*n\n lst=[]\n for i in range(n):\n if visited[i]==-1:\n self.soln(i,graph,lst,visited)\n lst.sort()\n return lst\n``` | 1 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
BEATS 99.12% IN SPACE OPTIMIZATION || EASY PYTHON SOLUTION | find-eventual-safe-states | 0 | 1 | # Code\n```\nclass Solution:\n def soln(self,node,graph,lst,visited):\n visited[node]=0\n ans=1\n for i in graph[node]:\n if visited[i]==-1:\n ans&=self.soln(i,graph,lst,visited)\n else:\n ans&=visited[i]\n # print(node,ans)\n visited[node]=ans\n if ans==1:\n lst.append(node)\n return 1\n return 0\n\n\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n=len(graph)\n visited=[-1]*n\n lst=[]\n for i in range(n):\n if visited[i]==-1:\n self.soln(i,graph,lst,visited)\n lst.sort()\n return lst\n``` | 1 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
🔥Best [C++,JAVA,🐍] Code🌟 || 🔥Commented || DFS💯 | find-eventual-safe-states | 1 | 1 | ### Connect with me on LinkedIn : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Intuition\n#### The code is based on the concept of finding eventual safe nodes in a directed graph. Here\'s the intuition behind the approach:\n\n1. The function `DFS` performs a depth-first search starting from a node `s` in the graph.\n2. The `visited` vector keeps track of nodes that have been visited during the DFS traversal.\n3. The `dfsVisited` vector keeps track of nodes that are visited in the current DFS path.\n4. The `checkCycle` vector is used to mark nodes that are part of a cycle.\n5. Initially, all nodes are marked as not visited (`visited` and `dfsVisited` vectors are `false`).\n6. For each node in the graph, if it has not been visited, the DFS function is called.\n7. During the DFS traversal, if an adjacent node is not visited, the DFS function is recursively called for that node.\n8. If the recursive call returns `true`, it means that a cycle is detected, and the current node `s` is marked as part of a cycle in the `checkCycle` vector.\n9. If an adjacent node is already visited and also part of the current DFS path (`dfsVisited` is `true`), it indicates a cycle, and the current node `s` is marked as part of a cycle in the `checkCycle` vector.\n10. After exploring all adjacent nodes, the current node `s` is marked as not visited in the current DFS path (`dfsVisited[s] = false`).\n11. Finally, the `eventualSafeNodes` function iterates over all nodes and adds the nodes that are not part of any cycle (marked as `false` in the `checkCycle` vector) to the `ans` vector.\n12. The `ans` vector is returned as the eventual safe nodes in the graph.\n\n#### The main idea is to perform a DFS traversal and detect cycles in the graph. Nodes that are not part of any cycle are considered eventual safe nodes. The `dfsVisited` vector is used to keep track of the current path and detect cycles. The `checkCycle` vector is used to mark nodes that are part of a cycle.\n# Code\n## An Upvote will be encouraging as it motivates me to post more such solutions\uD83E\uDD17\n```C++ []\nclass Solution {\npublic:\n bool DFS(int s, vector<vector<int>>& graph, vector<bool>& visited, vector<bool>& dfsVisited, vector<bool>& checkCycle) {\n visited[s] = dfsVisited[s] = true; // Mark the current node as visited and in the current DFS path\n for (auto it : graph[s]) {\n if (!visited[it]) { // If the adjacent node is not visited\n if (DFS(it, graph, visited, dfsVisited, checkCycle))\n return checkCycle[s] = true; // If a cycle is detected, mark the current node as part of a cycle\n } else if (dfsVisited[it]) { // If the adjacent node is visited and in the current DFS path\n return checkCycle[s] = true; // A cycle is detected, mark the current node as part of a cycle\n }\n }\n dfsVisited[s] = false; // Mark the current node as not visited in the current DFS path\n return false; // No cycle detected, current node is safe\n }\n \n vector<int> eventualSafeNodes(vector<vector<int>>& graph) {\n int v = graph.size();\n vector<bool> visited(v), dfsVisited(v), checkCycle(v);\n vector<int> ans;\n for (int i = 0; i < v; i++) {\n if (!visited[i])\n DFS(i, graph, visited, dfsVisited, checkCycle);\n }\n for (int i = 0; i < v; i++) {\n if (!checkCycle[i])\n ans.push_back(i); // Add the nodes that are not part of any cycle (eventual safe nodes) to the result\n }\n return ans;\n }\n};\n```\n```JAVA []\nclass Solution {\n public boolean DFS(int s, List<List<Integer>> graph, boolean[] visited, boolean[] dfsVisited, boolean[] checkCycle) {\n visited[s] = dfsVisited[s] = true; // Mark the current node as visited and in the current DFS path\n for (int it : graph.get(s)) {\n if (!visited[it]) { // If the adjacent node is not visited\n if (DFS(it, graph, visited, dfsVisited, checkCycle))\n return checkCycle[s] = true; // If a cycle is detected, mark the current node as part of a cycle\n } else if (dfsVisited[it]) { // If the adjacent node is visited and in the current DFS path\n return checkCycle[s] = true; // A cycle is detected, mark the current node as part of a cycle\n }\n }\n dfsVisited[s] = false; // Mark the current node as not visited in the current DFS path\n return false; // No cycle detected, current node is safe\n }\n\n public List<Integer> eventualSafeNodes(int[][] graph) {\n int v = graph.length;\n List<List<Integer>> adjList = new ArrayList<>();\n for (int i = 0; i < v; i++) {\n adjList.add(new ArrayList<>());\n }\n for (int i = 0; i < v; i++) {\n for (int j = 0; j < graph[i].length; j++) {\n adjList.get(i).add(graph[i][j]);\n }\n }\n\n boolean[] visited = new boolean[v];\n boolean[] dfsVisited = new boolean[v];\n boolean[] checkCycle = new boolean[v];\n List<Integer> ans = new ArrayList<>();\n\n for (int i = 0; i < v; i++) {\n if (!visited[i])\n DFS(i, adjList, visited, dfsVisited, checkCycle);\n }\n\n for (int i = 0; i < v; i++) {\n if (!checkCycle[i])\n ans.add(i); // Add the nodes that are not part of any cycle (eventual safe nodes) to the result\n }\n\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def isSafe(self, s, graph, visited, checkCycle):\n if visited[s] == 1:\n return True # Node is already visited and safe\n if visited[s] == -1:\n return False # Node is visited and part of a cycle\n\n visited[s] = -1 # Mark the current node as visited and part of a cycle\n for it in graph[s]:\n if not self.isSafe(it, graph, visited, checkCycle):\n return False # If any adjacent node is not safe, the current node is not safe\n\n visited[s] = 1 # Mark the current node as visited and safe\n return True\n\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n v = len(graph)\n visited = [0] * v\n checkCycle = []\n for i in range(v):\n if self.isSafe(i, graph, visited, checkCycle):\n checkCycle.append(i) # Add the nodes that are safe (eventual safe nodes) to the result\n return checkCycle\n\n```\n\n | 24 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
🔥Best [C++,JAVA,🐍] Code🌟 || 🔥Commented || DFS💯 | find-eventual-safe-states | 1 | 1 | ### Connect with me on LinkedIn : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n# Intuition\n#### The code is based on the concept of finding eventual safe nodes in a directed graph. Here\'s the intuition behind the approach:\n\n1. The function `DFS` performs a depth-first search starting from a node `s` in the graph.\n2. The `visited` vector keeps track of nodes that have been visited during the DFS traversal.\n3. The `dfsVisited` vector keeps track of nodes that are visited in the current DFS path.\n4. The `checkCycle` vector is used to mark nodes that are part of a cycle.\n5. Initially, all nodes are marked as not visited (`visited` and `dfsVisited` vectors are `false`).\n6. For each node in the graph, if it has not been visited, the DFS function is called.\n7. During the DFS traversal, if an adjacent node is not visited, the DFS function is recursively called for that node.\n8. If the recursive call returns `true`, it means that a cycle is detected, and the current node `s` is marked as part of a cycle in the `checkCycle` vector.\n9. If an adjacent node is already visited and also part of the current DFS path (`dfsVisited` is `true`), it indicates a cycle, and the current node `s` is marked as part of a cycle in the `checkCycle` vector.\n10. After exploring all adjacent nodes, the current node `s` is marked as not visited in the current DFS path (`dfsVisited[s] = false`).\n11. Finally, the `eventualSafeNodes` function iterates over all nodes and adds the nodes that are not part of any cycle (marked as `false` in the `checkCycle` vector) to the `ans` vector.\n12. The `ans` vector is returned as the eventual safe nodes in the graph.\n\n#### The main idea is to perform a DFS traversal and detect cycles in the graph. Nodes that are not part of any cycle are considered eventual safe nodes. The `dfsVisited` vector is used to keep track of the current path and detect cycles. The `checkCycle` vector is used to mark nodes that are part of a cycle.\n# Code\n## An Upvote will be encouraging as it motivates me to post more such solutions\uD83E\uDD17\n```C++ []\nclass Solution {\npublic:\n bool DFS(int s, vector<vector<int>>& graph, vector<bool>& visited, vector<bool>& dfsVisited, vector<bool>& checkCycle) {\n visited[s] = dfsVisited[s] = true; // Mark the current node as visited and in the current DFS path\n for (auto it : graph[s]) {\n if (!visited[it]) { // If the adjacent node is not visited\n if (DFS(it, graph, visited, dfsVisited, checkCycle))\n return checkCycle[s] = true; // If a cycle is detected, mark the current node as part of a cycle\n } else if (dfsVisited[it]) { // If the adjacent node is visited and in the current DFS path\n return checkCycle[s] = true; // A cycle is detected, mark the current node as part of a cycle\n }\n }\n dfsVisited[s] = false; // Mark the current node as not visited in the current DFS path\n return false; // No cycle detected, current node is safe\n }\n \n vector<int> eventualSafeNodes(vector<vector<int>>& graph) {\n int v = graph.size();\n vector<bool> visited(v), dfsVisited(v), checkCycle(v);\n vector<int> ans;\n for (int i = 0; i < v; i++) {\n if (!visited[i])\n DFS(i, graph, visited, dfsVisited, checkCycle);\n }\n for (int i = 0; i < v; i++) {\n if (!checkCycle[i])\n ans.push_back(i); // Add the nodes that are not part of any cycle (eventual safe nodes) to the result\n }\n return ans;\n }\n};\n```\n```JAVA []\nclass Solution {\n public boolean DFS(int s, List<List<Integer>> graph, boolean[] visited, boolean[] dfsVisited, boolean[] checkCycle) {\n visited[s] = dfsVisited[s] = true; // Mark the current node as visited and in the current DFS path\n for (int it : graph.get(s)) {\n if (!visited[it]) { // If the adjacent node is not visited\n if (DFS(it, graph, visited, dfsVisited, checkCycle))\n return checkCycle[s] = true; // If a cycle is detected, mark the current node as part of a cycle\n } else if (dfsVisited[it]) { // If the adjacent node is visited and in the current DFS path\n return checkCycle[s] = true; // A cycle is detected, mark the current node as part of a cycle\n }\n }\n dfsVisited[s] = false; // Mark the current node as not visited in the current DFS path\n return false; // No cycle detected, current node is safe\n }\n\n public List<Integer> eventualSafeNodes(int[][] graph) {\n int v = graph.length;\n List<List<Integer>> adjList = new ArrayList<>();\n for (int i = 0; i < v; i++) {\n adjList.add(new ArrayList<>());\n }\n for (int i = 0; i < v; i++) {\n for (int j = 0; j < graph[i].length; j++) {\n adjList.get(i).add(graph[i][j]);\n }\n }\n\n boolean[] visited = new boolean[v];\n boolean[] dfsVisited = new boolean[v];\n boolean[] checkCycle = new boolean[v];\n List<Integer> ans = new ArrayList<>();\n\n for (int i = 0; i < v; i++) {\n if (!visited[i])\n DFS(i, adjList, visited, dfsVisited, checkCycle);\n }\n\n for (int i = 0; i < v; i++) {\n if (!checkCycle[i])\n ans.add(i); // Add the nodes that are not part of any cycle (eventual safe nodes) to the result\n }\n\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def isSafe(self, s, graph, visited, checkCycle):\n if visited[s] == 1:\n return True # Node is already visited and safe\n if visited[s] == -1:\n return False # Node is visited and part of a cycle\n\n visited[s] = -1 # Mark the current node as visited and part of a cycle\n for it in graph[s]:\n if not self.isSafe(it, graph, visited, checkCycle):\n return False # If any adjacent node is not safe, the current node is not safe\n\n visited[s] = 1 # Mark the current node as visited and safe\n return True\n\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n v = len(graph)\n visited = [0] * v\n checkCycle = []\n for i in range(v):\n if self.isSafe(i, graph, visited, checkCycle):\n checkCycle.append(i) # Add the nodes that are safe (eventual safe nodes) to the result\n return checkCycle\n\n```\n\n | 24 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.