title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | linked-list-components | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numComponents(ListNode* head, vector<int>& nums) {\n ListNode* cur = head;\n int n = 0;\n while (cur) {\n n++;\n cur = cur->next;\n }\n std::vector<int> found (n);\n for (auto& val : nums) {\n found[val] = 1;\n }\n int ans = 0;\n cur = head;\n bool connected = false;\n while (cur) {\n if (connected and found[cur->val] == 0) {\n ans++;\n connected = false;\n }\n else if (!connected and found[cur->val] == 1) {\n connected = true;\n }\n cur = cur->next;\n }\n if (connected) {\n ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n numsSet:set = {num for num in nums}\n \n isInLoop = False\n componentsCounter = 0\n \n while (head != None):\n if head.val in numsSet:\n isInLoop = True\n else:\n if isInLoop:\n componentsCounter += 1\n isInLoop = False\n head = head.next\n \n if isInLoop:\n return componentsCounter+1\n return componentsCounter \n```\n\n```Java []\nclass Solution {\n public int numComponents(ListNode head, int[] nums) {\n boolean[] map = new boolean[10001];\n for (int num : nums) {\n map[num] = true;\n }\n ListNode it = head;\n int counter = 0;\n int len = 0;\n while (it != null) {\n if (map[it.val]) {\n len++;\n }\n else {\n if (len != 0) {\n counter++;\n }\n len = 0;\n }\n it = it.next;\n }\n if (len != 0) {\n counter++;\n }\n return counter;\n }\n}\n```\n | 2 | You are given the `head` of a linked list containing unique integer values and an integer array `nums` that is a subset of the linked list values.
Return _the number of connected components in_ `nums` _where two values are connected if they appear **consecutively** in the linked list_.
**Example 1:**
**Input:** head = \[0,1,2,3\], nums = \[0,1,3\]
**Output:** 2
**Explanation:** 0 and 1 are connected, so \[0, 1\] and \[3\] are the two connected components.
**Example 2:**
**Input:** head = \[0,1,2,3,4\], nums = \[0,3,1,4\]
**Output:** 2
**Explanation:** 0 and 1 are connected, 3 and 4 are connected, so \[0, 1\] and \[3, 4\] are the two connected components.
**Constraints:**
* The number of nodes in the linked list is `n`.
* `1 <= n <= 104`
* `0 <= Node.val < n`
* All the values `Node.val` are **unique**.
* `1 <= nums.length <= n`
* `0 <= nums[i] < n`
* All the values of `nums` are **unique**. | null |
Solution | linked-list-components | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numComponents(ListNode* head, vector<int>& nums) {\n ListNode* cur = head;\n int n = 0;\n while (cur) {\n n++;\n cur = cur->next;\n }\n std::vector<int> found (n);\n for (auto& val : nums) {\n found[val] = 1;\n }\n int ans = 0;\n cur = head;\n bool connected = false;\n while (cur) {\n if (connected and found[cur->val] == 0) {\n ans++;\n connected = false;\n }\n else if (!connected and found[cur->val] == 1) {\n connected = true;\n }\n cur = cur->next;\n }\n if (connected) {\n ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n numsSet:set = {num for num in nums}\n \n isInLoop = False\n componentsCounter = 0\n \n while (head != None):\n if head.val in numsSet:\n isInLoop = True\n else:\n if isInLoop:\n componentsCounter += 1\n isInLoop = False\n head = head.next\n \n if isInLoop:\n return componentsCounter+1\n return componentsCounter \n```\n\n```Java []\nclass Solution {\n public int numComponents(ListNode head, int[] nums) {\n boolean[] map = new boolean[10001];\n for (int num : nums) {\n map[num] = true;\n }\n ListNode it = head;\n int counter = 0;\n int len = 0;\n while (it != null) {\n if (map[it.val]) {\n len++;\n }\n else {\n if (len != 0) {\n counter++;\n }\n len = 0;\n }\n it = it.next;\n }\n if (len != 0) {\n counter++;\n }\n return counter;\n }\n}\n```\n | 2 | You are given two images, `img1` and `img2`, represented as binary, square matrices of size `n x n`. A binary matrix has only `0`s and `1`s as values.
We **translate** one image however we choose by sliding all the `1` bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the **overlap** by counting the number of positions that have a `1` in **both** images.
Note also that a translation does **not** include any kind of rotation. Any `1` bits that are translated outside of the matrix borders are erased.
Return _the largest possible overlap_.
**Example 1:**
**Input:** img1 = \[\[1,1,0\],\[0,1,0\],\[0,1,0\]\], img2 = \[\[0,0,0\],\[0,1,1\],\[0,0,1\]\]
**Output:** 3
**Explanation:** We translate img1 to right by 1 unit and down by 1 unit.
The number of positions that have a 1 in both images is 3 (shown in red).
**Example 2:**
**Input:** img1 = \[\[1\]\], img2 = \[\[1\]\]
**Output:** 1
**Example 3:**
**Input:** img1 = \[\[0\]\], img2 = \[\[0\]\]
**Output:** 0
**Constraints:**
* `n == img1.length == img1[i].length`
* `n == img2.length == img2[i].length`
* `1 <= n <= 30`
* `img1[i][j]` is either `0` or `1`.
* `img2[i][j]` is either `0` or `1`. | null |
89% TC and 77% SC easy python solution | linked-list-components | 0 | 1 | ```\ndef numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n\tcurr = head\n\tans = 0\n\ts = set(nums)\n\twhile(curr):\n\t\tif(curr.val in s and not(curr.next and curr.next.val in s)):\n\t\t\tans += 1\n\t\tcurr = curr.next\n\treturn ans\n``` | 4 | You are given the `head` of a linked list containing unique integer values and an integer array `nums` that is a subset of the linked list values.
Return _the number of connected components in_ `nums` _where two values are connected if they appear **consecutively** in the linked list_.
**Example 1:**
**Input:** head = \[0,1,2,3\], nums = \[0,1,3\]
**Output:** 2
**Explanation:** 0 and 1 are connected, so \[0, 1\] and \[3\] are the two connected components.
**Example 2:**
**Input:** head = \[0,1,2,3,4\], nums = \[0,3,1,4\]
**Output:** 2
**Explanation:** 0 and 1 are connected, 3 and 4 are connected, so \[0, 1\] and \[3, 4\] are the two connected components.
**Constraints:**
* The number of nodes in the linked list is `n`.
* `1 <= n <= 104`
* `0 <= Node.val < n`
* All the values `Node.val` are **unique**.
* `1 <= nums.length <= n`
* `0 <= nums[i] < n`
* All the values of `nums` are **unique**. | null |
89% TC and 77% SC easy python solution | linked-list-components | 0 | 1 | ```\ndef numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n\tcurr = head\n\tans = 0\n\ts = set(nums)\n\twhile(curr):\n\t\tif(curr.val in s and not(curr.next and curr.next.val in s)):\n\t\t\tans += 1\n\t\tcurr = curr.next\n\treturn ans\n``` | 4 | You are given two images, `img1` and `img2`, represented as binary, square matrices of size `n x n`. A binary matrix has only `0`s and `1`s as values.
We **translate** one image however we choose by sliding all the `1` bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the **overlap** by counting the number of positions that have a `1` in **both** images.
Note also that a translation does **not** include any kind of rotation. Any `1` bits that are translated outside of the matrix borders are erased.
Return _the largest possible overlap_.
**Example 1:**
**Input:** img1 = \[\[1,1,0\],\[0,1,0\],\[0,1,0\]\], img2 = \[\[0,0,0\],\[0,1,1\],\[0,0,1\]\]
**Output:** 3
**Explanation:** We translate img1 to right by 1 unit and down by 1 unit.
The number of positions that have a 1 in both images is 3 (shown in red).
**Example 2:**
**Input:** img1 = \[\[1\]\], img2 = \[\[1\]\]
**Output:** 1
**Example 3:**
**Input:** img1 = \[\[0\]\], img2 = \[\[0\]\]
**Output:** 0
**Constraints:**
* `n == img1.length == img1[i].length`
* `n == img2.length == img2[i].length`
* `1 <= n <= 30`
* `img1[i][j]` is either `0` or `1`.
* `img2[i][j]` is either `0` or `1`. | null |
Brute Force -> O(n) - Python/Java - Union Find | linked-list-components | 1 | 1 | > # Intuition\n\nThe "brute force" for this question is essentially Union Find. Understanding Union Find makes the O(n) for this question much more intuitive.\n\nWe perform a modified Union Find as we traverse the linked list, and decrement our total disjoint sets until we hit the end of the list. Also not sure why ordered set is tagged here, I\'m not seeing it.. \n\n---\n\n> # Union Find\n\n```python []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n #the pre-requisite to this problem is essentially Union Find \n #the idea here is to perform a modified Union Find as we go through the linked list\n UF = UnionFind(nums)\n\n #we first need to track what list nodes are in the subset nums\n uniqueValues= set(nums)\n \n #while we go through the linked list\n while head.next:\n #if the nodes are valid, i.e if they\'re in the subset\n if head.val in uniqueValues and head.next.val in uniqueValues:\n #then group them into 1 component, since in the linked list they\n #appear consecutively\n UF.union(head.val, head.next.val)\n head = head.next\n \n #the value sitting in UF.setCount is our answer. for the purposes of set count\n #every value in nums starts out as its own disjoint set. As we connect\n #components it becomes part of another disjoint set, so we subtract 1 from our total\n #to account for this joining\n return UF.setCount\n\n\nclass UnionFind:\n def __init__(self,nums):\n #our nodes here won\'t just be the len(nums) as we\'d expect in a typical union find\n #since the nodes can be any number and in any order we need to represent \n #our union find array as a map, where the index is the node value itself\n self.map = {nums[i] : nums[i] for i in range(len(nums))}\n #same for rank, except the node value is the key\n self.rank = {key : 0 for key in self.map.keys()}\n self.setCount = len(nums)\n \n #standard find with path compression\n def find(self, vertex):\n if vertex == self.map[vertex]:\n return vertex\n self.map[vertex] = self.find(self.map[vertex])\n return self.map[vertex]\n\n #standard union by rank, except for of course our setCount\n def union(self,vertex1,vertex2):\n parent1,parent2 = self.find(vertex1),self.find(vertex2)\n\n if parent1 == parent2:\n return\n elif self.rank[parent1]<self.rank[parent2]:\n self.map[parent1] = parent2\n self.rank[parent2] += 1\n else:\n self.map[parent2] = parent1\n self.rank[parent1] += 1\n self.setCount -= 1\n```\n```Java []\n#Java - Union Find\nclass Solution{\n public Solution(){};\n public int numComponents(ListNode head, int[] nums){\n UnionFind UF = new UnionFind(nums);\n Set<Integer> uniqueValues = Arrays.stream(nums).boxed().collect(Collectors.toSet());\n\n while (head.next != null){\n if (uniqueValues.contains(head.val)&&uniqueValues.contains(head.next.val)){\n UF.union(head.val, head.next.val);\n }\n head = head.next;\n }\n return UF.getSetCount();\n }\n}\n\n\nclass UnionFind{\n private Map<Integer,Integer> map;\n private Map<Integer,Integer> rank;\n private int setCount;\n\n public UnionFind(int[] nums){\n this.setCount = nums.length;\n this.map = Arrays.stream(nums).boxed().collect(Collectors.toMap(i -> i, i -> i));\n this.rank = map.keySet().stream().collect(Collectors.toMap(i->i, i->0));\n }\n\n public int find(int vertex){\n if (vertex == map.get(vertex)){\n return vertex;\n }\n map.put(vertex, find(map.get(vertex)));\n return map.get(vertex);\n }\n\n public void union(int vertex1, int vertex2){\n int parent1 = find(vertex1);\n int parent2 = find(vertex2);\n\n if (parent1 == parent2){\n return;\n } else if (rank.get(parent1) < rank.get(parent2)){\n map.put(parent1, parent2);\n } else if (rank.get(parent1) > rank.get(parent2)){\n map.put(parent2, parent1);\n } else {\n map.put(parent1, parent2);\n rank.put(parent2, rank.get(parent2) + 1);\n }\n setCount -= 1;\n }\n\n public int getSetCount(){\n return setCount;\n }\n}\n```\n\n---\n\n> # O(n)\n\n```python []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n #we can actually count the sets without using union find at all\n\n #we keep the same setCount as in the union find solution\n #holding the assumption every node in nums starts out as its own disjoint set\n numsSet,setCount = set(nums),len(nums)\n\n #go throught he linked list\n while head.next:\n #so long as it\'s a valid node in numsSet\n if head.val in numsSet and head.next.val in numsSet:\n #then make add it to an existing dijoint set, since it appears consecutively\n setCount -=1\n #exhaust the linked list\n head = head.next\n #the answer sits here\n return setCount\n \n```\n```Java []\nclass Solution{\n public Solution(){}\n public int numComponents(ListNode head,int[]nums){\n Set<Integer> numsSet = Arrays.stream(nums).boxed().collect(Collectors.toSet());\n int setCount = nums.length;\n\n while (head.next != null){\n if (numsSet.contains(head.val)&& numsSet.contains(head.next.val)){\n setCount-=1;\n }\n head = head.next;\n }\n return setCount;\n }\n}\n```\n | 0 | You are given the `head` of a linked list containing unique integer values and an integer array `nums` that is a subset of the linked list values.
Return _the number of connected components in_ `nums` _where two values are connected if they appear **consecutively** in the linked list_.
**Example 1:**
**Input:** head = \[0,1,2,3\], nums = \[0,1,3\]
**Output:** 2
**Explanation:** 0 and 1 are connected, so \[0, 1\] and \[3\] are the two connected components.
**Example 2:**
**Input:** head = \[0,1,2,3,4\], nums = \[0,3,1,4\]
**Output:** 2
**Explanation:** 0 and 1 are connected, 3 and 4 are connected, so \[0, 1\] and \[3, 4\] are the two connected components.
**Constraints:**
* The number of nodes in the linked list is `n`.
* `1 <= n <= 104`
* `0 <= Node.val < n`
* All the values `Node.val` are **unique**.
* `1 <= nums.length <= n`
* `0 <= nums[i] < n`
* All the values of `nums` are **unique**. | null |
Brute Force -> O(n) - Python/Java - Union Find | linked-list-components | 1 | 1 | > # Intuition\n\nThe "brute force" for this question is essentially Union Find. Understanding Union Find makes the O(n) for this question much more intuitive.\n\nWe perform a modified Union Find as we traverse the linked list, and decrement our total disjoint sets until we hit the end of the list. Also not sure why ordered set is tagged here, I\'m not seeing it.. \n\n---\n\n> # Union Find\n\n```python []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n #the pre-requisite to this problem is essentially Union Find \n #the idea here is to perform a modified Union Find as we go through the linked list\n UF = UnionFind(nums)\n\n #we first need to track what list nodes are in the subset nums\n uniqueValues= set(nums)\n \n #while we go through the linked list\n while head.next:\n #if the nodes are valid, i.e if they\'re in the subset\n if head.val in uniqueValues and head.next.val in uniqueValues:\n #then group them into 1 component, since in the linked list they\n #appear consecutively\n UF.union(head.val, head.next.val)\n head = head.next\n \n #the value sitting in UF.setCount is our answer. for the purposes of set count\n #every value in nums starts out as its own disjoint set. As we connect\n #components it becomes part of another disjoint set, so we subtract 1 from our total\n #to account for this joining\n return UF.setCount\n\n\nclass UnionFind:\n def __init__(self,nums):\n #our nodes here won\'t just be the len(nums) as we\'d expect in a typical union find\n #since the nodes can be any number and in any order we need to represent \n #our union find array as a map, where the index is the node value itself\n self.map = {nums[i] : nums[i] for i in range(len(nums))}\n #same for rank, except the node value is the key\n self.rank = {key : 0 for key in self.map.keys()}\n self.setCount = len(nums)\n \n #standard find with path compression\n def find(self, vertex):\n if vertex == self.map[vertex]:\n return vertex\n self.map[vertex] = self.find(self.map[vertex])\n return self.map[vertex]\n\n #standard union by rank, except for of course our setCount\n def union(self,vertex1,vertex2):\n parent1,parent2 = self.find(vertex1),self.find(vertex2)\n\n if parent1 == parent2:\n return\n elif self.rank[parent1]<self.rank[parent2]:\n self.map[parent1] = parent2\n self.rank[parent2] += 1\n else:\n self.map[parent2] = parent1\n self.rank[parent1] += 1\n self.setCount -= 1\n```\n```Java []\n#Java - Union Find\nclass Solution{\n public Solution(){};\n public int numComponents(ListNode head, int[] nums){\n UnionFind UF = new UnionFind(nums);\n Set<Integer> uniqueValues = Arrays.stream(nums).boxed().collect(Collectors.toSet());\n\n while (head.next != null){\n if (uniqueValues.contains(head.val)&&uniqueValues.contains(head.next.val)){\n UF.union(head.val, head.next.val);\n }\n head = head.next;\n }\n return UF.getSetCount();\n }\n}\n\n\nclass UnionFind{\n private Map<Integer,Integer> map;\n private Map<Integer,Integer> rank;\n private int setCount;\n\n public UnionFind(int[] nums){\n this.setCount = nums.length;\n this.map = Arrays.stream(nums).boxed().collect(Collectors.toMap(i -> i, i -> i));\n this.rank = map.keySet().stream().collect(Collectors.toMap(i->i, i->0));\n }\n\n public int find(int vertex){\n if (vertex == map.get(vertex)){\n return vertex;\n }\n map.put(vertex, find(map.get(vertex)));\n return map.get(vertex);\n }\n\n public void union(int vertex1, int vertex2){\n int parent1 = find(vertex1);\n int parent2 = find(vertex2);\n\n if (parent1 == parent2){\n return;\n } else if (rank.get(parent1) < rank.get(parent2)){\n map.put(parent1, parent2);\n } else if (rank.get(parent1) > rank.get(parent2)){\n map.put(parent2, parent1);\n } else {\n map.put(parent1, parent2);\n rank.put(parent2, rank.get(parent2) + 1);\n }\n setCount -= 1;\n }\n\n public int getSetCount(){\n return setCount;\n }\n}\n```\n\n---\n\n> # O(n)\n\n```python []\nclass Solution:\n def numComponents(self, head: Optional[ListNode], nums: List[int]) -> int:\n #we can actually count the sets without using union find at all\n\n #we keep the same setCount as in the union find solution\n #holding the assumption every node in nums starts out as its own disjoint set\n numsSet,setCount = set(nums),len(nums)\n\n #go throught he linked list\n while head.next:\n #so long as it\'s a valid node in numsSet\n if head.val in numsSet and head.next.val in numsSet:\n #then make add it to an existing dijoint set, since it appears consecutively\n setCount -=1\n #exhaust the linked list\n head = head.next\n #the answer sits here\n return setCount\n \n```\n```Java []\nclass Solution{\n public Solution(){}\n public int numComponents(ListNode head,int[]nums){\n Set<Integer> numsSet = Arrays.stream(nums).boxed().collect(Collectors.toSet());\n int setCount = nums.length;\n\n while (head.next != null){\n if (numsSet.contains(head.val)&& numsSet.contains(head.next.val)){\n setCount-=1;\n }\n head = head.next;\n }\n return setCount;\n }\n}\n```\n | 0 | You are given two images, `img1` and `img2`, represented as binary, square matrices of size `n x n`. A binary matrix has only `0`s and `1`s as values.
We **translate** one image however we choose by sliding all the `1` bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the **overlap** by counting the number of positions that have a `1` in **both** images.
Note also that a translation does **not** include any kind of rotation. Any `1` bits that are translated outside of the matrix borders are erased.
Return _the largest possible overlap_.
**Example 1:**
**Input:** img1 = \[\[1,1,0\],\[0,1,0\],\[0,1,0\]\], img2 = \[\[0,0,0\],\[0,1,1\],\[0,0,1\]\]
**Output:** 3
**Explanation:** We translate img1 to right by 1 unit and down by 1 unit.
The number of positions that have a 1 in both images is 3 (shown in red).
**Example 2:**
**Input:** img1 = \[\[1\]\], img2 = \[\[1\]\]
**Output:** 1
**Example 3:**
**Input:** img1 = \[\[0\]\], img2 = \[\[0\]\]
**Output:** 0
**Constraints:**
* `n == img1.length == img1[i].length`
* `n == img2.length == img2[i].length`
* `1 <= n <= 30`
* `img1[i][j]` is either `0` or `1`.
* `img2[i][j]` is either `0` or `1`. | null |
✅ Simple BFS Solution || Time and Space Complexity O(log n) 🚀😀 | race-car | 0 | 1 | # Intuition\nThis whole problem seems to be a shortest path question, where we have to reach from 0 to target position with minimum steps.\nAnd for this type of question it is better to proceed with BFS.\n\n# Approach\nMake decision of either accelerating or taking a reverse with the help of these conditions:\n- If our position < target, then we should accelerate\n- If our position > target, then we should reverse\nWe should keep on iterating these steps until we reach our target position.\n\n# Complexity\n- Time complexity:\nlog n, where n is target\n\n- Space complexity:\nlog n, where n is target\n\nBoth off the complexities are in log because when we are accelerating our speed is getting multiplied by 2 because of which the number of steps are getting reduced.\n\n# Video Explanation\nhttps://www.youtube.com/watch?v=qRizzFhEImM&t=21s\n\n# Code\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n queue = deque([(0,0,1)])\n visited = set()\n while queue:\n moves, position,speed = queue.popleft()\n if position == target:\n return moves\n if (position,speed) in visited:\n continue\n else:\n visited.add((position,speed))\n queue.append((moves+1,position+speed,speed*2))\n if (position+speed > target and speed > 0) or (position+speed < target and speed < 0):\n speed = -1 if speed > 0 else 1\n queue.append((moves+1,position,speed))\n return 0\n```\n[Video Explanation](https://www.youtube.com/watch?v=qRizzFhEImM) | 6 | Your car starts at position `0` and speed `+1` on an infinite number line. Your car can go into negative positions. Your car drives automatically according to a sequence of instructions `'A'` (accelerate) and `'R'` (reverse):
* When you get an instruction `'A'`, your car does the following:
* `position += speed`
* `speed *= 2`
* When you get an instruction `'R'`, your car does the following:
* If your speed is positive then `speed = -1`
* otherwise `speed = 1`Your position stays the same.
For example, after commands `"AAR "`, your car goes to positions `0 --> 1 --> 3 --> 3`, and your speed goes to `1 --> 2 --> 4 --> -1`.
Given a target position `target`, return _the length of the shortest sequence of instructions to get there_.
**Example 1:**
**Input:** target = 3
**Output:** 2
**Explanation:**
The shortest instruction sequence is "AA ".
Your position goes from 0 --> 1 --> 3.
**Example 2:**
**Input:** target = 6
**Output:** 5
**Explanation:**
The shortest instruction sequence is "AAARA ".
Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
**Constraints:**
* `1 <= target <= 104` | null |
✅ Simple BFS Solution || Time and Space Complexity O(log n) 🚀😀 | race-car | 0 | 1 | # Intuition\nThis whole problem seems to be a shortest path question, where we have to reach from 0 to target position with minimum steps.\nAnd for this type of question it is better to proceed with BFS.\n\n# Approach\nMake decision of either accelerating or taking a reverse with the help of these conditions:\n- If our position < target, then we should accelerate\n- If our position > target, then we should reverse\nWe should keep on iterating these steps until we reach our target position.\n\n# Complexity\n- Time complexity:\nlog n, where n is target\n\n- Space complexity:\nlog n, where n is target\n\nBoth off the complexities are in log because when we are accelerating our speed is getting multiplied by 2 because of which the number of steps are getting reduced.\n\n# Video Explanation\nhttps://www.youtube.com/watch?v=qRizzFhEImM&t=21s\n\n# Code\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n queue = deque([(0,0,1)])\n visited = set()\n while queue:\n moves, position,speed = queue.popleft()\n if position == target:\n return moves\n if (position,speed) in visited:\n continue\n else:\n visited.add((position,speed))\n queue.append((moves+1,position+speed,speed*2))\n if (position+speed > target and speed > 0) or (position+speed < target and speed < 0):\n speed = -1 if speed > 0 else 1\n queue.append((moves+1,position,speed))\n return 0\n```\n[Video Explanation](https://www.youtube.com/watch?v=qRizzFhEImM) | 6 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
BFS and DP with inline explanations | race-car | 0 | 1 | \n```python\n# Naive BFS\n# O(2^target)\n# TLE\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque([(0, 0, 1)])\n visited = set([0, 0, 1])\n \n while q:\n actions, x, v = q.popleft()\n if x == target:\n return actions\n \n actions += 1\n \n # Accelerate\n newx = x + v\n newv = v * 2\n if (state := (actions, newx, newv)) not in visited:\n visited.add(state)\n q.append(state)\n \n \n # Reverse\n newv = -1 if v > 0 else 1\n if (state := (actions, x, newv)) not in visited:\n visited.add(state)\n q.append(state)\n\n \n# Smart BFS\n# O(t*log(t))\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque([(0, 1)])\n visited = set([0, 1])\n actions = 0\n while q:\n size = len(q)\n for _ in range(size):\n x, v = q.popleft()\n if x == target:\n return actions\n \n # Accelerate\n # NOTE: if accelerating in the negative regions or passing the target by more than two times, \n # then this is never going to reach an answer\n # we won\'t add it to the queue\n newx = x + v\n newv = v * 2\n if 0 <= newx <= 2 * target and (state := (newx, newv)) not in visited:\n visited.add(state)\n q.append(state)\n\n\n # Reverse\n newv = -1 if v > 0 else 1\n if (state := (x, newv)) not in visited:\n visited.add(state)\n q.append(state)\n \n actions += 1\n \n# DP\n# O(t*log(t))\nclass Solution:\n def racecar(self, target: int) -> int:\n \n @cache\n def go(n):\n m = n.bit_length()\n # check if we can go directly to the target\n if 2 ** m - 1 == n:\n return m\n else:\n # otherwise we have two choices\n # we pass the point, and then we reverse (denoted by passing_moves)\n # or we go as close to the target as possible, reverse, go back up to m - 2 times, reverse again, and reach the point\n # note if we go back m - 1 times, we have reached the same point we started at.\n \n # 1. go past target (m moves), reverse (1 move), and reach the target (recurse)\n passing_moves = m + 1 + go(2 ** m - 1 - n)\n \n # 2. go as close to target as possible (m - 1 moves), reverse (1 move) and go back (i < m - 1 moves), reverse (1 move), and reach the target (recurse)\n closest_point = 2 ** (m - 1) - 1\n closest_moves = m - 1\n min_ = math.inf\n for i in range(m - 1):\n backward = 2 ** i - 1\n remain_moves = go(n - (closest_point - backward)) + i\n min_ = min(min_, remain_moves)\n \n closest_moves += min_ + 2\n \n return min(passing_moves, closest_moves)\n \n return go(target)\n``` | 12 | Your car starts at position `0` and speed `+1` on an infinite number line. Your car can go into negative positions. Your car drives automatically according to a sequence of instructions `'A'` (accelerate) and `'R'` (reverse):
* When you get an instruction `'A'`, your car does the following:
* `position += speed`
* `speed *= 2`
* When you get an instruction `'R'`, your car does the following:
* If your speed is positive then `speed = -1`
* otherwise `speed = 1`Your position stays the same.
For example, after commands `"AAR "`, your car goes to positions `0 --> 1 --> 3 --> 3`, and your speed goes to `1 --> 2 --> 4 --> -1`.
Given a target position `target`, return _the length of the shortest sequence of instructions to get there_.
**Example 1:**
**Input:** target = 3
**Output:** 2
**Explanation:**
The shortest instruction sequence is "AA ".
Your position goes from 0 --> 1 --> 3.
**Example 2:**
**Input:** target = 6
**Output:** 5
**Explanation:**
The shortest instruction sequence is "AAARA ".
Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
**Constraints:**
* `1 <= target <= 104` | null |
BFS and DP with inline explanations | race-car | 0 | 1 | \n```python\n# Naive BFS\n# O(2^target)\n# TLE\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque([(0, 0, 1)])\n visited = set([0, 0, 1])\n \n while q:\n actions, x, v = q.popleft()\n if x == target:\n return actions\n \n actions += 1\n \n # Accelerate\n newx = x + v\n newv = v * 2\n if (state := (actions, newx, newv)) not in visited:\n visited.add(state)\n q.append(state)\n \n \n # Reverse\n newv = -1 if v > 0 else 1\n if (state := (actions, x, newv)) not in visited:\n visited.add(state)\n q.append(state)\n\n \n# Smart BFS\n# O(t*log(t))\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque([(0, 1)])\n visited = set([0, 1])\n actions = 0\n while q:\n size = len(q)\n for _ in range(size):\n x, v = q.popleft()\n if x == target:\n return actions\n \n # Accelerate\n # NOTE: if accelerating in the negative regions or passing the target by more than two times, \n # then this is never going to reach an answer\n # we won\'t add it to the queue\n newx = x + v\n newv = v * 2\n if 0 <= newx <= 2 * target and (state := (newx, newv)) not in visited:\n visited.add(state)\n q.append(state)\n\n\n # Reverse\n newv = -1 if v > 0 else 1\n if (state := (x, newv)) not in visited:\n visited.add(state)\n q.append(state)\n \n actions += 1\n \n# DP\n# O(t*log(t))\nclass Solution:\n def racecar(self, target: int) -> int:\n \n @cache\n def go(n):\n m = n.bit_length()\n # check if we can go directly to the target\n if 2 ** m - 1 == n:\n return m\n else:\n # otherwise we have two choices\n # we pass the point, and then we reverse (denoted by passing_moves)\n # or we go as close to the target as possible, reverse, go back up to m - 2 times, reverse again, and reach the point\n # note if we go back m - 1 times, we have reached the same point we started at.\n \n # 1. go past target (m moves), reverse (1 move), and reach the target (recurse)\n passing_moves = m + 1 + go(2 ** m - 1 - n)\n \n # 2. go as close to target as possible (m - 1 moves), reverse (1 move) and go back (i < m - 1 moves), reverse (1 move), and reach the target (recurse)\n closest_point = 2 ** (m - 1) - 1\n closest_moves = m - 1\n min_ = math.inf\n for i in range(m - 1):\n backward = 2 ** i - 1\n remain_moves = go(n - (closest_point - backward)) + i\n min_ = min(min_, remain_moves)\n \n closest_moves += min_ + 2\n \n return min(passing_moves, closest_moves)\n \n return go(target)\n``` | 12 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Python3 BFS Explanation | race-car | 0 | 1 | At every position, we have two choice\n* Either accelerate\n* Or reverse\n\nNote: If you are thinking of accelerating till `curren position < target` and when `current position becomes > target to reverse`, it wont work because sometimes we would have to decelerate first and then accelerate even though` current position < target`.\nHence we need to consider both the options at every given position.\n\nBrute Force BFS Code\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque()\n q.append((0,1,0)) #curr pos, curr speed, number of moves\n \n while q:\n cp,cs,nm = q.popleft()\n \n if cp==target:\n return nm\n \n #every pos we have 2 choice\n #A or R\n q.append((cp+cs,cs*2,nm+1))\n \n if cs<0:\n q.append((cp,1,nm+1))\n else:\n q.append((cp,-1,nm+1))\n \n```\n\nBut this gives` MLE` since its complexity is` O(2^N)`. Hence to cut down on the brute force traversal, we need to wisely choose when we consider to move in opposite direction to the direction we are currently travelling in.\n\nWe need to CONSIDER moving in opposite direction only when we seem to cross the target and accelerating away from target or when we seem to move away from taregt and accelerating away from the target because we might never reach the target.\n\nHence:\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque()\n q.append((0,1,0)) #curr pos, curr speed, number of moves\n \n while q:\n cp,cs,nm = q.popleft()\n \n if cp==target:\n return nm\n \n #every pos we have 2 choice\n #A or R\n \n #Acceleration\n q.append((cp+cs,cs*2,nm+1))\n \n #Reverse\n if (cp+cs>target and cs>0) or (cp+cs<target and cs<0):\n if cs<0:\n q.append((cp,1,nm+1))\n else:\n q.append((cp,-1,nm+1))\n \n```\n\n\n | 15 | Your car starts at position `0` and speed `+1` on an infinite number line. Your car can go into negative positions. Your car drives automatically according to a sequence of instructions `'A'` (accelerate) and `'R'` (reverse):
* When you get an instruction `'A'`, your car does the following:
* `position += speed`
* `speed *= 2`
* When you get an instruction `'R'`, your car does the following:
* If your speed is positive then `speed = -1`
* otherwise `speed = 1`Your position stays the same.
For example, after commands `"AAR "`, your car goes to positions `0 --> 1 --> 3 --> 3`, and your speed goes to `1 --> 2 --> 4 --> -1`.
Given a target position `target`, return _the length of the shortest sequence of instructions to get there_.
**Example 1:**
**Input:** target = 3
**Output:** 2
**Explanation:**
The shortest instruction sequence is "AA ".
Your position goes from 0 --> 1 --> 3.
**Example 2:**
**Input:** target = 6
**Output:** 5
**Explanation:**
The shortest instruction sequence is "AAARA ".
Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
**Constraints:**
* `1 <= target <= 104` | null |
Python3 BFS Explanation | race-car | 0 | 1 | At every position, we have two choice\n* Either accelerate\n* Or reverse\n\nNote: If you are thinking of accelerating till `curren position < target` and when `current position becomes > target to reverse`, it wont work because sometimes we would have to decelerate first and then accelerate even though` current position < target`.\nHence we need to consider both the options at every given position.\n\nBrute Force BFS Code\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque()\n q.append((0,1,0)) #curr pos, curr speed, number of moves\n \n while q:\n cp,cs,nm = q.popleft()\n \n if cp==target:\n return nm\n \n #every pos we have 2 choice\n #A or R\n q.append((cp+cs,cs*2,nm+1))\n \n if cs<0:\n q.append((cp,1,nm+1))\n else:\n q.append((cp,-1,nm+1))\n \n```\n\nBut this gives` MLE` since its complexity is` O(2^N)`. Hence to cut down on the brute force traversal, we need to wisely choose when we consider to move in opposite direction to the direction we are currently travelling in.\n\nWe need to CONSIDER moving in opposite direction only when we seem to cross the target and accelerating away from target or when we seem to move away from taregt and accelerating away from the target because we might never reach the target.\n\nHence:\n```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = deque()\n q.append((0,1,0)) #curr pos, curr speed, number of moves\n \n while q:\n cp,cs,nm = q.popleft()\n \n if cp==target:\n return nm\n \n #every pos we have 2 choice\n #A or R\n \n #Acceleration\n q.append((cp+cs,cs*2,nm+1))\n \n #Reverse\n if (cp+cs>target and cs>0) or (cp+cs<target and cs<0):\n if cs<0:\n q.append((cp,1,nm+1))\n else:\n q.append((cp,-1,nm+1))\n \n```\n\n\n | 15 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Python easy to read and understand | BFS | race-car | 0 | 1 | ```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = [(0, 1)]\n steps = 0\n \n while q:\n num = len(q)\n for i in range(num):\n pos, speed = q.pop(0)\n if pos == target:\n return steps\n q.append((pos+speed, speed*2))\n rev_speed = -1 if speed > 0 else 1\n if (pos+speed) < target and speed < 0 or (pos+speed) > target and speed > 0:\n q.append((pos, rev_speed))\n steps += 1 | 2 | Your car starts at position `0` and speed `+1` on an infinite number line. Your car can go into negative positions. Your car drives automatically according to a sequence of instructions `'A'` (accelerate) and `'R'` (reverse):
* When you get an instruction `'A'`, your car does the following:
* `position += speed`
* `speed *= 2`
* When you get an instruction `'R'`, your car does the following:
* If your speed is positive then `speed = -1`
* otherwise `speed = 1`Your position stays the same.
For example, after commands `"AAR "`, your car goes to positions `0 --> 1 --> 3 --> 3`, and your speed goes to `1 --> 2 --> 4 --> -1`.
Given a target position `target`, return _the length of the shortest sequence of instructions to get there_.
**Example 1:**
**Input:** target = 3
**Output:** 2
**Explanation:**
The shortest instruction sequence is "AA ".
Your position goes from 0 --> 1 --> 3.
**Example 2:**
**Input:** target = 6
**Output:** 5
**Explanation:**
The shortest instruction sequence is "AAARA ".
Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
**Constraints:**
* `1 <= target <= 104` | null |
Python easy to read and understand | BFS | race-car | 0 | 1 | ```\nclass Solution:\n def racecar(self, target: int) -> int:\n q = [(0, 1)]\n steps = 0\n \n while q:\n num = len(q)\n for i in range(num):\n pos, speed = q.pop(0)\n if pos == target:\n return steps\n q.append((pos+speed, speed*2))\n rev_speed = -1 if speed > 0 else 1\n if (pos+speed) < target and speed < 0 or (pos+speed) > target and speed > 0:\n q.append((pos, rev_speed))\n steps += 1 | 2 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
📌📌 Greedy Approach || Normal conditions || 94% faster || Well-Coded 🐍 | race-car | 0 | 1 | ## IDEA:\n* The key point is move close to that point and then start reversing the gear based on conditions.\n\n* **If you are still before to the target and speed is reverse(i.e. deaccelerating) or if you are ahead of target and speed is positive (i.e. accelerating) then reverse the speed.**\n\nThere are two strategies to get to the target distance:\n\n\t1. We go pass it, then come back.\n\tfor example, the target is 2, we accelerate twice to 3, then reverse and come back (the new target is then 3 - 2 = 1.\n\t\n\t2. We get super close to it, then reverse accelerate a few times, then reverse back to the target\n\tfor example, the target is 2, we accelerate once to 1, then reverse to accelerate 0 times, and reverse again. The new target will be 1\n\n**Code :**\n\'\'\'\n\n\tclass Solution:\n def racecar(self, target: int) -> int:\n \n q = deque()\n q.append((0,0,1))\n while q:\n m,p,s = q.popleft()\n if p==target:\n return m\n rev = -1 if s>0 else 1\n\t\t\t\n q.append((m+1,p+s,s*2))\n \n if (p+s<target and s<0) or (p+s>target and s>0): # If you are back to the target and speed is reverse or if you are ahead of target and speed is positive then reverse the speed\n q.append((m+1,p,rev))\n \n return -1\n\n**Thanks & Upvote if you like the idea !!\uD83E\uDD1E** | 10 | Your car starts at position `0` and speed `+1` on an infinite number line. Your car can go into negative positions. Your car drives automatically according to a sequence of instructions `'A'` (accelerate) and `'R'` (reverse):
* When you get an instruction `'A'`, your car does the following:
* `position += speed`
* `speed *= 2`
* When you get an instruction `'R'`, your car does the following:
* If your speed is positive then `speed = -1`
* otherwise `speed = 1`Your position stays the same.
For example, after commands `"AAR "`, your car goes to positions `0 --> 1 --> 3 --> 3`, and your speed goes to `1 --> 2 --> 4 --> -1`.
Given a target position `target`, return _the length of the shortest sequence of instructions to get there_.
**Example 1:**
**Input:** target = 3
**Output:** 2
**Explanation:**
The shortest instruction sequence is "AA ".
Your position goes from 0 --> 1 --> 3.
**Example 2:**
**Input:** target = 6
**Output:** 5
**Explanation:**
The shortest instruction sequence is "AAARA ".
Your position goes from 0 --> 1 --> 3 --> 7 --> 7 --> 6.
**Constraints:**
* `1 <= target <= 104` | null |
📌📌 Greedy Approach || Normal conditions || 94% faster || Well-Coded 🐍 | race-car | 0 | 1 | ## IDEA:\n* The key point is move close to that point and then start reversing the gear based on conditions.\n\n* **If you are still before to the target and speed is reverse(i.e. deaccelerating) or if you are ahead of target and speed is positive (i.e. accelerating) then reverse the speed.**\n\nThere are two strategies to get to the target distance:\n\n\t1. We go pass it, then come back.\n\tfor example, the target is 2, we accelerate twice to 3, then reverse and come back (the new target is then 3 - 2 = 1.\n\t\n\t2. We get super close to it, then reverse accelerate a few times, then reverse back to the target\n\tfor example, the target is 2, we accelerate once to 1, then reverse to accelerate 0 times, and reverse again. The new target will be 1\n\n**Code :**\n\'\'\'\n\n\tclass Solution:\n def racecar(self, target: int) -> int:\n \n q = deque()\n q.append((0,0,1))\n while q:\n m,p,s = q.popleft()\n if p==target:\n return m\n rev = -1 if s>0 else 1\n\t\t\t\n q.append((m+1,p+s,s*2))\n \n if (p+s<target and s<0) or (p+s>target and s>0): # If you are back to the target and speed is reverse or if you are ahead of target and speed is positive then reverse the speed\n q.append((m+1,p,rev))\n \n return -1\n\n**Thanks & Upvote if you like the idea !!\uD83E\uDD1E** | 10 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Solution | most-common-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string mostCommonWord(string str, vector<string>& banned) {\n unordered_map<string, int> hash;\n for(auto& it : str)\n\t\t it = ispunct(it) ? \' \' : tolower(it);\n\n unordered_set<string> st(banned.begin(), banned.end()); \n string res, temp; \n int maxi =0;\n stringstream ss(str);\n while(ss >> temp) hash[temp]++;\n \n for(auto& it:hash){\n if(it.second > maxi && !st.count(it.first)){\n maxi = it.second;\n res = it.first;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n paragraph = paragraph.lower()\n symbol = "!?\',;."\n for s in symbol:\n paragraph = paragraph.replace(s, " ")\n paragraph = paragraph.split()\n\n from collections import Counter\n lst = sorted(Counter(paragraph).items(), key=lambda e: -e[1])\n for e, _ in lst:\n if e not in banned:\n return e\n break\n```\n\n```Java []\nclass Solution {\n public String mostCommonWord(String p, String[] ban) {\n var e = p.toLowerCase().toCharArray();\n var t = new Trie();\n var res = new char[0];\n int max = 0;\n int l = e.length;\n\n for (String w : ban) t.addW(w.toCharArray(), 0, true);\n\n for (int i = 0, j = 0; i < l; j = i) {\n while (i < l && e[i] > 64) i++;\n if (i > j) {\n var w = Arrays.copyOfRange(e, j, i);\n int x = t.addW(w, 0, false);\n if (x > max) {\n max = x;\n res = w;\n }\n j = i + 1;\n }\n while (i < l && e[i] < 64) i++;\n }\n return new String(res);\n }\n private static class Trie {\n private int c;\n private final Trie[] t = new Trie[26];\n\n public int addW(char[] w, int i, boolean ban) {\n if (i == w.length) {\n if (this.c == -1) return -1;\n return ban ? (this.c = -1) : ++this.c;\n }\n int idx = w[i] - \'a\';\n if (t[idx] == null) t[idx] = new Trie();\n return t[idx].addW(w, ++i, ban);\n }\n }\n}\n```\n | 1 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Solution | most-common-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string mostCommonWord(string str, vector<string>& banned) {\n unordered_map<string, int> hash;\n for(auto& it : str)\n\t\t it = ispunct(it) ? \' \' : tolower(it);\n\n unordered_set<string> st(banned.begin(), banned.end()); \n string res, temp; \n int maxi =0;\n stringstream ss(str);\n while(ss >> temp) hash[temp]++;\n \n for(auto& it:hash){\n if(it.second > maxi && !st.count(it.first)){\n maxi = it.second;\n res = it.first;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n paragraph = paragraph.lower()\n symbol = "!?\',;."\n for s in symbol:\n paragraph = paragraph.replace(s, " ")\n paragraph = paragraph.split()\n\n from collections import Counter\n lst = sorted(Counter(paragraph).items(), key=lambda e: -e[1])\n for e, _ in lst:\n if e not in banned:\n return e\n break\n```\n\n```Java []\nclass Solution {\n public String mostCommonWord(String p, String[] ban) {\n var e = p.toLowerCase().toCharArray();\n var t = new Trie();\n var res = new char[0];\n int max = 0;\n int l = e.length;\n\n for (String w : ban) t.addW(w.toCharArray(), 0, true);\n\n for (int i = 0, j = 0; i < l; j = i) {\n while (i < l && e[i] > 64) i++;\n if (i > j) {\n var w = Arrays.copyOfRange(e, j, i);\n int x = t.addW(w, 0, false);\n if (x > max) {\n max = x;\n res = w;\n }\n j = i + 1;\n }\n while (i < l && e[i] < 64) i++;\n }\n return new String(res);\n }\n private static class Trie {\n private int c;\n private final Trie[] t = new Trie[26];\n\n public int addW(char[] w, int i, boolean ban) {\n if (i == w.length) {\n if (this.c == -1) return -1;\n return ban ? (this.c = -1) : ++this.c;\n }\n int idx = w[i] - \'a\';\n if (t[idx] == null) t[idx] = new Trie();\n return t[idx].addW(w, ++i, ban);\n }\n }\n}\n```\n | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Simple Python Solution (Counter) | most-common-word | 0 | 1 | ```\n#Import RegEx\nimport re\n\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n #List words in paragraph, replacing punctuation with \' \' and all lower case\n paragraph = re.subn("[.,!?;\']", \' \', paragraph.lower())[0].split(\' \')\n \n #Remove any \'\' or words in banned from paragraph list\n paragraph = list(filter(lambda x: x not in banned + [\'\'], paragraph))\n \n #Return most common word in filtered list\n return Counter(paragraph).most_common(1)[0][0] | 1 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Simple Python Solution (Counter) | most-common-word | 0 | 1 | ```\n#Import RegEx\nimport re\n\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n #List words in paragraph, replacing punctuation with \' \' and all lower case\n paragraph = re.subn("[.,!?;\']", \' \', paragraph.lower())[0].split(\' \')\n \n #Remove any \'\' or words in banned from paragraph list\n paragraph = list(filter(lambda x: x not in banned + [\'\'], paragraph))\n \n #Return most common word in filtered list\n return Counter(paragraph).most_common(1)[0][0] | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
easy solution in python .... | most-common-word | 0 | 1 | \nimport re\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n res = re.sub(r\'[^\\w\\s]\', \' \', paragraph)\n dic={}\n c=1\n s=\'\'\n l=res.split(" ")\n print(l)\n for i in l:\n if(i!=""):\n i=i.lower()\n if i in banned:\n continue\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n if dic[i]>=c:\n c=dic[i]\n s=i\n return s\n``` | 1 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
easy solution in python .... | most-common-word | 0 | 1 | \nimport re\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n res = re.sub(r\'[^\\w\\s]\', \' \', paragraph)\n dic={}\n c=1\n s=\'\'\n l=res.split(" ")\n print(l)\n for i in l:\n if(i!=""):\n i=i.lower()\n if i in banned:\n continue\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n if dic[i]>=c:\n c=dic[i]\n s=i\n return s\n``` | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Python 3 three lines easy and explained | most-common-word | 0 | 1 | Runtime: 36 ms, faster than 40.27% of Python3 online submissions for Most Common Word.\nMemory Usage: 12.7 MB, less than 100.00% of Python3 online submissions for Most Common Word.\n\n```Python 3\nimport re\n\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n\t\t\n\t\t# convert to lower case and split string into words by spaces and punctuation\n a = re.split(r\'\\W+\', paragraph.lower())\n\t\t\n\t\t# make new list consisitng of words not in banned list (remove banned words)\n b = [w for w in a if w not in banned]\n\t\t\n\t\t# return value that counted max times in the new list\n return max(b, key = b.count)\n```\n\nPlease, upvote if you like it so that others can see and learn from it. Thanks! | 25 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Python 3 three lines easy and explained | most-common-word | 0 | 1 | Runtime: 36 ms, faster than 40.27% of Python3 online submissions for Most Common Word.\nMemory Usage: 12.7 MB, less than 100.00% of Python3 online submissions for Most Common Word.\n\n```Python 3\nimport re\n\nclass Solution:\n def mostCommonWord(self, paragraph: str, banned: List[str]) -> str:\n\t\t\n\t\t# convert to lower case and split string into words by spaces and punctuation\n a = re.split(r\'\\W+\', paragraph.lower())\n\t\t\n\t\t# make new list consisitng of words not in banned list (remove banned words)\n b = [w for w in a if w not in banned]\n\t\t\n\t\t# return value that counted max times in the new list\n return max(b, key = b.count)\n```\n\nPlease, upvote if you like it so that others can see and learn from it. Thanks! | 25 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Python3 library Function Runtime: 49ms 62.31% Memory: 14mb 37.05% | most-common-word | 0 | 1 | ```\nimport re\nfrom collections import Counter\n\n# Runtime: 49ms 62.31% Memory: 14mb 37.05%\nclass Solution:\n def mostCommonWord(self, string: str, banned: List[str]) -> str:\n string = re.sub(r"[^a-zA-Z]", \' \', string).lower()\n freq = Counter(string.split())\n for x in banned:\n if x in freq:\n freq.pop(x)\n \n return max(freq, key=freq.get)\n \n``` | 2 | Given a string `paragraph` and a string array of the banned words `banned`, return _the most frequent word that is not banned_. It is **guaranteed** there is **at least one word** that is not banned, and that the answer is **unique**.
The words in `paragraph` are **case-insensitive** and the answer should be returned in **lowercase**.
**Example 1:**
**Input:** paragraph = "Bob hit a ball, the hit BALL flew far after it was hit. ", banned = \[ "hit "\]
**Output:** "ball "
**Explanation:**
"hit " occurs 3 times, but it is a banned word.
"ball " occurs twice (and no other word does), so it is the most frequent non-banned word in the paragraph.
Note that words in the paragraph are not case sensitive,
that punctuation is ignored (even if adjacent to words, such as "ball, "),
and that "hit " isn't the answer even though it occurs more because it is banned.
**Example 2:**
**Input:** paragraph = "a. ", banned = \[\]
**Output:** "a "
**Constraints:**
* `1 <= paragraph.length <= 1000`
* paragraph consists of English letters, space `' '`, or one of the symbols: `"!?',;. "`.
* `0 <= banned.length <= 100`
* `1 <= banned[i].length <= 10`
* `banned[i]` consists of only lowercase English letters. | null |
Python3 library Function Runtime: 49ms 62.31% Memory: 14mb 37.05% | most-common-word | 0 | 1 | ```\nimport re\nfrom collections import Counter\n\n# Runtime: 49ms 62.31% Memory: 14mb 37.05%\nclass Solution:\n def mostCommonWord(self, string: str, banned: List[str]) -> str:\n string = re.sub(r"[^a-zA-Z]", \' \', string).lower()\n freq = Counter(string.split())\n for x in banned:\n if x in freq:\n freq.pop(x)\n \n return max(freq, key=freq.get)\n \n``` | 2 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Solution | short-encoding-of-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nstruct reverseComparer {\n bool operator()(const string& a, const string& b) {\n for (auto pa = a.rbegin(), pb = b.rbegin(); pa != a.rend() && pb != b.rend(); ++pa, ++pb) if (*pa != *pb) return *pa < *pb;\n return a.size() < b.size();\n }\n};\nint minimumLengthEncoding(vector<string>& ws, int res = 0) {\n sort(ws.begin(), ws.end(), reverseComparer());\n for (auto i = 0; i < ws.size() - 1; ++i) res += ws[i].size() <= ws[i + 1].size() \n && ws[i] == ws[i + 1].substr(ws[i + 1].size() - ws[i].size()) ? 0 : ws[i].size() + 1;\n return res + ws[ws.size() - 1].size() + 1;\n}\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n rev_words = list(map(lambda x: x[::-1], words))\n rev_words_list = sorted([word for i, word in enumerate(rev_words)])[::-1]\n ans = [rev_words_list[0]]\n for j in range(1, len(rev_words_list)):\n if rev_words_list[j - 1].startswith(rev_words_list[j]):\n continue\n else:\n ans.append(rev_words_list[j])\n num = len(ans)\n for j in ans:\n num = num + len(j)\n return num\n```\n\n```Java []\nclass Solution {\n TrieNode root;\n class TrieNode {\n TrieNode[] next = null;\n }\n public int minimumLengthEncoding(String[] words) {\n root = new TrieNode();\n root.next = new TrieNode[26];\n int res = 0;\n for (String w : words) {\n res += helper(w);\n }\n return res;\n }\n public int helper(String w) {\n int length = w.length();\n boolean newBranch = false;\n int create = 0;\n TrieNode current = root;\n for (int i = length - 1; i >= 0; --i) {\n boolean newLevel = false;\n int id = w.charAt(i) - \'a\';\n if (current.next == null) {\n newLevel = true;\n current.next = new TrieNode[26];\n }\n if (current.next[id] == null) {\n if (!newLevel) newBranch = true;\n current.next[id] = new TrieNode();\n create++;\n }\n current = current.next[id];\n }\n return newBranch ? length + 1 : create;\n }\n}\n```\n | 1 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Solution | short-encoding-of-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\nstruct reverseComparer {\n bool operator()(const string& a, const string& b) {\n for (auto pa = a.rbegin(), pb = b.rbegin(); pa != a.rend() && pb != b.rend(); ++pa, ++pb) if (*pa != *pb) return *pa < *pb;\n return a.size() < b.size();\n }\n};\nint minimumLengthEncoding(vector<string>& ws, int res = 0) {\n sort(ws.begin(), ws.end(), reverseComparer());\n for (auto i = 0; i < ws.size() - 1; ++i) res += ws[i].size() <= ws[i + 1].size() \n && ws[i] == ws[i + 1].substr(ws[i + 1].size() - ws[i].size()) ? 0 : ws[i].size() + 1;\n return res + ws[ws.size() - 1].size() + 1;\n}\n};\n```\n\n```Python3 []\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n rev_words = list(map(lambda x: x[::-1], words))\n rev_words_list = sorted([word for i, word in enumerate(rev_words)])[::-1]\n ans = [rev_words_list[0]]\n for j in range(1, len(rev_words_list)):\n if rev_words_list[j - 1].startswith(rev_words_list[j]):\n continue\n else:\n ans.append(rev_words_list[j])\n num = len(ans)\n for j in ans:\n num = num + len(j)\n return num\n```\n\n```Java []\nclass Solution {\n TrieNode root;\n class TrieNode {\n TrieNode[] next = null;\n }\n public int minimumLengthEncoding(String[] words) {\n root = new TrieNode();\n root.next = new TrieNode[26];\n int res = 0;\n for (String w : words) {\n res += helper(w);\n }\n return res;\n }\n public int helper(String w) {\n int length = w.length();\n boolean newBranch = false;\n int create = 0;\n TrieNode current = root;\n for (int i = length - 1; i >= 0; --i) {\n boolean newLevel = false;\n int id = w.charAt(i) - \'a\';\n if (current.next == null) {\n newLevel = true;\n current.next = new TrieNode[26];\n }\n if (current.next[id] == null) {\n if (!newLevel) newBranch = true;\n current.next[id] = new TrieNode();\n create++;\n }\n current = current.next[id];\n }\n return newBranch ? length + 1 : create;\n }\n}\n```\n | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
[Python] Concise Brute Force & Trie Solutions with Explanation | short-encoding-of-words | 0 | 1 | ### Introduction\n\nGiven a list of words, find the length of the shortest string which contains all the words in the list appended with a hash "#" symbol.\n\nRunning through some test cases, we quickly see that the only way for the resultant string to be shorter than the sum of all lengths of the words in the list is if **there are words in the list that are suffixes of other words in the list**. For example:\n\n```text\nwords = ["time","me"]\nresult = "time#"\n\nwords = ["time","meat"]\nresult = "time#meat#"\n(notice that it cannot be any variant of "timeat", since inserting a hash symbol will disrupt the words)\n```\n\nAs such, we require a solution that can **identify and group the words based on their suffixes**.\n\n---\n\n### Brute Force Approach\n\nThe simplest way to find out if a word `w1` is a suffix of another word `w2` is to check if `w2.endswith(w1)`. We can sort the list by word length in decreasing order, so that all words that are suffixes are guaranteed to be found.\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words.sort(key=len, reverse=True)\n res = []\n for suffix in words:\n if not any(word.endswith(suffix) for word in res): # check that this word is not actually a suffix\n res.append(suffix)\n return sum(len(word)+1 for word in res) # append hash \'#\' symbol to each word that is not a suffix\n```\n\n**TC: O(n<sup>2</sup>k)**, where `n` is the number of words in the list and `k` is the (maximum) length of the words; we check all words against one another in the worst case.\n**SC: O(n)**; for the resultant list of words.\n\n---\n\n### Optimised Brute Force Approach\n\nInstead of constantly having to compare two strings (which is slow), we can instead **loop through all possible suffixes of each word and count the number of occurrences of each suffix**. If a particular suffix only occurs once, that indicates that the \'suffix\' is actually a word to be added into the resultant string.\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words = set(words) # important - e.g. ["time","time"] -> "time#"\n counter = Counter(word[i:] for word in words for i in range(len(word)))\n return sum(len(word)+1 for word in words if counter[word] == 1)\n```\n\n**TC: O(nk)**; each character of each word is visited once.\n**SC: O(nk)**; each string has `k` substrings as keys in `d`.\n\n---\n\n### Trie Approach\n\nA trie is a specialised data structure that is useful for storing and searching for strings. [This article](https://towardsdatascience.com/implementing-a-trie-data-structure-in-python-in-less-than-100-lines-of-code-a877ea23c1a1) might help get you started if you\'re unfamiliar with the data structure.\n\nEssentially, we can find similar suffixes by **reversing each word and adding it to our trie**. Then, we can perform DFS on the tree-like structure to obtain all maximum-length chains; i.e., words that are not suffixes.\n\n```python\nclass TrieNode:\n def __init__(self, ch: Optional[str]=\'#\'):\n self.ch = ch\n self.cd = {} # children nodes\n self.end = False\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def add(self, word: str) -> None:\n curr = self.root\n for i in range(len(word)):\n if word[~i] not in curr.cd: # ~i = -i-1\n curr.cd[word[~i]] = TrieNode(word[~i])\n curr = curr.cd[word[~i]]\n curr.end = True # mark the end of the word\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n trie = Trie()\n for word in words:\n trie.add(word)\n def dfs(node: TrieNode, curr: int) -> int:\n return sum(dfs(adj, curr+1) for adj in node.cd.values()) if node.cd else curr\n return dfs(trie.root, 1)\n```\n\nA less verbose but more concise implementation:\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n trie = (d := lambda: defaultdict(d))() # multi-level collections.defaultdict\n for word in words:\n curr = trie\n for i in range(len(word)):\n curr = curr[word[~i]]\n return (dfs := lambda node, curr: sum(dfs(adj, curr+1) for adj in node.values()) if node else curr)(trie, 1)\n```\n\nA similar solution I found in the official solution post which uses a slightly different approach:\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words = list(set(words))\n trie = (d := lambda: defaultdict(d))()\n nodes = [reduce(dict.__getitem__, word[::-1], trie) for word in words] # equivalent to trie[word[-1]][word[-2]]...\n return sum((len(word)+1) for word, node in zip(words, nodes) if len(node) == 0)\n```\n\n> If the concise implementations are not sufficiently readable, please use the original implementation instead - it\'s the implementation that I first used when solving this problem! I just wanted to show that it is possible to write concise code for trie implementations even when it\'s not traditionally the way to write the code.\n\n**TC: O(nk)**; the worst-case scenario is if none of the words match with one another, in which case we have `n` chains of length `k`.\n**SC: O(nk)**; similar reasoning as above.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 25 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
[Python] Concise Brute Force & Trie Solutions with Explanation | short-encoding-of-words | 0 | 1 | ### Introduction\n\nGiven a list of words, find the length of the shortest string which contains all the words in the list appended with a hash "#" symbol.\n\nRunning through some test cases, we quickly see that the only way for the resultant string to be shorter than the sum of all lengths of the words in the list is if **there are words in the list that are suffixes of other words in the list**. For example:\n\n```text\nwords = ["time","me"]\nresult = "time#"\n\nwords = ["time","meat"]\nresult = "time#meat#"\n(notice that it cannot be any variant of "timeat", since inserting a hash symbol will disrupt the words)\n```\n\nAs such, we require a solution that can **identify and group the words based on their suffixes**.\n\n---\n\n### Brute Force Approach\n\nThe simplest way to find out if a word `w1` is a suffix of another word `w2` is to check if `w2.endswith(w1)`. We can sort the list by word length in decreasing order, so that all words that are suffixes are guaranteed to be found.\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words.sort(key=len, reverse=True)\n res = []\n for suffix in words:\n if not any(word.endswith(suffix) for word in res): # check that this word is not actually a suffix\n res.append(suffix)\n return sum(len(word)+1 for word in res) # append hash \'#\' symbol to each word that is not a suffix\n```\n\n**TC: O(n<sup>2</sup>k)**, where `n` is the number of words in the list and `k` is the (maximum) length of the words; we check all words against one another in the worst case.\n**SC: O(n)**; for the resultant list of words.\n\n---\n\n### Optimised Brute Force Approach\n\nInstead of constantly having to compare two strings (which is slow), we can instead **loop through all possible suffixes of each word and count the number of occurrences of each suffix**. If a particular suffix only occurs once, that indicates that the \'suffix\' is actually a word to be added into the resultant string.\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words = set(words) # important - e.g. ["time","time"] -> "time#"\n counter = Counter(word[i:] for word in words for i in range(len(word)))\n return sum(len(word)+1 for word in words if counter[word] == 1)\n```\n\n**TC: O(nk)**; each character of each word is visited once.\n**SC: O(nk)**; each string has `k` substrings as keys in `d`.\n\n---\n\n### Trie Approach\n\nA trie is a specialised data structure that is useful for storing and searching for strings. [This article](https://towardsdatascience.com/implementing-a-trie-data-structure-in-python-in-less-than-100-lines-of-code-a877ea23c1a1) might help get you started if you\'re unfamiliar with the data structure.\n\nEssentially, we can find similar suffixes by **reversing each word and adding it to our trie**. Then, we can perform DFS on the tree-like structure to obtain all maximum-length chains; i.e., words that are not suffixes.\n\n```python\nclass TrieNode:\n def __init__(self, ch: Optional[str]=\'#\'):\n self.ch = ch\n self.cd = {} # children nodes\n self.end = False\n \nclass Trie:\n def __init__(self):\n self.root = TrieNode()\n \n def add(self, word: str) -> None:\n curr = self.root\n for i in range(len(word)):\n if word[~i] not in curr.cd: # ~i = -i-1\n curr.cd[word[~i]] = TrieNode(word[~i])\n curr = curr.cd[word[~i]]\n curr.end = True # mark the end of the word\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n trie = Trie()\n for word in words:\n trie.add(word)\n def dfs(node: TrieNode, curr: int) -> int:\n return sum(dfs(adj, curr+1) for adj in node.cd.values()) if node.cd else curr\n return dfs(trie.root, 1)\n```\n\nA less verbose but more concise implementation:\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n trie = (d := lambda: defaultdict(d))() # multi-level collections.defaultdict\n for word in words:\n curr = trie\n for i in range(len(word)):\n curr = curr[word[~i]]\n return (dfs := lambda node, curr: sum(dfs(adj, curr+1) for adj in node.values()) if node else curr)(trie, 1)\n```\n\nA similar solution I found in the official solution post which uses a slightly different approach:\n\n```python\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words = list(set(words))\n trie = (d := lambda: defaultdict(d))()\n nodes = [reduce(dict.__getitem__, word[::-1], trie) for word in words] # equivalent to trie[word[-1]][word[-2]]...\n return sum((len(word)+1) for word, node in zip(words, nodes) if len(node) == 0)\n```\n\n> If the concise implementations are not sufficiently readable, please use the original implementation instead - it\'s the implementation that I first used when solving this problem! I just wanted to show that it is possible to write concise code for trie implementations even when it\'s not traditionally the way to write the code.\n\n**TC: O(nk)**; the worst-case scenario is if none of the words match with one another, in which case we have `n` chains of length `k`.\n**SC: O(nk)**; similar reasoning as above.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 25 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
📌 Python3 solution using Trie and DFS | short-encoding-of-words | 0 | 1 | ```\nclass TriNode:\n def __init__(self, val):\n self.val = val\n self.children = [0]*26\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n root = TriNode("")\n result = [0]\n \n def insertInTrie(word):\n curr = root\n for letter in word[::-1]:\n index = ord(letter)%97\n if curr.children[index] == 0:\n curr.children[index] = TriNode(letter)\n curr= curr.children[index]\n \n def traverseTrie(root,choosen):\n flag = 0\n for node in root.children:\n if node != 0:\n traverseTrie(node,choosen+node.val)\n flag=1\n if flag == 0:\n result[0]+=len(choosen)+1\n \n for word in words:\n insertInTrie(word)\n \n traverseTrie(root,"")\n \n return result[0]\n``` | 6 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
📌 Python3 solution using Trie and DFS | short-encoding-of-words | 0 | 1 | ```\nclass TriNode:\n def __init__(self, val):\n self.val = val\n self.children = [0]*26\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n root = TriNode("")\n result = [0]\n \n def insertInTrie(word):\n curr = root\n for letter in word[::-1]:\n index = ord(letter)%97\n if curr.children[index] == 0:\n curr.children[index] = TriNode(letter)\n curr= curr.children[index]\n \n def traverseTrie(root,choosen):\n flag = 0\n for node in root.children:\n if node != 0:\n traverseTrie(node,choosen+node.val)\n flag=1\n if flag == 0:\n result[0]+=len(choosen)+1\n \n for word in words:\n insertInTrie(word)\n \n traverseTrie(root,"")\n \n return result[0]\n``` | 6 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Without Trie || Sorting || Easy to Understand || Python | short-encoding-of-words | 0 | 1 | **The main idea is that larger string will never be suffix of smaller string.**\n* So,Simply sort (descending order) the list on the basis of length. \n* Then we\'ll traverse the array mantaining a string variable ( i.e st in code ) and \n\t* keep checking whether the current word + "#" is present in the string st or not\n\t* if it is **not** present in string st then we will add current word +"#" in the string st, Otherwise we won\'t add anything.\n* At last we\'ll return the length of string st.\n\n```\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words.sort(key=len,reverse=True)\n n=len(words)\n st=""\n for i in range(0,n):\n if words[i]+"#" not in st:\n st+=words[i]+"#"\n \n return len(st)\n \n``` | 4 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Without Trie || Sorting || Easy to Understand || Python | short-encoding-of-words | 0 | 1 | **The main idea is that larger string will never be suffix of smaller string.**\n* So,Simply sort (descending order) the list on the basis of length. \n* Then we\'ll traverse the array mantaining a string variable ( i.e st in code ) and \n\t* keep checking whether the current word + "#" is present in the string st or not\n\t* if it is **not** present in string st then we will add current word +"#" in the string st, Otherwise we won\'t add anything.\n* At last we\'ll return the length of string st.\n\n```\n\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n words.sort(key=len,reverse=True)\n n=len(words)\n st=""\n for i in range(0,n):\n if words[i]+"#" not in st:\n st+=words[i]+"#"\n \n return len(st)\n \n``` | 4 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Easy Python Solution using hashmap with Explanation and Comments | short-encoding-of-words | 0 | 1 | # Easy Python Solution using hashmap with Explanation and Comments\n\n**Question**\nThe question\'s phrasing is complex to understand.\n\nSimplifying the question:\n1. We have an array (`words`) of words\n2. Create another array `new_words` in which we have all the words which are not a suffix of any other word in `words`.\n3. Return the length of all the words in `new_words` + the number of words in `new_words`.\n\nE.g. \n`words = ["time", "me", "bell"]`\n`words_new = ["time", "bell"]` , removing `me` as it is already a suffix of `time` and we have already included `time`.\n\n\n**Time Complexity: O(n^2)\nSpace Complexity: O(n)**\n\n**Runtime: 170 ms.\nMemory Usage: 14.5 MB**\n\n\n```\nclass Solution:\n\n\tdef minimumLengthEncoding(self, words: List[str]) -> int:\n\t\t# hashmap to store all the non repeating words\n\t\tstore = {}\n\n\t\t# storing all the words in hashmap for faster access O(1)\n\t\tfor w in words:\n\t\t\tstore[w] = 1\n\n\t\t"""\n\t\tgoing through each word and checking if any of the \n\t\tsuffix is present as a different word in the initial array\n\t\t\n\t\tNote: the max length of array `words` = n\n\t\tand max length of any word in the array, i.e. `words[i].length` <= 7\n\t\tdeletion in hashmap worst case complexity: O(n); average/best case: O(1)\n\t\t\n\t\tTherefore the time complexity would be: O(n * 7 * n) = O(n^2)\n\t\t"""\n\t\tfor w in words:\n\t\t\tfor i in range(1, len(w)):\n\t\t\t # checking if suffix exists in O(1)\n\t\t\t\tif store.get(w[i:], None):\n\t\t\t\t\t# deleting the suffix if it exists: worst case complexity O(n)\n\t\t\t\t\tdel store[w[i:]]\n\n\t\t# getting the number of elements left in hashmap\n\t\tcnt = len(store)\n\n\t\t# getting lenght of each individual element and adding it to the variable\n\t\tfor k in store.keys():\n\t\t\tcnt += len(k)\n\n\t\treturn cnt\n``` | 4 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Easy Python Solution using hashmap with Explanation and Comments | short-encoding-of-words | 0 | 1 | # Easy Python Solution using hashmap with Explanation and Comments\n\n**Question**\nThe question\'s phrasing is complex to understand.\n\nSimplifying the question:\n1. We have an array (`words`) of words\n2. Create another array `new_words` in which we have all the words which are not a suffix of any other word in `words`.\n3. Return the length of all the words in `new_words` + the number of words in `new_words`.\n\nE.g. \n`words = ["time", "me", "bell"]`\n`words_new = ["time", "bell"]` , removing `me` as it is already a suffix of `time` and we have already included `time`.\n\n\n**Time Complexity: O(n^2)\nSpace Complexity: O(n)**\n\n**Runtime: 170 ms.\nMemory Usage: 14.5 MB**\n\n\n```\nclass Solution:\n\n\tdef minimumLengthEncoding(self, words: List[str]) -> int:\n\t\t# hashmap to store all the non repeating words\n\t\tstore = {}\n\n\t\t# storing all the words in hashmap for faster access O(1)\n\t\tfor w in words:\n\t\t\tstore[w] = 1\n\n\t\t"""\n\t\tgoing through each word and checking if any of the \n\t\tsuffix is present as a different word in the initial array\n\t\t\n\t\tNote: the max length of array `words` = n\n\t\tand max length of any word in the array, i.e. `words[i].length` <= 7\n\t\tdeletion in hashmap worst case complexity: O(n); average/best case: O(1)\n\t\t\n\t\tTherefore the time complexity would be: O(n * 7 * n) = O(n^2)\n\t\t"""\n\t\tfor w in words:\n\t\t\tfor i in range(1, len(w)):\n\t\t\t # checking if suffix exists in O(1)\n\t\t\t\tif store.get(w[i:], None):\n\t\t\t\t\t# deleting the suffix if it exists: worst case complexity O(n)\n\t\t\t\t\tdel store[w[i:]]\n\n\t\t# getting the number of elements left in hashmap\n\t\tcnt = len(store)\n\n\t\t# getting lenght of each individual element and adding it to the variable\n\t\tfor k in store.keys():\n\t\t\tcnt += len(k)\n\n\t\treturn cnt\n``` | 4 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Trie Solution| Industry Level Code | short-encoding-of-words | 0 | 1 | ```\nclass TreeNode:\n def __init__(self):\n self.children = [None]*26\n self.word = \'\'\nclass Trie:\n def __init__(self):\n self.root = TreeNode()\n def insert(self,word):\n cur_node = self.root\n for s in word:\n index = ord(s)-ord(\'a\')\n if cur_node.children[index] is None:\n cur_node.children[index] = TreeNode()\n cur_node = cur_node.children[index]\n if len(word)>len(cur_node.word):\n cur_node.word = word\n return\n def search(self,word):\n cur_node = self.root\n for s in word:\n index = ord(s)-ord(\'a\')\n cur_node = cur_node.children[index]\n return cur_node.word\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n res = set()\n root = Trie()\n for word in words:\n root.insert(word[::-1])\n for word in words:\n res.add(root.search(word[::-1]))\n count = 0\n for word in res:\n count+=len(word)+1\n return count\n```\nHope you like the above solution! | 2 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Trie Solution| Industry Level Code | short-encoding-of-words | 0 | 1 | ```\nclass TreeNode:\n def __init__(self):\n self.children = [None]*26\n self.word = \'\'\nclass Trie:\n def __init__(self):\n self.root = TreeNode()\n def insert(self,word):\n cur_node = self.root\n for s in word:\n index = ord(s)-ord(\'a\')\n if cur_node.children[index] is None:\n cur_node.children[index] = TreeNode()\n cur_node = cur_node.children[index]\n if len(word)>len(cur_node.word):\n cur_node.word = word\n return\n def search(self,word):\n cur_node = self.root\n for s in word:\n index = ord(s)-ord(\'a\')\n cur_node = cur_node.children[index]\n return cur_node.word\nclass Solution:\n def minimumLengthEncoding(self, words: List[str]) -> int:\n res = set()\n root = Trie()\n for word in words:\n root.insert(word[::-1])\n for word in words:\n res.add(root.search(word[::-1]))\n count = 0\n for word in res:\n count+=len(word)+1\n return count\n```\nHope you like the above solution! | 2 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Python, Trie | short-encoding-of-words | 0 | 1 | # Idea\nFirst, build the Trie data structure from the reversed words.\nThen, do a DFS and find out the total length of all the paths from the root to leaves:\n# Complexity:\nTime / Memory: O(N)\n\n```\ndef minimumLengthEncoding(self, words: List[str]) -> int:\n\ttrie = {}\n\tfor word in words:\n\t\tnode = trie\n\t\tfor ch in reversed(word):\n\t\t\tif ch not in node:\n\t\t\t\tnode[ch] = {}\n\t\t\tnode = node[ch]\n\n\tif not trie: return 0\n\n\tdef dfs(node=trie, curlvl=1):\n\t\tif not node: return curlvl\n\t\treturn sum([dfs(child, curlvl+1) for child in node.values()])\n\n\treturn dfs()\n``` | 12 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Python, Trie | short-encoding-of-words | 0 | 1 | # Idea\nFirst, build the Trie data structure from the reversed words.\nThen, do a DFS and find out the total length of all the paths from the root to leaves:\n# Complexity:\nTime / Memory: O(N)\n\n```\ndef minimumLengthEncoding(self, words: List[str]) -> int:\n\ttrie = {}\n\tfor word in words:\n\t\tnode = trie\n\t\tfor ch in reversed(word):\n\t\t\tif ch not in node:\n\t\t\t\tnode[ch] = {}\n\t\t\tnode = node[ch]\n\n\tif not trie: return 0\n\n\tdef dfs(node=trie, curlvl=1):\n\t\tif not node: return curlvl\n\t\treturn sum([dfs(child, curlvl+1) for child in node.values()])\n\n\treturn dfs()\n``` | 12 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
easy solution | shortest-distance-to-a-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n a=[]\n b=[]\n for i in range(len(s)):\n if s[i]==c:\n a.append(i)\n for i in range(len(s)):\n c=[]\n for j in a:\n c.append(abs(i-j))\n b.append(min(c))\n return b\n\n \n``` | 1 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
easy solution | shortest-distance-to-a-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n a=[]\n b=[]\n for i in range(len(s)):\n if s[i]==c:\n a.append(i)\n for i in range(len(s)):\n c=[]\n for j in a:\n c.append(abs(i-j))\n b.append(min(c))\n return b\n\n \n``` | 1 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python || 99.92% Faster || Two Pointers || O(n) Solution | shortest-distance-to-a-character | 0 | 1 | ```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n a,n=[],len(s)\n for i in range(n):\n if s[i]==c:\n a.append(i)\n answer=[]\n j=0\n for i in range(n):\n if s[i]==c:\n answer.append(0)\n j+=1\n elif i<a[0]:\n answer.append(a[0]-i)\n elif i>a[-1]:\n answer.append(i-a[-1])\n else:\n answer.append(min((a[j]-i),(i-a[j-1])))\n return answer\n```\n\n**An upvote will be encouraging** | 15 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python || 99.92% Faster || Two Pointers || O(n) Solution | shortest-distance-to-a-character | 0 | 1 | ```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n a,n=[],len(s)\n for i in range(n):\n if s[i]==c:\n a.append(i)\n answer=[]\n j=0\n for i in range(n):\n if s[i]==c:\n answer.append(0)\n j+=1\n elif i<a[0]:\n answer.append(a[0]-i)\n elif i>a[-1]:\n answer.append(i-a[-1])\n else:\n answer.append(min((a[j]-i),(i-a[j-1])))\n return answer\n```\n\n**An upvote will be encouraging** | 15 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python3 ✅✅✅ || Long but Fast || Faster than 97.10% | shortest-distance-to-a-character | 0 | 1 | # Code\n```\nclass Solution:\n def getIndicies(self, s, c):\n indicies = []\n for i in range(len(s)):\n if s[i] == c:\n indicies.append(i)\n return indicies\n def getShortest(self, idx, indicies):\n if idx in indicies: return 0\n if idx < indicies[0]: return abs(idx - indicies[0])\n elif idx > indicies[-1]: return abs(indicies[-1] - idx)\n for index in range(len(indicies)):\n if indicies[index] > idx:\n minDistance = min(abs(idx - indicies[index]), abs(idx - indicies[index - 1]))\n return minDistance\n def shortestToChar(self, s: str, c: str) -> List[int]:\n indicies = sorted(self.getIndicies(s, c), key=lambda x:x)\n result = []\n for i in range(len(s)):\n result.append(self.getShortest(i, indicies))\n return result\n```\n\n\n | 1 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python3 ✅✅✅ || Long but Fast || Faster than 97.10% | shortest-distance-to-a-character | 0 | 1 | # Code\n```\nclass Solution:\n def getIndicies(self, s, c):\n indicies = []\n for i in range(len(s)):\n if s[i] == c:\n indicies.append(i)\n return indicies\n def getShortest(self, idx, indicies):\n if idx in indicies: return 0\n if idx < indicies[0]: return abs(idx - indicies[0])\n elif idx > indicies[-1]: return abs(indicies[-1] - idx)\n for index in range(len(indicies)):\n if indicies[index] > idx:\n minDistance = min(abs(idx - indicies[index]), abs(idx - indicies[index - 1]))\n return minDistance\n def shortestToChar(self, s: str, c: str) -> List[int]:\n indicies = sorted(self.getIndicies(s, c), key=lambda x:x)\n result = []\n for i in range(len(s)):\n result.append(self.getShortest(i, indicies))\n return result\n```\n\n\n | 1 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python3 🐍 || explicit approach || memory 🤜🏻 88% | shortest-distance-to-a-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> list[int]:\n answer = []\n indexes = [i for i, val in enumerate(s) if val == c]\n low, high, index = indexes[0], indexes[1] if len(indexes) > 1 else indexes[0], 0\n last, first, second = indexes[-1], 0, 1\n for x in range(len(s)):\n if abs(x - low) < abs(x - high):\n index = low\n answer.append(abs(x - index))\n else:\n index = high\n answer.append(abs(x - index))\n if last != index:\n first += 1\n second += 1\n low = indexes[first ]\n high = indexes[second]\n return answer\n\n\nobj = Solution()\nprint(obj.shortestToChar(s="loveleetcode", c="e"))\n\n``` | 1 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python3 🐍 || explicit approach || memory 🤜🏻 88% | shortest-distance-to-a-character | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> list[int]:\n answer = []\n indexes = [i for i, val in enumerate(s) if val == c]\n low, high, index = indexes[0], indexes[1] if len(indexes) > 1 else indexes[0], 0\n last, first, second = indexes[-1], 0, 1\n for x in range(len(s)):\n if abs(x - low) < abs(x - high):\n index = low\n answer.append(abs(x - index))\n else:\n index = high\n answer.append(abs(x - index))\n if last != index:\n first += 1\n second += 1\n low = indexes[first ]\n high = indexes[second]\n return answer\n\n\nobj = Solution()\nprint(obj.shortestToChar(s="loveleetcode", c="e"))\n\n``` | 1 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python3 O(n) || O(n) # Runtime: 53ms 78.92% Memory: 13.9mb 91.60% | shortest-distance-to-a-character | 0 | 1 | ```\nclass Solution:\n def shortestToChar(self, string: str, char: str) -> List[int]:\n return self.optimalSolution(string, char)\n# O(n) || O(n)\n# Runtime: 53ms 78.92% Memory: 13.9mb 91.60%\n def optimalSolution(self, string, char):\n n = len(string)\n leftArray, rightArray, result = ([float(\'inf\')] * n, \n [float(\'inf\')] * n, \n [float(\'inf\')] * n)\n temp = float(\'inf\')\n for i in range(len(string)):\n if string[i] == char:\n temp = 0\n leftArray[i] = temp\n temp += 1\n\n temp = float(\'inf\')\n for i in reversed(range(len(string))):\n if string[i] == char:\n temp = 0\n rightArray[i] = temp\n temp += 1\n\n\n for i in range(len(result)):\n result[i] = min(leftArray[i], rightArray[i])\n\n return result\n\n \n# O(n^2) || O(n) Runtime: TLE\n def bruteForce(self, string, char):\n sequence = [float(\'inf\')] * len(string)\n newList = []\n for idx, val in enumerate(string):\n if val == char:\n newList.append(idx)\n\n for val1 in newList:\n for idx2, val2 in enumerate(string):\n sequence[idx2] = min(sequence[idx2], abs(idx2-val1))\n\n return sequence\n``` | 2 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python3 O(n) || O(n) # Runtime: 53ms 78.92% Memory: 13.9mb 91.60% | shortest-distance-to-a-character | 0 | 1 | ```\nclass Solution:\n def shortestToChar(self, string: str, char: str) -> List[int]:\n return self.optimalSolution(string, char)\n# O(n) || O(n)\n# Runtime: 53ms 78.92% Memory: 13.9mb 91.60%\n def optimalSolution(self, string, char):\n n = len(string)\n leftArray, rightArray, result = ([float(\'inf\')] * n, \n [float(\'inf\')] * n, \n [float(\'inf\')] * n)\n temp = float(\'inf\')\n for i in range(len(string)):\n if string[i] == char:\n temp = 0\n leftArray[i] = temp\n temp += 1\n\n temp = float(\'inf\')\n for i in reversed(range(len(string))):\n if string[i] == char:\n temp = 0\n rightArray[i] = temp\n temp += 1\n\n\n for i in range(len(result)):\n result[i] = min(leftArray[i], rightArray[i])\n\n return result\n\n \n# O(n^2) || O(n) Runtime: TLE\n def bruteForce(self, string, char):\n sequence = [float(\'inf\')] * len(string)\n newList = []\n for idx, val in enumerate(string):\n if val == char:\n newList.append(idx)\n\n for val1 in newList:\n for idx2, val2 in enumerate(string):\n sequence[idx2] = min(sequence[idx2], abs(idx2-val1))\n\n return sequence\n``` | 2 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Solution | shortest-distance-to-a-character | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> shortestToChar(string s, char c) {\n int n = s.length();\n\tvector<int>v;\n\tfor (int i = 0;i < n;i++) {\n\t\tint distance = 0;\n\t\tfor (int j = i, k = i;j < n || k >= 0;j++, k--) {\n\t\t\tif ((k >= 0 && s[k] == c) || (j < n && s[j] == c )) {\n\t\t\t\tv.push_back(distance);\n\t\t\t\tbreak;\n\t\t\t}\n\t\t\tdistance++;\n\t\t}\n\n\t}\n\treturn v;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n n=len(s)\n arr=[i for i in range(n) if s[i]==c]\n arr1=[]\n j=0\n for i in range(n):\n if s[i]==c:\n arr1.append(0)\n j=j+1\n elif i<arr[0]:\n arr1.append(arr[0]-i)\n elif i>arr[-1]:\n arr1.append(i-arr[-1])\n else:\n arr1.append(min(arr[j]-i,i-arr[j-1]))\n return arr1\n```\n\n```Java []\nclass Solution {\n public int[] shortestToChar(String s, char c) {\n int[] result = new int[s.length()];\n int currentIndex = -1; \n int leftIndex = findNextOccurance(s, -1, c);\n fillCreek(result, -leftIndex, leftIndex);\n while(true){\n int rightIndex = findNextOccurance( s, leftIndex, c);\n if( rightIndex == -1){\n fillCreek( result, leftIndex, s.length() + ( s.length()-1-leftIndex ));\n break;\n }\n fillCreek(result, leftIndex, rightIndex);\n leftIndex = rightIndex; \n }\n return result;\n }\n public int findNextOccurance(String s, int fromIndex, char c){\n for( int i = fromIndex+1; i< s.length(); i++){\n if( s.charAt(i) == c ) {\n return i;\n }\n }\n return -1;\n }\n public void fillCreek(int[] result, int leftIndex, int rightIndex){\n int from = Math.max( leftIndex, 0);\n int to = Math.min( rightIndex, result.length-1);\n for( int i = from ; i<= to; i++){\n result[i] = Math.min( i - leftIndex , rightIndex - i );\n }\n }\n}\n```\n | 2 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Solution | shortest-distance-to-a-character | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<int> shortestToChar(string s, char c) {\n int n = s.length();\n\tvector<int>v;\n\tfor (int i = 0;i < n;i++) {\n\t\tint distance = 0;\n\t\tfor (int j = i, k = i;j < n || k >= 0;j++, k--) {\n\t\t\tif ((k >= 0 && s[k] == c) || (j < n && s[j] == c )) {\n\t\t\t\tv.push_back(distance);\n\t\t\t\tbreak;\n\t\t\t}\n\t\t\tdistance++;\n\t\t}\n\n\t}\n\treturn v;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n n=len(s)\n arr=[i for i in range(n) if s[i]==c]\n arr1=[]\n j=0\n for i in range(n):\n if s[i]==c:\n arr1.append(0)\n j=j+1\n elif i<arr[0]:\n arr1.append(arr[0]-i)\n elif i>arr[-1]:\n arr1.append(i-arr[-1])\n else:\n arr1.append(min(arr[j]-i,i-arr[j-1]))\n return arr1\n```\n\n```Java []\nclass Solution {\n public int[] shortestToChar(String s, char c) {\n int[] result = new int[s.length()];\n int currentIndex = -1; \n int leftIndex = findNextOccurance(s, -1, c);\n fillCreek(result, -leftIndex, leftIndex);\n while(true){\n int rightIndex = findNextOccurance( s, leftIndex, c);\n if( rightIndex == -1){\n fillCreek( result, leftIndex, s.length() + ( s.length()-1-leftIndex ));\n break;\n }\n fillCreek(result, leftIndex, rightIndex);\n leftIndex = rightIndex; \n }\n return result;\n }\n public int findNextOccurance(String s, int fromIndex, char c){\n for( int i = fromIndex+1; i< s.length(); i++){\n if( s.charAt(i) == c ) {\n return i;\n }\n }\n return -1;\n }\n public void fillCreek(int[] result, int leftIndex, int rightIndex){\n int from = Math.max( leftIndex, 0);\n int to = Math.min( rightIndex, result.length-1);\n for( int i = from ; i<= to; i++){\n result[i] = Math.min( i - leftIndex , rightIndex - i );\n }\n }\n}\n```\n | 2 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python O(n) by propagation 85%+ [w/ Diagram] | shortest-distance-to-a-character | 0 | 1 | Python O(n) by propagation\n\n---\n\n**Hint**:\n\nImagine parameter C as a flag on the line.\n\nThink of propagation technique:\n**1st-pass** iteration **propagates distance** from C on the **left hand side**\n**2nd-pass** iteration **propagates distance** from C on the **right hand side** with min( 1st-pass result, 2nd-pass propagation distance ) in order to update with shortest path.\n\n---\n\n**Abstract Model**:\n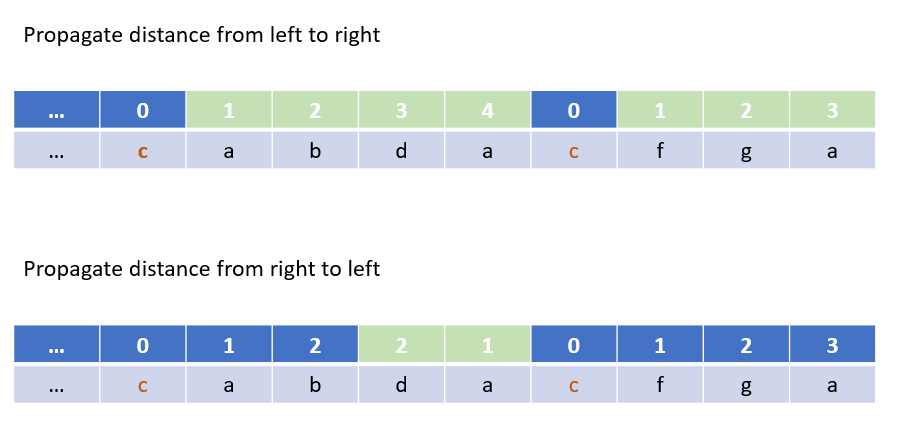\n\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def shortestToChar(self, S: str, C: str) -> List[int]:\n \n shortest_dist = []\n size = len(S)\n \n if size == 1:\n # Quick response for single character test case\n # Description guarantee that character C must exist in string S\n return [0]\n \n \n # Propagate distance from left to right\n for idx, char in enumerate(S):\n \n if char == C:\n shortest_dist.append(0)\n else:\n if idx == 0:\n shortest_dist.append( size )\n else:\n # Propagate distance from C on left hand side\n shortest_dist.append( shortest_dist[-1] + 1)\n \n \n \n # Propagate distance from right to left \n for idx in range(2, size+1):\n \n # Propagate distance from C on right hand side\n shortest_dist[-idx] = min(shortest_dist[-idx], shortest_dist[-idx+1]+1 )\n\n \n return shortest_dist\n``` | 16 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python O(n) by propagation 85%+ [w/ Diagram] | shortest-distance-to-a-character | 0 | 1 | Python O(n) by propagation\n\n---\n\n**Hint**:\n\nImagine parameter C as a flag on the line.\n\nThink of propagation technique:\n**1st-pass** iteration **propagates distance** from C on the **left hand side**\n**2nd-pass** iteration **propagates distance** from C on the **right hand side** with min( 1st-pass result, 2nd-pass propagation distance ) in order to update with shortest path.\n\n---\n\n**Abstract Model**:\n\n\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def shortestToChar(self, S: str, C: str) -> List[int]:\n \n shortest_dist = []\n size = len(S)\n \n if size == 1:\n # Quick response for single character test case\n # Description guarantee that character C must exist in string S\n return [0]\n \n \n # Propagate distance from left to right\n for idx, char in enumerate(S):\n \n if char == C:\n shortest_dist.append(0)\n else:\n if idx == 0:\n shortest_dist.append( size )\n else:\n # Propagate distance from C on left hand side\n shortest_dist.append( shortest_dist[-1] + 1)\n \n \n \n # Propagate distance from right to left \n for idx in range(2, size+1):\n \n # Propagate distance from C on right hand side\n shortest_dist[-idx] = min(shortest_dist[-idx], shortest_dist[-idx+1]+1 )\n\n \n return shortest_dist\n``` | 16 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Python 3 Solution, Brute Force and Two Pointers - 2 Solutions | shortest-distance-to-a-character | 0 | 1 | Brute Force:\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n req = []\n ind_list = []\n for i in range(len(s)):\n if s[i] == c:\n ind_list.append(i)\n min_dis = len(s)\n for j in range(len(s)):\n for k in range(len(ind_list)):\n min_dis = min(min_dis, abs(j - ind_list[k]))\n req.append(min_dis)\n min_dis = len(s)\n \n return req\n```\n\nTwo Pointers, O(n) Time and Space\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n# Travelling front to back\n result = ["*"] * len(s)\n i, j = 0, 0\n while i < len(s) and j < len(s):\n if s[i] == s[j] == c:\n result[i] = 0\n i += 1\n j += 1\n elif s[i] != c and s[j] == c:\n result[i] = abs(i-j)\n i += 1\n elif s[i] != c and s[j] != c:\n j += 1\n \n# Travelling back to front\n i = j = len(s) - 1\n while i >= 0 and j >= 0:\n if s[i] == s[j] == c:\n result[i] = 0\n i -= 1\n j -= 1\n elif s[i] != c and s[j] == c:\n if type(result[i]) == int:\n result[i] = min(result[i], abs(i-j))\n else:\n result[i] = abs(i-j)\n i -= 1\n elif s[i] != c and s[j] != c:\n j -= 1\n \n return result\n``` | 6 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python 3 Solution, Brute Force and Two Pointers - 2 Solutions | shortest-distance-to-a-character | 0 | 1 | Brute Force:\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n req = []\n ind_list = []\n for i in range(len(s)):\n if s[i] == c:\n ind_list.append(i)\n min_dis = len(s)\n for j in range(len(s)):\n for k in range(len(ind_list)):\n min_dis = min(min_dis, abs(j - ind_list[k]))\n req.append(min_dis)\n min_dis = len(s)\n \n return req\n```\n\nTwo Pointers, O(n) Time and Space\n```\nclass Solution:\n def shortestToChar(self, s: str, c: str) -> List[int]:\n# Travelling front to back\n result = ["*"] * len(s)\n i, j = 0, 0\n while i < len(s) and j < len(s):\n if s[i] == s[j] == c:\n result[i] = 0\n i += 1\n j += 1\n elif s[i] != c and s[j] == c:\n result[i] = abs(i-j)\n i += 1\n elif s[i] != c and s[j] != c:\n j += 1\n \n# Travelling back to front\n i = j = len(s) - 1\n while i >= 0 and j >= 0:\n if s[i] == s[j] == c:\n result[i] = 0\n i -= 1\n j -= 1\n elif s[i] != c and s[j] == c:\n if type(result[i]) == int:\n result[i] = min(result[i], abs(i-j))\n else:\n result[i] = abs(i-j)\n i -= 1\n elif s[i] != c and s[j] != c:\n j -= 1\n \n return result\n``` | 6 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Solution | card-flipping-game | 1 | 1 | ```C++ []\nclass Solution {\n void better(int &x, int y) {\n if (x == 0 || x > y) {\n x = y;\n }\n }\npublic:\n int flipgame(vector<int>& fronts, vector<int>& backs) {\n unordered_set<int> bad;\n const int n = backs.size();\n for (int i = 0; i < n; ++i) {\n if (fronts[i] == backs[i]) {\n bad.insert(backs[i]);\n }\n }\n int r = 0;\n for (int i = 0; i < n; ++i) {\n if (!bad.count(fronts[i])) {\n better(r, fronts[i]);\n }\n if (!bad.count(backs[i])) {\n better(r, backs[i]);\n }\n }\n return r;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n set_ = set(fronts + backs)\n\n for f,b in zip(fronts, backs):\n if f == b:\n set_.discard(f) # need discard instead of remove. ex. [1,1], [1,1]\n \n return min(set_, default = 0)\n```\n\n```Java []\nclass Solution {\n public int flipgame(int[] fronts, int[] backs) {\n int[] count = new int[2001];\n int n = fronts.length;\n for (int i = 0; i < n; i++) {\n if (fronts[i] == backs[i]) {\n count[fronts[i]]++;\n }\n }\n int res = Integer.MAX_VALUE;\n for (int i = 0; i < n; i++) {\n if (count[fronts[i]] == 0) {\n res = Math.min(res, fronts[i]);\n }\n if (count[backs[i]] == 0) {\n res = Math.min(res, backs[i]);\n }\n }\n return res == Integer.MAX_VALUE ? 0 : res;\n }\n}\n```\n | 1 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Solution | card-flipping-game | 1 | 1 | ```C++ []\nclass Solution {\n void better(int &x, int y) {\n if (x == 0 || x > y) {\n x = y;\n }\n }\npublic:\n int flipgame(vector<int>& fronts, vector<int>& backs) {\n unordered_set<int> bad;\n const int n = backs.size();\n for (int i = 0; i < n; ++i) {\n if (fronts[i] == backs[i]) {\n bad.insert(backs[i]);\n }\n }\n int r = 0;\n for (int i = 0; i < n; ++i) {\n if (!bad.count(fronts[i])) {\n better(r, fronts[i]);\n }\n if (!bad.count(backs[i])) {\n better(r, backs[i]);\n }\n }\n return r;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n set_ = set(fronts + backs)\n\n for f,b in zip(fronts, backs):\n if f == b:\n set_.discard(f) # need discard instead of remove. ex. [1,1], [1,1]\n \n return min(set_, default = 0)\n```\n\n```Java []\nclass Solution {\n public int flipgame(int[] fronts, int[] backs) {\n int[] count = new int[2001];\n int n = fronts.length;\n for (int i = 0; i < n; i++) {\n if (fronts[i] == backs[i]) {\n count[fronts[i]]++;\n }\n }\n int res = Integer.MAX_VALUE;\n for (int i = 0; i < n; i++) {\n if (count[fronts[i]] == 0) {\n res = Math.min(res, fronts[i]);\n }\n if (count[backs[i]] == 0) {\n res = Math.min(res, backs[i]);\n }\n }\n return res == Integer.MAX_VALUE ? 0 : res;\n }\n}\n```\n | 1 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Minimum Outside Doubles | card-flipping-game | 0 | 1 | # Intuition\nThe only exclusion criteria for a number in the pile is the existance of a card with that number on both the back and front. We simply take the minimum of the remaining numbers.\n\n# Approach\nGather the numbers that are on both the front and back of the same card (call that a "double") and find the minimum of numbers that are not doubles. We can build a set of the doubles (for constant time lookup when checking whether a number matches) and then grab the minimum number not in that set.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n doubles = {x for i, x in enumerate(fronts) if backs[i]==x}\n m = float("infinity")\n for x in fronts+backs:\n if x not in doubles:\n m = min(m,x)\n return m if m!=float("infinity") else 0\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Minimum Outside Doubles | card-flipping-game | 0 | 1 | # Intuition\nThe only exclusion criteria for a number in the pile is the existance of a card with that number on both the back and front. We simply take the minimum of the remaining numbers.\n\n# Approach\nGather the numbers that are on both the front and back of the same card (call that a "double") and find the minimum of numbers that are not doubles. We can build a set of the doubles (for constant time lookup when checking whether a number matches) and then grab the minimum number not in that set.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n doubles = {x for i, x in enumerate(fronts) if backs[i]==x}\n m = float("infinity")\n for x in fronts+backs:\n if x not in doubles:\n m = min(m,x)\n return m if m!=float("infinity") else 0\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Easy Python Solution | Beats 88% | Using Set | O(n) | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe fronts and backs are identical, i.e., we can flip any card to change its back to front and vice versa. Just try to see what if you have both the front and back values of a particular card same. In this case, that number cannot be good as it would be always up in all cases. Second thing is the good number should be faced down on atleast one card. This means that number should be present in either fronts or backs atleast once.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a set of numbers coming in fronts and backs. This would take all the unique numbers from them. Now iterate over fronts and backs and check if any card has the same value on front and back. Remove the card from set as it cannot be an answer.\nNow if length of the set is 0, this means we don\'t have any answer, so return 0. Else we just return the first element of set.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n s = set(fronts + backs)\n for i in range(len(fronts)):\n if fronts[i] == backs[i] and fronts[i] in s:\n s.remove(fronts[i])\n if len(s) == 0:\n return 0\n return s.pop()\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Easy Python Solution | Beats 88% | Using Set | O(n) | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe fronts and backs are identical, i.e., we can flip any card to change its back to front and vice versa. Just try to see what if you have both the front and back values of a particular card same. In this case, that number cannot be good as it would be always up in all cases. Second thing is the good number should be faced down on atleast one card. This means that number should be present in either fronts or backs atleast once.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a set of numbers coming in fronts and backs. This would take all the unique numbers from them. Now iterate over fronts and backs and check if any card has the same value on front and back. Remove the card from set as it cannot be an answer.\nNow if length of the set is 0, this means we don\'t have any answer, so return 0. Else we just return the first element of set.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n s = set(fronts + backs)\n for i in range(len(fronts)):\n if fronts[i] == backs[i] and fronts[i] in s:\n s.remove(fronts[i])\n if len(s) == 0:\n return 0\n return s.pop()\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python simple solution with set | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n nums=set(fronts+backs)\n for f,b in zip(fronts,backs):\n if f==b and f in nums:\n nums.remove(f)\n return sorted(nums)[0] if nums else 0\n\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python simple solution with set | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n nums=set(fronts+backs)\n for f,b in zip(fronts,backs):\n if f==b and f in nums:\n nums.remove(f)\n return sorted(nums)[0] if nums else 0\n\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
O(N) time and space, simple explanation of problem and approach | card-flipping-game | 0 | 1 | # Intuition\nThe only time a number CANNOT be good is if it appears on 2 sides of the SAME card, so you just have to find the smallest number that only appears on one side. It doesn\'t matter how many times the card appears, only that it is never on both sides of the same card.\ne.g. (front,back) (1,1), (3,2), (3,3), (2,4)\n- Could 1 be a good number? No, because if you were to put 1 face down, where would the other be? Pointing up.\n- Could 2 be a good number? Yes, because even though it appears more than once, any time it does appear, the opposite side of the card is not equal to 2.\n- Could 3 be a good number? No, for the same reason as 1\n- Could 4 be a good number? Yes, for the same reason as 2. But, since we want the minimum good number, 2 is the answer.\n\n# Approach\nMy idea is to store the \'state\' of any number, only setting it to True when it is first stored in the hashmap. Then, if I ever encounter a card with front = back, set its state to "False".\n\nSince the only time a number\'s state will change is when front = back, so in the end we just loop through the keys in our hashmap and find the smallest one with the value == True.\n\n\n# Complexity\n- Time complexity:\nO(N) since we have constant lookup time for hashmap and only one pass of the arrays.\n\n- Space complexity:\nO(N) in the worst case where the cards are (1,2), (3,4), (5,6), (7,8), ... or similar.\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n d = {}\n\n for i in range(len(fronts)):\n if fronts[i] != backs[i]:\n if fronts[i] not in d:\n d[fronts[i]] = True\n if backs[i] not in d:\n d[backs[i]] = True\n elif fronts[i] == backs[i]:\n d[fronts[i]] = False\n \n currmin = float(\'inf\')\n for key in d.keys():\n if d[key] == True:\n currmin = min(currmin, key)\n if currmin != float(\'inf\'):\n return currmin\n return 0\n \n \n \n\n \n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
O(N) time and space, simple explanation of problem and approach | card-flipping-game | 0 | 1 | # Intuition\nThe only time a number CANNOT be good is if it appears on 2 sides of the SAME card, so you just have to find the smallest number that only appears on one side. It doesn\'t matter how many times the card appears, only that it is never on both sides of the same card.\ne.g. (front,back) (1,1), (3,2), (3,3), (2,4)\n- Could 1 be a good number? No, because if you were to put 1 face down, where would the other be? Pointing up.\n- Could 2 be a good number? Yes, because even though it appears more than once, any time it does appear, the opposite side of the card is not equal to 2.\n- Could 3 be a good number? No, for the same reason as 1\n- Could 4 be a good number? Yes, for the same reason as 2. But, since we want the minimum good number, 2 is the answer.\n\n# Approach\nMy idea is to store the \'state\' of any number, only setting it to True when it is first stored in the hashmap. Then, if I ever encounter a card with front = back, set its state to "False".\n\nSince the only time a number\'s state will change is when front = back, so in the end we just loop through the keys in our hashmap and find the smallest one with the value == True.\n\n\n# Complexity\n- Time complexity:\nO(N) since we have constant lookup time for hashmap and only one pass of the arrays.\n\n- Space complexity:\nO(N) in the worst case where the cards are (1,2), (3,4), (5,6), (7,8), ... or similar.\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n d = {}\n\n for i in range(len(fronts)):\n if fronts[i] != backs[i]:\n if fronts[i] not in d:\n d[fronts[i]] = True\n if backs[i] not in d:\n d[backs[i]] = True\n elif fronts[i] == backs[i]:\n d[fronts[i]] = False\n \n currmin = float(\'inf\')\n for key in d.keys():\n if d[key] == True:\n currmin = min(currmin, key)\n if currmin != float(\'inf\'):\n return currmin\n return 0\n \n \n \n\n \n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Thought puzzle | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Proposition A: If the number $num$ satisfies the requirement, then among all the cards, there must be at least one side that is not equal to $num$.\n2. A is true.\n3. The inverse contrapositive proposition of A, denoted as A\': If on one of the cards, both sides are equal to $num$, then $num$ does not satisfy the requirement.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo, it will be more simple if we use the inverse contrapositive proposition. We just need to for loop all cards and check whether the two sides are equal. Then we get all bad $number$. We search all cards again and find which one is not a bad number and is the smallest one.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` cpp []\n/*\nCode generated by https://github.com/goodstudyqaq/leetcode-local-tester\n*/\n#if __has_include("../utils/cpp/help.hpp")\n#include "../utils/cpp/help.hpp"\n#elif __has_include("../../utils/cpp/help.hpp")\n#include "../../utils/cpp/help.hpp"\n#else\n#define debug(...) 42\n#endif\n\nclass Solution {\n public:\n int flipgame(vector<int>& fronts, vector<int>& backs) {\n int n = fronts.size();\n unordered_set<int> S;\n for (int i = 0; i < n; i++) {\n if (fronts[i] == backs[i]) {\n S.insert(fronts[i]);\n }\n }\n\n int res = 1e9;\n for (int i = 0; i < n; i++) {\n if (S.count(fronts[i]) == 0) {\n res = min(res, fronts[i]);\n }\n if (S.count(backs[i]) == 0) {\n res = min(res, backs[i]);\n }\n }\n if (res == 1e9) res = 0;\n return res;\n }\n};\n```\n``` python []\n"""\nCode generated by https://github.com/goodstudyqaq/leetcode-local-tester\n"""\ntry:\n from utils.python3.help import *\nexcept ImportError:\n pass # In leetcode environment, we don\'t need to import the help file.\n\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n s = set()\n for i in range(len(fronts)):\n if fronts[i] == backs[i]:\n s.add(fronts[i])\n ans = 2001\n for i in range(len(fronts)):\n if fronts[i] not in s:\n ans = min(ans, fronts[i])\n if backs[i] not in s:\n ans = min(ans, backs[i])\n \n return ans if ans != 2001 else 0\n\n\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Thought puzzle | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Proposition A: If the number $num$ satisfies the requirement, then among all the cards, there must be at least one side that is not equal to $num$.\n2. A is true.\n3. The inverse contrapositive proposition of A, denoted as A\': If on one of the cards, both sides are equal to $num$, then $num$ does not satisfy the requirement.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo, it will be more simple if we use the inverse contrapositive proposition. We just need to for loop all cards and check whether the two sides are equal. Then we get all bad $number$. We search all cards again and find which one is not a bad number and is the smallest one.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` cpp []\n/*\nCode generated by https://github.com/goodstudyqaq/leetcode-local-tester\n*/\n#if __has_include("../utils/cpp/help.hpp")\n#include "../utils/cpp/help.hpp"\n#elif __has_include("../../utils/cpp/help.hpp")\n#include "../../utils/cpp/help.hpp"\n#else\n#define debug(...) 42\n#endif\n\nclass Solution {\n public:\n int flipgame(vector<int>& fronts, vector<int>& backs) {\n int n = fronts.size();\n unordered_set<int> S;\n for (int i = 0; i < n; i++) {\n if (fronts[i] == backs[i]) {\n S.insert(fronts[i]);\n }\n }\n\n int res = 1e9;\n for (int i = 0; i < n; i++) {\n if (S.count(fronts[i]) == 0) {\n res = min(res, fronts[i]);\n }\n if (S.count(backs[i]) == 0) {\n res = min(res, backs[i]);\n }\n }\n if (res == 1e9) res = 0;\n return res;\n }\n};\n```\n``` python []\n"""\nCode generated by https://github.com/goodstudyqaq/leetcode-local-tester\n"""\ntry:\n from utils.python3.help import *\nexcept ImportError:\n pass # In leetcode environment, we don\'t need to import the help file.\n\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n s = set()\n for i in range(len(fronts)):\n if fronts[i] == backs[i]:\n s.add(fronts[i])\n ans = 2001\n for i in range(len(fronts)):\n if fronts[i] not in s:\n ans = min(ans, fronts[i])\n if backs[i] not in s:\n ans = min(ans, backs[i])\n \n return ans if ans != 2001 else 0\n\n\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python3 - Sorting + Set | card-flipping-game | 0 | 1 | # Intuition\nThe only way you can\'t have a good integer is if you have a card with it on both sides. You want the minimum, so just sort, giving you the lowest, and check if any card has it on both sides.\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n bad = set(i for i,j in zip(fronts, backs) if i==j)\n for i in sorted(set(fronts + backs)):\n if i in bad:\n continue\n return i\n return 0\n\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python3 - Sorting + Set | card-flipping-game | 0 | 1 | # Intuition\nThe only way you can\'t have a good integer is if you have a card with it on both sides. You want the minimum, so just sort, giving you the lowest, and check if any card has it on both sides.\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n bad = set(i for i,j in zip(fronts, backs) if i==j)\n for i in sorted(set(fronts + backs)):\n if i in bad:\n continue\n return i\n return 0\n\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python3 🐍 concise solution beats 99% | card-flipping-game | 0 | 1 | # Code\n```\nclass Solution:\n def flipgame(self, fronts, backs):\n dict1, res = defaultdict(int), []\n\n for i,j in zip(fronts,backs):\n dict1[i] += 1\n dict1[j] += 1\n\n for i,j in zip(fronts,backs):\n if i == j and i in dict1:\n del dict1[i]\n\n return min(dict1.keys()) if dict1 else 0\n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python3 🐍 concise solution beats 99% | card-flipping-game | 0 | 1 | # Code\n```\nclass Solution:\n def flipgame(self, fronts, backs):\n dict1, res = defaultdict(int), []\n\n for i,j in zip(fronts,backs):\n dict1[i] += 1\n dict1[j] += 1\n\n for i,j in zip(fronts,backs):\n if i == j and i in dict1:\n del dict1[i]\n\n return min(dict1.keys()) if dict1 else 0\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python (Simple Hashmap) | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts, backs):\n dict1, res = defaultdict(int), []\n\n for i,j in zip(fronts,backs):\n dict1[i] += 1\n dict1[j] += 1\n\n for i,j in zip(fronts,backs):\n if i == j and i in dict1:\n del dict1[i]\n\n return min(dict1.keys()) if dict1 else 0\n\n\n\n\n \n \n \n \n \n \n``` | 0 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python (Simple Hashmap) | card-flipping-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flipgame(self, fronts, backs):\n dict1, res = defaultdict(int), []\n\n for i,j in zip(fronts,backs):\n dict1[i] += 1\n dict1[j] += 1\n\n for i,j in zip(fronts,backs):\n if i == j and i in dict1:\n del dict1[i]\n\n return min(dict1.keys()) if dict1 else 0\n\n\n\n\n \n \n \n \n \n \n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python3 simple solution using a for() loop | card-flipping-game | 0 | 1 | ```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n """\n O(n) time complexity: n is length of fronts\n O(n) space complexity\n """\n same = {x for i, x in enumerate(fronts) if x == backs[i]}\n res = 9999\n for i in range(len(fronts)):\n if fronts[i] not in same: res = min(res, fronts[i])\n if backs[i] not in same: res = min(res, backs[i])\n return res % 9999\n``` | 2 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python3 simple solution using a for() loop | card-flipping-game | 0 | 1 | ```\nclass Solution:\n def flipgame(self, fronts: List[int], backs: List[int]) -> int:\n """\n O(n) time complexity: n is length of fronts\n O(n) space complexity\n """\n same = {x for i, x in enumerate(fronts) if x == backs[i]}\n res = 9999\n for i in range(len(fronts)):\n if fronts[i] not in same: res = min(res, fronts[i])\n if backs[i] not in same: res = min(res, backs[i])\n return res % 9999\n``` | 2 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
🔥🧭Beats 99.99% |🚩Optimised Code Using Dynamic Programming | 💡🚀🔥 | binary-trees-with-factors | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the number of binary trees that can be formed using a given array of integers. Each integer can be used multiple times, and the non-leaf nodes\' values should be the product of the values of their children. This suggests a dynamic programming approach. The code uses a bottom-up dynamic programming approach to count the number of binary trees for each value in the array.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the input array `arr` in ascending order. Sorting helps in ensuring that smaller numbers are processed before larger numbers, which is crucial for the dynamic programming approach.\n\n2. Initialize an unordered map `dp`, where the keys are values from `arr`, and the values are the number of binary trees that can be formed using that value.\n\n3. Iterate through the sorted `arr`. For each value `arr[i]`:\n\n- Initialize `dp[arr[i]]` to 1 because a single node tree with the value `arr[i]` is always possible.\n\n4. Nested within the loop from step 3, iterate over the values in `arr` before the current value (from `0` to `i - 1`). For each value `arr[j]`, check if it\'s a factor of `arr[i]`. If it is, then:\n\n- Calculate the factor as `factor = arr[i] / arr[j]`.\n- If `dp` already contains `factor`, it means that we have already computed the number of binary trees for `factor`.\n- Update `dp[arr[i]]` by adding the product of the number of trees for `arr[j]` and `factor` to it.\n\n5. After the loops, `dp` will contain the number of binary trees that can be formed for each value in `arr`.\n\n6. Sum up all the values in `dp` to get the total number of binary trees.\n\n7. Return the result modulo `10^9 + 7` to avoid integer overflow.\n\n---\n\n# Complexity\n## 1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Sorting the array takes O(n * log(n)) time.\n- The nested loop iterates through each element in `arr`, so it\'s O(n^2) in the worst case.\n- The final loop to calculate the result takes O(n).\n- Overall, the time complexity is O(n^2) due to the nested loop.\n## 2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The space complexity is O(n) for the unordered map `dp`.\n\n---\n\n# \uD83D\uDCA1If you have come this far, then i would like to request you to please upvote this solution\u2763\uFE0F\uD83D\uDCA1So that it could reach out to another one\uD83D\uDD25\uD83D\uDD25\n\n---\n\n\n# Code\n\n\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n int MOD = 1000000007;\n sort(arr.begin(), arr.end()); // Sort the array.\n\n unordered_map<int, long long> dp; // Use a map to store the number of trees for each value.\n\n for (int i = 0; i < arr.size(); i++) {\n dp[arr[i]] = 1; // A single node tree with the value arr[i].\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0) { // If arr[j] is a factor of arr[i].\n int factor = arr[i] / arr[j];\n if (dp.count(factor)) {\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD;\n }\n }\n }\n }\n\n long long result = 0;\n for (auto& entry : dp) {\n result = (result + entry.second) % MOD;\n }\n\n return static_cast<int>(result);\n }\n};\n```\n```Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int MOD = 1000000007;\n Arrays.sort(arr);\n Map<Integer, Long> dp = new HashMap<>();\n \n for (int i = 0; i < arr.length; i++) {\n dp.put(arr[i], 1L);\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0) {\n int factor = arr[i] / arr[j];\n if (dp.containsKey(factor)) {\n dp.put(arr[i], (dp.get(arr[i]) + dp.get(arr[j) * dp.get(factor)) % MOD);\n }\n }\n }\n }\n \n long result = 0;\n for (long value : dp.values()) {\n result = (result + value) % MOD;\n }\n \n return (int) result;\n }\n}\n\n```\n```Python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr):\n MOD = 10**9 + 7\n arr.sort()\n dp = {}\n \n for i in range(len(arr)):\n dp[arr[i]] = 1\n for j in range(i):\n if arr[i] % arr[j] == 0:\n factor = arr[i] // arr[j]\n if factor in dp:\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD\n \n result = 0\n for value in dp.values():\n result = (result + value) % MOD\n \n return result\n\n```\n```Javascript []\nvar numFactoredBinaryTrees = function(arr) {\n const MOD = 1000000007;\n arr.sort((a, b) => a - b);\n const dp = {};\n \n for (let i = 0; i < arr.length; i++) {\n dp[arr[i]] = 1;\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0) {\n const factor = arr[i] / arr[j];\n if (dp.hasOwnProperty(factor)) {\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD;\n }\n }\n }\n }\n \n let result = 0;\n for (const value of Object.values(dp)) {\n result = (result + value) % MOD;\n }\n \n return result;\n};\n\n```\n```Ruby []\ndef num_factored_binary_trees(arr)\n mod = 10**9 + 7\n arr.sort!\n dp = {}\n \n (0...arr.length).each do |i|\n dp[arr[i]] = 1\n (0...i).each do |j|\n if arr[i] % arr[j] == 0\n factor = arr[i] / arr[j]\n if dp.key?(factor)\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % mod\n end\n end\n end\n end\n \n result = 0\n dp.values.each do |value|\n result = (result + value) % mod\n end\n \n result\nend\n\n```\n\n\n\n\n | 11 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
🔥🧭Beats 99.99% |🚩Optimised Code Using Dynamic Programming | 💡🚀🔥 | binary-trees-with-factors | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the number of binary trees that can be formed using a given array of integers. Each integer can be used multiple times, and the non-leaf nodes\' values should be the product of the values of their children. This suggests a dynamic programming approach. The code uses a bottom-up dynamic programming approach to count the number of binary trees for each value in the array.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the input array `arr` in ascending order. Sorting helps in ensuring that smaller numbers are processed before larger numbers, which is crucial for the dynamic programming approach.\n\n2. Initialize an unordered map `dp`, where the keys are values from `arr`, and the values are the number of binary trees that can be formed using that value.\n\n3. Iterate through the sorted `arr`. For each value `arr[i]`:\n\n- Initialize `dp[arr[i]]` to 1 because a single node tree with the value `arr[i]` is always possible.\n\n4. Nested within the loop from step 3, iterate over the values in `arr` before the current value (from `0` to `i - 1`). For each value `arr[j]`, check if it\'s a factor of `arr[i]`. If it is, then:\n\n- Calculate the factor as `factor = arr[i] / arr[j]`.\n- If `dp` already contains `factor`, it means that we have already computed the number of binary trees for `factor`.\n- Update `dp[arr[i]]` by adding the product of the number of trees for `arr[j]` and `factor` to it.\n\n5. After the loops, `dp` will contain the number of binary trees that can be formed for each value in `arr`.\n\n6. Sum up all the values in `dp` to get the total number of binary trees.\n\n7. Return the result modulo `10^9 + 7` to avoid integer overflow.\n\n---\n\n# Complexity\n## 1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Sorting the array takes O(n * log(n)) time.\n- The nested loop iterates through each element in `arr`, so it\'s O(n^2) in the worst case.\n- The final loop to calculate the result takes O(n).\n- Overall, the time complexity is O(n^2) due to the nested loop.\n## 2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The space complexity is O(n) for the unordered map `dp`.\n\n---\n\n# \uD83D\uDCA1If you have come this far, then i would like to request you to please upvote this solution\u2763\uFE0F\uD83D\uDCA1So that it could reach out to another one\uD83D\uDD25\uD83D\uDD25\n\n---\n\n\n# Code\n\n\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n int MOD = 1000000007;\n sort(arr.begin(), arr.end()); // Sort the array.\n\n unordered_map<int, long long> dp; // Use a map to store the number of trees for each value.\n\n for (int i = 0; i < arr.size(); i++) {\n dp[arr[i]] = 1; // A single node tree with the value arr[i].\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0) { // If arr[j] is a factor of arr[i].\n int factor = arr[i] / arr[j];\n if (dp.count(factor)) {\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD;\n }\n }\n }\n }\n\n long long result = 0;\n for (auto& entry : dp) {\n result = (result + entry.second) % MOD;\n }\n\n return static_cast<int>(result);\n }\n};\n```\n```Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int MOD = 1000000007;\n Arrays.sort(arr);\n Map<Integer, Long> dp = new HashMap<>();\n \n for (int i = 0; i < arr.length; i++) {\n dp.put(arr[i], 1L);\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0) {\n int factor = arr[i] / arr[j];\n if (dp.containsKey(factor)) {\n dp.put(arr[i], (dp.get(arr[i]) + dp.get(arr[j) * dp.get(factor)) % MOD);\n }\n }\n }\n }\n \n long result = 0;\n for (long value : dp.values()) {\n result = (result + value) % MOD;\n }\n \n return (int) result;\n }\n}\n\n```\n```Python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr):\n MOD = 10**9 + 7\n arr.sort()\n dp = {}\n \n for i in range(len(arr)):\n dp[arr[i]] = 1\n for j in range(i):\n if arr[i] % arr[j] == 0:\n factor = arr[i] // arr[j]\n if factor in dp:\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD\n \n result = 0\n for value in dp.values():\n result = (result + value) % MOD\n \n return result\n\n```\n```Javascript []\nvar numFactoredBinaryTrees = function(arr) {\n const MOD = 1000000007;\n arr.sort((a, b) => a - b);\n const dp = {};\n \n for (let i = 0; i < arr.length; i++) {\n dp[arr[i]] = 1;\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0) {\n const factor = arr[i] / arr[j];\n if (dp.hasOwnProperty(factor)) {\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % MOD;\n }\n }\n }\n }\n \n let result = 0;\n for (const value of Object.values(dp)) {\n result = (result + value) % MOD;\n }\n \n return result;\n};\n\n```\n```Ruby []\ndef num_factored_binary_trees(arr)\n mod = 10**9 + 7\n arr.sort!\n dp = {}\n \n (0...arr.length).each do |i|\n dp[arr[i]] = 1\n (0...i).each do |j|\n if arr[i] % arr[j] == 0\n factor = arr[i] / arr[j]\n if dp.key?(factor)\n dp[arr[i]] = (dp[arr[i]] + dp[arr[j]] * dp[factor]) % mod\n end\n end\n end\n end\n \n result = 0\n dp.values.each do |value|\n result = (result + value) % mod\n end\n \n result\nend\n\n```\n\n\n\n\n | 11 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
🔥Efficient Method🔥| Explained Intuition & Approach | Java | C++ | Python | JavaScript | C# | PHP | binary-trees-with-factors | 1 | 1 | # Intuition \uD83D\uDE80\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key idea here is to use dynamic programming to count the number of valid binary trees efficiently. The intuition is as follows:\n\n1. Sort the input array: Start by sorting the array in ascending order because you need to consider factors from small to large values for dynamic programming.\n\n2. Initialize a dynamic programming map: Create a map to store the number of binary trees that can be formed with each element as the root node. Initialize the values in the map with 1 because each element can be a valid tree on its own.\n\n3. Dynamic Programming: Iterate through the sorted array, and for each element, iterate through all previous elements as potential factors. If a factor exists, update the number of binary trees ending with the current element by considering the factor\'s contribution. The dynamic programming formula used in this code is based on the principle that if you have two factors (j and i/j), you can form `dp[j] * dp[i/j]` new binary trees that end with the current element.\n\n4. Calculate the final result: Sum up all the values in the dynamic programming map to get the total number of valid binary trees.\n\n\n# Approach \uD83D\uDE80\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array in ascending order to consider factors from small to large values.\n\n2. Create a set to store unique numbers in the array. This set helps in faster containment checks.\n\n3. Initialize a dynamic programming map (`dp`) where the keys are array elements, and the values are the number of binary trees ending with that element. Initialize all values to 1, indicating that each element can form a single tree by itself.\n\n4. Iterate through the array elements:\n - For each element `i`, iterate through the elements that precede it (`j`).\n - If `j` is larger than the square root of `i`, break the loop because further `j` values won\'t be factors.\n - Check if `j` is a factor of `i` and if `i/j` is in the set of unique numbers.\n - Update the number of binary trees ending with `i` based on the factors `j` and `i/j` using the dynamic programming formula. This accounts for the new trees that can be formed using the factors.\n\n5. Calculate the final result by summing up all the values in the dynamic programming map and return the result modulo 1000000007 (as specified in the problem).\n\nThe below code is an efficient implementation of this approach, using dynamic programming to count the valid binary trees while considering all possible factors and combinations.\n\n\n# Complexity \uD83D\uDE81\n## \uD83C\uDFF9Time complexity: $$O(n * sqrt(max(arr)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. **Sorting:** The initial step involves sorting the input array. The time complexity for this is $$O(n * log(n))$$, where \'n\' is the number of elements in the array.\n\n2. **Dynamic Programming:** The main loop involves nested loops, where you iterate through all elements of the input array. In the worst case, for each element \'i\', you iterate through all previous elements \'j\' up to the square root of \'i\'. So, the time complexity of this part is $$O(n * sqrt(max(arr)))$$ where \'n\' is the number of elements in the array, and \'max(arr)\' is the maximum element in the array.\n\n3. **Final Summation:** After completing the dynamic programming, you iterate through all values in the `dp` map to calculate the final result. This requires iterating through \'n\' elements in the map. This step contributes $$O(n)$$ to the time complexity.\n\nCombining these steps, the overall time complexity is $$O(n * log(n)) + O(n * sqrt(max(arr))) + O(n)$$, which can be simplified to $$O(n * sqrt(max(arr))).$$\n\n\n## \uD83C\uDFF9Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n1. **Sorting:** Sorting the input array in-place doesn\'t require any additional space, so this step has a space complexity of $$O(1).$$\n\n2. **Set for Unique Numbers:** You create a set `uniqueNumbers` to store unique elements from the input array. In the worst case, if all elements are unique, this set would have \'n\' elements. Therefore, the space complexity of this set is $$O(n).$$\n\n3. **Dynamic Programming Map:** You create a map `dp` to store values for each element in the input array. In the worst case, there can be \'n\' key-value pairs in the map. So, the space complexity for the map is $$O(n).$$\n4. \nCombining these factors, the overall space complexity of the code is $$O(n)$$ due to the sets and maps created.\n\n# Code \u2712\uFE0F\n``` Java []\npublic class Solution {\n private static final int MOD = 1000000007;\n\n public int numFactoredBinaryTrees(int[] arr) {\n // Step 1: Sort the input array in ascending order.\n Arrays.sort(arr);\n \n // Create a set to make the containment check faster.\n Set<Integer> uniqueNumbers = new HashSet<>();\n for (int num : arr) {\n uniqueNumbers.add(num);\n }\n\n // Step 2: Initialize a map to store the number of binary trees that end with each element in the array.\n Map<Integer, Integer> dp = new HashMap<>();\n for (int num : arr) {\n dp.put(num, 1);\n }\n\n // Step 3: Dynamic Programming\n for (int i : arr) {\n for (int j : arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.sqrt(i)) break;\n \n // Check if j is a factor of i and i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.contains(i / j)) {\n long product = (long) dp.get(j) * dp.get(i / j);\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp.put(i, (int) ((dp.get(i) + (i / j == j ? product : product * 2)) % MOD));\n }\n }\n }\n\n // Step 4: Calculate the final result.\n int result = 0;\n for (int value : dp.values()) {\n result = (result + value) % MOD;\n }\n return result;\n }\n}\n\n``` \n``` C++ []\n\nclass Solution {\nconst int MOD = 1e9 + 7;\npublic:\n int numFactoredBinaryTrees(std::vector<int>& arr) {\n // Step 1: Sort the input array.\n std::sort(arr.begin(), arr.end());\n \n // Step 2: Create a set to store unique numbers in the array.\n std::unordered_set<int> uniqueNumbers(arr.begin(), arr.end());\n \n // Step 3: Initialize a dynamic programming map.\n std::unordered_map<int, int> dp;\n for (int num : arr) {\n dp[num] = 1;\n }\n \n // Step 4: Dynamic Programming\n for (int i : arr) {\n for (int j : arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > std::sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.find(i / j) != uniqueNumbers.end()) {\n long long temp = static_cast<long long>(dp[j]) * dp[i / j];\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n if (i / j == j) {\n dp[i] = (dp[i] + temp) % MOD;\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD;\n }\n }\n }\n }\n \n // Step 5: Calculate the final result.\n int result = 0;\n for (auto& [_, val] : dp) {\n result = (result + val) % MOD;\n }\n return result;\n }\n};\n```\n``` Python []\n\nMOD = 10**9 + 7\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n # Step 1: Sort the input array.\n arr.sort()\n \n # Step 2: Create a set to store unique numbers in the array.\n unique_numbers = set(arr)\n \n # Step 3: Initialize a dynamic programming dictionary.\n dp = {x: 1 for x in arr}\n \n # Step 4: Dynamic Programming\n for i in arr:\n for j in arr:\n # If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if j > i**0.5:\n break\n \n # Check if j is a factor of i and if i/j is in the set of unique numbers.\n if i % j == 0 and i // j in unique_numbers:\n if i // j == j:\n # If j and i/j are the same, update dp[i] accordingly.\n dp[i] += dp[j] * dp[j]\n else:\n # If j and i/j are different, update dp[i] accordingly.\n dp[i] += dp[j] * dp[i // j] * 2\n dp[i] %= MOD\n \n # Step 5: Calculate the final result.\n result = sum(dp.values()) % MOD\n return result\n\n```\n``` JavaScript []\nconst MOD = 10**9 + 7;\nvar numFactoredBinaryTrees = function(arr) {\n\n // Step 1: Sort the input array.\n arr.sort((a, b) => a - b);\n \n // Step 2: Create a set to store unique numbers in the array.\n const uniqueNumbers = new Set(arr);\n \n // Step 3: Initialize a dynamic programming object.\n const dp = {};\n for (let x of arr) {\n dp[x] = 1;\n }\n \n // Step 4: Dynamic Programming\n for (let i of arr) {\n for (let j of arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j === 0 && uniqueNumbers.has(i / j)) {\n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp[i] += (i / j === j ? dp[j] * dp[j] : dp[j] * dp[i / j] * 2);\n dp[i] %= MOD;\n }\n }\n }\n \n // Step 5: Calculate the final result.\n const result = Object.values(dp).reduce((acc, val) => (acc + val) % MOD, 0);\n return result;\n}\n\n```\n``` C# []\npublic class Solution {\n private const int MOD = 1000000007;\n\n public int NumFactoredBinaryTrees(int[] arr) {\n // Step 1: Sort the input array.\n Array.Sort(arr);\n \n // Step 2: Create a HashSet to store unique numbers in the array.\n HashSet<int> uniqueNumbers = new HashSet<int>(arr);\n \n // Step 3: Initialize a Dictionary for dynamic programming.\n Dictionary<int, long> dp = new Dictionary<int, long>();\n foreach (int num in arr) {\n dp[num] = 1;\n }\n \n // Step 4: Dynamic Programming\n foreach (int i in arr) {\n foreach (int j in arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.Sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.Contains(i / j)) {\n long temp = dp[j] * dp[i / j];\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp[i] = (dp[i] + (i / j == j ? temp : temp * 2)) % MOD;\n }\n }\n }\n \n // Step 5: Calculate the final result.\n long result = 0;\n foreach (long value in dp.Values) {\n result = (result + value) % MOD;\n }\n return (int)result;\n }\n}\n\n```\n``` PHP []\nclass Solution {\n function numFactoredBinaryTrees($arr) {\n // Step 1: Sort the input array in ascending order.\n sort($arr);\n \n // Step 2: Create a hash map for faster containment checks.\n $uniqueNumbers = array_flip($arr);\n \n // Step 3: Initialize a hash map for dynamic programming.\n $dp = [];\n foreach ($arr as $x) {\n $dp[$x] = 1;\n }\n\n // Step 4: Dynamic Programming\n foreach ($arr as $i) {\n foreach ($arr as $j) {\n // If $j is larger than the square root of $i, break the loop.\n if ($j > sqrt($i)) break;\n\n // Check if $j is a factor of $i and if $i/$j is in the unique numbers hash map.\n if ($i % $j == 0 && isset($uniqueNumbers[$i / $j])) {\n // Calculate the temporary result.\n $temp = (int)((($dp[$j] * $dp[$i / $j]) % 1000000007) * ($i / $j == $j ? 1 : 2));\n \n // Update the number of binary trees ending with $i based on the factors $j and $i/$j.\n $dp[$i] = ($dp[$i] + $temp) % 1000000007;\n }\n }\n }\n\n // Step 5: Calculate the final result.\n $result = 0;\n foreach ($dp as $val) {\n $result = ($result + $val) % 1000000007;\n }\n \n return $result;\n }\n}\n\n```\n\n\n | 32 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
🔥Efficient Method🔥| Explained Intuition & Approach | Java | C++ | Python | JavaScript | C# | PHP | binary-trees-with-factors | 1 | 1 | # Intuition \uD83D\uDE80\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key idea here is to use dynamic programming to count the number of valid binary trees efficiently. The intuition is as follows:\n\n1. Sort the input array: Start by sorting the array in ascending order because you need to consider factors from small to large values for dynamic programming.\n\n2. Initialize a dynamic programming map: Create a map to store the number of binary trees that can be formed with each element as the root node. Initialize the values in the map with 1 because each element can be a valid tree on its own.\n\n3. Dynamic Programming: Iterate through the sorted array, and for each element, iterate through all previous elements as potential factors. If a factor exists, update the number of binary trees ending with the current element by considering the factor\'s contribution. The dynamic programming formula used in this code is based on the principle that if you have two factors (j and i/j), you can form `dp[j] * dp[i/j]` new binary trees that end with the current element.\n\n4. Calculate the final result: Sum up all the values in the dynamic programming map to get the total number of valid binary trees.\n\n\n# Approach \uD83D\uDE80\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array in ascending order to consider factors from small to large values.\n\n2. Create a set to store unique numbers in the array. This set helps in faster containment checks.\n\n3. Initialize a dynamic programming map (`dp`) where the keys are array elements, and the values are the number of binary trees ending with that element. Initialize all values to 1, indicating that each element can form a single tree by itself.\n\n4. Iterate through the array elements:\n - For each element `i`, iterate through the elements that precede it (`j`).\n - If `j` is larger than the square root of `i`, break the loop because further `j` values won\'t be factors.\n - Check if `j` is a factor of `i` and if `i/j` is in the set of unique numbers.\n - Update the number of binary trees ending with `i` based on the factors `j` and `i/j` using the dynamic programming formula. This accounts for the new trees that can be formed using the factors.\n\n5. Calculate the final result by summing up all the values in the dynamic programming map and return the result modulo 1000000007 (as specified in the problem).\n\nThe below code is an efficient implementation of this approach, using dynamic programming to count the valid binary trees while considering all possible factors and combinations.\n\n\n# Complexity \uD83D\uDE81\n## \uD83C\uDFF9Time complexity: $$O(n * sqrt(max(arr)))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. **Sorting:** The initial step involves sorting the input array. The time complexity for this is $$O(n * log(n))$$, where \'n\' is the number of elements in the array.\n\n2. **Dynamic Programming:** The main loop involves nested loops, where you iterate through all elements of the input array. In the worst case, for each element \'i\', you iterate through all previous elements \'j\' up to the square root of \'i\'. So, the time complexity of this part is $$O(n * sqrt(max(arr)))$$ where \'n\' is the number of elements in the array, and \'max(arr)\' is the maximum element in the array.\n\n3. **Final Summation:** After completing the dynamic programming, you iterate through all values in the `dp` map to calculate the final result. This requires iterating through \'n\' elements in the map. This step contributes $$O(n)$$ to the time complexity.\n\nCombining these steps, the overall time complexity is $$O(n * log(n)) + O(n * sqrt(max(arr))) + O(n)$$, which can be simplified to $$O(n * sqrt(max(arr))).$$\n\n\n## \uD83C\uDFF9Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n1. **Sorting:** Sorting the input array in-place doesn\'t require any additional space, so this step has a space complexity of $$O(1).$$\n\n2. **Set for Unique Numbers:** You create a set `uniqueNumbers` to store unique elements from the input array. In the worst case, if all elements are unique, this set would have \'n\' elements. Therefore, the space complexity of this set is $$O(n).$$\n\n3. **Dynamic Programming Map:** You create a map `dp` to store values for each element in the input array. In the worst case, there can be \'n\' key-value pairs in the map. So, the space complexity for the map is $$O(n).$$\n4. \nCombining these factors, the overall space complexity of the code is $$O(n)$$ due to the sets and maps created.\n\n# Code \u2712\uFE0F\n``` Java []\npublic class Solution {\n private static final int MOD = 1000000007;\n\n public int numFactoredBinaryTrees(int[] arr) {\n // Step 1: Sort the input array in ascending order.\n Arrays.sort(arr);\n \n // Create a set to make the containment check faster.\n Set<Integer> uniqueNumbers = new HashSet<>();\n for (int num : arr) {\n uniqueNumbers.add(num);\n }\n\n // Step 2: Initialize a map to store the number of binary trees that end with each element in the array.\n Map<Integer, Integer> dp = new HashMap<>();\n for (int num : arr) {\n dp.put(num, 1);\n }\n\n // Step 3: Dynamic Programming\n for (int i : arr) {\n for (int j : arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.sqrt(i)) break;\n \n // Check if j is a factor of i and i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.contains(i / j)) {\n long product = (long) dp.get(j) * dp.get(i / j);\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp.put(i, (int) ((dp.get(i) + (i / j == j ? product : product * 2)) % MOD));\n }\n }\n }\n\n // Step 4: Calculate the final result.\n int result = 0;\n for (int value : dp.values()) {\n result = (result + value) % MOD;\n }\n return result;\n }\n}\n\n``` \n``` C++ []\n\nclass Solution {\nconst int MOD = 1e9 + 7;\npublic:\n int numFactoredBinaryTrees(std::vector<int>& arr) {\n // Step 1: Sort the input array.\n std::sort(arr.begin(), arr.end());\n \n // Step 2: Create a set to store unique numbers in the array.\n std::unordered_set<int> uniqueNumbers(arr.begin(), arr.end());\n \n // Step 3: Initialize a dynamic programming map.\n std::unordered_map<int, int> dp;\n for (int num : arr) {\n dp[num] = 1;\n }\n \n // Step 4: Dynamic Programming\n for (int i : arr) {\n for (int j : arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > std::sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.find(i / j) != uniqueNumbers.end()) {\n long long temp = static_cast<long long>(dp[j]) * dp[i / j];\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n if (i / j == j) {\n dp[i] = (dp[i] + temp) % MOD;\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD;\n }\n }\n }\n }\n \n // Step 5: Calculate the final result.\n int result = 0;\n for (auto& [_, val] : dp) {\n result = (result + val) % MOD;\n }\n return result;\n }\n};\n```\n``` Python []\n\nMOD = 10**9 + 7\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n # Step 1: Sort the input array.\n arr.sort()\n \n # Step 2: Create a set to store unique numbers in the array.\n unique_numbers = set(arr)\n \n # Step 3: Initialize a dynamic programming dictionary.\n dp = {x: 1 for x in arr}\n \n # Step 4: Dynamic Programming\n for i in arr:\n for j in arr:\n # If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if j > i**0.5:\n break\n \n # Check if j is a factor of i and if i/j is in the set of unique numbers.\n if i % j == 0 and i // j in unique_numbers:\n if i // j == j:\n # If j and i/j are the same, update dp[i] accordingly.\n dp[i] += dp[j] * dp[j]\n else:\n # If j and i/j are different, update dp[i] accordingly.\n dp[i] += dp[j] * dp[i // j] * 2\n dp[i] %= MOD\n \n # Step 5: Calculate the final result.\n result = sum(dp.values()) % MOD\n return result\n\n```\n``` JavaScript []\nconst MOD = 10**9 + 7;\nvar numFactoredBinaryTrees = function(arr) {\n\n // Step 1: Sort the input array.\n arr.sort((a, b) => a - b);\n \n // Step 2: Create a set to store unique numbers in the array.\n const uniqueNumbers = new Set(arr);\n \n // Step 3: Initialize a dynamic programming object.\n const dp = {};\n for (let x of arr) {\n dp[x] = 1;\n }\n \n // Step 4: Dynamic Programming\n for (let i of arr) {\n for (let j of arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j === 0 && uniqueNumbers.has(i / j)) {\n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp[i] += (i / j === j ? dp[j] * dp[j] : dp[j] * dp[i / j] * 2);\n dp[i] %= MOD;\n }\n }\n }\n \n // Step 5: Calculate the final result.\n const result = Object.values(dp).reduce((acc, val) => (acc + val) % MOD, 0);\n return result;\n}\n\n```\n``` C# []\npublic class Solution {\n private const int MOD = 1000000007;\n\n public int NumFactoredBinaryTrees(int[] arr) {\n // Step 1: Sort the input array.\n Array.Sort(arr);\n \n // Step 2: Create a HashSet to store unique numbers in the array.\n HashSet<int> uniqueNumbers = new HashSet<int>(arr);\n \n // Step 3: Initialize a Dictionary for dynamic programming.\n Dictionary<int, long> dp = new Dictionary<int, long>();\n foreach (int num in arr) {\n dp[num] = 1;\n }\n \n // Step 4: Dynamic Programming\n foreach (int i in arr) {\n foreach (int j in arr) {\n // If j is larger than the square root of i, break the loop because further j values won\'t be factors.\n if (j > Math.Sqrt(i)) break;\n \n // Check if j is a factor of i and if i/j is in the set of unique numbers.\n if (i % j == 0 && uniqueNumbers.Contains(i / j)) {\n long temp = dp[j] * dp[i / j];\n \n // Update the number of binary trees ending with i based on the factors j and i/j.\n dp[i] = (dp[i] + (i / j == j ? temp : temp * 2)) % MOD;\n }\n }\n }\n \n // Step 5: Calculate the final result.\n long result = 0;\n foreach (long value in dp.Values) {\n result = (result + value) % MOD;\n }\n return (int)result;\n }\n}\n\n```\n``` PHP []\nclass Solution {\n function numFactoredBinaryTrees($arr) {\n // Step 1: Sort the input array in ascending order.\n sort($arr);\n \n // Step 2: Create a hash map for faster containment checks.\n $uniqueNumbers = array_flip($arr);\n \n // Step 3: Initialize a hash map for dynamic programming.\n $dp = [];\n foreach ($arr as $x) {\n $dp[$x] = 1;\n }\n\n // Step 4: Dynamic Programming\n foreach ($arr as $i) {\n foreach ($arr as $j) {\n // If $j is larger than the square root of $i, break the loop.\n if ($j > sqrt($i)) break;\n\n // Check if $j is a factor of $i and if $i/$j is in the unique numbers hash map.\n if ($i % $j == 0 && isset($uniqueNumbers[$i / $j])) {\n // Calculate the temporary result.\n $temp = (int)((($dp[$j] * $dp[$i / $j]) % 1000000007) * ($i / $j == $j ? 1 : 2));\n \n // Update the number of binary trees ending with $i based on the factors $j and $i/$j.\n $dp[$i] = ($dp[$i] + $temp) % 1000000007;\n }\n }\n }\n\n // Step 5: Calculate the final result.\n $result = 0;\n foreach ($dp as $val) {\n $result = ($result + $val) % 1000000007;\n }\n \n return $result;\n }\n}\n\n```\n\n\n | 32 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | binary-trees-with-factors | 1 | 1 | # Intuition\nUse Dynamic Programming\n\n---\n\n# Solution Video\n\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,831\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nFirst of all, Let\'s understand question exactly.\n\n```\ninput: [2,3,4]\n```\nWhen input is `[2,3,4]`, we can create a binary tree. This is one of examples.\n```\n 24\n / \\\n 2 12\n / \\\n 3 4\n\nEach number may be used for any number of times.\n24 comes from 2 * 12\n2 comes from 2\n12 comes from 3 * 4\n3 comes from 3\n4 comes from 4\n```\n\nAll we have to do is to count this kind of tree we can make with input array. But difficulty is we don\'t know we will have `24` or `12` in the end. Do you calculate them one by one?\n\nActually, you don\'t have to calculate them exactly. Then how do we calculate them? We can take another approach.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to calculate number of subtree when each input number is root. \n\nLet\'s say we have 3 subtrees for some root number and 5 subtrees for the other root number. In that case, total number of trees are 8. Because each number may be used for any number of times, we can use any number for root or children.\n\n---\n\n- How can you calculate number of subtrees?\n\nWe have to multiply both sides of children for each non-leaf node. At least we can say\n\n---\n\n\u2B50\uFE0F Points\n\nThe number of the root must be a multiple of the current number. For example, root is `10`, current left child number is `5`. In that case there is possibiilty that we can create one of subtrees.\n\nWe can check it easily with 0 remainder.\n\n```[]\nif root % factor == 0\n```\n\n---\n\nBut we have one more important thing. Root is `10` and current left child number is `5`. In that case, what number do we need for right child number? Easy right? It\'s `2`\n\nSo, if we have node of value `2`, we can create at least one of subtrees.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to check if we have a number we need right now. Simply you can calculate it by division.\n\n```[]\nroot // factor\n```\n\nin the end,\n\n**number of subtree of the root = subtree of left side * subtree of right side**\n\nroot 10 = number of subtree of 5 * number of subtree of 2 + 1\n\n- Why +1?\n\nThat\'s because we can definitely create subtree of only 10. so in real solution code, we initialize each number of subtree with 1, so we don\'t write `+1` in solution code. \n\n---\n\n\nFrom the above idea, we need to keep previous numbers for future numbers, so seems like we can use Dynamic Programming.\n\n## How it works\n\nLet\'s think about this case again.\n\n```\ninput: [2,3,4]\n```\n\nWhen `2` is root. the rest of numbers are bigger than `2`. so we can create only `[2]`. subtree below is `HashMap`.\n\n```\nsubtree = {2: 1}\n\nkey: root number\nvalue: number of subtrees\n```\n\nHow about root is `3`. `2` and `4` doesn\'t meet this codition.\n\n```\nif root(3) % factor(2 or 4) == 0\n```\nSo, we will have only `[3]`.\n```\nsubtree = {2: 1, 3: 1}\n```\n\nHow about root is `4`. `2` meet the codition above, because we can create \n\n```\n 4\n / \\\n 2 2\n\nof course we can create subtree of only 4\n```\n\nDo you remember this point?\n\n---\n\n\u2B50\uFE0F Points\n\nnumber of subtree of the root = subtree of left side * subtree of right side\n\n---\n\nSo,\n\n```[]\nsubtree[root] += subtree[factor] * subtree[root // factor]\n\u2193\nsubtree[4] += subtree[2](=1) * subtree[4 // 2](=1)\n\u2193\nsubtree[4] = 2 \n\nall number of subtrees are initilized with 1,\nbacause of subtree of only root itself. We can definitely create it.\nIn this case, 1 + 1 = 2\n\n```\n\n```\nsubtree = {2: 1, 3: 1, 4: 2}\n```\n```\nOutput: 4 (1 + 1 + 2)\n```\n\n\n---\n\n\n\n## Visualization to understand easily and deeply\n\nTo understand easily and deeply. Let me explain this.\n```[]\nsubtree[4] += subtree[2](=1) * subtree[4 // 2](=1)\n```\n\n\n My shadow... lol\n\nWhen root is `4`, the `4` has two `2` nodes on the left and right side. In that case, Look at each triangle that has root 2 on left and right side.\n\n```\nsubtree = {2: 1, 3: 1}\n```\n\nWe know that if we have root 2 node, we can create only 1 subtree when input array is `[2,3,4]`(Look at `HashMap` above), so in the triangle parts, we can create 1 subtree from left triangle and 1 subtree from right triangle. That\'s why combination of the left side and right side should be `1 * 1 = 1`. Then add `+1` for the case where subtree of only root 4 itself.\n\nIn the end `1 + 1 = 2`.\n\nIf we have 2 subtrees on the right side. we can create 1 * 2 combinations.\n```\nleft side\nsubtree A\n\nright side\nsubtree B\nsubtree C\n\nall combinations of left and right should be AB and AC (= 1 * 2)\n```\nIf we have 2 subtrees on the left and right side. we can create 2 * 2 combinations.\n```\nleft side\nsubtree A\nsubtree D\n\nright side\nsubtree B\nsubtree C\n\nall combinations of left and right should be \nAB, AC, DB, DC (= 2 * 2)\n\n```\n\nEasy\uD83D\uDE06\n\n\nThis idea comes from a solution for unique binary search tree problem. I have a video. I took it last year.\n\nhttps://youtu.be/bTEcK_dh9QM\n\nI hope you understand main idea.\nLet\'s see real algorithm!\n\nI\'m rushed a little bit because I have a school event for my kids today. If I mistake something, let me know. Thank you!\n\n##### Algorithm Overview:\nThe algorithm aims to calculate the number of binary trees that can be formed using the elements in the input list `arr`, considering each element as a potential root. The result should be returned modulo `10^9 + 7`.\n\n##### Detailed Explanation:\n1. Sort the input list `arr` in ascending order.\n - This ensures that elements are processed in ascending order, which is crucial for the dynamic programming approach used.\n\n2. Initialize an empty dictionary called `subtree` to keep track of the number of binary trees that can be formed with each element as the root.\n - The keys of this dictionary will be the elements in `arr`, and the values will represent the number of binary trees that can be formed with the respective element as the root.\n\n3. Iterate through the sorted elements in `arr` with the variable `root`:\n a. Initialize the `subtree` count for the current `root` to 1.\n - This accounts for the possibility that the current element itself can be a single-node binary tree.\n\n4. Nested loop: Iterate through the elements in `arr` with the variable `factor`. This loop checks each element as a potential child node for the current `root`:\n a. If `factor` is greater than or equal to the current `root`, exit the loop.\n - This is because factors should be smaller than the root.\n b. Check if the current `root` is divisible by `factor` (i.e., `root % factor == 0`) and if the result of the division (`root // factor`) is already present in the `subtree` dictionary.\n - If both conditions are met, it means `factor` can be a child node of the current `root`.\n\n5. If the conditions in step 4 are met, update the `subtree` count for the current `root`:\n a. Increment the `subtree` count for the current `root` by multiplying the `subtree` count of the `factor` by the `subtree` count of the division result (`root // factor`).\n - This update accounts for the number of binary trees that can be formed with the current `root`.\n\n6. After processing all elements in the nested loop, you have calculated the number of binary trees that can be formed with the current `root` as the root node.\n\n7. The outer loop continues to the next `root` element, and the process repeats.\n\n8. Once all elements in `arr` have been processed, the `subtree` dictionary contains the number of binary trees that can be formed with each element as the root.\n\n9. Calculate the `total_trees` by summing up the values in the `subtree` dictionary.\n\n10. Finally, return `total_trees` modulo `(10^9 + 7)` to ensure the result is within the specified range.\n\nIn summary, this code iterates through the elements of `arr` while keeping track of the number of binary trees that can be formed with each element as the root node, taking advantage of previously calculated values for smaller factors.\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\nSorting the arr list takes $$O(n log n)$$ time, where "n" is the number of elements in the list.\n\nThe two nested loops iterate through the elements in arr. In the worst case, both loops will iterate over all elements. Therefore, the time complexity of this part is $$O(n^2)$$.\n\n\n- Space complexity: $$O(n)$$\n\nThe subtree dictionary stores values for each element in arr, so it has a space complexity of $$O(n)$$ to store the results for each element.\n\nThe other variables used in the code, such as root, factor, and total_trees, have constant space complexity and do not depend on the input size.\n\n```python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n subtree = {}\n\n for root in arr:\n subtree[root] = 1\n\n for factor in arr:\n if factor >= root:\n break\n \n if root % factor == 0 and root // factor in subtree:\n subtree[root] += subtree[factor] * subtree[root // factor]\n\n total_trees = sum(subtree.values())\n return total_trees % (10**9 + 7) \n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar numFactoredBinaryTrees = function(arr) {\n arr.sort((a, b) => a - b);\n const subtreeCount = {};\n\n for (const root of arr) {\n subtreeCount[root] = 1;\n\n for (const factor of arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor === 0 && subtreeCount[root / factor]) {\n subtreeCount[root] += subtreeCount[factor] * subtreeCount[root / factor];\n }\n }\n }\n\n let totalTrees = 0;\n for (const key in subtreeCount) {\n totalTrees += subtreeCount[key];\n }\n\n return totalTrees % (10 ** 9 + 7); \n};\n```\n```java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n Map<Integer, Long> subtreeCount = new HashMap<>();\n\n for (int root : arr) {\n subtreeCount.put(root, 1L);\n\n for (int factor : arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor == 0 && subtreeCount.containsKey(root / factor)) {\n subtreeCount.put(root, (subtreeCount.get(root) + subtreeCount.get(factor) * subtreeCount.get(root / factor)));\n }\n }\n }\n\n long totalTrees = 0L;\n for (int key : subtreeCount.keySet()) {\n totalTrees = (totalTrees + subtreeCount.get(key)) % 1_000_000_007;\n }\n\n return (int) totalTrees; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n sort(arr.begin(), arr.end());\n unordered_map<long, long> subtreeCount;\n\n for (long root : arr) {\n subtreeCount[root] = 1;\n\n for (long factor : arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor == 0 && subtreeCount.find(root / factor) != subtreeCount.end()) {\n subtreeCount[root] += subtreeCount[factor] * subtreeCount[root / factor];\n }\n }\n }\n\n long totalTrees = 0;\n for (const auto& entry : subtreeCount) {\n totalTrees += entry.second;\n }\n\n return totalTrees % static_cast<int>(pow(10, 9) + 7); \n }\n};\n```\n\n- Why do we sort input array?\n\nSorting the `arr` is done to comply with the constraints specified in the problem. The given constraint is that "each integer arr[i] is strictly greater than 1," which means that there are no integers in `arr` that are less than or equal to 1, and all integers are greater than or equal to 2.\n\nTo satisfy this condition, the array is sorted. Sorting the array ensures that the elements are processed in ascending order, from smaller integers to larger ones, which is essential for the effective application of the dynamic programming algorithm.\n\nBy sorting the array, you can solve the problem more efficiently, and it allows you to apply dynamic programming recursively, starting with smaller numbers and gradually progressing to larger numbers. This enables an efficient way to find the solution to the problem.\n\n\n---\n\n\n\nIf you are not familar with Dynamic Programming. This video might help you to understand it!\n\nhttps://youtu.be/MUU6tgywdPY\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/k-th-symbol-in-grammar/solutions/4205721/video-give-me-8-minutes-how-we-think-about-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/cCN38sMai-c\n\n\u25A0 Timeline of the video\n`0:04` Important Rules\n`0:17` How can you find the answer\n`1:13` How can you find the parent of the target pair\n`3:05` How can you know 0 or 1 in the target pair\n`3:40` How can you calculate the first position and the second position in the target pair\n`5:34` Coding\n`7:56` Time Complexity and Space Complexity\n\n\n | 58 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | binary-trees-with-factors | 1 | 1 | # Intuition\nUse Dynamic Programming\n\n---\n\n# Solution Video\n\nhttps://youtu.be/LrnKFjcjsqo\n\n\u25A0 Timeline of video\n`0:04` Understand question exactly and approach to solve this question\n`1:33` How can you calculate number of subtrees?\n`4:12` Demonstrate how it works\n`8:40` Coding\n`11:32` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,831\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nFirst of all, Let\'s understand question exactly.\n\n```\ninput: [2,3,4]\n```\nWhen input is `[2,3,4]`, we can create a binary tree. This is one of examples.\n```\n 24\n / \\\n 2 12\n / \\\n 3 4\n\nEach number may be used for any number of times.\n24 comes from 2 * 12\n2 comes from 2\n12 comes from 3 * 4\n3 comes from 3\n4 comes from 4\n```\n\nAll we have to do is to count this kind of tree we can make with input array. But difficulty is we don\'t know we will have `24` or `12` in the end. Do you calculate them one by one?\n\nActually, you don\'t have to calculate them exactly. Then how do we calculate them? We can take another approach.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to calculate number of subtree when each input number is root. \n\nLet\'s say we have 3 subtrees for some root number and 5 subtrees for the other root number. In that case, total number of trees are 8. Because each number may be used for any number of times, we can use any number for root or children.\n\n---\n\n- How can you calculate number of subtrees?\n\nWe have to multiply both sides of children for each non-leaf node. At least we can say\n\n---\n\n\u2B50\uFE0F Points\n\nThe number of the root must be a multiple of the current number. For example, root is `10`, current left child number is `5`. In that case there is possibiilty that we can create one of subtrees.\n\nWe can check it easily with 0 remainder.\n\n```[]\nif root % factor == 0\n```\n\n---\n\nBut we have one more important thing. Root is `10` and current left child number is `5`. In that case, what number do we need for right child number? Easy right? It\'s `2`\n\nSo, if we have node of value `2`, we can create at least one of subtrees.\n\n---\n\n\u2B50\uFE0F Points\n\nWe need to check if we have a number we need right now. Simply you can calculate it by division.\n\n```[]\nroot // factor\n```\n\nin the end,\n\n**number of subtree of the root = subtree of left side * subtree of right side**\n\nroot 10 = number of subtree of 5 * number of subtree of 2 + 1\n\n- Why +1?\n\nThat\'s because we can definitely create subtree of only 10. so in real solution code, we initialize each number of subtree with 1, so we don\'t write `+1` in solution code. \n\n---\n\n\nFrom the above idea, we need to keep previous numbers for future numbers, so seems like we can use Dynamic Programming.\n\n## How it works\n\nLet\'s think about this case again.\n\n```\ninput: [2,3,4]\n```\n\nWhen `2` is root. the rest of numbers are bigger than `2`. so we can create only `[2]`. subtree below is `HashMap`.\n\n```\nsubtree = {2: 1}\n\nkey: root number\nvalue: number of subtrees\n```\n\nHow about root is `3`. `2` and `4` doesn\'t meet this codition.\n\n```\nif root(3) % factor(2 or 4) == 0\n```\nSo, we will have only `[3]`.\n```\nsubtree = {2: 1, 3: 1}\n```\n\nHow about root is `4`. `2` meet the codition above, because we can create \n\n```\n 4\n / \\\n 2 2\n\nof course we can create subtree of only 4\n```\n\nDo you remember this point?\n\n---\n\n\u2B50\uFE0F Points\n\nnumber of subtree of the root = subtree of left side * subtree of right side\n\n---\n\nSo,\n\n```[]\nsubtree[root] += subtree[factor] * subtree[root // factor]\n\u2193\nsubtree[4] += subtree[2](=1) * subtree[4 // 2](=1)\n\u2193\nsubtree[4] = 2 \n\nall number of subtrees are initilized with 1,\nbacause of subtree of only root itself. We can definitely create it.\nIn this case, 1 + 1 = 2\n\n```\n\n```\nsubtree = {2: 1, 3: 1, 4: 2}\n```\n```\nOutput: 4 (1 + 1 + 2)\n```\n\n\n---\n\n\n\n## Visualization to understand easily and deeply\n\nTo understand easily and deeply. Let me explain this.\n```[]\nsubtree[4] += subtree[2](=1) * subtree[4 // 2](=1)\n```\n\n\n My shadow... lol\n\nWhen root is `4`, the `4` has two `2` nodes on the left and right side. In that case, Look at each triangle that has root 2 on left and right side.\n\n```\nsubtree = {2: 1, 3: 1}\n```\n\nWe know that if we have root 2 node, we can create only 1 subtree when input array is `[2,3,4]`(Look at `HashMap` above), so in the triangle parts, we can create 1 subtree from left triangle and 1 subtree from right triangle. That\'s why combination of the left side and right side should be `1 * 1 = 1`. Then add `+1` for the case where subtree of only root 4 itself.\n\nIn the end `1 + 1 = 2`.\n\nIf we have 2 subtrees on the right side. we can create 1 * 2 combinations.\n```\nleft side\nsubtree A\n\nright side\nsubtree B\nsubtree C\n\nall combinations of left and right should be AB and AC (= 1 * 2)\n```\nIf we have 2 subtrees on the left and right side. we can create 2 * 2 combinations.\n```\nleft side\nsubtree A\nsubtree D\n\nright side\nsubtree B\nsubtree C\n\nall combinations of left and right should be \nAB, AC, DB, DC (= 2 * 2)\n\n```\n\nEasy\uD83D\uDE06\n\n\nThis idea comes from a solution for unique binary search tree problem. I have a video. I took it last year.\n\nhttps://youtu.be/bTEcK_dh9QM\n\nI hope you understand main idea.\nLet\'s see real algorithm!\n\nI\'m rushed a little bit because I have a school event for my kids today. If I mistake something, let me know. Thank you!\n\n##### Algorithm Overview:\nThe algorithm aims to calculate the number of binary trees that can be formed using the elements in the input list `arr`, considering each element as a potential root. The result should be returned modulo `10^9 + 7`.\n\n##### Detailed Explanation:\n1. Sort the input list `arr` in ascending order.\n - This ensures that elements are processed in ascending order, which is crucial for the dynamic programming approach used.\n\n2. Initialize an empty dictionary called `subtree` to keep track of the number of binary trees that can be formed with each element as the root.\n - The keys of this dictionary will be the elements in `arr`, and the values will represent the number of binary trees that can be formed with the respective element as the root.\n\n3. Iterate through the sorted elements in `arr` with the variable `root`:\n a. Initialize the `subtree` count for the current `root` to 1.\n - This accounts for the possibility that the current element itself can be a single-node binary tree.\n\n4. Nested loop: Iterate through the elements in `arr` with the variable `factor`. This loop checks each element as a potential child node for the current `root`:\n a. If `factor` is greater than or equal to the current `root`, exit the loop.\n - This is because factors should be smaller than the root.\n b. Check if the current `root` is divisible by `factor` (i.e., `root % factor == 0`) and if the result of the division (`root // factor`) is already present in the `subtree` dictionary.\n - If both conditions are met, it means `factor` can be a child node of the current `root`.\n\n5. If the conditions in step 4 are met, update the `subtree` count for the current `root`:\n a. Increment the `subtree` count for the current `root` by multiplying the `subtree` count of the `factor` by the `subtree` count of the division result (`root // factor`).\n - This update accounts for the number of binary trees that can be formed with the current `root`.\n\n6. After processing all elements in the nested loop, you have calculated the number of binary trees that can be formed with the current `root` as the root node.\n\n7. The outer loop continues to the next `root` element, and the process repeats.\n\n8. Once all elements in `arr` have been processed, the `subtree` dictionary contains the number of binary trees that can be formed with each element as the root.\n\n9. Calculate the `total_trees` by summing up the values in the `subtree` dictionary.\n\n10. Finally, return `total_trees` modulo `(10^9 + 7)` to ensure the result is within the specified range.\n\nIn summary, this code iterates through the elements of `arr` while keeping track of the number of binary trees that can be formed with each element as the root node, taking advantage of previously calculated values for smaller factors.\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\nSorting the arr list takes $$O(n log n)$$ time, where "n" is the number of elements in the list.\n\nThe two nested loops iterate through the elements in arr. In the worst case, both loops will iterate over all elements. Therefore, the time complexity of this part is $$O(n^2)$$.\n\n\n- Space complexity: $$O(n)$$\n\nThe subtree dictionary stores values for each element in arr, so it has a space complexity of $$O(n)$$ to store the results for each element.\n\nThe other variables used in the code, such as root, factor, and total_trees, have constant space complexity and do not depend on the input size.\n\n```python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n subtree = {}\n\n for root in arr:\n subtree[root] = 1\n\n for factor in arr:\n if factor >= root:\n break\n \n if root % factor == 0 and root // factor in subtree:\n subtree[root] += subtree[factor] * subtree[root // factor]\n\n total_trees = sum(subtree.values())\n return total_trees % (10**9 + 7) \n```\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar numFactoredBinaryTrees = function(arr) {\n arr.sort((a, b) => a - b);\n const subtreeCount = {};\n\n for (const root of arr) {\n subtreeCount[root] = 1;\n\n for (const factor of arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor === 0 && subtreeCount[root / factor]) {\n subtreeCount[root] += subtreeCount[factor] * subtreeCount[root / factor];\n }\n }\n }\n\n let totalTrees = 0;\n for (const key in subtreeCount) {\n totalTrees += subtreeCount[key];\n }\n\n return totalTrees % (10 ** 9 + 7); \n};\n```\n```java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n Map<Integer, Long> subtreeCount = new HashMap<>();\n\n for (int root : arr) {\n subtreeCount.put(root, 1L);\n\n for (int factor : arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor == 0 && subtreeCount.containsKey(root / factor)) {\n subtreeCount.put(root, (subtreeCount.get(root) + subtreeCount.get(factor) * subtreeCount.get(root / factor)));\n }\n }\n }\n\n long totalTrees = 0L;\n for (int key : subtreeCount.keySet()) {\n totalTrees = (totalTrees + subtreeCount.get(key)) % 1_000_000_007;\n }\n\n return (int) totalTrees; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n sort(arr.begin(), arr.end());\n unordered_map<long, long> subtreeCount;\n\n for (long root : arr) {\n subtreeCount[root] = 1;\n\n for (long factor : arr) {\n if (factor >= root) {\n break;\n }\n\n if (root % factor == 0 && subtreeCount.find(root / factor) != subtreeCount.end()) {\n subtreeCount[root] += subtreeCount[factor] * subtreeCount[root / factor];\n }\n }\n }\n\n long totalTrees = 0;\n for (const auto& entry : subtreeCount) {\n totalTrees += entry.second;\n }\n\n return totalTrees % static_cast<int>(pow(10, 9) + 7); \n }\n};\n```\n\n- Why do we sort input array?\n\nSorting the `arr` is done to comply with the constraints specified in the problem. The given constraint is that "each integer arr[i] is strictly greater than 1," which means that there are no integers in `arr` that are less than or equal to 1, and all integers are greater than or equal to 2.\n\nTo satisfy this condition, the array is sorted. Sorting the array ensures that the elements are processed in ascending order, from smaller integers to larger ones, which is essential for the effective application of the dynamic programming algorithm.\n\nBy sorting the array, you can solve the problem more efficiently, and it allows you to apply dynamic programming recursively, starting with smaller numbers and gradually progressing to larger numbers. This enables an efficient way to find the solution to the problem.\n\n\n---\n\n\n\nIf you are not familar with Dynamic Programming. This video might help you to understand it!\n\nhttps://youtu.be/MUU6tgywdPY\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/k-th-symbol-in-grammar/solutions/4205721/video-give-me-8-minutes-how-we-think-about-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/cCN38sMai-c\n\n\u25A0 Timeline of the video\n`0:04` Important Rules\n`0:17` How can you find the answer\n`1:13` How can you find the parent of the target pair\n`3:05` How can you know 0 or 1 in the target pair\n`3:40` How can you calculate the first position and the second position in the target pair\n`5:34` Coding\n`7:56` Time Complexity and Space Complexity\n\n\n | 58 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
🌟[PYTHON] Simplest DP Solution Explained🌟 | binary-trees-with-factors | 0 | 1 | # Approach - DP\n<!-- Describe your approach to solving the problem. -->\n> NOTE --> DP array will store the number of tree that can be formed keeping that index element as the root\n\n1. Sort the given `arr` and then make another dp array `dp` of same length with all elements as `1` because every element will make atleast one tree consisting of itself only.\n2. Now start a loop from the second element of `arr` and see whether any element present before it can divide it completely.\n3. If yes, check whether the element which comes after their division (quotient) is present in the list.\n4. If yes, find its location (if present) and see its value in `dp` array and multiply both divident `dp`\'s array value and add it to `dp[i]`.\n5. Return the sum of `dp`, by taking modulo.\n\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n!!! Please Upvote if you understand \uD83D\uDE0A\uD83D\uDE0A !!!\n# Code\n```\nclass Solution(object):\n def numFactoredBinaryTrees(self, arr):\n mod = 10**9 + 7\n n = len(arr)\n arr.sort()\n dp = [1]*n \n for i in range(1,n):\n for j in range(i):\n if arr[i] % arr[j] == 0:\n temp = arr[i] // arr[j]\n try: k = arr.index(temp)\n except: continue\n dp[i] += (dp[j] * dp[k])\n return sum(dp) % mod\n \n``` | 1 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
🌟[PYTHON] Simplest DP Solution Explained🌟 | binary-trees-with-factors | 0 | 1 | # Approach - DP\n<!-- Describe your approach to solving the problem. -->\n> NOTE --> DP array will store the number of tree that can be formed keeping that index element as the root\n\n1. Sort the given `arr` and then make another dp array `dp` of same length with all elements as `1` because every element will make atleast one tree consisting of itself only.\n2. Now start a loop from the second element of `arr` and see whether any element present before it can divide it completely.\n3. If yes, check whether the element which comes after their division (quotient) is present in the list.\n4. If yes, find its location (if present) and see its value in `dp` array and multiply both divident `dp`\'s array value and add it to `dp[i]`.\n5. Return the sum of `dp`, by taking modulo.\n\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n!!! Please Upvote if you understand \uD83D\uDE0A\uD83D\uDE0A !!!\n# Code\n```\nclass Solution(object):\n def numFactoredBinaryTrees(self, arr):\n mod = 10**9 + 7\n n = len(arr)\n arr.sort()\n dp = [1]*n \n for i in range(1,n):\n for j in range(i):\n if arr[i] % arr[j] == 0:\n temp = arr[i] // arr[j]\n try: k = arr.index(temp)\n except: continue\n dp[i] += (dp[j] * dp[k])\n return sum(dp) % mod\n \n``` | 1 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
✅ Beats 100% 🔥 || Easiest Approach in 3 Points || DP & HashMap | binary-trees-with-factors | 1 | 1 | ##### TypeScript Result:\n\n\n\n# Intuition :\n**In order to build a tree, we need to know the number of left children and right children. \nIf we know the number of left children and right children, the total number of trees we can build is left * right.\nSo we can use a hashmap to store the number of trees we can build for each number.\nWe iterate the array from small to big, for each number, we iterate all the numbers smaller than it to find the left children,\nand we check if the right children exists in the hashmap.\nIf so, we can build left * right trees.\nFinally, we sum up the number of trees for each number.**\n\n# Algorithm :\n1. Sort the array "arr", and use a hashmap dp to record the number of trees we can build for each number.\n2. Iterate the array from small to big, for each number, we iterate all the numbers smaller than it to find the left children, and we check if the right children exists in the hashmap. If so, we can build left * right trees.\n3. Finally, we sum up the number of trees for each number.\n\n# Complexity Analysis :\n- $$Time Complexity$$: **O(N^2)**, where N is the length of arr. For each arr[i], we iterate arr[j] to find the left children, and check if arr[i] / arr[j] exists in the hashmap.\n- $$Space Complexity$$: **O(N)**, the space used by hashmap dp.\n\n### UpVote \u2B06\uFE0F if you found this helpful :)\n\n# Code\n``` Python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n dp = {}\n for i in range(len(arr)):\n dp[arr[i]] = 1\n for j in range(i):\n if arr[i] % arr[j] == 0 and arr[i] // arr[j] in dp:\n dp[arr[i]] += dp[arr[j]] * dp[arr[i] // arr[j]]\n return sum(dp.values()) % (10**9 + 7)\n```\n``` C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n std::sort(arr.begin(), arr.end());\n std::unordered_map<int, long> dp;\n\n for (int i = 0; i < arr.size(); i++) {\n dp[arr[i]] = 1;\n\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0 && dp.find(arr[i] / arr[j]) != dp.end()) {\n dp[arr[i]] += dp[arr[j]] * dp[arr[i] / arr[j]];\n }\n }\n }\n\n long result = 0;\n for (auto val : dp) {\n result += val.second;\n }\n\n return result % (int)(1e9 + 7);\n }\n};\n```\n``` Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n Map<Integer, Long> dp = new HashMap<>();\n\n for (int i = 0; i < arr.length; i++) {\n dp.put(arr[i], 1L);\n\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0 && dp.containsKey(arr[i] / arr[j])) {\n dp.put(arr[i], dp.get(arr[i]) + dp.get(arr[j]) * dp.get(arr[i] / arr[j]));\n }\n }\n }\n\n long result = 0;\n for (long val : dp.values()) {\n result += val;\n }\n\n return (int) (result % (Math.pow(10, 9) + 7));\n }\n}\n```\n``` C# []\npublic class Solution {\n public int NumFactoredBinaryTrees(int[] arr) {\n Array.Sort(arr);\n Dictionary<int, long> dp = new Dictionary<int, long>();\n\n foreach (int i in arr) {\n dp[i] = 1;\n\n foreach (int j in arr) {\n if (i % j == 0 && dp.ContainsKey(i / j)) {\n dp[i] += dp[j] * dp[i / j];\n }\n }\n }\n\n long result = 0;\n foreach (var val in dp.Values) {\n result += val;\n }\n\n return (int)(result % (Math.Pow(10, 9) + 7));\n }\n}\n```\n``` JavaScipt []\nvar numFactoredBinaryTrees = function(arr) {\n arr.sort((a, b) => a - b);\n const dp = new Map();\n\n for (let i = 0; i < arr.length; i++) {\n dp.set(arr[i], 1);\n\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0 && dp.has(arr[i] / arr[j])) {\n dp.set(arr[i], dp.get(arr[i]) + dp.get(arr[j]) * dp.get(arr[i] / arr[j]));\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result += val;\n }\n\n return result % (Math.pow(10, 9) + 7);\n};\n\n```\n``` TypeScipt []\nfunction numFactoredBinaryTrees(arr: number[]): number {\narr.sort((a, b) => a - b);\n const dp: Map<number, number> = new Map();\n\n for (let i = 0; i < arr.length; i++) {\n dp.set(arr[i], 1);\n\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0 && dp.has(arr[i] / arr[j])) {\n dp.set(arr[i], dp.get(arr[i])! + dp.get(arr[j])! * dp.get(arr[i] / arr[j])!);\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result += val;\n }\n\n return result % (Math.pow(10, 9) + 7);\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $arr\n * @return Integer\n */\n function numFactoredBinaryTrees($arr) {\n sort($arr);\n $dp = array();\n\n foreach ($arr as $i) {\n $dp[$i] = 1;\n\n foreach ($arr as $j) {\n if ($i % $j === 0 && isset($dp[$i / $j])) {\n $dp[$i] += $dp[$j] * $dp[$i / $j];\n }\n }\n }\n\n $result = 0;\n foreach ($dp as $val) {\n $result += $val;\n }\n\n return $result % (pow(10, 9) + 7);\n }\n}\n```\n``` Ruby []\n# @param {Integer[]} arr\n# @return {Integer}\ndef num_factored_binary_trees(arr)\n arr.sort!\n dp = {}\n\n arr.each do |i|\n dp[i] = 1\n\n arr.each do |j|\n if i % j == 0 && dp.key?(i / j)\n dp[i] += dp[j] * dp[i / j]\n end\n end\n end\n\n result = 0\n dp.values.each { |val| result += val }\n\n result % (10**9 + 7)\n end\n```\n\n\n | 15 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
✅ Beats 100% 🔥 || Easiest Approach in 3 Points || DP & HashMap | binary-trees-with-factors | 1 | 1 | ##### TypeScript Result:\n\n\n\n# Intuition :\n**In order to build a tree, we need to know the number of left children and right children. \nIf we know the number of left children and right children, the total number of trees we can build is left * right.\nSo we can use a hashmap to store the number of trees we can build for each number.\nWe iterate the array from small to big, for each number, we iterate all the numbers smaller than it to find the left children,\nand we check if the right children exists in the hashmap.\nIf so, we can build left * right trees.\nFinally, we sum up the number of trees for each number.**\n\n# Algorithm :\n1. Sort the array "arr", and use a hashmap dp to record the number of trees we can build for each number.\n2. Iterate the array from small to big, for each number, we iterate all the numbers smaller than it to find the left children, and we check if the right children exists in the hashmap. If so, we can build left * right trees.\n3. Finally, we sum up the number of trees for each number.\n\n# Complexity Analysis :\n- $$Time Complexity$$: **O(N^2)**, where N is the length of arr. For each arr[i], we iterate arr[j] to find the left children, and check if arr[i] / arr[j] exists in the hashmap.\n- $$Space Complexity$$: **O(N)**, the space used by hashmap dp.\n\n### UpVote \u2B06\uFE0F if you found this helpful :)\n\n# Code\n``` Python []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n dp = {}\n for i in range(len(arr)):\n dp[arr[i]] = 1\n for j in range(i):\n if arr[i] % arr[j] == 0 and arr[i] // arr[j] in dp:\n dp[arr[i]] += dp[arr[j]] * dp[arr[i] // arr[j]]\n return sum(dp.values()) % (10**9 + 7)\n```\n``` C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n std::sort(arr.begin(), arr.end());\n std::unordered_map<int, long> dp;\n\n for (int i = 0; i < arr.size(); i++) {\n dp[arr[i]] = 1;\n\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0 && dp.find(arr[i] / arr[j]) != dp.end()) {\n dp[arr[i]] += dp[arr[j]] * dp[arr[i] / arr[j]];\n }\n }\n }\n\n long result = 0;\n for (auto val : dp) {\n result += val.second;\n }\n\n return result % (int)(1e9 + 7);\n }\n};\n```\n``` Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n Map<Integer, Long> dp = new HashMap<>();\n\n for (int i = 0; i < arr.length; i++) {\n dp.put(arr[i], 1L);\n\n for (int j = 0; j < i; j++) {\n if (arr[i] % arr[j] == 0 && dp.containsKey(arr[i] / arr[j])) {\n dp.put(arr[i], dp.get(arr[i]) + dp.get(arr[j]) * dp.get(arr[i] / arr[j]));\n }\n }\n }\n\n long result = 0;\n for (long val : dp.values()) {\n result += val;\n }\n\n return (int) (result % (Math.pow(10, 9) + 7));\n }\n}\n```\n``` C# []\npublic class Solution {\n public int NumFactoredBinaryTrees(int[] arr) {\n Array.Sort(arr);\n Dictionary<int, long> dp = new Dictionary<int, long>();\n\n foreach (int i in arr) {\n dp[i] = 1;\n\n foreach (int j in arr) {\n if (i % j == 0 && dp.ContainsKey(i / j)) {\n dp[i] += dp[j] * dp[i / j];\n }\n }\n }\n\n long result = 0;\n foreach (var val in dp.Values) {\n result += val;\n }\n\n return (int)(result % (Math.Pow(10, 9) + 7));\n }\n}\n```\n``` JavaScipt []\nvar numFactoredBinaryTrees = function(arr) {\n arr.sort((a, b) => a - b);\n const dp = new Map();\n\n for (let i = 0; i < arr.length; i++) {\n dp.set(arr[i], 1);\n\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0 && dp.has(arr[i] / arr[j])) {\n dp.set(arr[i], dp.get(arr[i]) + dp.get(arr[j]) * dp.get(arr[i] / arr[j]));\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result += val;\n }\n\n return result % (Math.pow(10, 9) + 7);\n};\n\n```\n``` TypeScipt []\nfunction numFactoredBinaryTrees(arr: number[]): number {\narr.sort((a, b) => a - b);\n const dp: Map<number, number> = new Map();\n\n for (let i = 0; i < arr.length; i++) {\n dp.set(arr[i], 1);\n\n for (let j = 0; j < i; j++) {\n if (arr[i] % arr[j] === 0 && dp.has(arr[i] / arr[j])) {\n dp.set(arr[i], dp.get(arr[i])! + dp.get(arr[j])! * dp.get(arr[i] / arr[j])!);\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result += val;\n }\n\n return result % (Math.pow(10, 9) + 7);\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[] $arr\n * @return Integer\n */\n function numFactoredBinaryTrees($arr) {\n sort($arr);\n $dp = array();\n\n foreach ($arr as $i) {\n $dp[$i] = 1;\n\n foreach ($arr as $j) {\n if ($i % $j === 0 && isset($dp[$i / $j])) {\n $dp[$i] += $dp[$j] * $dp[$i / $j];\n }\n }\n }\n\n $result = 0;\n foreach ($dp as $val) {\n $result += $val;\n }\n\n return $result % (pow(10, 9) + 7);\n }\n}\n```\n``` Ruby []\n# @param {Integer[]} arr\n# @return {Integer}\ndef num_factored_binary_trees(arr)\n arr.sort!\n dp = {}\n\n arr.each do |i|\n dp[i] = 1\n\n arr.each do |j|\n if i % j == 0 && dp.key?(i / j)\n dp[i] += dp[j] * dp[i / j]\n end\n end\n end\n\n result = 0\n dp.values.each { |val| result += val }\n\n result % (10**9 + 7)\n end\n```\n\n\n | 15 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
EASY PYTHON SOLUTION | binary-trees-with-factors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nMOD = 10**9 + 7\n\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n s = set(arr)\n dp = {x: 1 for x in arr}\n \n for i in arr:\n for j in arr:\n if j > i**0.5:\n break\n if i % j == 0 and i // j in s:\n if i // j == j:\n dp[i] += dp[j] * dp[j]\n else:\n dp[i] += dp[j] * dp[i // j] * 2\n dp[i] %= MOD\n \n return sum(dp.values()) % MOD\n``` | 1 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
EASY PYTHON SOLUTION | binary-trees-with-factors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nMOD = 10**9 + 7\n\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n arr.sort()\n s = set(arr)\n dp = {x: 1 for x in arr}\n \n for i in arr:\n for j in arr:\n if j > i**0.5:\n break\n if i % j == 0 and i // j in s:\n if i // j == j:\n dp[i] += dp[j] * dp[j]\n else:\n dp[i] += dp[j] * dp[i // j] * 2\n dp[i] %= MOD\n \n return sum(dp.values()) % MOD\n``` | 1 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Solution | binary-trees-with-factors | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr)\n {\n sort(arr.begin(), arr.end());\n int len = arr.size();\n long ans = 0;\n unordered_map<int, long> fmap;\n for (int num : arr) {\n long ways = 1;\n double lim = sqrt(num);\n for (int j = 0, fA = arr[0]; fA <= lim; fA = arr[++j]) {\n if (num % fA != 0) continue;\n int fB = num / fA;\n if (fmap.find(fB) != fmap.end())\n ways = (ways + fmap[fA] * fmap[fB] * (fA == fB ? 1 : 2)) % 1000000007;\n }\n fmap[num] = ways;\n ans = (ans + ways) % 1000000007;\n }\n return (int)ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n total_nums = len(arr)\n moduler = 1000000007\n count_product_dict = {num: 1 for num in arr}\n arr.sort()\n\n for i in range(1, total_nums):\n for j in range(i):\n quotient = arr[i] // arr[j]\n if quotient < 2 or math.sqrt(arr[i]) > arr[i- 1]:\n break\n if arr[i] % arr[j] == 0:\n count_product_dict[arr[i]] += count_product_dict[arr[j]] * count_product_dict.get(quotient, 0)\n count_product_dict[arr[i]] %= moduler\n \n return sum(count_product_dict.values()) % moduler\n```\n\n```Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n long [] dp = new long[arr.length];\n Arrays.fill(dp,1);\n long MOD=(int)1e9+7,ans=1;\n dp[0]=1;\n Map<Integer,Integer> index = new HashMap<Integer,Integer>();\n index.put(arr[0],0);\n\n for(int i=1;i<dp.length;i++){\n index.put(arr[i],i);\n\n for(int j=0;arr[j]<=Math.sqrt(arr[i]);j++){\n if(arr[j]*(long )arr[j]==arr[i]){\n dp[i]+=dp[j] *(long ) dp[j]%MOD;\n dp[i]%=MOD;\n }\n else if(arr[i]%arr[j]==0&&index.containsKey(arr[i]/arr[j])){\n dp[i]+=dp[j]*dp[index.get(arr[i]/arr[j])]*2%MOD;\n }\n }\n ans=(ans+dp[i])%MOD;\n }\n return (int)ans;\n }\n}\n```\n | 1 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Solution | binary-trees-with-factors | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr)\n {\n sort(arr.begin(), arr.end());\n int len = arr.size();\n long ans = 0;\n unordered_map<int, long> fmap;\n for (int num : arr) {\n long ways = 1;\n double lim = sqrt(num);\n for (int j = 0, fA = arr[0]; fA <= lim; fA = arr[++j]) {\n if (num % fA != 0) continue;\n int fB = num / fA;\n if (fmap.find(fB) != fmap.end())\n ways = (ways + fmap[fA] * fmap[fB] * (fA == fB ? 1 : 2)) % 1000000007;\n }\n fmap[num] = ways;\n ans = (ans + ways) % 1000000007;\n }\n return (int)ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n total_nums = len(arr)\n moduler = 1000000007\n count_product_dict = {num: 1 for num in arr}\n arr.sort()\n\n for i in range(1, total_nums):\n for j in range(i):\n quotient = arr[i] // arr[j]\n if quotient < 2 or math.sqrt(arr[i]) > arr[i- 1]:\n break\n if arr[i] % arr[j] == 0:\n count_product_dict[arr[i]] += count_product_dict[arr[j]] * count_product_dict.get(quotient, 0)\n count_product_dict[arr[i]] %= moduler\n \n return sum(count_product_dict.values()) % moduler\n```\n\n```Java []\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n Arrays.sort(arr);\n long [] dp = new long[arr.length];\n Arrays.fill(dp,1);\n long MOD=(int)1e9+7,ans=1;\n dp[0]=1;\n Map<Integer,Integer> index = new HashMap<Integer,Integer>();\n index.put(arr[0],0);\n\n for(int i=1;i<dp.length;i++){\n index.put(arr[i],i);\n\n for(int j=0;arr[j]<=Math.sqrt(arr[i]);j++){\n if(arr[j]*(long )arr[j]==arr[i]){\n dp[i]+=dp[j] *(long ) dp[j]%MOD;\n dp[i]%=MOD;\n }\n else if(arr[i]%arr[j]==0&&index.containsKey(arr[i]/arr[j])){\n dp[i]+=dp[j]*dp[index.get(arr[i]/arr[j])]*2%MOD;\n }\n }\n ans=(ans+dp[i])%MOD;\n }\n return (int)ans;\n }\n}\n```\n | 1 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Python3 Solution | binary-trees-with-factors | 0 | 1 | \n```\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n mod=10**9+7\n arr.sort()\n ans=defaultdict(int)\n for a in arr:\n tmp=1\n for b in arr:\n if b>a:\n break\n tmp+=(ans[b]*ans[a/b])\n ans[a]=tmp\n return sum(ans.values())%mod \n \n``` | 5 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Python3 Solution | binary-trees-with-factors | 0 | 1 | \n```\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n mod=10**9+7\n arr.sort()\n ans=defaultdict(int)\n for a in arr:\n tmp=1\n for b in arr:\n if b>a:\n break\n tmp+=(ans[b]*ans[a/b])\n ans[a]=tmp\n return sum(ans.values())%mod \n \n``` | 5 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | binary-trees-with-factors | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Maps)***\n1. Initialize a modulo value `mod` to prevent integer overflow and create a map `mp` to store the count of factored binary trees for each number.\n1. `Sort` the input array in ascending order for efficient processing.\n1. Initialize the count for the first element in the array.\n1. Loop through the input array starting from the second element.\n1. For each element, iterate through the elements in the map and check if the current element is divisible by a map element and if the resulting factor is also present in the map.\n1. If the conditions are met, calculate the count for the current element by multiplying counts of factors and update the map.\n1. Calculate the total number of factored binary trees by summing up the counts in the map, using modulo to keep the result within bounds.\n1. Return the total number of factored binary trees.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n int mod = pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n map<int, long> mp; // Create a map to store the count of factored binary trees for each number.\n sort(arr.begin(), arr.end()); // Sort the input array in ascending order.\n mp[arr[0]] = 1; // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (int i = 1; i < arr.size(); i++) {\n long cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the map.\n for (auto x : mp) {\n int el = x.first; // Get an element from the map.\n\n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0 && mp.find(arr[i] / el) != mp.end()) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[el] * mp[arr[i] / el];\n }\n }\n\n mp[arr[i]] = cnt; // Store the computed count in the map for the current element.\n }\n\n int ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (auto a : mp) {\n ans = (ans + a.second) % mod; // Use modulo to keep the result within bounds.\n }\n\n return ans; // Return the total number of factored binary trees.\n }\n};\n\n\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n#include <math.h>\n\n// Define a structure to represent key-value pairs in the map\ntypedef struct {\n int key;\n long value;\n} KeyValuePair;\n\n// Function to compare two key-value pairs for sorting\nint compare(const void* a, const void* b) {\n return ((KeyValuePair*)a)->key - ((KeyValuePair*)b)->key;\n}\n\nint numFactoredBinaryTrees(int* arr, int arrSize) {\n long mod = (long)pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n \n // Create an array of key-value pairs to store the count of factored binary trees for each number.\n KeyValuePair* mp = (KeyValuePair*)malloc(arrSize * sizeof(KeyValuePair));\n \n // Sort the input array in ascending order.\n qsort(arr, arrSize, sizeof(int), compare);\n \n // Initialize the count for the first element in the array.\n mp[0].key = arr[0];\n mp[0].value = 1;\n \n // Loop through the input array starting from the second element.\n for (int i = 1; i < arrSize; i++) {\n long cnt = 1; // Initialize the count for the current element.\n \n // Iterate through the elements in the map.\n for (int j = 0; j < i; j++) {\n int el = mp[j].key; // Get an element from the map.\n \n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0) {\n int factor = arr[i] / el;\n for (int k = 0; k < i; k++) {\n if (mp[k].key == factor) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[j].value * mp[k].value;\n break;\n }\n }\n }\n }\n \n mp[i].key = arr[i];\n mp[i].value = cnt; // Store the computed count in the map for the current element.\n }\n \n long ans = 0; // Initialize the answer variable.\n \n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (int i = 0; i < arrSize; i++) {\n ans = (ans + mp[i].value) % mod; // Use modulo to keep the result within bounds.\n }\n \n free(mp); // Free the dynamically allocated memory.\n \n return (int)ans; // Return the total number of factored binary trees.\n}\n\nint main() {\n int arr[] = {2, 4, 5};\n int arrSize = sizeof(arr) / sizeof(arr[0]);\n int result = numFactoredBinaryTrees(arr, arrSize);\n printf("Total number of factored binary trees: %d\\n", result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nimport java.util.Arrays;\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int mod = (int) Math.pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n Arrays.sort(arr); // Sort the input array in ascending order.\n Map<Integer, Long> mp = new HashMap<>(); // Create a map to store the count of factored binary trees for each number.\n mp.put(arr[0], 1L); // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (int i = 1; i < arr.length; i++) {\n long cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the map.\n for (Map.Entry<Integer, Long> entry : mp.entrySet()) {\n int el = entry.getKey(); // Get an element from the map.\n\n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0 && mp.containsKey(arr[i] / el)) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += entry.getValue() * mp.get(arr[i] / el);\n }\n }\n\n mp.put(arr[i], cnt); // Store the computed count in the map for the current element.\n }\n\n long ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (long value : mp.values()) {\n ans = (ans + value) % mod; // Use modulo to keep the result within bounds.\n }\n\n return (int) ans; // Return the total number of factored binary trees.\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr):\n mod = 10**9 + 7 # Define a modulo value to prevent integer overflow.\n arr.sort() # Sort the input list in ascending order.\n mp = {} # Create a dictionary to store the count of factored binary trees for each number.\n mp[arr[0]] = 1 # Initialize the count for the first element in the list.\n\n # Loop through the input list starting from the second element.\n for i in range(1, len(arr)):\n cnt = 1 # Initialize the count for the current element.\n\n # Iterate through the elements in the dictionary.\n for el in mp:\n # Check if the current element in the list is divisible by the dictionary element\n # and if the resulting factor is also present in the dictionary.\n if arr[i] % el == 0 and arr[i] // el in mp:\n # Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[el] * mp[arr[i] // el]\n\n mp[arr[i]] = cnt # Store the computed count in the dictionary for the current element.\n\n ans = 0 # Initialize the answer variable.\n\n # Calculate the total number of factored binary trees by summing up the counts in the dictionary.\n for a in mp:\n ans = (ans + mp[a]) % mod # Use modulo to keep the result within bounds.\n\n return ans # Return the total number of factored binary trees.\n\n\n```\n\n```javascript []\nvar numFactoredBinaryTrees = function(arr) {\n const mod = 10**9 + 7; // Define a modulo value to prevent integer overflow.\n arr.sort((a, b) => a - b); // Sort the input array in ascending order.\n const mp = new Map(); // Create a Map to store the count of factored binary trees for each number.\n mp.set(arr[0], 1); // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (let i = 1; i < arr.length; i++) {\n let cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the Map.\n for (const [el, value] of mp) {\n // Check if the current element in the array is divisible by the Map element\n // and if the resulting factor is also present in the Map.\n if (arr[i] % el === 0 && mp.has(arr[i] / el)) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += value * mp.get(arr[i] / el);\n }\n }\n\n mp.set(arr[i], cnt); // Store the computed count in the Map for the current element.\n }\n\n let ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the Map.\n for (const value of mp.values()) {\n ans = (ans + value) % mod; // Use modulo to keep the result within bounds.\n }\n\n return ans; // Return the total number of factored binary trees.\n};\n\n```\n\n\n---\n#### ***Approach 2(DP)***\n1. The code uses dynamic programming to calculate the number of factored binary trees for each number in the input array.\n1. It sorts the input array for easier iteration and creates a set for efficient lookups.\n1. The `dp` map stores the count of factored binary trees for each number, initializing each count to 1.\n1. It iterates through each element in the array and checks for factors within the array. If factors are found, it calculates the count of binary trees by multiplying the counts of the factors.\n1. The modulo operation is used to keep the result within bounds to prevent integer overflow.\n1. Finally, it sums up all the counts in the map to obtain the total number of factored binary trees.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nconst int MOD = 1e9 + 7;\n\nclass Solution {\npublic:\n int numFactoredBinaryTrees(std::vector<int>& arr) {\n std::sort(arr.begin(), arr.end()); // Sort the input array in ascending order.\n std::unordered_set<int> s(arr.begin(), arr.end()); // Create a set for faster element lookup.\n std::unordered_map<int, int> dp; // Create a map to store the count of factored binary trees for each number.\n \n for (int x : arr)\n dp[x] = 1; // Initialize the count for each element to 1, representing the tree with just the element itself.\n \n for (int i : arr) {\n for (int j : arr) {\n if (j > std::sqrt(i))\n break; // If j is greater than the square root of i, we can break because further factors won\'t be found.\n \n if (i % j == 0 && s.find(i / j) != s.end()) {\n long long temp = (long long)dp[j] * dp[i / j]; // Calculate the count by multiplying counts of factors.\n \n if (i / j == j) {\n dp[i] = (dp[i] + temp) % MOD; // If the factor is the same, we add the count once.\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD; // If the factors are different, we add the count twice.\n }\n }\n }\n }\n \n int result = 0;\n for (auto& [_, val] : dp) {\n result = (result + val) % MOD; // Sum up all the counts in the map.\n }\n return result; // Return the total number of factored binary trees.\n }\n};\n\n\n```\n\n```C []\n#define MOD 1000000007\n\nint numFactoredBinaryTrees(int* arr, int arrSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n int s[arrSize];\n for (int i = 0; i < arrSize; i++) {\n s[i] = arr[i];\n }\n int dp[arrSize];\n for (int i = 0; i < arrSize; i++) {\n dp[i] = 1;\n }\n\n for (int i = 0; i < arrSize; i++) {\n for (int j = 0; j < arrSize; j++) {\n if (s[j] > sqrt(arr[i])) {\n break;\n }\n if (arr[i] % s[j] == 0) {\n long long temp = (long long)dp[j] * dp[binarySearch(s, arrSize, arr[i] / s[j])];\n if (arr[i] / s[j] == s[j]) {\n dp[i] = (dp[i] + temp) % MOD;\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD;\n }\n }\n }\n }\n\n int result = 0;\n for (int i = 0; i < arrSize; i++) {\n result = (result + dp[i]) % MOD;\n }\n return result;\n}\n\n\n\n```\n\n```Java []\nimport java.util.Arrays;\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int MOD = 1000000007;\n Arrays.sort(arr);\n Map<Integer, Integer> dp = new HashMap<>();\n int[] s = Arrays.copyOf(arr, arr.length);\n\n for (int x : arr) {\n dp.put(x, 1);\n }\n\n for (int i : arr) {\n for (int j : arr) {\n if (j > Math.sqrt(i)) {\n break;\n }\n if (i % j == 0 && Arrays.binarySearch(s, i / j) >= 0) {\n long temp = (long) dp.get(j) * dp.get(i / j);\n if (i / j == j) {\n dp.put(i, (int) ((dp.get(i) + temp) % MOD));\n } else {\n dp.put(i, (int) ((dp.get(i) + temp * 2) % MOD));\n }\n }\n }\n }\n\n int result = 0;\n for (int val : dp.values()) {\n result = (result + val) % MOD;\n }\n return result;\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n MOD = 1000000007\n arr.sort()\n dp = {}\n s = arr.copy()\n\n for x in arr:\n dp[x] = 1\n\n for i in arr:\n for j in arr:\n if j > int(i ** 0.5):\n break\n if i % j == 0 and i // j in s:\n temp = dp[j] * dp[i // j]\n if i // j == j:\n dp[i] = (dp[i] + temp) % MOD\n else:\n dp[i] = (dp[i] + temp * 2) % MOD\n\n result = 0\n for val in dp.values():\n result = (result + val) % MOD\n return result\n\n\n```\n\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar numFactoredBinaryTrees = function(arr) {\n const MOD = 1000000007;\n arr.sort((a, b) => a - b);\n const dp = new Map();\n const s = [...arr];\n\n for (const x of arr) {\n dp.set(x, 1);\n }\n\n for (const i of arr) {\n for (const j of arr) {\n if (j > Math.sqrt(i)) {\n break;\n }\n if (i % j === 0 && s.includes(i / j)) {\n const temp = BigInt(dp.get(j)) * BigInt(dp.get(i / j));\n if (i / j === j) {\n dp.set(i, (Number(dp.get(i)) + Number(temp)) % MOD);\n } else {\n dp.set(i, (Number(dp.get(i)) + Number(temp * 2n)) % MOD);\n }\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result = (result + val) % MOD;\n }\n return result;\n};\n\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥 | binary-trees-with-factors | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Maps)***\n1. Initialize a modulo value `mod` to prevent integer overflow and create a map `mp` to store the count of factored binary trees for each number.\n1. `Sort` the input array in ascending order for efficient processing.\n1. Initialize the count for the first element in the array.\n1. Loop through the input array starting from the second element.\n1. For each element, iterate through the elements in the map and check if the current element is divisible by a map element and if the resulting factor is also present in the map.\n1. If the conditions are met, calculate the count for the current element by multiplying counts of factors and update the map.\n1. Calculate the total number of factored binary trees by summing up the counts in the map, using modulo to keep the result within bounds.\n1. Return the total number of factored binary trees.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int numFactoredBinaryTrees(vector<int>& arr) {\n int mod = pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n map<int, long> mp; // Create a map to store the count of factored binary trees for each number.\n sort(arr.begin(), arr.end()); // Sort the input array in ascending order.\n mp[arr[0]] = 1; // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (int i = 1; i < arr.size(); i++) {\n long cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the map.\n for (auto x : mp) {\n int el = x.first; // Get an element from the map.\n\n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0 && mp.find(arr[i] / el) != mp.end()) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[el] * mp[arr[i] / el];\n }\n }\n\n mp[arr[i]] = cnt; // Store the computed count in the map for the current element.\n }\n\n int ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (auto a : mp) {\n ans = (ans + a.second) % mod; // Use modulo to keep the result within bounds.\n }\n\n return ans; // Return the total number of factored binary trees.\n }\n};\n\n\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n#include <math.h>\n\n// Define a structure to represent key-value pairs in the map\ntypedef struct {\n int key;\n long value;\n} KeyValuePair;\n\n// Function to compare two key-value pairs for sorting\nint compare(const void* a, const void* b) {\n return ((KeyValuePair*)a)->key - ((KeyValuePair*)b)->key;\n}\n\nint numFactoredBinaryTrees(int* arr, int arrSize) {\n long mod = (long)pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n \n // Create an array of key-value pairs to store the count of factored binary trees for each number.\n KeyValuePair* mp = (KeyValuePair*)malloc(arrSize * sizeof(KeyValuePair));\n \n // Sort the input array in ascending order.\n qsort(arr, arrSize, sizeof(int), compare);\n \n // Initialize the count for the first element in the array.\n mp[0].key = arr[0];\n mp[0].value = 1;\n \n // Loop through the input array starting from the second element.\n for (int i = 1; i < arrSize; i++) {\n long cnt = 1; // Initialize the count for the current element.\n \n // Iterate through the elements in the map.\n for (int j = 0; j < i; j++) {\n int el = mp[j].key; // Get an element from the map.\n \n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0) {\n int factor = arr[i] / el;\n for (int k = 0; k < i; k++) {\n if (mp[k].key == factor) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[j].value * mp[k].value;\n break;\n }\n }\n }\n }\n \n mp[i].key = arr[i];\n mp[i].value = cnt; // Store the computed count in the map for the current element.\n }\n \n long ans = 0; // Initialize the answer variable.\n \n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (int i = 0; i < arrSize; i++) {\n ans = (ans + mp[i].value) % mod; // Use modulo to keep the result within bounds.\n }\n \n free(mp); // Free the dynamically allocated memory.\n \n return (int)ans; // Return the total number of factored binary trees.\n}\n\nint main() {\n int arr[] = {2, 4, 5};\n int arrSize = sizeof(arr) / sizeof(arr[0]);\n int result = numFactoredBinaryTrees(arr, arrSize);\n printf("Total number of factored binary trees: %d\\n", result);\n return 0;\n}\n\n\n\n```\n\n```Java []\nimport java.util.Arrays;\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int mod = (int) Math.pow(10, 9) + 7; // Define a modulo value to prevent integer overflow.\n Arrays.sort(arr); // Sort the input array in ascending order.\n Map<Integer, Long> mp = new HashMap<>(); // Create a map to store the count of factored binary trees for each number.\n mp.put(arr[0], 1L); // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (int i = 1; i < arr.length; i++) {\n long cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the map.\n for (Map.Entry<Integer, Long> entry : mp.entrySet()) {\n int el = entry.getKey(); // Get an element from the map.\n\n // Check if the current element in the array is divisible by the map element\n // and if the resulting factor is also present in the map.\n if (arr[i] % el == 0 && mp.containsKey(arr[i] / el)) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += entry.getValue() * mp.get(arr[i] / el);\n }\n }\n\n mp.put(arr[i], cnt); // Store the computed count in the map for the current element.\n }\n\n long ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the map.\n for (long value : mp.values()) {\n ans = (ans + value) % mod; // Use modulo to keep the result within bounds.\n }\n\n return (int) ans; // Return the total number of factored binary trees.\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr):\n mod = 10**9 + 7 # Define a modulo value to prevent integer overflow.\n arr.sort() # Sort the input list in ascending order.\n mp = {} # Create a dictionary to store the count of factored binary trees for each number.\n mp[arr[0]] = 1 # Initialize the count for the first element in the list.\n\n # Loop through the input list starting from the second element.\n for i in range(1, len(arr)):\n cnt = 1 # Initialize the count for the current element.\n\n # Iterate through the elements in the dictionary.\n for el in mp:\n # Check if the current element in the list is divisible by the dictionary element\n # and if the resulting factor is also present in the dictionary.\n if arr[i] % el == 0 and arr[i] // el in mp:\n # Calculate the count for the current element by multiplying counts of factors.\n cnt += mp[el] * mp[arr[i] // el]\n\n mp[arr[i]] = cnt # Store the computed count in the dictionary for the current element.\n\n ans = 0 # Initialize the answer variable.\n\n # Calculate the total number of factored binary trees by summing up the counts in the dictionary.\n for a in mp:\n ans = (ans + mp[a]) % mod # Use modulo to keep the result within bounds.\n\n return ans # Return the total number of factored binary trees.\n\n\n```\n\n```javascript []\nvar numFactoredBinaryTrees = function(arr) {\n const mod = 10**9 + 7; // Define a modulo value to prevent integer overflow.\n arr.sort((a, b) => a - b); // Sort the input array in ascending order.\n const mp = new Map(); // Create a Map to store the count of factored binary trees for each number.\n mp.set(arr[0], 1); // Initialize the count for the first element in the array.\n\n // Loop through the input array starting from the second element.\n for (let i = 1; i < arr.length; i++) {\n let cnt = 1; // Initialize the count for the current element.\n\n // Iterate through the elements in the Map.\n for (const [el, value] of mp) {\n // Check if the current element in the array is divisible by the Map element\n // and if the resulting factor is also present in the Map.\n if (arr[i] % el === 0 && mp.has(arr[i] / el)) {\n // Calculate the count for the current element by multiplying counts of factors.\n cnt += value * mp.get(arr[i] / el);\n }\n }\n\n mp.set(arr[i], cnt); // Store the computed count in the Map for the current element.\n }\n\n let ans = 0; // Initialize the answer variable.\n\n // Calculate the total number of factored binary trees by summing up the counts in the Map.\n for (const value of mp.values()) {\n ans = (ans + value) % mod; // Use modulo to keep the result within bounds.\n }\n\n return ans; // Return the total number of factored binary trees.\n};\n\n```\n\n\n---\n#### ***Approach 2(DP)***\n1. The code uses dynamic programming to calculate the number of factored binary trees for each number in the input array.\n1. It sorts the input array for easier iteration and creates a set for efficient lookups.\n1. The `dp` map stores the count of factored binary trees for each number, initializing each count to 1.\n1. It iterates through each element in the array and checks for factors within the array. If factors are found, it calculates the count of binary trees by multiplying the counts of the factors.\n1. The modulo operation is used to keep the result within bounds to prevent integer overflow.\n1. Finally, it sums up all the counts in the map to obtain the total number of factored binary trees.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nconst int MOD = 1e9 + 7;\n\nclass Solution {\npublic:\n int numFactoredBinaryTrees(std::vector<int>& arr) {\n std::sort(arr.begin(), arr.end()); // Sort the input array in ascending order.\n std::unordered_set<int> s(arr.begin(), arr.end()); // Create a set for faster element lookup.\n std::unordered_map<int, int> dp; // Create a map to store the count of factored binary trees for each number.\n \n for (int x : arr)\n dp[x] = 1; // Initialize the count for each element to 1, representing the tree with just the element itself.\n \n for (int i : arr) {\n for (int j : arr) {\n if (j > std::sqrt(i))\n break; // If j is greater than the square root of i, we can break because further factors won\'t be found.\n \n if (i % j == 0 && s.find(i / j) != s.end()) {\n long long temp = (long long)dp[j] * dp[i / j]; // Calculate the count by multiplying counts of factors.\n \n if (i / j == j) {\n dp[i] = (dp[i] + temp) % MOD; // If the factor is the same, we add the count once.\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD; // If the factors are different, we add the count twice.\n }\n }\n }\n }\n \n int result = 0;\n for (auto& [_, val] : dp) {\n result = (result + val) % MOD; // Sum up all the counts in the map.\n }\n return result; // Return the total number of factored binary trees.\n }\n};\n\n\n```\n\n```C []\n#define MOD 1000000007\n\nint numFactoredBinaryTrees(int* arr, int arrSize) {\n qsort(arr, arrSize, sizeof(int), compare);\n int s[arrSize];\n for (int i = 0; i < arrSize; i++) {\n s[i] = arr[i];\n }\n int dp[arrSize];\n for (int i = 0; i < arrSize; i++) {\n dp[i] = 1;\n }\n\n for (int i = 0; i < arrSize; i++) {\n for (int j = 0; j < arrSize; j++) {\n if (s[j] > sqrt(arr[i])) {\n break;\n }\n if (arr[i] % s[j] == 0) {\n long long temp = (long long)dp[j] * dp[binarySearch(s, arrSize, arr[i] / s[j])];\n if (arr[i] / s[j] == s[j]) {\n dp[i] = (dp[i] + temp) % MOD;\n } else {\n dp[i] = (dp[i] + temp * 2) % MOD;\n }\n }\n }\n }\n\n int result = 0;\n for (int i = 0; i < arrSize; i++) {\n result = (result + dp[i]) % MOD;\n }\n return result;\n}\n\n\n\n```\n\n```Java []\nimport java.util.Arrays;\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public int numFactoredBinaryTrees(int[] arr) {\n int MOD = 1000000007;\n Arrays.sort(arr);\n Map<Integer, Integer> dp = new HashMap<>();\n int[] s = Arrays.copyOf(arr, arr.length);\n\n for (int x : arr) {\n dp.put(x, 1);\n }\n\n for (int i : arr) {\n for (int j : arr) {\n if (j > Math.sqrt(i)) {\n break;\n }\n if (i % j == 0 && Arrays.binarySearch(s, i / j) >= 0) {\n long temp = (long) dp.get(j) * dp.get(i / j);\n if (i / j == j) {\n dp.put(i, (int) ((dp.get(i) + temp) % MOD));\n } else {\n dp.put(i, (int) ((dp.get(i) + temp * 2) % MOD));\n }\n }\n }\n }\n\n int result = 0;\n for (int val : dp.values()) {\n result = (result + val) % MOD;\n }\n return result;\n }\n}\n\n\n```\n\n```python3 []\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n MOD = 1000000007\n arr.sort()\n dp = {}\n s = arr.copy()\n\n for x in arr:\n dp[x] = 1\n\n for i in arr:\n for j in arr:\n if j > int(i ** 0.5):\n break\n if i % j == 0 and i // j in s:\n temp = dp[j] * dp[i // j]\n if i // j == j:\n dp[i] = (dp[i] + temp) % MOD\n else:\n dp[i] = (dp[i] + temp * 2) % MOD\n\n result = 0\n for val in dp.values():\n result = (result + val) % MOD\n return result\n\n\n```\n\n```javascript []\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar numFactoredBinaryTrees = function(arr) {\n const MOD = 1000000007;\n arr.sort((a, b) => a - b);\n const dp = new Map();\n const s = [...arr];\n\n for (const x of arr) {\n dp.set(x, 1);\n }\n\n for (const i of arr) {\n for (const j of arr) {\n if (j > Math.sqrt(i)) {\n break;\n }\n if (i % j === 0 && s.includes(i / j)) {\n const temp = BigInt(dp.get(j)) * BigInt(dp.get(i / j));\n if (i / j === j) {\n dp.set(i, (Number(dp.get(i)) + Number(temp)) % MOD);\n } else {\n dp.set(i, (Number(dp.get(i)) + Number(temp * 2n)) % MOD);\n }\n }\n }\n }\n\n let result = 0;\n for (const val of dp.values()) {\n result = (result + val) % MOD;\n }\n return result;\n};\n\n```\n\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
🔥 Python || Detailed Explanation ✅ || Easily Understood || DP || O(n * sqrt(n)) | binary-trees-with-factors | 0 | 1 | **Appreciate if you could upvote this solution**\n\nMethod: `DP`\n\nSince the parent node is the product of the children, the value of the parent nodes must larger than the values of its children.\nThus, we can sort the `arr` first, and start to calculate the combination of products **from smallest node to the largest one**.\nFor example, `arr = [18, 3, 6, 2]`\nAfter sorting, `arr = [2, 3, 6, 18]`\nThen, a dict `count_product_dict` needs to be created to store the count of combinations and all the initial values should be `1`.\n\n```\nFor 2:\n\t- We can ignore the first number as the smallest number does not have a product of 2 smaller numbers.\n\nFor 3:\n\t- We can just scan the numbers smaller than 3\n\t\t- Since 2 is larger than half of 3, it is rejected as 3 must not be a product of 2 and a integer.\n\nFor 6:\n\t- We can just scan the numbers smaller than 6\n\t\t- 6 % 2 == 0 -> (2, 6 // 2)\n\t\t\t- count_product_dict[6] += count_product_dict[2] * count_product_dict[6 // 2]\n\t\t- 6 % 3 == 0 -> (3, 6 // 3)\n\t\t\t- count_product_dict[6] += count_product_dict[2] * count_product_dict[6 // 2]\n\nAnd so on...\nFinally, count_product_dict = {18: 7, 3: 1, 6: 3, 2: 1}\n```\n\nCode:\n```\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n total_nums = len(arr)\n moduler = 1000000007\n count_product_dict = {num: 1 for num in arr}\n arr.sort()\n\n for i in range(1, total_nums):\n for j in range(i):\n quotient = arr[i] // arr[j]\n if quotient < 2 or math.sqrt(arr[i]) > arr[i- 1]:\n break\n if arr[i] % arr[j] == 0:\n count_product_dict[arr[i]] += count_product_dict[arr[j]] * count_product_dict.get(quotient, 0)\n count_product_dict[arr[i]] %= moduler\n \n return sum(count_product_dict.values()) % moduler\n```\n\n**Time Complexity**: O(n ^ 2)\n**Space Complexity**: O(n)\n<br /> | 37 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
🔥 Python || Detailed Explanation ✅ || Easily Understood || DP || O(n * sqrt(n)) | binary-trees-with-factors | 0 | 1 | **Appreciate if you could upvote this solution**\n\nMethod: `DP`\n\nSince the parent node is the product of the children, the value of the parent nodes must larger than the values of its children.\nThus, we can sort the `arr` first, and start to calculate the combination of products **from smallest node to the largest one**.\nFor example, `arr = [18, 3, 6, 2]`\nAfter sorting, `arr = [2, 3, 6, 18]`\nThen, a dict `count_product_dict` needs to be created to store the count of combinations and all the initial values should be `1`.\n\n```\nFor 2:\n\t- We can ignore the first number as the smallest number does not have a product of 2 smaller numbers.\n\nFor 3:\n\t- We can just scan the numbers smaller than 3\n\t\t- Since 2 is larger than half of 3, it is rejected as 3 must not be a product of 2 and a integer.\n\nFor 6:\n\t- We can just scan the numbers smaller than 6\n\t\t- 6 % 2 == 0 -> (2, 6 // 2)\n\t\t\t- count_product_dict[6] += count_product_dict[2] * count_product_dict[6 // 2]\n\t\t- 6 % 3 == 0 -> (3, 6 // 3)\n\t\t\t- count_product_dict[6] += count_product_dict[2] * count_product_dict[6 // 2]\n\nAnd so on...\nFinally, count_product_dict = {18: 7, 3: 1, 6: 3, 2: 1}\n```\n\nCode:\n```\nclass Solution:\n def numFactoredBinaryTrees(self, arr: List[int]) -> int:\n total_nums = len(arr)\n moduler = 1000000007\n count_product_dict = {num: 1 for num in arr}\n arr.sort()\n\n for i in range(1, total_nums):\n for j in range(i):\n quotient = arr[i] // arr[j]\n if quotient < 2 or math.sqrt(arr[i]) > arr[i- 1]:\n break\n if arr[i] % arr[j] == 0:\n count_product_dict[arr[i]] += count_product_dict[arr[j]] * count_product_dict.get(quotient, 0)\n count_product_dict[arr[i]] %= moduler\n \n return sum(count_product_dict.values()) % moduler\n```\n\n**Time Complexity**: O(n ^ 2)\n**Space Complexity**: O(n)\n<br /> | 37 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Python3 code | goat-latin | 0 | 1 | # Intuition\n1.Split the input sentence into individual words using the .split() method, and store them in a list called w.\n2.Initialize empty lists l and v to store the modified words and the final modified words, respectively.\n3.Iterate over each word i in the list w.\n4.Check if the first letter of the word i is a vowel (either lowercase or uppercase). If it is, append the string "ma" to the end of the word i and add it to the list l.\n5.If the first letter of the word i is not a vowel, move the first letter to the end of the word, append "ma" to it, and add it to the list l.\n6.Iterate over the modified words in the list l. For each word at index i, append "a" repeated (i+1) times to the end of the word, and add it to the list v.\n7.Join all the modified words in the list v into a single string, separated by spaces, and store it in the variable m.\n8.Return the final modified string m.\n\n# Approach\nThe input string is first split into words, and then each word is processed individually. \nIf a word starts with a vowel (either lower or upper case), then the string "ma" is appended to the end of the word. Otherwise, the first letter of the word is moved to the end of the word, and then "ma" is appended.\nAfter processing all the words, each modified word is further modified by appending "a" characters to the end of the word, where the number of "a" characters depends on the position of the word in the sentence (starting from 1). \nFinally, all the modified words are joined together into a single string, separated by spaces, and returned as the output of the method.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n^2)\n\n# Code\n```\nclass Solution:\n def toGoatLatin(self, sentence: str) -> str:\n w = sentence.split()\n l=[]\n v=[]\n for i in w:\n a = 1*i \n if(i[0]==\'a\'or i[0]==\'e\'or i[0]==\'i\' or i[0]==\'o\' or i[0]==\'u\' or i[0]==\'A\'or i[0]==\'E\'or i[0]==\'I\' or i[0]==\'O\' or i[0]==\'U\'):\n i = i+"ma"\n l.append(i)\n else:\n w = i[1:]+i[0]+"ma"\n l.append(w)\n for i in range(len(l)):\n q = l[i]+"a"*(i+1)\n v.append(q)\n m = " ".join(v)\n\n \n return m\n \n``` | 1 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
Python3 code | goat-latin | 0 | 1 | # Intuition\n1.Split the input sentence into individual words using the .split() method, and store them in a list called w.\n2.Initialize empty lists l and v to store the modified words and the final modified words, respectively.\n3.Iterate over each word i in the list w.\n4.Check if the first letter of the word i is a vowel (either lowercase or uppercase). If it is, append the string "ma" to the end of the word i and add it to the list l.\n5.If the first letter of the word i is not a vowel, move the first letter to the end of the word, append "ma" to it, and add it to the list l.\n6.Iterate over the modified words in the list l. For each word at index i, append "a" repeated (i+1) times to the end of the word, and add it to the list v.\n7.Join all the modified words in the list v into a single string, separated by spaces, and store it in the variable m.\n8.Return the final modified string m.\n\n# Approach\nThe input string is first split into words, and then each word is processed individually. \nIf a word starts with a vowel (either lower or upper case), then the string "ma" is appended to the end of the word. Otherwise, the first letter of the word is moved to the end of the word, and then "ma" is appended.\nAfter processing all the words, each modified word is further modified by appending "a" characters to the end of the word, where the number of "a" characters depends on the position of the word in the sentence (starting from 1). \nFinally, all the modified words are joined together into a single string, separated by spaces, and returned as the output of the method.\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n^2)\n\n# Code\n```\nclass Solution:\n def toGoatLatin(self, sentence: str) -> str:\n w = sentence.split()\n l=[]\n v=[]\n for i in w:\n a = 1*i \n if(i[0]==\'a\'or i[0]==\'e\'or i[0]==\'i\' or i[0]==\'o\' or i[0]==\'u\' or i[0]==\'A\'or i[0]==\'E\'or i[0]==\'I\' or i[0]==\'O\' or i[0]==\'U\'):\n i = i+"ma"\n l.append(i)\n else:\n w = i[1:]+i[0]+"ma"\n l.append(w)\n for i in range(len(l)):\n q = l[i]+"a"*(i+1)\n v.append(q)\n m = " ".join(v)\n\n \n return m\n \n``` | 1 | There is a group of `n` people labeled from `0` to `n - 1` where each person has a different amount of money and a different level of quietness.
You are given an array `richer` where `richer[i] = [ai, bi]` indicates that `ai` has more money than `bi` and an integer array `quiet` where `quiet[i]` is the quietness of the `ith` person. All the given data in richer are **logically correct** (i.e., the data will not lead you to a situation where `x` is richer than `y` and `y` is richer than `x` at the same time).
Return _an integer array_ `answer` _where_ `answer[x] = y` _if_ `y` _is the least quiet person (that is, the person_ `y` _with the smallest value of_ `quiet[y]`_) among all people who definitely have equal to or more money than the person_ `x`.
**Example 1:**
**Input:** richer = \[\[1,0\],\[2,1\],\[3,1\],\[3,7\],\[4,3\],\[5,3\],\[6,3\]\], quiet = \[3,2,5,4,6,1,7,0\]
**Output:** \[5,5,2,5,4,5,6,7\]
**Explanation:**
answer\[0\] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet\[x\]) is person 7, but it is not clear if they have more money than person 0.
answer\[7\] = 7.
Among all people that definitely have equal to or more money than person 7 (which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet\[x\]) is person 7.
The other answers can be filled out with similar reasoning.
**Example 2:**
**Input:** richer = \[\], quiet = \[0\]
**Output:** \[0\]
**Constraints:**
* `n == quiet.length`
* `1 <= n <= 500`
* `0 <= quiet[i] < n`
* All the values of `quiet` are **unique**.
* `0 <= richer.length <= n * (n - 1) / 2`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs of `richer` are **unique**.
* The observations in `richer` are all logically consistent. | null |
Solution | goat-latin | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string toGoatLatin(string s) {\n string res;\n int count=0;\n for(int i=0; i<s.length(); i++){\n string temp;\n while(s[i]!=\' \' && i<s.length()){\n temp +=s[i];\n i++;\n }\n count++;\n if(temp[0]!=\'a\' && temp[0]!=\'e\' && temp[0]!=\'i\' && temp[0]!=\'o\' && temp[0]!=\'u\'&& temp[0]!=\'A\' && temp[0]!=\'E\' && temp[0]!=\'I\' && temp[0]!=\'O\' && temp[0]!=\'U\'){\n char t;\n t = temp[0];\n for(int k=0; k<temp.length()-1; k++){\n temp[k]=temp[k+1];\n }\n temp[temp.length()-1]=t;\n }\n temp+="ma";\n for(int j=0; j<count; j++){\n temp+="a";\n }\n res+=temp+" ";\n }\n return res.substr(0,res.length()-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def toGoatLatin(self, sentence: str) -> str:\n \n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\']\n words = sentence.split()\n for i in range(len(words)):\n if words[i][0] in vowels:\n words[i] += \'ma\'\n else:\n words[i] = words[i][1:] + words[i][0] + \'ma\'\n words[i] += \'a\' * (i+1)\n return \' \'.join(words)\n```\n\n```Java []\nclass Solution {\n static final char[] vowels = new char[10];\n static {\n vowels[0] = \'A\';\n vowels[1] = \'E\';\n vowels[2] = \'I\';\n vowels[3] = \'O\';\n vowels[4] = \'U\';\n vowels[5] = \'a\';\n vowels[6] = \'e\';\n vowels[7] = \'i\';\n vowels[8] = \'o\';\n vowels[9] = \'u\';\n }\n private static boolean isConsonant(char ch) {\n return Arrays.binarySearch(vowels, ch) < 0;\n }\n public String toGoatLatin(String sentence) {\n final StringBuilder sb = new StringBuilder();\n int count = 0;\n final char[] chars = sentence.toCharArray();\n final int length = chars.length;\n for (int index = 0; index < length;) {\n if (index > 0) {\n sb.append(\' \');\n }\n final char firstChar = chars[index];\n char next = firstChar;\n final boolean isConsonant = isConsonant(firstChar);\n if (isConsonant) {\n if (++index >= length) {\n next = \' \';\n } else {\n next = chars[index];\n }\n }\n while (next != \' \') {\n sb.append(next);\n if (++index >= length) {\n break;\n }\n next = chars[index];\n }\n if (isConsonant) {\n sb.append(firstChar);\n }\n sb.append("ma");\n ++count;\n for (int i = 0; i < count; i++) {\n sb.append(\'a\');\n }\n ++index;\n }\n return sb.toString();\n }\n}\n```\n | 1 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
Solution | goat-latin | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string toGoatLatin(string s) {\n string res;\n int count=0;\n for(int i=0; i<s.length(); i++){\n string temp;\n while(s[i]!=\' \' && i<s.length()){\n temp +=s[i];\n i++;\n }\n count++;\n if(temp[0]!=\'a\' && temp[0]!=\'e\' && temp[0]!=\'i\' && temp[0]!=\'o\' && temp[0]!=\'u\'&& temp[0]!=\'A\' && temp[0]!=\'E\' && temp[0]!=\'I\' && temp[0]!=\'O\' && temp[0]!=\'U\'){\n char t;\n t = temp[0];\n for(int k=0; k<temp.length()-1; k++){\n temp[k]=temp[k+1];\n }\n temp[temp.length()-1]=t;\n }\n temp+="ma";\n for(int j=0; j<count; j++){\n temp+="a";\n }\n res+=temp+" ";\n }\n return res.substr(0,res.length()-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def toGoatLatin(self, sentence: str) -> str:\n \n vowels = [\'a\', \'e\', \'i\', \'o\', \'u\', \'A\', \'E\', \'I\', \'O\', \'U\']\n words = sentence.split()\n for i in range(len(words)):\n if words[i][0] in vowels:\n words[i] += \'ma\'\n else:\n words[i] = words[i][1:] + words[i][0] + \'ma\'\n words[i] += \'a\' * (i+1)\n return \' \'.join(words)\n```\n\n```Java []\nclass Solution {\n static final char[] vowels = new char[10];\n static {\n vowels[0] = \'A\';\n vowels[1] = \'E\';\n vowels[2] = \'I\';\n vowels[3] = \'O\';\n vowels[4] = \'U\';\n vowels[5] = \'a\';\n vowels[6] = \'e\';\n vowels[7] = \'i\';\n vowels[8] = \'o\';\n vowels[9] = \'u\';\n }\n private static boolean isConsonant(char ch) {\n return Arrays.binarySearch(vowels, ch) < 0;\n }\n public String toGoatLatin(String sentence) {\n final StringBuilder sb = new StringBuilder();\n int count = 0;\n final char[] chars = sentence.toCharArray();\n final int length = chars.length;\n for (int index = 0; index < length;) {\n if (index > 0) {\n sb.append(\' \');\n }\n final char firstChar = chars[index];\n char next = firstChar;\n final boolean isConsonant = isConsonant(firstChar);\n if (isConsonant) {\n if (++index >= length) {\n next = \' \';\n } else {\n next = chars[index];\n }\n }\n while (next != \' \') {\n sb.append(next);\n if (++index >= length) {\n break;\n }\n next = chars[index];\n }\n if (isConsonant) {\n sb.append(firstChar);\n }\n sb.append("ma");\n ++count;\n for (int i = 0; i < count; i++) {\n sb.append(\'a\');\n }\n ++index;\n }\n return sb.toString();\n }\n}\n```\n | 1 | There is a group of `n` people labeled from `0` to `n - 1` where each person has a different amount of money and a different level of quietness.
You are given an array `richer` where `richer[i] = [ai, bi]` indicates that `ai` has more money than `bi` and an integer array `quiet` where `quiet[i]` is the quietness of the `ith` person. All the given data in richer are **logically correct** (i.e., the data will not lead you to a situation where `x` is richer than `y` and `y` is richer than `x` at the same time).
Return _an integer array_ `answer` _where_ `answer[x] = y` _if_ `y` _is the least quiet person (that is, the person_ `y` _with the smallest value of_ `quiet[y]`_) among all people who definitely have equal to or more money than the person_ `x`.
**Example 1:**
**Input:** richer = \[\[1,0\],\[2,1\],\[3,1\],\[3,7\],\[4,3\],\[5,3\],\[6,3\]\], quiet = \[3,2,5,4,6,1,7,0\]
**Output:** \[5,5,2,5,4,5,6,7\]
**Explanation:**
answer\[0\] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet\[x\]) is person 7, but it is not clear if they have more money than person 0.
answer\[7\] = 7.
Among all people that definitely have equal to or more money than person 7 (which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet\[x\]) is person 7.
The other answers can be filled out with similar reasoning.
**Example 2:**
**Input:** richer = \[\], quiet = \[0\]
**Output:** \[0\]
**Constraints:**
* `n == quiet.length`
* `1 <= n <= 500`
* `0 <= quiet[i] < n`
* All the values of `quiet` are **unique**.
* `0 <= richer.length <= n * (n - 1) / 2`
* `0 <= ai, bi < n`
* `ai != bi`
* All the pairs of `richer` are **unique**.
* The observations in `richer` are all logically consistent. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.