title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Easiest Solution | masking-personal-information | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public String maskPII(String s) {\n StringBuilder sb = new StringBuilder();\n\t\t //email handeling\n if((s.charAt(0) >= 97 && s.charAt(0) <= 122) || (s.charAt(0) >= 65 && s.charAt(0) <= 90)){\n\n s = s.toLowerCase();\n int indexofAt = s.indexOf(\'@\');\n String firstName = s.substring(0, indexofAt);\n sb.append(firstName.charAt(0)).append("*****").append(firstName.charAt(firstName.length()-1));\n sb.append(s.substring(indexofAt,s.length()));\n }\n //phone number handeling\n else{\n int digits = 0;\n for(int i = 0 ; i < s.length(); i++){\n if(Character.isDigit(s.charAt(i))){\n digits++;\n }\n }\n if(digits > 10){\n sb.append(\'+\');\n }\n while(digits > 10){\n sb.append(\'*\');\n digits--;\n }\n if(sb.toString().isEmpty() == false){\n sb.append(\'-\');\n }\n sb.append("***").append(\'-\').append("***-");\n StringBuilder last4 = new StringBuilder();\n int count = 0;\n for(int i = s.length()-1; i >=0; --i){\n if(count == 4){\n break;\n }\n if(Character.isDigit(s.charAt(i))){\n last4.append(s.charAt(i));\n count++;\n }\n }\n sb.append(last4.reverse());\n }\n\n return sb.toString();\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n string maskPII(string s) {\n \n string str;\n int c=0;\n for(auto val:s)\n {\n if(isalpha(val))\n {\n c++;\n }\n }\n if(c==0) //means a phone number\n {\n string str;\n for(int i=0;i<s.size();i++)\n {\n if(isdigit(s[i]))\n {\n str.push_back(s[i]);\n }\n }\n string ans;\n int t=str.size();\n // cout<<str<<" ";\n // cout<<t<<" "<<t-6;\n if(str.size()==10)\n {\n ans="***-***-";\n }\n else if(str.size()==11)\n {\n ans= "+*-***-***-";\n }\n else if(str.size()==12)\n {\n ans="+**-***-***-";\n }\n else\n {\n ans="+***-***-***-";\n }\n \n ans.push_back(str[t-4]);\n ans.push_back(str[t-3]);\n ans.push_back(str[t-2]);\n ans.push_back(str[t-1]);\n return ans;\n }\n else //an email\n {\n int c=0;\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'@\')\n {\n c=i;\n }\n }\n string ans;\n ans.push_back(tolower(s[0]));\n int t=5;\n while(t--)\n {\n ans.push_back(\'*\');\n }\n ans.push_back(tolower(s[c-1]));\n //cout<<c+1<<" ";\n for(int i=c;i<s.size();i++)\n {\n ans.push_back(tolower(s[i]));\n }\n return ans;\n }\n return s;\n }\n};\n```\n```python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n name, rest = s.split(\'@\')\n name = name[0] + \'*****\' + name[-1]\n return name + \'@\' + rest\n else:\n num = \'\'.join([n for n in s if n in \'1234567890\'])\n if len(num) == 10:\n return "***-***-" + num[-4:]\n elif len(num) == 11:\n return "+*-***-***-" + num[-4:]\n elif len(num) == 12:\n return "+**-***-***-" + num[-4:]\n else:\n return "+***-***-***-" + num[-4:]\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
Easiest Solution | masking-personal-information | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public String maskPII(String s) {\n StringBuilder sb = new StringBuilder();\n\t\t //email handeling\n if((s.charAt(0) >= 97 && s.charAt(0) <= 122) || (s.charAt(0) >= 65 && s.charAt(0) <= 90)){\n\n s = s.toLowerCase();\n int indexofAt = s.indexOf(\'@\');\n String firstName = s.substring(0, indexofAt);\n sb.append(firstName.charAt(0)).append("*****").append(firstName.charAt(firstName.length()-1));\n sb.append(s.substring(indexofAt,s.length()));\n }\n //phone number handeling\n else{\n int digits = 0;\n for(int i = 0 ; i < s.length(); i++){\n if(Character.isDigit(s.charAt(i))){\n digits++;\n }\n }\n if(digits > 10){\n sb.append(\'+\');\n }\n while(digits > 10){\n sb.append(\'*\');\n digits--;\n }\n if(sb.toString().isEmpty() == false){\n sb.append(\'-\');\n }\n sb.append("***").append(\'-\').append("***-");\n StringBuilder last4 = new StringBuilder();\n int count = 0;\n for(int i = s.length()-1; i >=0; --i){\n if(count == 4){\n break;\n }\n if(Character.isDigit(s.charAt(i))){\n last4.append(s.charAt(i));\n count++;\n }\n }\n sb.append(last4.reverse());\n }\n\n return sb.toString();\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n string maskPII(string s) {\n \n string str;\n int c=0;\n for(auto val:s)\n {\n if(isalpha(val))\n {\n c++;\n }\n }\n if(c==0) //means a phone number\n {\n string str;\n for(int i=0;i<s.size();i++)\n {\n if(isdigit(s[i]))\n {\n str.push_back(s[i]);\n }\n }\n string ans;\n int t=str.size();\n // cout<<str<<" ";\n // cout<<t<<" "<<t-6;\n if(str.size()==10)\n {\n ans="***-***-";\n }\n else if(str.size()==11)\n {\n ans= "+*-***-***-";\n }\n else if(str.size()==12)\n {\n ans="+**-***-***-";\n }\n else\n {\n ans="+***-***-***-";\n }\n \n ans.push_back(str[t-4]);\n ans.push_back(str[t-3]);\n ans.push_back(str[t-2]);\n ans.push_back(str[t-1]);\n return ans;\n }\n else //an email\n {\n int c=0;\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'@\')\n {\n c=i;\n }\n }\n string ans;\n ans.push_back(tolower(s[0]));\n int t=5;\n while(t--)\n {\n ans.push_back(\'*\');\n }\n ans.push_back(tolower(s[c-1]));\n //cout<<c+1<<" ";\n for(int i=c;i<s.size();i++)\n {\n ans.push_back(tolower(s[i]));\n }\n return ans;\n }\n return s;\n }\n};\n```\n```python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n name, rest = s.split(\'@\')\n name = name[0] + \'*****\' + name[-1]\n return name + \'@\' + rest\n else:\n num = \'\'.join([n for n in s if n in \'1234567890\'])\n if len(num) == 10:\n return "***-***-" + num[-4:]\n elif len(num) == 11:\n return "+*-***-***-" + num[-4:]\n elif len(num) == 12:\n return "+**-***-***-" + num[-4:]\n else:\n return "+***-***-***-" + num[-4:]\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
python simple solution beginner friendly 100% | masking-personal-information | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'.\' in s:\n s=s.lower()\n val1=s.index(\'@\')\n val2=s[:val1]\n l1=[\'*\']*7\n l1[0]=(s[0])\n l1[-1]=s[len(val2)-1]\n s1=\'\'.join(l1)\n s1=s1+s[len(val2):]\n print(s1)\n return s1\n else:\n l1=[]\n for i in range(len(s)):\n if s[i].isnumeric():\n l1.append(s[i])\n if len(l1)==10:\n s1=\'***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n elif len(l1)==11:\n s1="+*-***-***-"\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n elif len(l1)==12:\n s1=\'+**-***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n else:\n s1=\'+***-***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n\n\n # print(l1)\n return s1\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
python simple solution beginner friendly 100% | masking-personal-information | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'.\' in s:\n s=s.lower()\n val1=s.index(\'@\')\n val2=s[:val1]\n l1=[\'*\']*7\n l1[0]=(s[0])\n l1[-1]=s[len(val2)-1]\n s1=\'\'.join(l1)\n s1=s1+s[len(val2):]\n print(s1)\n return s1\n else:\n l1=[]\n for i in range(len(s)):\n if s[i].isnumeric():\n l1.append(s[i])\n if len(l1)==10:\n s1=\'***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n elif len(l1)==11:\n s1="+*-***-***-"\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n elif len(l1)==12:\n s1=\'+**-***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n else:\n s1=\'+***-***-***-\'\n k=len(l1)-4\n for i in range(4):\n s1=s1+l1[k]\n k=k+1\n\n\n # print(l1)\n return s1\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
[Python3] Good enough | masking-personal-information | 0 | 1 | ``` Python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n return f\'{s[0]}*****{s[s.index("@")-1:]}\'\n else:\n s = [x for x in s if x.isdigit()]\n return f\'{"+"+("*"*(len(s)-10))+"-" if len(s) > 10 else ""}***-***-{"".join(s[-4:])}\'\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
[Python3] Good enough | masking-personal-information | 0 | 1 | ``` Python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n return f\'{s[0]}*****{s[s.index("@")-1:]}\'\n else:\n s = [x for x in s if x.isdigit()]\n return f\'{"+"+("*"*(len(s)-10))+"-" if len(s) > 10 else ""}***-***-{"".join(s[-4:])}\'\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
[LC-831-M | Python3] A Plain Solution | masking-personal-information | 0 | 1 | Just write the process as requested.\n\n```Python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n ss = s.split(\'@\')\n return ss[0][0] + \'*****\' + ss[0][-1] + \'@\' + ss[1]\n \n k = len([int(x) for x in s if x.isdigit()]) - 10\n res, local_num = \'+\' + \'*\'*k + \'-\' if k > 0 else \'\', \'\' \n idx = -1\n while len(local_num) < 4:\n if (ch := s[idx]).isdigit():\n local_num += ch\n idx -= 1\n res += \'***-***-\' + local_num[::-1]\n\n return res\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
[LC-831-M | Python3] A Plain Solution | masking-personal-information | 0 | 1 | Just write the process as requested.\n\n```Python3 []\nclass Solution:\n def maskPII(self, s: str) -> str:\n if \'@\' in s:\n s = s.lower()\n ss = s.split(\'@\')\n return ss[0][0] + \'*****\' + ss[0][-1] + \'@\' + ss[1]\n \n k = len([int(x) for x in s if x.isdigit()]) - 10\n res, local_num = \'+\' + \'*\'*k + \'-\' if k > 0 else \'\', \'\' \n idx = -1\n while len(local_num) < 4:\n if (ch := s[idx]).isdigit():\n local_num += ch\n idx -= 1\n res += \'***-***-\' + local_num[::-1]\n\n return res\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
pyhon3 easy solution it`s just if and else | masking-personal-information | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n result = \'\'\n if "@" and \'.\' in s:\n char = s.find("@")\n result = s[0].lower() + "*****" + s[char-1].lower() + s[char:].lower()\n result2 = \'\'\n final_result = \'\'\n for i in s:\n if i.isalnum():\n result2+=i\n len_ = len(result2)\n if len_ == 10:\n final_result = "***-***-"+result2[-4:]\n elif len_ == 11:\n final_result = "+*-***-***-"+result2[-4:]\n elif len_ == 12:\n final_result = "+**-***-***-"+result2[-4:]\n elif len_ == 13:\n final_result = "+***-***-***-"+result2[-4:]\n return final_result if "@" not in s else result \n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
pyhon3 easy solution it`s just if and else | masking-personal-information | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n result = \'\'\n if "@" and \'.\' in s:\n char = s.find("@")\n result = s[0].lower() + "*****" + s[char-1].lower() + s[char:].lower()\n result2 = \'\'\n final_result = \'\'\n for i in s:\n if i.isalnum():\n result2+=i\n len_ = len(result2)\n if len_ == 10:\n final_result = "***-***-"+result2[-4:]\n elif len_ == 11:\n final_result = "+*-***-***-"+result2[-4:]\n elif len_ == 12:\n final_result = "+**-***-***-"+result2[-4:]\n elif len_ == 13:\n final_result = "+***-***-***-"+result2[-4:]\n return final_result if "@" not in s else result \n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
</> | masking-personal-information | 0 | 1 | # Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n def email(s):\n UserName, Domine = s.split("@")\n part1, part2 = Domine.split(".")\n ans = UserName[0].lower() + "*" * 5 + UserName[-1].lower()\n ans += "@"\n ans += part1.lower() + "." + part2.lower()\n return ans\n\n def phone_number(s):\n clean_s = ""\n for c in s:\n if c not in {\'+\', \'-\', \'(\', \')\', \' \'}:\n clean_s += c\n\n if len(clean_s) == 10:\n return "***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 11:\n return "+*-***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 12:\n return "+**-***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 13:\n return "+***-***-***-" + clean_s[-4:]\n\n\n if s[0].isalpha():\n return email(s)\n else:\n return phone_number(s)\n\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
</> | masking-personal-information | 0 | 1 | # Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n def email(s):\n UserName, Domine = s.split("@")\n part1, part2 = Domine.split(".")\n ans = UserName[0].lower() + "*" * 5 + UserName[-1].lower()\n ans += "@"\n ans += part1.lower() + "." + part2.lower()\n return ans\n\n def phone_number(s):\n clean_s = ""\n for c in s:\n if c not in {\'+\', \'-\', \'(\', \')\', \' \'}:\n clean_s += c\n\n if len(clean_s) == 10:\n return "***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 11:\n return "+*-***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 12:\n return "+**-***-***-" + clean_s[-4:]\n\n elif len(clean_s) == 13:\n return "+***-***-***-" + clean_s[-4:]\n\n\n if s[0].isalpha():\n return email(s)\n else:\n return phone_number(s)\n\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
Python Solution | masking-personal-information | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n arr = s.split(\'@\')\n if len(arr)==2:\n arr[0] = arr[0].lower()\n arr[1] = arr[1].lower()\n return arr[0][0]+\'*****\'+arr[0][-1] + \'@\' + arr[1]\n ph = []\n for ch in s:\n if ch != \'+\' and ch != \'-\' and ch != \'(\' and ch != \')\' and ch != \' \':\n ph.append(ch)\n if len(ph) == 10:\n return \'***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 11:\n return \'+*-***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 12:\n return \'+**-***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 13:\n return \'+***-***-***-\'+\'\'.join(ph[-4:])\n return \'\'\n``` | 0 | You are given a personal information string `s`, representing either an **email address** or a **phone number**. Return _the **masked** personal information using the below rules_.
**Email address:**
An email address is:
* A **name** consisting of uppercase and lowercase English letters, followed by
* The `'@'` symbol, followed by
* The **domain** consisting of uppercase and lowercase English letters with a dot `'.'` somewhere in the middle (not the first or last character).
To mask an email:
* The uppercase letters in the **name** and **domain** must be converted to lowercase letters.
* The middle letters of the **name** (i.e., all but the first and last letters) must be replaced by 5 asterisks `"***** "`.
**Phone number:**
A phone number is formatted as follows:
* The phone number contains 10-13 digits.
* The last 10 digits make up the **local number**.
* The remaining 0-3 digits, in the beginning, make up the **country code**.
* **Separation characters** from the set `{'+', '-', '(', ')', ' '}` separate the above digits in some way.
To mask a phone number:
* Remove all **separation characters**.
* The masked phone number should have the form:
* `"***-***-XXXX "` if the country code has 0 digits.
* `"+*-***-***-XXXX "` if the country code has 1 digit.
* `"+**-***-***-XXXX "` if the country code has 2 digits.
* `"+***-***-***-XXXX "` if the country code has 3 digits.
* `"XXXX "` is the last 4 digits of the **local number**.
**Example 1:**
**Input:** s = "[email protected] "
**Output:** "l\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
**Example 2:**
**Input:** s = "[email protected] "
**Output:** "a\*\*\*\*\*[email protected] "
**Explanation:** s is an email address.
The name and domain are converted to lowercase, and the middle of the name is replaced by 5 asterisks.
Note that even though "ab " is 2 characters, it still must have 5 asterisks in the middle.
**Example 3:**
**Input:** s = "1(234)567-890 "
**Output:** "\*\*\*-\*\*\*-7890 "
**Explanation:** s is a phone number.
There are 10 digits, so the local number is 10 digits and the country code is 0 digits.
Thus, the resulting masked number is "\*\*\*-\*\*\*-7890 ".
**Constraints:**
* `s` is either a **valid** email or a phone number.
* If `s` is an email:
* `8 <= s.length <= 40`
* `s` consists of uppercase and lowercase English letters and exactly one `'@'` symbol and `'.'` symbol.
* If `s` is a phone number:
* `10 <= s.length <= 20`
* `s` consists of digits, spaces, and the symbols `'('`, `')'`, `'-'`, and `'+'`. | null |
Python Solution | masking-personal-information | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maskPII(self, s: str) -> str:\n arr = s.split(\'@\')\n if len(arr)==2:\n arr[0] = arr[0].lower()\n arr[1] = arr[1].lower()\n return arr[0][0]+\'*****\'+arr[0][-1] + \'@\' + arr[1]\n ph = []\n for ch in s:\n if ch != \'+\' and ch != \'-\' and ch != \'(\' and ch != \')\' and ch != \' \':\n ph.append(ch)\n if len(ph) == 10:\n return \'***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 11:\n return \'+*-***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 12:\n return \'+**-***-***-\'+\'\'.join(ph[-4:])\n if len(ph) == 13:\n return \'+***-***-***-\'+\'\'.join(ph[-4:])\n return \'\'\n``` | 0 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
[Python] SIMPLE Forward O(N) Solution (32ms / 97%) | find-and-replace-in-string | 0 | 1 | First, create a dictionary that maps the index in `indexes` to its pair of strings in `sources` and `targets`.\n\nIterate through `S`, looking up the current index `i` to see if we can perform a replacement. Take a slice of `S` at our current index to see if it `.startswith()` the source string. If so, we perform a "replacement" by adding the target string to our `result` and incrementing `i` by the length of the source string.\n\nIf `i` isn\'t in `indexes` then just add a single character to `result` and move on.\n\n```\ndef findReplaceString(self, S: str, indexes: List[int], sources: List[str], targets: List[str]) -> str:\n\tlookup = {i: (src, tgt) for i, src, tgt in zip(indexes, sources, targets)}\n\ti, result = 0, ""\n\twhile i < len(S):\n\t\tif i in lookup and S[i:].startswith(lookup[i][0]):\n\t\t\tresult += lookup[i][1]\n\t\t\ti += len(lookup[i][0])\n\t\telse:\n\t\t\tresult += S[i]\n\t\t\ti += 1\n\treturn result\n```\n\n### Time Complexity\n* Let `N = len(S)` and `M = len(indexes)`\n* Building `lookup` ---> `O(M)`\n* Building `result` ---> `O(N)`\n\n### Space Complexity\n* Building `lookup` ---> `O(M)`\n* Building `result` ---> `O(N)` | 60 | You are given a **0-indexed** string `s` that you must perform `k` replacement operations on. The replacement operations are given as three **0-indexed** parallel arrays, `indices`, `sources`, and `targets`, all of length `k`.
To complete the `ith` replacement operation:
1. Check if the **substring** `sources[i]` occurs at index `indices[i]` in the **original string** `s`.
2. If it does not occur, **do nothing**.
3. Otherwise if it does occur, **replace** that substring with `targets[i]`.
For example, if `s = "abcd "`, `indices[i] = 0`, `sources[i] = "ab "`, and `targets[i] = "eee "`, then the result of this replacement will be `"eeecd "`.
All replacement operations must occur **simultaneously**, meaning the replacement operations should not affect the indexing of each other. The testcases will be generated such that the replacements will **not overlap**.
* For example, a testcase with `s = "abc "`, `indices = [0, 1]`, and `sources = [ "ab ", "bc "]` will not be generated because the `"ab "` and `"bc "` replacements overlap.
Return _the **resulting string** after performing all replacement operations on_ `s`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "a ", "cd "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeebffff "
**Explanation:**
"a " occurs at index 0 in s, so we replace it with "eee ".
"cd " occurs at index 2 in s, so we replace it with "ffff ".
**Example 2:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "ab ", "ec "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeecd "
**Explanation:**
"ab " occurs at index 0 in s, so we replace it with "eee ".
"ec " does not occur at index 2 in s, so we do nothing.
**Constraints:**
* `1 <= s.length <= 1000`
* `k == indices.length == sources.length == targets.length`
* `1 <= k <= 100`
* `0 <= indexes[i] < s.length`
* `1 <= sources[i].length, targets[i].length <= 50`
* `s` consists of only lowercase English letters.
* `sources[i]` and `targets[i]` consist of only lowercase English letters. | null |
[Python] SIMPLE Forward O(N) Solution (32ms / 97%) | find-and-replace-in-string | 0 | 1 | First, create a dictionary that maps the index in `indexes` to its pair of strings in `sources` and `targets`.\n\nIterate through `S`, looking up the current index `i` to see if we can perform a replacement. Take a slice of `S` at our current index to see if it `.startswith()` the source string. If so, we perform a "replacement" by adding the target string to our `result` and incrementing `i` by the length of the source string.\n\nIf `i` isn\'t in `indexes` then just add a single character to `result` and move on.\n\n```\ndef findReplaceString(self, S: str, indexes: List[int], sources: List[str], targets: List[str]) -> str:\n\tlookup = {i: (src, tgt) for i, src, tgt in zip(indexes, sources, targets)}\n\ti, result = 0, ""\n\twhile i < len(S):\n\t\tif i in lookup and S[i:].startswith(lookup[i][0]):\n\t\t\tresult += lookup[i][1]\n\t\t\ti += len(lookup[i][0])\n\t\telse:\n\t\t\tresult += S[i]\n\t\t\ti += 1\n\treturn result\n```\n\n### Time Complexity\n* Let `N = len(S)` and `M = len(indexes)`\n* Building `lookup` ---> `O(M)`\n* Building `result` ---> `O(N)`\n\n### Space Complexity\n* Building `lookup` ---> `O(M)`\n* Building `result` ---> `O(N)` | 60 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Solution | find-and-replace-in-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string findReplaceString(string s, vector<int>& indices, vector<string>& sources, vector<string>& targets) {\n int num_queries = indices.size();\n map<pair<int,int>, int> interval_set;\n for(int i = 0; i < num_queries; i++){\n\n int current_idx = indices[i];\n while(current_idx-indices[i] < sources[i].size() && current_idx < s.size() && s[current_idx] == sources[i][current_idx-indices[i]])\n current_idx++;\n\n if(current_idx-indices[i] == sources[i].size())\n interval_set[make_pair(indices[i],current_idx-1)] = i; \n }\n string res = "";\n int idx = 0;\n\n for(auto& elm : interval_set){\n while(idx < elm.first.first){\n res += s[idx];\n idx++;\n }\n res += targets[elm.second];\n idx = elm.first.second+1;\n }\n while(idx < s.size()){\n res += s[idx];\n idx++;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findReplaceString(self, s: str, indices: List[int], sources: List[str], targets: List[str]) -> str:\n ans=[]\n dic={}\n for i in range(len(indices)):\n ind=indices[i]\n dic[ind]=[sources[i],targets[i]]\n i=0\n while i<len(s):\n if i not in dic:\n ans.append(s[i])\n i+=1\n elif i in dic:\n j=i\n boo=True\n for el in dic[i][0]:\n if s[j]==el:\n j+=1\n else:\n boo=False\n break\n if boo:\n ans.append(dic[i][1])\n i=j\n else:\n ans.append(s[i])\n i+=1\n while i!=len(s):\n ans.append(s[i])\n i+=1\n return \'\'.join(ans)\n```\n\n```Java []\nclass Solution { \n public String findReplaceString(String S, int[] indexes, String[] sources, \nString[] targets) { \n Map<Integer, Integer> table = new HashMap<>(); \n for (int i=0; i<indexes.length; i++) { \n if (S.startsWith(sources[i], indexes[i])) { \n table.put(indexes[i], i); \n } \n } \n StringBuilder sb = new StringBuilder(); \n for (int i=0; i<S.length(); ) { \n if (table.containsKey(i)) { \n sb.append(targets[table.get(i)]); \n i+=sources[table.get(i)].length(); \n } else { \n sb.append(S.charAt(i)); \n i++; \n } \n } \n return sb.toString(); \n } \n}\n```\n | 2 | You are given a **0-indexed** string `s` that you must perform `k` replacement operations on. The replacement operations are given as three **0-indexed** parallel arrays, `indices`, `sources`, and `targets`, all of length `k`.
To complete the `ith` replacement operation:
1. Check if the **substring** `sources[i]` occurs at index `indices[i]` in the **original string** `s`.
2. If it does not occur, **do nothing**.
3. Otherwise if it does occur, **replace** that substring with `targets[i]`.
For example, if `s = "abcd "`, `indices[i] = 0`, `sources[i] = "ab "`, and `targets[i] = "eee "`, then the result of this replacement will be `"eeecd "`.
All replacement operations must occur **simultaneously**, meaning the replacement operations should not affect the indexing of each other. The testcases will be generated such that the replacements will **not overlap**.
* For example, a testcase with `s = "abc "`, `indices = [0, 1]`, and `sources = [ "ab ", "bc "]` will not be generated because the `"ab "` and `"bc "` replacements overlap.
Return _the **resulting string** after performing all replacement operations on_ `s`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "a ", "cd "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeebffff "
**Explanation:**
"a " occurs at index 0 in s, so we replace it with "eee ".
"cd " occurs at index 2 in s, so we replace it with "ffff ".
**Example 2:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "ab ", "ec "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeecd "
**Explanation:**
"ab " occurs at index 0 in s, so we replace it with "eee ".
"ec " does not occur at index 2 in s, so we do nothing.
**Constraints:**
* `1 <= s.length <= 1000`
* `k == indices.length == sources.length == targets.length`
* `1 <= k <= 100`
* `0 <= indexes[i] < s.length`
* `1 <= sources[i].length, targets[i].length <= 50`
* `s` consists of only lowercase English letters.
* `sources[i]` and `targets[i]` consist of only lowercase English letters. | null |
Solution | find-and-replace-in-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string findReplaceString(string s, vector<int>& indices, vector<string>& sources, vector<string>& targets) {\n int num_queries = indices.size();\n map<pair<int,int>, int> interval_set;\n for(int i = 0; i < num_queries; i++){\n\n int current_idx = indices[i];\n while(current_idx-indices[i] < sources[i].size() && current_idx < s.size() && s[current_idx] == sources[i][current_idx-indices[i]])\n current_idx++;\n\n if(current_idx-indices[i] == sources[i].size())\n interval_set[make_pair(indices[i],current_idx-1)] = i; \n }\n string res = "";\n int idx = 0;\n\n for(auto& elm : interval_set){\n while(idx < elm.first.first){\n res += s[idx];\n idx++;\n }\n res += targets[elm.second];\n idx = elm.first.second+1;\n }\n while(idx < s.size()){\n res += s[idx];\n idx++;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findReplaceString(self, s: str, indices: List[int], sources: List[str], targets: List[str]) -> str:\n ans=[]\n dic={}\n for i in range(len(indices)):\n ind=indices[i]\n dic[ind]=[sources[i],targets[i]]\n i=0\n while i<len(s):\n if i not in dic:\n ans.append(s[i])\n i+=1\n elif i in dic:\n j=i\n boo=True\n for el in dic[i][0]:\n if s[j]==el:\n j+=1\n else:\n boo=False\n break\n if boo:\n ans.append(dic[i][1])\n i=j\n else:\n ans.append(s[i])\n i+=1\n while i!=len(s):\n ans.append(s[i])\n i+=1\n return \'\'.join(ans)\n```\n\n```Java []\nclass Solution { \n public String findReplaceString(String S, int[] indexes, String[] sources, \nString[] targets) { \n Map<Integer, Integer> table = new HashMap<>(); \n for (int i=0; i<indexes.length; i++) { \n if (S.startsWith(sources[i], indexes[i])) { \n table.put(indexes[i], i); \n } \n } \n StringBuilder sb = new StringBuilder(); \n for (int i=0; i<S.length(); ) { \n if (table.containsKey(i)) { \n sb.append(targets[table.get(i)]); \n i+=sources[table.get(i)].length(); \n } else { \n sb.append(S.charAt(i)); \n i++; \n } \n } \n return sb.toString(); \n } \n}\n```\n | 2 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Python 3 | simple | 3 lines of code w/ explanation | find-and-replace-in-string | 0 | 1 | ```\nclass Solution:\n def findReplaceString(self, s: str, indices: List[int], sources: List[str], targets: List[str]) -> str:\n # iterate from the greater index to the smallest\n for i, src, tg in sorted(list(zip(indices, sources, targets)), reverse=True): \n # if found the pattern matches with the source, replace with the target accordingly\n if s[i:i+len(src)] == src: s = s[:i] + tg + s[i+len(src):] \n return s\n``` | 3 | You are given a **0-indexed** string `s` that you must perform `k` replacement operations on. The replacement operations are given as three **0-indexed** parallel arrays, `indices`, `sources`, and `targets`, all of length `k`.
To complete the `ith` replacement operation:
1. Check if the **substring** `sources[i]` occurs at index `indices[i]` in the **original string** `s`.
2. If it does not occur, **do nothing**.
3. Otherwise if it does occur, **replace** that substring with `targets[i]`.
For example, if `s = "abcd "`, `indices[i] = 0`, `sources[i] = "ab "`, and `targets[i] = "eee "`, then the result of this replacement will be `"eeecd "`.
All replacement operations must occur **simultaneously**, meaning the replacement operations should not affect the indexing of each other. The testcases will be generated such that the replacements will **not overlap**.
* For example, a testcase with `s = "abc "`, `indices = [0, 1]`, and `sources = [ "ab ", "bc "]` will not be generated because the `"ab "` and `"bc "` replacements overlap.
Return _the **resulting string** after performing all replacement operations on_ `s`.
A **substring** is a contiguous sequence of characters in a string.
**Example 1:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "a ", "cd "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeebffff "
**Explanation:**
"a " occurs at index 0 in s, so we replace it with "eee ".
"cd " occurs at index 2 in s, so we replace it with "ffff ".
**Example 2:**
**Input:** s = "abcd ", indices = \[0, 2\], sources = \[ "ab ", "ec "\], targets = \[ "eee ", "ffff "\]
**Output:** "eeecd "
**Explanation:**
"ab " occurs at index 0 in s, so we replace it with "eee ".
"ec " does not occur at index 2 in s, so we do nothing.
**Constraints:**
* `1 <= s.length <= 1000`
* `k == indices.length == sources.length == targets.length`
* `1 <= k <= 100`
* `0 <= indexes[i] < s.length`
* `1 <= sources[i].length, targets[i].length <= 50`
* `s` consists of only lowercase English letters.
* `sources[i]` and `targets[i]` consist of only lowercase English letters. | null |
Python 3 | simple | 3 lines of code w/ explanation | find-and-replace-in-string | 0 | 1 | ```\nclass Solution:\n def findReplaceString(self, s: str, indices: List[int], sources: List[str], targets: List[str]) -> str:\n # iterate from the greater index to the smallest\n for i, src, tg in sorted(list(zip(indices, sources, targets)), reverse=True): \n # if found the pattern matches with the source, replace with the target accordingly\n if s[i:i+len(src)] == src: s = s[:i] + tg + s[i+len(src):] \n return s\n``` | 3 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Two DFS | O(N) | Python Solution | Explained | sum-of-distances-in-tree | 0 | 1 | Hello **Tenno Leetcoders**,\n\nFor this problem we have a `bidirectional graph`, and we want to return the sum of the distances from the root node and all other nodes. \n\nOne simple way to do this is to build a graph with each given edges and choosing `0 to n-1` as the `root` and for each root, we will perform `DFS` to get the `total sum of distances` for that `root`. Doing it this way, our `Time Complexity` will be `O(N^2)` and this will give us a `TLE`.\n\n\nTurns out we can improve the performance by making our current parent root as a child. Once we do that, we will have some nodes closer to the parent node and some will become further away from the parent. \n\nOnce we have this concept down, we can actually create a formula out of this to help us. \n\nIn order to create a formula, we will need:\n\n #### 1) Current parent root\'s sum of distance \n \n #### 2) Sum of distance between the closer / further nodes of current root\n \nTo calculate the `further nodes` of child, we use `(N-1)`\n \nUsing this information, we can create a `formula` : `parent root sum - closer nodes + further nodes`\n\n#### However, the base of this formula changes with different root nodes\n\n\n\n\n\n\nWe can apply this math logic to help us implement `Two DFS`:\n\n 1) First DFS to calculate the S.O.D of our root node, which is node 0 for this problem and to pre-calculate sub nodes\n \n### Time Complexity: O(n)\n \n 2) Second DFS is to calculate S.O.D for each node\n \n### Time Complexity: O(n)\n\n### Space Complexity: O(n) \n\n# Code \n```\ndef sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]: \n # Our varaibles to store closer nodes and result\n result = [0] * n\n closer_nodes_count = [0] * n\n # keep track of our visited node\n seen = set()\n \n # Building our graph\n graph = [[] for _ in range(n)] \n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n # DFS to calculate closer nodes count and our parent nodes S.O.D\n def dfs(curr):\n closer_nodes = 1\n for child in graph[curr]:\n if child not in seen:\n seen.add(child)\n child_nodes_count = dfs(child)\n closer_nodes += child_nodes_count\n \n # To first get the S.O.D of our root node, which is node 0 for this problem\n result[0] += child_nodes_count\n \n closer_nodes_count[curr] = closer_nodes\n \n return closer_nodes\n \n def dfs2(curr):\n for child in graph[curr]:\n if child not in seen:\n seen.add(child) \n # Formula: parent_root_sum - closer_nodes + further_nodes\n result[child] = result[curr] - closer_nodes_count[child] + (n - closer_nodes_count[child]) \n # current child node becomes a parent node\n dfs2(child)\n \n \n seen.add(0)\n dfs(0)\n \n # reset seen for our dfs2 \n seen = set() \n seen.add(0)\n \n # Using result[0] (node 0) as base to populate all the other nodes\n dfs2(0)\n```\n\n | 2 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Two DFS | O(N) | Python Solution | Explained | sum-of-distances-in-tree | 0 | 1 | Hello **Tenno Leetcoders**,\n\nFor this problem we have a `bidirectional graph`, and we want to return the sum of the distances from the root node and all other nodes. \n\nOne simple way to do this is to build a graph with each given edges and choosing `0 to n-1` as the `root` and for each root, we will perform `DFS` to get the `total sum of distances` for that `root`. Doing it this way, our `Time Complexity` will be `O(N^2)` and this will give us a `TLE`.\n\n\nTurns out we can improve the performance by making our current parent root as a child. Once we do that, we will have some nodes closer to the parent node and some will become further away from the parent. \n\nOnce we have this concept down, we can actually create a formula out of this to help us. \n\nIn order to create a formula, we will need:\n\n #### 1) Current parent root\'s sum of distance \n \n #### 2) Sum of distance between the closer / further nodes of current root\n \nTo calculate the `further nodes` of child, we use `(N-1)`\n \nUsing this information, we can create a `formula` : `parent root sum - closer nodes + further nodes`\n\n#### However, the base of this formula changes with different root nodes\n\n\n\n\n\n\nWe can apply this math logic to help us implement `Two DFS`:\n\n 1) First DFS to calculate the S.O.D of our root node, which is node 0 for this problem and to pre-calculate sub nodes\n \n### Time Complexity: O(n)\n \n 2) Second DFS is to calculate S.O.D for each node\n \n### Time Complexity: O(n)\n\n### Space Complexity: O(n) \n\n# Code \n```\ndef sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]: \n # Our varaibles to store closer nodes and result\n result = [0] * n\n closer_nodes_count = [0] * n\n # keep track of our visited node\n seen = set()\n \n # Building our graph\n graph = [[] for _ in range(n)] \n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n \n # DFS to calculate closer nodes count and our parent nodes S.O.D\n def dfs(curr):\n closer_nodes = 1\n for child in graph[curr]:\n if child not in seen:\n seen.add(child)\n child_nodes_count = dfs(child)\n closer_nodes += child_nodes_count\n \n # To first get the S.O.D of our root node, which is node 0 for this problem\n result[0] += child_nodes_count\n \n closer_nodes_count[curr] = closer_nodes\n \n return closer_nodes\n \n def dfs2(curr):\n for child in graph[curr]:\n if child not in seen:\n seen.add(child) \n # Formula: parent_root_sum - closer_nodes + further_nodes\n result[child] = result[curr] - closer_nodes_count[child] + (n - closer_nodes_count[child]) \n # current child node becomes a parent node\n dfs2(child)\n \n \n seen.add(0)\n dfs(0)\n \n # reset seen for our dfs2 \n seen = set() \n seen.add(0)\n \n # Using result[0] (node 0) as base to populate all the other nodes\n dfs2(0)\n```\n\n | 2 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Solution | sum-of-distances-in-tree | 1 | 1 | ```C++ []\nclass Solution {\n int head[30010], end[60010], next[60010], idx;\n int siz[30010], n;\n vector<int> ans;\n void add (int a, int b) {\n end[idx] = b, next[idx] = head[a], head[a] = idx++;\n }\npublic:\n vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {\n memset(head, -1, 4 * n + 4);\n for (auto &edge : edges) {\n int a = edge[0], b = edge[1];\n add(a, b), add(b, a);\n }\n this -> n = n;\n this -> ans = vector<int> (n);\n dfs(0, -1, 0);\n dfs(0, -1);\n return ans;\n }\n void dfs(int u, int pre, int level) {\n ans[0] += level;\n siz[u] = 1;\n for (int e = head[u]; ~e; e = next[e]) {\n int v = end[e];\n if ((e ^ 1) != pre) {\n dfs(v, e, level + 1);\n siz[u] += siz[v];\n }\n }\n }\n void dfs(int u, int pre) {\n for (int e = head[u]; ~e; e = next[e]) {\n if ((e ^ 1) == pre) continue;\n int v = end[e];\n ans[v] = ans[u] + n - 2 * siz[v];\n dfs(v, e);\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n \n adj = [[] for _ in range(n)]\n for u, v in edges:\n adj[u].append(v)\n adj[v].append(u)\n \n child = [0] * n\n def dfs1(u, p):\n c, d = 1, 0\n for v in adj[u]:\n if v != p:\n x = dfs1(v, u)\n c += x[0]\n d += x[1]\n child[u] = c\n return c, d + c\n \n s = [0] * n\n s[0] = dfs1(0, -1)[1] - child[0]\n\n def dfs2(u, p):\n s[u] = s[p] - child[u] + (n - child[u])\n for v in adj[u]:\n if v != p:\n dfs2(v, u)\n \n for v in adj[0]:\n dfs2(v, 0)\n\n return s\n```\n\n```Java []\nclass Solution {\n int[][] graph;\n int[] count;\n int[] res;\n int N;\n \n public int[] sumOfDistancesInTree(int N, int[][] edges) {\n this.N = N;\n this.res = new int[N];\n this.graph = new int[N][];\n this.count = new int[N];\n \n for (int[] e : edges) {\n ++count[e[0]];\n ++count[e[1]];\n }\n for (int i = 0; i < N; i++) {\n graph[i] = new int[count[i]];\n }\n for (int[] e : edges) {\n graph[e[0]][--count[e[0]]] = e[1];\n graph[e[1]][--count[e[1]]] = e[0];\n }\n dfs1(0, -1);\n dfs2(0, -1);\n return res;\n }\n public void dfs1(int cur, int parent) {\n count[cur] = 1;\n for (int child : graph[cur]) {\n if (child != parent) {\n dfs1(child, cur);\n count[cur] += count[child];\n res[cur] += res[child] + count[child];\n }\n }\n }\n public void dfs2(int cur, int parent) {\n for (int child : graph[cur]) {\n if (child != parent) {\n res[child] = res[cur] + N - 2 * count[child];\n dfs2(child, cur);\n }\n }\n }\n}\n```\n | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Solution | sum-of-distances-in-tree | 1 | 1 | ```C++ []\nclass Solution {\n int head[30010], end[60010], next[60010], idx;\n int siz[30010], n;\n vector<int> ans;\n void add (int a, int b) {\n end[idx] = b, next[idx] = head[a], head[a] = idx++;\n }\npublic:\n vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {\n memset(head, -1, 4 * n + 4);\n for (auto &edge : edges) {\n int a = edge[0], b = edge[1];\n add(a, b), add(b, a);\n }\n this -> n = n;\n this -> ans = vector<int> (n);\n dfs(0, -1, 0);\n dfs(0, -1);\n return ans;\n }\n void dfs(int u, int pre, int level) {\n ans[0] += level;\n siz[u] = 1;\n for (int e = head[u]; ~e; e = next[e]) {\n int v = end[e];\n if ((e ^ 1) != pre) {\n dfs(v, e, level + 1);\n siz[u] += siz[v];\n }\n }\n }\n void dfs(int u, int pre) {\n for (int e = head[u]; ~e; e = next[e]) {\n if ((e ^ 1) == pre) continue;\n int v = end[e];\n ans[v] = ans[u] + n - 2 * siz[v];\n dfs(v, e);\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n \n adj = [[] for _ in range(n)]\n for u, v in edges:\n adj[u].append(v)\n adj[v].append(u)\n \n child = [0] * n\n def dfs1(u, p):\n c, d = 1, 0\n for v in adj[u]:\n if v != p:\n x = dfs1(v, u)\n c += x[0]\n d += x[1]\n child[u] = c\n return c, d + c\n \n s = [0] * n\n s[0] = dfs1(0, -1)[1] - child[0]\n\n def dfs2(u, p):\n s[u] = s[p] - child[u] + (n - child[u])\n for v in adj[u]:\n if v != p:\n dfs2(v, u)\n \n for v in adj[0]:\n dfs2(v, 0)\n\n return s\n```\n\n```Java []\nclass Solution {\n int[][] graph;\n int[] count;\n int[] res;\n int N;\n \n public int[] sumOfDistancesInTree(int N, int[][] edges) {\n this.N = N;\n this.res = new int[N];\n this.graph = new int[N][];\n this.count = new int[N];\n \n for (int[] e : edges) {\n ++count[e[0]];\n ++count[e[1]];\n }\n for (int i = 0; i < N; i++) {\n graph[i] = new int[count[i]];\n }\n for (int[] e : edges) {\n graph[e[0]][--count[e[0]]] = e[1];\n graph[e[1]][--count[e[1]]] = e[0];\n }\n dfs1(0, -1);\n dfs2(0, -1);\n return res;\n }\n public void dfs1(int cur, int parent) {\n count[cur] = 1;\n for (int child : graph[cur]) {\n if (child != parent) {\n dfs1(child, cur);\n count[cur] += count[child];\n res[cur] += res[child] + count[child];\n }\n }\n }\n public void dfs2(int cur, int parent) {\n for (int child : graph[cur]) {\n if (child != parent) {\n res[child] = res[cur] + N - 2 * count[child];\n dfs2(child, cur);\n }\n }\n }\n}\n```\n | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
One DFS O(N) | sum-of-distances-in-tree | 0 | 1 | # Intuition\nSuppose we have a tree A---B---C---D.\n\nTo calculate the sum of all paths for B we need to know the total sum of all paths and the number of paths for A and C but without, edges that connect them to B, we can just start a DFS from B.\nTo reduce the complexity we can use memorization.\n\ndfs(node, parent) -> (total sum of passes, total amount of paths)\n(node, parent) pair maps a node and parent to the sum of paths and count of paths from the node but without edge to the parent.\n\nIf we have all such states (neibor_node, parent=node) of the neighbors for a node it is simple to calculate (node, -1). -1 denotes the absence of a parent.\n\nEach edge connects 2 nodes, and each of them can be a parent to the other node, so in total, we need to compute (n-1)*2 such states and n states like (node, -1) for answers.\n(n-1)*3 states in total.\n\nFor each state, we need to perform the amount of work proportional to the number of edges connected to this node(if we know other states), but we have n-1 edges in total for all nodes, and each edge has two nodes connected, so the total amount of work for the whole tree is (n-1)*2 in total.\n\n# Complexity\n- Time complexity: O(n)\nAs such as we calculate the value of a state only once and memorize it, the complexities upper bound is O(n-1) = O(n).\n\n- Space complexity: O(n)\nThere are (n-1)*2 states.\nWe can do it with the help of recursion and memorise all states to use them again later.\n\n# Code\n```\nfrom functools import lru_cache\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n connections = defaultdict(list)\n for a, b in edges:\n connections[a].append(b)\n connections[b].append(a)\n\n @lru_cache(None)\n def dfs(node, parent_node = -1):\n pathes_total_length = 0\n pathes_count = 0\n for neibor_node in connections[node]:\n if neibor_node != parent_node:\n nlength, ncount = dfs(neibor_node, parent_node =node)\n pathes_total_length += nlength + ncount\n pathes_count += ncount\n return pathes_total_length, pathes_count+1\n\n return [dfs(i)[0] for i in range(n)]\n \n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
One DFS O(N) | sum-of-distances-in-tree | 0 | 1 | # Intuition\nSuppose we have a tree A---B---C---D.\n\nTo calculate the sum of all paths for B we need to know the total sum of all paths and the number of paths for A and C but without, edges that connect them to B, we can just start a DFS from B.\nTo reduce the complexity we can use memorization.\n\ndfs(node, parent) -> (total sum of passes, total amount of paths)\n(node, parent) pair maps a node and parent to the sum of paths and count of paths from the node but without edge to the parent.\n\nIf we have all such states (neibor_node, parent=node) of the neighbors for a node it is simple to calculate (node, -1). -1 denotes the absence of a parent.\n\nEach edge connects 2 nodes, and each of them can be a parent to the other node, so in total, we need to compute (n-1)*2 such states and n states like (node, -1) for answers.\n(n-1)*3 states in total.\n\nFor each state, we need to perform the amount of work proportional to the number of edges connected to this node(if we know other states), but we have n-1 edges in total for all nodes, and each edge has two nodes connected, so the total amount of work for the whole tree is (n-1)*2 in total.\n\n# Complexity\n- Time complexity: O(n)\nAs such as we calculate the value of a state only once and memorize it, the complexities upper bound is O(n-1) = O(n).\n\n- Space complexity: O(n)\nThere are (n-1)*2 states.\nWe can do it with the help of recursion and memorise all states to use them again later.\n\n# Code\n```\nfrom functools import lru_cache\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n connections = defaultdict(list)\n for a, b in edges:\n connections[a].append(b)\n connections[b].append(a)\n\n @lru_cache(None)\n def dfs(node, parent_node = -1):\n pathes_total_length = 0\n pathes_count = 0\n for neibor_node in connections[node]:\n if neibor_node != parent_node:\n nlength, ncount = dfs(neibor_node, parent_node =node)\n pathes_total_length += nlength + ncount\n pathes_count += ncount\n return pathes_total_length, pathes_count+1\n\n return [dfs(i)[0] for i in range(n)]\n \n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Updated: faster and less memory than 100% | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy initial approach was based on recursion. It was wrong, since it exceeded the time limit (it took $O(n^2)$ time).\nIt turns out that the problem can be solved in linear time, traversing the tree exactly 3 times.\n\nEdit: After optimizing the solution, now it is faster and takes less memory than 100%. The optimization consists in using neighbor lists instead of sets. Clearly, lists are faster.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDuring the depth-first traversal of the graph, for each vertex we compute its distance to the starting vertex (its level), then we sum these distances. This gives the answer for the starting vertex.\nOne could do the same for each vertex, but it would take too long ($O(n^2)$). However, it turns out that we only need to do this computation exactly once.\nSuppose we know the total distance (the answer) for a parent vertex. For each child, the total distance changes as follows: for all its descendants including itself, the distance decreases by 1, while for all other vertices in the graph the distance increases by 1. Hence the total distance changes, between parent to child, by\n$$\n-desc+(n-desc)=n-2desc,\n$$\nwhere desc is the child\'s number of descendants.\nWe then compute the total distance for each parent before each child, then add $n-2desc$ each time when going from parent to child. Since we already traversed the graph, this computation can be done in one pass, in the same order.\nFinally, the number of descendants of each vertex $desc$ can also be computed in one pass, recursively going from bottom to top. We can traverse the graph using the reverse of the previous order.\nThus, we only need 3 passes to get the answer.\n\n\n# Complexity\n- Time complexity: $O(n)$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n ans=[0]*n\n g=[[] for _ in range(n)]\n for e in edges:\n g[e[0]].append(e[1])\n g[e[1]].append(e[0])\n q=[(0, 0)]\n parent=[None]*n\n s=0\n for v2 in g[0]:\n q.append((v2, 1))\n parent[v2]=0\n for curs in range(1, n):\n v, lev=q[curs]\n s+=lev\n lev+=1\n g[v].remove(parent[v])\n for v2 in g[v]:\n q.append((v2, lev))\n parent[v2]=v\n lst=[it[0] for it in q]\n chil_ct=[-2]*n\n for v in lst[n-1:0:-1]:\n chil_ct[parent[v]]+=chil_ct[v]\n ans[0]=s\n for v in lst:\n tmp=ans[v]+n\n par=parent[v]\n for v2 in g[v]:\n ans[v2]=tmp+chil_ct[v2]\n return ans\n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Updated: faster and less memory than 100% | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy initial approach was based on recursion. It was wrong, since it exceeded the time limit (it took $O(n^2)$ time).\nIt turns out that the problem can be solved in linear time, traversing the tree exactly 3 times.\n\nEdit: After optimizing the solution, now it is faster and takes less memory than 100%. The optimization consists in using neighbor lists instead of sets. Clearly, lists are faster.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDuring the depth-first traversal of the graph, for each vertex we compute its distance to the starting vertex (its level), then we sum these distances. This gives the answer for the starting vertex.\nOne could do the same for each vertex, but it would take too long ($O(n^2)$). However, it turns out that we only need to do this computation exactly once.\nSuppose we know the total distance (the answer) for a parent vertex. For each child, the total distance changes as follows: for all its descendants including itself, the distance decreases by 1, while for all other vertices in the graph the distance increases by 1. Hence the total distance changes, between parent to child, by\n$$\n-desc+(n-desc)=n-2desc,\n$$\nwhere desc is the child\'s number of descendants.\nWe then compute the total distance for each parent before each child, then add $n-2desc$ each time when going from parent to child. Since we already traversed the graph, this computation can be done in one pass, in the same order.\nFinally, the number of descendants of each vertex $desc$ can also be computed in one pass, recursively going from bottom to top. We can traverse the graph using the reverse of the previous order.\nThus, we only need 3 passes to get the answer.\n\n\n# Complexity\n- Time complexity: $O(n)$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n ans=[0]*n\n g=[[] for _ in range(n)]\n for e in edges:\n g[e[0]].append(e[1])\n g[e[1]].append(e[0])\n q=[(0, 0)]\n parent=[None]*n\n s=0\n for v2 in g[0]:\n q.append((v2, 1))\n parent[v2]=0\n for curs in range(1, n):\n v, lev=q[curs]\n s+=lev\n lev+=1\n g[v].remove(parent[v])\n for v2 in g[v]:\n q.append((v2, lev))\n parent[v2]=v\n lst=[it[0] for it in q]\n chil_ct=[-2]*n\n for v in lst[n-1:0:-1]:\n chil_ct[parent[v]]+=chil_ct[v]\n ans[0]=s\n for v in lst:\n tmp=ans[v]+n\n par=parent[v]\n for v2 in g[v]:\n ans[v2]=tmp+chil_ct[v2]\n return ans\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python 3 || Beats 82.22% Memory 67.3 MB | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncount -> count list takes parent i\'th number of child\nans -> ans of ith positions\ndo comment out print(count) and print(ans) in order to Understand.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n tree = collections.defaultdict(set)\n count = [1]*n\n ans = [0]*n\n\n for x, y in edges:\n tree[x].add(y)\n tree[y].add(x)\n\n def dfs(node, parent, flag=True):\n for child in tree[node]:\n if flag and child != parent:\n dfs(child, node)\n count[node] += count[child]\n ans[node] += ans[child] + count[child]\n \n if not flag and child != parent:\n ans[child] = ans[node] - count[child] + n - count[child]\n dfs(child, node, False)\n \n dfs(0, None)\n // print(count)\n // print(ans)\n dfs(0, None, False)\n \n\n return ans\n\n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python 3 || Beats 82.22% Memory 67.3 MB | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncount -> count list takes parent i\'th number of child\nans -> ans of ith positions\ndo comment out print(count) and print(ans) in order to Understand.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n tree = collections.defaultdict(set)\n count = [1]*n\n ans = [0]*n\n\n for x, y in edges:\n tree[x].add(y)\n tree[y].add(x)\n\n def dfs(node, parent, flag=True):\n for child in tree[node]:\n if flag and child != parent:\n dfs(child, node)\n count[node] += count[child]\n ans[node] += ans[child] + count[child]\n \n if not flag and child != parent:\n ans[child] = ans[node] - count[child] + n - count[child]\n dfs(child, node, False)\n \n dfs(0, None)\n // print(count)\n // print(ans)\n dfs(0, None, False)\n \n\n return ans\n\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python3 | DFS, BFS, Math | Time beats 98.33% & Space beats 80.56% | Code and Explanation | sum-of-distances-in-tree | 0 | 1 | # Approach\nWe can calculate one node as root, and use this result to get other nodes\' result.\n\nYou can simply observe that the path calculation between one node and its parent node has a rule:\n\nLet\'s say that $$A$$ is the parent of $$B$$.\nWe can group nodes as: $$A$$ side and $$B$$ side.\nSo the path calculation is different from $$A$$ to $$B$$ side nodes and $$B$$ to $$A$$ side nodes.\nSo we can get a equation:\n$$Result_B = Result_A + (n - ChildAmount_B - 2) - ChildAmount_B = Result_A + n - 2 - ChildAmount_B * 2$$\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# https://leetcode.com/problems/sum-of-distances-in-tree/\n\nfrom typing import List\nfrom collections import deque\n\n\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n # Setup connection between nodes\n childNodes = [[] for i in range(n)]\n for x, y in edges:\n childNodes[x].append(y)\n childNodes[y].append(x)\n\n # The DFS do following steps:\n # 1. Find children nodes count for each node. (Store into childrenCnts)\n # 2. Setup parent node. (Store into parent)\n # 3. Cnt root node (node 0) answer (Store into result[0]).\n childrenCnts = [0] * n\n parent = [None] * n\n result = [0] * n\n seen = set()\n\n def dfs(node: int, rank: int) -> None:\n result[0] += rank\n childrenCnt = 0\n for childNode in childNodes[node]:\n if childNode not in seen:\n seen.add(childNode)\n parent[childNode] = node\n dfs(childNode, rank + 1)\n childrenCnt += childrenCnts[childNode] + 1\n childrenCnts[node] = childrenCnt\n\n seen.add(0)\n dfs(0, 0)\n\n # Use BFS to solve rest nodes\' answer by this formula:\n # result[i] = result[parent[i]] + n - 2 - childrenCnts[i] * 2\n q = deque(childNodes[0])\n seen.clear()\n seen.add(0)\n seen.union(childNodes[0])\n while len(q) > 0:\n node = q.popleft()\n result[node] = result[parent[node]] + n - 2 - childrenCnts[node] * 2\n for childNode in childNodes[node]:\n if childNode not in seen:\n seen.add(childNode)\n q.append(childNode)\n return result\n\n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python3 | DFS, BFS, Math | Time beats 98.33% & Space beats 80.56% | Code and Explanation | sum-of-distances-in-tree | 0 | 1 | # Approach\nWe can calculate one node as root, and use this result to get other nodes\' result.\n\nYou can simply observe that the path calculation between one node and its parent node has a rule:\n\nLet\'s say that $$A$$ is the parent of $$B$$.\nWe can group nodes as: $$A$$ side and $$B$$ side.\nSo the path calculation is different from $$A$$ to $$B$$ side nodes and $$B$$ to $$A$$ side nodes.\nSo we can get a equation:\n$$Result_B = Result_A + (n - ChildAmount_B - 2) - ChildAmount_B = Result_A + n - 2 - ChildAmount_B * 2$$\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# https://leetcode.com/problems/sum-of-distances-in-tree/\n\nfrom typing import List\nfrom collections import deque\n\n\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n # Setup connection between nodes\n childNodes = [[] for i in range(n)]\n for x, y in edges:\n childNodes[x].append(y)\n childNodes[y].append(x)\n\n # The DFS do following steps:\n # 1. Find children nodes count for each node. (Store into childrenCnts)\n # 2. Setup parent node. (Store into parent)\n # 3. Cnt root node (node 0) answer (Store into result[0]).\n childrenCnts = [0] * n\n parent = [None] * n\n result = [0] * n\n seen = set()\n\n def dfs(node: int, rank: int) -> None:\n result[0] += rank\n childrenCnt = 0\n for childNode in childNodes[node]:\n if childNode not in seen:\n seen.add(childNode)\n parent[childNode] = node\n dfs(childNode, rank + 1)\n childrenCnt += childrenCnts[childNode] + 1\n childrenCnts[node] = childrenCnt\n\n seen.add(0)\n dfs(0, 0)\n\n # Use BFS to solve rest nodes\' answer by this formula:\n # result[i] = result[parent[i]] + n - 2 - childrenCnts[i] * 2\n q = deque(childNodes[0])\n seen.clear()\n seen.add(0)\n seen.union(childNodes[0])\n while len(q) > 0:\n node = q.popleft()\n result[node] = result[parent[node]] + n - 2 - childrenCnts[node] * 2\n for childNode in childNodes[node]:\n if childNode not in seen:\n seen.add(childNode)\n q.append(childNode)\n return result\n\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Memoize partial trees for each node, simple and concise Python | sum-of-distances-in-tree | 0 | 1 | # Intuition\nSince this is a tree (acyclic) graph, there are only 2*(N-1) subtree possibilities, one subtree for either side of each edge. So we can define our memo as `dp[i][j]` where i is the root of the subtree and j is the connected node that should be considered the "parent" for the purposes of the query.\n\nThe memo values are tuples of `(size, total)` reflecting the number of nodes in the subtree and their total distance from the queried node. Then,\n\n**for leaf nodes** (meaning only one connection and that is `j`):\n\n dp[i][j] = (1, 0)\n\n**for all nodes**\n\n`dp[i][j][0]` is one plus the sum of all `dp[k][i][0]` for all k in `graph[i]` _except_ $$j$$.\n\n`dp[i][j][1]` is `dp[i][j][0]` plus the sum of all `dp[k][i][1]` for all $$k$$ in `graph[i]` _except_ $$j$$. That reflects the fact that each node in all the subtrees is one edge further from $$i$$ than it is from each connected node $$k$$.\n\n# Approach\nUsed `functools.cache` to memoize a `dp(i,j)` function.\nThe answer is, for each node, `(N-1)` plus the sum of all `dp(j, i)[1]` for each node $$j$$ that is connected to $$i$$.\n\n# Complexity\n\n- Time complexity:\n$$O(N)$$\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```\nfrom functools import cache\nclass Solution:\n def sumOfDistancesInTree(self, N: int, edges: List[List[int]]) -> List[int]:\n graph = [[] for i in range(N)]\n for i, j in edges:\n graph[i].append(j)\n graph[j].append(i)\n \n @cache\n def dp(i, j) -> tuple[int, int]:\n size, tot = map(\n sum, zip(*(dp(k, i) for k in graph[i] if k != j))\n ) if len(graph[i]) > 1 else (0, 0)\n return size + 1, tot + size\n \n return [\n N - 1 + sum(dp(edge, i)[1] for edge in graph[i])\n for i in range(N)\n ]\n\n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Memoize partial trees for each node, simple and concise Python | sum-of-distances-in-tree | 0 | 1 | # Intuition\nSince this is a tree (acyclic) graph, there are only 2*(N-1) subtree possibilities, one subtree for either side of each edge. So we can define our memo as `dp[i][j]` where i is the root of the subtree and j is the connected node that should be considered the "parent" for the purposes of the query.\n\nThe memo values are tuples of `(size, total)` reflecting the number of nodes in the subtree and their total distance from the queried node. Then,\n\n**for leaf nodes** (meaning only one connection and that is `j`):\n\n dp[i][j] = (1, 0)\n\n**for all nodes**\n\n`dp[i][j][0]` is one plus the sum of all `dp[k][i][0]` for all k in `graph[i]` _except_ $$j$$.\n\n`dp[i][j][1]` is `dp[i][j][0]` plus the sum of all `dp[k][i][1]` for all $$k$$ in `graph[i]` _except_ $$j$$. That reflects the fact that each node in all the subtrees is one edge further from $$i$$ than it is from each connected node $$k$$.\n\n# Approach\nUsed `functools.cache` to memoize a `dp(i,j)` function.\nThe answer is, for each node, `(N-1)` plus the sum of all `dp(j, i)[1]` for each node $$j$$ that is connected to $$i$$.\n\n# Complexity\n\n- Time complexity:\n$$O(N)$$\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```\nfrom functools import cache\nclass Solution:\n def sumOfDistancesInTree(self, N: int, edges: List[List[int]]) -> List[int]:\n graph = [[] for i in range(N)]\n for i, j in edges:\n graph[i].append(j)\n graph[j].append(i)\n \n @cache\n def dp(i, j) -> tuple[int, int]:\n size, tot = map(\n sum, zip(*(dp(k, i) for k in graph[i] if k != j))\n ) if len(graph[i]) > 1 else (0, 0)\n return size + 1, tot + size\n \n return [\n N - 1 + sum(dp(edge, i)[1] for edge in graph[i])\n for i in range(N)\n ]\n\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
[Python] Super Simple O(N) DP Solution | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe graph has no cycles, since it is tree. Hence, the graph is divided by each edges. \nGiven an edge consisting of A and B, Let\'s assumed we can be calculated that the sum of distances from all nodes which exist in A side.\nIn terms of node B, we can calculate total distance of A side as $$TotalDist_{A side} + NodeCnt_{A side}$$. This is because all nodes coming from side A cross one edge(A->B) to side B.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTherefore, we can define dp as follow.\nThere are the node $$n$$ and the source node $$s$$, which is visited before visit $$n$$.\nThen, the graph is divided $$(n, s)$$ edge.\n$$cnt[n][s] = $$ the number of nodes in $$n$$ side Graph.\n$$dist[n][s] =$$ the total distance from all nodes to $$n$$ in $$n$$ side Graph.\n\nAnd then, we can update as follow, \nlet $$G[n]$$ contain all the neighboring nodes of $$n$$.\n$$ dp[n][s] = sum_{i \\in G[n], i \\neq s}(dp[n][i] + cnt[n][i])$$\n$$ cnt[n][s] = sum_{i \\in G[n], i \\neq s}(cnt[n][i])$$\n\n# Complexity\nTime and space complexity are affected only by the number of edges.\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n self.G = [[] for i in range(n)]\n \n for e in edges:\n self.G[e[0]].append(e[1])\n self.G[e[1]].append(e[0])\n \n ans = []\n for i in range(n):\n ans.append(self.dp(i, -1)[0])\n return ans\n \n @cache\n def dp(self, pnode, source):\n dist = 0\n cnt = 0\n for n in self.G[pnode]:\n if n == source:\n continue\n n_dist, n_cnt = self.dp(n, pnode)\n dist += n_dist + n_cnt\n cnt += n_cnt\n cnt += 1\n return dist, cnt\n \n\n``` | 2 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
[Python] Super Simple O(N) DP Solution | sum-of-distances-in-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe graph has no cycles, since it is tree. Hence, the graph is divided by each edges. \nGiven an edge consisting of A and B, Let\'s assumed we can be calculated that the sum of distances from all nodes which exist in A side.\nIn terms of node B, we can calculate total distance of A side as $$TotalDist_{A side} + NodeCnt_{A side}$$. This is because all nodes coming from side A cross one edge(A->B) to side B.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTherefore, we can define dp as follow.\nThere are the node $$n$$ and the source node $$s$$, which is visited before visit $$n$$.\nThen, the graph is divided $$(n, s)$$ edge.\n$$cnt[n][s] = $$ the number of nodes in $$n$$ side Graph.\n$$dist[n][s] =$$ the total distance from all nodes to $$n$$ in $$n$$ side Graph.\n\nAnd then, we can update as follow, \nlet $$G[n]$$ contain all the neighboring nodes of $$n$$.\n$$ dp[n][s] = sum_{i \\in G[n], i \\neq s}(dp[n][i] + cnt[n][i])$$\n$$ cnt[n][s] = sum_{i \\in G[n], i \\neq s}(cnt[n][i])$$\n\n# Complexity\nTime and space complexity are affected only by the number of edges.\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n self.G = [[] for i in range(n)]\n \n for e in edges:\n self.G[e[0]].append(e[1])\n self.G[e[1]].append(e[0])\n \n ans = []\n for i in range(n):\n ans.append(self.dp(i, -1)[0])\n return ans\n \n @cache\n def dp(self, pnode, source):\n dist = 0\n cnt = 0\n for n in self.G[pnode]:\n if n == source:\n continue\n n_dist, n_cnt = self.dp(n, pnode)\n dist += n_dist + n_cnt\n cnt += n_cnt\n cnt += 1\n return dist, cnt\n \n\n``` | 2 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python3 || 1067 ms, faster than 83.89% of Python3 || Clean and Easy to Understand | sum-of-distances-in-tree | 0 | 1 | ```\ndef sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n d = {i:[1, 0] for i in range(n)}\n def dfs(root, prev):\n for x in g[root]:\n if x!= prev:\n dfs(x, root)\n d[root][0] += d[x][0]\n d[root][1] += (d[x][0] + d[x][1])\n def dfs2(root, prev):\n for x in g[root]:\n if x != prev:\n d[x][1] = d[root][1] - d[x][0] + (n-d[x][0])\n dfs2(x, root)\n dfs(0, -1)\n dfs2(0, -1)\n res = []\n for key in d:\n res.append(d[key][1])\n return res\n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python3 || 1067 ms, faster than 83.89% of Python3 || Clean and Easy to Understand | sum-of-distances-in-tree | 0 | 1 | ```\ndef sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n d = {i:[1, 0] for i in range(n)}\n def dfs(root, prev):\n for x in g[root]:\n if x!= prev:\n dfs(x, root)\n d[root][0] += d[x][0]\n d[root][1] += (d[x][0] + d[x][1])\n def dfs2(root, prev):\n for x in g[root]:\n if x != prev:\n d[x][1] = d[root][1] - d[x][0] + (n-d[x][0])\n dfs2(x, root)\n dfs(0, -1)\n dfs2(0, -1)\n res = []\n for key in d:\n res.append(d[key][1])\n return res\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python | sum-of-distances-in-tree | 0 | 1 | \n```\nclass Solution:\n def sumOfDistancesInTree(self, n,edges):\n result=[0]*n\n self.dist =0\n hashmap = self.create_map(edges)\n hashmap[0].append(0)\n base = {}\n self.r(0,hashmap,base,set(),0)\n result[0]=self.dist\n self.U(0,self.dist,hashmap,base,result,set())\n return result\n def r(self,key,hashmap,base,considered,count):\n if key not in considered:\n considered.add(key)\n self.dist +=count\n val=len(hashmap[key])-1\n for child in hashmap[key]:val+=self.r(child,hashmap,base,considered,count+1)\n base[key]=val\n return val\n return 0\n def create_map(self,edges):\n from collections import defaultdict\n hashmap=defaultdict(list)\n for x,y in edges:hashmap[x].append(y),hashmap[y].append(x)\n return hashmap\n def U(self,key,current,hashmap,base,result,considered):\n if key not in considered:\n considered.add(key)\n for i in hashmap[key]:\n if i not in considered:\n val=current + base[0] -(2*base[i])-1\n result[i]=val\n self.U(i,val,hashmap,base,result,considered)\n \n``` | 1 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python | sum-of-distances-in-tree | 0 | 1 | \n```\nclass Solution:\n def sumOfDistancesInTree(self, n,edges):\n result=[0]*n\n self.dist =0\n hashmap = self.create_map(edges)\n hashmap[0].append(0)\n base = {}\n self.r(0,hashmap,base,set(),0)\n result[0]=self.dist\n self.U(0,self.dist,hashmap,base,result,set())\n return result\n def r(self,key,hashmap,base,considered,count):\n if key not in considered:\n considered.add(key)\n self.dist +=count\n val=len(hashmap[key])-1\n for child in hashmap[key]:val+=self.r(child,hashmap,base,considered,count+1)\n base[key]=val\n return val\n return 0\n def create_map(self,edges):\n from collections import defaultdict\n hashmap=defaultdict(list)\n for x,y in edges:hashmap[x].append(y),hashmap[y].append(x)\n return hashmap\n def U(self,key,current,hashmap,base,result,considered):\n if key not in considered:\n considered.add(key)\n for i in hashmap[key]:\n if i not in considered:\n val=current + base[0] -(2*base[i])-1\n result[i]=val\n self.U(i,val,hashmap,base,result,considered)\n \n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python DFS with cache | sum-of-distances-in-tree | 0 | 1 | # I think this one approach is the only answer doable for a normal person during the interview \n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n graph = defaultdict(list)\n for x, y in edges:\n graph[x].append(y)\n graph[y].append(x)\n\n @cache\n def dfs(parent, child):\n total = 0\n count = 1\n for neighbor in graph[child]:\n if neighbor == parent: continue\n t, c = dfs(child, neighbor) \n total += t + c\n count += c\n return total, count\n return [dfs(-1, i)[0] for i in range(n)]\n``` | 2 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python DFS with cache | sum-of-distances-in-tree | 0 | 1 | # I think this one approach is the only answer doable for a normal person during the interview \n\n# Code\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n graph = defaultdict(list)\n for x, y in edges:\n graph[x].append(y)\n graph[y].append(x)\n\n @cache\n def dfs(parent, child):\n total = 0\n count = 1\n for neighbor in graph[child]:\n if neighbor == parent: continue\n t, c = dfs(child, neighbor) \n total += t + c\n count += c\n return total, count\n return [dfs(-1, i)[0] for i in range(n)]\n``` | 2 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Python easy to read and understand | graph | sum-of-distances-in-tree | 0 | 1 | **BRUTE(BFS)**\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n \n res = [0]*n\n for i in range(n):\n q = [i]\n visit = set()\n visit.add(i)\n step, cnt = 1, 0\n while q:\n num = len(q)\n for j in range(num):\n node = q.pop(0)\n for nei in g[node]:\n if nei not in visit:\n cnt += step\n visit.add(nei)\n q.append(nei)\n if q:step+=1\n res[i] = cnt\n \n return res\n```\n**DFS**\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n \n d = {i:[1, 0] for i in range(n)}\n \n def dfs(root, prev):\n for nei in g[root]:\n if nei != prev:\n dfs(nei, root)\n d[root][0] += d[nei][0]\n d[root][1] += (d[nei][0] + d[nei][1])\n \n def dfs2(root, prev):\n for nei in g[root]:\n if nei != prev:\n d[nei][1] = d[root][1] - d[nei][0] + (n-d[nei][0])\n dfs2(nei, root)\n \n dfs(0, -1)\n dfs2(0, -1)\n res = []\n for key in d:\n res.append(d[key][1])\n return res\n```\n | 3 | There is an undirected connected tree with `n` nodes labeled from `0` to `n - 1` and `n - 1` edges.
You are given the integer `n` and the array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between nodes `ai` and `bi` in the tree.
Return an array `answer` of length `n` where `answer[i]` is the sum of the distances between the `ith` node in the tree and all other nodes.
**Example 1:**
**Input:** n = 6, edges = \[\[0,1\],\[0,2\],\[2,3\],\[2,4\],\[2,5\]\]
**Output:** \[8,12,6,10,10,10\]
**Explanation:** The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer\[0\] = 8, and so on.
**Example 2:**
**Input:** n = 1, edges = \[\]
**Output:** \[0\]
**Example 3:**
**Input:** n = 2, edges = \[\[1,0\]\]
**Output:** \[1,1\]
**Constraints:**
* `1 <= n <= 3 * 104`
* `edges.length == n - 1`
* `edges[i].length == 2`
* `0 <= ai, bi < n`
* `ai != bi`
* The given input represents a valid tree. | null |
Python easy to read and understand | graph | sum-of-distances-in-tree | 0 | 1 | **BRUTE(BFS)**\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n \n res = [0]*n\n for i in range(n):\n q = [i]\n visit = set()\n visit.add(i)\n step, cnt = 1, 0\n while q:\n num = len(q)\n for j in range(num):\n node = q.pop(0)\n for nei in g[node]:\n if nei not in visit:\n cnt += step\n visit.add(nei)\n q.append(nei)\n if q:step+=1\n res[i] = cnt\n \n return res\n```\n**DFS**\n```\nclass Solution:\n def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:\n g = collections.defaultdict(list)\n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n \n d = {i:[1, 0] for i in range(n)}\n \n def dfs(root, prev):\n for nei in g[root]:\n if nei != prev:\n dfs(nei, root)\n d[root][0] += d[nei][0]\n d[root][1] += (d[nei][0] + d[nei][1])\n \n def dfs2(root, prev):\n for nei in g[root]:\n if nei != prev:\n d[nei][1] = d[root][1] - d[nei][0] + (n-d[nei][0])\n dfs2(nei, root)\n \n dfs(0, -1)\n dfs2(0, -1)\n res = []\n for key in d:\n res.append(d[key][1])\n return res\n```\n | 3 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
BFS + Bitmask -- runtime beats 94% | image-overlap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf two cells, $$c_1$$ and $$c_2$$ overlap one of the following happens:\n 1. If $c_1 = 0$ and $c_2 = 0$, we **don\'t count** the overlap.\n 2. If $c_1 = 1$ and $c_2 = 0$, we **don\'t count** the overlap.\n 3. If $c_1 = 0$ and $c_2 = 1$, we **don\'t count** the overlap.\n 4. If $c_1 = 1$ and $c_2 = 1$, we **count** the overlap.\n\nIf `n = 1`, then our final answer is $c_1 \\cdot c_2$, where $(\\cdot)$ is the bitwise and operation. We can certainly generalize this.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGiven an `n` by `n` binary grid, we can concatenate the entries of each row to create a single number to represent it. Thus, for the whole grid, we need one-dimensional bitmask array of length `n`. Then, we can count the overlap of two grids by counting the set bits of the bit-wise and of the correponding bitmask arrays of the two grids. This way of checking overlaps is what makes this approach more efficient than iterating over and counting one bits.\n\nHowever, we might need to shift one of the grids horizontally or vertically to maximize the overlaps. Vertical shift is easily simulated in the bitmask array by appending (or prepending) a `0` and popping out the bitmask at the opposite side of the bitmask array. Horizontal shift is done by dividing or multiplying each element of the bitmask array by `2` and setting the significant bit off to keep the bit length of the bitmasks at most `n`.\n\nOnce we know how to shift on our bitmask array, we can traverse through all possible shifts using breadth-first search (or depth-first search). To ease implementation, I maintained a tuple for each shift the tells me the number of horizontal and vertical shifts required make the current bitmask array from the original one. Negatives imply shifts in the left and up direction.\n\n\n# Complexity\n- Time complexity:\nThe BFS runs roughly $4n^2$ times while the inner loop costs $O(n)$, making the total runtime complexity $O(n^3)$\n- Space complexity(Excluding the input grids):\nThe bitmask arrays need $O(n)$ space each and the queue another $O(n)$. Thus, the overall space-complexity is $O(n).$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:\n\n n = len(img1)\n\n # convert to bits\n bit1 = []\n bit2 = []\n for i in range(n):\n b1 = int("0b" + "".join(map(str, img1[i])), 2)\n b2 = int("0b" + "".join(map(str, img2[i])), 2)\n\n bit1.append(b1)\n bit2.append(b2)\n \n # bfs on operations\n queue = deque([(bit1, (0, 0))])\n seen = set((0,0))\n max_overlaps = 0\n\n while queue:\n bit, op = queue.popleft()\n if all([True if b == 0 else False for b in bit]):\n continue\n\n overlaps = 0\n for i in range(n):\n overlaps+=(bit[i]&bit2[i]).bit_count()\n max_overlaps = max(max_overlaps, overlaps)\n\n \n # add translations\n if (op[0]+1, op[1]) not in seen:\n h_shifted_p = [b//2 for b in bit]\n queue.append((h_shifted_p, (op[0]+1, op[1])))\n seen.add((op[0]+1, op[1]))\n if (op[0]-1, op[1]) not in seen:\n h_shifted_n = [(2*b & ~(1<<(n+1))) for b in bit]\n seen.add((op[0]-1, op[1]))\n queue.append((h_shifted_n, (op[0]-1, op[1])))\n if (op[0], op[1]+1) not in seen:\n v_shifted_p = [0] + bit[:-1]\n seen.add((op[0], op[1]+1))\n queue.append((v_shifted_p, (op[0], op[1]+1)))\n if (op[0], op[1]-1) not in seen:\n v_shifted_n = bit[1:] + [0]\n queue.append((v_shifted_n, (op[0], op[1]-1)))\n seen.add((op[0], op[1]-1))\n\n\n\n return max_overlaps\n\n \n``` | 10 | You are given two images, `img1` and `img2`, represented as binary, square matrices of size `n x n`. A binary matrix has only `0`s and `1`s as values.
We **translate** one image however we choose by sliding all the `1` bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the **overlap** by counting the number of positions that have a `1` in **both** images.
Note also that a translation does **not** include any kind of rotation. Any `1` bits that are translated outside of the matrix borders are erased.
Return _the largest possible overlap_.
**Example 1:**
**Input:** img1 = \[\[1,1,0\],\[0,1,0\],\[0,1,0\]\], img2 = \[\[0,0,0\],\[0,1,1\],\[0,0,1\]\]
**Output:** 3
**Explanation:** We translate img1 to right by 1 unit and down by 1 unit.
The number of positions that have a 1 in both images is 3 (shown in red).
**Example 2:**
**Input:** img1 = \[\[1\]\], img2 = \[\[1\]\]
**Output:** 1
**Example 3:**
**Input:** img1 = \[\[0\]\], img2 = \[\[0\]\]
**Output:** 0
**Constraints:**
* `n == img1.length == img1[i].length`
* `n == img2.length == img2[i].length`
* `1 <= n <= 30`
* `img1[i][j]` is either `0` or `1`.
* `img2[i][j]` is either `0` or `1`. | null |
BFS + Bitmask -- runtime beats 94% | image-overlap | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf two cells, $$c_1$$ and $$c_2$$ overlap one of the following happens:\n 1. If $c_1 = 0$ and $c_2 = 0$, we **don\'t count** the overlap.\n 2. If $c_1 = 1$ and $c_2 = 0$, we **don\'t count** the overlap.\n 3. If $c_1 = 0$ and $c_2 = 1$, we **don\'t count** the overlap.\n 4. If $c_1 = 1$ and $c_2 = 1$, we **count** the overlap.\n\nIf `n = 1`, then our final answer is $c_1 \\cdot c_2$, where $(\\cdot)$ is the bitwise and operation. We can certainly generalize this.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGiven an `n` by `n` binary grid, we can concatenate the entries of each row to create a single number to represent it. Thus, for the whole grid, we need one-dimensional bitmask array of length `n`. Then, we can count the overlap of two grids by counting the set bits of the bit-wise and of the correponding bitmask arrays of the two grids. This way of checking overlaps is what makes this approach more efficient than iterating over and counting one bits.\n\nHowever, we might need to shift one of the grids horizontally or vertically to maximize the overlaps. Vertical shift is easily simulated in the bitmask array by appending (or prepending) a `0` and popping out the bitmask at the opposite side of the bitmask array. Horizontal shift is done by dividing or multiplying each element of the bitmask array by `2` and setting the significant bit off to keep the bit length of the bitmasks at most `n`.\n\nOnce we know how to shift on our bitmask array, we can traverse through all possible shifts using breadth-first search (or depth-first search). To ease implementation, I maintained a tuple for each shift the tells me the number of horizontal and vertical shifts required make the current bitmask array from the original one. Negatives imply shifts in the left and up direction.\n\n\n# Complexity\n- Time complexity:\nThe BFS runs roughly $4n^2$ times while the inner loop costs $O(n)$, making the total runtime complexity $O(n^3)$\n- Space complexity(Excluding the input grids):\nThe bitmask arrays need $O(n)$ space each and the queue another $O(n)$. Thus, the overall space-complexity is $O(n).$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:\n\n n = len(img1)\n\n # convert to bits\n bit1 = []\n bit2 = []\n for i in range(n):\n b1 = int("0b" + "".join(map(str, img1[i])), 2)\n b2 = int("0b" + "".join(map(str, img2[i])), 2)\n\n bit1.append(b1)\n bit2.append(b2)\n \n # bfs on operations\n queue = deque([(bit1, (0, 0))])\n seen = set((0,0))\n max_overlaps = 0\n\n while queue:\n bit, op = queue.popleft()\n if all([True if b == 0 else False for b in bit]):\n continue\n\n overlaps = 0\n for i in range(n):\n overlaps+=(bit[i]&bit2[i]).bit_count()\n max_overlaps = max(max_overlaps, overlaps)\n\n \n # add translations\n if (op[0]+1, op[1]) not in seen:\n h_shifted_p = [b//2 for b in bit]\n queue.append((h_shifted_p, (op[0]+1, op[1])))\n seen.add((op[0]+1, op[1]))\n if (op[0]-1, op[1]) not in seen:\n h_shifted_n = [(2*b & ~(1<<(n+1))) for b in bit]\n seen.add((op[0]-1, op[1]))\n queue.append((h_shifted_n, (op[0]-1, op[1])))\n if (op[0], op[1]+1) not in seen:\n v_shifted_p = [0] + bit[:-1]\n seen.add((op[0], op[1]+1))\n queue.append((v_shifted_p, (op[0], op[1]+1)))\n if (op[0], op[1]-1) not in seen:\n v_shifted_n = bit[1:] + [0]\n queue.append((v_shifted_n, (op[0], op[1]-1)))\n seen.add((op[0], op[1]-1))\n\n\n\n return max_overlaps\n\n \n``` | 10 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
Solution | image-overlap | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) {\n int n = img1.size();\n vector<unsigned int> small1(n, 0);\n vector<unsigned int> small2(n, 0);\n for(int row = 0; row < n; ++row) {\n for(int col = 0; col < n; ++col) {\n small1[row] |= img1[row][col] << col;\n small2[row] |= img2[row][col] << col;\n }\n }\n int maxOverlap = 0;\n for(int upMove = -n + 1; upMove < n; ++upMove) {\n for(int sideMove = 0; sideMove < n; ++sideMove) {\n int overlapL = 0, overlapR = 0;\n for(int row = 0; row + abs(upMove) < n; ++row) {\n int row1 = upMove < 0 ? row - upMove : row;\n int row2 = upMove < 0 ? row : row + upMove;\n overlapL += __builtin_popcount((small1[row1] << sideMove) & small2[row2]);\n overlapR += __builtin_popcount((small1[row1] >> sideMove) & small2[row2]);\n }\n maxOverlap = max(maxOverlap, max(overlapL, overlapR));\n }\n }\n return maxOverlap;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:\n def get_row_mask(row: List[int]) -> int: \n mask = 0\n for shift, value in enumerate(reversed(row)):\n if value:\n mask |= 1 << shift\n \n return mask\n \n img1_row_masks = [get_row_mask(row) for row in img1]\n img2_row_masks = [get_row_mask(row) for row in img2]\n n = len(img1)\n largest_overlap = 0\n \n for shift in range(n): \n for start_row in range(n):\n \n total_overlap_1 = 0\n total_overlap_2 = 0\n total_overlap_3 = 0\n total_overlap_4 = 0\n \n for idx in range(start_row, n): \n \n total_overlap_1 += (\n img1_row_masks[idx - start_row] >> shift & img2_row_masks[idx]\n ).bit_count()\n \n total_overlap_2 += (\n img1_row_masks[idx] >> shift & img2_row_masks[idx - start_row]\n ).bit_count()\n \n total_overlap_3 += (\n img1_row_masks[idx - start_row] & img2_row_masks[idx] >> shift\n ).bit_count()\n \n total_overlap_4 += (\n img1_row_masks[idx] & img2_row_masks[idx - start_row] >> shift\n ).bit_count()\n largest_overlap = max(\n largest_overlap, \n total_overlap_1,\n total_overlap_2,\n total_overlap_3,\n total_overlap_4,\n ) \n return largest_overlap\n```\n\n```Java []\nclass Solution {\n public int largestOverlap(int[][] img1, int[][] img2) {\n int n = img1.length;\n int[][] m = new int[2 * n + 1][2 * n + 1];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n if (img1[i][j] == 1) {\n for (int p = 0; p < n; p++) {\n for (int q = 0; q < n; q++) {\n if (img2[p][q] == 1) {\n m[i - p + n][j - q + n]++;\n }\n }\n }\n }\n }\n }\n int max = 0;\n for (int i = 0; i < m.length; i++) {\n for (int j = 0; j < m.length; j++) {\n max = Math.max(max, m[i][j]);\n }\n }\n return max;\n }\n}\n```\n | 1 | You are given two images, `img1` and `img2`, represented as binary, square matrices of size `n x n`. A binary matrix has only `0`s and `1`s as values.
We **translate** one image however we choose by sliding all the `1` bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the **overlap** by counting the number of positions that have a `1` in **both** images.
Note also that a translation does **not** include any kind of rotation. Any `1` bits that are translated outside of the matrix borders are erased.
Return _the largest possible overlap_.
**Example 1:**
**Input:** img1 = \[\[1,1,0\],\[0,1,0\],\[0,1,0\]\], img2 = \[\[0,0,0\],\[0,1,1\],\[0,0,1\]\]
**Output:** 3
**Explanation:** We translate img1 to right by 1 unit and down by 1 unit.
The number of positions that have a 1 in both images is 3 (shown in red).
**Example 2:**
**Input:** img1 = \[\[1\]\], img2 = \[\[1\]\]
**Output:** 1
**Example 3:**
**Input:** img1 = \[\[0\]\], img2 = \[\[0\]\]
**Output:** 0
**Constraints:**
* `n == img1.length == img1[i].length`
* `n == img2.length == img2[i].length`
* `1 <= n <= 30`
* `img1[i][j]` is either `0` or `1`.
* `img2[i][j]` is either `0` or `1`. | null |
Solution | image-overlap | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) {\n int n = img1.size();\n vector<unsigned int> small1(n, 0);\n vector<unsigned int> small2(n, 0);\n for(int row = 0; row < n; ++row) {\n for(int col = 0; col < n; ++col) {\n small1[row] |= img1[row][col] << col;\n small2[row] |= img2[row][col] << col;\n }\n }\n int maxOverlap = 0;\n for(int upMove = -n + 1; upMove < n; ++upMove) {\n for(int sideMove = 0; sideMove < n; ++sideMove) {\n int overlapL = 0, overlapR = 0;\n for(int row = 0; row + abs(upMove) < n; ++row) {\n int row1 = upMove < 0 ? row - upMove : row;\n int row2 = upMove < 0 ? row : row + upMove;\n overlapL += __builtin_popcount((small1[row1] << sideMove) & small2[row2]);\n overlapR += __builtin_popcount((small1[row1] >> sideMove) & small2[row2]);\n }\n maxOverlap = max(maxOverlap, max(overlapL, overlapR));\n }\n }\n return maxOverlap;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int:\n def get_row_mask(row: List[int]) -> int: \n mask = 0\n for shift, value in enumerate(reversed(row)):\n if value:\n mask |= 1 << shift\n \n return mask\n \n img1_row_masks = [get_row_mask(row) for row in img1]\n img2_row_masks = [get_row_mask(row) for row in img2]\n n = len(img1)\n largest_overlap = 0\n \n for shift in range(n): \n for start_row in range(n):\n \n total_overlap_1 = 0\n total_overlap_2 = 0\n total_overlap_3 = 0\n total_overlap_4 = 0\n \n for idx in range(start_row, n): \n \n total_overlap_1 += (\n img1_row_masks[idx - start_row] >> shift & img2_row_masks[idx]\n ).bit_count()\n \n total_overlap_2 += (\n img1_row_masks[idx] >> shift & img2_row_masks[idx - start_row]\n ).bit_count()\n \n total_overlap_3 += (\n img1_row_masks[idx - start_row] & img2_row_masks[idx] >> shift\n ).bit_count()\n \n total_overlap_4 += (\n img1_row_masks[idx] & img2_row_masks[idx - start_row] >> shift\n ).bit_count()\n largest_overlap = max(\n largest_overlap, \n total_overlap_1,\n total_overlap_2,\n total_overlap_3,\n total_overlap_4,\n ) \n return largest_overlap\n```\n\n```Java []\nclass Solution {\n public int largestOverlap(int[][] img1, int[][] img2) {\n int n = img1.length;\n int[][] m = new int[2 * n + 1][2 * n + 1];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n if (img1[i][j] == 1) {\n for (int p = 0; p < n; p++) {\n for (int q = 0; q < n; q++) {\n if (img2[p][q] == 1) {\n m[i - p + n][j - q + n]++;\n }\n }\n }\n }\n }\n }\n int max = 0;\n for (int i = 0; i < m.length; i++) {\n for (int j = 0; j < m.length; j++) {\n max = Math.max(max, m[i][j]);\n }\n }\n return max;\n }\n}\n```\n | 1 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
Solution | rectangle-overlap | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) {\n return rec1[0]<rec2[2] && rec1[1] < rec2[3] && rec2[0]<rec1[2] && rec2[1]< rec1[3];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isRectangleOverlap(self, rec1: List[int], rec2: List[int]) -> bool:\n \n width = min(rec1[2], rec2[2]) - max(rec1[0], rec2[0])\n height = min(rec1[3], rec2[3]) - max(rec1[1], rec2[1])\n return True if width > 0 and height > 0 else False\n```\n\n```Java []\nclass Solution {\n public boolean isRectangleOverlap(int[] rec1, int[] rec2) {\n return \n rec1[0] < rec2[2] &&\n rec1[1] < rec2[3] &&\n rec1[2] > rec2[0] &&\n rec1[3] > rec2[1]\n ;\n }\n}\n```\n | 2 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Solution | rectangle-overlap | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) {\n return rec1[0]<rec2[2] && rec1[1] < rec2[3] && rec2[0]<rec1[2] && rec2[1]< rec1[3];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isRectangleOverlap(self, rec1: List[int], rec2: List[int]) -> bool:\n \n width = min(rec1[2], rec2[2]) - max(rec1[0], rec2[0])\n height = min(rec1[3], rec2[3]) - max(rec1[1], rec2[1])\n return True if width > 0 and height > 0 else False\n```\n\n```Java []\nclass Solution {\n public boolean isRectangleOverlap(int[] rec1, int[] rec2) {\n return \n rec1[0] < rec2[2] &&\n rec1[1] < rec2[3] &&\n rec1[2] > rec2[0] &&\n rec1[3] > rec2[1]\n ;\n }\n}\n```\n | 2 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Python 3: Readable solution with comments | rectangle-overlap | 0 | 1 | ```\nclass Solution(object):\n def isRectangleOverlap(self, rec1, rec2):\n # TIME and SPACE Complexity: O(1)\n\t\t\n #Funtion checking if coordinate of Rec2 overlapped Rec1;\n def checkOverlapping(rec1_left, rec1_right, rec2_left, rec2_right):\n \n rec2_StartingCoordinate = max(rec1_left, rec2_left)\n rec1_EndingCoordinate = min(rec1_right, rec2_right)\n isOverlapped = rec2_StartingCoordinate < rec1_EndingCoordinate\n \n return isOverlapped\n \n \n #All Horizontal coordinates of Rec1 and Rec2;\n rec1HozlLeft = rec1[0]\n rec1HozlRight = rec1[2]\n rec2HozlLeft = rec2[0]\n rec2HozlRight = rec2[2]\n \n #All Vertical coordinates of Rec1 and Rec2;\n rec1VerBottom = rec1[1]\n rec1VerTop = rec1[3]\n rec2VerBottom = rec2[1]\n rec2VerTop = rec2[3]\n \n # 1st Check the Horizontal coordinates if Rec2 is overlapped Rec1;\n ## 2nd Check the Vertical coordinates if Rec2 is Overlapped Rec1; \n ### return True if both Horizontal and Vertical are Overlapped\n return checkOverlapping(rec1HozlLeft, rec1HozlRight, rec2HozlLeft, rec2HozlRight) and \\\n checkOverlapping(rec1VerBottom, rec1VerTop, rec2VerBottom, rec2VerTop) | 1 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Python 3: Readable solution with comments | rectangle-overlap | 0 | 1 | ```\nclass Solution(object):\n def isRectangleOverlap(self, rec1, rec2):\n # TIME and SPACE Complexity: O(1)\n\t\t\n #Funtion checking if coordinate of Rec2 overlapped Rec1;\n def checkOverlapping(rec1_left, rec1_right, rec2_left, rec2_right):\n \n rec2_StartingCoordinate = max(rec1_left, rec2_left)\n rec1_EndingCoordinate = min(rec1_right, rec2_right)\n isOverlapped = rec2_StartingCoordinate < rec1_EndingCoordinate\n \n return isOverlapped\n \n \n #All Horizontal coordinates of Rec1 and Rec2;\n rec1HozlLeft = rec1[0]\n rec1HozlRight = rec1[2]\n rec2HozlLeft = rec2[0]\n rec2HozlRight = rec2[2]\n \n #All Vertical coordinates of Rec1 and Rec2;\n rec1VerBottom = rec1[1]\n rec1VerTop = rec1[3]\n rec2VerBottom = rec2[1]\n rec2VerTop = rec2[3]\n \n # 1st Check the Horizontal coordinates if Rec2 is overlapped Rec1;\n ## 2nd Check the Vertical coordinates if Rec2 is Overlapped Rec1; \n ### return True if both Horizontal and Vertical are Overlapped\n return checkOverlapping(rec1HozlLeft, rec1HozlRight, rec2HozlLeft, rec2HozlRight) and \\\n checkOverlapping(rec1VerBottom, rec1VerTop, rec2VerBottom, rec2VerTop) | 1 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Single Line solution, beats 98.2%, Simple logic | rectangle-overlap | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can simplify the conditions by directly checking if rec1 is to the right, left, above, or below rec2. \n * If any of these conditions is true, it means the rectangles do not overlap. \n- If none of these conditions is met, the rectangles overlap.\n\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isRectangleOverlap(self, rec1: List[int], rec2: List[int]) -> bool:\n # Checking if rec1 is to the right, left, above, or below rec2\n return not (rec1[2] <= rec2[0] or # Left\n rec1[3] <= rec2[1] or # Bottom\n rec1[0] >= rec2[2] or # Right\n rec1[1] >= rec2[3]) # Top\n\n``` | 0 | An axis-aligned rectangle is represented as a list `[x1, y1, x2, y2]`, where `(x1, y1)` is the coordinate of its bottom-left corner, and `(x2, y2)` is the coordinate of its top-right corner. Its top and bottom edges are parallel to the X-axis, and its left and right edges are parallel to the Y-axis.
Two rectangles overlap if the area of their intersection is **positive**. To be clear, two rectangles that only touch at the corner or edges do not overlap.
Given two axis-aligned rectangles `rec1` and `rec2`, return `true` _if they overlap, otherwise return_ `false`.
**Example 1:**
**Input:** rec1 = \[0,0,2,2\], rec2 = \[1,1,3,3\]
**Output:** true
**Example 2:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[1,0,2,1\]
**Output:** false
**Example 3:**
**Input:** rec1 = \[0,0,1,1\], rec2 = \[2,2,3,3\]
**Output:** false
**Constraints:**
* `rec1.length == 4`
* `rec2.length == 4`
* `-109 <= rec1[i], rec2[i] <= 109`
* `rec1` and `rec2` represent a valid rectangle with a non-zero area. | null |
Single Line solution, beats 98.2%, Simple logic | rectangle-overlap | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can simplify the conditions by directly checking if rec1 is to the right, left, above, or below rec2. \n * If any of these conditions is true, it means the rectangles do not overlap. \n- If none of these conditions is met, the rectangles overlap.\n\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isRectangleOverlap(self, rec1: List[int], rec2: List[int]) -> bool:\n # Checking if rec1 is to the right, left, above, or below rec2\n return not (rec1[2] <= rec2[0] or # Left\n rec1[3] <= rec2[1] or # Bottom\n rec1[0] >= rec2[2] or # Right\n rec1[1] >= rec2[3]) # Top\n\n``` | 0 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
simple python code using hashmap | new-21-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0:\n return 1.0\n\n windowsum=0\n for i in range(k,k + maxPts):\n windowsum+= 1 if i<=n else 0\n\n dp={}\n for i in range(k-1,-1,-1):\n dp[i]=windowsum/maxPts\n remove=0\n if i+maxPts<=n:\n remove=dp.get(i+maxPts,1)\n windowsum+= dp[i]-remove\n return dp[0] \n``` | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
simple python code using hashmap | new-21-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0:\n return 1.0\n\n windowsum=0\n for i in range(k,k + maxPts):\n windowsum+= 1 if i<=n else 0\n\n dp={}\n for i in range(k-1,-1,-1):\n dp[i]=windowsum/maxPts\n remove=0\n if i+maxPts<=n:\n remove=dp.get(i+maxPts,1)\n windowsum+= dp[i]-remove\n return dp[0] \n``` | 1 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Python3 Solution | new-21-game | 0 | 1 | \n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0 or n>=k+maxPts:\n return 1\n\n dp=[1.0]+[0.0]*n\n maxPts_sum=1.0\n for i in range(1,n+1):\n dp[i]=maxPts_sum/maxPts\n if i<k:\n maxPts_sum+=dp[i]\n\n if i-maxPts>=0:\n maxPts_sum-=dp[i-maxPts]\n\n\n return sum(dp[k:]) \n``` | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Python3 Solution | new-21-game | 0 | 1 | \n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0 or n>=k+maxPts:\n return 1\n\n dp=[1.0]+[0.0]*n\n maxPts_sum=1.0\n for i in range(1,n+1):\n dp[i]=maxPts_sum/maxPts\n if i<k:\n maxPts_sum+=dp[i]\n\n if i-maxPts>=0:\n maxPts_sum-=dp[i-maxPts]\n\n\n return sum(dp[k:]) \n``` | 1 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Solution | new-21-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int mx) {\n if (k == 0 || n >= k + mx) return 1.0;\n vector<double> dp(n+1);\n dp[0] = 1.0;\n double pref = 1.0;\n double res = 0.0; \n for (int i = 1; i <= n; i++){\n dp[i] = pref / mx;\n if (i < k) pref += dp[i];\n if (i >= mx && i < k + mx) pref -= dp[i - mx];\n if (i >= k) res += dp[i];\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n```\n\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(n>=k+maxPts-1){\n return 1;\n }\n double[] dp =new double[k+maxPts];\n double p=1/(maxPts+0.0);\n dp[0]=1;\n double prev =0;\n for(int i=1;i<=k;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0)+dp[i-1];\n dp[i]=prev*p;\n }\n double res = dp[k];\n for(int i=k+1;i<=n;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0);\n dp[i]=prev*p;\n res+=dp[i];\n }\n return res;\n }\n}\n```\n | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Solution | new-21-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int mx) {\n if (k == 0 || n >= k + mx) return 1.0;\n vector<double> dp(n+1);\n dp[0] = 1.0;\n double pref = 1.0;\n double res = 0.0; \n for (int i = 1; i <= n; i++){\n dp[i] = pref / mx;\n if (i < k) pref += dp[i];\n if (i >= mx && i < k + mx) pref -= dp[i - mx];\n if (i >= k) res += dp[i];\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n```\n\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(n>=k+maxPts-1){\n return 1;\n }\n double[] dp =new double[k+maxPts];\n double p=1/(maxPts+0.0);\n dp[0]=1;\n double prev =0;\n for(int i=1;i<=k;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0)+dp[i-1];\n dp[i]=prev*p;\n }\n double res = dp[k];\n for(int i=k+1;i<=n;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0);\n dp[i]=prev*p;\n res+=dp[i];\n }\n return res;\n }\n}\n```\n | 1 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Image Explanation🏆- [Complete Intuition - Maths, Probability, DP, Sliding Window] - C++/Java/Python | new-21-game | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`New 21 Game` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n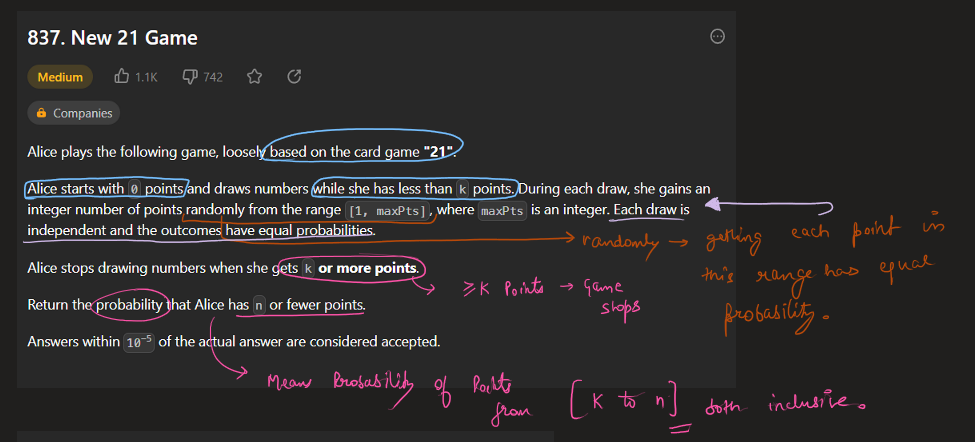\n\n\n\n\n\n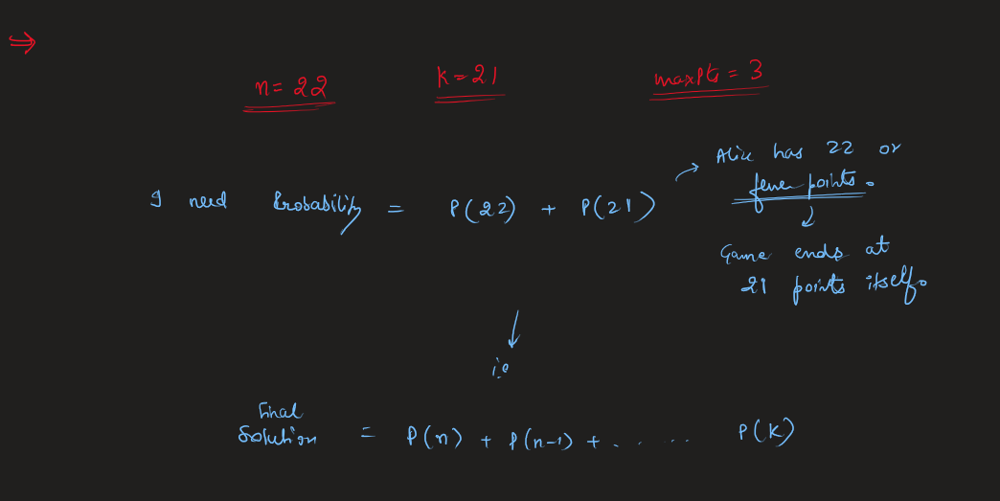\n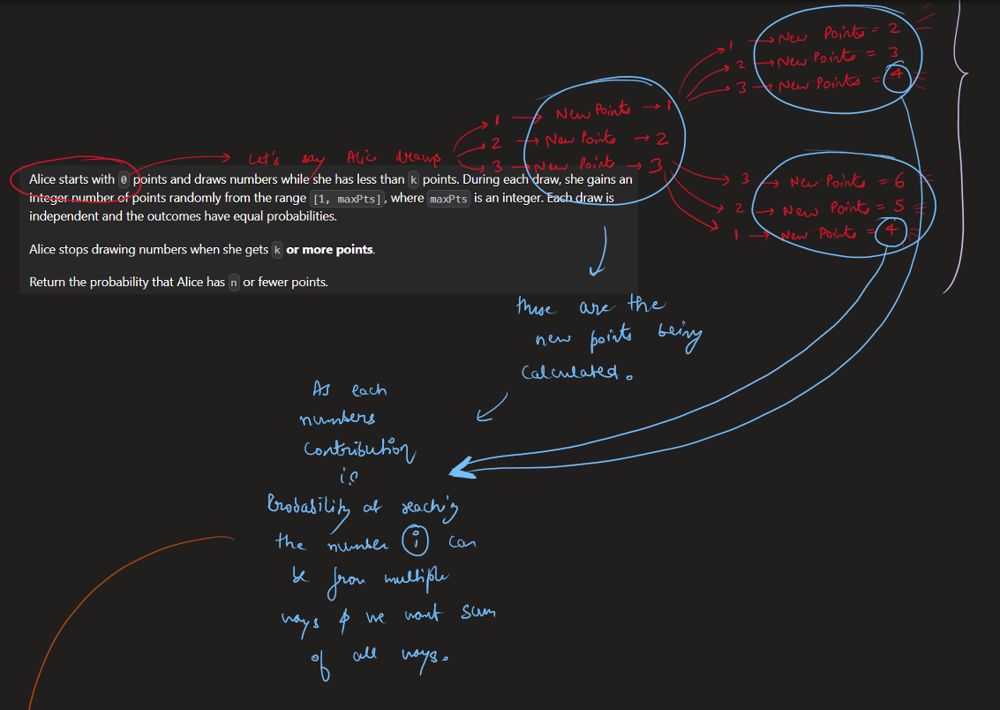\n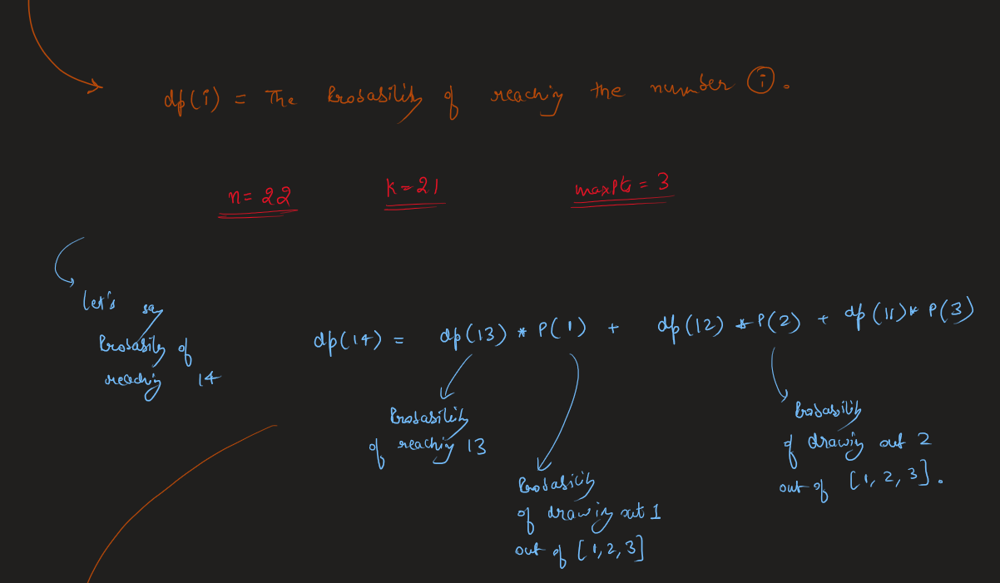\n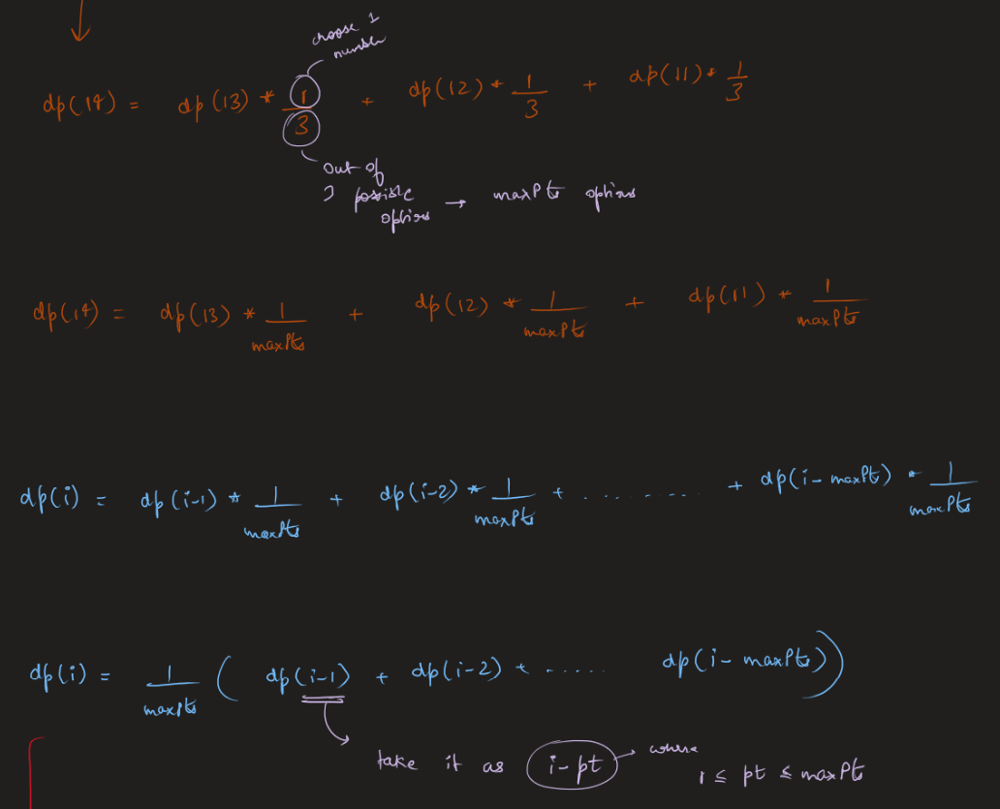\n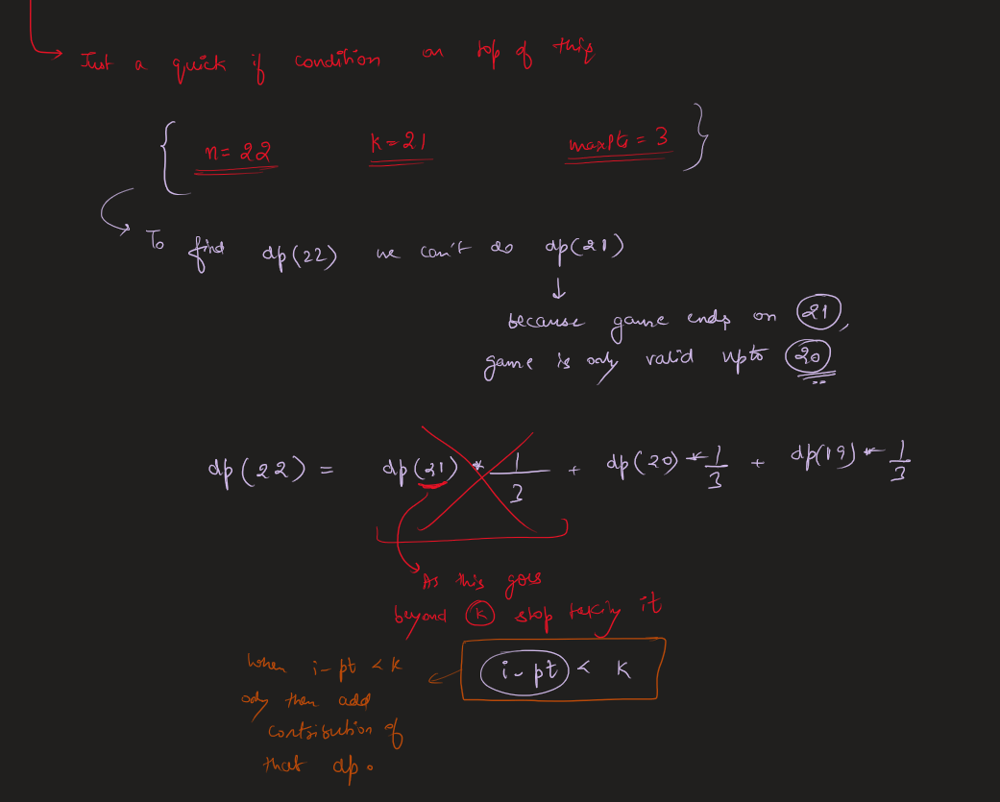\n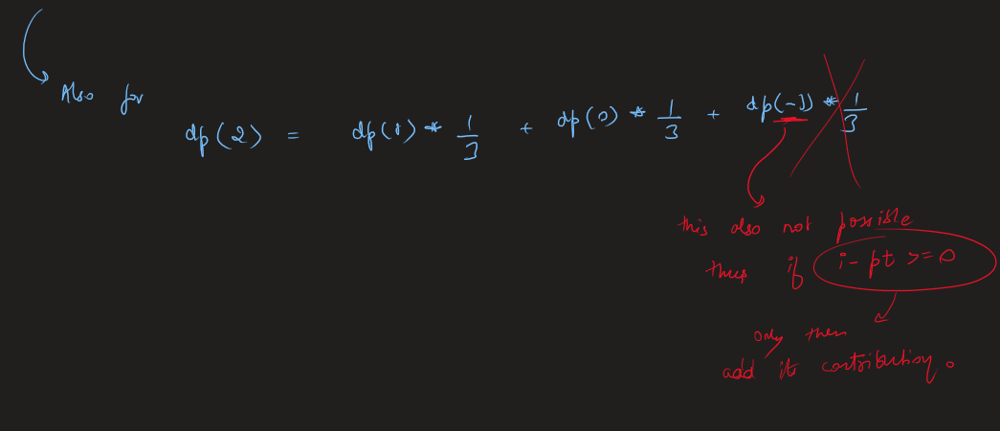\n\n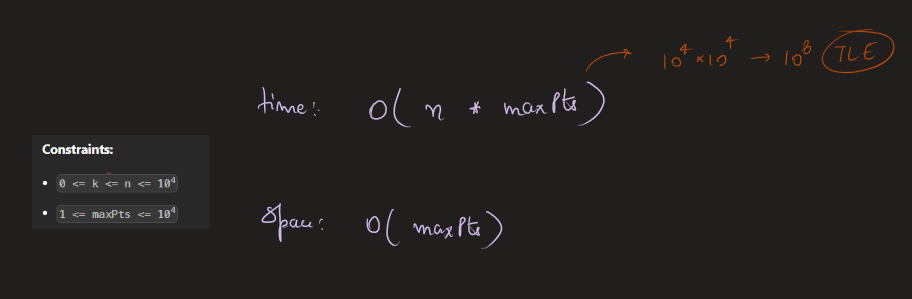\n\n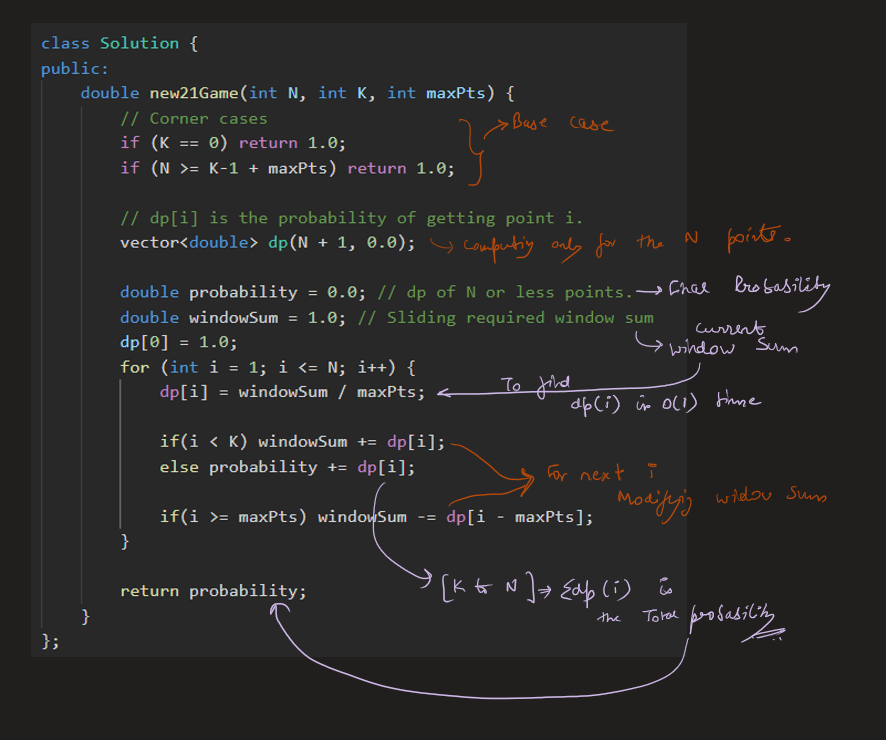\n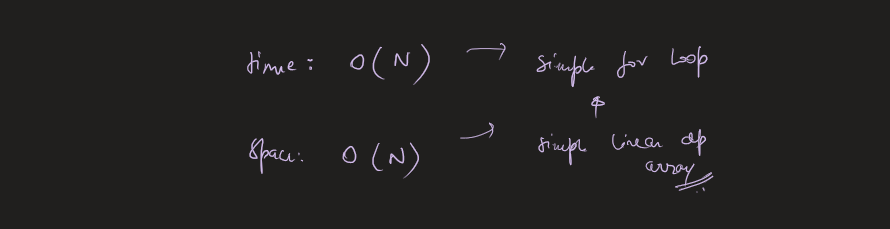\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K-1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n vector<double> dp(N + 1, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if(i < K) windowSum += dp[i];\n else probability += dp[i];\n \n if(i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n};\n```\n```Java []\nclass Solution {\n public double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K - 1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n double[] dp = new double[N + 1];\n Arrays.fill(dp, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if (i < K) windowSum += dp[i];\n else probability += dp[i];\n\n if (i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n}\n```\n```Python []\nclass Solution:\n def new21Game(self, N, K, maxPts):\n # Corner cases\n if K == 0:\n return 1.0\n if N >= K - 1 + maxPts:\n return 1.0\n\n # dp[i] is the probability of getting point i.\n dp = [0.0] * (N + 1)\n\n probability = 0.0 # dp of N or less points.\n windowSum = 1.0 # Sliding required window sum\n dp[0] = 1.0\n for i in range(1, N + 1):\n dp[i] = windowSum / maxPts\n\n if i < K:\n windowSum += dp[i]\n else:\n probability += dp[i]\n\n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n\n return probability\n``` | 70 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Image Explanation🏆- [Complete Intuition - Maths, Probability, DP, Sliding Window] - C++/Java/Python | new-21-game | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`New 21 Game` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n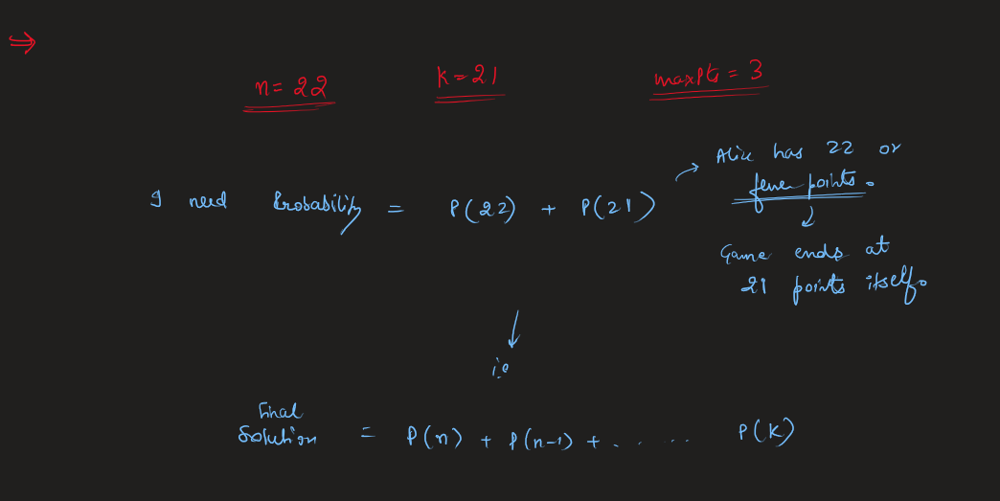\n\n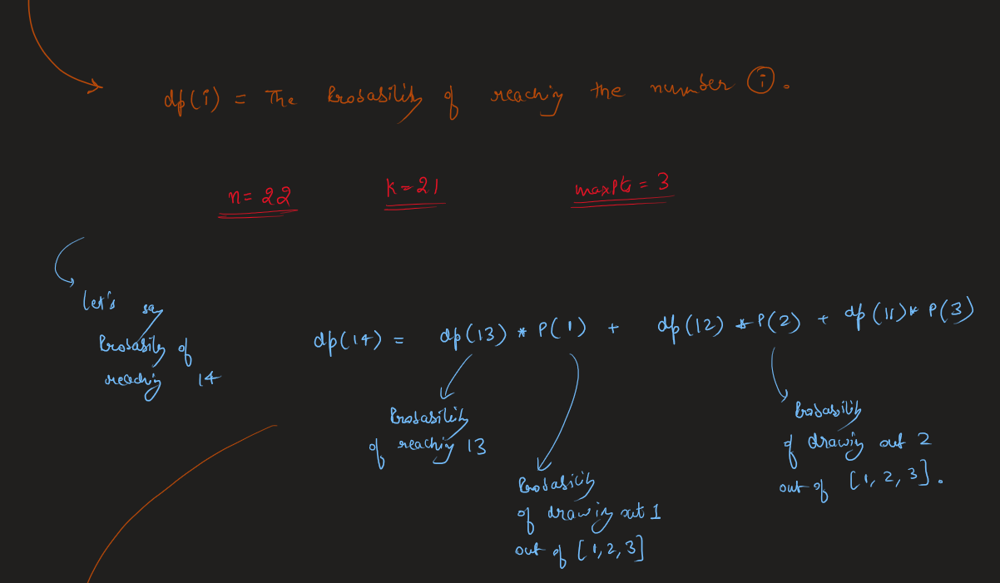\n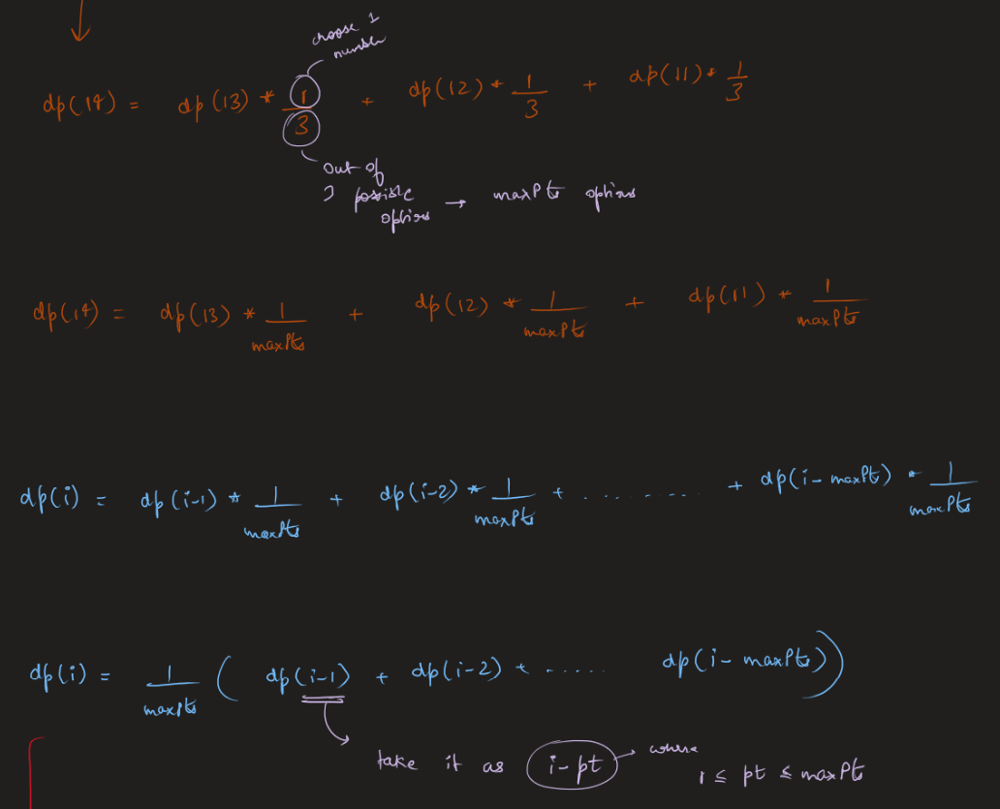\n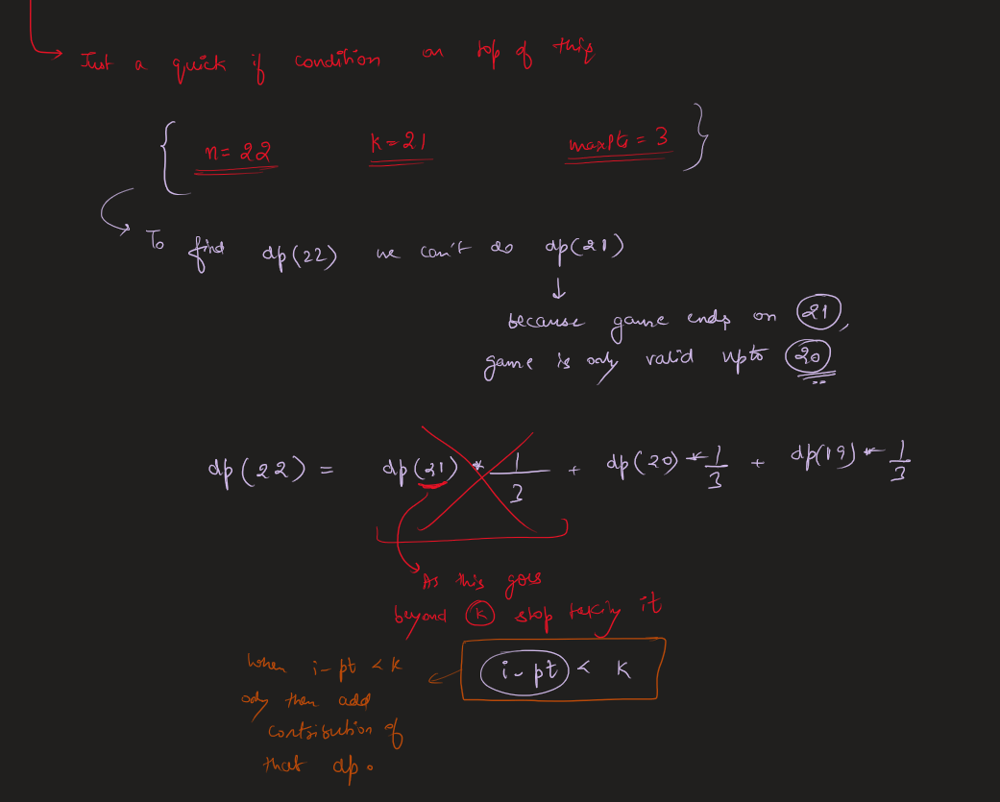\n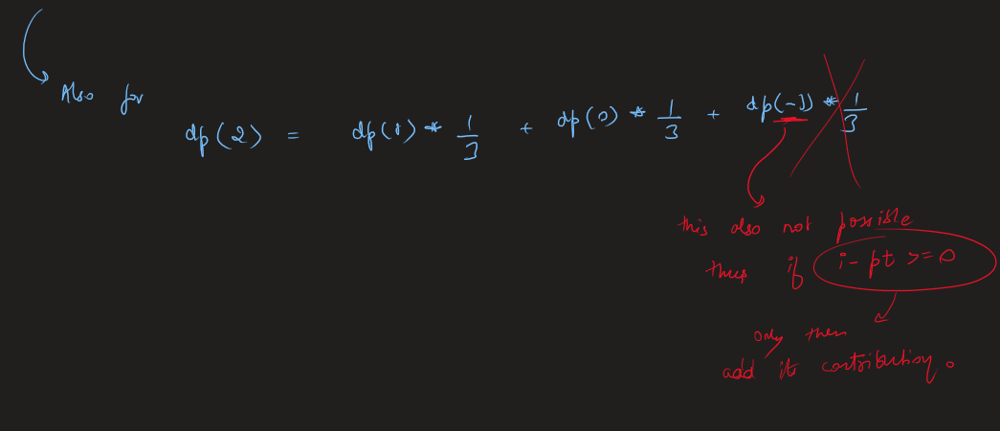\n\n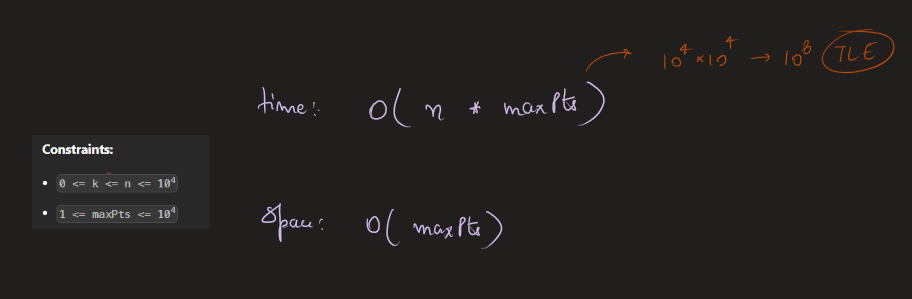\n\n\n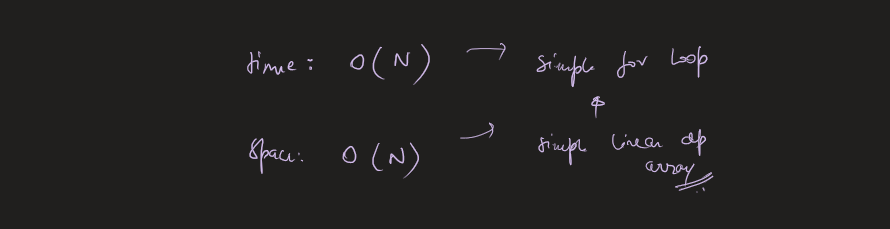\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K-1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n vector<double> dp(N + 1, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if(i < K) windowSum += dp[i];\n else probability += dp[i];\n \n if(i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n};\n```\n```Java []\nclass Solution {\n public double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K - 1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n double[] dp = new double[N + 1];\n Arrays.fill(dp, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if (i < K) windowSum += dp[i];\n else probability += dp[i];\n\n if (i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n}\n```\n```Python []\nclass Solution:\n def new21Game(self, N, K, maxPts):\n # Corner cases\n if K == 0:\n return 1.0\n if N >= K - 1 + maxPts:\n return 1.0\n\n # dp[i] is the probability of getting point i.\n dp = [0.0] * (N + 1)\n\n probability = 0.0 # dp of N or less points.\n windowSum = 1.0 # Sliding required window sum\n dp[0] = 1.0\n for i in range(1, N + 1):\n dp[i] = windowSum / maxPts\n\n if i < K:\n windowSum += dp[i]\n else:\n probability += dp[i]\n\n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n\n return probability\n``` | 70 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Python Easy Solution | new-21-game | 0 | 1 | # Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n``` | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Python Easy Solution | new-21-game | 0 | 1 | # Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n``` | 1 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Diagram & Image Explaination🥇 C++ Full Optimized🔥 DP | Well Explained | new-21-game | 1 | 1 | # Diagram\n<!-- Describe your first thoughts on how to solve this problem. -->\n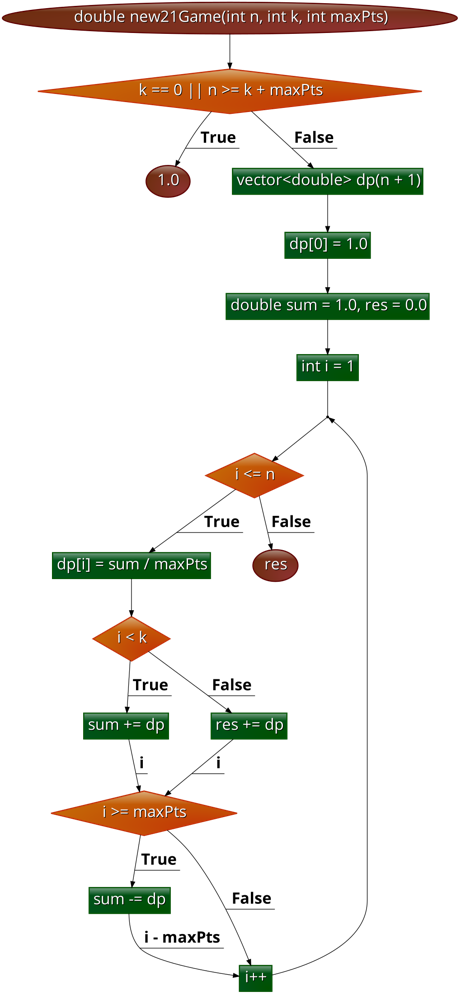\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck if Alice can always get k or more points. If so, return 1.0.\n\nCreate a vector dp of size n + 1 to store the probabilities of getting each point from 0 to n. Initialize dp[0] = 1.0.\n\nInitialize two variables, sum and res, to keep track of the sum of probabilities and the final result, respectively. Set sum = 1.0.\n\nLoop over all possible points from 1 to n. For each point i, calculate the probability of getting that point by taking the sum of the probabilities of getting the previous maxPts points and dividing by maxPts.\n\nIf i < k, add the probability of getting i points to sum.\n\nIf i >= k, add the probability of getting i points to res.\n\nUpdate sum by subtracting the probability of getting the point i - maxPts.\n\nReturn the value of res, which represents the probability of getting n or fewer points in the game.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * maxPts) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double sum = 1.0, res = 0.0;\n for (int i = 1; i <= n; i++) {\n dp[i] = sum / maxPts;\n if (i < k) {\n sum += dp[i];\n } else {\n res += dp[i];\n }\n if (i >= maxPts) {\n sum -= dp[i - maxPts];\n }\n }\n return res;\n }\n};\n\n```\n\n | 7 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Diagram & Image Explaination🥇 C++ Full Optimized🔥 DP | Well Explained | new-21-game | 1 | 1 | # Diagram\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck if Alice can always get k or more points. If so, return 1.0.\n\nCreate a vector dp of size n + 1 to store the probabilities of getting each point from 0 to n. Initialize dp[0] = 1.0.\n\nInitialize two variables, sum and res, to keep track of the sum of probabilities and the final result, respectively. Set sum = 1.0.\n\nLoop over all possible points from 1 to n. For each point i, calculate the probability of getting that point by taking the sum of the probabilities of getting the previous maxPts points and dividing by maxPts.\n\nIf i < k, add the probability of getting i points to sum.\n\nIf i >= k, add the probability of getting i points to res.\n\nUpdate sum by subtracting the probability of getting the point i - maxPts.\n\nReturn the value of res, which represents the probability of getting n or fewer points in the game.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * maxPts) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double sum = 1.0, res = 0.0;\n for (int i = 1; i <= n; i++) {\n dp[i] = sum / maxPts;\n if (i < k) {\n sum += dp[i];\n } else {\n res += dp[i];\n }\n if (i >= maxPts) {\n sum -= dp[i - maxPts];\n }\n }\n return res;\n }\n};\n\n```\n\n | 7 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | new-21-game | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n# Approach:\n\n- If the minimum target points K is 0 or the maximum total points N is greater than or equal to K + W, it is guaranteed to win, so return 1.0.\n- Create a dp array of size N + 1 to store the probabilities. \n- Initialize all elements to 0.0, except dp[0] which is set to 1.0.\n- Initialize windowSum to 1.0 to keep track of the sum of the previous maxPts probabilities.\n- Initialize probability to 0.0 to store the final probability of winning.\n- Iterate from 1 to N and calculate the probabilities using dynamic programming:\n- Update dp[i] as windowSum / maxPts.\n- If i is less than K, add dp[i] to windowSum.\n- If i is greater than or equal to K, add dp[i] to probability.\n- If i - maxPts is greater than or equal to 0, subtract dp[i - maxPts] from windowSum.\n- Return probability as the result.\n# Intuition:\n\n- We can think of the game as a series of draws, where at each draw we can draw any number from 1 to maxPts with equal probability.\n- To calculate the probability of winning, we use dynamic programming to keep track of the probabilities for each point.\n- Starting from point 0, we calculate the probabilities for each subsequent point up to N.\n- At each point i, the probability of reaching that point is the sum of probabilities from the previous maxPts points divided by maxPts.\n- If the current point i is less than K, we add the probability to the windowSum to keep track of the sum of previous probabilities.\n- If the current point i is greater than or equal to K, we add the probability to the probability variable, which represents the final probability of winning.\n- We maintain a sliding window of size maxPts to efficiently calculate the probabilities, removing the probability of the point that falls outside the window and adding the probability of the current point.\n- Finally, we return the probability as the result, which represents the probability of winning the game.\n\n```Python []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k == 0 or n >= k + maxPts:\n return 1.0\n \n windowSum = 1.0\n probability = 0.0\n \n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n```\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n double[] dp = new double[n + 1];\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n vector<double> dp(n + 1, 0.0);\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n};\n\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D | 16 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | new-21-game | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n# Approach:\n\n- If the minimum target points K is 0 or the maximum total points N is greater than or equal to K + W, it is guaranteed to win, so return 1.0.\n- Create a dp array of size N + 1 to store the probabilities. \n- Initialize all elements to 0.0, except dp[0] which is set to 1.0.\n- Initialize windowSum to 1.0 to keep track of the sum of the previous maxPts probabilities.\n- Initialize probability to 0.0 to store the final probability of winning.\n- Iterate from 1 to N and calculate the probabilities using dynamic programming:\n- Update dp[i] as windowSum / maxPts.\n- If i is less than K, add dp[i] to windowSum.\n- If i is greater than or equal to K, add dp[i] to probability.\n- If i - maxPts is greater than or equal to 0, subtract dp[i - maxPts] from windowSum.\n- Return probability as the result.\n# Intuition:\n\n- We can think of the game as a series of draws, where at each draw we can draw any number from 1 to maxPts with equal probability.\n- To calculate the probability of winning, we use dynamic programming to keep track of the probabilities for each point.\n- Starting from point 0, we calculate the probabilities for each subsequent point up to N.\n- At each point i, the probability of reaching that point is the sum of probabilities from the previous maxPts points divided by maxPts.\n- If the current point i is less than K, we add the probability to the windowSum to keep track of the sum of previous probabilities.\n- If the current point i is greater than or equal to K, we add the probability to the probability variable, which represents the final probability of winning.\n- We maintain a sliding window of size maxPts to efficiently calculate the probabilities, removing the probability of the point that falls outside the window and adding the probability of the current point.\n- Finally, we return the probability as the result, which represents the probability of winning the game.\n\n```Python []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k == 0 or n >= k + maxPts:\n return 1.0\n \n windowSum = 1.0\n probability = 0.0\n \n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n```\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n double[] dp = new double[n + 1];\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n vector<double> dp(n + 1, 0.0);\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n};\n\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D | 16 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Give it 2 hours . TRY it yourself for logic building from scratch ! ✔🐱🏍🙌 | new-21-game | 0 | 1 | # Intuition\n##### Build-up for the game :-\n\nIn this game, Alice starts with 0 points and draws numbers randomly. She wants to know the chance of having `n` or fewer points at the end.\n\nTo figure this out, we can use a trick called "counting." We start counting from 0 and keep track of the chance of having each number of points. \n\nWe use a list to remember the chances. At the beginning, the chance of having 0 points is 100% or 1.0. Then we look at the next number, 1, and think about how we can get there. We can get to 1 point by drawing a number from 1 to `maxPts`. We calculate the chances of each of those possibilities and add them up. \n\nNext, we move on to the number 2 and do the same thing. We consider all the ways to get to 2 points, based on the chances we already calculated for the previous numbers.\n\nWe keep doing this for each number up to `n`, using the chances we already know to figure out the chances for the next number.\n\nFinally, we add up all the chances from `k` to `n` to find the overall chance of having `n` or fewer points.\n\nSo, in simple terms, we\'re just counting and keeping track of the chances of having different numbers of points. We use the chances we already calculated to find the chances for the next numbers. By adding up all the chances, we get the answer Alice is looking for.\n\n----\n##### More Intuition in technical terms now :- \n\nIn this game, Alice starts with 0 points and draws numbers randomly until she reaches a certain number of points called `k`. We want to know the probability of Alice having `n` or fewer points at the end of the game.\n\nTo solve this problem, we can use a technique called Dynamic Programming, or DP for short. DP is like a special way of solving problems where we break down a big problem into smaller, easier-to-solve subproblems.\n\nIn this case, we can think of the problem like a puzzle. We start with the smallest subproblem: what is the probability of having 0 points? Since Alice starts with 0 points, the probability is 100% or 1.0.\n\nThen, we move on to the next subproblem: what is the probability of having 1 point? To solve this, we look at all the ways Alice can get 1 point. She can draw a number from 1 to `maxPts`, so we need to consider all those possibilities and calculate the probabilities. Once we know the probabilities of having 0 and 1 point, we can calculate the probability of having 2 points by adding up the probabilities of getting to 2 from the previous points (0 and 1).\n\nWe keep doing this for all the points up to `n`. Each time, we use the probabilities we already calculated for the previous points to calculate the probability for the current point. This is why we use a list or array called `dp` to store the probabilities. `dp` stands for "dynamic programming".\n\nBy building up the probabilities step by step, using the probabilities we already know, we can finally find the probability of having `n` or fewer points.\n\nSo, in summary, we use dynamic programming (DP) to solve this problem because it helps us break down the big problem into smaller, easier-to-solve subproblems. We calculate the probabilities for each point by using the probabilities we already calculated for the previous points. This way, we can find the final probability we\'re looking for.\n\n----\n##### Maths :-\n\nCertainly! Let\'s denote the probability that Alice has exactly `i` points as `P[i]`. We want to calculate the probability that Alice has `n` or fewer points, which can be expressed as:\n\n> P(n) = P[0] + P[1] + P[2] + ... + P[n]\n\nTo calculate `P[i]`, we can use dynamic programming and break it down into subproblems. Here\'s the recursive equation:\n\n> P[i] = (P[i-1] + P[i-2] + ... + P[i-maxPts]) / maxPts\n\nThe above equation states that the probability of having `i` points is equal to the sum of probabilities of reaching the current point from the previous `maxPts` points, divided by `maxPts`. This is because in each draw, Alice gains an integer number of points randomly from the range [1, maxPts] with equal probabilities.\n\nTo calculate `P[i]`, we iterate from 1 to `n` and use the above equation to fill in the probabilities in a dynamic programming array or list. We initialize `P[0] = 1` since Alice starts with 0 points. Then, we calculate `P[1]` using the equation, followed by `P[2]`, and so on, until we reach `P[n]`. Finally, we sum up the probabilities from `P[k]` to `P[n]` to obtain the desired probability.\n\nBy using dynamic programming, we avoid recalculating the same probabilities multiple times, leading to an efficient solution to the problem.\n\n----\n##### Intuition for the code :-\nThe given code calculates the probability that Alice will have `n` or fewer points in the game, where Alice starts with 0 points and draws numbers randomly until she reaches `k` or more points.\n\nHere\'s the intuition behind the code:\n\n1. First, the code checks for a special case where `k` is 0 or `n` is greater than or equal to `k + maxPts`. In these cases, it means that Alice is guaranteed to have `n` or fewer points, so the probability is 1.0. The code returns 1.0 in these cases.\n\n2. If the special cases don\'t apply, the code proceeds to calculate the probability using dynamic programming.\n\n3. A list `dp` is initialized with `n + 1` elements, representing the probabilities of having each number of points from 0 to `n`. All elements are initially set to 0.0, except for `dp[0]`, which is set to 1.0 since Alice starts with 0 points.\n\n4. The loop iterates from 1 to `n`, and for each index `i`, it calculates the probability `dp[i]` of having `i` or fewer points.\n\n5. The probability `dp[i]` is calculated by summing the probabilities of getting to `i` from the previous points. The probability of getting to `i` is equal to the sum of the probabilities of getting to `i - 1`, `i - 2`, ..., `i - maxPts`, divided by `maxPts`.\n\n6. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0 since `dp[0] = 1.0`.\n\n7. Within the loop, if `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n8. If `i - maxPts` is greater than or equal to 0, it means that the window of the previous `maxPts` probabilities has shifted, so the probability at `i - maxPts` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n9. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) since Alice stops drawing numbers when she reaches `k` or more points.\n\nThe code uses dynamic programming to efficiently calculate the probabilities by reusing the results of previous calculations. By iterating through the indices and updating the probabilities based on the previous results, it builds up the probability distribution for the desired range of points. \n\n# Approach\n\nIn this version, the circular buffer is replaced with a simple list `dp`, which stores the probabilities.\n\nHere\'s an explanation of the changes:\n\n1. The `if` condition `n >= k + maxPts` is used to determine whether the probability of winning is guaranteed to be 1. If true, the function directly returns 1.0.\n\n2. Instead of using a circular buffer, a regular list `dp` of size `n + 1` is initialized with all elements set to 0.0. The element `dp[0]` is set to 1.0 to represent the initial probability.\n\n3. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0.\n\n4. The loop iterates from 1 to `n`, and at each iteration, the probability for the current index `i` is calculated as `_sum / maxPts`. The `_sum` is divided by `maxPts` because there are `maxPts` possible outcomes, each with an equal probability of occurring.\n\n5. If `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n6. If `i - maxPts` is greater than or equal to 0, the probability `dp[i - maxPts]` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n7. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) and returned.\n\nThis version eliminates the need for a circular buffer and simplifies the code while maintaining efficiency.\n\n# Complexity\n- **Time complexity** : $$O(n)$$, here n is the value given as input.\n- **Space complexity** : $$O(n)$$, w here n is the value given as input. This is because the code uses a list `dp` of size `n + 1` to store the probabilities for each number of points from 0 to n.\n\nThe loop that iterates from 1 to n has a time complexity of $$O(n)$$. Within the loop, the calculations involve accessing elements of the `dp` list, which has a constant time complexity. Overall, the time complexity of the code is determined by the loop, resulting in $$O(n)$$.\n\nSimilarly, the space complexity is determined by the `dp` list, which has a size of n + 1. Therefore, the space complexity of the code is $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n \'\'\'\n if k == 0 or n >= k + maxPts:\n return 1\n \n windowSum = 1\n probability = 0\n \n dp = [0] * (n + 1)\n dp[0] = 1\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n \'\'\'\n\n# MLE\n\'\'\'\nclass CircularBuffer:\n def __init__(self, min_size):\n self.data = [None] * (1 << self.bit_len(min_size))\n self.mask = len(self.data) - 1\n\n @staticmethod\n def bit_len(min_size):\n return 32 - min_size.bit_length()\n\n def __getitem__(self, index):\n return self.data[index & self.mask]\n\n def __setitem__(self, index, value):\n self.data[index & self.mask] = value\n\n def capacity(self):\n return len(self.data)\n\n def get_mask(self):\n return self.mask\n\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n - k + 1 >= maxPts:\n return 1.0\n\n kFactor = 1.0 / maxPts\n if maxPts + 1 >= n:\n return pow(1 + kFactor, k - 1) / maxPts * (n - k + 1)\n\n dp = CircularBuffer(maxPts + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, k):\n dp[i] = _sum * kFactor\n _sum += dp[i] - dp[i - maxPts]\n\n answer = 0.0\n for i in range(k, n + 1):\n answer += _sum * kFactor\n _sum -= dp[i - maxPts]\n\n return answer\n\'\'\'\n\n# Efficient Solution:-\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n >= k + maxPts:\n return 1.0\n\n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, n + 1):\n dp[i] = _sum / maxPts\n if i < k:\n _sum += dp[i]\n if i - maxPts >= 0:\n _sum -= dp[i - maxPts]\n\n return sum(dp[k:])\n\n``` | 1 | Alice plays the following game, loosely based on the card game **"21 "**.
Alice starts with `0` points and draws numbers while she has less than `k` points. During each draw, she gains an integer number of points randomly from the range `[1, maxPts]`, where `maxPts` is an integer. Each draw is independent and the outcomes have equal probabilities.
Alice stops drawing numbers when she gets `k` **or more points**.
Return the probability that Alice has `n` or fewer points.
Answers within `10-5` of the actual answer are considered accepted.
**Example 1:**
**Input:** n = 10, k = 1, maxPts = 10
**Output:** 1.00000
**Explanation:** Alice gets a single card, then stops.
**Example 2:**
**Input:** n = 6, k = 1, maxPts = 10
**Output:** 0.60000
**Explanation:** Alice gets a single card, then stops.
In 6 out of 10 possibilities, she is at or below 6 points.
**Example 3:**
**Input:** n = 21, k = 17, maxPts = 10
**Output:** 0.73278
**Constraints:**
* `0 <= k <= n <= 104`
* `1 <= maxPts <= 104` | null |
Give it 2 hours . TRY it yourself for logic building from scratch ! ✔🐱🏍🙌 | new-21-game | 0 | 1 | # Intuition\n##### Build-up for the game :-\n\nIn this game, Alice starts with 0 points and draws numbers randomly. She wants to know the chance of having `n` or fewer points at the end.\n\nTo figure this out, we can use a trick called "counting." We start counting from 0 and keep track of the chance of having each number of points. \n\nWe use a list to remember the chances. At the beginning, the chance of having 0 points is 100% or 1.0. Then we look at the next number, 1, and think about how we can get there. We can get to 1 point by drawing a number from 1 to `maxPts`. We calculate the chances of each of those possibilities and add them up. \n\nNext, we move on to the number 2 and do the same thing. We consider all the ways to get to 2 points, based on the chances we already calculated for the previous numbers.\n\nWe keep doing this for each number up to `n`, using the chances we already know to figure out the chances for the next number.\n\nFinally, we add up all the chances from `k` to `n` to find the overall chance of having `n` or fewer points.\n\nSo, in simple terms, we\'re just counting and keeping track of the chances of having different numbers of points. We use the chances we already calculated to find the chances for the next numbers. By adding up all the chances, we get the answer Alice is looking for.\n\n----\n##### More Intuition in technical terms now :- \n\nIn this game, Alice starts with 0 points and draws numbers randomly until she reaches a certain number of points called `k`. We want to know the probability of Alice having `n` or fewer points at the end of the game.\n\nTo solve this problem, we can use a technique called Dynamic Programming, or DP for short. DP is like a special way of solving problems where we break down a big problem into smaller, easier-to-solve subproblems.\n\nIn this case, we can think of the problem like a puzzle. We start with the smallest subproblem: what is the probability of having 0 points? Since Alice starts with 0 points, the probability is 100% or 1.0.\n\nThen, we move on to the next subproblem: what is the probability of having 1 point? To solve this, we look at all the ways Alice can get 1 point. She can draw a number from 1 to `maxPts`, so we need to consider all those possibilities and calculate the probabilities. Once we know the probabilities of having 0 and 1 point, we can calculate the probability of having 2 points by adding up the probabilities of getting to 2 from the previous points (0 and 1).\n\nWe keep doing this for all the points up to `n`. Each time, we use the probabilities we already calculated for the previous points to calculate the probability for the current point. This is why we use a list or array called `dp` to store the probabilities. `dp` stands for "dynamic programming".\n\nBy building up the probabilities step by step, using the probabilities we already know, we can finally find the probability of having `n` or fewer points.\n\nSo, in summary, we use dynamic programming (DP) to solve this problem because it helps us break down the big problem into smaller, easier-to-solve subproblems. We calculate the probabilities for each point by using the probabilities we already calculated for the previous points. This way, we can find the final probability we\'re looking for.\n\n----\n##### Maths :-\n\nCertainly! Let\'s denote the probability that Alice has exactly `i` points as `P[i]`. We want to calculate the probability that Alice has `n` or fewer points, which can be expressed as:\n\n> P(n) = P[0] + P[1] + P[2] + ... + P[n]\n\nTo calculate `P[i]`, we can use dynamic programming and break it down into subproblems. Here\'s the recursive equation:\n\n> P[i] = (P[i-1] + P[i-2] + ... + P[i-maxPts]) / maxPts\n\nThe above equation states that the probability of having `i` points is equal to the sum of probabilities of reaching the current point from the previous `maxPts` points, divided by `maxPts`. This is because in each draw, Alice gains an integer number of points randomly from the range [1, maxPts] with equal probabilities.\n\nTo calculate `P[i]`, we iterate from 1 to `n` and use the above equation to fill in the probabilities in a dynamic programming array or list. We initialize `P[0] = 1` since Alice starts with 0 points. Then, we calculate `P[1]` using the equation, followed by `P[2]`, and so on, until we reach `P[n]`. Finally, we sum up the probabilities from `P[k]` to `P[n]` to obtain the desired probability.\n\nBy using dynamic programming, we avoid recalculating the same probabilities multiple times, leading to an efficient solution to the problem.\n\n----\n##### Intuition for the code :-\nThe given code calculates the probability that Alice will have `n` or fewer points in the game, where Alice starts with 0 points and draws numbers randomly until she reaches `k` or more points.\n\nHere\'s the intuition behind the code:\n\n1. First, the code checks for a special case where `k` is 0 or `n` is greater than or equal to `k + maxPts`. In these cases, it means that Alice is guaranteed to have `n` or fewer points, so the probability is 1.0. The code returns 1.0 in these cases.\n\n2. If the special cases don\'t apply, the code proceeds to calculate the probability using dynamic programming.\n\n3. A list `dp` is initialized with `n + 1` elements, representing the probabilities of having each number of points from 0 to `n`. All elements are initially set to 0.0, except for `dp[0]`, which is set to 1.0 since Alice starts with 0 points.\n\n4. The loop iterates from 1 to `n`, and for each index `i`, it calculates the probability `dp[i]` of having `i` or fewer points.\n\n5. The probability `dp[i]` is calculated by summing the probabilities of getting to `i` from the previous points. The probability of getting to `i` is equal to the sum of the probabilities of getting to `i - 1`, `i - 2`, ..., `i - maxPts`, divided by `maxPts`.\n\n6. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0 since `dp[0] = 1.0`.\n\n7. Within the loop, if `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n8. If `i - maxPts` is greater than or equal to 0, it means that the window of the previous `maxPts` probabilities has shifted, so the probability at `i - maxPts` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n9. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) since Alice stops drawing numbers when she reaches `k` or more points.\n\nThe code uses dynamic programming to efficiently calculate the probabilities by reusing the results of previous calculations. By iterating through the indices and updating the probabilities based on the previous results, it builds up the probability distribution for the desired range of points. \n\n# Approach\n\nIn this version, the circular buffer is replaced with a simple list `dp`, which stores the probabilities.\n\nHere\'s an explanation of the changes:\n\n1. The `if` condition `n >= k + maxPts` is used to determine whether the probability of winning is guaranteed to be 1. If true, the function directly returns 1.0.\n\n2. Instead of using a circular buffer, a regular list `dp` of size `n + 1` is initialized with all elements set to 0.0. The element `dp[0]` is set to 1.0 to represent the initial probability.\n\n3. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0.\n\n4. The loop iterates from 1 to `n`, and at each iteration, the probability for the current index `i` is calculated as `_sum / maxPts`. The `_sum` is divided by `maxPts` because there are `maxPts` possible outcomes, each with an equal probability of occurring.\n\n5. If `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n6. If `i - maxPts` is greater than or equal to 0, the probability `dp[i - maxPts]` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n7. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) and returned.\n\nThis version eliminates the need for a circular buffer and simplifies the code while maintaining efficiency.\n\n# Complexity\n- **Time complexity** : $$O(n)$$, here n is the value given as input.\n- **Space complexity** : $$O(n)$$, w here n is the value given as input. This is because the code uses a list `dp` of size `n + 1` to store the probabilities for each number of points from 0 to n.\n\nThe loop that iterates from 1 to n has a time complexity of $$O(n)$$. Within the loop, the calculations involve accessing elements of the `dp` list, which has a constant time complexity. Overall, the time complexity of the code is determined by the loop, resulting in $$O(n)$$.\n\nSimilarly, the space complexity is determined by the `dp` list, which has a size of n + 1. Therefore, the space complexity of the code is $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n \'\'\'\n if k == 0 or n >= k + maxPts:\n return 1\n \n windowSum = 1\n probability = 0\n \n dp = [0] * (n + 1)\n dp[0] = 1\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n \'\'\'\n\n# MLE\n\'\'\'\nclass CircularBuffer:\n def __init__(self, min_size):\n self.data = [None] * (1 << self.bit_len(min_size))\n self.mask = len(self.data) - 1\n\n @staticmethod\n def bit_len(min_size):\n return 32 - min_size.bit_length()\n\n def __getitem__(self, index):\n return self.data[index & self.mask]\n\n def __setitem__(self, index, value):\n self.data[index & self.mask] = value\n\n def capacity(self):\n return len(self.data)\n\n def get_mask(self):\n return self.mask\n\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n - k + 1 >= maxPts:\n return 1.0\n\n kFactor = 1.0 / maxPts\n if maxPts + 1 >= n:\n return pow(1 + kFactor, k - 1) / maxPts * (n - k + 1)\n\n dp = CircularBuffer(maxPts + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, k):\n dp[i] = _sum * kFactor\n _sum += dp[i] - dp[i - maxPts]\n\n answer = 0.0\n for i in range(k, n + 1):\n answer += _sum * kFactor\n _sum -= dp[i - maxPts]\n\n return answer\n\'\'\'\n\n# Efficient Solution:-\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n >= k + maxPts:\n return 1.0\n\n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, n + 1):\n dp[i] = _sum / maxPts\n if i < k:\n _sum += dp[i]\n if i - maxPts >= 0:\n _sum -= dp[i - maxPts]\n\n return sum(dp[k:])\n\n``` | 1 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Solution | push-dominoes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string pushDominoes(string s) {\n string ans=s;\n int n=ans.size(),r=-1;\n for(int i=0; i<n; i++) {\n if(s[i]==\'L\' && r==-1) {\n for(int l=i-1; l>=0 && s[l]==\'.\'; l--) {\n ans[l]=\'L\';\n }\n }\n else if(s[i]==\'R\') {\n while(r!=-1 && r<i)\n ans[r++]=\'R\';\n r=i;\n }\n else if(s[i]==\'L\') {\n int l=i;\n while(r<l) {\n ans[r++]=\'R\';\n ans[l--]=\'L\';\n }\n r=-1;\n }\n }\n while(r!=-1 && r<n)\n ans[r++]=\'R\';\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n arr = list(dominoes)\n n = len(arr)\n l = r = -1\n for i, c in enumerate(arr):\n if c is \'.\':\n continue\n if c is \'L\':\n if l >= r:\n while l < i:\n l += 1\n arr[l] = \'L\'\n else:\n l = i\n lo, hi = r + 1, l - 1\n while lo < hi:\n arr[lo] = \'R\'\n arr[hi] = \'L\'\n lo += 1\n hi -= 1\n else:\n if r > l:\n while r < i:\n arr[r] = \'R\'\n r += 1\n else:\n r = i\n if r > l:\n while r < n:\n arr[r] = \'R\'\n r += 1\n \n return \'\'.join(arr)\n```\n\n```Java []\nclass Solution {\n public String pushDominoes(String dominoes) {\n char[] dos = dominoes.toCharArray();\n int left = \'L\';\n int i = 0;\n while(i<dos.length){\n if(dos[i] == \'.\'){\n int j = i;\n while(j<dos.length && dos[j] == \'.\'){\n j++;\n }\n int right = j>=dos.length? \'R\': dos[j];\n if(right == left){\n while(i < j){\n dos[i++] = (char)right;\n }\n }else if(right == \'R\'){\n i = j-1;\n }else{\n j--;\n while(i < j){\n dos[i++] = (char)left;\n dos[j--] = (char)right;\n }\n }\n left = right;\n }else{\n left = dos[i];\n }\n i++;\n }\n return new String(dos);\n }\n public String pushDominoes1(String dominoes) {\n StringBuilder sb = new StringBuilder();\n char[] dos = dominoes.toCharArray();\n Stack<Character> stack = new Stack<>();\n int lastRight = -1;\n int lastLeft = -1;\n\n for(int i = 0; i<dos.length;){\n if(dos[i] == \'R\'){\n while(i<dos.length && dos[i] != \'L\'){\n stack.push(\'R\');\n if(dos[i] == \'R\'){\n lastRight = i;\n }\n i++;\n }\n }else if(dos[i] == \'L\'){\n int numOfPop = 0;\n if(lastLeft == -1 && lastRight == -1){\n numOfPop = i;\n }else{\n numOfPop = lastLeft > lastRight? (i- lastLeft):(i-lastRight)/2;\n }\n int count = numOfPop;\n while(count > 0){\n stack.pop();\n count--;\n }\n if(lastRight != -1 && lastRight > lastLeft && (i-lastRight)%2 == 0 && numOfPop >= 1) {\n stack.push(\'.\');\n numOfPop--;\n }\n while(count < numOfPop){\n stack.push(\'L\');\n count++;\n }\n stack.push(\'L\');\n lastLeft = i;\n i++;\n }else{\n stack.push(dos[i]);\n i++;\n }\n }\n while(!stack.isEmpty()){\n sb.append(stack.pop());\n }\n return sb.reverse().toString();\n }\n}\n```\n | 1 | There are `n` dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string `dominoes` representing the initial state where:
* `dominoes[i] = 'L'`, if the `ith` domino has been pushed to the left,
* `dominoes[i] = 'R'`, if the `ith` domino has been pushed to the right, and
* `dominoes[i] = '.'`, if the `ith` domino has not been pushed.
Return _a string representing the final state_.
**Example 1:**
**Input:** dominoes = "RR.L "
**Output:** "RR.L "
**Explanation:** The first domino expends no additional force on the second domino.
**Example 2:**
**Input:** dominoes = ".L.R...LR..L.. "
**Output:** "LL.RR.LLRRLL.. "
**Constraints:**
* `n == dominoes.length`
* `1 <= n <= 105`
* `dominoes[i]` is either `'L'`, `'R'`, or `'.'`. | null |
Solution | push-dominoes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string pushDominoes(string s) {\n string ans=s;\n int n=ans.size(),r=-1;\n for(int i=0; i<n; i++) {\n if(s[i]==\'L\' && r==-1) {\n for(int l=i-1; l>=0 && s[l]==\'.\'; l--) {\n ans[l]=\'L\';\n }\n }\n else if(s[i]==\'R\') {\n while(r!=-1 && r<i)\n ans[r++]=\'R\';\n r=i;\n }\n else if(s[i]==\'L\') {\n int l=i;\n while(r<l) {\n ans[r++]=\'R\';\n ans[l--]=\'L\';\n }\n r=-1;\n }\n }\n while(r!=-1 && r<n)\n ans[r++]=\'R\';\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n arr = list(dominoes)\n n = len(arr)\n l = r = -1\n for i, c in enumerate(arr):\n if c is \'.\':\n continue\n if c is \'L\':\n if l >= r:\n while l < i:\n l += 1\n arr[l] = \'L\'\n else:\n l = i\n lo, hi = r + 1, l - 1\n while lo < hi:\n arr[lo] = \'R\'\n arr[hi] = \'L\'\n lo += 1\n hi -= 1\n else:\n if r > l:\n while r < i:\n arr[r] = \'R\'\n r += 1\n else:\n r = i\n if r > l:\n while r < n:\n arr[r] = \'R\'\n r += 1\n \n return \'\'.join(arr)\n```\n\n```Java []\nclass Solution {\n public String pushDominoes(String dominoes) {\n char[] dos = dominoes.toCharArray();\n int left = \'L\';\n int i = 0;\n while(i<dos.length){\n if(dos[i] == \'.\'){\n int j = i;\n while(j<dos.length && dos[j] == \'.\'){\n j++;\n }\n int right = j>=dos.length? \'R\': dos[j];\n if(right == left){\n while(i < j){\n dos[i++] = (char)right;\n }\n }else if(right == \'R\'){\n i = j-1;\n }else{\n j--;\n while(i < j){\n dos[i++] = (char)left;\n dos[j--] = (char)right;\n }\n }\n left = right;\n }else{\n left = dos[i];\n }\n i++;\n }\n return new String(dos);\n }\n public String pushDominoes1(String dominoes) {\n StringBuilder sb = new StringBuilder();\n char[] dos = dominoes.toCharArray();\n Stack<Character> stack = new Stack<>();\n int lastRight = -1;\n int lastLeft = -1;\n\n for(int i = 0; i<dos.length;){\n if(dos[i] == \'R\'){\n while(i<dos.length && dos[i] != \'L\'){\n stack.push(\'R\');\n if(dos[i] == \'R\'){\n lastRight = i;\n }\n i++;\n }\n }else if(dos[i] == \'L\'){\n int numOfPop = 0;\n if(lastLeft == -1 && lastRight == -1){\n numOfPop = i;\n }else{\n numOfPop = lastLeft > lastRight? (i- lastLeft):(i-lastRight)/2;\n }\n int count = numOfPop;\n while(count > 0){\n stack.pop();\n count--;\n }\n if(lastRight != -1 && lastRight > lastLeft && (i-lastRight)%2 == 0 && numOfPop >= 1) {\n stack.push(\'.\');\n numOfPop--;\n }\n while(count < numOfPop){\n stack.push(\'L\');\n count++;\n }\n stack.push(\'L\');\n lastLeft = i;\n i++;\n }else{\n stack.push(dos[i]);\n i++;\n }\n }\n while(!stack.isEmpty()){\n sb.append(stack.pop());\n }\n return sb.reverse().toString();\n }\n}\n```\n | 1 | Given a positive integer `n`, find and return _the **longest distance** between any two **adjacent**_ `1`_'s in the binary representation of_ `n`_. If there are no two adjacent_ `1`_'s, return_ `0`_._
Two `1`'s are **adjacent** if there are only `0`'s separating them (possibly no `0`'s). The **distance** between two `1`'s is the absolute difference between their bit positions. For example, the two `1`'s in `"1001 "` have a distance of 3.
**Example 1:**
**Input:** n = 22
**Output:** 2
**Explanation:** 22 in binary is "10110 ".
The first adjacent pair of 1's is "10110 " with a distance of 2.
The second adjacent pair of 1's is "10110 " with a distance of 1.
The answer is the largest of these two distances, which is 2.
Note that "10110 " is not a valid pair since there is a 1 separating the two 1's underlined.
**Example 2:**
**Input:** n = 8
**Output:** 0
**Explanation:** 8 in binary is "1000 ".
There are not any adjacent pairs of 1's in the binary representation of 8, so we return 0.
**Example 3:**
**Input:** n = 5
**Output:** 2
**Explanation:** 5 in binary is "101 ".
**Constraints:**
* `1 <= n <= 109` | null |
[Python3] Multi-source BFS | push-dominoes | 0 | 1 | I know that a lot of great solutions have been discussed in the discussion, but I want to share mine as well -- a multi-source BFS solution.\n\nThe idea is pretty straightforward, we first add all position where the initial forces happen (i.e. add all "L" and "R"), and then does BFS.\n\nNotice that we need to take special care of collisions, so we need to modify BFS a littile bit. Here is my solution.\n\nSpace Complexity: O(N) because each position will only be added to the queue or to the collision dictionary once.\nTime Complexity: O(N) because we loop through each element once.\n\n```\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n ans = [\'.\' for _ in range(len(dominoes))]\n\n queue = deque()\n for i, d in enumerate(dominoes):\n if d == \'L\' or d == \'R\':\n queue.append((i, d))\n ans[i] = d\n \n while queue:\n size = len(queue)\n collision = defaultdict(list)\n for _ in range(size):\n i, d = queue.popleft()\n if d == \'L\' and i - 1 >= 0 and ans[i - 1] == \'.\':\n collision[i - 1].append(\'L\')\n elif d == \'R\' and i + 1 < len(ans) and ans[i + 1] == \'.\':\n collision[i + 1].append(\'R\')\n for pos in collision:\n if len(collision[pos]) == 2:\n ans[pos] = \'.\'\n else:\n ans[pos] = collision[pos][0]\n queue.append((pos, collision[pos][0]))\n \n return \'\'.join(ans)\n``` | 2 | There are `n` dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string `dominoes` representing the initial state where:
* `dominoes[i] = 'L'`, if the `ith` domino has been pushed to the left,
* `dominoes[i] = 'R'`, if the `ith` domino has been pushed to the right, and
* `dominoes[i] = '.'`, if the `ith` domino has not been pushed.
Return _a string representing the final state_.
**Example 1:**
**Input:** dominoes = "RR.L "
**Output:** "RR.L "
**Explanation:** The first domino expends no additional force on the second domino.
**Example 2:**
**Input:** dominoes = ".L.R...LR..L.. "
**Output:** "LL.RR.LLRRLL.. "
**Constraints:**
* `n == dominoes.length`
* `1 <= n <= 105`
* `dominoes[i]` is either `'L'`, `'R'`, or `'.'`. | null |
[Python3] Multi-source BFS | push-dominoes | 0 | 1 | I know that a lot of great solutions have been discussed in the discussion, but I want to share mine as well -- a multi-source BFS solution.\n\nThe idea is pretty straightforward, we first add all position where the initial forces happen (i.e. add all "L" and "R"), and then does BFS.\n\nNotice that we need to take special care of collisions, so we need to modify BFS a littile bit. Here is my solution.\n\nSpace Complexity: O(N) because each position will only be added to the queue or to the collision dictionary once.\nTime Complexity: O(N) because we loop through each element once.\n\n```\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n ans = [\'.\' for _ in range(len(dominoes))]\n\n queue = deque()\n for i, d in enumerate(dominoes):\n if d == \'L\' or d == \'R\':\n queue.append((i, d))\n ans[i] = d\n \n while queue:\n size = len(queue)\n collision = defaultdict(list)\n for _ in range(size):\n i, d = queue.popleft()\n if d == \'L\' and i - 1 >= 0 and ans[i - 1] == \'.\':\n collision[i - 1].append(\'L\')\n elif d == \'R\' and i + 1 < len(ans) and ans[i + 1] == \'.\':\n collision[i + 1].append(\'R\')\n for pos in collision:\n if len(collision[pos]) == 2:\n ans[pos] = \'.\'\n else:\n ans[pos] = collision[pos][0]\n queue.append((pos, collision[pos][0]))\n \n return \'\'.join(ans)\n``` | 2 | Given a positive integer `n`, find and return _the **longest distance** between any two **adjacent**_ `1`_'s in the binary representation of_ `n`_. If there are no two adjacent_ `1`_'s, return_ `0`_._
Two `1`'s are **adjacent** if there are only `0`'s separating them (possibly no `0`'s). The **distance** between two `1`'s is the absolute difference between their bit positions. For example, the two `1`'s in `"1001 "` have a distance of 3.
**Example 1:**
**Input:** n = 22
**Output:** 2
**Explanation:** 22 in binary is "10110 ".
The first adjacent pair of 1's is "10110 " with a distance of 2.
The second adjacent pair of 1's is "10110 " with a distance of 1.
The answer is the largest of these two distances, which is 2.
Note that "10110 " is not a valid pair since there is a 1 separating the two 1's underlined.
**Example 2:**
**Input:** n = 8
**Output:** 0
**Explanation:** 8 in binary is "1000 ".
There are not any adjacent pairs of 1's in the binary representation of 8, so we return 0.
**Example 3:**
**Input:** n = 5
**Output:** 2
**Explanation:** 5 in binary is "101 ".
**Constraints:**
* `1 <= n <= 109` | null |
Simple python solution | push-dominoes | 0 | 1 | ```\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n n = len(dominoes)\n \n right_force = [0] * n\n \n for i in range(n):\n if dominoes[i] == \'R\':\n right_force[i] = n\n elif dominoes[i] == \'L\':\n right_force[i] = 0\n else:\n if(i-1 >= 0):\n right_force[i] = max(right_force[i-1]-1, 0)\n\n left_force = [0] * n\n \n for i in range(n-1, -1, -1):\n if dominoes[i] == \'L\':\n left_force[i] = n\n elif dominoes[i] == \'R\':\n left_force[i] = 0\n else:\n if(i+1 < n):\n left_force[i] = max(left_force[i+1]-1, 0)\n \n return \'\'.join(\'.\' if right_force[i] == left_force[i] else \'R\' if right_force[i] > left_force[i] else \'L\' for i in range(n))\n \n``` | 1 | There are `n` dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string `dominoes` representing the initial state where:
* `dominoes[i] = 'L'`, if the `ith` domino has been pushed to the left,
* `dominoes[i] = 'R'`, if the `ith` domino has been pushed to the right, and
* `dominoes[i] = '.'`, if the `ith` domino has not been pushed.
Return _a string representing the final state_.
**Example 1:**
**Input:** dominoes = "RR.L "
**Output:** "RR.L "
**Explanation:** The first domino expends no additional force on the second domino.
**Example 2:**
**Input:** dominoes = ".L.R...LR..L.. "
**Output:** "LL.RR.LLRRLL.. "
**Constraints:**
* `n == dominoes.length`
* `1 <= n <= 105`
* `dominoes[i]` is either `'L'`, `'R'`, or `'.'`. | null |
Simple python solution | push-dominoes | 0 | 1 | ```\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n n = len(dominoes)\n \n right_force = [0] * n\n \n for i in range(n):\n if dominoes[i] == \'R\':\n right_force[i] = n\n elif dominoes[i] == \'L\':\n right_force[i] = 0\n else:\n if(i-1 >= 0):\n right_force[i] = max(right_force[i-1]-1, 0)\n\n left_force = [0] * n\n \n for i in range(n-1, -1, -1):\n if dominoes[i] == \'L\':\n left_force[i] = n\n elif dominoes[i] == \'R\':\n left_force[i] = 0\n else:\n if(i+1 < n):\n left_force[i] = max(left_force[i+1]-1, 0)\n \n return \'\'.join(\'.\' if right_force[i] == left_force[i] else \'R\' if right_force[i] > left_force[i] else \'L\' for i in range(n))\n \n``` | 1 | Given a positive integer `n`, find and return _the **longest distance** between any two **adjacent**_ `1`_'s in the binary representation of_ `n`_. If there are no two adjacent_ `1`_'s, return_ `0`_._
Two `1`'s are **adjacent** if there are only `0`'s separating them (possibly no `0`'s). The **distance** between two `1`'s is the absolute difference between their bit positions. For example, the two `1`'s in `"1001 "` have a distance of 3.
**Example 1:**
**Input:** n = 22
**Output:** 2
**Explanation:** 22 in binary is "10110 ".
The first adjacent pair of 1's is "10110 " with a distance of 2.
The second adjacent pair of 1's is "10110 " with a distance of 1.
The answer is the largest of these two distances, which is 2.
Note that "10110 " is not a valid pair since there is a 1 separating the two 1's underlined.
**Example 2:**
**Input:** n = 8
**Output:** 0
**Explanation:** 8 in binary is "1000 ".
There are not any adjacent pairs of 1's in the binary representation of 8, so we return 0.
**Example 3:**
**Input:** n = 5
**Output:** 2
**Explanation:** 5 in binary is "101 ".
**Constraints:**
* `1 <= n <= 109` | null |
Python | Neetcode | Queue Traversal | push-dominoes | 0 | 1 | ```\nfrom collections import deque\n\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n \n q=deque()\n dominoes=list(dominoes)\n for a,i in enumerate(dominoes):\n if i=="L"or i=="R":\n q.append((i,a))\n \n # print(q)\n \n while(q):\n val,ind=q.popleft()\n \n if val=="R" and ind+1<len(dominoes) and dominoes[ind+1]==".":\n if q and q[0][0]=="L" and ind+2==q[0][1]:\n q.popleft()\n else:\n dominoes[ind+1]="R"\n q.append(("R",ind+1))\n \n \n elif val=="L" and ind>0 and dominoes[ind-1]==".":\n dominoes[ind-1]="L"\n q.append(("L",ind-1))\n \n return "".join(dominoes)\n \n \n \n``` | 1 | There are `n` dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string `dominoes` representing the initial state where:
* `dominoes[i] = 'L'`, if the `ith` domino has been pushed to the left,
* `dominoes[i] = 'R'`, if the `ith` domino has been pushed to the right, and
* `dominoes[i] = '.'`, if the `ith` domino has not been pushed.
Return _a string representing the final state_.
**Example 1:**
**Input:** dominoes = "RR.L "
**Output:** "RR.L "
**Explanation:** The first domino expends no additional force on the second domino.
**Example 2:**
**Input:** dominoes = ".L.R...LR..L.. "
**Output:** "LL.RR.LLRRLL.. "
**Constraints:**
* `n == dominoes.length`
* `1 <= n <= 105`
* `dominoes[i]` is either `'L'`, `'R'`, or `'.'`. | null |
Python | Neetcode | Queue Traversal | push-dominoes | 0 | 1 | ```\nfrom collections import deque\n\nclass Solution:\n def pushDominoes(self, dominoes: str) -> str:\n \n q=deque()\n dominoes=list(dominoes)\n for a,i in enumerate(dominoes):\n if i=="L"or i=="R":\n q.append((i,a))\n \n # print(q)\n \n while(q):\n val,ind=q.popleft()\n \n if val=="R" and ind+1<len(dominoes) and dominoes[ind+1]==".":\n if q and q[0][0]=="L" and ind+2==q[0][1]:\n q.popleft()\n else:\n dominoes[ind+1]="R"\n q.append(("R",ind+1))\n \n \n elif val=="L" and ind>0 and dominoes[ind-1]==".":\n dominoes[ind-1]="L"\n q.append(("L",ind-1))\n \n return "".join(dominoes)\n \n \n \n``` | 1 | Given a positive integer `n`, find and return _the **longest distance** between any two **adjacent**_ `1`_'s in the binary representation of_ `n`_. If there are no two adjacent_ `1`_'s, return_ `0`_._
Two `1`'s are **adjacent** if there are only `0`'s separating them (possibly no `0`'s). The **distance** between two `1`'s is the absolute difference between their bit positions. For example, the two `1`'s in `"1001 "` have a distance of 3.
**Example 1:**
**Input:** n = 22
**Output:** 2
**Explanation:** 22 in binary is "10110 ".
The first adjacent pair of 1's is "10110 " with a distance of 2.
The second adjacent pair of 1's is "10110 " with a distance of 1.
The answer is the largest of these two distances, which is 2.
Note that "10110 " is not a valid pair since there is a 1 separating the two 1's underlined.
**Example 2:**
**Input:** n = 8
**Output:** 0
**Explanation:** 8 in binary is "1000 ".
There are not any adjacent pairs of 1's in the binary representation of 8, so we return 0.
**Example 3:**
**Input:** n = 5
**Output:** 2
**Explanation:** 5 in binary is "101 ".
**Constraints:**
* `1 <= n <= 109` | null |
python 3 - dsu + union by rank + path compression | similar-string-groups | 0 | 1 | # Intuition\nThe word "group" in description -> think about DSU is good intuition.\n\nOptimize:\n- skip checking if you know 2 strings are already in the same group\n- if >2 letter differences are found between 2 strings, stop checking because they are not the same group\n\n(When I first saw this question, I thought my answer\'s time complexity was too large that it couldn\'t get accepted. But turnout it passed...)\n\n# Approach\nDSU\n\n# Complexity\n- Time complexity:\nO(ll * ll * lw * inverse ackermann function of ll) -> triple loops on DSU structure\n\n- Space complexity:\nO(ll) -> dsu structure\'s space\n\nll = len of strs\nlw = len of strs[0]\n\n# Code\n```\nclass DSU:\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n\n def find(self, node):\n if self.par[node] != node:\n self.par[node] = self.find(self.par[node])\n return self.par[node]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if self.rank[px] > self.rank[py]: # py to px\n self.rank[px] += self.rank[py]\n self.par[py] = px\n else: # px to py\n self.rank[py] += self.rank[px]\n self.par[px] = py\n\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n\n ls = len(strs)\n dsu = DSU(ls)\n\n for i in range(ls):\n\n for j in range(i + 1, ls):\n\n \n if dsu.par[i] == dsu.par[j]: # same group\n continue\n \n diff = 0\n for k in range(len(strs[0])):\n if strs[i][k] != strs[j][k]:\n diff += 1\n if diff > 2: # not same group\n break\n if diff <= 2:\n dsu.union(i, j)\n \n for i in range(ls):\n dsu.find(i)\n \n return len(set(dsu.par))\n``` | 3 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
python 3 - dsu + union by rank + path compression | similar-string-groups | 0 | 1 | # Intuition\nThe word "group" in description -> think about DSU is good intuition.\n\nOptimize:\n- skip checking if you know 2 strings are already in the same group\n- if >2 letter differences are found between 2 strings, stop checking because they are not the same group\n\n(When I first saw this question, I thought my answer\'s time complexity was too large that it couldn\'t get accepted. But turnout it passed...)\n\n# Approach\nDSU\n\n# Complexity\n- Time complexity:\nO(ll * ll * lw * inverse ackermann function of ll) -> triple loops on DSU structure\n\n- Space complexity:\nO(ll) -> dsu structure\'s space\n\nll = len of strs\nlw = len of strs[0]\n\n# Code\n```\nclass DSU:\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n\n def find(self, node):\n if self.par[node] != node:\n self.par[node] = self.find(self.par[node])\n return self.par[node]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if self.rank[px] > self.rank[py]: # py to px\n self.rank[px] += self.rank[py]\n self.par[py] = px\n else: # px to py\n self.rank[py] += self.rank[px]\n self.par[px] = py\n\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n\n ls = len(strs)\n dsu = DSU(ls)\n\n for i in range(ls):\n\n for j in range(i + 1, ls):\n\n \n if dsu.par[i] == dsu.par[j]: # same group\n continue\n \n diff = 0\n for k in range(len(strs[0])):\n if strs[i][k] != strs[j][k]:\n diff += 1\n if diff > 2: # not same group\n break\n if diff <= 2:\n dsu.union(i, j)\n \n for i in range(ls):\n dsu.find(i)\n \n return len(set(dsu.par))\n``` | 3 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
[Python] Graph solution | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou can think this problem as calculating the number of connected graph.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a function that check 2 strings is similar.\nIf similiar connect them.\nUse BFS(or DFS or Unionfind ...) calculate the number of connected graph.\n\n# Complexity\n$$n$$ is the number of the string.\n$$m$$ is the length of string.\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2*m)$$\n\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nfrom collections import deque\n\ndef compare(s1, s2):\n N = len(s1)\n idx1 = -1\n idx2 = -1\n for i in range(N):\n ch1, ch2 = s1[i], s2[i]\n if ch1 != ch2:\n if idx1 == -1:\n idx1 = i\n elif idx2 == -1:\n idx2 = i\n else:\n return False\n\n if idx1 == -1:\n return True\n\n if idx2 == -1:\n return False\n\n return s1[idx1] == s2[idx2] and s1[idx2] == s2[idx1]\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n N = len(strs)\n graph = [[] for _ in range(N)]\n for i in range(N):\n for j in range(i+1, N):\n if compare(strs[i], strs[j]):\n graph[i].append(j)\n graph[j].append(i)\n\n visited = [False for _ in range(N)] \n ans = 0\n for i in range(N):\n if visited[i]:\n continue\n ans += 1 \n q = deque([i])\n while len(q) > 0:\n u = q.popleft()\n if visited[u]:\n continue\n visited[u] = True\n for v in graph[u]:\n if visited[v]:\n continue\n q.append(v) \n\n return ans\n\n``` | 2 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
[Python] Graph solution | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nYou can think this problem as calculating the number of connected graph.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCreate a function that check 2 strings is similar.\nIf similiar connect them.\nUse BFS(or DFS or Unionfind ...) calculate the number of connected graph.\n\n# Complexity\n$$n$$ is the number of the string.\n$$m$$ is the length of string.\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2*m)$$\n\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nfrom collections import deque\n\ndef compare(s1, s2):\n N = len(s1)\n idx1 = -1\n idx2 = -1\n for i in range(N):\n ch1, ch2 = s1[i], s2[i]\n if ch1 != ch2:\n if idx1 == -1:\n idx1 = i\n elif idx2 == -1:\n idx2 = i\n else:\n return False\n\n if idx1 == -1:\n return True\n\n if idx2 == -1:\n return False\n\n return s1[idx1] == s2[idx2] and s1[idx2] == s2[idx1]\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n N = len(strs)\n graph = [[] for _ in range(N)]\n for i in range(N):\n for j in range(i+1, N):\n if compare(strs[i], strs[j]):\n graph[i].append(j)\n graph[j].append(i)\n\n visited = [False for _ in range(N)] \n ans = 0\n for i in range(N):\n if visited[i]:\n continue\n ans += 1 \n q = deque([i])\n while len(q) > 0:\n u = q.popleft()\n if visited[u]:\n continue\n visited[u] = True\n for v in graph[u]:\n if visited[v]:\n continue\n q.append(v) \n\n return ans\n\n``` | 2 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Python3 beats 95.41% 🚀🚀 with explanation || quibler7 | similar-string-groups | 0 | 1 | \n\n\n\n# Code\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n def similar(a: str, b: str):\n diff1 = -1\n diff2 = -1\n\n for i in range(len(a)):\n if a[i] != b[i]:\n if diff1 == -1: diff1 = i\n elif diff2 == -1: diff2 = i\n else: return False #thirs diff has been found. \n # We know there are exactly 0 or 2 differences now since a and b\n # are defined by the problem to be anagrams\n return True\n \n # List of groups (2D List of Lists of strings)\n groupList = []\n\n # (2) Iterate through input list of strings\n for s in strs:\n # Variable for group assignment of s\n foundGroup = -1\n\n for i, group in enumerate(groupList):\n # (3) Iterate through groups to search for similar strings to s\n for s2 in group:\n if similar(s, s2):\n # (4) We\'ve found our first similar string\n if foundGroup == -1:\n # Assign s to group i\n foundGroup = i\n groupList[i].append(s)\n break\n # (5) We\'ve found another similar string\n else:\n # Combine group foundGroup and group i\n groupList[foundGroup] = groupList[foundGroup] + groupList[i]\n del groupList[i]\n break\n\n # (6) No similar string found in groups, add new group\n if foundGroup == -1:\n groupList.append([s])\n\n # (7) Profit\n return len(groupList)\n``` | 2 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Python3 beats 95.41% 🚀🚀 with explanation || quibler7 | similar-string-groups | 0 | 1 | \n\n\n\n# Code\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n def similar(a: str, b: str):\n diff1 = -1\n diff2 = -1\n\n for i in range(len(a)):\n if a[i] != b[i]:\n if diff1 == -1: diff1 = i\n elif diff2 == -1: diff2 = i\n else: return False #thirs diff has been found. \n # We know there are exactly 0 or 2 differences now since a and b\n # are defined by the problem to be anagrams\n return True\n \n # List of groups (2D List of Lists of strings)\n groupList = []\n\n # (2) Iterate through input list of strings\n for s in strs:\n # Variable for group assignment of s\n foundGroup = -1\n\n for i, group in enumerate(groupList):\n # (3) Iterate through groups to search for similar strings to s\n for s2 in group:\n if similar(s, s2):\n # (4) We\'ve found our first similar string\n if foundGroup == -1:\n # Assign s to group i\n foundGroup = i\n groupList[i].append(s)\n break\n # (5) We\'ve found another similar string\n else:\n # Combine group foundGroup and group i\n groupList[foundGroup] = groupList[foundGroup] + groupList[i]\n del groupList[i]\n break\n\n # (6) No similar string found in groups, add new group\n if foundGroup == -1:\n groupList.append([s])\n\n # (7) Profit\n return len(groupList)\n``` | 2 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Solution | similar-string-groups | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isNeighbor(string &a, string &b) {\n int diff = 0;\n for (int i = 0; i < a.size(); i++) {\n if (a[i] != b[i])\n if (++diff > 2) return false;\n }\n return true;\n }\n int numSimilarGroups(vector<string>& strs) {\n int n = strs.size();\n vector<vector<int>> g(n);\n for (int i = 0; i < n - 1; i++)\n for (int j = i+1; j < n; j++) {\n if (isNeighbor(strs[i], strs[j])) {\n g[i].push_back(j);\n g[j].push_back(i);\n }\n }\n vector<bool> v(n, false);\n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (v[i] == false) {\n dfs(g, v, i);\n ans++;\n }\n }\n return ans;\n }\n void dfs(vector<vector<int>>& g, vector<bool>& v, int x) {\n v[x] = true;\n for (int adj: g[x])\n if (v[adj] == false)\n dfs(g, v, adj);\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def similar(self, x, y):\n cnt = 0\n for i in range(len(x)):\n if x[i] != y[i]:\n cnt += 1\n if cnt > 2:\n return False\n return True \n\n def numSimilarGroups(self, A: List[str]) -> int:\n wordlen = len(A[0])\n A = set(A)\n divs = defaultdict(list)\n if wordlen > 6:\n for word in A:\n step = wordlen // 3\n for i in range(0, step * 3, step):\n divs[word[i:i+step] + str(i)].append(word)\n else:\n divs[\'all\'].extend(A)\n \n graph = defaultdict(set)\n for _list in divs.values():\n for i, a in enumerate(_list):\n for j, b in enumerate(_list[i+1:], i+1):\n if self.similar(a, b):\n graph[a].add(b)\n graph[b].add(a)\n ans = 0 \n cc = set()\n for word in A:\n if word not in cc:\n queue = [word]\n while queue:\n cur = queue.pop()\n cc.add(cur)\n for nx in graph[cur]:\n if nx not in cc:\n queue.append(nx)\n ans += 1\n return ans \n```\n\n```Java []\nclass Solution {\n char[][] ss;\n public int numSimilarGroups(String[] strs) {\n int ans = 0;\n boolean[] seen = new boolean[strs.length];\n\n ss = new char[strs.length][];\n for (int i = 0; i < strs.length; i++) \n ss[i] = strs[i].toCharArray();\n\n for (int i = 0; i < strs.length; ++i)\n if (!seen[i]) {\n dfs(strs, i, seen);\n ++ans;\n }\n return ans; \n }\n private void dfs(final String[] strs, int i, boolean[] seen) {\n seen[i] = true;\n for (int j = 0; j < strs.length; ++j)\n if (!seen[j] && isSimilar(i, j)){\n dfs(strs, j, seen);\n }\n }\n private boolean isSimilar( int s1, int s2) {\n char[] st1 = ss[s1];\n char[] st2 = ss[s2];\n int diff = 0;\n for (int i = 0; i < st1.length; ++i)\n if (st1[i] != st2[i] && ++diff > 2)\n return false;\n return true;\n }\n}\n```\n | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Solution | similar-string-groups | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isNeighbor(string &a, string &b) {\n int diff = 0;\n for (int i = 0; i < a.size(); i++) {\n if (a[i] != b[i])\n if (++diff > 2) return false;\n }\n return true;\n }\n int numSimilarGroups(vector<string>& strs) {\n int n = strs.size();\n vector<vector<int>> g(n);\n for (int i = 0; i < n - 1; i++)\n for (int j = i+1; j < n; j++) {\n if (isNeighbor(strs[i], strs[j])) {\n g[i].push_back(j);\n g[j].push_back(i);\n }\n }\n vector<bool> v(n, false);\n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (v[i] == false) {\n dfs(g, v, i);\n ans++;\n }\n }\n return ans;\n }\n void dfs(vector<vector<int>>& g, vector<bool>& v, int x) {\n v[x] = true;\n for (int adj: g[x])\n if (v[adj] == false)\n dfs(g, v, adj);\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def similar(self, x, y):\n cnt = 0\n for i in range(len(x)):\n if x[i] != y[i]:\n cnt += 1\n if cnt > 2:\n return False\n return True \n\n def numSimilarGroups(self, A: List[str]) -> int:\n wordlen = len(A[0])\n A = set(A)\n divs = defaultdict(list)\n if wordlen > 6:\n for word in A:\n step = wordlen // 3\n for i in range(0, step * 3, step):\n divs[word[i:i+step] + str(i)].append(word)\n else:\n divs[\'all\'].extend(A)\n \n graph = defaultdict(set)\n for _list in divs.values():\n for i, a in enumerate(_list):\n for j, b in enumerate(_list[i+1:], i+1):\n if self.similar(a, b):\n graph[a].add(b)\n graph[b].add(a)\n ans = 0 \n cc = set()\n for word in A:\n if word not in cc:\n queue = [word]\n while queue:\n cur = queue.pop()\n cc.add(cur)\n for nx in graph[cur]:\n if nx not in cc:\n queue.append(nx)\n ans += 1\n return ans \n```\n\n```Java []\nclass Solution {\n char[][] ss;\n public int numSimilarGroups(String[] strs) {\n int ans = 0;\n boolean[] seen = new boolean[strs.length];\n\n ss = new char[strs.length][];\n for (int i = 0; i < strs.length; i++) \n ss[i] = strs[i].toCharArray();\n\n for (int i = 0; i < strs.length; ++i)\n if (!seen[i]) {\n dfs(strs, i, seen);\n ++ans;\n }\n return ans; \n }\n private void dfs(final String[] strs, int i, boolean[] seen) {\n seen[i] = true;\n for (int j = 0; j < strs.length; ++j)\n if (!seen[j] && isSimilar(i, j)){\n dfs(strs, j, seen);\n }\n }\n private boolean isSimilar( int s1, int s2) {\n char[] st1 = ss[s1];\n char[] st2 = ss[s2];\n int diff = 0;\n for (int i = 0; i < st1.length; ++i)\n if (st1[i] != st2[i] && ++diff > 2)\n return false;\n return true;\n }\n}\n```\n | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
python 🐍 | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\uD83D\uDC0D PLZ UPVOTE\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n map_str= set(strs)\n res, visited = 0, set()\n for strs in map_str:\n if strs in visited:\n continue\n res += 1\n q = deque([strs])\n visited.add(strs)\n while(q):\n for _ in range(len(q)):\n s = q.popleft()\n for nxt in map_str:\n if nxt!=s and nxt not in visited:\n d = sum([s[i]!=nxt[i] for i in range(len(s))])\n if d==2:\n q.append(nxt)\n visited.add(nxt)\n \n return res\n``` | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
python 🐍 | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\uD83D\uDC0D PLZ UPVOTE\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n map_str= set(strs)\n res, visited = 0, set()\n for strs in map_str:\n if strs in visited:\n continue\n res += 1\n q = deque([strs])\n visited.add(strs)\n while(q):\n for _ in range(len(q)):\n s = q.popleft()\n for nxt in map_str:\n if nxt!=s and nxt not in visited:\n d = sum([s[i]!=nxt[i] for i in range(len(s))])\n if d==2:\n q.append(nxt)\n visited.add(nxt)\n \n return res\n``` | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
not easy to undrstand | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef check(tg,i,dc,dctg):\n if(dctg[i]!=-1):\n return\n dctg[i]=tg\n for a in dc[i]:\n check(tg,a,dc,dctg)\ndef fun(s1,s2):\n k=0\n for i in range(len(s1)):\n if(s1[i]!=s2[i]):\n k+=1\n return k<=2\n\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n ans=0\n dc=defaultdict(lambda:[])\n dctg=defaultdict(lambda:-1)\n gn=1\n for i in range(len(strs)):\n for j in range(i+1,len(strs)):\n if(fun(strs[i],strs[j])):\n dc[i].append(j)\n dc[j].append(i)\n\n tg=1\n # print(dc)\n for i in range(len(strs)):\n if(dctg[i]==-1):\n check(tg,i,dc,dctg)\n tg+=1\n return tg-1\n\n``` | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
not easy to undrstand | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef check(tg,i,dc,dctg):\n if(dctg[i]!=-1):\n return\n dctg[i]=tg\n for a in dc[i]:\n check(tg,a,dc,dctg)\ndef fun(s1,s2):\n k=0\n for i in range(len(s1)):\n if(s1[i]!=s2[i]):\n k+=1\n return k<=2\n\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n ans=0\n dc=defaultdict(lambda:[])\n dctg=defaultdict(lambda:-1)\n gn=1\n for i in range(len(strs)):\n for j in range(i+1,len(strs)):\n if(fun(strs[i],strs[j])):\n dc[i].append(j)\n dc[j].append(i)\n\n tg=1\n # print(dc)\n for i in range(len(strs)):\n if(dctg[i]==-1):\n check(tg,i,dc,dctg)\n tg+=1\n return tg-1\n\n``` | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Python easy working solution | similar-string-groups | 0 | 1 | \n\n# Code\n```\nclass UnionFindSet:\n def __init__(self, n):\n self.parents = list(range(n))\n \n def find(self, x):\n if self.parents[x] != x:\n return self.find(self.parents[x])\n return x\n \n def union(self, u, v):\n self.parents[self.find(u)] = self.find(v)\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int: \n def isSimilar(s, t):\n swaps = 0\n l, r = 0, len(s) - 1\n while l <= r:\n if (s[l] != t[l] and s[r] != t[r]):\n if s[l] != t[r] or s[r] != t[l]: return False\n l += 1\n r -= 1\n swaps += 1\n if s[l] == t[l]: l += 1\n if s[r] == t[r]: r -= 1\n return swaps <= 1\n\n seen = UnionFindSet(len(strs))\n for i in range(len(strs)):\n for j in range(len(strs)):\n if isSimilar(strs[i], strs[j]):\n seen.union(i, j)\n\n parents = set()\n for i in range(len(strs)):\n parent = seen.find(i)\n if parent not in parents:\n parents.add(parent)\n\n return len(set(parents))\n``` | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Python easy working solution | similar-string-groups | 0 | 1 | \n\n# Code\n```\nclass UnionFindSet:\n def __init__(self, n):\n self.parents = list(range(n))\n \n def find(self, x):\n if self.parents[x] != x:\n return self.find(self.parents[x])\n return x\n \n def union(self, u, v):\n self.parents[self.find(u)] = self.find(v)\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int: \n def isSimilar(s, t):\n swaps = 0\n l, r = 0, len(s) - 1\n while l <= r:\n if (s[l] != t[l] and s[r] != t[r]):\n if s[l] != t[r] or s[r] != t[l]: return False\n l += 1\n r -= 1\n swaps += 1\n if s[l] == t[l]: l += 1\n if s[r] == t[r]: r -= 1\n return swaps <= 1\n\n seen = UnionFindSet(len(strs))\n for i in range(len(strs)):\n for j in range(len(strs)):\n if isSimilar(strs[i], strs[j]):\n seen.union(i, j)\n\n parents = set()\n for i in range(len(strs)):\n parent = seen.find(i)\n if parent not in parents:\n parents.add(parent)\n\n return len(set(parents))\n``` | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Simple Solution that Actually Works! (Union Find Python3) | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe gotta use union find\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUnion find\n\n# Complexity\nnot complex\n\n# Code\n```\nclass UnionFindSet:\n def __init__(self, n):\n self.parents = list(range(n))\n \n def find(self, x):\n if self.parents[x] != x:\n return self.find(self.parents[x])\n return x\n \n def union(self, u, v):\n self.parents[self.find(u)] = self.find(v)\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int: \n def isSimilar(s, t):\n swaps = 0\n l, r = 0, len(s) - 1\n while l <= r:\n if (s[l] != t[l] and s[r] != t[r]):\n if s[l] != t[r] or s[r] != t[l]: return False\n l += 1\n r -= 1\n swaps += 1\n if s[l] == t[l]: l += 1\n if s[r] == t[r]: r -= 1\n return swaps <= 1\n\n seen = UnionFindSet(len(strs))\n for i in range(len(strs)):\n for j in range(len(strs)):\n if isSimilar(strs[i], strs[j]):\n seen.union(i, j)\n\n parents = set()\n for i in range(len(strs)):\n parent = seen.find(i)\n if parent not in parents:\n parents.add(parent)\n\n return len(set(parents))\n``` | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Simple Solution that Actually Works! (Union Find Python3) | similar-string-groups | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe gotta use union find\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUnion find\n\n# Complexity\nnot complex\n\n# Code\n```\nclass UnionFindSet:\n def __init__(self, n):\n self.parents = list(range(n))\n \n def find(self, x):\n if self.parents[x] != x:\n return self.find(self.parents[x])\n return x\n \n def union(self, u, v):\n self.parents[self.find(u)] = self.find(v)\n\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int: \n def isSimilar(s, t):\n swaps = 0\n l, r = 0, len(s) - 1\n while l <= r:\n if (s[l] != t[l] and s[r] != t[r]):\n if s[l] != t[r] or s[r] != t[l]: return False\n l += 1\n r -= 1\n swaps += 1\n if s[l] == t[l]: l += 1\n if s[r] == t[r]: r -= 1\n return swaps <= 1\n\n seen = UnionFindSet(len(strs))\n for i in range(len(strs)):\n for j in range(len(strs)):\n if isSimilar(strs[i], strs[j]):\n seen.union(i, j)\n\n parents = set()\n for i in range(len(strs)):\n parent = seen.find(i)\n if parent not in parents:\n parents.add(parent)\n\n return len(set(parents))\n``` | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Python Beats 96% Easy Solution Only Arrays Explained | similar-string-groups | 0 | 1 | # Intuition\nAt a high level, the algorithm needs to be able to:\n1. Compare strings to each other for similarity\n2. Go through the strings and assign them to groups\n3. Combine groups if necessary, when we process a new string with similarities to multiple groups\n\n\n# Approach\n1. Create helper function to check if two strings are similar\n2. Iterate through all of the strings\n3. For each string, compare it to strings in a list of groups we maintain\n4. If we find a similarity, assign the string to a group\n5. Continue to search the rest of the groups for similarities, and combine groups if found\n6. If string not assigned, create a new group\n7. Return the number of groups\n\nStep numbers added to code comments.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n # (1) Helper function to check if two strings are similar\n def similar(a: str, b: str):\n # Indices of different letters\n diff1 = -1\n diff2 = -1\n\n for i in range(len(a)):\n if a[i] != b[i]:\n if diff1 == -1:\n diff1 = i\n elif diff2 == -1:\n diff2 = i\n else:\n # A third difference has been found\n return False\n\n # We know there are exactly 0 or 2 differences now since a and b\n # are defined by the problem to be anagrams\n return True\n \n # List of groups (2D List of Lists of strings)\n groupList = []\n\n # (2) Iterate through input list of strings\n for s in strs:\n # Variable for group assignment of s\n foundGroup = -1\n\n for i, group in enumerate(groupList):\n # (3) Iterate through groups to search for similar strings to s\n for s2 in group:\n if similar(s, s2):\n # (4) We\'ve found our first similar string\n if foundGroup == -1:\n # Assign s to group i\n foundGroup = i\n groupList[i].append(s)\n break\n # (5) We\'ve found another similar string\n else:\n # Combine group foundGroup and group i\n groupList[foundGroup] = groupList[foundGroup] + groupList[i]\n del groupList[i]\n break\n\n # (6) No similar string found in groups, add new group\n if foundGroup == -1:\n groupList.append([s])\n\n # (7) Profit\n return len(groupList)\n``` | 1 | Two strings `X` and `Y` are similar if we can swap two letters (in different positions) of `X`, so that it equals `Y`. Also two strings `X` and `Y` are similar if they are equal.
For example, `"tars "` and `"rats "` are similar (swapping at positions `0` and `2`), and `"rats "` and `"arts "` are similar, but `"star "` is not similar to `"tars "`, `"rats "`, or `"arts "`.
Together, these form two connected groups by similarity: `{ "tars ", "rats ", "arts "}` and `{ "star "}`. Notice that `"tars "` and `"arts "` are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.
We are given a list `strs` of strings where every string in `strs` is an anagram of every other string in `strs`. How many groups are there?
**Example 1:**
**Input:** strs = \[ "tars ", "rats ", "arts ", "star "\]
**Output:** 2
**Example 2:**
**Input:** strs = \[ "omv ", "ovm "\]
**Output:** 1
**Constraints:**
* `1 <= strs.length <= 300`
* `1 <= strs[i].length <= 300`
* `strs[i]` consists of lowercase letters only.
* All words in `strs` have the same length and are anagrams of each other. | null |
Python Beats 96% Easy Solution Only Arrays Explained | similar-string-groups | 0 | 1 | # Intuition\nAt a high level, the algorithm needs to be able to:\n1. Compare strings to each other for similarity\n2. Go through the strings and assign them to groups\n3. Combine groups if necessary, when we process a new string with similarities to multiple groups\n\n\n# Approach\n1. Create helper function to check if two strings are similar\n2. Iterate through all of the strings\n3. For each string, compare it to strings in a list of groups we maintain\n4. If we find a similarity, assign the string to a group\n5. Continue to search the rest of the groups for similarities, and combine groups if found\n6. If string not assigned, create a new group\n7. Return the number of groups\n\nStep numbers added to code comments.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```\nclass Solution:\n def numSimilarGroups(self, strs: List[str]) -> int:\n # (1) Helper function to check if two strings are similar\n def similar(a: str, b: str):\n # Indices of different letters\n diff1 = -1\n diff2 = -1\n\n for i in range(len(a)):\n if a[i] != b[i]:\n if diff1 == -1:\n diff1 = i\n elif diff2 == -1:\n diff2 = i\n else:\n # A third difference has been found\n return False\n\n # We know there are exactly 0 or 2 differences now since a and b\n # are defined by the problem to be anagrams\n return True\n \n # List of groups (2D List of Lists of strings)\n groupList = []\n\n # (2) Iterate through input list of strings\n for s in strs:\n # Variable for group assignment of s\n foundGroup = -1\n\n for i, group in enumerate(groupList):\n # (3) Iterate through groups to search for similar strings to s\n for s2 in group:\n if similar(s, s2):\n # (4) We\'ve found our first similar string\n if foundGroup == -1:\n # Assign s to group i\n foundGroup = i\n groupList[i].append(s)\n break\n # (5) We\'ve found another similar string\n else:\n # Combine group foundGroup and group i\n groupList[foundGroup] = groupList[foundGroup] + groupList[i]\n del groupList[i]\n break\n\n # (6) No similar string found in groups, add new group\n if foundGroup == -1:\n groupList.append([s])\n\n # (7) Profit\n return len(groupList)\n``` | 1 | You are given an integer `n`. We reorder the digits in any order (including the original order) such that the leading digit is not zero.
Return `true` _if and only if we can do this so that the resulting number is a power of two_.
**Example 1:**
**Input:** n = 1
**Output:** true
**Example 2:**
**Input:** n = 10
**Output:** false
**Constraints:**
* `1 <= n <= 109` | null |
Solution | magic-squares-in-grid | 1 | 1 | ```C++ []\n#define DO(...) { __VA_ARGS__ do\n#define WHILE(...) while(__VA_ARGS__); }\n\nclass Solution {\n typedef unsigned int uInt;\n typedef const uInt c_uInt;\n static constexpr uInt\n magicSize = 3, magicSizeM1 = magicSize - 1;\n bool contained[10];\n bool isMagicSqr (const vector<vector<int>> &grid, c_uInt c_row, c_uInt c_col) {\n uInt sum, targetSum;\n DO ( uInt row = 0; ) {\n sum = 0;\n DO ( uInt col = 0; ) {\n uInt num = grid[c_row + row][c_col + col];\n if ((1 <= num) && (num <= 9)) {} else return false;\n bool &hasNum = contained[num];\n if (hasNum) return false;\n hasNum = true; sum += num;\n } WHILE (++col < magicSize);\n if (row) {\n if (targetSum != sum) return false;\n } else { targetSum = sum; }\n } WHILE (++row < magicSize);\n DO ( uInt col = 0; ) {\n sum = 0;\n DO ( uInt row = 0; ) {\n sum += grid[c_row + row][c_col + col];\n } WHILE (++row < magicSize);\n if (targetSum != sum) return false;\n } WHILE (++col < magicSize);\n sum = 0;\n DO ( uInt ctr = 0; ) {\n sum += grid[c_row + ctr][c_col + ctr];\n } WHILE (++ctr < magicSize);\n if (targetSum != sum) return false;\n sum = 0;\n DO ( uInt ctr = 0; ) {\n sum += grid[c_row + magicSizeM1 - ctr][c_col + ctr];\n } WHILE (++ctr < magicSize);\n return (targetSum == sum);\n }\npublic:\n uInt numMagicSquaresInside(const vector<vector<int>> &grid) {\n uInt magicCnt = 0;\n c_uInt rowCnt = grid.size(), colCnt = grid[0].size();\n for (uInt lstRow = magicSizeM1; lstRow < rowCnt; lstRow++) {\n for (uInt lstCol = magicSizeM1; lstCol < colCnt; lstCol++) {\n fill(contained + 1, contained + 10, false);\n if (isMagicSqr(grid, lstRow - magicSizeM1, lstCol - magicSizeM1)) { ++magicCnt; }\n }\n }\n return magicCnt;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n count = 0\n numset=set(range(1,10))\n for rowix in range(1,len(grid)-1):\n row =grid[rowix]\n fiveix = [ix for ix in range(1, len(row)-1) if row[ix] == 5]\n for five in fiveix:\n subgrid = [row[five-1:five+2] for row in grid]\n subgrid = subgrid[rowix-1:rowix+2]\n\n flatgrid=set([item for row in subgrid for item in row])\n diff = numset-flatgrid\n \n row_sum = [1 if sum(row)==15 else 0 for row in subgrid]\n col_sum = [1 if sum(col)==15 else 0 for col in zip(*subgrid)]\n if sum(row_sum) == 3 and sum(col_sum)==3 and len(diff)==0:\n count +=1\n \n return count\n```\n\n```Java []\nclass Solution {\n public int numMagicSquaresInside(int[][] grid) {\n if(grid.length < 3 || grid[0].length < 3) return 0;\n \n int magicBoxCount = 0;\n for(int i=0; i<=(grid.length-3); i++){\n for(int j=0; (j<=grid[0].length-3); j++){\n if(isAMagicBox(grid, i, j)) \n magicBoxCount++;\n }\n }\n return magicBoxCount;\n }\n private boolean isAMagicBox(int[][] grid, int x, int y){\n if(grid[x+1][y+1] != 5) return false;\n \n if(grid[x][y] %2 != 0 || grid[x+2][y] %2 != 0 ||\n grid[x][y+2] %2 != 0 || grid[x+2][y+2] %2 != 0 )\n {\n return false;\n }\n if(grid[x+1][y] %2 == 0 || grid[x][y+1] %2 == 0 ||\n grid[x+1][y+2] %2 == 0 || grid[x+2][y+1] %2 == 0 )\n {\n return false;\n }\n if ( (grid[x][y] + grid[x][y+1] + grid[x][y+2]) != 15 || \n (grid[x+2][y] + grid[x+2][y+1] + grid[x+2][y+2]) != 15 ||\n (grid[x][y] + grid[x+1][y] + grid[x+2][y]) != 15)\n {\n return false;\n }\n return true; \n }\n}\n```\n | 1 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Solution | magic-squares-in-grid | 1 | 1 | ```C++ []\n#define DO(...) { __VA_ARGS__ do\n#define WHILE(...) while(__VA_ARGS__); }\n\nclass Solution {\n typedef unsigned int uInt;\n typedef const uInt c_uInt;\n static constexpr uInt\n magicSize = 3, magicSizeM1 = magicSize - 1;\n bool contained[10];\n bool isMagicSqr (const vector<vector<int>> &grid, c_uInt c_row, c_uInt c_col) {\n uInt sum, targetSum;\n DO ( uInt row = 0; ) {\n sum = 0;\n DO ( uInt col = 0; ) {\n uInt num = grid[c_row + row][c_col + col];\n if ((1 <= num) && (num <= 9)) {} else return false;\n bool &hasNum = contained[num];\n if (hasNum) return false;\n hasNum = true; sum += num;\n } WHILE (++col < magicSize);\n if (row) {\n if (targetSum != sum) return false;\n } else { targetSum = sum; }\n } WHILE (++row < magicSize);\n DO ( uInt col = 0; ) {\n sum = 0;\n DO ( uInt row = 0; ) {\n sum += grid[c_row + row][c_col + col];\n } WHILE (++row < magicSize);\n if (targetSum != sum) return false;\n } WHILE (++col < magicSize);\n sum = 0;\n DO ( uInt ctr = 0; ) {\n sum += grid[c_row + ctr][c_col + ctr];\n } WHILE (++ctr < magicSize);\n if (targetSum != sum) return false;\n sum = 0;\n DO ( uInt ctr = 0; ) {\n sum += grid[c_row + magicSizeM1 - ctr][c_col + ctr];\n } WHILE (++ctr < magicSize);\n return (targetSum == sum);\n }\npublic:\n uInt numMagicSquaresInside(const vector<vector<int>> &grid) {\n uInt magicCnt = 0;\n c_uInt rowCnt = grid.size(), colCnt = grid[0].size();\n for (uInt lstRow = magicSizeM1; lstRow < rowCnt; lstRow++) {\n for (uInt lstCol = magicSizeM1; lstCol < colCnt; lstCol++) {\n fill(contained + 1, contained + 10, false);\n if (isMagicSqr(grid, lstRow - magicSizeM1, lstCol - magicSizeM1)) { ++magicCnt; }\n }\n }\n return magicCnt;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n count = 0\n numset=set(range(1,10))\n for rowix in range(1,len(grid)-1):\n row =grid[rowix]\n fiveix = [ix for ix in range(1, len(row)-1) if row[ix] == 5]\n for five in fiveix:\n subgrid = [row[five-1:five+2] for row in grid]\n subgrid = subgrid[rowix-1:rowix+2]\n\n flatgrid=set([item for row in subgrid for item in row])\n diff = numset-flatgrid\n \n row_sum = [1 if sum(row)==15 else 0 for row in subgrid]\n col_sum = [1 if sum(col)==15 else 0 for col in zip(*subgrid)]\n if sum(row_sum) == 3 and sum(col_sum)==3 and len(diff)==0:\n count +=1\n \n return count\n```\n\n```Java []\nclass Solution {\n public int numMagicSquaresInside(int[][] grid) {\n if(grid.length < 3 || grid[0].length < 3) return 0;\n \n int magicBoxCount = 0;\n for(int i=0; i<=(grid.length-3); i++){\n for(int j=0; (j<=grid[0].length-3); j++){\n if(isAMagicBox(grid, i, j)) \n magicBoxCount++;\n }\n }\n return magicBoxCount;\n }\n private boolean isAMagicBox(int[][] grid, int x, int y){\n if(grid[x+1][y+1] != 5) return false;\n \n if(grid[x][y] %2 != 0 || grid[x+2][y] %2 != 0 ||\n grid[x][y+2] %2 != 0 || grid[x+2][y+2] %2 != 0 )\n {\n return false;\n }\n if(grid[x+1][y] %2 == 0 || grid[x][y+1] %2 == 0 ||\n grid[x+1][y+2] %2 == 0 || grid[x+2][y+1] %2 == 0 )\n {\n return false;\n }\n if ( (grid[x][y] + grid[x][y+1] + grid[x][y+2]) != 15 || \n (grid[x+2][y] + grid[x+2][y+1] + grid[x+2][y+2]) != 15 ||\n (grid[x][y] + grid[x+1][y] + grid[x+2][y]) != 15)\n {\n return false;\n }\n return true; \n }\n}\n```\n | 1 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Beats 100%, approach explained. | magic-squares-in-grid | 1 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA 3x3 magic square is a square grid of numbers arranged in such a way that the sum of the numbers in each row, each column, and both main diagonals is the same. In the case of a 3x3 magic square, this sum is always equal to **15**. Additionally, the middle number in the square is always **5**. Let\'s prove these properties.\n\n1. **Property 1: Sum of numbers in a row, column, or diagonal is 15**\n\nConsider the following 3x3 magic square:\n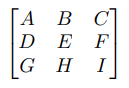\nLet `S` be the sum of the numbers in the magic square.\nThe sum of the rows is equal to :\n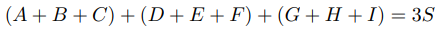\nSince the sum of the rows is equal to the sum of the numbers from 1 to 9, we have :\n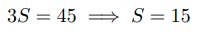\nUsing the same logic we can prove that for a given nxn matrix :\n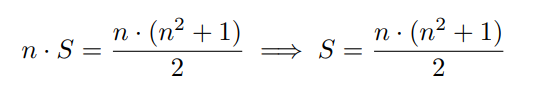\n\n2. **Property 2: Middle number is 5**\nUsing the equations that contains the middle number `E` :\n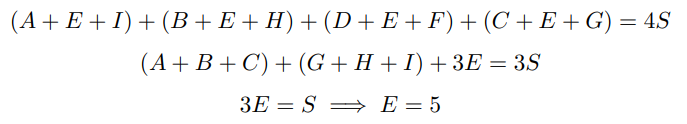\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the middle number `E` and the sum `S` are both odd, we can easily prove that the corners are even and the edges are odd.\nWith this understanding, all magic squares can be seen as variations achieved through rotations and transpositions of any other magic square.\nWe use the one in the description for example :\n\n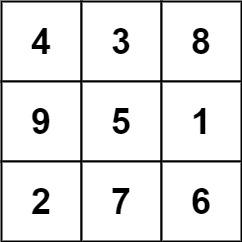\n\nSo the approach is we check if the middle number is equal to **5**, if it is we check if the grid is a rotation or a transposition of our magic square\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n n,m=len(grid),len(grid[0])\n magic_square=[\n [4,3,8],\n [9,5,1],\n [2,7,6]\n ]\n def grid_Rotation(grid,k):\n a=grid\n for _ in range(k):\n a=list(zip(*a[::-1]))\n return a\n def number_Of_Rotations(k):\n if k==4: return 0\n if k==2: return 1\n if k==6: return 2\n if k==8: return 3\n return -1\n def is_Identical(grid1,grid2):\n for i in range(3):\n for j in range(3):\n if grid1[i][j]!=grid2[i][j]:\n return False\n return True\n def is_transpose(grid1,grid2):\n for i in range(3):\n for j in range(3):\n if grid1[i][j]!=grid2[j][i]:\n return False\n return True\n def is_Magic_Square(i,j):\n if grid[i][j]!=5:\n return False\n if i<1 or i>n-2 or j<1 or j>m-2:\n return False\n k=number_Of_Rotations(grid[i-1][j-1])\n if k==-1:\n return False\n rotated=grid_Rotation(magic_square,k)\n return (is_Identical(rotated,[grid[i+x][j-1:j+2] for x in [-1,0,1]])) or (is_transpose(rotated,[grid[i+x][j-1:j+2] for x in [-1,0,1]]))\n\n\n if n<=2 or m<=2:\n return 0\n s=0\n for i in range(n):\n for j in range(m):\n if is_Magic_Square(i,j):\n s+=1\n return s\n``` | 2 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Beats 100%, approach explained. | magic-squares-in-grid | 1 | 1 | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA 3x3 magic square is a square grid of numbers arranged in such a way that the sum of the numbers in each row, each column, and both main diagonals is the same. In the case of a 3x3 magic square, this sum is always equal to **15**. Additionally, the middle number in the square is always **5**. Let\'s prove these properties.\n\n1. **Property 1: Sum of numbers in a row, column, or diagonal is 15**\n\nConsider the following 3x3 magic square:\n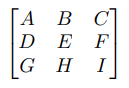\nLet `S` be the sum of the numbers in the magic square.\nThe sum of the rows is equal to :\n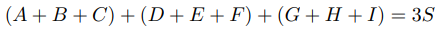\nSince the sum of the rows is equal to the sum of the numbers from 1 to 9, we have :\n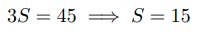\nUsing the same logic we can prove that for a given nxn matrix :\n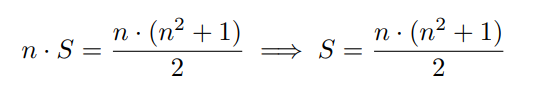\n\n2. **Property 2: Middle number is 5**\nUsing the equations that contains the middle number `E` :\n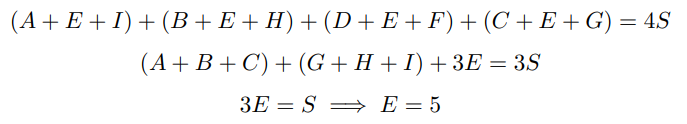\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince the middle number `E` and the sum `S` are both odd, we can easily prove that the corners are even and the edges are odd.\nWith this understanding, all magic squares can be seen as variations achieved through rotations and transpositions of any other magic square.\nWe use the one in the description for example :\n\n\n\nSo the approach is we check if the middle number is equal to **5**, if it is we check if the grid is a rotation or a transposition of our magic square\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n n,m=len(grid),len(grid[0])\n magic_square=[\n [4,3,8],\n [9,5,1],\n [2,7,6]\n ]\n def grid_Rotation(grid,k):\n a=grid\n for _ in range(k):\n a=list(zip(*a[::-1]))\n return a\n def number_Of_Rotations(k):\n if k==4: return 0\n if k==2: return 1\n if k==6: return 2\n if k==8: return 3\n return -1\n def is_Identical(grid1,grid2):\n for i in range(3):\n for j in range(3):\n if grid1[i][j]!=grid2[i][j]:\n return False\n return True\n def is_transpose(grid1,grid2):\n for i in range(3):\n for j in range(3):\n if grid1[i][j]!=grid2[j][i]:\n return False\n return True\n def is_Magic_Square(i,j):\n if grid[i][j]!=5:\n return False\n if i<1 or i>n-2 or j<1 or j>m-2:\n return False\n k=number_Of_Rotations(grid[i-1][j-1])\n if k==-1:\n return False\n rotated=grid_Rotation(magic_square,k)\n return (is_Identical(rotated,[grid[i+x][j-1:j+2] for x in [-1,0,1]])) or (is_transpose(rotated,[grid[i+x][j-1:j+2] for x in [-1,0,1]]))\n\n\n if n<=2 or m<=2:\n return 0\n s=0\n for i in range(n):\n for j in range(m):\n if is_Magic_Square(i,j):\n s+=1\n return s\n``` | 2 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.