title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Beat 94% in python | magic-squares-in-grid | 0 | 1 | # Idea\n- center has to be 5\n- check each number is there exact once\n- check row & col & diagonals\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n def checkMagic3x3(centerRow: int, centerCol: int) -> bool:\n # center one has to be 5 to make it magic\n if grid[centerRow][centerCol] != 5:\n return False\n\n\n # check each number is there exact once\n check = [0] * 9\n for i in [centerRow - 1, centerRow, centerRow + 1]:\n for j in [centerCol - 1, centerCol, centerCol + 1]:\n if grid[i][j] > 9:\n return False\n if check[grid[i][j]-1] == 1:\n return False\n check[grid[i][j]-1] = 1 \n\n\n\n # check row & col & diagonals\n cases = [\n # row\n [[-1, -1], [-1, 0], [-1, 1]],\n [[0, -1], [0, 0], [0, 1]],\n [[1, -1], [1, 0], [1, 1]],\n # col\n [[-1, -1], [0, -1], [1, -1]],\n [[-1, 0], [0, 0], [1, 0]],\n [[-1, 1], [0, 1], [1, 1]],\n # diagnals\n [[-1, -1], [0, 0], [1, 1]],\n [[1, -1], [0, 0], [-1, 1]],\n ]\n\n\n for x, y, z in cases:\n\n if grid[centerRow+x[0]][centerCol+x[1]] + grid[centerRow+y[0]][centerCol+y[1]] + grid[centerRow+z[0]][ centerCol+z[1]] != 15:\n return False\n\n\n return True\n\n num_row = len(grid)\n num_col = len(grid[0])\n\n if num_row < 3 or num_col < 3:\n return 0\n\n ans = 0\n for i in range(1, num_row - 1):\n for j in range(1, num_col - 1):\n if checkMagic3x3(i,j):\n ans += 1\n\n return ans \n\n\n\n\n \n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Beat 94% in python | magic-squares-in-grid | 0 | 1 | # Idea\n- center has to be 5\n- check each number is there exact once\n- check row & col & diagonals\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n def checkMagic3x3(centerRow: int, centerCol: int) -> bool:\n # center one has to be 5 to make it magic\n if grid[centerRow][centerCol] != 5:\n return False\n\n\n # check each number is there exact once\n check = [0] * 9\n for i in [centerRow - 1, centerRow, centerRow + 1]:\n for j in [centerCol - 1, centerCol, centerCol + 1]:\n if grid[i][j] > 9:\n return False\n if check[grid[i][j]-1] == 1:\n return False\n check[grid[i][j]-1] = 1 \n\n\n\n # check row & col & diagonals\n cases = [\n # row\n [[-1, -1], [-1, 0], [-1, 1]],\n [[0, -1], [0, 0], [0, 1]],\n [[1, -1], [1, 0], [1, 1]],\n # col\n [[-1, -1], [0, -1], [1, -1]],\n [[-1, 0], [0, 0], [1, 0]],\n [[-1, 1], [0, 1], [1, 1]],\n # diagnals\n [[-1, -1], [0, 0], [1, 1]],\n [[1, -1], [0, 0], [-1, 1]],\n ]\n\n\n for x, y, z in cases:\n\n if grid[centerRow+x[0]][centerCol+x[1]] + grid[centerRow+y[0]][centerCol+y[1]] + grid[centerRow+z[0]][ centerCol+z[1]] != 15:\n return False\n\n\n return True\n\n num_row = len(grid)\n num_col = len(grid[0])\n\n if num_row < 3 or num_col < 3:\n return 0\n\n ans = 0\n for i in range(1, num_row - 1):\n for j in range(1, num_col - 1):\n if checkMagic3x3(i,j):\n ans += 1\n\n return ans \n\n\n\n\n \n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Simple solution | magic-squares-in-grid | 0 | 1 | ```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n cnt = 0\n direct = [[(-1,0), (0,0), (1,0)], [(-1,-1), (0,-1), (1,-1)], [(-1,1), (0,1), (1,1)], [(0,-1), (0,0), (0,1)], [(-1,-1), (-1,0), (-1,1)], [(1,-1), (1,0), (1,1)], [(-1,-1), (0,0), (1,1)], [(1,-1), (0,0), (-1,1)]]\n\n for i, j in product(range(1, len(grid)-1), range(1, len(grid[0])-1)):\n if all(grid[i+x1][j+x2]+grid[i+y1][j+y2]+grid[i+z1][j+z2] == 15 for (x1,x2), (y1,y2), (z1, z2) in direct) and sum(1 << i for i in chain(grid[i-1][j-1:j+2], grid[i][j-1:j+2], grid[i+1][j-1:j+2])) == 1022:\n cnt += 1\n return cnt \n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Simple solution | magic-squares-in-grid | 0 | 1 | ```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n cnt = 0\n direct = [[(-1,0), (0,0), (1,0)], [(-1,-1), (0,-1), (1,-1)], [(-1,1), (0,1), (1,1)], [(0,-1), (0,0), (0,1)], [(-1,-1), (-1,0), (-1,1)], [(1,-1), (1,0), (1,1)], [(-1,-1), (0,0), (1,1)], [(1,-1), (0,0), (-1,1)]]\n\n for i, j in product(range(1, len(grid)-1), range(1, len(grid[0])-1)):\n if all(grid[i+x1][j+x2]+grid[i+y1][j+y2]+grid[i+z1][j+z2] == 15 for (x1,x2), (y1,y2), (z1, z2) in direct) and sum(1 << i for i in chain(grid[i-1][j-1:j+2], grid[i][j-1:j+2], grid[i+1][j-1:j+2])) == 1022:\n cnt += 1\n return cnt \n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Python3, intuitive but not most optimal -- beats 82.52% runtime and 85.44% memory | magic-squares-in-grid | 0 | 1 | # Intuition\nSlice down grid into 3x3 sub-grids and calculate sums for each:\n- rows\n- columns\n- diagonals\n\n# Approach\n1. Figure out row and column index range (i.e. highest value when slicing to 3x3 sub-grids)\n2. For each row index and column index in respective index_range\n2.1 calculate `expected_sum` (to be used when calculating rows/columns/diagonals sums)\n2.2 calculate sums for `rows`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n2.3 calculate sums for `columns`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n2.4 calculate sums for `diagonals`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n3. check if `len(rows) == 3 && len(columns) == 3 && len(diagonals) == 2`\n3.1 check if all values for `rows`, `columns` and `diagonals` are the same, if so, increase `results`\n4. return `results` value\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n result = 0\n\n no_rows = len(grid)\n no_columns = len(grid[0])\n\n if no_rows < 3:\n return 0\n if no_columns < 3:\n return 0\n\n row_index_range = 1 if no_columns == 3 else no_rows - 2\n column_index_range = 1 if no_columns == 3 else no_columns - 2\n for row_idx in range(row_index_range):\n for col_idx in range(column_index_range):\n expected_sum = sum(grid[row_idx][col_idx : col_idx + 3])\n rows = self.get_rows(grid[row_idx : row_idx + 3], col_idx, expected_sum)\n columns = self.get_columns(\n grid[row_idx : row_idx + 3], col_idx, expected_sum\n )\n diags = self.get_diags(\n grid[row_idx : row_idx + 3], col_idx, expected_sum\n )\n if len(rows) == 3 and len(columns) == 3 and len(diags) == 2:\n if all(rows) and all(columns) and all(diags):\n result += 1\n\n return result\n\n def get_rows(self, grid, column_index, expected_sum):\n result = []\n for idx in range(len(grid)):\n summ = sum(grid[idx][column_index : column_index + 3])\n if summ != expected_sum or any(\n el < 1 or el > 9 for el in grid[idx][column_index : column_index + 3]\n ) or len(set(grid[idx][column_index : column_index + 3])) < 3:\n return []\n result.append(summ)\n return result\n\n def get_columns(self, grid, column_index, expected_sum):\n result = []\n for idx_col in range(column_index, column_index + 3):\n tmp = []\n for idx_row in range(len(grid)):\n if 1 > grid[idx_row][idx_col] > 9:\n return []\n tmp.append(grid[idx_row][idx_col])\n if sum(tmp) != expected_sum or len(set(tmp)) < 3:\n return []\n result.append(sum(tmp))\n return result\n\n def get_diags(self, grid, column_index, expected_sum):\n result = []\n tmp = []\n for idx in range(len(grid)):\n if 1 > grid[idx][idx + column_index] > 9:\n return []\n tmp.append(grid[idx][idx + column_index])\n if sum(tmp) != expected_sum:\n return []\n result.append(sum(tmp))\n tmp = []\n for idx in range(len(grid)):\n if 1 > grid[idx][column_index + 2 - idx] > 9:\n return []\n tmp.append(grid[idx][column_index + 2 - idx])\n if sum(tmp) != expected_sum:\n return []\n result.append(sum(tmp))\n\n return result\n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Python3, intuitive but not most optimal -- beats 82.52% runtime and 85.44% memory | magic-squares-in-grid | 0 | 1 | # Intuition\nSlice down grid into 3x3 sub-grids and calculate sums for each:\n- rows\n- columns\n- diagonals\n\n# Approach\n1. Figure out row and column index range (i.e. highest value when slicing to 3x3 sub-grids)\n2. For each row index and column index in respective index_range\n2.1 calculate `expected_sum` (to be used when calculating rows/columns/diagonals sums)\n2.2 calculate sums for `rows`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n2.3 calculate sums for `columns`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n2.4 calculate sums for `diagonals`, while checking if the sums are equal to `expected_sum` from `2.1`, respective values are $$1 < x < 10$$ and values are distinct numbers\n3. check if `len(rows) == 3 && len(columns) == 3 && len(diagonals) == 2`\n3.1 check if all values for `rows`, `columns` and `diagonals` are the same, if so, increase `results`\n4. return `results` value\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n result = 0\n\n no_rows = len(grid)\n no_columns = len(grid[0])\n\n if no_rows < 3:\n return 0\n if no_columns < 3:\n return 0\n\n row_index_range = 1 if no_columns == 3 else no_rows - 2\n column_index_range = 1 if no_columns == 3 else no_columns - 2\n for row_idx in range(row_index_range):\n for col_idx in range(column_index_range):\n expected_sum = sum(grid[row_idx][col_idx : col_idx + 3])\n rows = self.get_rows(grid[row_idx : row_idx + 3], col_idx, expected_sum)\n columns = self.get_columns(\n grid[row_idx : row_idx + 3], col_idx, expected_sum\n )\n diags = self.get_diags(\n grid[row_idx : row_idx + 3], col_idx, expected_sum\n )\n if len(rows) == 3 and len(columns) == 3 and len(diags) == 2:\n if all(rows) and all(columns) and all(diags):\n result += 1\n\n return result\n\n def get_rows(self, grid, column_index, expected_sum):\n result = []\n for idx in range(len(grid)):\n summ = sum(grid[idx][column_index : column_index + 3])\n if summ != expected_sum or any(\n el < 1 or el > 9 for el in grid[idx][column_index : column_index + 3]\n ) or len(set(grid[idx][column_index : column_index + 3])) < 3:\n return []\n result.append(summ)\n return result\n\n def get_columns(self, grid, column_index, expected_sum):\n result = []\n for idx_col in range(column_index, column_index + 3):\n tmp = []\n for idx_row in range(len(grid)):\n if 1 > grid[idx_row][idx_col] > 9:\n return []\n tmp.append(grid[idx_row][idx_col])\n if sum(tmp) != expected_sum or len(set(tmp)) < 3:\n return []\n result.append(sum(tmp))\n return result\n\n def get_diags(self, grid, column_index, expected_sum):\n result = []\n tmp = []\n for idx in range(len(grid)):\n if 1 > grid[idx][idx + column_index] > 9:\n return []\n tmp.append(grid[idx][idx + column_index])\n if sum(tmp) != expected_sum:\n return []\n result.append(sum(tmp))\n tmp = []\n for idx in range(len(grid)):\n if 1 > grid[idx][column_index + 2 - idx] > 9:\n return []\n tmp.append(grid[idx][column_index + 2 - idx])\n if sum(tmp) != expected_sum:\n return []\n result.append(sum(tmp))\n\n return result\n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Python Medium | magic-squares-in-grid | 0 | 1 | ```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n M, N = len(grid), len(grid[0])\n res = 0\n\n solution = [((2, 7, 6), (4, 3, 8), (9, 5, 1)), ((3, 5, 7), (4, 9, 2), (8, 1, 6)), ((1, 5, 9), (6, 7, 2), (8, 3, 4)), ((1, 8, 6), (5, 3, 7), (9, 4, 2)), ((2, 9, 4), (6, 1, 8), (7, 5, 3))]\n\n\n for i in range(M):\n for j in range(N):\n arr = []\n\n for k in range(3):\n if k + i >= M:\n break\n arr.append(tuple(grid[i + k][j:j + 3]))\n \n arr.sort(key=lambda x: x[0])\n\n if tuple(arr) in solution:\n res += 1\n else:\n for row in arr:\n row = row[::-1]\n\n if tuple(arr) in solution:\n res += 1\n\n \n return res\n\n\n\n \'\'\'\n logic: find answer for 3 by 3 grid\n\n 4 3 8 \n 9 5 1\n 2 7 6\n\n\n 8 3 4\n 1 5 9 \n 2 7 6\n\n\n have a solution key with all possible answers\n iterate through matrix if from top left can build 3 x 3 chekc if in solution set if it is add one ot res\n\n\n \'\'\'\n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Python Medium | magic-squares-in-grid | 0 | 1 | ```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int:\n M, N = len(grid), len(grid[0])\n res = 0\n\n solution = [((2, 7, 6), (4, 3, 8), (9, 5, 1)), ((3, 5, 7), (4, 9, 2), (8, 1, 6)), ((1, 5, 9), (6, 7, 2), (8, 3, 4)), ((1, 8, 6), (5, 3, 7), (9, 4, 2)), ((2, 9, 4), (6, 1, 8), (7, 5, 3))]\n\n\n for i in range(M):\n for j in range(N):\n arr = []\n\n for k in range(3):\n if k + i >= M:\n break\n arr.append(tuple(grid[i + k][j:j + 3]))\n \n arr.sort(key=lambda x: x[0])\n\n if tuple(arr) in solution:\n res += 1\n else:\n for row in arr:\n row = row[::-1]\n\n if tuple(arr) in solution:\n res += 1\n\n \n return res\n\n\n\n \'\'\'\n logic: find answer for 3 by 3 grid\n\n 4 3 8 \n 9 5 1\n 2 7 6\n\n\n 8 3 4\n 1 5 9 \n 2 7 6\n\n\n have a solution key with all possible answers\n iterate through matrix if from top left can build 3 x 3 chekc if in solution set if it is add one ot res\n\n\n \'\'\'\n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Beats 92% of runtime !!! Detailed explanation 👨💻 | magic-squares-in-grid | 0 | 1 | \n# Approach\nWe divide the requirements and implement functions for each requirement. This way, it\'s easier to debug the code and also know what\'s happening at every step. From the problem, it can be seen that a 3*3 grid is classified as a magic square if:\n - all rows are equal\n - all columns are equal \n - all diagonals are equal\n - and the 3* *by 3 grid contains elements from 1-9 without repetition*.\n\nFor all the requirements we create the necessary functions for them. We then traverse the main matrix in a 3 * 3 grid mode and check if each grid satisfies all the requirements. We then output the number of grids in the matrix which satisfy all four requirements \n\n# Code\n```\nclass Solution:\n def check_diagonals(self, matrix): #Checks validity of sums of diagonals\n n = int(len(matrix)/2)+1\n front, back = [], []\n for i in range(n):\n for j in range(n):\n if i==j:\n front.extend([matrix[i][j],matrix[n-i][n-j]])\n back.extend([matrix[i][n-j],matrix[n-j][i]])\n if sum(front[:len(matrix)]) == sum(back[:len(matrix)]):\n return True\n return False\n\n def check_rows(self, matrix): #Checks validity of sums of rows\n top_row, middle_row, bottom_row = sum(matrix[0]), sum(matrix[1]), sum(matrix[2])\n if top_row==middle_row==bottom_row:\n return True\n return False\n \n def check_cols(self, matrix): #Checks validity of sums of columns\n right_col, middle_col, left_col = 0, 0, 0\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n right_col+=matrix[i][0]\n middle_col+=matrix[i][1]\n left_col+=matrix[i][2]\n if right_col==middle_col==left_col:\n return True\n return False\n \n def check_matrix(self, matrix): #Checks validity of sub_matrix or sub_grid\n nums = set()\n for i in matrix:\n for j in range(len(i)):\n if i[j]<10 and i[j]>0:\n nums.add(i[j])\n if len(nums)!= 9:\n return False\n return True\n\n def numMagicSquaresInside(self, grid: list[list[int]]): \n ans = 0\n for i in range(len(grid)-2):\n for j in range(0,len(grid[0])-2):\n sub_grid = grid[i:i+3]\n for k in range(len(sub_grid)):\n sub_grid[k] = sub_grid[k][j:j+3]\n if self.check_matrix(sub_grid) is False:\n continue\n else:\n if self.check_diagonals(sub_grid) and self.check_cols(sub_grid) and self.check_rows(sub_grid):\n ans+=1\n return ans\n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Beats 92% of runtime !!! Detailed explanation 👨💻 | magic-squares-in-grid | 0 | 1 | \n# Approach\nWe divide the requirements and implement functions for each requirement. This way, it\'s easier to debug the code and also know what\'s happening at every step. From the problem, it can be seen that a 3*3 grid is classified as a magic square if:\n - all rows are equal\n - all columns are equal \n - all diagonals are equal\n - and the 3* *by 3 grid contains elements from 1-9 without repetition*.\n\nFor all the requirements we create the necessary functions for them. We then traverse the main matrix in a 3 * 3 grid mode and check if each grid satisfies all the requirements. We then output the number of grids in the matrix which satisfy all four requirements \n\n# Code\n```\nclass Solution:\n def check_diagonals(self, matrix): #Checks validity of sums of diagonals\n n = int(len(matrix)/2)+1\n front, back = [], []\n for i in range(n):\n for j in range(n):\n if i==j:\n front.extend([matrix[i][j],matrix[n-i][n-j]])\n back.extend([matrix[i][n-j],matrix[n-j][i]])\n if sum(front[:len(matrix)]) == sum(back[:len(matrix)]):\n return True\n return False\n\n def check_rows(self, matrix): #Checks validity of sums of rows\n top_row, middle_row, bottom_row = sum(matrix[0]), sum(matrix[1]), sum(matrix[2])\n if top_row==middle_row==bottom_row:\n return True\n return False\n \n def check_cols(self, matrix): #Checks validity of sums of columns\n right_col, middle_col, left_col = 0, 0, 0\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n right_col+=matrix[i][0]\n middle_col+=matrix[i][1]\n left_col+=matrix[i][2]\n if right_col==middle_col==left_col:\n return True\n return False\n \n def check_matrix(self, matrix): #Checks validity of sub_matrix or sub_grid\n nums = set()\n for i in matrix:\n for j in range(len(i)):\n if i[j]<10 and i[j]>0:\n nums.add(i[j])\n if len(nums)!= 9:\n return False\n return True\n\n def numMagicSquaresInside(self, grid: list[list[int]]): \n ans = 0\n for i in range(len(grid)-2):\n for j in range(0,len(grid[0])-2):\n sub_grid = grid[i:i+3]\n for k in range(len(sub_grid)):\n sub_grid[k] = sub_grid[k][j:j+3]\n if self.check_matrix(sub_grid) is False:\n continue\n else:\n if self.check_diagonals(sub_grid) and self.check_cols(sub_grid) and self.check_rows(sub_grid):\n ans+=1\n return ans\n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Set theory and Memo's | 100% Time and Space Complexity on Average | Commented and Explained | magic-squares-in-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are only so many magic and non-magic squares we may encounter (though the latter is quite great!). Based on this, we can utilize memoization to speed up a set based approach to our problem. \n\nTo start, notice that we can use the order of the items in a square (called subgrid from here on) as a memo-key, which we can then mark after analysis as either a magic square or a non magic square. \n\nIf we know the number of magic squares, we also know when we can hit a real speed boost! To learn more, check this new york times article here : https://mindyourdecisions.com/blog/2015/11/08/how-many-3x3-magic-squares-are-there-sunday-puzzle/\n\nWith this in mind, we can outline our approach as follows \nWe are going to count the number of magic squares \nTo be a magic square, a square of 3 x 3 values in a grid must \n- have all values 1 to 9 \n- have all 3 rows sum to 15 \n- have all 3 cols sum to 15 \n\nFrom the article, we know there are only 8 magic squares. In the interest of fairness, we\'ll build these up as we go rather than simply enter them all at the start. \n\nThen, for each square subgrid in our grid \n- Get the subgrid key for the subgrid \n- If we have 8 magic keys already \n - increment number of magic squares by int cast of boolean of whether or not the subgrid key is in our magic keys \n - continue \n- otherwise if it is in our magic keys \n - increment number of magic squares by 1 and continue \n- otherwise if it is in our normal keys \n - continue \n- otherwise if it has all values 1 to 9 and has all rows sum to 15 and all cols sum to 15 \n - add the subgrid key to the magic squares set \n - increment number magic squares by 1 \n - continue \n- otherwise \n - add the subgrid key to the normal keys \n - continue \n\nAt end return number of magic squares \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is fairly laid out in the intuition, however, we\'ll note a few additions here \n\nIf you want the number of each type of magic square \n- change from magic square sets to magic square frequency dictionaries \n- make sure you increment on that as needed \n\nSimilar for the normal squares \n\nTo get each subgrid is actually a bit of a process. For our purposes we do the following \n- Loop row index in range 1 to rows - 1 \n - set row as grid at row index \n - set col indices as [index for index in range(1, cols-1) if row[index] == 5] (we can skip over those others in this way) \n - for col index in col indices \n - set a subgrid as the list of sub rows from col index - 1 to col index + 2 for sub row in grid from row index - 1 to row index + 2 \n - set a subgrid key as "".join([str(item) for row_s in subgrid for item in row_s]) \n - from here, above logic follows \n\n# Complexity\n- Time complexity : O(R * (C + c)) \n - We loop each row basically \n - In each row we do C work to loop each col and build col indices\n - Then we do c work for each col indices \n - Then we do O(1) work to build subgrid and get key \n - Then we do O(1) work for reset of processing \n - In total then we do O(R * (C + c)) \n\n- Space complexity : O(K) \n - We store at most 8 magic keys \n - We store at most the unique normal keys K \n - All other space is technically referential \n - O(K) is the final space, where K is the number of keys \n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int :\n # what we are after \n num_magic_squares = 0 \n # what a magic square must contain \n num_set = set(range(1, 10))\n # dimensions of our problem \n rows = len(grid)\n cols = len(grid[0])\n # square list of normal and magical keys respectively \n square_list = [set(), set()]\n # for row index in range 1 to rows - 1 \n for row_index in range(1, rows - 1) : \n # get the row \n row = grid[row_index]\n # only care about col indices where row at index is 5 as an optional skip\n col_indices = [index for index in range(1, cols-1) if row[index] == 5]\n # for col indices we care about \n for col_index in col_indices : \n # get the subgrid as sub row at col_index - 1 to col index + 2 for each sub row in grid \n subgrid = [row_s[col_index-1:col_index+2] for row_s in grid[row_index-1 : row_index + 2]]\n # build your subgrid key in order to utilize memo \n subgrid_key = "".join([str(item) for row_s in subgrid for item in row_s])\n # if you found them all, use that fact to skip out early \n if len(square_list[1]) == 8 : \n num_magic_squares += int(subgrid_key in square_list[1])\n continue\n elif subgrid_key in square_list[1] : \n # otherwise, if you found this one increment and continue to next col index\n num_magic_squares += 1 \n continue\n elif subgrid_key in square_list[0] : \n # or skip out early if you already know it\'s not magical \n continue\n else : \n # if we have all numbers in 0 - 9 and our row sum is 15 3 times and our col sum is 15 3 times, this is a magic square. Otherwise it is not. \n magical = (len(num_set-set([item for row_s in subgrid for item in row_s]))==0) and (sum([sum(row_s)==15 for row_s in subgrid])== sum([sum(col_s)==15 for col_s in zip(*subgrid)])==3)\n # increment based on status \n num_magic_squares += magical \n # and assign appropriately \n square_list[magical].add(subgrid_key)\n # then continue\n continue\n # return when done \n return num_magic_squares\n``` | 0 | A `3 x 3` magic square is a `3 x 3` grid filled with distinct numbers **from** `1` **to** `9` such that each row, column, and both diagonals all have the same sum.
Given a `row x col` `grid` of integers, how many `3 x 3` "magic square " subgrids are there? (Each subgrid is contiguous).
**Example 1:**
**Input:** grid = \[\[4,3,8,4\],\[9,5,1,9\],\[2,7,6,2\]\]
**Output:** 1
**Explanation:**
The following subgrid is a 3 x 3 magic square:
while this one is not:
In total, there is only one magic square inside the given grid.
**Example 2:**
**Input:** grid = \[\[8\]\]
**Output:** 0
**Constraints:**
* `row == grid.length`
* `col == grid[i].length`
* `1 <= row, col <= 10`
* `0 <= grid[i][j] <= 15` | null |
Set theory and Memo's | 100% Time and Space Complexity on Average | Commented and Explained | magic-squares-in-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are only so many magic and non-magic squares we may encounter (though the latter is quite great!). Based on this, we can utilize memoization to speed up a set based approach to our problem. \n\nTo start, notice that we can use the order of the items in a square (called subgrid from here on) as a memo-key, which we can then mark after analysis as either a magic square or a non magic square. \n\nIf we know the number of magic squares, we also know when we can hit a real speed boost! To learn more, check this new york times article here : https://mindyourdecisions.com/blog/2015/11/08/how-many-3x3-magic-squares-are-there-sunday-puzzle/\n\nWith this in mind, we can outline our approach as follows \nWe are going to count the number of magic squares \nTo be a magic square, a square of 3 x 3 values in a grid must \n- have all values 1 to 9 \n- have all 3 rows sum to 15 \n- have all 3 cols sum to 15 \n\nFrom the article, we know there are only 8 magic squares. In the interest of fairness, we\'ll build these up as we go rather than simply enter them all at the start. \n\nThen, for each square subgrid in our grid \n- Get the subgrid key for the subgrid \n- If we have 8 magic keys already \n - increment number of magic squares by int cast of boolean of whether or not the subgrid key is in our magic keys \n - continue \n- otherwise if it is in our magic keys \n - increment number of magic squares by 1 and continue \n- otherwise if it is in our normal keys \n - continue \n- otherwise if it has all values 1 to 9 and has all rows sum to 15 and all cols sum to 15 \n - add the subgrid key to the magic squares set \n - increment number magic squares by 1 \n - continue \n- otherwise \n - add the subgrid key to the normal keys \n - continue \n\nAt end return number of magic squares \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is fairly laid out in the intuition, however, we\'ll note a few additions here \n\nIf you want the number of each type of magic square \n- change from magic square sets to magic square frequency dictionaries \n- make sure you increment on that as needed \n\nSimilar for the normal squares \n\nTo get each subgrid is actually a bit of a process. For our purposes we do the following \n- Loop row index in range 1 to rows - 1 \n - set row as grid at row index \n - set col indices as [index for index in range(1, cols-1) if row[index] == 5] (we can skip over those others in this way) \n - for col index in col indices \n - set a subgrid as the list of sub rows from col index - 1 to col index + 2 for sub row in grid from row index - 1 to row index + 2 \n - set a subgrid key as "".join([str(item) for row_s in subgrid for item in row_s]) \n - from here, above logic follows \n\n# Complexity\n- Time complexity : O(R * (C + c)) \n - We loop each row basically \n - In each row we do C work to loop each col and build col indices\n - Then we do c work for each col indices \n - Then we do O(1) work to build subgrid and get key \n - Then we do O(1) work for reset of processing \n - In total then we do O(R * (C + c)) \n\n- Space complexity : O(K) \n - We store at most 8 magic keys \n - We store at most the unique normal keys K \n - All other space is technically referential \n - O(K) is the final space, where K is the number of keys \n\n# Code\n```\nclass Solution:\n def numMagicSquaresInside(self, grid: List[List[int]]) -> int :\n # what we are after \n num_magic_squares = 0 \n # what a magic square must contain \n num_set = set(range(1, 10))\n # dimensions of our problem \n rows = len(grid)\n cols = len(grid[0])\n # square list of normal and magical keys respectively \n square_list = [set(), set()]\n # for row index in range 1 to rows - 1 \n for row_index in range(1, rows - 1) : \n # get the row \n row = grid[row_index]\n # only care about col indices where row at index is 5 as an optional skip\n col_indices = [index for index in range(1, cols-1) if row[index] == 5]\n # for col indices we care about \n for col_index in col_indices : \n # get the subgrid as sub row at col_index - 1 to col index + 2 for each sub row in grid \n subgrid = [row_s[col_index-1:col_index+2] for row_s in grid[row_index-1 : row_index + 2]]\n # build your subgrid key in order to utilize memo \n subgrid_key = "".join([str(item) for row_s in subgrid for item in row_s])\n # if you found them all, use that fact to skip out early \n if len(square_list[1]) == 8 : \n num_magic_squares += int(subgrid_key in square_list[1])\n continue\n elif subgrid_key in square_list[1] : \n # otherwise, if you found this one increment and continue to next col index\n num_magic_squares += 1 \n continue\n elif subgrid_key in square_list[0] : \n # or skip out early if you already know it\'s not magical \n continue\n else : \n # if we have all numbers in 0 - 9 and our row sum is 15 3 times and our col sum is 15 3 times, this is a magic square. Otherwise it is not. \n magical = (len(num_set-set([item for row_s in subgrid for item in row_s]))==0) and (sum([sum(row_s)==15 for row_s in subgrid])== sum([sum(col_s)==15 for col_s in zip(*subgrid)])==3)\n # increment based on status \n num_magic_squares += magical \n # and assign appropriately \n square_list[magical].add(subgrid_key)\n # then continue\n continue\n # return when done \n return num_magic_squares\n``` | 0 | You are given two integer arrays `nums1` and `nums2` both of the same length. The **advantage** of `nums1` with respect to `nums2` is the number of indices `i` for which `nums1[i] > nums2[i]`.
Return _any permutation of_ `nums1` _that maximizes its **advantage** with respect to_ `nums2`.
**Example 1:**
**Input:** nums1 = \[2,7,11,15\], nums2 = \[1,10,4,11\]
**Output:** \[2,11,7,15\]
**Example 2:**
**Input:** nums1 = \[12,24,8,32\], nums2 = \[13,25,32,11\]
**Output:** \[24,32,8,12\]
**Constraints:**
* `1 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 109` | null |
Very easy to understand | python | keys-and-rooms | 0 | 1 | ```\nclass Solution:\n def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:\n n = len(rooms)\n keys = set()\n keys.add(0)\n k = 1\n while k!=0:\n k=len(keys)\n for i in range(n):\n if i in keys:\n keys.update(rooms[i])\n k = len(keys)-k\n return len(keys)==n\n``` | 1 | There are `n` rooms labeled from `0` to `n - 1` and all the rooms are locked except for room `0`. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of **distinct keys** in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array `rooms` where `rooms[i]` is the set of keys that you can obtain if you visited room `i`, return `true` _if you can visit **all** the rooms, or_ `false` _otherwise_.
**Example 1:**
**Input:** rooms = \[\[1\],\[2\],\[3\],\[\]\]
**Output:** true
**Explanation:**
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
**Example 2:**
**Input:** rooms = \[\[1,3\],\[3,0,1\],\[2\],\[0\]\]
**Output:** false
**Explanation:** We can not enter room number 2 since the only key that unlocks it is in that room.
**Constraints:**
* `n == rooms.length`
* `2 <= n <= 1000`
* `0 <= rooms[i].length <= 1000`
* `1 <= sum(rooms[i].length) <= 3000`
* `0 <= rooms[i][j] < n`
* All the values of `rooms[i]` are **unique**. | null |
Very easy to understand | python | keys-and-rooms | 0 | 1 | ```\nclass Solution:\n def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:\n n = len(rooms)\n keys = set()\n keys.add(0)\n k = 1\n while k!=0:\n k=len(keys)\n for i in range(n):\n if i in keys:\n keys.update(rooms[i])\n k = len(keys)-k\n return len(keys)==n\n``` | 1 | A car travels from a starting position to a destination which is `target` miles east of the starting position.
There are gas stations along the way. The gas stations are represented as an array `stations` where `stations[i] = [positioni, fueli]` indicates that the `ith` gas station is `positioni` miles east of the starting position and has `fueli` liters of gas.
The car starts with an infinite tank of gas, which initially has `startFuel` liters of fuel in it. It uses one liter of gas per one mile that it drives. When the car reaches a gas station, it may stop and refuel, transferring all the gas from the station into the car.
Return _the minimum number of refueling stops the car must make in order to reach its destination_. If it cannot reach the destination, return `-1`.
Note that if the car reaches a gas station with `0` fuel left, the car can still refuel there. If the car reaches the destination with `0` fuel left, it is still considered to have arrived.
**Example 1:**
**Input:** target = 1, startFuel = 1, stations = \[\]
**Output:** 0
**Explanation:** We can reach the target without refueling.
**Example 2:**
**Input:** target = 100, startFuel = 1, stations = \[\[10,100\]\]
**Output:** -1
**Explanation:** We can not reach the target (or even the first gas station).
**Example 3:**
**Input:** target = 100, startFuel = 10, stations = \[\[10,60\],\[20,30\],\[30,30\],\[60,40\]\]
**Output:** 2
**Explanation:** We start with 10 liters of fuel.
We drive to position 10, expending 10 liters of fuel. We refuel from 0 liters to 60 liters of gas.
Then, we drive from position 10 to position 60 (expending 50 liters of fuel),
and refuel from 10 liters to 50 liters of gas. We then drive to and reach the target.
We made 2 refueling stops along the way, so we return 2.
**Constraints:**
* `1 <= target, startFuel <= 109`
* `0 <= stations.length <= 500`
* `1 <= positioni < positioni+1 < target`
* `1 <= fueli < 109` | null |
Solution | split-array-into-fibonacci-sequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool helper(int ind,vector<int>& ds,string &numStr){\n if(ind==numStr.size() && ds.size()>2){\n return true;\n }\n for(int i=1;i<=10 && ind+i<=numStr.size() ;i++){\n string temp=numStr.substr(ind,i);\n long long num=stoll(temp);\n if((temp.size()>1) && (temp[0]==\'0\')) break;\n if(num>INT_MAX) break;\n if((ds.size()<2) || ((long long)ds[ds.size()-1]+(long long)ds[ds.size()-2]==num)){\n ds.push_back(num);\n if(helper(ind+i,ds,numStr)) return true;\n ds.pop_back();\n }\n else if(((long long)ds[ds.size()-1]+(long long)ds[ds.size()-2])<num) break;\n }\n return false;\n }\n vector<int> splitIntoFibonacci(string numStr) {\n vector<int>ds;\n helper(0,ds,numStr);\n return ds;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n N = len(num)\n MAX = 2 ** 31\n\n for i in range(1, N // 2 + 1):\n if i > 10:\n break\n if int(num[:i]) > MAX:\n break\n if i > 1 and num[0] == \'0\':\n break\n x = int(num[:i])\n\n for j in range(i + 1, i + N // 2):\n if j > 10:\n break\n if int(num[i:j]) > MAX:\n break\n if j > i + 1 and num[i] == \'0\':\n break\n y = int(num[i: j])\n\n res = []\n res.append(x)\n res.append(y)\n a, b, pos = x, y, j\n flag = 1\n\n while flag:\n c = a + b\n str_c = str(c)\n n = len(str_c)\n\n if c > MAX:\n flag = 0\n break\n if pos + n > N or str_c != num[pos:pos + n]:\n flag = 0\n break\n \n res.append(c)\n a = b\n b = c\n pos = pos + n\n\n if pos == N and len(res) > 2:\n return res\n\n return []\n```\n\n```Java []\nclass Solution {\n public List<Integer> splitIntoFibonacci(String num) {\n List<Integer> list = new ArrayList<>();\n dfs(num.toCharArray(), list, 0);\n return list;\n }\n public boolean dfs(char[] digit, List<Integer> list, int index) {\n if (index == digit.length && list.size() >= 3) {\n return true;\n }\n for (int i = index; i < digit.length; i++) {\n if (digit[index] == \'0\' && i > index) {\n break;\n }\n long num = subDigit(digit, index, i + 1);\n if (num > Integer.MAX_VALUE) {\n break;\n }\n int size = list.size();\n if (size >= 2 && num > list.get(size - 1) + list.get(size - 2)) {\n break;\n }\n if (size <= 1 || num == list.get(size - 1) + list.get(size - 2)) {\n list.add((int) num);\n if (dfs(digit, list, i + 1))\n return true;\n list.remove(list.size() - 1);\n }\n }\n return false;\n }\n private long subDigit(char[] digit, int start, int end) {\n long res = 0;\n for (int i = start; i < end; i++) {\n res = res * 10 + digit[i] - \'0\';\n }\n return res;\n }\n}\n```\n | 1 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Solution | split-array-into-fibonacci-sequence | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool helper(int ind,vector<int>& ds,string &numStr){\n if(ind==numStr.size() && ds.size()>2){\n return true;\n }\n for(int i=1;i<=10 && ind+i<=numStr.size() ;i++){\n string temp=numStr.substr(ind,i);\n long long num=stoll(temp);\n if((temp.size()>1) && (temp[0]==\'0\')) break;\n if(num>INT_MAX) break;\n if((ds.size()<2) || ((long long)ds[ds.size()-1]+(long long)ds[ds.size()-2]==num)){\n ds.push_back(num);\n if(helper(ind+i,ds,numStr)) return true;\n ds.pop_back();\n }\n else if(((long long)ds[ds.size()-1]+(long long)ds[ds.size()-2])<num) break;\n }\n return false;\n }\n vector<int> splitIntoFibonacci(string numStr) {\n vector<int>ds;\n helper(0,ds,numStr);\n return ds;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n N = len(num)\n MAX = 2 ** 31\n\n for i in range(1, N // 2 + 1):\n if i > 10:\n break\n if int(num[:i]) > MAX:\n break\n if i > 1 and num[0] == \'0\':\n break\n x = int(num[:i])\n\n for j in range(i + 1, i + N // 2):\n if j > 10:\n break\n if int(num[i:j]) > MAX:\n break\n if j > i + 1 and num[i] == \'0\':\n break\n y = int(num[i: j])\n\n res = []\n res.append(x)\n res.append(y)\n a, b, pos = x, y, j\n flag = 1\n\n while flag:\n c = a + b\n str_c = str(c)\n n = len(str_c)\n\n if c > MAX:\n flag = 0\n break\n if pos + n > N or str_c != num[pos:pos + n]:\n flag = 0\n break\n \n res.append(c)\n a = b\n b = c\n pos = pos + n\n\n if pos == N and len(res) > 2:\n return res\n\n return []\n```\n\n```Java []\nclass Solution {\n public List<Integer> splitIntoFibonacci(String num) {\n List<Integer> list = new ArrayList<>();\n dfs(num.toCharArray(), list, 0);\n return list;\n }\n public boolean dfs(char[] digit, List<Integer> list, int index) {\n if (index == digit.length && list.size() >= 3) {\n return true;\n }\n for (int i = index; i < digit.length; i++) {\n if (digit[index] == \'0\' && i > index) {\n break;\n }\n long num = subDigit(digit, index, i + 1);\n if (num > Integer.MAX_VALUE) {\n break;\n }\n int size = list.size();\n if (size >= 2 && num > list.get(size - 1) + list.get(size - 2)) {\n break;\n }\n if (size <= 1 || num == list.get(size - 1) + list.get(size - 2)) {\n list.add((int) num);\n if (dfs(digit, list, i + 1))\n return true;\n list.remove(list.size() - 1);\n }\n }\n return false;\n }\n private long subDigit(char[] digit, int start, int end) {\n long res = 0;\n for (int i = start; i < end; i++) {\n res = res * 10 + digit[i] - \'0\';\n }\n return res;\n }\n}\n```\n | 1 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
python3 clean easy understand code | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n\nBacktracking\n\n# Approach\n\n\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n size = len(num)\n self.result = None\n\n def dfs(start, path):\n if len(path) > 2 and path[-3] + path[-2] != path[-1]:\n return False\n if start == size:\n if len(path) > 2 and self.result is None:\n self.result = path.copy()\n return True\n return False\n for i in range(start, size):\n if num[start] == "0" and i > start:\n break\n if int(num[start : i + 1]) > (2**31):\n break\n path.append(int(num[start : i + 1]))\n if dfs(i + 1, path):\n return True\n path.pop()\n return False\n\n dfs(0, [])\n return self.result if self.result is not None else []\n\n``` | 1 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
python3 clean easy understand code | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n\nBacktracking\n\n# Approach\n\n\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n size = len(num)\n self.result = None\n\n def dfs(start, path):\n if len(path) > 2 and path[-3] + path[-2] != path[-1]:\n return False\n if start == size:\n if len(path) > 2 and self.result is None:\n self.result = path.copy()\n return True\n return False\n for i in range(start, size):\n if num[start] == "0" and i > start:\n break\n if int(num[start : i + 1]) > (2**31):\n break\n path.append(int(num[start : i + 1]))\n if dfs(i + 1, path):\n return True\n path.pop()\n return False\n\n dfs(0, [])\n return self.result if self.result is not None else []\n\n``` | 1 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Backtracking (R-94%+, M-87%+) | split-array-into-fibonacci-sequence | 0 | 1 | # Complexity\n- Time complexity: **O(n * n)**\nn - len of input string.\n\n- Space complexity: **O(n)**\nWorst case: all string values are 0, output list will have the same size as input string.\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n # We can\'t build anything from only zeroes, except [0, 0, ... 0]\n # So, it\'s unique case.\n if num.count(\'0\') == len(num):\n return [0 for _ in num]\n # Cull calc.\n limit: list[int] = [2 ** 31]\n\n def check(start: int, sequence: list[int]) -> list[int]:\n # Nothing left to build from.\n if start >= len(num):\n # We\'re building from (0 -> len(nums) - 1) for every option.\n # Even first number, need extra check for correct sequence >= 3.\n # And because all digits are positive we can\'t have 0 at the end.\n # Only unique case with 0 at the end checked before.\n if len(sequence) >= 3 and sequence[-1] != 0:\n return sequence\n return []\n # We can use 0, but not build with leading 0.\n if num[start] == \'0\':\n if correct := check(start + 1, sequence + [0]):\n return correct\n return []\n end: int = start\n # First two doesn\'t require correct sum of previous 2.\n if len(sequence) < 2:\n while end < len(num):\n cur_num: int = int(num[start:end + 1])\n if not 0 <= cur_num < limit[0]:\n return []\n # return -> list|none, so it\'s needs to be saved.\n # Either walrus or just variable.\n # We can insta return correct sequence if it\'s found:\n # ! Return any Fibonacci-like sequence split from num !\n if correct := check(end + 1, sequence + [cur_num]):\n return correct\n end += 1\n return []\n # Cull calc.\n expected: int = sequence[-2] + sequence[-1]\n while end < len(num):\n cur_num = int(num[start:end + 1])\n if not 0 <= cur_num < limit[0]:\n return []\n if expected == cur_num:\n if correct := check(end + 1, sequence + [cur_num]):\n return correct\n end += 1\n # Only positive values -> always increasing.\n # No reasons to check higher ones.\n if expected < cur_num:\n break\n return []\n\n return check(0, [])\n\n``` | 1 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Backtracking (R-94%+, M-87%+) | split-array-into-fibonacci-sequence | 0 | 1 | # Complexity\n- Time complexity: **O(n * n)**\nn - len of input string.\n\n- Space complexity: **O(n)**\nWorst case: all string values are 0, output list will have the same size as input string.\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n # We can\'t build anything from only zeroes, except [0, 0, ... 0]\n # So, it\'s unique case.\n if num.count(\'0\') == len(num):\n return [0 for _ in num]\n # Cull calc.\n limit: list[int] = [2 ** 31]\n\n def check(start: int, sequence: list[int]) -> list[int]:\n # Nothing left to build from.\n if start >= len(num):\n # We\'re building from (0 -> len(nums) - 1) for every option.\n # Even first number, need extra check for correct sequence >= 3.\n # And because all digits are positive we can\'t have 0 at the end.\n # Only unique case with 0 at the end checked before.\n if len(sequence) >= 3 and sequence[-1] != 0:\n return sequence\n return []\n # We can use 0, but not build with leading 0.\n if num[start] == \'0\':\n if correct := check(start + 1, sequence + [0]):\n return correct\n return []\n end: int = start\n # First two doesn\'t require correct sum of previous 2.\n if len(sequence) < 2:\n while end < len(num):\n cur_num: int = int(num[start:end + 1])\n if not 0 <= cur_num < limit[0]:\n return []\n # return -> list|none, so it\'s needs to be saved.\n # Either walrus or just variable.\n # We can insta return correct sequence if it\'s found:\n # ! Return any Fibonacci-like sequence split from num !\n if correct := check(end + 1, sequence + [cur_num]):\n return correct\n end += 1\n return []\n # Cull calc.\n expected: int = sequence[-2] + sequence[-1]\n while end < len(num):\n cur_num = int(num[start:end + 1])\n if not 0 <= cur_num < limit[0]:\n return []\n if expected == cur_num:\n if correct := check(end + 1, sequence + [cur_num]):\n return correct\n end += 1\n # Only positive values -> always increasing.\n # No reasons to check higher ones.\n if expected < cur_num:\n break\n return []\n\n return check(0, [])\n\n``` | 1 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Easiest Solution | split-array-into-fibonacci-sequence | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public List<Integer> splitIntoFibonacci(String num) {\n List<Integer> list = new ArrayList<>();\n helper(num, list, 0);\n return list;\n }\n\n public boolean helper(String str, List<Integer>list, int idx){\n if(idx == str.length()) return list.size() > 2;\n\n int num = 0;\n for(int i = idx; i < str.length(); i++) {\n num = (num*10) + (str.charAt(i) - \'0\');\n\n if(num < 0) return false;\n if(list.size() < 2 || (list.get(list.size()-1) + list.get(list.size()-2)) == num) {\n list.add(num);\n if(helper(str, list, i+1)) return true;\n list.remove(list.size()-1);\n }\n if(i == idx && str.charAt(i) == \'0\') return false;\n }\n return false;\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n void helper(vector<int>&res, vector<int>tmp, int index, string num)\n {\n if(index == num.size() && tmp.size()>=3 && res.size() < tmp.size())\n {\n res = tmp;\n return;\n }\n string x="";\n for(int i=index;i<num.size();++i)\n {\n if(i>index && num[index] == \'0\')\n {\n break;\n }\n x +=num[i];\n \n if(x.size() > num.size()/2)\n {\n break;\n }\n if(stoll(x)>INT_MAX)\n {\n break;\n }\n if(tmp.size()<2)\n {\n tmp.push_back(stoi(x));\n }\n else\n {\n if((long long)tmp[tmp.size()-2] + (long long)tmp[tmp.size()-1] < stoll(x))\n {\n break;\n }\n else if((long long)tmp[tmp.size()-2] + (long long)tmp[tmp.size()-1] == stoll(x))\n {\n tmp.push_back(stoi(x));\n }\n else\n {\n continue;\n }\n }\n helper(res,tmp,i+1,num);\n tmp.pop_back();\n }\n }\n vector<int> splitIntoFibonacci(string num) {\n vector<int>res,tmp;\n helper(res,tmp,0,num);\n return res;\n }\n};\n```\n```python3 []\nclass Solution:\n def splitIntoFibonacci(self, S: str) -> List[int]:\n for i in range(1, min(11, len(S))): # 2**31 limit \n if S[0] == "0" and i > 1: break \n for j in range(i+1, min(i+11, len(S))): # 2**31 limit \n if S[i] == "0" and j-i > 1: break \n x, y = int(S[:i]), int(S[i:j])\n ans = [x, y]\n while j < len(S):\n x, y = y, x+y\n if y <= 2**31 and S[j:j+len(str(y))] == str(y): \n ans.append(y)\n j += len(str(y))\n else: break \n else: \n if len(ans) > 2: return ans # no break encountered \n return []\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Easiest Solution | split-array-into-fibonacci-sequence | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public List<Integer> splitIntoFibonacci(String num) {\n List<Integer> list = new ArrayList<>();\n helper(num, list, 0);\n return list;\n }\n\n public boolean helper(String str, List<Integer>list, int idx){\n if(idx == str.length()) return list.size() > 2;\n\n int num = 0;\n for(int i = idx; i < str.length(); i++) {\n num = (num*10) + (str.charAt(i) - \'0\');\n\n if(num < 0) return false;\n if(list.size() < 2 || (list.get(list.size()-1) + list.get(list.size()-2)) == num) {\n list.add(num);\n if(helper(str, list, i+1)) return true;\n list.remove(list.size()-1);\n }\n if(i == idx && str.charAt(i) == \'0\') return false;\n }\n return false;\n }\n}\n```\n```c++ []\nclass Solution {\npublic:\n void helper(vector<int>&res, vector<int>tmp, int index, string num)\n {\n if(index == num.size() && tmp.size()>=3 && res.size() < tmp.size())\n {\n res = tmp;\n return;\n }\n string x="";\n for(int i=index;i<num.size();++i)\n {\n if(i>index && num[index] == \'0\')\n {\n break;\n }\n x +=num[i];\n \n if(x.size() > num.size()/2)\n {\n break;\n }\n if(stoll(x)>INT_MAX)\n {\n break;\n }\n if(tmp.size()<2)\n {\n tmp.push_back(stoi(x));\n }\n else\n {\n if((long long)tmp[tmp.size()-2] + (long long)tmp[tmp.size()-1] < stoll(x))\n {\n break;\n }\n else if((long long)tmp[tmp.size()-2] + (long long)tmp[tmp.size()-1] == stoll(x))\n {\n tmp.push_back(stoi(x));\n }\n else\n {\n continue;\n }\n }\n helper(res,tmp,i+1,num);\n tmp.pop_back();\n }\n }\n vector<int> splitIntoFibonacci(string num) {\n vector<int>res,tmp;\n helper(res,tmp,0,num);\n return res;\n }\n};\n```\n```python3 []\nclass Solution:\n def splitIntoFibonacci(self, S: str) -> List[int]:\n for i in range(1, min(11, len(S))): # 2**31 limit \n if S[0] == "0" and i > 1: break \n for j in range(i+1, min(i+11, len(S))): # 2**31 limit \n if S[i] == "0" and j-i > 1: break \n x, y = int(S[:i]), int(S[i:j])\n ans = [x, y]\n while j < len(S):\n x, y = y, x+y\n if y <= 2**31 and S[j:j+len(str(y))] == str(y): \n ans.append(y)\n j += len(str(y))\n else: break \n else: \n if len(ans) > 2: return ans # no break encountered \n return []\n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Non-Backtracking Iterative solution, O(N^3) | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIf we choose a partition for the first two numbers, we can uniquely derive what the rest of the sequence would look like.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nChoose indices $i, j$ so that the first two numbers are $num[0\\ldots i]$ and $num[i{+}1 \\ldots j]$. We can then construct the rest of the string until we hit the length of $num$, and compare our sequence with the original one.\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n for i in range(len(num) - 1):\n for j in range(i + 1, len(num) - 1):\n rest = num[j + 1:]\n fst = int(num[:i + 1])\n snd = int(num[i + 1:j + 1])\n \n tot = list(str(fst)) + list(str(snd))\n tot_lst = [fst, snd]\n while len(tot) < len(num):\n nxt = fst + snd\n tot.extend(list(str(nxt)))\n tot_lst.append(nxt)\n fst = snd\n snd = nxt\n\n if any(map(lambda x: x >= 2**31, tot_lst)):\n continue\n\n if \'\'.join(tot) == num:\n return tot_lst\n \n return []\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Non-Backtracking Iterative solution, O(N^3) | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nIf we choose a partition for the first two numbers, we can uniquely derive what the rest of the sequence would look like.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nChoose indices $i, j$ so that the first two numbers are $num[0\\ldots i]$ and $num[i{+}1 \\ldots j]$. We can then construct the rest of the string until we hit the length of $num$, and compare our sequence with the original one.\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n for i in range(len(num) - 1):\n for j in range(i + 1, len(num) - 1):\n rest = num[j + 1:]\n fst = int(num[:i + 1])\n snd = int(num[i + 1:j + 1])\n \n tot = list(str(fst)) + list(str(snd))\n tot_lst = [fst, snd]\n while len(tot) < len(num):\n nxt = fst + snd\n tot.extend(list(str(nxt)))\n tot_lst.append(nxt)\n fst = snd\n snd = nxt\n\n if any(map(lambda x: x >= 2**31, tot_lst)):\n continue\n\n if \'\'.join(tot) == num:\n return tot_lst\n \n return []\n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Backtracking - A clean and organized Python solution | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\nWe iterate over the search space using DFS. When we reach an invalid fibonacci index, we backtrack and continue searching.\n\n# Approach\nBacktracking\n\n# Complexity\n- Time complexity:\n?\n\n- Space complexity:\nO(n) - Just need to maintain the output array.\n\n# Code\n```\nclass Solution:\n \n def splitIntoFibonacci(self, num: str) -> List[int]:\n\n output = []\n\n def solve(j = 0):\n\n # Not Valid\n if len(output) > 2 and output[-3] + output[-2] != output[-1]:\n return False \n # Valid \n if len(output) > 2 and j == len(num) and output[-3] + output[-2] == output[-1]:\n return True\n \n # Loop through all possible first numbers \n for i in range(j + 1, len(num) + 1):\n\n # If we will never reach a solution on this branch\n if len(output) > 2 and output[-2] + output[-1] < int(num[j:i]):\n return False\n\n # Add the next number to the output\n if (num[j] != "0" or (i-j == 1 and num[j] == "0")) and int(num[j:i]) < pow(2, 31):\n output.append(int(num[j:i]))\n\n # Try to go down this branch\n if solve(i):\n return True \n\n # Backtrack\n output.pop()\n\n return False\n\n solve()\n\n return output\n\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Backtracking - A clean and organized Python solution | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\nWe iterate over the search space using DFS. When we reach an invalid fibonacci index, we backtrack and continue searching.\n\n# Approach\nBacktracking\n\n# Complexity\n- Time complexity:\n?\n\n- Space complexity:\nO(n) - Just need to maintain the output array.\n\n# Code\n```\nclass Solution:\n \n def splitIntoFibonacci(self, num: str) -> List[int]:\n\n output = []\n\n def solve(j = 0):\n\n # Not Valid\n if len(output) > 2 and output[-3] + output[-2] != output[-1]:\n return False \n # Valid \n if len(output) > 2 and j == len(num) and output[-3] + output[-2] == output[-1]:\n return True\n \n # Loop through all possible first numbers \n for i in range(j + 1, len(num) + 1):\n\n # If we will never reach a solution on this branch\n if len(output) > 2 and output[-2] + output[-1] < int(num[j:i]):\n return False\n\n # Add the next number to the output\n if (num[j] != "0" or (i-j == 1 and num[j] == "0")) and int(num[j:i]) < pow(2, 31):\n output.append(int(num[j:i]))\n\n # Try to go down this branch\n if solve(i):\n return True \n\n # Backtrack\n output.pop()\n\n return False\n\n solve()\n\n return output\n\n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Very easy to understand | split-array-into-fibonacci-sequence | 0 | 1 | \n# Approach\nBacktracking\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n \n n = len(num)\n res = []\n\n def backtrack(pos):\n\n if pos == n:\n if len(res) > 2 and res[-1] == res[-2] + res[-3]:\n return True\n return \n \n for i in range(pos+1, n+1):\n cur = num[pos:i]\n\n if cur[0] == \'0\' and i != pos+1: return\n \n if int(cur) > 2**31: return\n res.append(int(cur))\n if len(res) < 3 or res[-1] == res[-2] + res[-3]:\n if backtrack(i): return True\n \n res.pop()\n \n return \n\n backtrack(0)\n\n return res\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Very easy to understand | split-array-into-fibonacci-sequence | 0 | 1 | \n# Approach\nBacktracking\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n \n n = len(num)\n res = []\n\n def backtrack(pos):\n\n if pos == n:\n if len(res) > 2 and res[-1] == res[-2] + res[-3]:\n return True\n return \n \n for i in range(pos+1, n+1):\n cur = num[pos:i]\n\n if cur[0] == \'0\' and i != pos+1: return\n \n if int(cur) > 2**31: return\n res.append(int(cur))\n if len(res) < 3 or res[-1] == res[-2] + res[-3]:\n if backtrack(i): return True\n \n res.pop()\n \n return \n\n backtrack(0)\n\n return res\n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Python3 - Brute Force With Many Edge Cases | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\nWhat an interesting problem\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n c = Counter(num)\n mv = (2**31) - 1\n if c[\'0\'] == len(num):\n return [0] * len(num) # special case\n n = len(num)\n for i in range(1, 1 + n // 2):\n for j in range(1, 1 + n // 2):\n if i + j + max(i,j) > n:\n break\n n1 = num[0:i]\n n2 = num[i:i+j]\n if num[j+i] == \'0\':\n continue\n assert len(n1) == i and len(n2) == j\n if n1[0] == \'0\' and i > 1 or n2[0] == \'0\' and j > 1:\n continue\n fib, p = [int(n1), int(n2)], j + i\n if max(fib) > mv:\n break\n good = True\n while p < n and good:\n fib.append(fib[-1] + fib[-2])\n if fib[-1] > mv:\n good = False\n break\n nn = str(fib[-1])\n if num[p:p+len(nn)] != nn:\n good = False\n else:\n p += len(nn)\n if good and p == n:\n return fib\n return []\n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python3 - Brute Force With Many Edge Cases | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\nWhat an interesting problem\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num: str) -> List[int]:\n c = Counter(num)\n mv = (2**31) - 1\n if c[\'0\'] == len(num):\n return [0] * len(num) # special case\n n = len(num)\n for i in range(1, 1 + n // 2):\n for j in range(1, 1 + n // 2):\n if i + j + max(i,j) > n:\n break\n n1 = num[0:i]\n n2 = num[i:i+j]\n if num[j+i] == \'0\':\n continue\n assert len(n1) == i and len(n2) == j\n if n1[0] == \'0\' and i > 1 or n2[0] == \'0\' and j > 1:\n continue\n fib, p = [int(n1), int(n2)], j + i\n if max(fib) > mv:\n break\n good = True\n while p < n and good:\n fib.append(fib[-1] + fib[-2])\n if fib[-1] > mv:\n good = False\n break\n nn = str(fib[-1])\n if num[p:p+len(nn)] != nn:\n good = False\n else:\n p += len(nn)\n if good and p == n:\n return fib\n return []\n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Python (Simple Backtracking) | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num):\n n = len(num)\n\n def backtrack(num,path):\n if not num:\n if len(path) >= 3:\n res.append(path)\n\n for i in range(1,len(num)+1):\n if (int(num[:i]) >= 2**31 or str(int(num[:i])) != num[:i]): continue\n if len(path) >= 2 and int(num[:i]) != int(path[-1]) + int(path[-2]): continue\n backtrack(num[i:],path+[num[:i]])\n\n res = []\n backtrack(num,[])\n ans = res[0] if res else []\n return [int(i) for i in ans]\n\n \n``` | 0 | You are given a string of digits `num`, such as `"123456579 "`. We can split it into a Fibonacci-like sequence `[123, 456, 579]`.
Formally, a **Fibonacci-like** sequence is a list `f` of non-negative integers such that:
* `0 <= f[i] < 231`, (that is, each integer fits in a **32-bit** signed integer type),
* `f.length >= 3`, and
* `f[i] + f[i + 1] == f[i + 2]` for all `0 <= i < f.length - 2`.
Note that when splitting the string into pieces, each piece must not have extra leading zeroes, except if the piece is the number `0` itself.
Return any Fibonacci-like sequence split from `num`, or return `[]` if it cannot be done.
**Example 1:**
**Input:** num = "1101111 "
**Output:** \[11,0,11,11\]
**Explanation:** The output \[110, 1, 111\] would also be accepted.
**Example 2:**
**Input:** num = "112358130 "
**Output:** \[\]
**Explanation:** The task is impossible.
**Example 3:**
**Input:** num = "0123 "
**Output:** \[\]
**Explanation:** Leading zeroes are not allowed, so "01 ", "2 ", "3 " is not valid.
**Constraints:**
* `1 <= num.length <= 200`
* `num` contains only digits. | null |
Python (Simple Backtracking) | split-array-into-fibonacci-sequence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitIntoFibonacci(self, num):\n n = len(num)\n\n def backtrack(num,path):\n if not num:\n if len(path) >= 3:\n res.append(path)\n\n for i in range(1,len(num)+1):\n if (int(num[:i]) >= 2**31 or str(int(num[:i])) != num[:i]): continue\n if len(path) >= 2 and int(num[:i]) != int(path[-1]) + int(path[-2]): continue\n backtrack(num[i:],path+[num[:i]])\n\n res = []\n backtrack(num,[])\n ans = res[0] if res else []\n return [int(i) for i in ans]\n\n \n``` | 0 | Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a **leaf value sequence**_._
For example, in the given tree above, the leaf value sequence is `(6, 7, 4, 9, 8)`.
Two binary trees are considered _leaf-similar_ if their leaf value sequence is the same.
Return `true` if and only if the two given trees with head nodes `root1` and `root2` are leaf-similar.
**Example 1:**
**Input:** root1 = \[3,5,1,6,2,9,8,null,null,7,4\], root2 = \[3,5,1,6,7,4,2,null,null,null,null,null,null,9,8\]
**Output:** true
**Example 2:**
**Input:** root1 = \[1,2,3\], root2 = \[1,3,2\]
**Output:** false
**Constraints:**
* The number of nodes in each tree will be in the range `[1, 200]`.
* Both of the given trees will have values in the range `[0, 200]`. | null |
Python - Beats 99% | guess-the-word | 0 | 1 | I think this "interactive" problem may be over my head, but I found a lot of other solutions poorly explained or too theoretical, so here\'s my take.\n\nObservations:\n1) If `master.guess(guess_word)` returns 0 matches then any other word in `wordlist`that matches even 1 character with `guess_word` can be eliminated.\n2) If `master.guess(guess_word)` returns 6, then obviously we have our answer.\n3) If `master.guess(guess_word)` returns 1-5, then all remaining candidate need to match `guess_word` *exactly* that many times because the `secret` word is in the `wordlist` and matches the `guess_word` *exactly* that many times.\n\nApproach:\nTreat the `wordlist` as the candidate set. On each guess we can eliminate candidate words based on the guess. \n\nIf `master.guess(guess_word)` returns 0, it is better if `guess_word` was **not** very unique. Then it eliminates many similar words. \n\nIf `master.guess(guess_word)` returns 1-5, it is better if `guess_word` was very unique. Then it eliminates many unsimilar words.\n\nTo emphasize, if `master.guess(guess_word)` returns 0 and `guess_word = "zzzzzz"` but **no** other words in `wordlist` use the letter `"z"` then you cannot eliminate any other words! \n\nBut, if `master.guess("zzzzzz")` returned 4, and few other words in `wordlist` contained 4 `"z"`\'s, then you would eliminate many words.\n\nHere, I sort `wordlist` by uniqueness and change the end of the `wordlist` I am choosing `guess_word` from based on `matches`.\n\n```\nclass Solution:\n def findSecretWord(self, wordlist: List[str], master: \'Master\') -> None:\n place_counts = collections.defaultdict(int)\n for word in wordlist:\n for i, char in enumerate(word):\n place_counts[str(i)+char] += 1\n \n def word_uniqueness(word):\n score = 0\n for i, char in enumerate(word):\n score += place_counts[str(i)+char]\n return score\n \n # wordlist will be sorted from most to least unique.\n wordlist.sort(key=word_uniqueness)\n \n def word_is_possible(guess_word, word, matches):\n if guess_word == word:\n return False\n match_count = 0\n for a, b in zip(guess_word, word):\n if a == b:\n match_count += 1\n return match_count == matches\n \n end = -1\n for _ in range(10):\n guess_word = wordlist[end]\n matches = master.guess(guess_word)\n if matches == 6:\n break\n elif matches == 0:\n wordlist = [w for w in wordlist if not any(a==b for a, b in zip(guess_word, w))]\n if end == 0:\n end = -1\n else:\n wordlist = [w for w in wordlist if word_is_possible(guess_word, w, matches)]\n if end == -1:\n end = 0\n``` | 46 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Python - Beats 99% | guess-the-word | 0 | 1 | I think this "interactive" problem may be over my head, but I found a lot of other solutions poorly explained or too theoretical, so here\'s my take.\n\nObservations:\n1) If `master.guess(guess_word)` returns 0 matches then any other word in `wordlist`that matches even 1 character with `guess_word` can be eliminated.\n2) If `master.guess(guess_word)` returns 6, then obviously we have our answer.\n3) If `master.guess(guess_word)` returns 1-5, then all remaining candidate need to match `guess_word` *exactly* that many times because the `secret` word is in the `wordlist` and matches the `guess_word` *exactly* that many times.\n\nApproach:\nTreat the `wordlist` as the candidate set. On each guess we can eliminate candidate words based on the guess. \n\nIf `master.guess(guess_word)` returns 0, it is better if `guess_word` was **not** very unique. Then it eliminates many similar words. \n\nIf `master.guess(guess_word)` returns 1-5, it is better if `guess_word` was very unique. Then it eliminates many unsimilar words.\n\nTo emphasize, if `master.guess(guess_word)` returns 0 and `guess_word = "zzzzzz"` but **no** other words in `wordlist` use the letter `"z"` then you cannot eliminate any other words! \n\nBut, if `master.guess("zzzzzz")` returned 4, and few other words in `wordlist` contained 4 `"z"`\'s, then you would eliminate many words.\n\nHere, I sort `wordlist` by uniqueness and change the end of the `wordlist` I am choosing `guess_word` from based on `matches`.\n\n```\nclass Solution:\n def findSecretWord(self, wordlist: List[str], master: \'Master\') -> None:\n place_counts = collections.defaultdict(int)\n for word in wordlist:\n for i, char in enumerate(word):\n place_counts[str(i)+char] += 1\n \n def word_uniqueness(word):\n score = 0\n for i, char in enumerate(word):\n score += place_counts[str(i)+char]\n return score\n \n # wordlist will be sorted from most to least unique.\n wordlist.sort(key=word_uniqueness)\n \n def word_is_possible(guess_word, word, matches):\n if guess_word == word:\n return False\n match_count = 0\n for a, b in zip(guess_word, word):\n if a == b:\n match_count += 1\n return match_count == matches\n \n end = -1\n for _ in range(10):\n guess_word = wordlist[end]\n matches = master.guess(guess_word)\n if matches == 6:\n break\n elif matches == 0:\n wordlist = [w for w in wordlist if not any(a==b for a, b in zip(guess_word, w))]\n if end == 0:\n end = -1\n else:\n wordlist = [w for w in wordlist if word_is_possible(guess_word, w, matches)]\n if end == -1:\n end = 0\n``` | 46 | A sequence `x1, x2, ..., xn` is _Fibonacci-like_ if:
* `n >= 3`
* `xi + xi+1 == xi+2` for all `i + 2 <= n`
Given a **strictly increasing** array `arr` of positive integers forming a sequence, return _the **length** of the longest Fibonacci-like subsequence of_ `arr`. If one does not exist, return `0`.
A **subsequence** is derived from another sequence `arr` by deleting any number of elements (including none) from `arr`, without changing the order of the remaining elements. For example, `[3, 5, 8]` is a subsequence of `[3, 4, 5, 6, 7, 8]`.
**Example 1:**
**Input:** arr = \[1,2,3,4,5,6,7,8\]
**Output:** 5
**Explanation:** The longest subsequence that is fibonacci-like: \[1,2,3,5,8\].
**Example 2:**
**Input:** arr = \[1,3,7,11,12,14,18\]
**Output:** 3
**Explanation**: The longest subsequence that is fibonacci-like: \[1,11,12\], \[3,11,14\] or \[7,11,18\].
**Constraints:**
* `3 <= arr.length <= 1000`
* `1 <= arr[i] < arr[i + 1] <= 109` | null |
[Python] Solution with narrowed candidates and blacklist | guess-the-word | 0 | 1 | *Runtime: 48 ms, faster than 63.16% of Python3 online submissions for Guess the Word.\nMemory Usage: 14 MB, less than 62.02% of Python3 online submissions for Guess the Word.*\n\n1. Narrow the candidates as @qy9Mg did in [How to explain to interviewer - 843. Guess the Word](http://leetcode.com/problems/guess-the-word/discuss/556075/How-to-explain-to-interviewer-843.-Guess-the-Word)\n2. Create a blacklist for words with matches = 0\n\n```\nclass Solution:\n def findSecretWord(self, words: List[str], master: \'Master\') -> None: \n k = 1 # for tracing the number of loops\n matches = 0\n blacklists = [[] for i in range(6)]\n \n while matches != 6:\n n = len(words)\n r = random.randint(0, n - 1)\n matches = master.guess(words[r])\n key = words[r]\n # print(k, n, r, matches, key)\n \n words.pop(r)\n \n if matches == 0:\n for i in range(6):\n blacklists[i].append(key[i])\n # print(blacklists)\n \n elif matches > 0 and matches < 6:\n candidates = []\n for i in range(n - 1):\n count = 0\n for j in range(6):\n if words[i][j] not in blacklists[j] and words[i][j] == key[j]:\n count += 1\n if count >= matches:\n candidates.append(words[i])\n \n words = candidates.copy()\n # print(words)\n \n k += 1\n```\n\nThis problem depends on luck, kind of, lol.\nIf we find the secret in `k` times and `k` <= `allowedGuesses`, it shows `"You guessed the secret word correctly."`, \notherwise if `k` >`allowedGuesses`, it shows `"Either you took too many guesses, or you did not find the secret word."`\n\nBeginner\'s solution, please go easy. (\u25CF\'\u25E1\'\u25CF) | 2 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
[Python] Solution with narrowed candidates and blacklist | guess-the-word | 0 | 1 | *Runtime: 48 ms, faster than 63.16% of Python3 online submissions for Guess the Word.\nMemory Usage: 14 MB, less than 62.02% of Python3 online submissions for Guess the Word.*\n\n1. Narrow the candidates as @qy9Mg did in [How to explain to interviewer - 843. Guess the Word](http://leetcode.com/problems/guess-the-word/discuss/556075/How-to-explain-to-interviewer-843.-Guess-the-Word)\n2. Create a blacklist for words with matches = 0\n\n```\nclass Solution:\n def findSecretWord(self, words: List[str], master: \'Master\') -> None: \n k = 1 # for tracing the number of loops\n matches = 0\n blacklists = [[] for i in range(6)]\n \n while matches != 6:\n n = len(words)\n r = random.randint(0, n - 1)\n matches = master.guess(words[r])\n key = words[r]\n # print(k, n, r, matches, key)\n \n words.pop(r)\n \n if matches == 0:\n for i in range(6):\n blacklists[i].append(key[i])\n # print(blacklists)\n \n elif matches > 0 and matches < 6:\n candidates = []\n for i in range(n - 1):\n count = 0\n for j in range(6):\n if words[i][j] not in blacklists[j] and words[i][j] == key[j]:\n count += 1\n if count >= matches:\n candidates.append(words[i])\n \n words = candidates.copy()\n # print(words)\n \n k += 1\n```\n\nThis problem depends on luck, kind of, lol.\nIf we find the secret in `k` times and `k` <= `allowedGuesses`, it shows `"You guessed the secret word correctly."`, \notherwise if `k` >`allowedGuesses`, it shows `"Either you took too many guesses, or you did not find the secret word."`\n\nBeginner\'s solution, please go easy. (\u25CF\'\u25E1\'\u25CF) | 2 | A sequence `x1, x2, ..., xn` is _Fibonacci-like_ if:
* `n >= 3`
* `xi + xi+1 == xi+2` for all `i + 2 <= n`
Given a **strictly increasing** array `arr` of positive integers forming a sequence, return _the **length** of the longest Fibonacci-like subsequence of_ `arr`. If one does not exist, return `0`.
A **subsequence** is derived from another sequence `arr` by deleting any number of elements (including none) from `arr`, without changing the order of the remaining elements. For example, `[3, 5, 8]` is a subsequence of `[3, 4, 5, 6, 7, 8]`.
**Example 1:**
**Input:** arr = \[1,2,3,4,5,6,7,8\]
**Output:** 5
**Explanation:** The longest subsequence that is fibonacci-like: \[1,2,3,5,8\].
**Example 2:**
**Input:** arr = \[1,3,7,11,12,14,18\]
**Output:** 3
**Explanation**: The longest subsequence that is fibonacci-like: \[1,11,12\], \[3,11,14\] or \[7,11,18\].
**Constraints:**
* `3 <= arr.length <= 1000`
* `1 <= arr[i] < arr[i + 1] <= 109` | null |
Solution | guess-the-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int StringConstrain(const string& a, const string& b){\n int equals = 0;\n for (int i = 0 ; 6 > i ; i++){\n if (a[i] == b[i]){\n equals++;\n }\n }\n return equals;\n }\n void After_Compute(vector<string>& words, const string& guessed, int compute){ \n vector<string> new_words;\n if (compute == -1) compute = 0;\n for (int i = 0 ; words.size() > i ; i++){\n if (guessed != words[i]){\n if (StringConstrain(words[i], guessed) == compute){\n new_words.push_back(words[i]);\n }\n }\n }\n words = new_words;\n } \n void findSecretWord(vector<string>& words, Master& master) {\n int n = words.size();\n int curr = 0;\n for (int i = 0 ; curr != 6 ; i++){\n curr = master.guess(words[words.size() / 2]);\n After_Compute(words, words[words.size() / 2], curr);\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findSecretWord(self, words: List[str], master: \'Master\') -> None:\n freq_at_positions = []\n for i in range(6):\n pos_count = {}\n for word in words:\n if (word[i] in pos_count): pos_count[word[i]] += 1\n else: pos_count[word[i]] = 1\n freq_at_positions.append(pos_count)\n \n def calc_score(w):\n s = 0\n for i in range(len(w)):\n s += freq_at_positions[i][w[i]]\n return s\n\n words.sort(key=lambda word: calc_score(word))\n\n def find_common_sum(w1, w2):\n common_sum = 0\n for i in range(6):\n if (w1[i] == w2[i]): common_sum += 1\n return common_sum\n\n while (len(words) > 0):\n word = words.pop()\n matches = master.guess(word)\n\n if (matches == 6): break\n else:\n words = [w for w in words if matches == find_common_sum(w, word)]\n```\n\n```Java []\nclass Solution{\n\tpublic void findSecretWord(String[] words, Master master){\n\t\t\tint last = words.length-1;\n\t\t\twhile(true){\n\t\t\t\tint count = master.guess(words[0]);\n\t\t\t\tif(count==6) return;\n int i = 1;\n\t\t\t\twhile(i <= last){\n\t\t\t\t\tint c = 0;\n\t\t\t\t\tfor(int j = 0; j < 6; j++) if(words[i].charAt(j)==words[0].charAt(j)) c++;\n\t\t\t\t\tif(c!=count) words[i]=words[last--];\n\t\t\t\t\telse i++;\n\t\t\t\t}\n\t\t\t\twords[0]=words[last--];\n\t\t\t}\n\t\t}\n\t}\n```\n | 2 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Solution | guess-the-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int StringConstrain(const string& a, const string& b){\n int equals = 0;\n for (int i = 0 ; 6 > i ; i++){\n if (a[i] == b[i]){\n equals++;\n }\n }\n return equals;\n }\n void After_Compute(vector<string>& words, const string& guessed, int compute){ \n vector<string> new_words;\n if (compute == -1) compute = 0;\n for (int i = 0 ; words.size() > i ; i++){\n if (guessed != words[i]){\n if (StringConstrain(words[i], guessed) == compute){\n new_words.push_back(words[i]);\n }\n }\n }\n words = new_words;\n } \n void findSecretWord(vector<string>& words, Master& master) {\n int n = words.size();\n int curr = 0;\n for (int i = 0 ; curr != 6 ; i++){\n curr = master.guess(words[words.size() / 2]);\n After_Compute(words, words[words.size() / 2], curr);\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findSecretWord(self, words: List[str], master: \'Master\') -> None:\n freq_at_positions = []\n for i in range(6):\n pos_count = {}\n for word in words:\n if (word[i] in pos_count): pos_count[word[i]] += 1\n else: pos_count[word[i]] = 1\n freq_at_positions.append(pos_count)\n \n def calc_score(w):\n s = 0\n for i in range(len(w)):\n s += freq_at_positions[i][w[i]]\n return s\n\n words.sort(key=lambda word: calc_score(word))\n\n def find_common_sum(w1, w2):\n common_sum = 0\n for i in range(6):\n if (w1[i] == w2[i]): common_sum += 1\n return common_sum\n\n while (len(words) > 0):\n word = words.pop()\n matches = master.guess(word)\n\n if (matches == 6): break\n else:\n words = [w for w in words if matches == find_common_sum(w, word)]\n```\n\n```Java []\nclass Solution{\n\tpublic void findSecretWord(String[] words, Master master){\n\t\t\tint last = words.length-1;\n\t\t\twhile(true){\n\t\t\t\tint count = master.guess(words[0]);\n\t\t\t\tif(count==6) return;\n int i = 1;\n\t\t\t\twhile(i <= last){\n\t\t\t\t\tint c = 0;\n\t\t\t\t\tfor(int j = 0; j < 6; j++) if(words[i].charAt(j)==words[0].charAt(j)) c++;\n\t\t\t\t\tif(c!=count) words[i]=words[last--];\n\t\t\t\t\telse i++;\n\t\t\t\t}\n\t\t\t\twords[0]=words[last--];\n\t\t\t}\n\t\t}\n\t}\n```\n | 2 | A sequence `x1, x2, ..., xn` is _Fibonacci-like_ if:
* `n >= 3`
* `xi + xi+1 == xi+2` for all `i + 2 <= n`
Given a **strictly increasing** array `arr` of positive integers forming a sequence, return _the **length** of the longest Fibonacci-like subsequence of_ `arr`. If one does not exist, return `0`.
A **subsequence** is derived from another sequence `arr` by deleting any number of elements (including none) from `arr`, without changing the order of the remaining elements. For example, `[3, 5, 8]` is a subsequence of `[3, 4, 5, 6, 7, 8]`.
**Example 1:**
**Input:** arr = \[1,2,3,4,5,6,7,8\]
**Output:** 5
**Explanation:** The longest subsequence that is fibonacci-like: \[1,2,3,5,8\].
**Example 2:**
**Input:** arr = \[1,3,7,11,12,14,18\]
**Output:** 3
**Explanation**: The longest subsequence that is fibonacci-like: \[1,11,12\], \[3,11,14\] or \[7,11,18\].
**Constraints:**
* `3 <= arr.length <= 1000`
* `1 <= arr[i] < arr[i + 1] <= 109` | null |
Reduce by Hamming distance. 28 ms, faster than 91.22% & 14.2 MB, less than 92.67%. Python 3. | guess-the-word | 0 | 1 | ```\nclass Solution:\n def findSecretWord(self, wordlist: List[str], master: \'Master\') -> None:\n def hamming_distance(w1: str, w2: str) -> int:\n return sum(1 for k in range(6) if w1[k] != w2[k])\n\n current_guess = wordlist[0]\n curr_distance = 6 - Master.guess(master, current_guess)\n while curr_distance != 0:\n\t\t # Secret word have <current_distance> form our <current_guess>. \n\t\t\t# Therefore secret word is one of the words with Hamming distance <current_distance> from our <current_guess>.\n\t\t\t# So lets delete all other words.\n wordlist = [w for w in wordlist if hamming_distance(current_guess, w) == curr_distance]\n # current_guess = wordlist.pop(random.randint(0, len(wordlist) - 1))\n\t\t\t# You sould not use any random. In some random cases \n\t\t\t# number of guesses may be ecxeed 10, but in next attempt it\'s not, etc.\n current_guess = wordlist.pop()\n curr_distance = 6 - Master.guess(master, current_guess)\n``` | 2 | You are given an array of unique strings `words` where `words[i]` is six letters long. One word of `words` was chosen as a secret word.
You are also given the helper object `Master`. You may call `Master.guess(word)` where `word` is a six-letter-long string, and it must be from `words`. `Master.guess(word)` returns:
* `-1` if `word` is not from `words`, or
* an integer representing the number of exact matches (value and position) of your guess to the secret word.
There is a parameter `allowedGuesses` for each test case where `allowedGuesses` is the maximum number of times you can call `Master.guess(word)`.
For each test case, you should call `Master.guess` with the secret word without exceeding the maximum number of allowed guesses. You will get:
* **`"Either you took too many guesses, or you did not find the secret word. "`** if you called `Master.guess` more than `allowedGuesses` times or if you did not call `Master.guess` with the secret word, or
* **`"You guessed the secret word correctly. "`** if you called `Master.guess` with the secret word with the number of calls to `Master.guess` less than or equal to `allowedGuesses`.
The test cases are generated such that you can guess the secret word with a reasonable strategy (other than using the bruteforce method).
**Example 1:**
**Input:** secret = "acckzz ", words = \[ "acckzz ", "ccbazz ", "eiowzz ", "abcczz "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:**
master.guess( "aaaaaa ") returns -1, because "aaaaaa " is not in wordlist.
master.guess( "acckzz ") returns 6, because "acckzz " is secret and has all 6 matches.
master.guess( "ccbazz ") returns 3, because "ccbazz " has 3 matches.
master.guess( "eiowzz ") returns 2, because "eiowzz " has 2 matches.
master.guess( "abcczz ") returns 4, because "abcczz " has 4 matches.
We made 5 calls to master.guess, and one of them was the secret, so we pass the test case.
**Example 2:**
**Input:** secret = "hamada ", words = \[ "hamada ", "khaled "\], allowedGuesses = 10
**Output:** You guessed the secret word correctly.
**Explanation:** Since there are two words, you can guess both.
**Constraints:**
* `1 <= words.length <= 100`
* `words[i].length == 6`
* `words[i]` consist of lowercase English letters.
* All the strings of `wordlist` are **unique**.
* `secret` exists in `words`.
* `10 <= allowedGuesses <= 30` | null |
Reduce by Hamming distance. 28 ms, faster than 91.22% & 14.2 MB, less than 92.67%. Python 3. | guess-the-word | 0 | 1 | ```\nclass Solution:\n def findSecretWord(self, wordlist: List[str], master: \'Master\') -> None:\n def hamming_distance(w1: str, w2: str) -> int:\n return sum(1 for k in range(6) if w1[k] != w2[k])\n\n current_guess = wordlist[0]\n curr_distance = 6 - Master.guess(master, current_guess)\n while curr_distance != 0:\n\t\t # Secret word have <current_distance> form our <current_guess>. \n\t\t\t# Therefore secret word is one of the words with Hamming distance <current_distance> from our <current_guess>.\n\t\t\t# So lets delete all other words.\n wordlist = [w for w in wordlist if hamming_distance(current_guess, w) == curr_distance]\n # current_guess = wordlist.pop(random.randint(0, len(wordlist) - 1))\n\t\t\t# You sould not use any random. In some random cases \n\t\t\t# number of guesses may be ecxeed 10, but in next attempt it\'s not, etc.\n current_guess = wordlist.pop()\n curr_distance = 6 - Master.guess(master, current_guess)\n``` | 2 | A sequence `x1, x2, ..., xn` is _Fibonacci-like_ if:
* `n >= 3`
* `xi + xi+1 == xi+2` for all `i + 2 <= n`
Given a **strictly increasing** array `arr` of positive integers forming a sequence, return _the **length** of the longest Fibonacci-like subsequence of_ `arr`. If one does not exist, return `0`.
A **subsequence** is derived from another sequence `arr` by deleting any number of elements (including none) from `arr`, without changing the order of the remaining elements. For example, `[3, 5, 8]` is a subsequence of `[3, 4, 5, 6, 7, 8]`.
**Example 1:**
**Input:** arr = \[1,2,3,4,5,6,7,8\]
**Output:** 5
**Explanation:** The longest subsequence that is fibonacci-like: \[1,2,3,5,8\].
**Example 2:**
**Input:** arr = \[1,3,7,11,12,14,18\]
**Output:** 3
**Explanation**: The longest subsequence that is fibonacci-like: \[1,11,12\], \[3,11,14\] or \[7,11,18\].
**Constraints:**
* `3 <= arr.length <= 1000`
* `1 <= arr[i] < arr[i + 1] <= 109` | null |
✅Easy Solution using Stack Beats(90%) in O(N)✅ | backspace-string-compare | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n stack1= []\n stack2 = []\n for i in s:\n if i==\'#\':\n if stack1:\n stack1.pop()\n else:\n stack1.append(i)\n for i in t:\n if i==\'#\':\n if stack2:\n stack2.pop()\n else:\n stack2.append(i)\n return stack1==stack2\n\n\n``` | 2 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
✅Easy Solution using Stack Beats(90%) in O(N)✅ | backspace-string-compare | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n stack1= []\n stack2 = []\n for i in s:\n if i==\'#\':\n if stack1:\n stack1.pop()\n else:\n stack1.append(i)\n for i in t:\n if i==\'#\':\n if stack2:\n stack2.pop()\n else:\n stack2.append(i)\n return stack1==stack2\n\n\n``` | 2 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
ONE LINER PYTHON3 TRIVIAL / GOLF ✅ ✅ ✅ | backspace-string-compare | 0 | 1 | No explanation needed (trivial)\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n return [(z.append(c) or z) for z in [[]] for i, c in enumerate(s) if c != \'#\' or (i != 0 and (c == \'#\' and z and not z.pop()))][0] == [(z.append(c) or z) for z in [[]] for i, c in enumerate(t) if c != \'#\' or (i != 0 and (c == \'#\' and z and not z.pop()))][0]\n\n\n```\n\n | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
ONE LINER PYTHON3 TRIVIAL / GOLF ✅ ✅ ✅ | backspace-string-compare | 0 | 1 | No explanation needed (trivial)\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n return [(z.append(c) or z) for z in [[]] for i, c in enumerate(s) if c != \'#\' or (i != 0 and (c == \'#\' and z and not z.pop()))][0] == [(z.append(c) or z) for z in [[]] for i, c in enumerate(t) if c != \'#\' or (i != 0 and (c == \'#\' and z and not z.pop()))][0]\n\n\n```\n\n | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
Video Solution | Explanation With Drawings | Java | C++ | Python 3 | backspace-string-compare | 1 | 1 | # Intuition, approach, and complexity dicussed in detail in video solution\nhttps://youtu.be/UcRBFkfKK6w\n\n# Code\nC++\n```\n//TC : O(n)\n//SC : O(1)\nclass Solution {\npublic:\n bool backspaceCompare(string s, string t) {\n int szS = s.size(), szT = t.size();\n string sNew = findFinalString(s);\n string tNew = findFinalString(t);\n return sNew == tNew;\n }\n private:\n string findFinalString(string & str){\n int sz = str.size();\n\n int hashCnt = 0;\n string res = "";\n for(int indx = sz-1; indx > -1; indx--){\n if(str[indx] == \'#\'){\n hashCnt++;\n }else{\n if(hashCnt > 0){\n hashCnt--;\n }else{\n res += str[indx];\n }\n }\n }\n \n reverse(res.begin(), res.end());\n return res;\n } \n};\n```\nJava\n```\nclass Solution {\n public boolean backspaceCompare(String s, String t) {\n int szS = s.length(), szT = t.length();\n String sNew = findFinalString(s);\n String tNew = findFinalString(t);\n return sNew.equals(tNew);\n }\n \n private String findFinalString(String str) {\n int sz = str.length();\n int hashCnt = 0;\n StringBuilder res = new StringBuilder();\n for (int indx = sz - 1; indx > -1; indx--) {\n if (str.charAt(indx) == \'#\') {\n hashCnt++;\n } else {\n if (hashCnt > 0) {\n hashCnt--;\n } else {\n res.append(str.charAt(indx));\n }\n }\n }\n return res.reverse().toString();\n }\n}\n```\nPython 3\n```\nclass Solution:\n def backspaceCompare(self, s, t):\n szS = len(s)\n szT = len(t)\n sNew = self.findFinalString(s)\n tNew = self.findFinalString(t)\n return sNew == tNew\n\n def findFinalString(self, str):\n sz = len(str)\n hashCnt = 0\n res = []\n for indx in range(sz - 1, -1, -1):\n if str[indx] == \'#\':\n hashCnt += 1\n else:\n if hashCnt > 0:\n hashCnt -= 1\n else:\n res.append(str[indx])\n return \'\'.join(res[::-1])\n``` | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
Video Solution | Explanation With Drawings | Java | C++ | Python 3 | backspace-string-compare | 1 | 1 | # Intuition, approach, and complexity dicussed in detail in video solution\nhttps://youtu.be/UcRBFkfKK6w\n\n# Code\nC++\n```\n//TC : O(n)\n//SC : O(1)\nclass Solution {\npublic:\n bool backspaceCompare(string s, string t) {\n int szS = s.size(), szT = t.size();\n string sNew = findFinalString(s);\n string tNew = findFinalString(t);\n return sNew == tNew;\n }\n private:\n string findFinalString(string & str){\n int sz = str.size();\n\n int hashCnt = 0;\n string res = "";\n for(int indx = sz-1; indx > -1; indx--){\n if(str[indx] == \'#\'){\n hashCnt++;\n }else{\n if(hashCnt > 0){\n hashCnt--;\n }else{\n res += str[indx];\n }\n }\n }\n \n reverse(res.begin(), res.end());\n return res;\n } \n};\n```\nJava\n```\nclass Solution {\n public boolean backspaceCompare(String s, String t) {\n int szS = s.length(), szT = t.length();\n String sNew = findFinalString(s);\n String tNew = findFinalString(t);\n return sNew.equals(tNew);\n }\n \n private String findFinalString(String str) {\n int sz = str.length();\n int hashCnt = 0;\n StringBuilder res = new StringBuilder();\n for (int indx = sz - 1; indx > -1; indx--) {\n if (str.charAt(indx) == \'#\') {\n hashCnt++;\n } else {\n if (hashCnt > 0) {\n hashCnt--;\n } else {\n res.append(str.charAt(indx));\n }\n }\n }\n return res.reverse().toString();\n }\n}\n```\nPython 3\n```\nclass Solution:\n def backspaceCompare(self, s, t):\n szS = len(s)\n szT = len(t)\n sNew = self.findFinalString(s)\n tNew = self.findFinalString(t)\n return sNew == tNew\n\n def findFinalString(self, str):\n sz = len(str)\n hashCnt = 0\n res = []\n for indx in range(sz - 1, -1, -1):\n if str[indx] == \'#\':\n hashCnt += 1\n else:\n if hashCnt > 0:\n hashCnt -= 1\n else:\n res.append(str[indx])\n return \'\'.join(res[::-1])\n``` | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | backspace-string-compare | 1 | 1 | # Intuition\nUsing stack or pointers\n\n---\n\n# Solution Video\n\nhttps://youtu.be/YBt2dPL6z5o\n\n\u203B I put my son on my lap and recorded a video, so I\'m feeling a little rushed. lol Please leave a comment if you have any questions.\n\n\u25A0 Timeline of the video\n`0:04` Stack solution code\n`0:23` Explain key point with O(1) space\n`1:12` Consider 4 cases\n`3:14` Coding\n`7:20` Time Complexity and Space Complexity\n\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,734\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSimply, we can solve this question with `stack` like this.\n\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n\n def remove_characters(s):\n stack = []\n for char in s:\n if char == \'#\' and stack:\n stack.pop()\n elif char != \'#\':\n stack.append(char)\n return stack\n\n return remove_characters(s) == remove_characters(t)\n\n```\n\nBut we can improve space complexity to `O(1)`.\n\nWe use `pointers` for s and t but problem is\n\n\n---\n\nWe don\'t know whether we should keep these characters or not. \n\n---\n\nTo solve the problem, my idea is to iterate through both input strings from the end.\n\n---\n\n\u2B50\uFE0F Points\n\nIterate through the both strings from end. In that case, basically\n\nIf we meet alphabets, then we should keep them.\nIf we meet "#", then next character will be removed.\n\n---\n\n- Consider basic 4 cases\n\nI think there are 4 basic cases we should consider.\n\n---\n\n\u2B50\uFE0F Points\n\n1. The case where the same characters remain in the end\n Example case: `s = "ab#c"` `t = "ad#c"`\n Results: `true`\n2. The case where we remove all characters at the same time\n Example case: `s = "ab##"` `t = "c#d#"`\n Results: `true`\n3. The case where we remove all characters in one input string first, opposite of case 2\n Example case: `s = "ab#"` `t = "c#d#"`\n Results: `false`\n4. The case where different characters remain in the end, opposite of case 1\n Example case: `s = "a#c"` `t = "b"`\n Results: `false`\n---\n\n### Algorithm Overview:\n- The code is designed to determine whether two strings are equal after applying backspace operations. It compares the two strings character by character after processing the backspace operations.\n\n### Detailed Explanation:\n1. Define a function `get_next_valid_char_index` that takes two arguments: `s` (a string) and `end` (an integer representing the index to start from).\n - Initialize `backspace_count` to 0.\n - Start a while loop that runs while `end` is greater than or equal to 0.\n - Within the loop:\n - Check if the character at index `end` in string `s` is a \'#\' (backspace).\n - If it is a \'#\', increment `backspace_count`.\n - If `backspace_count` is greater than 0, decrement it to simulate the removal of a character.\n - If neither of the above conditions is met, break out of the loop. This indicates that you\'ve found the next valid character\'s index.\n - Decrement `end` by 1 in each iteration.\n\n2. Initialize two pointers, `ps` and `pt`, to the last index of strings `s` and `t`, respectively.\n\n3. Enter a while loop that continues as long as `ps` is greater than or equal to 0 or `pt` is greater than or equal to 0. This loop handles the comparison of the processed strings.\n\n4. In each iteration of the loop:\n - Update `ps` using the `get_next_valid_char_index` function for string `s`.\n - Update `pt` using the `get_next_valid_char_index` function for string `t`.\n\n5. After both `ps` and `pt` are updated:\n - If `ps` is less than 0 and `pt` is less than 0, it means both processed strings are empty. In this case, print "aaaaaa" as a debug message (you can remove it) and return `True` as the strings are equivalent after applying backspace operations.\n\n6. If either `ps` or `pt` is less than 0 but not both, it means one of the strings is empty while the other is not. In this case, return `False` as the strings are not equivalent.\n\n7. If neither of the above conditions is met, check if the characters at indices `ps` in string `s` and `pt` in string `t` are not equal. If they are not equal, return `False`.\n\n8. Decrement `ps` and `pt` by 1 to move on to the next character in both strings.\n\n9. Repeat the loop until both strings are fully processed.\n\n10. If none of the conditions for returning `False` are met throughout the loop, it means the strings are equivalent after applying backspace operations, and the function returns `True`.\n\n\n# Complexity\n- Time complexity: $$O(max(len(s), len(t))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n\n def get_next_valid_char_index(s, end):\n backspace_count = 0\n while end >= 0:\n if s[end] == \'#\':\n # find "#"\n backspace_count += 1\n elif backspace_count > 0:\n # find an alphabet but skip it because we have backspaces\n backspace_count -= 1\n else:\n # if we don\'t have backspaces and current character is alphabet\n # it\'s time to compare two characters from s and t\n break\n end -= 1\n return end # return current end pointer for the next iteration.\n\n ps = len(s) - 1\n pt = len(t) - 1\n\n while ps >= 0 or pt >= 0:\n ps = get_next_valid_char_index(s, ps)\n pt = get_next_valid_char_index(t, pt)\n\n if ps < 0 and pt < 0:\n # example case s = "ab##" t = "c#d#", case 2 \n return True\n if ps < 0 or pt < 0:\n # example case s = "ab#" t = "c#d#", case 3\n return False\n elif s[ps] != t[pt]:\n # example case s = "a#c" t = "b", case 4\n return False\n\n ps -= 1\n pt -= 1\n\n # example case s = "ab#c" t = "ad#c", case 1\n return True\n```\n```javascript []\n/**\n * @param {string} s\n * @param {string} t\n * @return {boolean}\n */\nvar backspaceCompare = function(s, t) {\n function get_next_valid_char_index(str, end) {\n let backspace_count = 0;\n while (end >= 0) {\n if (str.charAt(end) === \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n }\n\n let ps = s.length - 1;\n let pt = t.length - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s.charAt(ps) !== t.charAt(pt)) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n};\n```\n```java []\nclass Solution {\n public boolean backspaceCompare(String s, String t) {\n int ps = s.length() - 1;\n int pt = t.length() - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s.charAt(ps) != t.charAt(pt)) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n }\n\n private int get_next_valid_char_index(String str, int end) {\n int backspace_count = 0;\n while (end >= 0) {\n if (str.charAt(end) == \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n bool backspaceCompare(string s, string t) {\n int ps = s.length() - 1;\n int pt = t.length() - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s[ps] != t[pt]) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n }\n\nprivate:\n int get_next_valid_char_index(string str, int end) {\n int backspace_count = 0;\n while (end >= 0) {\n if (str[end] == \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n } \n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/backspace-string-compare/solutions/4184137/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/N8QehVXYSc0\n\n\u25A0 Timeline of the video\n`0:04` 2 Keys to solve this question\n`0:18` Explain the first key point\n`0:45` Explain the first key point\n`1:27` Explain the second key point\n`5:44` Coding\n`9:39` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/parallel-courses-iii/solutions/4180474/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/PWorxtrU6hY\n\n\u25A0 Timeline of the video\n`0:04` Key point to solve this question\n`0:23` Explain the first key point\n`1:12` Explain the second key point\n`1:39` Demonstrate real algorithms\n`6:36` Coding\n`10:33` Time Complexity and Space Complexity | 59 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
【Video】Give me 10 minutes - How we think about a solution - Python, JavaScript, Java, C++ | backspace-string-compare | 1 | 1 | # Intuition\nUsing stack or pointers\n\n---\n\n# Solution Video\n\nhttps://youtu.be/YBt2dPL6z5o\n\n\u203B I put my son on my lap and recorded a video, so I\'m feeling a little rushed. lol Please leave a comment if you have any questions.\n\n\u25A0 Timeline of the video\n`0:04` Stack solution code\n`0:23` Explain key point with O(1) space\n`1:12` Consider 4 cases\n`3:14` Coding\n`7:20` Time Complexity and Space Complexity\n\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,734\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSimply, we can solve this question with `stack` like this.\n\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n\n def remove_characters(s):\n stack = []\n for char in s:\n if char == \'#\' and stack:\n stack.pop()\n elif char != \'#\':\n stack.append(char)\n return stack\n\n return remove_characters(s) == remove_characters(t)\n\n```\n\nBut we can improve space complexity to `O(1)`.\n\nWe use `pointers` for s and t but problem is\n\n\n---\n\nWe don\'t know whether we should keep these characters or not. \n\n---\n\nTo solve the problem, my idea is to iterate through both input strings from the end.\n\n---\n\n\u2B50\uFE0F Points\n\nIterate through the both strings from end. In that case, basically\n\nIf we meet alphabets, then we should keep them.\nIf we meet "#", then next character will be removed.\n\n---\n\n- Consider basic 4 cases\n\nI think there are 4 basic cases we should consider.\n\n---\n\n\u2B50\uFE0F Points\n\n1. The case where the same characters remain in the end\n Example case: `s = "ab#c"` `t = "ad#c"`\n Results: `true`\n2. The case where we remove all characters at the same time\n Example case: `s = "ab##"` `t = "c#d#"`\n Results: `true`\n3. The case where we remove all characters in one input string first, opposite of case 2\n Example case: `s = "ab#"` `t = "c#d#"`\n Results: `false`\n4. The case where different characters remain in the end, opposite of case 1\n Example case: `s = "a#c"` `t = "b"`\n Results: `false`\n---\n\n### Algorithm Overview:\n- The code is designed to determine whether two strings are equal after applying backspace operations. It compares the two strings character by character after processing the backspace operations.\n\n### Detailed Explanation:\n1. Define a function `get_next_valid_char_index` that takes two arguments: `s` (a string) and `end` (an integer representing the index to start from).\n - Initialize `backspace_count` to 0.\n - Start a while loop that runs while `end` is greater than or equal to 0.\n - Within the loop:\n - Check if the character at index `end` in string `s` is a \'#\' (backspace).\n - If it is a \'#\', increment `backspace_count`.\n - If `backspace_count` is greater than 0, decrement it to simulate the removal of a character.\n - If neither of the above conditions is met, break out of the loop. This indicates that you\'ve found the next valid character\'s index.\n - Decrement `end` by 1 in each iteration.\n\n2. Initialize two pointers, `ps` and `pt`, to the last index of strings `s` and `t`, respectively.\n\n3. Enter a while loop that continues as long as `ps` is greater than or equal to 0 or `pt` is greater than or equal to 0. This loop handles the comparison of the processed strings.\n\n4. In each iteration of the loop:\n - Update `ps` using the `get_next_valid_char_index` function for string `s`.\n - Update `pt` using the `get_next_valid_char_index` function for string `t`.\n\n5. After both `ps` and `pt` are updated:\n - If `ps` is less than 0 and `pt` is less than 0, it means both processed strings are empty. In this case, print "aaaaaa" as a debug message (you can remove it) and return `True` as the strings are equivalent after applying backspace operations.\n\n6. If either `ps` or `pt` is less than 0 but not both, it means one of the strings is empty while the other is not. In this case, return `False` as the strings are not equivalent.\n\n7. If neither of the above conditions is met, check if the characters at indices `ps` in string `s` and `pt` in string `t` are not equal. If they are not equal, return `False`.\n\n8. Decrement `ps` and `pt` by 1 to move on to the next character in both strings.\n\n9. Repeat the loop until both strings are fully processed.\n\n10. If none of the conditions for returning `False` are met throughout the loop, it means the strings are equivalent after applying backspace operations, and the function returns `True`.\n\n\n# Complexity\n- Time complexity: $$O(max(len(s), len(t))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n\n def get_next_valid_char_index(s, end):\n backspace_count = 0\n while end >= 0:\n if s[end] == \'#\':\n # find "#"\n backspace_count += 1\n elif backspace_count > 0:\n # find an alphabet but skip it because we have backspaces\n backspace_count -= 1\n else:\n # if we don\'t have backspaces and current character is alphabet\n # it\'s time to compare two characters from s and t\n break\n end -= 1\n return end # return current end pointer for the next iteration.\n\n ps = len(s) - 1\n pt = len(t) - 1\n\n while ps >= 0 or pt >= 0:\n ps = get_next_valid_char_index(s, ps)\n pt = get_next_valid_char_index(t, pt)\n\n if ps < 0 and pt < 0:\n # example case s = "ab##" t = "c#d#", case 2 \n return True\n if ps < 0 or pt < 0:\n # example case s = "ab#" t = "c#d#", case 3\n return False\n elif s[ps] != t[pt]:\n # example case s = "a#c" t = "b", case 4\n return False\n\n ps -= 1\n pt -= 1\n\n # example case s = "ab#c" t = "ad#c", case 1\n return True\n```\n```javascript []\n/**\n * @param {string} s\n * @param {string} t\n * @return {boolean}\n */\nvar backspaceCompare = function(s, t) {\n function get_next_valid_char_index(str, end) {\n let backspace_count = 0;\n while (end >= 0) {\n if (str.charAt(end) === \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n }\n\n let ps = s.length - 1;\n let pt = t.length - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s.charAt(ps) !== t.charAt(pt)) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n};\n```\n```java []\nclass Solution {\n public boolean backspaceCompare(String s, String t) {\n int ps = s.length() - 1;\n int pt = t.length() - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s.charAt(ps) != t.charAt(pt)) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n }\n\n private int get_next_valid_char_index(String str, int end) {\n int backspace_count = 0;\n while (end >= 0) {\n if (str.charAt(end) == \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n bool backspaceCompare(string s, string t) {\n int ps = s.length() - 1;\n int pt = t.length() - 1;\n\n while (ps >= 0 || pt >= 0) {\n ps = get_next_valid_char_index(s, ps);\n pt = get_next_valid_char_index(t, pt);\n\n if (ps < 0 && pt < 0) {\n return true;\n }\n if (ps < 0 || pt < 0) {\n return false;\n } else if (s[ps] != t[pt]) {\n return false;\n }\n\n ps--;\n pt--;\n }\n\n return true; \n }\n\nprivate:\n int get_next_valid_char_index(string str, int end) {\n int backspace_count = 0;\n while (end >= 0) {\n if (str[end] == \'#\') {\n backspace_count++;\n } else if (backspace_count > 0) {\n backspace_count--;\n } else {\n break;\n }\n end--;\n }\n return end;\n } \n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/backspace-string-compare/solutions/4184137/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\nvideo\nhttps://youtu.be/N8QehVXYSc0\n\n\u25A0 Timeline of the video\n`0:04` 2 Keys to solve this question\n`0:18` Explain the first key point\n`0:45` Explain the first key point\n`1:27` Explain the second key point\n`5:44` Coding\n`9:39` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/parallel-courses-iii/solutions/4180474/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/PWorxtrU6hY\n\n\u25A0 Timeline of the video\n`0:04` Key point to solve this question\n`0:23` Explain the first key point\n`1:12` Explain the second key point\n`1:39` Demonstrate real algorithms\n`6:36` Coding\n`10:33` Time Complexity and Space Complexity | 59 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
Intuitive Approach Using Counting. Linear time & Constant Space. | backspace-string-compare | 0 | 1 | # Approach\n\nFor both s & t (string1 & string2 in my code)\n- Simply maintain the skip (count of # in a string).\n- Iterate from reverse,\n - If found #, increment skip and continue\n - If char is valid alpha but skip > 0: decrease skip and continue\n - If char is valid and skip == 0: do nothing\n- Do the above thing for s & t both\n- To do it together for both\n - use a while loop that will loop until there are unseen char in s or t\n - implement skip logic for s\n - implement skip logic for t\n - if your code reached this part, that means you found a valid character\n - If 2 valid characters: compare them & return False if not equal\n - If 1 valid character: return False (think why?)\n\nFollow the comments in the code to understand better! \n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, string1: str, string2: str) -> bool:\n s1, s2 = len(string1)-1, len(string2)-1\n skip1 = skip2 = 0\n\n while s1 > -1 or s2 > -1:\n # if we still have some elements to check in string1\n if s1 > -1:\n # if it is a valid alphabet\n if string1[s1].isalpha():\n # but we can skip it\n if skip1 > 0:\n skip1 -= 1\n s1 -= 1\n continue\n # valid alpha but can\'t skip (wrote this for clarity)\n else:\n pass\n else:\n # we found #, increment skip value and continue\n skip1 += 1\n s1 -= 1\n continue\n \n # if we still have some elements to check in string2\n # do same logic as done for string1\n if s2 > -1:\n if string2[s2].isalpha():\n if skip2 > 0:\n skip2 -= 1\n s2 -= 1\n continue\n else:\n pass\n else:\n skip2 += 1\n s2 -= 1\n continue\n\n # if we reached this end of the code\n # it means we found a valid character\n # but there could be 2 characters or 1 character\n # if we have 2 characters -> compare them to check if they are equal\n # if not equal -> return False\n # if only 1 valid character -> return False (think why?)\n if s1 > - 1 and s2 > -1:\n if string1[s1] != string2[s2]:\n return False\n else: \n pass\n else:\n return False\n \n # reduce the count of s1 & s2\n s1 -= 1\n s2 -= 1\n\n return True\n\n``` | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
Intuitive Approach Using Counting. Linear time & Constant Space. | backspace-string-compare | 0 | 1 | # Approach\n\nFor both s & t (string1 & string2 in my code)\n- Simply maintain the skip (count of # in a string).\n- Iterate from reverse,\n - If found #, increment skip and continue\n - If char is valid alpha but skip > 0: decrease skip and continue\n - If char is valid and skip == 0: do nothing\n- Do the above thing for s & t both\n- To do it together for both\n - use a while loop that will loop until there are unseen char in s or t\n - implement skip logic for s\n - implement skip logic for t\n - if your code reached this part, that means you found a valid character\n - If 2 valid characters: compare them & return False if not equal\n - If 1 valid character: return False (think why?)\n\nFollow the comments in the code to understand better! \n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, string1: str, string2: str) -> bool:\n s1, s2 = len(string1)-1, len(string2)-1\n skip1 = skip2 = 0\n\n while s1 > -1 or s2 > -1:\n # if we still have some elements to check in string1\n if s1 > -1:\n # if it is a valid alphabet\n if string1[s1].isalpha():\n # but we can skip it\n if skip1 > 0:\n skip1 -= 1\n s1 -= 1\n continue\n # valid alpha but can\'t skip (wrote this for clarity)\n else:\n pass\n else:\n # we found #, increment skip value and continue\n skip1 += 1\n s1 -= 1\n continue\n \n # if we still have some elements to check in string2\n # do same logic as done for string1\n if s2 > -1:\n if string2[s2].isalpha():\n if skip2 > 0:\n skip2 -= 1\n s2 -= 1\n continue\n else:\n pass\n else:\n skip2 += 1\n s2 -= 1\n continue\n\n # if we reached this end of the code\n # it means we found a valid character\n # but there could be 2 characters or 1 character\n # if we have 2 characters -> compare them to check if they are equal\n # if not equal -> return False\n # if only 1 valid character -> return False (think why?)\n if s1 > - 1 and s2 > -1:\n if string1[s1] != string2[s2]:\n return False\n else: \n pass\n else:\n return False\n \n # reduce the count of s1 & s2\n s1 -= 1\n s2 -= 1\n\n return True\n\n``` | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
Backspace String Compare | backspace-string-compare | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport copy\n\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def remove_backspace(string: str):\n backup = \'\'\n for i in range(len(string)):\n if string[i] == \'#\' and backup:\n backup = backup[:-1]\n elif string[i] == \'#\' and not backup:\n pass\n else:\n backup += string[i]\n return backup\n\n return remove_backspace(s) == remove_backspace(t)\n \n``` | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
Backspace String Compare | backspace-string-compare | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport copy\n\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def remove_backspace(string: str):\n backup = \'\'\n for i in range(len(string)):\n if string[i] == \'#\' and backup:\n backup = backup[:-1]\n elif string[i] == \'#\' and not backup:\n pass\n else:\n backup += string[i]\n return backup\n\n return remove_backspace(s) == remove_backspace(t)\n \n``` | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
🔥REAL O(1) space and O(n) time 🔥 JAVA 🔥PYTHON | backspace-string-compare | 1 | 1 | # Intuition\nWe will not use any additional structures to fit in memory. Only primitives, only hardcore.\n\n# Approach\n**Step 1**\nFirst of all, we count the number of characters not deleted after formatting in the strings S and T.\n```java []\npublic static int countRealSymbol(String s){\n int counter = 0;\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) != \'#\') {\n counter++;\n } else if (!(i < counter) && (counter - 1 >= 0)) {\n counter--;\n }\n }\n return counter;\n }\n```\n```python []\ndef countRealSymbol(s):\n counter = 0\n i = 0\n while i < len(s):\n if s[i] != \'#\':\n counter += 1\n elif not (i < counter) and (counter - 1 >= 0):\n counter -= 1\n i += 1\n return counter\n\n```\n\nIf the number of these characters is different, we immediately return false. \n\nIf their number is 0, that is, there will be no characters left after deletion, then we return true.\n\n```java []\nif (realSymbolInT != realSymbolInS) return false;\nif (realSymbolInT == 0) return true;\n```\n```python []\nif realSymbolInT != realSymbolInS:\n return False\nif realSymbolInT == 0:\n return True\n```\n\n**Step 2**\n\nThen it\'s more interesting. We will need two pointers to different strings. We will go from the end.\n\n```java []\nint counterI = 0; // count # in string S\nint counterJ = 0; // count # in string J\n\nfor (int i = s.length() - 1, j = t.length() - 1; j >= 0 && i >= 0; ) {\n}\n```\n```python []\ncounterI = 0 # count # in string S\ncounterJ = 0 # count # in string J\ni = len(s) - 1 \nj = len(t) - 1\nwhile j >= 0 and i >= 0:\n ***\n```\n**Inside loop :**\n\nIf we meet #, we will increase our counter # for the corresponding variable.\n\n```java []\nif (s.charAt(i) == \'#\' || t.charAt(j) == \'#\') {\n if (s.charAt(i) == \'#\') {\n counterI++;\n i--;\n }\n if (t.charAt(j) == \'#\') {\n counterJ++;\n j--;\n }\n}\n```\n```python []\nif s[i] == \'#\' or t[j] == \'#\':\n if s[i] == \'#\':\n counterI += 1\n i -= 1\n if t[j] == \'#\':\n counterJ += 1\n j -= 1\n```\n\nWhen we encounter a letter, we will check if our counter is empty.\nIf not, we will reduce its value and skip this letter as if we had deleted it.\nSimilarly for another counter.\n\n```java []\nelse if (counterI != 0 || counterJ != 0) {\n if (counterI != 0) {\n i--;\n counterI --;\n }else {\n j--;\n counterJ--;\n }\n}\n```\n```python []\nelif counterI != 0 or counterJ != 0:\n if counterI != 0:\n i -= 1\n counterI -= 1\n else:\n j -= 1\n counterJ -= 1\n```\n\nIf the counter of both is empty, then we can finally **compare** them!\nAnd go to the next character (to the left, do not forget).\n\n```java []\nelse {\n if (s.charAt(i) != t.charAt(j)) return false;\n i--;\n j--;\n}\n```\n```python []\nelse:\n if s[i] != t[j]:\n return False\n i -= 1\n j -= 1\n```\nThat\'s all! If it seems complicated, read it again\n\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n Only by the length of the string\n\n- Space complexity:\n $$O(1)$$ \nOnly primitives, only hardcore\n\n# Uprove it friends \uD83D\uDD25\n\n# Code\n```java []\npublic class Solution {\n public boolean backspaceCompare(String s, String t) {\n int realSymbolInS = countRealSymbol(s);\n int realSymbolInT = countRealSymbol(t);\n\n if (realSymbolInT != realSymbolInS) return false;\n if (realSymbolInT == 0) return true;\n\n int counterI = 0; // count # in string S\n int counterJ = 0; // count # in string J\n\n for (int i = s.length() - 1, j = t.length() - 1; j >= 0 && i >= 0; ) {\n if (s.charAt(i) == \'#\' || t.charAt(j) == \'#\') {\n if (s.charAt(i) == \'#\') {\n counterI++;\n i--;\n }\n if (t.charAt(j) == \'#\') {\n counterJ++;\n j--;\n }\n } else if (counterI != 0 || counterJ != 0) {\n if (counterI != 0) {\n i--;\n counterI --;\n }else {\n j--;\n counterJ--;\n }\n } else {\n if (s.charAt(i) != t.charAt(j)) return false;\n i--;\n j--;\n }\n }\n return true;\n }\n\n public static int countRealSymbol(String s){\n int counter = 0;\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) != \'#\') {\n counter++;\n } else if (!(i < counter) && (counter - 1 >= 0)) {\n counter--;\n }\n }\n return counter;\n }\n}\n```\n```python []\nclass Solution(object):\n def backspaceCompare(self, s, t):\n def countRealSymbol(s):\n counter = 0\n for i in range(len(s)):\n if s[i] != \'#\':\n counter += 1\n elif (not i < counter) and counter - 1 >= 0:\n counter -= 1\n return counter\n\n realSymbolInS = countRealSymbol(s)\n realSymbolInT = countRealSymbol(t)\n\n if realSymbolInT != realSymbolInS:\n return False\n if realSymbolInT == 0:\n return True\n\n counterI = 0 # count # in string S\n counterJ = 0 # count # in string J\n i = len(s) - 1 \n j = len(t) - 1\n\n while j >= 0 and i >= 0:\n if s[i] == \'#\' or t[j] == \'#\':\n if s[i] == \'#\':\n counterI += 1\n i -= 1\n if t[j] == \'#\':\n counterJ += 1\n j -= 1\n elif counterI != 0 or counterJ != 0:\n if counterI != 0:\n i -= 1\n counterI -= 1\n else:\n j -= 1\n counterJ -= 1\n else:\n if s[i] != t[j]:\n return False\n i -= 1\n j -= 1\n\n return True\n\n\n \n```\n\n# P.S.\n\nIf you remove the function call in python, and write down the functionality linearly, you can get such a runtime.\n\n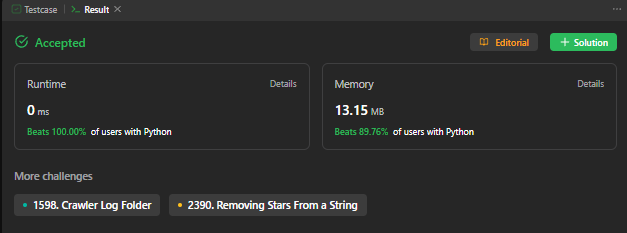\n\n\n | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
🔥REAL O(1) space and O(n) time 🔥 JAVA 🔥PYTHON | backspace-string-compare | 1 | 1 | # Intuition\nWe will not use any additional structures to fit in memory. Only primitives, only hardcore.\n\n# Approach\n**Step 1**\nFirst of all, we count the number of characters not deleted after formatting in the strings S and T.\n```java []\npublic static int countRealSymbol(String s){\n int counter = 0;\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) != \'#\') {\n counter++;\n } else if (!(i < counter) && (counter - 1 >= 0)) {\n counter--;\n }\n }\n return counter;\n }\n```\n```python []\ndef countRealSymbol(s):\n counter = 0\n i = 0\n while i < len(s):\n if s[i] != \'#\':\n counter += 1\n elif not (i < counter) and (counter - 1 >= 0):\n counter -= 1\n i += 1\n return counter\n\n```\n\nIf the number of these characters is different, we immediately return false. \n\nIf their number is 0, that is, there will be no characters left after deletion, then we return true.\n\n```java []\nif (realSymbolInT != realSymbolInS) return false;\nif (realSymbolInT == 0) return true;\n```\n```python []\nif realSymbolInT != realSymbolInS:\n return False\nif realSymbolInT == 0:\n return True\n```\n\n**Step 2**\n\nThen it\'s more interesting. We will need two pointers to different strings. We will go from the end.\n\n```java []\nint counterI = 0; // count # in string S\nint counterJ = 0; // count # in string J\n\nfor (int i = s.length() - 1, j = t.length() - 1; j >= 0 && i >= 0; ) {\n}\n```\n```python []\ncounterI = 0 # count # in string S\ncounterJ = 0 # count # in string J\ni = len(s) - 1 \nj = len(t) - 1\nwhile j >= 0 and i >= 0:\n ***\n```\n**Inside loop :**\n\nIf we meet #, we will increase our counter # for the corresponding variable.\n\n```java []\nif (s.charAt(i) == \'#\' || t.charAt(j) == \'#\') {\n if (s.charAt(i) == \'#\') {\n counterI++;\n i--;\n }\n if (t.charAt(j) == \'#\') {\n counterJ++;\n j--;\n }\n}\n```\n```python []\nif s[i] == \'#\' or t[j] == \'#\':\n if s[i] == \'#\':\n counterI += 1\n i -= 1\n if t[j] == \'#\':\n counterJ += 1\n j -= 1\n```\n\nWhen we encounter a letter, we will check if our counter is empty.\nIf not, we will reduce its value and skip this letter as if we had deleted it.\nSimilarly for another counter.\n\n```java []\nelse if (counterI != 0 || counterJ != 0) {\n if (counterI != 0) {\n i--;\n counterI --;\n }else {\n j--;\n counterJ--;\n }\n}\n```\n```python []\nelif counterI != 0 or counterJ != 0:\n if counterI != 0:\n i -= 1\n counterI -= 1\n else:\n j -= 1\n counterJ -= 1\n```\n\nIf the counter of both is empty, then we can finally **compare** them!\nAnd go to the next character (to the left, do not forget).\n\n```java []\nelse {\n if (s.charAt(i) != t.charAt(j)) return false;\n i--;\n j--;\n}\n```\n```python []\nelse:\n if s[i] != t[j]:\n return False\n i -= 1\n j -= 1\n```\nThat\'s all! If it seems complicated, read it again\n\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n Only by the length of the string\n\n- Space complexity:\n $$O(1)$$ \nOnly primitives, only hardcore\n\n# Uprove it friends \uD83D\uDD25\n\n# Code\n```java []\npublic class Solution {\n public boolean backspaceCompare(String s, String t) {\n int realSymbolInS = countRealSymbol(s);\n int realSymbolInT = countRealSymbol(t);\n\n if (realSymbolInT != realSymbolInS) return false;\n if (realSymbolInT == 0) return true;\n\n int counterI = 0; // count # in string S\n int counterJ = 0; // count # in string J\n\n for (int i = s.length() - 1, j = t.length() - 1; j >= 0 && i >= 0; ) {\n if (s.charAt(i) == \'#\' || t.charAt(j) == \'#\') {\n if (s.charAt(i) == \'#\') {\n counterI++;\n i--;\n }\n if (t.charAt(j) == \'#\') {\n counterJ++;\n j--;\n }\n } else if (counterI != 0 || counterJ != 0) {\n if (counterI != 0) {\n i--;\n counterI --;\n }else {\n j--;\n counterJ--;\n }\n } else {\n if (s.charAt(i) != t.charAt(j)) return false;\n i--;\n j--;\n }\n }\n return true;\n }\n\n public static int countRealSymbol(String s){\n int counter = 0;\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) != \'#\') {\n counter++;\n } else if (!(i < counter) && (counter - 1 >= 0)) {\n counter--;\n }\n }\n return counter;\n }\n}\n```\n```python []\nclass Solution(object):\n def backspaceCompare(self, s, t):\n def countRealSymbol(s):\n counter = 0\n for i in range(len(s)):\n if s[i] != \'#\':\n counter += 1\n elif (not i < counter) and counter - 1 >= 0:\n counter -= 1\n return counter\n\n realSymbolInS = countRealSymbol(s)\n realSymbolInT = countRealSymbol(t)\n\n if realSymbolInT != realSymbolInS:\n return False\n if realSymbolInT == 0:\n return True\n\n counterI = 0 # count # in string S\n counterJ = 0 # count # in string J\n i = len(s) - 1 \n j = len(t) - 1\n\n while j >= 0 and i >= 0:\n if s[i] == \'#\' or t[j] == \'#\':\n if s[i] == \'#\':\n counterI += 1\n i -= 1\n if t[j] == \'#\':\n counterJ += 1\n j -= 1\n elif counterI != 0 or counterJ != 0:\n if counterI != 0:\n i -= 1\n counterI -= 1\n else:\n j -= 1\n counterJ -= 1\n else:\n if s[i] != t[j]:\n return False\n i -= 1\n j -= 1\n\n return True\n\n\n \n```\n\n# P.S.\n\nIf you remove the function call in python, and write down the functionality linearly, you can get such a runtime.\n\n\n\n\n | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
Shortest, Fastest Solution, using regex 🔥 99% | backspace-string-compare | 0 | 1 | \n# Approach\n- We process both **input strings** using the `solve()` function, which efficiently handles backspaces using **regular expressions**. Then, we compare the processed strings to check for equality.\n# Complexity\n- Time complexity: $$O(max(n, m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(max(n, m))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def solve(string):\n while \'#\' in string:\n string = re.sub(r\'^#|[a-z]#\', \'\', string)\n return string\n return solve(s) == solve(t)\n```\n# Explanation\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def solve(string):\n # Define a function to process the input string.\n\n while \'#\' in string:\n # Continue as long as there are \'#\' characters in the string:\n string = re.sub(r\'^#|[a-z]#\', \'\', string)\n # Remove \'#\' at the start or after lowercase letters using regex.\n\n return string\n # Return the processed string.\n\n return solve(s) == solve(t)\n # Compare the processed versions of both input strings \n #and return True if they are equal, False otherwise.\n```\nplease upvote :D | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
Shortest, Fastest Solution, using regex 🔥 99% | backspace-string-compare | 0 | 1 | \n# Approach\n- We process both **input strings** using the `solve()` function, which efficiently handles backspaces using **regular expressions**. Then, we compare the processed strings to check for equality.\n# Complexity\n- Time complexity: $$O(max(n, m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(max(n, m))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def solve(string):\n while \'#\' in string:\n string = re.sub(r\'^#|[a-z]#\', \'\', string)\n return string\n return solve(s) == solve(t)\n```\n# Explanation\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def solve(string):\n # Define a function to process the input string.\n\n while \'#\' in string:\n # Continue as long as there are \'#\' characters in the string:\n string = re.sub(r\'^#|[a-z]#\', \'\', string)\n # Remove \'#\' at the start or after lowercase letters using regex.\n\n return string\n # Return the processed string.\n\n return solve(s) == solve(t)\n # Compare the processed versions of both input strings \n #and return True if they are equal, False otherwise.\n```\nplease upvote :D | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
🔥An Original in 🐍 || Beats 83% || Brute-Force🔥 | backspace-string-compare | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def rem_(st: str):\n while \'#\' in st:\n a = st.index(\'#\')\n if a == 0:\n st = st[1:]\n else:\n st = st[:a-1] + st[a+1:]\n return st\n \n s, t = rem_(s), rem_(t)\n return s == t\n``` | 1 | Given two strings `s` and `t`, return `true` _if they are equal when both are typed into empty text editors_. `'#'` means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
**Example 1:**
**Input:** s = "ab#c ", t = "ad#c "
**Output:** true
**Explanation:** Both s and t become "ac ".
**Example 2:**
**Input:** s = "ab## ", t = "c#d# "
**Output:** true
**Explanation:** Both s and t become " ".
**Example 3:**
**Input:** s = "a#c ", t = "b "
**Output:** false
**Explanation:** s becomes "c " while t becomes "b ".
**Constraints:**
* `1 <= s.length, t.length <= 200`
* `s` and `t` only contain lowercase letters and `'#'` characters.
**Follow up:** Can you solve it in `O(n)` time and `O(1)` space? | null |
🔥An Original in 🐍 || Beats 83% || Brute-Force🔥 | backspace-string-compare | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def backspaceCompare(self, s: str, t: str) -> bool:\n def rem_(st: str):\n while \'#\' in st:\n a = st.index(\'#\')\n if a == 0:\n st = st[1:]\n else:\n st = st[:a-1] + st[a+1:]\n return st\n \n s, t = rem_(s), rem_(t)\n return s == t\n``` | 1 | A robot on an infinite XY-plane starts at point `(0, 0)` facing north. The robot can receive a sequence of these three possible types of `commands`:
* `-2`: Turn left `90` degrees.
* `-1`: Turn right `90` degrees.
* `1 <= k <= 9`: Move forward `k` units, one unit at a time.
Some of the grid squares are `obstacles`. The `ith` obstacle is at grid point `obstacles[i] = (xi, yi)`. If the robot runs into an obstacle, then it will instead stay in its current location and move on to the next command.
Return _the **maximum Euclidean distance** that the robot ever gets from the origin **squared** (i.e. if the distance is_ `5`_, return_ `25`_)_.
**Note:**
* North means +Y direction.
* East means +X direction.
* South means -Y direction.
* West means -X direction.
**Example 1:**
**Input:** commands = \[4,-1,3\], obstacles = \[\]
**Output:** 25
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 3 units to (3, 4).
The furthest point the robot ever gets from the origin is (3, 4), which squared is 32 + 42 = 25 units away.
**Example 2:**
**Input:** commands = \[4,-1,4,-2,4\], obstacles = \[\[2,4\]\]
**Output:** 65
**Explanation:** The robot starts at (0, 0):
1. Move north 4 units to (0, 4).
2. Turn right.
3. Move east 1 unit and get blocked by the obstacle at (2, 4), robot is at (1, 4).
4. Turn left.
5. Move north 4 units to (1, 8).
The furthest point the robot ever gets from the origin is (1, 8), which squared is 12 + 82 = 65 units away.
**Example 3:**
**Input:** commands = \[6,-1,-1,6\], obstacles = \[\]
**Output:** 36
**Explanation:** The robot starts at (0, 0):
1. Move north 6 units to (0, 6).
2. Turn right.
3. Turn right.
4. Move south 6 units to (0, 0).
The furthest point the robot ever gets from the origin is (0, 6), which squared is 62 = 36 units away.
**Constraints:**
* `1 <= commands.length <= 104`
* `commands[i]` is either `-2`, `-1`, or an integer in the range `[1, 9]`.
* `0 <= obstacles.length <= 104`
* `-3 * 104 <= xi, yi <= 3 * 104`
* The answer is guaranteed to be less than `231`. | null |
Two Python Solution with O(n) time + O(n) space and second with O(1) space | longest-mountain-in-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n # n = len(arr)\n # incre, decre = [0]* n, [0]*n\n\n # for i in range(1, n):\n # if arr[i] > arr[i-1]:\n # incre[i] = incre[i-1] + 1\n\n # for i in range(n-1)[::-1]:\n # if arr[i] > arr[i+1]:\n # decre[i] = decre[i+1] + 1\n # maxi = 0 \n # for i in range(1, n):\n # if incre[i] and decre[i]:\n # maxi = max(maxi, incre[i] + decre[i] + 1)\n # return maxi\n # if len(arr) < 3:\n # return 0\n\n # In constant O(1) space\n incre,decre,ans = 0,0,0\n for i in range(1, len(arr)):\n if (decre and arr[i-1] < arr[i]) or arr[i-1] == arr[i]:\n incre,decre = 0, 0\n incre += arr[i-1] < arr[i]\n decre += arr[i-1] > arr[i]\n\n if incre and decre:\n ans = max(ans, incre + decre + 1)\n return ans \n\n``` | 1 | You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some index `i` (**0-indexed**) with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given an integer array `arr`, return _the length of the longest subarray, which is a mountain_. Return `0` if there is no mountain subarray.
**Example 1:**
**Input:** arr = \[2,1,4,7,3,2,5\]
**Output:** 5
**Explanation:** The largest mountain is \[1,4,7,3,2\] which has length 5.
**Example 2:**
**Input:** arr = \[2,2,2\]
**Output:** 0
**Explanation:** There is no mountain.
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 104`
**Follow up:**
* Can you solve it using only one pass?
* Can you solve it in `O(1)` space? | null |
Two Python Solution with O(n) time + O(n) space and second with O(1) space | longest-mountain-in-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n # n = len(arr)\n # incre, decre = [0]* n, [0]*n\n\n # for i in range(1, n):\n # if arr[i] > arr[i-1]:\n # incre[i] = incre[i-1] + 1\n\n # for i in range(n-1)[::-1]:\n # if arr[i] > arr[i+1]:\n # decre[i] = decre[i+1] + 1\n # maxi = 0 \n # for i in range(1, n):\n # if incre[i] and decre[i]:\n # maxi = max(maxi, incre[i] + decre[i] + 1)\n # return maxi\n # if len(arr) < 3:\n # return 0\n\n # In constant O(1) space\n incre,decre,ans = 0,0,0\n for i in range(1, len(arr)):\n if (decre and arr[i-1] < arr[i]) or arr[i-1] == arr[i]:\n incre,decre = 0, 0\n incre += arr[i-1] < arr[i]\n decre += arr[i-1] > arr[i]\n\n if incre and decre:\n ans = max(ans, incre + decre + 1)\n return ans \n\n``` | 1 | Koko loves to eat bananas. There are `n` piles of bananas, the `ith` pile has `piles[i]` bananas. The guards have gone and will come back in `h` hours.
Koko can decide her bananas-per-hour eating speed of `k`. Each hour, she chooses some pile of bananas and eats `k` bananas from that pile. If the pile has less than `k` bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return _the minimum integer_ `k` _such that she can eat all the bananas within_ `h` _hours_.
**Example 1:**
**Input:** piles = \[3,6,7,11\], h = 8
**Output:** 4
**Example 2:**
**Input:** piles = \[30,11,23,4,20\], h = 5
**Output:** 30
**Example 3:**
**Input:** piles = \[30,11,23,4,20\], h = 6
**Output:** 23
**Constraints:**
* `1 <= piles.length <= 104`
* `piles.length <= h <= 109`
* `1 <= piles[i] <= 109` | null |
[Python 3] Explained Solution (video + code) | longest-mountain-in-array | 0 | 1 | [](https://www.youtube.com/watch?v=FpO3fY-1mj8)\nhttps://www.youtube.com/watch?v=FpO3fY-1mj8\n```\nclass Solution:\n def longestMountain(self, A: List[int]) -> int:\n res = 0\n \n for indx in range(1, len(A) - 1):\n if A[indx - 1] < A[indx] > A[indx + 1]:\n \n l = r = indx\n \n while l > 0 and A[l] > A[l - 1]:\n l -= 1\n \n while r + 1 < len(A) and A[r] > A[r + 1]:\n r += 1\n \n res = max(res, (r - l + 1))\n \n return res\n``` | 15 | You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some index `i` (**0-indexed**) with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given an integer array `arr`, return _the length of the longest subarray, which is a mountain_. Return `0` if there is no mountain subarray.
**Example 1:**
**Input:** arr = \[2,1,4,7,3,2,5\]
**Output:** 5
**Explanation:** The largest mountain is \[1,4,7,3,2\] which has length 5.
**Example 2:**
**Input:** arr = \[2,2,2\]
**Output:** 0
**Explanation:** There is no mountain.
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 104`
**Follow up:**
* Can you solve it using only one pass?
* Can you solve it in `O(1)` space? | null |
[Python 3] Explained Solution (video + code) | longest-mountain-in-array | 0 | 1 | [](https://www.youtube.com/watch?v=FpO3fY-1mj8)\nhttps://www.youtube.com/watch?v=FpO3fY-1mj8\n```\nclass Solution:\n def longestMountain(self, A: List[int]) -> int:\n res = 0\n \n for indx in range(1, len(A) - 1):\n if A[indx - 1] < A[indx] > A[indx + 1]:\n \n l = r = indx\n \n while l > 0 and A[l] > A[l - 1]:\n l -= 1\n \n while r + 1 < len(A) and A[r] > A[r + 1]:\n r += 1\n \n res = max(res, (r - l + 1))\n \n return res\n``` | 15 | Koko loves to eat bananas. There are `n` piles of bananas, the `ith` pile has `piles[i]` bananas. The guards have gone and will come back in `h` hours.
Koko can decide her bananas-per-hour eating speed of `k`. Each hour, she chooses some pile of bananas and eats `k` bananas from that pile. If the pile has less than `k` bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return _the minimum integer_ `k` _such that she can eat all the bananas within_ `h` _hours_.
**Example 1:**
**Input:** piles = \[3,6,7,11\], h = 8
**Output:** 4
**Example 2:**
**Input:** piles = \[30,11,23,4,20\], h = 5
**Output:** 30
**Example 3:**
**Input:** piles = \[30,11,23,4,20\], h = 6
**Output:** 23
**Constraints:**
* `1 <= piles.length <= 104`
* `piles.length <= h <= 109`
* `1 <= piles[i] <= 109` | null |
Solution | longest-mountain-in-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestMountain(vector<int>& arr) {\n int n = arr.size(),ans=0,count;\n vector<int>peaks;\n for(int i=1;i<(n-1);i++){\n if(arr[i]>arr[i-1] && arr[i]>arr[i+1]){\n peaks.push_back(i);\n }\n }\n int m = peaks.size();\n for(int i=0;i<m;i++){\n count = 1;\n for(int j=peaks[i];j>0;j--){\n if(arr[j]>arr[j-1]){\n count++;\n }\n else{\n break;\n }\n }\n for(int j=peaks[i];j<(n-1);j++){\n if(arr[j]>arr[j+1]){\n count++;\n }\n else{\n break;\n }\n }\n if(ans<count){\n ans = count;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n longest_mountain = 0\n cur_mountain = 0\n NOTHING = 0\n GOING_UP = 1\n GOING_DOWN_AFTER_PEAK = 2\n state = NOTHING\n prev = arr[0]\n for a in arr[1:]:\n if a > prev:\n if state in (NOTHING, GOING_DOWN_AFTER_PEAK):\n state = GOING_UP\n cur_mountain = 1\n cur_mountain += 1\n elif a < prev:\n if state == GOING_UP:\n state = GOING_DOWN_AFTER_PEAK\n if state == GOING_DOWN_AFTER_PEAK:\n cur_mountain += 1\n longest_mountain = max(cur_mountain, longest_mountain)\n elif a == prev:\n state = NOTHING\n cur_mountain = 0\n prev = a\n return longest_mountain\n```\n\n```Java []\nclass Solution {\n public int longestMountain(int[] arr) {\n int maxLength = 0, i = 0;\n boolean uphill = false, downhill = false;\n while (i < arr.length - 1) {\n if (arr[i] < arr[i + 1]) {\n int start = i;\n while (i < arr.length - 1 && arr[i] < arr[i + 1]) {\n i++;\n uphill = true;\n }\n while (i < arr.length - 1 && arr[i] > arr[i + 1]) {\n i++;\n downhill = true;\n }\n if (uphill && downhill) {\n maxLength = Math.max(maxLength, i - start + 1);\n }\n uphill = downhill = false;\n } else {\n i++;\n }\n }\n return maxLength;\n }\n}\n```\n | 2 | You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some index `i` (**0-indexed**) with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given an integer array `arr`, return _the length of the longest subarray, which is a mountain_. Return `0` if there is no mountain subarray.
**Example 1:**
**Input:** arr = \[2,1,4,7,3,2,5\]
**Output:** 5
**Explanation:** The largest mountain is \[1,4,7,3,2\] which has length 5.
**Example 2:**
**Input:** arr = \[2,2,2\]
**Output:** 0
**Explanation:** There is no mountain.
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 104`
**Follow up:**
* Can you solve it using only one pass?
* Can you solve it in `O(1)` space? | null |
Solution | longest-mountain-in-array | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int longestMountain(vector<int>& arr) {\n int n = arr.size(),ans=0,count;\n vector<int>peaks;\n for(int i=1;i<(n-1);i++){\n if(arr[i]>arr[i-1] && arr[i]>arr[i+1]){\n peaks.push_back(i);\n }\n }\n int m = peaks.size();\n for(int i=0;i<m;i++){\n count = 1;\n for(int j=peaks[i];j>0;j--){\n if(arr[j]>arr[j-1]){\n count++;\n }\n else{\n break;\n }\n }\n for(int j=peaks[i];j<(n-1);j++){\n if(arr[j]>arr[j+1]){\n count++;\n }\n else{\n break;\n }\n }\n if(ans<count){\n ans = count;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n longest_mountain = 0\n cur_mountain = 0\n NOTHING = 0\n GOING_UP = 1\n GOING_DOWN_AFTER_PEAK = 2\n state = NOTHING\n prev = arr[0]\n for a in arr[1:]:\n if a > prev:\n if state in (NOTHING, GOING_DOWN_AFTER_PEAK):\n state = GOING_UP\n cur_mountain = 1\n cur_mountain += 1\n elif a < prev:\n if state == GOING_UP:\n state = GOING_DOWN_AFTER_PEAK\n if state == GOING_DOWN_AFTER_PEAK:\n cur_mountain += 1\n longest_mountain = max(cur_mountain, longest_mountain)\n elif a == prev:\n state = NOTHING\n cur_mountain = 0\n prev = a\n return longest_mountain\n```\n\n```Java []\nclass Solution {\n public int longestMountain(int[] arr) {\n int maxLength = 0, i = 0;\n boolean uphill = false, downhill = false;\n while (i < arr.length - 1) {\n if (arr[i] < arr[i + 1]) {\n int start = i;\n while (i < arr.length - 1 && arr[i] < arr[i + 1]) {\n i++;\n uphill = true;\n }\n while (i < arr.length - 1 && arr[i] > arr[i + 1]) {\n i++;\n downhill = true;\n }\n if (uphill && downhill) {\n maxLength = Math.max(maxLength, i - start + 1);\n }\n uphill = downhill = false;\n } else {\n i++;\n }\n }\n return maxLength;\n }\n}\n```\n | 2 | Koko loves to eat bananas. There are `n` piles of bananas, the `ith` pile has `piles[i]` bananas. The guards have gone and will come back in `h` hours.
Koko can decide her bananas-per-hour eating speed of `k`. Each hour, she chooses some pile of bananas and eats `k` bananas from that pile. If the pile has less than `k` bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return _the minimum integer_ `k` _such that she can eat all the bananas within_ `h` _hours_.
**Example 1:**
**Input:** piles = \[3,6,7,11\], h = 8
**Output:** 4
**Example 2:**
**Input:** piles = \[30,11,23,4,20\], h = 5
**Output:** 30
**Example 3:**
**Input:** piles = \[30,11,23,4,20\], h = 6
**Output:** 23
**Constraints:**
* `1 <= piles.length <= 104`
* `piles.length <= h <= 109`
* `1 <= piles[i] <= 109` | null |
Python3: One pass, O(1) Auxiliary Space | longest-mountain-in-array | 0 | 1 | ```\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n increasing = False\n increased = False\n mx = -math.inf\n curr = -math.inf\n for i in range(1, len(arr)):\n if arr[i] > arr[i-1]:\n if increasing:\n curr += 1\n increased = True\n else:\n mx = max(curr, mx)\n curr = 2\n increased = True\n increasing = True\n elif arr[i] < arr[i-1]:\n if increasing:\n increasing = False\n curr += 1\n else:\n if increased and not increasing:\n mx = max(mx, curr)\n curr = -math.inf\n increased = False\n increasing = False\n if not increasing and increased:\n mx = max(mx, curr)\n return 0 if mx == -math.inf else mx\n``` | 2 | You may recall that an array `arr` is a **mountain array** if and only if:
* `arr.length >= 3`
* There exists some index `i` (**0-indexed**) with `0 < i < arr.length - 1` such that:
* `arr[0] < arr[1] < ... < arr[i - 1] < arr[i]`
* `arr[i] > arr[i + 1] > ... > arr[arr.length - 1]`
Given an integer array `arr`, return _the length of the longest subarray, which is a mountain_. Return `0` if there is no mountain subarray.
**Example 1:**
**Input:** arr = \[2,1,4,7,3,2,5\]
**Output:** 5
**Explanation:** The largest mountain is \[1,4,7,3,2\] which has length 5.
**Example 2:**
**Input:** arr = \[2,2,2\]
**Output:** 0
**Explanation:** There is no mountain.
**Constraints:**
* `1 <= arr.length <= 104`
* `0 <= arr[i] <= 104`
**Follow up:**
* Can you solve it using only one pass?
* Can you solve it in `O(1)` space? | null |
Python3: One pass, O(1) Auxiliary Space | longest-mountain-in-array | 0 | 1 | ```\nclass Solution:\n def longestMountain(self, arr: List[int]) -> int:\n increasing = False\n increased = False\n mx = -math.inf\n curr = -math.inf\n for i in range(1, len(arr)):\n if arr[i] > arr[i-1]:\n if increasing:\n curr += 1\n increased = True\n else:\n mx = max(curr, mx)\n curr = 2\n increased = True\n increasing = True\n elif arr[i] < arr[i-1]:\n if increasing:\n increasing = False\n curr += 1\n else:\n if increased and not increasing:\n mx = max(mx, curr)\n curr = -math.inf\n increased = False\n increasing = False\n if not increasing and increased:\n mx = max(mx, curr)\n return 0 if mx == -math.inf else mx\n``` | 2 | Koko loves to eat bananas. There are `n` piles of bananas, the `ith` pile has `piles[i]` bananas. The guards have gone and will come back in `h` hours.
Koko can decide her bananas-per-hour eating speed of `k`. Each hour, she chooses some pile of bananas and eats `k` bananas from that pile. If the pile has less than `k` bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return _the minimum integer_ `k` _such that she can eat all the bananas within_ `h` _hours_.
**Example 1:**
**Input:** piles = \[3,6,7,11\], h = 8
**Output:** 4
**Example 2:**
**Input:** piles = \[30,11,23,4,20\], h = 5
**Output:** 30
**Example 3:**
**Input:** piles = \[30,11,23,4,20\], h = 6
**Output:** 23
**Constraints:**
* `1 <= piles.length <= 104`
* `piles.length <= h <= 109`
* `1 <= piles[i] <= 109` | null |
Solution | hand-of-straights | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isNStraightHand(vector<int>& hand, int sz) \n {\n int n = hand.size();\n if(n % sz) return 0;\n sort(hand.begin(), hand.end());\n for(int i=0; i<n; i++)\n {\n if(hand[i] == -1) continue;\n int k = i;\n for(int j=1; j<sz; j++)\n {\n while(k < n && hand[i] + j != hand[k]) k++;\n if(k == n) return 0;\n hand[k] = -1;\n }\n }\n return 1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n if len(hand)%groupSize >0:\n return False\n total_count = len(hand)//groupSize\n count =0\n hand.sort()\n while len(hand)>0:\n\n h = hand.pop()\n size = groupSize -1\n popi = len(hand)-1\n while popi>-1 and size >0:\n if hand[popi] == h:\n popi -=1\n elif hand[popi] != h -1:\n return False\n else:\n h = hand.pop(popi) \n popi -=1\n size -=1\n count +=1\n return count ==total_count\n```\n\n```Java []\nclass Solution {\n public boolean isNStraightHand(int[] hand, int groupSize) {\n Arrays.sort(hand);\n int len = hand.length;\n boolean[] visited = new boolean[len];\n for(int i = 0;i < len;i++){\n if(visited[i]) continue;\n visited[i] = true;\n int j = i + 1;\n int count = 1;\n int num = hand[i] + 1;\n for(count = 1;j < len && count < groupSize;j++){\n if(visited[j]) continue;\n if(hand[j] > num) break;\n if(hand[j] == num ) {\n num++;\n visited[j] = true;\n count++;\n }\n }\n if(count < groupSize) return false;\n }\n return true;\n }\n}\n```\n | 2 | Alice has some number of cards and she wants to rearrange the cards into groups so that each group is of size `groupSize`, and consists of `groupSize` consecutive cards.
Given an integer array `hand` where `hand[i]` is the value written on the `ith` card and an integer `groupSize`, return `true` if she can rearrange the cards, or `false` otherwise.
**Example 1:**
**Input:** hand = \[1,2,3,6,2,3,4,7,8\], groupSize = 3
**Output:** true
**Explanation:** Alice's hand can be rearranged as \[1,2,3\],\[2,3,4\],\[6,7,8\]
**Example 2:**
**Input:** hand = \[1,2,3,4,5\], groupSize = 4
**Output:** false
**Explanation:** Alice's hand can not be rearranged into groups of 4.
**Constraints:**
* `1 <= hand.length <= 104`
* `0 <= hand[i] <= 109`
* `1 <= groupSize <= hand.length`
**Note:** This question is the same as 1296: [https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/](https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/) | null |
Solution | hand-of-straights | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isNStraightHand(vector<int>& hand, int sz) \n {\n int n = hand.size();\n if(n % sz) return 0;\n sort(hand.begin(), hand.end());\n for(int i=0; i<n; i++)\n {\n if(hand[i] == -1) continue;\n int k = i;\n for(int j=1; j<sz; j++)\n {\n while(k < n && hand[i] + j != hand[k]) k++;\n if(k == n) return 0;\n hand[k] = -1;\n }\n }\n return 1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n if len(hand)%groupSize >0:\n return False\n total_count = len(hand)//groupSize\n count =0\n hand.sort()\n while len(hand)>0:\n\n h = hand.pop()\n size = groupSize -1\n popi = len(hand)-1\n while popi>-1 and size >0:\n if hand[popi] == h:\n popi -=1\n elif hand[popi] != h -1:\n return False\n else:\n h = hand.pop(popi) \n popi -=1\n size -=1\n count +=1\n return count ==total_count\n```\n\n```Java []\nclass Solution {\n public boolean isNStraightHand(int[] hand, int groupSize) {\n Arrays.sort(hand);\n int len = hand.length;\n boolean[] visited = new boolean[len];\n for(int i = 0;i < len;i++){\n if(visited[i]) continue;\n visited[i] = true;\n int j = i + 1;\n int count = 1;\n int num = hand[i] + 1;\n for(count = 1;j < len && count < groupSize;j++){\n if(visited[j]) continue;\n if(hand[j] > num) break;\n if(hand[j] == num ) {\n num++;\n visited[j] = true;\n count++;\n }\n }\n if(count < groupSize) return false;\n }\n return true;\n }\n}\n```\n | 2 | Given the `head` of a singly linked list, return _the middle node of the linked list_.
If there are two middle nodes, return **the second middle** node.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[3,4,5\]
**Explanation:** The middle node of the list is node 3.
**Example 2:**
**Input:** head = \[1,2,3,4,5,6\]
**Output:** \[4,5,6\]
**Explanation:** Since the list has two middle nodes with values 3 and 4, we return the second one.
**Constraints:**
* The number of nodes in the list is in the range `[1, 100]`.
* `1 <= Node.val <= 100` | null |
Simple O(n logn) Solution using Hash Table and Min Heap | hand-of-straights | 0 | 1 | ```\n#####################################################################################################################\n# Problem: Hand of Straights\n# Solution : Hash Table, Min Heap\n# Time Complexity : O(n logn)\n# Space Complexity : O(n)\n#####################################################################################################################\n\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n if len(hand) % groupSize:\n return False\n \n freq = collections.defaultdict(int)\n \n for num in hand:\n freq[num] += 1\n \n min_heap = list(freq.keys())\n heapq.heapify(min_heap)\n \n while min_heap:\n smallest = min_heap[0]\n for num in range(smallest, smallest + groupSize):\n if num not in freq:\n return False\n freq[num] -= 1\n \n if freq[num] == 0:\n if num != min_heap[0]:\n return False\n heapq.heappop(min_heap) \n return True\n``` | 9 | Alice has some number of cards and she wants to rearrange the cards into groups so that each group is of size `groupSize`, and consists of `groupSize` consecutive cards.
Given an integer array `hand` where `hand[i]` is the value written on the `ith` card and an integer `groupSize`, return `true` if she can rearrange the cards, or `false` otherwise.
**Example 1:**
**Input:** hand = \[1,2,3,6,2,3,4,7,8\], groupSize = 3
**Output:** true
**Explanation:** Alice's hand can be rearranged as \[1,2,3\],\[2,3,4\],\[6,7,8\]
**Example 2:**
**Input:** hand = \[1,2,3,4,5\], groupSize = 4
**Output:** false
**Explanation:** Alice's hand can not be rearranged into groups of 4.
**Constraints:**
* `1 <= hand.length <= 104`
* `0 <= hand[i] <= 109`
* `1 <= groupSize <= hand.length`
**Note:** This question is the same as 1296: [https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/](https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/) | null |
Simple O(n logn) Solution using Hash Table and Min Heap | hand-of-straights | 0 | 1 | ```\n#####################################################################################################################\n# Problem: Hand of Straights\n# Solution : Hash Table, Min Heap\n# Time Complexity : O(n logn)\n# Space Complexity : O(n)\n#####################################################################################################################\n\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n if len(hand) % groupSize:\n return False\n \n freq = collections.defaultdict(int)\n \n for num in hand:\n freq[num] += 1\n \n min_heap = list(freq.keys())\n heapq.heapify(min_heap)\n \n while min_heap:\n smallest = min_heap[0]\n for num in range(smallest, smallest + groupSize):\n if num not in freq:\n return False\n freq[num] -= 1\n \n if freq[num] == 0:\n if num != min_heap[0]:\n return False\n heapq.heappop(min_heap) \n return True\n``` | 9 | Given the `head` of a singly linked list, return _the middle node of the linked list_.
If there are two middle nodes, return **the second middle** node.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[3,4,5\]
**Explanation:** The middle node of the list is node 3.
**Example 2:**
**Input:** head = \[1,2,3,4,5,6\]
**Output:** \[4,5,6\]
**Explanation:** Since the list has two middle nodes with values 3 and 4, we return the second one.
**Constraints:**
* The number of nodes in the list is in the range `[1, 100]`.
* `1 <= Node.val <= 100` | null |
Python3 || Hashmap || 15-line easy to understand | hand-of-straights | 0 | 1 | ```\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n counter = Counter(hand)\n while counter:\n n = groupSize\n start = min(counter.keys())\n while n:\n if start not in counter:\n return False\n counter[start] -= 1\n if not counter[start]:\n del counter[start]\n start += 1\n n -= 1\n return True\n``` | 6 | Alice has some number of cards and she wants to rearrange the cards into groups so that each group is of size `groupSize`, and consists of `groupSize` consecutive cards.
Given an integer array `hand` where `hand[i]` is the value written on the `ith` card and an integer `groupSize`, return `true` if she can rearrange the cards, or `false` otherwise.
**Example 1:**
**Input:** hand = \[1,2,3,6,2,3,4,7,8\], groupSize = 3
**Output:** true
**Explanation:** Alice's hand can be rearranged as \[1,2,3\],\[2,3,4\],\[6,7,8\]
**Example 2:**
**Input:** hand = \[1,2,3,4,5\], groupSize = 4
**Output:** false
**Explanation:** Alice's hand can not be rearranged into groups of 4.
**Constraints:**
* `1 <= hand.length <= 104`
* `0 <= hand[i] <= 109`
* `1 <= groupSize <= hand.length`
**Note:** This question is the same as 1296: [https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/](https://leetcode.com/problems/divide-array-in-sets-of-k-consecutive-numbers/) | null |
Python3 || Hashmap || 15-line easy to understand | hand-of-straights | 0 | 1 | ```\nclass Solution:\n def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:\n counter = Counter(hand)\n while counter:\n n = groupSize\n start = min(counter.keys())\n while n:\n if start not in counter:\n return False\n counter[start] -= 1\n if not counter[start]:\n del counter[start]\n start += 1\n n -= 1\n return True\n``` | 6 | Given the `head` of a singly linked list, return _the middle node of the linked list_.
If there are two middle nodes, return **the second middle** node.
**Example 1:**
**Input:** head = \[1,2,3,4,5\]
**Output:** \[3,4,5\]
**Explanation:** The middle node of the list is node 3.
**Example 2:**
**Input:** head = \[1,2,3,4,5,6\]
**Output:** \[4,5,6\]
**Explanation:** Since the list has two middle nodes with values 3 and 4, we return the second one.
**Constraints:**
* The number of nodes in the list is in the range `[1, 100]`.
* `1 <= Node.val <= 100` | null |
✅ 94.74% BFS + Bitmask | shortest-path-visiting-all-nodes | 1 | 1 | # Comprehensive Guide to Solving "Shortest Path Visiting All Nodes"\n\n## Introduction & Problem Statement\n\nGreetings, coding enthusiasts! Today we embark on a fascinating journey through the realm of graphs. Our mission is to discover the shortest path that visits every node in an undirected, connected graph. Intriguing, isn\'t it? You can start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Graph Representation**:\n The problem is modeled as an undirected graph where each node has connections to other nodes. The graph is given in adjacency list format.\n\n2. **Bitmasking for State Representation**:\n The key to solving this problem efficiently lies in representing the set of visited nodes using a bitmask. This allows us to maintain a compact and efficient representation of our progress.\n\n3. **Constraints**: \n - $$ 1 \\leq n \\leq 12 $$\n - $$ 0 \\leq \\text{graph}[i].\\text{length} < n $$\n\n### Strategies to Tackle the Problem\n\n1. **Breadth-First Search (BFS)**:\n BFS is a classic algorithm for exploring a graph and can be adapted to solve this problem.\n\n---\n\n## Live Coding BFS & More\nhttps://youtu.be/1aJPYkZOuv8?si=wp2wcu-hPp7h-mJG\n\n## In-Depth Explanation of BFS Algorithm in "Shortest Path Visiting All Nodes"\n\n### What is Breadth-First Search (BFS)?\n\nBreadth-First Search (BFS) is a graph traversal algorithm that explores nodes level by level, moving through neighbors before going deeper. In this specific problem, we employ BFS not just to explore the graph but also to search through the different "states" that the graph can be in. Each state encapsulates a set of visited nodes, the current node, and the distance covered so far.\n\n### Detailed Breakdown of the Algorithm\n\n#### Initialize Variables\n\n1. **Number of Nodes (`n`)**: \n - The variable `n` stores the total number of nodes in the graph. It helps us create initial states and determine when all nodes have been visited.\n\n2. **Queue (`queue`)**: \n - We initialize a queue to store the states we need to explore. A deque is used for its efficient `O(1)` append and pop operations.\n\n3. **Visited Set (`visited`)**: \n - A set is used to keep track of states that have already been visited. This avoids redundant work and cycles.\n\n#### Initialization Step\n\n- **Initial States**: \n - Each node is used as a starting point, and for each starting node `i`, an initial state is enqueued. The state is represented as a tuple `(mask, node, dist)`. \n - `mask = 1 << i`: Only the `i`-th bit is set, indicating that only node `i` is visited.\n - `node = i`: The current node is `i`.\n - `dist = 0`: The distance traveled so far is zero.\n\n#### Main BFS Loop\n\n1. **Dequeue State**: \n - A state is dequeued from the front of the queue. This state contains:\n - `mask`: Bitmask representing the visited nodes.\n - `node`: The current node.\n - `dist`: The distance traveled to reach this state.\n\n2. **Check for Goal State**: \n - If the bitmask equals `(1 << n) - 1`, it means all nodes have been visited. In that case, the algorithm returns the distance for that state, effectively solving the problem.\n\n3. **Explore Neighbors**: \n - For the current node, all its neighbors in the graph are explored. For each neighbor, a new state is generated.\n - `new_mask = mask | (1 << neighbor)`: The new mask includes the neighbor as visited.\n - `new_node = neighbor`: The new current node is the neighbor.\n - `new_dist = dist + 1`: The distance is incremented by 1.\n\n4. **Check and Enqueue New States**: \n - Before enqueuing the new state, we check whether it has already been visited. If not, it\'s added to the `visited` set and enqueued for future exploration.\n\n#### Termination and Result\n\n- The BFS loop continues until the queue is empty or the goal state is reached. The shortest distance required to visit all nodes is then returned.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(2^n \\times n)$$, where $$n$$ is the number of nodes. This is because there are $$2^n$$ possible subsets of nodes and $$n$$ nodes to consider for each subset.\n- **Space Complexity**: $$O(2^n \\times n)$$, needed for the visited set and the queue.\n\n# Code\n``` Python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque([(1 << i, i, 0) for i in range(n)])\n visited = set((1 << i, i) for i in range(n))\n \n while queue:\n mask, node, dist = queue.popleft()\n if mask == (1 << n) - 1:\n return dist\n for neighbor in graph[node]:\n new_mask = mask | (1 << neighbor)\n if (new_mask, neighbor) not in visited:\n visited.add((new_mask, neighbor))\n queue.append((new_mask, neighbor, dist + 1))\n```\n``` Go []\ntype State struct {\n\tmask, node, dist int\n}\n\nfunc shortestPathLength(graph [][]int) int {\n\tn := len(graph)\n\tallVisited := (1 << n) - 1\n\tqueue := []State{}\n\tvisited := make(map[int]bool)\n\n\tfor i := 0; i < n; i++ {\n\t\tqueue = append(queue, State{1 << i, i, 0})\n\t\tvisited[(1<<i)*16+i] = true\n\t}\n\n\tfor len(queue) > 0 {\n\t\tcur := queue[0]\n\t\tqueue = queue[1:]\n\n\t\tif cur.mask == allVisited {\n\t\t\treturn cur.dist\n\t\t}\n\n\t\tfor _, neighbor := range graph[cur.node] {\n\t\t\tnewMask := cur.mask | (1 << neighbor)\n\t\t\thashValue := newMask*16 + neighbor\n\n\t\t\tif !visited[hashValue] {\n\t\t\t\tvisited[hashValue] = true\n\t\t\t\tqueue = append(queue, State{newMask, neighbor, cur.dist + 1})\n\t\t\t}\n\t\t}\n\t}\n\n\treturn -1\n}\n```\n``` Rust []\nuse std::collections::{HashSet, VecDeque}; \n\nimpl Solution {\n pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {\n let n = graph.len(); \n let all_visited = (1 << n) - 1; \n let mut queue: VecDeque<(i32, i32, i32)> = VecDeque::new(); \n let mut visited: HashSet<i32> = HashSet::new(); \n\n for i in 0..n as i32 { \n queue.push_back((1 << i, i, 0)); \n visited.insert((1 << i) * 16 + i); \n } \n\n while let Some((mask, node, dist)) = queue.pop_front() { \n if mask == all_visited as i32 { \n return dist; \n } \n\n for &neighbor in &graph[node as usize] { \n let new_mask = mask | (1 << neighbor); \n let hash_value = new_mask * 16 + neighbor; \n\n if visited.insert(hash_value) { \n queue.push_back((new_mask, neighbor, dist + 1)); \n } \n } \n } \n\n -1 \n\n }\n}\n```\n``` C++ []\nclass Solution {\n struct State {\n int mask, node, dist;\n };\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int n = graph.size();\n int all_visited = (1 << n) - 1;\n queue<State> q;\n unordered_set<int> visited;\n \n for (int i = 0; i < n; ++i) {\n q.push({1 << i, i, 0});\n visited.insert((1 << i) * 16 + i);\n }\n \n while (!q.empty()) {\n State cur = q.front(); q.pop();\n \n if (cur.mask == all_visited) {\n return cur.dist;\n }\n \n for (int neighbor : graph[cur.node]) {\n int new_mask = cur.mask | (1 << neighbor);\n int hash_value = new_mask * 16 + neighbor;\n \n if (visited.find(hash_value) == visited.end()) {\n visited.insert(hash_value);\n q.push({new_mask, neighbor, cur.dist + 1});\n }\n }\n }\n \n return -1;\n }\n};\n```\n``` Java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int n = graph.length;\n int allVisited = (1 << n) - 1;\n Queue<int[]> queue = new LinkedList<>();\n Set<Integer> visited = new HashSet<>();\n\n for (int i = 0; i < n; i++) {\n queue.offer(new int[]{1 << i, i, 0});\n visited.add((1 << i) * 16 + i);\n }\n\n while (!queue.isEmpty()) {\n int[] cur = queue.poll();\n\n if (cur[0] == allVisited) {\n return cur[2];\n }\n\n for (int neighbor : graph[cur[1]]) {\n int newMask = cur[0] | (1 << neighbor);\n int hashValue = newMask * 16 + neighbor;\n\n if (!visited.contains(hashValue)) {\n visited.add(hashValue);\n queue.offer(new int[]{newMask, neighbor, cur[2] + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int ShortestPathLength(int[][] graph) {\n int n = graph.Length;\n int allVisited = (1 << n) - 1;\n Queue<int[]> queue = new Queue<int[]>();\n HashSet<int> visited = new HashSet<int>();\n\n for (int i = 0; i < n; i++) {\n queue.Enqueue(new int[]{1 << i, i, 0});\n visited.Add((1 << i) * 16 + i);\n }\n\n while (queue.Count > 0) {\n int[] cur = queue.Dequeue();\n\n if (cur[0] == allVisited) {\n return cur[2];\n }\n\n foreach (int neighbor in graph[cur[1]]) {\n int newMask = cur[0] | (1 << neighbor);\n int hashValue = newMask * 16 + neighbor;\n\n if (!visited.Contains(hashValue)) {\n visited.Add(hashValue);\n queue.Enqueue(new int[]{newMask, neighbor, cur[2] + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const n = graph.length;\n const allVisited = (1 << n) - 1;\n const queue = [];\n const visited = new Set();\n\n for (let i = 0; i < n; i++) {\n queue.push([1 << i, i, 0]);\n visited.add((1 << i) * 16 + i);\n }\n\n while (queue.length > 0) {\n const [mask, node, dist] = queue.shift();\n\n if (mask === allVisited) {\n return dist;\n }\n\n for (const neighbor of graph[node]) {\n const newMask = mask | (1 << neighbor);\n const hashValue = newMask * 16 + neighbor;\n\n if (!visited.has(hashValue)) {\n visited.add(hashValue);\n queue.push([newMask, neighbor, dist + 1]);\n }\n }\n }\n\n return -1;\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[][] $graph\n * @return Integer\n */\n function shortestPathLength($graph) {\n $n = count($graph);\n $allVisited = (1 << $n) - 1;\n $queue = new SplQueue();\n $visited = [];\n\n for ($i = 0; $i < $n; $i++) {\n $queue->enqueue([1 << $i, $i, 0]);\n $visited[(1 << $i) * 16 + $i] = true;\n }\n\n while (!$queue->isEmpty()) {\n [$mask, $node, $dist] = $queue->dequeue();\n\n if ($mask === $allVisited) {\n return $dist;\n }\n\n foreach ($graph[$node] as $neighbor) {\n $newMask = $mask | (1 << $neighbor);\n $hashValue = $newMask * 16 + $neighbor;\n\n if (!isset($visited[$hashValue])) {\n $visited[$hashValue] = true;\n $queue->enqueue([$newMask, $neighbor, $dist + 1]);\n }\n }\n }\n\n return -1;\n}\n}\n```\n## Performance\n\n| Language | Fastest Runtime (ms) | Memory (MB) |\n|------------|----------------------|-------------|\n| Rust | 18 | 2.5 |\n| Go | 26 | 7.1 |\n| Java | 28 | 45.8 |\n| C++ | 43 | 18 |\n| PHP | 46 | 23.4 |\n| JavaScript | 68 | 51 |\n| C# | 97 | 47.7 |\n| Python3 | 151 | 21.2 |\n\n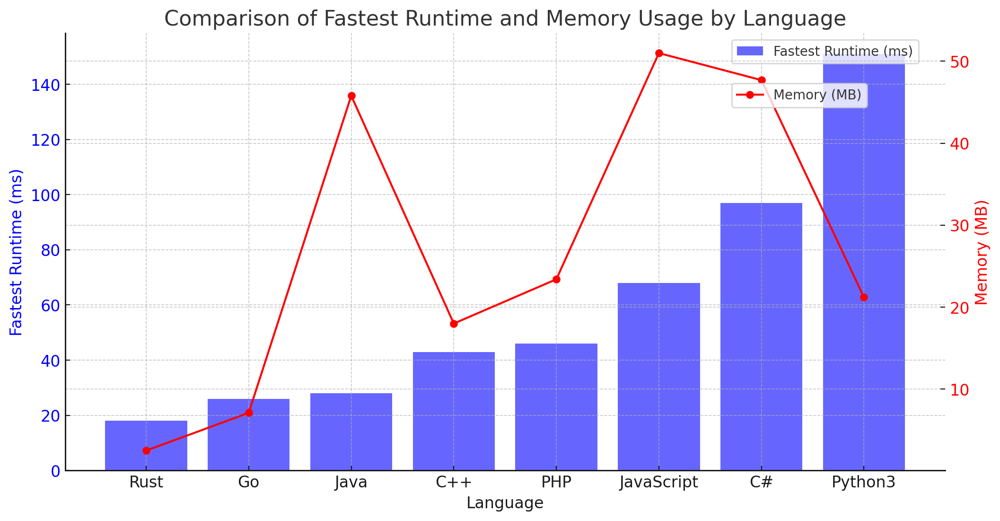\n\n\n## Live Coding + BFS in Rust\nhttps://youtu.be/rIdgnWYfA_w?si=accCEKNjtxdvfj48\n\n\n## Rust Code Highlights and Best Practices\n\n### Using `VecDeque` for Queue Operations\nIn Rust, we use the `VecDeque` data structure from the standard library for our queue. It provides efficient $$O(1)$$ operations for appending to and popping from both ends. This ensures that the queue operations in the BFS algorithm are as fast as possible, which is crucial for performance.\n\n### Using `HashSet` for Visited States\nTo keep track of the visited states, Rust\'s `HashSet` is employed. Hash sets offer $$O(1)$$ lookups, which is essential for ensuring that we don\'t revisit states that we have already processed. This helps to make the algorithm more efficient by avoiding redundant work.\n\n### Bit Manipulation for State Representation\nRust\'s excellent support for bit manipulation comes in handy for representing states efficiently. The `mask` variable serves as a compact representation of visited nodes, and bitwise operations like `|` and `<<` are used for updating it.\n\n### Hash Value Calculation: `mask * 16 + i`\nYou might wonder why we use `mask * 16 + i` as the hash value for each state. This specific hash function ensures a unique value for each state, considering both the mask and the current node. Multiplying by 16 (which is $$2^4$$) effectively shifts the bits of `mask` to the left by 4 bits, making space for the `i` value. This enables us to uniquely identify each state with a single integer.\n\n### Is the Hash Value used for preventing cycles?\nYes, the hash value is used to identify unique states that have been visited. By storing these in a `HashSet`, we can efficiently prevent cycles and avoid revisiting the same state, which is critical for the algorithm\'s performance.\n\nMastering this Rust implementation will not only deepen your understanding of graph algorithms and bit manipulation but also equip you with practical Rust programming skills. Are you ready to find the shortest path visiting all nodes in Rust? Let\'s get coding! \uD83D\uDE80 | 104 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
✅ 94.74% BFS + Bitmask | shortest-path-visiting-all-nodes | 1 | 1 | # Comprehensive Guide to Solving "Shortest Path Visiting All Nodes"\n\n## Introduction & Problem Statement\n\nGreetings, coding enthusiasts! Today we embark on a fascinating journey through the realm of graphs. Our mission is to discover the shortest path that visits every node in an undirected, connected graph. Intriguing, isn\'t it? You can start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.\n\n## Key Concepts and Constraints\n\n### What Makes This Problem Unique?\n\n1. **Graph Representation**:\n The problem is modeled as an undirected graph where each node has connections to other nodes. The graph is given in adjacency list format.\n\n2. **Bitmasking for State Representation**:\n The key to solving this problem efficiently lies in representing the set of visited nodes using a bitmask. This allows us to maintain a compact and efficient representation of our progress.\n\n3. **Constraints**: \n - $$ 1 \\leq n \\leq 12 $$\n - $$ 0 \\leq \\text{graph}[i].\\text{length} < n $$\n\n### Strategies to Tackle the Problem\n\n1. **Breadth-First Search (BFS)**:\n BFS is a classic algorithm for exploring a graph and can be adapted to solve this problem.\n\n---\n\n## Live Coding BFS & More\nhttps://youtu.be/1aJPYkZOuv8?si=wp2wcu-hPp7h-mJG\n\n## In-Depth Explanation of BFS Algorithm in "Shortest Path Visiting All Nodes"\n\n### What is Breadth-First Search (BFS)?\n\nBreadth-First Search (BFS) is a graph traversal algorithm that explores nodes level by level, moving through neighbors before going deeper. In this specific problem, we employ BFS not just to explore the graph but also to search through the different "states" that the graph can be in. Each state encapsulates a set of visited nodes, the current node, and the distance covered so far.\n\n### Detailed Breakdown of the Algorithm\n\n#### Initialize Variables\n\n1. **Number of Nodes (`n`)**: \n - The variable `n` stores the total number of nodes in the graph. It helps us create initial states and determine when all nodes have been visited.\n\n2. **Queue (`queue`)**: \n - We initialize a queue to store the states we need to explore. A deque is used for its efficient `O(1)` append and pop operations.\n\n3. **Visited Set (`visited`)**: \n - A set is used to keep track of states that have already been visited. This avoids redundant work and cycles.\n\n#### Initialization Step\n\n- **Initial States**: \n - Each node is used as a starting point, and for each starting node `i`, an initial state is enqueued. The state is represented as a tuple `(mask, node, dist)`. \n - `mask = 1 << i`: Only the `i`-th bit is set, indicating that only node `i` is visited.\n - `node = i`: The current node is `i`.\n - `dist = 0`: The distance traveled so far is zero.\n\n#### Main BFS Loop\n\n1. **Dequeue State**: \n - A state is dequeued from the front of the queue. This state contains:\n - `mask`: Bitmask representing the visited nodes.\n - `node`: The current node.\n - `dist`: The distance traveled to reach this state.\n\n2. **Check for Goal State**: \n - If the bitmask equals `(1 << n) - 1`, it means all nodes have been visited. In that case, the algorithm returns the distance for that state, effectively solving the problem.\n\n3. **Explore Neighbors**: \n - For the current node, all its neighbors in the graph are explored. For each neighbor, a new state is generated.\n - `new_mask = mask | (1 << neighbor)`: The new mask includes the neighbor as visited.\n - `new_node = neighbor`: The new current node is the neighbor.\n - `new_dist = dist + 1`: The distance is incremented by 1.\n\n4. **Check and Enqueue New States**: \n - Before enqueuing the new state, we check whether it has already been visited. If not, it\'s added to the `visited` set and enqueued for future exploration.\n\n#### Termination and Result\n\n- The BFS loop continues until the queue is empty or the goal state is reached. The shortest distance required to visit all nodes is then returned.\n\n### Time and Space Complexity\n\n- **Time Complexity**: $$O(2^n \\times n)$$, where $$n$$ is the number of nodes. This is because there are $$2^n$$ possible subsets of nodes and $$n$$ nodes to consider for each subset.\n- **Space Complexity**: $$O(2^n \\times n)$$, needed for the visited set and the queue.\n\n# Code\n``` Python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque([(1 << i, i, 0) for i in range(n)])\n visited = set((1 << i, i) for i in range(n))\n \n while queue:\n mask, node, dist = queue.popleft()\n if mask == (1 << n) - 1:\n return dist\n for neighbor in graph[node]:\n new_mask = mask | (1 << neighbor)\n if (new_mask, neighbor) not in visited:\n visited.add((new_mask, neighbor))\n queue.append((new_mask, neighbor, dist + 1))\n```\n``` Go []\ntype State struct {\n\tmask, node, dist int\n}\n\nfunc shortestPathLength(graph [][]int) int {\n\tn := len(graph)\n\tallVisited := (1 << n) - 1\n\tqueue := []State{}\n\tvisited := make(map[int]bool)\n\n\tfor i := 0; i < n; i++ {\n\t\tqueue = append(queue, State{1 << i, i, 0})\n\t\tvisited[(1<<i)*16+i] = true\n\t}\n\n\tfor len(queue) > 0 {\n\t\tcur := queue[0]\n\t\tqueue = queue[1:]\n\n\t\tif cur.mask == allVisited {\n\t\t\treturn cur.dist\n\t\t}\n\n\t\tfor _, neighbor := range graph[cur.node] {\n\t\t\tnewMask := cur.mask | (1 << neighbor)\n\t\t\thashValue := newMask*16 + neighbor\n\n\t\t\tif !visited[hashValue] {\n\t\t\t\tvisited[hashValue] = true\n\t\t\t\tqueue = append(queue, State{newMask, neighbor, cur.dist + 1})\n\t\t\t}\n\t\t}\n\t}\n\n\treturn -1\n}\n```\n``` Rust []\nuse std::collections::{HashSet, VecDeque}; \n\nimpl Solution {\n pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {\n let n = graph.len(); \n let all_visited = (1 << n) - 1; \n let mut queue: VecDeque<(i32, i32, i32)> = VecDeque::new(); \n let mut visited: HashSet<i32> = HashSet::new(); \n\n for i in 0..n as i32 { \n queue.push_back((1 << i, i, 0)); \n visited.insert((1 << i) * 16 + i); \n } \n\n while let Some((mask, node, dist)) = queue.pop_front() { \n if mask == all_visited as i32 { \n return dist; \n } \n\n for &neighbor in &graph[node as usize] { \n let new_mask = mask | (1 << neighbor); \n let hash_value = new_mask * 16 + neighbor; \n\n if visited.insert(hash_value) { \n queue.push_back((new_mask, neighbor, dist + 1)); \n } \n } \n } \n\n -1 \n\n }\n}\n```\n``` C++ []\nclass Solution {\n struct State {\n int mask, node, dist;\n };\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int n = graph.size();\n int all_visited = (1 << n) - 1;\n queue<State> q;\n unordered_set<int> visited;\n \n for (int i = 0; i < n; ++i) {\n q.push({1 << i, i, 0});\n visited.insert((1 << i) * 16 + i);\n }\n \n while (!q.empty()) {\n State cur = q.front(); q.pop();\n \n if (cur.mask == all_visited) {\n return cur.dist;\n }\n \n for (int neighbor : graph[cur.node]) {\n int new_mask = cur.mask | (1 << neighbor);\n int hash_value = new_mask * 16 + neighbor;\n \n if (visited.find(hash_value) == visited.end()) {\n visited.insert(hash_value);\n q.push({new_mask, neighbor, cur.dist + 1});\n }\n }\n }\n \n return -1;\n }\n};\n```\n``` Java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int n = graph.length;\n int allVisited = (1 << n) - 1;\n Queue<int[]> queue = new LinkedList<>();\n Set<Integer> visited = new HashSet<>();\n\n for (int i = 0; i < n; i++) {\n queue.offer(new int[]{1 << i, i, 0});\n visited.add((1 << i) * 16 + i);\n }\n\n while (!queue.isEmpty()) {\n int[] cur = queue.poll();\n\n if (cur[0] == allVisited) {\n return cur[2];\n }\n\n for (int neighbor : graph[cur[1]]) {\n int newMask = cur[0] | (1 << neighbor);\n int hashValue = newMask * 16 + neighbor;\n\n if (!visited.contains(hashValue)) {\n visited.add(hashValue);\n queue.offer(new int[]{newMask, neighbor, cur[2] + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int ShortestPathLength(int[][] graph) {\n int n = graph.Length;\n int allVisited = (1 << n) - 1;\n Queue<int[]> queue = new Queue<int[]>();\n HashSet<int> visited = new HashSet<int>();\n\n for (int i = 0; i < n; i++) {\n queue.Enqueue(new int[]{1 << i, i, 0});\n visited.Add((1 << i) * 16 + i);\n }\n\n while (queue.Count > 0) {\n int[] cur = queue.Dequeue();\n\n if (cur[0] == allVisited) {\n return cur[2];\n }\n\n foreach (int neighbor in graph[cur[1]]) {\n int newMask = cur[0] | (1 << neighbor);\n int hashValue = newMask * 16 + neighbor;\n\n if (!visited.Contains(hashValue)) {\n visited.Add(hashValue);\n queue.Enqueue(new int[]{newMask, neighbor, cur[2] + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const n = graph.length;\n const allVisited = (1 << n) - 1;\n const queue = [];\n const visited = new Set();\n\n for (let i = 0; i < n; i++) {\n queue.push([1 << i, i, 0]);\n visited.add((1 << i) * 16 + i);\n }\n\n while (queue.length > 0) {\n const [mask, node, dist] = queue.shift();\n\n if (mask === allVisited) {\n return dist;\n }\n\n for (const neighbor of graph[node]) {\n const newMask = mask | (1 << neighbor);\n const hashValue = newMask * 16 + neighbor;\n\n if (!visited.has(hashValue)) {\n visited.add(hashValue);\n queue.push([newMask, neighbor, dist + 1]);\n }\n }\n }\n\n return -1;\n}\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param Integer[][] $graph\n * @return Integer\n */\n function shortestPathLength($graph) {\n $n = count($graph);\n $allVisited = (1 << $n) - 1;\n $queue = new SplQueue();\n $visited = [];\n\n for ($i = 0; $i < $n; $i++) {\n $queue->enqueue([1 << $i, $i, 0]);\n $visited[(1 << $i) * 16 + $i] = true;\n }\n\n while (!$queue->isEmpty()) {\n [$mask, $node, $dist] = $queue->dequeue();\n\n if ($mask === $allVisited) {\n return $dist;\n }\n\n foreach ($graph[$node] as $neighbor) {\n $newMask = $mask | (1 << $neighbor);\n $hashValue = $newMask * 16 + $neighbor;\n\n if (!isset($visited[$hashValue])) {\n $visited[$hashValue] = true;\n $queue->enqueue([$newMask, $neighbor, $dist + 1]);\n }\n }\n }\n\n return -1;\n}\n}\n```\n## Performance\n\n| Language | Fastest Runtime (ms) | Memory (MB) |\n|------------|----------------------|-------------|\n| Rust | 18 | 2.5 |\n| Go | 26 | 7.1 |\n| Java | 28 | 45.8 |\n| C++ | 43 | 18 |\n| PHP | 46 | 23.4 |\n| JavaScript | 68 | 51 |\n| C# | 97 | 47.7 |\n| Python3 | 151 | 21.2 |\n\n\n\n\n## Live Coding + BFS in Rust\nhttps://youtu.be/rIdgnWYfA_w?si=accCEKNjtxdvfj48\n\n\n## Rust Code Highlights and Best Practices\n\n### Using `VecDeque` for Queue Operations\nIn Rust, we use the `VecDeque` data structure from the standard library for our queue. It provides efficient $$O(1)$$ operations for appending to and popping from both ends. This ensures that the queue operations in the BFS algorithm are as fast as possible, which is crucial for performance.\n\n### Using `HashSet` for Visited States\nTo keep track of the visited states, Rust\'s `HashSet` is employed. Hash sets offer $$O(1)$$ lookups, which is essential for ensuring that we don\'t revisit states that we have already processed. This helps to make the algorithm more efficient by avoiding redundant work.\n\n### Bit Manipulation for State Representation\nRust\'s excellent support for bit manipulation comes in handy for representing states efficiently. The `mask` variable serves as a compact representation of visited nodes, and bitwise operations like `|` and `<<` are used for updating it.\n\n### Hash Value Calculation: `mask * 16 + i`\nYou might wonder why we use `mask * 16 + i` as the hash value for each state. This specific hash function ensures a unique value for each state, considering both the mask and the current node. Multiplying by 16 (which is $$2^4$$) effectively shifts the bits of `mask` to the left by 4 bits, making space for the `i` value. This enables us to uniquely identify each state with a single integer.\n\n### Is the Hash Value used for preventing cycles?\nYes, the hash value is used to identify unique states that have been visited. By storing these in a `HashSet`, we can efficiently prevent cycles and avoid revisiting the same state, which is critical for the algorithm\'s performance.\n\nMastering this Rust implementation will not only deepen your understanding of graph algorithms and bit manipulation but also equip you with practical Rust programming skills. Are you ready to find the shortest path visiting all nodes in Rust? Let\'s get coding! \uD83D\uDE80 | 104 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
PYTHON solution (based on two other solutions) using Bit Masks, Queues, and Named Tuples | shortest-path-visiting-all-nodes | 0 | 1 | # **NOTE: This PYTHON solution was written based off two other solutions, linked below.**\n**This is a community where we are all learning together and by no means do I claim this as my own work. I always believe in giving credit to the original authors, especially the first one, who included detailed visuals to help you further understand the Bit Masking behind this. I would urge you all to view the links and upvote their hard work.**\n\nOriginal author wrote this in C++: https://leetcode.com/problems/shortest-path-visiting-all-nodes/solutions/1800180/c-detailed-explanation-answering-why-of-each-question-dry-run-bfs/\n\nAnother solution used the same C++ code (with no credit to the original, unfortunately), but also included a Python solution, which I primarily explained: https://leetcode.com/problems/shortest-path-visiting-all-nodes/solutions/4053538/98-92-detailed-explanation-with-example-bfs-method-easy-bitmask-method/\n\n***I have heavily commented explanations within the code. IF YOU FOUND THIS HELPFUL, PLEASE UPVOTE!***\n```\nfrom collections import deque, namedtuple\n\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n\n # We want to show that we have visited nodes 1-4\n # --> SO, we can have a binary number with 1\'s in positions 1 thru 4\n allMask = (1 << n) - 1 # Example: (1 << 4) - 1 = 10000 - 1 = 01111\n\n visited = set()\n Node = namedtuple("Node", ["id", "mask", "dist"])\n q = deque()\n \n # Since we can start from any of the nodes, we can add the initial state (mask)\n # of each of the nodes in our graph\n for i in range(n):\n currMask = (1 << i)\n currNode = Node(i, currMask, 0)\n q.append(currNode)\n # we can visited nodes more than once, so we keep a set of i, the node,\n # and the currMask, showing what we have already visited\n visited.add((i, currMask))\n \n\n while q:\n currNode = q.popleft()\n # whichever mask reaches our final state will take the shortest path\n if currNode.mask == allMask: \n return currNode.dist\n\n # nBor = neighbor(s) or adjacent nodes\n for nBor in graph[currNode.id]:\n # Bitwise OR will result in previous mask and newly visited node\'s mask\n newMask = currNode.mask | (1 << nBor)\n newNode = Node(nBor, newMask, currNode.dist + 1)\n\n # skip adjacent/neighboring nodes with same state/mask\n if (nBor, newMask) in visited:\n continue\n visited.add((nBor, newMask))\n q.append(newNode)\n\n# Since we are guaranteed to have a valid, connected path, as per \n# the problem description, we don\'t need another return value; otherwise,\n# you could just put "return -1" down here\n``` | 1 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
PYTHON solution (based on two other solutions) using Bit Masks, Queues, and Named Tuples | shortest-path-visiting-all-nodes | 0 | 1 | # **NOTE: This PYTHON solution was written based off two other solutions, linked below.**\n**This is a community where we are all learning together and by no means do I claim this as my own work. I always believe in giving credit to the original authors, especially the first one, who included detailed visuals to help you further understand the Bit Masking behind this. I would urge you all to view the links and upvote their hard work.**\n\nOriginal author wrote this in C++: https://leetcode.com/problems/shortest-path-visiting-all-nodes/solutions/1800180/c-detailed-explanation-answering-why-of-each-question-dry-run-bfs/\n\nAnother solution used the same C++ code (with no credit to the original, unfortunately), but also included a Python solution, which I primarily explained: https://leetcode.com/problems/shortest-path-visiting-all-nodes/solutions/4053538/98-92-detailed-explanation-with-example-bfs-method-easy-bitmask-method/\n\n***I have heavily commented explanations within the code. IF YOU FOUND THIS HELPFUL, PLEASE UPVOTE!***\n```\nfrom collections import deque, namedtuple\n\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n\n # We want to show that we have visited nodes 1-4\n # --> SO, we can have a binary number with 1\'s in positions 1 thru 4\n allMask = (1 << n) - 1 # Example: (1 << 4) - 1 = 10000 - 1 = 01111\n\n visited = set()\n Node = namedtuple("Node", ["id", "mask", "dist"])\n q = deque()\n \n # Since we can start from any of the nodes, we can add the initial state (mask)\n # of each of the nodes in our graph\n for i in range(n):\n currMask = (1 << i)\n currNode = Node(i, currMask, 0)\n q.append(currNode)\n # we can visited nodes more than once, so we keep a set of i, the node,\n # and the currMask, showing what we have already visited\n visited.add((i, currMask))\n \n\n while q:\n currNode = q.popleft()\n # whichever mask reaches our final state will take the shortest path\n if currNode.mask == allMask: \n return currNode.dist\n\n # nBor = neighbor(s) or adjacent nodes\n for nBor in graph[currNode.id]:\n # Bitwise OR will result in previous mask and newly visited node\'s mask\n newMask = currNode.mask | (1 << nBor)\n newNode = Node(nBor, newMask, currNode.dist + 1)\n\n # skip adjacent/neighboring nodes with same state/mask\n if (nBor, newMask) in visited:\n continue\n visited.add((nBor, newMask))\n q.append(newNode)\n\n# Since we are guaranteed to have a valid, connected path, as per \n# the problem description, we don\'t need another return value; otherwise,\n# you could just put "return -1" down here\n``` | 1 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Easy solution | shortest-path-visiting-all-nodes | 0 | 1 | # Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n visited = set()\n goal= (1 << n) - 1\n q = deque()\n ans = 0\n\n for i in range(n):\n q.append((i,1<<i))\n while q:\n for _ in range(len(q)):\n node , state = q.popleft()\n if (node , state) in visited:\n continue\n if state == goal:\n return ans\n visited.add((node,state))\n for nei in graph[node]:\n q.append((nei, state | 1 << nei))\n ans += 1\n \n return -1\n\n \n``` | 1 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Easy solution | shortest-path-visiting-all-nodes | 0 | 1 | # Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n visited = set()\n goal= (1 << n) - 1\n q = deque()\n ans = 0\n\n for i in range(n):\n q.append((i,1<<i))\n while q:\n for _ in range(len(q)):\n node , state = q.popleft()\n if (node , state) in visited:\n continue\n if state == goal:\n return ans\n visited.add((node,state))\n for nei in graph[node]:\n q.append((nei, state | 1 << nei))\n ans += 1\n \n return -1\n\n \n``` | 1 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Python accurated solution | shortest-path-visiting-all-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque([(1 << i, i, 0) for i in range(n)])\n visited = set((1 << i, i) for i in range(n))\n \n while queue:\n mask, node, dist = queue.popleft()\n if mask == (1 << n) - 1:\n return dist\n for neighbor in graph[node]:\n new_mask = mask | (1 << neighbor)\n if (new_mask, neighbor) not in visited:\n visited.add((new_mask, neighbor))\n queue.append((new_mask, neighbor, dist + 1))\n``` | 1 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Python accurated solution | shortest-path-visiting-all-nodes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque([(1 << i, i, 0) for i in range(n)])\n visited = set((1 << i, i) for i in range(n))\n \n while queue:\n mask, node, dist = queue.popleft()\n if mask == (1 << n) - 1:\n return dist\n for neighbor in graph[node]:\n new_mask = mask | (1 << neighbor)\n if (new_mask, neighbor) not in visited:\n visited.add((new_mask, neighbor))\n queue.append((new_mask, neighbor, dist + 1))\n``` | 1 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Python O( (n^2) * (2^n) ) by BFS + bitmask | shortest-path-visiting-all-nodes | 0 | 1 | [\u4E2D\u6587\u8A73\u89E3 \u89E3\u984C\u6587\u7AE0](https://vocus.cc/article/65069863fd897800018eb145)\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAll edge weight is equal, so we use BFS to find shortest path.\n\nTo avoid repeated traversal and looping in deadlock, we record the seach state pair( node index, search state) in visited set\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO( n^2 * 2^n )\nTraditional BFS takes O( V + E ) = O( n + n^2 ) at most in dense graph\n\nIn addition, each step in BFS takes extra O(2^n) to record search state (i.e., the bit mask of node discovered)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO( n * 2^n )\n\nTo sum up, we have n nodes, each node needs to record 2^n search state in traversal queue as well as visited set.\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n\n # n = total node count = height of adjacency matrix\n n = len(graph)\n\n # Initialize traversal queue\n # parameter of tuple: (node idx, state mask, visiting path length)\n traversal_queue = deque( [(node_idx, 1 << node_idx , 0) for node_idx in range(n) ] )\n\n # parameter of visited tuple: (node index, search state mask)\n visited = { (node_idx, 1 << node_idx ) for node_idx in range(n) }\n\n # Mask of all node visited\n all_node_visited = (1 << n) - 1\n\n # Launch BFS traversal from each node in graph G as source\n while traversal_queue:\n\n cur_node, cur_state, path_length = traversal_queue.popleft()\n\n # We\'ve visited all nodes in graph G at least once\n if cur_state == all_node_visited:\n return path_length\n \n # Visit neighbor of current node\n for neighbor_idx in graph[cur_node]:\n\n next_state = cur_state | (1 << neighbor_idx)\n next_length = path_length + 1\n\n # If pair (neighbor index, next state) is not seen before\n if (neighbor_idx, next_state) not in visited:\n\n traversal_queue.append( (neighbor_idx, next_state, next_length) )\n visited.add( (neighbor_idx, next_state) )\n\n \n return -1\n``` | 1 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Python O( (n^2) * (2^n) ) by BFS + bitmask | shortest-path-visiting-all-nodes | 0 | 1 | [\u4E2D\u6587\u8A73\u89E3 \u89E3\u984C\u6587\u7AE0](https://vocus.cc/article/65069863fd897800018eb145)\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAll edge weight is equal, so we use BFS to find shortest path.\n\nTo avoid repeated traversal and looping in deadlock, we record the seach state pair( node index, search state) in visited set\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO( n^2 * 2^n )\nTraditional BFS takes O( V + E ) = O( n + n^2 ) at most in dense graph\n\nIn addition, each step in BFS takes extra O(2^n) to record search state (i.e., the bit mask of node discovered)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO( n * 2^n )\n\nTo sum up, we have n nodes, each node needs to record 2^n search state in traversal queue as well as visited set.\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n\n # n = total node count = height of adjacency matrix\n n = len(graph)\n\n # Initialize traversal queue\n # parameter of tuple: (node idx, state mask, visiting path length)\n traversal_queue = deque( [(node_idx, 1 << node_idx , 0) for node_idx in range(n) ] )\n\n # parameter of visited tuple: (node index, search state mask)\n visited = { (node_idx, 1 << node_idx ) for node_idx in range(n) }\n\n # Mask of all node visited\n all_node_visited = (1 << n) - 1\n\n # Launch BFS traversal from each node in graph G as source\n while traversal_queue:\n\n cur_node, cur_state, path_length = traversal_queue.popleft()\n\n # We\'ve visited all nodes in graph G at least once\n if cur_state == all_node_visited:\n return path_length\n \n # Visit neighbor of current node\n for neighbor_idx in graph[cur_node]:\n\n next_state = cur_state | (1 << neighbor_idx)\n next_length = path_length + 1\n\n # If pair (neighbor index, next state) is not seen before\n if (neighbor_idx, next_state) not in visited:\n\n traversal_queue.append( (neighbor_idx, next_state, next_length) )\n visited.add( (neighbor_idx, next_state) )\n\n \n return -1\n``` | 1 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Easy Solution || Beginner Friendly || Line By Line Explanation || Beats 95%+ || Python || Java || C+ | shortest-path-visiting-all-nodes | 1 | 1 | # BEATS\n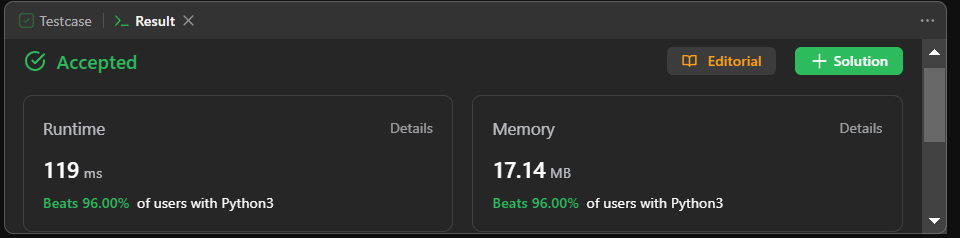\n\n# Intuition\nThe problem can be approached using Breadth-First Search (BFS) to explore different paths in the graph. The key insight is to use a bitmask to keep track of which nodes have been visited in a path. The goal is to find the shortest path that visits all nodes.\n<!-- Describe your first thoughts on how to solve this problem. -->\n# PLEASE UPVOTE IF U LIKE!!!\n# RUBY CODE BEATS 100%\n# Approach\nApproach:\n\n1. Calculate the number of vertices in the graph (V).\n\n2. Initialize a deque (double-ended queue) for BFS, initially visiting all vertices one by one. Each element in the deque is a tuple (u, bit_mask), where u is the current node, and bit_mask is a bitmask representing visited nodes.\n\n3. Calculate a bitmask where all vertices are visited (all_visited).\n\n4. Initialize a 2D array (visited) to track visited nodes. This array has dimensions (V x all_visited + 1), where each cell (u, bit_mask) is initially set to False.\n\n5. Mark the initial states of the BFS by setting corresponding cells in the visited array to True. Loop through all vertices (u) and set visited[u][1 << u] to True.\n\n6. Initialize the shortest path length (path_length) to 0.\n\n7. Start a BFS loop while the deque (curr_level) is not empty.\n\n - For each level of BFS, process nodes at that level:\n \n - Dequeue the current node (u) and its bitmask (bit_mask).\n \n - Check if all nodes are visited in this BFS level by comparing bit_mask to all_visited. If they match, return the current path_length as the shortest path.\n \n - Iterate through neighbors of the current node (u) in the graph:\n \n - Calculate the bitmask (next_bit_mask) after moving from u to v (a neighbor).\n \n - If v with the next bitmask has already been visited, skip to the next neighbor.\n \n - If all nodes are visited with the next bitmask (next_bit_mask equals all_visited), return path_length + 1 as the shortest path length.\n \n - Enqueue the neighbor v with the next bitmask for further exploration in the next BFS level.\n \n - Mark v as visited with the next bitmask (set visited[v][next_bit_mask] to True).\n \n - Decrement the counter (n) for the current BFS level.\n \n - Increment the path length (path_length) for the next level of BFS.\n\n8. If no valid path is found after exploring all possibilities, return -1 as there is no path that visits all nodes.\n\nThis approach effectively finds the shortest path that visits all nodes in the graph using BFS and bitmask-based node tracking.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: The algorithm uses BFS to explore the graph, so the time complexity is $$O(V * 2^V)$$, where V is the number of vertices in the graph.\n- Space complexity: The space complexity is $$O(V * 2^V)$$ as we store visited states in the 2D array and use a deque for BFS.\n\n\n# Code\n# Python\n```\nfrom collections import deque\n\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n # Calculate the number of vertices in the graph.\n V = len(graph)\n \n # Initialize a deque for BFS, initially visiting all vertices one by one.\n curr_level = deque([(u, 1 << u) for u in range(V)]) # BFS Queue\n \n # Calculate a bitmask where all vertices are visited.\n all_visited = (1 << V) - 1 # Bitmask for when all vertices are visited\n \n # Initialize a 2D array to track visited nodes.\n visited = [[False for bit_mask in range(0, all_visited + 1)] for _ in range(V)]\n \n # Mark the initial states of the BFS by setting corresponding cells in the visited array to True.\n for u in range(V):\n visited[u][1 << u] = True\n \n # Initialize the shortest path length.\n path_length = 0\n \n # Start a BFS loop.\n while curr_level:\n n = len(curr_level)\n while n:\n # Dequeue the current node and its bitmask.\n u, bit_mask = curr_level.popleft()\n \n # Check if all nodes are visited in this BFS level.\n if bit_mask == all_visited:\n return path_length \n \n # Iterate through neighbors of the current node.\n for v in graph[u]:\n # Calculate the bitmask after moving from u to v.\n next_bit_mask = bit_mask | (1 << v)\n \n # If v with the next bitmask has already been visited, skip to the next neighbor.\n if visited[v][next_bit_mask]:\n continue \n \n # If all nodes are visited with the next bitmask, return the shortest path length.\n if next_bit_mask == all_visited: \n return path_length + 1\n \n # Enqueue the neighbor v with the next bitmask for further exploration.\n curr_level.append((v, next_bit_mask))\n \n # Mark v as visited with the next bitmask.\n visited[v][next_bit_mask] = True \n \n n -= 1\n \n # Increment the path length for the next level of BFS.\n path_length += 1\n \n # If no valid path is found, return -1.\n return -1\n\n\n```\n# Java\n```\nimport java.util.*;\n\npublic class Solution {\n public int shortestPathLength(int[][] graph) {\n int V = graph.length;\n Queue<int[]> currLevel = new LinkedList<>();\n for (int u = 0; u < V; u++) {\n currLevel.offer(new int[]{u, 1 << u});\n }\n \n int allVisited = (1 << V) - 1;\n boolean[][] visited = new boolean[V][allVisited + 1];\n for (int u = 0; u < V; u++) {\n visited[u][1 << u] = true;\n }\n \n int pathLength = 0;\n \n while (!currLevel.isEmpty()) {\n int n = currLevel.size();\n while (n > 0) {\n int[] node = currLevel.poll();\n int u = node[0];\n int bitMask = node[1];\n \n if (bitMask == allVisited) {\n return pathLength;\n }\n \n for (int v : graph[u]) {\n int nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask == allVisited) {\n return pathLength + 1;\n }\n \n currLevel.offer(new int[]{v, nextBitMask});\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n }\n}\n\n```\n# C++\n```\n\n#include <vector>\n#include <queue>\nusing namespace std;\n\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int V = graph.size();\n queue<pair<int, int>> currLevel;\n for (int u = 0; u < V; u++) {\n currLevel.push({u, 1 << u});\n }\n \n int allVisited = (1 << V) - 1;\n vector<vector<bool>> visited(V, vector<bool>(allVisited + 1, false));\n for (int u = 0; u < V; u++) {\n visited[u][1 << u] = true;\n }\n \n int pathLength = 0;\n \n while (!currLevel.empty()) {\n int n = currLevel.size();\n while (n > 0) {\n pair<int, int> node = currLevel.front();\n currLevel.pop();\n int u = node.first;\n int bitMask = node.second;\n \n if (bitMask == allVisited) {\n return pathLength;\n }\n \n for (int v : graph[u]) {\n int nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask == allVisited) {\n return pathLength + 1;\n }\n \n currLevel.push({v, nextBitMask});\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n }\n};\n\n```\n# Ruby\n```\n# Define the method `shortest_path_length` that takes a 2D array `graph`.\ndef shortest_path_length(graph)\n v = graph.length # Calculate the number of vertices in the graph.\n curr_level = [] # Initialize an array for BFS.\n\n # Initialize the BFS queue, visiting all vertices one by one.\n (0...v).each do |u|\n curr_level << [u, 1 << u]\n end\n\n all_visited = (1 << v) - 1 # Calculate a bitmask where all vertices are visited.\n visited = Array.new(v) { Array.new(all_visited + 1, false) } # Initialize a 2D array to track visited nodes.\n\n # Mark the initial states of the BFS by setting corresponding cells in the visited array to `true`.\n (0...v).each do |u|\n visited[u][1 << u] = true\n end\n\n path_length = 0 # Initialize the shortest path length.\n\n # Start the BFS loop.\n until curr_level.empty?\n n = curr_level.length\n while n.positive?\n u, bit_mask = curr_level.shift # Dequeue the current node and its bitmask.\n\n return path_length if bit_mask == all_visited # Check if all nodes are visited.\n\n # Iterate through neighbors of the current node.\n graph[u].each do |v|\n next_bit_mask = bit_mask | (1 << v) # Calculate the bitmask after moving from `u` to `v`.\n\n next if visited[v][next_bit_mask] # Skip if `v` with the next bitmask has already been visited.\n\n return path_length + 1 if next_bit_mask == all_visited # If all nodes are visited, return the shortest path length.\n\n curr_level << [v, next_bit_mask] # Enqueue the neighbor `v` with the next bitmask for further exploration.\n visited[v][next_bit_mask] = true # Mark `v` as visited with the next bitmask.\n end\n\n n -= 1\n end\n\n path_length += 1 # Increment the path length for the next level of BFS.\n end\n\n -1 # If no valid path is found, return -1.\nend\n```\n# JavaScript\n```\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const V = graph.length;\n const currLevel = [];\n \n // Initialize the visited array.\n const allVisited = (1 << V) - 1;\n const visited = new Array(V).fill(null).map(() => new Array(allVisited + 1).fill(false));\n \n // Initialize the queue with initial states.\n for (let u = 0; u < V; u++) {\n currLevel.push([u, 1 << u]);\n visited[u][1 << u] = true;\n }\n \n let pathLength = 0;\n \n while (currLevel.length > 0) {\n let n = currLevel.length;\n \n while (n > 0) {\n const [u, bitMask] = currLevel.shift();\n \n if (bitMask === allVisited) {\n return pathLength;\n }\n \n for (const v of graph[u]) {\n const nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask === allVisited) {\n return pathLength + 1;\n }\n \n currLevel.push([v, nextBitMask]);\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n};\n``` | 28 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Easy Solution || Beginner Friendly || Line By Line Explanation || Beats 95%+ || Python || Java || C+ | shortest-path-visiting-all-nodes | 1 | 1 | # BEATS\n\n\n# Intuition\nThe problem can be approached using Breadth-First Search (BFS) to explore different paths in the graph. The key insight is to use a bitmask to keep track of which nodes have been visited in a path. The goal is to find the shortest path that visits all nodes.\n<!-- Describe your first thoughts on how to solve this problem. -->\n# PLEASE UPVOTE IF U LIKE!!!\n# RUBY CODE BEATS 100%\n# Approach\nApproach:\n\n1. Calculate the number of vertices in the graph (V).\n\n2. Initialize a deque (double-ended queue) for BFS, initially visiting all vertices one by one. Each element in the deque is a tuple (u, bit_mask), where u is the current node, and bit_mask is a bitmask representing visited nodes.\n\n3. Calculate a bitmask where all vertices are visited (all_visited).\n\n4. Initialize a 2D array (visited) to track visited nodes. This array has dimensions (V x all_visited + 1), where each cell (u, bit_mask) is initially set to False.\n\n5. Mark the initial states of the BFS by setting corresponding cells in the visited array to True. Loop through all vertices (u) and set visited[u][1 << u] to True.\n\n6. Initialize the shortest path length (path_length) to 0.\n\n7. Start a BFS loop while the deque (curr_level) is not empty.\n\n - For each level of BFS, process nodes at that level:\n \n - Dequeue the current node (u) and its bitmask (bit_mask).\n \n - Check if all nodes are visited in this BFS level by comparing bit_mask to all_visited. If they match, return the current path_length as the shortest path.\n \n - Iterate through neighbors of the current node (u) in the graph:\n \n - Calculate the bitmask (next_bit_mask) after moving from u to v (a neighbor).\n \n - If v with the next bitmask has already been visited, skip to the next neighbor.\n \n - If all nodes are visited with the next bitmask (next_bit_mask equals all_visited), return path_length + 1 as the shortest path length.\n \n - Enqueue the neighbor v with the next bitmask for further exploration in the next BFS level.\n \n - Mark v as visited with the next bitmask (set visited[v][next_bit_mask] to True).\n \n - Decrement the counter (n) for the current BFS level.\n \n - Increment the path length (path_length) for the next level of BFS.\n\n8. If no valid path is found after exploring all possibilities, return -1 as there is no path that visits all nodes.\n\nThis approach effectively finds the shortest path that visits all nodes in the graph using BFS and bitmask-based node tracking.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: The algorithm uses BFS to explore the graph, so the time complexity is $$O(V * 2^V)$$, where V is the number of vertices in the graph.\n- Space complexity: The space complexity is $$O(V * 2^V)$$ as we store visited states in the 2D array and use a deque for BFS.\n\n\n# Code\n# Python\n```\nfrom collections import deque\n\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n # Calculate the number of vertices in the graph.\n V = len(graph)\n \n # Initialize a deque for BFS, initially visiting all vertices one by one.\n curr_level = deque([(u, 1 << u) for u in range(V)]) # BFS Queue\n \n # Calculate a bitmask where all vertices are visited.\n all_visited = (1 << V) - 1 # Bitmask for when all vertices are visited\n \n # Initialize a 2D array to track visited nodes.\n visited = [[False for bit_mask in range(0, all_visited + 1)] for _ in range(V)]\n \n # Mark the initial states of the BFS by setting corresponding cells in the visited array to True.\n for u in range(V):\n visited[u][1 << u] = True\n \n # Initialize the shortest path length.\n path_length = 0\n \n # Start a BFS loop.\n while curr_level:\n n = len(curr_level)\n while n:\n # Dequeue the current node and its bitmask.\n u, bit_mask = curr_level.popleft()\n \n # Check if all nodes are visited in this BFS level.\n if bit_mask == all_visited:\n return path_length \n \n # Iterate through neighbors of the current node.\n for v in graph[u]:\n # Calculate the bitmask after moving from u to v.\n next_bit_mask = bit_mask | (1 << v)\n \n # If v with the next bitmask has already been visited, skip to the next neighbor.\n if visited[v][next_bit_mask]:\n continue \n \n # If all nodes are visited with the next bitmask, return the shortest path length.\n if next_bit_mask == all_visited: \n return path_length + 1\n \n # Enqueue the neighbor v with the next bitmask for further exploration.\n curr_level.append((v, next_bit_mask))\n \n # Mark v as visited with the next bitmask.\n visited[v][next_bit_mask] = True \n \n n -= 1\n \n # Increment the path length for the next level of BFS.\n path_length += 1\n \n # If no valid path is found, return -1.\n return -1\n\n\n```\n# Java\n```\nimport java.util.*;\n\npublic class Solution {\n public int shortestPathLength(int[][] graph) {\n int V = graph.length;\n Queue<int[]> currLevel = new LinkedList<>();\n for (int u = 0; u < V; u++) {\n currLevel.offer(new int[]{u, 1 << u});\n }\n \n int allVisited = (1 << V) - 1;\n boolean[][] visited = new boolean[V][allVisited + 1];\n for (int u = 0; u < V; u++) {\n visited[u][1 << u] = true;\n }\n \n int pathLength = 0;\n \n while (!currLevel.isEmpty()) {\n int n = currLevel.size();\n while (n > 0) {\n int[] node = currLevel.poll();\n int u = node[0];\n int bitMask = node[1];\n \n if (bitMask == allVisited) {\n return pathLength;\n }\n \n for (int v : graph[u]) {\n int nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask == allVisited) {\n return pathLength + 1;\n }\n \n currLevel.offer(new int[]{v, nextBitMask});\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n }\n}\n\n```\n# C++\n```\n\n#include <vector>\n#include <queue>\nusing namespace std;\n\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int V = graph.size();\n queue<pair<int, int>> currLevel;\n for (int u = 0; u < V; u++) {\n currLevel.push({u, 1 << u});\n }\n \n int allVisited = (1 << V) - 1;\n vector<vector<bool>> visited(V, vector<bool>(allVisited + 1, false));\n for (int u = 0; u < V; u++) {\n visited[u][1 << u] = true;\n }\n \n int pathLength = 0;\n \n while (!currLevel.empty()) {\n int n = currLevel.size();\n while (n > 0) {\n pair<int, int> node = currLevel.front();\n currLevel.pop();\n int u = node.first;\n int bitMask = node.second;\n \n if (bitMask == allVisited) {\n return pathLength;\n }\n \n for (int v : graph[u]) {\n int nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask == allVisited) {\n return pathLength + 1;\n }\n \n currLevel.push({v, nextBitMask});\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n }\n};\n\n```\n# Ruby\n```\n# Define the method `shortest_path_length` that takes a 2D array `graph`.\ndef shortest_path_length(graph)\n v = graph.length # Calculate the number of vertices in the graph.\n curr_level = [] # Initialize an array for BFS.\n\n # Initialize the BFS queue, visiting all vertices one by one.\n (0...v).each do |u|\n curr_level << [u, 1 << u]\n end\n\n all_visited = (1 << v) - 1 # Calculate a bitmask where all vertices are visited.\n visited = Array.new(v) { Array.new(all_visited + 1, false) } # Initialize a 2D array to track visited nodes.\n\n # Mark the initial states of the BFS by setting corresponding cells in the visited array to `true`.\n (0...v).each do |u|\n visited[u][1 << u] = true\n end\n\n path_length = 0 # Initialize the shortest path length.\n\n # Start the BFS loop.\n until curr_level.empty?\n n = curr_level.length\n while n.positive?\n u, bit_mask = curr_level.shift # Dequeue the current node and its bitmask.\n\n return path_length if bit_mask == all_visited # Check if all nodes are visited.\n\n # Iterate through neighbors of the current node.\n graph[u].each do |v|\n next_bit_mask = bit_mask | (1 << v) # Calculate the bitmask after moving from `u` to `v`.\n\n next if visited[v][next_bit_mask] # Skip if `v` with the next bitmask has already been visited.\n\n return path_length + 1 if next_bit_mask == all_visited # If all nodes are visited, return the shortest path length.\n\n curr_level << [v, next_bit_mask] # Enqueue the neighbor `v` with the next bitmask for further exploration.\n visited[v][next_bit_mask] = true # Mark `v` as visited with the next bitmask.\n end\n\n n -= 1\n end\n\n path_length += 1 # Increment the path length for the next level of BFS.\n end\n\n -1 # If no valid path is found, return -1.\nend\n```\n# JavaScript\n```\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const V = graph.length;\n const currLevel = [];\n \n // Initialize the visited array.\n const allVisited = (1 << V) - 1;\n const visited = new Array(V).fill(null).map(() => new Array(allVisited + 1).fill(false));\n \n // Initialize the queue with initial states.\n for (let u = 0; u < V; u++) {\n currLevel.push([u, 1 << u]);\n visited[u][1 << u] = true;\n }\n \n let pathLength = 0;\n \n while (currLevel.length > 0) {\n let n = currLevel.length;\n \n while (n > 0) {\n const [u, bitMask] = currLevel.shift();\n \n if (bitMask === allVisited) {\n return pathLength;\n }\n \n for (const v of graph[u]) {\n const nextBitMask = bitMask | (1 << v);\n \n if (visited[v][nextBitMask]) {\n continue;\n }\n \n if (nextBitMask === allVisited) {\n return pathLength + 1;\n }\n \n currLevel.push([v, nextBitMask]);\n visited[v][nextBitMask] = true;\n }\n \n n--;\n }\n \n pathLength++;\n }\n \n return -1;\n};\n``` | 28 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
🚀 97.92% || BFS + Bitmask || Explained Intuition || Commented Code 🚀 | shortest-path-visiting-all-nodes | 1 | 1 | # Probelm Description\nGiven an **undirected**, **connected** graph with `n` nodes labeled from `0` to `n - 1`, represented by an **adjacency list** in the form of an array graph, where `graph[i]` is a **list** of nodes **connected** to node `i`.\nThe task is to find the length of the **shortest path** that visits every node. You can start and stop at any node, **revisit** nodes multiple times, and **reuse** edges.\n\n- **Constraints:**\n - `n` == graph.length\n - `1 <= n <= 12`\n - `0 <= graph[i].length < n`\n - The input graph is **connected**.\n - `graph[i]` does not contain `i`.\n - If `graph[a]` contains `b`, then `graph[b]` contains `a`.\n - The input **graph** is always **connected**.\n - You may **reuse** edges.\n - You may **revisit** nodes.\n\n---\n\n\n# Intuition\n\nHello There\uD83D\uDE00\nLet\'s take a look on our interesting but yet challenging problem\uD83D\uDE80\n\nThe problem is that given a **adjacency lis**t of a graph, the task is to find the **shortest** path that visits **all** the nodes.\nThere are **two important** properties of the given graph: The graph is **undirected** and it is **unweighted** graph.\n\nShortest **path** and **unweighted** graph ? \uD83E\uDD14\nIt looks like a mission for **BFS** !\uD83D\uDC31\u200D\uD83C\uDFCD\n\nLet\'s try BFS on the first example:\n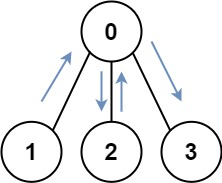\nlet\'s use normal BFS\n```\ngraph = [[1,2,3],[0],[0],[0]]\nStarting from node `1` : output is [1, 0, 2, 3]\nStarting from node `0` : output is [0, 1, 2, 3]\n```\nHuh, That doesn\'t seem right\uD83E\uDD14 since we are not storing a path but only nodes let\'s try to store path.\n```\nStarting from node `1` : output is [1, 0, 2]\n -> 0 is visited and we won\'t visit it again\nStarting from node `0` : output is [0, 1]\n -> 0 is visited and we won\'t visit it again\n```\nAlso, doesn\'t seem right !!\uD83D\uDE20\nThe problem now is with our **visited** array. The problem states that we can **revisit** nodes but **BFS** can\'t do that due to the **visited** array.\nBut if we can\'t **delete** visited array since we will run into loops !!\uD83E\uDD2F\n\nWhat can we do ??\uD83E\uDD14\nwe can use visited array but in another way.\uD83D\uDE33\nInstead of storing visited **nodes** why don\'t we store visited **pathes**...\uD83E\uDD28\n- The visited path is indicated by **two things**:\n - the **last node** visited\n - **boolean** of the nodes **visited** so far (using bitmask)\n\n> -> Bitmask: for an integer value we will store for each bit in it if the corresponding node is visited or not\n-> For nodes (0, 1, 2, 3, 4, 5)\n-> The bitmask will be something like [1 0 1 0 0 0]\n-> The value of the integer holding it equals =\n1 * 1 + 2 * 0 + 4 * 1 + 8 * 0 + 16 * 0 + 32 * 0 = 5\n\nHow will that help?\n- In our previous example, if we look into pathes using our new visited array:\n - `[1, 0, 2, 0, 3]` we can find that the **bitmask** for this path is `[1 1 1 1]` and the **last** node is `3`\n - `[1 0 1 0 1 0]` we can say it\'s **loop** for sure. The **bitmask** is `[1 1 0 0]` and the **last** node is `0`\n - `[1 0]` this is **not** a **loop** but yet is has the **same** bitmask and last node of previous example\n - `[0 1 0]` this also is **not** a **loop** and also has the **same** bitmask and last node of the two previous example\n\nI think we got something here...\uD83D\uDE80\nYes, The **bitmasking** with **tracking** of last node visited helps us to determine if a given path is visited before or not.\n\nLet\'s start from node `1`\n```\n-> node 1 : bitmask [0 1 0 0] , last visited : 1 (Not visited)\n-> node 0 : bitmask [1 1 0 0] , last visited : 0 (Not visited)\n-> node 1 : bitmask [1 1 0 0] , last visited : 1 (Not visited)\n-> node 0 : bitmask [1 1 0 0] , last visited : 0 (Visited before !!)\n```\n\nwe can see that the **third** line and **second** line are **same** in **bitmask** but what **distinguish** each of them that the **last** visited node.\nand this is the point, we don\'t care about the last visited node alone or the bitmask alone.\nWe care about **both**.\n\nWow, we really did it!!\uD83D\uDC4F\nwe used the visited array in another way to track loops and let us revisit nodes.\nWith using this visited array, we can afterwards use a normal **BFS** and this is our solution to the problem. \n\nLet\'s talk about some **implementation** Details \uD83D\uDD28\n\nWhich node we **start** from our **BFS**?\nSince the goal is to **minimize** our path then the answer can be found starting from **any node** of them but we don\'t know which...\nSo, We will try BFS from each node.\n- We have **two** approaches:\n - use a **for loop** indicates that we are starting from some node each iteration.\n - Use **multi-souce BFS**. It is simply instead of pushing one starting node to the queue push **multiple** nodes and the shortest path will appear from anyone of them eventually.\n\nHow can we implement our **visited data structure**?\n- we have **two** ways:\n - Use **2d array** `visited[bitmask][last_visited]` if it true it indicates that the path that visited the nodes in `bitmask` and ended with `last_visited` is true.\n - Use **set** of `pairs<bitmask, last_visited>`.\n\nWhat are the **elements** we use in our **Queue**?\n- We can use data structure that have 3 elements:\n - the **length** of the path \n - the visited nodes so far using **bitmask** \n - the **last** node visited\n\nThis is the full explanation. I hope everything is clear now\uD83D\uDE4F\n\n---\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialization:\n - `numNodes` -> number of nodes in the graph.\n - `allVisitedMask` -> representing all nodes visited.\n - `visited` -> track visited states.\n2. Starting Node Initialization:\n - For each node, set an **initial mask** representing that node as visited.\n - Push the **node** and its **state** into the queue.\n - Mark this **state** as **visited**.\n3. Breadth-First Search (BFS):\n - **Pop** a node and its state from the queue.\n - **Check** if **all nodes** have been **visited**. If true, return the `current length - 1`.\n - For each neighbor, calculate a **new state mask** by marking the neighbor as visited.\n - If this new state has **not visited**, push the neighbor and its updated state into the queue and mark the state as visited.\n4. If the loop completes **without finding a valid path**, return `-1` to indicate that no valid path was found.\n\n---\n\n\n\n# Complexity\n- **Time complexity:**$$O(N * 2^N)$$\nSince we are maintaining `visited` matrix then we are sure that we won\'t visit more that `(possible number of states * leading nodes)` which is `O(N * 2^N)` where `N` is the number of nodes in our graph.\n- **Space complexity:**$$O(N * 2^N)$$\nSince we are storing `visited` matrix that indicating if we visited specific state with some leading node so space complexity is `O(N * 2^N)` where `N` is the number of nodes in our graph.\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int numNodes = graph.size();\n int allVisitedMask = (1 << numNodes) - 1;\n queue<pair<int, pair<int, int>>> q;\n \n // Initialize visited array\n bool visited[allVisitedMask + 1][numNodes];\n memset(visited, false, sizeof visited);\n\n // Start from each node and add it to the queue as a starting point\n for (int node = 0; node < numNodes; ++node) {\n int initialMask = (1 << node);\n q.push({node, {initialMask, 1}});\n visited[initialMask][node] = true;\n }\n\n while (!q.empty()) {\n auto current = q.front();\n q.pop();\n\n int currentNode = current.first;\n int currentMask = current.second.first;\n int currentLength = current.second.second;\n\n // Check if all nodes have been visited\n if (currentMask == allVisitedMask)\n return currentLength - 1;\n\n // Explore the neighbors of the current node\n for (int i = 0; i < graph[currentNode].size(); ++i) {\n int neighbor = graph[currentNode][i];\n int newMask = currentMask | (1 << neighbor);\n\n // Check if this state has been visited before\n if (visited[newMask][neighbor])\n continue;\n\n // Add the neighbor to the queue with updated state\n q.push({neighbor, {newMask, currentLength + 1}});\n visited[newMask][neighbor] = true;\n }\n }\n return -1; // No valid path found\n }\n};\n```\n```Java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int numNodes = graph.length;\n int allVisitedMask = (1 << numNodes) - 1;\n Queue<int[]> q = new LinkedList<>();\n\n // Initialize visited array\n boolean[][] visited = new boolean[allVisitedMask + 1][numNodes];\n for (boolean[] row : visited) {\n Arrays.fill(row, false);\n }\n\n // Start from each node and add it to the queue as a starting point\n for (int node = 0; node < numNodes; ++node) {\n int initialMask = (1 << node);\n q.add(new int[] { node, initialMask, 1 });\n visited[initialMask][node] = true;\n }\n\n while (!q.isEmpty()) {\n int[] current = q.poll();\n\n int currentNode = current[0];\n int currentMask = current[1];\n int currentLength = current[2];\n\n // Check if all nodes have been visited\n if (currentMask == allVisitedMask)\n return currentLength - 1;\n\n // Explore the neighbors of the current node\n for (int i = 0; i < graph[currentNode].length; ++i) {\n int neighbor = graph[currentNode][i];\n int newMask = currentMask | (1 << neighbor);\n\n // Check if this state has been visited before\n if (visited[newMask][neighbor])\n continue;\n\n // Add the neighbor to the queue with updated state\n q.add(new int[] { neighbor, newMask, currentLength + 1 });\n visited[newMask][neighbor] = true;\n }\n }\n return -1; // No valid path found\n }\n}\n```\n```Python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n num_nodes = len(graph)\n all_visited_mask = (1 << num_nodes) - 1\n q = deque()\n\n # Initialize visited array\n visited = [[False for _ in range(num_nodes)] for _ in range(all_visited_mask + 1)]\n\n # Start from each node and add it to the queue as a starting point\n for node in range(num_nodes):\n initial_mask = (1 << node)\n q.append((node, initial_mask, 1))\n visited[initial_mask][node] = True\n\n while q:\n current = q.popleft()\n current_node, current_mask, current_length = current\n\n # Check if all nodes have been visited\n if current_mask == all_visited_mask:\n return current_length - 1\n\n # Explore the neighbors of the current node\n for neighbor in graph[current_node]:\n new_mask = current_mask | (1 << neighbor)\n\n # Check if this state has been visited before\n if visited[new_mask][neighbor]:\n continue\n\n # Add the neighbor to the queue with updated state\n q.append((neighbor, new_mask, current_length + 1))\n visited[new_mask][neighbor] = True\n\n return -1 # No valid path found\n```\n\n\n | 47 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
🚀 97.92% || BFS + Bitmask || Explained Intuition || Commented Code 🚀 | shortest-path-visiting-all-nodes | 1 | 1 | # Probelm Description\nGiven an **undirected**, **connected** graph with `n` nodes labeled from `0` to `n - 1`, represented by an **adjacency list** in the form of an array graph, where `graph[i]` is a **list** of nodes **connected** to node `i`.\nThe task is to find the length of the **shortest path** that visits every node. You can start and stop at any node, **revisit** nodes multiple times, and **reuse** edges.\n\n- **Constraints:**\n - `n` == graph.length\n - `1 <= n <= 12`\n - `0 <= graph[i].length < n`\n - The input graph is **connected**.\n - `graph[i]` does not contain `i`.\n - If `graph[a]` contains `b`, then `graph[b]` contains `a`.\n - The input **graph** is always **connected**.\n - You may **reuse** edges.\n - You may **revisit** nodes.\n\n---\n\n\n# Intuition\n\nHello There\uD83D\uDE00\nLet\'s take a look on our interesting but yet challenging problem\uD83D\uDE80\n\nThe problem is that given a **adjacency lis**t of a graph, the task is to find the **shortest** path that visits **all** the nodes.\nThere are **two important** properties of the given graph: The graph is **undirected** and it is **unweighted** graph.\n\nShortest **path** and **unweighted** graph ? \uD83E\uDD14\nIt looks like a mission for **BFS** !\uD83D\uDC31\u200D\uD83C\uDFCD\n\nLet\'s try BFS on the first example:\n\nlet\'s use normal BFS\n```\ngraph = [[1,2,3],[0],[0],[0]]\nStarting from node `1` : output is [1, 0, 2, 3]\nStarting from node `0` : output is [0, 1, 2, 3]\n```\nHuh, That doesn\'t seem right\uD83E\uDD14 since we are not storing a path but only nodes let\'s try to store path.\n```\nStarting from node `1` : output is [1, 0, 2]\n -> 0 is visited and we won\'t visit it again\nStarting from node `0` : output is [0, 1]\n -> 0 is visited and we won\'t visit it again\n```\nAlso, doesn\'t seem right !!\uD83D\uDE20\nThe problem now is with our **visited** array. The problem states that we can **revisit** nodes but **BFS** can\'t do that due to the **visited** array.\nBut if we can\'t **delete** visited array since we will run into loops !!\uD83E\uDD2F\n\nWhat can we do ??\uD83E\uDD14\nwe can use visited array but in another way.\uD83D\uDE33\nInstead of storing visited **nodes** why don\'t we store visited **pathes**...\uD83E\uDD28\n- The visited path is indicated by **two things**:\n - the **last node** visited\n - **boolean** of the nodes **visited** so far (using bitmask)\n\n> -> Bitmask: for an integer value we will store for each bit in it if the corresponding node is visited or not\n-> For nodes (0, 1, 2, 3, 4, 5)\n-> The bitmask will be something like [1 0 1 0 0 0]\n-> The value of the integer holding it equals =\n1 * 1 + 2 * 0 + 4 * 1 + 8 * 0 + 16 * 0 + 32 * 0 = 5\n\nHow will that help?\n- In our previous example, if we look into pathes using our new visited array:\n - `[1, 0, 2, 0, 3]` we can find that the **bitmask** for this path is `[1 1 1 1]` and the **last** node is `3`\n - `[1 0 1 0 1 0]` we can say it\'s **loop** for sure. The **bitmask** is `[1 1 0 0]` and the **last** node is `0`\n - `[1 0]` this is **not** a **loop** but yet is has the **same** bitmask and last node of previous example\n - `[0 1 0]` this also is **not** a **loop** and also has the **same** bitmask and last node of the two previous example\n\nI think we got something here...\uD83D\uDE80\nYes, The **bitmasking** with **tracking** of last node visited helps us to determine if a given path is visited before or not.\n\nLet\'s start from node `1`\n```\n-> node 1 : bitmask [0 1 0 0] , last visited : 1 (Not visited)\n-> node 0 : bitmask [1 1 0 0] , last visited : 0 (Not visited)\n-> node 1 : bitmask [1 1 0 0] , last visited : 1 (Not visited)\n-> node 0 : bitmask [1 1 0 0] , last visited : 0 (Visited before !!)\n```\n\nwe can see that the **third** line and **second** line are **same** in **bitmask** but what **distinguish** each of them that the **last** visited node.\nand this is the point, we don\'t care about the last visited node alone or the bitmask alone.\nWe care about **both**.\n\nWow, we really did it!!\uD83D\uDC4F\nwe used the visited array in another way to track loops and let us revisit nodes.\nWith using this visited array, we can afterwards use a normal **BFS** and this is our solution to the problem. \n\nLet\'s talk about some **implementation** Details \uD83D\uDD28\n\nWhich node we **start** from our **BFS**?\nSince the goal is to **minimize** our path then the answer can be found starting from **any node** of them but we don\'t know which...\nSo, We will try BFS from each node.\n- We have **two** approaches:\n - use a **for loop** indicates that we are starting from some node each iteration.\n - Use **multi-souce BFS**. It is simply instead of pushing one starting node to the queue push **multiple** nodes and the shortest path will appear from anyone of them eventually.\n\nHow can we implement our **visited data structure**?\n- we have **two** ways:\n - Use **2d array** `visited[bitmask][last_visited]` if it true it indicates that the path that visited the nodes in `bitmask` and ended with `last_visited` is true.\n - Use **set** of `pairs<bitmask, last_visited>`.\n\nWhat are the **elements** we use in our **Queue**?\n- We can use data structure that have 3 elements:\n - the **length** of the path \n - the visited nodes so far using **bitmask** \n - the **last** node visited\n\nThis is the full explanation. I hope everything is clear now\uD83D\uDE4F\n\n---\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialization:\n - `numNodes` -> number of nodes in the graph.\n - `allVisitedMask` -> representing all nodes visited.\n - `visited` -> track visited states.\n2. Starting Node Initialization:\n - For each node, set an **initial mask** representing that node as visited.\n - Push the **node** and its **state** into the queue.\n - Mark this **state** as **visited**.\n3. Breadth-First Search (BFS):\n - **Pop** a node and its state from the queue.\n - **Check** if **all nodes** have been **visited**. If true, return the `current length - 1`.\n - For each neighbor, calculate a **new state mask** by marking the neighbor as visited.\n - If this new state has **not visited**, push the neighbor and its updated state into the queue and mark the state as visited.\n4. If the loop completes **without finding a valid path**, return `-1` to indicate that no valid path was found.\n\n---\n\n\n\n# Complexity\n- **Time complexity:**$$O(N * 2^N)$$\nSince we are maintaining `visited` matrix then we are sure that we won\'t visit more that `(possible number of states * leading nodes)` which is `O(N * 2^N)` where `N` is the number of nodes in our graph.\n- **Space complexity:**$$O(N * 2^N)$$\nSince we are storing `visited` matrix that indicating if we visited specific state with some leading node so space complexity is `O(N * 2^N)` where `N` is the number of nodes in our graph.\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int numNodes = graph.size();\n int allVisitedMask = (1 << numNodes) - 1;\n queue<pair<int, pair<int, int>>> q;\n \n // Initialize visited array\n bool visited[allVisitedMask + 1][numNodes];\n memset(visited, false, sizeof visited);\n\n // Start from each node and add it to the queue as a starting point\n for (int node = 0; node < numNodes; ++node) {\n int initialMask = (1 << node);\n q.push({node, {initialMask, 1}});\n visited[initialMask][node] = true;\n }\n\n while (!q.empty()) {\n auto current = q.front();\n q.pop();\n\n int currentNode = current.first;\n int currentMask = current.second.first;\n int currentLength = current.second.second;\n\n // Check if all nodes have been visited\n if (currentMask == allVisitedMask)\n return currentLength - 1;\n\n // Explore the neighbors of the current node\n for (int i = 0; i < graph[currentNode].size(); ++i) {\n int neighbor = graph[currentNode][i];\n int newMask = currentMask | (1 << neighbor);\n\n // Check if this state has been visited before\n if (visited[newMask][neighbor])\n continue;\n\n // Add the neighbor to the queue with updated state\n q.push({neighbor, {newMask, currentLength + 1}});\n visited[newMask][neighbor] = true;\n }\n }\n return -1; // No valid path found\n }\n};\n```\n```Java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int numNodes = graph.length;\n int allVisitedMask = (1 << numNodes) - 1;\n Queue<int[]> q = new LinkedList<>();\n\n // Initialize visited array\n boolean[][] visited = new boolean[allVisitedMask + 1][numNodes];\n for (boolean[] row : visited) {\n Arrays.fill(row, false);\n }\n\n // Start from each node and add it to the queue as a starting point\n for (int node = 0; node < numNodes; ++node) {\n int initialMask = (1 << node);\n q.add(new int[] { node, initialMask, 1 });\n visited[initialMask][node] = true;\n }\n\n while (!q.isEmpty()) {\n int[] current = q.poll();\n\n int currentNode = current[0];\n int currentMask = current[1];\n int currentLength = current[2];\n\n // Check if all nodes have been visited\n if (currentMask == allVisitedMask)\n return currentLength - 1;\n\n // Explore the neighbors of the current node\n for (int i = 0; i < graph[currentNode].length; ++i) {\n int neighbor = graph[currentNode][i];\n int newMask = currentMask | (1 << neighbor);\n\n // Check if this state has been visited before\n if (visited[newMask][neighbor])\n continue;\n\n // Add the neighbor to the queue with updated state\n q.add(new int[] { neighbor, newMask, currentLength + 1 });\n visited[newMask][neighbor] = true;\n }\n }\n return -1; // No valid path found\n }\n}\n```\n```Python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n num_nodes = len(graph)\n all_visited_mask = (1 << num_nodes) - 1\n q = deque()\n\n # Initialize visited array\n visited = [[False for _ in range(num_nodes)] for _ in range(all_visited_mask + 1)]\n\n # Start from each node and add it to the queue as a starting point\n for node in range(num_nodes):\n initial_mask = (1 << node)\n q.append((node, initial_mask, 1))\n visited[initial_mask][node] = True\n\n while q:\n current = q.popleft()\n current_node, current_mask, current_length = current\n\n # Check if all nodes have been visited\n if current_mask == all_visited_mask:\n return current_length - 1\n\n # Explore the neighbors of the current node\n for neighbor in graph[current_node]:\n new_mask = current_mask | (1 << neighbor)\n\n # Check if this state has been visited before\n if visited[new_mask][neighbor]:\n continue\n\n # Add the neighbor to the queue with updated state\n q.append((neighbor, new_mask, current_length + 1))\n visited[new_mask][neighbor] = True\n\n return -1 # No valid path found\n```\n\n\n | 47 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Python Simplest solution You will ever find for this problem | shortest-path-visiting-all-nodes | 0 | 1 | \n\n# Code\n```\nclass Solution:\n\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n q=deque()\n s=set()\n n=len(graph)\n for i in range(n):\n q.append([i,0,1<<i])\n s.add((i,i<<i))\n reached=(1<<n) - 1\n while len(q)>0:\n node,dis,mask=q.popleft()\n if mask==reached:\n return dis\n for nei in graph[node]:\n tempMask=mask|1<<nei\n if (nei,tempMask) not in s:\n s.add((nei,tempMask))\n q.append([nei,dis+1,tempMask])\n return 0\n \n \n\n \n``` | 0 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Python Simplest solution You will ever find for this problem | shortest-path-visiting-all-nodes | 0 | 1 | \n\n# Code\n```\nclass Solution:\n\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n q=deque()\n s=set()\n n=len(graph)\n for i in range(n):\n q.append([i,0,1<<i])\n s.add((i,i<<i))\n reached=(1<<n) - 1\n while len(q)>0:\n node,dis,mask=q.popleft()\n if mask==reached:\n return dis\n for nei in graph[node]:\n tempMask=mask|1<<nei\n if (nei,tempMask) not in s:\n s.add((nei,tempMask))\n q.append([nei,dis+1,tempMask])\n return 0\n \n \n\n \n``` | 0 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Efficient Algorithm for Shortest Path Visiting All Nodes using Bitmasking and BFS | shortest-path-visiting-all-nodes | 1 | 1 | # Intuition\nThe main point of the algorithm is to find the shortest path that visits all nodes in a given graph. This is achieved by utilizing a bitmask to keep track of visited nodes and their states during a breadth-first search (BFS) traversal. The algorithm explores the graph, updating the state of visited nodes using bitwise operations to represent the visited status. The traversal continues until all nodes have been visited (indicated by a specific bitmask), and the shortest path length is determined. Key steps include:\n\n1. **Initialization:**\n - Calculate the total number of nodes and set up initial data structures, including the target bitmask and the BFS queue.\n\n2. **BFS Traversal:**\n - Begin BFS traversal from each node, considering its state represented by a bitmask.\n - Explore neighbors, updating the state and distance accordingly, and continue traversal until the target bitmask (indicating all nodes visited) is reached.\n\n3. **Goal:**\n - Return the shortest path length that covers all nodes, determined by the BFS traversal and reaching the target bitmask.\n\nThe algorithm efficiently explores the graph using BFS and utilizes bitmasks to keep track of visited nodes and states, providing an effective way to find the shortest path that visits all nodes.\n\n---\n\n# Solution Video\n\nI usually upload a solution video to youtube but today, I didn\'t have time to create a video because I took care of my kis all day.\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,358\nMy inital goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\nAlgorithm Overview:\n1. Calculate the total number of nodes `n` in the graph.\n2. Set the `target_mask` to a value where all `n` bits are set to 1.\n3. Initialize a BFS queue `queue` with starting positions (node, state, distance) for each node.\n4. Initialize a set `visited` to keep track of visited nodes with their state.\n\nDetailed Explanation:\n1. **Initialization**:\n - Set `n` to the length of the `graph`.\n - Calculate `target_mask` by left shifting 1 by `n` bits and then subtracting 1.\n\n2. **BFS Initialization**:\n - Create a queue `queue`.\n - Create a set `visited`.\n - For each node `i` from 0 to `n-1`, add the tuple `(i, 1 << i, 0)` to `queue` to represent the starting positions for BFS, where each node is considered visited in its own state.\n\n3. **BFS traversal**:\n - While the `queue` is not empty, do the following:\n - Pop the front element from the `queue` and extract `node`, `state`, and `distance`.\n - Check if `state` is equal to `target_mask`. If true, return the current `distance` as this represents the shortest path that visits all nodes.\n - Explore neighbors of the current `node`.\n - For each neighbor in the `graph[node]`, calculate the new state by setting the corresponding bit for that neighbor in `state`.\n - If `(neighbor, new_state)` is not in `visited`, add it to `visited`, and push `(neighbor, new_state, distance + 1)` to the `queue` to continue BFS.\n\nThe algorithm uses BFS to traverse the graph, considering each node and its state (represented by a bitmask). It explores neighbors, updating the state and distance accordingly, until it finds a state where all nodes have been visited (represented by `target_mask`), indicating the shortest path.\n\n\n```python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n target_mask = (1 << n) - 1\n\n # Initialize the BFS queue with starting positions (node, state, distance)\n queue = deque((i, 1 << i, 0) for i in range(n))\n\n # Use a set to keep track of visited nodes with their state\n visited = set((i, 1 << i) for i in range(n))\n \n while queue:\n node, state, distance = queue.popleft()\n \n # Check if we have visited all nodes\n if state == target_mask:\n return distance\n \n # Explore neighbors\n for neighbor in graph[node]:\n # Update the state to include the neighbor\n new_state = state | (1 << neighbor)\n # Check visited set for the current node and state\n if (neighbor, new_state) not in visited:\n visited.add((neighbor, new_state))\n queue.append((neighbor, new_state, distance + 1))\n```\n```javascript []\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const n = graph.length;\n const targetMask = (1 << n) - 1;\n \n const queue = [];\n const visited = new Set();\n \n for (let i = 0; i < n; i++) {\n queue.push([i, 1 << i, 0]);\n visited.add(`${i},${1 << i}`);\n }\n \n while (queue.length > 0) {\n const [node, state, distance] = queue.shift();\n \n if (state === targetMask) {\n return distance;\n }\n \n for (const neighbor of graph[node]) {\n const newState = state | (1 << neighbor);\n const key = `${neighbor},${newState}`;\n \n if (!visited.has(key)) {\n visited.add(key);\n queue.push([neighbor, newState, distance + 1]);\n }\n }\n } \n};\n```\n```java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int n = graph.length;\n int targetMask = (1 << n) - 1;\n\n Queue<int[]> queue = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n\n for (int i = 0; i < n; i++) {\n queue.offer(new int[]{i, 1 << i, 0});\n visited.add(i + "," + (1 << i));\n }\n\n while (!queue.isEmpty()) {\n int[] curr = queue.poll();\n int node = curr[0];\n int state = curr[1];\n int distance = curr[2];\n\n if (state == targetMask) {\n return distance;\n }\n\n for (int neighbor : graph[node]) {\n int newState = state | (1 << neighbor);\n String key = neighbor + "," + newState;\n\n if (!visited.contains(key)) {\n visited.add(key);\n queue.offer(new int[]{neighbor, newState, distance + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int n = graph.size();\n int targetMask = (1 << n) - 1;\n\n std::queue<std::vector<int>> queue;\n std::unordered_set<std::string> visited;\n\n for (int i = 0; i < n; i++) {\n queue.push({i, 1 << i, 0});\n visited.insert(std::to_string(i) + "," + std::to_string(1 << i));\n }\n\n while (!queue.empty()) {\n auto curr = queue.front();\n queue.pop();\n int node = curr[0];\n int state = curr[1];\n int distance = curr[2];\n\n if (state == targetMask) {\n return distance;\n }\n\n for (int neighbor : graph[node]) {\n int newState = state | (1 << neighbor);\n std::string key = std::to_string(neighbor) + "," + std::to_string(newState);\n\n if (visited.find(key) == visited.end()) {\n visited.insert(key);\n queue.push({neighbor, newState, distance + 1});\n }\n }\n }\n\n return -1; \n }\n};\n```\n | 10 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Efficient Algorithm for Shortest Path Visiting All Nodes using Bitmasking and BFS | shortest-path-visiting-all-nodes | 1 | 1 | # Intuition\nThe main point of the algorithm is to find the shortest path that visits all nodes in a given graph. This is achieved by utilizing a bitmask to keep track of visited nodes and their states during a breadth-first search (BFS) traversal. The algorithm explores the graph, updating the state of visited nodes using bitwise operations to represent the visited status. The traversal continues until all nodes have been visited (indicated by a specific bitmask), and the shortest path length is determined. Key steps include:\n\n1. **Initialization:**\n - Calculate the total number of nodes and set up initial data structures, including the target bitmask and the BFS queue.\n\n2. **BFS Traversal:**\n - Begin BFS traversal from each node, considering its state represented by a bitmask.\n - Explore neighbors, updating the state and distance accordingly, and continue traversal until the target bitmask (indicating all nodes visited) is reached.\n\n3. **Goal:**\n - Return the shortest path length that covers all nodes, determined by the BFS traversal and reaching the target bitmask.\n\nThe algorithm efficiently explores the graph using BFS and utilizes bitmasks to keep track of visited nodes and states, providing an effective way to find the shortest path that visits all nodes.\n\n---\n\n# Solution Video\n\nI usually upload a solution video to youtube but today, I didn\'t have time to create a video because I took care of my kis all day.\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,358\nMy inital goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\nAlgorithm Overview:\n1. Calculate the total number of nodes `n` in the graph.\n2. Set the `target_mask` to a value where all `n` bits are set to 1.\n3. Initialize a BFS queue `queue` with starting positions (node, state, distance) for each node.\n4. Initialize a set `visited` to keep track of visited nodes with their state.\n\nDetailed Explanation:\n1. **Initialization**:\n - Set `n` to the length of the `graph`.\n - Calculate `target_mask` by left shifting 1 by `n` bits and then subtracting 1.\n\n2. **BFS Initialization**:\n - Create a queue `queue`.\n - Create a set `visited`.\n - For each node `i` from 0 to `n-1`, add the tuple `(i, 1 << i, 0)` to `queue` to represent the starting positions for BFS, where each node is considered visited in its own state.\n\n3. **BFS traversal**:\n - While the `queue` is not empty, do the following:\n - Pop the front element from the `queue` and extract `node`, `state`, and `distance`.\n - Check if `state` is equal to `target_mask`. If true, return the current `distance` as this represents the shortest path that visits all nodes.\n - Explore neighbors of the current `node`.\n - For each neighbor in the `graph[node]`, calculate the new state by setting the corresponding bit for that neighbor in `state`.\n - If `(neighbor, new_state)` is not in `visited`, add it to `visited`, and push `(neighbor, new_state, distance + 1)` to the `queue` to continue BFS.\n\nThe algorithm uses BFS to traverse the graph, considering each node and its state (represented by a bitmask). It explores neighbors, updating the state and distance accordingly, until it finds a state where all nodes have been visited (represented by `target_mask`), indicating the shortest path.\n\n\n```python []\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n target_mask = (1 << n) - 1\n\n # Initialize the BFS queue with starting positions (node, state, distance)\n queue = deque((i, 1 << i, 0) for i in range(n))\n\n # Use a set to keep track of visited nodes with their state\n visited = set((i, 1 << i) for i in range(n))\n \n while queue:\n node, state, distance = queue.popleft()\n \n # Check if we have visited all nodes\n if state == target_mask:\n return distance\n \n # Explore neighbors\n for neighbor in graph[node]:\n # Update the state to include the neighbor\n new_state = state | (1 << neighbor)\n # Check visited set for the current node and state\n if (neighbor, new_state) not in visited:\n visited.add((neighbor, new_state))\n queue.append((neighbor, new_state, distance + 1))\n```\n```javascript []\n/**\n * @param {number[][]} graph\n * @return {number}\n */\nvar shortestPathLength = function(graph) {\n const n = graph.length;\n const targetMask = (1 << n) - 1;\n \n const queue = [];\n const visited = new Set();\n \n for (let i = 0; i < n; i++) {\n queue.push([i, 1 << i, 0]);\n visited.add(`${i},${1 << i}`);\n }\n \n while (queue.length > 0) {\n const [node, state, distance] = queue.shift();\n \n if (state === targetMask) {\n return distance;\n }\n \n for (const neighbor of graph[node]) {\n const newState = state | (1 << neighbor);\n const key = `${neighbor},${newState}`;\n \n if (!visited.has(key)) {\n visited.add(key);\n queue.push([neighbor, newState, distance + 1]);\n }\n }\n } \n};\n```\n```java []\nclass Solution {\n public int shortestPathLength(int[][] graph) {\n int n = graph.length;\n int targetMask = (1 << n) - 1;\n\n Queue<int[]> queue = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n\n for (int i = 0; i < n; i++) {\n queue.offer(new int[]{i, 1 << i, 0});\n visited.add(i + "," + (1 << i));\n }\n\n while (!queue.isEmpty()) {\n int[] curr = queue.poll();\n int node = curr[0];\n int state = curr[1];\n int distance = curr[2];\n\n if (state == targetMask) {\n return distance;\n }\n\n for (int neighbor : graph[node]) {\n int newState = state | (1 << neighbor);\n String key = neighbor + "," + newState;\n\n if (!visited.contains(key)) {\n visited.add(key);\n queue.offer(new int[]{neighbor, newState, distance + 1});\n }\n }\n }\n\n return -1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int shortestPathLength(vector<vector<int>>& graph) {\n int n = graph.size();\n int targetMask = (1 << n) - 1;\n\n std::queue<std::vector<int>> queue;\n std::unordered_set<std::string> visited;\n\n for (int i = 0; i < n; i++) {\n queue.push({i, 1 << i, 0});\n visited.insert(std::to_string(i) + "," + std::to_string(1 << i));\n }\n\n while (!queue.empty()) {\n auto curr = queue.front();\n queue.pop();\n int node = curr[0];\n int state = curr[1];\n int distance = curr[2];\n\n if (state == targetMask) {\n return distance;\n }\n\n for (int neighbor : graph[node]) {\n int newState = state | (1 << neighbor);\n std::string key = std::to_string(neighbor) + "," + std::to_string(newState);\n\n if (visited.find(key) == visited.end()) {\n visited.insert(key);\n queue.push({neighbor, newState, distance + 1});\n }\n }\n }\n\n return -1; \n }\n};\n```\n | 10 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Python3 Solution | shortest-path-visiting-all-nodes | 0 | 1 | \n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n=len(graph)\n queue=deque([(i,1<<i) for i in range(n)])\n seen=set(queue)\n ans=0\n while queue:\n for _ in range(len(queue)):\n u,m=queue.popleft()\n if m==(1<<n)-1:\n return ans\n for v in graph[u]:\n if (v,m|1<<v) not in seen:\n queue.append((v,m|1<<v))\n seen.add((v,m|1<<v))\n ans+=1 \n``` | 6 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
Python3 Solution | shortest-path-visiting-all-nodes | 0 | 1 | \n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n=len(graph)\n queue=deque([(i,1<<i) for i in range(n)])\n seen=set(queue)\n ans=0\n while queue:\n for _ in range(len(queue)):\n u,m=queue.popleft()\n if m==(1<<n)-1:\n return ans\n for v in graph[u]:\n if (v,m|1<<v) not in seen:\n queue.append((v,m|1<<v))\n seen.add((v,m|1<<v))\n ans+=1 \n``` | 6 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
🚀Most Efficient Python Code 🐍 || Beats 95% 🔥🔥 | shortest-path-visiting-all-nodes | 0 | 1 | # Intuition\nThe intuition behind the code is to use a combination of bitmasking and breadth-first search (BFS) to explore all possible paths in the graph efficiently. The goal is to find the shortest path that visits all nodes in the graph at least once. The code maintains a state for each visited node and the bitmask represents which nodes have been visited so far.\n\n\n\n\n\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque()\n visited = [[False] * (1 << n) for _ in range(n)]\n \n for i in range(n):\n queue.append((1 << i, i, 0))\n visited[i][1 << i] = True\n \n while queue:\n mask, x, dist = queue.popleft()\n \n if mask == (1 << n) - 1:\n return dist\n \n for neighbor in graph[x]:\n new_mask = mask | (1 << neighbor)\n \n if not visited[neighbor][new_mask]:\n queue.append((new_mask, neighbor, dist + 1))\n visited[neighbor][new_mask] = True\n\n``` | 3 | You have an undirected, connected graph of `n` nodes labeled from `0` to `n - 1`. You are given an array `graph` where `graph[i]` is a list of all the nodes connected with node `i` by an edge.
Return _the length of the shortest path that visits every node_. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0\],\[0\],\[0\]\]
**Output:** 4
**Explanation:** One possible path is \[1,0,2,0,3\]
**Example 2:**
**Input:** graph = \[\[1\],\[0,2,4\],\[1,3,4\],\[2\],\[1,2\]\]
**Output:** 4
**Explanation:** One possible path is \[0,1,4,2,3\]
**Constraints:**
* `n == graph.length`
* `1 <= n <= 12`
* `0 <= graph[i].length < n`
* `graph[i]` does not contain `i`.
* If `graph[a]` contains `b`, then `graph[b]` contains `a`.
* The input graph is always connected. | null |
🚀Most Efficient Python Code 🐍 || Beats 95% 🔥🔥 | shortest-path-visiting-all-nodes | 0 | 1 | # Intuition\nThe intuition behind the code is to use a combination of bitmasking and breadth-first search (BFS) to explore all possible paths in the graph efficiently. The goal is to find the shortest path that visits all nodes in the graph at least once. The code maintains a state for each visited node and the bitmask represents which nodes have been visited so far.\n\n\n\n\n\n\n# Code\n```\nclass Solution:\n def shortestPathLength(self, graph: List[List[int]]) -> int:\n n = len(graph)\n queue = deque()\n visited = [[False] * (1 << n) for _ in range(n)]\n \n for i in range(n):\n queue.append((1 << i, i, 0))\n visited[i][1 << i] = True\n \n while queue:\n mask, x, dist = queue.popleft()\n \n if mask == (1 << n) - 1:\n return dist\n \n for neighbor in graph[x]:\n new_mask = mask | (1 << neighbor)\n \n if not visited[neighbor][new_mask]:\n queue.append((new_mask, neighbor, dist + 1))\n visited[neighbor][new_mask] = True\n\n``` | 3 | Alice and Bob play a game with piles of stones. There are an **even** number of piles arranged in a row, and each pile has a **positive** integer number of stones `piles[i]`.
The objective of the game is to end with the most stones. The **total** number of stones across all the piles is **odd**, so there are no ties.
Alice and Bob take turns, with **Alice starting first**. Each turn, a player takes the entire pile of stones either from the **beginning** or from the **end** of the row. This continues until there are no more piles left, at which point the person with the **most stones wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins the game, or_ `false` _if Bob wins_.
**Example 1:**
**Input:** piles = \[5,3,4,5\]
**Output:** true
**Explanation:**
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes \[3, 4, 5\].
If Bob takes 3, then the board is \[4, 5\], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is \[3, 4\], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.
**Example 2:**
**Input:** piles = \[3,7,2,3\]
**Output:** true
**Constraints:**
* `2 <= piles.length <= 500`
* `piles.length` is **even**.
* `1 <= piles[i] <= 500`
* `sum(piles[i])` is **odd**. | null |
Python Easy To Understand | shifting-letters | 0 | 1 | # Code\n```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n sumArr=[shifts[len(s)-1]%26]\n new=""\n for i in range(1,len(s)):\n sumArr.insert(0,(sumArr[0]+shifts[len(s)-i-1])%26)\n for i in range(len(s)):\n n=ord(s[i])+sumArr[i]\n if n>ord("z"):\n n-=26\n new+=chr(n)\n return new\n``` | 1 | You are given a string `s` of lowercase English letters and an integer array `shifts` of the same length.
Call the `shift()` of a letter, the next letter in the alphabet, (wrapping around so that `'z'` becomes `'a'`).
* For example, `shift('a') = 'b'`, `shift('t') = 'u'`, and `shift('z') = 'a'`.
Now for each `shifts[i] = x`, we want to shift the first `i + 1` letters of `s`, `x` times.
Return _the final string after all such shifts to s are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[3,5,9\]
**Output:** "rpl "
**Explanation:** We start with "abc ".
After shifting the first 1 letters of s by 3, we have "dbc ".
After shifting the first 2 letters of s by 5, we have "igc ".
After shifting the first 3 letters of s by 9, we have "rpl ", the answer.
**Example 2:**
**Input:** s = "aaa ", shifts = \[1,2,3\]
**Output:** "gfd "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `shifts.length == s.length`
* `0 <= shifts[i] <= 109` | null |
Python Easy To Understand | shifting-letters | 0 | 1 | # Code\n```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n sumArr=[shifts[len(s)-1]%26]\n new=""\n for i in range(1,len(s)):\n sumArr.insert(0,(sumArr[0]+shifts[len(s)-i-1])%26)\n for i in range(len(s)):\n n=ord(s[i])+sumArr[i]\n if n>ord("z"):\n n-=26\n new+=chr(n)\n return new\n``` | 1 | A positive integer is _magical_ if it is divisible by either `a` or `b`.
Given the three integers `n`, `a`, and `b`, return the `nth` magical number. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, a = 2, b = 3
**Output:** 2
**Example 2:**
**Input:** n = 4, a = 2, b = 3
**Output:** 6
**Constraints:**
* `1 <= n <= 109`
* `2 <= a, b <= 4 * 104` | null |
[Python 3] Reversed prefix sum || beats 100% || 610ms 🥷🏼 | shifting-letters | 0 | 1 | ```python3 []\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n shifts = list(accumulate(shifts[::-1]))\n\n res = []\n for c, k in zip(s, shifts[::-1]):\n pos = (ord(c) - 97 + k) % 26 + 97\n res.append(chr(pos))\n\n return \'\'.join(res)\n```\n\n | 3 | You are given a string `s` of lowercase English letters and an integer array `shifts` of the same length.
Call the `shift()` of a letter, the next letter in the alphabet, (wrapping around so that `'z'` becomes `'a'`).
* For example, `shift('a') = 'b'`, `shift('t') = 'u'`, and `shift('z') = 'a'`.
Now for each `shifts[i] = x`, we want to shift the first `i + 1` letters of `s`, `x` times.
Return _the final string after all such shifts to s are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[3,5,9\]
**Output:** "rpl "
**Explanation:** We start with "abc ".
After shifting the first 1 letters of s by 3, we have "dbc ".
After shifting the first 2 letters of s by 5, we have "igc ".
After shifting the first 3 letters of s by 9, we have "rpl ", the answer.
**Example 2:**
**Input:** s = "aaa ", shifts = \[1,2,3\]
**Output:** "gfd "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `shifts.length == s.length`
* `0 <= shifts[i] <= 109` | null |
[Python 3] Reversed prefix sum || beats 100% || 610ms 🥷🏼 | shifting-letters | 0 | 1 | ```python3 []\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n shifts = list(accumulate(shifts[::-1]))\n\n res = []\n for c, k in zip(s, shifts[::-1]):\n pos = (ord(c) - 97 + k) % 26 + 97\n res.append(chr(pos))\n\n return \'\'.join(res)\n```\n\n | 3 | A positive integer is _magical_ if it is divisible by either `a` or `b`.
Given the three integers `n`, `a`, and `b`, return the `nth` magical number. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, a = 2, b = 3
**Output:** 2
**Example 2:**
**Input:** n = 4, a = 2, b = 3
**Output:** 6
**Constraints:**
* `1 <= n <= 109`
* `2 <= a, b <= 4 * 104` | null |
python easy to understand solution for beginner | shifting-letters | 0 | 1 | ```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n self.letters = {chr(97+i):i for i in range(26)}\n ans = \'\'\n summ = sum(shifts)\n for elm,i in zip(s,shifts):\n ans += self.shift(elm,summ%26)\n summ -= i\n return ans\n \n def shift(self,letter,bit):\n letter = (self.letters[letter] + bit)%26\n return chr(97+letter)\n``` | 1 | You are given a string `s` of lowercase English letters and an integer array `shifts` of the same length.
Call the `shift()` of a letter, the next letter in the alphabet, (wrapping around so that `'z'` becomes `'a'`).
* For example, `shift('a') = 'b'`, `shift('t') = 'u'`, and `shift('z') = 'a'`.
Now for each `shifts[i] = x`, we want to shift the first `i + 1` letters of `s`, `x` times.
Return _the final string after all such shifts to s are applied_.
**Example 1:**
**Input:** s = "abc ", shifts = \[3,5,9\]
**Output:** "rpl "
**Explanation:** We start with "abc ".
After shifting the first 1 letters of s by 3, we have "dbc ".
After shifting the first 2 letters of s by 5, we have "igc ".
After shifting the first 3 letters of s by 9, we have "rpl ", the answer.
**Example 2:**
**Input:** s = "aaa ", shifts = \[1,2,3\]
**Output:** "gfd "
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `shifts.length == s.length`
* `0 <= shifts[i] <= 109` | null |
python easy to understand solution for beginner | shifting-letters | 0 | 1 | ```\nclass Solution:\n def shiftingLetters(self, s: str, shifts: List[int]) -> str:\n self.letters = {chr(97+i):i for i in range(26)}\n ans = \'\'\n summ = sum(shifts)\n for elm,i in zip(s,shifts):\n ans += self.shift(elm,summ%26)\n summ -= i\n return ans\n \n def shift(self,letter,bit):\n letter = (self.letters[letter] + bit)%26\n return chr(97+letter)\n``` | 1 | A positive integer is _magical_ if it is divisible by either `a` or `b`.
Given the three integers `n`, `a`, and `b`, return the `nth` magical number. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1, a = 2, b = 3
**Output:** 2
**Example 2:**
**Input:** n = 4, a = 2, b = 3
**Output:** 6
**Constraints:**
* `1 <= n <= 109`
* `2 <= a, b <= 4 * 104` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.