title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python | faster than 83% | easy-understanding | explaining with comments | score-of-parentheses | 0 | 1 | ```\nclass Solution:\n def scoreOfParentheses(self, s: str) -> int:\n stk = [0] # temp value to help us\n\n for char in s:\n if char == \'(\':\n stk.append(0) # new parent: current sum = 0\n else:\n # An expression will be closed\n # Find its value: either 1 for empty () or 2 * its sub-expressions\n # we can calc both with a simple max()\n value = max(2 * stk.pop(), 1)\n\n # Add the expression sum to its parent current sum\n # Assume we have expression E that is (CHD)\n # where C, H, D are valid-subexpressions with values 5, 10, 4\n # then E is (5+10+4) = (19) = 38\n # Every time we finish an expression, we add its value to its parent\n # get the parent and update its sum with a finished sub-expression\n stk[-1] += value\n\n return stk.pop()\n\t\t``` | 8 | Given a balanced parentheses string `s`, return _the **score** of the string_.
The **score** of a balanced parentheses string is based on the following rule:
* `"() "` has score `1`.
* `AB` has score `A + B`, where `A` and `B` are balanced parentheses strings.
* `(A)` has score `2 * A`, where `A` is a balanced parentheses string.
**Example 1:**
**Input:** s = "() "
**Output:** 1
**Example 2:**
**Input:** s = "(()) "
**Output:** 2
**Example 3:**
**Input:** s = "()() "
**Output:** 2
**Constraints:**
* `2 <= s.length <= 50`
* `s` consists of only `'('` and `')'`.
* `s` is a balanced parentheses string. | null |
Python | faster than 83% | easy-understanding | explaining with comments | score-of-parentheses | 0 | 1 | ```\nclass Solution:\n def scoreOfParentheses(self, s: str) -> int:\n stk = [0] # temp value to help us\n\n for char in s:\n if char == \'(\':\n stk.append(0) # new parent: current sum = 0\n else:\n # An expression will be closed\n # Find its value: either 1 for empty () or 2 * its sub-expressions\n # we can calc both with a simple max()\n value = max(2 * stk.pop(), 1)\n\n # Add the expression sum to its parent current sum\n # Assume we have expression E that is (CHD)\n # where C, H, D are valid-subexpressions with values 5, 10, 4\n # then E is (5+10+4) = (19) = 38\n # Every time we finish an expression, we add its value to its parent\n # get the parent and update its sum with a finished sub-expression\n stk[-1] += value\n\n return stk.pop()\n\t\t``` | 8 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Solution | minimum-cost-to-hire-k-workers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double mincostToHireWorkers(vector<int>& quality, vector<int>& wage, int k) {\n struct Worker\n {\n int quality;\n int wage;\n Worker() : quality(0), wage(0) {}\n Worker(int q, int w) : quality(q), wage(w) {}\n double ratio() const { return double(wage) / quality; }\n bool operator < (const Worker& o) { return ratio() < o.ratio(); }\n };\n int i, j;\n double ans = 1e9;\n vector<Worker> W;\n for (i = 0; i < quality.size(); ++i)\n {\n W.emplace_back(Worker(quality[i], wage[i]));\n }\n std::sort(W.begin(), W.end());\n priority_queue<int> heap;\n int sumq = 0;\n for (const Worker& worker : W)\n {\n heap.push(worker.quality);\n sumq += worker.quality;\n if (heap.size() > k)\n {\n sumq -= heap.top();\n heap.pop();\n }\n if (heap.size() == k)\n {\n ans = std::min(ans, worker.ratio() * sumq);\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n = len(quality)\n unit_cost_lookup = [pay / q for pay, q in zip(wage, quality)]\n sorted_by_unit_cost = sorted(range(n), key = lambda worker_ID: unit_cost_lookup[worker_ID])\n pool = [0] * k\n total_quality_purchased = 0\n for rank in range(k):\n worker_ID = sorted_by_unit_cost[rank]\n quality_purchased = quality[worker_ID]\n total_quality_purchased += quality_purchased\n pool[rank] = -quality_purchased\n \n heapify(pool)\n unit_cost_for_group = unit_cost_lookup[worker_ID]\n res = unit_cost_for_group * total_quality_purchased\n \n for rank in range(k, n):\n worker_ID = sorted_by_unit_cost[rank]\n quality_purchased = quality[worker_ID]\n unit_cost = unit_cost_lookup[worker_ID]\n total_quality_purchased += quality_purchased + heapreplace(pool, -quality_purchased)\n res = min(res, unit_cost * total_quality_purchased)\n return res\n```\n\n```Java []\nclass Worker implements Comparable<Worker> {\n final int q, w;\n public Worker(int q, int w) {\n this.q = q;\n this.w = w;\n }\n @Override\n public int compareTo(Worker other) {\n return Integer.compare(w * other.q, q * other.w);\n }\n}\nclass Solution {\n public double mincostToHireWorkers(int[] quality, int[] wage, int k) {\n int n = quality.length;\n Worker[] a = new Worker[n];\n for (int i = 0; i < n; ++i) {\n a[i] = new Worker(quality[i], wage[i]);\n }\n Arrays.sort(a);\n int s = 0;\n double res = 1e15;\n PriorityQueue<Integer> q = new PriorityQueue<>();\n for (Worker worker: a) {\n q.add(-worker.q);\n s += worker.q;\n if (q.size() > k) s += q.poll();\n if (q.size() == k) res = Math.min(res, (double) s * worker.w / worker.q);\n }\n return res;\n }\n}\n```\n | 1 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
Solution | minimum-cost-to-hire-k-workers | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double mincostToHireWorkers(vector<int>& quality, vector<int>& wage, int k) {\n struct Worker\n {\n int quality;\n int wage;\n Worker() : quality(0), wage(0) {}\n Worker(int q, int w) : quality(q), wage(w) {}\n double ratio() const { return double(wage) / quality; }\n bool operator < (const Worker& o) { return ratio() < o.ratio(); }\n };\n int i, j;\n double ans = 1e9;\n vector<Worker> W;\n for (i = 0; i < quality.size(); ++i)\n {\n W.emplace_back(Worker(quality[i], wage[i]));\n }\n std::sort(W.begin(), W.end());\n priority_queue<int> heap;\n int sumq = 0;\n for (const Worker& worker : W)\n {\n heap.push(worker.quality);\n sumq += worker.quality;\n if (heap.size() > k)\n {\n sumq -= heap.top();\n heap.pop();\n }\n if (heap.size() == k)\n {\n ans = std::min(ans, worker.ratio() * sumq);\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n = len(quality)\n unit_cost_lookup = [pay / q for pay, q in zip(wage, quality)]\n sorted_by_unit_cost = sorted(range(n), key = lambda worker_ID: unit_cost_lookup[worker_ID])\n pool = [0] * k\n total_quality_purchased = 0\n for rank in range(k):\n worker_ID = sorted_by_unit_cost[rank]\n quality_purchased = quality[worker_ID]\n total_quality_purchased += quality_purchased\n pool[rank] = -quality_purchased\n \n heapify(pool)\n unit_cost_for_group = unit_cost_lookup[worker_ID]\n res = unit_cost_for_group * total_quality_purchased\n \n for rank in range(k, n):\n worker_ID = sorted_by_unit_cost[rank]\n quality_purchased = quality[worker_ID]\n unit_cost = unit_cost_lookup[worker_ID]\n total_quality_purchased += quality_purchased + heapreplace(pool, -quality_purchased)\n res = min(res, unit_cost * total_quality_purchased)\n return res\n```\n\n```Java []\nclass Worker implements Comparable<Worker> {\n final int q, w;\n public Worker(int q, int w) {\n this.q = q;\n this.w = w;\n }\n @Override\n public int compareTo(Worker other) {\n return Integer.compare(w * other.q, q * other.w);\n }\n}\nclass Solution {\n public double mincostToHireWorkers(int[] quality, int[] wage, int k) {\n int n = quality.length;\n Worker[] a = new Worker[n];\n for (int i = 0; i < n; ++i) {\n a[i] = new Worker(quality[i], wage[i]);\n }\n Arrays.sort(a);\n int s = 0;\n double res = 1e15;\n PriorityQueue<Integer> q = new PriorityQueue<>();\n for (Worker worker: a) {\n q.add(-worker.q);\n s += worker.q;\n if (q.size() > k) s += q.poll();\n if (q.size() == k) res = Math.min(res, (double) s * worker.w / worker.q);\n }\n return res;\n }\n}\n```\n | 1 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
Here I use simple Priority heapq and sorting method which beats 100% | minimum-cost-to-hire-k-workers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# **o**(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n = len(quality)\n workers = sorted([(w / q, q) for w, q in zip(wage, quality)]) \n heap = []\n total_quality = 0\n result = float(\'inf\')\n\n for ratio, q in workers:\n total_quality += q\n heapq.heappush(heap, -q) \n\n if len(heap) > k:\n total_quality += heapq.heappop(heap)\n\n if len(heap) == k:\n result = min(result, total_quality * ratio)\n\n return result\n\n``` | 1 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
Here I use simple Priority heapq and sorting method which beats 100% | minimum-cost-to-hire-k-workers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# **o**(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n = len(quality)\n workers = sorted([(w / q, q) for w, q in zip(wage, quality)]) \n heap = []\n total_quality = 0\n result = float(\'inf\')\n\n for ratio, q in workers:\n total_quality += q\n heapq.heappush(heap, -q) \n\n if len(heap) > k:\n total_quality += heapq.heappop(heap)\n\n if len(heap) == k:\n result = min(result, total_quality * ratio)\n\n return result\n\n``` | 1 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
[Python3] | Priority Queue | minimum-cost-to-hire-k-workers | 0 | 1 | ```\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n=len(wage)\n arr=[[wage[i]/quality[i],quality[i]] for i in range(n)]\n arr.sort(key=lambda x:x[0])\n kSmallest=0\n pq=[]\n for i in range(k):\n heapq.heappush(pq,-arr[i][1])\n kSmallest+=arr[i][1]\n minCost=arr[k-1][0]*kSmallest\n for c in range(k,n):\n if pq and abs(pq[0])>arr[c][1]:\n qRem=-heappop(pq)\n kSmallest-=qRem\n kSmallest+=arr[c][1]\n heappush(pq,-arr[c][1])\n minCost=min(minCost,arr[c][0]*kSmallest)\n return minCost\n \n \n \n```\nRefer for Explanation -> https://www.youtube.com/watch?v=o8emK4ehhq0 | 1 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
[Python3] | Priority Queue | minimum-cost-to-hire-k-workers | 0 | 1 | ```\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n n=len(wage)\n arr=[[wage[i]/quality[i],quality[i]] for i in range(n)]\n arr.sort(key=lambda x:x[0])\n kSmallest=0\n pq=[]\n for i in range(k):\n heapq.heappush(pq,-arr[i][1])\n kSmallest+=arr[i][1]\n minCost=arr[k-1][0]*kSmallest\n for c in range(k,n):\n if pq and abs(pq[0])>arr[c][1]:\n qRem=-heappop(pq)\n kSmallest-=qRem\n kSmallest+=arr[c][1]\n heappush(pq,-arr[c][1])\n minCost=min(minCost,arr[c][0]*kSmallest)\n return minCost\n \n \n \n```\nRefer for Explanation -> https://www.youtube.com/watch?v=o8emK4ehhq0 | 1 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
Python -- Faster than 99%, Memory < 86% | minimum-cost-to-hire-k-workers | 0 | 1 | ```python\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n \n # --- Sort Workers by Ratio\n workers = [(w/q, q) for w, q in zip(wage, quality)]\n workers.sort()\n\n # --- Initialize Quality Max-Heap\n paid_group = [-1*q for r, q in workers[:k]]\n heapq.heapify(paid_group)\n sum_q = -1 * sum(paid_group)\n\n # --- Initialize Cost with Captain = K\n cost = sum_q * workers[k-1][0]\n\n # --- Test more expensive Captains.\n # higher captain\'s ratio may be worth it if we can reduce sum_q\n for ratio, q in workers[k:]:\n sum_q += q + heapq.heappushpop(paid_group, -q)\n temp = ratio * sum_q\n cost = min(cost, temp)\n\n return cost\n\t``` | 1 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
Python -- Faster than 99%, Memory < 86% | minimum-cost-to-hire-k-workers | 0 | 1 | ```python\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n \n # --- Sort Workers by Ratio\n workers = [(w/q, q) for w, q in zip(wage, quality)]\n workers.sort()\n\n # --- Initialize Quality Max-Heap\n paid_group = [-1*q for r, q in workers[:k]]\n heapq.heapify(paid_group)\n sum_q = -1 * sum(paid_group)\n\n # --- Initialize Cost with Captain = K\n cost = sum_q * workers[k-1][0]\n\n # --- Test more expensive Captains.\n # higher captain\'s ratio may be worth it if we can reduce sum_q\n for ratio, q in workers[k:]:\n sum_q += q + heapq.heappushpop(paid_group, -q)\n temp = ratio * sum_q\n cost = min(cost, temp)\n\n return cost\n\t``` | 1 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
O(n log n) solution with a detailed explanation and commented code | minimum-cost-to-hire-k-workers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe first make the observation that in an optimal solution of $k$ workers there is at least one worker that gets paid exactly their minimum wage requirement.\nIf that would not be the case and all $k$ workers get paid more, we could construct a more efficient solution by scaling down all the wages by the smallest excess fraction. This brings one worker exactly to their minimum requirement and scales down the others accordingly and thus overall producing a cheaper solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGiven the observation above, we try each worker as the base - the worker that gets exactly their minimal requirement, and find the cheapest solution overall.\n\nNotation:\nLet the index of the base wage worker be $0$ and $1, ... , k-1$ the others.\n\nThe base wage worker gets paid $wage_0$ and every other gets paid proportionally by relative quality: $wage_0 * \\frac{quality_i}{quality_0}$ (note that: $wage_0 * \\frac{quality_0}{quality_0} = wage_0$).\nThis satisfies the proportionality requirement as for two workers $i$ and $j$ their wages are $$\\frac{wage_i}{wage_j} = \\frac{wage_0 * \\frac{quality_i}{quality_0}}{wage_0 * \\frac{quality_h}{quality_0}} = \\frac{quality_i}{quality_j}$$.\n\nThen the total cost is:\n\n$$\\sum_{i=0}^{k-1} wage_0 * \\frac{quality_i}{quality_0} = \\frac{wage_0}{quality_0}\\sum_{i=0}^{k-1}quality_i$$\n\nHow do we pick the workers $1,...,k-1$? They need to satisfy two conditions:\n* Minimize $\\sum_{i=0}^{k-1}quality_i$ (to minimize total cost).\n* Get paid enough, that is $wage_0 * \\frac{quality_i}{quality_0} >= wage_i$.\n\nThe last condition can be restated as $\\frac{wage_0}{quality_0} >= \\frac{wage_i}{quality_i}$.\nLet us call this the wage to quality _ratio_.\n\n**That means to find a cheapest solution that has worker $0$ defining the base salary, we need to find the $k-1$ lowest quality workers with a _smaller_ wage to quality ratio.**\n\nIn the solution, we simply test each worker as base salary worker.\nIf we _order_ the workers by increasing wage to quality ratio, we can go through them linearly and only need to keep track of the $k-1$ lowest quality values seen. For each candidate $i$ as the base salary worker, we get the total cost as $wage_i + \\frac{wage_i}{quality_i} * Q$, where $Q$ is the sum of the $k-1$ lowest quality values so far.\n\nWe can use a _max_ heap to keep track of the $k-1$ smallest quality values: At each point we insert the new value and remove the max, always keeping the $k-1$ smallest values.\n\n# Complexity\n- Time complexity: $$\\mathcal{O}(n \\log n)$$. Sorting is $\\mathcal{O}(n \\log n)$, then we do a linear sweep and update a heap of $k$ elements, so $\\mathcal{O}(n \\log n + n \\log k) = \\mathcal{O}(n \\log n)$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$\\mathcal{O}(n)$$ (could be improved to $$\\mathcal{O}(k)$$ if we use inplace sorting of the input rather than creating a workers array as in the code below. This could further be improved to $$\\mathcal{O}(1)$$ if we do the heap inplace as well)\n\nIf we would use **insertion sort** instead of using a max heap (and do everything inplace), we can arrive at a $$\\mathcal{O}(n^2)$$ time but $$\\mathcal{O}(1)$$ space solution.\n\n# Code\n```\nimport dataclasses\nimport heapq\n\n\[email protected]\nclass Worker:\n quality: int\n wage: int\n\n def r(self) -> float:\n return self.wage / self.quality\n\n\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n # Consider the workers in order of wage / quality.\n # This way, if worker i defines the base salary, we know that\n # we would pay any worker j (0 ... i-1) enough if we pay them\n # wage_i * (quality_j / quality_i) >= wage_j.\n # Pick the k-1 smallest (by quality) among 0 ... i-1, if worker i\n # defines the base salary to get an optimal solution.\n # We try all workers as defining the base salary to get the global optimum.\n workers = sorted([Worker(quality=q, wage=w) for q, w in zip(quality, wage)], key=lambda worker: worker.r())\n\n # Keep track of the k smallest quality values so far.\n # We use a max heap, as we want to incrementally keep the k lowest ones.\n h = [-worker.quality for worker in workers[:k-1]]\n heapq.heapify(h)\n total_q = -sum(h)\n\n # Test each base salary candidate.\n result = float("inf")\n for worker in workers[k-1:]:\n candidate = worker.wage + total_q * worker.r()\n if candidate < result:\n result = candidate\n\n # Add the worker.\n total_q += worker.quality\n heapq.heappush(h, -worker.quality)\n\n # Shrink heap to the k smallest by removing. the max.\n # Update new total.\n total_q += heapq.heappop(h)\n\n return result\n``` | 0 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
O(n log n) solution with a detailed explanation and commented code | minimum-cost-to-hire-k-workers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe first make the observation that in an optimal solution of $k$ workers there is at least one worker that gets paid exactly their minimum wage requirement.\nIf that would not be the case and all $k$ workers get paid more, we could construct a more efficient solution by scaling down all the wages by the smallest excess fraction. This brings one worker exactly to their minimum requirement and scales down the others accordingly and thus overall producing a cheaper solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGiven the observation above, we try each worker as the base - the worker that gets exactly their minimal requirement, and find the cheapest solution overall.\n\nNotation:\nLet the index of the base wage worker be $0$ and $1, ... , k-1$ the others.\n\nThe base wage worker gets paid $wage_0$ and every other gets paid proportionally by relative quality: $wage_0 * \\frac{quality_i}{quality_0}$ (note that: $wage_0 * \\frac{quality_0}{quality_0} = wage_0$).\nThis satisfies the proportionality requirement as for two workers $i$ and $j$ their wages are $$\\frac{wage_i}{wage_j} = \\frac{wage_0 * \\frac{quality_i}{quality_0}}{wage_0 * \\frac{quality_h}{quality_0}} = \\frac{quality_i}{quality_j}$$.\n\nThen the total cost is:\n\n$$\\sum_{i=0}^{k-1} wage_0 * \\frac{quality_i}{quality_0} = \\frac{wage_0}{quality_0}\\sum_{i=0}^{k-1}quality_i$$\n\nHow do we pick the workers $1,...,k-1$? They need to satisfy two conditions:\n* Minimize $\\sum_{i=0}^{k-1}quality_i$ (to minimize total cost).\n* Get paid enough, that is $wage_0 * \\frac{quality_i}{quality_0} >= wage_i$.\n\nThe last condition can be restated as $\\frac{wage_0}{quality_0} >= \\frac{wage_i}{quality_i}$.\nLet us call this the wage to quality _ratio_.\n\n**That means to find a cheapest solution that has worker $0$ defining the base salary, we need to find the $k-1$ lowest quality workers with a _smaller_ wage to quality ratio.**\n\nIn the solution, we simply test each worker as base salary worker.\nIf we _order_ the workers by increasing wage to quality ratio, we can go through them linearly and only need to keep track of the $k-1$ lowest quality values seen. For each candidate $i$ as the base salary worker, we get the total cost as $wage_i + \\frac{wage_i}{quality_i} * Q$, where $Q$ is the sum of the $k-1$ lowest quality values so far.\n\nWe can use a _max_ heap to keep track of the $k-1$ smallest quality values: At each point we insert the new value and remove the max, always keeping the $k-1$ smallest values.\n\n# Complexity\n- Time complexity: $$\\mathcal{O}(n \\log n)$$. Sorting is $\\mathcal{O}(n \\log n)$, then we do a linear sweep and update a heap of $k$ elements, so $\\mathcal{O}(n \\log n + n \\log k) = \\mathcal{O}(n \\log n)$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$\\mathcal{O}(n)$$ (could be improved to $$\\mathcal{O}(k)$$ if we use inplace sorting of the input rather than creating a workers array as in the code below. This could further be improved to $$\\mathcal{O}(1)$$ if we do the heap inplace as well)\n\nIf we would use **insertion sort** instead of using a max heap (and do everything inplace), we can arrive at a $$\\mathcal{O}(n^2)$$ time but $$\\mathcal{O}(1)$$ space solution.\n\n# Code\n```\nimport dataclasses\nimport heapq\n\n\[email protected]\nclass Worker:\n quality: int\n wage: int\n\n def r(self) -> float:\n return self.wage / self.quality\n\n\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n # Consider the workers in order of wage / quality.\n # This way, if worker i defines the base salary, we know that\n # we would pay any worker j (0 ... i-1) enough if we pay them\n # wage_i * (quality_j / quality_i) >= wage_j.\n # Pick the k-1 smallest (by quality) among 0 ... i-1, if worker i\n # defines the base salary to get an optimal solution.\n # We try all workers as defining the base salary to get the global optimum.\n workers = sorted([Worker(quality=q, wage=w) for q, w in zip(quality, wage)], key=lambda worker: worker.r())\n\n # Keep track of the k smallest quality values so far.\n # We use a max heap, as we want to incrementally keep the k lowest ones.\n h = [-worker.quality for worker in workers[:k-1]]\n heapq.heapify(h)\n total_q = -sum(h)\n\n # Test each base salary candidate.\n result = float("inf")\n for worker in workers[k-1:]:\n candidate = worker.wage + total_q * worker.r()\n if candidate < result:\n result = candidate\n\n # Add the worker.\n total_q += worker.quality\n heapq.heappush(h, -worker.quality)\n\n # Shrink heap to the k smallest by removing. the max.\n # Update new total.\n total_q += heapq.heappop(h)\n\n return result\n``` | 0 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
Using heap and sorting of wage/quality | Explained | minimum-cost-to-hire-k-workers | 0 | 1 | ```\nimport heapq\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n """\n This is a mind f**k problem\n Problem Statement:\n Given the quality of workers and minimum wage, we need to hire k workers using least \n amount of money such that two conditions are met:\n \n for any two workers among the k workers:\n \n offer[i] offer[j]\n ---------- = ----------\n quality[i] quality[j]\n \n offer[i] >= minimum_expected_wage[i]\n \n Approach 1: (which will give TLE)\n Assign one as caption, capture it\'s ratio\n using the same ratio, identify the offer that needs to be rolled out for remaining workers\n identify the workers whose offer are greater than their minimum expected wage\n if there are less than k such workers, then with current captian we cannot hire k workers\n if there are more than k such workers, identify the minimum sum of k elements for them\n \n Repeat the above process for each worker as the captain once, keep track of minimum sum needed\n and return the minimum sum of money\n \n Above approach will give TLE\n \n Optimization 1:\n when we assign one as captian, we compute the offer of other workers based on the ratio of assigned captain\n offer[j] = quality[j] * min_wage_of_current_captain\n ----------------------------\n quality_of_current_captain\n \n offer[j] = quality[j] * captain_ratio \n if min_wage[j] \n ------------- > offer[j]\n quality[j]\n \n worker cannot be hired \n hence, instead of doing same computations, we can create an array of ratios\n sort those ratios and if ratio1 < ratio2, then if worker 2 is captain, then worker1 hire offer will meet it\'s minimum expected wage criteria but not vice versa\n """\n ratios = []\n heap = []\n for q, w in zip(quality, wage):\n ratios.append((w/q, q))\n ratios.sort() \n # create a heap of quality[0] to quality[k-1]\n for i in range(k):\n heapq.heappush(heap, -ratios[i][1])\n \n min_sum_of_money = -1 * sum(heap) * ratios[k-1][0]\n \n for i in range(k, len(ratios)):\n ratio, quality = ratios[i][:]\n if -1 * heap[0] > quality:\n heapq.heappop(heap)\n heapq.heappush(heap, -quality)\n min_sum_of_money = min(min_sum_of_money, -1 * sum(heap)*ratio)\n return min_sum_of_money \n \n \n``` | 0 | There are `n` workers. You are given two integer arrays `quality` and `wage` where `quality[i]` is the quality of the `ith` worker and `wage[i]` is the minimum wage expectation for the `ith` worker.
We want to hire exactly `k` workers to form a paid group. To hire a group of `k` workers, we must pay them according to the following rules:
1. Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
2. Every worker in the paid group must be paid at least their minimum wage expectation.
Given the integer `k`, return _the least amount of money needed to form a paid group satisfying the above conditions_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** quality = \[10,20,5\], wage = \[70,50,30\], k = 2
**Output:** 105.00000
**Explanation:** We pay 70 to 0th worker and 35 to 2nd worker.
**Example 2:**
**Input:** quality = \[3,1,10,10,1\], wage = \[4,8,2,2,7\], k = 3
**Output:** 30.66667
**Explanation:** We pay 4 to 0th worker, 13.33333 to 2nd and 3rd workers separately.
**Constraints:**
* `n == quality.length == wage.length`
* `1 <= k <= n <= 104`
* `1 <= quality[i], wage[i] <= 104` | null |
Using heap and sorting of wage/quality | Explained | minimum-cost-to-hire-k-workers | 0 | 1 | ```\nimport heapq\nclass Solution:\n def mincostToHireWorkers(self, quality: List[int], wage: List[int], k: int) -> float:\n """\n This is a mind f**k problem\n Problem Statement:\n Given the quality of workers and minimum wage, we need to hire k workers using least \n amount of money such that two conditions are met:\n \n for any two workers among the k workers:\n \n offer[i] offer[j]\n ---------- = ----------\n quality[i] quality[j]\n \n offer[i] >= minimum_expected_wage[i]\n \n Approach 1: (which will give TLE)\n Assign one as caption, capture it\'s ratio\n using the same ratio, identify the offer that needs to be rolled out for remaining workers\n identify the workers whose offer are greater than their minimum expected wage\n if there are less than k such workers, then with current captian we cannot hire k workers\n if there are more than k such workers, identify the minimum sum of k elements for them\n \n Repeat the above process for each worker as the captain once, keep track of minimum sum needed\n and return the minimum sum of money\n \n Above approach will give TLE\n \n Optimization 1:\n when we assign one as captian, we compute the offer of other workers based on the ratio of assigned captain\n offer[j] = quality[j] * min_wage_of_current_captain\n ----------------------------\n quality_of_current_captain\n \n offer[j] = quality[j] * captain_ratio \n if min_wage[j] \n ------------- > offer[j]\n quality[j]\n \n worker cannot be hired \n hence, instead of doing same computations, we can create an array of ratios\n sort those ratios and if ratio1 < ratio2, then if worker 2 is captain, then worker1 hire offer will meet it\'s minimum expected wage criteria but not vice versa\n """\n ratios = []\n heap = []\n for q, w in zip(quality, wage):\n ratios.append((w/q, q))\n ratios.sort() \n # create a heap of quality[0] to quality[k-1]\n for i in range(k):\n heapq.heappush(heap, -ratios[i][1])\n \n min_sum_of_money = -1 * sum(heap) * ratios[k-1][0]\n \n for i in range(k, len(ratios)):\n ratio, quality = ratios[i][:]\n if -1 * heap[0] > quality:\n heapq.heappop(heap)\n heapq.heappush(heap, -quality)\n min_sum_of_money = min(min_sum_of_money, -1 * sum(heap)*ratio)\n return min_sum_of_money \n \n \n``` | 0 | You are given `k` identical eggs and you have access to a building with `n` floors labeled from `1` to `n`.
You know that there exists a floor `f` where `0 <= f <= n` such that any egg dropped at a floor **higher** than `f` will **break**, and any egg dropped **at or below** floor `f` will **not break**.
Each move, you may take an unbroken egg and drop it from any floor `x` (where `1 <= x <= n`). If the egg breaks, you can no longer use it. However, if the egg does not break, you may **reuse** it in future moves.
Return _the **minimum number of moves** that you need to determine **with certainty** what the value of_ `f` is.
**Example 1:**
**Input:** k = 1, n = 2
**Output:** 2
**Explanation:**
Drop the egg from floor 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from floor 2. If it breaks, we know that f = 1.
If it does not break, then we know f = 2.
Hence, we need at minimum 2 moves to determine with certainty what the value of f is.
**Example 2:**
**Input:** k = 2, n = 6
**Output:** 3
**Example 3:**
**Input:** k = 3, n = 14
**Output:** 4
**Constraints:**
* `1 <= k <= 100`
* `1 <= n <= 104` | null |
Solution | mirror-reflection | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 0)\n return 2;\n if (q % 2 == 0)\n return 0;\n return 1;\n }\n};\n```\n\n```Python3 []\nimport math\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n y = q\n x = p\n gcd = math.gcd(y, x)\n y //= gcd\n x //= gcd\n\n if y % 2 == 0:\n return 0\n else:\n if x % 2 == 1:\n return 1\n else:\n return 2\n```\n\n```Java []\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(((p|q)&1) == 0){\n p >>= 1;\n q >>= 1;\n }\n return (q&1) + ((p&1)^1);\n }\n}\n```\n | 1 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
Solution | mirror-reflection | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int mirrorReflection(int p, int q) {\n while (p % 2 == 0 && q % 2 == 0) {\n p /= 2;\n q /= 2;\n }\n if (p % 2 == 0)\n return 2;\n if (q % 2 == 0)\n return 0;\n return 1;\n }\n};\n```\n\n```Python3 []\nimport math\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n y = q\n x = p\n gcd = math.gcd(y, x)\n y //= gcd\n x //= gcd\n\n if y % 2 == 0:\n return 0\n else:\n if x % 2 == 1:\n return 1\n else:\n return 2\n```\n\n```Java []\nclass Solution {\n public int mirrorReflection(int p, int q) {\n while(((p|q)&1) == 0){\n p >>= 1;\n q >>= 1;\n }\n return (q&1) + ((p&1)^1);\n }\n}\n```\n | 1 | Alice and Bob have a different total number of candies. You are given two integer arrays `aliceSizes` and `bobSizes` where `aliceSizes[i]` is the number of candies of the `ith` box of candy that Alice has and `bobSizes[j]` is the number of candies of the `jth` box of candy that Bob has.
Since they are friends, they would like to exchange one candy box each so that after the exchange, they both have the same total amount of candy. The total amount of candy a person has is the sum of the number of candies in each box they have.
Return a_n integer array_ `answer` _where_ `answer[0]` _is the number of candies in the box that Alice must exchange, and_ `answer[1]` _is the number of candies in the box that Bob must exchange_. If there are multiple answers, you may **return any** one of them. It is guaranteed that at least one answer exists.
**Example 1:**
**Input:** aliceSizes = \[1,1\], bobSizes = \[2,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** aliceSizes = \[1,2\], bobSizes = \[2,3\]
**Output:** \[1,2\]
**Example 3:**
**Input:** aliceSizes = \[2\], bobSizes = \[1,3\]
**Output:** \[2,3\]
**Constraints:**
* `1 <= aliceSizes.length, bobSizes.length <= 104`
* `1 <= aliceSizes[i], bobSizes[j] <= 105`
* Alice and Bob have a different total number of candies.
* There will be at least one valid answer for the given input. | null |
Python3 || 4 lines, geometry, w/ explanation || T/M: 92%/81% | mirror-reflection | 0 | 1 | Instead of imagining one room with mirrored walls, imagine an infinite cluster of rooms with glass walls; the light passes through to the next room and on and on until it evenually hits a corner. \n\n Suppose for example: p = 6, q = 4, which is demonstrated in the figure below.\n\t \n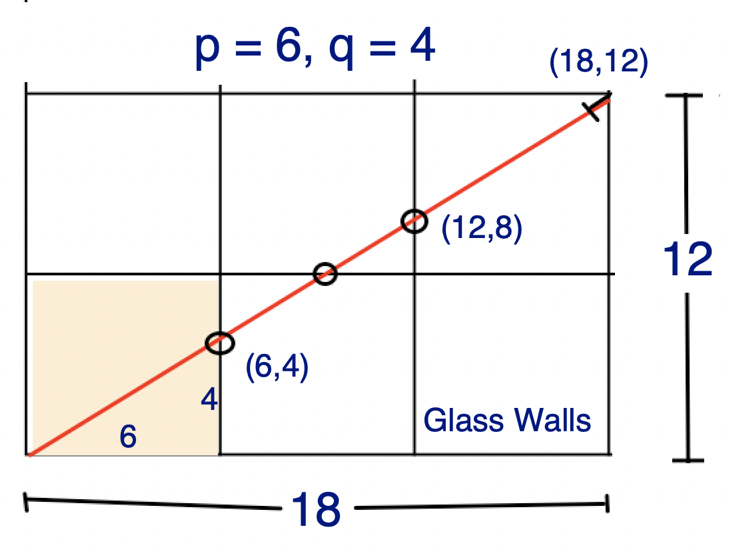\n\nThe least common multiple of 4 and 6 is 12, and 3x4 = 12, so the light will have to pass thru three walls before a multiple of 4 and a multiple of 6 coincide. In the mirrored room, the light would reflect off of three walls before hitting a corner, and three bounces bring us to receptor zero in the bottom right corner\n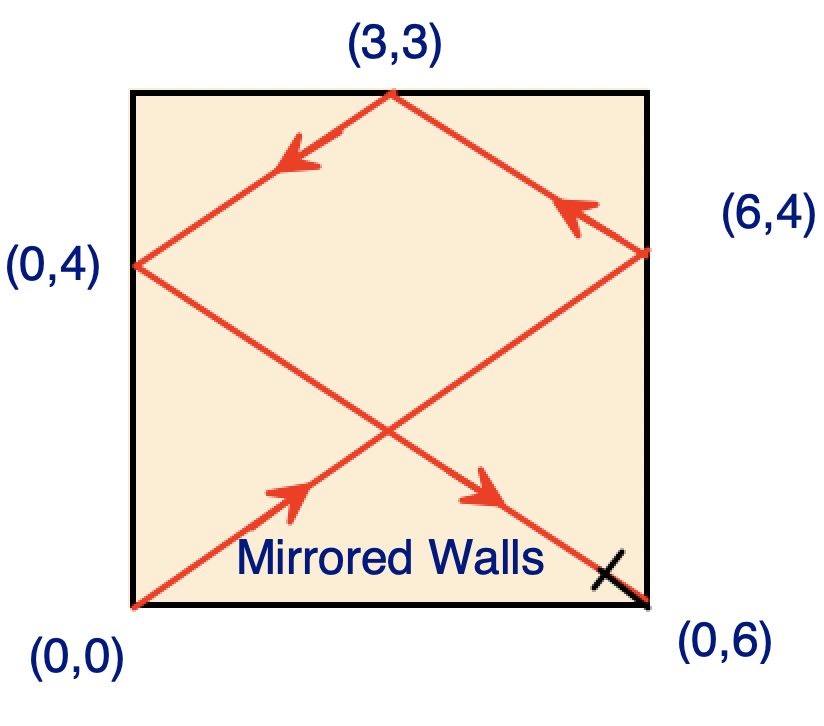\n\nThere\'s still some similar triangles and some other geometry to wrestle with, but the algorithm emerges eventually.\n\nHere\'s my code:\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n if (L//q)%2 == 0:\n return 2\n\n return (L//p)%2\n```\nHere\'s another version using the identity lcm(p,q) x gcd(p,q) == p x q:\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n # L*G = p*q <=> L/q = p/G <=> L/p = q/G\n\n G = gcd(p,q)\n p//= G\n q//= G\n \n if p%2 == 0:\n return 2\n\n return q%2 | 78 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
Python3 || 4 lines, geometry, w/ explanation || T/M: 92%/81% | mirror-reflection | 0 | 1 | Instead of imagining one room with mirrored walls, imagine an infinite cluster of rooms with glass walls; the light passes through to the next room and on and on until it evenually hits a corner. \n\n Suppose for example: p = 6, q = 4, which is demonstrated in the figure below.\n\t \n\n\nThe least common multiple of 4 and 6 is 12, and 3x4 = 12, so the light will have to pass thru three walls before a multiple of 4 and a multiple of 6 coincide. In the mirrored room, the light would reflect off of three walls before hitting a corner, and three bounces bring us to receptor zero in the bottom right corner\n\n\nThere\'s still some similar triangles and some other geometry to wrestle with, but the algorithm emerges eventually.\n\nHere\'s my code:\n\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n\n L = lcm(p,q)\n\n if (L//q)%2 == 0:\n return 2\n\n return (L//p)%2\n```\nHere\'s another version using the identity lcm(p,q) x gcd(p,q) == p x q:\n```\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n # L*G = p*q <=> L/q = p/G <=> L/p = q/G\n\n G = gcd(p,q)\n p//= G\n q//= G\n \n if p%2 == 0:\n return 2\n\n return q%2 | 78 | Alice and Bob have a different total number of candies. You are given two integer arrays `aliceSizes` and `bobSizes` where `aliceSizes[i]` is the number of candies of the `ith` box of candy that Alice has and `bobSizes[j]` is the number of candies of the `jth` box of candy that Bob has.
Since they are friends, they would like to exchange one candy box each so that after the exchange, they both have the same total amount of candy. The total amount of candy a person has is the sum of the number of candies in each box they have.
Return a_n integer array_ `answer` _where_ `answer[0]` _is the number of candies in the box that Alice must exchange, and_ `answer[1]` _is the number of candies in the box that Bob must exchange_. If there are multiple answers, you may **return any** one of them. It is guaranteed that at least one answer exists.
**Example 1:**
**Input:** aliceSizes = \[1,1\], bobSizes = \[2,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** aliceSizes = \[1,2\], bobSizes = \[2,3\]
**Output:** \[1,2\]
**Example 3:**
**Input:** aliceSizes = \[2\], bobSizes = \[1,3\]
**Output:** \[2,3\]
**Constraints:**
* `1 <= aliceSizes.length, bobSizes.length <= 104`
* `1 <= aliceSizes[i], bobSizes[j] <= 105`
* Alice and Bob have a different total number of candies.
* There will be at least one valid answer for the given input. | null |
Simple O(log n) Easy to understand Solution | mirror-reflection | 0 | 1 | ```\n#####################################################################################################################\n# Problem: Mirror Reflection\n# Solution : Maths\n# Time Complexity : O(log n) \n# Space Complexity : O(1)\n#####################################################################################################################\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while p % 2 == 0 and q % 2 == 0:\n q /= 2\n p /= 2\n \n if p % 2 == 0:\n return 2\n elif q % 2 == 0:\n return 0\n else:\n return 1\n``` | 4 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
Simple O(log n) Easy to understand Solution | mirror-reflection | 0 | 1 | ```\n#####################################################################################################################\n# Problem: Mirror Reflection\n# Solution : Maths\n# Time Complexity : O(log n) \n# Space Complexity : O(1)\n#####################################################################################################################\n\nclass Solution:\n def mirrorReflection(self, p: int, q: int) -> int:\n while p % 2 == 0 and q % 2 == 0:\n q /= 2\n p /= 2\n \n if p % 2 == 0:\n return 2\n elif q % 2 == 0:\n return 0\n else:\n return 1\n``` | 4 | Alice and Bob have a different total number of candies. You are given two integer arrays `aliceSizes` and `bobSizes` where `aliceSizes[i]` is the number of candies of the `ith` box of candy that Alice has and `bobSizes[j]` is the number of candies of the `jth` box of candy that Bob has.
Since they are friends, they would like to exchange one candy box each so that after the exchange, they both have the same total amount of candy. The total amount of candy a person has is the sum of the number of candies in each box they have.
Return a_n integer array_ `answer` _where_ `answer[0]` _is the number of candies in the box that Alice must exchange, and_ `answer[1]` _is the number of candies in the box that Bob must exchange_. If there are multiple answers, you may **return any** one of them. It is guaranteed that at least one answer exists.
**Example 1:**
**Input:** aliceSizes = \[1,1\], bobSizes = \[2,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** aliceSizes = \[1,2\], bobSizes = \[2,3\]
**Output:** \[1,2\]
**Example 3:**
**Input:** aliceSizes = \[2\], bobSizes = \[1,3\]
**Output:** \[2,3\]
**Constraints:**
* `1 <= aliceSizes.length, bobSizes.length <= 104`
* `1 <= aliceSizes[i], bobSizes[j] <= 105`
* Alice and Bob have a different total number of candies.
* There will be at least one valid answer for the given input. | null |
Faster than 100%😍🎆 python users || Easy Python Solution🤑 || GCD ,LCM Solution😎 | mirror-reflection | 0 | 1 | \n\n\n\n\n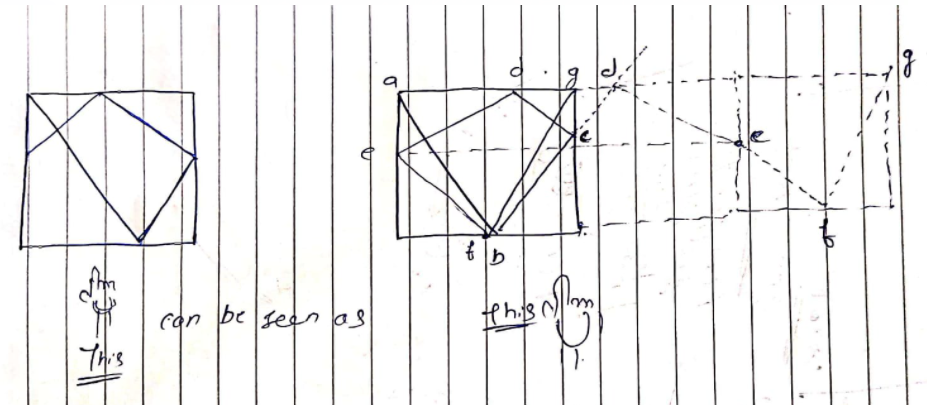\n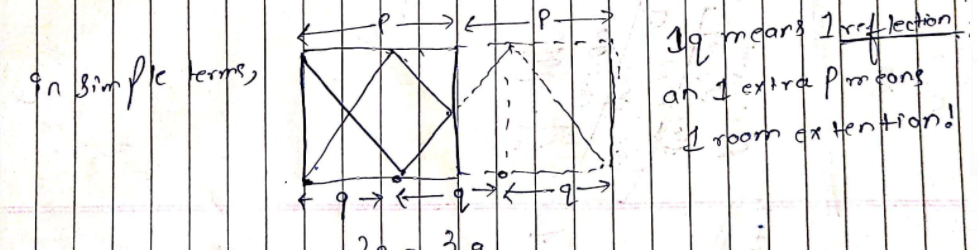\n\n\n\n\n\nWe just have to find m&n which satisfy the given equation m * p = n * q, where\nm = the number of room extension \nn = the number q extentions or the number of reflection\n\nIf the number of light reflection is odd (which means n is even), it means the corner is on west side so out answer can only be 2 in that case.\nOtherwise, the corner is on the right-hand side. The possible corners are 0 and 1.\nSo if n is odd, \nIf the number of total room extension (+the room itself) is even , it means the corner is 0. Otherwise, the corner is 1.\nNow in order to find m and n, we have to find the LCM of p &q and as we know,\nx*y=lcm(x,y)*gcd(x,y)\nso lcm=gdc//x*y\nhence, m=lcm//p || n=lcm//q\n\n**CODE**\n\n```\nclass Solution(object):\n def gcd(self,a,b):\n if a == 0:\n return b\n return self.gcd(b % a, a)\n def lcm(self,a,b):\n return (a / self.gcd(a,b))* b\n def mirrorReflection(self, p,q):\n \n lcm=self.lcm(p,q)\n m=lcm//p\n n=lcm//q\n if n%2==0:\n return 2\n if m%2==0:\n return 0\n return 1\n \n \n# basically you can just ignore the north wall and imagine the mirrors \n# as two parallel mirrors with just extending east and west walls and the end points of east walls are made of 0 reflector then 1 reflector the oth the 1th and so onn....\n# eventually we gotta find the point where m*p=n*q\n# and we can find m and n by lcm of p and q \n# now the consept is simple .....\n# if number of extensions of q(ie n) is even that means the end reflection must have happened on west wall ie. reflector 2 else \n# else there are two possibility reflector 1 or 0 which depends on the value of m(ie. the full fledged square extentions) if its even or odd\n```\n | 3 | There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered `0`, `1`, and `2`.
The square room has walls of length `p` and a laser ray from the southwest corner first meets the east wall at a distance `q` from the `0th` receptor.
Given the two integers `p` and `q`, return _the number of the receptor that the ray meets first_.
The test cases are guaranteed so that the ray will meet a receptor eventually.
**Example 1:**
**Input:** p = 2, q = 1
**Output:** 2
**Explanation:** The ray meets receptor 2 the first time it gets reflected back to the left wall.
**Example 2:**
**Input:** p = 3, q = 1
**Output:** 1
**Constraints:**
* `1 <= q <= p <= 1000` | null |
Faster than 100%😍🎆 python users || Easy Python Solution🤑 || GCD ,LCM Solution😎 | mirror-reflection | 0 | 1 | \n\n\n\n\n\n\n\n\n\n\n\nWe just have to find m&n which satisfy the given equation m * p = n * q, where\nm = the number of room extension \nn = the number q extentions or the number of reflection\n\nIf the number of light reflection is odd (which means n is even), it means the corner is on west side so out answer can only be 2 in that case.\nOtherwise, the corner is on the right-hand side. The possible corners are 0 and 1.\nSo if n is odd, \nIf the number of total room extension (+the room itself) is even , it means the corner is 0. Otherwise, the corner is 1.\nNow in order to find m and n, we have to find the LCM of p &q and as we know,\nx*y=lcm(x,y)*gcd(x,y)\nso lcm=gdc//x*y\nhence, m=lcm//p || n=lcm//q\n\n**CODE**\n\n```\nclass Solution(object):\n def gcd(self,a,b):\n if a == 0:\n return b\n return self.gcd(b % a, a)\n def lcm(self,a,b):\n return (a / self.gcd(a,b))* b\n def mirrorReflection(self, p,q):\n \n lcm=self.lcm(p,q)\n m=lcm//p\n n=lcm//q\n if n%2==0:\n return 2\n if m%2==0:\n return 0\n return 1\n \n \n# basically you can just ignore the north wall and imagine the mirrors \n# as two parallel mirrors with just extending east and west walls and the end points of east walls are made of 0 reflector then 1 reflector the oth the 1th and so onn....\n# eventually we gotta find the point where m*p=n*q\n# and we can find m and n by lcm of p and q \n# now the consept is simple .....\n# if number of extensions of q(ie n) is even that means the end reflection must have happened on west wall ie. reflector 2 else \n# else there are two possibility reflector 1 or 0 which depends on the value of m(ie. the full fledged square extentions) if its even or odd\n```\n | 3 | Alice and Bob have a different total number of candies. You are given two integer arrays `aliceSizes` and `bobSizes` where `aliceSizes[i]` is the number of candies of the `ith` box of candy that Alice has and `bobSizes[j]` is the number of candies of the `jth` box of candy that Bob has.
Since they are friends, they would like to exchange one candy box each so that after the exchange, they both have the same total amount of candy. The total amount of candy a person has is the sum of the number of candies in each box they have.
Return a_n integer array_ `answer` _where_ `answer[0]` _is the number of candies in the box that Alice must exchange, and_ `answer[1]` _is the number of candies in the box that Bob must exchange_. If there are multiple answers, you may **return any** one of them. It is guaranteed that at least one answer exists.
**Example 1:**
**Input:** aliceSizes = \[1,1\], bobSizes = \[2,2\]
**Output:** \[1,2\]
**Example 2:**
**Input:** aliceSizes = \[1,2\], bobSizes = \[2,3\]
**Output:** \[1,2\]
**Example 3:**
**Input:** aliceSizes = \[2\], bobSizes = \[1,3\]
**Output:** \[2,3\]
**Constraints:**
* `1 <= aliceSizes.length, bobSizes.length <= 104`
* `1 <= aliceSizes[i], bobSizes[j] <= 105`
* Alice and Bob have a different total number of candies.
* There will be at least one valid answer for the given input. | null |
✅Beat's 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | buddy-strings | 1 | 1 | # Intuition:\nThe Intuition is to check if it is possible to swap two characters in string `s` to make it equal to string `goal`. It first handles the case where `s` and `goal` are identical by checking for duplicate characters. If they are not identical, it looks for the first pair of mismatched characters and tries swapping them to achieve equality. The code provides a solution by considering these two scenarios and returns `true` if swapping is successful, otherwise `false`.\n\n# Explanation:\n1. First, it checks if `s` is equal to `goal` using the `==` operator. If they are equal, it means the strings are identical.\n\n2. If `s` is equal to `goal`, the code creates a temporary set called `temp` to store the unique characters present in `s`. It does this by converting the string `s` to a set of characters using the `set` constructor.\n\n3. The code then returns the result of the comparison `temp.size() < goal.size()`. This comparison checks if the size of the set `temp` (number of unique characters in `s`) is less than the size of the string `goal`. If it is, it means there are duplicate characters in `s`, and swapping any two of them would result in `s` becoming equal to `goal`. In this case, the function returns `true`; otherwise, it returns `false`.\n\n4. If `s` is not equal to `goal`, the code proceeds to find the indices `i` and `j` such that `s[i]` and `goal[i]` are the first pair of characters that are different from each other when scanning from the left, and `s[j]` and `goal[j]` are the first pair of characters that are different from each other when scanning from the right.\n5. The code uses a `while` loop to increment the `i` index from left to right until it finds a mismatch between `s[i]` and `goal[i]`. Similarly, it uses another `while` loop to decrement the `j` index from right to left until it finds a mismatch between `s[j]` and `goal[j]`.\n6. After finding the mismatched indices, the code checks if `i` is less than `j`. If it is, it means there is a pair of characters that can be swapped to make `s` equal to `goal`. In this case, the code uses the `swap` function to swap the characters `s[i]` and `s[j]`.\n\n7. Finally, the code checks if `s` is equal to `goal` after the potential swap. If they are equal, it means we have successfully swapped two characters to make `s` equal to `goal`, and the function returns `true`. Otherwise, it returns `false`.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool buddyStrings(string s, string goal) {\n int n = s.length();\n \n if(goal.length() != n){\n return false;\n }\n\n if(s == goal){\n set<char> temp(s.begin(), s.end());\n return temp.size() < goal.size(); // Swapping same characters\n }\n\n int i = 0;\n int j = n - 1;\n\n while(i < j && s[i] == goal[i]){\n i++;\n }\n\n while(j >= 0 && s[j] == goal[j]){\n j--;\n }\n\n if(i < j){\n swap(s[i], s[j]);\n }\n\n return s == goal;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean buddyStrings(String s, String goal) {\n if(s.length() != goal.length()){\n return false;\n }\n\n int n = s.length();\n if (s.equals(goal)) {\n Set<Character> temp = new HashSet<>();\n for (char c : s.toCharArray()) {\n temp.add(c);\n }\n return temp.size() < goal.length(); // Swapping same characters\n }\n\n int i = 0;\n int j = n - 1;\n\n while (i < j && s.charAt(i) == goal.charAt(i)) {\n i++;\n }\n\n while (j >= 0 && s.charAt(j) == goal.charAt(j)) {\n j--;\n }\n\n if (i < j) {\n char[] sArr = s.toCharArray();\n char temp = sArr[i];\n sArr[i] = sArr[j];\n sArr[j] = temp;\n s = new String(sArr);\n }\n\n return s.equals(goal);\n }\n}\n```\n```Python3 []\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n n = len(s)\n\n if len(goal) != n:\n return False;\n\n if s == goal:\n temp = set(s)\n return len(temp) < len(goal) # Swapping same characters\n\n i = 0\n j = n - 1\n\n while i < j and s[i] == goal[i]:\n i += 1\n\n while j >= 0 and s[j] == goal[j]:\n j -= 1\n\n if i < j:\n s_list = list(s)\n s_list[i], s_list[j] = s_list[j], s_list[i]\n s = \'\'.join(s_list)\n\n return s == goal\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 206 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
✅Beat's 100% || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | buddy-strings | 1 | 1 | # Intuition:\nThe Intuition is to check if it is possible to swap two characters in string `s` to make it equal to string `goal`. It first handles the case where `s` and `goal` are identical by checking for duplicate characters. If they are not identical, it looks for the first pair of mismatched characters and tries swapping them to achieve equality. The code provides a solution by considering these two scenarios and returns `true` if swapping is successful, otherwise `false`.\n\n# Explanation:\n1. First, it checks if `s` is equal to `goal` using the `==` operator. If they are equal, it means the strings are identical.\n\n2. If `s` is equal to `goal`, the code creates a temporary set called `temp` to store the unique characters present in `s`. It does this by converting the string `s` to a set of characters using the `set` constructor.\n\n3. The code then returns the result of the comparison `temp.size() < goal.size()`. This comparison checks if the size of the set `temp` (number of unique characters in `s`) is less than the size of the string `goal`. If it is, it means there are duplicate characters in `s`, and swapping any two of them would result in `s` becoming equal to `goal`. In this case, the function returns `true`; otherwise, it returns `false`.\n\n4. If `s` is not equal to `goal`, the code proceeds to find the indices `i` and `j` such that `s[i]` and `goal[i]` are the first pair of characters that are different from each other when scanning from the left, and `s[j]` and `goal[j]` are the first pair of characters that are different from each other when scanning from the right.\n5. The code uses a `while` loop to increment the `i` index from left to right until it finds a mismatch between `s[i]` and `goal[i]`. Similarly, it uses another `while` loop to decrement the `j` index from right to left until it finds a mismatch between `s[j]` and `goal[j]`.\n6. After finding the mismatched indices, the code checks if `i` is less than `j`. If it is, it means there is a pair of characters that can be swapped to make `s` equal to `goal`. In this case, the code uses the `swap` function to swap the characters `s[i]` and `s[j]`.\n\n7. Finally, the code checks if `s` is equal to `goal` after the potential swap. If they are equal, it means we have successfully swapped two characters to make `s` equal to `goal`, and the function returns `true`. Otherwise, it returns `false`.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool buddyStrings(string s, string goal) {\n int n = s.length();\n \n if(goal.length() != n){\n return false;\n }\n\n if(s == goal){\n set<char> temp(s.begin(), s.end());\n return temp.size() < goal.size(); // Swapping same characters\n }\n\n int i = 0;\n int j = n - 1;\n\n while(i < j && s[i] == goal[i]){\n i++;\n }\n\n while(j >= 0 && s[j] == goal[j]){\n j--;\n }\n\n if(i < j){\n swap(s[i], s[j]);\n }\n\n return s == goal;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean buddyStrings(String s, String goal) {\n if(s.length() != goal.length()){\n return false;\n }\n\n int n = s.length();\n if (s.equals(goal)) {\n Set<Character> temp = new HashSet<>();\n for (char c : s.toCharArray()) {\n temp.add(c);\n }\n return temp.size() < goal.length(); // Swapping same characters\n }\n\n int i = 0;\n int j = n - 1;\n\n while (i < j && s.charAt(i) == goal.charAt(i)) {\n i++;\n }\n\n while (j >= 0 && s.charAt(j) == goal.charAt(j)) {\n j--;\n }\n\n if (i < j) {\n char[] sArr = s.toCharArray();\n char temp = sArr[i];\n sArr[i] = sArr[j];\n sArr[j] = temp;\n s = new String(sArr);\n }\n\n return s.equals(goal);\n }\n}\n```\n```Python3 []\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n n = len(s)\n\n if len(goal) != n:\n return False;\n\n if s == goal:\n temp = set(s)\n return len(temp) < len(goal) # Swapping same characters\n\n i = 0\n j = n - 1\n\n while i < j and s[i] == goal[i]:\n i += 1\n\n while j >= 0 and s[j] == goal[j]:\n j -= 1\n\n if i < j:\n s_list = list(s)\n s_list[i], s_list[j] = s_list[j], s_list[i]\n s = \'\'.join(s_list)\n\n return s == goal\n```\n\n\n\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.** | 206 | Given two integer arrays, `preorder` and `postorder` where `preorder` is the preorder traversal of a binary tree of **distinct** values and `postorder` is the postorder traversal of the same tree, reconstruct and return _the binary tree_.
If there exist multiple answers, you can **return any** of them.
**Example 1:**
**Input:** preorder = \[1,2,4,5,3,6,7\], postorder = \[4,5,2,6,7,3,1\]
**Output:** \[1,2,3,4,5,6,7\]
**Example 2:**
**Input:** preorder = \[1\], postorder = \[1\]
**Output:** \[1\]
**Constraints:**
* `1 <= preorder.length <= 30`
* `1 <= preorder[i] <= preorder.length`
* All the values of `preorder` are **unique**.
* `postorder.length == preorder.length`
* `1 <= postorder[i] <= postorder.length`
* All the values of `postorder` are **unique**.
* It is guaranteed that `preorder` and `postorder` are the preorder traversal and postorder traversal of the same binary tree. | null |
Python3 Solution | buddy-strings | 0 | 1 | \n```\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n c1=Counter(s)\n c2=Counter(goal)\n if c1!=c2:\n return False\n\n diff=sum([1 for i in range(len(s)) if s[i]!=goal[i]])\n if diff==2:\n return True\n\n elif diff==0:\n return any([cont>1 for char,cont in c1.items()])\n\n else:\n return False \n``` | 1 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Python3 Solution | buddy-strings | 0 | 1 | \n```\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n c1=Counter(s)\n c2=Counter(goal)\n if c1!=c2:\n return False\n\n diff=sum([1 for i in range(len(s)) if s[i]!=goal[i]])\n if diff==2:\n return True\n\n elif diff==0:\n return any([cont>1 for char,cont in c1.items()])\n\n else:\n return False \n``` | 1 | Given two integer arrays, `preorder` and `postorder` where `preorder` is the preorder traversal of a binary tree of **distinct** values and `postorder` is the postorder traversal of the same tree, reconstruct and return _the binary tree_.
If there exist multiple answers, you can **return any** of them.
**Example 1:**
**Input:** preorder = \[1,2,4,5,3,6,7\], postorder = \[4,5,2,6,7,3,1\]
**Output:** \[1,2,3,4,5,6,7\]
**Example 2:**
**Input:** preorder = \[1\], postorder = \[1\]
**Output:** \[1\]
**Constraints:**
* `1 <= preorder.length <= 30`
* `1 <= preorder[i] <= preorder.length`
* All the values of `preorder` are **unique**.
* `postorder.length == preorder.length`
* `1 <= postorder[i] <= postorder.length`
* All the values of `postorder` are **unique**.
* It is guaranteed that `preorder` and `postorder` are the preorder traversal and postorder traversal of the same binary tree. | null |
Easy code 100% fast | Strings |Explanation in video| C++ Java Python | buddy-strings | 1 | 1 | For detailed explanation you can refer to my youtube channel (Hindi Language)\nhttps://youtube.com/@LetsCodeTogether72?sub_confirmation=1\n or link in comment.Here,you can find any solution in playlists monthwise from june 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\nor\nsearch \uD83D\uDC49`Buddy Strings` on youtube\n\n# C++ Code\n```\nclass Solution {\npublic:\n bool buddyStrings(string s, string goal) {\n int ns=s.size(),ng=goal.size();\n if(ns != ng ) {\n return 0;\n }\n if(s == goal ) {\n vector<int>farr(26,0);\n for(auto &x:s){\n farr[x-\'a\']++;\n if(farr[x-\'a\']==2)\n return true;\n }\n return false;;\n }\n vector<int> ans;\n for(int i=0;i<ns;i++)\n {\n if(s[i] != goal[i]) {\n ans.push_back(i);\n }\n if(ans.size()>2)\n return false;\n }\n \n return ans.size()==2&&s[ans[0]]==goal[ans[1]] && s[ans[1]]==goal[ans[0]];\n }\n};\n```\n# Java Code\n```\n\nclass Solution {\n public boolean buddyStrings(String s, String goal) {\n int ns = s.length();\n int ng = goal.length();\n \n if (ns != ng) {\n return false;\n }\n \n if (s.equals(goal)) {\n int[] farr = new int[26];\n for (char ch : s.toCharArray()) {\n farr[ch - \'a\']++;\n if (farr[ch - \'a\'] == 2) {\n return true;\n }\n }\n return false;\n }\n \n ArrayList<Integer>ans=new ArrayList<>();\n //int count = 0;\n for (int i = 0; i < ns; i++) {\n if (s.charAt(i) != goal.charAt(i)) {\n ans.add(i);\n if (ans.size()> 2) {\n return false;\n }\n }\n }\n \n return ans.size() == 2 && s.charAt(ans.get(0)) == goal.charAt(ans.get(1)) && s.charAt(ans.get(1)) == goal.charAt(ans.get(0));\n }\n}\n```\n# Python3 Code\n\n```\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n ns = len(s)\n ng = len(goal)\n\n if ns != ng:\n return False\n\n if s == goal:\n farr = [0] * 26\n for ch in s:\n farr[ord(ch) - ord(\'a\')] += 1\n \n for count in farr:\n if count > 1:\n return True\n \n return False\n\n ans = []\n for i in range(ns):\n if s[i] != goal[i]:\n ans.append(i)\n if len(ans) > 2:\n return False\n\n return len(ans) == 2 and s[ans[0]] == goal[ans[1]] and s[ans[1]] == goal[ans[0]]\n\n````\n# please upvote if u like this | 30 | Given two strings `s` and `goal`, return `true` _if you can swap two letters in_ `s` _so the result is equal to_ `goal`_, otherwise, return_ `false`_._
Swapping letters is defined as taking two indices `i` and `j` (0-indexed) such that `i != j` and swapping the characters at `s[i]` and `s[j]`.
* For example, swapping at indices `0` and `2` in `"abcd "` results in `"cbad "`.
**Example 1:**
**Input:** s = "ab ", goal = "ba "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'b' to get "ba ", which is equal to goal.
**Example 2:**
**Input:** s = "ab ", goal = "ab "
**Output:** false
**Explanation:** The only letters you can swap are s\[0\] = 'a' and s\[1\] = 'b', which results in "ba " != goal.
**Example 3:**
**Input:** s = "aa ", goal = "aa "
**Output:** true
**Explanation:** You can swap s\[0\] = 'a' and s\[1\] = 'a' to get "aa ", which is equal to goal.
**Constraints:**
* `1 <= s.length, goal.length <= 2 * 104`
* `s` and `goal` consist of lowercase letters. | null |
Easy code 100% fast | Strings |Explanation in video| C++ Java Python | buddy-strings | 1 | 1 | For detailed explanation you can refer to my youtube channel (Hindi Language)\nhttps://youtube.com/@LetsCodeTogether72?sub_confirmation=1\n or link in comment.Here,you can find any solution in playlists monthwise from june 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\nor\nsearch \uD83D\uDC49`Buddy Strings` on youtube\n\n# C++ Code\n```\nclass Solution {\npublic:\n bool buddyStrings(string s, string goal) {\n int ns=s.size(),ng=goal.size();\n if(ns != ng ) {\n return 0;\n }\n if(s == goal ) {\n vector<int>farr(26,0);\n for(auto &x:s){\n farr[x-\'a\']++;\n if(farr[x-\'a\']==2)\n return true;\n }\n return false;;\n }\n vector<int> ans;\n for(int i=0;i<ns;i++)\n {\n if(s[i] != goal[i]) {\n ans.push_back(i);\n }\n if(ans.size()>2)\n return false;\n }\n \n return ans.size()==2&&s[ans[0]]==goal[ans[1]] && s[ans[1]]==goal[ans[0]];\n }\n};\n```\n# Java Code\n```\n\nclass Solution {\n public boolean buddyStrings(String s, String goal) {\n int ns = s.length();\n int ng = goal.length();\n \n if (ns != ng) {\n return false;\n }\n \n if (s.equals(goal)) {\n int[] farr = new int[26];\n for (char ch : s.toCharArray()) {\n farr[ch - \'a\']++;\n if (farr[ch - \'a\'] == 2) {\n return true;\n }\n }\n return false;\n }\n \n ArrayList<Integer>ans=new ArrayList<>();\n //int count = 0;\n for (int i = 0; i < ns; i++) {\n if (s.charAt(i) != goal.charAt(i)) {\n ans.add(i);\n if (ans.size()> 2) {\n return false;\n }\n }\n }\n \n return ans.size() == 2 && s.charAt(ans.get(0)) == goal.charAt(ans.get(1)) && s.charAt(ans.get(1)) == goal.charAt(ans.get(0));\n }\n}\n```\n# Python3 Code\n\n```\nclass Solution:\n def buddyStrings(self, s: str, goal: str) -> bool:\n ns = len(s)\n ng = len(goal)\n\n if ns != ng:\n return False\n\n if s == goal:\n farr = [0] * 26\n for ch in s:\n farr[ord(ch) - ord(\'a\')] += 1\n \n for count in farr:\n if count > 1:\n return True\n \n return False\n\n ans = []\n for i in range(ns):\n if s[i] != goal[i]:\n ans.append(i)\n if len(ans) > 2:\n return False\n\n return len(ans) == 2 and s[ans[0]] == goal[ans[1]] and s[ans[1]] == goal[ans[0]]\n\n````\n# please upvote if u like this | 30 | Given two integer arrays, `preorder` and `postorder` where `preorder` is the preorder traversal of a binary tree of **distinct** values and `postorder` is the postorder traversal of the same tree, reconstruct and return _the binary tree_.
If there exist multiple answers, you can **return any** of them.
**Example 1:**
**Input:** preorder = \[1,2,4,5,3,6,7\], postorder = \[4,5,2,6,7,3,1\]
**Output:** \[1,2,3,4,5,6,7\]
**Example 2:**
**Input:** preorder = \[1\], postorder = \[1\]
**Output:** \[1\]
**Constraints:**
* `1 <= preorder.length <= 30`
* `1 <= preorder[i] <= preorder.length`
* All the values of `preorder` are **unique**.
* `postorder.length == preorder.length`
* `1 <= postorder[i] <= postorder.length`
* All the values of `postorder` are **unique**.
* It is guaranteed that `preorder` and `postorder` are the preorder traversal and postorder traversal of the same binary tree. | null |
Python self explanatory solution | lemonade-change | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n exchange = {5:0, 10:0}\n for bill in bills:\n if bill == 5 : \n exchange[5] +=1\n elif bill == 10 and exchange[5]: \n exchange[10] +=1\n exchange[5] -= 1\n elif bill == 20 and ((exchange[5] and exchange[10]) or exchange[5] >=3):\n if exchange[5] and exchange[10]:\n exchange[5] -= 1\n exchange[10] -=1\n else: \n exchange[5] -=3\n else : return False\n return True\n \n``` | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python self explanatory solution | lemonade-change | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n exchange = {5:0, 10:0}\n for bill in bills:\n if bill == 5 : \n exchange[5] +=1\n elif bill == 10 and exchange[5]: \n exchange[10] +=1\n exchange[5] -= 1\n elif bill == 20 and ((exchange[5] and exchange[10]) or exchange[5] >=3):\n if exchange[5] and exchange[10]:\n exchange[5] -= 1\n exchange[10] -=1\n else: \n exchange[5] -=3\n else : return False\n return True\n \n``` | 1 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Python 97.19% faster | Simplest solution with explanation | Beg to Adv | Greedy | lemonade-change | 0 | 1 | ```python\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n count5 = 0 # taking counter for $5\n count10 = 0 # taking counter for $10\n for b in bills: # treversing the list of bills.\n if b == 5: \n count5+=1 # if the bill is 5, incresing the 5 counter.\n elif b == 10:\n if count5 == 0: # if the bill is 10 & we dont have change to return, then its false.\n return False\n count10+=1 # increasing the 10 counter\n count5-=1 # decreasing 5 counter as we`ll give 5 as change. \n else: # if the bill is of $20\n if (count5>=1 and count10>=1):# checking if we have enough change to return\n count5-=1 # if its a $20 , then $5 as change and \n count10-=1 # one $10\n elif count5>=3: # fi we dont have $10 as change, though we have three $3.\n count5-=3 # decresing the $3 counter. \n else:\n return False\n return True\n \n ```\n***Found helpful, Do upvote !!***\n | 15 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python 97.19% faster | Simplest solution with explanation | Beg to Adv | Greedy | lemonade-change | 0 | 1 | ```python\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n count5 = 0 # taking counter for $5\n count10 = 0 # taking counter for $10\n for b in bills: # treversing the list of bills.\n if b == 5: \n count5+=1 # if the bill is 5, incresing the 5 counter.\n elif b == 10:\n if count5 == 0: # if the bill is 10 & we dont have change to return, then its false.\n return False\n count10+=1 # increasing the 10 counter\n count5-=1 # decreasing 5 counter as we`ll give 5 as change. \n else: # if the bill is of $20\n if (count5>=1 and count10>=1):# checking if we have enough change to return\n count5-=1 # if its a $20 , then $5 as change and \n count10-=1 # one $10\n elif count5>=3: # fi we dont have $10 as change, though we have three $3.\n count5-=3 # decresing the $3 counter. \n else:\n return False\n return True\n \n ```\n***Found helpful, Do upvote !!***\n | 15 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Python3 | lemonade-change | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n salary = {5: 0, 10: 0}\n\n for i in bills:\n if i == 5:\n salary[5] += 1\n elif i == 10:\n if salary[5] == 0:\n return False\n salary[5] -= 1\n salary[10] += 1\n elif i == 20:\n if salary[10] > 0 and salary[5] > 0:\n salary[10] -= 1\n salary[5] -= 1\n elif salary[5] >= 3:\n salary[5] -= 3\n else:\n return False\n \n return True\n``` | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python3 | lemonade-change | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n salary = {5: 0, 10: 0}\n\n for i in bills:\n if i == 5:\n salary[5] += 1\n elif i == 10:\n if salary[5] == 0:\n return False\n salary[5] -= 1\n salary[10] += 1\n elif i == 20:\n if salary[10] > 0 and salary[5] > 0:\n salary[10] -= 1\n salary[5] -= 1\n elif salary[5] >= 3:\n salary[5] -= 3\n else:\n return False\n \n return True\n``` | 1 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Python3 O(n) || O(1) # Runtime: 1159ms 49.65% Memory: 18mb 49.96% | lemonade-change | 0 | 1 | ```\nclass Solution:\n# O(n) || O(1)\n# Runtime: 1159ms 49.65% Memory: 18mb 49.96%\n def lemonadeChange(self, bills: List[int]) -> bool:\n fiveBills, tenBills = 0, 0\n\n for i in bills:\n if i == 5:\n fiveBills += 1\n elif i == 10:\n tenBills += 1\n fiveBills -= 1\n elif tenBills > 0:\n tenBills -= 1\n fiveBills -= 1\n else:\n fiveBills -= 3\n\n if fiveBills < 0:\n return False\n\n\n return True \n``` | 2 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python3 O(n) || O(1) # Runtime: 1159ms 49.65% Memory: 18mb 49.96% | lemonade-change | 0 | 1 | ```\nclass Solution:\n# O(n) || O(1)\n# Runtime: 1159ms 49.65% Memory: 18mb 49.96%\n def lemonadeChange(self, bills: List[int]) -> bool:\n fiveBills, tenBills = 0, 0\n\n for i in bills:\n if i == 5:\n fiveBills += 1\n elif i == 10:\n tenBills += 1\n fiveBills -= 1\n elif tenBills > 0:\n tenBills -= 1\n fiveBills -= 1\n else:\n fiveBills -= 3\n\n if fiveBills < 0:\n return False\n\n\n return True \n``` | 2 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
✅✅✅ very easy solution. 97% on memory and 89% on time | lemonade-change | 0 | 1 | \n\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n a, b = 0, 0\n for i in bills:\n if i==5: a+=1\n elif i==10:\n if a>0:\n b+=1\n a-=1\n else: return False\n else:\n if b>0 and a>0:\n b-=1\n a-=1\n elif a>2:\n a-=3\n else: return False\n return True\n``` | 2 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
✅✅✅ very easy solution. 97% on memory and 89% on time | lemonade-change | 0 | 1 | \n\n```\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n a, b = 0, 0\n for i in bills:\n if i==5: a+=1\n elif i==10:\n if a>0:\n b+=1\n a-=1\n else: return False\n else:\n if b>0 and a>0:\n b-=1\n a-=1\n elif a>2:\n a-=3\n else: return False\n return True\n``` | 2 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Solution | lemonade-change | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool lemonadeChange(vector<int>& bills) {\n int cnt1 = 0, cnt2 = 0;\n for(int a : bills)\n {\n if(a == 5) cnt1++;\n else if(a == 10)\n {\n if(cnt1 < 1) return false;\n cnt2++; cnt1--;\n }\n else if(a == 20)\n {\n if(cnt2 > 0 && cnt1 > 0){cnt2--; cnt1--;}\n else if(cnt1 > 2) cnt1 -= 3;\n else return false;\n }\n else return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n if bills[0] != 5:\n return False\n else:\n num_5 = 0\n num_10 = 0\n for i in range(len(bills)):\n if bills[i] == 5:\n num_5 += 1\n continue\n else:\n change = bills[i] - 5\n if change == 5:\n num_5 -= 1\n num_10 += 1\n else:\n num_5 -= 1\n if num_10 != 0:\n num_10 -= 1\n else:\n num_5 -=2\n if num_5 < 0 or num_10 < 0:\n return False\n return True\n```\n\n```Java []\nclass Solution {\n public boolean lemonadeChange(int[] bills) {\n int fives = 0, tens = 0;\n for (int bill : bills) {\n if (bill == 5) {\n fives++;\n } else if (bill == 10) {\n if (fives == 0) {\n return false;\n }\n fives--;\n tens++;\n } else {\n if (tens > 0 && fives > 0) {\n tens--;\n fives--;\n } else if (fives >= 3) {\n fives -= 3;\n } else {\n return false;\n }\n }\n }\n return true;\n }\n}\n```\n | 2 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Solution | lemonade-change | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool lemonadeChange(vector<int>& bills) {\n int cnt1 = 0, cnt2 = 0;\n for(int a : bills)\n {\n if(a == 5) cnt1++;\n else if(a == 10)\n {\n if(cnt1 < 1) return false;\n cnt2++; cnt1--;\n }\n else if(a == 20)\n {\n if(cnt2 > 0 && cnt1 > 0){cnt2--; cnt1--;}\n else if(cnt1 > 2) cnt1 -= 3;\n else return false;\n }\n else return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n if bills[0] != 5:\n return False\n else:\n num_5 = 0\n num_10 = 0\n for i in range(len(bills)):\n if bills[i] == 5:\n num_5 += 1\n continue\n else:\n change = bills[i] - 5\n if change == 5:\n num_5 -= 1\n num_10 += 1\n else:\n num_5 -= 1\n if num_10 != 0:\n num_10 -= 1\n else:\n num_5 -=2\n if num_5 < 0 or num_10 < 0:\n return False\n return True\n```\n\n```Java []\nclass Solution {\n public boolean lemonadeChange(int[] bills) {\n int fives = 0, tens = 0;\n for (int bill : bills) {\n if (bill == 5) {\n fives++;\n } else if (bill == 10) {\n if (fives == 0) {\n return false;\n }\n fives--;\n tens++;\n } else {\n if (tens > 0 && fives > 0) {\n tens--;\n fives--;\n } else if (fives >= 3) {\n fives -= 3;\n } else {\n return false;\n }\n }\n }\n return true;\n }\n}\n```\n | 2 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Python - Beats 93% | lemonade-change | 0 | 1 | class Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n \n change = {5:0, 10:0}\n\n for bill in bills:\n if bill == 5:\n change[5] += 1\n elif bill == 10:\n if change[5] > 0:\n change[5] -= 1\n change[10] += 1\n else:\n return False\n else:\n if change[10]>0 and change[5]>0:\n change[10] -= 1\n change[5] -= 1\n elif change[5] >=3:\n change[5] -= 3\n else:\n return False\n return True\n | 1 | At a lemonade stand, each lemonade costs `$5`. Customers are standing in a queue to buy from you and order one at a time (in the order specified by bills). Each customer will only buy one lemonade and pay with either a `$5`, `$10`, or `$20` bill. You must provide the correct change to each customer so that the net transaction is that the customer pays `$5`.
Note that you do not have any change in hand at first.
Given an integer array `bills` where `bills[i]` is the bill the `ith` customer pays, return `true` _if you can provide every customer with the correct change, or_ `false` _otherwise_.
**Example 1:**
**Input:** bills = \[5,5,5,10,20\]
**Output:** true
**Explanation:**
From the first 3 customers, we collect three $5 bills in order.
From the fourth customer, we collect a $10 bill and give back a $5.
From the fifth customer, we give a $10 bill and a $5 bill.
Since all customers got correct change, we output true.
**Example 2:**
**Input:** bills = \[5,5,10,10,20\]
**Output:** false
**Explanation:**
From the first two customers in order, we collect two $5 bills.
For the next two customers in order, we collect a $10 bill and give back a $5 bill.
For the last customer, we can not give the change of $15 back because we only have two $10 bills.
Since not every customer received the correct change, the answer is false.
**Constraints:**
* `1 <= bills.length <= 105`
* `bills[i]` is either `5`, `10`, or `20`. | null |
Python - Beats 93% | lemonade-change | 0 | 1 | class Solution:\n def lemonadeChange(self, bills: List[int]) -> bool:\n \n change = {5:0, 10:0}\n\n for bill in bills:\n if bill == 5:\n change[5] += 1\n elif bill == 10:\n if change[5] > 0:\n change[5] -= 1\n change[10] += 1\n else:\n return False\n else:\n if change[10]>0 and change[5]>0:\n change[10] -= 1\n change[5] -= 1\n elif change[5] >=3:\n change[5] -= 3\n else:\n return False\n return True\n | 1 | Given a list of strings `words` and a string `pattern`, return _a list of_ `words[i]` _that match_ `pattern`. You may return the answer in **any order**.
A word matches the pattern if there exists a permutation of letters `p` so that after replacing every letter `x` in the pattern with `p(x)`, we get the desired word.
Recall that a permutation of letters is a bijection from letters to letters: every letter maps to another letter, and no two letters map to the same letter.
**Example 1:**
**Input:** words = \[ "abc ", "deq ", "mee ", "aqq ", "dkd ", "ccc "\], pattern = "abb "
**Output:** \[ "mee ", "aqq "\]
**Explanation:** "mee " matches the pattern because there is a permutation {a -> m, b -> e, ...}.
"ccc " does not match the pattern because {a -> c, b -> c, ...} is not a permutation, since a and b map to the same letter.
**Example 2:**
**Input:** words = \[ "a ", "b ", "c "\], pattern = "a "
**Output:** \[ "a ", "b ", "c "\]
**Constraints:**
* `1 <= pattern.length <= 20`
* `1 <= words.length <= 50`
* `words[i].length == pattern.length`
* `pattern` and `words[i]` are lowercase English letters. | null |
Solution | score-after-flipping-matrix | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int matrixScore(vector<vector<int>>& grid) {\n int rows=grid.size();\n int cols=grid[0].size();\n for(int i=0;i<rows;i++){\n if(grid[i][0]==0){\n for(int j=0;j<cols;j++){\n if(grid[i][j]==0) grid[i][j]=1;\n else grid[i][j]=0;\n }\n }\n }\n for(int j=0;j<cols;j++){ \n int noz=0;\n int no1=0;\n for(int i=0;i<rows;i++){\n if(grid[i][j]==0) noz++;\n else no1++;\n }\n if(noz>no1){\n for(int i=0;i<rows;i++){\n if(grid[i][j]==0) grid[i][j]=1;\n else grid[i][j]=0;\n }\n }\n }\n int sum1=0;\n for(int i=0;i<rows;i++){\n int x=1;\n for(int j=cols-1;j>=0;j--){\n sum1=sum1+grid[i][j]*x;\n x=x*2;\n }\n }\n return sum1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n for row in range(m):\n if grid[row][0] == 0:\n for col in range(n):\n grid[row][col] = 1 - grid[row][col]\n \n for col in range(1, n):\n num_bit_ones = 0\n for row in range(m):\n if grid[row][col] == 1:\n num_bit_ones += 1\n if num_bit_ones < m - num_bit_ones:\n for row in range(m):\n grid[row][col] = 1 - grid[row][col]\n \n score = 0\n for col in range(n):\n num_bit_ones = 0\n for row in range(m):\n if grid[row][col] == 1:\n num_bit_ones += 1\n \n score += num_bit_ones * 2 ** (n-1 - col)\n\n return score \n```\n\n```Java []\nclass Solution {\n public int matrixScore(int[][] grid) {\n int score = 0;\n boolean[] rowFlipped = new boolean[grid.length];\n\n for (int i = 0; i < grid.length; i++) {\n int current = 0;\n int flipped = 0;\n for (int j = 0; j < grid[i].length; j++) {\n current <<= 1;\n flipped <<= 1;\n current += grid[i][j];\n flipped += grid[i][j] == 0 ? 1 : 0;\n }\n rowFlipped[i] = current < flipped;\n score += Math.max(current, flipped);\n }\n for (int i = 0; i < grid[0].length; i++) {\n int count = 0;\n for (int j = 0; j < grid.length; j++) {\n count += rowFlipped[j] ? grid[j][i] == 0 ? 1 : 0 : grid[j][i];\n }\n if (count < (grid.length - count)) {\n score += ((grid.length - count) - count) * (1 << grid[0].length - 1 - i);\n }\n }\n return score;\n }\n}\n```\n | 1 | You are given an `m x n` binary matrix `grid`.
A **move** consists of choosing any row or column and toggling each value in that row or column (i.e., changing all `0`'s to `1`'s, and all `1`'s to `0`'s).
Every row of the matrix is interpreted as a binary number, and the **score** of the matrix is the sum of these numbers.
Return _the highest possible **score** after making any number of **moves** (including zero moves)_.
**Example 1:**
**Input:** grid = \[\[0,0,1,1\],\[1,0,1,0\],\[1,1,0,0\]\]
**Output:** 39
**Explanation:** 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
**Example 2:**
**Input:** grid = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid[i][j]` is either `0` or `1`. | null |
Solution | score-after-flipping-matrix | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int matrixScore(vector<vector<int>>& grid) {\n int rows=grid.size();\n int cols=grid[0].size();\n for(int i=0;i<rows;i++){\n if(grid[i][0]==0){\n for(int j=0;j<cols;j++){\n if(grid[i][j]==0) grid[i][j]=1;\n else grid[i][j]=0;\n }\n }\n }\n for(int j=0;j<cols;j++){ \n int noz=0;\n int no1=0;\n for(int i=0;i<rows;i++){\n if(grid[i][j]==0) noz++;\n else no1++;\n }\n if(noz>no1){\n for(int i=0;i<rows;i++){\n if(grid[i][j]==0) grid[i][j]=1;\n else grid[i][j]=0;\n }\n }\n }\n int sum1=0;\n for(int i=0;i<rows;i++){\n int x=1;\n for(int j=cols-1;j>=0;j--){\n sum1=sum1+grid[i][j]*x;\n x=x*2;\n }\n }\n return sum1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n for row in range(m):\n if grid[row][0] == 0:\n for col in range(n):\n grid[row][col] = 1 - grid[row][col]\n \n for col in range(1, n):\n num_bit_ones = 0\n for row in range(m):\n if grid[row][col] == 1:\n num_bit_ones += 1\n if num_bit_ones < m - num_bit_ones:\n for row in range(m):\n grid[row][col] = 1 - grid[row][col]\n \n score = 0\n for col in range(n):\n num_bit_ones = 0\n for row in range(m):\n if grid[row][col] == 1:\n num_bit_ones += 1\n \n score += num_bit_ones * 2 ** (n-1 - col)\n\n return score \n```\n\n```Java []\nclass Solution {\n public int matrixScore(int[][] grid) {\n int score = 0;\n boolean[] rowFlipped = new boolean[grid.length];\n\n for (int i = 0; i < grid.length; i++) {\n int current = 0;\n int flipped = 0;\n for (int j = 0; j < grid[i].length; j++) {\n current <<= 1;\n flipped <<= 1;\n current += grid[i][j];\n flipped += grid[i][j] == 0 ? 1 : 0;\n }\n rowFlipped[i] = current < flipped;\n score += Math.max(current, flipped);\n }\n for (int i = 0; i < grid[0].length; i++) {\n int count = 0;\n for (int j = 0; j < grid.length; j++) {\n count += rowFlipped[j] ? grid[j][i] == 0 ? 1 : 0 : grid[j][i];\n }\n if (count < (grid.length - count)) {\n score += ((grid.length - count) - count) * (1 << grid[0].length - 1 - i);\n }\n }\n return score;\n }\n}\n```\n | 1 | The **width** of a sequence is the difference between the maximum and minimum elements in the sequence.
Given an array of integers `nums`, return _the sum of the **widths** of all the non-empty **subsequences** of_ `nums`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, `[3,6,2,7]` is a subsequence of the array `[0,3,1,6,2,2,7]`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 6
Explanation: The subsequences are \[1\], \[2\], \[3\], \[2,1\], \[2,3\], \[1,3\], \[2,1,3\].
The corresponding widths are 0, 0, 0, 1, 1, 2, 2.
The sum of these widths is 6.
**Example 2:**
**Input:** nums = \[2\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Simple Approach beats 97% O(n) | score-after-flipping-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n ans = [0] * n\n for r in grid:\n if r[0]:\n for i in range(n):\n ans[i] += r[i]\n else:\n for i in range(n):\n ans[i] += 1-r[i]\n ret = 0\n for i in range(n):\n ret += max(ans[-1-i], m-ans[-1-i]) * (1<<i)\n return ret\n\n``` | 2 | You are given an `m x n` binary matrix `grid`.
A **move** consists of choosing any row or column and toggling each value in that row or column (i.e., changing all `0`'s to `1`'s, and all `1`'s to `0`'s).
Every row of the matrix is interpreted as a binary number, and the **score** of the matrix is the sum of these numbers.
Return _the highest possible **score** after making any number of **moves** (including zero moves)_.
**Example 1:**
**Input:** grid = \[\[0,0,1,1\],\[1,0,1,0\],\[1,1,0,0\]\]
**Output:** 39
**Explanation:** 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
**Example 2:**
**Input:** grid = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid[i][j]` is either `0` or `1`. | null |
Simple Approach beats 97% O(n) | score-after-flipping-matrix | 0 | 1 | # Code\n```\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n ans = [0] * n\n for r in grid:\n if r[0]:\n for i in range(n):\n ans[i] += r[i]\n else:\n for i in range(n):\n ans[i] += 1-r[i]\n ret = 0\n for i in range(n):\n ret += max(ans[-1-i], m-ans[-1-i]) * (1<<i)\n return ret\n\n``` | 2 | The **width** of a sequence is the difference between the maximum and minimum elements in the sequence.
Given an array of integers `nums`, return _the sum of the **widths** of all the non-empty **subsequences** of_ `nums`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, `[3,6,2,7]` is a subsequence of the array `[0,3,1,6,2,2,7]`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 6
Explanation: The subsequences are \[1\], \[2\], \[3\], \[2,1\], \[2,3\], \[1,3\], \[2,1,3\].
The corresponding widths are 0, 0, 0, 1, 1, 2, 2.
The sum of these widths is 6.
**Example 2:**
**Input:** nums = \[2\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
[Python3] Greedy O(MN) | score-after-flipping-matrix | 0 | 1 | **Algo** \nTwo key observations\nIf a row starts with 0, you should flip the row;\nIf a column has more 0 than 1, you shold flip the column. \n\n**Implementation**\n```\nclass Solution:\n def matrixScore(self, A: List[List[int]]) -> int:\n m, n = len(A), len(A[0])\n for i in range(m):\n if A[i][0] == 0: \n for j in range(n): A[i][j] ^= 1 \n \n for j in range(n): \n cnt = sum(A[i][j] for i in range(m))\n if cnt < m - cnt: \n for i in range(m): A[i][j] ^= 1\n \n return sum(int("".join(map(str, A[i])), 2) for i in range(m))\n```\n\n**Analysis**\nTime complexity `O(MN)`\nSpace complexity `O(1)` | 16 | You are given an `m x n` binary matrix `grid`.
A **move** consists of choosing any row or column and toggling each value in that row or column (i.e., changing all `0`'s to `1`'s, and all `1`'s to `0`'s).
Every row of the matrix is interpreted as a binary number, and the **score** of the matrix is the sum of these numbers.
Return _the highest possible **score** after making any number of **moves** (including zero moves)_.
**Example 1:**
**Input:** grid = \[\[0,0,1,1\],\[1,0,1,0\],\[1,1,0,0\]\]
**Output:** 39
**Explanation:** 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
**Example 2:**
**Input:** grid = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid[i][j]` is either `0` or `1`. | null |
[Python3] Greedy O(MN) | score-after-flipping-matrix | 0 | 1 | **Algo** \nTwo key observations\nIf a row starts with 0, you should flip the row;\nIf a column has more 0 than 1, you shold flip the column. \n\n**Implementation**\n```\nclass Solution:\n def matrixScore(self, A: List[List[int]]) -> int:\n m, n = len(A), len(A[0])\n for i in range(m):\n if A[i][0] == 0: \n for j in range(n): A[i][j] ^= 1 \n \n for j in range(n): \n cnt = sum(A[i][j] for i in range(m))\n if cnt < m - cnt: \n for i in range(m): A[i][j] ^= 1\n \n return sum(int("".join(map(str, A[i])), 2) for i in range(m))\n```\n\n**Analysis**\nTime complexity `O(MN)`\nSpace complexity `O(1)` | 16 | The **width** of a sequence is the difference between the maximum and minimum elements in the sequence.
Given an array of integers `nums`, return _the sum of the **widths** of all the non-empty **subsequences** of_ `nums`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, `[3,6,2,7]` is a subsequence of the array `[0,3,1,6,2,2,7]`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 6
Explanation: The subsequences are \[1\], \[2\], \[3\], \[2,1\], \[2,3\], \[1,3\], \[2,1,3\].
The corresponding widths are 0, 0, 0, 1, 1, 2, 2.
The sum of these widths is 6.
**Example 2:**
**Input:** nums = \[2\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
[Python3] Good enough | score-after-flipping-matrix | 0 | 1 | ``` Python3 []\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n for i in range(len(grid)):\n if not grid[i][0]:\n for j in range(len(grid[i])):\n grid[i][j] = abs(grid[i][j]-1)\n \n for j in range(len(grid[0])):\n ones = sum(grid[i][j] for i in range(len(grid)))\n if ones<len(grid)/2:\n for i in range(len(grid)):\n grid[i][j] = abs(grid[i][j]-1)\n\n return sum(int(\'\'.join([str(y) for y in x]),2) for x in grid)\n``` | 0 | You are given an `m x n` binary matrix `grid`.
A **move** consists of choosing any row or column and toggling each value in that row or column (i.e., changing all `0`'s to `1`'s, and all `1`'s to `0`'s).
Every row of the matrix is interpreted as a binary number, and the **score** of the matrix is the sum of these numbers.
Return _the highest possible **score** after making any number of **moves** (including zero moves)_.
**Example 1:**
**Input:** grid = \[\[0,0,1,1\],\[1,0,1,0\],\[1,1,0,0\]\]
**Output:** 39
**Explanation:** 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
**Example 2:**
**Input:** grid = \[\[0\]\]
**Output:** 1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 20`
* `grid[i][j]` is either `0` or `1`. | null |
[Python3] Good enough | score-after-flipping-matrix | 0 | 1 | ``` Python3 []\nclass Solution:\n def matrixScore(self, grid: List[List[int]]) -> int:\n for i in range(len(grid)):\n if not grid[i][0]:\n for j in range(len(grid[i])):\n grid[i][j] = abs(grid[i][j]-1)\n \n for j in range(len(grid[0])):\n ones = sum(grid[i][j] for i in range(len(grid)))\n if ones<len(grid)/2:\n for i in range(len(grid)):\n grid[i][j] = abs(grid[i][j]-1)\n\n return sum(int(\'\'.join([str(y) for y in x]),2) for x in grid)\n``` | 0 | The **width** of a sequence is the difference between the maximum and minimum elements in the sequence.
Given an array of integers `nums`, return _the sum of the **widths** of all the non-empty **subsequences** of_ `nums`. Since the answer may be very large, return it **modulo** `109 + 7`.
A **subsequence** is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, `[3,6,2,7]` is a subsequence of the array `[0,3,1,6,2,2,7]`.
**Example 1:**
**Input:** nums = \[2,1,3\]
**Output:** 6
Explanation: The subsequences are \[1\], \[2\], \[3\], \[2,1\], \[2,3\], \[1,3\], \[2,1,3\].
The corresponding widths are 0, 0, 0, 1, 1, 2, 2.
The sum of these widths is 6.
**Example 2:**
**Input:** nums = \[2\]
**Output:** 0
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | null |
Solution | shortest-subarray-with-sum-at-least-k | 1 | 1 | ```C++ []\n#pragma GCC optimize("Ofast","inline","-ffast-math")\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\n\nclass Solution {\npublic:\n int shortestSubarray(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int n = nums.size();\n long pref[n + 1];\n \n pref[0] = 0;\n for(int i = 1; i != n + 1; ++i)\n pref[i] = pref[i - 1] + nums[i - 1];\n \n deque<int> dq;\n int res = INT_MAX;\n \n dq.push_back(0);\n for(int i = 1; i != n + 1; ++i) {\n while(!dq.empty() && pref[dq.back()] >= pref[i])\n dq.pop_back();\n while(!dq.empty() && pref[i] - pref[dq.front()] >= k) {\n res = min(res, i - dq.front());\n dq.pop_front();\n }\n dq.push_back(i);\n }\n return res == INT_MAX ? -1 : res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n n = len(nums)\n preSum = 0\n queue = collections.deque([(-1,0)])\n res = n + 1\n for i in range(n):\n preSum += nums[i]\n if nums[i] > 0:\n while queue and preSum - queue[0][1] >= k:\n res = min(res, i - queue.popleft()[0])\n else:\n while queue and preSum < queue[-1][1]:\n queue.pop()\n queue.append((i, preSum))\n return res if res <= n else -1\n```\n\n```Java []\nclass Solution {\n public int shortestSubarray(int[] nums, int k) {\n int len = nums.length;\n\t\tlong[] sum = new long[len + 1];\n\t\tfor (int i = 0; i < len; i++) {\n\t\t\tsum[i + 1] = sum[i] + nums[i];\n\t\t}\n\t\tint start = 0;\n int end = -1;\n int dp[] = new int[len + 1];\n int res = len + 1;\n for (int i = 0; i<=len; i++) {\n while (end - start + 1 > 0 && sum[i] <= sum[dp[end]]) {\n end--;\n }\n while (end - start + 1 > 0 && sum[i] >= sum[dp[start]] + k) {\n res = Math.min(res, i - dp[start++]);\n }\n dp[++end] = i;\n }\n return res == len + 1 ? -1 : res;\n }\n}\n```\n | 1 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Solution | shortest-subarray-with-sum-at-least-k | 1 | 1 | ```C++ []\n#pragma GCC optimize("Ofast","inline","-ffast-math")\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\n\nclass Solution {\npublic:\n int shortestSubarray(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int n = nums.size();\n long pref[n + 1];\n \n pref[0] = 0;\n for(int i = 1; i != n + 1; ++i)\n pref[i] = pref[i - 1] + nums[i - 1];\n \n deque<int> dq;\n int res = INT_MAX;\n \n dq.push_back(0);\n for(int i = 1; i != n + 1; ++i) {\n while(!dq.empty() && pref[dq.back()] >= pref[i])\n dq.pop_back();\n while(!dq.empty() && pref[i] - pref[dq.front()] >= k) {\n res = min(res, i - dq.front());\n dq.pop_front();\n }\n dq.push_back(i);\n }\n return res == INT_MAX ? -1 : res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n n = len(nums)\n preSum = 0\n queue = collections.deque([(-1,0)])\n res = n + 1\n for i in range(n):\n preSum += nums[i]\n if nums[i] > 0:\n while queue and preSum - queue[0][1] >= k:\n res = min(res, i - queue.popleft()[0])\n else:\n while queue and preSum < queue[-1][1]:\n queue.pop()\n queue.append((i, preSum))\n return res if res <= n else -1\n```\n\n```Java []\nclass Solution {\n public int shortestSubarray(int[] nums, int k) {\n int len = nums.length;\n\t\tlong[] sum = new long[len + 1];\n\t\tfor (int i = 0; i < len; i++) {\n\t\t\tsum[i + 1] = sum[i] + nums[i];\n\t\t}\n\t\tint start = 0;\n int end = -1;\n int dp[] = new int[len + 1];\n int res = len + 1;\n for (int i = 0; i<=len; i++) {\n while (end - start + 1 > 0 && sum[i] <= sum[dp[end]]) {\n end--;\n }\n while (end - start + 1 > 0 && sum[i] >= sum[dp[start]] + k) {\n res = Math.min(res, i - dp[start++]);\n }\n dp[++end] = i;\n }\n return res == len + 1 ? -1 : res;\n }\n}\n```\n | 1 | You are given an `n x n` `grid` where you have placed some `1 x 1 x 1` cubes. Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of cell `(i, j)`.
After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.
Return _the total surface area of the resulting shapes_.
**Note:** The bottom face of each shape counts toward its surface area.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 34
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 32
**Example 3:**
**Input:** grid = \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Output:** 46
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Queue with Explanation | shortest-subarray-with-sum-at-least-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNeeds a monotonic queue as we are going to find the minimal length and need to care about the value reaching k. As such, we are bounded on two sides so that sliding window / two pointer is not going to cut it. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBased on intuition, we start by finding the length of the nums, and determine if we are edge case of a length of 1 before proceeding. \n\nAfter edge case, we set up our queue and our prefix sums, filling with the values in the array as needed. Our minimum size needs to start outside of range, so we begin with a range of N+1. \n\nNow, we enumerate our prefix sums, and track indices and values by doing so. As we do\n- While we have a queue and our current value is less than our prefix_sums mosts recent value added we pop from the front. \n- Afterwards, while we have a queue and our current value minus our starting value is greater than or equal to k, we want to recast our minimum size as the minimum of itself and the popleft of the queue, removing from the front. \n - We do the first while loop to ensure that our prefix sums approach K without going too far past it. We are trying to limit this to only the size needed. \n - Similarly, we are concerned that our value with the front most item may end up past K, so we consider the same while loop process using the difference and recasting min size as we do so. \n - Together then, we limit on both ends of the queue as we move thorugh the prefix sums, thus finding the correct length through this process. \n\n\nAt the end we will check to see if min size was ever changed. If it was not, not possible, return -1. Otherwise, return minimum size.\n\n# Complexity\n- Time complexity: O(2N), one loop through the nums for prefix sums and one loop again for minimum size \n\n- Space complexity: O(N) as we needed to store the prefix sum. The queue size may add another O(N) in worst case, and as such O(2N) as well. \n\n\n# Code\n```\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n N = len(nums)\n # edge case of one entry \n if N == 1 : \n if nums[0] == k : \n return 1 \n return -1 \n # queue of indices of prefix sums \n queue = collections.deque()\n # zeroth sum of no values \n prefix_sums = [0]\n # loop over nums \n for num in nums :\n # get the sum value by using value up to here process \n prefix_sums.append(prefix_sums[-1] + num)\n # if it is this size, we never found it \n min_size = N + 1 \n # enumerate prefix sums to keep indices as you go \n for index, value in enumerate(prefix_sums) : \n # while you have a queue and the value current is less than the value of the prefix sums most recently queued \n while queue and value <= prefix_sums[queue[-1]] : \n # remove the item most recently queued\n queue.pop()\n # while you have a queue and the value minus the front value is greater than or equal to k\n while queue and value - prefix_sums[queue[0]] >= k : \n # set min size to the min of itself and the distance between index and leftmost index of queue \n min_size = min(min_size, index - queue.popleft())\n # append the index at the end of the loop to the queue \n queue.append(index)\n # if it changed, you found it \n if min_size != N + 1 : \n return min_size\n # if it did not, you never found it \n return -1 \n``` | 1 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Queue with Explanation | shortest-subarray-with-sum-at-least-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNeeds a monotonic queue as we are going to find the minimal length and need to care about the value reaching k. As such, we are bounded on two sides so that sliding window / two pointer is not going to cut it. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBased on intuition, we start by finding the length of the nums, and determine if we are edge case of a length of 1 before proceeding. \n\nAfter edge case, we set up our queue and our prefix sums, filling with the values in the array as needed. Our minimum size needs to start outside of range, so we begin with a range of N+1. \n\nNow, we enumerate our prefix sums, and track indices and values by doing so. As we do\n- While we have a queue and our current value is less than our prefix_sums mosts recent value added we pop from the front. \n- Afterwards, while we have a queue and our current value minus our starting value is greater than or equal to k, we want to recast our minimum size as the minimum of itself and the popleft of the queue, removing from the front. \n - We do the first while loop to ensure that our prefix sums approach K without going too far past it. We are trying to limit this to only the size needed. \n - Similarly, we are concerned that our value with the front most item may end up past K, so we consider the same while loop process using the difference and recasting min size as we do so. \n - Together then, we limit on both ends of the queue as we move thorugh the prefix sums, thus finding the correct length through this process. \n\n\nAt the end we will check to see if min size was ever changed. If it was not, not possible, return -1. Otherwise, return minimum size.\n\n# Complexity\n- Time complexity: O(2N), one loop through the nums for prefix sums and one loop again for minimum size \n\n- Space complexity: O(N) as we needed to store the prefix sum. The queue size may add another O(N) in worst case, and as such O(2N) as well. \n\n\n# Code\n```\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n N = len(nums)\n # edge case of one entry \n if N == 1 : \n if nums[0] == k : \n return 1 \n return -1 \n # queue of indices of prefix sums \n queue = collections.deque()\n # zeroth sum of no values \n prefix_sums = [0]\n # loop over nums \n for num in nums :\n # get the sum value by using value up to here process \n prefix_sums.append(prefix_sums[-1] + num)\n # if it is this size, we never found it \n min_size = N + 1 \n # enumerate prefix sums to keep indices as you go \n for index, value in enumerate(prefix_sums) : \n # while you have a queue and the value current is less than the value of the prefix sums most recently queued \n while queue and value <= prefix_sums[queue[-1]] : \n # remove the item most recently queued\n queue.pop()\n # while you have a queue and the value minus the front value is greater than or equal to k\n while queue and value - prefix_sums[queue[0]] >= k : \n # set min size to the min of itself and the distance between index and leftmost index of queue \n min_size = min(min_size, index - queue.popleft())\n # append the index at the end of the loop to the queue \n queue.append(index)\n # if it changed, you found it \n if min_size != N + 1 : \n return min_size\n # if it did not, you never found it \n return -1 \n``` | 1 | You are given an `n x n` `grid` where you have placed some `1 x 1 x 1` cubes. Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of cell `(i, j)`.
After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.
Return _the total surface area of the resulting shapes_.
**Note:** The bottom face of each shape counts toward its surface area.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 34
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 32
**Example 3:**
**Input:** grid = \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Output:** 46
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Python - using deque- with explaination | shortest-subarray-with-sum-at-least-k | 0 | 1 | At first, I used sliding window, but got TLE - O(N^2)\nAnd then I look into the discuss and thinking how can use deque to achieve O(N).\n\nSome Tips:\n1. dealing with sum, construct sum array may help.\n2. using deque may leads to a O(N) solution.\n\nusing deque:\n\t\t1. think about that should it be increasing or decreasing? since we want to minimize the window size, no need to save one has bigger sum but smaller index ==> choose increasing\n\t\t2. think about what we need to save in the deque? we need index to compute window size, it is fine to not save the sum value in deque, because you can get it by pre[i], but I save it too \n\t\t3. when add/ delete our deque: \n\\ \t\t\t\tadd => usually at the end of every loop \n\\\t\t\t\tdelete=> \na. keeping deque increasing, so when current sum_ <= sum_[deque[-1]], deque.pop()\nb. every time we check from the begining of the queue(smallest sum), if it is satisfied with K difference we can pop it, because there will no any other window satistify K and start with queue[0] have a smaller size when sum_[i] - sum_[deque[0]] >= K, deque.popleft(0)\n```\nclass Solution:\n def shortestSubarray(self, A: List[int], K: int) -> int:\n pre = [0]\n for num in A:\n pre.append(pre[-1]+num)\n \n deque = collections.deque()\n result = float(inf)\n for i,sum_ in enumerate(pre):\n \n while(deque and deque[-1][1] >=sum_):\n deque.pop()\n \n while deque and sum_ - deque[0][1] >= K:\n result = min(i-deque[0][0], result)\n deque.popleft()\n \n deque.append([i,sum_])\n return result if result!= float(inf) else -1 \n\n``` | 14 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Python - using deque- with explaination | shortest-subarray-with-sum-at-least-k | 0 | 1 | At first, I used sliding window, but got TLE - O(N^2)\nAnd then I look into the discuss and thinking how can use deque to achieve O(N).\n\nSome Tips:\n1. dealing with sum, construct sum array may help.\n2. using deque may leads to a O(N) solution.\n\nusing deque:\n\t\t1. think about that should it be increasing or decreasing? since we want to minimize the window size, no need to save one has bigger sum but smaller index ==> choose increasing\n\t\t2. think about what we need to save in the deque? we need index to compute window size, it is fine to not save the sum value in deque, because you can get it by pre[i], but I save it too \n\t\t3. when add/ delete our deque: \n\\ \t\t\t\tadd => usually at the end of every loop \n\\\t\t\t\tdelete=> \na. keeping deque increasing, so when current sum_ <= sum_[deque[-1]], deque.pop()\nb. every time we check from the begining of the queue(smallest sum), if it is satisfied with K difference we can pop it, because there will no any other window satistify K and start with queue[0] have a smaller size when sum_[i] - sum_[deque[0]] >= K, deque.popleft(0)\n```\nclass Solution:\n def shortestSubarray(self, A: List[int], K: int) -> int:\n pre = [0]\n for num in A:\n pre.append(pre[-1]+num)\n \n deque = collections.deque()\n result = float(inf)\n for i,sum_ in enumerate(pre):\n \n while(deque and deque[-1][1] >=sum_):\n deque.pop()\n \n while deque and sum_ - deque[0][1] >= K:\n result = min(i-deque[0][0], result)\n deque.popleft()\n \n deque.append([i,sum_])\n return result if result!= float(inf) else -1 \n\n``` | 14 | You are given an `n x n` `grid` where you have placed some `1 x 1 x 1` cubes. Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of cell `(i, j)`.
After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.
Return _the total surface area of the resulting shapes_.
**Note:** The bottom face of each shape counts toward its surface area.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 34
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 32
**Example 3:**
**Input:** grid = \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Output:** 46
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Explained why is works | shortest-subarray-with-sum-at-least-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSo I could\'t come up with this approach , read some post and spend way to long to understand does this works.\n\nQ : What would we do if the question was to find the Sortest sub array and we had only position integer.\nA : We can take two pointers i and j and increse j if the sum is smaller and increse i if the sum we want to reduce the window to check if we can find some smaller window .\n\nIn this question we have -ve values so there is no way of telling if incresing j,i will inc or dec our sum.\n\nTo solve this issue we will pre compute preSum[i] such that preSum[i]=nums[0]+nums[1]...nums[i]\n\nNow lets think this problem in terms of preSum .\n\npreSum[3]-preSum[1] = num[3]+num[2] so we can say that preSum[j]-preSum[i] = sum(num[i+1]...num[j]).\n\nWhat we need to find ?\nWe need to find **preSum[j]-preSum[i] >= k {and we want to minimize k, for same value of k we want to min j-i}**\n\nlets rewrite it to preSum[j]-k>=preSum[i]\n\nSo when i am at an index j I need to find preSum[i] which satisfies the above equation.\n\nWe will use an Incresing Deque to do the same. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nSo given that you somehow magicaly we have a deque that stores all the preSum that are before j in an incrsesing order how will you find the answer when you are at j.\n\n***Case 1*** : preSum[j]<= deque.top()\n\nYou find and element at the top the deque that is greatr that current elemnt .\nQ: Can it even stisfy the equation ? \nA : No,bcz preSum[i] should be less than preSum[j] .\nQ : Can we have a case where we find some u > j further down the line and preSum[i] is a valid cndidate for it ?\nA : It can but since we are min minimize index2-index1 , If we find some preSum[j] < preSum[u] , j<u if preSum[i]\n staisfies the condition preSum[u]-preSum[i]>=k then preSum[u]-preSum[j]>=k will also satisfy since preSum[j] < preSum[i] (in this case )and we are trying to min index2-index1 so preSum[u]-preSum[i] is useless if we found preSum[u]-preSum[j].\n\nSo we simply keep removing such elemnt for the queue.\n\n\n***Case 2*** : preSum[j] > deque.top() \n\n Now in this case you can\'t remove the top elemnt bcz it can be a probable ans for some future preSum[u] value.\n\nNow lets think how we will find our optimal preSum[i] in this case .\n\nSince we are maintaining an Incresing dequeue and if the top element is smaller that preSum[j] all the elemnt below the top of deque will be even smaller than top and we want to find min preSum[i] for an preSum[j].\n\nSo left start for the smallst preSum[i] that is from left of the deque. \nif preSum[j]-k>=dequeu[0] we still want to go forward and minimize (j-i) so we keep removing element from the deque from the left .\n\nQ Why are we removing dequeu[0] can\'t stisfy some preSum[u] , j<u ?\nA : It can but since we are min minimize (j-i) and u >j then it is useless for us.\n\n\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n n= len(nums)\n deque=collections.deque()\n preSum=[0]*n\n preSum[0]=nums[0]\n\n mini=float(inf)\n\n for i in range(1,n):\n preSum[i]=preSum[i-1]+nums[i]\n \n deque.append([0,-1])\n for i,num in enumerate(preSum):\n\n while deque and deque[-1][0]>=num:\n deque.pop()\n \n deque.append([num,i])\n\n while deque and deque[0][0] <= preSum[i]-k:\n mini=min(mini,i-deque[0][1])\n deque.popleft()\n\n \n return mini if mini!=float(inf) else -1\n\n\n \n``` | 1 | Given an integer array `nums` and an integer `k`, return _the length of the shortest non-empty **subarray** of_ `nums` _with a sum of at least_ `k`. If there is no such **subarray**, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1\], k = 1
**Output:** 1
**Example 2:**
**Input:** nums = \[1,2\], k = 4
**Output:** -1
**Example 3:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 3
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* `1 <= k <= 109` | null |
Explained why is works | shortest-subarray-with-sum-at-least-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSo I could\'t come up with this approach , read some post and spend way to long to understand does this works.\n\nQ : What would we do if the question was to find the Sortest sub array and we had only position integer.\nA : We can take two pointers i and j and increse j if the sum is smaller and increse i if the sum we want to reduce the window to check if we can find some smaller window .\n\nIn this question we have -ve values so there is no way of telling if incresing j,i will inc or dec our sum.\n\nTo solve this issue we will pre compute preSum[i] such that preSum[i]=nums[0]+nums[1]...nums[i]\n\nNow lets think this problem in terms of preSum .\n\npreSum[3]-preSum[1] = num[3]+num[2] so we can say that preSum[j]-preSum[i] = sum(num[i+1]...num[j]).\n\nWhat we need to find ?\nWe need to find **preSum[j]-preSum[i] >= k {and we want to minimize k, for same value of k we want to min j-i}**\n\nlets rewrite it to preSum[j]-k>=preSum[i]\n\nSo when i am at an index j I need to find preSum[i] which satisfies the above equation.\n\nWe will use an Incresing Deque to do the same. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nSo given that you somehow magicaly we have a deque that stores all the preSum that are before j in an incrsesing order how will you find the answer when you are at j.\n\n***Case 1*** : preSum[j]<= deque.top()\n\nYou find and element at the top the deque that is greatr that current elemnt .\nQ: Can it even stisfy the equation ? \nA : No,bcz preSum[i] should be less than preSum[j] .\nQ : Can we have a case where we find some u > j further down the line and preSum[i] is a valid cndidate for it ?\nA : It can but since we are min minimize index2-index1 , If we find some preSum[j] < preSum[u] , j<u if preSum[i]\n staisfies the condition preSum[u]-preSum[i]>=k then preSum[u]-preSum[j]>=k will also satisfy since preSum[j] < preSum[i] (in this case )and we are trying to min index2-index1 so preSum[u]-preSum[i] is useless if we found preSum[u]-preSum[j].\n\nSo we simply keep removing such elemnt for the queue.\n\n\n***Case 2*** : preSum[j] > deque.top() \n\n Now in this case you can\'t remove the top elemnt bcz it can be a probable ans for some future preSum[u] value.\n\nNow lets think how we will find our optimal preSum[i] in this case .\n\nSince we are maintaining an Incresing dequeue and if the top element is smaller that preSum[j] all the elemnt below the top of deque will be even smaller than top and we want to find min preSum[i] for an preSum[j].\n\nSo left start for the smallst preSum[i] that is from left of the deque. \nif preSum[j]-k>=dequeu[0] we still want to go forward and minimize (j-i) so we keep removing element from the deque from the left .\n\nQ Why are we removing dequeu[0] can\'t stisfy some preSum[u] , j<u ?\nA : It can but since we are min minimize (j-i) and u >j then it is useless for us.\n\n\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def shortestSubarray(self, nums: List[int], k: int) -> int:\n n= len(nums)\n deque=collections.deque()\n preSum=[0]*n\n preSum[0]=nums[0]\n\n mini=float(inf)\n\n for i in range(1,n):\n preSum[i]=preSum[i-1]+nums[i]\n \n deque.append([0,-1])\n for i,num in enumerate(preSum):\n\n while deque and deque[-1][0]>=num:\n deque.pop()\n \n deque.append([num,i])\n\n while deque and deque[0][0] <= preSum[i]-k:\n mini=min(mini,i-deque[0][1])\n deque.popleft()\n\n \n return mini if mini!=float(inf) else -1\n\n\n \n``` | 1 | You are given an `n x n` `grid` where you have placed some `1 x 1 x 1` cubes. Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of cell `(i, j)`.
After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.
Return _the total surface area of the resulting shapes_.
**Note:** The bottom face of each shape counts toward its surface area.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 34
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,0,1\],\[1,1,1\]\]
**Output:** 32
**Example 3:**
**Input:** grid = \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Output:** 46
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
EASY PYTHON SOLUTION || BINARY TREE | all-nodes-distance-k-in-binary-tree | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def getTarget(self,root,target):\n if root is None:\n return float("infinity"),\'\'\n if root==target:\n return 0,\'\'\n x,path1=self.getTarget(root.left,target)\n y,path2=self.getTarget(root.right,target)\n if x<y:\n return x+1,\'L\'+path1\n else:\n return y+1,\'R\'+path2\n\n def addNeighbor(self,root,k,path,lst,lvl,target):\n if root is None:\n return\n if path==\'\':\n if k==lvl:\n lst.append(root.val)\n return\n self.addNeighbor(root.left,k,path,lst,lvl+1,target)\n self.addNeighbor(root.right,k,path,lst,lvl+1,target)\n return\n x=path[0]\n if k==lvl:\n lst.append(root.val)\n if x==\'L\':\n self.addNeighbor(root.left,k,path[1:],lst,lvl-1,target)\n self.addNeighbor(root.right,k,\'\',lst,lvl+1,target)\n else:\n self.addNeighbor(root.right,k,path[1:],lst,lvl-1,target)\n self.addNeighbor(root.left,k,\'\',lst,lvl+1,target)\n\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n lvl,path=self.getTarget(root,target)\n lst=[]\n self.addNeighbor(root,k,path,lst,lvl,target)\n return lst\n\n``` | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
EASY PYTHON SOLUTION || BINARY TREE | all-nodes-distance-k-in-binary-tree | 0 | 1 | \n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def getTarget(self,root,target):\n if root is None:\n return float("infinity"),\'\'\n if root==target:\n return 0,\'\'\n x,path1=self.getTarget(root.left,target)\n y,path2=self.getTarget(root.right,target)\n if x<y:\n return x+1,\'L\'+path1\n else:\n return y+1,\'R\'+path2\n\n def addNeighbor(self,root,k,path,lst,lvl,target):\n if root is None:\n return\n if path==\'\':\n if k==lvl:\n lst.append(root.val)\n return\n self.addNeighbor(root.left,k,path,lst,lvl+1,target)\n self.addNeighbor(root.right,k,path,lst,lvl+1,target)\n return\n x=path[0]\n if k==lvl:\n lst.append(root.val)\n if x==\'L\':\n self.addNeighbor(root.left,k,path[1:],lst,lvl-1,target)\n self.addNeighbor(root.right,k,\'\',lst,lvl+1,target)\n else:\n self.addNeighbor(root.right,k,path[1:],lst,lvl-1,target)\n self.addNeighbor(root.left,k,\'\',lst,lvl+1,target)\n\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n lvl,path=self.getTarget(root,target)\n lst=[]\n self.addNeighbor(root,k,path,lst,lvl,target)\n return lst\n\n``` | 1 | You are given an array of strings of the same length `words`.
In one **move**, you can swap any two even indexed characters or any two odd indexed characters of a string `words[i]`.
Two strings `words[i]` and `words[j]` are **special-equivalent** if after any number of moves, `words[i] == words[j]`.
* For example, `words[i] = "zzxy "` and `words[j] = "xyzz "` are **special-equivalent** because we may make the moves `"zzxy " -> "xzzy " -> "xyzz "`.
A **group of special-equivalent strings** from `words` is a non-empty subset of words such that:
* Every pair of strings in the group are special equivalent, and
* The group is the largest size possible (i.e., there is not a string `words[i]` not in the group such that `words[i]` is special-equivalent to every string in the group).
Return _the number of **groups of special-equivalent strings** from_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "cdab ", "cbad ", "xyzz ", "zzxy ", "zzyx "\]
**Output:** 3
**Explanation:**
One group is \[ "abcd ", "cdab ", "cbad "\], since they are all pairwise special equivalent, and none of the other strings is all pairwise special equivalent to these.
The other two groups are \[ "xyzz ", "zzxy "\] and \[ "zzyx "\].
Note that in particular, "zzxy " is not special equivalent to "zzyx ".
**Example 2:**
**Input:** words = \[ "abc ", "acb ", "bac ", "bca ", "cab ", "cba "\]
**Output:** 3
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 20`
* `words[i]` consist of lowercase English letters.
* All the strings are of the same length. | null |
Solution | all-nodes-distance-k-in-binary-tree | 1 | 1 | ```C++ []\n#define pp pair<int, TreeNode*>\n\nclass Solution {\npublic:\n unordered_map<TreeNode*, TreeNode*> nodeParent;\n void makeParent(TreeNode* root, TreeNode* parent){\n nodeParent[root] = parent; \n if(root->left) makeParent(root->left, root);\n if(root->right) makeParent(root->right, root);\n }\n vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {\n TreeNode* dummy = new TreeNode(501);\n makeParent(root, dummy);\n \n vector<int> ans = {};\n if(!root) return ans;\n\n priority_queue< pp, vector<pp>, greater<pp>> pq;\n pq.push({0, target});\n vector<bool> vis(501 ,false);\n vis[target->val] = true;\n while(!pq.empty()){\n auto [ dis, Node] = pq.top(); \n pq.pop();\n if(dis == k and Node->val!=501) ans.push_back(Node->val);\n\n if(Node->left && !vis[Node->left->val]){\n pq.push({dis+1, Node->left});\n vis[Node->left->val] = true;\n }\n if(Node->right && !vis[Node->right->val]){\n pq.push({dis+1, Node->right});\n vis[Node->right->val] =true;\n }\n if(nodeParent[Node] && !vis[nodeParent[Node]->val]){\n pq.push({dis+1, nodeParent[Node]});\n vis[nodeParent[Node]->val] = true;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass Solution:\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n if not root or not target:\n return []\n if k==0:\n return [target.val]\n \n parent={root: None}\n def dfs(root):\n if not root:\n return\n if root.left:\n parent[root.left]=root\n dfs(root.left)\n if root.right:\n parent[root.right]=root\n dfs(root.right)\n dfs(root)\n\n def bfs(root, level, visited):\n if not root or level<0:\n return []\n if root in visited:\n return []\n pool=deque()\n pool.append(root)\n visited.add(root)\n cnt=0\n while pool and cnt<level:\n tp=deque()\n while pool:\n cur=pool.popleft()\n if cur.left and cur.left not in visited:\n tp.append(cur.left)\n visited.add(cur.left)\n if cur.right and cur.right not in visited:\n tp.append(cur.right)\n visited.add(cur.right)\n pool=tp\n cnt+=1\n ans=[]\n while pool:\n cur=pool.popleft()\n ans.append(cur.val)\n return ans\n \n tp=target\n ans=[]\n visited=set()\n for l in range(k+1):\n ans.extend(bfs(tp, k-l, visited))\n tp=parent[tp]\n if not tp:\n break\n return ans\n```\n\n```Java []\nclass Solution {\n List<Integer> ans = new ArrayList();\n int k;\n public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {\n this.k = k;\n find(root, target.val, 0);\n return ans;\n }\n int find(TreeNode root, int target, int depth) {\n if (root == null) {\n return -1;\n }\n if (root.val == target) {\n traverse(root, 0, k);\n return depth;\n }\n int foundDepth = find(root.left, target, depth + 1);\n if (foundDepth != -1) {\n if (foundDepth - depth == k) {\n ans.add(root.val);\n } else if (foundDepth - depth < k) {\n traverse(root.right, 1, k - (foundDepth - depth));\n }\n return foundDepth;\n }\n foundDepth = find(root.right, target, depth + 1);\n if (foundDepth != -1) {\n if (foundDepth - depth == k) {\n ans.add(root.val);\n } else if (foundDepth - depth < k) {\n traverse(root.left, 1, k - (foundDepth - depth));\n }\n }\n return foundDepth;\n }\n void traverse(TreeNode root, int depth, int targetDepth) {\n if (root == null) {\n return;\n }\n if (depth == targetDepth) {\n ans.add(root.val);\n return;\n }\n traverse(root.left, depth + 1, targetDepth);\n traverse(root.right, depth + 1, targetDepth);\n }\n}\n```\n | 1 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
Solution | all-nodes-distance-k-in-binary-tree | 1 | 1 | ```C++ []\n#define pp pair<int, TreeNode*>\n\nclass Solution {\npublic:\n unordered_map<TreeNode*, TreeNode*> nodeParent;\n void makeParent(TreeNode* root, TreeNode* parent){\n nodeParent[root] = parent; \n if(root->left) makeParent(root->left, root);\n if(root->right) makeParent(root->right, root);\n }\n vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {\n TreeNode* dummy = new TreeNode(501);\n makeParent(root, dummy);\n \n vector<int> ans = {};\n if(!root) return ans;\n\n priority_queue< pp, vector<pp>, greater<pp>> pq;\n pq.push({0, target});\n vector<bool> vis(501 ,false);\n vis[target->val] = true;\n while(!pq.empty()){\n auto [ dis, Node] = pq.top(); \n pq.pop();\n if(dis == k and Node->val!=501) ans.push_back(Node->val);\n\n if(Node->left && !vis[Node->left->val]){\n pq.push({dis+1, Node->left});\n vis[Node->left->val] = true;\n }\n if(Node->right && !vis[Node->right->val]){\n pq.push({dis+1, Node->right});\n vis[Node->right->val] =true;\n }\n if(nodeParent[Node] && !vis[nodeParent[Node]->val]){\n pq.push({dis+1, nodeParent[Node]});\n vis[nodeParent[Node]->val] = true;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\n\nclass Solution:\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n if not root or not target:\n return []\n if k==0:\n return [target.val]\n \n parent={root: None}\n def dfs(root):\n if not root:\n return\n if root.left:\n parent[root.left]=root\n dfs(root.left)\n if root.right:\n parent[root.right]=root\n dfs(root.right)\n dfs(root)\n\n def bfs(root, level, visited):\n if not root or level<0:\n return []\n if root in visited:\n return []\n pool=deque()\n pool.append(root)\n visited.add(root)\n cnt=0\n while pool and cnt<level:\n tp=deque()\n while pool:\n cur=pool.popleft()\n if cur.left and cur.left not in visited:\n tp.append(cur.left)\n visited.add(cur.left)\n if cur.right and cur.right not in visited:\n tp.append(cur.right)\n visited.add(cur.right)\n pool=tp\n cnt+=1\n ans=[]\n while pool:\n cur=pool.popleft()\n ans.append(cur.val)\n return ans\n \n tp=target\n ans=[]\n visited=set()\n for l in range(k+1):\n ans.extend(bfs(tp, k-l, visited))\n tp=parent[tp]\n if not tp:\n break\n return ans\n```\n\n```Java []\nclass Solution {\n List<Integer> ans = new ArrayList();\n int k;\n public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {\n this.k = k;\n find(root, target.val, 0);\n return ans;\n }\n int find(TreeNode root, int target, int depth) {\n if (root == null) {\n return -1;\n }\n if (root.val == target) {\n traverse(root, 0, k);\n return depth;\n }\n int foundDepth = find(root.left, target, depth + 1);\n if (foundDepth != -1) {\n if (foundDepth - depth == k) {\n ans.add(root.val);\n } else if (foundDepth - depth < k) {\n traverse(root.right, 1, k - (foundDepth - depth));\n }\n return foundDepth;\n }\n foundDepth = find(root.right, target, depth + 1);\n if (foundDepth != -1) {\n if (foundDepth - depth == k) {\n ans.add(root.val);\n } else if (foundDepth - depth < k) {\n traverse(root.left, 1, k - (foundDepth - depth));\n }\n }\n return foundDepth;\n }\n void traverse(TreeNode root, int depth, int targetDepth) {\n if (root == null) {\n return;\n }\n if (depth == targetDepth) {\n ans.add(root.val);\n return;\n }\n traverse(root.left, depth + 1, targetDepth);\n traverse(root.right, depth + 1, targetDepth);\n }\n}\n```\n | 1 | You are given an array of strings of the same length `words`.
In one **move**, you can swap any two even indexed characters or any two odd indexed characters of a string `words[i]`.
Two strings `words[i]` and `words[j]` are **special-equivalent** if after any number of moves, `words[i] == words[j]`.
* For example, `words[i] = "zzxy "` and `words[j] = "xyzz "` are **special-equivalent** because we may make the moves `"zzxy " -> "xzzy " -> "xyzz "`.
A **group of special-equivalent strings** from `words` is a non-empty subset of words such that:
* Every pair of strings in the group are special equivalent, and
* The group is the largest size possible (i.e., there is not a string `words[i]` not in the group such that `words[i]` is special-equivalent to every string in the group).
Return _the number of **groups of special-equivalent strings** from_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "cdab ", "cbad ", "xyzz ", "zzxy ", "zzyx "\]
**Output:** 3
**Explanation:**
One group is \[ "abcd ", "cdab ", "cbad "\], since they are all pairwise special equivalent, and none of the other strings is all pairwise special equivalent to these.
The other two groups are \[ "xyzz ", "zzxy "\] and \[ "zzyx "\].
Note that in particular, "zzxy " is not special equivalent to "zzyx ".
**Example 2:**
**Input:** words = \[ "abc ", "acb ", "bac ", "bca ", "cab ", "cba "\]
**Output:** 3
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 20`
* `words[i]` consist of lowercase English letters.
* All the strings are of the same length. | null |
✅Two BFS || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | all-nodes-distance-k-in-binary-tree | 1 | 1 | # Intuition:\nThe Intuition is to perform two BFS traversals: one to build the parent-child relationship and another to find all nodes at a distance of k from the target node.\n\n# Explanation:\n\n1. Start a BFS from the root node of the binary tree. We will use a queue to perform the BFS traversal. Initialize an empty queue and push the root node into it.\n\n2. While the queue is not empty, perform the following steps:\n - Get the current size of the queue (number of nodes at the current level).\n - Iterate through all the nodes at the current level.\n - For each node, check if it has a left child. If it does, store the parent-child relationship by mapping the left child\'s value to its parent node in an unordered_map called "parent".\n - Similarly, if the current node has a right child, store the parent-child relationship for the right child.\n - After processing the children of the current node, remove it from the queue.\n\n3. After the BFS traversal, we will have the parent-child relationship stored in the "parent" unordered_map.\n\n4. Now, we need to perform another BFS traversal to find all the nodes at a distance of k from the target node. Initialize another empty queue and push the target node into it.\n\n5. While the value of k is greater than 0 and the queue is not empty, perform the following steps:\n - Get the current size of the queue (number of nodes at the current level).\n - Iterate through all the nodes at the current level.\n - Mark the current node as visited by adding its value to the "visited" unordered_map.\n - If the current node has a left child and it has not been visited yet, push it into the queue.\n - If the current node has a right child and it has not been visited yet, push it into the queue.\n - If the current node has a parent and the parent node has not been visited yet, push the parent node into the queue.\n - After processing the current node and its children/parent, remove it from the queue.\n\n6. After the BFS traversal, we will have all the nodes at a distance of k from the target node stored in the queue.\n\n7. Finally, we can extract the values of the nodes from the queue and store them in a vector called "ans". Return the "ans" vector as the result.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {\n vector<int> ans;\n unordered_map<int, TreeNode*> parent;\n queue<TreeNode*> q;\n q.push(root);\n\n while(!q.empty()){\n int si = q.size();\n for(int i = 0; i < si; i++){\n auto top = q.front();\n q.pop();\n \n if(top -> left){\n parent[top->left->val] = top;\n q.push(top->left); \n }\n\n if(top -> right){\n parent[top->right->val] = top;\n q.push(top->right); \n }\n }\n }\n\n unordered_map<int, int> visited;\n q.push(target);\n while(k-- && !q.empty()){\n int size = q.size();\n\n for(int i = 0; i < size; i++){\n auto top = q.front();\n q.pop();\n\n visited[top -> val] = 1;\n\n if(top -> left && !visited[top->left->val]){\n q.push(top -> left);\n }\n\n if(top -> right && !visited[top->right->val]){\n q.push(top -> right);\n }\n\n if(parent[top->val] && !visited[parent[top->val] -> val]){\n q.push(parent[top->val]);\n }\n\n }\n }\n\n while(!q.empty()){\n ans.push_back(q.front()->val);\n q.pop();\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {\n List<Integer> ans = new ArrayList<>();\n Map<Integer, TreeNode> parent = new HashMap<>();\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n\n while (!queue.isEmpty()) {\n int size = queue.size();\n for (int i = 0; i < size; i++) {\n TreeNode top = queue.poll();\n\n if (top.left != null) {\n parent.put(top.left.val, top);\n queue.offer(top.left);\n }\n\n if (top.right != null) {\n parent.put(top.right.val, top);\n queue.offer(top.right);\n }\n }\n }\n\n Map<Integer, Integer> visited = new HashMap<>();\n queue.offer(target);\n while (k > 0 && !queue.isEmpty()) {\n int size = queue.size();\n\n for (int i = 0; i < size; i++) {\n TreeNode top = queue.poll();\n\n visited.put(top.val, 1);\n\n if (top.left != null && !visited.containsKey(top.left.val)) {\n queue.offer(top.left);\n }\n\n if (top.right != null && !visited.containsKey(top.right.val)) {\n queue.offer(top.right);\n }\n\n if (parent.containsKey(top.val) && !visited.containsKey(parent.get(top.val).val)) {\n queue.offer(parent.get(top.val));\n }\n }\n\n k--;\n }\n\n while (!queue.isEmpty()) {\n ans.add(queue.poll().val);\n }\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n ans = []\n parent = {}\n queue = deque()\n queue.append(root)\n\n while queue:\n size = len(queue)\n for _ in range(size):\n top = queue.popleft()\n\n if top.left:\n parent[top.left.val] = top\n queue.append(top.left)\n\n if top.right:\n parent[top.right.val] = top\n queue.append(top.right)\n\n visited = {}\n queue.append(target)\n while k > 0 and queue:\n size = len(queue)\n\n for _ in range(size):\n top = queue.popleft()\n\n visited[top.val] = 1\n\n if top.left and top.left.val not in visited:\n queue.append(top.left)\n\n if top.right and top.right.val not in visited:\n queue.append(top.right)\n\n if top.val in parent and parent[top.val].val not in visited:\n queue.append(parent[top.val])\n\n k -= 1\n\n while queue:\n ans.append(queue.popleft().val)\n\n return ans\n```\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 104 | Given the `root` of a binary tree, the value of a target node `target`, and an integer `k`, return _an array of the values of all nodes that have a distance_ `k` _from the target node._
You can return the answer in **any order**.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\], target = 5, k = 2
**Output:** \[7,4,1\]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
**Example 2:**
**Input:** root = \[1\], target = 1, k = 3
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* All the values `Node.val` are **unique**.
* `target` is the value of one of the nodes in the tree.
* `0 <= k <= 1000` | null |
✅Two BFS || C++ || JAVA || PYTHON || Beginner Friendly🔥🔥🔥 | all-nodes-distance-k-in-binary-tree | 1 | 1 | # Intuition:\nThe Intuition is to perform two BFS traversals: one to build the parent-child relationship and another to find all nodes at a distance of k from the target node.\n\n# Explanation:\n\n1. Start a BFS from the root node of the binary tree. We will use a queue to perform the BFS traversal. Initialize an empty queue and push the root node into it.\n\n2. While the queue is not empty, perform the following steps:\n - Get the current size of the queue (number of nodes at the current level).\n - Iterate through all the nodes at the current level.\n - For each node, check if it has a left child. If it does, store the parent-child relationship by mapping the left child\'s value to its parent node in an unordered_map called "parent".\n - Similarly, if the current node has a right child, store the parent-child relationship for the right child.\n - After processing the children of the current node, remove it from the queue.\n\n3. After the BFS traversal, we will have the parent-child relationship stored in the "parent" unordered_map.\n\n4. Now, we need to perform another BFS traversal to find all the nodes at a distance of k from the target node. Initialize another empty queue and push the target node into it.\n\n5. While the value of k is greater than 0 and the queue is not empty, perform the following steps:\n - Get the current size of the queue (number of nodes at the current level).\n - Iterate through all the nodes at the current level.\n - Mark the current node as visited by adding its value to the "visited" unordered_map.\n - If the current node has a left child and it has not been visited yet, push it into the queue.\n - If the current node has a right child and it has not been visited yet, push it into the queue.\n - If the current node has a parent and the parent node has not been visited yet, push the parent node into the queue.\n - After processing the current node and its children/parent, remove it from the queue.\n\n6. After the BFS traversal, we will have all the nodes at a distance of k from the target node stored in the queue.\n\n7. Finally, we can extract the values of the nodes from the queue and store them in a vector called "ans". Return the "ans" vector as the result.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {\n vector<int> ans;\n unordered_map<int, TreeNode*> parent;\n queue<TreeNode*> q;\n q.push(root);\n\n while(!q.empty()){\n int si = q.size();\n for(int i = 0; i < si; i++){\n auto top = q.front();\n q.pop();\n \n if(top -> left){\n parent[top->left->val] = top;\n q.push(top->left); \n }\n\n if(top -> right){\n parent[top->right->val] = top;\n q.push(top->right); \n }\n }\n }\n\n unordered_map<int, int> visited;\n q.push(target);\n while(k-- && !q.empty()){\n int size = q.size();\n\n for(int i = 0; i < size; i++){\n auto top = q.front();\n q.pop();\n\n visited[top -> val] = 1;\n\n if(top -> left && !visited[top->left->val]){\n q.push(top -> left);\n }\n\n if(top -> right && !visited[top->right->val]){\n q.push(top -> right);\n }\n\n if(parent[top->val] && !visited[parent[top->val] -> val]){\n q.push(parent[top->val]);\n }\n\n }\n }\n\n while(!q.empty()){\n ans.push_back(q.front()->val);\n q.pop();\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {\n List<Integer> ans = new ArrayList<>();\n Map<Integer, TreeNode> parent = new HashMap<>();\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n\n while (!queue.isEmpty()) {\n int size = queue.size();\n for (int i = 0; i < size; i++) {\n TreeNode top = queue.poll();\n\n if (top.left != null) {\n parent.put(top.left.val, top);\n queue.offer(top.left);\n }\n\n if (top.right != null) {\n parent.put(top.right.val, top);\n queue.offer(top.right);\n }\n }\n }\n\n Map<Integer, Integer> visited = new HashMap<>();\n queue.offer(target);\n while (k > 0 && !queue.isEmpty()) {\n int size = queue.size();\n\n for (int i = 0; i < size; i++) {\n TreeNode top = queue.poll();\n\n visited.put(top.val, 1);\n\n if (top.left != null && !visited.containsKey(top.left.val)) {\n queue.offer(top.left);\n }\n\n if (top.right != null && !visited.containsKey(top.right.val)) {\n queue.offer(top.right);\n }\n\n if (parent.containsKey(top.val) && !visited.containsKey(parent.get(top.val).val)) {\n queue.offer(parent.get(top.val));\n }\n }\n\n k--;\n }\n\n while (!queue.isEmpty()) {\n ans.add(queue.poll().val);\n }\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:\n ans = []\n parent = {}\n queue = deque()\n queue.append(root)\n\n while queue:\n size = len(queue)\n for _ in range(size):\n top = queue.popleft()\n\n if top.left:\n parent[top.left.val] = top\n queue.append(top.left)\n\n if top.right:\n parent[top.right.val] = top\n queue.append(top.right)\n\n visited = {}\n queue.append(target)\n while k > 0 and queue:\n size = len(queue)\n\n for _ in range(size):\n top = queue.popleft()\n\n visited[top.val] = 1\n\n if top.left and top.left.val not in visited:\n queue.append(top.left)\n\n if top.right and top.right.val not in visited:\n queue.append(top.right)\n\n if top.val in parent and parent[top.val].val not in visited:\n queue.append(parent[top.val])\n\n k -= 1\n\n while queue:\n ans.append(queue.popleft().val)\n\n return ans\n```\n\n**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions.**\n\n | 104 | You are given an array of strings of the same length `words`.
In one **move**, you can swap any two even indexed characters or any two odd indexed characters of a string `words[i]`.
Two strings `words[i]` and `words[j]` are **special-equivalent** if after any number of moves, `words[i] == words[j]`.
* For example, `words[i] = "zzxy "` and `words[j] = "xyzz "` are **special-equivalent** because we may make the moves `"zzxy " -> "xzzy " -> "xyzz "`.
A **group of special-equivalent strings** from `words` is a non-empty subset of words such that:
* Every pair of strings in the group are special equivalent, and
* The group is the largest size possible (i.e., there is not a string `words[i]` not in the group such that `words[i]` is special-equivalent to every string in the group).
Return _the number of **groups of special-equivalent strings** from_ `words`.
**Example 1:**
**Input:** words = \[ "abcd ", "cdab ", "cbad ", "xyzz ", "zzxy ", "zzyx "\]
**Output:** 3
**Explanation:**
One group is \[ "abcd ", "cdab ", "cbad "\], since they are all pairwise special equivalent, and none of the other strings is all pairwise special equivalent to these.
The other two groups are \[ "xyzz ", "zzxy "\] and \[ "zzyx "\].
Note that in particular, "zzxy " is not special equivalent to "zzyx ".
**Example 2:**
**Input:** words = \[ "abc ", "acb ", "bac ", "bca ", "cab ", "cba "\]
**Output:** 3
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length <= 20`
* `words[i]` consist of lowercase English letters.
* All the strings are of the same length. | null |
Python3 Solution | shortest-path-to-get-all-keys | 0 | 1 | \n```\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n m=len(grid)\n n=len(grid[0])\n arr=deque([])\n numOfKeys=0\n keys={\'a\':0,\'b\':1,\'c\':2,\'d\':3,\'e\':4,\'f\':5}\n locks={\'A\':0,\'B\':1,\'C\':2,\'D\':3,\'E\':4,\'F\':5}\n for i in range(m):\n for j in range(n):\n if grid[i][j]==\'@\':\n arr.append((i,j,0,0))\n elif grid[i][j] in keys:\n numOfKeys+=1\n\n visited=set()\n while arr:\n size=len(arr)\n for _ in range(size):\n i,j,found,steps=arr.popleft()\n curr=grid[i][j]\n if curr in locks and not (found>>locks[curr]) & 1 or curr==\'#\':\n continue\n\n if curr in keys:\n found |=1<<keys[curr]\n if found==(1<<numOfKeys)-1:\n return steps\n\n for x,y in [(i+1,j),(i,j+1),(i-1,j),(i,j-1)]:\n if 0<=x<m and 0<=y<n and (x,y,found) not in visited:\n visited.add((x,y,found))\n arr.append((x,y,found,steps+1))\n\n return -1 \n``` | 15 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
Python3 Solution | shortest-path-to-get-all-keys | 0 | 1 | \n```\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n m=len(grid)\n n=len(grid[0])\n arr=deque([])\n numOfKeys=0\n keys={\'a\':0,\'b\':1,\'c\':2,\'d\':3,\'e\':4,\'f\':5}\n locks={\'A\':0,\'B\':1,\'C\':2,\'D\':3,\'E\':4,\'F\':5}\n for i in range(m):\n for j in range(n):\n if grid[i][j]==\'@\':\n arr.append((i,j,0,0))\n elif grid[i][j] in keys:\n numOfKeys+=1\n\n visited=set()\n while arr:\n size=len(arr)\n for _ in range(size):\n i,j,found,steps=arr.popleft()\n curr=grid[i][j]\n if curr in locks and not (found>>locks[curr]) & 1 or curr==\'#\':\n continue\n\n if curr in keys:\n found |=1<<keys[curr]\n if found==(1<<numOfKeys)-1:\n return steps\n\n for x,y in [(i+1,j),(i,j+1),(i-1,j),(i,j-1)]:\n if 0<=x<m and 0<=y<n and (x,y,found) not in visited:\n visited.add((x,y,found))\n arr.append((x,y,found,steps+1))\n\n return -1 \n``` | 15 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Python | Contract to weighted component graph then djikstra's | shortest-path-to-get-all-keys | 0 | 1 | # Intuition\n\nThe original idea I had came from a comment left on the leetcode editorial. Someone said you might be able to use the connected components graph. This is true, but you end up having to solve the same problem as the original, but with a weighted graph instead of an unweighted graph.\n\n# Approach\nThe approach is a modification of the editorial solution. We will instead first contract the graph into a weighted version. The way I went about this is using breadth first search from every "important location" to find the distances to the other important locations.\n\nAfter building this contracted weighted graph we apply djisktra\'s algorithm to search for the state where all keys have been found (similar to the editorial, but they use bfs).\n\n# Complexity\n- Time complexity:\nThe graph contraction takes: $$ O(k^2 \\cdot m \\cdot n) $$ where $k$ is number of keys, and the grid is $m \\times n$.\nThe worst case complexity for djiktra\'s part is more complicated. Let the number of nodes and edges in the contracted graph be V, E. Then we have:\n\n$$O(E + V \\cdot 2^k \\cdot \\log(V \\cdot2^k)) = E + kV2^k + 2^kV\\log(V)$$\n\nBut we also know that $E$, $V$ are actually bounded by $k^2$:\n\n$$ k^2 + k^3 2^k + 2^k k^2 \\log(k^2) = k^2 + k^3 2^k + 2^k k^2 \\log(k)$$.\n\nMaybe this could be tightened through some analysis, but otherwise the dominating factor is: $k^32^k$. This isn\'t much better then the editorial, but for some graphs it is.\n\n- Space complexity:\nWe have an additional $k^2$ plus the original $O(mn2^k)$\n\n# Code\n```\ndef neighbors(grid, r, c):\n H, W = len(grid), len(grid[0])\n for dr, dc in [(-1, 0), (1, 0), (0, -1), (0, 1)]:\n nr = r + dr\n nc = c + dc\n if 0 <= nr < H and 0 <= nc < W and grid[nr][nc] != \'#\':\n yield nr, nc\n\ndef locations(grid):\n for r in range(len(grid)):\n for c in range(len(grid[0])):\n if grid[r][c] not in "#.":\n yield r, c\n\ndef targets_and_num_keys(grid):\n result = "".join(grid).replace("#", "").replace(".", "") \n return result, (len(result) - 1) // 2\n\ndef bfs(grid, loc, targets, keys=None):\n q = deque([(0, loc)])\n visited = set([loc])\n result = defaultdict(lambda: -1)\n\n while q:\n distance, curr = q.pop()\n r, c = curr\n cell = grid[r][c]\n \n if cell in targets:\n result[cell] = distance\n \n for succ in neighbors(grid, r, c):\n nr, nc = succ\n cell = grid[nr][nc]\n\n if cell.isupper() and (not keys or cell.lower() not in keys):\n result[cell] = min(result.get(cell, float(\'inf\')), distance + 1)\n continue\n\n if succ not in visited:\n q.appendleft((distance + 1, succ))\n visited.add(succ)\n\n return result\n\ndef djikstra(graph, loc, state, desired_state):\n distances = defaultdict(lambda: float(\'inf\'))\n distances[loc, state] = 0\n q = [(0, loc, state)]\n visited = set([])\n\n while q:\n distance, curr, state = heapq.heappop(q)\n if state == desired_state: return distance\n visited.add((curr, state))\n\n if distance < distances[curr, state]:\n distances[curr, state] = distance\n \n for succ, weight in graph[curr].items():\n if succ.isupper() and not (state & (1 << (ord(succ.lower()) - ord(\'a\')))):\n continue\n\n new_state = state\n if succ.islower():\n new_state |= (1 << (ord(succ) - ord(\'a\')))\n \n if (succ, new_state) in visited: continue\n\n if distance + weight < distances[succ, new_state]:\n distances[succ] = distance + weight\n heapq.heappush(q, (distance + weight, succ, new_state))\n\n return -1\n\n\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n targets, key_count = targets_and_num_keys(grid)\n graph = {}\n\n for r, c in locations(grid):\n cell = grid[r][c]\n distances = bfs(grid, (r, c), targets)\n del distances[cell]\n graph[cell] = distances\n\n desired_state = (1 << key_count) - 1\n return djikstra(graph, \'@\', 0, desired_state)\n``` | 1 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
Python | Contract to weighted component graph then djikstra's | shortest-path-to-get-all-keys | 0 | 1 | # Intuition\n\nThe original idea I had came from a comment left on the leetcode editorial. Someone said you might be able to use the connected components graph. This is true, but you end up having to solve the same problem as the original, but with a weighted graph instead of an unweighted graph.\n\n# Approach\nThe approach is a modification of the editorial solution. We will instead first contract the graph into a weighted version. The way I went about this is using breadth first search from every "important location" to find the distances to the other important locations.\n\nAfter building this contracted weighted graph we apply djisktra\'s algorithm to search for the state where all keys have been found (similar to the editorial, but they use bfs).\n\n# Complexity\n- Time complexity:\nThe graph contraction takes: $$ O(k^2 \\cdot m \\cdot n) $$ where $k$ is number of keys, and the grid is $m \\times n$.\nThe worst case complexity for djiktra\'s part is more complicated. Let the number of nodes and edges in the contracted graph be V, E. Then we have:\n\n$$O(E + V \\cdot 2^k \\cdot \\log(V \\cdot2^k)) = E + kV2^k + 2^kV\\log(V)$$\n\nBut we also know that $E$, $V$ are actually bounded by $k^2$:\n\n$$ k^2 + k^3 2^k + 2^k k^2 \\log(k^2) = k^2 + k^3 2^k + 2^k k^2 \\log(k)$$.\n\nMaybe this could be tightened through some analysis, but otherwise the dominating factor is: $k^32^k$. This isn\'t much better then the editorial, but for some graphs it is.\n\n- Space complexity:\nWe have an additional $k^2$ plus the original $O(mn2^k)$\n\n# Code\n```\ndef neighbors(grid, r, c):\n H, W = len(grid), len(grid[0])\n for dr, dc in [(-1, 0), (1, 0), (0, -1), (0, 1)]:\n nr = r + dr\n nc = c + dc\n if 0 <= nr < H and 0 <= nc < W and grid[nr][nc] != \'#\':\n yield nr, nc\n\ndef locations(grid):\n for r in range(len(grid)):\n for c in range(len(grid[0])):\n if grid[r][c] not in "#.":\n yield r, c\n\ndef targets_and_num_keys(grid):\n result = "".join(grid).replace("#", "").replace(".", "") \n return result, (len(result) - 1) // 2\n\ndef bfs(grid, loc, targets, keys=None):\n q = deque([(0, loc)])\n visited = set([loc])\n result = defaultdict(lambda: -1)\n\n while q:\n distance, curr = q.pop()\n r, c = curr\n cell = grid[r][c]\n \n if cell in targets:\n result[cell] = distance\n \n for succ in neighbors(grid, r, c):\n nr, nc = succ\n cell = grid[nr][nc]\n\n if cell.isupper() and (not keys or cell.lower() not in keys):\n result[cell] = min(result.get(cell, float(\'inf\')), distance + 1)\n continue\n\n if succ not in visited:\n q.appendleft((distance + 1, succ))\n visited.add(succ)\n\n return result\n\ndef djikstra(graph, loc, state, desired_state):\n distances = defaultdict(lambda: float(\'inf\'))\n distances[loc, state] = 0\n q = [(0, loc, state)]\n visited = set([])\n\n while q:\n distance, curr, state = heapq.heappop(q)\n if state == desired_state: return distance\n visited.add((curr, state))\n\n if distance < distances[curr, state]:\n distances[curr, state] = distance\n \n for succ, weight in graph[curr].items():\n if succ.isupper() and not (state & (1 << (ord(succ.lower()) - ord(\'a\')))):\n continue\n\n new_state = state\n if succ.islower():\n new_state |= (1 << (ord(succ) - ord(\'a\')))\n \n if (succ, new_state) in visited: continue\n\n if distance + weight < distances[succ, new_state]:\n distances[succ] = distance + weight\n heapq.heappush(q, (distance + weight, succ, new_state))\n\n return -1\n\n\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n targets, key_count = targets_and_num_keys(grid)\n graph = {}\n\n for r, c in locations(grid):\n cell = grid[r][c]\n distances = bfs(grid, (r, c), targets)\n del distances[cell]\n graph[cell] = distances\n\n desired_state = (1 << key_count) - 1\n return djikstra(graph, \'@\', 0, desired_state)\n``` | 1 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
python 3 - bfs + bitmask | shortest-path-to-get-all-keys | 0 | 1 | # Intuition\nThis question is BFS question but allowing you to go back. The question is: you can\'t revisit the same cell infinitely.\n\nIf you think about the key_state and unlocked_state, you should take these 2 into account. For a certain cell, it can\'t be revisited with the same (key_state, unlocked_state).\n\n# Approach\nBFS with bitmask\n\n# Complexity\n- Time complexity:\nO(mn * 2^k * 2^k) -> Visit m * n grid and there are 2^k * 2^k possibility of bitmask\n\n- Space complexity:\nO(mn * 2^k * 2^k) -> visited_state dict with m * n dimension. In each cell, there is a set with 2^k * 2^k size.\n\n# Code\n```\nimport collections\n\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n\n m, n = len(grid), len(grid[0])\n\n # prevent revisit with the same key_state, unlocked state\n visited_state = [[set() for _ in range(n)] for _ in range(m)] # set of (key_state, unlocked state)\n\n key = 0\n starti, startj = -1, -1\n\n for i in range(m):\n for j in range(n):\n if grid[i][j] in \'abcdef\':\n key += 1\n if grid[i][j] == \'@\':\n starti, startj = i, j\n\n # bitmask after getting all keys\n key_final_state = 0\n for i in range(key):\n key_final_state ^= 1 << i\n\n step = 0\n\n queue = collections.deque() # queue of [i, j, key_state, unlocked state]\n queue.append([starti, startj, 0, 0])\n\n while queue:\n\n for _ in range(len(queue)):\n\n i, j, key_state, unlocked_state = queue.popleft()\n\n if key_state == key_final_state:\n return step\n\n # move in 4 directions\n for ii, jj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:\n ni, nj = i + ii, j + jj\n\n if not (0 <= ni < m and 0 <= nj < n) or grid[ni][nj] == \'#\': # exceed grid / wall\n continue\n\n # update unlocked_state\n new_unlocked_state = unlocked_state\n if grid[ni][nj] in "ABCDEF": # lock\n bit_shift = ord(grid[ni][nj]) - ord("A")\n if not (key_state & 1 << bit_shift): # but you dont have the key\n continue\n\n new_unlocked_state |= 1 << i\n\n # update key_state\n new_key_state = key_state\n if grid[ni][nj] in \'abcdef\': # key\n bit_shift = ord(grid[ni][nj]) - ord(\'a\')\n new_key_state |= 1 << bit_shift\n\n # prevent going back / multiple count\n state = (new_key_state, new_unlocked_state)\n if state in visited_state[ni][nj]:\n continue\n visited_state[ni][nj].add(state)\n\n # \'.@\' -> walk through\n queue.append([ni, nj, new_key_state, new_unlocked_state])\n\n step += 1\n\n return -1\n``` | 1 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
python 3 - bfs + bitmask | shortest-path-to-get-all-keys | 0 | 1 | # Intuition\nThis question is BFS question but allowing you to go back. The question is: you can\'t revisit the same cell infinitely.\n\nIf you think about the key_state and unlocked_state, you should take these 2 into account. For a certain cell, it can\'t be revisited with the same (key_state, unlocked_state).\n\n# Approach\nBFS with bitmask\n\n# Complexity\n- Time complexity:\nO(mn * 2^k * 2^k) -> Visit m * n grid and there are 2^k * 2^k possibility of bitmask\n\n- Space complexity:\nO(mn * 2^k * 2^k) -> visited_state dict with m * n dimension. In each cell, there is a set with 2^k * 2^k size.\n\n# Code\n```\nimport collections\n\nclass Solution:\n def shortestPathAllKeys(self, grid: List[str]) -> int:\n\n m, n = len(grid), len(grid[0])\n\n # prevent revisit with the same key_state, unlocked state\n visited_state = [[set() for _ in range(n)] for _ in range(m)] # set of (key_state, unlocked state)\n\n key = 0\n starti, startj = -1, -1\n\n for i in range(m):\n for j in range(n):\n if grid[i][j] in \'abcdef\':\n key += 1\n if grid[i][j] == \'@\':\n starti, startj = i, j\n\n # bitmask after getting all keys\n key_final_state = 0\n for i in range(key):\n key_final_state ^= 1 << i\n\n step = 0\n\n queue = collections.deque() # queue of [i, j, key_state, unlocked state]\n queue.append([starti, startj, 0, 0])\n\n while queue:\n\n for _ in range(len(queue)):\n\n i, j, key_state, unlocked_state = queue.popleft()\n\n if key_state == key_final_state:\n return step\n\n # move in 4 directions\n for ii, jj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:\n ni, nj = i + ii, j + jj\n\n if not (0 <= ni < m and 0 <= nj < n) or grid[ni][nj] == \'#\': # exceed grid / wall\n continue\n\n # update unlocked_state\n new_unlocked_state = unlocked_state\n if grid[ni][nj] in "ABCDEF": # lock\n bit_shift = ord(grid[ni][nj]) - ord("A")\n if not (key_state & 1 << bit_shift): # but you dont have the key\n continue\n\n new_unlocked_state |= 1 << i\n\n # update key_state\n new_key_state = key_state\n if grid[ni][nj] in \'abcdef\': # key\n bit_shift = ord(grid[ni][nj]) - ord(\'a\')\n new_key_state |= 1 << bit_shift\n\n # prevent going back / multiple count\n state = (new_key_state, new_unlocked_state)\n if state in visited_state[ni][nj]:\n continue\n visited_state[ni][nj].add(state)\n\n # \'.@\' -> walk through\n queue.append([ni, nj, new_key_state, new_unlocked_state])\n\n step += 1\n\n return -1\n``` | 1 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Python short and clean. Functional programming. | shortest-path-to-get-all-keys | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/shortest-path-to-get-all-keys/editorial/) but clean and functional.\n\n# Complexity\n- Time complexity: $$O(2^6 \\cdot m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\nwhere, `m x n is the dimensions of grid`.\n\n# Code\n```python\nclass Solution:\n def shortestPathAllKeys(self, grid: list[str]) -> int:\n m, n = len(grid), len(grid[0])\n dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))\n\n in_bounds = lambda i, j: 0 <= i < m and 0 <= j < n\n nbrs = lambda i, j: ((i + di, j + dj) for di, dj in dirs)\n\n starfilter = lambda f, xs: filter(lambda args: f(*args), xs)\n starfilterfalse = lambda f, xs: filterfalse(lambda args: f(*args), xs)\n\n is_x = lambda val, x: val in x\n is_empty = partial(is_x, x=\'.\')\n is_wall = partial(is_x, x=\'#\')\n is_start = partial(is_x, x=\'@\')\n is_key = partial(is_x, x=\'abcdef\')\n is_lock = partial(is_x, x=\'ABCDEF\')\n\n matrix2d_get = lambda i, j, mtx: mtx[i][j]\n get = partial(matrix2d_get, mtx=grid)\n\n k = sum(map(is_key, chain.from_iterable(grid))) # Total number of keys in grid.\n start = next(filter(lambda ij: is_start(get(*ij)), product(range(m), range(n))))\n \n frontier = deque([(start, 0, frozenset())])\n seen = {(indices, keys) for indices, d, keys in frontier}\n\n while frontier:\n (i, j), d, keys = frontier.popleft()\n\n nbrs_ = starfilter(in_bounds, nbrs(i, j)) # Keep only inbound nbrs.\n nbrs_ = filter(lambda nbr: (nbr, keys) not in seen, nbrs_) # Keep only nbr not seen with same keys.\n\n nbr_and_vals = map(lambda nbr: (nbr, get(*nbr)), nbrs_) # Pair up nbr and containing value.\n nbr_and_vals = starfilterfalse(lambda _, val: is_wall(val), nbr_and_vals) # Remove nbr with WALL as value.\n nbr_and_vals = starfilterfalse(lambda _, val: is_lock(val) and val.lower() not in keys, nbr_and_vals) # Remove nbr with LOCK to which we don\'t have key yet, as value. \n\n for nbr, val in nbr_and_vals:\n new_d, new_keys = d + 1, (keys | {val} if is_key(val) else keys)\n if len(new_keys) == k: return new_d\n\n frontier.append((nbr, new_d, new_keys))\n seen.add((nbr, new_keys))\n \n return -1\n\n\n``` | 2 | You are given an `m x n` grid `grid` where:
* `'.'` is an empty cell.
* `'#'` is a wall.
* `'@'` is the starting point.
* Lowercase letters represent keys.
* Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some `1 <= k <= 6`, there is exactly one lowercase and one uppercase letter of the first `k` letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return _the lowest number of moves to acquire all keys_. If it is impossible, return `-1`.
**Example 1:**
**Input:** grid = \[ "@.a.. ", "###.# ", "b.A.B "\]
**Output:** 8
**Explanation:** Note that the goal is to obtain all the keys not to open all the locks.
**Example 2:**
**Input:** grid = \[ "@..aA ", "..B#. ", "....b "\]
**Output:** 6
**Example 3:**
**Input:** grid = \[ "@Aa "\]
**Output:** -1
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 30`
* `grid[i][j]` is either an English letter, `'.'`, `'#'`, or `'@'`.
* The number of keys in the grid is in the range `[1, 6]`.
* Each key in the grid is **unique**.
* Each key in the grid has a matching lock. | null |
Python short and clean. Functional programming. | shortest-path-to-get-all-keys | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/shortest-path-to-get-all-keys/editorial/) but clean and functional.\n\n# Complexity\n- Time complexity: $$O(2^6 \\cdot m \\cdot n)$$\n\n- Space complexity: $$O(m \\cdot n)$$\n\nwhere, `m x n is the dimensions of grid`.\n\n# Code\n```python\nclass Solution:\n def shortestPathAllKeys(self, grid: list[str]) -> int:\n m, n = len(grid), len(grid[0])\n dirs = ((0, 1), (1, 0), (0, -1), (-1, 0))\n\n in_bounds = lambda i, j: 0 <= i < m and 0 <= j < n\n nbrs = lambda i, j: ((i + di, j + dj) for di, dj in dirs)\n\n starfilter = lambda f, xs: filter(lambda args: f(*args), xs)\n starfilterfalse = lambda f, xs: filterfalse(lambda args: f(*args), xs)\n\n is_x = lambda val, x: val in x\n is_empty = partial(is_x, x=\'.\')\n is_wall = partial(is_x, x=\'#\')\n is_start = partial(is_x, x=\'@\')\n is_key = partial(is_x, x=\'abcdef\')\n is_lock = partial(is_x, x=\'ABCDEF\')\n\n matrix2d_get = lambda i, j, mtx: mtx[i][j]\n get = partial(matrix2d_get, mtx=grid)\n\n k = sum(map(is_key, chain.from_iterable(grid))) # Total number of keys in grid.\n start = next(filter(lambda ij: is_start(get(*ij)), product(range(m), range(n))))\n \n frontier = deque([(start, 0, frozenset())])\n seen = {(indices, keys) for indices, d, keys in frontier}\n\n while frontier:\n (i, j), d, keys = frontier.popleft()\n\n nbrs_ = starfilter(in_bounds, nbrs(i, j)) # Keep only inbound nbrs.\n nbrs_ = filter(lambda nbr: (nbr, keys) not in seen, nbrs_) # Keep only nbr not seen with same keys.\n\n nbr_and_vals = map(lambda nbr: (nbr, get(*nbr)), nbrs_) # Pair up nbr and containing value.\n nbr_and_vals = starfilterfalse(lambda _, val: is_wall(val), nbr_and_vals) # Remove nbr with WALL as value.\n nbr_and_vals = starfilterfalse(lambda _, val: is_lock(val) and val.lower() not in keys, nbr_and_vals) # Remove nbr with LOCK to which we don\'t have key yet, as value. \n\n for nbr, val in nbr_and_vals:\n new_d, new_keys = d + 1, (keys | {val} if is_key(val) else keys)\n if len(new_keys) == k: return new_d\n\n frontier.append((nbr, new_d, new_keys))\n seen.add((nbr, new_keys))\n \n return -1\n\n\n``` | 2 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Solution | smallest-subtree-with-all-the-deepest-nodes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int height(TreeNode* root) {\n if (!root) return 0;\n return max(height(root->left) + 1, height(root->right) + 1); \n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if (!root) return NULL;\n\n int left = height(root->left); \n int right = height(root->right);\n\n if (left == right) return root;\n if (left > right) return subtreeWithAllDeepest(root->left);\n return subtreeWithAllDeepest(root->right);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n found = False\n ans = TreeNode(-1)\n \n def dfs(node,p,q):\n nonlocal found, ans\n if not node: return []\n \n left = dfs(node.left,left_node,right_node)\n right = dfs(node.right,left_node,right_node)\n \n total = [*left,*right]\n total.append(node.val)\n \n if p.val in total and q.val in total and not found: \n ans = (node)\n found = True\n \n return total\n\n def find_depth(root):\n q = deque()\n q.append(root)\n\n while q:\n l,r = None,None\n no_nodes = len(q)\n for i in range(len(q)):\n a = q.popleft()\n if i == 0: l = a\n if i == no_nodes-1: r = a\n\n if a.left: q.append(a.left)\n if a.right: q.append(a.right)\n \n return l,r\n \n left_node,right_node = find_depth(root)\n dfs(root,left_node,right_node)\n \n return ans\n```\n\n```Java []\nclass Solution {\n int maxDepth = Integer.MIN_VALUE;\n TreeNode result = null;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n postOrder(root, 0);\n return result;\n }\n public int postOrder(TreeNode node, int deep) {\n if (node == null) {\n return deep;\n }\n int left = postOrder(node.left, deep + 1);\n int right = postOrder(node.right, deep + 1);\n int curDepth = Math.max(left, right);\n maxDepth = Math.max(maxDepth, curDepth);\n if (left == maxDepth && right == maxDepth) {\n result = node;\n }\n return curDepth;\n }\n}\n```\n | 3 | Given the `root` of a binary tree, the depth of each node is **the shortest distance to the root**.
Return _the smallest subtree_ such that it contains **all the deepest nodes** in the original tree.
A node is called **the deepest** if it has the largest depth possible among any node in the entire tree.
The **subtree** of a node is a tree consisting of that node, plus the set of all descendants of that node.
**Example 1:**
**Input:** root = \[3,5,1,6,2,0,8,null,null,7,4\]
**Output:** \[2,7,4\]
**Explanation:** We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.
**Example 2:**
**Input:** root = \[1\]
**Output:** \[1\]
**Explanation:** The root is the deepest node in the tree.
**Example 3:**
**Input:** root = \[0,1,3,null,2\]
**Output:** \[2\]
**Explanation:** The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 500]`.
* `0 <= Node.val <= 500`
* The values of the nodes in the tree are **unique**.
**Note:** This question is the same as 1123: [https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/](https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/) | null |
Solution | smallest-subtree-with-all-the-deepest-nodes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int height(TreeNode* root) {\n if (!root) return 0;\n return max(height(root->left) + 1, height(root->right) + 1); \n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if (!root) return NULL;\n\n int left = height(root->left); \n int right = height(root->right);\n\n if (left == right) return root;\n if (left > right) return subtreeWithAllDeepest(root->left);\n return subtreeWithAllDeepest(root->right);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n found = False\n ans = TreeNode(-1)\n \n def dfs(node,p,q):\n nonlocal found, ans\n if not node: return []\n \n left = dfs(node.left,left_node,right_node)\n right = dfs(node.right,left_node,right_node)\n \n total = [*left,*right]\n total.append(node.val)\n \n if p.val in total and q.val in total and not found: \n ans = (node)\n found = True\n \n return total\n\n def find_depth(root):\n q = deque()\n q.append(root)\n\n while q:\n l,r = None,None\n no_nodes = len(q)\n for i in range(len(q)):\n a = q.popleft()\n if i == 0: l = a\n if i == no_nodes-1: r = a\n\n if a.left: q.append(a.left)\n if a.right: q.append(a.right)\n \n return l,r\n \n left_node,right_node = find_depth(root)\n dfs(root,left_node,right_node)\n \n return ans\n```\n\n```Java []\nclass Solution {\n int maxDepth = Integer.MIN_VALUE;\n TreeNode result = null;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n postOrder(root, 0);\n return result;\n }\n public int postOrder(TreeNode node, int deep) {\n if (node == null) {\n return deep;\n }\n int left = postOrder(node.left, deep + 1);\n int right = postOrder(node.right, deep + 1);\n int curDepth = Math.max(left, right);\n maxDepth = Math.max(maxDepth, curDepth);\n if (left == maxDepth && right == maxDepth) {\n result = node;\n }\n return curDepth;\n }\n}\n```\n | 3 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Solution | prime-palindrome | 1 | 1 | ```C++ []\nclass Solution {\n bool isPrime(int val){\n if(val == 1 ) \n return false ;\n if(val == 2)\n return true ;\n int limit = sqrt(val) ;\n for(int i = 2; i <= limit; i++){\n if(val % i == 0)\n return false ;\n }\n return true ;\n }\npublic:\n int primePalindrome(int n) {\n if(n >= 8 && n <= 11)\n return 11 ;\n for(int i = 1; i <= 1e5; i++){\n string s = to_string(i) ;\n string t(s.rbegin(), s.rend()) ;\n int val = stoi(s + t.substr(1)) ;\n if(val >= n && isPrime(val))\n return val ;\n }\n return -1 ;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isPrime(self, num):\n from math import sqrt\n if num < 2 or num % 2 == 0:\n return num == 2\n for i in range(3, int(sqrt(num)) + 1, 2):\n if num % i == 0:\n return False\n return True\n\n def primePalindrome(self, n: int) -> int:\n if 8 <= n <= 11:\n return 11\n if len(str(n)) % 2 == 0:\n limit = pow(10, len(str(n)) // 2)\n else:\n n_string = str(n)\n limit = n_string[:len(str(n)) // 2 + 1]\n for i in range(int(limit), 20000):\n y = int(str(i) + str(i)[:-1][::-1])\n if y >= n and self.isPrime(y):\n return y\n```\n\n```Java []\nclass Solution {\n private int n;\n private int numDigits;\n private static ArrayList<Integer> primes;\n private static int lastChecked = 1;\n public int primePalindrome(int nInput) {\n n = nInput;\n if (n==1 || n==2){\n return 2;\n }\n if (n==4 || n==5){\n return 5;\n }\n if (primes == null){\n primes = new ArrayList<Integer>();\n primes.add(2);\n }\n numDigits = 1;\n while (n >= Math.pow(10, numDigits)){\n numDigits++;\n }\n if (numDigits%2 == 0 && n > 11){\n n = (int)Math.pow(10, numDigits)+1;\n numDigits++;\n }\n int msd = getDigit(numDigits);\n if (msd%2 == 0 || msd == 5){\n if (msd >= 4 && msd <= 6){\n msd = 7;\n } else {\n msd++;\n }\n n = msd;\n if (numDigits!=1){\n n+=msd * (int)Math.pow(10, numDigits-1);\n }\n } else {\n for (int i = (numDigits+1)/2; i > 0; i--){\n setDigit(i, getDigit(numDigits-i+1));\n }\n if (n < nInput){\n increment();\n }\n }\n while (!isPrime()){\n increment();\n }\n return n;\n }\n private int getDigit(int i) {\n return (n%(int)Math.pow(10, i))/(int)Math.pow(10, i-1);\n }\n private void setDigit(int i, int m) {\n int first = n-n%(int)Math.pow(10, numDigits-i+1);\n int middle = Math.max(0, n%(int)Math.pow(10, numDigits-i)\n - n%(int)Math.pow(10, i));\n int last = n%(int)Math.pow(10, i-1);\n n = first + middle + last + m*(int)Math.pow(10, i-1);\n if (i != numDigits-i+1){\n n += m*(int)Math.pow(10, numDigits-i);\n }\n }\n private void increment(){\n for (int i = (numDigits+1)/2; i > 0; i--){\n int curDigit = getDigit(i);\n if (i == 1 && curDigit == 9){\n if (numDigits == 1){\n n = 11;\n numDigits = 2;\n return;\n } else {\n n = (int)Math.pow(10, numDigits+1)+1;\n numDigits+=2;\n return;\n }\n } else if (curDigit == 9){\n setDigit(i, 0);\n } else {\n curDigit++;\n if (i == 1){\n if (curDigit%2 == 0 || curDigit == 5){\n if (curDigit >= 4 && curDigit <= 6){\n curDigit = 7;\n } else {\n curDigit++;\n }\n }\n }\n setDigit(i, curDigit);\n return;\n }\n }\n }\n private boolean isPrime() {\n int end = (int)Math.sqrt(n);\n for (int i = lastChecked+2; i <= end; i+=2){\n if (isPrimeLookup(i)){\n primes.add(i);\n }\n lastChecked = i;\n }\n return isPrimeLookup(n);\n }\n private boolean isPrimeLookup(int m){\n int end = (int)Math.sqrt(m);\n for (int i = 0; i < primes.size() && primes.get(i) <= end; i++){\n if (m%primes.get(i) == 0){\n return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Solution | prime-palindrome | 1 | 1 | ```C++ []\nclass Solution {\n bool isPrime(int val){\n if(val == 1 ) \n return false ;\n if(val == 2)\n return true ;\n int limit = sqrt(val) ;\n for(int i = 2; i <= limit; i++){\n if(val % i == 0)\n return false ;\n }\n return true ;\n }\npublic:\n int primePalindrome(int n) {\n if(n >= 8 && n <= 11)\n return 11 ;\n for(int i = 1; i <= 1e5; i++){\n string s = to_string(i) ;\n string t(s.rbegin(), s.rend()) ;\n int val = stoi(s + t.substr(1)) ;\n if(val >= n && isPrime(val))\n return val ;\n }\n return -1 ;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isPrime(self, num):\n from math import sqrt\n if num < 2 or num % 2 == 0:\n return num == 2\n for i in range(3, int(sqrt(num)) + 1, 2):\n if num % i == 0:\n return False\n return True\n\n def primePalindrome(self, n: int) -> int:\n if 8 <= n <= 11:\n return 11\n if len(str(n)) % 2 == 0:\n limit = pow(10, len(str(n)) // 2)\n else:\n n_string = str(n)\n limit = n_string[:len(str(n)) // 2 + 1]\n for i in range(int(limit), 20000):\n y = int(str(i) + str(i)[:-1][::-1])\n if y >= n and self.isPrime(y):\n return y\n```\n\n```Java []\nclass Solution {\n private int n;\n private int numDigits;\n private static ArrayList<Integer> primes;\n private static int lastChecked = 1;\n public int primePalindrome(int nInput) {\n n = nInput;\n if (n==1 || n==2){\n return 2;\n }\n if (n==4 || n==5){\n return 5;\n }\n if (primes == null){\n primes = new ArrayList<Integer>();\n primes.add(2);\n }\n numDigits = 1;\n while (n >= Math.pow(10, numDigits)){\n numDigits++;\n }\n if (numDigits%2 == 0 && n > 11){\n n = (int)Math.pow(10, numDigits)+1;\n numDigits++;\n }\n int msd = getDigit(numDigits);\n if (msd%2 == 0 || msd == 5){\n if (msd >= 4 && msd <= 6){\n msd = 7;\n } else {\n msd++;\n }\n n = msd;\n if (numDigits!=1){\n n+=msd * (int)Math.pow(10, numDigits-1);\n }\n } else {\n for (int i = (numDigits+1)/2; i > 0; i--){\n setDigit(i, getDigit(numDigits-i+1));\n }\n if (n < nInput){\n increment();\n }\n }\n while (!isPrime()){\n increment();\n }\n return n;\n }\n private int getDigit(int i) {\n return (n%(int)Math.pow(10, i))/(int)Math.pow(10, i-1);\n }\n private void setDigit(int i, int m) {\n int first = n-n%(int)Math.pow(10, numDigits-i+1);\n int middle = Math.max(0, n%(int)Math.pow(10, numDigits-i)\n - n%(int)Math.pow(10, i));\n int last = n%(int)Math.pow(10, i-1);\n n = first + middle + last + m*(int)Math.pow(10, i-1);\n if (i != numDigits-i+1){\n n += m*(int)Math.pow(10, numDigits-i);\n }\n }\n private void increment(){\n for (int i = (numDigits+1)/2; i > 0; i--){\n int curDigit = getDigit(i);\n if (i == 1 && curDigit == 9){\n if (numDigits == 1){\n n = 11;\n numDigits = 2;\n return;\n } else {\n n = (int)Math.pow(10, numDigits+1)+1;\n numDigits+=2;\n return;\n }\n } else if (curDigit == 9){\n setDigit(i, 0);\n } else {\n curDigit++;\n if (i == 1){\n if (curDigit%2 == 0 || curDigit == 5){\n if (curDigit >= 4 && curDigit <= 6){\n curDigit = 7;\n } else {\n curDigit++;\n }\n }\n }\n setDigit(i, curDigit);\n return;\n }\n }\n }\n private boolean isPrime() {\n int end = (int)Math.sqrt(n);\n for (int i = lastChecked+2; i <= end; i+=2){\n if (isPrimeLookup(i)){\n primes.add(i);\n }\n lastChecked = i;\n }\n return isPrimeLookup(n);\n }\n private boolean isPrimeLookup(int m){\n int end = (int)Math.sqrt(m);\n for (int i = 0; i < primes.size() && primes.get(i) <= end; i++){\n if (m%primes.get(i) == 0){\n return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Python Simple Solution | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1>Check if n is a palindrome. If it is, check if it is a prime number. If it is, return n.\n2>Otherwise, increment n by 1 and repeat step 1 until a palindrome prime is found.\n\n# Complexity\n- Time complexity:\nThe time complexity of this algorithm depends on the number of steps it takes to find a palindrome prime greater than or equal to n. The worst-case scenario is when n is a large prime number and the next palindrome prime is much large.\n\n- Space complexity:\nThe space complexity of this algorithm is O(1) .\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n#1 best \n def is_palindrome(x):\n return str(x) == str(x)[::-1]\n \n def is_prime(x):\n if x < 2:\n return False\n for i in range(2, int(x ** 0.5) + 1):\n if x % i == 0:\n return False\n return True\n \n while True:\n if is_palindrome(n) and is_prime(n):\n return n\n n += 1\n if 10**7 < n < 10**8:\n n = 10**8\n \n\n\n\n\n\n\n\n\n #2 TLE\n # def is_prime(number):\n # if number > 1:\n # for num in range(2, number):\n # if number % num == 0:\n # return False\n # return True\n # return False\n\n # n_str = str(n)\n # l = len(n_str) \n # for k in range(max(0, l//2-1), 5):\n # for i in range(10**k, 10**(k+1)): # odd length\n # i_str = str(i)\n # if k > 0 and i_str[0] in [\'2\',\'4\',\'5\',\'6\',\'8\']: continue # pruning\n # cur = i_str + i_str[-2::-1]\n # cur_int = int(cur)\n # if cur_int >= n and is_prime(cur_int): \n # return cur_int\n \n # for i in range(10**k, 10**(k+1)): # even length\n # i_str = str(i)\n # if i_str[0] in [\'2\',\'4\',\'5\',\'6\',\'8\']: continue # pruning\n # cur = i_str + i_str[::-1]\n # cur_int = int(cur)\n # if cur_int >= n and is_prime(cur_int): \n # return cur_int\n # return -1\n\n\n\n\n\n\n\n\n # #3 TLE\n # if 8 <= n <= 11: return 11\n # for x in range(10 ** (len(str(n))// 2), 10**5):\n # y = int(str(x) + str(x)[-2::-1])\n # if y >= n and is_prime(y): return y\n\n\n\n\n\n\n\n\n\n\n\n # #4 it gives TLE\n # res=n\n # c=1\n # while c:\n # if str(res)==str(res)[::-1] and is_prime(res)==True:\n # c=0\n # else:\n # res+=1\n # return res\n \n\n \n``` | 2 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Python Simple Solution | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1>Check if n is a palindrome. If it is, check if it is a prime number. If it is, return n.\n2>Otherwise, increment n by 1 and repeat step 1 until a palindrome prime is found.\n\n# Complexity\n- Time complexity:\nThe time complexity of this algorithm depends on the number of steps it takes to find a palindrome prime greater than or equal to n. The worst-case scenario is when n is a large prime number and the next palindrome prime is much large.\n\n- Space complexity:\nThe space complexity of this algorithm is O(1) .\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n#1 best \n def is_palindrome(x):\n return str(x) == str(x)[::-1]\n \n def is_prime(x):\n if x < 2:\n return False\n for i in range(2, int(x ** 0.5) + 1):\n if x % i == 0:\n return False\n return True\n \n while True:\n if is_palindrome(n) and is_prime(n):\n return n\n n += 1\n if 10**7 < n < 10**8:\n n = 10**8\n \n\n\n\n\n\n\n\n\n #2 TLE\n # def is_prime(number):\n # if number > 1:\n # for num in range(2, number):\n # if number % num == 0:\n # return False\n # return True\n # return False\n\n # n_str = str(n)\n # l = len(n_str) \n # for k in range(max(0, l//2-1), 5):\n # for i in range(10**k, 10**(k+1)): # odd length\n # i_str = str(i)\n # if k > 0 and i_str[0] in [\'2\',\'4\',\'5\',\'6\',\'8\']: continue # pruning\n # cur = i_str + i_str[-2::-1]\n # cur_int = int(cur)\n # if cur_int >= n and is_prime(cur_int): \n # return cur_int\n \n # for i in range(10**k, 10**(k+1)): # even length\n # i_str = str(i)\n # if i_str[0] in [\'2\',\'4\',\'5\',\'6\',\'8\']: continue # pruning\n # cur = i_str + i_str[::-1]\n # cur_int = int(cur)\n # if cur_int >= n and is_prime(cur_int): \n # return cur_int\n # return -1\n\n\n\n\n\n\n\n\n # #3 TLE\n # if 8 <= n <= 11: return 11\n # for x in range(10 ** (len(str(n))// 2), 10**5):\n # y = int(str(x) + str(x)[-2::-1])\n # if y >= n and is_prime(y): return y\n\n\n\n\n\n\n\n\n\n\n\n # #4 it gives TLE\n # res=n\n # c=1\n # while c:\n # if str(res)==str(res)[::-1] and is_prime(res)==True:\n # c=0\n # else:\n # res+=1\n # return res\n \n\n \n``` | 2 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Who did? GOD DID | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n if n>=9989900:\n return 100030001\n if n == 101101:\n return 1003001\n def is_prime(n):\n if n==1: return False\n x= 2\n while x <=int(n**0.5):\n if n % x == 0:\n return False\n x+=1\n return True\n while True:\n if is_prime(n) and str(n) == str(n)[::-1]:\n return n\n n+=1\n \n\n \n\n``` | 0 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Who did? GOD DID | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n if n>=9989900:\n return 100030001\n if n == 101101:\n return 1003001\n def is_prime(n):\n if n==1: return False\n x= 2\n while x <=int(n**0.5):\n if n % x == 0:\n return False\n x+=1\n return True\n while True:\n if is_prime(n) and str(n) == str(n)[::-1]:\n return n\n n+=1\n \n\n \n\n``` | 0 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Easiest Solution | prime-palindrome | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int primePalindrome(int n) {\n \n \n boolean l=false;\n\n if(n==1||n==0)\n return 2;\n\n\n while(l!=true)\n {\n\n if( n > 11 && n < 100 )\n {\n n = 101 ;\n }\n if( n > 999 && n < 10000 )\n {\n n = 10001 ;\n }\n if( n > 99999 && n < 1000000 )\n {\n n = 1000001 ;\n }\n if( n > 9999999 && n < 100000000 )\n {\n n = 100000001 ;\n }\n\n else if(pal(n)&&prime(n))\n break;\n\n else\n n++;\n\n }\n\n return n;\n\n }\n\n public static boolean prime(int N)\n {\n\n int i ;\n\n if( ( N & 1 ) == 0 && N != 2 )\n {\n return false ;\n }\n\n else if( N % 3 == 0 && N != 3 )\n {\n return false ;\n }\n\n else if( N % 11 == 0 && N != 11 )\n {\n return false ;\n }\n\n else if( N % 13 == 0 && N != 13 )\n {\n return false ;\n }\n\n else if( N % 17 == 0 && N != 17 )\n {\n return false ;\n }\n\n else\n {\n for( i = 3 ; i <= Math.sqrt(N) ; i += 2 )\n {\n if( N % i == 0 )\n {\n return false ;\n }\n }\n }\n\n return true ;\n\n }\n public static boolean pal(int u)\n {\n\n int z=Integer.toString(u).length()-1;\n int w=0;\n int ans=u;\n\n while(u>0)\n {\n\n int k=u%10;\n w=w+k*(int)Math.pow(10,z);\n z--;\n u=u/10;\n\n }\n\n if(w==ans)\n return true;\n\n else\n return false;\n\n }\n\n}\n```\n```c++ []\nclass Solution {\npublic:\n int primePalindrome(int n) {\n if(n==2|| n==1)return 2;\n if(n>=9989900)return 100030001;\n if(n%2==0)n++;\n while(!palin(n) ||!prime(n))n+=2;\n return n;\n }\n bool palin(int n){\n string s=to_string(n);\n int i=0,j=s.length();\n while(i<j){\n if(s[i]!=s[j-1])return false;\n i++;j--;\n }\n return true;\n }\n bool prime(int n){\n for(int i=2;i<=sqrt(n);i++){\n if(n%i==0)return false;\n }\n return true;\n }\n};\n```\n```python3 []\nclass Solution:\n def primePalindrome(self, N: int) -> int:\n \'\'\'\n 1. If N<=11, then the result is the first prime number greater than or equal N\n 2. If 11<N<=101, then the result is 101\n 3. Otherwise, there are no prime palindromes of even length\n 4. Let N is a x\' digit number. If x\' is even, then set N=10^x\'. Now N is x=x\'+1 digit number where x is odd. If x\' is odd, then don\'t change N and here x=x\'.\n 5. Starting from N, generate palindromes and check if it is prime\n 6. If not, then set N = value of first floor(x//2) digits + 1, and go back to step 4 and generate new palindromes from new N.\n \'\'\'\n \n def isPrime(n): \n i=3 #don\'t need to check any even number, so start checking from 3\n while i*i<=n: #if n is not prime, then it will be divisible by a number at most sqrt(n)\n if n%i==0:\n return False #has divisor, so not prime\n i+=2 #only check if there are odd divisors, as n is odd\n \n return True #n is prime\n \n if N==1 or N==2: #nearest prime number of N in {1,2} is 2 which is palindrome\n return 2\n \n elif N==3: #3 is a prime palindrome\n return 3\n \n elif N==4 or N==5: #nearest prime number of N in {4,5} is 5 which is palindrome\n return 5\n \n elif N==6 or N==7: #nearest prime number of N in {6,7} is 7 which is palindrome\n return 7\n \n elif N>7 and N<=11: #nearest prime number of N greater than 7 is 11 which is palindrome\n return 11\n \n elif N>11 and N<=101: #for all two digit numbers greater than 11, and for 100,101\n return 101 #nearest prime palindrome is 101\n \n start=(N+1)*(N%2==0)+N*(N%2==1) #prime number must be odd, so start checking from the odd number nearest to N\n len_string =len(str(start))\n str_N = str(start)\n \n if str_N==str_N[::-1] and isPrime(start): #if N or (N+1) is prime, then don\'t need to check further\n return start\n \n else: \n while(True):\n if len_string%2==0:\n start=10**(len_string) #convert even length starting number to odd length\n str_N=str(start) #store the string representation of starting number\n \n if int(str_N[0])%2==0: #if the first digit is even, then the palindrome will also be even\n start+=10**(len_string-1) #start from the nearest number whose first digit is odd \n str_N=str(start)\n \n if int(str_N[0])==5: #if the first digit is 5, then the palindrome is divisible by 5\n start=7*(10**(len_string-1)) #the nearest prime palindrome starts with 7 \n str_N=str(start)\n \n str_N = str_N[0:len_string//2]+str_N[len_string//2]+str_N[0:len_string//2][::-1] #create palindrome closest to starting number\n \n if int(str_N)>=N and isPrime(int(str_N)):\n return int(str_N) #got a palindrome greater than or equal N, return the palindrome\n else:\n start=int(str_N[0:len_string//2+1])+1 #increase the value of starting floor(len_string//2) digits by one \n start*=10**(len_string//2) #append necessary 0\'s to start and this will be the new starting position\n \n str_N=str(start) #convert start to string\n len_string=len(str_N) #store the length\n``` | 0 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Easiest Solution | prime-palindrome | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int primePalindrome(int n) {\n \n \n boolean l=false;\n\n if(n==1||n==0)\n return 2;\n\n\n while(l!=true)\n {\n\n if( n > 11 && n < 100 )\n {\n n = 101 ;\n }\n if( n > 999 && n < 10000 )\n {\n n = 10001 ;\n }\n if( n > 99999 && n < 1000000 )\n {\n n = 1000001 ;\n }\n if( n > 9999999 && n < 100000000 )\n {\n n = 100000001 ;\n }\n\n else if(pal(n)&&prime(n))\n break;\n\n else\n n++;\n\n }\n\n return n;\n\n }\n\n public static boolean prime(int N)\n {\n\n int i ;\n\n if( ( N & 1 ) == 0 && N != 2 )\n {\n return false ;\n }\n\n else if( N % 3 == 0 && N != 3 )\n {\n return false ;\n }\n\n else if( N % 11 == 0 && N != 11 )\n {\n return false ;\n }\n\n else if( N % 13 == 0 && N != 13 )\n {\n return false ;\n }\n\n else if( N % 17 == 0 && N != 17 )\n {\n return false ;\n }\n\n else\n {\n for( i = 3 ; i <= Math.sqrt(N) ; i += 2 )\n {\n if( N % i == 0 )\n {\n return false ;\n }\n }\n }\n\n return true ;\n\n }\n public static boolean pal(int u)\n {\n\n int z=Integer.toString(u).length()-1;\n int w=0;\n int ans=u;\n\n while(u>0)\n {\n\n int k=u%10;\n w=w+k*(int)Math.pow(10,z);\n z--;\n u=u/10;\n\n }\n\n if(w==ans)\n return true;\n\n else\n return false;\n\n }\n\n}\n```\n```c++ []\nclass Solution {\npublic:\n int primePalindrome(int n) {\n if(n==2|| n==1)return 2;\n if(n>=9989900)return 100030001;\n if(n%2==0)n++;\n while(!palin(n) ||!prime(n))n+=2;\n return n;\n }\n bool palin(int n){\n string s=to_string(n);\n int i=0,j=s.length();\n while(i<j){\n if(s[i]!=s[j-1])return false;\n i++;j--;\n }\n return true;\n }\n bool prime(int n){\n for(int i=2;i<=sqrt(n);i++){\n if(n%i==0)return false;\n }\n return true;\n }\n};\n```\n```python3 []\nclass Solution:\n def primePalindrome(self, N: int) -> int:\n \'\'\'\n 1. If N<=11, then the result is the first prime number greater than or equal N\n 2. If 11<N<=101, then the result is 101\n 3. Otherwise, there are no prime palindromes of even length\n 4. Let N is a x\' digit number. If x\' is even, then set N=10^x\'. Now N is x=x\'+1 digit number where x is odd. If x\' is odd, then don\'t change N and here x=x\'.\n 5. Starting from N, generate palindromes and check if it is prime\n 6. If not, then set N = value of first floor(x//2) digits + 1, and go back to step 4 and generate new palindromes from new N.\n \'\'\'\n \n def isPrime(n): \n i=3 #don\'t need to check any even number, so start checking from 3\n while i*i<=n: #if n is not prime, then it will be divisible by a number at most sqrt(n)\n if n%i==0:\n return False #has divisor, so not prime\n i+=2 #only check if there are odd divisors, as n is odd\n \n return True #n is prime\n \n if N==1 or N==2: #nearest prime number of N in {1,2} is 2 which is palindrome\n return 2\n \n elif N==3: #3 is a prime palindrome\n return 3\n \n elif N==4 or N==5: #nearest prime number of N in {4,5} is 5 which is palindrome\n return 5\n \n elif N==6 or N==7: #nearest prime number of N in {6,7} is 7 which is palindrome\n return 7\n \n elif N>7 and N<=11: #nearest prime number of N greater than 7 is 11 which is palindrome\n return 11\n \n elif N>11 and N<=101: #for all two digit numbers greater than 11, and for 100,101\n return 101 #nearest prime palindrome is 101\n \n start=(N+1)*(N%2==0)+N*(N%2==1) #prime number must be odd, so start checking from the odd number nearest to N\n len_string =len(str(start))\n str_N = str(start)\n \n if str_N==str_N[::-1] and isPrime(start): #if N or (N+1) is prime, then don\'t need to check further\n return start\n \n else: \n while(True):\n if len_string%2==0:\n start=10**(len_string) #convert even length starting number to odd length\n str_N=str(start) #store the string representation of starting number\n \n if int(str_N[0])%2==0: #if the first digit is even, then the palindrome will also be even\n start+=10**(len_string-1) #start from the nearest number whose first digit is odd \n str_N=str(start)\n \n if int(str_N[0])==5: #if the first digit is 5, then the palindrome is divisible by 5\n start=7*(10**(len_string-1)) #the nearest prime palindrome starts with 7 \n str_N=str(start)\n \n str_N = str_N[0:len_string//2]+str_N[len_string//2]+str_N[0:len_string//2][::-1] #create palindrome closest to starting number\n \n if int(str_N)>=N and isPrime(int(str_N)):\n return int(str_N) #got a palindrome greater than or equal N, return the palindrome\n else:\n start=int(str_N[0:len_string//2+1])+1 #increase the value of starting floor(len_string//2) digits by one \n start*=10**(len_string//2) #append necessary 0\'s to start and this will be the new starting position\n \n str_N=str(start) #convert start to string\n len_string=len(str_N) #store the length\n``` | 0 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Python 100%, Light | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import sqrt\nclass Solution:\n def isPrime(self, num):\n if num < 2 or num % 2 == 0:\n return num == 2\n for i in range(3, int(sqrt(num)) + 1, 2):\n if num % i == 0:\n return False\n return True\n def primePalindrome(self, n: int) -> int:\n if 8 <= n <= 11:\n return 11\n if len(str(n)) % 2 == 0:\n l = pow(10, len(str(n))//2)\n else:\n n_string = str(n)\n l = n_string[:len(str(n)) // 2 + 1]\n for i in range(int(l), 20000):\n tr = int(str(i)+ str(i)[:-1][::-1])\n if tr >= n and self.isPrime(tr):\n return tr\n``` | 0 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
Python 100%, Light | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import sqrt\nclass Solution:\n def isPrime(self, num):\n if num < 2 or num % 2 == 0:\n return num == 2\n for i in range(3, int(sqrt(num)) + 1, 2):\n if num % i == 0:\n return False\n return True\n def primePalindrome(self, n: int) -> int:\n if 8 <= n <= 11:\n return 11\n if len(str(n)) % 2 == 0:\n l = pow(10, len(str(n))//2)\n else:\n n_string = str(n)\n l = n_string[:len(str(n)) // 2 + 1]\n for i in range(int(l), 20000):\n tr = int(str(i)+ str(i)[:-1][::-1])\n if tr >= n and self.isPrime(tr):\n return tr\n``` | 0 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
by PRODONiK (py) | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n def isPrime(num: int) -> bool:\n if num < 2:\n return False\n for i in range(2, int(num ** 0.5) + 1):\n if num % i == 0:\n return False\n return True\n def reversion(num: int) -> bool:\n return str(num)[::-1] == str(num)\n if n <= 2:\n return 2\n while True:\n if reversion(n) and isPrime(n):\n return n\n n += 1\n if 10**7 < n < 10**8:\n n = 10**8\n \n\n\n``` | 0 | Given an integer n, return _the smallest **prime palindrome** greater than or equal to_ `n`.
An integer is **prime** if it has exactly two divisors: `1` and itself. Note that `1` is not a prime number.
* For example, `2`, `3`, `5`, `7`, `11`, and `13` are all primes.
An integer is a **palindrome** if it reads the same from left to right as it does from right to left.
* For example, `101` and `12321` are palindromes.
The test cases are generated so that the answer always exists and is in the range `[2, 2 * 108]`.
**Example 1:**
**Input:** n = 6
**Output:** 7
**Example 2:**
**Input:** n = 8
**Output:** 11
**Example 3:**
**Input:** n = 13
**Output:** 101
**Constraints:**
* `1 <= n <= 108` | null |
by PRODONiK (py) | prime-palindrome | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def primePalindrome(self, n: int) -> int:\n def isPrime(num: int) -> bool:\n if num < 2:\n return False\n for i in range(2, int(num ** 0.5) + 1):\n if num % i == 0:\n return False\n return True\n def reversion(num: int) -> bool:\n return str(num)[::-1] == str(num)\n if n <= 2:\n return 2\n while True:\n if reversion(n) and isPrime(n):\n return n\n n += 1\n if 10**7 < n < 10**8:\n n = 10**8\n \n\n\n``` | 0 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Easy transpose C/C++/Python->zip 1 line | transpose-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust the definition t[i][j]=m[j][i]\n# Approach\n<!-- Describe your approach to solving the problem. -->\nC/C++/Python codes are implemented.\n\nFor the reason of mallocating memory, the order for outer loop & inner loop in C code is different from others.\n\nPython can use zip to build a 1-line solution.\n\n[Please turn English subtitles if necessary]\n[https://youtu.be/DvD1r0IOxPQ?si=dv4dPKZqWdTd28FE](https://youtu.be/DvD1r0IOxPQ?si=dv4dPKZqWdTd28FE)\n\n# Why zip(*matrix) works?\nThe python `zip` function has the similar behavior like transpose!\n\nFor test case `marix=[[1,2,3],[4,5,6]]`\n\nConsider\n```\nrow=matrix[0]\nprint(*row)\n```\none has `1 2 3`\nApplying \n`print(*matrix)`\none has \n`[1, 2, 3] [4, 5, 6]`\nwhere each row is separated. Using `zip` to aggregate elements as tuples.\nFor example \n```\nx=[\'a\', \'b\', \'c\']\ny=[1, 2, 3]\nprint(list(zip(x, y)))\n```\nOne has\n```\n[(\'a\', 1), (\'b\', 2), (\'c\', 3)]\n```\nTherefor, on can obtain a 1-line code\n```\nreturn zip(*matrix)\n```\nIn a more precise way, it can be written by\n```\nreturn list(zip(*matrix))\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n int n=matrix.size(), m=matrix[0].size();\n vector<vector<int>> t(m, vector<int>(n));\n for(int i=0; i<n; i++)\n for(int j=0; j<m; j++)\n t[j][i]=matrix[i][j];\n return t;\n }\n};\n```\n# Python solution\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n n=len(matrix)\n m=len(matrix[0])\n t=[[0]*n for _ in range(m)]\n for i in range(n):\n for j in range(m):\n t[j][i]=matrix[i][j]\n return t\n\n```\n# C code\n```\n/**\n * Return an array of arrays of size *returnSize.\n * The sizes of the arrays are returned as *returnColumnSizes array.\n * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().\n */\n#pragma GCC optimize("O3", "unroll-loops")\nint** transpose(int** matrix, int n, int* col, int* returnSize, int** returnColumnSizes) {\n int m=*col;\n *returnSize=m;\n int** t=(int**)malloc(sizeof(int*)*m);\n *returnColumnSizes=(int*)malloc(sizeof(int)*m);\n for(register int i=0; i<m; i++){\n t[i]=(int*)malloc(sizeof(int)*n);\n (*returnColumnSizes)[i] = n;\n for(register int j=0; j<n; j++)\n t[i][j]=matrix[j][i];\n }\n return t;\n}\n```\n# Python 1 line\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n return zip(*matrix)\n```\n | 17 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Easy transpose C/C++/Python->zip 1 line | transpose-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust the definition t[i][j]=m[j][i]\n# Approach\n<!-- Describe your approach to solving the problem. -->\nC/C++/Python codes are implemented.\n\nFor the reason of mallocating memory, the order for outer loop & inner loop in C code is different from others.\n\nPython can use zip to build a 1-line solution.\n\n[Please turn English subtitles if necessary]\n[https://youtu.be/DvD1r0IOxPQ?si=dv4dPKZqWdTd28FE](https://youtu.be/DvD1r0IOxPQ?si=dv4dPKZqWdTd28FE)\n\n# Why zip(*matrix) works?\nThe python `zip` function has the similar behavior like transpose!\n\nFor test case `marix=[[1,2,3],[4,5,6]]`\n\nConsider\n```\nrow=matrix[0]\nprint(*row)\n```\none has `1 2 3`\nApplying \n`print(*matrix)`\none has \n`[1, 2, 3] [4, 5, 6]`\nwhere each row is separated. Using `zip` to aggregate elements as tuples.\nFor example \n```\nx=[\'a\', \'b\', \'c\']\ny=[1, 2, 3]\nprint(list(zip(x, y)))\n```\nOne has\n```\n[(\'a\', 1), (\'b\', 2), (\'c\', 3)]\n```\nTherefor, on can obtain a 1-line code\n```\nreturn zip(*matrix)\n```\nIn a more precise way, it can be written by\n```\nreturn list(zip(*matrix))\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n int n=matrix.size(), m=matrix[0].size();\n vector<vector<int>> t(m, vector<int>(n));\n for(int i=0; i<n; i++)\n for(int j=0; j<m; j++)\n t[j][i]=matrix[i][j];\n return t;\n }\n};\n```\n# Python solution\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n n=len(matrix)\n m=len(matrix[0])\n t=[[0]*n for _ in range(m)]\n for i in range(n):\n for j in range(m):\n t[j][i]=matrix[i][j]\n return t\n\n```\n# C code\n```\n/**\n * Return an array of arrays of size *returnSize.\n * The sizes of the arrays are returned as *returnColumnSizes array.\n * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().\n */\n#pragma GCC optimize("O3", "unroll-loops")\nint** transpose(int** matrix, int n, int* col, int* returnSize, int** returnColumnSizes) {\n int m=*col;\n *returnSize=m;\n int** t=(int**)malloc(sizeof(int*)*m);\n *returnColumnSizes=(int*)malloc(sizeof(int)*m);\n for(register int i=0; i<m; i++){\n t[i]=(int*)malloc(sizeof(int)*n);\n (*returnColumnSizes)[i] = n;\n for(register int j=0; j<n; j++)\n t[i][j]=matrix[j][i];\n }\n return t;\n}\n```\n# Python 1 line\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n return zip(*matrix)\n```\n | 17 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
【Video】Give me 5 minutes - 2 solutions - How we think about a solution. | transpose-matrix | 1 | 1 | # Intuition\nIterate the matrix vertically.\n\n# Approach\n\n---\n\n# Solution Video\n\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,401\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n## How we think about a solution.\n\n## Solution 1\n\nI think most people do like this.\n\n```python []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = [[0] * len(matrix) for _ in range(len(matrix[0]))]\n\n for r in range(len(matrix)):\n for c in range(len(matrix[0])):\n res[c][r] = matrix[r][c]\n \n return res\n```\n```javascript []\nvar transpose = function(matrix) {\n const res = Array.from({ length: matrix[0].length }, () => Array(matrix.length).fill(0));\n\n for (let r = 0; r < matrix.length; r++) {\n for (let c = 0; c < matrix[0].length; c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int[][] res = new int[matrix[0].length][matrix.length];\n\n for (int r = 0; r < matrix.length; r++) {\n for (int c = 0; c < matrix[0].length; c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n vector<vector<int>> res(matrix[0].size(), vector<int>(matrix.size(), 0));\n\n for (size_t r = 0; r < matrix.size(); r++) {\n for (size_t c = 0; c < matrix[0].size(); c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n }\n};\n```\n\nIf I write the same algorithm, it\'s boring. So I\'ll show you different way.\n(I explain an algorithm of this solution in the video)\n\n---\n\n## Solution 2\n\n\n\nLook at the picure carefully. What if we iterate the matrix vertically? We can create the target matrix.\n\n```\nLeft matrix\n\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n```\nWe iterate it vertically, so\n\n```\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [2, -10, 18]\n\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [4, 5, -7]\n\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [-1, 11, 6]\n```\nGet all arrays together we created\n```\nOutput:\n\n[2, -10, 18]\n[4, 5, -7]\n[-1, 11, 6]\n\n= right matrix in the picture\n```\n \nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n# Step by step Algorithm\n\n1. **Initialize an empty list for the result (`res`):**\n ```python\n res = []\n ```\n This list will hold the transposed matrix.\n\n2. **Iterate over each column of the input matrix:**\n ```python\n for c in range(len(matrix[0])):\n ```\n This outer loop iterates over each column of the input matrix. `c` represents the current column index.\n\n3. **Initialize a temporary list for the current transposed row (`temp`):**\n ```python\n temp = []\n ```\n This list will hold the elements of the current transposed row.\n\n4. **Iterate over each row of the input matrix:**\n ```python\n for r in range(len(matrix)):\n ```\n This inner loop iterates over each row of the input matrix. `r` represents the current row index.\n\n5. **Append the element at the current (r, c) position to the temporary list:**\n ```python\n temp.append(matrix[r][c])\n ```\n This line adds the element at the current position in the input matrix to the temporary list. This is a key step in transposing the matrix.\n\n6. **Append the temporary list (representing a transposed row) to the result:**\n ```python\n res.append(temp)\n ```\n After the inner loop completes for a specific column (`c`), the temporary list `temp` is added to the result `res`. This represents a transposed row.\n\n7. **Return the transposed matrix (`res`):**\n ```python\n return res\n ```\n After the outer loop completes for all columns, the transposed matrix is returned as the final result.\n\nIn summary, the algorithm transposes the input matrix by iterating over its columns and rows, creating a new matrix where the rows become columns and vice versa. The result is a transposed matrix.\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(r * c)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(r * c)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = []\n\n for c in range(len(matrix[0])):\n temp = []\n\n for r in range(len(matrix)):\n temp.append(matrix[r][c])\n\n res.append(temp)\n\n return res\n\n```\n```javascript []\nvar transpose = function(matrix) {\n const res = [];\n\n for (let c = 0; c < matrix[0].length; c++) {\n const temp = [];\n\n for (let r = 0; r < matrix.length; r++) {\n temp.push(matrix[r][c]);\n }\n\n res.push(temp);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n List<List<Integer>> resList = new ArrayList<>();\n\n for (int c = 0; c < matrix[0].length; c++) {\n List<Integer> temp = new ArrayList<>();\n\n for (int r = 0; r < matrix.length; r++) {\n temp.add(matrix[r][c]);\n }\n\n resList.add(temp);\n }\n\n // Convert List<List<Integer>> to int[][]\n int[][] res = new int[resList.size()][];\n for (int i = 0; i < resList.size(); i++) {\n List<Integer> row = resList.get(i);\n res[i] = row.stream().mapToInt(Integer::intValue).toArray();\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n vector<vector<int>> res;\n\n for (size_t c = 0; c < matrix[0].size(); c++) {\n vector<int> temp;\n\n for (size_t r = 0; r < matrix.size(); r++) {\n temp.push_back(matrix[r][c]);\n }\n\n res.push_back(temp);\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/solutions/4388310/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-tree-inorder-traversal/solutions/4380244/video-give-me-5-minutes-recursion-and-stackbonus-solution-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/TKMxiXRzDZ0\n\n\u25A0 Timeline\n`0:04` How to implement inorder, preorder and postorder\n`1:16` Coding (Recursive)\n`2:14` Time Complexity and Space Complexity\n`2:37` Explain Stack solution\n`7:22` Coding (Stack)\n`8:45` Time Complexity and Space Complexity\n`8:59` Step by step algorithm with my stack solution code\n\n | 28 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
【Video】Give me 5 minutes - 2 solutions - How we think about a solution. | transpose-matrix | 1 | 1 | # Intuition\nIterate the matrix vertically.\n\n# Approach\n\n---\n\n# Solution Video\n\nhttps://youtu.be/lsAZepsNRPo\n\n\u25A0 Timeline of the video\n\n`0:04` Explain algorithm of Solution 1\n`1:12` Coding of solution 1\n`2:30` Time Complexity and Space Complexity of solution 1\n`2:54` Explain algorithm of Solution 2\n`3:49` Coding of Solution 2\n`4:53` Time Complexity and Space Complexity of Solution 2\n`5:12` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,401\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n## How we think about a solution.\n\n## Solution 1\n\nI think most people do like this.\n\n```python []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = [[0] * len(matrix) for _ in range(len(matrix[0]))]\n\n for r in range(len(matrix)):\n for c in range(len(matrix[0])):\n res[c][r] = matrix[r][c]\n \n return res\n```\n```javascript []\nvar transpose = function(matrix) {\n const res = Array.from({ length: matrix[0].length }, () => Array(matrix.length).fill(0));\n\n for (let r = 0; r < matrix.length; r++) {\n for (let c = 0; c < matrix[0].length; c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int[][] res = new int[matrix[0].length][matrix.length];\n\n for (int r = 0; r < matrix.length; r++) {\n for (int c = 0; c < matrix[0].length; c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n vector<vector<int>> res(matrix[0].size(), vector<int>(matrix.size(), 0));\n\n for (size_t r = 0; r < matrix.size(); r++) {\n for (size_t c = 0; c < matrix[0].size(); c++) {\n res[c][r] = matrix[r][c];\n }\n }\n\n return res; \n }\n};\n```\n\nIf I write the same algorithm, it\'s boring. So I\'ll show you different way.\n(I explain an algorithm of this solution in the video)\n\n---\n\n## Solution 2\n\n\n\nLook at the picure carefully. What if we iterate the matrix vertically? We can create the target matrix.\n\n```\nLeft matrix\n\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n```\nWe iterate it vertically, so\n\n```\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [2, -10, 18]\n\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [4, 5, -7]\n\n \u2193\n[2, 4, -1]\n[-10, 5, 11]\n[18, -7, 6]\n\nWe can create [-1, 11, 6]\n```\nGet all arrays together we created\n```\nOutput:\n\n[2, -10, 18]\n[4, 5, -7]\n[-1, 11, 6]\n\n= right matrix in the picture\n```\n \nEasy!\uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n# Step by step Algorithm\n\n1. **Initialize an empty list for the result (`res`):**\n ```python\n res = []\n ```\n This list will hold the transposed matrix.\n\n2. **Iterate over each column of the input matrix:**\n ```python\n for c in range(len(matrix[0])):\n ```\n This outer loop iterates over each column of the input matrix. `c` represents the current column index.\n\n3. **Initialize a temporary list for the current transposed row (`temp`):**\n ```python\n temp = []\n ```\n This list will hold the elements of the current transposed row.\n\n4. **Iterate over each row of the input matrix:**\n ```python\n for r in range(len(matrix)):\n ```\n This inner loop iterates over each row of the input matrix. `r` represents the current row index.\n\n5. **Append the element at the current (r, c) position to the temporary list:**\n ```python\n temp.append(matrix[r][c])\n ```\n This line adds the element at the current position in the input matrix to the temporary list. This is a key step in transposing the matrix.\n\n6. **Append the temporary list (representing a transposed row) to the result:**\n ```python\n res.append(temp)\n ```\n After the inner loop completes for a specific column (`c`), the temporary list `temp` is added to the result `res`. This represents a transposed row.\n\n7. **Return the transposed matrix (`res`):**\n ```python\n return res\n ```\n After the outer loop completes for all columns, the transposed matrix is returned as the final result.\n\nIn summary, the algorithm transposes the input matrix by iterating over its columns and rows, creating a new matrix where the rows become columns and vice versa. The result is a transposed matrix.\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(r * c)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(r * c)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = []\n\n for c in range(len(matrix[0])):\n temp = []\n\n for r in range(len(matrix)):\n temp.append(matrix[r][c])\n\n res.append(temp)\n\n return res\n\n```\n```javascript []\nvar transpose = function(matrix) {\n const res = [];\n\n for (let c = 0; c < matrix[0].length; c++) {\n const temp = [];\n\n for (let r = 0; r < matrix.length; r++) {\n temp.push(matrix[r][c]);\n }\n\n res.push(temp);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n List<List<Integer>> resList = new ArrayList<>();\n\n for (int c = 0; c < matrix[0].length; c++) {\n List<Integer> temp = new ArrayList<>();\n\n for (int r = 0; r < matrix.length; r++) {\n temp.add(matrix[r][c]);\n }\n\n resList.add(temp);\n }\n\n // Convert List<List<Integer>> to int[][]\n int[][] res = new int[resList.size()][];\n for (int i = 0; i < resList.size(); i++) {\n List<Integer> row = resList.get(i);\n res[i] = row.stream().mapToInt(Integer::intValue).toArray();\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n vector<vector<int>> res;\n\n for (size_t c = 0; c < matrix[0].size(); c++) {\n vector<int> temp;\n\n for (size_t r = 0; r < matrix.size(); r++) {\n temp.push_back(matrix[r][c]);\n }\n\n res.push_back(temp);\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/solutions/4388310/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/binary-tree-inorder-traversal/solutions/4380244/video-give-me-5-minutes-recursion-and-stackbonus-solution-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/TKMxiXRzDZ0\n\n\u25A0 Timeline\n`0:04` How to implement inorder, preorder and postorder\n`1:16` Coding (Recursive)\n`2:14` Time Complexity and Space Complexity\n`2:37` Explain Stack solution\n`7:22` Coding (Stack)\n`8:45` Time Complexity and Space Complexity\n`8:59` Step by step algorithm with my stack solution code\n\n | 28 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
🚀🚀 867. 𝕿𝖗𝖆𝖓𝖘𝖕𝖔𝖘𝖊 𝕸𝖆𝖙𝖗𝖎𝖝 | 𝕭𝖊𝖆𝖙𝖘 100% | 𝕱𝖚𝖑𝖑𝖞 𝕰𝖝𝖕𝖑𝖆𝖎𝖓𝖊𝖉 🔥💖 | transpose-matrix | 1 | 1 | # Intuition\nThe task is to find the transpose of a given matrix, which is like doing a dance move with the rows and columns, switching their positions. Imagine a joyful matrix flip!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. \uD83D\uDD75\uFE0F\u200D\u2642\uFE0F **Investigate the Matrix Dimensions:** Identify the number of rows and columns in the original matrix and save them as `row` and `col`, respectively.\n2. \uD83C\uDFA8 **Create a Blank Canvas:** Set up a new matrix called `Transpose` with dimensions `col x row` to serve as our artistic canvas for the transposed matrix. Fill it with a placeholder value (e.g., -1).\n3. \uD83D\uDE80 **Launch the Loop Rocket:** Use nested loops to traverse the elements of the original matrix.\n4. \uD83D\uDD04 **Swap the Rows and Columns:** Within the loops, perform a magical switch by assigning the value at `matrix[j][i]` to `Transpose[i][j]`.\n5. \uD83C\uDFAD **Admire the Art:** Behold! The transposed matrix is now a beautiful creation.\n6. \uD83C\uDF89 **Showcase the Masterpiece:** Present the transposed matrix to the world with a triumphant return.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nvector<vector<int>> transpose(vector<vector<int>>& matrix) {\n // \uD83D\uDD75\uFE0F\u200D\u2642\uFE0F Get the number of rows and columns in the original matrix\n int row = matrix.size();\n int col = matrix[0].size();\n\n // \uD83C\uDFA8 Create a new matrix to store the transposed matrix\n vector<vector<int>> Transpose(col, vector<int>(row, -1));\n\n // \uD83D\uDE80 Iterate over the elements of the original matrix\n for(int i = 0; i < col; i++)\n {\n for(int j = 0; j < row; j++)\n {\n // \uD83D\uDD04 Swap rows and columns to get the transposed matrix\n Transpose[i][j] = matrix[j][i];\n }\n }\n\n // \uD83C\uDF89 Return the transposed matrix\n return Transpose;\n}\n```\n\n | 3 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
🚀🚀 867. 𝕿𝖗𝖆𝖓𝖘𝖕𝖔𝖘𝖊 𝕸𝖆𝖙𝖗𝖎𝖝 | 𝕭𝖊𝖆𝖙𝖘 100% | 𝕱𝖚𝖑𝖑𝖞 𝕰𝖝𝖕𝖑𝖆𝖎𝖓𝖊𝖉 🔥💖 | transpose-matrix | 1 | 1 | # Intuition\nThe task is to find the transpose of a given matrix, which is like doing a dance move with the rows and columns, switching their positions. Imagine a joyful matrix flip!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. \uD83D\uDD75\uFE0F\u200D\u2642\uFE0F **Investigate the Matrix Dimensions:** Identify the number of rows and columns in the original matrix and save them as `row` and `col`, respectively.\n2. \uD83C\uDFA8 **Create a Blank Canvas:** Set up a new matrix called `Transpose` with dimensions `col x row` to serve as our artistic canvas for the transposed matrix. Fill it with a placeholder value (e.g., -1).\n3. \uD83D\uDE80 **Launch the Loop Rocket:** Use nested loops to traverse the elements of the original matrix.\n4. \uD83D\uDD04 **Swap the Rows and Columns:** Within the loops, perform a magical switch by assigning the value at `matrix[j][i]` to `Transpose[i][j]`.\n5. \uD83C\uDFAD **Admire the Art:** Behold! The transposed matrix is now a beautiful creation.\n6. \uD83C\uDF89 **Showcase the Masterpiece:** Present the transposed matrix to the world with a triumphant return.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nvector<vector<int>> transpose(vector<vector<int>>& matrix) {\n // \uD83D\uDD75\uFE0F\u200D\u2642\uFE0F Get the number of rows and columns in the original matrix\n int row = matrix.size();\n int col = matrix[0].size();\n\n // \uD83C\uDFA8 Create a new matrix to store the transposed matrix\n vector<vector<int>> Transpose(col, vector<int>(row, -1));\n\n // \uD83D\uDE80 Iterate over the elements of the original matrix\n for(int i = 0; i < col; i++)\n {\n for(int j = 0; j < row; j++)\n {\n // \uD83D\uDD04 Swap rows and columns to get the transposed matrix\n Transpose[i][j] = matrix[j][i];\n }\n }\n\n // \uD83C\uDF89 Return the transposed matrix\n return Transpose;\n}\n```\n\n | 3 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Straightforward transpose! | transpose-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = [[0 for _ in range(len(matrix))] for _ in range(len(matrix[0]))]\n #print(res)\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n res[j][i]=matrix[i][j]\n return res\n \n``` | 3 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Straightforward transpose! | transpose-matrix | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n res = [[0 for _ in range(len(matrix))] for _ in range(len(matrix[0]))]\n #print(res)\n for i in range(len(matrix)):\n for j in range(len(matrix[0])):\n res[j][i]=matrix[i][j]\n return res\n \n``` | 3 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || EXPLAINED🔥 | transpose-matrix | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n1. **Input:** It takes a 2D vector `matrix` as input, representing the original matrix.\n\n1. **Output:** Returns a new 2D vector `ans`, which stores the transposed elements.\n\n1. **Transposing the Matrix:** It iterates through the original matrix, assigning the transposed elements (swapping row and column indices) to the new matrix `ans`.\n\n1. **Variables:**\n\n - `row` and `col`: Store the number of rows and columns in the original matrix, respectively.\n - `ans`: Represents the matrix to store the transposed elements, with dimensions `col` x `row`.\n1. Return: Finally, it returns the transposed matrix `ans`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(row*col)$$\n \n\n- *Space complexity:*\n $$O(row*col)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n // Function to compute the transpose of a given matrix\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n int row = matrix.size(); // Get the number of rows in the original matrix\n int col = matrix[0].size(); // Get the number of columns in the original matrix\n\n // Create a new matrix to store the transposed elements\n vector<vector<int>> ans(col, vector<int>(row)); // New matrix with dimensions col x row\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to compute the transpose of a given matrix\nint** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes) {\n int row = matrixSize; // Get the number of rows in the original matrix\n int col = *matrixColSize; // Get the number of columns in the original matrix\n\n // Create a new matrix to store the transposed elements\n int** ans = (int**)malloc(col * sizeof(int*)); // Allocate memory for rows\n *returnSize = col; // Set returnSize to the number of columns in the transposed matrix\n\n // Create and initialize the returnColumnSizes array\n *returnColumnSizes = (int*)malloc(col * sizeof(int));\n for (int i = 0; i < col; i++) {\n (*returnColumnSizes)[i] = row; // Each column will have \'row\' elements\n ans[i] = (int*)malloc(row * sizeof(int)); // Allocate memory for each row\n }\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n}\n\n\n\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int row = matrix.length;\n int col = matrix[0].length;\n\n // Create a new matrix to store the transposed elements\n int[][] ans = new int[col][row]; // New matrix with dimensions col x row\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n row = len(matrix)\n col = len(matrix[0])\n\n # Create a new matrix to store the transposed elements\n ans = [[0 for _ in range(row)] for _ in range(col)] # New matrix with dimensions col x row\n\n # Traverse through the original matrix\n for i in range(row):\n for j in range(col):\n # Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j] # Transpose by swapping row and column indices\n\n return ans # Return the transposed matrix\n\n\n\n```\n```javascript []\nfunction transpose(matrix) {\n const row = matrix.length;\n const col = matrix[0].length;\n\n // Create a new matrix to store the transposed elements\n const ans = Array.from({ length: col }, () => Array(row).fill(0));\n\n // Traverse through the original matrix\n for (let i = 0; i < row; i++) {\n for (let j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n\n return ans; // Return the transposed matrix\n}\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || EXPLAINED🔥 | transpose-matrix | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n1. **Input:** It takes a 2D vector `matrix` as input, representing the original matrix.\n\n1. **Output:** Returns a new 2D vector `ans`, which stores the transposed elements.\n\n1. **Transposing the Matrix:** It iterates through the original matrix, assigning the transposed elements (swapping row and column indices) to the new matrix `ans`.\n\n1. **Variables:**\n\n - `row` and `col`: Store the number of rows and columns in the original matrix, respectively.\n - `ans`: Represents the matrix to store the transposed elements, with dimensions `col` x `row`.\n1. Return: Finally, it returns the transposed matrix `ans`.\n\n\n# Complexity\n- *Time complexity:*\n $$O(row*col)$$\n \n\n- *Space complexity:*\n $$O(row*col)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n // Function to compute the transpose of a given matrix\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n int row = matrix.size(); // Get the number of rows in the original matrix\n int col = matrix[0].size(); // Get the number of columns in the original matrix\n\n // Create a new matrix to store the transposed elements\n vector<vector<int>> ans(col, vector<int>(row)); // New matrix with dimensions col x row\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n }\n};\n\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to compute the transpose of a given matrix\nint** transpose(int** matrix, int matrixSize, int* matrixColSize, int* returnSize, int** returnColumnSizes) {\n int row = matrixSize; // Get the number of rows in the original matrix\n int col = *matrixColSize; // Get the number of columns in the original matrix\n\n // Create a new matrix to store the transposed elements\n int** ans = (int**)malloc(col * sizeof(int*)); // Allocate memory for rows\n *returnSize = col; // Set returnSize to the number of columns in the transposed matrix\n\n // Create and initialize the returnColumnSizes array\n *returnColumnSizes = (int*)malloc(col * sizeof(int));\n for (int i = 0; i < col; i++) {\n (*returnColumnSizes)[i] = row; // Each column will have \'row\' elements\n ans[i] = (int*)malloc(row * sizeof(int)); // Allocate memory for each row\n }\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n}\n\n\n\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.List;\n\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int row = matrix.length;\n int col = matrix[0].length;\n\n // Create a new matrix to store the transposed elements\n int[][] ans = new int[col][row]; // New matrix with dimensions col x row\n\n // Traverse through the original matrix\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n return ans; // Return the transposed matrix\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n row = len(matrix)\n col = len(matrix[0])\n\n # Create a new matrix to store the transposed elements\n ans = [[0 for _ in range(row)] for _ in range(col)] # New matrix with dimensions col x row\n\n # Traverse through the original matrix\n for i in range(row):\n for j in range(col):\n # Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j] # Transpose by swapping row and column indices\n\n return ans # Return the transposed matrix\n\n\n\n```\n```javascript []\nfunction transpose(matrix) {\n const row = matrix.length;\n const col = matrix[0].length;\n\n // Create a new matrix to store the transposed elements\n const ans = Array.from({ length: col }, () => Array(row).fill(0));\n\n // Traverse through the original matrix\n for (let i = 0; i < row; i++) {\n for (let j = 0; j < col; j++) {\n // Assign transposed elements to the new matrix\n ans[j][i] = matrix[i][j]; // Transpose by swapping row and column indices\n }\n }\n\n return ans; // Return the transposed matrix\n}\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Python3 Solution | transpose-matrix | 0 | 1 | \n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n n=len(matrix)\n m=len(matrix[0])\n ans=[[0]*n for _ in range(m)]\n for i in range(m):\n for j in range(n):\n ans[i][j]=matrix[j][i]\n return ans \n \n``` | 2 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
Python3 Solution | transpose-matrix | 0 | 1 | \n```\nclass Solution:\n def transpose(self, matrix: List[List[int]]) -> List[List[int]]:\n n=len(matrix)\n m=len(matrix[0])\n ans=[[0]*n for _ in range(m)]\n for i in range(m):\n for j in range(n):\n ans[i][j]=matrix[j][i]\n return ans \n \n``` | 2 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
🔥|| BEGINNER FRIENDLY || EXPLAINED || 9ms || OPTIMAL || 🔥 | transpose-matrix | 1 | 1 | # INTUTION\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCertainly! Here\'s an explanation of the provided C++ code in points:\n\n**Algorithm: Transpose Matrix**\n\n1. **Input:**\n - `matrix`: a 2D vector representing the original matrix.\n\n2. **Initialize Variables:**\n - `n`: Number of rows in the original matrix (`matrix.size()`).\n - `m`: Number of columns in the original matrix (`matrix[0].size()`).\n\n3. **Create Transposed Matrix:**\n - Initialize a new 2D vector (`ans`) with dimensions swapped (`m` rows and `n` columns) to store the transposed matrix.\n - `vector<vector<int>> ans(m, vector<int>(n, 0));`\n\n4. **Transpose the Matrix:**\n - Use nested loops to iterate over each element in the original matrix.\n - Swap the row and column indices during assignment to the transposed matrix.\n ```cpp\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < m; ++j) {\n ans[j][i] = matrix[i][j];\n }\n }\n ```\n\n5. **Return Transposed Matrix:**\n - Return the transposed matrix (`ans`) as the result.\n - `return ans;`\n\n\n\nThe provided C++ code follows a similar approach to the Python solution, efficiently transposing the input matrix and returning the transposed result. The use of nested loops and swapping row and column indices is a common strategy for solving this problem.\n\n# Complexity\n- Time complexity: O(m * n), where m is the number of rows and n is the number of columns in the matrix. Each element needs to be visited once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m * n), as a new matrix of the transposed dimensions is created.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n\n int n=matrix.size();\n int m=matrix[0].size(); // no. of rows\n\n vector<vector<int>>ans(m,vector<int>(n,0));\n\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n\n ans[j][i]=matrix[i][j];\n \n }\n }\n return ans;\n \n }\n};\n```\n```python []\nclass Solution(object):\n def transpose(self, matrix):\n row = len(matrix)\n col = len(matrix[0])\n result = [[0] * row for _ in range(col)]\n \n for i in range(col):\n for j in range(row):\n result[i][j] = matrix[j][i]\n \n return result\n \n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int row=matrix.length;\n int col=matrix[0].length;\n int arr[][]=new int[col][row];\n for(int i=0;i<col;i++)\n {\n for(int j=0;j<row;j++)\n {\n arr[i][j]=matrix[j][i];\n }\n }\n return arr;\n }\n}\n```\n | 2 | Given a 2D integer array `matrix`, return _the **transpose** of_ `matrix`.
The **transpose** of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
**Example 1:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\],\[7,8,9\]\]
**Output:** \[\[1,4,7\],\[2,5,8\],\[3,6,9\]\]
**Example 2:**
**Input:** matrix = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\[1,4\],\[2,5\],\[3,6\]\]
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `-109 <= matrix[i][j] <= 109` | null |
🔥|| BEGINNER FRIENDLY || EXPLAINED || 9ms || OPTIMAL || 🔥 | transpose-matrix | 1 | 1 | # INTUTION\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCertainly! Here\'s an explanation of the provided C++ code in points:\n\n**Algorithm: Transpose Matrix**\n\n1. **Input:**\n - `matrix`: a 2D vector representing the original matrix.\n\n2. **Initialize Variables:**\n - `n`: Number of rows in the original matrix (`matrix.size()`).\n - `m`: Number of columns in the original matrix (`matrix[0].size()`).\n\n3. **Create Transposed Matrix:**\n - Initialize a new 2D vector (`ans`) with dimensions swapped (`m` rows and `n` columns) to store the transposed matrix.\n - `vector<vector<int>> ans(m, vector<int>(n, 0));`\n\n4. **Transpose the Matrix:**\n - Use nested loops to iterate over each element in the original matrix.\n - Swap the row and column indices during assignment to the transposed matrix.\n ```cpp\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < m; ++j) {\n ans[j][i] = matrix[i][j];\n }\n }\n ```\n\n5. **Return Transposed Matrix:**\n - Return the transposed matrix (`ans`) as the result.\n - `return ans;`\n\n\n\nThe provided C++ code follows a similar approach to the Python solution, efficiently transposing the input matrix and returning the transposed result. The use of nested loops and swapping row and column indices is a common strategy for solving this problem.\n\n# Complexity\n- Time complexity: O(m * n), where m is the number of rows and n is the number of columns in the matrix. Each element needs to be visited once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m * n), as a new matrix of the transposed dimensions is created.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> transpose(vector<vector<int>>& matrix) {\n\n int n=matrix.size();\n int m=matrix[0].size(); // no. of rows\n\n vector<vector<int>>ans(m,vector<int>(n,0));\n\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n\n ans[j][i]=matrix[i][j];\n \n }\n }\n return ans;\n \n }\n};\n```\n```python []\nclass Solution(object):\n def transpose(self, matrix):\n row = len(matrix)\n col = len(matrix[0])\n result = [[0] * row for _ in range(col)]\n \n for i in range(col):\n for j in range(row):\n result[i][j] = matrix[j][i]\n \n return result\n \n```\n```java []\nclass Solution {\n public int[][] transpose(int[][] matrix) {\n int row=matrix.length;\n int col=matrix[0].length;\n int arr[][]=new int[col][row];\n for(int i=0;i<col;i++)\n {\n for(int j=0;j<row;j++)\n {\n arr[i][j]=matrix[j][i];\n }\n }\n return arr;\n }\n}\n```\n | 2 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.