title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | profitable-schemes | 1 | 1 | ```C++ []\nconstexpr int MAX = 128;\nconstexpr int MOD = 1000000007;\nint sum[MAX], dp[MAX][MAX];\nint Add(int a, int b, int p = MOD) {\n int c = a + b;\n return c < p ? c : c - p;\n}\nint Sub(int a, int b, int p = MOD) {\n int c = a - b;\n return c < 0 ? c + p : c;\n}\nclass Solution {\npublic:\n int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {\n int m = group.size(), p = minProfit - 1, ret = 0;\n memset(sum, 0, sizeof(sum));\n memset(dp, 0, sizeof(dp));\n sum[0] = 1;\n dp[0][0] = 1;\n for (int i = 0; i < m; ++i) {\n int v = group[i], w = profit[i];\n for (int j = n; j >= v; --j) {\n sum[j] = Add(sum[j], sum[j - v]);\n for (int k = p; k >= w; --k) {\n dp[j][k] = Add(dp[j][k], dp[j - v][k - w]);\n }\n }\n }\n for (int i = 0; i <= n; ++i) {\n int cur = sum[i];\n for (int j = 0; j <= p; ++j) {\n cur = Sub(cur, dp[i][j]);\n }\n ret = Add(ret, cur);\n }\n return ret;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n mod = 1000000007\n dp = [[0]*(n+1) for i in range(minProfit+1)]\n dp[0][0] = 1\n for g,p in zip(group,profit):\n for j in range(n,g-1,-1):\n dp[minProfit][j] += dp[minProfit][j-g]\n for i in range(max(0,minProfit-p),minProfit):\n for j in range(g,n+1):\n dp[minProfit][j] += dp[i][j-g]\n for i in range(minProfit-1,p-1,-1):\n dp[i][g:] = [(x+y) for x,y in zip(dp[i][g:],dp[i-p])]\n return sum(dp[minProfit])%mod\n```\n\n```Java []\nclass Solution {\n private static final long MOD = 1_000_000_007L;\n public int profitableSchemes(int n, int m, int[] group, int[] profit) {\n long[][] dp = new long[n + 1][m + 1];\n dp[0][0] = 1;\n for (int i = 0; i < group.length; i++) {\n int g = group[i], p = profit[i];\n for (int j = n - g; j >= 0; j--) {\n for (int k = m; k >= 0; k--) {\n dp[j + g][Math.min(k + p, m)] += dp[j][k];\n }\n }\n for (int j = 0; j <= n; j++) dp[j][m] %= MOD;\n }\n long res = 0L;\n for (int j = 0; j <= n; j++) res = (res + dp[j][m]) % MOD;\n return (int) res;\n }\n}\n```\n | 1 | There is a group of `n` members, and a list of various crimes they could commit. The `ith` crime generates a `profit[i]` and requires `group[i]` members to participate in it. If a member participates in one crime, that member can't participate in another crime.
Let's call a **profitable scheme** any subset of these crimes that generates at least `minProfit` profit, and the total number of members participating in that subset of crimes is at most `n`.
Return the number of schemes that can be chosen. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, minProfit = 3, group = \[2,2\], profit = \[2,3\]
**Output:** 2
**Explanation:** To make a profit of at least 3, the group could either commit crimes 0 and 1, or just crime 1.
In total, there are 2 schemes.
**Example 2:**
**Input:** n = 10, minProfit = 5, group = \[2,3,5\], profit = \[6,7,8\]
**Output:** 7
**Explanation:** To make a profit of at least 5, the group could commit any crimes, as long as they commit one.
There are 7 possible schemes: (0), (1), (2), (0,1), (0,2), (1,2), and (0,1,2).
**Constraints:**
* `1 <= n <= 100`
* `0 <= minProfit <= 100`
* `1 <= group.length <= 100`
* `1 <= group[i] <= 100`
* `profit.length == group.length`
* `0 <= profit[i] <= 100` | null |
Solution | profitable-schemes | 1 | 1 | ```C++ []\nconstexpr int MAX = 128;\nconstexpr int MOD = 1000000007;\nint sum[MAX], dp[MAX][MAX];\nint Add(int a, int b, int p = MOD) {\n int c = a + b;\n return c < p ? c : c - p;\n}\nint Sub(int a, int b, int p = MOD) {\n int c = a - b;\n return c < 0 ? c + p : c;\n}\nclass Solution {\npublic:\n int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {\n int m = group.size(), p = minProfit - 1, ret = 0;\n memset(sum, 0, sizeof(sum));\n memset(dp, 0, sizeof(dp));\n sum[0] = 1;\n dp[0][0] = 1;\n for (int i = 0; i < m; ++i) {\n int v = group[i], w = profit[i];\n for (int j = n; j >= v; --j) {\n sum[j] = Add(sum[j], sum[j - v]);\n for (int k = p; k >= w; --k) {\n dp[j][k] = Add(dp[j][k], dp[j - v][k - w]);\n }\n }\n }\n for (int i = 0; i <= n; ++i) {\n int cur = sum[i];\n for (int j = 0; j <= p; ++j) {\n cur = Sub(cur, dp[i][j]);\n }\n ret = Add(ret, cur);\n }\n return ret;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n mod = 1000000007\n dp = [[0]*(n+1) for i in range(minProfit+1)]\n dp[0][0] = 1\n for g,p in zip(group,profit):\n for j in range(n,g-1,-1):\n dp[minProfit][j] += dp[minProfit][j-g]\n for i in range(max(0,minProfit-p),minProfit):\n for j in range(g,n+1):\n dp[minProfit][j] += dp[i][j-g]\n for i in range(minProfit-1,p-1,-1):\n dp[i][g:] = [(x+y) for x,y in zip(dp[i][g:],dp[i-p])]\n return sum(dp[minProfit])%mod\n```\n\n```Java []\nclass Solution {\n private static final long MOD = 1_000_000_007L;\n public int profitableSchemes(int n, int m, int[] group, int[] profit) {\n long[][] dp = new long[n + 1][m + 1];\n dp[0][0] = 1;\n for (int i = 0; i < group.length; i++) {\n int g = group[i], p = profit[i];\n for (int j = n - g; j >= 0; j--) {\n for (int k = m; k >= 0; k--) {\n dp[j + g][Math.min(k + p, m)] += dp[j][k];\n }\n }\n for (int j = 0; j <= n; j++) dp[j][m] %= MOD;\n }\n long res = 0L;\n for (int j = 0; j <= n; j++) res = (res + dp[j][m]) % MOD;\n return (int) res;\n }\n}\n```\n | 1 | You are given two integer arrays `persons` and `times`. In an election, the `ith` vote was cast for `persons[i]` at time `times[i]`.
For each query at a time `t`, find the person that was leading the election at time `t`. Votes cast at time `t` will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.
Implement the `TopVotedCandidate` class:
* `TopVotedCandidate(int[] persons, int[] times)` Initializes the object with the `persons` and `times` arrays.
* `int q(int t)` Returns the number of the person that was leading the election at time `t` according to the mentioned rules.
**Example 1:**
**Input**
\[ "TopVotedCandidate ", "q ", "q ", "q ", "q ", "q ", "q "\]
\[\[\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]\], \[3\], \[12\], \[25\], \[15\], \[24\], \[8\]\]
**Output**
\[null, 0, 1, 1, 0, 0, 1\]
**Explanation**
TopVotedCandidate topVotedCandidate = new TopVotedCandidate(\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]);
topVotedCandidate.q(3); // return 0, At time 3, the votes are \[0\], and 0 is leading.
topVotedCandidate.q(12); // return 1, At time 12, the votes are \[0,1,1\], and 1 is leading.
topVotedCandidate.q(25); // return 1, At time 25, the votes are \[0,1,1,0,0,1\], and 1 is leading (as ties go to the most recent vote.)
topVotedCandidate.q(15); // return 0
topVotedCandidate.q(24); // return 0
topVotedCandidate.q(8); // return 1
**Constraints:**
* `1 <= persons.length <= 5000`
* `times.length == persons.length`
* `0 <= persons[i] < persons.length`
* `0 <= times[i] <= 109`
* `times` is sorted in a strictly increasing order.
* `times[0] <= t <= 109`
* At most `104` calls will be made to `q`. | null |
✔️✔️Easy Solutions in Python ✔️✔️with Explanation | profitable-schemes | 0 | 1 | # Intuition - Use dfs and dp - by bruteforcing\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach - knapsack problem with additional check\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n \n @lru_cache(None)\n \n def dfs(i,pro,people):\n if i>=len(group):\n return pro>=minProfit\n\n ways = 0\n\n if people+group[i]<=n:\n ways+=dfs(i+1,min(minProfit,pro+profit[i]),people+group[i])\n\n ways+=dfs(i+1,pro,people)\n\n return ways\n \n return dfs(0,0,0)%(10**9+7)\n\n``` | 1 | There is a group of `n` members, and a list of various crimes they could commit. The `ith` crime generates a `profit[i]` and requires `group[i]` members to participate in it. If a member participates in one crime, that member can't participate in another crime.
Let's call a **profitable scheme** any subset of these crimes that generates at least `minProfit` profit, and the total number of members participating in that subset of crimes is at most `n`.
Return the number of schemes that can be chosen. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, minProfit = 3, group = \[2,2\], profit = \[2,3\]
**Output:** 2
**Explanation:** To make a profit of at least 3, the group could either commit crimes 0 and 1, or just crime 1.
In total, there are 2 schemes.
**Example 2:**
**Input:** n = 10, minProfit = 5, group = \[2,3,5\], profit = \[6,7,8\]
**Output:** 7
**Explanation:** To make a profit of at least 5, the group could commit any crimes, as long as they commit one.
There are 7 possible schemes: (0), (1), (2), (0,1), (0,2), (1,2), and (0,1,2).
**Constraints:**
* `1 <= n <= 100`
* `0 <= minProfit <= 100`
* `1 <= group.length <= 100`
* `1 <= group[i] <= 100`
* `profit.length == group.length`
* `0 <= profit[i] <= 100` | null |
✔️✔️Easy Solutions in Python ✔️✔️with Explanation | profitable-schemes | 0 | 1 | # Intuition - Use dfs and dp - by bruteforcing\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach - knapsack problem with additional check\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n \n @lru_cache(None)\n \n def dfs(i,pro,people):\n if i>=len(group):\n return pro>=minProfit\n\n ways = 0\n\n if people+group[i]<=n:\n ways+=dfs(i+1,min(minProfit,pro+profit[i]),people+group[i])\n\n ways+=dfs(i+1,pro,people)\n\n return ways\n \n return dfs(0,0,0)%(10**9+7)\n\n``` | 1 | You are given two integer arrays `persons` and `times`. In an election, the `ith` vote was cast for `persons[i]` at time `times[i]`.
For each query at a time `t`, find the person that was leading the election at time `t`. Votes cast at time `t` will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.
Implement the `TopVotedCandidate` class:
* `TopVotedCandidate(int[] persons, int[] times)` Initializes the object with the `persons` and `times` arrays.
* `int q(int t)` Returns the number of the person that was leading the election at time `t` according to the mentioned rules.
**Example 1:**
**Input**
\[ "TopVotedCandidate ", "q ", "q ", "q ", "q ", "q ", "q "\]
\[\[\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]\], \[3\], \[12\], \[25\], \[15\], \[24\], \[8\]\]
**Output**
\[null, 0, 1, 1, 0, 0, 1\]
**Explanation**
TopVotedCandidate topVotedCandidate = new TopVotedCandidate(\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]);
topVotedCandidate.q(3); // return 0, At time 3, the votes are \[0\], and 0 is leading.
topVotedCandidate.q(12); // return 1, At time 12, the votes are \[0,1,1\], and 1 is leading.
topVotedCandidate.q(25); // return 1, At time 25, the votes are \[0,1,1,0,0,1\], and 1 is leading (as ties go to the most recent vote.)
topVotedCandidate.q(15); // return 0
topVotedCandidate.q(24); // return 0
topVotedCandidate.q(8); // return 1
**Constraints:**
* `1 <= persons.length <= 5000`
* `times.length == persons.length`
* `0 <= persons[i] < persons.length`
* `0 <= times[i] <= 109`
* `times` is sorted in a strictly increasing order.
* `times[0] <= t <= 109`
* At most `104` calls will be made to `q`. | null |
Short Python Solution | profitable-schemes | 0 | 1 | \n# Complexity\n- Time complexity: $$ O(n*minProfit*len(group))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O(n*minProfit*len(group))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n MOD = 10**9 + 7\n \n @functools.lru_cache(None)\n def solve(members,i,minProfit):\n if i == 0:\n return 1 if minProfit <= 0 else 0\n if minProfit <= 0:\n minProfit = 0\n result = solve(members,i-1,minProfit)\n if group[i - 1] <= members:\n result += solve(members - group[i-1],i - 1,minProfit - profit[i-1])\n\n result %= MOD\n return result\n\n return solve(n,len(group),minProfit)\n``` | 1 | There is a group of `n` members, and a list of various crimes they could commit. The `ith` crime generates a `profit[i]` and requires `group[i]` members to participate in it. If a member participates in one crime, that member can't participate in another crime.
Let's call a **profitable scheme** any subset of these crimes that generates at least `minProfit` profit, and the total number of members participating in that subset of crimes is at most `n`.
Return the number of schemes that can be chosen. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, minProfit = 3, group = \[2,2\], profit = \[2,3\]
**Output:** 2
**Explanation:** To make a profit of at least 3, the group could either commit crimes 0 and 1, or just crime 1.
In total, there are 2 schemes.
**Example 2:**
**Input:** n = 10, minProfit = 5, group = \[2,3,5\], profit = \[6,7,8\]
**Output:** 7
**Explanation:** To make a profit of at least 5, the group could commit any crimes, as long as they commit one.
There are 7 possible schemes: (0), (1), (2), (0,1), (0,2), (1,2), and (0,1,2).
**Constraints:**
* `1 <= n <= 100`
* `0 <= minProfit <= 100`
* `1 <= group.length <= 100`
* `1 <= group[i] <= 100`
* `profit.length == group.length`
* `0 <= profit[i] <= 100` | null |
Short Python Solution | profitable-schemes | 0 | 1 | \n# Complexity\n- Time complexity: $$ O(n*minProfit*len(group))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$ O(n*minProfit*len(group))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n MOD = 10**9 + 7\n \n @functools.lru_cache(None)\n def solve(members,i,minProfit):\n if i == 0:\n return 1 if minProfit <= 0 else 0\n if minProfit <= 0:\n minProfit = 0\n result = solve(members,i-1,minProfit)\n if group[i - 1] <= members:\n result += solve(members - group[i-1],i - 1,minProfit - profit[i-1])\n\n result %= MOD\n return result\n\n return solve(n,len(group),minProfit)\n``` | 1 | You are given two integer arrays `persons` and `times`. In an election, the `ith` vote was cast for `persons[i]` at time `times[i]`.
For each query at a time `t`, find the person that was leading the election at time `t`. Votes cast at time `t` will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.
Implement the `TopVotedCandidate` class:
* `TopVotedCandidate(int[] persons, int[] times)` Initializes the object with the `persons` and `times` arrays.
* `int q(int t)` Returns the number of the person that was leading the election at time `t` according to the mentioned rules.
**Example 1:**
**Input**
\[ "TopVotedCandidate ", "q ", "q ", "q ", "q ", "q ", "q "\]
\[\[\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]\], \[3\], \[12\], \[25\], \[15\], \[24\], \[8\]\]
**Output**
\[null, 0, 1, 1, 0, 0, 1\]
**Explanation**
TopVotedCandidate topVotedCandidate = new TopVotedCandidate(\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]);
topVotedCandidate.q(3); // return 0, At time 3, the votes are \[0\], and 0 is leading.
topVotedCandidate.q(12); // return 1, At time 12, the votes are \[0,1,1\], and 1 is leading.
topVotedCandidate.q(25); // return 1, At time 25, the votes are \[0,1,1,0,0,1\], and 1 is leading (as ties go to the most recent vote.)
topVotedCandidate.q(15); // return 0
topVotedCandidate.q(24); // return 0
topVotedCandidate.q(8); // return 1
**Constraints:**
* `1 <= persons.length <= 5000`
* `times.length == persons.length`
* `0 <= persons[i] < persons.length`
* `0 <= times[i] <= 109`
* `times` is sorted in a strictly increasing order.
* `times[0] <= t <= 109`
* At most `104` calls will be made to `q`. | null |
Python Solution Top Down DFS with 3D Cache | profitable-schemes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n def dfs(i, n, minProfit, cache):\n if (i, n, minProfit) in cache:\n return cache[(i, n,minProfit)]%(10**9+7)\n if i == len(group):\n if n >= 0 and minProfit <= 0:\n cache[(i, n, minProfit)] = 1\n return 1\n else:\n cache[(i, n, minProfit)] = 0\n return 0\n commit = 0\n if n-group[i]>=0: #only commit if still have people left\n commit = dfs(i+1, n-group[i], max(minProfit-profit[i],0), cache)\n no_commit = dfs(i+1, n, minProfit, cache)\n cache[(i, n, minProfit)] = commit + no_commit\n return (commit + no_commit)%(10**9+7)\n cache = {}\n res = dfs(0, n, minProfit, cache)\n return res \n\n``` | 1 | There is a group of `n` members, and a list of various crimes they could commit. The `ith` crime generates a `profit[i]` and requires `group[i]` members to participate in it. If a member participates in one crime, that member can't participate in another crime.
Let's call a **profitable scheme** any subset of these crimes that generates at least `minProfit` profit, and the total number of members participating in that subset of crimes is at most `n`.
Return the number of schemes that can be chosen. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, minProfit = 3, group = \[2,2\], profit = \[2,3\]
**Output:** 2
**Explanation:** To make a profit of at least 3, the group could either commit crimes 0 and 1, or just crime 1.
In total, there are 2 schemes.
**Example 2:**
**Input:** n = 10, minProfit = 5, group = \[2,3,5\], profit = \[6,7,8\]
**Output:** 7
**Explanation:** To make a profit of at least 5, the group could commit any crimes, as long as they commit one.
There are 7 possible schemes: (0), (1), (2), (0,1), (0,2), (1,2), and (0,1,2).
**Constraints:**
* `1 <= n <= 100`
* `0 <= minProfit <= 100`
* `1 <= group.length <= 100`
* `1 <= group[i] <= 100`
* `profit.length == group.length`
* `0 <= profit[i] <= 100` | null |
Python Solution Top Down DFS with 3D Cache | profitable-schemes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:\n def dfs(i, n, minProfit, cache):\n if (i, n, minProfit) in cache:\n return cache[(i, n,minProfit)]%(10**9+7)\n if i == len(group):\n if n >= 0 and minProfit <= 0:\n cache[(i, n, minProfit)] = 1\n return 1\n else:\n cache[(i, n, minProfit)] = 0\n return 0\n commit = 0\n if n-group[i]>=0: #only commit if still have people left\n commit = dfs(i+1, n-group[i], max(minProfit-profit[i],0), cache)\n no_commit = dfs(i+1, n, minProfit, cache)\n cache[(i, n, minProfit)] = commit + no_commit\n return (commit + no_commit)%(10**9+7)\n cache = {}\n res = dfs(0, n, minProfit, cache)\n return res \n\n``` | 1 | You are given two integer arrays `persons` and `times`. In an election, the `ith` vote was cast for `persons[i]` at time `times[i]`.
For each query at a time `t`, find the person that was leading the election at time `t`. Votes cast at time `t` will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.
Implement the `TopVotedCandidate` class:
* `TopVotedCandidate(int[] persons, int[] times)` Initializes the object with the `persons` and `times` arrays.
* `int q(int t)` Returns the number of the person that was leading the election at time `t` according to the mentioned rules.
**Example 1:**
**Input**
\[ "TopVotedCandidate ", "q ", "q ", "q ", "q ", "q ", "q "\]
\[\[\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]\], \[3\], \[12\], \[25\], \[15\], \[24\], \[8\]\]
**Output**
\[null, 0, 1, 1, 0, 0, 1\]
**Explanation**
TopVotedCandidate topVotedCandidate = new TopVotedCandidate(\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]);
topVotedCandidate.q(3); // return 0, At time 3, the votes are \[0\], and 0 is leading.
topVotedCandidate.q(12); // return 1, At time 12, the votes are \[0,1,1\], and 1 is leading.
topVotedCandidate.q(25); // return 1, At time 25, the votes are \[0,1,1,0,0,1\], and 1 is leading (as ties go to the most recent vote.)
topVotedCandidate.q(15); // return 0
topVotedCandidate.q(24); // return 0
topVotedCandidate.q(8); // return 1
**Constraints:**
* `1 <= persons.length <= 5000`
* `times.length == persons.length`
* `0 <= persons[i] < persons.length`
* `0 <= times[i] <= 109`
* `times` is sorted in a strictly increasing order.
* `times[0] <= t <= 109`
* At most `104` calls will be made to `q`. | null |
Python short and clean 1-liner. DP. Functional programming. | profitable-schemes | 0 | 1 | # Approach\nTry both, picking and skipping, for each `group` until there are no more `people` or `group` left.\n\nSince there are overlappimg subproblems, and optimal sub-structure, cache / memoize the results. (DP)\n\n# Complexity\n- Time complexity: $$O(n * k * m)$$\n\n- Space complexity: $$O(n * k * m)$$\n\nwhere,\n`n is number of people`,\n`k is min_profit`,\n`m is number of groups`.\n\n# Code\n1-liner recursive function:\n```python\nclass Solution:\n def profitableSchemes(self, n_: int, min_profit: int, group: list[int], profit: list[int]) -> int:\n @cache\n def schemes(n: int, k: int, i: int) -> int: return (schemes(n, k, i + 1) + schemes(n - group[i], max(k - profit[i], 0), i + 1)) % 1_000_000_007 if i < len(group) and n >= 0 else n >= 0 and k == 0\n return schemes(n_, min_profit, 0)\n\n\n```\nFormated to multiline for clarity:\n```python\nclass Solution:\n def profitableSchemes(self, n_: int, min_profit: int, group: list[int], profit: list[int]) -> int:\n @cache\n def schemes(n: int, k: int, i: int) -> int:\n return (\n schemes(n, k, i + 1) + # Skip group\n schemes(n - group[i], max(k - profit[i], 0), i + 1) # Pick group\n ) % 1_000_000_007 if i < len(group) and n >= 0 else n >= 0 and k == 0\n\n return schemes(n_, min_profit, 0)\n\n\n``` | 3 | There is a group of `n` members, and a list of various crimes they could commit. The `ith` crime generates a `profit[i]` and requires `group[i]` members to participate in it. If a member participates in one crime, that member can't participate in another crime.
Let's call a **profitable scheme** any subset of these crimes that generates at least `minProfit` profit, and the total number of members participating in that subset of crimes is at most `n`.
Return the number of schemes that can be chosen. Since the answer may be very large, **return it modulo** `109 + 7`.
**Example 1:**
**Input:** n = 5, minProfit = 3, group = \[2,2\], profit = \[2,3\]
**Output:** 2
**Explanation:** To make a profit of at least 3, the group could either commit crimes 0 and 1, or just crime 1.
In total, there are 2 schemes.
**Example 2:**
**Input:** n = 10, minProfit = 5, group = \[2,3,5\], profit = \[6,7,8\]
**Output:** 7
**Explanation:** To make a profit of at least 5, the group could commit any crimes, as long as they commit one.
There are 7 possible schemes: (0), (1), (2), (0,1), (0,2), (1,2), and (0,1,2).
**Constraints:**
* `1 <= n <= 100`
* `0 <= minProfit <= 100`
* `1 <= group.length <= 100`
* `1 <= group[i] <= 100`
* `profit.length == group.length`
* `0 <= profit[i] <= 100` | null |
Python short and clean 1-liner. DP. Functional programming. | profitable-schemes | 0 | 1 | # Approach\nTry both, picking and skipping, for each `group` until there are no more `people` or `group` left.\n\nSince there are overlappimg subproblems, and optimal sub-structure, cache / memoize the results. (DP)\n\n# Complexity\n- Time complexity: $$O(n * k * m)$$\n\n- Space complexity: $$O(n * k * m)$$\n\nwhere,\n`n is number of people`,\n`k is min_profit`,\n`m is number of groups`.\n\n# Code\n1-liner recursive function:\n```python\nclass Solution:\n def profitableSchemes(self, n_: int, min_profit: int, group: list[int], profit: list[int]) -> int:\n @cache\n def schemes(n: int, k: int, i: int) -> int: return (schemes(n, k, i + 1) + schemes(n - group[i], max(k - profit[i], 0), i + 1)) % 1_000_000_007 if i < len(group) and n >= 0 else n >= 0 and k == 0\n return schemes(n_, min_profit, 0)\n\n\n```\nFormated to multiline for clarity:\n```python\nclass Solution:\n def profitableSchemes(self, n_: int, min_profit: int, group: list[int], profit: list[int]) -> int:\n @cache\n def schemes(n: int, k: int, i: int) -> int:\n return (\n schemes(n, k, i + 1) + # Skip group\n schemes(n - group[i], max(k - profit[i], 0), i + 1) # Pick group\n ) % 1_000_000_007 if i < len(group) and n >= 0 else n >= 0 and k == 0\n\n return schemes(n_, min_profit, 0)\n\n\n``` | 3 | You are given two integer arrays `persons` and `times`. In an election, the `ith` vote was cast for `persons[i]` at time `times[i]`.
For each query at a time `t`, find the person that was leading the election at time `t`. Votes cast at time `t` will count towards our query. In the case of a tie, the most recent vote (among tied candidates) wins.
Implement the `TopVotedCandidate` class:
* `TopVotedCandidate(int[] persons, int[] times)` Initializes the object with the `persons` and `times` arrays.
* `int q(int t)` Returns the number of the person that was leading the election at time `t` according to the mentioned rules.
**Example 1:**
**Input**
\[ "TopVotedCandidate ", "q ", "q ", "q ", "q ", "q ", "q "\]
\[\[\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]\], \[3\], \[12\], \[25\], \[15\], \[24\], \[8\]\]
**Output**
\[null, 0, 1, 1, 0, 0, 1\]
**Explanation**
TopVotedCandidate topVotedCandidate = new TopVotedCandidate(\[0, 1, 1, 0, 0, 1, 0\], \[0, 5, 10, 15, 20, 25, 30\]);
topVotedCandidate.q(3); // return 0, At time 3, the votes are \[0\], and 0 is leading.
topVotedCandidate.q(12); // return 1, At time 12, the votes are \[0,1,1\], and 1 is leading.
topVotedCandidate.q(25); // return 1, At time 25, the votes are \[0,1,1,0,0,1\], and 1 is leading (as ties go to the most recent vote.)
topVotedCandidate.q(15); // return 0
topVotedCandidate.q(24); // return 0
topVotedCandidate.q(8); // return 1
**Constraints:**
* `1 <= persons.length <= 5000`
* `times.length == persons.length`
* `0 <= persons[i] < persons.length`
* `0 <= times[i] <= 109`
* `times` is sorted in a strictly increasing order.
* `times[0] <= t <= 109`
* At most `104` calls will be made to `q`. | null |
Detailed Explanation Ever - Most Optimised code with 100% Runtime and Memory Acceptance in C++ | decoded-string-at-index | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to decode an encoded string by iteratively expanding it based on the digits found in the string. The goal is to find the kth character (1-indexed) in the decoded string efficiently.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize totalSize to keep track of the total size of the decoded string.\n2. Iterate through the input string s to calculate totalSize by considering both letters and digits.\n- If a character is a digit, multiply totalSize by that digit.\n- If a character is a letter, increment totalSize by 1, as each letter contributes to the size by 1.\n3. Decode the string in reverse order by iterating through s from the last character.\n- If a character is a digit, update totalSize by dividing it by the digit value and update k by taking its modulo with the updated totalSize.\n- If a character is a letter, check if k is 0 or equal to totalSize. If so, return the current character as it is the kth character.\n- If k is not found yet, decrease totalSize by 1, as each letter contributes to the size by 1.\n4. If the loop finishes without finding the kth character, return an empty string.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. The first loop through the string s to calculate totalSize takes O(N) time, where N is the length of the input string.\n2. The second loop through the string s in reverse order also takes O(N) time.\n3. Overall, the time complexity is O(N).\n\n\n---\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. The code uses a single integer variable totalSize to keep track of the size, which requires constant space.\n2. Other variables used within the loops also require constant space.\nThe space complexity is O(1).\n3. The code efficiently decodes the string and finds the kth character without the need for additional memory allocation, making it memory-efficient.\n\n\n---\n\n# **Do Upvote if you liked the explanation \uD83E\uDD1E**\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalSize = 0; // To keep track of the total size of the decoded string.\n \n // Calculate the total size of the decoded string.\n for (char c : s) {\n if (isdigit(c)) {\n int digit = c - \'0\';\n totalSize *= digit;\n } else {\n totalSize++;\n }\n }\n \n // Decode the string in reverse order.\n for (int i = s.size() - 1; i >= 0; i--) {\n char currentChar = s[i];\n if (isdigit(currentChar)) {\n int digit = currentChar - \'0\';\n totalSize /= digit;\n k %= totalSize;\n } else {\n if (k == 0 || k == totalSize) {\n return string(1, currentChar); // Found the character at k.\n }\n totalSize--; // Decrease the size for a single character.\n }\n }\n \n return ""; // This line should never be reached.\n }\n};\n\n``` | 12 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
Detailed Explanation Ever - Most Optimised code with 100% Runtime and Memory Acceptance in C++ | decoded-string-at-index | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to decode an encoded string by iteratively expanding it based on the digits found in the string. The goal is to find the kth character (1-indexed) in the decoded string efficiently.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize totalSize to keep track of the total size of the decoded string.\n2. Iterate through the input string s to calculate totalSize by considering both letters and digits.\n- If a character is a digit, multiply totalSize by that digit.\n- If a character is a letter, increment totalSize by 1, as each letter contributes to the size by 1.\n3. Decode the string in reverse order by iterating through s from the last character.\n- If a character is a digit, update totalSize by dividing it by the digit value and update k by taking its modulo with the updated totalSize.\n- If a character is a letter, check if k is 0 or equal to totalSize. If so, return the current character as it is the kth character.\n- If k is not found yet, decrease totalSize by 1, as each letter contributes to the size by 1.\n4. If the loop finishes without finding the kth character, return an empty string.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. The first loop through the string s to calculate totalSize takes O(N) time, where N is the length of the input string.\n2. The second loop through the string s in reverse order also takes O(N) time.\n3. Overall, the time complexity is O(N).\n\n\n---\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n1. The code uses a single integer variable totalSize to keep track of the size, which requires constant space.\n2. Other variables used within the loops also require constant space.\nThe space complexity is O(1).\n3. The code efficiently decodes the string and finds the kth character without the need for additional memory allocation, making it memory-efficient.\n\n\n---\n\n# **Do Upvote if you liked the explanation \uD83E\uDD1E**\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalSize = 0; // To keep track of the total size of the decoded string.\n \n // Calculate the total size of the decoded string.\n for (char c : s) {\n if (isdigit(c)) {\n int digit = c - \'0\';\n totalSize *= digit;\n } else {\n totalSize++;\n }\n }\n \n // Decode the string in reverse order.\n for (int i = s.size() - 1; i >= 0; i--) {\n char currentChar = s[i];\n if (isdigit(currentChar)) {\n int digit = currentChar - \'0\';\n totalSize /= digit;\n k %= totalSize;\n } else {\n if (k == 0 || k == totalSize) {\n return string(1, currentChar); // Found the character at k.\n }\n totalSize--; // Decrease the size for a single character.\n }\n }\n \n return ""; // This line should never be reached.\n }\n};\n\n``` | 12 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
🚀100% || Reverse || Stack || Commented Code🚀 | decoded-string-at-index | 1 | 1 | # Problem Description\nThe tasked is **decoding** an encoded string following specific **rules**. \n- The encoded string is read character by character, and actions are taken accordingly: \n - letters are directly written to a tape,\n - digits determine how many times the current content of the tape is repeated. \n \nGiven an encoded string and an integer `k`, you need to determine the `kth` letter (1-indexed) in the decoded string.\n\n**Example:**\nFor a given encoded string `leet2code3` and `k = 10`.\n the decoded string is `leetleetcodeleetleetcodeleetleetcode`\nthe `10th` letter in the decoded string is `o`.\n\n---\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s unique problem\uD83D\uDE80\n\nIn our problem, we have an **encoded** string and we have to **decode** it then to find the `kth` character.\nSeems Interesting.\uD83E\uDD29\nThe naive solution that can come in mind that we **first** encode the string by appending the **repeated** characters and then return the `kth` character.\nlike `leet2code3` and `k` = `10`.\nwe can intialize another vairable and construct the decoded string into it which will be `leetleetcodeleetleetcodeleetleetcode` then return `kth` character which is `o`.\n\nThis approach is **correct** but has one problem that it has **high** time complexity and will give you **time limit**.\uD83D\uDE14\nThen how can we think out of box for this problem.\uD83D\uDCE6\n\nThe **valid** thing to think of is can we get the `kth` character without **storing** the **encoded** string?\uD83E\uDD14\nLet\'s observe `leet2code3` and `k` = `10` example and see what happen to lengths when we traverse it.\n```\n1) string: l -> length: 1 \n2) string: le -> length: 2\n3) string: lee -> length: 3\n4) string: leet -> length: 4\n5) string: leetleet -> length: 8\n6) string: leetleetc -> length: 9 \n7) string: leetleetco -> length: 10\n8) string: leetleetcod -> length: 11\n9) string: leetleetcode -> length: 12\n10)string: leetleetcodeleetleetcodeleetleetcode -> length: 36 \n```\n\nI think that we all **observed** something.\uD83E\uDD2F\nThe total encoded string is `leetleetcode-leetleetcode-leetleetcode`can be divided into three parts since the last character in the **decoded** string is `3`.\nand because of that we have kind of **cycle** (this cycle feature is important in our problem).\n\nasssume that we have different k.\n```\nk = 10 -> answer = o\nk = 14 -> answer = e\nk = 20 -> answer = t\nk = 28 -> answer = t\n```\nThe main **observation** to solve this problem is that we **multiply** string by some digit and `k` will always land in the **original** string\n\nHOW TO GET K IF WE DON\'T WANT TO ENCODE OUR STRING ?\uD83D\uDE20\nif we have our string `leetleetcode` and number of multiplication `3` why don\'t we use **modulus** ?\n```\nlength of encoded string = 36\nlength of desired string = 36 / 3 = 12 -> leetleetcode\n\nk = 10 -> 10 % 12 = 10 -> o\nk = 14 -> 14 % 12 = 2 -> e\nk = 20 -> 20 % 12 = 8 -> t\nk = 28 -> 28 % 12 = 4 -> t\n``` \nDid you noticed how we always our final `k = (k % length of decoded string)`\nthis is the way to get the `kth` char without **encode** our string, only see the length of encoded string and take mod out of it.\uD83E\uDD2F\n\n- and to do that we have two steps\n - **traverse** the whole string and get the **total length** of encoded string\n - **reverse traversing** the string and apply the two operations, **division** and **mod** to the length until we get `k`\n\nlet\'s take an example ?\nstring = `prob3slve4` , `k` = `31`\n```\nlength of encoded string = ( 3 * 4 + 4 )* 4 = 64 \n-without really encoding it-\n```\nnow let\'s reverse traverse\nstring = `prob3slve4`\n\n```\nlentgh = 64, k = 31\nat 10th char = 4 -> length = 64 / 4 = 16\nk = 31 % 16 = 15\n```\n```\nlentgh = 16, k = 15\nat 9th char = e\nlength = 16 - 1 = 15\n```\n```\nlentgh = 15, k = 15\nat 8th char = v\nk == length -> then our desire char is v\n```\n\n- this solution can be done using **two** approaches\n - **first** one by doint like the **intuition** exactly \n - **second** one by using a **stack**\n\nThe **stack** solution can be little **tricky** but it is totally **like** the first one except for each char we traverse we are storing the size of the encoded string we have reached so far.\nand when emptying the **stack** we are doing the **reverse travers**e and actually we won\'t need the division operation here since we have the **correct** lengths for all chars.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n# Proposed Solutions\n## 1. Reverse\n- Initialize `decodedLength` to `0`, representing the **total length** of the decoded string.\n- **Iterate** through each character in the input string.\n - If the character is a **digit**, update `decodedLength` by **multiplying** it with the digit.\n - If the character is a **letter**, **increment** `decodedLength`.\n- **Traverse** the input string in **reverse** order.\n- For each character:\n - If it\'s a **digit** adjust `decodedLength` and `k` accordingly.\n - If it\'s a **letter** Check if it\'s the `kth` character or if `k` is `0`.\n - If **yes**, **return** the character as a string.\n - If **not**, **decrement** decodedLength.\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the string twice, one time to calculate lengths for each character in the encoded string and another time to get `kth` character then time complexity is `2*N` which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are only storing couple of constant variables.\n---\n\n## 2. Stack\n- Initialize a **stack** to store the lengths of characters in the decoded string.\n- **Iterate** through each character in the encoded string.\n - If the character is a **digit**, **update** the length in the stack based on the digit.\n - If the character is a **letter**, **increment** the length in the stack.\n- Traverse the character lengths in **reverse** order.\n- For each character length:\n - Adjust `k` based on the current character length.\n - If `k` is `0` and the character is an alphabet letter, **return** it.\nMove to the **previous** character length.\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the string twice, one time to calculate `decodedLength` and another time to get `kth` character then time complexity is `2*N` which is `O(N)`.\n- **Space complexity:** $$O(N)$$\nSince we are storing the lengths if each character in a `stack` then the space complexity is `O(N)`\n\n---\n\n\n# Code\n## 1. Reverse\n```C++ []\nclass Solution {\npublic:\n std::string decodeAtIndex(std::string inputString, int k) {\n long long decodedLength = 0; // Total length of the decoded string\n for (auto character : inputString) {\n if (isdigit(character)) {\n // If the character is a digit, update the decoded length accordingly\n decodedLength *= character - \'0\';\n } else {\n // If the character is a letter, increment the decoded length\n decodedLength++;\n }\n }\n\n // Traverse the input string in reverse to decode and find the kth character\n for (int i = inputString.size() - 1; i >= 0; i--) {\n if (isdigit(inputString[i])) {\n // If the character is a digit, adjust the length and k accordingly\n decodedLength /= (inputString[i] - \'0\');\n k = k % decodedLength;\n } else {\n // If the character is a letter, check if it\'s the kth character\n if (k == 0 || decodedLength == k)\n return string("") + inputString[i]; // Return the kth character as a string\n decodedLength--;\n }\n }\n\n return ""; // Return an empty string if no character is found\n }\n};\n```\n```Java []\npublic class Solution {\n public String decodeAtIndex(String inputString, int k) {\n long decodedLength = 0; // Total length of the decoded string\n\n for (char character : inputString.toCharArray()) {\n if (Character.isDigit(character)) {\n // If the character is a digit, update the decoded length accordingly\n decodedLength *= (character - \'0\');\n } else {\n // If the character is a letter, increment the decoded length\n decodedLength++;\n }\n }\n\n // Traverse the input string in reverse to decode and find the kth character\n for (int i = inputString.length() - 1; i >= 0; i--) {\n char currentChar = inputString.charAt(i);\n\n if (Character.isDigit(currentChar)) {\n // If the character is a digit, adjust the length and k accordingly\n decodedLength /= (currentChar - \'0\');\n k %= decodedLength;\n } else {\n // If the character is a letter, check if it\'s the kth character\n if (k == 0 || decodedLength == k) {\n return String.valueOf(currentChar); // Return the kth character as a string\n }\n decodedLength--;\n }\n }\n\n return ""; // Return an empty string if no character is found\n }\n}\n```\n```Python []\nclass Solution:\n def decodeAtIndex(self, inputString: str, k: int) -> str:\n decoded_length = 0 # Total length of the decoded string\n\n for char in inputString:\n if char.isdigit():\n # If the character is a digit, update the decoded length accordingly\n decoded_length *= int(char)\n else:\n # If the character is a letter, increment the decoded length\n decoded_length += 1\n\n # Traverse the input string in reverse to decode and find the kth character\n for i in range(len(inputString) - 1, -1, -1):\n current_char = inputString[i]\n\n if current_char.isdigit():\n # If the character is a digit, adjust the length and k accordingly\n decoded_length //= int(current_char)\n k %= decoded_length\n else:\n # If the character is a letter, check if it\'s the kth character\n if k == 0 or decoded_length == k:\n return current_char # Return the kth character as a string\n\n decoded_length -= 1\n\n return "" # Return an empty string if no character is found\n```\n\n\n---\n\n\n## 2. Stack\n```C++ []\nclass Solution {\npublic:\n string decodeAtIndex(string encodedString, int k) {\n stack<long long> characterLengths; // Stores the lengths of characters in the decoded string\n\n // Calculate lengths for each character in the encoded string\n characterLengths.push(0); // Start with 0 length\n\n for (size_t i = 0; i < encodedString.length(); ++i) {\n if (isdigit(encodedString[i])) {\n // If the character is a digit, update the length based on the digit\n long long length = characterLengths.top() * (encodedString[i] - \'0\');\n characterLengths.push(length);\n } else {\n // If the character is a letter, increment the length\n long long length = characterLengths.top() + 1;\n characterLengths.push(length);\n }\n }\n\n // Traverse the character lengths to decode and find the kth character\n size_t ln = characterLengths.size();\n while (!characterLengths.empty()) {\n k %= characterLengths.top(); // Adjust k based on the character length\n ln--;\n // If k is 0 and the character is an alphabet letter, return it\n if (k == 0 && isalpha(encodedString[ln - 1])) {\n return string(1, encodedString[ln - 1]);\n }\n\n // Move to the previous character length\n characterLengths.pop();\n }\n\n return ""; // Return an empty string if no character is found\n }\n};\n```\n```Java []\nclass Solution {\n public String decodeAtIndex(String encodedString, int k) {\n Stack<Long> characterLengths = new Stack<>(); // Stores the lengths of characters in the decoded string\n\n // Calculate lengths for each character in the encoded string\n characterLengths.push(0L); // Start with 0 length\n\n for (int i = 0; i < encodedString.length(); i++) {\n char c = encodedString.charAt(i);\n if (Character.isDigit(c)) {\n // If the character is a digit, update the length based on the digit\n long length = characterLengths.peek() * (c - \'0\');\n characterLengths.push(length);\n } else {\n // If the character is a letter, increment the length\n long length = characterLengths.peek() + 1;\n characterLengths.push(length);\n }\n }\n\n // Traverse the character lengths to decode and find the kth character\n int ln = characterLengths.size();\n while (!characterLengths.isEmpty()) {\n k %= characterLengths.peek(); // Adjust k based on the character length\n ln--;\n // If k is 0 and the character is an alphabet letter, return it\n if (k == 0 && Character.isLetter(encodedString.charAt(ln - 1))) {\n return String.valueOf(encodedString.charAt(ln - 1));\n }\n\n // Move to the previous character length\n characterLengths.pop();\n }\n\n return ""; // Return an empty string if no character is found\n }\n}\n```\n```Python []\nclass Solution:\n def decodeAtIndex(self, encodedString: str, k: int) -> str:\n character_lengths = [0] # Stores the lengths of characters in the decoded string\n\n for i in range(len(encodedString)):\n if encodedString[i].isdigit():\n # If the character is a digit, update the length based on the digit\n length = character_lengths[-1] * int(encodedString[i])\n character_lengths.append(length)\n else:\n # If the character is a letter, increment the length\n length = character_lengths[-1] + 1\n character_lengths.append(length)\n\n # Traverse the character lengths to decode and find the kth character\n ln = len(character_lengths)\n while character_lengths:\n k %= character_lengths[-1] # Adjust k based on the character length\n ln -= 1\n # If k is 0 and the character is an alphabet letter, return it\n if k == 0 and encodedString[ln - 1].isalpha():\n return encodedString[ln - 1]\n\n # Move to the previous character length\n character_lengths.pop()\n\n return "" # Return an empty string if no character is found\n```\n\n\n\n\n | 242 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
🚀100% || Reverse || Stack || Commented Code🚀 | decoded-string-at-index | 1 | 1 | # Problem Description\nThe tasked is **decoding** an encoded string following specific **rules**. \n- The encoded string is read character by character, and actions are taken accordingly: \n - letters are directly written to a tape,\n - digits determine how many times the current content of the tape is repeated. \n \nGiven an encoded string and an integer `k`, you need to determine the `kth` letter (1-indexed) in the decoded string.\n\n**Example:**\nFor a given encoded string `leet2code3` and `k = 10`.\n the decoded string is `leetleetcodeleetleetcodeleetleetcode`\nthe `10th` letter in the decoded string is `o`.\n\n---\n\n\n# Intuition\nHello There\uD83D\uDE00\nLet\'s take a look on our today\'s unique problem\uD83D\uDE80\n\nIn our problem, we have an **encoded** string and we have to **decode** it then to find the `kth` character.\nSeems Interesting.\uD83E\uDD29\nThe naive solution that can come in mind that we **first** encode the string by appending the **repeated** characters and then return the `kth` character.\nlike `leet2code3` and `k` = `10`.\nwe can intialize another vairable and construct the decoded string into it which will be `leetleetcodeleetleetcodeleetleetcode` then return `kth` character which is `o`.\n\nThis approach is **correct** but has one problem that it has **high** time complexity and will give you **time limit**.\uD83D\uDE14\nThen how can we think out of box for this problem.\uD83D\uDCE6\n\nThe **valid** thing to think of is can we get the `kth` character without **storing** the **encoded** string?\uD83E\uDD14\nLet\'s observe `leet2code3` and `k` = `10` example and see what happen to lengths when we traverse it.\n```\n1) string: l -> length: 1 \n2) string: le -> length: 2\n3) string: lee -> length: 3\n4) string: leet -> length: 4\n5) string: leetleet -> length: 8\n6) string: leetleetc -> length: 9 \n7) string: leetleetco -> length: 10\n8) string: leetleetcod -> length: 11\n9) string: leetleetcode -> length: 12\n10)string: leetleetcodeleetleetcodeleetleetcode -> length: 36 \n```\n\nI think that we all **observed** something.\uD83E\uDD2F\nThe total encoded string is `leetleetcode-leetleetcode-leetleetcode`can be divided into three parts since the last character in the **decoded** string is `3`.\nand because of that we have kind of **cycle** (this cycle feature is important in our problem).\n\nasssume that we have different k.\n```\nk = 10 -> answer = o\nk = 14 -> answer = e\nk = 20 -> answer = t\nk = 28 -> answer = t\n```\nThe main **observation** to solve this problem is that we **multiply** string by some digit and `k` will always land in the **original** string\n\nHOW TO GET K IF WE DON\'T WANT TO ENCODE OUR STRING ?\uD83D\uDE20\nif we have our string `leetleetcode` and number of multiplication `3` why don\'t we use **modulus** ?\n```\nlength of encoded string = 36\nlength of desired string = 36 / 3 = 12 -> leetleetcode\n\nk = 10 -> 10 % 12 = 10 -> o\nk = 14 -> 14 % 12 = 2 -> e\nk = 20 -> 20 % 12 = 8 -> t\nk = 28 -> 28 % 12 = 4 -> t\n``` \nDid you noticed how we always our final `k = (k % length of decoded string)`\nthis is the way to get the `kth` char without **encode** our string, only see the length of encoded string and take mod out of it.\uD83E\uDD2F\n\n- and to do that we have two steps\n - **traverse** the whole string and get the **total length** of encoded string\n - **reverse traversing** the string and apply the two operations, **division** and **mod** to the length until we get `k`\n\nlet\'s take an example ?\nstring = `prob3slve4` , `k` = `31`\n```\nlength of encoded string = ( 3 * 4 + 4 )* 4 = 64 \n-without really encoding it-\n```\nnow let\'s reverse traverse\nstring = `prob3slve4`\n\n```\nlentgh = 64, k = 31\nat 10th char = 4 -> length = 64 / 4 = 16\nk = 31 % 16 = 15\n```\n```\nlentgh = 16, k = 15\nat 9th char = e\nlength = 16 - 1 = 15\n```\n```\nlentgh = 15, k = 15\nat 8th char = v\nk == length -> then our desire char is v\n```\n\n- this solution can be done using **two** approaches\n - **first** one by doint like the **intuition** exactly \n - **second** one by using a **stack**\n\nThe **stack** solution can be little **tricky** but it is totally **like** the first one except for each char we traverse we are storing the size of the encoded string we have reached so far.\nand when emptying the **stack** we are doing the **reverse travers**e and actually we won\'t need the division operation here since we have the **correct** lengths for all chars.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n# Proposed Solutions\n## 1. Reverse\n- Initialize `decodedLength` to `0`, representing the **total length** of the decoded string.\n- **Iterate** through each character in the input string.\n - If the character is a **digit**, update `decodedLength` by **multiplying** it with the digit.\n - If the character is a **letter**, **increment** `decodedLength`.\n- **Traverse** the input string in **reverse** order.\n- For each character:\n - If it\'s a **digit** adjust `decodedLength` and `k` accordingly.\n - If it\'s a **letter** Check if it\'s the `kth` character or if `k` is `0`.\n - If **yes**, **return** the character as a string.\n - If **not**, **decrement** decodedLength.\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the string twice, one time to calculate lengths for each character in the encoded string and another time to get `kth` character then time complexity is `2*N` which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are only storing couple of constant variables.\n---\n\n## 2. Stack\n- Initialize a **stack** to store the lengths of characters in the decoded string.\n- **Iterate** through each character in the encoded string.\n - If the character is a **digit**, **update** the length in the stack based on the digit.\n - If the character is a **letter**, **increment** the length in the stack.\n- Traverse the character lengths in **reverse** order.\n- For each character length:\n - Adjust `k` based on the current character length.\n - If `k` is `0` and the character is an alphabet letter, **return** it.\nMove to the **previous** character length.\n\n## Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over the string twice, one time to calculate `decodedLength` and another time to get `kth` character then time complexity is `2*N` which is `O(N)`.\n- **Space complexity:** $$O(N)$$\nSince we are storing the lengths if each character in a `stack` then the space complexity is `O(N)`\n\n---\n\n\n# Code\n## 1. Reverse\n```C++ []\nclass Solution {\npublic:\n std::string decodeAtIndex(std::string inputString, int k) {\n long long decodedLength = 0; // Total length of the decoded string\n for (auto character : inputString) {\n if (isdigit(character)) {\n // If the character is a digit, update the decoded length accordingly\n decodedLength *= character - \'0\';\n } else {\n // If the character is a letter, increment the decoded length\n decodedLength++;\n }\n }\n\n // Traverse the input string in reverse to decode and find the kth character\n for (int i = inputString.size() - 1; i >= 0; i--) {\n if (isdigit(inputString[i])) {\n // If the character is a digit, adjust the length and k accordingly\n decodedLength /= (inputString[i] - \'0\');\n k = k % decodedLength;\n } else {\n // If the character is a letter, check if it\'s the kth character\n if (k == 0 || decodedLength == k)\n return string("") + inputString[i]; // Return the kth character as a string\n decodedLength--;\n }\n }\n\n return ""; // Return an empty string if no character is found\n }\n};\n```\n```Java []\npublic class Solution {\n public String decodeAtIndex(String inputString, int k) {\n long decodedLength = 0; // Total length of the decoded string\n\n for (char character : inputString.toCharArray()) {\n if (Character.isDigit(character)) {\n // If the character is a digit, update the decoded length accordingly\n decodedLength *= (character - \'0\');\n } else {\n // If the character is a letter, increment the decoded length\n decodedLength++;\n }\n }\n\n // Traverse the input string in reverse to decode and find the kth character\n for (int i = inputString.length() - 1; i >= 0; i--) {\n char currentChar = inputString.charAt(i);\n\n if (Character.isDigit(currentChar)) {\n // If the character is a digit, adjust the length and k accordingly\n decodedLength /= (currentChar - \'0\');\n k %= decodedLength;\n } else {\n // If the character is a letter, check if it\'s the kth character\n if (k == 0 || decodedLength == k) {\n return String.valueOf(currentChar); // Return the kth character as a string\n }\n decodedLength--;\n }\n }\n\n return ""; // Return an empty string if no character is found\n }\n}\n```\n```Python []\nclass Solution:\n def decodeAtIndex(self, inputString: str, k: int) -> str:\n decoded_length = 0 # Total length of the decoded string\n\n for char in inputString:\n if char.isdigit():\n # If the character is a digit, update the decoded length accordingly\n decoded_length *= int(char)\n else:\n # If the character is a letter, increment the decoded length\n decoded_length += 1\n\n # Traverse the input string in reverse to decode and find the kth character\n for i in range(len(inputString) - 1, -1, -1):\n current_char = inputString[i]\n\n if current_char.isdigit():\n # If the character is a digit, adjust the length and k accordingly\n decoded_length //= int(current_char)\n k %= decoded_length\n else:\n # If the character is a letter, check if it\'s the kth character\n if k == 0 or decoded_length == k:\n return current_char # Return the kth character as a string\n\n decoded_length -= 1\n\n return "" # Return an empty string if no character is found\n```\n\n\n---\n\n\n## 2. Stack\n```C++ []\nclass Solution {\npublic:\n string decodeAtIndex(string encodedString, int k) {\n stack<long long> characterLengths; // Stores the lengths of characters in the decoded string\n\n // Calculate lengths for each character in the encoded string\n characterLengths.push(0); // Start with 0 length\n\n for (size_t i = 0; i < encodedString.length(); ++i) {\n if (isdigit(encodedString[i])) {\n // If the character is a digit, update the length based on the digit\n long long length = characterLengths.top() * (encodedString[i] - \'0\');\n characterLengths.push(length);\n } else {\n // If the character is a letter, increment the length\n long long length = characterLengths.top() + 1;\n characterLengths.push(length);\n }\n }\n\n // Traverse the character lengths to decode and find the kth character\n size_t ln = characterLengths.size();\n while (!characterLengths.empty()) {\n k %= characterLengths.top(); // Adjust k based on the character length\n ln--;\n // If k is 0 and the character is an alphabet letter, return it\n if (k == 0 && isalpha(encodedString[ln - 1])) {\n return string(1, encodedString[ln - 1]);\n }\n\n // Move to the previous character length\n characterLengths.pop();\n }\n\n return ""; // Return an empty string if no character is found\n }\n};\n```\n```Java []\nclass Solution {\n public String decodeAtIndex(String encodedString, int k) {\n Stack<Long> characterLengths = new Stack<>(); // Stores the lengths of characters in the decoded string\n\n // Calculate lengths for each character in the encoded string\n characterLengths.push(0L); // Start with 0 length\n\n for (int i = 0; i < encodedString.length(); i++) {\n char c = encodedString.charAt(i);\n if (Character.isDigit(c)) {\n // If the character is a digit, update the length based on the digit\n long length = characterLengths.peek() * (c - \'0\');\n characterLengths.push(length);\n } else {\n // If the character is a letter, increment the length\n long length = characterLengths.peek() + 1;\n characterLengths.push(length);\n }\n }\n\n // Traverse the character lengths to decode and find the kth character\n int ln = characterLengths.size();\n while (!characterLengths.isEmpty()) {\n k %= characterLengths.peek(); // Adjust k based on the character length\n ln--;\n // If k is 0 and the character is an alphabet letter, return it\n if (k == 0 && Character.isLetter(encodedString.charAt(ln - 1))) {\n return String.valueOf(encodedString.charAt(ln - 1));\n }\n\n // Move to the previous character length\n characterLengths.pop();\n }\n\n return ""; // Return an empty string if no character is found\n }\n}\n```\n```Python []\nclass Solution:\n def decodeAtIndex(self, encodedString: str, k: int) -> str:\n character_lengths = [0] # Stores the lengths of characters in the decoded string\n\n for i in range(len(encodedString)):\n if encodedString[i].isdigit():\n # If the character is a digit, update the length based on the digit\n length = character_lengths[-1] * int(encodedString[i])\n character_lengths.append(length)\n else:\n # If the character is a letter, increment the length\n length = character_lengths[-1] + 1\n character_lengths.append(length)\n\n # Traverse the character lengths to decode and find the kth character\n ln = len(character_lengths)\n while character_lengths:\n k %= character_lengths[-1] # Adjust k based on the character length\n ln -= 1\n # If k is 0 and the character is an alphabet letter, return it\n if k == 0 and encodedString[ln - 1].isalpha():\n return encodedString[ln - 1]\n\n # Move to the previous character length\n character_lengths.pop()\n\n return "" # Return an empty string if no character is found\n```\n\n\n\n\n | 242 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
✅ 97.47% Reverse Traversal | decoded-string-at-index | 1 | 1 | # Interview Guide: "Decoded String at Index" Problem\n\n## Problem Understanding\n\nThe "Decoded String at Index" problem requires you to decode a given string based on specific rules. When a letter is encountered, it\'s written as is; when a digit is encountered, the decoded string so far is repeated that many times. Your task is to return the $$k$$th character in the decoded string.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore starting with the solution, grasp the constraints. The length of string `s` is between 2 and 100, and `s` consists of lowercase English letters and digits from 2 to 9. This provides insight into feasible solutions in terms of time and space complexity.\n\n### 2. Reverse Traversal\n\nOne of the efficient methods to solve this problem is to traverse the string in reverse, starting from the end and moving toward the beginning. This avoids having to actually build the complete decoded string, which can be very long.\n\n### 3. Handling Digits and Letters\n\nWhen traversing the string, if a letter is encountered, the length of the decoded string reduces by one. If a digit is encountered, the length of the decoded string is divided by that digit. This simulates the decoding process in reverse.\n\n### 4. Explain Your Thought Process\n\nAlways articulate the rationale behind your approach. Explain why reverse traversal is efficient and how you simulate the decoding process without actually forming the full string.\n\n## Conclusion\n\nThe "Decoded String at Index" problem demonstrates the importance of understanding the problem\'s constraints and requirements. By simulating the decoding process in reverse, you avoid memory issues and provide an efficient solution.\n\n---\n\n## Live Coding & Explain\nhttps://youtu.be/UgSrm6LwXqk?si=WzBk-tHvhzNO8cNI\n\n# Approach: Reverse Traversal\n\nTo tackle the "Decoded String at Index" problem using reverse traversal, we simulate the decoding process in reverse:\n\n## Key Data Structures:\n\n- **length**: An integer variable to keep track of the current length of the decoded string.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize the length variable to 0.\n \n2. **Forward Traversal**:\n - Traverse the string from start to end, updating the length based on whether you encounter a letter or a digit.\n\n3. **Reverse Traversal**:\n - Start from the end of the string. If you encounter a digit, divide the length by the digit and update $$k$$ using modulo operation. If you encounter a letter and $$k$$ equals 0 or length, return the letter.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution involves two traversals over the string, leading to a time complexity of $$ O(n) $$, where `n` is the length of the string `s`.\n\n**Space Complexity:** \n- The space complexity is $$ O(1) $$ since the solution doesn\'t use any additional data structures that scale with the input size. \n\n# Code Reverse Traversal\n``` Python []\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n length = 0\n i = 0\n \n while length < k:\n if s[i].isdigit():\n length *= int(s[i])\n else:\n length += 1\n i += 1\n \n for j in range(i-1, -1, -1):\n char = s[j]\n if char.isdigit():\n length //= int(char)\n k %= length\n else:\n if k == 0 or k == length:\n return char\n length -= 1\n```\n``` Go []\nfunc decodeAtIndex(s string, k int) string {\n length := int64(0)\n i := 0\n\n for length < int64(k) {\n if s[i] >= \'0\' && s[i] <= \'9\' {\n length *= int64(s[i] - \'0\')\n } else {\n length++\n }\n i++\n }\n\n for j := i - 1; j >= 0; j-- {\n if s[j] >= \'0\' && s[j] <= \'9\' {\n length /= int64(s[j] - \'0\')\n k %= int(length)\n } else {\n if k == 0 || k == int(length) {\n return string(s[j])\n }\n length--\n }\n }\n\n return ""\n}\n```\n``` Rust []\nimpl Solution {\n pub fn decode_at_index(s: String, mut k: i32) -> String {\n let mut length: i64 = 0;\n let mut i = 0;\n let bytes = s.as_bytes();\n\n while length < k as i64 {\n if bytes[i].is_ascii_digit() {\n length *= (bytes[i] as char).to_digit(10).unwrap() as i64;\n } else {\n length += 1;\n }\n i += 1;\n }\n\n for j in (0..i).rev() {\n if bytes[j].is_ascii_digit() {\n length /= (bytes[j] as char).to_digit(10).unwrap() as i64;\n k = (k as i64 % length) as i32;\n } else {\n if k == 0 || k as i64 == length {\n return (bytes[j] as char).to_string();\n }\n length -= 1;\n }\n }\n\n return "".to_string();\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string decodeAtIndex(string s, int k) {\n long long length = 0;\n int i = 0;\n \n while (length < k) {\n if (isdigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n \n for (int j = i - 1; j >= 0; j--) {\n if (isdigit(s[j])) {\n length /= s[j] - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n return std::string(1, s[j]); // Convert char to std::string\n }\n length--;\n }\n }\n \n return ""; // Default return, should never reach here given problem constraints\n }\n};\n```\n``` C []\nchar* decodeAtIndex(char* s, int k) {\n long long length = 0;\n int i = 0;\n\n while (length < k) {\n if (isdigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n static char result[2]; // static to return a local array, initialized to hold one character and a null terminator\n for (int j = i - 1; j >= 0; j--) {\n if (isdigit(s[j])) {\n length /= s[j] - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n result[0] = s[j];\n return result;\n }\n length--;\n }\n }\n\n return "";\n}\n```\n``` Java []\npublic class Solution {\n public String decodeAtIndex(String s, int k) {\n long length = 0;\n int i = 0;\n\n while (length < k) {\n if (Character.isDigit(s.charAt(i))) {\n length *= s.charAt(i) - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n for (int j = i - 1; j >= 0; j--) {\n if (Character.isDigit(s.charAt(j))) {\n length /= s.charAt(j) - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n return Character.toString(s.charAt(j));\n }\n length--;\n }\n }\n\n return "";\n }\n}\n```\n``` JavaScript []\nvar decodeAtIndex = function(s, k) {\n let length = 0;\n let i = 0;\n\n while (length < k) {\n if (!isNaN(s[i])) {\n length *= Number(s[i]);\n } else {\n length++;\n }\n i++;\n }\n\n for (let j = i - 1; j >= 0; j--) {\n if (!isNaN(s[j])) {\n length /= Number(s[j]);\n k %= length;\n } else {\n if (k === 0 || k === length) {\n return s[j];\n }\n length--;\n }\n }\n\n return "";\n};\n```\n``` C# []\npublic class Solution {\n public string DecodeAtIndex(string s, int k) {\n long length = 0;\n int i = 0;\n\n while (length < k) {\n if (char.IsDigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n for (int j = i - 1; j >= 0; j--) {\n if (char.IsDigit(s[j])) {\n length /= s[j] - \'0\';\n k %= (int)length;\n } else {\n if (k == 0 || k == length) {\n return s[j].ToString();\n }\n length--;\n }\n }\n\n return "";\n }\n}\n```\n``` PHP []\nclass Solution {\n function decodeAtIndex($s, $k) {\n $length = 0;\n $i = 0;\n\n while ($length < $k) {\n if (is_numeric($s[$i])) {\n $length *= intval($s[$i]);\n } else {\n $length++;\n }\n $i++;\n }\n\n for ($j = $i - 1; $j >= 0; $j--) {\n if (is_numeric($s[$j])) {\n $length /= intval($s[$j]);\n $k %= $length;\n } else {\n if ($k == 0 || $k == $length) {\n return $s[$j];\n }\n $length--;\n }\n }\n\n return "";\n }\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 0 ms | 2 MB |\n| C | 0 ms | 6.4 MB |\n| C++ | 0 ms | 6.4 MB |\n| Java | 0 ms | 40.5 MB |\n| Go | 1 ms | 1.9 MB |\n| PHP | 3 ms | 19.1 MB |\n| Python3 | 22 ms | 16.1 MB |\n| JavaScript | 49 ms | 41.9 MB |\n| C# | 68 ms | 37 MB |\n\n\n\n\nThe "Decoded String at Index" problem emphasizes the importance of simulating processes and thinking in reverse to find efficient solutions. It\'s a testament to the idea that sometimes, the direct approach isn\'t the most efficient one. \uD83D\uDE80\uD83E\uDDE0\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB.\n | 146 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
✅ 97.47% Reverse Traversal | decoded-string-at-index | 1 | 1 | # Interview Guide: "Decoded String at Index" Problem\n\n## Problem Understanding\n\nThe "Decoded String at Index" problem requires you to decode a given string based on specific rules. When a letter is encountered, it\'s written as is; when a digit is encountered, the decoded string so far is repeated that many times. Your task is to return the $$k$$th character in the decoded string.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore starting with the solution, grasp the constraints. The length of string `s` is between 2 and 100, and `s` consists of lowercase English letters and digits from 2 to 9. This provides insight into feasible solutions in terms of time and space complexity.\n\n### 2. Reverse Traversal\n\nOne of the efficient methods to solve this problem is to traverse the string in reverse, starting from the end and moving toward the beginning. This avoids having to actually build the complete decoded string, which can be very long.\n\n### 3. Handling Digits and Letters\n\nWhen traversing the string, if a letter is encountered, the length of the decoded string reduces by one. If a digit is encountered, the length of the decoded string is divided by that digit. This simulates the decoding process in reverse.\n\n### 4. Explain Your Thought Process\n\nAlways articulate the rationale behind your approach. Explain why reverse traversal is efficient and how you simulate the decoding process without actually forming the full string.\n\n## Conclusion\n\nThe "Decoded String at Index" problem demonstrates the importance of understanding the problem\'s constraints and requirements. By simulating the decoding process in reverse, you avoid memory issues and provide an efficient solution.\n\n---\n\n## Live Coding & Explain\nhttps://youtu.be/UgSrm6LwXqk?si=WzBk-tHvhzNO8cNI\n\n# Approach: Reverse Traversal\n\nTo tackle the "Decoded String at Index" problem using reverse traversal, we simulate the decoding process in reverse:\n\n## Key Data Structures:\n\n- **length**: An integer variable to keep track of the current length of the decoded string.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize the length variable to 0.\n \n2. **Forward Traversal**:\n - Traverse the string from start to end, updating the length based on whether you encounter a letter or a digit.\n\n3. **Reverse Traversal**:\n - Start from the end of the string. If you encounter a digit, divide the length by the digit and update $$k$$ using modulo operation. If you encounter a letter and $$k$$ equals 0 or length, return the letter.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution involves two traversals over the string, leading to a time complexity of $$ O(n) $$, where `n` is the length of the string `s`.\n\n**Space Complexity:** \n- The space complexity is $$ O(1) $$ since the solution doesn\'t use any additional data structures that scale with the input size. \n\n# Code Reverse Traversal\n``` Python []\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n length = 0\n i = 0\n \n while length < k:\n if s[i].isdigit():\n length *= int(s[i])\n else:\n length += 1\n i += 1\n \n for j in range(i-1, -1, -1):\n char = s[j]\n if char.isdigit():\n length //= int(char)\n k %= length\n else:\n if k == 0 or k == length:\n return char\n length -= 1\n```\n``` Go []\nfunc decodeAtIndex(s string, k int) string {\n length := int64(0)\n i := 0\n\n for length < int64(k) {\n if s[i] >= \'0\' && s[i] <= \'9\' {\n length *= int64(s[i] - \'0\')\n } else {\n length++\n }\n i++\n }\n\n for j := i - 1; j >= 0; j-- {\n if s[j] >= \'0\' && s[j] <= \'9\' {\n length /= int64(s[j] - \'0\')\n k %= int(length)\n } else {\n if k == 0 || k == int(length) {\n return string(s[j])\n }\n length--\n }\n }\n\n return ""\n}\n```\n``` Rust []\nimpl Solution {\n pub fn decode_at_index(s: String, mut k: i32) -> String {\n let mut length: i64 = 0;\n let mut i = 0;\n let bytes = s.as_bytes();\n\n while length < k as i64 {\n if bytes[i].is_ascii_digit() {\n length *= (bytes[i] as char).to_digit(10).unwrap() as i64;\n } else {\n length += 1;\n }\n i += 1;\n }\n\n for j in (0..i).rev() {\n if bytes[j].is_ascii_digit() {\n length /= (bytes[j] as char).to_digit(10).unwrap() as i64;\n k = (k as i64 % length) as i32;\n } else {\n if k == 0 || k as i64 == length {\n return (bytes[j] as char).to_string();\n }\n length -= 1;\n }\n }\n\n return "".to_string();\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n std::string decodeAtIndex(string s, int k) {\n long long length = 0;\n int i = 0;\n \n while (length < k) {\n if (isdigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n \n for (int j = i - 1; j >= 0; j--) {\n if (isdigit(s[j])) {\n length /= s[j] - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n return std::string(1, s[j]); // Convert char to std::string\n }\n length--;\n }\n }\n \n return ""; // Default return, should never reach here given problem constraints\n }\n};\n```\n``` C []\nchar* decodeAtIndex(char* s, int k) {\n long long length = 0;\n int i = 0;\n\n while (length < k) {\n if (isdigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n static char result[2]; // static to return a local array, initialized to hold one character and a null terminator\n for (int j = i - 1; j >= 0; j--) {\n if (isdigit(s[j])) {\n length /= s[j] - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n result[0] = s[j];\n return result;\n }\n length--;\n }\n }\n\n return "";\n}\n```\n``` Java []\npublic class Solution {\n public String decodeAtIndex(String s, int k) {\n long length = 0;\n int i = 0;\n\n while (length < k) {\n if (Character.isDigit(s.charAt(i))) {\n length *= s.charAt(i) - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n for (int j = i - 1; j >= 0; j--) {\n if (Character.isDigit(s.charAt(j))) {\n length /= s.charAt(j) - \'0\';\n k %= length;\n } else {\n if (k == 0 || k == length) {\n return Character.toString(s.charAt(j));\n }\n length--;\n }\n }\n\n return "";\n }\n}\n```\n``` JavaScript []\nvar decodeAtIndex = function(s, k) {\n let length = 0;\n let i = 0;\n\n while (length < k) {\n if (!isNaN(s[i])) {\n length *= Number(s[i]);\n } else {\n length++;\n }\n i++;\n }\n\n for (let j = i - 1; j >= 0; j--) {\n if (!isNaN(s[j])) {\n length /= Number(s[j]);\n k %= length;\n } else {\n if (k === 0 || k === length) {\n return s[j];\n }\n length--;\n }\n }\n\n return "";\n};\n```\n``` C# []\npublic class Solution {\n public string DecodeAtIndex(string s, int k) {\n long length = 0;\n int i = 0;\n\n while (length < k) {\n if (char.IsDigit(s[i])) {\n length *= s[i] - \'0\';\n } else {\n length++;\n }\n i++;\n }\n\n for (int j = i - 1; j >= 0; j--) {\n if (char.IsDigit(s[j])) {\n length /= s[j] - \'0\';\n k %= (int)length;\n } else {\n if (k == 0 || k == length) {\n return s[j].ToString();\n }\n length--;\n }\n }\n\n return "";\n }\n}\n```\n``` PHP []\nclass Solution {\n function decodeAtIndex($s, $k) {\n $length = 0;\n $i = 0;\n\n while ($length < $k) {\n if (is_numeric($s[$i])) {\n $length *= intval($s[$i]);\n } else {\n $length++;\n }\n $i++;\n }\n\n for ($j = $i - 1; $j >= 0; $j--) {\n if (is_numeric($s[$j])) {\n $length /= intval($s[$j]);\n $k %= $length;\n } else {\n if ($k == 0 || $k == $length) {\n return $s[$j];\n }\n $length--;\n }\n }\n\n return "";\n }\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Memory (MB) |\n|------------|-----------|-------------|\n| Rust | 0 ms | 2 MB |\n| C | 0 ms | 6.4 MB |\n| C++ | 0 ms | 6.4 MB |\n| Java | 0 ms | 40.5 MB |\n| Go | 1 ms | 1.9 MB |\n| PHP | 3 ms | 19.1 MB |\n| Python3 | 22 ms | 16.1 MB |\n| JavaScript | 49 ms | 41.9 MB |\n| C# | 68 ms | 37 MB |\n\n\n\n\nThe "Decoded String at Index" problem emphasizes the importance of simulating processes and thinking in reverse to find efficient solutions. It\'s a testament to the idea that sometimes, the direct approach isn\'t the most efficient one. \uD83D\uDE80\uD83E\uDDE0\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB.\n | 146 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
Easy to Understand python solution (beats 80%) | decoded-string-at-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSave the length of actual array ending at each index. (lArray)\nRecursively Find the index where it is same as k.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2) (n = length of array)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n # leet2code3\n # 1234 8 9 10 11 12 36\n def getNew(self,k):\n for i in range(len(self.s)):\n if self.lArray[i]>=k:\n if k%self.lArray[i-1]==0:\n return self.lArray[i-1]\n else:\n return k%self.lArray[i-1]\n \n def decodeAtIndex(self, s: str, k: int) -> str:\n lArray=[1]\n seet={1: s[0]}\n for i in range(1,len(s)):\n if s[i] in \'0123456789\':\n lArray.append(lArray[-1]*int(s[i]))\n else:\n lArray.append(lArray[-1]+1)\n seet[lArray[-1]]=s[i]\n self.lArray=lArray\n self.s=s\n while seet.get(k)==None:\n k=self.getNew(k)\n return seet[k]\n \n\n \n``` | 1 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
Easy to Understand python solution (beats 80%) | decoded-string-at-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSave the length of actual array ending at each index. (lArray)\nRecursively Find the index where it is same as k.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^2) (n = length of array)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n # leet2code3\n # 1234 8 9 10 11 12 36\n def getNew(self,k):\n for i in range(len(self.s)):\n if self.lArray[i]>=k:\n if k%self.lArray[i-1]==0:\n return self.lArray[i-1]\n else:\n return k%self.lArray[i-1]\n \n def decodeAtIndex(self, s: str, k: int) -> str:\n lArray=[1]\n seet={1: s[0]}\n for i in range(1,len(s)):\n if s[i] in \'0123456789\':\n lArray.append(lArray[-1]*int(s[i]))\n else:\n lArray.append(lArray[-1]+1)\n seet[lArray[-1]]=s[i]\n self.lArray=lArray\n self.s=s\n while seet.get(k)==None:\n k=self.getNew(k)\n return seet[k]\n \n\n \n``` | 1 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
Decode At Index Solution in Python3 | decoded-string-at-index | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code:\n\n1. Initialize variables:\n\n- n stores the length of the input string s.\n- i is an index variable used to iterate through the string s.\n- count is a variable used to keep track of the length of the decoded string as characters are processed.\n2. Enter a while loop that iterates through the string s character by character until i reaches the end of the string.\n\n3. Check if the current character s[i] is numeric:\n\n- If it is numeric, it means that there is a repetition factor for the substring. For example, "abc2" means the substring "abc" should be repeated twice.\n- Calculate the effective length of the string if this substring is repeated (int(s[i])-1) * count.\n4. Compare the calculated effective length with k:\n\n- If the calculated effective length is greater than or equal to k, it means that the k-th character falls within the current repetition. In this case, the loop restarts (setting i back to 0 and resetting count to 0) to process the substring from the beginning.\n- If the calculated effective length is less than k, subtract it from k and update the count by adding the calculated effective length. This is done to keep track of the length of the decoded string.\n5. If the current character s[i] is not numeric (i.e., it\'s a regular character):\n\n- Decrement k by 1 to indicate that one character has been processed.\n- Increment count by 1 to account for the processed character.\n- Check if k has reached 0. If it has, return the current character s[i], which is the k-th character of the decoded string.\n6. Increment i to move to the next character in the string s.\n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n n=len(s)\n i=0\n count=0\n while i<n:\n if s[i].isnumeric():\n if (int(s[i])-1)*count>=k:\n i=0\n count=0\n continue\n else:\n k-=(int(s[i])-1)*count\n count+=(int(s[i])-1)*count\n else:\n k-=1\n count+=1\n if k==0:\n return s[i]\n i+=1 \n``` | 1 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
Decode At Index Solution in Python3 | decoded-string-at-index | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code:\n\n1. Initialize variables:\n\n- n stores the length of the input string s.\n- i is an index variable used to iterate through the string s.\n- count is a variable used to keep track of the length of the decoded string as characters are processed.\n2. Enter a while loop that iterates through the string s character by character until i reaches the end of the string.\n\n3. Check if the current character s[i] is numeric:\n\n- If it is numeric, it means that there is a repetition factor for the substring. For example, "abc2" means the substring "abc" should be repeated twice.\n- Calculate the effective length of the string if this substring is repeated (int(s[i])-1) * count.\n4. Compare the calculated effective length with k:\n\n- If the calculated effective length is greater than or equal to k, it means that the k-th character falls within the current repetition. In this case, the loop restarts (setting i back to 0 and resetting count to 0) to process the substring from the beginning.\n- If the calculated effective length is less than k, subtract it from k and update the count by adding the calculated effective length. This is done to keep track of the length of the decoded string.\n5. If the current character s[i] is not numeric (i.e., it\'s a regular character):\n\n- Decrement k by 1 to indicate that one character has been processed.\n- Increment count by 1 to account for the processed character.\n- Check if k has reached 0. If it has, return the current character s[i], which is the k-th character of the decoded string.\n6. Increment i to move to the next character in the string s.\n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n n=len(s)\n i=0\n count=0\n while i<n:\n if s[i].isnumeric():\n if (int(s[i])-1)*count>=k:\n i=0\n count=0\n continue\n else:\n k-=(int(s[i])-1)*count\n count+=(int(s[i])-1)*count\n else:\n k-=1\n count+=1\n if k==0:\n return s[i]\n i+=1 \n``` | 1 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
📈Beats🧭 99.73% ✅ | 🔥Clean & Concise Code | Easy Understanding🔥 | decoded-string-at-index | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to decode an encoded string by iteratively expanding it based on the digits found in the string. The goal is to find the kth character (1-indexed) in the decoded string efficiently.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize totalSize to keep track of the total size of the decoded string.\n2. Iterate through the input string s to calculate totalSize by considering both letters and digits.\n- If a character is a digit, multiply totalSize by that digit.\n- If a character is a letter, increment totalSize by 1, as each letter contributes to the size by 1.\n3. Decode the string in reverse order by iterating through s from the last character.\n- If a character is a digit, update totalSize by dividing it by the digit value and update k by taking its modulo with the updated totalSize.\n- If a character is a letter, check if k is 0 or equal to totalSize. If so, return the current character as it is the kth character.\n- If k is not found yet, decrease totalSize by 1, as each letter contributes to the size by 1.\n4. If the loop finishes without finding the kth character, return an empty string.\n\n---\n\n\n# Complexity\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The first loop through the string s to calculate totalSize takes O(N) time, where N is the length of the input string.\n- The second loop through the string s in reverse order also takes O(N) time.\n- Overall, the time complexity is O(N).\n\n---\n\n2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The code uses a single integer variable totalSize to keep track of the size, which requires constant space.\n- Other variables used within the loops also require constant space.\nThe space complexity is O(1).\n- The code efficiently decodes the string and finds the kth character without the need for additional memory allocation, making it memory-efficient.\n\n---\n\n\n# Do Upvote if you liked the explanation \uD83E\uDD1E\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalSize = 0; // To keep track of the total size of the decoded string.\n \n // Calculate the total size of the decoded string.\n for (char c : s) {\n if (isdigit(c)) {\n int digit = c - \'0\';\n totalSize *= digit;\n } else {\n totalSize++;\n }\n }\n \n // Decode the string in reverse order.\n for (int i = s.size() - 1; i >= 0; i--) {\n char currentChar = s[i];\n if (isdigit(currentChar)) {\n int digit = currentChar - \'0\';\n totalSize /= digit;\n k %= totalSize;\n } else {\n if (k == 0 || k == totalSize) {\n return string(1, currentChar); // Found the character at k.\n }\n totalSize--; // Decrease the size for a single character.\n }\n }\n \n return ""; // This line should never be reached.\n }\n};\n\n``` | 2 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
📈Beats🧭 99.73% ✅ | 🔥Clean & Concise Code | Easy Understanding🔥 | decoded-string-at-index | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code aims to decode an encoded string by iteratively expanding it based on the digits found in the string. The goal is to find the kth character (1-indexed) in the decoded string efficiently.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize totalSize to keep track of the total size of the decoded string.\n2. Iterate through the input string s to calculate totalSize by considering both letters and digits.\n- If a character is a digit, multiply totalSize by that digit.\n- If a character is a letter, increment totalSize by 1, as each letter contributes to the size by 1.\n3. Decode the string in reverse order by iterating through s from the last character.\n- If a character is a digit, update totalSize by dividing it by the digit value and update k by taking its modulo with the updated totalSize.\n- If a character is a letter, check if k is 0 or equal to totalSize. If so, return the current character as it is the kth character.\n- If k is not found yet, decrease totalSize by 1, as each letter contributes to the size by 1.\n4. If the loop finishes without finding the kth character, return an empty string.\n\n---\n\n\n# Complexity\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The first loop through the string s to calculate totalSize takes O(N) time, where N is the length of the input string.\n- The second loop through the string s in reverse order also takes O(N) time.\n- Overall, the time complexity is O(N).\n\n---\n\n2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The code uses a single integer variable totalSize to keep track of the size, which requires constant space.\n- Other variables used within the loops also require constant space.\nThe space complexity is O(1).\n- The code efficiently decodes the string and finds the kth character without the need for additional memory allocation, making it memory-efficient.\n\n---\n\n\n# Do Upvote if you liked the explanation \uD83E\uDD1E\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalSize = 0; // To keep track of the total size of the decoded string.\n \n // Calculate the total size of the decoded string.\n for (char c : s) {\n if (isdigit(c)) {\n int digit = c - \'0\';\n totalSize *= digit;\n } else {\n totalSize++;\n }\n }\n \n // Decode the string in reverse order.\n for (int i = s.size() - 1; i >= 0; i--) {\n char currentChar = s[i];\n if (isdigit(currentChar)) {\n int digit = currentChar - \'0\';\n totalSize /= digit;\n k %= totalSize;\n } else {\n if (k == 0 || k == totalSize) {\n return string(1, currentChar); // Found the character at k.\n }\n totalSize--; // Decrease the size for a single character.\n }\n }\n \n return ""; // This line should never be reached.\n }\n};\n\n``` | 2 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
Python3 Solution | decoded-string-at-index | 0 | 1 | \n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n n=len(s)\n i=0\n count=0\n while i<n:\n if s[i].isnumeric():\n if (int(s[i])-1)*count>=k:\n i=0\n count=0\n continue\n else:\n k-=(int(s[i])-1)*count\n count+=(int(s[i])-1)*count\n else:\n k-=1\n count+=1\n if k==0:\n return s[i]\n i+=1 \n``` | 0 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
Python3 Solution | decoded-string-at-index | 0 | 1 | \n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n n=len(s)\n i=0\n count=0\n while i<n:\n if s[i].isnumeric():\n if (int(s[i])-1)*count>=k:\n i=0\n count=0\n continue\n else:\n k-=(int(s[i])-1)*count\n count+=(int(s[i])-1)*count\n else:\n k-=1\n count+=1\n if k==0:\n return s[i]\n i+=1 \n``` | 0 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
【Video】How I think about a solution - Python Java, C++ | decoded-string-at-index | 1 | 1 | Welcome to my article! This artcle starts with "How we think about a solution". In other words, that is my thought process to solve the question. This article explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope this aricle is helpful for someone.\n\n# Intuition\ntraverse input `s` with thinking about decoded length.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/zdHBMnztG3A\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Decoded String at Index\n`1:39` How we think about a solution\n`7:12` Demonstrate solution with an example.\n`12:09` Coding\n`14:17` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,512\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n#### How I think about a solution\nFirst of all, I just try brute force solution like this.\n\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n decoded_str = "" # Initialize an empty string to store the decoded characters\n i = 0 # Initialize an index for the input string\n\n # Continue decoding characters until the length of the decoded string is less than k\n while len(decoded_str) < k:\n # If the current character is a digit, repeat the decoded string by the digit\n if s[i].isdigit():\n decoded_str *= int(s[i])\n else:\n # If the current character is a letter, add it to the decoded string\n decoded_str += s[i]\n i += 1 # Move to the next character in the input string\n\n # Return the k-th character (1-based index) from the decoded string\n return decoded_str[k - 1]\n```\nbut I got `Memory Limit Exceeded`, so I thought I have to solve this question with efficient space. That\'s how I started thinking a solution with $$O(1)$$.\n\n```\nInput: s = "leet2code3", k = 10\n```\nIn this case, the decoded string is\n```\n"leetleetcodeleetleetcodeleetleetcode"\n```\nI looked at the string for a while and realized that this is a repeated string. The last letter in input `s` is `3`, so the original decoded string is `leetleetcode` which means I have 3 `leetleetcode`.\n\n```\n"leetleetcode leetleetcode leetleetcode"\n```\nI thought if I have only `leetleetcode`, we can get `k` character.\nLet\'s see this\n```\nl e e t l e e t c o d e \n1 2 3 4 5 6 7 8 9 10 11 12\n\nl e e t l e e t c o d e\n13 14 15 16 17 18 19 20 21 22 23 24\n\nl e e t l e e t c o d e\n25 26 27 28 29 30 31 32 33 34 35 36\n\nthe numbers are "k"\n```\nIf I use only the original decoded string `leetleetcode`, I can calculate the position like this.\n\n```\nl e e t l e e t c o d e \n1 2 3 4 5 6 7 8 9 10 11 12\n13 14 15 16 17 18 19 20 21 22 23 24\n25 26 27 28 29 30 31 32 33 34 35 36\n```\nQuestion is how I can calcuate each position? My answer is to use `modulo`. Let\'s see a few examples.\n\n```\nk = 10, 10 % 12 = 10(o) \nk = 17, 17 % 12 = 5(l)\nk = 33, 33 % 12 = 9(c)\n```\n\nFrom this idea, I need current length of decoded string. At first, I have `leetleetcodeleetleetcodeleetleetcode` which is `36`.\n```\n10 % 36 = 10\n```\n`k` is still `10`. The reason why I have `36 letters` is that I have `3` at the last position of an `input s`, so if I divide length of decoded string by `3`, I can get `12` which is the length of original decoded string.\n\nBy the way, somebody is wondering why we traverse input string `s` from the end. There are a few reasons.\n\n---\n\n\n- Efficiently reaching the last repeating pattern:\n\nReversing allows us to easily start from the first character of the last repeating pattern, because `number is always after some characters and we repeat a previous string n times`. This helps us efficiently determine how many times this pattern repeats.\n\n- Find the last repeating pattern easily:\n\nBy reversing the string, we can efficiently progress and focus on the end of the string, which corresponds to the beginning of the final decoded string. This is where the last repeating pattern is, and it is a crucial part in efficiently determining the k-th character.\n\nFor example,\n`leetleetcodeleetleetcodeleetleetcode` \u2192 `leetleetcode`\n`leetleetcode` is coming from `"leet2code`(`input s`)\n\n---\n\nTo get `leetleetcode` from `leetleetcodeleetleetcodeleetleetcode`, just divide current length by a number I found.\n\n```\n36 / 3 = 12 which is length of "leetleetcode"\n``` \nSeems like when I find a number in input `s`, I should divide current length of decoded string by the number.\n\nAnd I have one more pattern. what if I find a character instead of a number. In that case, just subtract `1` from current length to shorten range of the current length. No wonder.\n\nLet\'s continue. Now\n```\nk = 10\nlength of decoded string = 12 ("leetleetcode")\ninput s = "leet2code"\n```\nRepeat the same process above.\n```\n10 % 12 = 10\ntarget character is 10 position in decoded string\n\nCurrent character is "e" from input s, so just subtract 1\nfrom current decoded length which is 11\n\nIn the end,\nk = 10\nlength of decoded string = 11 ("leetleetcod")\ninput s = "leet2cod"\n```\n\n```\n10 % 11 = 10\ntarget character is 10 position in decoded string\n\nk = 10\nCurrent character is "d" from input s, so just subtract 1\nfrom current decoded length which is 10\n\nIn the end,\n\nk = 10\nlength of decoded string = 10 ("leetleetco")\ninput s = "leet2co"\n```\nHere is an important point.\n```\n10 % 10 = 0\n```\nSo now `k = 0` which means I found a target character in the last position of decoded string. If current character is English character, then we should return current character which is `o` .\n\nThis is `k = 10` case. If you try `k = 15`, we will understand modulo like what if `k` is over the original decoded string.\n\nIn that case, at some point, we calculate `15 % 12 = 3`. All we have to do is to find `k = 3` instead of `k = 15` and when length of decoded string is `3`, you will get `k = 0` and then get `e`.\n\n\n---\n\n**We can say "k" is a target position in the range of current decoded string. It can be changed to be located inside of the new length of decoded string when length of decoded string is changed.**\n\n---\n\n\n\nAlgorithm Overview:\n1. Initialize `total_length` to 0.\n2. Calculate the total length of the decoded string by iterating through each character in the input string `s`. Multiply the length by the numeric value if the character is a digit; otherwise, increment the length by 1.\n\nDetailed Explanation:\n1. Start with `total_length` initialized to 0.\n2. Iterate through each character, `char`, in the input string `s`.\n a. If `char` is a digit, multiply `total_length` by the numeric value of `char`.\n b. If `char` is an alphabet character, increment `total_length` by 1.\n3. Traverse the string in reverse.\n4. Calculate the modified index `k` by taking the modulo of `k` with `total_length`.\n5. Check if `k` is 0 and the current character is an alphabet character:\n a. If true, return the current character as the answer.\n6. Update `total_length` based on the current character:\n a. If the current character is a digit, divide `total_length` by the numeric value of the character.\n b. If the current character is an alphabet character, decrement `total_length` by 1.\n\n\n---\n\n\n\n# Complexity\n\nTime Complexity:\n- The first loop that calculates the total length of the decoded string iterates through each character in the input string `s`, resulting in a time complexity of O(n), where n is the length of the input string `s`.\n- The second loop that traverses the string in reverse also iterates through each character, resulting in an additional time complexity of O(n).\n\nOverall time complexity: O(n).\n\nSpace Complexity:\n- The algorithm uses a constant amount of extra space, regardless of the size of the input string `s`. It only uses a few variables to store intermediate values, and the space they consume is not dependent on the size of the input.\n\nOverall space complexity: O(1).\n\n```python []\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n total_length = 0\n\n # Calculate the total length of the decoded string\n for char in s:\n if char.isdigit():\n total_length *= int(char)\n else:\n total_length += 1\n\n # Traverse the string in reverse to find the character at index k\n for char in reversed(s):\n k %= total_length # Reduce index based on the length\n\n # Check if the current character is the answer\n if k == 0 and char.isalpha():\n return char\n\n # Update the length based on the current character\n if char.isdigit():\n total_length //= int(char)\n else:\n total_length -= 1\n```\n```java []\nclass Solution {\n public String decodeAtIndex(String s, int k) {\n long totalLength = 0;\n\n // Calculate the total length of the decoded string\n for (char c : s.toCharArray()) {\n if (Character.isDigit(c)) {\n totalLength *= Character.getNumericValue(c);\n } else {\n totalLength += 1;\n }\n }\n\n // Traverse the string in reverse to find the character at index k\n for (int i = s.length() - 1; i >= 0; i--) {\n k %= totalLength;\n\n if (k == 0 && Character.isLetter(s.charAt(i))) {\n return String.valueOf(s.charAt(i));\n }\n\n if (Character.isDigit(s.charAt(i))) {\n totalLength /= Character.getNumericValue(s.charAt(i));\n } else {\n totalLength -= 1;\n }\n }\n\n return ""; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalLength = 0;\n\n // Calculate the total length of the decoded string\n for (char c : s) {\n if (isdigit(c)) {\n totalLength *= (c - \'0\');\n } else {\n totalLength += 1;\n }\n }\n\n // Traverse the string in reverse to find the character at index k\n for (int i = s.length() - 1; i >= 0; i--) {\n k %= totalLength;\n\n if (k == 0 && isalpha(s[i])) {\n string result(1, s[i]);\n return result;\n }\n\n if (isdigit(s[i])) {\n totalLength /= (s[i] - \'0\');\n } else {\n totalLength -= 1;\n }\n }\n\n return ""; \n }\n};\n```\n\n\n---\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 28th, 2023\nhttps://leetcode.com/problems/sort-array-by-parity/solutions/4098282/video-how-we-think-about-a-solution-one-pointer-python-javascript-java-c/ | 40 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
【Video】How I think about a solution - Python Java, C++ | decoded-string-at-index | 1 | 1 | Welcome to my article! This artcle starts with "How we think about a solution". In other words, that is my thought process to solve the question. This article explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope this aricle is helpful for someone.\n\n# Intuition\ntraverse input `s` with thinking about decoded length.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/zdHBMnztG3A\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Decoded String at Index\n`1:39` How we think about a solution\n`7:12` Demonstrate solution with an example.\n`12:09` Coding\n`14:17` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,512\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n#### How I think about a solution\nFirst of all, I just try brute force solution like this.\n\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n decoded_str = "" # Initialize an empty string to store the decoded characters\n i = 0 # Initialize an index for the input string\n\n # Continue decoding characters until the length of the decoded string is less than k\n while len(decoded_str) < k:\n # If the current character is a digit, repeat the decoded string by the digit\n if s[i].isdigit():\n decoded_str *= int(s[i])\n else:\n # If the current character is a letter, add it to the decoded string\n decoded_str += s[i]\n i += 1 # Move to the next character in the input string\n\n # Return the k-th character (1-based index) from the decoded string\n return decoded_str[k - 1]\n```\nbut I got `Memory Limit Exceeded`, so I thought I have to solve this question with efficient space. That\'s how I started thinking a solution with $$O(1)$$.\n\n```\nInput: s = "leet2code3", k = 10\n```\nIn this case, the decoded string is\n```\n"leetleetcodeleetleetcodeleetleetcode"\n```\nI looked at the string for a while and realized that this is a repeated string. The last letter in input `s` is `3`, so the original decoded string is `leetleetcode` which means I have 3 `leetleetcode`.\n\n```\n"leetleetcode leetleetcode leetleetcode"\n```\nI thought if I have only `leetleetcode`, we can get `k` character.\nLet\'s see this\n```\nl e e t l e e t c o d e \n1 2 3 4 5 6 7 8 9 10 11 12\n\nl e e t l e e t c o d e\n13 14 15 16 17 18 19 20 21 22 23 24\n\nl e e t l e e t c o d e\n25 26 27 28 29 30 31 32 33 34 35 36\n\nthe numbers are "k"\n```\nIf I use only the original decoded string `leetleetcode`, I can calculate the position like this.\n\n```\nl e e t l e e t c o d e \n1 2 3 4 5 6 7 8 9 10 11 12\n13 14 15 16 17 18 19 20 21 22 23 24\n25 26 27 28 29 30 31 32 33 34 35 36\n```\nQuestion is how I can calcuate each position? My answer is to use `modulo`. Let\'s see a few examples.\n\n```\nk = 10, 10 % 12 = 10(o) \nk = 17, 17 % 12 = 5(l)\nk = 33, 33 % 12 = 9(c)\n```\n\nFrom this idea, I need current length of decoded string. At first, I have `leetleetcodeleetleetcodeleetleetcode` which is `36`.\n```\n10 % 36 = 10\n```\n`k` is still `10`. The reason why I have `36 letters` is that I have `3` at the last position of an `input s`, so if I divide length of decoded string by `3`, I can get `12` which is the length of original decoded string.\n\nBy the way, somebody is wondering why we traverse input string `s` from the end. There are a few reasons.\n\n---\n\n\n- Efficiently reaching the last repeating pattern:\n\nReversing allows us to easily start from the first character of the last repeating pattern, because `number is always after some characters and we repeat a previous string n times`. This helps us efficiently determine how many times this pattern repeats.\n\n- Find the last repeating pattern easily:\n\nBy reversing the string, we can efficiently progress and focus on the end of the string, which corresponds to the beginning of the final decoded string. This is where the last repeating pattern is, and it is a crucial part in efficiently determining the k-th character.\n\nFor example,\n`leetleetcodeleetleetcodeleetleetcode` \u2192 `leetleetcode`\n`leetleetcode` is coming from `"leet2code`(`input s`)\n\n---\n\nTo get `leetleetcode` from `leetleetcodeleetleetcodeleetleetcode`, just divide current length by a number I found.\n\n```\n36 / 3 = 12 which is length of "leetleetcode"\n``` \nSeems like when I find a number in input `s`, I should divide current length of decoded string by the number.\n\nAnd I have one more pattern. what if I find a character instead of a number. In that case, just subtract `1` from current length to shorten range of the current length. No wonder.\n\nLet\'s continue. Now\n```\nk = 10\nlength of decoded string = 12 ("leetleetcode")\ninput s = "leet2code"\n```\nRepeat the same process above.\n```\n10 % 12 = 10\ntarget character is 10 position in decoded string\n\nCurrent character is "e" from input s, so just subtract 1\nfrom current decoded length which is 11\n\nIn the end,\nk = 10\nlength of decoded string = 11 ("leetleetcod")\ninput s = "leet2cod"\n```\n\n```\n10 % 11 = 10\ntarget character is 10 position in decoded string\n\nk = 10\nCurrent character is "d" from input s, so just subtract 1\nfrom current decoded length which is 10\n\nIn the end,\n\nk = 10\nlength of decoded string = 10 ("leetleetco")\ninput s = "leet2co"\n```\nHere is an important point.\n```\n10 % 10 = 0\n```\nSo now `k = 0` which means I found a target character in the last position of decoded string. If current character is English character, then we should return current character which is `o` .\n\nThis is `k = 10` case. If you try `k = 15`, we will understand modulo like what if `k` is over the original decoded string.\n\nIn that case, at some point, we calculate `15 % 12 = 3`. All we have to do is to find `k = 3` instead of `k = 15` and when length of decoded string is `3`, you will get `k = 0` and then get `e`.\n\n\n---\n\n**We can say "k" is a target position in the range of current decoded string. It can be changed to be located inside of the new length of decoded string when length of decoded string is changed.**\n\n---\n\n\n\nAlgorithm Overview:\n1. Initialize `total_length` to 0.\n2. Calculate the total length of the decoded string by iterating through each character in the input string `s`. Multiply the length by the numeric value if the character is a digit; otherwise, increment the length by 1.\n\nDetailed Explanation:\n1. Start with `total_length` initialized to 0.\n2. Iterate through each character, `char`, in the input string `s`.\n a. If `char` is a digit, multiply `total_length` by the numeric value of `char`.\n b. If `char` is an alphabet character, increment `total_length` by 1.\n3. Traverse the string in reverse.\n4. Calculate the modified index `k` by taking the modulo of `k` with `total_length`.\n5. Check if `k` is 0 and the current character is an alphabet character:\n a. If true, return the current character as the answer.\n6. Update `total_length` based on the current character:\n a. If the current character is a digit, divide `total_length` by the numeric value of the character.\n b. If the current character is an alphabet character, decrement `total_length` by 1.\n\n\n---\n\n\n\n# Complexity\n\nTime Complexity:\n- The first loop that calculates the total length of the decoded string iterates through each character in the input string `s`, resulting in a time complexity of O(n), where n is the length of the input string `s`.\n- The second loop that traverses the string in reverse also iterates through each character, resulting in an additional time complexity of O(n).\n\nOverall time complexity: O(n).\n\nSpace Complexity:\n- The algorithm uses a constant amount of extra space, regardless of the size of the input string `s`. It only uses a few variables to store intermediate values, and the space they consume is not dependent on the size of the input.\n\nOverall space complexity: O(1).\n\n```python []\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n total_length = 0\n\n # Calculate the total length of the decoded string\n for char in s:\n if char.isdigit():\n total_length *= int(char)\n else:\n total_length += 1\n\n # Traverse the string in reverse to find the character at index k\n for char in reversed(s):\n k %= total_length # Reduce index based on the length\n\n # Check if the current character is the answer\n if k == 0 and char.isalpha():\n return char\n\n # Update the length based on the current character\n if char.isdigit():\n total_length //= int(char)\n else:\n total_length -= 1\n```\n```java []\nclass Solution {\n public String decodeAtIndex(String s, int k) {\n long totalLength = 0;\n\n // Calculate the total length of the decoded string\n for (char c : s.toCharArray()) {\n if (Character.isDigit(c)) {\n totalLength *= Character.getNumericValue(c);\n } else {\n totalLength += 1;\n }\n }\n\n // Traverse the string in reverse to find the character at index k\n for (int i = s.length() - 1; i >= 0; i--) {\n k %= totalLength;\n\n if (k == 0 && Character.isLetter(s.charAt(i))) {\n return String.valueOf(s.charAt(i));\n }\n\n if (Character.isDigit(s.charAt(i))) {\n totalLength /= Character.getNumericValue(s.charAt(i));\n } else {\n totalLength -= 1;\n }\n }\n\n return ""; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string decodeAtIndex(string s, int k) {\n long long totalLength = 0;\n\n // Calculate the total length of the decoded string\n for (char c : s) {\n if (isdigit(c)) {\n totalLength *= (c - \'0\');\n } else {\n totalLength += 1;\n }\n }\n\n // Traverse the string in reverse to find the character at index k\n for (int i = s.length() - 1; i >= 0; i--) {\n k %= totalLength;\n\n if (k == 0 && isalpha(s[i])) {\n string result(1, s[i]);\n return result;\n }\n\n if (isdigit(s[i])) {\n totalLength /= (s[i] - \'0\');\n } else {\n totalLength -= 1;\n }\n }\n\n return ""; \n }\n};\n```\n\n\n---\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\nMy next post for daily coding challenge on Sep 28th, 2023\nhttps://leetcode.com/problems/sort-array-by-parity/solutions/4098282/video-how-we-think-about-a-solution-one-pointer-python-javascript-java-c/ | 40 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
Explain to solution in easiest method......Try it..(^_^) | decoded-string-at-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n size=0\n for it in s: # Calculate the all string size\n if it.isdigit():\n size=int(it)*size\n else:\n size+=1\n i=len(s) \n for i in range(i-1,-1,-1): # Reverse string counting because it\'s will be help to short string length\n if(size<=k):\n if(s[i].isalpha()):\n k=k%size\n if(k==0 and (\'a\'<=s[i]<=\'z\')):\n return s[i]\n\n if (s[i].isdigit()):\n size=size//int(s[i])\n else:\n size-=1 \n if size==0:\n return s[i] \n``` | 0 | You are given an encoded string `s`. To decode the string to a tape, the encoded string is read one character at a time and the following steps are taken:
* If the character read is a letter, that letter is written onto the tape.
* If the character read is a digit `d`, the entire current tape is repeatedly written `d - 1` more times in total.
Given an integer `k`, return _the_ `kth` _letter (**1-indexed)** in the decoded string_.
**Example 1:**
**Input:** s = "leet2code3 ", k = 10
**Output:** "o "
**Explanation:** The decoded string is "leetleetcodeleetleetcodeleetleetcode ".
The 10th letter in the string is "o ".
**Example 2:**
**Input:** s = "ha22 ", k = 5
**Output:** "h "
**Explanation:** The decoded string is "hahahaha ".
The 5th letter is "h ".
**Example 3:**
**Input:** s = "a2345678999999999999999 ", k = 1
**Output:** "a "
**Explanation:** The decoded string is "a " repeated 8301530446056247680 times.
The 1st letter is "a ".
**Constraints:**
* `2 <= s.length <= 100`
* `s` consists of lowercase English letters and digits `2` through `9`.
* `s` starts with a letter.
* `1 <= k <= 109`
* It is guaranteed that `k` is less than or equal to the length of the decoded string.
* The decoded string is guaranteed to have less than `263` letters. | null |
Explain to solution in easiest method......Try it..(^_^) | decoded-string-at-index | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def decodeAtIndex(self, s: str, k: int) -> str:\n size=0\n for it in s: # Calculate the all string size\n if it.isdigit():\n size=int(it)*size\n else:\n size+=1\n i=len(s) \n for i in range(i-1,-1,-1): # Reverse string counting because it\'s will be help to short string length\n if(size<=k):\n if(s[i].isalpha()):\n k=k%size\n if(k==0 and (\'a\'<=s[i]<=\'z\')):\n return s[i]\n\n if (s[i].isdigit()):\n size=size//int(s[i])\n else:\n size-=1 \n if size==0:\n return s[i] \n``` | 0 | You are given two string arrays `words1` and `words2`.
A string `b` is a **subset** of string `a` if every letter in `b` occurs in `a` including multiplicity.
* For example, `"wrr "` is a subset of `"warrior "` but is not a subset of `"world "`.
A string `a` from `words1` is **universal** if for every string `b` in `words2`, `b` is a subset of `a`.
Return an array of all the **universal** strings in `words1`. You may return the answer in **any order**.
**Example 1:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "e ", "o "\]
**Output:** \[ "facebook ", "google ", "leetcode "\]
**Example 2:**
**Input:** words1 = \[ "amazon ", "apple ", "facebook ", "google ", "leetcode "\], words2 = \[ "l ", "e "\]
**Output:** \[ "apple ", "google ", "leetcode "\]
**Constraints:**
* `1 <= words1.length, words2.length <= 104`
* `1 <= words1[i].length, words2[i].length <= 10`
* `words1[i]` and `words2[i]` consist only of lowercase English letters.
* All the strings of `words1` are **unique**. | null |
⭐Explained Python 2 Pointers Solution | boats-to-save-people | 0 | 1 | **OBSERVATIONS:**\n```\nLets take an example: People = [1, 1, 2, 3, 9, 10, 11, 12] and Limit = 12\n```\n\n1. Since we want to minimise the number of boats used, we must try to form pair of largest and smallest numbers to fit them into one boat if possible. Taking two smaller weight people and adding them to one boat might waste some precious space.\n2. Now we can see that as 12 tries to form a pair. Logically being the largest number it should start from the smallest. So it goes to 1\'s, then 2 then 3 and so on to form a pair. Now one thing to note is that if 12 cannot form a pair with the smallest number(that is 1), then there is no point looking forward to 2, 3 ... as it is certain that numbers beyond 1 will be equal to or larger than 1 and will definitely exceed the boats rated capacity if it did with 1 in the first place. \n3. Thus if the `people[hi]` cannot be seated with `people[lo]` in one boat then that means that people[hi] cannot form a pair with any of the remaining people, and we will thus stop looking for a partner for that person and give him a boat for him/her self.\n\n**STEPS:**\n1. Maintain 2 pointers `lo` and `hi` set to 0 and n-1 respectively.\n2. Sort the array `people`.\n3. Now traverse till `lo <= hi`.\n4. If people[lo] + people[hi] <= target. That means they can form a pair and can sit in the same boat. \n5. If not then the people[hi] that is the person with the higher weight is the problem and must be given his own boat as we observed above. \n\n**CODE**\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n lo = 0\n hi = len(people)-1\n boats = 0\n while lo <= hi:\n if people[lo] + people[hi] <= limit:\n lo += 1\n hi -= 1\n else:\n hi -= 1\n boats += 1\n return boats\n```\n**SPACE & TIME COMPLEXITY:**\nO(NlogN) time as we only traverse the array once but require NlogN to sort it in the first place.\nand O(N) space in worst case as we only use 3 variables: `lo`, `hi` and `boats` **however Python sorting has a space complexity of `\u03A9(n)` {Upperbound at N or O(n) in the worst case}.** \n\n\n | 53 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
⭐Explained Python 2 Pointers Solution | boats-to-save-people | 0 | 1 | **OBSERVATIONS:**\n```\nLets take an example: People = [1, 1, 2, 3, 9, 10, 11, 12] and Limit = 12\n```\n\n1. Since we want to minimise the number of boats used, we must try to form pair of largest and smallest numbers to fit them into one boat if possible. Taking two smaller weight people and adding them to one boat might waste some precious space.\n2. Now we can see that as 12 tries to form a pair. Logically being the largest number it should start from the smallest. So it goes to 1\'s, then 2 then 3 and so on to form a pair. Now one thing to note is that if 12 cannot form a pair with the smallest number(that is 1), then there is no point looking forward to 2, 3 ... as it is certain that numbers beyond 1 will be equal to or larger than 1 and will definitely exceed the boats rated capacity if it did with 1 in the first place. \n3. Thus if the `people[hi]` cannot be seated with `people[lo]` in one boat then that means that people[hi] cannot form a pair with any of the remaining people, and we will thus stop looking for a partner for that person and give him a boat for him/her self.\n\n**STEPS:**\n1. Maintain 2 pointers `lo` and `hi` set to 0 and n-1 respectively.\n2. Sort the array `people`.\n3. Now traverse till `lo <= hi`.\n4. If people[lo] + people[hi] <= target. That means they can form a pair and can sit in the same boat. \n5. If not then the people[hi] that is the person with the higher weight is the problem and must be given his own boat as we observed above. \n\n**CODE**\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n lo = 0\n hi = len(people)-1\n boats = 0\n while lo <= hi:\n if people[lo] + people[hi] <= limit:\n lo += 1\n hi -= 1\n else:\n hi -= 1\n boats += 1\n return boats\n```\n**SPACE & TIME COMPLEXITY:**\nO(NlogN) time as we only traverse the array once but require NlogN to sort it in the first place.\nand O(N) space in worst case as we only use 3 variables: `lo`, `hi` and `boats` **however Python sorting has a space complexity of `\u03A9(n)` {Upperbound at N or O(n) in the worst case}.** \n\n\n | 53 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
[Java, Python & C++] Easy to Understand and Efficient Solutions. | boats-to-save-people | 1 | 1 | # Approach\nTwo Pointer Approach\n\n\n# Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n\n# Code\n### Java\n```\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n Arrays.sort(people);\n int start = 0; \n int end = people.length - 1;\n int res = 0;\n\n while (start <= end) {\n if (people[start] + people[end] <= limit){\n start++;\n }\n end--;\n res++;\n }\n\n return res;\n }\n}\n```\n\n### Python\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n start = 0\n end = len(people) - 1\n res = 0\n\n while start <= end:\n if people[start] + people[end] <= limit:\n start += 1\n end -= 1\n res += 1\n\n return res\n\n```\n\n### C++\n```\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n sort(people.begin(), people.end());\n int start = 0; \n int end = people.size() - 1;\n int res = 0;\n\n while (start <= end) {\n if (people[start] + people[end] <= limit){\n start++;\n }\n end--;\n res++;\n }\n\n return res;\n }\n};\n``` | 6 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
[Java, Python & C++] Easy to Understand and Efficient Solutions. | boats-to-save-people | 1 | 1 | # Approach\nTwo Pointer Approach\n\n\n# Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n\n# Code\n### Java\n```\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n Arrays.sort(people);\n int start = 0; \n int end = people.length - 1;\n int res = 0;\n\n while (start <= end) {\n if (people[start] + people[end] <= limit){\n start++;\n }\n end--;\n res++;\n }\n\n return res;\n }\n}\n```\n\n### Python\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n start = 0\n end = len(people) - 1\n res = 0\n\n while start <= end:\n if people[start] + people[end] <= limit:\n start += 1\n end -= 1\n res += 1\n\n return res\n\n```\n\n### C++\n```\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n sort(people.begin(), people.end());\n int start = 0; \n int end = people.size() - 1;\n int res = 0;\n\n while (start <= end) {\n if (people[start] + people[end] <= limit){\n start++;\n }\n end--;\n res++;\n }\n\n return res;\n }\n};\n``` | 6 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
✅✅Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand🔥 | boats-to-save-people | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Video Solution\n**Search \uD83D\uDC49 `Boats to Save People by Tech Wired` on YouTube**\n\n\n\n\n# Approach:\n\n- One possible approach to solving this problem is to sort the people by weight, and then use two pointers to traverse the sorted array from both ends. We can start with the heaviest person and the lightest person, and try to pair them up. If their combined weight is less than or equal to the boat\'s weight limit, we add them to a boat and move the lightest person\'s pointer to the next person. Otherwise, we only add the heaviest person to a boat.\n\n- We continue this process until all the people are either in a boat or have been paired up. The number of boats required is then the total number of iterations required to complete this process.\n\n# Intuition:\n\n- The intuition behind this approach is that we want to maximize the number of people we can put on a boat while ensuring that we don\'t exceed the weight limit of the boat. By starting with the heaviest and lightest person and pairing them up, we can ensure that we use the weight capacity of the boat as efficiently as possible. We then repeat this process with the next heaviest and lightest person, and so on, until we have either used all the people or run out of boats.\n\n- Sorting the people by weight is important because it allows us to pair up the heaviest and lightest person efficiently. If the people are not sorted, we might miss an optimal pairing and end up using more boats than necessary.\n\n- Overall, the time complexity of this approach is O(nlogn) due to the sorting step, where n is the number of people.\n\n```Python []\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n i, j = 0, len(people) - 1\n boats = 0\n while i <= j:\n if people[j] + people[i] <= limit:\n i += 1\n j -= 1\n boats += 1\n return boats\n\n```\n```Java []\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n Arrays.sort(people);\n int i = 0, j = people.length - 1;\n int boats = 0;\n while (i <= j) {\n if (people[j] + people[i] <= limit) {\n i++;\n }\n j--;\n boats++;\n }\n return boats;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n sort(people.begin(), people.end());\n int i = 0, j = people.size() - 1;\n int boats = 0;\n while (i <= j) {\n if (people[j] + people[i] <= limit) {\n i++;\n }\n j--;\n boats++;\n }\n return boats;\n }\n};\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D\n | 18 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
✅✅Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand🔥 | boats-to-save-people | 1 | 1 | # Please UPVOTE \uD83D\uDC4D\n\n**!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers this week. I planned to give for next 10,000 Subscribers as well. So **DON\'T FORGET** to Subscribe\n\n**Search \uD83D\uDC49`Tech Wired leetcode` on YouTube to Subscribe**\n# OR \n**Click the Link in my Leetcode Profile to Subscribe**\n\nHappy Learning, Cheers Guys \uD83D\uDE0A\n\n# Video Solution\n**Search \uD83D\uDC49 `Boats to Save People by Tech Wired` on YouTube**\n\n\n\n\n# Approach:\n\n- One possible approach to solving this problem is to sort the people by weight, and then use two pointers to traverse the sorted array from both ends. We can start with the heaviest person and the lightest person, and try to pair them up. If their combined weight is less than or equal to the boat\'s weight limit, we add them to a boat and move the lightest person\'s pointer to the next person. Otherwise, we only add the heaviest person to a boat.\n\n- We continue this process until all the people are either in a boat or have been paired up. The number of boats required is then the total number of iterations required to complete this process.\n\n# Intuition:\n\n- The intuition behind this approach is that we want to maximize the number of people we can put on a boat while ensuring that we don\'t exceed the weight limit of the boat. By starting with the heaviest and lightest person and pairing them up, we can ensure that we use the weight capacity of the boat as efficiently as possible. We then repeat this process with the next heaviest and lightest person, and so on, until we have either used all the people or run out of boats.\n\n- Sorting the people by weight is important because it allows us to pair up the heaviest and lightest person efficiently. If the people are not sorted, we might miss an optimal pairing and end up using more boats than necessary.\n\n- Overall, the time complexity of this approach is O(nlogn) due to the sorting step, where n is the number of people.\n\n```Python []\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n i, j = 0, len(people) - 1\n boats = 0\n while i <= j:\n if people[j] + people[i] <= limit:\n i += 1\n j -= 1\n boats += 1\n return boats\n\n```\n```Java []\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n Arrays.sort(people);\n int i = 0, j = people.length - 1;\n int boats = 0;\n while (i <= j) {\n if (people[j] + people[i] <= limit) {\n i++;\n }\n j--;\n boats++;\n }\n return boats;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n sort(people.begin(), people.end());\n int i = 0, j = people.size() - 1;\n int boats = 0;\n while (i <= j) {\n if (people[j] + people[i] <= limit) {\n i++;\n }\n j--;\n boats++;\n }\n return boats;\n }\n};\n\n```\n\n\n# Please UPVOTE \uD83D\uDC4D\n | 18 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
Solution | boats-to-save-people | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n std::ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);\n int freq[30001] = {0};\n int hv = INT_MIN;\n int lt = INT_MAX;\n for(int i : people){\n hv = max(hv, i);\n lt = min(lt, i);\n freq[i]++;\n }\n int cnt = 0;\n while(lt < hv){\n while(lt < hv && freq[hv]==0)\n hv--;\n\n while(lt < hv && freq[lt]==0)\n lt++;\n\n if (lt == hv)\n break;\n if (lt + hv <= limit)\n freq[lt]--;\n freq[hv]--;\n cnt++;\n }\n if (lt == hv){\n if(lt*2>limit) cnt+=freq[lt]; \n else cnt+=(freq[lt]+1)/2;\n }\n return cnt;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n ans = lo = 0\n hi = len(people) - 1\n\n while lo <= hi:\n if people[lo] + people[hi] <= limit:\n lo += 1\n \n hi -= 1\n ans += 1\n \n return ans\n```\n\n```Java []\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n int min = people[0], max = people[0];\n for(int i=1;i<people.length;i++)\n {\n min = Math.min(min, people[i]);\n max = Math.max(max, people[i]);\n }\n int[] arr = new int[max - min + 1];\n int res = 0;\n for(int num : people)\n {\n arr[num - min]++;\n }\n int l = min, r = max;\n while(l < r)\n {\n if(r + l > limit)\n {\n res += arr[r - min];\n r--;\n while(l < r && arr[r - min]==0)r--;\n }\n else{\n int diff = (arr[l - min] > arr[r - min]) ? arr[r - min] : arr[l-min];\n arr[l - min] -= diff; arr[r - min] -= diff; res += diff;\n while(l < r && arr[l - min]==0)l++;while(l < r && arr[r - min]==0)r--;\n }\n }\n if(arr[l - min]!= 0)\n {\n int q = limit/l;\n if(q == 1)\n {\n res += arr[l - min];\n }else{\n res += arr[l - min]/2 + arr[l - min] % 2;\n }\n }\n return res;\n }\n}\n```\n | 1 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
Solution | boats-to-save-people | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numRescueBoats(vector<int>& people, int limit) {\n std::ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);\n int freq[30001] = {0};\n int hv = INT_MIN;\n int lt = INT_MAX;\n for(int i : people){\n hv = max(hv, i);\n lt = min(lt, i);\n freq[i]++;\n }\n int cnt = 0;\n while(lt < hv){\n while(lt < hv && freq[hv]==0)\n hv--;\n\n while(lt < hv && freq[lt]==0)\n lt++;\n\n if (lt == hv)\n break;\n if (lt + hv <= limit)\n freq[lt]--;\n freq[hv]--;\n cnt++;\n }\n if (lt == hv){\n if(lt*2>limit) cnt+=freq[lt]; \n else cnt+=(freq[lt]+1)/2;\n }\n return cnt;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n ans = lo = 0\n hi = len(people) - 1\n\n while lo <= hi:\n if people[lo] + people[hi] <= limit:\n lo += 1\n \n hi -= 1\n ans += 1\n \n return ans\n```\n\n```Java []\nclass Solution {\n public int numRescueBoats(int[] people, int limit) {\n int min = people[0], max = people[0];\n for(int i=1;i<people.length;i++)\n {\n min = Math.min(min, people[i]);\n max = Math.max(max, people[i]);\n }\n int[] arr = new int[max - min + 1];\n int res = 0;\n for(int num : people)\n {\n arr[num - min]++;\n }\n int l = min, r = max;\n while(l < r)\n {\n if(r + l > limit)\n {\n res += arr[r - min];\n r--;\n while(l < r && arr[r - min]==0)r--;\n }\n else{\n int diff = (arr[l - min] > arr[r - min]) ? arr[r - min] : arr[l-min];\n arr[l - min] -= diff; arr[r - min] -= diff; res += diff;\n while(l < r && arr[l - min]==0)l++;while(l < r && arr[r - min]==0)r--;\n }\n }\n if(arr[l - min]!= 0)\n {\n int q = limit/l;\n if(q == 1)\n {\n res += arr[l - min];\n }else{\n res += arr[l - min]/2 + arr[l - min] % 2;\n }\n }\n return res;\n }\n}\n```\n | 1 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
Python BS-paring with heaviest within limit O(n^2) worsest O(nlogn) ave | boats-to-save-people | 0 | 1 | # Intuition\nI know pairing the heaviest with the next heaviest within limit is an overkill and the following code using BS is not as efficient as pairing with the lightest. But to me, it\'s really more intuitive that the more greedy way to pair the heaviest with the next heaviest within limit.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing binary search to find the next heaviest within limit in the remaining people. I used a set to maintain the alreay on-boat people. It does in the worest case take O(n) time to search if the heaviest pairing within limit is aleady paired with others. Please post your ideas if a better way to get rid of this.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2) worsest O(nlogn) ave. Accepted with 5% time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n\n people.sort()\n n = len(people)\n check = set()\n res = 0\n for i in range(n-1,-1,-1):\n if i in check:\n continue\n res += 1\n check.add(i)\n x = people[i]\n cap = limit - x\n l,r = 0,i-1\n while l<=r: # binary search to find the heaviest pairing within limit\n m = l+(r-l)//2\n if people[m] <= cap:\n l = m+1\n else:\n r = m-1\n if not r in check: # -1 can be added to check as well\n check.add(r)\n else:\n while r>=0 and r in check: # worest case O(n)\n r -= 1\n if r>=0:\n check.add(r)\n return res\n\n\n\n\n\n``` | 1 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
Python BS-paring with heaviest within limit O(n^2) worsest O(nlogn) ave | boats-to-save-people | 0 | 1 | # Intuition\nI know pairing the heaviest with the next heaviest within limit is an overkill and the following code using BS is not as efficient as pairing with the lightest. But to me, it\'s really more intuitive that the more greedy way to pair the heaviest with the next heaviest within limit.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsing binary search to find the next heaviest within limit in the remaining people. I used a set to maintain the alreay on-boat people. It does in the worest case take O(n) time to search if the heaviest pairing within limit is aleady paired with others. Please post your ideas if a better way to get rid of this.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2) worsest O(nlogn) ave. Accepted with 5% time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n\n people.sort()\n n = len(people)\n check = set()\n res = 0\n for i in range(n-1,-1,-1):\n if i in check:\n continue\n res += 1\n check.add(i)\n x = people[i]\n cap = limit - x\n l,r = 0,i-1\n while l<=r: # binary search to find the heaviest pairing within limit\n m = l+(r-l)//2\n if people[m] <= cap:\n l = m+1\n else:\n r = m-1\n if not r in check: # -1 can be added to check as well\n check.add(r)\n else:\n while r>=0 and r in check: # worest case O(n)\n r -= 1\n if r>=0:\n check.add(r)\n return res\n\n\n\n\n\n``` | 1 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
April 3rd Daily Challenge | | 🐍 | | Two pointer approach | | Fastest | boats-to-save-people | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> Sort the given array\n-> Take two pointers on either side of the array\n-> If sum of items on both sides <= Limit , then i+=1 and j-=1\n-> Else decrease right pointer by 1\n-> Increment the result by repeating the above process until starting pointer <= Ending Pointer\n# Complexity\n- Time complexity:O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n i,j=0,len(people)-1\n ans=0\n while i<=j:\n if people[i]+people[j]<=limit:\n i+=1\n j-=1\n else:\n j-=1\n ans+=1\n return ans\n \n``` | 1 | You are given an array `people` where `people[i]` is the weight of the `ith` person, and an **infinite number of boats** where each boat can carry a maximum weight of `limit`. Each boat carries at most two people at the same time, provided the sum of the weight of those people is at most `limit`.
Return _the minimum number of boats to carry every given person_.
**Example 1:**
**Input:** people = \[1,2\], limit = 3
**Output:** 1
**Explanation:** 1 boat (1, 2)
**Example 2:**
**Input:** people = \[3,2,2,1\], limit = 3
**Output:** 3
**Explanation:** 3 boats (1, 2), (2) and (3)
**Example 3:**
**Input:** people = \[3,5,3,4\], limit = 5
**Output:** 4
**Explanation:** 4 boats (3), (3), (4), (5)
**Constraints:**
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= limit <= 3 * 104` | null |
April 3rd Daily Challenge | | 🐍 | | Two pointer approach | | Fastest | boats-to-save-people | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> Sort the given array\n-> Take two pointers on either side of the array\n-> If sum of items on both sides <= Limit , then i+=1 and j-=1\n-> Else decrease right pointer by 1\n-> Increment the result by repeating the above process until starting pointer <= Ending Pointer\n# Complexity\n- Time complexity:O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRescueBoats(self, people: List[int], limit: int) -> int:\n people.sort()\n i,j=0,len(people)-1\n ans=0\n while i<=j:\n if people[i]+people[j]<=limit:\n i+=1\n j-=1\n else:\n j-=1\n ans+=1\n return ans\n \n``` | 1 | Given a string `s`, reverse the string according to the following rules:
* All the characters that are not English letters remain in the same position.
* All the English letters (lowercase or uppercase) should be reversed.
Return `s` _after reversing it_.
**Example 1:**
**Input:** s = "ab-cd"
**Output:** "dc-ba"
**Example 2:**
**Input:** s = "a-bC-dEf-ghIj"
**Output:** "j-Ih-gfE-dCba"
**Example 3:**
**Input:** s = "Test1ng-Leet=code-Q!"
**Output:** "Qedo1ct-eeLg=ntse-T!"
**Constraints:**
* `1 <= s.length <= 100`
* `s` consists of characters with ASCII values in the range `[33, 122]`.
* `s` does not contain `'\ "'` or `'\\'`. | null |
Solution | reachable-nodes-in-subdivided-graph | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {\n vector<vector<pair<int, int>>> graph(n);\n vector<int> dist(graph.size(), maxMoves + 1);\n\n for (const vector<int>& edge : edges) {\n const int u = edge[0];\n const int v = edge[1];\n const int cnt = edge[2];\n graph[u].emplace_back(v, cnt);\n graph[v].emplace_back(u, cnt);\n }\n const int reachableNodes = dijkstra(graph, 0, maxMoves, dist);\n int reachableSubnodes = 0;\n\n for (const vector<int>& edge : edges) {\n const int u = edge[0];\n const int v = edge[1];\n const int cnt = edge[2];\n const int a = dist[u] > maxMoves ? 0 : min(maxMoves - dist[u], cnt);\n const int b = dist[v] > maxMoves ? 0 : min(maxMoves - dist[v], cnt);\n reachableSubnodes += min(a + b, cnt);\n }\n return reachableNodes + reachableSubnodes;\n }\n private:\n int dijkstra(const vector<vector<pair<int, int>>>& graph, int src,\n int maxMoves, vector<int>& dist) {\n using P = pair<int, int>;\n priority_queue<P, vector<P>, greater<>> minHeap;\n\n dist[src] = 0;\n minHeap.emplace(dist[src], src);\n\n while (!minHeap.empty()) {\n const auto [d, u] = minHeap.top();\n minHeap.pop();\n for (const auto& [v, w] : graph[u])\n if (d + w + 1 < dist[v]) {\n dist[v] = d + w + 1;\n minHeap.emplace(dist[v], v);\n }\n }\n return count_if(begin(dist), end(dist),\n [&](int d) { return d <= maxMoves; });\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph = defaultdict(dict)\n for u,v,cnt in edges:\n graph[u][v]=graph[v][u]=cnt\n \n cur = [(0,0)]\n heapify(cur)\n visited, added = set(), {0}\n sol, addn = 1, n+1\n\n while cur:\n c,v = heappop(cur)\n if v in visited:\n continue\n visited.add(v)\n for u in graph[v]:\n if u not in visited:\n if c + graph[v][u] + 1 <= maxMoves:\n sol += graph[v][u]\n if u not in added:\n sol += 1\n added.add(u)\n if u <= n:\n heappush(cur,(c + graph[v][u] + 1, u))\n else:\n sol += maxMoves-c\n graph[u][addn] = graph[v][u]-(maxMoves-c)-1\n graph[u].pop(v,None)\n addn += 1\n\n return sol\n```\n\n```Java []\nclass Node implements Comparable<Node>{\n int u;\n int w;\n Node(int u, int w){\n this.u = u;\n this.w = w;\n }\n @Override\n public int compareTo(Node o) {\n return this.w-o.w;\n }\n}\nclass Solution {\n public int reachableNodes(int[][] edges, int maxMoves, int n) {\n PriorityQueue<Node> pq = new PriorityQueue<>();\n int[] dis = new int[n];\n List<List<Node>> adj = new ArrayList<>();\n for(int i=0;i<n;i++){\n dis[i] = Integer.MAX_VALUE;\n adj.add(new ArrayList<>());\n }\n dis[0] = 0 ;\n for(int[] edge: edges){\n adj.get(edge[0]).add(new Node(edge[1], edge[2]+1));\n adj.get(edge[1]).add(new Node(edge[0], edge[2]+1));\n }\n pq.add(new Node(0, 0 ));\n while (!pq.isEmpty()){\n Node node = pq.poll();\n int u = node.u;\n for(Node x : adj.get(u)){\n if(dis[x.u]== Integer.MAX_VALUE || dis[u]+x.w < dis[x.u]){\n dis[x.u] = dis[u] + x.w;\n pq.add(new Node(x.u, dis[x.u]));\n }\n }\n }\n int ans = 0;\n for(int i=0;i < edges.length;i++){\n int u=edges[i][0];\n int v = edges[i][1];\n int w = edges[i][2];\n int t1 = Math.min(Math.max(maxMoves-dis[u], 0), w);\n int t2 = Math.min(Math.max(maxMoves-dis[v], 0), w);\n ans += Math.min(w,t1+t2);\n }\n for(int i=0;i<n;i++)if(dis[i]<=maxMoves)ans++;\n return ans;\n }\n}\n```\n | 1 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
Solution | reachable-nodes-in-subdivided-graph | 1 | 1 | ```C++ []\nclass Solution {\n public:\n int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {\n vector<vector<pair<int, int>>> graph(n);\n vector<int> dist(graph.size(), maxMoves + 1);\n\n for (const vector<int>& edge : edges) {\n const int u = edge[0];\n const int v = edge[1];\n const int cnt = edge[2];\n graph[u].emplace_back(v, cnt);\n graph[v].emplace_back(u, cnt);\n }\n const int reachableNodes = dijkstra(graph, 0, maxMoves, dist);\n int reachableSubnodes = 0;\n\n for (const vector<int>& edge : edges) {\n const int u = edge[0];\n const int v = edge[1];\n const int cnt = edge[2];\n const int a = dist[u] > maxMoves ? 0 : min(maxMoves - dist[u], cnt);\n const int b = dist[v] > maxMoves ? 0 : min(maxMoves - dist[v], cnt);\n reachableSubnodes += min(a + b, cnt);\n }\n return reachableNodes + reachableSubnodes;\n }\n private:\n int dijkstra(const vector<vector<pair<int, int>>>& graph, int src,\n int maxMoves, vector<int>& dist) {\n using P = pair<int, int>;\n priority_queue<P, vector<P>, greater<>> minHeap;\n\n dist[src] = 0;\n minHeap.emplace(dist[src], src);\n\n while (!minHeap.empty()) {\n const auto [d, u] = minHeap.top();\n minHeap.pop();\n for (const auto& [v, w] : graph[u])\n if (d + w + 1 < dist[v]) {\n dist[v] = d + w + 1;\n minHeap.emplace(dist[v], v);\n }\n }\n return count_if(begin(dist), end(dist),\n [&](int d) { return d <= maxMoves; });\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph = defaultdict(dict)\n for u,v,cnt in edges:\n graph[u][v]=graph[v][u]=cnt\n \n cur = [(0,0)]\n heapify(cur)\n visited, added = set(), {0}\n sol, addn = 1, n+1\n\n while cur:\n c,v = heappop(cur)\n if v in visited:\n continue\n visited.add(v)\n for u in graph[v]:\n if u not in visited:\n if c + graph[v][u] + 1 <= maxMoves:\n sol += graph[v][u]\n if u not in added:\n sol += 1\n added.add(u)\n if u <= n:\n heappush(cur,(c + graph[v][u] + 1, u))\n else:\n sol += maxMoves-c\n graph[u][addn] = graph[v][u]-(maxMoves-c)-1\n graph[u].pop(v,None)\n addn += 1\n\n return sol\n```\n\n```Java []\nclass Node implements Comparable<Node>{\n int u;\n int w;\n Node(int u, int w){\n this.u = u;\n this.w = w;\n }\n @Override\n public int compareTo(Node o) {\n return this.w-o.w;\n }\n}\nclass Solution {\n public int reachableNodes(int[][] edges, int maxMoves, int n) {\n PriorityQueue<Node> pq = new PriorityQueue<>();\n int[] dis = new int[n];\n List<List<Node>> adj = new ArrayList<>();\n for(int i=0;i<n;i++){\n dis[i] = Integer.MAX_VALUE;\n adj.add(new ArrayList<>());\n }\n dis[0] = 0 ;\n for(int[] edge: edges){\n adj.get(edge[0]).add(new Node(edge[1], edge[2]+1));\n adj.get(edge[1]).add(new Node(edge[0], edge[2]+1));\n }\n pq.add(new Node(0, 0 ));\n while (!pq.isEmpty()){\n Node node = pq.poll();\n int u = node.u;\n for(Node x : adj.get(u)){\n if(dis[x.u]== Integer.MAX_VALUE || dis[u]+x.w < dis[x.u]){\n dis[x.u] = dis[u] + x.w;\n pq.add(new Node(x.u, dis[x.u]));\n }\n }\n }\n int ans = 0;\n for(int i=0;i < edges.length;i++){\n int u=edges[i][0];\n int v = edges[i][1];\n int w = edges[i][2];\n int t1 = Math.min(Math.max(maxMoves-dis[u], 0), w);\n int t2 = Math.min(Math.max(maxMoves-dis[v], 0), w);\n ans += Math.min(w,t1+t2);\n }\n for(int i=0;i<n;i++)if(dis[i]<=maxMoves)ans++;\n return ans;\n }\n}\n```\n | 1 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
Clear and simple python3 solution | Dijkstra's algorithm + additional count | reachable-nodes-in-subdivided-graph | 0 | 1 | # Complexity\n\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n vs = defaultdict(dict)\n for u, v, cnt in edges:\n vs[u][v] = cnt\n vs[v][u] = cnt\n \n def dijkstra(n, vs, max_moves, start_node):\n h = [(0, 0)] # distance, u\n\n inf = float(\'inf\')\n dist = [inf for _ in range(n)]\n dist[start_node] = 0\n\n while h:\n distance, u = heapq.heappop(h)\n if distance > max_moves:\n break\n\n for v, cnt in vs[u].items():\n if dist[v] < distance:\n continue\n new_distance = distance + cnt + 1\n if new_distance < dist[v]:\n dist[v] = new_distance\n heapq.heappush(h, (new_distance, v))\n \n return dist\n\n dist = dijkstra(n, vs, maxMoves, 0)\n\n # count original nodes\n result = sum(1 for distance in dist if distance <= maxMoves)\n\n # count new nodes\n for u, v_cnt in vs.items():\n for v, cnt in v_cnt.items():\n if cnt == 0 or u > v:\n continue\n result += min(\n cnt, \n min(cnt, max(0, maxMoves - dist[u])) \n + min(cnt, max(0, maxMoves - dist[v])),\n )\n \n return result\n\n``` | 1 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
Clear and simple python3 solution | Dijkstra's algorithm + additional count | reachable-nodes-in-subdivided-graph | 0 | 1 | # Complexity\n\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nimport heapq\n\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n vs = defaultdict(dict)\n for u, v, cnt in edges:\n vs[u][v] = cnt\n vs[v][u] = cnt\n \n def dijkstra(n, vs, max_moves, start_node):\n h = [(0, 0)] # distance, u\n\n inf = float(\'inf\')\n dist = [inf for _ in range(n)]\n dist[start_node] = 0\n\n while h:\n distance, u = heapq.heappop(h)\n if distance > max_moves:\n break\n\n for v, cnt in vs[u].items():\n if dist[v] < distance:\n continue\n new_distance = distance + cnt + 1\n if new_distance < dist[v]:\n dist[v] = new_distance\n heapq.heappush(h, (new_distance, v))\n \n return dist\n\n dist = dijkstra(n, vs, maxMoves, 0)\n\n # count original nodes\n result = sum(1 for distance in dist if distance <= maxMoves)\n\n # count new nodes\n for u, v_cnt in vs.items():\n for v, cnt in v_cnt.items():\n if cnt == 0 or u > v:\n continue\n result += min(\n cnt, \n min(cnt, max(0, maxMoves - dist[u])) \n + min(cnt, max(0, maxMoves - dist[v])),\n )\n \n return result\n\n``` | 1 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
[Python] BFS - 3 Steps | reachable-nodes-in-subdivided-graph | 0 | 1 | **Approach:**\n\nPerform BFS (starting with M steps at node 0) to find the \nmaximum number of steps remaining after reaching each node.\n```v``` is a map of node to maximum steps remaining after reaching node.\n\nFor each pair of original nodes, the number of new nodes between them is ```n```.\nSay node ```a``` and ```b``` are separated by 10 nodes.\nIf ```v[a] = 3``` and ```v[b] = 7``` then we can reach every node between ```a``` and ```b```.\n\nFor each pair of nodes if ```v[a] + v[b] >= n``` then we can reach every node between ```a``` and ```b```.\nIf ```v[a] + v[b] < n``` then we can reach ```v[a] + v[b]``` nodes between ```a``` and ```b```.\nCheck this for every pair of original nodes.\nThe total nodes visited is: ```original_nodes_visited + new_nodes_visited```\n\n\n<br>\n\n```python\ndef reachableNodes(self, edges: List[List[int]], M: int, N: int) -> int:\n\n\tdef bfs():\n\t\t"""Find the maximum remaining steps after reaching each node."""\n\t\tq = [(M, 0, -1)] # (m) steps remaining, (n) node, (p) parent\n\t\tv = {0: M} # visited: v[node] = steps remaining after reaching node\n\t\twhile q:\n\t\t\tnext_level = []\n\t\t\tfor m, n, p in q:\n\t\t\t\tv[n] = max(v.get(n, -math.inf), m)\n\t\t\t\tfor neigh in g[n]:\n\t\t\t\t\tc = cost[(n, neigh)]\n\t\t\t\t\tif (neigh != p) and (c <= m) and (v.get(neigh, -math.inf) < (m - c)):\n\t\t\t\t\t\tnext_level.append((m-c, neigh, n))\n\t\t\tq = next_level\n\t\treturn v\n\n\t# 1. Convert list of edges to a graph\n\tcost = collections.defaultdict(int) \n\tg = collections.defaultdict(list)\n\tfor a, b, n in edges:\n\t\tg[a].append(b)\n\t\tg[b].append(a)\n\t\tcost[(a,b)] = cost[(b,a)] = n + 1\n\n\t# 2. Make a map v where v[node] = number of steps remaining after reaching node\n\tv = bfs()\n\n\t# 3. From each pair of original nodes try to visit all of the new nodes that connect them.\n\tnew_nodes = sum(min(v.get(a, 0) + v.get(b, 0), n) for a, b, n in edges)\n\toriginal_nodes = len(v)\n\t\n\treturn original_nodes + new_nodes\n``` | 10 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
[Python] BFS - 3 Steps | reachable-nodes-in-subdivided-graph | 0 | 1 | **Approach:**\n\nPerform BFS (starting with M steps at node 0) to find the \nmaximum number of steps remaining after reaching each node.\n```v``` is a map of node to maximum steps remaining after reaching node.\n\nFor each pair of original nodes, the number of new nodes between them is ```n```.\nSay node ```a``` and ```b``` are separated by 10 nodes.\nIf ```v[a] = 3``` and ```v[b] = 7``` then we can reach every node between ```a``` and ```b```.\n\nFor each pair of nodes if ```v[a] + v[b] >= n``` then we can reach every node between ```a``` and ```b```.\nIf ```v[a] + v[b] < n``` then we can reach ```v[a] + v[b]``` nodes between ```a``` and ```b```.\nCheck this for every pair of original nodes.\nThe total nodes visited is: ```original_nodes_visited + new_nodes_visited```\n\n\n<br>\n\n```python\ndef reachableNodes(self, edges: List[List[int]], M: int, N: int) -> int:\n\n\tdef bfs():\n\t\t"""Find the maximum remaining steps after reaching each node."""\n\t\tq = [(M, 0, -1)] # (m) steps remaining, (n) node, (p) parent\n\t\tv = {0: M} # visited: v[node] = steps remaining after reaching node\n\t\twhile q:\n\t\t\tnext_level = []\n\t\t\tfor m, n, p in q:\n\t\t\t\tv[n] = max(v.get(n, -math.inf), m)\n\t\t\t\tfor neigh in g[n]:\n\t\t\t\t\tc = cost[(n, neigh)]\n\t\t\t\t\tif (neigh != p) and (c <= m) and (v.get(neigh, -math.inf) < (m - c)):\n\t\t\t\t\t\tnext_level.append((m-c, neigh, n))\n\t\t\tq = next_level\n\t\treturn v\n\n\t# 1. Convert list of edges to a graph\n\tcost = collections.defaultdict(int) \n\tg = collections.defaultdict(list)\n\tfor a, b, n in edges:\n\t\tg[a].append(b)\n\t\tg[b].append(a)\n\t\tcost[(a,b)] = cost[(b,a)] = n + 1\n\n\t# 2. Make a map v where v[node] = number of steps remaining after reaching node\n\tv = bfs()\n\n\t# 3. From each pair of original nodes try to visit all of the new nodes that connect them.\n\tnew_nodes = sum(min(v.get(a, 0) + v.get(b, 0), n) for a, b, n in edges)\n\toriginal_nodes = len(v)\n\t\n\treturn original_nodes + new_nodes\n``` | 10 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
✅BFS || Python | reachable-nodes-in-subdivided-graph | 0 | 1 | \n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph=[[0 for i in range(n)]for i in range(n)]\n for v in edges:\n graph[v[0]][v[1]]=v[2]+1\n graph[v[1]][v[0]]=v[2]+1\n q=[[0,0]]\n heapify(q)\n vis=[0 for i in range(n)]\n ans=1\n while(len(q)!=0):\n a,i=heappop(q)\n # print(a,i,ans,q)\n if(vis[i]):\n ans-=1\n continue\n vis[i]=1\n for j in range(n):\n if(graph[i][j]==0):continue\n if((graph[i][j]+a)>maxMoves):\n steps=maxMoves-a\n ans+=steps\n graph[j][i]-=steps\n graph[i][j]-=steps\n else:\n ans+=graph[i][j]\n heappush(q,[(graph[i][j]+a),j])\n graph[i][j]=0\n graph[j][i]=0\n # print(i,j,ans)\n return ans\n``` | 0 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
✅BFS || Python | reachable-nodes-in-subdivided-graph | 0 | 1 | \n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph=[[0 for i in range(n)]for i in range(n)]\n for v in edges:\n graph[v[0]][v[1]]=v[2]+1\n graph[v[1]][v[0]]=v[2]+1\n q=[[0,0]]\n heapify(q)\n vis=[0 for i in range(n)]\n ans=1\n while(len(q)!=0):\n a,i=heappop(q)\n # print(a,i,ans,q)\n if(vis[i]):\n ans-=1\n continue\n vis[i]=1\n for j in range(n):\n if(graph[i][j]==0):continue\n if((graph[i][j]+a)>maxMoves):\n steps=maxMoves-a\n ans+=steps\n graph[j][i]-=steps\n graph[i][j]-=steps\n else:\n ans+=graph[i][j]\n heappush(q,[(graph[i][j]+a),j])\n graph[i][j]=0\n graph[j][i]=0\n # print(i,j,ans)\n return ans\n``` | 0 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
Python 3: Dijkstra's solution with comments | reachable-nodes-in-subdivided-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n \n # edges between the two are distance between the two nodes\n # add; \n # nodes we can visit from the 0\n # nodes in between we can visit from u, v\n # if distance to u is bigger than the maxMoves, 0 from u\n # if distance to v is bigger than the maxMoves, 0 from v\n # otherwise, sum of the two, and min of the nodes in between\n \n # build adjList with weight\n adjList = defaultdict(list)\n for u, v, d in edges:\n adjList[u].append((v, d + 1))\n adjList[v].append((u, d + 1))\n\n # dijkstra\'s to find the distance from 0 to all nodes\n minHeap = []\n heapq.heappush(minHeap, (0, 0)) # dist, node 0\n visit = set()\n dist = [float(\'inf\')] * n\n dist[0] = 0\n\n while minHeap:\n d, node = heapq.heappop(minHeap)\n visit.add(node)\n\n # add to the heap all the edges\n # that was not visited and that can be relaxed\n for nei, w in adjList[node]:\n if (nei not in visit) and (d + w < dist[nei]):\n dist[nei] = d + w\n heapq.heappush(minHeap, (d + w, nei))\n \n res = 0\n # check if each node can be visited within the maxMoves\n for d in dist:\n if d <= maxMoves:\n res += 1\n \n # for each edges that contain the between nodes, check how many can be\n # visited from each node\n for u, v, d in edges:\n from_u = 0 if dist[u] > maxMoves else maxMoves - dist[u]\n from_v = 0 if dist[v] > maxMoves else maxMoves - dist[v]\n res += min(d, from_u + from_v)\n return res\n``` | 0 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
Python 3: Dijkstra's solution with comments | reachable-nodes-in-subdivided-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n \n # edges between the two are distance between the two nodes\n # add; \n # nodes we can visit from the 0\n # nodes in between we can visit from u, v\n # if distance to u is bigger than the maxMoves, 0 from u\n # if distance to v is bigger than the maxMoves, 0 from v\n # otherwise, sum of the two, and min of the nodes in between\n \n # build adjList with weight\n adjList = defaultdict(list)\n for u, v, d in edges:\n adjList[u].append((v, d + 1))\n adjList[v].append((u, d + 1))\n\n # dijkstra\'s to find the distance from 0 to all nodes\n minHeap = []\n heapq.heappush(minHeap, (0, 0)) # dist, node 0\n visit = set()\n dist = [float(\'inf\')] * n\n dist[0] = 0\n\n while minHeap:\n d, node = heapq.heappop(minHeap)\n visit.add(node)\n\n # add to the heap all the edges\n # that was not visited and that can be relaxed\n for nei, w in adjList[node]:\n if (nei not in visit) and (d + w < dist[nei]):\n dist[nei] = d + w\n heapq.heappush(minHeap, (d + w, nei))\n \n res = 0\n # check if each node can be visited within the maxMoves\n for d in dist:\n if d <= maxMoves:\n res += 1\n \n # for each edges that contain the between nodes, check how many can be\n # visited from each node\n for u, v, d in edges:\n from_u = 0 if dist[u] > maxMoves else maxMoves - dist[u]\n from_v = 0 if dist[v] > maxMoves else maxMoves - dist[v]\n res += min(d, from_u + from_v)\n return res\n``` | 0 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
Why is everyone complicating the solution <My Solution> | reachable-nodes-in-subdivided-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe extra nodes that we have to add in between can be considered as the edge length between the two nodes. If there is edge from ```u``` to ```v``` with edge length ```w```, then ```v``` is at the ```w+1``` moves from ```u```.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Run the Dijkstra\'s Algorithm directly the graph as usual. We will get ```distance``` array which contain the distances of all the nodes from ```node 0```.\n2. Now to count the number of nodes reachable from ```node 0```\n2.1 For the nodes in the graph : If ```distance[node] <= maxMoves``` then it is reachable.\n2.2 For the nodes that we have to add inbetween : Loop the ```edges``` array. For each edge :-\n $$u----cnt1----cnt2----cnt3.......----cntn----v.$$\nSome nodes are reachable from ```u``` and some from ```v```. To count only the valid nodes not duplicates we can do the following :-\n```min(cnt, nodes_reachable_from_u + nodes_reachable_from_v)```.\nThe number of nodes reachable from ```u``` is ```maxMoves - distance[u]```. (if u is reachable)\nThe number of nodes reachable from ```v``` is ```maxMoves - distance[v]```. (if v is reachable)\n\n# Complexity\n- Time complexity: O(Elog(V))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph = [[] for _ in range(n)]\n for u,v,cnt in edges:\n graph[u].append((v,cnt + 1))\n graph[v].append((u,cnt + 1))\n \n distance = [float(\'inf\')]*n\n pq = [(0,0)]\n visited = [False]*n\n distance[0] = 0 \n while pq:\n dist,curr = heapq.heappop(pq)\n visited[curr] = True\n for node,edge_length in graph[curr]:\n if visited[node]:\n continue\n if distance[node] > distance[curr] + edge_length:\n distance[node] = distance[curr] + edge_length\n heapq.heappush(pq,(distance[node],node))\n \n ans = 0\n for d in distance:\n if d <= maxMoves:\n ans += 1\n for u,v,cnt in edges:\n nodes_reachable_from_u = maxMoves - distance[u]\n if distance[u] > maxMoves:\n nodes_reachable_from_u = 0\n nodes_reachable_from_v = maxMoves - distance[v]\n if distance[v] > maxMoves:\n nodes_reachable_from_v = 0\n ans += min(cnt, nodes_reachable_from_u + nodes_reachable_from_v)\n\n return ans\n``` | 0 | You are given an undirected graph (the **"original graph "**) with `n` nodes labeled from `0` to `n - 1`. You decide to **subdivide** each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.
The graph is given as a 2D array of `edges` where `edges[i] = [ui, vi, cnti]` indicates that there is an edge between nodes `ui` and `vi` in the original graph, and `cnti` is the total number of new nodes that you will **subdivide** the edge into. Note that `cnti == 0` means you will not subdivide the edge.
To **subdivide** the edge `[ui, vi]`, replace it with `(cnti + 1)` new edges and `cnti` new nodes. The new nodes are `x1`, `x2`, ..., `xcnti`, and the new edges are `[ui, x1]`, `[x1, x2]`, `[x2, x3]`, ..., `[xcnti-1, xcnti]`, `[xcnti, vi]`.
In this **new graph**, you want to know how many nodes are **reachable** from the node `0`, where a node is **reachable** if the distance is `maxMoves` or less.
Given the original graph and `maxMoves`, return _the number of nodes that are **reachable** from node_ `0` _in the new graph_.
**Example 1:**
**Input:** edges = \[\[0,1,10\],\[0,2,1\],\[1,2,2\]\], maxMoves = 6, n = 3
**Output:** 13
**Explanation:** The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.
**Example 2:**
**Input:** edges = \[\[0,1,4\],\[1,2,6\],\[0,2,8\],\[1,3,1\]\], maxMoves = 10, n = 4
**Output:** 23
**Example 3:**
**Input:** edges = \[\[1,2,4\],\[1,4,5\],\[1,3,1\],\[2,3,4\],\[3,4,5\]\], maxMoves = 17, n = 5
**Output:** 1
**Explanation:** Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.
**Constraints:**
* `0 <= edges.length <= min(n * (n - 1) / 2, 104)`
* `edges[i].length == 3`
* `0 <= ui < vi < n`
* There are **no multiple edges** in the graph.
* `0 <= cnti <= 104`
* `0 <= maxMoves <= 109`
* `1 <= n <= 3000` | null |
Why is everyone complicating the solution <My Solution> | reachable-nodes-in-subdivided-graph | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe extra nodes that we have to add in between can be considered as the edge length between the two nodes. If there is edge from ```u``` to ```v``` with edge length ```w```, then ```v``` is at the ```w+1``` moves from ```u```.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Run the Dijkstra\'s Algorithm directly the graph as usual. We will get ```distance``` array which contain the distances of all the nodes from ```node 0```.\n2. Now to count the number of nodes reachable from ```node 0```\n2.1 For the nodes in the graph : If ```distance[node] <= maxMoves``` then it is reachable.\n2.2 For the nodes that we have to add inbetween : Loop the ```edges``` array. For each edge :-\n $$u----cnt1----cnt2----cnt3.......----cntn----v.$$\nSome nodes are reachable from ```u``` and some from ```v```. To count only the valid nodes not duplicates we can do the following :-\n```min(cnt, nodes_reachable_from_u + nodes_reachable_from_v)```.\nThe number of nodes reachable from ```u``` is ```maxMoves - distance[u]```. (if u is reachable)\nThe number of nodes reachable from ```v``` is ```maxMoves - distance[v]```. (if v is reachable)\n\n# Complexity\n- Time complexity: O(Elog(V))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:\n graph = [[] for _ in range(n)]\n for u,v,cnt in edges:\n graph[u].append((v,cnt + 1))\n graph[v].append((u,cnt + 1))\n \n distance = [float(\'inf\')]*n\n pq = [(0,0)]\n visited = [False]*n\n distance[0] = 0 \n while pq:\n dist,curr = heapq.heappop(pq)\n visited[curr] = True\n for node,edge_length in graph[curr]:\n if visited[node]:\n continue\n if distance[node] > distance[curr] + edge_length:\n distance[node] = distance[curr] + edge_length\n heapq.heappush(pq,(distance[node],node))\n \n ans = 0\n for d in distance:\n if d <= maxMoves:\n ans += 1\n for u,v,cnt in edges:\n nodes_reachable_from_u = maxMoves - distance[u]\n if distance[u] > maxMoves:\n nodes_reachable_from_u = 0\n nodes_reachable_from_v = maxMoves - distance[v]\n if distance[v] > maxMoves:\n nodes_reachable_from_v = 0\n ans += min(cnt, nodes_reachable_from_u + nodes_reachable_from_v)\n\n return ans\n``` | 0 | Given a **circular integer array** `nums` of length `n`, return _the maximum possible sum of a non-empty **subarray** of_ `nums`.
A **circular array** means the end of the array connects to the beginning of the array. Formally, the next element of `nums[i]` is `nums[(i + 1) % n]` and the previous element of `nums[i]` is `nums[(i - 1 + n) % n]`.
A **subarray** may only include each element of the fixed buffer `nums` at most once. Formally, for a subarray `nums[i], nums[i + 1], ..., nums[j]`, there does not exist `i <= k1`, `k2 <= j` with `k1 % n == k2 % n`.
**Example 1:**
**Input:** nums = \[1,-2,3,-2\]
**Output:** 3
**Explanation:** Subarray \[3\] has maximum sum 3.
**Example 2:**
**Input:** nums = \[5,-3,5\]
**Output:** 10
**Explanation:** Subarray \[5,5\] has maximum sum 5 + 5 = 10.
**Example 3:**
**Input:** nums = \[-3,-2,-3\]
**Output:** -2
**Explanation:** Subarray \[-2\] has maximum sum -2.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 3 * 104`
* `-3 * 104 <= nums[i] <= 3 * 104` | null |
Solution | projection-area-of-3d-shapes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int projectionArea(vector<vector<int>>& grid) {\n int n = grid.size(), area = 0;\n vector<int> x_v(n), y_v(n);\n for (int x = 0; x < n; x++) {\n for (int y = 0; y < n; y++) {\n int v = grid[x][y];\n if (v) {\n area++;\n if (x_v[x] < v) x_v[x] = v;\n if (y_v[y] < v) y_v[y] = v;\n }\n }\n area += x_v[x];\n }\n for (int y = 0; y < n; y++)\n area += y_v[y];\n return area;\n }\n};\n```\n\n```Python3 []\nclass Solution: \n def projectionArea(self, grid: List[List[int]]) -> int:\n xy = sum(i > 0 for s in grid for i in s)\n xz = sum(max(s) for s in grid)\n yz = sum(max(s[i] for s in grid) for i in range(len(grid)))\n return xy + xz + yz\n```\n\n```Java []\nclass Solution {\n public int projectionArea(int[][] grid) {\n int a=0,x=0;\n for(int i=0;i<grid.length;i++)\n {\n int mr=Integer.MIN_VALUE;\n int mc=Integer.MIN_VALUE;\n for(int j=0;j<grid[0].length;j++)\n {\n if(grid[i][j]!=0)x+=1;\n if(grid[i][j]>mr)mr=grid[i][j];\n if(grid[j][i]>mc)mc=grid[j][i];\n }\n a+=mr+mc;\n }\n return (a+x);\n }\n}\n```\n | 2 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Solution | projection-area-of-3d-shapes | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int projectionArea(vector<vector<int>>& grid) {\n int n = grid.size(), area = 0;\n vector<int> x_v(n), y_v(n);\n for (int x = 0; x < n; x++) {\n for (int y = 0; y < n; y++) {\n int v = grid[x][y];\n if (v) {\n area++;\n if (x_v[x] < v) x_v[x] = v;\n if (y_v[y] < v) y_v[y] = v;\n }\n }\n area += x_v[x];\n }\n for (int y = 0; y < n; y++)\n area += y_v[y];\n return area;\n }\n};\n```\n\n```Python3 []\nclass Solution: \n def projectionArea(self, grid: List[List[int]]) -> int:\n xy = sum(i > 0 for s in grid for i in s)\n xz = sum(max(s) for s in grid)\n yz = sum(max(s[i] for s in grid) for i in range(len(grid)))\n return xy + xz + yz\n```\n\n```Java []\nclass Solution {\n public int projectionArea(int[][] grid) {\n int a=0,x=0;\n for(int i=0;i<grid.length;i++)\n {\n int mr=Integer.MIN_VALUE;\n int mc=Integer.MIN_VALUE;\n for(int j=0;j<grid[0].length;j++)\n {\n if(grid[i][j]!=0)x+=1;\n if(grid[i][j]>mr)mr=grid[i][j];\n if(grid[j][i]>mc)mc=grid[j][i];\n }\n a+=mr+mc;\n }\n return (a+x);\n }\n}\n```\n | 2 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
“You don't have to be a mathematician to have a feel for numbers.” - John Forbes Nash | projection-area-of-3d-shapes | 0 | 1 | \n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n \n if len(grid)==1:\n return 1+grid[0][0]*2\n s=0\n l=[]\n for j in range(len(grid)):\n f2=0\n for i in range(len(grid)):\n f2=max(grid[i][j],f2)\n if grid[i][j]!=0:\n l.append(grid[i][j])\n s+=f2+max(grid[j])\n\n return len(l)+s\n \n\n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
“You don't have to be a mathematician to have a feel for numbers.” - John Forbes Nash | projection-area-of-3d-shapes | 0 | 1 | \n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n \n if len(grid)==1:\n return 1+grid[0][0]*2\n s=0\n l=[]\n for j in range(len(grid)):\n f2=0\n for i in range(len(grid)):\n f2=max(grid[i][j],f2)\n if grid[i][j]!=0:\n l.append(grid[i][j])\n s+=f2+max(grid[j])\n\n return len(l)+s\n \n\n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
python || bruteforce solution | projection-area-of-3d-shapes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n gridlen=len(grid)\n ans =0\n for i in range(gridlen):\n gridrow=0\n gridcol=0\n for j in range(gridlen):\n if grid[i][j] > 0:\n ans +=1\n gridrow= max(gridrow,grid[i][j])\n gridcol=max(gridcol,grid[j][i])\n ans +=gridrow+gridcol\n return ans\n\n \n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
python || bruteforce solution | projection-area-of-3d-shapes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n gridlen=len(grid)\n ans =0\n for i in range(gridlen):\n gridrow=0\n gridcol=0\n for j in range(gridlen):\n if grid[i][j] > 0:\n ans +=1\n gridrow= max(gridrow,grid[i][j])\n gridcol=max(gridcol,grid[j][i])\n ans +=gridrow+gridcol\n return ans\n\n \n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
Easiest Solution | projection-area-of-3d-shapes | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int projectionArea(int[][] grid) \n {\n int x=0,y=0,z=0;\n\n for(int i=0;i<grid.length;i++)\n {\n for(int j=0;j<grid[0].length;j++)\n {\n if(grid[i][j]!=0) x++;\n }\n }\n\n for(int i=0;i<grid.length;i++)\n {\n int max=grid[i][0];\n for(int j=0;j<grid[i].length;j++)\n {\n if(grid[i][j]>=max) max=grid[i][j];\n }\n y+=max;\n }\n \n for(int i=0;i<grid.length;i++)\n {\n int max=grid[0][i];\n for(int j=0;j<grid[i].length;j++)\n {\n if(grid[j][i]>=max) max=grid[j][i];\n }\n z+=max;\n }\n\n return x+y+z;\n \n }\n}\n```\n```c++ []\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n area = 0\n \n for x in grid:\n maxx = 0\n for y in x:\n if y:\n maxx = max(y,maxx)\n area += 1\n area += maxx\n \n for j in range(len(grid[0])):\n area += max(grid[i][j] for i in range(len(grid)))\n\n return area\n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Easiest Solution | projection-area-of-3d-shapes | 1 | 1 | \n\n# Code\n```java []\nclass Solution {\n public int projectionArea(int[][] grid) \n {\n int x=0,y=0,z=0;\n\n for(int i=0;i<grid.length;i++)\n {\n for(int j=0;j<grid[0].length;j++)\n {\n if(grid[i][j]!=0) x++;\n }\n }\n\n for(int i=0;i<grid.length;i++)\n {\n int max=grid[i][0];\n for(int j=0;j<grid[i].length;j++)\n {\n if(grid[i][j]>=max) max=grid[i][j];\n }\n y+=max;\n }\n \n for(int i=0;i<grid.length;i++)\n {\n int max=grid[0][i];\n for(int j=0;j<grid[i].length;j++)\n {\n if(grid[j][i]>=max) max=grid[j][i];\n }\n z+=max;\n }\n\n return x+y+z;\n \n }\n}\n```\n```c++ []\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n area = 0\n \n for x in grid:\n maxx = 0\n for y in x:\n if y:\n maxx = max(y,maxx)\n area += 1\n area += maxx\n \n for j in range(len(grid[0])):\n area += max(grid[i][j] for i in range(len(grid)))\n\n return area\n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
Python: two one-liners | projection-area-of-3d-shapes | 0 | 1 | \n# Complexity\n- Time complexity: Both solutions are $$O(n^2)$$ which is the time needed to iterate over the matrix anyways.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Both are technically $$O(n)$$ due to the unpacking in the `zip(*grid)` call, but this is probably optimized by the Python interpreter as it is qiute a common approach to iterate over a matrix\'s columns.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n return sum(map(bool, chain.from_iterable(grid))) + sum(map(max, grid)) + sum(map(max, zip(*grid)))\n```\n\nOr, if you prefer list comprehension:\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n sum(x != 0 for row in grid for x in row) + sum(map(max, grid)) + sum(map(max, zip(*grid)))\n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Python: two one-liners | projection-area-of-3d-shapes | 0 | 1 | \n# Complexity\n- Time complexity: Both solutions are $$O(n^2)$$ which is the time needed to iterate over the matrix anyways.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Both are technically $$O(n)$$ due to the unpacking in the `zip(*grid)` call, but this is probably optimized by the Python interpreter as it is qiute a common approach to iterate over a matrix\'s columns.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n return sum(map(bool, chain.from_iterable(grid))) + sum(map(max, grid)) + sum(map(max, zip(*grid)))\n```\n\nOr, if you prefer list comprehension:\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n sum(x != 0 for row in grid for x in row) + sum(map(max, grid)) + sum(map(max, zip(*grid)))\n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
a lot of loops | projection-area-of-3d-shapes | 0 | 1 | \n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n [\n [1,2],\n [3,4]\n ]\n todown = 0\n for row in grid:\n for el in row:\n if el!=0:\n todown+=1\n toright = 0\n for row in grid:\n toright += max(row)\n tostraight = 0\n for j in range(len(grid[0])):\n mx = 0\n for i in range(len(grid)):\n mx=max(grid[i][j],mx)\n tostraight += mx\n return todown+toright+tostraight\n\n \n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
a lot of loops | projection-area-of-3d-shapes | 0 | 1 | \n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n [\n [1,2],\n [3,4]\n ]\n todown = 0\n for row in grid:\n for el in row:\n if el!=0:\n todown+=1\n toright = 0\n for row in grid:\n toright += max(row)\n tostraight = 0\n for j in range(len(grid[0])):\n mx = 0\n for i in range(len(grid)):\n mx=max(grid[i][j],mx)\n tostraight += mx\n return todown+toright+tostraight\n\n \n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
Sol | projection-area-of-3d-shapes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n xy = 0\n yz = 0\n zx = 0\n for i in range(n):\n max_row = 0\n max_col = 0\n for j in range(n):\n if grid[i][j] > 0:\n xy += 1\n max_row = max(max_row, grid[i][j])\n max_col = max(max_col, grid[j][i])\n yz += max_row\n zx += max_col\n\n return xy + yz + zx\n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Sol | projection-area-of-3d-shapes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def projectionArea(self, grid: List[List[int]]) -> int:\n n = len(grid)\n xy = 0\n yz = 0\n zx = 0\n for i in range(n):\n max_row = 0\n max_col = 0\n for j in range(n):\n if grid[i][j] > 0:\n xy += 1\n max_row = max(max_row, grid[i][j])\n max_col = max(max_col, grid[j][i])\n yz += max_row\n zx += max_col\n\n return xy + yz + zx\n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
Simple Solution | 30 ms | Beats 99% | Accepted 🔥🚀🚀 | projection-area-of-3d-shapes | 0 | 1 | # Code\n```\nclass Solution:\n def projectionArea(self, x: List[List[int]]) -> int:\n s=len(x)*len(x[0])\n y=list(zip(*x))\n for i in x: s-=i.count(0)\n y=[list(y[i]) for i in range(len(y))]\n for i in x: s+=max(i)\n for i in y: s+=max(i)\n return s\n``` | 0 | You are given an `n x n` `grid` where we place some `1 x 1 x 1` cubes that are axis-aligned with the `x`, `y`, and `z` axes.
Each value `v = grid[i][j]` represents a tower of `v` cubes placed on top of the cell `(i, j)`.
We view the projection of these cubes onto the `xy`, `yz`, and `zx` planes.
A **projection** is like a shadow, that maps our **3-dimensional** figure to a **2-dimensional** plane. We are viewing the "shadow " when looking at the cubes from the top, the front, and the side.
Return _the total area of all three projections_.
**Example 1:**
**Input:** grid = \[\[1,2\],\[3,4\]\]
**Output:** 17
**Explanation:** Here are the three projections ( "shadows ") of the shape made with each axis-aligned plane.
**Example 2:**
**Input:** grid = \[\[2\]\]
**Output:** 5
**Example 3:**
**Input:** grid = \[\[1,0\],\[0,2\]\]
**Output:** 8
**Constraints:**
* `n == grid.length == grid[i].length`
* `1 <= n <= 50`
* `0 <= grid[i][j] <= 50` | null |
Simple Solution | 30 ms | Beats 99% | Accepted 🔥🚀🚀 | projection-area-of-3d-shapes | 0 | 1 | # Code\n```\nclass Solution:\n def projectionArea(self, x: List[List[int]]) -> int:\n s=len(x)*len(x[0])\n y=list(zip(*x))\n for i in x: s-=i.count(0)\n y=[list(y[i]) for i in range(len(y))]\n for i in x: s+=max(i)\n for i in y: s+=max(i)\n return s\n``` | 0 | A **complete binary tree** is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.
Implement the `CBTInserter` class:
* `CBTInserter(TreeNode root)` Initializes the data structure with the `root` of the complete binary tree.
* `int insert(int v)` Inserts a `TreeNode` into the tree with value `Node.val == val` so that the tree remains complete, and returns the value of the parent of the inserted `TreeNode`.
* `TreeNode get_root()` Returns the root node of the tree.
**Example 1:**
**Input**
\[ "CBTInserter ", "insert ", "insert ", "get\_root "\]
\[\[\[1, 2\]\], \[3\], \[4\], \[\]\]
**Output**
\[null, 1, 2, \[1, 2, 3, 4\]\]
**Explanation**
CBTInserter cBTInserter = new CBTInserter(\[1, 2\]);
cBTInserter.insert(3); // return 1
cBTInserter.insert(4); // return 2
cBTInserter.get\_root(); // return \[1, 2, 3, 4\]
**Constraints:**
* The number of nodes in the tree will be in the range `[1, 1000]`.
* `0 <= Node.val <= 5000`
* `root` is a complete binary tree.
* `0 <= val <= 5000`
* At most `104` calls will be made to `insert` and `get_root`. | null |
FREE BOBI python solution using counter | uncommon-words-from-two-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n s = s1 + " "+ s2\n ans = Counter(s.split())\n arr = []\n for key,v in (ans.items()):\n if v==1:\n arr.append(key)\n return arr\n \n``` | 1 | A **sentence** is a string of single-space separated words where each word consists only of lowercase letters.
A word is **uncommon** if it appears exactly once in one of the sentences, and **does not appear** in the other sentence.
Given two **sentences** `s1` and `s2`, return _a list of all the **uncommon words**_. You may return the answer in **any order**.
**Example 1:**
**Input:** s1 = "this apple is sweet", s2 = "this apple is sour"
**Output:** \["sweet","sour"\]
**Example 2:**
**Input:** s1 = "apple apple", s2 = "banana"
**Output:** \["banana"\]
**Constraints:**
* `1 <= s1.length, s2.length <= 200`
* `s1` and `s2` consist of lowercase English letters and spaces.
* `s1` and `s2` do not have leading or trailing spaces.
* All the words in `s1` and `s2` are separated by a single space. | null |
FREE BOBI python solution using counter | uncommon-words-from-two-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n s = s1 + " "+ s2\n ans = Counter(s.split())\n arr = []\n for key,v in (ans.items()):\n if v==1:\n arr.append(key)\n return arr\n \n``` | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Python3 easy solution | uncommon-words-from-two-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n s1_list=s1.split()\n s2_list=s2.split()\n count=0\n op=[]\n\n for i in s1_list:\n if i not in s2_list and s1_list.count(i)==1:\n op.append(i)\n for i in s2_list:\n if i not in s1_list and s2_list.count(i)==1:\n op.append(i)\n return op\n\n \n``` | 1 | A **sentence** is a string of single-space separated words where each word consists only of lowercase letters.
A word is **uncommon** if it appears exactly once in one of the sentences, and **does not appear** in the other sentence.
Given two **sentences** `s1` and `s2`, return _a list of all the **uncommon words**_. You may return the answer in **any order**.
**Example 1:**
**Input:** s1 = "this apple is sweet", s2 = "this apple is sour"
**Output:** \["sweet","sour"\]
**Example 2:**
**Input:** s1 = "apple apple", s2 = "banana"
**Output:** \["banana"\]
**Constraints:**
* `1 <= s1.length, s2.length <= 200`
* `s1` and `s2` consist of lowercase English letters and spaces.
* `s1` and `s2` do not have leading or trailing spaces.
* All the words in `s1` and `s2` are separated by a single space. | null |
Python3 easy solution | uncommon-words-from-two-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n s1_list=s1.split()\n s2_list=s2.split()\n count=0\n op=[]\n\n for i in s1_list:\n if i not in s2_list and s1_list.count(i)==1:\n op.append(i)\n for i in s2_list:\n if i not in s1_list and s2_list.count(i)==1:\n op.append(i)\n return op\n\n \n``` | 1 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Python Easy Solution || Hash Table | uncommon-words-from-two-sentences | 0 | 1 | # Complexity\n- Time complexity:\nO(n+m)\n\n- Space complexity:\nO(n+m)\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n dic={}\n res=[]\n s1=s1.rsplit()\n s2=s2.rsplit()\n for i in s1+s2:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n \n for i in dic:\n if dic[i]==1:\n res.append(i)\n return res\n``` | 3 | A **sentence** is a string of single-space separated words where each word consists only of lowercase letters.
A word is **uncommon** if it appears exactly once in one of the sentences, and **does not appear** in the other sentence.
Given two **sentences** `s1` and `s2`, return _a list of all the **uncommon words**_. You may return the answer in **any order**.
**Example 1:**
**Input:** s1 = "this apple is sweet", s2 = "this apple is sour"
**Output:** \["sweet","sour"\]
**Example 2:**
**Input:** s1 = "apple apple", s2 = "banana"
**Output:** \["banana"\]
**Constraints:**
* `1 <= s1.length, s2.length <= 200`
* `s1` and `s2` consist of lowercase English letters and spaces.
* `s1` and `s2` do not have leading or trailing spaces.
* All the words in `s1` and `s2` are separated by a single space. | null |
Python Easy Solution || Hash Table | uncommon-words-from-two-sentences | 0 | 1 | # Complexity\n- Time complexity:\nO(n+m)\n\n- Space complexity:\nO(n+m)\n\n# Code\n```\nclass Solution:\n def uncommonFromSentences(self, s1: str, s2: str) -> List[str]:\n dic={}\n res=[]\n s1=s1.rsplit()\n s2=s2.rsplit()\n for i in s1+s2:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n \n for i in dic:\n if dic[i]==1:\n res.append(i)\n return res\n``` | 3 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Accepted Python3: One-Liner using Counter from collections | uncommon-words-from-two-sentences | 0 | 1 | ```\nfrom collections import Counter as c\n\nclass Solution:\n def uncommonFromSentences(self, A: str, B: str) -> List[str]:\n return [k for k, v in c(A.split() + B.split()).items() if v == 1]\n``` | 14 | A **sentence** is a string of single-space separated words where each word consists only of lowercase letters.
A word is **uncommon** if it appears exactly once in one of the sentences, and **does not appear** in the other sentence.
Given two **sentences** `s1` and `s2`, return _a list of all the **uncommon words**_. You may return the answer in **any order**.
**Example 1:**
**Input:** s1 = "this apple is sweet", s2 = "this apple is sour"
**Output:** \["sweet","sour"\]
**Example 2:**
**Input:** s1 = "apple apple", s2 = "banana"
**Output:** \["banana"\]
**Constraints:**
* `1 <= s1.length, s2.length <= 200`
* `s1` and `s2` consist of lowercase English letters and spaces.
* `s1` and `s2` do not have leading or trailing spaces.
* All the words in `s1` and `s2` are separated by a single space. | null |
Accepted Python3: One-Liner using Counter from collections | uncommon-words-from-two-sentences | 0 | 1 | ```\nfrom collections import Counter as c\n\nclass Solution:\n def uncommonFromSentences(self, A: str, B: str) -> List[str]:\n return [k for k, v in c(A.split() + B.split()).items() if v == 1]\n``` | 14 | Your music player contains `n` different songs. You want to listen to `goal` songs (not necessarily different) during your trip. To avoid boredom, you will create a playlist so that:
* Every song is played **at least once**.
* A song can only be played again only if `k` other songs have been played.
Given `n`, `goal`, and `k`, return _the number of possible playlists that you can create_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** n = 3, goal = 3, k = 1
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 2, 3\], \[1, 3, 2\], \[2, 1, 3\], \[2, 3, 1\], \[3, 1, 2\], and \[3, 2, 1\].
**Example 2:**
**Input:** n = 2, goal = 3, k = 0
**Output:** 6
**Explanation:** There are 6 possible playlists: \[1, 1, 2\], \[1, 2, 1\], \[2, 1, 1\], \[2, 2, 1\], \[2, 1, 2\], and \[1, 2, 2\].
**Example 3:**
**Input:** n = 2, goal = 3, k = 1
**Output:** 2
**Explanation:** There are 2 possible playlists: \[1, 2, 1\] and \[2, 1, 2\].
**Constraints:**
* `0 <= k < n <= goal <= 100` | null |
Solution | spiral-matrix-iii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n \n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n\n vector<vector<int>> result;\n int total = 0;\n\n int rowStart = rStart;\n int rowEnd = rStart;\n\n int colStart = cStart;\n int colEnd = cStart;\n\n while(true){\n for(int i=colStart; i<=colEnd; i++){\n if(i >= 0 && i < cols && rowStart >= 0){\n result.push_back({rowStart, i});\n total++;\n }\n }\n colEnd++;\n if(total == (rows * cols))\n break;\n for(int i=rowStart; i<=rowEnd; i++){\n if(i >= 0 && i < rows && colEnd < cols){\n result.push_back({i, colEnd});\n total++;\n }\n }\n rowEnd++;\n if(total == (rows * cols))\n break;\n for(int i=colEnd; i>=colStart; i--){\n if(i >= 0 && i < cols && rowEnd < rows){\n result.push_back({rowEnd, i});\n total++;\n }\n }\n colStart--;\n if(total == (rows * cols))\n break;\n for(int i=rowEnd; i>=rowStart; i--){\n if(i >= 0 && i < rows && colStart >= 0){\n result.push_back({i, colStart});\n total++;\n }\n }\n rowStart--;\n if(total == (rows * cols))\n break;\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n visits = []\n top, bottom, left, right = rStart, rStart + 1, cStart, cStart + 1\n\n self.incr = 1\n direction = 0\n\n def place(row, col):\n visits.append([row, col])\n self.incr += 1\n \n while self.incr != (1 + rows * cols):\n if direction == 0:\n if top >= 0:\n row = top\n for col in range(max(left, 0), min(right, cols)):\n place(row, col)\n right += 1\n if direction == 1:\n if right <= cols:\n col = right - 1\n for row in range(max(top, 0), min(bottom, rows)):\n place(row, col)\n bottom += 1\n if direction == 2:\n if bottom <= rows:\n row = bottom - 1\n for col in range(min(right - 1, cols - 1), max(left - 1, -1), -1):\n place(row, col)\n left -= 1\n if direction == 3:\n if left >= 0:\n col = left\n for row in range(min(bottom - 1, rows - 1), max(top - 1, -1), -1):\n place(row, col)\n top -= 1\n direction = (direction + 1) % 4\n return visits\n```\n\n```Java []\nclass Solution {\n int index = 1;\n int row;\n int col;\n int rows;\n int cols;\n\n public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n int[][] result = new int[rows * cols][2];\n int moves = 0;\n row = rStart;\n col = cStart;\n this.rows = rows;\n this.cols = cols;\n result[0] = new int[] { rStart, cStart };\n while (index < result.length) {\n ++moves;\n addToResult(result, moves, 1, 0);\n addToResult(result, moves, 0, 1);\n ++moves;\n addToResult(result, moves, -1, 0);\n addToResult(result, moves, 0, -1);\n }\n return result;\n }\n public void addToResult(int[][] result, int moves, int horizontal, int vertical) {\n for (int i = 0; i < moves; ++i) {\n row += vertical;\n col += horizontal;\n if (row < rows && row > -1 && col < cols && col > -1) {\n result[index] = new int[] { row, col };\n ++index;\n }\n }\n }\n}\n```\n | 1 | You start at the cell `(rStart, cStart)` of an `rows x cols` grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all `rows * cols` spaces of the grid.
Return _an array of coordinates representing the positions of the grid in the order you visited them_.
**Example 1:**
**Input:** rows = 1, cols = 4, rStart = 0, cStart = 0
**Output:** \[\[0,0\],\[0,1\],\[0,2\],\[0,3\]\]
**Example 2:**
**Input:** rows = 5, cols = 6, rStart = 1, cStart = 4
**Output:** \[\[1,4\],\[1,5\],\[2,5\],\[2,4\],\[2,3\],\[1,3\],\[0,3\],\[0,4\],\[0,5\],\[3,5\],\[3,4\],\[3,3\],\[3,2\],\[2,2\],\[1,2\],\[0,2\],\[4,5\],\[4,4\],\[4,3\],\[4,2\],\[4,1\],\[3,1\],\[2,1\],\[1,1\],\[0,1\],\[4,0\],\[3,0\],\[2,0\],\[1,0\],\[0,0\]\]
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rStart < rows`
* `0 <= cStart < cols` | null |
Solution | spiral-matrix-iii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n \n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n\n vector<vector<int>> result;\n int total = 0;\n\n int rowStart = rStart;\n int rowEnd = rStart;\n\n int colStart = cStart;\n int colEnd = cStart;\n\n while(true){\n for(int i=colStart; i<=colEnd; i++){\n if(i >= 0 && i < cols && rowStart >= 0){\n result.push_back({rowStart, i});\n total++;\n }\n }\n colEnd++;\n if(total == (rows * cols))\n break;\n for(int i=rowStart; i<=rowEnd; i++){\n if(i >= 0 && i < rows && colEnd < cols){\n result.push_back({i, colEnd});\n total++;\n }\n }\n rowEnd++;\n if(total == (rows * cols))\n break;\n for(int i=colEnd; i>=colStart; i--){\n if(i >= 0 && i < cols && rowEnd < rows){\n result.push_back({rowEnd, i});\n total++;\n }\n }\n colStart--;\n if(total == (rows * cols))\n break;\n for(int i=rowEnd; i>=rowStart; i--){\n if(i >= 0 && i < rows && colStart >= 0){\n result.push_back({i, colStart});\n total++;\n }\n }\n rowStart--;\n if(total == (rows * cols))\n break;\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n visits = []\n top, bottom, left, right = rStart, rStart + 1, cStart, cStart + 1\n\n self.incr = 1\n direction = 0\n\n def place(row, col):\n visits.append([row, col])\n self.incr += 1\n \n while self.incr != (1 + rows * cols):\n if direction == 0:\n if top >= 0:\n row = top\n for col in range(max(left, 0), min(right, cols)):\n place(row, col)\n right += 1\n if direction == 1:\n if right <= cols:\n col = right - 1\n for row in range(max(top, 0), min(bottom, rows)):\n place(row, col)\n bottom += 1\n if direction == 2:\n if bottom <= rows:\n row = bottom - 1\n for col in range(min(right - 1, cols - 1), max(left - 1, -1), -1):\n place(row, col)\n left -= 1\n if direction == 3:\n if left >= 0:\n col = left\n for row in range(min(bottom - 1, rows - 1), max(top - 1, -1), -1):\n place(row, col)\n top -= 1\n direction = (direction + 1) % 4\n return visits\n```\n\n```Java []\nclass Solution {\n int index = 1;\n int row;\n int col;\n int rows;\n int cols;\n\n public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n int[][] result = new int[rows * cols][2];\n int moves = 0;\n row = rStart;\n col = cStart;\n this.rows = rows;\n this.cols = cols;\n result[0] = new int[] { rStart, cStart };\n while (index < result.length) {\n ++moves;\n addToResult(result, moves, 1, 0);\n addToResult(result, moves, 0, 1);\n ++moves;\n addToResult(result, moves, -1, 0);\n addToResult(result, moves, 0, -1);\n }\n return result;\n }\n public void addToResult(int[][] result, int moves, int horizontal, int vertical) {\n for (int i = 0; i < moves; ++i) {\n row += vertical;\n col += horizontal;\n if (row < rows && row > -1 && col < cols && col > -1) {\n result[index] = new int[] { row, col };\n ++index;\n }\n }\n }\n}\n```\n | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Easy Python Solution Based on Spiral Matrix I and II | spiral-matrix-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter every iteration of a row or column we need to widen our range.\nIf the first row we\'re reading is length of two when we read if in reverse direction we need to add one more element to it.\nEg. Lets read a row in to the left direction then when we eventually try to read in the reverse that is to the right direction. We include one more element. 1->2 then 5<-4<-3\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n ans = []\n left, right = cStart, cStart+1\n top, bottom = rStart, rStart+1\n current = 1\n move = 0\n while current <= rows*cols:\n # fill top\n for i in range(left+move, right+1):\n if self.inbound(top, i, rows, cols):\n ans.append([top, i])\n current += 1\n left -= 1\n # fill right\n for i in range(top+1, bottom+1):\n if self.inbound(i, right, rows, cols):\n ans.append([i, right])\n current += 1\n top -= 1\n # fill bottom\n for i in range(right-1, left-1, -1):\n if self.inbound(bottom, i, rows, cols):\n ans.append([bottom, i])\n current += 1\n right += 1\n # fill left\n for i in range(bottom-1, top-1, -1):\n if self.inbound(i, left, rows, cols):\n ans.append([i, left])\n current += 1\n bottom += 1\n move = 1\n return ans\n def inbound(self, r, c, rows, cols):\n return 0<=r<rows and 0<=c<cols\n``` | 3 | You start at the cell `(rStart, cStart)` of an `rows x cols` grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all `rows * cols` spaces of the grid.
Return _an array of coordinates representing the positions of the grid in the order you visited them_.
**Example 1:**
**Input:** rows = 1, cols = 4, rStart = 0, cStart = 0
**Output:** \[\[0,0\],\[0,1\],\[0,2\],\[0,3\]\]
**Example 2:**
**Input:** rows = 5, cols = 6, rStart = 1, cStart = 4
**Output:** \[\[1,4\],\[1,5\],\[2,5\],\[2,4\],\[2,3\],\[1,3\],\[0,3\],\[0,4\],\[0,5\],\[3,5\],\[3,4\],\[3,3\],\[3,2\],\[2,2\],\[1,2\],\[0,2\],\[4,5\],\[4,4\],\[4,3\],\[4,2\],\[4,1\],\[3,1\],\[2,1\],\[1,1\],\[0,1\],\[4,0\],\[3,0\],\[2,0\],\[1,0\],\[0,0\]\]
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rStart < rows`
* `0 <= cStart < cols` | null |
Easy Python Solution Based on Spiral Matrix I and II | spiral-matrix-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter every iteration of a row or column we need to widen our range.\nIf the first row we\'re reading is length of two when we read if in reverse direction we need to add one more element to it.\nEg. Lets read a row in to the left direction then when we eventually try to read in the reverse that is to the right direction. We include one more element. 1->2 then 5<-4<-3\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n ans = []\n left, right = cStart, cStart+1\n top, bottom = rStart, rStart+1\n current = 1\n move = 0\n while current <= rows*cols:\n # fill top\n for i in range(left+move, right+1):\n if self.inbound(top, i, rows, cols):\n ans.append([top, i])\n current += 1\n left -= 1\n # fill right\n for i in range(top+1, bottom+1):\n if self.inbound(i, right, rows, cols):\n ans.append([i, right])\n current += 1\n top -= 1\n # fill bottom\n for i in range(right-1, left-1, -1):\n if self.inbound(bottom, i, rows, cols):\n ans.append([bottom, i])\n current += 1\n right += 1\n # fill left\n for i in range(bottom-1, top-1, -1):\n if self.inbound(i, left, rows, cols):\n ans.append([i, left])\n current += 1\n bottom += 1\n move = 1\n return ans\n def inbound(self, r, c, rows, cols):\n return 0<=r<rows and 0<=c<cols\n``` | 3 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
simple simulation solution || python | spiral-matrix-iii | 1 | 1 | # Intuition and Approach\n* start the simulation from starting cell and insert position of cells in to ans which lie within the matrix\n\n# Complexity\n- Time complexity: O(N^2)\n\n- Space complexity: O(N^2)\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, m: int, n: int, i: int, j: int) -> List[List[int]]:\n ans=[]\n lb,rb,tb,bb=j,j,i,i\n while(len(ans)<m*n):\n while(j<rb+1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n j+=1\n rb+=1\n while(i<bb+1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n i+=1\n bb+=1\n while(j>lb-1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n j-=1\n lb-=1\n while(i>tb-1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n i-=1\n tb-=1\n return ans\n\n``` | 1 | You start at the cell `(rStart, cStart)` of an `rows x cols` grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all `rows * cols` spaces of the grid.
Return _an array of coordinates representing the positions of the grid in the order you visited them_.
**Example 1:**
**Input:** rows = 1, cols = 4, rStart = 0, cStart = 0
**Output:** \[\[0,0\],\[0,1\],\[0,2\],\[0,3\]\]
**Example 2:**
**Input:** rows = 5, cols = 6, rStart = 1, cStart = 4
**Output:** \[\[1,4\],\[1,5\],\[2,5\],\[2,4\],\[2,3\],\[1,3\],\[0,3\],\[0,4\],\[0,5\],\[3,5\],\[3,4\],\[3,3\],\[3,2\],\[2,2\],\[1,2\],\[0,2\],\[4,5\],\[4,4\],\[4,3\],\[4,2\],\[4,1\],\[3,1\],\[2,1\],\[1,1\],\[0,1\],\[4,0\],\[3,0\],\[2,0\],\[1,0\],\[0,0\]\]
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rStart < rows`
* `0 <= cStart < cols` | null |
simple simulation solution || python | spiral-matrix-iii | 1 | 1 | # Intuition and Approach\n* start the simulation from starting cell and insert position of cells in to ans which lie within the matrix\n\n# Complexity\n- Time complexity: O(N^2)\n\n- Space complexity: O(N^2)\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, m: int, n: int, i: int, j: int) -> List[List[int]]:\n ans=[]\n lb,rb,tb,bb=j,j,i,i\n while(len(ans)<m*n):\n while(j<rb+1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n j+=1\n rb+=1\n while(i<bb+1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n i+=1\n bb+=1\n while(j>lb-1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n j-=1\n lb-=1\n while(i>tb-1):\n if(i<m and j<n and i>=0 and j>=0):ans.append([i,j])\n i-=1\n tb-=1\n return ans\n\n``` | 1 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
easy understanding for beginners | spiral-matrix-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(rows * cols)\n\n- Space complexity:\nO(rows * cols)\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n dirs=[(0,1),(1,0),(0,-1),(-1,0)]\n #[(east),(south),(west),(north)]\n #[right,down,left,up]\n #(row,column)#(if row number increase (1,0) and so on........)\n #(-1,0)\n # (0,-1) (0,0) (0,1)\n # (1,0)\n dir_idx=0\n total=rows*cols\n res=[[rStart,cStart]]\n increment=1\n steps=1\n while len(res)<total:\n for i in range(increment):\n rStart,cStart=rStart+dirs[dir_idx][0],cStart+dirs[dir_idx][1]\n if rStart>=0 and rStart<rows and cStart>=0 and cStart<cols:\n res.append([rStart,cStart])\n dir_idx=(dir_idx+1)%4\n if steps%2==0:\n increment+=1\n steps+=1\n return res\n \n\n\n \n \n``` | 0 | You start at the cell `(rStart, cStart)` of an `rows x cols` grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all `rows * cols` spaces of the grid.
Return _an array of coordinates representing the positions of the grid in the order you visited them_.
**Example 1:**
**Input:** rows = 1, cols = 4, rStart = 0, cStart = 0
**Output:** \[\[0,0\],\[0,1\],\[0,2\],\[0,3\]\]
**Example 2:**
**Input:** rows = 5, cols = 6, rStart = 1, cStart = 4
**Output:** \[\[1,4\],\[1,5\],\[2,5\],\[2,4\],\[2,3\],\[1,3\],\[0,3\],\[0,4\],\[0,5\],\[3,5\],\[3,4\],\[3,3\],\[3,2\],\[2,2\],\[1,2\],\[0,2\],\[4,5\],\[4,4\],\[4,3\],\[4,2\],\[4,1\],\[3,1\],\[2,1\],\[1,1\],\[0,1\],\[4,0\],\[3,0\],\[2,0\],\[1,0\],\[0,0\]\]
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rStart < rows`
* `0 <= cStart < cols` | null |
easy understanding for beginners | spiral-matrix-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(rows * cols)\n\n- Space complexity:\nO(rows * cols)\n\n# Code\n```\nclass Solution:\n def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:\n dirs=[(0,1),(1,0),(0,-1),(-1,0)]\n #[(east),(south),(west),(north)]\n #[right,down,left,up]\n #(row,column)#(if row number increase (1,0) and so on........)\n #(-1,0)\n # (0,-1) (0,0) (0,1)\n # (1,0)\n dir_idx=0\n total=rows*cols\n res=[[rStart,cStart]]\n increment=1\n steps=1\n while len(res)<total:\n for i in range(increment):\n rStart,cStart=rStart+dirs[dir_idx][0],cStart+dirs[dir_idx][1]\n if rStart>=0 and rStart<rows and cStart>=0 and cStart<cols:\n res.append([rStart,cStart])\n dir_idx=(dir_idx+1)%4\n if steps%2==0:\n increment+=1\n steps+=1\n return res\n \n\n\n \n \n``` | 0 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Best java submission with 99.9% beat | spiral-matrix-iii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(m*n) where m = no. of rows and n = no. of columns\n99.6% beat \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(1) constant space complexity\n\n# Code\n```\nclass Solution {\n public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n int left = rStart, down = left + 1, top = cStart, k = 0, right = top + 1;\n int[][] ans = new int[rows * cols][2];\n while (true) {\n if (left >= 0) {\n for (int i = (top >= 0) ? top : 0; i <= ((right <= cols - 1) ? right : cols - 1); i++) {\n ans[k][0] = left;\n ans[k++][1] = i;\n }\n }\n top--;\n if (right < cols) {\n for (int i = ((left + 1) >= 0 ? left + 1 : 0); i <= ((down < rows) ? down : rows - 1); i++) {\n ans[k][0] = i;\n ans[k++][1] = right;\n }\n }\n right++;\n left--;\n if (down < rows) {\n for (int i = ((right - 2) < cols ? right - 2 : cols - 1); i >= ((top >= 0) ? top : 0); i--) {\n ans[k][0] = down;\n ans[k++][1] = i;\n }\n }\n down++;\n if (top >= 0) {\n for (int i = ((down - 2) < rows ? down - 2 : rows - 1); i > ((left >= 0) ? left : -1); i--) {\n ans[k][0] = i;\n ans[k++][1] = top;\n }\n }\n if (left < 0 && right >= cols && down >= rows && top < 0)\n break;\n }\n return ans;\n }\n}\n``` | 0 | You start at the cell `(rStart, cStart)` of an `rows x cols` grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.
You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid's boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all `rows * cols` spaces of the grid.
Return _an array of coordinates representing the positions of the grid in the order you visited them_.
**Example 1:**
**Input:** rows = 1, cols = 4, rStart = 0, cStart = 0
**Output:** \[\[0,0\],\[0,1\],\[0,2\],\[0,3\]\]
**Example 2:**
**Input:** rows = 5, cols = 6, rStart = 1, cStart = 4
**Output:** \[\[1,4\],\[1,5\],\[2,5\],\[2,4\],\[2,3\],\[1,3\],\[0,3\],\[0,4\],\[0,5\],\[3,5\],\[3,4\],\[3,3\],\[3,2\],\[2,2\],\[1,2\],\[0,2\],\[4,5\],\[4,4\],\[4,3\],\[4,2\],\[4,1\],\[3,1\],\[2,1\],\[1,1\],\[0,1\],\[4,0\],\[3,0\],\[2,0\],\[1,0\],\[0,0\]\]
**Constraints:**
* `1 <= rows, cols <= 100`
* `0 <= rStart < rows`
* `0 <= cStart < cols` | null |
Best java submission with 99.9% beat | spiral-matrix-iii | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(m*n) where m = no. of rows and n = no. of columns\n99.6% beat \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(1) constant space complexity\n\n# Code\n```\nclass Solution {\n public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {\n int left = rStart, down = left + 1, top = cStart, k = 0, right = top + 1;\n int[][] ans = new int[rows * cols][2];\n while (true) {\n if (left >= 0) {\n for (int i = (top >= 0) ? top : 0; i <= ((right <= cols - 1) ? right : cols - 1); i++) {\n ans[k][0] = left;\n ans[k++][1] = i;\n }\n }\n top--;\n if (right < cols) {\n for (int i = ((left + 1) >= 0 ? left + 1 : 0); i <= ((down < rows) ? down : rows - 1); i++) {\n ans[k][0] = i;\n ans[k++][1] = right;\n }\n }\n right++;\n left--;\n if (down < rows) {\n for (int i = ((right - 2) < cols ? right - 2 : cols - 1); i >= ((top >= 0) ? top : 0); i--) {\n ans[k][0] = down;\n ans[k++][1] = i;\n }\n }\n down++;\n if (top >= 0) {\n for (int i = ((down - 2) < rows ? down - 2 : rows - 1); i > ((left >= 0) ? left : -1); i--) {\n ans[k][0] = i;\n ans[k++][1] = top;\n }\n }\n if (left < 0 && right >= cols && down >= rows && top < 0)\n break;\n }\n return ans;\n }\n}\n``` | 0 | A parentheses string is valid if and only if:
* It is the empty string,
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid strings, or
* It can be written as `(A)`, where `A` is a valid string.
You are given a parentheses string `s`. In one move, you can insert a parenthesis at any position of the string.
* For example, if `s = "())) "`, you can insert an opening parenthesis to be `"(**(**))) "` or a closing parenthesis to be `"())**)**) "`.
Return _the minimum number of moves required to make_ `s` _valid_.
**Example 1:**
**Input:** s = "()) "
**Output:** 1
**Example 2:**
**Input:** s = "((( "
**Output:** 3
**Constraints:**
* `1 <= s.length <= 1000`
* `s[i]` is either `'('` or `')'`. | null |
Python - Color Solution - Video Solution | possible-bipartition | 0 | 1 | I have explained this [here](https://youtu.be/Zqvdg0TmAnE).\n\n```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n \n g = defaultdict(list)\n for x,y in dislikes:\n g[x].append(y)\n g[y].append(x)\n \n color = {}\n \n def dfs(i, c):\n color[i] = c\n for enemy in g[i]:\n if enemy in color:\n # if enemy has same color, then return False directly\n if color[enemy]==c:\n return False\n else:\n # assign inverted color to enemy and check for anomalies\n if not dfs(enemy, 1-c):\n return False\n return True\n \n for i in range(1, n+1):\n if i not in color:\n # assign color 1 and check for anomalies\n if not dfs(i, 1):\n return False\n \n\t\t # We found no anomaly, so return True\n return True | 2 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Python - Color Solution - Video Solution | possible-bipartition | 0 | 1 | I have explained this [here](https://youtu.be/Zqvdg0TmAnE).\n\n```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n \n g = defaultdict(list)\n for x,y in dislikes:\n g[x].append(y)\n g[y].append(x)\n \n color = {}\n \n def dfs(i, c):\n color[i] = c\n for enemy in g[i]:\n if enemy in color:\n # if enemy has same color, then return False directly\n if color[enemy]==c:\n return False\n else:\n # assign inverted color to enemy and check for anomalies\n if not dfs(enemy, 1-c):\n return False\n return True\n \n for i in range(1, n+1):\n if i not in color:\n # assign color 1 and check for anomalies\n if not dfs(i, 1):\n return False\n \n\t\t # We found no anomaly, so return True\n return True | 2 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Solution | possible-bipartition | 1 | 1 | ```C++ []\nvoid make(int n,int size[],int par[]){\n for(int i=0;i<n;i++){\n size[i] = 1;\n par[i] = i;\n }\n}\nint find(int a,int par[]){\n if(par[a]==a){\n return a;\n }\n par[a] = find(par[a],par);\n return par[a];\n}\nvoid Union(int a,int b,int size[],int par[]){\n a = find(a,par);\n b = find(b,par);\n if(a!=b){\n if(size[a]<size[b]){\n swap(a,b);\n }\n size[a]+=size[b];\n par[b] = a;\n }\n}\nclass Solution {\npublic:\n bool possibleBipartition(int n, vector<vector<int>>& dislikes) {\n int size[n+2];\n int par[n+2];\n make(n+2,size,par);\n int exchange[n];\n for(int i=0;i<n;i++){\n exchange[i] = -1;\n }\n for(int i=0;i<dislikes.size();i++){\n int aa = dislikes[i][0];\n int bb = dislikes[i][1];\n aa--;\n bb--;\n if(exchange[aa]==-1 and exchange[bb]==-1){\n exchange[aa] = bb;\n exchange[bb] = aa;\n }\n else if(exchange[aa]==-1){\n exchange[aa] = bb;\n Union(exchange[bb],aa,size,par);\n }\n else if(exchange[bb]==-1){\n exchange[bb] = aa;\n Union(exchange[aa],bb,size,par);\n }\n else{\n if(find(aa,par)==find(bb,par)){\n return 0;\n }\n Union(exchange[aa],bb,size,par);\n Union(exchange[bb],aa,size,par);\n }\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n adj = [[] for _ in range(n+1)]\n\n for p1, p2 in dislikes:\n adj[p1].append(p2)\n adj[p2].append(p1)\n \n colors = [-1] * (n+1)\n\n def bfs(color_idx):\n q = collections.deque([color_idx])\n colors[color_idx] = 0\n\n while q:\n person = q.popleft()\n for neighbor in adj[person]:\n if colors[neighbor] == colors[person]:\n return False\n if colors[neighbor] == -1:\n colors[neighbor] = 1 - colors[person]\n q.append(neighbor)\n \n return True\n\n for idx in range(1, len(colors)):\n if colors[idx] == -1:\n if not bfs(idx):\n return False\n \n return True\n```\n\n```Java []\nclass Solution {\n public boolean possibleBipartition(int n, int[][] dislikes) {\n int len = dislikes.length;\n boolean[] check = new boolean[len];\n int[] arr = new int[n + 1];\n boolean foundNew;\n for(int i = 0; i < len; i++){\n if(check[i]) continue;\n arr[dislikes[i][0]] = 1;\n arr[dislikes[i][1]] = 2;\n foundNew = true;\n while(foundNew){\n foundNew = false;\n for(int j = i + 1; j < len; j++){\n if(check[j]) continue;\n int x = arr[dislikes[j][0]];\n int y = arr[dislikes[j][1]];\n if(x == 0 && y == 0) continue;\n if(x > 0 && y > 0){\n if((x - y) % 2 == 0) return false;\n }\n else if(x > 0) arr[dislikes[j][1]] = x + 1;\n else arr[dislikes[j][0]] = y + 1;\n foundNew = true;\n check[j] = true;\n }\n }\n }\n return true;\n }\n}\n```\n | 1 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Solution | possible-bipartition | 1 | 1 | ```C++ []\nvoid make(int n,int size[],int par[]){\n for(int i=0;i<n;i++){\n size[i] = 1;\n par[i] = i;\n }\n}\nint find(int a,int par[]){\n if(par[a]==a){\n return a;\n }\n par[a] = find(par[a],par);\n return par[a];\n}\nvoid Union(int a,int b,int size[],int par[]){\n a = find(a,par);\n b = find(b,par);\n if(a!=b){\n if(size[a]<size[b]){\n swap(a,b);\n }\n size[a]+=size[b];\n par[b] = a;\n }\n}\nclass Solution {\npublic:\n bool possibleBipartition(int n, vector<vector<int>>& dislikes) {\n int size[n+2];\n int par[n+2];\n make(n+2,size,par);\n int exchange[n];\n for(int i=0;i<n;i++){\n exchange[i] = -1;\n }\n for(int i=0;i<dislikes.size();i++){\n int aa = dislikes[i][0];\n int bb = dislikes[i][1];\n aa--;\n bb--;\n if(exchange[aa]==-1 and exchange[bb]==-1){\n exchange[aa] = bb;\n exchange[bb] = aa;\n }\n else if(exchange[aa]==-1){\n exchange[aa] = bb;\n Union(exchange[bb],aa,size,par);\n }\n else if(exchange[bb]==-1){\n exchange[bb] = aa;\n Union(exchange[aa],bb,size,par);\n }\n else{\n if(find(aa,par)==find(bb,par)){\n return 0;\n }\n Union(exchange[aa],bb,size,par);\n Union(exchange[bb],aa,size,par);\n }\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n adj = [[] for _ in range(n+1)]\n\n for p1, p2 in dislikes:\n adj[p1].append(p2)\n adj[p2].append(p1)\n \n colors = [-1] * (n+1)\n\n def bfs(color_idx):\n q = collections.deque([color_idx])\n colors[color_idx] = 0\n\n while q:\n person = q.popleft()\n for neighbor in adj[person]:\n if colors[neighbor] == colors[person]:\n return False\n if colors[neighbor] == -1:\n colors[neighbor] = 1 - colors[person]\n q.append(neighbor)\n \n return True\n\n for idx in range(1, len(colors)):\n if colors[idx] == -1:\n if not bfs(idx):\n return False\n \n return True\n```\n\n```Java []\nclass Solution {\n public boolean possibleBipartition(int n, int[][] dislikes) {\n int len = dislikes.length;\n boolean[] check = new boolean[len];\n int[] arr = new int[n + 1];\n boolean foundNew;\n for(int i = 0; i < len; i++){\n if(check[i]) continue;\n arr[dislikes[i][0]] = 1;\n arr[dislikes[i][1]] = 2;\n foundNew = true;\n while(foundNew){\n foundNew = false;\n for(int j = i + 1; j < len; j++){\n if(check[j]) continue;\n int x = arr[dislikes[j][0]];\n int y = arr[dislikes[j][1]];\n if(x == 0 && y == 0) continue;\n if(x > 0 && y > 0){\n if((x - y) % 2 == 0) return false;\n }\n else if(x > 0) arr[dislikes[j][1]] = x + 1;\n else arr[dislikes[j][0]] = y + 1;\n foundNew = true;\n check[j] = true;\n }\n }\n }\n return true;\n }\n}\n```\n | 1 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
[Python] Union-Find in O(E), The Best | possible-bipartition | 0 | 1 | # Approach\nKeeping root and rank arrays of size $$n$$ is unnecessary. The hashmap-based union-find implementation below supports all value types, and keeps neither single-node ranks nor roots of root nodes in the maps.\n\nThe Best!\n\n# Complexity\n- Time complexity: $$O(E \\cdot\\alpha(E)) \\approx O(E)$$\n- Space complexity: $$O(E)$$\n\n# Code\n```python\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: list[list[int]]) -> bool:\n graph, uf = collections.defaultdict(list), UnionFind()\n for u, v in dislikes:\n graph[u].append(v)\n graph[v].append(u)\n for u, vs in graph.items():\n for v in vs:\n if uf[u] == uf[v]:\n return False\n uf.union(v, vs[0])\n return True\n\nclass UnionFind:\n def __init__(self):\n self.root, self.rank = {}, {}\n def __getitem__(self, x):\n path = []\n while (root_x := self.root.get(x, path)) is not path:\n path.append(x)\n x = root_x\n for y in path:\n self.root[y] = x\n return x\n def union(self, x, y):\n if (root_low := self[x]) != (root_high := self[y]):\n if (rank_low := self.rank.get(root_low, 1)) > (rank_high := self.rank.get(root_high, 1)):\n root_low, root_high, rank_low, rank_high = root_high, root_low, rank_high, rank_low\n self.root[root_low], self.rank[root_high] = root_high, rank_high + rank_low\n if rank_low != 1:\n del self.rank[root_low]\n``` | 1 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
[Python] Union-Find in O(E), The Best | possible-bipartition | 0 | 1 | # Approach\nKeeping root and rank arrays of size $$n$$ is unnecessary. The hashmap-based union-find implementation below supports all value types, and keeps neither single-node ranks nor roots of root nodes in the maps.\n\nThe Best!\n\n# Complexity\n- Time complexity: $$O(E \\cdot\\alpha(E)) \\approx O(E)$$\n- Space complexity: $$O(E)$$\n\n# Code\n```python\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: list[list[int]]) -> bool:\n graph, uf = collections.defaultdict(list), UnionFind()\n for u, v in dislikes:\n graph[u].append(v)\n graph[v].append(u)\n for u, vs in graph.items():\n for v in vs:\n if uf[u] == uf[v]:\n return False\n uf.union(v, vs[0])\n return True\n\nclass UnionFind:\n def __init__(self):\n self.root, self.rank = {}, {}\n def __getitem__(self, x):\n path = []\n while (root_x := self.root.get(x, path)) is not path:\n path.append(x)\n x = root_x\n for y in path:\n self.root[y] = x\n return x\n def union(self, x, y):\n if (root_low := self[x]) != (root_high := self[y]):\n if (rank_low := self.rank.get(root_low, 1)) > (rank_high := self.rank.get(root_high, 1)):\n root_low, root_high, rank_low, rank_high = root_high, root_low, rank_high, rank_low\n self.root[root_low], self.rank[root_high] = root_high, rank_high + rank_low\n if rank_low != 1:\n del self.rank[root_low]\n``` | 1 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Python || DFS, BFS, Union-Find & Odd-Cycle Solutions | possible-bipartition | 0 | 1 | # Code\n```\nfrom collections import deque\nfrom dataclasses import dataclass\nfrom functools import cached_property\nfrom typing import Optional\n\nUNEXPLORED = None\n\n\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: list[list[int]]) -> bool:\n """\n we first create a graph, say g, from given "dislikes" list of edges. In it, each vertex\n represents corresponding person. Two vertices are adjacent (neighbors) then, they dislike\n each other.\n\n In all the solutions, except "no_odd_cycle", we will use graph coloring methodology.\n We will try coloring neighbors with different colors, representing they dislike each other\n and if this can not be done then graph can not be bi-partitioned (we will not choose more\n than two color)\n :param n:\n :param dislikes:\n :return:\n """\n graph = [[] for _ in range(n + 1)]\n\n for u, v in dislikes:\n graph[u].append(v)\n graph[v].append(u)\n\n # return self.dfs(graph)\n # return self.bfs(graph)\n # return self.no_odd_cycle(graph)\n return self.union_find(graph)\n\n @staticmethod\n def union_find(graph: list[list[int]]) -> bool:\n """\n :param graph:\n :return:\n """\n n = len(graph)\n uf = UF(n)\n\n for u, neighbors in enumerate(graph):\n u_color = uf.find(u)\n\n if not neighbors: # "u" is an isolated node, so it can be painted with any color\n continue\n\n # As we need to create a bi-partition graph so each vertex will either be in the\n # same group as that of "u" (say, group A) or will be in another group (say, group B), since\n # neighbors of "u" can not be in A, so they should be in B (assuming the graph is bi-partitioned).\n # As we are coloring groups A and B so all neighbors of "u" will have same color as that of the group B.\n # So, we are picking a neighbor (say opposite_group_representative_node) and merging all of them\n opposite_group_representative_node = neighbors[0] # any neighbor can become the representative node\n\n for v in neighbors:\n v_color = uf.find(v) # each node is represented by a color\n\n if u_color == v_color:\n return False\n else:\n uf.union(opposite_group_representative_node, v) # node and v will have same color\n\n # below statements are equivalent to above line of code\n # uf.union(opposite_group_representative_node, v_color)\n # uf.union(uf.find(opposite_group_representative_node), v)\n # uf.union(uf.find(opposite_group_representative_node), v_color)\n\n return True\n\n @staticmethod\n def dfs(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # To begin with, color of each node will be None, representing that it has not been colored/explored.\n # The color would be changed to True or False later on\n node_color: list[Optional[bool]] = [UNEXPLORED] * n\n\n def is_bipartite(u: int) -> bool:\n color_u = node_color[u]\n\n for v in graph[u]:\n if (color_v := node_color[v]) == UNEXPLORED:\n node_color[v] = not color_u\n\n if not is_bipartite(v):\n return False\n elif color_v == color_u:\n return False\n\n return True\n\n for i in range(n):\n if node_color[i] == UNEXPLORED:\n node_color[i] = True # we could assign False as well, does not matter\n\n if not is_bipartite(i):\n return False\n\n return True\n\n @staticmethod\n def bfs(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # To begin with, color of each node will be None, representing that it has not been colored/explored.\n # The color would be changed to True or False later on\n node_color: list[Optional[bool]] = [UNEXPLORED] * n\n\n q = deque()\n\n def is_bipartite(s: int) -> bool:\n q.append(s)\n\n while q:\n u = q.popleft()\n color_u = node_color[u]\n\n for v in graph[u]:\n if (color_v := node_color[v]) == UNEXPLORED:\n node_color[v] = not color_u\n q.append(v)\n elif color_u == color_v:\n return False\n\n return True\n\n for i in range(n):\n if node_color[i] == UNEXPLORED:\n node_color[i] = True # we could assign False as well, does not matter\n\n if not is_bipartite(i):\n return False\n\n return True\n\n @staticmethod\n def no_odd_cycle(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # Bipartite graph can never have odd cycles (https://en.wikipedia.org/wiki/Bipartite_graph#Characterization)\n depths: list[Optional[int]] = [UNEXPLORED] * n\n q = deque()\n\n def append(s: int):\n q.append((s, depths[s]))\n\n def is_bipartite(s: int) -> bool:\n append(s)\n\n while q:\n u, depth_u = q.popleft()\n\n for v in graph[u]:\n if (depth_v := depths[v]) == UNEXPLORED:\n depths[v] = depth_u + 1\n append(v)\n elif (depth_u - depth_v) % 2 == 0:\n return False\n\n return True\n\n for i in range(n):\n if depths[i] == UNEXPLORED:\n depths[i] = 0\n\n if not is_bipartite(i):\n return False\n\n return True\n```\n\n\nDefinion of **Union-Find**,\n\n```python\n@dataclass(frozen=True)\nclass UF:\n """\n Implementing union find algorithm\n """\n node_count: int\n\n def find(self, u: int) -> int:\n """\n :return: representative node of cluster containing node "u"\n """\n parent = self._parent\n\n if u != (pu := parent[u]):\n parent[u] = self.find(pu) # path compression\n\n return parent[u]\n\n def union(self, u: int, v: int) -> bool:\n """\n merging clusters containing node "u" and node "v"\n :param u:\n :param v:\n :return: True if union/merge is needed else False\n """\n root_u, root_v = self.find(u), self.find(v)\n\n if root_u == root_v:\n # merge not required as they belong to same cluster\n return False\n else:\n self._merge_roots(root_u, root_v)\n return True\n\n def _merge_roots(self, u: int, v: int):\n """\n "u" and "v" are root nodes of two different clusters and the two\n clusters are to be merged. In this function, we determine which\n node should be made parent using rank and update parent accordingly.\n\n Node with higher rank is made parent and in case of tie, "v" ("u" can\n also be chosen) node is chosen as parent and its rank is incremented\n by 1\n\n :param u:\n :param v:\n """\n rank = self._rank\n\n if rank[u] > rank[v]:\n self._parent[v] = u\n else:\n self._parent[u] = v\n\n if rank[u] == rank[v]:\n self._rank[v] += 1\n\n @cached_property\n def _parent(self) -> list[int]:\n """\n :return: list in which ith index is the ith element and value\n is its corresponding parent\n """\n return list(range(self.node_count))\n\n @cached_property\n def _rank(self) -> list[int]:\n """\n :return: list in which ith index is ith node element and value\n is its rank. Rank is used while merging clusters\n """\n return [1] * self.node_count\n``` | 1 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Python || DFS, BFS, Union-Find & Odd-Cycle Solutions | possible-bipartition | 0 | 1 | # Code\n```\nfrom collections import deque\nfrom dataclasses import dataclass\nfrom functools import cached_property\nfrom typing import Optional\n\nUNEXPLORED = None\n\n\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: list[list[int]]) -> bool:\n """\n we first create a graph, say g, from given "dislikes" list of edges. In it, each vertex\n represents corresponding person. Two vertices are adjacent (neighbors) then, they dislike\n each other.\n\n In all the solutions, except "no_odd_cycle", we will use graph coloring methodology.\n We will try coloring neighbors with different colors, representing they dislike each other\n and if this can not be done then graph can not be bi-partitioned (we will not choose more\n than two color)\n :param n:\n :param dislikes:\n :return:\n """\n graph = [[] for _ in range(n + 1)]\n\n for u, v in dislikes:\n graph[u].append(v)\n graph[v].append(u)\n\n # return self.dfs(graph)\n # return self.bfs(graph)\n # return self.no_odd_cycle(graph)\n return self.union_find(graph)\n\n @staticmethod\n def union_find(graph: list[list[int]]) -> bool:\n """\n :param graph:\n :return:\n """\n n = len(graph)\n uf = UF(n)\n\n for u, neighbors in enumerate(graph):\n u_color = uf.find(u)\n\n if not neighbors: # "u" is an isolated node, so it can be painted with any color\n continue\n\n # As we need to create a bi-partition graph so each vertex will either be in the\n # same group as that of "u" (say, group A) or will be in another group (say, group B), since\n # neighbors of "u" can not be in A, so they should be in B (assuming the graph is bi-partitioned).\n # As we are coloring groups A and B so all neighbors of "u" will have same color as that of the group B.\n # So, we are picking a neighbor (say opposite_group_representative_node) and merging all of them\n opposite_group_representative_node = neighbors[0] # any neighbor can become the representative node\n\n for v in neighbors:\n v_color = uf.find(v) # each node is represented by a color\n\n if u_color == v_color:\n return False\n else:\n uf.union(opposite_group_representative_node, v) # node and v will have same color\n\n # below statements are equivalent to above line of code\n # uf.union(opposite_group_representative_node, v_color)\n # uf.union(uf.find(opposite_group_representative_node), v)\n # uf.union(uf.find(opposite_group_representative_node), v_color)\n\n return True\n\n @staticmethod\n def dfs(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # To begin with, color of each node will be None, representing that it has not been colored/explored.\n # The color would be changed to True or False later on\n node_color: list[Optional[bool]] = [UNEXPLORED] * n\n\n def is_bipartite(u: int) -> bool:\n color_u = node_color[u]\n\n for v in graph[u]:\n if (color_v := node_color[v]) == UNEXPLORED:\n node_color[v] = not color_u\n\n if not is_bipartite(v):\n return False\n elif color_v == color_u:\n return False\n\n return True\n\n for i in range(n):\n if node_color[i] == UNEXPLORED:\n node_color[i] = True # we could assign False as well, does not matter\n\n if not is_bipartite(i):\n return False\n\n return True\n\n @staticmethod\n def bfs(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # To begin with, color of each node will be None, representing that it has not been colored/explored.\n # The color would be changed to True or False later on\n node_color: list[Optional[bool]] = [UNEXPLORED] * n\n\n q = deque()\n\n def is_bipartite(s: int) -> bool:\n q.append(s)\n\n while q:\n u = q.popleft()\n color_u = node_color[u]\n\n for v in graph[u]:\n if (color_v := node_color[v]) == UNEXPLORED:\n node_color[v] = not color_u\n q.append(v)\n elif color_u == color_v:\n return False\n\n return True\n\n for i in range(n):\n if node_color[i] == UNEXPLORED:\n node_color[i] = True # we could assign False as well, does not matter\n\n if not is_bipartite(i):\n return False\n\n return True\n\n @staticmethod\n def no_odd_cycle(graph: list[list[int]]) -> bool:\n n = len(graph)\n\n # Bipartite graph can never have odd cycles (https://en.wikipedia.org/wiki/Bipartite_graph#Characterization)\n depths: list[Optional[int]] = [UNEXPLORED] * n\n q = deque()\n\n def append(s: int):\n q.append((s, depths[s]))\n\n def is_bipartite(s: int) -> bool:\n append(s)\n\n while q:\n u, depth_u = q.popleft()\n\n for v in graph[u]:\n if (depth_v := depths[v]) == UNEXPLORED:\n depths[v] = depth_u + 1\n append(v)\n elif (depth_u - depth_v) % 2 == 0:\n return False\n\n return True\n\n for i in range(n):\n if depths[i] == UNEXPLORED:\n depths[i] = 0\n\n if not is_bipartite(i):\n return False\n\n return True\n```\n\n\nDefinion of **Union-Find**,\n\n```python\n@dataclass(frozen=True)\nclass UF:\n """\n Implementing union find algorithm\n """\n node_count: int\n\n def find(self, u: int) -> int:\n """\n :return: representative node of cluster containing node "u"\n """\n parent = self._parent\n\n if u != (pu := parent[u]):\n parent[u] = self.find(pu) # path compression\n\n return parent[u]\n\n def union(self, u: int, v: int) -> bool:\n """\n merging clusters containing node "u" and node "v"\n :param u:\n :param v:\n :return: True if union/merge is needed else False\n """\n root_u, root_v = self.find(u), self.find(v)\n\n if root_u == root_v:\n # merge not required as they belong to same cluster\n return False\n else:\n self._merge_roots(root_u, root_v)\n return True\n\n def _merge_roots(self, u: int, v: int):\n """\n "u" and "v" are root nodes of two different clusters and the two\n clusters are to be merged. In this function, we determine which\n node should be made parent using rank and update parent accordingly.\n\n Node with higher rank is made parent and in case of tie, "v" ("u" can\n also be chosen) node is chosen as parent and its rank is incremented\n by 1\n\n :param u:\n :param v:\n """\n rank = self._rank\n\n if rank[u] > rank[v]:\n self._parent[v] = u\n else:\n self._parent[u] = v\n\n if rank[u] == rank[v]:\n self._rank[v] += 1\n\n @cached_property\n def _parent(self) -> list[int]:\n """\n :return: list in which ith index is the ith element and value\n is its corresponding parent\n """\n return list(range(self.node_count))\n\n @cached_property\n def _rank(self) -> list[int]:\n """\n :return: list in which ith index is ith node element and value\n is its rank. Rank is used while merging clusters\n """\n return [1] * self.node_count\n``` | 1 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Python BFS solution | possible-bipartition | 0 | 1 | ```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n visited=[0]*n\n group=[-1]*n\n adj=[[] for _ in range(n)]\n for i,j in dislikes:\n adj[i-1].append(j-1)\n adj[j-1].append(i-1)\n \n for k in range(n):\n if visited[k]==0:\n lst=[[k,0]]\n visited[k]=1\n group[k]=0\n while lst:\n x,c=lst.pop(0)\n for i in adj[x]:\n if visited[i]==0:\n lst.append([i,(c+1)%2])\n visited[i]=1\n group[i]=(c+1)%2\n else:\n if group[i]!=(c+1)%2:\n return False\n \n return True\n``` | 1 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Python BFS solution | possible-bipartition | 0 | 1 | ```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:\n visited=[0]*n\n group=[-1]*n\n adj=[[] for _ in range(n)]\n for i,j in dislikes:\n adj[i-1].append(j-1)\n adj[j-1].append(i-1)\n \n for k in range(n):\n if visited[k]==0:\n lst=[[k,0]]\n visited[k]=1\n group[k]=0\n while lst:\n x,c=lst.pop(0)\n for i in adj[x]:\n if visited[i]==0:\n lst.append([i,(c+1)%2])\n visited[i]=1\n group[i]=(c+1)%2\n else:\n if group[i]!=(c+1)%2:\n return False\n \n return True\n``` | 1 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Beats 100% | CodeDominar Solution | possible-bipartition | 0 | 1 | - **Time complexity:** `O(V + E), where V is the number of vertices and E is the number of edges in the graph.`\n\n# Code\n```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool: \n # Create an adjacency list representation of the graph\n adj_list = [[] for _ in range(n)]\n for a, b in dislikes:\n adj_list[a - 1].append(b - 1)\n adj_list[b - 1].append(a - 1)\n \n # Initialize a colors array to store the colors of the vertices\n # 0 = not visited, 1 = set A, 2 = set B\n colors = [0] * n\n \n # Perform BFS starting from each vertex\n for start in range(n):\n # If the vertex has not been visited, perform BFS\n if colors[start] == 0:\n # Initialize the queue with the starting vertex\n queue = deque([start])\n colors[start] = 1\n \n # Perform BFS\n while queue:\n vertex = queue.popleft()\n for neighbor in adj_list[vertex]:\n # If the neighbor has not been visited, assign it to the other set and add it to the queue\n if colors[neighbor] == 0:\n colors[neighbor] = 3 - colors[vertex]\n queue.append(neighbor)\n # If the neighbor is in the same set as the current vertex, return False (not bipartite)\n elif colors[neighbor] == colors[vertex]:\n return False\n # If BFS was successful for all vertices, return True (bipartite)\n return True\n\n \n``` | 37 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Beats 100% | CodeDominar Solution | possible-bipartition | 0 | 1 | - **Time complexity:** `O(V + E), where V is the number of vertices and E is the number of edges in the graph.`\n\n# Code\n```\nclass Solution:\n def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool: \n # Create an adjacency list representation of the graph\n adj_list = [[] for _ in range(n)]\n for a, b in dislikes:\n adj_list[a - 1].append(b - 1)\n adj_list[b - 1].append(a - 1)\n \n # Initialize a colors array to store the colors of the vertices\n # 0 = not visited, 1 = set A, 2 = set B\n colors = [0] * n\n \n # Perform BFS starting from each vertex\n for start in range(n):\n # If the vertex has not been visited, perform BFS\n if colors[start] == 0:\n # Initialize the queue with the starting vertex\n queue = deque([start])\n colors[start] = 1\n \n # Perform BFS\n while queue:\n vertex = queue.popleft()\n for neighbor in adj_list[vertex]:\n # If the neighbor has not been visited, assign it to the other set and add it to the queue\n if colors[neighbor] == 0:\n colors[neighbor] = 3 - colors[vertex]\n queue.append(neighbor)\n # If the neighbor is in the same set as the current vertex, return False (not bipartite)\n elif colors[neighbor] == colors[vertex]:\n return False\n # If BFS was successful for all vertices, return True (bipartite)\n return True\n\n \n``` | 37 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Python/C++/Java sol by DFS and coloring. [w/ Graph] | possible-bipartition | 1 | 1 | Sol by DFS and coloring.\n\n---\n\n**Hint**:\n\nThink of **graph**, **node coloring**, and **DFS**.\n\nAbstract model transformation:\n\n**Person** <-> **Node**\n\nP1 **dislikes P2** <-> Node 1 and Node 2 **share one edge**, and they should be **drawed with different two colors** (i.e., for dislike relation)\n\n\nIf we can **draw each dislike pair** with **different two colors**, and **keep the dislike relationship always**, then there exists at least one possible **bipartition**.\n\n---\n\n**Illustration** and **Visualization**:\n\n\n\n---\n\n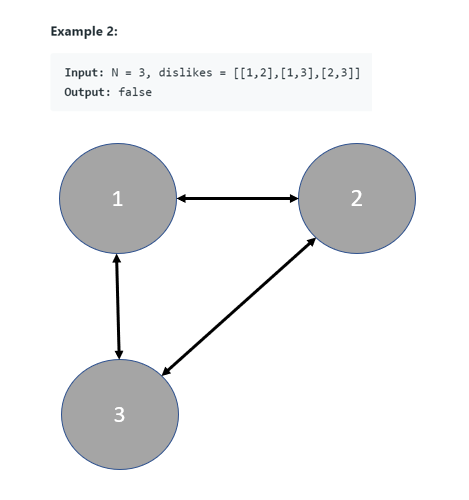\n\n\n---\n\n**Implementation** by DFS and coloring:\n\n**Special thanks to @ezpzm9\'s contribution** in discussion.\n\n```python []\nclass Solution:\n def possibleBipartition(self, N: int, dislikes: List[List[int]]) -> bool:\n \n # Constant defined for color drawing to person\n BLUE, GREEN = 1, -1\n # -------------------------------------\n \n def draw( person_id, color ):\n \n # Draw person_id as color\n color_of[person_id] = color\n \n # Draw the_other, with opposite color, in dislike table of current person_id\n for the_other in dislike_table[ person_id ]:\n \n if color_of[the_other] == color:\n # the_other has the same color of current person_id\n # Reject due to breaking the relationship of dislike\n return False\n\n if (not color_of[the_other]) and (not draw( the_other, -color)):\n # Other people can not be colored with two different colors. \n\t\t\t\t\t# Therefore, it is impossible to keep dis-like relationship with bipartition.\n return False\n \n return True\n \n \n # ------------------------------------------------\n\t\t\n\t\t\n if N == 1 or not dislikes:\n # Quick response for simple cases\n return True\n \n # each person maintain a list of dislike\n dislike_table = defaultdict( list )\n \n # key: person ID\n # value: color of person\n color_of = defaultdict(int)\n \n for p1, p2 in dislikes:\n \n # P1 dislikes P2\n # P1 and P2 should be painted with two different color\n dislike_table[p1].append( p2 )\n dislike_table[p2].append( p1 )\n \n \n # Try to draw dislike pair with different colors in DFS\n for person_id in range(1, N+1):\n \n if (not color_of[person_id]) and (not draw( person_id, BLUE)):\n # Other people can not be colored with two different colors. \n\t\t\t\t# Therefore, it is impossible to keep dis-like relationship with bipartition.\n return False \n \n return True\n```\n```C++ []\nclass Solution {\npublic:\n bool possibleBipartition(int n, vector<vector<int>>& dislikes) {\n \n enum COLOR_CONSTANT{\n GREEN = -1, // -1\n NOT_COLORDED, // 0\n BLUE // 1\n };\n \n \n if( n == 1 || dislikes.size() == 0 ){\n \n // Quick response for simple cases\n return true;\n }\n \n // each person maintains a list of dislike\n unordered_map< int, vector<int> > dislikeTable;\n \n // key: personID\n // value: color of person\n unordered_map< int, int> colorTable;\n \n // -----------------------\n \n std::function< bool( int, int ) > helper;\n helper = [&]( int personID, int color)->bool{\n \n // Draw personID as color\n colorTable[personID] = color;\n \n // Draw theOther, with opposite color, in dislike table of current personID\n for( const int& theOther : dislikeTable[ personID ] ){\n \n if( colorTable[theOther] == color ){\n // the_other has the same color of current person_id\n // Reject due to breaking the relationship of dislike\n return false;\n }\n \n if( colorTable[theOther] == NOT_COLORDED && ( !helper(theOther, -color) ) ){\n // Other people can not be colored with two different colors. \n // Therefore, it is impossible to keep dis-like relationship with bipartition.\n return false;\n }\n }\n \n return true;\n \n };\n \n // -----------------------\n \n \n // update dislike table\n for( const auto& relation : dislikes ){\n \n int p1 = relation[0], p2 = relation[1];\n \n dislikeTable[p1].emplace_back( p2 );\n dislikeTable[p2].emplace_back( p1 );\n \n }\n \n // Try to draw dislike pair with different color in DFS\n for( int personID = 1 ; personID <= n ; personID++){\n \n if( colorTable[personID] == NOT_COLORDED && ( !helper(personID, BLUE) ) ){\n // Other people can not be colored with two different colors. \n\t\t\t\t // Therefore, it is impossible to keep dis-like relationship with bipartition.\n return false;\n }\n }\n \n\n return true; \n }\n};\n```\n```Java []\nclass Solution {\n public boolean possibleBipartition(int N, int[][] dislikes) { \n List<Integer>[] graph = new List[N + 1]; \n\n for (int i = 1; i <= N; ++i) graph[i] = new ArrayList<>(); \n\n for (int[] dislike : dislikes) {\n graph[dislike[0]].add(dislike[1]);\n graph[dislike[1]].add(dislike[0]);\n }\n\n Integer[] colors = new Integer[N + 1];\n\n for (int i = 1; i <= N; ++i) {\n // If the connected component that node i belongs to hasn\'t been colored yet then try coloring it.\n if (colors[i] == null && !dfs(graph, colors, i, 1)) return false;\n }\n return true; \n }\n\n private boolean dfs(List<Integer>[] graph, Integer[] colors, int currNode, int currColor) {\n colors[currNode] = currColor;\n\n // Color all uncolored adjacent nodes.\n for (Integer adjacentNode : graph[currNode]) {\n\n if (colors[adjacentNode] == null) {\n if (!dfs(graph, colors, adjacentNode, currColor * -1)) return false; \n\n } else if (colors[adjacentNode] == currColor) {\n return false; \n }\n }\n return true; \n }\n}\n```\n\n---\n\nSupplement material:\n\n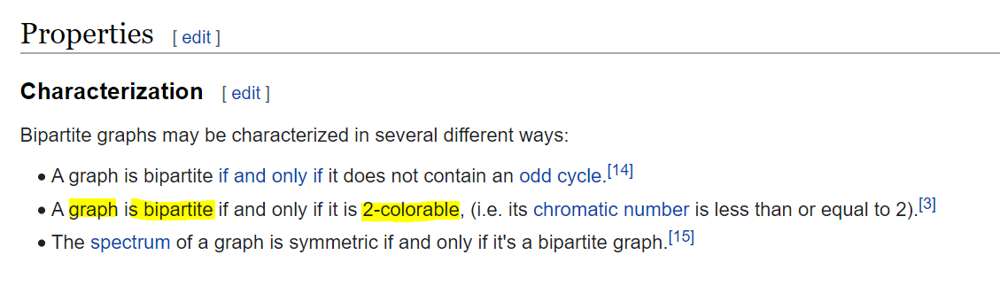\n\n---\n\nReference:\n\n[1] [Wiki: Bipartite graph](https://en.wikipedia.org/wiki/Bipartite_graph) | 251 | We want to split a group of `n` people (labeled from `1` to `n`) into two groups of **any size**. Each person may dislike some other people, and they should not go into the same group.
Given the integer `n` and the array `dislikes` where `dislikes[i] = [ai, bi]` indicates that the person labeled `ai` does not like the person labeled `bi`, return `true` _if it is possible to split everyone into two groups in this way_.
**Example 1:**
**Input:** n = 4, dislikes = \[\[1,2\],\[1,3\],\[2,4\]\]
**Output:** true
**Explanation:** The first group has \[1,4\], and the second group has \[2,3\].
**Example 2:**
**Input:** n = 3, dislikes = \[\[1,2\],\[1,3\],\[2,3\]\]
**Output:** false
**Explanation:** We need at least 3 groups to divide them. We cannot put them in two groups.
**Constraints:**
* `1 <= n <= 2000`
* `0 <= dislikes.length <= 104`
* `dislikes[i].length == 2`
* `1 <= ai < bi <= n`
* All the pairs of `dislikes` are **unique**. | null |
Python/C++/Java sol by DFS and coloring. [w/ Graph] | possible-bipartition | 1 | 1 | Sol by DFS and coloring.\n\n---\n\n**Hint**:\n\nThink of **graph**, **node coloring**, and **DFS**.\n\nAbstract model transformation:\n\n**Person** <-> **Node**\n\nP1 **dislikes P2** <-> Node 1 and Node 2 **share one edge**, and they should be **drawed with different two colors** (i.e., for dislike relation)\n\n\nIf we can **draw each dislike pair** with **different two colors**, and **keep the dislike relationship always**, then there exists at least one possible **bipartition**.\n\n---\n\n**Illustration** and **Visualization**:\n\n\n\n---\n\n\n\n\n---\n\n**Implementation** by DFS and coloring:\n\n**Special thanks to @ezpzm9\'s contribution** in discussion.\n\n```python []\nclass Solution:\n def possibleBipartition(self, N: int, dislikes: List[List[int]]) -> bool:\n \n # Constant defined for color drawing to person\n BLUE, GREEN = 1, -1\n # -------------------------------------\n \n def draw( person_id, color ):\n \n # Draw person_id as color\n color_of[person_id] = color\n \n # Draw the_other, with opposite color, in dislike table of current person_id\n for the_other in dislike_table[ person_id ]:\n \n if color_of[the_other] == color:\n # the_other has the same color of current person_id\n # Reject due to breaking the relationship of dislike\n return False\n\n if (not color_of[the_other]) and (not draw( the_other, -color)):\n # Other people can not be colored with two different colors. \n\t\t\t\t\t# Therefore, it is impossible to keep dis-like relationship with bipartition.\n return False\n \n return True\n \n \n # ------------------------------------------------\n\t\t\n\t\t\n if N == 1 or not dislikes:\n # Quick response for simple cases\n return True\n \n # each person maintain a list of dislike\n dislike_table = defaultdict( list )\n \n # key: person ID\n # value: color of person\n color_of = defaultdict(int)\n \n for p1, p2 in dislikes:\n \n # P1 dislikes P2\n # P1 and P2 should be painted with two different color\n dislike_table[p1].append( p2 )\n dislike_table[p2].append( p1 )\n \n \n # Try to draw dislike pair with different colors in DFS\n for person_id in range(1, N+1):\n \n if (not color_of[person_id]) and (not draw( person_id, BLUE)):\n # Other people can not be colored with two different colors. \n\t\t\t\t# Therefore, it is impossible to keep dis-like relationship with bipartition.\n return False \n \n return True\n```\n```C++ []\nclass Solution {\npublic:\n bool possibleBipartition(int n, vector<vector<int>>& dislikes) {\n \n enum COLOR_CONSTANT{\n GREEN = -1, // -1\n NOT_COLORDED, // 0\n BLUE // 1\n };\n \n \n if( n == 1 || dislikes.size() == 0 ){\n \n // Quick response for simple cases\n return true;\n }\n \n // each person maintains a list of dislike\n unordered_map< int, vector<int> > dislikeTable;\n \n // key: personID\n // value: color of person\n unordered_map< int, int> colorTable;\n \n // -----------------------\n \n std::function< bool( int, int ) > helper;\n helper = [&]( int personID, int color)->bool{\n \n // Draw personID as color\n colorTable[personID] = color;\n \n // Draw theOther, with opposite color, in dislike table of current personID\n for( const int& theOther : dislikeTable[ personID ] ){\n \n if( colorTable[theOther] == color ){\n // the_other has the same color of current person_id\n // Reject due to breaking the relationship of dislike\n return false;\n }\n \n if( colorTable[theOther] == NOT_COLORDED && ( !helper(theOther, -color) ) ){\n // Other people can not be colored with two different colors. \n // Therefore, it is impossible to keep dis-like relationship with bipartition.\n return false;\n }\n }\n \n return true;\n \n };\n \n // -----------------------\n \n \n // update dislike table\n for( const auto& relation : dislikes ){\n \n int p1 = relation[0], p2 = relation[1];\n \n dislikeTable[p1].emplace_back( p2 );\n dislikeTable[p2].emplace_back( p1 );\n \n }\n \n // Try to draw dislike pair with different color in DFS\n for( int personID = 1 ; personID <= n ; personID++){\n \n if( colorTable[personID] == NOT_COLORDED && ( !helper(personID, BLUE) ) ){\n // Other people can not be colored with two different colors. \n\t\t\t\t // Therefore, it is impossible to keep dis-like relationship with bipartition.\n return false;\n }\n }\n \n\n return true; \n }\n};\n```\n```Java []\nclass Solution {\n public boolean possibleBipartition(int N, int[][] dislikes) { \n List<Integer>[] graph = new List[N + 1]; \n\n for (int i = 1; i <= N; ++i) graph[i] = new ArrayList<>(); \n\n for (int[] dislike : dislikes) {\n graph[dislike[0]].add(dislike[1]);\n graph[dislike[1]].add(dislike[0]);\n }\n\n Integer[] colors = new Integer[N + 1];\n\n for (int i = 1; i <= N; ++i) {\n // If the connected component that node i belongs to hasn\'t been colored yet then try coloring it.\n if (colors[i] == null && !dfs(graph, colors, i, 1)) return false;\n }\n return true; \n }\n\n private boolean dfs(List<Integer>[] graph, Integer[] colors, int currNode, int currColor) {\n colors[currNode] = currColor;\n\n // Color all uncolored adjacent nodes.\n for (Integer adjacentNode : graph[currNode]) {\n\n if (colors[adjacentNode] == null) {\n if (!dfs(graph, colors, adjacentNode, currColor * -1)) return false; \n\n } else if (colors[adjacentNode] == currColor) {\n return false; \n }\n }\n return true; \n }\n}\n```\n\n---\n\nSupplement material:\n\n\n\n---\n\nReference:\n\n[1] [Wiki: Bipartite graph](https://en.wikipedia.org/wiki/Bipartite_graph) | 251 | Given an array of integers `nums`, half of the integers in `nums` are **odd**, and the other half are **even**.
Sort the array so that whenever `nums[i]` is odd, `i` is **odd**, and whenever `nums[i]` is even, `i` is **even**.
Return _any answer array that satisfies this condition_.
**Example 1:**
**Input:** nums = \[4,2,5,7\]
**Output:** \[4,5,2,7\]
**Explanation:** \[4,7,2,5\], \[2,5,4,7\], \[2,7,4,5\] would also have been accepted.
**Example 2:**
**Input:** nums = \[2,3\]
**Output:** \[2,3\]
**Constraints:**
* `2 <= nums.length <= 2 * 104`
* `nums.length` is even.
* Half of the integers in `nums` are even.
* `0 <= nums[i] <= 1000`
**Follow Up:** Could you solve it in-place? | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.