title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
🦧 PYTHON3 BEATS 80% 🦧 Recursion + Caching Solution | all-possible-full-binary-trees | 0 | 1 | # Intuition\n1. The first important thing to realize about this problem is that there are various repeated sub problems. \n2. For example, if we have n = 7, we know that we must recursively try every odd split from the root note ((1, 5), (3, 3), (5, 1)), which means starting from the root node, we collect all combinations of n = 1 on the left side and n = 5 for the right side. Then, we try every combination of n = 3 on the left side and n = 3 on the right side, etc. For 1, 3, and 5, each of these subproblems are double-computed. \n3. This hints at the possibliity of using a cached solution to prevent repeat computations, where we can use lru_cache. \n4. Finally, we need to determine the mechanism for the recursion. Say we have n = 7. For the first tuple (1, 5), we calculate all possible full binary trees with n = 1 for the left side, and n = 5 for the right side. We then use every combination of each from the left and right side to output in the current recursive step\n\n# Complexity\n- Time complexity: $$O(2^{n/2})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*2^{n/2})$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\nfrom functools import lru_cache\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n @lru_cache(None)\n def recurse(count):\n if count == 1: return [TreeNode()]\n output = []\n for i in range((count - 1) // 2):\n l_output, r_output = recurse(i * 2 + 1), recurse(count - 2 - i * 2)\n for j in range(len(l_output)):\n for k in range(len(r_output)):\n output.append(TreeNode(val=0, left=l_output[j], right=r_output[k]))\n return output\n return recurse(n)\n``` | 1 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🦧 PYTHON3 BEATS 80% 🦧 Recursion + Caching Solution | all-possible-full-binary-trees | 0 | 1 | # Intuition\n1. The first important thing to realize about this problem is that there are various repeated sub problems. \n2. For example, if we have n = 7, we know that we must recursively try every odd split from the root note ((1, 5), (3, 3), (5, 1)), which means starting from the root node, we collect all combinations of n = 1 on the left side and n = 5 for the right side. Then, we try every combination of n = 3 on the left side and n = 3 on the right side, etc. For 1, 3, and 5, each of these subproblems are double-computed. \n3. This hints at the possibliity of using a cached solution to prevent repeat computations, where we can use lru_cache. \n4. Finally, we need to determine the mechanism for the recursion. Say we have n = 7. For the first tuple (1, 5), we calculate all possible full binary trees with n = 1 for the left side, and n = 5 for the right side. We then use every combination of each from the left and right side to output in the current recursive step\n\n# Complexity\n- Time complexity: $$O(2^{n/2})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*2^{n/2})$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\nfrom functools import lru_cache\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n @lru_cache(None)\n def recurse(count):\n if count == 1: return [TreeNode()]\n output = []\n for i in range((count - 1) // 2):\n l_output, r_output = recurse(i * 2 + 1), recurse(count - 2 - i * 2)\n for j in range(len(l_output)):\n for k in range(len(r_output)):\n output.append(TreeNode(val=0, left=l_output[j], right=r_output[k]))\n return output\n return recurse(n)\n``` | 1 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
🥳 Runtime 1ms | Beats 98.7% | Recursion | Memoization | all-possible-full-binary-trees | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe recursion works by first generating all possible full binary trees with i nodes, and then all possible full binary trees with n - i - 1 nodes. For each pair of trees, a new tree is created with the first tree as the left subtree and the second tree as the right subtree. This process is repeated until all possible trees with n nodes have been generated.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a hash table to store the generated trees.\n2. If n is even, return an empty list.\n3. If n is 1, add a new tree to the hash table.\n4. For i from 1 to n - 1, do:\n- Generate all possible full binary trees with i nodes.\n- Generate all possible full binary trees with n - i - 1 nodes.\n- For each pair of trees, create a new tree with the first tree as the left subtree and the second tree as the right subtree.\n- Add the new tree to the hash table.\n5. Return the list of trees in the hash table.\n\n# Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n static Map<Integer, List<TreeNode>> saved = new HashMap<>();\n \n public List<TreeNode> allPossibleFBT(int n) {\n if (n%2==0)\n return new ArrayList<>();\n\n if (!saved.containsKey(n)) {\n List<TreeNode> list = new ArrayList<>();\n \n if (n==1)\n list.add(new TreeNode(0));\n else {\n for (int i=1; i<=n-1; i+=2) {\n List<TreeNode> lTrees = allPossibleFBT(i);\n List<TreeNode> rTrees = allPossibleFBT(n-i-1);\n\n for (TreeNode lt: lTrees) {\n for (TreeNode rt: rTrees) {\n list.add(new TreeNode(0, lt, rt));\n }\n }\n }\n }\n\n saved.put(n, list);\n }\n return saved.get(n);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<TreeNode*> allPossibleFBT(int n) {\n if (n % 2 == 0) {\n return {};\n }\n\n vector<TreeNode*> list;\n if (n == 1) {\n list.push_back(new TreeNode(0));\n } else {\n for (int i = 1; i <= n - 1; i += 2) {\n vector<TreeNode*> lTrees = allPossibleFBT(i);\n vector<TreeNode*> rTrees = allPossibleFBT(n - i - 1);\n\n for (TreeNode* lt : lTrees) {\n for (TreeNode* rt : rTrees) {\n list.push_back(new TreeNode(0, lt, rt));\n }\n }\n }\n }\n\n return list;\n }\n};\n```\n```Python3 []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n if n % 2 == 0:\n return []\n\n memo = {}\n\n def _allPossibleFBT(n):\n if n in memo:\n return memo[n]\n\n list = []\n if n == 1:\n list.append(TreeNode(0))\n else:\n for i in range(1, n - 1, 2):\n lTrees = _allPossibleFBT(i)\n rTrees = _allPossibleFBT(n - i - 1)\n\n for lt in lTrees:\n for rt in rTrees:\n list.append(TreeNode(0, lt, rt))\n\n memo[n] = list\n return list\n\n return _allPossibleFBT(n)\n```\n\n> If you find my solution helpful, I would greatly appreciate your one upvote.\n\n | 58 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🥳 Runtime 1ms | Beats 98.7% | Recursion | Memoization | all-possible-full-binary-trees | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe recursion works by first generating all possible full binary trees with i nodes, and then all possible full binary trees with n - i - 1 nodes. For each pair of trees, a new tree is created with the first tree as the left subtree and the second tree as the right subtree. This process is repeated until all possible trees with n nodes have been generated.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a hash table to store the generated trees.\n2. If n is even, return an empty list.\n3. If n is 1, add a new tree to the hash table.\n4. For i from 1 to n - 1, do:\n- Generate all possible full binary trees with i nodes.\n- Generate all possible full binary trees with n - i - 1 nodes.\n- For each pair of trees, create a new tree with the first tree as the left subtree and the second tree as the right subtree.\n- Add the new tree to the hash table.\n5. Return the list of trees in the hash table.\n\n# Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n static Map<Integer, List<TreeNode>> saved = new HashMap<>();\n \n public List<TreeNode> allPossibleFBT(int n) {\n if (n%2==0)\n return new ArrayList<>();\n\n if (!saved.containsKey(n)) {\n List<TreeNode> list = new ArrayList<>();\n \n if (n==1)\n list.add(new TreeNode(0));\n else {\n for (int i=1; i<=n-1; i+=2) {\n List<TreeNode> lTrees = allPossibleFBT(i);\n List<TreeNode> rTrees = allPossibleFBT(n-i-1);\n\n for (TreeNode lt: lTrees) {\n for (TreeNode rt: rTrees) {\n list.add(new TreeNode(0, lt, rt));\n }\n }\n }\n }\n\n saved.put(n, list);\n }\n return saved.get(n);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<TreeNode*> allPossibleFBT(int n) {\n if (n % 2 == 0) {\n return {};\n }\n\n vector<TreeNode*> list;\n if (n == 1) {\n list.push_back(new TreeNode(0));\n } else {\n for (int i = 1; i <= n - 1; i += 2) {\n vector<TreeNode*> lTrees = allPossibleFBT(i);\n vector<TreeNode*> rTrees = allPossibleFBT(n - i - 1);\n\n for (TreeNode* lt : lTrees) {\n for (TreeNode* rt : rTrees) {\n list.push_back(new TreeNode(0, lt, rt));\n }\n }\n }\n }\n\n return list;\n }\n};\n```\n```Python3 []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n if n % 2 == 0:\n return []\n\n memo = {}\n\n def _allPossibleFBT(n):\n if n in memo:\n return memo[n]\n\n list = []\n if n == 1:\n list.append(TreeNode(0))\n else:\n for i in range(1, n - 1, 2):\n lTrees = _allPossibleFBT(i)\n rTrees = _allPossibleFBT(n - i - 1)\n\n for lt in lTrees:\n for rt in rTrees:\n list.append(TreeNode(0, lt, rt))\n\n memo[n] = list\n return list\n\n return _allPossibleFBT(n)\n```\n\n> If you find my solution helpful, I would greatly appreciate your one upvote.\n\n | 58 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Recursion+DP+Video Explanation in depth || Very Easy to Understand || C++ || Java || Python | all-possible-full-binary-trees | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTake every odd node from 1 to n as a tree and make a full binary tree.\nNote: if there are even nodes then we cant make a full binary tree.\n\nFor detailed explanation you can refer to my youtube channel (hindi Language)\nhttps://youtu.be/iSnz3DvPEnM\n or link in my profile.Here,you can find any solution in playlists monthwise from June 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The function `allPossibleFBT(n)` takes an integer `n` as input, representing the desired number of nodes in the Full Binary Trees.\n2. Initialize a 2D array `dp` to store the results of subproblems to avoid redundant calculations.\n3. Base case: If `n` is even, there are no possible Full Binary Trees with an even number of nodes, so return an empty list `[]`.\n4. If `n` is 1, return a list containing a single FBT with one node: `TreeNode(0)`.\n5. If the result for `n` is already computed and stored in `dp`, return it to avoid redundant calculations.\n6. Initialize an empty list `res` to store the results for the current value of `n`.\n7. Iterate from 1 to `n` with a step of 2, as the number of nodes in left and right subtrees of an FBT will be odd to maintain the full binary tree property.\n8. For each odd value `i` in the loop, recursively generate all possible left and right subtrees with `i` nodes and `n-i-1` nodes, respectively.\n9. For each combination of left and right subtrees, create a new FBT with the current root node having value 0 and left and right subtrees as computed in the previous step.\n10. Append the new FBT to the `res` list.\n11. Store the result `res` in the `dp` array for the current value of `n`.\n12. Return the `res` list containing all possible Full Binary Trees with `n` nodes.\n\n# Complexity\n- Time complexity:$$O(2^ \nn/2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n\u22C52^\nn/2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n vector<vector<TreeNode*>>dp;\n \n vector<TreeNode*> solve(int n)\n {\n \n \n if(n % 2 == 0)\n return {};\n \n if(dp[n].size()!=0)\n return dp[n];\n \n if(n == 1) \n {\n TreeNode* new_node = new TreeNode(0);\n \n return {new_node};\n }\n \n vector<TreeNode*> res;\n \n for(int i = 1; i < n; i+=2)\n {\n \n vector<TreeNode*>left = solve(i);\n \n \n vector<TreeNode*>right = solve(n - i - 1);\n \n for( TreeNode*l: left)\n {\n for(TreeNode*r : right)\n {\n \n TreeNode* root = new TreeNode(0);\n \n root -> left = l;\n \n root -> right = r;\n \n \n res.push_back(root);\n }\n }\n }\n \n \n \n return dp[n]=res;\n }\n \n vector<TreeNode*> allPossibleFBT(int n) {\n dp.resize(n+1);\n return solve(n);\n }\n};\n```\n```Java []\n\nclass Solution {\n List<List<TreeNode>> dp = new ArrayList<>();\n \n List<TreeNode> solve(int n) {\n if (n % 2 == 0)\n return new ArrayList<>();\n \n if (!dp.get(n).isEmpty())\n return dp.get(n);\n \n if (n == 1) {\n TreeNode new_node = new TreeNode(0);\n List<TreeNode> result = new ArrayList<>();\n result.add(new_node);\n return result;\n }\n \n List<TreeNode> res = new ArrayList<>();\n \n for (int i = 1; i < n; i += 2) {\n List<TreeNode> left = solve(i);\n List<TreeNode> right = solve(n - i - 1);\n \n for (TreeNode l : left) {\n for (TreeNode r : right) {\n TreeNode root = new TreeNode(0);\n root.left = l;\n root.right = r;\n res.add(root);\n }\n }\n }\n \n dp.set(n, res);\n return res;\n }\n \n public List<TreeNode> allPossibleFBT(int n) {\n for (int i = 0; i <= n; i++) {\n dp.add(new ArrayList<>());\n }\n return solve(n);\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.dp = []\n\n def solve(self, n):\n if n % 2 == 0:\n return []\n\n if self.dp[n]:\n return self.dp[n]\n\n if n == 1:\n new_node = TreeNode(0)\n return [new_node]\n\n res = []\n for i in range(1, n, 2):\n left = self.solve(i)\n right = self.solve(n - i - 1)\n\n for l in left:\n for r in right:\n root = TreeNode(0)\n root.left = l\n root.right = r\n res.append(root)\n\n self.dp[n] = res\n return res\n\n def allPossibleFBT(self, n: int):\n self.dp = [[] for _ in range(n + 1)]\n return self.solve(n)\n\n```\n\n | 38 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Recursion+DP+Video Explanation in depth || Very Easy to Understand || C++ || Java || Python | all-possible-full-binary-trees | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTake every odd node from 1 to n as a tree and make a full binary tree.\nNote: if there are even nodes then we cant make a full binary tree.\n\nFor detailed explanation you can refer to my youtube channel (hindi Language)\nhttps://youtu.be/iSnz3DvPEnM\n or link in my profile.Here,you can find any solution in playlists monthwise from June 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The function `allPossibleFBT(n)` takes an integer `n` as input, representing the desired number of nodes in the Full Binary Trees.\n2. Initialize a 2D array `dp` to store the results of subproblems to avoid redundant calculations.\n3. Base case: If `n` is even, there are no possible Full Binary Trees with an even number of nodes, so return an empty list `[]`.\n4. If `n` is 1, return a list containing a single FBT with one node: `TreeNode(0)`.\n5. If the result for `n` is already computed and stored in `dp`, return it to avoid redundant calculations.\n6. Initialize an empty list `res` to store the results for the current value of `n`.\n7. Iterate from 1 to `n` with a step of 2, as the number of nodes in left and right subtrees of an FBT will be odd to maintain the full binary tree property.\n8. For each odd value `i` in the loop, recursively generate all possible left and right subtrees with `i` nodes and `n-i-1` nodes, respectively.\n9. For each combination of left and right subtrees, create a new FBT with the current root node having value 0 and left and right subtrees as computed in the previous step.\n10. Append the new FBT to the `res` list.\n11. Store the result `res` in the `dp` array for the current value of `n`.\n12. Return the `res` list containing all possible Full Binary Trees with `n` nodes.\n\n# Complexity\n- Time complexity:$$O(2^ \nn/2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n\u22C52^\nn/2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n vector<vector<TreeNode*>>dp;\n \n vector<TreeNode*> solve(int n)\n {\n \n \n if(n % 2 == 0)\n return {};\n \n if(dp[n].size()!=0)\n return dp[n];\n \n if(n == 1) \n {\n TreeNode* new_node = new TreeNode(0);\n \n return {new_node};\n }\n \n vector<TreeNode*> res;\n \n for(int i = 1; i < n; i+=2)\n {\n \n vector<TreeNode*>left = solve(i);\n \n \n vector<TreeNode*>right = solve(n - i - 1);\n \n for( TreeNode*l: left)\n {\n for(TreeNode*r : right)\n {\n \n TreeNode* root = new TreeNode(0);\n \n root -> left = l;\n \n root -> right = r;\n \n \n res.push_back(root);\n }\n }\n }\n \n \n \n return dp[n]=res;\n }\n \n vector<TreeNode*> allPossibleFBT(int n) {\n dp.resize(n+1);\n return solve(n);\n }\n};\n```\n```Java []\n\nclass Solution {\n List<List<TreeNode>> dp = new ArrayList<>();\n \n List<TreeNode> solve(int n) {\n if (n % 2 == 0)\n return new ArrayList<>();\n \n if (!dp.get(n).isEmpty())\n return dp.get(n);\n \n if (n == 1) {\n TreeNode new_node = new TreeNode(0);\n List<TreeNode> result = new ArrayList<>();\n result.add(new_node);\n return result;\n }\n \n List<TreeNode> res = new ArrayList<>();\n \n for (int i = 1; i < n; i += 2) {\n List<TreeNode> left = solve(i);\n List<TreeNode> right = solve(n - i - 1);\n \n for (TreeNode l : left) {\n for (TreeNode r : right) {\n TreeNode root = new TreeNode(0);\n root.left = l;\n root.right = r;\n res.add(root);\n }\n }\n }\n \n dp.set(n, res);\n return res;\n }\n \n public List<TreeNode> allPossibleFBT(int n) {\n for (int i = 0; i <= n; i++) {\n dp.add(new ArrayList<>());\n }\n return solve(n);\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.dp = []\n\n def solve(self, n):\n if n % 2 == 0:\n return []\n\n if self.dp[n]:\n return self.dp[n]\n\n if n == 1:\n new_node = TreeNode(0)\n return [new_node]\n\n res = []\n for i in range(1, n, 2):\n left = self.solve(i)\n right = self.solve(n - i - 1)\n\n for l in left:\n for r in right:\n root = TreeNode(0)\n root.left = l\n root.right = r\n res.append(root)\n\n self.dp[n] = res\n return res\n\n def allPossibleFBT(self, n: int):\n self.dp = [[] for _ in range(n + 1)]\n return self.solve(n)\n\n```\n\n | 38 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
🔥One Line Solution🔥 | all-possible-full-binary-trees | 0 | 1 | # Complexity\n- Time complexity: $$O(2^{n/2})$$.\n\n- Space complexity: $$O(n*2^{n/2})$$.\n\n# Code in One Line\n```\nclass Solution:\n @cache\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n return [TreeNode(0, left, right) for k in range(1, n-1, 2) for left in self.allPossibleFBT(k) for right in self.allPossibleFBT(n-1-k)] if n != 1 else [TreeNode()]\n```\n\n# Code in More Readable Way\n```\nclass Solution:\n @cache\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n if n == 1:\n return [TreeNode()]\n \n result = []\n for k in range(1, n-1, 2):\n for left in self.allPossibleFBT(k):\n for right in self.allPossibleFBT(n-1-k):\n result.append(TreeNode(0, left, right))\n \n return result\n``` | 14 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🔥One Line Solution🔥 | all-possible-full-binary-trees | 0 | 1 | # Complexity\n- Time complexity: $$O(2^{n/2})$$.\n\n- Space complexity: $$O(n*2^{n/2})$$.\n\n# Code in One Line\n```\nclass Solution:\n @cache\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n return [TreeNode(0, left, right) for k in range(1, n-1, 2) for left in self.allPossibleFBT(k) for right in self.allPossibleFBT(n-1-k)] if n != 1 else [TreeNode()]\n```\n\n# Code in More Readable Way\n```\nclass Solution:\n @cache\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n if n == 1:\n return [TreeNode()]\n \n result = []\n for k in range(1, n-1, 2):\n for left in self.allPossibleFBT(k):\n for right in self.allPossibleFBT(n-1-k):\n result.append(TreeNode(0, left, right))\n \n return result\n``` | 14 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Easy, detailed Python solution, beats 96%. Recursion + dictionary | all-possible-full-binary-trees | 0 | 1 | \n\n\nInspired by this Java solution: [https://leetcode.com/problems/all-possible-full-binary-trees/solutions/216853/java-easy-with-examples/]()\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Every full binary tree can be broken down into smaller full binary trees.\n- The smaller full binary trees would contain i, n-i-1 nodes where I would be in the range(1,n,2) - this is shown in the below comments\n- The smaller full binary trees can be mapped and stored in a dictionary so that it does not have to be computed again (key = n, value = TreeNode object)\n- Thus, the tree is broken down into smaller trees recursively and solved for.\n\n #1. if N = 3 , the number of nodes combination are as follows\n #left root right\n #1 1 1 \n #--------------N = 3, res = 1----------\n \n #2. if N = 5 , the number of nodes combination are as follows\n #left root right\n #1 1 3 (recursion)\n #3 1 1 \n #--------------N = 5, res = 1 + 1 = 2----------\n \n #3. if N = 7 , the number of nodes combination are as follows\n #left root right\n #1 1 5 (recursion)\n #3 1 3 \n #5 1 1\n #--------------N = 7, res = 2 + 1 + 2 = 5----------\n \n #4. in order to make full binary tree, the node number must increase by 2\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n map1 = {}\n\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n res = []\n if n%2 == 0:\n return[]\n if n == 1:\n return [TreeNode(),]#default value is 0 \n if n in self.map1.keys():\n return self.map1[n]\n\n for i in range(1, n, 2):\n left = self.allPossibleFBT(i)#left subtree\n right = self.allPossibleFBT(n-i-1)#right subtree\n #2 loops to cover all combinations of left and right subtrees\n for l in left:\n for r in right:\n root = TreeNode(0,l,r)\n res.append(root)\n \n self.map1[n] = res \n return res\n\n``` | 2 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Easy, detailed Python solution, beats 96%. Recursion + dictionary | all-possible-full-binary-trees | 0 | 1 | \n\n\nInspired by this Java solution: [https://leetcode.com/problems/all-possible-full-binary-trees/solutions/216853/java-easy-with-examples/]()\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Every full binary tree can be broken down into smaller full binary trees.\n- The smaller full binary trees would contain i, n-i-1 nodes where I would be in the range(1,n,2) - this is shown in the below comments\n- The smaller full binary trees can be mapped and stored in a dictionary so that it does not have to be computed again (key = n, value = TreeNode object)\n- Thus, the tree is broken down into smaller trees recursively and solved for.\n\n #1. if N = 3 , the number of nodes combination are as follows\n #left root right\n #1 1 1 \n #--------------N = 3, res = 1----------\n \n #2. if N = 5 , the number of nodes combination are as follows\n #left root right\n #1 1 3 (recursion)\n #3 1 1 \n #--------------N = 5, res = 1 + 1 = 2----------\n \n #3. if N = 7 , the number of nodes combination are as follows\n #left root right\n #1 1 5 (recursion)\n #3 1 3 \n #5 1 1\n #--------------N = 7, res = 2 + 1 + 2 = 5----------\n \n #4. in order to make full binary tree, the node number must increase by 2\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n map1 = {}\n\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n res = []\n if n%2 == 0:\n return[]\n if n == 1:\n return [TreeNode(),]#default value is 0 \n if n in self.map1.keys():\n return self.map1[n]\n\n for i in range(1, n, 2):\n left = self.allPossibleFBT(i)#left subtree\n right = self.allPossibleFBT(n-i-1)#right subtree\n #2 loops to cover all combinations of left and right subtrees\n for l in left:\n for r in right:\n root = TreeNode(0,l,r)\n res.append(root)\n \n self.map1[n] = res \n return res\n\n``` | 2 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
🚀 [ VIDEO] Master Full Binary Trees 🌳 | Step-by-Step LeetCode Guide | all-possible-full-binary-trees | 1 | 1 | # Intuition\nAt first glance, this problem might seem complex due to its requirement for generating all possible full binary trees. However, it\'s clear that the problem can be approached via dynamic programming, breaking down the larger problem into smaller sub-problems and using memoization to prevent redundant computations. \n\nhttps://youtu.be/jLnWQe4Hzps\n\n# Approach\nWe start by understanding that a full binary tree always has an odd number of nodes. So, we can directly return an empty list for even numbers. For the number 1, we return a list with a single node tree. For numbers greater than 1, we iterate over all odd numbers less than `n`, and for each number `i`, we generate all pairs of trees with `i` and `n - i - 1` nodes. We then create a new tree for each pair by adding a new root node and attaching the pair as its left and right child respectively. We use a memoization dictionary to store and retrieve previously computed results.\n\n# Complexity\n- Time complexity: \\(O(4^n / n^{3/2})\\) The time complexity of this problem is governed by the Catalan number, which grows rapidly with `n`.\n\n- Space complexity: \\(O(4^n / n^{3/2})\\) This is because we need to store each generated tree.\n\n# Code\n```Python []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n memo = {0: [], 1: [TreeNode(0)]}\n \n def helper(n):\n if n not in memo:\n memo[n] = [TreeNode(0, left, right)\n for i in range(1, n, 2)\n for left in helper(i)\n for right in helper(n - i - 1)]\n return memo[n]\n \n return helper(n)\n```\n``` C++ []\nclass Solution {\npublic:\n unordered_map<int, vector<TreeNode*>> memo;\n \n vector<TreeNode*> allPossibleFBT(int n) {\n if (memo.find(n) == memo.end()) {\n vector<TreeNode*> list;\n if (n == 1) {\n list.push_back(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int x = 0; x < n; ++x) {\n int y = n - 1 - x;\n for (TreeNode* left: allPossibleFBT(x)) {\n for (TreeNode* right: allPossibleFBT(y)) {\n TreeNode* root = new TreeNode(0);\n root->left = left;\n root->right = right;\n list.push_back(root);\n }\n }\n }\n }\n memo[n] = list;\n }\n return memo[n];\n }\n};\n```\n``` Java []\nclass Solution {\n Map<Integer, List<TreeNode>> memo = new HashMap<>();\n \n public List<TreeNode> allPossibleFBT(int n) {\n if (!memo.containsKey(n)) {\n List<TreeNode> list = new LinkedList<>();\n if (n == 1) {\n list.add(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int i = 0; i < n; ++i) {\n int j = n - 1 - i;\n for (TreeNode left: allPossibleFBT(i)) {\n for (TreeNode right: allPossibleFBT(j)) {\n TreeNode root = new TreeNode(0);\n root.left = left;\n root.right = right;\n list.add(root);\n }\n }\n }\n }\n memo.put(n, list);\n }\n return memo.get(n);\n }\n}\n```\n``` JavaScript []\nvar allPossibleFBT = function(n) {\n let memo = new Map();\n \n function helper(n) {\n if (memo.has(n)) return memo.get(n);\n let res = [];\n if (n === 1) {\n res.push(new TreeNode(0));\n } else if (n % 2 === 1) {\n for (let i = 0; i < n; i++) {\n let j = n - 1 - i;\n for (let left of helper(i)) {\n for (let right of helper(j)) {\n let root = new TreeNode(0);\n root.left = left;\n root.right = right;\n res.push(root);\n }\n }\n }\n }\n memo.set(n, res);\n return res;\n }\n \n return helper(n); \n};\n```\n``` C# []\npublic class Solution {\n Dictionary<int, IList<TreeNode>> memo = new Dictionary<int, IList<TreeNode>>();\n \n public IList<TreeNode> AllPossibleFBT(int n) {\n if (!memo.ContainsKey(n)) {\n List<TreeNode> list = new List<TreeNode>();\n if (n == 1) {\n list.Add(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int i = 0; i < n; ++i) {\n int j = n - 1 - i;\n foreach (TreeNode left in AllPossibleFBT(i)) {\n foreach (TreeNode right in AllPossibleFBT(j)) {\n TreeNode root = new TreeNode(0);\n root.left = left;\n root.right = right;\n list.Add(root);\n }\n }\n }\n }\n memo[n] = list;\n }\n return memo[n];\n }\n}\n```\n\nRemember, this problem is a great example of how dynamic programming can help solve complex problems by breaking them down into simpler sub-problems. Happy coding! \uD83D\uDE80 | 7 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🚀 [ VIDEO] Master Full Binary Trees 🌳 | Step-by-Step LeetCode Guide | all-possible-full-binary-trees | 1 | 1 | # Intuition\nAt first glance, this problem might seem complex due to its requirement for generating all possible full binary trees. However, it\'s clear that the problem can be approached via dynamic programming, breaking down the larger problem into smaller sub-problems and using memoization to prevent redundant computations. \n\nhttps://youtu.be/jLnWQe4Hzps\n\n# Approach\nWe start by understanding that a full binary tree always has an odd number of nodes. So, we can directly return an empty list for even numbers. For the number 1, we return a list with a single node tree. For numbers greater than 1, we iterate over all odd numbers less than `n`, and for each number `i`, we generate all pairs of trees with `i` and `n - i - 1` nodes. We then create a new tree for each pair by adding a new root node and attaching the pair as its left and right child respectively. We use a memoization dictionary to store and retrieve previously computed results.\n\n# Complexity\n- Time complexity: \\(O(4^n / n^{3/2})\\) The time complexity of this problem is governed by the Catalan number, which grows rapidly with `n`.\n\n- Space complexity: \\(O(4^n / n^{3/2})\\) This is because we need to store each generated tree.\n\n# Code\n```Python []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n memo = {0: [], 1: [TreeNode(0)]}\n \n def helper(n):\n if n not in memo:\n memo[n] = [TreeNode(0, left, right)\n for i in range(1, n, 2)\n for left in helper(i)\n for right in helper(n - i - 1)]\n return memo[n]\n \n return helper(n)\n```\n``` C++ []\nclass Solution {\npublic:\n unordered_map<int, vector<TreeNode*>> memo;\n \n vector<TreeNode*> allPossibleFBT(int n) {\n if (memo.find(n) == memo.end()) {\n vector<TreeNode*> list;\n if (n == 1) {\n list.push_back(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int x = 0; x < n; ++x) {\n int y = n - 1 - x;\n for (TreeNode* left: allPossibleFBT(x)) {\n for (TreeNode* right: allPossibleFBT(y)) {\n TreeNode* root = new TreeNode(0);\n root->left = left;\n root->right = right;\n list.push_back(root);\n }\n }\n }\n }\n memo[n] = list;\n }\n return memo[n];\n }\n};\n```\n``` Java []\nclass Solution {\n Map<Integer, List<TreeNode>> memo = new HashMap<>();\n \n public List<TreeNode> allPossibleFBT(int n) {\n if (!memo.containsKey(n)) {\n List<TreeNode> list = new LinkedList<>();\n if (n == 1) {\n list.add(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int i = 0; i < n; ++i) {\n int j = n - 1 - i;\n for (TreeNode left: allPossibleFBT(i)) {\n for (TreeNode right: allPossibleFBT(j)) {\n TreeNode root = new TreeNode(0);\n root.left = left;\n root.right = right;\n list.add(root);\n }\n }\n }\n }\n memo.put(n, list);\n }\n return memo.get(n);\n }\n}\n```\n``` JavaScript []\nvar allPossibleFBT = function(n) {\n let memo = new Map();\n \n function helper(n) {\n if (memo.has(n)) return memo.get(n);\n let res = [];\n if (n === 1) {\n res.push(new TreeNode(0));\n } else if (n % 2 === 1) {\n for (let i = 0; i < n; i++) {\n let j = n - 1 - i;\n for (let left of helper(i)) {\n for (let right of helper(j)) {\n let root = new TreeNode(0);\n root.left = left;\n root.right = right;\n res.push(root);\n }\n }\n }\n }\n memo.set(n, res);\n return res;\n }\n \n return helper(n); \n};\n```\n``` C# []\npublic class Solution {\n Dictionary<int, IList<TreeNode>> memo = new Dictionary<int, IList<TreeNode>>();\n \n public IList<TreeNode> AllPossibleFBT(int n) {\n if (!memo.ContainsKey(n)) {\n List<TreeNode> list = new List<TreeNode>();\n if (n == 1) {\n list.Add(new TreeNode(0));\n } else if (n % 2 == 1) {\n for (int i = 0; i < n; ++i) {\n int j = n - 1 - i;\n foreach (TreeNode left in AllPossibleFBT(i)) {\n foreach (TreeNode right in AllPossibleFBT(j)) {\n TreeNode root = new TreeNode(0);\n root.left = left;\n root.right = right;\n list.Add(root);\n }\n }\n }\n }\n memo[n] = list;\n }\n return memo[n];\n }\n}\n```\n\nRemember, this problem is a great example of how dynamic programming can help solve complex problems by breaking them down into simpler sub-problems. Happy coding! \uD83D\uDE80 | 7 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
🐍 python, dynamic programming solutions || faster than 100% | all-possible-full-binary-trees | 0 | 1 | # Approach\nI highly recommend that you solve [96. Unique Binary Search Trees\n](https://leetcode.com/problems/unique-binary-search-trees/solutions/2947716/python-two-approaches-1-recursive-2-iterative-both-o-n-faster-than-97-with-explanation/) and [95. Unique Binary Search Trees II](https://leetcode.com/problems/unique-binary-search-trees-ii/post-solution/3831090/) before solving this since the core is the same. \n\nAlso, this is a very exceptional case that we can use DP for printing all combinations (usually we use DP for counnting or optimziation problems)\n\n# Complexity\n- Time complexity: The actual number of unique trees is the Catalan(N) and each tree has N nodes so N*Cat(N)\n\n- Space complexity: N*Cat(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n\n\n @lru_cache(None)\n def helper(n):\n if n==0:\n return [None]\n if n==1:\n return [TreeNode(0)]\n ans = []\n for i in range(1, n+1):\n left_trees = helper(i-1)\n right_trees = helper(n-i)\n for l in left_trees:\n for r in right_trees:\n if not (l is None)^(r is None):\n ans.append(TreeNode(0, l, r))\n return ans\n\n return helper(n)\n```\n\n\n\n\n\n\nwhile this is very fast, we can optimize a bit mroe. We know that full tree always have odd number of nodes. Then\n\n```\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n\n\n @lru_cache(None)\n def helper(n):\n if n==0:\n return [None]\n if n==1:\n return [TreeNode(0)]\n if n%2==0:\n return []\n ans = []\n for i in range(1, n+1):\n left_trees = helper(i-1)\n right_trees = helper(n-i)\n for l in left_trees:\n for r in right_trees:\n if not (l is None)^(r is None):\n ans.append(TreeNode(0, l, r))\n return ans\n\n return helper(n)\n```\n\n\n\n\n | 1 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
🐍 python, dynamic programming solutions || faster than 100% | all-possible-full-binary-trees | 0 | 1 | # Approach\nI highly recommend that you solve [96. Unique Binary Search Trees\n](https://leetcode.com/problems/unique-binary-search-trees/solutions/2947716/python-two-approaches-1-recursive-2-iterative-both-o-n-faster-than-97-with-explanation/) and [95. Unique Binary Search Trees II](https://leetcode.com/problems/unique-binary-search-trees-ii/post-solution/3831090/) before solving this since the core is the same. \n\nAlso, this is a very exceptional case that we can use DP for printing all combinations (usually we use DP for counnting or optimziation problems)\n\n# Complexity\n- Time complexity: The actual number of unique trees is the Catalan(N) and each tree has N nodes so N*Cat(N)\n\n- Space complexity: N*Cat(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n\n\n @lru_cache(None)\n def helper(n):\n if n==0:\n return [None]\n if n==1:\n return [TreeNode(0)]\n ans = []\n for i in range(1, n+1):\n left_trees = helper(i-1)\n right_trees = helper(n-i)\n for l in left_trees:\n for r in right_trees:\n if not (l is None)^(r is None):\n ans.append(TreeNode(0, l, r))\n return ans\n\n return helper(n)\n```\n\n\n\n\n\n\nwhile this is very fast, we can optimize a bit mroe. We know that full tree always have odd number of nodes. Then\n\n```\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n\n\n @lru_cache(None)\n def helper(n):\n if n==0:\n return [None]\n if n==1:\n return [TreeNode(0)]\n if n%2==0:\n return []\n ans = []\n for i in range(1, n+1):\n left_trees = helper(i-1)\n right_trees = helper(n-i)\n for l in left_trees:\n for r in right_trees:\n if not (l is None)^(r is None):\n ans.append(TreeNode(0, l, r))\n return ans\n\n return helper(n)\n```\n\n\n\n\n | 1 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Solution | all-possible-full-binary-trees | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n unordered_map<int, vector<TreeNode *>> dp;\n vector<TreeNode*> allPossibleFBT(int n) {\n vector<TreeNode*> ans;\n if(n%2==0)return {};\n if(n==1){\n ans.push_back(new TreeNode(0));\n return dp[1]=ans;\n }\n if(dp.find(n)!=dp.end()){\n return dp[n];\n }\n for(int i=1;i<n;i+=2){\n vector<TreeNode*> left=allPossibleFBT(i);\n vector<TreeNode*> right=allPossibleFBT(n-1-i);\n for(auto l:left){\n for(auto r:right){\n TreeNode* root=new TreeNode(0);\n root->left=l;\n root->right=r;\n ans.push_back(root);\n }\n }\n }\n return dp[n]=ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n cache = {\n 1: [TreeNode(0)]\n }\n def rec(n, cache):\n res = []\n if n % 2 == 0:\n return []\n if n in cache:\n return cache[n]\n for i in range(1, n, 2):\n for left in rec(i, cache):\n j = n-1-i\n for right in rec(j, cache):\n\n root = TreeNode(0)\n root.left = left\n root.right = right\n res.append(root)\n\n cache[n] = res\n return res\n\n return rec(n, cache) \n```\n\n```Java []\nclass Solution {\n static final int MAX_N = 20;\n static TreeNode[][] trees = new TreeNode[MAX_N + 1][];\n public List<TreeNode> allPossibleFBT(int n) {\n if (trees[1] == null) {\n trees[0] = new TreeNode[0];\n for (int i = 0; i <= MAX_N; i += 2) trees[i] = trees[0];\n trees[1] = new TreeNode[1];\n trees[1][0] = new TreeNode();\n trees[3] = new TreeNode[1];\n trees[3][0] = new TreeNode();\n trees[3][0].left = trees[3][0].right = trees[1][0];\n for (int m = 5; m <= MAX_N; m += 2) {\n int configCount = 0;\n for (int i = 1; i < m; i++)\n configCount += trees[i].length * trees[m - i - 1].length;\n TreeNode[] configs = trees[m] = new TreeNode[configCount];\n int configsIdx = 0;\n for (int i = 1; i < m; i++) {\n for (TreeNode left : trees[i]) {\n for (TreeNode right : trees[m - i - 1]) {\n configs[configsIdx] = new TreeNode();\n configs[configsIdx].left = left;\n configs[configsIdx++].right = right;\n }\n }\n }\n }\n }\n return Arrays.asList(trees[n]);\n }\n}\n```\n | 2 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
Solution | all-possible-full-binary-trees | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n unordered_map<int, vector<TreeNode *>> dp;\n vector<TreeNode*> allPossibleFBT(int n) {\n vector<TreeNode*> ans;\n if(n%2==0)return {};\n if(n==1){\n ans.push_back(new TreeNode(0));\n return dp[1]=ans;\n }\n if(dp.find(n)!=dp.end()){\n return dp[n];\n }\n for(int i=1;i<n;i+=2){\n vector<TreeNode*> left=allPossibleFBT(i);\n vector<TreeNode*> right=allPossibleFBT(n-1-i);\n for(auto l:left){\n for(auto r:right){\n TreeNode* root=new TreeNode(0);\n root->left=l;\n root->right=r;\n ans.push_back(root);\n }\n }\n }\n return dp[n]=ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n cache = {\n 1: [TreeNode(0)]\n }\n def rec(n, cache):\n res = []\n if n % 2 == 0:\n return []\n if n in cache:\n return cache[n]\n for i in range(1, n, 2):\n for left in rec(i, cache):\n j = n-1-i\n for right in rec(j, cache):\n\n root = TreeNode(0)\n root.left = left\n root.right = right\n res.append(root)\n\n cache[n] = res\n return res\n\n return rec(n, cache) \n```\n\n```Java []\nclass Solution {\n static final int MAX_N = 20;\n static TreeNode[][] trees = new TreeNode[MAX_N + 1][];\n public List<TreeNode> allPossibleFBT(int n) {\n if (trees[1] == null) {\n trees[0] = new TreeNode[0];\n for (int i = 0; i <= MAX_N; i += 2) trees[i] = trees[0];\n trees[1] = new TreeNode[1];\n trees[1][0] = new TreeNode();\n trees[3] = new TreeNode[1];\n trees[3][0] = new TreeNode();\n trees[3][0].left = trees[3][0].right = trees[1][0];\n for (int m = 5; m <= MAX_N; m += 2) {\n int configCount = 0;\n for (int i = 1; i < m; i++)\n configCount += trees[i].length * trees[m - i - 1].length;\n TreeNode[] configs = trees[m] = new TreeNode[configCount];\n int configsIdx = 0;\n for (int i = 1; i < m; i++) {\n for (TreeNode left : trees[i]) {\n for (TreeNode right : trees[m - i - 1]) {\n configs[configsIdx] = new TreeNode();\n configs[configsIdx].left = left;\n configs[configsIdx++].right = right;\n }\n }\n }\n }\n }\n return Arrays.asList(trees[n]);\n }\n}\n```\n | 2 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
FAST Solution With DP | all-possible-full-binary-trees | 0 | 1 | # Code\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n trees = defaultdict(list)\n trees[1].append(TreeNode(0))\n \n for lvl in range(3, n + 1, 2):\n for left in range(1, lvl, 2):\n for left_subtree in d[left]:\n for right_subtree in d[lvl - left - 1]:\n trees[lvl].append(\n TreeNode(0, left_subtree, right_subtree))\n \n return trees[n]\n\n``` | 3 | Given an integer `n`, return _a list of all possible **full binary trees** with_ `n` _nodes_. Each node of each tree in the answer must have `Node.val == 0`.
Each element of the answer is the root node of one possible tree. You may return the final list of trees in **any order**.
A **full binary tree** is a binary tree where each node has exactly `0` or `2` children.
**Example 1:**
**Input:** n = 7
**Output:** \[\[0,0,0,null,null,0,0,null,null,0,0\],\[0,0,0,null,null,0,0,0,0\],\[0,0,0,0,0,0,0\],\[0,0,0,0,0,null,null,null,null,0,0\],\[0,0,0,0,0,null,null,0,0\]\]
**Example 2:**
**Input:** n = 3
**Output:** \[\[0,0,0\]\]
**Constraints:**
* `1 <= n <= 20` | null |
FAST Solution With DP | all-possible-full-binary-trees | 0 | 1 | # Code\n```python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:\n trees = defaultdict(list)\n trees[1].append(TreeNode(0))\n \n for lvl in range(3, n + 1, 2):\n for left in range(1, lvl, 2):\n for left_subtree in d[left]:\n for right_subtree in d[lvl - left - 1]:\n trees[lvl].append(\n TreeNode(0, left_subtree, right_subtree))\n \n return trees[n]\n\n``` | 3 | Given a binary array `nums` and an integer `goal`, return _the number of non-empty **subarrays** with a sum_ `goal`.
A **subarray** is a contiguous part of the array.
**Example 1:**
**Input:** nums = \[1,0,1,0,1\], goal = 2
**Output:** 4
**Explanation:** The 4 subarrays are bolded and underlined below:
\[**1,0,1**,0,1\]
\[**1,0,1,0**,1\]
\[1,**0,1,0,1**\]
\[1,0,**1,0,1**\]
**Example 2:**
**Input:** nums = \[0,0,0,0,0\], goal = 0
**Output:** 15
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `nums[i]` is either `0` or `1`.
* `0 <= goal <= nums.length` | null |
Solution | maximum-frequency-stack | 1 | 1 | ```C++ []\nclass FreqStack {\npublic:\n unordered_map<int,int> freq;\n unordered_map<int,stack<int>> m;\n int maxFreq;\n FreqStack() {\n maxFreq=0;\n }\n void push(int val) {\n maxFreq=max(maxFreq,++freq[val]);\n m[freq[val]].push(val);\n }\n int pop() {\n int ele = m[maxFreq].top();\n m[maxFreq].pop();\n freq[ele]--;\n if(!m[maxFreq].size()) maxFreq--;\n return ele;\n }\n};\n```\n\n```Python3 []\nclass FreqStack:\n\n def __init__(self):\n self.freq = 0\n self.numToFreq = {}\n self.freqToNum = {}\n\n def push(self, val: int) -> None:\n if val not in self.numToFreq:\n self.numToFreq[val] = 1\n else:\n self.numToFreq[val] += 1\n\n if self.numToFreq[val] > self.freq:\n self.freq = self.numToFreq[val]\n \n if self.numToFreq[val] not in self.freqToNum:\n self.freqToNum[self.numToFreq[val]] = [val]\n else:\n self.freqToNum[self.numToFreq[val]].append(val)\n \n def pop(self) -> int:\n ret = self.freqToNum[self.freq].pop()\n if not self.freqToNum[self.freq]:\n self.freq -= 1\n self.numToFreq[ret] -= 1\n return ret\n```\n\n```Java []\nclass FreqStack {\n HashMap<Integer,Integer> freq_map;\n int max_freq;\n ArrayList<ArrayList<Integer>> freq_stack;\n\n public FreqStack() {\n freq_map= new HashMap<>();\n freq_stack= new ArrayList<>();\n freq_stack.add(new ArrayList<>());\n max_freq=0; \n }\n public void push(int val) {\n int freq=freq_map.getOrDefault(val,0)+1;\n freq_map.put(val,freq);\n if(freq>max_freq)max_freq=freq;\n \n if(freq_stack.size()<=freq)freq_stack.add(new ArrayList<>());\n freq_stack.get(freq).add(val); \n }\n public int pop(){\n ArrayList<Integer> s= freq_stack.get(max_freq);\n int top= s.remove(s.size()-1);\n if(s.isEmpty()){\n max_freq--;\n }\n freq_map.put(top,freq_map.get(top)-1);\n return top;\n }\n}\n```\n | 1 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Solution | maximum-frequency-stack | 1 | 1 | ```C++ []\nclass FreqStack {\npublic:\n unordered_map<int,int> freq;\n unordered_map<int,stack<int>> m;\n int maxFreq;\n FreqStack() {\n maxFreq=0;\n }\n void push(int val) {\n maxFreq=max(maxFreq,++freq[val]);\n m[freq[val]].push(val);\n }\n int pop() {\n int ele = m[maxFreq].top();\n m[maxFreq].pop();\n freq[ele]--;\n if(!m[maxFreq].size()) maxFreq--;\n return ele;\n }\n};\n```\n\n```Python3 []\nclass FreqStack:\n\n def __init__(self):\n self.freq = 0\n self.numToFreq = {}\n self.freqToNum = {}\n\n def push(self, val: int) -> None:\n if val not in self.numToFreq:\n self.numToFreq[val] = 1\n else:\n self.numToFreq[val] += 1\n\n if self.numToFreq[val] > self.freq:\n self.freq = self.numToFreq[val]\n \n if self.numToFreq[val] not in self.freqToNum:\n self.freqToNum[self.numToFreq[val]] = [val]\n else:\n self.freqToNum[self.numToFreq[val]].append(val)\n \n def pop(self) -> int:\n ret = self.freqToNum[self.freq].pop()\n if not self.freqToNum[self.freq]:\n self.freq -= 1\n self.numToFreq[ret] -= 1\n return ret\n```\n\n```Java []\nclass FreqStack {\n HashMap<Integer,Integer> freq_map;\n int max_freq;\n ArrayList<ArrayList<Integer>> freq_stack;\n\n public FreqStack() {\n freq_map= new HashMap<>();\n freq_stack= new ArrayList<>();\n freq_stack.add(new ArrayList<>());\n max_freq=0; \n }\n public void push(int val) {\n int freq=freq_map.getOrDefault(val,0)+1;\n freq_map.put(val,freq);\n if(freq>max_freq)max_freq=freq;\n \n if(freq_stack.size()<=freq)freq_stack.add(new ArrayList<>());\n freq_stack.get(freq).add(val); \n }\n public int pop(){\n ArrayList<Integer> s= freq_stack.get(max_freq);\n int top= s.remove(s.size()-1);\n if(s.isEmpty()){\n max_freq--;\n }\n freq_map.put(top,freq_map.get(top)-1);\n return top;\n }\n}\n```\n | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Solution with Stack in Python3 | maximum-frequency-stack | 0 | 1 | # Intuition\nHere we need to implement **Frequency Stack**.\nAccording to a problem definition it has **two methods**:\n- `push` to insert a val into `stack`\n- `pop` to extract **most frequent** element in stack \n\nThe first way to maintain an order with frequency is **Max Priority Queue (MPQ)**.\nThough this solution is **accepted**, it costs at least **O(N log N)** to work with MPQ.\n\nTo improve this approach we could use **separate stacks** for **each** frequency.\nThis helps us to maintain **order**, in which we pop **tie** frequencies.\n\n```\n# Example\n\nstack = [1, 2, 1, 0, 6], groups = {1: [1, 2, 0, 6], 2: [1]} \n\n# First pop = 1\nstack = [1, 2, 0, 6], groups = {1: [1, 2, 0, 6], 2: []} \n\n# Second pop = 6\nstack = [1, 2, 0], groups = {1: [1, 2, 0], 2: []} \n```\n\n# Approach\n1. initialize `freq` as frequencies of each inserted integer\n2. initialize `groups` to store mapping as `freq: [...vals]`\n3. initialize `maxFreq`, we\'ll use this each time we **pop** an integer from stack\n4. while `push` increment `freq` and update `maxFreq`, if we needed\n5. while `pop` extract the first element on top of a stack from `groups` and decrease `maxFreq` if `groups[maxFreq]` don\'t have **any** vals with this freq\n\n# Complexity\n- Time complexity: **O(1)**\n\n- Space complexity: **O(N)** in worst-case scenario \n\n# Code\n```\nclass FreqStack:\n\n def __init__(self):\n self.freq = defaultdict(int)\n self.groups = defaultdict(list)\n self.maxFreq = 0\n \n\n def push(self, val: int) -> None:\n self.freq[val] += 1\n\n if self.freq[val] > self.maxFreq: self.maxFreq = self.freq[val]\n\n self.groups[self.freq[val]].append(val)\n\n def pop(self) -> int:\n first = self.groups[self.maxFreq].pop()\n self.freq[first] -= 1\n\n if not self.groups[self.maxFreq]:\n self.maxFreq -= 1\n\n return first\n``` | 2 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Solution with Stack in Python3 | maximum-frequency-stack | 0 | 1 | # Intuition\nHere we need to implement **Frequency Stack**.\nAccording to a problem definition it has **two methods**:\n- `push` to insert a val into `stack`\n- `pop` to extract **most frequent** element in stack \n\nThe first way to maintain an order with frequency is **Max Priority Queue (MPQ)**.\nThough this solution is **accepted**, it costs at least **O(N log N)** to work with MPQ.\n\nTo improve this approach we could use **separate stacks** for **each** frequency.\nThis helps us to maintain **order**, in which we pop **tie** frequencies.\n\n```\n# Example\n\nstack = [1, 2, 1, 0, 6], groups = {1: [1, 2, 0, 6], 2: [1]} \n\n# First pop = 1\nstack = [1, 2, 0, 6], groups = {1: [1, 2, 0, 6], 2: []} \n\n# Second pop = 6\nstack = [1, 2, 0], groups = {1: [1, 2, 0], 2: []} \n```\n\n# Approach\n1. initialize `freq` as frequencies of each inserted integer\n2. initialize `groups` to store mapping as `freq: [...vals]`\n3. initialize `maxFreq`, we\'ll use this each time we **pop** an integer from stack\n4. while `push` increment `freq` and update `maxFreq`, if we needed\n5. while `pop` extract the first element on top of a stack from `groups` and decrease `maxFreq` if `groups[maxFreq]` don\'t have **any** vals with this freq\n\n# Complexity\n- Time complexity: **O(1)**\n\n- Space complexity: **O(N)** in worst-case scenario \n\n# Code\n```\nclass FreqStack:\n\n def __init__(self):\n self.freq = defaultdict(int)\n self.groups = defaultdict(list)\n self.maxFreq = 0\n \n\n def push(self, val: int) -> None:\n self.freq[val] += 1\n\n if self.freq[val] > self.maxFreq: self.maxFreq = self.freq[val]\n\n self.groups[self.freq[val]].append(val)\n\n def pop(self) -> int:\n first = self.groups[self.maxFreq].pop()\n self.freq[first] -= 1\n\n if not self.groups[self.maxFreq]:\n self.maxFreq -= 1\n\n return first\n``` | 2 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
67% Tc and 76% Sc easy python solution | maximum-frequency-stack | 0 | 1 | ```\nclass FreqStack:\n\tdef __init__(self):\n\t\tself.freq = defaultdict(int)\n\t\tself.freqEle = defaultdict(list)\n\t\tself.maxx = -1\n\n\tdef push(self, val: int) -> None:\n\t\tself.freq[val] += 1\n\t\tself.freqEle[self.freq[val]].append(val)\n\t\tself.maxx = max(self.maxx, self.freq[val])\n\n\tdef pop(self) -> int:\n\t\ttemp = self.freqEle[self.maxx].pop()\n\t\tself.freq[temp] -= 1\n\t\tif(self.freqEle[self.maxx] == []):\n\t\t\tself.maxx -= 1\n\t\treturn temp\n``` | 1 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
67% Tc and 76% Sc easy python solution | maximum-frequency-stack | 0 | 1 | ```\nclass FreqStack:\n\tdef __init__(self):\n\t\tself.freq = defaultdict(int)\n\t\tself.freqEle = defaultdict(list)\n\t\tself.maxx = -1\n\n\tdef push(self, val: int) -> None:\n\t\tself.freq[val] += 1\n\t\tself.freqEle[self.freq[val]].append(val)\n\t\tself.maxx = max(self.maxx, self.freq[val])\n\n\tdef pop(self) -> int:\n\t\ttemp = self.freqEle[self.maxx].pop()\n\t\tself.freq[temp] -= 1\n\t\tif(self.freqEle[self.maxx] == []):\n\t\t\tself.maxx -= 1\n\t\treturn temp\n``` | 1 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
Python O(1) Solution using two dictionaries with explanation | maximum-frequency-stack | 0 | 1 | Initialise two dictionaries **set** and **freq** and a variable **max_freq**.\n**freq** is used to store the frequency of the elements provided, i.e., Key: Element; Value: Count of that element\n**set** is used to store the group of elements having the same frequency. Key: Count; Value: List of elements\n**max_freq** is used to store the frequency of most common element.\nFor example, let\'s say we have an input stack and we start adding the following elements:\n**Push 5:** freq: {5: 1}; set: {1: [5]}; max_freq = 1\n**Push 7:** freq: {5: 1, 7: 1}; set: {1: [5, 7]}; max_freq = 1\n**Push 5:** freq: {5: 2, 7: 1}; set: {1: [5, 7], 2:[5]}; max_freq = 2\n**Pop**: \n- Use max_freq to access the set dictionary and pop the last element from the list.\n- val = set[max_freq].pop()\n- Since, our set[2] is empty, decrement max_freq by 1.\n- Also, decrement freq[val] by 1.\n- freq: {5:1, 7: 1}; set: {1: [5, 7], 2: []}; max_freq = 1\n- return val\n\n```\nclass FreqStack:\n\n def __init__(self):\n self.set = defaultdict(list)\n self.freq = defaultdict(int)\n self.max_freq = 0\n\n def push(self, val: int) -> None:\n self.freq[val] += 1\n self.max_freq = max(self.max_freq, self.freq[val])\n self.set[self.freq[val]].append(val)\n\n def pop(self) -> int:\n val = self.set[self.max_freq].pop()\n self.freq[val] -= 1\n if not self.set[self.max_freq]:\n self.max_freq -= 1\n return val\n``` | 16 | Design a stack-like data structure to push elements to the stack and pop the most frequent element from the stack.
Implement the `FreqStack` class:
* `FreqStack()` constructs an empty frequency stack.
* `void push(int val)` pushes an integer `val` onto the top of the stack.
* `int pop()` removes and returns the most frequent element in the stack.
* If there is a tie for the most frequent element, the element closest to the stack's top is removed and returned.
**Example 1:**
**Input**
\[ "FreqStack ", "push ", "push ", "push ", "push ", "push ", "push ", "pop ", "pop ", "pop ", "pop "\]
\[\[\], \[5\], \[7\], \[5\], \[7\], \[4\], \[5\], \[\], \[\], \[\], \[\]\]
**Output**
\[null, null, null, null, null, null, null, 5, 7, 5, 4\]
**Explanation**
FreqStack freqStack = new FreqStack();
freqStack.push(5); // The stack is \[5\]
freqStack.push(7); // The stack is \[5,7\]
freqStack.push(5); // The stack is \[5,7,5\]
freqStack.push(7); // The stack is \[5,7,5,7\]
freqStack.push(4); // The stack is \[5,7,5,7,4\]
freqStack.push(5); // The stack is \[5,7,5,7,4,5\]
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,5,7,4\].
freqStack.pop(); // return 7, as 5 and 7 is the most frequent, but 7 is closest to the top. The stack becomes \[5,7,5,4\].
freqStack.pop(); // return 5, as 5 is the most frequent. The stack becomes \[5,7,4\].
freqStack.pop(); // return 4, as 4, 5 and 7 is the most frequent, but 4 is closest to the top. The stack becomes \[5,7\].
**Constraints:**
* `0 <= val <= 109`
* At most `2 * 104` calls will be made to `push` and `pop`.
* It is guaranteed that there will be at least one element in the stack before calling `pop`. | null |
Python O(1) Solution using two dictionaries with explanation | maximum-frequency-stack | 0 | 1 | Initialise two dictionaries **set** and **freq** and a variable **max_freq**.\n**freq** is used to store the frequency of the elements provided, i.e., Key: Element; Value: Count of that element\n**set** is used to store the group of elements having the same frequency. Key: Count; Value: List of elements\n**max_freq** is used to store the frequency of most common element.\nFor example, let\'s say we have an input stack and we start adding the following elements:\n**Push 5:** freq: {5: 1}; set: {1: [5]}; max_freq = 1\n**Push 7:** freq: {5: 1, 7: 1}; set: {1: [5, 7]}; max_freq = 1\n**Push 5:** freq: {5: 2, 7: 1}; set: {1: [5, 7], 2:[5]}; max_freq = 2\n**Pop**: \n- Use max_freq to access the set dictionary and pop the last element from the list.\n- val = set[max_freq].pop()\n- Since, our set[2] is empty, decrement max_freq by 1.\n- Also, decrement freq[val] by 1.\n- freq: {5:1, 7: 1}; set: {1: [5, 7], 2: []}; max_freq = 1\n- return val\n\n```\nclass FreqStack:\n\n def __init__(self):\n self.set = defaultdict(list)\n self.freq = defaultdict(int)\n self.max_freq = 0\n\n def push(self, val: int) -> None:\n self.freq[val] += 1\n self.max_freq = max(self.max_freq, self.freq[val])\n self.set[self.freq[val]].append(val)\n\n def pop(self) -> int:\n val = self.set[self.max_freq].pop()\n self.freq[val] -= 1\n if not self.set[self.max_freq]:\n self.max_freq -= 1\n return val\n``` | 16 | Given an `n x n` array of integers `matrix`, return _the **minimum sum** of any **falling path** through_ `matrix`.
A **falling path** starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position `(row, col)` will be `(row + 1, col - 1)`, `(row + 1, col)`, or `(row + 1, col + 1)`.
**Example 1:**
**Input:** matrix = \[\[2,1,3\],\[6,5,4\],\[7,8,9\]\]
**Output:** 13
**Explanation:** There are two falling paths with a minimum sum as shown.
**Example 2:**
**Input:** matrix = \[\[-19,57\],\[-40,-5\]\]
**Output:** -59
**Explanation:** The falling path with a minimum sum is shown.
**Constraints:**
* `n == matrix.length == matrix[i].length`
* `1 <= n <= 100`
* `-100 <= matrix[i][j] <= 100` | null |
NOOB CODE : Easy to understand | monotonic-array | 0 | 1 | \n# Approach\n1. `o` is initialized to `False`. This variable will be used to store the result indicating whether the list is monotonic.\n\n2. An empty list `k` is initialized.\n\n3. A loop is used to iterate through each element `i` in the input list `nums`. Inside the loop, each element `i` is appended to the list `k`.\n\n4. The list `k` is sorted in ascending order using `k.sort()`. This sorting operation doesn\'t modify the original `nums` list.\n\n5. The code checks if the first element of the sorted list `k` is equal to the last element of the input `nums`. This comparison is used to determine whether the list is non-increasing or non-decreasing. If they are equal, it suggests that the list is non-increasing, and if they are not equal, it suggests that the list is non-decreasing.\n\n6. Two separate loops are used based on the comparison result:\n - If `k[0] == nums[-1]`, it means the list is non-increasing. In this case, a loop iterates through the `nums` list from the first element to the second-to-last element. If it finds any element that is greater than or equal to the next element, it sets `o` to `True`, indicating that the list is non-increasing. If any element is less than the next element, it sets `o` to `False` and breaks the loop.\n - If `k[0] != nums[-1]`, it means the list is non-decreasing. In this case, a loop iterates through the `nums` list from the first element to the second-to-last element. If it finds any element that is less than or equal to the next element, it sets `o` to `True`, indicating that the list is non-decreasing. If any element is greater than the next element, it sets `o` to `False` and breaks the loop.\n\n7. There\'s a special case check for lists with only one element (`len(nums) == 1`). In this case, the list is considered monotonic by default, so `o` is set to `True`.\n\n8. Finally, the function returns the value of `o`, which indicates whether the input list `nums` is monotonic or not.\n\n\n# Complexity\n- Time complexity: ***O(n x log(n))*** \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***o(n)***\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n o=False\n k=[]\n for i in nums:\n k.append(i)\n k.sort()\n if(k[0]==nums[-1]):\n for i in range(len(nums)-1):\n print(1)\n if nums[i]>=nums[i+1]:\n o=True\n else:\n o=False\n break\n else:\n for i in range(len(nums)-1):\n print(nums[i])\n if nums[i]<=nums[i+1]:\n o=True\n else:\n o=False\n break\n if(len(nums)==1):\n o=True\n return(o)\n \n\n``` | 3 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
NOOB CODE : Easy to understand | monotonic-array | 0 | 1 | \n# Approach\n1. `o` is initialized to `False`. This variable will be used to store the result indicating whether the list is monotonic.\n\n2. An empty list `k` is initialized.\n\n3. A loop is used to iterate through each element `i` in the input list `nums`. Inside the loop, each element `i` is appended to the list `k`.\n\n4. The list `k` is sorted in ascending order using `k.sort()`. This sorting operation doesn\'t modify the original `nums` list.\n\n5. The code checks if the first element of the sorted list `k` is equal to the last element of the input `nums`. This comparison is used to determine whether the list is non-increasing or non-decreasing. If they are equal, it suggests that the list is non-increasing, and if they are not equal, it suggests that the list is non-decreasing.\n\n6. Two separate loops are used based on the comparison result:\n - If `k[0] == nums[-1]`, it means the list is non-increasing. In this case, a loop iterates through the `nums` list from the first element to the second-to-last element. If it finds any element that is greater than or equal to the next element, it sets `o` to `True`, indicating that the list is non-increasing. If any element is less than the next element, it sets `o` to `False` and breaks the loop.\n - If `k[0] != nums[-1]`, it means the list is non-decreasing. In this case, a loop iterates through the `nums` list from the first element to the second-to-last element. If it finds any element that is less than or equal to the next element, it sets `o` to `True`, indicating that the list is non-decreasing. If any element is greater than the next element, it sets `o` to `False` and breaks the loop.\n\n7. There\'s a special case check for lists with only one element (`len(nums) == 1`). In this case, the list is considered monotonic by default, so `o` is set to `True`.\n\n8. Finally, the function returns the value of `o`, which indicates whether the input list `nums` is monotonic or not.\n\n\n# Complexity\n- Time complexity: ***O(n x log(n))*** \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***o(n)***\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n o=False\n k=[]\n for i in nums:\n k.append(i)\n k.sort()\n if(k[0]==nums[-1]):\n for i in range(len(nums)-1):\n print(1)\n if nums[i]>=nums[i+1]:\n o=True\n else:\n o=False\n break\n else:\n for i in range(len(nums)-1):\n print(nums[i])\n if nums[i]<=nums[i+1]:\n o=True\n else:\n o=False\n break\n if(len(nums)==1):\n o=True\n return(o)\n \n\n``` | 3 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
✅ Detailed Explanation with Solution using Two Pointer Approach (O(n)) - with 100% Acceptance Rate | monotonic-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to determine whether the given array is monotonic, i.e., either monotone increasing or monotone decreasing. It uses a two-pointer approach to skip identical elements at the beginning and end of the array and then checks if the remaining elements are consistent with either a monotone increasing or decreasing pattern.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Check if the size of the input array nums is less than or equal to 1. If it is, return true because a single-element array is considered monotonic.\n\n2. Initialize two pointers, left and right, initially pointing to the first and last elements of the array, respectively.\n\n3. Use the left pointer to skip identical elements at the beginning of the array. Increment left while the current element is equal to the next element.\n\n4. Use the right pointer to skip identical elements at the end of the array. Decrement right while the current element is equal to the previous element.\n\n5. Check if left is greater than or equal to right. If it is, it means all elements in the array are identical, and the array is considered monotonic. Return true.\n\n6. Determine whether the array is increasing or decreasing based on the values at left and left + 1.\n\n7. Iterate from left to right - 1 and compare each element with its next element:\n\n- If the array is increasing and the current element is greater than the next element, return false (not monotonic).\n\n- If the array is decreasing and the current element is less than the next element, return false (not monotonic).\n8. If the loop completes without returning false, return true because the array is monotonic.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the input array nums once, either from left to right or from right to left, depending on the direction of monotonicity. The time complexity is O(n), where n is the number of elements in the array.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses a constant amount of extra space for variables (left, right, n). Therefore, the space complexity is O(1), indicating constant space usage regardless of the input array\'s size.\n\n# Do Upvote if you liked the explanation \uD83E\uDD1E\n\n# Code\n```\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n int n = nums.size();\n \n if (n <= 1) {\n return true; // A single element array is considered monotonic.\n }\n \n int left = 0;\n int right = n - 1;\n \n while (left < n - 1 && nums[left] == nums[left + 1]) {\n left++; // Skip identical elements at the beginning.\n }\n \n while (right > 0 && nums[right] == nums[right - 1]) {\n right--; // Skip identical elements at the end.\n }\n \n if (left >= right) {\n return true; // All elements are identical; the array is monotonic.\n }\n \n bool increasing = nums[left] < nums[left + 1];\n \n for (int i = left; i < right; i++) {\n if (increasing && nums[i] > nums[i + 1]) {\n return false; // Not monotonic if it decreases.\n } else if (!increasing && nums[i] < nums[i + 1]) {\n return false; // Not monotonic if it increases.\n }\n }\n \n return true;\n }\n};\n\n``` | 3 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
✅ Detailed Explanation with Solution using Two Pointer Approach (O(n)) - with 100% Acceptance Rate | monotonic-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to determine whether the given array is monotonic, i.e., either monotone increasing or monotone decreasing. It uses a two-pointer approach to skip identical elements at the beginning and end of the array and then checks if the remaining elements are consistent with either a monotone increasing or decreasing pattern.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Check if the size of the input array nums is less than or equal to 1. If it is, return true because a single-element array is considered monotonic.\n\n2. Initialize two pointers, left and right, initially pointing to the first and last elements of the array, respectively.\n\n3. Use the left pointer to skip identical elements at the beginning of the array. Increment left while the current element is equal to the next element.\n\n4. Use the right pointer to skip identical elements at the end of the array. Decrement right while the current element is equal to the previous element.\n\n5. Check if left is greater than or equal to right. If it is, it means all elements in the array are identical, and the array is considered monotonic. Return true.\n\n6. Determine whether the array is increasing or decreasing based on the values at left and left + 1.\n\n7. Iterate from left to right - 1 and compare each element with its next element:\n\n- If the array is increasing and the current element is greater than the next element, return false (not monotonic).\n\n- If the array is decreasing and the current element is less than the next element, return false (not monotonic).\n8. If the loop completes without returning false, return true because the array is monotonic.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code iterates through the input array nums once, either from left to right or from right to left, depending on the direction of monotonicity. The time complexity is O(n), where n is the number of elements in the array.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe code uses a constant amount of extra space for variables (left, right, n). Therefore, the space complexity is O(1), indicating constant space usage regardless of the input array\'s size.\n\n# Do Upvote if you liked the explanation \uD83E\uDD1E\n\n# Code\n```\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n int n = nums.size();\n \n if (n <= 1) {\n return true; // A single element array is considered monotonic.\n }\n \n int left = 0;\n int right = n - 1;\n \n while (left < n - 1 && nums[left] == nums[left + 1]) {\n left++; // Skip identical elements at the beginning.\n }\n \n while (right > 0 && nums[right] == nums[right - 1]) {\n right--; // Skip identical elements at the end.\n }\n \n if (left >= right) {\n return true; // All elements are identical; the array is monotonic.\n }\n \n bool increasing = nums[left] < nums[left + 1];\n \n for (int i = left; i < right; i++) {\n if (increasing && nums[i] > nums[i + 1]) {\n return false; // Not monotonic if it decreases.\n } else if (!increasing && nums[i] < nums[i + 1]) {\n return false; // Not monotonic if it increases.\n }\n }\n \n return true;\n }\n};\n\n``` | 3 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
✅97.44%🔥Increasing & Decreasing🔥1 line code🔥 | monotonic-array | 1 | 1 | # Problem\n#### The problem statement asks you to determine whether a given array nums is monotonic. An array is considered monotonic if it is either monotone increasing or monotone decreasing.\n\n **1.** **Monotone Increasing :** An array is considered monotone increasing if for all indices i and j where i <= j, the element at index i is less than or equal to the element at index j. In other words, the values in the array are non-decreasing as you move from left to right.\n\n**2.** **Monotone Decreasing :** An array is considered monotone decreasing if for all indices i and j where i <= j, the element at index i is greater than or equal to the element at index j. In other words, the values in the array are non-increasing as you move from left to right.\n\n#### The task is to check if the given nums array satisfies either of these conditions. If it does, the function should return true, indicating that the array is monotonic. Otherwise, it should return false.\n---\n# Solution\n#### 1. Initialize two boolean variables, increasing and decreasing, to true. These variables will be used to track whether the array is monotone increasing or monotone decreasing.\n\n#### 2.Iterate through the array from the second element (i = 1) to the last element (i = nums.length - 1).\n\n#### 3.For each pair of adjacent elements at indices i and i - 1, compare them:\n\n- ***If nums[i] is greater than nums[i - 1], set decreasing to false. This means the array is not monotone decreasing.***\n\n- ***If nums[i] is less than nums[i - 1], set increasing to false. This means the array is not monotone increasing.***\n\n#### 4. During the iteration, if at any point both increasing and decreasing become false, you can immediately return false because the array is neither monotone increasing nor monotone decreasing.\n\n#### 5.After the loop, if either increasing or decreasing is still true, it means the array is either monotone increasing or monotone decreasing, so you return true. Otherwise, you return false because the array is not monotonic.\n---\n\n```python []\nclass Solution:\n def isMonotonic(self, A: List[int]) -> bool:\n return all(A[i] <= A[i + 1] for i in range(len(A) - 1)) or all(A[i] >= A[i + 1] for i in range(len(A) - 1))\n\n```\n```C# []\npublic class Solution {\n public bool IsMonotonic(int[] nums) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < nums.Length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < nums.size(); ++i) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n return true;\n }\n};\n\n```\n```C []\nbool isMonotonic(int* nums, int numsSize) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < numsSize; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n}\n\n```\n```Java []\nclass Solution {\n public boolean isMonotonic(int[] nums) {\n boolean increasing = true;\n boolean decreasing = true;\n\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true;\n }\n}\n\n```\n```javascript []\nvar isMonotonic = function(nums) {\n let increasing = true;\n let decreasing = true;\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n};\n\n```\n```typescript []\nfunction isMonotonic(nums: number[]): boolean {\n let increasing = true;\n let decreasing = true;\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true;\n}\n\n```\n```Go []\nfunc isMonotonic(nums []int) bool {\n increasing := true\n decreasing := true\n for i := 1; i < len(nums); i++ {\n if nums[i] > nums[i-1] {\n decreasing = false\n } else if nums[i] < nums[i-1] {\n increasing = false\n }\n if !increasing && !decreasing {\n return false\n }\n }\n return true \n}\n```\n```rust []\nimpl Solution {\n pub fn is_monotonic(nums: Vec<i32>) -> bool {\n let mut increasing = true;\n let mut decreasing = true;\n\n for i in 1..nums.len() {\n if nums[i] > nums[i - 1] {\n decreasing = false;\n } else if nums[i] < nums[i - 1] {\n increasing = false;\n }\n if !increasing && !decreasing {\n return false;\n }\n }\n true \n }\n}\n```\n | 94 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
✅97.44%🔥Increasing & Decreasing🔥1 line code🔥 | monotonic-array | 1 | 1 | # Problem\n#### The problem statement asks you to determine whether a given array nums is monotonic. An array is considered monotonic if it is either monotone increasing or monotone decreasing.\n\n **1.** **Monotone Increasing :** An array is considered monotone increasing if for all indices i and j where i <= j, the element at index i is less than or equal to the element at index j. In other words, the values in the array are non-decreasing as you move from left to right.\n\n**2.** **Monotone Decreasing :** An array is considered monotone decreasing if for all indices i and j where i <= j, the element at index i is greater than or equal to the element at index j. In other words, the values in the array are non-increasing as you move from left to right.\n\n#### The task is to check if the given nums array satisfies either of these conditions. If it does, the function should return true, indicating that the array is monotonic. Otherwise, it should return false.\n---\n# Solution\n#### 1. Initialize two boolean variables, increasing and decreasing, to true. These variables will be used to track whether the array is monotone increasing or monotone decreasing.\n\n#### 2.Iterate through the array from the second element (i = 1) to the last element (i = nums.length - 1).\n\n#### 3.For each pair of adjacent elements at indices i and i - 1, compare them:\n\n- ***If nums[i] is greater than nums[i - 1], set decreasing to false. This means the array is not monotone decreasing.***\n\n- ***If nums[i] is less than nums[i - 1], set increasing to false. This means the array is not monotone increasing.***\n\n#### 4. During the iteration, if at any point both increasing and decreasing become false, you can immediately return false because the array is neither monotone increasing nor monotone decreasing.\n\n#### 5.After the loop, if either increasing or decreasing is still true, it means the array is either monotone increasing or monotone decreasing, so you return true. Otherwise, you return false because the array is not monotonic.\n---\n\n```python []\nclass Solution:\n def isMonotonic(self, A: List[int]) -> bool:\n return all(A[i] <= A[i + 1] for i in range(len(A) - 1)) or all(A[i] >= A[i + 1] for i in range(len(A) - 1))\n\n```\n```C# []\npublic class Solution {\n public bool IsMonotonic(int[] nums) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < nums.Length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < nums.size(); ++i) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n return true;\n }\n};\n\n```\n```C []\nbool isMonotonic(int* nums, int numsSize) {\n bool increasing = true;\n bool decreasing = true;\n\n for (int i = 1; i < numsSize; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n}\n\n```\n```Java []\nclass Solution {\n public boolean isMonotonic(int[] nums) {\n boolean increasing = true;\n boolean decreasing = true;\n\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true;\n }\n}\n\n```\n```javascript []\nvar isMonotonic = function(nums) {\n let increasing = true;\n let decreasing = true;\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true; \n};\n\n```\n```typescript []\nfunction isMonotonic(nums: number[]): boolean {\n let increasing = true;\n let decreasing = true;\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i - 1]) {\n decreasing = false;\n } else if (nums[i] < nums[i - 1]) {\n increasing = false;\n }\n\n if (!increasing && !decreasing) {\n return false;\n }\n }\n\n return true;\n}\n\n```\n```Go []\nfunc isMonotonic(nums []int) bool {\n increasing := true\n decreasing := true\n for i := 1; i < len(nums); i++ {\n if nums[i] > nums[i-1] {\n decreasing = false\n } else if nums[i] < nums[i-1] {\n increasing = false\n }\n if !increasing && !decreasing {\n return false\n }\n }\n return true \n}\n```\n```rust []\nimpl Solution {\n pub fn is_monotonic(nums: Vec<i32>) -> bool {\n let mut increasing = true;\n let mut decreasing = true;\n\n for i in 1..nums.len() {\n if nums[i] > nums[i - 1] {\n decreasing = false;\n } else if nums[i] < nums[i - 1] {\n increasing = false;\n }\n if !increasing && !decreasing {\n return false;\n }\n }\n true \n }\n}\n```\n | 94 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python 3 || O(n) time, O(1) Space | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n\n # If last elemnt is greater than first\n # Conisdeirng it as monotonically increasing\n if nums[-1]>nums[0]:\n for i in range(len(nums)-1):\n if nums[i+1]<nums[i]:\n return False\n return True\n # Else monotonically decreasing\n else:\n for i in range(len(nums)-1):\n if nums[i+1]>nums[i]:\n return False\n return True\n\n \n \n``` | 2 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Python 3 || O(n) time, O(1) Space | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n\n # If last elemnt is greater than first\n # Conisdeirng it as monotonically increasing\n if nums[-1]>nums[0]:\n for i in range(len(nums)-1):\n if nums[i+1]<nums[i]:\n return False\n return True\n # Else monotonically decreasing\n else:\n for i in range(len(nums)-1):\n if nums[i+1]>nums[i]:\n return False\n return True\n\n \n \n``` | 2 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python 3 || Sorting | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n rev=sorted(nums,reverse=True)\n so=sorted(nums)\n\n return nums==so or nums==rev\n \n``` | 2 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Python 3 || Sorting | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n rev=sorted(nums,reverse=True)\n so=sorted(nums)\n\n return nums==so or nums==rev\n \n``` | 2 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Simple map reduce | monotonic-array | 0 | 1 | # Intuition\nCould check `nums[0]` and `nums[len(nums)-1]` to determine increasing / decreasing / constant upfront, but there is no meaningful difference.\n\n# Approach\n- Create an iterator for `is_increasing` and `is_decreasing`.\n- Use `all()` to reduce them.\n- Return `True` if either of them reduces to `True`.\n\n# Complexity\n- Time complexity: $$O(n)$$\n > worst case two passes (`nums[len(nums)-2]` > `nums[len(nums)-1]`)\n\n- Space complexity: $$O(1)$$\n > iterators are nice\n\n# Code\n- Using `map` and `lambda`:\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n is_increasing = map(lambda a, b: a <= b, nums[:len(nums)], nums[1:])\n is_decreasing = map(lambda a, b: a >= b, nums[:len(nums)], nums[1:])\n return all(is_increasing) or all(is_decreasing)\n```\n- Using `generator expression`:\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n is_increasing = (a <= b for (a, b) in zip(nums[:len(nums)], nums[1:]))\n is_decreasing = (a >= b for (a, b) in zip(nums[:len(nums)], nums[1:]))\n return all(is_increasing) or all(is_decreasing)\n``` | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Simple map reduce | monotonic-array | 0 | 1 | # Intuition\nCould check `nums[0]` and `nums[len(nums)-1]` to determine increasing / decreasing / constant upfront, but there is no meaningful difference.\n\n# Approach\n- Create an iterator for `is_increasing` and `is_decreasing`.\n- Use `all()` to reduce them.\n- Return `True` if either of them reduces to `True`.\n\n# Complexity\n- Time complexity: $$O(n)$$\n > worst case two passes (`nums[len(nums)-2]` > `nums[len(nums)-1]`)\n\n- Space complexity: $$O(1)$$\n > iterators are nice\n\n# Code\n- Using `map` and `lambda`:\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n is_increasing = map(lambda a, b: a <= b, nums[:len(nums)], nums[1:])\n is_decreasing = map(lambda a, b: a >= b, nums[:len(nums)], nums[1:])\n return all(is_increasing) or all(is_decreasing)\n```\n- Using `generator expression`:\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n is_increasing = (a <= b for (a, b) in zip(nums[:len(nums)], nums[1:]))\n is_decreasing = (a >= b for (a, b) in zip(nums[:len(nums)], nums[1:]))\n return all(is_increasing) or all(is_decreasing)\n``` | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
🔥 Easy solution in 1 line | Python 3 🔥 | monotonic-array | 0 | 1 | # Intuition\nA list is considered monotonic if it is entirely non-increasing (every element is less than or equal to the next) or entirely non-decreasing (every element is greater than or equal to the next)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. The function defines a single parameter nums, which is a list of integers.\n\n1. Inside the function, there are two parts connected by or:\n\n 1. The first part checks if all elements in the list nums are in non-decreasing order (monotonic increasing). It does this using a generator expression and the all function. It iterates through the elements of nums using a for loop, and for each pair of consecutive elements (using range(len(nums) - 1)), it checks if the current element is less than or equal to the next element. If this condition holds for all pairs, it returns True.\n\n 1. The second part does the opposite; it checks if all elements in the list nums are in non-increasing order (monotonic decreasing). Similar to the first part, it uses a generator expression and the all function to iterate through the elements and check if the current element is greater than or equal to the next element. If this condition holds for all pairs, it returns True.\n\n1. The or operator is used to combine the results of both parts. If either the increasing or decreasing condition holds for all pairs of elements in the list, the function returns True, indicating that the list is monotonic. Otherwise, it returns False.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n return (all(nums[i] <= nums[i + 1] for i in range(len(nums) - 1)) or all(nums[i] >= nums[i + 1] for i in range(len(nums) - 1))) \n \n \n``` | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
🔥 Easy solution in 1 line | Python 3 🔥 | monotonic-array | 0 | 1 | # Intuition\nA list is considered monotonic if it is entirely non-increasing (every element is less than or equal to the next) or entirely non-decreasing (every element is greater than or equal to the next)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. The function defines a single parameter nums, which is a list of integers.\n\n1. Inside the function, there are two parts connected by or:\n\n 1. The first part checks if all elements in the list nums are in non-decreasing order (monotonic increasing). It does this using a generator expression and the all function. It iterates through the elements of nums using a for loop, and for each pair of consecutive elements (using range(len(nums) - 1)), it checks if the current element is less than or equal to the next element. If this condition holds for all pairs, it returns True.\n\n 1. The second part does the opposite; it checks if all elements in the list nums are in non-increasing order (monotonic decreasing). Similar to the first part, it uses a generator expression and the all function to iterate through the elements and check if the current element is greater than or equal to the next element. If this condition holds for all pairs, it returns True.\n\n1. The or operator is used to combine the results of both parts. If either the increasing or decreasing condition holds for all pairs of elements in the list, the function returns True, indicating that the list is monotonic. Otherwise, it returns False.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n return (all(nums[i] <= nums[i + 1] for i in range(len(nums) - 1)) or all(nums[i] >= nums[i + 1] for i in range(len(nums) - 1))) \n \n \n``` | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
✅ 95.15% Single Pass Check | monotonic-array | 1 | 1 | # Interview Guide: "Check Monotonic Array" Problem\n\n## Problem Understanding\n\nThe "Check Monotonic Array" problem requires evaluating whether a given array is either entirely non-decreasing (monotonically increasing) or non-increasing (monotonically decreasing). The objective is to return a boolean value indicating the array\'s monotonicity.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore diving into the solution, it\'s crucial to recognize the problem\'s constraints. The length of the array `nums` is between 1 and $$10^5$$, and the integers in `nums` range between $$-10^5$$ and $$10^5$$. These constraints offer insights into potential solutions in terms of time and space complexity.\n\n### 2. Single Pass Check\n\nOne efficient way to solve this problem is to use a single pass through the array to determine if it\'s increasing, decreasing, or neither. This approach reduces the number of checks and can potentially exit early if the array is neither increasing nor decreasing.\n\n### 3. Understand Array Characteristics\n\nA key observation is that if an array starts by increasing, it should not switch to decreasing later and vice versa. This observation forms the basis of the solution.\n\n### 4. Explain Your Thought Process\n\nAlways articulate the rationale behind your approach. Describe the importance of determining the direction of monotonicity early on and how it can help in making the solution more efficient.\n\n## Conclusion\n\nThe "Check Monotonic Array" problem emphasizes the significance of understanding array traversal and condition checks. By performing a single pass through the array, you can efficiently determine its monotonicity.\n\n---\n\n## Live Coding & Explain\nhttps://youtu.be/INyEvNkNRcg?si=R2VWH4FxIb_nHWoH\n\n# Approach: Single Pass Check\n\nTo solve the "Check Monotonic Array" problem using the single pass check:\n\n## Key Data Structures:\n\n- **direction**: A variable to keep track of the array\'s direction (increasing, decreasing, or unknown).\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - If the array\'s length is less than 2, return `True` (arrays with 0 or 1 elements are always monotonic).\n - Initialize the `direction` as 0 (unknown).\n \n2. **Traverse the Array**:\n - For every pair of adjacent elements, determine if the array is increasing, decreasing, or neither.\n - If the direction is set to increasing and a decreasing pattern is found, return `False`, and vice versa.\n \n3. **Return the Result**:\n - If no violation of monotonicity is found during traversal, return `True`.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution involves traversing the array once, leading to a time complexity of $$O(n)$$, where `n` is the length of the array `nums`.\n\n**Space Complexity:** \n- The space complexity is $$O(1)$$ since the solution doesn\'t use any additional data structures that scale with the input size.\n\n# Code Single Pass Check\n``` Python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return True\n \n direction = 0 # 0 means unknown, 1 means increasing, -1 means decreasing\n \n for i in range(1, len(nums)):\n if nums[i] > nums[i-1]: # increasing\n if direction == 0:\n direction = 1\n elif direction == -1:\n return False\n elif nums[i] < nums[i-1]: # decreasing\n if direction == 0:\n direction = -1\n elif direction == 1:\n return False\n \n return True\n```\n``` Go []\nfunc isMonotonic(nums []int) bool {\n if len(nums) < 2 {\n return true\n }\n\n direction := 0 // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for i := 1; i < len(nums); i++ {\n if nums[i] > nums[i-1] { // increasing\n if direction == 0 {\n direction = 1\n } else if direction == -1 {\n return false\n }\n } else if nums[i] < nums[i-1] { // decreasing\n if direction == 0 {\n direction = -1\n } else if direction == 1 {\n return false\n }\n }\n }\n\n return true\n}\n```\n``` Rust []\nimpl Solution {\n pub fn is_monotonic(nums: Vec<i32>) -> bool {\n if nums.len() < 2 {\n return true;\n }\n\n let mut direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for i in 1..nums.len() {\n if nums[i] > nums[i-1] { // increasing\n if direction == 0 {\n direction = 1;\n } else if direction == -1 {\n return false;\n }\n } else if nums[i] < nums[i-1] { // decreasing\n if direction == 0 {\n direction = -1;\n } else if direction == 1 {\n return false;\n }\n }\n }\n\n true\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n bool isMonotonic(std::vector<int>& nums) {\n if (nums.size() < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (size_t i = 1; i < nums.size(); i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean isMonotonic(int[] nums) {\n if (nums.length < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n``` JavaScript []\nvar isMonotonic = function(nums) {\n if (nums.length < 2) return true;\n\n let direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction === 0) direction = 1;\n else if (direction === -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction === 0) direction = -1;\n else if (direction === 1) return false;\n }\n }\n\n return true;\n};\n```\n``` PHP []\nclass Solution {\n function isMonotonic($nums) {\n if (count($nums) < 2) return true;\n\n $direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for ($i = 1; $i < count($nums); $i++) {\n if ($nums[$i] > $nums[$i-1]) { // increasing\n if ($direction == 0) $direction = 1;\n else if ($direction == -1) return false;\n } else if ($nums[$i] < $nums[$i-1]) { // decreasing\n if ($direction == 0) $direction = -1;\n else if ($direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool IsMonotonic(int[] nums) {\n if (nums.Length < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (int i = 1; i < nums.Length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Memory |\n|------------|-----------|-----------|\n| Java | 1 ms | 55.4 MB |\n| Rust | 12 ms | 3.3 MB |\n| JavaScript | 80 ms | 52.4 MB |\n| C++ | 131 ms | 96.8 MB |\n| Go | 135 ms | 9.8 MB |\n| C# | 241 ms | 61.4 MB |\n| PHP | 277 ms | 31.7 MB |\n| Python3 | 812 ms | 30.4 MB |\n\n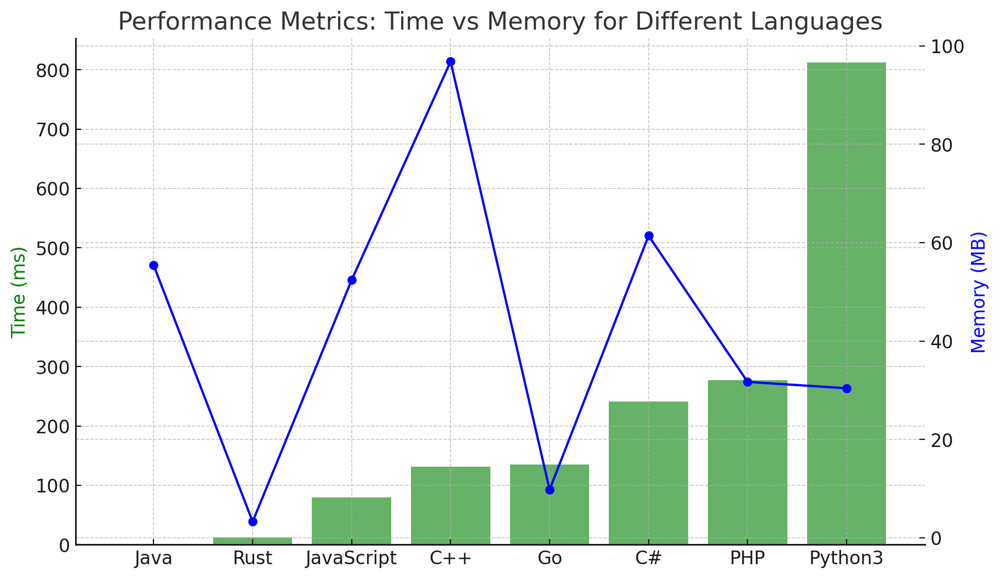\n\nThe "Check Monotonic Array" problem is an interesting array traversal problem that tests the ability to keep track of a property (monotonicity) while traversing an array. It showcases the importance of efficient array traversal and conditional checks. \uD83D\uDE80\uD83E\uDDE0\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB. | 112 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
✅ 95.15% Single Pass Check | monotonic-array | 1 | 1 | # Interview Guide: "Check Monotonic Array" Problem\n\n## Problem Understanding\n\nThe "Check Monotonic Array" problem requires evaluating whether a given array is either entirely non-decreasing (monotonically increasing) or non-increasing (monotonically decreasing). The objective is to return a boolean value indicating the array\'s monotonicity.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nBefore diving into the solution, it\'s crucial to recognize the problem\'s constraints. The length of the array `nums` is between 1 and $$10^5$$, and the integers in `nums` range between $$-10^5$$ and $$10^5$$. These constraints offer insights into potential solutions in terms of time and space complexity.\n\n### 2. Single Pass Check\n\nOne efficient way to solve this problem is to use a single pass through the array to determine if it\'s increasing, decreasing, or neither. This approach reduces the number of checks and can potentially exit early if the array is neither increasing nor decreasing.\n\n### 3. Understand Array Characteristics\n\nA key observation is that if an array starts by increasing, it should not switch to decreasing later and vice versa. This observation forms the basis of the solution.\n\n### 4. Explain Your Thought Process\n\nAlways articulate the rationale behind your approach. Describe the importance of determining the direction of monotonicity early on and how it can help in making the solution more efficient.\n\n## Conclusion\n\nThe "Check Monotonic Array" problem emphasizes the significance of understanding array traversal and condition checks. By performing a single pass through the array, you can efficiently determine its monotonicity.\n\n---\n\n## Live Coding & Explain\nhttps://youtu.be/INyEvNkNRcg?si=R2VWH4FxIb_nHWoH\n\n# Approach: Single Pass Check\n\nTo solve the "Check Monotonic Array" problem using the single pass check:\n\n## Key Data Structures:\n\n- **direction**: A variable to keep track of the array\'s direction (increasing, decreasing, or unknown).\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - If the array\'s length is less than 2, return `True` (arrays with 0 or 1 elements are always monotonic).\n - Initialize the `direction` as 0 (unknown).\n \n2. **Traverse the Array**:\n - For every pair of adjacent elements, determine if the array is increasing, decreasing, or neither.\n - If the direction is set to increasing and a decreasing pattern is found, return `False`, and vice versa.\n \n3. **Return the Result**:\n - If no violation of monotonicity is found during traversal, return `True`.\n\n# Complexity:\n\n**Time Complexity:** \n- The solution involves traversing the array once, leading to a time complexity of $$O(n)$$, where `n` is the length of the array `nums`.\n\n**Space Complexity:** \n- The space complexity is $$O(1)$$ since the solution doesn\'t use any additional data structures that scale with the input size.\n\n# Code Single Pass Check\n``` Python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n if len(nums) < 2:\n return True\n \n direction = 0 # 0 means unknown, 1 means increasing, -1 means decreasing\n \n for i in range(1, len(nums)):\n if nums[i] > nums[i-1]: # increasing\n if direction == 0:\n direction = 1\n elif direction == -1:\n return False\n elif nums[i] < nums[i-1]: # decreasing\n if direction == 0:\n direction = -1\n elif direction == 1:\n return False\n \n return True\n```\n``` Go []\nfunc isMonotonic(nums []int) bool {\n if len(nums) < 2 {\n return true\n }\n\n direction := 0 // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for i := 1; i < len(nums); i++ {\n if nums[i] > nums[i-1] { // increasing\n if direction == 0 {\n direction = 1\n } else if direction == -1 {\n return false\n }\n } else if nums[i] < nums[i-1] { // decreasing\n if direction == 0 {\n direction = -1\n } else if direction == 1 {\n return false\n }\n }\n }\n\n return true\n}\n```\n``` Rust []\nimpl Solution {\n pub fn is_monotonic(nums: Vec<i32>) -> bool {\n if nums.len() < 2 {\n return true;\n }\n\n let mut direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for i in 1..nums.len() {\n if nums[i] > nums[i-1] { // increasing\n if direction == 0 {\n direction = 1;\n } else if direction == -1 {\n return false;\n }\n } else if nums[i] < nums[i-1] { // decreasing\n if direction == 0 {\n direction = -1;\n } else if direction == 1 {\n return false;\n }\n }\n }\n\n true\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n bool isMonotonic(std::vector<int>& nums) {\n if (nums.size() < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (size_t i = 1; i < nums.size(); i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean isMonotonic(int[] nums) {\n if (nums.length < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (int i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n``` JavaScript []\nvar isMonotonic = function(nums) {\n if (nums.length < 2) return true;\n\n let direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (let i = 1; i < nums.length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction === 0) direction = 1;\n else if (direction === -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction === 0) direction = -1;\n else if (direction === 1) return false;\n }\n }\n\n return true;\n};\n```\n``` PHP []\nclass Solution {\n function isMonotonic($nums) {\n if (count($nums) < 2) return true;\n\n $direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for ($i = 1; $i < count($nums); $i++) {\n if ($nums[$i] > $nums[$i-1]) { // increasing\n if ($direction == 0) $direction = 1;\n else if ($direction == -1) return false;\n } else if ($nums[$i] < $nums[$i-1]) { // decreasing\n if ($direction == 0) $direction = -1;\n else if ($direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n``` C# []\npublic class Solution {\n public bool IsMonotonic(int[] nums) {\n if (nums.Length < 2) return true;\n\n int direction = 0; // 0 means unknown, 1 means increasing, -1 means decreasing\n\n for (int i = 1; i < nums.Length; i++) {\n if (nums[i] > nums[i-1]) { // increasing\n if (direction == 0) direction = 1;\n else if (direction == -1) return false;\n } else if (nums[i] < nums[i-1]) { // decreasing\n if (direction == 0) direction = -1;\n else if (direction == 1) return false;\n }\n }\n\n return true;\n }\n}\n```\n\n## Performance\n\n| Language | Time (ms) | Memory |\n|------------|-----------|-----------|\n| Java | 1 ms | 55.4 MB |\n| Rust | 12 ms | 3.3 MB |\n| JavaScript | 80 ms | 52.4 MB |\n| C++ | 131 ms | 96.8 MB |\n| Go | 135 ms | 9.8 MB |\n| C# | 241 ms | 61.4 MB |\n| PHP | 277 ms | 31.7 MB |\n| Python3 | 812 ms | 30.4 MB |\n\n\n\nThe "Check Monotonic Array" problem is an interesting array traversal problem that tests the ability to keep track of a property (monotonicity) while traversing an array. It showcases the importance of efficient array traversal and conditional checks. \uD83D\uDE80\uD83E\uDDE0\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB. | 112 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Monotonic Solution in Python3 with one liner also | monotonic-array | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code:\n\n1. increasing_index and decreasing_index are initialized as True. These variables will be used to keep track of whether the list is increasing or decreasing.\n\n2. A for loop iterates through the elements of the nums list, starting from the second element (index 1) and going to the end of the list.\n\n3. Inside the loop, it compares the current element nums[i] with the previous element nums[i - 1].\n\n4. If nums[i] is greater than nums[i - 1], it sets decreasing_index to False. This indicates that the list is not decreasing.\n\n5. If nums[i] is less than nums[i - 1], it sets increasing_index to False. This indicates that the list is not increasing.\n\n6. After iterating through all elements in the list, the method returns True if either increasing_index or decreasing_index is True. This means that the list is either entirely non-increasing or non-decreasing, which makes it monotonic.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums:list[int]) -> bool:\n increasing_index = True\n decreasing_index = True\n\n for i in range(1, len(nums)):\n if nums[i] > nums[i - 1]:\n decreasing_index = False\n elif nums[i] < nums[i - 1]:\n increasing_index = False\n\n return increasing_index or decreasing_index\n```\n\n```\nclass Solution:\n def isMonotonic(self, A: list[int]) -> bool:\n return all(A[i] <= A[i + 1] for i in range(len(A) - 1)) or all(A[i] >= A[i + 1] for i in range(len(A) - 1))\n``` | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Monotonic Solution in Python3 with one liner also | monotonic-array | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s a step-by-step explanation of the code:\n\n1. increasing_index and decreasing_index are initialized as True. These variables will be used to keep track of whether the list is increasing or decreasing.\n\n2. A for loop iterates through the elements of the nums list, starting from the second element (index 1) and going to the end of the list.\n\n3. Inside the loop, it compares the current element nums[i] with the previous element nums[i - 1].\n\n4. If nums[i] is greater than nums[i - 1], it sets decreasing_index to False. This indicates that the list is not decreasing.\n\n5. If nums[i] is less than nums[i - 1], it sets increasing_index to False. This indicates that the list is not increasing.\n\n6. After iterating through all elements in the list, the method returns True if either increasing_index or decreasing_index is True. This means that the list is either entirely non-increasing or non-decreasing, which makes it monotonic.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums:list[int]) -> bool:\n increasing_index = True\n decreasing_index = True\n\n for i in range(1, len(nums)):\n if nums[i] > nums[i - 1]:\n decreasing_index = False\n elif nums[i] < nums[i - 1]:\n increasing_index = False\n\n return increasing_index or decreasing_index\n```\n\n```\nclass Solution:\n def isMonotonic(self, A: list[int]) -> bool:\n return all(A[i] <= A[i + 1] for i in range(len(A) - 1)) or all(A[i] >= A[i + 1] for i in range(len(A) - 1))\n``` | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Monotonic Array | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is a simple monotonic array, So there is no intuition for this problem this is direct approach problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitally initate two terms that is increasing and decreasing set to True iterate the array check if A[i] > A[i+1] increasing = False,\nif A[i] < A[i+1] decreasing = False then last return increasing or decreasing\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n# Code\n```\nclass Solution(object):\n def isMonotonic(self, A):\n increasing = decreasing = True\n\n for i in range(len(A)-1):\n if A[i] > A[i+1]:\n increasing = False\n if A[i] < A[i+1]:\n decreasing = False\n\n return increasing or decreasing\n``` | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Monotonic Array | monotonic-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is a simple monotonic array, So there is no intuition for this problem this is direct approach problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitally initate two terms that is increasing and decreasing set to True iterate the array check if A[i] > A[i+1] increasing = False,\nif A[i] < A[i+1] decreasing = False then last return increasing or decreasing\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n# Code\n```\nclass Solution(object):\n def isMonotonic(self, A):\n increasing = decreasing = True\n\n for i in range(len(A)-1):\n if A[i] > A[i+1]:\n increasing = False\n if A[i] < A[i+1]:\n decreasing = False\n\n return increasing or decreasing\n``` | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python two-liner | monotonic-array | 0 | 1 | # Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n $$O(1)$$\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n op = operator.le if nums[0] <= nums[-1] else operator.ge\n return all(op(nums[i], nums[i + 1]) for i in range(len(nums) - 1))\n``` | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Python two-liner | monotonic-array | 0 | 1 | # Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n $$O(1)$$\n\n# Code\n```\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n op = operator.le if nums[0] <= nums[-1] else operator.ge\n return all(op(nums[i], nums[i + 1]) for i in range(len(nums) - 1))\n``` | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
100% - ONE LINE TRAVERSAL APPROACH IN C++/JAVA/PYTHON/PYTHON3( TIME - O(N) SPACE - O(1)) | monotonic-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n \n Empty or Single-Element Array:\n The function first checks if the array has fewer than or equal to 1 element. In such cases, an array of this size is considered monotonic (both non-increasing and non-decreasing). This is a base case.\n\n Checking Non-Increasing Property:\n The code then iterates through the array, comparing each element with the previous one. If it finds any element that is greater than the previous one, it means the array is not non-increasing, so it sets the nonIncreasing flag to false and breaks the loop. If the loop completes without encountering this, the array is non-increasing.\n\n Checking Non-Decreasing Property:\n Similarly, the code iterates through the array to check if it is non-decreasing. If it finds any element that is less than the previous one, it means the array is not non-decreasing, so it sets the nonDecreasing flag to false and breaks the loop. If the loop completes without encountering this, the array is non-decreasing.\n\n Returning Monotonicity:\n The function returns true if either the array is non-increasing or non-decreasing, indicating that the array is monotonic. If neither of the properties holds, it returns false, indicating that the array is not monotonic.\n\nThe key idea is to determine if the array is monotonic by checking both non-increasing and non-decreasing properties independently. If either property holds, the array is considered monotonic. The code uses simple comparisons and flags to achieve this.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe provided code is a straightforward approach to determine whether an array is monotonic or not. Let\'s break down the approach step by step:\n\n Base Case Check:\n If the size of the array (n) is less than or equal to 1, the array is considered monotonic (both non-increasing and non-decreasing), so the function returns true.\n\n Check for Non-Increasing Property:\n The code iterates through the array, comparing each element with its previous element.\n If it finds any element that is greater than the previous one, it sets the nonIncreasing flag to false and breaks the loop.\n If the loop completes without encountering this, it means the array is non-increasing.\n\n Check for Non-Decreasing Property:\n Similarly, the code iterates through the array, comparing each element with its previous element.\n If it finds any element that is less than the previous one, it sets the nonDecreasing flag to false and breaks the loop.\n If the loop completes without encountering this, it means the array is non-decreasing.\n\n Return Monotonicity:\n The function returns true if either the array is non-increasing or non-decreasing, indicating that the array is monotonic.\n If neither of the properties holds, it returns false, indicating that the array is not monotonic.\n\nIn summary, the code checks for both non-increasing and non-decreasing properties independently, and if either property holds, it concludes that the array is monotonic. The logic is simple and easy to follow, making it an effective approach to solving the problem\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n The time complexity of the code is O(n), where n is the size of the input array.\n\nExplanation:\n\n The two loops that iterate through the array to check for non-increasing and non-decreasing properties both have a time complexity of O(n) since they iterate through each element in the array once.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n The space complexity of the code is O(1), which is constant.\n\nExplanation:\n\n The code uses a constant amount of extra space, regardless of the size of the input array. The variables n, nonIncreasing, nonDecreasing, and the loop counters use a constant amount of space. The space used does not grow with the input size, so it is O(1), or constant space.\n\n# Code\n```java []\nimport java.util.List;\n\nclass Solution {\n public boolean isMonotonic(int[] nums){\n int n = nums.size();\n if (n <= 1)\n return true; \n\n boolean nonIncreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums.get(i) > nums.get(i - 1)) {\n nonIncreasing = false;\n break;\n }\n }\n\n boolean nonDecreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums.get(i) < nums.get(i - 1)) {\n nonDecreasing = false;\n break;\n }\n }\n return nonIncreasing || nonDecreasing;\n }\n}\n```\n```python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n \n increasing = False\n decreasing = False\n \n for i in range(0, len(nums) - 1):\n num1 = nums[i]\n num2 = nums[i+1]\n \n if num1 < num2:\n if decreasing:\n return False\n increasing = True\n if num1 > num2:\n if increasing:\n return False\n decreasing = True\n \n return True\n```\n```C++ []\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n int n = nums.size();\n \n if (n <= 1)\n return true; // An empty or single-element array is considered monotonic\n \n // Check if the array is non-increasing\n bool nonIncreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums[i] > nums[i - 1]) {\n nonIncreasing = false;\n break;\n }\n }\n \n // Check if the array is non-decreasing\n bool nonDecreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums[i] < nums[i - 1]) {\n nonDecreasing = false;\n break;\n }\n }\n \n return nonIncreasing || nonDecreasing;\n }\n```\n```python3 []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n if nums==sorted(nums) or nums==sorted(nums,reverse=True):\n return True\n else:\n return False\n```\n\n | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
100% - ONE LINE TRAVERSAL APPROACH IN C++/JAVA/PYTHON/PYTHON3( TIME - O(N) SPACE - O(1)) | monotonic-array | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n \n Empty or Single-Element Array:\n The function first checks if the array has fewer than or equal to 1 element. In such cases, an array of this size is considered monotonic (both non-increasing and non-decreasing). This is a base case.\n\n Checking Non-Increasing Property:\n The code then iterates through the array, comparing each element with the previous one. If it finds any element that is greater than the previous one, it means the array is not non-increasing, so it sets the nonIncreasing flag to false and breaks the loop. If the loop completes without encountering this, the array is non-increasing.\n\n Checking Non-Decreasing Property:\n Similarly, the code iterates through the array to check if it is non-decreasing. If it finds any element that is less than the previous one, it means the array is not non-decreasing, so it sets the nonDecreasing flag to false and breaks the loop. If the loop completes without encountering this, the array is non-decreasing.\n\n Returning Monotonicity:\n The function returns true if either the array is non-increasing or non-decreasing, indicating that the array is monotonic. If neither of the properties holds, it returns false, indicating that the array is not monotonic.\n\nThe key idea is to determine if the array is monotonic by checking both non-increasing and non-decreasing properties independently. If either property holds, the array is considered monotonic. The code uses simple comparisons and flags to achieve this.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe provided code is a straightforward approach to determine whether an array is monotonic or not. Let\'s break down the approach step by step:\n\n Base Case Check:\n If the size of the array (n) is less than or equal to 1, the array is considered monotonic (both non-increasing and non-decreasing), so the function returns true.\n\n Check for Non-Increasing Property:\n The code iterates through the array, comparing each element with its previous element.\n If it finds any element that is greater than the previous one, it sets the nonIncreasing flag to false and breaks the loop.\n If the loop completes without encountering this, it means the array is non-increasing.\n\n Check for Non-Decreasing Property:\n Similarly, the code iterates through the array, comparing each element with its previous element.\n If it finds any element that is less than the previous one, it sets the nonDecreasing flag to false and breaks the loop.\n If the loop completes without encountering this, it means the array is non-decreasing.\n\n Return Monotonicity:\n The function returns true if either the array is non-increasing or non-decreasing, indicating that the array is monotonic.\n If neither of the properties holds, it returns false, indicating that the array is not monotonic.\n\nIn summary, the code checks for both non-increasing and non-decreasing properties independently, and if either property holds, it concludes that the array is monotonic. The logic is simple and easy to follow, making it an effective approach to solving the problem\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n The time complexity of the code is O(n), where n is the size of the input array.\n\nExplanation:\n\n The two loops that iterate through the array to check for non-increasing and non-decreasing properties both have a time complexity of O(n) since they iterate through each element in the array once.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n The space complexity of the code is O(1), which is constant.\n\nExplanation:\n\n The code uses a constant amount of extra space, regardless of the size of the input array. The variables n, nonIncreasing, nonDecreasing, and the loop counters use a constant amount of space. The space used does not grow with the input size, so it is O(1), or constant space.\n\n# Code\n```java []\nimport java.util.List;\n\nclass Solution {\n public boolean isMonotonic(int[] nums){\n int n = nums.size();\n if (n <= 1)\n return true; \n\n boolean nonIncreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums.get(i) > nums.get(i - 1)) {\n nonIncreasing = false;\n break;\n }\n }\n\n boolean nonDecreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums.get(i) < nums.get(i - 1)) {\n nonDecreasing = false;\n break;\n }\n }\n return nonIncreasing || nonDecreasing;\n }\n}\n```\n```python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n \n increasing = False\n decreasing = False\n \n for i in range(0, len(nums) - 1):\n num1 = nums[i]\n num2 = nums[i+1]\n \n if num1 < num2:\n if decreasing:\n return False\n increasing = True\n if num1 > num2:\n if increasing:\n return False\n decreasing = True\n \n return True\n```\n```C++ []\nclass Solution {\npublic:\n bool isMonotonic(vector<int>& nums) {\n int n = nums.size();\n \n if (n <= 1)\n return true; // An empty or single-element array is considered monotonic\n \n // Check if the array is non-increasing\n bool nonIncreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums[i] > nums[i - 1]) {\n nonIncreasing = false;\n break;\n }\n }\n \n // Check if the array is non-decreasing\n bool nonDecreasing = true;\n for (int i = 1; i < n; ++i) {\n if (nums[i] < nums[i - 1]) {\n nonDecreasing = false;\n break;\n }\n }\n \n return nonIncreasing || nonDecreasing;\n }\n```\n```python3 []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n if nums==sorted(nums) or nums==sorted(nums,reverse=True):\n return True\n else:\n return False\n```\n\n | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Easy to understand approach | monotonic-array | 0 | 1 | \n```python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n m = 1 # Initialize the monotonicity variable\n \n # Check for non-increasing monotonicity\n for i in range(1, len(nums)):\n if nums[i - 1] >= nums[i]: # If the previous element is greater or equal to the current element\n m += 1\n else:\n break # If not, break the loop\n \n if m == len(nums):\n return True # If the entire array is non-increasing, return True\n else:\n m = 1 # Reset the monotonicity variable\n \n # Check for non-decreasing monotonicity\n for i in range(1, len(nums)):\n if nums[i - 1] <= nums[i]: # If the previous element is smaller or equal to the current element\n m += 1\n else:\n break # If not, break the loop\n \n return (m == len(nums)) # Return True if the entire array is non-decreasing\n```\n# Intuition\n We want to check if the given array is either non-increasing or non-decreasing, which means it\'s monotonic.\n We can do this by iterating through the array once in both directions and checking if the condition holds.\n\n# Approach\n 1. Initialize a monotonicity variable `m` to 1.\n 2. Check for non-increasing monotonicity:\n - Iterate through the array from left to right.\n - If the previous element is greater or equal to the current element, increment `m`.\n - If not, break the loop.\n 3. If `m` becomes equal to the length of the array, return True because it\'s non-increasing.\n 4. Otherwise, reset `m` to 1.\n 5. Check for non-decreasing monotonicity:\n - Iterate through the array from left to right again.\n - If the previous element is smaller or equal to the current element, increment `m`.\n - If not, break the loop.\n 6. Finally, return True if `m` becomes equal to the length of the array because it\'s non-decreasing.\n\n# Complexity\n - Time complexity: O(n), where n is the length of the input array `nums`. We iterate through the array twice.\n - Space complexity: O(1), as we only use a single variable `m` to keep track of monotonicity.\n\n\n\n | 1 | An array is **monotonic** if it is either monotone increasing or monotone decreasing.
An array `nums` is monotone increasing if for all `i <= j`, `nums[i] <= nums[j]`. An array `nums` is monotone decreasing if for all `i <= j`, `nums[i] >= nums[j]`.
Given an integer array `nums`, return `true` _if the given array is monotonic, or_ `false` _otherwise_.
**Example 1:**
**Input:** nums = \[1,2,2,3\]
**Output:** true
**Example 2:**
**Input:** nums = \[6,5,4,4\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,3,2\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105` | null |
Easy to understand approach | monotonic-array | 0 | 1 | \n```python []\nclass Solution:\n def isMonotonic(self, nums: List[int]) -> bool:\n m = 1 # Initialize the monotonicity variable\n \n # Check for non-increasing monotonicity\n for i in range(1, len(nums)):\n if nums[i - 1] >= nums[i]: # If the previous element is greater or equal to the current element\n m += 1\n else:\n break # If not, break the loop\n \n if m == len(nums):\n return True # If the entire array is non-increasing, return True\n else:\n m = 1 # Reset the monotonicity variable\n \n # Check for non-decreasing monotonicity\n for i in range(1, len(nums)):\n if nums[i - 1] <= nums[i]: # If the previous element is smaller or equal to the current element\n m += 1\n else:\n break # If not, break the loop\n \n return (m == len(nums)) # Return True if the entire array is non-decreasing\n```\n# Intuition\n We want to check if the given array is either non-increasing or non-decreasing, which means it\'s monotonic.\n We can do this by iterating through the array once in both directions and checking if the condition holds.\n\n# Approach\n 1. Initialize a monotonicity variable `m` to 1.\n 2. Check for non-increasing monotonicity:\n - Iterate through the array from left to right.\n - If the previous element is greater or equal to the current element, increment `m`.\n - If not, break the loop.\n 3. If `m` becomes equal to the length of the array, return True because it\'s non-increasing.\n 4. Otherwise, reset `m` to 1.\n 5. Check for non-decreasing monotonicity:\n - Iterate through the array from left to right again.\n - If the previous element is smaller or equal to the current element, increment `m`.\n - If not, break the loop.\n 6. Finally, return True if `m` becomes equal to the length of the array because it\'s non-decreasing.\n\n# Complexity\n - Time complexity: O(n), where n is the length of the input array `nums`. We iterate through the array twice.\n - Space complexity: O(1), as we only use a single variable `m` to keep track of monotonicity.\n\n\n\n | 1 | An array `nums` of length `n` is **beautiful** if:
* `nums` is a permutation of the integers in the range `[1, n]`.
* For every `0 <= i < j < n`, there is no index `k` with `i < k < j` where `2 * nums[k] == nums[i] + nums[j]`.
Given the integer `n`, return _any **beautiful** array_ `nums` _of length_ `n`. There will be at least one valid answer for the given `n`.
**Example 1:**
**Input:** n = 4
**Output:** \[2,1,4,3\]
**Example 2:**
**Input:** n = 5
**Output:** \[3,1,2,5,4\]
**Constraints:**
* `1 <= n <= 1000` | null |
Python3 One Pass beat 94.57% 26ms Iterative BFS | increasing-order-search-tree | 0 | 1 | \n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def increasingBST(self, root: TreeNode) -> TreeNode:\n stack, a, curr, prev = [], [], root, None\n while curr or stack:\n while curr:\n stack.append(curr)\n curr = curr.right\n curr = stack.pop()\n a.append(curr.val)\n new = TreeNode(curr.val)\n new.right = prev\n prev = new\n curr = curr.left\n return prev\n \n``` | 1 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Python3 One Pass beat 94.57% 26ms Iterative BFS | increasing-order-search-tree | 0 | 1 | \n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def increasingBST(self, root: TreeNode) -> TreeNode:\n stack, a, curr, prev = [], [], root, None\n while curr or stack:\n while curr:\n stack.append(curr)\n curr = curr.right\n curr = stack.pop()\n a.append(curr.val)\n new = TreeNode(curr.val)\n new.right = prev\n prev = new\n curr = curr.left\n return prev\n \n``` | 1 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Morris In-order traversal (Python 3, O(n) time / O(1) space) | increasing-order-search-tree | 0 | 1 | Hi everyone and thank you for showing interest in reading this article \uD83D\uDE4C.\n\n**Morris In-order traversal algorithm**\nHave you ever asked yourself why do we use the stack when it comes to traversing a tree? Lets answer to this question! Stacks are used in [traversal algorithms](https://en.wikipedia.org/wiki/Tree_traversal) to keep track of parent-nodes that are not explored completely. This algorithm gets rid of the need for a stack and uses ```left``` and ```right``` links instead. Usually, this algorithm is used to collect only values, but we can do a slight modification to do relinking among different subtrees.\n\n**The workflow**\n* create variables ```dummy``` and ```tail``` that will hold a link to a new node\n* start iterating the tree with a while loop\n\t* if the current node has left child\n\t\t* find the rightmost node in the left subtree (the predecessor)\n\t\t* make the current node as the sibling\'s right child\n\t\t* delete the link between the current node and its left child\n\t\t* mark the left child as a current node\n\t* if the current node does not have left child\n\t\t* make the current node as the right child of the ```tail```\n\t\t* mark current node as the ```tail```\n\t\t* mark the right child of the current node as a current node\n5. return the right child of the ```dummy```\n\n**The code**\n```\nclass Solution:\n def increasingBST(self, node: TreeNode) -> TreeNode:\n dummy = tail = TreeNode()\n while node is not None:\n if node.left is not None:\n predecessor = node.left\n while predecessor.right is not None:\n predecessor = predecessor.right\n \n predecessor.right = node\n left, node.left = node.left, None\n node = left\n else:\n tail.right = tail = node\n node = node.right\n \n return dummy.right\n```\n\n**Complexity analysis**\nO(n) time - we traverse each node at most two times\nO(1) space - no additional data structures were used\n\n**In conclusion**\nThis is one of the most remarkably interesting algorithms I have ever learned \uD83D\uDC98. This algorithm does not only give you the possibility to collect all the nodes\' values of the tree (without using any space) but also can rearrange the whole tree where nodes are present in order and each node has only the right child.\n\n\uD83D\uDCE2 *If you think that that solution is good enough to be recommended to other LeetCoders then upvote.* | 51 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Morris In-order traversal (Python 3, O(n) time / O(1) space) | increasing-order-search-tree | 0 | 1 | Hi everyone and thank you for showing interest in reading this article \uD83D\uDE4C.\n\n**Morris In-order traversal algorithm**\nHave you ever asked yourself why do we use the stack when it comes to traversing a tree? Lets answer to this question! Stacks are used in [traversal algorithms](https://en.wikipedia.org/wiki/Tree_traversal) to keep track of parent-nodes that are not explored completely. This algorithm gets rid of the need for a stack and uses ```left``` and ```right``` links instead. Usually, this algorithm is used to collect only values, but we can do a slight modification to do relinking among different subtrees.\n\n**The workflow**\n* create variables ```dummy``` and ```tail``` that will hold a link to a new node\n* start iterating the tree with a while loop\n\t* if the current node has left child\n\t\t* find the rightmost node in the left subtree (the predecessor)\n\t\t* make the current node as the sibling\'s right child\n\t\t* delete the link between the current node and its left child\n\t\t* mark the left child as a current node\n\t* if the current node does not have left child\n\t\t* make the current node as the right child of the ```tail```\n\t\t* mark current node as the ```tail```\n\t\t* mark the right child of the current node as a current node\n5. return the right child of the ```dummy```\n\n**The code**\n```\nclass Solution:\n def increasingBST(self, node: TreeNode) -> TreeNode:\n dummy = tail = TreeNode()\n while node is not None:\n if node.left is not None:\n predecessor = node.left\n while predecessor.right is not None:\n predecessor = predecessor.right\n \n predecessor.right = node\n left, node.left = node.left, None\n node = left\n else:\n tail.right = tail = node\n node = node.right\n \n return dummy.right\n```\n\n**Complexity analysis**\nO(n) time - we traverse each node at most two times\nO(1) space - no additional data structures were used\n\n**In conclusion**\nThis is one of the most remarkably interesting algorithms I have ever learned \uD83D\uDC98. This algorithm does not only give you the possibility to collect all the nodes\' values of the tree (without using any space) but also can rearrange the whole tree where nodes are present in order and each node has only the right child.\n\n\uD83D\uDCE2 *If you think that that solution is good enough to be recommended to other LeetCoders then upvote.* | 51 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Solution | increasing-order-search-tree | 1 | 1 | ```C++ []\nclass Solution {\n public:\n TreeNode* increasingBST(TreeNode* root, TreeNode* tail = nullptr) {\n if (root == nullptr)\n return tail;\n TreeNode* ans = increasingBST(root->left, root);\n root->left = nullptr;\n root->right = increasingBST(root->right, tail);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def dfsInorder(self, root):\n if root is None: return\n self.dfsInorder(root.left)\n self.represented.append(root.val)\n self.dfsInorder(root.right)\n\n def increasingBST(self, root: TreeNode) -> TreeNode:\n self.represented = []\n self.dfsInorder(root)\n\n pointer = answer = TreeNode(self.represented[0])\n for node in self.represented[1:]:\n pointer.right = TreeNode(node)\n pointer = pointer.right\n\n return answer\n```\n\n```Java []\nclass Solution {\n TreeNode arr = new TreeNode(0, null, null);\n TreeNode pointer = arr;\n public TreeNode increasingBST(TreeNode root) {\n func(root);\n return arr.right;\n }\n void func (TreeNode root) {\n if (root==null) return;\n func(root.left);\n TreeNode temp = new TreeNode (root.val, null, null);\n pointer.right = temp;\n pointer = pointer.right;\n func(root.right);\n }\n}\n```\n | 4 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Solution | increasing-order-search-tree | 1 | 1 | ```C++ []\nclass Solution {\n public:\n TreeNode* increasingBST(TreeNode* root, TreeNode* tail = nullptr) {\n if (root == nullptr)\n return tail;\n TreeNode* ans = increasingBST(root->left, root);\n root->left = nullptr;\n root->right = increasingBST(root->right, tail);\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def dfsInorder(self, root):\n if root is None: return\n self.dfsInorder(root.left)\n self.represented.append(root.val)\n self.dfsInorder(root.right)\n\n def increasingBST(self, root: TreeNode) -> TreeNode:\n self.represented = []\n self.dfsInorder(root)\n\n pointer = answer = TreeNode(self.represented[0])\n for node in self.represented[1:]:\n pointer.right = TreeNode(node)\n pointer = pointer.right\n\n return answer\n```\n\n```Java []\nclass Solution {\n TreeNode arr = new TreeNode(0, null, null);\n TreeNode pointer = arr;\n public TreeNode increasingBST(TreeNode root) {\n func(root);\n return arr.right;\n }\n void func (TreeNode root) {\n if (root==null) return;\n func(root.left);\n TreeNode temp = new TreeNode (root.val, null, null);\n pointer.right = temp;\n pointer = pointer.right;\n func(root.right);\n }\n}\n```\n | 4 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Easy Python Solution beats 90% with Comments! | increasing-order-search-tree | 0 | 1 | ```\nclass Solution:\n def increasingBST(self, root: TreeNode) -> TreeNode:\n \n vals = []\n # Easy recursive Inorder Traversal to get our values to insert.\n def inord(node):\n if not node:\n return\n inord(node.left)\n vals.append(node.val)\n inord(node.right)\n \n inord(root)\n # Create a new tree to return.\n tree = TreeNode(val=vals[0])\n\t\t# Use a sentinel so we dont lose our tree location in memory.\n tmp = tree\n\t\t# Iterate through our vals, creating a new right node with the current val.\n for i in vals[1:]:\n tmp.right = TreeNode(val=i)\n\t\t\t# Move the sentinel to the next node.\n tmp = tmp.right\n \n return tree\n``` | 36 | Given the `root` of a binary search tree, rearrange the tree in **in-order** so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
**Example 1:**
**Input:** root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]
**Output:** \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]
**Example 2:**
**Input:** root = \[5,1,7\]
**Output:** \[1,null,5,null,7\]
**Constraints:**
* The number of nodes in the given tree will be in the range `[1, 100]`.
* `0 <= Node.val <= 1000` | null |
Easy Python Solution beats 90% with Comments! | increasing-order-search-tree | 0 | 1 | ```\nclass Solution:\n def increasingBST(self, root: TreeNode) -> TreeNode:\n \n vals = []\n # Easy recursive Inorder Traversal to get our values to insert.\n def inord(node):\n if not node:\n return\n inord(node.left)\n vals.append(node.val)\n inord(node.right)\n \n inord(root)\n # Create a new tree to return.\n tree = TreeNode(val=vals[0])\n\t\t# Use a sentinel so we dont lose our tree location in memory.\n tmp = tree\n\t\t# Iterate through our vals, creating a new right node with the current val.\n for i in vals[1:]:\n tmp.right = TreeNode(val=i)\n\t\t\t# Move the sentinel to the next node.\n tmp = tmp.right\n \n return tree\n``` | 36 | You have a `RecentCounter` class which counts the number of recent requests within a certain time frame.
Implement the `RecentCounter` class:
* `RecentCounter()` Initializes the counter with zero recent requests.
* `int ping(int t)` Adds a new request at time `t`, where `t` represents some time in milliseconds, and returns the number of requests that has happened in the past `3000` milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range `[t - 3000, t]`.
It is **guaranteed** that every call to `ping` uses a strictly larger value of `t` than the previous call.
**Example 1:**
**Input**
\[ "RecentCounter ", "ping ", "ping ", "ping ", "ping "\]
\[\[\], \[1\], \[100\], \[3001\], \[3002\]\]
**Output**
\[null, 1, 2, 3, 3\]
**Explanation**
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = \[1\], range is \[-2999,1\], return 1
recentCounter.ping(100); // requests = \[1, 100\], range is \[-2900,100\], return 2
recentCounter.ping(3001); // requests = \[1, 100, 3001\], range is \[1,3001\], return 3
recentCounter.ping(3002); // requests = \[1, 100, 3001, 3002\], range is \[2,3002\], return 3
**Constraints:**
* `1 <= t <= 109`
* Each test case will call `ping` with **strictly increasing** values of `t`.
* At most `104` calls will be made to `ping`. | null |
Solution | bitwise-ors-of-subarrays | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int subarrayBitwiseORs(vector<int>& arr) {\n vector<int> or_results;\n int i = 0, j = 0;\n int start,a2;\n for (auto a: arr) {\n start = or_results.size();\n or_results.emplace_back(a);\n for (int k = i; k < j; k++) {\n a2 = or_results[k] | a;\n if (a2 > or_results.back()) {\n or_results.emplace_back(a2);\n }\n }\n i = start, j = or_results.size();\n }\n return unordered_set<int>(or_results.begin(), or_results.end()).size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n res = set()\n main = set()\n\n for a in arr:\n local = set()\n local.add(a)\n for b in main:\n local.add(b|a)\n main = local\n res |= main\n \n return len(res)\n```\n\n```Java []\nclass Solution {\n public int subarrayBitwiseORs(int[] arr) {\n Set<Integer> ors= new HashSet<>();\n\n for(int i=arr.length-1; i>=0; i--) {\n ors.add(arr[i]);\n for(int j=i+1; j<arr.length; j++) {\n if((arr[j] | arr[i]) == arr[j]) {\n break;\n }\n arr[j] |= arr[i];\n ors.add(arr[j]);\n }\n }\n return ors.size();\n }\n}\n```\n | 1 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Solution | bitwise-ors-of-subarrays | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int subarrayBitwiseORs(vector<int>& arr) {\n vector<int> or_results;\n int i = 0, j = 0;\n int start,a2;\n for (auto a: arr) {\n start = or_results.size();\n or_results.emplace_back(a);\n for (int k = i; k < j; k++) {\n a2 = or_results[k] | a;\n if (a2 > or_results.back()) {\n or_results.emplace_back(a2);\n }\n }\n i = start, j = or_results.size();\n }\n return unordered_set<int>(or_results.begin(), or_results.end()).size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n res = set()\n main = set()\n\n for a in arr:\n local = set()\n local.add(a)\n for b in main:\n local.add(b|a)\n main = local\n res |= main\n \n return len(res)\n```\n\n```Java []\nclass Solution {\n public int subarrayBitwiseORs(int[] arr) {\n Set<Integer> ors= new HashSet<>();\n\n for(int i=arr.length-1; i>=0; i--) {\n ors.add(arr[i]);\n for(int j=i+1; j<arr.length; j++) {\n if((arr[j] | arr[i]) == arr[j]) {\n break;\n }\n arr[j] |= arr[i];\n ors.add(arr[j]);\n }\n }\n return ors.size();\n }\n}\n```\n | 1 | You are given an `n x n` binary matrix `grid` where `1` represents land and `0` represents water.
An **island** is a 4-directionally connected group of `1`'s not connected to any other `1`'s. There are **exactly two islands** in `grid`.
You may change `0`'s to `1`'s to connect the two islands to form **one island**.
Return _the smallest number of_ `0`_'s you must flip to connect the two islands_.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** 1
**Example 2:**
**Input:** grid = \[\[0,1,0\],\[0,0,0\],\[0,0,1\]\]
**Output:** 2
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,0,0,0,1\],\[1,0,1,0,1\],\[1,0,0,0,1\],\[1,1,1,1,1\]\]
**Output:** 1
**Constraints:**
* `n == grid.length == grid[i].length`
* `2 <= n <= 100`
* `grid[i][j]` is either `0` or `1`.
* There are exactly two islands in `grid`. | null |
Simple approach with Example | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\nFind all possible subarraies and get the number of unique sums for those subarraies\n\n# Approach\nIterate the array and built all possible subarrys with unique OR sums\n\n\n# Code\n```\nclass Solution(object):\n def subarrayBitwiseORs(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n\n result = tmp = set()\n for n in arr:\n tmp = {num | n for num in tmp} | {n}\n result |= tmp\n return len(result)\n```\n\n# Example \n\narr = [1, 2, 4]\n\n----level 1------\n[1]\n----level 2------\n[1, 2], [2]\n----level 3------\n[1, 2, 4], [2, 4], [4]\n\nThen the result will become the number of unique OR sums for all subarrays in level 1, 2 and 3. \n\n**Hint:** [1, 4] is not valid subarray, so using a single set to store intermidiate values won\'t work.\n | 0 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Simple approach with Example | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\nFind all possible subarraies and get the number of unique sums for those subarraies\n\n# Approach\nIterate the array and built all possible subarrys with unique OR sums\n\n\n# Code\n```\nclass Solution(object):\n def subarrayBitwiseORs(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n\n result = tmp = set()\n for n in arr:\n tmp = {num | n for num in tmp} | {n}\n result |= tmp\n return len(result)\n```\n\n# Example \n\narr = [1, 2, 4]\n\n----level 1------\n[1]\n----level 2------\n[1, 2], [2]\n----level 3------\n[1, 2, 4], [2, 4], [4]\n\nThen the result will become the number of unique OR sums for all subarrays in level 1, 2 and 3. \n\n**Hint:** [1, 4] is not valid subarray, so using a single set to store intermidiate values won\'t work.\n | 0 | You are given an `n x n` binary matrix `grid` where `1` represents land and `0` represents water.
An **island** is a 4-directionally connected group of `1`'s not connected to any other `1`'s. There are **exactly two islands** in `grid`.
You may change `0`'s to `1`'s to connect the two islands to form **one island**.
Return _the smallest number of_ `0`_'s you must flip to connect the two islands_.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** 1
**Example 2:**
**Input:** grid = \[\[0,1,0\],\[0,0,0\],\[0,0,1\]\]
**Output:** 2
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,0,0,0,1\],\[1,0,1,0,1\],\[1,0,0,0,1\],\[1,1,1,1,1\]\]
**Output:** 1
**Constraints:**
* `n == grid.length == grid[i].length`
* `2 <= n <= 100`
* `grid[i][j]` is either `0` or `1`.
* There are exactly two islands in `grid`. | null |
set | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe idea is dynamic programing\n- ans = {n | i for i in ans} | {n}\n- {n} for current number\n- ans is the previous set before n\n- [1, 2, 3], while i = 2, ans = {2, 2 | 1}\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n res, ans = set(), set()\n for n in arr:\n ans = {n | i for i in ans} | {n}\n res |= ans\n return len(res)\n``` | 0 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
set | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe idea is dynamic programing\n- ans = {n | i for i in ans} | {n}\n- {n} for current number\n- ans is the previous set before n\n- [1, 2, 3], while i = 2, ans = {2, 2 | 1}\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n res, ans = set(), set()\n for n in arr:\n ans = {n | i for i in ans} | {n}\n res |= ans\n return len(res)\n``` | 0 | You are given an `n x n` binary matrix `grid` where `1` represents land and `0` represents water.
An **island** is a 4-directionally connected group of `1`'s not connected to any other `1`'s. There are **exactly two islands** in `grid`.
You may change `0`'s to `1`'s to connect the two islands to form **one island**.
Return _the smallest number of_ `0`_'s you must flip to connect the two islands_.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** 1
**Example 2:**
**Input:** grid = \[\[0,1,0\],\[0,0,0\],\[0,0,1\]\]
**Output:** 2
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,0,0,0,1\],\[1,0,1,0,1\],\[1,0,0,0,1\],\[1,1,1,1,1\]\]
**Output:** 1
**Constraints:**
* `n == grid.length == grid[i].length`
* `2 <= n <= 100`
* `grid[i][j]` is either `0` or `1`.
* There are exactly two islands in `grid`. | null |
🚀 Time: O(n * w) Space: O(n * w) | 📚 Detailed Explanations | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\nWe need to find the number of distinct bitwise ORs of all non-empty subarrays of the input array. A brute-force approach would be to iterate through all possible subarrays, calculate their bitwise OR, and store unique results in a set. However, this approach will have a high time complexity. We can optimize it by using dynamic programming to store and reuse the results of previous calculations.\n\n# Approach\n1. Initialize an empty set `ans` to store unique bitwise ORs of subarrays.\n2. Initialize an empty set `endwithThis` to store bitwise ORs of subarrays ending at the current element.\n3. Iterate through the input array `arr`:\n a. For each element `n` in `arr`, update the `endwithThis` set by applying bitwise OR of `n` with all the elements in the `endwithThis` set, and then add `n` itself to the set.\n b. Update the `ans` set with the union of `ans` and `endwithThis` sets.\n4. Return the length of the `ans` set, which represents the number of unique bitwise ORs of subarrays.\n\n# Complexity\n- Time complexity: The time complexity is $$O(n * w)$$, where n is the length of the input array, and w is the maximum number of bits required to represent the largest integer in the array. This is because, in the worst case, we need to calculate the bitwise OR for all subarrays ending at each element, and for each calculation, we need to perform bitwise OR operations for up to w bits.\n- Space complexity: The space complexity is also $$O(n * w)$$, as we store the bitwise ORs of subarrays in the `ans` and `endwithThis` sets, and each set can store up to n * w elements.\n\n# Code\n```python\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n ans = set()\n endwithThis = set()\n for n in arr:\n endwithThis = {n | x for x in endwithThis}\n endwithThis.add(n)\n ans |= endwithThis\n return len(ans)\n | 0 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
🚀 Time: O(n * w) Space: O(n * w) | 📚 Detailed Explanations | bitwise-ors-of-subarrays | 0 | 1 | # Intuition\nWe need to find the number of distinct bitwise ORs of all non-empty subarrays of the input array. A brute-force approach would be to iterate through all possible subarrays, calculate their bitwise OR, and store unique results in a set. However, this approach will have a high time complexity. We can optimize it by using dynamic programming to store and reuse the results of previous calculations.\n\n# Approach\n1. Initialize an empty set `ans` to store unique bitwise ORs of subarrays.\n2. Initialize an empty set `endwithThis` to store bitwise ORs of subarrays ending at the current element.\n3. Iterate through the input array `arr`:\n a. For each element `n` in `arr`, update the `endwithThis` set by applying bitwise OR of `n` with all the elements in the `endwithThis` set, and then add `n` itself to the set.\n b. Update the `ans` set with the union of `ans` and `endwithThis` sets.\n4. Return the length of the `ans` set, which represents the number of unique bitwise ORs of subarrays.\n\n# Complexity\n- Time complexity: The time complexity is $$O(n * w)$$, where n is the length of the input array, and w is the maximum number of bits required to represent the largest integer in the array. This is because, in the worst case, we need to calculate the bitwise OR for all subarrays ending at each element, and for each calculation, we need to perform bitwise OR operations for up to w bits.\n- Space complexity: The space complexity is also $$O(n * w)$$, as we store the bitwise ORs of subarrays in the `ans` and `endwithThis` sets, and each set can store up to n * w elements.\n\n# Code\n```python\nclass Solution:\n def subarrayBitwiseORs(self, arr: List[int]) -> int:\n ans = set()\n endwithThis = set()\n for n in arr:\n endwithThis = {n | x for x in endwithThis}\n endwithThis.add(n)\n ans |= endwithThis\n return len(ans)\n | 0 | You are given an `n x n` binary matrix `grid` where `1` represents land and `0` represents water.
An **island** is a 4-directionally connected group of `1`'s not connected to any other `1`'s. There are **exactly two islands** in `grid`.
You may change `0`'s to `1`'s to connect the two islands to form **one island**.
Return _the smallest number of_ `0`_'s you must flip to connect the two islands_.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** 1
**Example 2:**
**Input:** grid = \[\[0,1,0\],\[0,0,0\],\[0,0,1\]\]
**Output:** 2
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,0,0,0,1\],\[1,0,1,0,1\],\[1,0,0,0,1\],\[1,1,1,1,1\]\]
**Output:** 1
**Constraints:**
* `n == grid.length == grid[i].length`
* `2 <= n <= 100`
* `grid[i][j]` is either `0` or `1`.
* There are exactly two islands in `grid`. | null |
Python short and clean solution | bitwise-ors-of-subarrays | 0 | 1 | ```\nclass Solution:\n def subarrayBitwiseORs(self, A: List[int]) -> int:\n my_set = set(A)\n curr = 0\n prev = set()\n prev.add(A[0])\n for num in A[1:]:\n temp = set()\n for p in prev:\n temp.add(num | p)\n my_set.add(num | p)\n prev = temp\n prev.add(num)\n\n return len(my_set)\n \n``` | 8 | Given an integer array `arr`, return _the number of distinct bitwise ORs of all the non-empty subarrays of_ `arr`.
The bitwise OR of a subarray is the bitwise OR of each integer in the subarray. The bitwise OR of a subarray of one integer is that integer.
A **subarray** is a contiguous non-empty sequence of elements within an array.
**Example 1:**
**Input:** arr = \[0\]
**Output:** 1
**Explanation:** There is only one possible result: 0.
**Example 2:**
**Input:** arr = \[1,1,2\]
**Output:** 3
**Explanation:** The possible subarrays are \[1\], \[1\], \[2\], \[1, 1\], \[1, 2\], \[1, 1, 2\].
These yield the results 1, 1, 2, 1, 3, 3.
There are 3 unique values, so the answer is 3.
**Example 3:**
**Input:** arr = \[1,2,4\]
**Output:** 6
**Explanation:** The possible results are 1, 2, 3, 4, 6, and 7.
**Constraints:**
* `1 <= arr.length <= 5 * 104`
* `0 <= arr[i] <= 109` | We don't need any special algorithms to do this. You just need to know what the transpose of a matrix looks like. Rows become columns and vice versa! |
Python short and clean solution | bitwise-ors-of-subarrays | 0 | 1 | ```\nclass Solution:\n def subarrayBitwiseORs(self, A: List[int]) -> int:\n my_set = set(A)\n curr = 0\n prev = set()\n prev.add(A[0])\n for num in A[1:]:\n temp = set()\n for p in prev:\n temp.add(num | p)\n my_set.add(num | p)\n prev = temp\n prev.add(num)\n\n return len(my_set)\n \n``` | 8 | You are given an `n x n` binary matrix `grid` where `1` represents land and `0` represents water.
An **island** is a 4-directionally connected group of `1`'s not connected to any other `1`'s. There are **exactly two islands** in `grid`.
You may change `0`'s to `1`'s to connect the two islands to form **one island**.
Return _the smallest number of_ `0`_'s you must flip to connect the two islands_.
**Example 1:**
**Input:** grid = \[\[0,1\],\[1,0\]\]
**Output:** 1
**Example 2:**
**Input:** grid = \[\[0,1,0\],\[0,0,0\],\[0,0,1\]\]
**Output:** 2
**Example 3:**
**Input:** grid = \[\[1,1,1,1,1\],\[1,0,0,0,1\],\[1,0,1,0,1\],\[1,0,0,0,1\],\[1,1,1,1,1\]\]
**Output:** 1
**Constraints:**
* `n == grid.length == grid[i].length`
* `2 <= n <= 100`
* `grid[i][j]` is either `0` or `1`.
* There are exactly two islands in `grid`. | null |
Very Simple Approach, Beginner Friendly!!!!!! | orderly-queue | 0 | 1 | # Intuition\nThe questions seems to be very tricky at first but its all about recognizing the pattern. My initial thoughts were to sort the string for k > 1 and think of a way to write a solution for k == 1.\n\n# Approach\n1. for k == 1 we can try generating all the variations and store it in a set until the strings being generated starts repeating. Once you encounter such situation simply return the min from set. That will be our answer.\n2. For k > 1, we can simply sort the string and return our answer\n\n# Complexity\n- Time complexity:\nO(N ^ 2) # NOT SURE\n\n- Space complexity:\nO(len(visited))\n\n# Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n visited = set()\n if k == 1:\n arr = list(s)\n\n while "".join(arr) not in visited:\n visited.add("".join(arr))\n ele = arr.pop(0)\n arr.append(ele)\n \n \n\n return min(visited)\n\n ans = sorted(s)\n return "".join(ans)\n``` | 2 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
Very Simple Approach, Beginner Friendly!!!!!! | orderly-queue | 0 | 1 | # Intuition\nThe questions seems to be very tricky at first but its all about recognizing the pattern. My initial thoughts were to sort the string for k > 1 and think of a way to write a solution for k == 1.\n\n# Approach\n1. for k == 1 we can try generating all the variations and store it in a set until the strings being generated starts repeating. Once you encounter such situation simply return the min from set. That will be our answer.\n2. For k > 1, we can simply sort the string and return our answer\n\n# Complexity\n- Time complexity:\nO(N ^ 2) # NOT SURE\n\n- Space complexity:\nO(len(visited))\n\n# Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n visited = set()\n if k == 1:\n arr = list(s)\n\n while "".join(arr) not in visited:\n visited.add("".join(arr))\n ele = arr.pop(0)\n arr.append(ele)\n \n \n\n return min(visited)\n\n ans = sorted(s)\n return "".join(ans)\n``` | 2 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
Simple Solution beats 97% | orderly-queue | 0 | 1 | # Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k > 1: return \'\'.join(sorted(s))\n m = s\n for i in range(1, len(s)):\n # print(s[i: ]+s[: i])\n m = min(m, s[i: ]+s[: i])\n return m\n``` | 1 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
Simple Solution beats 97% | orderly-queue | 0 | 1 | # Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k > 1: return \'\'.join(sorted(s))\n m = s\n for i in range(1, len(s)):\n # print(s[i: ]+s[: i])\n m = min(m, s[i: ]+s[: i])\n return m\n``` | 1 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
Solution | orderly-queue | 1 | 1 | ```C++ []\n#pragma once\n#include <algorithm>\n#include <string>\n\nclass Solution {\nprivate:\n static bool less(const std::string &s, size_t l, size_t r) {\n for (size_t i = 0; i < s.size(); ++i) {\n const auto s1 = s[(l + i) % s.size()];\n const auto s2 = s[(r + i) % s.size()];\n if (s1 != s2) {\n return s1 < s2;\n }\n }\n return true;\n }\n static size_t min_position(const std::string &s) {\n size_t i = 0;\n for (size_t j = 1; j < s.size(); ++j) {\n if (less(s, j, i)) {\n i = j;\n }\n }\n return i;\n }\npublic:\n static std::string orderlyQueue(std::string s, int k) {\n if (k == 1) {\n std::rotate(s.begin(), s.begin() + min_position(s), s.end());\n } else {\n std::sort(s.begin(), s.end());\n }\n return s;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k == 1:\n return min(s[i:]+s[:i] for i in range(len(s)))\n\n else :\n return \'\'.join(sorted(s))\n```\n\n```Java []\nclass Solution {\n public String orderlyQueue(String s, int k) {\n int[] countChar = new int[26];\n int length = s.length();\n for(int i = 0 ; i < length ; ++i) {\n countChar[s.charAt(i) - \'a\']++;\n }\n if(k > 1) {\n StringBuilder sb = new StringBuilder();\n for(int i = 0 ; i < 26 ; ++i) {\n int appearance = countChar[i];\n char c = (char)(\'a\' + i);\n for(int r = 0 ; r < appearance ; ++r) {\n sb.append(c);\n }\n }\n return sb.toString();\n }\n char startChar = \'a\';\n for(int i = 0 ; i < 26 ; ++i) {\n if(countChar[i] > 0) {\n startChar = (char)(\'a\' + i);\n break;\n }\n }\n List<String> beginWithStartChar = new ArrayList<>();\n for(int i = 0 ; i < length ; ++i) {\n if(s.charAt(i) == startChar) {\n beginWithStartChar.add(s.substring(i) + s.substring(0, i));\n }\n }\n String min = beginWithStartChar.get(0);\n for(String strBeginWithStartChar : beginWithStartChar) {\n if(strBeginWithStartChar.compareTo(min) < 0) min = strBeginWithStartChar;\n }\n return min;\n }\n}\n```\n | 1 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
Solution | orderly-queue | 1 | 1 | ```C++ []\n#pragma once\n#include <algorithm>\n#include <string>\n\nclass Solution {\nprivate:\n static bool less(const std::string &s, size_t l, size_t r) {\n for (size_t i = 0; i < s.size(); ++i) {\n const auto s1 = s[(l + i) % s.size()];\n const auto s2 = s[(r + i) % s.size()];\n if (s1 != s2) {\n return s1 < s2;\n }\n }\n return true;\n }\n static size_t min_position(const std::string &s) {\n size_t i = 0;\n for (size_t j = 1; j < s.size(); ++j) {\n if (less(s, j, i)) {\n i = j;\n }\n }\n return i;\n }\npublic:\n static std::string orderlyQueue(std::string s, int k) {\n if (k == 1) {\n std::rotate(s.begin(), s.begin() + min_position(s), s.end());\n } else {\n std::sort(s.begin(), s.end());\n }\n return s;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k == 1:\n return min(s[i:]+s[:i] for i in range(len(s)))\n\n else :\n return \'\'.join(sorted(s))\n```\n\n```Java []\nclass Solution {\n public String orderlyQueue(String s, int k) {\n int[] countChar = new int[26];\n int length = s.length();\n for(int i = 0 ; i < length ; ++i) {\n countChar[s.charAt(i) - \'a\']++;\n }\n if(k > 1) {\n StringBuilder sb = new StringBuilder();\n for(int i = 0 ; i < 26 ; ++i) {\n int appearance = countChar[i];\n char c = (char)(\'a\' + i);\n for(int r = 0 ; r < appearance ; ++r) {\n sb.append(c);\n }\n }\n return sb.toString();\n }\n char startChar = \'a\';\n for(int i = 0 ; i < 26 ; ++i) {\n if(countChar[i] > 0) {\n startChar = (char)(\'a\' + i);\n break;\n }\n }\n List<String> beginWithStartChar = new ArrayList<>();\n for(int i = 0 ; i < length ; ++i) {\n if(s.charAt(i) == startChar) {\n beginWithStartChar.add(s.substring(i) + s.substring(0, i));\n }\n }\n String min = beginWithStartChar.get(0);\n for(String strBeginWithStartChar : beginWithStartChar) {\n if(strBeginWithStartChar.compareTo(min) < 0) min = strBeginWithStartChar;\n }\n return min;\n }\n}\n```\n | 1 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
This is not a hard problem [no ds or algorithm applied] | orderly-queue | 0 | 1 | # Intuition\nI posted this so that you don\'t waste time, as I did behind this problem using heapq or any fancy algorithm.\n\n# Approach\nJust return sorted string if k > 1: yes, they should remove "hard" badge!\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k == 1:\n ans = s\n for _ in range(len(s)):\n s = s[1:] + s[0]\n ans = min(ans, s)\n return ans\n else:\n return \'\'.join(sorted(s))\n\n\n\n``` | 1 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
This is not a hard problem [no ds or algorithm applied] | orderly-queue | 0 | 1 | # Intuition\nI posted this so that you don\'t waste time, as I did behind this problem using heapq or any fancy algorithm.\n\n# Approach\nJust return sorted string if k > 1: yes, they should remove "hard" badge!\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k == 1:\n ans = s\n for _ in range(len(s)):\n s = s[1:] + s[0]\n ans = min(ans, s)\n return ans\n else:\n return \'\'.join(sorted(s))\n\n\n\n``` | 1 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
Easy python solution using queue || TC: O(K^2+Nlog(N)), SC: O(N) | orderly-queue | 0 | 1 | ```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n st=""\n lst=list(s)\n lst.sort()\n queue=list(s)\n flg=defaultdict(lambda :0)\n if k==1:\n pt=[z for z in range(len(lst)) if s[z]==lst[0]]\n mn=s[pt[0]:]+s[:pt[0]]\n for p in range(len(pt)):\n mn=min(mn,s[pt[p]:]+s[:pt[p]])\n return mn\n ct=k\n if k==len(s):\n return "".join(lst)\n while k>0:\n if queue[0][0]==lst[0]:\n st+=queue.pop(0)[0]\n lst.pop(0)\n k-=1\n for nm in flg:\n flg[nm]=0\n else:\n mn=queue[0]\n ind=0\n for i in range(1,min(ct,len(queue)-1)):\n if queue[i]<mn and queue[i]!=lst[0] and flg[queue[i]]!=1:\n ind=i\n x=queue.pop(ind)\n queue.append(x)\n flg[x]=1\n if ct>1:\n queue.sort()\n return st+"".join(queue)\n``` | 6 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
Easy python solution using queue || TC: O(K^2+Nlog(N)), SC: O(N) | orderly-queue | 0 | 1 | ```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n st=""\n lst=list(s)\n lst.sort()\n queue=list(s)\n flg=defaultdict(lambda :0)\n if k==1:\n pt=[z for z in range(len(lst)) if s[z]==lst[0]]\n mn=s[pt[0]:]+s[:pt[0]]\n for p in range(len(pt)):\n mn=min(mn,s[pt[p]:]+s[:pt[p]])\n return mn\n ct=k\n if k==len(s):\n return "".join(lst)\n while k>0:\n if queue[0][0]==lst[0]:\n st+=queue.pop(0)[0]\n lst.pop(0)\n k-=1\n for nm in flg:\n flg[nm]=0\n else:\n mn=queue[0]\n ind=0\n for i in range(1,min(ct,len(queue)-1)):\n if queue[i]<mn and queue[i]!=lst[0] and flg[queue[i]]!=1:\n ind=i\n x=queue.pop(ind)\n queue.append(x)\n flg[x]=1\n if ct>1:\n queue.sort()\n return st+"".join(queue)\n``` | 6 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
Python Easy Solution : Expalined | orderly-queue | 0 | 1 | ```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k>1:\n return \'\'.join(sorted(s))\n n=len(s)\n t=s*2 # t=cbacba\n ans=s # ans=cba\n for i in range(1,n):\n s1=t[i:i+n] # 1st move : s1=t[1:1+3] = bac\n ans=min(ans,s1) # 2nd move : s1=t[2:2+3] = acb\n return ans\n```\n\n**Upvote if you like the solution or ask if there is any query** | 1 | You are given a string `s` and an integer `k`. You can choose one of the first `k` letters of `s` and append it at the end of the string..
Return _the lexicographically smallest string you could have after applying the mentioned step any number of moves_.
**Example 1:**
**Input:** s = "cba ", k = 1
**Output:** "acb "
**Explanation:**
In the first move, we move the 1st character 'c' to the end, obtaining the string "bac ".
In the second move, we move the 1st character 'b' to the end, obtaining the final result "acb ".
**Example 2:**
**Input:** s = "baaca ", k = 3
**Output:** "aaabc "
**Explanation:**
In the first move, we move the 1st character 'b' to the end, obtaining the string "aacab ".
In the second move, we move the 3rd character 'c' to the end, obtaining the final result "aaabc ".
**Constraints:**
* `1 <= k <= s.length <= 1000`
* `s` consist of lowercase English letters. | null |
Python Easy Solution : Expalined | orderly-queue | 0 | 1 | ```\nclass Solution:\n def orderlyQueue(self, s: str, k: int) -> str:\n if k>1:\n return \'\'.join(sorted(s))\n n=len(s)\n t=s*2 # t=cbacba\n ans=s # ans=cba\n for i in range(1,n):\n s1=t[i:i+n] # 1st move : s1=t[1:1+3] = bac\n ans=min(ans,s1) # 2nd move : s1=t[2:2+3] = acb\n return ans\n```\n\n**Upvote if you like the solution or ask if there is any query** | 1 | The chess knight has a **unique movement**, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an **L**). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
We have a chess knight and a phone pad as shown below, the knight **can only stand on a numeric cell** (i.e. blue cell).
Given an integer `n`, return how many distinct phone numbers of length `n` we can dial.
You are allowed to place the knight **on any numeric cell** initially and then you should perform `n - 1` jumps to dial a number of length `n`. All jumps should be **valid** knight jumps.
As the answer may be very large, **return the answer modulo** `109 + 7`.
**Example 1:**
**Input:** n = 1
**Output:** 10
**Explanation:** We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
**Example 2:**
**Input:** n = 2
**Output:** 20
**Explanation:** All the valid number we can dial are \[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94\]
**Example 3:**
**Input:** n = 3131
**Output:** 136006598
**Explanation:** Please take care of the mod.
**Constraints:**
* `1 <= n <= 5000` | null |
Solution | rle-iterator | 1 | 1 | ```C++ []\nclass RLEIterator {\npublic:\n RLEIterator(const std::vector<int>& encoding)\n {\n m_encodings.reserve(encoding.size() / 2);\n for (int i = 0; i < encoding.size(); i += 2) {\n const int count = encoding[i];\n const int number = encoding[i + 1];\n m_encodings.emplace_back(count, number);\n }\n }\n int next(int n)\n {\n while (m_current_idx < m_encodings.size() && m_encodings[m_current_idx].first < n) {\n n -= m_encodings[m_current_idx].first;\n m_encodings[m_current_idx].first = 0;\n ++m_current_idx;\n }\n if (m_current_idx >= m_encodings.size())\n return -1;\n m_encodings[m_current_idx].first -= n;\n return m_encodings[m_current_idx].second;\n }\nprivate:\n int m_current_idx = 0;\n std::vector<std::pair<int, int>> m_encodings;\n};\n```\n\n```Python3 []\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n```\n\n```Java []\nclass RLEIterator {\n public int[] encoding;\n public int index;\n public RLEIterator(int[] encoding) {\n this.encoding = encoding;\n this.index = 0;\n }\n public int next(int n) { \n while (n > 0 && index < encoding.length) {\n if (encoding[index] < n) {\n n -= encoding[index];\n encoding[index] = 0;\n index += 2;\n } else {\n encoding[index] -= n;\n n = 0;\n }\n }\n if (index >= encoding.length) return -1;\n return encoding[index + 1];\n }\n}\n```\n | 1 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Solution | rle-iterator | 1 | 1 | ```C++ []\nclass RLEIterator {\npublic:\n RLEIterator(const std::vector<int>& encoding)\n {\n m_encodings.reserve(encoding.size() / 2);\n for (int i = 0; i < encoding.size(); i += 2) {\n const int count = encoding[i];\n const int number = encoding[i + 1];\n m_encodings.emplace_back(count, number);\n }\n }\n int next(int n)\n {\n while (m_current_idx < m_encodings.size() && m_encodings[m_current_idx].first < n) {\n n -= m_encodings[m_current_idx].first;\n m_encodings[m_current_idx].first = 0;\n ++m_current_idx;\n }\n if (m_current_idx >= m_encodings.size())\n return -1;\n m_encodings[m_current_idx].first -= n;\n return m_encodings[m_current_idx].second;\n }\nprivate:\n int m_current_idx = 0;\n std::vector<std::pair<int, int>> m_encodings;\n};\n```\n\n```Python3 []\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n```\n\n```Java []\nclass RLEIterator {\n public int[] encoding;\n public int index;\n public RLEIterator(int[] encoding) {\n this.encoding = encoding;\n this.index = 0;\n }\n public int next(int n) { \n while (n > 0 && index < encoding.length) {\n if (encoding[index] < n) {\n n -= encoding[index];\n encoding[index] = 0;\n index += 2;\n } else {\n encoding[index] -= n;\n n = 0;\n }\n }\n if (index >= encoding.length) return -1;\n return encoding[index + 1];\n }\n}\n```\n | 1 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Easy python solution | rle-iterator | 0 | 1 | ```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n``` | 1 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Easy python solution | rle-iterator | 0 | 1 | ```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n``` | 1 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
fastest solution possible in python | rle-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n``` | 5 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
fastest solution possible in python | rle-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n``` | 5 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Python3 simple solution - RLE Iterator | rle-iterator | 0 | 1 | ```\nclass RLEIterator:\n\n def __init__(self, A: List[int]):\n self.A = A[::-1]\n\n def next(self, n: int) -> int:\n acc = 0\n while acc < n:\n if not self.A:\n return -1\n times, num = self.A.pop(), self.A.pop()\n acc += times\n if acc > n:\n self.A.append(num)\n self.A.append(acc - n)\n return num\n``` | 6 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Python3 simple solution - RLE Iterator | rle-iterator | 0 | 1 | ```\nclass RLEIterator:\n\n def __init__(self, A: List[int]):\n self.A = A[::-1]\n\n def next(self, n: int) -> int:\n acc = 0\n while acc < n:\n if not self.A:\n return -1\n times, num = self.A.pop(), self.A.pop()\n acc += times\n if acc > n:\n self.A.append(num)\n self.A.append(acc - n)\n return num\n``` | 6 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Keep a global pointer and handle three separate cases | rle-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIndexing and edge cases need to be handled correctly. Keep an idx pointer on which val we are currently. If n required is greater than current cnt, move idx and decrement leftover with diff, else decrement current cnt. We stay at the same idx and return this val. One edge case can be if leftover = currCnt. In that case we return current val but also move the idx for next iteration. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) n = len. of RLE\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) n = len. of RLE as we stored cnt, val separately just for convenience, can be done using 2 pointers as well to make it O(1)\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.cnts = [] \n self.vals = [] \n for i in range(0,len(encoding),2):\n self.cnts.append(encoding[i])\n self.vals.append(encoding[i+1])\n self.idx = 0\n self.nCnts = len(self.cnts)\n \n def next(self, n: int) -> int:\n if self.idx >= self.nCnts:\n return -1 \n \n leftover = n \n while leftover: \n if leftover > self.cnts[self.idx]:\n leftover -= self.cnts[self.idx]\n self.idx += 1 \n if self.idx >= self.nCnts:\n return -1 \n elif leftover < self.cnts[self.idx]: \n self.cnts[self.idx] -= leftover \n return self.vals[self.idx]\n else:\n self.idx += 1 \n return self.vals[self.idx - 1]\n \n\n\n\n \n \n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Keep a global pointer and handle three separate cases | rle-iterator | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIndexing and edge cases need to be handled correctly. Keep an idx pointer on which val we are currently. If n required is greater than current cnt, move idx and decrement leftover with diff, else decrement current cnt. We stay at the same idx and return this val. One edge case can be if leftover = currCnt. In that case we return current val but also move the idx for next iteration. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) n = len. of RLE\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) n = len. of RLE as we stored cnt, val separately just for convenience, can be done using 2 pointers as well to make it O(1)\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.cnts = [] \n self.vals = [] \n for i in range(0,len(encoding),2):\n self.cnts.append(encoding[i])\n self.vals.append(encoding[i+1])\n self.idx = 0\n self.nCnts = len(self.cnts)\n \n def next(self, n: int) -> int:\n if self.idx >= self.nCnts:\n return -1 \n \n leftover = n \n while leftover: \n if leftover > self.cnts[self.idx]:\n leftover -= self.cnts[self.idx]\n self.idx += 1 \n if self.idx >= self.nCnts:\n return -1 \n elif leftover < self.cnts[self.idx]: \n self.cnts[self.idx] -= leftover \n return self.vals[self.idx]\n else:\n self.idx += 1 \n return self.vals[self.idx - 1]\n \n\n\n\n \n \n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Noob simple solution | rle-iterator | 0 | 1 | # Intuition\nThe encoding allows 0s, so we\'ll leverage that.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n\n def next(self, n: int) -> int:\n while self.encoding:\n if n <= self.encoding[0]:\n self.encoding[0] -= n\n return self.encoding[1]\n else:\n n -= self.encoding[0]\n self.encoding = self.encoding[2:]\n return -1\n\n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Noob simple solution | rle-iterator | 0 | 1 | # Intuition\nThe encoding allows 0s, so we\'ll leverage that.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n\n def next(self, n: int) -> int:\n while self.encoding:\n if n <= self.encoding[0]:\n self.encoding[0] -= n\n return self.encoding[1]\n else:\n n -= self.encoding[0]\n self.encoding = self.encoding[2:]\n return -1\n\n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
✅ Simple Python Solution | O(1) space | rle-iterator | 0 | 1 | - Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n i = 0\n while i < len(encoding):\n if encoding[i] == 0:\n encoding.pop(i)\n encoding.pop(i)\n else:\n i += 2\n\n def next(self, n: int) -> int:\n ans = 0\n if self.encoding:\n if n <= self.encoding[0]:\n ans = self.encoding[1]\n self.encoding[0] -= n\n if self.encoding[0] <= 0:\n self.encoding.pop(0)\n self.encoding.pop(0)\n else:\n while self.encoding and n > self.encoding[0]:\n n -= self.encoding[0]\n self.encoding.pop(0)\n self.encoding.pop(0)\n if self.encoding:\n ans = self.encoding[1]\n self.encoding[0] -= n\n if self.encoding[0] <= 0:\n self.encoding.pop(0)\n self.encoding.pop(0)\n else:\n return -1\n return ans \n else:\n return -1 \n \n \n \n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
✅ Simple Python Solution | O(1) space | rle-iterator | 0 | 1 | - Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n i = 0\n while i < len(encoding):\n if encoding[i] == 0:\n encoding.pop(i)\n encoding.pop(i)\n else:\n i += 2\n\n def next(self, n: int) -> int:\n ans = 0\n if self.encoding:\n if n <= self.encoding[0]:\n ans = self.encoding[1]\n self.encoding[0] -= n\n if self.encoding[0] <= 0:\n self.encoding.pop(0)\n self.encoding.pop(0)\n else:\n while self.encoding and n > self.encoding[0]:\n n -= self.encoding[0]\n self.encoding.pop(0)\n self.encoding.pop(0)\n if self.encoding:\n ans = self.encoding[1]\n self.encoding[0] -= n\n if self.encoding[0] <= 0:\n self.encoding.pop(0)\n self.encoding.pop(0)\n else:\n return -1\n return ans \n else:\n return -1 \n \n \n \n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Python Prefix Sum Binary Search | rle-iterator | 0 | 1 | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. --> Similar to random pick with weight leetcode problem. Build the prefix sum on the frequencies. And perform binary search.\n\n\n# Complexity\n- Time complexity: O(logn) each call.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.freq=[]\n self.val=[]\n self.count=0\n\n prefixSum=0\n for i in range(0, len(encoding)-1, 2):\n if encoding[i]!=0:\n prefixSum+=encoding[i]\n self.freq.append(prefixSum)\n self.val.append(encoding[i+1])\n\n\n def next(self, n: int) -> int:\n self.count+=n\n if self.count>self.freq[-1]:\n return -1\n\n # Binary Search on prefix index sums\n l=0\n r=len(self.freq)-1\n \n while(l<=r):\n\n mid=(l+r)//2\n\n if self.count>self.freq[mid]:\n l=mid+1\n else:\n r=mid-1\n \n\n return self.val[l]\n\n\n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Python Prefix Sum Binary Search | rle-iterator | 0 | 1 | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. --> Similar to random pick with weight leetcode problem. Build the prefix sum on the frequencies. And perform binary search.\n\n\n# Complexity\n- Time complexity: O(logn) each call.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.freq=[]\n self.val=[]\n self.count=0\n\n prefixSum=0\n for i in range(0, len(encoding)-1, 2):\n if encoding[i]!=0:\n prefixSum+=encoding[i]\n self.freq.append(prefixSum)\n self.val.append(encoding[i+1])\n\n\n def next(self, n: int) -> int:\n self.count+=n\n if self.count>self.freq[-1]:\n return -1\n\n # Binary Search on prefix index sums\n l=0\n r=len(self.freq)-1\n \n while(l<=r):\n\n mid=(l+r)//2\n\n if self.count>self.freq[mid]:\n l=mid+1\n else:\n r=mid-1\n \n\n return self.val[l]\n\n\n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Readable Python; knowing the problem is 90% of the battle! | rle-iterator | 0 | 1 | # Intuition\nAt first, I thought what would happen if I expanded the RLE out. Iterating through the decoded data is straightforward. Well, the tests have diabolical inputs and run out of memory! That is, the repeated elements could be in the hundreds of thousands or millions!\n\nSo you can operate on the encoded input directly. Just keep subtracting the repeat values in order up to n count, then return the appropriate last value.\n\n\n# Approach\nI converted the input into a deque of 2-sized lists representing the [run_count, value]. This isn\'t really necessary, and adds some overhead, but doesn\'t affect overall runtime. It\'s just for some readability as I only have to worry about popping the first item off the deque when I\'ve exhausted its repeated count. Remember, you can\'t mutate tuples, so that\'s why I use a two-sized list for [run_count, value]. \n\nAlso, I hate using pointers in Python so avoiding them sure is nice (though you can\'t get away from it in Leetcode-style questions). However, if I were to go into an interview tomorrow, I\'d probably use the deque to simplify the problem at first and to avoid having to deal with pointers. Then, I\'d probably say "this can be optimized by just operating on the input directly and keeping track of where you are instead of popping off the first item in a double-ended queue".\n\n# Complexity\n- Time complexity: $$O(n)$$ to create the deque; the next() method $$O(n)$$, as you may have to visit the entire encoded data (note that popping an item off the end of a deque is $$O(1)$$); the overall runtime is $$O(n)$$.\n\n- Space complexity: $$O(n)$$ to store the data in a deque. We can do this in $$O(1)$$ extra space by just operating on the input directly.\n\n# Code\n```\nfrom collections import deque\n\nK = 0\nVALUE = 1\n\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.data = deque()\n i = 0\n while i < len(encoding):\n k = encoding[i]\n value = encoding[i+1]\n self.data.append([k, value])\n i += 2\n\n def next(self, n: int) -> int:\n value = -1\n if self.data:\n while True:\n if not self.data:\n break\n item = self.data[0]\n if item[K] >= n:\n item[K] -= n\n value = item[VALUE]\n break\n else:\n n -= item[K]\n self.data.popleft()\n return value\n\n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | We can use run-length encoding (i.e., **RLE**) to encode a sequence of integers. In a run-length encoded array of even length `encoding` (**0-indexed**), for all even `i`, `encoding[i]` tells us the number of times that the non-negative integer value `encoding[i + 1]` is repeated in the sequence.
* For example, the sequence `arr = [8,8,8,5,5]` can be encoded to be `encoding = [3,8,2,5]`. `encoding = [3,8,0,9,2,5]` and `encoding = [2,8,1,8,2,5]` are also valid **RLE** of `arr`.
Given a run-length encoded array, design an iterator that iterates through it.
Implement the `RLEIterator` class:
* `RLEIterator(int[] encoded)` Initializes the object with the encoded array `encoded`.
* `int next(int n)` Exhausts the next `n` elements and returns the last element exhausted in this way. If there is no element left to exhaust, return `-1` instead.
**Example 1:**
**Input**
\[ "RLEIterator ", "next ", "next ", "next ", "next "\]
\[\[\[3, 8, 0, 9, 2, 5\]\], \[2\], \[1\], \[1\], \[2\]\]
**Output**
\[null, 8, 8, 5, -1\]
**Explanation**
RLEIterator rLEIterator = new RLEIterator(\[3, 8, 0, 9, 2, 5\]); // This maps to the sequence \[8,8,8,5,5\].
rLEIterator.next(2); // exhausts 2 terms of the sequence, returning 8. The remaining sequence is now \[8, 5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 8. The remaining sequence is now \[5, 5\].
rLEIterator.next(1); // exhausts 1 term of the sequence, returning 5. The remaining sequence is now \[5\].
rLEIterator.next(2); // exhausts 2 terms, returning -1. This is because the first term exhausted was 5,
but the second term did not exist. Since the last term exhausted does not exist, we return -1.
**Constraints:**
* `2 <= encoding.length <= 1000`
* `encoding.length` is even.
* `0 <= encoding[i] <= 109`
* `1 <= n <= 109`
* At most `1000` calls will be made to `next`. | null |
Readable Python; knowing the problem is 90% of the battle! | rle-iterator | 0 | 1 | # Intuition\nAt first, I thought what would happen if I expanded the RLE out. Iterating through the decoded data is straightforward. Well, the tests have diabolical inputs and run out of memory! That is, the repeated elements could be in the hundreds of thousands or millions!\n\nSo you can operate on the encoded input directly. Just keep subtracting the repeat values in order up to n count, then return the appropriate last value.\n\n\n# Approach\nI converted the input into a deque of 2-sized lists representing the [run_count, value]. This isn\'t really necessary, and adds some overhead, but doesn\'t affect overall runtime. It\'s just for some readability as I only have to worry about popping the first item off the deque when I\'ve exhausted its repeated count. Remember, you can\'t mutate tuples, so that\'s why I use a two-sized list for [run_count, value]. \n\nAlso, I hate using pointers in Python so avoiding them sure is nice (though you can\'t get away from it in Leetcode-style questions). However, if I were to go into an interview tomorrow, I\'d probably use the deque to simplify the problem at first and to avoid having to deal with pointers. Then, I\'d probably say "this can be optimized by just operating on the input directly and keeping track of where you are instead of popping off the first item in a double-ended queue".\n\n# Complexity\n- Time complexity: $$O(n)$$ to create the deque; the next() method $$O(n)$$, as you may have to visit the entire encoded data (note that popping an item off the end of a deque is $$O(1)$$); the overall runtime is $$O(n)$$.\n\n- Space complexity: $$O(n)$$ to store the data in a deque. We can do this in $$O(1)$$ extra space by just operating on the input directly.\n\n# Code\n```\nfrom collections import deque\n\nK = 0\nVALUE = 1\n\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.data = deque()\n i = 0\n while i < len(encoding):\n k = encoding[i]\n value = encoding[i+1]\n self.data.append([k, value])\n i += 2\n\n def next(self, n: int) -> int:\n value = -1\n if self.data:\n while True:\n if not self.data:\n break\n item = self.data[0]\n if item[K] >= n:\n item[K] -= n\n value = item[VALUE]\n break\n else:\n n -= item[K]\n self.data.popleft()\n return value\n\n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n``` | 0 | You are given two strings `stamp` and `target`. Initially, there is a string `s` of length `target.length` with all `s[i] == '?'`.
In one turn, you can place `stamp` over `s` and replace every letter in the `s` with the corresponding letter from `stamp`.
* For example, if `stamp = "abc "` and `target = "abcba "`, then `s` is `"????? "` initially. In one turn you can:
* place `stamp` at index `0` of `s` to obtain `"abc?? "`,
* place `stamp` at index `1` of `s` to obtain `"?abc? "`, or
* place `stamp` at index `2` of `s` to obtain `"??abc "`.
Note that `stamp` must be fully contained in the boundaries of `s` in order to stamp (i.e., you cannot place `stamp` at index `3` of `s`).
We want to convert `s` to `target` using **at most** `10 * target.length` turns.
Return _an array of the index of the left-most letter being stamped at each turn_. If we cannot obtain `target` from `s` within `10 * target.length` turns, return an empty array.
**Example 1:**
**Input:** stamp = "abc ", target = "ababc "
**Output:** \[0,2\]
**Explanation:** Initially s = "????? ".
- Place stamp at index 0 to get "abc?? ".
- Place stamp at index 2 to get "ababc ".
\[1,0,2\] would also be accepted as an answer, as well as some other answers.
**Example 2:**
**Input:** stamp = "abca ", target = "aabcaca "
**Output:** \[3,0,1\]
**Explanation:** Initially s = "??????? ".
- Place stamp at index 3 to get "???abca ".
- Place stamp at index 0 to get "abcabca ".
- Place stamp at index 1 to get "aabcaca ".
**Constraints:**
* `1 <= stamp.length <= target.length <= 1000`
* `stamp` and `target` consist of lowercase English letters. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.